Submitted:
08 August 2023
Posted:
09 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
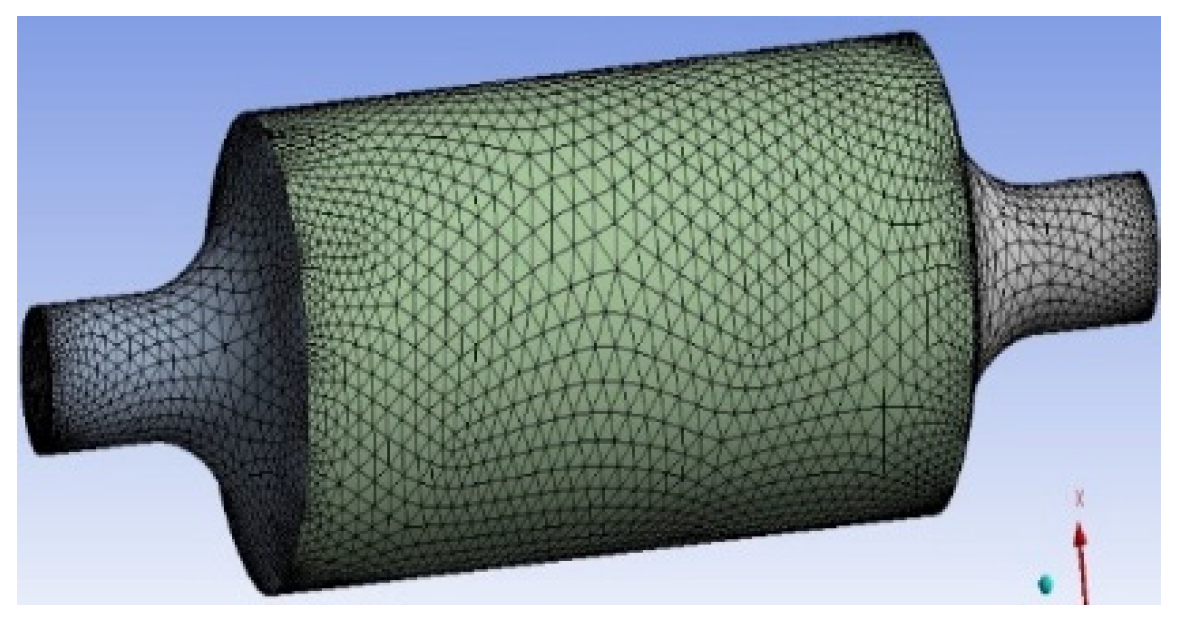
2.1. Geometry and discretization
2.2. Kinetic model
2.2.1. Reactions scheme
- I.
- Biomass is converted to CO, CO2, H2 and CH4, with traces of coke and tar.
- I.
- II. The CO, CO2, H2, CH4 and H2O are adsorbed on the catalyst surface, which react until they desorb and form part of the product.
- I.
- III. The dominant reactions in the reaction are water-gas shift (WGS), dry reforming of methane (DRM) and steam reforming of methane (SRM) reactions.
| Reaction | Stoichiometry | |
|---|---|---|
| The water-gas shift (WGS) | (3) | |
| Steam methane reforming (SMR) | (4) | |
| Reverse dry methane reforming (RDRM) | (5) | |
2.2.1. Steam reforming of methane (SRM)
2.2.1.2. The water-gas shift
2.2.1.3. Reverse dry methane reforming reaction
2.2.2. Reaction rate constants and adsorption rate constant.
2.2.3. Dynamic and Steady-State material balance
3. Results and Discussion
3.1. Fluid behavior inside the reactor
3.1.1. Velocity through the reactor
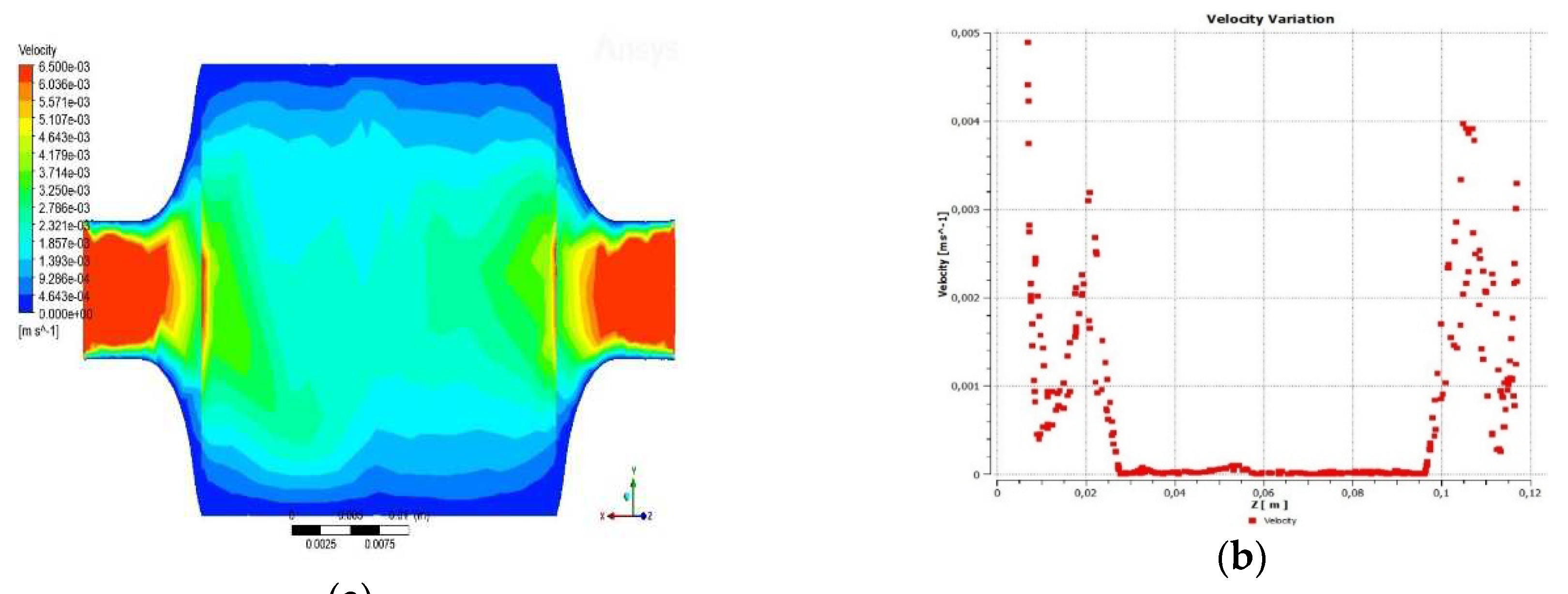
3.1.2. Temperature across the reactor
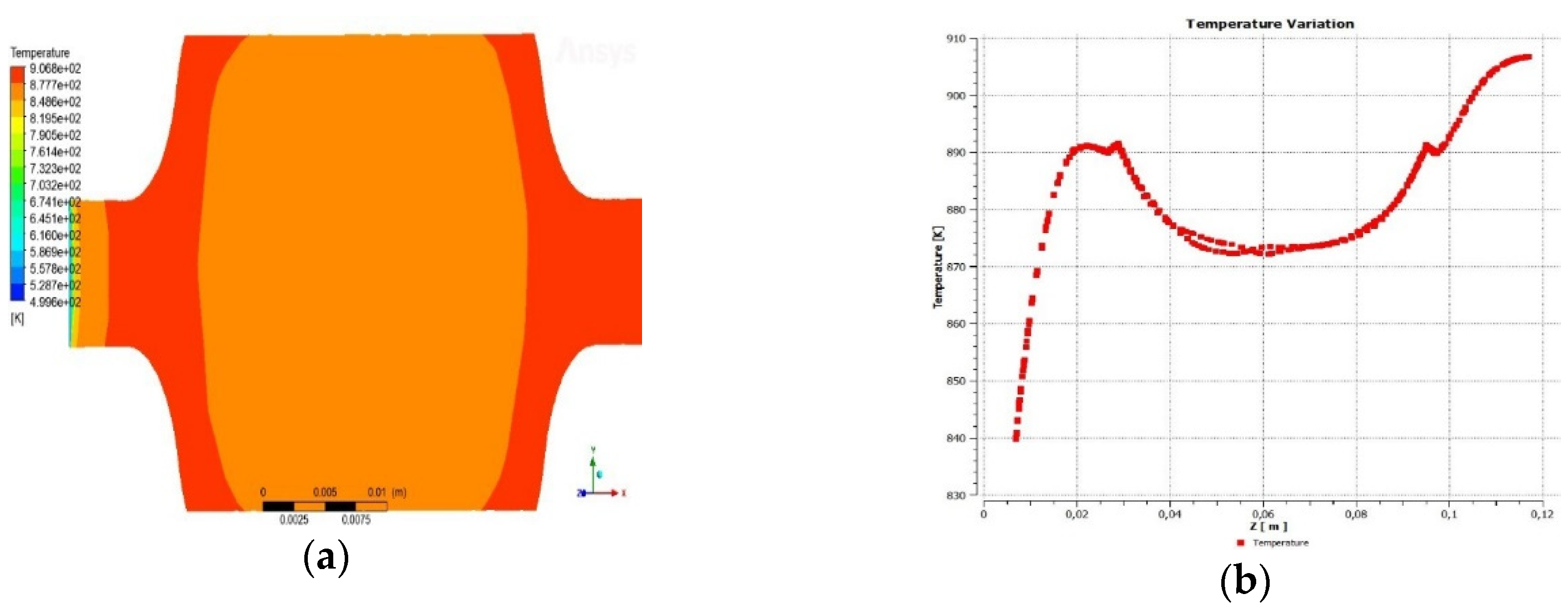
3.1.3. Pressure drop across the reactor
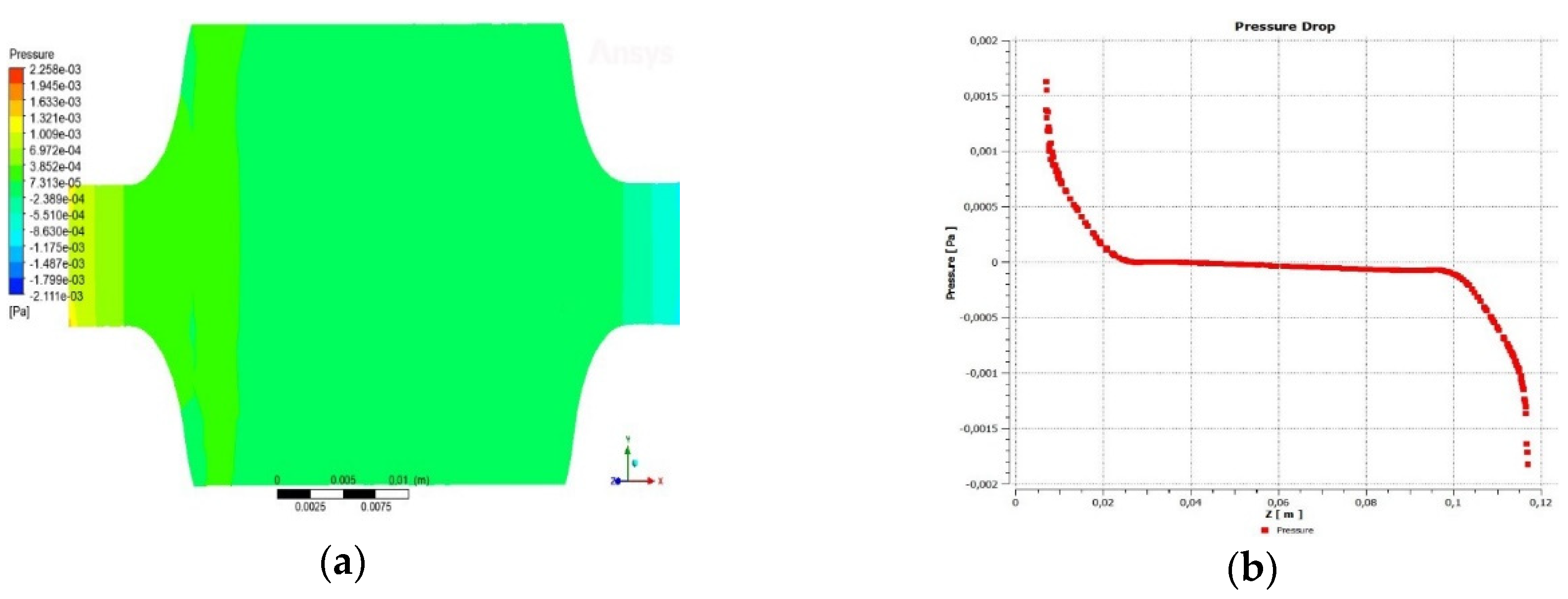
3.2. Simulation of the gasification reaction
3.2.1. Evolution of the number of moles with respect to time
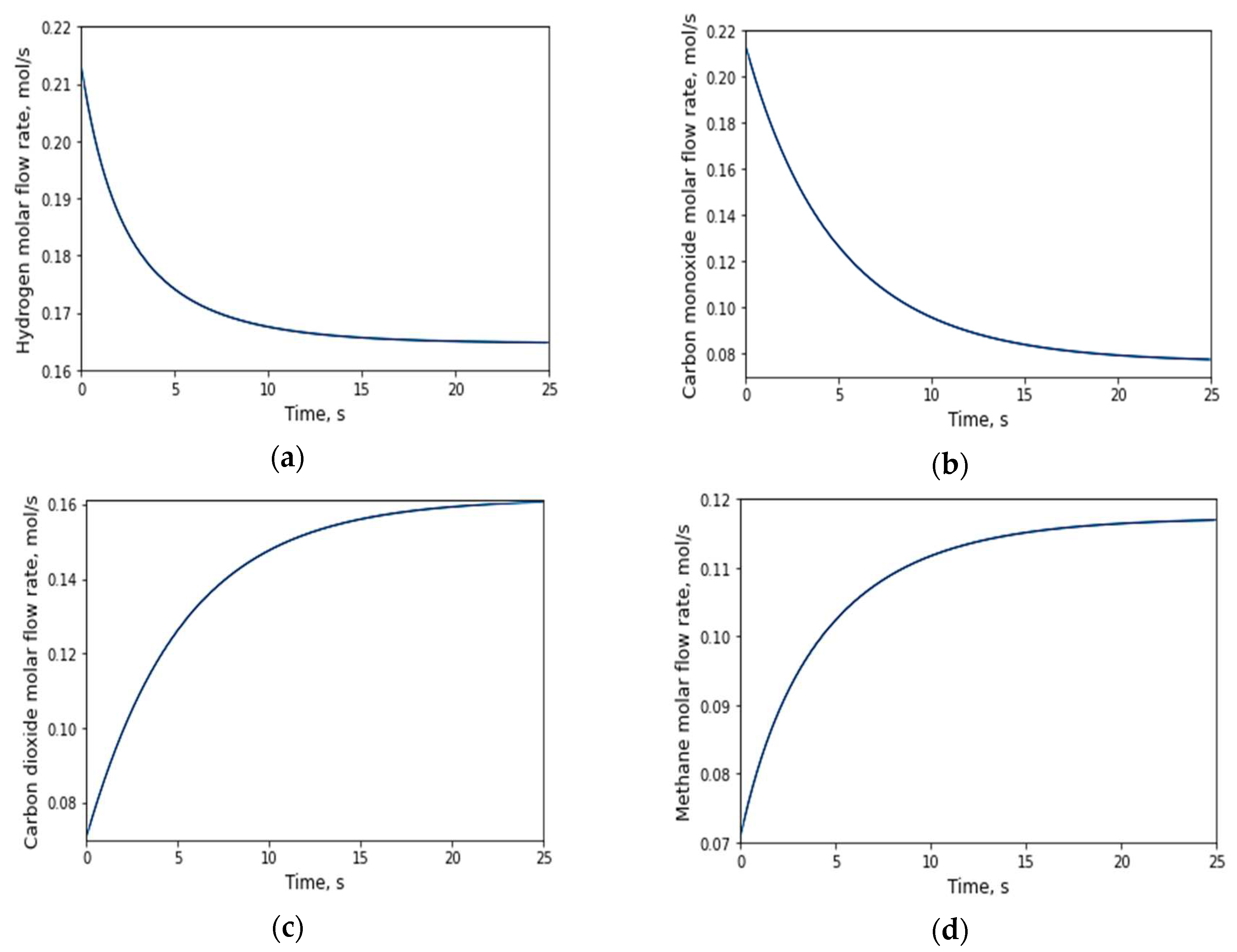
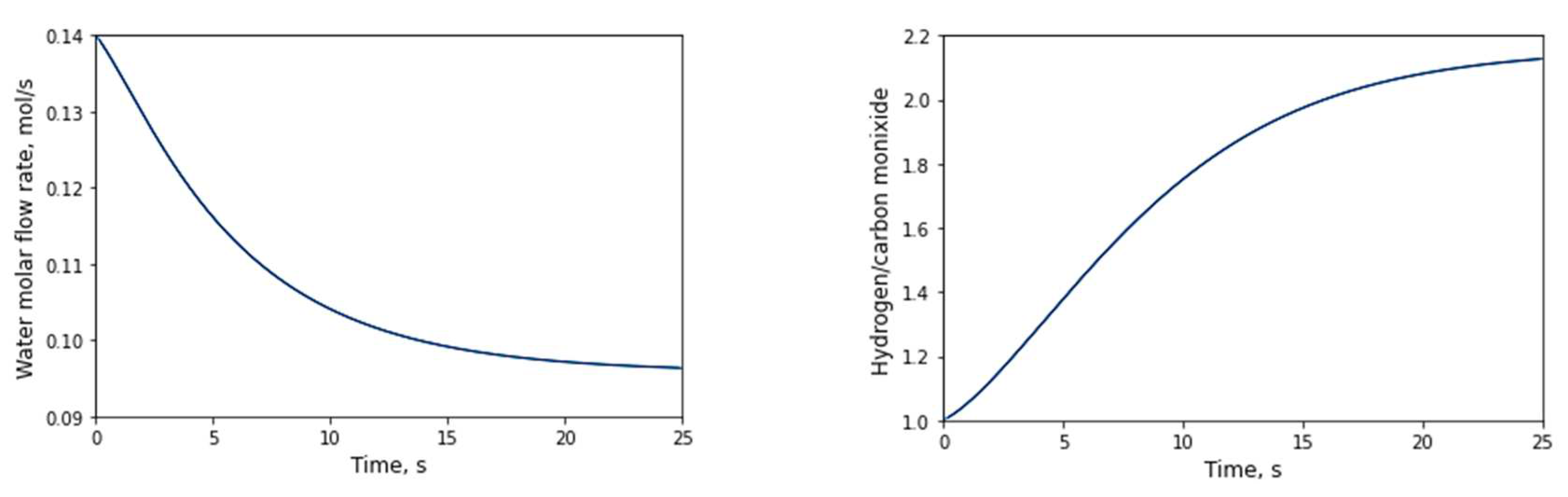
3.2.2. Evolution of the number of moles with respect to the longitudinal axis
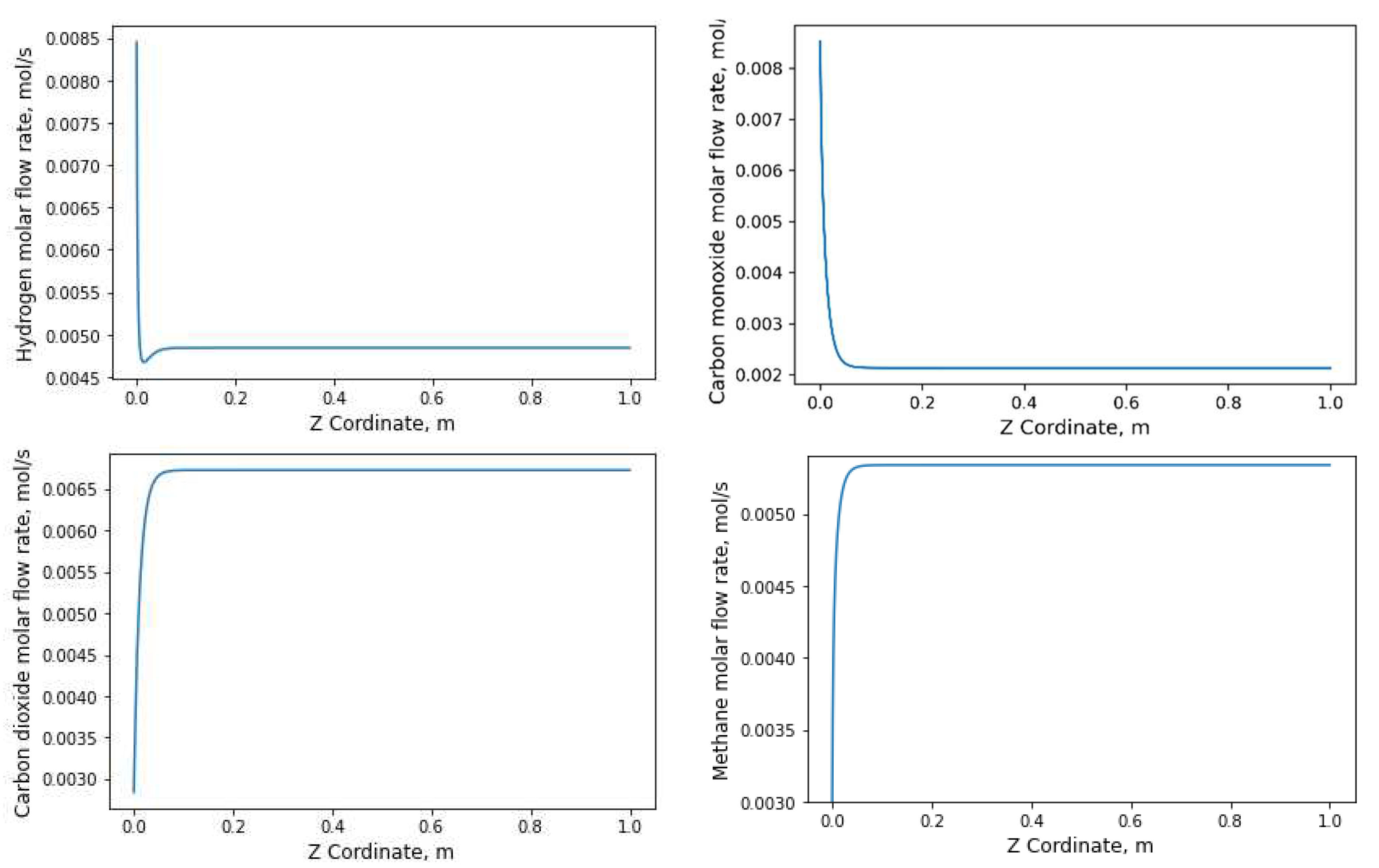
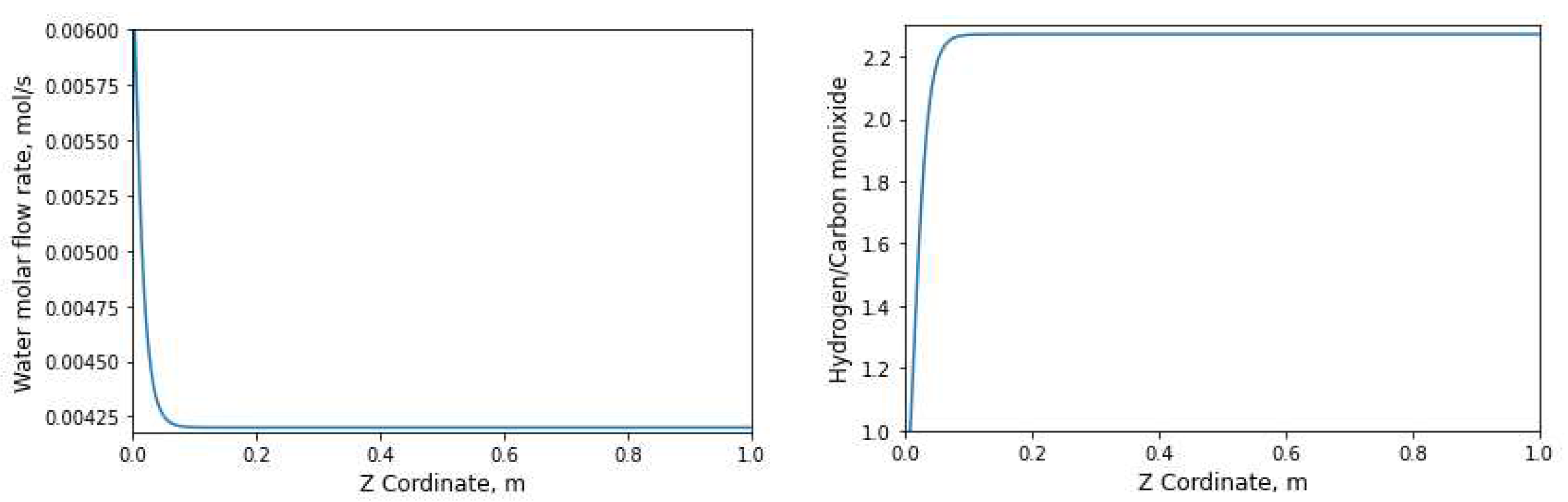
4. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Olabi, A.G.; Abdelkareem, M.A. Renewable energy and climate change. Renewable and Sustainable Energy Reviews 2022, 158, 2022. [Google Scholar] [CrossRef]
- Feng, C.-Y.; Yang, X.; Afshan, S. , and M. Irfan. Can renewable energy technology innovation promote mineral resources’ green utilization efficiency? Novel insights from regional development inequality. Resources Policy 2023, 82, 103449. [Google Scholar] [CrossRef]
- Solaymani, S.; Zada, E.R. , and A. Gatto. A Review on Energy and Renewable Energy Policies in Iran. Sustainability 2021, 13, 7328. [Google Scholar] [CrossRef]
- Djellouli, N.; Abdelli, L.; Elheddad, M.; Ahmed, R. , and H. Mahmood. The effects of non-renewable energy, renewable energy, economic growth, and foreign direct investment on the sustainability of African countries. Renew Energy 2022, 183, 676–686. [Google Scholar] [CrossRef]
- Elavarasan, R.M. A Comprehensive Review on Renewable Energy Development, Challenges, and Policies of Leading Indian States with an International Perspective. IEEE Access 2020, 8, 74432–74457. [Google Scholar] [CrossRef]
- Saleem, M. Possibility of utilizing agriculture biomass as a renewable and sustainable future energy source. Heliyon 2022, 8, e08905. [Google Scholar] [CrossRef]
- Ahmed, A.; Ge, T.; Peng, J.; Yan, W.C.; Tee, B.T. , and S. You. Assessment of the renewable energy generation towards net-zero energy buildings: A review. Energy Build 2022, 256, 111755. [Google Scholar] [CrossRef]
- Amjith, L.R.; Bavanish, B. A review on biomass and wind as renewable energy for sustainable environment. Chemosphere 2022, 293, 133579. [Google Scholar] [CrossRef]
- Rahman, A.; Farrok, O. , and M. M. Haque. Environmental impact of renewable energy source based electrical power plants: Solar, wind, hydroelectric, biomass, geothermal, tidal, ocean, and osmotic. Renewable and Sustainable Energy Reviews 2022, 161, 112279. [Google Scholar] [CrossRef]
- Yana, S.; Nizar, M.; Irhamni, and D. Mulyati. Biomass waste as a renewable energy in developing bio-based economies in Indonesia: A review. Renewable and Sustainable Energy Reviews 2022, 160, 112268. [Google Scholar] [CrossRef]
- Tezer, Ö.; Karabağ, N.; Öngen, A.; Çolpan, C.Ö. , and A. Ayol. Biomass gasification for sustainable energy production: A review. Int J Hydrogen Energy 2022, 47, 15419–15433. [Google Scholar] [CrossRef]
- Fiallos-Cárdenas, M.; Pérez-Martínez, S. , and A. D. Ramirez. Prospectives for the development of a circular bioeconomy around the banana value chain. Sustain Prod Consum 2022, 30, 541–555. [Google Scholar] [CrossRef]
- Verma, M.; Mishra, V. Bioelectricity generation by microbial degradation of banana peel waste biomass in a dual-chamber S. cerevisiae-based microbial fuel cell. Biomass Bioenergy 2023, 168, 106677. [Google Scholar] [CrossRef]
- Singh, R.K.; Patil, T.; Pandey, D.; Tekade, S.P. , and A. N. Sawarkar. Co-pyrolysis of petroleum coke and banana leaves biomass: Kinetics, reaction mechanism, and thermodynamic analysis. J Environ Manage 2022, 301, 113854. [Google Scholar] [CrossRef]
- Dayton, D.C.; Foust, T.D. Analytical methods for biomass characterization and conversion. Analytical Methods for Biomass Characterization and Conversion, 2020; 1–260. [Google Scholar] [CrossRef]
- Wang, X.; Yang, S.; Shen, B.; Yang, J. , and L. Xu. Pyrolysis of Biomass Pineapple Residue and Banana Pseudo-Stem: Kinetics, Mechanism and Valorization of Bio-Char. Catalysts 2022, 12, 840. [Google Scholar] [CrossRef]
- Subramanian, P.; Sriramajayam, S.; Vijayakumary, P.; Raja, K.; Reddy, M., and P. G. Research. Extraction of cellulose from banana sheath and its characterization. The Pharma Innovation Journal 2022, 11, 1861–1867.
- Francisco; Salinas, G.; Obtener, P.; De, G.; Mario, I.Q., and A. G. Gallardo. Producción de hidrógeno a través de la gasificación de glucosa usando catalizadores de 5%Ni con 2% de La, Ce y Mg y deducción de una ecuación de velocidad de reacción intrínseca. 2019, Accessed: Apr. 04, 2023. [Online]. Available: http://ricaxcan.uaz.edu.mx/jspui/handle/20.500.11845/2306.
- Jara-Cobos, L.; Abril-González, M. , and V. Pinos-Vélez. Production of Hydrogen from Lignocellulosic Biomass: A Review of Technologies. Catalysts 2023, 13. [Google Scholar] [CrossRef]
- Jara-Cobos, L.; Abril-González, M. , and V. Pinos-Vélez. Production of Hydrogen from Lignocellulosic Biomass: A Review of Technologies. Catalysts 2023, 13. [Google Scholar] [CrossRef]
- Tacuri, D. Design and Development of a Catalytic Fixed-Bed Reactor for Gasification of Banana Biomass in Hydrogen Production. Catalysts 2022, 12. [Google Scholar] [CrossRef]
- Yu, J.; Guo, Q.; Gong, Y.; Ding, L.; Wang, J. , and G. Yu. A review of the effects of alkali and alkaline earth metal species on biomass gasification. Fuel Processing Technology 2021, 214, 106723. [Google Scholar] [CrossRef]
- Adamu, S.; Hossain, M.M. Kinetics of Steam Gasification of Glucose as a Biomass Surrogate over Ni/Ce-Mesoporous Al2O3 in a Fluidized Bed Reactor. Ind Eng Chem Res 2018, 57, 3128–3137. [Google Scholar] [CrossRef]
- Bhushan, S.; Rana, M.S. ; Mamta; Nandan, N., and S. K. Prajapati. Energy harnessing from banana plant wastes: A review. Bioresource Technology Reports 2019, 7. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.; Xu, P.; Liu, B.; Shuai, Y. , and B. Li. Hydrogen production through biomass gasification in supercritical water: A review from exergy aspect. Int J Hydrogen Energy 2019, 44, 15727–15736. [Google Scholar] [CrossRef]
- García-Jarana, M.B.; Portela, J.R.; Sánchez-Oneto, J.; de la Ossa, E.J.M. , and B. Al-Duri. Analysis of the supercriticalwater gasification of cellulose in a continuous system using short residence times. Analysis of the supercriticalwater gasification of cellulose in a continuous system using short residence times. Applied Sciences (Switzerland) 2020, 10. [Google Scholar] [CrossRef]
- Guamán, F.R.F. Determinación de la capacidad calorífica de biomasas residuales de la producción agrícola del Ecuador. Universidad Central de Ecuador, 2022.
- Situmorang, Y.A.; Zhao, Z.; Yoshida, A.; Abudula, A. , and G. Guan. Small-scale biomass gasification systems for power generation (<200 kW class): A review. Renewable and Sustainable Energy Reviews 2020, 117, 109486. [Google Scholar] [CrossRef]
- Ang, T.-Z.; Salem, M.; Kamarol, M.; Das, H.S.; Nazari, M.A. , and N. Prabaharan. A comprehensive study of renewable energy sources: Classifications, challenges and suggestions. Energy Strategy Rev. 2022, 43, 100939. [Google Scholar] [CrossRef]
- Zalamea, S.; William, M. , and J. Serrano. Kinetic and mathematical modeling of the catalytic supercritical water gasification of the glucose for the hydrogen production. Revista de la Facultad de Ciencias Químicas, 2016, 1–11.
- Peña, F.J.E. Elaboración de un modelo 3D de una turbina de vapor. 2019, Accessed: Apr. 06, 2023. [Online]. Available: https://riull.ull.es/xmlui/handle/915/13373.
- Escobar, J.O.C.; Jurado, F. , and D. Vera. Simulation of an active indirect hybrid dehydrator using ANSYS software. Enfoque UTE 2021, 12, 29–44. [Google Scholar] [CrossRef]
- A.B. Parrilla. Simulación 2D de la rotura de Presa de Malpasset con los modelos Iber y RiverFlow2D. 2019.
- J. Carlos and J. Bedolla. Métodos numéricos usando Python con aplicaciones a la Ingeniería Química”.
- Lemus-Contreras, S.A.; Pavón-Silva, T.B.; Alva, M.L.H. , and Y. Zarazúa-Aguilar. Desarrollo de un programa con Python para la determinación de datos cinéticos en reacciones irreversibles de un solo componente en reactores intermitentes. Journal of Basic Sciences 2022, 8, 11–34. [Google Scholar] [CrossRef]
- Adamu, S.; Hossain, M.M. Kinetics of Steam Gasification of Glucose as a Biomass Surrogate over Ni/Ce-Mesoporous Al2O3 in a Fluidized Bed Reactor. Ind Eng Chem Res 2018, 57, 3128–3137. [Google Scholar] [CrossRef]
- Li, A. A novel sludge pyrolysis and biomass gasification integrated method to enhance hydrogen-rich gas generation. Energy Convers Manag 2022, 254, 115205. [Google Scholar] [CrossRef]
- Salinas, F.; García, G. Producción de hidrógeno a través de la gasificación de glucosa usando catalizadores de 5%Ni con 2% de La, Ce y Mg y deducción de una ecuación de velocidad de reacción intrínseca. 2019, Accessed: Sep. 12, 2022. [Online]. Available: http://ricaxcan.uaz.edu.mx/jspui/handle/20.500.11845/2306.
- Cruz, I. Producción de hidrógeno a través de la gasificación de glucosa usando catalizadores de γ-Al2O3 con Ni, Ce y La e interpretación de resultados usando un modelo No-estequiométrico. 2018. Accessed: Sep. 17, 2022. [Online]. Available: https://1library.co/document/y4jjvj9y-produccion-hidrogeno-traves-gasificacion-catalizadores-interpretacion-resultados-estequiometrico.html.
- Song, X.; Guo, Z. Technologies for direct production of flexible H2/CO synthesis gas. Energy Convers Manag 2006, 47, 560–569. [Google Scholar] [CrossRef]

| Zone | Temperature Range | Type of Material |
|---|---|---|
| I | <373 K | Humidity evolution. |
| II | 373 – 523 K | It takes place at the beginning of the decomposition of hemicellulose. |
| III | 523 – 633 K | Decomposition of cellulose. |
| IV | 633 – 733 K | Lignin decomposition. |
| V | >733 K | Fixed carbon oxidation. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





