Preprint
Article
Maximal Bell Violations with Independent Classical Observables
Altmetrics
Downloads
269
Views
167
Comments
1
This version is not peer-reviewed
Submitted:
10 January 2024
Posted:
10 January 2024
You are already at the latest version
Alerts
Abstract
Sequential properties can violate Bell-type inequalities without direct influence on each other, but only if detected in pairs. This is demonstrated below with theoretical arguments, and with a straightforward toy model. Rotating arrows can have transient qualities that produce maximal Bell violations with predetermined values. Any non-signaling phenomenon (classical, or non-classical) can also be interpreted as local.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
1. Introduction
Many quantum properties are fundamentally contextual. The question is: how do they relate to the act of measurement? Are they “created” during exposure, or are they merely “confirmed” after preparation? As will be shown below, Bell’s Theorem [1] entails different conclusions for each answer. From a mathematical point of view, Bell’s argument is based on the statistical properties of jointly distributed (and therefore simultaneous) variables [2,3]. However, simultaneity is only equivalent to locality if measurements are defined as creative operations. Hence, Bell’s inequality is either the ceiling for local correlations, or just a test of simultaneous existence, depending on the starting assumptions. Indeed, it is possible to violate Bell-type inequalities with independent sequential observables. No influence between preceding and succeeding events is required for this to work. Instead, the order of events is sufficient, by enabling inconsistent pairwise combinations. This will be demonstrated below with an arrow, rotating above a clockface with 8 sectors. Recurrent chains of pairwise measurements produce Popescu-Rohrlich (PR Box) [4] correlations between the properties of a single system. By extension, the same result can be achieved with separated twin systems, in adequate conditions. Therefore, quantum correlations [5], “super-quantum” correlations [4] and “quantum monogamy” [6] are classical phenomena. This conclusion falsifies Bell’s Theorem as an argument for quantum nonlocality.
Sequential binary properties are very different from simultaneous properties, both physically and statistically. First of all, they describe individual states that only exist one at a time. For example, the arm of an analogue clock is forced to rotate continuously, from one digit to the next. When the arm is in the state of “1 o’clock”, it cannot also show some other time of the day. Every value has to “wait for its turn”. Accordingly, if an observer wants to “measure” the next value for a given inclination of the clock arm, the relevant property cannot be produced on the spot. Detection events can only happen when and where they are possible. This is the essence of physical contextuality. Secondly, the association between opposite values along a single orientation (such as 12 o’clock and 6 o'clock, 3 o'clock and 9 o'clock, etc.) is purely abstract. The arm of the clock does not jump between one pair of opposites to another, in any physically meaningful way. It always rotates around the clock, one sector at a time. Before it reaches 6 o’clock (starting at 12), it has to pass through 5 other sectors. Accordingly, the correlations between different “angles of measurement” cannot be the same as for permanent binary properties. Indeed, as will be shown below, Bell violations are natural for them. In contrast, if time markers are artificially divided into opposite pairs, expected to manifest at will, then classical rules of analysis no longer hold. This is particularly relevant, given the qualitative similarity between rotating classical arrows and spin-like quantum properties. On closer inspection, quantum behavior looks “weird” because of circular reasoning. If observables are presumed to materialize when they are measured (as if by magic), then any relationship between them can also seem magical. Unfortunately, magical assumptions are often implicit in the analysis of quantum behavior, even if they are explicitly rejected.
Quantum mechanics is often described as if it constrains the existence of basic particle properties. Presumably, one can choose to create momentum states for a quantum, or position states, but not both. The problem with this description is that quantum theory is not about intrinsic particle properties. It uses wave-functions (or their matrix equivalents) to predict wave-like distributions. In the same vein, quantum experiments do not inspect the particles with magnifying glasses. They count the detection events at different coordinates, in order to confirm the amplitudes of corresponding wave-functions. More importantly, these distributions do not “become real” because they are chosen for observation. Instead, they have to be “tracked down” with high precision. This is particularly clear in the Einstein-Podolsky-Rosen (EPR) experiment [7], when realized with photons. In this case [8], the spectrum of “momentum” is sharp in the focal plane of a lens, just as seen in classical optical projections [9]. At the same time, the spectrum of “position” is sharp in the image plane of the same lens (conjugated to the plane of emission). Thus, in order to detect one property or another, the physical preparation is practically the same. The state of mind of the observer for each choice also does not matter. Instead, the photon counter needs to be moved from one plane of detection to another, depending on which distribution is selected (Figure 1). Just like in the double-slit experiment, the choice is “where to place the detector”, not “what property to create”. Accordingly, EPR systems appear paradoxical, but only if measurements are assumed to create physical reality. If we acknowledge the existence of objective sequential qualities, then the mystery vanishes. At first sight, this is a purely interpretive problem. What does it matter what people assume? The facts are what they are. As it turns out, facts require conceptual frameworks for analysis and their significance can be lost out of context. In the case of Bell’s Theorem, interpretive assumptions blocked the consideration of relevant facts, distorting the essence of both classical mechanics and quantum mechanics.
2.“. Locality” without “Local Realism”
Bell’s inequality is a well-known marker for “Local Realism”. Yet, what is the physical meaning of this concept? At first sight, it seems to include any process that is “local” and “real”, but this is not true in discussions about quantum mechanics. As clarified by Einstein, Podolsky and Rosen (EPR) [7], any physical property must be accepted as real if its values can be predicted with certainty. However, EPR also insisted that real properties should always exist at the same time in any “reasonable definition of reality”. In their opinion, quantum correlations required action at a distance, if non-commuting properties were assumed to exist only one at a time. Accordingly, “Local Realism” is just a different word for “Simultaneous Realism”. As will be shown below, Bell-type inequalities are indeed constrained in the same way, and only work as tests of concomitant existence. They only apply when relevant properties obey the principle of transitivity. For this reason, they are unsuitable as tests of locality, especially in the case of sequential observables with hidden variables.
In what follows, measurement choices (and corresponding experimental settings) shall be denoted with capital letters, such as A1, A2, B1 or B2. Following modern conventions, measurement outcomes shall be denoted with small letters, such as a1, a2, b1 or b2. Let us begin with the basics. Correlated phenomena are statistically dependent on each other, and their joint probability cannot be factorized:
However, statistical dependence is not equivalent to physical dependence. Even when observables are correlated, they can be conditionally independent by virtue of some prior causal mechanism. The set of relevant causal influences can be denoted by the parameter “λ”, commonly used as a symbol for “hidden variables” in this context of analysis:
This expression is commonly referred to as the Locality Criterion. A known consequence of this property is that:
In other words, the probability of one event is altogether independent from the choice to measure or not to measure the other one, given the effect of unspecified hidden variables. The two events are causally independent from each other. Though, is it possible to derive a Bell-type inequality merely on the basis of this property? Before giving the answer, let us recall that quantum theory is fundamentally non-signaling. In order to avoid the possibility of superluminal signaling, two observers (Alice and Bob) can only have events that obey the rules:
In plain language, the probability of Alice’s event does not depend in any way on Bob’s choice of measurement, and vice versa. This entails the conditional independence relationships:
There is a striking similarity between expressions (9), (10) and expressions (3), (4). The Non-Signaling Criterion is more general, compared to the Locality Criterion, but the two situations are experimentally indistinguishable. After all, the hidden parameter λ can have any value, including a null effect. For this reason, measurement outcomes do not reveal any information about the physical behavior at the opposite station in both cases. Yet, the expressions (9) and (10) do not obey Bell’s inequality. As shown by Popescu and Rohrlich, they even allow for maximal (“super-quantum”) violations. Therefore, we do not have the necessary grounds to derive a marker for local behavior, on the basis of correlation analysis. This conclusion is not just intuitive. It is well supported by recent theoretical advancements. For instance, Raymond-Robichaud has written a treatise on the equivalence between non-signaling behavior and local realist behavior [10,11]. He showed that the non-signaling condition is indeed more general. Any local relationship is automatically non-signaling, and the reverse is not necessarily true, in a general sense. However, the two conditions are physically equivalent. Any theory with invertible dynamics (including quantum mechanics) can be given a local interpretation. This conclusion is further supported by the recent work of Cetto and collaborators [12,13]. They performed a rigorous analysis of the bi-partite quantum correlation function and discovered that it is local. Similarly, Khrennikov analyzed the properties of quantum correlations directly, without any assumptions about hidden variables [14,15]. His conclusion was that Bell’s inequality is a test of physical compatibility. It does not justify belief in action at a distance, either in space or time.
This leads to the question: how did Bell produce his theorem? Which condition did he use to derive the inequality? In his original seminal paper [1], Bell started with the relationship in expression (2), emphasizing the separability of two local variables. However, when he moved on to introduce a third variable, he used the tacit assumption that all the observables are jointly distributed [2,3]. In other words, Bell’s inequality requires two conditions:
- All the properties of the relevant system are local, and
- All the properties exist at the same time.
This is the EPR notion of “Local Realism” (meaning “Simultaneous Realism”), as explained above. In other words, Bell’s inequality is actually derived from the following condition:
An interesting question to ask is whether expression (11) is observationally equivalent to expression (2). Could it be that we automatically get (11) if (2) is true? In particular, if we have two joint observations (a,b) and (b,c), while the value of b is the same in both cases, does it not follow that all the events are jointly distributed? This does sound intuitively appealing when we think about classical properties that are permanent, and therefore simultaneous. However, classical realism also includes properties that are transient and mutually exclusive. In this case, it is necessary to devise special schemes for measurement, enabling the joint observation of incompatible properties. In theory, we could make three copies of a single system, enabling the simultaneous measurement of all the relevant observables for a Bell experiment. In this case, expression (11) would be true by default. However, it is well known that quantum theory does not predict Bell violations in this case. In any experiment where three variables or more are measured at the same time, we get the so-called phenomenon of “quantum monogamy” [6]. The only way to achieve violations is by designing dedicated experiments that only measure relevant observables in pairs. Accordingly, expression (2) would be empirically equivalent to expression (11), and Bell’s inequality would be a universal test of locality, if the following condition was true: for any three observable A, B and C, if A is jointly distributed with B, and B is jointly distributed with C, then A is always jointly distributed with C.
It is a well-known fact in probability theory that such an assumption cannot be correct [16,17]. A simple way to explain this in the context of quantum mechanics is to recall that Bell’s inequality is violated by variables that do not commute. To make such joint measurements possible, two entangled quanta are used, thereby forcing these variables to commute, but only two at a time. For example, suppose that Bob is studying observable B, while Alice has a choice between A and C. It is conceivable that Bob’s distribution is the same in both combinations (and therefore local). Is it necessary to exclude this possibility when Bell’s inequality is violated? For something like that to be true, it should be mathematically impossible for Bob’s distribution to be compatible with two different measurements, unless all the observables of this system commuted with each other. In other words, if A commutes with B, and B commutes with C, then it should always be true that A commutes with C. Again, it is textbook knowledge that such a rule does not hold in linear algebra (see, for example, [18,19]). Here, this can be illustrated by considering three Pauli operators:
One can easily verify that AB=BA, and BC=CB, since B is the identity matrix. However, AC≠CA, which is a known property of the Pauli matrices (and other operators that obey Heisenberg’s Uncertainty Principle). Therefore, it is possible for Bob to have the same distribution of events regardless of Alice’s choice of observation, even in cases where Bell’s inequality does not apply.
After careful consideration, this type of behavior can be given a straightforward intuitive explanation. When several properties occur at the same time, they obey the so-called transitive rule. For example, if we have three permanent properties X, Y, and Z, then two pairwise correlations automatically determine the third. To visualize the logical structure of this process, consider a pile of shirts, such that “all the white shirts are made from cotton” and “all the cotton shirts are short-sleeved”. It follows with necessity that “all the white shirts are short-sleeved” in the same group. It would be a contradiction to have even one white shirt with long sleeves. Accordingly, Bell violations are logically impossible because they entail contradictory properties for one and the same object. As shown in Figure 2a, several observables can be detected at the same time, in which case the same exact value for each measurement outcome is used in all the pairwise combinations. In contrast, when we have mutually exclusive events that are staggered in time, the transitive rule does not apply. Instead, simultaneous measurements are replaced with extended coincidence windows that only allow for the detection of two events at a time. In this case, it is logically impossible to arrange four sequential observations (or more), such that all of them are adjacent to each other. As seen in Figure 2b, the same value of b1 is used in (a1, b1) and (b1, a2). The same value of b2 is used in (a2, b2) and (b2, a1). Hence, we have independence between the measurement settings of Alice and Bob. However, different values of a1 are used in different parts of this chain (one at T1 and one at T5). The predetermined order of observables is such that different events are paired in different combinations, simply because of the sequential nature of this process. In conclusion, simultaneous properties cannot produce Bell violations. This would contradict their definition as being simultaneous. At the same time, sequential properties cannot always obey the inequalities. This would contradict their definition as being sequential. Furthermore, as will be shown in the next section, staggered independent events can produce maximal Bell violations. This confirms the equivalence between non-signaling behavior and local behavior, because both types of events exhaust the range of possible combinations in a CHSH experiment (0≤S≤4). To sum up, all the lines of analysis converge on the same conclusion: “Local Realism” only means “Simultaneous Realism” in discussions about quantum entanglement. As defined in expression (2), the Locality Criterion is insufficient to derive the Bell inequalities. For any practical purpose, “non-signaling” means “local”, in any meaningful physical theory.
3. Super-quantum Bell violations in classical systems
Sequential physical properties require a little bit of “intuition training” for analysis, or else they might seem “weird”. For instance, playing cards have several binary properties that exist simultaneously. Any one of them can be marked with numbers that are odd or even, red or black, etc. – all at the same time. In the same way, coins always have two sides (“heads” and “tails”), such that one of them is always observable on top, when at rest. In contrast, sequential properties are mutually exclusive. They can only exist one at a time. Therefore, a finite time budget must always be divided between them, such that every property can manifest alone, in its designated time segment. Analogue clocks are the best way to visualize this process. The time segment 1 o’clock happens alone, followed by 2 o’clock, and so on. More importantly, opposite values along an axis of “measurement” are also sequential, relative to each other, and also manifest in order, in designated time slots. Hence, any time marker on a clockface has an opposite match, but they are noticeably remote from each other. As the arms of a clock move around, they scan all the values continuously. After a long period of time, all the opposite values will be expressed with equal frequency. Ergo, their distribution is 50-50, just like for coin tosses. However, it is very important to remember that coins can be measured on the spot, but sequential properties require patience. The system has to pass through all the intermediate phases (with corresponding statistical implications) before alternative events can manifest on the same axis. This feature of sequential events can demystify a lot of quantum phenomena, especially with regard to quantum entanglement.
Bell experiments are designed to make closed chains of pairwise measurements. For example, if we designate four observables as A, B, C and D (for the sake of clarity), then the four relevant pairs are (A,B), (B,C), (C,D) and finally (D,A). These joint observations can be made in continuous cycles or at random, without any difference on the final outcome, at least in ideal conditions. Though, it bears repeating that sequential properties cannot exist at the same time by default. Therefore, it is not possible to make simultaneous pairwise measurements. Instead, a window of coincidence needs to be defined, such that only two events in a chain are detectable for measurement. When the sequence of alternative properties is designed to work like clockwork, the necessary time window is determined by the period of a complete cycle of events. For example, if the minute arm goes around the clock in 60 minutes, then a time window of 5 minutes can be used to isolate two consecutive events for joint detection. In the same manner, a clockface can be divided into 6 sectors or 8 sectors, or as many pairs as necessary to replicate the properties of a chosen measurement protocol.
Another well-known feature of quantum Bell experiments is the emphasis on space-like separation between joint measurements. The stations of Alice and Bob are always as far as technology allows (the trend being to increase the distance with each generation). This is perceived as necessary, in order to close interpretive loopholes for non-locality. Quantum behavior is unobservable, while the standard presumption is that Bell violations require action at a distance. Nonetheless, Bells inequality is derived from abstract considerations that have nothing to do with communication between measurements. The proof is merely that statistical predictions of a certain sort do not depend on the distance between measurements. If it was possible to have a “God’s eye view” on the underlying mechanism, such precautions would not be necessary. Indeed, macroscopic classical systems can be perfectly transparent. For example, the time markers on a clockface are printed in advance of operation and stay permanently fixed. By default, such properties cannot influence each other. They operate as if they are “space-like separated”. Thus, if a set of coefficients can (or cannot) violate a Bell-type inequality as part of a single system, then the same behavior will be replicated by using two copies of the same system. If Bob measures a copy of Alice’s clock, without any disturbance, then he can only get the same events (and corresponding correlations) that he would get by measuring Alice’s clock directly. In short, the mechanism of Bell violations can be determined simply by studying the properties of a single classical system.
With this in mind, let us consider a macroscopic system with four sequential binary properties. As shown in Figure 3, this can be done by dividing a round table into 8 equal sectors. The sectors on the right side are colored in blue and assigned “+” values. The sectors on the left side are colored green and marked with “−“ values. Each of the four observables (A1, B1, A2 and B2) has two opposite sectors on the table. The arrow above the table is forced to rotate continuously, like clockwork. At any point in time, the orientation of the arrow corresponds to a value that can be treated as a “measurement outcome”. For example, when the arrow points at the blue sector A1, it expresses the event “a1+”. If it points at the green sector B2, it expresses the event “b2− ”. Joint measurements are conducted by isolating consecutive pairs of events in a narrow window of coincidence. For example, if the period of rotation of the arrow is 1 second, then the required window is 1/8 second long. The binary properties are interlaced, such that any pairwise measurement includes an “Alice” event and a “Bob” event. Notably, every Alice event is flanked by two alternative Bob events. Therefore, Alice’s events are the same, regardless of Bob’s choice of observation. The same is true for Bob. However, it is a necessary feature of this arrangement that b1 and b2 events cannot be adjacent to the same a1 event. Therefore, unusual correlations are possible: A1 is correlated with B1, B1 with A2, and A2 with B2, but B2 and A1 are anti-correlated. The latter are always on opposite-colored sides of the table.
A typical Bell experiment with four binary properties is usually designed to test the Clauser-Horne-Shimony-Holt (CHSH) inequality [20]. In order to capture the details of the described toy model, the main prediction can be expressed as follows:
As explained in the previous section, Ai and Bj correspond to measurement settings, while E(Ai, Bj) is the expectation value for the product of outcomes in the selected settings. This expectation value is commonly referred to as the coefficient of correlation, and it is calculated by processing the marginal probabilities of each possible combination of outcomes, as follows:
Or, in more intuitive terms:
In the case of our rotating arrow, coincidence windows allow exclusively for (+,+) and (-,-) observations between three pairs of variables. Hence,
In contrast, the remaining pair is always anticorrelated, since it can only display (-,+) and (+,-) coincidences:
Accordingly, the final tally is:
Not only is this result larger than S≤2, but it also corresponds to the maximal possible value that is allowed by the CHSH formula. This conclusion is identical to the result of Popescu and Rohrlich [4], with regard to the range of “non-signaling” physical behavior. Yet, in this case the violation was achieved in a transparent classical system, without any room for speculation about non-locality. All the measurement outcomes were fixed in advance, and no mutual interactions between events were allowed. This type of behavior is natural for sequential events, as explained in the preceding section. Ergo, non-signaling interactions are physically equivalent to local interactions, in any form. If quantum theory is acknowledged as non-signaling, then it must also be treated as local by default. Surprisingly, no physical theory can make non-local predictions that are statistically distinguishable from local events. Or, to put it differently, empirical evidence cannot falsify local behavior, at least with regard to pairwise correlations.
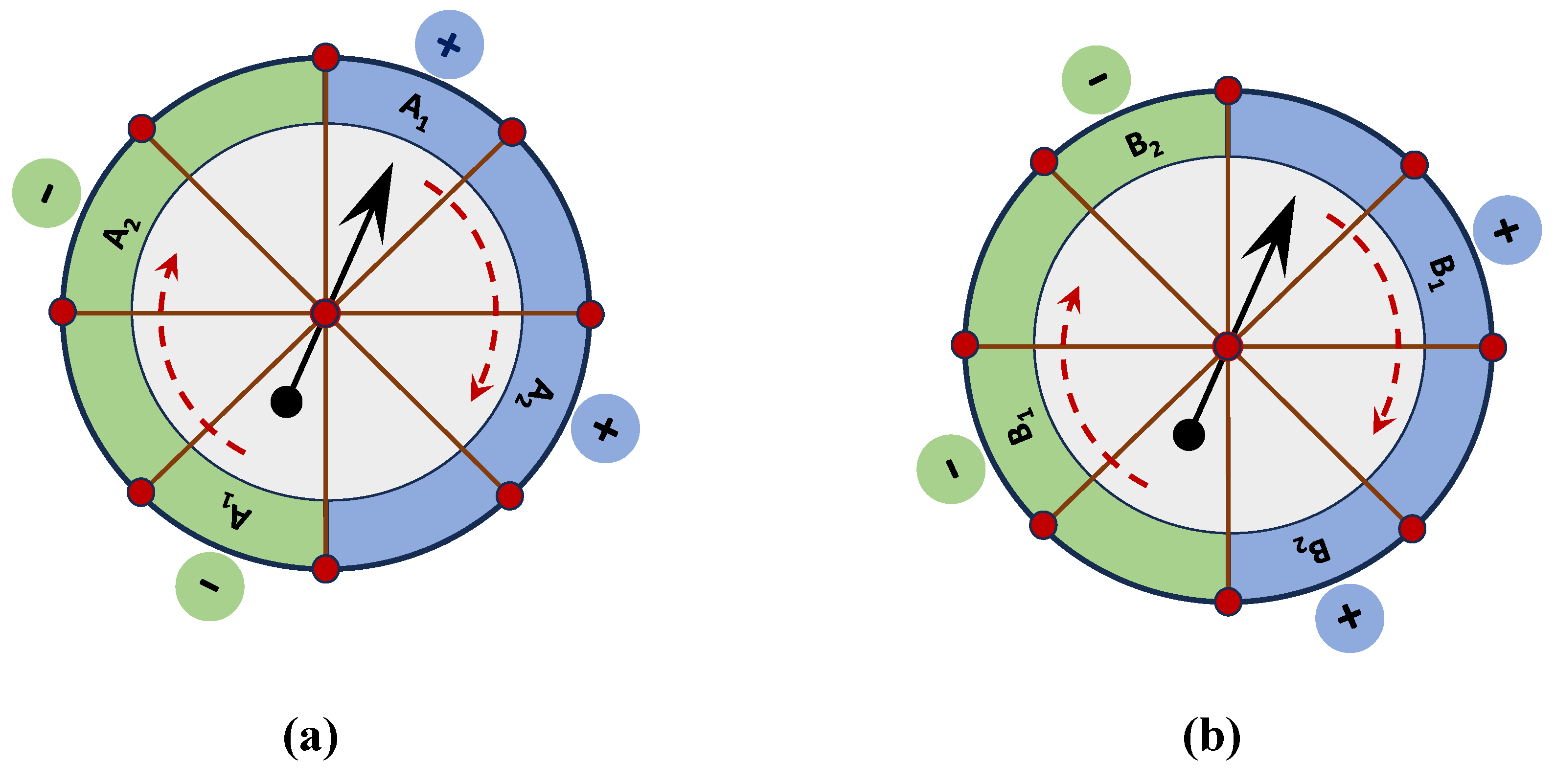
The effect described above was achieved with a single rotating arrow, in order to bring out the physical mechanism behind these patterns of correlation. However, it is not a challenge to express the same type of behavior with remote measurements. As shown in Figure 4a and 4b, it is possible to make tailored versions of this system for Alice and Bob, such that Alice only has access to Ai settings, while Bob is only free to record the Bj settings. As long as the two arrows are synchronized, joint measurements are going to produce the same behavior as in the case of a single arrow. Alternatively, the two arrows can be programmed to spin at the same rate, but out of phase by half a period, in order to mimic the anti-correlation between the spin of entangled electrons. In both cases, maximal CHSH violations are the natural result, if measurements are conducted in suitable coincidence windows. Though, it should be noted that sequential properties only express this behavior when measured in pairs. For instance, it is possible to make four copies of this arrow system, in order to detect all the properties at the same time (A1, A2, B1 and B2). In this case, observers end up producing isolated groups of four events, just as shown in Figure 2a. The cycle of staggered events is artificially broken into simultaneous bunches. Instead of pairing different events in different combinations, all the combinations in a batch are forced to use the same events for analysis. In this case, equation (5) becomes:
In short, Bell violations are no longer possible. Yet, this is not a consequence of interactions between measurements. This outcome is forced by the method of analysis, given that pairwise combinations are produced by different rules. By implication, “quantum monogamy” [6] is also an ordinary classical phenomenon. To generalize what was shown above, there is nothing special or non-classical about Bell violations, be they “quantum” or “super-quantum”. Indeed, it is misleading to even describe these correlations as “quantum”. They are natural properties of all sequential properties, both classical and non-classical [21].
4. Discussion
Non-commuting quantum properties can be interpreted in two ways. On the one hand, they can emerge as a result of preparation, before detection. For example, a photon can be polarized by a beam-splitter, in one of two orthogonal planes. The outcome of this transformation is verified downstream, by one of two detectors. On the other hand, the same properties can “become real” at the moment of detection. For example, a photon can pass through a beam-splitter, but only becomes polarized when it is registered by a detector. This interpretation is phantasmagoric, but the founders of quantum mechanics were deeply influenced by it, even when this nuance was not explicitly acknowledged. In particular, Niels Bohr and his supporters opposed the notion of classical realism at the quantum level [22,23]. They justified this position with references to non-commutativity. If complementary properties become real one at a time, at the moment of measurement, then nothing needed to exist prior to measurement. Such a position only makes sense with the second interpretation in mind. Otherwise, it is possible to explain consecutive properties in terms of objective evolving processes. In the same vein, Einstein and his supporters [7,24] insisted that non-commuting properties should exist at the same time. If “momentum” and “position” become real one at a time, then quantum correlations require action at a distance. This mechanism sounded “unreasonable”, as suggested in the EPR paper, but only in the context of the second interpretation. Again, an objective process of evolution, independent of measurement, can remove any basis for non-locality (as shown in Figure 1), but somehow this alternative did not seem relevant in that historical context. Today, Bell’s inequality is widely perceived as the boundary to non-locality. Granted, it was not previously known that sequential events can violate Bell’s inequality without action. Nonetheless, it was a known fact that Bell’s Theorem is limited to properties that exist at the same time. In retrospect, if we look at the facts with fresh eyes, the conclusion is straightforward: Bell’s Theorem only makes sense, as formulated, if “creation by observation” is taken for granted. It is quite impressive that the Copenhagen interpretation had such a deep impact. Even its opponents felt constrained to adopt the same mystical assumptions about the process of measurement, whether explicitly or implicitly.
Looking back at the origins of this debate, we can see that “team Bohr” and “team Einstein” were engaged in an “all-or-nothing” confrontation. One side insisted that contextuality is everything. If quantum properties are conditional, then nothing is real outside of measurement. The other side insisted that everything is real at the same time, with no room for contextuality. The two positions sounded like perfect opposites, but they shared a common misconception. The only way to justify either of them is by taking it for granted that detectors (or, in extreme cases, human minds) are the source of conditional physical behavior. In contrast, if we allow for the emergence of objective contextual behavior, then the conflict disappears. For example, time markers follow each other like clockwork, one at a time. Clocks are built by humans, but the flow of time is an objective real process. It is not 1 o’clock because we look at the clock. Quite the contrary: we see it because it happens to be real. As shown above, sequential events produce maximal Bell violations, even if they are predetermined and even if measurements are non-invasive. Therefore, quantum properties can also be real and contextual at the same time. This means that quantum theory is correct, as insisted by Bohr, and ontologically incomplete, as shown by Einstein. The two sides can finally shake hands in agreement.
The overlooked detail of quantum entanglement is that non-commuting variables are never real at the same time. They seem to be observable at the same time with two correlated systems, but the relevant effects are still determined by incompatible mechanisms of preparation. If both systems are prepared in the same way, then Alice and Bob are forced to make their measurements at different stages of wave-function evolution (or else they can only measure identical properties). Hence, twin systems produce the same type of correlations that are possible in a single system with consecutive non-destructive measurements. Their incompatibility is objective, and this is what determines their patterns of correlation. Though, as shown above, maximal Bell violations require special conditions. The delay between paired measurements must be constant, such that any combination of two observables can fall within the same coincidence window. Positive (negative) values have to be grouped together, ensuring maximal coefficients of correlation between adjacent events. There is an instructive difference between the solution presented above and the observable features of photon polarization. In the latter case, there is a gradual increase in phase delay between optical components, as the angle between measurements is increased. Real Bell experiments maintain constant differences between observables by choosing four measurements at equal angular intervals from each other (22.5°). Furthermore, rotations of the plane of polarization introduce a gradual (and non-linear) loss of correlation, as dictated by Malus’ Law. This explains the gap between the maximal Bell violations that are numerically possible and the ones that are physically possible with quantum projections. Accordingly, we can now resolve the ongoing debates about the limited nature of quantum entanglement. From the perspective of Bell’s argument [1], the apparent problem was that quantum correlations were “too high”. Yet, as suggested by Popescu and Rohrlich [4], the true physical puzzle was that they were “too low”. In retrospect, there is nothing uniquely “quantum” about quantum correlations. As shown above, “local” and “non-signaling” types of behavior are physically equivalent at any level of analysis.
A major obstacle on the path to this solution was the confusing nature of quantum dualism. Solid bodies, such as bowling balls, have simultaneous values for momentum and position at every stage of motion. How can they possibly exist only one at a time? The trick was to realize that quantum experiments do not measure particles. They count them, in order to verify the parameters of wave-like phenomena. As it turns out, wave properties can have the same names as particle properties, but they have radically different connotations. For instance, wave “position” and wave “momentum” describe virtual components of macroscopic projections [9]. As shown with Fourier analysis, the spectrum of position can only be well-defined in a plane of measurement where the spectrum of momentum is maximally undefined, and vice versa. Though, Fourier transforms cannot tell us where to look for these phenomena. An independent model of wave mechanics is required, in order to understand their sequential nature. In the same way, matrix mechanics did not result in a meaningful mechanism for quantum non-commutativity. Conjugate variables were perceived as abstract alternatives to each other. One needs to study quantum wavefunctions in experimental contexts [8], in order to avoid distorted interpretations. Though, it appears that Schrodinger’s “undulatory theory” – despite being published in 1926 [25] – entered the public arena too late, when the framework for analysis was already cemented by the Copenhagen interpretation. It may be that Kuhn [26] was right: scientific ideas require conceptual structures for meaning. Once a paradigm is institutionalized, alternative concepts are hard to process or even imagine. In extreme cases, it may take a global scientific revolution just to correct a simple misconception.
5. Conclusion
Bell violations cannot falsify locality. They only serve to identify incompatible physical properties. This was demonstrated above with three complementary arguments. First of all, quantum theory is distorted by arbitrary interpretive assumptions. Chief among them is the principle that measurements create reality. This is the source of confusion between “locality” and “simultaneity”. Secondly, Bell’s Theorem is an argument about simultaneous existence, not about locality. Bell-type inequalities are always obeyed by simultaneous properties, but they can be maximally violated by sequential properties. Finally, a chain of pairwise measurements was described, revealing the mechanism for maximal Bell violations with hidden (and not so hidden) variables. This made it clear that “quantum correlations”, “super-quantum correlations” and “quantum monogamy” are all classical phenomena. The underlying problem was, indeed, interpretive, but the missing piece of the puzzle was factual: sequential events can express any combination of correlations that is numerically possible in a Bell protocol. They can do it locally, without mutual interactions. Ergo, there is no such thing as “non-signaling nonlocality”. This result does not contradict quantum theory. It only corrects the assumptions that distorted its physical essence and opens the path towards a deeper understanding of quantum phenomena.
Acknowledgments
The search for this solution was inspired by a series of discussions with Jan-Åke Larsson, Gregor Weihs, Sergey Polyakov, Andrei Khrennikov, Ana-María Cetto, Richard Gill, OpenAI ChatGPT, and France Čop.
References:
- Bell, J. S. Speakable and unspeakable in quantum mechanics (Cambridge UP, 1987).
- Fine, A. Joint Distributions, Quantum Correlations, and Commuting Observables. J. Math. Phys. 23, 1306 (1982). [CrossRef]
- Kujala, J. V.; Dzhafarov, E. N.; Larsson, J-A. Necessary and Sufficient Conditions for an Extended Noncontextuality in a Broad Class of Quantum Mechanical Systems, Phys. Rev. Lett. 115, 150401 (2015). [CrossRef]
- Popescu, S.; Rohrlich, D. Quantum Nonlocality as an Axiom. Found. Phys. 24, 379 (1994). [CrossRef]
- Peres, A. Quantum Theory: Concepts and Methods (Kluwer, 1993).
- Dhar, H. S.; Pal, A. K.; Rakshit, D.; Sen (De), A.; Sen, U. Monogamy of Quantum Correlations - A Review. In: F. Fanchini, D. Soares Pinto, and G. Adesso (eds), Lectures on General Quantum Correlations and their Applications (Springer, 2017).
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 47, 777 (1935). [CrossRef]
- Howell, J. C.; Bennink, R. S.; Bentley, S. J.; Boyd, R. W. Realization of the Einstein-Podolsky-Rosen paradox using momentum- and position-entangled photons from spontaneous parametric down conversion. Phys. Rev. Lett., 92, 210403 (2004). [CrossRef]
- Hecht, E. Optics (Addison-Wesley, 2001).
- Raymond-Robichaud, P. The Equivalence of Local-Realistic and No-Signalling Theories. Preprint: arXiv:quant-ph/1710.01380. https://arxiv.org/abs/1710.01380.
- Raymond-Robichaud, P. L’équivalence entre le local-réalisme et le principe de non-signalement. PhD Thesis (Université de Montréal, 2017). https://papyrus.bib.umontreal.ca/xmlui/handle/1866/20497.
- Cetto, A. M.; Valdés-Hernández, A.; de la Peña, L. On the Spin Projection Operator and the Probabilistic Meaning of the Bipartite Correlation Function. Found. Phys. 50, 27 (2020). [CrossRef]
- Cetto, A.M. Electron Spin Correlations: Probabilistic Description and Geometric Representation. Entropy 24, 1439 (2022). [CrossRef]
- Khrennikov, A. Bell-Boole Inequality: Nonlocality or Probabilistic Incompatibility of Random Variables? Entropy, 10, 19 (2008). [CrossRef]
- Khrennikov, A. Get Rid of Nonlocality from Quantum Physics. Entropy 21, 806 (2019). [CrossRef]
- DeGroot, M. H.; Schervish, M. J. Probability and Statistics (Addison-Wesley, 2010).
- Durrett, R. Probability: Theory and Examples (Cambridge UP, 2019).
- Adler, S. J. Linear Algebra Done Right (Springer, 1997).
- Meyer, C. D. Matrix Analysis and Applied Linear Algebra (SIAM, 2000).
- Clauser, J. F.; Horne, M. A.; Shimony, A.; Holt, R. A. Proposed Experiment to Test Local Hidden-Variable Theories. Phys. Rev. Lett. 23, 880 (1969). [CrossRef]
- Mardari, G. N. Experimental Counterexample to Bell’s Locality Criterion. Entropy 24, 1742 (2022). [CrossRef]
- Bohr, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 48, 696 (1935). [CrossRef]
- Jammer, M. The Conceptual Development of Quantum Mechanics (McGraw Hill, 1966).
- Einstein, A. Physics and Reality, in Einstein, A. Ideas and Opinions, 290-323 (Crown, 1954).
- Schrödinger, E. An undulatory theory of the mechanics of atoms and molecules. Phys. Rev. 28, 1049 (1926). [CrossRef]
- Kuhn, T. S. The Structure of Scientific Revolutions (Chicago UP, 1962).
Figure 1.
Quantum momentum and quantum position are objectively sequential properties. In classical optics, wave momentum and wave position are defined in reference to spatial frequency k-vectors. Ideally, component wave vectors with parallel directions intersect at a common point in the focal plane of a lens. (Only two pairs are shown for clarity). Component wave vectors from a common source-point converge onto a small area in the image plane. The two types of distributions are connected by a Fourier transform. Quantum behavior is identical, for large numbers of events, since it obeys the Correspondence Principle. Accordingly, photon “momentum” information is extracted by placing an event counter in the focal plane of a lens. Photon “position” information is extracted by moving the same detector to the image plane. Thus, an observer cannot “collapse” the photon for each property at random coordinates. These properties can only be resolved in adequate planes of detection, when and where they are able to manifest. More importantly, the photons do not reveal information about their “particle” properties. Instead, the proportion of photons at each coordinate provides information about the corresponding wave-function amplitudes. NB: this diagram is made with optical rays, in order to express the geometry of relevant macroscopic features. These rays should not be mistaken for “photon trajectories”, or else contradictions with classical and quantum mechanics will follow. The trajectories of individual quanta are unobservable. The only verifiable detail is that a given number of quanta can arrive at a selected coordinate per unit of time, with a probability that is determined by Born’s rule.
Figure 1.
Quantum momentum and quantum position are objectively sequential properties. In classical optics, wave momentum and wave position are defined in reference to spatial frequency k-vectors. Ideally, component wave vectors with parallel directions intersect at a common point in the focal plane of a lens. (Only two pairs are shown for clarity). Component wave vectors from a common source-point converge onto a small area in the image plane. The two types of distributions are connected by a Fourier transform. Quantum behavior is identical, for large numbers of events, since it obeys the Correspondence Principle. Accordingly, photon “momentum” information is extracted by placing an event counter in the focal plane of a lens. Photon “position” information is extracted by moving the same detector to the image plane. Thus, an observer cannot “collapse” the photon for each property at random coordinates. These properties can only be resolved in adequate planes of detection, when and where they are able to manifest. More importantly, the photons do not reveal information about their “particle” properties. Instead, the proportion of photons at each coordinate provides information about the corresponding wave-function amplitudes. NB: this diagram is made with optical rays, in order to express the geometry of relevant macroscopic features. These rays should not be mistaken for “photon trajectories”, or else contradictions with classical and quantum mechanics will follow. The trajectories of individual quanta are unobservable. The only verifiable detail is that a given number of quanta can arrive at a selected coordinate per unit of time, with a probability that is determined by Born’s rule.
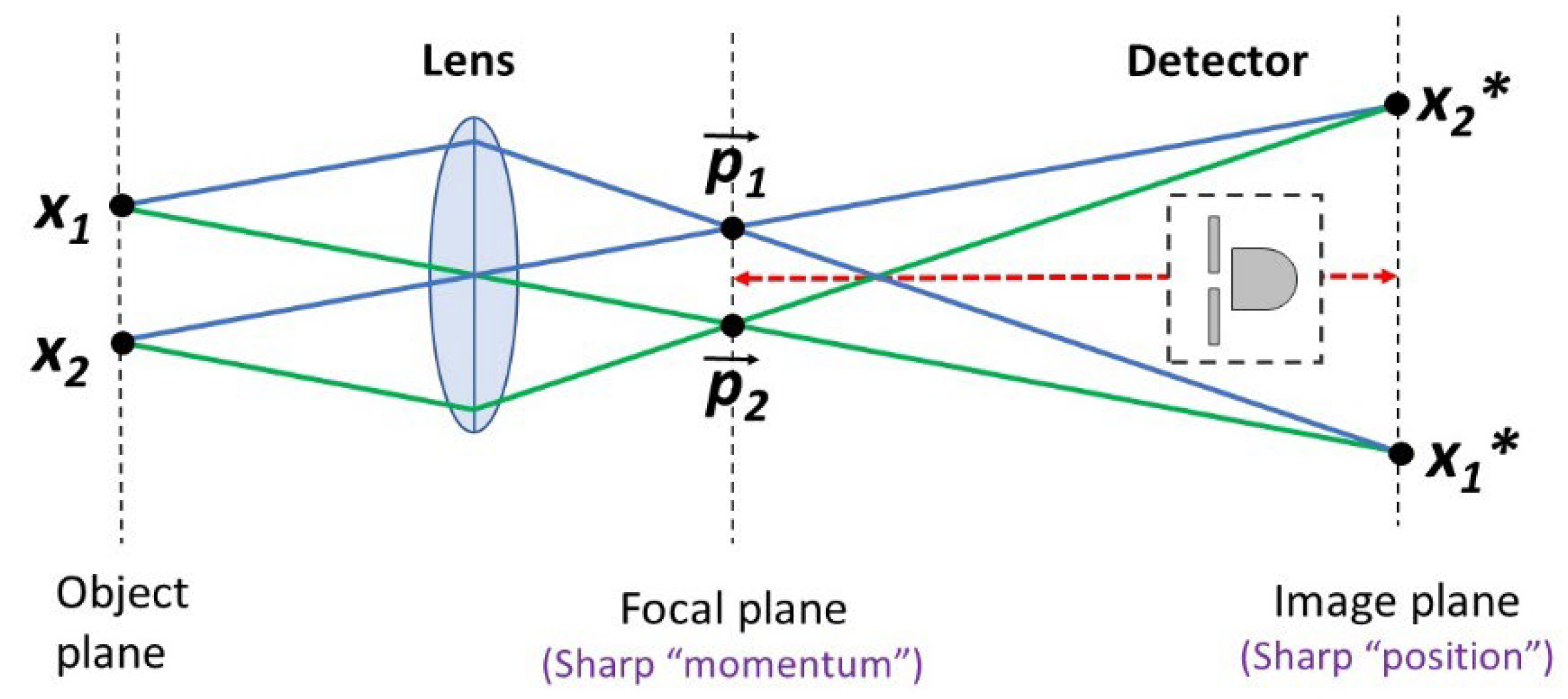
Figure 2.
Simultaneous and sequential events can have different rules of pairwise combination. Some patterns of coincidence cannot violate Bell-type inequalities. As shown in table (a), simultaneous events are blocked into fixed groups. The same event is paired repeatedly with any other observable from the same group. Therefore, coefficients of correlation cannot contradict each other. In contrast, sequential events allow for pairwise combinations outside of the group. As seen in table (b), it is impossible for four different events in a row to be adjacent to each other. Instead, a narrow window of coincidence forces the emergence of incompatible pairings. Maximal Bell violations become possible. On the other hand, if four different events are recorded at the same time, this pairwise inconsistency is erased, and pattern (b) switches back to pattern (a). This explains the shift from “super-quantum correlations” to “quantum monogamy”.
Figure 2.
Simultaneous and sequential events can have different rules of pairwise combination. Some patterns of coincidence cannot violate Bell-type inequalities. As shown in table (a), simultaneous events are blocked into fixed groups. The same event is paired repeatedly with any other observable from the same group. Therefore, coefficients of correlation cannot contradict each other. In contrast, sequential events allow for pairwise combinations outside of the group. As seen in table (b), it is impossible for four different events in a row to be adjacent to each other. Instead, a narrow window of coincidence forces the emergence of incompatible pairings. Maximal Bell violations become possible. On the other hand, if four different events are recorded at the same time, this pairwise inconsistency is erased, and pattern (b) switches back to pattern (a). This explains the shift from “super-quantum correlations” to “quantum monogamy”.
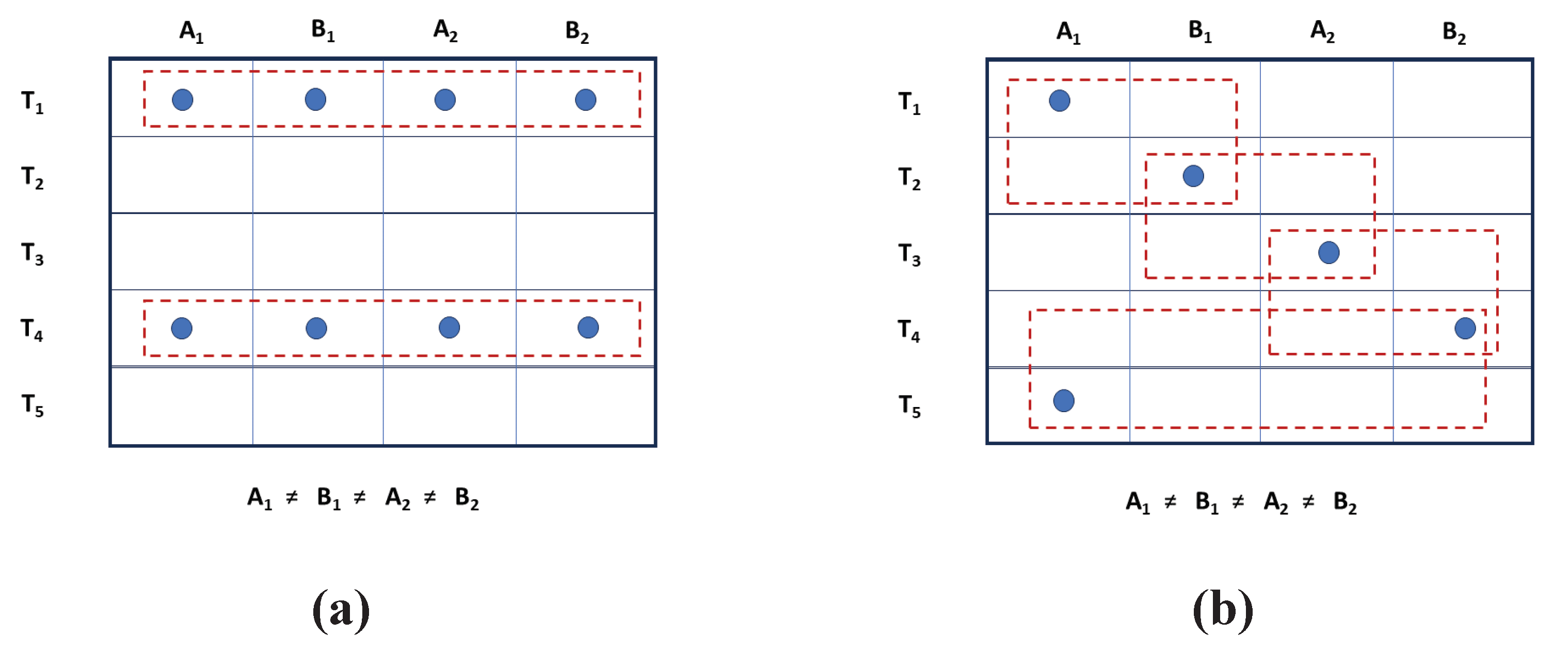
Figure 3.
Toy model for maximal Bell violations with sequential properties. Spinning arrows can have arbitrarily large numbers of sequential properties, one for each relevant angle of inclination. This is analogous to the rotation of wave polarization, or the precession of the axis of spin for rotating bodies. In this case, the arrow is placed above a table with markers for 4 binary properties, each one along a designated axis of measurement. Two “Alice” settings are interlaced with two “Bob” settings, enabling pairwise measurements between consecutive events, as if in a Bell experiment. Notably, the value markers are permanently fixed on the table. All the measurements are non-invasive and no interactions between the events are possible. The arrow is simply pointing at each sector one at a time, expressing the corresponding quality, like clockwork. The crucial detail is that such properties are not “created” by measurement. They only become real when the arrow is able to express them. As explained in the text, this mechanism entails maximal violations of the CHSH inequality.
Figure 3.
Toy model for maximal Bell violations with sequential properties. Spinning arrows can have arbitrarily large numbers of sequential properties, one for each relevant angle of inclination. This is analogous to the rotation of wave polarization, or the precession of the axis of spin for rotating bodies. In this case, the arrow is placed above a table with markers for 4 binary properties, each one along a designated axis of measurement. Two “Alice” settings are interlaced with two “Bob” settings, enabling pairwise measurements between consecutive events, as if in a Bell experiment. Notably, the value markers are permanently fixed on the table. All the measurements are non-invasive and no interactions between the events are possible. The arrow is simply pointing at each sector one at a time, expressing the corresponding quality, like clockwork. The crucial detail is that such properties are not “created” by measurement. They only become real when the arrow is able to express them. As explained in the text, this mechanism entails maximal violations of the CHSH inequality.
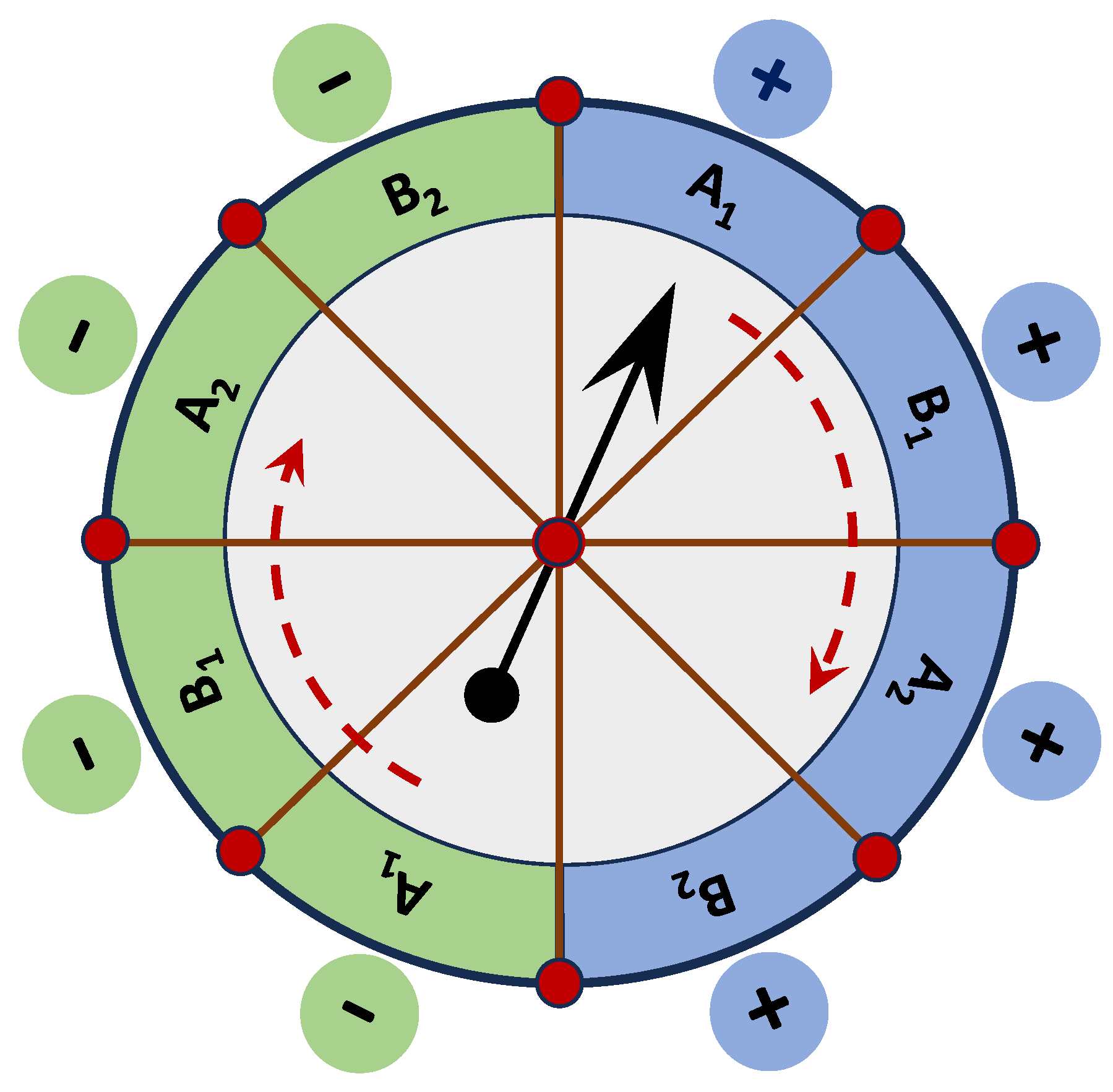
Figure 4.
Bell experiment with correlated spinning arrows. The transient properties of a single system can produce maximal Bell violations. Therefore, it is possible to obtain the same result by studying the properties of two identical systems, with correlated internal dynamics. (a) Alice receives a set-up with Bob’s settings erased from the reference table. (b) Bob receives a copy with Alice’s settings removed. As longs as the two systems are synchronized, consecutive remote events will be correlated (or anti-correlated), just as in the case of a single system. Hence, Alice and Bob can record all of their events, in sequence, with corresponding time markers, for an agreed period of time. Afterwords, they can meet to reconcile their records and to identify coincidences for each combination of properties. Alternatively, they can make random measurements with the same final outcome since the whole process is perfectly deterministic. (There is no difference between sampling live events or sampling recorded events in this case.) The only requirement is for Alice and Bob to select adjacent qualities for measurement, or else the correlations would be lost. This matches the requirement to target entangled quanta (as opposed to arbitrary pairings) in real Bell experiments.
Figure 4.
Bell experiment with correlated spinning arrows. The transient properties of a single system can produce maximal Bell violations. Therefore, it is possible to obtain the same result by studying the properties of two identical systems, with correlated internal dynamics. (a) Alice receives a set-up with Bob’s settings erased from the reference table. (b) Bob receives a copy with Alice’s settings removed. As longs as the two systems are synchronized, consecutive remote events will be correlated (or anti-correlated), just as in the case of a single system. Hence, Alice and Bob can record all of their events, in sequence, with corresponding time markers, for an agreed period of time. Afterwords, they can meet to reconcile their records and to identify coincidences for each combination of properties. Alternatively, they can make random measurements with the same final outcome since the whole process is perfectly deterministic. (There is no difference between sampling live events or sampling recorded events in this case.) The only requirement is for Alice and Bob to select adjacent qualities for measurement, or else the correlations would be lost. This matches the requirement to target entangled quanta (as opposed to arbitrary pairings) in real Bell experiments.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





