Puppis: Hardware Accelerator of Single-Shot Multibox Detectors for Edge-Based Applications

Object detection is a popular image processing technique, widely used in numerous applications for detecting and locating objects in images or videos. While being one of the fastest algorithms for object detection, Single-Shot Multibox Detection (SSD) networks are also computationally very demanding, which limits their usage in real-time edge applications. Even though the SSD post-processing algorithm is not the most complex segment of the overall SSD object detection network, it is still computationally demanding and can become a bottleneck with respect to processing latency and power consumption, especially in edge applications with limited resources. When using hardware accelerators to accelerate backbone CNN processing, the SSD post-processing step implemented in software can become critical for high-end applications where high frame rates are required, as this paper shows. To overcome this problem, we propose Puppis, an architecture for hardware acceleration of SSD post-processing algorithm. As experiments will show, our solution will lead to an average SSD post-processing speedup of 34.42 when compared with a software implementation. Furthermore, execution of a complete SSD network will be on average 45.39 times faster than software implementation when the proposed Puppis SSD hardware accelerator is used together with some existing CNN accelerators.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Object detection is a computer vision and image processing technique, widely used in many applications, such as face detection, video surveillance, image annotation, activity recognition, autonomous driving, quality inspection, etc. Among several object detection algorithms, the most popular and the fastest algorithm is a Single-Shot Multibox Detector (SSD) algorithm [1]. SSD is used for detecting objects from a predefined set of detection classes in images and videos, by a single Deep Neural Network. The main idea of the proposed object detector is to discretize the output space of so called bounding boxes into a set of default ones, using different scales and aspect ratios. During the inference, SSD network outputs the probability that each detection class is being detected within each of default bounding boxes, but also outputs the coordinate adjustments with respect to coordinates of default boxes to better "match" detected objects. By combining predictions from feature maps of different resolutions, proposed object detector leads to accurate detection of both large and small objects from a detection class set. As shown in [1], SSD architecture is significantly faster than multi-stage object detectors, like Faster R-CNN [2], while having significantly better accuracy compared to other single shot object detectors, like Yolo [3]. Even though SSD post-processing algorithm is not the most complex segment of overall object detection network, it is very computationally demanding and can be a bottleneck with respect to processing latency and power consumption, especially in the edge applications with limited resources. Motivated by that, in this paper we propose Puppis , an architecture of SSD hardware accelerator, which will reduce the duration of a software implemented SSD post-processing by 97%, on average, as we will show in the section presenting experimental results.

Despite the evolution of original object detectors [4,5,6] deep networks for detecting objects based on SSD are still one of the most widely used, while the scientific community proposed a lot of original SSD algorithm improvements, during years that followed. Authors in [7] propose slightly slower, but more accurate object detector based on enhanced SSD with a feature fusion module, while authors in [8] additionally optimize their SSD based network for small object detection. In [9] the classification accuracy of SSD architecture is improved by the introduction of Inception block which replaces extra layers in the original SSD approach, as well as an improved non-maximum suppression method. Attentive Single-Shot Multibox detector is proposed in [10], where irrelevant information within feature maps are suppressed in favour of the useful feature map regions. There are also multiple real-time system proposals based on the Single-shot Multibox Detector algorithm, where either modified convolutional layers are used as in [11], complete backbone CNN is simplified as in [12], or a multistage bidirectional feature fusion network based on Single-shot Multibox Detector is used for object detection as in [13].

While there are numerous proposals for algorithmic improvements of the original SSD algorithm available, there are not many proposals for the hardware acceleration of a Single-shot Multibox Detector algorithm in the available literature. Authors in [14] and [15] present the acceleration of the convolution blocks within the SSD network. In this paper, we propose a system for hardware acceleration of a complete Single-shot Multibox Detector algorithm and show how it can be integrated with a slightly modified backbone classifier (Mobilenet V1) to obtain fast and accurate object detector architecture, when implemented in FPGA. When using hardware accelerators for the implementation of backbone CNN in low-end, low frame-rate applications, SSD post-processing implemented in software is acceptable since the introduced latency is significantly shorter than the latency of the backbone CNN processing. Hence, it can be either neglected or even hidden by a pipelining to increase the throughput, even though the latency remains the same. Our work was motivated by the fact that SSD post-processing becomes critical for high-end applications where high frame rates are required. Results from the experimental section will show how our proposal results in SSD post-processing speedup up to 40.28 times and complete CNN network processing speedup up to 52.39 times, compared with pure software implementation, when MobilenetV1 SSD network is used for the object detection. The rest of the paper is structured as follows: after introductory section, in section 2 we will elaborate general structure of SSD network and the purpose of accelerating the SSD post-processing algorithm. In section 3, we will show which algorithms from SSD post-processing are accelerated and how, while the accelerator architecture is presented in section 4. Experimental results are shown in section 5, while the conclusion is given in the last section.

2. Overview of Proposed System for Hardware Accelerator of Complete SSD Network

2.1. General structure of SSD network

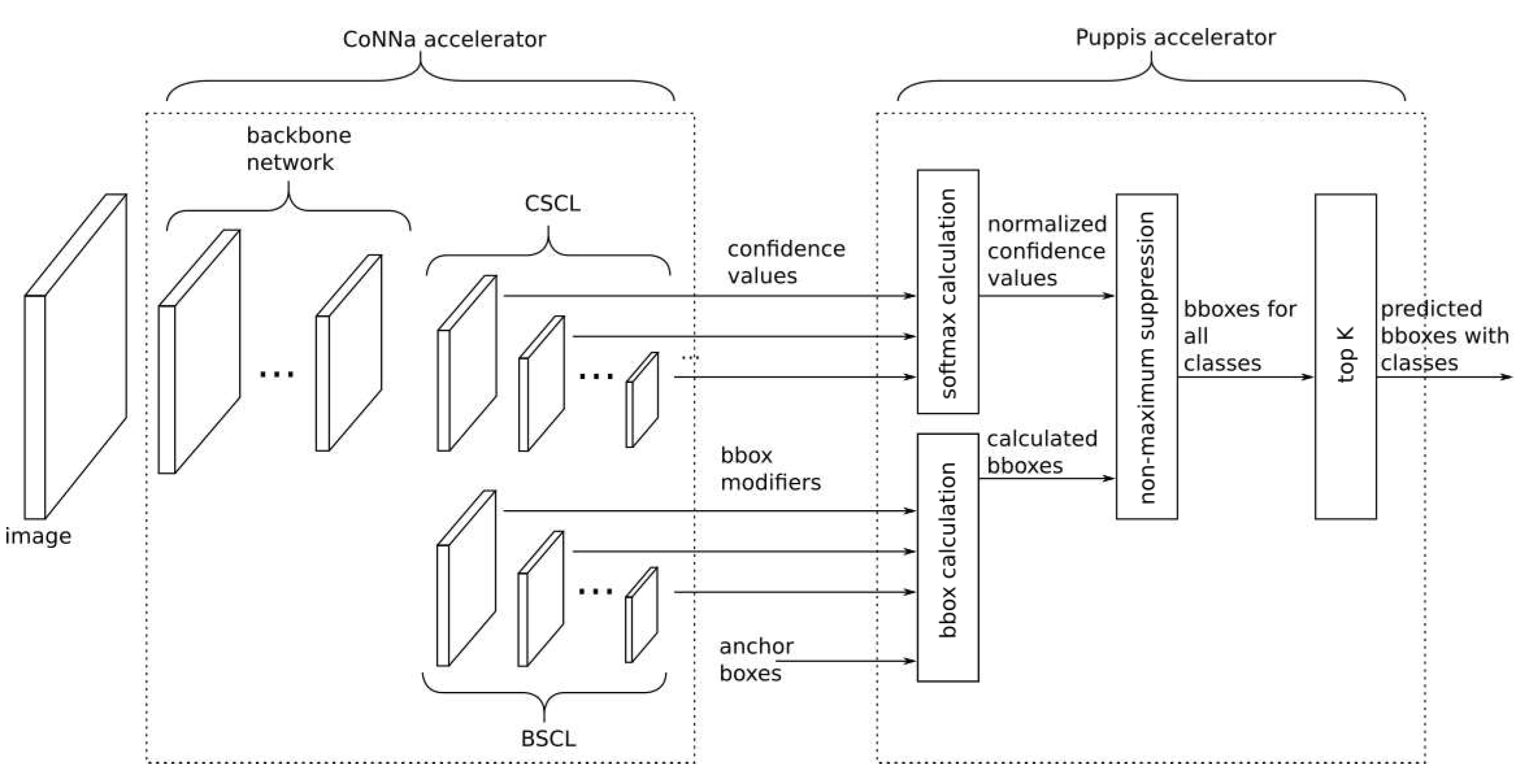
Figure 1 shows a general structure of the SSD network. The first part of SSD network is called a backbone network. Some standard Convolutional Neural Network (CNN) is used as backbone network, like VGG, MobileNet, ResNet, Inception, EfficientNet, etc. The purpose of the backbone network is to automatically extract the features from the input image so that the rest of the system can successfully determine bounding boxes.

The second part of the SSD network is the Single-shot Multibox Detector, SSD Head, for short. The purpose of the SSD Head is to calculate the bounding boxes for every class from the results computed by the backbone part of the network. The SSD Head consists of additional convolution layers and four other functions: softmax calculation, bounding-box calculation, Non-Maximum Suppression (NMS) function, and top-K sorting.

The additional convolutional layers in SSD Head always come in pairs. One layer calculates confidence values - Confidence SSD Convolution Layer (CSCL), and the other calculates the bounding-box modifiers - Bounding-Box SSD Convolution Layer (BSCL). The SSD Head also has a third layer which calculates anchor boxes. The anchor boxes are trainable parameters of the network, but for every SSD network, after training, they are constant.

2.2. System for HW acceleration of complete SSD arhitecture

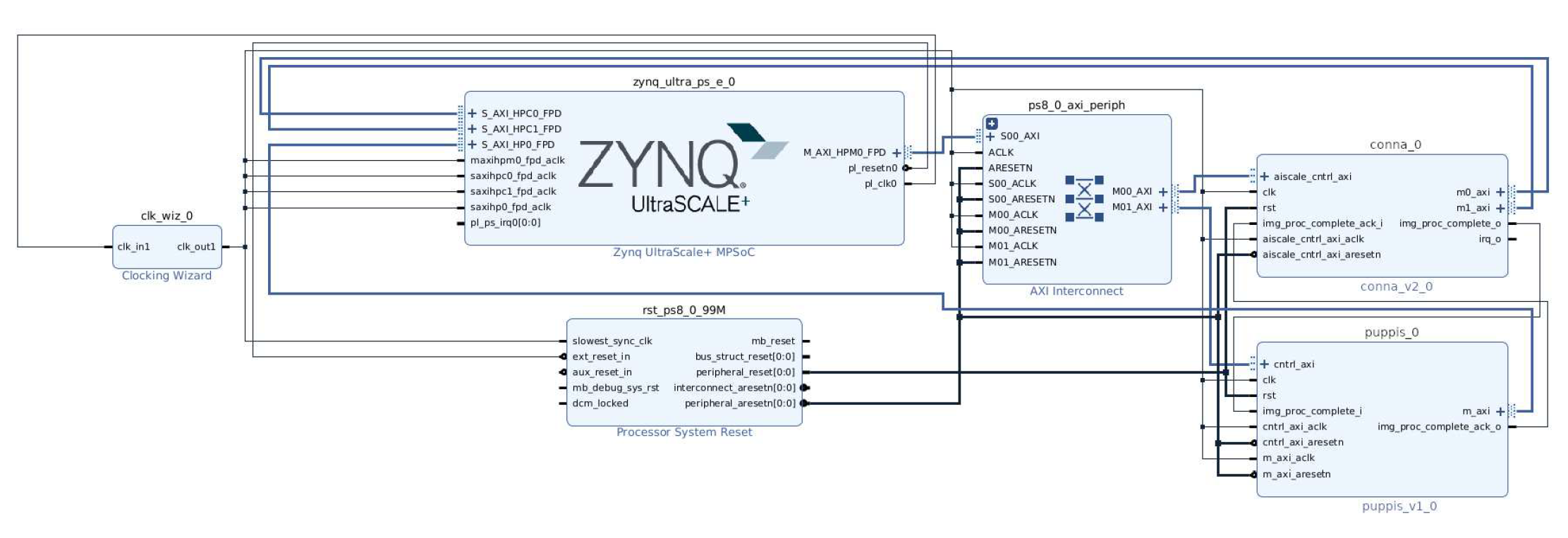
Figure 2 illustrates how the Puppis , an SSD Head hardware accelerator we are proposing in this paper, is integrated into the overall flow of CNN calculation. To enable complete SSD network acceleration in hardware, Puppis HW accelerator must be coupled with some of previously proposed CNN HW accelerators. CNN accelerator will be used to accelerate the backbone CNN network, as well as additional convolutional layers located in the SSD head. In this paper a modified version of CoNNa CNN HW accelerator, proposed in [16], has been used for this purpose. In contrast, Puppis HW accelerator will be used to accelerate remaining calculating functions from the SSD Head: softmax, bounding-box, non-maximum suppression and top-K sort. By working together, CoNNa and Puppis enable hardware acceleration of complete SSD network.

The Puppis uses two generic handshake interfaces, enabling easy and generic way of connecting to selected HW CNN accelerator. Please notice that if the CNN accelerator does not already have this handshake interface it must be adapted to support it. However, due to the simplicity of the used handshake interface, this poses no significant problem. Figure 3 shows the proposed interfaces between the two accelerators. These two interfaces will be called SSD-CNN handshake.

Both interfaces contain only two signals. In Figure 3 the first one consists of cnn_done and ssd_ack signals. When cnn_done is asserted, that means that the CNN accelerator is finished with processing backbone CNN, using current input image. The Puppis asserts cnn_ack to acknowledge that, and starts executing its part of the complete SSD algorithm using the feature maps provided by the backbone CNN, computed using the last input image.

The second interface includes ssd_done and cnn_ack signals. Here ssd_done indicates that Puppis is finished with the processing, and cnn_ack is asserted when CNN accelerator acknowledged that, and it can start with processing of the next input feature map.

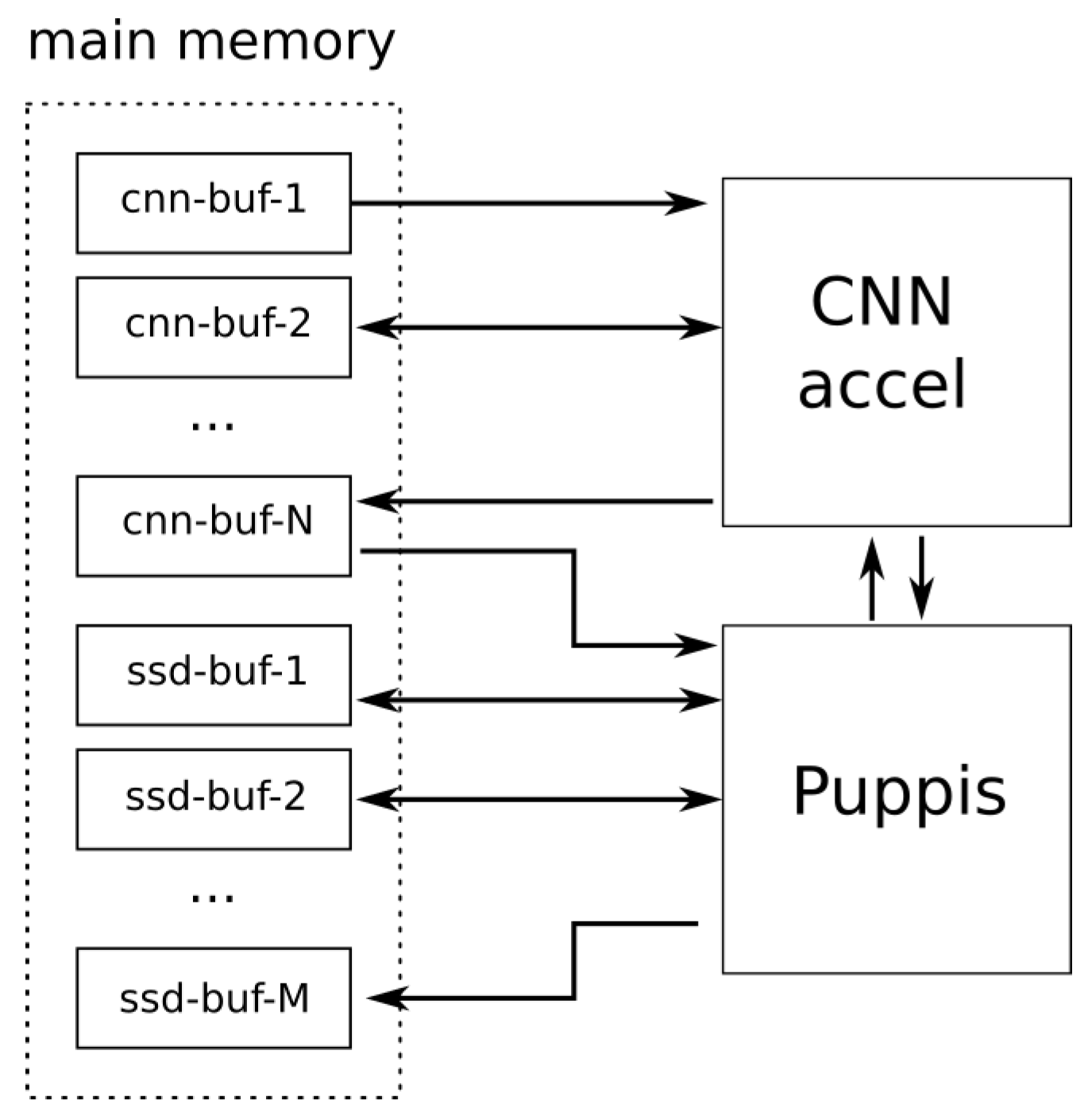
As can be seen from the previous explanation, these two interfaces enable synchronisation and reliable transfer of data between the selected CNN accelerator and Puppis SSD Head accelerator. Feature maps computed by the CNN accelerator are transferred to the Puppis using a shared memory buffer. This is illustrated in Figure 4. The buffer cnn-buf-1 is used as the input buffer. The input image that needs to be processed by the SSD network is stored in this buffer. The results after processing the first layer are stored in the buffer cnn-buf-2. That buffer is then input for the next layer, and so on.

The results of processing final layers from CSCL and BSCL layers are stored in couple of last cnn-buf buffers, depending on the number of these final layers. For example, if there are k final layers then cnn-buf-N-k up to cnn-buf-N buffers would be used to store their output values. These buffers are actually the input buffers for the Puppis HW accelerator. During its operation, Puppis uses additional memory buffers: ssd-buf-1 up to ssd-buf-M. These buffers are used to store intermediate results, computed as the Puppis HW accelerator operates on input data. The final results are stored in the output buffer ssd-buf-M. From this buffer, the software can read the final results of SSD network processing, containing the detected objects bounding boxes information.

Please notice that described setup enables the implementation of a coarse-grained pipelining technique during the processing of a complete SSD network by the proposed system. While the Puppis HW accelerator processes CNN-generated information for the input image i, CNN HW accelerator can already start processing input image i+1. This setup can significantly increase the processing throughput of the complete system, although the processing latency will remain unchanged. In applications where achieving high frame-rate is of interest, this could prove highly beneficial.

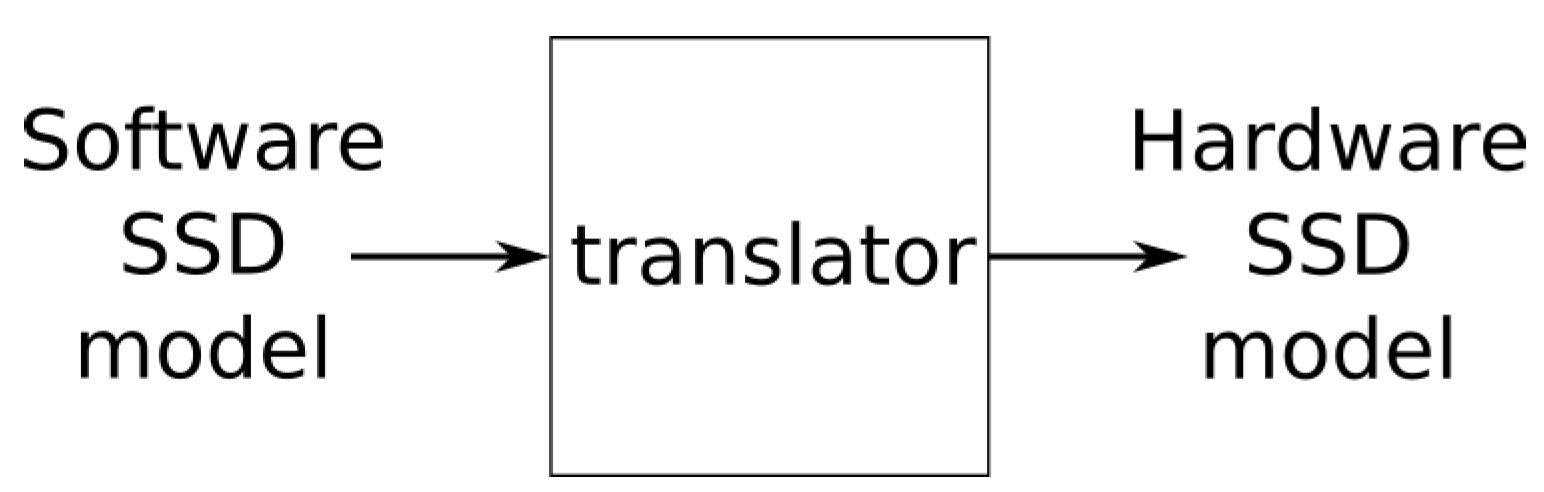
In order to be able to process selected SSD network, both the CNN and Puppis HW accelerators require that the SSD network is represented in an accelerator-specific binary format, as shown in Figure 5. During the development of Puppis , such a tool for translating the high-level model of SSD network (developed for example using Keras, PyTorch, or some other framework) into this accelerator-specific binary model was also developed.

In the process of SSD model translation, the translator tool also determines the optimal fixed-point number format that will be used to store various SSD-model related data during the SSD network processing. Then it translates the model parameters to this number format and stores them in buffers, which are located in the main memory of the SSD system. For anchor boxes, it prepares special buffers for the Puppies, so that it can just load those values from the memory system, without any calculation. In short, this tool prepares the model to be successfully processed by the CoNNa , and Puppis accelerators.

3. Accelerated SSD Head Computation Algorithms

The part of Single-shot Multibox Detector algorithm which is implemented by the Puppis HW accelerator contains four main computational steps:

(1): Softmax calculation
(2): Bounding-Box calculation
(3): NMS calculation
(4): TopK sorting

The first three steps are more computationally complex, and they will described in more datails in the following chapters. The last part of the calculation, TopK sorting, determines the best K bounding boxes within the results calculated in the non-maximum suppression block. This is done using a simple bubble-sort algorithm.

3.1. The Softmax calculation

The Softmax calculation is the first step executed by the Puppis accelerator. The inputs for Softmax calculation are confidence values of SSD convolution layers, and Exponential Confidence Look-up Tables (ECLUT). The outputs are score predictions for all boxes. The confidence values are outputs from the backbone network and CSCL. In our setup of the complete SSD network hardware accelerator, the modified CoNNa CNN accelerator will provide these as its output. The ECLUT is an array of samples of exponential functions in the floating point format. This array is calculated by the translator and stored in main memory.

In this step, for all results of the confidence layers, for all the anchor boxes, and for all the classes the following normalized values are calculated:

n_{k} = \frac{e^{S_{k}}}{\sum_{i = 1}^{i = N} e^{S_{i}}}

(1)

where k is index of the current class, the S are inputs from the confidence layers, N in the number of the classes, and

n_{k}

is the normalized confidence score.

In implementation of hardware accelerators, two number formats are mostly used: fixed-point and floating point. The fixed point format is used for hardware simplicity and energy efficiency. The floating point format is used in an application needing a wide dynamic range. In this architecture, we used a hybrid approach which will be described in more details. Softmax calculation uses an exponential function over a wide range of values. On one hand, the hardware is simpler when using a fixed point format for real values. On the other hand, this calculation requires a wide range of values. So if only a fixed format is used, it will require a large number of bits to cover the required dynamic number range. Using only the floating point hardware is not feasible, because the floating point calculation uses too many hardware resources. So, a mix of floating point and fixed point numbers is used in the calculation. We decided to use floating point representation for comparison operations only. In that way, we keep hardware utilization close to fixed-point representation, and still cover the required range of values, as if floating-point number representation was used.

Inside the Puppis HW accelerator, there are hardware blocks that determine the format used for representing fixed point numbers. The pseudocode of the algorithm for the equation calculation 1, with some hardware-related details, is shown below.

Listing 1. Softmax pseudocode

The parameter SCN is the current number of SSD convolution layer pairs that the network uses. It is a run-time time parameter that can be configured by the user. The confs is an input array which contains confidence values. That array is located in the main memory of the system. The variable box_cnt counts all boxes for which score prediction values are calculated.

The algorithm iterates through output feature maps, generated by each CSCL that is shown in Figure 1. For every output point of any CSCL, and for all boxes corresponding to that layer, the list of confidence values is read from memory for each class (conf_box = conf[i][j][k]). For all confidence values, the corresponding floating point value from ECLUT is read, and the maximum value is determined. The comparison between exp_vals[cls] > exp_val_max is a floating point comparison. According to the result of the comparison, the fixed-point representation used later in the calculation is determined. The ECLUT contains samples of exponential functions for every class used in the network. There are 4096 samples in the ECLUT for every class. The translator determines which samples should be stored in the table. All fixed point numbers in this block are 16 bits wide. The computed format is stored in the exp_sum_reduce variable. This number determines how much the values are shifted during the calculation, so this number represents the number of bits after the fixed point. The floating point numbers are represented with 32 bits using the IEEE 754 standard.

The function getFormatFromFloat determines the format according to the value of exp_val_max variable. The next loop in the code determines the sum of all exponential function values, computing the value of the denominator from equation 1. That is needed to determine soft-max score box predictions. If, during sum calculation, there is an overflow, then the fixed point is moved one point to the left exp_sum_reduce += 1, and the sum is divided by 2, to be correctly interpreted by a new fixed point format.

Finally, for all classes, the new normalized score predictions,

n_{k}

, are calculated. For every class, the confidence value is divided by a computed denominator value, and the result is stored in a score prediction array. This array is also located in the main memory of the system.

3.2. The Bounding-box calculation

The Bounding-box calculation is the next step in the accelerator calculation flow. For every output point in the convolution layer that calculates the bounding-box modifiers, and for every anchor box, the accelerator calculates one resulting bounding box. The chance that this bounding box is the result of a prediction is stored, for every class, in the soft-max calculation step.

The bounding box calculation procedure is expressed with these formulas:

C_{x b} = X_{p} X_{v} W_{a} + C_{x a}

(2)

C_{y b} = Y_{p} Y_{v} H_{a} + C_{y a}

(3)

W_{b} = e^{W_{p} W_{v}} H_{a}

(4)

H_{b} = e^{H_{p} H_{v}} W_{a}

(5)

X_{m i n} = C_{x b} - W_{b}

(6)

X_{m a x} = C_{x b} + W_{b}

(7)

Y_{m i n} = C_{y b} - H_{b}

(8)

Y_{m a x} = C_{y b} + H_{b}

(9)

where

C_{x b}

and

C_{y b}

are the coordinates of a predicted bounding box center. The

X_{p}

and

Y_{p}

are two of four predicted input values from the convolutional layers. The

X_{v}

and

Y_{v}

are so-called variance values. Those are trainable parameters of the SSD network, and they are recorded in the binary description of the network with the help of the translator. The values

W_{a}

and

H_{a}

are the width and height of the current anchor box, and the values

C_{x a}

C_{y a}

specify the center of the current anchor box. The values

W_{b}

and

H_{b}

are output values of the convolution layer used to calculate the width and height of the bounding box. The values

W_{v}

and

H_{v}

are variance values determined during the training. Finally, the values

X_{m i n}

, and

Y_{m i n}

specify the upper left corner of the predicted bounding box, and

X_{m a x}

Y_{m a x}

specify the lower right corner, thus specifying the exact location and size of computed bounding box.

The Puppis uses 16-bit fixed-point number representation for all calculations 2 - 9. The translator determines the exact position of the decimal point, which is then set with barrel-shifters. The exponential functions from equations 4 and 5 are again calculated using the look-up table approach. But this time the number dynamic range is small enough, so that a predetermined number format can be used.

3.3. The NMS calculation

The third step is the NMS calculation. This algorithm removes overlapping boxes around the same object. The output of the bounding-box calculation can put several boxes around the same object with high confidence. The purpose of this step is to remove the boxes around the same object which overlap enough (algorithm parameter). The aim is to have only one bounding box around one object. In short, ideally, before this step, there can be several bounding boxes around the same object, and after it, there will be only one.

The pseudo-code for this algorithm is listed below. The input for this algorithm are confidence values after soft-max calculation, calculated in step one, and the bounding boxes locations calculated in the second step. These inputs are represented as in_confs variable for the confidences, and in_bboxes for the bounding boxes. The confs is a 2d array, because it holds the normalized confidence values for all the classes and for all the bounding boxes.

Listing 2. NMS pseudocode

The algorithm iterates over all classes. The current class is represented by the variable cnt_class. The variable box_ind represents the indices of all confidence values which are greater than the input parameter threshold TVAL. The variable confs are all confidence values which are greater than TVAL and the variable bboxes are the corresponding bounding boxes. If there are no confidence values greater than TVAL then the algorithm iterates to the next class. The variable areas represent areas of all bboxes. The variable sort_ind is a sorted version of box_ind where indices are sorted corresponding to their confidence value. The value gt_ind represents the index of the bounding box with the greatest confidence value for the current class. The bounding box, its class, and confidence values are stored into the final result of the algorithm. For all other bounding boxes, the overlap area with the current best bounding box is calculated. For the next while-iteration, only indices with overlaps less than a threshold value TOVER are chosen. This while loop is terminated when there are no more indices in the sort_ind list. The output of the algorithm is all possible bounding boxes for all classes, with a confidence value greater than the parameter TOVER, and with overlap less than TOVER from the better confidence boxes.

Function calc_overlap calculates overlap between two boxes. This function receives two rectangles as input. The first rectangle is defined by two points:

(X_{m i n 1}, Y_{m i n 1})

and

(X_{m a x 1}, Y_{m a x 1})

for the first rectangle, and

(X_{m i n 2}, Y_{m i n 2})

and

(X_{m a x 2}, Y_{m a x 2})

for the second. The function calculates overlap according to these formulas:

X_{m i n} = max (X_{m i n 1}, X_{m i n 2})

(10)

Y_{m i n} = max (Y_{m i n 1}, Y_{m i n 2})

(11)

X_{m a x} = min (X_{m a x 1}, X_{m a x 2})

(12)

Y_{m a x} = min (Y_{m a x 1}, Y_{m a x 2})

(13)

A_{i} = (X_{m a x} - X_{m i n}) (Y_{m a x} - Y_{m i n})

(14)

A_{u} = A_{1} + A_{2} - A_{i}

(15)

O = \frac{A_{i}}{A_{u}}

(16)

where the points

(X_{m i n}, Y_{m i n})

and

(X_{m a x}, Y_{m a x})

define an overlapping rectangle. The overlapping area is

A_{i}

, and

A_{u}

is a non-overlapping area. The values

A_{1}

and

A_{2}

are the areas of the two bounding boxes, for which the calculation is done. The value

A_{1}

is always the area of the bounding box with the greatest confidence value for the current class. The O is the result of the function and it represents a ratio between

A_{i}

and

A_{u}

4. Puppis HW Accelerator Architecture

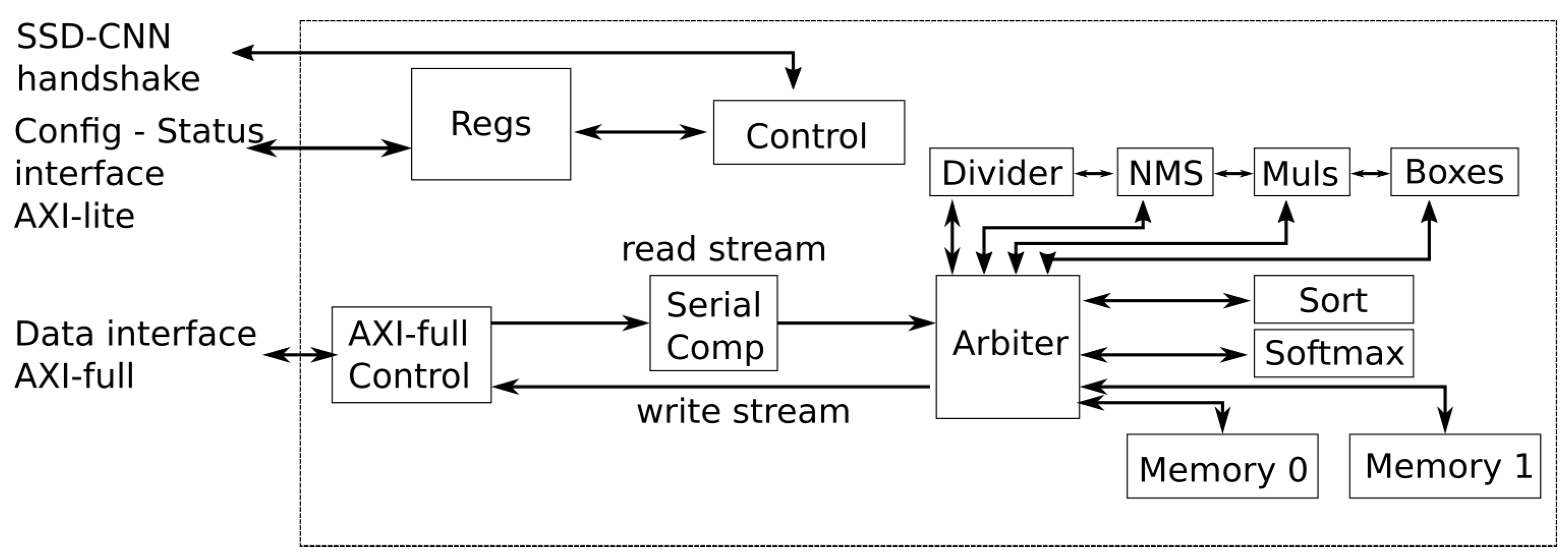
Figure 6 shows an overview of the Puppis HW accelerator architecture. Interfaces of the accelerator, as well as main building blocks at the top level are presented.

The Puppis uses three interfaces to connect to surrounding modules: the configuration and status AXI-lite interface, the data transfer AXI-full interface, and the SSD-CNN handshake, explained earlier in Chapter 2.2. The AXI-lite interface is used for the Puppis configuration, and for inspecting the status of the accelerator. The AXI-Full interface is used for the data transfers in and out of the accelerator. The received and transferred data are routed through the Arbiter module. Finally, the SSD-CNN handshake interface is introduced to Puppis to enable the calculation of the whole SSD CNN without processor intervention. It was shown in Figure 3.

Puppis contains several modules at the top level. There is the Regs module, which contains the configuration registers of the accelerator. Also, the Puppis has status registers, which can be accessed through AXI-lite interface. The configuration affects how main controller module, Control in the Figure 6, works.

The Control module coordinates the operation of all other modules, to compute the SSD Head output. Sequentially, depending on the configuration and the state of calculation, this module controls the routing and timing of data transfers through the calculation modules of the accelerator, as well as, their internal pipeline stages. This module has connections to all other modules, but for clarity, those connections are not illustrated in Figure 6. This module will be described in more details in the following chapter.

The main data-routing unit inside Puppis is the Arbiter module. It implements an interconnect architecture which enables all required routing of data from source to destination. In other words, it enables the data transfers inside Puppis accelerator. It is controlled by the main Control module.

The main calculation modules of the Puppis are Softmax, Boxes, and NMS. The Softmax module is used for calculating the softmax function, given by equation 1, and listing 1. The Boxes module calculates bounding boxes, equations 2 - 9. The NMS module calculates the NMS function of the SSD calculation, listing 2. All of these modules will be described in more details in the following chapters.

The other, helper calculation modules of Puppis are: Divider, Muls, and Sort. The Divider module implements division operation of two fixed-point numbers, which is used in the Softmax, and NMS computational steps of the SSD algorithm. It uses pipelined architecture, in order to reach the operating frequency of other modules. The Muls module is used for calculating multiplication of two fixed-point numbers, represented with the same number of bits. This module is pipelined, and has four lanes, so that four multiplications can be done at once. The Sort module sorts values, and it is used during the NMS calculation, as well as for selecting final top K results.

The Puppis uses two internal caching memories: Memory 0 and 1. They are used for storing configuration parameters and intermediate results during the SSD calculation. The memories are configurable and have several purposes during the SSD calculation process, which will be described in more details, in the following chapters.

The Arbiter module enables communication between the calculation modules and the memories. Additionally, some communication lines connect the calculation modules directly: Divider to NMS, NMS to Muls, and finally Muls to Boxes. These lines stream intermediate results, without buffering, between modules.

An AXI-Full interface enables the communication to the external main memory. The AXI-Full Control module implements the AXI-Full protocol. This module receives two AXI-Stream data streams, a read stream, and a write stream, and combines them into a single AXI-Full interface.

The Serial Comp module connects to the Arbiter and the AXI-Full Control module’s read interface. The module reads the confidence predictions from the main memory and passes only those predictions that are greater than the predefined threshold to the Arbiter module. Furthermore, the Serial Comp module can transfer other data types without discrimination.

4.1. The Control module

The Control module sends control signals to all the other modules in the architecture. It implements Finite State Machine (FSM) which sequentially processes the input through several steps of the SSD Head computation algorithm explained earlier. The simplified FSM is shown in Figure 7.

In the READY state, the Puppis is ready to receive the next input. In this state, it can be configured using the AXI-Lite interface to be prepared for processing the next input. In the next state, SOFTMAX, the Control module sends control signals to read the input confidence values from memory, calculate the softmax algorithm with those inputs, and write the output normalized values into the main memory. In the BOXES state, Puppis reads the bounding box modifiers from the main memory, and also anchor boxes, and then calculates the bounding boxes. The resulting bounding boxes are stored into the internal Memory modules. In the NMS state, the Control unit sends control signals, so that the normalized confidence values are read from the main memory, and the bounding boxes are read from the internal Memory. Then the NMS algorithm is processed on those inputs. The resulting output is stored in the internal Memory. In the SORT state, the inputs from the NMS step are read from the internal Memory, they are sorted, and the best K results are stored into the main memory, as the final result of the input processing. Then the Puppis accelerator switches to the READY state, where it is prepared to take the next input.

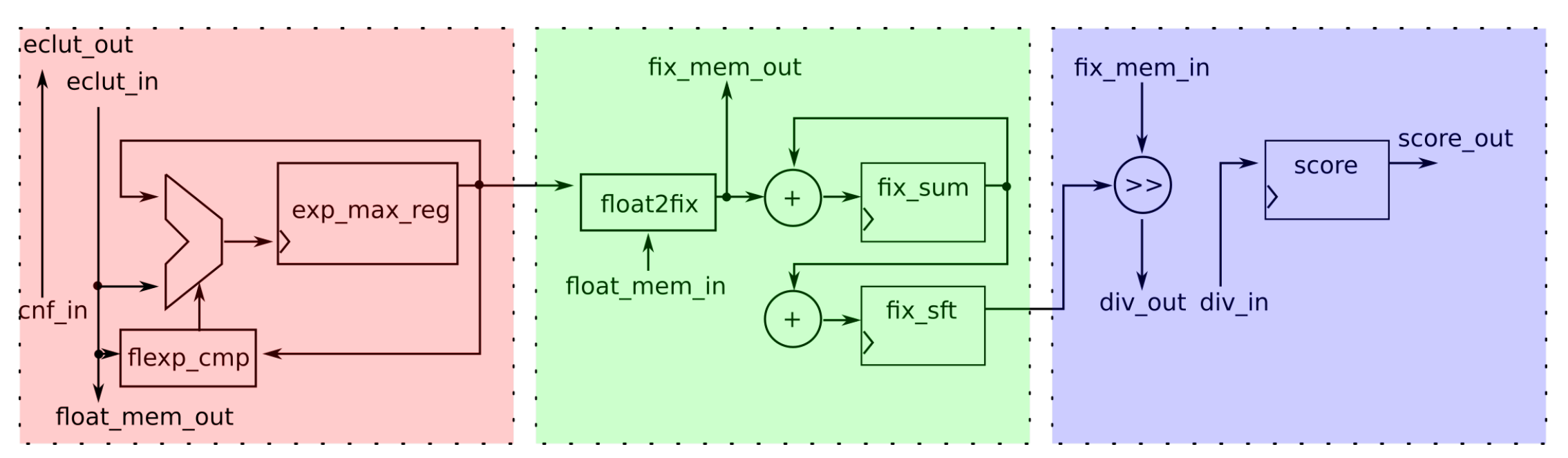
4.2. The Softmax module

Figure 8 shows the top-level block diagram of the Softmax module. The block diagram presents a model of the Softmax module close to the Register Transfer Level (RTL) level, but some details are abstracted. In this way, model is easier to explain. For example, the model does not show the control signals from the Control module. We will call this kind of model abstracted RTL model. The Softmax module contains three pipeline stages.

In the first stage, the module receives the confidence value inputs, cnf_in, from the main memory, the

S_{i}

from the equation 1. The module sends this value to the ECLUT - eclut_out, and receives exponents of floating points - eclut_in. The internal memory stores ECLUT samples. The calculated values, which represent

e^{S_{k}}

from the equation 1 in floating point number format, are also stored in the internal memory. The internal memory receives them through the port float_mem_out. The module compares the exponents of those numbers and stores the current maximum exponent in the register exp_max_reg. The component flexp_cmp is the exponent comparator. After the processing is finished at the first stage, in the exp_max_reg register is the maximum exponent of all confidence values. That is also the input for the next pipeline stage.

In the second stage, the module receives the floating point values

e^{S_{k}}

from the internal memory, and converts them to the fixed-point format. Converted numbers are sent to the intermediate memory, and are used in the third stage. These values are

e^{S_{k}}

from the equation 1, but in the fixed-point number format. The exp_max_reg register stores the current value and determines the exact fixed-point number format. These converted numbers are then sent to the memories Memory 0 or Memory 1, shown in Figure 6.

In the third stage, the values are read from the intermediate memories through the fix_mem_in input port. These are

e^{S_{k}}

from the equation 1. They are then shifted by the parameter number, determined by the translator. The shifted value is sent to the divider, and then, the result of the division is stored in the register - score_out. This value, that actually represents the

n_{k}

from equation 1 is sent to the internal memory, because it will be used in the following steps of SSD calculation.

4.3. The Bounding-box module

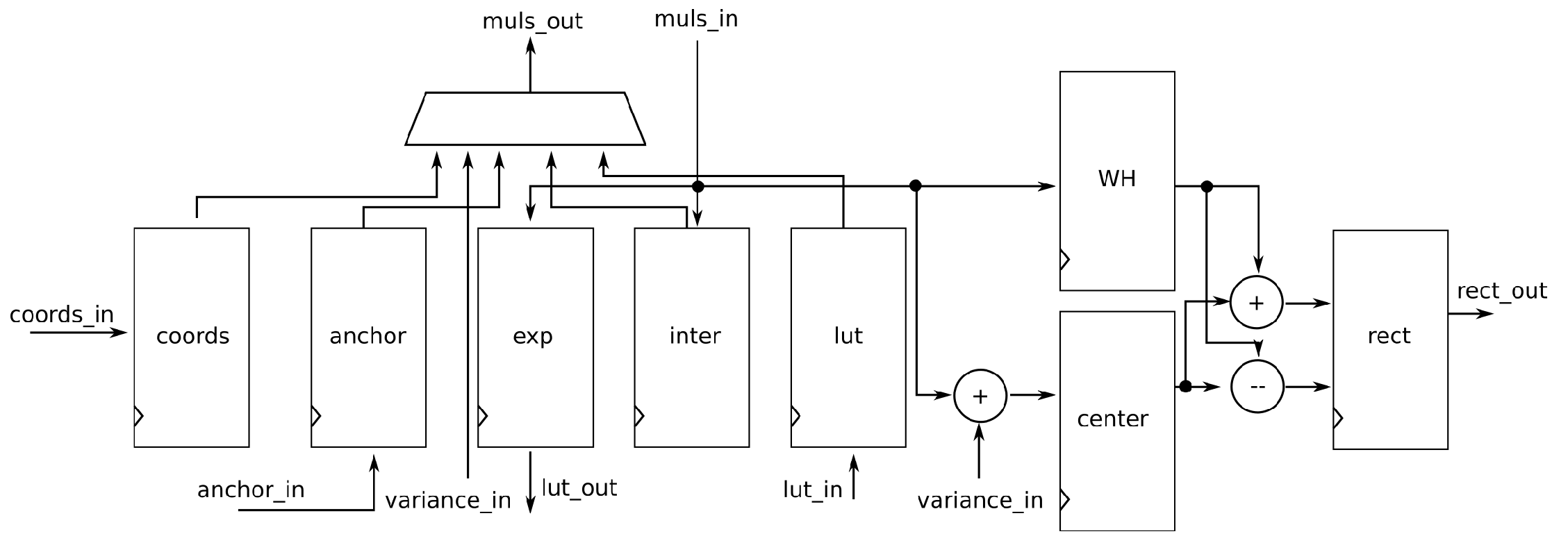
Figure 9 shows the abstracted RTL model for the Bounding-box module. The module uses several registers to store intermediate calculation results for equations 2 - 9.

At the top of the Figure 9, the multiplexer is shown. The Control module uses this component to select which arguments to send to the Muls module.

The coord stores input values from the BSCL:

X_{p}

Y_{p}

W_{p}

, and

H_{p}

. The anchor stores values from the anchor boxes:

X_{a}

Y_{a}

W_{a}

, and

H_{a}

. The variance values come from the input variance_in, and those are values:

X_{v}

Y_{v}

W_{v}

, and

H_{v}

. First, the values

X_{p}

W_{a}

Y_{p}

, and

H_{a}

are sent to multiplexer, so that the inter receives input from multipliers and stores the intermediate results:

X_{p} W_{a}

, and

Y_{p} H_{a}

. The terms which are input for exponential function are stored in the register exp:

W_{p} W_{v}

, and

H_{p} H_{v}

. The values from exp are sent to look-up tables, and from lut_in the values

e^{W_{p} W_{v}}

, and

e^{H_{p} H_{v}}

are received. The received values are stored in the register lut. Then the values from the inter register are sent to the multipliers, along with variance values :

X_{v}

and

Y_{v}

. The results from multipliers are summed-up with the anchor boxes center:

C_{x a}

, and

C_{y a}

, and the final result are stored into the register center. Those are the values

C_{x b}

, and

X_{y b}

. The values from the lut are then send to multipliers, along with width and height of the anchor boxes:

H_{a}

and

W_{a}

. The results are

W_{b}

and

H_{b}

from the formulas and they are stored in the register WH. The final calculations are done with internal adders, and subtractors, which calculate the formulas for

X_{m i n}

X_{m a x}

Y_{m i n}

, and

Y_{m a x}

. Those results are stored into register rect, and then they are forwarded to the internal memories.

4.4. The NMS module

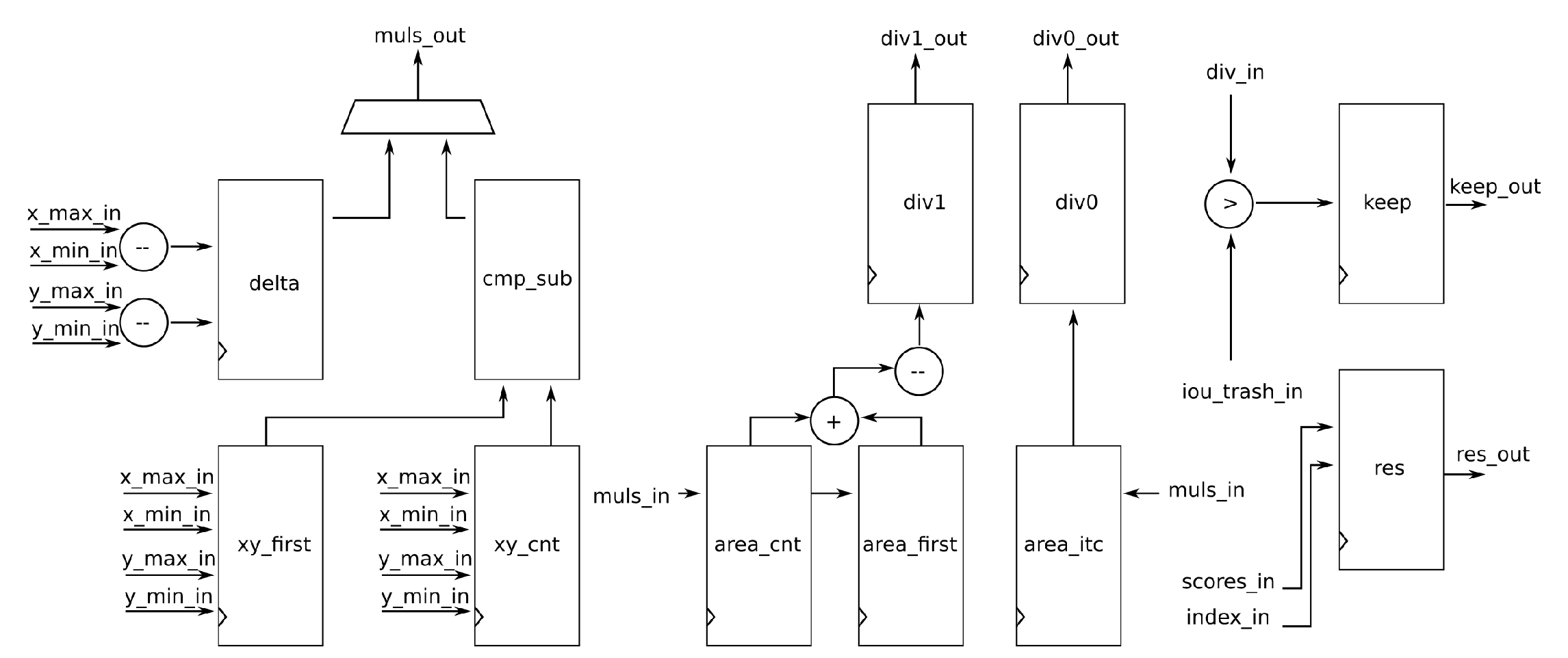
The Control module guides the NMS module through algorithm 2. The core of that algorithm are equations 10 - 16. Figure 10 shows abstract RTL schematic of the NMS module. The following is a description of how the module calculates these equations.

The areas are calculated using the Muls module. First, the area of all the boxes is calculated using datapath through the register delta. The register contains the length of the sizes of the boxes. Those values are then sent to the Muls modules, using the output muls_out. The area is then stored in the register area_cnt. In case the first bounding box is processed, then the area is, after delay, also stored in the register area_first. That first bounding box is referenced in the algorithm 2 with index gt_ind. Then, for all other bounding boxes, the equations 10 - 13, and the right side of 14 are calculated using combinatorial network cmp_sub. That network has 4 comparators and two subtractors which are needed to evaluate the left side of the equation 14. The final multiplication in equation 14 is done using the Muls module. The values

A_{i}

are stored in the register area_itc. The equation 15 is calculated using the values stored in the registers area_cnt and area_first. The output is stored in the register div1 which represents the values

A_{u}

in equations 15 and 16. The register div0 takes the value

A_{i}

from the register area_its. The division in equation 16 is done using the Divider module. The values from the register div0 and div1 are sent to the Divider module. The output of the Divider module is sent back using the input div_in. If that value is greater than the threshold value TOVER in the algorithm (iou_trash_in in Figure 10), the output flag keep_out is asserted, otherwise it stays zero. The confidence score corresponding to the current box is stored in the register res. Those values are delayed for several clock cycles, so they are written to this register at the same time as corresponding keep values are written to the register keep. The output values which have the “keep output” set to one will be stored in the internal memory and will be sorted in the last part of the SSD calculation.

4.5. The Sort module

The final stage of the computation involves TopK sorting, which identifies the top K bounding boxes among the results obtained from the non-maximum suppression block. This process is accomplished using a straightforward bubble-sort algorithm. This step is non-computationally critical, thereby leading to the adoption of a simple sequential architecture for the module.

5. Experimental results

In order to evaluate Puppis and compare it’s performance with the software implementation of MobilenetV1 SSD network, experiments were conducted on Zynq Ultrascale+ MPSoC ZCU102 Evaluation Board [19]. All results shown in this section are measured timings obtained from the experimental setup and not the values obtained by simulations.

5.1. Hardware setup

To test the efficiency of the proposed architecture, the complete SSD network hardware acceleration system was implemented using an FPGA development platform. For design and implementation Xilinx Vivado Design Suite [18] was used. The development platform on which the system was implemented and experiments were conducted has been Zynq Ultrascale+ MPSoC ZCU102 Evaluation Board [19]. The implementation tools have been used with default settings for synthesis and implementation. The top level block diagram of developed system used in experiments, taken from Vivado’s IP Integrator tool, is shown in Figure 11.

The main part of the system are processing system of Zynq, CoNNa , and Puppis HW accelerators. The achieved maximum operating frequency of complete system after implementation was 180 MHz. The resource utilization is shown in the Table 1.

As can be seen from Table 1 Puppis HW accelerator uses only a fraction of consumed hardware resources required to implement complete SSD network accelerating system. It uses mix of all FPGA resources, which is desirable feature. Compared to the whole system the utilization of LUTs is 3.91%, BRAM is on 5.36%, and DSP is below 1%. Most hardware resources have been utilized by the CoNNa accelerator. Please notice that this would be the case even if some other CNN HW accelerator would be used, instead of CoNNa. This means that the integration of Puppis SSD Head HW accelerator will not increase the overall HW resource consumption by any significant number that would prevent the complete system to be successfully implemented for most of existing AI systems that already use hardware acceleration of CNNs. On the other hand, which will be clearly demonstrated in the next chapter, having Puppis HW accelerator in the system can significantly increase the processing speed of SSD networks.

5.2. Software comparison

In order to evaluate Puppis , a comparison with software SSD network processing is performed. Additionally, to obtain relevant results, software is run on Ultrascale+ MPSoC ZCU102 evaluation board [19] running Ubuntu 20.04 Operating System. SSD network chosen for comparison is MobilenetV1 SSD network, trained on Pascal VOC dataset [17]. MobilenetV1 SSD network model is built using Tensorflow framework [20], but split into backbone CNN part, accelerated by CoNNa CNN accelerator, and the part of the network which will be run using Puppis accelerator. This split was performed to accurately evaluate the performance of each submodule. During evaluation, images from Pascal VOC dataset were used, both for the inference in software and hardware accelerator. Processing latencies during detecting objects in the image using hardware accelerators CoNNa and Puppis are shown in the table below.

As it can be seen from the Table 2 processing latencies for both CoNNa and Puppis have a minimum deviation and are executed in almost constant time, independently from the image being processed or the number of detected objects within the image. This feature represents the additional benefit of using hardware accelerators for CNN processing, since the constant processing time is highly appreciated in most applications. Table 3 presents processing latencies for the backbone CNN network and Single-shot Multibox Detector when both of them are executed by the embedded ARM processor, present in the Zynq MPSoC system. As in the case of hardware measurements MobilenetV1 SSD network was used.

It can be seen from the Table 3 that the execution of SSD network using an embedded processor, as expected, takes significantly more time, when compared to hardware accelerated processing of the same set of images.

Table 4 shows SSD Head processing latency reduction and SSD head processing speedup obtained as a result of using Puppis , when compared to pure SW implementation. Those two are calculated as:

L R_{1} = (t_{s w_S S D_h e a d_p r o c} - t_{a c c_S S D_h e a d_p r o c}) / t_{s w_S S D_h e a d_p r o c} * 100

(17)

S p e e d u p_{1} = t_{s w_S S D_h e a d_p r o c} / t_{a c c_S S D_h e a d_p r o c}

(18)

where

t_{s w_S S D_h e a d_p r o c}

represents the duration of SSD post-processing algorithm execution in software (column 3 from Table 3) and, similarly,

t_{a c c_S S D_h e a d_p r o c}

represents the duration of the SSD post-processing algorithm execution performed by Puppis (column 3 from Table 2).

Table 5 presents comparison between MobilenetV1 SSD network running in software and on developed system for complete SSD network HW acceleration (comprising of CoNNa CNN accelerator and Puppis Single-shot Multibox Detector accelerator). Latency reduction and speedup shown in table are calculated as:

L R_{2} = (t_{s w_M o b i l e n e t V 1_S S D} - t_{a c c_M o b i l e n e t V 1_S S D}) / t_{s w_M o b i l e n e t V 1_S S D} * 100

(19)

S p e e d u p_{2} = t_{s w_M o b i l e n e t V 1_S S D} / t_{a c c_M o b i l e n e t V 1_S S D}

(20)

where

t_{s w_M o b i l e n e t V 1_S S D}

represents the duration of MobilenetV1 SSD inference when executed in software (sum of columns 2 and 3 from Table 3) and, similarly,

t_{a c c_M o b i l e n e t V 1_S S D}

represents the duration of the MobilenetV1 SSD processing when executed on CoNNa and Puppis (sum of columns 2 and 3 from Table 2).

Finally, Table 6 shows the latency reduction and speedup in a setup where backbone network processing is executed by CoNNa hardware accelerator, while SSD post-processing is executed by SW in the first scenario, and executed by Puppis in the second scenario. Hence, the latency reduction and the speedup are calculated as:

L R_{3} = (t_{a c c_b a c k b o n e_s w_S S D} - t_{a c c_M o b i l e n e t V 1_S S D}) / t_{a c c_b a c k b o n e_s w_S S D} * 100

(21)

S p e e d u p_{3} = t_{a c c_b a c k b o n e_s w_S S D} / t_{a c c_M o b i l e n e t V 1_S S D}

(22)

where

t_{a c c_b a c k b o n e_s w_S S D}

represents the duration of MobilenetV1 SSD inference when backbone network is executed on CoNNa but SSD post-processing is executed in software (sum of columns 2 from Table 2 and 3 from Table 3) and

t_{a c c_M o b i l e n e t V 1_S S D}

represents the duration of the MobilenetV1 SSD processing when executed on CoNNa and Puppis (sum of columns 2 and 3 from Table 2).

From Table 4 it can be seen that using Puppis for acceleration of SSD Head reduces time by 97.08% on average and leads to average speedup of 34.42 times, when compared with SW implementation executed using embedded ARM processor. Table 5 shows that the average MobilenetV1 SSD execution duration reduction is 97.76% when hardware accelerators CoNNa and Puppis are used for running backbone network and SSD post-processing, compared to a software implementation, while average speedup is 45.39 in this scenario. Finally, performance improvement due to using Puppis to execute SSD Head, instead of software, can be observed from Table 6. This Table shows that the average MobilenetV1 SSD network execution duration reduction is 51.11%, with average speedup of 2.05, when Puppis is used for SSD post-processing instead of a software implementation, while the backbone network is running on CoNNa in both cases.

6. Conclusion

This paper presents the Puppis, hardware accelerator of the Single-shot Multibox Detector, popular network architecture for the object detection. Our research was motivated by the fact that the software implementation of Single-shot Multibox Detector algorithm has become a bottleneck for both throughput and latency, after the backbone CNN processing latency has been shortened significantly recently, by using dedicated CNN hardware accelerators. Hence, to overcome this issue, the target for proposed hardware accelerator was to shorten the execution of all processing blocks within the SSD Head algorithm: Softmax, Bounding-box and Non-maximum suppression calculation, as well as Top-K sorting. Even though the proposed solution can be integrated with any classifier backbone CNN, during our experiments we have used MobilenetV1 SSD network. By performing tests on images from Pascal VOC dataset [17], results show that hardware accelerated Single-shot Multibox Detector part of a complete SSD network reduces SSD Head execution time by 97.08% on average, resulting in average speedup of 34.42 times, when compared to the software implementation. Performance improvement is even higher when complete MobilenetV1 SSD network is running on CoNNa and Puppis hardware accelerators, instead in software: processing latency is reduced by 97.76% on average, leading to the average speedup of 45.39 times.

Funding

This work has received partial funding from the European Union’s Horizon 2020 research and innovation programme under Grant Agreement number 856967 and has been supported by the Ministry of Education, Science and Technological Development through project no. 451-03-47/2023-01/200156 “Innovative scientific and artistic research from the FTS (activity) domain”

References

Liu, Wei and Anguelov, Dragomir and Erhan, Dumitru and Szegedy, Christian and Reed, Scott and Fu, Cheng-Yang and Berg, Alexander C.: Ssd: Single shot multibox detector, Computer Vision–ECCV 2016; 2016; 21-37.
Ren, Shaoquing and He, Kaiming and Girshick, Ross and Sun, Jian: Faster r-cnn: Towards real-time object detection with region proposal networks, Advances in neural information processing systems; 28.
Redmon, Joseph and Divvala, Santosh and Girshick, Ross and Farhadi, Ali: You only look once: Unified, real-time object detection, Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR); 2016; 779-788.
Redmon, Joseph and Farhadi, Ali: Yolov3: An incremental improvement, arXiv preprint;arXiv:1804.02767; 2018.
Bochkovskiy, Alexey and Wang, Chien-Yao and Liao, Hong-Yuan M.: Yolov4: Optimal speed and accuracy of object detection, arXiv preprint;arXiv:2004.10934;2020.
Carion, Nicolas and Massa, Francisco and Synnaeve, Gabriel and Usunier, Nicolas and Kirillov, Alexander and Zagoruyko, Sergey: End-to-end object detection with transformers, In European conference on computer vision; 2020; 213-229.
Li, Zuo-Xin and Zhou, Fu-Qiang: FSSD: feature fusion single shot multibox detector, arXiv preprint; arXiv:1712.00960; 2017.
Jiang, Deng and Sun, Bei and Su, Shaojing and Zuo, Zhen and Wu, Peng and Tan, Xiaopeng: FASSD: A feature fusion and spatial attention-based single shot detector for small object detection, Electronics,2020 9(9), 1536. [CrossRef]
Ning, Chengcheng and Zhou, Huajun and Song, Yan and Tang, Jinhui: Inception single shot multibox detector for object detection, 2017 IEEE International Conference on Multimedia and Expo Workshops (ICMEW); 2017; 549-554. [CrossRef]
Yi, Jingru and Wu, Pengxiang and Metaxas, Dimitris N.: ASSD: Attentive single shot multibox detector, Computer Vision and Image Understanding; 2019; 189:102827. [CrossRef]
Kumar, Ashwani and Zhang, Zuopeng Justin and Lyu, Hongbo: Object detection in real time based on improved single shot multi-box detector algorithm, EURASIP Journal on Wireless Communications and Networking, 2020, 1-18. [CrossRef]
Kanimozhi, S. and Gayathri, G. and Mala, T: Multiple Real-time object identification using Single shot Multi-Box detection, 2019 International Conference on Computational Intelligence in Data Science (ICCIDS); 2019; 1-5. [CrossRef]
Wu, Shixiao and Xinghuan, Wang and Chengcheng, Guo: Application of Feature Pyramid Network and Feature Fusion Single Shot Multibox Detector for Real-Time Prostate Capsule Detection, Electronics 2023 12(4), 1060.
Ma, Yufei and Zheng, Tu and Cao, Yu and Vrudhula, Sarma and Seo: Algorithm-Hardware Co-Design of Single Shot Detector for Fast Object Detection on FPGAs, 2018 IEEE/ACM International Conference on Computer-Aided Design (ICCAD); 2018; 1-8.
Cai, Liang and Dong, Feng and Chen, Ke and Yu, Kehua and Qu, Wei and Jiang, Jianfei: An FPGA Based Heterogeneous Accelerator for Single Shot MultiBox Detector (SSD), 2020 IEEE 15th International Conference on Solid-State & Integrated Circuit Technology (ICSICT); 2020; 1-3.
Struharik, Rastislav and Vukobratović, Bogdan and Erdeljan, Andrea and Rakanović, Damjan: CoNNa–Hardware accelerator for compressed convolutional neural networks, Microprocessors and Microsystems 2020, 73. [CrossRef]
The PASCAL Visual Object Classes Homepage. Available online: http://host.robots.ox.ac.uk/pascal/VOC (accessed on 27 07 2023).
Xilinx Vivado Design Suite. Available online: https://www.xilinx.com/developer/products/vivado.html (accessed on 27 07 2023).
Zynq UltraScale+ MPSoC ZCU102 Evaluation Kit. Available online: https://www.xilinx.com/products/boards-and-kits/ek-u1-zcu102-g.html (accessed on 27 07 2023).
Tensorflow. Available online: http://www.tensorflow.org (accessed on 27 07 2023).

Figure 1. SSD Calculation Flow.

Figure 2. Accelerator in SSD Calculation Flow.

Figure 3. Handshake connection of CNN Accelerator and Puppis Accelerator.

Figure 4. Shared buffer connection of CNN Accelerator and Puppis Accelerator.

Figure 5. Translator tool.

Figure 6. Accelerator Architecture Overview.

Figure 7. The Control FSM.

Figure 8. The abstract schematic of the Softmax module.

Figure 9. The abstract schematic of the Bounding-box module.

Figure 10. The abstract schematic of the NMS module.

Figure 11. Vivado’s IP Integrator view of the Complete System.

Table 1. FPGA implementation results.

Component	LUT	BRAM	DSP
Puppis	4055	17.5	4
System	103766	326.5	446

Table 2. Processing latency when detecting objects in images from [17] by CoNNa and Puppis

Image	CoNNa latency [ms]	Puppis latency [ms]	Number of boxes
001996.jpg	16.6061	0.5313	2
001760.jpg	16.6085	0.5597	6
002301.jpg	16.6109	0.5589	17
003626.jpg	16.6032	0.5343	4
004795.jpg	16.6025	0.5310	3
005095.jpg	16.6007	0.5308	1
006040.jpg	16.6045	0.5368	7
006324.jpg	16.6083	0.5315	3
006741.jpg	16.6088	0.5304	1
009910.jpg	16.6180	0.5310	5

Table 3. Processing latency when detecting objects in images from [17] using software implementation of MobilenetV1 SSD network

Image	Backbone CNN	SSD Head	Number of boxes
	latency SW [ms]	latency SW [ms]
001996.jpg	723.18	18.80	2
001760.jpg	667.57	17.91	7
002301.jpg	672.47	18.05	12
003626.jpg	878.43	18.22	2
004795.jpg	875.64	17.92	2
005095.jpg	683.90	21.38	1
006040.jpg	673.04	17.87	7
006324.jpg	663.84	17.79	3
006741.jpg	879.81	18.09	1
009910.jpg	879.47	18.89	3

Table 4. Single-shot Multibox Detector processing latency reduction and speedup when using Puppis HW accelerator

Image	SSD head latency reduction [perc]	SSD head speedup
001996.jpg	97.17	35.38
001760.jpg	96.87	32.00
002301.jpg	96.90	32.30
003626.jpg	97.07	34.10
004795.jpg	97.04	33.75
005095.jpg	97.52	40.28
006040.jpg	97.00	33.29
006324.jpg	97.01	33.47
006741.jpg	97.07	34.11
009910.jpg	97.19	35.57

Table 5. MobilenetV1 SSD latency reduction and processing speedup

Image	MobilenetV1 SSD network	MobilenetV1 SSD
	latency reduction [perc]	network speedup
001996.jpg	97.69	43.30
001760.jpg	97.50	39.93
002301.jpg	97.51	40.22
003626.jpg	98.09	52.32
004795.jpg	98.08	52.15
005095.jpg	97.57	41.17
006040.jpg	97.52	40.31
006324.jpg	97.49	39.77
006741.jpg	98.09	52.39
009910.jpg	98.09	52.39

Table 6. MobilenetV1 SSD latency reduction and processing speedup

Image	MobilenetV1 SSD network	MobilenetV1 SSD
	latency reduction [perc]	network speedup
001996.jpg	51.60	2.07
001760.jpg	50.26	2.01
002301.jpg	50.46	2.02
003626.jpg	50.79	2.03
004795.jpg	50.37	2.01
005095.jpg	54.89	2.22
006040.jpg	50.28	2.01
006324.jpg	50.17	2.01
006741.jpg	50.61	2.02
009910.jpg	51.70	2.07

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Puppis: Hardware Accelerator of Single-Shot Multibox Detectors for Edge-Based Applications

Abstract

1. Introduction

2. Overview of Proposed System for Hardware Accelerator of Complete SSD Network

2.1. General structure of SSD network

2.2. System for HW acceleration of complete SSD arhitecture

3. Accelerated SSD Head Computation Algorithms

3.1. The Softmax calculation

3.2. The Bounding-box calculation

3.3. The NMS calculation

4. Puppis HW Accelerator Architecture

4.1. The Control module

4.2. The Softmax module

4.3. The Bounding-box module

4.4. The NMS module

4.5. The Sort module

5. Experimental results

5.1. Hardware setup

5.2. Software comparison

6. Conclusion

Funding

References

MDPI Initiatives

Important Links

Subscribe