Preprint
Article
Application of DEM Coupled with CFD to Predict the Erosive Wear Behavior of Arctic Vessel Hulls Subjected to Ice Impacts
Altmetrics
Downloads
129
Views
20
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
09 August 2023
Posted:
11 August 2023
You are already at the latest version
Alerts
Abstract
Marine vessels operating on the Arctic Sea route are constantly prone to collisions and friction with ice. This study discusses the wear of the hull plate caused by the collision of ice against vessels operating in Arctic Sea routes. The abrasive wear of the hull due to ice impact was numerically assessed based on both the incident behavior of ice particles interacting with the flow around the hull and the wear loss of the hull surface caused by the contact force of ice particles. A multi-phase approach was adopted to account for the behavior of ice particles continuously affected by the fluid force around the hull. The fluid force acting on the ice floe was evaluated using computational fluid dynamics (CFD) and the dynamic motion of the drift ice was evaluated using the discrete element method (DEM). The motion of the floating ice particles was updated in real time by iteratively coupling the fluid force and the motion of the ice floe at each time step of the numerical simulation. The results of the wear simulation models were presented in terms of the shape change of the hull surface due to wear. At first, the wear was evaluated for cases in which only the surface paint of the hull was damaged. Thereafter, a computation model considering the shape change of the hull surface experiencing long-term friction of ice particles was introduced. Finally, the numerical procedures to predict the abrasive wear of the hull surface by ice impact were discussed.
Keywords:
Subject: Engineering - Marine Engineering
1. Introduction
The ice covering Arctic shipping routes is constantly broken up into numerous floating ice floes, which damages the hull of the vessels that operate in these waters. Such ice-floe fields are generally considered the most important challenge for Arctic shipping. This has motivated various studies on the interaction between marine vessels and ice floes. Particularly, the floes can induce not only significant resistance on the ship but also impact forces on the hull surface. Therefore, predicting the effect of ice-induced collision is crucial. Considering the high costs of experimental analyses and the shortage of field-measurement data, numerical models offer a cost-effective means to investigate the effect of ice floes on vessels. Since damage to ships operating in the Arctic route causes severe environmental and property problems, the structural capacity of vessels against ice collisions must be assessed at the design stage. Therefore, various studies have conducted structural safety assessments to determine the effects of environmental loads on ships. Particularly, these studies (e.g., Fabrice et al. [1]; Riska et al. [2]; Adumene et al. [3]) have assessed the effects of cargo load, wave load, and harsh fluid impact applied to a ship, and the evaluation procedures have been curated by shipping classification societies [4,5,6,7]. For ships operating in Arctic regions, collisions caused by ice floes are the most important risk. Nonetheless, few efforts have been made to assess the impact of drift ice of both the impact load and structural safety of Arctic vessels. The ice impact load can be inversely estimated based on the reactive stress measured on a ship operating in a specified route. However, the measured data can only be used to estimate the impact load in a specific route. Therefore, the ice impact load measured on the ship can be applied only to ships that have a similar hull form and operate in the same route. Therefore, many attempts (e.g., Gao et al. [8]; Kim et al. [9]; Liu et al. [10]; van den Berg [11]; Sun and Shen [12]) have been made to predict ice impact loads and evaluate the impact resistance of the hull using numerical analysis to contribute to arctic ship design.
Vessels operating in Arctic routes experience various types of damage from interaction with drift ice. The type of hull damage is related to the magnitude of the impact energy of the drift ice. When a ship collides with a large fragment of drift ice at high speed, the hull completely collapses. An ice impact with small energy may cause localized hull damage and deformation. Even if the collision energy induces stresses below the yield stress, repeated ice collisions may cause fatigue damage or wear damage to the hull. Vessels operating on Arctic routes with abundant drift ice experience continuous frictional forces as they advance while resisting the drift ice. Once the coating is separated from the hull surface by frictional force, the wear load caused by friction begins to accumulate on the surface of the hull plate. Afterward, wear damage due to abrasive force, which peels off the steel of the hull, spreads out onto the hull surface. The accumulated abrasion of the hull plates can eventually cause corrosion damage, in addition to deteriorating the structural strength of the hull. Various theoretical approaches and shipping classification criteria have enabled the analysis of structural stress and deformation response due to ice impact (Kwon et al. [13]; Nho et al. [14]). However, very few studies have actively sought to predict the wear damage of the hull due to ice impact.
The purpose of this study was to develop a numerical model to enable the estimation of the wear of a vessel hull undergoing collision with drift ice based on three key considerations. The first consideration is the influence of the sea environmental load in the Arctic route on the ice floes. Given that both vessels and ice floes are subjected to the Arctic environment loads during their lifetime, the numerical model would also have to reflect the hydrodynamic behavior of drift ice. The second consideration is the behavior of ice floes continuously experiencing fluid flow and their interactive loads. The behavior of ice fragments can be expressed by solving a multi-phase problem consisting of a fluid phase, which numerically represents the environmental load, and a particle phase, which represents the motion of the ice fragments. The last consideration is the development of a reasonable wear assessment method. Since wear is caused by continuous contact friction between the ice fragments and the hull surface, it can be simulated by a contact element in the FEA. However, FEA including contact elements is a typical nonlinear problem, which not only demands large computation times but also cannot easily render a stable converging solution. In addition, it is practically impossible to set a contact condition by predicting the behavior of a large number of irregular flowing ice. In this study, we discuss the three aforementioned considerations and present a numerical implementation procedure for predicting abrasive wear damage on hull surfaces subjected to cumulative ice impact. However, the implementation of numerical analysis is focused on reflecting physical characteristics rather than quantitatively accurate predictions of wear. The effects of hull shape, operating conditions, and wear-inducing material properties that affect wear are not covered in this study.
2. State of the Art
Studies on the structural safety of vessels operating in Arctic routes have been conducted in terms of the dynamic material properties of ice, the motion of ice floes, impact forces and friction loads, and structural responses. Han et al. [15] conducted a compression test of conical ice specimens to obtain the strain-load relationship. Additionally, the load-displacement relationship of the conical ice predicted by the FEA was compared with the experimental results. By applying this relationship to FEA, the spalling of ice under the crushable compression was simulated. Cai et al. [16] and Zhu et al. [17] estimated the dynamic stress-strain relationship of steel and ice using the Cowper-Symonds model and the Crushable Foam model, respectively. The authors demonstrated that the dynamic material properties of both steel and ice can be applied to FEA to predict the fracture shape of ice subjected to impact.
The estimation of ice impact loads requires an a priori knowledge of the ice floe motion, which represented the first major concern of the present study. Kim et al. [18] modeled the behavior of a ship, drift ice, and seawater using the arbitrary Lagrangian-Eulerian (ALE) technique and calculated the ship resistance using FEA. The ice resistance of the icebreaker was measured and compared with that of ALE based FEA by conducting an ice breaking towing-test in the ice basin. The authors ultimately aimed to calculate the ice resistance of the icebreaker. An alternative approach to FEA is to couple computational fluid dynamics (CFD) with a particle model such as DEM (discrete element method) or SPH (smoothed particle hydrodynamics), which allows for fully non-linear solutions including complex geometries to investigate structure-flow-ice interactions. In other words, CFD and DEM have been coupled to model the ship-flow-ice interaction. Robb et al. [19] presented a SPH-DEM coupling model to numerically simulate the behavior of an ice floe on a free surface. Moreover, Huang et al. [20] constructed a CFD model to calculate the ship resistance in response to ice collision. The flow generated by the operating vessel was calculated using CFD, and the behavior of the drift ice was simulated by adding pancake ice to the flow field. Liu et al. [21] also performed CFD-DEM coupling analysis to evaluate hull resistance by accounting for the motion of ice floes. By assuming that the drift ice particles were spherical, a CFD-DEM model was used to predict the hull resistance applied to the vessel. The authors tested both one-way and two-way coupling schemes to the CFD-DEM model and calculated the velocity and pressure of ice particles experiencing the flow of surrounding sea water. Their results demonstrated that the two-way coupling analysis could simulate the motion of the ice floe more accurately than one-way analysis. However, the result of the one-way coupling method was estimated to be only approximately 5% different from the two-way coupling analysis. Therefore, although the two-way coupling method provides estimates that are close to experiment-derived values, it should be noted that it takes more computation time than the one-way coupling method. Therefore, the authors suggested that the one-way coupling method can be practical. Particularly, as the ship moves at a lower speed, the difference in simulated results according to the coupling method becomes smaller, and the one-way coupling provides a more conservative result from the perspective of impact forces. Therefore, the one-way coupling method may be more reasonable for predicting wear generated at low-velocity impacts. Liu et al. [22] and Zhang et al. [23] also simulated the behavior of ice floes surrounding a moving ship by coupling CFD and DEM. Particularly, CFD was applied to simulate the fluid surrounding the ice floes, whereas DEM was incorporated to account for the ice motions and ship-to-ice or ice-to-ice collisions. By integrating these approaches, the proposed method could account for the influence of ship-generated fluid flow on the ship-ice interactions.
The hull damage caused by large icebergs in high-speed collisions is not much different from ship-to-ship collision in terms of structural deformation caused by the excessive collision energy, except that the colliding object is ice and the behavior of ice should be predicted. Suyuthi et al. [24] developed a probability model that assesses the collision loads of ice with various thicknesses and velocities. Cho et al. [25] investigated the wear of hull coatings through ice friction experiments. Changes in the coated surface of the hull were measured by varying the friction force, surface roughness, and coefficient of friction. Kietzig et al. [26] summarized the friction coefficient of ice collected by relevant studies and presented the factors that affect the friction force of contacting ice, including ice temperature, sliding speed, and vertical load. The main purpose of this study is to determine the effect of various external factors on the friction of ice. Several other studies have also applied FEM to wear assessment (Shimizu [27]; Xie [28]). However, the applicability of FEM for the evaluation of wear caused by contact between metal planes is limited and the wear force of impacting particles cannot be easily accounted for when using this model. Chen et al. [29], Xu et al. [30], and Zhang et al. [31] suggested that the friction behavior derived from the interaction between fluid and solid particles could be efficiently predicted by applying the CFD-DEM coupling method. Walker et al. [32] also demonstrated that the particle shape has a great influence on wear through several friction experiments. Huang et al. [20], Luo et al. [21], Zhang et al. [23] and Shunying et al. [33] analyzed the collision between the hull and the ice floe by coupling CFD and DEM. However, they simulated the collision of the ice floe with the hull by assuming that the ice particles were spherical and free shapes were obtained by combining several spherical particles. Therefore, their study could not efficiently reflect the wear caused by sharp edges or vertices of ice particles. When the surface geometry of the impact object changes due to wear, the flow of the colliding particles changes. Furthermore, as the particle flow changes, regions with high wear energy shift non-linearly. Shunying et al. [33] analyzed the effect of changes in the geometry of the worn surface on particle flow and the effects that these variables had on the final wear pattern. However, to the best of our knowledge, no previous studies have examined the effects of the changes in the hull shape due collision-induced wear on ice flow and ductility.
Our study sought to develop a numerical model to evaluate the wear of a vessel hull by considering the particle shape and changes in the particle motion due to wear-induced changes in the shape of the impacted object. Finally, this study presents a practical approach for the estimation of Arctic ship wear, which could be used as a basis for the design of safer and more resilient Arctic vessels.
3. Numerical Scheme
3.1. Analysis Process
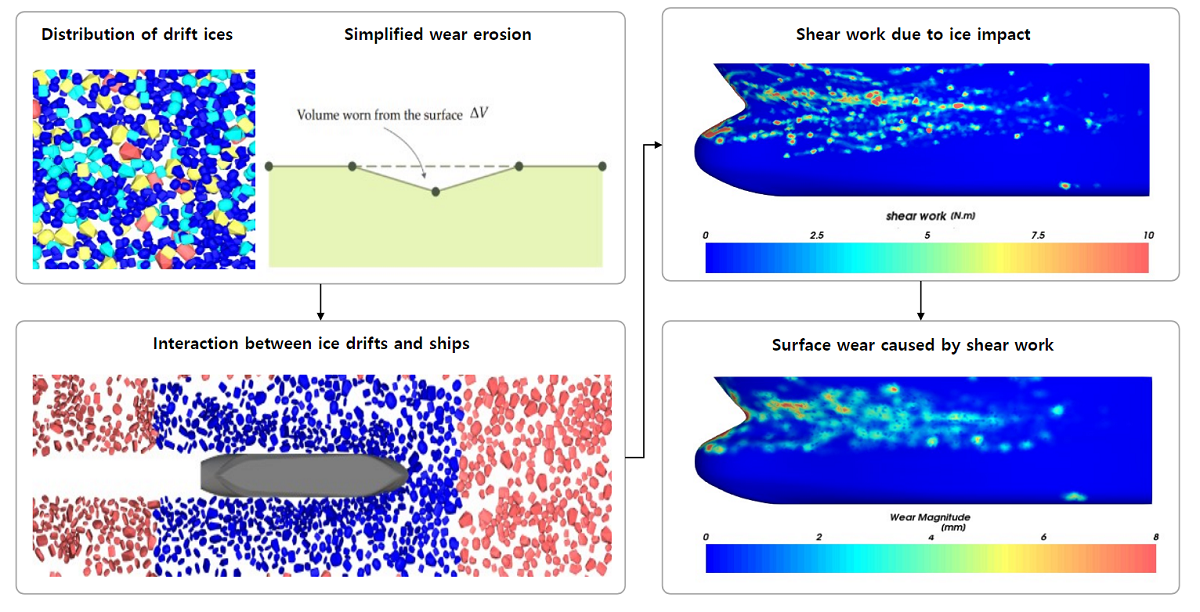
Our study sought to develop a reasonable numerical model to predict the behavior of drift ice and estimate the wear caused by the collision between drift ice and a vessel’s hull. The environmental load of the Arctic route can be modeled with the CFD scheme, after which the computed load is transferred to the ice floes. The motion of many ice particles colliding on a ship can be modeled with the DEM scheme. The impact computed with the DEM algorithm can be used to construct models to describe the scattering of ice floes approaching an object, as well as to assess the contact forces on the hull surface. Afterward, the wear magnitude was evaluated based on the collision mechanism between the hull surface and the ice floe, and was simulated with three-dimensional DEM. In this study, we sought to predict hull wear caused by a set of ice floe collisions by taking advantage of the unique strengths of the CFD and DEM methods. The flow-induced load was computed using the continuum method and the behavior of drift ice was simulated with the discrete method, whereas the continuum and discrete methods were implemented using the Ansys Fluent code and Rocky-DEM code, respectively. Ansys Fluent is a VOF (volume of fluid)-based CFD code that simulates the hydrodynamic load of seawater on ice, whereas the Rocky-DEM is a particle behavior analysis solver that can accurately predict the load and behavior of particles colliding with other particles, as well as particles colliding with hulls. From the perspective of particle geometry, the Rocky-DEM approach can be used to model the free shape of the particles whereas other DEM schemes (Cleary et al., [34]; Morrison and Cleary [35]) exclusively assume that the particles are spherical, resulting in unrealistic results.
In the coupling analysis method, hydrodynamic loads such as drag force and buoyancy caused by seawater are calculated through CFD analysis and then transferred to the DEM analysis. In the DEM analysis, the load calculated from the CFD analysis is applied to evaluate the behavior and collision load of the particles. In this approach, the fluid phase and particle phase are analyzed through each specialized solver, which greatly enhances the accuracy of the analysis. Coupling analysis can be classified as one-way and two-way according to the interrelationships between the fluid phase and the particle phase. One-way coupling analysis is suitable when particles are exposed to the flow environment but the particle behavior does not have a substantial influence on the flow. In contrast, two-way coupling analysis may be suitable when the behavior and flow of particles closely affect each other. The flow of the route acts as the dominant load on the drift ice. However, the behavior of the drift ice can slightly affect the flow of the route but has no effect on the overall flow. Therefore, the one-way coupling analysis is reasonably well suited as a basis for the wear evaluation model due to the collision between the drift ice and the hull.
Figure 1.
Schematic diagram of numerical codes to simulate the CFD – DEM coupling behavior.

3.2. Theoretical Background of DEM
DEM is a numerical method that is often used to compute the motion and behavior of a large number of particles. In the DEM analysis, the load applied to the particle is defined as the combination of the contact load (surface force) caused by the collision and the non-contact load (body force). Non-contact load can be defined as a load that affects particles regardless of whether collision occurs, such as gravity and ambient fluid forces. The inertia force due to particle motion and the effects of the marine environment are applied as a non-contact load to the center of gravity of the particles. The speed and direction of motion are changed by the collision of particles, and some kinetic energy is dissipated. DEM analysis can be defined as the repeated process of calculating particle behavior (body force) and collision (surface force) during the analysis [36].
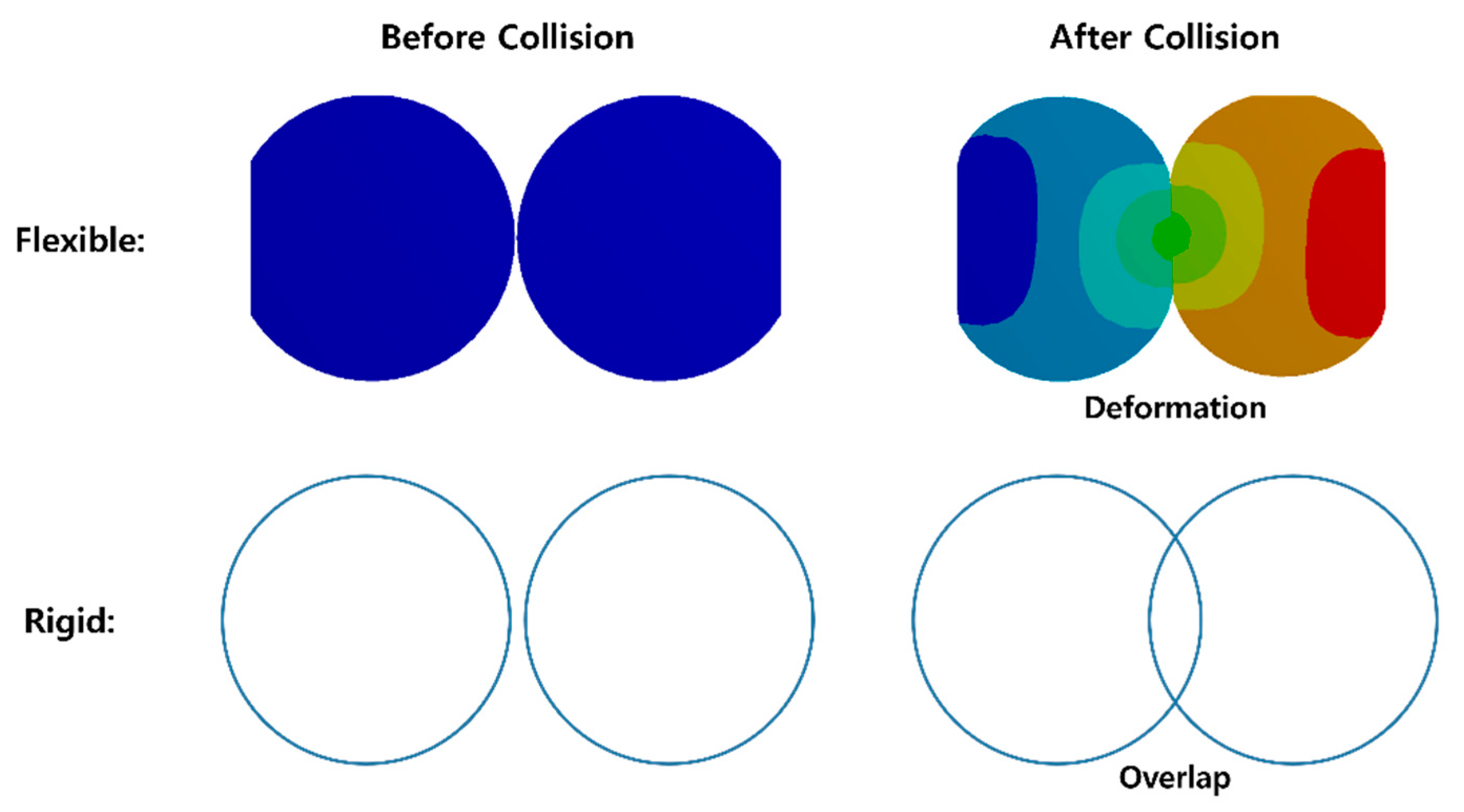
Although some particles are modeled as flexible in the DEM algorithm, particles are generally modeled as rigid objects to make the analysis more efficient. When a particle collides with other particles and structures, deformation occurs due to the collision energy. Particles modeled as rigid objects do not deform even when a collision occurs. The deformation caused by the collision was replaced by an overlap of particles because the DEM algorithm generally uses rigid particles. The relationship between load and displacement is defined as a function of either or when describing the behavior of a flexible body or a rigid particle, respectively. Where F denotes force, is stiffness, is deformation, and represents the overlap distance.
Figure 2.
Comparison of the behavior of flexible and rigid particles.
Collision load is defined as the component of normal force and tangential force, and each load is defined as a function of stiffness and overlap. In this study, the normal force was defined using the hysteretic linear spring model (HLS). The HLS model is an elastoplastic model that is used by separately defining the loading stiffness, in which the direction of motion is maintained in the direction of the initial collision, and the un-loading stiffness, where the direction of motion is reversed after the initial collision. In Figure 3, the slope of is the loading stiffness, whereas represents the un-loading stiffness. , which is an overlap that remains after being completely numerically un-loaded, is plastic deformation, and the area of the triangle is the energy lost due to noise, heat, and other factors after collision.
The linear spring Coulomb limit (LSCL) model was used to evaluate the tangential force that directly affects the wear. The Coulomb friction model, which defines the tangential force as the product of the friction coefficient () and the normal force (), is widely used to calculate the tangential forces between contact surfaces. However, unlike the LSCL model, it cannot account for contact area and sliding stiffness (Figure 5). Therefore, the tangential force calculated through the Coulomb friction model was applied as a limitation of the LSCL model. The normal force model and tangential force model are shown in Figure 4 and Figure 5, respectively.
In Figure 4, the loading stiffness and the unloading stiffness are respectively defined as follows:
where and represent the stiffness of the particle, L is the particle size, and represents the bulk Young's modulus of the particles. Moreover, ε denotes the restitution coefficient, which is not an individual property of particles but a relative property of a collision pair.
where represents the sliding stiffness and is defined as the product of (tangential stiffness ratio) and , as shown in the following equation:
3.3. Theoretical Background of CFD [38]
In this study, the flow of routes was predicted using Ansys Fluent, and the continuous equation and the motion equation were defined as follows:
where is the density, is the velocity of the fluid, is the pressure, is the fluid viscosity, is the volume force, and is the shear stress. The RANS (Reynolds-averaged Navier–Stokes) equation converted using the average velocity in Equation (6) was assumed using the following equation:
where represents the fluctuation speed. The k-ε model was applied for turbulence, and the equations for turbulent kinetic energy and viscous dissipation were assumed as follows:
where is the strain and is the fluid viscosity in Equation (9) and (10), is assumed to be 1.00, is 1.30, is 1.44, and is 1.92.
3.4. Theoretical Background of DEM-CFD Coupling [39]
The flow of the route was calculated through CFD analysis in which the conservation equations for the mass and momentum of the fluid were solved using the finite volume method and the continuum method. The drift ice particles in the route were modeled using the DEM approach. The behavior of the particles is determined by the interaction between the flow and particles. To numerically evaluate the behavior of drift ice, we must first understand the numerical models of each fluid phase and particle phase, as well as the governing equations for the interaction. The translational and rotational motions of all particles can be defined using Euler’s first and second laws as follows:
where is the mass of the particle, is the gravitational acceleration, is the particle contact force, is the angular velocity vector, is the moment of inertia tensor, and is the net torque. and are added to define the interrelationship between particles and flow. defines the load and relationship that induces the particle's translational motion, and defines the load and relationship that causes the particle's rotation. can be defined as the sum of the drag force () and other loads as shown in the following equation:
where is defined as the sum of the pressure gradient force (), the added mass force (), and the lift force ().
In this study, was defined as Equation (15) because the effects of loads other than and are relatively insignificant when the particle density is significantly greater than the fluid density.
can thus be defined as Equation (16).
where is the volume of the particle and is the local pressure gradient. The buoyancy force acting on the drift ice is reflected by the pressure gradient force. is defined by the drag coefficient () as in Equation (17).
where is the relative velocity of the particle and the flow and is the projected area. Various equations for are presented according to the Reynolds number (), which is defined by the relative velocity between particles and flow. is defined as follows:
In this study we used as suggested by Ganser [40], which is applicable to both spherical and shaped particles. The Ganser drag model is defined as follows:
where is the diameter of a spherical particle with the same projected area of the actual particle in the direction of the flow, is the diameter of a spherical particle with the same volume of the actual particle, and D is the diameter of the container. is sphericity, which is defined as the ratio of the surface area of a spherical particle having the same volume as the real particle to the surface area of the real particle.
3.5. Archard Wear Law
The Archard wear law (Archard [41]) was used to evaluate the amount of wear caused by the collision between the hull and the floating ice particles. Archard's wear law evaluates wear through the relationship between the shear work by frictional forces on the surface and the lost volume. Equation (22) is a numerical model of Archard's wear law.
where is the total volume lost due to wear, is the tangential force, is the sliding distance, is the material hardness, and is an experimental constant. and are values that can be calculated through DEM analysis, and and are material property values. In Equation (22), the product of and is defined as shear work as in Equation (23).
where is the shear work generated in each time step. The amount of wear by depends on the material. Moreover, the amount of wear evaluated by is determined by , which is defined as the ratio of to as in Equation 24. The unit of is defined as .
If Equations (23) and (24) are substituted into Equation (22), it can be rearranged in Equation (25). Equation (22) can thus be reorganized as follows.
If the amount of wear is not too high, the deformation caused by material loss does not significantly affect the flow of particles. However, when material loss increases due to wear, the flow of particles changes non-linearly. Therefore, when material loss occurs due to wear, the changes in the surface shape must be accounted for. calculated through Equation (25) was applied to the evaluation model every 0.005 seconds to reflect the shape change process due to material loss. Given that the area of the grid composed on the surface of the hull model was determined, the grid was moved in the direction of the material loss based on the lost volume. The wear shape evaluation method is shown in Figure 6.
4. Evaluation of Hull Wear Due to Collision with Ice Floes
To evaluate the wear of arctic operating vessels in ice floes, multi-phase problems consisting of particles and flow can be solved numerically. In this study, the flow of the sailing route was modeled as a fluid phase, whereas the behavior of the ice floes was modeled as a particle phase. The flow of the route acts as a dominant load on the ice floes but the behavior of the ice floe does not have a significant effect on the flow of the route. To reflect these behavioral characteristics, the one-way coupling method is reasonable. The fluid phase acts as the load of the particle phase, and the hull is defined as the boundary condition. The hull wear is evaluated by extracting the load component that causes wear from the impact energy generated in the particle phase. Hull wear due to collision with particles was evaluated by applying the Archard wear law, which is defined based on shear work and the volume loss ratio.
Wear is a failure that occurs when energy is continuously transferred from ice floe to the hull surface over a long period of time. Therefore, it is impossible to evaluate wear on a real-time scale and over an operational distance. To overcome this limitation, a method for numerically accelerated analysis is needed. Considering the characteristics of wear, it has been shown that the wear can be efficiently predicted by converting long-term loads into equivalent material constants. In Lee et al. [37], the specimen was moved 208 km for 20 hours in the experiment, while in the numerical model, the wear was evaluated by moving 3 m in 1.18 seconds with the same specimen geometry and travel speed. Although the analysis was accelerated, the wear shape could be accurately predicted. In Equation (25), the amount of wear volume per unit time is defined as the product of the material constant and the shear work accumulated per unit time. The material constant C is defined as the volume lost due to the accumulated shear work per unit time. If C is increased by N times, there is an effect of increase in the unit time, as shown in Equation (26).
where is enlarged material constant for accelerated analysis, is actual material constant and N is enlargement factor. is defined as shear work accumulated over N times the unit time. Through this relationship, micro material loss cannot be evaluated, but it can be evaluated from a macro perspective.
The purpose of this study is to develop a numerical model for assessing wear in ships traveling Arctic routes. The shape of ship, operating conditions, and wear-inducing material properties were not of primary interest in this study. Therefore, the wear magnitude evaluated in this study is not representative of actual operational ships.
4.1. Evaluation Conditions
In the early stages of operation, the painted hull surface is damaged by friction with the floating ice. Since the shape of the hull does not change, there is no need to account for the shape change due to wear. If the operation is prolonged, friction with the ice floe accumulates and the material of the hull is lost. Since the shape of the hull changes due to material loss, the shape change due to wear must now be accounted for. Evaluation models suitable for each situation were thus presented. The evaluation was conducted assuming a scenario in which a vessel sails 200 m on a route with ice floes. To calculate the fluid force of the route, an evaluation model was constructed with Ansys Fluent. It was assumed that there was no seawater flow, and the buoyancy force was considered by implementing the pressure gradient of the fluid force. To simulate buoyancy and conditions in which there is no fluid flow, an arbitrary speed was applied upward from the lower part of the CFD model and analyzed, after which the speeds in all directions were patched to 0. The velocity in all directions was fixed to 0 to prevent particle movement due to seawater flow, and the depth direction pressure gradient was implemented to define the buoyancy force. The results of CFD analysis were applied as the load of DEM analysis. For the coupling of CFD and DEM, the Ganser drag law was applied to calculate drag force. The density of water was defined as 1000 kg/m3 and the viscosity as 0.001003 kg/m-s.
Transport Canada [42], a Canadian company that operates through the Arctic Ocean, suggests a range of safe operating speeds to avoid potential accidents from ice collision. Therefore, our evaluations were carried out based on the safe speeds of 4, 6, and 10 knots suggested by Transport Canada (AMNS) [42].
According to the Arctic Ice Regime Shipping System (AIRSS) [43] developed by Transport Canada, one of the main factors defining the ice regime that affects ships operating in polar regions is ice concentration, which is defined according to the percentage of space occupied by ice in the route. In this study, ice concentrations of 60% and 80% were evaluated, as illustrated in Figure 7. Ice concentration was defined as the area ratio of particles in the evaluation area. The method for the evaluation of ice concentration is shown in Figure 8.
The shape of the ice particles was defined as described by Zhang et al. [23]. The ice particle modeling results are shown in Figure 9. The size distribution of the ice particles was determined by Liu and Ji [22]: 25% of 1.0 m particles, 50% of particles larger than 1 m and smaller than 1.5 m, and 25% of particles larger than 1.5 m and smaller than 2.0 m. This size distribution was used for the three particle shapes. The sizes of the three different particle shapes were defined as the sizes of spherical particles having the same volume. Figure 9 illustrates the ice particle shape modeling.
An oil tanker with a length of 43 m, a width of 6.5 m, a depth of 3.6 m, and a draft of 2.4 m was evaluated. The material properties applied to the analysis are shown in Table 1 and Table 2.
Figure 10.
Ship modeling.

The DEM analysis conditions reflecting the above conditions are shown in Figure 11. The evaluation models were constructed by initially placing particles according to the ice concentration on the surface of the 200 m route and then moving the hull. The blue area in Figure 11 is the seawater area defined by the CFD analysis result. To perform the evaluation in the same ice arrangement for each ice concentration, the particle arrangement was stored and used as an initial condition for each evaluation case. The initial arrangements of drift ice according to ice concentration are shown in Figure 12 and Figure 13.
4.2. Coating Material Wear Assessment
The evaluations were performed assuming a scenario in which a coating material such as paint was separated from the hull by friction between the ice and the hull. Evaluations were performed at ice concentration of 60% and 80% and ship speeds of 4, 6, and 10 knots.
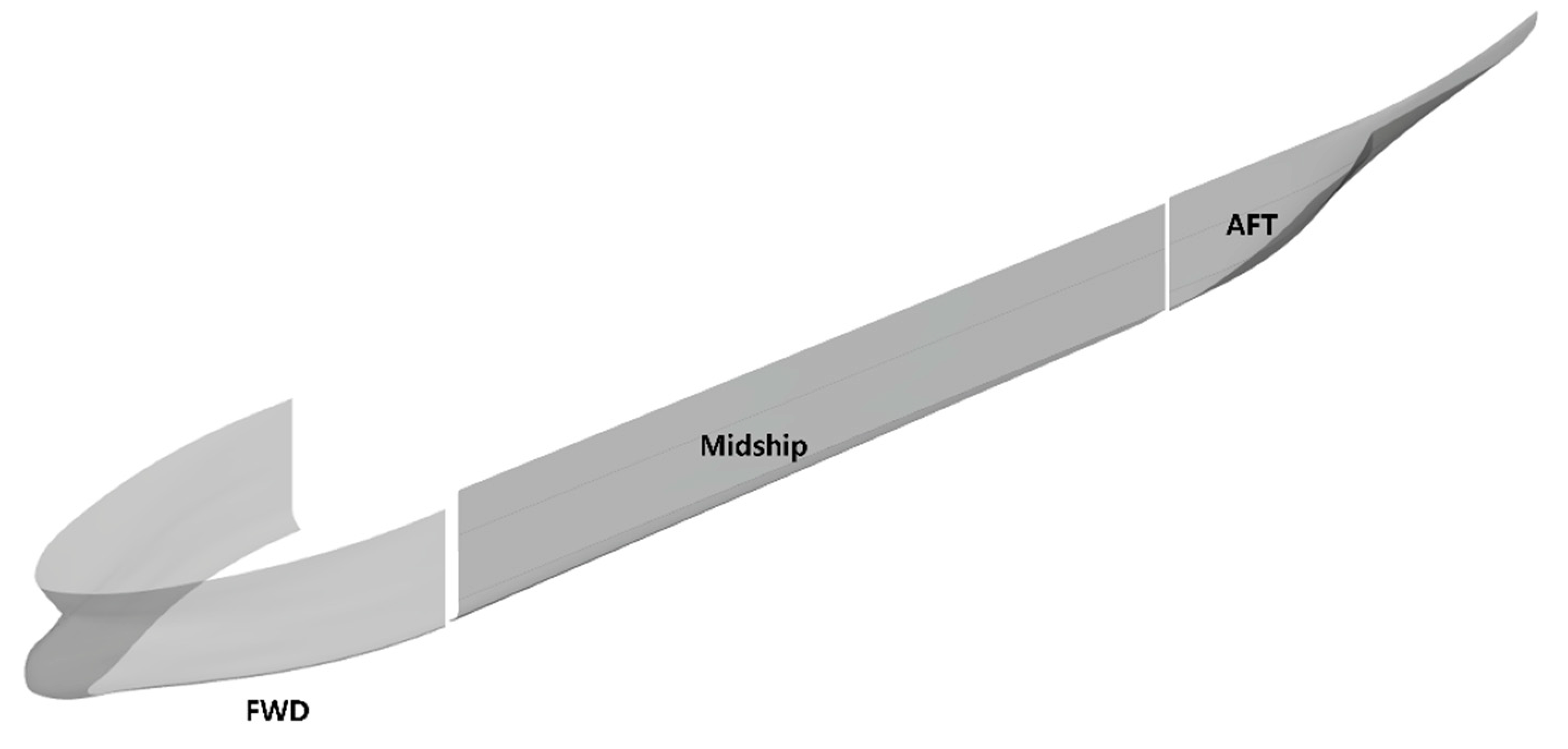
Given that the coating material is very thin compared to the thickness of the hull, the effect of material loss on the flow and behavior of ice is negligible. Therefore, the analysis was performed without reflecting the shape change, and the wear was evaluated based on the shear work according to Archard's wear law. Given that wear is a type of damage that occurs over a long period, it was not evaluated as a result of a specific point in time but was evaluated as an accumulated value on the hull after passing a 200 m route. Shear work, tangential force, and sliding distance were evaluated in the form of cumulative values for each evaluation condition according to the Archard wear law. The hull was divided into three regions to conduct the evaluations: forward (FWD; i.e., the bow), midship, and after (AFT; i.e., the stern) of port.
Figure 14.
Evaluation area.
Six analysis scenarios were simulated by combining three cases of ship speed and two cases of ice concentration. Among the six simulated scenarios, Figure 15 and Figure 16 show the simulation results of the scenario with the slowest ship speed and the lowest ice concentration (4 knots, 60%), whereas Figure 17 and Figure 18 illustrate the scenario with the fastest ship speed and the highest ice concentration (10 knots, 80%).
The average, maximum, and total cumulative shear work causing wear on the FWD, midship, and AFT are shown in Figure 19, Figure 20 and Figure 21.
The average, maximum, and total cumulative tangential force, which are components of shear work, at the FWD, midship, and AFT are shown in Figure 22, Figure 23 and Figure 24.
The average, maximum, and total cumulative sliding distance, which are components of shear work, at the FWD, midship, and AFT are shown in Figure 25, Figure 26 and Figure 27. The total area affected by wear is shown in Figure 28.
Our findings indicated that the accumulated total shear work, tangential force, and sliding distance in all areas at 80% ice concentration was greater than 60%. As the ice concentration increases, the cumulative results of each item increase because the number of collisions also increases.
Our results also demonstrated that as the ship speed increases, the cumulative shear work, tangential force, sliding distance of the drift ice per unit time, and wear affected area at the FWD also increased. These results indicate that the wear occurs in a deep and wide area as the ship speed and the ice concentration increases. Since the direct collision between drift ice and the hull is dominant in the FWD, the tangential force and sliding distance generated in each collision increases as the ship speed increases. Therefore, the cumulative average, maximum, and total amounts of each evaluation item tended to increase.
In the midship and AFT, as the ship speed increases, the cumulative shear work, tangential force, sliding distance, and the area affected by wear tend to decrease inversely. This is because the drift ice, which first collided with FWD, rubs against the hull while flowing along the outer wall. When the ship speed is relatively slow, the drift ice that first collided with FWD moves smoothly along the outer wall of the hull. However, as the ship speed increases, it tends to move away from the hull rather than flowing along the outer wall.
This trend is clearly shown in Table 3, which summarizes the total cumulative shear work per unit area as a ratio of FWD. Given that the total volume of wear according to the Archard's wear law is proportional to the shear work, the results are summarized based on the shear work. The total shear work accumulated per unit area of the midship and AFT relative to the FWD region was evaluated to be as high as 4.99%, and the ratio tends to decrease as the speed increases. As expected, our results demonstrated that FWD directly collides with the drift ice, and therefore the amount of wear and the ship speed are directly related. In contrast, midship and AFT wear was not related to ship speed because the particles that first collided with the FWD induced wear while moving along the outer wall of the hull. Therefore, to prevent abrasion in the FWD, the ship speed must be reduced, or sufficient reinforcement must be provided according to the ship speed. Moreover, to prevent midship and AFT wear, the outer shape of the hull could be redesigned to minimize the damage caused the drift ice that first collides with the FWD.
Models without shape changes due to wear-induced material loss can also evaluate the wear depth by applying the accumulated shear work to the Archard wear law. As shown in Equation (27), the wear depth was evaluated by multiplying the accumulated shear work by the volume loss ratio C according to the Archard wear law. The wear depth was evaluated by dividing the evaluated wear volume by the individual cell area of the hull surface. The volume loss ratio C per unit shear work was defined as 5e-7m3/J, which is the same as the value applied in the following section. The wear depth according to ship speed and ice concentration for each hull position was evaluated as shown in Table 4.
4.3. Hull Material Wear Assessment
In this section, the simulations were conducted assuming that the material of the hull is lost due to the accumulation of friction with the drift ice. The evaluations were performed at ice concentrations of 60% and 80% and ship speeds of 4, 6, and 10 knots. Wear-induced material loss leads to changes in the hull shape. In turn, these deformations can affect the flow of drift ice. To account for these dynamic changes, the analyses were performed by updating the shape change in real time, and the amount of material loss due to shear work was evaluated according to the Archard wear law. In Equation (25), C, which represents the volume lost per unit of shear work, was defined as m3/J, and the shape deformed by wear was automatically updated every 0.005 seconds. That is, the shape change due to abrasive wear was added in the analysis conditions described in Section 4.1.
Among the six simulation scenarios, the analysis results of the scenario with the slowest ship speed and the lowest ice concentration (4 knots, 60%) and the scenario with the fastest ship speed and the highest ice concentration (10 knots, 80%) are shown in Figure 29 and Figure 30, respectively.
For each evaluation condition, the average, maximum wear depth, and total area affected by wear in the FWD, midship, and AFT are shown in Figure 31, Figure 32 and Figure 33.
In the evaluation model considering material loss due to wear, as the ice concentration increases, the frequency of collisions with drift ice increases, and therefore the amount of wear tends to increase. The effect of ship speed tends to be different for each area. In the FWD area, as the speed of the ship increases, the average and maximum wear depth increases, and the area affected by wear also widens. In other words, the ice particles wear the hull more deeply and over a wider area. In the case of the midship, as the ship speed increases, the average wear depth and area tend to decrease, and the maximum wear depth tends to increase. If the ship speed is slow, a relatively large area is worn because the particles that first collide with the FWD move smoothly and accumulate along the outer wall of the hull. At the point where the shape of the vessel changes from the curved surface of the FWD to the straight walls of the midship, the maximum wear depth tends to increase as the ship speed increases because the drift ice that first collided with the FWD surface moves along the hull and is repeatedly separated. Similarly, since the same behavior appears at the point where the shape changes from the straight midship to the curved AFT region, our findings confirmed that the wear depth increased as the ship speed increased.
4.4. Comparison of the Results According to the Evaluation Method
Two evaluation models were examined in this study according to two different phases of hull wear. The first was the painting surface wear that may occur in the early stages of the operation, and the second was the loss of hull material due to the accumulation of friction with drift ice with extended operation periods. In terms of numerical analysis, the first method was used to evaluate wear based on shear work without considering the change in hull shape due to wear, whereas the second method was used to evaluate wear by accounting for the effect of wear-induced shape changes of the hull on the dynamics of the ice particles. Our results confirmed that the wear of the FWD area was significantly greater than that of the midship and AFT. The characteristics according to the evaluation method were analyzed based on the results of the FWD area. In the case of the model that accounted for hull deformation, the results cannot be compared with the same value as the model without hull deformation because the mesh constituting the hull model is continuously deformed. Therefore, our study compared the amount of hull deformation due to wear in the model with hull deformation and the shear work that causes wear in the model without hull deformation. To compare the wear patterns for each numerical model, the evaluation results of the two analysis methods were compared. The coefficient of variation (CoV) was used to compare wear patterns with different physical indices. The CoV is an index that is commonly used to compare two sample groups with a large difference in mean values or to compare data with different units. It is defined as the ratio of the standard deviation to the mean.
The analysis results were compared in the scenario with low ice concentration (4 knots, 60%) and the scenario with the fastest line speed and the highest ice concentration (10 knots, 80%).
Figure 34 and Figure 35 illustrate the wear shape and shear work for each numerical model. Since the structural boundary conditions do not change from the perspective of the drift ice in the model that does not consider the shape change, the area where most of the shear work occurs in the early stage did not change substantially and it continuously received a large load. Therefore, a band shape tended to form because the shear work was concentrated in a specific area over time. In the case of the model considering accounting for wear-induced shape change, the structural boundary conditions of the ice continuously changed, and therefore the areas that received the highest levels of shear work changed continuously. Thus, the model that accounted for shape change was evenly worn in a relatively wide area. Due to the characteristics of the numerical models used for wear evaluation, the model that does not consider the dynamic shape change of the hull exhibited a pattern of deep wear in limited areas, whereas the model that did account for shape change exhibited a more even wear over a wide area. The same trend can be seen in Table 5, which compares the average, maximum wear depth, and wear area of the two numerical models. In the model that did not account for the shape changes due to wear, the average wear depth was low, but the maximum wear depth was relatively high. Moreover, the area affected by wear was also relatively narrow.
These above-described characteristics are shown in Figure 36, Figure 37 and Figure 38. A low CoV means that a relatively large area was evenly worn. From the evaluation results, it was confirmed that the CoV was relatively low when the shape change due to wear was considered. Given the clear differences between the two evaluation models, their application would greatly depend on the evaluation scenario. Since the loss of the coating material due to wear does not cause a significant shape change, the model that does not consider the shape change is reasonable. In contrast, the model that accounts for shape changes is more suited for cases with material loss due to long-term operation.
5. Conclusions
This study sought to develop a model to numerically evaluate the environmental load of the Arctic route and evaluate hull wear caused by repeated collisions with drift ice, a representative environmental load in Arctic routes. For this purpose, it is necessary to predict the environmental load of the route, the behavior of the drift ice, and the wear caused by repeated collisions. To solve this problem, a method coupling DEM and CFD was proposed, and the wear was evaluated based on the Archard wear law. The evaluation model was presented separately depending on the material loss. The shape change due to the loss of the paint material was not large enough to affect the behavior of the ice flakes. Therefore, to evaluate the loss of the paint material due to wear, an evaluation model that does not account for shape change was presented. Since the structural boundary condition does not change in the model that does not account for shape change, the region where most shear work occurred did not change and a large load was continuously applied to the same areas. Therefore, as the period of shear work accumulation increases, the wear is concentrated in a specific area and the wear pattern exhibited a band shape. In cases where the hull material is lost due to wear (i.e., cases where wear exceeds the superficial paint layer), substantial damage may occur in a localized area and therefore a more conservative design may be required in terms of material strength.
In contrast, when evaluating a situation where material loss due to wear occurs, shape changes should be accounted for in real time during the analysis. Because the structural boundary conditions are constantly changing as material loss is reflected, the area where shear work occurs changes constantly. Therefore, material loss due to wear occurs evenly over a relatively wide area. If this evaluation model is applied in a situation where the painting material is lost, repairs might not be necessary because the damage is evenly distributed over a relatively wide area. Nevertheless, given that a specific model cannot be considered suitable for all situations, selecting an appropriate evaluation model suitable for each scenario is crucial to ensure a reasonable wear evaluation.
Author Contributions
Conceptualization and methodology, S.-J.L. and J.-H.L.; validation, formal analysis, investigation, and data curation, S.-J.L. and J.-H.L.; research administration, J.-H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a grant from National R&D Project "Development of fixed offshore green hydrogen production technology connected to marine renewable energy" funded by the Ministry of Oceans and Fisheries (1525013967).
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. The data derived from the present study are only partially available for research purposes.
Acknowledgments
This research was supported by a grant from National R&D Project "Development of fixed offshore green hydrogen production technology connected to marine renewable energy" funded by the Ministry of Oceans and Fisheries (1525013967).
Conflicts of Interest
The authors have no conflicts of interest to declare.
References
- Ardhuin, F.; Sutherland, P.; Doble, M.; Wadhams, P. Ocean waves across the Arctic: Attenuation due to dissipation dominates over scattering for periods longer than 19s. Geophys. Res. Lett. 2016, 43, 5775–5783. [Google Scholar] [CrossRef]
- Riska, K.; Bridges, R. Limit state design and methodologies in ice class rules for ships and standards for Arctic offshore structures. Mar. Struct. 2019, 63, 462–479. [Google Scholar] [CrossRef]
- Adumene, S.; Ikue-John, H. Offshore system safety and operational challenges in harsh Arctic operations. J. Saf. Sci. Resil. 2022, 3, 153–168. [Google Scholar] [CrossRef]
- International Association of Classification Societies (IACS). Polar ship rules, URI. 2016.
- International Association of Classification Societies (IACS). Technical background (TB) documents for URs concerning polar class (UR I). 2016.
- International Maritime Organization (IMO). Descriptions of polar classes, submitted by the international association of classification Societies (IACS), development of a mandatory code for ships operating in polar waters, DE 55/12/10. 2011.
- International Maritime Organization (IMO). International code for ships operating in polar waters (polar code), resolution MEPC.264(68). 2014. adopted on. 15 May.
- Gao, Y.; Hu, Z.; Wang, J. Sensitivity analysis for iceberg geometry shape in ship–iceberg collision in view of different material models. Math. Probl. Eng. 2014, 2014, 11. [Google Scholar] [CrossRef]
- Kim, H.; Daley, C.; Colbourne, B. A numerical model for ice crushing on concave surfaces. Ocean. Eng. 2015, 106, 289–297. [Google Scholar] [CrossRef]
- Liu, L.; Sun, S.; Ji, S. Interaction between Floater and Sea Ice Simulated with Dilated Polyhedral DEM, DEM 2016: Proceedings of the 7th International Conference on Discrete Element Methods, 1-. 4 August.
- van den Berg, M. Discrete Numerical Modelling of the Interaction Between Broken Ice Fields and Structures, Norwegian University of Science and Technology, 2019.
- Sun, S.; Shen, H. Simulation of pancake ice load in a circular cylinder in a wave and current field. Cold Reg. Sci. Technol. 2012, 78, 31–39. [Google Scholar] [CrossRef]
- Kwon, J.; Jeon, B.; Kim, J.; Bo Wang, H.Y.; Basu, R.; Lee, H.; Kendrick, A. Structural Integrity Assessment of Cargo Containment Systems in Arctic LNG Carriers under Ice Loads. In Fourth Annual Arctic Shipping St. Petersburg, Russia.
- Nho, I.S.; Lim, S.J.; Kang, K.J. Safe Speed Estimation of Arctic Ships considering Structural Safety. J. Soc. Nav. Archit. Korea 2018, 55, 236–242. [Google Scholar] [CrossRef]
- Han, Y.; Sawamura, J. Fatigue Damage Calculation for Ship Hulls Operating in Pack Ice, Proceeding of the 24th International Conference on Port and Ocean Engineering under Arctic Conditions, 11–16 June.
- Cai, W.; Zhu, L.; Yu, T.X.; Li, Y. Numerical simulations for plates under ice impact based on a concrete constitutive ice model. Int. J. Impact Eng. 2020, 143, 103594. [Google Scholar] [CrossRef]
- Zhu, L.; Qiu, X.; Chen, M.; Yu, T.X. Simplified ship-ice collision numerical simulations, In The 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 16. 20 June.
- Kim, M.; Lee, S.; Lee, W.; Wang, J. Numerical and experimental investigation of the resistance performance of an icebreaking cargo vessel in pack ice conditions. Int. J. Nav. Archit. Ocean. Eng. 2013, 5, 116–131. [Google Scholar] [CrossRef]
- Robb, D.M.; Gaskin, S.J.; Marongiu, J.C. SPH-DEM model for free-surface flows containing solids applied to river ice jams. J. Hydraulic Research 2016, 54, 27–40. [Google Scholar] [CrossRef]
- Huang, L.; Tuhkuri, L.; Igrec, B.; Li, M.; Stagonas, D.; Toffoli, A.; Cardiff, P.; Thomas, G. Ship resistance when operating in floating ice floes: A combined CFD&DEM approach. Mar. Struct. 2020, 74, 102817. [Google Scholar]
- Luo, W.; Jiang, D.; Wu, T.; Guo, C.; Wang, C.; Deng, R.; Dai, S. Numerical simulation of an ice-strengthened bulk carrier in brash ice channel. Ocean Eng. 2020, 196, 106830. [Google Scholar] [CrossRef]
- Liu, L.; Ji, S. Dilated-polyhedron-based DEM analysis of the ice resistance on ship hulls in escort operations in level ice. Mar. Struct. 2021, 80, 103092. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Shang, Y.; Jin, Q.; Zhang, L. CFD-DEM based full-scale ship-ice interaction research under FSICR ice condition in restricted brash ice channel. Cold Reg. Sci. Technol. 2022, 194, 103454. [Google Scholar] [CrossRef]
- Suyuthi, A.; Leira, B.J.; Riska, K. Fatigue damage of ship hulls due to local ice-induced stresses. Appl. Ocean. Res. 2013, 42, 87–104. [Google Scholar] [CrossRef]
- Cho, S.; Chun, E.; Yoo, C.; Jeong, S.; Lee, C. The measuring methodology of friction coefficient between ice and ship hull. J. Soc. Nav. Archit. Korea 2011, 48, 363–367. [Google Scholar] [CrossRef]
- Kietzig, A.M.; Hatzikiriakos, S.G.; Englezos, P. Physics of ice friction. J. Appl. Phys. 2010, 107, 081101. [Google Scholar] [CrossRef]
- Shimizu, K.; Noguchi, T.; Seitoh, H.; Okada, M.; Matsubara, Y. FEM Analysis of Erosive Wear. Wear 2001, 250, 779–784. [Google Scholar] [CrossRef]
- Xie, L.-J.; Schmidt, J.; Schmidt, C.; Biesinger, F. 2D FEM estimate of tool wear in turning operation. Wear 2005, 258, 1479–1490. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y.; Li, X.; He, R.; Han, S.; Chen, Y. Erosion prediction of liquid-particle two-phase flow in pipeline elbows via CFD–DEM coupling method. Powder Technol. 2015, 282, 25–31. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, Q.; Zheng, J.; Zhao, Y. Numerical prediction of erosion in elbow based on CFD-DEM simulation. Powder Technol. 2016, 302, 236–246. [Google Scholar] [CrossRef]
- Zhang, D.M.; Gao, C.P.; Yin, Z.Y. CFD-DEM modeling of seepage erosion around shield tunnels. Tunn. Undergr. Space Technol. 2019, 83, 60–72. [Google Scholar] [CrossRef]
- Walker, C.I.; Hambe, M. Influence of particle shape on slurry wear of white iron. Wear 2015, 332, 1021–1027. [Google Scholar] [CrossRef]
- Shunying, J.I.; Zilin, L.I.; Chunhua, L.I.; Shang, J. Discrete element modeling of ice loads on ship hulls in broken ice fields. Acta Oceanol. Sin. 2013, 32, 50–58. [Google Scholar]
- Cleary, P.W.; Morrisson, R.; Morrell, S. Comparison of DEM and experiment for a scale model SAG mill. Int. J. Miner. Process. 2003, 68, 129–165. [Google Scholar] [CrossRef]
- Morrison, R.D.; Cleary, P.W. Using DEM to model ore breakage within a pilot scale SAG mill. Miner. Eng. 2004, 17, 1117–1124. [Google Scholar] [CrossRef]
- ESSS Rocky, Release 2022 R1.1, DEM Technical Manual, ESSS Rocky DEM, S.R.L.
- Lee, S.; Lee, J.; Hwang, S. Suggestion of Practical Application of Discrete Element Method for Long-Term Wear of Metallic Materials. Appl. Sci. 2022, 12, 10423. [Google Scholar] [CrossRef]
- Ansys Inc., Fluent Theory Guide Release 2020, Ansys Inc.
- ESSS Rocky, Release 2022 R1.1, CFD Coupling Technical Manual, ESSS Rocky DEM, S.R.L.
- Ganser, G.H. A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Archard, J.F. Wear theory and mechanisms. In Wear control handbook; American Society of Mechanical Engineers, 1980. [Google Scholar]
- Transport Canada, Safe speed in ice: an analysis of transit speed and ice decision numerals. Ship Safety Northern (AMNS), 1996.
- Transport Canada, Arctic Ice Regime Shipping System (AIRSS), Pictorial Guide, 03. 20 January.
Figure 3.
Overlap-normal force relationship in the HLS model [37].
Figure 3.
Overlap-normal force relationship in the HLS model [37].
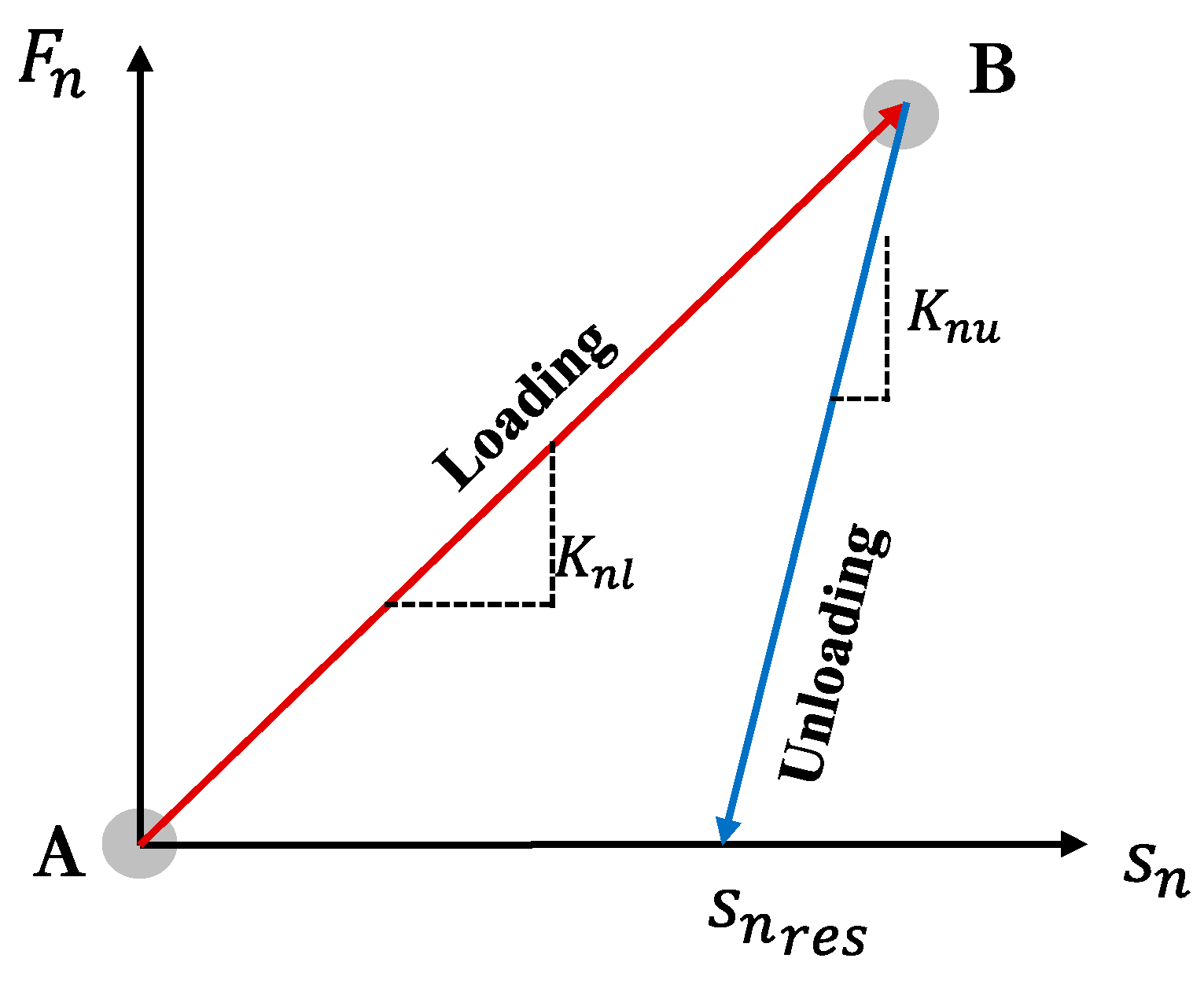
Figure 4.
HLS normal force model (ESSS Rocky [36]).
Figure 4.
HLS normal force model (ESSS Rocky [36]).

Figure 5.
LSCL tangential force model (ESSS Rocky [36]).
Figure 5.
LSCL tangential force model (ESSS Rocky [36]).
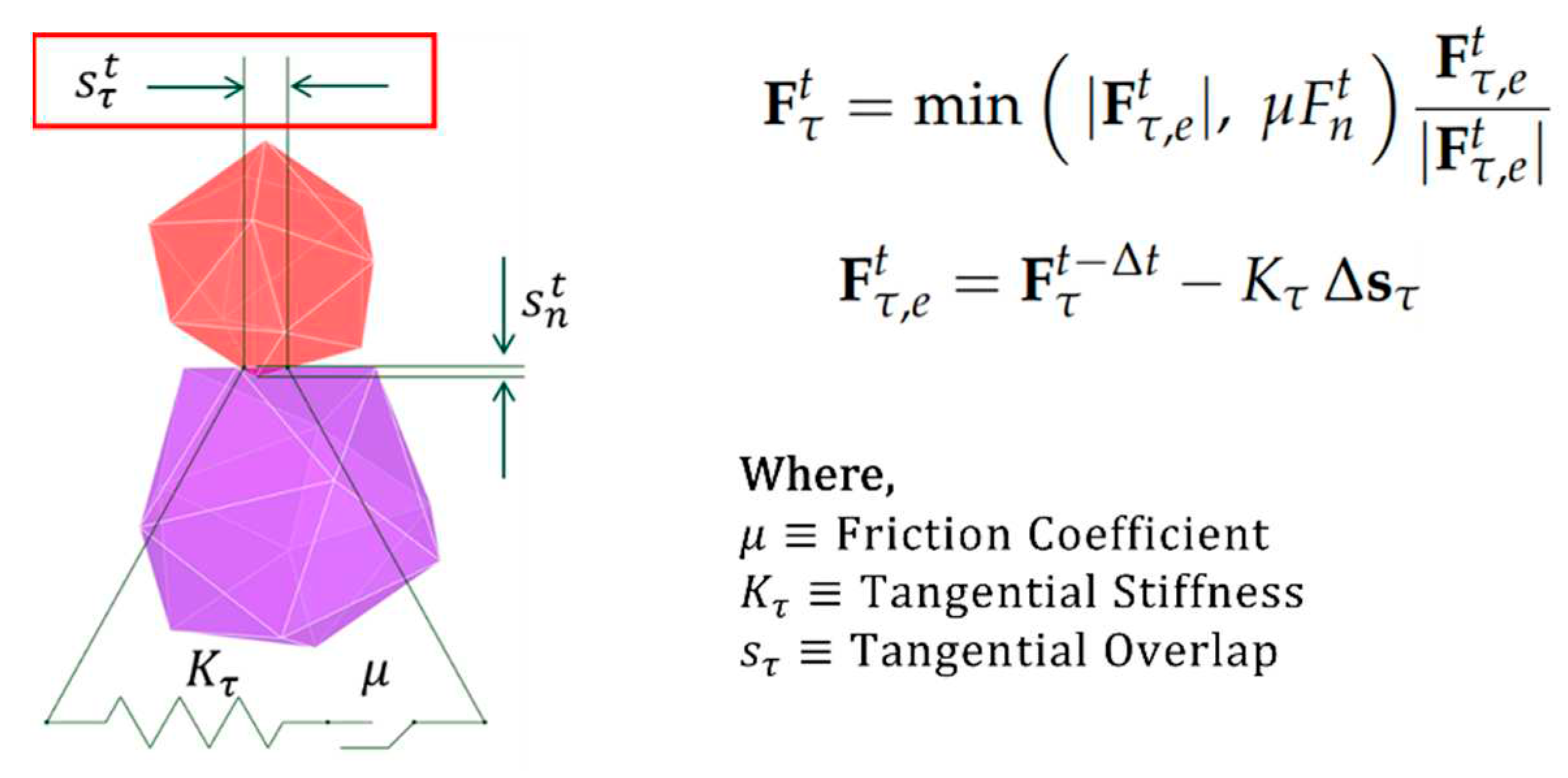
Figure 6.
Mechanism of shape change caused by wear (ESSS Rocky [36]).
Figure 6.
Mechanism of shape change caused by wear (ESSS Rocky [36]).
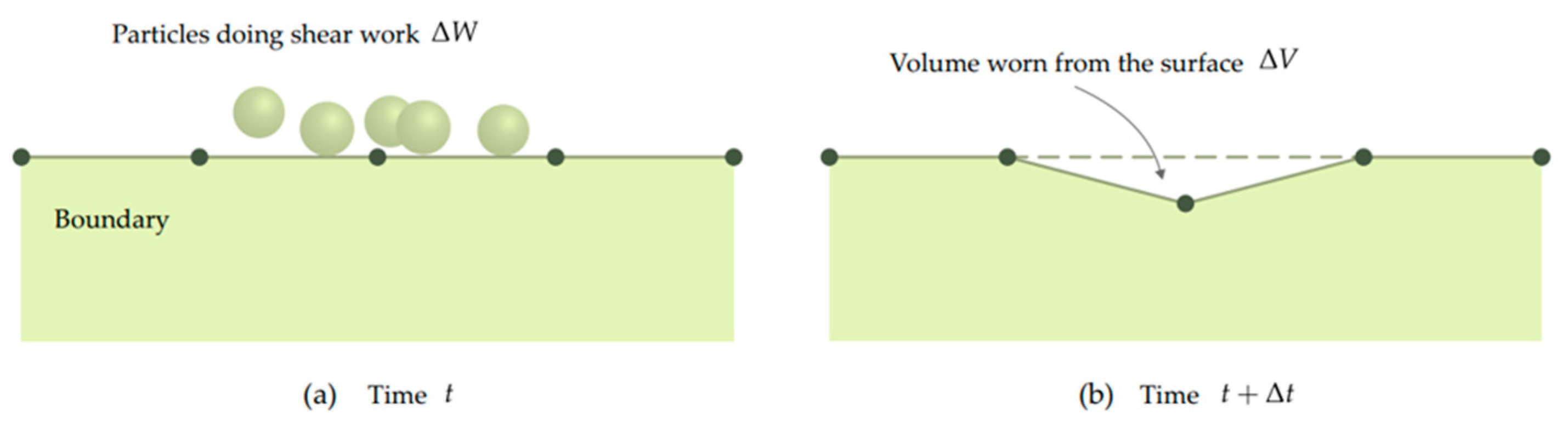
Figure 7.
Ice concentration (Transport Canada [43]).
Figure 7.
Ice concentration (Transport Canada [43]).

Figure 8.
Ice concentration evaluation method.
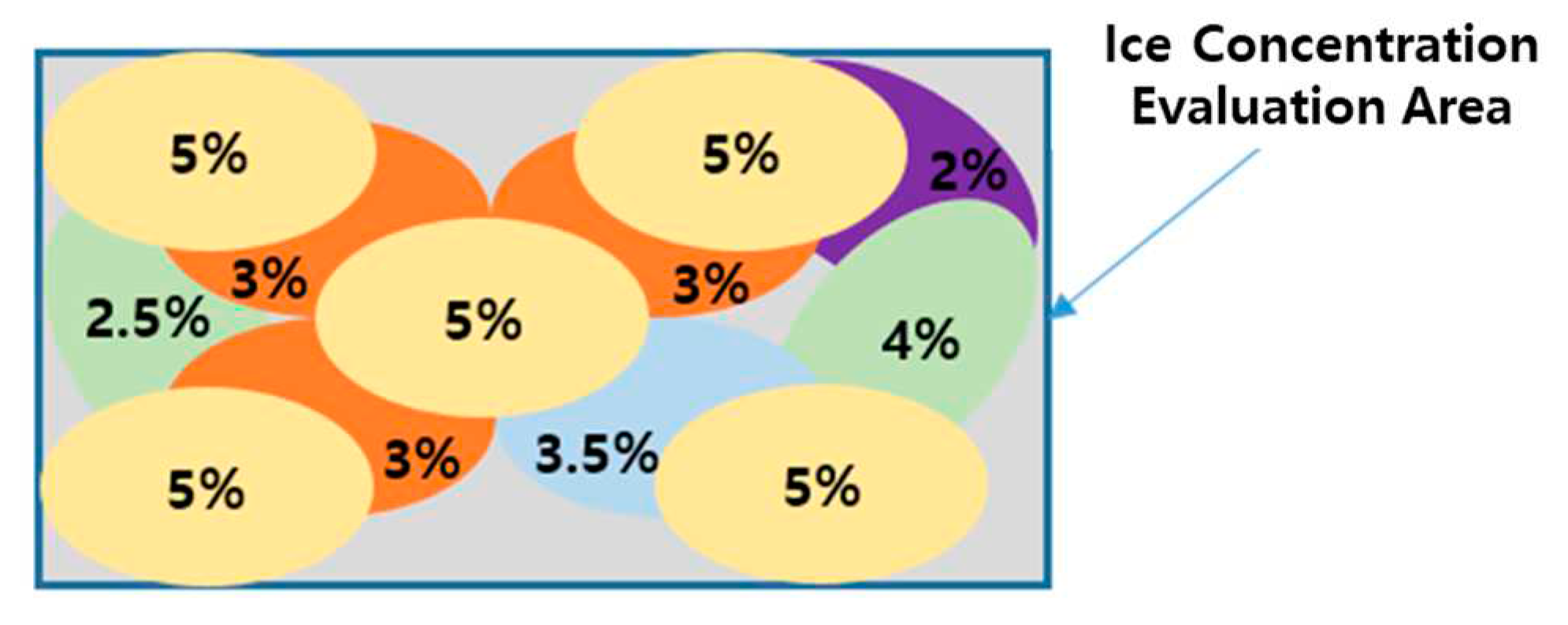
Figure 9.
Ice particle modeling.
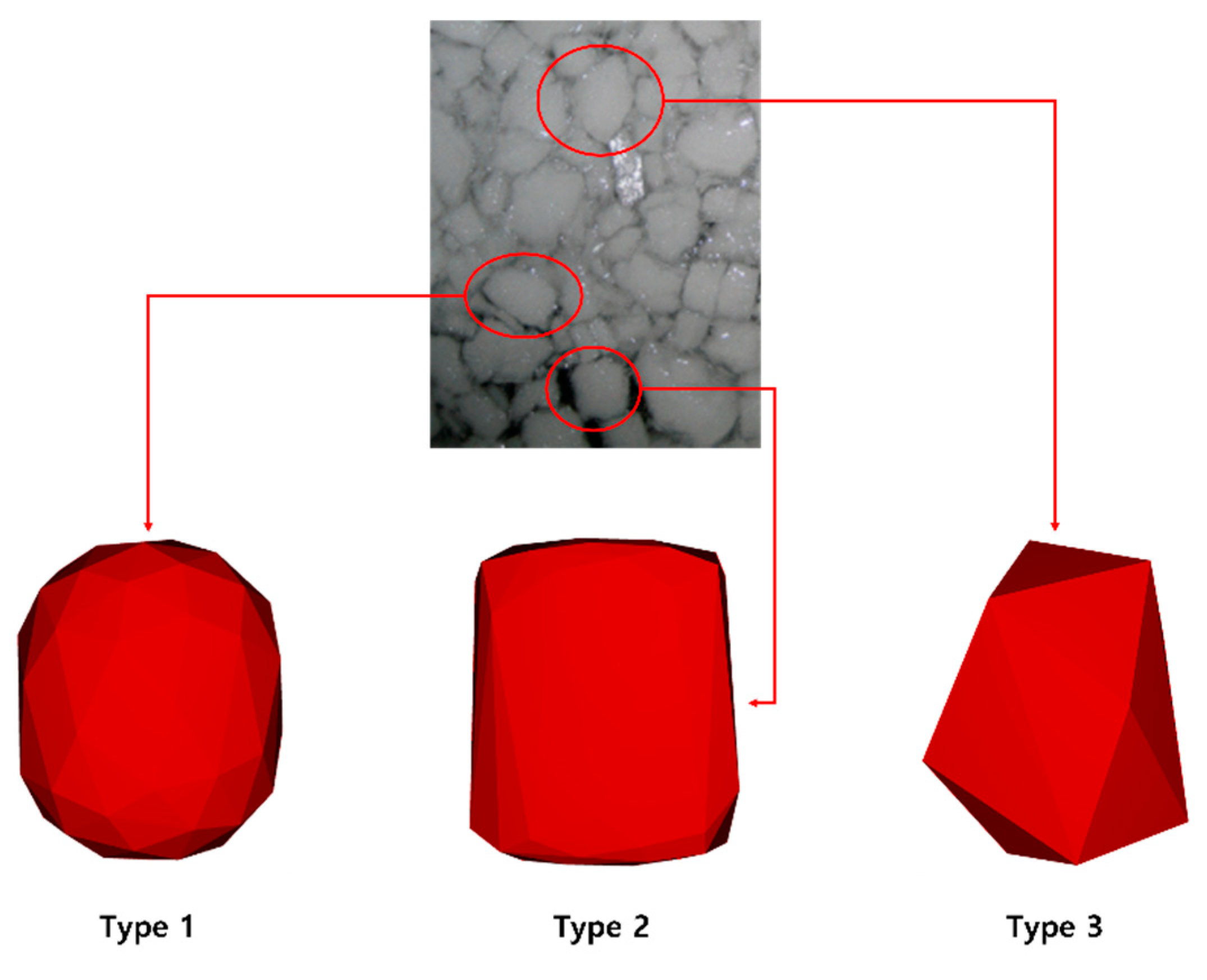
Figure 11.
Initial condition of DEM analysis.
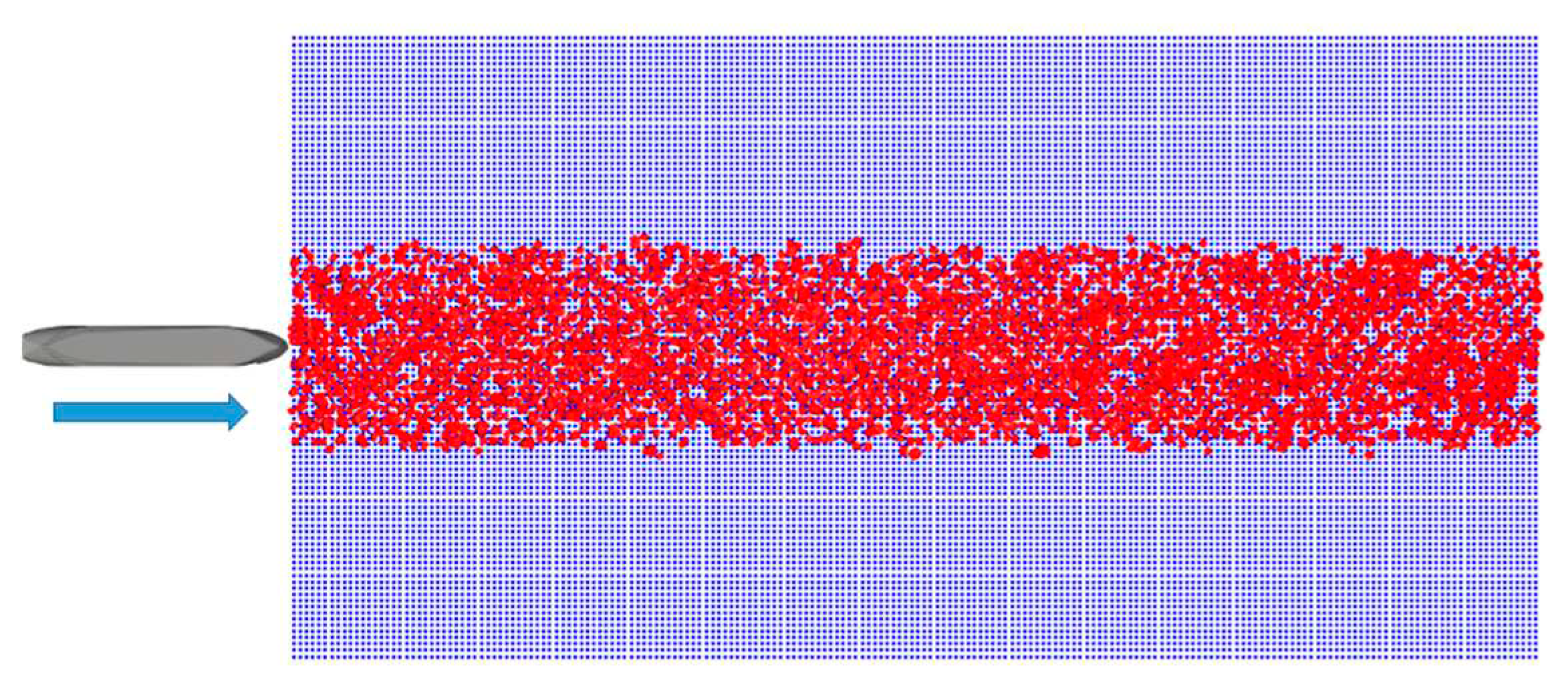
Figure 12.
Ice concentration 60% initial condition.
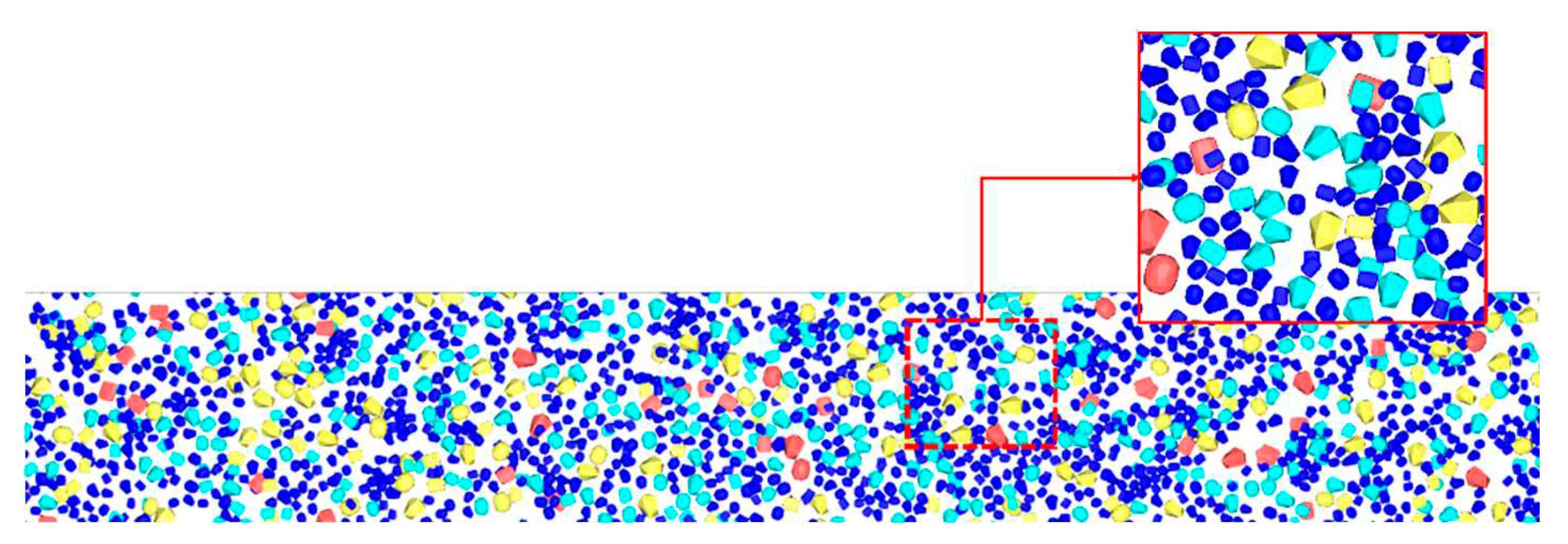
Figure 13.
Ice concentration 80% initial condition.
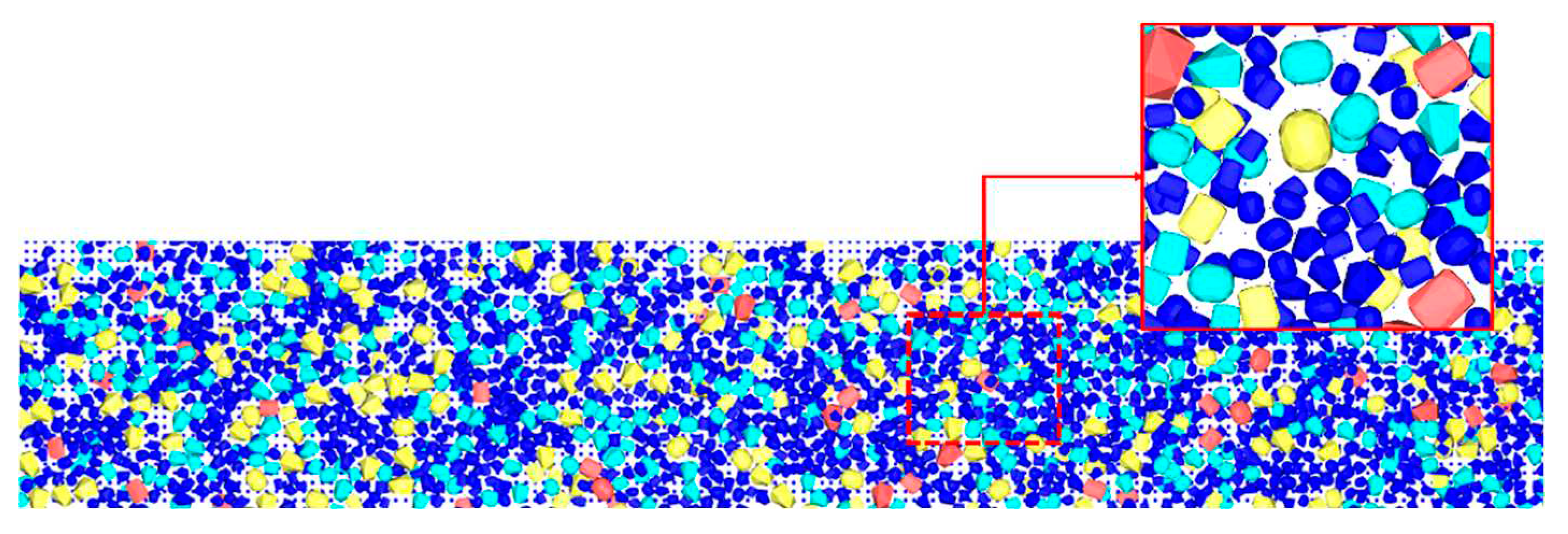
Figure 15.
Snapshots of simulation: 4 knots, 60%.
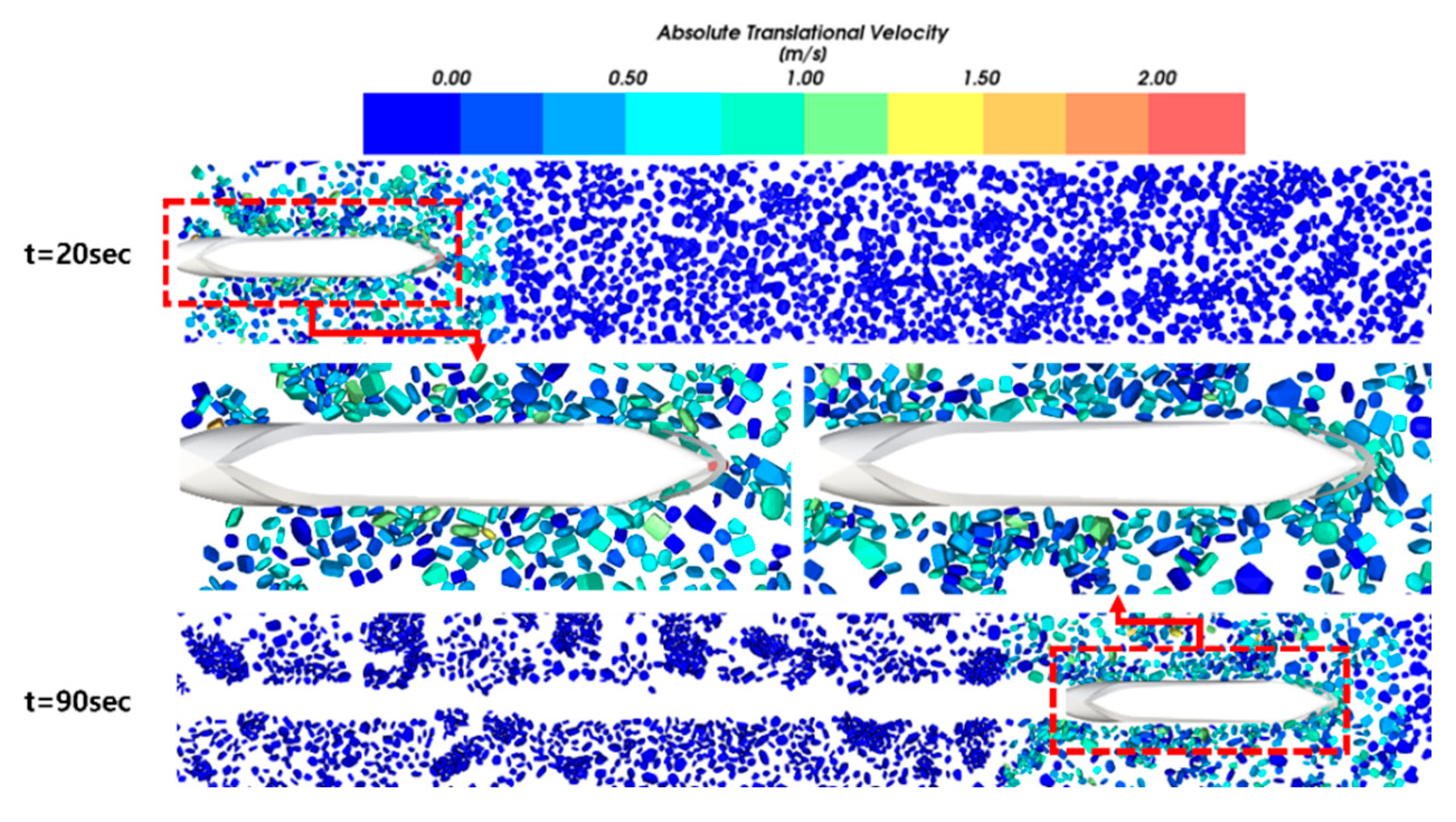
Figure 16.
Cumulative shear work: 4 knots, 60%.
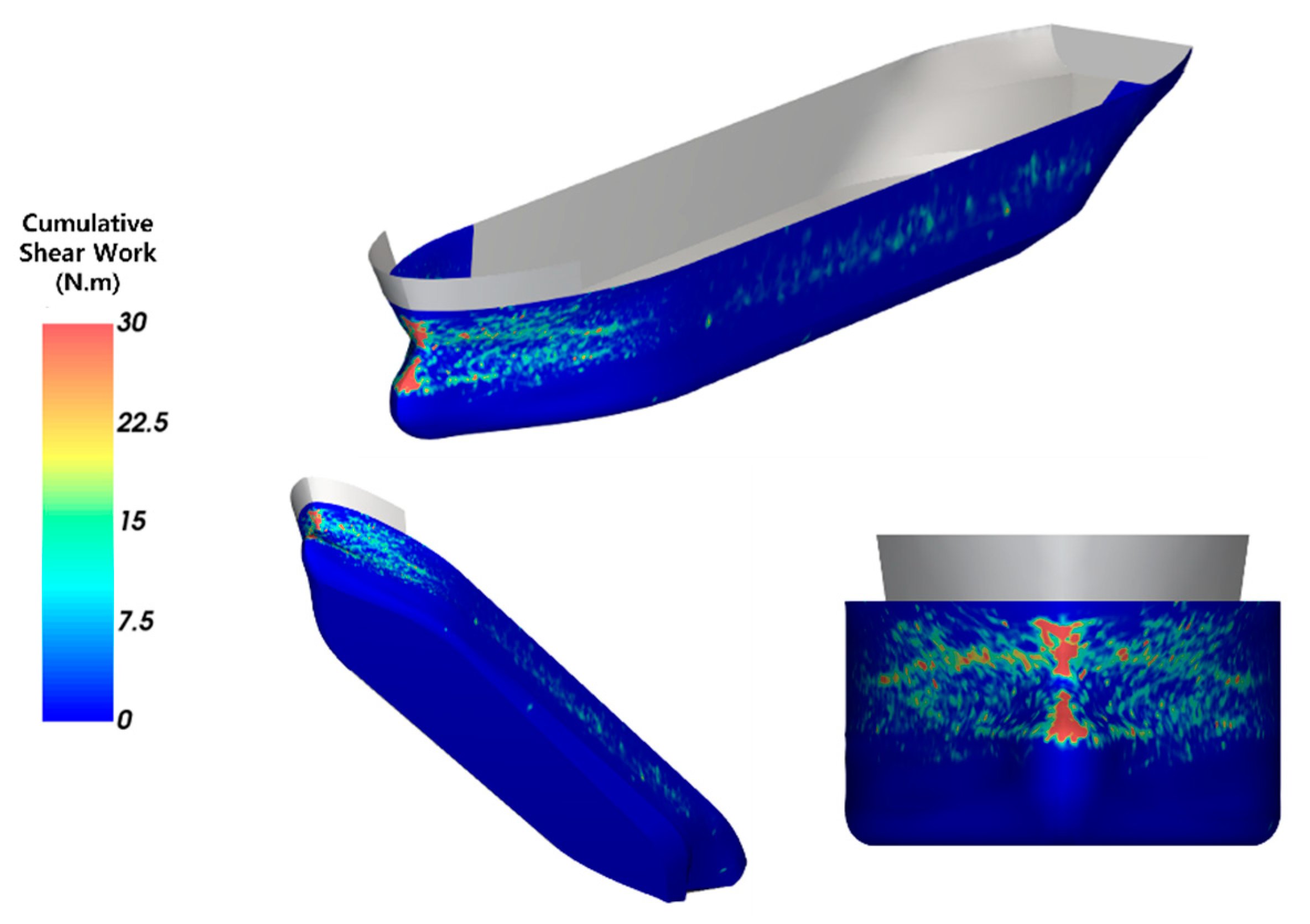
Figure 17.
Snapshots of simulation: 10 knots, 80%.
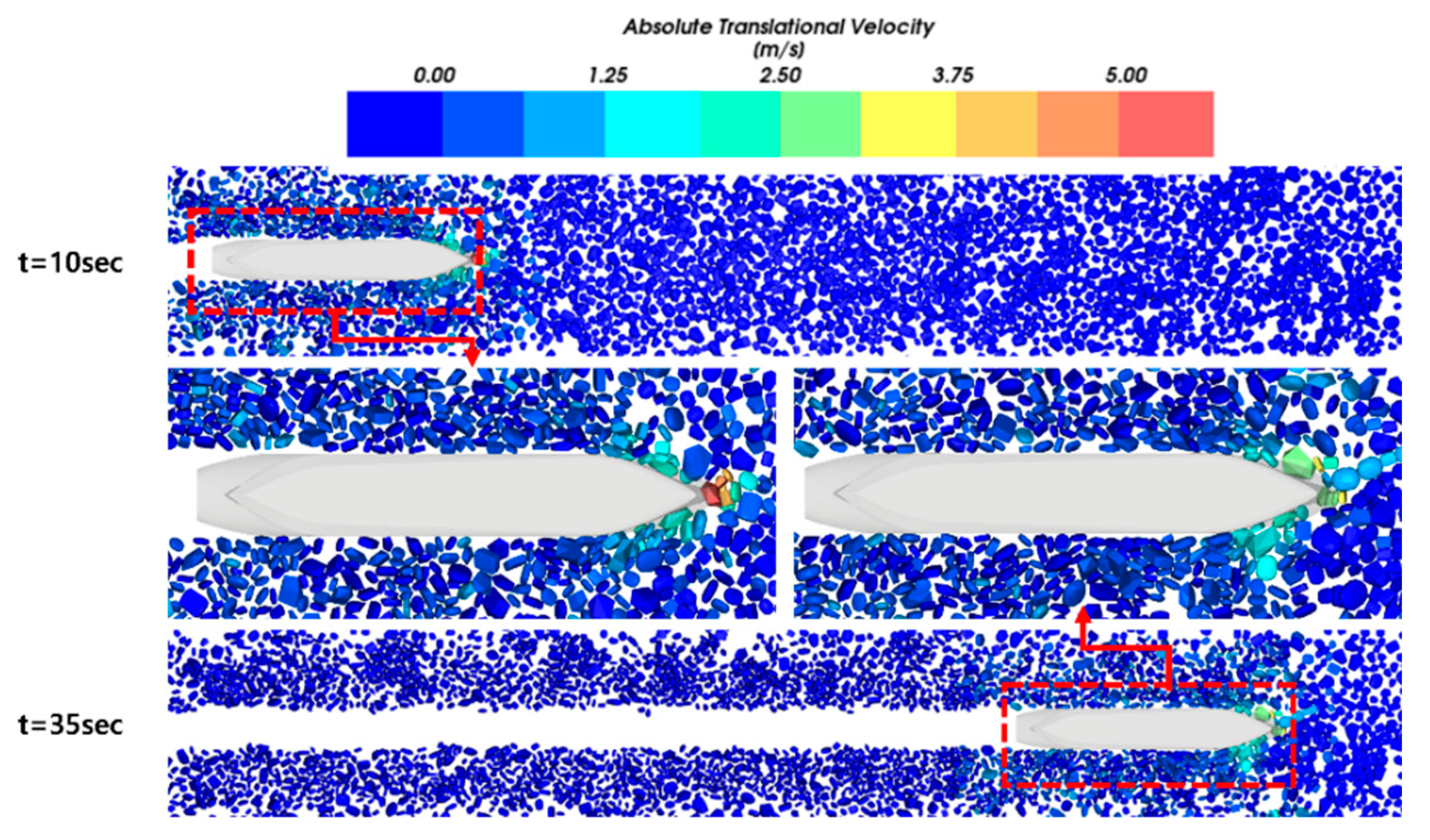
Figure 18.
Cumulative shear work: 10 knots, 80%.
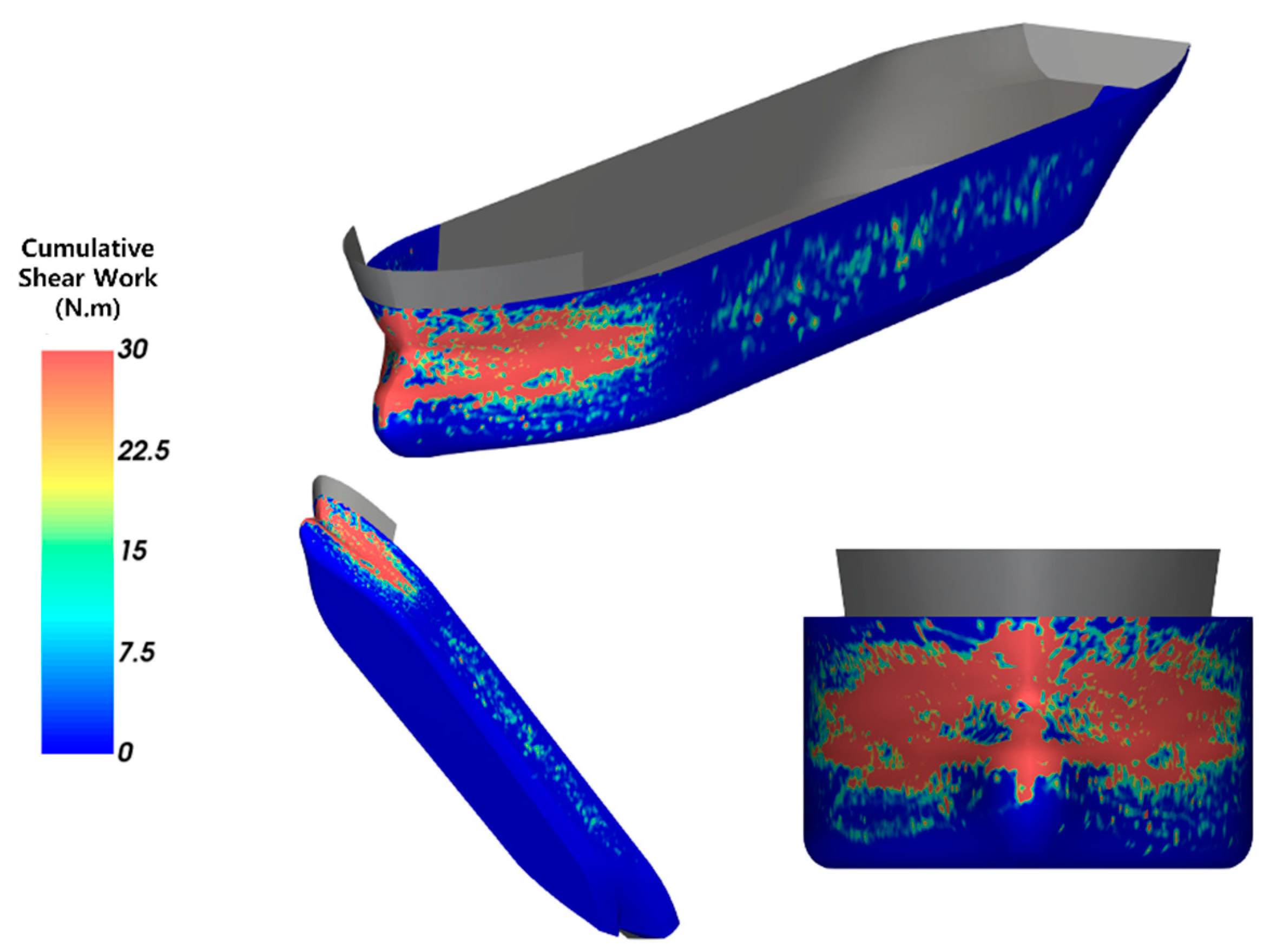
Figure 19.
Cumulative average shear work.
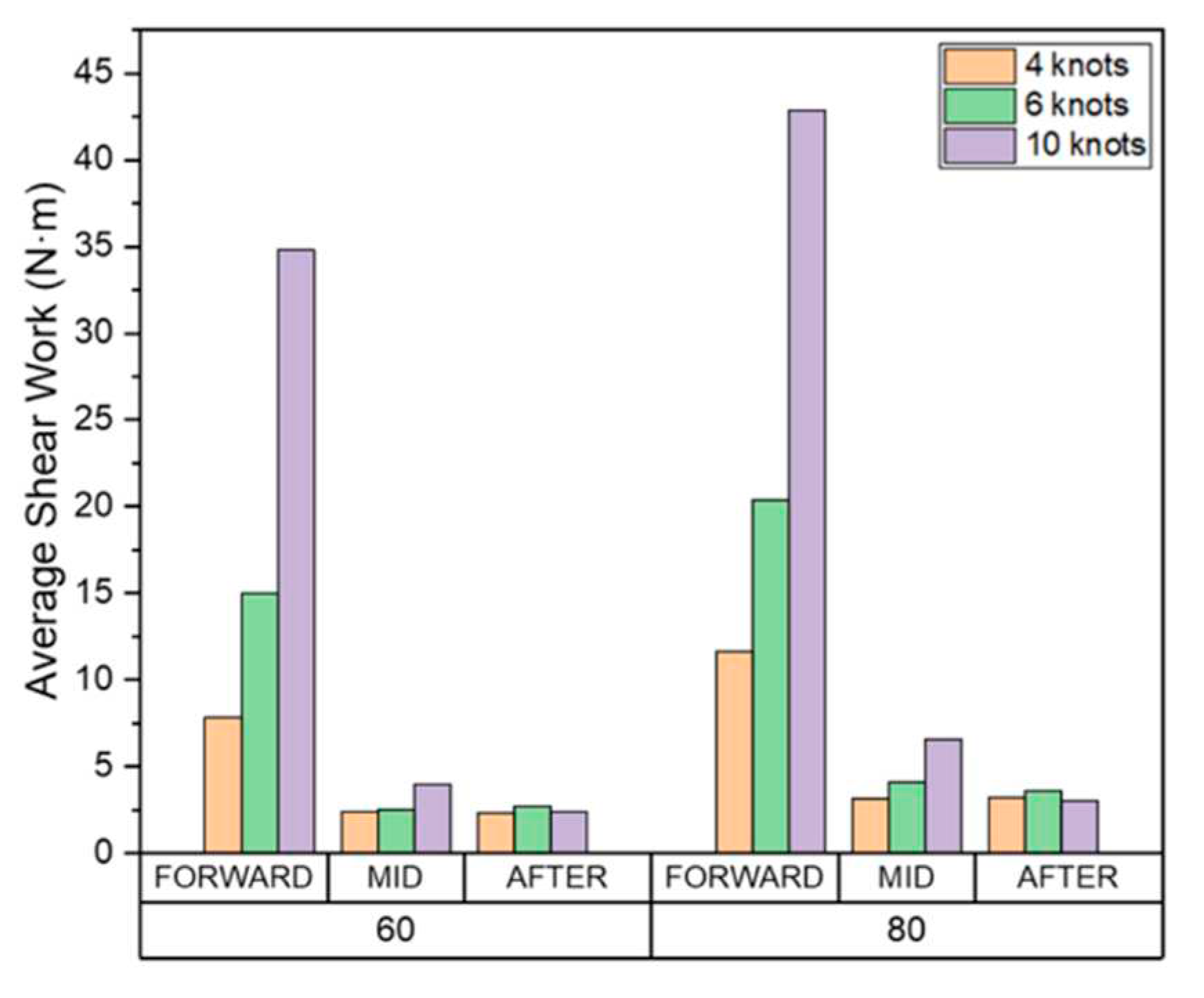
Figure 20.
Cumulative maximum shear work.
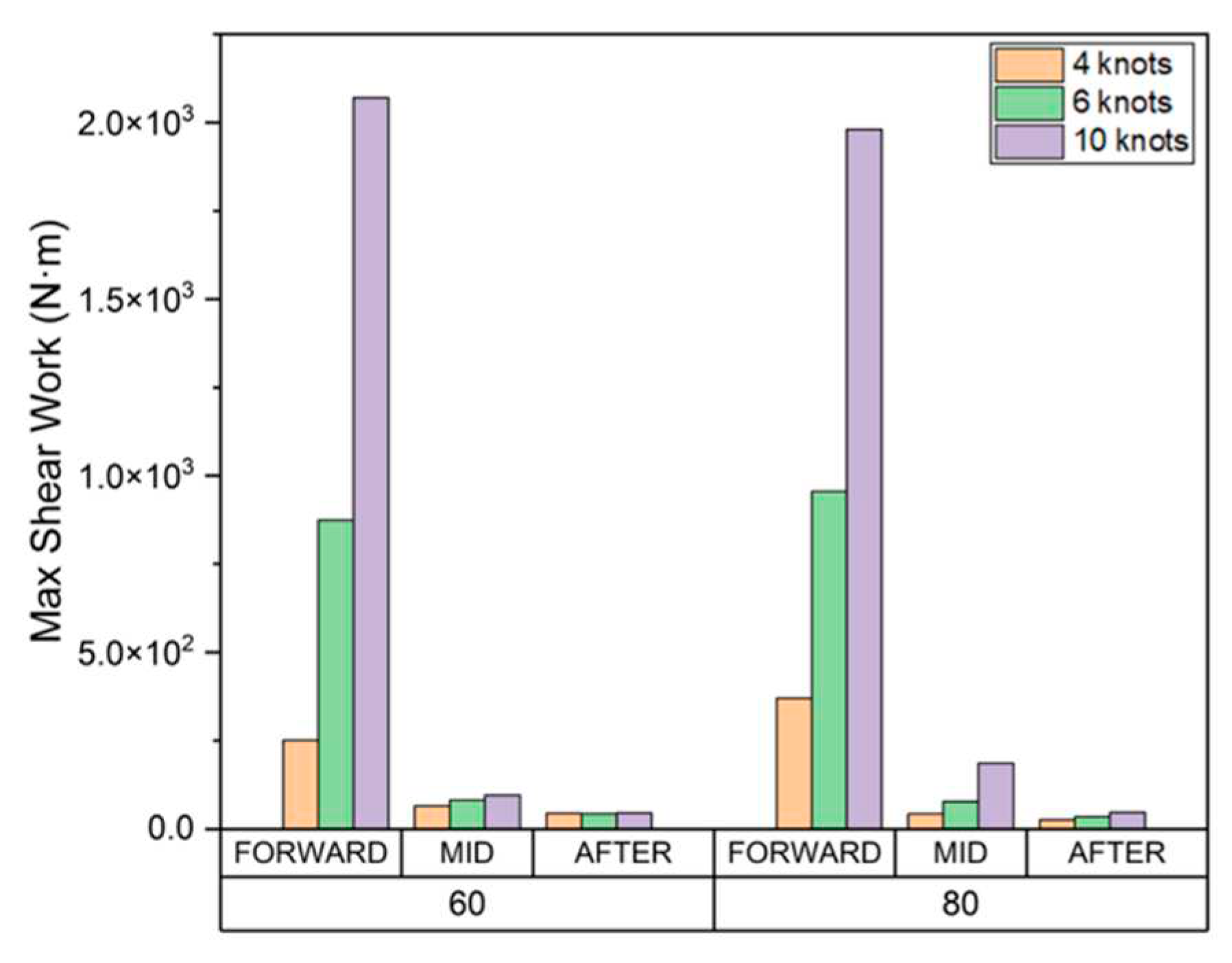
Figure 21.
Cumulative total shear work.
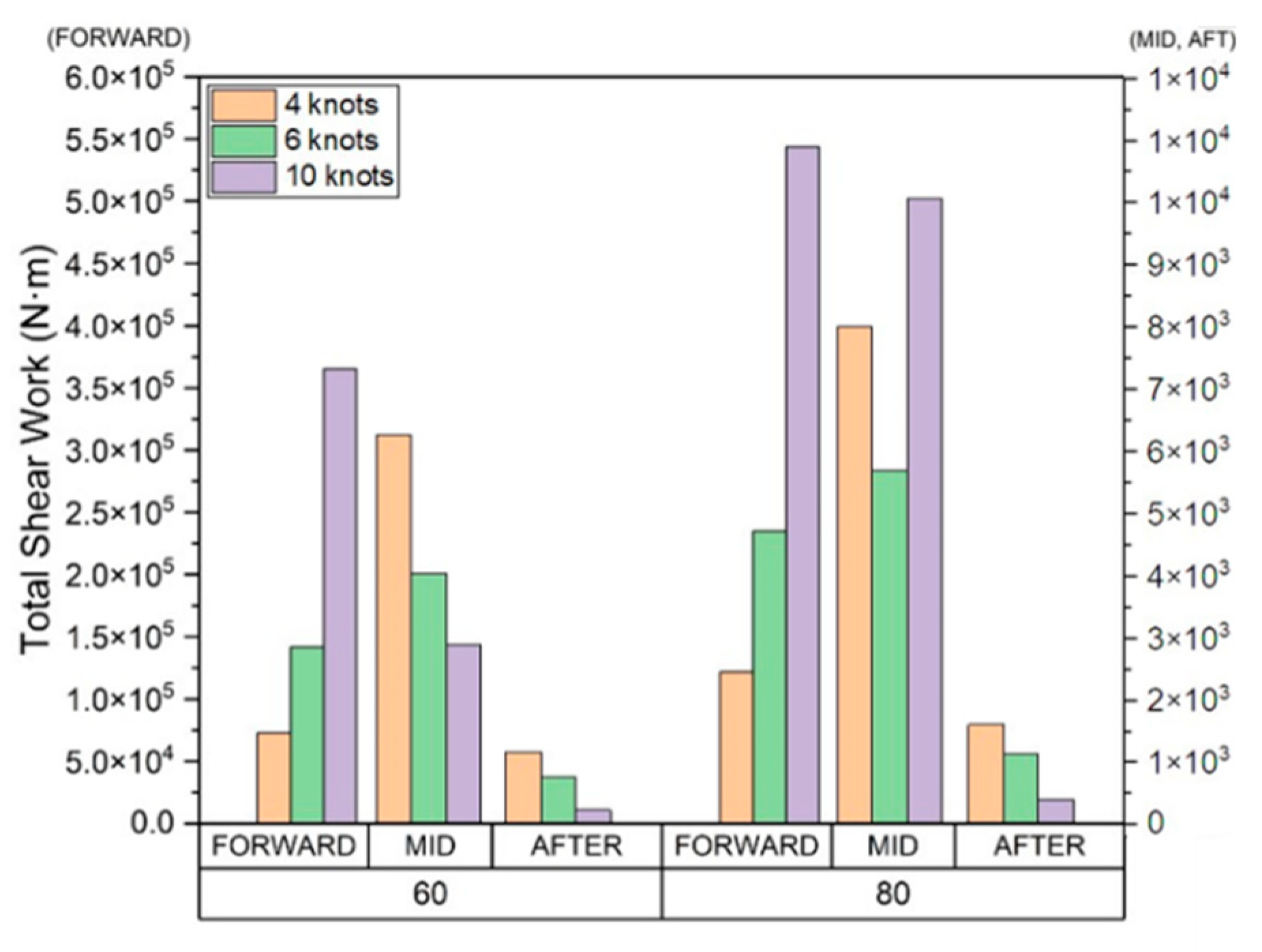
Figure 22.
Cumulative average tangential force.
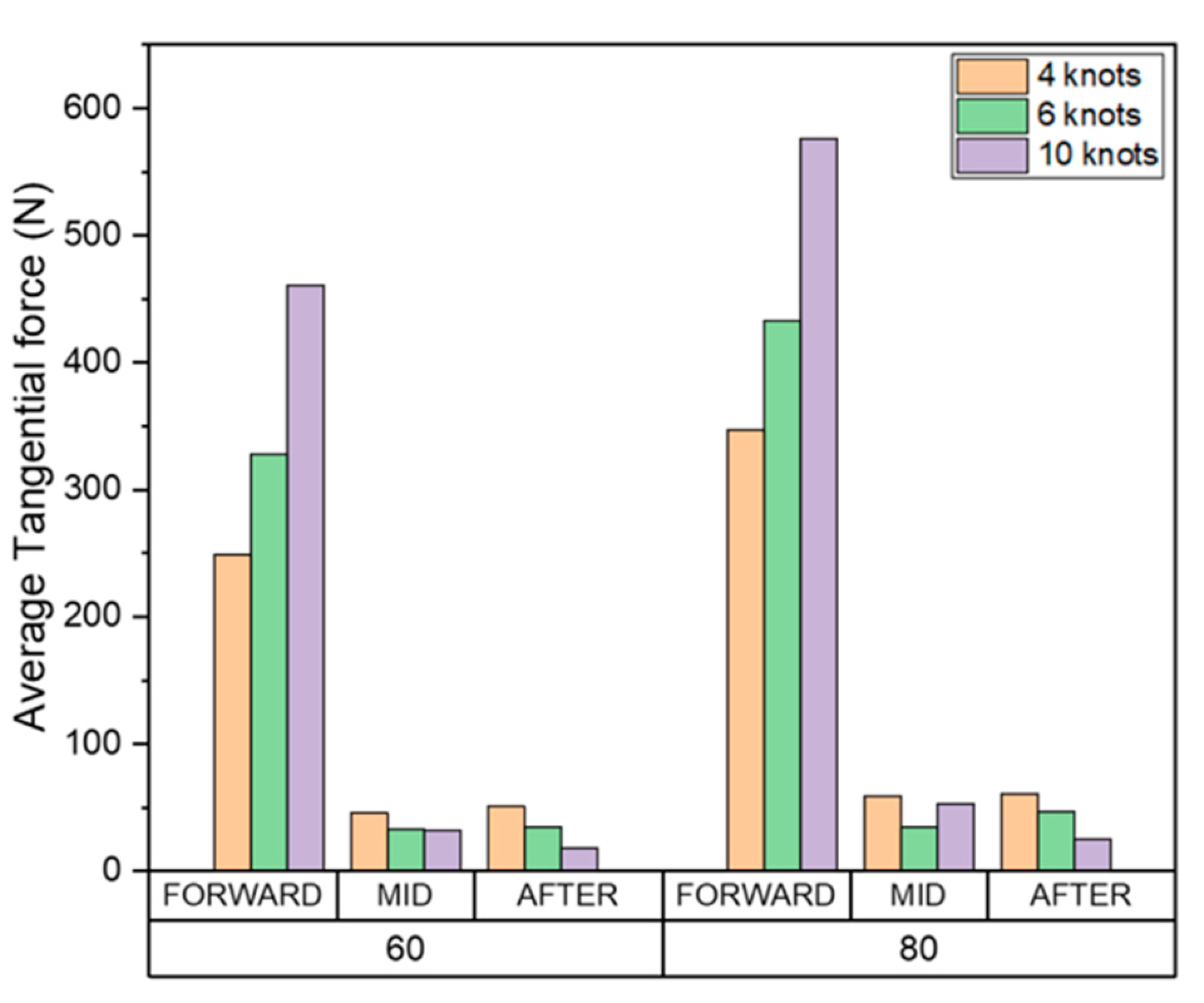
Figure 23.
Cumulative maximum tangential force.
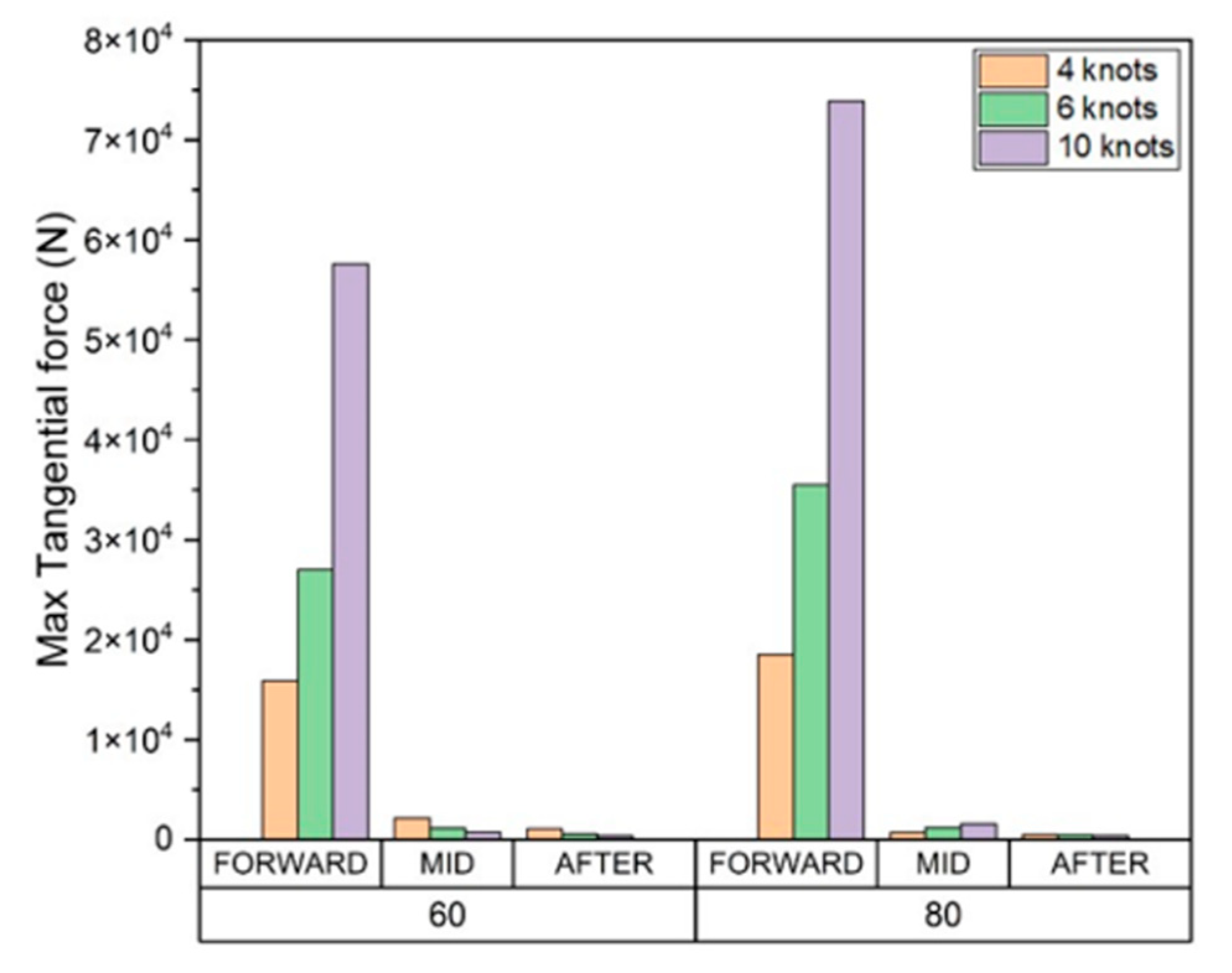
Figure 24.
Cumulative total tangential force.
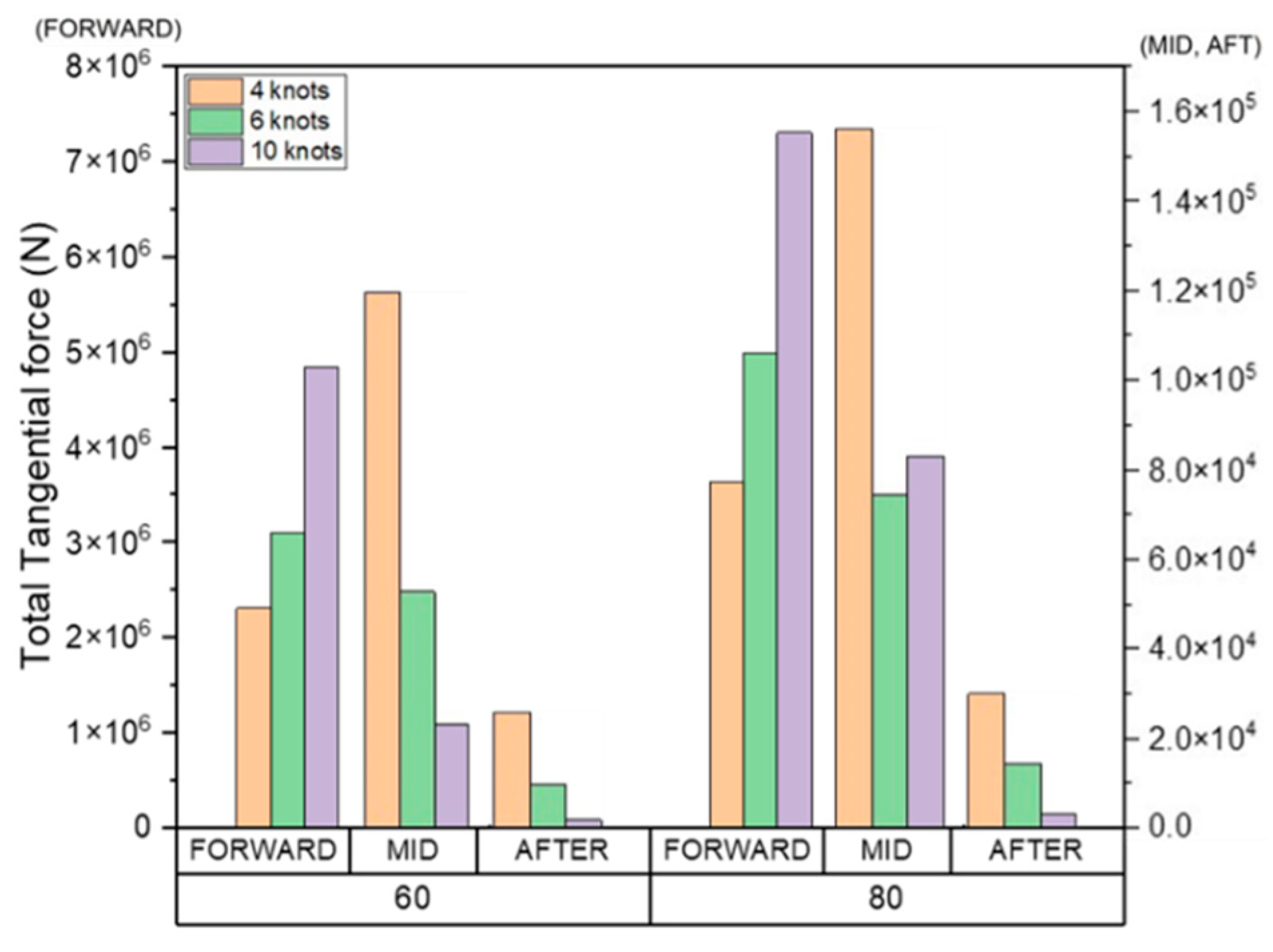
Figure 25.
Cumulative average sliding distance.
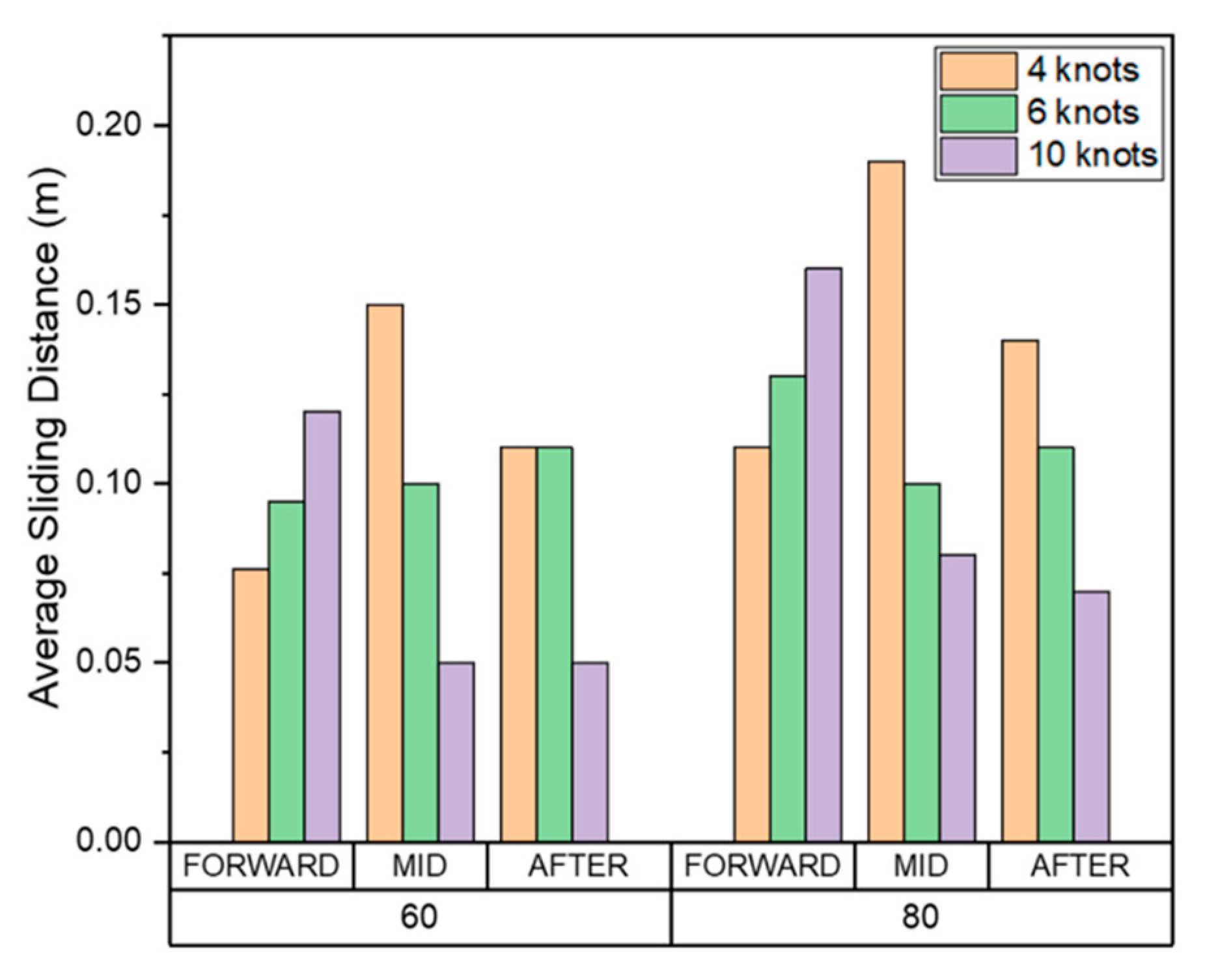
Figure 26.
Cumulative maximum sliding distance.
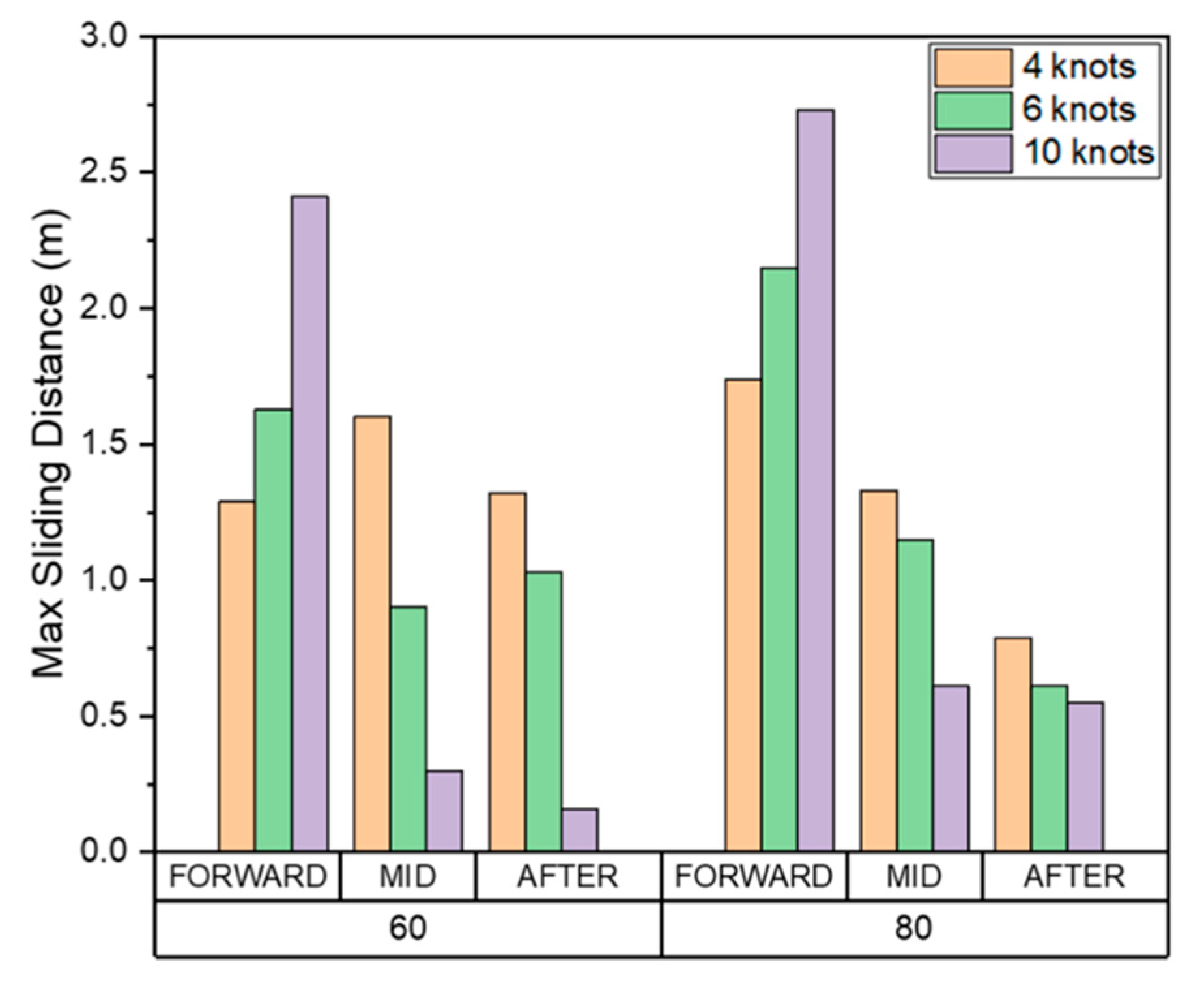
Figure 27.
Cumulative total sliding distance.
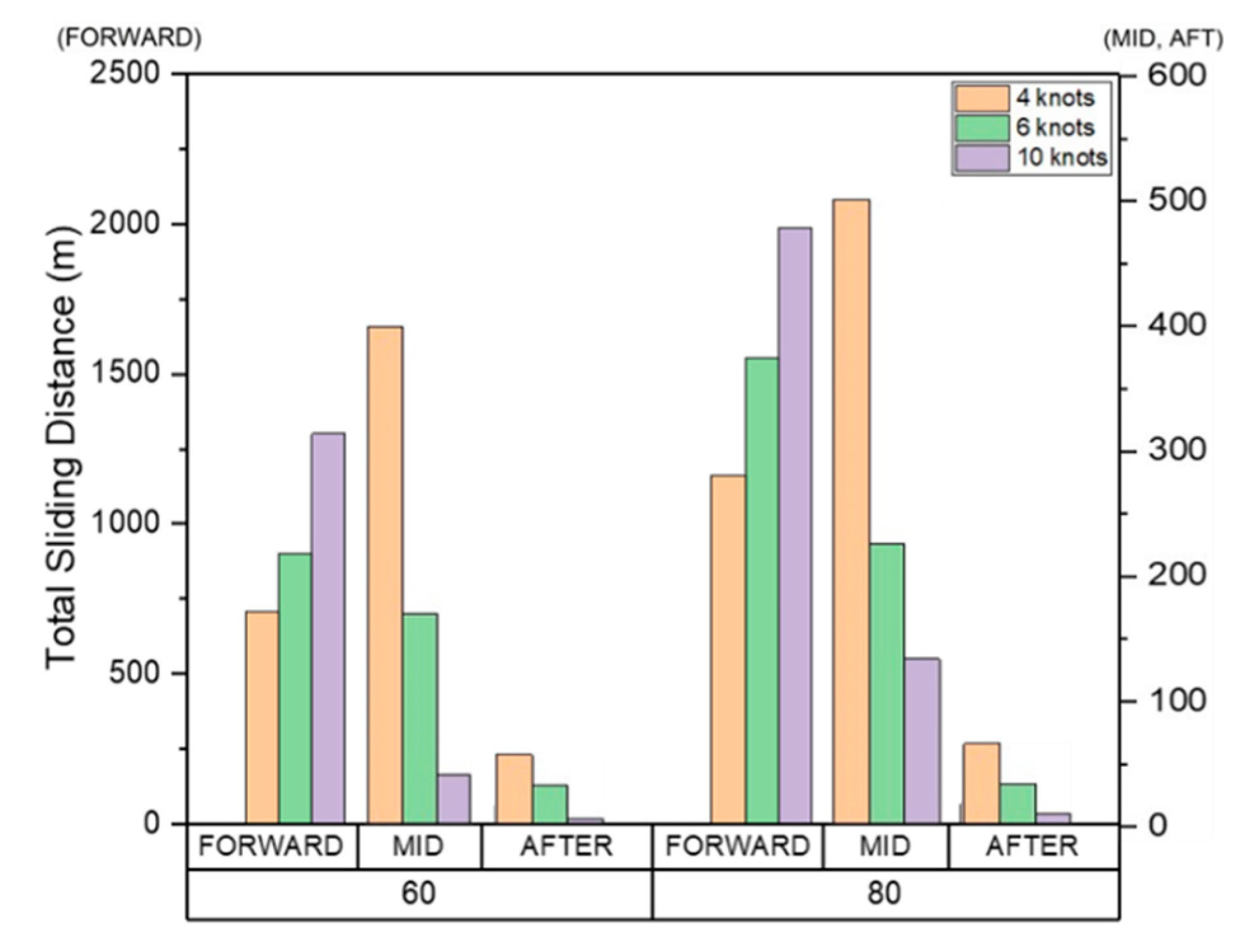
Figure 28.
Total area affected by wear.
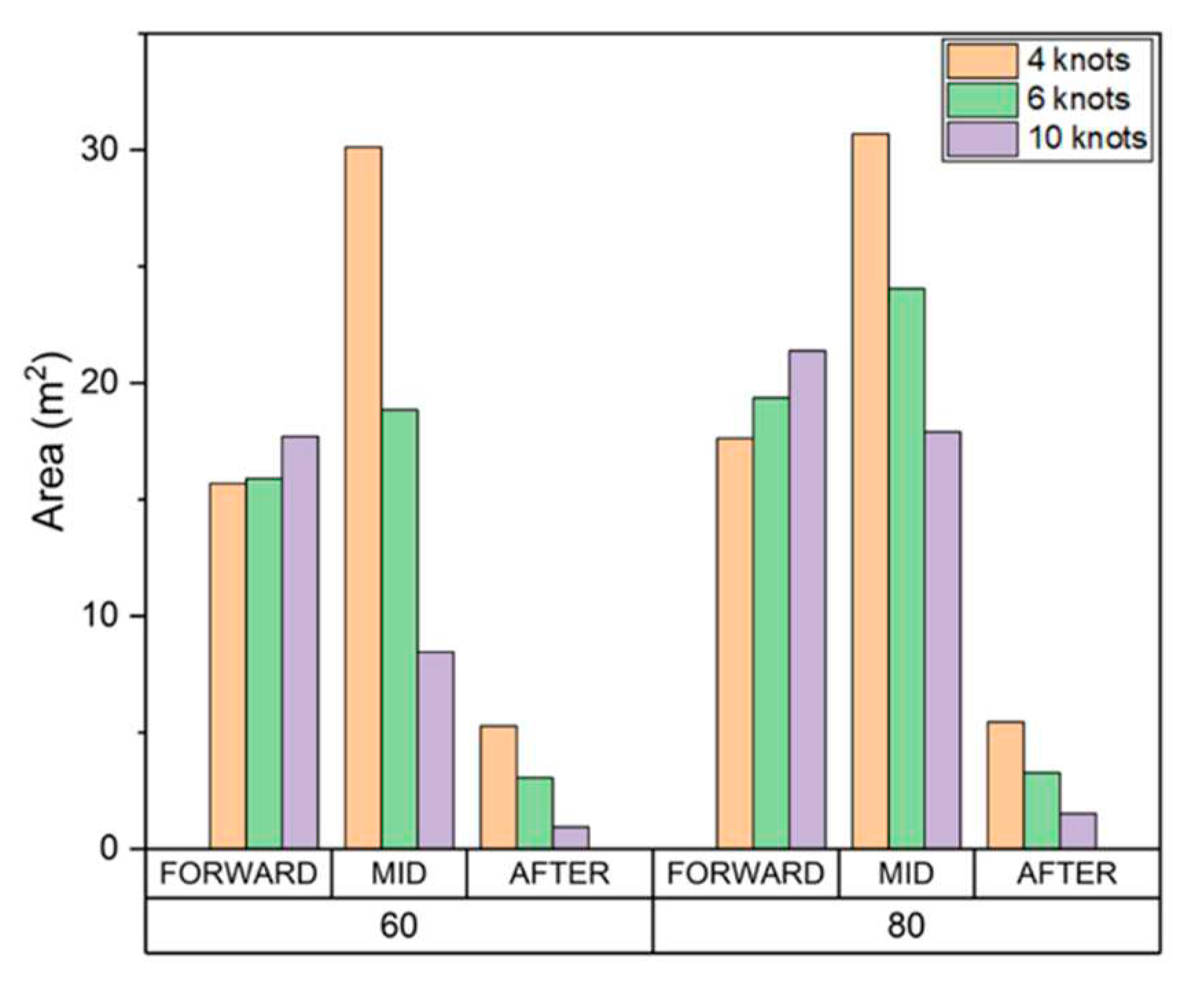
Figure 29.
Cumulative wear magnitude: 4 knots, 60%.

Figure 30.
Cumulative wear magnitude: 10 knots, 80%.

Figure 31.
Average wear depth.
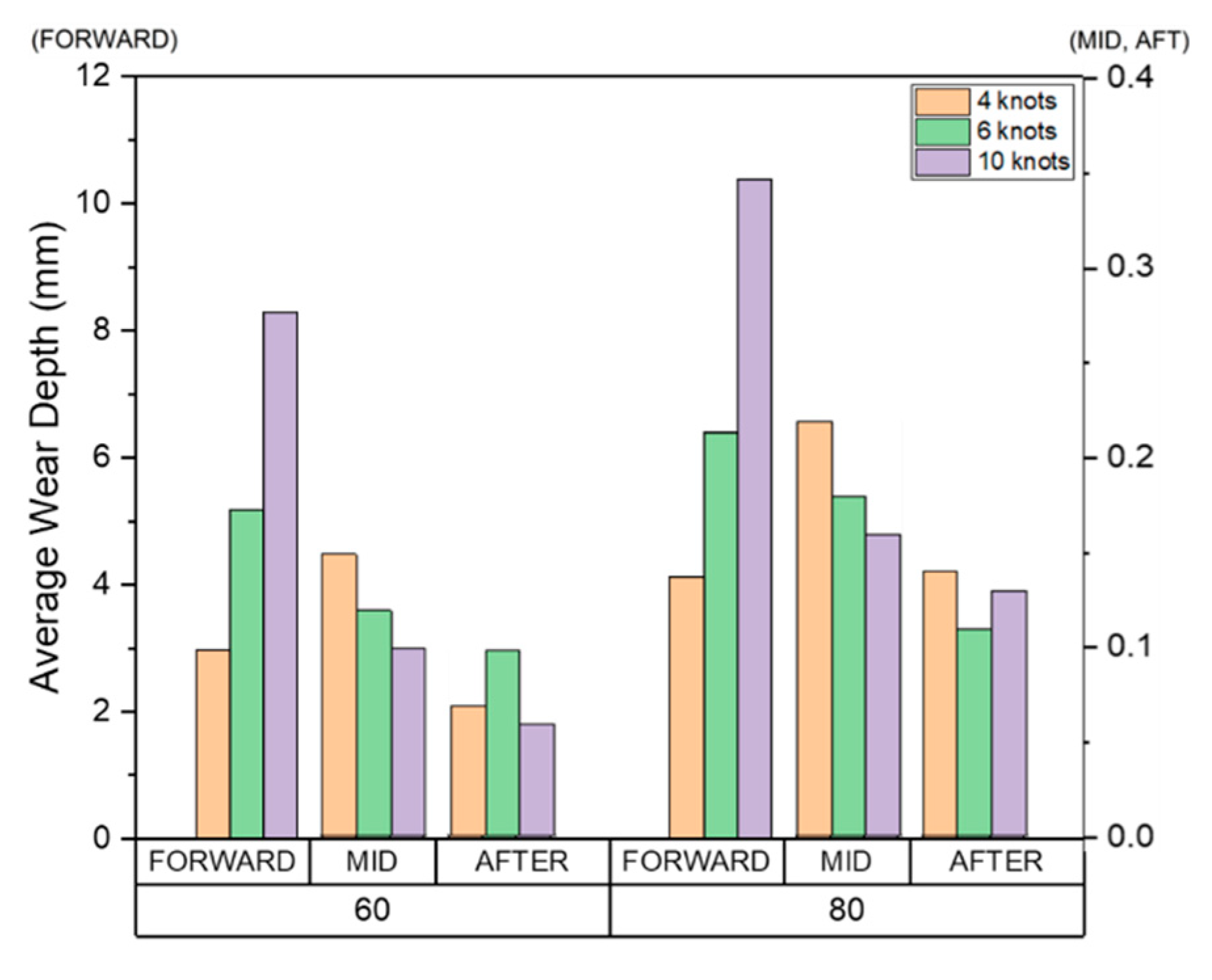
Figure 32.
Maximum wear depth.
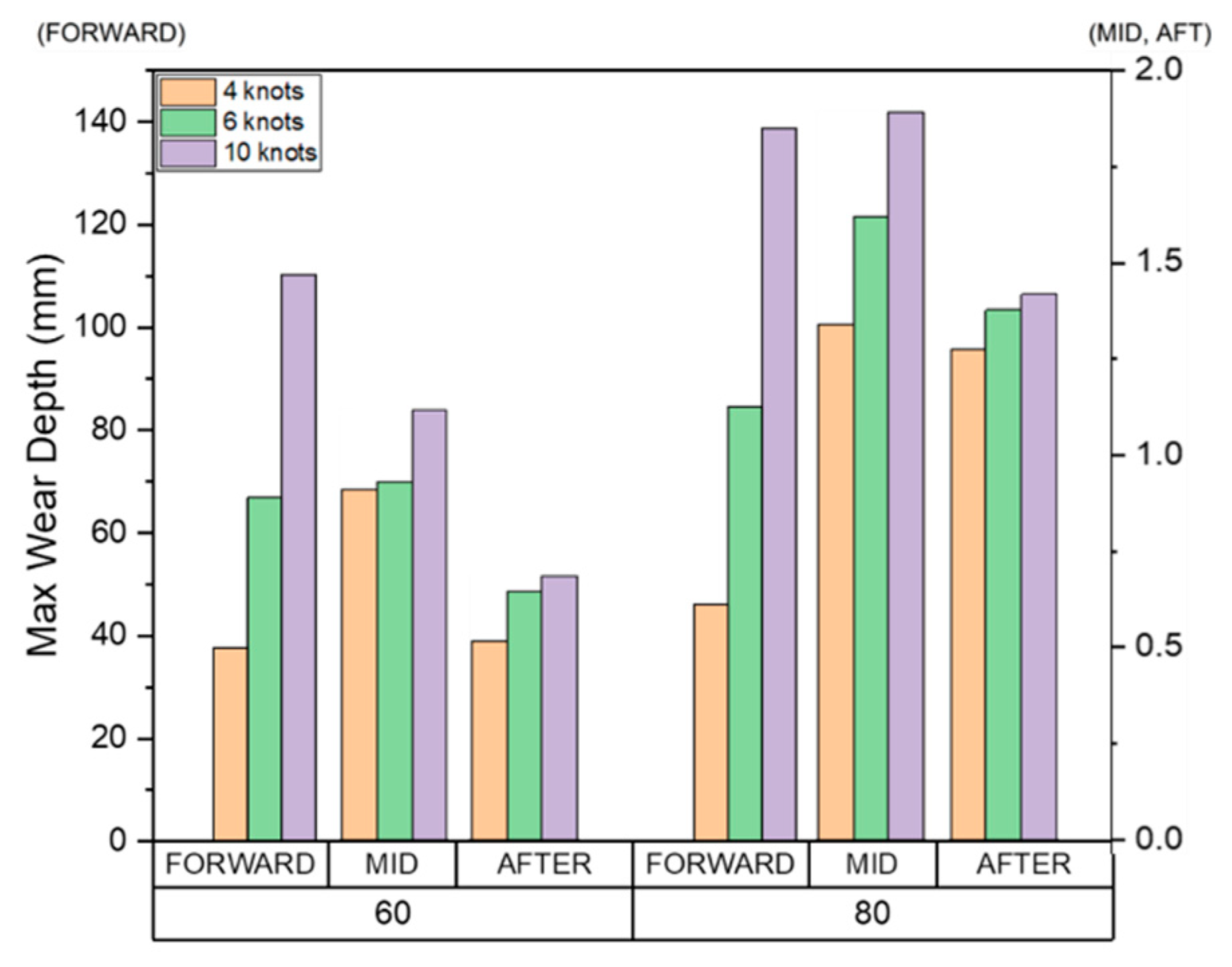
Figure 33.
Total wear area.
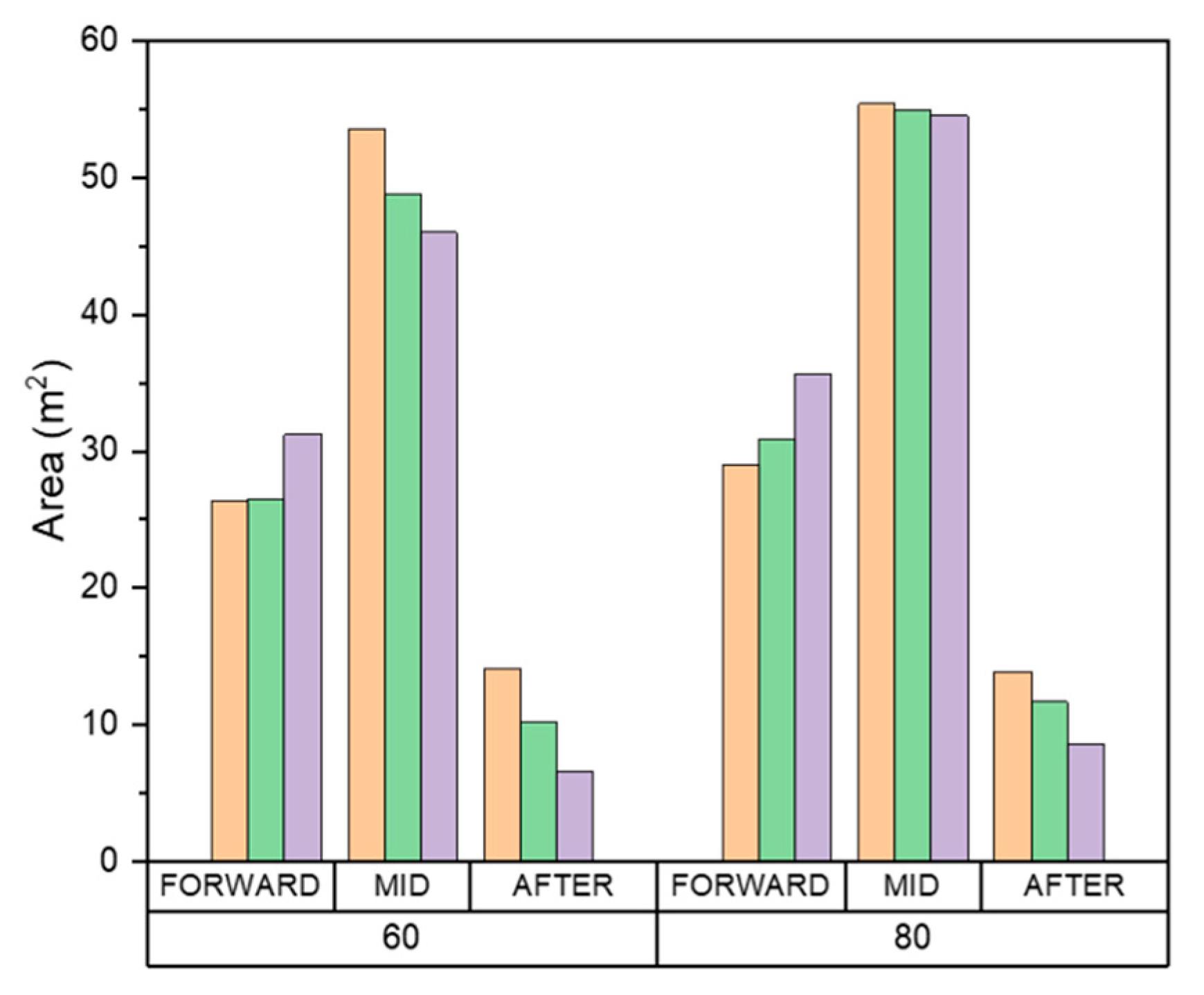
Figure 34.
Accumulated wear process of the shape change reflection model (left) and non-reflected models (right) (4 knots, 60%).
Figure 34.
Accumulated wear process of the shape change reflection model (left) and non-reflected models (right) (4 knots, 60%).
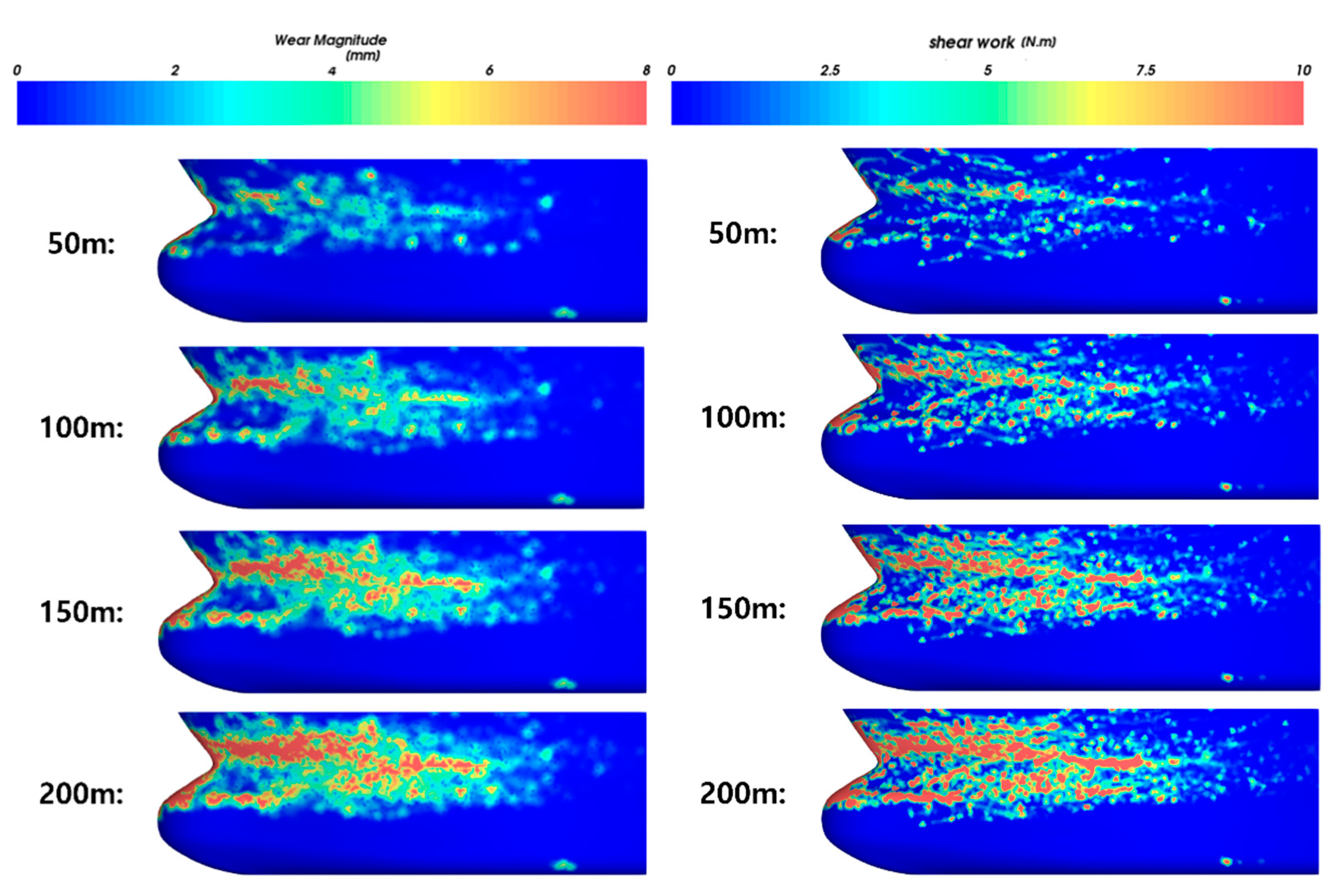
Figure 35.
Accumulated wear process of the shape change reflection model (left) and non-reflected models (right) (10 knots, 80%).
Figure 35.
Accumulated wear process of the shape change reflection model (left) and non-reflected models (right) (10 knots, 80%).
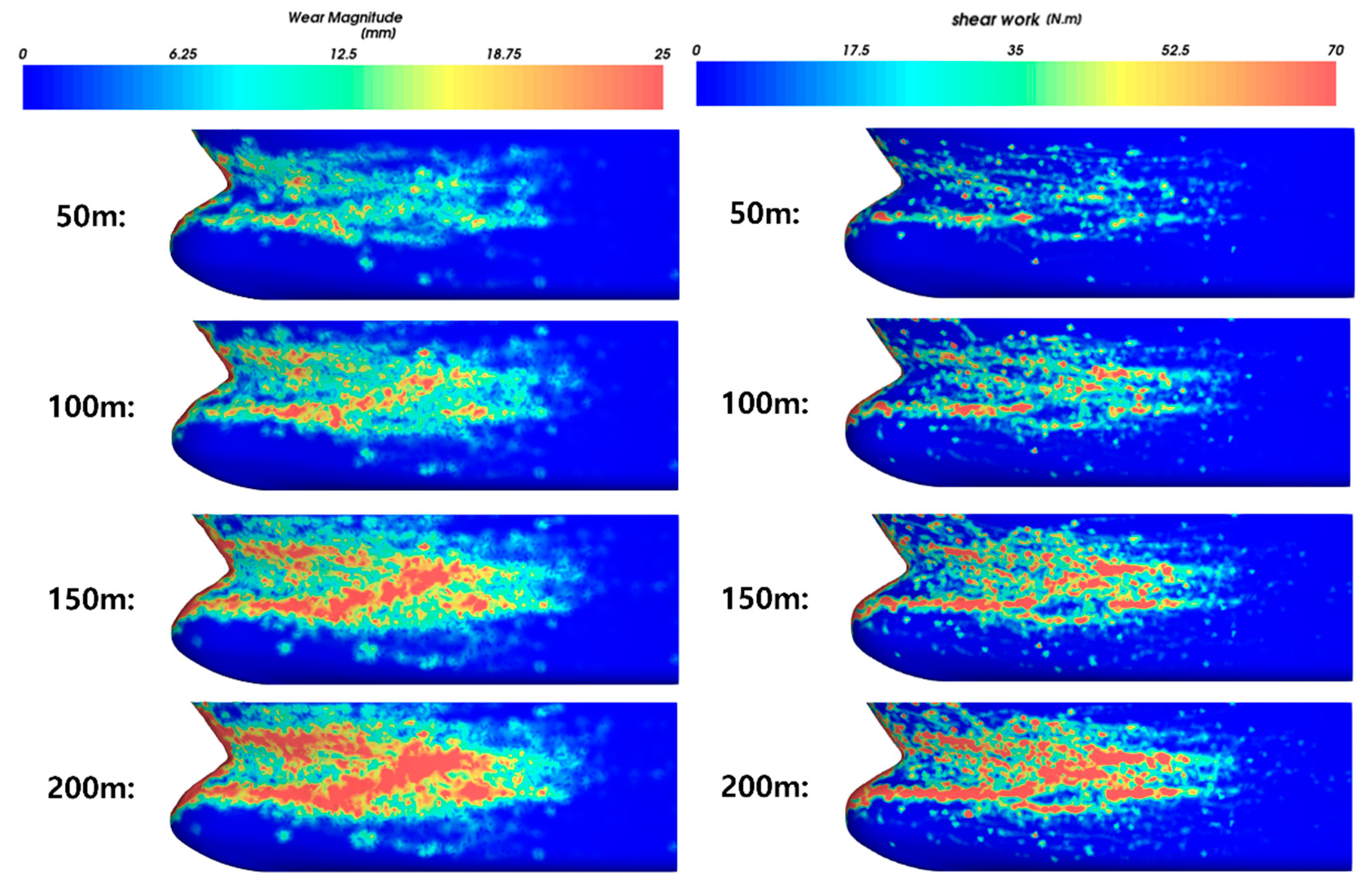
Figure 36.
CoV: 4 knots.
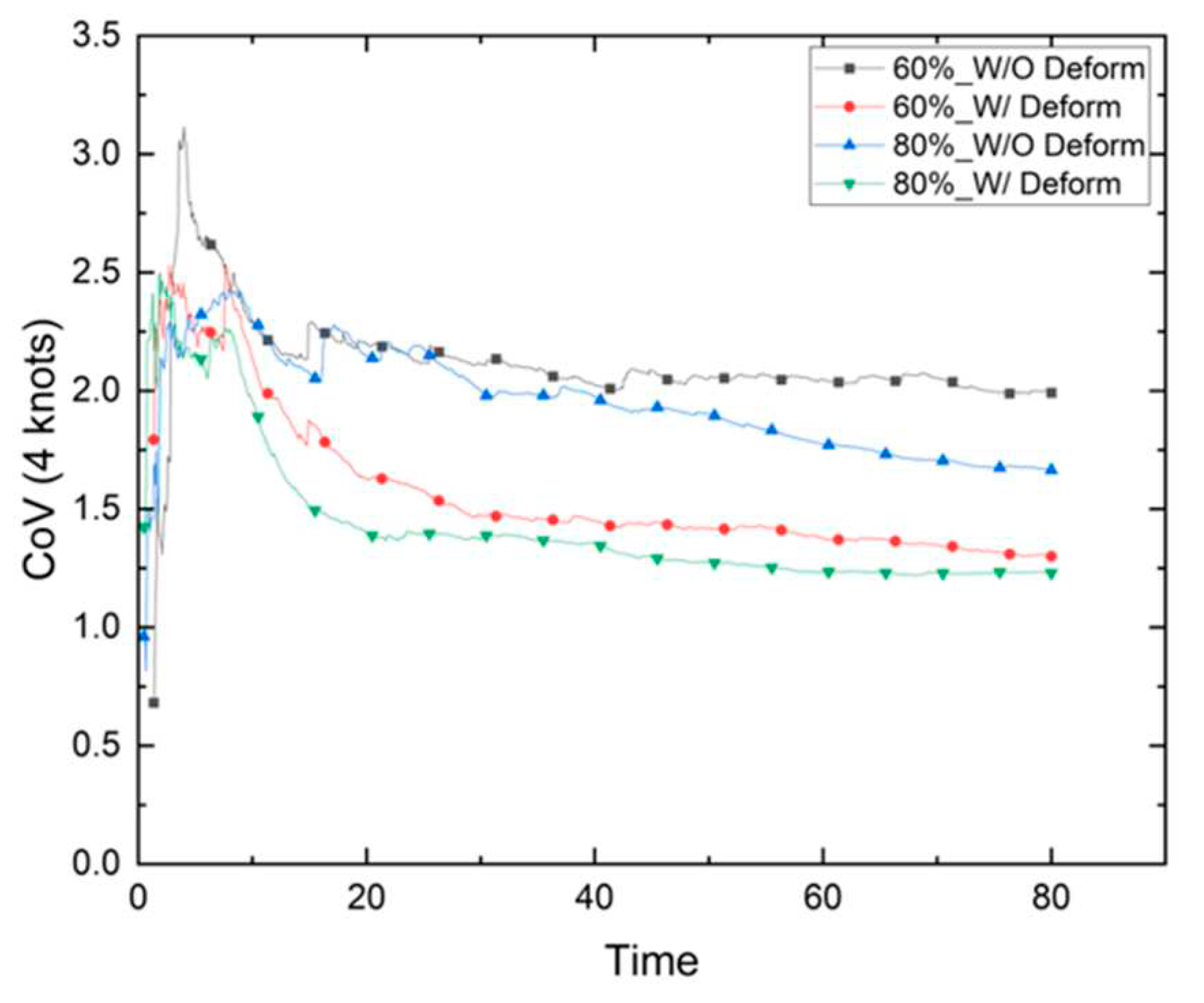
Figure 37.
CoV: 6 knots.
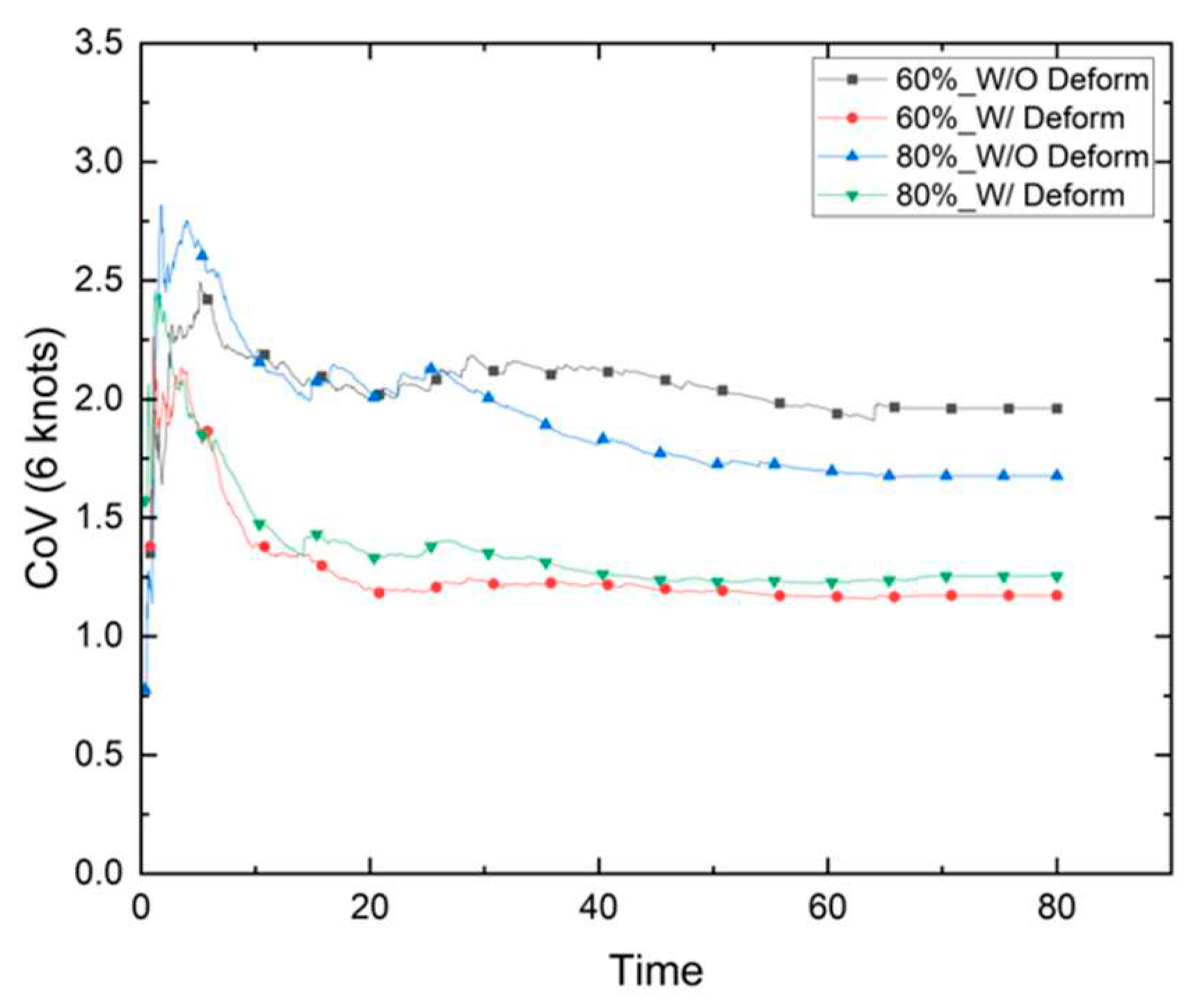
Figure 38.
CoV: 10 knots.
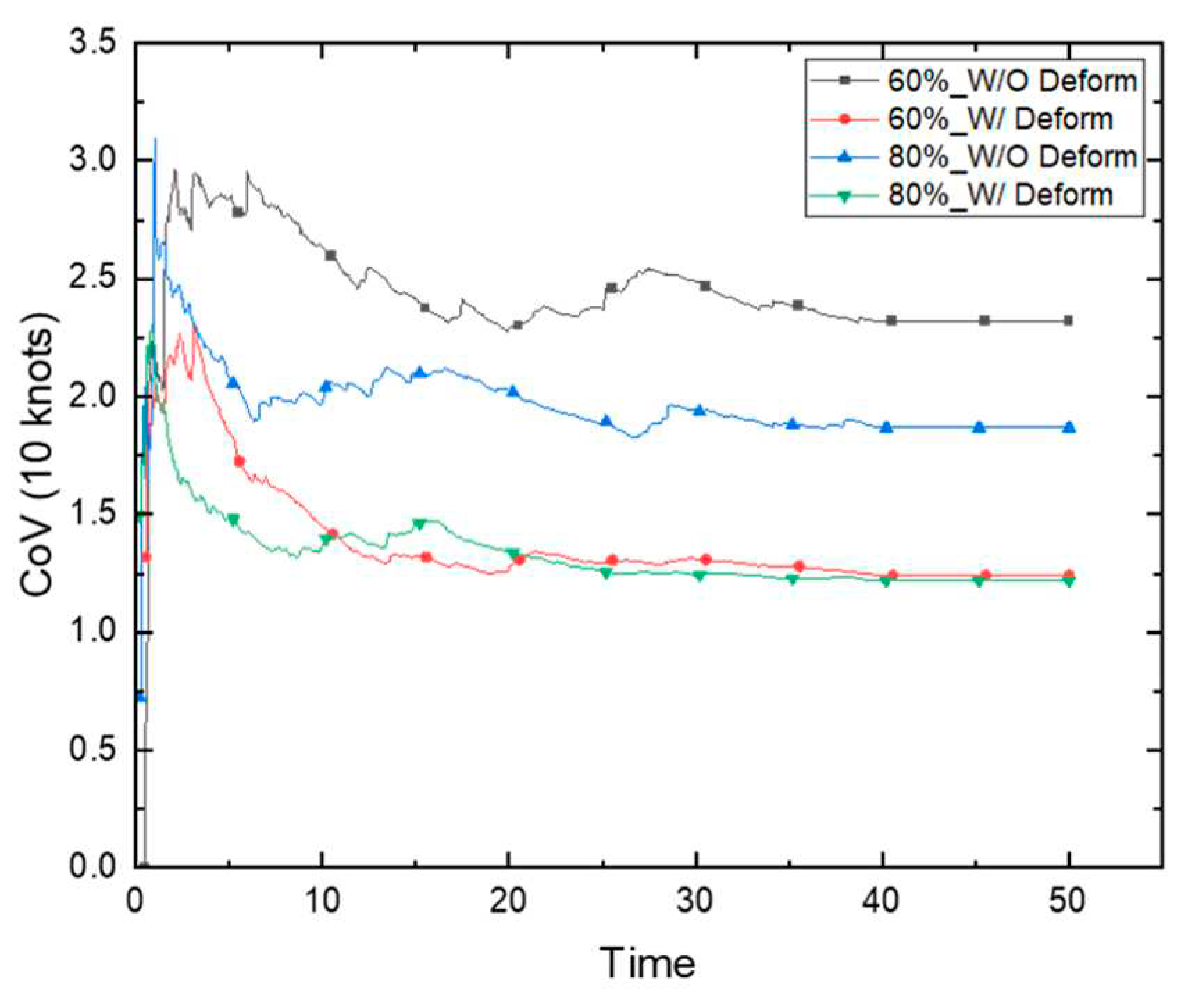
Table 1.
Material properties.
| Ice | Ship | |
|---|---|---|
| Density (kg/m3) | 900 | 7850 |
| Bulk Young’s modulus (MPa) | 61 | 2.0e5 |
| Poisson’s ratio | 0.003 | 0.3 |
Table 2.
Material interaction properties.
| Ice-Ice | Ice-Ship | |
|---|---|---|
| Friction coefficient | 0.1 | 0.131 |
| Tangential stiffness ratio | 1 | 1 |
| Restitution coefficient | 0.1 | 0.2 |
Table 3.
Ratio of affected area to FWD (%).
| Speed [knots] |
[1] Affected Area [m2] |
[2] Total shear work/[1] [N·m/m2] |
[3] Ratio to Bow in [2] (%) |
||||
|---|---|---|---|---|---|---|---|
| Ice Concentration | |||||||
| 60% | 80% | 60% | 80% | 60% | 80% | ||
| Bow (Forward) |
4 | 15.69 | 19.63 | 4.60E+3 | 6.90E+3 | - | - |
| 6 | 15.90 | 19.36 | 8.92E+3 | 1.21E+4 | - | - | |
| 10 | 17.71 | 21.38 | 2.06E+4 | 2.54E+4 | - | - | |
| Midship | 4 | 30.12 | 30.69 | 209.72 | 270.49 | 4.56 | 3.92 |
| 6 | 18.85 | 24.05 | 215.60 | 244.86 | 2.42 | 2.02 | |
| 10 | 8.46 | 17.90 | 343.09 | 583.56 | 1.67 | 2.30 | |
| Stern (After) |
4 | 5.28 | 5.44 | 229.31 | 296.24 | 4.99 | 4.29 |
| 6 | 3.06 | 3.28 | 254.47 | 346.18 | 2.85 | 2.86 | |
| 10 | 0.95 | 1.52 | 247.15 | 264.33 | 1.20 | 1.04 | |
Table 4.
Evaluated Wear Depth.
| Speed [knots] |
Ice concentration = 60% | Ice concentration = 80% | |||
|---|---|---|---|---|---|
| Average | Max | Average | Max | ||
| Bow (Forward) |
4 | 2.38 | 90.83 | 3.51 | 109.81 |
| 6 | 4.59 | 284.00 | 6.20 | 412.03 | |
| 10 | 10.76 | 863.34 | 13.06 | 953.36 | |
| Mid Ship | 4 | 0.11 | 5.78 | 0.14 | 4.14 |
| 6 | 0.11 | 5.00 | 0.13 | 3.38 | |
| 10 | 0.19 | 4.83 | 0.30 | 10.38 | |
| Stern (AFTER) |
4 | 0.12 | 1.90 | 0.16 | 2.22 |
| 6 | 0.14 | 2.39 | 0.25 | 9.95 | |
| 10 | 0.12 | 2.63 | 0.13 | 2.52 | |
Table 5.
Comparison of wear depth and area evaluation results.
| Ice concentration |
Numerical model |
Average wear depth [mm] |
Maximum wear depth [mm] |
Area [m2] |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 4 knots |
6 knots |
10 knots |
4 knots |
6 knots |
10 knots |
4 knots |
6 knots |
10 knots |
||
| 60% | With deformed geometry |
2.97 | 5.18 | 8.28 | 37.73 | 66.89 | 110.3 | 26.38 | 26.56 | 31.25 |
| Without deformed geometry |
2.38 | 4.59 | 10.76 | 90.83 | 284.0 | 863.3 | 15.69 | 15.90 | 19.36 | |
| 80% | With deformed geometry |
4.13 | 6.39 | 10.38 | 46.10 | 84.53 | 138.8 | 29.00 | 30.88 | 35.65 |
| Without deformed geometry |
3.51 | 6.20 | 13.06 | 109.8 | 512.0 | 953.4 | 19.63 | 19.36 | 21.38 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







