Prerpints.org logo
Preprint
Article

Prediction of Crack Width in RC Piles Exposed to Local Corrosion in Chloride Environment

Altmetrics

Downloads

115

Views

19

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

10 August 2023

Posted:

10 August 2023

You are already at the latest version

Alerts
Abstract
A novel prediction model for crack development of reinforced concrete (RC) piles with localized chloride corrosion in marine environment is proposed. A discrete method is used to solve the corrosion pit radius model and a crack extension model is developed to investigate the initiation and extension of cracks. The maximum corrosion degree of reinforced concrete pile is predicted according to the limit crack criterion, and finally a sensitivity analysis is carried out on the important parameters of crack extension. The results show that the radius of corrosion pit, the depth corrosion pit and cross-sectional area loss of reinforcement gradually increase as the corrosion level increases. The loss of local reinforcement section at crack initiation decreases with the increase of the ratio of concrete cover to initial diameter, and increases with the increase of pitting factor. The required pit depth for reinforcement cracking increases with the increase of the ratio of concrete cover thickness to diameter. The loss of cross-sectional area of reinforcement and the radius of corrosion pit increase with the increase of initial diameter of reinforcement. Increasing the pitting factor will reduce the pit depth and make the crack width develop faster before reaching the limit crack width. Increasing the concrete cover thickness can provide an improvement in the propagation of cracks. A comparative analysis shows that the localized corrosion pattern is more in conformity with marine engineering practice.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

In recent years, the corrosion of reinforced concrete (RC) structures in marine environment has received great concern. RC structures can be affected by chloride, air, seawater splash, wind and other external factors during service, which can cause corrosion of reinforced concrete structures. Corrosion can produce some corrosion products on the surface of RC structures, which can cause the volume increase and create tensile stress around the reinforced concrete. When the maximum tensile strength exceeds the tensile stress of the concrete, the cracking of concrete cover initiates. The concrete cracking may cause early intrusion of local chloride ions and corrosion of reinforcement, Concrete cracking may cause early localized chloride ion ingress and reinforcement corrosion, corrosion-induced cracks penetrate the concrete cover and provide a way for corrosive media such as chloride ions and oxygen to rapidly enter the reinforcement [1,2]. The cracks start to spread outwards from the steel-concrete interface and finally lead to complete cracking of the concrete cover.
The mechanism of damage and crack expansion in RC structures caused by corrosion and expansion of reinforcement has always been a hot topic of research in this field. Reinforcement corrosion can affect the safety and durability of RC structures. Many scholars have studied the bearing capacity of RC structures locally corroded by chloride [3,4,5,6,7,8,9]. In the actual marine environment, chlorides generally penetrate into the concrete in one direction, and corrosion may start from the outermost layer of the reinforcement, so the steel bar may not corrode uniformly in cross sections [10], Corrosion pits of varying sizes are randomly produced on the reinforcement surface. The development of corrosion pits is related to the generation of cracks. In fact, longitudinal cracks provide the clearest visual representation of steel corrosion. Shao et al. [11] proposed an analysis model for durability life of RC piles with chloride local corrosion considering the impact of crack growth stage on the structure. Guzmán and Gálvez [12] used embedded cohesive cracking finite element analysis to study the effect of localized corrosion on the cracking of concrete cover, deriving different cracking patterns. Kim and Kim [13] estimated the maximum corrosion depth of local corrosion of reinforcement considering chloride ion diffusion. Li et al. [14] conducted tests on pit corrosion of reinforcement in chloride ion corroded concrete and analyzed the relationship between pit depth, residual sectional area and area of the smaller planar principal moment of inertia and corrosion grade. Darowicki et al. [15] investigated localized corrosion of stainless steel using optical surface measurement technology and deduced the cumulative distribution function of pitting corrosion. Kioumarsi et al. [16] studied the influence of corrosion pit disturbance on the damage probability of reinforced concrete beams after localized corrosion. Vidal et al. [17] predicted the crack width of corrosion in reinforced concrete structures and proposed a relationship between reinforcement section loss and cracking. Zhang et al. [18] measured the crack initiation, maximum load, fracture energy and other parameters of short cut basalt fiber concrete through tests, and studied the crack resistance of concrete. Zhang et al. [19] presented a new model to predict steel corrosion from corrosion cracks based on the average steel section loss parameter. Li et al. [20] inferred a theoretical model for the corrosion crack width of reinforced concrete structures. Zhao et al. [21] presented a concrete cracking model to investigate stress and cracks in concrete cover caused by reinforcing steel corrosion. Many scholars have conducted a great number of studies on the corrosion initiation and concrete cracking of RC structures. Chernin and Val [22] provided a review of existing models for predicting corrosion-induced cracking times in concrete cover. Xu et al. [23] studied the cracking of concrete protective layers caused by non-uniform corrosion of reinforcement. In fact, defining the initiation of corrosion or the appearance of the first crack as the end of the functional life of a RC structure underestimates the real life of a reinforced concrete structure. This method of predicting the durability life of RC structures is too conservative. When cracks develop to the limit crack, the structure fails. Although the above studies have studied the development of corrosion cracks in reinforced concrete, these studies have not combined the pit depth, corrosion degree and crack development. To predict the durability life of RC structures partially corroded by chloride more comprehensively, the mechanism of corrosion crater development and crack propagation should be studied in depth. Therefore, it is very meaningful to study the development of cracks for the durability life prediction and repair of RC structures.
In this paper, a novel prediction model for crack development of RC piles with localized chloride corrosion in marine environment is proposed. The maximum corrosion degree of RC pile is predicted according to the limit crack criterion. A discrete method is used to solve the corrosion pit radius model, then crack initiation and extension are investigated based on the crack extension model, and finally a sensitivity analyses were conducted on the important parameters of crack extension.

2. Localized corrosion modelling

2.1. Geometry model

RC piles exposed to the marine environment are easily corroded by chloride ions. The corrosion of RC structure is generally divided into uniform corrosion and local corrosion, and local corrosion is the key factor for predicting the durability life of RC piles. When reinforced concrete is corroded, corrosion pits are created on the surface of the reinforcement. The location and shape of these corrosion pits are formed randomly and they are related to factors such as the environment and the level of corrosion. In this paper, the non-uniform corrosion model proposed by Alami et al. [24] is used to study the development of corrosion crater. It is assumed that the shape of the corrosion pit is semi-circular, and the center of the corrosion crater is located at the edge of the reinforcement.

2.2. Modelling of corrosion pits

As corrosion process proceeds, corrosion products can be produced on the surface of reinforcement, and corrosion products can expand on the surface of reinforcement. In this paper, the distribution of corrosion pits on the surface of reinforcement is regarded as a simple geometric distribution. As shown in Figure 1, it is assumed that the centre O’ of the corrosion crater is directly above the center O of the reinforcement. The intersection points of corrosion pit and reinforcement are Q and Q’, respectively, the intersection of OO’ and QQ’ is I, and the radius of corrosion pit is R’. According to Figure 1, the shadow area is the corrosion pit area, which is composed of two semicircles with different radii. The pit area is the sum of the areas of zone 1 and zone 2.
In the corrosion pit model, it is assumed that
I Q = I Q '
The area of zone 1 can be expressed as
A 1 = A S O Q Q ' − A T O Q Q '
The area of triangle OQQ ‘obtained from geometric knowledge can be expressed as
A T O Q Q ' = I Q × I O
IO can be expressed as
I O = O Q 2 − Q I 2 = R 2 − R ' 2
Therefore, the area of the triangle OQQ’ is expressed as
A T O Q Q ' = R ' × R 2 − R ' 2
The expression for the area of the sector OQQ’ can be expressed as
A S O Q Q ' = 2 π R 2 α 360
The angle α can be expressed as
sin α = R ' R
Therefore, the expression for α is
α = arcsin R ' R
Therefore, the area of sector OQQ’ is calculated as
A S O Q Q ' = 2 π R 2 360 ⋅ arcsin R ' R
In summary, the area of region 1 is obtained as
A 1 = A S O Q Q ' − A T O Q Q ' = ( 2 π R 2 360 ⋅ arcsin R ' R ) − ( R ' × R 2 − R ' 2 )
Based on the same analysis method, the area of zone 2 can be obtained as
A 2 = A S O ' Q Q ' − A T O ' Q Q '
IO’ can be expressed as
I O ' = O O ' − O I = R − R 2 − R ' 2
The relationship between angle β and angle α is given by
β = 90 ∘ − α
Therefore, the area of the sector O’QQ’ is obtained as
A S O ' Q Q ' = 2 π R ' 2 360 ( 90 ∘ − α )
The area of triangle O’QQ’ is given by
A T O ' Q Q ' = R ' × ( R − R 2 − R ' 2 )
According to Eq. (14) and Eq. (15), the area of zone 2 is
A 2 = A S O ' Q Q ' − A T O ' Q Q ' = 2 π R ' 2 360 ⋅ ( 90 − α ) − R ' × ( R − R 2 − R ' 2 )
Therefore, the corrosion pit area can be expressed as
Δ A s = A 1 + A 2 = 2 π [ R ' 2 360 ⋅ ( 90 − α ) + R 2 360 ⋅ α ] − R ' ⋅ [ R 2 − R ' 2 + ( R − R 2 − R ' 2 ) ]
Eq. (17) can be simplified as
Δ A s = 2 π [ R ' 2 360 ⋅ ( 90 ∘ − α ) + R 2 360 ⋅ α ] − R R '
where ΔAs is the area of the corrosion pit and denotes the loss of cross-sectional area of the reinforcement, R’ is the corrosion pit radius and R is the initial radius of the reinforcement. In general, the degree of corrosion of reinforced concrete piles is expressed as the percentage mass loss of reinforcement ρ, and ρ can be calculated as
ρ = M 1 − M 2 M 1
where M1 and M2 are the masses of the reinforcement bars before corrosion and the mass after corrosion, respectively. Eq. (19) can be rewritten as [25]
ρ = M 1 − M 2 M 1 = ρ r e b a r ⋅ Δ A s ρ r e b a r ⋅ A r e b a r = Δ A s A r e b a r
According to Eq. (18) and Eq. (20), the following equation can be obtained as
ρ A r e b a r = 2 π [ R ' 2 360 ( 90 ∘ − α ) + R 2 360 α ] − R R '
where ρ is the degree of corrosion of the reinforcement, and Arebar is the initial area of the reinforcement. Eq. (21) involves two unknown parameters ρ and R’, when the degree of corrosion ρ is known, the radius of pit radius R’ can be obtained for different corrosion degrees. However, since the unknown parameter R’ is present in the trigonometric function, the radius of the corrosion pit cannot be solved by simple reduction. The relevant programming software is used to scatter countless points in the feasibility domain of radius R’ to find the closest solution. The variation of the corrosion pit radius R’ and the loss of reinforcement cross-sectional area ΔAs with the degree of corrosion are analyzed. Because the discrete approach generates a certain amount of error, the model calculation error E is also analyzed in this study.

2.3. Analysis of crack width

After the onset of cracking in RC structures, the corrosion products on the surface can first fill the local pores and then be deposited at the interface between the reinforcement and the concrete. The depth of corrosion pit required for reinforcement cracking is calculated by [26]
x 0 = 7.53 + 9.32 c D 0
where x0 is the corrosion pit depth required for cracking, c is the concrete cover thickness (mm) and D0 is the initial diameter of the reinforcement. The above equation shows that the depth of corrosion pit required for cracking is related to the ratio of the concrete cover thickness and the initial diameter of the reinforcement. The relationship between the depth of corrosion crater and reinforcement cross-section loss can be obtained by [17]
x = D 0 α [ 1 − 1 − Δ A s A r e b a r ] ⋅ 10 3
where α is the pitting factor, is the ratio of localized corrosion depth to uniform corrosion depth, α=2, for uniform corrosion, 4<α<8, for localized corrosion, D0 is the initial diameter of the reinforcement (mm), Arebar is the initial area of the reinforcement and ΔAs is the loss of reinforcement cross-section. The relationship between the corrosion pit depth x and the corrosion pit radius R’ is shown in Figure 4. According to Eqs. (22) and (23), the local steel section loss at the beginning of cracking can be obtained as [19]
Δ A s 0 = A r e b a r [ 1 − [ 1 − α D 0 ( 7.53 + 9.32 c D 0 ) ⋅ 10 − 3 ] 2 ]
It should be noted that the local reinforcement section loss at the onset of cracking obtained by Eq. (24) is obtained without taking into account the properties of the concrete. Based on the experimental data, a linear regression formula obtained by Vidal et al. [17] is used for predicting crack width as
w = K ( Δ A s − Δ A s 0 )
where ΔAs0 is the loss of local steel cross-section at the beginning of cracking, and K is the slope of the curve (K =0.0575). According to the limit crack criterion, when the crack width exceeds the limit crack value, the reinforced concrete pile loses stability.

3. Analysis results

In this paper, the selected limit crack width is wlim=0.4 mm. The values of model parameters used in this analysis are shown in Table 1. According to Eq. (22), the pit depth at the beginning of reinforcement cracking is 0.054 mm, according to Eq. (24), the local steel section loss at the beginning of cracking is 4.73 mm2. The relationship between the radius of the corrosion pit and the loss of reinforcement cross-section with the degree of corrosion is shown in Figure 2. When the corrosion degree increases, the corrosion pit radius gradually increases and the reinforcement section loss gradually increases. This is consistent with the findings of the experiment by Li et al. [14]. The error analysis caused by solving the corrosion pit radius with discrete method is shown in Figure 3. The error varies randomly and irregularly as the corrosion level increases from 1% to 16%, while each error is very small, therefore, the influence of the error formed by the discrete method on the results can be ignored. Figure 4 shows the relationship between corrosion crater radius and corrosion crater depth. The depth of corrosion pit increases with increasing pit radius.
The effect of pitting factor on corrosion crater depth is shown in Figure 5. When the corrosion degree is 8%, the pit depth decreases from 115.50 mm to 57.75 mm as the pitting factor increases from 4 to 8. The crater depth decreases with the increase of pitting factor. This is because when the corrosion degree is certain, the cross-sectional loss of reinforcement is also a fixed value, and the depth of the corrosion pit is inversely proportional to the pitting factor. When the pitting factor is 6, the pit depth increases from 50.81 mm to 76.99 mm as the corrosion degree increases from 6% to 9%. The corrosion degree increases from 6% to 7%, from 7% to 8%, and from 8% to 9%, the pit depth increases by 16.53%, 14.69%, and 13.27%, respectively. The depth of corrosion crater increases slowly. This is because with the increase of corrosion level, the local corrosion of reinforcement becomes more and more serious. The corrosion products generated by corrosion attach to the surface of reinforcement, and blocks the flow of media required for corrosion such as chlorine ion and oxygen, thus slowing down the development of corrosion to a certain extent.
The effect of the pitting factor on the crack width is shown in Figure 6. When the corrosion degree is 9%, the crack width reduces from 0.21 mm to 0.025 mm as the pitting factor increases from 4 to 8. The crack width decreases with the increase of pitting factor. When the pitting factor is 5, the crack width increases from 0.03 mm to 0.17 mm as the corrosion degree increases from 6% to 9%. The crack width increases 4.67 times. The crack width increases with the increase of corrosion degree. This is because with the progress of corrosion, air, oxygen and other corrosive media are sufficient, and corrosion will develop rapidly at the beginning. The crack width will expand rapidly before reaching the limit crack width, but after the crack width reaches the threshold, the corrosion rate will slow down because the accumulation of corrosion products restricts the flow of air and so on.
The influence of the concrete cover thickness on the required pit depth at the initiation of reinforcement cracking is shown in Figure 7. When concrete cover thickness increases from 40 mm to 60 mm, the corrosion pit depth at the beginning of reinforcement cracking increases from 44.81 mm to 63.45 mm. The depth of the pit required for the initiation of reinforcement cracking increases with the concrete cover thickness. This is because increasing the concrete cover thickness not only increases the diffusion path of the chloride, but also decreases the tensile stresses on the outer surface of the concrete cover due to the radial expansion of the corroded reinforcement, thus delaying the initiation of cracking the concrete cover.
The influence of the thickness of concrete cover on crack width is shown in Figure 8. When corrosion degree is 8%, the crack width decreases from 0.14 mm to 0.04 mm as the concrete cover thickness increases from 40 mm to 60 mm. The crack width decreases with the increase of concrete cover thickness. This is because the increase in the thickness of the concrete cover improves the impermeability, corrosion resistance and other durability of the reinforced concrete, so the crack expansion is improved. Generally speaking, the greater the thickness of the concrete cover, the longer it takes for the external corrosive medium to reach the surface of the steel, the less likely it is for the reinforcement to rust, and the better the durability of the concrete. However, the concrete cover should not be too thick, as the shrinkage and temperature stresses are not well controlled during the hardening process.
The effect of initial diameter of reinforcement on the radius of corrosion pit and the loss of reinforcement section is shown in Figure 9. When the corrosion degree is 6%, the radius of corrosion pit increases from 1.56 mm to 3.12 mm with the reinforcement diameter increasing from 8 mm to 16 mm. At the same corrosion degree, the radius of corrosion pit tends to increase with the increase of initial diameter of reinforcement. When the initial diameter is 10 mm, the corrosion pit radius increases from 1.95 mm to 2.49 mm as corrosion level increases from 6% to 9%. At the same initial diameter, the radius of corrosion pit tends to increase with the increase of corrosion degree. This shows that the corrosion radius and the loss of cross-sectional area of reinforcement increase with the increase of initial diameter of reinforcement.
Figure 10 shows the influence of initial diameter of reinforcement on the depth of corrosion pit at the beginning of reinforcement cracking and in the process of corrosion. When the corrosion degree is 6%, 7%, 8% and 9%, the corrosion pit depth increases from 43.16 mm to 86.32 mm, from 50.61 mm to 100.71 mm, from 57.85 mm to 115.70 mm, and from 65.31 mm to 130.61 mm, as the initial diameter of reinforcement increases from 8 mm to 16 mm. At the same corrosion degree, the pit depth increases with the increase of the initial diameter of the reinforcement. When the initial diameter of the reinforcement increases from 8 mm to 16 mm, the required corrosion pit depth for cracking of the reinforcement decreases from 65.78 mm to 36.66 mm. The depth of corrosion pit required for reinforcement cracking reduces as the initial diameter of the reinforcement increases.
The relationship between the localized reinforcement cross-section loss at the beginning of reinforcement cracking and the ratio of concrete cover thickness to initial diameter is shown in Figure 11(a). The localized loss of reinforcement cross-section at the onset of cracking decreases as the ratio of concrete cover thickness to initial diameter increases. The relationship between local reinforcement section loss and pitting factor at the beginning of reinforcement cracking is shown in Figure 11(b). The localized reinforcement cross-section loss at the beginning of reinforcement cracking increases with the pitting factor. This is because the increase of pitting factor means that the ratio of local corrosion degree to uniform corrosion degree increases, and the local corrosion degree increases, and then the loss of cross sectional area of reinforcement at the beginning of reinforcement cracking increases.
The influence of corrosion degree on crack width is shown in Figure 12(a). When the corrosion level is approximately 15%, the crack width reaches the ultimate crack width of 0.4 mm, and the structure becomes unstable. The influence of the loss of cross-sectional area of reinforcement on the crack width is shown in Figure 12(b). When the crack width reaches the limit crack width, the loss of cross-sectional area of reinforcement is about 11.79 mm2. The crack width increases with the increase of corrosion degree. This is because the reinforcement corrosion becomes more serious with the increase of corrosion degree. The crack gradually expands with the reinforcement corrosion until the structure is unstable.
Figure 13 shows the influence of initial diameter of reinforcement on model error of corrosion pit radius. As the corrosion level increases from 1% to 16%, the error curves follow very similar trends for initial steel diameters of 8 mm, 10 mm and 12 mm. The error varies within the range from 0 to 2%. Therefore, it can be concluded that the initial diameter of reinforcement has little effect on the variation trend of the error of the pit radius model, and the error caused by the solution of the pit radius model can be ignored.

4. Discussion

Comparison of localized and uniform corrosion: Kim and Kim [13] carried out a numerical analysis of localized corrosion (two-dimensional corrosion) of reinforced concrete structures. The results show that the depth of localized corrosion is 3.5 times greater than the depth of uniform corrosion after 3.5 years from the onset of corrosion. The results of Santiago and Jaime’s study show that the concrete surface cracking time in localized corrosion mode is earlier and the vertical surface displacement is much greater than in uniform corrosion [12]. It has been shown that in the localized corrosion mode, cracks appear earlier on the concrete surface and the pressure to crack the concrete surface is much less than in the uniform corrosion mode. In addition, localized corrosion requires less loss of reinforcement section and shorter periods to study the limit state of the concrete structure [8,10,29]. In conclusion, the uniform corrosion model to study the corrosion of reinforced concrete structures is too conservative, and there is a gap with the actual engineering conditions. The cracking time of the concrete surface, the crack initiation time and the time when the cracks reach the ultimate crack are much later in the uniform corrosion model than in the localized corrosion model. Therefore, in order to be more relevant to the actual marine engineering, the crack analysis of reinforced concrete structures in localized corrosion mode should be developed as much as possible. This paper only proposes a new method for predicting cracks in concrete piles under localized corrosion of chloride in marine environment, and the predicted results in this paper are in conformity with many experimental results. However, the shape, size and spatial distribution of the specific corrosion pits and cracks need to be investigated in more depth.

5. Conclusions

In this paper, a novel prediction model for crack development of RC piles with local chloride corrosion in marine environment is proposed. The generation and extension of cracks are studied and a sensitivity analysis of the important parameters of the cracking phase is carried out. Therefore, the following conclusions can be obtained.
(1) The radius of corrosion pit, loss of cross-sectional area of reinforcement and corrosion pit depth increase as the corrosion level increases. The corrosion pit depth decreases with increasing pitting factor and the crack width develops more rapidly before the ultimate crack width is reached. The increased thickness of the protective concrete cover delays the cracking of the concrete surface and provides an improvement in the propagation of cracks.
(2) The required pit depth for reinforcement cracking increases with the increase of the ratio of concrete cover thickness to diameter. The loss of cross-sectional area of reinforcement and the radius of corrosion pit increase with the increase of initial diameter of reinforcement. The loss of local reinforcement section at the beginning of reinforcement cracking decreases with the increase of the ratio of concrete cover thickness to initial diameter, and increases with the increase of pitting factor.
(3) According to the limit crack criterion, the maximum corrosion degree of reinforced concrete pile is about 15%. The error caused by the discrete method can be ignored.
(4) A comparative analysis of the results of existing studies shows that chloride corrosion of reinforced concrete piles under the assumption of uniform corrosion is too conservative and that localized corrosion would be more in conformity with engineering practice. This paper only proposes a new method to predict the cracking of concrete piles by localized corrosion of chloride in the marine environment, and the predicted results are consistent with many experimental results. However, the shape, size and spatial distribution of specific corrosion pits and cracks need to be developed for more in-depth study.

Author Contributions

Conceptualization, W.S and D.S.; methodology, W.S and X.H.; writing-original draft, X.H.; formal analysis, X.H.; investigation, D.S.; visualization, D.S.; writing-review & editing, W.S.; supervision, W.S.; funding acquisition, W.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was financially supported by the National Natural Science Foundation of China (Grant No. 52078289), the Shanghai International Science and Technology Cooperation Project (Grant No. 19520744100), State Key Laboratory of Hydraulic Engineering Simulation and Safety (Tianjin University) (Grant No. HESS-2321), and State Key Laboratory of Coastal and Offshore Engineering (Dalian University of Technology) (Grant No. LP2111).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zhao, Y.; Wu, Y.; Jin, W. Distribution of millscale on corroded steel bars and penetration of steel corrosion products in concrete. Corros. Sci. 2013, 66, 160–168. [Google Scholar] [CrossRef]
  2. Chao, Z.; Dang, Y.; Pan, Y.; Wang, F.; Wang, M.; Zhang, J.; Yang, C. Prediction of the shale gas permeability: A data mining approach. Géoméch. Energy Environ. 2023, 33. [Google Scholar] [CrossRef]
  3. Cao, C. 3D simulation of localized steel corrosion in chloride contaminated reinforced concrete. Constr. Build. Mater. 2014, 72, 434–443. [Google Scholar] [CrossRef]
  4. Chen, E.; Berrocal, C.G.; Fernandez, I.; Löfgren, I.; Lundgren, K. Assessment of the mechanical behaviour of reinforcement bars with localized pitting corrosion by digital image correlation. Engineering Structures. 2020, 219, 110936. [Google Scholar] [CrossRef]
  5. Moreno, E.; Cobo, A.; Palomo, G.; González, M.N. Mathematical models to predict the mechanical behavior of reinforcements depending on their degree of corrosion and the diameter of the rebars. Constr. Build. Mater. 2014, 61, 156–163. [Google Scholar] [CrossRef]
  6. Tang, F.; Lin, Z.; Chen, G.; Yi, W. Three-dimensional corrosion pit measurement and statistical mechanical degradation analysis of deformed steel bars subjected to accelerated corrosion. Constr. Build. Mater. 2014, 70, 104–117. [Google Scholar] [CrossRef]
  7. Jin, L.; Wang, Z.; Zhang, R.; Du, X. Mesoscopic simulation on flexural behavior of single-way reinforced concrete slab with rebars subjected to localized corrosion. Structures 2021, 31, 815–827. [Google Scholar] [CrossRef]
  8. Xia, N.; ASCE, A.M.; Ren, Q.W.; ASCE, M.; Liang, R.Y.; ASCE, F.; Payer, J.; Patnaik, A.; ASCE, M. Nonuniform corrosion-induced stresses in steel-reinforced concrete. Journal of Engineering Mechanics. 2012, 138, 338–346. [Google Scholar] [CrossRef]
  9. Zhao, Y.; Hu, B.; Yu, J.; Jin, W. Non-uniform distribution of rust layer around steel bar in concrete. Corros. Sci. 2011, 53, 4300–4308. [Google Scholar] [CrossRef]
  10. Jang, B.S.; Oh, B.H. Effects of non-uniform corrosion on the cracking and service life of reinforced concrete structures. Cem. Concr. Res. 2010, 40, 1441–1450. [Google Scholar] [CrossRef]
  11. Shao, W.; He, X.; Shi, D. Durability life prediction of RC piles subjected to localized corrosion in chloride environments. Eng. Fail. Anal. 2022, 136. [Google Scholar] [CrossRef]
  12. Guzmán, S.; Gálvez, J.C. Modelling of concrete cover cracking due to non-uniform corrosion of reinforcing steel. Constr. Build. Mater. 2017, 155, 1063–1071. [Google Scholar] [CrossRef]
  13. Kim, C.-Y.; Kim, J.-K. Numerical analysis of localized steel corrosion in concrete. Constr. Build. Mater. 2008, 22, 1129–1136. [Google Scholar] [CrossRef]
  14. Li, D.; Wei, R.; Li, L.; Guan, X.; Mi, X. Pitting corrosion of reinforcing steel bars in chloride contaminated concrete. Constr. Build. Mater. 2018, 199, 359–368. [Google Scholar] [CrossRef]
  15. Darowicki, K.; Mirakowski, A.; Krakowiak, S. Investigation of pitting corrosion of stainless steel by means of acoustic emission and potentiodynamic methods. Corros. Sci. 2003, 45, 1747–1756. [Google Scholar] [CrossRef]
  16. Kioumarsi, M.M.; Hendriks, M.A.; Kohler, J.; Geiker, M.R. The effect of interference of corrosion pits on the failure probability of a reinforced concrete beam. Eng. Struct. 2016, 114, 113–121. [Google Scholar] [CrossRef]
  17. Vidal, T.; Castel, A.; François, R. Analyzing crack width to predict corrosion in reinforced concrete. Cem. Concr. Res. 2004, 34, 165–174. [Google Scholar] [CrossRef]
  18. Zhang, W.; Shi, D.; Shen, Z.; Zhang, J.; Zhao, S.; Gan, L.; Li, Q.; Chen, Y.; Tang, P. Influence of chopped basalt fibers on the fracture performance of concrete subjected to calcium leaching. Theor. Appl. Fract. Mech. 2023, 125. [Google Scholar] [CrossRef]
  19. Zhang, R.; Castel, A.; François, R. Concrete cover cracking with reinforcement corrosion of RC beam during chloride-induced corrosion process. Cem. Concr. Res. 2010, 40, 415–425. [Google Scholar] [CrossRef]
  20. Li, C.Q.; Lawanwisut, W.; Zheng, J.J.; Kijawatworawet, W. Crack width due to corroded bar in reinforced concrete structures. International Journal of Materials & Structural Reliability. 2005, 3, 87–94. [Google Scholar]
  21. Zhao, Y.; Yu, J.; Jin, W. Damage analysis and cracking model of reinforced concrete structures with rebar corrosion. Corros. Sci. 2011, 53, 3388–3397. [Google Scholar] [CrossRef]
  22. Chernin, L.; Val, D.V. Prediction of corrosion-induced cover cracking in reinforced concrete structures. Constr. Build. Mater. 2011, 25, 1854–1869. [Google Scholar] [CrossRef]
  23. Xu, G.; Wei, J.; Liu, H.Q. The experimental study of the non-uniform corrosion of steel bars. Journal of Huazhong University of Science and Technology (Nature Science Edition). 2006, 34, 111–114. [Google Scholar]
  24. Eliass, E.A.; Fekak, F.E.; Garibaldi, L.; Ahmed, E. A numerical study of pitting corrosion in reinforced concrete structures. Journal of Building Engineering. 2021, 43, 102789. [Google Scholar]
  25. Sun, J.; Ding, Z.; Huang, Q. Corrosion fatigue life prediction for steel bar in concrete based on fatigue crack propagation and equivalent initial flaw size. Constr. Build. Mater. 2018, 195, 208–217. [Google Scholar] [CrossRef]
  26. Alonso, C.; Andrade, C.; Rodriguez, J.; Diez, J.M. Factors controlling cracking of concrete affected by reinforcement corrosion. Mater. Struct. 1998, 31, 435–441. [Google Scholar] [CrossRef]
  27. Stewart, M.G.; Mullard, J.A. Spatial time-dependent reliability analysis of corrosion damage and the timing of first repair for RC structures. Eng. Struct. 2007, 29, 1457–1464. [Google Scholar] [CrossRef]
  28. Stewart, M.G. Spatial variability of pitting corrosion and its influence on structural fragility and reliability of RC beams in flexure. Struct. Saf. 2004, 26, 453–470. [Google Scholar] [CrossRef]
  29. Zhao, Y.; Karimi, A.R.; Wong, H.S.; Hu, B.; Buenfeld, N.R.; Jin, W. Comparison of uniform and non-uniform corrosion induced damage in reinforced concrete based on a Gaussian description of the corrosion layer. Corros. Sci. 2011, 53, 2803–2814. [Google Scholar] [CrossRef]
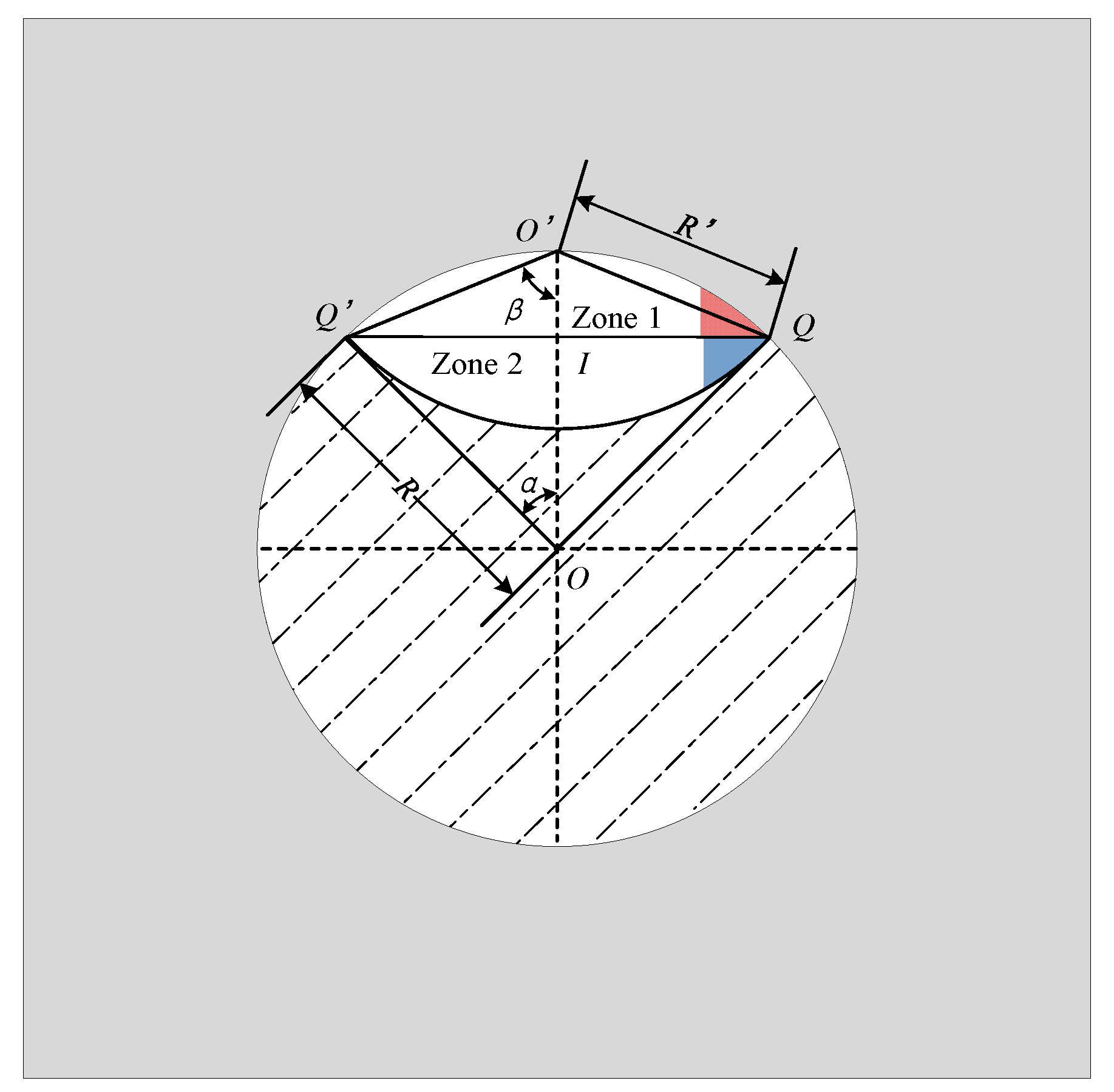
Preprints 82104 g001
Figure 1. Area loss of reinforcement.
Figure 1. Area loss of reinforcement.
Preprints 82104 g001
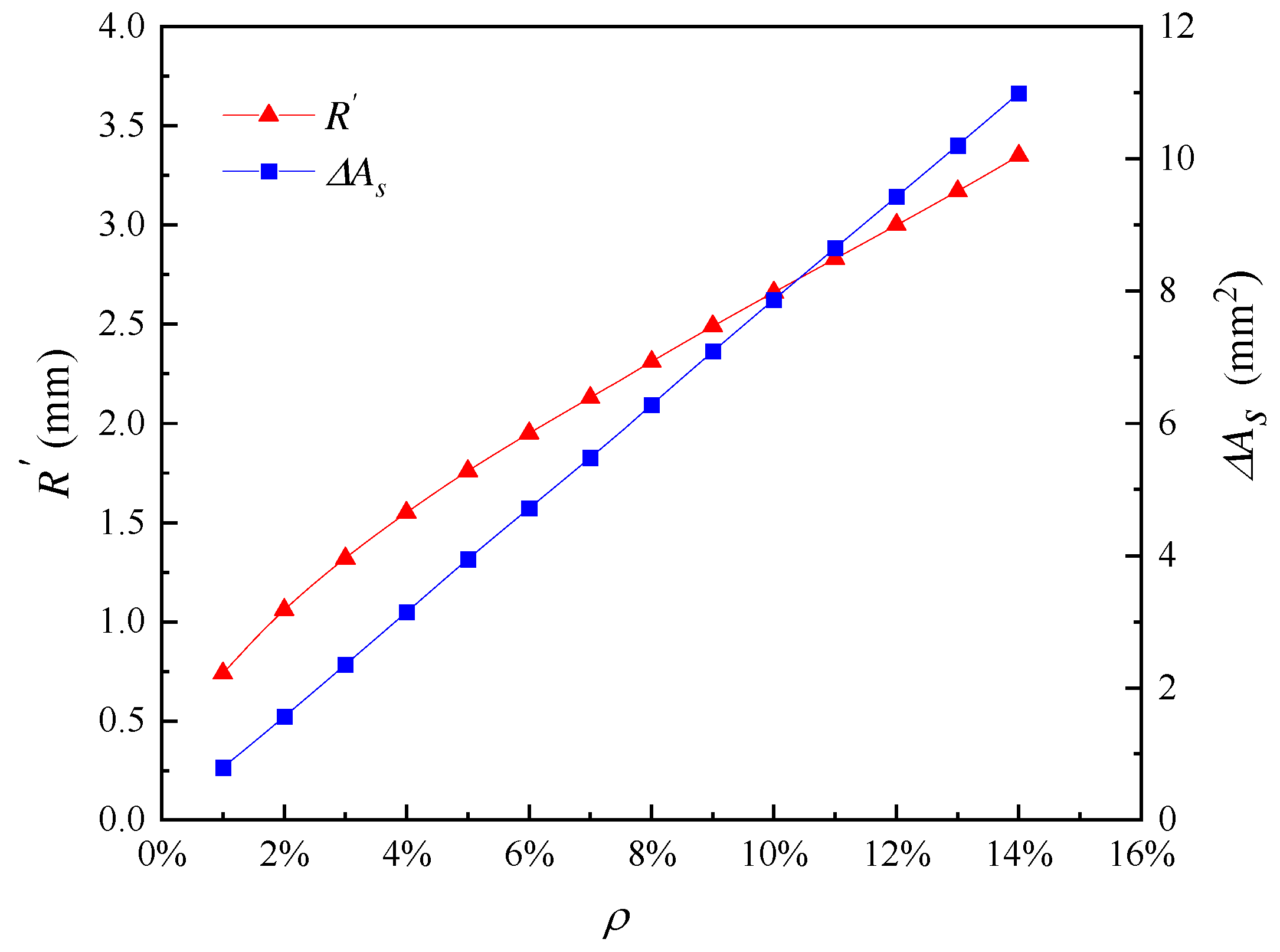
Preprints 82104 g002
Figure 2. Influence of corrosion degree on radius of corrosion pit and cross-sectional area loss of reinforcement.
Figure 2. Influence of corrosion degree on radius of corrosion pit and cross-sectional area loss of reinforcement.
Preprints 82104 g002
Preprints 82104 g003
Figure 3. Calculation error of corrosion pit radius.
Figure 3. Calculation error of corrosion pit radius.
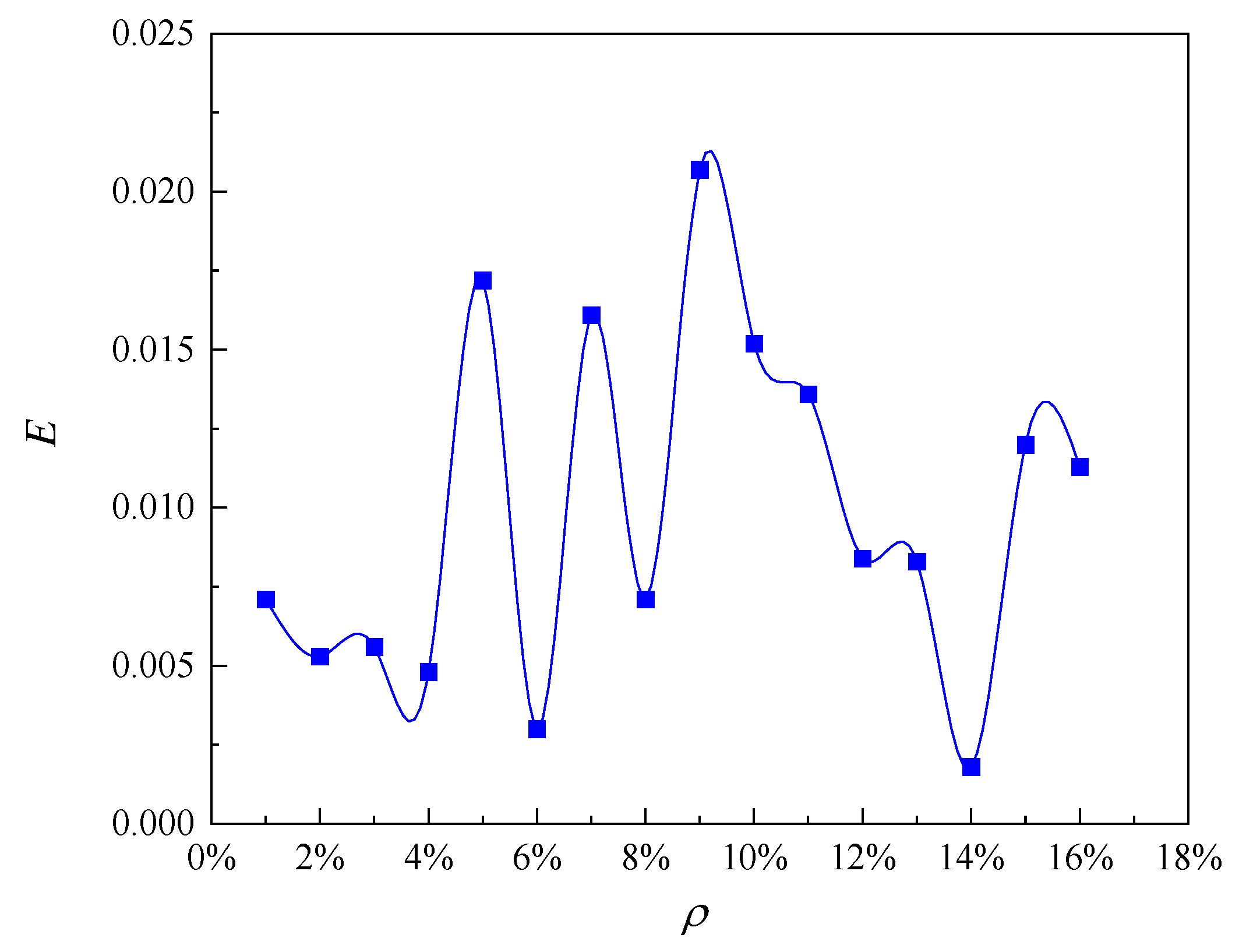
Preprints 82104 g003
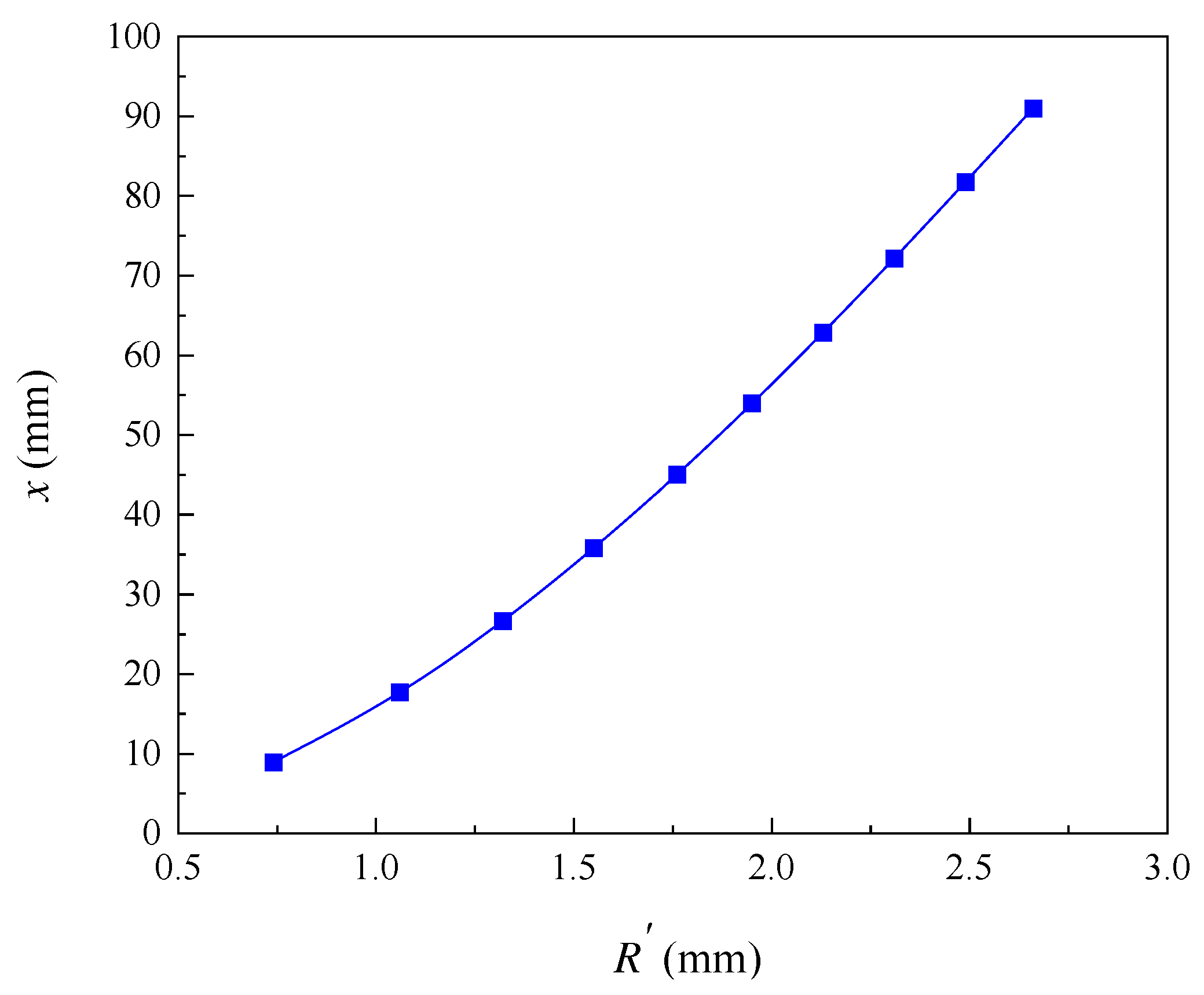
Preprints 82104 g004
Figure 4. Influence of pit radius variation on corrosion pit depth.
Figure 4. Influence of pit radius variation on corrosion pit depth.
Preprints 82104 g004
Preprints 82104 g005
Figure 5. Influence of pitting factor on pit depth.
Figure 5. Influence of pitting factor on pit depth.
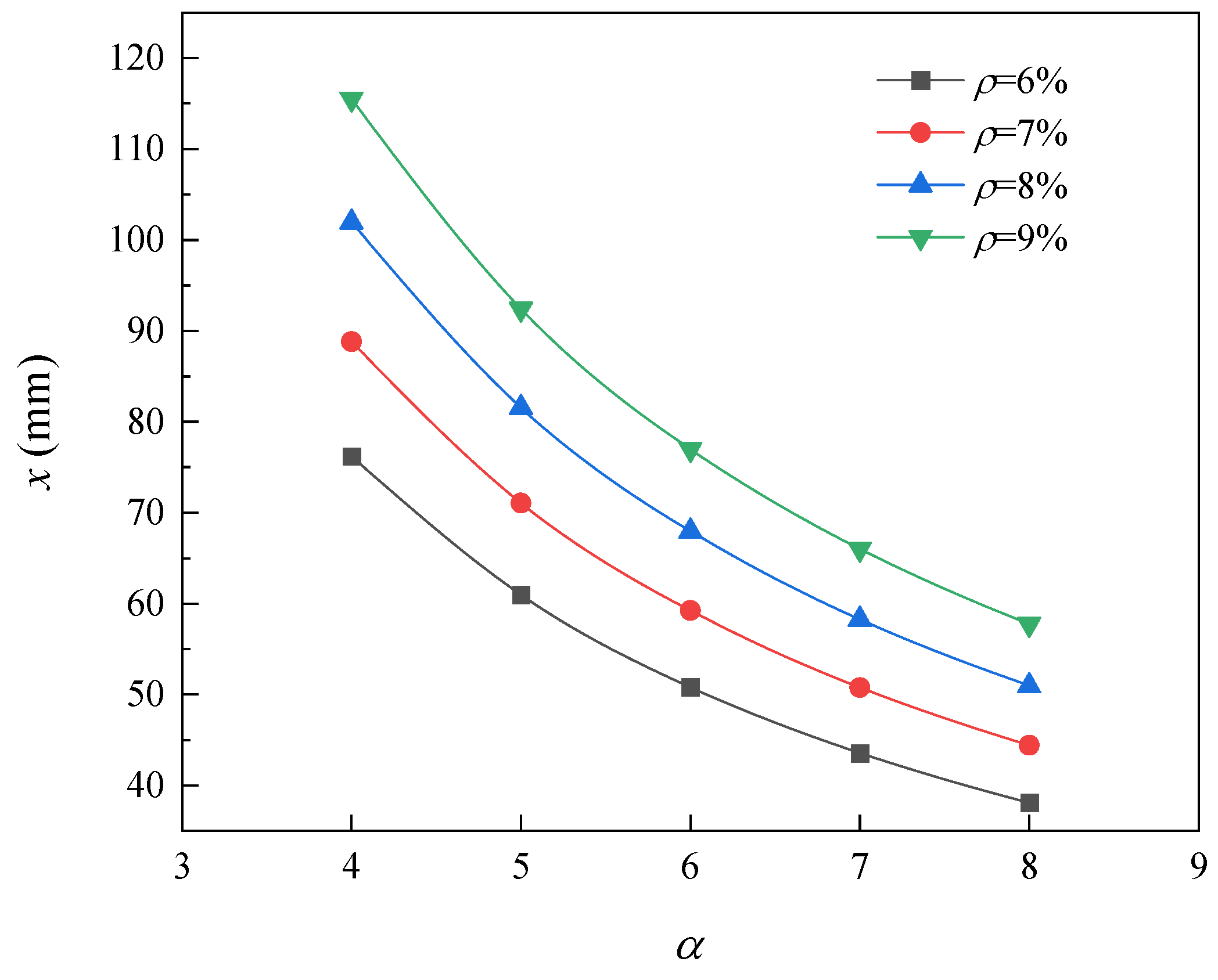
Preprints 82104 g005
Preprints 82104 g006
Figure 6. Effect of pitting factor on crack width.
Figure 6. Effect of pitting factor on crack width.
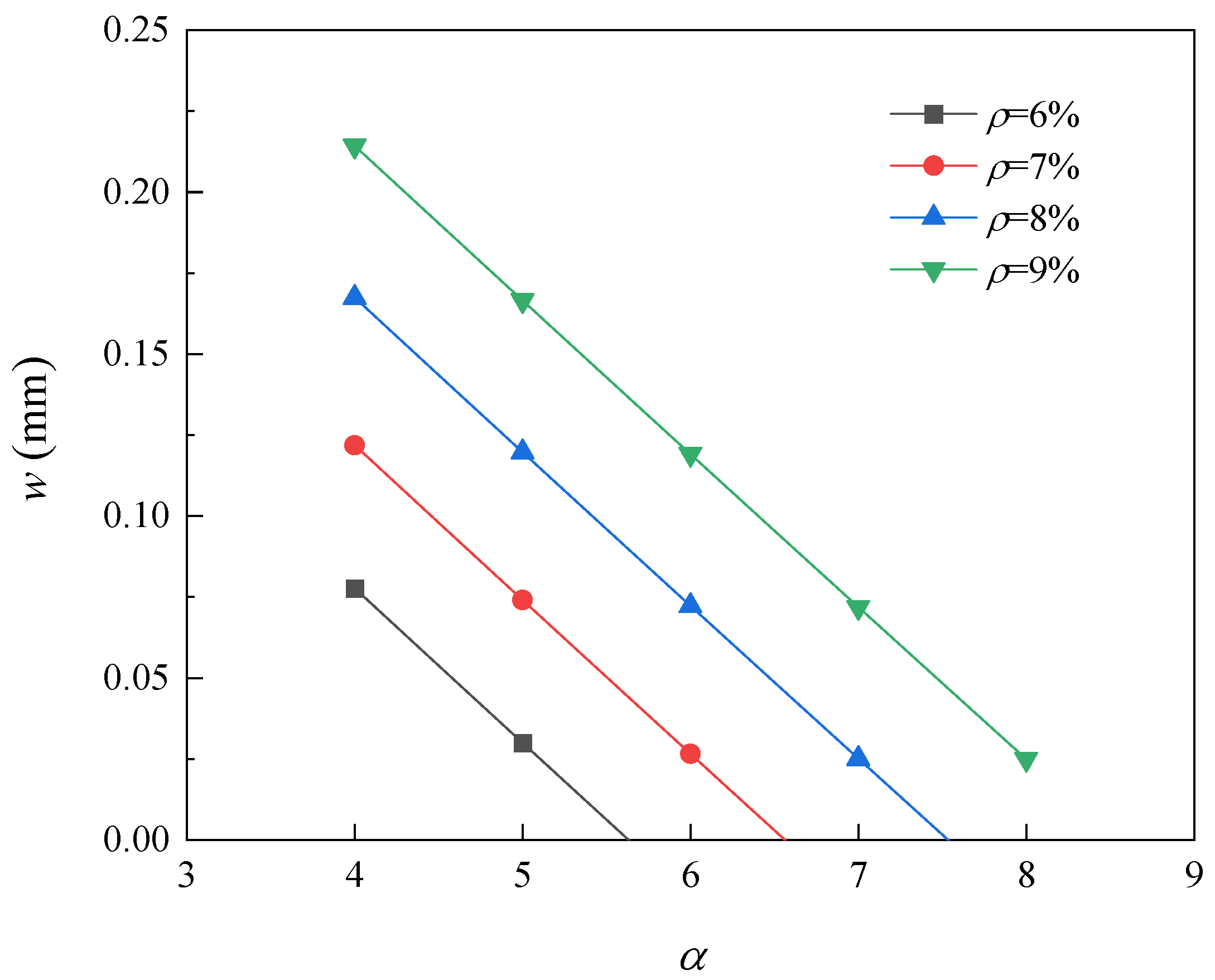
Preprints 82104 g006
Preprints 82104 g007
Figure 7. Influence of concrete cover thickness on pit depth during cracking.
Figure 7. Influence of concrete cover thickness on pit depth during cracking.
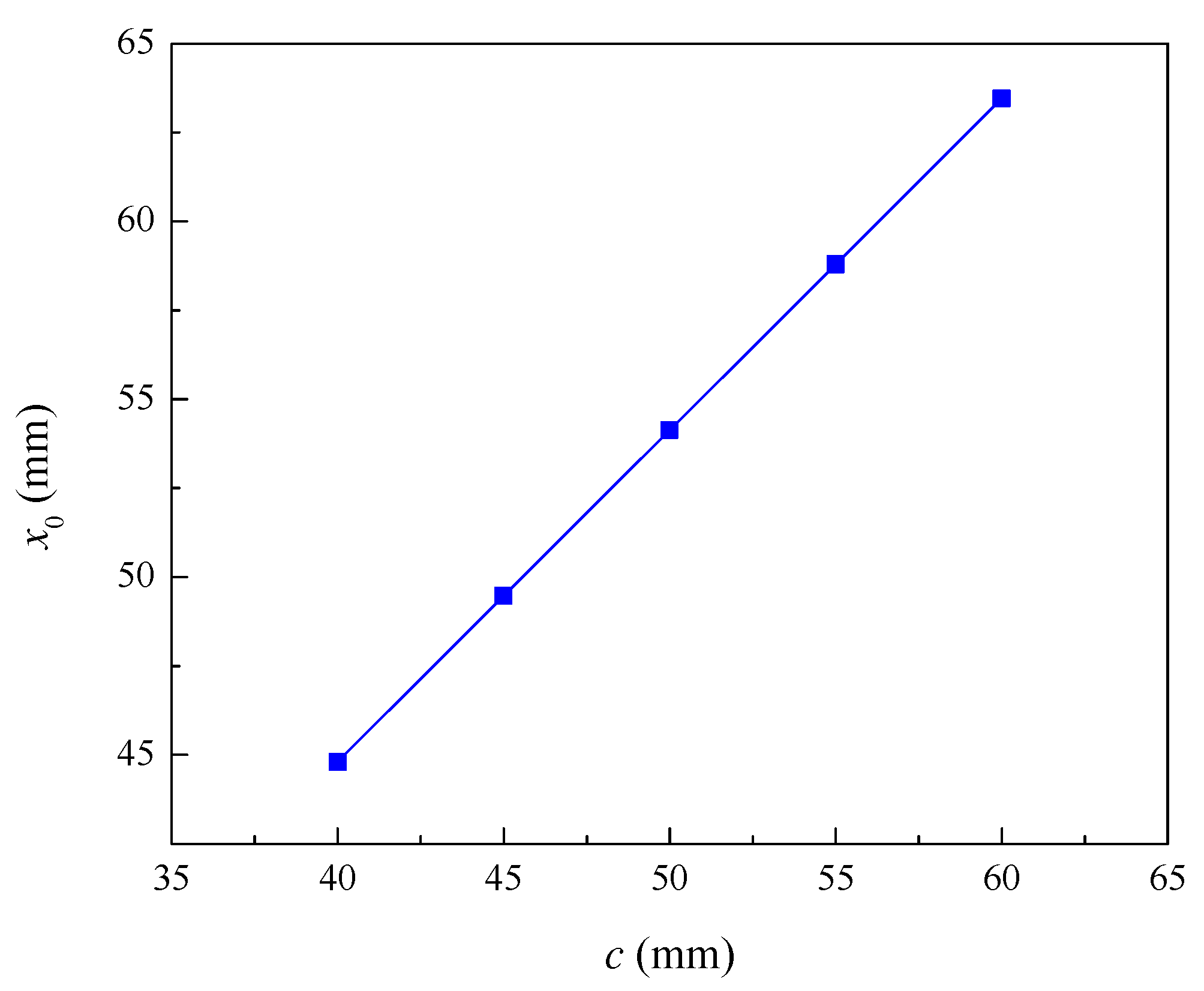
Preprints 82104 g007
Preprints 82104 g008
Figure 8. Effect of concrete cover thickness on crack width.
Figure 8. Effect of concrete cover thickness on crack width.
Preprints 82104 g008
Preprints 82104 g009
Figure 9. Effect of initial diameter on corrosion pit radius and loss of reinforcement cross-section.
Figure 9. Effect of initial diameter on corrosion pit radius and loss of reinforcement cross-section.
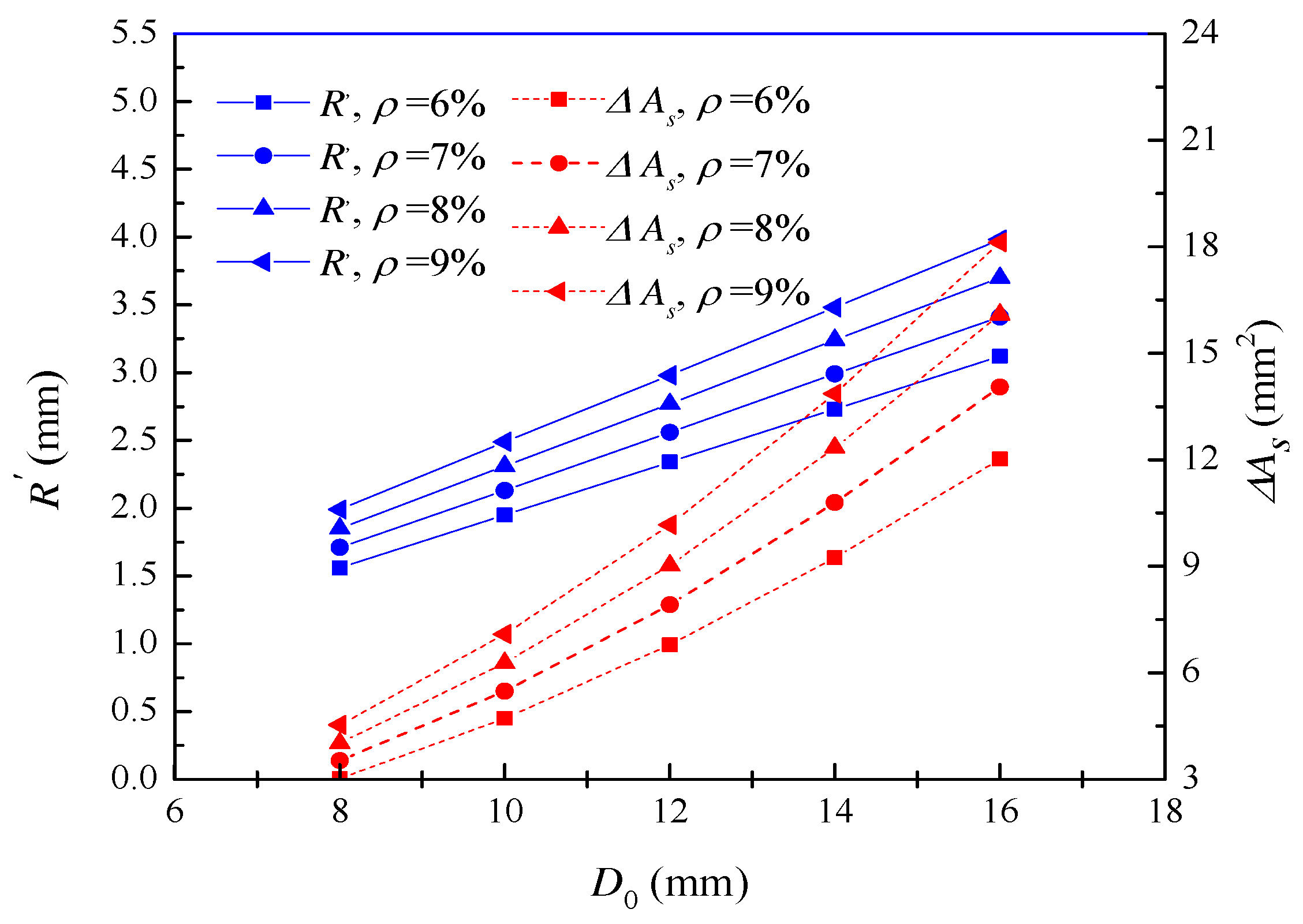
Preprints 82104 g009
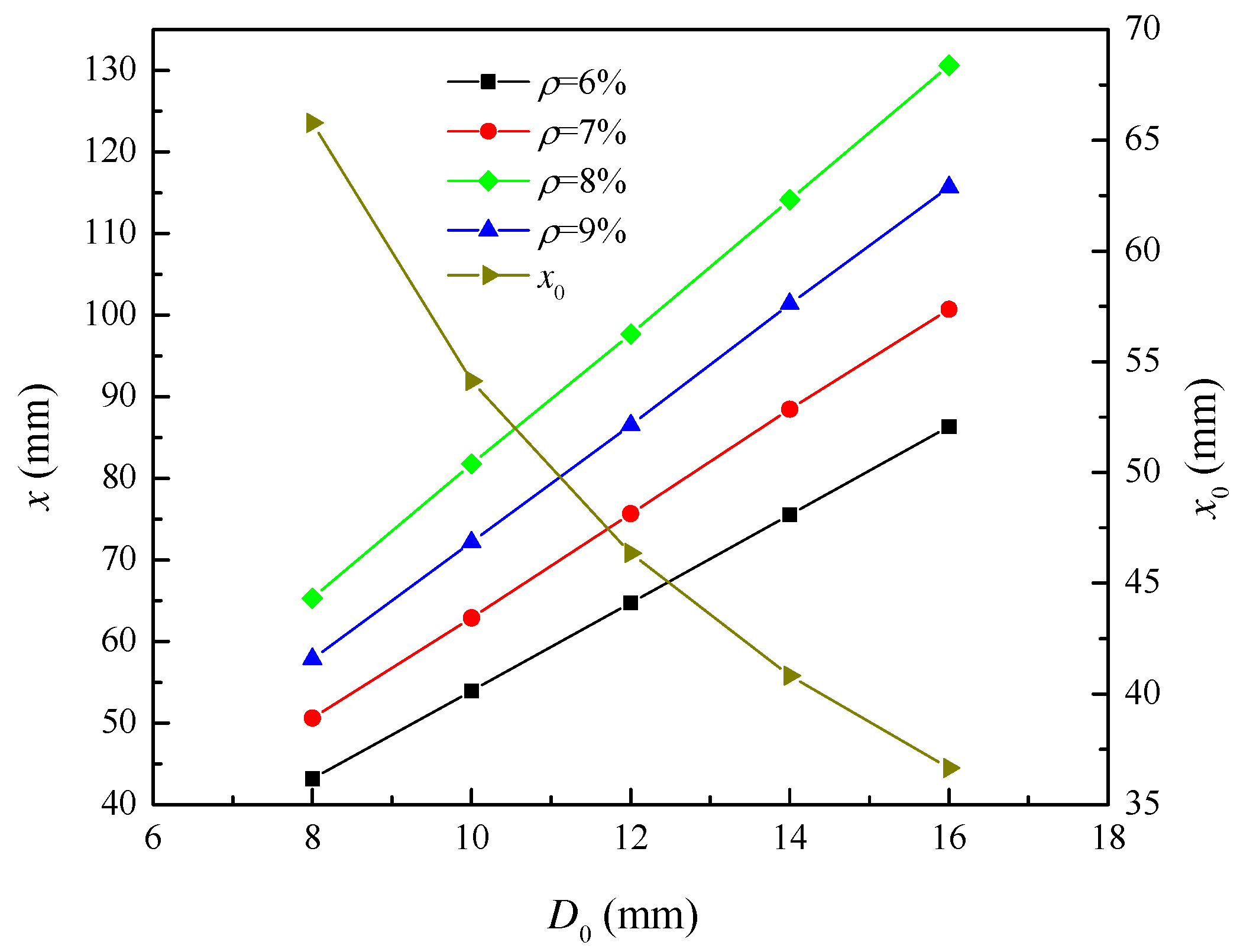
Preprints 82104 g010
Figure 10. Influence of initial diameter on the pit depth at the initiation of cracking and the pit depth during corrosion.
Figure 10. Influence of initial diameter on the pit depth at the initiation of cracking and the pit depth during corrosion.
Preprints 82104 g010
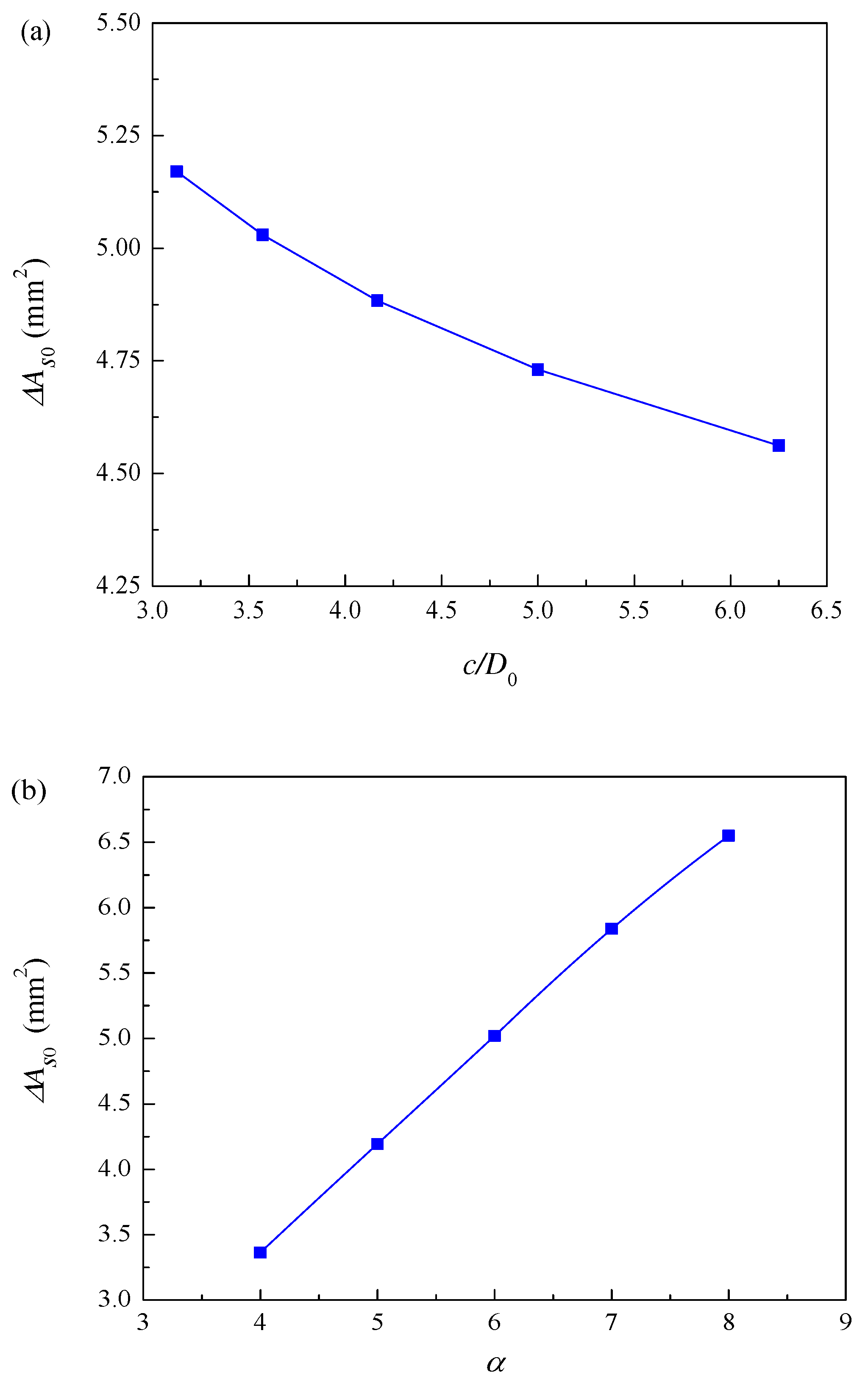
Preprints 82104 g011
Figure 11. Influence of factors on the local reinforcement cross-section loss at the initiation of cracking: (a) the ratio of cover thickness to initial diameter; and (b) pitting factor.
Figure 11. Influence of factors on the local reinforcement cross-section loss at the initiation of cracking: (a) the ratio of cover thickness to initial diameter; and (b) pitting factor.
Preprints 82104 g011
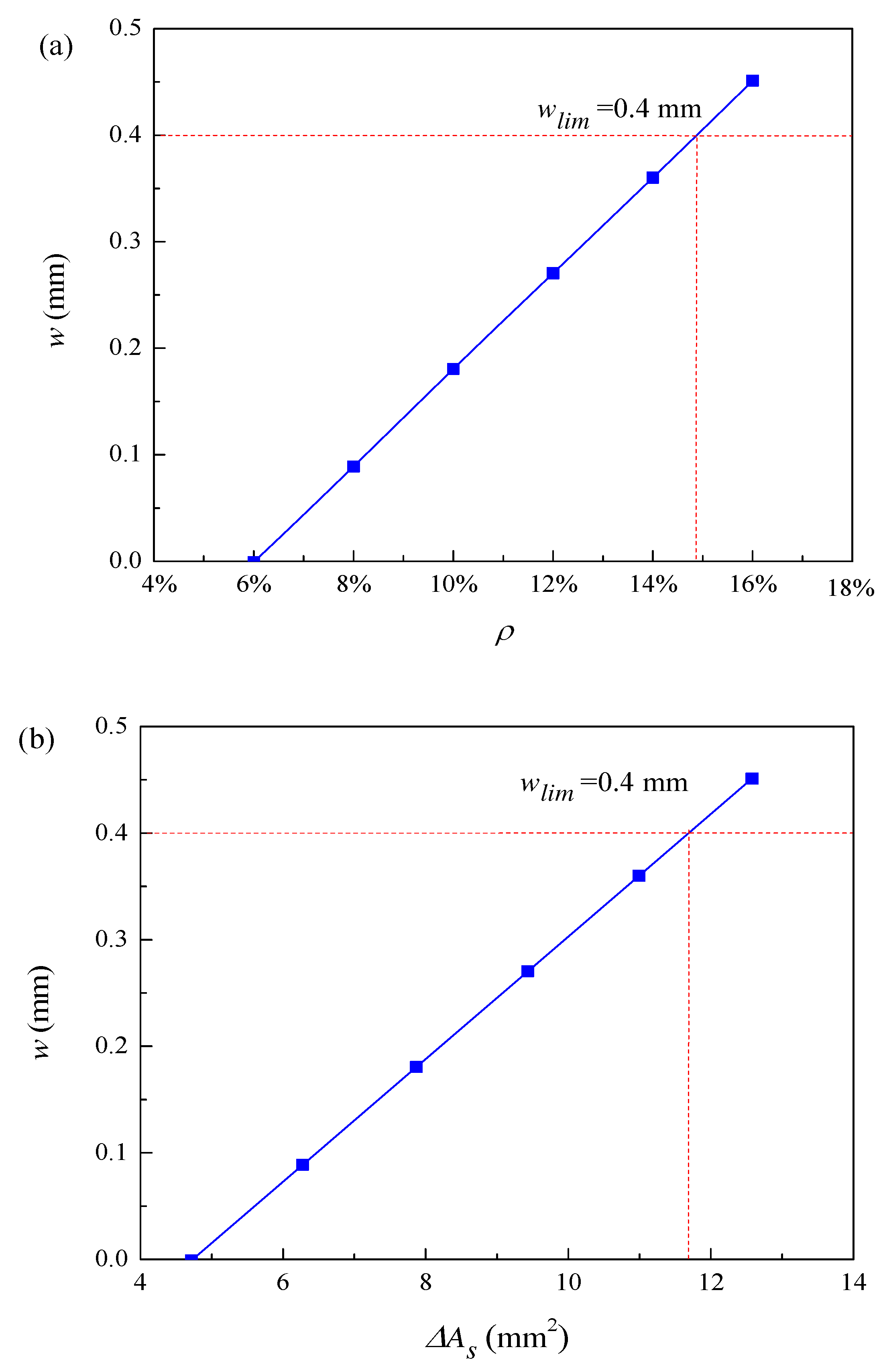
Preprints 82104 g012
Figure 12. Effect of different factors on crack width: (a) corrosion degree; and (b) Loss of reinforcement cross-sectional area.
Figure 12. Effect of different factors on crack width: (a) corrosion degree; and (b) Loss of reinforcement cross-sectional area.
Preprints 82104 g012
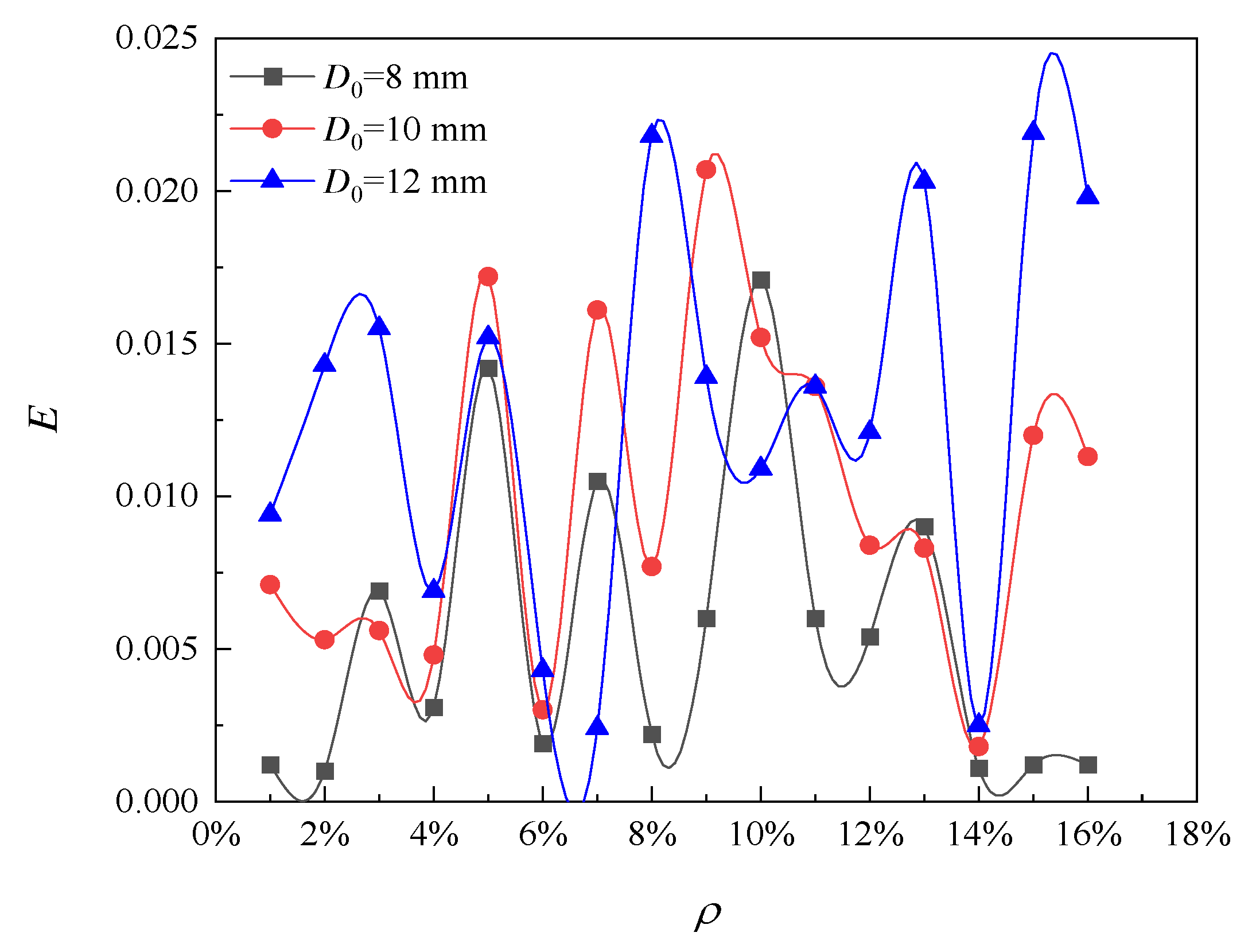
Preprints 82104 g013
Figure 13. Effect of diameter change on error.
Figure 13. Effect of diameter change on error.
Preprints 82104 g013
Table 1. Values of main parameters used in the analysis.
Table 1. Values of main parameters used in the analysis.
Parameters Unit Values Description Reference
a mm 190 Inner radius of pile
b mm 300 Outside radius of pile
D0 mm 10 Initial diameter of steel bar
c mm 50 Concrete cover thickness
wlim mm 0.4 Limit crack width [27]
α 5.65 Pitting factor [17]
K 0.0575 slope of curve [28]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated