Preprint
Article
Marcus Cross-Relationship Probed by Time-Resolved CIDNP
Altmetrics
Downloads
103
Views
34
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.docx (14.69KB )
This version is not peer-reviewed
Submitted:
10 August 2023
Posted:
10 August 2023
You are already at the latest version
Alerts
Abstract
The time-resolved CIDNP method can provide information about degenerate exchange reactions (DEE) involving short-lived radicals. In the temperature range from 8 to 65°C, the DEE reactions of the guanosine-5’-monophosphate anion GMP(-H)- with the neutral radical GMP(-H)•, of the N-acetyl tyrosine anion NacTyrO- with a neutral radical NacTyrO• and of the tyrosine anion TyrO- with a neutral radical TyrO• were studied. In all the studied cases, the radicals were formed in the reaction of quenching triplet 2,2’-dipyridyl. The reorganization energies were obtained from Arrhenius plots. The rate constant of the reductive electron-transfer reaction in pair GMP(-H)•/TyrO- was determined at T = 25°C. Rate constants of GMP(-H)• radical reduction reactions with TyrO- and NacTyrO- anions calculated by the Marcus cross relation differ from the experimental ones by two orders of magnitude. The rate constants of several other electron transfer reactions involving GMP(-H)-/•, NacTyrO-/•, and TyrO-/• pairs calculated by cross relation agree well with the experimental values. The rate of nuclear paramagnetic relaxation was found for the 3,5 and β-protons TyrO• and NacTyrO•, the 8-proton GMP(-H)• the 3,4-protons DPH• at each temperature. In all cases, the dependences of the rate of nuclear paramagnetic relaxation on temperature are described by the Arrhenius dependence.
Keywords:
Subject: Chemistry and Materials Science - Physical Chemistry
1. Introduction
The kinetics of electron transfer reactions is described by Marcus' theory [1]. According to this theory, the rate constant of the electron transfer reaction is expressed as follows:
where λ is the reorganization energy, ΔG° is the driving force of the reaction.
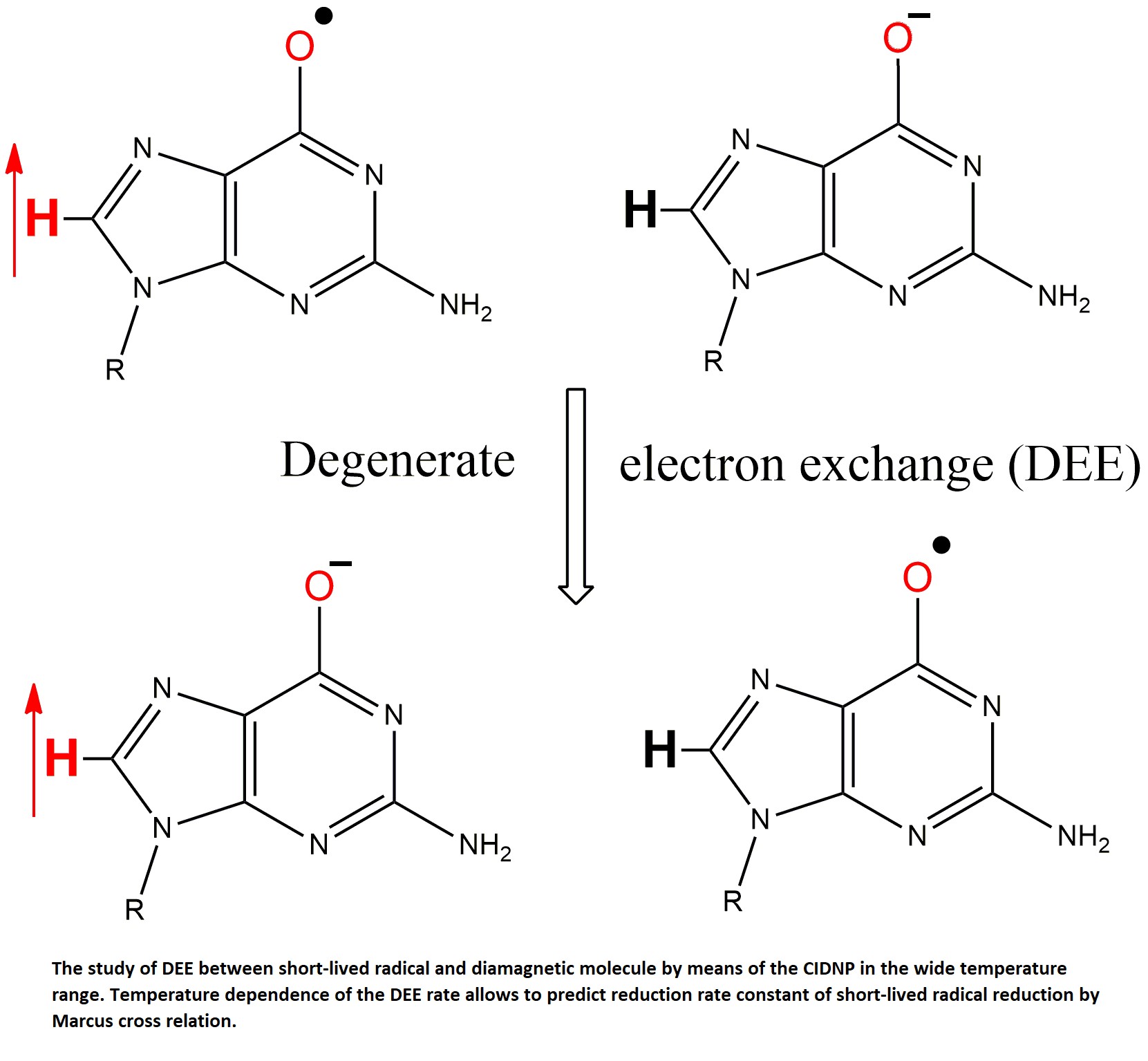
The electron transfer reaction is called degenerate if the donor and acceptor differ by only one electron. Degenerate reactions of electron exchange constitute a special section of Marcus theory because the rate constant k12 and the reorganization energy λ12 of an arbitrary electron transfer reaction can be estimated through the equilibrium constant of the cross-reaction K12 and the rate constants k11, k22 and the reorganization energies λ11, λ22 of the corresponding degenerate electron exchange (DEE) reactions [1]:
Equations 2-4 are used to estimate the DEE rate constants if the cross-reaction rate constant and one of the DEE rate constants are known [2,3,4]. When the rate constants are known only at a single temperature then A11 = A22 = 1011 M-1s-1 is often assumed, that introduce an error in the value being determined.
The purpose of this work is to probe the applicability of the Marcus cross-relation with the better accuracy that is provided by knowing of the temperature dependences of the corresponding DEE rate constants. In this case the value of the rate constant of reductive electron transfer to short-lived radical calculated from the cross-relation does not contain the errors due to the uncertainty of the pre-exponent values of the DEE rate constants, since the latter are determined from the temperature dependences of the rates.
To test the Marcus cross-relation, we chose the reduction reactions of the short-lived GMP(-H)• radical by tyrosine (TyrO-) and N-acetyl tyrosine (NacTyrO-) anions. The DEE reactions cannot be studied using optical methods, since there is no change of reactants concentration in course of the reaction, thus the total optical density does not change. The methods for studying DEE reactions between stable reactants (transition metal complexes in different oxidation states, long-lived radicals with the corresponding diamagnetic molecules) usually employ modification one of the reactants. Such methods include the use of deuterated ligands [5], optical isomers [6], and radioactive isotopes [7]. All these methods are not suitable for studying DEE involving short-lived radicals. The DEE reactions between stable reagents can also be studied using line broadening in EPR spectrum [8,9,10,11] or in NMR spectra [12,13,14]. These methods are also not applicable to short-lived radicals, when the lifetime of the radicals is so short that it is impossible to record their EPR or NMR spectra under normal conditions.
The photoinduced time-resolved chemical induced nuclear polarization (tr-CIDNP) method [15,16,17,18,19,20,21,22,23] fortunately allows to study degenerate exchange reactions involving short-lived radical intermediates [24,25,26]. It is an indirect way of radical intermediates detection that are formed by short laser pulse via quantitative analysis of anomalous enhancement or emission of NMR lines of the diamagnetic reaction products and their dependence on time after a laser pulse.
The reduction reaction of the neutral radical GMP(-H)• by the anions of tyrosine TyrO- and N-acetyltyrosine NacTyrO-, was studied by the tr-CIDNP method; dipyridyl (DP) was used as a dye. The CIDNP kinetics for the systems GMP + DP [27], NacTyrOH + DP [28] and GMP + NacTyrOH + DP [29] were previously studied at t = 25ºC in a wide pH range. The temperature dependence for the DEE rate constant in the GMPH+/GMPH++• pair was also measured earlier [30]. In the temperature range 8-65ºC we measured the DEE rate constants in the pairs GMP(-H)-/GMP(-H)•, TyrO-/TyrO• and NacTyrO-/NacTyrO•. From these temperature dependences of the rate constants the reorganization energies were determined; and with use of their values and Marcus cross relation, the rate constants of the GMP(-H)• radical reduction reaction by TyrO- and NacTyrO- anions were calculated. We compared the calculated rate constants with the measured at t = 25ºC electron transfer reaction rate constant for GMP(-H)• + TyrO- and the previously determined reaction rate constant for the reactants GMP(-H)• + NacTyrO- [29].
2. Results
2.1. Mechanism of CIDNP effect
The CIDNP spectra recorded during irradiation of solutions containing DP + GMP(-H)-, DP + TyrO- with signal attribution are shown in Figure 1. The spectra were recorded with zero delay after the laser pulse, without internal standard, the dependence of water chemical shifts on temperature was used: δ(HDO) = 5.060 – 0.0122t + (2.11*10-5)t2 (t in ºC) [31] to relate the chemical shifts.
The CIDNP signal origins as follows. The dye molecule D absorbs a quantum of light and transition from the ground singlet state S0 to the excited singlet state S1 occurs. Due to inter system crossing (ISC) the S1 molecule state converts to the triplet electronic state. Then, as a result of diffusion motion, the dye molecule D in the triplet state encounter the quencher Q, which quenches the dye triplet state by means of electron transfer with a rate constant kq. The radical pair formed in course of this reaction preserves the triplet electron state of the precursor. At the instant of their formation, the radicals are situated in the solvent “cage”. They cannot react back to the ground diamagnetic states due to the conservation of the total electron spin. In order for this to happen, the radical pair must change to the singlet state. Such a transition from the triplet to singlet state (and vice versa) can happen due to the difference of Larmor frequencies of the radicals in the field of the NMR spectrometer (at different g- factors) and due to hyperfine couplings of electron spins of the radicals with magnetic nuclei. Thus, in the high field of NMR spectrometer the rate of singlet-triplet transitions depends, besides of g-factor difference, on the nuclear spin projections along the magnetic field, configuration of nuclei spins (S-T0 mechanism of CIDNP formation in strong magnetic fields). Therefore, the in-cage, geminate, recombination products are enriched in those nuclear spin states that have a higher singlet-triplet interconversion rate. However, the total polarization of nuclear spins does not change since the geminate reaction gives rise only to the sorting between the nuclear polarization of geminate diamagnetic products and the polarization of the radicals which escaped into the bulk of solution. Consequently, at the initial instant of time (on the scale of T1 nuclear relaxation time in radicals) the nuclear polarization of radicals escaped in the bulk of solution is equal in magnitude and opposite in sign to the polarization of diamagnetic products formed in the course of geminate recombination.
The sign of CIDNP signal Г of geminate diamagnetic products is determined by the Kaptein rule [32] Г = μ•sgn(Δg)•sgn(A), where μ = +1 in the case of a triplet precursor and μ = –1 in the case of a singlet one; sgn(Δg) is the sign of the g-factor difference of the radicals; sgn(A) is the sign of the hfi-coupling constant of the corresponding nucleus. The value of the g-factor of the neutral GMP(-H)• radical is equal to 2.0034 [33], g-factors for the TyrO• and NacTyrO• radicals are 2.0041 [34] and 2.0055 [35], respectively. The sign of the hfi-coupling constant of the H-8 proton of the GMP(-H)• radical is negative [33], for TyrO• and NacTyrO• the sign of the hfi-coupling constants of the H-3,5 protons is also negative, and of the H-2,6,β protons is positive [34, 35]. There are no experimental data for the DPH• radical, the calculated hfi-coupling constants of the H-3,4,5,6 protons are negative [32], and the value of the g-factor of the DP-• radical anion is equal to 2.0030 [33]. Kaptein's rule holds for all signals in all 1H CIDNP spectra obtained in this work.
2.2. Experimental data processing
Theoretical fitting of the CIDNP kinetics measured for the systems GMP(-H)- + DP, NacTyrO- + DP, TyrO- + DP was performed within the Fisher model [36]. The model takes into account the nuclear polarization transfer from radical into diamagnetic molecule due to the second-order radical recombination, paramagnetic nuclear relaxation in radicals, arising of polarization within re-contacts of radicals in the bulk, and polarization transfer from radical to molecule as a result of DEE. The system of three Eqns. (5-7) describes the time evolution of the radical pair concentration R(t), the nuclear polarization in radicals PR(t), and the experimentally registered nuclear polarization in diamagnetic molecules PPr(t):
with initial condition: PPr(t=0) = –PR(t=0) = PG.
here R0 is the initial concentration of radical pairs; kR is the rate constant for the second-order radical recombination; T1 is the nuclear spin relaxation time in radicals; kobs is the rate constant for DEE; Cq is the concentration of diamagnetic quencher molecules; parameter β = γPG/R0 shows the amount of polarization arising in one secondary radical pair (the radical pairs formed by radicals escaped from different geminate pairs, so-called F-pairs); γ is the ratio of CIDNP polarization formed in the secondary radical pair to the polarization in the geminate pair, in the case of a triplet precursor one has γ ≈ 3, usually is taken γ = 2.8 [27]; PG is the geminate polarization.
The system of Eqns. (5-7) is written assuming that the fraction of geminate recombination of radical pairs is negligible and that the radical formation due to quenching of the triplet state of the dye occurs instantaneously. Eq. (5) describes the time dependence of the radical concentration, which decreases according to the second-order recombination kinetics. The first terms in Eqns. (6-7) describe transfer of polarization from radicals to diamagnetic molecules due to the recombination of radicals, the third terms in both Eqns. (6-7) describe transfer of polarization from radicals to diamagnetic molecules due to DEE process. The second terms in Eqns. (6-7) describe the polarization forming as a result of radicals encounter in the bulk, i.e. in F-pairs. The fourth term in Eq. (6) describes the decay of nuclear polarization in radicals as a result of nuclear paramagnetic relaxation.
Under experimental conditions, there is a DPH•/DP pair (pKa(DPH•) > 14, [37]) . The possible electron and proton transfer (PCET) is much slower than the electron transfer and cannot affect the CIDNP kinetics of DP protons. Therefore, when modeling the kinetic curves for nuclear polarization of DP, we took kobs = 0.
In the system GMP(-H)- + TyrO- + DP, the kinetics of nuclear polarization is also affected by the reduction reaction of the GMP(-H)• radical by the TyrO- anion. Then, the time evolution of the concentrations of GMP(-H)•, TyrO• and DPH• radicals and the polarizations of the nuclei in PRGMP, PRTyr radicals, and PPrGMP, PPrTyr diamagnetic molecules are described by the following equations:
with initial conditions: PPrGMP(t=0) = –PRGMP(t=0) = PGGMP, PPr Tyr(t=0) = –PRTyr(t=0) = PGTyr, here kRGMP, kRTyr are the recombination rate constants of the radicals DPH• with GMP(-H)• and TyrO• radicals respectively, kobsred is the observed rate constant of reduction of the GMP(-H)• radical by tyrosinate-anion, βGMP = γPGGMP/R0GMP, βTyr = γPGTyr/R0Tyr .
In the process of solving this system of equations, the parameters kRGMP/kRTyr and kqGMP/kqTyr are introduced, through the latter the ratio of initial concentrations of GMP(-H)• and TyrO• radicals is expressed.
The initial concentration of radical pairs R0 is proportional to the fraction of light absorbed by the dye. The TyrO-, NacTyrO- compounds absorb at λ = 308 nm, as the concentration of tyrosine in the solution increases, the fraction of light absorbed by DP decreases and, accordingly, the initial concentration of radical pairs decreases as well. The ratio of initial concentrations of radical pairs in two experiments with different concentrations of tyrosine is as follows:
In Eq. (15) εDP, εTyr are the extinction coefficients at λ = 308 nm; CDP is DP concentration; C1Tyr, C2Tyr are tyrosine concentrations; εDP = 1.2*103 M-1cm-1 [38], εTyrOˉ = εNacTyrOˉ = 790±8 M-1cm-1 was determined in this work. This effect was taken into account when modeling CIDNP kinetics in systems containing TyrO- and NacTyrO-.
The duration of the RF pulse (1-2 μs) is comparable with the characteristic time of the CIDNP decay, so it is necessary to take into account the polarization evolution during the RF pulse. Consideration of the CIDNP kinetics during the RF pulse for the special case of an ideal rectangular pulse is considered in [39], the case of an RF pulse of arbitrary shape is considered in [40]. The similar approach was used in the works of Morozova and Yurkovskaya [41,42,43,44,45,46,47,48].
To take into account the CIDNP kinetics during the application of the RF pulse along the x-axis, we considered the following system of equations that takes into account the polarization of the nuclei along the y, z axes:
where w(t) is the pulse shape, the equation for dPPr/dt is given by Eq. (7), before the pulse PPry = 0. The signal observed in the experiment is proportional to the after pulse value of PPry. The expression for polarization along the y-axis after the pulse is as follows [39]:
where t0 is the start time of the RF pulse, T is its duration.
The duration of the π pulse is equal to tπ = 12.70 µs. The shapes of RF pulses of 1 and 2 µs duration used in this work were determined using an oscilloscope.
2.3. Results of CIDNP kinetics treatment
In the GMP(-H)- + DP system, the polarization-time dependences were modeled for 8-th GMP protons and 3,4 DP protons. In the TyrO- + DP, NacTyrO- + DP systems, the dependences were modeled for 3,5 and β-protons of tyrosine, and 3,4 protons of DP – the other signals have too low signal-to-noise ratio. In the GMP(-H)- + TyrO- + DP system, CIDNP polarization time dependences were modeled for 8-th GMP protons and 3,5 tyrosine protons. Values of the degenerate electron exchange rate constants and paramagnetic nuclear relaxation times obtained from the best agreement between the calculated and experimental curves are given in Table 1, Table 2 and Table 3; Figure 2(a-c) shows the examples of simulations of these experimental data.
For the GMP(-H)- + DP we did not determine T1 for 3,4 protons of DP at 65°C because perdeuterated d8-DP was used due to the overlapping the 1H NMR signals of H-8 of GMP and H-3,4 of DP. For NacTyrO- + DP at 65°C and TyrO- + DP at 45°C we failed to determine T1 for H-β.
For GMP(-H)- + DP at 25ºC, the value of the DEE rate constant differs from the literature data, while the paramagnetic relaxation time of the 8-th proton in the GMP(-H)• radical coincides well with the literature data: kobs = 4.0*107 M-1s-1, T1 =20 μs [27]. Moreover, the T1 for the 8-th proton in the GMP(-H)• radical coincides with the previously found T1 for the 8-th proton in the GMPH++• radical over the entire temperature range [30]. For the NacTyrO- + DP at t = 25ºC the values of the DEE rate constant and paramagnetic relaxation time of 3,5 protons coincide with the literature data: kobs = 6.0*107 M-1s-1, T1 =63 µs [29]; = 4*107 M-1s-1, T1 = 60 µs [49]. However, the best fit values of nuclear paramagnetic relaxation times for 3,4 protons in the DPH• radical do not coincide with the literature data T1 = 44 µs [28, 38, 50] and T1 = 45 µs [49].
Simulation of the experimental data for DP + GMP(-H)- + TyrO- is shown in Figure 2-d, the parameters found are: kobsred = 1.5*108 M-1s-1, kqGMP/kqTyr = 0.3, kRGMP/kRTyr = 1.3. The parameters kobsGMP, kobsTyr, T1GMP, and T1Tyr found in this work were used in the calculation. There are literature data for the reduction of GMP(-H)• radical by NacTyrO- anion: kobsred = 1.6*108 M-1s-1, kqGMP/kqTyr = 0.56, kRGMP/kRTyr = 0.9 [29].
- a) TyrO- + DP at t = 65°C, kinetics for H-3.5 TyrO-, black – C(TyrO-) = 1.5 mM, blue – C(TyrO-) = 2.5 mM, red – C(TyrO-) = 3.5 mM;.
- b) TyrO- + DP at t = 65°C, kinetics for H-β TyrO-, black – C(TyrO-) = 1.5 mM, blue – C(TyrO-) = 2.5 mM, red – C(TyrO-) = 3.5 mM;.
- c) GMP(-H)- + DP at t = 45°C, kinetics for H-8 GMP(-H)-, black – C(GMP) = 6.5 mM, red – C(GMP) = 13 mM;.
- d) GMP(-H)- + TyrO- + DP at t = 25ºC, kinetics for H-8 GMP(-H)-, black – C(TyrO-) = 1.3 mM, red – C(TyrO-) = 2.5 mM, insert – kinetics for H-3.5 TyrO-, black – C(TyrO-) = 1.3 mM, red – C(TyrO-) = 2.5 mM.
2.4. Temperature dependence of the DEE rate constants
For the estimation of the effect of diffusion the following DEE kinetic scheme was considered (using tyrosine as an example):
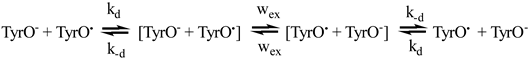
where the first-order DEE rate wex is related to the second-order rate constant ket as:
kobs is the observable DEE rate constant, kobs it is expressed through ket and kd as follows:
The diffusion rate constant kd was estimated by the Smoluchowski equation, taking into account the charges of the reactants:
where r1, r2 are the radii of the reagents; wr is the work function of approach charged reactants to each other:
we assume that the reactants approaches to the distance equal to the sum of their radii. The factor takes into account the ionic strength of the solution:
where B = (2NAe2/(ε0k))1/2 = 50.345 l1/2K1/2Å-1M-1/2.
The viscosity values of D2O were taken from [51, 52], dielectric permittivity from [53]. The average elliptical radii of the reactants were used to estimate r1 and r2. An ellipsoid of the smallest volume was described around the molecule and the radius was expressed as [54]:
where F(φ,α) is an elliptic integral of the first kind; φ = arcsin((a2 – c2)1/2/a); α = ((a2 – c2)/(a2 – b2))1/2; a, b, c are the semiaxes of the ellipsoid, a ≥ b ≥ c.
The ellipsoid semiaxes were calculated using the algorithm N. Shor [55] with the molecular geometries of the crystal structures of DL-tyrosine [56], N-acetyl-L-tyrosine and guanosine-5'-monophosphate trihydrate [57]. The molecular radii found: r(GMP(-H)-) = 4.18 Å, r(NacTyrO-) = 3.82 Å, r(TyrO-) = 3.06 Å, we assumed that the radii of the radicals do not differ from those of the corresponding diamagnetic particles.
When calculating wr, the negatively charged carboxyl and phosphate groups in the reactants were taken into account: z(GMP(-H)-) = -3, z(TyrO-) = -2.
The ket values calculated by Eq.(20) are given in the last columns of Table Error! Reference source not found.-Error! Reference source not found..
The first-order DEE rate constant wex depends on temperature as [1]:
The second-order DEE rate constant ket is expressed as follows:
The KA in Eq. (26) is the equilibrium constant of pre-reaction complex formation; it depends on temperature as follows [58] :
where is the reaction zone thickness. Then the second-order rate constant ket depends on temperature as:
The work function wr depends on the temperature through dependence on temperature of the D2O dielectric permittivity, at each temperature wr can be calculated by Eq. (22). To find the pre-exponent A and the reorganization energy λ, we plot the values of ln[ket√Texp(wr/RT)], where the ket values are experimental ones, versus 1/T (Figure 3) and and approximated these points by linear dependence. The values of A and λ found from the approximation are given in Table 4.
Previously we studied [30] the temperature dependence of the DEE rate constant between the GMPH+ cation and the GMPH++•, dication radical, the reorganization energy found for this reaction is λ = 0.79 ± 0.11 eV [21] and coincides with the value for GMP(-H)- + GMP(-H)• (see Table Error! Reference source not found.).
2.5. The Marcus cross-relation equation
To account for the effects of diffusion the following kinetic scheme of electron transfer was considered (for the radical GMP(-H)• reduction by anion TyrO- as an example):
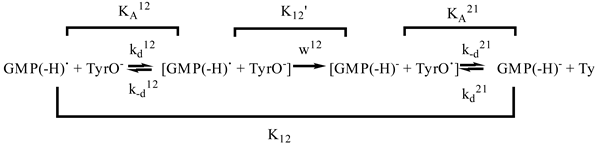
where the first-order rate w12 is related to the second-order rate constant k12 as:
The observable second-order rate constant kobs12 is expressed through k12 and kd12 as follows:
The rate constants k12(TyrO-) and k12(NacTyrO-) of GMP(-H)• reduction by TyrO- and NacTyrO- respectively after correction for diffusion (kd was calculated according Eq. (21)) are the following: k12(TyrO-) = 1.7*108 M-1s-1 and k12(NacTyrO-) = 1.8*108 M-1s-1 [29]. Thus, the values of the reduction rate constants are very close.
The rate constant w12 depends on the temperature as follows:
where ΔG12º’ is the driving force of the first-order redox reaction.
The equilibrium constant between the initial reactants and reaction products K12 is expressed as:
here KA12 and KA21 are the equilibrium constants of the formation of pre-reaction and post-reaction complexes, expressed by Eq. (27). Assuming the radii of radicals and corresponding diamagnetic particles are the same, the pre-exponents in Eq. (32) the factors KA12 and KA21 can be shortened (reduced). The ΔG12º value is expressed through standard electrode potentials, thus, ΔG12º’ can be calculated.
The expression for the second-order electron transfer rate constant k12 is given as follows:
If the electron transfer occurs over a relatively long distance with a weak force interaction between the reactants, then one can assume that λ12 = (λ11 + λ22)/2 that is the Marcus cross relation, where λ11, λ22 are the reorganization energies for the respective DEE reactions.
If we additionally assume the following ratio between the pre-exponents: A12 = (A11A22)1/2, then we can express k12 through the temperature dependence parameters of the DEE rate constants. Thus, the cross-reaction rate constant kcalc12 was calculated employing the following formula:
2.5.1. Reactants parameters for the Marcus cross-relation calculations
The cross-relation calculations require the values of the difference of standard electrode potentials, the reorganization energy and the pre-exponent for the corresponding DEE reactions, as well as the radii of all reactants and products to calculate the work function. In all the cases, we assume that the radii of radicals and corresponding diamagnetic particles are the same.
If only the DEE rate constant at a certain temperature is known, we estimate the pre-exponent as: A11 = 1011 M-1s-1 and calculate the reorganization energy by Eq. (35).
All the parameters of the reactants are given in Table 5. The Zred column shows the charge of the reduced form of each reactant. The structures of some reactants are shown in Figure 4.
The TyrO•/TyrO- case. The standard electrode potential is E° = 0.72 V [59]. The radius calculation is described above, the pre-exponent and reorganization energy for the DEE reaction were found experimentally in this work.
The NacTyrO•/NacTyrO- case. We use the value of the standard electrode potential for N-acetyltyrosine methyl ester at pH = 7, E7 = 0.97 V [60]. pKa(NacTyrOH) = 10.1, then Eº = 0.79 V. The calculation of the radius is described above; the pre-exponent and reorganization energy for the DEE reaction were found experimentally in this work.
The GMP(-H)•/GMP(-H)- case. The standard electrode potential of GMP at pH = 7, E7 = 1.31 V [61], determined from photoinduced electron transfer reaction rates, that agrees well with that of guanosine at pH = 7, E7 = 1.29 V [62], determined by pulsed radiolysis. The acidity constants of GMP [63] and its radical [64,65,66] are shown in Figure 4. For GMP(-H)•/GMP(-H)- the calculated potential is: Eº = 1.23 V.
The GMPH++•/GMPH+ case. The standard electrode potential E° = 1.55 V, calculated from E7 = 1.29 V [62]. The pre-exponent and reorganization energy for the DEE reaction were found earlier [30]. Average elliptical radius r = 4.19 Å, calculated by the method described above, the geometry was taken from the crystal structure of guanosine-5'-monophosphate trihydrate [57]
The NacTrpH+•/NacTrpH case, we use the value of the standard electrode potential for tryptophan, E° = 1.15 V [59]. The DEE rate constant at 25°C is k11 = 9*108 M-1s-1 was determined experimentally by CIDNP with microsecond resolution [38]. After correction for diffusion by Eq. (20) one has: k11 = 1.3*109 M-1s-1. The mean elliptical radius r = 3.83 Å was calculated by the method described above, geometry from was taken from the NacTrpH crystal structure [67]. We assume that A11/√T = 1011 M-1s-1, then λ = 0.45 eV.
The ClO2•/ClO2- case. The standard electrode potential E° = 0.934 V [68]. The DEE constant at 25°C is k11 = 3.3*104 M-1s-1, determined from a cross relation with parameters A11/√T = 1011 M-1s-1, r = 1.5 Å [69]. Then λ11 = 1.53 eV.
The N3•/N3- case. The standard electrode potential E° = 1.33 V [68]. The DEE rate constant at 25°C k11 = 3.7*106 M-1s-1, determined from a cross relation with parameters A11/√T = 1011 M-1s-1, r = 2 Å [69]. Then λ11 = 1.05 eV.
The NO2•/NO2- case. The standard electrode potential E° = 1.04 V [68]. The DEE rate constant at 25°C k11 = 580 M-1s-1, determined experimentally by isotopic substitution [70]. We assume that A11/√T = 1011 M-1s-1, then λ = 1.95 eV. The radius r = 1.9 Å [69].
The [IrCl6]2-/[IrCl6]3- case. The standard electrode potential E° = 0.892 V [71]. The DEE constant at 25°C k11 = 2.3*105 M-1s-1, determined experimentally by isotopic substitution [72]. We assume that A11/√T = 1011 M-1s-1. Radius r = 4.4 Å [73], DEE rate constant measured at μ = 0.1 M. Then λ = 1.04 eV.
The CysS•/CysS- case. The standard electrode potential E° = 0.76 V [74]. The DEE rate constant at 25°C k11 = 5.4*103 M-1s-1, determined from the Marcus cross relation with parameters A11/√T = 1011 M-1s-1, r = 3.0 Å, the k12 cross-reaction rate constant was measured at μ = 0.1 M [74]. Then λ = 1.48 eV.
The TEMPO+/TEMPO• case. The standard electrode potential E° = 0.745 V [75]. The DEE rate constant at 25°C kobs = 8.6*107 M-1s-1, determined experimentally by line broadening in the EPR spectrum [76]. After correction for diffusion by Eq. (20), k11 = 8.8*107 M-1s-1. We assume that A11/√T = 1011 M-1s-1. Then λ = 0.72 eV. The radius r = 3.67 Å [76].
Figure 5.
Structures of N-acetyltryptophan (NacTrpH), guanosine-5'-monophosphate cation (GMPH+), cysteine anion (CysS-), stable free radical TEMPO – (2,2,6,6-tetramethylpiperidin-1-yl)oxyl.
Figure 5.
Structures of N-acetyltryptophan (NacTrpH), guanosine-5'-monophosphate cation (GMPH+), cysteine anion (CysS-), stable free radical TEMPO – (2,2,6,6-tetramethylpiperidin-1-yl)oxyl.
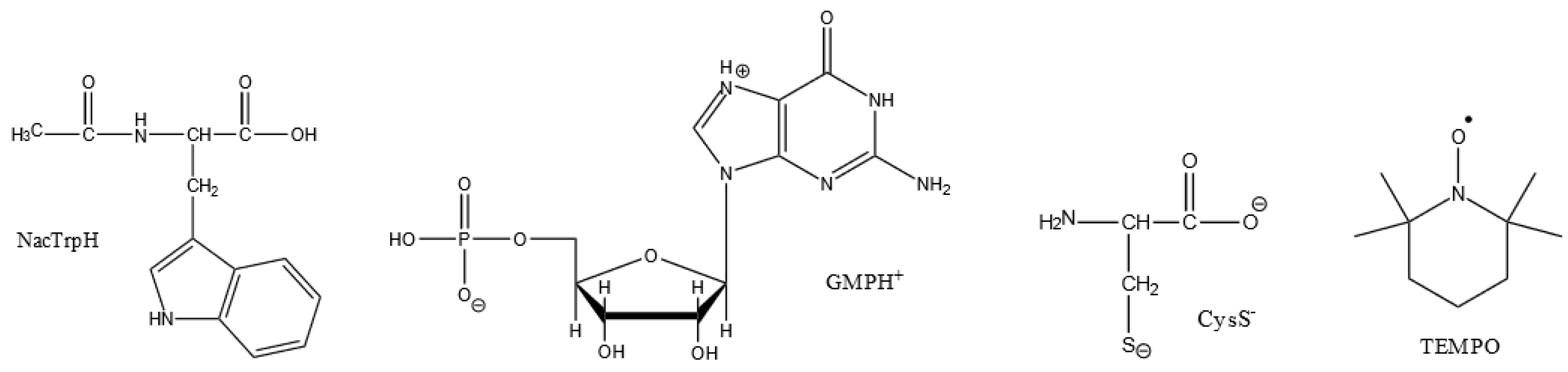
Table 5.
Parameters of the reactants for the Marcus cross-relation calculations.
| DEE reaction | E°, V | ln(A) | λ, eV | r, Å | Zred |
|---|---|---|---|---|---|
| GMP(-H)- + GMP(-H)• | 1.23 | 31.7 | 0.82 | 4.18 | -3 |
| GMPH+ + GMPH++• | 1.55 | 29.2 | 0.79 | 4.19 | 0 |
| NacTyrO- + NacTyrO• | 0.79 | 27.0 | 0.50 | 3.82 | -2 |
| TyrO- + TyrO• | 0.72 | 30.2 | 0.81 | 3.06 | -2 |
| ClO2- + ClO2• | 0.934 | 28.2 | 1.53 | 1.5 | -1 |
| N3- + N3• | 1.33 | 28.2 | 1.05 | 2.0 | -1 |
| NO2• + NO2- | 1.04 | 28.2 | 1.95 | 1.9 | -1 |
| [IrCl6]2- + [IrCl6]3- | 0.892 | 28.2 | 1.04 | 4.4 | -3 |
| TEMPO• + TEMPO+ | 0.745 | 28.2 | 0.72 | 3.67 | 0 |
| CysS- + CysS• | 0.76 | 28.2 | 1.57 | 3.0 | -2 |
| NacTrpH + NacTrpH+• | 1.15 | 28.2 | 0.45 | 3.83 | 0 |
2.6. The T1 temperature dependence.
The temperature dependences of the nuclear paramagnetic relaxation times T1 were obtained by means of the CIDNP kinetics simulation. We assume that the main mechanism of relaxation is modulation of the hyperfine interaction (hfi) tensor due to the stochastic rotation of the molecule as a whole. Then the nuclear paramagnetic relaxation time T1 should depend on the magnetic field B and the rotational correlation time of the molecule as follows:
If the diffusive stochastic rotation of the radical is fast, , then the nuclear paramagnetic relaxation rate 1/T1 is proportional to ; the value of can be estimated from the Stokes-Einstein-Debye equation:
According to [51, 52], the temperature dependence of D2O viscosity in the temperature range 8 - 65ºC is well described by the following equation:
where E/R = 2059 K, η0 = 1.14*10-6 Pa*s.
Then the T1 temperature dependence should be described by the following equation:
where C, E/R are parameters, E/R = 2059 K.
The T1 temperature dependence, Eq. (39) is linearized in the coordinates ln(T/T1) vs 1/T (Figure 6).
While fitting by straight lines we discarded by the dropout values. Found values from the slopes of the straight lines E/R are summarized in Table 6. For 3,5 protons NacTyrO•, 8-th proton GMP(-H)•, H3,4 DPH• protons the slopes coincide within an error with the slope from viscosity dependence. The slope for ТyrO• 3,5 protons is almost twice as different from that for viscosity. Earlier we found the slope for the 8-th proton GMPH++•, it also coincides with the slope from viscosity dependence.
For the H-3,5 of NacTyrO•, H-8 of GMP(-H)•, and H-3,4 of DPH• the slopes of the fitted straight lines coincide with the slope for viscosity within an error margin, indicating that rotational modulation of the hfi tensor is the main mechanism of nuclear paramagnetic relaxation of these protons.
The defined energy value E for the 3,5 TyrO• protons is notably different from that for the viscosity dependence. This result can be rationalized assuming that for these protons two mechanisms gives rise to paramagnetic relaxation: modulation of the hfi tensor due to stochastic rotation of the molecule as a whole and modulation of the hfi tensor due to stochastic rotation of the phenolic ring. Assuming that the ring rotation has a small activation energy, the temperature dependence of the correlation time τe for this rotation is as follows:
while the temperature dependence of the rotational correlation time τM is:
Then the nuclear relaxation time T1 can be expressed employing Lipari-Szabo [77, 78] equation:
where S2 is an order parameter, playing the role of the dimensionless amplitude of molecular motion: the smaller S2, the larger the amplitude; Th is the temperature when the correlation times τe and τM coincide, C2 = C1exp(E/(R·Th).
The temperature dependence of the ln(T/T1) on 1/T has the form:
here E/R = 2059 K is the activation energy for D2O viscosity. There are three fit parameters: C, S2, Th. The value S2 = 0.01 was taken for the fit. The best fit of the experimental data is then achieved at Th = 850 K, see Figure 7.
The paramagnetic relaxation time T1 of the methylene protons (β-CH2 protons) in the NacTyrO• and ТyrO• radicals is almost independent on temperature (Tables Error! Reference source not found.-Error! Reference source not found.). We assume that probably the paramagnetic relaxation of β-CH2 protons occurs also due to the modulation of hfi tensor by intramolecular rotations around the aliphatic bonds. These rotations can have low activation energy, so in a small range of temperatures the rotational frequency changes weakly, which causes the apparent independence of the relaxation time T1 on the temperature.
3. Discussion
3.1. Comparison of the calculation and experiment
A comparison of the electron transfer reaction rate constants calculated from the Marcus cross relation and those found in the experiment are shown in Table 7 The experimental rate constants were corrected for diffusion by Eq. (30).
Rate constants were calculated by Eq. (34) with parameters from the Table 7. All experimental rate constants were measured at 25°C. We assume that parameters of the dipeptide Gly-TyrO- do not differ from those of the NacTyrO- and parameters of the amide N-acetyltyrosine NacTyrO--NH2 differ from those of NacTyrO- only in charge.
The agreement with the experiment for reactions involving GMPH+/++•, GMP(-H)-/• is noticeably worse than for reactions involving TyrO-/•, NacTyrO-/•. If GMP is an oxidizing agent, the calculated rate value is overestimated, and when GMP is a reducing agent, the calculated value is underestimated. Perhaps the values of standard potentials for GMPH+/++•, GMP(-H)-/• are overestimated, if the error would be in the pre-exponent or in the reorganization energy of GMP, the values would be overestimated or underestimated in all reactions involving GMP, regardless of whether it is oxidation or reduction.
For the reactions TyrO- + GMP(-H)•, NacTyrO- + GMP(-H)• the calculated rate values notably differ from the experimental values than in other GMP involving reactions. Probably this difference can be explained not only by the overestimation of potential of GMP(-H)-/•, but also by other causes.
For reactions involving TyrO-/•, NacTyrO-/• the calculated values agree well with the experimental values. In the case of the reaction TyrO- + N3•, the experimental rate constant is close to the diffusion rate constant; the calculation shows that the reaction occurs in the diffusion control limit; the calculation shows good agreement with the experiment.
3.2. The possible reasons for the failure of the Marcus cross-relation in the reactions of GMP(-H)• radical reduction by TyrO-, NacTyrO- anions.
The Marcus cross-relation is fulfilled under the following conditions: the value of ΔG12° is not too large, the reaction is far from the inverted region; the reactants and products are in the ground state; the electron transfer is adiabatic [1, 88]. Also the size difference of the reactants should not be very large (2λ12 ≈ λ11 + λ22 requires 2(r11r22)1/2 ≈ r11 + r22), otherwise the expression for the cross relation should be modified [89] .
The Marcus cross-relation for reactions of transition metal complexes was verified in [90,91,92] and for reactions of organic molecules in [93, 94]. The Marcus cross-relation for redox reactions between organic TMPPD and various inorganic oxidating ions was tested in [95]. A good linear relation over a range of seven orders of magnitudes was found. As a rule, the calculated according to the cross-relation reaction rate constant turns out to be greater than the experimental one; the error increases with the growth of K12. In the above-mentioned works, verification of the cross-relation was done for rate constants measured only at one temperature with the employment of Eqns. (2-4). In these equations, the parameter ln(f12) = -(ΔG12°)2/(2RTλ12), f12 ≈ 1 at ΔG12° << λ12. But at large ΔG12° this parameter contributes significantly, and its calculation requires values of the pre-exponents for DEE reactions. In these works, estimates on the order of 1011 were taken for the values of the pre-exponents. We believe that this can introduce an error when K12 is large. In this work, the values of the pre-exponents and reorganization energies of DEE were determined experimentally; that allows to exclude this error. In particular, it turned out that the pre-exponent in the case of GMP is two orders of magnitude greater than the 1011 M-1s-1.
In the course of reactions no any isomer product is formed since as it is seen from the CIDNP spectra the electron is transferred only within the aromatic π-systems of the reactants.
When describing the kinetics of electron transfer, the pre-exponent includes the factor κ, which has the meaning of the probability of electron transfer while passing into transition state. For adiabatic reactions κ = 1, the parameter κ is close to unity if there is substantial overlap of the reactant orbitals [96]. For reactions of organic molecules, κ = 1 is usually assumed [93, 97]. In addition, possible nonadiabaticity is taken into account in the cross relation as κ12 = (κ11κ22)1/2.
The steric cross-reacting factor is included in the pre-exponent A12 and is estimated as the geometric mean of the steric factors of the DEE, i.e. A12 = (A11A22)1/2.
Another possible reason for the failure of the Marcus cross-relation can be effect of non-electrostatic interactions between the reactants. In the pairs TyrO-/TyrO•, GMP(-H)-/GMP(-H)•, TyrO-/GMP(-H)• the stacking interactions increasing the stability of pre-reaction complexes are possible. Assume that contribution ΔHº of the stacking-interaction to the enthalpy change of the pre-reaction complex formation is independent of temperature and ΔHº < 0. Then the expressions for the DEE and cross-reaction rate constants taking into account the stacking-interaction are as follows:
In Eq. (47), we assume that ΔH12º ≈ ΔH21º. The Eq.(46) shows that when treating the temperature dependence of the DEE rate constants by the method described above (i.e. considering only the electrostatic interactions), the found values of the reorganization energies λ11obs will be underestimated: λ11obs = λ11 + 4ΔH11º.
Consideration of the stacking-interaction on the one hand increases the calculated cross-reaction rate constant kcalcred due to the factor exp(-ΔH 12º/RT), on the other hand it decreases, as the calculated reorganization energy increases. The final result depends on the values of ΔH11º, ΔH22º, ΔH12º. When ΔH11º = ΔH22º = ΔH12º = -RT the calculated value of kcalcred increases by 1.4 times, when ΔH11º = ΔH22º = -RT, ΔH12º = 0 it decreases by 2 times.
Marcus cross-relation fails if the electron transfer reaction produces products in the vibrationally-excited state.
When we assume that the overlap of the orbitals in the TyrO-/GMP(-H)• pair is less than in the TyrO-/TyrO•, GMP(-H)-/GMP(-H)• pairs, then the electronic factor of the cross-reaction appears to be less than that calculated from the cross relation, κ12 < (κ11κ22)1/2. The enthalpy of the stacking-interaction for the cross-reaction turns out to be lower than for the DEE reactions. This gives rise to the fact that the cross-reaction rate constant is less than the one we calculated without taking these effects into account.
4. Materials and Methods
The set-up for time-resolved CIDNP experiments was based on a Bruker DRX-200 NMR spectrometer (magnetic field 4.7 Tesla, resonance frequency of protons 200 MHz). A detailed scheme of the setup and methodology of the experiment were published in a review devoted to the application of time-resolved CPNR for studying the kinetics and mechanism of reactions of biologically important molecules [98].
The 1H CIDNP spectra were recorded as follows. First, the sample in a standard 5 mm NMR Pyrex ampule was barbotaged with argon for 7 min to remove dissolved oxygen. Then, the sample was placed in the NMR spectrometer sensor and broadband homonuclear de-coupler pulses were applied for a few seconds on channel 1H to suppress the thermal magnetization of the sample. The pulse sequence WALTZ16 was used. The parameters of the sequence were chosen so that the 1H NMR signals were completely absent from the spectrum without laser irradiation. After that, the sample in the ampoule was irradiated with a single laser pulse of the excimer XeCl-laser COMPEX Lambda Physik (wavelength 308 nm, pulse energy up to 120 mJ, pulse duration ~15 ns), and after time interval τ a registering radiofrequency (RF) pulse with a maximum allowable power -4 dB and duration 1 or 2 μs was applied. After the pulse was applied, the decay of the free induction signal was recorded in the same way as in the conventional NMR experiment. The delay τ was varied in the range from 0 to 100 µs.
The temperature was calibrated by the difference of chemical shifts in the 1H NMR spectrum of methanol, the temperature measurement error 1K [99].
The pH of the NMR samples was adjusted by addition of NaOD. No correction was made for the deuterium isotope effect on the pH. Experiments with TyrO- and NacTyrO- were performed at pH = 11.7, with GMP(-H)- and GMP(-H)- + TyrO- at pH = 11.3. At t = 25ºC the pKa of phenol groups TyrOH and NacTyrOH are 10.1 and 10.2 [100], pKa(GMP) = 9.4 [63], pKa(GMP(-H)•) = 10.8 [64], but deprotonation is slow and the GMP(-H)- radical is stable at pH = 11.8 for at least 1000 µs [27]. The 2,2'-dipyridyl (DP) was used as a dye (photosensitizer); its concentration was 15 mM in all experiments. The concentrations of quencher Cq were chosen so that the characteristic quenching time kq-1Cq-1 was shorter than the duration of the recording RF pulse (1-2 μs), and so that a rapid decline in polarization due to too high a product of the observed DEE rate constant and the quencher concentration, kobsCq, was avoided. The compositions of all samples are given in supplementary information.
The GMP in the form of sodium salt hydrate (mass fraction of water 23.4% was determined by 1H NMR), NacTyrOH, TyrOH, D2O from "Sigma-Aldrich" were used without additional purification, DP was recrystallized from hexane. For the experiment GMP(-H)- + DP at 65ºC, d8-DP was used because the signals from DP and GMP overlapped each other. The structures of the studied diamagnetic particles GMP(-H)-, NacTyrO-, TyrO-, DP, and the previously studied GMPH+ are shown in Figure 8.
At each temperature, two or three kinetic curves differing in the quencher concentration were recorded. To record each kinetic curve, 4 samples were used for the GMP(-H)- + DP, NacTyrO- + DP, TyrO- + DP systems and 8 samples for the GMP(-H)- + TyrO- + DP system. Each sample was used twice, the delays were followed in increasing order and in decreasing order to reduce the error from depletion. At each time delay, 4 scans (6 for TyrO- + DP at 55°C and 65°C) were taken, so each point of the kinetic curve corresponds to 64 signal accumulations for GMP(-H)- + TyrO- + DP, 48 signal accumulations for TyrO- + DP at T = 55°C, 65°C, 32 signal accumulations for GMP(-H)- + DP, NacTyrO- + DP, TyrO- + DP at T = 8-45°C. A 2 μs RF pulse was used for GMP(-H)- + TyrO- + DP and TyrO- + DP at T = 55°C, 65°C; otherwise, a 1 μs RF pulse was used.
All standard electrode potentials Eo used are reported versus NHE.
5. Conclusions.
The CIDNP technique with microsecond time resolution makes it possible to study the kinetics of DEE reactions for the short-lived radicals and determine the DEE reaction rate constant by performing the reaction at different concentrations of the diamagnetic reactant.
The degenerate electron exchange reactions of the neutral radicals GMP(-H)•, TyrO•, NacTyrO• with anions GMP(-H)-, TyrO-, NacTyrO- in alkaline aqueous media were studied by CIDNP in the temperature range 8-65ºC.
At each temperature chosen in this range, all parameters of CIDNP kinetics were determined, and the experimental values of reorganization energies for the DEE rate constants were found. At the t = 25ºC the rate constant of GMP(-H)• reduction by TyrO- anion was measured.
The agreement of the calculated rate constants employing Marcus cross relation approach with the experimental ones for the reactions involving GMPH+/++•, GMP(-H)-/• is poor, perhaps an overestimated values of the standard electrode potentials for GMPH+/++•, GMP(-H)-/• are used.
The rate constants of GMP(-H)• radical reduction by tyrosine and N-acetyltyrosine anions calculated from the cross relation differ by almost two orders of magnitude from those found experimentally, which is a notably greater difference than that for the other reactions involving GMP-• species. Possible causes for this difference are the not taking into account the nonadiabaticity of the cross-reaction and the enthalpy of the stacking interaction between the reactants in the calculation.
At the same time, the calculated rate constants according to the cross-relation of electron transfer reactions involving TyrO-/•, NacTyrO-/• coincide well with the literature values.
It was also found that the dependences of the nuclear paramagnetic relaxation rate T1 on temperature are described by the Arrhenius dependence; for the methylene protons in the tyrosine and N-acetyltyrosine radicals TyrO• and NacTyrO• these dependencies are almost activationless, while for the NacTyrO• 3,5 protons, GMP(-H)• 8-th proton and 3,4 protons of DPH• the activation energy value coincides with the solvent (D2O) activation energy. This indicates a difference in relaxation mechanisms for these protons: relaxation in the methylene protons of the TyrO• and NacTyrO• radicals occurs due to the modulation of the hfi tensor due to ring inversion, while relaxation in the 3,5 protons of NacTyrO• and 8-th proton of the GMP(-H)• occurs due to modulation of the hfi tensor due to stochastic rotation of the molecule as a whole. The intermediate type of the temperature dependence of the nuclear paramagnetic relaxation rate T1 is observed for the 3,5 protons of the TyrO• radical: the activation energy was about half the activation energy for the solvent viscosity. We assume that the both relaxation mechanisms manifest themselves in this case.
Author Contributions
Conceptualization, M.P.G, A.V.Y, G.G, N.N.L.; validation, M.P.G, A.V.Y, G.G, N.N.L..; investigation, O.B.M, A.V.Y, M.P.G; writing— original draft preparation M.P.G, A.V.Y, G.G, N.N.L.; writing—review and editing, M.P.G, A.V.Y, G.G, N.N.L; project administration, A.V.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ministry of Science and Higher Education of the Russian Federation grant 075-15-2020-779.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Marcus, R.A.; Sutin, N. Electron transfers in chemistry and biology. Biochimica et Biophysica Acta (BBA)-Reviews on Bioenergetics 1985, 811, 265–322. [Google Scholar] [CrossRef]
- Zerk, T.J.; Saouma, C.T.; Mayer, J.M.; Tolman, W.B. Low Reorganization Energy for Electron Self-Exchange by a Formally Copper (III, II) Redox Couple. Inorganic chemistry 2019, 58, 14151–14158. [Google Scholar] [CrossRef]
- Xie, B.; Wilson, L.J.; Stanbury, D.M. Cross-Electron-Transfer Reactions of the [CuII/I(bite)]2+/+ Redox Couple. Inorganic Chemistry 2001, 40, 3606–3614. [Google Scholar] [CrossRef] [PubMed]
- Ganesan, M.; Sivasubramanian, V.K.; Rajagopal, S.; Ramaraj, R. Electron transfer reactions of organic sulfoxides with photochemically generated ruthenium(III)–polypyridyl complexes. Tetrahedron 2004, 60, 1921–1929. [Google Scholar] [CrossRef]
- Meyer, T.J.; Taube, H. Electron-transfer reactions of ruthenium ammines. Inorganic Chemistry 1968, 7, 2369–2379. [Google Scholar] [CrossRef]
- Dwyer, F.P.; Sargeson, A.M. The Rate of Electron Transfer Between the Tris-(Ethylenediamine)-Cobalt (II) and Cobalt (III) Ions. The Journal of Physical Chemistry 1961, 65, 1892–1894. [Google Scholar] [CrossRef]
- Krishnamurty, K.V.; Waiil, A.C. Kinetics of the Vanadium(II)-Vanadium(III) Isotopic Exchange Reaction. Journal of the American Chemical Society 1958, 80, 5921–5924. [Google Scholar] [CrossRef]
- Grampp, G.; Landgraf, S.; Rasmussen, K. Electron self-exchange kinetics between 2,3-dicyano-5,6-dichloro-p-benzoquinone (DDQ) and its radical anion. Part 1. Solvent dynamical effects. Journal of the Chemical Society, Perkin Transactions 2 1999, 9, 1897–1899. [Google Scholar] [CrossRef]
- Grampp, G.; Rasmussen, K. Solvent dynamical effects on the electron self-exchange rate of the TEMPO/TEMPO+ Couple (TEMPO= 2, 2, 6, 6-Tetramethyl-1-Piperidinyloxy Radical) Part I. ESR-Linebroadening measurements at T= 298 K. Physical Chemistry Chemical Physics 2002, 4, 5546–5549. [Google Scholar] [CrossRef]
- Mladenova, B.; Kattnig, D.R.; Kaiser, C.; Schäfer, J.; Lambert, C.; Grampp, G. n. Investigations of the Degenerate Intramolecular Charge Exchange in Symmetric Organic Mixed Valence Compounds: Solvent Dynamics of Bis (triarylamine) paracyclophane Redox Systems. The Journal of Physical Chemistry C 2015, 119, 8547–8553. [Google Scholar] [CrossRef]
- Grampp, G.; Mladenova, B.Y.; Kattnig, D.; Landgraf, S. ESR and ENDOR investigations of the degenerate electron exchange reactions of various viologens in solution. Solvent dynamical effects. Applied Magnetic Resonance 2006, 30, 145–164. [Google Scholar] [CrossRef]
- Chan, M.-S.; Wahl, A.C. Rate of electron exchange between iron, ruthenium, and osmium complexes containing 1, 10-phenanthroline, 2, 2'-bipyridyl, or their derivatives from nuclear magnetic resonance studies. The Journal of Physical Chemistry 1978, 82, 2542–2549. [Google Scholar] [CrossRef]
- Koval, C.A.; Margerum, D.W. Determination of the self-exchange electron-transfer rate constant for a copper (III/II) tripeptide complex by proton NMR line broadening. Inorganic Chemistry 1981, 20, 2311–2318. [Google Scholar] [CrossRef]
- Parker, J.F.; Choi, J.-P.; Wang, W.; Murray, R.W. Electron Self-exchange Dynamics of the Nanoparticle Couple [Au25(SC2Ph)18]0/1− By Nuclear Magnetic Resonance Line-Broadening. The Journal of Physical Chemistry C 2008, 112, 13976–13981. [Google Scholar] [CrossRef]
- Closs, G.L.; Miller, R.J. Laser flash photolysis with NMR detection. Microsecond time-resolved CIDNP: separation of geminate and random-phase processes. J. Am. Chem. Soc. 1979, 101, 1639–41. [Google Scholar] [CrossRef]
- Closs, G.L.; Miller, R.J.; Redwine, O.D. Time-resolved CIDNP: applications to radical and biradical chemistry. Acc. Chem. Res. 1985, 18, 196–202. [Google Scholar] [CrossRef]
- Morozova, O.B.; Yurkovskaya, A.V.; Tsentalovich, Y.P.; Forbes, M.D.E.; Hore, P.J.; Sagdeev, R.Z. Time resolved CIDNP study of electron transfer reactions in proteins and model compounds. Mol. Phys. 2002, 100, 1187–1195. [Google Scholar] [CrossRef]
- Morozova, O.B.; Yurkovskaya, A.V.; Tsentalovich, Y.P.; Forbes, M.D.E.; Sagdeev, R.Z. Time-Resolved CIDNP Study of Intramolecular Charge Transfer in the Dipeptide Tryptophan-Tyrosine. J. Phys. Chem. B 2002, 106, 1455–1460. [Google Scholar] [CrossRef]
- Goez, M.; Kuprov, I.; Hore, P.J. Increasing the sensitivity of time-resolved photo-CIDNP experiments by multiple laser flashes and temporary storage in the rotating frame. J. Magn. Reson. 2005, 177, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Morozova, O.B.; Korchak, S.E.; Sagdeev, R.Z.; Yurkovskaya, A.V. Time-Resolved Chemically Induced Dynamic Nuclear Polarization Studies of Structure and Reactivity of Methionine Radical Cations in Aqueous Solution as a Function of pH. J. Phys. Chem. A 2005, 109, 10459–10466. [Google Scholar] [CrossRef]
- Kuprov, I.; Goez, M.; Abbott, P.A.; Hore, P.J. Design and performance of a microsecond time-resolved photo-chemically induced dynamic nuclear polarization add-on for a high-field nuclear magnetic resonance spectrometer. Rev. Sci. Instrum. 2005, 76, 084103/1-084103/7. [Google Scholar] [CrossRef]
- Wörner, J.; Chen, J.; Bacher, A.; Weber, S. Non-classical disproportionation revealed by photo-chemically induced dynamic nuclear polarization NMR. Magn. Reson. 2021, 2, 281–290. [Google Scholar] [CrossRef]
- Pompe, N.; Illarionov, B.; Fischer, M.; Bacher, A.; Weber, S. Completing the Picture: Determination of 13C Hyperfine Coupling Constants of Flavin Semiquinone Radicals by Photochemically Induced Dynamic Nuclear Polarization Spectroscopy. J. Phys. Chem. Lett. 2022, 13, 5160–5167. [Google Scholar] [CrossRef] [PubMed]
- Goez, M. The Degenerate Electron Exchange between N, N-Dimethylanilines and their Radical Cations. Zeitschrift für Physikalische Chemie 1990, 169, 133–145. [Google Scholar] [CrossRef]
- Schael, F.; Löhmannsröben, H.-G. The deactivation of singlet excited all-trans-1, 6-diphenylhexa-1, 3, 5-triene by intermolecular charge transfer processes. 1. Mechanisms of fluorescence quenching and of triplet and cation formation. Chemical physics 1996, 206, (1-2), 193-210.
- Closs, G.L.; Sitzmann, E.V. Measurements of degenerate radical ion-neutral molecule electron exchange by microsecond time-resolved CIDNP. Determination of relative hyperfine coupling constants of radical cations of chlorophylls and derivatives. J. Am. Chem. Soc. 1981, 103, 3217–19. [Google Scholar] [CrossRef]
- Yurkovskaya, A.V.; Snytnikova, O.A.; Morozova, O.B.; Tsentalovich, Y.P.; Sagdeev, R.Z. Time-resolved CIDNP and laser flash photolysis study of the photoreaction between triplet 2, 2′-dipyridyl and guanosine-5′-monophosphate in water. Physical chemistry chemical physics 2003, 5, 3653–3659. [Google Scholar] [CrossRef]
- Tsentalovich, Y.P.; Morozova, O.B.; Yurkovskaya, A.V.; Hore, P.J.; Sagdeev, R.Z. Time-Resolved CIDNP and Laser Flash Photolysis Study of the Photoreactions of N-Acetyl Histidine with 2,2'-Dipyridyl in Aqueous Solution. J. Phys. Chem. A 2000, 104, 6912–6916. [Google Scholar] [CrossRef]
- Morozova, O.B.; Kiryutin, A.S.; Sagdeev, R.Z.; Yurkovskaya, A.V. Electron transfer between guanosine radical and amino acids in aqueous solution. 1. Reduction of guanosine radical by tyrosine. The Journal of Physical Chemistry B 2007, 111, 7439–7448. [Google Scholar] [CrossRef]
- Geniman, M.; Panov, M.; Morozova, O.; Kiryutin, A.; Fishman, N.; Yurkovskaya, A. Temperature dependence of the degenerate electron exchange between guanosine-5′-monophosphate cation and its short-lived radical dication in aqueous solution. Russian Chemical Bulletin 2021, 70, 2375–2381. [Google Scholar] [CrossRef]
- Gottlieb, H.; Kotlyar, V.; Nudelman, A. NMR Chemical Shifts of Common Laboratory Solvents as Trace Impurities. The Journal of organic chemistry 1997, 62, 7512–7515. [Google Scholar] [CrossRef]
- Kaptein, R. Simple rules for chemically induced dynamic nuclear polarization. J. Chem. Soc. Chem Commun. 1971, (14), 732–733. [Google Scholar] [CrossRef]
- Adhikary, A.; Kumar, A.; Becker, D.; Sevilla, M.D. The Guanine Cation Radical: Investigation of Deprotonation States by ESR and DFT. The Journal of Physical Chemistry B 2006, 110, 24171–24180. [Google Scholar] [CrossRef] [PubMed]
- Tomkiewicz, M.; McAlpine, R.D.; Cocivera, M. Photooxidation and Decarboxylation of Tyrosine Studied by E.P.R. and C.I.D.N.P. Techniques. Canadian Journal of Chemistry 1972, 50, 3849–3856. [Google Scholar] [CrossRef]
- Mezzetti, A.; Maniero, A.L.; Brustolon, M.; Giacometti, G.; Brunel, L.C. A tyrosyl radical in an irradiated single crystal of N-acetyl-L-tyrosine studied by X-band cw-EPR, high-frequency EPR, and ENDOR spectroscopies. The Journal of Physical Chemistry A 1999, 103, 9636–9643. [Google Scholar] [CrossRef]
- Vollenweider, J.-K.; Fischer, H.; Hennig, J.; Leuschner, R. Time-resolved CIDNP in laser flash photolysis of aliphatic ketones. A quantitative analysis. Chemical physics 1985, 97, (2-3), 217-234.
- Mulazzani, Q.G.; Emmi, S.; Fuochi, P.G.; Venturi, M.; Hoffman, M.Z.; Simic, M.G. One-electron reduction of aromatic nitrogen heterocycles in aqueous solution. 2,2'-Bipyridine and 1,10-phenanthroline. The Journal of Physical Chemistry 1979, 10, 1582–1590. [Google Scholar] [CrossRef]
- Tsentalovich, Y.P.; Morozova, O.B.; Yurkovskaya, A.V.; Hore, P. Kinetics and Mechanism of the Photochemical Reaction of 2, 2 ‘-Dipyridyl with Tryptophan in Water: Time-Resolved CIDNP and Laser Flash Photolysis Study. The Journal of Physical Chemistry A 1999, 103, 5362–5368. [Google Scholar] [CrossRef]
- Läufer, M. Increasing the time resolution of flash CIDNP by numerical analysis: photoreduction of anthraquinone by N, N-dimethylaniline. Chemical physics letters 1986, 127, 136–140. [Google Scholar] [CrossRef]
- Goez, M. Evaluation of flash CIDNP experiments by iterative reconvolution. Chemical Physics Letters 1990, 165, 11–14. [Google Scholar] [CrossRef]
- Morozova, O.B.; Tsentalovich, Y.P.; Yurkovskaya, A.V.; Sagdeev, R.Z. Consecutive biradicals during the photolysis of 2,12-dihydroxy-2,12-dimethylcyclododecanone: low- and high-field chemically induced dynamic nuclear polarizations (CIDNP) study. J. Phys. Chem. A 1998, 102, 3492–3497. [Google Scholar] [CrossRef]
- Morozova, O.B.; Yurkovskaya, A.V.; Tsentalovich, Y.P.; Sagdeev, R.Z.; Wu, T.; Forbes, M.D.E. Study of Consecutive Biradicals from 2-Hydroxy-2,12-dimethylcyclododecanone by TR-CIDNP, TREPR, and Laser Flash Photolysis. J. Phys. Chem. A 1997, 101, 8803–8808. [Google Scholar] [CrossRef]
- Morozova, O.B.; Yurkovskaya, A.V.; Tsentalovich, Y.P.; Vieth, H.-M. 1H and 13C Nuclear Polarization in Consecutive Biradicals during the Photolysis of 2,2,12,12-Tetramethylcyclododecanone. J. Phys. Chem. A 1997, 101, 399–406. [Google Scholar] [CrossRef]
- Tsentalovich, Y.P.; Forbes, M.D.E.; Morozova, O.B.; Plotnikov, I.A.; McCaffrey, V.P.; Yurkovskaya, A.V. Spin and Molecular Dynamics in Acyl-Containing Biradicals: Time-Resolved Electron Paramagnetic Resonance and Laser Flash Photolysis Study. J. Phys. Chem. A 2002, 106, 7121–7129. [Google Scholar] [CrossRef]
- Tsentalovich, Y.P.; Morozova, O.B.; Avdievich, N.I.; Ananchenko, G.S.; Yurkovskaya, A.V.; Ball, J.D.; Forbes, M.D.E. Influence of Molecular Structure on the Rate of Intersystem Crossing in Flexible Biradicals. J. Phys. Chem. A 1997, 101, 8809–8816. [Google Scholar] [CrossRef]
- Tsentalovich, Y.P.; Yurkovskaya, A.V.; Sagdeev, R.Z.; Obynochny, A.A.; Purtov, P.A.; Shargorodsky, A.A. Kinetics of Nuclear-Polarization in the Geminate Recombination of Biradicals. Chem. Phys. 1989, 139, (2-3), 307-315.
- Yurkovskaya, A.; Grosse, S.; Dvinskikh, S.; Morozova, O.; Vieth, H.-M. Spin and molecular dynamics of biradicals as studied by low field nuclear polarization at variable temperature. J. Phys. Chem. A 1999, 103, 980–988. [Google Scholar] [CrossRef]
- Yurkovskaya, A.V.; Morozova, O.B.; Sagdeev, R.Z.; Dvinskih, S.V.; Buntkowsky, G.; Vieth, H.-M. The influence of scavenging on CIDNP field dependences in biradicals during the photolysis of large-ring cycloalkanones. Chem. Phys. 1995, 197, 157–66. [Google Scholar] [CrossRef]
- Babenko, S.V.; Kruppa, A.I. Probing the inclusion complexes of short-lived radicals with β-cyclodextrin by CIDNP. Journal of Inclusion Phenomena and Macrocyclic Chemistry 2019, 95, 321–330. [Google Scholar] [CrossRef]
- Tsentalovich, Y.P.; Morozova, O.B.; Yurkovskaya, A.V.; Hore, P.J.; Sagdeev, R.Z. Time-Resolved CIDNP and Laser Flash Photolysis Study of the Photoreactions of N-Acetyl Histidine with 2,2‘-Dipyridyl in Aqueous Solution. The Journal of Physical Chemistry A 2000, 104, 6912–6916. [Google Scholar] [CrossRef]
- Hardy, R.C.; Cottington, R.L. Viscosity of deuterium oxide and water in the range 5 to 125°C. J. Res. Natl. Bur. Stand 1949, 42, 573. [Google Scholar] [CrossRef]
- Nikol’skii, B.P.R.V.A. Spravochnik khimika [Chemist’s Handbook]. Khimiya: Moscow—Leningrad, 1962; Vol. 1, p 1075.
- Malmberg, C.G. Dielectric constant of deuterium oxide. Journal of Research of the National Bureau of Standards 1958, 60, 609–612. [Google Scholar] [CrossRef]
- German, E.; Kuznetsov, A. Outer sphere energy of reorganization in charge transfer processes. Electrochimica Acta 1981, 26, 1595–1608. [Google Scholar] [CrossRef]
- Shor, N.; Berezovskii, O. Algorithms to construct a minimum-volume invariant ellipsoid for a stable dynamic system. Cybernetics and Systems Analysis 1995, 31, 421–427. [Google Scholar] [CrossRef]
- Mostad, A.; Rømming, C.; Graver, H.; Husebye, S.; Klæboe, P.; Swahn, C. Crystal-structure of DL-tyrosine. Acta Chem. Scand 1973, 27, 401–410. [Google Scholar] [CrossRef]
- Emerson, J.; Sundaralingam, M. Zwitterionic character of guanosine 5'-monophosphate (5'-GMP): Redetermination of the structure of 5'-GMP trihydrate. Acta Crystallographica Section B: Structural Crystallography and Crystal Chemistry 1980, 36, 1510–1513. [Google Scholar] [CrossRef]
- Brunschwig, B.S.; Creutz, C.; Macartney, D.H.; Sham, T.; Sutin, N. The role of inner-sphere configuration changes in electron-exchange reactions of metal complexes. Faraday Discussions of the Chemical Society 1982, 74, 113–127. [Google Scholar] [CrossRef]
- Harriman, A. Further comments on the redox potentials of tryptophan and tyrosine. Journal of Physical Chemistry 1987, 91, 6102–6104. [Google Scholar] [CrossRef]
- Mahmoudi, L.; Kissner, R.; Nauser, T.; Koppenol, W.H. Electrode Potentials of l-Tryptophan, l-Tyrosine, 3-Nitro-l-tyrosine, 2,3-Difluoro-l-tyrosine, and 2,3,5-Trifluoro-l-tyrosine. Biochemistry 2016, 55, 2849–2856. [Google Scholar] [CrossRef]
- Fukuzumi, S.; Miyao, H.; Ohkubo, K.; Suenobu, T. Electron-transfer oxidation properties of DNA bases and DNA oligomers. The Journal of Physical Chemistry A 2005, 109, 3285–3294. [Google Scholar] [CrossRef]
- Steenken, S.; Jovanovic, S.V. How Easily Oxidizable Is DNA? One-Electron Reduction Potentials of Adenosine and Guanosine Radicals in Aqueous Solution. J. Am. Chem. Soc. 1997, 119, 617–618. [Google Scholar] [CrossRef]
- Asimov, I. Data for Biochemical Research (Dawson, RMC.; Elliott, Daphne C.; Elliott, WH.; Jones, KM; eds.). In ACS Publications: 1960.
- Candeias, L.; Steenken, S. Structure and acid-base properties of one-electron-oxidized deoxyguanosine, guanosine, and 1-methylguanosine. Journal of the American Chemical Society 1989, 111, 1094–1099. [Google Scholar] [CrossRef]
- Morozova, O.B.; Fishman, N.N.; Yurkovskaya, A.V. Kinetics of reversible protonation of transient neutral guanine radical in neutral aqueous solution. ChemPhysChem 2018, 19, 2696–2702. [Google Scholar] [CrossRef]
- Saprygina, N.N.; Morozova, O.B.; Abramova, T.V.; Grampp, G. n.; Yurkovskaya, A.V. Oxidation of Purine Nucleotides by Triplet 3, 3′, 4, 4′-Benzophenone Tetracarboxylic Acid in Aqueous Solution: pH-Dependence. The Journal of Physical Chemistry A 2014, 118, 4966–4974. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Oldfield, E. Tryptophan Chemical Shift in Peptides and Proteins: A Solid State Carbon-13 Nuclear Magnetic Resonance Spectroscopic and Quantum Chemical Investigation. Journal of the American Chemical Society 2004, 126, 4726–4734. [Google Scholar] [CrossRef] [PubMed]
- Stanbury, D.M. Reduction Potentials Involving Inorganic Free Radicals in Aqueous Solution. In Advances in Inorganic Chemistry, Sykes, A.G. Ed. Academic Press: 1989; Vol. 33, pp 69-138.
- Awad, H.H.; Stanbury, D.M. Electron transfer between azide and chlorine dioxide: the effect of solvent barrier nonadditivity. Journal of the American Chemical Society 1993, 115, 3636–3642. [Google Scholar] [CrossRef]
- Stanbury, D.M.; DeMaine, M.M.; Goodloe, G. Reactive dissolution of nitrogen dioxide in aqueous 15NO2-: the first experimental determination of a main-group electron-exchange rate in solution. Journal of the American Chemical Society 1989, 111, 5496–5498. [Google Scholar] [CrossRef]
- Margerum, D.W.; Chellappa, K.L.; Bossu, F.P.; Burce, G.L. Characterization of a readily accessible copper(III)-peptide complex. Journal of the American Chemical Society 1975, 97, 6894–6896. [Google Scholar] [CrossRef]
- Hurwitz, P.; Kustin, K. Kinetic study of the reaction IrCl62–+ IrBr63– ⇌ IrCl63–+ IrBr62–. Transactions of the Faraday Society 1966, 62, 427–432. [Google Scholar] [CrossRef]
- Stanbury, D.M.; Lednicky, L.A. Outer-sphere electron-transfer reactions involving the chlorite/chlorine dioxide couple. Activation barriers for bent triatomic species. Journal of the American Chemical Society 1984, 106, 2847–2853. [Google Scholar] [CrossRef]
- Hung, M.; Stanbury, D.M. Catalytic and Direct Oxidation of Cysteine by Octacyanomolybdate(V). Inorganic Chemistry 2005, 44, 3541–3550. [Google Scholar] [CrossRef]
- Gerken, J.B.; Pang, Y.Q.; Lauber, M.B.; Stahl, S.S. Structural Effects on the pH-Dependent Redox Properties of Organic Nitroxyls: Pourbaix Diagrams for TEMPO, ABNO, and Three TEMPO Analogs. The Journal of Organic Chemistry 2018, 83, 7323–7330. [Google Scholar] [CrossRef]
- Grampp, G.; Rasmussen, K. Solvent dynamical effects on the electron self-exchange rate of the TEMPO˙/TEMPO+ couple (TEMPO = 2,2,6,6-tetramethyl-1-piperidinyloxy radical) Part I. ESR-linebroadening measurements at T = 298 K. Phys. Chem. Chem. Phys. 2002, 4, 5546–5549. [Google Scholar] [CrossRef]
- Lipari, G.; Szabo, A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982, 104, 4546–59. [Google Scholar] [CrossRef]
- Lipari, G.; Szabo, A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 2. Analysis of experimental results. J. Am. Chem. Soc. 1982, 104, 4559–70. [Google Scholar] [CrossRef]
- Morozova, O.B.; Kiryutin, A.S.; Yurkovskaya, A.V. Electron transfer between guanosine radicals and amino acids in aqueous solution. II. Reduction of guanosine radicals by tryptophan. The Journal of Physical Chemistry B 2008, 112, 2747–2754. [Google Scholar] [CrossRef] [PubMed]
- Morozova, O.B.; Kaptein, R.; Yurkovskaya, A.V. Reduction of Guanosyl Radical by Cysteine and Cysteine-Glycine Studied by Time-Resolved CIDNP. The Journal of Physical Chemistry B 2012, 116, 8058–8063. [Google Scholar] [CrossRef] [PubMed]
- Napolitano, M.J.; Stewart, D.J.; Margerum, D.W. Chlorine Dioxide Oxidation of Guanosine 5 ‘-Monophosphate. Chemical research in toxicology 2006, 19, 1451–1458. [Google Scholar] [CrossRef]
- Faraggi, M.; Broitman, F.; Trent, J.B.; Klapper, M.H. One-Electron Oxidation Reactions of Some Purine and Pyrimidine Bases in Aqueous Solutions. Electrochemical and Pulse Radiolysis Studies. The Journal of Physical Chemistry 1996, 100, 14751–14761. [Google Scholar] [CrossRef]
- Napolitano, M.J.; Green, B.J.; Nicoson, J.S.; Margerum, D.W. Chlorine Dioxide Oxidations of Tyrosine, N-Acetyltyrosine, and Dopa. Chemical Research in Toxicology 2005, 18, 501–508. [Google Scholar] [CrossRef]
- Land, E.J.; Prütz, W. Reaction of azide radicals with amino acids and proteins. International Journal of Radiation Biology and Related Studies in Physics, Chemistry and Medicine 1979, 36, 75–83. [Google Scholar] [CrossRef]
- Prütz, W.A.; Mönig, H.; Butler, J.; Land, E.J. Reactions of nitrogen dioxide in aqueous model systems: Oxidation of tyrosine units in peptides and proteins. Archives of Biochemistry and Biophysics 1985, 243, 125–134. [Google Scholar] [CrossRef]
- Song, N. Mechanisms and Kinetics of Proton-Coupled Electron-Transfer Oxidation of Phenols. 2011.
- Pattison, D.I.; Lam, M.; Shinde, S.S.; Anderson, R.F.; Davies, M.J. The nitroxide TEMPO is an efficient scavenger of protein radicals: Cellular and kinetic studies. Free Radical Biology and Medicine 2012, 53, 1664–1674. [Google Scholar] [CrossRef]
- Marcus, R.A. Electron transfer reactions in chemistry: theory and experiment (Nobel lecture). Angewandte Chemie International Edition in English 1993, 32, 1111–1121. [Google Scholar] [CrossRef]
- Weinstock, I.A. Outer-Sphere Oxidation of the Superoxide Radical Anion. Inorganic Chemistry 2008, 47, 404–406. [Google Scholar] [CrossRef] [PubMed]
- Chou, M.; Creutz, C.; Sutin, N. Rate constants and activation parameters for outer-sphere electron-transfer reactions and comparisons with the predictions of Marcus theory. Journal of the American Chemical Society 1977, 99, 5615–5623. [Google Scholar] [CrossRef]
- Weaver, M.J.; Yee, E.L. Activation parameters for homogeneous outer-sphere electron-transfer reactions. Comparisons between self-exchange and cross reactions using Marcus' theory. Inorganic Chemistry 1980, 19, 1936–1945. [Google Scholar] [CrossRef]
- Hupp, J.T.; Weaver, M.J. Electrochemical and homogeneous exchange kinetics for transition-metal aqua couples: anomalous behavior of hexaaquairon(III/II). Inorganic Chemistry 1983, 22, 2557–2564. [Google Scholar] [CrossRef]
- Eberson, L. Electron-transfer reactions in organic chemistry. In Advances in physical organic chemistry, Elsevier: 1982; Vol. 18, pp 79-185.
- Nelsen, S.F.; Ramm, M.T.; Ismagilov, R.F.; Nagy, M.A.; Trieber, D.A.; Powell, D.R.; Chen, X.; Gengler, J.J.; Qu, Q.; Brandt, J.L.; Pladziewicz, J.R. Estimation of Self-Exchange Electron Transfer Rate Constants for Organic Compounds from Stopped-Flow Studies. Journal of the American Chemical Society 1997, 119, 5900–5907. [Google Scholar] [CrossRef]
- Grampp, G.; Landgraf, S.; Sabou, D.; Dvoranova, D. Application of Marcus cross-relation to mixed inorganic–organic redox couples. A stopped-flow study of the oxidation of N, N, N′, N′-tetramethyl-p-phenylenediamine with various oxidants. Journal of the Chemical Society, Perkin Transactions 2 2002, (1), 178-180.
- Sutin, N. Theory of Electron Transfer Reactions: Insights and Hindsights. Progress in Inorganic Chemistry: An Appreciation of Henry Taube 1983, 441-498.
- Marcus, R. On the theory of oxidation-reduction reactions involving electron transfer. III. Applications to data on the rates of organic redox reactions. The Journal of Chemical Physics 1957, 26, 872–877. [Google Scholar] [CrossRef]
- Morozova, O.B.; Ivanov, K.L. Time-Resolved Chemically Induced Dynamic Nuclear Polarization of Biologically Important Molecules. ChemPhysChem 2019, 20, 197–215. [Google Scholar] [CrossRef]
- Raiford, D.S.; Fisk, C.L.; Becker, E.D. Calibration of methanol and ethylene glycol nuclear magnetic resonance thermometers. Analytical Chemistry 1979, 51, 2050–2051. [Google Scholar] [CrossRef]
- Nelson, D.L.; Lehninger, A.L.; Cox, M.M. Lehninger principles of biochemistry. Macmillan: 2008.
Figure 1.
The 1H CIDNP spectra obtained by photo-irradiation of solutions containing a) 15 mM DP and 9, 7.5, 6.5, 4 mM GMP(-H)- at 8, 25, 45, 65ºC and pH = 11.3; b) 15 mM DP and 6.5, 6, 6, 2.5 mM TyrO- at 8, 25, 45, 65ºC and pH = 11.7.
Figure 1.
The 1H CIDNP spectra obtained by photo-irradiation of solutions containing a) 15 mM DP and 9, 7.5, 6.5, 4 mM GMP(-H)- at 8, 25, 45, 65ºC and pH = 11.3; b) 15 mM DP and 6.5, 6, 6, 2.5 mM TyrO- at 8, 25, 45, 65ºC and pH = 11.7.
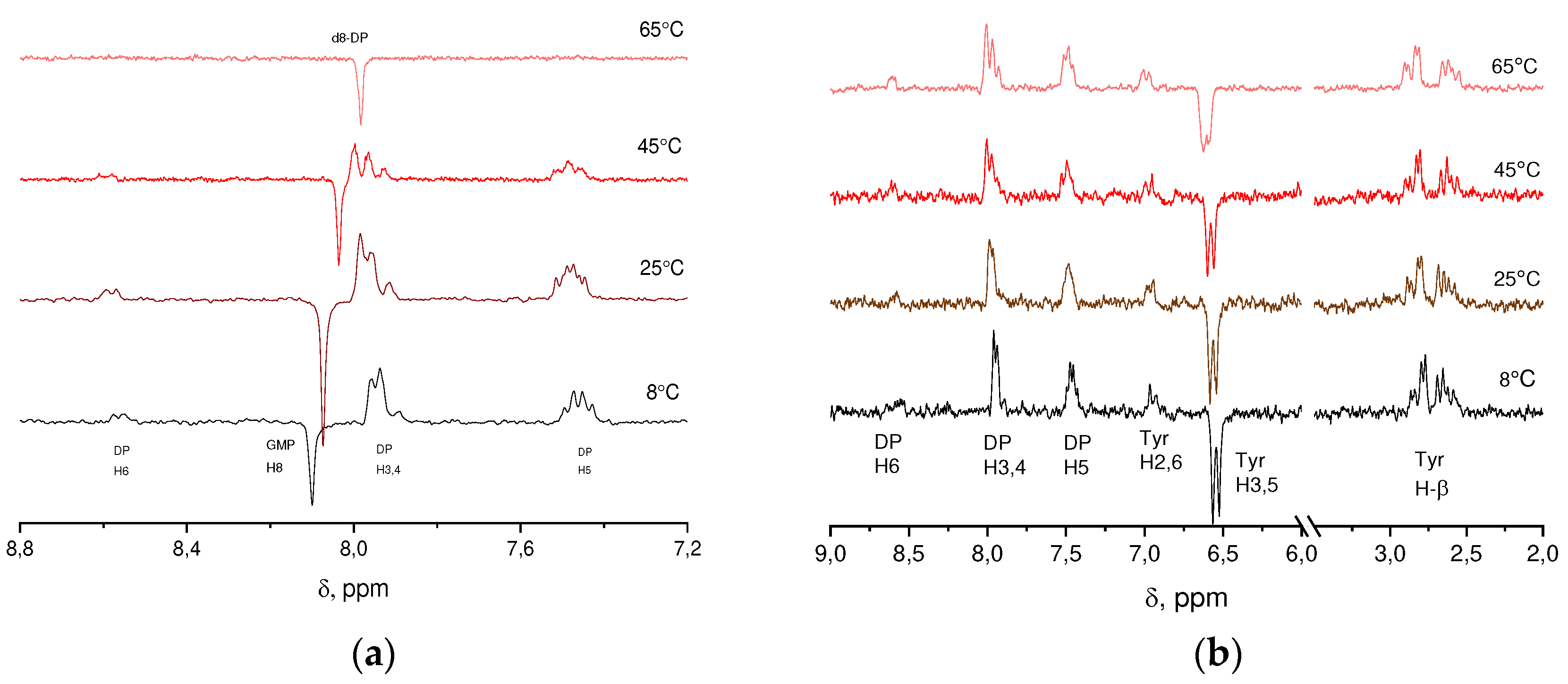
Figure 2.
Experimental data (dots) and simulation curves (solid lines) for:.
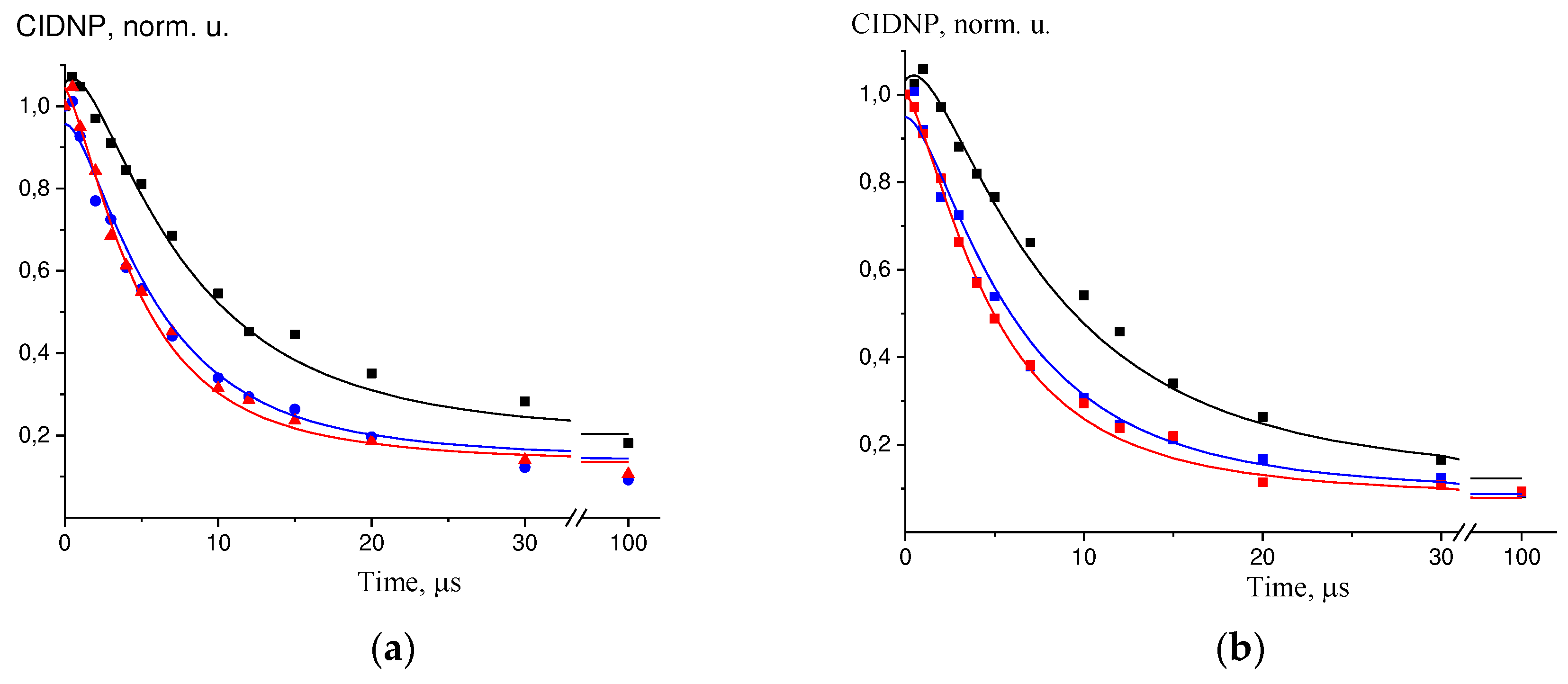
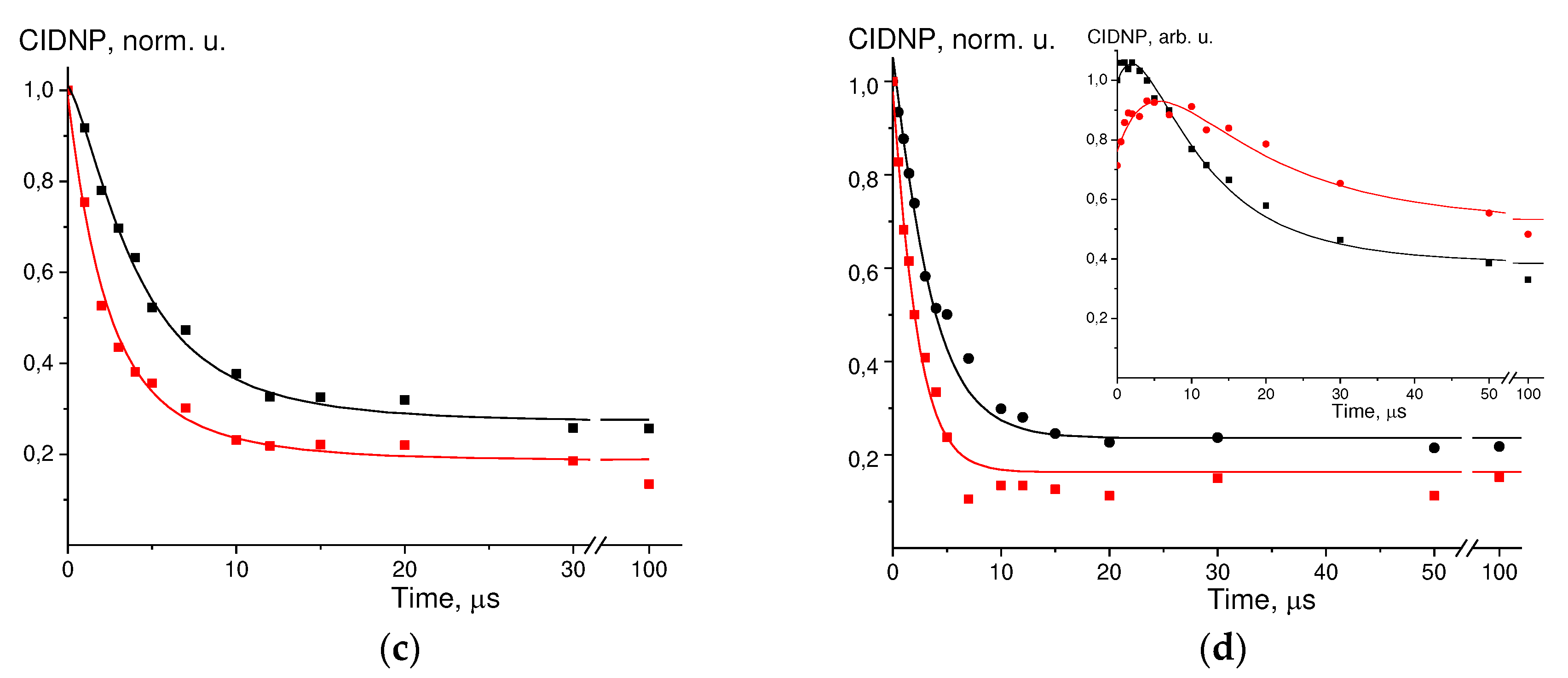
Figure 3.
Temperature dependences of the DEE rate constants ket in the coordinates ln[ket√Texp(wr/RT)] vs 1/T for: a) GMP(-H)• + GMP(-H)- b) NacTyrO• + NacTyrO- c) TyrO• + TyrO-.
Figure 3.
Temperature dependences of the DEE rate constants ket in the coordinates ln[ket√Texp(wr/RT)] vs 1/T for: a) GMP(-H)• + GMP(-H)- b) NacTyrO• + NacTyrO- c) TyrO• + TyrO-.
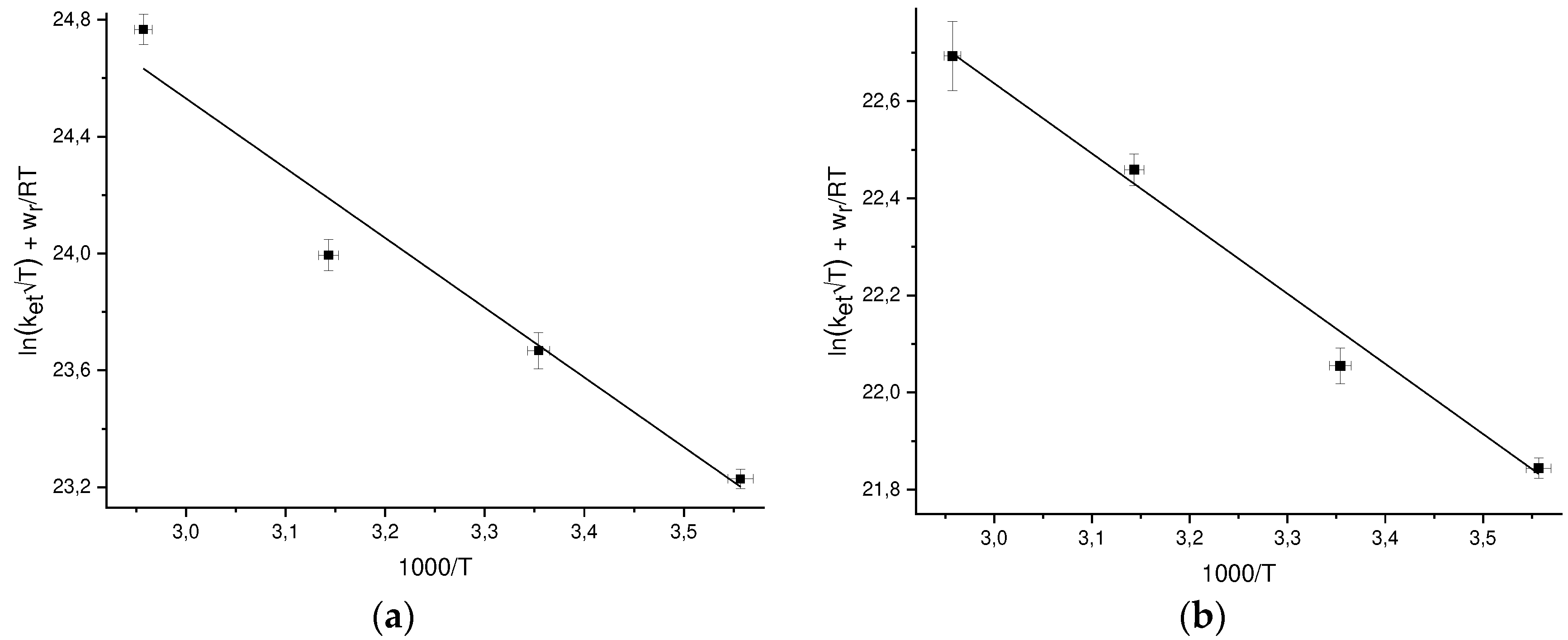
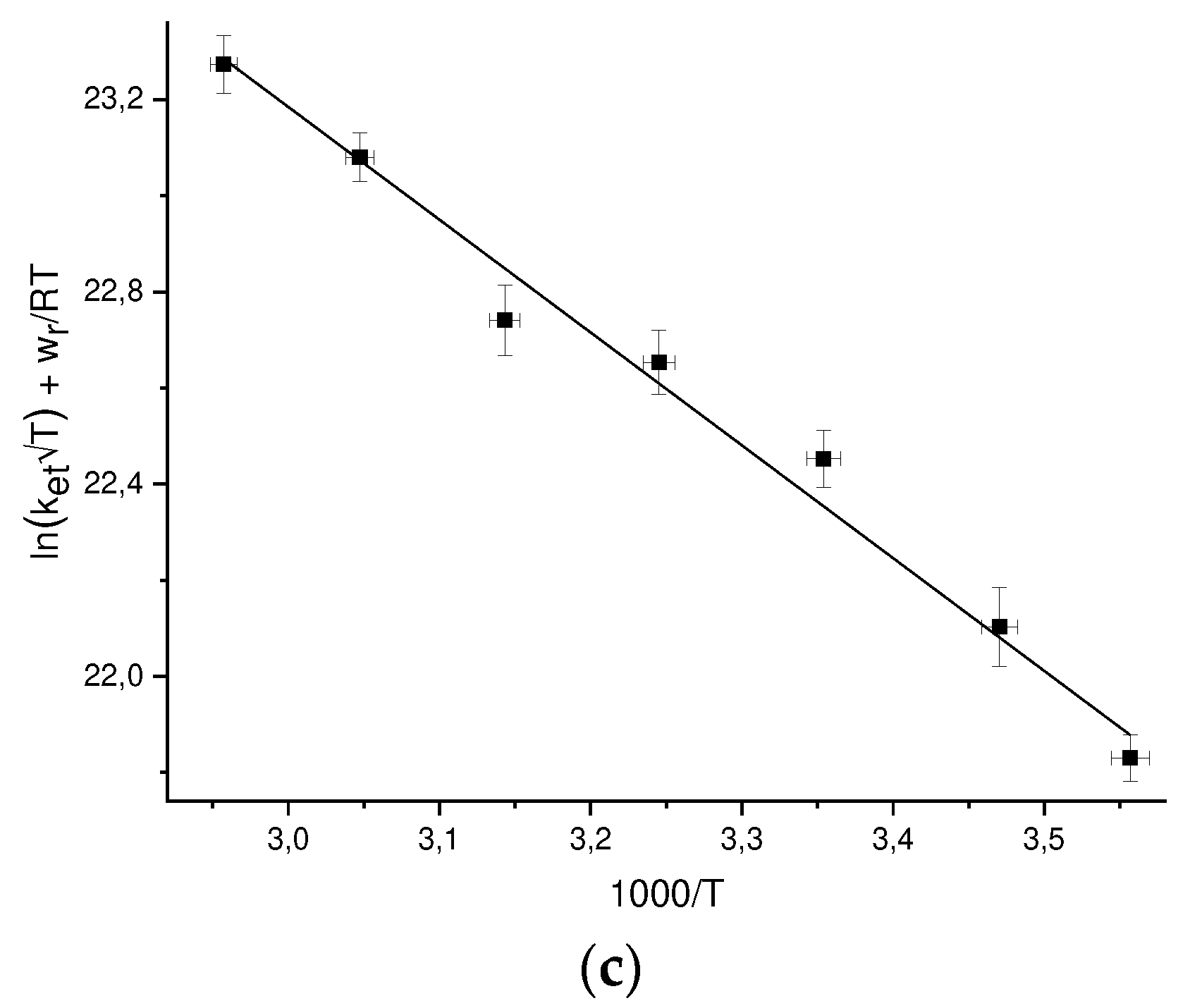
Figure 4.
Acid-base equilibria for GMP and radical GMP•.
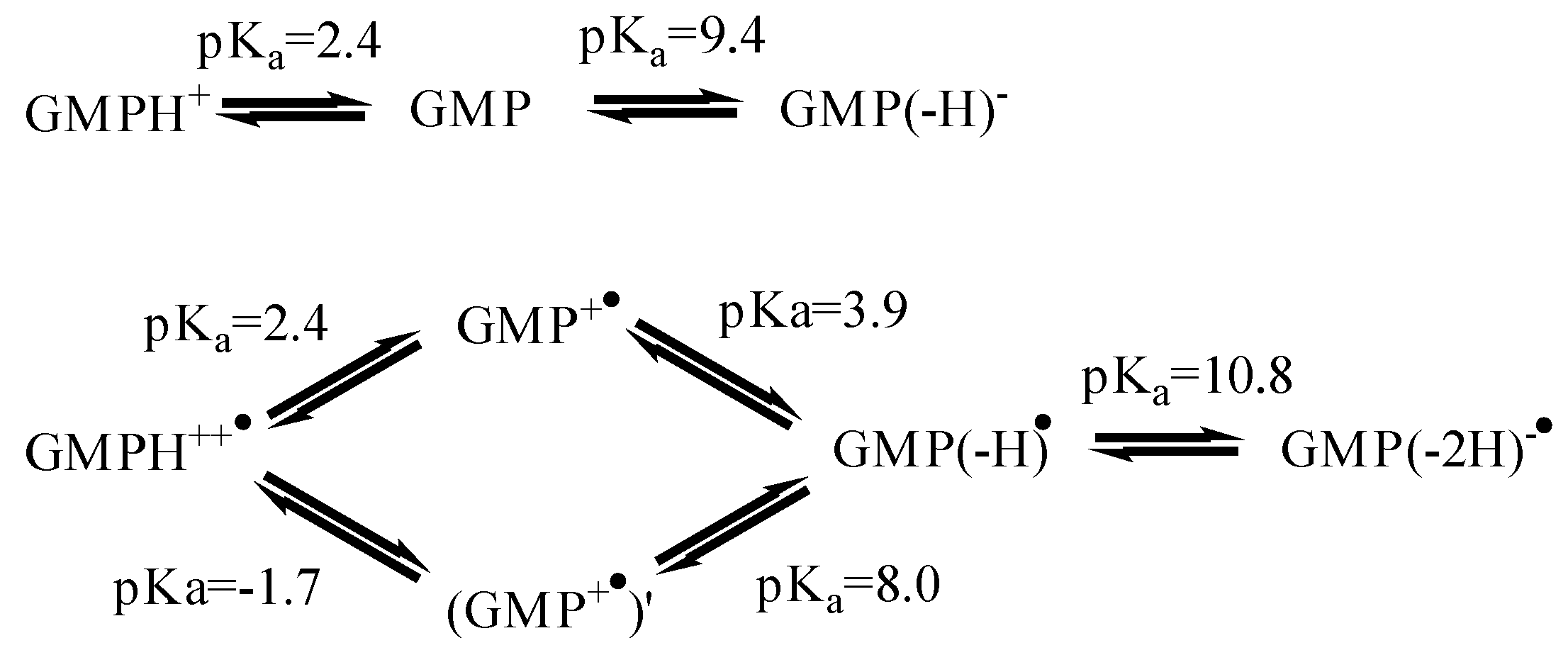
Figure 6.
Temperature dependences of the nuclear relaxation time T1 in coordinates ln(T/T1) vs 1/T for: a) H-8 in the radical GMP(-H)• b) H-3,5 in the radical NacTyrO• (black dots) and ТyrO• (red dots); c) H-3,4 in the radical DPH• according to the data for systems GMP(-H)- + DP (black dots), NacTyrO- + DP (red dots), TyrO- + DP (blue dots).
Figure 6.
Temperature dependences of the nuclear relaxation time T1 in coordinates ln(T/T1) vs 1/T for: a) H-8 in the radical GMP(-H)• b) H-3,5 in the radical NacTyrO• (black dots) and ТyrO• (red dots); c) H-3,4 in the radical DPH• according to the data for systems GMP(-H)- + DP (black dots), NacTyrO- + DP (red dots), TyrO- + DP (blue dots).
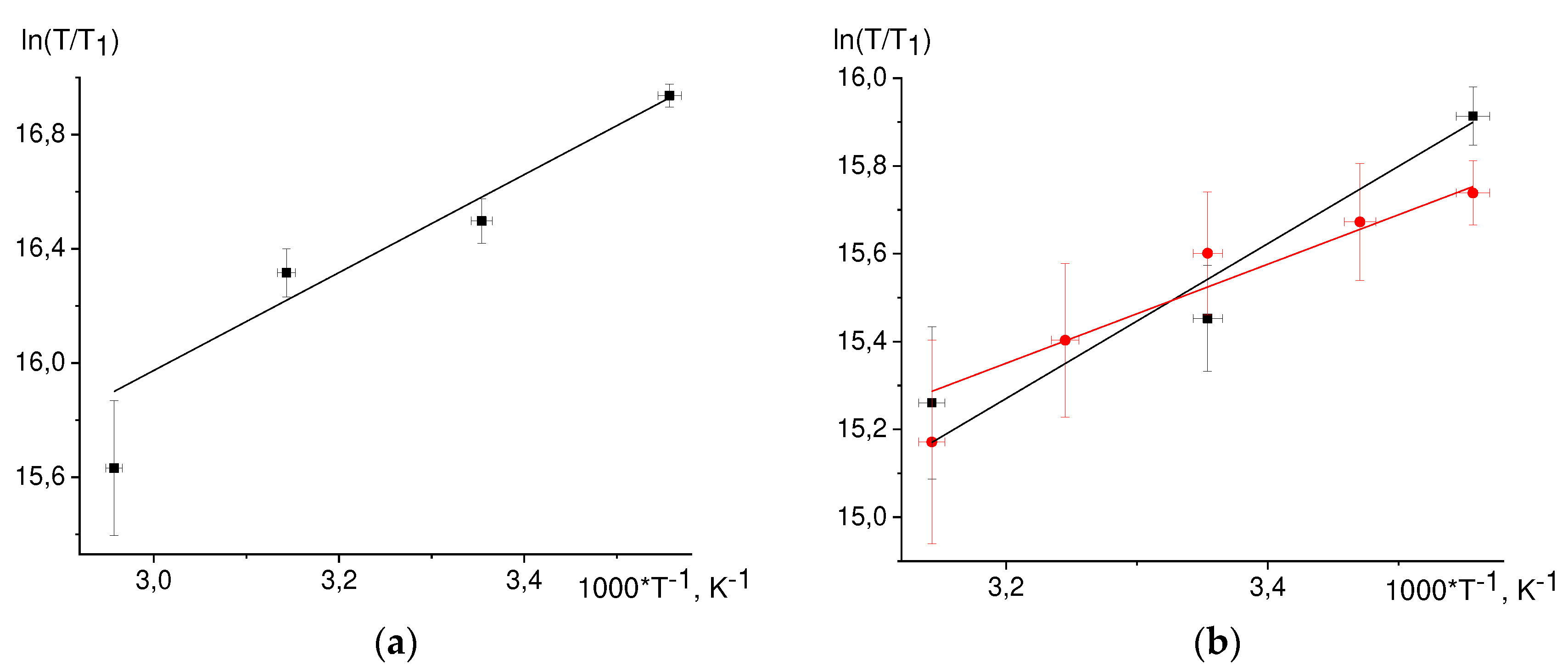
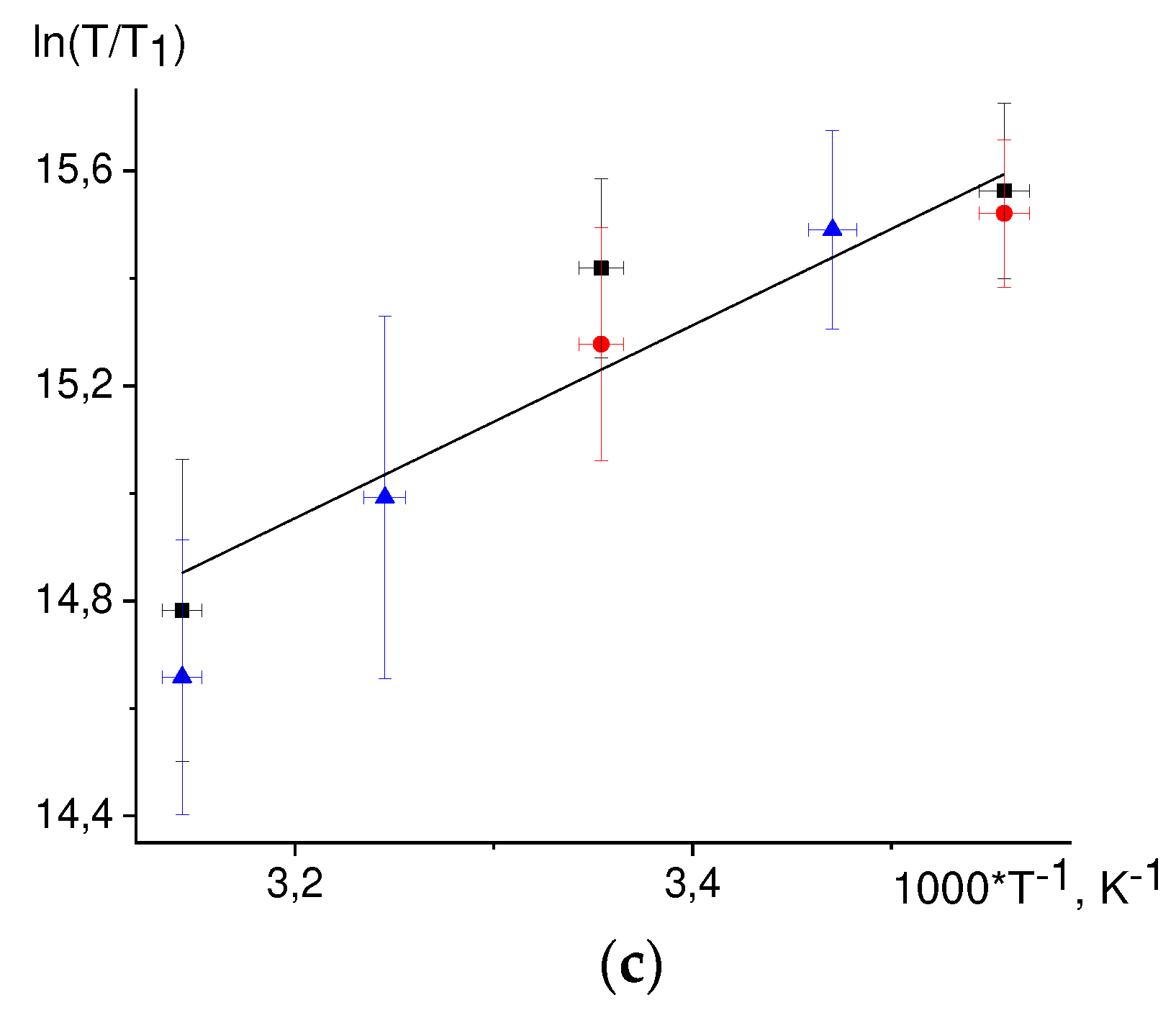
Figure 7.
Fitting of the nuclear paramagnetic relaxation temperature dependence of 3,5 protons of radical TyrO• according to the Eq. (44) with a fixed value of S2 = 0.01.
Figure 7.
Fitting of the nuclear paramagnetic relaxation temperature dependence of 3,5 protons of radical TyrO• according to the Eq. (44) with a fixed value of S2 = 0.01.
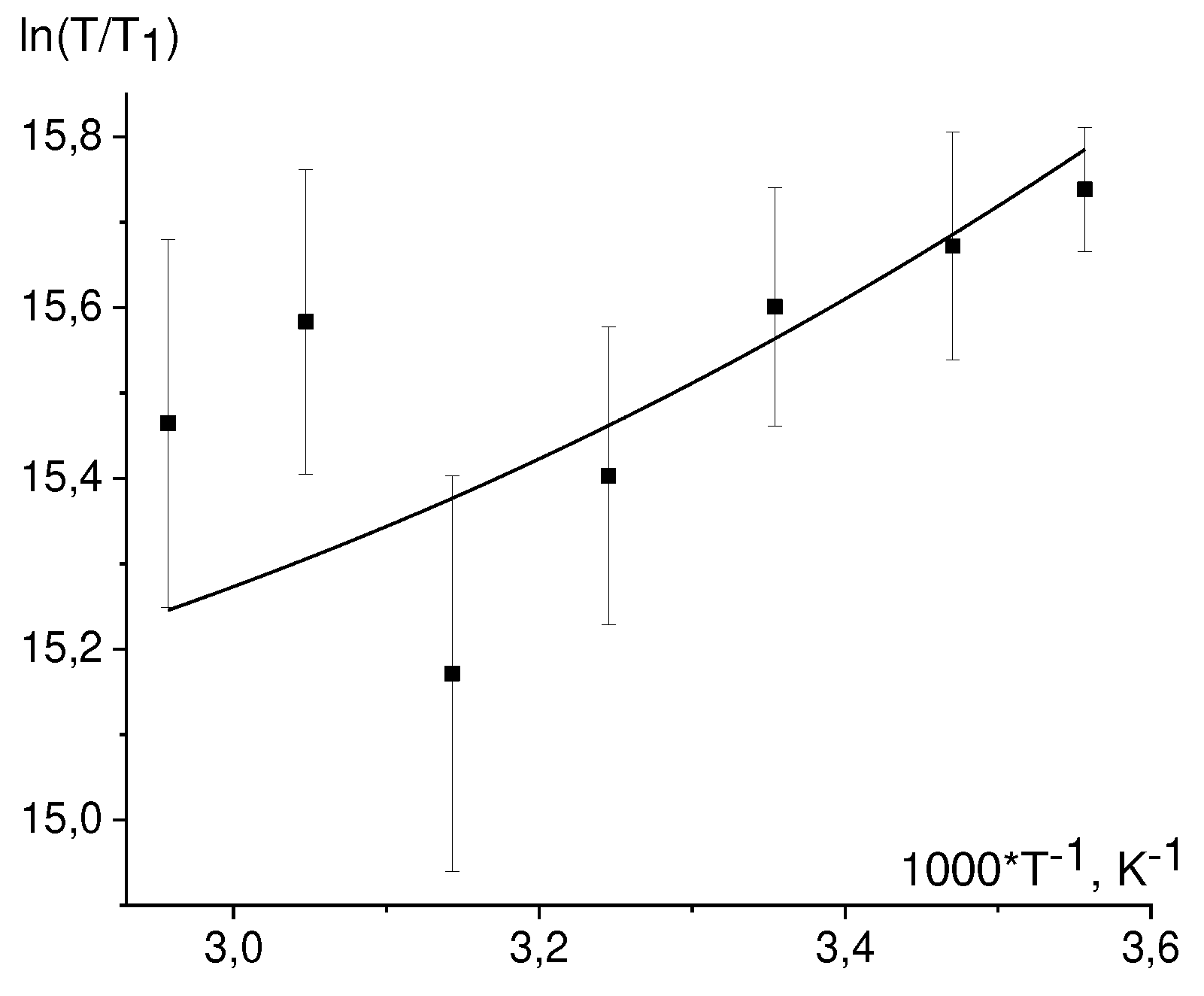
Figure 8.
The structures of diamagnetic reactants and products and GMPH+.
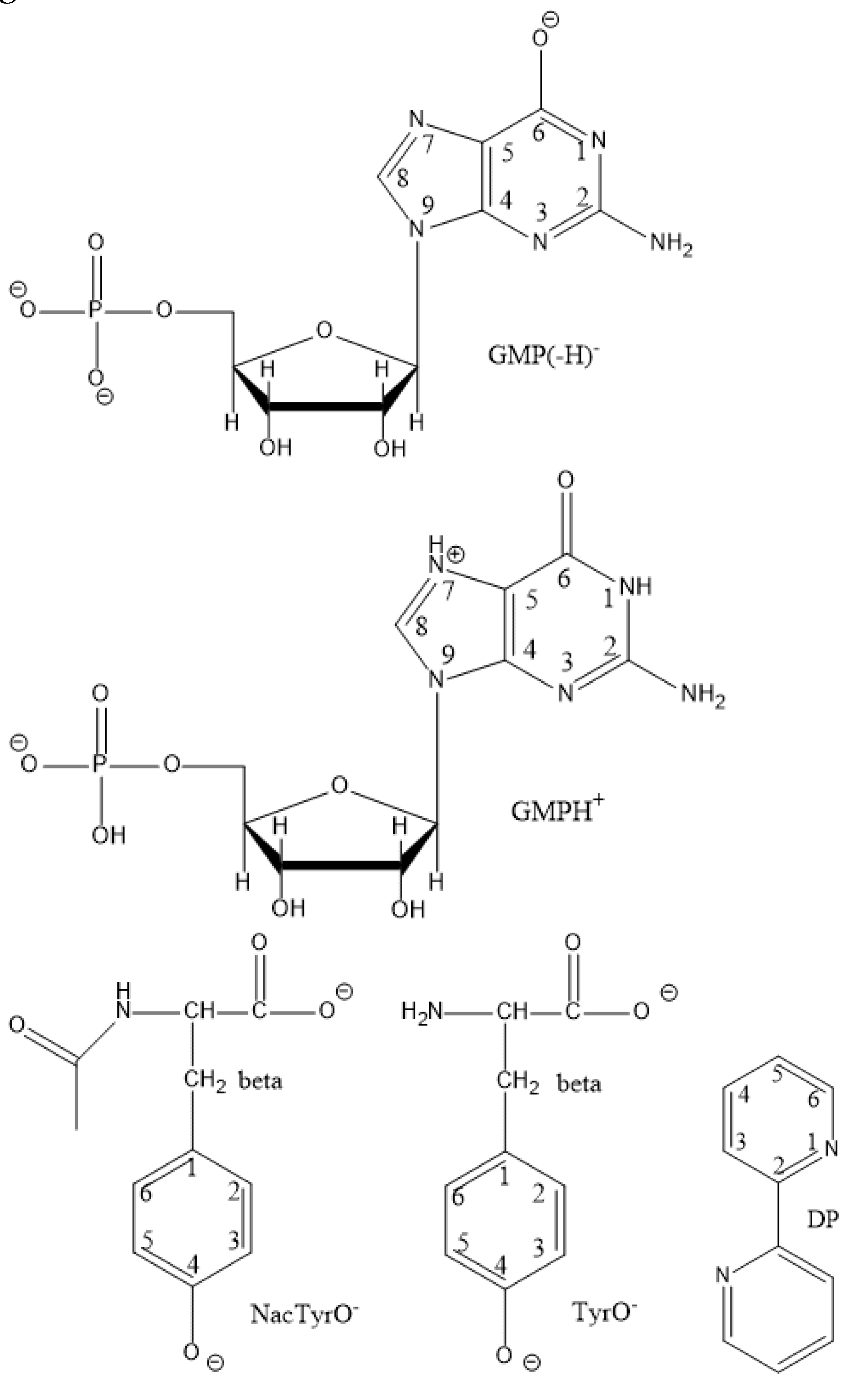
Table 1.
Fitting parameters for the GMP(-H)- + DP system.
| t°C | kobs, M-1s-1 | T1(H8), µs | T1(H3,4 DP), µs | ket, M-1s-1 |
|---|---|---|---|---|
| 8 | (3.77±0.11)*107 | 12.4±0.5 | 49±8 | (4.27±0.14)*107 |
| 25 | (4.91±0.27)*107 | 20.4±1.6 | 60±10 | (5.50±0.32)*107 |
| 45 | (5.78±0.28)*107 | 26.1±2.2 | 121±34 | (6.32±0.32)*107 |
| 65 | (8.12±0.38)*107 | 55±13 | -- (d8-DP) | (9.04±0.45)*107 |
Table 2.
Fitting parameters for the NacTyrO- + DP system.
| t°C | kobs, M-1s-1 | T1(H3,5), µs | T1(Hβ), µs | T1(H3,4 DP), µs | ket, M-1s-1 |
|---|---|---|---|---|---|
| 8 | (4.46±0.09)*107 | 34.5±2.3 | 111±16 | 51.1±7 | (4.71±0.10)*107 |
| 25 | (5.07±0.18)*107 | 58±7 | 119±24 | 69.1±15 | (5.27±0.19)*107 |
| 45 | (6.95±0.22)*107 | 75±13 | 129±35 | 73.2±24 | (7.19±0.23)*107 |
| 65 | (8.24±0.57)*107 | 50±9 | -- | 42.1±19 | (8.46±0.60)*107 |
Table 3.
Fitting parameters for the TyrO- + DP system.
| t°C | kobs, M-1s-1 | T1(H3,5), µs | T1(Hβ), µs | T1(H3,4 DP), µs | ket, M-1s-1 |
|---|---|---|---|---|---|
| 8 | (2.81±0.13)*107 | 41.1±3 | 118±25 | 98±22 | (2.94±0.14)*107 |
| 15 | (3.59±0.28)*107 | 45±6 | 138±21 | 54±10 | (3.76±0.30)*107 |
| 25 | (4.78±0.27)*107 | 50±7 | 139±26 | 199±81 | (5.02±0.29)*107 |
| 35 | (5.64±0.36)*107 | 63±11 | 149±36 | 95±32 | (5.90±0.39)*107 |
| 45 | (5.96±0.42)*107 | 82±19 | -- | 137±35 | (6.19±0.45)*107 |
| 55 | (7.60±0.37)*107 | 56±10 | 121±32 | 48±16 | (7.92±0.40)*107 |
| 65 | (8.53±0.49)*107 | 65±14 | 106±30 | 67±22 | (8.87±0.52)*107 |
Table 4.
The found pre-exponents and reorganization energies for DEE reactions.
| DEE reaction | ln(A) | λ, eV |
|---|---|---|
| GMP(-H)- + GMP(-H)• | 31.7 ± 1.0 | 0.82 ± 0.11 |
| NacTyrO- + NacTyrO• | 27.0 ± 0.4 | 0.50 ± 0.04 |
| TyrO- + TyrO• | 30.2 ± 0.4 | 0.81 ± 0.04 |
Table 6.
The energy E values (see Eq. (42)) defined from the linear fitting of ln(T/T1) vs 1/T dependencies.
Table 6.
The energy E values (see Eq. (42)) defined from the linear fitting of ln(T/T1) vs 1/T dependencies.
| radical, nucleus | E/R, K |
|---|---|
| GMPH++•, H-8 [30] | 1993 ± 650 |
| GMP(-H)•, H-8 | 1720 ± 270 |
| NacTyrO•, H-3,5 | 1760 ± 370 |
| TyrO•, H-3,5 | 1130 ± 210 |
| DPH•, H-3,4 | 1790 ± 300 |
| η(D2O) [51, 52] | 2059 ± 81 |
Table 7.
Comparison of the rate constants calculated from the cross relation and those found in the experiment.
Table 7.
Comparison of the rate constants calculated from the cross relation and those found in the experiment.
| Reaction | k12expt, M-1s-1 | k12calc, M-1s-1 | Reference |
|---|---|---|---|
| NacTrpH + GMPH++• | 1.2*109 | 7.9*1010 | [79] |
| TyrO- + GMP(-H)• | 1.7*108 | 3.7*1010 | this work |
| NacTyrO- + GMP(-H)• | 1.8*108 | 1.6*1010 | [29] |
| CysS- + GMP(-H)• | 1.9*108 | 6.4*108 | [80] |
| GMP(-H)- + ClO2• | 1.1*105 | 5.6*103 | [81] |
| GMP(-H)- + N3• | 3.2*109 | 2.0*108 | [82] |
| TyrO- + ClO2• | 1.8*108 | 1.1*108 | [83] |
| NacTyrO- + ClO2 • | 7.6*107 | 3.2*107 | [83] |
| TyrO- + N3• | 6.7*109 | 8.1*1010 | [84] |
| Gly-TyrO- + NO2• | 2.0*107 | 1.9*107 | [85] |
| NacTyrO--NH2 + [IrCl6]2- | 3.6*107 | 1.2*108 | [86] |
| TEMPO• + NacTyrO•-NH2 | 1.5*108 a | 4.1*108 | [87] |
athe rate constant measured at 22°C.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







