A Hydroacoustic Adversarial Strategy Based on the Matrix Game Theory

Preprint

Article

A Hydroacoustic Adversarial Strategy Based on the Matrix Game Theory

This version is not peer-reviewed.

Yu Chen^*

Yu Chen^*

This version is not peer-reviewed.

Altmetrics

Downloads

162

Views

Comments

Submitted:

10 August 2023

Posted:

11 August 2023

Read the latest preprint version here

Abstract

Aiming at the decision-making problem in the anti-torpedo hydroacoustic countermeasure scenarios, this paper proposes an intelligent adversarial strategy based on the game theory. By discretizing the strategy space of both sides, a matrix game model is established with the payoff characterized by the capture probability of attacking torpedo. An improved simplex algorithm is developed to get the mixed-strategy Nash equilibrium of the game model, by which preferred avoiding strategies can be obtained to minimize the risk of being captured by the attacking torpedo. Considering the urgent stage when the sonar equipment detects the torpedo without identification of its attacking direction, the proposed intelligent strategy provides an probabilistic overview on the countermeasure scenarios, which could improve the success capability of surface warships for the anti-torpedo cases.

Keywords:

Subject:

Computer Science and Mathematics - Applied Mathematics

1. Introduction

With the development of the international situation, as well as the emergence of new types of confrontation targets, it is urgent to re-examine the hydroacoustic confrontation to adapt to the needs of naval operations in the new situation [1]. Hydroacoustic countermeasures are devoted to using hydroacoustic equipment and devices [2], luring, interfering with the enemy acoustic guided torpedo detection and attack, to avoid enemy torpedo attacks, and thereby improving their own survival capability [3,4,5,6,7]. Hydroacoustic countermeasures technology has been investigated for more than 60 years since the Second World War, which contributes to some representative systems such as the United States / Britain joint Surface Ship Torpedo Defence (SSTD) system, the France Systeme-de Lutte Anti-Torpille (SLAT) system, the Israel Torpedo Self Defence System (TSDS) system, the United States / United Kingdom joint Surface Ship Torpedo Defence (SSTD) system, the French system, the Israeli Torpedo Self Defence System (TSDS) system, the United States and United Kingdom joint Surface Ship Torpedo Defence (SSTD) system, the Defence System (TSDS) system of France, the Torpedo Self Defence System (TSDS) system of Israel, as well as the research of the USSR and its post-dissolution republics [8]. Recently, there are popular researches on anti-submarine search mode abroad [9], and a few researches on submarine countermeasures against torpedoes are reported on the countermeasure characteristics of individual countermeasures [10,11]. Based on the Mote-Carlo simulating method and the manoeuvre evasion strategy, some preliminary researches have been reported for the anti-torpedo scenarios [12,13].

Some researches have implemented the game theory to develop intelligent strategies of naval warfare. Levine [14] studied aspects of naval warfare in the previous centuries using concepts from game theory. Since the powerful nations in the 18th and 19th centuries built warships with cannons positioned along their sides, neither fleet would gain from turning towards the enemy and neither would get ahead. Levine concluded that this strategy—forming a line of battle and sailing parallel to the other fleet—was each fleet’s best response, and thus represented a Nash equilibrium.

Maskery et al. [15] investigated the problem of deploying counter-measures against anti-ship missiles using a network-enabled operations framework, where multiple ships communicate and coordinate to defend against a missile threat. Here, the missile threats were modelled as a discrete Markov process, and the ships which are equipped with countermeasures were modelled as the players of a transient stochastic game, where the actions of the individual players include the use of countermeasures to maximize their own safety while cooperating with other players which are essentially aiming to achieve the same objective. The optimal strategy of this game-theoretic problem is a correlated equilibrium strategy and is shown to be achieved via an optimization problem with bilinear constraints. In [16], Maskery et al. considered the problem of network-centric force protection of a task group against anti-ship missiles. The decision-makers in this model are the ships equipped with hard-kill/soft-kill weapons (counter-measures) and these ships are also considered the players in the formulation of this problem in a game-theoretic setting. Here, the ships play a game with each other instead of with a missile. This approach naturally lends itself to decentralised solutions which may be implemented when full communication is not feasible. Moreover, this formulation leads to an interpretation of the problem as a stochastic shortest past game for which Nash Equilibrium solutions are known to exist.

Bachmann et al. [17] analyzed the interaction between radar and jammer using a noncooperative two-player zero-sum game. In their approach, the radar and jammer were considered ‘players’ with opposing goals: the radar tries to maximize the probability of detection of the target while the jammer attempts to minimize its detection by the radar by jamming it. This game-theoretic formulation was solved by optimizing these utility functions subject to constraints in the control variables (strategies), which for the jammer are jammer power and the spatial extent of jamming while for the radar the available strategies include the threshold parameter and reference window size. The resulting matrix-form games were solved for optimal strategies of both radar and jammer from which they identify conditions under which the radar and jammer are effective in achieving their individual goals.

Consider the scenario that a surface ship encounter with an enemy submarine, where the submarine would like to launch a torpedo attacking the ship. While the coming torpedo is alarmed by sonar equipments of the ship, the defensive crew of ship would take some countermeasure strategies to survive from the dangerous situation. For most cases, the enemy submarine would maintain silence for a long time to attack in a advantageous situation, and accordingly, this scenario of hydroacoustic confrontation is very emergent, due to the faster maneuvering speed and unknown attacking direction of the torpedo. Thus, it is of great help to improvement of its survival capability by predicting the attacking intention of the enemy torpedo. In this paper, we address it based on the theory of matrix game [18,19]. Taking the avoidance angle and the attacking advance angle as the antagonizing strategies of the defensive surface ship and the attacking torpedo, respectively, a matrix game model is constructed by discretizing them in their value ranges, taking the payoff as the probability of being captured by the torpedo. Then, the linear programming (LP) model for matrix game is proposed, and an improved initialization strategy of the simplex method to get the Nash equilibrium solution to the game model as soon as possible. In this way, a realtime antagonizing strategy can be generated to address the emergent scenario of Hydroacoustic countermeasure.

Rest of this paper is organized as follows. Section 2 presents some preliminary introductions on the theory of matrix game and the simplex method for LP, and a matrix game model for the investrigated hydroacoustic countermeasure scenario is proposed in Section 3. To efficiently put into practice the proposed game model, Section 4 validate the construction of payoff matrix and an improved initialization method for the simplex method (SM) is put forward in Section 5. Then, numerical simulation is implemented in Section 6 to demonstrate the applicability of the proposed strategy, and Section 7 presents conclusions and discussions.

2. Preliminaries

2.1. Introduction to the Game Theory

Pure vs. mixed strategies [20]

A game typically consists of two or more players, a set of strategies available to these players, and a corresponding set of payoff values for each player. A pure strategy in a game provides a complete definition of how a player will play a game, and a mixed strategy is a combination of pure strategies where a particular probability p (where

0 \leq p \leq 1

) is associated with each of these pure strategies. Therefore, any pure strategy is actually a degenerate case of a mixed strategy, in which that particular strategy is selected with probability 1 and every other strategy is selected with probability 0.

Nash equilibrium [20]

The solution to a game model refers to the Nash equilibrium (solution). Let

(S, f)

be a game with n players, where

S_{i}

is the strategy set of a given player i. Thus, the stragety profile S consisting of the strategy sets of all players would be

S = S_{1} \times S_{2} \times \dots \times S_{n}

. Let

f (x) = (f_{1} (x), \dots, f_{n} (x))

be the payoff function for strategy set

x \in S

. Suppose

x_{i}

is the strategy of player i and

x_{- i}

is the strategy set of all players except player i. Thus, when each player

i \in {1, \dots, n}

chooses strategy

x_{i}

that would result in the strategy set

x = (x_{1}, \dots, x_{n})

, giving a payoff of

f_{i} (x)

to that particular player, which depends on both the strategy chosen by that player

(x_{i})

and the strategies chosen by other players

(x_{- i})

. A strategy set

x^{*} \in S

is in Nash equilibrium if no unilateral deviation in strategy by any single player would return a higher utility for that particular player. Formally put,

x^{*}

is in Nash equilibrium if and only if:

\forall i, x_{i} \in S_{i} : f_{i} (x_{i}^{*}, x_{- i}^{*}) \geq f_{i} (x_{i}, x_{- i}^{*}) .

(1)

x^{*}

is called a pure/mixed-strategy Nash equilibrium when

x_{i}^{*}

is pure/mixed-strategy for any player i,

i \in {1, \dots, n}

Matrix (Two-person zero-sum) games [20]

Zero-sum games are a class of competitive games where the total of the payoffs of all players is zero. In two-player games, this implies that one player’s loss in the payoff is equal to another player’s gain in the payoff. A maxtrix (two-player zero-sum) game can therefore be represented by a payoff matrix that shows only the payoffs of one player. The mini-max theorem [21] states that in a zero-sum game there is a set of strategies that minimizes the maximum losses (or maximises the minimum payoff) of each player, which can be addressed by solving LP problems. Note that the linear programming problems given for both players are dual to each other. The optimal mixed strategies for both players can be found by solving only one of the linear programming problems because the optimal dual solution is an automatic by-product of the simplex method calculations to find the optimal primal solution. In general, you always can find optimal mixed strategies for both players by choosing just one of the models (either one) and then using the simplex method to solve for both an optimal solution and an optimal dual solution [22].

2.2. The Simplex Method for LP Problems [23]

An LP problem with

n^{'}

variables and r constraints takes the form

\begin{matrix} max z^{'} = c^{' T} x^{'} \\ s . t . \{\begin{matrix} A^{'} x^{'} \leq b, \\ x^{'} \geq 0, b \geq 0 \end{matrix} \end{matrix}

where

n^{'}

and r are positive integers,

c^{'} \in R

x^{'} \in R^{n^{'}}

A^{'} \in R^{n^{'} \times n^{'}}

, and

b \in R^{r}

. Let

N^{'} = {1, \dots, n}

be the set of variable indices and

R = {1, \dots, r}

be the set of constraint indices. The feasible region of an LP is denoted by

S^{'} = {x^{'} \in R_{+}^{n^{'}} : A^{'} x^{'} \leq b}

and the optimal solution of an LP is

x^{' *} \in S

such that

z^{' *} = c^{' T} x^{' *} \geq c^{' T} x^{''}

for all

x^{''} \in S

One of the most popular algorithms to LP problems is the simplex method (SM) created by George Dantzig [24]. Given an LP, the SM requires that all constraints be converted into linear equations by adding r slack variables. This new problem is called the canonical linear program (CLP) and is defined as

\begin{matrix} max z = c^{T} x \\ s . t . \{\begin{matrix} A x = b, \\ x \geq 0, b \geq 0, \end{matrix} \end{matrix}

where

x \in R^{n + r}

c \in R^{n + r}

c^{'}

augmented with r zeros, and

A \in R^{r \times (n + r)}

A^{'}

augmented with an

r \times r

identity matrix. Let

N = {1, \dots, n + r}

be the variable indices and

S = {x \in R_{+}^{n + r} : A x = b}

be the feasible region of an CLP.

Initially, SM requires a starting basic feasible solution. Formally,

B V \subseteq N

is called a basis if

| B V | = | R |

and

A_{. B V}

is nonsigular. The set of nonbasic indices is

N B V = N ∖ B V

. The corresponding vasic and nonbasic variables are

x_{B V}

and

x_{N B V}

, respectively. If

A_{. B V}^{- 1} b \geq 0

, then

B V

is a feasible basis with

x_{B V} = A_{. B V}^{- 1} b

and

x_{N B V} = 0

being the corresponding vasic feasible solution. Here,

A_{. B V}

represents the columns of A restricted to the indices in

B V

, and

x_{B V}

is the x values of the indices in

B V

The input to SM is an CLP and a feasible basise

B V \subseteq N

that produces a feasible basis solution. The algorithm evaluates each nonbasis variable’s reduced cost, which is euql to

c_{B V} A_{. B V}^{- 1} A_{. i} - c_{i}

for all

i \in N B V

. If all nonbasic reduced costs are nonnegative, then the corresponding vasic feasible solution represents an optimal solution of CLP. Furthermore,

B V

is said to be an optimal basis. If

B V

is not optimal, then there exists an entering variable with index

p \in N B V

such that its reduced cost is negative. In order to determine the leaving variable, define

R^{+} = {j \in R : {(A_{. B V}^{- 1} A_{. p})}_{j} > 0}

. If

R^{+} = \emptyset

, then the problem is unbounded. If not, SM performs the ratio test and identifies

j^{*} \in R^{+}

such that

\frac{{(A_{. B V}^{- 1} b)}_{j^{*}}}{{(A_{. B V}^{- 1} A_{. p})}_{j^{*}}} \leq \frac{{(A_{. B V}^{- 1} b)}_{j}}{{(A_{. B V}^{- 1} A_{. p})}_{j}}

for all

j \in R^{+}

. SM replaces the

j^{*}

th element in

B V

with p. This process is referred to as a pivot. The algorithm continues pivoting until an optimal basis of CLP is identified or CLP is shown to be unbounded.

3. The Matrix Game Model for Hydroacoustic Countermeasure

Knowing that both sides of the hydroacoustic countermeasure would like to maximize their own profits, we construct a matrix game model to simulate the adversarial scenario, where the game strategies of the two opposing sides in the static game are their own sailing/attacking directions. Because the sailing speed of torpedo is much greater than that of the surface ship, we construct the payoff matrix by the maximum capturing probabilities corresponding to pairs of sailing directions. Since the capturing probability depend on relative positions of the opposite objects, we can get the functional relationship between the relative positions of the torpedo and the ship under each game situation as a function of time. Then, a component of the payoff matrix is obtained by taking the maximum capture probability for a pair of sailing settings. If the probability of capture is less than the given threshold, no evasion operation is carried out; otherwise, it is necessary to determine the evasion strategy of the red ship.

To model the scenario of hydroacoustic confrontation, we establish a planar rectangular coordinate system based on the relative positions of the torpedo and the ship. Assuming that the detected position of the torpedo and the location of surface ship obey the normal distribution, we always place the surface ship at the origin of the coordinate system. Then, the position of torpedo can be taken as a two-dimensional random vector obeying a normal distribution.

The hydroacoustic confrontation situations when the sonar system of the red ship detects the incoming torpedo are shown in Figure 1, where the avoidance direction angle

θ

of the red surface ship and the advance angle

ϕ

of the blue torpedo attack are supposed to be regulated to perform the countermeasure game. For a strategy pair (

ϕ, θ

), the relative position of the mine-ship can be calculated as a function of time according to the sailing speed of the red ship and the attack advance angle and attack speed of the incoming torpedo. By incorporating a calculation method of capture probability, one can get the capture probability function of sailing time, and take its maximum value as the probability that an attacking torpedo captures the red ship.

Accordingly, the game model of hydroacoustic confrontation between red and blue parties can be constructed, and the game strategy pair is

(ϕ, θ)

. As illustrated in Figure 1, let

θ \in [- θ_{0}, θ_{0}]

ϕ \in [0, ϕ_{0}]

. To construct a discrete matrix game model, intervals

[- θ_{0}, θ_{0}]

and

[0, ϕ_{0}]

are discretized as collections of finite feasible values, that is, we set

θ \in {θ_{1}, \dots, θ_{m}}

and

ϕ \in {ϕ_{1}, \dots, ϕ_{n}}

. Then, we get the

n \times m

payoff matrix

P = {(p_{i, j})}_{n \times m}

, where the payoff

p_{i, j}

is the probability that a red ship is captured by a blue torpedo when the adversarial strategy pair is

(ϕ_{i}, θ_{j})

(

i = 1, \dots, n, j = 1, \dots, m

A mixed/pure-strategy Nash equilibrium solution to this matrix game model can be obtained by solving the linear programming model [22]

\begin{matrix} max z = \sum_{j = 1}^{m} r_{j} \\ s . t . \{\begin{matrix} \sum_{j = 1}^{m} p_{i j} r_{j} \leq 1, i = 1, \dots, n, \\ r_{j} \geq 0, j = 1, \dots, m . \end{matrix} \end{matrix}

(2)

According to the optimal solution

\vec{r} = (r_{1}, \dots, r_{m})

of model (1), the sum of components

v = \sum_{j = 1}^{m} r_{j}

is the optimal payment corresponding to the mixed-strategy Nash equilibrium, and the probability distribution

σ^{*} = (\frac{r_{1}}{v}, \dots, \frac{r_{m}}{v})

is the pure/mixed-strategy Nash equilibrium.

4. Calculation of the Payoff Corresponding to a Strategy Pair ( $ϕ$ , $θ$ )

4.1. The Gaussian Model for Payoff of a Strategy Pair ( $ϕ$ , $θ$ )

Figure 1 illustrates the confrontation posture at the time of alarm. We establish an inertial coordinate system where the surface ship’s position is set as the origin of the coordinate system, denoted by O. The sailing direction of the ship is set as the positive direction of the Y axis, labelled as the due north direction, and the due east direction is taken as the positive direction of the X axis. Denote the sailing speed of the surface ship by

v_{w a r s h i p}

, and the deflection angle to avoid the attack of torpedo by

θ

. For the acoustic self-guided torpedo, let q and

d_{0}

be its relative bearing angle and the distance from the surface ship, respectively. While the torpedo attack with the speed

v_{t o r p e d o}

uniform linear search, the attacking direction can be computed by

C = q + ϕ + π,

(3)

where

ϕ

is the favourable advance angle,

φ

is the angle between the torpedo heading extension line and the Y-axis angle.

Set

t = 0

for the moment when the sonar equipment reports attack of the torpedo. We get the position

M (t) = (x_{w a r s h i p} (t), y_{w a r s h i p} (t))

of the red warship at time t, where

x_{w a r s h i p} (t) = \int_{0}^{t} v_{w a r s h i p} sin θ d t,

(4)

y_{w a r s h i p} (t) = \int_{0}^{t} v_{w a r s h i p} cos θ d t .

(5)

Similarly, the torpedo’s position

T (t) = (x_{t o r p e d o} (t), y_{t o r p e d o} (t))

can be identified by

x_{t o r p e d o} (t) = d_{0} sin q + \int_{0}^{t} v_{t o r p e d o} sin C d t,

(6)

y_{t o r p e d o} (t) = d_{0} cos q + \int_{0}^{t} v_{t o r p e d o} cos C d t .

(7)

The distance between the surface ship and the torpedo is

d (t) = \sqrt{{(x_{t o r p e d o} (t) - x_{w a r s h i p} (t))}^{2} + {(y_{t o r p e d o} (t) - y_{w a r s h i p} (t))}^{2}} .

(8)

The lead angle is changing with time t by

ϕ (t) = π - arccos \frac{r_{1} (t) r_{2} (t)}{∥ r_{1} (t) ∥ ∥ r_{2} (t) ∥},

(9)

where

r_{1} (t) = T (0) - T (t), r_{2} (t) = M (t) - T (t) .

Since the positions of both surface ship and torpedo could not be precisely located, it is assumed that their coordinate positions obey the two-dimensional normal distribution:

r_{M} (t) \sim N (M (t), Σ_{w a r s h i p}),

(10)

r_{T} (t) \sim N (T (t), Σ_{t o r p e d o}) .

(11)

In case that

r_{M} (t)

and

r_{T} (t)

are independent, we know

r (t) = r_{M} (t) - r_{T} (t)

is a Gaussian random vector with

r (t) \sim N (r_{0} (t), Σ),

where

r_{0} (t) = M (t) - T (t),

(12)

Σ = Σ_{w a r s h i p} + Σ_{t o r p e d o} .

(13)

The probability density function (PDF) of

r (t)

f (r, t) = \frac{1}{2 π {| Σ |}^{\frac{1}{2}}} exp [- \frac{1}{2} {(r - r_{0} (t))}^{T} Σ^{- 1} (r - r_{0} (t))] .

(14)

While the surface ship is located in the self-guided sector S of the torpedo, it would be captured by the torpedo. Thus, the capture probability

P_{c} (t)

can be computed by a double integral

P_{C} (t) = {\int \int}_{S_{1}} \frac{1}{2 π {| Σ |}^{\frac{1}{2}}} exp [- \frac{1}{2} {(r - r_{0} (t))}^{T} Σ^{- 1} (r - r_{0} (t))] d x d y

(15)

where

S_{1}

is the sector illustrated in Figure 2. Maximizing

P_{C} (t)

for time t we can get the payoff (capture probability) corresponding to a strategy pair

(θ, ϕ) .

4.2. Approximation of the Payoff Corresponding to a Strategy Pair $(θ, ϕ)$

Since the integral included in (15) cannot be analytically computed, we would like to get an analytical approximation of

P_{C} (t)

to get the payoff corresponding to a strategy pair

(θ, ϕ)

Assuming that the position error in the x-direction is uncorrelated to the position error in the y-direction, we get a diagonal covariance matrix

P = [\begin{matrix} σ_{x}^{2} & 0 \\ 0 & σ_{y}^{2} \end{matrix}] .

(16)

For any time moment t, denote

r_{0} (t) = (x_{0} (t), y_{0} (t))

, and Equation (15) implies

P_{C} (t) = \frac{1}{2 π σ_{x} σ_{y}} {\int \int}_{S_{1}} exp [- \frac{1}{2} (\frac{x^{2}}{σ_{x}^{2}} + \frac{y^{2}}{σ_{y}^{2}})] d x d y .

(17)

Denote the radius and the sector angle of

S_{1}

L_{m a x}

and

λ

, respectively. As illustrated in Figure 2, any

(x, y) \in S_{1}

satisfies

\{\begin{matrix} x^{2} + y^{2} \leq {L_{m a x}}^{2}, \\ - y t a n (\frac{λ}{2}) \leq x \leq y t a n (\frac{λ}{2}), \\ y \geq 0 . \end{matrix}

Since the self-conducting sector of torpedo is usually a sector with a large radius

L_{m a x}

and a comparatively small angle

λ

, we can approximate

P_{C} (t)

by integrating the PDF in a rectangle

S_{2}

that is illustrated in Figure 2 by dashed lines, which is confirmed by

S_{2} = {(x, y) | - y t a n (\frac{λ}{2}) \leq x \leq y t a n (\frac{λ}{2}), 0 < y < L_{m a x}} .

(18)

Thus, Equations (17) and (18) implies that the probability can be approximated by

P_{C_{A}} (t) \approx \frac{1}{2 π σ_{x} σ_{y}} {\int \int}_{S_{1}} exp [- \frac{1}{2} (\frac{x^{2}}{σ_{x}^{2}} + \frac{y^{2}}{σ_{y}^{2}})] d x d y = P_{C x} (t) \cdot P_{C y} (t),

where

\begin{matrix} P_{C x} (t) & = & \int_{- L_{m a x} tan (\frac{λ}{2})}^{L_{m a x} tan (\frac{λ}{2})} \frac{1}{\sqrt{2 π} σ_{x}} exp (- \frac{{(x - x_{0} (t))}^{2}}{2 σ_{x}^{2}}) d x, \\ = & Φ (\frac{L_{m a x} tan (\frac{λ}{2}) - x_{0} (t)}{σ_{x}}) + Φ (\frac{L_{m a x} tan (\frac{λ}{2}) + x_{0} (t)}{σ_{x}}) - 1, \end{matrix}

P_{C y} (t) = \int_{0}^{L_{m a x}} \frac{1}{\sqrt{2 π} σ_{y}} exp (- \frac{{(y - y_{0} (t))}^{2}}{2 σ_{y}^{2}}) d y = Φ (\frac{L_{m a x} - y_{0} (t)}{σ_{y}}) + Φ (\frac{y_{0} (t)}{σ_{y}}) - 1,

and

Φ (\cdot)

is the cumulative distribution function (CDF) of the standard normal distribution. In summary, the capture probability can be approximated by

P_{C} (t) \approx [Φ (\frac{L_{m a x} tan (\frac{λ}{2}) - x_{0} (t)}{σ_{x}}) + Φ (\frac{L_{m a x} tan (\frac{λ}{2}) + x_{0} (t)}{σ_{x}}) - 1] \cdot [Φ (\frac{L_{m a x} - y_{0} (t)}{σ_{y}}) + Φ (\frac{y_{0} (t)}{σ_{y}}) - 1] .

(19)

5. The Generation Strategy of Initial Feasible Solution

To get real-time countermeasure strategy for the constructed matrix game model, an improved simplex method algorithm addressing the linear programming model (2) is developed to get a (mixed/pure) Nash equilibrium solution of the game model.

The simplex method can address the canonical form of a linear programming problem

\begin{matrix} max z = C^{T} X \\ s . t . \{\begin{matrix} A X = b, \\ X \geq 0, b \geq 0 . \end{matrix} \end{matrix}

(20)

Starting with an initial basic feasible solution, the simplex method iterates successively to get the optimal solution of (20). In this paper, we incorporate a tailored strategy included in Algorithm 1 to accelerate the iteration process of the simplex method. By resorting the decision variables according components of C, problem (20) is transformed to a reformed linear programming problem

\begin{matrix} max w = {C^{^{'}}}^{T} X^{^{'}} \\ s . t . \{\begin{matrix} A^{^{'}} X^{^{'}} = b^{^{'}}, \\ X^{^{'}} \geq 0, b \geq 0, \end{matrix} \end{matrix}

and a promising basis feasible solution

X_{0}

is generated by the Gaussian elimination method with partial pivoting. Accordingly, the initial feasible basis can be obtained by picking up columns of

A^{^{'}}

that correspond to its leading entries.

The proposed method generates an initial feasible solution with a promising objective value and tries to incorporate in it artificial variables as few as possible, which not only reduces the time complexity of each iteration, but also reduces the number of iterations before the optimal solution is achieved.

6. Numerical Simulation

In this section, we perform numerical simulation to validate the effectiveness of our proposed method.

Algorithm 1 Initialization for the Simplex Method

Input:: $A = {(a_{i, j})}_{n \times m}, C = {(c_{1}, \dots, c_{m})}^{T}, X = {(x_{1}, \dots, x_{m})}^{T}, b = {(b_{1}, \dots, b_{n})}^{T}$ .
Output:: $A^{^{'}}, C^{^{'}}, X^{^{'}}, b^{^{'}}, X_{0}$ .
1:: Sort the components of C in descending order to get the reformed problem

$max w = {C^{^{'}}}^{T} X^{^{'}} s . t . A^{^{'}} X^{^{'}} = b^{^{'}},$

where $A^{^{'}} = {(a_{i, k_{j}})}_{n \times m}$ , $X^{^{'}} = {(x_{k_{1}}, \dots, x_{k_{m}})}^{T}$ , $b^{^{'}} = b$ , $C^{^{'}} = {(c_{k_{1}}, \dots, c_{k_{m}})}^{T}$ , $c_{k_{1}} \geq \dots \geq c_{k_{m}}$ ;
2:: Perform the Gaussian elimination method with partial pivoting on the linear system $A^{^{'}} X^{^{'}} = b^{^{'}}$ , obtaining a linear system $A^{^{″}} X^{^{'}} = b^{^{″}}$ , where $A^{^{''}}$ is a reduced row echelon form of matrix $A^{^{'}}$ ;
3:: Set $A^{^{'}} = A^{^{''}}, b^{^{'}} = b^{^{''}}, X_{0} = {({b^{^{'}}}^{T}, 0^{T})}^{T}$ .

6.1. Simulation Settings

Numerical simulation is carried out based on the settings presented as follows.

Torpedo:

The torpedo attacks at a speed of

50 k n

1. When the sonar equipment alarms its attack, it is

28 c a b

2 far away from the surface ship, and the outboard angle is

30^{\circ}

. The standard deviation of the reported position is

150 m

for both the x-coordinate and the y-coordinate. The maximum self-guiding distance of torpedo is

1500 m

, and the self-guiding sector angle is

30^{\circ}

. The value of advance angle

ϕ

of the torpedo ranges in

[0^{\circ}, 35^{\circ}]

with a stepsize of

5^{\circ}

surface ship:

The sailing speed of surface ship is

18 k n

. The value of avoidance angle

θ

of the surface ship ranges in

[- 35^{\circ}, 35^{\circ}]

with a stepsize of

5^{\circ}

6.2. Simulation Results

According to the discretization of

(ϕ, θ)

, we can maximize

P_{C} (t)

for time t to obtain the payoff (capture probability) corresponding to each pair of game strategy

(ϕ, θ)

, which contributes to a

8 \times 15

payoff matrix. While numerical results demonstrate that when

ϕ

is greater than

25^{\circ}

, the capture probabilities are very small, which is ignored and deleted from the payoff matrix. Accordingly, we get the payoff matrix presented in Table 1.

The linear programming problem (2) is addressed by the simplex method with an initialization method presented in Algorithm 1, and we get the Nash equilibrium solution, which demonstrates that the ship-side mixed strategy is

S_{M} = (0.40, 0.00, 0.00, 0.00, 0.00, 0.00, 0.20, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.4)

and the torpedo-side mixed strategy is

S_{T} = (0.47, 0.00, 0.21, 0.32, 0.00, 0.00) .

The corresponding equilibrium value is

V_{G} = 0.46

The torpedo-side mixed strategy shows that the torpedo would attack the surface ship in the directions characterized the advanced angles

0^{\circ}

10^{\circ}

and

15^{\circ}

, and the corresponding probabilities are

0.47

0.21

and

0.35

, respectively. Meanwhile, the ship-side mixed strategy suggests that the preferred avoidance angles of surface ship are

- 35^{\circ}

5^{\circ}

, and

15^{\circ}

, and the corresponding probabilities are

0.4

0.2

and

0.4

, respectively. The Nash equilibrium solutions could lead to a preliminary decision for the hydroacoustic countermeasure scenario: the advance angle of attacking torpedo could range in

[10^{\circ}, 15^{\circ}]

, and the preferred avoidance strategy could be turning right for about

5^{\circ} - 15^{\circ}

, which could provide a suggestive action before the attacking direction of torpedo is addressed, and in turn improve the survival probabilities of surface ship for the emergent scenarios of hydroacoustic countermeasure.

7. Conclusions and Discussions

In order to improve the survival capability of surface ship in the scenarios of anti-torpedo hydroacoustic countermeasure, this paper proposes a game-based strategy to predict possible attacking directions of the hostile torpedoes. Based on the matrix game theory with the capture probabilities as payoffs, our method can output a real-time Nash equilibrium solution that reports the probabilities of all possible attacking directions. With this result, the defensive side can take actions before the sonar equipment identifies the attack intention of the hostile torpedoes. However, the predicting probability distribution does not given a definitive answer on what is the avoidance strategy of surface ship. Thus, our future work will investigate how a definitive countermeasure strategy is derived from the Nash equilibrium solution of the game model.

Author Contributions

Conceptualization, Y. Chen; formal analysis, Y. Chen; writing—original draft preparation, H. Zhao and H. Cheng; writing—review and editing, H. Cheng; funding acquisition, Y. Chen. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Open Fund of the National Key Laboratory of Science and Technology on Underwater Acoustic Antagonizing (No. 2021-JCJQ-LB033-02).

Conflicts of Interest

The authors declare no conflict of interest.

References

Liu, Haiyang.;Tang, Yubo.;Hu,Xiaofeng.;et al.Research on the assessment framework of joint combat programmes based on military chess projections.Journal of System Simulation.2018,30(11), 92–99.
Cheng, Jian.; Zhang, Hui. Optimal model and model solving strategy of submarine torpedo defence using acoustic counter measure equipment. Command Control and Simulation.2019, 41(6),48–51.
Lu, Wan.; Li, Zhao. Foreign anti-torpedo hydro-acoustic electronic warfare technology and its development trend. Shipboard Electronic Countermeasure. 2008,31(1), 50–53.
Wang, Xinhua.; Gao, Honglin.;Mu Lianyun.; et al.Research on warship anti-torpedo technology.Ship Science and Technology. 2011, 33(9), 86–90.
Gao, Xueqiang.; Song, Qiang.; Yang, Rijie. A review of key hard-kill techniques in acoustic warfare. Ship Science and Technology. 2007,29(2), 28–31.
Li, Benchang.; Liu, Chunyue.; Zheng, Yuan. Development of modern acoustic countermeasure equipments and its effect on sea warfare.Torpedo Technology.2011,19(6), 468–472.
George, J.; Sinchu, P.; Kumar, K. A.; et al. Towed acoustic countermeasures for defending acoustic homing torpedoes.Defence Science Journal.2019,69(6), 607–612. [CrossRef]
Zhao, Lianfang. Anti-torpedo defense system and technology of surface and underwater warship.Intelligence Command Control and Simulation Techniques.2001,6(2), 1–14.
Kierstead, D.; Delbalzo, D. A genetic algorithm applied search paths in complicated environments.Military Operations Research.2003,8(2), 45–59.
Jia, Yue.; Song, Baowei.; Liang, Qingwei. Evadable optimization model and survival probability analysis of warship with rocket assist acoustic decoy countering torpedo.Acta Armamentar.2008,29(5), 637–640.
Jia, Yue.; Song, Baowei.; Cui Shaobo. The mathematical and simulation model of countering the acoustic homing torpedo with the acoustic decoy.Journal of System Simulation.2008,20(2), 267–269.
Li,Minghui.;Min,Shaorong.;Xie,Hongsheng.Derivative assessment of torpedo avoidance effectiveness of ships based on the Monte Carlo method.Ship Electronics Engineering.2014,34(2),136–140.
Malinowski, M.; Gopakumar, K.; Rodriguz, J.; et al. A survey on cascaded multilevel inverters.IEEE Transactions on Industry Electronics.2010,57(7), 2197–2206. [CrossRef]
Levine, A.J. The Pacific War: Japan versus the Allies; Greenwood Publishing Group: Westport, CT, USA, 1995; Volume 130.
Maskery, M.; Krishnamurthy, V. Network-enabled missile deflection: Games and correlation equilibrium. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 843–863. [CrossRef]
Maskery, M.; Krishnamurthy, V.; O’Regan, C. Decentralized algorithms for netcentric force protection against antiship missiles. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1351–1372. [CrossRef]
Bachmann, D.J.; Evans, R.J.; Moran, B. Game theoretic analysis of adaptive radar jamming. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1081–1100. [CrossRef]
Xia,Zhijun.;Zhang, Xinhua.;Xiao Jigang.;et al.Requirement Analysis of Hydroacoustic Countermeasures System for Ship Formation.Ship Science and Technology.2007,29(6),66–69.
Ma, Fei.; Cao, Zeyang.; Liu, Hui. Construction and search of strategy space of target assignment based on game theory.Journal of Systems Engineering and Electronics. 2010,32(9), 1941–1945.
Edwin Ho, Arvind Rajagopalan, Alex Skvortsov, Sanjeev Arulampalam and Mahendra Piraveenan. Game Theory in Defence Application: A Review. Sensors. 2022,22(3), 1032. [CrossRef]
Kuhn, H.; Arrow, K.; Tucker, A. Contributions to the Theory of Games. Number v. 2 in Annals of Mathematics Studies; Princeton University Press: Princeton, NJ, USA, 1953.
Hillier, F. S.;Lieberman, G. J.Introduction to operations research, 7rd ed.; McGraw-Hill: New York, USA, 2001; pp.726–741.
Vitor, F., Easton, T. The double pivot simplex method. Mathematical Methods of Operations Research, 2017,87, 109–137. [CrossRef]
Dantzig G. Maximization of a linear function of variables subject to linear inequalities. In: Koopmans TC (ed) Activity analysis of production and allocation, 1951. Wiley, New York, pp 339–347.

1	1 kn = 1n mile/h= 0.514 m/s.
2	1cab=0.1 n mile=185.2m.

Figure 1. Scenarios of hydroacoustic countermeasures.

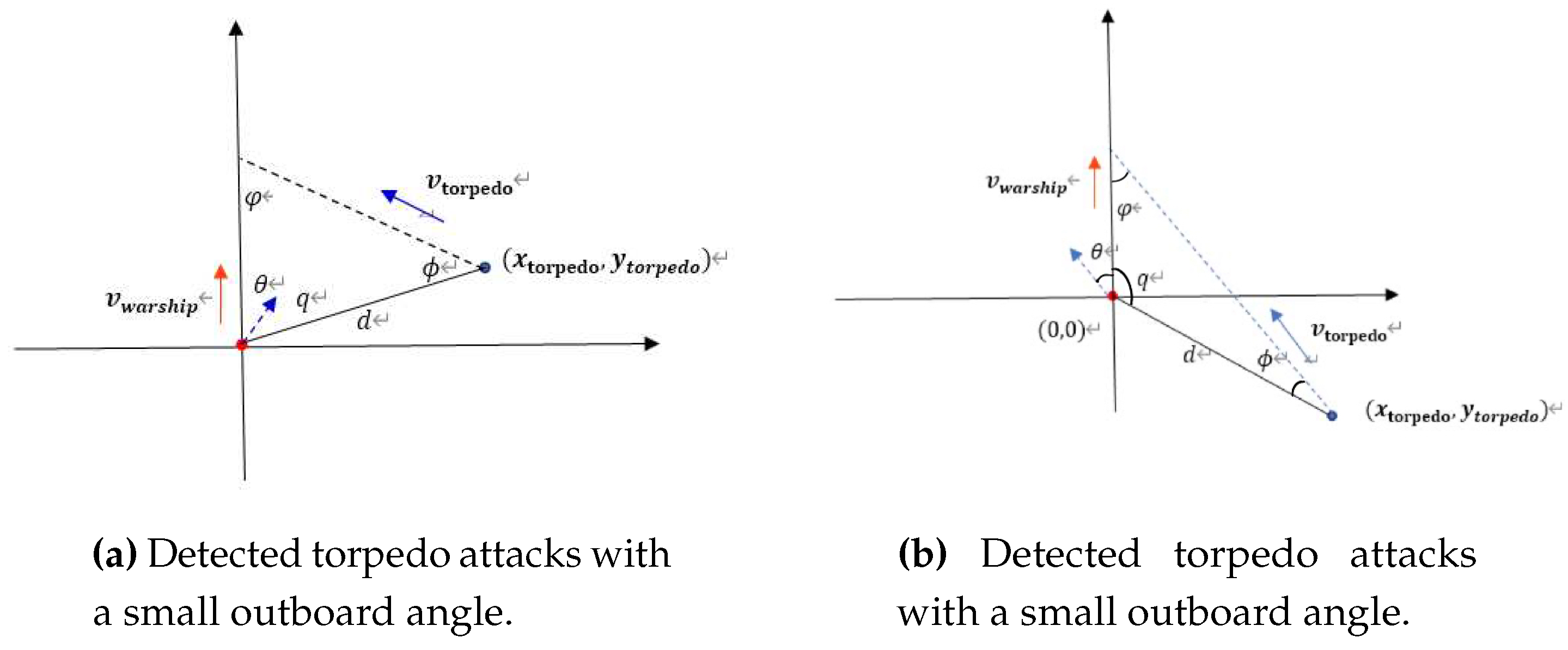
Figure 2. The self-guided sector for calculation of the capture probability.

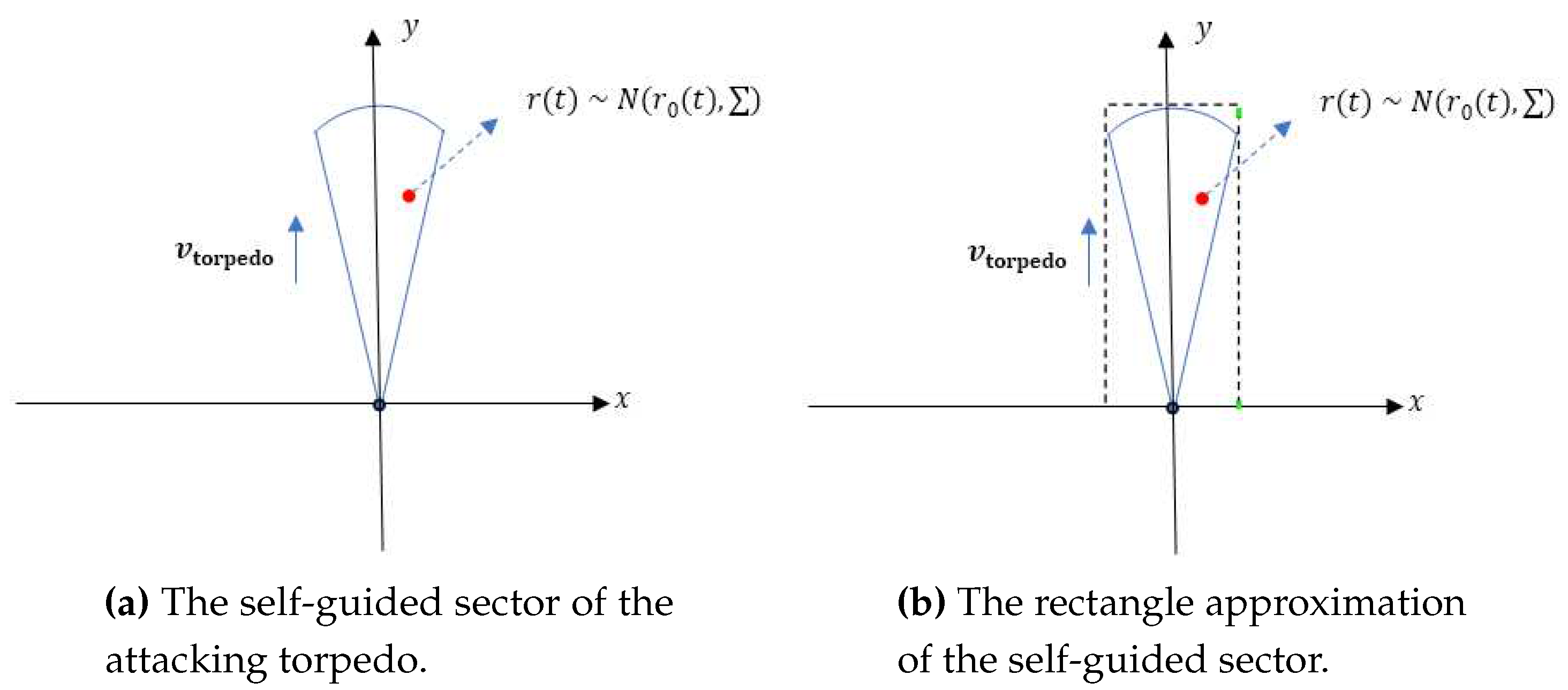
Table 1. The payoff matrix of game model.

ϕ	θ
ϕ	$- 35^{\circ}$	$- 30^{\circ}$	$- 25^{\circ}$	$- 20^{\circ}$	$- 15^{\circ}$	$- 10^{\circ}$	$- 5^{\circ}$	$0^{\circ}$	$5^{\circ}$	$10^{\circ}$	$15^{\circ}$	$20^{\circ}$	$25^{\circ}$	$30^{\circ}$	$35^{\circ}$
$0^{\circ}$	0.00	0.00	0.00	0.00	0.00	0.02	0.06	0.17	0.35	0.58	0.79	0.92	0.98	0.99	0.98
$5^{\circ}$	0.02	0.06	0.13	0.25	0.43	0.62	0.80	0.91	0.97	0.99	0.99	0.97	0.87	0.65	0.34
$10^{\circ}$	0.66	0.79	0.89	0.95	0.98	0.99	0.99	0.99	0.95	0.84	0.62	0.35	0.13	0.03	0.00
$15^{\circ}$	0.99	0.99	0.99	0.99	0.96	0.90	0.76	0.54	0.30	0.11	0.03	0.00	0.00	0.00	0.00
$20^{\circ}$	0.91	0.83	0.71	0.54	0.34	0.17	0.06	0.02	0.00	0.00	0.00	0.00	0.00	0.00	0.00
$25^{\circ}$	0.14	0.08	0.04	0.01	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Hydroacoustic Adversarial Strategy Based on the Matrix Game Theory

Abstract

Keywords:

Subject:

1. Introduction

2. Preliminaries

2.1. Introduction to the Game Theory

2.2. The Simplex Method for LP Problems [23]

3. The Matrix Game Model for Hydroacoustic Countermeasure

4. Calculation of the Payoff Corresponding to a Strategy Pair ( ϕ , θ )

4.1. The Gaussian Model for Payoff of a Strategy Pair ( ϕ , θ )

4.2. Approximation of the Payoff Corresponding to a Strategy Pair ( θ , ϕ )

5. The Generation Strategy of Initial Feasible Solution

6. Numerical Simulation

6.1. Simulation Settings

6.2. Simulation Results

7. Conclusions and Discussions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4. Calculation of the Payoff Corresponding to a Strategy Pair ( $ϕ$ , $θ$ )

4.1. The Gaussian Model for Payoff of a Strategy Pair ( $ϕ$ , $θ$ )

4.2. Approximation of the Payoff Corresponding to a Strategy Pair $(θ, ϕ)$