Prerpints.org logo
Preprint
Article

Optimizing Inference Distribution for Efficient Kidney Tumor Segmentation using a UNet-PWP Deep Learning Model on CT Scan Images

Altmetrics

Downloads

115

Views

93

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 August 2023

Posted:

11 August 2023

You are already at the latest version

Alerts
Abstract
Motivation: It is essential for the diagnosis and treatment of renal cancers to segment kidney tumours precisely and effectively. In medical image segmentation tasks, deep learning models have demonstrated promising results, and the UNet model is widely employed in this field. However, optimising the UNet model for kidney tumour segmentation further can improve its efficacy and deployment feasibility. Related Works: Previous works have explored various techniques to improve the efficiency of deep learning models in medical image segmentation. Image partitioning methods divides the input image into smaller regions, enabling parallel processing and reducing memory requirements. Pruning techniques eliminates redundant or insignificant weights, neurons and connections, resulting in a more compact and efficient model architecture. However, the UNet model architecture and its complexity in the context of kidney tumor segmentation using UNet remains unexplored. Methodology: The proposed methodology consists of adaptive partitioning and weight pruning. Adaptive partitioning divides the UNet model into smaller sub-models, facilitating parallel processing and accelerating inference without compromising segmentation accuracy. Weight pruning techniques remove redundant or less significant weights from the UNet-P model, reducing complexity and improving inference time by eliminating unnecessary computations. The adaptive partitioning and weight pruning processes are seamlessly integrated within the UNet-P architecture, resulting in an optimized model for kidney tumor segmentation. Results: We performed experiments utilising a dataset of KiT 23 CT scan images containing images of kidney malignancies. Compared to the standard UNet model, the optimised UNet-PWP model with adaptive partitioning and weight pruning obtained significant efficiency gains. The adaptive partitioning permitted parallel computation of sub-models, which accelerated inference times. Weight pruning decreased the UNet-PWP model’s complexity without compromising segmentation accuracy, thereby enhancing efficiency. The results of our experiments demonstrated the efficacy of the proposed method with 98% accuracy, demonstrating its potential for deployment in health sector.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

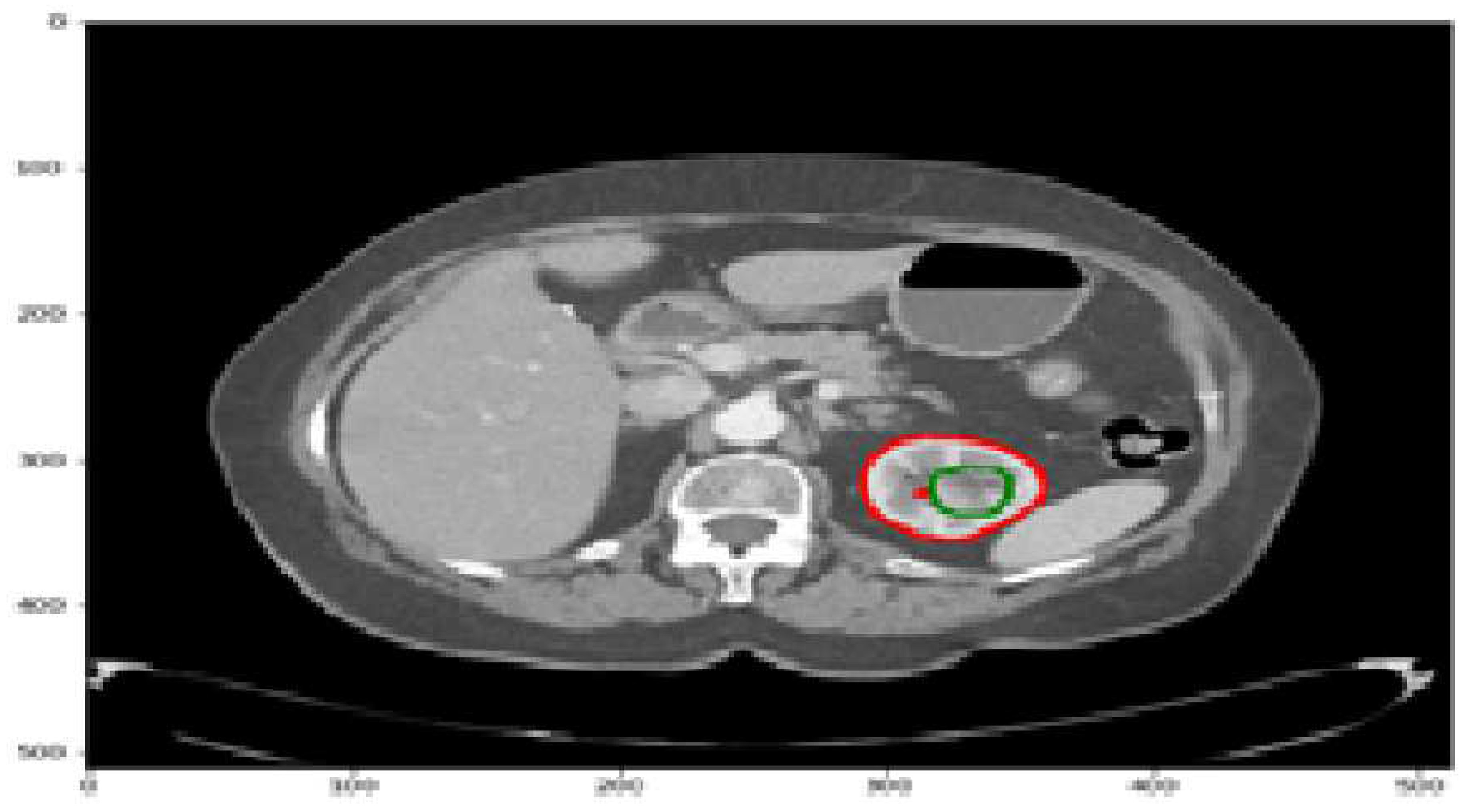
The kidneys play a crucial role in maintaining fluid and solute balance, hormone secretion, and blood pressure regulation. However, kidney diseases and cancer pose significant health challenges, with a lifetime risk of approximately 1 in 75 individuals [19]. Kidney malignancies are a prevalent form of cancer, affecting over 400,000 people annually and contributing to around 175,000 deaths [19]. They account for the majority of kidney tumors, with 80-90% attributed to kidney malignancies. Detecting kidney tumors [18] as shown in Figure 1 at an early stage is challenging since they can grow for an extended period without displaying symptoms. Various clinical procedures, including imaging techniques such as CT scans, aid in detecting kidney tumors or abnormalities. Accurately identifying and segmenting tumors in CT images can be challenging due to their irregular shapes and sizes. To address the complexities of kidney tumor segmentation, deep learning techniques have shown promise, particularly the use of convolutional neural networks (CNNs) [20]. In this study, we aim to develop an efficient approach for kidney tumor segmentation in CT images using deep learning, specifically CNNs. Our focus is on achieving fast inference times to overcome computational resource limitations [21] and improve the practical usability of the UNet [1] algorithm.
While deep learning models like UNet [1] have demonstrated high performance in medical image segmentation, their computational complexity can be a limiting factor, especially when processing large datasets or when deployed on resource-constrained systems. Thus, it is crucial to optimize the inference time of the UNet [1] model for efficient kidney tumor segmentation. By reducing the computational requirements [22] and improving inference speed, we can enable real-time or near-real-time segmentation, enhancing the usability and practicality of the model in clinical settings.
In this research study, we will explore techniques such as adaptive partitioning and weight pruning to optimize the UNet [1] model. Adaptive partitioning involves dividing the UNet [1] model into sub-models based on computational complexity, enabling parallel processing and accelerating inference. Weight pruning [4] focuses on eliminating redundant or less significant weights from the UNet [1] model, reducing its complexity and improving inference time. By integrating these techniques into the UNet [1] architecture, we aim to achieve faster inference times while maintaining accurate segmentation results.
The proposed approach has significant implications for kidney tumor segmentation, as it enables faster and more efficient processing of CT images. The optimized UNet [1] model with fast inference times can overcome computational resource limitations and make it feasible to deploy the model on various systems, including those with limited computational capabilities. This, in turn, enhances the practical usability of the UNet [1] algorithm for kidney tumor segmentation in clinical practice. In summary, this study focuses on developing an efficient approach for kidney tumor segmentation in CT images using deep learning, specifically CNNs [20]. By optimizing the UNet [1] model to achieve fast inference times, we aim to overcome computational resource limitations and improve the practical usability of the algorithm. The proposed methodology will contribute to more efficient and accurate kidney tumor segmentation, enabling enhanced diagnosis and treatment planning for patients with renal malignancies.
The reminder of this paper is organized as follows Section 2 presents the related work to detect CT images and clinical records. Section 3 describes the materials and methods applied on CT scan image dataset KiTs 23 using UNet-PWP distributed partition model [22]. Section 4 shows the experiments and results. Lastly section 5 presents the conclusions.

2. Related Works

Deep learning models have become widely employed in medical imaging analysis tasks such as segmentation, progression assessment, prediction, and tumor size estimation, providing valuable support to radiologists and healthcare professionals. However, these models often consist of complex architectures that may not be suitable for deployment on limited computational resources [3–7]. To address these challenges, researchers have focused on developing distributed strategies based on model complexity [7], aiming to achieve faster inference and efficient resource utilization [22]. By partitioning and optimizing the complexity of deep learning models [6], these approaches enable the deployment of accurate and efficient medical imaging analysis tools in real-world clinical settings.

2.1. Model Complexity

The complexity of a machine learning model or deep learning model [21] plays a crucial role in understanding its capabilities, resource requirements, and performance. In the context of a UNet [1] model used for tumor segmentation in CT scan image datasets, model complexity can be assessed using several key factors. These factors include the number of parameters, network depth, computational operations, and FLOPs (Floating Point Operations) [21].
Number of Parameters:
The number of parameters [7–9] in a UNet [1] model can be calculated by summing up the parameters in each layer. Let’s denote the number of parameters in a particular layer as P l a y e r . Assuming the UNet [1] model has L layers, the total number of parameters (P) can be computed as shown in Equation (1): P = P 1 + P 2 + . . . + P L ( 1 ) In a convolutional layer, the number of parameters is determined by the size of the kernel or filter and the number of input and output channels. For example, if a convolutional layer has a kernel size of K x K and Cin input channels, and Cout output channels, the number of parameters ( P l a y e r .) in that layer would be: P l a y e r . = K ∗ K ∗ C i n ∗ C o u t ( 2 )
Network Depth: The network depth [15] of a UNet [1] model refers to the number of encoder and decoder blocks/stages. Let’s assume the UNet [1] model has N stages [9]. In each stage, there are typically two convolutional layers followed by a downsampling operation (such as max pooling or stride-2 convolution) in the encoder and an upsampling operation (such as transposed convolution or bilinear upsampling) in the decoder. Thus, the network depth (D) [15] is equal to the number of stages as D = N (3).
Computational Operations: The computational operations [9] in a UNet [1] model depend on the operations in each layer, including convolutions, pooling, and upsampling. Let’s denote the number of operations [9] in a specific layer as Olayer. The total number of operations (C) can be calculated by summing up the operations in each layer: C = O 1 + O 2 + . . . + O L ( 4 ) The number of operations in a convolutional layer depends on the input and output feature map sizes, the kernel size, and the number of input and output channels. The specific calculation can vary based on the operations used and the hardware optimizations implemented.
FLOPs (Floating Point Operations): FLOPs (Floating Point Operations) [8,25] represent the number of floating-point operations required for a forward pass through the UNet [1] model. It provides an estimate of the computational complexity of the model. The FLOPs can be calculated by summing up the FLOPs in each layer: F L O P s = F L O P s 1 + F L O P s 2 + . . . + F L O P s L ( 5 ) The exact calculation of FLOPs depends on the specific operations performed in each layer. For convolutional layers, the FLOPs [8,25] can be estimated by considering the number of multiply-accumulate (MAC) operations[25] required based on the input and output feature map sizes and the kernel size.

2.2. Model Partitioning Strategies

Partitioning strategy [10] in the context of deep learning refers to the process of dividing a computational model into smaller sub-models or partitions. The objective is to distribute the computational workload across multiple resources or devices [10], allowing for efficient processing in resource-constrained environments or scenarios where parallel processing can provide performance benefits. The partitioning strategy [10] aims to strike a balance between maintaining the model’s overall functionality and minimizing the computational complexity of each partition. The goal is to create sub-models that are smaller and less computationally demanding while preserving the overall model’s performance to the best extent possible. The partitioning strategy can vary depending on the specific model architecture and the requirements of the application. Some common partitioning strategies include:
Layer-based Partitioning: Layer-based partitioning is a strategy introduced in Saguil, D., & Azim, A. (2020), where the model is divided into partitions based on individual layers. Each partition comprises a subset of layers that can be processed independently [11]. This approach is relatively straightforward to implement; however, it may lead to imbalanced computational workloads if certain layers are more computationally intensive than others. Further exploration and optimization of workload distribution techniques are necessary to overcome these limitations.
Block-based Partitioning: Block-based partitioning, as proposed in Kariyam, Abdurakhman, Subanar, Utami, H., & Effendie, A. R. (2022), involves dividing the model into blocks or segments of layers. Each block consists of a group of logically connected layers that can be processed together. This partitioning strategy [12] allows for a more balanced distribution of computational workloads and improved utilization of computational resources. By efficiently assigning layers into blocks, the model’s performance can be enhanced while ensuring effective utilization of available hardware resources.
Channel-based Partitioning: In Hui, C., Liu, S., & Jiang, F. (2022), channel-based partitioning is presented as a strategy for dividing the model based on the number of channels or feature maps in the layers. By allocating subsets of channels to different partitions, the computational workload can be evenly distributed [13], particularly in models with a large number of channels. Channel-based partitioning provides a means to efficiently parallelize the computation process, allowing for improved scalability and faster inference times in models with complex channel structures.
Data-based Partitioning: Data-based partitioning, described in Rota, J., Malm, T., Chazot, N., Peña, C., & Wahlberg, N. (2018), is a strategy that involves dividing the model based on the input data. This partitioning approach is commonly utilized in distributed machine learning frameworks [14]. In data-based partitioning, the input data is partitioned or distributed among multiple sub-models, with each sub-model processing its assigned data independently. This strategy enables parallel processing of data across multiple compute resources, facilitating efficient utilization of distributed computing environments for improved scalability and performance in large-scale machine learning tasks.

3. Materials and Methods

The U-Net model [1] is widely utilized in medical imaging tasks, offering a symmetric encoder-decoder architecture with skip connections. This architecture incorporates a contracting path (encoder) and an expanding path (decoder) to capture both low-level and high-level features in the input image. To understand the computational complexity of the U-Net model [1], we examine its components. The encoder consists of four blocks, each containing two 3x3 convolutional layers followed by max pooling. The number of filters increases gradually from 64 to 512. The bottleneck layer acts as a bridge between the encoder and decoder, comprising a 3x3 convolutional layer with 1024 filters to capture high-level features. The decoder, also consisting of four blocks, follows a similar structure as the encoder but with the number of filters decreasing from 512 to 64. Up-sampling operations double the spatial dimensions of the feature maps in the decoder. The output layer employs a 1x1 convolutional layer with 3 filters, applying a sigmoid activation function for pixel-wise segmentation predictions [13–15]. Assessing the computational complexity involves estimating the number of parameters and FLOPs required for each convolutional layer, max pooling, and up-sampling operation. Understanding the complexity of the U-Net [1] model facilitates resource management and optimization for efficient medical image segmentation applications. In our study, we conducted a comprehensive analysis of the computational requirements for the UNet [1] model employed in tumor segmentation tasks. To determine the exact computational demands, we meticulously calculated the total number of parameters [13–15] and Floating-Point operations (FLOPs) [9]. Our findings revealed that the model consists of a total of 31,030,723 parameters, encompassing both trainable (31,030,723) and non-trainable (0) parameters. Trainable parameters are updated during the model training process, while non-trainable parameters represent fixed components, such as biases or batch normalization statistics. Moreover, we estimated the total FLOPs for the model, amounting to approximately 109,133,365,256. FLOPs signify the number of floating-point operations needed for model inference. The precise calculation of FLOPs takes into account the specific operations and input size utilized in each layer. Our meticulous assessment of the UNet [1] model’s computational requirements provides valuable insights for resource allocation [23,24] and optimization strategies in tumor segmentation applications.

3.1. Data Preprocessing

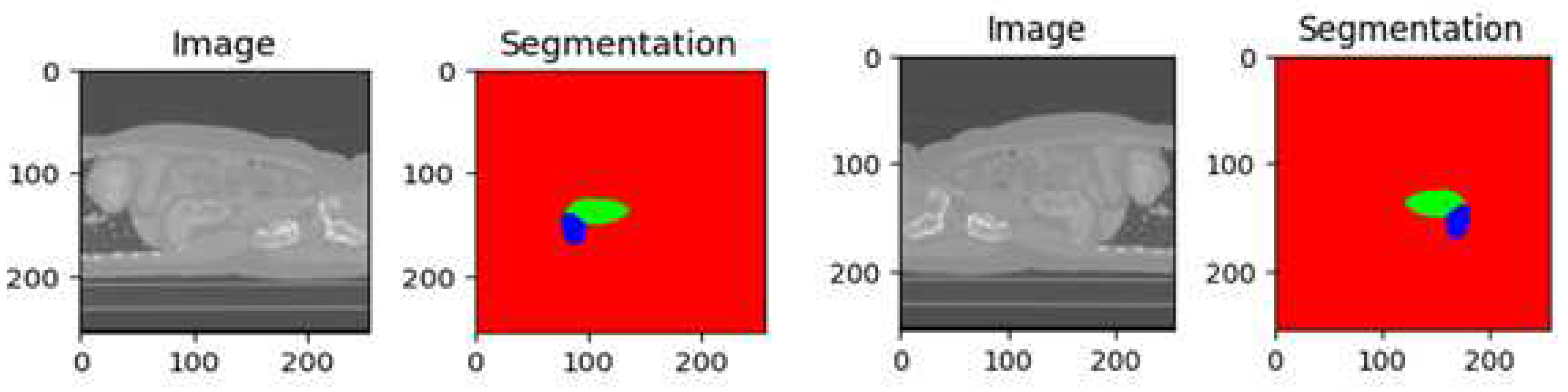
The KiTs23 dataset is often used for evaluating kidney tumor segmentation techniques. It consists of high-contrast CT images [2] taken between 2010 and 2020 at the University of Minnesota Medical Center [2], involving 548 patients who underwent partial or radical nephrectomy for one or more kidney tumors. The dataset contains scans with varying in-plane resolutions (ranging from 0.437 to 1.04 mm) and slice thicknesses (ranging from 0.5 to 5.0 mm). Each instance in the dataset includes ground-truth masks for both malignant tumors and healthy kidney tissue, as shown in Figure 2. These masks were manually created by medical students under the guidance of expert radiologists, using only the axial projections of the CT images. The dataset is provided in the NIFTI format and has dimensions specified as the number of slices, height, and width. It has been widely utilized as a benchmark for assessing kidney tumor segmentation methods, including the proposed model evaluated on this dataset.
The utilization of the KiTs23 [2] dataset offers several advantages. Firstly, it provides a diverse collection of CT scans with varying resolutions and slice thicknesses, allowing for the evaluation of the robustness and generalizability of segmentation techniques. Additionally, the ground-truth masks were created under the supervision of experts, ensuring the accuracy and reliability of the annotations.

3.2. Adaptive Partitioning

Deep learning models, particularly UNet [1], have demonstrated exceptional performance in tumor segmentation tasks using CT scan image datasets. However, their computational demands can hinder their practical implementation in resource-limited [24] settings. To tackle this challenge, we propose Adaptive Model Partitioning [16] (UNet-P)described in algorithm I, an algorithm that intelligently partitions a UNet model into sub-models, each with reduced complexity while maintaining high segmentation accuracy.UNet-P leverages key complexity metrics such as the number of parameters, network depth, computational operations, and FLOPs [21] to guide the partitioning process. By incorporating user-defined constraints on maximum complexity and the number of partitions, UNet-P provides a flexible and adaptive approach. The algorithm enables efficient utilization of computational resources by distributing the model’s complexity across multiple sub-models. The core of UNet-P lies in the analysis of layer-level complexities within the UNet architecture. By calculating the complexity of each layer and estimating the total complexity of the model, UNet-P determines the target complexity for each sub-model. Through an iterative process, the algorithm identifies partitioning points in the model where complexity thresholds are exceeded, ensuring that each sub-model adheres to the defined constraints. The resulting sub-models obtained from UNet-P exhibit reduced complexity, making them suitable for deployment on resource-constrained devices or distributed computing environments. These sub-models maintain the ability to accurately segment tumors in CT scan images while significantly reducing the computational burden.
The resulting ‘ s u b m o d e l s ’ list will contain the partitioned sub-models of the UNet model [1] [4], each representing a portion of the original model based on the specified maximum complexity and number of partitions.

3.3. Proposed UNet-PWP

Weight pruning UNet [4] involves removing redundant or less important connections in a deep learning model. By setting certain weights to zero, weight pruning [4] achieves sparsity in the network, effectively reducing the number of parameters and the overall complexity of the model. This process can be guided by various criteria, including magnitude-based pruning or structured pruning, depending on the desired level of sparsity and the specific characteristics of the model. In this section we introduce an extended version of the Adaptive Model Partitioning [15] algorithm called UNet-P with Weight Pruning [4] (UNet-PWP)described in algorithm II (Figure 4).
The resulting ‘ s u b m o d e l s ’ list will contain the partitioned sub-models of the UNet model, with weight pruning applied to each sub-model. This combined approach allows for efficient utilization of computational resources by reducing model complexity through partitioning and eliminating unnecessary connections through weight pruning [4]. The resulting sub-models maintain accuracy while being more suitable for deployment on resource-constrained devices or distributed computing environments.

4. Results

The UNet model [1], a popular choice for tumor segmentation in medical imaging, utilizes a standard architecture with distinct encoder and decoder pathways. The encoder consists of several convolutional layers with pooling operations [17], gradually reducing the spatial dimensions while increasing the number of feature maps. This process helps extract hierarchical representations of the input image. The decoder pathway then employs transposed convolutions or upsampling operations to progressively recover the spatial resolution, accompanied by skip connections [17] that concatenate feature maps from the encoder path to preserve finer details. This aids in localizing and segmenting tumors accurately.
To refine the predictions, additional convolutional layers can be incorporated, followed by an output layer employing a suitable activation function such as sigmoid or softmax [17]. During training, the model optimizes a loss function [17], such as binary cross-entropy or dice coefficient [18], by comparing the predicted segmentation masks with the ground truth annotations. Efficient implementations of UNet [1] often utilize parallelization techniques and GPU acceleration to expedite the computational operations involved as shown in Table 1, enabling faster training and inference times [4,7–9]. In this article, we applied an adaptive partitioning UNet-P framework that incorporates weight pruning techniques to reduce the model complexity and improve the efficiency of tumor segmentation. The adaptive partitioning approach divides the UNet-P model into submodels based on the importance of each parameter, allowing for fine-grained control over the number of parameters and computational operations. Through weight pruning, we selectively remove less significant connections in UNet-PWP architecture, thereby reducing the overall model size while preserving its performance. The results presented in Table 2 demonstrate the effectiveness of our approach, showcasing a substantial reduction in the number of parameters and computational operations, such as floating-point operations (FLOPs) [25]. This reduction leads to faster inference times, enabling real-time segmentation in clinical settings. By combining adaptive partitioning and weight pruning, we achieve a more resource-efficient and faster tumor segmentation model without compromising accuracy, demonstrating the potential of our proposed approach for practical medical image analysis applications.
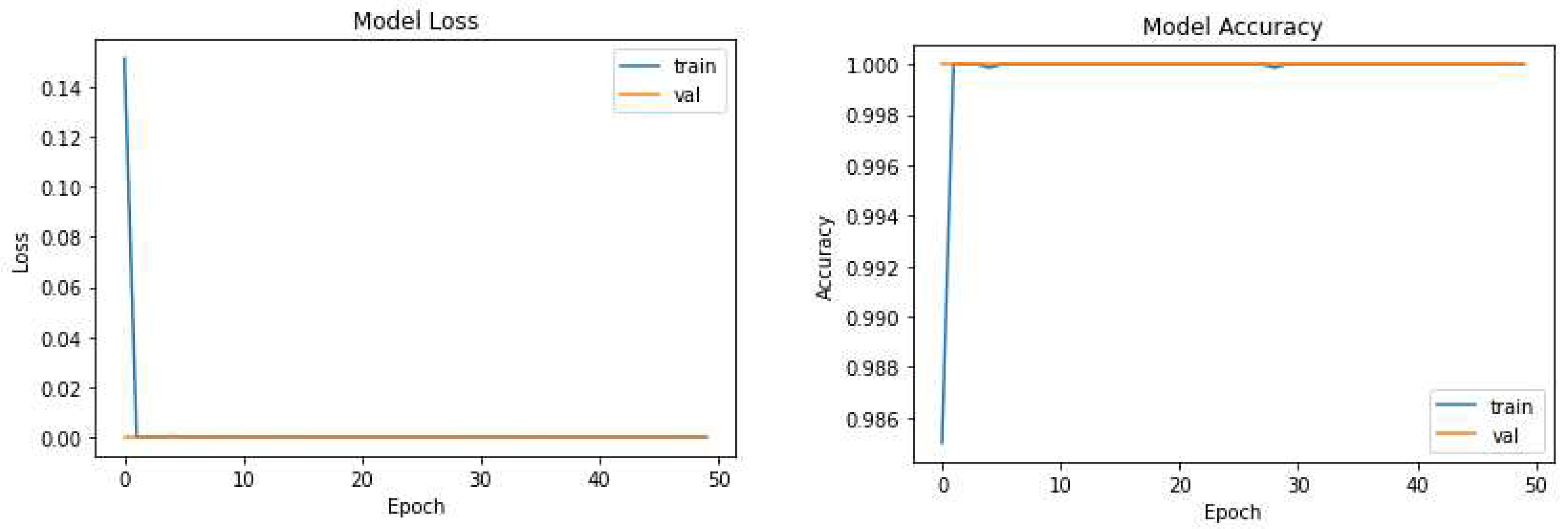
We further investigated two variants: UNet-P and UNet-PWP algorithms. UNet-P incorporates a modified training strategy by adjusting the number of epochs and optimizing the loss parameters. UNet-P partitioned the UNet model into 17 sub model with different FlOPs and parameters as shown in Table 2. While training the proposed model by carefully tuning parameters, we achieved a remarkable accuracy of 97.3%. This improvement can be attributed to the enhanced convergence and better utilization of the training and validating the KiTs 23 dataset.
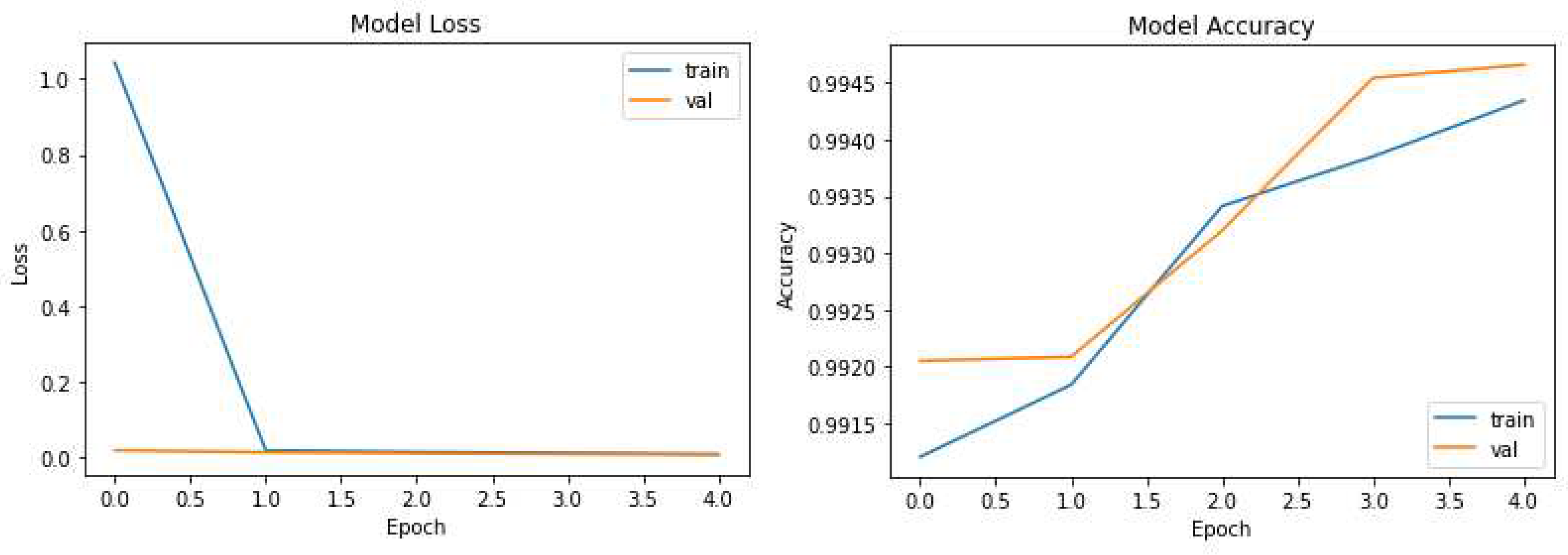
The pruning process selectively removes redundant connections, resulting in a more compact model while maintaining high segmentation accuracy. Remarkably, UNet-PWP achieved an even higher accuracy of 97.91%. These results shown in Figure 5 and Figure 6 highlight the effectiveness of our proposed algorithms in significantly reducing model complexity while preserving or even surpassing the accuracy achieved by the original UNet model. These findings underscore the potential of UNet-P and UNet-PWP for efficient and accurate tumor segmentation in medical imaging applications.
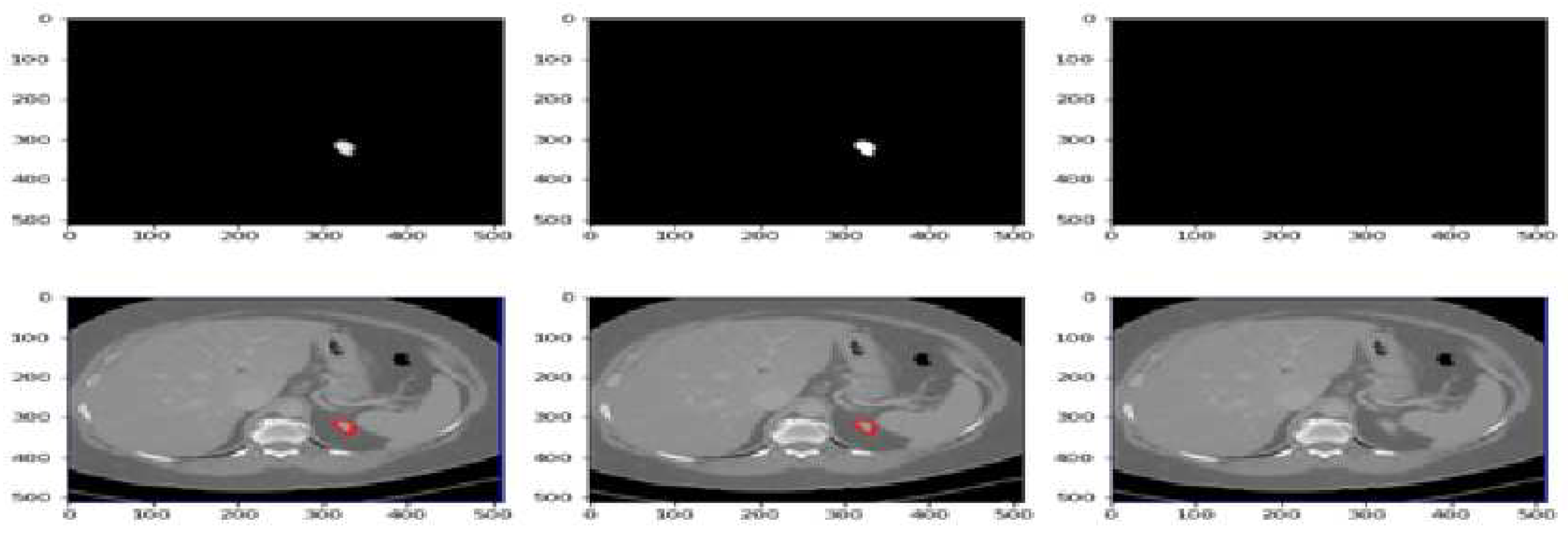
Figure 7 displays the segmentation predictions generated by the UNet-PWP model on the KiTs23 dataset. The model achieves an impressive accuracy of 97.91% in accurately segmenting kidney tumors. The predictions showcase the model’s ability to precisely delineate tumor boundaries and differentiate them from the surrounding healthy kidney tissue. With high accuracy, the UNet-PWP model demonstrates its potential as a robust tool for kidney tumor segmentation, providing valuable support in clinical applications such as tumor detection, monitoring, and treatment planning.

5. Conclusion

In conclusion, our study presents an optimized approach for kidney tumor segmentation using the UNet-PWP (partitioned UNet with weight pruning) model. With an accuracy of 97.8%, the UNet-PWP achieves highly accurate segmentation while reducing the number of floating-point operations (FLOPs) and enabling fast inference.The integration of adaptive partitioning in the UNet-P architecture allows for efficient computation by dividing the model into smaller submodels. Weight pruning techniques further enhance efficiency by reducing computational complexity. This optimized approach is beneficial for real-time clinical applications and offers a balance between accuracy and computational efficiency.The accurate segmentation provided by the UNet-PWP model is crucial for diagnosing and monitoring kidney tumors. Medical professionals can rely on the segmentation results to assess tumor progression, plan treatments, and evaluate their effectiveness.Our findings have implications beyond kidney tumor segmentation, as the methodology can be applied to other medical image segmentation tasks. The approach opens opportunities for efficient and accurate segmentation in diverse clinical scenarios, improving decision-making and patient care. To summarize, our study introduces an optimized approach using the UNet-PWP model for kidney tumor segmentation. It achieves high accuracy while reducing FLOPs and enabling fast inference. The approach has the potential to enhance medical image segmentation tasks and benefit clinical practice.

Author Contributions

Conceptualization: P.K.R. and S.C. conceived the idea of fusing graph and tabular deep learning models for enhanced CKD prediction. S.B.K. provided valuable input and suggestions to refine the concept. Model Implementation and Experimentation: P.K.R. and S.C. implemented the graph and tabular deep learning models and the fusion layer, while S.B.K. optimized model hyperparameters and conducted the experiments. Writing—Review and Editing: A.I.A. and A.A. participated in the review and editing process, providing feedback and suggestions for improving the manuscript’s clarity, coherence, and scientific rigor. Data curation, K.N. All authors have read and agreed to the published version of the manuscript.

Funding

Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R151), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia

Institutional Review Board Statement

“Not applicable” for studies not involving humans or animals.

Informed Consent Statement

“Not applicable” for studies not involving humans.

Acknowledgments

The datasets generated and/or analysed during the current study are available in the KiTs 23 [2] repository, Data – KiTS23 - Grand Challenge (grand-challenge.org) (Link: Data – KiTS23 - Grand Challenge (grand-challenge.org))

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
WP Weight Pruning
CT Computer Tomography
BN Batch Normalization
FLOPs Floating Point Operations
KiTs 23 [2] KiTs 23 [2] World Challenge Dataset
NIFTI Neuroimaging Informatics Technology Initiative
ADP Adaptive Partitioning
UNet-P Unet model with Partitions
UNet-PWP Unet Model with Pruned Partitions

References

  1. Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
  2. Heller, N.; Isensee, F.; Maier-Hein, K.H.; Hou, X.; Xie, C.; Li, F.; Nan, Y.; Mu, G.; Lin, Z.; Han, M.; et al. The state of the art in kidney and kidney tumor segmentation in contrast-enhanced CT imaging: Results of the KiTS19 challenge. Medical Image Analysis 2021. [Google Scholar] [CrossRef] [PubMed]
  3. Gadosey, P.K.; Li, Y.; Agyekum, E.A.; Zhang, T.; Liu, Z.; Yamak, P.T.; Essaf, F. SD-UNET: Stripping down U-net for segmentation of biomedical images on platforms with low computational budgets. Diagnostics 2020, 110. [Google Scholar] [CrossRef] [PubMed]
  4. Rao, P.; Chatterjee, S.; Sharma, S. Weight pruning-UNet: Weight pruning UNet with depth-wise separable convolutions for semantic segmentation of kidney tumors. Journal of Medical Signals and Sensors 2022. [Google Scholar] [CrossRef] [PubMed]
  5. Shah, B.; Bhavsar, H. Time Complexity in Deep Learning Models. Procedia Computer Science 2022. [Google Scholar] [CrossRef]
  6. Grebenkova, O.S.; Bakhteev, O.Y.; Strijov, V.V. Variational deep learning model optimization with complexity control. Informatika i Ee Primeneniya 2021. [Google Scholar] [CrossRef]
  7. Hu, X.; Chu, L.; Pei, J.; Liu, W.; Bian, J. Model complexity of deep learning: a survey. Knowledge and Information Systems 2021. [Google Scholar] [CrossRef]
  8. Yang, Y.; Deng, L.; Wu, S.; Yan, T.; Xie, Y.; Li, G. Training high-performance and large-scale deep neural networks with full 8-bit integers. Neural Networks 2020. [Google Scholar] [CrossRef] [PubMed]
  9. Wei, T.; Tian, Y.; Wang, Y.; Liang, Y.; Chen, C.W. Optimized separable convolution: Yet another efficient convolution operator. AI Open 2022. [Google Scholar] [CrossRef]
  10. Mahmud, M.S.; Huang, J.Z.; Salloum, S.; Emara, T.Z.; Sadatdiynov, K. A survey of data partitioning and sampling methods to support big data analysis. Big Data Mining and Analytics 2020. [Google Scholar] [CrossRef]
  11. Saguil, D.; Azim, A. A Layer-Partitioning Approach for Faster Execution of Neural Network-Based Embedded Applications in Edge Networks. IEEE Access 2020. [Google Scholar] [CrossRef]
  12. Kariyam; Abdurakhman; Subanar; Utami, H.; Effendie, A.R. Block-Based K-Medoids Partitioning Method with Standardized Data to Improve Clustering Accuracy. Mathematical Modelling of Engineering Problems 2022. [Google Scholar] [CrossRef]
  13. Hui, C.; Liu, S.; Jiang, F. Multi-Channel Adaptive Partitioning Network for Block-Based Image Compressive Sensing. In Proceedings of the IEEE International Conference on Multimedia and Expo; 2022. [Google Scholar] [CrossRef]
  14. Rota, J.; Malm, T.; Chazot, N.; Peña, C.; Wahlberg, N. A simple method for data partitioning based on relative evolutionary rates. PeerJ 2018. [Google Scholar] [CrossRef] [PubMed]
  15. Shi, S.; Wang, Q.; Chu, X. Performance modeling and evaluation of distributed deep learning frameworks on GPUs. In Proceedings of the IEEE 16th International Conference on Dependable, Autonomic and Secure Computing, IEEE 16th International Conference on Pervasive Intelligence and Computing, IEEE 4th International Conference on Big Data Intelligence and Computing and IEEE 3rd Cyber Science and Technology Congress, DASC-PICom-DataCom-CyberSciTec 2018; 2018. [Google Scholar]
  16. Zhou, L.; Samavatian, M.H.; Bacha, A.; Majumdar, S.; Teodorescu, R. Adaptive parallel execution of deep neural networks on heterogeneous edge devices. In Proceedings of the 4th ACM/IEEE Symposium on Edge Computing, SEC 2019. [CrossRef]
  17. Mert, İ. Activation functions for deep learning in smart manufacturing. In Optimization and Robotic Applications; 2019. [Google Scholar]
  18. Abdelrahman, A.; Viriri, S. Kidney Tumor Semantic Segmentation Using Deep Learning: A Survey of State-of-the-Art. Journal of Imaging 2022, 55. [Google Scholar] [CrossRef] [PubMed]
  19. Chatterjee, S.; Kiran; Rao, P. Diagnosis of kidney renal cell tumor through clinical data mining and CT scan image processing: A survey. International Journal of Research in Pharmaceutical Sciences 2020. [Google Scholar] [CrossRef]
  20. Parvathi, S.S.L.; Jonnadula, H. An Efficient and Optimal Deep Learning Architecture using Custom U-Net and Mask R-CNN Models for Kidney Tumor Semantic Segmentation. International Journal of Advanced Computer Science and Applications 2022. [Google Scholar] [CrossRef]
  21. Hu, X.; Chu, L.; Pei, J.; Liu, W.; Bian, J. Model complexity of deep learning: a survey. Knowledge and Information Systems 2021. [Google Scholar] [CrossRef]
  22. Langer, M.; He, Z.; Rahayu, W.; Xue, Y. Distributed Training of Deep Learning Models: A Taxonomic Perspective. IEEE Transactions on Parallel and Distributed Systems 2020. [Google Scholar] [CrossRef]
  23. Ahmed, U.; Lin, J.C.W.; Srivastava, G. A resource allocation deep active learning based on load balancer for network intrusion detection in SDN sensors. Computer Communications 2022. [Google Scholar] [CrossRef]
  24. Seetharam, K.; Kagiyama, N.; Sengupta, P.P. Application of mobile health, telemedicine and artificial intelligence to echocardiography. Echo Research and Practice 2019. [Google Scholar] [CrossRef] [PubMed]
  25. Nousi, P.; Patsiouras, E.; Tefas, A.; Pitas, I. Convolutional neural networks for visual information analysis with limited computing resources. In Proceedings of the International Conference on Image Processing, ICIP; 2018. [Google Scholar] [CrossRef]
Preprints 82093 g001
Figure 1. Sample CT scan image with Kidney and Kidney tumor region segmentation.
Figure 1. Sample CT scan image with Kidney and Kidney tumor region segmentation.
Preprints 82093 g001
Preprints 82093 g002
Figure 2. KiTs 23 [2] sample dataset with Kidney and Kidney tumor segmentation.
Figure 2. KiTs 23 [2] sample dataset with Kidney and Kidney tumor segmentation.
Preprints 82093 g002
Preprints 82093 g003
Figure 3. Adaptive Model Partitioning (UNet-P).
Figure 3. Adaptive Model Partitioning (UNet-P).
Preprints 82093 g003
Preprints 82093 g004
Figure 4. Adaptive Model Partitioning (UNet-PWP).
Figure 4. Adaptive Model Partitioning (UNet-PWP).
Preprints 82093 g004
Preprints 82093 g005
Figure 5. UNet-P architecture loss and accuracy on KiTs 23 [2] dataset with training and validation steps.
Figure 5. UNet-P architecture loss and accuracy on KiTs 23 [2] dataset with training and validation steps.
Preprints 82093 g005
Preprints 82093 g006
Figure 6. UNet-PWP architecture loss and accuracy on KiTs 23 [2] dataset with training and validation steps.
Figure 6. UNet-PWP architecture loss and accuracy on KiTs 23 [2] dataset with training and validation steps.
Preprints 82093 g006
Preprints 82093 g007
Figure 7. Visualization of the UNet-PWP model’s segmentation predictions on the KiTs23 dataset.
Figure 7. Visualization of the UNet-PWP model’s segmentation predictions on the KiTs23 dataset.
Preprints 82093 g007
Table 1. Standard UNet model for tumor segmentation with required computational operations.
Table 1. Standard UNet model for tumor segmentation with required computational operations.
Model Total Parameters Trainable Parameters Non-Trainable Parameters FLOPs
UNet 31,030,723 31,030,723 0.0 96,200,556,544
Table 2. UNet Sub Models Parameters and Complexity.
Table 2. UNet Sub Models Parameters and Complexity.
SNO Sub Model Total Parameters Trainable Parameters FLOPs
1 UNet Sub Model 1 4.68422e+06 4.68422e+06 2961178624
2 UNet Sub Model 2 9.40384e+06 9.40384e+06 3229614080
3 UNet Sub Model 3 2.56588e+07 2.56588e+07 5108662272
4 UNet Sub Model 4 2.80186e+07 2.80186e+07 5645533184
5 UNet Sub Model 5 2.85432e+07 2.85432e+07 5913968640
6 UNet Sub Model 6 2.85432e+07 2.85432e+07 5913968640
7 UNet Sub Model 7 2.97231e+07 2.97231e+07 6987710464
8 UNet Sub Model 8 3.03132e+07 3.03132e+07 7524581376
9 UNet Sub Model 9 3.04444e+07 3.04444e+07 7793016832
10 UNet Sub Model 10 3.04444e+07 3.04444e+07 7793016832
11 UNet Sub Model 11 3.07394e+07 3.07394e+07 8866758656
12 UNet Sub Model 12 3.0887e+07 3.0887e+07 9403629568
13 UNet Sub Model 13 3.09198e+07 3.09198e+07 9672065024
14 UNet Sub Model 14 3.09198e+07 3.09198e+07 9672065024
15 UNet Sub Model 15 3.09936e+07 3.09936e+07 10745806848
16 UNet Sub Model 16 3.10305e+07 3.10305e+07 11282677760
17 UNet Sub Model 17 3.10307e+07 3.10307e+07 11307843584
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated