A Classification of Elements of Function Space F(R,R)

Preprint

Article

A Classification of Elements of Function Space F(R,R)

Altmetrics

Downloads

Views

116

Comments

A peer-reviewed article of this preprint also exists.

Mohsen Soltanifar^*

This version is not peer-reviewed

Submitted:

10 August 2023

Posted:

11 August 2023

You are already at the latest version

Alerts

Abstract

In this paper, we classify the function space of all real-valued functions on R denoted as F(R,R) into 28 distinct blocks. Each block contains elements that share common features in terms of the cardinality of their sets of continuity and differentiability. Alongside this classification, we introduce the concept of the Connection, which reveals a special relationship structure between four well-known real-valued functions in real analysis: the Cantor function, Dirichlet function, the Thomae function, and the Weierstrass function. Despite the significance of this field, several perspectives remain unexplored.

Keywords:

Subject: Computer Science and Mathematics - Analysis

MSC: 05A18; 26A15; 26A21; 26A24; 26A30; 03E10

From the paradise, that Cantor created for us, no-one shall be able to expel us.

David Hilbert-1925

1. Introduction

1.1. Real Valued Functions

The theory of functions of a real variable was first treated by the Italian mathematician Ulisse Dini in 1878 [1]. This theory was constructed through the enlargement and deepening of set theory and was later developed separately and in parallel [1]. The development of this theory can be divided into three periods: the first period (1867-1902) saw extensive investigation into various topics of classical analysis, such as integrals, derivatives, and point set theory; the second period (1902-1930) marked the solidification of the theory of functions of a real variable as an independent mathematical discipline; and, the third period (1930-present) is characterized by the study of the theory of real-valued functions in connection with functional analysis [1].

1.2. Motivation

"The function space of all real-valued functions on the real line (

F (R, R)

) is an infinite-dimensional vector space with a nonconstructive basis. It encompasses various types of functions with pathological and chaotic structures. As researchers’ attention has shifted from pure existential mathematics to constructive mathematics [2,3], mathematicians have made numerous attempts to focus on special subsets of this vast vector space (e.g., all real-valued continuous functions [4]) or to classify this vector space using novel ancillary concepts. Examples of such classifications include those based on (i) set theory (surjective, injective, bijective, etc.), (ii) operators (additive, multiplicative, even, odd, etc.), (iii) topology (continuous, open, closed, etc.), (iv) properties concerning real numbers (differentiable, smooth, convex, etc.), and (v) measurability (Borel status, Baire status, etc.) [5,6,7].

This work presents another attempt to describe the vector space of real-valued functions on the real line in a constructive manner. Specifically, it aims to classify the elements of this vector space using their associated information on cardinality, continuity, and differentiability. Furthermore, based on this classification, it establishes a particular relationship among four of them: the Cantor function, the Dirichlet function, the Thomae function, and the Weierstrass function."

1.3. Study Outline

This paper is divided into four sections. The first section provides the necessary preliminaries in set theory, linear algebra, and special functions, which are essential for the following sections. In the second section, we discuss the partition of

F (R, R)

into 28 blocks of functions, presenting constructive examples for each block. The third section focuses on the relationship between these 28 blocks of functions using graph theory, with a specific emphasis on the four main plausible functions. Finally, we conclude the work with a discussion section on the current results and future directions.

2. Preliminaries

Readers who have studied the key topics of Analysis and Linear Algebra are well-equipped with the following notations, definitions, and results in the areas of "Set Theory" [8,9,10], "Linear Algebra" [8,11,12,13], and "Special Functions" [14,15,16,17].

2.1. Set Theory

Proposition 2.1.

Let

R

denote the set of real numbers and

A \subseteq R .

Then, either A is empty, non-empty finite, denumerable, or uncountable. In these cases, we denote the cardinality of A by

0, n (n \in N), ℵ_{0},

c,

respectively.

Remark 2.2.

Henceforth, we assume there are only four types of subsets in the real line given Proposition 2.1, and considering all non-empty finite sets of one category with symbol n as their cardinal number.

Proposition 2.3.

(i) Let

A \subseteq R

be uncountable and

A = A_{1} \dot{\cup} A_{2}

Then,

A_{1}

A_{2}

is uncountable.

(ii) Let

A \subseteq B \subseteq R .

Then,

0 \leq C a r d (A) \leq C a r d (B) \leq c .

Proposition 2.4.

Let C be the ternary Cantor set, i.e

C = {x \in [0, 1] | x : = \sum_{n = 1}^{\infty} \frac{a_{n}}{3^{n}} : a_{n} = 0, 2 (n \in N)}

. Then, one can write

C = \cap_{n = 1}^{\infty} C_{n}

where

C_{n}

is the disjoint union of

2^{n}

intervals of the form

I_{n, k} : = [a_{n, k}, b_{n, k}] (1 \leq k \leq n)

each of the length

3^{- n}, (n \geq 1) .

Remark 2.5.

Given

C_{u n c} = {A \subseteq C | C a r d (A) = c}

we have:

C a r d (C_{u n c}) = 2^{c} .

2.2. Linear Algebra

Definition 2.6.

Let

R

denote the set of real numbers. We define (i)

F (R, R) = {f : R \to R | f i s a f u n c t i o n .};

(ii)

C (R, R) = {f : R \to R | f i s a c o n t i n u o u s f u n c t i o n e v e r y w h e r e .}

; and, (iii)

D (R, R) = {f : R \to R | f i s a d i f f e r e n t i a b l e f u n c t i o n e v e r y w h e r e .}

Remark 2.7.

The function space

F (R, R)

equipped with conventional addition + and scalar multiplication • constitutes the vector space

(F (R, R), R, +, •)

. In addition, the vector spaces

(C (R, R), R, +, •)

, and

(D (R, R), R, +, •)

are its sub-spaces.

Proposition 2.8.

Given the sets introduced in Definition2.6 we have: (i)

D (R, R) ⊊ C (R, R) ⊊ F (R, R);

(ii)

C a r d (F (R, R)) = 2^{c};

(iii)

C a r d (C (R, R)) = c;

and, (iv)

C a r d (D (R, R)) = c .

Proposition 2.9.

dim (F (R, R)) = 2^{c} .

2.3. Special Functions

Definition 2.10.

Given indicator function

1_{A} (A \subseteq R),

and the ternary Cantor set

C .

Then, the Cantor function

C (.),

the Dirichlet function

D (.),

the Thomae function

T (.),

and the Weierstrass function

W (.)

are defined on closed unit interval as:

\begin{matrix} C (x : = \sum_{n = 1}^{\infty} \frac{a_{n, x}}{3^{n}}) & = & \frac{1}{2^{N_{x}}} + \sum_{n = 1}^{N_{x} - 1} \frac{a_{n, x}}{2^{n + 1}} : N_{x} = min {n \in N : a_{n, x} = 1}, \end{matrix}

(1)

\begin{matrix} D (x) & = & 1_{Q} (x), \end{matrix}

(2)

\begin{matrix} T (\frac{m}{n} 1_{Q} (x : = \frac{m}{n}) + x 1_{Q^{c}} (x)) & = & \frac{1}{n} 1_{Q} (x) : (m, n) = 1, \end{matrix}

(3)

\begin{matrix} W (x) & = & \sum_{n = 0}^{\infty} \frac{cos (21^{n} π x)}{3^{n}} . \end{matrix}

(4)

Remark 2.11.

We note that the definitions of the above functions have straightforward extension from the closed unit interval to the entire real line. Also, the introduced Weierstrass function here is special case of the general form for

a = \frac{1}{3}, b = 21 .

Definition 2.12.

Let C be the ternary Cantor set,

D (.)

be the Dirichlet function, and,

- \infty < a < b < \infty .

Then, for the triangular function

T^{(1)} (.)

given by

T_{a, b}^{(1)} (x) = \sqrt{3} (\frac{b - a}{2} - | x - \frac{b + a}{2} |) 1_{[a, b]} (x),

and the transformed cosine function

T^{(2)} (.)

given by

T_{a, b}^{(2)} (x) = (b - a) * (1 - c o s (2 π (\frac{x - a}{b - a}))) 1_{[a, b]} (x)

we define two functions

f_{C}

and

g_{C}

on the real line as:

\begin{matrix} f_{C} (x) & = & (\sum_{n = 1}^{\infty} f_{n} (x)) D (x) : f_{n} (x) = \sum_{k = 1}^{2^{n}} T_{a_{n, k}, b_{n, k}}^{(1)} (x) 1_{[a_{n, k}, b_{n, k}]} (x) (n \geq 1) \end{matrix}

(5)

\begin{matrix} g_{C} (x) & = & (\sum_{n = 1}^{\infty} g_{n} (x)) D (x) : g_{n} (x) = \sum_{k = 1}^{2^{n}} T_{a_{n, k}, b_{n, k}}^{(2)} (x) 1_{[a_{n, k}, b_{n, k}]} (x) (n \geq 1) . \end{matrix}

(6)

Remark 2.13.

While the triangular function is continuous everywhere and has no derivative at points

x = a, b,

the linear transformed cosine function is differentiable everywhere and in particular it derivative at points

x = a, b

is zero. These properties will be inherited by the associated functions

f_{C}

and

g_{C},

respectively.

3. Main Results

3.1. Partition of $F (R, R)$ with Scenario Classification & Examples

Theorem 3.1.

The function space

F (R, R)

may be partitioned into 28 unique distinct blocks of functions:

\begin{matrix} F (R, R) & = & {\dot{\cup}}_{i = 1}^{28} [f_{i}] \end{matrix}

(7)

where in which

\begin{matrix} [f_{i}] & = & {f \in F (R, R) | C a r d (C_{f}) = C a r d (C_{f_{i}}), C a r d (D_{f}) = C a r d (D_{f_{i}})} (1 \leq i \leq 28), \end{matrix}

(8)

\begin{matrix} C_{f} & = & the set of continuity points of the function f, \end{matrix}

(9)

\begin{matrix} D_{f} & = & the set of differentiability points of the function f . \end{matrix}

(10)

Proof.

First, let

f \in F (R, R),

and consider its set of continuity points

C_{f}

. Then, given

R = C_{f} \dot{\cup} C_{f}^{c},

by an application of Proposition 2.3 (i) it follows that at least

C_{f}

C_{f}^{c}

in uncountable. Subsequently, by Proposition 2.3 (ii) there are seven different scenarios for the cardinality of the pair

(C_{f}, C_{f}^{c})

including

(0, c), (n, c), (ℵ_{0}, c), (c, c), (c, ℵ_{0}), (c, n), (c, 0) .

A similar argument for the set of differentiabilities

D_{f}

with seven blocks holds. Second, by multiplication principle, it appears that there are

7 \times 7 = 49

blocks of functions. However, by two applications of Proposition 2.3 (ii) for

A = D_{f}

and

B = C_{f},

and, for

A = C_{f}^{c}

and

B = D_{f}^{c},

only

(1 + 2 + \dots + 7) = 28

blocks exist. Table 1 enlists these blocks.□

Corollary 3.2.

Each of the blocks of functions with most chaotic structure (

[f_{1}]

) and functions of the least chaotic structure (

[f_{28}] = D (R, R)

) constitutes only 3.5% (1/28) of all blocks. Hence, 93% of blocks of functions fall between these two opposite extremes. Furthermore, the vector space of everywhere continuous functions on the real line (

C (R, R)

) constitutes 25% (7/28) of all blocks.

Theorem 3.3.

There is at least one constructive example representing each of 28 unique distinct blocks of functions in

F (R, R) .

Proof.

We provide the representative functions as listed in Table 2. □

Remark 3.4.

The block of functions with least chaotic structure (

[f_{28}]

) represented by the identity function I in the Table 2 enlists many well known functions including all polynomials

p_{m} (.) (m \geq 0)

, the trigonometric functions

s i n (.), c o s (.),

the exponential function

exp (.),

and the Volterra’s function [18].

Remark 3.5.

The ternary Cantor set C appears in the construction of representatives of

17.9 % (5 / 28)

of the blocks. This shows that the ternary Cantor set has remarkable presence in the representative blocks of the space of real valued functions on the real line.

Remark 3.6.

The four well-known functions

C (.), D (.), T (.),

and

W (.)

show up in

64.3 % (18 / 28)

of the blocks where for given representative function

f_{i} = (h_{i 1} + h_{i 2}) h_{i 3}

at least one of

h_{i j} (j = 1, 2, 3)

is one of these four functions.

Lemma 3.7.

Let

F_{1} (R, R) = \cup_{i = 1}^{10} [f_{i}]

and

F_{2} (R, R) = \cup_{i = 11}^{28} [f_{i}]

. Then:

(i)

C a r d (F_{1} (R, R)) = 2^{c}

(ii)

C a r d (F_{2} (R, R)) = c .

Proof.

First, given

F (R, R) = F_{1} (R, R) \dot{\cup} F_{2} (R, R),

we have

2^{c} = C a r d (F_{1} (R, R)) + C a r d (F_{2} (R, R)) .

Hence, proving claim (ii) yields proving claim (i). Second, to prove claim (ii) let

X_{c o u n t} \subset R

be countable. Then, given

C a r d (C (X_{c o u n t}^{c}, R)) = c

[19] we have

C a r d (\cup_{X_{c o u n t} \subset R} C (X_{c o u n t}^{c}, R)) = c .

Consequently,

C a r d (F (N, R) \times \cup_{X_{c o u n t} \subset R} C (X_{c o u n t}^{c}, R)) = c .

(11)

Finally, using the result in equation 11 it is sufficient to consider the mapping

F_{2} (R, R) \mapsto (F (N, R) \times \cup_{X_{c o u n t} \subset R} C (X_{c o u n t}^{c}, R))

which maps

f \in F_{2} (R, R)

(f |_{C_{f}^{c}}, f |_{C_{f}}) .

This complete the proof. □

Theorem 3.8.

\begin{matrix} C a r d ([f_{i}]) & = & 1_{[1, 10]} (i) \times 2^{c} + 1_{[11, 28]} (i) \times c (1 \leq i \leq 28) . \end{matrix}

(12)

Proof.

First, let

f \in F (Q^{c}, R_{0}^{-})

. Then, we can extend f to

R

f (Q) = {1}

. A straightforward verification shows that

f \in [f_{1}]

. Thus, given the mapping

F (Q^{c}, R_{0}^{-}) \mapsto [f_{1}]

we have

2^{c} = C a r d (F (Q^{c}, R_{0}^{-})) \leq C a r d ([f_{1}]) \leq C a r d (F (R, R)) = 2^{c}

. This yields,

C a r d ([f_{1}]) = 2^{c}

. Next, let

f \in [f_{1}]

and define

g_{i} (.) (2 \leq i \leq 6)

g_{i} (x) = (\prod_{k = 1}^{n} (x - k)), (\prod_{k = 1}^{n} {(x - k)}^{2}), sin (π x), (sin (π x) \prod_{k = 1}^{n} (x - k)), ({sin}^{2} (π x))

for

(2 \leq i \leq 6),

respectively. Then, using the CDF of the normal distribution

Φ,

we have

g_{i} Φ (f) \in [f_{i}]

for

(2 \leq i \leq 6),

respectively. Thus, given the mapping

[f_{1}] \mapsto [f_{i}]

we have

2^{c} = C a r d ([f_{1}]) \leq C a r d ([f_{i}]) \leq C a r d (F (R, R)) = 2^{c},

implying

C a r d ([f_{i}]) = 2^{c}

for

(2 \leq i \leq 6),

respectively.

Second, let

A \in C_{u n c}

and consider the modified

f_{i}^{A} (.) (7 \leq i \leq 10)

in Table 2 by

f_{i}^{A} (x) = f_{A} (x), (\prod_{k = 1}^{n} (x - 1 / 3^{k})) f_{A} (x), ({sin}^{2} (\frac{π}{x})) f_{A} (x), g_{A} (x)

for

(7 \leq i \leq 10),

respectively. Thus, given the mapping

C_{u n c} \mapsto [f_{i}]

we have

2^{c} = C a r d (C_{u n c}) \leq C a r d ([f_{i}]) \leq C a r d (F (R, R)) = 2^{c},

implying

C a r d ([f_{i}]) = 2^{c}

for

(7 \leq i \leq 10),

respectively.

Third, let

p \in R^{+} .

Then, using function

f_{i} (11 \leq i \leq 28)

in the Table 2 we have

p f_{i} \in [f_{i}] (11 \leq i \leq 28) .

Hence, given the mapping

R^{+} \mapsto [f_{i}]

we have

c = C a r d (R^{+}) \leq C a r d ([f_{i}]),

for

(11 \leq i \leq 28),

respectively. Next, given

[f_{i}] \subseteq F_{2} (R, R),

for

(11 \leq i \leq 28),

and Lemma3.7 (ii) we have:

C a r d ([f_{i}]) \leq c

for

(11 \leq i \leq 28),

respectively. Accordingly, by the last two inequalities on the cardinals, it follows that:

C a r d ([f_{i}]) = c (11 \leq i \leq 28) .

In particular, for

[f_{28}] = D (R, R)

we have

C a r d ([f_{28}]) = c .

This completes the proof. □

Remark 3.9.

The cardinality of

35.7 % (10 / 28)

of the blocks is

2^{c}

while that of

64.3 % (18 / 28)

of blocks is

c .

This indicates that the cardinal number c has almost double frequency of that of cardinal number

2^{c}

in representing the size of blocks of the space of real valued functions on the real line.

3.2. The Relationship between the Big Four

In the previous section, we observed that any given function

f \in F (R, R)

belongs to one of the 28 blocks of its partitions. In particular, the four well-known functions—the Cantor function, Dirichlet function, Thomae function, and the Weierstrass function—each represent one of these blocks. Now, one may wonder how to connect these four key functions. Trivially, the equivalence relation induced by the aforementioned partition is unhelpful in this regard. Hence, we consider an alternative approach. We begin with a definition:

Definition 3.10.

Given two functions

f_{1}, f_{2} \in F (R, R) .

Then,

f_{1}

is called connected to

f_{2}

denoted by

f_{1} \overset{c o n n}{\sim} f_{2}

whenever for some function

g \in F (R, R),

we have

f_{1} g \in [f_{2}] .

Remark 3.11.

Additional restrictions on g: When

g = 1

in Definition 3.10,

\overset{c o n n}{\sim}

is transformed into the induced equivalence relation by the above partition. Furthermore, if g is a positive everywhere-differentiable function on

R

, the aforementioned relation becomes an equivalence relation.

It is trivial that in Theorem 3.1,

f_{i} \overset{c o n n}{\sim} f_{28}

for all

(1 \leq i \leq 27) .

Figure 1 presents these relationships. As shown, the block of everywhere differentiable functions

[f_{28}]

is the sink node with the highest in-degree connectivity among all blocks of functions.

As there are

4^{C_{2}^{28}} = 3.790327 \times 10^{227}

potential scenarios for the complete graph in Figure 1, finding the relationships between all nodes of the graph appears to be a tedious and difficult task. However, we can identify the relationships between four of them, i.e.,

f_{1} = D, f_{11} = T, f_{22} = W,

and

f_{25} = C,

where there are only

4^{C_{2}^{4}} = 4096

potential scenarios. Equipped with Definition 3.10, we have:

Theorem 3.12.

Given above notations and definitions we have: (i)

W \overset{c o n n}{\sim} T,

(ii)

W \overset{c o n n}{\sim} C,

(iii)

W \overset{c o n n}{\sim} D,

(iv)

T \overset{c o n n}{\sim} D,

and, (v)

C \overset{c o n n}{\sim} D .

Proof.

It is sufficient for each case to present the g function in the Definition 3.10 as follows: (i)

g (x) = x + \sum_{n = 1}^{+ \infty} π^{n} 1_{{π^{n}}} (x)

; (ii)

g (x) = x (x - 1) 1_{[0, 1]} (x)

; (iii)-(v)

g (x) = \sum_{- \infty}^{+ \infty} 1_{A + 2 n} (x) : A = {(sin (n))}_{n = 1}^{+ \infty}

dense in

[- 1, 1]

. □

Figure 2 presents a graphical overview of the results in Theorem 3.12. As it is shown, the Weierstrass function (W) is the source-universal node with the highest out-degree connectivity; the Cantor function (C) and the Thomae function (T) are the bridging nodes; and, the Dirichlet function (D) is the sink node with the highest in-degree connectivity.

4. Discussion

4.1. Summary & Contributions

This work presents a finite partition of the function spaces of all real-valued functions on

R

based on cardinality, continuity, and differentiability, along with constructive examples representing each block of the partition. In particular, it shows that the well-known Cantor function, Dirichlet function, Thomae function, and the Weierstrass function each represent a unique block of this partition. An additional aspect adding more importance to these four functions is that they collectively appear in representation of almost two-thirds of the blocks. Furthermore, the concept of connection among real-valued functions is introduced, and the unique connection relation between the aforementioned functions was investigated.

Finally, this work findings adds more prominence to the Cantor set C as well. While it has a remarkable presence in the construction of the representative functions of blocks, its size (e.g., Cardinal number c) has the highest presence in the size of representative blocks.

4.2. Limitations & Future Work

The limitations of this work are clear, and they open up new perspectives for further investigations. Firstly, we merged the cardinal number of all finite subsets of

R

with given symbol

n .

While this inaccuracy is a minimal price to pay for enabling the creation of the aforementioned finite partition, it should be noted. Secondly, the presented graph in Figure 1 needs to be completed for all its involved nodes. Thirdly, the connection relation in Definition 3.10 is not an equivalence, making it suboptimal. One open problem in this regard is investigating the results in Figure 1 and Figure 2 when considering the equivalence relations mentioned in Remark 3.11. Finally, it is worth exploring how the presented partition in this work changes in terms of the number of blocks and the representative function for each block when one replaces some key features, such as continuity and differentiability, with other properties of real-valued functions on the real line, such as integrability, measurability, etc.

4.3. Conclusion

This work presented a constructive description of the function space of all real-valued functions on

R

in terms of four concepts: partition, cardinality, continuity, and differentiability. Additionally, it established a special relationship between the well-known representative functions of four of the blocks.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declares no conflict of interest.

References

Medvedev, F. A. Scenes from the History of Real Functions, 1st ed.; In Birkhäuser Basel eBooks. Springer Basel AG, Switzerland, 1991; pp. 11–14.
Waaldijk, F. On the Foundations of Constructive Mathematics–Especially in Relation to the Theory of Continuous Functions. Found. Sci. 2005, 10, 249–324. [CrossRef]
Troelstra, A.S.; van Dalen, D. Constructivism in Mathematics: An Introduction, 1st ed.; (Two Volumes); Elsevier Science, Amsterdam: North Holland, The Netherlands, 1988.
Pugh, C. C. Real Mathematical Analysis, 1st ed.;In Undergraduate texts in mathematics. Springer Science Business Media, New York, USA, 2002; pp. 223–225.
Hairer, E.; Wanner, G. Analysis by Its History, 1st ed.; Springer Science+Business Media, LLC, NY, USA, 2008.
Stillwell, J. The real numbers: An Introduction to Set Theory and Analysis, 1st ed.; Springer. Switzerland, 2013.
Royden, H. L.; Fitzpatrick, P. Real Analysis. 5th ed, Pearson, USA, 2023.
Lin, S.T. and, Lin, Y. Set Theory with Applications, 2ed ed. Manner Publishing Company Inc., Tampa, FL, USA, 1981; pp. 147–149.
Soltanifar, M. On A Sequence of Cantor Fractals. Rose-Hulman Undergraduate Mathematics Journal 2006, 7(1), Article 9.
Soltanifar, M. A Different Description of A Family of Middle-a Cantor Sets. American Journal of Undergraduate Research 2006, 5(2), 9–12.
Lipshutz, S. Schaum’s Ouline of Theory and Problems of Linear Algebra, SI ed. McGraw Hill International, Singapore, 1981; pp. 64,83.
Ventre, A.G.S. Calculus and Linear Algebra: Fundamentals and Applications. Springer, Switzerland, 2023; p.338.
Aron, R. M.; Gurariy, V. I., & Seoane, J. Lineability and spaceability of sets of functions on R. Proceedings of the American Mathematical Society 2004, 133(3), 795-–803. [CrossRef]
Dunham, W. The Calculus Gallery: Masterpieces from Newton to Lebesgue. Princeton University Press, NJ, USA, 2018; pp.100,142,149.
Bass, Richard Franklin. Real analysis for Graduate Students, 2ed ed. Createspace Independent Publishing, USA, 2013; pp.28,29.
Gelbaum, B. R.; Olmsted, J. M. H. Counterexamples in Analysis. Courier Corporation. Dover Publications, Inc. Mineola, New York, USA, 2003; pp. 22,27,38–39.
Bourchtein, A.; Bourchtein, L. Counterexamples: From Elementary Calculus to the Beginnings of Analysis. CRC Press, Boca Raton, FL, USA, 2014; pp. 37,45,65.
Bressoud, D. A Radical Approach to Lebesgue’s Theory of Integration. Cambridge: Cambridge University Press/Mathematical Association of America, USA, 2008; pp. 91–94.
Hodel, R. "Chapter 1: Cardinal Functions I." Handbook of Set-Theoretic Topology. Elsevier Science Publishers B.V., USA, 1984; pp.39–40.

Figure 1. The graphical presentation of the relationship between all representatives of blocks of

F (R, R)

and

f_{28}

the identity function.

Figure 1. The graphical presentation of the relationship between all representatives of blocks of

F (R, R)

and

f_{28}

the identity function.

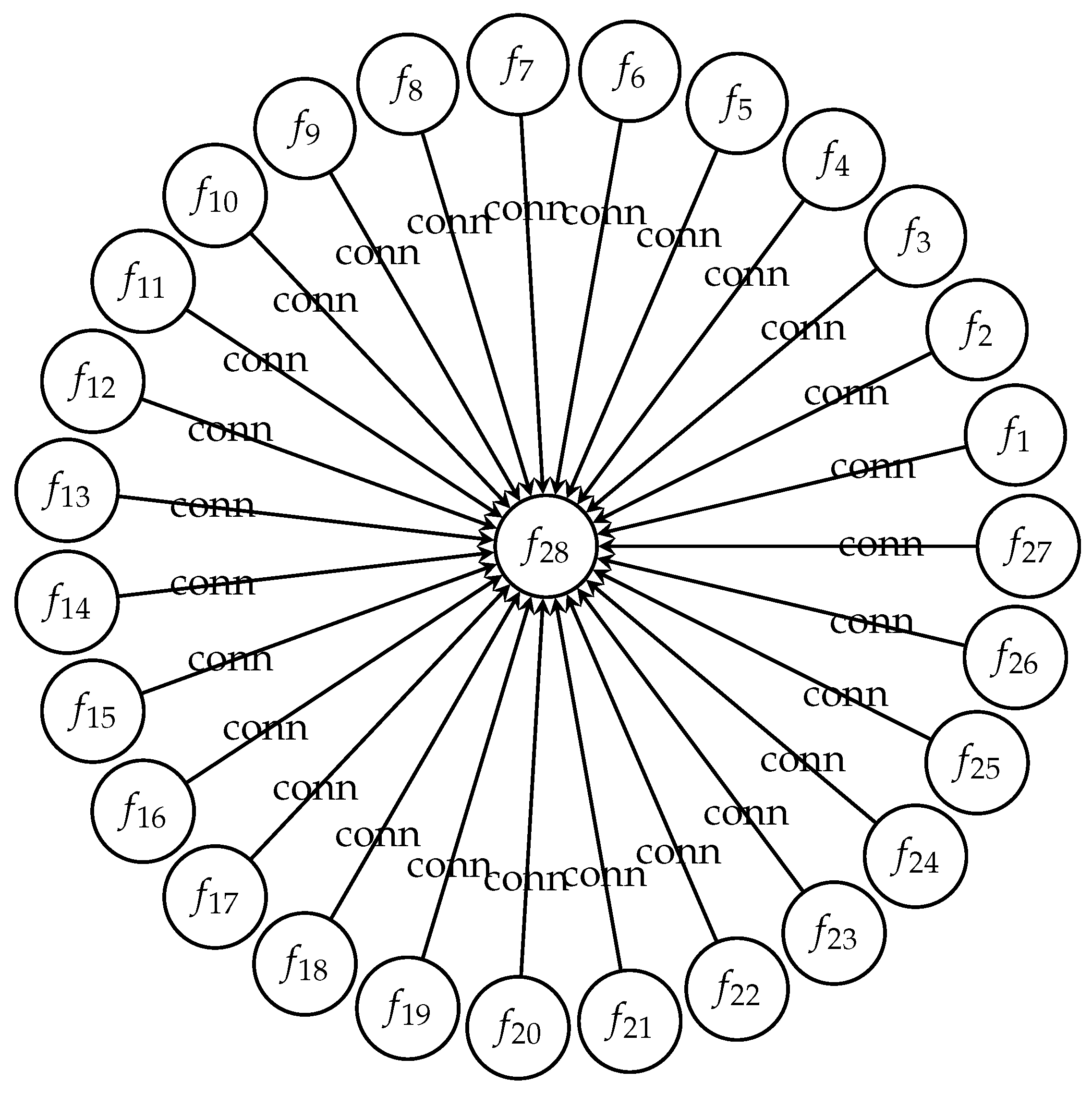
Figure 2. The graphical presentation of the relationship between well-known functions: the Cantor function (C), the Dirichlet function (D), the Thomae function (T), and, the Weierstrass function (W).

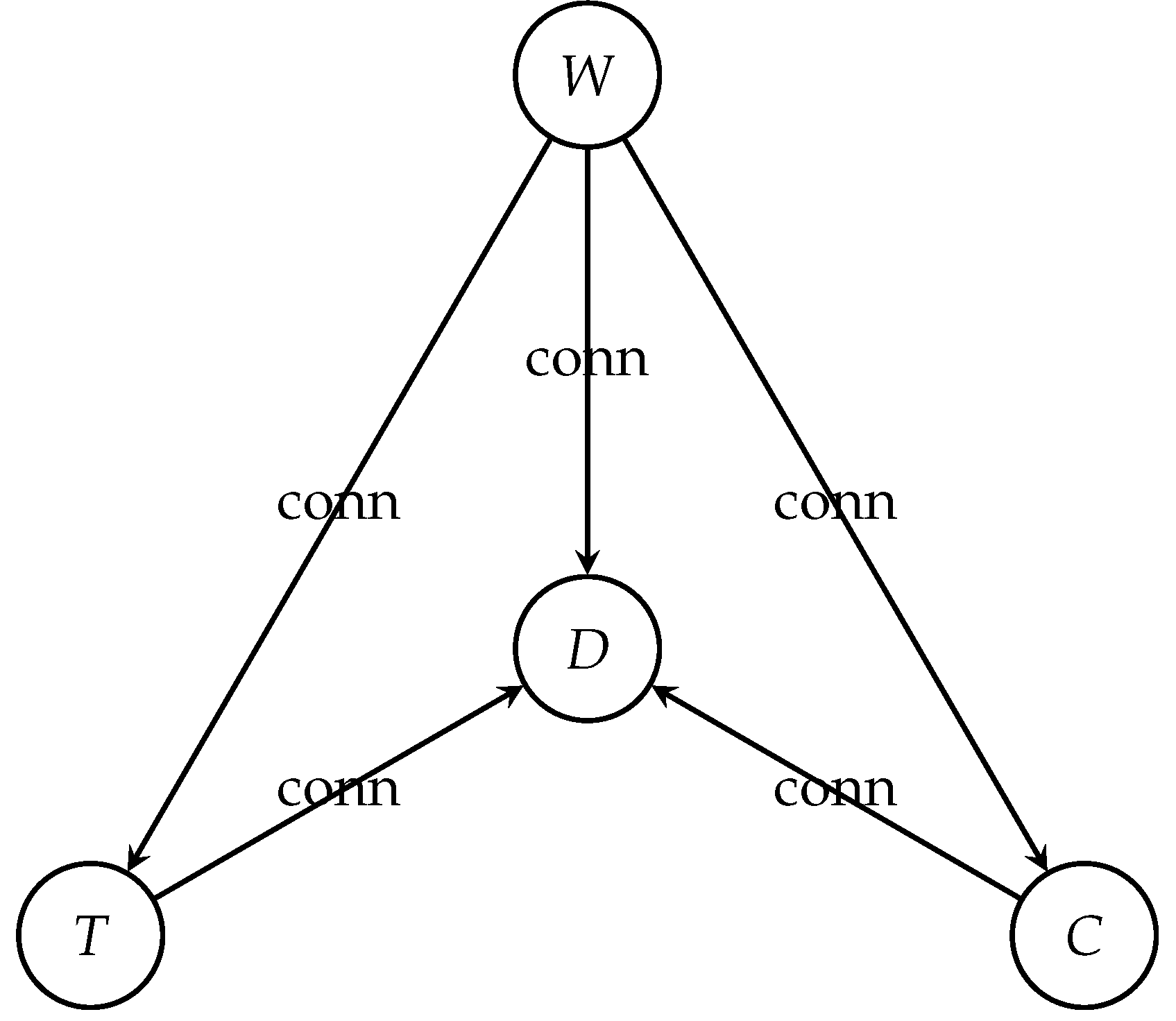
Table 1. List of 28 representatives blocks of partition of

F (R, R)

Table 1. List of 28 representatives blocks of partition of

F (R, R)

		Continuity		Differentiability
#	Case	$C a r d (C_{f})$	$C a r d (C_{f}^{c})$	$C a r d (D_{f})$	$C a r d (D_{f}^{c})$
1	1-1	0	c	0	c
2	2-1	n	c	0	c
3	2-2	−	−	n	c
4	3-1	$ℵ_{0}$	c	0	c
5	3-2	−	−	n	c
6	3-3	−	−	$ℵ_{0}$	c
7	4-1	c	c	0	c
8	4-2	−	−	n	c
9	4-3	−	−	$ℵ_{0}$	c
10	4-4	−	−	c	c
11	5-1	c	$ℵ_{0}$	0	c
12	5-2	−	−	n	c
13	5-3	−	−	$ℵ_{0}$	c
14	5-4	−	−	c	c
15	5-5	−	−	c	$ℵ_{0}$
16	6-1	c	n	0	c
17	6-2	−	−	n	c
18	6-3	−	−	$ℵ_{0}$	c
19	6-4	−	−	c	c
20	6-5	−	−	c	$ℵ_{0}$
21	6-6	−	−	c	n
22	7-1	c	0	0	c
23	7-2	−	−	n	c
24	7-3	−	−	$ℵ_{0}$	c
25	7-4	−	−	c	c
26	7-5	−	−	c	$ℵ_{0}$
27	7-6	−	−	c	n
28	7-7	−	−	c	0

Table 2. List of 28 representatives functions for each of 28 blocks

F (R, R)

Table 2. List of 28 representatives functions for each of 28 blocks

F (R, R)

#	Case	Representative $f (x)$	Comments	$C a r d ([f])$
1	1-1	$D (x)$	Dirichlet Function	$2^{c}$
2	2-1	$(\prod_{k = 1}^{n} (x - k)) D (x)$		$2^{c}$
3	2-2	$(\prod_{k = 1}^{n} {(x - k)}^{2}) D (x)$		$2^{c}$
4	3-1	$sin (π x) D (x)$		$2^{c}$
5	3-2	$(sin (π x) \prod_{k = 1}^{n} (x - k)) D (x)$		$2^{c}$
6	3-3	$({sin}^{2} (π x)) D (x)$		$2^{c}$
7	4-1	$f_{C} (x)$	$C_{f} = C$	$2^{c}$
8	4-2	$(\prod_{k = 1}^{n} {(x - \frac{1}{3^{k}})}^{2}) f_{C} (x)$		$2^{c}$
9	4-3	$({sin}^{2} (\frac{π}{x})) f_{C} (x)$		$2^{c}$
10	4-4	$g_{C} (x)$	$C_{f} = D_{f} = C$	$2^{c}$
11	5-1	$T (x)$	Thomae Function	c
12	5-2	$(\prod_{k = 1}^{n} {(x - k)}^{2}) T (x)$		c
13	5-3	$({sin}^{2} (π x)) T (x)$		c
14	5-4	$T (x) 1_{[0, 1]} (x)$		c
15	5-5	$\sum_{n = 1}^{+ \infty} π^{n} 1_{{π^{n}}} (x)$		c
16	6-1	$W (x) + \sum_{k = 1}^{n} π^{k} 1_{{π^{k}}} (x)$		c
17	6-2	$(\prod_{k = 1}^{n} {(x - k)}^{2}) (W (x) + \sum_{k = 1}^{n} π^{k} 1_{{π^{k}}} (x))$		c
18	6-3	$({sin}^{2} (π x)) (W (x) + \sum_{k = 1}^{n} π^{k} 1_{{π^{k}}} (x))$		c
19	6-4	$(W (x) + \sum_{k = 1}^{n} π^{- k} 1_{{π^{- k}}} (x)) 1_{[0, 1]} (x)$		c
20	6-5	$\| sin (π x) \| + \sum_{k = 1}^{n} π^{k} 1_{{π^{k}}} (x)$		c
21	6-6	$\sum_{k = 1}^{n} π^{k} 1_{{π^{k}}} (x)$		c
22	7-1	$W (x)$	Weierstrass Function	c
23	7-2	$(\prod_{k = 1}^{n} {(x - k)}^{2}) W (x)$		c
24	7-3	$({sin}^{2} (π x)) W (x)$		c
25	7-4	$C (x)$	Cantor Function	c
26	7-5	$\| sin (π x) \|$		c
27	7-6	$\| \prod_{k = 1}^{n} (x - k) \|$		c
28	7-7	x		c

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Classification of Elements of Function Space F(R,R)

Abstract

1. Introduction

1.1. Real Valued Functions

1.2. Motivation

1.3. Study Outline

2. Preliminaries

2.1. Set Theory

2.2. Linear Algebra

2.3. Special Functions

3. Main Results

3.1. Partition of F ( R , R ) with Scenario Classification & Examples

3.2. The Relationship between the Big Four

4. Discussion

4.1. Summary & Contributions

4.2. Limitations & Future Work

4.3. Conclusion

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3.1. Partition of $F (R, R)$ with Scenario Classification & Examples