Prerpints.org logo
Preprint
Review

Emergent Information Processing: Observations, Experiments, and Future Directions

Altmetrics

Downloads

140

Views

45

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 August 2023

Posted:

11 August 2023

You are already at the latest version

Alerts
Abstract
Scientists are gradually becoming aware of the challenges in the understanding of the very root mechanisms of massively parallel computations that are observed in literally all scientific disciplines ranging from cosmology, physics, across chemistry, biochemistry, and ending in biology. This leads us to the main motivation and simultaneously to the central thesis of this review: “Can we design artificial, massively-parallel, self-organized, emergent, error-resilient, computational environments?” A large number of simulations along with examples and counter-examples, finalized by a list of the future directions, are giving hints and partial answers to the main thesis. This all together is opening the crucial question whether there is existing a deeper, beyond the Turing machine theoretical description of massively-parallel computing. Important information dealing with this topic is reviewed along with highly expressive animations generated by the open-source, Python software GoL-N24. The perspective, future directions including applications in robotics and biology of this research are discussed in the light of known information.
Keywords: 
Subject: Computer Science and Mathematics  -   Data Structures, Algorithms and Complexity

1. Introduction

Currently, the science as the whole is facing an underlying challenge in the form of understanding of emergent, error-resilient information processing environments that have a potential of eventually becoming artificial analogs of natural phenomena observed within virtually all physical & biological systems. Such descriptions can become workhorses of the future information processing devices.
This challenge should be decomposed into three distinct steps: decoding, understanding, and finally design of artificial systems based on massively-parallel computations, e.g., see documented examples withing various systems and observed natural phenomena in biology [1,2] and physics [3,4,5].
The text is composed of the following parts: (a) The introduction contains a brief explanation of the emergence [6], describing the difference between classical and massively-parallel models/ information processing, and a brief introduction into cellular automata. (b) The main thesis of the review. (c) The section dealing with examples and descriptions of various instances of massively-parallel computations: ’Game of Life’ (GoL), GoL-N24, logic-gates in GoL, error resilient emergents in rGoL, gliders, ships, and emergents of the 2nd order. (d) Simulation of massively-parallel systems using cellular automata. (e) Counter-examples to the proposed approach, (f) which are followed by a number of arguments/examples confirming it. (g) All is finalized by the section describing the perspective, future directions, which is followed by conclusions.

1.1. Emergence Observed in Natural Systems

Emergence is found in many, if not all, observed natural phenomena that operate on the scales ranging from quantum mechanics, across atoms, molecules, bio-molecules, towards cells, organs, bodies, and ecosystems in biology, and in non-living matter from quantum mechanics, across atoms, molecules, solids, and liquids, towards rocks, celestial bodies, stars, galaxies, and the Universe.
An important subclass of emergent systems is created by self-organized criticality (SOC) expressing systems [7,8]: simply said, they are fed by energy continuously by the same amount of input energy, which is released in irregularly-timed bursts of released energy, that leads to a power-law distribution of avalanches of released energy. Examples encompass earthquakes, stock market crashes, multi-scale plasma instabilities, traffic flow jams creation[9], laser operation, and so on.
Another important class is represented by agent-based models (ABM) that are applied to morphological development and embryogenesis [10], societal systems, stock markets, economic systems, opinion pols, and the list goes on.
Emergence is standing behind the occurrence of mechanical properties present in solids, metals, biological systems, societal opinions, electromagnetic properties of materials, or information processing in material and biological systems.

1.2. Distinguishing between Traditional and Massively-Parallel Computing

A side-by-side comparison of two major computational methods known in the ry of computation: (a) the classical, von Neumann architecture that is based on the sequential processing of information using logic-gates, and (b) the emergent one [6] that is based on utilization of massively-parallel computations (cellular automata, movable agents, atoms, molecules, etc.), see Table 1.

1.3. Brief Introduction into Cellular Automata and Complex Systems Simulations

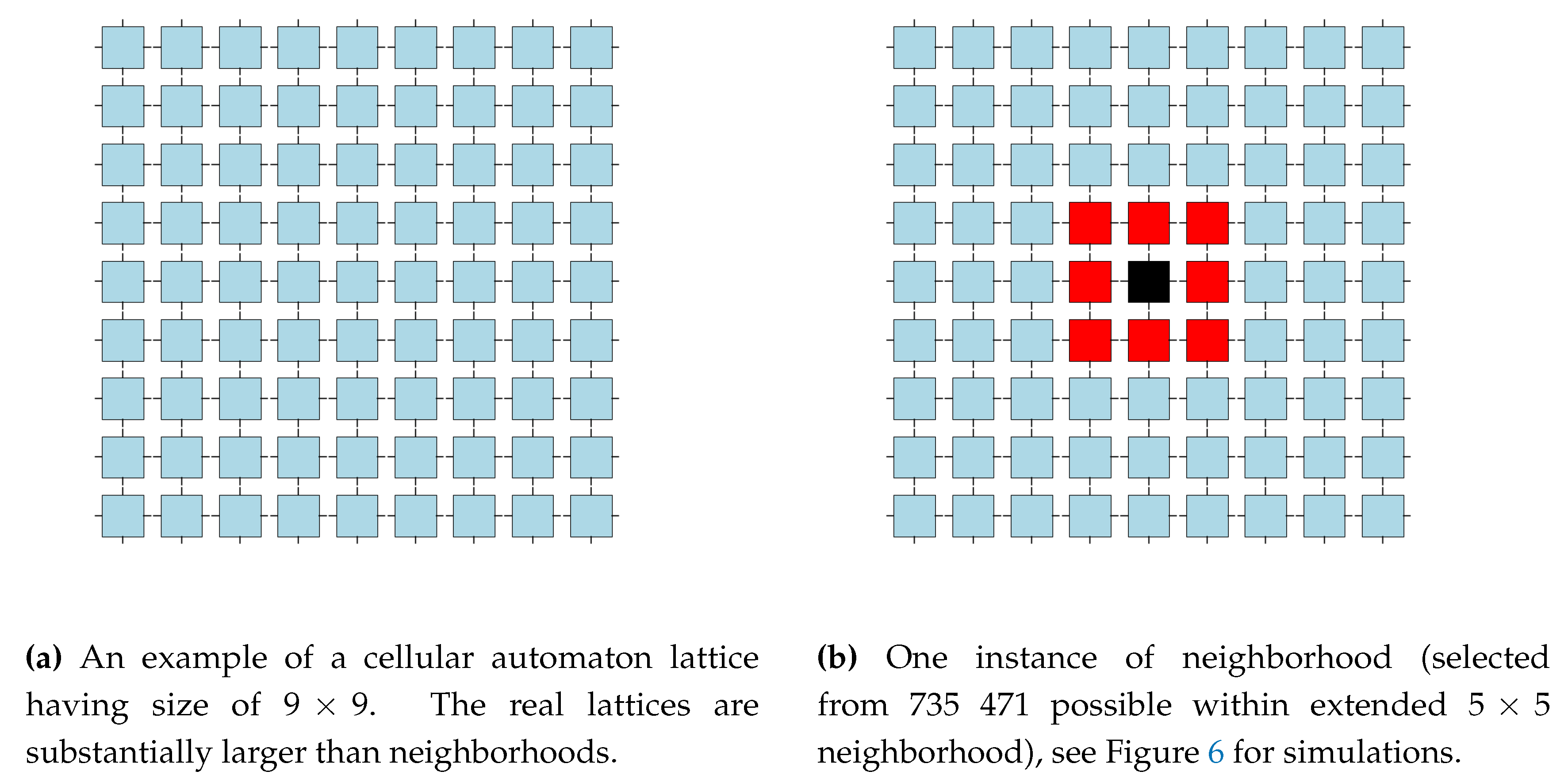
The Figure 1 depicts the very principle of massively-parallel computation demonstrated on cellular automata: (a) uniform lattice of square cells defining the computational medium, and (b) uniform, cell’s neighborhood identical to each cell.
The cellular space L is in this description defined by the 2-dimensional lattice of square cells □ i , j (see the more general definition in [11])
L = { □ i , j | ∀ i ∈ 〈 1 , N 〉 , ∀ j ∈ 〈 1 , N 〉 }
where each cell □ i , j has the associated state s i , j . The top & down, and left & right edges of the lattice are connected together, which creates a toroid.
In our case, the state of each cell can attain only two values
s i , j = { 0 , 1 } ,
where the 0 state (depicted as a white square, □ i , j ) is often called as the dead state and the 1 state (depicted as a black square, ▪ i , j ) is called the alive one.
The uniform neighborhood, which is identical for each cell, is defined by eight neighbors N, which are selected from the extended neighborhood N r a d i u s = { given i , j | ∀ i ∈ 〈 i − 2 , i + 2 〉 , ∀ j ∈ 〈 j − 2 , j + 2 〉 } = 5 × 5 − 1 = 24 cells, see Figure 1. This gives the total of n k = 735 471 possible neighborhoods:
N = { n i , j | ∀ i , j ∈ { 8 pre - selected □ i , j from - within N r a d i u s } } .
The uniform evolution rule E (known as the transition function or local rule) defines the change of the state of each cell going from the step N to the step N + 1 independently among all cells (the evaluation of the next cell’s state is always centripetal: no change of the state of any neighboring cell is allowed):
s t + 1 = E ( { s i , j t | ∀ cells □ i , j ∈ N } ) .
The global transition function, which is describing the evolution of the whole system:
G N + 1 = E ( G N ) = { E ( s i , j ) | ∀ i ∈ 〈 1 , N 〉 , ∀ j ∈ 〈 1 , N 〉 ) }
has no closed analytic solution in the vast majority of cases.
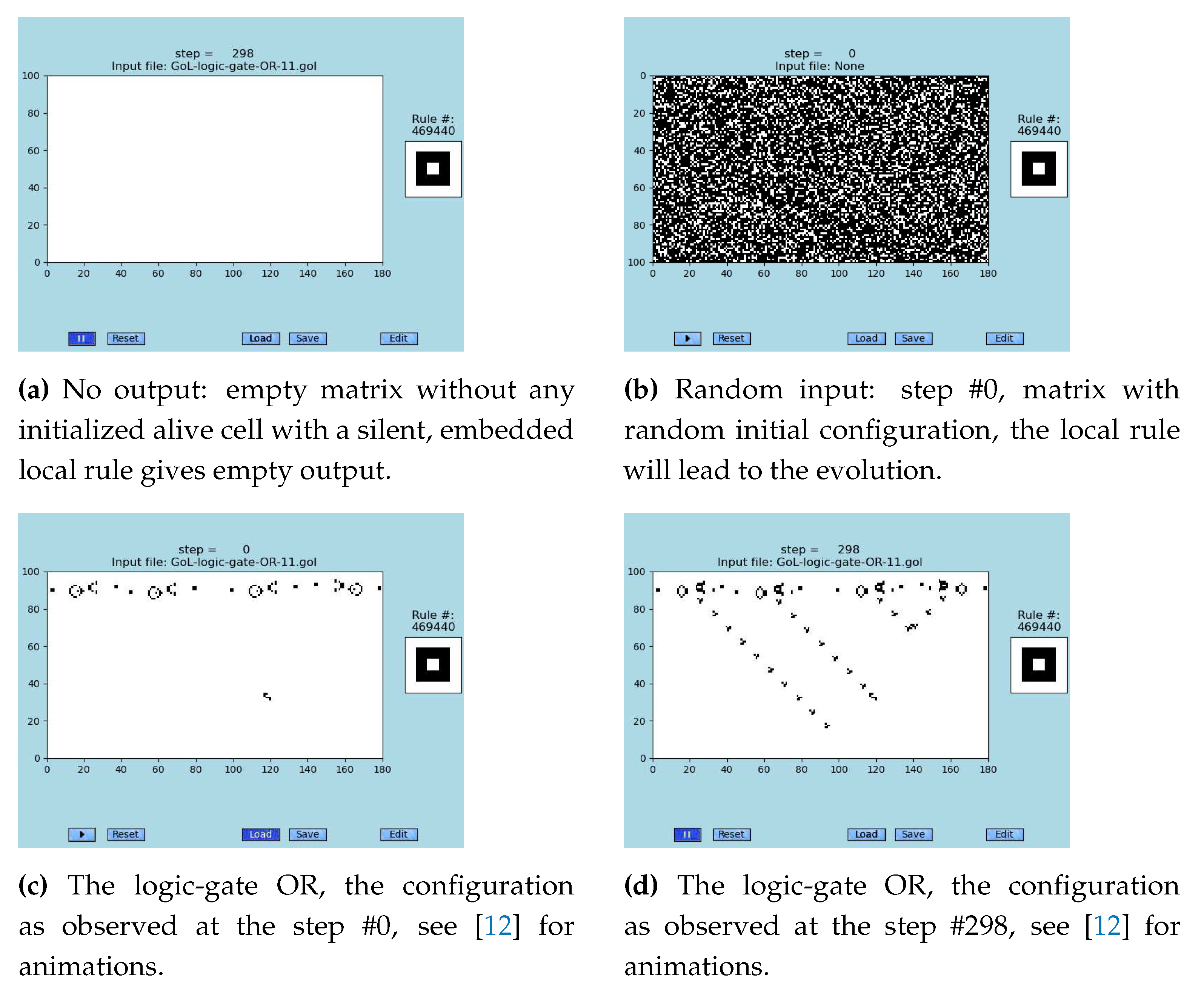
Preprints 82162 g002
Figure 2. The principles of CA-simulations and emergence are explained on the simulation of the cellular automaton ’Game of Life’ [4,13]: (a) empty matrix, step #298, (b) random matrix, step #0, (c) predefined initial configuration, step #0, and (d) simulation of the case c, step #298. Those simulations are not error-resilient!
Figure 2. The principles of CA-simulations and emergence are explained on the simulation of the cellular automaton ’Game of Life’ [4,13]: (a) empty matrix, step #298, (b) random matrix, step #0, (c) predefined initial configuration, step #0, and (d) simulation of the case c, step #298. Those simulations are not error-resilient!
Preprints 82162 g002

2. Thesis: Existence of Emergent Information Processing

Preprints 82162 i001
The most wanted properties in such design are emergent and error-resilient ones: they, when achieved, will eventually lead to self-healing information processing environments.
The main motivation of the Thesis is delivered by biological systems, as they have exactly the very same properties. It is known that biological systems are running the same ’program’—that is composed of many interdependent processes—on the top of always reconstructing, re-configuring, rebuilding, and fluid wetware. Is it possible to build such systems artificially?

3. Simulations of Massively-Parallel Computations Using Cellular Automata

A concise introduction into cellular automata (CA) [14] along with CA-books covering quite diverse topics & CA-examples [11,15] are provided to allow a quick start in the field. This learning stage is recommended to be followed and even accompanied by the following software, which together will assist in building a strong skill set in CA-design and programming.
A recommended, easy to-think-through starting point to understand the very principles of CA-computations and programming is the following, less than one hundred lines long Python program simulating the John. H. Conway’s ’Game of Life’ [16] along with CA-theory covered, e.g., in [14]. This is recommended to be followed by books [17] and more advanced software [13,18,19]. The combination of experimenting with CA-codes along with studying their applications is representing the fundamental approach to reach the cutting-edge of knowledge in this field fast and efficiently. The open-source Python software GoL-N24 [13] was used to create all simulations (initial configurations are open-source) except the simulations of r-GoL in Figure 4 and Figure 5, which were simulated by [18].

3.1. Neighborhood Definition Within GoL-N24 Cellular Automaton Implementation

Each rule number is defined in the following way. The extended neighborhood is numbered as 2 x 1 + 2 x 2 + 2 x 3 + 2 x 4 + 2 x 5 + 2 x 6 + 2 x 7 + 2 x 8 where the numbers { x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 , x 8 } represents the ordering number of the given cell in the neighborhood: counting starts at the lower-left corners and proceeds in rows upwards to the upper-right corner (the left-lower corner has position 0 and contributes by the value of 2 0 = 1 and finally, upper-right corner has the position 24 and by contributes by the value of 2 24 = 16777216 ). The central cell is not part of the neighborhood!

3.2. Implementation of Logic-Gates in the ’Game of Life’ Cellular Automaton

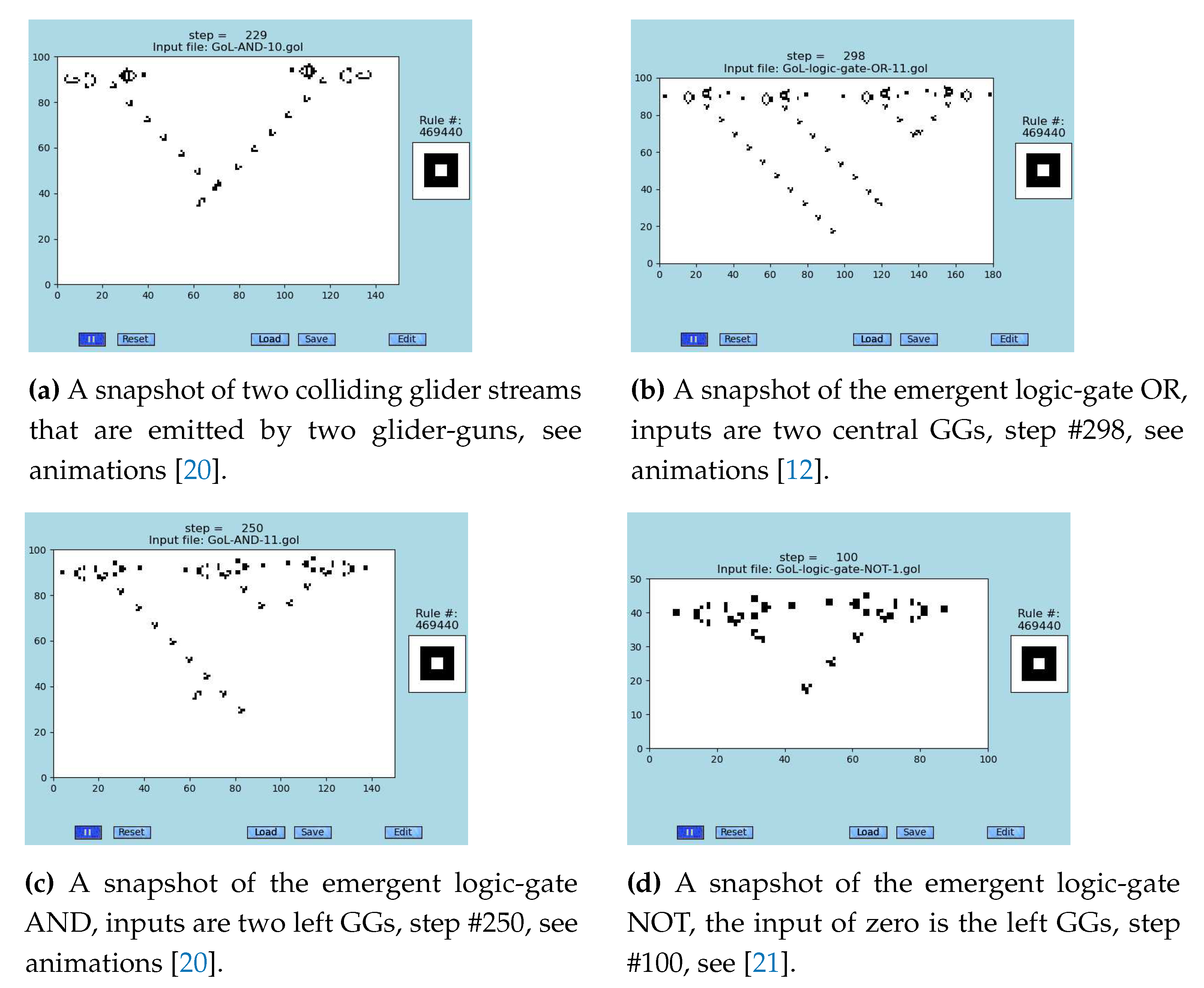
Glider-gun generated emergents—when designed in precisely aligned geometrical configurations—can carry on logic operations by utilizing collisions of glider-streams, which is demonstrated in Figure 3 that was created by the program [13] with details covered in [4] and animations provided in [12,20,21].
Each glider gun is composed of two counter-wise moving parts, which emits gliders in regular moments, that propagate further independently. The specific topology of glider-streams, which can be switched on or off using various glider-streams blockers defines the actual output of the logic-gate under the consideration, see Figure 3.

3.3. Error-Resilient Emergents Observed in Cellular Automata

The hypothesis of the existence of error-resilient emergents—which are utilizing generalized local rules—was tested and confirmed in CA named r-GoL [4] using software [18]: animations are available in [24].
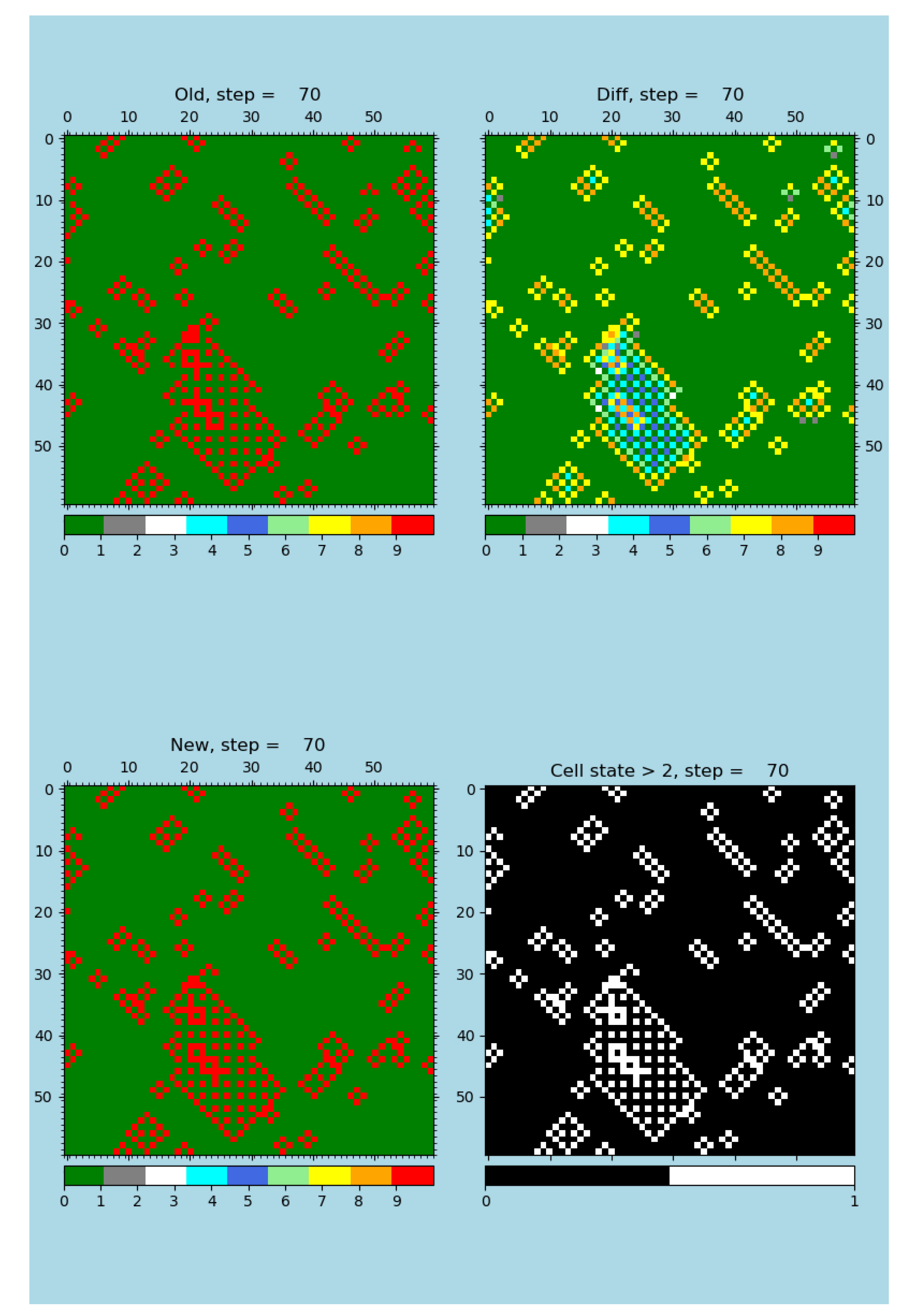
In the modified GoL called r-GoL, it was observed that contrary to the GoL rule some emergents express resilience against injection of 1% of errors in the evaluation process of the rule, see details in Figure 4 and Figure 5.
Preprints 82162 g004
Figure 4. A demonstration of the effect of changed rule (r-GoL) and the identical neighborhood. A snapshot of error-resistant (resilient) emergents operating within a rule variant of the ’Game of Life’, rGoL is shown: an undisturbed error-resilient rule, see the publication [4], software [18], and animations [24]. There are shown old, diffusion, new, and the state > 2 sub-figures at the step 70.
Figure 4. A demonstration of the effect of changed rule (r-GoL) and the identical neighborhood. A snapshot of error-resistant (resilient) emergents operating within a rule variant of the ’Game of Life’, rGoL is shown: an undisturbed error-resilient rule, see the publication [4], software [18], and animations [24]. There are shown old, diffusion, new, and the state > 2 sub-figures at the step 70.
Preprints 82162 g004
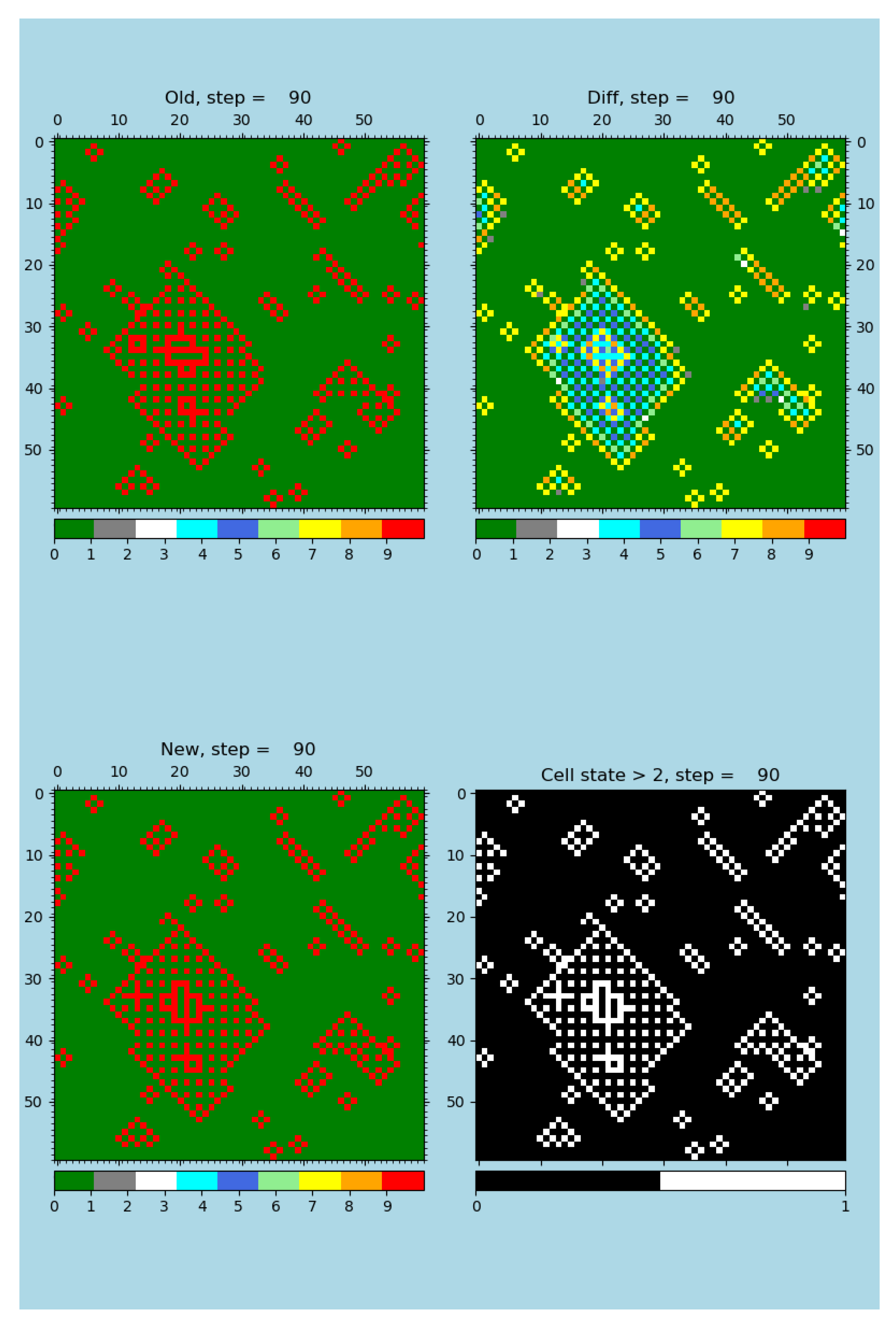
Preprints 82162 g005
Figure 5. The same error-resilient rule and simulation as in Figure 4 with the only difference: there are injected 1% of faulty evaluations, see the publication [4], software [18], and animations [24] for details. In both figures showing r-GoL simulations, old and new steps demonstrate the existence of alternating states.
Figure 5. The same error-resilient rule and simulation as in Figure 4 with the only difference: there are injected 1% of faulty evaluations, see the publication [4], software [18], and animations [24] for details. In both figures showing r-GoL simulations, old and new steps demonstrate the existence of alternating states.
Preprints 82162 g005

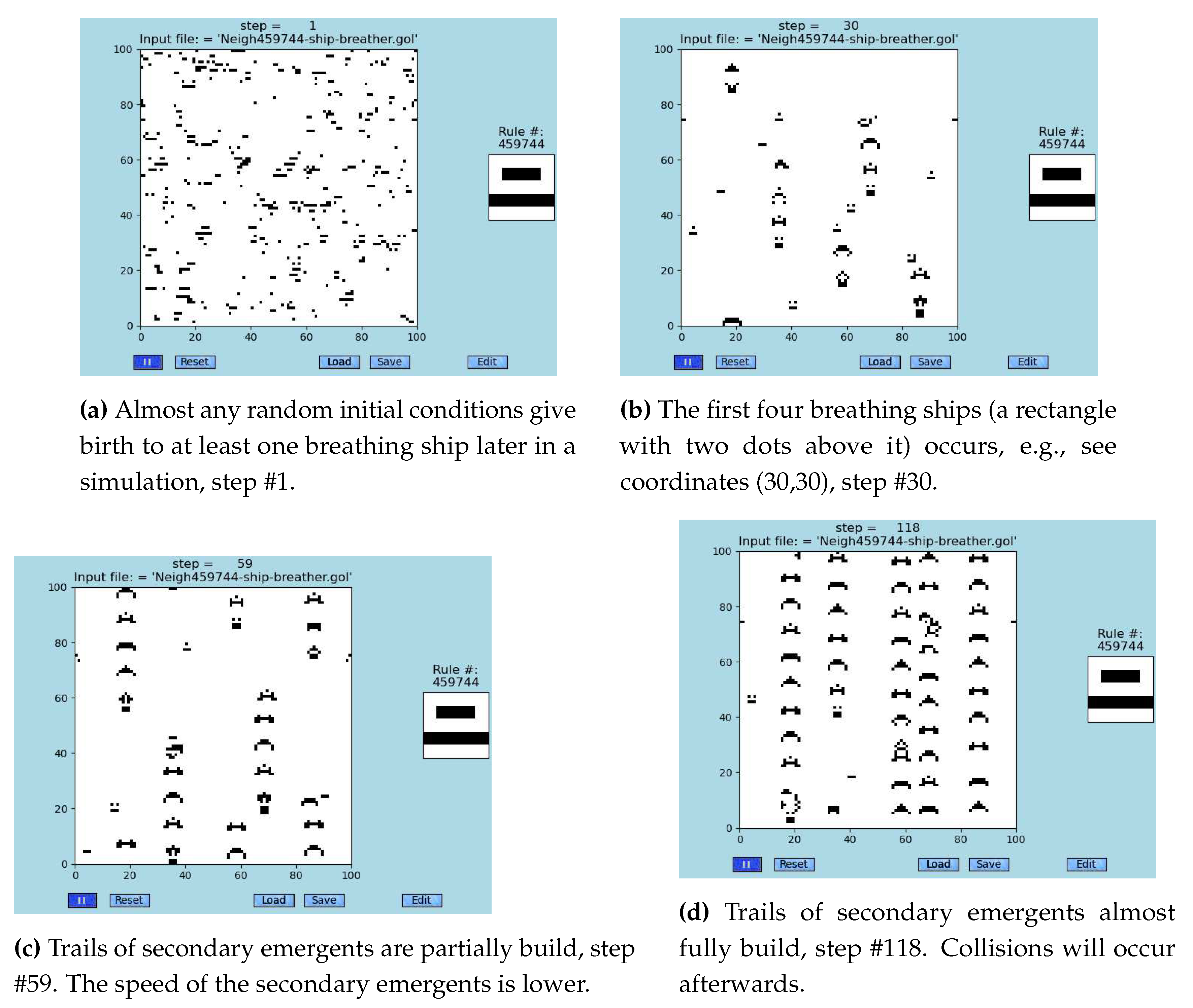
3.4. Ship Breathing Ships Found in GoL-N24: Second-Order Emergence Confirmed

Unexpectedly, important components of emergent information processing were already found, see Figure 6 and animations [25]. The first-order emergents are generating a stream of the second-order emergents are observed. This opens a window to the exploration of unconventional self-assembling circuitry design, see other examples in [4], which is a highly challenging task requiring novel computational approaches.

3.5. Gliders Observed in Different GoL-N24 Neighborhoods.

An important observation within simulations that were carried on a whole range of different neighborhoods in GoL-N24 is the fact that important components of emergent information processing had been found in many of those tested neighborhoods: gliders are emerging from random conditions, see Figure 7 for selected examples. Hence, one of the most critical component of the emergent computation is proving to be abundant in GoL-N24.

4. Counter-Examples

A number of possible counter-examples to the hypothesis—where it is initially assumed that all are true; each of them is followed by supporting evidence and subsequently by its refute—are provided and discussed in this section.

4.1. Genes Are Encoding All Processes Observed Within Bodies of All Living Entities

Everyone knows that it is well-known from a huge number of research papers dealing with genetics that genes are encoding all processes occurring and operating within living organisms.
Evidence. The functions of cells, tissues, organs, and bodies are defined and solely driven by the expression of genetic material and nothing else, as disruption of the genetic code leads to disruption of cellular and bodily functions.
Refute. Gradually, it was demonstrated that epigenetics plays an indispensable role in health and disease of living organisms. On the top of that, it is experimentally proven that physiology, cellular regulation, tissues, organs, and the body-plan are defined by the value and distribution of the electric potentials on cellular membranes [2,27].

4.2. Genes Are Encoding All Body Plans Observed Within Bodies of Living Entities

It is a widely accepted idea that morphological development and from it resulting body-plans are encoded by genes locally.
Evidence. Defects in gene-encoding leads to dysfunctions, as is known from and proven by experiments with knock-out genes, which in turn leads to malformations within tissues, organs, and body growth.
Refute. The tissues, organs, and bodies growth and morphological development can be manipulated by the electric potential changes on the surface of cells is larger volumes. Additionally, it is proven that the number of legs, heads, tails, two-headed, two-tailed using plantar worms and lizards can be arbitrary engineered by mere changes in the electric potential on cell surfaces [2,27]! The body plan is defined by the electric potential on cell membranes within tissue of developing living entities.
Preprints 82162 i002

4.3. Resilience of Emergents against Perturbation of Neighborhood

The problem with emergence is that emergents are not resilient when the neighborhood is perturbed.
Evidence. Emergents cannot maintain their shape even after even the slightest change of the GoL-neighborhood, see [4] for logic-gate simulations (an example of OR logic-gate in Figure 3) that are working with emergent glider-guns and gliders.
Refute. As the counter-example, serve the resilience of emergents, which were demonstrated to persist even when the underlying neighborhood was gradually changed Figure 8. Additionally, it was demonstrated in [4] that special design of the evolution function enables emergents to resist injection of 1% of evaluation errors into the simulation. Hence, it had been demonstrated that there is existing a class of emergents, which are resistant against perturbations of either neighborhood or evolution function.

5. Arguments/Examples

The hypothesis is supported by the following observations and phenomena observed across the whole spectrum of scientific fields including biology where it should be tested in depth.

5.1. Emergents Operating Within GoL Carrying on Computations

It is known for a long time that AND, OR, and NOT logic-gates can be constructed within GoL using glider-guns, gliders, and stop-structures. Promising attempts to design emergent processing units and memories in this way within GoL are in progress [23].
Supporting examples. GoL was proven to be Turing machine equivalent [22], which creates a solid basis for its future applications in emergent computations.

5.2. Gliders are Observed in Modified GoL-N24 with Extended Neighborhood

From the proven Turing equivalence of GoL [22], there is existing a hypothesis that each presence of gliders in modified GoL (see Figure 7) indicates that there exist a high probability of discovery/design of glider-guns. Once those emergents are found, any type of classic logic can be designed.
Supporting examples. Many randomly tested neighborhoods within GoL-N24 contain gliders, ships, and in some cases there are observed even more complicated emergent structures (e.g., second-order emergents in the neighborhood #459744, see Figure 6).

5.3. Emergent Information Processing Produces Morphology

MPCs has the proven potential [1,29,30,31] to process information in so far poorly understood, distributed forms, which are computationally richer and simultaneously very robust when compared to classical logic-gates used in designed computing devices.
Supporting examples. The proof is provided by many known natural systems that are, including biological systems. Morphological growth of living organisms represent the best example. It is known that Dictyostelium discoideum [1,29] (slime mold) is solving complicated spatio-temporal tasks during searching for food, the same goes for ants and other social insects [30]. Additionally, D. discoideum is capable to assembly single cells into a fruiting body using simple signaling techniques, which serves as an example of primitive anatomy plan.
Some organisms and even cells use the external environment as a kind of external memory, e.g., ant pheromone-trails and bees-comb’s structure—they make local, independent decisions accordingly to the interactions with the surrounding environment, which is leading to self-organization and emergence [31] without the presence of the internal memory. Flocking behavior of birds express similar features.

5.4. EIP Produce Tissues, Organs, and Bodies

It is known that bodies, organs, and tissues exist through the entire life-span of each living organism, while its constituting elements are being continuously repaired and replaced. In humans, on average, this might take about 1 year to replace the majority of cells in the whole body: some are replaced within days like square cells in the colon, and others may take many years like long sensory and motor nerve connections. Persistence of the function and maintaining the identity of the whole while the constituting parts are being continuously replaced represents an excellent example of emergence, which is expressing error-resilience and self-repair.
Supporting examples. Stem and senescent cells replacement, and cellular regeneration are insufficient to perform tissue’s, organ’s, and body’s regeneration as morphology is not fully defined by them. Those questions are being already addressed in biomedical research for over two decades by trying to uncover the role of cell-membrane potentials in the genesis and maintenance of living organisms, e.g., [2,27]. Well-defined changes of cell-membrane potentials are capable to initiate regrowth of lost limbs in lower-level vertebrae, and even heal breast cancer in humans.
There is existing an increasing number of researchers of consciousness, e.g., [32,33], who are exploring the origins of all living and even those non-living forms using various ways combining quantum approaches, emergence, and consciousness.

5.5. Physical Laws Are Emergent

Contrary to our beliefs based on daily experiences, physical laws themselves are emergent and not fixed. For example, a solid material made from atoms is an emergent arising through interactions of its constituting components called atoms, which are resulting in a specific crystal lattice. Very complicated dependencies cannot be explained in any other way to apply massively-parallel interactions: one example are non-Newtonian liquids [34].
Supporting examples. For example, strength, stiffness, lattice type, temperature are emerging properties of solids. Non-Newtonian liquids have a very different response to physical loading during slow deformations (liquid-like) and fast deformations (solid-like). This type of behavior is reached in liquid materials containing long strings like starches or polymers, which are smoothly sliding on each other during slow deformation speeds but are getting mutually interlocked during fast deformation speeds.
Another examples can be found in statistical physics, Hook’s law, DRX [3,35] and many other natural phenomena, which are expressing self-organizing and emergent properties.

5.6. Artificial Morphology Growth and Embryogenesis as Proxy to Uncover Principles of Emergent Design of Computation

Artificial morphology is representing means to recreate the processes that are observed during embryonic growth of living organisms, which in turn enrich our understanding of phenomena observed in health and disease because it can be compared with real biology, and as a bonus it will improve our theory of EIP and MPCs.
Supporting examples. Morphogenesis [27,36], swarm behavior [30], along with other observed phenomena, which are operating within biological systems, give us means to validate the tested models.
The understanding of this area of biological phenomena is still not settled down. Top-down models [2] dealing with pattern formation, growth, and embryogenetic regulation, are complementing bottom-up developmental models that are discussed in this paper and, e.g., [4], in mathematical description of biological systems.

5.7. Error-Resilient Emergent Information Processing as Alternative to VLSI Technology

There is rising a chance of the following very important application. Contrary to VLSI chips that are artificially designed by humans, emergent computation and information processing due to their error-resilience are not prone to the occurrence of local errors within the local rule and neighborhood (partially proven here and in [4]).
Supporting examples. All morphologically growing living entities that are maintaining emergents at many hierarchical levels. Did anyone ever observed a biological entity—e.g., a vertebrae species—which after failure of a single neuron cease to function? It is just the opposite with our current VLSI technology, a failure of a single-chip constituting element is often detrimental to the performance of the whole processor, or it can become even fatal.

6. Future Directions

As already shown, emergent, error-resilient structures are existing within relatively simple CAs. This is opening the doors towards the development of novel descriptive tools capable of morphological-development-like description of biological systems: such approaches can be as well applied in the description of simpler chemical and physical systems.

6.1. Realization Hypothesis: Description of Emergent Information Processing from the First Principles

What would be the line of attack along which it is possible to resolve the Existence of EIP Thesis? As already demonstrated, there are known examples of such systems (see this text), but there is not existing any theory enabling to design them systematically. All the presented emergents were discovered by the following procedure—called the forward task: randomly choosing a rule → applying it to the matrix → observing occurrence of emergents and their operation.
The opposite direction—called the reverse task—where the desired emergent structure initiates the search for local rules that are generating those emergents is currently unavailable. It requires deep, future theoretical studies due to its intractability using brutal force approaches.
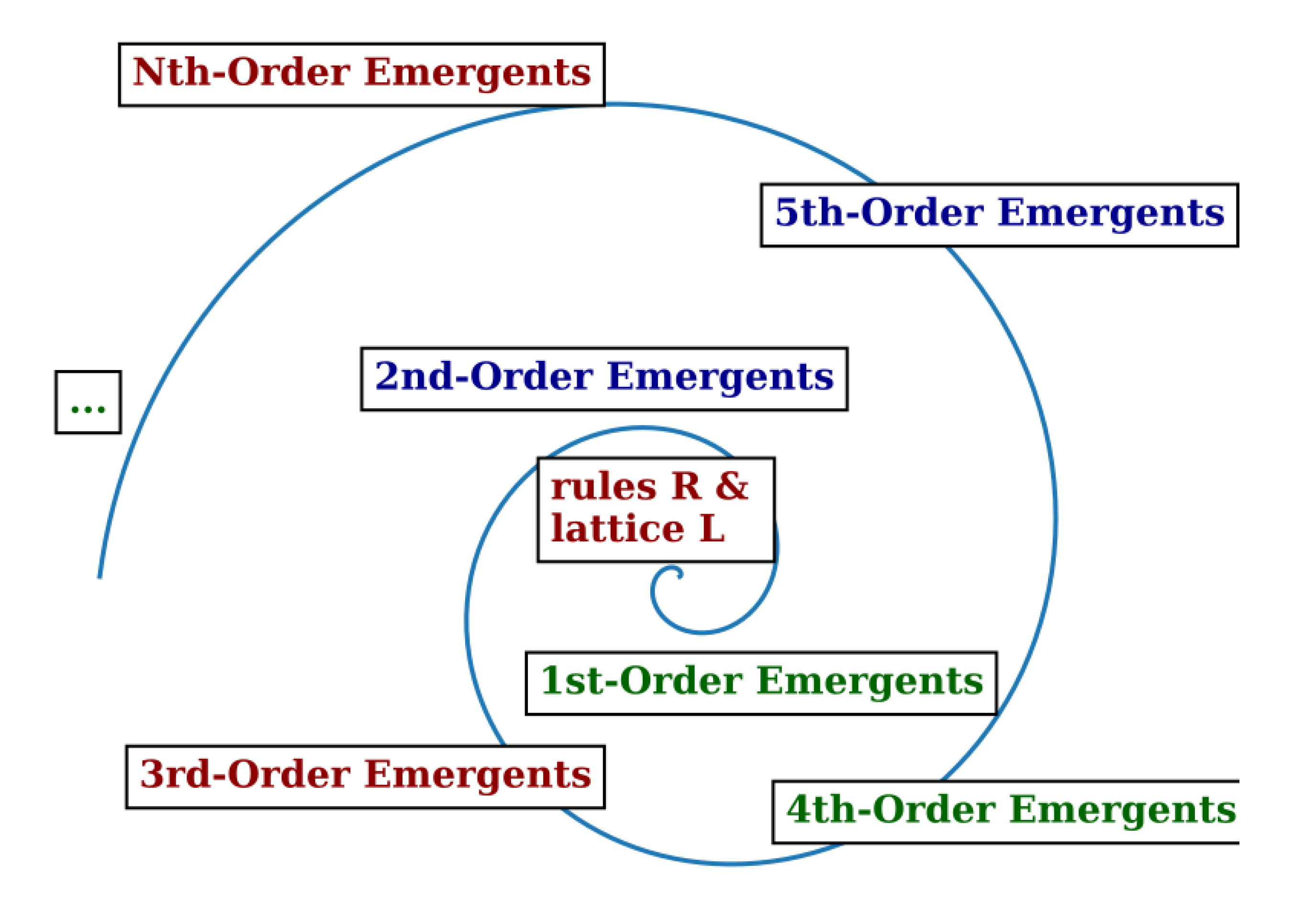
Preprints 82162 g009
Figure 9. A spiral depicting emergence of the hierarchy of emergents, as observed within various emergent-levels of the generalized ’Game of Life’, GoL-N24 and other complex systems. The emergence is resulting from the core rules & processes without any additional design. In this paper we documented the first- and second-order emergents only, some of those are artificially designed others are pure emergents.
Figure 9. A spiral depicting emergence of the hierarchy of emergents, as observed within various emergent-levels of the generalized ’Game of Life’, GoL-N24 and other complex systems. The emergence is resulting from the core rules & processes without any additional design. In this paper we documented the first- and second-order emergents only, some of those are artificially designed others are pure emergents.
Preprints 82162 g009

6.2. Emergent-Logic Hypothesis: Beyond Gödel’s Theorem of Incompletenss

From the simulations of logic-gates, see Figure 3, significant implicit and not immediately obvious consequences are arising.
Preprints 82162 i003
We just proved by an example that massively-parallel interactions are capable to generate standard logic operations [4,22,23]. This leads to the conclusion that logic is arising from and through a medium of low-level massively-parallel interactions. The big question is how is it realized? The sequence of design of logic-gates within GoL is: a rule → projection into matrix → logic.
It seems to be that our mathematical logic is coarse-grained and human-readable whereas the MPC-logic is fine-grained and beyond standard human perception due to its inherent massive parallelism. The search for rules governing the MPC-logic is one of the cornerstones in theory & design of future models of living systems and error-resilient information processing devices, including computers.

6.3. Emergent-Logic Hypothesis: What Are Means of Decision-Making in CSs?

From all so far presented results and as an extension of the previous subsection, it is proven that logic can be simulated by MPC logic-gates in GoL (see e.g., [22,23]). This implies the fact that there must exist a richer, elusive, massively-parallel ’logic system’, which is going to be called emergent-logic (= MPC-logic), that in some special cases collapses to us already known mathematical logic (in our case, it collapses into emergent logic-gates, see Figure 3). Currently, it is only possible to speculate what is the character and theory of this emergent, massively-parallel emergent-logic.
From the work of Kurt Gödel, it is known that some logical statements are impossible to evaluate within any axiomatic system. A very important question is: "Is the underlying, massively-parallel, emergent-logic complete or incomplete?” What is occurring to be quite important check in depth is a possibility that all living systems are operating at the level of emergent-logic. When this is true, we can look at logic-operations without even noticing them due to their massively-parallel nature. The author’s personal hypothesis is that massively-parallel emergent-logic is error-resilient and hence, the issue of completeness/incompleteness is avoided in this way.
Preprints 82162 i004

6.4. Emergence of Natural Laws’ Hypothesis: Are Physical, Biological, and Other Observed Natural Laws Just Emergents Originating in Lover-Level Processes?

Statistical physics is serving as the first example of a theory where collective emergent properties (temperature, pressure, information, etc.) are arising from microstates of atoms or molecules without necessity to trace the energy and position of each single atom. As we know, Ludwig Boltzmann [37,38] had proven that it is not necessary to trace every microstate of the system, instead emergent properties are derived from collective statistical properties based on microstates.
Following the above example, when we assume the emergence of natural laws’ hypothesis being true, it means that there is existing a much larger set of emergent behaviors originating in MPCs, which are not describable by standard analytical and computational approaches used to define natural laws in the closed analytical form we are used to, see Table 2 and Table 3.
An MPC example can be observed within the well-documented DRX model [3,35] where only the MPC model—despite centuries of trying to derive a heuristic, probabilistic, or analytic model—is capable to describe observed stress-strain curves expressing oscillations or single-peak response to the imposed deformation under varying deformation conditions and elevated temperatures. Centuries of failures in creation heuristics, statistic, and analytic models had been successfully replaced by MPC models.

6.5. No-Law-Describable Natural Phenomena Hypothesis: Are There Existing Processes Contradicting Causality and Determinism?

To extend the Emergence of the Natural Laws’ Hypothesis further, a question is given: “Is the nature allowing no-law-describable interactions?” Does it mean that the standard notion of sequences of events known as the causality does not hold always? This opens doors to novel approaches in the description of observed natural phenomena that seems to be too ’messy’ to be described by the standard approaches used by our contemporary mathematical descriptions within science; the book [39] describes the paradigm shifts in science. Currently, there are known two possible proxies of such descriptions: massively-parallel distributed causality, and those descriptions that are potentially contradicting causality (this is just a hypothesis, which deserves a deeper study on its own).
As proven in the case of DRX [3], the broader, no-laws-describable natural phenomena hypothesis holds because MPC are allowing descriptions impossible to achieve by standard analytic and computational descriptions, and hence, MPC environments are richer and more expressive due to their huge flexibility in definition of local interactions (each computational element is making an independent decision from the rest, see [40,41] for details). The existence of non-causal natural phenomena should be addressed in serious studies specially designed to this purpose.
A question for the future studies is: “Are processes & matrix arising from realms of the ocean of unknown, which is undescribable, beyond-the-reach by our common senses and detecting devices.” The quantum-mechanical description using wave function, delocalization, entanglement, and localization with delocalization are pointing towards a possibility of such description. All is open.

6.6. Hypothesis Creation

Preprints 82162 i005
The scope of the standard description of the observed phenomena is limited [39]; this had been, is, and always will be true in science. Hence, in recent decade the science started to use novel methods to create hypotheses using machine learning, AI, deep learning, data mining, and other methods of inference of relationships among data. The quantum-mechanical description of natural phenomena is facing similar issues. The problem with AI, ML, and DM methods is that they are typically utilizing the black-box methods that are not human understandable.
EIP provide us means to develop deeper methods of description of natural phenomena—i.e., get closer to the primary causes—that goes beyond by-the-equations-based ones. Brain functioning can become one of such areas of research where from-the-first-sight random neuronal activity patterns can have some underlying mechanism exploiting EIP. The first step would be to find some of those emergent information processing configurations, in the ideal case, error-resilient ones.

6.7. Frontiers of Our Understanding: Where Theories and Applications in Biology and Robotics Meet Each Other?

When we observe the scientific efforts to build life-like entities named robots1 from the meta-level, it becomes obvious that there are currently existing two major research strategies, which are approaching the goal from two opposite ends.
The first approach, the top-down one, is building macroscopic systems that perform similar actions as humans and animals do: locomotion, manipulation by limbs, vision, sensing, evaluation, etc. The second approach, the bottom-up one, is utilizing self-organization and emergence in building larger structures from the tiniest ones: atoms, molecules, bio-molecules, DNA-strands, etc.
Therefore, in the top-down approach, we do have (hard-) robots utilizing macroscopic mechanical, hydraulics, and electromagnetic systems, as we know them from industry and remote-controlled applications. Below them are being developed soft robotic-materials and soft robots [43] working at the intermediate levels, which inherently rely on the development of coupling of sensing, computation, and communication [44] at the mesoscopic level. One example can be gellular automata [45] and related approaches that utilize separated gell cells, which are facilitating computation. The mesoscopic level suffers from one huge deficiency: the existence computational bottleneck between local sensors and effectors on one side and the centralized computation due to necessity to connect both sides (too much wires and too little space).
The above-mentioned case leads to the lowest level, the bottom-up approach, there are being developed robots operating at the microscopic level, which are utilizing atoms, molecules, DNA, proteins, and cells. DNA-computing , DNA designed structures, and DNA origami [46] that are representing a very promising biologically, mathematically, and technologically challenging approach, see details on DNA computing [47]. DNA computing provides us a window into the ways the biology is ’thinking’ and solving problems locally using to us so far unknown mathematics within uncharted parts of theories of graphs, NP-hard problems, and manifolds, and complex systems.
After preparing the hypotheses, perspectives, and future directions about emergent information processing presented in this paper, the scientific literature was scanned to find some links to already-known research implementations of soft robotic materials, soft robots, and bio-computing, which can confirm the validity of the approach implemented within GoL-N24 [13] and r-GoL [18] software. As mentioned above [43,44,45,46,47], links between the software and applications are already existing. For example Gellular Automata [45] are representing one-to-one representation with GoL-N24 whereas DNA computing and origami structures [46] can be implemented in networked automata.
Important observations were made from the comparison of the software and robotic & DNA implementations. Generalizations of the neighborhood implemented within CAs can help to implement networked automata. GoL-N24 & r-GoL software is working with regular lattices (regular networks), which can be relaxed and use networked automata instead of cellular automata (some links within the neighborhood are missing, others are distant).
Within this context, it is necessary to remind the research about the effects of the electric potentials of living cell membranes on the development of living cells, tissues, organs, and whole bodies [2,27], which can be simulated using GoL-N24.

7. Conclusions

The main purpose of this publication is to review the current knowledge about, capabilities to reproduce, means of defining the input data & local processes, means of solution, and future lines of attack to find "Artificial, massively-parallel, self-organized, emergent, error-resilient computational environments.”
Two main streams of research along those lines are demonstrated: the existence of error-resilient emergents, and resilience of emergents against variations of the neighborhood. That all beside other features such as the proof of the existence of the second-order emergents. Reviewed approaches provide proofs of possibility and partially even means of achievement of the goal of this type of research. The above is built upon the top of and broadening of known proof of Turing equivalence of the ’Game of Life’ cellular automaton.
After providing examples and counter-examples, the possible future research paths along with a number of hypotheses are given in order to sufficiently cover as many scientific disciplines as possible. This allows everyone to apply those ideas in their respective field of research. Some of those hypotheses are going beyond what is currently known and understood.

Funding

This research received no external funding.

Data Availability Statement

All data and software created and used in this review can be found on the RG profile of the author: www.researchgate.net/profile/Jiri-Kroc.

Acknowledgments

This work is entirely dedicated to the people of the Czech Republic, and is the result of independent research that had been fully sponsored by the author himself without any kind of external support.

Conflicts of Interest

“The authors declare no conflict of interest.”

Sample Availability

The open-source, Python software GoL-N24 & r-Gol are avaiable at RG profile: www.researchgate.net/profile/Jiri-Kroc

Abbreviations

The following abbreviations are used in this manuscript:
CA Cellular automata
GoL ’Game of Life’
SOC Self organized criticality
CS Complex systems
EIP Emergent information processing
ABM Agent-based models
AND AND logic-gate
OR OR logic-gate
NOT NOT logic-gate
r-GoL Resilient GoL software
GoL-N24 GoL software using extended neigborhoods of 24 cells

References

  1. Adamatzky, A. A brief history of liquid computers. Philosophical Transactions of the Royal Society B: Biological Sciences 2019, 374, 20180372. [Google Scholar] [CrossRef] [PubMed]
  2. Pezzulo, G.; Levin, M. Top-dow models in biology: explanation and control of complex living systems above the molecular level. J.R.Soc. Interface 2016, 13, 20160555. [Google Scholar] [CrossRef] [PubMed]
  3. Kroc, J. Application of Cellular Automata to Modelling of Dynamic Recrystallization. Computational Science – ICCS 2002; Sloot, P.; Hoekstra, A.; Tan, C.J.K., C.; Dongarra, J., Eds. Springer Berlin Heidelberg, 2002, Vol. 2329, pp. 773–782. [CrossRef]
  4. Kroc, J. Robust massive parallel information processing environments in biology and medicine: case study. Journal of Problems of Information Society 2022, 13, 12–22. [Google Scholar] [CrossRef]
  5. Guisado, J.L.; Jimenés-Morales, F.; Guerra, J.M. Cellular automaton to model for simulation of laser dynamics. Physics Review E 2003, 67, 066708. [Google Scholar] [CrossRef] [PubMed]
  6. Johnson, S. Emergence: The Connected Lives of Ants, Brains, Cities and Software; Penguin Books, 2001; p. 288.
  7. Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f-noise. Phys.Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef] [PubMed]
  8. Bak, P. How Nature Works: the science of self-organized criticality; Copernicus New York, NY, 1996; p. 212. [CrossRef]
  9. Nagel, K.; Shreckenberg, M. A cellular automaton model for freeway traffic. Journal de Physique I 1992, 2, 2221–2229. [Google Scholar] [CrossRef]
  10. Glen, C.; Kemp, M.; Voit, E. Agent-based modelling of morphogenetic systems: Advantages and challenges. PLoS Comput Biol 2019, 15, e1006577. [Google Scholar] [CrossRef]
  11. Kroc, J.; Sloot, P.; Hoekstra, A. Simulating Complex Systems by Cellular Automata; Understanding Complex Systems, Springer Berlin, Heidelberg, 2010; p. 384.
  12. Kroc, J. Emergent computations: simulations of logic-gate OR using cellular automaton GoL-N24 implemented in Python. https://www.researchgate.net/publication/367380336/, 2023. Accessed as on 043-01-2023.
  13. Kroc, J. Exploring Emergence: Python program GoL-N24 simulating the ’Game of Life’ using 8 Neighbors from 24 Possible. https://www.researchgate.net/publication/365477118, 2022. Accessed as on 03-25-2023.
  14. Kroc, J.; Sloot, P.; Hoekstra, A., Simulating Complex Systems by Cellular Automata; Understanding Complex Systems, Springer, 2010; chapter Introduction to Modeling of Complex Systems Using Cellular Automata.
  15. Illachinski, A. Cellular Automata: A Discrete Universe; World Scientific Publishing Company, 2001; p. 808.
  16. Kroc, J. The simplest Python program simulating a cellular automaton model of a complex system: the ’Game of Life’. https://www.researchgate.net/publication/355043921, 2021. Accessed as on 03-25-2023.
  17. Resnick, M. Turtles, Termits,and Traffic Jams: Explorations in Massively Parallel Microvorlds; Complex Adaptive Systems, MIT Press, RI, 1997.
  18. Kroc, J. Python program simulating cellular automaton r-GoL that represents robust generalization of ’Game of Life’. https://www.researchgate.net/publication/358445347, 2022. Accessed as on 03-25-2023.
  19. Wilensky, U. NetLogo. https://ccl.northwestern.edu/netlogo/, 1999. Center for Connected Learning and Computer-Based Modeling, Northwestern University. Evanson, IL.
  20. Kroc, J. Emergent computations: simulations of logic-gate AND using cellular automaton GoL-N24 implemented in Python. https://www.researchgate.net/publication/368300518/, 2023. Accessed as on 03-25-2023.
  21. Kroc, J. Emergent computations: simulations of logic-gate NOT using cellular automaton GoL-N24 implemented in Python. https://www.researchgate.net/publication/368300097, 2023. Accessed as on 03-25-2023.
  22. Wainwright, R.; Winter Simulation Conference: Washington, DC, 1974; Vol. 2, chapter Life is Universal!, pp. 449–459. [CrossRef]
  23. Carlini, N. Multiplexing Circuits on the Game of Life – part 5. https://nicholas.carlini.com/writing/2022/multiplexing-circuits-game-of-life.html, 2022. Accessed as on 04-01-2023.
  24. Kroc, J. Python program simulating cellular automaton r-GoL that represents robust generalization of ’Game of Life’: sample runs. https://www.researchgate.net/publication/357285926, 2022. Accessed as on 03-25-2023.
  25. Kroc, J. Emergent Computations: Emergents Are Breeding Emergents as Demonstrated on Ships Breding Trains of Ships Occuring in Modified GoL Using Program GoL-N24. https://www.researchgate.net/publication/368635079/, 2023. Accessed as on 04-01-2023.
  26. Kroc, J. Exploring Emergence: Database of Initial Configurations of Modified GoL Using Program GoL-N24. https://www.researchgate.net/publication/372187009/, 2023. Accessed as on 07-07-2023.
  27. Whiteld, J.; Levin, M. Bioelectrical controls of morphogenesis: from ancient mechanisms of cell coordination to biomedical oportunities. Current Opinion in Genetics & Development 2019, 57, 61–69. [Google Scholar] [CrossRef]
  28. Kroc, J. Robust emergents within GoL resisting perturbation of neighborhood. https://www.researchgate.net/publication/372364849/, 2023. Accessed as on 07-14-2023.
  29. Pears, C.; Gross, J. Microbe Profile: Dictyostelium discoideum: model system fordevelopment, chemotaxis, and biomedical research. Microbiology 2021, 167. [Google Scholar] [CrossRef]
  30. Ahmed, H.; Glasgow, J. Swarm Intellligence: Concepts, Models and Applications. Conference: Queen’s University, School of Computing Technical Reports;, 2012; Vol. 2012-585. [CrossRef]
  31. Heylighen, F. Stigmergy as a universal coordination mechanism I: Definition and components. Cognitive Systems Research 2016, 38, 4–13, Special Issue of Cognitive Systems Research – Human-Human Stigmergy. [Google Scholar] [CrossRef]
  32. Theise, N.; Kafatos, M. Sentience Everywhere: Complexity Theory, Panpsychism & the Role of Science in Self-Organization of the Universe. Journal of Consciousness Exploration & Research 2013, 4, 378–390. [Google Scholar]
  33. Li, T.; Tang, H.; Zhu, J.; Zhang, J. The finer scale of consciousness: quantum theory. Annals of Translational Medicine 2019, 7, 585. [Google Scholar] [CrossRef] [PubMed]
  34. Zhou, J.; Papautsky, I. Viscoelastic microfluids: progress and challenges. Microsystems & Nanoengineering 2020, 6, 113. [Google Scholar] [CrossRef]
  35. Tkáč, J.; Kroc, J. Cellular Automaton Simulations of Dynamic Recrystallization: Introduction into Self-Organization and Emergence. https://www.researchgate.net/publication/316989956/, 2017. Accessed as on 04-11-2023. [CrossRef]
  36. Doursat, R.; Sayama, H.; Mitchel, O. A review of morphogenetic engineering. Natural Computing 2013, 12, 517–535. [Google Scholar] [CrossRef]
  37. Boltzmann, L. Vorlensungen über Gastheorie; Vol. I, J.A. Barth, 1896.
  38. Boltzmann, L. Vorlensungen über Gastheorie; Vol. II, J.A. Barth, 1896.
  39. Kuhn, T.; Hacking, I. The Structure of Scientific Revolutions, 4th ed.; University of Chicago Press, 2012; p. 212.
  40. Vichniac, G. Simulating physics with cellular automata. Physica D: Nonlinear Phenomena 1984, 10, 96–116. [Google Scholar] [CrossRef]
  41. Toffoli, T. Cellular automata as an alternative to (rather than and approaximation of) differential equations in modeling physics. Physica D: Nonlinear Phenomena 1984, 10, 117–127. [Google Scholar] [CrossRef]
  42. Popper, K. The Logic of Scientific Discovery; Routledge Classics, Taylor & Francis, 2005; p. 544.
  43. Schmitt, F.; Piccin, O.; Barbé, L.; Bayle, B. Soft Robots Manufacturing: A Review. Frontiers of Robotics and AI 2018, 5, 00084. [Google Scholar] [CrossRef] [PubMed]
  44. McEvoy, M.; Correll, N. Materials that couple sensing, computation, and communication. Science 2015, 347, 1261689. [Google Scholar] [CrossRef] [PubMed]
  45. Hagiya, M. ; T., H., Visions of DNA Nanotechnology at 40 for the Next 40: A Tribute to Nadrian C. Seeman; Springer Nature Singapore: Singapore, 2023; chapter Models of Gellular Automata, pp. 397–410. [Google Scholar] [CrossRef]
  46. Ellis-Monaghan, J.; Jonoska, N. , Visions of DNA Nanotechnology at 40 for the Next 40: A Tribute to Nadrian C. Seeman; Springer Nature Singapore: Singapore, 2023; chapter From Molecules to Mathematic, pp. 189–206. [Google Scholar] [CrossRef]
  47. Jonoska, N.; Winfree, E. Visions of DNA Nanotechnology at 40 for the Next 40: A Tribute to Nadrian C. Seeman; Natural Computing Series, Springer Nature Singapore, 2023; p. 431. [CrossRef]
1
The word robot was created by the Czech visionary writer Karel Čapek: the word originates in the Czech word ’robota’ that means forced labor.
Preprints 82162 g001
Figure 1. The principles of massively-parallel information processing are described on the prototype of all such systems: a cellular automaton. (a) The lattice definition. (b) From the extended neighborhood of 24 cells are chosen 8 of them that are assigned as neighbors to each cell (the neighbourhood of just one cell is shown). Each cell is evaluating its next state in the next step according to the states of itself and its defined neighbors.
Figure 1. The principles of massively-parallel information processing are described on the prototype of all such systems: a cellular automaton. (a) The lattice definition. (b) From the extended neighborhood of 24 cells are chosen 8 of them that are assigned as neighbors to each cell (the neighbourhood of just one cell is shown). Each cell is evaluating its next state in the next step according to the states of itself and its defined neighbors.
Preprints 82162 g001
Preprints 82162 g003
Figure 3. The Turing machine equivalence of the GoL (rule #469440) is demonstrated on snapshots of a glider-gun generating gliders of logic-gates AND, OR, and NOT. Those gates enable to construct emergent logic circuits and memory within the original cellular automaton ’Game of Life’ [22,23], simulated by [4,13]. Those simulations are not error-resilient!
Figure 3. The Turing machine equivalence of the GoL (rule #469440) is demonstrated on snapshots of a glider-gun generating gliders of logic-gates AND, OR, and NOT. Those gates enable to construct emergent logic circuits and memory within the original cellular automaton ’Game of Life’ [22,23], simulated by [4,13]. Those simulations are not error-resilient!
Preprints 82162 g003
Preprints 82162 g006
Figure 6. Four snapshots of ships breathing ships that are observed within the modified ’Game of Life’, GoL-N24, rule #459744, see animations [25]. An important observation is that almost any simulation breeds those two-level emergent structures from the random initial conditions.
Figure 6. Four snapshots of ships breathing ships that are observed within the modified ’Game of Life’, GoL-N24, rule #459744, see animations [25]. An important observation is that almost any simulation breeds those two-level emergent structures from the random initial conditions.
Preprints 82162 g006
Preprints 82162 g007
Figure 7. The effect of different neighborhoods on the identical rule (GoL) is demonstrated by various types of gliders that were originally generated from the random initial conditions. (a)-(c) propagates in the speed of one cell per one time step.
Figure 7. The effect of different neighborhoods on the identical rule (GoL) is demonstrated by various types of gliders that were originally generated from the random initial conditions. (a)-(c) propagates in the speed of one cell per one time step.
Preprints 82162 g007
Preprints 82162 g008
Figure 8. Resilience of emergents is demonstrated on three different neighborhoods, which are generating the very same emergent arrow-glider from the identical initial conditions (a). Computations in sub-figures (e) & (f) are initiated by the arrow pointing down where in (f) is the symmetry gets broken, and the evolution is alternating between the initial arrow and a diagonal line, the computation in the figure (c) has only seven neighbors, see GoL-N24 [13], and animations [28].
Figure 8. Resilience of emergents is demonstrated on three different neighborhoods, which are generating the very same emergent arrow-glider from the identical initial conditions (a). Computations in sub-figures (e) & (f) are initiated by the arrow pointing down where in (f) is the symmetry gets broken, and the evolution is alternating between the initial arrow and a diagonal line, the computation in the figure (c) has only seven neighbors, see GoL-N24 [13], and animations [28].
Preprints 82162 g008
Table 1. A side-by-side comparison of two major approaches known in the theory of computing: (a) the standard, classical, sequential von Neumann architecture, and (b) the future, massively-parallel information processing observed in natural phenomena and living systems (as well-developed by S. Ulam & J. von Neumann in 40ies).
Table 1. A side-by-side comparison of two major approaches known in the theory of computing: (a) the standard, classical, sequential von Neumann architecture, and (b) the future, massively-parallel information processing observed in natural phenomena and living systems (as well-developed by S. Ulam & J. von Neumann in 40ies).
Computation Type Classical Emergent
Implementation method artificial, designed, engineered, sequential, mechanical, liquid, in silico natural, self-assembling, automatic, massively-parallel, in physical and biological systems
Constituting units AND, OR, NOT, XOR logic-gates atoms, molecules, cells, agents, graph nodes ...
Evaluation methods fixed wiring of logic-gates in fixed circuits self-organized and emergent information processing circuits
Design micro-mechanic, micro-flow, micro-electric elements & connective paths any medium enabling massive parallelism and definition of the local rules
Information flow predominantly sequential or slightly parallel inherently massively-parallel
Output single state or value everything between single value and multidimensional array
Error-resilience virtually non-existent quite high in a subset of generalized r-GoL
Table 2. The abstract concept of the hierarchy of emergents where processes operating in the parent-medium (emergents of the ( N − 1 ) t h order) creates emergents of the N t h order in the child-medium. Each next-level (child-medium) and processes are based on principles different from the parent-medium.
Table 2. The abstract concept of the hierarchy of emergents where processes operating in the parent-medium (emergents of the ( N − 1 ) t h order) creates emergents of the N t h order in the child-medium. Each next-level (child-medium) and processes are based on principles different from the parent-medium.
Process Matrix Emerging Phenomenon
Cellular automaton rules periodic lattice of identical elements glider-guns, gliders (1st-level emergents)
Rules of movable agents continuous space collisions, crowds (1st-level emergents)
...
Interactions of 1st-level emergents 1st-level emergent medium 2nd-level emergents
Interactions of 2nd-level emergents 2nd-level emergent medium 3rd-level emergents
... . .
Interactions of N − 1 t h -level emergents N − 1 t h -level emergent medium N t h -level emergents
Table 3. The hierarchy of emergents explained on well-known natural phenomena within physics, bio-chemistry, and biology that are expressing emergent behavior.
Table 3. The hierarchy of emergents explained on well-known natural phenomena within physics, bio-chemistry, and biology that are expressing emergent behavior.
Process Matrix Emerging Phenomenon
Atomic bonds space metallic lattice
Atomic bonds space chemical compounds
Bonds among chemicals chemicals & catalysts biochemicals
mRNA ribosomes proteins
Proteins cellular functional-units cells
Cells cellular interior & exterior tissues
Tissues cellular ensembles organs
Organs organ systems & physiology bodies
... . .
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated