Prerpints.org logo
Preprint
Article

Mechanical Properties and Non-isothermal Crystallization Kinetics of Polylactic Acid Modified by Polyacrylic Elastomer and Cellulose Nanocrystalline

Altmetrics

Downloads

134

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 August 2023

Posted:

11 August 2023

You are already at the latest version

Alerts
Abstract
In this paper, a polyacrylic elastomer latex with butyl acrylate (BA) as the core and methyl methacrylate (MMA) copolymerized with glycidyl methacrylate (GMA) as the shell, named poly(BA-MMA-GMA) (PBMG), was synthesized by seeded emulsion polymerization. Cellulose nanocrystal (CNC) was dispersed in the polyacrylic latex to prepare PBMG/CNC dispersions with different CNC contents. The dried product was mixed with polylactic acid (PLA) to fabricate PLA/PBMG/CNC blends. The addition of PBMG and PBMG/CNC improved the mechanical properties of the PLA matrix. Differential scanning calorimetry (DSC) was used to investigate the non-isothermal crystallization kinetics. The Avrami equation modified by Jeziorny, and the Ozawa, and Mo’s equations were used to analyze the nonisothermal crystallization kinetics of PLA and its blends. Analysis of crystallization halftime of nonisothermal conditions indicated that the overall rate of crystallization increased significantly at 1 wt% content of CNC. This seemed to result from the increase of nucleation density and the acceleration of segment movement in the presence of CNC component. This phenomenon was verified by polarizing microscope observation.
Keywords: 
Subject: Chemistry and Materials Science  -   Polymers and Plastics

1. Introduction

With the increase in environmental protection awareness, the demand for use of biodegradable polymers is increasing. Polylactic acid (PLA), a biodegradable polymer derived from renewable resources [1], is considered to be one of the most competitive renewable bio-based polymers because of its excellent biocompatibility, good biodegradability [2-3]. As an environmentally friendly, biodegradable plastic, PLA shows great potential as an alternative to petroleum-based plastics in various applications. However, the wide application of PLA is limited due to some inherent shortcomings such as low impact strength, low heat distortion temperature, and slow crystallization rate [4-5]. Therefore, recently many researchers have been working on modification of PLA to improve these properties.
Blending method is the most simple, feasible and economical way to modify PLA [6-7]. Mazidi modified PLA with PB-g-SAN core-shell impact modifier [8]. Although toughness was improved, tensile strength and Young's modulus decreased significantly. Zhao obtained the same results using poly(ethylene-butyl acrylate-glycidyl methacrylate) components [9]. Yeo introduced multifunctional polyhydroxybutyrate rubber copolymer into PLA to act as an effective nucleating agent to accelerate the crystallization of PLA, but the storage modulus decreased significantly [10]. In order to improve the toughness of PLA, a higher content of plasticizers or rubber fillers was required, which is often accompanied by the sacrifice of tensile strength and modulus [11-15]. Meanwhile PLA is a semi-crystalline polymer, secondary crystallization during heating leads to different physical properties. Therefore, crystallization and crystallization kinetics play an important role in the manufacturing process and product performance [16]. Jin prepared ramie fiber-reinforced PLA biocomposites using non-woven ramie fibers (RF) and PLA staple fibers as raw materials [17]. In order to understand the effect of RF on the crystallization behavior of PLA, the non-isothermal crystallization kinetics of PLA and PLA/RF biocomposites were studied. The results showed that RF, as a heterogeneous nucleating agent, weakened the interaction between PLA polymer chains during the crystallization process, and reduced the energy barrier of PLA. So, to promote the crystallization performance of PLA, nanocellulose [18-19], a high-performance nanomaterial, has attracted the interest of researchers because of its adjustable aspect ratio, controllable morphology, improved mechanical properties [20]. Nanocellulose is mainly composed of crystalline domains of cellulose, an abundantly available biopolymer, and is divided into three different types according to the degree of crystallinity and the morphology of crystalline segments. Cellulose nanocrystals (CNCs) or cellulose nanowhiskers (CNWs) with high crystallinity are mainly prepared by controlled acid hydrolysis [21]. CNCs, rigid rod-shaped single crystal cellulose with diameters of 1-100 nm and lengths of 10-1000 nm [22-26] have attracted widespread attention due to their crystal structure, high aspect ratio and large surface area (about 150 m2/g) [27]. Cao improved the mechanical properties and shape memory properties of polylactic acid (PLA)/epoxidized natural rubber (ENR) thermoplastic vulcanizates (TPVs) by using CNCs as an additive [28]. Borkotoky explored the thermal degradation and crystallization behavior of PLA and PLA/CNC [29]. Nonisothermal crystallization experiments show that low loading CNC can act as heterogeneous nucleating agent in the matrix, but high loading CNC is easy to agglomerate in the PLA matrix, which hinders the migration of PLA molecular chain and inhibits the crystallization of PLA.
Most studies have shown that plasticizers or rubber fillers can effectively improve the toughness of PLA [30-31], but they often have a non-negligible effect on their tensile strength and modulus [32]. Crystallization can improve the modulus, strength, and heat resistance of PLA [33], but usually at the expense of ductility [34]. Therefore, this article combined polyacrylic elastomer (PBMG) with reinforced component (CNC) at different contents (1%, 2%, 3%, 4%) to modify PLA. The mechanical properties and nonisothermal crystallization kinetics of the blends were investigated. The goal is to maintain or even improve the strength while toughening PLA.

2. Experimental

2.1. Materials

Polylactic acid (PLA), (Injection grade, Mw=1×105g/mol) was supplied from Haizheng Biomaterials Co., Zhejiang, China. Cellulose nanocrystalline (CNC) was obtained from Tianjin Mujingling Biotechnology Co. Butyl acrylate (BA) and methyl methacrylate (MMA) (Analytical purity) were purchased from Tianjin Damao Chemical Reagent Factory. Potassium persulfate (K2S2O8, Analytical purity), was obtained from Tianjin Hongyan Chemical Reagent Factory. Anionic surfactant (Chemical purity) was supplied from Tianjin Reagent Factory. Glycidyl methacrylate (GMA, Analytical purity) was purchased from Tianjin Heans Biochemical Technology Co. Allyl methacrylate (ALMA, Analytical purity) was received from Tokyo Chemical Industry Co., Ltd. 1,4-Butanediol diacrylate (BDDA, Analytical purity) was supplied from Tianjiao Chemical Co., Ltd. Deionized water (DIW) was used for all polymerization processes.

2.2. Synthesis of PBMG and PBMG/CNC

The poly(BA-MMA-GMA) PBMG latex was synthesized by the same procedure developed by Qu et al. [35, 36] with minor modifications using higher stirring speed and shorter time. The CNC aqueous dispersion was prepared by dispersing CNC in DIW (1/3, w/w) with magnetic stirring and ultrasonic treatment for 0.5 h, respectively. Then, the CNC dispersion was poured into a five-fold diluted PBMG latex and stirred for 1 h. The content of CNC was 1%, 2%, 3%, and 4% of PBMG latex. PBMG/CNC powders were obtained by freeze-drying under vacuum.

2.3. Preparation of PLA/PBMG/CNC Blends

PLA, freeze-dried PBMG powder, and PBMG/CNC powder were dried under a vacuum oven at 60℃ for 12 h. A TE-34 twin screw extruder (Nanjing Institute of Extrusion Machinery, China) was used to prepare blends with weight ratios of 90/10/0, 90/10/1, 90/10/2, 90/10/3, 90/10/4, designated as PLA/PBMG (PLB), PLA/PBMG/CNC1 (PLBC1), PLA/PBMG/CNC2 (PLBC2), PLA/PBMG/CNC3 (PLBC3), PLA/PBMG/CNC4 (PLBC4), respectively, at a screw speed of 60 rpm and barrel temperatures of 160oC, 165oC, 165oC, 165oC, 160oC, and 160oC. The palletized particles were dried and molded in an injection-molding machine (JPH-30, Guangdong Hongli Machine Co., China) at 160℃.

2.4. Measurement and Characterization

The monomers’ weight conversions, including instantaneous conversions and overall conversions of PBMG latexes at seed emulsion polymerization process and their particles were calculated and measured according to Qu et al. [37, 38].
A field emission scanning electron microscope (FE-SEM, Nova Nano SEM 450, FEI) was used to examine the PMBG and PBMG/CNC latexes’ morphologies. The fractured surfaces of PLA/PBMG/CNC blends were coated with gold before observation. The detailed procedure referred the reference 37.
Tensile tests of PLA, PLA/PBMG and PLA/PBMG/CNC blends were performed according to Qu et al. [37, 38] DSC tests of the samples (about 5-8 mg) were conducted on a PE Diamond DSC. The samples were heated from 20oC to 200oC at a heating rate of 10oC/min in a nitrogen atmosphere and kept for 3 min to eliminate the thermal history. After that, the temperature was cooled to 20oC at a rate of 20oC/min and then increased to 200oC at a rate of 10oC/min. Finally, the samples were cooled to 20oC at the rates of 1.0oC/min, 1.5oC/min, 2oC/min, and 3oC/min, respectively.
Samples of a small rice-grain size were inserted between the two slides of the heating table and observed under an Axioskop 40 hot stage polarizing microscope (POM, Karl Zeiss, Germany). First, the samples were heated to 200oC at the rate of 30oC/min for 3min to eliminate the thermal history. Then, the samples were cooled to 115oC at the rate of 30oC/min, and the spherulites were observed by isothermal crystallization at 115oC.

3. Results and Discussion

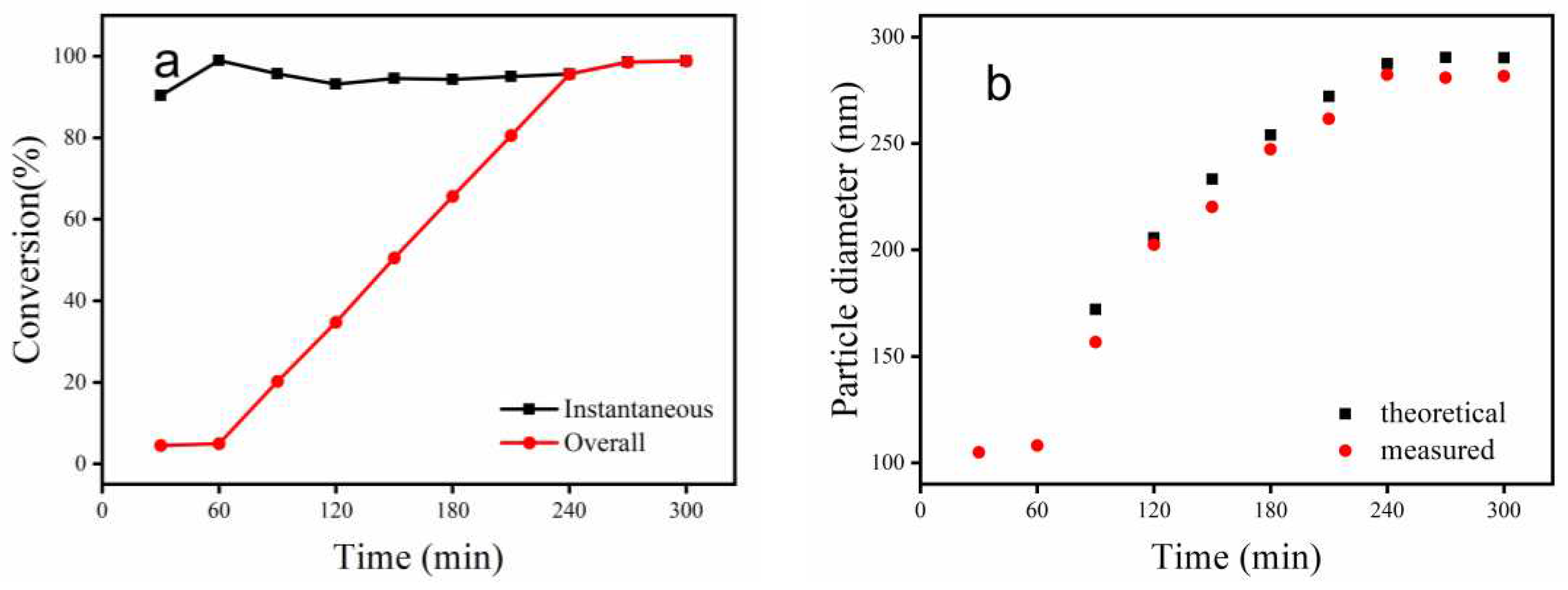
3.1. Conversion and Particle Diameter Analysis of Emulsion Polymerization

The instantaneous conversion and overall conversion versus reaction time during the emulsion polymerization process are shown in Figure 1(a). It can be seen that the instantaneous conversion was over 90%, and the final conversion rate is 98.82%. The overall conversion increased linearly with the reaction time at the growth stage, indicating that the drip-feeding rate of the monomers was appropriate in this reaction. Figure 1(b) shows the variation of theoretical and measured latex particle diameter versus reaction time. The results showed that the theoretical values were consistent with the measured ones. This indicated that all the added monomers were polymerized on the surfaces of the original latex particles without secondary nucleation, and the surfactant dosage supplemented in the pre-mixed monomers was appropriate. This also showed that during the growth stage, the particles grew under monomer-starved conditions. Under these conditions, the copolymer composition in the diameter direction would be uniform and approximately equal to the composition of the comonomer feed mixture. Similar results were obtained in a previous study by the authors [36]. The final particle diameter was 282 nm. Meanwhile, the particle diameter index (PDI) of the final latex was 0.06, meaning that all particle sizes were uniform. The same particle size and the distribution of PBMG/CNC composite latexes were obtained after the addition of CNC dispersions, that is to say there was no effect on the final PBMG latex as the CNC dispersion was added.

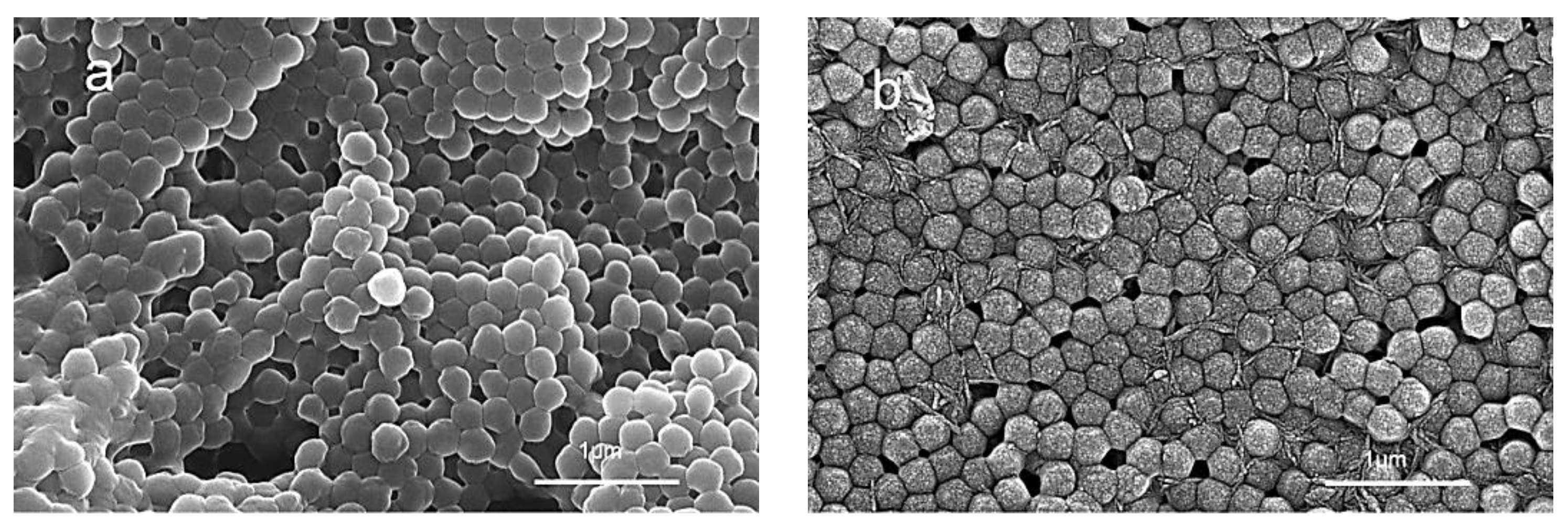
3.2. Particle Morphology and Structure

The SEM images of PBMG and PBMG/CNC1 powders are shown in Figure 2. It can be seen in Figure 2(a) that the particle diameter of PBMG is consistent and evenly distributed. The particle diameter was consistent with the DLS test results. As can be seen in Figure 2(b), the PBMG latex dispersed with CNC1 has a uniform particle size, indicating that CNC does not affect the morphology of PBMG. In addition, the CNC is wrapped on the surface of PBMG particles or dispersed between PBMG particles.

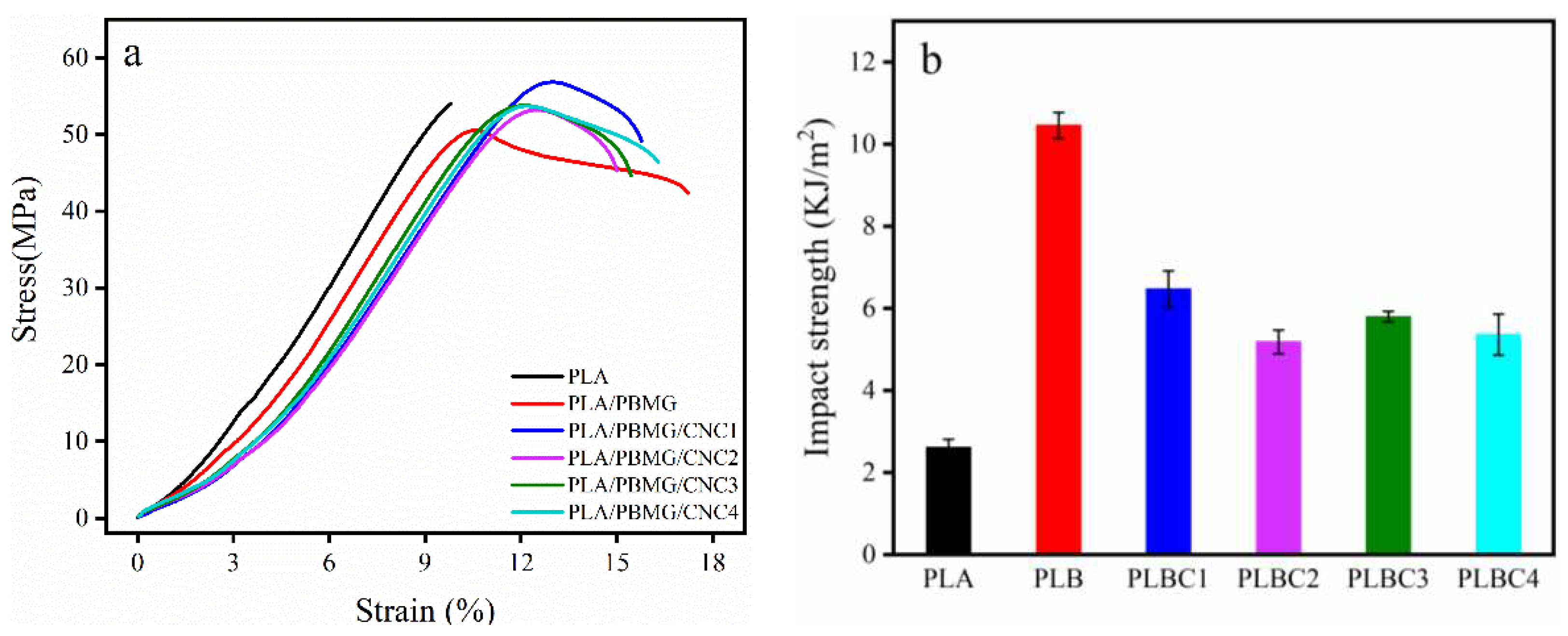
3.3. Mechanical Properties

Figure 3 shows the mechanical properties of PLA and its blends, in which PLB and PLBC represent PLA/PBMG blend and PLA/PBMG/CNC blends, respectively. It can be seen from the stress-strain curve in Figure 3(a) that PLA is a brittle material without a yield point. The PLA/PBMG blend shows a yield point, and the elongation at break increases from 9.80% to 17.22%. This indicates that the PLA undergoes a brittle-ductile transition and the PLA/PBMG blend gains toughness. The notched impact strength of PLA/PBMG blend increases from 2.60 kJ/m2 of PLA to 10.45 kJ/m2, while the tensile strength decreases from 54.23 MPa to 49.79 MPa, as shown in Figure 3(b) and 3(a). Notably the tensile strength of the blend increases and elongation at break decreases slightly after the CNC component was added. When the amount of CNC is 1 wt%, the tensile strength increases to 56.96 MPa, which is more than that of the PLA matrix. This indicates that CNC has significant reinforcing properties. At the same time, the impact strength (6.47 kJ/m2) is about 3 times higher than that of the PLA. This is attributed to the following two points. First, CNC has higher aspect ratio, higher modulus and higher crystallinity [39]. Secondly, there are hydrogen bonds between the CNC and PLA [40]. However, the CNC powder was easy to agglomerate [41,42] when the amount of CNC added in the matrix was high, which leads to uneven dispersion of the filler and decline of the properties of the blends. Overall, Figure 3 shows that the PLA/PBMG/CNC1 had the best mechanical and toughness properties of all the blends. Therefore, the following discussion will focus on the properties of PLA/PBMG/CNC1 blend.

3.4. Crystallization

Figure 4 (a) and (b) show the secondary heating DSC curves, and the cooling crystallization curves of the PLA blends, respectively. The glass transition temperature (Tg), cold crystallization temperature (Tcc), and melting temperature (Tm) of the polymer can be seen in Figure 4(a), and the specific values are shown in Table 1. Compared with PLA, the heating curves of PLA/PBMG and PLA/PBMG/CNC1 blends do not change significantly, which indicates that the fillers do not affect the crystallization process of PLA. The Tg of PLA/PBMG and PLA/PBMG/CNC1 blends shift to lower temperature, which is consistent with the results of the DMA test. At the same time, Tcc and Tm also move towards lower temperature, which is attributed to the heterophase nucleation effect of the PBMG and PBMG/CNC1. This indicates that the addition of PBMG and PBMG/CNC1 promoted the movement of PLA chain segments [43], so that the PLA chain segments have sufficient movement ability to conduct regular arrangement and crystallize at low temperature. The lower the cold crystallization temperature, the more imperfect the crystal form would be, which leads to the melting peak moving to the low temperature direction. Moreover, there are two different melting peaks in the PLA, which indicates that incomplete crystals are formed during crystallization [44].
The crystallinity (Xc) [45] can be calculated by Equation (2):
X c = ∆ H m - ∆ H c / f × ∆ H m 0
Where ΔHm0 is the melting heat of 100% crystallization of PLA, f is the weight percentage of PLA, where the content of powder is 10%, so f is 0.9. The ΔHm0 of pure PLA is 93.7 J/g [45]. Relevant values are summarized in Table 1. It can be seen that the addition of fillers has improved the crystallization of PLA, and more so with the PLA/PBMG/CNC1 blend.
Figure 4(b) is the DSC curves of cooling crystallization at a cooling rate of 1.5oC/min. The crystallization temperature (Tc) of PLA/PBMG and PLA/PBMG/CNC1 blends are higher than that of PLA. This indicates that PBMG and PBMG/CNC1 act as nucleating agents in PLA and provide more nucleation sites to induce crystallization, which makes it possible to crystallize at a higher temperature during the cooling process.

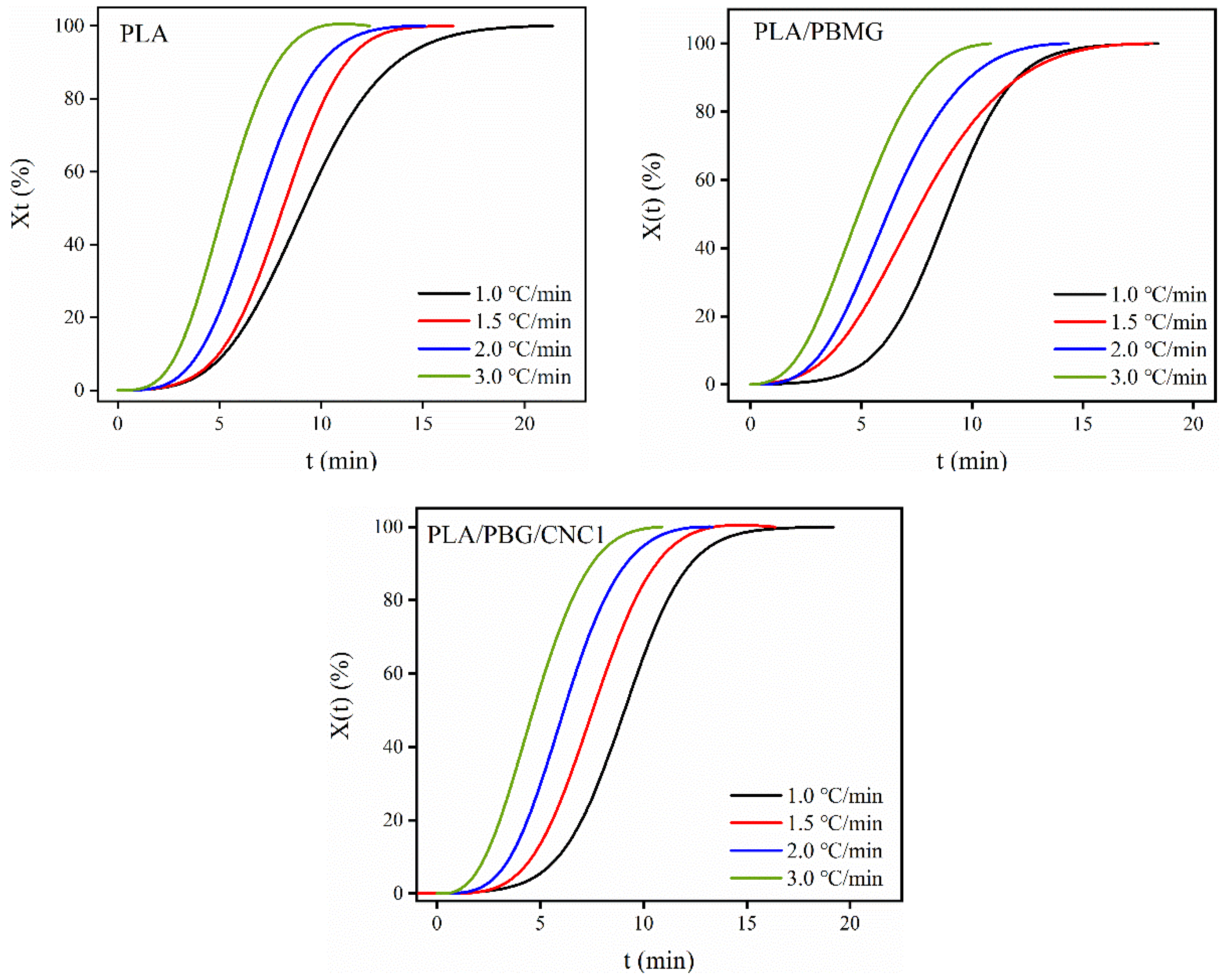
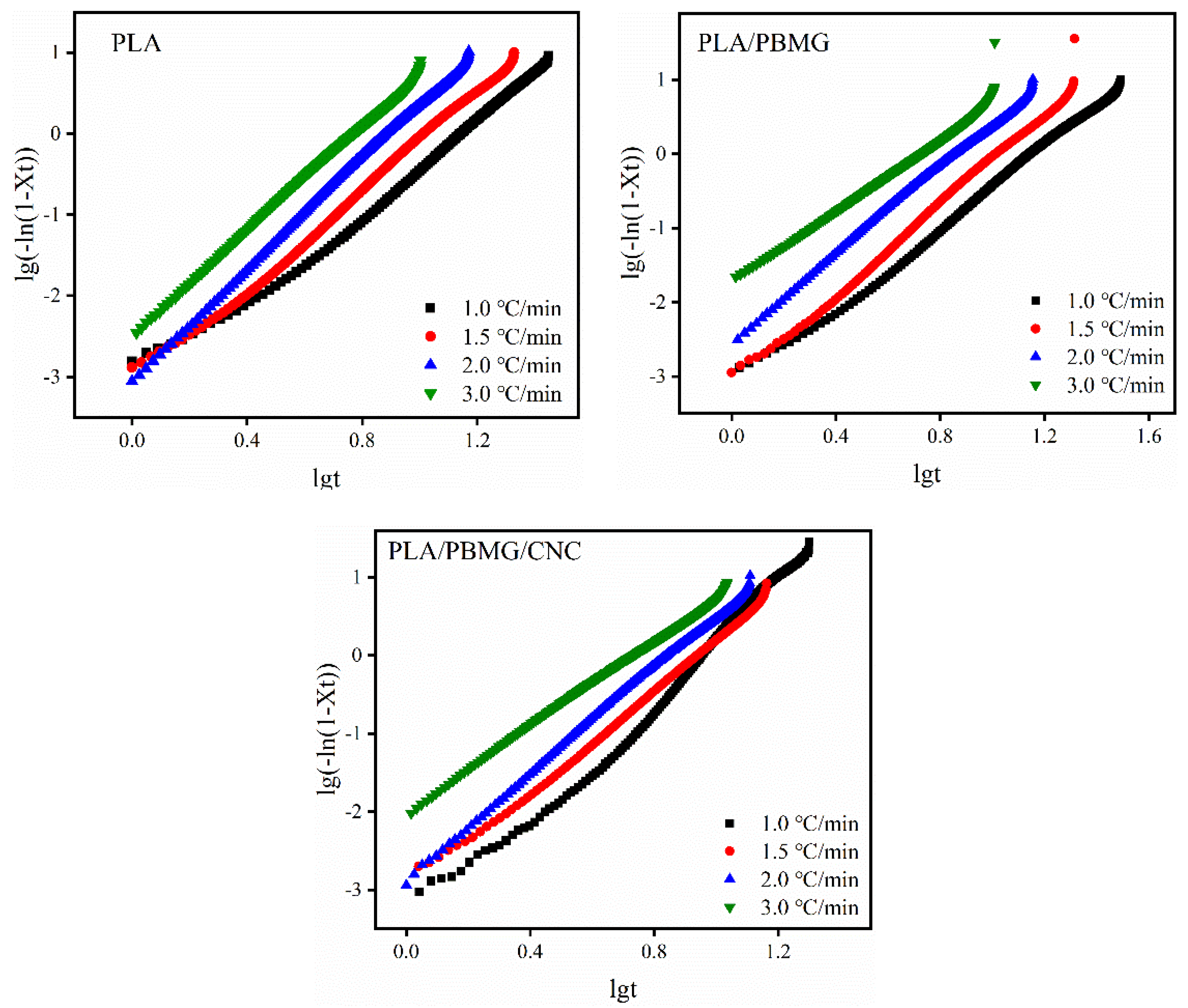
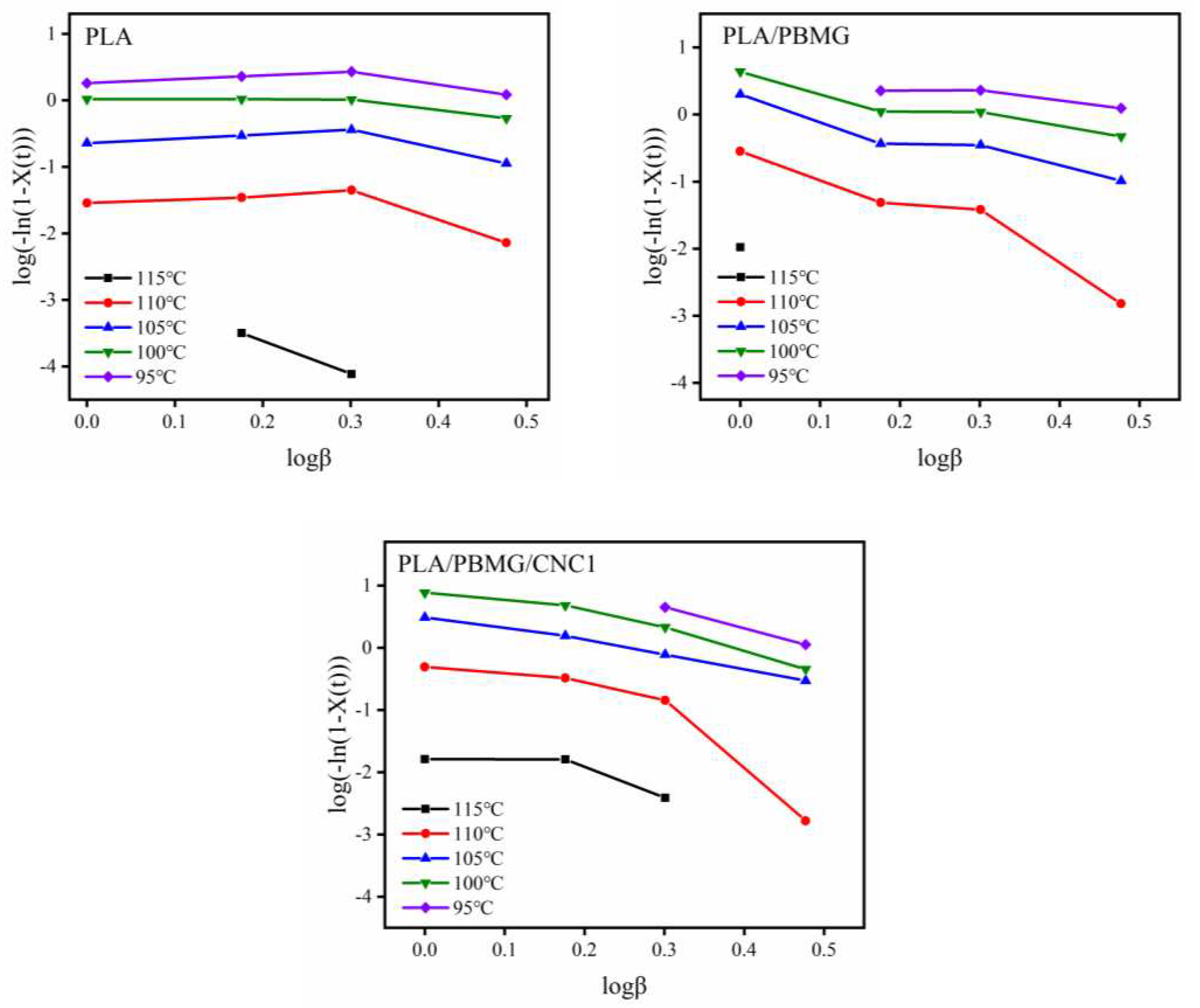
3.5. Nonisothermal crystallization kinetics

A crystallization kinetics study was performed to investigate the effects of time, temperature, and cooling rate on crystallization behavior. The crystallization behavior of polymers is usually performed under non-isothermal conditions, so in this study non-isothermal crystallization kinetics of PLA and its blends were explored. Figure 5 shows the DSC curves of the PLA and its blends with a cooling rate of 1.0, 1.5, 2.0, and 3.0oC/min, respectively. Tp is the crystallization peak temperature where the crystallization rate reaches the maximum, and T0 is the temperature when crystallization starts. It can be seen from Figure 5 that both Tp and T0 of PLA move to the lower temperature and the crystallization peak becomes wider as the cooling rate increases. At a lower cooling rate, there is enough time to activate the nucleus at a higher temperature. During this time, the movement speed of the polymer segment is faster than the cooling speed, and there is enough time to complete the crystallization, so the crystallization temperature becomes higher. On the other hand, at a faster cooling rate, TP moves to low temperature at which the mobility of molecular chains is poor, and the degree of perfection of crystallization is lower. It takes more time for the polymer chains to arrange into crystal lattices, and the crystallization peak becomes wider.
The relative crystallinity X(t) is the ratio of the peak area from the initial crystallization temperature(T0) to any temperature(T) and the peak area from T0 to the end crystallization temperature(T∞) [46], which can be calculated by Equation (3).
X t = ∫ T 0 T d H C d T d T ∫ T 0 T ∞ ( d H c d T ) d T
The temperature (T) can be converted into time (t) by Equation (4), where T is the temperature at t and β is the cooling rate. Then the X(t)-t curve is obtained, as shown in Figure 6.
t = T 0 - T / β
Half crystallization time(t1/2) defined as the time to complete 50% of crystallization is an important parameter of crystallization performance. Table 2 shows the t1/2 under different cooling rates. As the cooling rate increased, the crystallization time decreased. In other words, the time to reach the same crystallinity became shorter, as shown in Figure 6. At the same cooling rate, the t1/2 of the modified PLA blends was shorter than that of PLA. Moreover, with the increase of cooling rate, the t1/2 of PLA/PBMG/CNC1 blend continued to decrease, especially at higher cooling rates, which indicates that PBMG/CNC1 had greater influence on the crystallization properties at higher cooling rate.
The Avrami equation [46,47], Equation (5), is commonly used in isothermal crystallization process. The equation can be written in double logarithmic form as shown in Equation (6).
1 - X t = exp ( - K t n )
lg - ln 1 - X t = lg   K + n   lg   t
Where K is a composite rate constant involving both nucleation and growth rate parameters; n is the Avrami index, a mechanism constant, which depends on the type of nucleation and growth rate parameters.
However, the non-isothermal crystallization process is more complex than the isothermal crystallization process, and it is closer to the actual fabrication process. Therefore, Jeziorny [48] extended the Avrami equation to the process of non-isothermal crystallization [49]. The modified Avrami equation is shown in Equations (7) and (8).
l g   K c = l g   K β
t 1 / 2 = ln   2 K 1 / n
Where Kc is the modified crystallization rate constant, and β is the cooling rate. The graphs of lg[-ln(1-X(t))] versus lgt are shown in Figure 7. They demonstrate that the polymer and the blends have similar properties, and the curves slightly deviate from linearity. This is because of secondary crystallization in the polymer and the two different crystal growth rates in the low crystalline region and the high crystalline region [29]. The intercept and slope, namely lgK and n, can be obtained by curve fitting, and Kc and t1/2 can be calculated using Equations (7) and (8) giving the results shown in Table 3. In Table 3, the value of n is between 2.5-3.4, that is closer to 3, which indicates that the spherulites grew in a plate-shape with time [50]. As the cooling rate increased, the crystallization rate constant, Kc, increased and t1/2 decreased, indicating that the crystallization rate of PLA gradually increased. Compared with pure PLA at the same cooling rate, the Kcs of PLA/PBMG and PLA/PBMG/CNC1 blends increased, and t1/2 values decreased, which show that PBMG and PBMG/CNC1 acted as heterogeneous nucleating agents, and produced more nucleation sites in the PLA matrix, thereby accelerating the crystallization rate of PLA.
Ozawa’s equation [51] is also used to describe the non-isothermal crystallization process [52]. Ozawa considered that the linear growth rate of spherulites was a function of temperature, and proposed an equation similar to the Avrami equation, as shown in Equation (9).
l g - l n 1 - X t = l g   K T + m   l g   β
Where KT is the cooling function related to the crystallization rate, and m is the Ozawa index. Although the Ozawa model was derived from the Avrami model, the Ozawa model ignores the secondary crystallization and impact of spherulites [53], and under different cooling rates, the temperature range of polymer crystallization varies greatly, so lg[-ln(1-X(t))] did not have a linear relationship with lg β, as shown in Figure 8. In addition, the physical meaning of its cooling crystallization function is not clear. Similar phenomena have been described in other articles [47,54].
Therefore, Mo [55] et al. combined the Avrami equation with the Ozawa equation and proposed a new method to analyze crystallization kinetics parameters, establishing the relationship between cooling rate and crystallization time [56], as shown in Equations (10) and (11).
lg   K + n lg   t = lg   K T - m lg   β
lg   β = lg   Z - a lg   t
where Z=KT/K is the cooling rate per unit crystallization time when the system reaches a certain degree of crystallinity, and a (n/m) is the ratio of Avrami index n to Ozawa exponent m.
Figure 9 shows the lgβ-lgt curves of PLA/PBMG and PL/PBMG/CNC1 blends at different crystallinities. It can be seen that there is a good linear relationship between lgβ and lgt, which indicates that Mo’s equation can well describe the non-isothermal crystallization process of PLA and its blends. The values of the ratio a, and cooling rate per unit crystallization time Z can be obtained from the curves, as shown in Table 4. Z increases with the increase of relative crystallinity in the same system indicating that the cooling rate required to reach a certain crystallinity in unit crystallization time is increasing.
Considering the effect of cooling rate on non-isothermal crystallization process, Kissinger [57] proposed a theoretical model that could determine quantitatively the crystallization activation energy (ΔE) in the non-isothermal crystallization process, as shown in Equation (12).
d [ ln ( β / T P 2 ) ] d 1 / T P = - ∆ E / R
where β is the cooling rate, Tp is the temperature corresponding to the crystallization peak, and R is the gas constant (8.314 J·mol-1·K-1). As shown in Figure 10, a ln(β/Tp2)-1/Tp graph with good linear relationship was obtained. After fitting, the slope of the curve, -ΔE/R, and the calculated ΔE values are listed in Table 4. It can be observed that the |ΔE| of PLA/PBMG and PLA/PBMG/CNC1 blends is reduced to 155.80 kJ/mol and 147.57 kJ/mol, respectively, compared with the |ΔE| of PLA (156.64 kJ/mol). This indicates that the addition of PBMG or PBMG/CNC1 fillers reduced the crystallization energy barrier and increased the crystallization rate in non-isothermal crystallization process [52], which in turn improved the crystallization properties of the PLA blends.

Polarizing Microscope

The POM images of isothermal crystallization of PLA and its blends at 115oC are shown in Figure 11. It can be seen from the figures that PLA crystals mainly exist in the form of spherulites with uniform size. Compared with PLA, the number of spherulites in PLA/PBMG and PLA/PBMG/CNC1 blends increased, while the size of spherulites decreased after isothermal crystallization for 3 mins. The images show that the spherulites of PLA/PBMG and PLA/PBMG/CNC1 blends have covered the whole region after isothermal crystallization for 10 min. This is because the addition of PBMG and PBMG/CNC1 to PLA matrix plays the role of a heterogeneous nucleating agent, providing more nucleation sites. The fillers accelerated the movement of PLA segment and increased the crystallization rate of PLA, which made the crystal fully crystallized in a shorter time, which is consistent with the analysis results of non-isothermal crystallization process. In addition, the PLA/PBMG/CNC1 blend has higher nucleation density, which indicates that the addition of CNC provides more nucleation sites [44,52].

4. Conclusions

In this paper, PBMG emulsion with uniform particle diameter was successfully synthesized by seed emulsion polymerization. CNC was dispersed in the emulsion by stirring and ultrasound, and PLA/PBMG and PLA/PBMG/CNC blends with different CNC contents were prepared by twin screw extrusion. When the content of CNC was 1%, the mechanical properties of PLA/PBMG/CNC1 blend were best, the impact strength was 300% higher than that of pure PLA, the elongation at break was 60% higher, and the tensile strength was increased by 5%. DSC tests showed that PBMG and PBMG/CNC1 improved the crystallization performance of PLA. The crystallinity of PLA/PBMG and PLA/PBMG/CNC1 blends increased from 3.92% of PLA to 12.65% and 14.05%, respectively. The Avrami equation modified by the Jeziorny and Ozawa equations, and Mo’s method were used to study the non-isothermal crystallization kinetics of PLA and its blends. It was found that, as heterogeneous nucleating agents, PBMG and PBMG/CNC1 provided more nucleation for the PLA matrix. Furthermore, the addition of CNCs acted as heterogeneous nucleating agents and increased the density of nucleating sites. The CNCs seem to weaken the force between the segments in the PLA polymer chains and accelerate the movement of the segments, thus reducing the activation energy of crystallization and accelerating the growth rate of spherulites.

Acknowledgments

We acknowledge the financial support from the National Natural Science Foundation of China (No. U20A20260), Government Guide the Development of Local Science and Technology Special Funds (226Z1203G, 226Z1202G), Natural Science Foundation of Hebei Province (E2016202036).

References

  1. Rasal, R. M.; Janorkar, A.V.; Hirt, D. E. ; Poly(lactic acid) modifications. Prog. Polym. Sci. 2010, 35, 338–356. [Google Scholar] [CrossRef]
  2. Gupta, B.; Revagade, N.; Hilborn, J. ; Poly(lactic acid) fiber: An overview. Prog. Polym. Sci. 2007, 32, 455–482. [Google Scholar] [CrossRef]
  3. Chen, Y.; Han, L.; Chen, H.; Jia, S.; Dong, L. ; Effect of nanoscale dispersed silica on the fabrication of microporous poly(L-lactic acid) by uniaxial stretching. Compos. Part A-Appl. S. 2018, 112, 423–431. [Google Scholar] [CrossRef]
  4. Tan, B. H.; Muiruri, J. K.; Li, Z.; He, C. ; Recent progress in using stereocomplexation for enhancement of thermal and mechanical property of polylactide. ACS Sustain. Chem. Eng. 2016, 4, 5370–5391. [Google Scholar] [CrossRef]
  5. Saeidlou, S.; Huneault, M. A.; Li, H.; Park, C. B. ; Poly(lactic acid) crystallization. Prog. Polym. Sci. 2012, 37, 1657–1677. [Google Scholar] [CrossRef]
  6. Qiu, J.; Liu, F.; Zhang, J.; Na, H.; Zhu, J. ; Non-planar ring contained polyester modifying polylactide to pursue high toughness. Compos. Sci. Technol. 2016, 128, 41–48. [Google Scholar] [CrossRef]
  7. Yang, Y.; Zhang, L.; Xiong, Z.; Tang, Z.; Zhang, R.; Zhu, J. ; Research progress in the heat resistance, toughening and filling modification of PLA. Sci. China Chem. 2016, 59, 1355–1368. [Google Scholar] [CrossRef]
  8. Mazidi, M. M.; Edalat, A.; Berahman, R.; Hosseini, F.S. ; Highly-toughened polylactide-(PLA-) based ternary blends with significantly enhanced glass transition and melt strength: tailoring the interfacial interactions, phase morphology, and performance. Macromolecules 2018, 51, 4298–4314. [Google Scholar] [CrossRef]
  9. Zhao, J.; Pan, H.; Yang, H.; Bian, J.; Zhang, H.; Gao, G.; Dong, L. ; Study on miscibility, thermal properties, degradation behaviors, and toughening mechanism of poly(lactic acid)/poly (ethylene-butylacrylate-glycidyl methacrylate) blends. Int. J. Biol. Macromol. 2020, 143, 443–452. [Google Scholar] [CrossRef] [PubMed]
  10. Yeo, J. C. C.; Muiruri, J. K.; Koh, J. J.; Thitsartarn, W.; Zhang, X.; Kong, J.; Lin, T. T.; Li, Z.; He, C. ; Bend, twist, and turn: first bendable and malleable toughened PLA green composites. Adv. Funct. Mater. 2020, 30, 2001565. [Google Scholar] [CrossRef]
  11. He, H.; Duan, Z.; Wang, Z. ; Anomalously enhanced toughness of poly(lactic acid) nanocomposites by core-shell particles with high thickness soft shell. Compos. Part A-Appl. S. 2020, 128, 105676. [Google Scholar] [CrossRef]
  12. Rasselet, D.; Caro-Bretelle, A.-S.; Taguet, A.; Lopez-Cuesta, J.-M. ; Reactive compatibilization of PLA/PA11 blends and their application in additive manufacturing. Materials 2019, 12, 485. [Google Scholar] [CrossRef]
  13. Lee, J. Y.; Kwon, S. H.; Chin, I.-J.; Choi, H. J. ; Toughness and rheological characteristics of poly(lactic acid)/acrylic core-shell rubber blends. Polym. Bull. 2019, 76, 5483–5497. [Google Scholar] [CrossRef]
  14. Jariyasakoolroj, P.; Rojanaton, N.; Jarupan, L. ; Crystallization behavior of plasticized poly(lactide) film by poly(l-lactic acid)-poly(ethylene glycol)-poly(l-lactic acid) triblock copolymer. Polym. Bull. 2020, 77, 2309–2323. [Google Scholar] [CrossRef]
  15. Ritchie, R. O. ; The Conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef]
  16. Chen, P.-Y.; Lian, H.-Y.; Shih, Y.-F.; Chen-Wei, S.-M.; Jeng, R.-J. ; Preparation, characterization and crystallization kinetics of kenaf fiber/multi-walled carbon nanotube/polylactic acid (PLA) Green Composites. Mater. Chem. Phys. 2017, 196, 249–255. [Google Scholar] [CrossRef]
  17. Jin, X.; Chen, X.; Cheng, Q.; Zhang, N.; Cai, S.; Ren, J. ; Non-isothermal crystallization kinetics of Ramie fiber-reinforced polylactic acid biocomposite. RSC Adv. 2017, 7, 46014–46021. [Google Scholar] [CrossRef]
  18. Klemm, D.; Kramer, F.; Moritz, S.; Lindstrom, T.; Ankerfors, M.; Gray, D.; Dorris, A. ; Nanocelluloses: A new family of nature-based materials. Angew. Chem. Int. Edit. 2011, 50, 5438–5466. [Google Scholar] [CrossRef]
  19. Maiti, S.; Jayaramudu, J.; Das, K.; Reddy, S.M.; Sadiku, R.; Ray, S.S.; Liu, D. ; Preparation and characterization of nano-cellulose with new shape from different precursor. Carbohyd. Polym. 2013, 98, 562–567. [Google Scholar] [CrossRef]
  20. Habibi, Y.; Lucia, L.A.; Rojas, O.J. ; Cellulose nanocrystals: chemistry, self-assembly, and applications. Chem. Rev. 2010, 110, 3479–3500. [Google Scholar] [CrossRef]
  21. Abitbol, T.; Rivkin, A.; Cao, Y.; Nevo, Y.; Abraham, E.; Ben-Shalom, T.; Lapidot, S.; Shoseyov, O. ; Nanocellulose, a tiny fiber with huge applications. Curr. Opin. Biotech. 2016, 39, 76–88. [Google Scholar] [CrossRef]
  22. Gong, J.; Mo, L.; Li, J. ; A comparative study on the preparation and characterization of cellulose nanocrystals with various polymorphs. Carbohyd. Polym. 2018, 195, 18–28. [Google Scholar] [CrossRef]
  23. Samir, M.; Alloin, F.; Dufresne, A. ; Review of recent research into cellulosic whiskers, their properties and their application in nanocomposite field. Biomacromolecules 2005, 6, 612–626. [Google Scholar] [CrossRef]
  24. Fortunati, E.; Armentano, I.; Zhou, Q.; Iannoni, A.; Saino, E.; Visai, L.; Berglund, L.A.; Kenny, J.M. ; Multifunctional bionanocomposite films of poly(lactic acid), cellulose nanocrystals and silver nanoparticles. Carbohyd. Polym. 2012, 87, 1596–1605. [Google Scholar] [CrossRef]
  25. Borkotoky, S.S.; Dhar, P.; Katiyar, V. ; Biodegradable poly(lactic acid)/cellulose nanocrystals (CNCs) composite microcellular foam: effect of nanofillers on foam cellular morphology, thermal and wettability behavior. Int. J. Biol. Macromol. 2018, 106, 433–446. [Google Scholar] [CrossRef]
  26. Dhar, P.; Tarafder, D.; Kumar, A.; Katiyar, V. ; Effect of cellulose nanocrystal polymorphs on mechanical, barrier and thermal properties of poly(lactic acid) based bionanocomposites. RSC Adv. 2015, 5, 60426–60440. [Google Scholar] [CrossRef]
  27. Ruiz, M. M.; Cavaille, J. Y.; Dufresne, A.; Gerard, J. F.; Graillat, C. ; Processing and characterization of new thermoset nanocomposites based on cellulose whiskers. Compos. Interface. 2000, 7, 117–131. [Google Scholar] [CrossRef]
  28. Cao, L.; Liu, C.; Zou, D.; Zhang, S.; Chen, Y. ; Using cellulose nanocrystals as sustainable additive to enhance mechanical and shape memory properties of PLA/ENR thermoplastic vulcanizates. Carbohyd. Polym. 2020, 230, 115618. [Google Scholar] [CrossRef]
  29. Borkotoky, S. S.; Chakraborty, G.; Katiyar, V. ; Thermal degradation behaviour and crystallization kinetics of poly(lactic acid) and cellulose nanocrystals (CNC) based microcellular composite foams. Int. J. Biol. Macromol. 2018, 118, 1518–1531. [Google Scholar] [CrossRef]
  30. Lebarbe, T.; Grau, E.; Alfos, C.; Cramail, H. ; Fatty acid-based thermoplastic poly(ester-amide) as toughening and crystallization improver of poly(L-lactide). Eur. Polym. J. 2015, 65, 276–285. [Google Scholar] [CrossRef]
  31. Feng, F.; Ye, L. ; Morphologies and mechanical properties of polylactide/thermoplastic polyurethane elastomer blends. J. Appl. Polym. Sci. 2011, 119, 2778–2783. [Google Scholar] [CrossRef]
  32. Han, J.-J.; Huang, H.-X. ; Preparation and characterization of biodegradable polylactide/thermoplastic polyurethane elastomer blends. J. Appl. Polym. Sci. 2011, 120, 3217–3223. [Google Scholar] [CrossRef]
  33. Kulinski, Z.; Piorkowska, E. ; Crystallization, structure and properties of plasticized poly(L-lactide). Polymer 2005, 46, 10290–10300. [Google Scholar] [CrossRef]
  34. Liu, G.; Zhang, X.; Wang, D. ; Tailoring crystallization: towards high-performance poly(lactic acid). Adv. Mater. 2014, 26, 6905–6911. [Google Scholar] [CrossRef] [PubMed]
  35. Gao, W. S.; Li, C.; Li, J. W.; Zhang, Q. X.; Wang, N. Y.; Abdel-Magid, B.; Qu, X. W. ; Effect of the crosslinking agent content on the emulsion polymerization process and adhesive properties of poly(n-butyl acrylate-co-methacrylic acid), J. Adhes. Sci. Technol., 2019, 33, 2031–2046. [Google Scholar] [CrossRef]
  36. Xu, C.; Qu, T. G.; Zhang, X. J.; Qu, X. W.; Wang, N. Y.; Zhang, Q. X.; Abdel-Magid, B.; Li, G. H. ; Enhanced toughness and thermal conductivity for epoxy resin with a core–shell structured polyacrylic modifier and modified boron nitride. RSC Adv. 2019, 9, 8654–8663. [Google Scholar] [CrossRef]
  37. Fu, N.; Li, G.; Yao, Y.; Wang, N.; Grami, M. E.; Zhang Q., X.; Qu, X. W. ; Super-tough poly(butylene terephthalate) materials: blending with CSSP nanoparticles, Soft Mater. 2015, 13, 86-92. /: https. [CrossRef]
  38. Qu, X.; Wang, N.; Lovell, P. A. ; Preparation and characterization of the latexes with different particle sizes by semibatch emulsion polymerization and the influence on properties of waterborne pressure-sensitive adhesives. J. Appl. Polym. Sci. 2009, 112, 3030–3040. [Google Scholar] [CrossRef]
  39. Pei, A.; Zhou, Q.; Berglund, L.A. ; Functionalized cellulose nanocrystals as biobased nucleation agents in poly(L-lactide) (PLLA)-crystallization and mechanical property effects. Compos. Sci. Technol. 2010, 70, 815–821. [Google Scholar] [CrossRef]
  40. Clarkson, C. M.; Azrak, S. M. E. A.; Chowdhury, R.; Shuvo, S. N.; Snyder, J.; Schueneman, G.; Ortalan, V.; Youngblood, J. P. ; Melt spinning of cellulose nanofibril/polylactic acid (CNF/PLA) composite fibers for high stiffness. ACS Appl. Polym. Mater. 2019, 1, 160–168. [Google Scholar] [CrossRef]
  41. Vatansever, E.; Arslan, D.; Sarul, D.S.; Kahraman, Y.; Gunes, G.; Durmus, A.; Nofar, M. ; Development of CNC-reinforced PBAT nanocomposites with reduced percolation threshold: a comparative sudy on the preparation method. J. Mater. Sci. 2020, 55, 15523–15537. [Google Scholar] [CrossRef]
  42. Arslan, D.; Vatansever, E.; Sarul, D. S.; Kahraman, Y.; Gunes, G.; Durmus, A.; Nofar, M. ; Effect of preparation method on the properties of polylactide/cellulose nanocrystal nanocomposites. Polym. Compos. 2020, 41, 4170–4180. [Google Scholar] [CrossRef]
  43. Yu, H.-y.; Qin, Z.-y.; Zhou, Z. ; Cellulose nanocrystals as green fllers to improve crystallization and hydrophilic property of poly(3-hydroxybutyrate-co-3-hydroxyvalerate). Prog. Nat. Sci-Mater. 2011, 21, 478–484. [Google Scholar] [CrossRef]
  44. Dhar, P.; Bhasney, S.M.; Kumar, A.; Katiyar, V. ; Acid functionalized cellulose nanocrystals and its effect on mechanical, thermal, crystallization and surfaces properties of poly(lactic acid) bionanocomposites films: a comprehensive study. Polymer 2016, 101, 75–92. [Google Scholar] [CrossRef]
  45. Suksut, B.; Deeprasertkul, C. ; Effect of nucleating agents on physical properties of poly(lactic acid) and its blend with natural rubber. J. Polym. Environ. 2011, 19, 288–296. [Google Scholar] [CrossRef]
  46. Avrami, M. Kinetics of phase change. I General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
  47. Kuo, M.C.; Huang, J.C.; Chen, M. ; Non-isothermal crystallization kinetic behavior of alumina nanoparticle filled poly(ether ether ketone). Mater. Chem. Phys. 2006, 99, 258–268. [Google Scholar] [CrossRef]
  48. Jeziorny, A. ; Parameters characterizing the kinetics of the non-isothermal crystallization of poly (ethylene terephthalate) determined by DSC. Polymer 1978, 19, 1142–1144. [Google Scholar] [CrossRef]
  49. Jain, S.; Goossens, H.; van Duin, M.; Lemstra, P. ; Effect of in situ prepared silica nano-particles on non-isothermal crystallization of polypropylene. Polymer 2005, 46, 8805–8818. [Google Scholar] [CrossRef]
  50. Battegazzore, D.; Bocchini, S.; Frache, A. ; Crystallization kinetics of poly(lactic acid)-talc composites. Express Polym. Lett. 2011, 5, 849–858. [Google Scholar] [CrossRef]
  51. Ozawa, T. ; Kinetics of non-isothermal crystallization. Polymer 1971, 12, 150–158. [Google Scholar] [CrossRef]
  52. Xu, W. B.; Ge, M. L.; He, P. S. ; Nonisothermal crystallization kinetics of polypropylene/montmorillonite nanocomposites. J. Polym. Sci. Part B-Polym. Phys. 2002, 40, 408–414. [Google Scholar] [CrossRef]
  53. Qiao, Y.; Jalali, A.; Yang, J.; Chen, Y.; Wang, S.; Jiang, Y.; Hou, J.; Jiang, J.; Li, Q.; Park, C.B. ; Non-isothermal crystallization kinetics of polypropylene/polytetrafluoroethylene fibrillated composites. J. Mater. Sci. 2021, 56, 3562–3575. [Google Scholar] [CrossRef]
  54. Xu, X.; Zhen, W. ; Preparation, performance and non-isothermal crystallization kinetics of poly(lactic acid)/amidated humic acid composites. Polym. Bull. 2018, 75, 3753–3780. [Google Scholar] [CrossRef]
  55. Liu, T.; Mo, Z.; Wang. S.; Nonisothermal melt and cold crystallization kinetics of poly(aryl ether ether ketone ketone). Polym. Eng. Sci. 1997, 37, 568–575. [Google Scholar] [CrossRef]
  56. Layachi, A.; Frihi, D.; Satha, H.; Seguela, R.; Gherib, S. ; Non-isothermal crystallization kinetics of polyamide 66/glass fibers/carbon black composites. J. Therm. Anal. Calorim. 2016, 124, 1319–1329. [Google Scholar] [CrossRef]
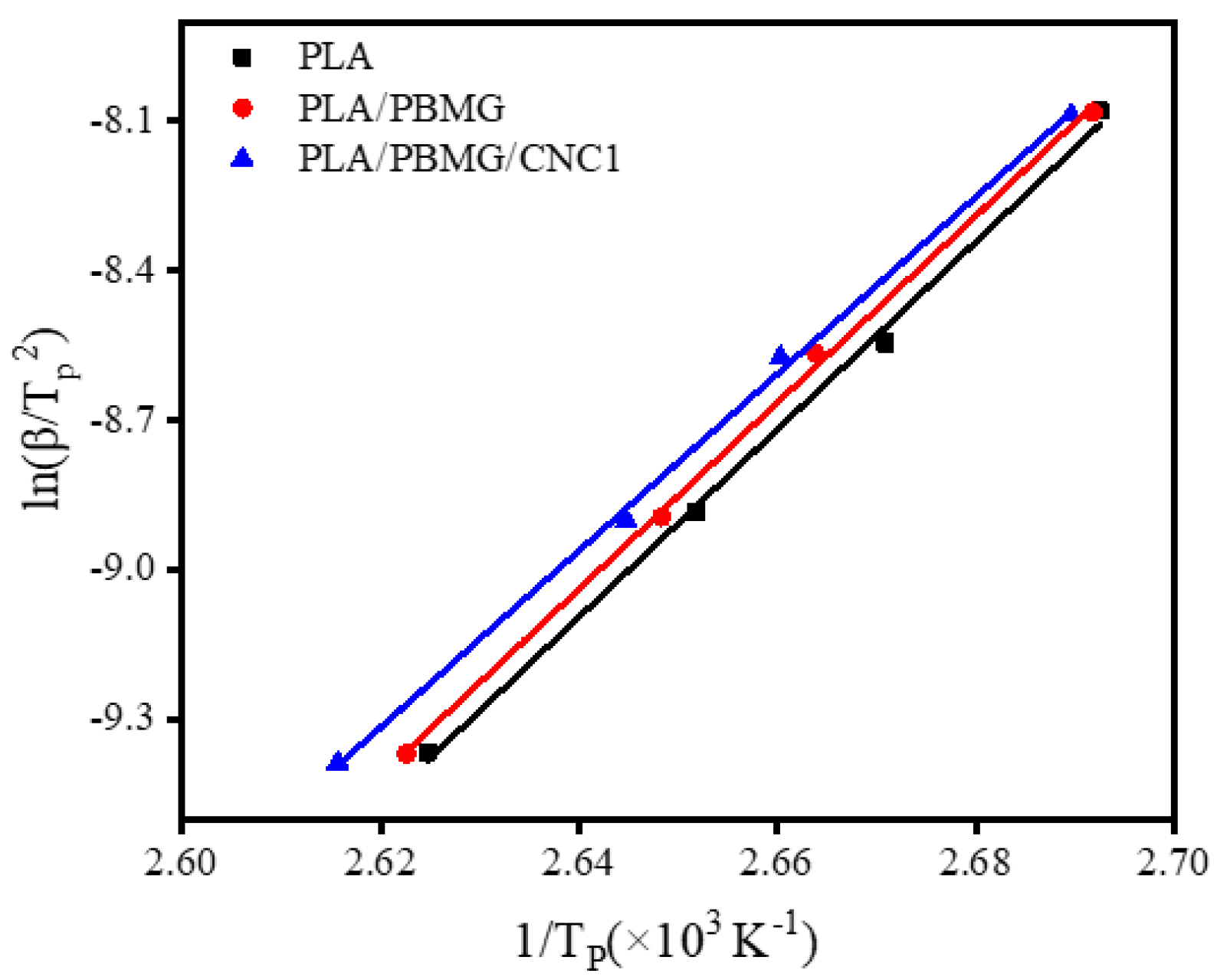
  57. Kissinger, H. E. ; Variation of peak temperature with heating rate in differential thermal analysis. J. Res. Natl. Bur. Stand. 1956, 57, 217–221. [Google Scholar] [CrossRef]
Preprints 82114 g001
Figure 1. Variation with reaction time: (a) overall and instantaneous conversion; (b) measured and theoretical particle diameter.
Figure 1. Variation with reaction time: (a) overall and instantaneous conversion; (b) measured and theoretical particle diameter.
Preprints 82114 g001
Preprints 82114 g002
Figure 2. SEM images of PBMG (a) and PBMG/CNC1 (b).
Figure 2. SEM images of PBMG (a) and PBMG/CNC1 (b).
Preprints 82114 g002
Preprints 82114 g003
Figure 3. Mechanical properties of PLA blends, a: stress-strain graphs, b: notched impact strength of cantilever beam.
Figure 3. Mechanical properties of PLA blends, a: stress-strain graphs, b: notched impact strength of cantilever beam.
Preprints 82114 g003
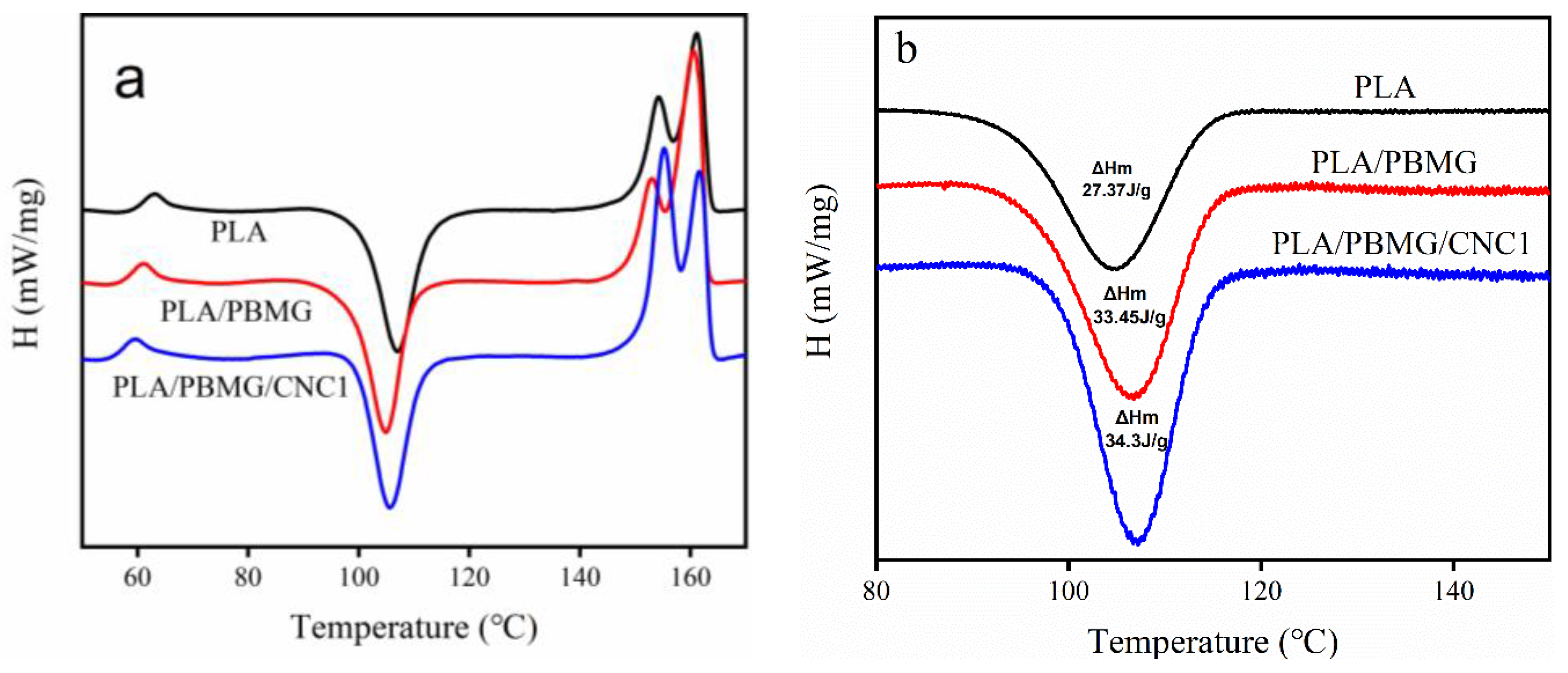
Preprints 82114 g004
Figure 4. (a) Secondary heating curves, (b) Cooling crystallization curves at 1.5oC/min of PLA, PLA/PBMG, and PLA/PBMG/CNC1 blends.
Figure 4. (a) Secondary heating curves, (b) Cooling crystallization curves at 1.5oC/min of PLA, PLA/PBMG, and PLA/PBMG/CNC1 blends.
Preprints 82114 g004
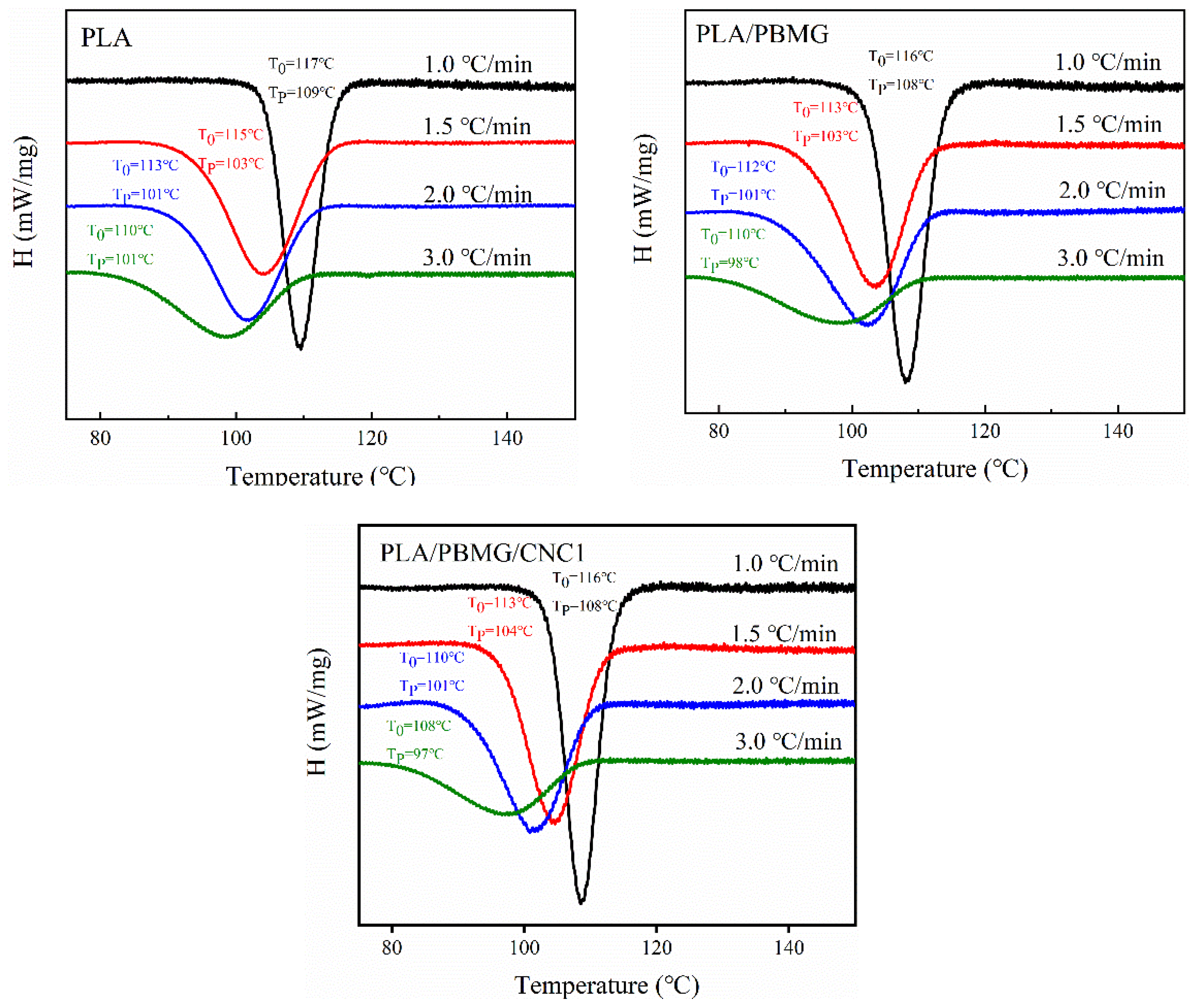
Preprints 82114 g005
Figure 5. Nonisothermal crystallization curves of PLA, PLA/PBMG, and PLA/PBMG/CNC1 blends.
Figure 5. Nonisothermal crystallization curves of PLA, PLA/PBMG, and PLA/PBMG/CNC1 blends.
Preprints 82114 g005
Preprints 82114 g006
Figure 6. X(t)-t curves of PLA, PLA/PBMG, and PLA/PBMG/CNC1 blends.
Figure 6. X(t)-t curves of PLA, PLA/PBMG, and PLA/PBMG/CNC1 blends.
Preprints 82114 g006
Preprints 82114 g007
Figure 7. lg(-ln(1-X(t))-lg t graphs of PLA, PLA/BMG and PLA/PBMG/CNC1 blends modified by Jeziorny equation.
Figure 7. lg(-ln(1-X(t))-lg t graphs of PLA, PLA/BMG and PLA/PBMG/CNC1 blends modified by Jeziorny equation.
Preprints 82114 g007
Preprints 82114 g008
Figure 8. lg(-ln(1-X(t))-lgβ curves of PLA, PLA/PBMG and PLA/PBMG/CNC1 blends by Ozawa equation.
Figure 8. lg(-ln(1-X(t))-lgβ curves of PLA, PLA/PBMG and PLA/PBMG/CNC1 blends by Ozawa equation.
Preprints 82114 g008
Preprints 82114 g009
Figure 9. lgβ-lgt curves of PLA, PLA/PBMG and PLA/PBMG/CNC1 blends at different crystallinities using Mo’s method.
Figure 9. lgβ-lgt curves of PLA, PLA/PBMG and PLA/PBMG/CNC1 blends at different crystallinities using Mo’s method.
Preprints 82114 g009
Preprints 82114 g010
Figure 10. ln(β/Tp2)-1/TP curves of PLA, and PLA/PBMG, PLA/PBMG/CNC1 blends.
Figure 10. ln(β/Tp2)-1/TP curves of PLA, and PLA/PBMG, PLA/PBMG/CNC1 blends.
Preprints 82114 g010
Preprints 82114 g011
Figure 11. Polarizing microscopic images of isothermal crystallization with different times for PLA (a-c), PLA/PBMG (d-f) and PLA/PBMG/CNC1 (g-i) blends at 115 ℃.
Figure 11. Polarizing microscopic images of isothermal crystallization with different times for PLA (a-c), PLA/PBMG (d-f) and PLA/PBMG/CNC1 (g-i) blends at 115 ℃.
Preprints 82114 g011
Table 1. Summary of crystallization parameters of PLA blends.
Table 1. Summary of crystallization parameters of PLA blends.
Tg(oC) Tcc(oC) Tm (oC) ΔHc ((J/g) ΔHm (J/g) Xc (%)
PLA 63.62 107.43 161.43 23.7 27.37 4.35
PLA/PBMG 60.75 104.70 160.30 22.78 33.45 12.65
PLB/PBMG/CNC1 59.52 105.63 155.15 22.45 34.30 14.05
Table 2. t1/2 values of PLA, PLA/PBMG and PLA/PBMG/CNC1 blends.
Table 2. t1/2 values of PLA, PLA/PBMG and PLA/PBMG/CNC1 blends.
t1/2(min)
PLA PLA/PBMG PLA/PBMG/CNC1
1.0oC/min 9.16 8.86 9.10
1.5oC/min 8.14 7.48 7.50
2.0oC/min 6.80 6.18 6.14
3.0oC/min 5.18 4.84 4.59
Table 3. Nonisothermal crystallization kinetics parameters of PLA, PLA/PBMG, and PLA/PBMG/CNC1 blends.
Table 3. Nonisothermal crystallization kinetics parameters of PLA, PLA/PBMG, and PLA/PBMG/CNC1 blends.
β (oC/min) n K Kc t1/2
PLA 1.0 3.20 0.0003 0.0003 11.25
1.5 3.20 0.0006 0.0071 9.06
2.0 3.39 0.0010 0.0317 6.88
3.0 3.20 0.0034 0.1503 5.27
PLA/PBMG 1.0 3.15 0.0006 0.0006 9.38
1.5 3.10 0.0008 0.0086 8.86
2.0 2.93 0.0030 0.0547 6.41
3.0 2.36 0.0195 0.2693 4.54
PLA/PBMG/CNC1 1.0 3.27 0.0004 0.0004 9.78
1.5 3.32 0.0008 0.0086 7.67
2.0 3.40 0.0013 0.0362 6.33
3.0 2.78 0.0107 0.2205 4.48
Table 4. Mo’s parameters for non-isothermal crystallization kinetics of PLA, PLA/PBMG, and PLA/PBMG/CNC1 blends.
Table 4. Mo’s parameters for non-isothermal crystallization kinetics of PLA, PLA/PBMG, and PLA/PBMG/CNC1 blends.
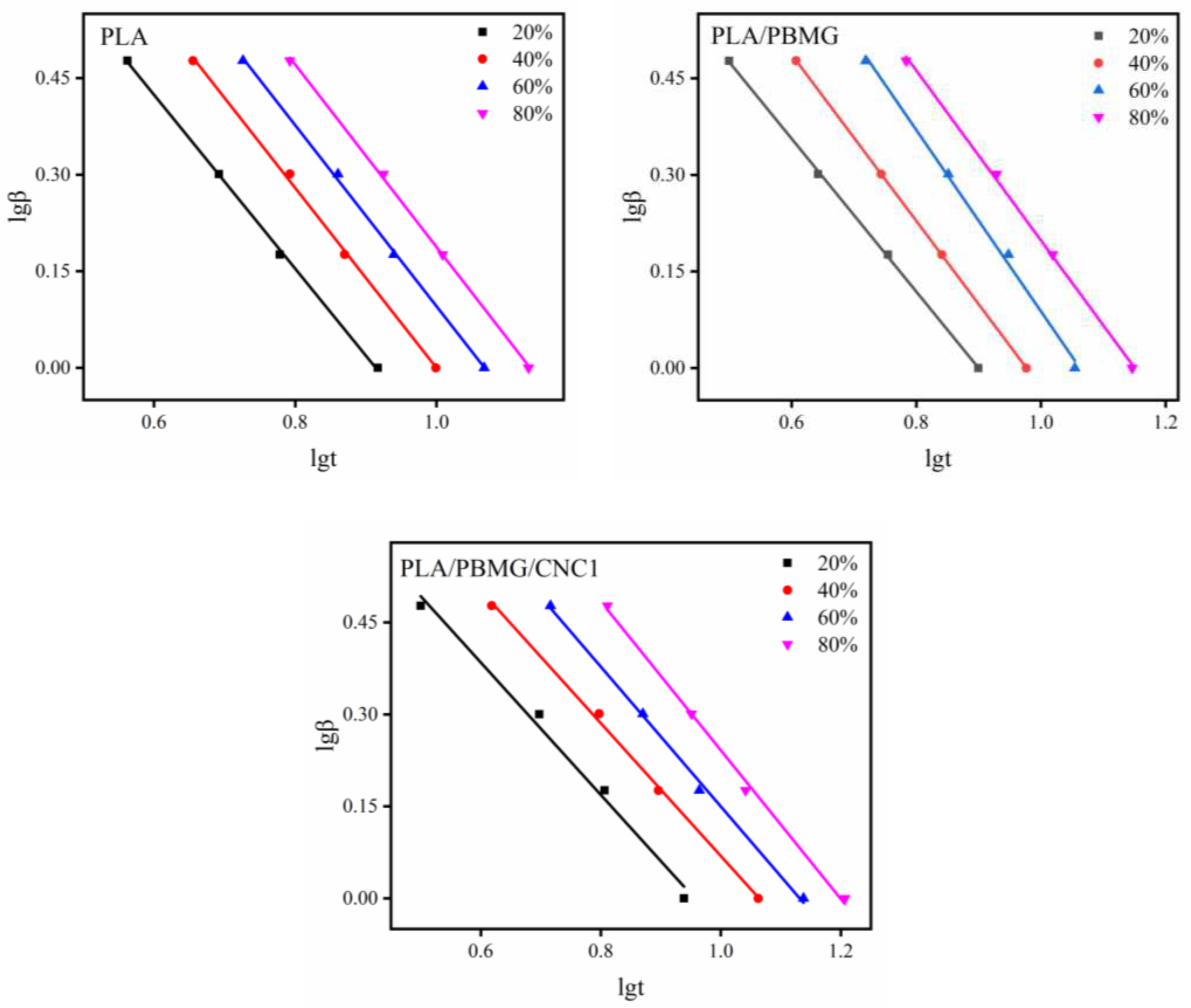
X(t) (%) α log Z Z ΔE (KJ/mol)
PLA 20 1.18 1.1351 13.65 -156.64
40 1.14 1.2190 16.56
60 1.12 1.2800 19.05
80 1.05 1.3030 20.09
PLA/PBMG 20 0.96 0.9387 8.68 -155.80
40 1.08 1.1515 14.17
60 1.16 1.2129 16.33
80 1.17 1.2849 19.27
PLA/PBMG/CNC1 20 1.12 1.0791 11.75 -147.57
40 1.11 1.1741 14.79
60 1.34 1.2166 16.47
80 1.54 1.2891 19.46
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated