Prerpints.org logo
Preprint
Article

H(N3)dap (Hdap = 2,6-diaminopurine) Recognition by Cu2(EGTA): Structure, Physical Properties and DFT-Calculations of [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2]·7H2O

Altmetrics

Downloads

88

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (16.09MB )

Submitted:

11 August 2023

Posted:

14 August 2023

You are already at the latest version

Alerts
Abstract
Reactions in water between the Cu2(µ-EGTA) chelate (EGTA = ethylene-bis(oxyethyleneimino)tetraacetate(4-) ion) and 2,6-diaminopurine (Hdap) in molar ratios 1:1 and 1:2 yield only blue crystals of the ternary compound [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2]·7H2O (1) that has been studied by single crystal X-ray diffractometry, various physical methods (thermal stability, spectral and magnetic properties), as well as DFT theoretical calculations. In the crystal, uncoordinated water is disordered. The tetranuclear complex molecule also has some irrelevant disorder in an EGTA-ethylene moiety. In the complex molecule, both bridging organic molecules act as binucleating ligands. There are two distorted five- (type 4+1) and two six- (type 4+1+1) Cu(II) centres. Each half EGTA acts as a tripodal tetradentate Cu(II) chelator, with mer-NO2+O(ether, distal) conformation. Hdap exhibits the tautomer H(N3)dap, with the dissociable H-atom on its less basic N-heterocyclic atom. These features favour the efficient cooperation between Cu-N7 or Cu-N9 bonds with appropriate O-EGTA atoms, as N6-H···O or N3-H···O interligand interactions respectively. Bridging role of both organics determines the tetranuclear dimensionality of the complex in 1. In this crystal, such molecules associate in zig-zag chains, built by alternating ,-interactions between the five- or six-atom rings of Hdap ligands of adjacent molecules. DFT theoretical calculations (using two different theoretical models and characterized by the quantum theory of “atoms in molecules”) reveal the importance of these ,-interactions between Hdap ligands, as well as that corresponding to the referred hydrogen bonds in the contributed tetranuclear molecule.
Keywords: 
Subject: Chemistry and Materials Science  -   Inorganic and Nuclear Chemistry

1. Introduction

In a recent contribution from our group, the universal criteria on which the concept of molecular recognition is based are highlighted as something universal and always reciprocal. Obviously, this does not exclude biological systems. Based on this work, the purpose of this contribution is to design a system using a copper(II) chelate where the chelator increases the dinucleating potential of EDTA (ethylenediaminetetraacetic acid) and make it react with an aminopurine that is currently arousing much interest. For these purposes, Figure 1 shows the schematics of the ligands EDTA, EGTA (ethylene-bis(oxyethyleneimino)tetraacetate(4-) ion), and Hdap (2,6-diaminopurine). The consideration of EGTA as a chelator resides in the fact that each half can act with a tetradentate character, using an N-substituted iminodiacetic group that includes an oxygen ether as an additional donor. On the other hand, 2,6-diaminopurine is currently considered a biological precursor of the other purines of nucleosides, nucleotides, and nucleic acids [3,4,5,6,7,8,9]. It is interesting to highlight the recognition of Hdap as a promoter of DNA lesion repair under prebiotic conditions [4,5,6]. They also highlight the capacity of Hdap nucleosides as broad-spectrum antiviral and antibacterial agents [7], also, efforts have been made for the preparation of this type of nucleosides [8]. Moreover, there are results available on synthetic nucleotides with Hdap as prodrugs [9,10,11]. On the other hand, a review of the acid H4EGTA and its complexes with metal ions in the Cambridge Structural Database (CSD) reveals that the crystalline structure of the acid itself is available [12] and around 50 crystalline structures containing the tetravalent anion EGTA4- or its partially protonated form H4EGTA3- as a ligand are available as well [13,14,15,16,17,18,19,20,21,22]. A detailed examination of these structures leads to three general types of compounds: (1) Complexes where EGTA essentially acts as a chelator of a metal center, without excluding dinuclearization or polymerization situations in particular cases. This group of compounds, where the coordination index is high (from 8 to 10), include complexes of yttrium(III) and most of trivalent lanthanides, Ln = La-Lu, excepting praseodymium, promethium (all its isotopes being radioactive, with short half-lives) or lutetium (see a nice example for Gd [13]) as well as calcium [14], strontium, barium, cadmium, hafnium and zirconium. (2) Complexes where EGTA acts as a dinucleating bridge for two copper(II) [16,17,18,19] or two nickel(II) centers. (3) Another type of heterometallic combinations that include sophisticated clusters [20,21,22].
Diaminopurine (Hdap) has been investigated with about 40 structures including its protonated form, its molecular form or its anionic form [23,24,25,26]. Both the molecular and the anionic form generate a diversity of structures affected by two circumstances that are also typical of other purines. Without going into detail, on the one hand it consists of the well-known basicity of adenine nitrogens (6-aminopurine) according to the sequence N9 > N1 > N7 > N3 >> -N(6)H2, and on the other hand, the possibility of tautomerism that motivates the migration of the proton normally attached to N9 to other N-heterocyclic donors. In addition, the steric factor associated with the hexocyclic amino groups cannot be ignored, which for Hdap represents serious difficulties in its coordination by N1.
With these considerations in mind, the purpose of this work was to obtain a compound where EGTA acts as a Cu(II) dinucleating bridge, capable of admitting in Cu2(μ-EGTA) a pair of Hdap ligands at its ends.

2. Results and Discussion

2.1. The synthesis of the Binary Precursor and the Novel Compound 1

The synthesis of the novel compound was carried out according to the usual strategy followed by our research group. The chelating compound is always available in its acid form, which applies to various first-row transition metals (Mn-Zn) or post-transition metals (Cd, Pb), with more or less success. For Cu(II) azurite type (bluish) or malachite type (greenish) could be used, upon the assumption that the Cu2CO3(OH)2 (mw 221.1) formula is reasonable in practice for the calculation of the quantity of the copper(II) sources. This strategy is founded in the idea that the reaction of the copper hydroxy-carbonate with the acid form of the chelator (amino-polycarboxylic acids, amino acids, small peptides, etc.) will yield CO2 as an easily removable by-product (stirring and heating the reaction mixture, as well as applying controlled vacuum environment, usually working in aqueous medium). Two relevant comments need to be added regarding this work (and closely related ones): (1) The use of bluish copper hydroxy-carbonate can yield to unreacted dark CuO, whereas malachite only leaves unreacted apple green residue. (2) It is convenient to remove the small amount of unreacted material by careful filtration prior to adding other(s) coligands(s) to the binary complex solution This general strategy has the advantage of avoiding undesired by-products (i.e., alkaline salts). At the same time, it seems to favor good crystallizations. Moreover, when the amounts of reagents used do not match the stoichiometry of the final product according to molecular recognition criteria, it´s because the mother liquors can retain the excess of a free-ligand.
Our experiment, reported in the experimental section of this work, illustrates a case-study where the use of a significant excess of Hdap prevents the initial crystallization of the novel compound 1, though with a less practical yield.

2.2. Molecular and Supramolecular Structures in the Crystal

The structure established in the crystallographic study, with a single crystal, runs into the difficulty that the uncoordinated water molecules are highly disordered, which is why they are not taken into account in determining the molecular structure of the compound. Furthermore, the Figure 2a reveals that one of the EGTA chelating ligands shows some disorder in an ethylene unit. This circumstance is of minor importance in relation to the molecular recognition between the Cu2(EGTA) chelate and the Hdap nucleobase, although it must somehow influence the fact that the four metal centers of the tetranuclear molecule are non-equivalent (Figure 2b). The data in Table 1 indicate that the crystallographic quality is quite good.
Table 2 provides the data of bond distances and relevant trans angles in the coordination environments. Briefly, each µ-EGTA bridging chelator generates an elongated octahedral environment (4+2 type) and a penta-coordinate environment (4+1 type). Thus, there is an EGTA-1 with the Cu1 (4+1) and Cu4 (4+2) centers; and on the other hand, EGTA-2 has the Cu2 (4+1) and Cu3 (4+2) centers. Both the 4+1 and 4+2 environments contain the H(N3)dap N7 or N9 donors (with conventional notation for purines). The tetranuclear nature of the compound 1 is essentially due to the bridging mode of the H(N3)dap ligands. This means that compound 1 is formed from the bridging mode of molecular recognition of the Hdap ligands, instead of having obtained a different compound where the Cu2(µ-EGTA) chelate coordinated an Hdap ligand to each metal center. The formation of the tetranuclear molecule is made possible by the tautomerization of the 2,6-diaminourine proton from its more basic donor (N9) to its less basic heterocyclic donor (N3). Therefore, tautomerization efficiently contributes to the molecular recognition mode in the investigated compound.
Table 3 shows the data of the distances and angles in the hydrogen bonds that were determined in this crystallographic study. Evidently, it includes N3-H···O and N6-H···O-type interactions between the Hdap ligands and coordinated oxygen atoms of EGTA.
The crystallographic study further reveals a supramolecular recognition that is illustrated in the most simplified way in Figure 3, despite the uncoordinated water delocalization and the disorder in an EGTA chelator. For this reason, locating the uncoordinated water was sacrificed in order to achieve a high structural resolution (SQUEEZE). Figure 3 shows the involvement of the H(N3)dap ligands in stacking interactions that affect their 5- and 6-atom aromatic rings, but in such a way that two 5-atom rings of the Hdap ligand interact with each other at one end, and in the other something similar happens with the 6-atom rings. The aforementioned stacking interactions are shown in the figure by dashed lines that join the centroids of the rings involved.
The coordination of the H(N3)dap tautomer has been provided by five compounds prior to the present study. The available data are collected in the Table 4 emphasizing two aspects: the molecular or polymeric nature of the compound and, where available, the formation of hydrogen bonds N3-H···O and N6-H··· O by cooperating with M-N9 or M-N7 coordinate bonds (M is transition metal). The very limited data available suggest the existence of known analogous compounds with copper, zinc or cobalt. Of a molecular nature, they are only available from data on the MULCED compound [23], while the other compounds are polymers (1D or 2D) or metal organic frameworks (MOF) (3D). Available data indicates that the style of molecular recognition of compound 1 and its analogues is feasible regardless of the molecular or polymeric nature of the known compounds.

2.3. Physical properties

The physical properties studies are the thermal, spectral and magnetic stability which are described in detail below.
For comparison purposes, Figure S1 (Supplementary file) shows the FT-IR spectra of the binary compound [Cu2(µ-EGTA)(H2O)2]·2H2O (without Hdap) and of compound 1, [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O.
It can be observed that above 3000 cm-1 the spectrum of compound 1 permits us to determine different absorptions due to antisymmetric and symmetric water stretching modes and the primary amino group, in addition to two bands at 3194 and 3139 cm-1 due to N-H group stretching modes. Within this region of the spectrum we can determine the presence of water in the compound, as well as the presence of two non-equivalent N-H groups that correspond to the N3-H group of the two slightly different tautomers of H(N3)dap present in the crystal. On the other hand, a broad band is observed between 1650 and 1620 cm-1 due to the scissor’s deformation of the water molecules and the hexocyclic amino groups of Hdap. This band also includes the antisymmetric stretching of the EGTA carboxylate groups.
Of particular diagnostic value is a weak band at 1534 cm-1 that indicates the deformation in the plane of the N3-H group, δ (N-H). This band appears in a region where few other absorptions take place. At 1372 cm-1 the symmetric stretching of the carboxylate groups is observed. Two other interesting bands are observed at 1114 and 850 cm-1 corresponding to the antisymmetric and symmetric stretchings of the C-O-C group. These bands are normally observed at 1300-1000 and 890-820 cm-1; while in the binary compound, they’re observed at 1088 and 856 cm-1. The aromatic CHs of Hdap gives a deformation band out-of-plane π-CH at 850 cm-1. This band is always very defined and appears between 900-860 cm-1, which is a normal range, especially in hydrocarbons.
Figure 4 shows the TGA (in air) and DSC (in N2 atmosphere) curves. As is often the case, the seven (uncoordinated) water molecules and the two distal aqua ligands are lost in an overlapping process that corresponds to steps 1 and 2 indicated in Table 5.
These processes occur within three thermal decomposition stages that produce carbon dioxide, carbon monoxide, water and the three oxides of nitrogen normally observed (N2O, NO, NO2) with traces of methane at 520 degrees, an oxide of copper is obtained with an experimental value higher than what was calculated, with the difference of these values being lesser than 1%. The decomposition of N2O in the atmosphere clearly shows the dynamics of heat absorption that essentially corresponds to the coordinated or uncoordinated loss of water between 30 degrees and 180 degrees, reflecting that the overlapping loss of the uncoordinated and the coordinated is a global and complex process. Above 180 degrees, a reasonable compensation of the absorption and heat loss processes occurs, as corresponds to the thermal decomposition of the organic ligands. It is important to note that complete loss of water initiates thermal decomposition above approximately 200 degrees in order to generate copper oxide at 520 degrees.
The electronic spectrum, obtained by diffuse reflectance, shows an asymmetric d-d band with maximum absorption at 685 nm (see Figure 5). The barycenter of intensity of this band is located at 735 nm, a value that is below the maximum absorption of the corresponding electronic spectrum of hexaaqua-cation (~800 nm) [29]. In short, this comparison reflects that the metal environment in compound 1 has a stronger ligand field than the aqua-cation.
For the measurements of the electronic spin resonance (ESR), X and Q band ESR measurements were carried out in the 5-300 K range. The X-band ESR spectra exhibit near axial symmetries, but a considerable rhombicity can be detected operating at Q-band (Figure 6 and Figure 7). With a computer program working at the second order of the perturbation theory, the spectra could be fitted with a unique g tensor. Therefore, the exchange interaction between copper ions is large enough to collapse the spectra of the magnetically non-equivalent sites [30]. It is noteworthy to mention that the intensity of the ESR signal drastically decreases below 20 K, suggesting that the exchange interactions are mainly antiferromagnetic. The main components of the calculated g tensor are: g1 = 2.235, g2 = 2.071 and g3 = 2.052 (gII = 2.235; g⊥ = 2.061). The G parameter, defined as G = (gII-2)/(g⊥-2), is 3.8, less than 4, confirming the existence of exchange interactions and a small misalignment between the main axes of the individual g tensors in compound 1 [31]. In any case, the lowest g value indicates a dx2-y2 ground electronic for all the Cu(II) centers, as correspond to axially elongated 4+1 and 4+2 environments.
The thermal evolution of the magnetic molar susceptibility is shown in Figure 8. As the temperature is lowered, the susceptibility increases until a maximum of 0.0369 cm3/mol is reached at 23 K, which then rapidly decreases (0.003 cm3/mol at 5 K). The χmT product lies practically constant (1.56 cm3K/mol) between 300 and 100 K and decreases swiftly when cooling down to 5 K (0.016 cm3K/mol). The high temperature data (T>50K) is well described by a Curie-Weiss law (χm = Cm/T-θ), with Cm = 1.62 cm3K/mol and θ = -9.7 K (Figure 8, right). The observed Curie constant (Cm) agrees well with the calculations for four non-interacting S = 1/2 ions, with the g value deduced from de ESR study (g = 2.12). The negative θ value and the overall appearance of the χmT vs. T curve indicate the predominance of short-range antiferromagnetic interactions between the Cu(II) ions leading to a S = 0 spin ground state.
Considering the tetranuclear nature of compound 1, different magnetic exchange pathways through the H(N3)dap and EGTA organic ligands must be taken into account: Cu1···Cu2 (5.783 Å), Cu3···Cu4 (5.676 Å), Cu1···Cu4 (7.453 Å) and Cu2···Cu3 (7.233 Å). Therefore, the following spin Hamiltonian should be used to analyze the magnetic properties, including only isotropic interactions and the Zeeman term:
H ^ = − J 12 ( S 1 . S 2 ) − J 34 ( S 3 . S 4 ) − J 14 ( S 1 . S 4 ) − J 23 ( S 2 . S 3 ) + μ β ∑ i = 1 4 B . g i . S i (1)
However, due to the large number of adjustable parameters, fitting the magnetic curves using the above expression does not provide reliable values for the exchange coupling constants. Therefore, it is necessary to put some constraints to the Jij and g parameters. In this sense, it has been considered that despite the small differences in the super-exchange pathway, the two interactions propagated by the EGTA ligand are similar (J12 = J34 = JA), and the same is applicable for the two interactions propagated by the H(N3)dap ligand (J14 = J23 = JB In addition, taking into account the ESR results, it was assumed that all the local g-values are equal. Under these conditions, the fit of the experimental susceptibility data using the full-matrix diagonalization PHI program [32] provided the following set of parameters: JA = -12.4 cm-1, JB = -0.33 cm-1 and g = 2.102 with R = 1.3x10-4. The calculated curve matches very well with the experimental data in the complete temperature range studied (Figure 8, left). The smaller coupling constant can be unambiguously attributed to the interactions propagated through the EGTA ligand, since the magnetic orbitals (mainly dx2-y2) lie in planes parallel to each other and perpendicular to the exchange pathway. The overlap between the orbitals bearing the unpaired electrons is significantly better through the H(N3)dap ligands in this compound, hence the stronger antiferromagnetic couplings.

2.4. DFT calculations

In the solid state, compound 1 forms infinite 1D assemblies that propagate via two different π-stacking interactions (see Figure 9a). One is established between the 2,6-diaminopurine bases that are coordinated to the pseudo-octahedral Cu-atoms (denoted as A···A in Figure 9a) and the other binding mode involves the 2,6-diaminopurine rings that are coordinated to the square-pyramidal Cu-atoms (denoted as B···B). The theoretical study is devoted to the energetic analysis of both π-stacking modes and the characterization of some additional H-bonds that are formed in the A···A binding mode. In order to keep the model computationally approachable and to simplify the description and DFT analysis of both interaction modes, the tetranuclear complex has been divided in two halves by cutting the μ-EGTA chelate as indicated in Figure 9b, resulting in two dinuclear complexes denoted as “A” and “B”, see Figure 9b.
First, the MEP surfaces of fragments A and B have been computed to explore the most electron rich and poor parts of the molecules, which are represented in Figure 10. As expected, the minima are located at the noncoordinated atoms of the carboxylate groups (–75 and –63 kcal/mol in A and B, respectively) and the MEP maxima are located at the amino group bonded to C2 (ranging +54 to +60 kcal/mol). The MEP value at the H-atoms of the Cu-coordinated water molecules is similar (+53 kcal/mol), revealing that both the NH2 groups and water molecules are strong H-bond donors. The MEP value at the available NH bond of the NH2 group at C6 is also large and positive (+46 and +44 kcal/mol in A and B, respectively) but significantly smaller than those at the NH2 groups due to the formation of the intramolecular NH···O H-bond in the former. The MEP is also positive at the –CH2– groups of the chelate ligand (+26 kcal/mol) and over the six membered ring of the 2,6-diaminopurine.
The coordination by N7 and N9 in combination with the N3-H tautomer instead of the coordination via the more basic N1 or N3 in combination with the N9-H tautomer is likely due to the formation of extra H-bonds that compensate the different coordination ability of the six and five-membered ring N-atoms. This has been confirmed by performing QTAIM analysis. The distributions of bond critical points (CPs, fuchsia spheres) and bond paths of the Cu(II) complexes A and B are shown in Figure 11, confirming the existence of the NH···O contacts (via N3H3 and N6H6). The interaction energies of these NH···O HBs derived from the potential energy density (Vr) measured at the bond CPs range from –6.06 kcal/mol to –9.07 kcal/mol, confirming the energetic relevance of these contacts. Interestingly, the QTAIM analysis also evidences the presence of a weaker CH···O contact in the Cu(II)-atom coordinated by N7 in both models, where a bond CP and bond path connects the C8–H bond of the imidazole ring to the Cu-coordinated O-atom of the carboxylate group. The energy associated to these contacts are weaker (–5.08 and –3.70 kcal/mol in A and B, respectively).
As commented above, two different π-stacking modes have been analyzed theoretically. They are shown in Figure 12 along with the QTAIM and NCIplot analyses. The combined QTAIM and NCIplot representations are very useful to visualize NCIs in real space, including their attractive/repulsive nature (provided by the color of the isosurfaces). It can be observed that the self-assembled A···A dimer shown in Figure 12a combines two strong and symmetrically equivalent OH···N interactions (established between the coordinated water molecules and the N1-atom of 2,6-diaminopurine) with an antiparallel π-stacking interaction. The latter is characterized by four bond CPs and bond paths interconnecting C and N atoms and includes the exocyclic NH2 group. Moreover, a green (attractive) reduced density gradient (RDG) isosurface is located between the 2,6-diaminopurine moieties, further characterizing the π···π interaction. The dimerization energy is large and negative (–17.00 kcal/mol), confirming the importance of this assembly in the solid state of compound 2. The contribution of the HBs is –14.4 kcal/mol, thus supporting the strong nature of these HBs, in line with the blue RDG isosurfaces located between the OH groups and N1-atoms. This energetic analysis reveals that in fact the HBs dominate the formation of this dimer. The other stacking binding mode (B····B) that involves the 2,6-diaminopurine coordinated to the square-pyramidal Cu(II) metal centre is much complicated. The RDG isosurface is very extended and occupies most of the space between the monomers, disclosing a strong complementarity. Moreover, there is an intricate combination of interactions taking place, explaining the very large dimerization energy (–44.5 kcal/mol), more than twice the A···A. This is due to the existence of multiple CH··O contacts between the carboxylate groups and the CH bonds of the chelator. Moreover, two ancillary anion–π interactions (indicated as O···π in Figure 12b) are also observed, characterized by a bond CP and bond path connecting one O-atom of the carboxylate group to the pyrimidine ring, in line with the MEP analysis that revealed the π-acidity of this ring. The large binding energy observed for the B···B dimer likely explains the pentacoordination of these Cu(II) in B since the formation of the B···B staking mode is able to compensate the stabilization that would be obtained by the coordination of the water molecules.

3. Materials and methods

3.1. Reagents and synthesis for the dicopper(ii)-egta chelate and the novel compound 1.

These products have been obtained by the reaction between Cu2CO3(OH)2 (green-malachite, Aldrich) and H4EGTA (Aldrich), in the absence of presence of 2,6-diaminopurine (Aldrich).
The binary dicopper(II)-EGTA chelate [Cu2(µ-EGTA)(H2O)2]·2H2O (mw 575.47) has been prepared in good yields by the strategy previously reported from our group [16]. In a recent essay, 0.44 g (2 mmol) of green malachite was reacted with H4EGTA (0.76 g, 2 mmol) in 125 mL of distilled water, inside a stoppered Kitasato flask of 500 mL, in such a manner that its side outlet allows the escape of CO2 (the only by-product!) preventing possible splashes. The mixture is continuously heated (45-50 °C) and stirred for about two hours, until the unreacted malachite is no longer observed. The stoichiometry of the reaction is:
Cu2CO3(OH)2 + H4EGTA + H2O → [Cu2(µ-EGTA)(H2O)2]·2H2O + CO2↑.
The blue solution is left to cool at room temperature, and then filtered (without vacuum) through a Bücher into a 250 mL crystallization flask. It was then covered with a perforated plastic film to control the evaporation of the solvent. After two months, the chelate was collected and air dried (0.87 g, 1.52 mmol, 75.6%).
Initially, a similar process carried out the synthesis of novel compound 1, with the difference of using above-referred amounts of malachite and H4EGTA in a larger volume of distilled water (175 mL). In order to remove the trace amounts of unreacted malachite, the resulting solution of the Cu2(µ-EGTA) chelate was filtered into an Erlenmeyer. Hadp (0.30 g, 2 mmol) was then added to this solution in successive small portions at room temperature and posteriorly filtered into an appropriate crystallization flask. This procedure represents the use of Hdap in a 100% excess versus the stoichiometry of compound 1!
2 Cu2CO3(OH)2 + 2 H4EGTA + 2 Hdap + 15 H2O → 2 [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O + CO2↑
The excess of Hdap remained in the mother liquors, decreasing the practical yield (up to ~50%) but enabling the obtaining of only high-quality compound 1 (Figure 14). In contrast, the use on a ‘stoichiometric amount’ of Hdap (that is using 1 mmol of Hdap, 0.15 g) firstly produced crystals of the binary chelate, as can be easily assesses by single-crystal X-ray diffraction.
Elemental analysis (%): Calc. for C38H70Cu4N16O29, C 31.06, H 4.80, N 15.19. Found, C 31.02, H, 4.85, N, 15.19.

3.2. Physical measurements

The elemental analysis was performed with a Thermo Scientific Flash 2000 (Thermo Fisher Scientific Inc., Waltham, MA, USA). Infrared spectra (samples in KBr pellets) were recorded using a Jasco FT-IR 6300 spectrometer (Jasco Analítica, Madrid, Spain). Electronic spectra (diffuse reflectance) were obtained in a Varian Cary-5E spectrophotometer (Agilent Scientific Instruments, Santa Clara, CA, USA) from a grinded crystalline sample. Thermogravimetric analyses (TGA) were carried out (10 °C/min) under air-dry flow (100 mL/min) with a thermobalance Mettler-Toledo TGA/DSC1 (Mettler-Toledo, Columbus, OH, USA), and a series of 30 time-spaced FT-IR spectra were recorded to identify evolved gasses throughout the experiment, using a coupled FT-IR Nicolet 550 spectrometer (Thermo Fisher Scientific Inc., Waltham, MA, USA). Differential scanning calorimetry (DSC) measurement was recorded on a DSC-SHIMADZU mod. DSC-50Q instrument (Shimadzu Europe, F.R. Germany GbmH,) in an N2 atmosphere, at 30-400 °C (heating rate 10 °C/min). Room temperature X-band electron spin resonance (ESR) spectra of powdered samples were recorded on a Bruker ELEXSYS E500 spectrometer, equipped with a super-high-Q resonator ER-4123-SHQ. The magnetic field was calibrated by a NMR probe and the frequency inside the cavity was determined with an integrated MW-frequency counter. Q-band measurements were carried out by a Bruker ESP300 spectrometer equipped with an ER-510-QT resonator, a Bruker BNM 200 gaussmeter and a Hewlett-Packard 5352B microwave frequency counter. Data was collected and processed using the Bruker Xepr suite. Magnetic measurements of powdered samples were performed in the 5-300 K temperature range by using a Quantum Design MPMS-7 SQUID magnetometer with a magnetic field of 0.1 T. Diamagnetic corrections were calculated from Pascal tables.

3.3. Crystallography

A Blue plate crystal of {[Cu2(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O} was mounted on a glass fiber and used for data collection. Crystal data were collected at 298(2) K, using a Bruker D8 VENTURE diffractometer. Graphite monochromated CuK (α radiation) (λ = 1.54184 angstrom's) was used throughout. The data were processed with APEX3 [33] and corrected for absorption using SADABS (transmissions factors: 1.000 - 0.714) [34]. The structure was solved by direct methods using the program XT [35] and refined by full-matrix least-squares techniques against F2 using XL [35]. Positional and anisotropic atomic displacement parameters were refined for all non-hydrogen atoms. Hydrogen atoms were located in difference maps and included as fixed contributions riding on attached atoms with isotropic thermal parameters 1.2/1.5 times those of their carrier atoms. The contribution of the density of the disordered solvent molecules was subtracted from the measured structure factors with use of the SQUEEZE option [35]. This indicated that there were approximately seven water molecules per asymmetric unit. The subsequent refinement then converged with R factors and parameter errors significantly improved for all attempts to model the solvent disorder. The criteria of a satisfactory complete analysis were the ratios of root-mean-square shift to standard deviation less than 0.001 and no significant features in the final difference maps. The atomic scattering factors were from "International Tables for Crystallography" [36], and the molecular graphics from PLATON [37]. A summary of the crystal data, experimental details and refinement results are listed in Table 1.

3.4. Computational details

Non-covalent interaction calculations were conducted utilizing Gaussian-16 [38] at the PBE0-D3/def2-TZVP level [39,40,41,42,43,44,45]. Solid-state interactions were evaluated using crystallographic coordinates. Binding energies were determined by comparing isolated monomer energies with their assemblies, while the Boys–Bernardi method [42] corrected for basis set superposition error (BSSE). Bader's "Atoms in molecules" theory (QTAIM) [43], through the AIMAll calculation package [44], explored π-hole and H-bonding interactions. Molecular electrostatic potential surfaces (isosurface 0.001 a.u.) were generated using Gaussian-16 [38].
To assess the nature of interactions in terms of attraction or repulsion and visualize them in real space, the NCIPLOT index was employed [45]. This method, based on the NCI (Non-Covalent Interactions) visualization index derived from electronic density, utilizes the reduced density gradient (RDG) derived from density and its first derivative. This RDG is plotted against the density (represented as isosurfaces) across the molecule of interest.
Identifying attractive/stabilizing (blue-green isosurfaces) or repulsive (yellow-red isosurfaces) interactions is achieved using 3D-plots through the sign of the second Hessian eigenvalue multiplied by the electron density (sign(λ2)ρ in atomic units). The specific NCIplot index parameters are: RDG = 0.5; ρ cutoff = 0.04 a.u.; color range: –0.04 a.u. ≤ sign(λ2)ρ ≤ 0.04 a.u.

4. Concluding remarks

In this manuscript, we report the synthesis and X-ray characterization of a novel tetranuclear Cu(II) complex molecule having two μ-EGTA chelators as binding ligands and two 2,6-diaminopurine molecules as the tautomer H(N3)dap. In the crystal, non-coordinated water is disordered but our results allow the discussion of molecular recognition, which justifies the tetranuclear nature of the complex molecule, and also of the supramolecular recognition in chains generated by π,π-interactions of a pair of rings of 5 or 6 atoms of H(N3)dap. The spectral, magnetic, or thermal stability properties of the compound are rationalized on the basis of the tetranuclear molecule.
The theoretical DFT study also reveals the importance of π-stacking and H-bonding interactions in the solid state using two representative models. In particular, O···π interactions and extra CH···O interactions in the B···B binding mode justify the very large dimerization energy and also explain the different coordination of the Cu(II) atoms (without the distal water molecules) that facilitate the approximation of the 2,6-diaminopurine units, leading to a more efficient approximation of the monomers. The quantification of the intramolecular H-bonds in both model complexes by using the QTAIM analysis allows to rationalize the complexation via N7 and N9 to the metal centers.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Figure S1: FT-IR spectra of the binary compound [Cu2(µ-EGTA)(H2O)2]·2H2O (up) and the novel ternary compound 1 [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O (down). Figure S2: Photos of crystals of [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O (1).

Author Contributions

Conceptualization, M.E.G.-R and J.N.-G.; methodology, all authors; software, A.C. and A.F.; investigation, H.M.; writing—original draft preparation, all authors, writing—review and editing, all authors; visualization, A.C., D.C.-L., A.F. and J.N.-G. project administration, A.C., A.F., and J.N.-G.; funding acquisition, A.C., A.F., D.C.-L. and J.N.-G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by MICIU/AEI of Spain project PID2020-115637GB-I00 FEDER, MICINN of Spain project PGC2018-102047-B-I00, Project B-FQM-478-UGR20 (FEDER-Universidad de Granada, Spain). Funds and instrumental support of research group FQM-283 (Junta de Andalucía, Spain) are also acknowledged.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article or supplementary material

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rosales-Martínez, C.; Matilla-Hernádez, A.; Choquesillo-Lazarte, D.; Frontera, A.; Castiñeiras, A.; Niclós-Gutiérrez, J. The copper(II)-thiodiacetate (tda) chelate as efficient receptor of N9-(2-hydroxyethyl)adenine (9heade). Synthesis, molecular and crystal structures, physical properties and DFT calculations of [Cu(tda)(9heade)(H2O)]·2H2O. Molecules, 2023, 28, 5830. [Google Scholar] [CrossRef] [PubMed]
  2. García-Rubiño, M.E.; Matilla-Hernández, A.; Frontera, A.; Lezama, L.; Niclós-Gutiérrez, J.; Choquesillo-Lazarte, D. Dicopper(II)-EDTA Chelate as a bicephalic receptor model for a synthetic adenine nucleoside. Pharmaceuticals 2021, 14, 426. [Google Scholar] [CrossRef] [PubMed]
  3. Bendich, A.; Furst, S.S.; Brown, G.B. On the role of 2,6-diaminopurine in the biosynthesis of nucleic acid guanine. J. Biol. Chem. 1950, 185, 423–33. [Google Scholar] [CrossRef] [PubMed]
  4. Szabla, R.; Zdrowowicz, M.; Spisz, P; Green, N. J.; Stadlbauer, P.; Kruse, H.; Šponer, J.; Rak, J. 2,6-diaminopurine promotes repair of DNA lesions under prebiotic conditions. Nat. Commun. 2021, 12, 3018. [Google Scholar] [CrossRef] [PubMed]
  5. Madaoui, M.; Datta, D.; Wassarman, K.; Zlatev, I.; Egli, M.; Ross, B.S. Manoharan, M.; A Chemical Approach to Introduce 2,6-Diaminopurine and 2-Aminoadenine Conjugates into Oligonucleotides without Need for Protecting Groups. Org. Lett. 2022, 24, 6111–6116. [Google Scholar] [CrossRef] [PubMed]
  6. Kim, H.-J.; Benner, S.A. Prebiotic stereoselective synthesis of purine and noncanonical pyrimidine nucleotide from nucleobases and phosphorylated carbohydrates. PNAS, 2017, 114, 11315–11320. [Google Scholar] [CrossRef] [PubMed]
  7. Martina, M.G.; Giammarino, F.; Vicenti, I.; Groaz, E.; Rozenski, J.; Incerti, M.; Sannio, F.; J. ; Docquier, D.; Zazzi, M.; Radi, M.; Nucleoside Derivatives of 2,6-diaminopurine Antivirals: Base-Modified Nucleosides with Broad-Spectrum Antimicrobial Properties. ChemMedChem 2023, e202300200. [Google Scholar] [CrossRef]
  8. XiaoHua, X.; Zhiyuan, S.; Ramachandra, S.H. A versatile synthetic precursor for introduction of specific N6-modifications in 2,6-diaminopurine nucleosides: N2-acetyl-2',3',5'-tri-O-acetyl-N6-(1,2,4-triazol-1-yl)-2,6-diaminopurine -9-ribofuranoside. Proceedings of ECSOC-3, The Third International Electronic Conference on Synthetic Organic Chemistry, Basel, Switzerland, 1-30 September 1999. [Google Scholar]
  9. Krečmerová, M.; Jansa, P.; Dračínský, M.; Sázelová, P.; Kašička, V.; Neyts, J.; Auwerx, J.; Kiss, E.; Goris, N.; Stepan, G.; Janeba, Z. 9-[2-(R)-(phosphonomethoxy)propyl]-2,6-diaminopurine (R)-PMPDAP and its prodrugs: optimized preparation, including identification of by-products formed, and antiviral evaluation in vitro. Bioorg. Med. Chem. 2013, 21, 1199–208. [Google Scholar] [CrossRef]
  10. Furman, Ph.A.; Jeffrey, J.; Kiefer, L.L.; Feng, J.Y.; Anderson, K.S.; Borroto-Esoda, K.; Hill, E.; Copeland, W.C.; Chu, Ch.K.; Sommadossi, J.-P.; Liberman, I.; Schinazi, R.F.; Painter, G.R. Mechanism of action of 1-β-d-2,6-diaminopurine dioxolane, a prodrug of the human immunodeficiency virus type 1 Inhibitor 1-β-d-dioxolane guanosine. Antimicrob. Agents Chemother. 2001, 45, 158–165. [Google Scholar] [CrossRef]
  11. Pasternak, A.; Kierzek, E.; Pasternak, K.; Turner, D.H.; Kierzek, R. A chemical synthesis of LNA-2,6-diaminopurine riboside, and the influence of 2'-O-methyl-2,6-diaminopurine and LNA-2,6-diaminopurine ribosides on the thermodynamic properties of 2'-O-methyl RNA/RNA heteroduplexes. Nucleic Acids Res. 2007, 35, 4055–4063. [Google Scholar] [CrossRef]
  12. Schauer, C.K.; Anderson, O.P. Calcium-selective ligands. 1. Structure of 3,12-bis (carboxymethyl)-6,9-dioxa-3,12-diazatetradecanedioic acid (H4egta). Acta Crystallogr., 1986, C42, 760–762. [Google Scholar] [CrossRef]
  13. Yerly, F.; Hardcastle, K.I.; Helm, L.; Aime, S.; Botta, M.; Merbach, A.E. Molecular dynamics simulation of [Gd(egta)(H2O)]− in aqueous solution: Internal motions of the poly(amino carboxylate) and water ligands, and rotational correlation times. Chem. Eur. J. 2002, 8, 1031–1039. [Google Scholar] [CrossRef] [PubMed]
  14. Schauer, C.K.; Anderson, O.P. Highly polydentate ligands. 5. Structures of alkaline-earth complexes of the calcium-selective ligand EGTA4- (H4EGTA = 3,12- bis (carboxymethyl)-6,9-dioxa-3,12-diazatetradecanedioic acid). Inorg. Chem., 1988, 27, 3118–3130. [Google Scholar] [CrossRef]
  15. Gaur, R. Selective anionic dye adsorption, topology and luminescence study of structurally diverse cadmium(II) coordination polymers. Inorg. Chem. Front., 2019, 6, 278–286. [Google Scholar] [CrossRef]
  16. Alarcón-Payer, C.; Bugella-Altamirano, E.; Choquesillo-Lazarte, D.; Castineiras, A.; González-Pérez, J.M.; Niclós-Gutiérrez, J. Dinuclear EGTA-copper(II) chelates with imidazole as auxiliary ligand. Inorg. Chem. Commun. 2006, 9, 903–906. [Google Scholar] [CrossRef]
  17. Gaur, R.; Roy, S.; Kallem, P.; Banat,F. Experimental and theoretical investigation of hydrogen bonded supramolecular assemblies through water molecules in a copper(II)-EGTA complex. J. Mol. Struct. 2022, 1265, 133400. [Google Scholar] [CrossRef]
  18. Escriva, E.; Server-Carrio, J.; Garcia-Lozano, J.; Folgado, J.-V.; Sapina, F.; Lezama, L. Exchange interactions through hydrogen-bond bridges. Crystal structure, spectroscopic characterisation and magnetic properties of the complex [{Cu(en)}2(μ-egta)]·4H2O (H4egta = 3,12-bis(carboxymethyl)-6,9-dioxa-3,12-diazatetradecanedionic acid). Inorg. Chim. Acta, 1998, 279, 58–64. [Google Scholar] [CrossRef]
  19. Wu, Y.-P.; Wang, Y.-Y.; Wang, C.-J.; Li, D.-S.; Guo, C.-Y.; Wen, G.-L.; Shi, Q.-Z. From 1D polymeric chain to two-fold parallel interpenetration of (4,4) net: Synthesis and characterization of two new copper(II) complexes derived from highly polydentate aminopolycarboxylate ligand. Chin. J. Chem. 2008, 26, 1233–1238. [Google Scholar] [CrossRef]
  20. Zhang, C.-H.; Chen, Y.-G.; Liu, S.-X. Weakley sandwich-type anion in organic–inorganic hybrid compound with 3D framework. Inorg. Chem. Commun. 2013, 29, 45–48. [Google Scholar] [CrossRef]
  21. Zhang, C.-H.; Chen, Y.-G. A flexible chelate ligand in dodecatungstoborate-based supramolecular compounds. J. Inclusion Phenom. Macrocyclic Chem. 2014, 79, 171–176. [Google Scholar] [CrossRef]
  22. Yang, E.-C.; Chan, Y.-N.; Liu, H.; Wang, Z.-C.; Zhao, X.-J. Unusual polymeric ZnII/CdII complexes with 2,6-diaminopurine by synergistic coordination of nucleobases and polycarboxylate anions: Binding behavior, self-assembled pattern of the nucleobase, and luminscent properties. Cryst. Growth Des., 2009, 9, 4933–4944. [Google Scholar] [CrossRef]
  23. González-Pérez, J.M.; Choquesillo-Lazarte, D.; Domínguez-Martín, A.; El Bakkali, H.; García-Rubiño, M.E.; Pérez-Toro, I.; Vílchez-Rodríguez, E.; Castiñeiras, A.; Marina Nurchi, V.; Niclós-Gutiérrez, J. Molecular recognition between adenine or 2,6-diaminopurine and copper(II) chelates with N,O2,S-tripodal tetradentate chelators having thioether or disulfide donor groups. J. Inorg. Biochem. 2015, 151, 75–86. [Google Scholar] [CrossRef] [PubMed]
  24. Xu, L.-L.; Zhang, H.-F.; Li, M.; Ng, S.W.; Feng, J.-H.; Mao, J.-G.; Li, D. Chiroptical Activity from an Achiral Biological Metal−Organic Framework. J. Am. Chem. Soc. 2018, 140, 11569–11572. [Google Scholar] [CrossRef] [PubMed]
  25. Zhao, H.-K; Yang, H.-W.; Wang, X.-G.; Ding, B.; Liu, Z.-Y.; Zhao, X.-J.; Yang, E.-C. An unusual 2D polymeric Co(II) complex with 2,6-diaminopurine: Synthesis, crystal structure, and magnetic behavior. Inorg. Chem. Commun. 2019, 107, 107483. [Google Scholar] [CrossRef]
  26. Bai, J.-P.; Huang, Y.-L.; Xie, M.; Zhao, Y.; Luo, D.; Li, Y.Y.; Lu, W.; Li, D. Reversible multiphase transition in a BioMOF and its distinctive luminescence turn-on in alcohol vapor. ACS Appl. Mater. Interfaces 2019, 11, 38503–38509. [Google Scholar] [CrossRef] [PubMed]
  27. Addison, A.W.; Nageswara Rao, T.; Reedijk, J.; van Rijn, J. Verschoor, G.C., Synthesis, structure, and spectroscopic properties of copper(II) compounds containing nitrogen-sulphur donor ligands ; the crystal and molecular structure of aqua[l,7-bis(N-methylbenzimidazol-2'-yl)-2,6-dithiaheptane]copper(II) perchlorate. J. Chem. Soc., Dalton Trans. 1984, 1349–1356. [Google Scholar] [CrossRef]
  28. Blackman, A.G.; Schenk, E.B.; Jelley, R.E.; Krensked, E.H.; Gahan, L.R. Five-coordinate transition metal complexes and the value of τ5: observations and caveats. Dalton Trans., 2020, 49, 14798–14806. [Google Scholar] [CrossRef] [PubMed]
  29. Sutton, D. Electronic spectra of transition metal complexes: An introductory text; McGraw-Hill Book Co.: New York & London, 1968. [Google Scholar]
  30. Calvo, R.; Mesa, M.A. EPR study of electronic and magnetic properties of bis(DL-α-amino-n-butyrato)copper(II). A layered magnetic system. Phys. Rev. B 1983, 28, 1244–1248. [Google Scholar] [CrossRef]
  31. Hathaway, B.J. A new look at the stereochemistry and electronic properties of complexes of the copper(II) ion. Struct. Bonding 1984, 57, 55–118. [Google Scholar]
  32. Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef]
  33. Bruker, APEX3 Software, Bruker AXS Inc. v2018.7-2, Madison, Wisconsin, USA. 2019.
  34. Sheldrick, G.M. SADABS. Program for Empirical Absorption Correction of Area Detector Data. ( 1997, 1997). University of Goettingen, Germany. [Google Scholar]
  35. Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. 2008, A64, 112–122. [Google Scholar] [CrossRef] [PubMed]
  36. Wilson, A.J.C. International Tables for Crystallography. Vol. C, Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995.
  37. Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. 2009, D65, 148–155. [Google Scholar] [CrossRef] [PubMed]
  38. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision A.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  39. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104–154122. [Google Scholar] [CrossRef] [PubMed]
  40. Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
  41. Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
  42. Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys., 1970, 19, 553–566. [Google Scholar] [CrossRef]
  43. Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893928. [Google Scholar] [CrossRef]
  44. Keith, T.A. TK Gristmill Software, version 13.05.06; AIMAll: Overland Park, KS, USA, 2013. [Google Scholar]
  45. Contreras-Garcia, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.P.; Beratan, D.N.; Yang, W. NCIPLOT: A program for plotting non-covalent interaction regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef]
Preprints 82202 g001
Figure 1. Schematics of H4EDTA (left) and H4EGTA (center) and H(N9)dap (right).
Figure 1. Schematics of H4EDTA (left) and H4EGTA (center) and H(N9)dap (right).
Preprints 82202 g001
Preprints 82202 g002
Figure 2. (a) EGTA chelating ligands with disorder in an ethylene unit. (b) The tetranuclear molecule [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2] with its four metal centers that are non-equivalent.
Figure 2. (a) EGTA chelating ligands with disorder in an ethylene unit. (b) The tetranuclear molecule [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2] with its four metal centers that are non-equivalent.
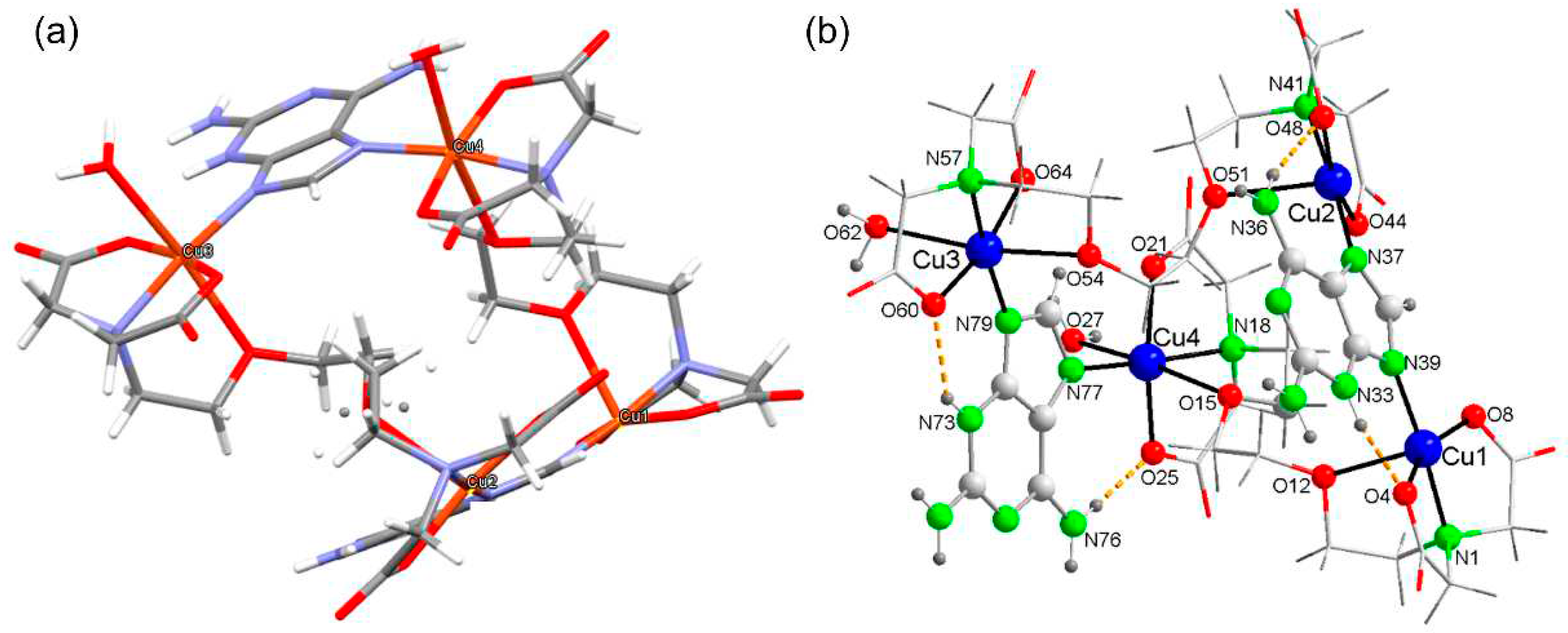
Preprints 82202 g002
Preprints 82202 g003
Figure 3. Schematics of the supramolecular recognition of [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2]·7H2O.
Figure 3. Schematics of the supramolecular recognition of [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2]·7H2O.
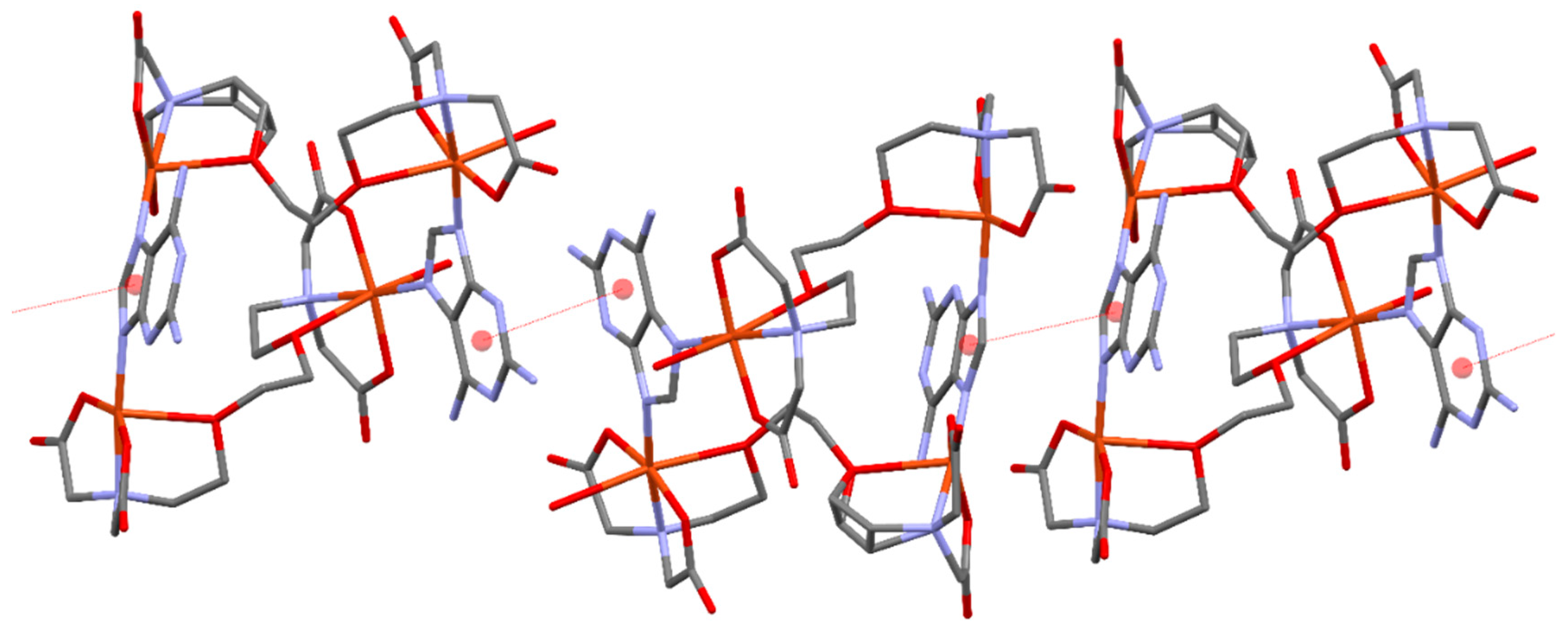
Preprints 82202 g003
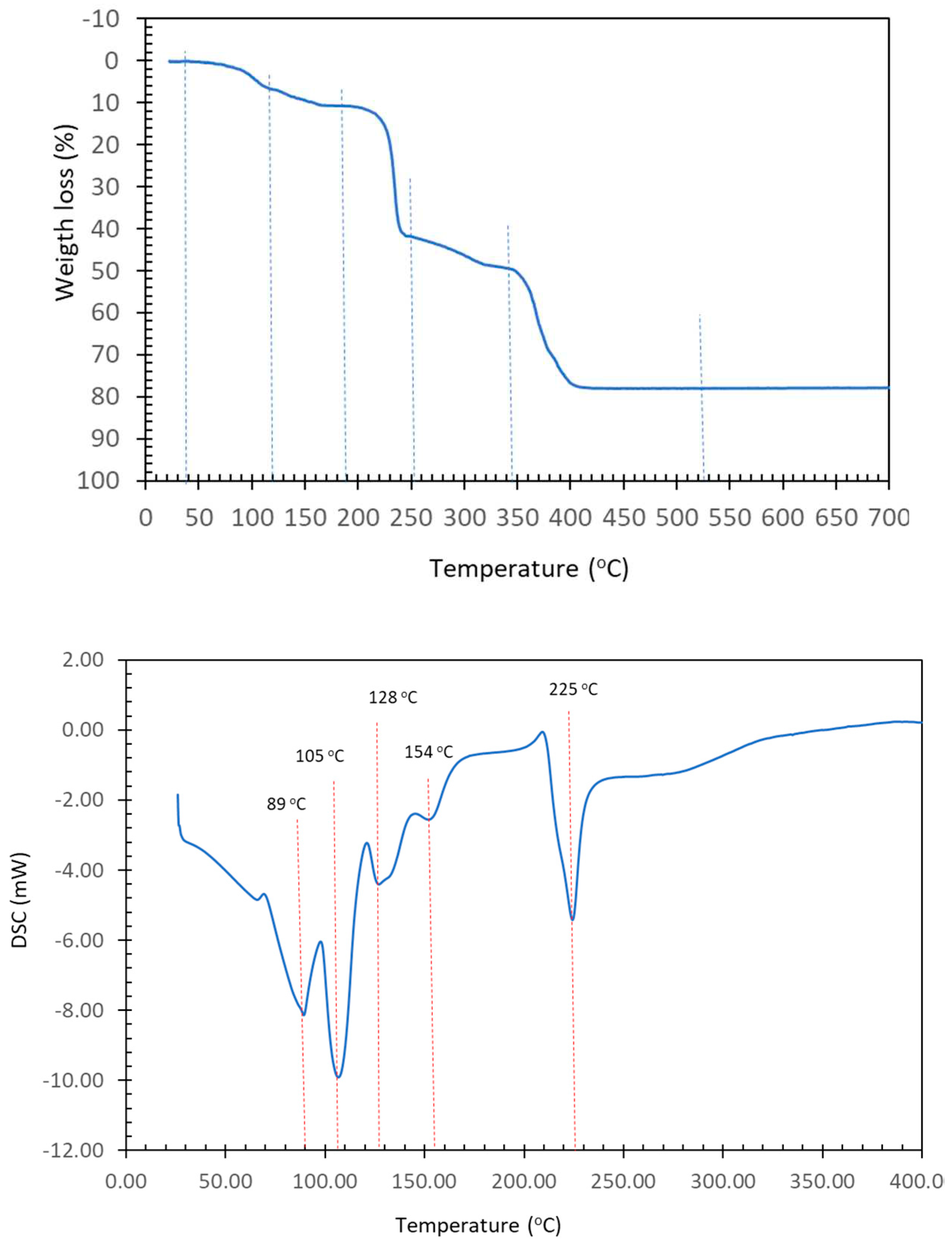
Preprints 82202 g004
Figure 4. TGA (up) and DSC (down) curves of compound [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O (1).
Figure 4. TGA (up) and DSC (down) curves of compound [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O (1).
Preprints 82202 g004
Preprints 82202 g005
Figure 5. Electronic spectrum (diffuse reflectance) of [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O (1).
Figure 5. Electronic spectrum (diffuse reflectance) of [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O (1).
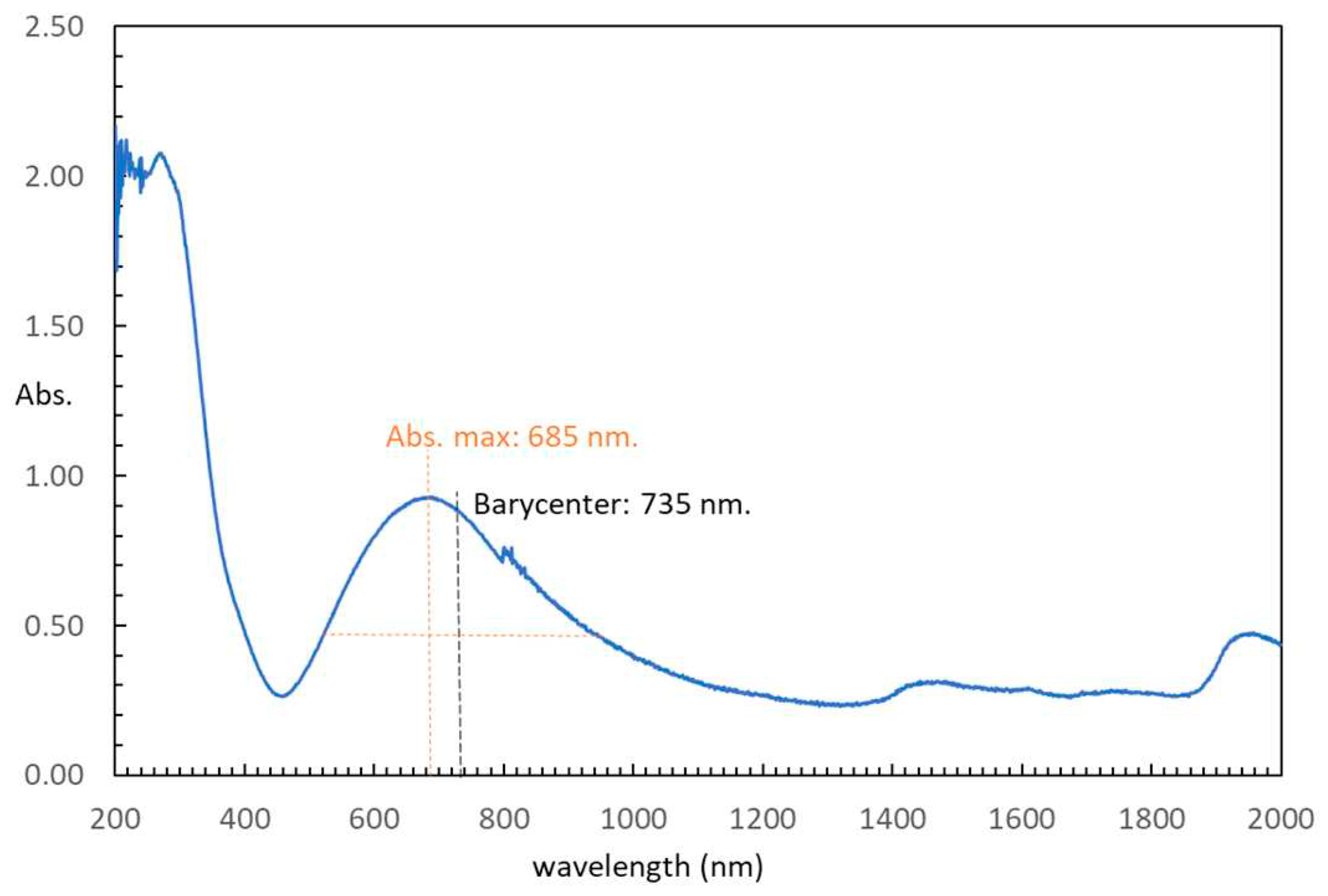
Preprints 82202 g005
Preprints 82202 g006
Figure 6. Experimental (continuous line) and simulated (dashed line) Q-band room temperature ESR spectrum for compound [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O.
Figure 6. Experimental (continuous line) and simulated (dashed line) Q-band room temperature ESR spectrum for compound [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O.
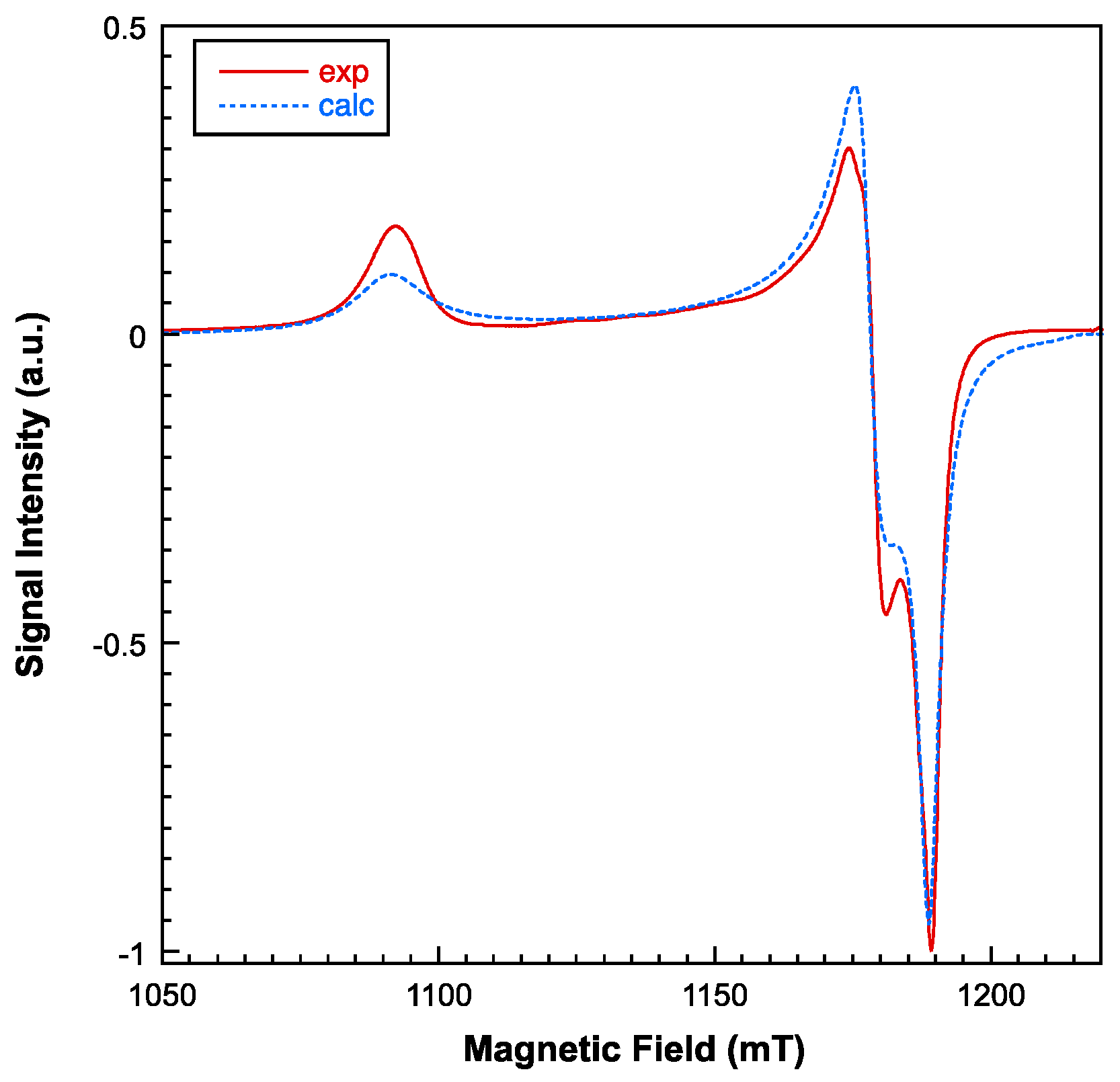
Preprints 82202 g006
Preprints 82202 g007
Figure 7. Experimental (continuous line) and simulated (dashed line) X-band room temperature EPR spectrum for compound 1 (left). Thermal evolution of the signal at low temperatures (right).
Figure 7. Experimental (continuous line) and simulated (dashed line) X-band room temperature EPR spectrum for compound 1 (left). Thermal evolution of the signal at low temperatures (right).
Preprints 82202 g007
Preprints 82202 g008
Figure 8. Left: Magnetic behavior of compound 1 (see text for the details of fit). Right: Thermal dependence of the reciprocal molar susceptibility for compound 1. Continuous line corresponds to the Curie-Weiss fit for T>50 K.
Figure 8. Left: Magnetic behavior of compound 1 (see text for the details of fit). Right: Thermal dependence of the reciprocal molar susceptibility for compound 1. Continuous line corresponds to the Curie-Weiss fit for T>50 K.
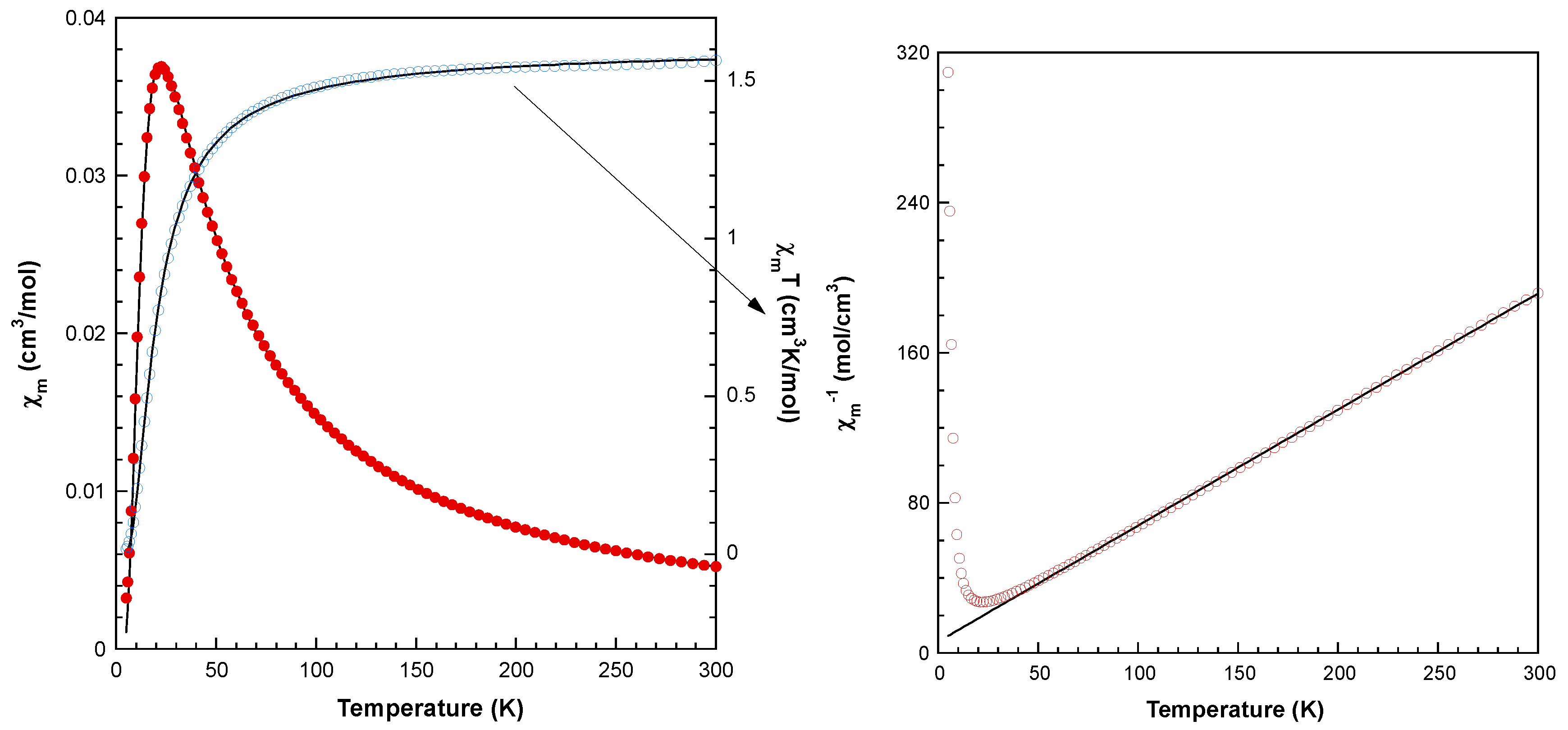
Preprints 82202 g008
Preprints 82202 g009
Figure 9. (a). Partial view of the X-ray structure of compound 1 where the 1D supramolecular chain is represented. (b) Dinuclear models A and B generated from the tetranuclear macrocycle.
Figure 9. (a). Partial view of the X-ray structure of compound 1 where the 1D supramolecular chain is represented. (b) Dinuclear models A and B generated from the tetranuclear macrocycle.
Preprints 82202 g009
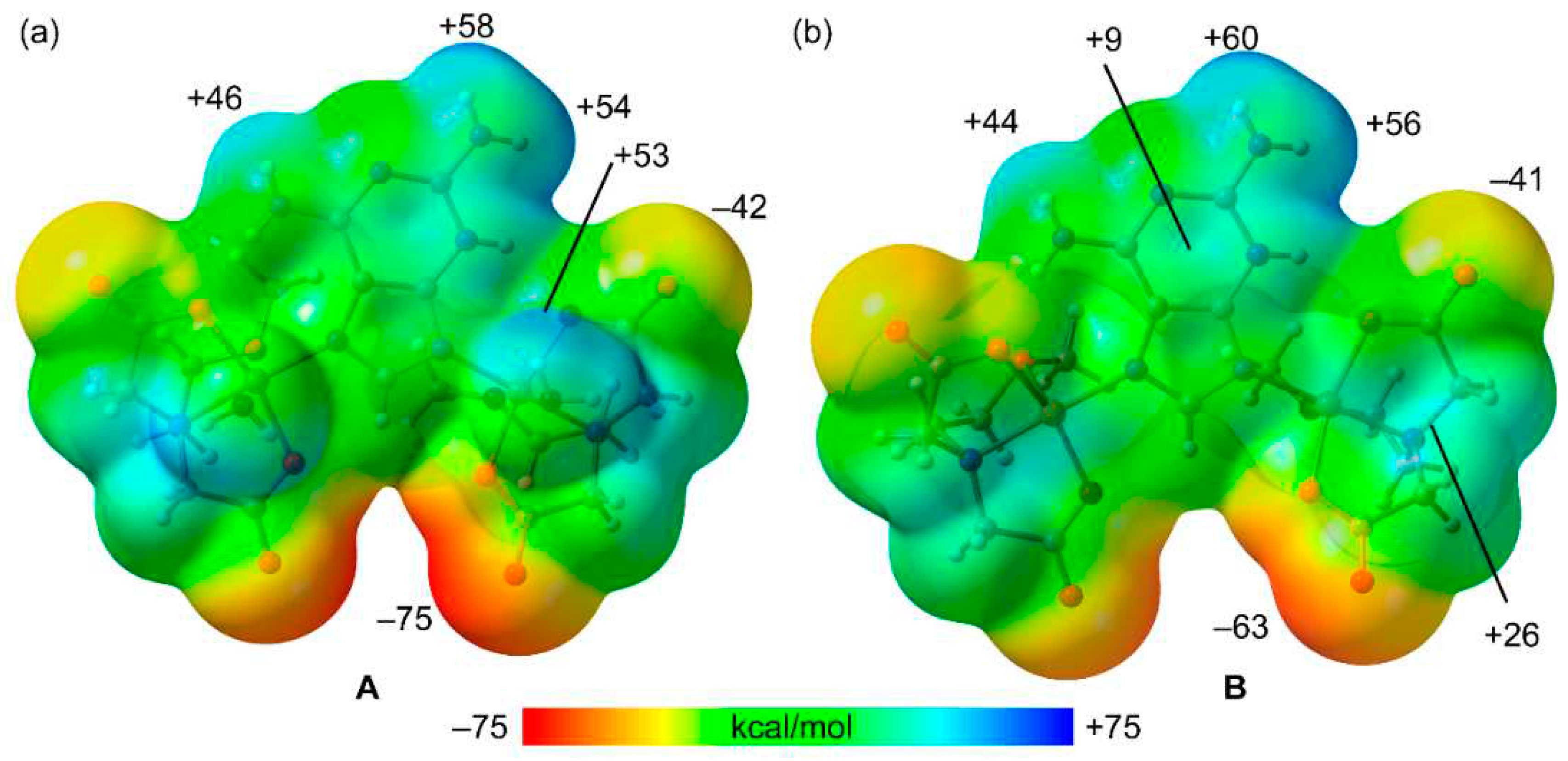
Preprints 82202 g010
Figure 10. MEP surfaces of dinuclear model systems A (a)and B (b) at the PBE0-D3/def2-TZVP level of theory (density isovalue 0.001 a.u.). The energies are given in kcal/mol.
Figure 10. MEP surfaces of dinuclear model systems A (a)and B (b) at the PBE0-D3/def2-TZVP level of theory (density isovalue 0.001 a.u.). The energies are given in kcal/mol.
Preprints 82202 g010
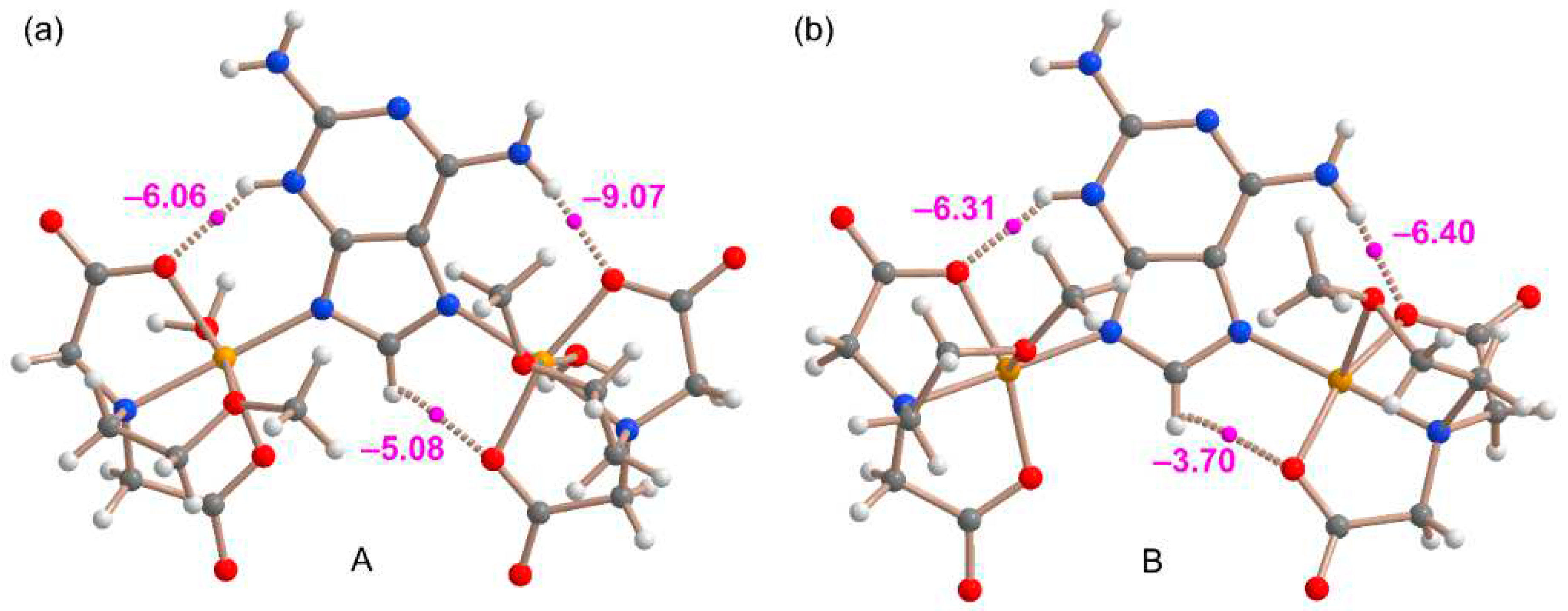
Preprints 82202 g011
Figure 11. QTAIM analysis of the complexes A (a) and B (b) where the bond critical points (CPs, fuchsia spheres) and bond paths (dashed bonds) of the noncovalent interactions are shown. The energy of the HBs is indicated using a fuchsia colored font adjacent to the bond CPs.
Figure 11. QTAIM analysis of the complexes A (a) and B (b) where the bond critical points (CPs, fuchsia spheres) and bond paths (dashed bonds) of the noncovalent interactions are shown. The energy of the HBs is indicated using a fuchsia colored font adjacent to the bond CPs.
Preprints 82202 g011
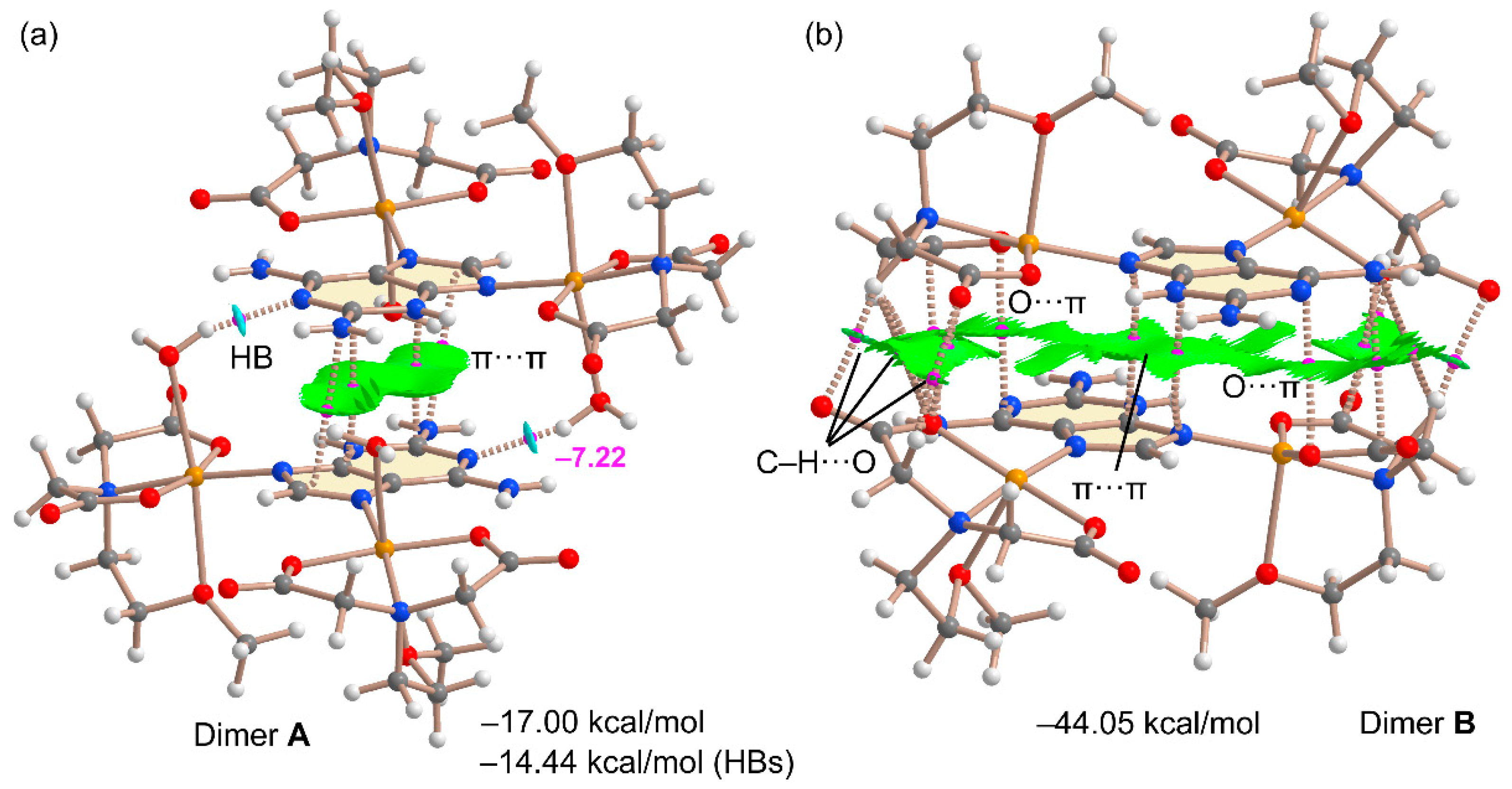
Preprints 82202 g012
Figure 12. QTAIM/NCIPlot analysis of intermolecular bond CPs (fuchsia spheres), bond paths and RDG isosurfaces of the A···A (a) and B···B (b) π-stacking binding modes of 1compound 2. The individual interaction energies of the H-bonds are indicated using a red font next to the bond CPs.
Figure 12. QTAIM/NCIPlot analysis of intermolecular bond CPs (fuchsia spheres), bond paths and RDG isosurfaces of the A···A (a) and B···B (b) π-stacking binding modes of 1compound 2. The individual interaction energies of the H-bonds are indicated using a red font next to the bond CPs.
Preprints 82202 g012
Table 1. Crystal data and structure refinement for [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2]·7H2O (1).
Table 1. Crystal data and structure refinement for [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2]·7H2O (1).
Empirical formula C38H70Cu4N16O29
Formula weight 1469.24
Temperature 298(2) K
Wavelength 1.54178 Å
Crystal system Triclinic
Space group P 1 ¯
Unit cell dimensions a = 12.9272(4) Å α = 104.372(1)°
b = 13.1727(4) Å β = 94.015(2)°
c = 19.6298(6) Å γ = 95.213(2)°
Volume 3209.80(17) Å3
Z 2
Calculated density 1.520 Mg/m3
Absorption coefficient 2.396 mm–1
F(000) 1516
Crystal size 0.10 × 0.10 × 0.09 mm
θ range for data collection (°) 2.334 to 66.591.
Limiting indices 14 ≤  h  ≤ 15, -15 ≤  k  ≤ 15, -23 ≤  l  ≤ 23
Reflections collected / unique 23305 / 10915 [Rint = 0.0287]
Completeness to theta = 66.591° 96.2 %
Absorption correction Semi-empirical from equivalents
Max. and min. transmission 1.000 and 0.714
Refinement method Full-matrix least-squares on F2
Data / restraints / parameters 10915 / 1 / 742
Goodness-of-fit on F2 1.038
Final R indices [I>2σ(I)] R1 = 0.0354, wR2 = 0.0956
R indices (all data) R1 = 0.0394 wR2 = 0.0986
Largest diff. peak and hole 0.462 and -0.429 e·Å–3
CCSD code 2287840
Table 2. Selected coordination bond lengths [Å] and trans-angles [°] for [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2]·7H2O (1).
Table 2. Selected coordination bond lengths [Å] and trans-angles [°] for [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2]·7H2O (1).
Cu(1)-N(1) 2.000(2) Cu(2)-N(37) 1.973(2)
Cu(1)-O(4) 1.934(2) Cu(2)-N(41) 2.004(3)
Cu(1)-O(8) 1.930(2) Cu(2)-O(44) 1.939(2)
Cu(1)-N(39) 1.961(2) Cu(2)-O(48) 1.951(2)
Cu(1)-O(12) 2.337(2) Cu(2)-O(51) 2.424(2)
N(39)-Cu(1)-N(1) θ = 175.67(10) N(37)-Cu(2)-N(41) θ = 174.95(10)
O(8)-Cu(1)-O(4) φ = 158.40(11 O(44)-Cu(2)-O(48) φ = 163.30(10)
τ = (θ-φ)/60* 0.29 τ = (θ-φ)/60 0.19
Cu(3)-N(57) 1.997(2) Cu(4)-N(77) 1.9801(2)
Cu(3)-O(60) 1.969(2) Cu(4)-N(18) 2.010(2)
Cu(3)-O(64) 1.955(2) Cu(4)-O(21) 1.959(2)
Cu(3)-N(79) 1.944(2) Cu(4)-O(25) 1.959(2)
Cu(3)-O(54) 2.417(2) Cu(4)-O(27) 2.499(2)
Cu(3)-O(62) 2.552(3) Cu(4)-O(15) 2.561(2)
N(79)-Cu(3)-N(57) 172.71(8) O(27)-Cu(4)-O(15) 172.58(6)
O(54)-Cu(3)-O(62) 171.82(8) N(77)-Cu(4)-N(18) 170.55(8)
O(64)-Cu(3)-O(60) 167.33(7) O(21)-Cu(4)-O(25) 166.11(6)
* Addison-Reedijk parameter [27,28].
Table 3. Distances (D···A, Å) and angles (<, °) for hydrogen bindings in the crystal of [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2]·7H2O (1).
Table 3. Distances (D···A, Å) and angles (<, °) for hydrogen bindings in the crystal of [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2]·7H2O (1).
D-H···A d(D···A) <(D-H···A)
O(27)-H(27A)···O(65)#1 2.833(3) 159.4
O(27)-H(27B)···O(22)#1 2.917(3) 142.7
N(33)-H(33)···O(4) 2.760(3) 138.6
N(36)-H(36A)···O(26)#2 2.938(3) 159.4
N(36)-H(36B)···O(48) 2.844(4) 160.3
O(62)-H(62B)···N(71)#3 2.947(3) 162.0
N(72)-H(72A)···O(22)#4 2.751(3) 133.2
N(73)-H(73)···O(60) 2.781(2) 140.3
N(76)-H(76B)···O(25) 2.825(3) 170.4
Symmetry transformations to generate equivalent atoms: #1 = -x+1,-y+1,-z; #2 = x,y+1,z; #3 = -x,-y+1,-z; #4 = x-1,y,z.
Table 4. Relevant H-bonding data for mixed-ligand metal complexes having as μ2-N7,N9 the tautomer H(N3)dap.
Table 4. Relevant H-bonding data for mixed-ligand metal complexes having as μ2-N7,N9 the tautomer H(N3)dap.
Compound § Formula* N3-H···O (Å, °) N6-H···O (Å, °) Ref.
1 (this work) [Cu4(μ-EGTA)2(μ-H(N3)dap)2(H2O)2]·7H2O 2.760(3), 139
2.781(2), 140		 2.844(4), 139
2.825(3), 170.4		 -
QUDKEG [Zn2(μ2-Hdap)(tp)2]n (3D MOF) 2.739(2), 173 3.003(2), 162
2.912(2), 155		 [22]
QUDKIK {[Zn2(μ2-Hdap)(tm)(μ2-OH)]·3H2O}n
(1D polymer)		 2.559(2), 176 2.935(3), 172 [22]
MULCED [Cu2(BCBC)2(μ2-N7,N9)Hdap)(H2O)2]·4H2O 2.732(7), 140 2.774(7), 169 [23]
FINDAC [Zn(FDC)(μ2-N7,N9)Hdap)]·0.5H2O (3D MOF) N/A N/A [24]
KOZNAR [Co(Hdap)(ip)]n (2D layers) N/A N/A [25]
§Acronyms in CSD for previously reported compounds. * Ligands: Hdap . tp = terephthalate(2-) ion. tm = trimesicate(3-) ion. BCBC = N,N-bis(carboxymethyl)-S-benzyl-cysteaminate(2-) anion. FDC = H2FDC = 2,5-furandicarboxylilate(2-) ion. ip = isophthalate(2-) ion.
Table 5. Data for the thermogravimetric analysis of [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O (1).
Table 5. Data for the thermogravimetric analysis of [Cu4(µ-EGTA)2(µ-Hdap)2(H2O)2]·7H2O (1).
Step or R Temp.
(°C)		 Time
(min)		 Weight loss (%)
Exp. Calc.		 Evolved gases or residue (R)
1 30-115 0-12 6.905 8.098 ~6 H2O*, CO2 (t*)
2 115-185 12-17 3.681 4.049 ~3 H2O, CO2 (t*)
(1+2) (30-185) (0-17) (10.586) 11.035 9 H2O
3 185-255 17-23 31.177 - CO2, H2O
4 255-335 23-32 7.128 - CO2, CO, H2O
5 335-450 32-45 28.922 - CO2, CO, H2O, N2O, NO, NO2, CH4 (t*)
R 520 95 19.532 17.879 4 CuO
*t = trace amounts. R = solid residue.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated