Indirect Solution Modeling of Melting Behavior of SiO2 Based on the Image Processing Technology

The utilization of tempered blast furnace (BF) slag through the direct fiber forming process to create high-value thermal insulation materials offers a dual benefit: it efficiently harnesses the latent heat within unused slag and substantially enhances the value of blast-furnace slag utilization. However, gauging the melting properties of iron slag under high temperatures is a challenge. In this study, we explore the melting behavior of SiO2 within a high-temperature molten pool. We employ dynamic visual data (video stream) captured via a non-contact charge coupled device (CCD) video recording system to extract SiO2 contours through image processing. The change in image centroid characteristics is used to establish a convolution function relationship, and MATLAB's traversal search algorithm determines SiO2's centroid position. Given that SiO2 is proportionate to crucible pixels, the area of SiO2 is calculated through pixel statistics within these contours. Subsequently, we propose a new indirect method to process image information, yielding SiO2 volume and mass at different time points. An exponential fitting yields the melting rate function of SiO2. Finally, we compare this indirect method with shape from shading (SFS), quantitative characterization, and dimensional analysis techniques. We also discuss the strengths and limitations of each method. Our findings reveal that the indirect solution method presented here boasts straightforward calculation steps and imposes minimal image format requirements. This research provides theoretical and technical support for blast-furnace slag's direct fiber forming process.

Keywords:

Subject: Engineering - Industrial and Manufacturing Engineering

1. Introduction

Iron tailings are the waste that remains after separation of the iron ore concentrate in the beneficiation process. Iron tailings are usually dumped for a long time due to technical limitations. Dumping the iron tailings not only occupies land, but also causes environmental pollution and safety problems. Therefore, the best solution is to reuse the iron tailings [1].

Blast furnace (BF) slag is a by-product of the ironmaking process and could be used to produce slag fibers by adding iron ore tailings [2]. This method can not only efficiently utilize the sensible heat of the slag, which is currently unutilized [3], but also significantly increase the value added of blast-furnace slag utilization. The crystallization behavior of the modified BF slag is important for the fiberization process. However, due to the difficulty of measuring the high-temperature process, the process cannot be applied industrially, and the melting characteristics of ferrous scrap under high-temperature conditions need more in-depth research.

At present, the relevant studies mainly focus on the dissolution behavior of CaO, MgO, SiO₂, Al₂O₃ in slag and the influence of various factors on its melting behavior[4, 5], while few studies have been conducted on the homogenization behavior. The homogenization process includes two processes, melting and diffusion, both of which are very important in homogenizing the conditioned slag. The melting process was investigated by in-situ observation experiment [6] to study the dissolution behavior of the modifier in BF slag and to analyze the dynamic factors.

To investigate the influence of basicity on the crystallization behavior, BF slag was modified by the addition of iron ore tailings at room temperature and melted at 1500 °C by Ren et al. [7]. The influence of basicity on the initial crystallization temperature during cooling was investigated using various techniques such as X-ray diffraction (XRD), scanning electron microscope backscattered electron imaging (SEMBSE), energy dispersive spectrometer (EDS), and hot thermocouple technique (HTT), etc. The effect of acidity coefficient on the crystallization behavior of modified BF slag was investigated by Cai et al. [8] using Factage software, HTT and XRD, with the conclusion that the crystal growth rate is controlled by diffusion driving force and undercooling driving force. Most of the above similar studies focus on experimental measurement, which is difficult to operate and requires high demands on instruments and equipment. Studying the melting dynamic process requires repeated rapid cooling of the sample, which results in wasted experimental cost and time. More importantly, it is difficult to repeat an experiment many times to ensure that other conditions (such as particle size, the state of two-phase flow during the dissolution process, cooling rate, etc.) are exactly the same.

The main component of the iron tailings is SiO₂, and SiO₂ is the most difficult part of the iron tailings to melt, and the melting behavior of the iron tailings can be expressed by the melting behavior of SiO₂. However, the temperature of the high-temperature melting groove is more than 1500℃, and the service life of the conventional testing equipment in this environment is very short. To solve this problem, high-temperature laser scanning confocal microscopy (CSLM) [9] is usually used to obtain dynamic visualization data of SiO₂ in the high-temperature melting pool in a non-contact way, observe the dissolution phenomenon in situ during the high-temperature process, and observe the melting state of SiO₂ in time series in real time through video analysis.

For the same problem, some scholars have used different methods to conduct research, such as: Dai et al. [10] proposed to use image matching, moving state target tracking, gray scale and binary method to build a multiple linear regression model to study the melting process of silica, use generalized radius and area to reflect the changes in the melting process of silica, and finally get the melting rate of silica. Sun et al. [11] selected shape, perimeter, area and generalized radius as objects. By independently analyzing the influence of these four indices on the melting rate, area and shape were selected as the characteristic parameters of the edge profile of silica particles. Then, the actual melting rate of silica was estimated by using the characteristic index of the edge profile. Ma et al. [12] established the piecewise function and exponential function of the angle between the crucible center of mass and the crucible center, studied the position of the center of mass and its motion trajectory, used the generalized diameter method to effectively describe the morphology and area of SiO₂ in the melting process, used the microelement method to calculate the phase between the generalized diameter and the velocity, and used the correlation function to quantitatively characterize the melting rate at different times. Zhu et al. [13] used the optimized convolutional neural network (CNN) to track the moving target in the charge-coupled device (CCD) camera system, and used the coordinate translation transformation theory to describe the melting behavior of SiO₂. The characteristic parameters of SiO₂ melting process were extracted by hierarchical clustering (HAC) and Delaunay triangulation. Least square fitting (LSF) and dimensional analysis are used to establish the prediction model of the melting rate of SiO₂ at high temperature, and the actual melting rate of SiO₂ is compared with that obtained by experiment. By establishing a pixel clustering model, Guo et al. [14] analyzed the contour changes in the melting process of silica, proposed the centroid calculation method, plotted the centroid trajectory, established the change model of silica sample area and perimeter over time, and then obtained the change rate of silica mass. Zheng et al. [15] used the snake active contour algorithm combined with the Sobel operator to extract indicators representing the edge contour characteristics of silica during the melting process, including shape, perimeter, and area. Using the extracted skeleton features, a 3D skeleton generation model was built. From the skeleton data, the volume of silica was estimated and the parameter formula of the actual melting rate of silica was determined. For the same issue, Yang et al. [16] constructed the 3D image according to the 2D image by constructing a shape from shading (SFS) model. The melting rate of silica was calculated by polynomial curve fitting. The above literatures all use image processing related methods to study the melting rate of SiO₂, and the differences in the research methods are mainly reflected in the determination of the position of the center of mass and the solution of the area.

The solution methods for determining the volume and mass of SiO₂ are relatively straightforward, yet their accuracy and applicability warrant an in-depth examination and potential refinement. Building upon the aforementioned research approaches, this paper introduces an indirect method to ascertain the volume of SiO₂ during the iron waste melting process. Subsequently, it investigates the dissolution rate of SiO₂ through exponential fitting and contrasts the outcomes with the previously discussed primary algorithms. The key contributions of this paper are outlined as follows:

Utilization of image processing technology: The extraction of SiO₂ contours, centroid tracking, and area determination are facilitated through advanced image processing techniques.

Introduction of the indirect method: The paper introduces an indirect approach to derive the volume and mass of SiO₂, subsequently estimating the SiO₂ melting rate over a defined time sequence. These outcomes are compared against those generated by three other methods.

The paper's structure is as follows: Section 2 elaborates on the data sources and the data collection procedures employed in the research. Section 3 details the methods used for calculating SiO₂'s area, volume, and melting rate, accompanied by the entire modeling process. Section 4 provides a presentation of the obtained results. In Section 5, the outcomes of the two different methods are discussed, the proposed model's performance is juxtaposed with other typical advanced methods, and the model's validity and accuracy are scrutinized. Lastly, Section 6 concludes the full-text by summarizing the findings and looking ahead to future research directions.

2. Experimental set-up and data acquisition

There is a 1000W tungsten lamp at the bottom of the high-temperature copolymer coke oven to provide the light source, which is reflected by the gold-plated layer on the inner wall of the furnace, the light source is focused on the bottom of the crucible to heat the crucible, After the furnace slag is melted in the crucible at a constant temperature, the pure reagent iron waste is added to the crucible, a camera is installed on the top of the high-temperature copolymer coke oven, and an image is collected and stored with the camera every 1s during the melting process.

The data used in this paper are sequential images of the melting process of SiO₂. These sequential images were collected in the 497 ~ 610 seconds of the experiment, and the file sequence number generated one image per second according to the collection time order. The duration of each experiment was approximately 114 s [17]. Images of the SiO₂ process in the high-temperature melt pools at different times are shown in Figure 1(a)-(f). The 6 images correspond to 6 of physical change time points in the sequence images of the melting process, and the accumulation of dynamic differences between adjacent images can be used to characterize the melting process of SiO₂. The experimental setup and some of the collected images are shown in Figure 1.

3. Methods

The images of SiO₂ melting are first classified according to their time series, and then image processing technology is used to perform a series of processing on the given images, extract feature information from the images, and solve the volume of SiO₂. The structural block diagram investigated in this paper is shown in Figure 2.

To extract SiO₂ contours, a series of processing on the original image data is required. Since not all the existing data are grayscale images, grayscale image processing and enhancement are first performed on the image [18], and then K-means clustering algorithm [19] is used to further process the image. Finally, Canny filter function [20] and expansion corrosion are used to smooth the image [21]. To calculate the motion trajectory of the center of mass, first, a rectangular coordinate system based on the whole image system is set up so that one pixel represents one coordinate, and then the center of mass position model is set up to minimize the convolution integral of the horizontal and vertical coordinates, respectively, and the position of the center of mass is obtained. After the position of the center of mass is obtained, the edge contour of SiO₂ is extracted, and the cross-sectional area of SiO₂ in the melting process is calculated according to the ratio of pixels equal to the ratio of area. Before solving the melting rate, it is necessary to calculate the volume of SiO₂. The gray value difference between each pixel is used to assume the height of each point, and the volume of SiO₂ is solved by using the method of large volume reduction groove. However, this method can only obtain the volume of the upper half of SiO₂, assuming that SiO₂ is symmetrical about the maximum section plane in the melting process. After obtaining the volume data, the density is multiplied and the equation is obtained by fitting. The melting rate of SiO₂ can be obtained by deriving the equation.

3.1. Determination of the contour area of SiO₂

First, K-means algorithm is used to process the image to get the approximate contour, then Canny filtering technology is used to eliminate the noise outside the contour, and corrosion operation is used to eliminate the burrs around the contour to get the specific contour. The horizontal and vertical coordinates of the center of mass are determined by binarization and convolution. Then find out the contour of the crucible, get the relationship between SiO₂ and the cross-sectional area of the crucible, through the binary image digital matrix to represent the area of SiO₂.

3.1.1. Extraction of the SiO₂ profile

First, the original image is converted to a grayscale image so that the image becomes a classic grayscale image. Since the obtained gray image contrast is low, that is, the difference between the SiO₂ image and the background image is small, image enhancement is needed for low contrast images to highlight the difference between the SiO₂ image and the background image. In this paper, an image enhancement method based on fuzzy sets is adopted to extract fuzzy features of gray image, and a mathematical model of conversion from spatial domain to fuzzy domain is established. Then, the K-means algorithm is used to divide the existing data into many different categories through multiple iterations, and the clustering center is gradually updated several times to achieve the expected goal. The data similarity in the sample cluster is calculated. Assuming that the data sample has k clustering subsets, the data object is randomly assigned to k sample clusters, and the average value of each cluster is further calculated. That's the eigenvalue of that cluster. Finally, in the process of applying the model, it is found that after image segmentation, there are still some interference factors such as burrs and noise in the contours of SiO₂ images, and it is difficult to extract effective information from the images. To solve this problem, the Canny filter function is used to eliminate the noise outside the contour, and the corrosion operation technology is used to basically eliminate the burrs around the contour. To modify the shadow part of the SiO₂ image, this paper uses the expansion theory to effectively fill the shadow part and improve the accuracy of the effective area. To improve the SiO₂ shadow and ensure the integrity of the image, morphological open and close operations are performed on the later image, and elements C and D of two different structures are recorded.

3.1.2. Extraction of the SiO₂ profile

Since the image size processed by this model is M×N, a two-dimensional planar rectangular coordinate system XOY is established to divide the image into M×N grids, where each pixel block represents a coordinate (x_i, y_j) (i=1, 2, ... , M, j=1, 2, ... , N), as shown in Figure 3.

In the process of image processing, the feature contour of SiO₂ image is A binary image, assuming that the binary image is R(x_i, y_j), the white area in the image is A, the black area is B, and the area A and area B can be expressed as:

{\begin{cases} R_{(x_{i}, y_{j})} = {\begin{cases} 0, (x_{i}, y_{j}) \in A \\ 1, (x_{i}, y_{j}) \in A \end{cases} \\ R_{B}_{(x_{i}, y_{j})} = {\begin{cases} \emptyset, (x_{i}, y_{j}) \in B \\ \emptyset, (x_{i}, y_{j}) \in B \end{cases} \end{cases}

(1)

Assuming that the centroid coordinate of SiO₂ is R₀(x₀, y₀), its horizontal and vertical coordinates are defined as:

{\begin{cases} x_{0} = \sum_{(x_{i}, y_{j}) \in A}^{A} x \cdot R (x_{i}, y_{j}) / \sum_{(x_{i}, y_{j}) \in A}^{A} R (x_{i}, y_{j}) \\ y_{0} = \sum_{(x_{i}, y_{j}) \in A}^{A} y \cdot R (x_{i}, y_{j}) / \sum_{(x_{i}, y_{j}) \in A}^{A} R (x_{i}, y_{j}) \end{cases}

(2)

The position of any point in a region is represented by R(m, n), then the convolution integral of the shortest distance between any two points in the horizontal coordinate is defined as:

f_{x} (k) = \sum_{m = 1}^{M} \sum_{n = 1}^{N} {(k - x_{i})}^{2} \cdot R (m, n) = d (k, x_{i}) \cdot R (x_{i}, y_{j})

(3)

Similarly, the convolution integral of the ordinate is expressed as:

f_{y} (l) = \sum_{m = 1}^{M} \sum_{n = 1}^{N} {(l - y_{i})}^{2} \cdot R (m, n) = d (l, y_{i}) \cdot R (x_{i}, y_{j})

(4)

When the two convolution integrals are minimum values, k and l are the horizontal and vertical coordinates of the image center, respectively.

3.1.3. Modeling of SiO₂ area

Based on the effective segmentation image obtained above, image processing technology is first used to remove the black background of the entire image, and only the crucible outline image and the SiO₂ outline image are retained. After segmentation, an image containing only the SiO₂ profile and an image containing only the crucible profile can be obtained to facilitate the subsequent solution of the area of the crucible and the SiO₂ profile. The ratio of the cross-sectional area of the SiO₂ to the cross-sectional area of the crucible is equal to the ratio of the number of pixels of the two, which can be expressed as：

\frac{S_{c}}{S_{d}} = N_{c} {[\sum_{i = 1}^{N} n_{i}]}^{- 1} = \frac{1}{λ_{0}}

(5)

where λ₀ is the proportional coefficient between S_c and S_d; S_c is the cross-sectional area of the crucible; S_d is the area surrounded by the contour edge of SiO₂, n_i is a number of possible contour areas of SiO₂, this is because some of the edge contour of the silica image is not completely closed, then it is necessary to separate the small contour and the main contour of the sum to achieve higher accuracy.

If the radius of the crucible is defined as R', the expression for the cross-sectional area of the crucible is:

S_{c} = π R'^{2}

(6)

By substituting formula (6) into formula (5), the relationship between SiO₂ and the cross-sectional area of the crucible is as follows:

\frac{π R'^{2}}{S_{d}} = N_{c} {[\sum_{i = 1}^{N} n_{i}]}^{- 1} = \frac{1}{λ_{0}}

(7)

S_{d} = \frac{π R'^{2}}{N_{c} {[\sum_{i = 1}^{N} n_{i}]}^{- 1}} = π \frac{R'^{2}}{N_{c}} [\sum_{i = 1}^{N} n_{i}]

(8)

The binary digital image is represented by a matrix to realize the effective number of pixels, and its matrix is represented as:

{(G_{ab})}_{w h o l e f i e l d} = [\begin{array}{l} G_{00} G_{01} G_{02} \dots G_{0 j} \dots G_{0 b} \\ G_{10} G_{11} G_{12} \dots G_{1 j} \dots G_{1 b} \\ G_{20} G_{21} G_{22} \dots G_{2 j} \dots G_{2 b} \\ ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ \\ G_{i 0} G_{i 1} G_{i 2} \dots G_{ij} \dots G_{ib} \\ ⋮ ⋮ ⋮ \dots ⋮ ⋱ ⋮ \\ G_{a 0} G_{a 1} G_{a 2} \dots G_{aj} \dots G_{ab} \end{array}]

(9)

where, G_ij=0 or G_ij=1. According to this binary principle, the computer is made to search the entire image field for the numerical values "0" and "1" of the binary image. The digital value "1" represents the image within the SiO₂ contour in the entire image area. When the computer searches for the digital value "1", it records the coordinates of the pixel. Then the search continues, and the number of coordinate points calculated is the number of pixels. In the same way, you can get the number of pixels in the crucible.

3.2. Establishment of a volume solution model for SiO₂

In establishing the SiO₂ volume model, the indirect method is used to solve the SiO₂ volume, and the obtained volume is plotted on a scatter plot. The relationship between the volume and time of SiO₂ is obtained by using function fitting in MATLAB.

3.2.1. Image processing

First, the piecewise linear transformation is performed. The matplotlib library of the PYTHON software [22] was used to obtain the histogram of the image, highlighting the desired gray intervals, and reducing other gray intervals. First, the image is cropped and the unwanted black areas are subtracted. The color image is extracted, then the gray value obtained by the averaging method replaces the value of the three primary colors in the original color image, and the processed image is pasted back into the original position. Taking the 0497 image modification as an example, the modification process is shown in Figure 4.

The hist function in PYTHON's matplotlib library is used to extract the gray values in the image, and the resulting gray values are plotted in a histogram. The gray values in the SiO₂ profile determined above are plotted as a separate histogram. By analyzing the histogram, it can be seen that the difference in gray values is large, and the place with large gray values is the gully, which needs to be highlighted. For other gray values that are not needed, interval compression can increase the gray value difference of the image so that the discrimination of SiO₂ in the image is higher.

3.2.2. Indirect solver-based volume solution model

The gray value difference between each pixel is used to define the height of each point, and the volume of SiO₂ is solved by subtracting the groove with large volume. This model can only obtain the volume above and below the cross section. Here it is assumed that the volume above and below the cross section is symmetrical with respect to the cross section. As shown in Figure 5, at some point the plane is artificially assigned a spatial height H. If H is a constant, then the volume of the SiO₂ particles can be expressed as the volume of a cylinder:

V_{1} = H \iint_{D} d x d y = H S_{d}

(10)

S_d is the area of the SiO₂ profile. Note that the cylinder volume is the direct volume of the SiO₂ particles, not the actual volume of the SiO₂ particles, but the direct volume and the actual volume have the same geometric height H, as shown in Figure 5:

The graph is filtered twice using the edge filtering technique. The purpose of this filtering is to mine the undetected spatial region in the binary image to obtain the gullies on the surface of the SiO₂ stereoscopic image, which indirectly plays the role of mining the three-dimensional coordinates of the image surface. The effective volume of the direct volume, also subtracted from the volume of its surface gully, is expressed as:

V_{m} = V_{1} - V_{g} = H \iint_{D} d x d y - h \int_{c} d x = H S_{d} - h S_{g}

(11)

where, H is the average height of the trench; Sg is the area at the bottom of the trench. The bottom area of the trench is generally considered to be a finite pixel band, so the specific calculation method of the bottom area is consistent with Sd, which must be related to the crucible cross-sectional area and the number of pixels, expressed as:

S_{g} = \frac{π R'^{2}}{N_{c} {[\sum_{i = 1}^{N} n_{gi}]}^{- 1}} = π \frac{R'^{2}}{N_{c}} [\sum_{i = 1}^{N} n_{gi}]]

(12)

In formula (12), the contents in parentheses represent the total number of pixels contained in the bottom region of the trench. For the sake of simplicity, the actual volume of SiO₂ is standardized. Assuming that the actual volume of SiO₂ is an ellipse, its volume is expressed as:

V_{s} = \iint_{D} H (x, y) d x d y = \frac{4 π}{3} a b c

(14)

Subtracting the trench volume gives the actual effective volume of SiO₂:

V_{c} = V_{s} - h S_{g} = \frac{4 π}{3} a b c - h π \frac{R'^{2}}{N_{c}} [\sum_{i = 1}^{N} n_{gi}]

(14)

When the CCD camera is facing the S2 plane, the height h of the trench can be related to the height H of the ellipsoid, expressed as:

\frac{H}{h} = {[\sum_{i = 1}^{N} n_{gi}]}^{- 1} \sum_{i = 1}^{N} n_{i}

(15)

Substituting equation (15) into equation (14), Vc can be expressed as:

\begin{array}{l} V_{c} = \frac{4 π}{3} a b c - [\sum_{i = 1}^{N} n_{i}] \sum_{i = 1}^{N} n_{gi} H π \frac{R'^{2}}{N_{c}} [\sum_{i = 1}^{N} n_{gi}] \\ = \frac{4 π}{3} a b c - [\sum_{i = 1}^{N} n_{i}] H π \frac{R'^{2}}{N_{c}} {[\sum_{i = 1}^{N} n_{gi}]}^{2} \end{array}

(16)

If H=2c and Sd=πab, the actual effective volume of SiO₂ can be further expressed as:

V_{c} = \frac{2}{3} H π \frac{R'^{2}}{N_{c}} [\sum_{i = 1}^{N} n_{i}] - {[\sum_{i = 1}^{N} n_{i}]}^{- 1} H π \frac{R'^{2}}{N_{c}} {[\sum_{i = 1}^{N} n_{gi}]}^{2}

(17)

When R' and H are connected, we get:

\frac{R'}{H} = \frac{N_{R^{'}}}{N_{H}}, H = \frac{R' N_{H}}{N_{R^{'}}}

(18)

where, N_R' and N_H are image elements of crucible radius R' and stereoscopic image height H, respectively. Substituting the formula into V_c, we obtain:

V_{c} = \frac{2}{3} \frac{N_{H}}{N_{R'}} π \frac{R'^{3}}{N_{c}} [\sum_{i = 1}^{N} n_{i}] - {[\sum_{i = 1}^{N} n_{i}]}^{- 1} \frac{N_{H}}{N_{R'}} π \frac{R'^{3}}{N_{c}} {[\sum_{i = 1}^{N} n_{gi}]}^{2}

(19)

In the above formula, R' is a known quantity, and other parameters represent the corresponding image parameters that can be directly counted by the computer. On this basis, the actual volume of SiO₂ corresponding to different times can be calculated. If the density of SiO₂ is ρ, then the mass μ per second of SiO₂ can be expressed as:

μ = ρ V_{c} = ρ {\frac{2}{3} \frac{N_{H}}{N_{R'}} π \frac{R'^{3}}{N_{c}} [\sum_{i = 1}^{N} n_{i}] - {[\sum_{i = 1}^{N} n_{i}]}^{- 1} \frac{N_{H}}{N_{R'}} π \frac{R'^{3}}{N_{c}} {[\sum_{i = 1}^{N} n_{gi}]}^{2}}

(20)

3.3. Modeling of SiO₂ melting rate

The dissolution behavior of oxide in slag has a major impact on metal cleanliness, refractory erosion and slag formation in metallurgical processes. For example, to reduce refractory erosion, a slow and indirect melting model can be established to improve refractory life. For typical clean steel production, the oxides must melt quickly into the slag phase, and if the melting is not fast enough, the undissolved inclusions will remain near the slag/steel interface, increasing the risk of entrainment of the molten steel. Therefore, the melting rate model of SiO₂ is established to study its melting behavior.

Set the density of SiO₂ as ρ and the mass of SiO₂ as μ, given the volume Vc of SiO₂ when it is melted:

μ = ρ V_{c}

(21)

The function of SiO₂ volume change with time t can be expressed as:

V = λ e^{γ t}

(22)

where, λ, γ are the parameters of the function, SiO₂ mass μ change function with time:

μ = ρ λ e^{γ t}

(23)

By deriving equation (23), the melting rate function of SiO₂ can be obtained:

V_{c}' = ρ λ γ e^{γ t}

(24)

4. Results

According to the model established above, and the traversal search algorithm of MATLAB is used to obtain the centroid coordinates and area of SiO₂. The solution of SiO₂ volume is to idealize SiO₂ into an ellipsoid, take the obtained area as the maximum cross-sectional area of the ellipsoid, and then calculate the volume. The Fitting Toolbox is used to fit the functional relationship between volume and time, and the relationship function between mass and time is obtained according to the physical relationship between volume and mass. The first derivative of this function is the melting rate of SiO₂.

4.1. The result of SiO₂ area

According to the centroid coordinate model established above, the centroid coordinates are obtained by using the ergodic search algorithm, and then the plot function is called to plot the centroid motion trajectory, as shown in Figure 6(a).

The number of crucible pixels and the number of SiO₂ profile pixels are substituted into formula (8) to obtain the area data of SiO₂ profile per second. The plot function in MATLAB is used to draw an image of the SiO₂ area change, as shown in Figure 6(b).

4.2. Results of Volume and Melting Rate of SiO₂

Among the 114 images collected in this paper, SiO₂ has basically melted completely in the last 14 images, and SiO₂ images are not obvious in the images, so the position of SiO₂ cannot be determined, and it is difficult to extract relevant data. Therefore, the first 100 images are selected for relevant calculation and solution. Assuming that the density of SiO₂ is 2.2g/cm³, the mass of SiO₂ in each image is obtained by the above model, and then the trajectory function of the quality data is established. MATLAB software was used to draw the mass scatter point, and then the function fitting toolbox was used to perform exponential function fitting on the scatter point. The goodness of fit of the quadratic exponential function fitting (R²=0.930) was better than that of the primary exponential function fitting (R²=0.927), and the exponential fitting function obtained was as follows:

V = - 429.9 e^{- 0.4425 t} + 430.1 e^{- 0.4426 t}

(25)

The function image obtained by fitting is shown in Figure 7(a):

The melting rate of SiO₂ is obtained by deriving the formula (25):

μ' = 0.4185 e^{- 0.4425 t} - 0.4188 e^{- 0.4425 t}

(26)

The average rate obtained is 0.086g/s, and the image of the melting rate change is shown in Figure 7(b).

5. Discussion

Based on the indirect solution model, this paper solves the functional relationship between volume and time, and then obtains the dissolution rate of SiO₂. In this part, the indirect solution method is compared with the SFS method, dimensional analysis method and quantitative characterization method, and the pros and cons of each are summarized.

5.1. Solution of SiO₂ volume based on SFS model

SFS three-dimensional reconstruction [16] uses Lambert's reflection principle and Lambert's cosine theorem to find the angle between incident light, reflected light and normal when Lambert's reflector is the origin, and then solves the distance between image pixels and CCD plane under the established three-dimensional coordinate system with CCD as the origin according to the transformation formula of the light source coordinate system and the imaging coordinate system. Finally, the volume of SiO₂ can be obtained by taking the crucible as the horizontal plane to obtain the height of SiO₂.

The SFS model is applied to all the images, taking the processing of the first image as an example, the image is first cropped to the appropriate size and the SiO₂ is included in the graph. Then, using the SFS algorithm and XOY as a plane, the corresponding height value of each pixel was obtained according to the SFS model, and the 3D reconstructed graph as shown in Figure 8 (a) was drawn:

Through the SFS model, the obtained SiO₂ volume data shows that at the end of the melting of SiO₂, the difference in SiO₂ volume change is less than 0.0001, and it is infinitely close to 0. Therefore, all the data less than 0.0002 were discarded, and the obtained data were drawn into a scatter plot, and the fitting function image drawn is shown in Figure 8(b).

The scatter plot was fitted by a primary and a secondary exponential function, respectively, and the relevant data obtained showed that the goodness of fit of the quadratic exponential function fit (R²=0.945) was equivalent to that of the primary exponential function fit (R²=0.946). In this case, the final fit function obtained was as follows:

V = 0.6209 e^{- 0.02438 t}

(27)

Using the mass-volume relationship, the mass μ of SiO₂ can be obtained, and the relationship function between melting rate μ' and time can be obtained by mass derivative:

{\begin{cases} μ = 0.0014 e^{- 0.02438 t} \\ μ' = 0.000033 e^{- 0.02438 t} \end{cases}

(28)

The SFS algorithm is used to reconstruct the three-dimensional model and extract the volume value, which is also realized based on the assumption that the volume above the cross-section of SiO₂ is symmetrical with the volume below the cross-section. Since the image is a CCD image, this method can easily realize the three-dimensional reconstruction and volume solution of SiO₂. The melting rate of SiO₂ obtained by this method is 0.083g/s.

5.2. Comparing the results of different methods

In this section, the results obtained by this method are compared with SFS method, quantitative characterization method and dimensional analysis method, respectively, and the advantages and disadvantages of different models are analyzed.

Based on the three-dimensional reconstructed volume results obtained by the SFS method [16], polynomial or exponential fitting can be used to obtain the functional relationship between volume and time, and then the functional relationship between mass and time is obtained according to mass is equal to volume multiplied by density, and finally the melting rate of SiO₂ is calculated by derivation. However, because the volume obtained by polynomial fitting cannot accurately reflect the change of melting rate after derivation, there is a large error. Therefore, in this paper, the melting rate is analyzed by exponential function fitting, and the melting rate results obtained by solving are shown in the blue line in Figure 9.

In the quantitative characterization method model [12], SiO₂ is idealized as a sphere, its generalized diameter is taken as the diameter of the sphere, and the problem of solving the melting rate of SiO₂ is transformed into a function of solving the relationship between diameter and time. Since SiO₂ is not a sphere in real life, the results obtained by the quantitative characterization method are bound to be biased, as shown by the green line in Figure 9.

Zhu et al [13] used dimensional analysis to solve the same problem, which assumes that every physical law has one or more uncorrelated dimensionless variables. Buckingham's π theorem [23] states that the number of uncorrelated dimensionless quantities is equal to the total number of variables involved minus the number of uncorrelated fundamental quantities. In setting up the model, the expressions of functions S(t), C(t) and R(t) of SiO₂ area, perimeter, generalized radius and time are known, and the density of pure SiO₂ particles is ρ. The change rule of SiO₂ particle mass µ(t) can be determined according to dimensional analysis. The result of SiO₂ dissolution rate in this problem is shown by the black line in Figure 9. Because the dimensional analysis method obtained a small number of characteristic physical quantities of SiO₂ in the analysis process, it could not fully display the mass dimension of SiO₂, and the obtained results were not fitted in the end, but simply traced the points, so the result graph has a certain deviation from the result graph of other methods in this paper. Table 1 lists several methods used in different literature and compares their advantages and disadvantages.

To compare the result graphs of different methods with those obtained in this paper, the result curves of the indirect solution method in this paper are red lines, as shown in Figure 9.

As shown in Table 1, the quantitative characterization method and the indirect method in this paper are easy to calculate and have low requirements on the number and format of photographs. Dimensional analysis can directly obtain the functional relationship between SiO₂ mass and time, but the number of physical quantities that reflect the physical properties of SiO₂ is large. The SFS method can obtain three-dimensional images of SiO₂, and the melting rate is more reasonable, but it requires high photo quantity and photo format, and CCD images must be analyzed. The melting rate trend of SFS method with polynomial fitting will be abnormal, if exponential fitting is used, the melting rate trend is reasonable.

6. Conclusions

Aiming at the melting behavior of iron tailings in high-temperature molten pool, this paper uses a non-contact CCD video recording system to obtain dynamic visual data (video stream) of solvent dissolution in high-temperature molten pool. With the help of computer vision recognition technology and data modeling theory, the indirect solution method is applied to analyze the melting process of iron tailings in molten slag. The rate is determined to provide theoretical and technical support for the direct fiber forming process of BF slag. Through the research of this paper, the following aspects are completed: (1) The image processing technology is used to solve the centroid and area of SiO₂; (2) An indirect solution method is proposed, and the volume of SiO₂ is well obtained, and the melting rate of SiO₂ is obtained by exponential fitting. (3) The current relevant methods are fully compared, and the results show that the indirect solution method or SFS method with exponential fitting has a relatively good effect.

This study still has some shortcomings: (1) In the discussion section, the possible sources of error of different methods are explained. Although the results of different methods are compared, due to the nature of the problem, each method has its advantages and disadvantages. Under different backgrounds, it is difficult to evaluate which method is the best, and the overall error is controllable, but the error still exists. In the future, research on the accuracy of different evaluation methods can be considered to better evaluate the accuracy of different methods. (2) There is still room for improvement and perfection of the correlation fitting method. Polynomial fitting is not very suitable for solving the melting rate, but whether exponential fitting is perfect can also be further discussed. (3) The study proposed in this paper used only images of one cycle and did not compare images of multiple sets of parallel experiments. Although one set of experimental images may support the conclusions of this paper, the study of multiple sets of parallel control groups is also a direction worth exploring in the future.

Author Contributions

Conceptualization, C.L., J.C.; methodology, C.L., J.C.; software, Y.Z., J.Z and. W.S.; validation, C.L., Y.Z, W.S. and Q.Z.; formal analysis, C.L., Y.Z, J.Z., W.S. and J.C.; investigation, C.L., Y.Z, J.Z., W.S. and J.C.; resources, J.C.; data curation, C.L. and J.C.; writing—original draft preparation, M.Z., C.L. and J.C.; writing—review and editing, C.L., M.Z. and J.C.; visualization, C.L. and J.C.; supervision, J.C.; project administration, A.X., J.C.; funding acquisition, C.L., A.X., J.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Natural Science Foundation of Jiangsu Province (grant number: BK20190873), the Postgraduate Education Reform Project of Yangzhou University (grant number: JGLX2021_002), the Undergraduate Education Reform Project of Yangzhou University (Special Funding for Mathematical Contest in Modeling) (grant number: xkjs2023049), as well as the Lvyang Jinfeng Plan for Excellent Doctors of Yangzhou City.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available upon request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

Carmignano, O., S. Vieira, A. Teixeira, F. Lameiras, P. Brandao and R. Lago. "Iron ore tailings: Characterization and applications. Journal of the Brazilian Chemical Society, 32 (2021): 10.21577/0103-5053.20210100. [CrossRef]
Ding, B., H. Wang, X. Zhu, X.-Y. He, Q. Liao and Y. Tan. "Crystallization behaviors of blast furnace (bf) slag in a phase-change cooling process." Energy & Fuels 30 (2016): 3331-39. 10.1021/acs.energyfuels.5b03000. [CrossRef]
Qin, Y., X. Lv, C. Bai, G. Qiu and P. Chen. "Waste heat recovery from blast furnace slag by chemical reactions." JOM 64 (2012): 997-1001. 10.1007/s11837-012-0392-3. [CrossRef]
Wang, W., S. Dai, L. Zhou, J. Zhang, W. Tian and J. Xu. "Viscosity and structure of mgo–sio2-based slag melt with varying b2o3 content. Ceramics International, 46 (2019): 10.1016/j.ceramint.2019.10.082. [CrossRef]
Ren, Q., Y. Zhang, Y. Long, Z. Zou, S. Chen and J. Li. "Investigation on the effect of mgo content on the crystallization behavior of synthetic bf slag." Materials and Manufacturing Processes 33 (2018): 1654-60. 10.1080/10426914.2018.1424903. [CrossRef]
Chen, J., C. Liang, J. Chen and Q. Zhou. "Modeling analysis of melting and crystallization process of mold flux based on the image processing technology." Crystals 13 (2023): 594. https://www.mdpi.com/2073-4352/13/4/594.
Ren, Q., Y. Zhang, Y. Long, S. Chen, Z. Zou, J. Li and C. Xu. "Crystallization behavior of blast furnace slag modified by adding iron ore tailing." Journal of Iron and Steel Research International 24 (2017): 601-07. 10.1016/S1006-706X(17)30091-2. [CrossRef]
Cai, S., T. -l. Tian, Z.-H. Guo and Y.-z. Zhang. "Effect of acidity coefficient on crystallization behaviour of modified blast furnace slag." Ironmaking & Steelmaking 49 (2022): 555-61. 10.1080/03019233.2021.2014170. [CrossRef]
Komizo, Y. and H. Terasaki. "Optical observation of real materials using laser scanning confocal microscopy part 1 – techniques and observed examples of microstructural changes." Science and Technology of Welding and Joining 16 (2011): 56-60. 10.1179/136217110X12785889549868. [CrossRef]
Dai, P., Y. Gu, R. Zhou, J. Guo, R. Li, Y. He, W. Ji and S. Chen. "Research questions on silica melting based on image analysis." Presented at 2020 IEEE Conference on Telecommunications, Optics and Computer Science (TOCS), 2020. 168-71. [CrossRef]
Sun, Y. "Solving the problem of silicon dioxide melting based on deviation model. Non-Metallic Material Science, 2 (2020): 10.30564/omms.v2i1.1653. [CrossRef]
Ma, X., H. Lv and K. Zhang. "Image analysis of high temperature melting process of iron tailings based on clustering model." Presented at 2020.
Zhu, Y., P. He, X. Ma, K. Zhang, H. Li, H.-Y. Mi, X.-Z. Xiong, Z. Li and Y. Li. "Perspective and prediction of the rule of high temperature melting of sio₂ via visual analysis." IEEE Access 8 (2020): 171334-49. [CrossRef]
Guo, J., X. Zhang, Y. Zhang and Z. Pan. "Melting representation model of silicon dioxide analyzed based on image." Presented at 2021 IEEE International Conference on Computer Science, Electronic Information Engineering and Intelligent Control Technology (CEI), 2021. 450-54. [CrossRef]
Zheng, T., S. Li and L. Zhang. "Characterization model of silicon dioxide melting based on image analysis." Journal of Intelligent & Fuzzy Systems 43 (2022): 3655-77. [CrossRef]
Yang, A., L. -J. Wang, W.-N. Ma, M. Tang and J. Chen. "Shape from shading-based study of silica fusion characterization problems." Minerals 12 (2022): 1286. https://www.mdpi.com/2075-163X/12/10/1286.
"Asia and pacific mathematical contest in modeling, question 2022a.." Beijing Society of Image and Graphics., 2022. https://www.saikr.com/c/nd/6277. August 10th 2023.
Qi, Y., Z. Yang, W. Sun, M. Lou, J. Lian, W. Zhao, X. Deng and Y. Ma. "A comprehensive overview of image enhancement techniques." Archives of Computational Methods in Engineering 29 (2022): 583-607. 10.1007/s11831-021-09587-6. [CrossRef]
MacQueen, J. "Some methods for classification and analysis of multivariate observations." Presented at 1967.
Canny, J. "A computational approach to edge detection." IEEE Transactions on Pattern Analysis and Machine Intelligence PAMI-8 (1986): 679-98. [CrossRef]
MathWorks. "Types of morphological operations." The MathWorks, Inc., https://ww2.mathworks.cn/help/images/morphological-dilation-and-erosion.html. August 10th 2023.
Matplotlib. "Matplotlib: Visualization with python." The Matplotlib development team, https://matplotlib.org/. August 10th 2023.
Gupta, G. S., S. Sarkar, A. Chychko, L. D. Teng, M. Nzotta and S. Seetharaman. "Chapter 3.1 - process concept for scaling-up and plant studies." In Treatise on process metallurgy. S. Seetharaman. Boston: Elsevier, 2014, 1100-44.

Figure 1. Schematic diagram of the experimental equipment and some of the collected images. On the left is the high temperature copolymer coke oven and CCD image acquisition equipment, on the right (a)~(f) are some images taken under different time series and corresponding observed SiO₂ melting state images.

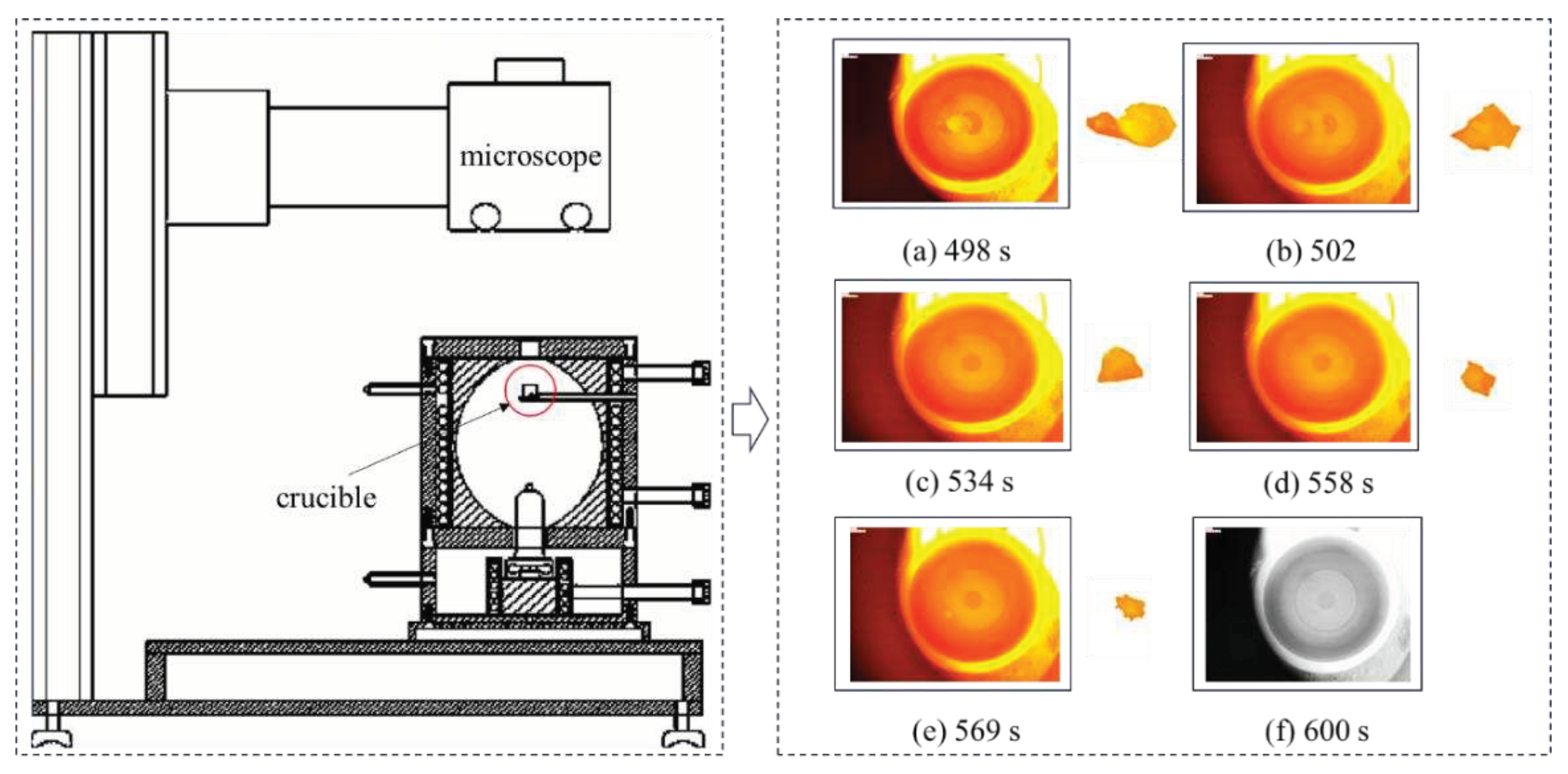
Figure 2. Schematic diagram of the structure of this paper.

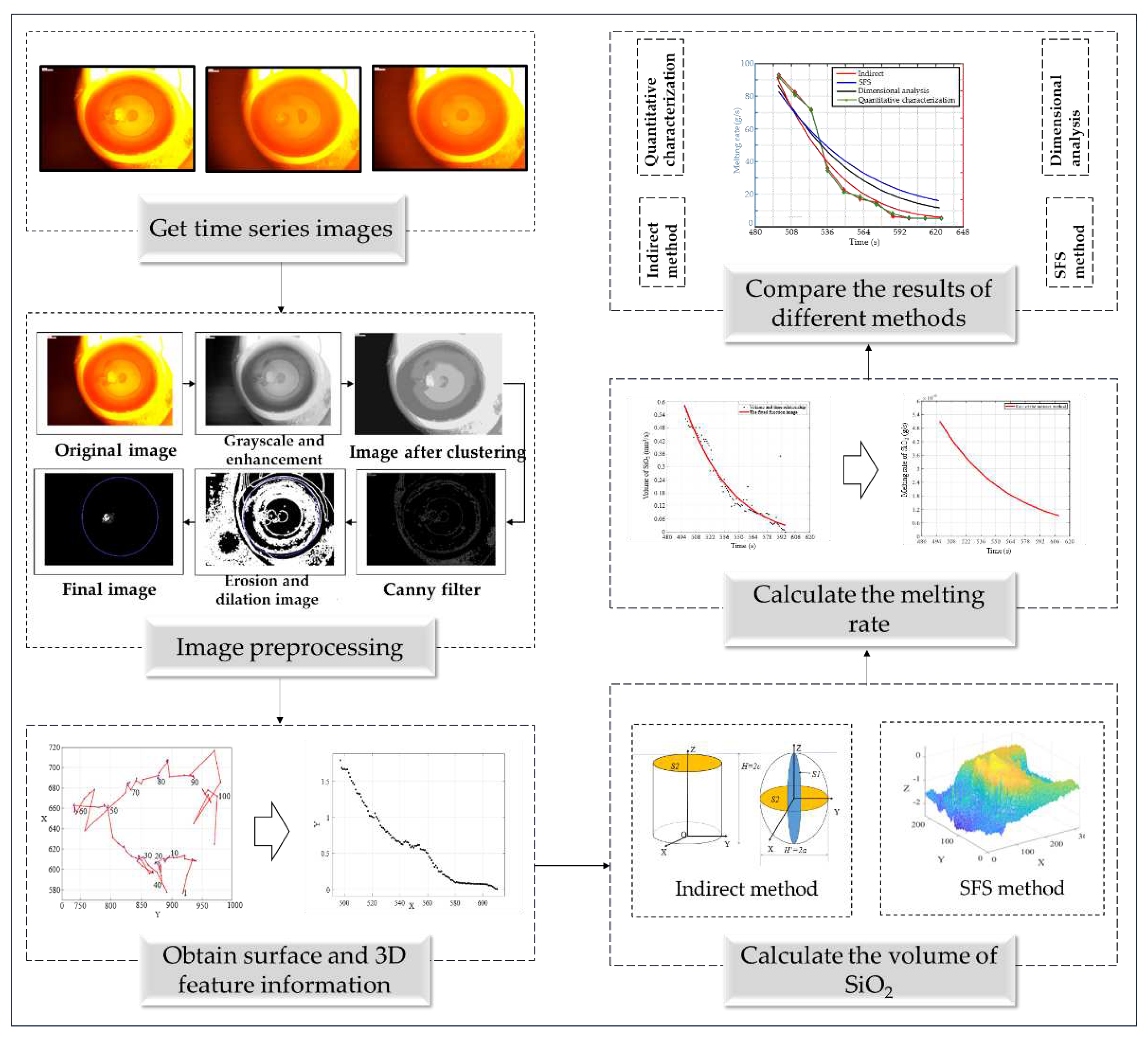
Figure 3. Schematic representation of the Cartesian coordinate system established over the entire image area.

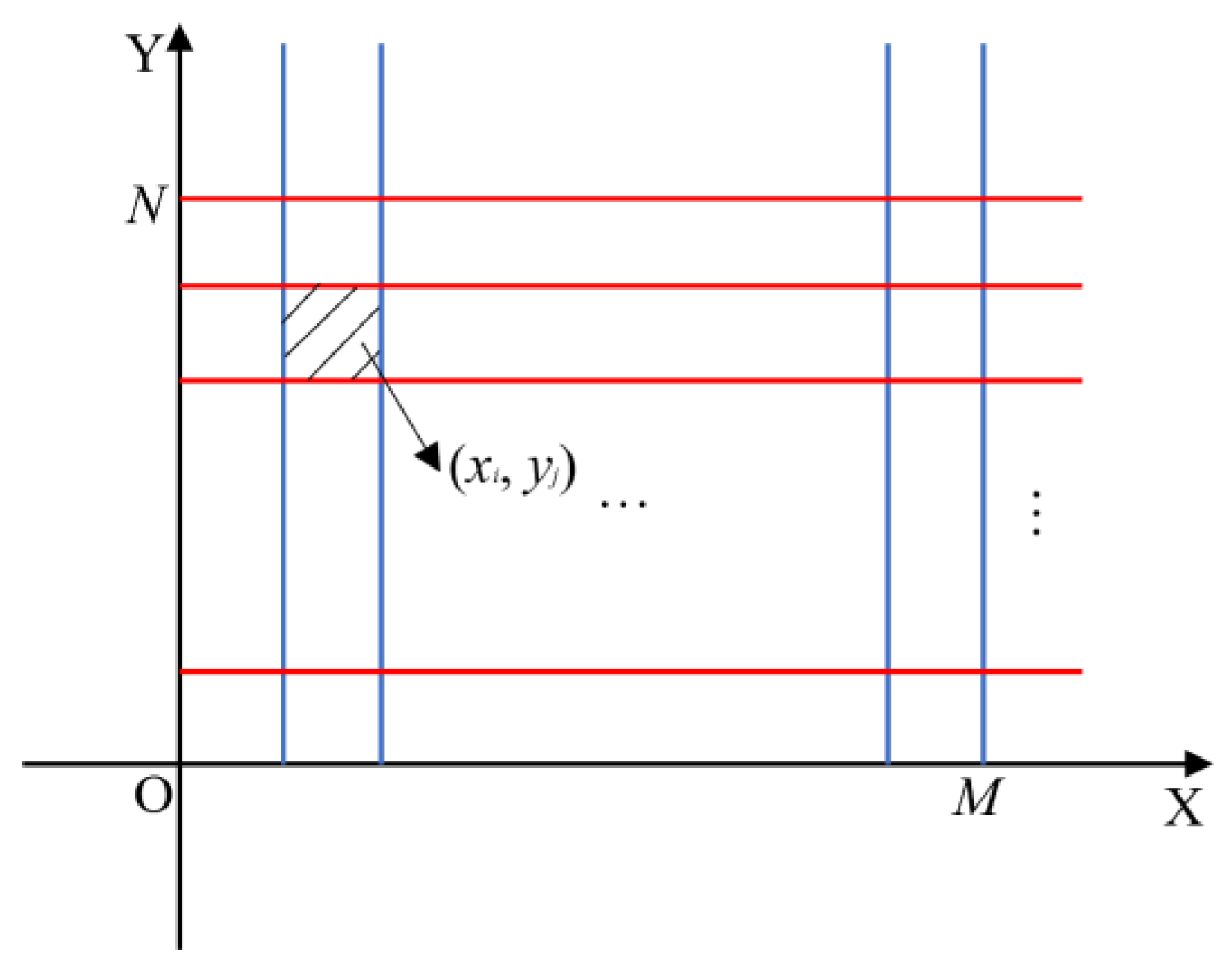
Figure 4. Processing images of picture with series number 0497.

Figure 5. Schematic diagram of SiO2 volume calculation.

Figure 6. Trajectory diagram of centroid motion and variation diagram of SiO₂ area. (a) is the trajectory diagram of SiO₂ centroid motion; (b) is the variation diagram of SiO₂ area with time.

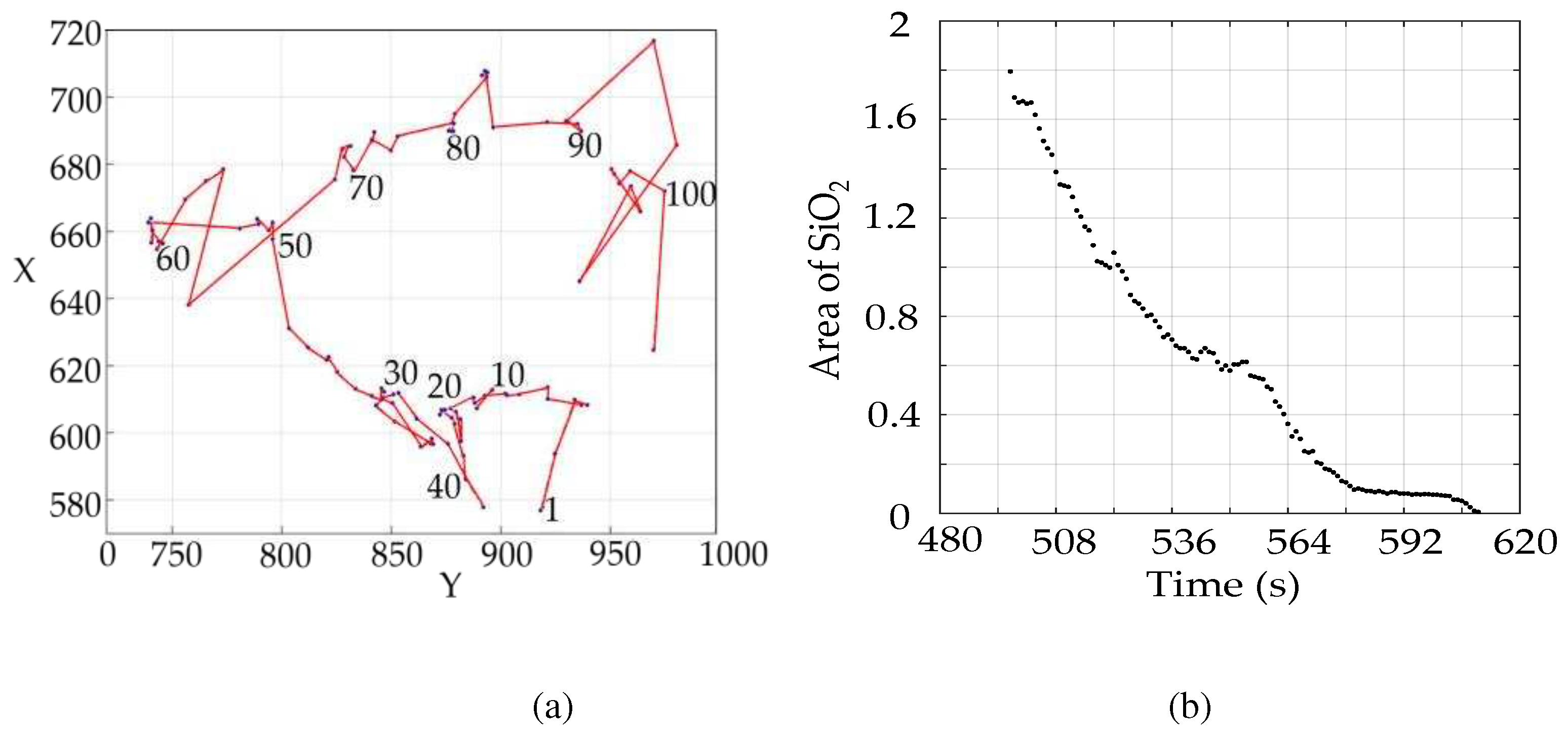
Figure 7. Volume change image and melting rate results. where (a) is the volume change image obtained by fitting the scatter plot, and (b) is the melting rate change image of SiO2.

Figure 8. Results of the SFS method. (a) 3D reconstruction of the image with serial number 0497, (b) is the scatter plot of SiO₂ volume versus time and the fitting curve.

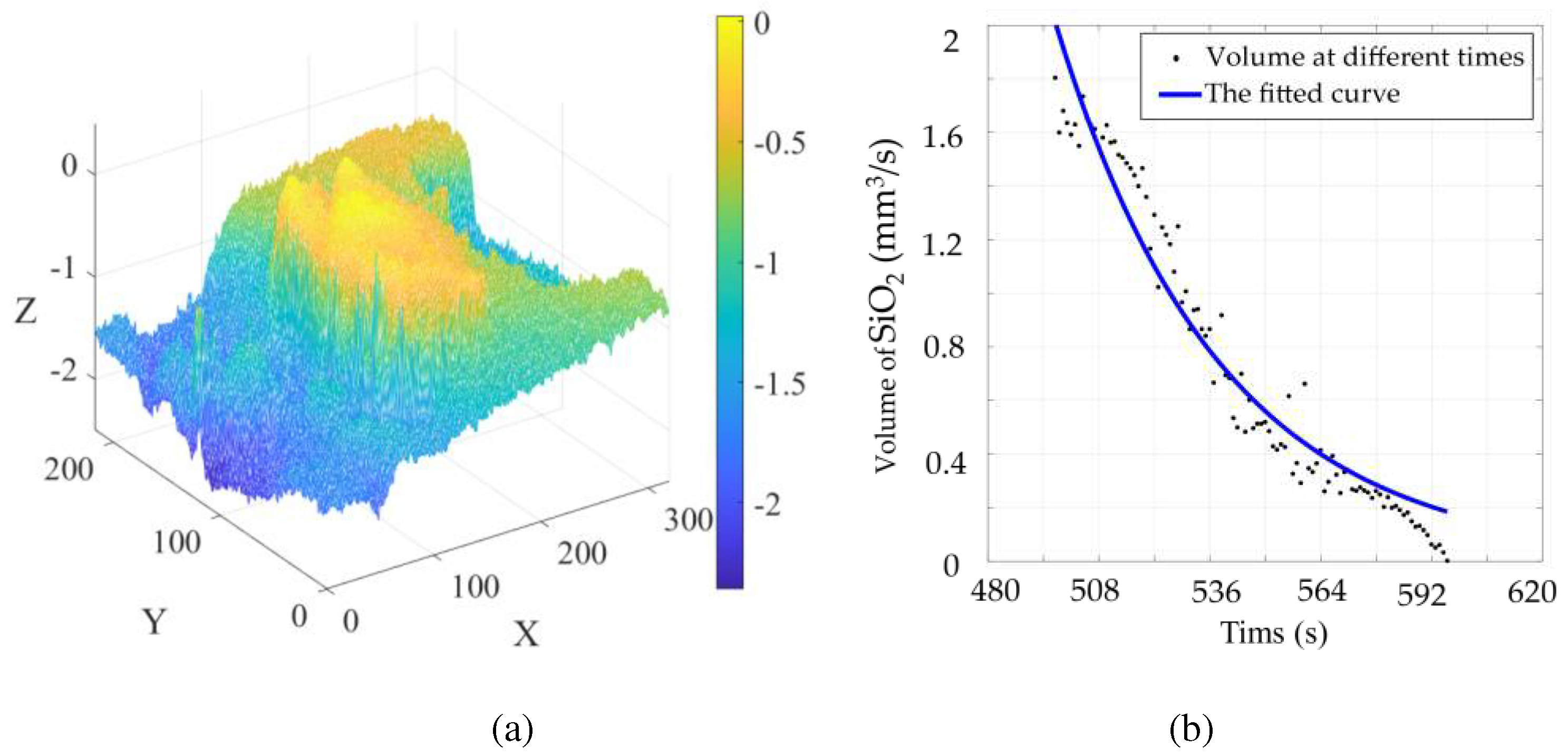
Figure 9. Comparison of the results from different analytical methods. The red, blue, black, and green lines represent the results obtained by the indirect solution, the SFS, the dimensional analysis and the quantitative characterization methods, respectively.

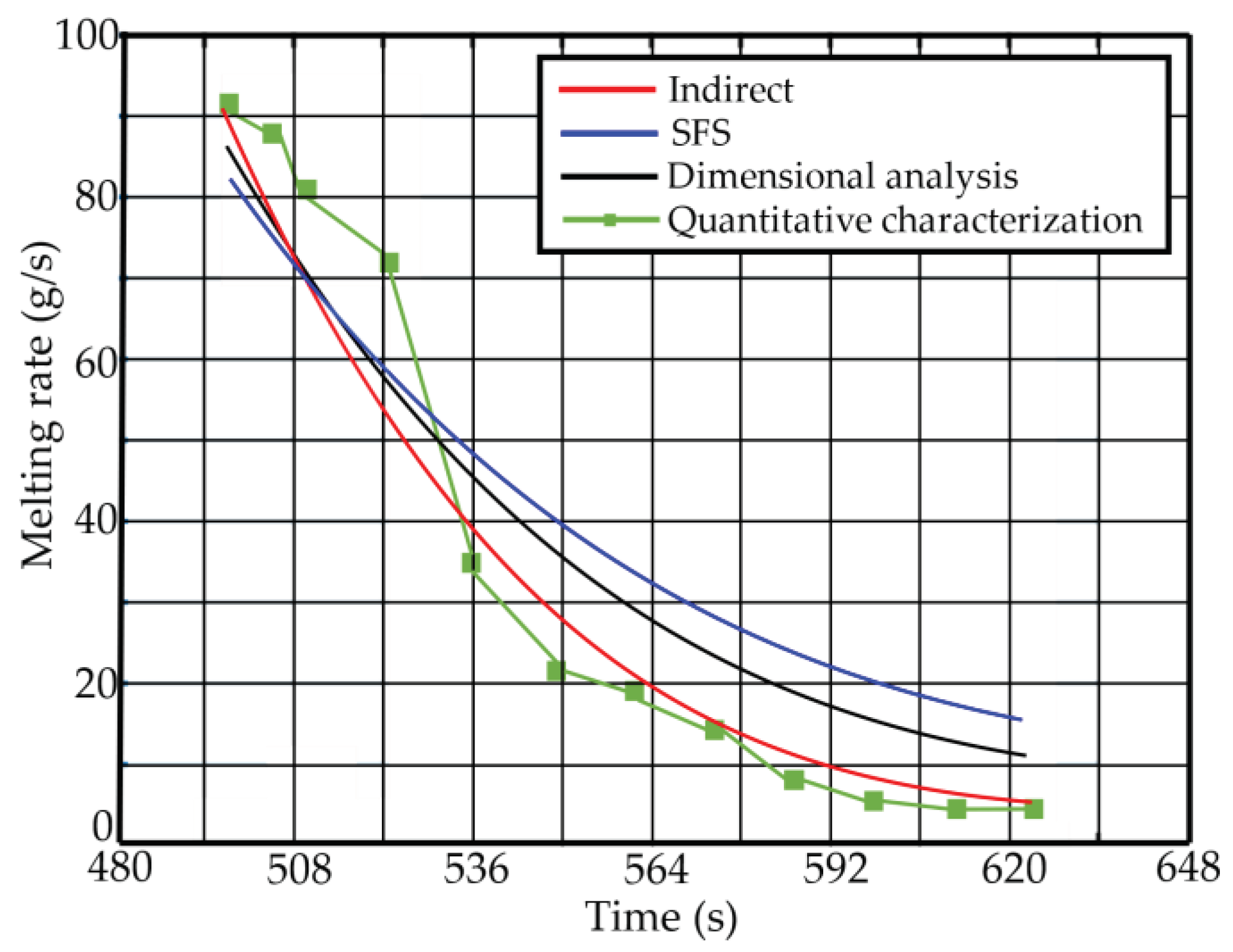
Table 1. Compares the advantages and disadvantages of different analysis methods.

Number	Reference	Method used	Advantage	Disadvantage
1	Ma et al. [12]	Quantitative characterization combined with exponential fitting	Easy calculation, number of photos and format requirements not high.	SiO₂ is assumed to be a sphere, the accuracy of volume calculation is low.
2	Zhu et al. [13]	Dimensional analysis combined with tracing points	The functional relationship between SiO₂ mass and time can be obtained directly, and the steps are simple.	The more physical quantities that reflect the physical properties of SiO₂, the more accurate.
3	Yang et al. [16]	SFS method combined with polynomial fitting	3D image of SiO₂ can be obtained.	The trend of melting rate will be abnormal, and the number and format of photos are required, which must be CCD images.
4	Method used in this paper.	Indirect method combined with exponential fitting	Calculating is easy, and the number and size of photos required is small.	The accuracy is not as precise as SFS, but it can meet the analysis requirements.
5	Method used in this paper.	SFS method combined with exponential fitting	3D image of SiO₂ can be obtained. The melting rate results are more reasonable.	High requirements for the amount of photos and the format of photos, CCD images must be required.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer