1. Introduction

Figure 1. Modified on a phylogenetic tree built on Nextstarin (2023-3-27) [2], consisting of 2775 SARS-CoV-2 genomes from the GISAID database evolving in chronological order, with bright colors representing the most noteworthy variants of the moment, such as red dots.

Figure 1. Modified on a phylogenetic tree built on Nextstarin (2023-3-27) [2], consisting of 2775 SARS-CoV-2 genomes from the GISAID database evolving in chronological order, with bright colors representing the most noteworthy variants of the moment, such as red dots.

Figure 2. SARS-CoV-2 Structure [9].

Figure 2. SARS-CoV-2 Structure [9].

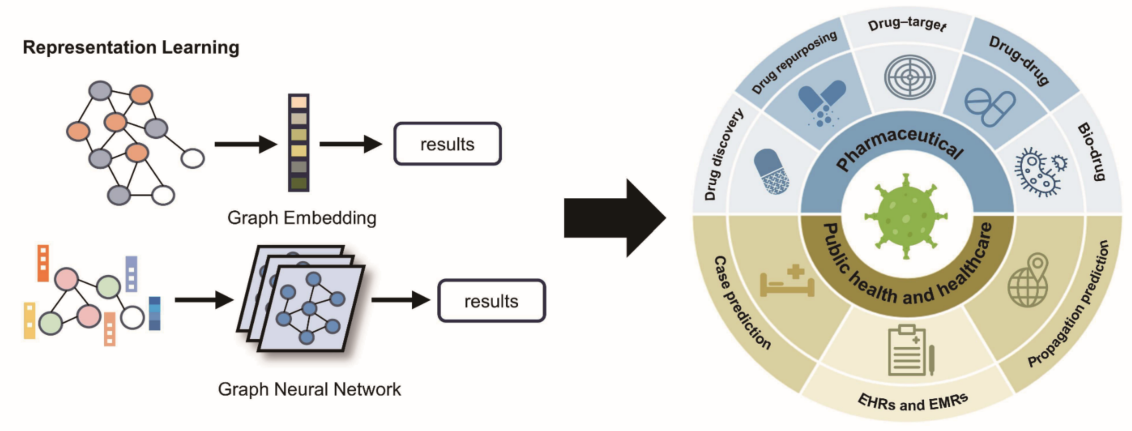
2. Representation Learning

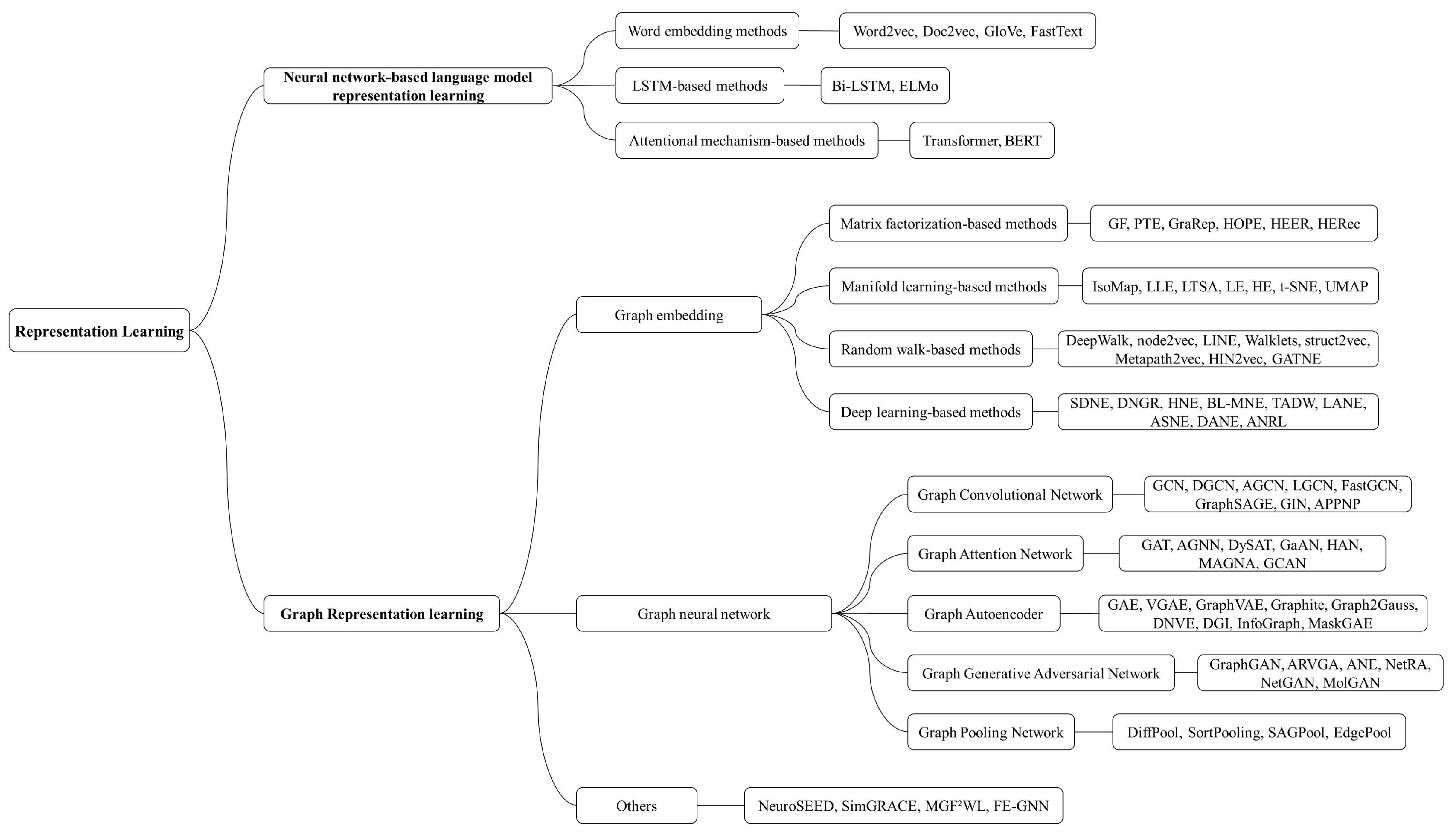
3. Overview of Representation Learning Methods

3.2. Graph Representation Learning

Graph representation learning is a technique that aims to learn low-dimensional vector representations of nodes and edges in graph data. Its overarching objective is to encode the structural and semantic information of graph data in a compact form that can be used for various downstream tasks. In this section, we introduce graph embedding methods and graph neural network methods. In the end, some other methods were introduced in an expanded manner.

3.2.1. Graph Embedding

The objective of graph embedding is to find a low-dimensional vector representation of a high-dimensional graph while preserving the connectivity and interactions between nodes in the graph, which typically retains some key information about the nodes in the original graph. We categorize these graph embedding methods into four major types: matrix factorization-based methods, manifold learning-based methods, random walk-based methods and deep learning-based methods.

Matrix factorization-based methods. A common graph embedding method is matrix factorization, which learns the low-dimensional representation of nodes by dissecting the adjacency matrix or laplacian matrix of the graph. The graph factorization (GF) [52] learns the low-dimensional representation of nodes in a graph by decomposing the graph’s adjacency matrix or Laplacian matrix. While maintaining the advantages of unsupervised text embedding, Predictive Text Embedding (PTE) [53] learns features from labeled data while using both labeled and unlabeled data for representation learning. Matrix factorization is used by both GraRep [54] and HOPE [55] to extract the higher-order neighborhood information from the graph. However, GraRep constructs the higher-order proximity matrix by concatenating k-hop transition probability matrices, while HOPE constructs the higher-order proximity matrix by measuring the pairwise similarity between nodes in subgraphs of varying sizes and orders. By generating edge representations and learning heterogeneous metrics, HEER [56] decomposes the network into low-dimensional embeddings and captures both structural and semantic information. A joint embedding matrix can be constructed by HERec [57] using meta-path-guided sampling to capture semantic and structural similarities between nodes of different types, which can then be factorized into low-dimensional embeddings.

Manifold learning-based methods. In high-dimensional spaces, the sparsity and noise of graph data can pose challenges for model training and lead to overfitting. Manifold learning methods address this issue by mapping high-dimensional graph data to a lower-dimensional manifold space, which preserves the local properties and structural information of the original data while reducing its dimensionality. The main idea of isometric mapping (IsoMap) [58] is to preserve the shortest path between data points to maintain the manifold structure. Both locally linear embedding (LLE) [59] and local tangent space alignment (LTSA) [60] are local information manifold learning methods. A local linear reconstruction is carried out in the neighborhood of each data point by LLE to maintain the flow structure. LTSA preserves the manifold structure by aligning the data in each point’s local tangent space. Laplacian eigenmaps (LE) [61] and hessian eigenmaps (HE) [62] are both manifold learning methods based on spectral analysis. Specifically, LE utilizes the Laplacian matrix to perform local weight assignment on the data’s neighborhood for preserving the manifold structure, while HE models the curvature and geometry of the data by leveraging the Hessian matrix. t-Distributed stochastic neighbor embedding (t-SNE) [63] uses a probabilistic approach to model the similarity between points in high-dimensional space and maps them to low-dimensional space while preserving pairwise similarities. Both uniform manifold approximation and projection (UMAP) [64] and t-SNE use graph layout algorithms to arrange data in low-dimensional space, which makes them very similar. The distinction is that UMAP builds a low-dimensional representation using an optimization technique based on the nearest neighbor graph.

Random walk-based methods. Inspired by the word vector model in the field of NLP, the researchers consider that the nodes on the graph can be analogized to words and the node sequences to sentences, and then the node sequences can be generated by random walk sampling on the graph to learn the representation vectors of the nodes using the Skip-gram model. DeepWalk [65] is the origin of the random walk approach, employing a simple, unbiased random walk followed by skip-gram representation learning of the walk sequences. Similarly, node2vec [66] is a biased random walk that introduces two parameters to regulate the search strategy of random walks, aiming to achieve a better balance between capturing graph structural features and node similarity features and improving the quality of node representations. By maximizing the likelihood functions of first-order proximity and second-order proximity, large-scale information network embedding (LINE) [67] learns the embedding of nodes. Additionally, LINE employs negative sampling strategies to boost training effectiveness. Walklets [68], which concentrates on higher-order structural information, splits joint random walk sequences of various lengths to obtain structural data on nodes at various scales. The similarity of the structural roles of nodes in the network is taken into account by struct2vec [69], not just the probability of contribution between nodes. Traditional node embedding techniques typically employ a co-occurrence probability-based methodology, which makes it difficult to adequately capture the semantic and structural information between nodes in heterogeneous information networks. By limiting the direction of random walk, meta-paths direct the generation of node sequences related to particular meta-paths, thereby capturing semantic and structural information between nodes. Metapath2vec [70] uses skip-gram to learn node embeddings after defining meta-paths to describe the semantic relationships between nodes and create heterogeneous neighborhoods of nodes. Using the defined meta-paths, HIN2vec [71] also creates diverse node neighborhoods. The crucial distinction is that it reconstructs the neighborhood using a self-encoder model and learns the embedding vector of the nodes by minimizing the reconstruction error. GATNE [72] combines the ideas of graph attention network (GAN) and neighborhood aggregation embedding (NAE). It employs the GAT model for node representation learning in heterogeneous graphs and the NAE method for node neighborhood aggregation. Setting the proper number of walks and walk lengths is crucial when learning node embedding in various heterogeneous networks.

Deep learning-based methods. Traditional machine learning techniques rely heavily on manually created feature representations, which have a priori knowledge restrictions and limit the expressiveness of the models. Deep learning techniques can enhance data representation by learning multi-level feature representations and reducing the need for manual features. To encode and decode the nodes and obtain the details of the graph structure, SDNE [73] employs a deep self-encoder architecture. First- and second-order proximity are simultaneously optimized, and overfitting is prevented by sparse regularization. The advantage of SDNE is that it learns the relationships between the nodes while retaining the graph’s structural information, improving the graph’s representation. DNGR [74] directly obtains graph structural information using a random walk model and learns node representations using stacked denoising autoencoders. The nonlinear features of the graph can be learned using these two techniques, but they do not perform well on non-Euclidean graphs. To encode the text, HNE [75] employs recursive neural networks, which can model the hierarchical structure of the text. Both image and text encoders are optimized using a joint training approach to learn better matching. A deep-aligned autoencoder-based embedding method for heterogeneous graphs was introduced by BL-MNE [76] to embed different types of nodes into the same low-dimensional space. TADW [77] learns low-dimensional embedding representations of network nodes using DeepWalk and latent dirichlet allocation (LDA) methods, and it introduces the attention mechanism to weigh the nodes’ textual information. Three different attention mechanisms—node attention, attribute attention, and neighbor attention—are introduced by the LANE [78] method, which adaptively adjusts the weights on different embedding layers to better capture the similarities and differences between nodes and improve the quality of embedding. ASNE [79] creates supernodes by combining the structural and attribute information of the nodes, employs an attention-based framework to regulate the weights between the different supernodes in the embedding space, and employs adaptive sparse methods to learn the representation of the nodes. DANE [80] can simultaneously capture highly nonlinear node attributes and topological relationships while preserving their proximity. The expressiveness and generalization performance of the node representation are improved by ANRL [81], which uses adaptive neighborhood regularization to dynamically adjust the weights of each node’s neighbors using the relationships between neighboring nodes.

3.2.2. Graph Neural Network-Based Methods

Currently, GNNs have emerged as a prominent research field in graph representation learning, especially in handling non-Euclidean data. Their capacity to effectively process such data makes them a suitable choice for various real-world applications. GNNs differ from traditional neural network methods in that they can effectively model the interactions between nodes and edges, thereby exhibiting superior performance in tasks related to the analysis and prediction of graph-structured data. Drawing upon prior research [82,83], we present a taxonomy of graph neural networks in this section, organized into five distinct categories based on their architectural design and unique approaches to processing structured graph data: GCNs, GATs, GAEs, GGANs, and GPNs.

GCNs. GCNs define a convolution operation on a graph that aggregates the features of a node’s neighboring nodes and the node itself to generate a new node feature. Graph convolution methods can be classified into spectral methods and spatial methods. In graph data, the relationships between nodes are irregular. GCN [84] introduces learnable convolutional parameters to extract and learn features from graph data. By stacking multiple graph convolutional layers, GCN obtains more abundant and complex node feature representations. DGCN [85] employs distinct graph convolution operations on the primal and dual graphs to obtain node representations on both graphs. To address the issue of traditional graph neural networks requiring the definition of static adjacency matrices in advance, AGCN [86] introduces adaptive adjacency matrices and gate mechanisms, avoiding the computational burden brought by multiple convolutional operations. LGCN [87] utilizes a learnable graph convolutional layer (LGCL) and a subgraph training technique for handling large-scale graph data, thereby circumventing the computational limitations of traditional graph convolutional operations that necessitate computing the entire graph. In addition, FastGCN [88] was proposed to address the issue of high computational and memory overheads in traditional graph convolutional methods by introducing importance sampling and mini-batch training. The GraphSAGE [89] approach is considered a significant milestone in the field of graph neural networks. It uses a sampler to randomly sample subgraphs from the graph data that contain the target node, enabling inductive representation learning and prediction on unseen nodes. GIN [90] incorporates a global sorted pooling operation in its aggregation process, endowing the GIN method with a certain degree of graph isomorphism invariance, thereby avoiding the mapping of isomorphic graphs to different vector representations. APPNP [91] uses the personalized PageRank algorithm to achieve personalized propagation and prediction of nodes and utilizes a larger receptive field for node classification tasks.

GATs. To address the issue of information aggregation in traditional graph neural networks, GATs introduced attention mechanisms [46] that enable different weighting of neighboring nodes around each node, thus better capturing the relationships between nodes. The attention mechanism in GAT [92] adaptively calculates the weights between nodes and further incorporates multi-head attention mechanisms to better capture the structural information of graphs and effectively handle large-scale graph data. AGNN [93] utilizes an attention mechanism to dynamically learn the relationships between each node and its neighboring nodes, thereby enhancing the model’s performance. DySAT [94] computes node representations through joint self-attention along the two dimensions of the structural neighborhood and temporal dynamics, more effectively capturing the relationships and features in dynamic graph data. GaAN [95] introduced an adaptive receptive field mechanism to dynamically adjust the neighborhood size of each node, enabling the receptive field size to adaptively fit the density and distribution of its surrounding nodes, thus enhancing the model’s flexibility and adaptability to different graph structures. HAN [96] utilizes distinct attention mechanisms to model different types of nodes and edges, learning complex relationships between nodes and the structural information of heterogeneous graphs by adaptively computing weights and representations of nodes. MAGNA [97] adopts a multi-hop attention mechanism that utilizes diffusive priors on attention values to consider all paths between non-connected node pairs, enabling the dynamic capture of complex relationships between nodes. High-order attention mechanisms and adversarial regularization constraints are employed by GCAN [98] to fully utilize both low-order and high-order information of nodes for representation learning.

GAEs. The encoder-decoder architecture has also been widely applied in graph generation and reconstruction tasks. GAE [99] initially employs this architecture by utilizing an encoder to compress the raw graph data into low-dimensional vectors and a decoder to decode these low-dimensional vectors back into the original graph. The structures of both the encoder and decoder are composed of multiple layers of GCN. VGAE [99] is an extension of GAE that introduces a variational inference method on top of GAE, enabling VGAE to learn more robust and interpretable low-dimensional representations. GraphVAE [100] adopts a similar structure to VAE, where the encoder transforms the graph information into a vector that approximates a normal distribution, and the decoder then transforms this vector back into a new graph. Graphite [101] utilizes graph neural networks to parameterize a variational autoencoder and employs a novel iterative graph refinement strategy for decoding. Graph2Gauss [102] builds upon VGAE by modeling node representations using Gaussian distributions and improving the distance metric to better capture complex category structures. In addition, DNVE [103] introduces deep generative models into graph autoencoders, embedding the network through deep encoders and decoders. Contrastive learning has also been applied to graph embedding methods. For example, DGI [104] uses a mutual information maximization method to learn node representations, which can learn high-order relationships between nodes without reconstructing the input graph. Another approach, InfoGraph [105], learns graph-level representations by maximizing the mutual information between the graph-level representation and representations of substructures at different scales within the graph. There is also a novel approach called MaskGAE [106], which combines the Masked Graph Model (MGM) with the graph autoencoder to achieve self-supervised graph representation learning and capture node features and structural information in the graph.

GGANs. GGANs are a type of generative model based on adversarial training that extends conventional generative adversarial networks (GANs) [107] and can be used for generating and learning embedded representations of graph data. The generator network can generate realistic graph data, while the discriminator network can evaluate the quality of the generated graph data. Through adversarial training between the two networks, GGANs can continuously optimize their ability to generate and learn graph data. An earlier method, GraphGAN [108], uses GAN to learn graph embedding representations and employs a loss function based on pairwise similarity to preserve the continuity of the embedding space. ARVGA [109] uses adversarial regularization to regularize node embeddings in the embedding space, thereby improving the continuity and robustness of embedding representations. By introducing an additional regularization term in adversarial training, ANE [110] enhances existing graph embedding methods by treating the prior distribution as real data and embedding vectors as generated samples. NetRA [111] is a network representation learning method based on an encoder-decoder framework and adversarial training. It encodes and decodes random walks on nodes, utilizes adversarial training to regularize embeddings, and introduces a prior distribution to improve the model’s generalization performance. In addition, there is an implicit generative model called NetGAN [112], which is used to simulate real-world networks. It uses GAN to train a generator and utilizes random walk loss in the graph to learn node-level representations. MolGAN [113] is an implicit generative model used for generating small molecule graphs. It combines GAN and policy gradient reinforcement learning methods to improve the quality and diversity of generated molecular graphs.

GPNs. GPNs use two operations, graph pooling and graph convolution, to process input graph data, with the main goal of reducing the size of the graph data and extracting global features. A general differentiable pooling operation called DiffPool [114] has been proposed, which can optimize node representations and pooling matrices through backpropagation to better capture the hierarchical structure of graph data. Zhang et al. [115] proposed a novel SortPooling operation that sorts each node’s feature vector along with the node’s degree and then uses the sorted result as the pooling result to better capture the global features of graph data. A method different from other graph pooling methods is SAGPool [116], which dynamically selects a subset of nodes using self-attention scores without the need to specify a fixed-size node subset. This approach enables more accurate learned graph representations that can adapt to different graph structures. Diehl et al. [117] proposed a pooling method called EdgePool, which relies on the edge contraction concept to learn localized and sparse hard pooling transformations. This method calculates importance scores for each edge to select representative edges and compress them together to form new nodes.

In addition, research on embedding methods for non-Euclidean spaces, contrastive learning for graph neural networks, and feature processing is worth noting. Corso et al. [118] proposed a neural distance embedding model, NeuroSEED, which embeds biological sequences into hyperbolic space for improved capture of hierarchical structure. A simple graph contrastive learning framework called SimGRACE [119] was proposed, which does not require data augmentation and enhances the robustness of graph contrastive learning using an adversarial scheme. Tang et al. [120] proposed a novel unsupervised feature selection method, MGF²WL, which combines multiple image fusion and feature weight learning to address poor-quality similarity graphs and designed an effective feature reconstruction model. Sun et al. Sun et al. [121] proposed a feature expanded graph neural network model FE-GNN that utilizes feature subspace flattening and structural principal components to expand the feature space and improve model performance.

We also summarize the representation learning method implementations reviewed in the paper in Table 1, most of which are official implementations.

Table 1. Summary of Representation Learning Methods.

Table 1. Summary of Representation Learning Methods.

Category	Method Name	Code Link
Neural network-based language model representation learning	Word2vec [37]	https://code.google.com/archive/p/word2vec/
	Doc2vec [38]	https://nbviewer.org/github/danielfrg/ word2vec/blob/main/examples/doc2vec.ipynb
	GloVe [39]	https://nlp.stanford.edu/projects/glove/
	FastText [40]	https://github.com/facebookresearch/fastText
	Bi-LSTM [42]	-
	ELMo [43]	https://allenai.org/allennlp/software/elmo
	Transformer [46]	https://github.com/tensorflow/tensorflow
	BERT [50]	https://github.com/google-research/bert
Graph representation learning
Graph embedding	GF [52]	-
	PTE [53]	https://github.com/mnqu/PTE
	GraRep [54]	https://github.com/ShelsonCao/GraRep
	HOPE [55]	http://git.thumedia.org/embedding/HOPE
	HEER [56]	https://github.com/GentleZhu/HEER
	HERec [57]	https://github.com/librahu/HERec
	IsoMap [58]	https://github.com/scikit-learn/scikit-learn/blob/ main/sklearn/manifold/_isomap.py
	LLE [59]	-
	LTSA [60]	-
	LE [61]	-
	HE [62]	-
	t-SNE [63]	https://lvdmaaten.github.io/tsne/
	UMAP [64]	https://github.com/lmcinnes/umap
	DeepWalk [65]	https://github.com/phanein/deepwalk
	node2vec [66]	https://github.com/aditya-grover/node2vec
	LINE [67]	https://github.com/tangjianpku/LINE
	Walklets [68]	https://github.com/benedekrozemberczki/ walklets
	struct2vec [69]	https://github.com/leoribeiro/struc2vec
	Metapath2vec [70]	https://ericdongyx.github.io/metapath2vec/ m2v.html
	HIN2vec [71]	https://github.com/csiesheep/hin2vec
	GATNE [72]	https://github.com/THUDM/GATNE
	SDNE [73]	https://github.com/suanrong/SDNE
	DNGR [74]	https://github.com/ShelsonCao/DNGR
	HNE [75]	-
	BL-MNE [76]	-
	TADW [77]	https://github.com/thunlp/tadw
	LANE [78]	https://github.com/xhuang31/LANE
	ASNE [79]	https://github.com/lizi-git/ASNE
	DANE [80]	https://github.com/gaoghc/DANE
	ANRL [81]	https://github.com/cszhangzhen/ANRL
Graph neural network	GCN [84]	https://github.com/tkipf/gcn
	DGCN [85]	https://github.com/ZhuangCY/DGCN
	AGCN [86]	https://github.com/yimutianyang/AGCN
	LGCN [87]	https://github.com/divelab/lgcn
	FastGCN [88]	https://github.com/matenure/FastGCN
	GraphSAGE [89]	https://github.com/williamleif/GraphSAGE
	GIN [90]	https://github.com/weihua916/powerful-gnns
	APPNP [91]	https://github.com/gasteigerjo/ppnp
	GAT [92]	https://github.com/PetarV-/GAT
	AGNN [93]	-
	DySAT [94]	https://github.com/aravindsankar28/DySAT
	GaAN [95]	https://github.com/jennyzhang0215/GaAN
	HAN [96]	https://github.com/Jhy1993/HAN
	MAGNA [97]	https://github.com/xjtuwgt/GNN-MAGNA
	GCAN [98]	-
	GAE [99]	https://github.com/tkipf/gae
	VGAE [99]	https://github.com/tkipf/gae
Graph neural network	GraphVAE [100]	https://github.com/snap-stanford/GraphRNN/ tree/master/baselines/graphvae
	Graphite [101]	https://github.com/ermongroup/graphite
	Graph2Gauss [102]	https://github.com/abojchevski/gra ph2gauss
	DNVE [103]	-
	DGI [104]	https://github.com/PetarV-/DGI
	InfoGraph [105]	https://github.com/fanyun-sun/Info Graph
	MaskGAE [106]	https://github.com/EdisonLeeeee/Mas kGAE
	GraphGAN [108]	https://github.com/hwwang55/GraphGAN
	ARVGA [109]	-
	ANE [110]	-
	NetRA [111]	https://github.com/chengw07/NetRA
	NetGAN [112]	https://github.com/danielzuegner/ne tgan
	MolGAN [113]	https://github.com/nicola-decao/Mol GAN
	DiffPool [114]	https://github.com/RexYing/diffpool
	SortPooling [115]	https://github.com/muhanzhang/DGCNN
	SAGPool [116]	https://github.com/inyeoplee77/SAG Pool
	EdgePool [117]	-
Others	NeuroSEED [118]	https://github.com/gcorso/NeuroSEED
	SimGRACE [119]	https://github.com/mpanpan/SimGRACE
	MGF²WL [120]	-
	FE-GNN [121]	https://github.com/sajqavril/Featur e-Extension-Graph-Neural-Networks

4. Representation Learning Methods for COVID-19

5. Challenges and Prospects

6. Conclusions

References

1. William T Harvey, Alessandro M Carabelli, Ben Jackson, Ravindra K Gupta, Emma C Thomson, Ewan M Harrison, Catherine Ludden, Richard Reeve, Andrew Rambaut, COVID-19 Genomics UK (COG-UK) Consortium, et al. Sars-cov-2 variants, spike mutations and immune escape. Nature Reviews Microbiology, 19(7):409–424, 2021.
2. James Hadfield, Colin Megill, Sidney M Bell, John Huddleston, Barney Potter, Charlton Callender, Pavel Sagulenko, Trevor Bedford, and Richard A Neher. Nextstrain: real-time tracking of pathogen evolution. Bioinformatics, 34(23):4121–4123, 2018. [CrossRef]
3. David M Morens, Gregory K Folkers, and Anthony S Fauci. The concept of classical herd immunity may not apply to covid-19. The Journal of infectious diseases, 226(2):195–198, 2022. [CrossRef]
4. Leiwen Fu, Bingyi Wang, Tanwei Yuan, Xiaoting Chen, Yunlong Ao, Thomas Fitzpatrick, Peiyang Li, Yiguo Zhou, Yi-fan Lin, Qibin Duan, et al. Clinical characteristics of coronavirus disease 2019 (covid-19) in china: a systematic review and meta-analysis. Journal of Infection, 80(6):656–665, 2020. [CrossRef]
5. Elizabeth J Williamson, Alex J Walker, Krishnan Bhaskaran, Seb Bacon, Chris Bates, Caroline E Morton, Helen J Curtis, Amir Mehrkar, David Evans, Peter Inglesby, et al. Opensafely: factors associated with covid-19 death in 17 million patients. Nature, 584(7821):430, 2020.
6. Yan-Rong Guo, Qing-Dong Cao, Zhong-Si Hong, Yuan-Yang Tan, Shou-Deng Chen, Hong-Jun Jin, Kai-Sen Tan, De-Yun Wang, and Yan Yan. The origin, transmission and clinical therapies on coronavirus disease 2019 (covid-19) outbreak–an update on the status. Military medical research, 7:1–10, 2020.
7. Chaolin Huang, Yeming Wang, Xingwang Li, Lili Ren, Jianping Zhao, Yi Hu, Li Zhang, Guohui Fan, Jiuyang Xu, Xiaoying Gu, et al. Clinical features of patients infected with 2019 novel coronavirus in wuhan, china. The lancet, 395(10223):497–506, 2020.
8. Thanh Thi Nguyen, Mohamed Abdelrazek, Dung Tien Nguyen, Sunil Aryal, Duc Thanh Nguyen, Sandeep Reddy, Quoc Viet Hung Nguyen, Amin Khatami, Edbert B Hsu, and Samuel Yang. Origin of novel coronavirus (covid-19): a computational biology study using artificial intelligence. BioRxiv, pages 2020–05, 2020. [CrossRef]
9. Marco Cascella, Michael Rajnik, Abdul Aleem, Scott C Dulebohn, and Raffaela Di Napoli. Features, evaluation, and treatment of coronavirus (covid-19). Statpearls [internet], 2022.
10. Shibo Jiang, Christopher Hillyer, and Lanying Du. Neutralizing antibodies against sars-cov-2 and other human coronaviruses. Trends in immunology, 41(5):355–359, 2020.
11. Lok Bahadur Shrestha, Charles Foster, William Rawlinson, Nicodemus Tedla, and Rowena A Bull. Evolution of the sars-cov-2 omicron variants ba. 1 to ba. 5: Implications for immune escape and transmission. Reviews in Medical Virology, 32(5):e2381, 2022. [CrossRef]
12. Bette Korber, Will M Fischer, Sandrasegaram Gnanakaran, Hyejin Yoon, James Theiler, Werner Abfalterer, Nick Hengartner, Elena E Giorgi, Tanmoy Bhattacharya, Brian Foley, et al. Tracking changes in sars-cov-2 spike: evidence that d614g increases infectivity of the covid-19 virus. Cell, 182(4):812–827, 2020.
13. Yunlong Cao, Jing Wang, Fanchong Jian, Tianhe Xiao, Weiliang Song, Ayijiang Yisimayi, Weijin Huang, Qianqian Li, Peng Wang, Ran An, et al. Omicron escapes the majority of existing sars-cov-2 neutralizing antibodies. Nature, 602(7898):657–663, 2022.
14. Manojit Bhattacharya, Ashish Ranjan Sharma, Kuldeep Dhama, Govindasamy Agoramoorthy, and Chiranjib Chakraborty. Omicron variant (b. 1.1. 529) of sars-cov-2: understanding mutations in the genome, s-glycoprotein, and antibody-binding regions. GeroScience, 44(2):619–637, 2022.
15. Dhiraj Mannar, James W Saville, Xing Zhu, Shanti S Srivastava, Alison M Berezuk, Katharine S Tuttle, Ana Citlali Marquez, Inna Sekirov, and Sriram Subramaniam. Sars-cov-2 omicron variant: Antibody evasion and cryo-em structure of spike protein–ace2 complex. Science, 375(6582):760–764, 2022.
16. Dinah V Parums. The xbb. 1.5 (‘kraken’) subvariant of omicron sars-cov-2 and its rapid global spread. Medical Science Monitor, 29, 2023.
17. Imad A Basheer and Maha Hajmeer. Artificial neural networks: fundamentals, computing, design, and application. Journal of microbiological methods, 43(1):3–31, 2000. [CrossRef]
18. Yifei Chen, Yi Li, Rajiv Narayan, Aravind Subramanian, and Xiaohui Xie. Gene expression inference with deep learning. Bioinformatics, 32(12):1832–1839, 2016. [CrossRef]
19. Hongming Chen, Ola Engkvist, Yinhai Wang, Marcus Olivecrona, and Thomas Blaschke. The rise of deep learning in drug discovery. Drug discovery today, 23(6):1241–1250, 2018. [CrossRef]
20. Mihalj Bakator and Dragica Radosav. Deep learning and medical diagnosis: A review of literature. Multimodal Technologies and Interaction, 2(3):47, 2018. [CrossRef]
21. Jie Zhou, Ganqu Cui, Shengding Hu, Zhengyan Zhang, Cheng Yang, Zhiyuan Liu, Lifeng Wang, Changcheng Li, and Maosong Sun. Graph neural networks: A review of methods and applications. AI open, 1:57–81, 2020. [CrossRef]
22. Jiacheng Xiong, Zhaoping Xiong, Kaixian Chen, Hualiang Jiang, and Mingyue Zheng. Graph neural networks for automated de novo drug design. Drug Discovery Today, 26(6):1382–1393, 2021. [CrossRef]
23. Fang Yang, Kunjie Fan, Dandan Song, and Huakang Lin. Graph-based prediction of protein-protein interactions with attributed signed graph embedding. BMC bioinformatics, 21(1):1–16, 2020. [CrossRef]
24. Xiao-Meng Zhang, Li Liang, Lin Liu, and Ming-Jing Tang. Graph neural networks and their current applications in bioinformatics. Frontiers in genetics, 12:690049, 2021. [CrossRef]
25. Daniele Mercatelli, Laura Scalambra, Luca Triboli, Forest Ray, and Federico M Giorgi. Gene regulatory network inference resources: A practical overview. Biochimica et Biophysica Acta (BBA)-Gene Regulatory Mechanisms, 1863(6):194430, 2020. [CrossRef]
26. Hongyun Cai, Vincent W Zheng, and Kevin Chen-Chuan Chang. A comprehensive survey of graph embedding: Problems, techniques, and applications. IEEE transactions on knowledge and data engineering, 30(9):1616–1637, 2018. [CrossRef]
27. Mengjia Xu. Understanding graph embedding methods and their applications. SIAM Review, 63(4):825–853, 2021. [CrossRef]
28. James Kotary, Ferdinando Fioretto, Pascal Van Hentenryck, and Bryan Wilder. End-to-end constrained optimization learning: A survey. arXiv preprint arXiv:2103.16378, 2021. [CrossRef]
29. Xiao Wang, Deyu Bo, Chuan Shi, Shaohua Fan, Yanfang Ye, and S Yu Philip. A survey on heterogeneous graph embedding: methods, techniques, applications and sources. IEEE Transactions on Big Data, 2022. [CrossRef]
30. Giulia Muzio, Leslie O’Bray, and Karsten Borgwardt. Biological network analysis with deep learning. Briefings in bioinformatics, 22(2):1515–1530, 2021.
31. Zehong Zhang, Lifan Chen, Feisheng Zhong, Dingyan Wang, Jiaxin Jiang, Sulin Zhang, Hualiang Jiang, Mingyue Zheng, and Xutong Li. Graph neural network approaches for drug-target interactions. Current Opinion in Structural Biology, 73:102327, 2022. [CrossRef]
32. Sezin Kircali Ata, Min Wu, Yuan Fang, Le Ou-Yang, Chee Keong Kwoh, and Xiao-Li Li. Recent advances in network-based methods for disease gene prediction. Briefings in bioinformatics, 22(4):bbaa303, 2021. [CrossRef]
33. Oliver Wieder, Stefan Kohlbacher, Mélaine Kuenemann, Arthur Garon, Pierre Ducrot, Thomas Seidel, and Thierry Langer. A compact review of molecular property prediction with graph neural networks. Drug Discovery Today: Technologies, 37:1–12, 2020. [CrossRef]
34. World. Statement on the fifteenth meeting of the ihr (2005) emergency committee on the covid-19 pandemic, May 2023.
35. Ruiwei Feng, Yufeng Xie, Minshan Lai, Danny Z Chen, Ji Cao, and Jian Wu. Agmi: Attention-guided multi-omics integration for drug response prediction with graph neural networks. In 2021 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), pages 1295–1298. IEEE, 2021. [CrossRef]
36. Yaxin Zhu, Peisheng Qian, Ziyuan Zhao, and Zeng Zeng. Deep feature fusion via graph convolutional network for intracranial artery labeling. In 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), pages 467–470. IEEE, 2022.
37. Tomas Mikolov, Ilya Sutskever, Kai Chen, Greg S Corrado, and Jeff Dean. Distributed representations of words and phrases and their compositionality. Advances in neural information processing systems, 26, 2013.
38. Quoc Le and Tomas Mikolov. Distributed representations of sentences and documents. In International conference on machine learning, pages 1188–1196. PMLR, 2014.
39. Jeffrey Pennington, Richard Socher, and Christopher D Manning. Glove: Global vectors for word representation. In Proceedings of the 2014 conference on empirical methods in natural language processing (EMNLP), pages 1532–1543, 2014.
40. Piotr Bojanowski, Edouard Grave, Armand Joulin, and Tomas Mikolov. Enriching word vectors with subword information. Transactions of the association for computational linguistics, 5:135–146, 2017.
41. Sepp Hochreiter and Jürgen Schmidhuber. Long short-term memory. Neural computation, 9(8):1735–1780, 1997.
42. Zhiheng Huang, Wei Xu, and Kai Yu. Bidirectional lstm-crf models for sequence tagging. arXiv preprint arXiv:1508.01991, 2015.
43. Matthew E. Peters, Mark Neumann, Mohit Iyyer, Matt Gardner, Christopher Clark, Kenton Lee, and Luke Zettlemoyer. Deep contextualized word representations, 2018.
44. Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio. Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473, 2014.
45. Yoon Kim, Carl Denton, Luong Hoang, and Alexander M Rush. Structured attention networks. arXiv preprint arXiv:1702.00887, 2017.
46. Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, ukasz Kaiser, and Illia Polosukhin. Attention is all you need. Advances in neural information processing systems, 30, 2017.
47. Jonas Gehring, Michael Auli, David Grangier, Denis Yarats, and Yann N Dauphin. Convolutional sequence to sequence learning. In International conference on machine learning, pages 1243–1252. PMLR, 2017.
48. Sainbayar Sukhbaatar, Jason Weston, Rob Fergus, et al. End-to-end memory networks. Advances in neural information processing systems, 28, 2015.
49. Alexander Miller, Adam Fisch, Jesse Dodge, Amir-Hossein Karimi, Antoine Bordes, and Jason Weston. Key-value memory networks for directly reading documents. arXiv preprint arXiv:1606.03126, 2016.
50. Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805, 2018.
51. Minh-Thang Luong, Hieu Pham, and Christopher D Manning. Effective approaches to attention-based neural machine translation. arXiv preprint arXiv:1508.04025, 2015.
52. Amr Ahmed, Nino Shervashidze, Shravan Narayanamurthy, Vanja Josifovski, and Alexander J Smola. Distributed large-scale natural graph factorization. In Proceedings of the 22nd international conference on World Wide Web, pages 37–48, 2013.
53. Jian Tang, Meng Qu, and Qiaozhu Mei. Pte: Predictive text embedding through large-scale heterogeneous text networks. In Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining, pages 1165–1174, 2015.
54. Shaosheng Cao, Wei Lu, and Qiongkai Xu. Grarep: Learning graph representations with global structural information. In Proceedings of the 24th ACM international on conference on information and knowledge management, pages 891–900, 2015.
55. Mingdong Ou, Peng Cui, Jian Pei, Ziwei Zhang, and Wenwu Zhu. Asymmetric transitivity preserving graph embedding. In Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining, pages 1105–1114, 2016.
56. Yu Shi, Qi Zhu, Fang Guo, Chao Zhang, and Jiawei Han. Easing embedding learning by comprehensive transcription of heterogeneous information networks. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pages 2190–2199, 2018.
57. Chuan Shi, Binbin Hu, Wayne Xin Zhao, and S Yu Philip. Heterogeneous information network embedding for recommendation. IEEE Transactions on Knowledge and Data Engineering, 31(2):357–370, 2018. [CrossRef]
58. Joshua B Tenenbaum, Vin de Silva, and John C Langford. A global geometric framework for nonlinear dimensionality reduction. science, 290(5500):2319–2323, 2000. [CrossRef]
59. Sam T Roweis and Lawrence K Saul. Nonlinear dimensionality reduction by locally linear embedding. science, 290(5500):2323–2326, 2000. [CrossRef]
60. Zhenyue Zhang and Hongyuan Zha. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment. SIAM journal on scientific computing, 26(1):313–338, 2004. [CrossRef]
61. Mikhail Belkin and Partha Niyogi. Laplacian eigenmaps for dimensionality reduction and data representation. Neural computation, 15(6):1373–1396, 2003. [CrossRef]
62. David L Donoho and Carrie Grimes. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data. Proceedings of the National Academy of Sciences, 100(10):5591–5596, 2003. [CrossRef]
63. Laurens Van der Maaten and Geoffrey Hinton. Visualizing data using t-sne. Journal of machine learning research, 9(11), 2008.
64. Leland McInnes, John Healy, and James Melville. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv preprint arXiv:1802.03426, 2018.
65. Bryan Perozzi, Rami Al-Rfou, and Steven Skiena. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining, pages 701–710, 2014.
66. Aditya Grover and Jure Leskovec. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining, pages 855–864, 2016.
67. Jian Tang, Meng Qu, Mingzhe Wang, Ming Zhang, Jun Yan, and Qiaozhu Mei. Line: Large-scale information network embedding. In Proceedings of the 24th international conference on world wide web, pages 1067–1077, 2015.
68. Bryan Perozzi, Vivek Kulkarni, Haochen Chen, and Steven Skiena. Don’t walk, skip! online learning of multi-scale network embeddings. In Proceedings of the 2017 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining 2017, pages 258–265, 2017.
69. Leonardo FR Ribeiro, Pedro HP Saverese, and Daniel R Figueiredo. struc2vec: Learning node representations from structural identity. In Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining, pages 385–394, 2017.
70. Yuxiao Dong, Nitesh V Chawla, and Ananthram Swami. metapath2vec: Scalable representation learning for heterogeneous networks. In Proceedings of the 23rd ACM SIGKDD international conference on knowledge discovery and data mining, pages 135–144, 2017.
71. Tao-yang Fu, Wang-Chien Lee, and Zhen Lei. Hin2vec: Explore meta-paths in heterogeneous information networks for representation learning. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, pages 1797–1806, 2017.
72. Yukuo Cen, Xu Zou, Jianwei Zhang, Hongxia Yang, Jingren Zhou, and Jie Tang. Representation learning for attributed multiplex heterogeneous network. In Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining, pages 1358–1368, 2019.
73. Daixin Wang, Peng Cui, and Wenwu Zhu. Structural deep network embedding. In Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining, pages 1225–1234, 2016.
74. Shaosheng Cao, Wei Lu, and Qiongkai Xu. Deep neural networks for learning graph representations. In Proceedings of the AAAI conference on artificial intelligence, volume 30, 2016.
75. Shiyu Chang, Wei Han, Jiliang Tang, Guo-Jun Qi, Charu C Aggarwal, and Thomas S Huang. Heterogeneous network embedding via deep architectures. In Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining, pages 119–128, 2015.
76. Jiawei Zhang, Congying Xia, Chenwei Zhang, Limeng Cui, Yanjie Fu, and S Yu Philip. Bl-mne: emerging heterogeneous social network embedding through broad learning with aligned autoencoder. In 2017 IEEE International Conference on Data Mining (ICDM), pages 605–614. IEEE, 2017. [CrossRef]
77. Cheng Yang, Zhiyuan Liu, Deli Zhao, Maosong Sun, and Edward Y Chang. Network representation learning with rich text information. In IJCAI, volume 2015, pages 2111–2117, 2015.
78. Xiao Huang, Jundong Li, and Xia Hu. Label informed attributed network embedding. In Proceedings of the tenth ACM international conference on web search and data mining, pages 731–739, 2017.
79. Lizi Liao, Xiangnan He, Hanwang Zhang, and Tat-Seng Chua. Attributed social network embedding. IEEE Transactions on Knowledge and Data Engineering, 30(12):2257–2270, 2018.
80. Hongchang Gao and Heng Huang. Deep attributed network embedding. In Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI)), 2018.
81. Zhen Zhang, Hongxia Yang, Jiajun Bu, Sheng Zhou, Pinggang Yu, Jianwei Zhang, Martin Ester, and Can Wang. Anrl: attributed network representation learning via deep neural networks. In Ijcai, volume 18, pages 3155–3161, 2018. [CrossRef]
82. Hitoshi Iuchi, Taro Matsutani, Keisuke Yamada, Natsuki Iwano, Shunsuke Sumi, Shion Hosoda, Shitao Zhao, Tsukasa Fukunaga, and Michiaki Hamada. Representation learning applications in biological sequence analysis. Computational and Structural Biotechnology Journal, 19:3198–3208, 2021. [CrossRef]
83. Hai-Cheng Yi, Zhu-Hong You, De-Shuang Huang, and Chee Keong Kwoh. Graph representation learning in bioinformatics: trends, methods and applications. Briefings in Bioinformatics, 23(1):bbab340, 2022. [CrossRef]
84. Thomas N Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907, 2016.
85. Chenyi Zhuang and Qiang Ma. Dual graph convolutional networks for graph-based semi-supervised classification. In Proceedings of the 2018 world wide web conference, pages 499–508, 2018. [CrossRef]
86. Ruoyu Li, Sheng Wang, Feiyun Zhu, and Junzhou Huang. Adaptive graph convolutional neural networks. In Proceedings of the AAAI conference on artificial intelligence, volume 32, 2018.
87. Hongyang Gao, Zhengyang Wang, and Shuiwang Ji. Large-scale learnable graph convolutional networks. In Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery & data mining, pages 1416–1424, 2018.
88. Jie Chen, Tengfei Ma, and Cao Xiao. Fastgcn: fast learning with graph convolutional networks via importance sampling. arXiv preprint arXiv:1801.10247, 2018.
89. Will Hamilton, Zhitao Ying, and Jure Leskovec. Inductive representation learning on large graphs. Advances in neural information processing systems, 30, 2017.
90. Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. How powerful are graph neural networks? arXiv preprint arXiv:1810.00826, 2018.
91. Johannes Gasteiger, Aleksandar Bojchevski, and Stephan Günnemann. Predict then propagate: Graph neural networks meet personalized pagerank. arXiv preprint arXiv:1810.05997, 2018.
92. Petar Velickovic, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, Yoshua Bengio, et al. Graph attention networks. stat, 1050(20):10–48550, 2017.
93. Kiran K Thekumparampil, Chong Wang, Sewoong Oh, and Li-Jia Li. Attention-based graph neural network for semi-supervised learning. arXiv preprint arXiv:1803.03735, 2018.
94. Aravind Sankar, Yanhong Wu, Liang Gou, Wei Zhang, and Hao Yang. Dynamic graph representation learning via self-attention networks. arXiv preprint arXiv:1812.09430, 2018.
95. Jiani Zhang, Xingjian Shi, Junyuan Xie, Hao Ma, Irwin King, and Dit-Yan Yeung. Gaan: Gated attention networks for learning on large and spatiotemporal graphs. arXiv preprint arXiv:1803.07294, 2018.
96. Xiao Wang, Houye Ji, Chuan Shi, Bai Wang, Yanfang Ye, Peng Cui, and Philip S Yu. Heterogeneous graph attention network. In The world wide web conference, pages 2022–2032, 2019. [CrossRef]
97. Guangtao Wang, Rex Ying, Jing Huang, and Jure Leskovec. Multi-hop attention graph neural network. arXiv preprint arXiv:2009.14332, 2020. [CrossRef]
98. Haiyun Xu, Shaojie Zhang, Bo Jiang, and Jin Tang. Graph context-attention network via low and high order aggregation. Neurocomputing, 2023. [CrossRef]
99. Thomas N Kipf and Max Welling. Variational graph auto-encoders. arXiv preprint arXiv:1611.07308, 2016.
100. Martin Simonovsky and Nikos Komodakis. Graphvae: Towards generation of small graphs using variational autoencoders. In Artificial Neural Networks and Machine Learning–ICANN 2018: 27th International Conference on Artificial Neural Networks, Rhodes, Greece, October 4-7, 2018, Proceedings, Part I 27, pages 412–422. Springer, 2018.
101. Aditya Grover, Aaron Zweig, and Stefano Ermon. Graphite: Iterative generative modeling of graphs. In International conference on machine learning, pages 2434–2444. PMLR, 2019.
102. Aleksandar Bojchevski and Stephan Günnemann. Deep gaussian embedding of graphs: Unsupervised inductive learning via ranking. arXiv preprint arXiv:1707.03815, 2017.
103. Dingyuan Zhu, Peng Cui, Daixin Wang, and Wenwu Zhu. Deep variational network embedding in wasserstein space. In Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery & data mining, pages 2827–2836, 2018.
104. Petar Velickovic, William Fedus, William L Hamilton, Pietro Liò, Yoshua Bengio, and R Devon Hjelm. Deep graph infomax. ICLR (Poster), 2(3):4, 2019.
105. Fan-Yun Sun, Jordan Hoffmann, Vikas Verma, and Jian Tang. Infograph: Unsupervised and semi-supervised graph-level representation learning via mutual information maximization. arXiv preprint arXiv:1908.01000, 2019.
106. Jintang Li, Ruofan Wu, Wangbin Sun, Liang Chen, Sheng Tian, Liang Zhu, Changhua Meng, Zibin Zheng, and Weiqiang Wang. Maskgae: masked graph modeling meets graph autoencoders. arXiv preprint arXiv:2205.10053, 2022.
107. Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio. Generative adversarial networks. Communications of the ACM, 63(11):139–144, 2020.
108. Hongwei Wang, Jia Wang, Jialin Wang, Miao Zhao, Weinan Zhang, Fuzheng Zhang, Xing Xie, and Minyi Guo. Graphgan: Graph representation learning with generative adversarial nets. In Proceedings of the AAAI conference on artificial intelligence, volume 32, 2018. [CrossRef]
109. Shirui Pan, Ruiqi Hu, Sai-fu Fung, Guodong Long, Jing Jiang, and Chengqi Zhang. Learning graph embedding with adversarial training methods. IEEE transactions on cybernetics, 50(6):2475–2487, 2019. [CrossRef]
110. Quanyu Dai, Qiang Li, Jian Tang, and Dan Wang. Adversarial network embedding. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 32, 2018.
111. Wenchao Yu, Cheng Zheng, Wei Cheng, Charu C Aggarwal, Dongjin Song, Bo Zong, Haifeng Chen, and Wei Wang. Learning deep network representations with adversarially regularized autoencoders. In Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery & data mining, pages 2663–2671, 2018.
112. Aleksandar Bojchevski, Oleksandr Shchur, Daniel Zügner, and Stephan Günnemann. Netgan: Generating graphs via random walks. In International conference on machine learning, pages 610–619. PMLR, 2018.
113. Nicola De Cao and Thomas Kipf. Molgan: An implicit generative model for small molecular graphs. arXiv preprint arXiv:1805.11973, 2018.
114. Zhitao Ying, Jiaxuan You, Christopher Morris, Xiang Ren, Will Hamilton, and Jure Leskovec. Hierarchical graph representation learning with differentiable pooling. Advances in neural information processing systems, 31, 2018.
115. Muhan Zhang, Zhicheng Cui, Marion Neumann, and Yixin Chen. An end-to-end deep learning architecture for graph classification. In Proceedings of the AAAI conference on artificial intelligence, volume 32, 2018. [CrossRef]
116. Junhyun Lee, Inyeop Lee, and Jaewoo Kang. Self-attention graph pooling. In International conference on machine learning, pages 3734–3743. PMLR, 2019.
117. Frederik Diehl, Thomas Brunner, Michael Truong Le, and Alois Knoll. Towards graph pooling by edge contraction. In ICML 2019 workshop on learning and reasoning with graph-structured data, 2019.
118. Gabriele Corso, Zhitao Ying, Michal Pándy, Petar Veličković, Jure Leskovec, and Pietro Liò. Neural distance embeddings for biological sequences. Advances in Neural Information Processing Systems, 34:18539–18551, 2021.
119. Jun Xia, Lirong Wu, Jintao Chen, Bozhen Hu, and Stan Z Li. Simgrace: A simple framework for graph contrastive learning without data augmentation. In Proceedings of the ACM Web Conference 2022, pages 1070–1079, 2022. [CrossRef]
120. Chang Tang, Xiao Zheng, Wei Zhang, Xinwang Liu, Xinzhong Zhu, and En Zhu. Unsupervised feature selection via multiple graph fusion and feature weight learning. Science China Information Sciences, 66(5):1–17, 2023. [CrossRef]
121. Jiaqi Sun, Lin Zhang, Guangyi Chen, Kun Zhang, Peng XU, and Yujiu Yang. Feature expansion for graph neural networks. arXiv preprint arXiv:2305.06142, 2023.
122. Anh-Tien Ton, Francesco Gentile, Michael Hsing, Fuqiang Ban, and Artem Cherkasov. Rapid identification of potential inhibitors of sars-cov-2 main protease by deep docking of 1.3 billion compounds. Molecular informatics, 39(8):2000028, 2020.
123. Konda Mani Saravanan, Haiping Zhang, Md Tofazzal Hossain, Md Selim Reza, and Yanjie Wei. Deep learning-based drug screening for covid-19 and case studies. In Silico Modeling of Drugs Against Coronaviruses: Computational Tools and Protocols, pages 631–660, 2021.
124. Deshan Zhou, Shaoliang Peng, Dong-Qing Wei, Wu Zhong, Yutao Dou, and Xiaolan Xie. Lunar: drug screening for novel coronavirus based on representation learning graph convolutional network. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 18(4):1290–1298, 2021. [CrossRef]
125. Zhengyang Wang, Meng Liu, Youzhi Luo, Zhao Xu, Yaochen Xie, Limei Wang, Lei Cai, Qi Qi, Zhuoning Yuan, Tianbao Yang, et al. Advanced graph and sequence neural networks for molecular property prediction and drug discovery. Bioinformatics, 38(9):2579–2586, 2022. [CrossRef]
126. Xiao-Shuang Li, Xiang Liu, Le Lu, Xian-Sheng Hua, Ying Chi, and Kelin Xia. Multiphysical graph neural network (mp-gnn) for covid-19 drug design. Briefings in Bioinformatics, 23(4), 2022. [CrossRef]
127. Jiangsheng Pi, Peishun Jiao, Yang Zhang, and Junyi Li. Mdgnn: Microbial drug prediction based on heterogeneous multi-attention graph neural network. Frontiers in Microbiology, 13, 2022. [CrossRef]
128. Yiyue Ge, Tingzhong Tian, Suling Huang, Fangping Wan, Jingxin Li, Shuya Li, Hui Yang, Lixiang Hong, Nian Wu, Enming Yuan, et al. A data-driven drug repositioning framework discovered a potential therapeutic agent targeting covid-19. BioRxiv, pages 2020–03, 2020.
129. Raghvendra Mall, Abdurrahman Elbasir, Hossam Al Meer, Sanjay Chawla, and Ehsan Ullah. Data-driven drug repurposing for covid-19. 2020.
130. Seyed Aghil Hooshmand, Mohadeseh Zarei Ghobadi, Seyyed Emad Hooshmand, Sadegh Azimzadeh Jamalkandi, Seyed Mehdi Alavi, and Ali Masoudi-Nejad. A multimodal deep learning-based drug repurposing approach for treatment of covid-19. Molecular diversity, 25:1717–1730, 2021. [CrossRef]
131. Rosa Aghdam, Mahnaz Habibi, and Golnaz Taheri. Using informative features in machine learning based method for covid-19 drug repurposing. Journal of cheminformatics, 13:1–14, 2021. [CrossRef]
132. Kanglin Hsieh, Yinyin Wang, Luyao Chen, Zhongming Zhao, Sean Savitz, Xiaoqian Jiang, Jing Tang, and Yejin Kim. Drug repurposing for covid-19 using graph neural network with genetic, mechanistic, and epidemiological validation. Research Square, 2020.
133. Thai-Hoang Pham, Yue Qiu, Jucheng Zeng, Lei Xie, and Ping Zhang. A deep learning framework for high-throughput mechanism-driven phenotype compound screening and its application to covid-19 drug repurposing. Nature machine intelligence, 3(3):247–257, 2021. [CrossRef]
134. Kanglin Hsieh, Yinyin Wang, Luyao Chen, Zhongming Zhao, Sean Savitz, Xiaoqian Jiang, Jing Tang, and Yejin Kim. Drug repurposing for covid-19 using graph neural network and harmonizing multiple evidence. Scientific reports, 11(1):23179, 2021. [CrossRef]
135. Siddhant Doshi and Sundeep Prabhakar Chepuri. A computational approach to drug repurposing using graph neural networks. Computers in Biology and Medicine, 150:105992, 2022. [CrossRef]
136. Bo Ram Beck, Bonggun Shin, Yoonjung Choi, Sungsoo Park, and Keunsoo Kang. Predicting commercially available antiviral drugs that may act on the novel coronavirus (sars-cov-2) through a drug-target interaction deep learning model. Computational and structural biotechnology journal, 18:784–790, 2020.
137. Sovan Saha, Piyali Chatterjee, Anup Kumar Halder, Mita Nasipuri, Subhadip Basu, and Dariusz Plewczynski. Ml-dtd: Machine learning-based drug target discovery for the potential treatment of covid-19. Vaccines, 10(10):1643, 2022. [CrossRef]
138. Xianfang Wang, Qimeng Li, Yifeng Liu, Zhiyong Du, and Ruixia Jin. Drug repositioning of covid-19 based on mixed graph network and ion channel. Mathematical Biosciences and Engineering, 19(4):3269–3284, 2022. [CrossRef]
139. Peiliang Zhang, Ziqi Wei, Chao Che, and Bo Jin. Deepmgt-dti: Transformer network incorporating multilayer graph information for drug–target interaction prediction. Computers in biology and medicine, 142:105214, 2022.
140. Guodong Li, Weicheng Sun, Jinsheng Xu, Lun Hu, Weihan Zhang, and Ping Zhang. Ga-ens: A novel drug–target interactions prediction method by incorporating prior knowledge graph into dual wasserstein generative adversarial network with gradient penalty. Applied Soft Computing, 139:110151, 2023. [CrossRef]
141. Zhenchao Tang, Guanxing Chen, Hualin Yang, Weihe Zhong, and Calvin Yu-Chian Chen. Dsil-ddi: A domain-invariant substructure interaction learning for generalizable drug–drug interaction prediction. IEEE Transactions on Neural Networks and Learning Systems, 2023. [CrossRef]
142. Sarina Sefidgarhoseini, Leila Safari, and Zanyar Mohammady. Drug-drug interaction extraction using transformer-based ensemble model. 2023.
143. Zhong-Hao Ren, Zhu-Hong You, Chang-Qing Yu, Li-Ping Li, Yong-Jian Guan, Lu-Xiang Guo, and Jie Pan. A biomedical knowledge graph-based method for drug–drug interactions prediction through combining local and global features with deep neural networks. Briefings in Bioinformatics, 23(5), 2022. [CrossRef]
144. Yujie Chen, Tengfei Ma, Xixi Yang, Jianmin Wang, Bosheng Song, and Xiangxiang Zeng. Muffin: multi-scale feature fusion for drug–drug interaction prediction. Bioinformatics, 37(17):2651–2658, 2021. [CrossRef]
145. Deng Pan, Lijun Quan, Zhi Jin, Taoning Chen, Xuejiao Wang, Jingxin Xie, Tingfang Wu, and Qiang Lyu. Multisource attention-mechanism-based encoder–decoder model for predicting drug–drug interaction events. Journal of Chemical Information and Modeling, 62(23):6258–6270, 2022. [CrossRef]
146. Zimeng Li, Shichao Zhu, Bin Shao, Tie-Yan Liu, Xiangxiang Zeng, and Tong Wang. Multi-view substructure learning for drug-drug interaction prediction. arXiv preprint arXiv:2203.14513, 2022.
147. Mei Ma and Xiujuan Lei. A dual graph neural network for drug–drug interactions prediction based on molecular structure and interactions. PLOS Computational Biology, 19(1):e1010812, 2023. [CrossRef]
148. Lopamudra Dey, Sanjay Chakraborty, and Anirban Mukhopadhyay. Machine learning techniques for sequence-based prediction of viral–host interactions between sars-cov-2 and human proteins. Biomedical journal, 43(5):438–450, 2020.
149. Hangyu Du, Feng Chen, Hongfu Liu, and Pengyu Hong. Network-based virus-host interaction prediction with application to sars-cov-2. Patterns, 2(5):100242, 2021.
150. Hongpeng Yang, Yijie Ding, Jijun Tang, and Fei Guo. Inferring human microbe–drug associations via multiple kernel fusion on graph neural network. Knowledge-Based Systems, 238:107888, 2022. [CrossRef]
151. Bihter Das, Mucahit Kutsal, and Resul Das. A geometric deep learning model for display and prediction of potential drug-virus interactions against sars-cov-2. Chemometrics and Intelligent Laboratory Systems, 229:104640, 2022.
152. Farah Shahid, Aneela Zameer, and Muhammad Muneeb. Predictions for covid-19 with deep learning models of lstm, gru and bi-lstm. Chaos, Solitons & Fractals, 140:110212, 2020. [CrossRef]
153. Hossein Abbasimehr and Reza Paki. Prediction of covid-19 confirmed cases combining deep learning methods and bayesian optimization. Chaos, Solitons & Fractals, 142:110511, 2021. [CrossRef]
154. Trisha Sinha, Titash Chowdhury, Rabindra Nath Shaw, and Ankush Ghosh. Analysis and prediction of covid-19 confirmed cases using deep learning models: a comparative study. In Advanced Computing and Intelligent Technologies: Proceedings of ICACIT 2021, pages 207–218. Springer, 2022. [CrossRef]
155. Junyi Gao, Rakshith Sharma, Cheng Qian, Lucas M Glass, Jeffrey Spaeder, Justin Romberg, Jimeng Sun, and Cao Xiao. Stan: spatio-temporal attention network for pandemic prediction using real-world evidence. Journal of the American Medical Informatics Association, 28(4):733–743, 2021. [CrossRef]
156. Myrsini Ntemi, Ioannis Sarridis, and Constantine Kotropoulos. An autoregressive graph convolutional long short-term memory hybrid neural network for accurate prediction of covid-19 cases. IEEE Transactions on Computational Social Systems, 2022. [CrossRef]
157. Dong Li, Xiaofei Ren, and Yunze Su. Predicting covid-19 using lioness optimization algorithm and graph convolution network. Soft Computing, pages 1–65, 2023. [CrossRef]
158. Konstantinos Skianis, Giannis Nikolentzos, Benoit Gallix, Rodolphe Thiebaut, and Georgios Exarchakis. Predicting covid-19 positivity and hospitalization with multi-scale graph neural networks. Scientific Reports, 13(1):5235, 2023. [CrossRef]
159. Zohair Malki, El-Sayed Atlam, Ashraf Ewis, Guesh Dagnew, Osama A Ghoneim, Abdallah A Mohamed, Mohamed M Abdel-Daim, and Ibrahim Gad. The covid-19 pandemic: prediction study based on machine learning models. Environmental science and pollution research, 28:40496–40506, 2021. [CrossRef]
160. Dixizi Liu, Weiping Ding, Zhijie Sasha Dong, and Witold Pedrycz. Optimizing deep neural networks to predict the effect of social distancing on covid-19 spread. Computers & Industrial Engineering, 166:107970, 2022. [CrossRef]
161. Devante Ayris, Maleeha Imtiaz, Kye Horbury, Blake Williams, Mitchell Blackney, Celine Shi Hui See, and Syed Afaq Ali Shah. Novel deep learning approach to model and predict the spread of covid-19. Intelligent Systems with Applications, 14:200068, 2022. [CrossRef]
162. Valerio La Gatta, Vincenzo Moscato, Marco Postiglione, and Giancarlo Sperli. An epidemiological neural network exploiting dynamic graph structured data applied to the covid-19 outbreak. IEEE Transactions on Big Data, 7(1):45–55, 2020. [CrossRef]
163. Truong Son Hy, Viet Bach Nguyen, Long Tran-Thanh, and Risi Kondor. Temporal multiresolution graph neural networks for epidemic prediction. In Workshop on Healthcare AI and COVID-19, pages 21–32. PMLR, 2022.
164. Ru Geng, Yixian Gao, Hongkun Zhang, and Jian Zu. Analysis of the spatio-temporal dynamics of covid-19 in massachusetts via spectral graph wavelet theory. IEEE Transactions on Signal and Information Processing over Networks, 8:670–683, 2022. [CrossRef]
165. Baoling Shan, Xin Yuan, Wei Ni, Xin Wang, and Ren Ping Liu. Novel graph topology learning for spatio-temporal analysis of covid-19 spread. IEEE Journal of Biomedical and Health Informatics, 2023. [CrossRef]
166. Jose Luis Izquierdo, Julio Ancochea, Savana COVID-19 Research Group, and Joan B Soriano. Clinical characteristics and prognostic factors for intensive care unit admission of patients with covid-19: retrospective study using machine learning and natural language processing. Journal of medical Internet research, 22(10):e21801, 2020. [CrossRef]
167. Isotta Landi, Benjamin S Glicksberg, Hao-Chih Lee, Sarah Cherng, Giulia Landi, Matteo Danieletto, Joel T Dudley, Cesare Furlanello, and Riccardo Miotto. Deep representation learning of electronic health records to unlock patient stratification at scale. NPJ digital medicine, 3(1):96, 2020. [CrossRef]
168. Tyler Wagner, FNU Shweta, Karthik Murugadoss, Samir Awasthi, AJ Venkatakrishnan, Sairam Bade, Arjun Puranik, Martin Kang, Brian W Pickering, John C O’Horo, et al. Augmented curation of clinical notes from a massive ehr system reveals symptoms of impending covid-19 diagnosis. Elife, 9:e58227, 2020.
169. Tingyi Wanyan, Hossein Honarvar, Suraj K Jaladanki, Chengxi Zang, Nidhi Naik, Sulaiman Somani, Jessica K De Freitas, Ishan Paranjpe, Akhil Vaid, Jing Zhang, et al. Contrastive learning improves critical event prediction in covid-19 patients. Patterns, 2(12):100389, 2021. [CrossRef]
170. Tingyi Wanyan, Mingquan Lin, Eyal Klang, Kartikeya M Menon, Faris F Gulamali, Ariful Azad, Yiye Zhang, Ying Ding, Zhangyang Wang, Fei Wang, et al. Supervised pretraining through contrastive categorical positive samplings to improve covid-19 mortality prediction. In Proceedings of the 13th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, pages 1–9, 2022. [CrossRef]
171. Liantao Ma, Xinyu Ma, Junyi Gao, Xianfeng Jiao, Zhihao Yu, Chaohe Zhang, Wenjie Ruan, Yasha Wang, Wen Tang, and Jiangtao Wang. Distilling knowledge from publicly available online emr data to emerging epidemic for prognosis. In Proceedings of the Web Conference 2021, pages 3558–3568, 2021. [CrossRef]
172. Tingyi Wanyan, Akhil Vaid, Jessica K De Freitas, Sulaiman Somani, Riccardo Miotto, Girish N Nadkarni, Ariful Azad, Ying Ding, and Benjamin S Glicksberg. Relational learning improves prediction of mortality in covid-19 in the intensive care unit. IEEE transactions on big data, 7(1):38–44, 2020. [CrossRef]
173. Doudou Zhou, Ziming Gan, Xu Shi, Alina Patwari, Everett Rush, Clara-Lea Bonzel, Vidul A Panickan, Chuan Hong, Yuk-Lam Ho, Tianrun Cai, et al. Multiview incomplete knowledge graph integration with application to cross-institutional ehr data harmonization. Journal of Biomedical Informatics, 133:104147, 2022. [CrossRef]
174. Junyi Gao, Chaoqi Yang, Joerg Heintz, Scott Barrows, Elise Albers, Mary Stapel, Sara Warfield, Adam Cross, Jimeng Sun, et al. Medml: Fusing medical knowledge and machine learning models for early pediatric covid-19 hospitalization and severity prediction. Iscience, 25(9):104970, 2022. [CrossRef]
175. Kaize Ding, Zhe Xu, Hanghang Tong, and Huan Liu. Data augmentation for deep graph learning: A survey. ACM SIGKDD Explorations Newsletter, 24(2):61–77, 2022. [CrossRef]
176. Travers Ching, Daniel S Himmelstein, Brett K Beaulieu-Jones, Alexandr A Kalinin, Brian T Do, Gregory P Way, Enrico Ferrero, Paul-Michael Agapow, Michael Zietz, Michael M Hoffman, et al. Opportunities and obstacles for deep learning in biology and medicine. Journal of The Royal Society Interface, 15(141):20170387, 2018.
177. Riccardo Miotto, Fei Wang, Shuang Wang, Xiaoqian Jiang, and Joel T Dudley. Deep learning for healthcare: review, opportunities and challenges. Briefings in bioinformatics, 19(6):1236–1246, 2018. [CrossRef]
178. Guido Zampieri, Supreeta Vijayakumar, Elisabeth Yaneske, and Claudio Angione. Machine and deep learning meet genome-scale metabolic modeling. PLoS computational biology, 15(7):e1007084, 2019. [CrossRef]