Preprint
Article
Generalized Rough Neighborhood Approximations and Related Topological Approaches
This version is not peer-reviewed.
Submitted:
13 August 2023
Posted:
15 August 2023
You are already at the latest version
Abstract
This work aims to generate some types of M_(j )–neighborhoods. Relationships among these M_(j )-neighborhoods and some other types of neighborhoods are discussed. Additionally, M_(j )-lower, M_(j )-upper approximations and M_(j )-accuracy in terms of M_(j )-neighborhoods are presented. Their properties, with some examples, are investigated. Finally, We addressed the comparisons among M_(j )approach and other approaches.
Keywords:
Subject:
Computer Science and Mathematics - Information Systems1. Introduction
Topology and rough sets are two distinct mathematical frameworks, but many con nections exist. Rough set theory [1,2,3,4,5] is a good non-statistical tool for big data. It depends essentially on binary relations that are equivalence. These types of relations are often hard to satisfy because of their restrictions and application limitations. The philosophy of rough set theory depends on two approximations of categories. This theory can extend to many other approaches related to topological notations, such as near-open sets and neighborhoods. Topology is an important branch of mathematics that is rich with logical relations. These relations can make use of many generalizations and useful applications. It has many near-open logical notations, such as alpha and beta open sets, that generate new real-life applications. More studies had done to use topology with rough set theory in different ways [6,7,8,9,10,11]. Topologically, rough approximations are motivated by different types of neighborhoods. Some studies [12,13,14,15] used generalized binary relations to generate new rough-set approaches. Others used topological neighborhood systems to generate granules used in many applications [16,17,18,19]. Also, some introduced a mixed neighborhood system for rough approximations and developed eight different types of neighborhoods. These types of neighborhood systems are studied and generalized by to -neighborhoods, -neighborhoods, -neighborhoods, and recently -neighborhoods. The connection between rough set theory and topology is studied in various directions depending on the suitable applications [8]. The following manuscript is formulated as follows: Sections 1&2 are the introduction and preliminaries of the work. Section 3 introduces the concepts of neighborhoods systems. Section 4 introduces the relations between these neighborhoods, and Section 5 communicates and revision the notions -lower and -upper approximations, -boundary region, -positive and -negative regions, and -accuracy measure, and generate their –topologies in section 6. We studied the relations among the generated topologies in Section 7. Some approximations operators induced by the topologies studied in Section 8, and we investigate the concepts from a topological concept, and its main properties are explored. Moreover, Section 9 compares our approaches and previous approaches concerning different j types. Finally, we give a conclusion in Section 10.
2. Preliminaries
We rewrite some important definitions and notations for non-specific readers to help them read this work easily. These definitions spotlight on different types of neighborhoods and relations.
2.1. Pawlak Approximation Space
Definition 2.1.1. [1,20] The relation on universe is a subset of . Two elements, p and r, are in relation (in symbols ) when (p, r) . The relation is called:
- Reflexive if pQp for each pU.
- Symmetric if pQr↔rQp.
- Transitive if pQn whenever pQr and rQn.
- Equivalence is when it is reflexive, transitive, and symmetric.
Definition 2.1.2. [1,20] We assume Q is an equivalence relation. A pair (U, Q) is called an approximation space, where U is the universe, and Q is an equivalence relation on U. Let P be a subset of U, i.e., P U. Our goal is to characterize the set P concerning Q.
- ={ V| VP}.
- ={ VU | V ∩ P ≠}.
The two sets and are respectively called lower and upper approximations of P, and P is said to be a rough set if . Otherwise, it is definable (or exact).
The boundary and accuracy of Pawlak approximations are defined, respectively, by:
- BND(P) = − and = , Where .
Proposition 2.1.1. [1,20] Pawlak supposes that (U, Q) be an approximation space, represents an empty set and represents a complement of P in U. Then, the lower approximations and the upper approximations have the followings properties:
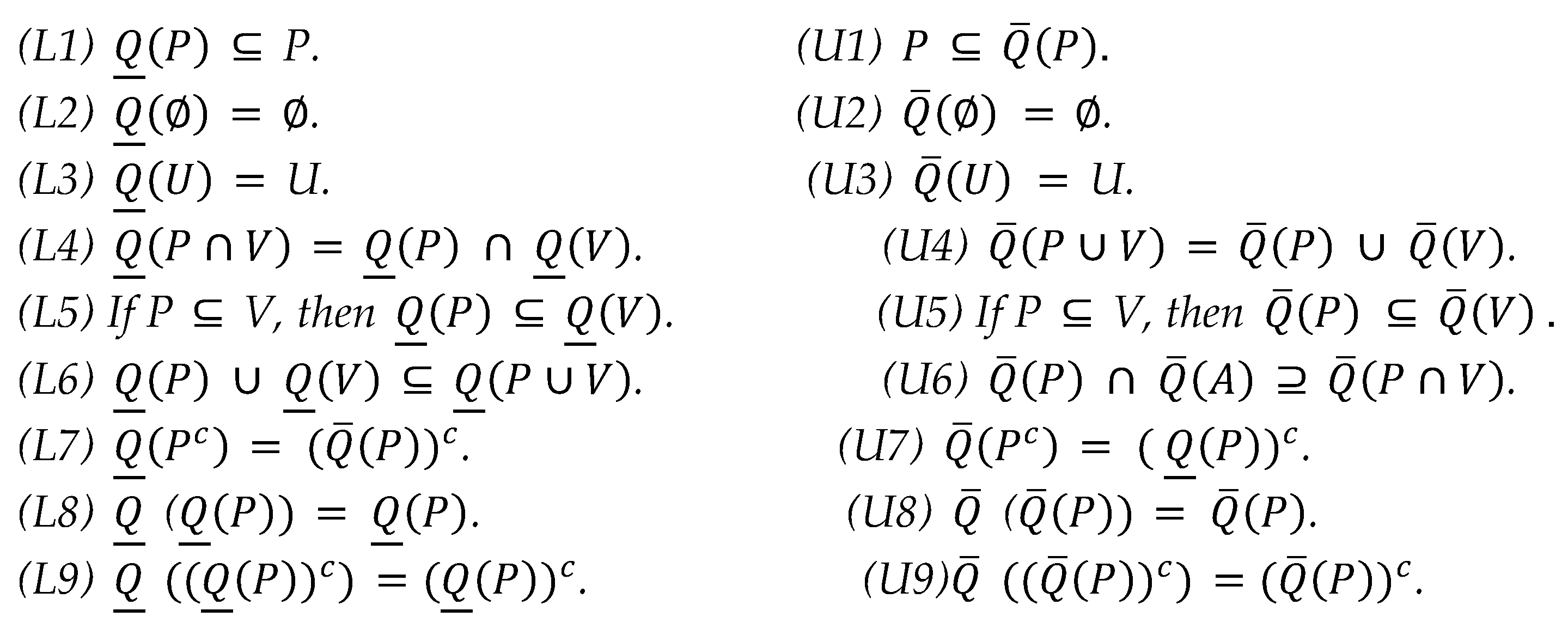
2.2. j-Neighborhood space
Definition 2.2.1. [12] For any binary relation Q on U. The following j-neighborhood sets are defined for p ∪ ((p)), j {r, l, ‹ r ›, ‹ l ›, i, u, ‹ i ›, ‹ u ›} as follows:
- The r-Neighborhood when,(p) = {vU | p Q v}.
- The l-Neighborhood when,(p) = {vU | v Q p}.
- The ‹ r ›-Neighborhood when,(p) =(v).
- The ‹ l ›-Neighborhood when,(p) =(v).
- The i-Neighborhood when,(p) =(p) ∩(p).
- The u-Neighborhood when,(p) =(p)∪(p).
- The ‹ i ›-Neighborhood when,(p) =(p) ∩(p).
- The ‹ u ›-Neighborhood when,(p) =(p)∪(p).
Definition 2.2.2. [12] Let Q be an arbitrary binary relation on U and ξj : U→ P(U) be a mapping which assigns for each p U its (p) in the P(U) . Then, the triple (U, Q, ξj ) called a j-neighborhood space (briefly, j-NS).
Theorem 2.2.1. [12] Let (U, Q, ξj ) be a j-NS and P U. Then, for each j {r, l, ‹ r ›, ‹ l ›, i, u, ‹ i ›, ‹ u ›}the group = {(v) P} is a topology on U.
Definition 2.2.3. [12] Let (U, Q, ξj ) be a j-NS. Then, a subset P U is called a j-open set if P . The complement of a j-open set is called j-closed, and the family of all j-closed sets is given by { F | } and the j-interior (resp. j-closure) operator of A is given by
- = ∪ {G: GP}.
- ={ H: PH}.
Definition 2.2.4. [12] Let (U, Q, ξj ) be a j-NS and P U. Then, the (j-lower and j-upper) approximations, (j-boundary, j-positive and j-negative) regions, and j-accuracy of the approximations of P U are given, respectively, by
- (P) = ∪ { G: GP } = j-interior of P.
- (P) ={ H: PH } = j-closure of P.
- =(P) _(P).
- (P) =(P).
- =(P).
- =, where
Definition 2.2.5. [18] For any binary relation Q on U. The group of -neighborhoods of PU are defined as follows:
- (P) = {vU:(v) ∩(P) ≠∅}.
- (P) = {vU:(v) ∩(P) ≠∅}.
- (P) =(P) ∩(P).
- (P) =(P) ∪(P).
- (P) = {v∈U:(v) ∩(P) ≠∅}.
- (P) = {v∈U(v) ∩(P) ≠∅}.
- (P) =(P) ∩(P).
- (P) =(P) ∪(P).
-Neighborhoods in the j -neighborhood space
In this section, we define the concepts ofneighborhoods By inclusion relations between -neighborhoods and -neighborhoods. An illustrative example is given to support the obtained results and relationships. The study of-neighborhoods aims to increase the accuracy of approximations.
Definition 3.1. For any binary relation Q on U. The class of-neighborhoods of PU ((P)) are defined, for each as follows:
- (P) = { vU:(P) (P) }.
- (P) = { vU:(P) (P) }.
- (P) =
- (P) =.
- (P) = { vU:(P) }.
- (P) = { vU(P) (P)}.
- (P) = { vU(P) (P)}.
- (P) =
The following example will show the behavior of these neighborhoods, help us show the relationships among them, and illustrates the method of Mj-neighborhood.
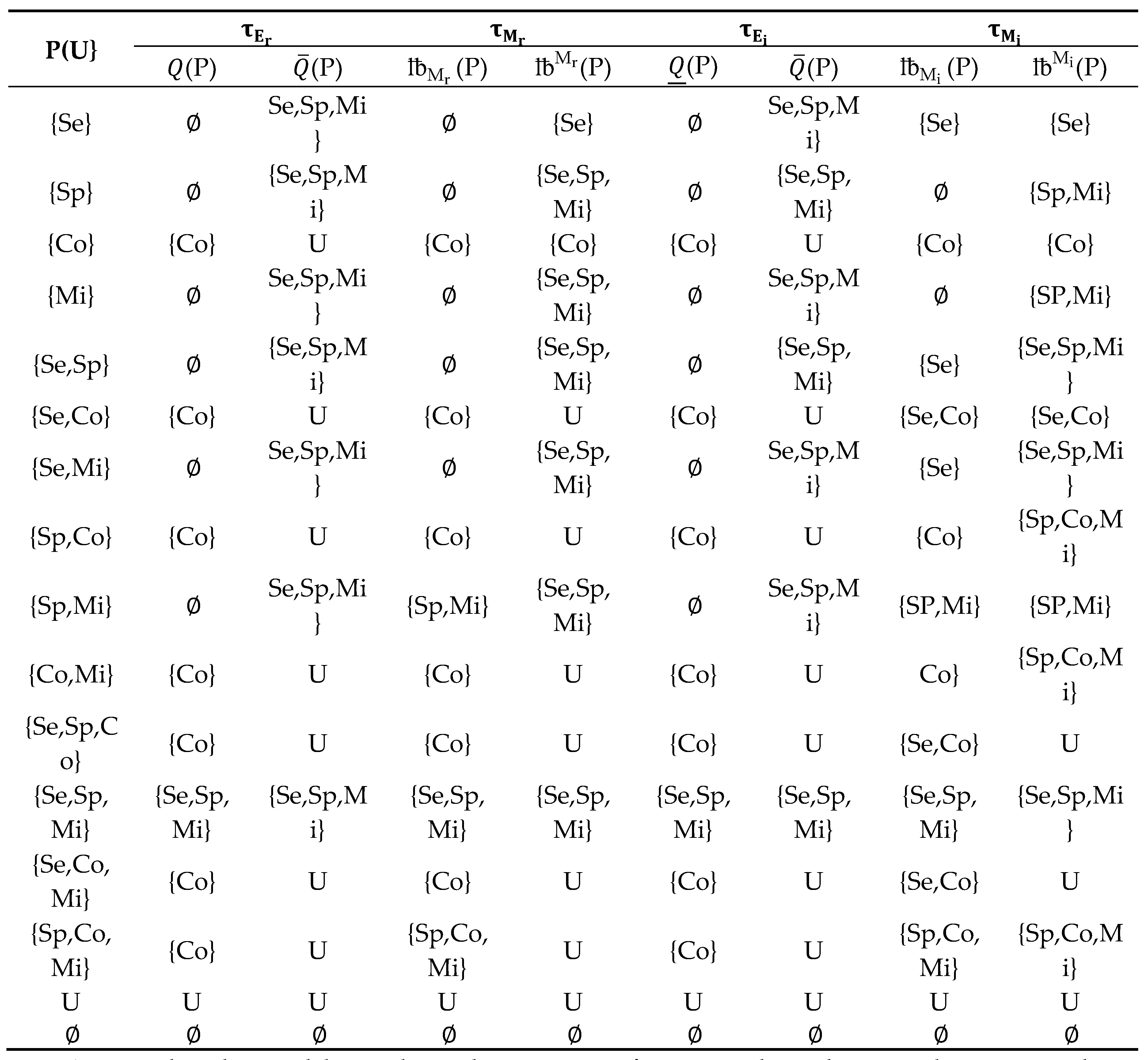
Example 3.1. Suppose the universe of some types of characters in a storyas an initial set of objects. We suppose the relationthat defined on U. The classesneighborhoods,-neighborhoods and-neighborhoods are shown inTable 1.
4. The Relationships Among –neighborhoods
The following results show the relationships between the different types of Mj-neighborhoods.
Proposition 4.1. Let (U, Q, ξj) be a j-approximation space. Then for each vthe following relations hold.
- v (v) for each j.
- (v) (v) (v).
- (v) (v) (v).
- (v) (v) (v).
- (v) (v) (v).
- If Q is symmetric, then(v) =(v) =(v)(v) and(v) =(v)=(v) (v).
Proof. The proof of (1) comes from the fact (v) (v) and (v)(v) for The proof of (2)-(5) come from the Definition 3.1.
The proof of (6): Since Q is symmetric, then (v) = (v). This leads to (v) (v) as well and (v) = (v). This leads to (v) (v). Therefore, (v) = (v) = (v) (v) . Similarly, one can prove that and (v) = (v) = (v) (v). □
5. Generalized Rough Approximations Based on –neighborhoods
In this section, New concepts of -lower approximations and -upper approximations, -boundary region, –positive regions, -negative regions and -accuracy measure of a subset based on –neighborhoods. We reveal the main properties with the help of some examples.
Definition 5.1. Let (U, Q, ξj) be a j-approximation Space, given a set PU. The lower(P) and the upper(P) approximations based on-neighborhoods defined as follows:
- (P) = { v U , (v) P } Called lower approximation of P.
- (P) = { v U , (v) P ≠ } Called upper approximation of P.
Definition 5.2. Let (U, Q, ξj) be a j-approximation Space, given a set PU. The-boundary region,-positive region,-negative region and-accuracy of P is defined as follows:
- = (P) _ (P)
- (P) = (P)
- (P) = (P)
- = , where
In the next example, we calculate the lower approximation of P, upper approximation of P, -boundary region, -positive region, -negative region and -accuracy measure of P.
Example 5.1. Suppose the universe U= {e, f, g, h} as an initial set of objects and PU. We suppose the relation Q = {(e,e),(e,h),(f,e),(f,g),(g,f),(g,g),(g,h),(h,e)} that defined on U.
Let P ={e,f,h}. Then we calculate (P), (P), and for j=(r,l,i,u) as follows:
- For j = r, we have (P) ={e,h} ,(P) = U,{f,g} and = ½.
- For j = l, we have (P) ={e} ,(P) = {e,g,h},{g,h} and = 1/3.
- For j = i, we have (P) ={e,h} ,(P) = {e,g,h},{g} and = 2/3
- For j = u, we have (P) ={e} ,(P) = U,{f,g,h} and = 1/3.
Proposition 5.1. For any j and each non-empty subset P of U, we have [0,1].
Proof. Let P be a non-empty subset of U. It follows from (1) of Proposition 4.1 that v (v) for each j. Then (v) for each v P; consequently, (P) . Thus, . □
Now, we have two cases:
Case 1: (P) = . Then = 0.
Case 2: . Then v (P). Then v (v) . Therefore, v (P). Thus (P) (P). This means that 0 ≤ ≤ 1. Hence, we obtain from the two cases above that 0 ≤ ≤ 1 as required.
In the following results, we present the main properties of -lower approximations and -upper approximations for each j.
Theorem 5.2. Let (U, Q, ξj) be a j-approximation space, given a set PU. Then the following properties hold for each j.
- (P) P
- () = and = .
- (U) = U and = U.
- If P W, then (P) (W) .
- If P W, then
- (P W) = (P) (W).
- (P ∪W) = (P) (W .
- () = .
- () = .
Proof. We prove (1) ,(2),(3),(4),(6) and (8) and the other cases similarly.
- Let v (P) . Then (v) P. It follows from the item (1) of Proposition 4.1 that v (v) therefore, v P. Thus, (P) P.
- Since (v) . For each v U, then () = .
- Since v (v) U for each v U, then {v} (v) U thus (U) = U.
- Since P W, then (P) = {(v) P } {(v) W } = (W).
- It follows from (iv) that (P W) = (P) (W). Conversely, let v (P) (W). Then v (P) and v (W) so that (v) P and (v) W thus (v) P W, Hence v (P W).
- v () ↔ (v) ↔(v) P = ↔ v not belong ↔ v
Corollary 5.3. Let (U, Q, ξj) be a j-approximation space and P, VQ. Then(P) (V) (P V). The next example shows that the converse of the above corollary need not be true.
Example 5.2. According to Example 5.1. Let P = {e}, V = {f, h} and PV = {e,f,h}. Then(PV) ={e},(P) ={e} and(V) = .(P V) (P) (V).
Remark 5.1. The converse of Theorem 5.2. that(P) P need not be true. The following example shows this remark.
Example 5.3. According to Example 5.1. Let P = {f, g}, we have= {g} then P(P).
Remark 5.2. The converse of the item (4) of Theorem 5.2. that If PW, then(P) (W) need not be true as shown in Example 5.4.
Example 5.4. According to Example 5.1. Let P = {e,f,h} and W = {e,g,h}. Then(P) = {e,h} (W) = {e,f,h} although PW.
Some properties of Pawlak’s lower approximations are not realized for -lower approximation such as . To clarify this fact, consider a subset P = {e, f, h}. Then = {e}, But given in Example 5.1.
Corollary5.4. Let (U, Q, ξj) be a j-approximation space and P, VQ. Then(P) (V). The next example show that the converse of the above corollary need not be true.
Example 5.5. According to Example 5.1. Let P = {f, h}, V = {e, g, h} and PV = {h}. Then(P) = {e, g},(V) = and(PV) ={e}.(P) (V)(PV).
Remark 5.3.The converse or the item (1) of Theorem 5.2. that P Need not be true as shown in the following example.
Example 5.6. According to Example 5.1. Let P = {f, g}, we have={g} then P.
Remark 5.4. The converse of item (5) of Theorem 5.2. need not be true as shown in Example 5.7.
Example 5.7. According to Example 5.1. Let P = {g, h} and V = {e,g,h}. Then ={e,f,h} = U although PV.
Some properties of Pawlak’s upper approximations are not realized for -Upper approximation such as . To clarify this fact, consider a subset P = {f}. Then = {g} But given in example 5.1.
Proposition 5.5. Let (U, Q, ξj) be a j-approximation space, given a set PU. Then the following proposition gives the relationships between the-lower approximations(P) and-upper approximations(P) where.
- (P) (P) (P) .
- (P) (P) (P) .
- (P) (P) (P)
- (P) (P) (P)
- (P) (P) (P) .
- (P) (P) (P) .
- (P) (P) (P) .
- (P) (P) (P) .
Proof.
- We prove (1): Let v (P) then v (v) P. Since (v) (v), then v (P) therefore (P) (P). □
similarly, we prove that (P) (P) and the other cases (2),(3) and (4) can be proved similarly.
- We prove (v): let v then v (v). Such that (v) Since (v) (v). Then (v) , therefore . □
similarly, we prove that and the other cases (6),(7) and (8) can be proved similarly.
Proposition 5.6. Let (U, Q, ξj) be a j-approximation space, given a non-empty set PU
- .
- .
- .
- .
Proof. We prove (1) and one can prove the other cases similarly.
Since (P) (P) (P) then
Since (P) (P) (P) then
By hypothesis, P is non-empty, so that > 0 for each j. Therefore:
. Then . □
To support the above results, we present the following example.
Example 5.8. According to Example 5.1, we calculate the approximations and their accuracy measure foras inTable 2, and we calculate the approximations and their accuracy measureas inTable 3.
6.
Using the following theorem, we can generate eight different topologies via
-neighborhoods.
Theorem 6.1. Ifis a j-approximation space, Then the collection
,is a topology
On U.
Proof.
- U and Ø belong to .
- If {| i } is a family of elements in and v . Then there exists such that v . Thus, (v) this lead to (v) and .
- If and P Then, v and v which lead to (v) and (v) Thus, (v) and hence . Then is a topology on U. □
Example 6.1. According to Example 3.1, the classes of-topologies are given as follows:
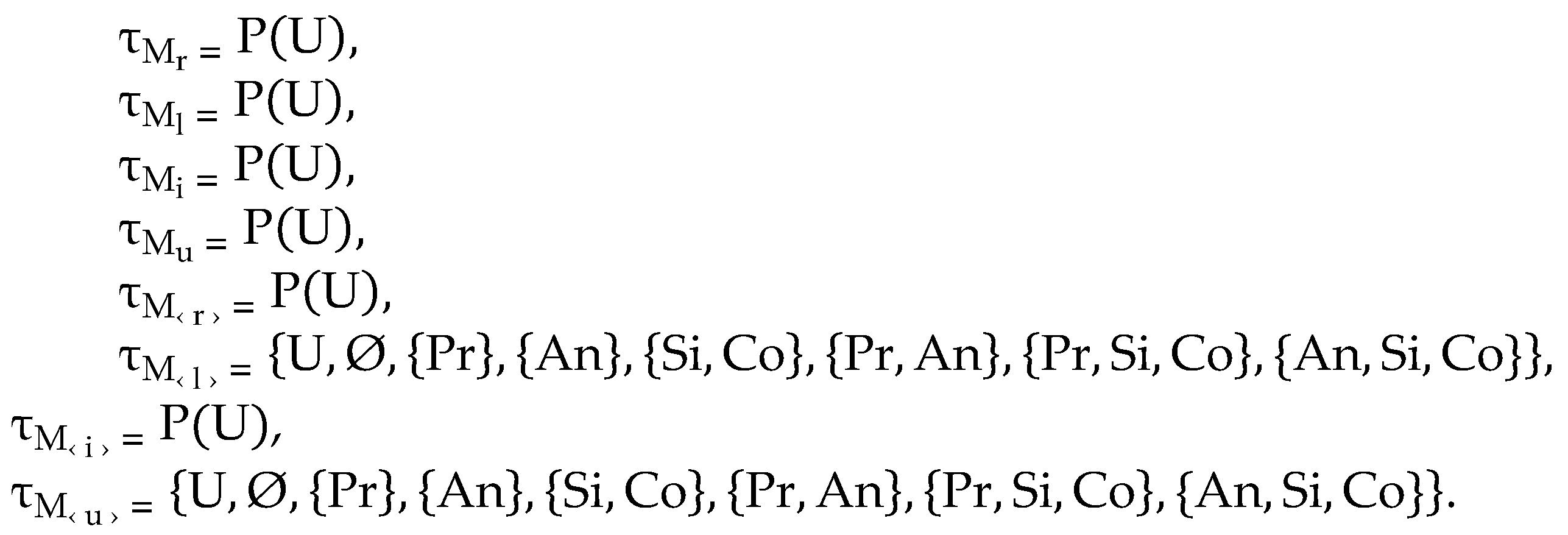
7. The Relations Among Topologies
We study the relationships among the topologies ,,,, ,,and
Proposition 7.1. In a j-NS (U, R, ξj),is the dual topology of.
Proof. Firstly, let A then ∀v A , (v) A. Suppose that q B, then (q)= {y .
Now, let (q) ∩ A ≠ then x ∈ U such that x ∈ A and x ∈ (q) ⇒ x∈A and xRq ⇒ x∈A and q ∈ (x) Since x ∈A ⇒(x) ⊆ A and so q ∈ A which contradicts with q ∈ B. Thus, (q) ∩ A = this implies (q) ⊆ B. Now, we have ∀q ∈ B, (q) ⊆ B. Hence, B ∈ . Similarly, we can prove that if B ∈ . Then, ∈ . Consequently, is the dual topology of □
The following example shows Proposition 7.1
Exemple7.1. Let U = {e, f, g, h} and R = {(e, e),(e, h),(f, e),(f, g),(g, f),(g, g),(g, h),(h, e)}.
Then, we have
= {U, Ø, {e, h}},
={U,Ø,{f, g}}.
Obviously, is the dual topology of .
Proposition 7.2. Let (U, Q, ξj) is a j-approximation space , then
.
.
Proof. Let B ∈, then ∀ v ∈ B, (v) ⊆ B. Thus (v) (v) ⊆ B and so ∀ v ∈ B, (v) ⊆ B ,Hence B ∈ and , similarly, we can deduce that . □
Remark 7.1. Let (U, R, ξj) be a j-NS and then the following are not necessarily true.
Proposition 7.3. Let (U, Q, ξj) is a j-approximation space. Then
Proof. Let B ∈ , then ∀ v ∈ B, (v) ⊆ B. Thus, ∀p ∈ B, (v) U (v) ⊆ B and so ∀ v ∈ B, (v) ⊆ B,(v) ⊆ B. Then, B ∈ and B ∈ and ⊆ and ⊆ . Using Proposition 7.2. we have ⊆ . □
Remark 7.2: Let (U, R, ξj) be a j-NS, then the following is not necessarily true.
The following example explains Remark 7.1 and Remark 7.2.
Example 7.2. Let U = {e, f, g, h, k} and R = {(e, e), (f, g), (f, h), (g, h), (g, k), (h, e), (h, k), (k, f), (k, k)}.
Then, we have = {U, Ø, {e},{k},{e, k},{e, h, k},{e, g, h, k}},
={U,Ø,{e},{g},{g, h},{g, h, k},{e, g, h, k} {f, g, h, k}}
= P(U) and = {U, Ø , {e},{e, g, h, k}}.
Proposition 7.4. Let (U, Q, ξj) is a j-approximation space. Then
Proof. Let B ∈ , then ∀ v ∈ B, (v) ⊆ B. Thus ∀ v ∈ B, (v)(v) ⊆ B and so ∀ v ∈ B, (v) ⊆ B ,Then B ∈ and . we can prove that similarly. □
Remark 7.3. Let (U, R, ξj) be a j-NS, then the following is not necessarily true.
Remark 7.4. In a j-NS,andare not necessarily comparable.
The following example explains remarks Remark 7.3 and Remark 7.4.
Example 7.3. Let U = {e, f, g, h} and R = {(e, h), (f, f), (f, g), (g, f), (h, e), (h, g)}.
Then, we have
= {U, Ø, {f},{g}, {h}, {e, g},{f, g},{f, h},{g, h},{e, f, g},{e, g, h},{f, g, h}},
={U,Ø,{e},{f},{h},{e, f},{e, h},{f, g},{f, h},{e, f, g},{e, f, h},{f, g, h}} and
= P(U).
Proposition 7.5. Let (U, Q, ξj) is a j-approximation space. Then
Proof. Let B ∈ , then ∀ v ∈ B, (v) ⊆ B. Thus, ∀ v ∈ B , (v) U (v) ⊆ B. and so ∀ v ∈ B, (v) ⊆ B and (v) ⊆ B. Then, B ∈ and B ∈ and hence ⊆ and ⊆ . Similarly, we can prove that ⊆ . □
Remark 7.5. Let (U, R, ξj) be a j-NS; then the following are not necessarily true.
The following example shows Remark 7.5.
Example 7.4. Let U = {e, f, g, h} and R = {(e, e), (e, f), (f, g), (f, h), (g, e), (h, e)}.
Then, we have
= {U, Ø, {e},{e, f},{g, h},{e, g, h}},
={U,Ø,{e},{f},{e, f},{e, g, h}},
= { U,Ø,{e},{f},{e, f},{g, h},{e, g, h},{f, g, h}} and
={U,Ø,{e},{e, f},{e, g, h}}.
Remark 7.6. In a j-NS,andare not necessarily comparable. Also,andare not necessarily comparable, as the following example illustrates.
Example 7.5. Let U = {e, f, g, h} and R = {(e, e), (f, f), (g, g), (g, h), (h, e)}.
Then, we have
= {U, Ø, {e},{f},{g},{e, f},{e, g},{e, h},{f, g},{e, f, g},{e, f, h},{e, g, h}},
={U,Ø,{e},{f},{e, f},{g, h},{e, g, h},{f, g, h}},
= {U, Ø, {e},{f},{g},{e, f},{e, g},{f, h},{g, h},{e, f, g},{e, g, h},{f, g, h}} and
={U,Ø,{f},{g},{e, h},{f, g},{e, f, h},{e, g, h}}.
Proposition 7.6. Let (U, Q, ξj) is a j-approximation space. Then
Proof. By using Propositions 7.2, 7.3, 7.4, and 7.5, the proof is obvious. □
8. Rough Approximations Generated by-Topologies
We introduced the rough approximations by using -neighborhoods. Let (U, Q, ξj) be j-approximation space. We employ -neighborhoods to generate classes of topologies (called -topologies).
Rough approximations using interior and closure operators in the topology , are defined.
Definition 8.1. Let (U, Q, ξj) be a j-approximation space. The subset BU is said to be-open set if B and the supplement of-open sets are called-closed sets. The familyof all-closed sets are defined as{ F|}.
Definition 8.2. Let (U, Q, ξj) be a j-approximation space and PU. The-lower approximations(P) and-upper approximations(P) are defined by:
- (P) = ∪{G : G P} = -interior of P.
- (P) = { H : P H} = - closure of P.
Definition 8.3. Let (U, Q, ξj) be a j-approximation space and PU. The-boundary region,-positive region and-negative region of P are defined as follows:
- = (P) _ (P).
- (P) = (P).
- = (P).
Definition 8.4. Let (U, Q, ξj) be a j-approximation space. The-accuracy of the approximations of PU is defined by:
= , where
It is clear that 0 ≤ ≤ 1. if ) = 1, then P is called -exact set. Otherwise, P called -rough.
9. Comparison between our approach and previous approaches.
According to data given in Example 3.1. Table 7 and Table 8 provide a comparison between Yao’s method [21], Abd El-Monsef et al.’s method [12], and the current methods in case of respectively.
From the Table 7 and Table 8, it is clear that the best of these methods given by using The boundary regions, in this case, are canceled. The results are so important for eliminating the imprecision of rough sets.
Example 9.1. We give the following example to illuminate some consequences.
Suppose that our universe is a set of carsand our relationship is given as. The different types of neighborhoods are given inTable 9as follows:
The -Topologies as follows:
.
.
.
Table 10 give -lower approximations and - upper approximations for each . Table 11 shows the comparison between Tareq M. Al-shami [18] approach and approach in case of j {r,i} as given in Example 9.1. The -accuracy for each are given in
We complete this work by studying these concepts from a topological view and comparing them. In all comparisons, we obtain higher accurate approximations in our approach.
10. Conclusions
This paper generated some classes of neighborhood systems that we call them -neighborhoods. We introduced some examples to discuss the main structures and their main concepts. We generalized these concepts to the topological case. We addressed many possible comparisons among them. We obtained refinement results that can be useful in real-life applications.
Author Contributions
Conceptualization, A.S. Salama and M. S. Bondok.; methodology, A.S. Salama.; software, A. A. El Atik and O.A. Embaby.; validation, A.S. Salama and M.S. Bondok.; formal analysis, A.M. Hussein.; investigation, A.S. Salama.; resources, A.S. Salama and M. S. Bondok.; data curation, M.S. Bondok; writing—original draft preparation, A.S. Salama.; writing—review and editing, A.S. Salama.; visualization, A. A. El Atik and O.A. Embaby; supervision, A.S. Salama; project administration, A.M.Hussein; funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
MDPI Research Data Policies at https://www.mdpi.com/ethics.
Acknowledgments
The author sincerely thank the editor and to anonymous reviewers for their valuable comments and suggestions that helped in improving this paper. The authors would like to thank all Tanta Topological Seminar colleagues ‘‘under the leadership of Prof. Dr. A. M. Kozae’’ for their interests.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Z. Pawlak, Rough sets, Int. J. Inf. Comput. Sci. 11 (5) (1982) 341–356.
- Z. Pawlak, A. Skowron, Rough sets, Some extensions, Information Sciences, 177 (2007) 28–40.
- K. Qin, J. Yang, Z. Pei, Generalized rough sets based on reflexive and transitive relations, Information Sciences, 178 (2008) 4138–4144.
- W. Zhu, F. Wang, Reduction and axiomatization of covering generalized rough sets, Information Sciences, 152 (2003) 217–230.
- W. Zhu, F. Wang, Binary relation based rough sets, Lecture Notes in Computer Sciences, 4223 (2006) 276–285.
- A. S. Salama, Generalizations of Rough Sets Using two Topological Spaces with Medical Applications, INFORMATION, 19 (7A) (2016) 2425-2440.
- A.S. Salama, Sequences of Topological Near Open and Near Closed Sets with Rough Applications, Filomat, 34(1) (2020), 51–58.
- A.S. Salama, Bitopological Approximation Space with Application to Data Reduction in Multi-valued Information Systems, Filomat, 34 (1) (2020), 99–110.
- A.S. Salama, Topological solution of missing attribute values problem in incomplete information tables, Information Sciences, 180 (2010) 631-639.
- A.S. Salama, Topologies induced by relations with applications, Journal of Computer Science, 4(10) (2008), 877–887.
- A.S. Salama, Abd El-Monsef, M. M. E., New topological approach of rough set generalizations, International Journal of Computer Mathematics, 88(7) (2011), 1347–1357.
- M.E. Abd El-Monsef, O.A. Embaby, M.K. El-Bably, Comparison between rough set approximations based on different topologies, International Journal of Granular Computing, Rough Set and Intelligent Systems, 3(4) (2014), 292–305.
- M.E. Abd El-Monsef, A.S. Salama and O.A. Embaby, Granular computing using mixed neighborhood systems, Journal of Institute of Mathematics and Computer Sciences, 20 (2) (2009), 233–243. O.G.
- El Barbary, A.S. Salama, Feature selection for document classification based on topology, Egyptian Informatics Journal, 19(2) (2018), 129–132.
- Wiweger, On topological rough sets, Bulletin of the Polish Academy of Sciences Mathematics, 37 (1989) 89–93.
- Tareq M. Al-shami, An improvement of rough sets’ accuracy measure using containment neighborhoods with a medical application. Inf Sci, 569 (2021),110–124.
- Tareq, M. Al-shami, Ciucci D, Subset neighborhood rough sets. Knowl Based Syst, 237 (2022), 107868.
- Tareq, M. Al-shami, Fu WQ, Abo-Tabl E. A., New rough approximations based on E-neighborhoods. Complexity, 6666853 (2021), 1-6.
- Mareay R, Generalized rough sets based on neighborhood systems and topological spaces, Journal of Egyptian Math Soc, 24 (2016) 603–608.
- Z. Pawlak, Rough Sets, Theoretical Aspects of Reasoning About Data, Kluwer Acadmic Publishers Dordrecht, 1991.
- Yao YY, Two views of the theory of rough sets in finite universes. Int J Approx Reason, (1996), 15:291–317.
Table 1.
Classes of -neighborhoods, Ej-neighborhoods and Mj -neighborhoods.

Table 2.
The approximations and accuracy measure in cases of
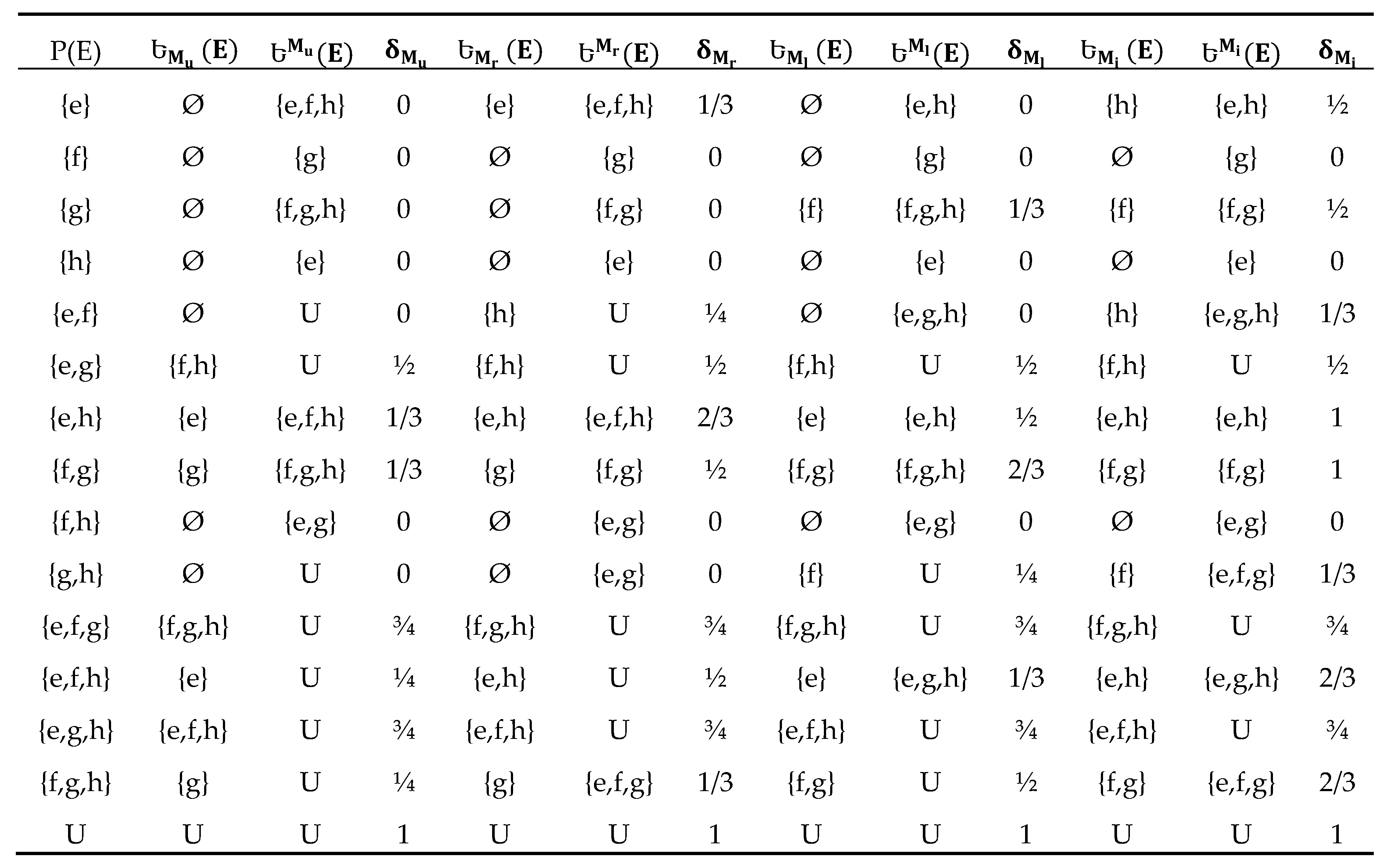
Table 3.
The approximations and accuracy measure in cases of
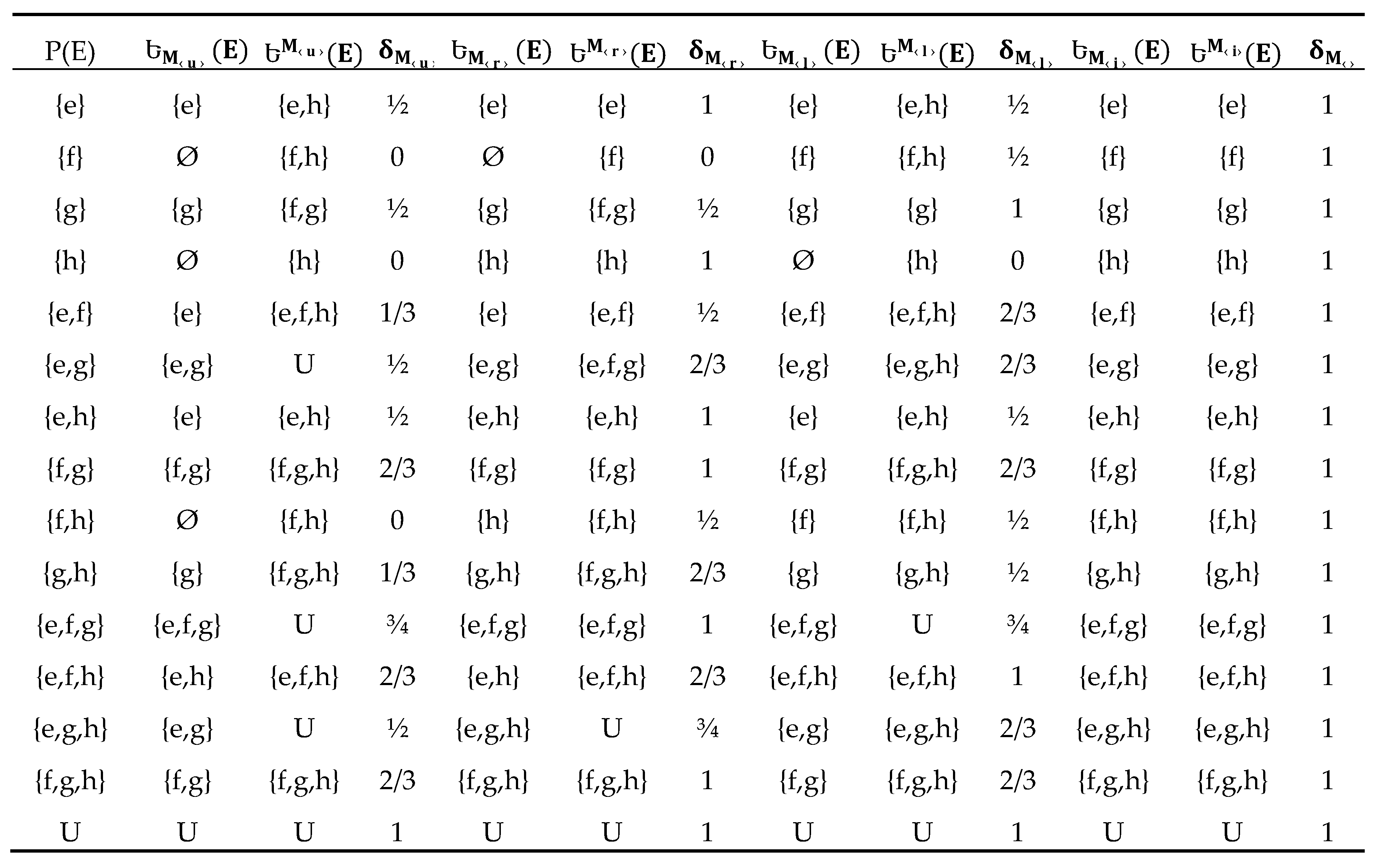
Table 4.
The -approximations for each .
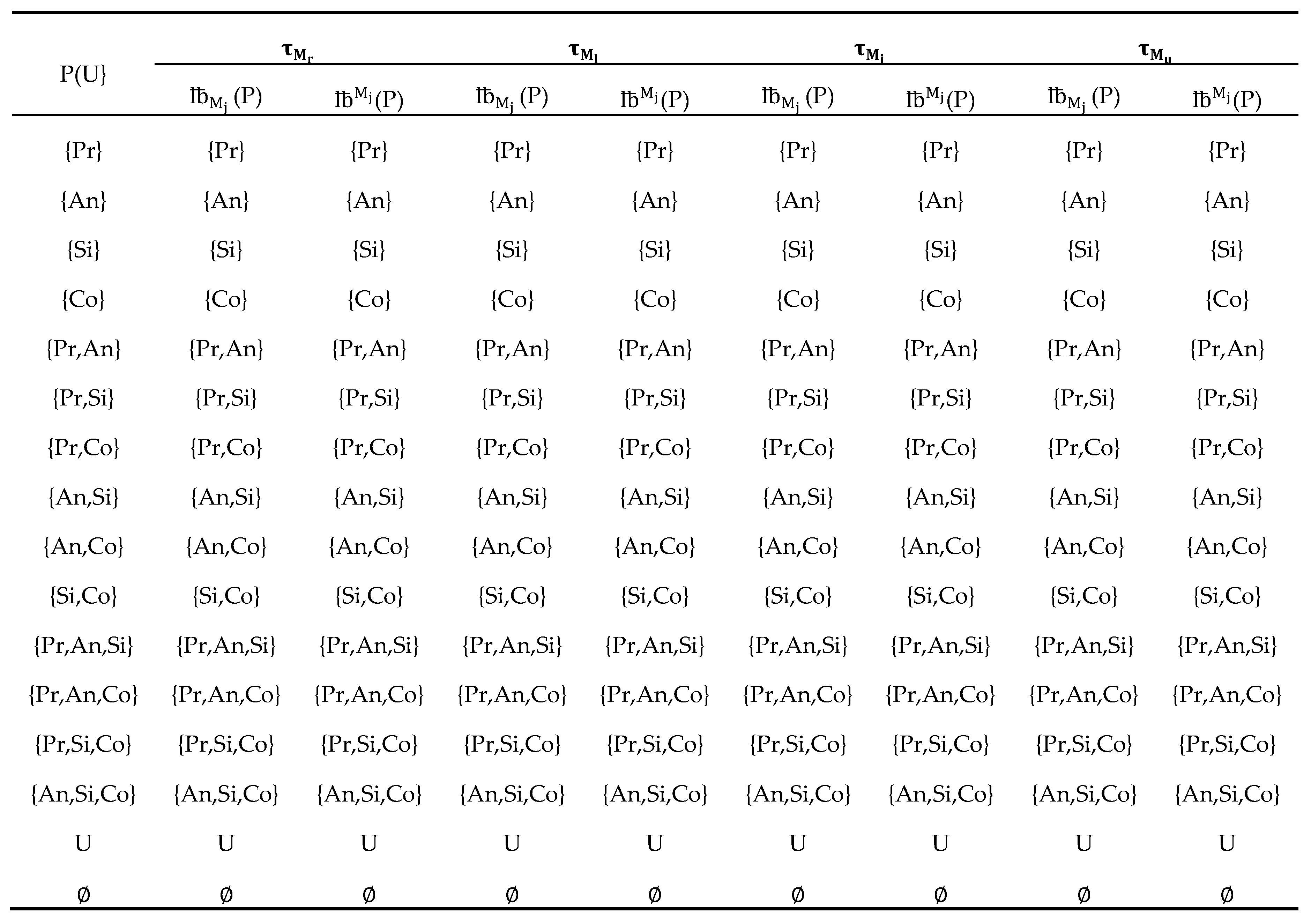
Table 5.
The -approximations for each

Table 6.
The
-accuracy for
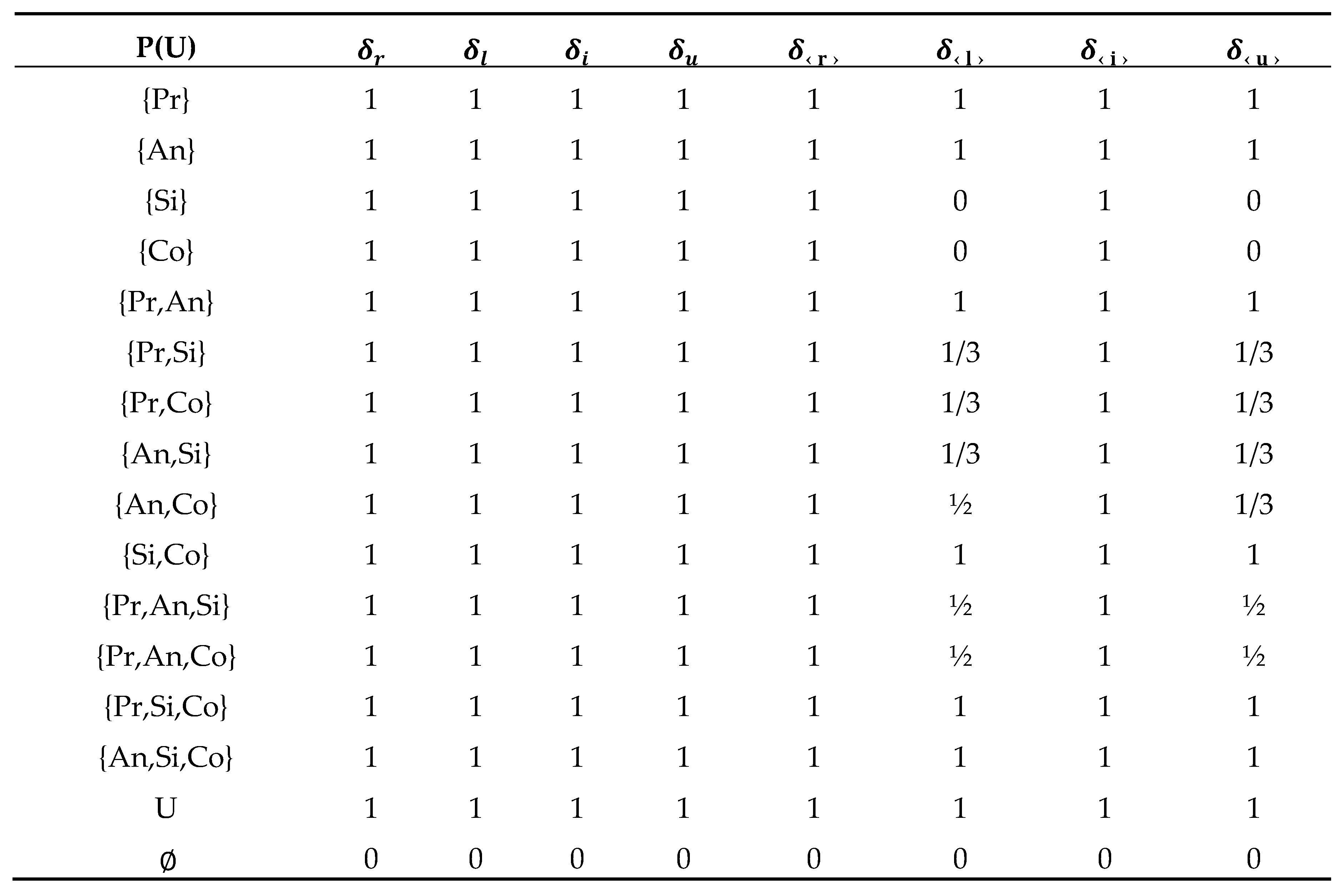
Table 7.
Comparison between Yao, and Mj approaches for j = (r, l).

Table 8.
Comparison between Yao, and Mj approaches for j = (r, l).
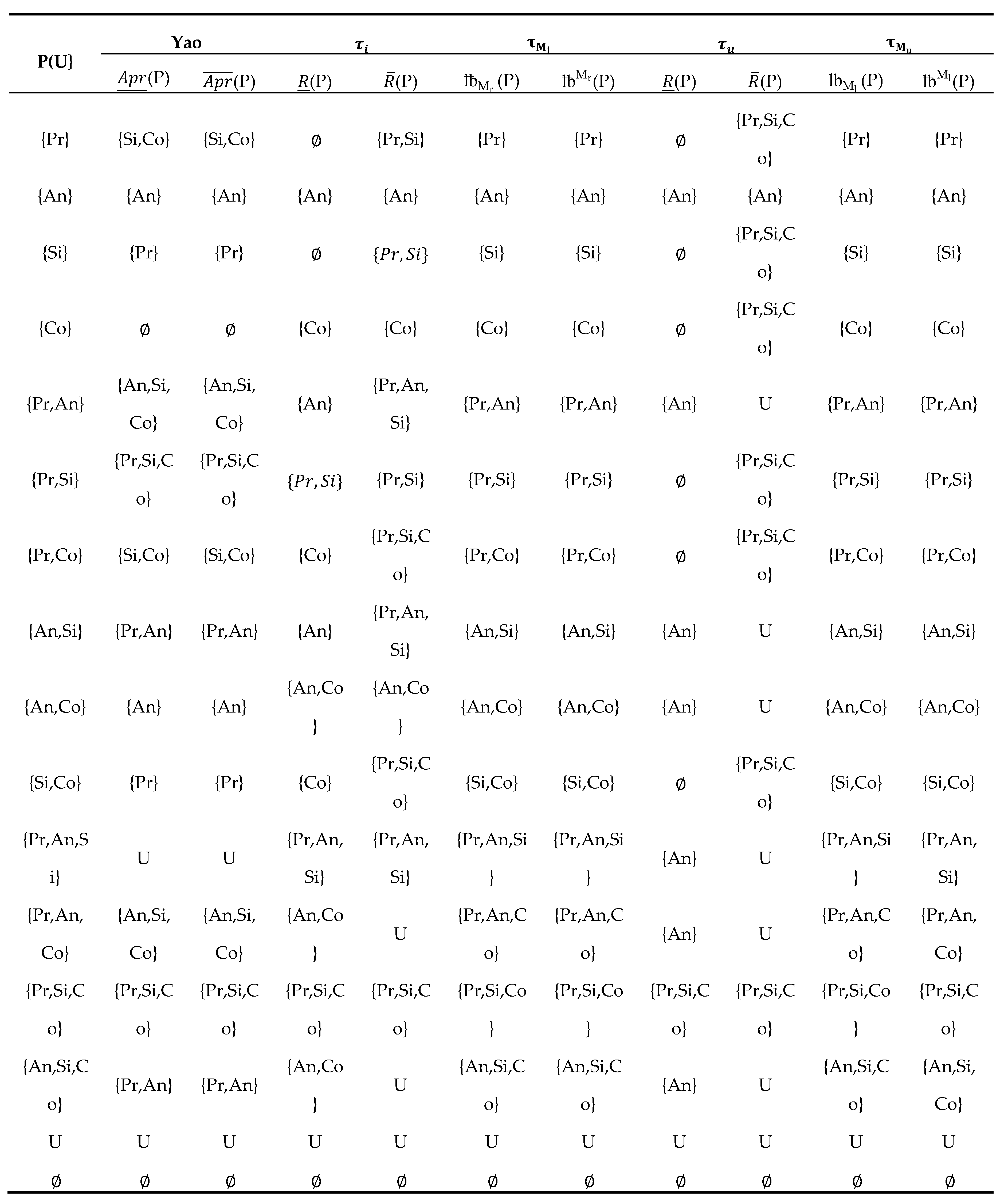
Table 9.
Different types of neighborhoods.
| U | Sedan | Sports Car | Coupe | Minivan |
| {Se,Co,Mi} | {Mi} | {Sp,Mi} | ||
| {Se} | {Mi} | {Se} | {Se,Sp,Mi} | |
| {Se} | {Mi} | {Sp,Mi} | ||
| {Se,Co,Mi} | {Mi} | {Se} | {Se,Sp,Mi} | |
| {Se,Co,Mi} | {Sp,Mi} | {Se,Co,Mi} | {Mi} | |
| {Se} | {Se,Sp,Mi} | {Mi} | ||
| {Se} | {Sp,Mi} | {Mi} | ||
| {Se,Co,Mi} | {Se,Sp,Mi} | {Se,Co,Mi} | {Mi} | |
| {Se,Sp,Mi} | {Se,Sp,Mi} | {Se,Sp,Mi} | ||
| {Se,Co,Mi} | {Sp,Mi} | {Se,Co,Mi} | U | |
| {Se,Mi} | {Sp,Mi} | {Se,Sp,Mi} | ||
| U | {Se,Sp,Mi} | {Se,Co,Mi} | U | |
| U | U | U | U | |
| {Se,Sp} | {Se,Sp,Mi} | {Sp,Mi} | ||
| {Se,Sp} | {Se,Sp,Mi} | {Sp,Mi} | ||
| U | U | U | U | |
| {Se,Mi} | {Mi} | {Sp,Mi} | ||
| {Se} | {Mi} | {Se} | {Se,Sp,Mi} | |
| {Se} | {Mi} | {Sp,Mi} | ||
| {Se,Mi} | {Mi} | {Se} | {Se,Sp,Mi} | |
| {Se,Co,Mi} | {Sp,Mi} | {Se,Co,Mi} | {Mi} | |
| {Se} | {Se,Sp,Mi} | {Mi} | ||
| {Se} | {Sp,Mi} | {Mi} | ||
| {Se,Co,Mi} | {Se,Sp,Mi} | {Se,Co,Mi} | {Mi} |
Table 10.
Approximations operators based on for some subsets of U.
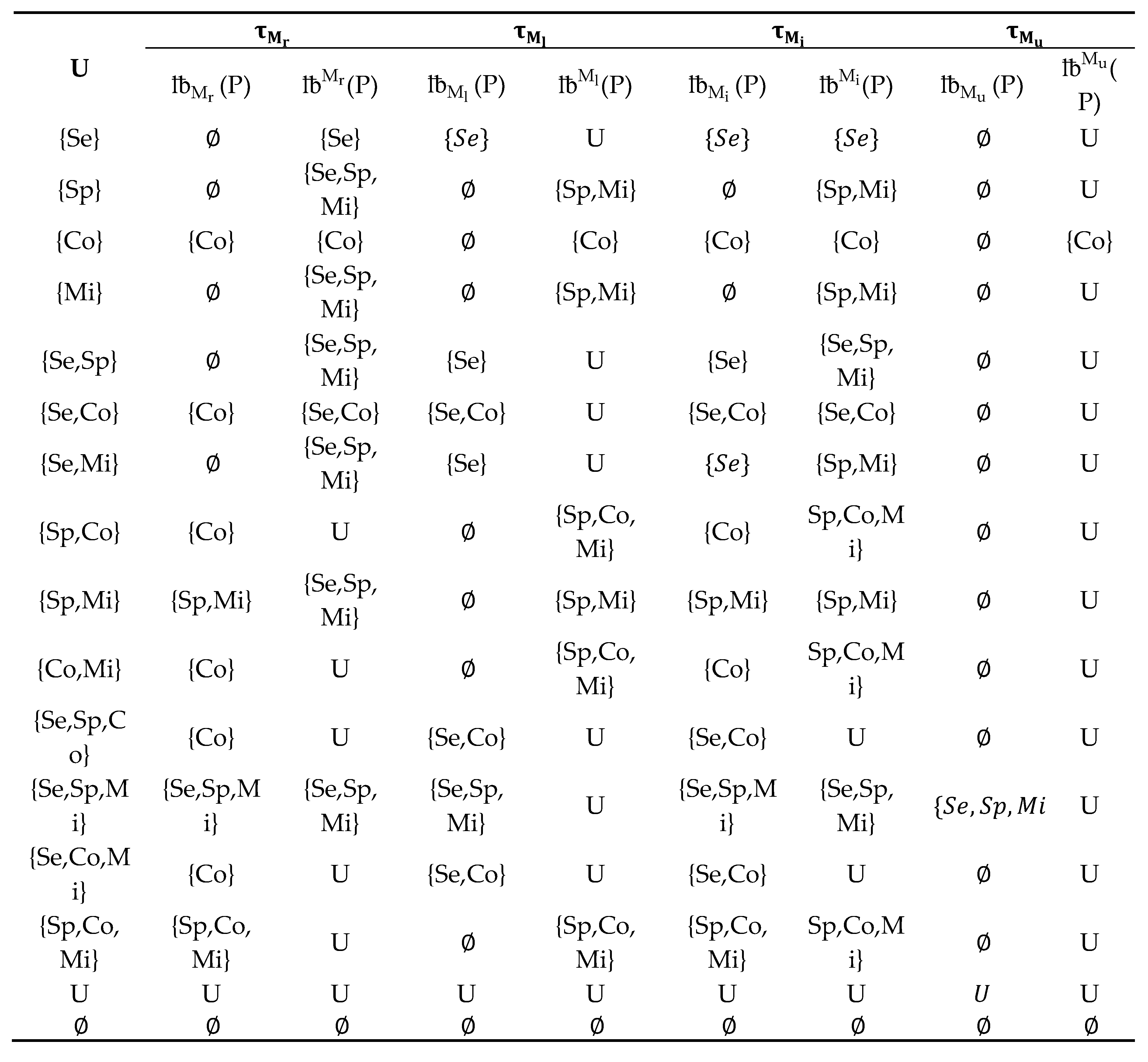
Table 11.
Comparison among and Mi approaches for some subsets of U.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated






