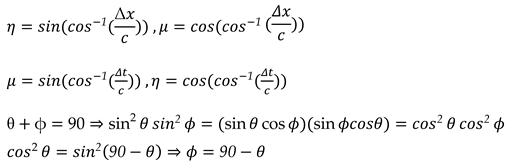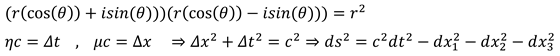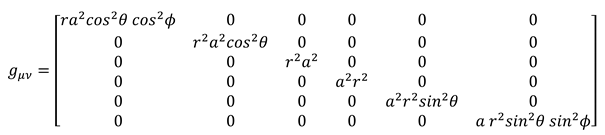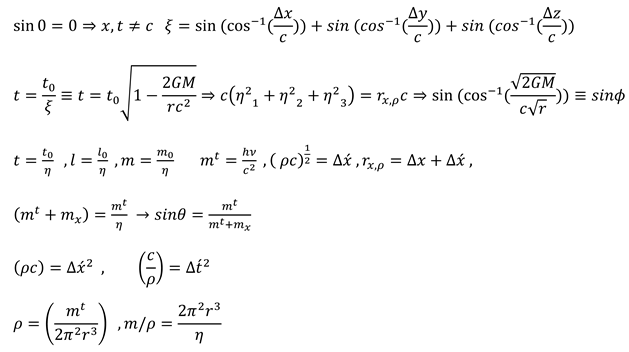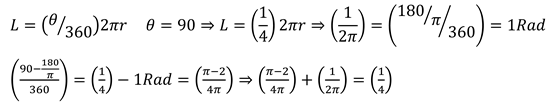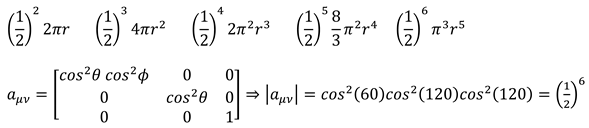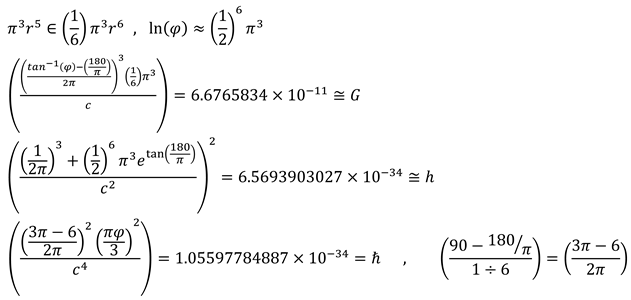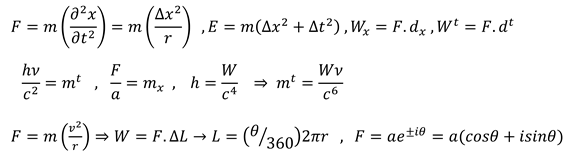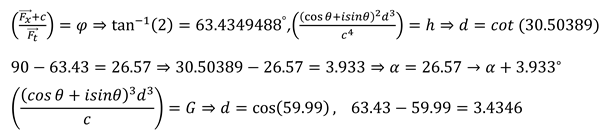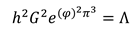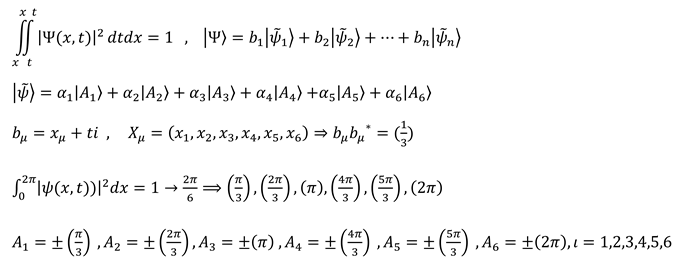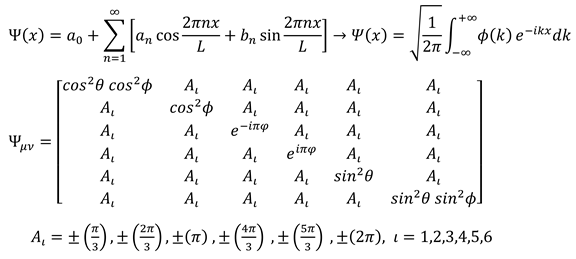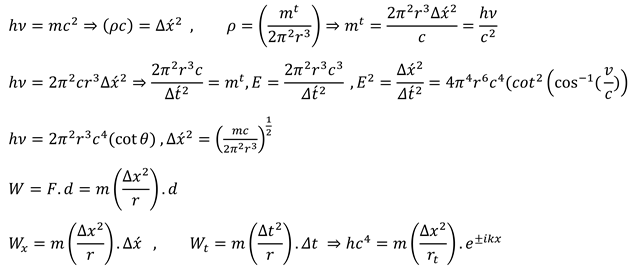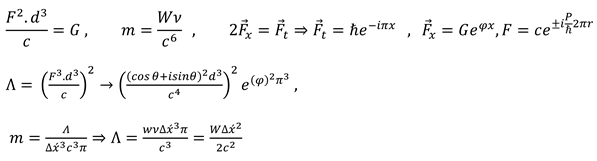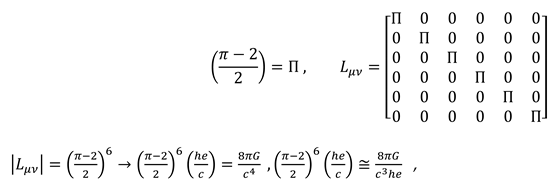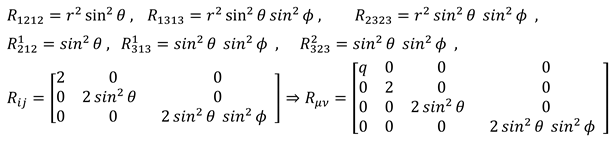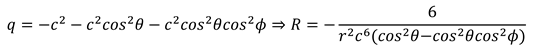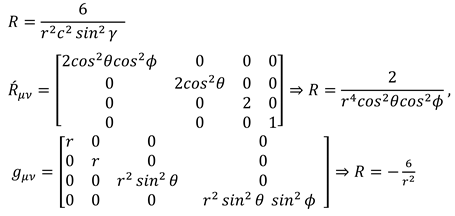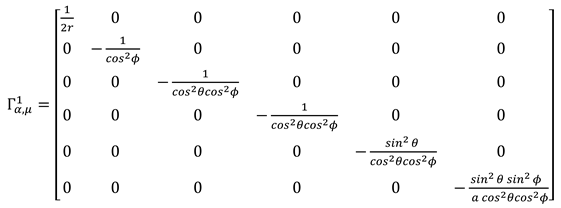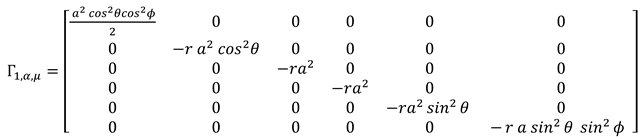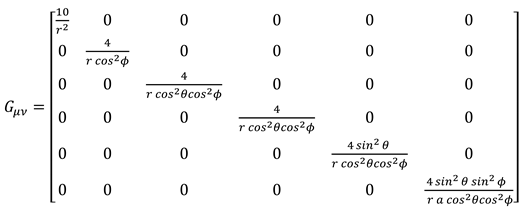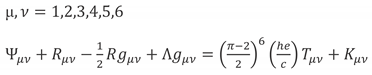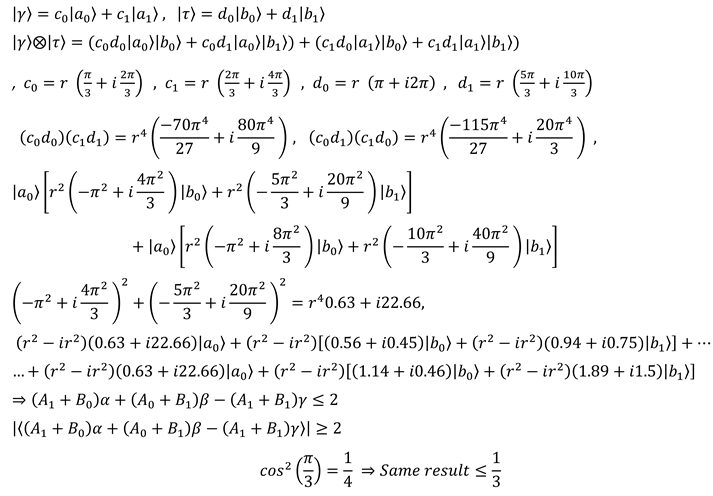The General Balance in the Six Dimensional of Space-Time

Preprint

Article

The General Balance in the Six Dimensional of Space-Time

Altmetrics

Downloads

168

Views

Comments

seyed kazem mousavi^*

This version is not peer-reviewed

Submitted:

13 August 2023

Posted:

16 August 2023

You are already at the latest version

Alerts

Abstract

On the basis of the findings of this paper, the theories of quantum mechanics and general relativity can be expressed in a comprehensive theory. The events were surveyed length of the time, in the Euclidean six-dimensional space-time (R6=x1+x2+x3+t1+t2+t3). Previous studies have not studied the relationship between the origin of matter's inherent properties, fundamental constants, and quantum mechanics phenomenon with space-time geometry. This theory prediction the with certainty obtained probabilistic results of quantum mechanics. This prediction is on the basis of metric resulting from the Eccentricity of the Ellipse due to the object density, in the length of time. The cause and nature of dark matter and dark energy are the findings of this article.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

During the recent century, much effort was made to unite quantum mechanics and general relativity. The non-classical nature of quantum mechanics phenomena is the cause of the incompatibility between quantum mechanics and general relativity. the main reason for the incompatibility of quantum mechanics with general relativity is the unrealized quantum mechanics phenomena. Considering Einstein’s view that ‘reality of a physical quantity is materialized with the possibility of forecasting that reality with certainty without creating any disorder in the system [1]. It shall be mentioned that for uniting two theories, the two theories shall have identic attitudes concerning physical quantities. Understanding the phenomenon of quantum mechanics is possible by knowing the origin of mass, spin, electric charge, etc. [2,3,4,5,6]. With consideration of quantum mechanics’ successes, describing time nature can be an essential strategy for the evolution of the theory of everything [7]. A new attitude to space–time nature for explaining quantum mechanics phenomena is only possible with time nature description. Studying events out of time is a new discussion. This attitude in physics is a different glance at the universe’s world. The papers and research in this field are based on descriptions of various metrics in six-dimensional space [8,9,10,11,12]. Even though introducing six-dimensional space for space–time has some problems, it is very useful for explaining several quantum mechanics phenomena [13].The metric description of space-time, based on elliptical Eccentricity solves some problems [14,15]. The description of all quantum mechanics phenomena is possible in six-dimensional space-time [16].

If we imagine time as an independent dimension from space, we will be able to define a type of ‘motion’ in time. From the viewpoint of extrinsic geometry, motion in time is a ‘real’ distance. The time arrow expresses one-directionality of time, and objects move at different speeds in time. The rate of objects’ movement during time is in relation with their mass. Gravitational time dilation and Time dilation for the moving object expresses the object density change in space-time. Denser objects move slower in the time dimension. The balance theory discusses the balance of events and quantities between three-time dimensions and three space dimensions within six dimensions of space–time [17]. Meanwhile, this theory has some defects which were removed in this paper. This theory establishes balance, equilibrium, and parity between time, space, and physical quantities. For example, the mass resulted from movement in time, gravitational mass, and the mass resulted from movement in space ،In total, they are the mass of the object. On the basis of this attitude, time can be ignored for the sub-atomic world. For example, a particle attends within the limit of its field in the three times of past, present, and future, and it passes from two fissures in a moment. The wave function expresses particle attendance in dimensions more than 3 dimensions and entanglement expresses the closeness of particles’ state in higher dimensions, even though they have distance in space from each other. The measurement can equate the dimension of the particle with the dimensions of the observing world. This paper discusses about the manner of possibility for the independence of three-time dimensions from three space dimensions and also deep relations between these 2 worlds for analyzing and describing the phenomena of quantum mechanics and general relativity in a unit theory. The nature and cause of quantum mechanical phenomena lies in the relationship between fundamental constants, such as Planck’s constant, gravitational constant, and cosmological constant with three numbers, Pi, Phi, and Euler’s number. Geometrical interpretation of quantum mechanics phenomena is the factor for uniting quantum mechanics with general relativity.

2. Six-Dimensional Space-Time

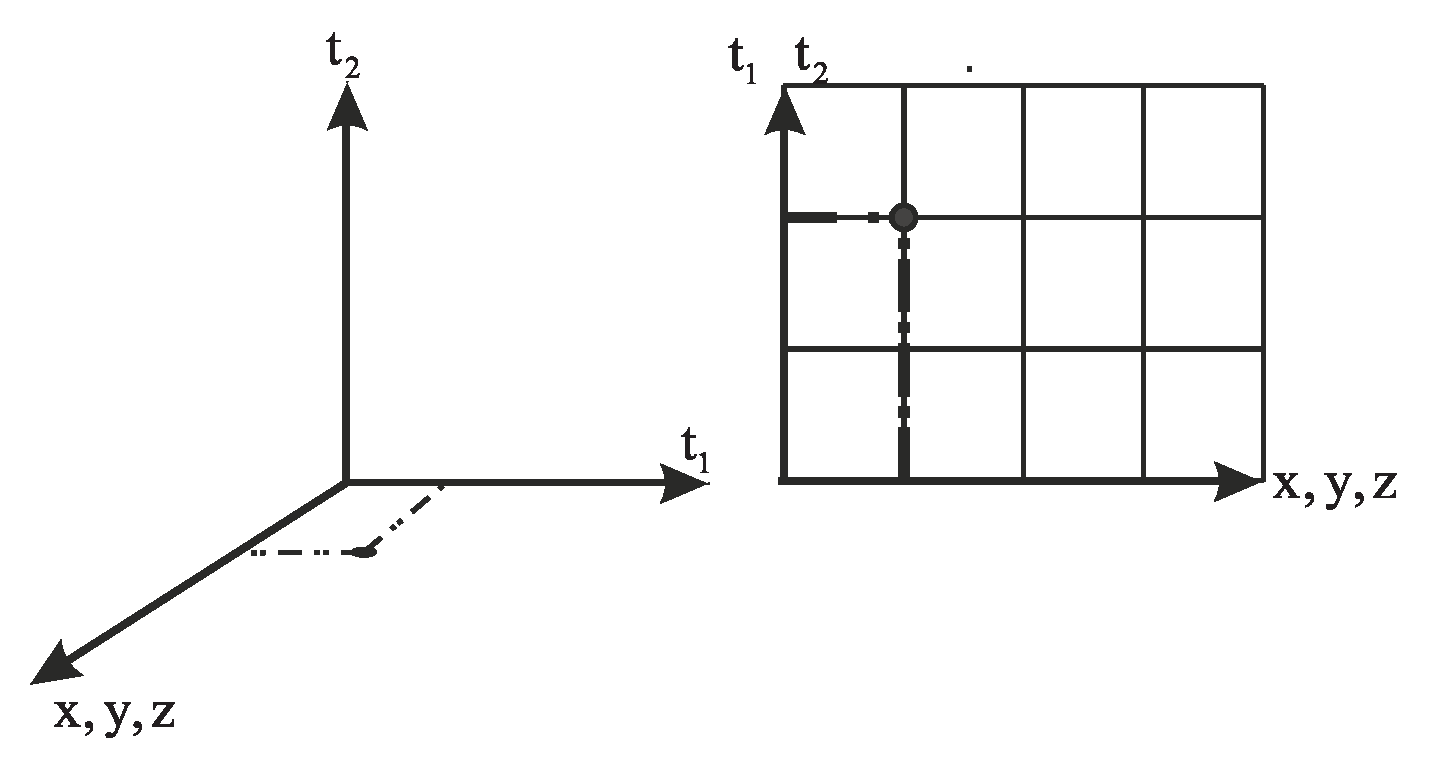
Space-time is a Euclidian space 3+3 consisting of three space dimensions (x,y,z) and three-time dimensions(t-, t, t+). (2.1) Time dimensions are imaginary 3- dimensional from the perspective of a supervisor and they are observed only in one dimension. (1.2) (2.2)

X = (x_{1}, x_{2}, x_{3}, t_{1}, t_{2}, t_{3}) \in R^{6}

(1.2)

d s^{2} = d x_{1}^{2} + d x_{2}^{2} + d x_{3}^{2} - (c^{2} d t_{1}^{2} + c^{2} d t_{2}^{2} + c^{2} d t_{3}^{2})

(2.2)

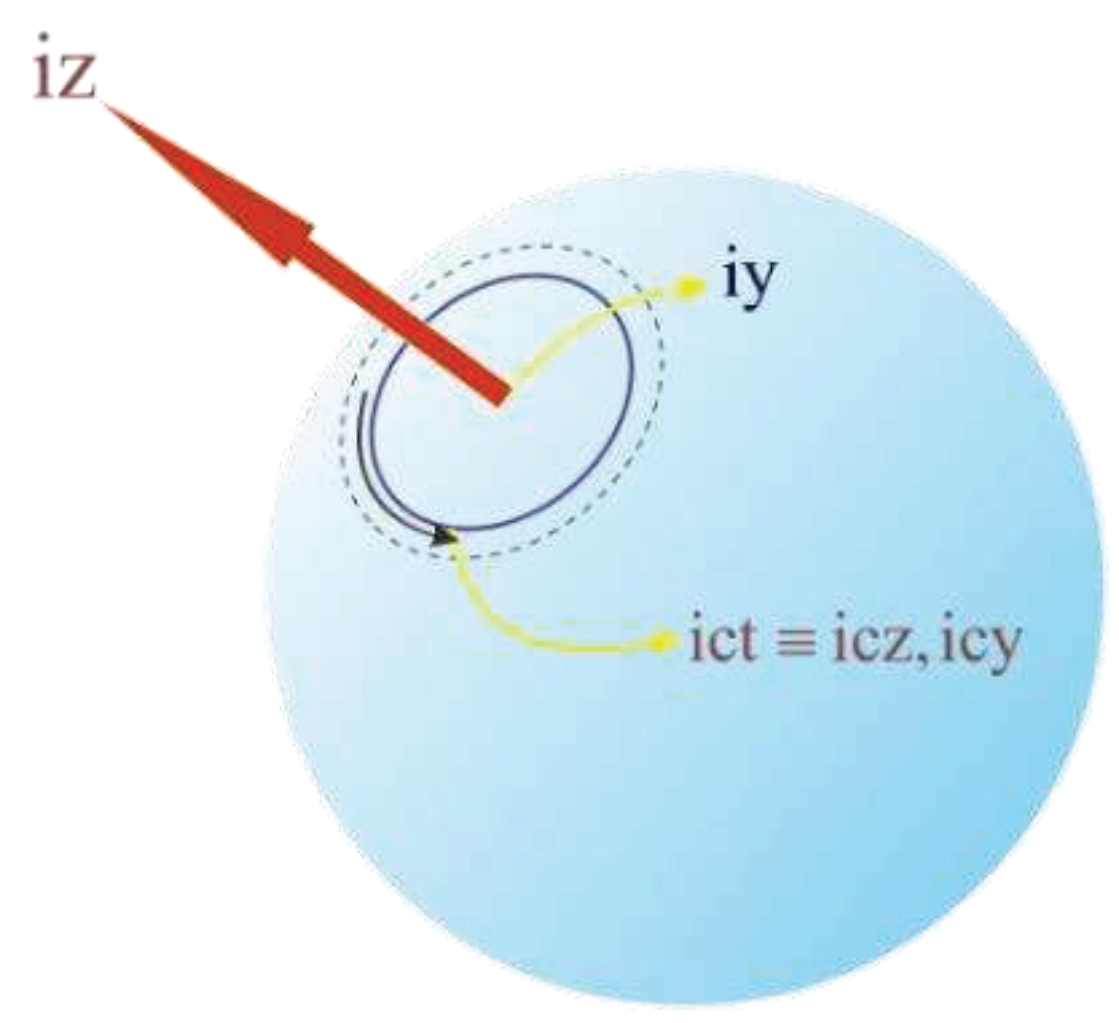
The y and z there are imaginary for creatures one- dimensional on a circle. This circle is embedded in the surface of a 3-dimensional sphere. also, This sphere is expanding. Figure 1.

Consequently, of the parallaxes of one -dimensional creatures, two imaginary dimensions are observed in the direction of one imaginary dimension. also, Time has an internal dimension as well.

Time dilation depends on the mass and speed of the observer. Time dilation (the speed of movement in the time dimension) depends on the mass and speed of the observer. The mass and speed of the observer are directly related to the eccentricity of the ellipse. Figure 2.

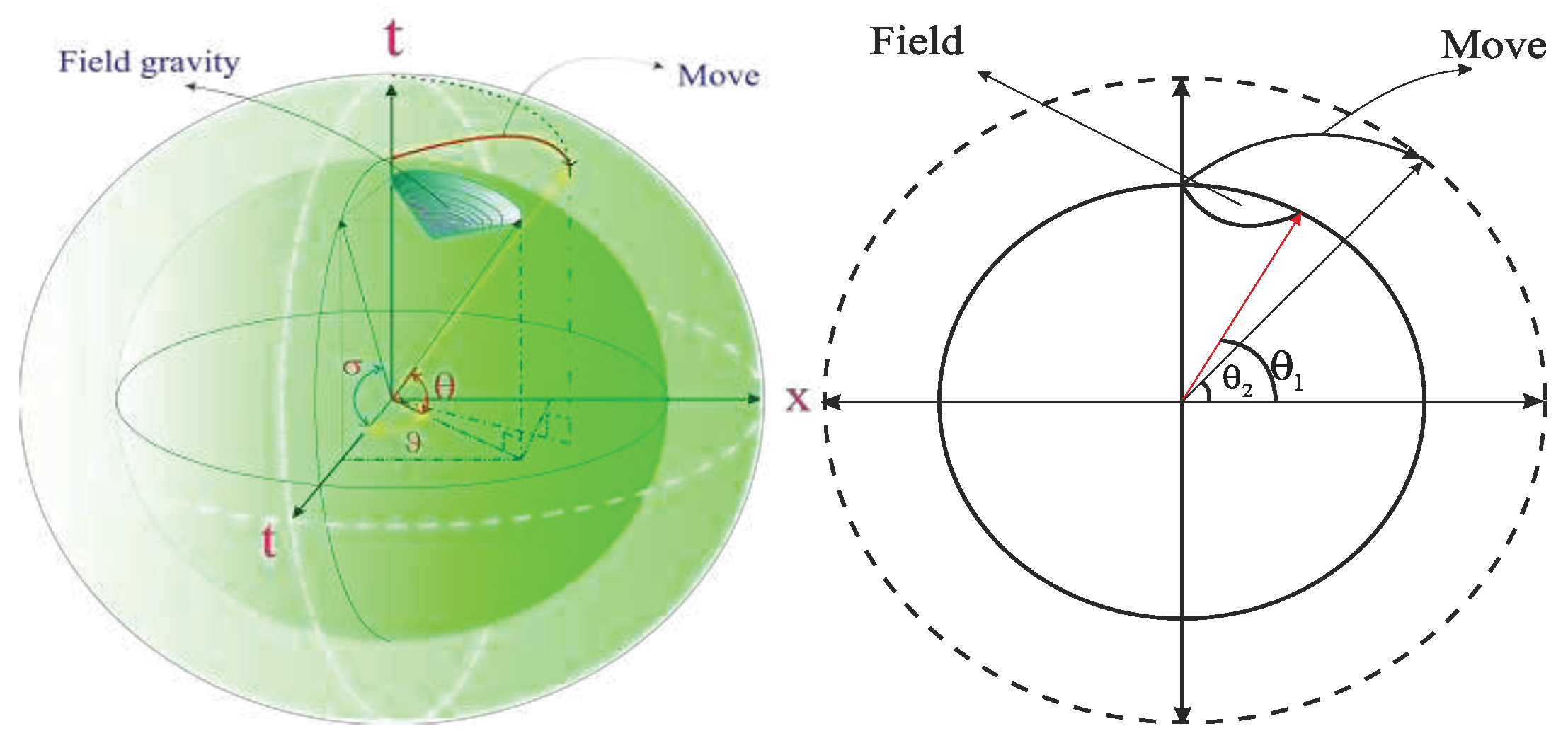
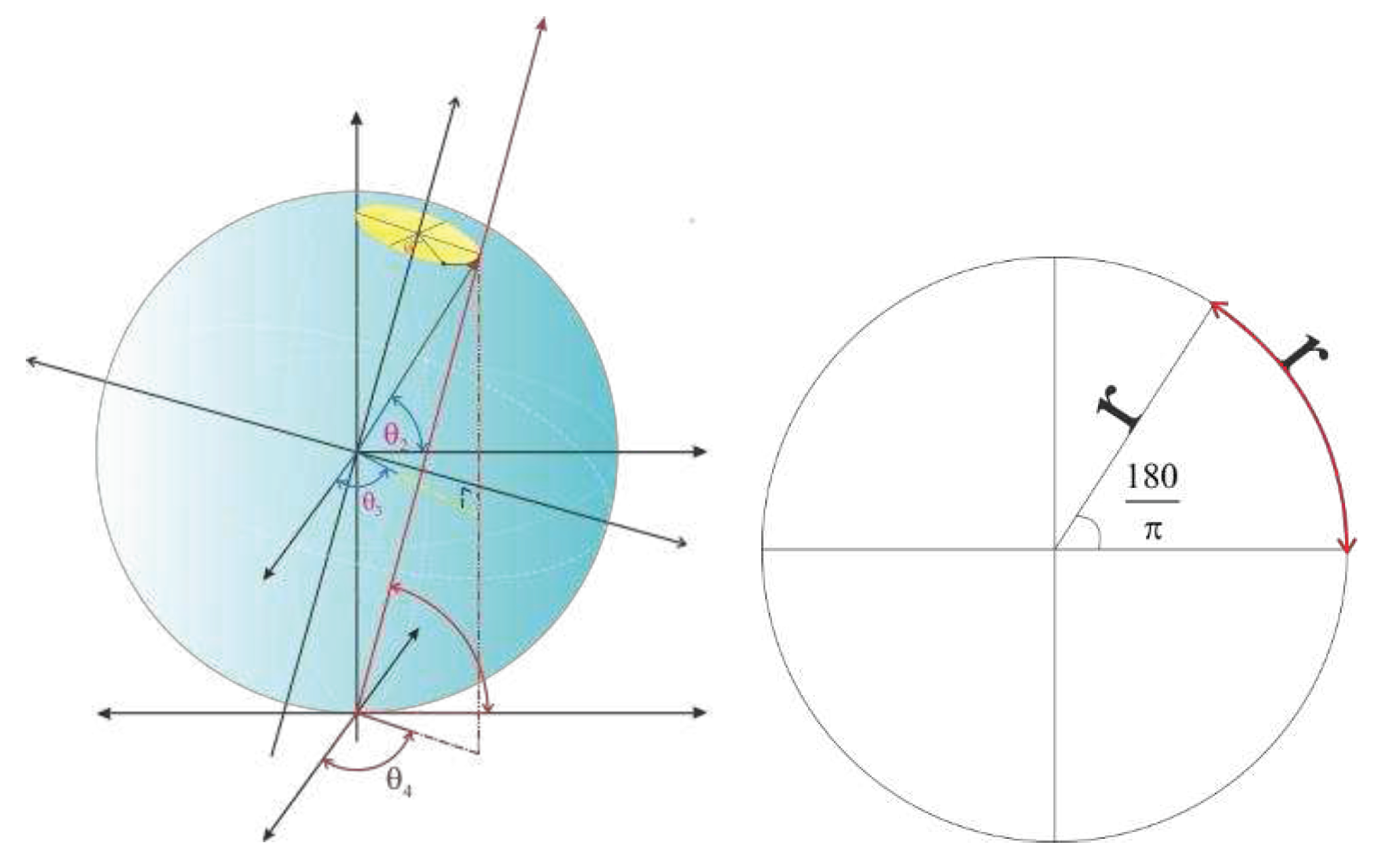
Eccentricity in the space dimensions has an effect on the time dimensions as well. From the perspective of extrinsic geometry, the time dilation of the moving object and also Gravitational time dilation in the gravitational field are expressed based on the angle θ. (2.3) . Figure 2

Density or speed can create eccentricity in space-time dimensions.

\sqrt{1 - \frac{v^{2}}{c^{2}}} = \sin (\cos^{- 1} (\frac{v}{c})) t = \frac{t_{0}}{\sin θ} t = t_{0} \sqrt{1 - \frac{2 G M}{r c^{2}}}

(2.3)

The passed distance in space is real six–dimensional from the perspective of space-time. But the distance from perspective. of 4 or 5 –dimensional space-time is expressed in hyperbolic geometry. (2.4) (2.5)

i n t r i n s i c g e o m e t r y d s^{2} = d x_{1}^{2} + d x_{2}^{2} + d x_{3}^{2} + c^{2} d t_{1}^{2} + c^{2} d t_{2}^{2} - c^{2} d t_{3}^{2}

(2.4)

e x t r i n s i c g e o m e t r y d s^{2} = d x_{1}^{2} + d x_{2}^{2} + d x_{3}^{2} + d t_{1}^{2} + d t_{2}^{2} + d t_{3}^{2}

(2.5)

Eccentricity in one axis causes eccentricity in other axes. As a result of this eccentricity, the path traversed in space-time has a rotation equal to ¼ of the circumference of the hypothetical circle with the radius of the density (field). Figure 3

As a result of defining the passed distance in space-time is dependent on the space-time expansion, the light speed as well as eccentricity in six-dimensional space-time.(2.6)

(2.6)

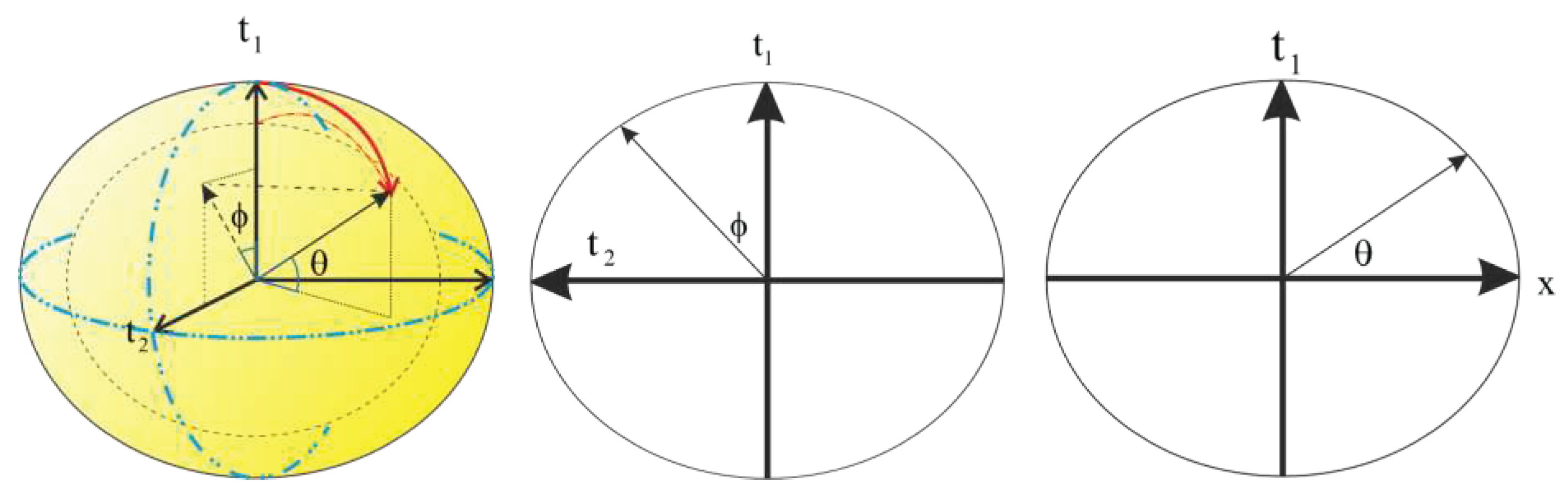
In six-dimensional space, there are five degrees of freedom. From the perspective of 4 –dimensional space-time, two-time dimensions are observed in one dimension. Consequently, the two angles, related to eccentricity are expressed by the angle

θ

. The angle

κ

is also for expansion and final movement in time. Figure 4

While moving the rigid body in space, the radius of the field and object lengths change which is proportional to density. The angles related to eccentricity exist in equilibrium in the two-time dimensions. (2.7)

(2.7)

With consideration of the two time axles, the matter is stressed by space–time. The exerted stress on the matter from time dimensions is twice the exerted stress from space dimensions. This twice proportion has a direct connection with the golden constant. (2.8) Figure 5

φ = \frac{x + \sqrt{x^{2} + {(2 x)}^{2}}}{2 x} = \frac{{\vec{F}}_{X} + \sqrt{{\vec{F}}_{X}^{2} + {\vec{F}}_{t}^{2}}}{{\vec{F}}_{t}}

(2.8)

From the perspective of extrinsic geometry, the illusory dimension of time is a real dimension. And the distance traveled in space-time is a real path over time. (2.9)

(2.9)

The angles θ and ϕ indicate the extent of eccentricity. The metric of space-time is expressed based on the two angles of θ, according to the surface metric of the sphere (3sphere). (2.10)

(2.10)

Matter with 3-dimensional nature creates heterogeneity in the space density with higher dimensions. As a result of existing this heterogeneity, the matter moves in space–time. Meanwhile, heterogeneity is a factor for creating eccentricity and stress to the material. On the basis of creating heterogeneity in space –time structure by matter and energy, density can be expressed in the form of passed distance in space –time.

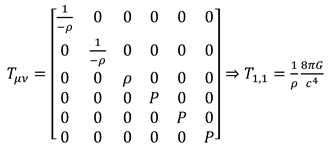
The oscillation of heterogeneity in space-time creates gravitational mass. mass cannot exist in the past or future, as a result expressing negative density is necessary for the Energy momentum tensor (2.11).

(2.11)

(2.11)

Objects in space-time rotate around a field with a radius that matches their density radius in higher dimensions. This radius is equivalent to the density in two dimensions of one radian. Figure 6.The matter field is rotating and moving simultaneously by rotating around a field which its radius varies with space expansion as well. Figure 7

The length of density or heterogeneity is like the length of one Radian on the circle circumference. a sum of density and the negative of density in the 2 dimensions is equal to¼ of the circle circumference. On the basis of Figure 3, the object route in one dimension is changed in the direction of geodesics of space–time in another dimension as well. As a result, the object rotates equal to¼ of the circle circumference in 3- dimensional space. This rotation was generalized to higher dimensions. (2.12). This rotation is due to the constancy of object density and causes to create eccentricity in other space–time expansion axles. Figure 3

(2.12)

3. Geometry and Fundamental Constants of Physics

The rotating of objects in 5- dimensional space was expressed by the Golden proportion. (3.13) Golden constant, π, and e have a geometrical connection with physics fundamental constants like the gravity constant and Planck constant in 6- dimensional space-time. (3.13)

(3.13)

The resulting force from rotating objects around the field and then the performed work in six-dimensional space were calculated by Planck constant coefficient. (3.14) Planck constant is in relation to object movement in space-time and the gravity constant is in relation to object resistance versus expansion of space-time. Figure 7

(3.14)

Two forces are exerted on the rigid object by the higher dimensions. One force causes the object to move perpendicular to the axis of expansion, and the other force applies force to the object against the direction of expansion of space-time. As a whole, the object is rotating around a field, and the field is also rotating around an expanding sphere. Changing angles of ɑ and β indicate rigid object motion around a field with higher dimensions. (3.15)

(3.15)

Cosmology constant established a direct connection with the Planck constant, the gravity constant, and 3 natural numbers. (3.16)

(3.16)

Observations related to the planets movement express a deep geometrical relationship between fundamental constants. (3.17)

{(\frac{π - 2}{2})}^{6} (\frac{h e}{c}) = \frac{8 π G}{c^{4}} \Rightarrow {(\frac{π - 2}{2})}^{6} ≅ \frac{8 π G}{c^{3} h e}

(3.17)

The radius of the object field in space–time has a direct relationship with exerted force by the higher dimensions. As a result of this direct relationship, the proportions between these forces have a constant with density. These proportions follow the golden constant, Euler’s number, and π. Figure 8

4. Wave Function

The wave function in quantum mechanics has expanded over time. With regard to the object field, the eccentricity of space-time dimensional, negative density, object rotation around the field, and field rotation, the structure of wave function was expressed in the 6- dimensional space-time (4.18) Quantization depends on two types of rotations in space. Figure 9

(4.18)

Due to the affine transformation, elliptic parametric equation, Fourier Series,eccentricity of elliptic, and metric of 6- dimensional space-time, the relationship between wave function and wave tensor was expressed.(4.19).meanwhile, the tensor Ψ expresses the created rotation stress by space-time to the matter.(4.19). Positive and negative amounts that have a relationship with object rotation in higher dimensions are variable depending on the phase, speed, and density.

(4.19)

5. Field Structure and Force

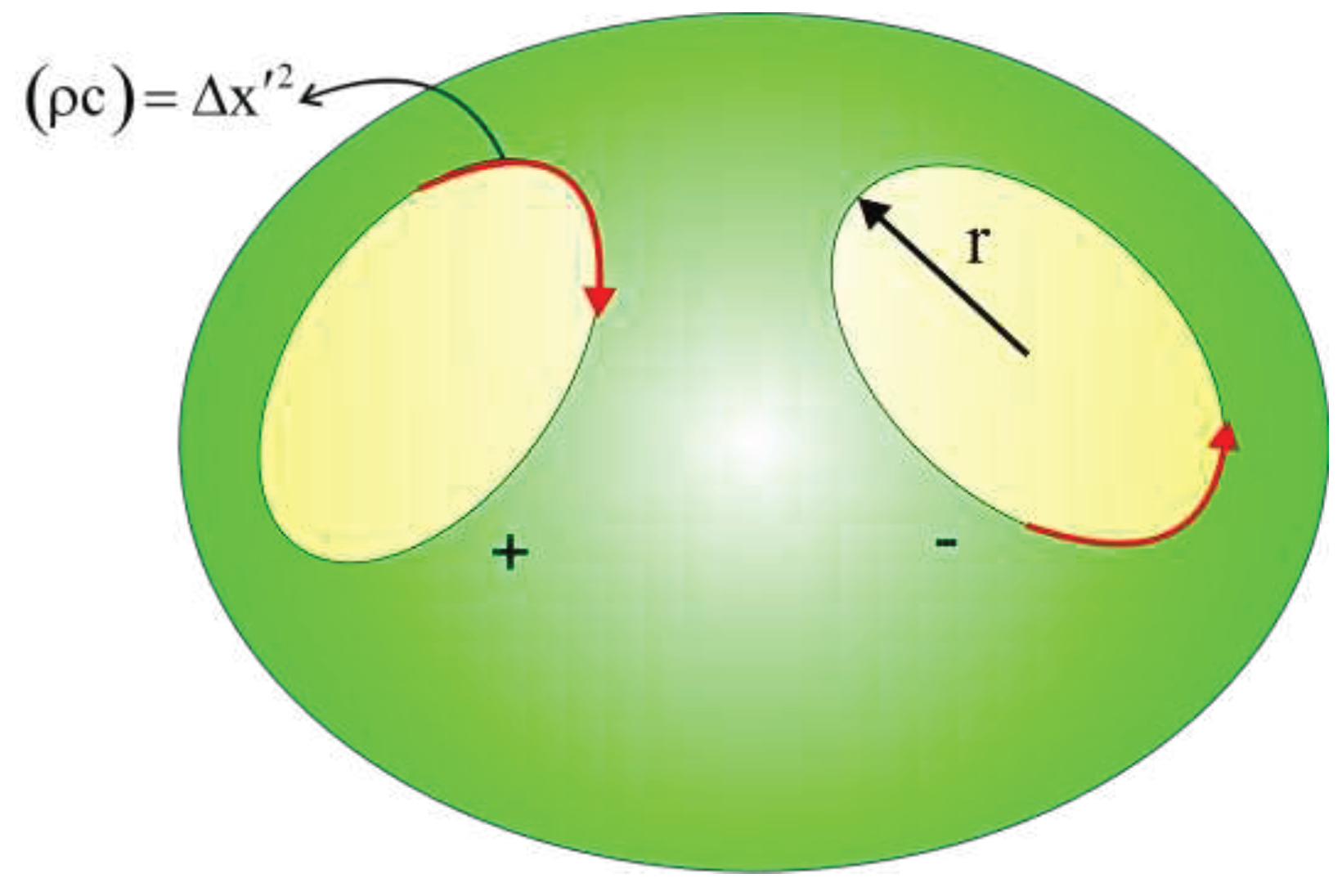
The electrical load has a direct relationship with the phase of object field rotation. Particleswith no mass or without loads like photons and neutrons have two opposite rotation phases. Photons are a length of density without phase in space-time. They transport energy and follow from the geodesics of quantized space-time. the photons can be decomposed into a pair couple of electron-positron fields. Each pack of energy has a particular geometric structure, and on this basis, the field radius and the 2nd radius can be calculated with consideration of the performed work in space and time. (5.20) Electrical load has a direct relationship with the phase of the field in higher dimensions. Figure 10

(5.20)

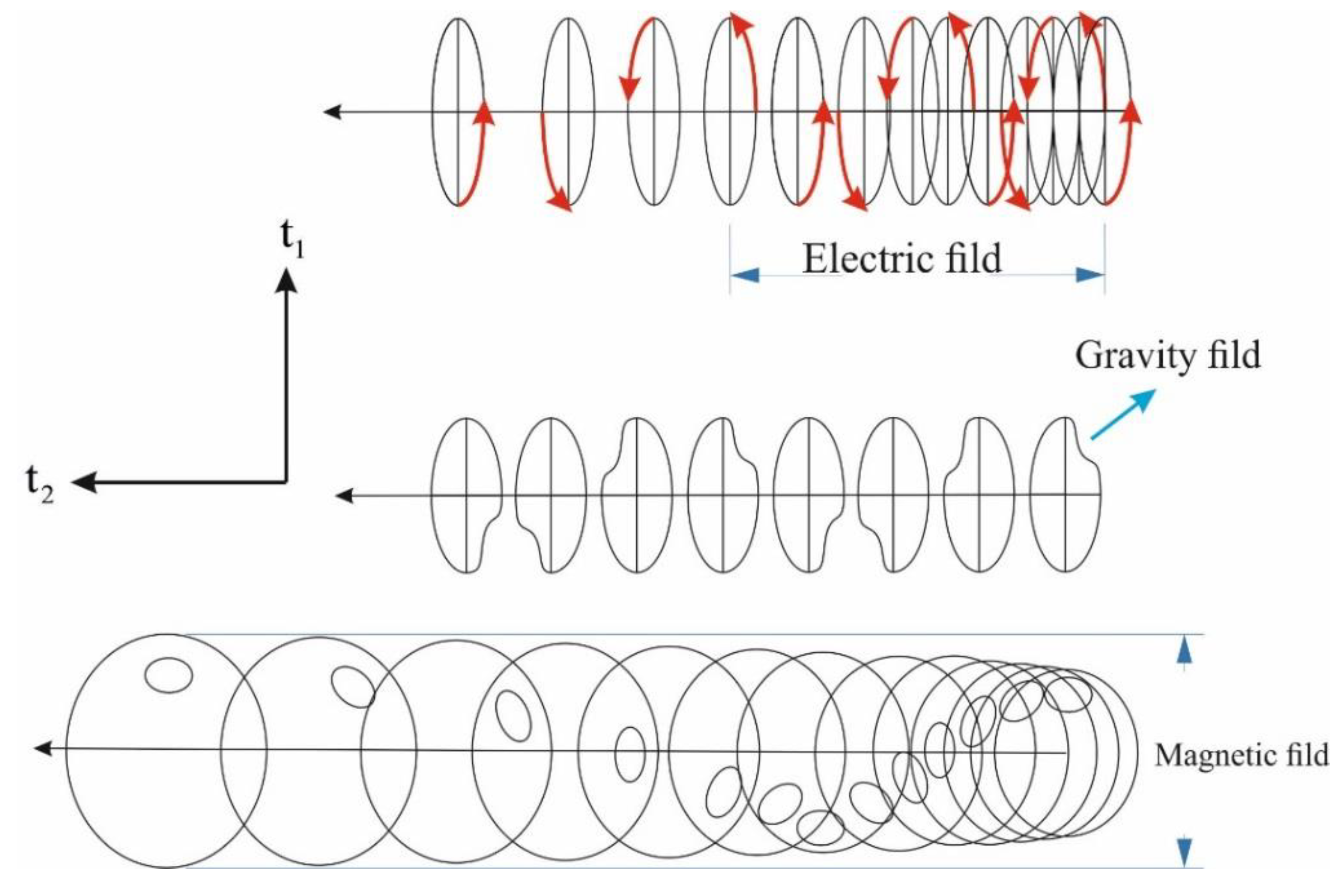
Changing the speed of rotation phases in the electromagnetics field is more than other space-time points. Each particle follows space-time geodesics within the limits of an electrical field. Eccentricity, in the gravitational field and electromagnetic fields, creates phase-changing speed. Figure 11

The mass obtained from motion in space is (inertial mass) and the mass obtained from motion in time is (gravitational mass). The exerted stress from space-time to matter is in relation with Planck constant and gravitation constant. This stress intensity is very insignificant. But the exerted stress is observable with regard to the rotation around field and the passage of time. Tensor for space-time stress based on Planck constant, gravitation constant, and cosmology constant indicate the quantum Structure of space-time. (5.21) (5.22)

The “K” tensor expresses the exerted stress to matter in space-time by higher dimensions. This Stress is, therefore, a factor for producing spin, electrical load & electromagnetic fields. K tensor has a direct relationship with wavelength and cosmology constant. (5.22) The radius equal to density length(field radius) is ‘

r_{x}

’ and radius for the variable of field rotation is ‘

r_{t}

’. is not able to be greater than a specified amount that is dependent on the object mass. Consequently,

’ r_{t}

’ is periodic.

(5.21)

(5.22)

On the basis of Movement in time dimensions and also work definition, the relationship of Planck constant and gravitation constant is specified with cosmology constant. (5.23)

(5.23)

Type and intensity of electrical load and magnetic field depend on other components of k tensor.

Momentum tensor and energy with new coefficient make general relativity equation more complete. (5.24).Mass in space-time can cause inhomogeneity, which is represented by negative density. (5.24)

(5.24)

(5.25)

6. Curvature in Six-Dimensional space Time

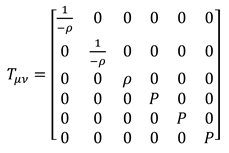
Ricci tensor expresses curvature in 4-dimensional space-time; by adding two Dimensions of time another definition of curvature is formed. Expressing the sphere surface curvature by Riemann tensor and Ricci tensor in six-dimensional space-time can’t be comprehensive. (6.26)

(6.26)

With regard to space rotation, the Ricci tensor expresses curvature in the time dimension length, and space dimensions.. Curvature in time means changing wavelength in higher dimensions as well as becoming closer or farther the states of space-time from each other. Generally, Ricci’s 6-dimensional tensor can only be defined during the time in the case of existing various masses. (6.27)

(6.27)

Using the introduced metric, two types of Christoffel symbols were expressed in 6-dimensional space. (6.28) (6.29)

(6.28)

(6.29)

Einstein tensor, Scaler Ricci, and Ricci tensor obtained using Christoffel symbols. (6.30) (6.31) Geometrical connection is hidden between space curvature and length time curvature in Scaler Ricci. (6.30)

(6.30)

(6.31)

The general equation obtained for general relativity and quantum mechanics. (6.32) that Whenever mass is high (not in the scale of black holes), wave function and electromagnetic field are disappeared, and whenever mass and density are low, quantum behavior is observed (6.32)

(6.32)

7. Quantum Mechanics

Hilbert space is a complex of various states for a particle in a time loop. particle rotates around the field with a density radius in higher dimensions. In a moment a particle can have two upper and lower spins. Measurement causes a particle’s dimensions to become collapsed into a four-dimensional. Figure 12

Measuring a phenomenon in higher dimensions causes the wave function to collapse to the lower dimensions, resulting in different observable states. Figure 13

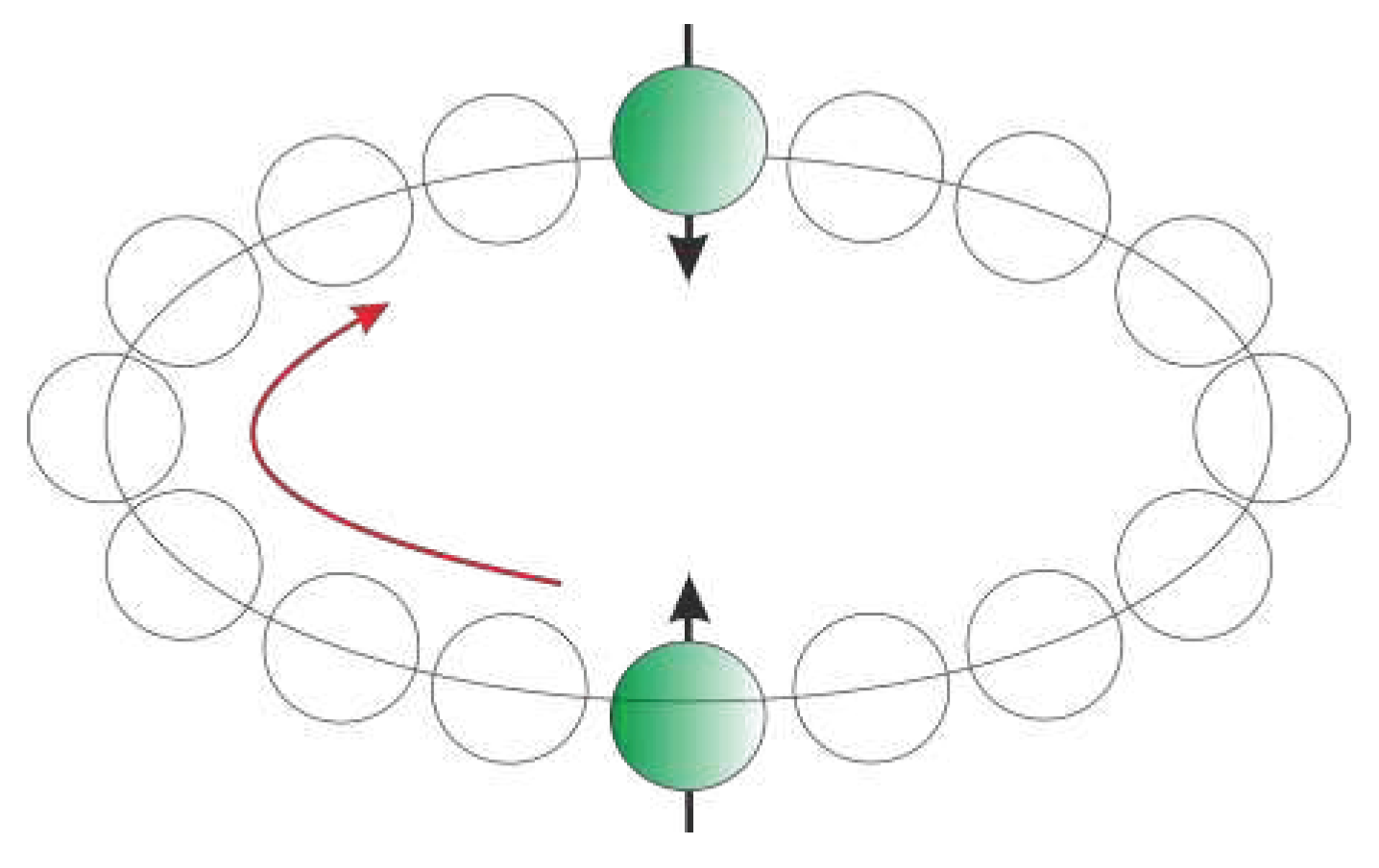
Despite the distance of the two objects from each other, they can have similar states. Regarding the masses with similar densities, these states are contrariwise. Figure 14

Due to direct relationship of mass and momentum with wave function and direct relationship of wave function with space-time structure, the whole similar particles like electrons, photons, and protons,.... follow space geodesics. When one of the entangled particles are measured, another particle’s all states can be foreseen with certainty. Figure 15

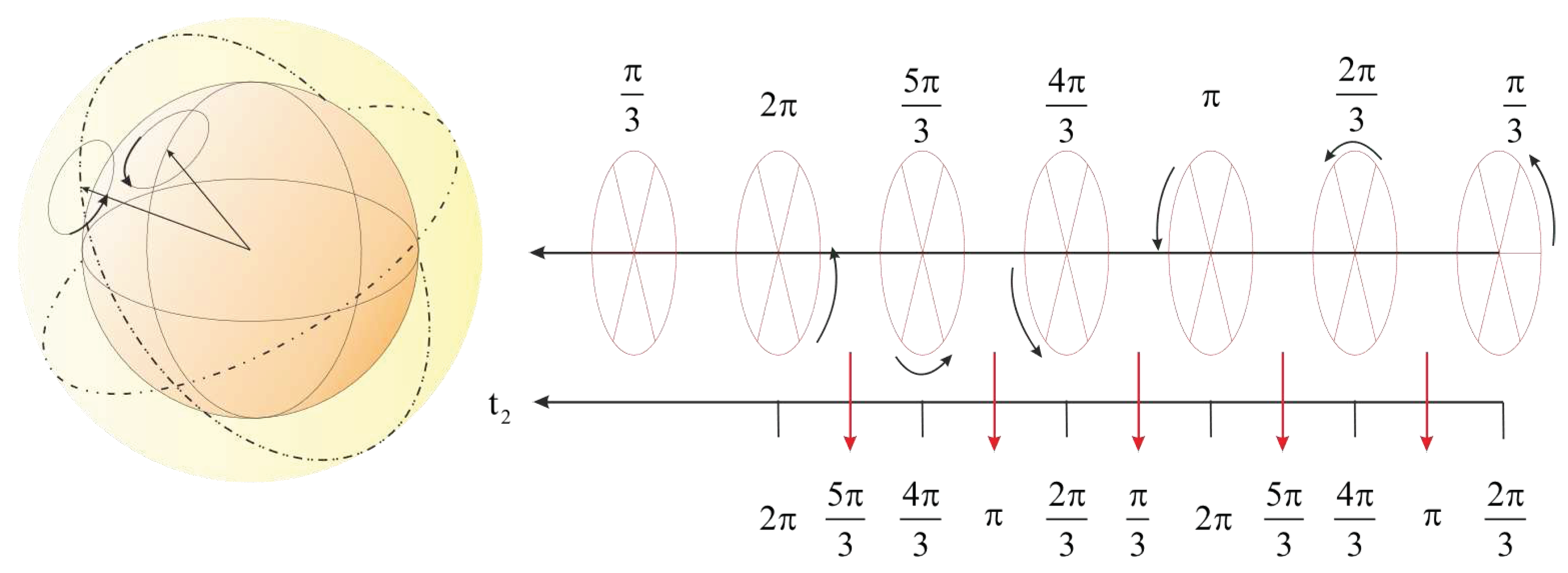
Before measuring a particle, there is no orientation in 3-dimensional space. measuring In the time state π/3 makes the particle’s dimension collapses to a four-dimensional space, as a result, we select the states from the tensor

Ψ

which are constant for all the particles with a specific momentum. As a result, entanglement will never occur between two particles in the coordinate system of relativistic. Entanglement has been institutionalized in the space-time structure. Bell’s Inequality defect is due to the existence of similar states in the space-time rotating structure. (7.33)

(7.33)

8. Resule

The relationship of physics fundamental constants with 3 numbers of π, ȹ and ɐ express the relationship of electromagnetic field and space-time geometry. It seems that in the relationship of space-time geometry with electromagnetic field, agents and nature of inherent properties of matter such as spin, mass, Polarization, and load are exposed. The mass resulting from motion in space (inertial mass)and the mass resulting from motion in time (gravitational mass) express the subject that equilibrium exists between the whole physical quantities in symmetrical space-time. Orthogonality, separability, and reality are the results obtained from the investigation of events during time. In this direction, the non-certainty principle, Commutative property, and the Bell inequality Violation are dependent on time passage. On the basis of quantum mechanics’ general equation and general relativity, an electromagnetic field rotating in space-time is capable of producing a positive or negative gravitational field. Dark matter and dark energy have a direct relationship with the geometry of space-time.

Acknowledgements

The author expresses gratitude to God, P.R. Masoud Naseri, Dr. L.R and their professors for their helpful discussions and valuable comments.

References

Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
Brody, D.C.; Graefe, E.-M. Six-dimensional space-time from quaternionic quantum mechanics. Phys. Rev. D 2011, 84. [Google Scholar] [CrossRef]
Bonezzi, R.; Latini, E.; Waldron, A. Gravity, two times, tractors, Weyl invariance, and six-dimensional quantum mechanics. Phys. Rev. D 2010, 82. [Google Scholar] [CrossRef]
Halliwell, J. The quantum cosmology of Einstein-Maxwell theory in six dimensions. Nucl. Phys. B 1986, 266, 228–244. [Google Scholar] [CrossRef]
Randjbar-Daemi, S.; Salam, A.; Strathdee, J. Spontaneous compactification in six-dimensional Einstein-Maxwell theory. Nucl. Phys. B 1983, 214, 491–512. [Google Scholar] [CrossRef]
Córdova, C.; Dumitrescu, T.T.; Intriligator, K. 2-Group global symmetries and anomalies in six-dimensional quantum field theories. J. High Energy Phys. 2021, 2021, 1–46. [Google Scholar] [CrossRef]
Maxwell, N. Relativity Theory May not Have the Last Word on the Nature of Time: Quantum Theory and Probabilism. 2017; 109–124. [Google Scholar] [CrossRef]
Mkhize, N.; Hansraj, S. de Sitter potential in six dimensional Einstein–Gauss–Bonnet isotropic fluids. Ann. Phys. 2023, 454, 169328. [Google Scholar] [CrossRef]
Wu, Y.-L. Maximal symmetry and mass generation of Dirac fermions and gravitational gauge field theory in six-dimensional spacetime. Chin. Phys. C 2017, 41, 103106. [Google Scholar] [CrossRef]
Yerra, P.K.; Bhamidipati, C. Topology of black hole thermodynamics in Gauss-Bonnet gravity. Phys. Rev. D 2022, 105, 104053. [Google Scholar] [CrossRef]
Barvinsky, A.O.; Kurov, A.V.; Sibiryakov, S.M. Beta functions of (3+ 1)-dimensional projectable Hořava gravity. Phys. Rev. D 2022, 105, 044009. [Google Scholar] [CrossRef]
Ganchev, B.; Houppe, A.; Warner, N.P. New superstrata from three-dimensional supergravity. J. High Energy Phys. 2022, 2022, 1–40. [Google Scholar] [CrossRef]
Popov, N.; Matveev, I. Six-Dimensional Space with Symmetric Signature and Some Properties of Elementary Particles. Axioms 2022, 11, 650. [Google Scholar] [CrossRef]
Brahma, R.; Sen, A.K. The space–time line element for static ellipsoidal objects. Gen. Relativ. Gravit. 2023, 55, 1–21. [Google Scholar] [CrossRef]
Zhang, C.; Gong, Y.; Liang, D.; Wang, B. Gravitational waves from eccentric extreme mass-ratio inspirals as probes of scalar fields. J. Cosmol. Astropart. Phys. 2023, 2023. [Google Scholar] [CrossRef]
Buchbinder, I.L.; Fedoruk, S.A.; Isaev, A.P. Light-front description of infinite spin fields in six-dimensional Minkowski space. Eur. Phys. J. C 2022, 82, 1–11. [Google Scholar] [CrossRef]
Mousavi, S. K. The balance In the six dimensions of space-time description of quantum mechanics phenomena and nature of time. Journal of Physics: Theories and Applications, 7(1).

Figure 1. The circle on the surface of the sphere is also expanded with the expansion of the sphere, and as a result, the dimensions y & z are observed from the perspective of the points on the circle’s surface in the form of an imaginary dimension.

Figure 2. Time dilation of the moving object and Gravitational time dilation express the direct relationship between mass & density with time.

Figure 3. Eccentricity in space causes to create time dilation for the moving object compared to the 2-time axles.

Figure 4. The density of each object has a length in the time dimension and it is embedded around a sphere with a radius equal to the density which is called a “mass field”. .

Figure 5. Two dimensions of time are seen from the perspective of three-dimensional space in one dimension, and as a result, This causes the material to experience double stress from the time dimensions.

Figure 6. The rigid body is rotating in a field with a radius equal to the object density simultaneously by space –time expansion. Negative density is meaningful with passing time.

Figure 7. The object field in the space-time expanding is rotating and moving by the two forces perpendicular to each other.

Figure 8. The proportion of exerted stress from space–time has a relationship with the object density. This proportion has a relationship with three natural numbers of π, e, and

φ

Figure 8. The proportion of exerted stress from space–time has a relationship with the object density. This proportion has a relationship with three natural numbers of π, e, and

φ

Figure 9. Quantization has been entangled in space-time structure, and it depends on the object’s momentum.

Figure 10. Electrical load results from density phase in higher dimensions. Neutrons has consisted of two out of phase quarks.

Figure 11. Phase changing speed is more in electrical and magnetic fields compared to the gravitational field, and the effective range of the gravitational field is more compared to electrical and magnetic fields.

Figure 12. when a particle is in the time loop around a field, it exists in Hilbert space.

Figure 13. With continuous changing of supervisor states or objects in space, with each time a measurement is created new result.

Figure 14. Particles with different charge and mass can have similar states in space simultaneously.

Figure 15. In case of having sufficient information from mass and particle speed, other States can be foreseen as well.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The General Balance in the Six Dimensional of Space-Time

Abstract

1. Introduction

2. Six-Dimensional Space-Time

3. Geometry and Fundamental Constants of Physics

4. Wave Function

5. Field Structure and Force

6. Curvature in Six-Dimensional space Time

7. Quantum Mechanics

8. Resule

Acknowledgements

References

MDPI Initiatives

Important Links

Subscribe