Preprint
Article
Instability during Stepping and Distance between the Center of Mass and the Minimal Moment Axis: Effect of Age and Speed
Altmetrics
Downloads
82
Views
26
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
15 August 2023
Posted:
16 August 2023
You are already at the latest version
Alerts
Abstract
The goal of this study was to analyze the instability during stepping of young and older adults at fast and spontaneous speed. To this aim, the anteroposterior and the mediolateral distances between the body center of mass (COM) and the minimum moment axis (MMA) were computed. A total of 15 young adults (25y.o. [19-29]) and 15 older adults 68.7y.o. [63-77] volunteered for this study. For the computation of the distances, a complete biomechanical protocol combining two force platforms and a 3D motion capture analysis system was setup. The subjects were equipped with 47 reflective markers and were modeled as a frictionless multibody with 19 segments, 18 joints and 42 degrees of freedom and were asked to perform a stepping at both speeds. The stepping was divided in 5 phases with successive swing and double stance phases. The greater instability was observed during the swing phases. The distances indicate a significant higher instability at fast speed for both groups (p < 0.001) for all the phases. The anteroposterior distance also increases significantly for older adults highlighting greater instability while no differences were observed for the mediolateral distance all along the 5 phases suggesting higher risks of backward of forward falls during stepping.
Keywords:
Subject: Biology and Life Sciences - Life Sciences
1. Introduction
Autonomous locomotion is largely related to quality of life. The lack of autonomous gait has been shown to be the first indicator of decline in motor skills but also in the cognitive abilities of individuals [1]. In this context, a better understanding of the factors that affect locomotion is essential to detect and prevent the loss of autonomy [2].
The ability to walk indoor and outdoor without falling is a key element in maintaining the autonomy of people whose locomotor system is impaired due to ageing, disability or pathology. Falling can occur for different reasons such as tripping (34%) and slipping (25%) and incorrect weight shifting [3,4], which cause strong perturbations to balance during steady-state gait cycle. For non-impaired individuals, balance recovery following these perturbations is performed by changes in the moments generated at all joints of the support limb, resulting in a modification of the contact forces with the ground [5]. This control of the contact forces depends on the balance control system, which generate appropriate muscular actions on the basis of the sensory information from the visual, the vestibular and somatosensory systems. The vestibular system senses the acceleration and angular velocity of the head and the somatosensory system senses ground reaction forces and body positioning [6]. When impaired, the balance control system no more performs its regulatory role and recovery from the aforementioned perturbations is not guaranteed anymore. Considering the mechanical nature of the signals implied in the balance control, it seems reasonable to focus the understanding of balance on biomechanical analysis of the body which should provide essential information for personalized rehabilitation interventions [7].
During gait, the external mechanical actions that apply on the body are gravity and ground contact forces that are regularly broken (toe off) and recovered (heel strike) and that can be modulated so that the system efficiently performs a specific movement. Numerous studies have been carried out to define criteria for the assessment of the greater or lesser instability of the gait during steady-state walking. The trajectory of the Center Of Pressure (COP) has been first widely used as an indicator to qualify the healthy gait [8]. Since then, several indicators, considering the whole-body dynamics of the musculoskeletal system, have been proposed. Hof et al [9], proposed to use the extrapolated COM as the limit of the surface in which the center of mass should be located thus defining the margin of stability during locomotion. This parameter is based on the modeling, often proposed in the literature, of the gait as an inverted pendulum [10]. The angular momentum or the derivative of the angular momentum at the COM have been particularly studied during walking and have been shown to increase significantly during unstable phases of gait [10,11,12]. In particular, the reduction in angular momentum variation during walking, consistent with limitation of uncontrolled whole-body rotations, appears a realistic goal to achieve to globally enhance balance capacities of the impaired population. In the same idea, Bailly et al. [13], studied the distance between the COM and the Minimum Moment Axis (MMA) intimately related to the derivate of the angular momentum of the subjects at the COM: the greater the distance, the greater the angular acceleration of the body around the center of mass. This criterion, easily understood in a clinical context, has made it possible to discriminate healthy subjects walking in unstable conditions compared to level-ground walking. A noticeable strength of the MMA-COM index is that it can be computed under various conditions, including when all contact points are not on the same horizontal surface (slope, stair, when using assistive devices, uneven terrain…), contrary to classical COM or COP indexes. Al. Abiad et al. [14] have thus taken up this parameter and highlighted the greater instability of locomotion of subjects wearing transfemoral prothesis.
Gait initiation and stepping, which consist of a voluntary transition from a quiet standing position to a dynamic phase, are known to be a particularly critical phase of locomotion. Observations revealed that most falls in older adults occurred during these transitional tasks [4]. In particular, research has shown that anticipatory postural adjustments developed during the double support phase are crucial elements to guarantee and prepare the correct execution of the first step [15]. Indeed, at the time of the takeoff of the foot, a medio-lateral gap is created between the COP located under the foot of the stance leg and the projection of the COM. This natural gap induces a fall of the body toward the swing leg side which stops at the time of swing foot contact [16]. The authors then showed, at the time of the anticipatory postural adjustment, an initial shift of the center of pressure laterally toward the swing leg which accelerates the center mass toward the contralateral leg in order to decrease the amplitude of the lateral fall [16,17]. Furthermore, they observed a forward displacement of the center of mass induced by the backward shift of the center of pressure. The anteroposterior gap between the center of mass and the center of pressure, observed during the double support phase, induces a forward imbalance and contributes to the generation of propulsive forces [18,19]. The sum of these antero-posterior and lateral movements must lead the individual to segmental movements creating a complete body dynamic modifying the variation of the angular momentum in order to initiate and continue the gait.
In this context, some authors recently studied the instability during stepping. Using the COP trajectory R. Watanabe and T. Higuchi [20] demonstrated that action costs for maintaining postural stability are considered dominantly for planning the stepping. The margin of stability [21] was also analyzed during stepping in different situations and could highlight the higher risks of falls in frail individuals such as older adults. Muijres et al. [22] also studied the stepping instability in older adults using foot placement error, step duration, and mediolateral center of pressure path. The results showed that compared to young adults, older adults exhibited a higher foot placement error, suggesting a reduction in the ability to control balance with age. However, while foot placement error increased with step execution velocity, the authors did not find an age-related difference at higher speeds. Interestingly, studies focusing on angular momentum during stepping revealed age-related changes in angular momentum [23,24]. Compared to young adults, older adults exhibited higher values of angular momentum during stepping, emphasizing greater difficulties in balance control during stepping. It is noteworthy that these age-related changes were more pronounced in the sagittal plane. Furthermore, although both age groups increased angular momentum with increasing speed during stepping, the age-related changes previously observed at spontaneous speed were exacerbated at faster speeds [20]. Taken together, these results suggest that the greater variation in angular momentum with age and speed generates larger values of angular momentum derivatives and consequently contributes to increasing the distance between the COM and the MMA. However, to the best of our knowledge, no studies focused on the stepping instability using the distance between the COM and the MMA.
This study aimed, therefore, to investigate the distance between the MMA and the COM in young and older adults at different speeds during stepping. We hypothesize that due to the greater variation in sagittal angular momentum in older adults, the derivative of the angular momentum should increase. As a consequence, the anteroposterior distance between the MMA and the COM should also increase. Similarly, we hypothesize that increasing speed should generate a greater distance between the MMA and the COM due to a greater variation in angular momentum. Finally, in this study, we will test the ability of the distance between the MMA and the COM to quantify this greater instability.
2. Materials and Methods
2.1. Participants
Thirty adults participated to this research and were assigned into two groups. Fifteen of them were young adults (25y.o. [19-29]; 62.3kg [44.8-76.1]; 170.2cm [155-186]) and the fifteen others were older adults (68.7y.o. [63-77]; 58.7kg [37.1-77.1]; 157.6cm [147-172]). None of them reported a history of locomotor pathologies. The study protocol was conducted in accordance with the Declaration of Helsinki and approved by the local institutional review board.
2.2. Experimental procedure
Data collection methods have been previously described by Begue et al. [23] and are summarized here.
Initially, the volunteers stood motionless on a force plate (AMTI, USA). After a verbal signal from the experimenter, they were asked to initiate a first step with their dominant leg up to a second force plate (SENSIX, France) located in front of the first force-plate. All initiated the first step with their right leg, with the exception of two young adults. Initial feet position was marked on the ground and standardized [25]. The participants were equipped with 49 reflective passive markers placed on anatomical bony landmarks based on the recommendations of the International Society of Biomechanics (ISB) [26,27]. Kinematics were collected with a Vicon system (200Hz) until the end of the second step, where participants had to stop in a natural upright posture with their arm alongside their body. Stepping was completed under two randomized speed conditions: at spontaneous speed and as fast as possible. For each participant, at least 9 trials were achieved at both speeds. Both force plates were synchronized with the Vicon system and their data were collected at a frequency of 1000Hz.
2.3. Skeletal model
The human model included 42 degrees of freedom, 18 joints and 19 segments as presented by Maldonado et al. [28]. The skeleton is modeled as a friction-less articulated multi-body dynamic system. The pelvis, thighs, shanks and feet segments mass and inertia were set according to the model of [29]. Anthropometry of the torso and head segments, including the neck, were estimated from the regression equations of [30]. Hands anthropomorphic data are based on regression equations of De Leva [31].
2.4. Data analysis
Kinematics and kinetics were processed with a cut-off frequency using a low-pass Butterworth digital filter of 4th order applied in a zero-phase. A cutoff frequency of 6Hz was used after a residual analysis for the kinematics and at 10Hz for the force-plate data. Euler XYZ body-fixed rotation angles are used to express the orientation using OpenSim [32] after an inverse kinematics process with body frames defined according to ISB recommendations [26,27]. The COM position of the whole-body was also extracted after the inverse kinematics process. In the coordinate system used, X is the anteroposterior axis, Y is vertical and Z is the mediolateral axis.
The stepping motion was divided into five phases [23]: anticipatory postural adjustments (APAs) and first double support phase (P1), swing phase of the dominant leg (P2), second double support phase (P3), swing phase of the second step (P4) and third double support phase until the end of the movement (P5), also named restabilization phase. The APAs were considered to begin when one of the anteroposterior and mediolateral accelerations of the COM deviated 2.5 standard deviations from its baseline value until the toe off of the dominant foot. The end of the motion was defined as the time-point at which the mediolateral COM velocity remained within 2 standard deviations of the mean calculated during the terminal-stance quiet standing after the end of the stepping. Each phase was normalized from 0 to 100%.
The resulting subject-specific kinematics data i.e., positions, orientations and velocities of body segments, and the inertial parameters were exported to a custom-made Matlab program for the angular momentum computation. The whole-body angular momentum at the COM (HCOM) was calculated in the three dimensions as described by Begue et al. [23]. Then the derivative of the angular momentum was extracted using classical methodology by finite difference (KCOM = dHCOM/dt). Finally, distance between the MMA and the COM was computed as explained below.
2.5. Theoretical Background
It is current in biomechanics to represent the resulting ground reaction forces as a vector located under the foot at the COP. The COP is defined as the barycenter of the vertical pressure under the foot. It does not take into account friction forces in the horizontal plane (XZ). Thus, at the COP, the ground reaction moments are null alongside X and Z. Only the vertical free moment is not null. Another interesting point on the ground is the point where the moment is minimal. At this point Q of the ground, the moment is not vertical but collinear to the reaction forces. Let us denote, MQ the moment at this point and R the reaction force.
MQ = λR
Where λ is a given real value. According to the Varignon theorem, we can compute the moment at another point P:
MP = MQ+R×QP = λR+R×QP
Where × denotes the cross product. The square of the equation 2 leads to:
(MP)2 = (λR+R×QP)2 = (λR)2+2λR.(R×QP)+(R×QP)2
Where . denotes the scalar product. It is clear that 2λR.(R×QP) = 0 since R×QP is orthogonal to R. Finally:
(MP)2 = (λR)2+(R×QP)2 = (MQ)2+(R×QP)2
And:
(MP)2 ≥ (MQ)2
Thus, the square-norm of the moment at point Q is minimal. One can note that this moment is constant alongside an axis colinear to R, named Minimal Moment Axis (MMA). Indeed, if M is a point along this axis:
QM=aR with a∈]- ∞, + ∞[
MM = MQ+ R×QM = MQ+ R×(aR) = MQ
Now, if A is any point in space, it is possible to localize this minimal moment axis according to A. If we define the point B as:
AB = (R×MA)/R2
The moment at point B is:
MB = MA+R×AB = MA+R×(R×MA)/R2
Using the properties of the double cross product:
R×(R×MA)/R2 = [(R.MA)R–(R.R)MA]/R2 = (R.MA)R/R2–MA = λR–MA
Considering λ=(R.MA)/R2
Finally, the moment at point B is:
MB = MA+λR–MA = λR
Accordingly, it is possible to determine one point of the MMA from any other point given the reaction force and the moment at this point. Moreover, this MMA exists regardless of the conditions of the gait. Indeed, this axis is not defined only when walking on flat ground like the COP and can take into account all external mechanical actions: swing phase, double stance, contact with a cane, staircase ramp, etc. Moreover, the vector AB = (R×MA)/R2 represents the shortest distance between A and the MMA (the orthogonal projection of A on the MMA). Indeed, it is clear that AB is perpendicular to R and thus, to the direction of the MMA.
In the present study we computed the derivative of the angular momentum at the COM as presented above. According to Newton’s equation the derivate of the angular momentum (KCOM) at the COM is equal to the moment at the COM (MCOM), i.e.:.
KCOM = MCOM
Thus, the shortest vector between the COM (point G) and its orthogonal projection on the MMA (point M) is denoted dCOM-MMA and was computed as follows:
dCOM-MMA = GM = (R×MCOM)/R2 = (R×KCOM)/R2
Where R are the total reaction forces obtained with the force plates. Accordingly, all other things being equal, the greater the derivative of the angular momentum, the greater the distance. In this circumstance, the distance is related with the whole-body variation of the angular momentum and could reflect the instability of the gait.
As a vector in space, dCOM-MMA was projected onto the anteroposterior axis dAP, he vertical axis dVERT and the mediolateral axis dML. According to our hypothesis, only dAPand dML were studied here. Both distances were then divided by the subject’s height to obtain them in a dimensionless form. For each phase and for the total duration of the motion, the range of each dimensionless distance was computed.
3. Results
3.1. Spatiotemporal parameters
Spatiotemporal parameters are presented in the Table 1. ANOVA results highlighted a significant speed effect (p < 0.001), but no group effect for the forward speed. Forward speed increased with stepping speed. A significant Group×Speed interaction was also found for the forward speed. Post hoc analysis revealed significant differences in this parameter for all pairwise comparisons, except for the comparison between both age groups in the spontaneous speed condition (p > 0.05).
Regarding the temporal parameters, a significant group effect was found for the duration of the phases P1 and P5 (p = 0.003). Compared to young adults, older adults exhibited smaller duration of P1 and conversely, longer duration of P5. ANOVA revealed a significant speed effect for the total duration of the five phases, duration of the phases P1, P2, P3 and P4 (p < 0.001). The durations of these phases decreased with speed. A significant Group×Speed interaction was found for the duration of the phase P3 (p = 0.004). Post hoc analysis indicated significant differences in P3 duration for all pairwise comparisons, except for the comparisons between young and older adults in both the spontaneous and fast speed conditions (p > 0.05).
3.2. Distances between the COM and the MMA
The time evolution of the antero-posterior and medio-lateral distances over the five phases is presented in Figure 1.
Along the antero-posterior axis, for both age groups and both speed conditions, the minimal distance throughout the entire stepping is observed at the end of the first swing phase (P2) while the maximum distance is observed at the beginning of the second swing phase (P4). Statistical analysis revealed that the minimal and maximal distances are significantly impacted by group and speed conditions (Table 2). The negative minimal distance increased with age (p = 0.009) and speed (p < 0.001). Similarly, the maximal distance increased with age (p = 0.004) and speed (p < 0.001).
Along the medio-lateral axis, the minimal distance occurred at the end of the first swing phase (P2) and the maximal occurred at the transition between the double stance phase (P3) and the second swing phase (P4), as observed along the antero-posterior axis. ANOVA revealed no group effect for both minimal and maximal distances (Table 2). Nevertheless, a significant speed effect was found (Table 2). Both minimal (p < 0.001) and maximal (p < 0.001) absolute distances increased significantly with increasing speed. Also, a significant Group×Speed interaction was found for the minimal medio-lateral distance. Post hoc analysis revealed significant differences in the minimal medio-lateral for all pairwise comparisons, with the exception of the comparison between young and older adults in the fast speed condition (p > 0.05).
The range of the distances along the antero-posterior and medio-lateral axes for all phases and over the entire stepping are presented in Table 3.
Along the antero-posterior axis, a significant group effect was found for the ranges of the distance COM-MMA in all phases, with the exception of P1 (p>0.05). Compared to young adults, older adults exhibited larger range of the antero-posterior distance for P2, P3, P4, P5 and throughout the entire stepping. In addition, the results highlighted a significant effect of the speed on ranges of the distance along the antero-posterior axis. Range of the distances increased with speed for all the phases. Statistical analysis revealed no effect of group×speed interaction for the ranges of the distance between COM and MMA along the antero-posterior axis (p > 0.05).
Along medio-lateral axis, no group effect was revealed for range of the distance between COM and MMA. However, ANOVA revealed a significant speed effect for the ranges of the distance along the mediolateral axis, with an increase in this distance with increasing speed for all phases. Furthermore, a significant effect of Group×speed interaction was observed for the ranges of mediolateral distance during P2 and P3. For these two phases, post hoc analysis indicated significant differences in the mediolateral distance for all pairwise comparisons, except for the comparison between young and older adults at fast speed (p > 0.05).
4. Discussion
The aim of the present study was to investigate the distance between the MMA and the COM in young and older adults at different speeds during stepping. Consistent with our hypotheses, results revealed that (1) older adults exhibited higher antero-posterior distances than their younger counterparts and (2) both antero-posterior and mediolateral distances increased with increasing speed during stepping. These results are further discussed in the following paragraphs.
Regarding the spatiotemporal results, it is interesting to note that the forward speed of the stepping was not different between both groups at spontaneous speed, but was slower in older adults than their young counterparts in the fast speed condition. This result is in line with the literature, which has already shown that there were no significant differences in spontaneous walking speeds up to the age of 80 [33]. Thus, it appears justified to compare the dynamics of both groups throughout the entire motion. Although there is no group effect for the total duration, the results highlight a significant group effect for the duration of the phases P1 (anticipatory postural adjustments and stepping initiation) and P5 (restabilization phase). Compared to young adults, older adults decreased the duration of the first phase (p = 0.003) and, on the contrary, increased the duration of the restabilization phase (p = 0.003). This result confirms previous findings of the literature [34] which showed that the time required to stop the locomotion was longer in older adults. Conversely, one can note that speed effect is observed for all the spatiotemporal parameters meaning that the volunteers correctly followed the instructions accelerating the stepping during the fast speed condition.
The time evolution of the antero-posterior distance observed during stepping, describes a profile consistent with that presented by Al-Abiad et al. [14] for healthy people. The minimal distance (i.e., the largest negative distance) is observed at the end of the single support phase of the first step (i.e. the swing phase of the dominant leg - phase P2). This result is consistent with the fact that during the swing phase, the base of support is reduced, thus increasing the difficulty of instability control. In addition, just before the contralateral heel strike (i.e., during the swing phase of the non-dominant leg – phase P4), COP and COM undergo significant shifts in order to position themselves between the two supporting feet, further increasing instability. In the context of stepping, a lower negative antero-posterior distance is observed during the second swing phase (P4). This result is probably related with the beginning of the deceleration phase and the decrease of the dynamics of the participants. Indeed, participants were instructed to stop just after P4 phase at the phase P5. The negative values observed during P2 and P4 indicate that the MMA shifts behind the center of mass. Knowing that the external vertical force acts upwards, it means that, according to the equation 13, the derivative of the angular momentum is negative and generates global forward angular acceleration of the body. This angular acceleration is stopped at the time of the heel strike which marks the onset of the double support phase. Concerning the maximum values of the antero-posterior distance, they are observed at the beginning of the swing phases (P2 and P4). At this time, the MMA shifts beyond of the COM and the positive value indicates a significant backward angular acceleration, meaning that insufficient global positive angular speed of the body at the beginning of the swing phase could lead to fall backwards. This result is in accordance with the previous works of [35].
In a similar manner, the minimal distance along the medio lateral axis is observed at the end of the first swing phase (P2). Accordingly, it means that the MMA is located more laterally towards the non-dominant leg than the COM, while the dominant leg is swinging. It confirms global positive angular acceleration around the antero-posterior axis and the fall of the body toward the swing leg. This lateral fall stops during the double stance phase (P3). Conversely, the maximal mediolateral distance is observed during the swing phase of the non-dominant leg (P4). During this phase, the mediolateral distance is positive, meaning an ipsilateral fall of the body, i.e., toward the non-dominant leg. In the middle of the double stance phase P3, the distance changes from negative to positive value. This result highlights the transition of the COM from the dominant to the non-dominant side. All these results are in accordance with previous data [36,37]. Another interesting result is the evolution of the medio-lateral distance during the anticipatory postural adjustments. During large part of the phase P1, the distance along the medio-lateral axis is positive and becomes negative at the time of heel lift of the dominant leg. This positive value highlights a displacement of the COM towards the non-dominant side before the swing of the dominant leg, which is in line with previous observations during the anticipatory postural adjustments [15,16,17].
Finally, whatever the phase, the variations of the distance along the antero-posterior axis are approximatively twice the variations along the medio-lateral axis. This reflects the larger variations of the tangential forces which orient alternatively the MMA forwards and backwards in the direction of the propulsive and braking forces.
Interestingly, our results showed a significant effect of group for antero-posterior distances, but not for mediolateral distances. Indeed, compared to their younger counterparts, older adults increased both minimal and maximal antero-posterior distances, which explains the larger range of the antero-posterior distance between COM and MMA during stepping. The larger range of antero-posterior distance in older adults is potentially associated with the larger range of angular momentum in the sagittal plane already observed in a previous study [23]. The detailed analysis of each phase also revealed an effect of age for the range of the distance along antero-posterior axis. These significant differences are observed for all stepping phases, except for phase 1, during which APAs are developed. This interesting result reveals larger reorientations of the MMA with respect to the position of the COM that could explain a poorest ability of older adults to control propulsion and braking forces. This result is in accordance with Al-Abiad et al. [14] which previously demonstrated larger antero-posterior distances between the COM and the MMA for at-risk populations with transfemoral amputations and the preponderant role of the control of the antero-posterior force for the instrumented and healthy lower limb. Given the absence of significant differences with age along the mediolateral axis, present results suggest that the risk of falling forwards or backwards is higher than the risk of falling laterally during stepping in older adults. This result could explain the contradictory results obtained by the authors regarding the gait instability in the elderly compared to young adults [38,39]. However, it is worth noting that the lack of difference along the mediolateral axis could be explained by the fact that older adults included in the study were relatively young (68.7 years on average) and physically active.
Our results revealed a significant speed effect on the maximal and the minimal values of the antero-posterior and medio-lateral distances. The results highlighted a mean increase of 66% of the absolute values of the minimal and maximal distances between the spontaneous and the fast speed conditions. This result is consistent with those of previous studies, which highlighted an increase in the variation of angular momentum with speed during stepping [24] . Indeed, a larger angular momentum during the same time interval will lead to higher derivative of the angular momentum and according to equation 13 to higher distance.
The detailed analysis of each phase revealed that during the phase P1, the range of medio-lateral and antero-posterior distances increased with speed. The increase with speed is particularly more important for young adults (+109%) than older adults (+ 66%) along the antero-posterior axis. Conversely, along the medio-lateral axis, the speed effect is more moderate, with an average increase of 19% for both age groups combined. As previously described [18,40], this period presents dynamics adjustments with variations of both the antero-posterior and medio-lateral distances. This result confirms the COM displacement and the reorientation of the external forces before the toe off. It allows the subject to generate the force propulsion and the placement of the COM above the supporting foot at the beginning of the swing phase.
During the phases P2, P3 and P4, a speed effect was observed for the range of the medio-lateral and the antero-posterior distances. However, this speed effect is higher along the medio-lateral axis (+85%) compared to the antero-posterior axis (+70%). These increases in range occur while phase durations decrease, with a mean of 29%. It therefore corresponds to larger dynamics variations in shortest times. Along the antero-posterior axis, the larger variations of the distances are observed during the second swing phase P4, while the larger variations along the medio-lateral axis occur during the double stance phase P3. This result corroborates the previous studies which revealed the large lateral displacement of the COM during this phase [36]. Finally, the analysis of the restabilization phase (phase P5) shows that the subjects anticipate the end of the stepping. Indeed, in this phase, the variations of the antero-posterior and medio-lateral distances present the lowest values until the end of the motion. However, in this phase there is no decrease in duration with the speed condition. For the entire stepping, the differences between the maximal and the minimal values of the distances confirm our hypothesis about the speed effect while a group effect is observed only along the antero-posterior direction. Moreover, these larger variations of the distance are globally realized with a shorter time (-13%) at fast speed leading to greater dynamics variables of the subject and potentially higher instability.
5. Conclusions
The main results of this study revealed an effect of age and speed on the distance between COM and MMA during a stepping task. Older adults exhibited larger distances between COM and MMA along the antero-posterior direction, compared to young adults. In particular, older adults displayed larger minimal and maximal antero-posterior distances, resulting in a larger range of the distance over the entire stepping movement. These age-related differences underscore that older adults may have higher difficulties to control instability during stepping movement. With increasing speed, both older and younger adults increased their body dynamic, resulting in larger antero-posterior and mediolateral distances. Finally, these results confirm that the distance between COM and MMA appears to be able to discriminate individuals at risk of falling and the most unstable phases of the locomotion, as it increases during the most critical phase with reduced support surface. This result is in line with the previous work of Bailly et al. [13]. Therefore, further works should determine the thresholds of the distance along both antero-posterior and medio-lateral axis which could inevitably lead to falls.
Author Contributions
Conceptualization, B.W., J.B., T.C. and H.P.; methodology, B.W., J.B., T.C. and H.P.; validation, B.W. and H.P.; formal analysis, B.W. and H.P.; investigation, B.W.; resources, J.B. and T.C.; data curation, J.B. and B.W.; writing—original draft preparation, B.W.; writing—review and editing, B.W., J.B., T.C. and H.P.; visualization, B.W.; supervision, B.W.; project administration, B.W. and T.C.; funding acquisition, T.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the French national research agency (ANR), through the HoBiS [ANR -18-CE27-0010], eWALKING [ANR-22-CE19-0009-01] and BAC2WALK [ANR-22-CE19-0003] projects.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of IRISSE, EA 4075.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study. Written informed consent has been obtained from the volunteers to publish this paper.
Data Availability Statement
Data available on reasonable request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Rowland, D.M.; Lewek, M.D. Linking Gait Mechanics with Perceived Quality of Life and Participation after Stroke. PLoS ONE 2022, 17, e0274511. [Google Scholar] [CrossRef]
- Pin, S.; Spini, D. Impact of Falling on Social Participation and Social Support Trajectories in a Middle-Aged and Elderly European Sample. SSM - Population Health 2016, 2, 382–389. [Google Scholar] [CrossRef]
- Berg, W.P.; Alessio, H.M.; Mills, E.M.; Tong, C. Circumstances and Consequences of Falls in Independent Community-Dwelling Older Adults. Age Ageing 1997, 26, 261–268. [Google Scholar] [CrossRef]
- Robinovitch, S.N.; Feldman, F.; Yang, Y.; Schonnop, R.; Leung, P.M.; Sarraf, T.; Sims-Gould, J.; Loughin, M. Video Capture of the Circumstances of Falls in Elderly People Residing in Long-Term Care: An Observational Study. The Lancet 2013, 381, 47–54. [Google Scholar] [CrossRef]
- Pijnappels, M.; Bobbert, M.F.; Dieën, J.H.V. Push-off Reactions in Recovery after Tripping Discriminate Young Subjects, Older Non-Fallers and Older Fallers. Gait & Posture 2005, 21, 388–394. [Google Scholar] [CrossRef]
- Müller, B.; wolf, S.I. Handbook of Human Motion; Springer Cham.; Springer Berlin Heidelberg: New York, NY, 2018; ISBN 978-3-319-14417-7. [Google Scholar]
- Neptune, R.R.; Vistamehr, A. Dynamic Balance During Human Movement: Measurement and Control Mechanisms. Journal of Biomechanical Engineering 2019, 141. [Google Scholar] [CrossRef]
- Grundy, M.; Tosh, P.A.; McLeish, R.D.; Smidt, L. An Investigation of the Centres of Pressure under the Foot While Walking. The Journal of Bone and Joint Surgery. British volume. [CrossRef]
- Hof, A.L.; Gazendam, M.G.J.; Sinke, W.E. The Condition for Dynamic Stability. Journal of Biomechanics 2005, 38, 1–8. [Google Scholar] [CrossRef]
- Herr, H.; Popovic, M. Angular Momentum in Human Walking. Journal of Experimental Biology 2008, 211, 467–481. [Google Scholar] [CrossRef] [PubMed]
- Neptune, R.R.; Vistamehr, A. Dynamic Balance During Human Movement: Measurement and Control Mechanisms. Journal of Biomechanical Engineering 2019, 141, 070801. [Google Scholar] [CrossRef] [PubMed]
- Vistamehr, A.; Neptune, R.R. Differences in Balance Control between Healthy Younger and Older Adults during Steady-State Walking. Journal of Biomechanics 2021, 128, 110717. [Google Scholar] [CrossRef]
- Bailly, F.; Carpentier, J.; Pinet, B.; Soueres, P.; Watier, B. A Mechanical Descriptor of Human Locomotion and Its Application to Multi-Contact Walking in Humanoids. In Proceedings of the 2018 7th IEEE International Conference on Biomedical Robotics and Biomechatronics (Biorob); IEEE: Enschede, August, 2018; pp. 350–356. [Google Scholar]
- Al Abiad; Pillet; Watier A Mechanical Descriptor of Instability in Human Locomotion: Experimental Findings in Control Subjects and People with Transfemoral Amputation. Applied Sciences 2020, 10, 840. [CrossRef]
- Yiou, E.; Caderby, T.; Delafontaine, A.; Fourcade, P.; Honeine, J.-L. Balance Control during Gait Initiation: State-of-the-Art and Research Perspectives. WJO 2017, 8, 815–828. [Google Scholar] [CrossRef]
- Lyon, I.N.; Day, B.L. Control of Frontal Plane Body Motion in Human Stepping: Exp Brain Res 1997, 115, 345–356. 115. [CrossRef]
- Zettel, J.L.; McIlroy, W.E.; Maki, B.E. Environmental Constraints on Foot Trajectory Reveal the Capacity for Modulation of Anticipatory Postural Adjustments during Rapid Triggered Stepping Reactions. Exp Brain Res 2002, 146, 38–47. [Google Scholar] [CrossRef]
- Brenière, Y.; Cuong Do, M.; Bouisset, S. Are Dynamic Phenomena Prior to Stepping Essential to Walking? Journal of Motor Behavior 1987, 19, 62–76. [Google Scholar] [CrossRef]
- Lepers, R.; Brenière, Y. The Role of Anticipatory Postural Adjustments and Gravity in Gait Initiation. Exp Brain Res 1995, 107. [Google Scholar] [CrossRef]
- Watanabe, R.; Higuchi, T. Anticipatory Action Planning for Stepping onto Competing Potential Targets. Front. Hum. Neurosci. 2022, 16, 875249. [Google Scholar] [CrossRef]
- Monaghan, A.S.; Hooyman, A.; Dibble, L.E.; Mehta, S.H.; Peterson, D.S. Stability Changes in Fall-Prone Individuals With Parkinson Disease Following Reactive Step Training. Journal of Neurologic Physical Therapy 9900. [Google Scholar] [CrossRef]
- Muijres, W.; Arnalsteen, S.; Daenens, C.; Afschrift, M.; De Groote, F. Accuracy-Speed-Stability Trade-Offs in a Targeted Stepping Task Are Similar in Young and Older Adults. Front. Aging Neurosci. 2023, 15, 1130707. [Google Scholar] [CrossRef]
- Begue, J.; Peyrot, N.; Lesport, A.; Turpin, N.A.; Watier, B.; Dalleau, G.; Caderby, T. Segmental Contribution to Whole-Body Angular Momentum during Stepping in Healthy Young and Old Adults. Sci Rep 2021, 11, 19969. [Google Scholar] [CrossRef]
- Begue, J.; Peyrot, N.; Dalleau, G.; Caderby, T. Age-Related Changes in the Control of Whole-Body Angular Momentum during Stepping. Experimental Gerontology 2019, 127, 110714. [Google Scholar] [CrossRef]
- McIlroy, W.; Maki, B. Preferred Placement of the Feet during Quiet Stance: Development of a Standardized Foot Placement for Balance Testing. Clinical Biomechanics 1997, 12, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Siegler, S.; Allard, P.; Kirtley, C.; Leardini, A.; Rosenbaum, D.; Whittle, M.; D’Lima, D.D.; Cristofolini, L.; Witte, H. ISB Recommendation on Definitions of Joint Coordinate System of Various Joints for the Reporting of Human Joint Motion—Part I: Ankle, Hip, and Spine. Journal of biomechanics 2002, 35, 543–548. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; van der Helm, F.C.T.; (DirkJan) Veeger, H.E.J.; Makhsous, M.; Van Roy, P.; Anglin, C.; Nagels, J.; Karduna, A.R.; McQuade, K.; Wang, X.; et al. ISB Recommendation on Definitions of Joint Coordinate Systems of Various Joints for the Reporting of Human Joint Motion—Part II: Shoulder, Elbow, Wrist and Hand. Journal of Biomechanics 2005, 38, 981–992. [Google Scholar] [CrossRef] [PubMed]
- Maldonado, G.; Bailly, F.; Souères, P.; Watier, B. On the Coordination of Highly Dynamic Human Movements: An Extension of the Uncontrolled Manifold Approach Applied to Precision Jump in Parkour. Scientific Reports 2018, 8. [Google Scholar] [CrossRef] [PubMed]
- Anderson, F.C.; Pandy, M.G. A Dynamic Optimization Solution for Vertical Jumping in Three Dimensions. Computer Methods in Biomechanics and Biomedical Engineering 1999, 2, 201–231. [Google Scholar] [CrossRef]
- Dumas, R.; Chèze, L.; Verriest, J.-P. Adjustments to McConville et al. and Young et al. Body Segment Inertial Parameters. Journal of Biomechanics 2007, 40, 543–553. [Google Scholar] [CrossRef]
- de Leva, P. Adjustments to Zatsiorsky-Seluyanov’s Segment Inertia Parameters. Journal of Biomechanics 1996, 29, 1223–1230. [Google Scholar] [CrossRef]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-Source Software to Create and Analyze Dynamic Simulations of Movement. IEEE Transactions on Biomedical Engineering 2007, 54, 1940–1950. [Google Scholar] [CrossRef]
- Sloot, L.H.; Malheiros, S.; Truijen, S.; Saeys, W.; Mombaur, K.; Hallemans, A.; Van Criekinge, T. Decline in Gait Propulsion in Older Adults over Age Decades. Gait & Posture 2021, 90, 475–482. [Google Scholar] [CrossRef]
- Menant, J.C.; Steele, J.R.; Menz, H.B.; Munro, B.J.; Lord, S.R. Rapid Gait Termination: Effects of Age, Walking Surfaces and Footwear Characteristics. Gait & Posture 2009, 30, 65–70. [Google Scholar] [CrossRef]
- Manckoundia Backward Disequilibrium in Elderly Subjects. CIA 2008, Volume 3, 667–672. [CrossRef]
- Tesio, L.; Rota, V.; Chessa, C.; Perucca, L. The 3D Path of Body Centre of Mass during Adult Human Walking on Force Treadmill. Journal of Biomechanics 2010, 43, 938–944. [Google Scholar] [CrossRef]
- Orendurff, M.S.; Segal, A.D.; Klute, G.K.; Berge, J.S.; Rohr, E.S.; Kadel, N.J. The Effect of Walking Speed on Center of Mass Displacement. JRRD 2004, 41, 829. [Google Scholar] [CrossRef]
- Ohtsu, H.; Yoshida, S.; Minamisawa, T.; Katagiri, N.; Yamaguchi, T.; Takahashi, T.; Yomogida, S.; Kanzaki, H. Does the Balance Strategy during Walking in Elderly Persons Show an Association with Fall Risk Assessment? Journal of Biomechanics 2020, 103, 109657. [Google Scholar] [CrossRef]
- Lockhart, T.E.; Smith, J.L.; Woldstad, J.C. Effects of Aging on the Biomechanics of Slips and Falls. 2010.
- Bouisset, S.; Do, M.-C. Posture, Dynamic Stability, and Voluntary Movement. Neurophysiologie Clinique/Clinical Neurophysiology 2008, 38, 345–362. [Google Scholar] [CrossRef]
Figure 1.
Means of the dimensionless distances between the COM and the MMA along the antero-posterior and medio-lateral axis for older and young participants in both speed conditions. From the left to the right, the five phases (P1 to P5) are presented. Each phase is normalized from 0 to 100%. Minimal distances are observed at the end of the first swing phase (P2). Maximal distances are observed at the transition between the phases P3 and P4. The amplitudes on the ordinate axes are different in the antero-posterior [-0.04;0.04] and medio-lateral [-0.02;0.01] directions.
Figure 1.
Means of the dimensionless distances between the COM and the MMA along the antero-posterior and medio-lateral axis for older and young participants in both speed conditions. From the left to the right, the five phases (P1 to P5) are presented. Each phase is normalized from 0 to 100%. Minimal distances are observed at the end of the first swing phase (P2). Maximal distances are observed at the transition between the phases P3 and P4. The amplitudes on the ordinate axes are different in the antero-posterior [-0.04;0.04] and medio-lateral [-0.02;0.01] directions.
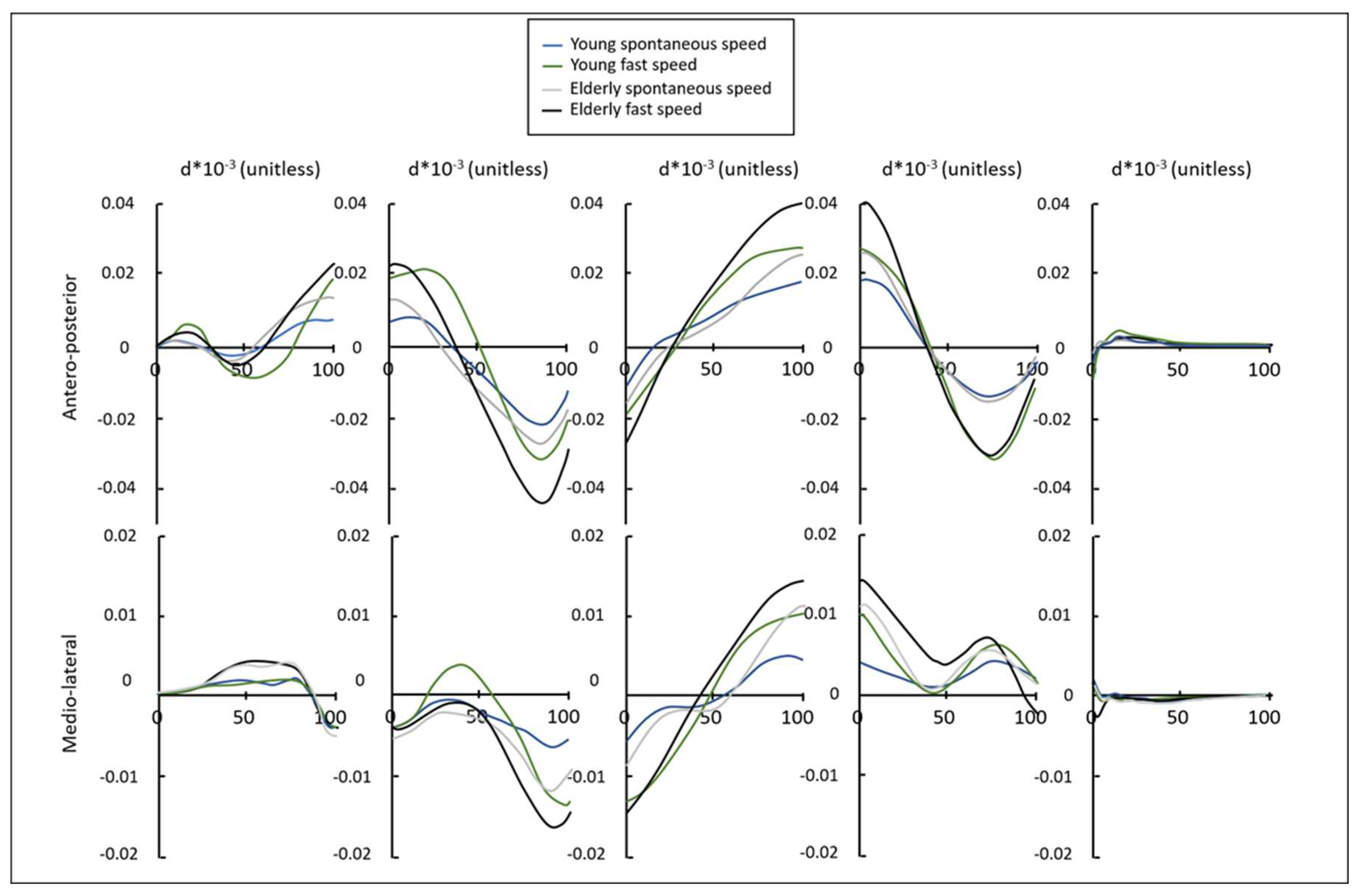
Table 1.
Mean±Std spatiotemporal parameters for young and older adults at spontaneous and fast speed. ‘ns’ indicates a non-significant effect (p > 0.05).
Table 1.
Mean±Std spatiotemporal parameters for young and older adults at spontaneous and fast speed. ‘ns’ indicates a non-significant effect (p > 0.05).
| Young adults | Older adults | Effect | |||||
|---|---|---|---|---|---|---|---|
| Parameters | spontaneous | fast | spontaneous | fast | speed | group | speed×group |
| Total duration (s) | 3.21±0.15 | 2.75±0.17 | 3.18±0.32 | 2.89±0.28 | p < 0.001 | ns | ns |
| P1 duration (s) | 0.62±0.09 | 0.49±0.08 | 0.51±0.08 | 0.43±0.08 | p < 0.001 | p = 0.003 | ns |
| P2 duration (s) | 0.43±0.06 | 0.34±0.04 | 0.40±0.06 | 0.33±0.04 | p < 0.001 | ns | ns |
| P3 duration (s) | 0.29±0.07 | 0.13±0.03 | 0.25±0.05 | 0.16±0.02 | p < 0.001 | ns | p = 0.004 |
| P4 duration (s) | 0.46±0.05 | 0.36±0.03 | 0.48±0.05 | 0.38±0.06 | p < 0.001 | ns | ns |
| P5 duration (s) | 1.42±0.11 | 1.42±0.13 | 1.54±0.17 | 1.58±0.18 | ns | p = 0.003 | ns |
| Forward speed (m/s) | 0.71±0.16 | 1.18±0.19 | 0.73±0.12 | 0.99±0.21 | p < 0.001 | ns | p < 0.001 |
Table 2.
Minimal and maximal dimensionless distances (×100) along the antero-posterior (AP) and medio-lateral (ML) axis throughout the entire stepping. ‘ns’ indicates a non-significant effect (p > 0.05).
Table 2.
Minimal and maximal dimensionless distances (×100) along the antero-posterior (AP) and medio-lateral (ML) axis throughout the entire stepping. ‘ns’ indicates a non-significant effect (p > 0.05).
| Young adults | Older adults | Effect | |||||
|---|---|---|---|---|---|---|---|
| Parameters | spontaneous | fast | spontaneous | fast | speed | group | speed×group |
| Minimal AP distance | -2.27±0.35 | -3.87±0.78 | -2.81±0.47 | -4.71±1.29 | p < 0.001 | p = 0.009 | ns |
| Maximal AP distance | 2.00±0.37 | 3.48±0.97 | 2.75±0.58 | 4.39±1.33 | p < 0.001 | p = 0.004 | ns |
| Minimal ML distance | -1.15±0.35 | -2.21±0.64 | -1.35±0.17 | -1.92±0.36 | p < 0.001 | ns | p = 0.017 |
| Maximal ML distance | 1.10±0.36 | 1.85±0.61 | 1.32±0.25 | 1.89±0.60 | p < 0.001 | ns | ns |
Table 3.
Range of the dimensionless distances along the antero-posterior (AP) and medio lateral (ML) axis (×100) for each phase and throughout the entire stepping. ‘ns’ indicates a non-significant effect (p > 0.05).
Table 3.
Range of the dimensionless distances along the antero-posterior (AP) and medio lateral (ML) axis (×100) for each phase and throughout the entire stepping. ‘ns’ indicates a non-significant effect (p > 0.05).
| Young adults | Older adults | Effect | ||||||
|---|---|---|---|---|---|---|---|---|
| Phase | Parameters | spontaneous | fast | spontaneous | fast | speed | group | speed×group |
| P1 | AP | 1.48±0.48 | 3.10±1.02 | 2.18±0.78 | 3.62±1.34 | p < 0.001 | ns | ns |
| ML | 0.97±0.28 | 1.21±0.56 | 1.23±0.42 | 1.40±0.54 | p = 0.026 | ns | ns | |
| P2 | AP | 3.14±0.59 | 6.02±1.79 | 4.19±0.95 | 7.02±2.26 | p < 0.001 | p = 0.036 | ns |
| ML | 1.13±0.31 | 2.69±0.68 | 1.42±0.32 | 2.36±0.71 | p < 0.001 | ns | p = 0.013 | |
| P3 | AP | 3.08±0.73 | 5.00±1.70 | 4.30±0.81 | 6.95±2.58 | p < 0.001 | p = 0.004 | ns |
| ML | 1.64±0.47 | 3.47±1.44 | 2.11±0.40 | 3.06±1.01 | p < 0.001 | ns | p = 0.04 | |
| P4 | AP | 3.54±0.56 | 6.23±1.21 | 4.46±0.93 | 7.49±1.83 | p < 0.001 | p = 0.007 | ns |
| ML | 1.07±0.43 | 2.13±0.87 | 1.53±0.32 | 2.33±0.72 | p < 0.001 | ns | ns | |
| P5 | AP | 1.09±0.21 | 1.85±0.51 | 0.90±0.21 | 1.52±0.49 | p < 0.001 | p = 0.031 | ns |
| ML | 0.69±0.25 | 0.86±0.25 | 0.59±0.14 | 0.82±0.24 | p < 0.001 | ns | ns | |
| Total | AP | 4.27±0.64 | 7.35±1.64 | 5.56±0.95 | 9.10±2.53 | p < 0.001 | p = 0.005 | ns |
| ML | 2.21±0.63 | 4.06±1.27 | 2.67±0.34 | 3.82±0.87 | p < 0.001 | ns | ns | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







