Research on Short-Term Passenger Flow Prediction of LSTM Rail Transit Based on Wavelet Denoising

1. Introduction

Urban rail transit, as an important part of urban public transportation, is greatly significant for improving urban passenger flow and transportation efficiency, as well as alleviating traffic congestion. Scientific passenger flow prediction plays an extremely important role in feasibility studies for urban rail transit, layout planning of urban rail transit networks, decision-making around urban rail transit construction scale and levels, and contributes to better management of urban transit systems and timely countermeasures.

The research on the traditional forecasting model of rail transit passenger flow is quite mature. Jérémy Roos [1] proposed a dynamic Bayesian network approach to forecast the short-term passenger flows of the urban rail network of Paris, which could deal with the incompleteness of the data caused by failures or lack of collection systems. Zhao Yutang [2] used support vector machine to predict the passenger flow of Xinzhuang subway station, and concluded that the nonlinear support vector machine model can predict the working day better. Anl Utku [3] developed a long short-term memory-based(LTSM-based) deep learning model to predict short-term transit passenger volume on transport routes in Istanbul using a dataset that included the number of people who used different transit routes at one-hour interval between January and December 2020, and compared that with popular models such as random forest (RF), support vector machines, autoregressive integrated moving average, multilayer perceptron, and convolutional neural networks.

There are also many scholars who studied the application of neural network and nonlinear model for forecast short-term passenger flow. Alghamdi [4] proposed an end-to-end deep learning-based framework with a novel architecture to predict multi-step-ahead real time travel demand, along with uncertainty estimation. Asce [5] presented a novel nonparametric dynamic time-delay recurrent wavelet neural network model for forecasting traffic flow, which exploited the concept of wavelet in the model to provide flexibility and extra adaptable translation parameters in traffic flow forecasting model. Alireza Ermagun [6] examined spatiotemporal dependency between traffic links, proposed a two-step algorithm to search and identify the best look-back time window for upstream links, indicated the best look-back time window depends on the travel time between two study detctors. Dong Shengwei [7] used genetic algorithm to optimize the BP model, which significantly improved the prediction accuracy of short-term passenger flow of Beijing Line 4. Pekel [8] developed two hybrid methods: parliamentary optimization algorithm-artificial neural network (POA-ANN), and intelligent water drops algorithm-ANN (IWD-ANN), to illustrate the effect of precise prediction for passenger queues. Mirzahossein [9] proposed a novel hybrid method based on deep learning to estimate short-term traffic volume at three adjacent intersections, combined with time window and normal distribution of WND-LSTM for traffic flow prediction, and the MAPE obtained was 60%-90% lower than that of ARIMA, LR and other models.

This paper examines Shantang Street station in Suzhou, chosen for its high commercial nature and weekday/weekend passenger differences. Wavelet denoising processed the short-term flow data, which an LSTM model used to predict volumes versus standalone LSTM and SVR. The wavelet-denoised LSTM model significantly improved accuracy, indicating effectiveness for real-world rail transit forecasting.

2. Research Methods

2.1. Wavelet denoising analysis

2.1.1. Principle of wavelet denoising analysis

Wavelet denoising analysis [10,11,12] has been successfully utilized in many fields. Due to the irregularity of short-term passenger flow data at stations, prediction error for short-term rail transit passenger flow may be substantial. Therefore, wavelet denoising analysis was selected to improve prediction accuracy based on data characteristics.

The short-term passenger flow data of rail transit stations fluctuates constantly, with a certain level of noise. High-frequency signals can be denoised through threshold values, then data reconstructed to achieve denoising. The traffic signal for short-term traffic volume containing noise can be formulated as follows:

$$S(x)=f(x)+\sigma e(x)$$

(1)

f(x): data after noise removal

e(x): contained noise

σ: noise intensity

S(x): short-term passenger flow data of rail transit with noise signal

2.1.2. Wavelet denoising process

The basic process of wavelet denoising analysis is shown in the figure below:

Figure 1. Flow chart of wavelet denoising.

Figure 1. Flow chart of wavelet denoising.

Therefore, when utilizing wavelet denoising to analyze short-term passenger flow data for rail transit, it can be simplified into five processes: selecting the wavelet function, wavelet base order, threshold function, decomposition layer, and wavelet reconstruction.

2.2. Basic principles of long term memory networks

2.2.1. LSTM process

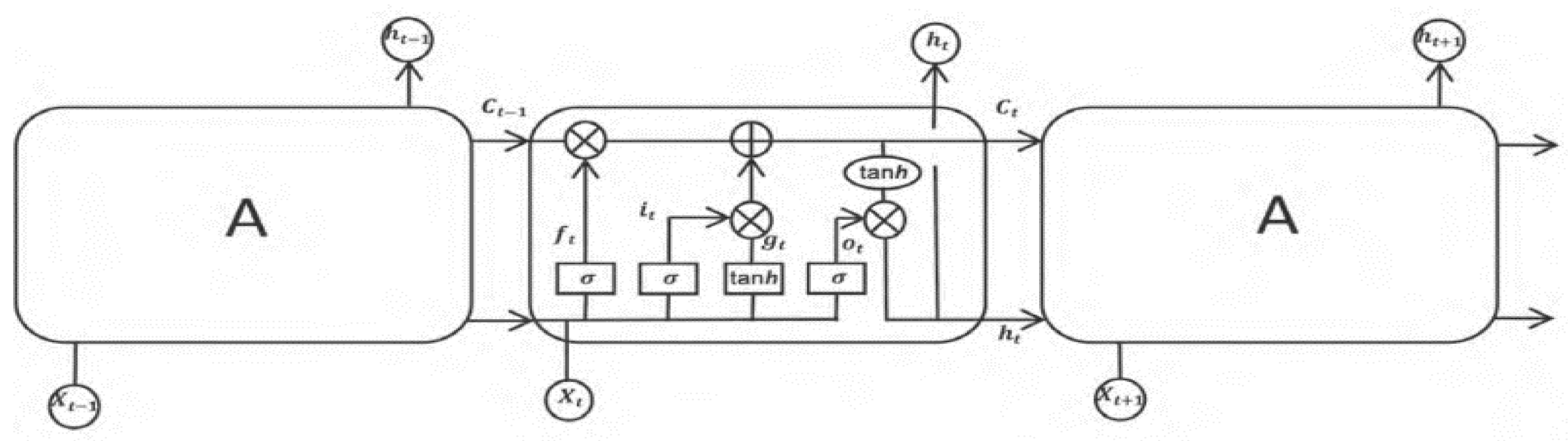
The LSTM neural network [13] has four structures: forgetting gate, input gate, output gate and memory unit. The cell structure of the unit is controlled through the forgetting and input gates. The LSTM process is:

Figure 2. LSTM process structure diagram.

Figure 2. LSTM process structure diagram.

The arrows in the figure above represent vectors, showing input from the previous node to the node the arrows point to. LSTM controls information flow through three gate structures, consisting of sigmoid activation functions and a multiplicative structure with an output of 0 or 1. The sigmoid activation function in the gate is equations (2) and (3), with the tanh functions being (4) and (5).

$$\sigma (z)=y=\frac{1}{1+e^{-z}}$$

(2)

$$\sigma \text{'}(z)=y(1-y)$$

(3)

$$\tanh (z)=y=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$

(4)

$$\tanh \text{'}(z)=1-y^2$$

(5)

$C_{t-1}$：The cell state passed in at the previous time.

$x_t$：The new value of information that is read at the present moment causes the module to generate a new memory.

$h_{t-1}$：The output value of the previous hidden neuron module.

$C_t$： Belongs to the current time output information, to the next time transmitted unit state.

$h_t$：New output at the current time.

2.2.2. Calculation of LSTM forward propagation

The LSTM forward propagation calculation process is from the forgetting gate to the input gate, updating the unit state, and finally to the output gate [14].

The forgetting gate determines how much information can be retained from the previous moment to the current one. After $h_{t-1}$ and $x_t$ are activated by activation function, $f_t$ is obtained, representing the degree of retention of the previous hidden neuron state. The activation function is sigma, with the $f_t$ expression being:

$$f_t=\sigma (W_f{h}_{t-1}+U_f{x}_t+b_f)$$

(6)

$W_f$：Represents the weight of the input forgetting gate of the previous hidden neuron module.

$U_f$：The information value of the input layer flows into the weight of the forgetting gate.

$b_f$：Calculate the bias parameters of the forgetting door.

The input gate determines how much information will be received and can determine the new information generated and what percentage of the new information will be used. The calculation process is as follows:

$$i_t=\sigma (W_i[h_{t-1},x_t]+b_i)$$

(7)

$${\tilde{C}}_t=\tan h(W_c\left[h_{t-1},x_t\right]+b_c)$$

(8)

After passing through the input gate, the output of the input gate is: $i_t*C_t$.

The updating of memory cell state means that the output $f_t$of the forgetting gate is multiplied by the cell state $C_{t-1}$ at the previous time and combined with the output of the input gate to get a new cell state $C_t$, so $C_t$is formed by combining the retained part of the information at the previous time and the newly generated information. The expression of $C_t$is as follows:

$$C_t=f_t*C_{t-1}+i_t*{\tilde{C}}_t$$

(9)

Finally, need to go through the output door, which is composed of two parts calculation, partly by the current information combined with short-term memory thus calculated $o_t$, another part is calculated combined with long-term memory and concluded $h_t$, $o_t$by the module of a hidden neurons on the output value of $h_{t-1}$ combined with the current input value $x_t$ and activated by sigma function. The calculation process is as follows:

$$o_t=\sigma (W_o[h_{t-1},x_t]+b_o)$$

(10)

The final output after LSTM model is as follows:

$$h_t=o_t。(\tanh ((C_t))$$

(11)

2.2.3. Reverse calculation of LSTM

After LSTM model forward propagation, the weight set and relevant bias terms must be updated, so reverse calculation can be performed by propagating the error up the layer.

2.3. Principle of Support vector machine regression

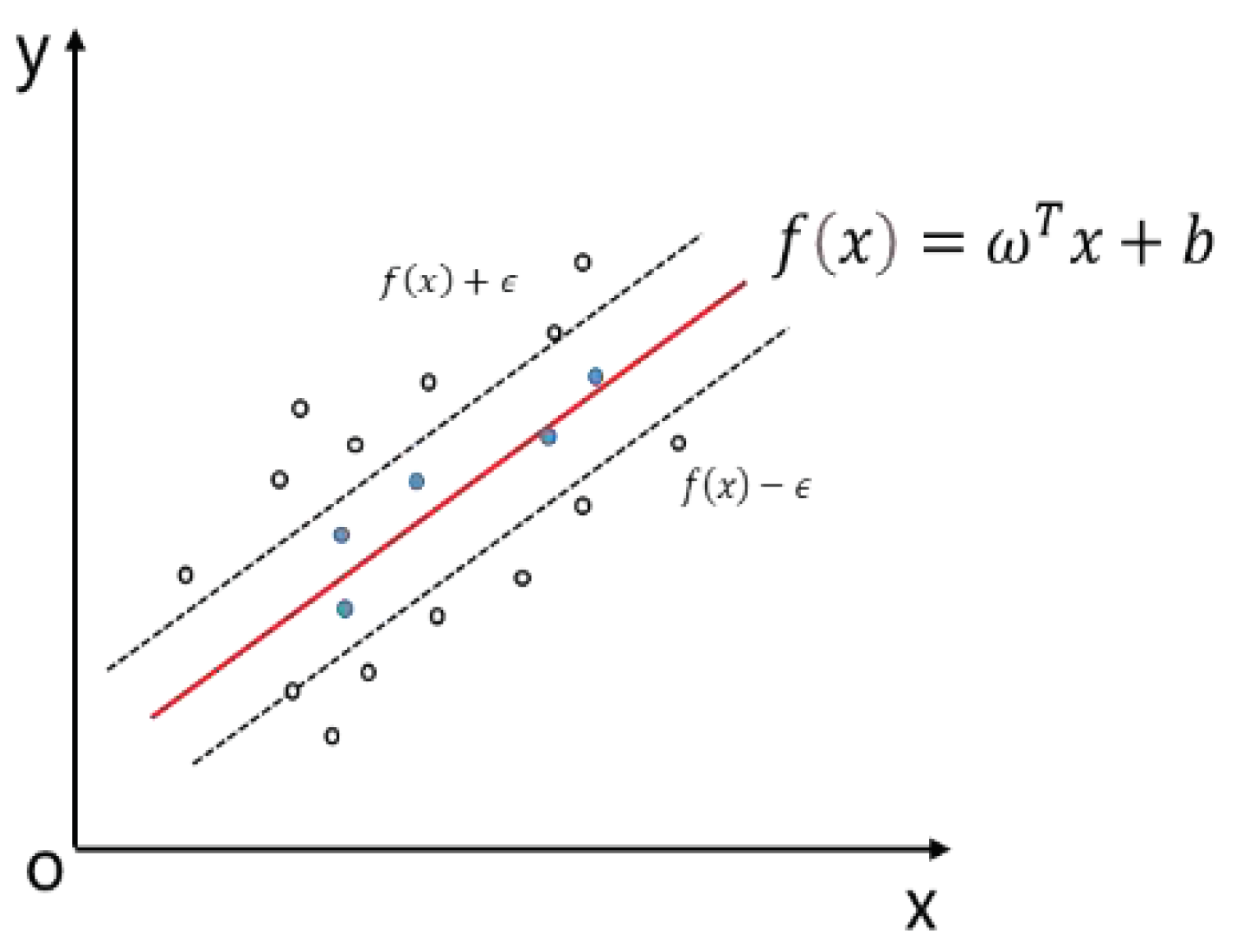
The training samples of SVR model [15,16,17] are D={(x1,y1),(x2,y2)..., (xn,yn)}, with yi∈R. The goal is to learn a model f(x) with a value close to y. When model f(x) exactly matches y, the final loss is 0. In the SVR model, the deviation between f(x) and y is set at most to ε. When the difference between f(x) and y is greater than ε, the loss is calculated; otherwise, the loss is ignored. This is equivalent to establishing a 2ε wide tolerance band centered on f(x). If sample data falls within the tolerance bands, the prediction is accurate, as shown:

Figure 3. Support vector machine regression display.

Figure 3. Support vector machine regression display.

Parameters involved in support vector machine (SVM) regression include ε and C. ε is the loss function and affects model precision and training speed - an important index for measuring SVR model accuracy. Parameter C is a penalty factor, aiming to balance the model. The smaller C, the lower model complexity and penalty. The choice of C should not be too large or small, otherwise overfitting or underfitting may occur.

3. Empirical Study

3.1. Data Preprocessing

This article examines short-term traffic prediction for the Shantang Street station of the Suzhou Rail Transit system. The data utilized in this study were obtained from the Suzhou Rail Transit AFC system and include transaction time, ticket ID and type, inbound and outbound station codes and names, and inbound and outbound times. The experiments in this article were conducted on a Windows 10 64-bit operating system. The hardware used includes an AMD Ryzen 7 5800H with Radeon Graphics 3.20 GHz processor and 16GB of memory. The programming language used is Python 3.7, and the Matplotlib 3.0.2 plotting tool was utilized for generating plots.

MySQL was used to clean the raw data. Relevant database rules were applied to extract the required information, resulting in over 14 million data points for the month of July that were used in this analysis. Given the high commercial nature and distinct weekday versus weekend ridership patterns, outbound passenger traffic from Shantang Street station was selected as the prediction target. The July 1st to 27th inbound passenger flow was used as the training set, while the July 28th and 29th (Monday and Sunday) data were held out as the test set. Hourly passenger volumes for Shantang Street station are shown in part in the table below:

Table 1. Hourly passenger flow data of Shantang Street station.

Time	Station	Monday	Tuesday	Wednesday	Thursday	Friday	Saturday	Sunday
5:00:00	Shantang Street	4	2	4	12	3	9	10
6:00:00	Shantang Street	220	235	203	250	237	198	133
7:00:00	Shantang Street	472	471	495	470	471	432	410
8:00:00	Shantang Street	519	491	467	543	491	601	513
9:00:00	Shantang Street	497	525	595	596	552	655	572
10:00:00	Shantang Street	461	538	537	531	516	583	656
18:00:00	Shantang Street	415	360	317	382	409	527	621
19:00:00	Shantang Street	391	396	400	425	466	640	636
20:00:00	Shantang Street	407	479	536	497	494	845	772
21:00:00	Shantang Street	306	365	371	431	463	703	551
22:00:00	Shantang Street	77	81	129	94	149	100	171

Table 1. Hourly passenger flow data of Shantang Street station.

Time	Station	Monday	Tuesday	Wednesday	Thursday	Friday	Saturday	Sunday
5:00:00	Shantang Street	4	2	4	12	3	9	10
6:00:00	Shantang Street	220	235	203	250	237	198	133
7:00:00	Shantang Street	472	471	495	470	471	432	410
8:00:00	Shantang Street	519	491	467	543	491	601	513
9:00:00	Shantang Street	497	525	595	596	552	655	572
10:00:00	Shantang Street	461	538	537	531	516	583	656
18:00:00	Shantang Street	415	360	317	382	409	527	621
19:00:00	Shantang Street	391	396	400	425	466	640	636
20:00:00	Shantang Street	407	479	536	497	494	845	772
21:00:00	Shantang Street	306	365	371	431	463	703	551
22:00:00	Shantang Street	77	81	129	94	149	100	171

3.2. LSTM model construction and prediction analysis

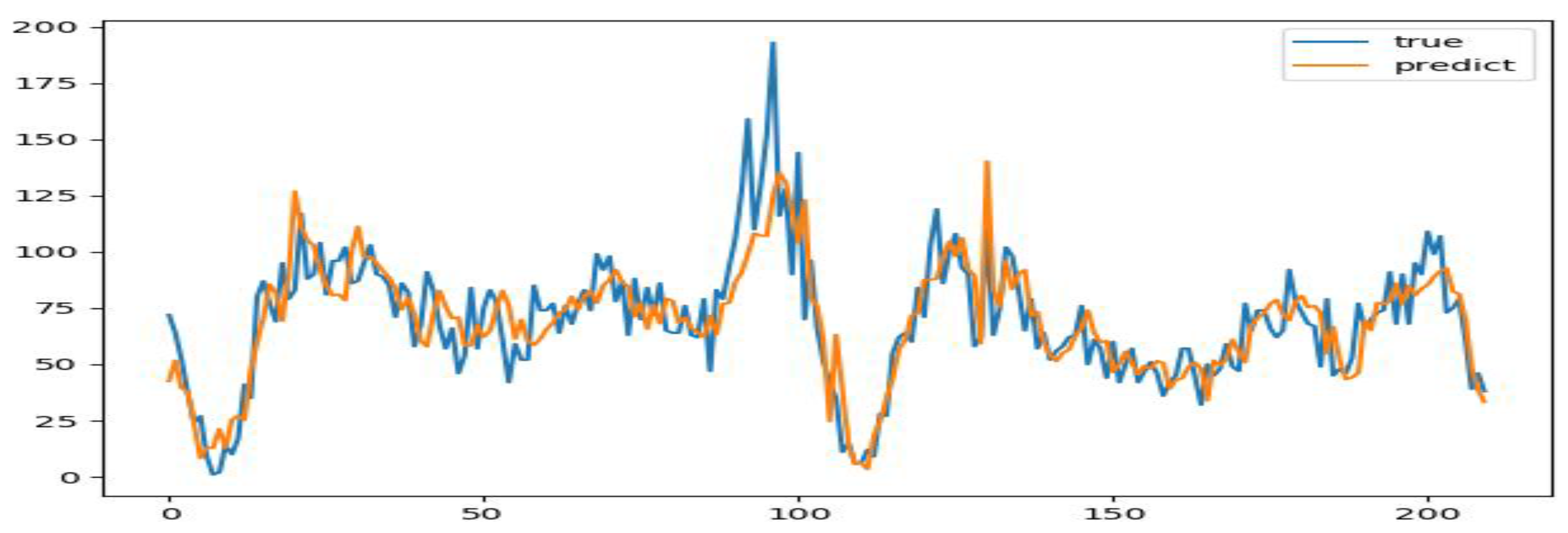
The LSTM neural network model was implemented using the Shantang Street training data as input. The output layer dimension was set to 1, with 4 hidden layers and 1000 training iterations. To capture traffic patterns, a historical time step of 30 was used. A batch size of 10 and dropout layers were incorporated to improve accuracy and prevent overfitting. Sigmoid activation functions were utilized for all fully connected layers during training., the prediction results are compared as follows:

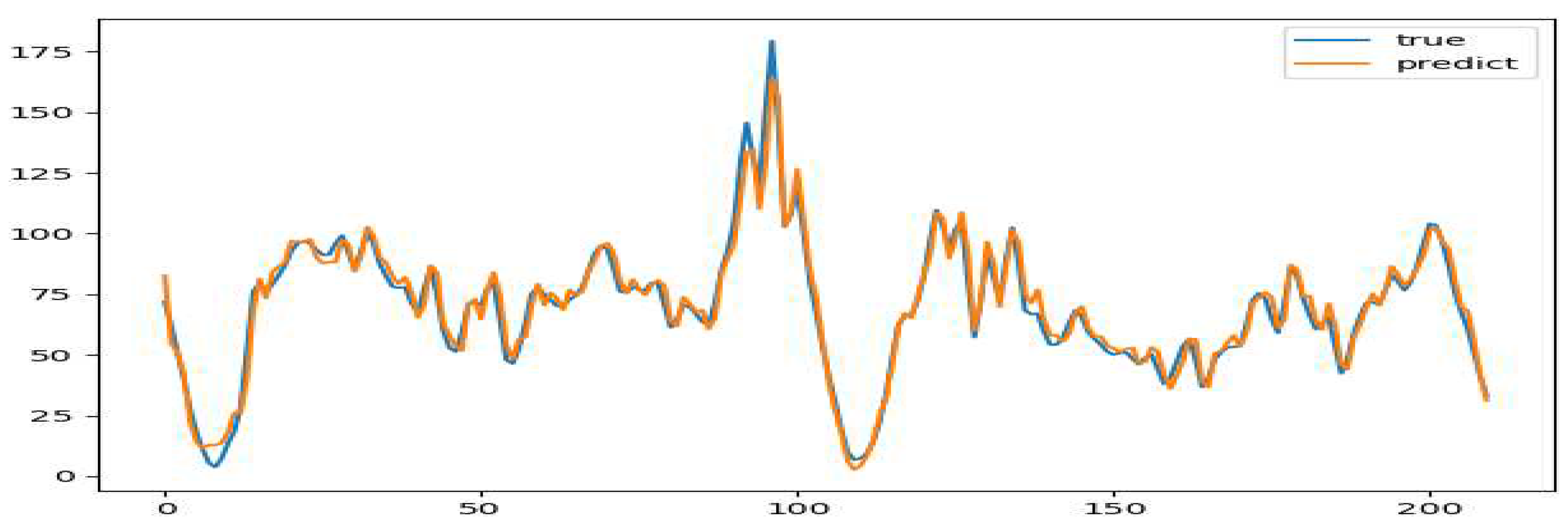
Figure 4. Comparison of actual data and test set prediction results.

Figure 4. Comparison of actual data and test set prediction results.

Table 2. LSTM model prediction results index values.

Method	Index	Monday (7.29)	Sunday (7.28)
LSTM	RMSE	12.86	19.78
	MAE	10.27	15.35
	MAPE	18%	31%

Table 2. LSTM model prediction results index values.

Method	Index	Monday (7.29)	Sunday (7.28)
LSTM	RMSE	12.86	19.78
	MAE	10.27	15.35
	MAPE	18%	31%

This model configuration was trained and used to predict the test set ridership. The results were compared to the actual values using the RMSE, MAE, and MAPE metrics for both weekdays and weekends. As seen in the figure, the LSTM model predictions did not match the true values very closely, indicating poor performance that needs improvement across all accuracy metrics.

3.3. LSTM model construction and prediction analysis of wavelet denoising

3.3.1. Steps of model construction and prediction

To address these limitations, a wavelet denoising approach was applied prior to LSTM modeling. The key steps were:

• Perform a 3-level discrete wavelet transform on the time series data using the db6 wavelet.
• Decompose the signal into low and high frequency components.
• Apply soft thresholding denoising to the 3 high frequency signals.
• Reconstruct the denoised signal.
• Split data into training and test sets.
• Train LSTM model on denoised training data
• Validate model performance on denoised test data.

The visualizations below depict the original noisy data versus the smoothed denoised signal after wavelet decomposition and thresholding.

3.3.2. Predictive analysis

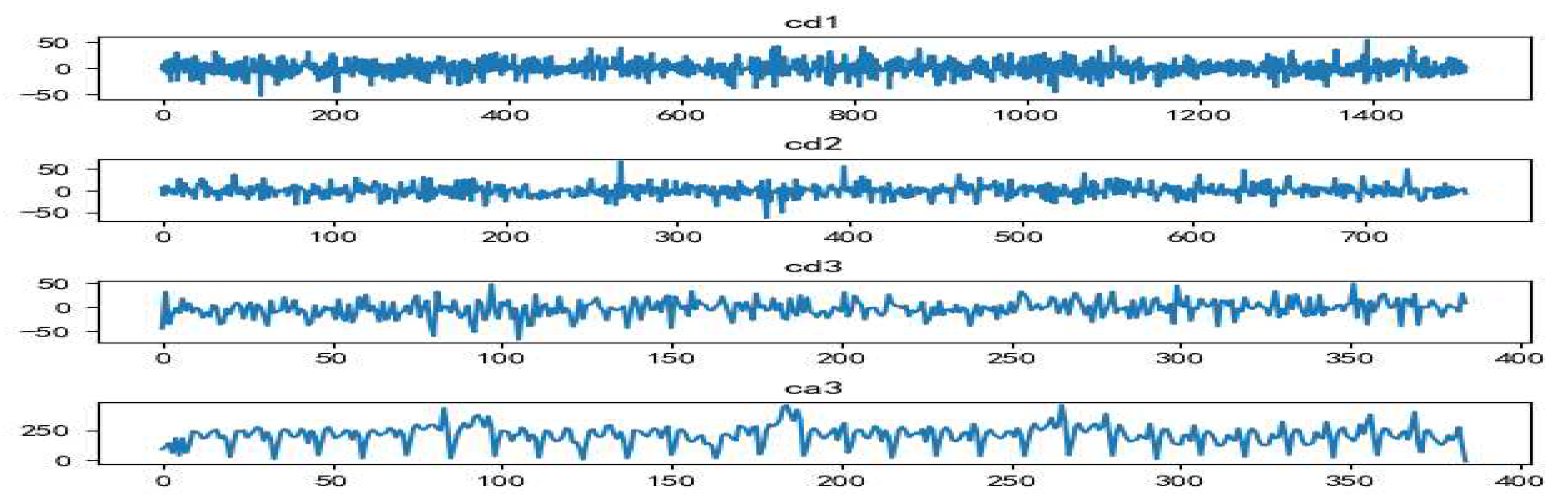
First, the db6 wavelet basis function is selected to decompose the three-layer wavelet of July inbound passenger flow data of Shantang Street station with a time interval of 10min [15], and the results are shown in Figure 5 below.

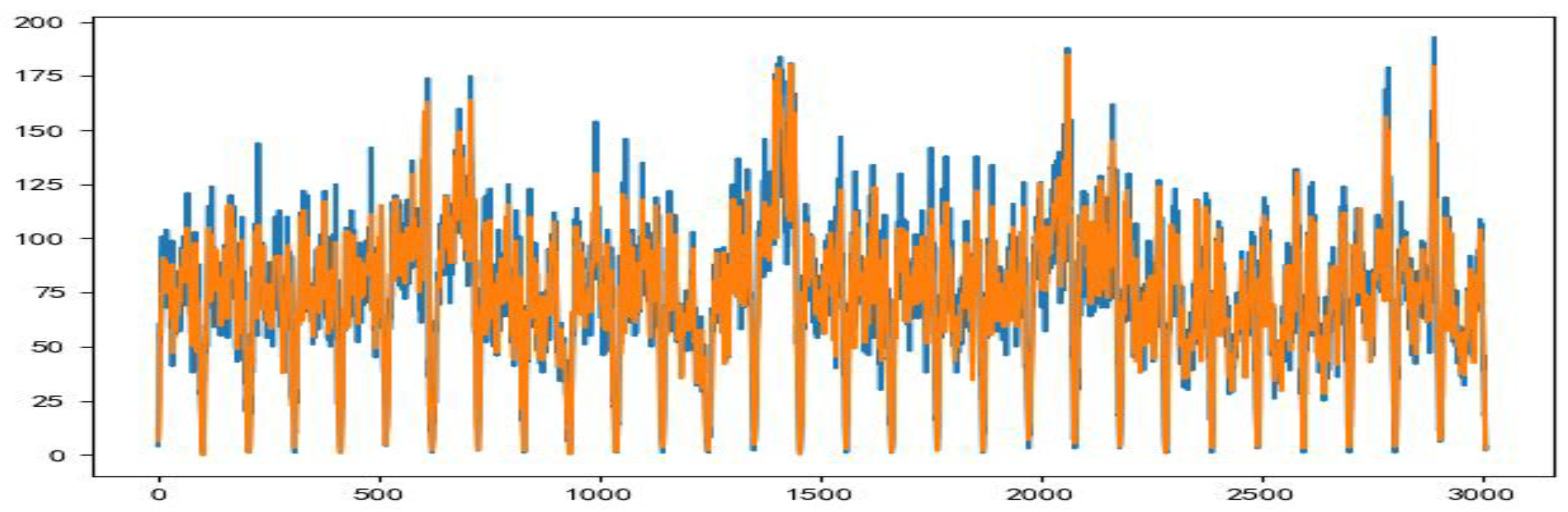
After wavelet decomposition and soft threshold denoising, the denoised data and the original data are visualized, as shown in Figure 6. It can be seen that the denoised data is smoother.

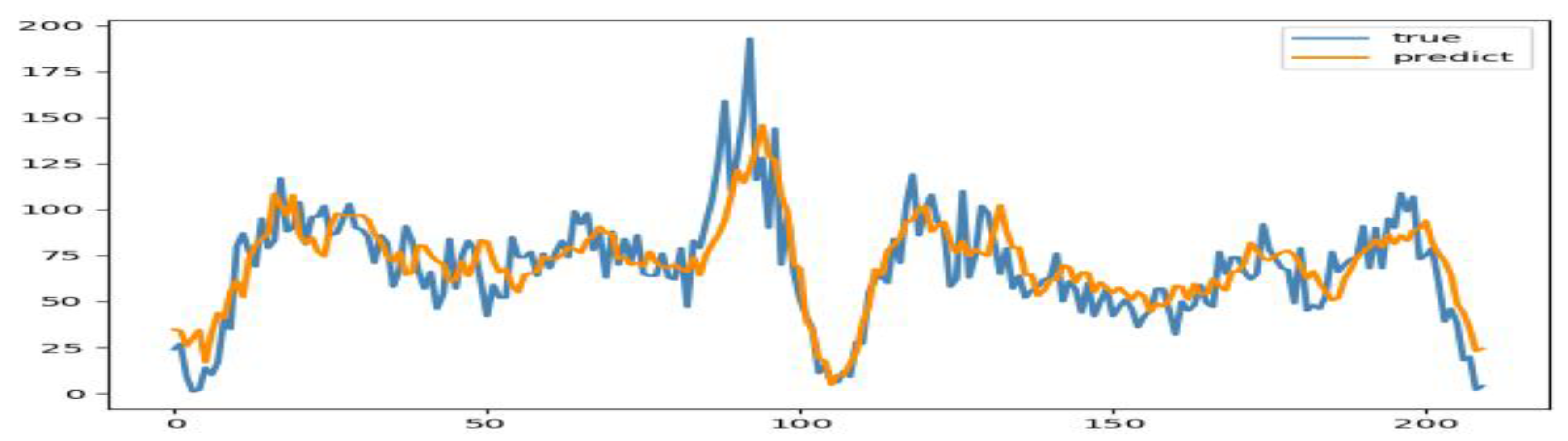
The inbound short-time passenger flow training set data of Shantang Street station after noise removal is used as the input of the LSTM network. The dimension of the input layer is set to 1, the time step is set to 1, the dimension of the output layer is set to 1, the hidden layer is set to 4, the number of iterations is set to 1000, and the historical time step is set to 30. For accurate training, the batch_size is set to 10 and the dropout layer is added. It is better to set the probability to 0.1. Based on the above Settings, the training of the model is expanded, and the comparison figure of the prediction results is as follows:

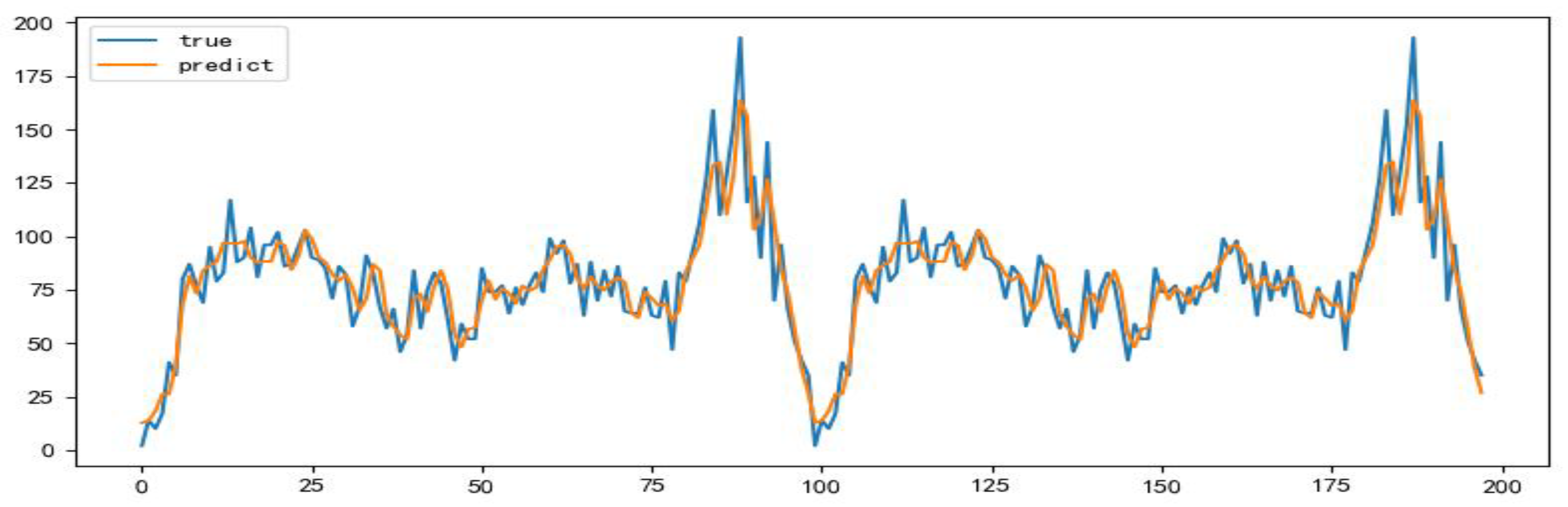
According to Figure 7 and Figure 8, it can be seen that there is almost no difference between the prediction results of the test set data and the data after noise removal, and the prediction model effect of the processed data is more significant.

Table 3. Prediction result index value of LSTM model based on wavelet denoising.

Index	Monday (7.29)	Sunday (7.28)
RMSE	8.94	12.32
MAE	7.22	9.88
MAPE	12%	19%

Table 3. Prediction result index value of LSTM model based on wavelet denoising.

Index	Monday (7.29)	Sunday (7.28)
RMSE	8.94	12.32
MAE	7.22	9.88
MAPE	12%	19%

With the denoised data, the LSTM model was re-trained using the same configuration described previously. As evident in the figure, the predictions closely matched the denoised test set values, demonstrating significantly improved model performance compared to the non-denoised data. The RMSE, MAE, and MAPE were substantially lower for both weekday and weekend results as shown in the table, confirming the benefits of preprocessing with wavelets prior to LSTM modeling for this application. It has great significance for forecasting.

3.4. SVR model construction and prediction analysis

According to the existing experimental results, it can be found that the SVR model has a good fitting ability, and has a good effect on solving some complex nonlinear problems. The short-term passenger flow of rail transit has the characteristic of complexity, so support vector machine model can be used to deal with the problem of short-term passenger flow prediction.

3.4.1. Steps of SVR model construction and prediction

Given the ability of support vector machines (SVMs) to model complex nonlinear patterns, an SVM approach was also evaluated. The key steps were:

• Separate data into training (July 1st - 27th) and test sets (July 28th and 29th).
• Train SVM models with different kernels, selecting RBF based on best fit.
• Initialize hyperparameter values for penalty factor C and gamma.
• Refine hyperparameters via grid search cross-validation to minimize MSE.
• Assess model on test data.

3.4.2. Predictive analysis

The step of prediction is set as 1. It is proved that the first 30 data are used to predict the next data, and the calculated error is relatively small. Firstly, the penalty factor parameter C was set as 1,5,10,30,100, and the parameter gamma was set as 0.1,0.12,0.01, 0.05, 0.001,1,0.5,0.9. rbf function was selected as the kernel function, and mean square error was selected as the standard to judge the quality of the model. Finally, C=5 and gamma=0.1 were determined to predict the test set data based on the parameters, and the prediction result was as follows:

Figure 9. Comparison of actual data and test set prediction result.

Figure 9. Comparison of actual data and test set prediction result.

Table 4. Index values of prediction results based on the SVR model.

Index	Monday (7.29)	Sunday (7.28)
RMSE	14.15	19.25
MAE	11.78	14.72
MAPE	21%	38%

Table 4. Index values of prediction results based on the SVR model.

Index	Monday (7.29)	Sunday (7.28)
RMSE	14.15	19.25
MAE	11.78	14.72
MAPE	21%	38%

By calculating the predicted results, it can be seen that the predicted results do not deviate much from the actual values, but there is still a certain gap compared with the LSTM model of wavelet denoising. But in general, SVR model is relatively reasonable for the prediction of short-term passenger flow.

3.5. Comparison of Results

Visually inspecting the Shantang Street station predictions reveals the estimated volumes from all methods stayed relatively close to the true values. This suggests the selected techniques were appropriate for modeling this station’s ridership. Across both weekday and weekend results, the denoised LSTM predictions aligned most tightly with the real data.

Table 5. Index values of prediction results under different models.

Method	Index	Monday (7.29)	Sunday (7.28)
LSTM	RMSE	12.86	19.78
	MAE	10.27	15.35
	MAPE	18%	31%
The wavelet +LSTM	RMSE	8.94	12.32
	MAE	7.22	9.88
	MAPE	12%	19%
SVR	RMSE	14.15	19.25
	MAE	11.78	14.72
	MAPE	21%	38%

Table 5. Index values of prediction results under different models.

Method	Index	Monday (7.29)	Sunday (7.28)
LSTM	RMSE	12.86	19.78
	MAE	10.27	15.35
	MAPE	18%	31%
The wavelet +LSTM	RMSE	8.94	12.32
	MAE	7.22	9.88
	MAPE	12%	19%
SVR	RMSE	14.15	19.25
	MAE	11.78	14.72
	MAPE	21%	38%

The wavelet-denoised LSTM achieved RMSE values around 4-5 lower, MAE values 3-4 lower, and more substantially improved MAPE versus other techniques. This indicates clear advantages in accuracy for this approach, further confirmed by the lower errors on Monday compared to the higher-volume Sunday. Considering both predictive power and practicality, the integrated wavelet denoising with LSTM emerges as the superior methodology, demonstrating applicability to real-world forecasting.

4. Conclusion

This study focused on applying different short-term forecasting techniques to predict passenger volumes at Suzhou Rail Transit’s Shantang Street station. The goal was analyzing whether the proposed denoised LSTM method provided higher accuracy and effectiveness.

For short-term prediction research, wavelet denoising processed the time series data before LSTM modeling. Based on signal-to-noise ratios and rail transit passenger flow characteristics, 3-level decomposition via soft thresholding and the db6 wavelet filtered out noise. This denoised data was used to train the LSTM model and compare its forecasts against the original noisy LSTM and SVR results. The wavelet-enhanced LSTM significantly improved prediction quality, providing a new perspective for rail transit volume forecasting. Leveraging big data and scientific modeling in this manner can produce practical gains, demonstrating the value of this integrated approach.