Preprint
Communication
Solar Disc Concentrator: Material Selection for the Receiver
Altmetrics
Downloads
99
Views
31
Comments
0
This version is not peer-reviewed
Submitted:
15 August 2023
Posted:
17 August 2023
You are already at the latest version
Alerts
Abstract
Solar concentration is the ability to harness solar radiation to increase the temperature of a receiver. The receiver is the component into which a heat transfer fluid can be flowed for an ORC system and produce electricity, or it can be used for high-temperature thermal storage, or even to implement thermochemical cycles. The choice of material is critical to ensure optimal performance and long-lasting operation. It is also essential that such material can operate at high temperatures and high thermal gradients. In short, material identification involves high thermal stresses that result in structural deformation. Different metal alloys were used to verify that the yield strength limit was not exceeded due to thermal stress induced by concentrated solar radiation. The problem was implemented in Matlab starting from the general heat equation. The purpose is to test whether thermal stress exceeds the yield strength, which is the condition in which elastic bonds in the material are changed, causing deformation. The best material identified was Inconel 740H, which had a high yield strength value and the lowest temperature difference. Under extreme working conditions, it can withstand thermally induced shocks.
Keywords:
Subject: Engineering - Energy and Fuel Technology
1. Introduction
The development of renewable resources is a topic of continuous and growing interest in the current energy and environmental context. Within which the solar source is crucial, a rapidly developing technology is related to the exploitation of solar concentration for energy purposes [1]. The development of concentrating solar power (CSP) systems is continuous and growing [1,2]. Islam et al., showed the growth of CSP systems, with a steady increase of brevets up to 1600 patents/year in 2015. The exploitation of solar radiation, however, is better when considering photovoltaic (PV) technology, because both direct and diffuse radiation are exploited. This is not the case with CSP systems. Another limiting factor of CSP technology lies in its inherent difficulty to be distributed, which is favourable to PV systems. The worldwide installation of PV systems stands at around 1185 GW by the end of 2022 [3], while power installation for CSPs is around 7 GW [4]. There are, however, aspects in favour of the concentration technique, i.e. for the same area occupied, CSP systems generate more electricity than photovoltaic systems. This shows that the economic return of CSP is greater [5]. Several reviews in the industry highlight the latest developments and steps forward in research to lower the cost per installed power and compete more with other power generation systems [1,5,6]. Alami et al., tried to highlight the main critical aspects of such systems [6].
Concentration systems can be used directly or indirectly for the production of thermal energy [7,8,9,10], fresh water [11,12] and synthesis gas [13,14,15]. A further use is for the production of electrical energy using Stirling engines inserted in the focal zone of the concentrator [16,17,18,19]. Considerable research studies point out interesting aspects and points for improvement. For example, the efficiency of thermochemical cycles must be improved [20,21]. Considerable improvements, also in terms of cyclability and repeatability must be achieved, not only for solar-driven thermochemical cycles but also for other applications. In the study of Borghero et al., a critical aspect was shown: the difficulty of working under real conditions by the receiver placed in the focal point of a CSP disc [22].
This aspect is common to all possible uses of solar concentration. The choice of material to be placed at the focal point and to be used as a receiver is an important choice for the good functionality of the system. They must be both resistant to high temperatures and able to withstand extreme temperature gradients. These aspects are highly stressed for thermochemical cycles, where operating temperatures can exceed 1000 °C [23] and thermal gradients can be as high as 300 °C/min. The strong thermal gradient shows the fragility of ceramic materials, while the high-temperature conditions limit the functionality of metal alloys. In Borghero et al., it was shown that the use of sintered alumina is almost impossible to achieve the operating conditions for the reduction reaction for Fe2O3 [22]. Li et al., Liu et al., and Erasmus et al. showed similar issues [24,25,26]. Research in the field of synthesis gas production from thermochemical cycles is driven by electrical systems (industrial furnaces) and the focus is on the production and realisation of the best catalyst capable of cycling and withstanding such reactions. The research gap is therefore related to the identification and choice of material that can withstand the extreme operating conditions of thermochemical cycles. Possible solutions, identified in the literature, show the possibility of realising systems capable of working at high temperatures and high pressures, using composite materials, even if the costs and processing techniques are prohibitive. Solar tubes under a non-uniform solar flux were employed by Du et al., using two layers of protective metal material, placed on a Nickel-based receiver with high thermal conductivity [27].
Encouraging results are shown at low thermal gradients and peak temperatures not exceeding 600 - 700 °C. This work was focused on the identification and behavioural study of the thermal stresses induced by certain metal alloys that can be used as solar receivers. Especially considering low-cost solutions. The solar concentrator at the Energy Center was used, in which temperature higher than 1000 °C can be recorded, with temperature gradients of around 300 °C/min.
The main objective of this work is to identify materials, selected within selected metal alloys, to highlight their ability to withstand the thermal stresses associated with strong thermal gradients.
2. Materials and Methods
The receiver is the most critical component of the entire CSP structure because it must withstand high temperatures that sometimes exceed 1000 °C and large thermal gradients. The purpose of the project is to investigate different materials to select the most suitable one to withstand high-temperature conditions. This is the reason why special attention has been paid to researching the most suitable materials to accomplish this task. Metal alloys were selected due to lower costs than composite materials. The receiver must first and foremost satisfy the optical properties as can be seen from the discussion so far, but it is essential that it also have good thermal and mechanical characteristics: it must have high conductivity values for heat to reach the heat transfer fluid (which is precisely the purpose of the whole apparatus), it must also possess great resistance to mechanical and thermally induced stresses and resist corrosion. However, it is appropriate to explain what causes of material breakdown or weakening are to be avoided before analyzing them individually.
The solar concentrator was described elsewhere [19,28], and the following Figure 1, Figure 2 and Figure 3 focused on the main receiver elements. Figure 1 shows the receiver illuminated by concentrated solar radiation; each receiver will be placed in the housing indicated.
Figure 2 highlights the experimental set-up without the receiver, the B thermocouple “T0” (Tersid Srl, Italy) is placed inside the receiver and located in the middle point.
The geometrical parameters of the solar concentrator (Elma. Net srl, Italy) are described in figure 3. They are used for the model implemented in Matlab R2023b (Mathworks, USA).
Table 1 shows the relevant geometrical data to model the solar concentrator and solar receiver. The solar concentrator was modelled using the previous model implemented in Comsol Multiphysics 6.0 (Sweden) and presented by Marra et al. [29].
The metal alloy properties used and implemented in the present study are described in Table 2.
The main simplifying hypotheses are listed below:
Gas flowing inside the receiver has been approximated to air, with a minimum airflow fixed to = 1.66 10-5 m3/s (calm air condition)
- Heat transport in the fluid (air) due to only advection while thermal diffusion phenomena in this region are considered negligible
- Fully developed airflow
- Spatially and temporally constant properties assessed at a temperature of 800 °C
- One-way heat transfer along the axial direction
- Average radiation equal to I0= 800 W/m2
The useful available energy of the concentrator obtained through an energy balance on this can be calculated considering the irradiation from the sun, as:
Where, the first term is associated with the optical losses (), and the second term to the thermal losses. The overall performance of the concentrator thus results in equation 2:
The fluid flow regime was evaluated using the Reynolds number:
This turns out to be less than 100, confirming that it is a laminar regime problem. Consequently, given the calm air, we can set Nusselt's number equal to 3.66.
The problem from the thermofluidodynamic point of view can be described by the following relations, see equations 5 and 6. This is a case of coupled conduction and advection since the material composing the receiver receives heat from solar radiation (which has been assumed to be constant throughout the year and equal to an average value) and gives it up to the air, which, entering the receiver at a lower temperature, also cools the material by licking the inner walls. The goal is to analyze how the problem behaves as time varies until a steady-state situation is reached where the only thermal gradients will be those induced by the geometry-that is, spatial gradients. They were discretized using an explicit Euler time derivative discretization method and spatially using the centred finite difference method for the conduction and an upwind scheme for the advective term.
The receiver was described using the following equation:
Receiver
Internal of the receiver
The initial conditions are fixed using the Dirichlet boundary condition:
While the material boundary conditions (Neumann condition) are fixed as adiabatic extremities
The spatial course of the temperature at the end of the transient and the temporal course of the most stressed section is the model Output.
The thermal stress induced by the temperature gradient is evaluated at the end of the transient (most extreme working condition), using the following formula (equation 9).
If this stress () exceeds the yield stress ()), i.e., the condition in which the elastic bonds of the material change, the material deformation and material failure occur (fatigue behaviour is omitted).
3. Results and Discussion
3.1. Preliminary Temperature Receiver Recording
An experimental campaign was conducted in March and April 2023. The median value, blue line and interquartile range were shown, in figure 4. The latter describes how far the values deviate from a central value. The fairly high variability is a function of non-fixed solar radiation. Solar radiation in March is more variable than in April, and consequently the receiver temperature.
The curve measured is normally a Gaussian curve with the maximum values recorded during the hottest hours of the day, corresponding to the highest value of solar radiation, as shown in previous research [22,30]. In March, the variability is greater, in the hottest hours of the day it is close to 500 °C with a low just above 100 °C. In April the minimum value at similar hours is just above 300 °C, while the maximum recorded rises to around 550 - 600 °C.
As previously reported in our research work the temperature registered increased in the spring and summer seasons [29]. The maximum recorded temperature can reach as high as 1100 to 1200 °C. The variability of the data shown in Figure 4 showcases the important value of the thermal gradient. These two aspects affect the receiver structure and its deformation up to achieve the point of structural failure.
3.2. Thermal Stress Induced by the Temperature on the Receiver
Many thermodynamic problems can be solved simply if it is assumed that the internal temperature difference of the body is negligible compared with that between the body and the outside. This assumption, which translates numerically into a Bi < 0.1, allows the temperature distribution in the solid to be approximated as uniform. This condition is called the concentrated parameter assumption. For all materials used for the receiver the Biot number was lower than 0.1, see Table 3.
Using equation 9 was evaluated the thermal stress induced by the temperature level variation in the receiver. The thermal stress is a function of the material related to the coefficient of linear expansion.
Figure 5 compares the induced efforts in alloy 625. The thermal stress reached about 6 108 Pa, while the yield stress is almost around 4 108 Pa. Figure 9 (b) confirms this result, it is showed the collapse of the structure. The maximum temperature imposed, 800 °C, is excessively high, as shown by the experimental studies of Suave et al. [33]. They found that the alloy 625 without any prior aging is unstable increasing the temperature above 700 – 750 °C. Thermal ageing at 650 °C for 500 h induced a stress of around 1000 MPa with a strain of 52%.
Figure 6 compares the induced efforts in the alloy 800H. The thermal stress reached about 7.7 108 Pa, while the yield stress is almost around 1 108 Pa. The maximum temperature imposed, 800 °C, is excessively high, as shown by the experimental studies of Cao et al. [34]. Cao et al. studied the hot deformation behaviour of alloy 800H in the temperature range of 825 – 975 °C [35]. The microstructure was shown to be deformed at 875 °C with elongated parent grains. When the deformation temperature was increased to 975 °C, the degree of recrystallization is higher, and the deformed grains affect the structure of the material.
Figure 7 compares the induced efforts in the haynes 230. The thermal stress reached about 6 108 Pa, while the yield stress is almost around 3 108 Pa. Figure 9 (c) confirms this result, it is showed the collapse of the structure. The maximum temperature imposed, 800 °C, is excessively high, as shown by the experimental studies of Pataky et al. [36]. They studied the creed deformation and mechanisms in haynes 230 at 800 and 900 °C. Intergranular failure was observed in all samples, secondary and tertiary creep were investigated. To improve the operating lifetime, the grain boundary serrations restrict grain boundary sliding working at high temperature. Too bad that this process is quite expensive.
Figure 8 compares the induced efforts in the Inconel 740H. The thermal stress is slightly below the yield stress. Figure 9 (a) confirms this result, it is showed the non-collapse of the structure. This result can be compared to previous researchers, such as Kim et al. and de Barbadillo [37,38]. Kim et al., illustrate the deformation behaviour of carbides during the creep investigation at 750 °C for 5000 h. They found that the Inconel 740K was able to maintain the mechanical structure avoiding the collapse, even if the Ὺ particles gradually increase.
It is superfluous to test the receiver with alloy 800H, since the thermal stress induced is much greater than the yield strength, comparing the situation achieved with the "similar" alloy 625. For that alloy, which is better than alloy 800H, we experimentally reach the failure, as shown in Figure 9 (b). Figure 9 (a) shows, on the other hand, the non-breakage of alloy Inconel 740H, the goodness of the alloy in resisting extreme conditions of temperature and strong thermal gradient is then experimentally verified.
4. Conclusions
Solar concentration can be exploited in depth in the near future, and the material selection for the receiver element is crucial. High temperatures and high thermal gradients are important issues to be analyzed. Different metal alloys were used to verify that the yield strength limit was not exceeded due to thermal stress induced by concentrated solar radiation. The following conclusions have been made:
- − Alloy 625 was considered, and the model implemented showed the collapse of the structure. This result can be experimentally verified as reported in figure 9b.
- − Alloy 800H was considered, and the model implemented showed the collapse of the structure. The thermal stress was higher than the yield stress.
- − Haynes 230 was considered, and the model implemented showed the collapse of the structure. This result can be experimentally verified as reported in figure 9c.
- − Inconel 740H was considered, and the model implemented showed the non-collapse of the structure. This result can be experimentally verified as reported in figure 9a.
Future works will focus on composite materials considering metal alloys and ceramic materials, used as receiver coatings.
Author Contributions
Conceptualization, M.P. and D.P.; methodology, D.P.; software, M.P. and D.P.; formal analysis, D.P.; resources, D.P.; writing—original draft preparation, D.P.; writing—review and editing, D.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available on request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
yield stress [Pa] |
|
thermally induced stress [Pa] |
|
coefficient of linear expansion [m/mK] |
|
| Aa | concentrator area [] |
| Ar | receiver area [] |
| Ari | internal receiver area [] |
| cp | specific heat at constant pressure [J/kgK] |
| CR0 | optical concentration ratio |
| d | receiver diameter [m] |
| D | solar concentrator diameter [m] |
| E | elastic modulus of material [Pa] |
| f | focal length [m] |
| I0 | constant solar radiation [W/] |
| Ir | receiver flow from the solar concentration factor [W/] |
| k | thermal conductivity [W/mK] |
| L | receiver length [m] |
| m | subscript for the material side |
heat transfer fluid mass flow rate [kg/s] |
|
| Ta | temperature for the air fluid [°C] |
| Tin | heat transfer fluid inlet temperature [°C] |
| Tm | material temperature of the receiver [°C] |
| Tout | heat transfer fluid outlet temperature [°C] |
| Uc | receiver heat transfer coefficient [W/K] |
| Vm | receiver volume [m3] |
| Va | internal receiver volume [m3] |
| α | solar altitude [rad] |
| γ | intercept factor |
| μ | dynamic viscosity [Pa s] |
| ρ | density [kg/] |
| τ | receiver coverage transmittance |
| ϕrim | angle between reflected radiation and vertex-focus junction |
| ψ1 | slope error |
| ψ2 | solar radius error |
| ψ3 | error in solar tracking |
| αr | absorbance receiver |
| η0 | optimal concentrator performance |
| ηreceiver | receiver performance |
| τb | direct optical length |
| τd | diffused optical length |
References
- M.T. Islam, N. M.T. Islam, N. Huda, A.B. Abdullah, R. Saidur, A comprehensive review of state-of-the-art concentrating solar power (CSP) technologies: Current status and research trends, Renew. Sustain. Energy Rev. 91 (2018) 987–1018. [CrossRef]
- Q. Chen, Y. Wang, J. Zhang, Z. Wang, The Knowledge Mapping of Concentrating Solar Power Development Based on Literature Analysis Technology, Energies. 13 (2020) 1988. [CrossRef]
- Solar, IEA. (n.d.). https://www.iea.org/energy-system/renewables/solar-pv (accessed , 2023). 13 July.
- Renewable electricity – Renewables 2022 – Analysis, IEA. (n.d.). https://www.iea.org/reports/renewables-2022/renewable-electricity (accessed , 2023). 13 July.
- V.K. Sharma, R. V.K. Sharma, R. Singh, A. Gehlot, D. Buddhi, S. Braccio, N. Priyadarshi, B. Khan, Imperative Role of Photovoltaic and Concentrating Solar Power Technologies towards Renewable Energy Generation, Int. J. Photoenergy. 2022 (2022) e3852484. [CrossRef]
- A.H. Alami, A.G. A.H. Alami, A.G. Olabi, A. Mdallal, A. Rezk, A. Radwan, S.M.A. Rahman, S.K. Shah, M.A. Abdelkareem, Concentrating solar power (CSP) technologies: Status and analysis, Int. J. Thermofluids. 18 (2023) 100340. [CrossRef]
- M.I. Soomro, A. M.I. Soomro, A. Mengal, Y.A. Memon, M.W.A. Khan, Q.N. Shafiq, N.H. Mirjat, Performance and Economic Analysis of Concentrated Solar Power Generation for Pakistan, Processes. 7 (2019) 575. [CrossRef]
- D. Borge-Diez, E. D. Borge-Diez, E. Rosales-Asensio, A.I. Palmero-Marrero, E. Acikkalp, Optimization of CSP Plants with Thermal Energy Storage for Electricity Price Stability in Spot Markets, Energies. 15 (2022) 1672. [CrossRef]
- S. Kuravi, Y. S. Kuravi, Y. Goswami, E.K. Stefanakos, M. Ram, C. Jotshi, S. Pendyala, J. Trahan, P. Sridharan, M. Rahman, B. Krakow, THERMAL ENERGY STORAGE FOR CONCENTRATING SOLAR POWER PLANTS, Technol. Innov. 14 (2012) 81–91. [CrossRef]
- L. Qoaider, A. L. Qoaider, A. Liqreina, Optimization of dry cooled parabolic trough (CSP) plants for the desert regions of the Middle East and North Africa (MENA), Sol. Energy. 122 (2015) 976–985. [CrossRef]
- M.A. Abdelkareem, M. M.A. Abdelkareem, M. El Haj Assad, E.T. Sayed, B. Soudan, Recent progress in the use of renewable energy sources to power water desalination plants, Desalination. 435 (2018) 97–113. [CrossRef]
- K. Mohammadi, M. K. Mohammadi, M. Saghafifar, K. Ellingwood, K. Powell, Hybrid concentrated solar power (CSP)-desalination systems: A review, Desalination. 468 (2019) 114083. [CrossRef]
- C. Agrafiotis, M. C. Agrafiotis, M. Roeb, C. Sattler, A review on solar thermal syngas production via redox pair-based water/carbon dioxide splitting thermochemical cycles, Renew. Sustain. Energy Rev. 42 (2015) 254–285. [CrossRef]
- S. Chuayboon, S. S. Chuayboon, S. Abanades, An overview of solar decarbonization processes, reacting oxide materials, and thermochemical reactors for hydrogen and syngas production, Int. J. Hydrog. Energy. 45 (2020) 25783–25810. [CrossRef]
- J.P. Sharma, R. J.P. Sharma, R. Kumar, M.H. Ahmadi, A. Mukhtar, A.S.H.M. Yasir, M. Sharifpur, B. Ongar, A. Yegzekova, Chemical and thermal performance analysis of a solar thermochemical reactor for hydrogen production via two-step WS cycle, Energy Rep. 10 (2023) 99–113. [CrossRef]
- G. Barreto, P. G. Barreto, P. Canhoto, Modelling of a Stirling engine with parabolic dish for thermal to electric conversion of solar energy, Energy Convers. Manag. 132 (2017) 119–135. [CrossRef]
- G.E. Carrillo Caballero, L.S. G.E. Carrillo Caballero, L.S. Mendoza, A.M. Martinez, E.E. Silva, V.R. Melian, O.J. Venturini, O.A. del Olmo, Optimization of a Dish Stirling system working with DIR-type receiver using multi-objective techniques, Appl. Energy. 204 (2017) 271–286. [CrossRef]
- T. Mancini, P. T. Mancini, P. Heller, B. Butler, B. Osborn, W. Schiel, V. Goldberg, R. Buck, R. Diver, C. Andraka, J. Moreno, Dish-Stirling Systems: An Overview of Development and Status, J. Sol. Energy Eng. 125 (2003) 135–151. [CrossRef]
- D. Papurello, D. D. Papurello, D. Bertino, M. Santarelli, CFD Performance Analysis of a Dish-Stirling System for Microgeneration, Processes. 9 (2021) 1142. [CrossRef]
- Bose, A. Farooqui, D. Ferrero, M. Santarelli, J. Llorca, Thermodynamic assessment of non-catalytic Ceria for syngas production by methane reduction and CO2 + H2O oxidation, Mater. Renew. Sustain. Energy. 8 (2019) 5. [CrossRef]
- Farooqui, A. Bose, M. Boaro, J. Llorca, M. Santarelli, Assessment of integration of methane-reduced ceria chemical looping CO2/H2O splitting cycle to an oxy-fired power plant, Int. J. Hydrog. Energy. 45 (2020) 6184–6206. [CrossRef]
- L. Borghero, M. L. Borghero, M. Bressan, D. Ferrero, M. Santarelli, D. Papurello, Methane-Assisted Iron Oxides Chemical Looping in a Solar Concentrator: A Real Case Study, Catalysts. 12 (2022) 1477. [CrossRef]
- Boretti, Which thermochemical water-splitting cycle is more suitable for high-temperature concentrated solar energy? J. Hydrog. Energy. 47 (2022) 20462–20474. [CrossRef]
- J.-Q. Li, J.-T. Kwon, S.-J. Jang, The Power and Efficiency Analyses of the Cylindrical Cavity Receiver on the Solar Stirling Engine, Energies. 13 (2020) 5798. [CrossRef]
- S. Liu, B. S. Liu, B. Yang, X. Yu, Impact of installation error and tracking error on the thermal-mechanical properties of parabolic trough receivers, Renew. Energy. 212 (2023) 197–211. [CrossRef]
- D.J. Erasmus, A. D.J. Erasmus, A. Sánchez-González, M. Lubkoll, K.J. Craig, T.W. von Backström, Thermal performance characteristics of a tessellated-impinging central receiver, Appl. Therm. Eng. 229 (2023) 120529. [CrossRef]
- S. Du, Z. S. Du, Z. Wang, S. Shen, Thermal and structural evaluation of composite solar receiver tubes for Gen3 concentrated solar power systems, Renew. Energy. 189 (2022) 117–128. [CrossRef]
- L. Ricci, D. L. Ricci, D. Papurello, A Prediction Model for Energy Production in a Solar Concentrator Using Artificial Neural Networks, Int. J. Energy Res. 2023 (2023) 1–20. [CrossRef]
- Marra, M. Santarelli, D. Papurello, Solar Dish Concentrator: A Case Study at the Energy Center Rooftop, Int. J. Energy Res. 2023 (2023) 1–18. [CrossRef]
- E. Montà, M. E. Montà, M. Santarelli, D. Papurello, Synthetic-Gas Production through Chemical Looping Process with Concentrating Solar Dish: Temperature-Distribution Evaluation, Processes. 10 (2022) 1698. [CrossRef]
- R. Kumar Goyal, EswaramoorthyMuthusamy, Thermo-physical properties of heat storage material required for effective heat storage and heat transfer enhancement techniques for the solar cooking applications, Sustain. Energy Technol. Assess. 56 (2023) 103078. [CrossRef]
- M. Al-Nimr, S.A. M. Al-Nimr, S.A. Khashan, H. Al-Oqla, Novel techniques to enhance the performance of Stirling engines integrated with solar systems, Renew. Energy. 202 (2023) 894–906. [CrossRef]
- L. Mataveli Suave, J. L. Mataveli Suave, J. Cormier, D. Bertheau, P. Villechaise, A. Soula, Z. Hervier, F. Hamon, High temperature low cycle fatigue properties of alloy 625, Mater. Sci. Eng. A. 650 (2016) 161–170. [CrossRef]
- Y. Cao, H. Y. Cao, H. Di, J. Zhang, Y. Yang, Dynamic behavior and microstructural evolution during moderate to high strain rate hot deformation of a Fe–Ni–Cr alloy (alloy 800H), J. Nucl. Mater. 456 (2015) 133–141. [CrossRef]
- Y. Cao, H.S. Di, R.D.K. Misra, J. Zhang, Hot Deformation Behavior of Alloy 800H at Intermediate Temperatures: Constitutive Models and Microstructure Analysis, J. Mater. Eng. Perform. 23 (2014) 4298–4308. [CrossRef]
- G.J. Pataky, H. G.J. Pataky, H. Sehitoglu, H.J. Maier, Creep deformation and mechanisms in Haynes 230 at 800°C and 900°C, J. Nucl. Mater. 443 (2013) 484–490. [CrossRef]
- D.-M. Kim, C. Kim, C.-H. Yang, J.-U. Park, H.-W. Jeong, K.-H. Yim, H.-U. Hong, Heat treatment design of Inconel 740H superalloy for microstructure stability and enhanced creep properties, J. Alloys Compd. 946 (2023) 169341. [CrossRef]
- J.J. deBarbadillo, 14 - INCONEL alloy 740H, in: A. Di Gianfrancesco (Ed.), Mater. Ultra-Supercrit. Adv. Ultra-Supercrit. Power Plants, Woodhead Publishing, 2017: pp. 469–510. [CrossRef]
Figure 1.
Solar concentrator, focus of the receiver housing.

Figure 2.
Thermocouple T0 (type B) inside the receiver.

Figure 3.
Main geometrical parameters of the solar concentrator.

Figure 4.
Example of the temperature recorded in the central receiver point (T0) for March and April 2023.
Figure 4.
Example of the temperature recorded in the central receiver point (T0) for March and April 2023.
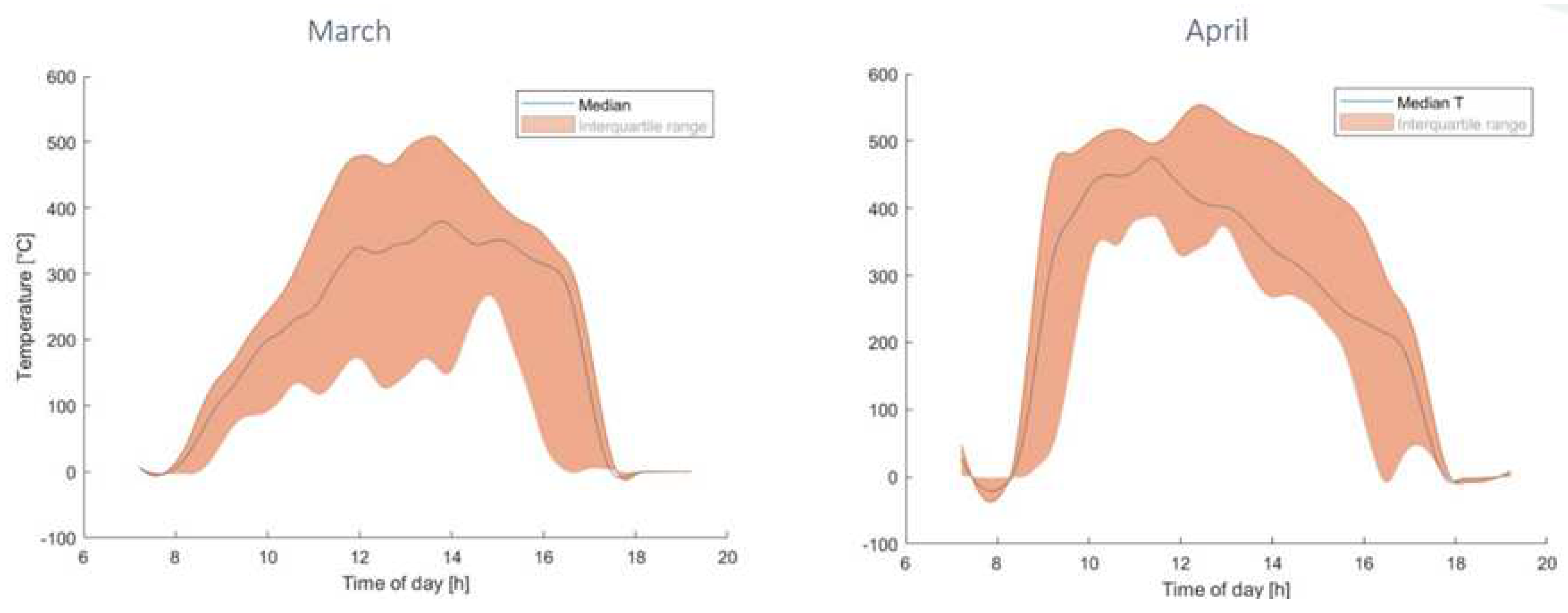
Figure 5.
Evaluation of the induced effort for the metallic alloy 625 – thermal stress versus yield stress.
Figure 5.
Evaluation of the induced effort for the metallic alloy 625 – thermal stress versus yield stress.
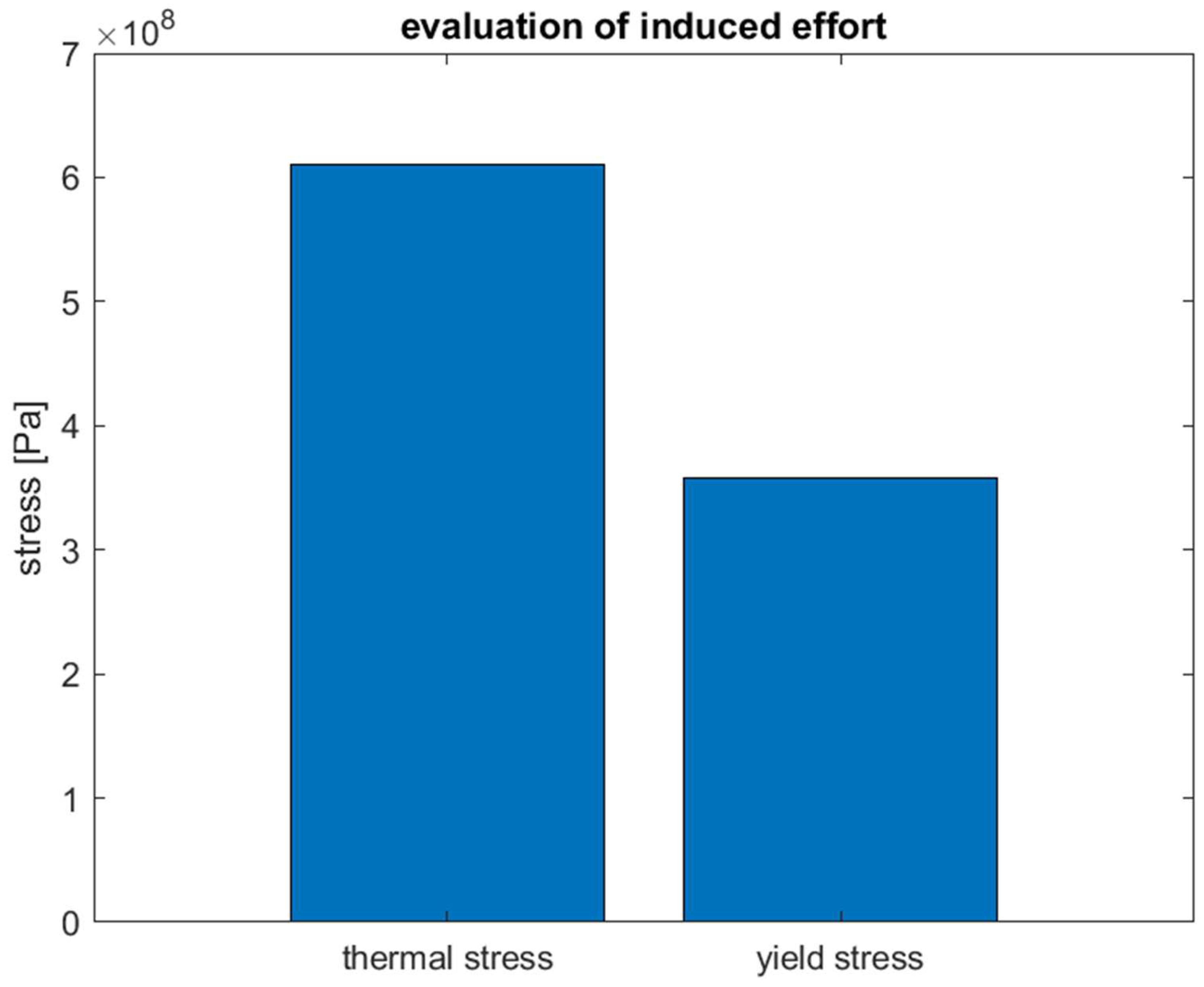
Figure 6.
Evaluation of the induced effort for the metallic alloy 800H – thermal stress versus yield stress.
Figure 6.
Evaluation of the induced effort for the metallic alloy 800H – thermal stress versus yield stress.
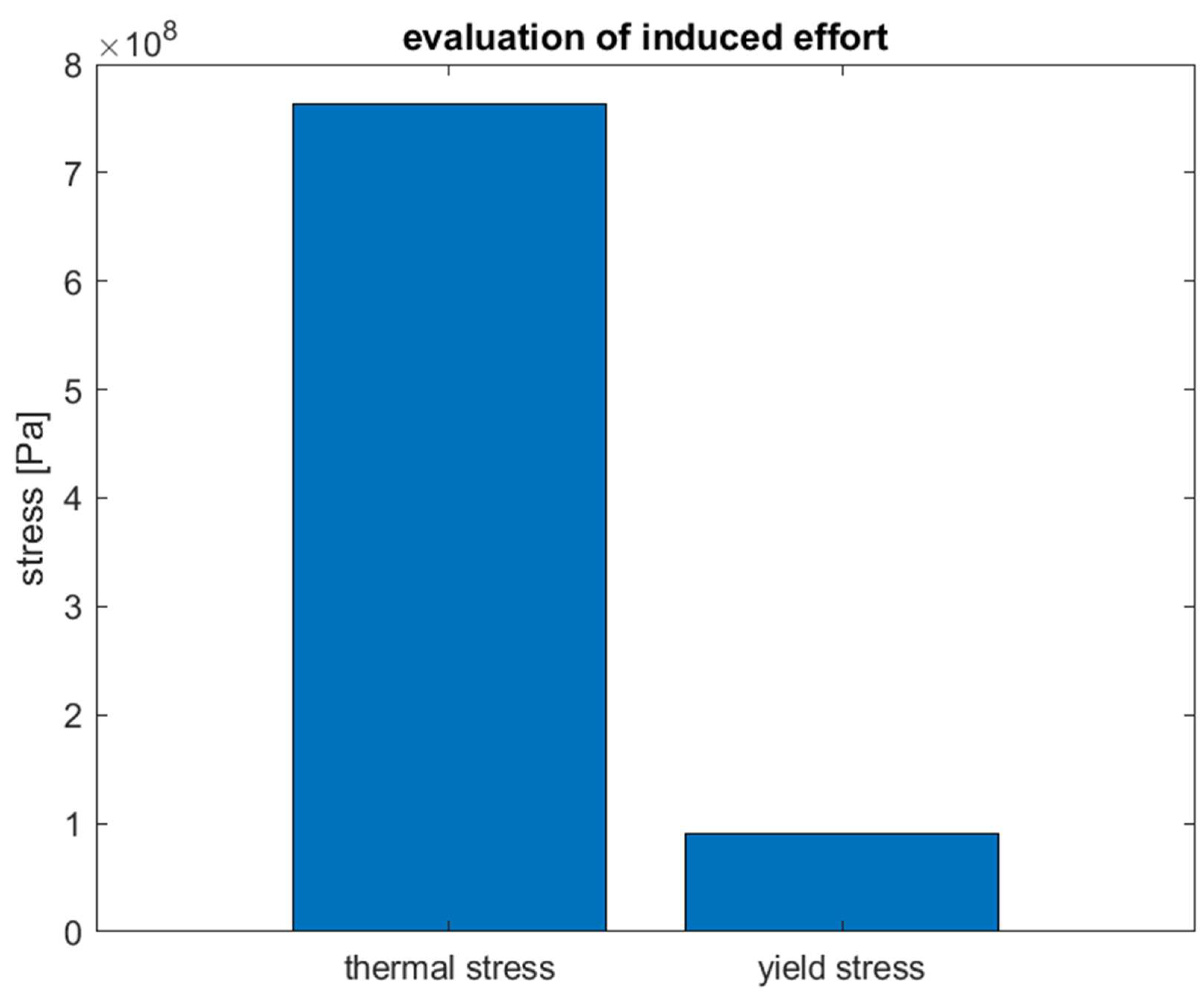
Figure 7.
Evaluation of the induced effort for the metallic alloy Haynes 230 – thermal stress versus yield stress.
Figure 7.
Evaluation of the induced effort for the metallic alloy Haynes 230 – thermal stress versus yield stress.
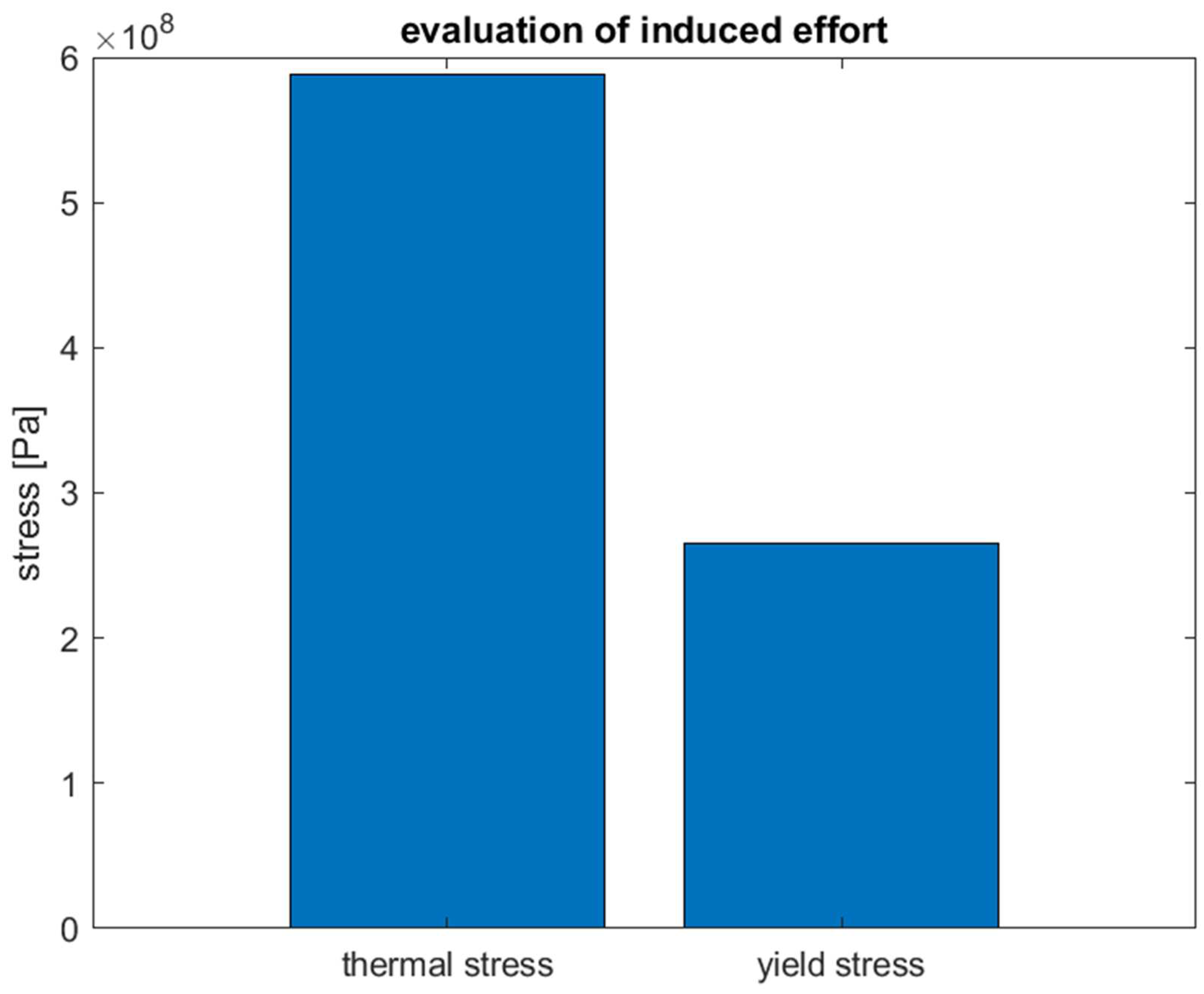
Figure 8.
Evaluation of the induced effort for the metallic alloy Inconel 740H – thermal stress versus yield stress.
Figure 8.
Evaluation of the induced effort for the metallic alloy Inconel 740H – thermal stress versus yield stress.
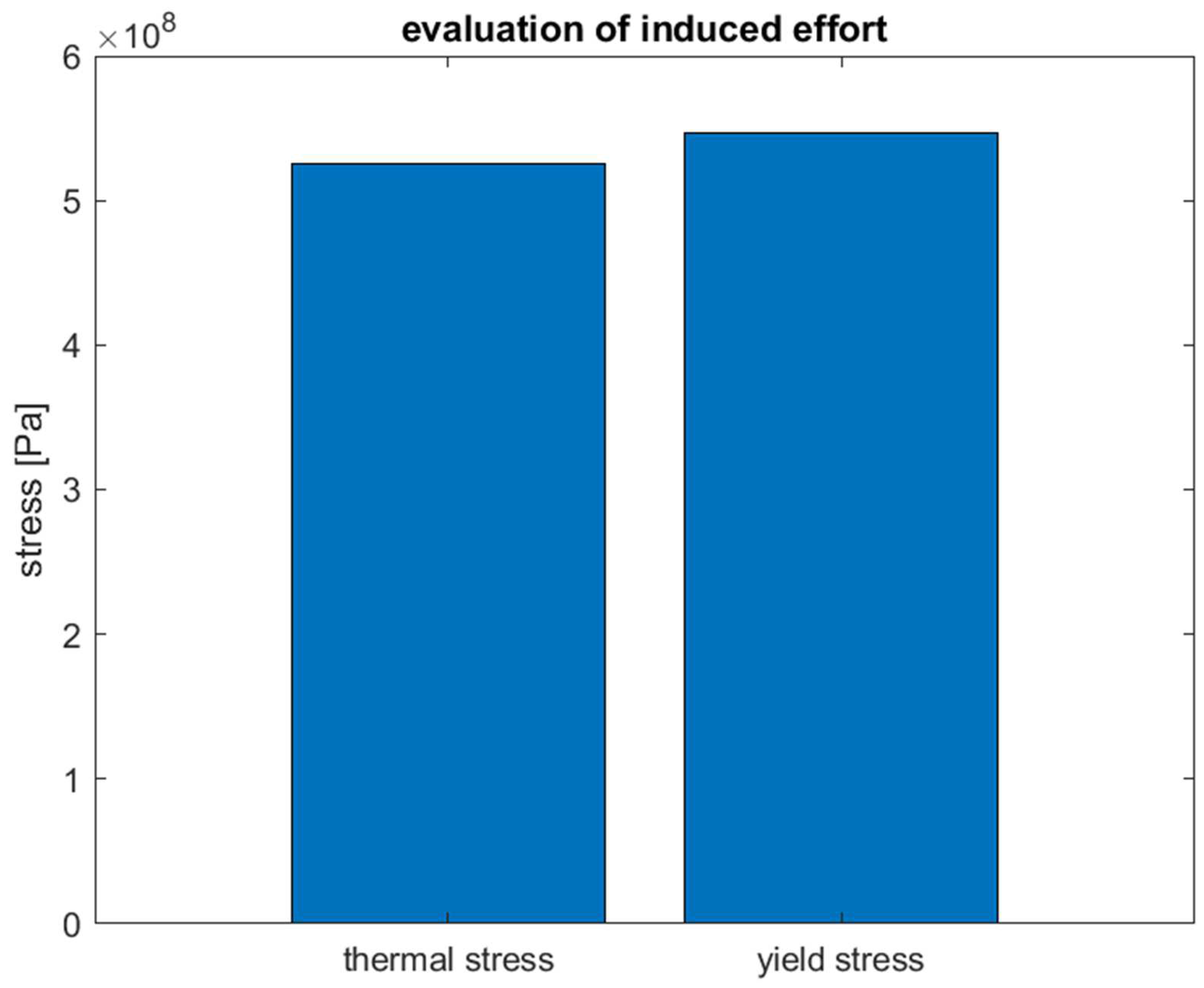
Figure 9.
Experimental activity for the metal alloys used a: Inconel 740H; b: alloy 625; c: Haynes 230.
Figure 9.
Experimental activity for the metal alloys used a: Inconel 740H; b: alloy 625; c: Haynes 230.

Table 1.
Geometrical data for the solar concentrator.
| Name | Expression | Value | Description |
|---|---|---|---|
| 0.92 m | Focal length | ||
| 45° | 0.7854 rad | Rim Angle | |
| - | 2.37 m | Diameter of the concentrator | |
| 2.54 m2 | Capturing Area of the concentrator | ||
| d | - | 18.06 10-3 m | Receiver diameter (outer) |
| L | - | 0.2 m | Receiver length |
| CR0 | - | 8013 | Optical concentration ratio |
Table 2.
Properties of the metal alloys used in the study.
| Inconel 740H | Alloy 625 | Alloy 800H | Haynes 230 | |
| T melting | 1288-1362 °C | 1290-1350 °C | 1357-1385 °C | 1301-1371 °C |
| Elastic modulus (E) | 186 GPa (@T=600 °C) 178 GPa (@T=700 °C) 169 GPa (@T=800 °C) |
170 GPa (@T=650 °C) 160 GPa (@T=760 °C) 148 GPa (@T=870 °C) |
157.7 GPa (@T=600 °C) 150.1 GPa (@T=700 °C) 141.3 GPa (@T=800 °C) |
175 GPa (@T=600 °C) 168 GPa (@T=700 °C) 159 GPa (@T=800 °C) |
| ) | 742 MPa (@Tamb) 608 Mpa (@T=700 °C) 547 MPa (@T=800 °C) |
414-517 MPa (annealed, @Tamb) 357.2 MPa (@T=800 °C) |
150 MPa (@Tamb) 109 MPa (@T=700 °C) 90 MPa (@T=760 °C) |
415 MPa (@Tamb) 265 MPa (@871 °C) 294 Mpa (@T=1000 °C) |
| Density (ρ) | 7940 kg/m3 | |||
| Specific heat (c) | 573 J/kgK | 600 J/kgK | 460 J/kgK | 465 J/kgK |
| Thermal conductivity (k) | 22.1 W/mK | 15.7 W/mK | 11.5 W/mK | 16.4 W/mK |
Table 3.
Biot number evaluated for all the materials.
| Material | Biot |
|---|---|
| Alloy 625 | 0.0019 |
| Alloy 800H | 0.0026 |
| Haynes 230 | 0.0018 |
| Inconel 740H | 0.0013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






