Preprint
Article
Explainable Approaches for Forecasting Building Electricity Consumption
Altmetrics
Downloads
113
Views
76
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
16 August 2023
Posted:
17 August 2023
You are already at the latest version
Alerts
Abstract
Building electric energy is characterized by a significant increase of its uses (e.g. vehicle charging), a rapidly declining cost of all related data collection and a proliferation of smart grid concepts, including diverse and flexible electricity pricing schemes. Not surprisingly, an increased number of approaches have been proposed for its modeling and forecasting. In this work, we place our emphasis on three forecasting related issues. First, on the forecasting explainability, i.e. the ability to understand and explain to the user what shapes the forecast. To this extent we rely on concepts and approaches that are inherently explainable, such as the evolutionary approach of genetic programming (GP) and its associated symbolic expressions, as well as the so-called SHAP (SHapley Additive eXplanations) values, which is a well established model agnostic approach for explainability, especially in terms of feature importance. Second, we investigate the impact of the training timeframe on the forecasting accuracy; this is driven by the realization that a fast training would allow for faster deployment of forecasting in real life solutions. And third, we explore the concept of counterfactual analysis on actionable features, i.e. features that the user can really act upon and which therefore present an inherent advantage when it comes to decision support. We have found that SHAP values can provide important insights into the model explainability. As for GP models, we have found comparable and in some cases superior accuracy when compared to its neural-network and time-series counterparts but a rather questionable potential to produce crisp and insightful symbolic expressions, allowing a better insight into the model performance. We have also found, and report here on an important potential especially for practical, decision support, solutions of counterfactuals built on actionable features and short training timeframes.
Keywords:
Subject: Engineering - Energy and Fuel Technology
1. Introduction
1.1. The forecasting timeframe and scope of our current application
Literature building electricity forecasting approaches differ with regard to the envisaged timeframe. Typically, we have short-term forecasts (timeframe ranging from minutes up to 1 week), mid term forecasts (timeframe ranging from 1 week up to months), long-term forecasts (timeframe of years), useful for planning for infrastructure and grid investments (Tadahiro N., Shigeyuki H., 2010), and also very long-term, policy-oriented forecasting exercises. TIMES (an acronym for The Integrated Markal Efom System) allows us to model supply and anticipated technology shifts over such a very long-term horizon, often extending as far away in time as 2100 where anticipated changes of technology are accounted for. Forecasts may also differ based on the scope of their application, which can range from a single building (to be reviewed in detail below), to a collection of buildings (e.g. neighborhood, district, etc.) (Johannesen N.J, et al, 2019), up to countries (Suganthi L., et al 2012; Pessanha J.F.M, et al 2015; Sakkas N., et al, 2021). The forecasting timeframe selection, the forecasting application context and the envisaged decision support are all tightly linked together. For example, decisions related to building operational aspects are typically linked to more short-term investigations and timeframes as well as the scope of the particular building. Decisions on policy action, such as fuel taxation, may be supported by long-term timeframes and the scope of the particular country.
In our investigation the overarching decision framework is that of demand response. Demand response is, in its narrow sense, about adapting consumption patterns to make the most of the pricing scheme in place (Schreiber M. et al, 2015, Asadinejad A. et al, 2017). However, the term is also used in a broader sense, whereby demand response may be any user action and response informed by electricity prices. For example, a lowering of the winter thermostat settings in time slots when prices rise is also referred to in the literature (Yoona J.I et al, 2014) as a demand response scheme; it is indeed a response, even if not a time shift response. Thus, demand response is more broadly about the user who takes action in response to changing prices.
Thus, a demand response related forecasting timeframe must necessarily follow the respective building electricity price change timeframe. As we move to more fast changing and flexible pricing schemes it follows that our case is clearly that of a short-term timeframe. There are however also cases where the price change impact manifests over longer timeframes. For example, in the chase of consumption tier pricing, prices are determined according to the consumption levels within the billing period, which typically spans several months. In such a case, a forecast spanning a timeframe that equals the billing period also becomes pertinent.
We also need to set the timeframe in a way that is unambiguously user friendly. Along with the above considerations, the timeframe for our investigation is set in two different and alternative ways. First, there is an hourly forecast for the next full calendar day. This means that when a user runs the forecast she will receive 24 hourly forecasts corresponding to the consumption of the very next calendar day. Second, there is a remaining day forecast. In this alternative formulation the user would receive forecasts for the remainder of the day. Thus, if the forecast is run at 17.15, the user would receive 6 hourly forecasts, corresponding to the six full hours remaining from 18.00 to 23.00. (Note: the forecast of 18.00 is the consumption between 18.00 and 19.00.) A forecast for, literally, the next 24 hours was not considered as it is essentially a subset of the two above schemes and rather less intuitive in itself. Additionally, a third timeframe that in principle needs to be considered is that of the billing period. As explained above, this may be pertinent in the case of consumption tier pricing.
In the description below we have opted to focus on one of these three pertinent timeframes and in particular that of the next day's 24h forecast. The benchmarking that will be attempted in the following will be conducted on data collected and modeled on this timeframe.
1.2. The key modeling approaches and features used in short term forecasting
Forecasting in short timeframes has been consistently addressed in the literature via a number of different approaches, both with regard to the model type and to the parameters (features) used (Karatasou S., et.al 2006; Escrivá-Escrivá G., et al 2011; Roldán-Blay C., et al, 2013; Daut M.A.M, et. al 2017; Deng H., et al, 2017). Approaches in the literature have evolved in two main directions. On the one hand, there are methods that rely on conventional approaches (e.g. regression, stochastic time series, ARIMA, etc.) which, due to their relative simplicity, still receive some interest in the literature. And, on other hand, there are artificial intelligence (AI)-based methods (Raza M.Q, et al. 2015; Darbellay GA, et al, 2019). Indeed, AI approaches have received increased attention and a lot of sophisticated approaches have been proposed; there is a wide consensus on the nonlinearity of the underlying phenomena in building energy, which renders AI approaches particularly pertinent.
Islam (Islam B, 2011) has provided a comparison of these two broad approaches. In the recent decade, among AI approaches, support vector machine (SVM) has been popular with researchers, due to the fact that it may rely on small quantities of training data. This SVM is a typical supervised learning method applied for categorization and regression, and has a solid legacy, having been introduced by Cortes and Vapnik in the 1990s (Cortes C., et al, 1995). It ranks high in the context of accuracy and can solve nonlinear problems using small quantities of training data. The SVM is based on the structure risk minimization (SRM) with the idea of minimizing the upper bounds of error of the object function.
More recently, hybrid methods have also been introduced by researchers (Zhang Z., et al, 2021), in an attempt to combine more than one modeling approach. Swarm intelligence (SI) approaches have been combined with ANNs as well as SVM in search of better forecasting accuracy. SI has been inspired by the behavior of insects and other animals, and comes in various forms such as particle swarm optimization (PSO), ant colony optimization (ACO) and artificial bee colony (ABC).
Similarly, Mohammad Azhar Mat Daut (Daut M.A.M, et. al 2017) has provided for an exhaustive summary of the SVM and ANN as well as hybrid approaches pursued. These authors conclude that the hybrid methods (ANN and SAI and even more SVM and SI) have shown some improvement in the performance of the accuracy of building load forecasting. Indeed, ANN has been widely utilized in different applications, but its hybridization with other methods seems to improve the accuracy of forecasting electrical load of buildings. The same authors expanded also into reviewing the type of features typically used in the modeling exercise. Indeed, a great diversity of possible combinations have been tried out in the literature. In a categorization of 17 approaches, these authors have found that historical consumption loads are used across all of them. Diverse weather data (Temperature, Dry Bulb Temperature, Dew Point Temperature, Wet Point Temperature, Air Temperature, Humidity, Wind Speed, Wind Direction, Brightness of Sun, Precipitation, Vapor Pressure, Global/Solar Radiation, Sky Condition) have been used in the modeling, although only a few appear consistently across the models (temperature in 11 out of the 17 cases, Global/Solar Radiation in 9 out of the 17 cases and humidity in 8 out of the 17 cases). Finally, indoor conditions (temperature, occupancy) as well as calendar data are also used in the modeling, albeit less frequently.
Bourdeau (Bourdeau et al, 2019) has also provided for a review and a classification of methods for building energy consumption modeling and forecasting. He addressed both physical and data driven approaches. As far as the latter are concerned, they also confirm the two main approaches and orientations, i.e. they are mostly time-series reliant as well as machine learning based. The authors analyzed 110 papers in the period between 2007 and 2019, and reported that 22 among them were based on ANN approaches, 20 on SVM approaches, 17 on time series and regression approaches and 16 combining more than one approach. These authors referred to this last category as ensemble approaches, while reserving the term hybrid to describe the combined use of data and physical approaches. Although this represents a notable semantic difference with regard to the previous, exclusively data-driven work reviewed, the results between this team and the previous one (Daut M.A.M, et. al, 2017) converge overall. The authors also provide a thorough analysis of the features used in the modeling exercise. First in frequency is the outdoor temperature that is included in 32 of the papers reviewed; humidity and solar radiation also appear often (19 and 18 instances respectively). Past loads are again found to be intensely used (21 instances). As to calendar data, here the authors provide some more detailed analysis considering four types of calendar data, and in particular type of day (13 instances), day of the week (13 instances), time of the day (12 instances) and month of the year (8 instances). Occupancy data appear in 7 instances while indoor temperature only in 1 instance (although other types of indoor data appear in 2 more instances). Overall, there seems to be a good convergence with the related analysis of feature frequency presented by the previous researchers. This is also confirmed by Isaac Kofi Nti (Nti, 2020), who examined the various aspects of electricity load forecasting. The findings indicated that weather factors are employed in 50% of the electricity demand predictions, while 38.33% rely on historical energy usage. Additionally, 8.33% of the forecasts consider household lifestyle, with 3.33% taking even stock indices into account.
1.3. Approaches used for explainable demand forecasts
All approaches reviewed above aim at reducing the forecasting error, by means of the typical error metrics used: the Root Mean Squared Error- RMSE, the Mean Absolute Error- MAE, the Mean Average Percentage Error- MAPE. Thus, accuracy is typically the sole optimization criterion. In time, however, it became apparent that there are also other important issues, besides accuracy, related to the forecasting. In particular, explainability considerations, implying the ability to understand why the forecast works the way it does and get this understanding over to the user in a user-friendly way, have started receiving increased attention over the last few years.
Mouakher (Mouakher A., et al, 2022) introduced a framework seeking to provide explainable daily, weekly and monthly predictions for the electricity consumption of building users of a LSTM-based neural network model, based on consumption data as well as external information, and in particular weather conditions and dwelling type. To this extent, in addition to their predictive model the authors also developed an explainable layer that could explain to users why the predicted model forecast the particular, every time, energy consumption. The proposed explainable layer was based on graphic interpretation by the user, by means of partial dependence plots (PDPs) which unveiled what happens to energy consumption whenever a feature changes while keeping all other features constant.
Kim (Kim J.Y., et al, 2022) attempted to explain the feature dependence of a deep learning model by taking account of the long-term and short-term properties of the time-series forecasting. The model consisted of two encoders that represented the power information for prediction and explanation, a decoder to predict the power demand from the concatenated outputs of encoders, and an explainer to identify the most significant attributes for predicting the energy consumption.
Shajalal (Shahjalal Md, et al, 2022) also embarked on the task of energy demand forecasting and its explainability. The focus was on household energy consumption, for which they trained an LSTM-based model. For the interpretability component, they combined DeepLIFT and SHAP, two techniques that explain the output of a machine learning model. This approach enabled the illustration of time association with the contributions of individual features.
2. Concept and setup
The pertinence of explainability varies from case to case and should by no means be considered as an ubiquitous modeling requirement. Thus, there may well be cases where the concept is irrelevant and its consideration would add little, if any, value. Undoubtedly, health applications of AI is an area where explainability is greatly important (Aniek F. Markus et al, 2020). Indeed, the ability to explain to the patient the suggested approach may be key to her decision and eventually to her medical treatment.
Admittedly, energy applications do not represent such a clear cut case for explainability. We would, however, argue that there are cases where the concept would indeed add value. Such is, in particular, the case of demand response, the overarching application context of this work. Demand response, at least in the narrow sense of the term, implies responding to energy price signals. Literature clearly identifies user risk as a main factor preventing a wider adoption of such demand response schemes (Dutta, G., Krishnendranath, M., 2017; Borenstein, S., 2013) and benefiting from the many advantages they may bring to users, energy retailers and grid operators, in terms of lower costs, as well as to renewable deployment planners who will find more opportunity for viable renewable energy. Thus, in this particular application context we would argue that explainability indeed comes with a clear potential to mitigate this well identified risk; this would come with important and unique value, increasing the chances of demand response adoption.
In an attempt to gain more insight on what would be important information for the users as regards the forecast they receive, we carried out interviews with four building energy experts/facility managers to discuss in more depth what information and functionality would add value to them or their building users when delivering the forecasting results. What came out in these discussions were the following two requirements: first, the concept of feature importance, i.e. information on how exactly each feature contributed to the forecast, perhaps with a seasonal variation; and second, the concept of counterfactuals, i.e. the empowerment of users to consider what-if scenarios. At this point the issue of actionability was also raised. Counterfactuals built around actionable features were highlighted as having a higher potential. Indeed, users cannot affect the weather; therefore, a weather counterfactual can only be of an indirect use and cannot contribute to any direct action. On the contrary, the indoor conditions (temperature, humidity, etc.) are actionable features as the user can typically act upon them, e.g. via thermostat settings. Surprisingly, as shown in the above literature review regarding features used in the forecasting, the indoor conditions are relatively rarely used among the selected feature set. Because of the inherent actionability of indoor conditions, a decision was made at this point to prioritize them in the modeling.
Indeed, as shown above in paragraph 1.3, there is a gradual and rather recent appreciation of explainability and its importance in forecasting. A number of explainable approaches that have very recently appeared in the energy literature were discussed there; as shown, these were variants of neural networks which incidentally are also the predominant approach used in energy forecasting exercises. However, neural networks inherently perform very poorly as regards explainability. Their complex and black box structure makes it impossible to gain insight and therefore confidence in their performance.
In this work we consider two distinct approaches to explainability. First, we will use genetic programming (GP) modeling. In artificial intelligence, GP is an evolutionary approach, i.e. a technique of evolving programs, starting from a population of random programs, fit for a particular task. Operations analogous to natural genetic processes are then applied; such are the selection of the fittest programs for reproduction (called crossover) and mutation according to a predefined fitness measure. Crossover swaps random parts of selected pairs (parents) to produce new and different offspring that become part of the new generation of programs, while mutation involves substitution of some random part of a program with some other random part of a program. GP is a distinct modeling approach that results in symbolic expressions which can potentially offer insights to the model performance. In addition, GP is a classical case of so-called global level explainability. It provides insights on the overall model performance. Up to this moment and to the best of our knowledge GP has not been used in the building energy forecasting literature. On the contrary, counterfactuals are referred to as instance or local level explainability as they do not relate to the model itself but only to a particular instance.
A second approach that we will use for explainability purposes will be that of SHAP — which stands for SHapley Additive exPlanations. This approach was first published in 2017 by Lundberg (Lundberg S. and Lee S, 2017). In short, SHAP values provide for a quantification of the contribution that each feature brings to the model. Thus, it is an excellent way to track feature importance, which has already been highlighted above as a key mandate for explainability, especially within the demand response application context.
Therefore, although GP is a distinct modeling approach, SHAP values are not anything close; they are an approach that can be used regardless of the underlying model and its purpose is to highlight feature importance. For this reason they are called model agnostic; they are equally relevant regardless of the model used, which could be a gradient boosting, a neural network or anything that takes some features as input and produces some forecasts as output.
Interestingly, SHAP values have been recently (Emanuele Albini, 2022) employed in a counterfactual context, making them also appropriate for our second explainability use case. The proposed method generates counterfactual explanations that show how changing the values of a feature would impact the prediction of a machine learning model.
Also, it may be that explainability comes with an accuracy tradeoff. Thus, we considered it important to benchmark the GP performance in terms of accuracy and for this purpose we opted for two mainstream modeling approaches in the forecasting literature. First, there are the structural time series (STS) models which are a family of probability models for time series that include and generalize many standard time-series modeling ideas, including: autoregressive processes, moving averages, local linear trends, seasonality, and regression and variable selection on external covariates (other time series potentially related to the series of interest). And, second, there are the neural networks and in particular their LSTM variant which is often used in the energy forecasting literature.
We have opted not to use hybrid models; although it is often reported that they come with some increased accuracy they would be a very poor selection in terms of explainability as we would also need to understand the relative impact of every model for the various space instances. This would be an impressive task also if SHAP were to be applied. Overall, without denying the accuracy benefits that hybrid approaches may bring, we consider them an inappropriate path when explainability considerations are deemed important, as they are in our use case.
Finally, as the investigation was prompted by the design needs of a demand response controller, additionally to the GP and SHAP related explainability investigations, there were two further issues that were deemed important. Indeed, if a demand response controller seeks to provide user support, then seeking to run counterfactuals on actionable features seems to be a preferable and value adding approach. Actionable features are those that the user of the controller can act upon. Such is, for example, the case of indoor temperature that can be acted upon by changing the thermostat settings. Conversely, features such as weather, or consumption history, or day of the week and hour of the day, features that dominate the forecasting literature, are inherently non actionable. Also, the fast deployment of a real life controller would be directly impacted upon by the duration of the training period. Thus, the investigation of a fast training option of the forecasting algorithm would come at a clear benefit and would be preferable, provided performance is not overtly eroded.
3. The methodological approach; an overview
Yearly real time data were collected via a smart meter and a set of indoor environmental sensors in an office building of around 1300 square meters at the Hellenic Mediterranean University in Crete, Greece. The energy meter was a Shelly 3M, 3x 120A (with an accuracy of 2%) reporting energy data every four minutes. The three indoor environmental sensors were Shelly H&T type (with an accuracy of 2% for temperature and 4% for humidity) and were used to collect measurements of temperature and humidity. The resolution of this data collection was not fixed. To secure battery longevity these sensors report only when there is a 0.5 degrees change of temperature or 2% change of humidity. This typically occurred between 1/2 an hour and 5 hours. Additionally, weather data were sourced from a local weather station, via the open weather map provider https://openweathermap.org/ API. Although temperature, humidity, wind and cloud coverage data were collected, a preliminary analysis revealed that the predominant weather driver of electricity consumption was that of air temperature, something that converges well with the literature.
Data were split into the four seasons. In the first two seasons (winter and spring months) we tested all three approaches (STS, NN-LSTM and GP) to investigate and validate the relative performance of the GP approach with regard to the more traditional time series and NN approaches. Different feature subsets were used to train models, including various combinations of weather, past consumption, hour of the day, day of the week and indoor temperature (monitored and averaged across three points in the building). This latter selection was considered important if we were to achieve models that could be actionable. Indeed, from all other parameters tried, indoor temperature was the only actionable one.
As far as the training validation and test sets the approach was as follows:
After we collected evidence that GP was performing well, in the next two seasons we restricted the modeling on GP alone and shifted the focus onto investigating SHAP explainability and feature importance, running counterfactuals on actionable features (indoor temperature) and analyzing the impact of the training duration on model performance.
All primary sensor data can be visualized via a public dashboard at the address https://wsn.wirelessthings.biz/v2/stef. Data exported from this dashboard were cleaned and then used to calculate hourly values of all features used.
Data (in excel sheets) as well as models (as Jupyter notebooks) including a model index are publicly available at the Open Science Framework, at https://osf.io/epw4n/.
The following table provides a summary of all the models that have been used in this work and can be downloaded from the above URL. Not all of these models will be reviewed below as we will selectively browse through the most important findings.
Table 1.
List of models used.
| Winter models | |||
| Model code | Type | Features used | |
| Model 1 | LSTM | Weekly history | |
| Model 2a | LSTM | Weekly history, Day of week | |
| Model 2b | LSTM | Weekly history, Indoor temperature | |
| Model 2c | LSTM | Weekly history, Day of week, Indoor temperature | |
| Model 2c’ | LSTM | Weekly history, Indoor temperature, Day of week, Hour of day | |
| Model 3a | LSTM | Weekly history, Day of week, Outdoor temperature, Wind | |
| Model 3b | LSTM | Weekly history, Day of week, Outdoor temperature | |
| Model 3c | LSTM | Weekly history, Day of week, Wind | |
| Model 4a | LSTM | Weekly history, Day of week, Outdoor temperature, Indoor temperature | |
| Model 4b | LSTM | Weekly history, Day of week, Wind, Indoor temperature | |
| Model 4c | LSTM | Weekly history, Day of week, Outdoor temperature, Wind, Indoor temperature | |
| Model 4a’ | LSTM | Weekly history, Day of week, Outdoor temperature, Indoor temperature, Hour of day | |
| Model 5 | LSTM | Same day past week consumption | |
| Model 6a | LSTM | Same day past week consumption, Outdoor temperature, Wind, Indoor temperature | |
| Model 6b | LSTM | Same day past week consumption, Outdoor temperature, Wind, Day of week | |
| Model 7a | LSTM | Same day past week consumption, Outdoor temperature, Wind, Indoor temperature | |
| Model 7b | LSTM | Same day past week consumption, Outdoor temperature, Wind, Indoor temperature, Day of week | |
| Model 7c | LSTM | Same day past week consumption, Indoor temperature | |
| Model 7d | LSTM | Same day past week consumption, Indoor temperature, Day of week | |
| Model 2c | GP | Weekly history, Day of week, Indoor temperature | |
| Model 2c’ | GP | Weekly history, Day of week, Hour of day, Indoor temperature | |
| Model 3a | GP | Weekly history, Day of week, Hour of day, Outdoor temperature | |
| Model 3a’ | GP | Weekly history, Day of week, Hour of day, ABS (absolute value of difference between indoor and outdoor temperature) | |
| Model 3a’’ | GP | Weekly history, Day of week, ABS | |
| Model 8 | STS | Consumption, Day of week, Indoor temperature | |
| Model 8’ | STS | Consumption, Day of week, Hour of day, Indoor temperature | |
| Spring models | |||
| Model code | Type | Features used | |
| Model 2c | LSTM | Weekly history, Day of week, Indoor temperature | |
| Model 2c’ | LSTM | Weekly history, Indoor temperature, Day of week, Hour of day | |
| Model 3a | LSTM | Weekly history, Day of week, Outdoor temperature | |
| Model 3a’ | LSTM | Weekly history, Outdoor temperature, Day of week, Hour of day | |
| Model 4a | LSTM | Weekly history, Day of week, Outdoor temperature, Indoor temperature | |
| Model 4a’ | LSTM | Weekly history, Indoor temperature, Outdoor temperature, Day of week, Hour of day | |
| Model 6b | LSTM | Same day past week consumption, Outdoor temperature, Day of week | |
| Model 7b | LSTM | Same day past week consumption, Outdoor temperature, Indoor temperature, Day of week | |
| Model 2c | GP | Weekly history, Day of week, Indoor temperature | |
| Model 2c’ | GP | Weekly history, Day of week, Hour of day, Indoor temperature | |
| Model 3a | GP | Weekly history, Day of week, Hour of day, Outdoor temperature | |
| Model 3a’ | GP | Weekly history, Day of week, Hour of day, ABS | |
| Model 3a’’ | GP | Weekly history, Day of week, ABS | |
| Model 8 | STS | Consumption, Day of week, Indoor temperature | |
| Model 8’ | STS | Consumption, Day of week, Hour of day, Indoor temperature | |
| Summer models | |||
| Model code | Type | Features used | |
| Model 8 | STS | Consumption, Holiday, ABS, Hour of day | |
| Model 9 | GP | Weekly history, ABS, Holiday(includes weekends too) | |
| Model 10 | GP | Weekly history, Holiday(includes weekends too) | |
| Model 11 | GP | 3-day history, ABS, Hour of day, Holiday(includes weekends) | |
| Model 12 | GP | 3-hour history, ABS, Hour of day, Holiday(includes weekends) | |
| Model 13 | GP | active_electricity(t-23), ABS, Holiday(includes weekends) | |
| Model 14 | GP | active_electricity(t-23), Indoor temperature, Outdoor temperature, Holiday(includes weekends) | |
| Model 15 | GP | active_electricity(t-23), Indoor temperature, Outdoor temperature, Work hour | |
| Autumn models | |||
| Model code | Type | Features used | |
| Model 16a1 | GP | active_electricity(t-7), Indoor temperature, Outdoor temperature,(only work hours of workdays considered) | |
| Model 16b1 | GP | active_electricity(t-15)(non-work hours of workdays considered) | |
| Model 16b2 | GP | active_electricity(t-23)(non-work hours of holidays considered) | |
The reader is reminded that the ‘hour’ was the resolution of the forecasting and the hourly forecast of the next day was the key objective.
3.1. The recursive approach pursued
Although in the case of LSTM block, 24h forecasts are possible, in the case of GP only next-hour forecasts are possible. To this extent, and in order to abide by the mandate for next-day forecasting, a recursive approach was necessary. Depending on the features used there are various approaches to this recursion. For example, let us consider that our forecast of consumption, denoted as Con [t], uses the feature of past hour consumption, denoted as Con [t-1], for its training. Let us imagine now that we are at 17.15 and run the daily forecast. We would first forecast the consumption for Con [17.00] (which corresponds to the consumption between 17.00 and 18.00 of the same day) based on the actual value of Con [16.00]. We would then forecast Con [18.00] by using the previously forecasted value of Con [17.00]. We would carry on similarly until Con [24.00] of the next day. In this approach, our recursion would be heavily relying on forecasts rather than actual values.
An alternative and better formulation of recursion would be to use history data in the modeling not as Con [t-1] but, in principle, rather as Con [t-24], which corresponds to the observed consumption at the same hour of the past day. We say here ‘in principle’ because one may also have to account for the difference between work and non work days. We will come back to this issue in the next section. For now it suffices to realize that our new formulation of ‘history’ has the advantage that it implicitly takes account of the ‘hour of the day’ and does not require this to be entered as an additional feature, as often occurs in the forecasting literature. This recursion setup also has the additional advantage that the next-hour forecast will now rely far more on actual data rather than forecast data. Indeed, in this recursive approach our next-day forecasting of Con [t], and from t = 0 … 16, would now rely on actual, measured data. Only the Con [t], from t = 17 … 23, would rely on forecasted data.
To conclude with the discussion of the recursive approach pursued we also need to describe the approach pursued as regards weather data. Whenever weather [t] was used among the features for the forecasting of Con [t] we used the forecast provided by the weather station itself. We found this approach more intuitive than treating weather [t] in a recursive fashion as in the case of history data.
4. Results and discussion
4.1. Comparing STS, LSTM and GP performance; winter and spring data
As said above, the approach in the first two seasons aimed at benchmarking the GP approach against the more traditional STS and LSTM approaches. Overall, we validated that GP was performing in a comparable way, even with a better performance when compared to its two ‘competitors’. We will present below the best-performing models in all three cases for winter and spring.
4.1.1. Winter models
The table below summarizes the relative performance of the three approaches.
Table 2.
Relative performance of GP, LSTM and STS approaches for the winter data.
| Winter period | ||
|---|---|---|
| Modelling approach | Best performing model | RMSE |
| GP | model 3a’ | 4460 |
| LSTM | model 2c’ | 5441 |
| STS | model 8 | 5529 |
4.1.2. Spring models
The four tables below summarize the relative performance of the three approaches.
Table 3.
Relative performance of GP, LSTM and STS approaches for the spring data.
| Spring period | ||
|---|---|---|
| Modelling approach | Best performing model | RMSE |
| GP | model 3a’ | 2798 |
| LSTM | model 2c’ | 3824 |
| STS | model 8 | 4566 |
4.1.3. The training duration
In order to test how a faster model training would affect performance we tested fast training protocols with the spring data: one week and two weeks of training data. The following table illustrates the findings.
Table 4.
Impact of training period duration on GP models. The test set comprises one week of data for all cases.
Table 4.
Impact of training period duration on GP models. The test set comprises one week of data for all cases.
| MAPE | |
| GP model 3a'' ; training on 71 days | 25.45% |
| GP model 3a'' ; one week training (7 days) | 25.78% |
| GP model 3a'' ; two weeks training (14 days) | 30.11% |
The impact on performance was insignificant in the case of GP models. However, in the case of STS, model 8, fast training performance rapidly declined. Again, the test set comprises one week of data for all cases. This is shown below.
Table 5.
Impact of training period duration on STS models.
| MAPE | |
| STS model 8; training on 71 days | 26.22% |
| STS model 8; one week training (7 days) | 39.51% |
| STS model 8; two weeks training (14 days) | 46.07% |
4.1.4. Results
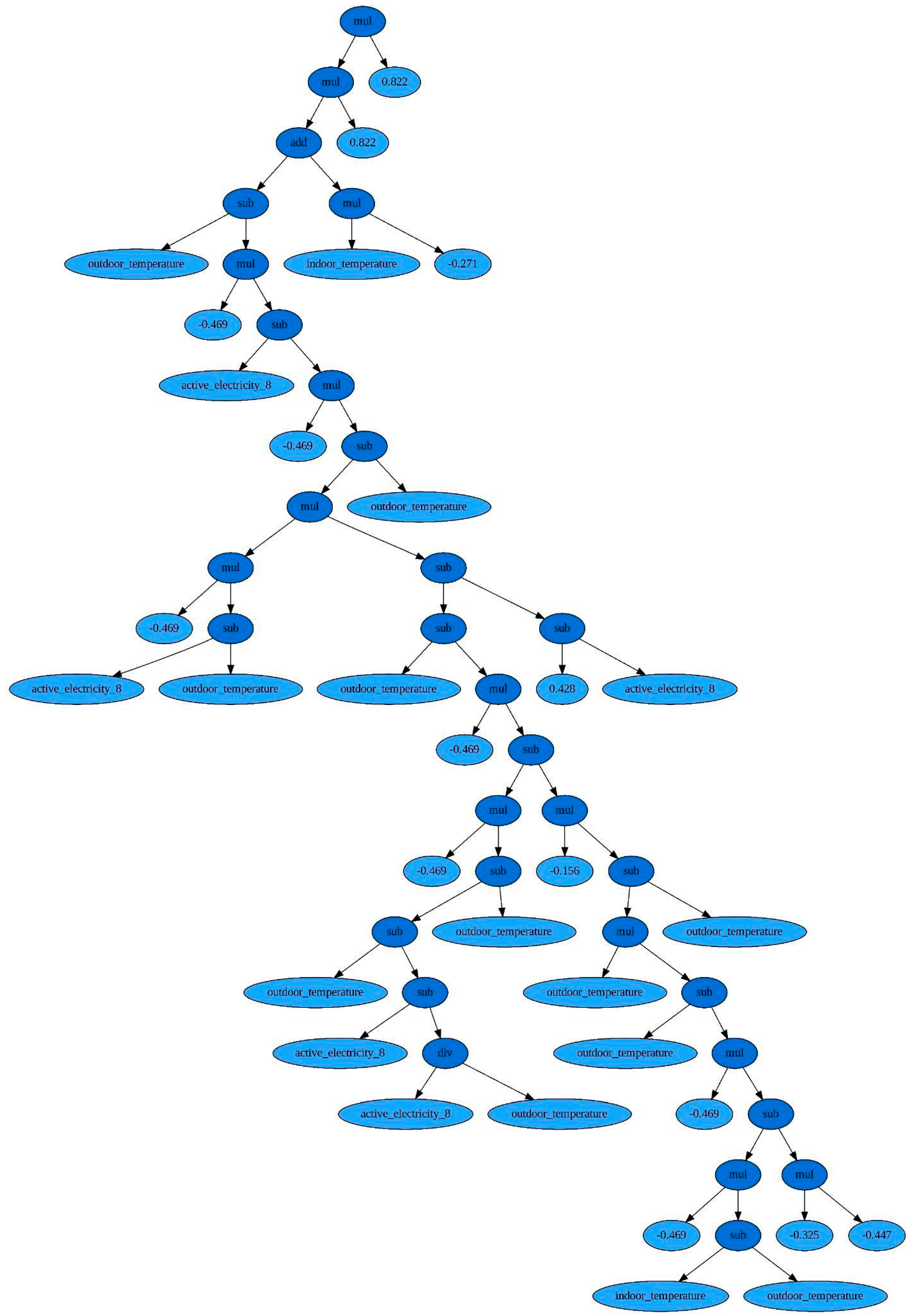
On the one hand, GP appears to perform well and outperform other, well-established approaches (STS, LSTM). However, the associated symbolic expressions that have resulted appear to be very complex and quite useless in providing explainable insights at the model level. The following figure illustrates such a daunting symbolic expression.
Thus, although in terms of accuracy it appears that GP approaches are quite promising, in terms of their global explainability potential the results have been quite disappointing. Of course, this was a very first attempt at touching the surface of the issue. It remains to be seen how potentially a guided pruning of the symbolic expressions into more simple forms would affect performance. This is an exercise we are currently working on in the framework of the EU TRUST AI project, where an environment that can prune and manipulate symbolic expressions in a guided way is implemented. This environment will then allow us to reduce the complexity, assess the accuracy trade off and exploit the explainable potential of the resulting, more simple and crisp symbolic expressions.
Some encouraging first evidence was collected that the length of training did not affect the GP model performance in any significant way. This was not the case for the STS approach, where the accuracy rapidly deteriorated as short timeframes were used in place of the typical ones.
Figure 1.
The complex structure of the symbolic expression underlying the GP model.
4.2. SHAP analysis and actionability considerations: summer and autumn data
In the next two seasons the investigation shifted towards concepts of local explainability, feature importance and counterfactual analysis, along with a further assessment of the impact of the reduction of the training time. In both summer and autumn we used only GP models.
4.2.1. The case of summer
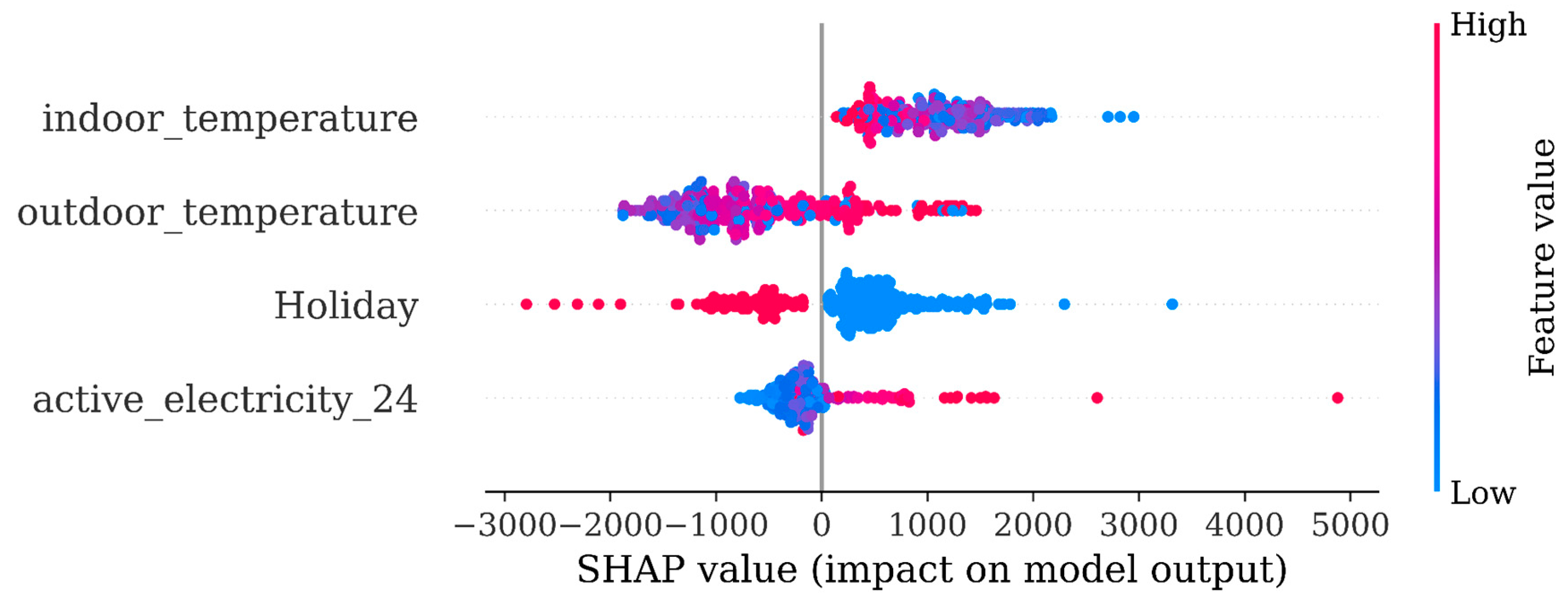
A first GP model that was developed for the summer (model 13) was based on the introduction of a combined parameter called ABS and defined as the absolute value of the difference between indoor and outdoor temperatures. The idea was that this temperature difference is essentially driving cooling requirements and would allow us to end up with a more compact feature set. Second, because of holidays in this season we also introduced a holiday feature (boolean; 1- holiday, 0- work day). The third feature was the past 24h consumption.
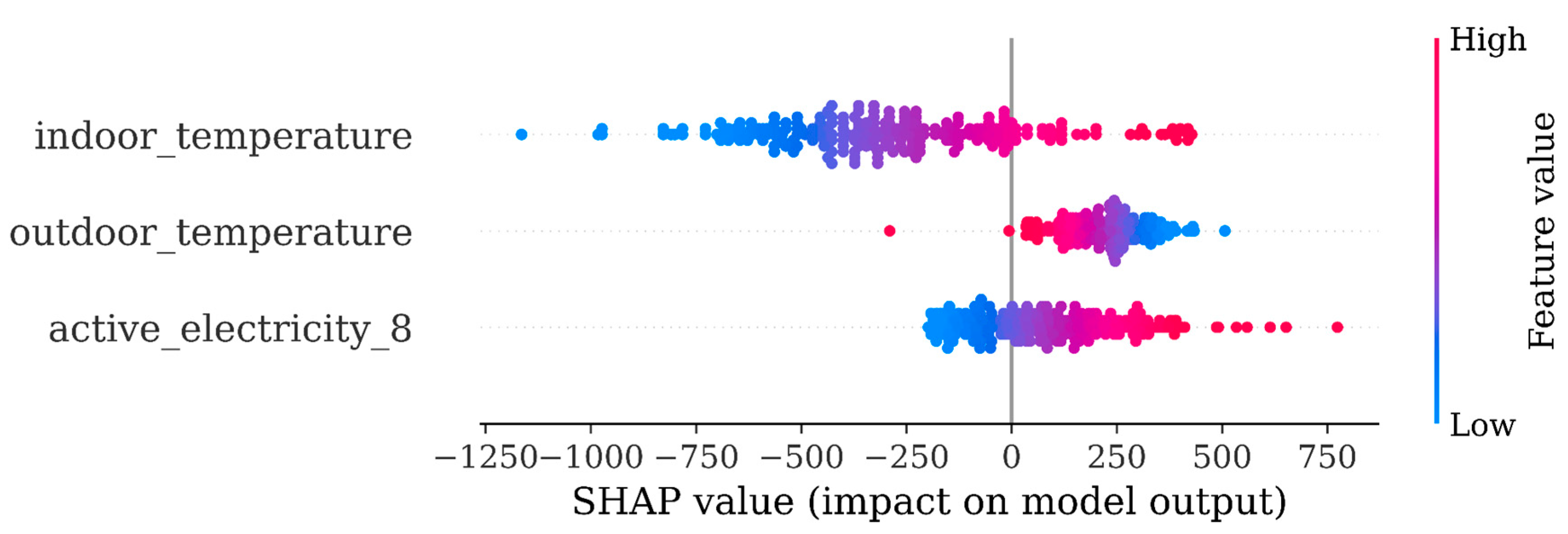
We carried out our first SHAP analysis on this model wishing to investigate the relative significance of these three features.
The SHAP plots that follow below illustrate on the vertical axis the feature importance. Also, a feature that turns from blue (low values) to red (high values) as the SHAP values increase on the horizontal axis, signifies that an increase of the feature value also increases the predicted value.
The SHAP analysis (see Figure 2 below) in this case was particularly counterintuitive. It indicated no clear trend of the SHAP values for our ABS feature. Even worse, in Figure 3 the ABS feature, although of high importance in the model, appeared to turn from red into blue as the SHAP increases, implying a reverse relationship between this feature and electricity consumption, something not acceptable for the summer season.
The reason for this behavior was that our compact ABS feature did not account for building thermal inertia. This was most apparent in the early afternoon hours, after people left work. In this period consumption went down; however, due to thermal inertia the ABS feature was still on the rise.
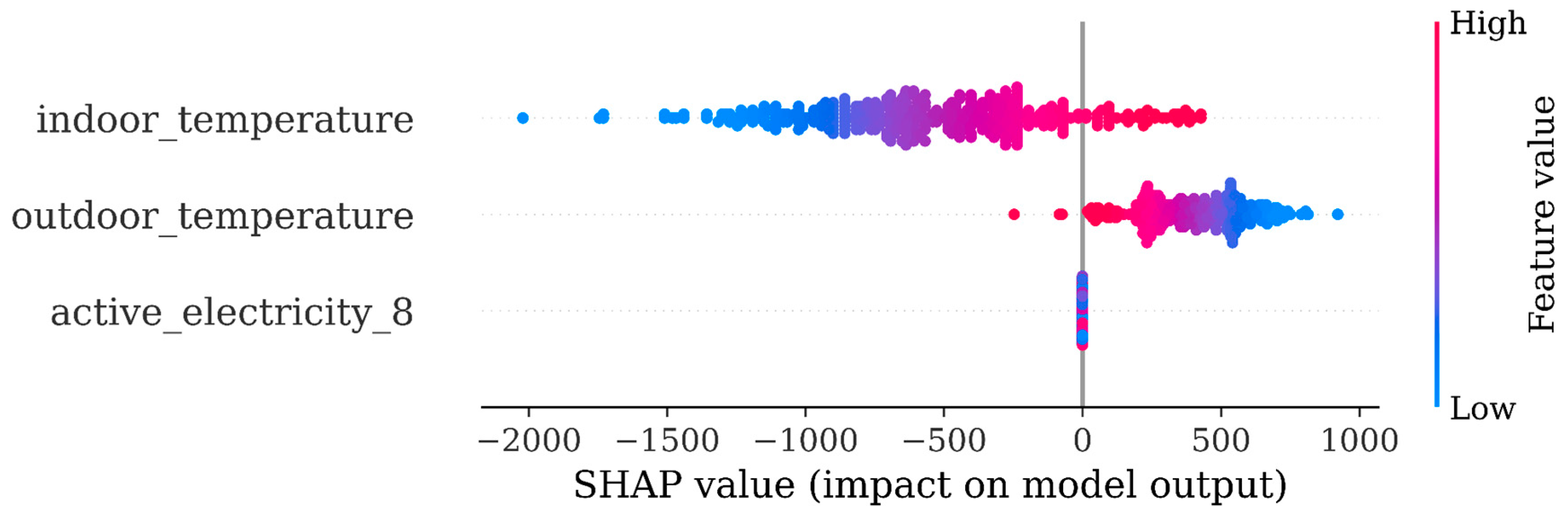
Following this finding we concluded that we should abandon any effort to jointly include the indoor and outdoor temperatures in one feature like the ABS. In following modeling these two features were separately considered, as distinct features.
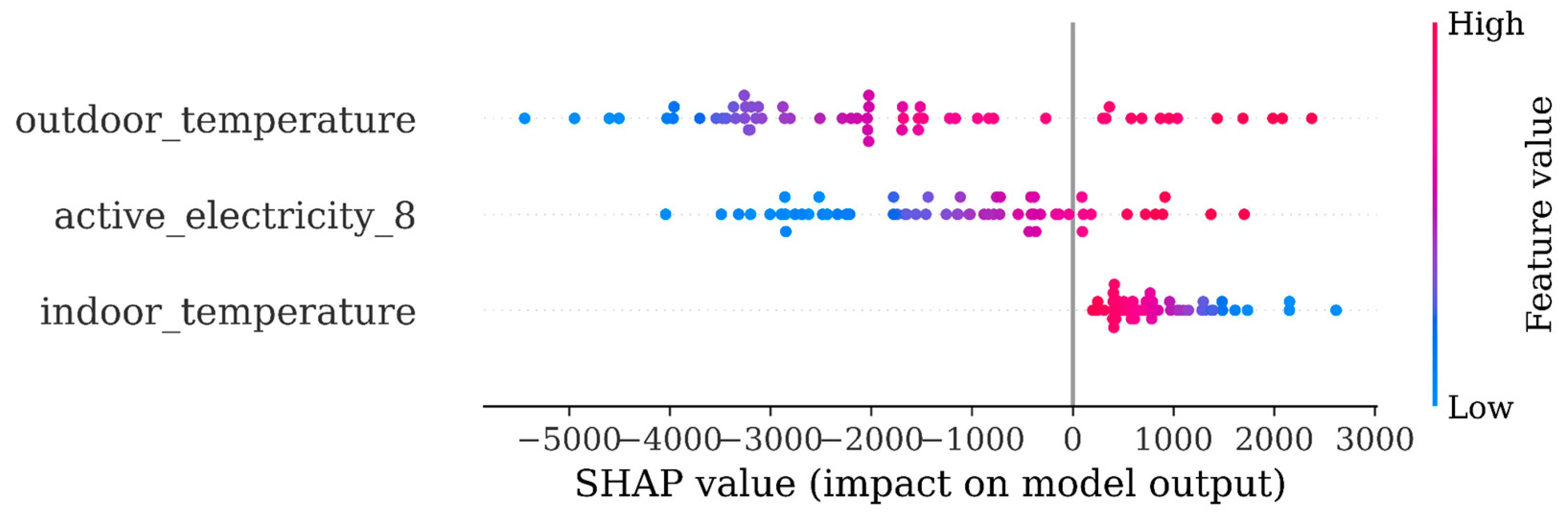
Thus the amended model 14 was based on four features: indoor temperature, outdoor temperature, holiday and past consumption. The SHAP analysis is shown in the next figure. An important result was that the indoor temperature was now the main driver of the forecast and of course in the right direction, i.e. dots turn from red into blue implying that as the indoor temperature decreases the predicted variable will increase. Indeed, this was the first meaningful and useful result of our SHAP analysis, highlighting the high importance of indoor temperature on the forecast, which indeed now appeared as its key driver.
Figure 4.
Model 14 SHAP plot.
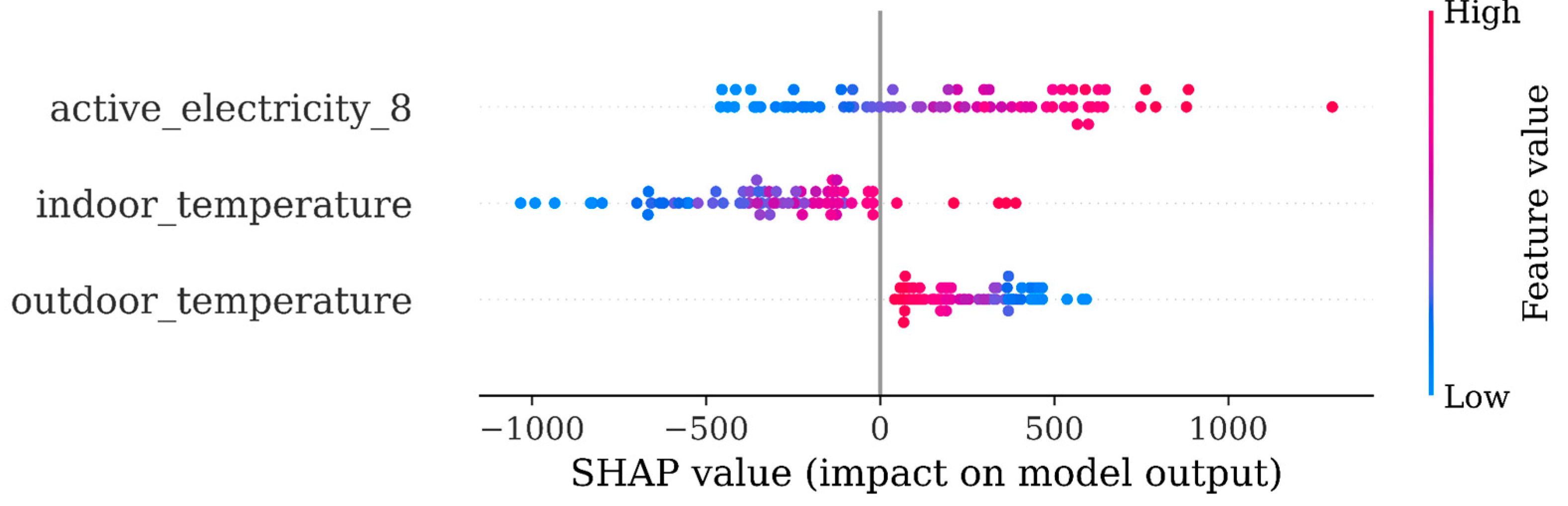
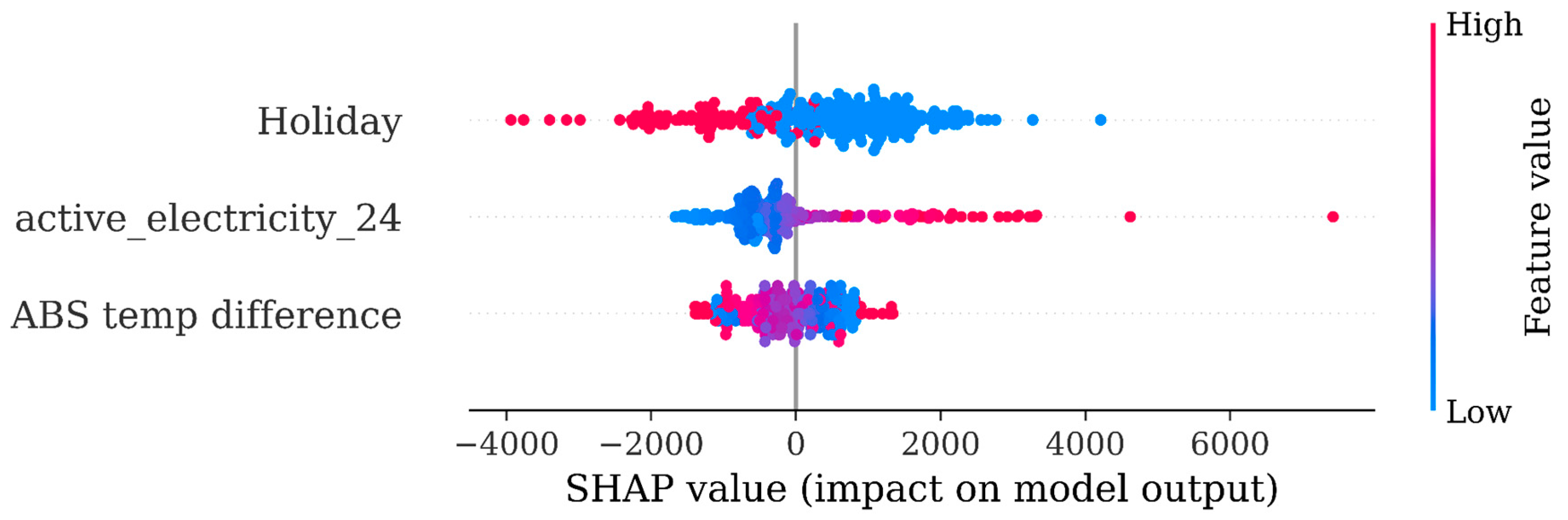
Following this finding we set up model 15, wherein we introduced the ‘work hour’ feature to signify whether a given hour was a work hour or non-work hour. This feature eliminated the need for the holiday feature, too, as they were included as non-work hours.
In this case SHAP analysis showed the newly introduced work hour as the most significantly contributing feature to the model output. The importance of indoor temperature in this model now has been much reduced. Additionally, there is no conclusive evidence that the increase of indoor temperature (dots turning in red color) would have some impact on the predicted variable (SHAP value clearly increasing or decreasing). These remarks prompted us to adapt the model features so that we could potentially raise the importance of indoor temperature in the model forecasts.
Figure 5.
Model 15 SHAP plot.
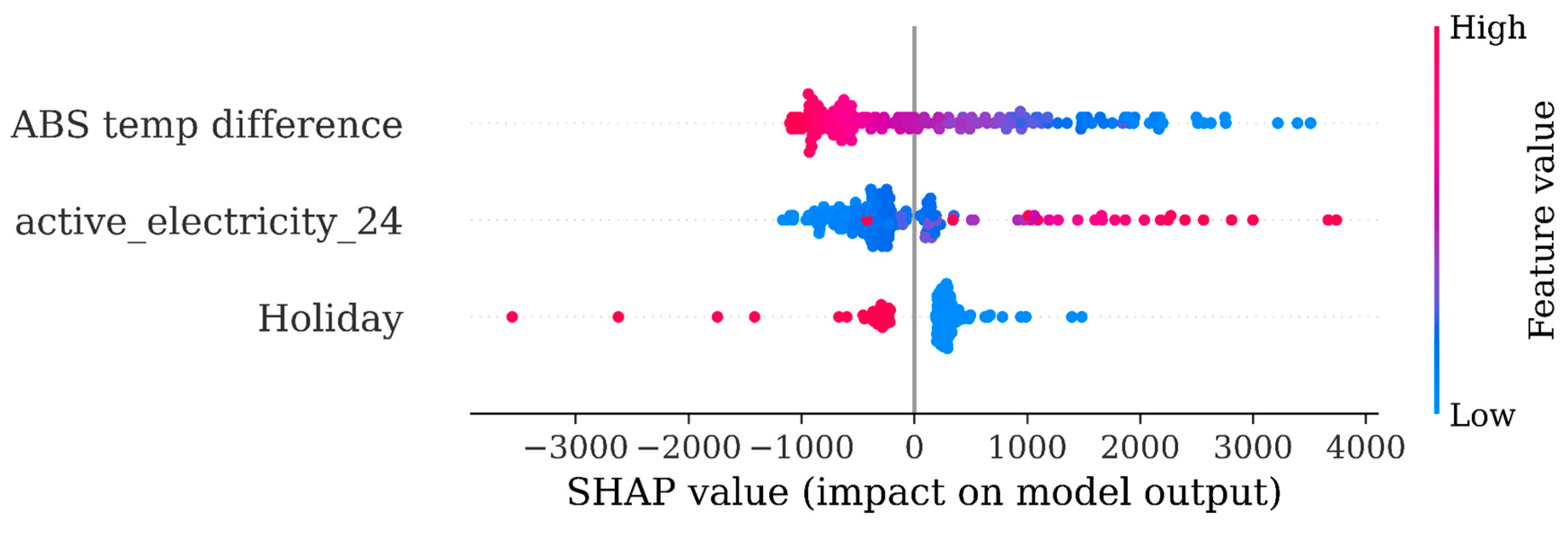
As the work hour appeared now to be the key driver, we considered building separate models for work/non-work hours and holidays denoted as 16a1, 16b1 and 16b2 respectively. Because of the 24h recursive approach pursued it was necessary to have separate models for holidays and non-work hours.
SHAP analysis in model 16a1 revealed now (figure below) that outdoor temperature was the most important driver while indoor came third. However, in this plot indoor temperature dots turn from red into blue as SHAP values increase, indicating that as indoor temperature is lowered (increased cooling) consumption will rise. This is now clearly in line with our intuition.
Figure 6.
Model 16a1 long training SHAP plot.
We also tried changing the training duration of these three models. We experimented with three training to test sizes: 85/15 (long training), 50/50 (medium training) and (15/85) short training. Again, we found that there was no notable impact on the MAPE values calculated, which once again suggests that the GP models do not deteriorate when the training timeframe reduces. The following table summarizes these results.
Table 6.
Impact of training period duration of GP models on MAPE values.
| Model | Train/ Test = 85/15 | Train/ Test = 50/50 | Train/ Test = 15/85 |
| 16a1 | 30% | 30% | 30% |
| 16b1 | 18% | 18% | 18% |
| 16b2 | 20% | 13% | 13% |
4.2.2. The autumn data and models
The same models 16a1, 16b1 and 16b2 were used in the autumn period. The SHAP analysis of the 16a1 model (work hours) highlighted the indoor temperature as an important contributor both in the long and short timeframe models.
Figure 7.
Model 16a1 long training SHAP plot.
Figure 8.
Model 16a1 medium training 50/50 train/test SHAP plot.
Figure 9.
Model 16a1 short training 15/85 train/test SHAP plot.
Interestingly, SHAP analysis revealed that indoor impact has now shifted to positive. This means that an increase in indoor temperature (dots turning from blue into red) results in an increase in consumption. This of course is no surprise and is due to the autumn period (defined as the October, November and December calendar months). Indeed, an increase of indoor temperature is now associated with heating and will be reflected in an increased consumption.
As in summer, in the autumn period once again no noticeable change occurred when reducing the training timeframe.
4.2.3. Results
SHAP analysis proved helpful in figuring out the important drivers in every model. Thus they were found to provide important insights into feature importance. Indoor temperature appeared to be an important driver, often the most important one, but at other times surpassed by outdoor temperature. Also, the SHAP sign in all cases coincided with intuition. SHAP analysis helped us to understand the inherent error in trying to combine indoor and outdoor temperature in just one parameter and avoid any such modeling approach.
Having analytically firmly established that indoor settings are important, and keeping in mind that indoor temperature is actionable, we have confirmed that counterfactual analysis is pertinent. If indoor is important and actionable then one may consider ‘what if’ I change indoor temperature? How would the forecast evolve?
These investigations are the focus of the section below.
4.3. Counterfactual analysis
In this section we present results from the counterfactuals run both for the winter and for the summer period. The model used in both cases was the work hour model 16a1. Indeed, it is when building users are at work that counterfactual findings may result in user action.
For what-if counterfactuals to be meaningful they must be generated on conditions that really make sense. As we will see, setting such conditions is a key aspect of the counterfactual analysis and can itself reveal important findings.
Let us look at the case of summer. For summer data we have opted to generate counterfactuals on meaningful instances where: Tin<25 && Tin<Tout-2 .
The condition Tin<25 aims at defining ‘excessive’ cooling, which are the instances where what-if analysis leading to user action may make sense. In this case, by selecting 25 degrees we have defined that if the indoor temperature is above 25 degrees no claim for ‘excessive’ cooling can possibly be made so any ‘what if’ would be of no practical purpose. Indeed, we could have set this value lower at 23 deg, in which case we would have limited the sample space where meaningful counterfactuals could be generated.
The condition Tin<Tout-2 aims at excluding instances where indoor temperature may be low but not due to ‘excessive’ cooling but due to a relatively cool summer day.
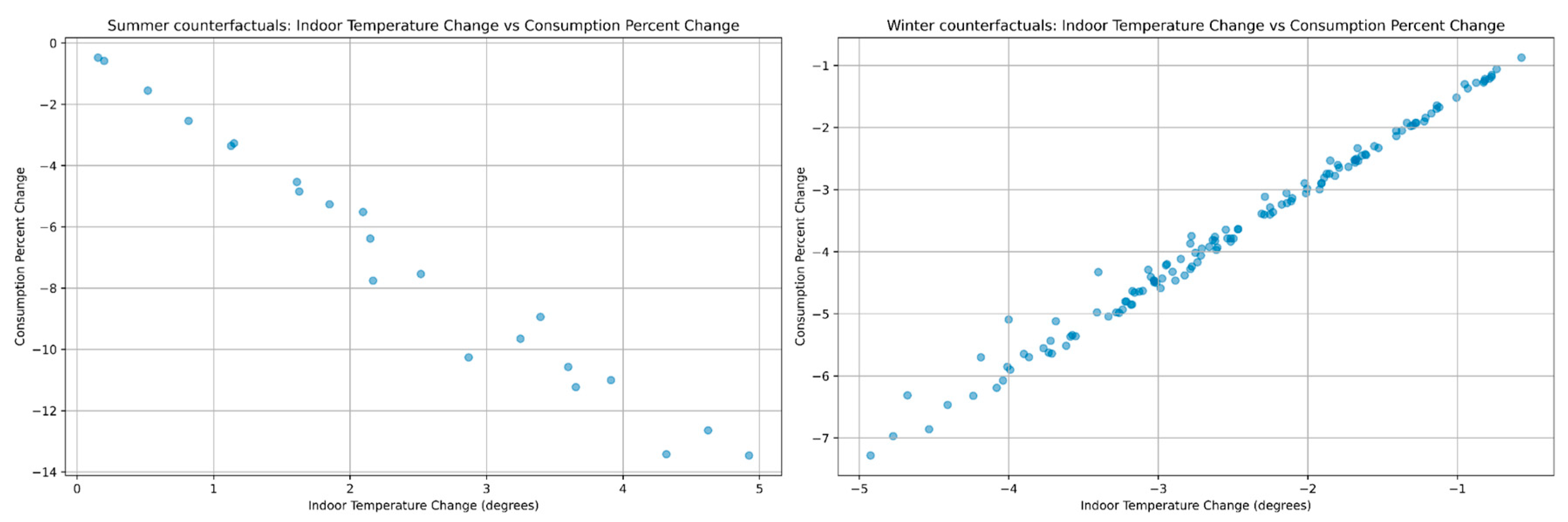
Thus, the counterfactual analysis under this condition revealed that
increasing indoor temperature by an average of 2.15 degrees causes a mean decrease in consumption by 6.44%.
Similarly for the winter period the condition for the counterfactual instances to be meaningful was
Tin>21 && Tin>Tout+2
In this case the result was as follows:
decreasing indoor temperature by an average of 2.3 degrees causes a mean decrease in consumption by 3.4%.
The table below illustrates the results of the counterfactual analysis. The above two key statements can be tracked in the ‘mean’ rows.
Table 7.
Counterfactual analysis.
| Indoor temperature initial | Outdoor temperature | Predicted consumption | New Indoor temperature | Consumption prediction for new Indoor temperature | Change in Indoor temperature by degrees | Percent change in consumption | |
| Summer Model 16a1 | |||||||
| count | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| mean | 24.36 | 27.65 | 16740.58 | 26.51 | 15671.90 | 2.15 | -6.44 |
| std | 0.25 | 0.71 | 1053.16 | 0.92 | 1193.52 | 0.75 | 2.38 |
| Winter Model 16a1 | |||||||
| count | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| mean | 22.84 | 16.91 | 11927.82 | 20.55 | 11523.75 | -2.3 | -3.4 |
| std | 0.58 | 1.89 | 1412.25 | 0.74 | 1383.14 | 0.68 | 1.0 |
In Figure 10 below we illustrate the generated counterfactuals and the effect on consumption that will result from changing the indoor temperature. As one can see, in the summer season an increase in indoor temperature by 1 degree causes a decrease of consumption of approximately 3.36%; an increase by 2 degrees a consumption reduction by 5.52% and by 3 degrees a reduction by 9.65%. Similarly, for the winter season decreasing indoor temperature by 1 degree causes a decrease of consumption of 1.52%; a decrease by 2 degrees a reduction of 2.98% and by 3 degrees a reduction by 4.50%.
Of course these counterfactuals above apply only to the valid counterfactual instances, i.e. that part of the test set that fulfills the conditions set. The following table illustrates the conditions and how they effectively reduce the counterfactual space.
Table 8.
Impact of conditions set on the counterfactual space.
| SUMMER | valid counterfactual instances from test set | WINTER | valid counterfactual instances from test set |
| Tin<25 | 11 | Tin>21 | 67 |
| Tin<24 | 2 | Tin>22 | 64 |
| Tin<23 | 0 | Tin>23 | 28 |
As can be seen, the conditions set affect the scope of counterfactual analysis and help us to understand to what extent the particular building/user interaction context could benefit from the analysis. The more valid instances there are, the greater the potential of counterfactual analysis in the specific context.
4.3.1. Results
Counterfactuals applied on the demand forecasting allows users to be supported in decisions as regards their energy use. Additionally, they can reveal important information related to building operation.
The average figures calculated and reported above demonstrate the average impact on consumption when acting upon the indoor temperature. In this way, the figures are important in understanding building performance and especially what the impact of a more energy conscious behavior would eventually be.
These figures should of course always be assessed together with the enumeration of the valid counterfactual instances (called counterfactual space), which again is a direct result of the conditions set. If this space is too limited then the scope for action driven by counterfactuals is limited. One should also realize that the conditions set should reflect the thermal comfort as perceived by the users and should only be set by taking strong account of them.
These are side benefits of the counterfactual analysis. Of course the key aspired benefit in our demand response context is not closely related to the average values; the use of counterfactuals in the demand response context would be instance centered and would work as follows:
If a valid counterfactual instance is identified, one that fulfills the conditions that have been set up, then
run the instance counterfactual and calculate the impact on consumption of 1/2/3 degrees change respectively
communicate this information to the building users, especially those able to act upon the thermostat and make effective use of the information communicated
Last, we have introduced here the counterfactual analysis with regard to the indoor temperature, a feature that we have beforehand established as important in the forecasting analysis of the specific building in question.
Indoor temperature is by no means the only building parameter users can act upon. Whenever a user can interact with a building feature (e.g. act on drapes to reduce/increase heat gains, switch lights on/off, turn on/off the aeration, etc.) counterfactuals are pertinent. Perhaps these may not be pertinent for the building overall, but in smaller and more targeted forecasting scopes. However, we believe they deserve more attention in the various building modeling aspects as they can link to tangible action that is the heart of effective decision support.
5. Conclusions and currently ongoing work
In this work we focussed on forecasting explainability, and we sought to test a number of approaches of global (model) or local (instance) level explainability.
At the model level we started with a number of modeling approaches including LSTM and STS as well as purely explainable models based on genetic programming (GP). We found that GP typically outperformed LSTM and STS in terms of accuracy. However, the symbolic expressions that resulted were very complex and would not allow us to reach any insight on the model performance. We also found that GP quality, contrary to STS, does not deteriorate when shorter training timeframes are selected. This is an important result, at least from a practical point of view, as a demand response controller would be able to train a GP model and become productive in a short period of time, one or two weeks.
At the instance explainability level we introduced SHAP analysis in order to investigate the critical issue of feature importance. Although we applied this in general and across all features we were particularly interested in the indoor temperature feature as this was an actionable one. Indoor temperature often, in terms of its SHAP value, emerged as an important feature, and in some models even as the most important one. SHAP values of indoor temperature were also always intuitive: negative in summer when a decrease of indoor temperature results, because of the cooling, in an increase of consumption; and positive in winter, when an increase of indoor temperature results in increased consumption due to heating.
After having verifiably, via SHAP, established the importance of indoor temperature in the forecasting, we introduced counterfactual (or what-if) analysis seeking to gain a numerical indication of the change of consumption, with a respective change of indoor temperature. Of course, in order to run meaningful counterfactual analyses, one has first to set some specific conditions that secure the validity and meaningfulness of the counterfactual. These conditions also reflect our perception of thermal comfort. If, for example, we consider an indoor temperature of 24 degrees as an overheating event, we might be interested in restricting the counterfactual space to instances where indoor temperature is greater than 24 degrees.
The counterfactual analysis is useful from two distinct perspectives.
First, at a building level, it provides insight into the true scope of counterfactuals’ driven action. It allows us to answer questions such as: What economy will I have on average, if in winter time I reduce the set point by 1 (2 or 3, etc.) degrees in all instances where according to the conditions set, an overheating event is identified. One can also change the conditions, and see how things develop. Of course, changing the conditions is equivalent to redefining the thermal comfort in the building and it should only be done with this kept in mind. Besides the insight into the building performance, such questions can also allow users to make and implement informed decisions about thermostat settings.
And second, in a (demand) controller environment, counterfactual analysis allows us to answer questions such as: What economy will I have if at the specific moment that I am notified of an overheating event I reduce the set point by 1 (2 or 3, etc.) degrees?
Finally, counterfactuals have in our case been set up with regard to the indoor temperature alone, because this was the only essentially actionable feature considered. Could we, for example, have set up counterfactuals for the outdoor temperature, which was also consistently used in the modeling? The answer is, in principle, yes, but there would be some important limitations. At the building level, similarly to the above description of the indoor temperature, we would now be still able to ask questions such as: How will my building consumption evolve if tomorrow I will have outdoor temperature that is 2 degrees higher? But now, contrary to the indoor temperature case, there is nothing here that I, as a building user, can do about this; I cannot act upon the outdoor temperature or set up any building policy with regards to it. Therefore, my analysis is of limited importance. Similarly, in the second use case discussed above (controller case) a counterfactual based on the outdoor temperature would be meaningless, as the building user has again no possibility of acting upon the outdoor temperature.
Taking a broader perspective on counterfactuals in the building energy forecasting context, we would argue that they can be particularly useful when actionable parameters, such as indoor temperature, humidity, lighting levels, aeration, etc. are included in the model. Therefore, an important result is that the inclusion of such parameters would empower our model with the additional capabilities summarized above. This result calls into question the relatively limited use of such parameters in forecasting models as discussed in the literature review. Currently we are exploring such additional uses of counterfactuals on actionable features.
Additionally, a key focus is on the GP symbolic expressions. At the moment we have found them to be complex and of no true insight. In TRUST AI, a framework for working with symbolic expressions, for pruning and more generally editing them, is being developed. We are looking forward to exploiting it to see if the symbolic expressions can be edited and shortened so that they may result in some explainable models. In addition, we will examine what the performance expense of such a symbolic expression compacting exercise would eventually be.
CRediT authorship contribution statement:
Nikos Sakkas: Methodology, Investigation, Sofia Yfanti: Building contact point, writing - review & editing, Pooja Shah: Modeling, Nikitas Sakkas, Modeling and data pretreatment, Christina Chaniotakis: Integration of results with demand response controller, Costas Daskalakis: Data collection, curation and visualization, Eduard Barbu: Explainability and counterfactual analysis, Marharyta Domnich: Explainability and counterfactual analysis.
Declaration of competing interest:
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The work presented in this paper is funded by the European Commission within the HORIZON Programme (TRUST AI Project, Contract No.: 952060).
References
- Ailin Asadinejad and Kevin Tomsovic, Optimal use of incentive and price based demand response to reduce costs and price volatility, Electric Power Systems Research 144 (2017) 215–223. [CrossRef]
- Amira Mouakher, Wissem Inoubli, Chahinez Ounoughi and Andrea Ko, EXPECT: EXplainable Prediction Model for Energy ConsumpTion, Mathematics 2022, 10, 248. [CrossRef]
- Aniek F. Markus, Jan A. Kors and Peter R. Rijnbeek, The role of explainability in creating trustworthy artificial intelligence for health care: A comprehensive survey of the terminology, design choices, and evaluation strategies, Journal of Biomedical Informatics, Volume 113, 2021. [CrossRef]
- Badar Islam, Comparison of conventional and modern load forecasting techniques based on artificial intelligence and expert systems. Int J Comput Sci Issues 2011;8(5):504–513.
- Carlos Roldán-Blay, Guillermo Escrivá-Escrivá, Carlos Álvarez-Bel, Carlos Roldán-Porta, and Javier Rodríguez-García, Upgrade of an artificial neural network prediction method for electrical consumption forecasting using an hourly temperature curve model, Energy and Buildings 60 (2013) 38–46.
- Corinna Cortes and Valdimir Vapnik, Support-vector networks. Mach Learn 1995;20(3):273–97.
- Georges Darbellay and Marek Slama, Forecasting the short-term demand for electricity: do neural networks stand a better chance?. Int J Forecast 2000;16(1):71–83.
- Goutam Dutta and Krishnendranath Mitra, A literature review on dynamic pricing of electricity, Journal of the Operational Research Society 68 (2017) 1131–1145. [CrossRef]
- Guillermo Escrivá-Escrivá, Carlos Álvarez-Bel, Carlos Roldán-Blay and Manuel Alcázar-Ortega, New artificial neural network prediction method for electrical consumption forecasting based on building end-uses, Energy and Buildings 43 (2011) 3112–3119.
- Hengfang Deng, David Fannon and Matthew J. Eckelman, Predictive modeling for US commercial building energy use: A comparison of existing statistical and machine learning algorithms using CBECS microdata, Energy and Buildings 163 (2018) 34–43. [CrossRef]
- Isaac K. Nti, Moses Teimeh, Owusu Nyarko-Boateng and Adebayo Felix Adekoya, Electricity load forecasting: a systematic review, Journal of Electrical Systems and Inf Technol 7, 13 (2020). [CrossRef]
- Ji Hoon Yoon, Ross Bladicka and Atila Novoselac, Demand response for residential buildings based on dynamic price of electricity, Energy and Buildings 80 (2014) 531–541. [CrossRef]
- Jin-Young Kim and Sung-Bae Cho, Predicting Residential Energy Consumption by Explainable Deep Learning with Long-Term and Short-Term Latent Variables, Cybernetics and Systems 2022. [CrossRef]
- José Francisco Moreira Pessanha and Nelson Leon, 2015. Forecasting long-term electricity demand in the residential sector. Procedia Computer Science. 55, 529–538. [CrossRef]
- L. Suganthi and Anand A. Samuel, 2012. Energy models for demand forecasting—A review, Renewable and Sustainable Energy Reviews. 16 (2), 1223-1240. [CrossRef]
- Mathieu Bourdeau, Xiao Qiang Zhai, Elyes Nefzaoui, Xiaofeng Guo and Patrice Chatellier, Modeling and forecasting building energy consumption: A review of data driven techniques, Sustainable Cities and Society 2019; 48: 101533. [CrossRef]
- Md Shahjalal, Alexander Boden, and Gunnar Stevens, Towards user-centered explainable energy demand forecasting systems, Proceedings of the Thirteenth ACM International Conference on Future Energy Systems (e-Energy '22). Association for Computing Machinery, New York, NY, USA, 446–447. [CrossRef]
- Michael Schreiber, Martin E. Wainstein, Patrick Hochloff and Roger Dargaville, Flexible electricity tariffs: Power and energy price signals designed for a smarter grid, Energy 93 (2015) 2568-2581. [CrossRef]
- Mohammad Azhar Mat Daut, Mohammad Yusri Hassan, Hayati Abdullah, Hasimah Abdul Rahman, Pauzi Abdullah and Faridah Hussin, Building electrical energy consumption forecasting analysis using conventional and artificial intelligence methods: A review, Renewable and Sustainable Energy Reviews 70 (2017) 1108-1118. [CrossRef]
- Muhammad Qamar Raza & Abbas Khosravi, A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings, Renew Sustain Energy Rev 2015;50:1352–72. [CrossRef]
- Nikos Sakkas, Sofia Yfanti, Costas Daskalakis, Eduard Barbu and Margarita Domnich, Interpretable Forecasting of Energy Demand in the Residential Sector. Energies 14 (2021) 6568. [CrossRef]
- Nils Jakob Johannesen, Mohan Kolhe and Morten Goodwin, Relative evaluation of regression tools for urban area electrical energy demand forecasting, Journal of Cleaner Production 218 (2019) 555- 564. [CrossRef]
- Sandra Wachter, Brent Mittelstadt and Chris Russell, Counterfactual Explanations without Opening the Black Box: Automated Decisions and the GDPR, 2018, https://arxiv.org/abs/1711.00399.
- Scott M. Lundberg and Su-In Lee, 2017, A Unified Approach to Interpreting Model Predictions, 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA.
- Severin Borenstein, Effective and Equitable Adoption of Opt-In Residential Dynamic Electricity Pricing, Rev Ind Organ 42 (2013) 127–160. [CrossRef]
- Stavroula Karatasou, Mattheos Santamouris and Vassilis Geros, Modeling and predicting building’s energy use with artificial neural networks: Methods and results, Energy and Buildings 38 (2006) 949–958. [CrossRef]
- Tadahiro Nakajima and Shigeyuki Hamori, 2010. Change in consumer sensitivity to electricity prices in response to retail deregulation: A panel empirical analysis of the residential demand for electricity in the United States. Energy Policy. 38 (5), 2470-2476. [CrossRef]
- Tim Miller, Explanation in artificial intelligence: Insights from the social sciences, Artificial Intelligence, Volume 267, 2019, Pages 1-38, ISSN 0004-3702. [CrossRef]
- Zichen Zhang and Wei-Chiang Hong, Application of variational mode decomposition and chaotic gray wolf optimizer with support vector regression for forecasting electric loads, Knowledge-Based Systems 228 (2021) 1-16.
Figure 2.
Model 13 long training SHAP plot.
Figure 3.
Model 13 short training SHAP plot.
Figure 10.
Indoor temperature change effect on consumption percent change from generated summer and winter counterfactuals.
Figure 10.
Indoor temperature change effect on consumption percent change from generated summer and winter counterfactuals.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated