1. Introduction
Identification of damage in reinforced concrete (RC) structures can be done by detection of variations in their dynamic characteristics with reference to the undamaged state. To detect the Eigen-Frequencies (and mode-shapes) of existing RC structures, instrumental monitoring of the structure by an installed local multichannel network system of accelerometers is necessary, and then, an analytic processing of the recorded response should be performed by using various stochastic and deterministic procedures developed in the past [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11]. Recent research effort has led to the development of theories, methods, and techniques for the detection of damage in existing structures, such as the rank perturbation theory (MRPT) [
12,
13], a technique about the discontinuity of forms of mode-shapes [
14,
15], an artificial neural network technique [
16], the method of the damage stiffness matrix [
17,
18], a comprehensive review of data-driven damage indicators for rapid seismic structural health monitoring [
19] and a combination of traditional structural health monitoring techniques with novel machine learning tools [
20]. Furthermore, recently, a hybrid procedure for the damage identification in existing planar RC frame has been developed [
21], mainly for the case of seismic loadings or wind loadings. The last methodology is based, on the one hand, on the development of Eigen-Frequencies curves by performing two pushover analyses in a suitable nonlinear model of the planar moment-frame, and, on the other hand, on the fundamental Eigen-Frequency of the damaged frame, which is identified by the instrumental monitoring of its structural integrity. Using the fundamental Eigen-Frequency of the damaged moment-frame that arise by the instrumental monitoring, all the other higher Eigen-Frequencies of the moment-frame are determined from the diagram of the instantaneous Eigen-Frequencies of the frame in the nonlinear regime (namely the key-diagram). Furthermore, the modal shapes of the damaged frame are determined with instantaneous modal analysis (at the examined step of pushover analysis), where all calculations are performed into the examined step of the nonlinear area of analysis. Last, the damage stiffness matrix of the moment-frame is calculated at the examined step considering all plastic hinges and the degradation of member stiffness, and therefore it determines the extent of damage of the moment-frame. Finally, the damage image of the planar RC moment-frame, i.e. the location and the magnitude of damage, is obtained from the state of the developed plastic hinges at the corresponding step of the pushover analysis. It is noting that in planar frames, two pushover analyses, with lateral floor forces with triangular (or according to the first mode-shape) distribution in elevation, are needed, where the second pushover analysis has negative sign on the lateral floor forces with reference to the first one.
To verify the abovementioned recently proposed methodology [
21] in frames that develop a beam-sway plastic mechanism, a group of existing ductile, multi-storey, multi-span, planar RC frames with various lengths and storey heights is examined in this paper in order to determine the damage state. Here, a numerical example of a five-storey moment-frame with three unequal spans is presented. All the steps of the proposed methodology are clearly presented in the corresponding section below and applied during the presentation of the numerical example. The article focuses, on the one hand, on the determination of the Eigen-Frequencies curves of the damaged moment-frame as a function of the seismic roof displacement, which are drawn by performing a sequence of pushover and instantaneous modal analyses with gradually increasing target displacement, and, on the other hand, on the evaluation of the damage stiffness matrix of the moment-frame. In addition, a new load pattern appropriate for tall multi-storey frames is incorporated in pushover analysis to take account of the effects of higher modes in the distribution of damage along the height of the frame. Finally, for each case, the damage matrix of the frame is calculated, and the damage image of the frame is illustrated.
2. Materials and Methods
The free vibration differential equation of motion of a multi-degree of freedom system (MDOF) without damping due to an initial forced displacement or velocity is:
where m is the mass matrix of the frame, is the stiffness matrix of the frame while and are the time-varying displacement and acceleration vectors of the system respectively.
Next, it is assumed that this is an existing system that presents a damage image due to any cause. Then, the stiffness matrix at any time step
i will change by
, so it follows that:
where is the Damage Stiffness Matrix.
Moreover, the instantaneous mode-shapes at each inelastic
i-step of the analysis can be defined if a modal linear analysis is performed using the instantaneous stiffness matrix
, which includes the damage effects on stiffness. Therefore, the equation of motion is written:
That is, a modal analysis is performed using as initial conditions the inelastic response of the frame structure at the
i-step. Hence, considering that the mass matrix
m does not vary, the eigenvalue problem at the inelastic
i-step is written:
where
(rad/s) is the instantaneous eigenvalues and
is the instantaneous mode-shape vectors of the frame structure at the inelastic
i-step of the analysis. The solution of the eigenvalue problem is given by setting the following determinant to zero and finding the roots
of the resulting algebraic equation:
Then, the instantaneous mode-shape vector
can be calculated by Equation (4) for each value of
, where
in an N-degrees of freedom system. Moreover, with a known eigenvalue
, Equation (4) is pre-multiplied by the
:
Rearranging the terms in Equation (6), it can be rewritten as following:
It is noted that it is impossible to identify the instantaneous frequency
and the instantaneous mode-shape vector
of the structure at the inelastic
i-step by analysis of the records (time-history analysis with accelerograms) using the Random Data Processing, since these procedures require the existence of a sufficient time-window, where the eigenfrequencies remain constant. Instead, the obtained records by an installed monitoring multichannel network system of accelerometers must come from the ambient vibration of an existing (with damage) calm structure, without motion. Therefore, if
are known by the recently proposed methodology [
21], then Equation (7) can be used at the end for verification reasons.
In summary, the recently proposed methodology [
21] on multi-storey planar frames, using a hybrid technique (that we call “
M and P” technique, where the
M means “Monitoring” and the
P means “Pushover”) that combines an identification system and a numerical model, consists of the following phases:
- (a)
The fundamental Eigen-Frequency of the existing damaged structure is identified by monitoring with a local network of uniaxial accelerometers located at the characteristic positions along the degrees of freedom of the system.
- (b)
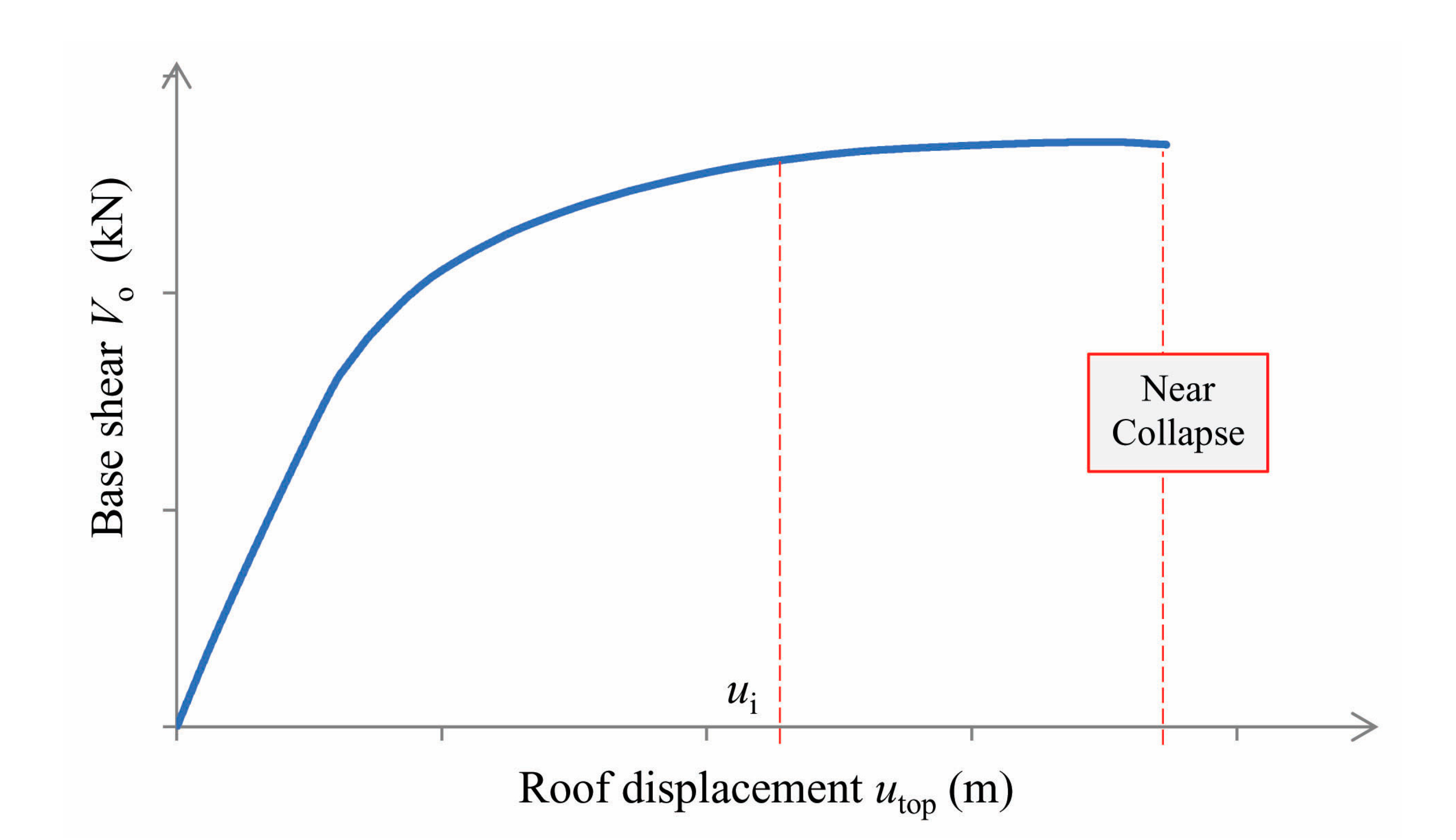
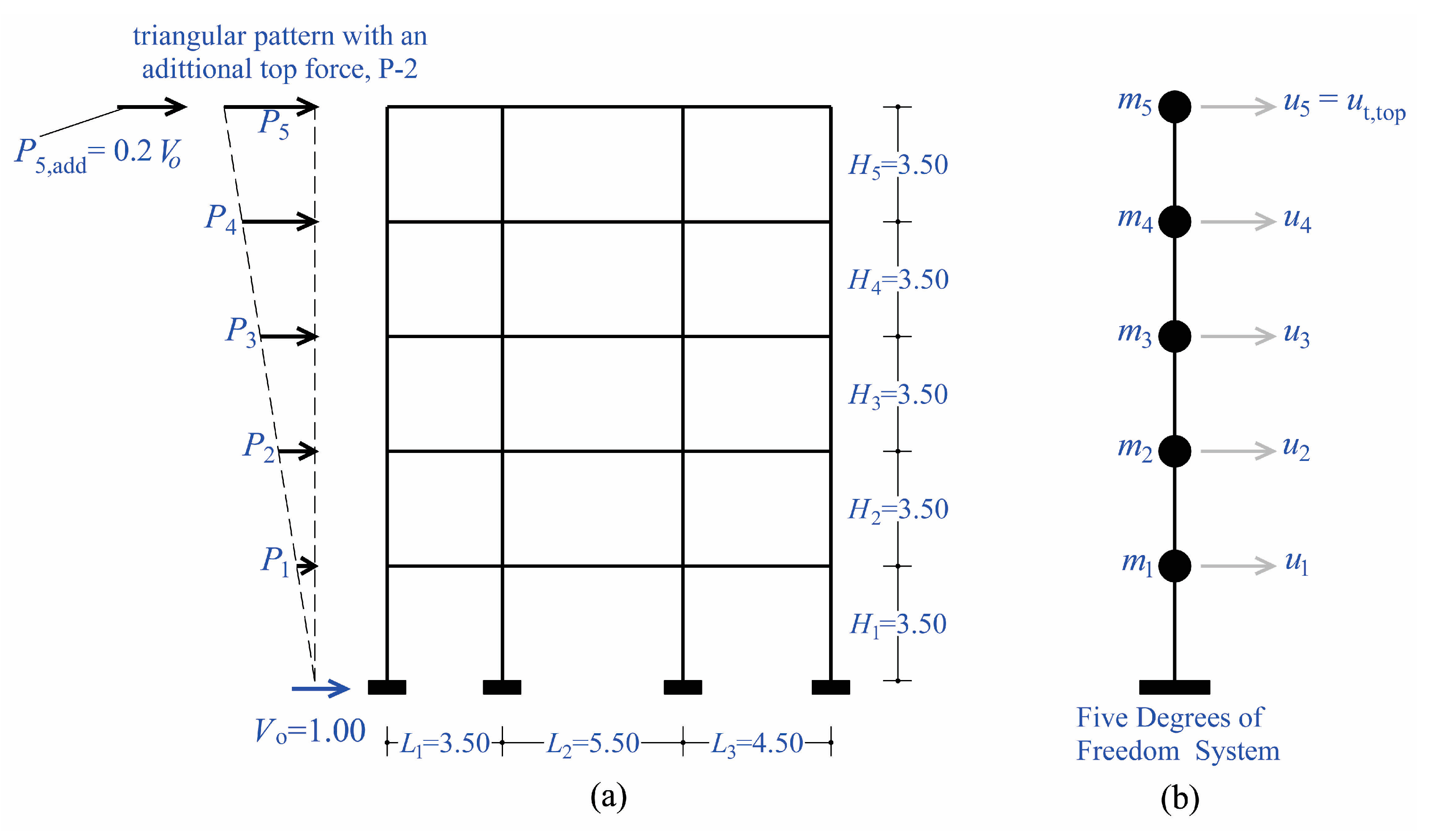
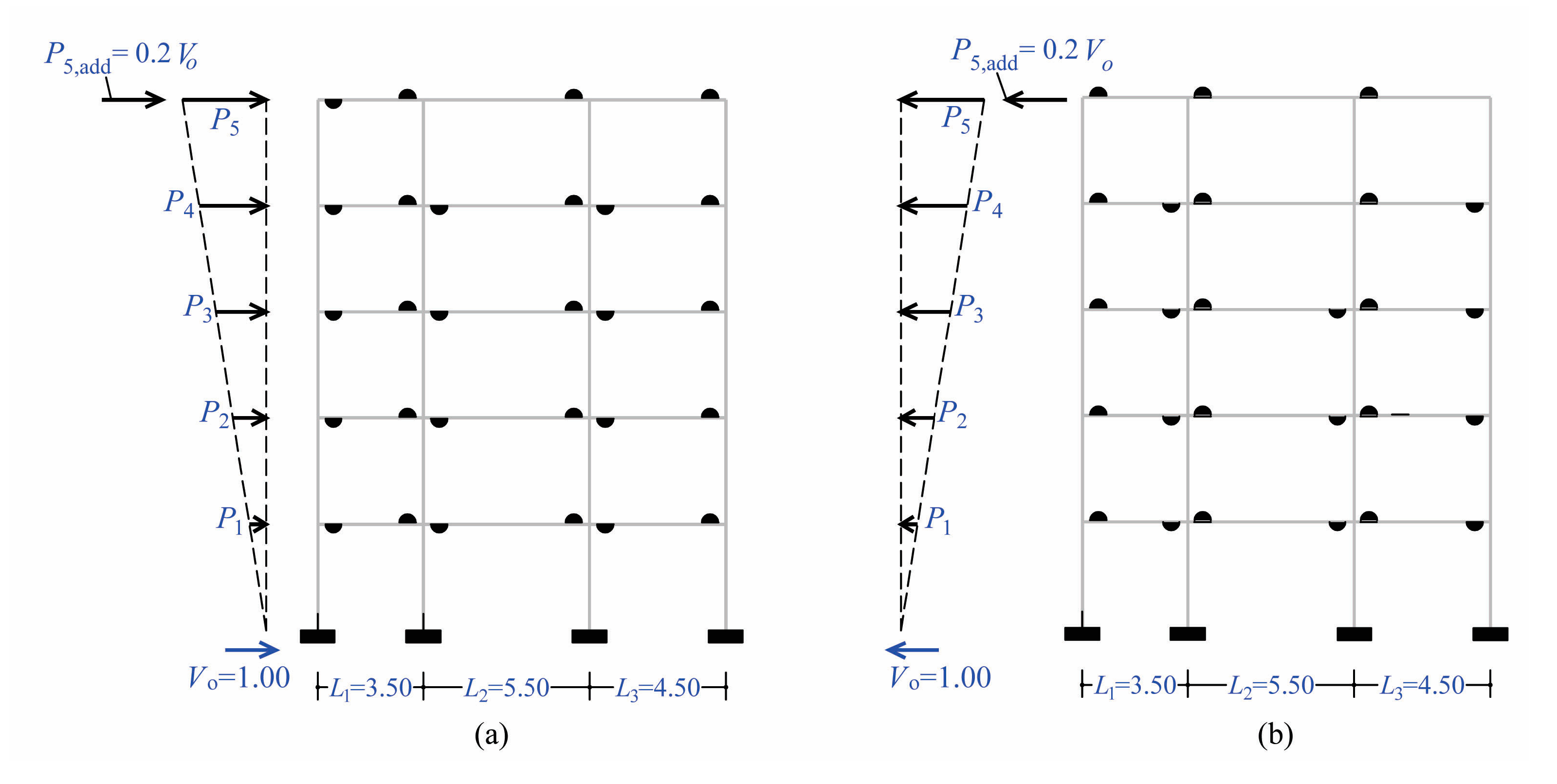
A suitable numerical non-linear model of the structure is obtained, and two pushover analyses are performed, with positive and negative floor forces, leading to the drawing of the capacity curves of the structure in terms of base shear and roof displacement (
Figure 1). As regards the floor lateral force pattern used in pushover analysis, the triangular or the first mode pattern of forces is suitable for building structures up to four floors. For higher buildings, an additional second-floor force pattern is proposed with a unit base shear (
), in which an additional force equal to
is applied at the top floor [
22] and the rest of the base shear (namely the
) is distributed (in floor forces) according to the triangular or to the first mode pattern. The goal here is to consider the higher mode effects of tall buildings into the linear and non-linear area, which can be significant especially for more flexible structures, such as moment-frames. Another important point in the application of pushover analysis is that P-D effects should always be considered in the nonlinear area, especially for frame structures which are more flexible.
- (c)
By performing Modal analysis at each
i-step (or at various characteristic steps) of the pushover analysis, using the stiffness matrix of the damaged structure obtained at the last
i-step in pushover analysis, the diagram of the instantaneous (step) cyclic Eigen-Frequencies
(in Hz) of the damaged structure is drawn as a function of the roof displacement
of the structure (
Figure 2). In this diagram, that is the novel key point of the proposed methodology, the value of the inelastic roof displacement
is the abscissa and the value of the Eigen-Frequencies
of the damaged structure is the ordinate.
It is emphasized that that the sequence of pushover and instantaneous modal analyses of the structure, targeting each time at a gradual increasing roof displacement, should be performed in a nonlinear model of the structure with discrete values
(
is the elastic modulus of concrete) of the effective bending stiffness of RC structural elements, that correspond to different damage states at each
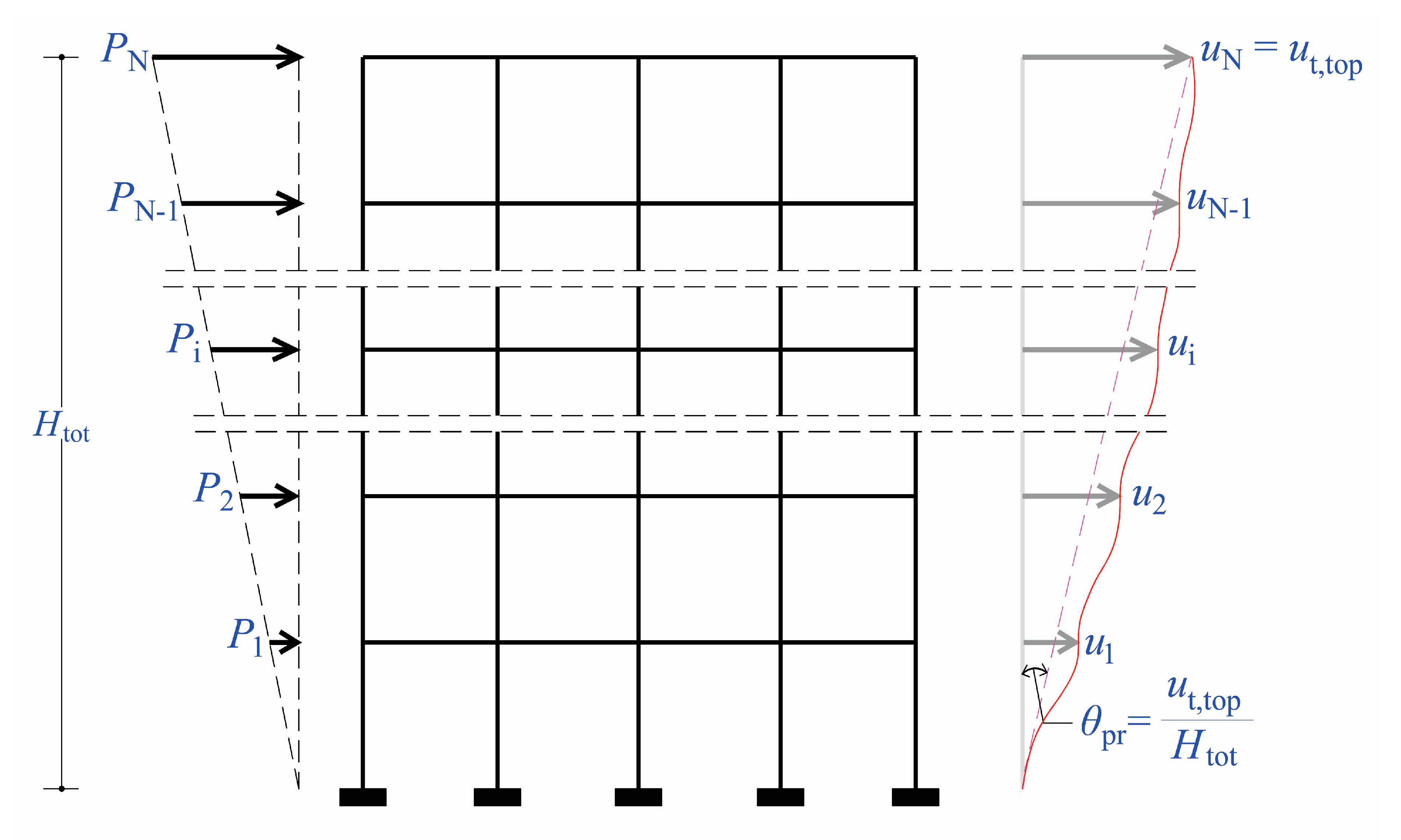
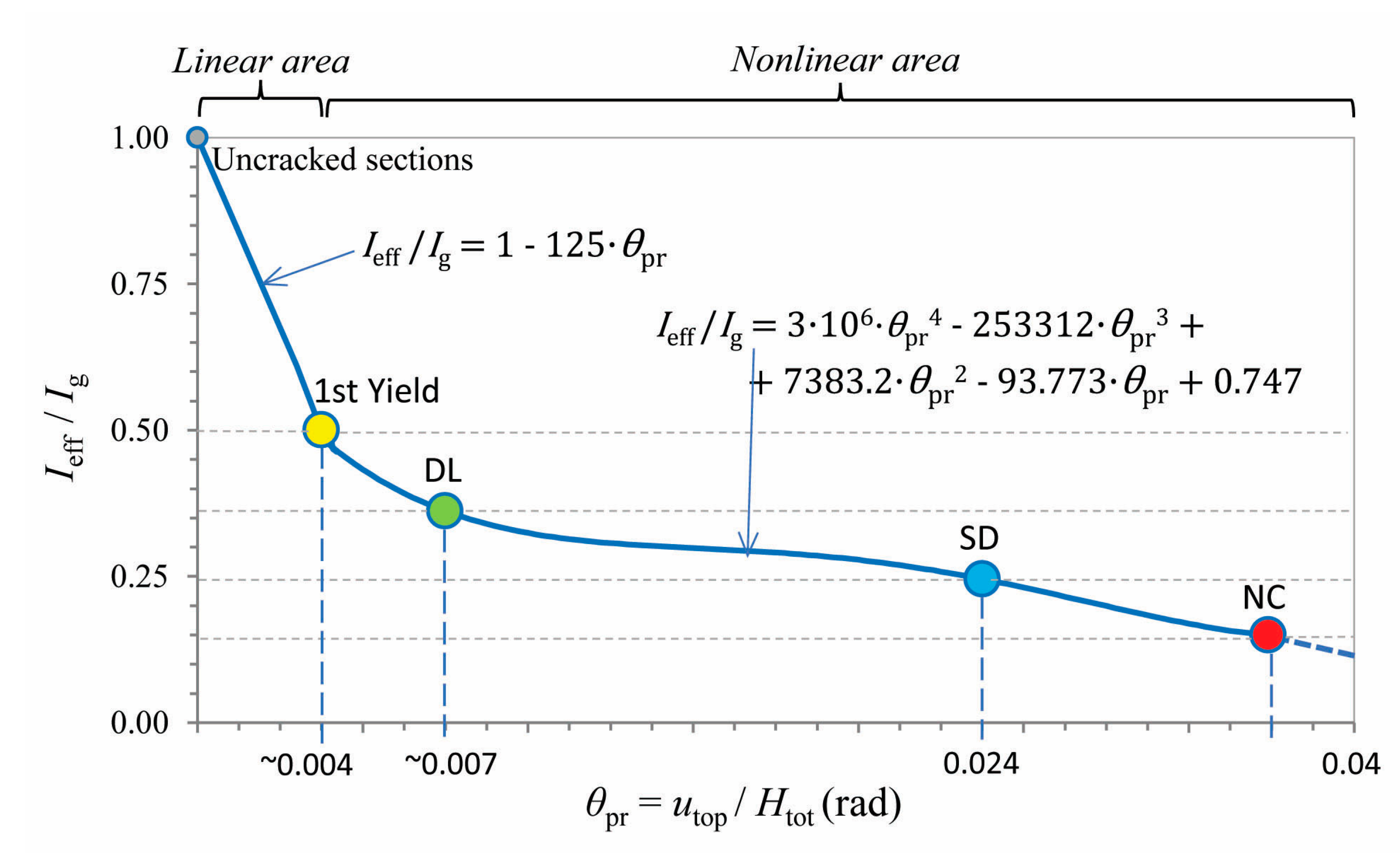
i-step, due to stiffness degradation because of damage. The damage state corresponds to various performance levels: undamaged state, first Yield (first plastic hinge formation), Damage Limitation (DL), Significant Damage (SD), Near Collapse (NC), and all the intermediate ones. Hence, an effective stiffness scenario in terms of the effective moment of inertia ratio
(where
is the moment of inertia of the geometric section) must be prepared before performing pushover and modal analyses, as a function of the mean (chord) rotation of the frame structure,
, where the subscript
pr,i refers to the chord rotation profile of the moment-frame at the examined
i-step. This is equal to
, where
is the seismic (target) roof displacement at the
i-step and
is the total building height (
Figure 3). As shown in
Figure 4, the effective moment of inertia
of RC structural elements (as the mean value for their two end-sections) that corresponds to the NC performance level is too low, and it can be calculated from an equation given in EN 1998-3 [
23]:
where
is the plastic moment of the section determined through an elastoplastic idealization of the Moment-Curvature diagram
Μ-φ of the section,
is the shear length of the RC element taken equal to the half clear-length of the element [
22,
23], and
is the available chord rotation of the shear length of the element at yield state that is given approximately by Equation A.10 of Eurocode EN 1998-3. In fact, EN 1998-3 impose these low values of the effective bending stiffness on all RC structural elements, in order to perform nonlinear analysis targeting all performance levels, from DL to NC. Since this is too conservative, a scaling is proposed in
Figure 4 when pushover analysis targets other higher seismic performance levels, such as DL or SD or all other intermediate ones [
22]. Another point in Equation (8) is that it provides different values of effective stiffness at various structural elements. To simplify this, the mean effective stiffness at NC state is assigned to each structural element of the nonlinear model according to the proposed methodology. Moreover, the effective stiffness scenario of
Figure 4 proposes discrete
values from the uncracked state towards the 1
st Yield (when the 1
st plastic hinge is shown) and from there to DL. Additionally, two proposed lines (with the corresponding equations) for the effective stiffness into the linear and nonlinear area are also presented into
Figure 4:
For the linear area,
:
For the nonlinear area,
:
For the nonlinear area in the vicinity of (near) collapse,
- (d)
The known fundamental Eigen-Frequency of the damaged structure of phase (a),
, is inserted in the instantaneous Eigen-Frequencies diagram (
Figure 2) and, hence, the respective inelastic seismic (target) roof displacement
is determined. All the rest instantaneous higher Eigen-Frequencies
lie on the same vertical line passing through the target-displacement
.
- (e)
The damage state of the structure can be identified by the results of two pushover analyses (with floor forces along the positive and negative direction) at the i-step where the roof displacement is shown. The location and the state of the plastic hinges at this i-step of each pushover analysis indicate the damaged state of the structure, while the final requested damaged state of the structure will result from the superposition of the damage states of the two pushovers.
- (f)
Moreover, a linear modal analysis is performed at the i-step of pushover analysis (phase e), using as initial conditions the instantaneous stiffness matrix of the i-step. From this modal analysis, all the circular Eigen-Frequencies and all the instantaneous mode-shapes of the damaged structure are calculated.
- (g)
At the end, the instantaneous stiffness matrix of the structure at the examined inelastic i-step is determined. Hence, the Damage Stiffness Matrix at the same i-step is calculated from the general relationship , where is the known Initial Stiffness Matrix of the undamaged structure.
3. Numerical Example
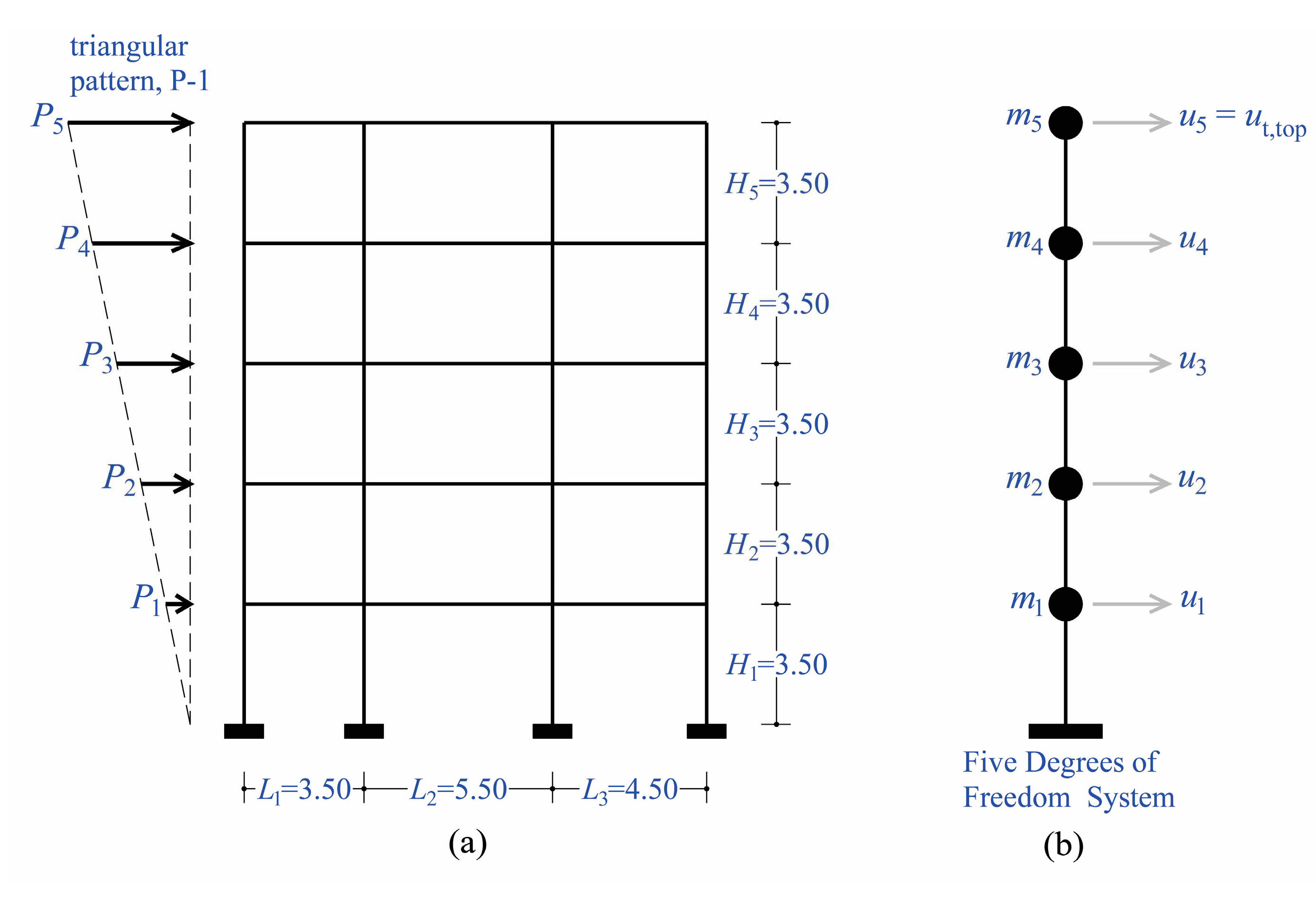
We consider the existing five-storey planar RC frame of
Figure 5, with three unequal spans, with dimensions
and
. The strorey height is equal to 3.5 m in all floors, and the total height of the frame is 17.5 m. The total vertical uniformly distributed loads of the seismic combination
(where
is the dead load,
is the quasi-live load and
[
24]) applied on the spans of each floor are respectively equal to
and
kN/m. These loads contribute to a floor mass of approximately 45 tn and to a total frame mass of 225 tns. The floor mass and the degrees of freedom of the five-storey planar frame for the modal analysis are illustrated in
Figure 5b and
Figure 6b. Additionally,
Figure 5a and
Figure 6a present the two patterns (P-1 and P-2) of lateral floor forces that will be used in pushover analysis. The frame was constructed with concrete grade C25/30 and steel grade B500s, with mean compressive and tensile strengths, respectively equal to
and
. The Elasticity Modulus of the concrete is equal to
, while that of the steel is
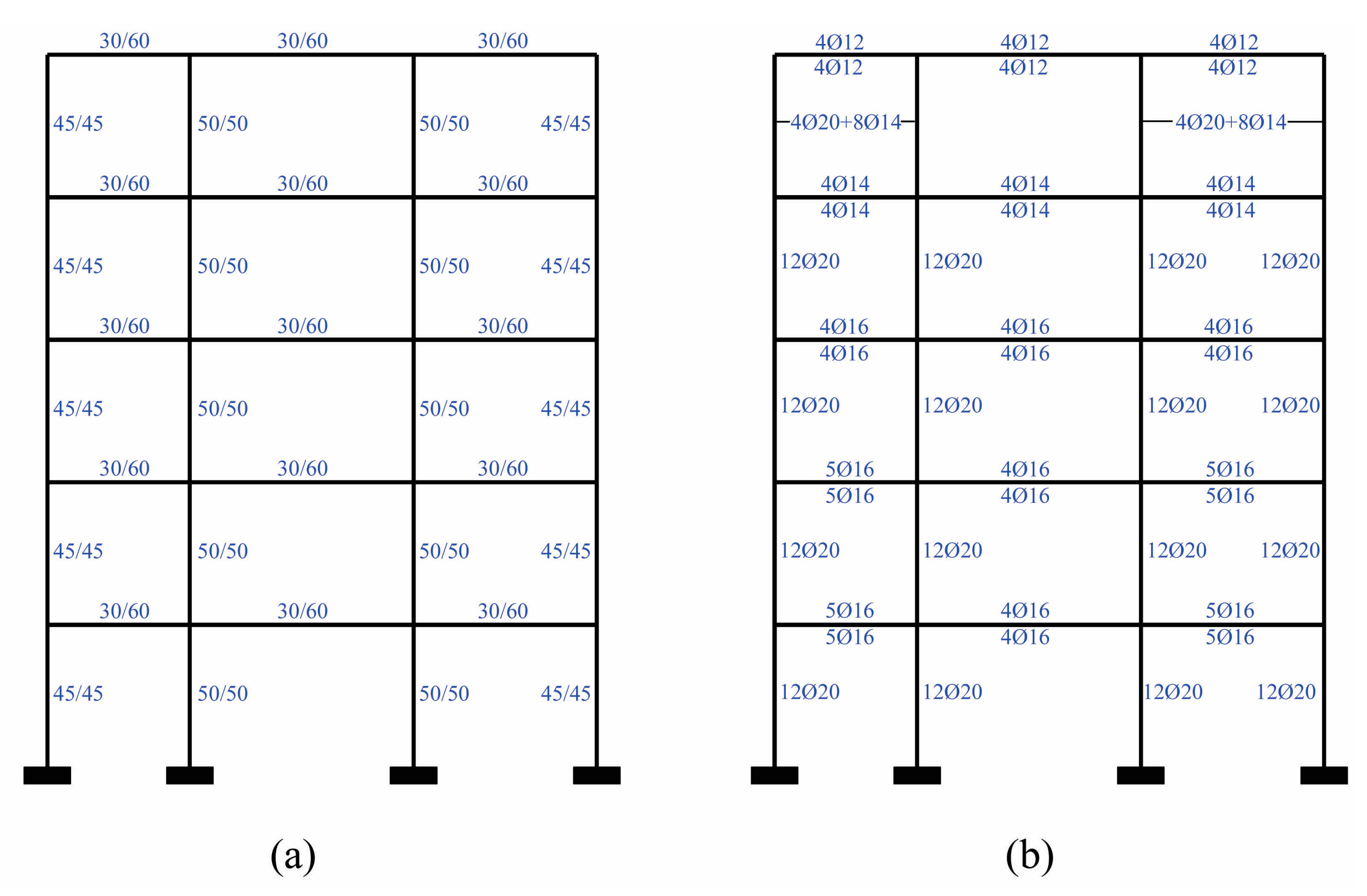
. There are two different column sections, with dimensions
equal to
and
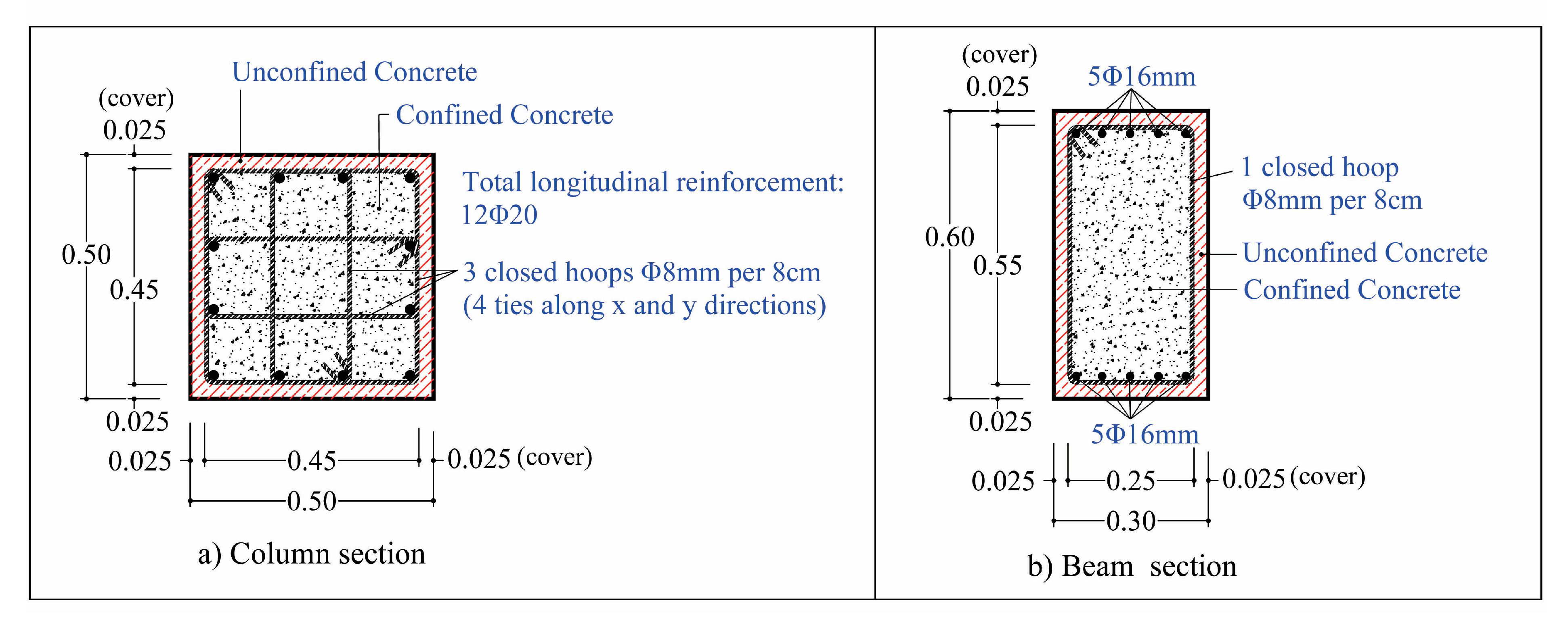
m, respectively. All column sections are symmetrically reinforced with 12 steel bars of 20 mm diameter (or 12Ø20) at all floors, except the top floor where the total steel bars are 4Ø20+8Ø14 (
Figure 7). The confinement reinforcement in all columns, in every floor, consists of closed hoops with 4 ties of 8 mm diameter, evenly spaced per 8 cm axially at the critical end sections. The beams of the frame have a rectangular section of dimension
m and are symmetrically reinforced at the upper and the lower fibers but have different steel bars at various floors (
Figure 7). The beams in all floors have a perimetric closed hoop of 8mm diameter, evenly spaced per 8cm axially at the critical end sections, which acts as shear reinforcement and provides a low confinement state. Steel reinforcement details of typical column and beam sections are shown in
Figure 8. It is noting that the planar RC frame has been designed according to EN 1998-1 [
24] for the high ductility class (DCH) and, hence, it is expected to demonstrate a beam-sway plastic mechanism in the nonlinear area.
In order to apply the proposed methodology [
21] for the identification of the structural damage, a sequence of pushover and instantaneous modal analyses should be performed. The nonlinear model of the planar RC frame was created in the FEM analysis software SAP2000 [
25] using fiber hinges to simulate the locations of the possible developing plastic hinges at the end-sections of the elements, with plastic hinge length calculated by Equation (A.9) of EN 1998-3 [
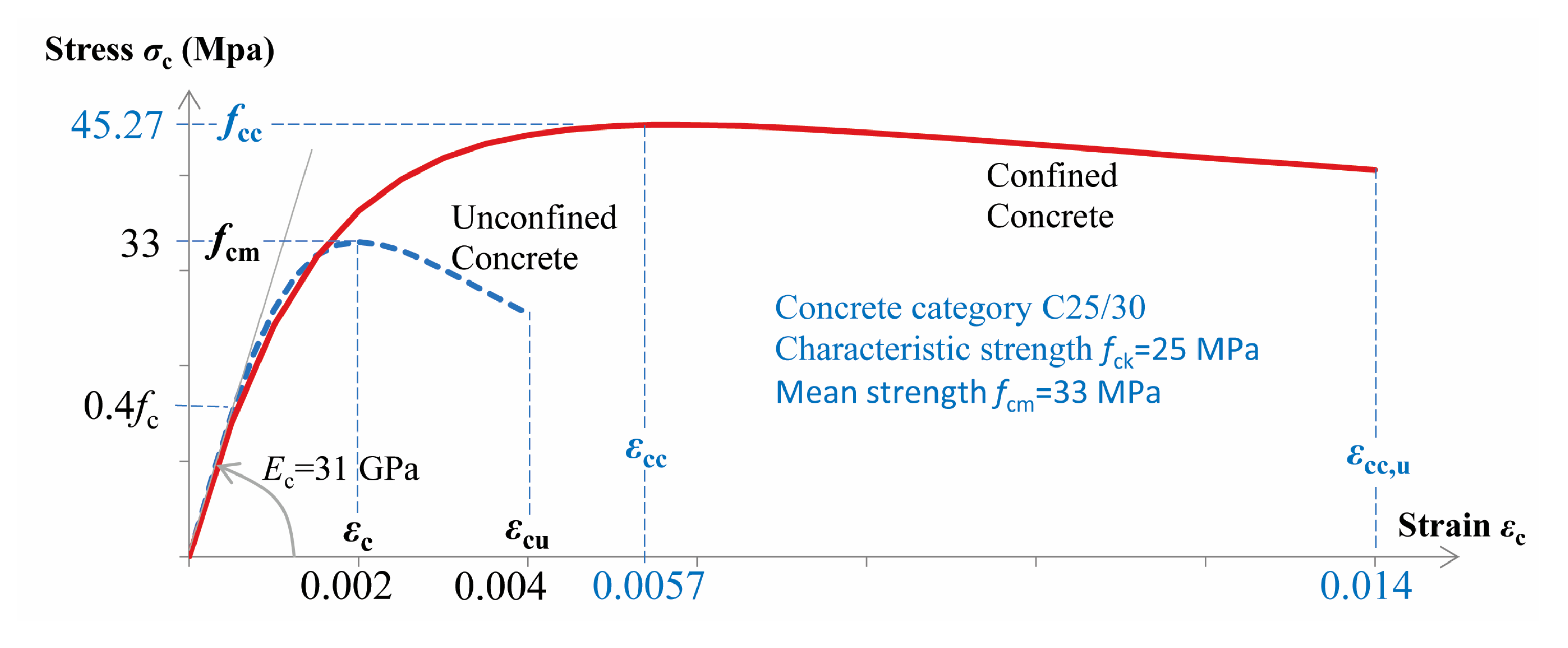
23]. The material constitutive relationships used in nonlinear analyses are consistent with: (a) the uniaxial unconfined and confined model for the concrete proposed by Mander, Priestley and Park (1988) [
26] (
Figure 9), and (b) the steel reinforcement model (parabolic at strain hardening region) proposed by Park and Paulay (1975) [
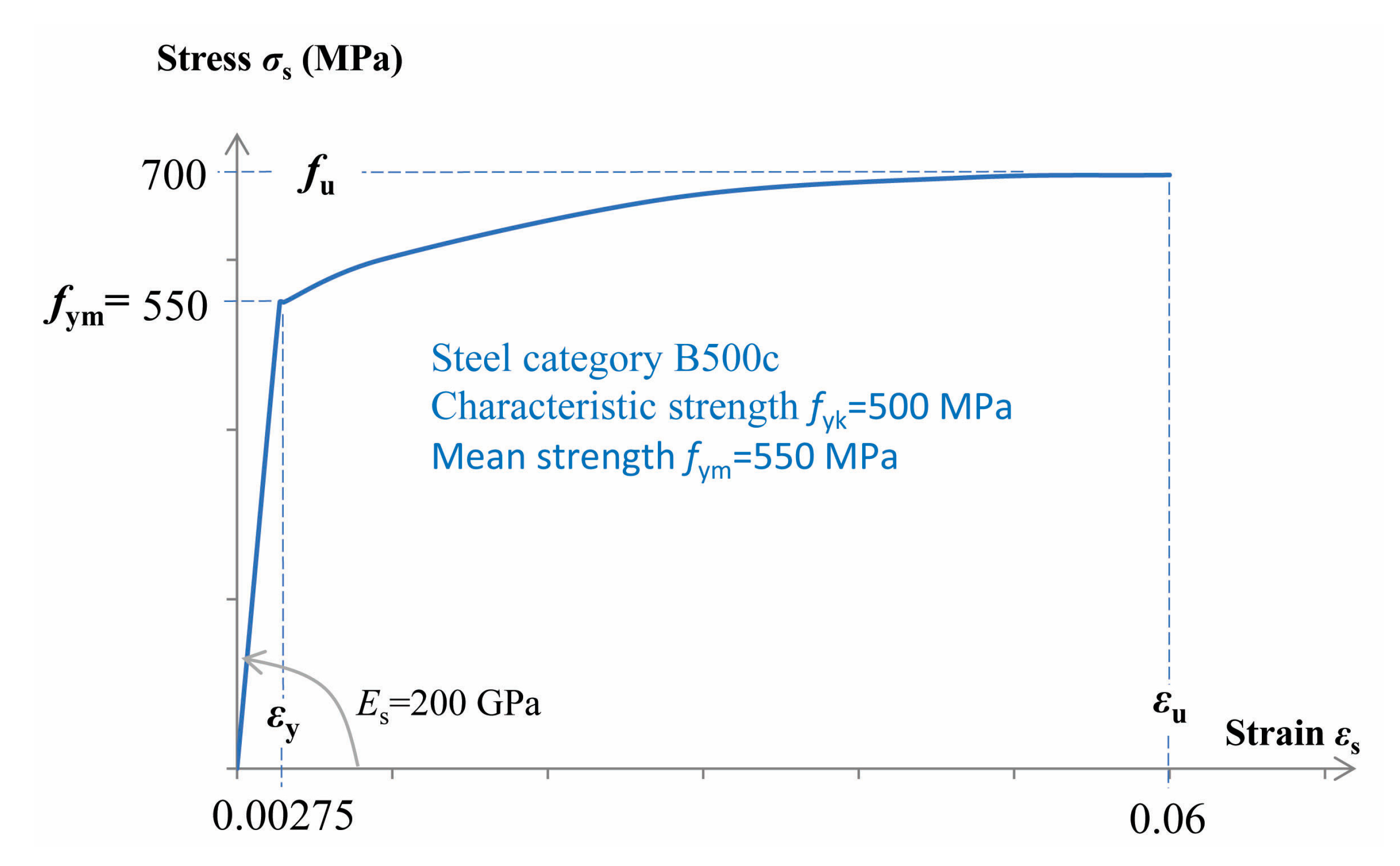
27] (
Figure 10).
A section analysis [
25] should be performed first, in order to calculate the effective bending stiffness
of the structural elements at the NC state, using Equation (8). Then, the stiffness scenario used in the sequence of pushover analyses of the frame -with gradually increasing target roof displacement- is established (phase c), which is presented in
Table 1 as a function of the profile angle
(
Figure 3). The discrete values of the effective moment of inertia
assigned to all RC structural elements of the nonlinear model of the frame depend on the seismic (target) roof displacement of the pushover analysis, i.e. on the target performance level (
Figure 4). For example, if the target roof displacement
corresponds to a value of
equal to 0.028, i.e.
, then the value of
that should be assigned to all structural elements of the nonlinear model is equal to
according to
Table 1.
To obtain the capacity curve of the planar frame, two pushover analyses are performed targeting the NC state, with positive and negative signs of the floor lateral forces. In these analyses, the effective moment of inertia
of
Table 1 that correspond to the NC state is used (Equation 8), i.e. the value 0.15
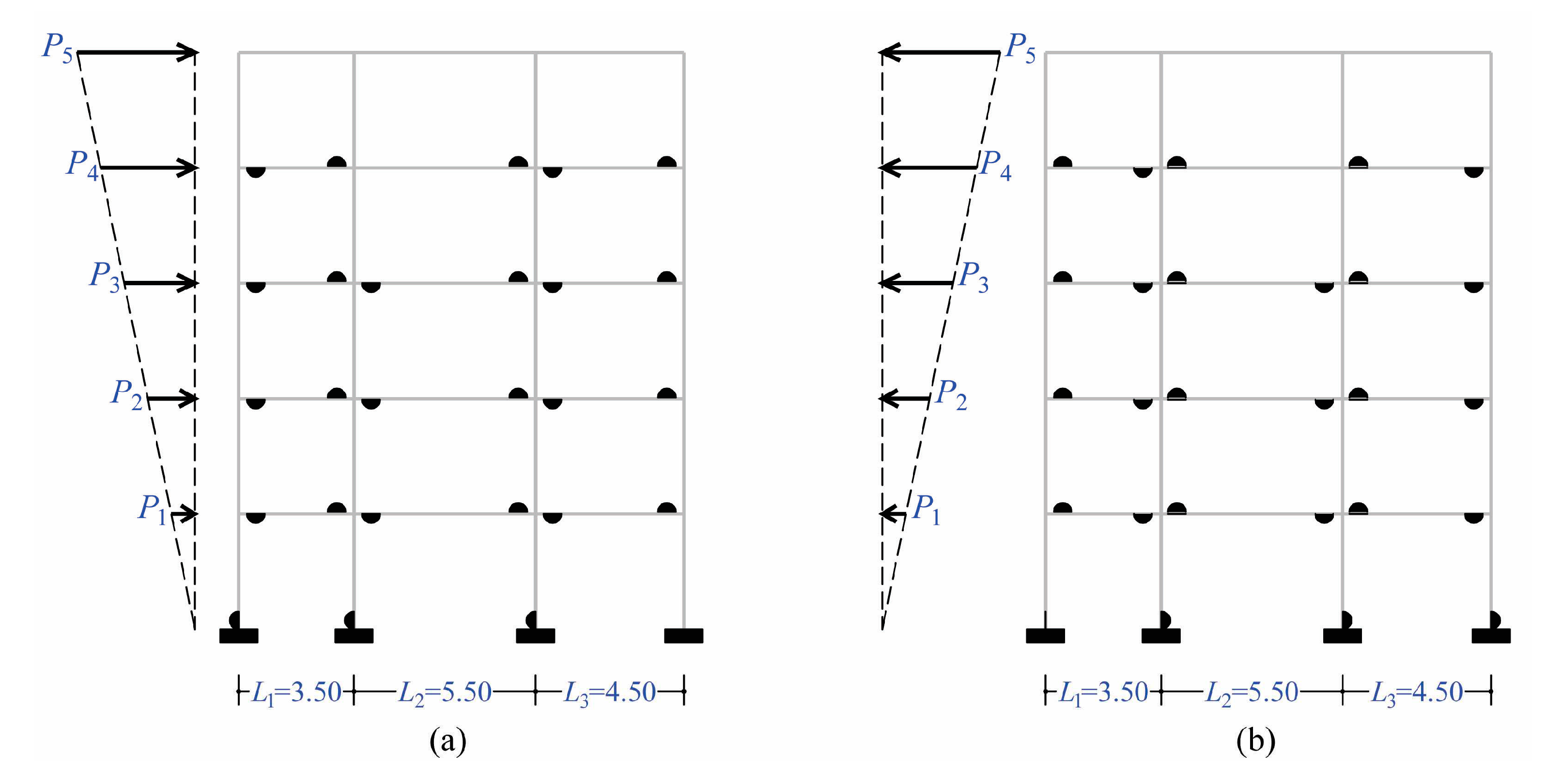
. Since the planar frame has more than four floors, two floor force patterns are used in pushover analysis according to phase (b): (i) the triangular pattern (
Figure 5a), (ii) the triangular pattern but with an additional top force equal to
for a unit base shear (
Figure 6a). These two force patterns will be referred to, from now on, as P-1 and P-2. The two capacity curves of the planar frame for the two pushover sets are illustrated in
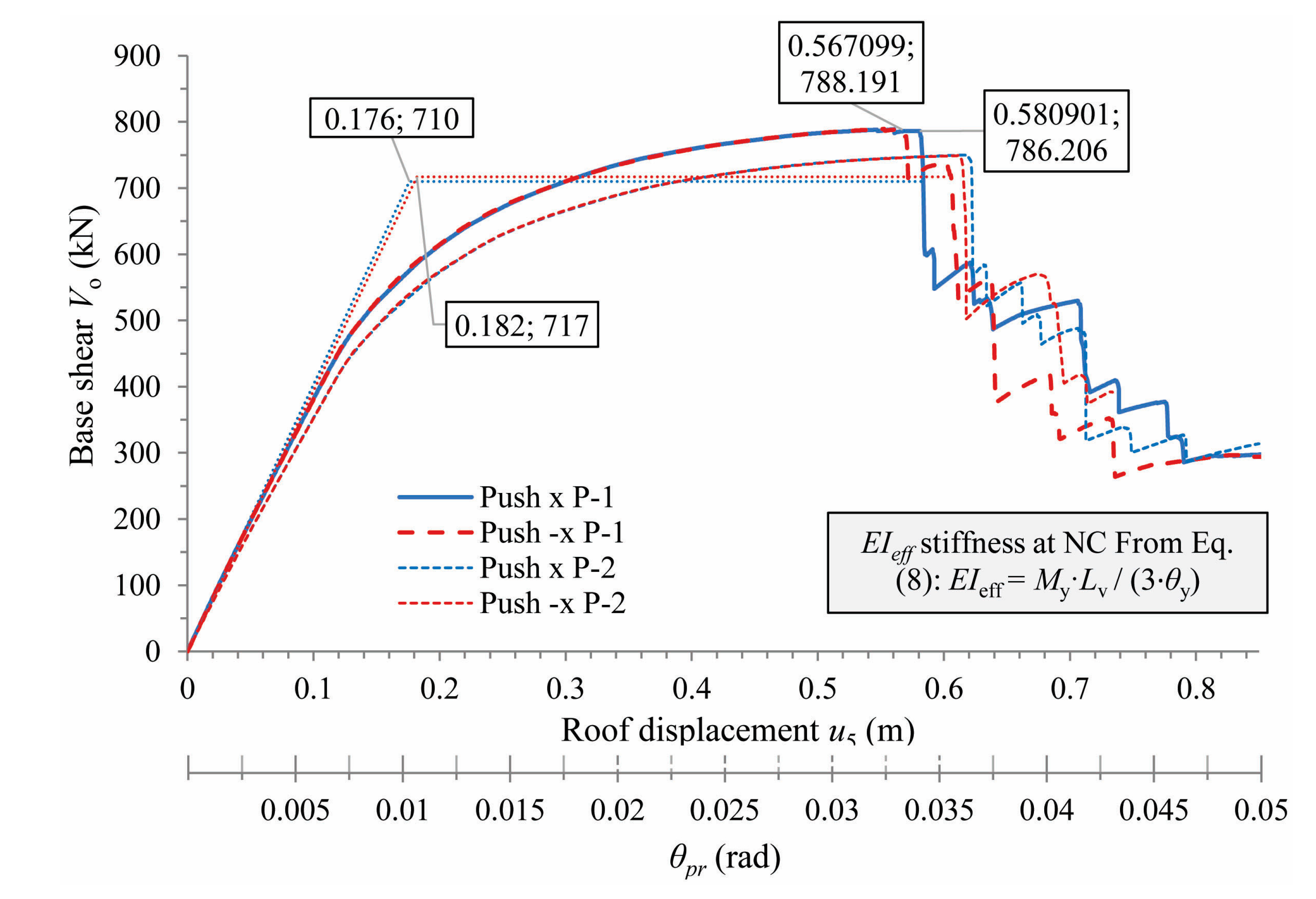
Figure 11, together with bi-linearization lines for the first set P-1 that mark the DL state at a value of
about equal to
. As shown in this figure, the NC state of the frame is conservatively shown at a value of
equal to
, i.e., that in the last line of
Table 1. The capacity curves for the second pushover set P-2 present higher ultimate displacements and lower elastic stiffness.
Next, a sequence of pushover analyses of the existing planar frame is performed, where each one targets a seismic roof displacement which corresponds to the discrete values of the profile angle
of
Table 1, from 0 to 0.032 rad. In each pushover analysis, the effective moment of inertia
assigned to the structural elements of the nonlinear model of the frame is that shown in
Table 1, which corresponds to the same discrete values of the target profile angle
. At the last step of the separate pushover analyses, an instantaneous modal analysis is running with initial condition the damage state of this last step, i.e. using the stiffness matrix of the damaged frame at the last step of each pushover analysis. From the sequence of modal analyses of the planar frame, the instantaneous cyclic Eigen-Frequencies of the system are recorded (
F1 to
F5) and the diagram of the instantaneous cyclic Eigen-Frequencies (in Hz) of the planar frame in the nonlinear area is obtained as a function of the roof displacement
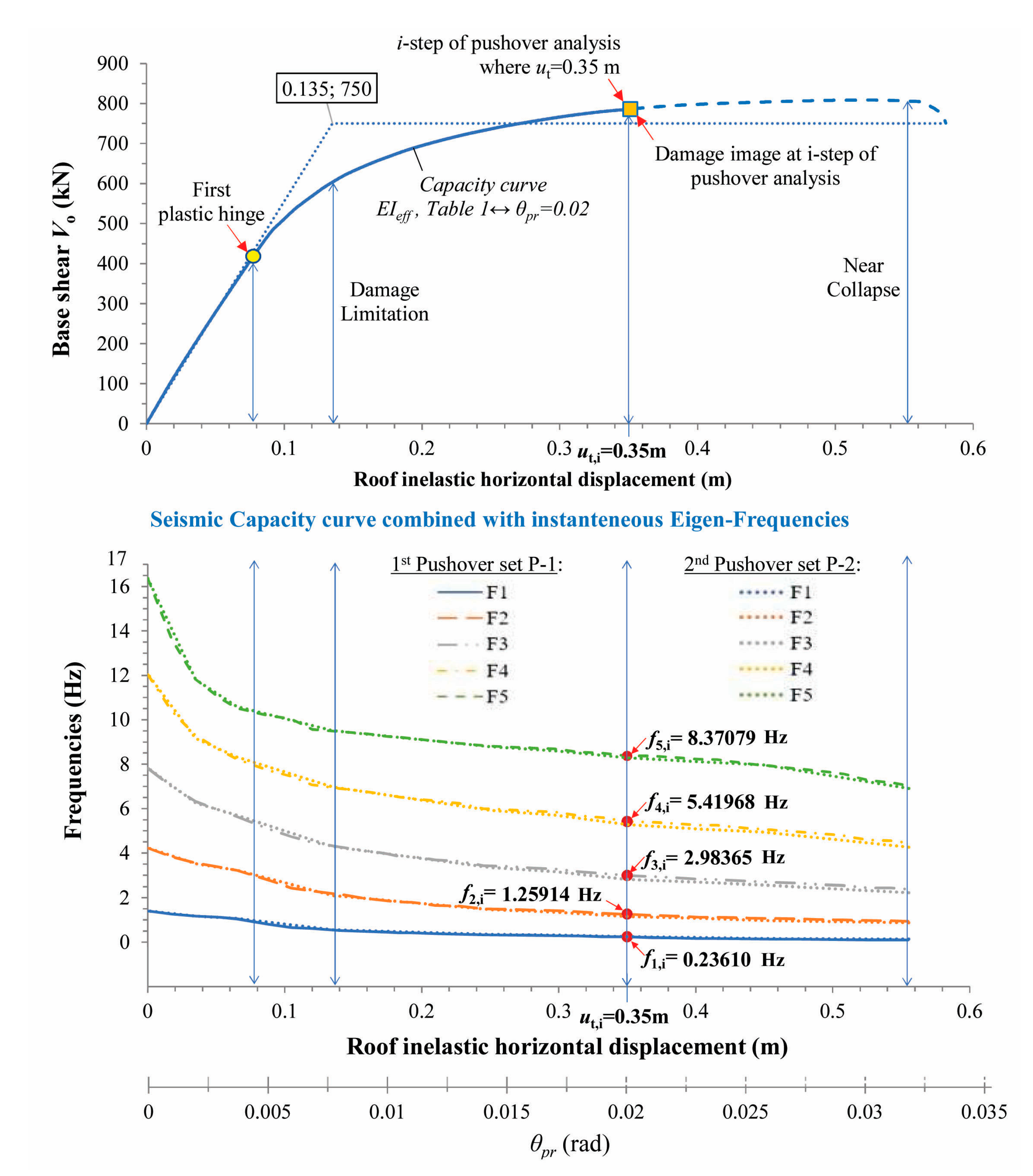
. This is done for the two directions of application of the floor forces and the mean values of the instantaneous cyclic Eigen-Frequencies (in Hz) of the planar frame are calculated, for both pushover sets with the different floor force patterns P-1 and P-2. In
Figure 12, the diagram of the instantaneous cyclic Eigen-Frequencies (in Hz) is combined with the capacity curve of the planar RC frame. For figure clarity, only one capacity curve is presented, that for the pushover with positive floor forces following a triangular pattern (P-1). This curve was determined using a nonlinear model of the frame in which the
value of
Table 1 that corresponds to
has been assigned to all RC structural elements. As is shown in
Figure 12, the two pushover sets P-1 and P-2 provide similar results for the instantaneous cyclic Eigen-Frequencies in this planar frame. At
, the second pushover set (P-2) provides a value for
f1 (Hz) which is 3% higher while for the other frequencies lower values up to 8% are shown. Generally speaking, the difference for
f1 (Hz) increase linearly with the damage state for the second pushover set, up to 30% at the NC state. Finally, the mean values of the instantaneous cyclic Eigen-Frequencies (Hz) of the multi-storey frame resulted from four pushovers along the positive and negative directions (P-2 and P-3) should be used in the diagram.
According to phase (a) of the methodology for existing structures, an identification multi-channel system of uniaxial accelerometers is installed in the 5-storey planar RC frame and response accelerations when the frame is quasi-calm are recorded. From the analysis of the records, the fundamental Eigen-Frequency for the i-step of pushover analysis is determined.
Then, according to phase (d) of the methodology, the fundamental Eigen-Frequency
is inserted in the Eigen-Frequencies diagram of
Figure 12 (see also the key-
Figure 2) and the respective displacement
of the frame roof is determined, which corresponds to
. All the other higher frequencies (
) can also be found from
Figure 12 at the same
i-step. The first three instantaneous mode shapes (φ
1,i to φ
3,i) of the multi-storey frame at the corresponding
i-step where
is equal to 0.02 rad are illustrated in
Figure 13. Moreover, at the
i-step of the pushover analyses where the roof displacement
appears, two damage images are obtained, one for the positive and one for the negative application of floor forces, for each one of the two pushovers sets P-1 and P-2. By these two damage images for each one pushover set and by taking the envelope damage image from the two sets, the final requested estimation of the damage is obtained. In
Figure 14 the damage image for the first pushover set P-1 is shown, separately for the positive and negative direction of the lateral floor forces. In this figure, the developed plastic hinges are illustrated with a black semicircle at the upper or lower fibers of the beams. As shown in this figure, the multi-storey planar frame develops a beam-sway type plastic mechanism, with plastic hinges at the end-sections of the beams in all floors (except the top floor) and at the base of the columns of the ground floor. Τhis is fully in line with the seismic design objective for high ductility [
24]. For the second set P-2 of pushover analysis, the damage is distributed throughout the frame, at the end-sections of the beams in all floors, but the magnitude of damage is a little higher in the upper half of the frame and a little lower in the lower half (
Figure 15). Also, no plastic hinges appear at the base of the columns of the ground floor.
It is noting that in an earthquake event, the actual seismic load on the structure is different and this loading varies in each time step. Hence, the damage distribution on the frame can be different from that obtained by the pushover analysis. However, the critical parameter in the recently proposed methodology is the fundamental Eigen-Frequency, which is identified by monitoring with a local network of uniaxial accelerometers. Knowing the fundamental Eigen-Frequency of the structure, the equivalent lateral displacement of the monitoring point on the roof of the building can be estimated by
Figure 12 and then the capacity curve is considered to identify the damage state. On the other hand, the second set of pushover analysis, with the load pattern with an additional top force, should always be considered in tall moment-frames with more than four floors, to take account of the higher mode effects on the damage potential. In this frame, both pushover sets provide similar values for the fundamental instantaneous cyclic Eigen-Frequency
and for the damage image, but, if the frame was taller, then these results might have been different.
Finally, according to phase (g) of the methodology, the instantaneous stiffness matrix
of the frame structure at the examined inelastic
i-step (
) is calculated for the case of pushover analysis with positive floor forces following the triangular pattern (P-1):
Therefore, the Damage Stiffness Matrix
at the same
i-step is calculated from the general relationship
, where
is the known Initial Stiffness Matrix of the planar frame in the health state without damage. The later can be calculated from the nonlinear model of the frame in which the geometric moment of inertia
has been assigned to all RC structural elements and the gravity loads are applying gradually:
Hence, the Damage Stiffness Matrix
of the planar frame, at the same
i-step, is calculated as following:
For the pushover analysis with positive floor forces following the triangular pattern but with an additional top force (P-2), the corresponding Damage Stiffness Matrix
of the planar frame, at the same
i-step (
), is calculated as abovementioned and is equal to:
Figure 1.
Pushover Capacity Curve of the multi-storey planar frame structure.
Figure 1.
Pushover Capacity Curve of the multi-storey planar frame structure.
Figure 2.
Instantaneous Eigen-Frequencies diagram, in the nonlinear area.
Figure 2.
Instantaneous Eigen-Frequencies diagram, in the nonlinear area.
Figure 3.
The profile angle of the frame structure in pushover analysis with floor lateral forces.
Figure 3.
The profile angle of the frame structure in pushover analysis with floor lateral forces.
Figure 4.
Effective moment of inertia ratio with reference to the geometric moment of inertia of RC structural elements at discrete damage states as a function of the mean (chord) rotation of the frame structure (rad).
Figure 4.
Effective moment of inertia ratio with reference to the geometric moment of inertia of RC structural elements at discrete damage states as a function of the mean (chord) rotation of the frame structure (rad).
Figure 5.
Five-storey planar RC frame with three unequal spans: (a) static simulation for the first pushover set (P-1) with a triangular force pattern, (b) dynamic simulation.
Figure 5.
Five-storey planar RC frame with three unequal spans: (a) static simulation for the first pushover set (P-1) with a triangular force pattern, (b) dynamic simulation.
Figure 6.
(a) Static simulation of the five-storey planar RC frame for the second pushover set (P-2) with a triangular force pattern and an additional top force, (b) dynamic simulation.
Figure 6.
(a) Static simulation of the five-storey planar RC frame for the second pushover set (P-2) with a triangular force pattern and an additional top force, (b) dynamic simulation.
Figure 7.
(a) Sections of RC structural elements, (b) longitudinal steel bars.
Figure 7.
(a) Sections of RC structural elements, (b) longitudinal steel bars.
Figure 8.
Steel reinforcement details of typical column and beam sections.
Figure 8.
Steel reinforcement details of typical column and beam sections.
Figure 9.
Stress-strain diagram for unconfined and confined concrete.
Figure 9.
Stress-strain diagram for unconfined and confined concrete.
Figure 10.
Stress-strain diagram for steel bars.
Figure 10.
Stress-strain diagram for steel bars.
Figure 11.
Capacity curves of the planar frame along the +x and -x axis (
at NC,
Table 1), for the two force patterns P-1 & P-2.
Figure 11.
Capacity curves of the planar frame along the +x and -x axis (
at NC,
Table 1), for the two force patterns P-1 & P-2.
Figure 12.
Diagram of the instantaneous Eigen-Frequencies in Nonlinear Area combined with the Seismic Capacity Curve for the two pushover sets.
Figure 12.
Diagram of the instantaneous Eigen-Frequencies in Nonlinear Area combined with the Seismic Capacity Curve for the two pushover sets.
Figure 13.
The first three instantaneous modes φ1,i to φ3,i at rad.
Figure 13.
The first three instantaneous modes φ1,i to φ3,i at rad.
Figure 14.
Plastic mechanism of the planar RC moment-frame by the 1st set P-1 of pushover analysis, with (a) positive and (b) negative signs of floor forces, at seismic (target) displacement 0.35 m () corresponding to the fundamental Eigen-Frequency of the damaged frame. Evaluation of Damage Locations.
Figure 14.
Plastic mechanism of the planar RC moment-frame by the 1st set P-1 of pushover analysis, with (a) positive and (b) negative signs of floor forces, at seismic (target) displacement 0.35 m () corresponding to the fundamental Eigen-Frequency of the damaged frame. Evaluation of Damage Locations.
Figure 15.
Plastic mechanism of the planar RC moment-frame by the 2nd set P-2 of pushover analysis, with (a) positive and (b) negative signs of floor forces, at seismic (target) displacement 0.35 m () corresponding to the fundamental Eigen-Frequency of the damaged frame. Evaluation of Damage Locations.
Figure 15.
Plastic mechanism of the planar RC moment-frame by the 2nd set P-2 of pushover analysis, with (a) positive and (b) negative signs of floor forces, at seismic (target) displacement 0.35 m () corresponding to the fundamental Eigen-Frequency of the damaged frame. Evaluation of Damage Locations.
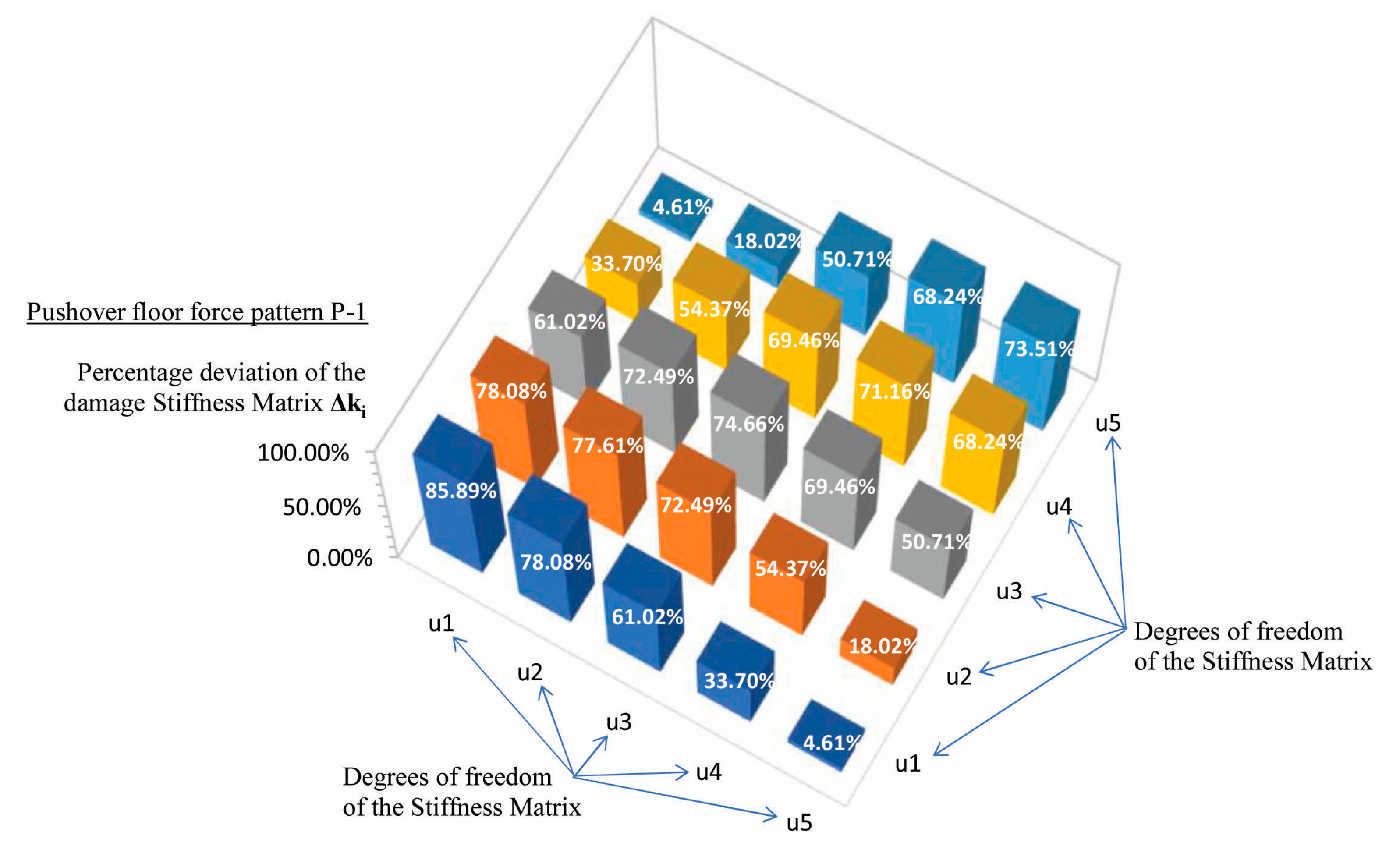
Figure 16.
Percentage deviation of the Damage Stiffness matrix at the i-step (), for the triangular force pattern (P-1).
Figure 16.
Percentage deviation of the Damage Stiffness matrix at the i-step (), for the triangular force pattern (P-1).
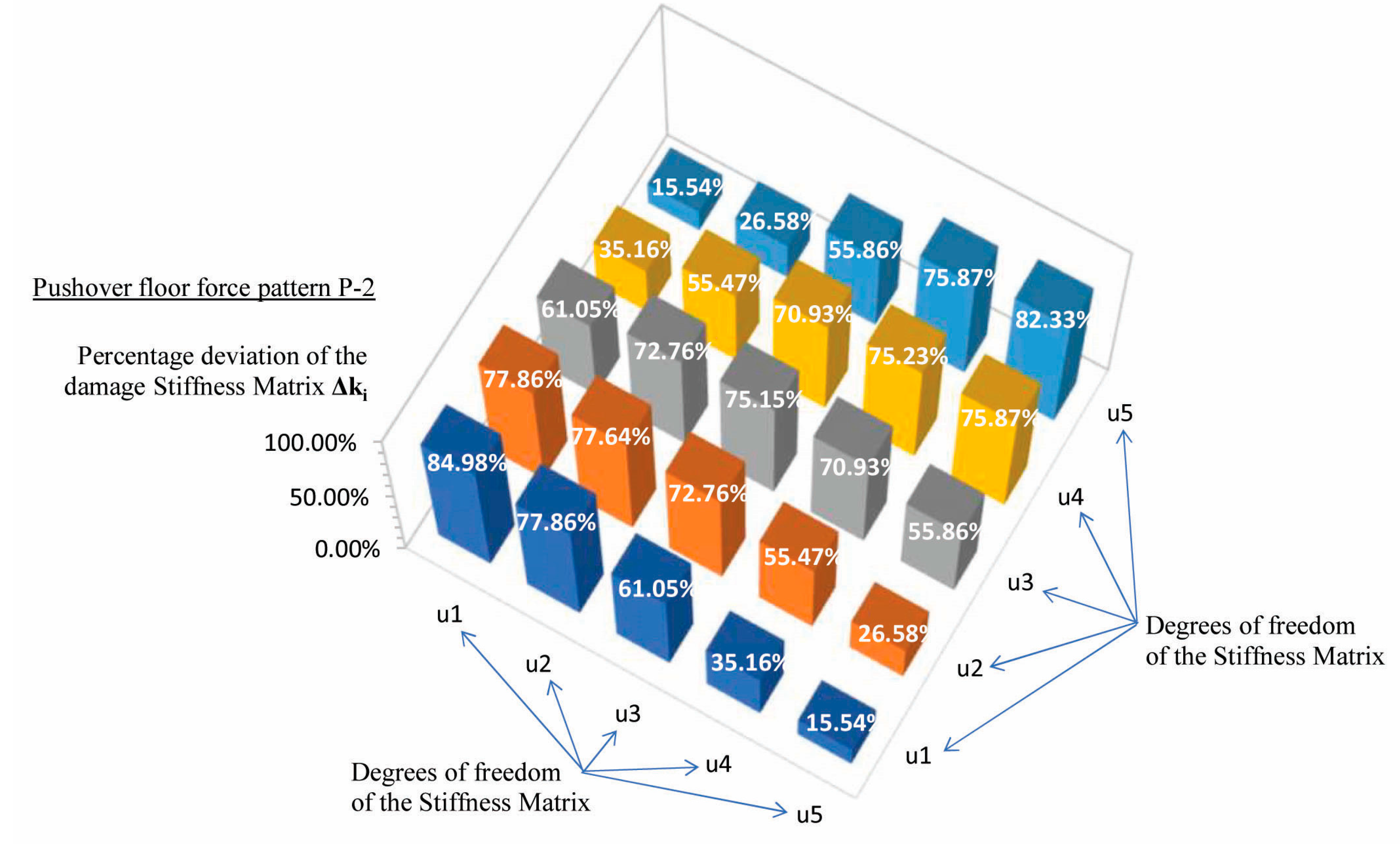
Figure 17.
Percentage deviation of the Damage Stiffness matrix at the i-step (), for the triangular force pattern with an additional top force (P-2).
Figure 17.
Percentage deviation of the Damage Stiffness matrix at the i-step (), for the triangular force pattern with an additional top force (P-2).
Table 1.
Effective moment of inertia ratio () of RC structural elements as a function of the mean (chord) rotation of the frame structure (rad).
Table 1.
Effective moment of inertia ratio () of RC structural elements as a function of the mean (chord) rotation of the frame structure (rad).
|
|
|
|
|
|
|
|
|
|
|
| 0.000 |
1.00 |
|
0.010 |
0.32 |
|
0.020 |
0.28 |
|
0.030 |
0.17 |
| 0.001 |
0.87 |
|
0.011 |
0.32 |
|
0.021 |
0.27 |
|
0.031 |
0.16 |
| 0.002 |
0.74 |
|
0.012 |
0.31 |
|
0.022 |
0.26 |
|
0.032 |
0.15 |
| 0.003 |
0.61 |
|
0.013 |
0.30 |
|
0.023 |
0.25 |
|
0.032+ |
Eq. (8) |
| 0.004 |
0.50 |
|
0.014 |
0.30 |
|
0.024 |
0.24 |
|
|
|
| 0.005 |
0.43 |
|
0.015 |
0.30 |
|
0.025 |
0.23 |
|
|
|
| 0.006 |
0.40 |
|
0.016 |
0.30 |
|
0.026 |
0.22 |
|
|
|
| 0.007 |
0.37 |
|
0.017 |
0.29 |
|
0.027 |
0.21 |
|
|
|
| 0.008 |
0.35 |
|
0.018 |
0.29 |
|
0.028 |
0.19 |
|
|
|
| 0.009 |
0.34 |
|
0.019 |
0.28 |
|
0.029 |
0.18 |
|
|
|
Table 2.
Percentage deviation of the Damage Stiffness matrix at the i-step (), for the triangular force pattern (P-1).
Table 2.
Percentage deviation of the Damage Stiffness matrix at the i-step (), for the triangular force pattern (P-1).
| Degrees offreedom |
|
|
|
|
|
|
85.89% |
78.08% |
61.02% |
33.70% |
4.61% |
|
78.08% |
77.61% |
72.49% |
54.37% |
18.02% |
|
61.02% |
72.49% |
74.66% |
69.46% |
50.71% |
|
33.70% |
54.37% |
69.46% |
71.16% |
68.24% |
|
4.61% |
18.02% |
50.71% |
68.24% |
73.51% |
Table 3.
Percentage deviation of the Damage Stiffness matrix , at the i-step (), for the triangular force pattern with an additional top force (P-2).
Table 3.
Percentage deviation of the Damage Stiffness matrix , at the i-step (), for the triangular force pattern with an additional top force (P-2).
| Degrees offreedom |
|
|
|
|
|
|
84.98% |
77.86% |
61.05% |
35.16% |
15.54% |
|
77.86% |
77.64% |
72.76% |
55.47% |
26.58% |
|
61.05% |
72.76% |
75.15% |
70.93% |
55.86% |
|
35.16% |
55.47% |
70.93% |
75.23% |
75.87% |
|
15.54% |
26.58% |
55.86% |
75.87% |
82.33% |