Prerpints.org logo
Preprint
Article

Simulation of Regular Operating Modes of Oil and Oil Product Pipelines

Altmetrics

Downloads

134

Views

52

Comments

1

This version is not peer-reviewed

Submitted:

16 August 2023

Posted:

17 August 2023

You are already at the latest version

Alerts
Abstract
Regular regimes of oil and oil products pipelines are studied. The problem is to develop an algorithm of effective pipeline system control that ensures the fulfillment of specified boundary conditions at the system boundaries. The product is pumped in batches, the flow is characterized by a change in temperature and pressure flow parameters over time. The developed solution method uses the principle of decomposition in the sense that each computational iteration is im-plemented in 3 stages, in three nested loops. The inner cycle is connected with the material bal-ance relations, at the next cycle the flow equations are introduced and the fulfillment of the 2nd Kirchhoff's law is monitored. If the flow process is significantly affected by temperature, then an external cycle is also implemented, correcting the solution so that the energy conservation equa-tion is satisfied. In the calculation procedure, some computational difficulties may arise, which consist in choosing an appropriate optimization method. On a specific example, the possibility of using various library programs to solve the problem was checked. The developed method is suita-ble for the analysis of systems of arbitrary topology. Since the method is not time-consuming, it can be recommended for online control of oil and oil products supply systems. The paper opens a new direction in the theory of hydraulic circuits. It uses both traditional methods of continuum mechanics and stochastic models.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

Multi-product pipelines are an inalienable part of the transport infrastructure of modern energy. They make it possible to transport large volumes of oil and oil products in a wide range from sources - places of extraction and production - to places of processing and markets. The pumping of the product by the considered pipelines is carried out in successive batches. For product pipelines, a batch is a certain type of product, for example, products from an oil refinery. A batch of product for an oil pipeline is characterized by the invariability of the properties of oil at the inlet to the pipeline system. Oil properties depend on grade. The grade of oil is characterized by its viscosity, density, and component composition. Even components whose concentration is very low, such as sulfur compounds, which degrade the quality of oil, play a role. The grade is also determined by the presence and percentage of antifriction additives.
Companies operating multi-product pipelines have to deal with numerous problems when planning modes and operational cjuntrol. First of all, it is a rational choice of the sequence of pumped products and the amount of product in each batch. Existing studies have focused mainly on solving this problem, which is especially significant for oil product pipelines.
The actual modes of pumping oil and oil products through main pipelines are characterized by constant changes in flow parameters. They are initiated by a change in the grade and thermobaric parameters of the product entering the system, switching of pumps and valves, changes in the technical condition of the equipment, volatility of external conditions: weather factors, consumer demand, etc.
The dynamics of flow processes through pipelines can be significantly affected by thermal effects. Especially significant are the thermal effects during the transport of oil, which is explained by its viscosity. With a decrease in temperature, the oil passes into a visco-plastic state, the flow rate drops, and pumping may stop, which is a systemic failure, the timing of which is difficult to predict. To prevent such failures, oil pipelines are equipped with heating furnaces. When the fluid moves through the pipeline, the transported product heats up due to internal friction and advection – mixing in the horizontal direction. Cooling of the fluid occurs due to the outflow of heat into the environment. To reduce the intensity of the outflow, heat-insulating coatings in one or more layers are used. The physical processes of heat transfer have different time scales. The heat transfer by the moving fluid is much faster than the outflow process, the intensity of which depends on the pipe insulation and the thermal conductivity of the soil. Thermal processes directly affect hydrodynamic processes, the higher the temperature, the lower the friction resistance. There is also an inverse relationship: with an increase in the flow velocity, the heating of the fluid intensifies due to internal friction. Therefore, flow models in "hot" pipelines must be thermodynamic.
The transition of the temperature of the incoming flow from one level to another can also be regarded as a change of batches, since the properties of oil, primarily viscosity, depend on temperature. In regular modes, these changes are usually not large. Small in absolute value, but not in rate of change. Parameters such as density and viscosity change abruptly at the boundary of the batches of the transported product.
Slow changes in modes are also caused by the evolution of the technical condition of the pipeline equipment in operation. The deterioration of the technical condition of pipes is manifested in a decrease in the flow area of the pipe due to the deposition of paraffins, in violation of the integrity of the pipe and the appearance of leaks. The technical condition of power equipment is deteriorating due to wear and is manifested in the drawdown of the pressure and power characteristics of the pumps. During repairs, on the contrary, the technical condition of the equipment usually improves.
The purpose of this work is to develop a mathematical model for simulating the described regular flow processes in oil and oil product pipelines. The significance of the model is determined by the fact that these pipeline systems are in normal modes for the vast majority of the time. The model gives a short-term forecast of changes in the technological situation. Dispatching services also get the opportunity to compare the regular development of the situation with the actual one and, if necessary, take measures to prevent the regime from falling into the risk zone.
A flow model that satisfies these conditions will be called quasi-stationary 1. Its hydrodynamic component is reduced to the study of stationary flows at some points in time, characterizing the movement of batches of the transported product through the pipelines of the system. The quasi-stationary model (QSM) uses piecewise constant and piecewise linear functions. Discontinuities of functions describing regime parameters take place at the boundaries of product batches. Discontinuous functions adequately describe the process for the following reasons. With sequential pumping of fluids at the boundary of batches, due to the processes of advection and diffusion, a mixture zone is formed. However, it is known that the size of this zone is negligible compared to the size of the batches and does not have a significant effect on the thermobaric calculation of flows in industrial oil and oil product pipelines. Therefore, the proposed model is built using piecewise constant functions, that is, under the assumption that the extent of the mixture zone is zero. The quasi-stationary model is applicable to simulate normal flow regimes, which do not include start/stop modes in the pumping directions, system switching, and other modes with sharp and significant pressure drops.
Thus, the range of technological situations where slow changes in the mode parameters take place is quite wide. We single out 3 groups of such situations, differing in the reasons for their occurrence.
I. Changing the conditions at the entrances to the system. The situation of the 1st group is observed, for example, when batches of a product that differ in grade, for example, oil from different fields or from different deposits of one field, alternately enter the system (one of the inputs). Disturbance (change of flow parameters) from the source is transmitted along the flow with the speed of the fluid flow. Changing the conditions at the entrances to the system. The situation of the 1st group is observed, for example, when batches of a product that differ in grade, for example, oil from different fields or from different deposits of the same field, alternately arrive at one of the inputs to the system. Disturbance (change of flow parameters) from the source is transmitted along the flow with the speed of the fluid flow.
II. Turning on / off or changing the control settings of pumps as part of the normal regulation of modes. The situation of the II group is characterized by a change in pressure at some points of the pipeline system, which is transmitted along the flow.
III. Enabling and disabling or changing the control settings of furnaces at oil heating points. A change in fluid temperature affects the viscosity, which leads to a change in the flow regime.
The mathematical apparatus used in the construction of the CSM differs from that traditionally used to simulate flows and the optimal choice of control actions on pipeline systems. In the vast majority of publications, the study of flows in pipelines is carried out by methods of continuum mechanics. The apparatus of the constructed QSM is based, firstly, on the theory of flows in networks [2], modified to apply to dynamic problems of incompressible fluid flows and, secondly, it includes stochastic models for describing temperature effects in the technogenic complex: pipeline - environment. Both approaches are not new, but examples of their application in combination are not known to us. There is hope that the method found will be productive in other applications.

2. Review of publications

The main subject of research in this work is the regular regimes of oil and oil product pipelines. A large number of publications are devoted to the topic. Below is a brief review of publications in some of its three close areas: stationary models of flow distribution, sequential pumping of different batches of the product, thermal interaction of components in the natural-technogenic triad: pipeline – pumped product – environment.
Models of stationary flow distribution. The theoretical basis for modeling stationary flows in pipeline systems is the theory of hydraulic circuits (THC). THC is an effective tool for studying the problems of operational control, design, medium and long-term planning of pipeline systems. The significance of the THC is determined by its multifunctional orientation, the possibility of application to water, oil and gas supply systems, not to mention electric power systems. The classical works of G. Kirchhoff on electrical circuits, dating back to the middle of the 19th century, immortalized his name and formed the foundation on which the THC was built a century later.
The theory of hydraulic circuits is an apparatus for calculating the static modes of network objects. The problem formulations most studied in the THC are reduced in mathematical terms to solving nonlinear algebraic equations or optimizing a criterion function in the presence of constraints in the form of algebraic equations. THC, as a branch of science demanded by the industry, despite its considerable age, is intensively developing. New directions in other cases turn out to be important for functionally different pipeline systems, while in others their appearance is due to the specific features of one of them.
The canonical THC problem is the problem of determining the unknown parameters of the stationary flow regime under given boundary conditions (BC). Moreover, the number and composition of the BC should be such as to uniquely determine the solution [3,4]. Several methods have been developed to solve the canonical problem, the best known are the (Newton loop method) [3,4,5,6], the nodal potential method (Newton nodal method) [1,2,3,4], and the global gradient method [4,7]. All 3 methods are iterative and based on Newtonian linearization. For isothermal problems, the THC model includes the equations of momentum and material balance, and the space of unknowns (phase space) is formed by flow rates along arcs, and at the nodes by those pressures and inflows/extractions that are not part of the BC. For nonisothermal problems, one also has to consider the energy conservation equation, and supplement the phase space with temperatures at the nodes, and the boundary conditions with the temperatures at the sources.
The solution is constructed by an iterative method with nested cycles of multiplicity 2 or 3. To solve an isothermal problem, 2 the basis of the calculation algorithm is a cyclic procedure with a multiplicity of 2. If the contour flow method is used, then the approximation at the entrance to the external cycle satisfies the conditions of the material balance (Kirchhoff's 1st law). The outer loop serves to consistently reduce the discrepancy of the equations of the 2nd Kirchhoff law without violating these conditions.
To solve a nonisothermal problem, one has to use a cyclic procedure with a multiplicity of 3. Two inner cycles provide a solution to the problem for some fixed temperature distribution. On the outer cycle, the temperature distribution is corrected in such a way as to reduce the discrepancy in the energy conservation equations. The practice of calculating engineering pipeline networks indicates that the outer cycle converges very quickly. This is natural, since the influence of temperature on the distribution of flows is usually less than the influence of pressure.
The listed information characterizing the physical processes and features of computational procedures for static formulations of the problem is well known. The main subject of this paper is the study of a certain class of non-stationary processes. The above information about known facts makes it possible to identify an analogy and understand the relationship of problems that seem to be far from each other in mathematical terms.
Sequential pumping of the transported product batches. The tasks of sequential pumping are very complex and diverse [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Studies of these processes began at least half a century ago, monographs were written, and many priority technological problems were solved [5]. The flow of work does not dry out, they are mainly devoted to problems that have arisen due to changes in the conditions for the operation of pipelines and the emergence of new technologies. Let us give a brief description of some works [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. A description of the technology, current state and problems of sequential pumping of oil and oil products can be found in the monograph [8]. The article [9], written in the form of a methodological guide, discusses the main problems associated with the sequential pumping of oils. As a criterion for choosing the optimal operating mode, the total cost of pumping the product is used. At the same time takes into account changes in electricity tariffs during the day. The following are found: volumes of product supply to the pipeline inlet, points in time, place and amount of introduction of antifriction additives for the lead period (forecast horizon). In the full formulation, the optimization problem turns out to be very complex, and the possibility of its mathematically rigorous solution is problematic. However, the basic formulation can be simplified, which makes it possible to increase the speed and productivity of optimization procedures, while retaining the most essential features of the problem and its practical significance.
Published about 20 years ago, paper [10] is one of many that uses partially integer linear programming. and much attention is paid to the rationalization of the computational procedure. The publication [11] proposes a decomposition approach that combines heuristic procedures and mixed integer linear programming models. This approach provides for inventory management and process control, taking into account such operational aspects as simultaneous deliveries and predetermined maintenance periods for tanks and pipelines. The following works are devoted to the problems of sequential pumping. In [12], a method is proposed for calculating the mixture zone at the junctions of pumped batches of products. Milano and Goyal [13] showed how to take into account the terrain (altitude of the route above sea level) and changes in the internal diameter of the pipe, in particular due to the deposition of paraffins on the pipe walls. It is argued that significant simplifications can be made in the mathematical model without practically changing the simulation results. The main goal of the paper [14] is to maximize the throughput of the pipeline system in sequential pumping. A large-scale pipeline system is being considered: an 808-mile pipeline with a 155-mile branch. The calculation model contains non-stationary equations of continuity and momentum, the energy balance is considered approximately. In [15], an example of sequential pumping of oils of different grades through a system with two sources and one outlet is given. The model includes all objects of the system: tank farms, pumps, check valves - and the main technological limitations. In stationary and non-stationary modes, flow rates, temperature and density profiles were calculated for such operations as shutting down a pumping station, stopping and starting a pipeline, switching valves, adjusting pressure and flow.
The article [16] compares two different models for tracking batches during their sequential transfer. One of them is a model of an incompressible fluid, the other considers the formation of a gas phase and the transition to a two-layer flow. For the study, mainly finite-difference methods for solving partial differential equations are used. The advantage of the work is the fact that the model is designed to search for the best variant of operational control based on continuously incoming information. The effectiveness of the recommendations received with its help has been tested in practice. In [17], the equations describing serial pumping are linearized; and this makes it possible to apply the methods of the theory of automatic control with the Laplace transform.
The problem considered in this article is related to a number of works on modeling the flows of viscous fluids. In [18], methods for studying multiphase flow in pipelines are presented. The emphasis is on the tools, the possibilities of which are opened up in the framework of computer simulation: information is given on commercial products Pipesim and. In most cases, the research apparatus is finite-difference methods for integrating a system of nonlinear partial differential equations.
New tasks appear in connection with changes in the conditions for the operation of pipelines and the emergence of new technologies. The publication [19] draws attention to the fact that the formulation and, consequently, the results of solving the problems of sequential pumping largely depend on the economic paradigm. With the development of the oil products market, a market-oriented regime of pipeline transport enterprises has been formed. Market demand is characterized by great uncertainty. The article proposes a method that takes into account the uncertainty of market demand and allows you to find options for reliable inventory management. In [20], the planning of the operation of a multi-product transportation system with several inputs and outputs is considered. It is noted that the main difficulty in solving this problem is caused by a large number of technological limitations, which often force one to resort to heuristic approaches and fuzzy formulations. The authors see the novelty of the study in the strict consideration of forbidden sequences of products and the rational construction of the computational procedure.
In [21], an operating pipeline system for transporting liquids is considered. Due to the large number of restrictions that are difficult to formalize, a method is proposed that consists in checking the feasibility of the system work plan drawn up by experts, drawn up for the upcoming time interval of up to 1 month. Characteristically, the authors failed to select any of the existing software systems for their methodological development; it was required to draw up their own program. The publication [22] studies the contamination of products, which inevitably arises during their sequential pumping. Best control methods are recommended to minimize contamination losses. The effectiveness of these methods is demonstrated on concrete examples.
The publication [23] draws attention to the importance of timely detection of emergency situations in multi-product pipelines. A deep learning method is proposed for detecting anomalies in the operation of a technological object. One of the many articles where artificial intelligence techniques are applied to solving serial pumping problems. In [24], one of the latest in sequential pumping, a mixed integer linear programming model and an algorithm similar to a greedy randomized adaptive search procedure are proposed. Contains, in particular, an extensive bibliography indicating the place of each of the 51 refereed papers in the study of the problem. This list can serve as an addition to the short list of the present work.
Non-isothermal models. Let's move on to works where the temperature regimes of the fluid are considered during flows in pipelines and results are obtained that seem useful in connection with the development and application of QSM. An analysis of non-isothermal flows in both stationary and non-stationary cases using the methods of continuum mechanics is contained in the monograph by Lurie [1]. The review publication Modisette [25] compares different approaches to the thermal calculations of pipelines. The need for simplified models, which, however, do not go beyond the acceptable level of accuracy, is emphasized. The principal statement is that all errors arising due to various assumptions under which the model is built should be compared with the inevitable errors in setting information about the thermophysical parameters of the soil. 4 simplifying models are compared: isothermal, a sequence of steady states, Leapfrog – alternate solution of hydraulic and thermal equations, pseudo-stationary scheme with moving nodes 3 (nodes of finite difference grids for approximating the equations). The importance of determining the thermal characteristics of the soil as accurately as possible is repeatedly emphasized, since the error due to the simplification of the model is less than the difference between the solutions for dry and wet soil.
The paper [26] lists the most important technological problems of industrial oil and oil product pipelines in conjunction with the theory of hydraulic circuits. Lurie and Chuprakova [27] propose a model that takes into account the dynamics of the thermal interaction of the pipeline with the environment, analyze the non-stationary process of replacing pumped oil batches with temperature changes in the “hot” oil pipeline. It is taken into account that with a change in the temperature of the pumped oil along the length of the pipeline, a gradual cooling (or heating) of the soil mass occurs. It is shown that when the heating conditions change, the temperature of the pumped oil, as well as the time for the oil pipeline to reach a new stationary temperature and hydraulic regime, depend significantly on the inertia of the thermal field of the soil.
In [28], a thermodynamic analysis of "frictional heating" and changes in the internal energy of a viscous liquid during pumping through a pipeline is given. This is important at high flow rates, which can lead to a significant increase in temperature, but the heating effect cannot be ignored in the quasi-stationary models we are considering. The work [29] raises practically important issues of modeling pipeline systems for pumping liquid fluids, in particular, the question of when it is necessary to include the study of heat transfer processes in the model. In [30], stationary, non-stationary, and successive change of steady state models are compared. For each of these classes, the area of applicability is indicated. In particular, the possibility of using steady-state transition models to track batches of transported product and the influence of temperature effects when pumping viscous liquids is being investigated. In particular, the possibility of using model of successive change of steady states to track batches of transported product and the influence of temperature effects when pumping viscous liquids is being investigated.
Some aspects of the temperature regimes of gas pipelines are also of interest for oil and product pipelines. The subject of research in [31] are offshore gas pipelines. The factors influencing the fluid temperature distribution are listed. The option of partial immersion of the pipe into the sea soil is considered. In [32], models of stationary and non-stationary modes are compared. It turns out that in the thermal calculation of gas pipelines, as well as for oil pipelines, the main source of uncertainty is the unreliability of knowledge of soil properties, primarily, changes in the heat transfer coefficient of КТ along the route.
Conceptually, the methodology of [33] approaches that used in this article, although its subject is unsteady flows in gas pipelines. Its authors formulate the main contribution [33] as an expansion of the statistical space to eliminate the uncertainty of knowledge about the technical condition of pipelines – friction coefficients. Not without reason, it is noted that such an approach improves the overall accuracy of modeling and contributes to an increase in the reliability of the results. The tasks associated with the operational management of pipeline systems for the transport of oil and petroleum products are close to a certain extent to similar tasks of heat supply. In both cases, the significant factors that determine the flow process are the weak compressibility of the liquid and the thermal interaction of the pipeline with the environment [34].
Barros et al. [35] collected representative material on temperature processes in soils. A method is proposed for determining the ambient temperature and the heat transfer coefficient Tsoil, КТ for use in thermal-hydraulic modeling of flows in pipelines. A harmonic approximation is considered for the annual temperature variation. Approximation coefficients are estimated depending on the type (composition) of the soil.
Thus, many researchers [25,32,33,34] agree that the weak link in justifying the adequacy of decisions on the temperature regimes of pipelines is the unreliability of knowing the heat transfer coefficient of КТ and temperature soil Tsoil. The monograph [36] is devoted to the problem of identifying the parameters of hydraulic circuits. Christie [37] provides a model for estimating the efficiency factors of a large pipeline system and an example of its application to a specific system in operation.
We note an important methodological feature characteristic of most publications. In connection with the transportation of oil and oil products through pipelines, one has to turn to the study of complex processes of a physical, technological and economic nature. The multicomponent composition of the pumped product, the presence of phase transitions liquid – gas, liquid – viscous-plastic medium up to solidification, the length of pipeline systems, the diversity of equipment, the technical condition of which changes during operation, and many other factors cause the fundamental impossibility of reliable knowledge of all the details of the technological process. This implies the fundamental impossibility of building "exact" models; it is expedient to build several models adapted to take into account certain operating conditions. For each specific pipeline system, the model must be calibrated, adapted to its specifics and operating modes. The focus should not be on the "accuracy" of the model (a priori accounting for all influencing factors), but on the possibility of its adaptation.
Summarizing the analysis of publications on the subject, we note the following:
○
There are no approaches that would be focused on a comprehensive accounting of all factors that have a significant impact on the processes of pumping oil and oil products through pipelines.
○
Most of the research is based on continuum mechanics models, while a combination of traditional continuum mechanics models with methods of discrete mathematics may be more productive.
○
Despite the fact that in many works it is noted the expediency of identifying the parameters of the thermal model (primarily Tsoil, КТ), the number of meaningful publications on this issue is not numerous.
○
Among the methods used for identification, there are virtually no methods that are based on the most available operational information – measurements of temperature (and, possibly, pressure) in real time.
Poor coverage of identification methods based on the most available operational information – measurements of flow parameters (temperature and pressure) in real time.
1. A model has been built in the work that allows predicting the reaction of a pipeline system to a change in the mode parameters at its inlets and outlets – boundary conditions. Unlike most works on sequential pumping, the boundary conditions are not found as a solution to the optimization problem, but are considered given. Regular modes of operation are considered that are not related to the starts/stops of pumping directions and flow maneuvering. At the same time, no restrictions are imposed on the topology of the pipeline system and methods of controlling it within the framework of the formulated assumptions.
2. The model is built using, in addition to the methods of continuum mechanics, methods of discrete mathematics (flows on networks).
3. Accounting for temperature effects is combined with the estimation of the model coefficients (identification of state parameters), which is carried out according to regular dispatcher measurements of operating parameters.

3. Modeling algorithm

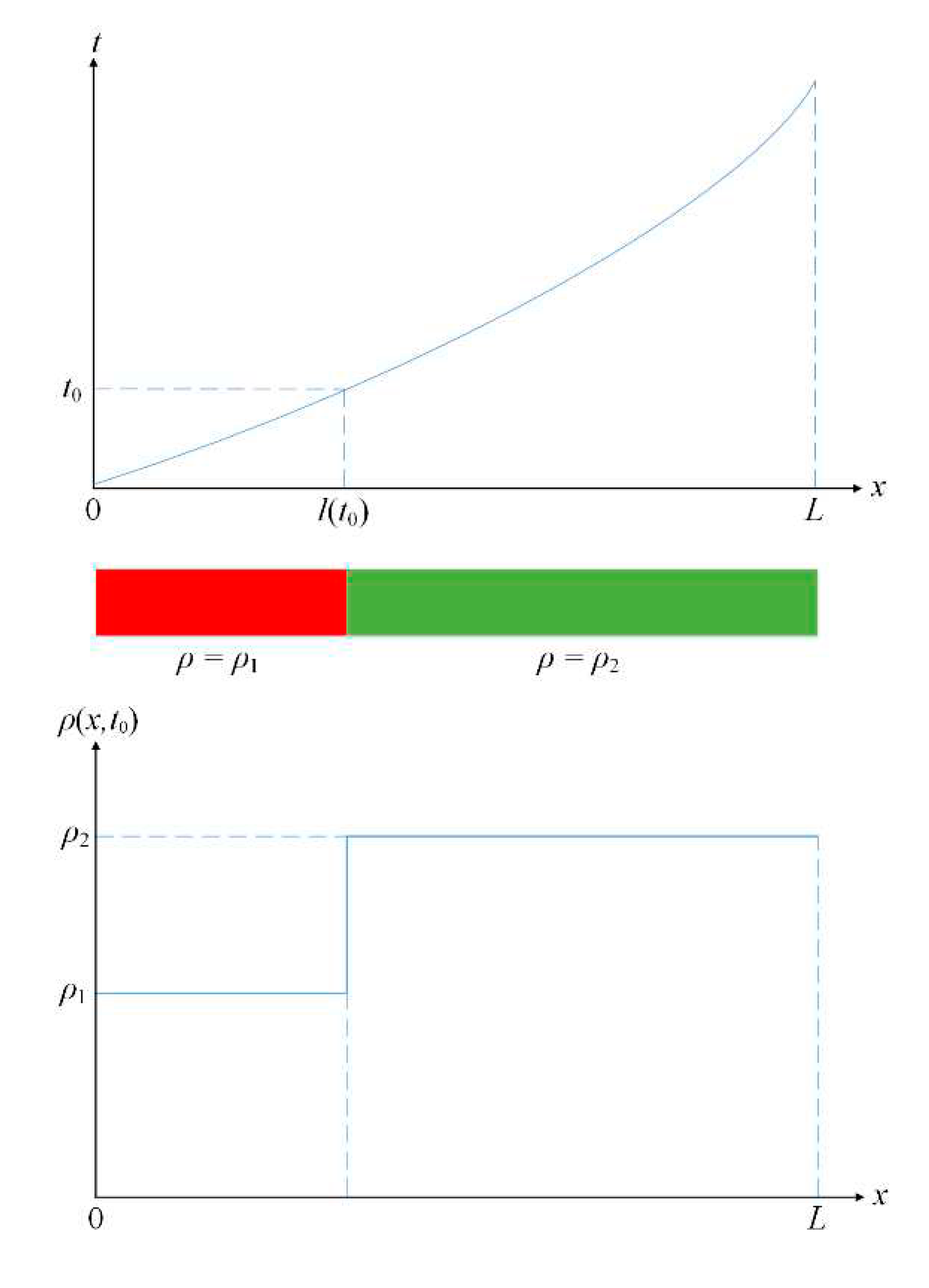
Simple pipeline4, isothermal flow. The quasi-stationary model is built on the assumptions that the flow is one-dimensional and the fluid is incompressible. The functions that determine the flow process depend only on one spatial coordinate x – the distance measured along the axis of the pipeline, and time t. For the mode parameters, we introduce the notations: p ( x , t ) – pressure, ρ ( x , t ) – density, υ ( x , t ) – viscosity, v(x,t) – velocity, T ( x , t ) – temperature, all values are average over the pipe section. The vector quantity – the set of all parameters – will be denoted by Ω ( x , t ) . In addition to the above, the coordinates Ω ( x , t ) , can also include there may also be other characteristics of the pumped products, for example, component composition. The effect of fluid compressibility can be neglected. In QSM the density ρ ( x , t ) is a piecewise constant function of each argument, with a fixed value of the other (Figure 1). The figure shows the position of the batch boundary at the moment t=t0, the density of the displacing batch 𝜌1 is less than the density of the displaced batch 𝜌2. The curve t(х) characterizes the displacement of the interface: l(t0) is the position of the interface at the moment t0. the other being fixed In the area (x,t), where the product grade does not change, ρ=const.
To carry out hydraulic calculation of the pipeline system, it is necessary to set the boundary conditions (BC). 5 Hydraulic calculation is the determination of all isothermal flow parameters Ω ( x , t ) by given BCs. For a simple pipeline, the BC should include such values that allow you to calculate the hydraulics throughout the pipeline. The minimum required composition of the BC: velocity v ( 0 , t ) , density ρ(0,t), and viscosity υ ( 0 , t ) in the initial section x=0. The proposed algorithm is designed to calculate Ω ( x , t ) – simulation of flow in a pipeline. This means that at the initial moment 0 the inlet pressure is known. Let us assume that at t=0, a new batch of oil of a different grade begins to flow into the pipeline. To clarify the procedure, consider the case when the oil of the displacing batch is heavier ρ2>ρ1. Filling the pipe with a new batch can be carried out under different inlet conditions.
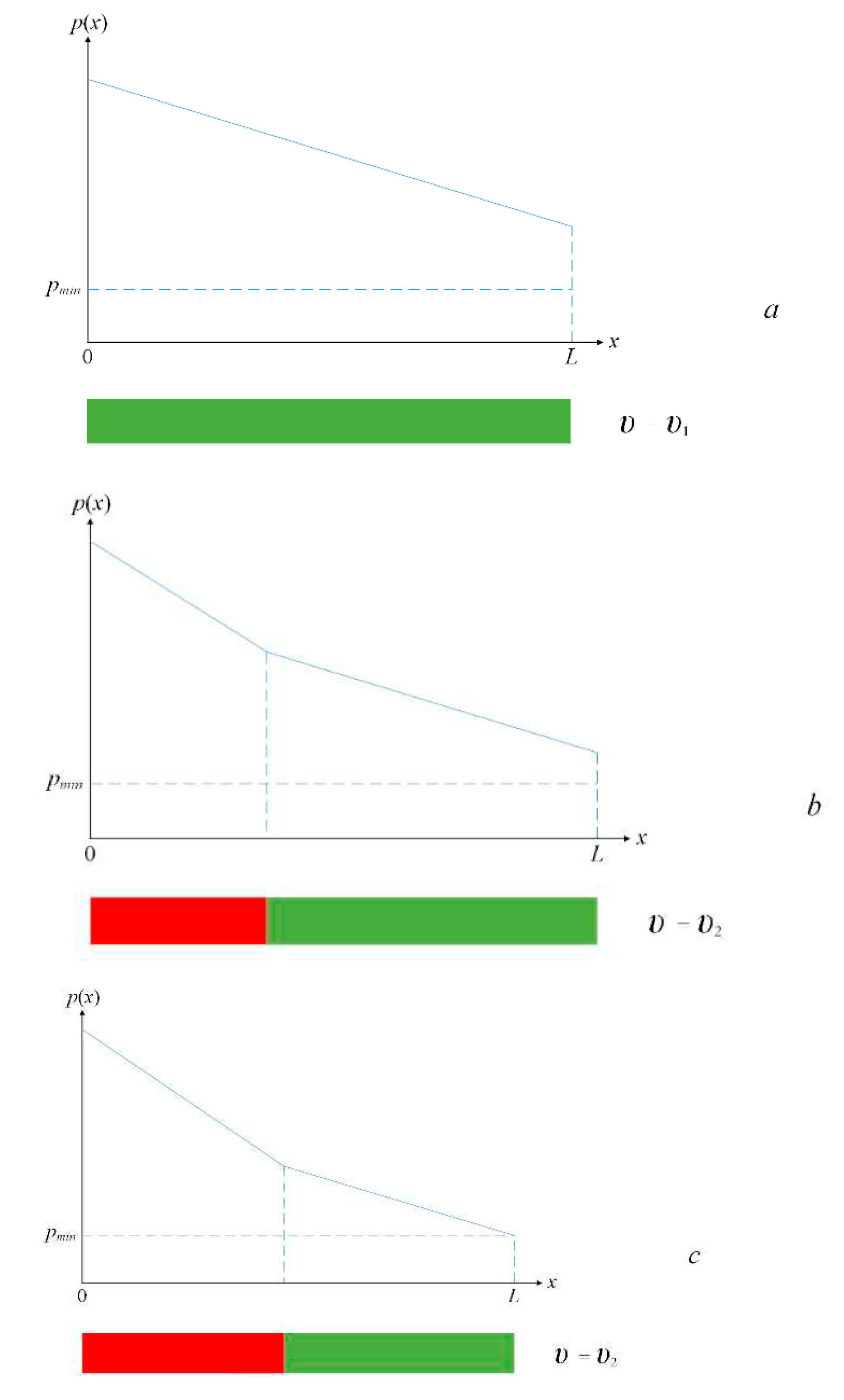
The purpose of hydraulic calculation is to find a regime that satisfies all technological constraints. Figure 2 shows how the consideration of the constraint affects the pressure minimum p(L,t)≥ pmin.. The process of displacement of several grades by heavier oil ρ2>ρ1 is considered. The displacement started at time t= t1. At the initial moment, ρ(х,0)=ρ1 (Figure 2a). If the process runs at a constant inlet pressure, while maintaining a constant inlet flow rate, the pressure at the end of the pipeline will decrease (Figure 2b) until (at time t3) it reaches the technologically acceptable minimum pmin. After that (Figure 2c), from the moment t3 to the moment t4 when the pipe is completely filled with oil of the 2nd batch, the inlet velocity must decrease so that the mode satisfies the requirement for the minimum pressure pmin. Thus, the period of replacement of one batch by another is divided into 2 intervals [t1, t3] and [t3, t4].
Other technological constraints are taken into account in the model in a similar way. The description is omitted so as not to overload the text with technological details that do not affect the principles of constructing the methodology.
If the process takes place at a constant inlet pressure, while maintaining a constant inlet flow rate, the pressure at the end of the pipeline will decrease until (at time t1) it reaches 6 the technologically acceptable minimum pmin. After that, until the moment t2 of the complete filling of the pipe with the 2nd batch, the inlet velocity must decrease so that the mode satisfies the requirement for pmin. Thus, the period of replacement of one batch by another is divided into 2 intervals [0, t1] and [t1, t2].
At the stage of hydraulic calculation, only the 1st and 2nd Kirchhoff laws are taken into account, that is, the equations of balance and momentum. In this case, all parameters of the Ω ( x , t ) mode as functions of time are determined by the results of calculating stationary modes for two crucial moments t1, t2. Let's find t1, t2. At a fixed point in time, due to incompressibility, the fluid velocity is the same for any 0≤х≤L where L is the length of the pipeline. Until the moment t1 v ( x , t ) = v ( x , 0 ) = v1. The value of t1 is determined by hydraulic calculation as the time required for the pressure at the interface of batches to become equal to the value pmin – the minimum allowable pressure at the end of the pipeline. The fluid velocity at the moment the interface reaches the end of the pipeline v2=V(х,t2) is determined by hydraulic calculation, since the entire pipeline at the time t2 is filled with a displacing liquid and the pressures at its ends are known. Under the QSM assumptions, the change in the flow velocity over the interval [t1, t2] can be considered linear. Hence, the average speed on the interval τ=t2−t1 is equal to 0.5(v1+ v2) and the relation from which t2 is calculated.
L − v1t1 =0.5(v1 +v2) (t2− t1) = 0.5(v1 + v2)τ
At the moments t1, t2, the BC at the pipe inlet changes. Let's call these moments key points. The term will be needed in the next section when describing the algorithm for an arbitrary configuration system. At key moments, the regime parameters – the components of the vector Ω ( x , t ) or their derivatives – in the QSM can suffer a discontinuity.
The considered case ρ2>ρ1 serves as a model by analogy with which other options for the ratio of parameters at the interface of two batches are studied. The situation when there are 3 batches of fluid in a simple pipeline at the same time is relatively rare in practice. Nevertheless, an analytical study of such a situation does not encounter fundamental difficulties.

4. Hydraulic calculation of a pipeline system of arbitrary configuration (isothermal model)

We characterize the structure of the system by a directed graph G(V,E), V is the set of its vertices (nodes), E is the set of arcs.. The movements of batches of the pumped product will be identified with the process of coloring the arcs and nodes of the graph. We will assume that at those moment when a new batch of product arrives at one of the inputs, the input node is colored with some color that does not match the colors currently involved in coloring other elements of the graph. In those moments when a new batch of product arrives at one of the inputs, the input node is colored. 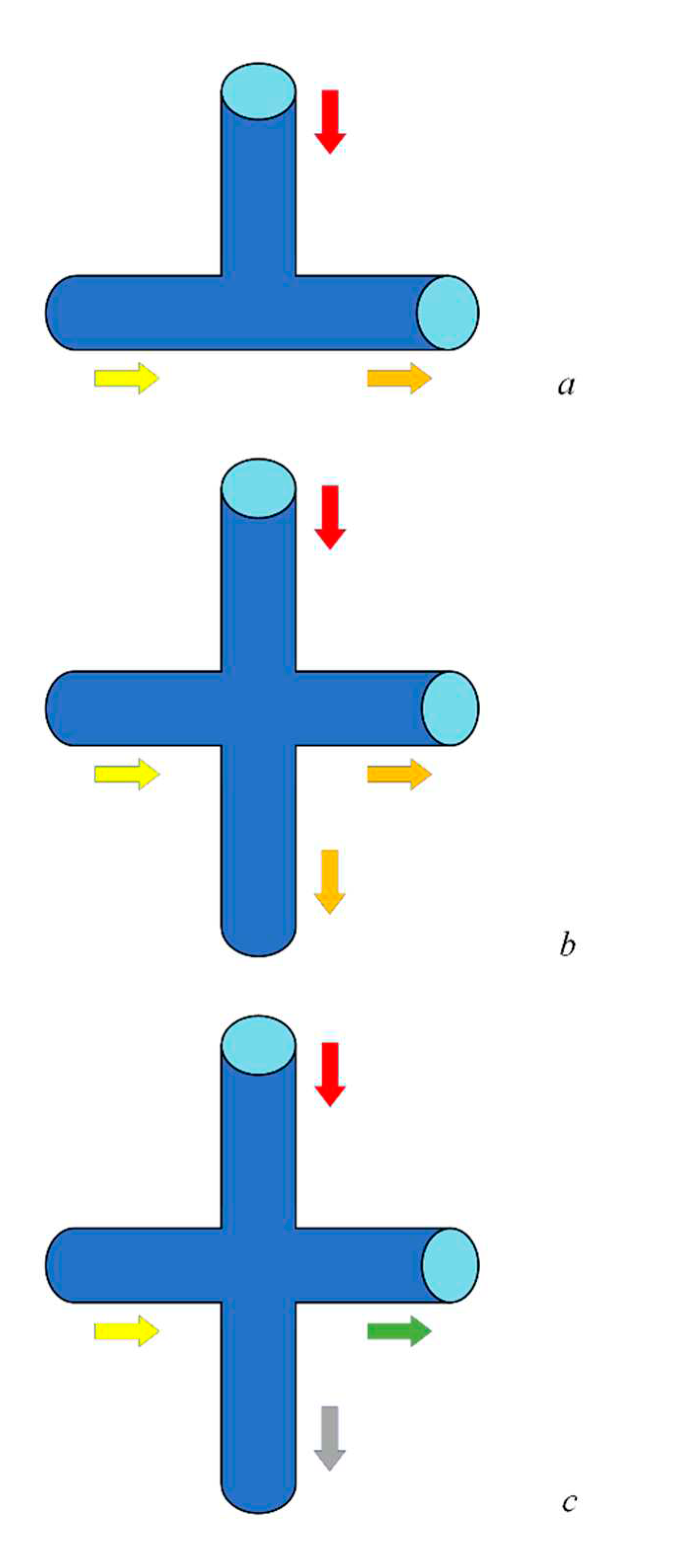Figure 3. illustrates the staining procedure during the passage of batch boundaries through butt nodes. Comments are necessary for the case when both the number of arcs entering the butt joint and the number of arcs leaving the joint are greater than 1 (Figure 3b,c). Due to the technological features of the local pipeline connection scheme in the butt joint, mixing may be complete or incomplete. In the 1st case (Figure 3b), the component composition of the product and, consequently, its properties in the pipelines outgoing from the node are the same and can be determined. For density and temperature as a weighted average for all incoming pipelines, for viscosity according to empirically established laws. In the 2nd case (Figure 3c), the component composition of the products (and their properties) in the pipelines outgoing from the node are different. In order to determine them, it is necessary to carry out measurements on the outgoing pipelines. Hydraulic calculation in the 2nd case is impossible without this additional information. In the 2nd case (Figure 3c), the component composition of the product (and its properties) in the pipelines outgoing from the node are different. In order to determine the properties, it is necessary to carry out measurements on the outgoing pipelines. Hydraulic calculation in the 2nd case is impossible without this additional information.
The order of hydraulic calculation of objects of the pipeline system – arcs and nodes of the graph – is conveniently described by introducing a virtual (imaginary) coloring procedure. The coloring procedure can be applied not only to hydraulic, but also to thermobaric calculations. To do this, it suffices to expand the concept of a product batch: to approximate the temperature increase at the inlet to the system with a piecewise constant function and to attribute the moments of transition to a new temperature level also to the moments of changing product batches. In this case, in the process of coloring, both hydraulic and thermal calculations are carried out (see below, p. 5). As the product advances, the arc(s) outgoing from the node is (are) colored. A node i∈V is colored when all arcs entering it are colored. Each new batch is assigned its own color, which is not in the color palette at the time the batch arrives. When two streams of different colors merge in a node, they are mixed. The mixture uses its own color. In order not to be distracted by the details, we will further consider the mixing to be complete. 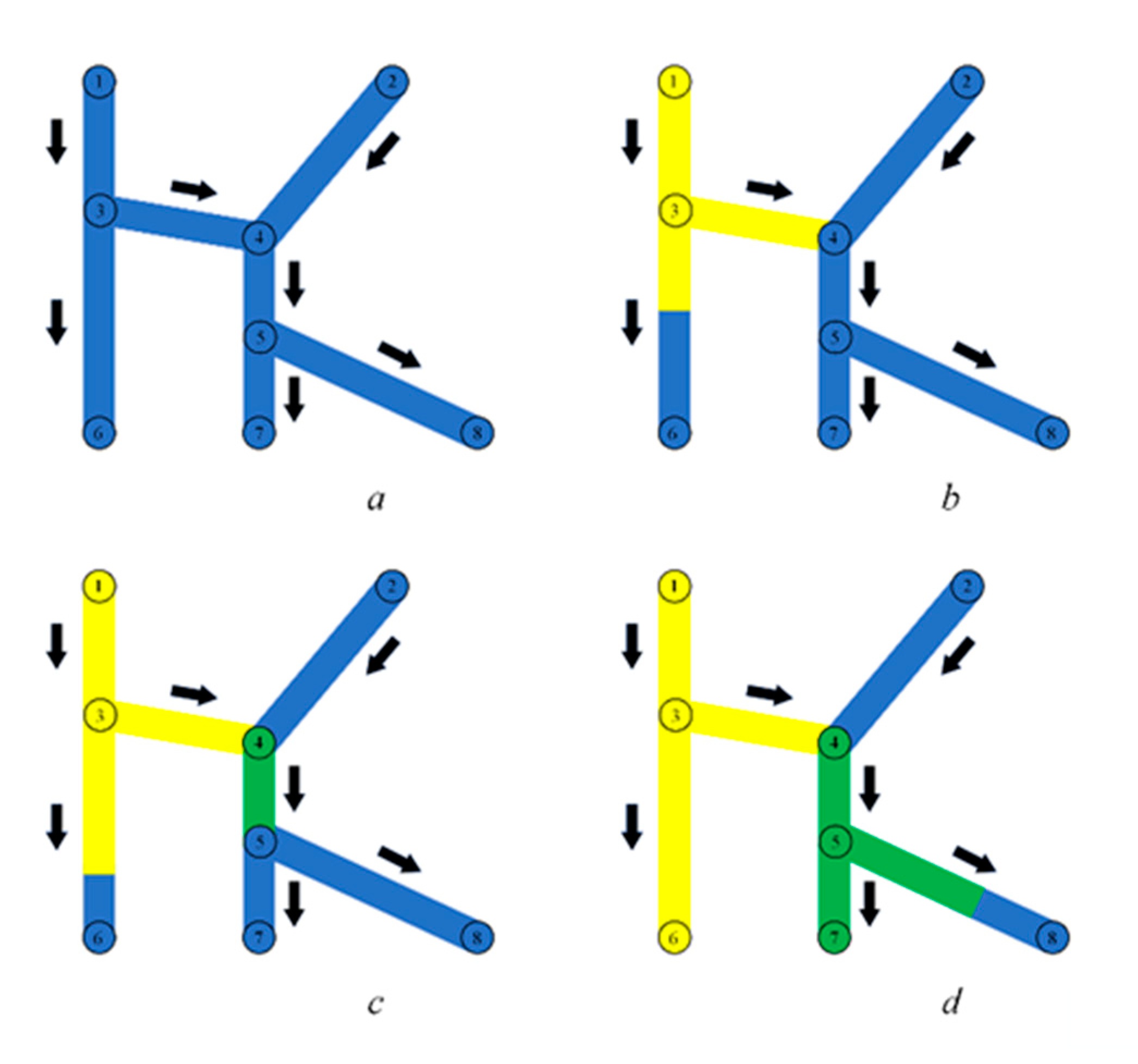Figure 4 shows an example of coloring a graph that is simple in structure.
The parameters of the mixture are calculated according to the relevant laws. For example, density, speed and temperature as weighted averages (according to the laws of conservation of mass and heat), while viscosity is in accordance with a more complex empirically established relationship. The resulting fluid is colored in its own color (of combined stream), the propagation of this color from the parent node of the merge is tracked.
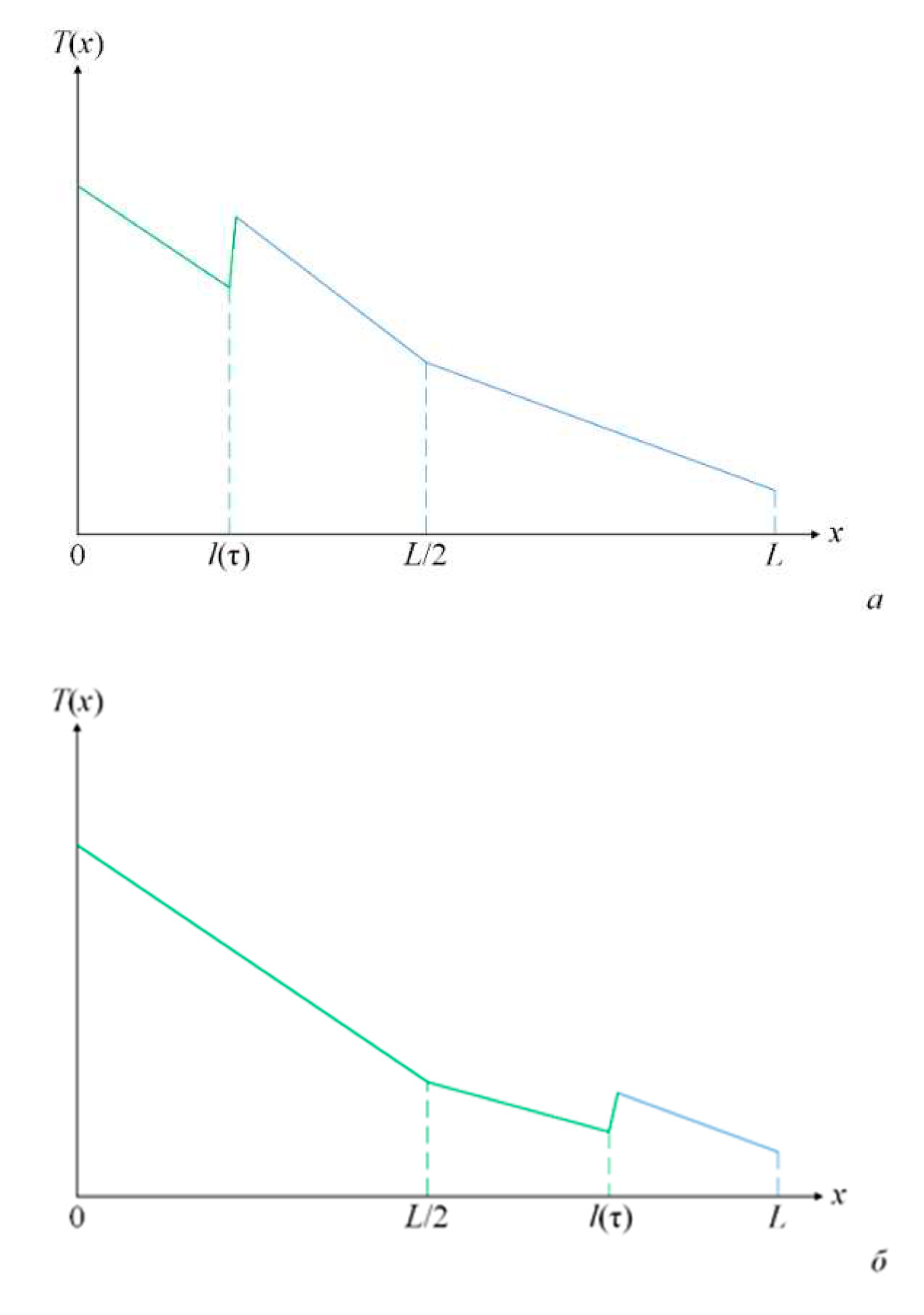
Let's denote the set of graph elements, colored by the moment t in some definite color ϰ, by Γ ϰ ( t ) . Γ ϰ ( t ) is a subgraph of G. Γ ϰ ( t ) can be thought of as a function on the graph, the number of Γ ϰ ( t ) functions is equal to the number of colors used for coloring at time t. At the beginning of coloring of arc i with length Li, according to the method of the previous paragraph, the time interval τi required for coloring and the end time of coloring Τi are calculated in accordance with (1). When the running area Γ ϰ ( t ) reaches a sink or joint node, this sink or joint node is colored. The arcs emanating from the newly painted node j are added to the list of arcs ready for painting. For each such arc j→i, the coloring termination time Τji is calculated. The arcs ready for coloring are ordered in ascending order of the values0 Τji (j∈ V, i∈E). The coloring of the arcs is carried out in a certain order, which is established in the process of implementing the calculation procedure. A list 𝔈(t) of arcs is compiled and constantly updated, which determines the order of coloring for the moment t. Each arc j → i in the list is represented by the end time 𝔗ji of coloring. The arcs are sorted in ascending order of 𝔗ji. The moments when the coloring of some arc is completed are called key moments. At the moment of completion of the coloring of the arc entering the node j, all arcs j → i are considered, the repainting of which begins at the given moment; i∈Е(j), where Е(j) is the set of arcs outgoing from j. For each arc j → i, according to the method of the previous paragraph, in accordance with (1), the time interval ti required for coloring and the end time of coloring 𝔗ji are estimated. The arcs j → i, i∈Е(j) are introduced into the list 𝔈(t). For the next in turn coloring, the first arc of this list is selected, after which the arc is removed from the list. When the last uncolored arc outgoing from a node falls under coloring, that node is colored.
Let's look at an example (Figure 4). At the end of the coloring of the arc 1 → 3, the values 𝔗34 and 𝔗36 are entered into the list 𝔈. Since 𝔗34 < 𝔗36, the next key moment will be the moment Τ13+Τ34. The last key moment in the example is determined by the coloring of node 8 (it is assumed that up to this point the parameters of the injected products at inputs 1 and 2 have not been changed.
Denote by Τ the set of key moments of the calculation procedure Τ={τs}, s=1,2,…,S. The moments of the set Τ are ordered in ascending order τs≤ τs+1. The subgraph colored by the time τs is denoted by Γs=Γ(τs). On all arcs colored by the moment Τs, the velocities are calculated using the above methods, and in all colored nodes, the heads are calculated. Only at moments of the set Τ do discontinuities arise in the flow parameters, i.e. in the coordinates of the vector Ω ( x , t ) . The search for a solution Ω(τs) that satisfies Kirchhoff's laws is combined with the coloring process. At each step s→s+1, the current solution Ω(τs) is used as an initial guess for finding Ω(τs+1). For the transition Ω(τs)⟹Ω(τs+1), we can apply any of the methods of the theory of hydraulic circuits [3,4,5,6] to solve stationary problems. Only at moments of the set Τ do discontinuities arise in the flow parameters, i.e., the coordinates of the vectorΩ(x,t). Their appearance is explained by abrupt changes in the boundary conditions during the transition from one key moment to another τs⟹ τs+1.
The coloring process implements the search for a solution Ω ( x , t ) that satisfies Kirchhoff's laws. At each step s→s+1, the current flow distribution Q(Γs+1) is used as an initial approximation. The current solution Ω(Τs) is corrected using the methods of the theory of hydraulic circuits for solving stationary problems, as a result, a solution Ω(Γs+1), is obtained on Γs+1 , but also the 2nd Kirchhoff law. The components of the vector Ω(t) outside the discontinuity points are continuous; by virtue of the QSM assumptions, they can be considered linear on any interval [τs, τs+1].

5. Inclusion of the energy conservation equation in the model

In some cases, when temperature changes along the pipeline route are small, the flow regime in the CSM can be considered isothermal. Thermal effects can significantly affect both steady-state flows and the dynamics of flow processes through pipelines. The specificity of nonisothermal problems is determined by two circumstances. First, the fluid temperature affects the flow hydraulics only through viscosity. With relatively small temperature changes that are possible within the framework of QSM, this effect is insignificant. Secondly, models that take into account the physics of thermal interaction processes in the system fluid – pipe with thermal insulation – environment are complex. When modeling, one cannot do without such quantities as: coefficient of heat transfer and ambient temperature. Reliable knowledge of that parameters is fundamentally impossible [25,32,33,34]. The most motivated approach for modeling temperature effects is to use the entire set of current fluid temperature measurements and trends.
Thermal processes directly affect hydrodynamic processes: the higher the temperature, the lower the friction resistance. There is also an inverse relationship: with an increase in the flow velocity, the heating of the fluid intensifies due to internal friction. Therefore, flow models in "hot" pipelines must be thermodynamic. To reflect the influence of temperature on flow processes in continuum mechanics, an equation is used that follows from the law of energy conservation. For a one-dimensional flow through a pipeline, it is written as [1,25]
ρ C v D T D t     = 4 K T d ( T − T s o i l ) − λ R e , ε 1 d ρ v 3 2 .
Here Cv is the isochoric (at constant volume) specific heat thermal of the fluid, Tsoil is the soil temperature, KT is the heat transfer coefficient from the pipe to the soil. The total time derivative D/Dt is required to characterize the heat transfer process in the direction of the pipeline axis. This process occurs due to the thermal conductivity of the fluid and advection, i.e. horizontal mixing during fluid movement. This process is initiated by advection. The first term on the right side of equality (2) characterizes the outflow of heat transfer from the pipe into the ground. Newton's law is used to quantify this outflow in equation (2).To quantitatively characterize this outflow in equation (2), Newton's law is used - a linear dependence of the amount of heat on the temperature difference between the fluid and soil T-T_{soil}. Equation (2) uses Newton's law: the heat outflow linearly depends on the temperature difference between the fluid and the soil T − T s o i l . Newton's law is the simplest approximation of the heat transfer process, which contains a single parameter КТ. If you want to clarify the description of thermal processes, different methods are used. With multilayer insulation, the coefficient КТ is determined so that it integrally characterizes all heat-insulating layers [27]. The outflow of heat depends on the properties and moisture content of the soil. It usually varies significantly along the path and over the time КТ= КТ(x,t) [29]. The second term on the right side characterizes the heating of the moving fluid from friction between the layers. As follows from formula (2), the heating depends substantially, proportionally to v3, on the speed [37]. Generally speaking, the temperature T(x,t) should be determined together with other flow parameters: pressure p(x,t), velocity v(x,t), density ρ(x,t), viscosity υ ( x , t ) . The temperature T affects the flow process through the Reynolds number Re. However, this dependence is weak and, as computational experiments show, this allows using the decomposition method in the calculation. Equation (2) can be simplified if the physical features of the flow process are taken into account. The total time derivative on the left side of the equation is written as D T D t     = ∂ T ∂ t     + v ∂ T ∂ x     . Here, the term 𝜕T/𝜕t is due to diffusion heat transfer, and the term v ∂ T ∂ x     is due to advection. The transfer of heat from a heated body to a colder one in a medium at rest is a much slower process than the process of fluid flow in a pipeline under normal conditions, i.e.   ∂ T ∂ t     ≪ v ∂ T ∂ x     . Usually, whether the total derivative DT/Dt or v ∂ T ∂ x     is used in the equation, the result practically does not change [1]. That is, the energy equation (2) for a pipeline filled with a homogeneous fluid 7, under the conditions of QSM applicability, can be replaced by the equation
ρ C v v ∂ T ∂ x     = − 4 K T d ( T − T s o i l ) + λ R e , ε 1 d ρ v 3 2 .
Thus, the model for determining the regime parameters of an isothermal flow is refined by taking into account temperature effects. Let us call the Correction of the solution when the energy conservation equation is included in the model is the final stage of the algorithm (plus iterative cycles of Section 4). This stage is realized by introducing one more iterative cycle into the algorithm. For its formal notation, we denote by the symbol Ω(Т) the solution of the hydraulic problem, that is, the set of functions p(x,t), v ( x , t ) , ρ(x,t), υ ( x , t ) , for a given distribution temperature T(x,t). The decomposition procedure is implemented as an iterative process
Ω(1)= Ω(Т(0))→ Т(1)= Т(Ω(1)) → Ω(2)= Ω(Т(1))→ Т(2)= Т(Ω(2))
(4)
This notation means that the procedure begins with the choice of the approximation Т(0). With Т(0) chosen, the algorithm of Section 4 is used to find the remaining components of the solution Ω(1). The temperature distribution is corrected, more precisely, the temperature distribution Т(1) corresponding to Ω(1) is found. The process continues until at some iteration k the distance between two successive approximations becomes less than the preselected accuracy δ: ‖Ω(k) − Ω(k−1)‖ < δ. As evidenced by the experience of calculating pipeline networks for various functional purposes [2], iterative procedures for determining the temperature of type (4) are not sensitive to the choice of the initial approximation and quickly converge. 8 As in static models of the theory of hydraulic circuits, it is advisable to take into account the effect of temperature on the regime parameters by introducing an external iterative cycle at each key moment from T. The initial approximation for the temperature distribution at step s+1 should be the temperature component of the vector Ω (Τs). To correct the solution Ω (Τs+1) on the outer loop, a small number of iterations will suffice.
There is a fundamental difference between the algorithmic QSM procedures at the stage of solving the isothermal problem and at the final stage, when the model is supplemented with the temperature effect taken into account. At the isothermal stage, the algorithm includes only logical-combinatorial procedures for theory of flows in networks [2] and hydraulic calculation of the stationary regime of the pipeline. At the final stage, it is required to analyze the dynamics of the interaction of temperature fields in the pipeline and the environment [14,15,16,17,21,22,23]. It would seem that the natural way to carry out such an analysis would be to solve the problem of the theory of heat conduction, in which the situation is simulated by setting the appropriate boundary conditions. However, this path is unreasonably difficult. The solution of such a problem will require significant labor costs and computation time. This is explained by the fact that the processes of temperature change in the transported product and in the soil are characterized by very differentscales of calendar time. 9 And – the main argument – the initial information for thermal conductivity models, the coefficients T s o i l ,  КТ, can only in principle cannot be determined with a low high degree of certainty. One of the basic principles of mathematical modeling is that all components of the model must be comparable in accuracy. Thus, in order not to make a methodological error, it is necessary to abandon attempts to apply models of continuum mechanics to the study of temperature fields. That is, it is based on instrumental measurements of flow parameters, primarily the temperature of the transported product and, perhaps, pressure. The logic of constructing the calculation procedure is as follows.
Therefore, the final stage of the proposed algorithm is based only on information that is promptly received by the pipeline system mode control centers, that is, it is based on instrumental measurements of flow parameters, primarily the temperature of the transported product. The logic of constructing the calculation procedure construction is as follows. By the time τs, according to the prehistory of temperature change up to this moment, the parameters are estimated, which is extrapolated to the time interval [𝜏s, 𝜏s+1]. These parameters are the coefficient KT(x,t) in Newton's formula and Tsoil(x,t) – the soil temperature. Both of these functions are considered piecewise constant: an extended section of the pipeline is divided into several parts so that these coefficients can be considered constant on each part. Thus, the problem of estimating KT(x,t) and Tsoil(x,t) is reduced to estimating a finite number of coefficients. The algorithm assumes that these coefficients do not change on the interval [𝜏s, 𝜏s+1]. This assumption is quite justified due to the inertia of thermal processes in the soil. With known KT(x,t) and Tsoil(x,t), the fluid temperature distribution over the interval [𝜏s, 𝜏s+1] is calculated in relation to the distribution of flow rates and pressures. With this logic of constructing the computational procedure in mind, let's move on to describing its details.
The temperature of the transported product changes due to the temperature difference between the incoming and preceding batches of the product, due to the switching on / off of the heating furnaces, due to heat exchange between the pipeline and the environment, or, finally, due to a change in fluid flow rate. Of these reasons, the first three cause an abrupt or close to an abrupt change in temperature. If the speed changes, even changes abruptly, for example, when moving from one batch of product to another, the rate of temperature change due to internal friction of the layers of the moving product is not high. Thus, QSM considers both abrupt changes in flow parameters and continuous, evolutionary changes. When changing batches of the pumped product, the transition process time for the case of a simple pipeline is equal to the interval of passing the interface between the batches from the beginning to the end of the pipeline. These changes are relatively slow, that is, they certainly satisfy the QSM assumptions.
3.4. Simple pipeline. Relation (3) Relation (3) can be further simplified [1] by neglecting the term λ R e , ε 1 d ρ v 3 2 compared to 4 K T d ( T − T s o i l ) , that is, assuming a priori that the heat outflow through the surface of the pipe is much higher than the intensity of heat generation in the moving fluid due to frictional resistance. Then (for KT (x)=const) the solution of equation (3) is found in elementary functions
  T ( x ) = T s o i l + ( T 0 − T s o i l )   e x p ( − π K T d C v M ) x ,     0 ≤ x ≤ L .
Here M = ρ v S is the mass flow rate of fluid, 10 S is the area of the internal section of the pipe. Analytical solution (5) from the point of view of calculations is not much better than an ordinary differential equation, but, using it, it iseasier to present the ideological side of the final stage of the algorithm. The accuracy of the model is in this case less important than the accuracy of determining the heat transfer coefficient KT(x). 11
As already noted, KT(x) can be considered a piecewise constant function. Then the function T(x) can also be written in analytical form. Consider, for example, the case when the coefficient of thermal conductivity along the route of a simple pipeline 0≤x≤L, takes 2 values K1 and K2, that is, the function KT(x), is approximated by a piecewise constant function
K T   ( x ) = K 1 ,   0 ≤ x ≤ l K 2 ,   l ≤ x ≤ L .
Then
T ( x ) = T s o i l + ( T 0 − T     s o i l )   e x p ( − π K 1 d C v M ) x ,   0 ≤ x ≤ l T s o i l + ( T l − T s o i l )   e x p ( − π K 2 d C v M ) x ,   l ≤ x ≤ L .
where T0 is the temperature at the pipeline inlet, and Tl is calculated by the upper formula (7) Tl =T(l). Formulas for T(x) are also obtained for any piecewise constant functions KT (x) and Tsoil(x).
Instead of the analytical representation (7), one can use the differential equation (2). Integrate equation (2) over the interval 0≤x≤l with KT =K1 and take the resulting value T1=T(l) as the initial condition for integration over the interval l≤x≤L. This procedure is somewhat more accurate than the analytical representation (7). Instead of Shukhov's formula (7), it would now be natural to indicate which program from the standard package is recommended to be used for numerical integration of equation (2) and calculation of the function Т ( x ) = T ( x ; T 0 , T s o i l , K 1 , K 2 ) . Instead of (7) or (2), one could use other, more accurate formulas for T(x), which, however, in our opinion, is inappropriate given the low level of reliability of information about the thermophysical properties of the soil.
In the thermobaric calculation of a simple pipeline, iterative procedure (4) must also be used. T ( 0 ) ( x ) allows calculating [1,38] the corrected value of viscosity υ(1), and then the corrected value of all parameters that define the expression λ R e , ε 1 d ρ v 3 2 . Now it becomes possible to calculate the approximation T ( 1 ) ( x ) using formula (5). Process (4) is repeated until the norm of the difference between two successive approximations becomes less than the specified calculation accuracy.
Figure 5 illustrates the movement of the interface of 2 oil batches along the pipeline section L = 80 km long and 700 mm in diameter. The heat transfer coefficient KT varies along the route according to the formula (6), where l= L /2, K1=3.5 W/(m2 ∙ 0С), K2=1.5 W/(m2 ∙ 0С). On Figure 2 moments of temperature jump propagation along the route are shown. At the initial moment of time, the temperature of the displacing batch is 7 0С lower than the temperature of the displaced batch.
3.5. 6..
As noted, information support for temperature calculations is the most problematic place in the simulation of flow processes in specific oil and oil product pipelines. In order to bring the results of calculations closer to the actual modes of the technogenic system, it is necessary to evaluate the parameters of the model using real current information. On main pipelines, information is usually collected and transmitted by SCADA systems. The coefficients KT, Tsoil can be estimated from temperature and pressure measurements T*={ T i , n * } ; p * = { p i , n * } ; i = 0,1 , . . . , I ;   n = 0,1 , . . . , N of the pumped product. 12 The number of measurement points is I+1, and the number of measurement transfer sessions is N+1. 13 The informational value of the measurements T* ; p * is different. The temperature enters directly into the energy equation (2) or (3) and into the Shukhov formula (7) for the temperature distribution T(x) along the pipeline. The pressure p(x) depends on temperature indirectly through viscosity, which affects the hydraulic resistance during fluid motion. Dependence T(p(x)) can be easily taken into account in the estimation procedure, but we do not do this, trying to focus on the presentation of fundamental points.
Usually, in mathematical statistics, The vector of unknown parameters to be estimated is will be denoted by 𝜽={ θ j } ; j = 0,1 , . . . , J . Denote by θ ^ the required estimate. Let us consider the problem when θ ^ is searched by the totality of temperature measurements T*={ T i , n * } ; i = 0,1 , . . . , I ;   n = 0,1 , . . . , N . Along with the numbers of communication sessions, we need the time moments t 0=0, t1,…,tN, when the measurements were taken. If the sessions are held at regular intervals h, then t0=0, t1=h, …, tN=Nh. To determine θ ^ , we use the maximum likelihood method, which reduces the problem to conditional optimization of a quadratic function with constraints in the form of equalities. When solving problems of this kind, computational difficulties may occur due to the presence of many extremum points and ravines of the criterion function. Therefore, when setting the problem, it is desirable to limit ourselves to the smallest possible number J of estimated coefficients. In our case, the variants options 𝜽= { K 1 , K 2 ,   T s o i l } and 𝜽={ K 1 , K 2 ,   K 3 ,   T s o i l } are of practical importance. In the 1st variant, the heat transfer coefficient is represented by formula (6), in the 2nd, KT (x) is piecewise constant function with three values, the soil temperature is considered unchanged throughout the pipeline. It is hoped that the computational difficulties in estimating 3-4 parameters will not be excessive. However, this cannot be guaranteed in advance. It is necessary to carry out computational experiments (CE). The purpose of the CE is to select a suitable apparatus (program) from a general-purpose package or, having established that there are no suitable programs in such packages, continue the search among commercial optimization packages.
Temperature measurements are random variables T i , n * = T i , n + δ T i , n ;  i=0,1, ..., I; n=0,1,...,N. Here T i , n are the true, albeit unknown, temperature values, and δ T i , n are the measurement errors, which, as is customary in error theory, we will consider distributed according to the normal law with zero mean and variance σ2, that is
δ T i , n ∈ N ( 0 , σ 2 ) .
According to the maximum likelihood method, the estimate θ ^ of the parameter θ should maximize the probability density of the sample, subject to the constraints in the form of equalities, which we write in symbolic form Φ ( T , θ ) = 0 . In the case under consideration, when a sample of temperature measurements T i , n * is processed, the likelihood function has the form f ( T * , T ) = ∏ i , n 1 σ 2 π e x p { − 1 2 ( T i , n * − T i n ) 2 σ 2 } . Obviously, the maximum of f(T*,T) is reached when the sum ∑ i , n ( T i , n * − T i n ) 2 takes the minimum value. Relationships Φ(T, θ)=0 can be chosen in the form (2), (3) or (7). Let us dwell on version (7), since the analytical representation of the function T(x) makes it possible to demonstrate the ideological side of the method in a simpler form. Thus, all quantities T i , n   ( i = 0,1 , . . . , I ;   n = 0,1 , . . . , N ) are determined by formula (7). The unknowns to be estimated are the true values of the regime parameters T i , n and the vector of estimated coefficients θ={ K 1 , K 2 ,   T s o i l } .. The optimization problem has the form
∑ i , n ( T i , n * − T i n ) 2 ⇒ T , θ m i n   under   the   condition   Φ ( T , θ ) = 0
The role of constraints Φ(T,θ)=0 is played by relations (7). To find the estimate T ^ 0 of the parameter T0 for fixed θ, one should solve the problem of unconstrained optimization of the quadratic function. This function is obtained by substituting into the sum ∑ i , n ( T i , n * − T i n ) 2 the expression for T i , i = 0,1 , . . . , I through T0.
It is known that the solution of identification problems often encounters computational difficulties. Experience in solving a number of identification problems has shown that the Levenberg-Marquardt method often serves as an effective tool for this. We have carried out a computational experiment on the example of a simple oil pipeline 80 km long and 700 mm in inner diameter, through which 2 batches of oil of different grades are pumped successively. The heat transfer coefficients K1, K2 were estimated for two parts of the pipeline, each 40 km long. The measurements were modeled as noisy calculation results. The error is distributed according to the (8) with a standard deviation σ 2 =0.2135. The Levenberg-Marquardt method gave unsatisfactory results: the deviation of estimates from the true values of the coefficients was unacceptably large.
The solution of the optimization problem is obtained by the Nelder-Mead deformable polyhedron method. When varying the noise dispersion and the number of measurements, the method invariably led to estimates close to the true values of the coefficients. The results of the computational experiment should be considered encouraging, but not exhaustive. The experiment showed that the optimization problem of estimating 3 thermophysical parameters in a particular case of a simple pipeline can be solved using a program from a general-purpose package. It does not follow from this that the same program is suitable for solving any similar problem. The complexity of computational problems depends on the specific features of the problem, the structure of the pipeline system, on the range of possible changes in numerical parameters, and on the adequacy of the representation of the QSM of the flow process. However, the computational experiment proved the fundamental efficiency of the technique. Its application to a specific system should be preceded by testing in the range of parameter changes characteristic of the real modes of the production facility. In the process of preparing for the application of the proposed procedure online, the developers will be able to solve in advance the technical issues related to the selection of the parameters of the computational procedure.

7. Conclusion

Models for the calculation and optimization of pipeline systems are combined under the name of the theory of hydraulic circuits. The main content of this theory is the study of the regimes of industrial pipelines with a stationary flow of the target product. This paper considers unsteady flows in oil and oil product pipelines that take place under normal operating conditions. An algorithm for modeling technological processes containing several nested iterative loops is proposed. On internal cycles, a solution is determined that satisfies Kirchhoff's laws, but under the assumption that the flow is isothermal. On the outer iteration cycle of the algorithm, the solution is corrected in order to take into account heat exchange processes. In this case, traditional methods adopted in continuum mechanics are not used. The expediency of this approach is explained by the fundamental impossibility of reliable knowledge of the thermophysical parameters of the anthropogenic system fluid – pipe – soil. The normal modes of oil and oil product pipelines are characterized by the arrival of the product at the inputs in batches. Batches differ in product grade or temperature. Correction of the solution on the outer iteration cycle of the algorithm is focused on the use of current measurements of the regime parameters of the flow. The constructed model is stochastic, since it takes into account possible errors of measuring instruments. To estimate the parameters of the model, the maximum likelihood method was applied, which reduces to solving an optimization problem with constraints in the form of equalities. The implementation of the model is associated with some computational difficulties related to the choice of an appropriate optimization method. On a specific example, the possibility of using various programs to solve the problem was checked. It turned out that such programs are available even in general-purpose packages.
The technique proposed in the paper opens up a new direction in modeling the regimes of industrial pipeline systems designed to transport weakly compressible liquids. If the changes in the flow regime of a weakly compressible fluid are regular, then the simulation of unsteady flows is reduced to the calculation of stationary regimes at some points in time, determined by the movement of batches of the transported product. This innovation – the apparatus of hydraulic calculations using sequential pumping – represents the development of the theory of flows in networks. If it is necessary to take into account thermal effects, it is proposed to supplement hydraulic models with models for assessing the state of the natural-technogenic system pipeline – environment. The assessment is made on the basis of measurements of regime parameters of the flow. This approach is the only justified one in the conditions of constant change and blurring of information about the environment.

References

  1. Lurie, M.V. Theoretical foundations of pipeline transportation of oil, oil products and gas. Moscow: Nedra Publishing House LLC, 2017. 477 p. [in Russian].
  2. Christofides, N. Graph Theory. An Algorithmic Approach. Academic Press. 1975. 424 p.
  3. Merenkov, A.P. , Khasilev V.Ya. Theory of hydraulic circuits. – M.: Nauka, 1985. – 278.
  4. Sukharev, M.G. , Samoilov R.V. Analysis and management stationary and non-stationary modes of gas transport. – M.: Ed. Center of the Gubkina State University of Oil and Gas 2016. - 399 p.
  5. Osiadacz, A.J. Simulation and Analysis of Gas Network. First Edition. London: D and F.N. Spon Ltd. 1987. – 176 p.
  6. Poh Hong Hwee. Application of computer based simulation in gas network system using graph theory algorithms and numerical methods. Universiti teknologi Malaysia 2008. http://eprints.utm.my/id/eprint/6801/1/PohHonhHweeMFKKKSA2007.pdf 2018 г. 4: 25 Nov 09.
  7. Nechval, M.V. , Novoselov V.F., Tugunov P.I. Sequential pumping of oils and oil products through main pipelines. M.: 1976. [in Russian] Todini E., Pilati S. Un metodo del gradiente per la verifica reti idrauliche // Bollettino degli Ingengneri della Toscana. – 1979. № 11: pp. 11 – 14.
  8. Metwally, M. , Modisette J. The Atmos book of pipeline simulation. 2022. 545 p.
  9. Nicholas, E. Simulation of Slack Line Flow. A Tutorial. PSIG 9505. 1995. 18 p.
  10. Cafaro, D.C. , Cerdá J. Optimal scheduling of multiproduct pipeline systems using a non-discrete MILP formulation. Comput. Chem. Eng. 2004. 2: 28 (10), 2053. [Google Scholar] [CrossRef]
  11. Meira, W.H.T. , Magatão L., Neves F. Jr., et al. A solution framework for the long-term scheduling and inventory management of straight pipeline systems with multiple-sources. Eur. J. Oper. Res. 2021. 268 (2): 665–687. [CrossRef]
  12. Manning, W. , Lind G. Data Analysis and Discussion of Product Interface Size on a Batched Crude Oil Pipeline. PSIG 1411. Baltimore. 2014. 9 p.
  13. Milano, G. , Goyal N. Tracking Batches Accurately in a Multiproduct Pipeline with Large Elevation Changes and Prominent Slack. IPC 2018.
  14. Stanley, G. , Ford M.H. Throughput Maximization and Verification for Batched Liquid Pipelines. PSIG 1216. New Mexico. 2012. 16 p.
  15. Garcia-Hernandez, A. Modeling and Simulation Case Study of a Batching Operation of Crude Oils in a Pipeline System. PSIG 1111. California. 2011. 14 p.
  16. Milano, G. Evaluating Different Approaches for Tracking Batches in a Multi-product Pipeline During the Presence of Slack. PSIG 1904. London, 2019. 9 p.
  17. Matko, D.S. , Geiger G. Simulation of Multi-product Pipelines. Int. journal of math. models and methods in applied sciences. Issue 2, Volume 1, 2007. P. 62 – 69.
  18. Ellul, I.R. , Saether G., Shippen M. E. The Modeling of Multiphase Systems Under Steady-State and Transient Conditions PSIG 0403. California, 2004. 21 p.
  19. Li, Z. , Liang Y. Scheduling of a branched multiproduct pipeline system with robust inventory management. Comput. Ind. Eng. 162 2021. [CrossRef]
  20. Mostafaei, H. , Castro P.M., Relvas S., Harjunkoski I. A holistic (целoстный) MILP model for scheduling and inventory management of a multiproduct oil distribution system. Omega (Westport), 98. 2021, Article 102110.
  21. Csontos, B. , Halász L., Heckl I. Event-driven simulation method for fuel transport in a mesh-like pipeline network. Computers & Chemical Engineering. Vol. 157, 2022. 17 p.
  22. Xu Bin Xu, Y. , Song J., Li Zh. et al. Scheduling of Straight Multiproduct Pipelines Considering the Contamination Control. Jun 22, 2023. Journal of Pipeline Systems Engineering and Practice. Vol. 14, No. 4. [CrossRef]
  23. Zheng, J. , Wang C., Liang Y., Liao Q., Li Z., Wang B. Deeppipe: A deep-learning method for anomaly detection of multi-product pipelines. Energy 2022. 259 (Nov): 125025. [CrossRef]
  24. Bamoumen, M. , Elfirdoussi S., Ren L., Tchernev N. An efficient GRASP-like algorithm for the multi-product straight pipeline scheduling problem. Computers & Operations Research. Vol. 150, 2023. [CrossRef]
  25. Modisette, J. Pipeline Thermal Models, PSIG 0204 Annual Meeting, Portland, Oregon, 2002.
  26. Sukharev, M.G. , Yuzhanin V.V. Modeling of the oil supply system as a problem of the theory of hydraulic circuits. Automation, telemechanization and communications in the oil industry 3(572)-2021. pp. 40 –51. [in Russian].
  27. Lurie, M.V. , Chuprakova N.P. Non-stationary modes of operation of a "hot" oil pipeline, taking into account the thermal field of the surrounding soil. Science and Technology of Pipeline Transportation of Oil and Petroleum Products 2021 11(3):276–283. pp. 276 - 283. [in Russian].
  28. Blazic, S. , Matko D., Geiger G. Simple model of a multi-batch driven pipeline, Math. Comput. Simul. 64 (2004) 617–630.
  29. Bennett, J.A. , Garcia-Hernandez A., Alvarado A. From Pipelines to Manifolds: Practical Considerations for Modeling Liquid Systems. PSIG 1607. Columbia, 2016. 11 p.
  30. Modisette, J. L Modisette J.P. Transient and Succession-of-Steady-States Pipeline Flow Models PSIG 0108 2001, 15 р.
  31. Ramsen, J. , Losnegård S.-E., Langelandsvik L.-I., Simonsen A. J., Postvoll W. Important Aspects of Gas Temperature Modeling in Long Subsea Pipelines. PSIG 0901. Texas, 2009.
  32. Vostry, Z. , Styblo M. Gas Network Simulation and Uncertainty of Pipe Leg Surroundings Parameters, PSIG 09A3 Annual Meeting, Galveston, Texas. 2009.
  33. Allen, C.W. , Holcomb Ch., Zamotorin R., Kurz R. Optimal parameter estimation for efficient transient pipeline simulation. PSIG 2118. 2021. 12 p.
  34. Chertkov, M. , Novitsky N.N. Thermal Transients in District Heating Systems Energy. Vol.184. P.22-23. [CrossRef]
  35. Barros, D. , Cathcart B., Tawney E. Ambient Ground Temperature and Heat Transfer Coefficient Derivation Method for Use in Hydraulic Modeling. PSIG 2002. San Antonio, Texas, 2020. 21 p.
  36. Novitsky, N. Estimation of parameters of hydraulic chains. Novosibirsk: Nauka; 1998. [in Russian].
  37. Christie, B. Analysis of the Frictional Heating Effect in Pipelines, PSIG 0702 Annual Meeting, Calgary, Alberta, 2007.
  38. Mohinder LN 2000. "PIPING HANDBOOK, 7th Edition" The McGraw-Hill Companies, Inc. 201 p.
1
The concept of quasi-stationary (quasi-steady) does not have an unambiguous interpretation. For example, in a standard university textbook [1], processes that are formally unsteady but occur rather slowly are called quasi-stationary. Then this qualitative definition is refined in the mathematical notation adopted in continuum mechanics.
2
The task is to solve the system of equations of the 1st and 2nd Kirchhoff laws. In hydraulics (unlike electrical circuits with Ohm's law), this task is not linear.
3
We are talking about nodes of finite difference grids for approximating equations.
4
A simple pipeline is a pipeline of constant diameter without interstitial inflows/outflows.
5
Reference information about the pipeline: diameter, wall thickness, pipeline profile along the route z(x), roughness coefficient – is known, that is, it is included in the initial QSM data.
6
If the pressure remains above pmin before the end of pumping, then the speed will not change.
7
Homogeneous fluid means oil of the same batch, that is, of the same grade.
8
Procedure (4) in [5] is called leapfrog («transient thermal model with fixed knots which alternates solution of the hydraulic model and solution of the thermal model»).
9
It takes no more than 10 hours to move oil in the normal mode for 50 km. The characteristic time for the effect of a change in soil temperature on the mode to become noticeable is measured in weeks.
10
Formula (5) was proposed by the Russian engineer Vladimir Shukhov at the beginning of the 20th century and was successfully used by him to calculate the first product pipeline in Russia. There are modifications of that formula, one of them allows to take into account the influence of internal friction, that is, the influence of the term λ R e , ε 1 d ρ v 3 2 in equation (3) [7].
11
The increased attention paid to the coefficient KT is quite natural: the 1st term on the right side of formulas (2, 3), as a rule, prevails (in absolute value) over the 2nd term. This means that KT, and not the flow velocity or frictional resistance, have a decisive influence on the temperature distribution T(x).
12
Here i is the index of the measuring point, n is the number of information transfer sessions, an asterisk (*) here and below denotes the measured value. In the introduced notation, the number of temperature and pressure measurements is the same and equals (I+1)∙(N+1).
13
It is assumed that the temperature is necessarily measured at the entrance of the section, the 1st measurement is taken at the initial time and is marked with index 0.
14
On Figure 5 the function T(x) is represented by points T(0), T(l), T(L/2), T(L), which, for clarity, are connected by line segments.
Preprints 82599 g001
Figure 1. Function l(t) (top); in the middle – the position of the batches of the product at the moment (t=t0); function 𝜌(х,t0) (below).
Figure 1. Function l(t) (top); in the middle – the position of the batches of the product at the moment (t=t0); function 𝜌(х,t0) (below).
Preprints 82599 g001
Preprints 82599 g002
Figure 2. Moving the interface between batches. a – the initial time t= t1, b is the time t2> t1, c is the time t3> t2.
Figure 2. Moving the interface between batches. a – the initial time t= t1, b is the time t2> t1, c is the time t3> t2.
Preprints 82599 g002
Preprints 82599 g003
Figure 3. Distribution of flows in the butt joint. a is the merging of two streams, b is the complete mixing of merging streams of different grades, c is the incomplete mixing of merging streams of different grades.
Figure 3. Distribution of flows in the butt joint. a is the merging of two streams, b is the complete mixing of merging streams of different grades, c is the incomplete mixing of merging streams of different grades.
Preprints 82599 g003
Preprints 82599 g004
Figure 4. Illustration of the staining procedure when a batch of product of a different grade arrives.
Figure 4. Illustration of the staining procedure when a batch of product of a different grade arrives.
Preprints 82599 g004
Preprints 82599 g005
Figure 5. Moving the interface of two oil batches. 14
Figure 5. Moving the interface of two oil batches. 14
Preprints 82599 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated