Prerpints.org logo
Preprint
Article

Using the Commercial RO Spire Data in the Neutral Atmosphere for Climate and Weather Prediction Studies

Altmetrics

Downloads

147

Views

60

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

16 August 2023

Posted:

18 August 2023

You are already at the latest version

Alerts
Abstract
Recently, NOAA has included GNSS (Global Navigation Satellite System) Radio Occultation (RO) data as one of the crucial long-term observables for weather and climate applications. To include more GNSS RO data in the numerical weather prediction system, the NOAA Commercial Weather Data Pilot program (CWDP) started to explore the commercial RO data available on the market. After two rounds of pilot studies, the CDWP decided to award the first Indefinite Delivery Indefinite Quantity (IDIQ) contract to GeoOptics and Spire Incs. in 2020. This study examines the quality of Spire data products for weather and climate applications. Spire RO data are collected from commercial CubeSats through careful comparison with the data from Formosa Satellite Mission 7–Constellation Observing System for Meteorology, Ionosphere, and Climate-2 (COSMIC-2), ERA-5, and high-quality radiosonde data. The results demonstrated that although with lower Signal-Noise-Ratio (SNR) in general, the pattern of the lowest penetration height for Spire is similar to those for COSMIC-2. The Spire and COSMIC-2 penetrate heights are between 0.6 and 0.8 km altitude at the tropical oceans. Although using different GNSS RO receivers, the precision of Spire STRASP receivers is of the same quality as those of COSMIC-2 Global Positioning System - GPS, GALILEO, and GLObal NAvigation Satellite System – GLONASS (TGRS) receivers. The retrieval accuracy from Spire is very compatible with those from COSMIC-2. We validated Spire temperature and water vapor profiles by comparing them with collocated radiosonde data. Generally, over the height region between 8 km and 16.5 km, the Spire temperature profiles match those from RS41 RAOB very well with temperature biases < 0.02 K. Over the height range from 17.8 to 26.4 km, the temperature differences are ~-0.034 K with RS41 RAOB being warmer. We also estimated the error covariance matrix for Spire, COSMIC-2, and KOMPSAT-5. Results showed that the COSMIC-2 estimated error covariance values are slightly more significant over the oceans at the mid-latitudes (45oN-30oN and 30oS-45oS), which may also be owing to COSMIC-2 SNR being lower at those latitudinal zones.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

GNSS (Global Navigation Satellite System) Radio Occultation (RO) technique provides unique measurements of atmospheric density vertical distribution, which is a function of temperature, moisture, and pressure in the neutral atmosphere [1,2,3]. [4] and [5] demonstrated that the RO-derived temperature profiles in the lower stratosphere and water vapor profiles in the troposphere are instrumental in identifying the calibration biases from the satellite infrared (IR) and microwave (MW) sensors, respectively. The raw RO observation is the time delay owing to the ray path occurring through the atmosphere between the GNSS RO emitters and receivers. The RO receivers are onboard Low Earth Orbit (LEO) satellites. Unlike IR and MW sensors, RO measurements are of a very high vertical resolution (~300 – 600 meters) and are unaffected by clouds and precipitations [1,2]. As a result, the RO data products are very suitable for atmospheric studies for all weather conditions [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. In addition, because the clocks on GNSS and LEO satellites are traceable to the International System of Unit (SI) of time (SI-traceable), RO data are also very suitable for climate studies [20,21,22,23,24,25,26,27,28]. In the global operational numerical weather prediction (NWP) centers, GNSS RO data were used as in-space references to correct other satellite data [1,2,29].
Many new GNSS RO missions were launched in the past five years, implementing different RO receivers and covering different orbits. The new missions included Taiwan/US Formosat-7/Constellation Observing System for Meteorology, Ionosphere, and Climate-2 (COSMIC-2), the European Space Agency (ESA)/European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT)/US Sentinel-6, and commercial RO missions from GeoOptics, Inc. and Spire Global, Inc. [30]. NOAA has included GNSS RO data as one of the crucial long-term observables for weather and climate applications, just as those from IR and MW measurements [30,31]. NOAA National Center for Environmental Prediction (NCEP) has assimilated the RO data from NOAA missions (i.e., COSMIC-2 and Sentinel-6) and partners’ missions (i.e., Korea Multi-Purpose Satellite/Arirang-5 (KOMPSAT-5), Meteorological Operational Satellite-A, -B, and -C (Metop-A, -B, and -C)) into their NWP system. Around 10K daily occultation profiles were ingested into the NCEP global NWP system. The RO data demonstrated apparent impacts on the NCEP global NWP, especially in the lower stratosphere [29]. The International Radio Occultation Working Group (IROWG) from World Meteorology Organization (WMO) recommended the optimal occultation number for NWP and climate applications is at least 20K per day with a uniform spatial and temporal distribution [30].
To include more GNSS RO data in the NWP system, NOAA initiated the Commercial Weather Data Pilot (CWDP) program to assess commercial GNSS RO data available on the market. After two rounds of pilot studies, the CDWP decided to award the first Indefinite Delivery Indefinite Quantity (IDIQ) contract to GeoOptics and Spire Incs. in 2020. Unlike those national-supported RO missions with more expensive receivers and larger antennae (see below), GeoOptics and Spire used CubeSats. Using the miniature 6U CubeSat version onboard the Community Initiative for Cellular Earth Remote Observation (CICERO) satellites, GeoOptics can collect approximately 1000 to 2000 occultation profiles per day. While GeoOptics data are collected from ten CubeSats, Spire GNSS RO data are collected from over thirty CubeSats. Currently, Spire can collect around 20K occultation profiles per day. COSMIC-2 used the TriG (Global Positioning System - GPS, GALILEO, and GLObal NAvigation Satellite System - GLONASS) RO Receiver System (TGRS) receiver. The Spire STRATOS RO antenna-receiver payload can track GNSS signals from GPS, GLONASS, and GALILEO, and Quasi-Zenith Satellite System (QZSS).
To use the RO data collected from commercial CubeSats in the neutral atmosphere for climate and weather prediction studies, we must first quantify their observation quality and retrieval data product quality. More specifically, we need to provide detailed quantitative analyses to answer the following questions:
1)
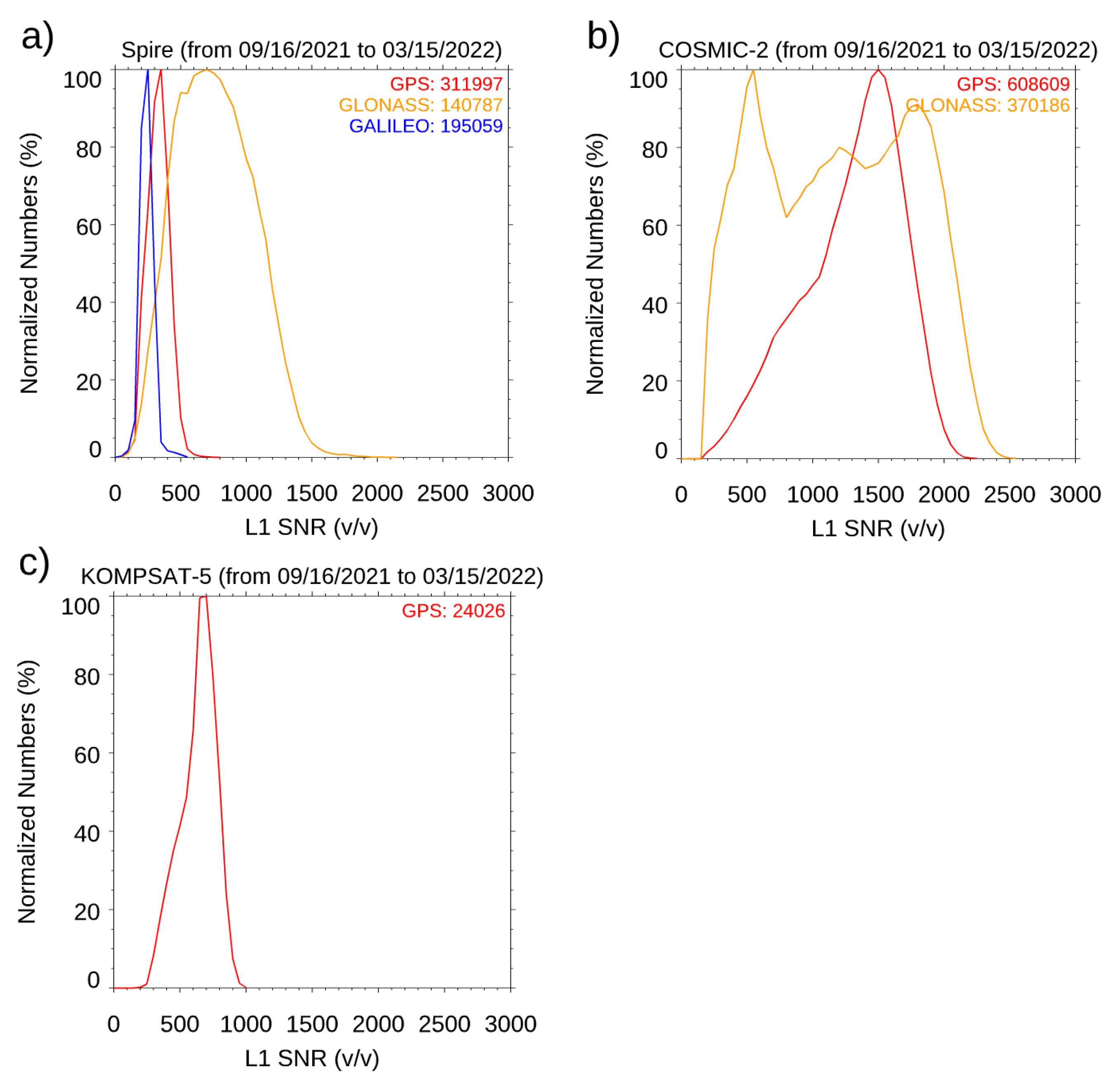
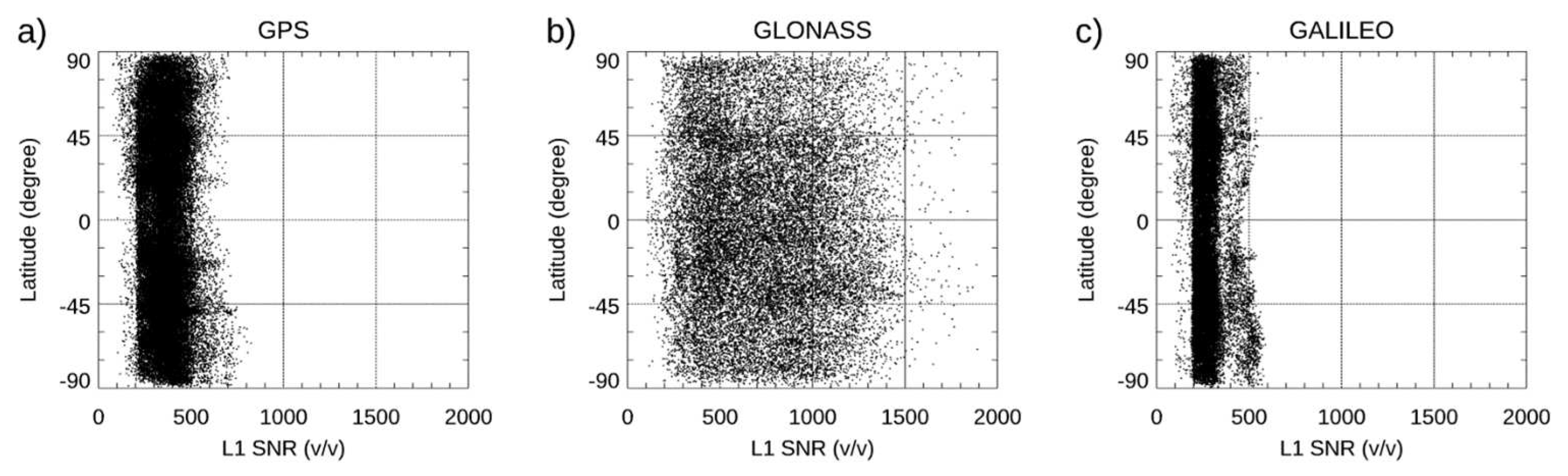
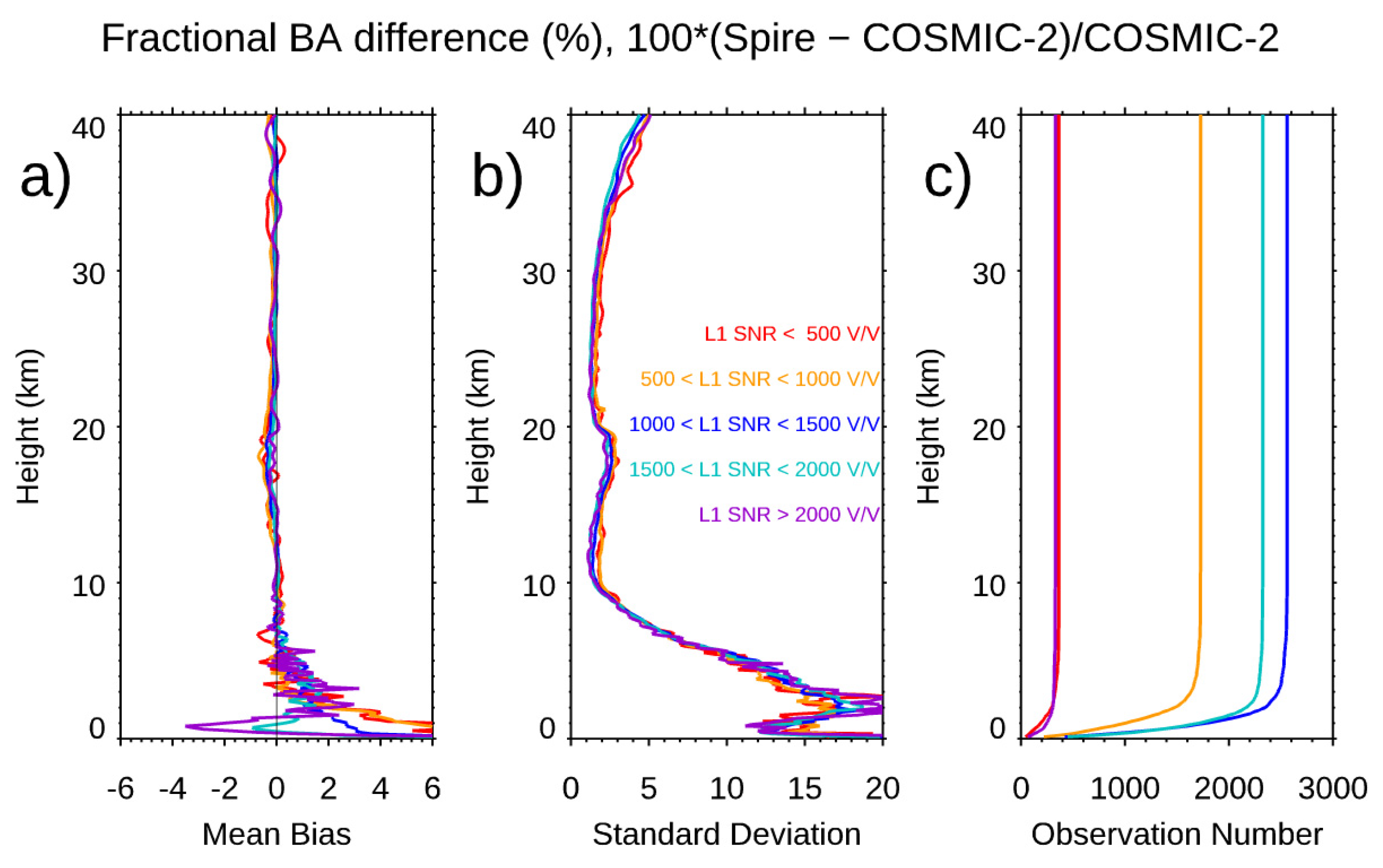
Does lower Signal-Noise-Ratio (SNR) commercial CubeSats RO data lead to lower precision and more significant observation errors? The SNR is defined as the magnitude of the RO signals divided by the noise level from that receiver in the voltage-to-voltage unit (V/V). The SNR of the RO signal is one of the critical parameters to indicate the quality of RO measurements (i.e., time delay and excess phases) and L2 data products (i.e., bending angle (BA), refractivity, temperature, and moisture profiles). When RO signals are stronger, or the noise level is smaller, the magnitude of the SNR will be larger, which may indicate an improved observation quality. While Formosa Satellite Mission 3–Constellation Observing System for Meteorology, Ionosphere, and Climate (COSMIC-1 hereafter) and COSMIC-2 used an antenna of 2 feet, the antenna from CubeSat is only 1 foot. Figure 1 depicts the SNR histogram of Spire, COSMIC-2, and KOMPSAT-5 for the corresponding emitters. The sample numbers are normalized to the maximum number of the SNR bin. With the TGRS receiver, COSMIC-2 has a larger mean SNR than Spire and KOMPSAT-5. The mean COSMIC-2 L1 SNR ranges from 250 to 2500 V/V [31,32], and the L1 SNR for Spire ranges from 200 V/V to 1500 V/V, lower than those from COSMIC-2 (Figure 1). The mean L1 SNR for KOMPAST-5 is 570 V/V. With higher SNR than other RO missions, COSMIC-2 is expected to penetrate deeper into the lower troposphere [30]. With such a smaller antenna size for the Spire, one might expect the detected SNR to be much smaller than those from a larger antenna, which may lead to higher measurement and retrieval uncertainty. The antenna’s geometry may also influence the SNR distribution (see Section 2). The RO signals received from different receivers may also introduce extra retrieval uncertainty [31,32,33].
2)
Does lower SNR Spire RO data lead to less accurate retrieval results? Whether the RO data products derived from lower SNR signals obtained from the commercial CubeSats are as accurate as those from high SNR signals is a significant concern for the RO community and climate and atmospheric scientists. The causes of the retrieval uncertainty may include receiver quality, antenna geometry, the accuracy of Precise Orbit Determination (POD) estimation, L0 to L1a processing, L1a-L1b (excess phase) processing, and L1b-L2 (bending angle and refractivity profiles) processing [33]. Because RO data quality and retrieval uncertainty may also be affected by atmospheric conditions, especially in the lower troposphere, assessing RO data accuracy and identifying the accuracy uncertainty from different RO missions is still a significant challenge.
3)
How to optimize Spire RO data in the NWP system through data assimilation? As mentioned above, because RO bending angle and refractivity uncertainty, especially in the lower troposphere, are highly related to the atmospheric condition, we must carefully examine the observation uncertainty for each RO mission to use RO data optimally in the NWP through data assimilation (DA). An accurate estimate of retrieval uncertainty is also critical for optimizing the RO impacts in the NWP through the data assimilation system [1,2].
This study aims to use COSMIC-2, ERA-5, and high-quality radiosonde data to quantify the Spire RO data quality. NOAA Center for Satellite Applications and Research (STAR) has developed capabilities as a GNSS RO science and data center (STAR RO DSC, see https://www.star.nesdis.noaa.gov/smcd/GNSSRO/RO/index.php, also see [31,32,33,34,35,36,37,38,39,40,41]). STAR RO DSC aims to develop enterprise RO processing algorithms for all RO missions, like other NOAA infrared and microwave satellite missions. STAR has developed the RO inversion package for COSMIC-2 [33,35]. In addition to the Spire RO data processed by UCAR, STAR also processed Spire data using an independently developed inversion package (see Appendix A). In this study, we will compare the STAR-processed Spire products with those from UCAR to evaluate the uncertainty due to the differences in the processing algorithm implementation. This study examines the Spire data processed by UCAR (see http://cdaac-www.cosmic.ucar.edu/cdaac/doc/documents/ Sokolovskiy_newroam.pdf). We will examine the Spire data quality during the CWDP Delivery-Order 3 (DO3, from September 8, 2021, to March 15, 2022) and Delivery-Order 4 (DO4, from March 16, 2022, to January 16, 2023). NOAA purchased about 3000 Spire RO profiles daily in DO3 and about ~5000-6000 in DO4 (not shown). We will conduct the quality assessment of the UCAR Spire neutral atmospheric profiles regarding their stability, precision, and accuracy.
We first describe the Spire data spatial and temporal distribution in Section 2. We also detail the data used to validate the Spire retrievals in Section 2. The procedures to obtain the simultaneous limb overpass RO (SRO) were introduced by [32,42]. Section 3 presents the SRO method for our studies to collect the Spire-Spire pairs, Spire-other RO mission pairs, and COSMIC-2 – COSMIC-2 pairs. Because the Spire satellites are in the Sun-synchronized orbits, which also cover the globe, we can collect many coplanar Spire-Spire pairs and Spire-COSMIC-2 pair at all latitudes during the performance period. This provides an excellent opportunity to examine the climate quality regarding each RO mission’s precision, stability, and accuracy. We quantify the Spire penetration, precision, and stability in Section 4. Section 5 quantified the Spire retrieval accuracy and uncertainties using STAR Spire retrievals, the fifth generation European Centre for Medium-Range Weather Forecasts (ECMWF) atmospheric reanalysis (ERA5), and RS41 radiosondes. We compared Spire BA profiles with ERA5 and the Spire temperature and water vapor profiles with those of RS41 in Section 5.2 and Section 5.3, respectively. We further estimated the Spire error covariance matrix for NWP data assimilation in Section 6. We concluded this paper in Section 7.

2. Data

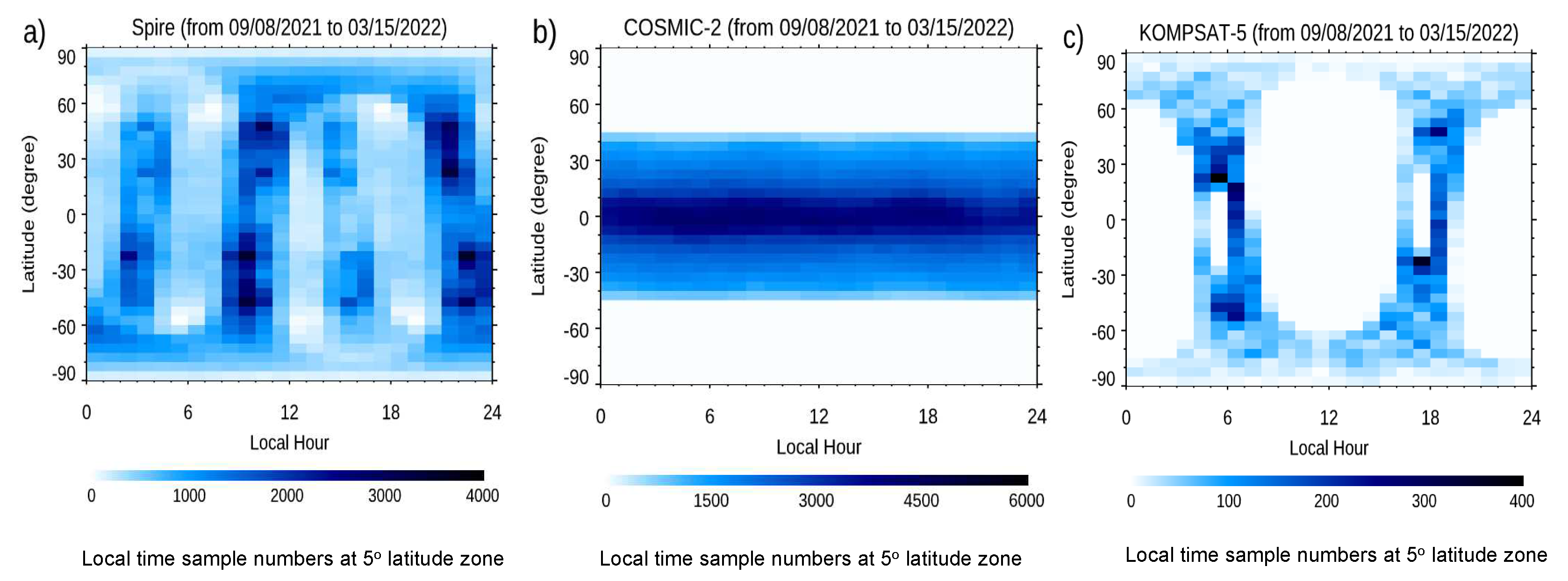
2.1. Spatial and Local Time Distribution of Spire and Other RO Missions

For the Spire constellation, there are thirty satellites to provide RO observations during the DO3 and DO4 periods, where twenty-five satellites are in high inclination angle orbit covering the globe and five satellites are in low inclination angle orbit covering mid-latitude and tropical regions (see below). To demonstrate the spatial distribution for different RO missions, we generate the RO sample numbers for each 5o×5o grid for Spire, COSMIC-2, and KOMPSAT-5 for the whole DO3 period in Figure 2a–c, respectively. Figure 2 depicts that while Spire and KOMPSAT-5 have the global spatial distribution, COSMIC-2 data cover mainly from 45°N to 45°S. The observation numbers at each box are indicated by the color bar. Although CWDP purchases more Spire data in DO4 than those from DO3, the spatial distribution for Spire DO4 data is very similar to Figure 2a.
Figure 3a–c show the local time distribution for the DO3 period binned at every 5o latitude and every local time for Spire, COSMIC-2, and KOMPSAT-5 observations, respectively. Since COSMIC-2 satellites have a low inclination angle (24o), the observation can cover all latitudes within [45oS, 45oN] for a given local time (Figure 3b). While KOMPSAT-5 observations mainly distribute on 5-7 and 17-19 local time, Spire observations mainly distribute on 2-3, 9-10, 14-15, and 21-22 local time. With more than thirty satellites, Spire collected approximately 15K-20K RO profiles daily during the DO3 and DO4 periods.

2.2. Spire Signal-to-Noise (SNR) Latitudinal Distribution

We usually use the SNR to indicate the strength of RO signals to penetrate to the lower troposphere (see section 4.1). Note that many factors affect the magnitude of SNRs and their spatial distribution. The most dominant factors include i) the GNSS emitter’s signal power, ii) the receiver intermediate frequency bandwidth, iii) RO antenna design, iv) the antenna gain pattern related to the viewing geometry, and v) the azimuth angle (the angle between the occultation plane and the direction to the true North). Each Spire flight module equips a STRATOS GNSS RO receiver with a high-gain side-mounted antenna for both L1 and L2 frequencies. With the antenna beam peak at 20o electronic beam tilt and about 36o vertical beamwidth [43], the Spire SNR for GPS, GLONASS, and GALILEO are uniformly distributed at all latitudes (Figure 4), where the Spire SNR from GLONASS is higher than those from GPS and GALILEO. The mean Spire SNR for tracking from GPS, GLONASS, and GALILEO are equal to around 300 V/V, 850 V/V, and 250 V/V, respectively.
However, with different antenna geometry, the spatial distribution of COSMIC-2 SNR differs from those of Spire. Each of the COSMIC-2 flighting modules equips two TGRS RO antennas, one for antenna (+X) and one aft antenna (–X). Unlike the Spire’s side-mounted RO antenna, the COSMIC-2 RO antenna points to the nadir, and the position-tracking antenna points to the sideway. Because COSMIC-2 forward and backward antennas are within [23o, 66o] and [115o, 158o], respectively [32], the RO sample distribution has a maximum RO event at 24o for the forwarding antenna and 157o for the backward. As a result, the COSMIC-2 SNR is smaller in the mid-latitude (see Figure 5), and it has a broader distribution (from 200 V/V to 2000 V/V) from 30oN-30oS. The COSMIC-2 event distribution as a function of the antenna view angle was also shown by [32]. The geolocation distribution of COSMIC-2 SNR may affect the COSMIC-2 penetration depth at different latitudes (see Section 4.1).

2.3. STAR processed Spire data, Global Radiosonde data, and Reanalysis Data

To further evaluate the UCAR Spire RO data, we compared the UCAR Spire data with the Spire data products derived from the STAR independently developed inversion package. The STAR RO package was designed to quantify how the observation uncertainty from clock error and geometry determination may propagate to bending angle/refractivity and temperature/humidity profiles [33]. The package consists of GNSS RO L1a (phase and pseudo-range) to L1b (excess phase) processing module (see Appendix), Full-Spectrum Inversion (FSI) based L1b to L2 (bending angle and refractivity) data inversion module [35], and the neutral atmospheric temperature and humidity profiles derived by using the one-dimension variational (1D-Var) inversion module [37]. We will compare the STAR-processed Spire bending angle data with those from UCAR to quantify the retrieval structure uncertainty due to the differences in the algorithm implementations [22,23,24,25,44].
In this study, we will evaluate UCAR Spire RO temperature and water vapor accuracy and uncertainty through comparison with the Vaisala RS41 radiosonde data, which were downloaded from the National Center of Environmental Prediction (NCEP) Automated Data Processing (ADP) Global Upper Air Observational Weather Data (ds351.0, http://rda.ucar.edu/datasets/ds351.0/). As mentioned in [26,31], the RAOB measurement quality may vary with sensor types. The RAOB temperature measurements are affected by solar radiation effect on the sensor [26]. Introduced in 2013, the Vaisala RS41 is currently the most accurate radiosonde observation system, which is of improved precision and accuracy compared to RS92 (see [26 and 31]). With an advanced manufacturer’s correction, the RS41 radiation effect on the sensor is significantly diminished compared to RS92. The NCEP RAOB dataset contains information such as pressure, geopotential height, air temperature, dew point temperature, wind direction, and wind speed. Including a few significant levels, the radiosonde data are available at up to 20 mandatory levels, ranging from 1000 millibars to about 10 millibars. Complete daily data can be downloaded in Binary Universal Form for the Representation of meteorological data (BUFR) format. The software library NCEPLIBS-bufr (also often referred to as BUFRLIB) is used in this study to decode the BUFR radiosonde data.
This study will use the ERA-5 reanalysis model data as the background for the observation-minus-background (O-B) (Spire vs. ERA-5) bending angle/refractivity difference and uncertainty analysis. The data used in this paper has been gridded to a regular latitude-longitude grid of 0.25 degrees for the reanalysis. ERA-5 is updated daily with a latency of about five days. The background data from ERA-5 used for comparison with Spire are refractivity as a function of geopotential height and bending angle as a function of impact parameter. The O-B comparison requires forward modeling to derive refractivity/bending angle from atmospheric background temperature, humidity, and pressure profiles. In the forward modeling, refractivity is first calculated from the interpolated pressure, temperature, and water vapor profiles and then converted into the refractive index n to compute the bending angle using the Abel integral.

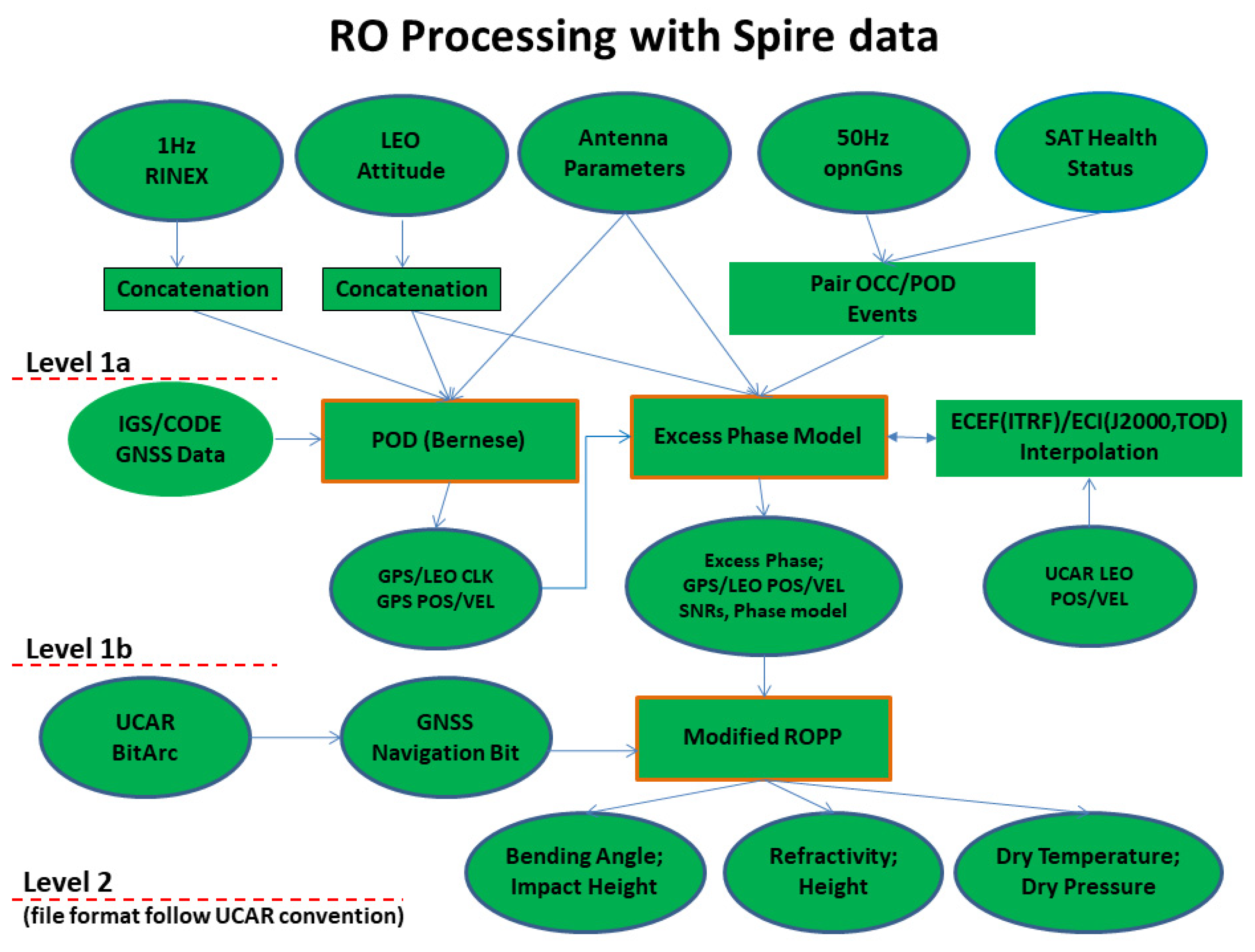
3. SRO Methodology

To better compare the RO retrievals profiles from two missions, we developed an efficient method for predicting RO limb-sounding events between GNSS emitters and LEO RO receivers for inter-satellite comparison purposes [32]. The procedures to obtain the simultaneous limb overpass RO (SRO) events from two receivers on different LEOs with the same GNSS satellite are detailed in [32] and are not described further here. The main advantage of SRO comparisons of RO data products is that the method significantly reduces the collocation uncertainties due to the much shorter time and minor atmospheric path differences than traditional RO comparisons (150-250 km distance and within a 3-hour time window). The SRO events are very close to the coplanar.
UCAR-processed Spire data are collected and assessed in this study. We have collected over 50000 Spire-COSMIC-2 SRO pairs and 20K Spire-Metop GRAS coplanar pairs since 2020 during the DO3 and DO4 periods. [22,23,24,25,44] specified that structural uncertainty owing to the initial implementation and processing assumption choices might affect the retrieval results. All the RO data used in this study are generated by UCAR, which can efficiently remove the RO data processing uncertainty from different data processing centers [22,23,24,25,44] so that we can focus on the systematic biases from the instruments and processing algorithm performance for SNR, penetration height, and bending angle retrieval uncertainty in the SRO inter-comparisons.

4. Assessment of Spire Data Characteristics

This section assesses Spire data characteristics regarding penetration, precision, and stability. We summarized the penetration height (cut-off height) of Spire and COSMIC-2 in Section 4.1. We used the SRO method to collect the Spire-Spire and COSMIC2 -COSMIC-2 pairs and calculate their precision in Section 4.2. We also use the SRO approach to collect Spire-other RO mission pairs and quantify the Spire stability in Section 4.3. We quantified the accuracy of Spire data in Section 5.

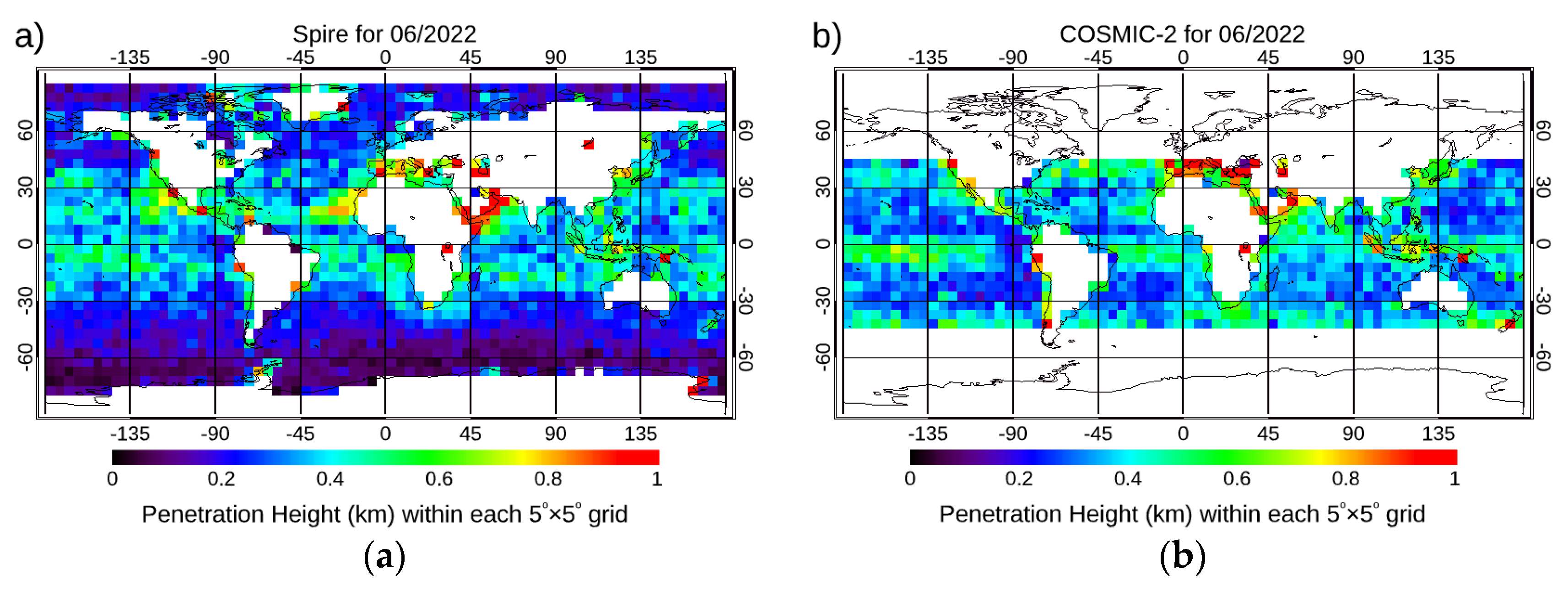
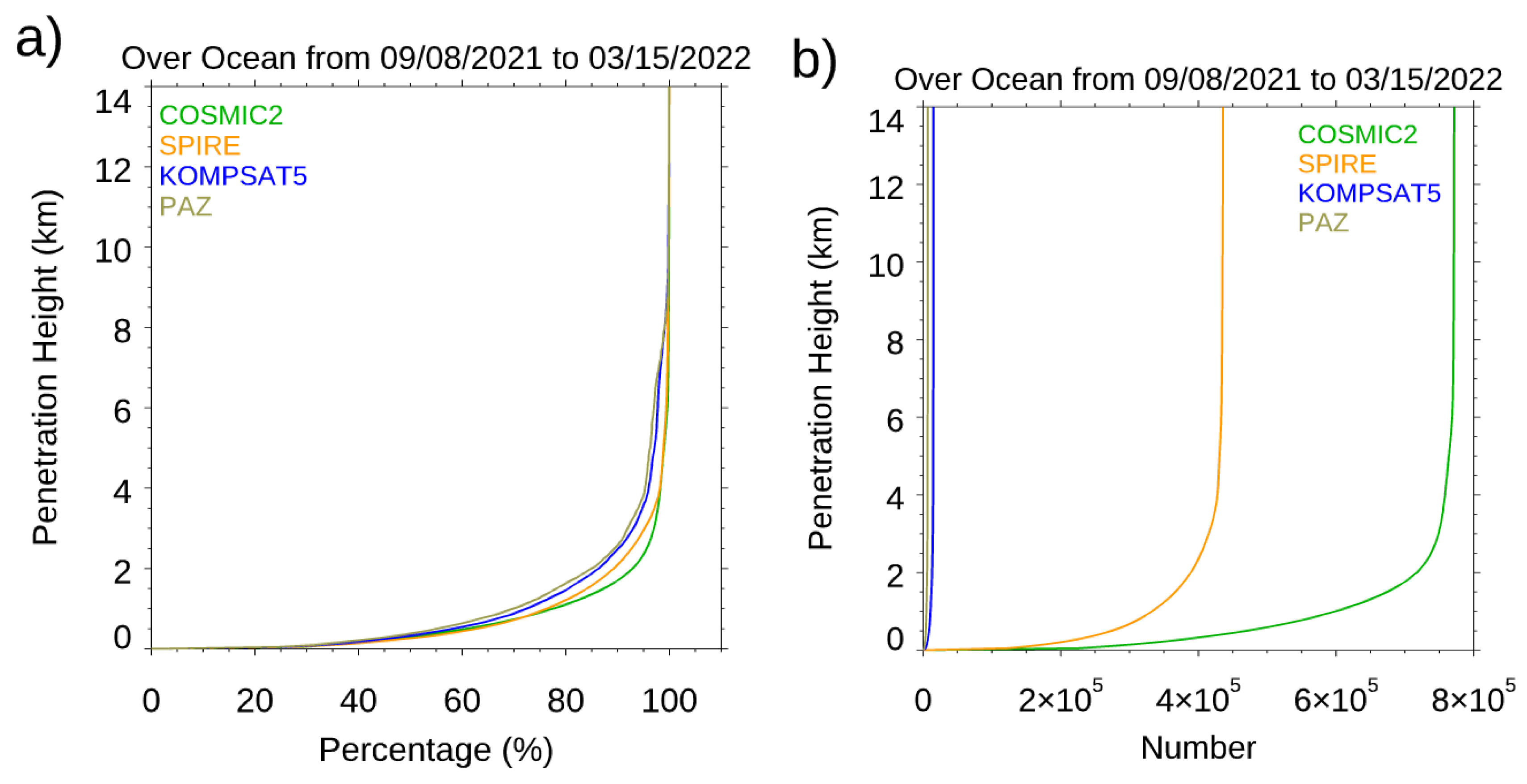
4.1. The Lowest Penetration Height

In the RO inversion procedures, we need to use the RO tracking information and derived excess phase to determine the cut-off height of RO retrievals to obtain the best RO bending angle and refractivity retrievals [33]. Therefore, the lowest penetration height is an essential indicator of RO data quality. The lowest penetration height of RO tracking is usually related to the data’s SNR and the atmosphere’s dryness. Generally, the observations with higher SNR usually penetrate deeper than those of lower SNR [31]. Figure 6a,b depict the global mean of the lowest penetration height in June 2022 binned into 5º × 5º grid for COSMIC-2 (from 45 ºN-45 ºS) and Spire (from 90ºN-90ºS), respectively. With a 200 km horizontal resolution, RO’s lowest penetration height may be affected by mountains and uneven topography along the tracks. Here we showed penetration height only over the oceans. Figure 6 shows that although COSMIC-2 has a relatively more uniform spatial distribution in general than Spire, the pattern of the lowest penetration height for COSMIC-2 is similar to those for Spire. The Spire and COSMIC-2 data generally penetrate to lower troposphere at higher (and drier) latitudes. The Spire and COSMIC-2 penetrate heights are around 0.6 to 0.8 km near the tropical region. The lowest penetration heights for Spire are approximately 0.2 to 0.3 km altitude in mid-latitudes and high latitudes (Figure 6b).
5º grid for a) Spire (from 90ºN-90ºS) and b) COSMIC-2 (from 45ºN-45ºS).
Figure 7 depicts the penetration height for different RO missions over oceans within [45oN, 45oS] during the DO3 period. It shows that the Spire data penetrate to a similar height as those of COSMIC-2 over oceans within this latitude range. Although not shown, the Spire data penetration heights are also very close to those of COSMIC-2 over lands.
Table 1 summarizes the lowest penetration height of 80% of the total data (defined as the 80% penetration height) for different RO missions at different latitudinal zones during the DO3 period. The Spire 80% penetration height is slightly higher than that of COSMIC-2 at latitudinal zones within [10oN, 10oS], but they are the same for latitudinal zones of [30oN, 10oN] and [10oS, 30oS]. Spire has lower penetration heights than COSMIC-2 at latitudinal zones [30oS, 45oS] and [45oN, 30oN]. This may be owing to COSMIC-2 SNR being lower at those latitudinal zones (See Figure 5). Because of the frequent occurrence of the super-refraction over most of the stratocumulus cloud-dominated areas (i.e., the southeast of the Pacific, Atlantic, and South China seas), the COSMIC-2 and Spire penetration heights are about 0.5 to 0.8 km altitudes over those regions (not shown).
Although not shown, the SRO pairs of COSMIC-2 and Spire also showed that Spire penetration height is about 100 meters lower than those of COSMIC-2 at latitudinal zones [30oS, 45oS] and [45oN, 30oN]. The lowest penetration height of 80% of the total data for COSMIC-2 and Spire SRO pairs are very similar to Table 1 and are not further detailed here.

4.2. Precision

Precision is one of the most crucial qualities for using RO data for climate studies [1,2,3,4,5,20,21,22,23,24,25]. For climate analysis, the precision of the RO data is quantified as the mean differences of the retrieved variables derived for the SRO pairs when viewing the same emitter. The uncertainty of the mean (standard deviation, STD) at the vertical level indicates how well one can use RO data to detect climate signals. [42] and [32] have demonstrated how the SRO pairs are matched. The coplanar (SRO pairs) eliminate the potential comparison uncertainty owing to the viewing geometry.
About 26 - 30 satellites are in the Spire constellation over the DO3 and DO4 periods. Therefore, Spire provided plenty of opportunities for inter-comparison of the RO observations between two flight modules from the SRO pairs. We have collocated these observations from two receivers only 20 minutes and 300 km apart but viewing the identical emitters. Figure 8 shows the fractional bending angle, dry temperature, and water vapor mixing ratio comparison between the collocated Spire S128 and S119 receivers. The mean differences are very close to zero from the surface to 40 km altitude for all three physical quantities. The standard deviations from the bending angle, dry temperature, and water vapor mixing ratio are similar to those from other RO missions, such as COSMIC-2 and COSMIC-1 [31]. Although it is not shown, the mean bending angle difference and STD of the differences for SRO pairs between any Spire flight modules are consistent with that between S128 and S119. This indicates that the Spire receiver quality is all in high precision.
Because the Spire SNR range varies when tracking different GNSS systems (see Figure 4), Figure 9 also examines how Spire precision may differ with different SNR ranges. To see how the Spire precision may change when tracking other GNSS systems, we compare the fractional mean BA difference for Spire S124 and S120 from surface to 40 km altitudes but separated with GPS, GLONASS, and GALILEO, respectively (Figure 9a). The corresponding standard deviations and sample numbers at each vertical level are shown in Figure 9b,c, respectively. Although the SNRs from different emitters ranges are different, the mean difference for GPS, GLONASS, and GALILEO are all close to zero with the STD of 1.81, 1.78, and 1.78, respectively.
Using a similar approach, we further compare the precision of Spire with those of COSMIC-2 and COSMIC-1. Because the uncertainty of the mean difference may vary with atmospheric moisture distribution, we limit our comparisons to the same period from October 1 to November 30 but with different years and over the same latitudinal zones (the tropical region from 20°N-20°S, mid-latitudes from 20°S-45°S and 45°N-20°N) (Figure 10). The Spire, COSMIC-2, and COSMIC-1 data are collected from 2022, 2019, and 2006, respectively. In general, the STD of Spire is very close to those from COSMIC-2 over the tropical region, especially in the troposphere (Figure 10b). With fewer observations in the lower troposphere, the COSMIC-1 STD is smaller than those of Spire and COSMIC-2. COSMIC-2 STDs over mid-latitude are slightly more significant than those from Spire, which may be owing to their lower SNR over the same regions (see Figure 5). The Spire STD above 10 km altitude is marginally larger than COSMIC-2 over the mid-latitudes but somewhat smaller than those from COSMIC-2.

4.3. Stability

To quantify the stability of the Spire data, we compare the fractional bending angle profiles for the Spire-PAZ, Spire-KOMPSAT-5, Spire-Metop-B, Spire-Metop-C, and Spire-Terrsar-X SRO pairs during the D04 period in this section (Figure 11). Although the satellite SNR and equator crossing time differ, we do not see a systematic difference for each Spire-RO comparison. Note that, with higher SNR, the Spire-Metop-A/-B GRAS STD is smaller than Spire-other RO missions, especially above 30 km altitude. Table 2 lists the mean BA fractional difference and the corresponding standard deviations for the Spire-PAZ, Spire-KOMPSAT-5, Spire-Metop-B, Spire-Metop-C, and Spire-Terrsar-X SRO pairs from surface to 40 km altitude. With high SNR, the STD for the Spire-Metop-A and Spire-Metop-B is smaller than others above 30 km altitude. The STDs for Spire-Metop-A and Spire-Metop-B SRO pairs are 1.94% and 2.89%, respectively, and those for the Spire-PAZ, Spire-KOMPSAT-5, and Spire-TerraSAR-X SRO pairs are 3.25%, 3.20%, and 3.35%, respectively.
To see whether the retrieval quality of lower SNR Spire may differ from those of COSMIC-2, we further compared the bending angle profiles between Spire and COSMIC-2 (Spire-COSMIC-2 SRO pairs) in the DO4 period for different COSMIC-2 SNR groups (i.e., 0–500 V/V, 500–1000 V/V, 1000–1500 V/V, 1500–2000 V/V, >2000 V/V) in Figure 12. Table 3 lists the mean fractional BA difference, the standard deviation of the mean difference, and the sample number at 10 km altitude for each of the five SNR groups for the Spire-COSMIC-2 SRO pairs.
The bending angle profiles generally show a good agreement between Spire and COSMIC-2 from 8 to 40 km, with an absolute mean of less than 0.2% and a standard deviation close to 4% for all five groups (see below). Above 30 km, the mean differences are minimal (less than 0.5%), but the standard deviations gradually increase with the height and reach 5% at 40 km. Below 10 km, the mean relative bending angle difference increases with height decreasing and more significant oscillation toward the surface owing to the sharp decrease of the sample pairs. At the same time, the standard deviations dramatically increase toward the lower impact height and reach the maximum (~20%) at about 3 km. Below 30 km impact height, there is no noticeable difference in the standard deviation for these 5 SNR groups. COSMIC-2 SNR level slightly affects the mean bias at a low level. Higher COSMIC-2 SNR introduced a more negligible bias in the height range close to the surface; however, the standard deviations relative to the mean BA fractional Spire-COSMIC-2 difference for all the five groups are all around 4.0% from the surface to 40 km impact height, which is larger than those of Spire-RO pairs.

5. Quantify the Spire Retrieval Accuracy and Uncertainty

While the above sections quantify the Spire retrievals’ penetration, precision, and stability, we assess the Spire retrieval accuracy and uncertainty from Sections 5.1 to 5.3. To evaluate the UCAR Spire bending angle quality, we compared them with the STAR Spire retrievals in Section 5.1. We interpolated ERA-5 refractivity profiles onto the locations and times of Spire data and summarized the comparison results in Section 5.2. Because we also want to compare the Spire retrieval accuracy with those from COSMIC-2, we limit our comparisons from 45°N to 45°S in Section 5.2. We also compared the UCAR Spire global (90°N to 90°S) temperature and moisture profiles with those of collocated RS41 measurements, mainly over lands and islands in Section 5.3. We also generate the Spire- RS41 temperature and water vapor difference time series in. the same section.

5.1. Initial Comparison of UCAR Spire Products with STAR Spire Retrievals

The RO retrievals may vary when implementing different processing procedures [20,21,22,23,24,25]. To quantify the UCAR retrieval uncertainty owing to RO processing, we also compare the UCAR Spire data with STAR Spire retrievals (see Appendix A). STAR has become a RO processing and science center [31,33,34,35,36,37,38,39,40,41]. We developed the RO inversion packages for COSMIC-1, KOMPSAT-5, COSMIC-2, and GeoOptics data [33,35]. In addition, we also developed a processing package for the CWDP Spire mission (see Appendix A). Like the approaches used to derive the COSMIC-2 data products, we use a similar inversion package to derive the STAR Spire bending angle and refractivity profiles. The STAR Spire BA is close to the ERA5 data interpolated at the Spire location and time (see Appendix Figure 1).
Figure 13 shows the relative bending angle difference between STAR and UCAR Spire retrievals from 8 km to 40 km is close to zero. Table 4 depicts the mean and standard of STAR-UCAR Spire fractional refractivity for GPS, GLONASS, and GALILEO. The mean fractional refractivity difference is less than 0.06% from surface to 40 km altitudes for GPS, GLONASS, and GALILEO signals. GLONASS’s mean difference and standard deviation are larger than GPS and GALILEO’s.

5.2. Assessment of the Spire Bending Angle Accuracy by Comparing ERA-5

With a similar lowest penetration height to those from COSMIC-2 (see Section 4.1), Spire data can also explore the atmosphere in the lower troposphere. Figure 14 shows the Spire-ERA5 and COSMCI-2-ERA-5 BA fractional differences at different latitudinal zones from 45°N to 45°S. Here the Spire-COSMIC-2 SRO pairs (compared to the ERA5 profiles interpolated unto Spire-COSMSIC-2 locations and times) are used in the comparisons. Figure 14 shows that although Spire data are of lower SNR, there is no noticeable difference for the Spire-ERA-5 and COSMIC-2- ERA-5 pairs in different latitudinal zones. The Spire - COSMSIC-2 SRO pairs from August 1-31, 2022, are used in the comparisons.
We also compared Spire-ERA-5 and COSMIC-2 -ERA-5 BA comparisons for different SNR groups. Again, the mean differences for Spire-ERA-5 and COSMIC-2 -ERA-5 have no significant differences among the five SNR groups (not shown).

5.3. Assessment of Spire Temperature and Water Vapor Accuracy by Comparing to RS41 Radiosonde Observation

The Spire’s geographic location is determined by the longitude and latitude of the perigee point at the occultation point. This study collected collocated Spire retrievals and RS41 RAOB data within position and time ranges of 150 km and 2 hours, respectively. Any Spire RO profiles with a bad attribute flag (equal to 1) are excluded.
We collected 16 months of Spire and RAOB data covering the DO3 and DO4 periods. About 19000 collocated Spire and RS41 pairs were collected for this study. We use the hydrostatic equation to convert the RAOB pressure level to the geometric height. Then we interpolate the Spire temperature data to the radiosonde’s geometric heights at 8, 9.6, 11, 12.5, 14.5, 16.5, 17.5, 20, 23, 26.5, and 30 km altitudes for the temperature comparison. RO and RAOB humidity data are also interpolated to fixed levels for comparison, and the vertical sampling interval is 0.6 km over the height region of interest below 8.4 km. Using this approach, we maintained a high vertical resolution below 8.4 km for humidity comparison.
Figure 15 shows the height-dependent mean temperature/humidity differences (UCAR Spire - RS41) and associated uncertainties. Table 3 shows the mean temperature differences over three height layers, e.g., 8-11 km, 12.5-16.5 km, and 17.8-26.4 km altitude, which are derived from the comparison of retrieval with RS41 RAOB observations shown in Figure 15a).
Above 4.2 km altitude, the humidity difference (Spire – RS41) between UCAR Spire retrievals and RS41 RAOB is relatively small, which is equal to -0.04g/kg (Figure 15b). Below 4.2 km, UCAR Spire humidity retrievals deviate from RS41 observations with increasing negative humidity differences approaching the surface, and the mean difference below 4.2 km reaches -0.19 g/kg. This may indicate systematic dry biases in RO humidity retrievals due to the negativity biases caused by the super-refraction near the Planetary Boundary Layer (PBL) when high temperature and moisture gradients are present.
Table 5 also shows the mean humidity difference (uncertainties) over two height ranges (below and above 4.2 km) between Spire retrievals and RS41. Generally, over the height region between 8 km and 16.5 km, the Spire temperature profiles match RS41 very well with a mean temperature difference of < 0.02 K. In the altitude range of 17.8 to 26.4 km, the average temperature difference is -0.01 K. However, small fluctuations can be seen in this height range, particularly the negative temperature difference (Spire temperature < RS41 Temperature) over the height from 18 to 24 km.
Because the quality of RS41 may be affected by the solar zenith angle (SZA) (see Ho et al., 2014), we compared Spire retrievals versus RS41 observations on the SZA. The Spire-RS41 temperature/humidity differences are divided into three SZA groups for daytime (SZA <= 80o), dusk/dawn (80o< SZA <100o), and nighttime (SZA >= 100o). Figure 16 shows the height-dependent mean temperature differences and uncertainties over three SZA groups. Table 5 listed the mean temperature differences and uncertainties over three height ranges (8-11 km, 12.5-16.5 km, and 17.8-26.4 km) and three SZA groups. The number of Spire and RAOB collocations over the dusk/dawn zone is relatively small compared to daytime and nighttime groups.
From Figure 16 and Table 6, over the height range of 8-26.4 km, the temperature between Spire and RS41 during daytime and nighttime is consistent with being within 0.06 K. However, a warm difference, i.e., Spire is warmer than RS41, in temperature is shown at different altitudes during the daytime. In contrast, a cold difference in temperature is shown at nighttime, which can come from the temperature correction scheme implemented for RS41.
We also analyzed the humidity biases between Spire retrievals and RS41 RAOB observation according to daytime, dusk/dawn, and nighttime SZA groups. The results are summarized in Table 7. In particular, the height-dependent humidity differences over these three SZA groups are shown in Figure 17. The mean humidity biases over two height regions (below 4.2 km and 4.8-8.4 km) are calculated from the data shown in Figure 17. Over the height range above 4.8 km, the mean humidity differences between UCAR Spire retrievals and RS41 are all less than 0.06 g/kg for both daytime and nighttime, which suggests that the day and nighttime UCAR Spire retrieval agrees well with RS41. Over the height range below 4.2 km, Figure 17 shows that the Spire - RS41 humidity differences are all negative over the three SZA groups, and the nighttime difference is the largest (-0.23 g/kg), which is about 0.07 g/Kg more negative than the daytime difference.

6. Estimates of the Error Covariance Matrix for NWP Data Assimilation

The observation error matrix is an important component of any NWP model data assimilation (DA) algorithm because it modulates the relative weighting assigned to individual observations and the background state when generating the analysis solution, regardless of whether the algorithm is variational, ensemble Kalman filter (EnKF), or hybrid flavored. RO profiles from different receiver satellite platforms may have systematic differences in their observation uncertainty, which must be specified in the RO DA system. Based on the calibration and validation results, we can provide the RO data quality information to NWP centers and collaborate to optimize RO data assimilation. We also use NWP diagnostic tools to analyze RO data usage from our forecast experiment datasets and provide feedback to NCEP for assessing RO DA impacts on the current NCEP data assimilation system.
Accurate estimates of RO observation errors and their dependence on the platform, observation location, and meteorological fields are needed for optimal usage of RO data assimilated into an NWP model. In the operational NCEP Global Forecast System (GFS) model’s Gridpoint Statistical Interpolation (GSI) DA system, BA instead of refractivity data are assimilated [45]. RO observation error sources associated with signal measurement and processing into bending angle profiles can be grouped into measurement and calibration errors [46]. The measurement errors include SNR performance, open-loop tracking error, clock instability, and local multipath propagation; calibration errors include residual ionospheric effects, orbit determination accuracy, and clock error removal. In an NWP framework, “representativeness errors” arising from uncertainties in simulating observations from the background forecast field – i.e., forward operator errors – provide an additional observation error source. The perturbation method can theoretically predict the observation error for the individual error sources and then assemble it to establish an overall accuracy estimate.
The differences (aka apparent or perceived error) between observations and their corresponding values estimated from the background forecast contain contributions from observation and model forecast errors. One method of estimating observation error variance uses observation innovation (i.e., observation-minus-background) and short-term forecast error statistics, as [47] described. Under the assumption that the observation errors are uncorrelated with the forecast errors, the apparent error variance ( σ a 2 ) can be divided into model forecast error variance ( σ b 2 ) and observation error variance ( σ o 2 ) components:
σ a 2 = σ b 2 + σ o 2
Therefore, if the model forecast error could be reasonably well estimated, one can estimate the observation error by subtracting the model forecast error variance from the apparent error variance. Our work calculates the model forecast error using the National Meteorological Center (NMC) method [48], which approximates σ b 2 using the differences between sets of 12-h and 24-h GFS forecasts verifying simultaneously. The apparent error was calculated using the difference between the RO observations and 6-h GFS forecasts.
A recent STAR’s RO DSC study estimated the bending angle observation error for four RO missions: COSMIC-2, KOMPSAT-5, GeoOptics, and Spire, from December 15, 2022, to January 15, 2023. Note that because the Spire quality does not change at different Delivery Orders, the estimated errors from the DO3 are very similar to those from other Delivery Orders and are not repeated here. A bending angle forward model developed by the STAR RO DSC (see [33]) was used to calculate a corresponding model background forecast bending angle for each RO observation by (i) interpolating the GFS 6-h forecast pressure, temperature, and water vapor fields to a grid column at the RO observation’s latitude/longitude location and time; (ii) computing the forecast BA/refractivity from these fields; and then (iii) integrating the forecast BA/refractivity field’s vertical gradient from the model top down to the observation impact height. The observation errors are estimated from the observation-minus-background sample variance ( σ a ) and the model error variance estimate ( σ b ) using Eq. (1). Figure 18 shows estimates of the four RO missions’ bending angle observation errors (normalized by the mean BA profile, aka the relative BA error (%)) based on one month of observations and the corresponding GFS forecasts from 45oS to 45oN over oceans (Figure 18a), land (Figure 18b), and both oceans and land (Figure 18c). The observation errors are less than 4% above 9 km and below 36 km. We also depict the relative BA error over oceans for Mid-latitude South Hemisphere (from 20oS to 45oS, Figure 20d), the tropical region (from 20oN to 20oS, Figure 18e), and Mid-latitude North Hemisphere (from 45oN to 20oN, Figure 20f).
Below 9 km, the observation errors increase with decreasing height and peak at around 2 km. For all four missions, the lower troposphere peak value over the ocean (~15%) is larger than that over land (~12%). These significant errors in the lower troposphere may result from greater RO retrieval uncertainty relative to the middle and upper troposphere due to multipath propagation and a smaller SNR over the mid-latitudes for COSMIC-2. Larger observation errors also exist in the upper stratosphere above 36 km. This likely results from larger GFS forecast field errors at these altitudes and RO retrieval uncertainty (i.e., residual ionospheric errors). The over-land observation errors (Figure 18b) are generally smaller than those over oceans. Owing to the significantly larger number of RO observations over the oceans than over land, the full-sample observation errors (Figure 18c) are similar to the over-ocean observation errors shown in Figure 18a. We can implement the defined COSMIC-2, PAZ, Metop-C, KOMPSAT-5, and Sentinel-6 RO observation errors and updated forward operator (including QC settings) generated based on these results into STAR’s offline RO data assessment system. The NCEP can also use these results for the global NWP through DA. The relative BA error over oceans is larger for the tropical region and mid-latitude summer (in the southern hemisphere) than in the mid-latitude winter region (in the northern hemisphere) (see Figure 18d–f).

7. Conclusions, Discussions, and Future Work

Recently, NOAA has included GNSS RO data as one of the crucial long-term observables for weather and climate applications, just as those from IR and MW measurements. To include more GNSS RO data in the NWP system, the NOAA CWDP program started to explore the commercial RO data available on the market. CWDP awarded the first IDIQ contract to GeoOptics and Spire Incs. in 2020. Both GeoOptics and Spire RO data were collected from commercial CubeSats. [32] examined the GeoOptics data quality. This study examines the specific quality of Spire data products during the DO3 and DO4 periods (from September 8, 2021, to January 16, 2023) for climate and weather applications. We carefully examined the Spire data penetration, precision, stability, and accuracy. We also quantified the Spire BA vertical error uncertainty (the diagonal terms in the error covariance matrix), which is crucial for the RO NWP through DA. We reach the following conclusions.
1)
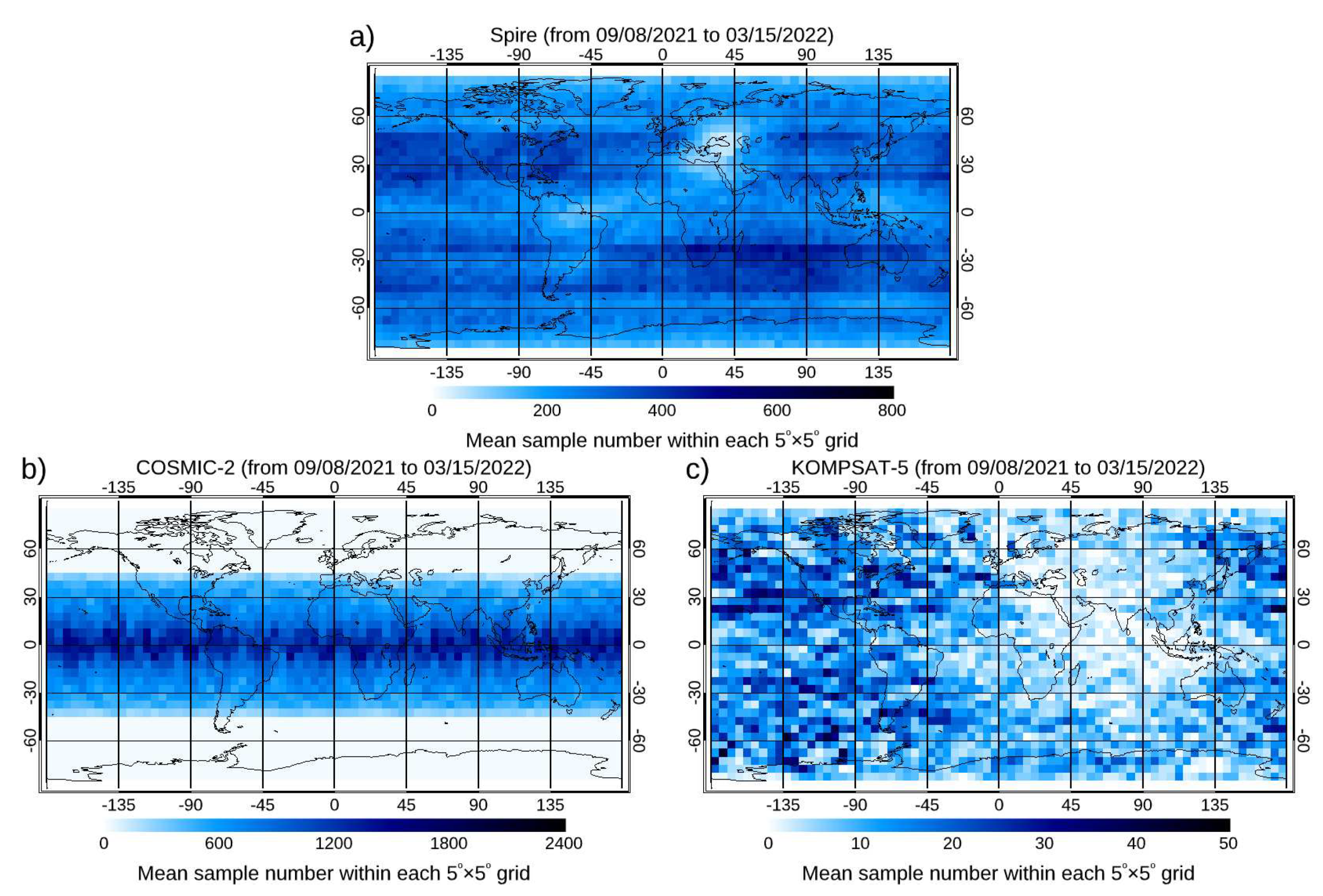
The spatial and temporal coverage. Spire has close to 30 satellites at LEO orbits during the DO3 and DO4. Although the complete global Spire RO occultation is around 20K per day during the performance periods, CWDP purchased about 3000 Spire occultation profiles per day during the DO3 and 5500 Spire per day in DO4. While COSMIC-2 has an inclination angle of 24o, Spire is at the Sun-synchronized orbits. While Spire data cover the globe and are distributed relatively evenly across all latitudes, COSMIC-2 observation can cover all latitudes within [45oS, 45oN]. The Spire has observations peaking local time ranges in 2-3, 9-10, 14-15, and 21-22, while KOMPSAT5 observation peaking local time is located at 6 and 18, and COSMIC-2 observations are independent of the local time.
2)
The effect of SNR on Spire data penetration. The lowest penetration height is an essential indicator of RO data quality. The lowest penetration height of RO tracking is usually related to the data’s SNR and the atmosphere’s dryness. Although with lower SNR in general, the pattern of the lowest penetration height for Spire is similar to those for COSMIC-2. The Spire and COSMIC-2 penetrate heights are around 0.6 to 0.8 km altitude at the tropical oceans. We also compared the lowest penetration height of 80% of the total data for different RO missions at different latitudinal zones. GeoOptics and Spire have lower penetration heights (for 80% of the total data) than COSMIC-2 at latitudinal zones [45oS, 30oS] and [30oN, 45oN]. This may be owing to COSMIC-2 SNR being lower at latitudinal zones [45oS, 30oS] and [30oN, 45oN].
3)
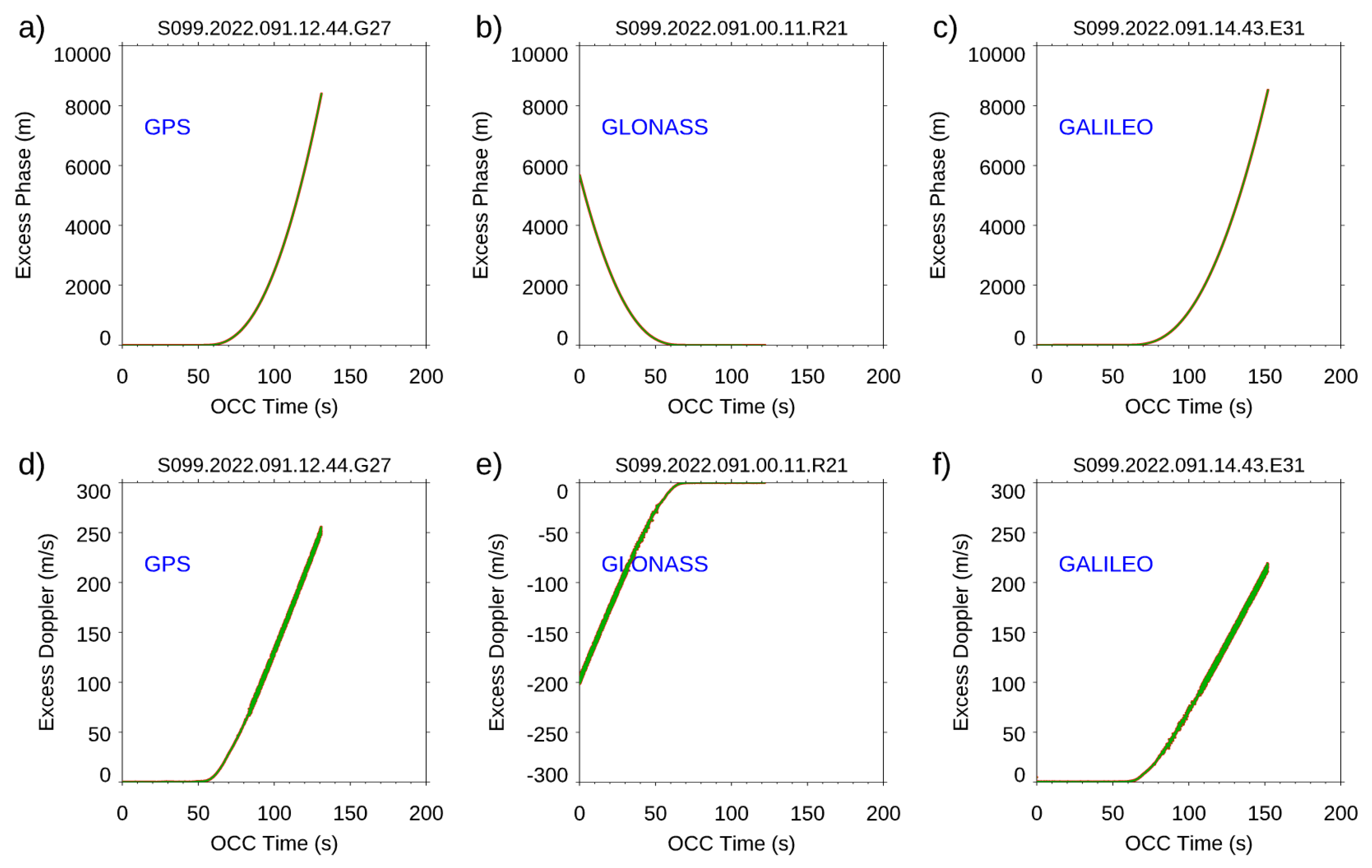
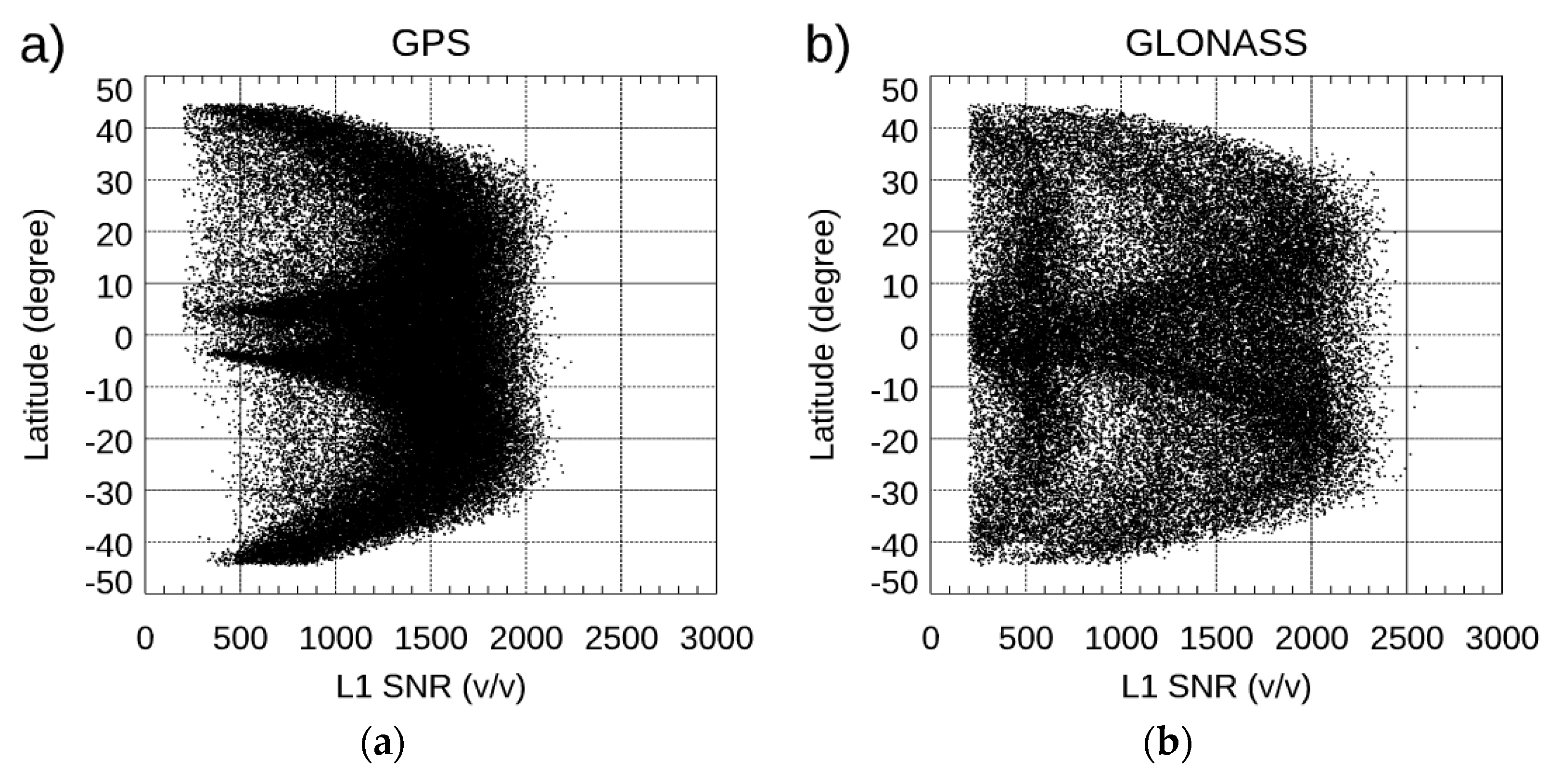
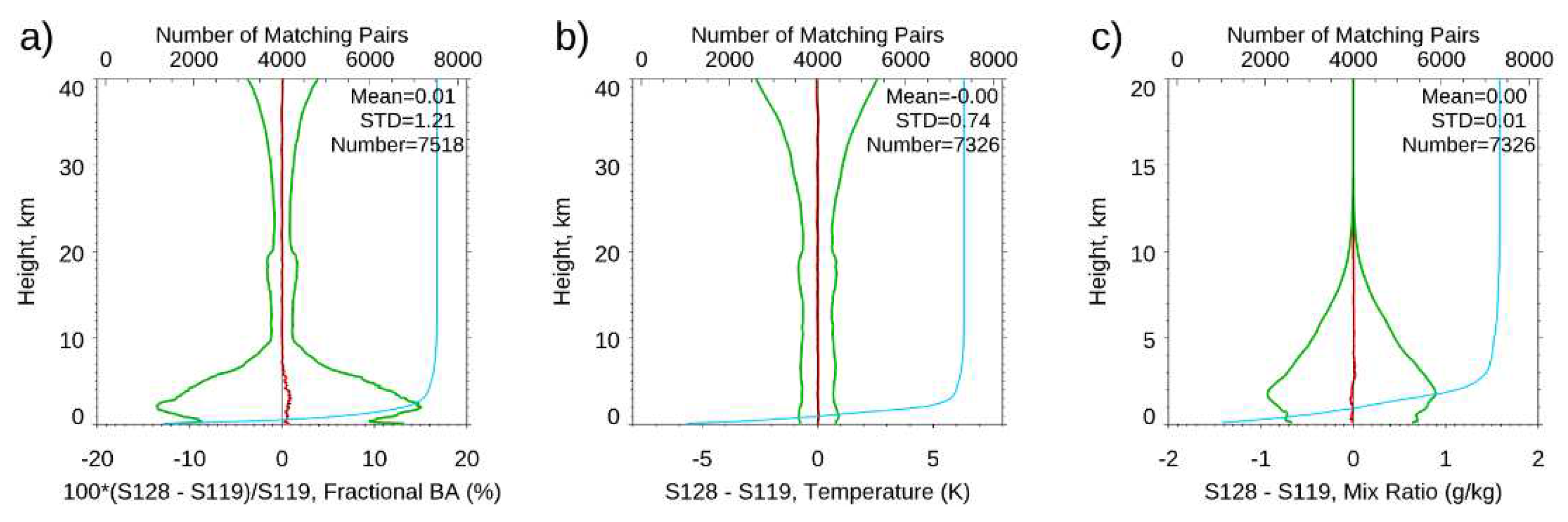
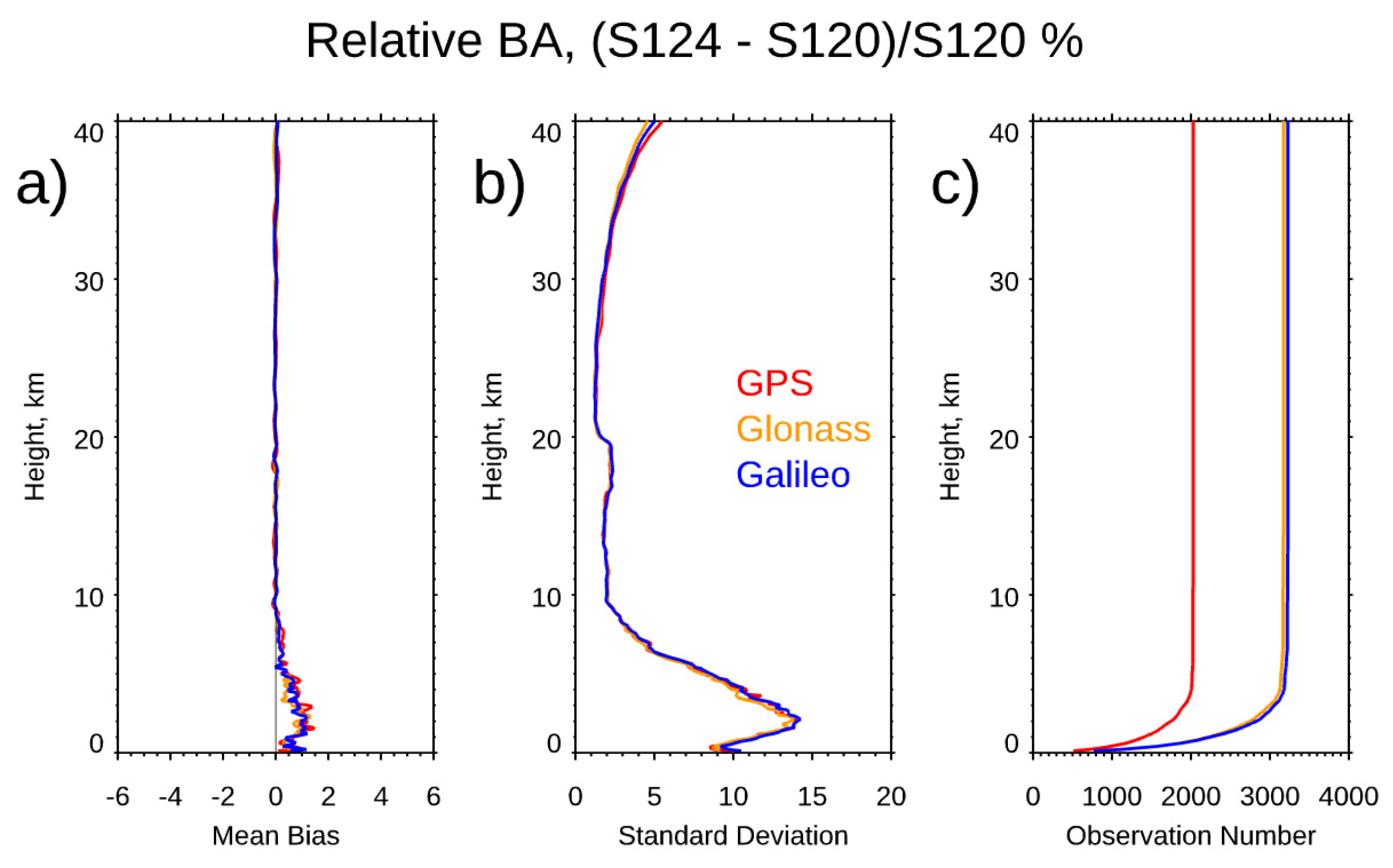
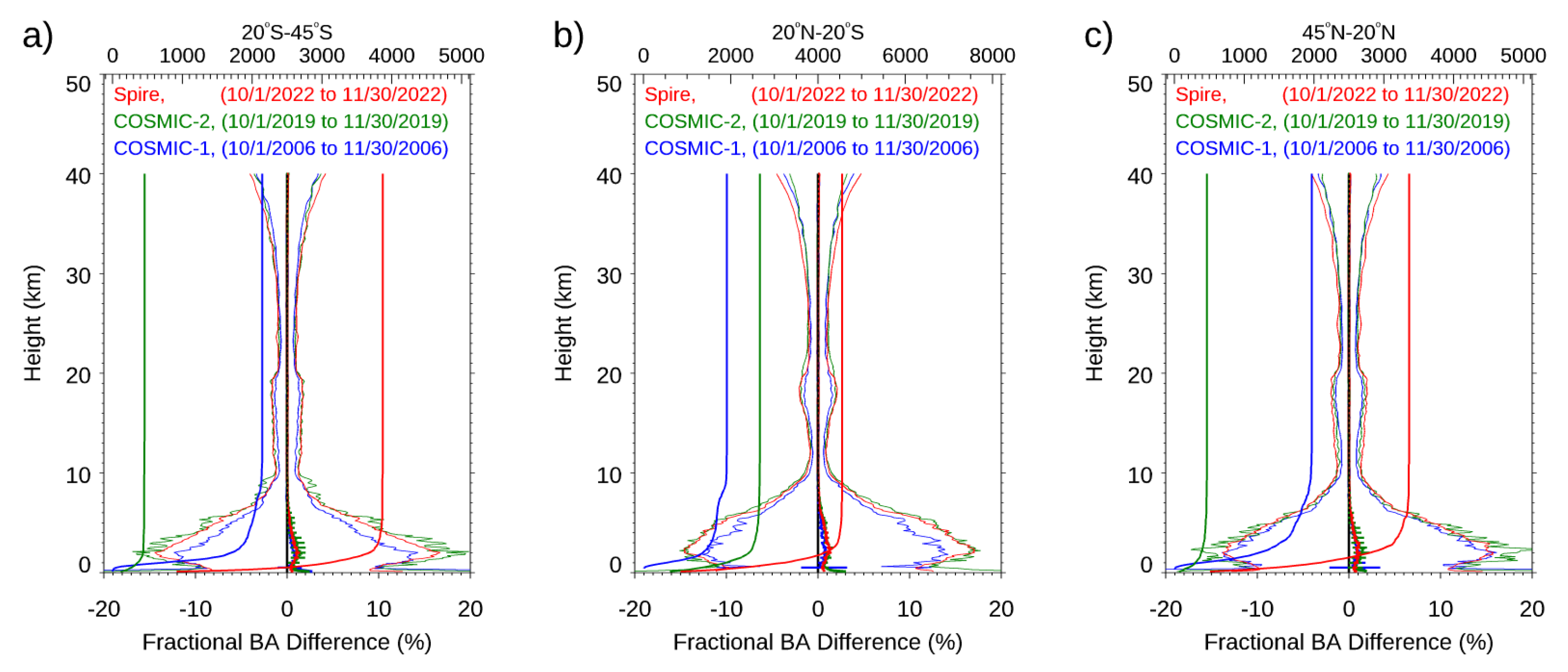
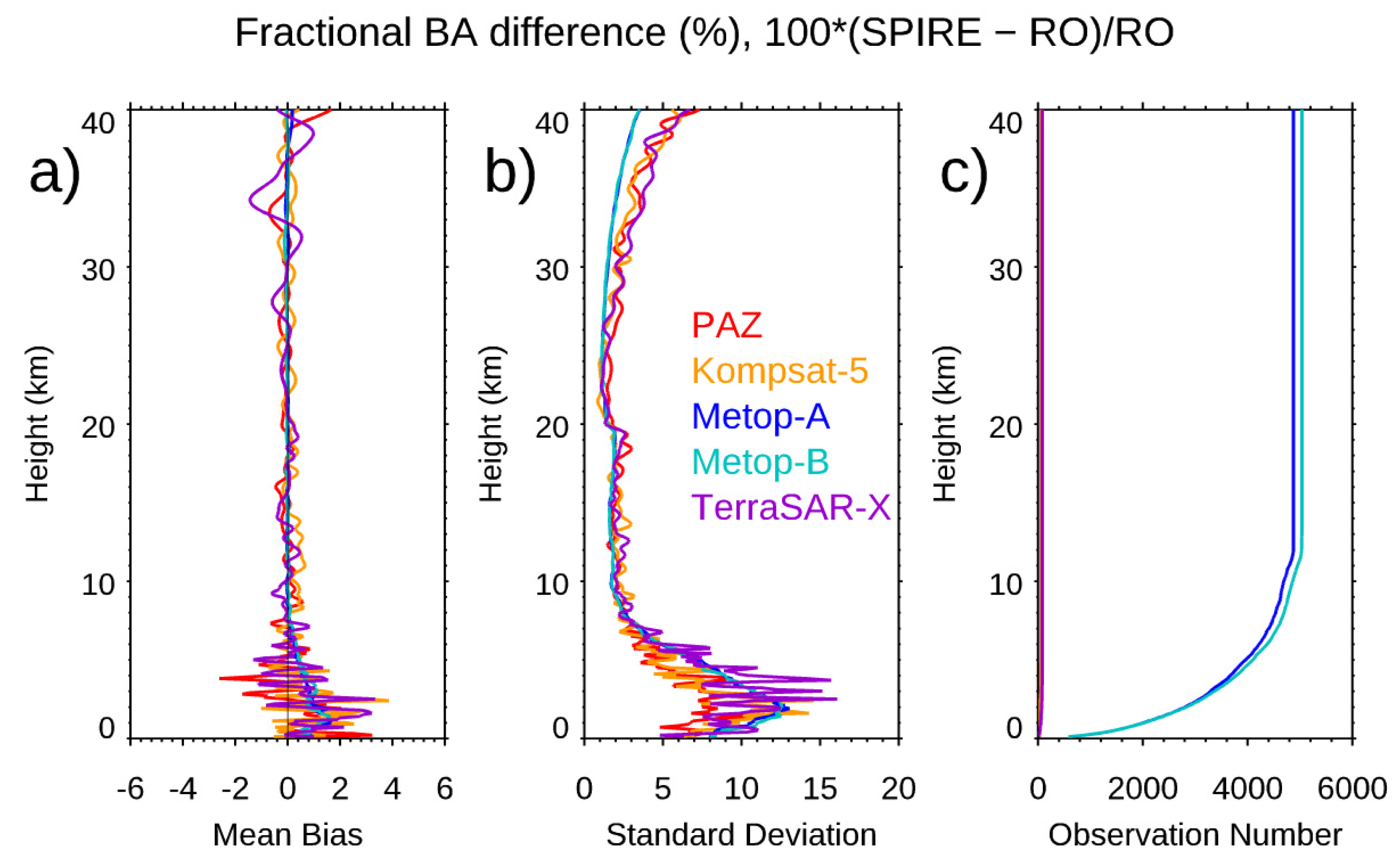
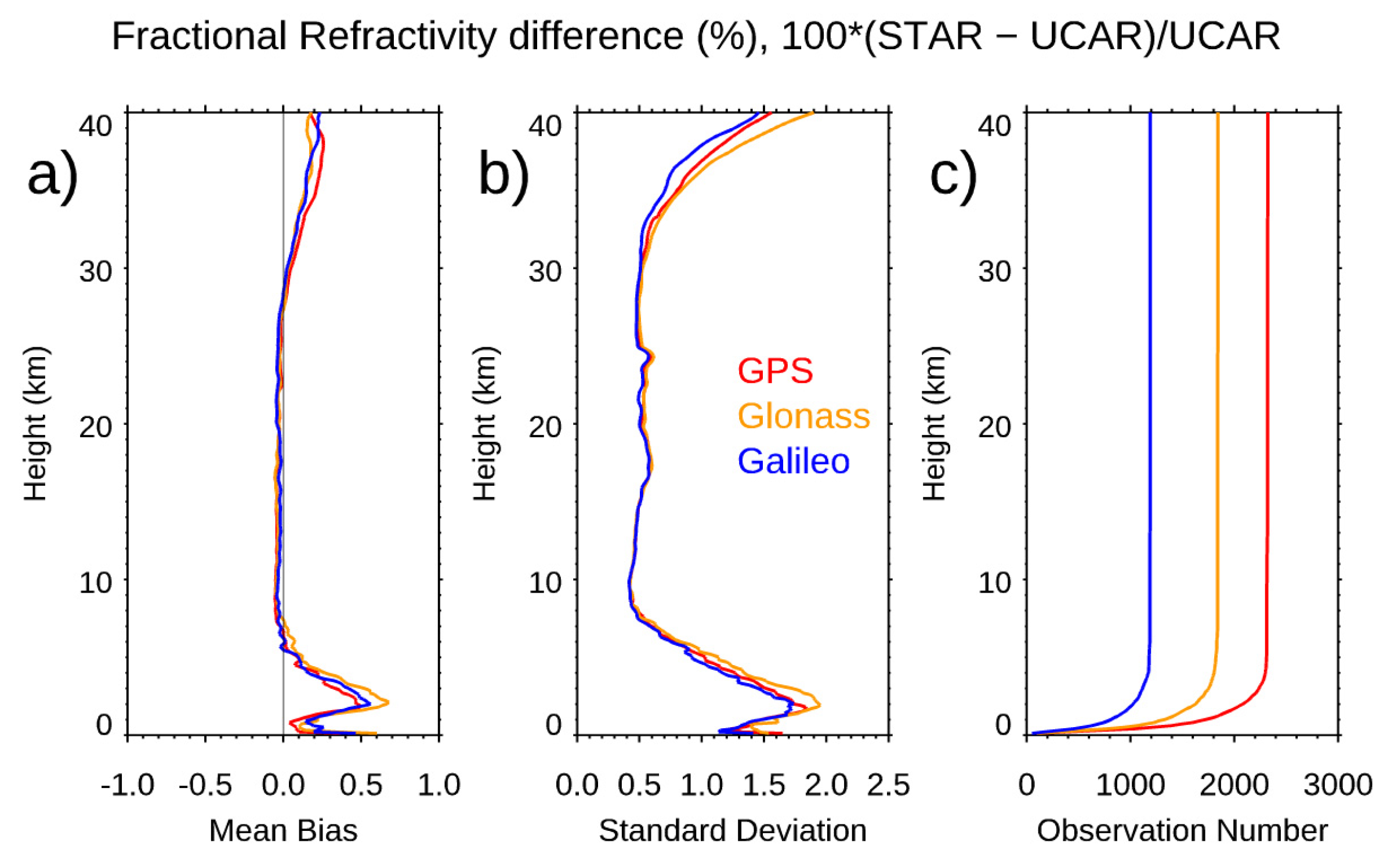
The Spire data precision and stability. We used the Spire-Spire SRO pairs to quantify the Spire precision for bending angle, dry temperature, and water vapor mixing ratio. Results showed that the mean differences are very close to zero from the surface to 40 km altitude for all three physical quantities. The standard deviations from the bending angle, dry temperature, and water vapor mixing ratio are similar to those from other RO missions, such as COSMIC-2 and COSMIC-1. We also compare the fractional mean BA difference for Spire S124 and S120 from surface to 40 km altitudes but separated with GPS, GLONASS, and GALILEO, respectively. Although the SNRs from different emitters ranges are different, the mean difference for GPS, GLONASS, and GALILEO are all close to zero with the STD of 1.81, 1.78, and 1.78, respectively. We also compared the precision of COSMIC-1 (SRO pairs collected from 2006) and COSMIC-2 (SRO pairs collected from 2021) and compared with those from Spire (SRO pairs collected from 2022). All comparisons are within [45oN-45oS]. We found that COSMIC-2 STDs over mid-latitude are slightly more significant than those from Spire, which may be owing to their lower SNR over the same regions. Although it was not shown in this paper, the receiver quality for different flight modules is very close. Although using slightly different receivers, the precision of Spire STRASP receivers is of the same quality as those of COSMIC-2 TGRS receivers.
4)
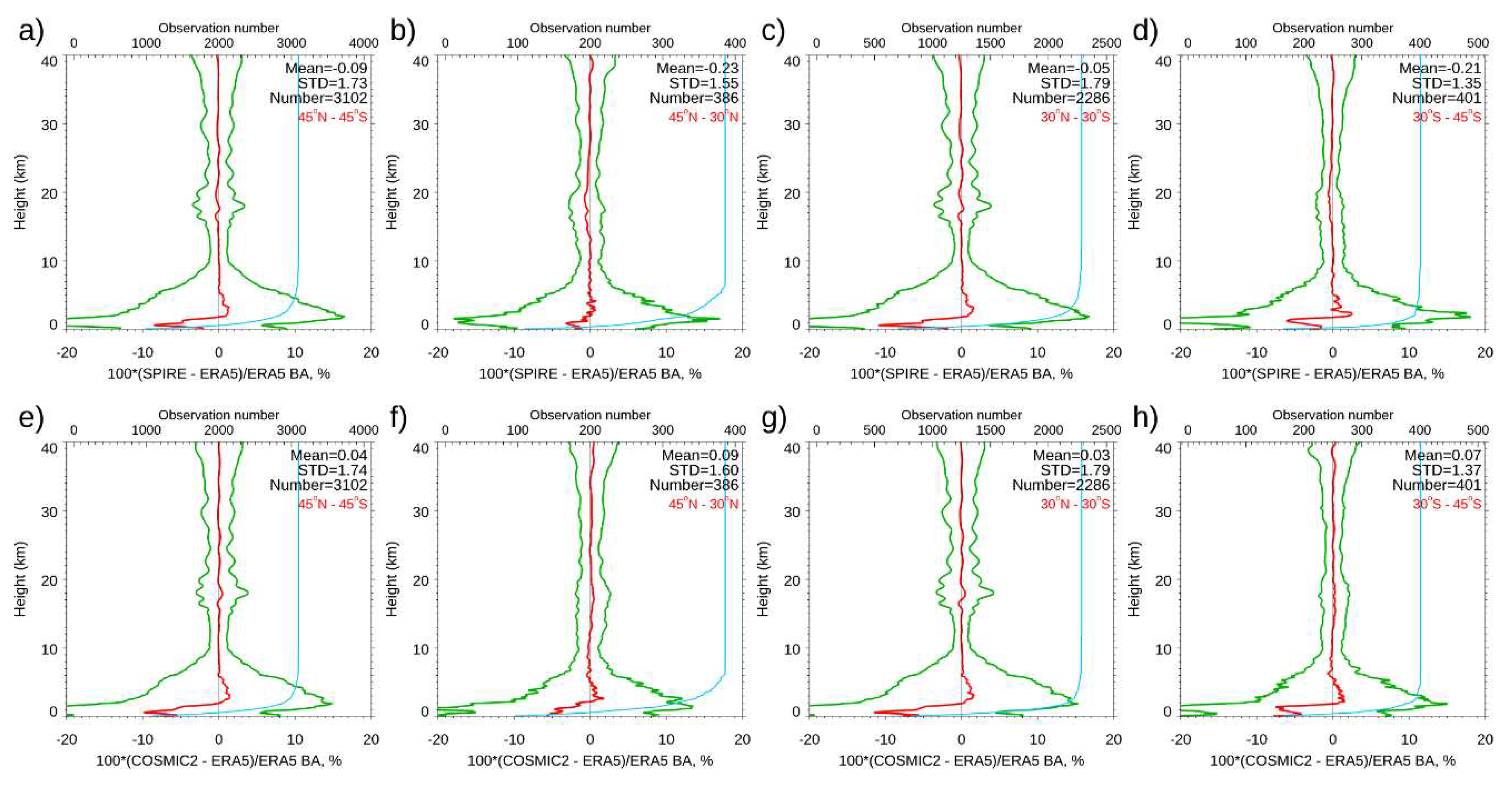
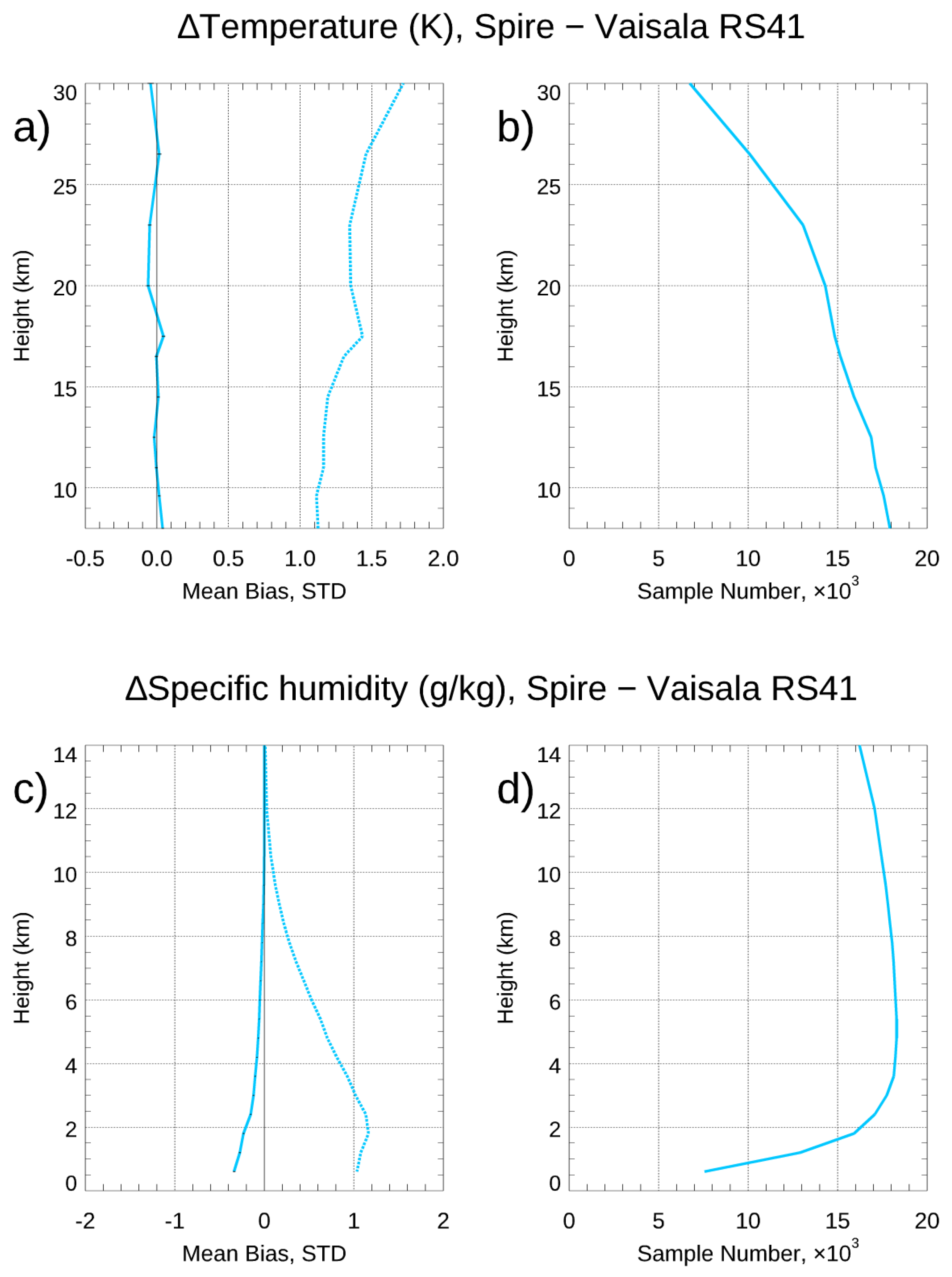
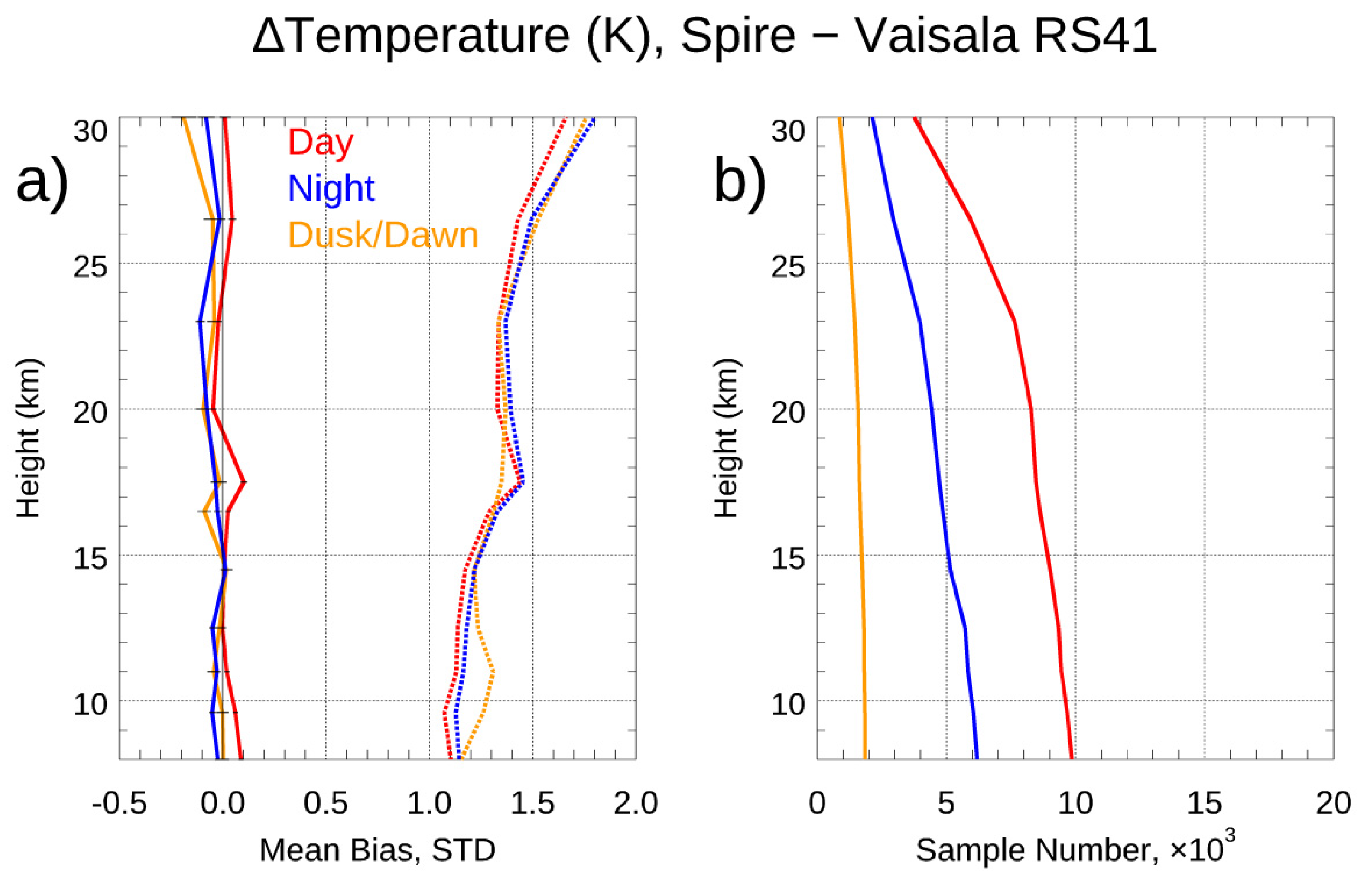
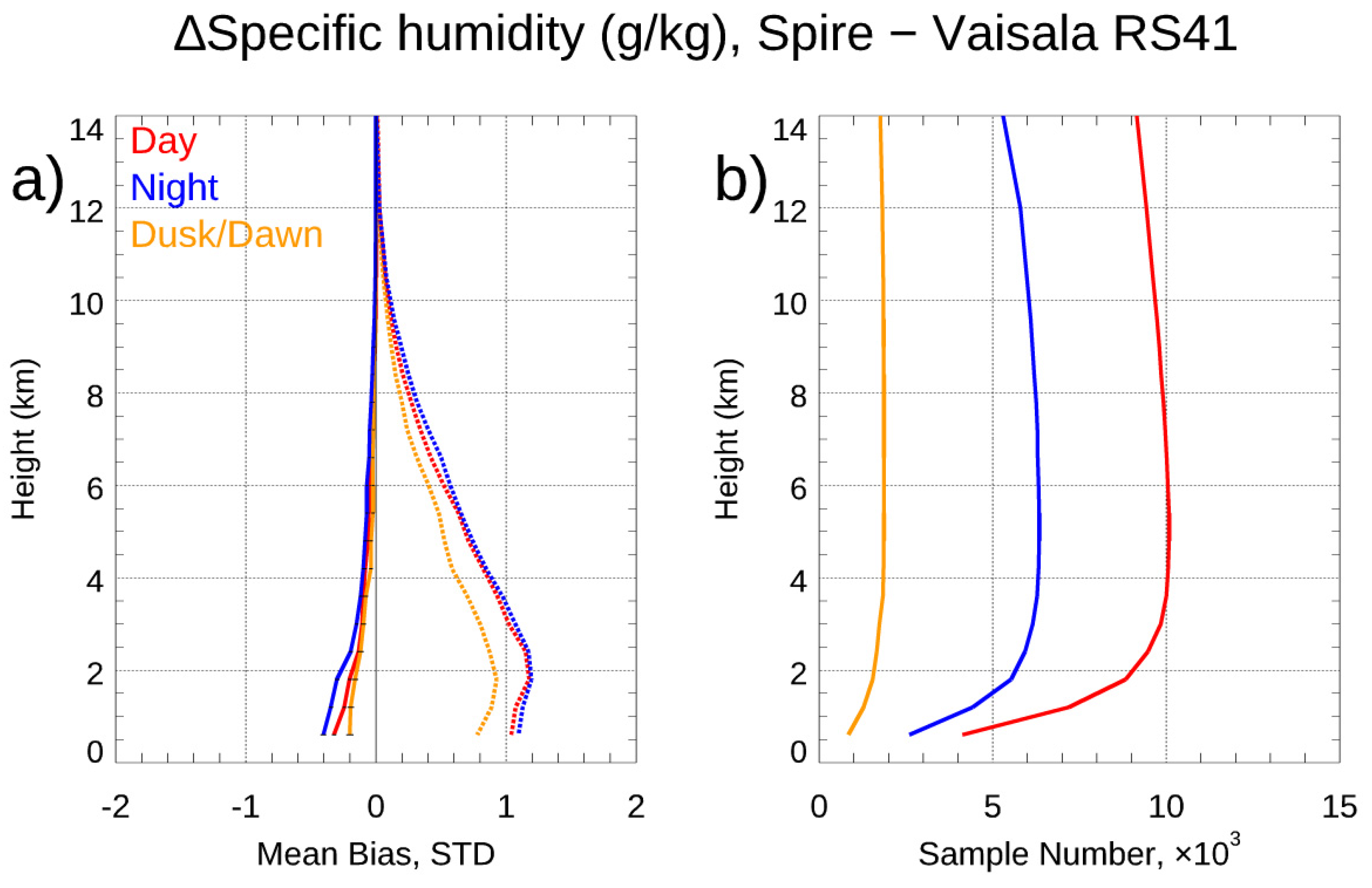
The effect of SNR on Spire retrieval accuracy. The UCAR Spire retrievals are consistent with those from STAR-independent derived BA retrievals. The independent statistical analysis and validation from ERA5 and direct bending angle profile comparison from these SRO cases above 35 km suggest: i) RO bending angle profiles retrieved from GPS satellites are, in general, better than those from GLONASS satellites; ii) Significant uncertainty exists for RO bending angle profiles from GLONASS, which may indicate potential RO phase issue related to the clock, residual ionospheric effects, receiver noise, and orbit determination errors for GLONASS. We validated Spire temperature and water vapor profiles by comparing them with collocated radiosonde in-situ data. Generally, over the height region between 8 km and 16.5 km, the RS41 RAOB matches Spire temperature profiles very well with temperature biases < 0.02 K. Over the height range from 17.8 to 26.4 km, the temperature biases are ~-0.034 K with RS41 RAOB being warmer.
5)
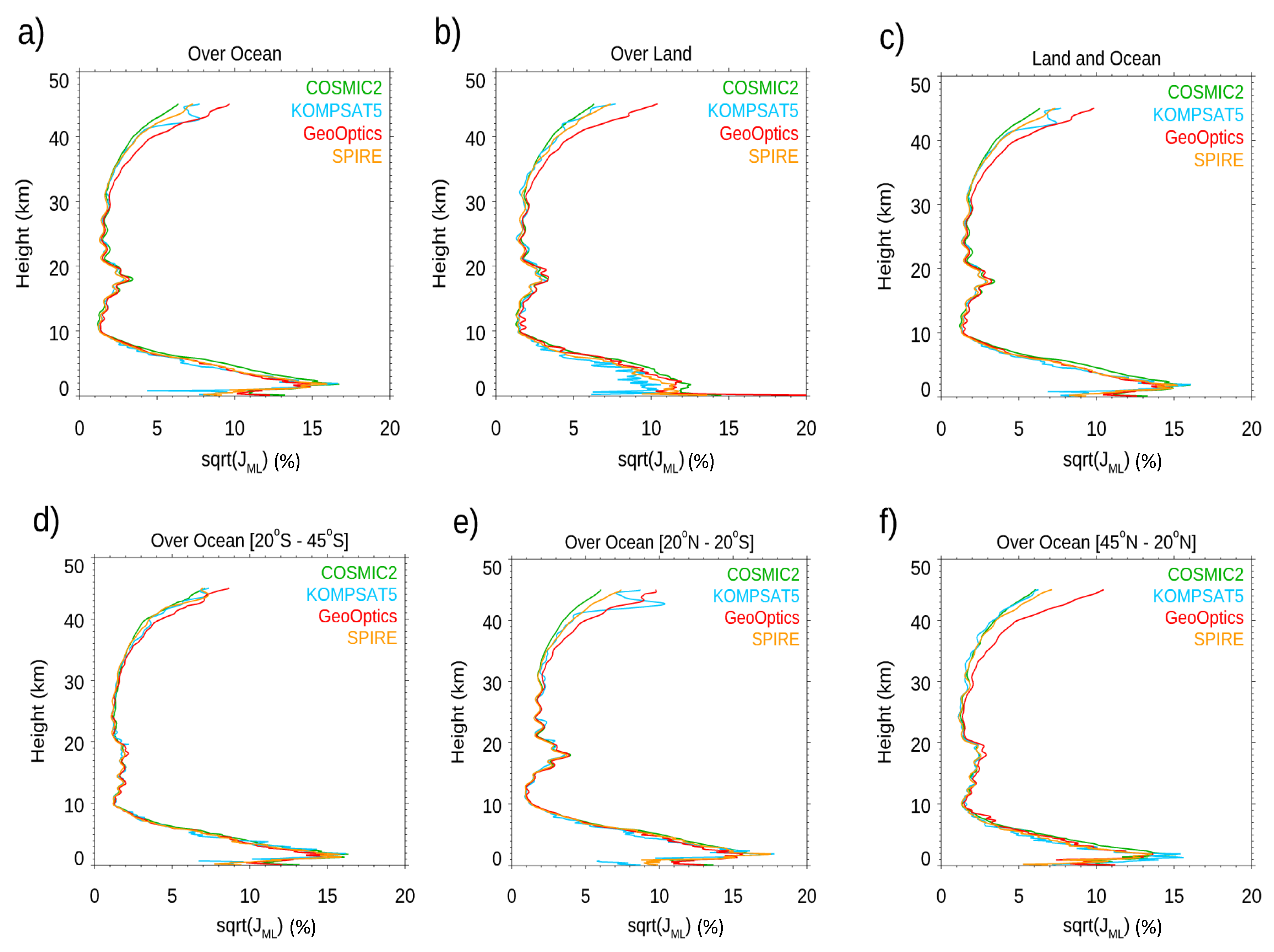
Estimates of the error covariance matrix for NWP. Below 9 km, the RO observation errors increase with decreasing height and peak at around 2 km. For all Spire, COSMIC-2, KOMPSAT-5, and GeoOptics missions, the lower troposphere peak value over the ocean (~15%) is more significant than that over land (~12%). These significant errors in the lower troposphere may result from greater RO retrieval uncertainty relative to the middle and upper troposphere due to multipath propagation and a smaller SNR over the mid-latitudes for COSMIC-2. The COSMIC-2 retrieval uncertainty is slightly more significant over the oceans at the mid-latitudes (45oN-30oN and 30 oS-45oS), which may also be owing to COSMIC-2 SNR being lower at those latitudinal zones.
[31] has demonstrated that the accuracy and uncertainty of retrieved water vapor and refractivity profiles for COSMIC-2 from higher SNR (> 2000 V/V) signals are similar to those from the lower SNR (less than 1000 V/V) signals. [51] demonstrated that even with smaller SNR the retrievals uncertainty from COSMIC (SNR ~1200V/V) is almost identical to that of COSMIC-2. However, the SNR may not be the only factor that affects the RO retrieval uncertainty. For example, the horizontal water vapor irregularity and turbulence may also affect the RO retrieval uncertainty (JPL, personal communication), especially in the lower troposphere. A simulation study showed that the retrieval biases and uncertainty are identical for all SNR groups while we increase the turbulence effect.
In this study, we also notice that the antenna’s viewing geometry affects the SNRs’ latitudinal distribution, affecting the observation error distribution. As discussed in Section 3, the factors that affect the SNR include i) the GNSS emitter’s signal power, ii) the receiver intermediate frequency bandwidth, iii) RO antenna design, iv) the antenna gain pattern related to the viewing geometry, and v) the azimuth angle, where the antenna viewing geometry directly affects the SNR latitudinal distribution. With the high-gain side-mounted antenna for both L1 and L2 frequencies, the Spire SNR for GPS, GLONASS, and GALILEO are uniformly distributed at all latitudes. Unlike Spire, the COSMIC-2 RO antenna points to the nadir, and the position-tracking antenna points to the sideway. As a result, the COSMIC-2 SNR is smaller in the mid-latitude. Generally, COSMIC-2 SNR has a broader distribution (from 200 V/V to 2000 V/V) from 30oN-30oS. The COSMIC-2 event distribution as a function of the antenna view angle was also shown by Chen et al. (2021). The geolocation distribution of COSMIC-2 SNR may affect the COSMIC-2 penetration depth at different latitudes. We demonstrated that owing to the viewing geometry, the COSMIC-2 SNR is lowest (~1000 V/V) in mid-latitudes (45oN-30oN and 30 oS-45oS). As a result, the COSMIC-2 retrieval uncertainty at the mid-latitudes is higher than those from Spire and other RO missions.
The GNSS landscape has been rapidly evolving. Besides GeoOptics and Spire, more commercial RO data are available on the market (i.e., PlanetiQ and others). More than 100 GNSS RO sensors are currently in orbit to track more signals (i.e., GPS, GLONASS, QZSS, IRNSS, GALILEO, Beidou, and GPS III). To use all the above different tracking and receiver system for climate and NWP applications, we need to carefully examine the quality of each receiver and the inter-consistency of the retrieved data products. NOAA STAR has become a GNSS RO DSC (see https://www.star.nesdis.noaa.gov/smcd/GNSSRO/RO/index.php and [31,32,33,34,35,36,37,38,39,40,41]. We will continue developing the RO processing packages for PlanetiQ and other RO missions and use our validation system (see [37]) to provide independent validation results. That will be for future work.

Acknowledgments

The authors would like to thank three reviewers for their comments and suggestions to improve the quality of this manuscript. The manuscript contents are solely the opinions of the authors and do not constitute a statement of policy, decision, or position on behalf of NOAA or the U.S. government.

Appendix A. STAR Spire Data Products

In addition to COSMIC-1, KOMPSAT-5, COSMIC-2, and GeoOptics, we also developed a processing package for the CWDP SPIRE mission. Figure A1 details the STAR SPIRE RO data processing flow chart. The Spire data processing procedures are similar to COSMIC-2. This processing is detailed in [33], except the SPIRE has high-rate reference link observations from the POD antenna. It has only one POD antenna and two OCC antennas for setting and rising measurements. While LEO POD uses only GPS signals, including GALILEO signals in the OCC observations requires orbital interpolation with GALILEO satellites.
Preprints 82628 g0a1
Figure A1. The STAR Spire RO data processing flow chart.
Figure A1. The STAR Spire RO data processing flow chart.
Preprints 82628 g0a1
There are more than 20 small satellite data available during the DO3 period. Processing of more than 20 other satellites requires parallel processing. We have developed code for the parallel processing multiple LEO POD solutions to retrieve orbit and clock information. We have retrieved all needed satellite parameters, including COSPAR ID, satellite launch dates, satellite antenna offset and phase center variations, and satellite mass, and assigned each satellite a unique processing ID.
One more distinct feature of SPIRE different from COSMIC-2 and other missions is that it has GALILEO satellite signals in the OCC antenna observations. The two frequencies used are L1C and L7Q. The occultation also includes GPS and GLONASS signals, but POD observation only has GPS signals. Thus, this makes the POD processing relatively easier. However, including GALILEO signals with OCC observations requires additional code development to process excess phase and bending angles. One caveat for GALILEO processing is that we do not have GNSS bit time series. In the long run, a global ground station network must collect the GALILEO broadcasting word and decipher the bit time series based on the spatial and temporal availability when OCC observation occurs. UCAR or another agency can provide such a database. However, the ROPP [49] provided GNSS bit internal time series routine can still be used in bending angle inversion.
The Spire clock bias can be significant with high-rate POD observation. The single differencing removes the clock bias with the excess phase calculation. The excess phase is calculated by eliminating the geometric distance between the receiver and transmitter antennas, the receiver and transmitter clock bias, and corrections to other terms [50]. Then the excess phase, the SNR, and receiver/transmitter position information are written into a netCDF file for each profile. Figure A2 shows excess phase comparisons between STAR and UCAR processes for three GNSS systems. An excellent agreement between these two processes can be achieved for all three satellite systems.
Preprints 82628 g0a2
Figure A2. STAR processed Spire RO excess phase comparison with those processed by UCAR for three cases representing RO tracking to (left) GPS, (middle) GLONASS, and (right) GALILEO systems, respectively. The a), b), and c) are for the excess phase comparison for GPS, GLONASS, and GALILEO, respectively. The d), e), and f) are for the excess Doppler comparison for GPS, GLONASS, and GALILEO.
Figure A2. STAR processed Spire RO excess phase comparison with those processed by UCAR for three cases representing RO tracking to (left) GPS, (middle) GLONASS, and (right) GALILEO systems, respectively. The a), b), and c) are for the excess phase comparison for GPS, GLONASS, and GALILEO, respectively. The d), e), and f) are for the excess Doppler comparison for GPS, GLONASS, and GALILEO.
Preprints 82628 g0a2

References

  1. Anthes, R.A.; Bernhardt, P.A.; Chen, Y.; Cucurull, L.; Dymond, K.F.; Ector, D.; Healy, S.B.; Ho, S.-P.; Hunt, D.C.; Kuo, Y.; et al. The COSMIC/FORMOSAT-3 Mission: Early Results. Bull. Am. Meteorol. Soc. 2008, 89, 313–334. [Google Scholar] [CrossRef]
  2. Ho, S.-P.; Anthes, R.A.; Ao, C.O.; Healy, S.; Horanyi, A.; Hunt, D.; Mannucci, A.J.; Pedatella, N.; Randel, W.J.; Simmons, A. The COSMIC/FORMOSAT-3 Radio Occultation Mission after 12 Years: Accomplishments, Remaining Challenges, and Potential Impacts of COSMIC-2. Bull. Amer. Meteor. Soc. 2020, 101, E1107–E1136. [Google Scholar] [CrossRef]
  3. Bean, B.R.; Dutton, E.J. Radio Meteorology. National Bureau of Standards Monogr., no. 92; U.S. Government Printing Office: Washington, DC, USA, 1966; p. 435. [Google Scholar]
  4. Ho, S.-P.; Goldberg, M.; Kuo, Y.-H.; Zou, C.-Z.; Shiau, W. Calibration of Temperature in the Lower Stratosphere from Microwave Measurements Using COSMIC Radio Occultation Data: Preliminary Results. Terr. Atmos. Ocean. Sci. 2009, 20, 87. [Google Scholar] [CrossRef]
  5. Ho, S.-P.; Zhou, X.; Kuo, Y.-H.; Hunt, D.; Wang, J.-H. Global Evaluation of Radiosonde Water Vapor Systematic Biases using GPS Radio Occultation from COSMIC and ECMWF Analysis. Remote Sens. 2010, 2, 1320–1330. [Google Scholar] [CrossRef]
  6. Huang, C.; Teng, W.; Ho, S.; Kuo, Y. Global variation of COSMIC precipitable water over land: Comparisons with ground-based GPS measurements and NCEP reanalyses. Geophys. Res. Lett. 2013, 40, 5327–5331. [Google Scholar] [CrossRef]
  7. Teng, W.-H.; Huang, C.-Y.; Ho, S.-P.; Kuo, Y.-H.; Zhou, X.-J. Characteristics of global precipitable water in ENSO events revealed by COSMIC measurements. J. Geophys. Res. Atmos. 2013, 118, 8411–8425. [Google Scholar] [CrossRef]
  8. Biondi, R.; Randel, W.J.; Ho, S.-P.; Neubert, T.; Syndergaard, S. Thermal structure of intense convective clouds derived from GPS radio occultations. Atmospheric Chem. Phys. 2012, 12, 5309–5318. [Google Scholar] [CrossRef]
  9. Biondi, R.; Ho, S.-P.; Randel, W.; Syndergaard, S.; Neubert, T. Tropical cyclone cloud-top height and vertical temperature structure detection using GPS radio occultation measurements. J. Geophys. Res. Atmos. 2013, 118, 5247–5259. [Google Scholar] [CrossRef]
  10. Xue, Y.H.; Li, J.; Menzel, P.; Borbas, E.; Ho, S.-P.; Li, Z. Impact of Sampling Biases on the Global Trend of Total Precipitable Water Derived from the Latest 10-Year Data of COSMIC, SSMIS and HIRS Observations. J. Geophys. Res. Atmos. 2018, 124, 6966–6981. [Google Scholar] [CrossRef]
  11. Zeng, Z.; Ho, S.-P.; Sokolovskiy, S. The Structure and Evolution of Madden- Julian Oscillation from FORMOSAT-3/COSMIC Radio Occultation Data. J. Geophys. Res. 2012, 117, D22108. [Google Scholar] [CrossRef]
  12. Schröder, M.; Lockhoff, M.; Shi, L.; August, T.; Bennartz, R.; Brogniez, H.; Calbet, X.; Fell, F.; Forsythe, J.; Gambacorta, A.; et al. The GEWEX water vapor assessment: Overview and introduction to results and recommendations. Remote Sens. 2018, 11, 251. [Google Scholar] [CrossRef]
  13. Mears, C.; Ho, S.P.; Wang, J.; Huelsing, H.; Peng, L. Total Column Water Vapor [In “States of the Climate in 2018“]. Bull. Amer. Meteor. Soc. 2019, 98, S24–S25. [Google Scholar] [CrossRef]
  14. Mears, C. ; J. Wang, J.; Ho, S.P.; Zhang, L.; Zhou, X. Total Column Water Vapor [In “States of the Climate in 2020”]. Bul. Amer. Meteor. Sci. 2021, in press.
  15. Rieckh, T.; Anthes, R.; Randel, W.; Ho, S.-P.; Foelsche, U. Tropospheric dry layers in the tropical western Pacific: comparisons of GPS radio occultation with multiple data sets. Atmospheric Meas. Tech. 2017, 10, 1093–1110. [Google Scholar] [CrossRef]
  16. Rieckh, T.; Anthes, R.; Randel, W.; Ho, S.-P.; Foelsche, U. Evaluating tropospheric humidity from GPS radio occultation, radiosonde, and AIRS from high-resolution time series. Atmospheric Meas. Tech. 2018, 11, 3091–3109. [Google Scholar] [CrossRef]
  17. Liu, C.-Y.; Li, J.; Ho, S.-P.; Liu, G.-R.; Lin, T.-H.; Young, C.-C. Retrieval of Atmospheric Thermodynamic State From Synergistic Use of Radio Occultation and Hyperspectral Infrared Radiances Observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 744–756. [Google Scholar] [CrossRef]
  18. Ho, S.-P.; Peng, L.; Mears, C.; Anthes, R.A. Comparison of global observations and trends of total precipitable water derived from microwave radiometers and COSMIC radio occultation from 2006 to 2013. Atmospheric Chem. Phys. 2018, 18, 259–274. [Google Scholar] [CrossRef]
  19. Ho, S.P.; Kuo, Y.H.; Sokolovskiy, S. Improvement of the temperature and moisture retrievals in the lower troposphere using AIRS and GPS radio occultation measurements. J. Atmos. Ocean. Technol. 2007, 24, 1726–1739. [Google Scholar] [CrossRef]
  20. Ho, S.-P.; Kuo, Y.-H.; Schreiner, W.; Zhou, X. Using SI-traceable global positioning system radio occultation measurements for climate monitoring In "State of the Climate in 2009". Bull. Am. Meteorol. Soc. 2010, 91, S36–S37. [Google Scholar]
  21. Ho, S.P.; Yue, X.; Zeng, Z.; Ao, C.O.; Huang, C.Y.; Kursinski, E.R.; Kuo, Y.H. Applications of COSMIC radio occultation data from the troposphere to ionosphere and potential impacts of COSMIC-2 data. Bull. Am. Meteorol. Soc. 2014, 95, ES18–ES22. [Google Scholar] [CrossRef]
  22. Ho, S.-P.; Peng, L.; Anthes, R.A.; Kuo, Y.-H.; Lin, H.-C. Marine Boundary Layer Heights and Their Longitudinal, Diurnal, and Interseasonal Variability in the Southeastern Pacific Using COSMIC, CALIOP, and Radiosonde Data. J. Clim. 2015, 28, 2856–2872. [Google Scholar] [CrossRef]
  23. Ho, S.-P.; Kirchengast, G.; Leroy, S.; Wickert, J.; Mannucci, A.J.; Steiner, A.; Hunt, D.; Schreiner, W.; Sokolovskiy, S.; Ao, C.; et al. Estimating the uncertainty of using GPS radio occultation data for climate monitoring: Intercomparison of CHAMP refractivity climate records from 2002 to 2006 from different data centers. J. Geophys. Res. Earth Surf. 2009, 114, D23107. [Google Scholar] [CrossRef]
  24. Ho, S.-P.; Hunt, D.; Steiner, A.; Mannucci, A.J.; Kirchengast, G.; Gleisner, H.; Heise, S.; Von Engeln, A.; Marquardt, C.; Sokolovskiy, S.; et al. Reproducibility of GPS radio occultation data for climate monitoring: Profile-to-profile inter-comparison of CHAMP climate records 2002 to 2008 from six data centers. J. Geophys. Res. Earth Surf. 2012, 117, D18111. [Google Scholar] [CrossRef]
  25. Steiner, A.K.; Ladstädter, F.; Ao, C.O.; Gleisner, H.; Ho, S.-P.; Hunt, D.; Schmidt, T.; Foelsche, U.; Kirchengast, G.; Kuo, Y.-H.; et al. Consistency and structural uncertainty of multi-mission GPS radio occultation records. Atmospheric Meas. Tech. 2020, 13, 2547–2575. [Google Scholar] [CrossRef]
  26. Ho, S.-P.; Peng, L.; Vömel, H. Characterization of the long-term radiosonde temperature biases in the upper troposphere and lower stratosphere using COSMIC and Metop-A/GRAS data from 2006 to 2014. Atmospheric Chem. Phys. 2017, 17, 4493–4511. [Google Scholar] [CrossRef]
  27. Ho, S.-P.; Peng, L. Global water vapor estimates from measurements from active GPS RO sensors and passive infrared and microwave sounders. In Green Chemistry Applications; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
  28. Lin, C.C.; Yang, S.C.; Ho, S.P.; Pedatella, N.M. Exploring the terrestrial and space weather using an operational radio occultation satellite constellation—A FORMOSAT-7/COSMIC-2 Special Issue after 1-year on orbit. Terr. Atmos. Ocean. Sci. 2022, 32, 1–3. [Google Scholar] [CrossRef]
  29. Cucurull, L; Derber; J. C.; Purser, R. J.; A bending angle forward operator for global positioning system radio occultation measurements. J. Geophys. Res. Atmos. 2013; 118, 14–28. [CrossRef]
  30. Ho, S.-P.; Pedatella, N.; Foelsche, U.; Healy, S.; Weiss, J.P.; Ullman, R. Using Radio Occultation Data for Atmospheric Numerical Weather Prediction, Climate Sciences, and Ionospheric Studies and Initial Results from COSMIC-2, Commercial RO Data, and Recent RO Missions. Bul. Amer. Meteor. Sci. 2022. [Google Scholar] [CrossRef]
  31. Ho, S.-P.; Zhou, X.; Shao, X.; Zhang, B.; Adhikari, L.; Kireev, S.; He, Y.; Yoe, J.; Xia-Serafino, W.; Lynch, E. Initial Assessment of the COSMIC-2/FORMOSAT-7 Neutral Atmosphere Data Quality in NESDIS/STAR Using In Situ and Satellite Data. Remote Sens. 2020, 12, 4099. [Google Scholar] [CrossRef]
  32. Chen, Y.; Shao, X.; Cao, C.-Y.; Ho, S.-P. Simultaneous Radio Occultation Predictions for Inter-Satellite Comparison of Bending Angle Profiles from COSMIC-2 and GeoOptics. Remote Sens. 2021, 13, 3644. [Google Scholar] [CrossRef]
  33. Zhang, B.; Ho, S.-P.; Cao, C.; Shao, X.; Dong, D. ; Chen. Y. Verification and Validation of the COSMIC-2 Excess Phase and Bending Angle Algorithms for Data Quality Assurance at STAR. Remote Sens. 2022, 14, 3288.
  34. Chen, Y.; Han, Y.; Weng, F. Characterization of Long-Term Stability of Suomi NPP Cross-Track Infrared Sounder Spectral Calibration. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1147–1159. [Google Scholar] [CrossRef]
  35. Adhikari, L.; Ho, S.-P.; Zhou, X. Inverting COSMIC-2 Phase Data to Bending Angle and Refractivity Profiles Using the Full Spectrum Inversion Method. Remote Sens. 2021, 13, 1793. [Google Scholar] [CrossRef]
  36. Chen, Y.; Cao, C.; Shao, X.; Ho, S.-P. Assessment of the Consistency and Stability of CrIS Infrared Observations Using COSMIC-2 Radio Occultation Data over Ocean. Remote Sens. 2022, 14, 2721. [Google Scholar] [CrossRef]
  37. Ho, S.-p.; Kireev, S.; Shao, X.; Zhou, X.; Jing, X. Processing and Validation of the STAR COSMIC-2 Temperature and Water Vapor Profiles in the Neural Atmosphere. Remote Sens. 2022, 14, 5588. [Google Scholar] [CrossRef]
  38. Jing, X.; Shao, X.; Liu, T.-C.; Zhang, B. Comparison of GRUAN RS92 and RS41 Radiosonde Temperature Biases. Atmosphere 2021, 12, 857. [Google Scholar] [CrossRef]
  39. Miller, W. J. , Y. Chen, S.-P. Ho, and X. Shao, Evaluating the impacts of COSMIC-2 GNSS RO bending angle assimilation on Atlantic hurricane forecasts using the HWRF model. Mon. Wea. Rev., under review, 2023. [Google Scholar]
  40. Shao, X. , Shu-Peng Ho, Bin Zhang, Changyong Cao, and Yong Chen, Consistency and Stability of SNPP ATMS Microwave Observations and COSMIC-2 Radio Occultation over Oceans, Remote Sens. 2021a, 13, 3754. [CrossRef]
  41. Shao, X. S.-P. Ho, B. Zhang, X. Zhou, S. Kireev, Y. Chen, and C. Cao, 2021b: Comparison of COSMIC-2 radio occultation retrievals with RS41 and RS92 radiosonde humidity and temperature measurements. Terr. Atmos. Ocean. Sci., 2021b, 32, 1015-1032. [CrossRef]
  42. Cao, C.; Wang, W.; Lynch, E.; Bai, Y.; Ho, S.-P.; Zhang, B. Simultaneous Radio Occultation for intersatellite comparison of bending angle toward more accurate atmospheric sounding. J. Atmos. Ocean. Technol. 2020, 37, 2307–2320. [Google Scholar] [CrossRef]
  43. Dallas Masters, Seizing Opportunity: Spire’s CubeSat Constellation of GNSS, AIS, and ADS-B Sensors, Stanford PNT Symposium, 2018-11-08. http://web.stanford.edu/group/scpnt/pnt/PNT18/presentation_files/I07-Masters-Spire_GNSS_AIS_ADS-B.pdf.
  44. Andrea, K.S.; et al. Consistency and structural uncertainty of multi-mission GPS radio occultation records. Atmos. Meas. Tech. 2020, 13, 2547–2575. [Google Scholar] [CrossRef]
  45. Cucurull, L.; Derber, J. C.; and Purser, R. J. A bending angle forward operator for global positioning system radio occultation measurements. J. Geophys. Res. Atmos., 118, 2013,14–28. [CrossRef]
  46. Kursinski, E. R.; Gebhardt, T. A method to deconvolve errors in GPS RO- derived water vapor histograms. J. Atmos. Oceanic Technol., 31, 2014, 2606–2628. [CrossRef]
  47. Kuo, Y.-H.; Wee, T.-K.; Sokolovskiy, S.; Rocken, C.; Schreiner, W.; Hunt, D.; Anthes, R. A. Inversion and error estimation of GPS radio occultation data. J. Meteor. Soc. Japan, 82, 2004, 507–531. [CrossRef]
  48. Parrish, D. F.; Derber J., C. The National Meteorological Center’s Spectral Statistical-Interpolation Analysis System, Monthly Weather Review, 120, 1992, 1747-1763. [CrossRef]
  49. Culverwell, I.D.; Lewis, H.W.; Offiler, D.; Marquardt, C.; Burrows, C.P. The Radio Occultation Processing Package, ROPP. Atmos. Meas. Tech. 2015, 8, 1887–1899. [Google Scholar] [CrossRef]
  50. Schreiner, W.; Rocken, C.; Sokolovskiy, S.; Hunt, D. Quality assessment of COSMIC/FORMOSAT-3 GPS radio occultation data derived from single- and double-difference atmospheric excess phase processing. GPS Solut. 2009, 14, 13–22. [Google Scholar] [CrossRef]
  51. Anthes, R.; Sjoberg, J.; Feng, X. L.; and Syndergaard, S. Comparison of COSMIC and COSMIC-2 Radio Occultation Refractivity and Bending Angle Uncertainties in August 2006 and 2021, Atmosphere 2022, 13(5), 790. [CrossRef]
Preprints 82628 g001
Figure 1. The distribution of the normalized SNR frequency sample numbers (defined as the sample numbers for each SNR bin normalized to the maximum number of the SNR bin) for GPS (in red line), GLONASS (in orange line), and GALILEO (in blue line) signals on a) Spire, b) COSMIC-2, and c) KOMPSAT-5 over the CWDP Delivery-Order 3 (DO3, from September 8, 2021 to March 15, 2022). The total number of observations from each GNSS satellite is listed in the Figures.
Figure 1. The distribution of the normalized SNR frequency sample numbers (defined as the sample numbers for each SNR bin normalized to the maximum number of the SNR bin) for GPS (in red line), GLONASS (in orange line), and GALILEO (in blue line) signals on a) Spire, b) COSMIC-2, and c) KOMPSAT-5 over the CWDP Delivery-Order 3 (DO3, from September 8, 2021 to March 15, 2022). The total number of observations from each GNSS satellite is listed in the Figures.
Preprints 82628 g001
Preprints 82628 g002
Figure 2. Spatial distribution of the RO sample numbers for each 5o×5o grid for a) Spire, b) COSMIC-2, and c) KOMPSAT-5 for the whole DO3 period.
Figure 2. Spatial distribution of the RO sample numbers for each 5o×5o grid for a) Spire, b) COSMIC-2, and c) KOMPSAT-5 for the whole DO3 period.
Preprints 82628 g002
Preprints 82628 g003
Figure 3. Same as Figure 2, but for the hourly local time distribution binned at 5o latitude bin for a) Spire, b) COSMIC-2, and c) KOMPSAT-5 for the DO3 period. The observation numbers at each box are indicated by the color bar.
Figure 3. Same as Figure 2, but for the hourly local time distribution binned at 5o latitude bin for a) Spire, b) COSMIC-2, and c) KOMPSAT-5 for the DO3 period. The observation numbers at each box are indicated by the color bar.
Preprints 82628 g003
Preprints 82628 g004
Figure 4. Latitudinal distribution for Spire L1 SNR from February 15 to March 15, 2022 for a) GPS, b) GLONASS, and c) GALILEO.
Figure 4. Latitudinal distribution for Spire L1 SNR from February 15 to March 15, 2022 for a) GPS, b) GLONASS, and c) GALILEO.
Preprints 82628 g004
Preprints 82628 g005
Figure 5. Latitudinal distribution for COSMIC-2 L1 SNR from February 15 to March 15, 2022, for a) GPS and b) GLONASS. .
Figure 5. Latitudinal distribution for COSMIC-2 L1 SNR from February 15 to March 15, 2022, for a) GPS and b) GLONASS. .
Preprints 82628 g005
Preprints 82628 g006
Figure 6. The global mean of the lowest penetration height in June 2022 binned into 5º ×
Figure 6. The global mean of the lowest penetration height in June 2022 binned into 5º ×
Preprints 82628 g006
Preprints 82628 g007
Figure 7. a) the RO penetration percentage (defined as the observation number at each penetration depth relative to the observation number at 8 km) over oceans within [45oN, 45oS] during the DO3 period and b) the corresponding numbers of observations from surface to 14 km altitude for COSMIC-2, Spire, KOMPSAT5, and PAZ.
Figure 7. a) the RO penetration percentage (defined as the observation number at each penetration depth relative to the observation number at 8 km) over oceans within [45oN, 45oS] during the DO3 period and b) the corresponding numbers of observations from surface to 14 km altitude for COSMIC-2, Spire, KOMPSAT5, and PAZ.
Preprints 82628 g007
Preprints 82628 g008
Figure 8. The mean difference (in red line) and standard deviation (in green line) for a) fractional bending angle, b) dry temperature, and c) water vapor mixing ratio comparison for the Spire S128 and S119 DO3 SRO pairs. .
Figure 8. The mean difference (in red line) and standard deviation (in green line) for a) fractional bending angle, b) dry temperature, and c) water vapor mixing ratio comparison for the Spire S128 and S119 DO3 SRO pairs. .
Preprints 82628 g008
Preprints 82628 g009
Figure 9. The DO3 SRO fractional BA comparison for Spire S120 and S124 receivers for GPS (in red line), GLONASS (in orange line), and GALILEO (in blue line) for a) the fractional mean difference, b) the standard deviation, and c) the observation numbers from surface to 40 km altitude.
Figure 9. The DO3 SRO fractional BA comparison for Spire S120 and S124 receivers for GPS (in red line), GLONASS (in orange line), and GALILEO (in blue line) for a) the fractional mean difference, b) the standard deviation, and c) the observation numbers from surface to 40 km altitude.
Preprints 82628 g009
Preprints 82628 g010
Figure 10. The fractional BA difference, the corresponding standard deviation, and the sample number at each vertical level from surface to 40 km altitude for Spire (in red line), COSMIC-2 (in green line), and COSMIC-1 (in blue line) for a) mid-latitude for the southern hemisphere (20°S-45°S), b) tropical region (20°N-20°S), and c) mid-latitude northern hemisphere (45°N-20°N). We also compute the standard error of the mean (SEM) in a vertical line superimposed on the mean. .
Figure 10. The fractional BA difference, the corresponding standard deviation, and the sample number at each vertical level from surface to 40 km altitude for Spire (in red line), COSMIC-2 (in green line), and COSMIC-1 (in blue line) for a) mid-latitude for the southern hemisphere (20°S-45°S), b) tropical region (20°N-20°S), and c) mid-latitude northern hemisphere (45°N-20°N). We also compute the standard error of the mean (SEM) in a vertical line superimposed on the mean. .
Preprints 82628 g010
Preprints 82628 g011
Figure 11. The fractional BA Spire-RO comparison for a) mean differences, b) the standard deviations, and c) observation numbers for the Spire-PAZ, Spire-KOMPSAT-5, Spire-Metop-B, Spire-Metop-C, and Spire-TerraSAR-X SRO pairs during the D04 period.
Figure 11. The fractional BA Spire-RO comparison for a) mean differences, b) the standard deviations, and c) observation numbers for the Spire-PAZ, Spire-KOMPSAT-5, Spire-Metop-B, Spire-Metop-C, and Spire-TerraSAR-X SRO pairs during the D04 period.
Preprints 82628 g011
Preprints 82628 g012
Figure 12. Bending angle profile comparison between COSMIC-2 and Spire for a) fractional BA profile differences, b) the standard deviations, and c) vertical observation numbers for five COSMIC-2 SNR groups (i.e., 0–500 V/V, 500–1000 V/V, 1000–1500 V/V, 1500–2000 V/V, >2000 V/V).
Figure 12. Bending angle profile comparison between COSMIC-2 and Spire for a) fractional BA profile differences, b) the standard deviations, and c) vertical observation numbers for five COSMIC-2 SNR groups (i.e., 0–500 V/V, 500–1000 V/V, 1000–1500 V/V, 1500–2000 V/V, >2000 V/V).
Preprints 82628 g012
Preprints 82628 g013
Figure 13. Bending angle profile comparison between STAR and UCAR Spire for GPS (in red line), GLONASS (in orange line), and GALILEO (in blue line) for a) the fractional mean difference, b) the standard deviation, and c) the observation numbers from surface to 40 km altitude. .
Figure 13. Bending angle profile comparison between STAR and UCAR Spire for GPS (in red line), GLONASS (in orange line), and GALILEO (in blue line) for a) the fractional mean difference, b) the standard deviation, and c) the observation numbers from surface to 40 km altitude. .
Preprints 82628 g013
Preprints 82628 g014
Figure 14. Spire-ERA-5 mean BA fractional difference and corresponding standard deviations for a) 45°N to 45°S, b) 45°N to 30°N, c) 30°N to 30°S, and d) 30°S to 45°S. Similar to a)-d), we also compared the COSMIC-2 and ERA-5 BA fractional difference and corresponding standard deviations in e) 45°N to 45°S, f) 45°N to 30°N, g) 30°N to 30°S, and h) 30°S to 45°S.
Figure 14. Spire-ERA-5 mean BA fractional difference and corresponding standard deviations for a) 45°N to 45°S, b) 45°N to 30°N, c) 30°N to 30°S, and d) 30°S to 45°S. Similar to a)-d), we also compared the COSMIC-2 and ERA-5 BA fractional difference and corresponding standard deviations in e) 45°N to 45°S, f) 45°N to 30°N, g) 30°N to 30°S, and h) 30°S to 45°S.
Preprints 82628 g014
Preprints 82628 g015
Figure 15. a) Differences (dash lines) and uncertainties (dot lines) of Spire temperature profiles retrieved by UCAR wetPf2 compared to RS41 RAOB data. c) Differences (dash lines) and uncertainties (dot lines) of Spire-specific humidity profiles retrieved by UCAR wetPf2 compared to RS41 RAOB data. b) shows the number of collocated Spire-RAOB temperature profiles, and d) is the number of Spire-RAOB water vapor profiles. .
Figure 15. a) Differences (dash lines) and uncertainties (dot lines) of Spire temperature profiles retrieved by UCAR wetPf2 compared to RS41 RAOB data. c) Differences (dash lines) and uncertainties (dot lines) of Spire-specific humidity profiles retrieved by UCAR wetPf2 compared to RS41 RAOB data. b) shows the number of collocated Spire-RAOB temperature profiles, and d) is the number of Spire-RAOB water vapor profiles. .
Preprints 82628 g015
Preprints 82628 g016
Figure 16. a) height-dependent mean temperature differences (K) of UCAR wetPf2 versus RS41 RAOB in the zones of daytime (SZA < 80o), nighttime (SZA > 100o), and dusk/dawn (80o < SZA <100o) in the upper troposphere and lower stratosphere. b) the height-dependent profile numbers for the analysis.
Figure 16. a) height-dependent mean temperature differences (K) of UCAR wetPf2 versus RS41 RAOB in the zones of daytime (SZA < 80o), nighttime (SZA > 100o), and dusk/dawn (80o < SZA <100o) in the upper troposphere and lower stratosphere. b) the height-dependent profile numbers for the analysis.
Preprints 82628 g016
Preprints 82628 g017
Figure 17. a) the height-dependent mean humidity differences (g/kg) of UCAR wetPf2 versus RS41 RAOB for daytime (SZA < 80o), nighttime (SZA > 100o), and dusk/dawn (80o < SZA <100o). Corresponding profile numbers are shown in b).
Figure 17. a) the height-dependent mean humidity differences (g/kg) of UCAR wetPf2 versus RS41 RAOB for daytime (SZA < 80o), nighttime (SZA > 100o), and dusk/dawn (80o < SZA <100o). Corresponding profile numbers are shown in b).
Preprints 82628 g017
Preprints 82628 g018
Figure 18. Fractional BA observation errors (in %) estimated for the region within [45oS, 45oN] for a) over oceans, b) over land, and c) over oceans and land, d) over ocean [45oS, 20oS], e) over ocean [20oS, 20oN], f) over ocean [20oN, 45oN]. One month (from December 15, 2020, to January 15, 2021) of COSMIC-2, KOMPSAT-5, GeoOptics, and Spire bending angle observations were used for generating these figures.
Figure 18. Fractional BA observation errors (in %) estimated for the region within [45oS, 45oN] for a) over oceans, b) over land, and c) over oceans and land, d) over ocean [45oS, 20oS], e) over ocean [20oS, 20oN], f) over ocean [20oN, 45oN]. One month (from December 15, 2020, to January 15, 2021) of COSMIC-2, KOMPSAT-5, GeoOptics, and Spire bending angle observations were used for generating these figures.
Preprints 82628 g018
Table 1. The lowest penetration height of 80% of the total data for different RO missions at different latitudinal zones.
Table 1. The lowest penetration height of 80% of the total data for different RO missions at different latitudinal zones.
10oN-10oS 30oN-10oN 10oS-30oS 45oN-30oN 30oS-45oS 60oN-45oN 45oN-60oS 90oN-60oN 60oS-90oS
COSMIC-2 0.85 0.90 0.75 1.35 1.10
Spire 0.90 0.90 0.75 0.80 0.55 0.45 0.25 0.45 0.20
KOMPSAT-5 1.85 1.50 1.15 0.40 0.95 0.35 0.40 0.25 0.20
PAZ 2.65 1.85 2.05 0.90 1.30 0.45 0.45 0.35 0.35
Table 2. The mean BA fractional difference and the corresponding standard deviations, and the sample number at 10 km altitude for the Spire-PAZ, Spire-KOMPSAT-5, Spire-Metop-B, Spire-Metop-C, and Spire-TerraSAR-X SRO pairs from surface to 40 km altitude.
Table 2. The mean BA fractional difference and the corresponding standard deviations, and the sample number at 10 km altitude for the Spire-PAZ, Spire-KOMPSAT-5, Spire-Metop-B, Spire-Metop-C, and Spire-TerraSAR-X SRO pairs from surface to 40 km altitude.
Mean Difference standard deviation Sample Number at 10 km altitude
Spire -PAZ 0.01% 3.25% 113
Spire -KOMSAT-5 0.18% 3.20% 54
Spire -Metop-A GRAS 0.12% 1.94% 816
Spire - Metop-B GRAS 0.06% 2.89% 792
Spire -TerraSAR-X -0.13% 3.35% 42
Table 3. The mean fractional BA difference, standard deviation of the mean difference, and sample number at 10 km altitude for Spire-COSMIC-2 SRO pairs for different COSMIC-2 SNR groups (i.e., 0–500 V/V, 500–1000 V/V, 1000–1500 V/V, 1500–2000 V/V, >2000 V/V).
Table 3. The mean fractional BA difference, standard deviation of the mean difference, and sample number at 10 km altitude for Spire-COSMIC-2 SRO pairs for different COSMIC-2 SNR groups (i.e., 0–500 V/V, 500–1000 V/V, 1000–1500 V/V, 1500–2000 V/V, >2000 V/V).
Mean standard deviation Sample Number at 10 km altitude
0–500 V/V 0.12% 4.15% 364
500–1000 V/V 0.10% 4.14% 1727
1000–1500 V/V 0.24% 3.97% 2559
1500–2000 V/V 0.16% 3.87% 2325
> 2000 V/V 0.19% 4.07% 332
Table 4. The mean and standard deviation for the fractional refractivity difference between STAR and UCAR Spire for GPS, GLONASS, and GALILEO.
Table 4. The mean and standard deviation for the fractional refractivity difference between STAR and UCAR Spire for GPS, GLONASS, and GALILEO.
Mean standard deviation
GPS 0.06% 0.73%
GLONASS 0.06% 0.78%
GALILEO 0.06% 0.69%
Table 5. Mean temperature biases (uncertainties) (K) and mean humidity biases (uncertainties) (g/kg) between Spire RO retrievals and RS41 RAOB observations over different height regions.
Table 5. Mean temperature biases (uncertainties) (K) and mean humidity biases (uncertainties) (g/kg) between Spire RO retrievals and RS41 RAOB observations over different height regions.
Spire Retrieval µ(ΔT) (σ(ΔT))(K)
(8-11 km)		 µ(ΔT) (σ(ΔT)) (K)
(12.5-16.5 km)		 µ(ΔT) (σ(ΔT)) (K)
(17.8-26.4 km)		 µ(ΔH) (σ(ΔH))
(g/kg) (below 4.2 km)		 µ(ΔH) (σ(ΔH)) (g/kg) (4.8-8.4 km)
UCAR wetPf2 0.02(1.13) -0.00(1.22) -0.01(1.40) -0.19(1.02) -0.04(0.45)
Table 6. The mean temperature bias (uncertainty) (K) of UCAR Spire wetPf2 versus RS41 RAOB comparisons in three SZA zones over three height regions in the upper and lower stratosphere.
Table 6. The mean temperature bias (uncertainty) (K) of UCAR Spire wetPf2 versus RS41 RAOB comparisons in three SZA zones over three height regions in the upper and lower stratosphere.
Height Range Day Night Dusk/Dawn
8-11 km 0.06(1.10) -0.04(1.15) -0.01(1.21)
12.5-16.5 km 0.01(1.20) -0.02(1.25) -0.02(1.25)
17.8-26.4 km 0.02(1.38) -0.05(1.46) -0.06(1.35)
Table 7. Mean humidity differences (uncertainties) (g/kg) between RO retrievals and RS41 RAOB observations over two height regions and three SZA zones.
Table 7. Mean humidity differences (uncertainties) (g/kg) between RO retrievals and RS41 RAOB observations over two height regions and three SZA zones.
Height Range Day Night Dusk/Dawn
Below 4.2 km -0.17(1.03) -0.23(1.07) -0.15(0.89)
4.8-8.4 km -0.04(0.45) -0.06(0.49) -0.02(0.39)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated