Prerpints.org logo
Preprint
Article

Is Drug Delivery System a Deterministic or Probabilistic Approach? A Theoretical Model Based in the Sequence Electrodynamics-Diffusion-Bayes

Altmetrics

Downloads

110

Views

17

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 August 2023

Posted:

18 August 2023

You are already at the latest version

Alerts
Abstract
The paradigm of molecular communications is applied to the concrete case for delivering electrically charged nanoparticles to tumor. Once them have been injecetd in blood it is expecetd an optimal outcome as to reduce toxicity and minimal dispersion of drugs in the blood stream. With a fraction of nanoparticles arrives to surface of tumor, the scattered part of injected ones can minimize the success of scheme of drug delivery. In this paper is presented a theory based at the sequence electrodynamics-diffusion-Bayes theorem. The resulting probability of Bayes at the end of sequence, might be telling us that dynamical processes based in the injection of electrically charged nanoparticles might be dictated by stochastic formalism more that biochemical approaches by which makes impossible to know the success or fail of drug delivery dynamics. Illustrations demonstrating the transition of a linear to nonlinear scenario are presented
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematical and Computational Biology

1. Introduction

The technique known as Targeted Drug Delivery (TDD) constitutes a promising and advantageous therapy against the progress of diseases related to cancer. Thus, one can perceives that there is still a wide debate is seen in literature as to the pros and cons in the injection into the blood stream of metal-based nanoparticles [1]. In fact, in order to accomplish with the objectives of therapy it is required the longevity of nanoparticles while transits over the blood stream. Nevertheless, the sustainability of nanoparticles is affected by wrong binding that would decrease the effectiveness of anticancer strategy [2]. On the other hand, some nanoparticles (as for example made of gold), have shown undesirable side effects leading to noteworthy changes on the mechanisms of blood coagulation. As investigated by [3] physical effects at the injected nanoparticles might be exhibited transformation into a type known as "corona". At the other hand, nanoparticles under interaction with proteins (such as albumin) triggers new states such as protein corona [4]. It is actually logic to expect sustainable chain of events (against the central objective of TDD). The exposure of surface’s nanoparticles lead to interaction with biomolecules as well as the nanoparticles itself have the capability to reconfigure the biochemistry of proteins [5,6]. In [7] it was studied the effects of electric charge in colloidal coated gold nanoparticles to unfold FibriGen (FG) by producing inflammatory events, demonstrating that the surface of coated nanoparticles might be playing a crucial role in the degradation of the TDD schemes. In this manner, electrodynamics emerges as a key point to understand the role of coated nanoparticles whose surface charge density has a direct influence on the cellular uptake. As investigated in [8] the issue of effect of electric sign in the internalization of nanoparticles,was boarded. In [9,10] it was found that systems with positively charged nanoparticles reach the target (tumors or cells) to continue with the uptake by molecular systems belonging to tumor tissue. Adsorption of proteins would generate layers over the nanoparticles surface emphasizing the event that gives place to potential stability of colloidal system in according to the magnitude of so-called zeta-function [11]. In this way, one can see that a model describing diffusive phenomenologies might be incomplete and the theoretical implementation of classical electrodynamics, would be an accurate approach to some extent. This is the opted avenue of this paper: the generation of hybrid model that combines the diffusion in conjunction to electrical events at the pathway of nanoparticles towards their target. Moreover, to complete the description the hypothetical scenario is considered: uptake as well internalization of electrically charged nanoparticles would be dictated by probabilistic rules. This might be a fair consequence of the confluence of a plethora of variables that converts the TDD scheme in a nonlinear system by which is far of being boarded by deterministic equations. A sketch of the central idea of paper is displayed in Figure 1. The rest of paper is as follows: In second section by using the concept of Eq.1 the transition of efficiency to probability is presented. In third section, the Coulomb force is used to derive probabilistic relations involving surface of nanoparticles as well as distances. In fourth section, the 1-dimension diffusion equation is introduced and their closed-for solutions are incorporated at the efficiency of system. Contour plots indicating the map of probabilities are presented. In fifth section, the efficiency of drug delivery scheme is established with the solutions of diffusion equations and the resulting electrodynamics. From it a Bayes-like expression is derived. Analysis and discussions from the contour plots are presented. Finally, the conclusion is presented.

2. The Electrodynamics Model

While nanoparticles are made of metals, the promising citrate-coated gold nanoparticles have shown to be stable in aqueous solution while they bear negative charge [17]. Thus, due to the surface electrically charge flip, repulsive forces can emerge as well as them can constitute a attractor volume of albumin proteins that are negatively charged proteins. By following this view, a description based in electrodynamics would complement the construction of a theoretical model of targeted drug delivery based so far in probabilities as displayed in Figure 2. Consider that nanoparticles have a spheric shape with a surface charge density given by: σ = q / 4 π r 2 . The charge of nanoparticles can be written as q = 4 π σ r 2 with σ surface charge density (assumed to be constant for all nanoparticles). One can wonder if once the nanoparticles traveling along the blood stream loses its initial geometry [18]. In this sense the radius might be varying in time. Then in this scenario one gets below:
q ( t ) = 8 π σ ∫ 0 r ( t ) r d r = 4 π σ r 2 ( t ) .
Thus, for a couple of nanoparticles separated by distance R with different radius, then the corresponding Coulomb repulsion force with ϵ B the dielectric constant of interstitial fluid (see again Ref. [16]) reads:
F = 4 π σ 1 σ 2 r 1 2 ( t ) r 2 2 ( t ) ϵ B R 2 .
With proteins like albumin with negative electric charge, the aggregation of nanoparticles would not undergoes repulsion among them but also electric work. With this, the electric work done to move a charge a displacement x can be written as:
W = F x = 4 π σ 1 σ 2 r 1 2 ( t ) r 2 2 ( t ) x ϵ B ( R + x ) 2 = 4 π σ 1 σ 2 r 1 2 ( t ) r 2 2 ( t ) ϵ B R 2 ( 1 + x R ) 2 .
With the energy given above is possible to derive the energy distribution based on the well-known Boltzmann-Maxwell distribution. While all nanoparticles have same charge density σ 1 = σ 2 = σ such distribution is:
B ( σ ) = N π σ Exp − 4 π σ 2 r 1 2 ( t ) r 2 2 ( t ) k T ϵ B R 2 ( 1 + x R ) 2 ,
(that can be directly compared to flux of Eq.19). N is a normalization constant depending on the electric characteristics. This is to some extent analogue to case of plasma physics where electrodynamics adjust well to kinetic theory, yielding Boltzmann-Maxwell statistics [19]. With this probability of energy, B ( σ ) has its associate Shannon’s entropy [20] so that an universal probability distribution function reads:
P ( σ ) = Exp − 1 N σ π 4 π σ 2 r 1 2 ( t ) r 2 2 ( t ) k T ϵ B R 2 ( 1 + x R ) 2 N π σ .
Entropy would emerge from the lapse of time by which same-sign nanoparticles are exerting forces each other distorting their transit towards target. (Although it goes beyond the scope of paper, the electrical behavior of nanoparticles might be investigated directly from the usage of theories based on entropy). In this manner, the electric work done by nanoparticles acquires the mathematical structure of entropy so that W= Log P . On the other hand, the Coulomb force can incorporate the concept of volumetric charge density under the assumption that exist a cargo of nanoparticles containing a net charge as commonly employed at TDD schemes [21]. With this the net charge q = ∫ ρ d V suggests to write down the Coulomb force as:
F = 1 4 π ϵ B ∫ ρ 1 d V 1 ∫ ρ 2 d V 2 ( R + x ) 2 = 1 4 π ϵ B ∫ ρ 1 d V 1 ∫ ρ 2 d V 2 R 1 + x R 2 .
By using the sum with the restriction ∑ p ≥ 2 1 p ! x R p = 0, then one gets below:
1 + x R = 1 + x R + ∑ p ≥ 2 1 p ! x R p = e | x | R ,
so that Eq.30 can be written as:
F = 1 4 π ϵ R ∫ ρ 1 d V 1 ∫ ρ 2 d V 2 e − 2 | x | R .
The focus of interest is the case when cargo have spherical geometry, so that the force is written as:
F = 4 π ϵ R ∫ ρ 1 ( r 1 , t ) r 1 2 d r 1 ∫ ρ 2 ( r 2 , t ) r 2 2 d r 2 e − 2 | x | R .
Consider the scenario that the densities are only dependent on s and t then Eq.33 acquires a simplified form:
F = 4 π ϵ R ( r 1 r 2 ) 3 9 ρ 1 ( s , t ) ρ 2 ( s , t ) e − 2 x R .
Moreover, the case that consider the homogenization of all densities in nanoparticles, then Eq.34 reads:
F = 4 π ϵ R ( r 1 r 2 ) 3 9 | ρ ( s , t ) | 2 e − 2 x R .
Since all electrical forces along the blood stream can be called instantaneous interactions, then Eq.35 is expressed as function of a Dirac-Delta function in the sense that:
F ( T ) = 4 π ϵ R ( r 1 r 2 ) 3 9 e − 2 x R δ ( t − T ) | ρ ( s , T ) | 2 .
Therefore, the transported impulse I is given by:
I = ∫ d T F ( T ) = 4 π ϵ R ( r 1 r 2 ) 3 9 e − 2 x R × × ∫ d T δ ( t − T ) | ρ ( r , T ) | 2 .

3. The Diffusion Model

The scenario of study at this paper is the pass of injected nanoparticles at a limited segment of blood stream. Although at the case of nanoparticles, molecular effects might emerge, but this is discarded since it is assumed a macroscopic scenario where classical laws applies well [22]. It is also feasible to assume that the direction of velocity of blood flowing is parallel to longitudinal symmetry of artery or veins. This is an important argument to neglect effects of drag forces (as well as Brownian motion), so that the usage of Fokker-Planck equation might not be fitted in the context of present study. The dynamics of the injected nanoparticles into the blood flowing can be seen for example as an exact equation of transport. Under this view then the Fick’s first law applies well. Thus, the mass current J ( s , t ) and nanoparticles density ρ ( s , t ) are related through J ( s , t ) = − D ∇ ρ ( s , t ) with D the diffusion constant. As written so far s has units of distance. One can demand continuity in the sense that nanoparticles are unstoppable while are at the blood stream. In this manner, Fick’s first law is combined with continuity equation d ρ / d t + ∇ · J ( s , t ) =0. In this way one gets the diffusion equation d ρ / d t = D ∇ 2 n ( s , t ) [23]. It clearly demonstrates the equivalence between Fick’s first law and diffusion equation [24]. At the other hand, the diffusion equation has been and is being used as a trusted first approximation for the transit of nanoparticles moving along the blood stream [25–28]. On the other hand one can see that Eq.35 is still incomplete because not any specific information of volumetric charge densities ρ ( s , t ) is known. As sketched in Figure 1 the central idea of this paper consists in the parallel displacement of nanoparticles along the arteries. Therefore it logically suggests to employ the diffusion equation in its simplest representation (1-dimension) for densities of Eq.35:
d ρ d t = D d 2 ρ d s 2 .
This can be rewritten as d ρ d s d s d t = D d 2 ρ d s 2 ⇒ d ρ d s = D v d 2 ρ d s 2 , where only the longitudinal displacement is considered so that it is defined: v = d s d t (again is remarked whose direction is parallel to artery). Therefore Eq.38 can be written as d 2 ρ d s 2 − v D d ρ d s = 0 yielding the trivial closed-form solutions:
ρ ( s ) = a 1 Exp v D s + a 2 Exp − v D s .
It should be noted that a 1 and a 2 have units of charge per unit of volume. Solution Eq.39 is inserted into Eq.35 yielding the Coulomb force depending on the solutions of diffusion equation. Thus one can write down:
F = 4 π ( r 1 r 2 ) 3 e − 2 x R 9 ϵ R a 1 e v D s + a 2 e − v D s 2 .
Turning back to Eq.3, the solution given at Eq.40 can enter since the coefficients a 1 , 2 pass to be replaced by the ones that have arrived, free of interactions, and been rejected. Therefore the efficiency now it is composed by diffusion and electrodynamics, with the coefficients with units of number of nanoparticles per unitr of volume.

4. Efficiency of Drug Delivery Based in Probabilities

The success of an event of drug delivery can be measured in terms of number of nanoparticles that have been internalized into tumor. Consider n nanoparticles injected in the blood stream at the time t. It is expected that in a subsequent time t + t M a fraction of them can arrive to tumor. Here t M the time by which nanoparticles have arrived to the surface of tumor. Thus, only a fraction of them arrives to target due to interactions with blood plasm, cells, proteins, etc [13]. Therefore a new quantity is defined as the efficiency of delivery and it can be written as:
E ( t ) = n AR ( t ) n FR ( t ) + n RE ( t )
with n AR ( t ) , n FR ( t ) and n RE ( t ) , the number of effective nanoparticles that have arrived to target, the ones that are free of interactions (that are not undergoing electrical interactions), and the ones that have had chemical or electrical rejection along their path to tumor, respectively. It should be remarked that n AR ( t ) + n FR ( t ) + n RE ( t ) = n TO the total number of injected nanoparticles. Eq.3 can be seen from another angle in the sense that this efficiency abandons its deterministic status and departures to a probabilistic territory. Then, it can write down as:
E ( t ) = n AR ( t ) n FR ( t ) 1 + n RE ( t ) n FR ( t ) .
Under the assumption that ∑ m 1 / m ! ( n RE ( t ) n FR ( t ) ) m = 0 for m ≥ 2 then Eq.4 can be written again as:
E ( t ) = n AR ( t ) n FR ( t ) Exp − n RE ( t ) n FR ( t ) .
If the rate n RE / n FR is proportional to t, then the negative exponential might be seen as a pessimistic scenario in which the efficiency falls down in time. Eq.5 manifests that the entire process of drug delivery would be in risk. Therefore, biochemical compounds and proteins like albumin would decrease the chance to maximize the efficiency of sent doses. Then it is strongly desired that such efficiency exhibits the highest values. Mathematically speaking it is desired the efficiency behaves as a peaked distribution [9].
With the existence of negative aspects then it is logical to assume events against the success of TDD scheme. A crude view of TDD scheme might to consider to the system nanoparticles-tumor through the formulation of signal and background. Therefore it is defined efficiency as n a / n SEN with n a (signal) the ones that have arrived to target and n SEN the total that were sent. The efficiency can be written in an explicit manner to another equation that reads:
P = n a n a + n r ,
with n r (background) the ones that were rejected by the target. Thus, one can wonder about the probability that a number of injected nanoparticles can reach their target conserving their biochemical and electrical properties? Inspired at probabilistic matrix factorization (Eq.3 of Ref. [12] by which it was anticipated a form of conditional probability), one can expect a large product of probabilities. So that the probability of internalization can be written as a function of a finite number of probabilistic variables ξ L (including the random ones if any):
P ( ξ 1 , ξ 2 , . . . , ξ L ) = ∏ ℓ = 1 L p ℓ ( ξ ℓ ) .

4.1. Gaussian Distributions

From Eq.5 the well-known Gaussian distributions can be derived inside the context of TDD. Consider the assumption that:
n RE ( t ) n FR ( t ) = β t ℓ ,
with β a free parameter, so that from Eq.5 one gets the following:
E ( t ) = n AR ( t ) n FR ( t ) Exp − β t ℓ ,
by which one can recognize the case of ℓ=2 as the Gaussian profile. When β = 1 Δ 2 then Eq.7 can be written as:
E ( t ) = n AR ( t ) n FR ( t ) Exp − ( t − t C ) 2 Δ 2 ,
with t C the critical time that yields the highest probability of event. But of course it would not be the only one probabilistic manifestation of an event of drug delivery [14]. Aside, one can impose limitations to the general assumption Eq.5 under a time-dependent scenario. In order to explore another derivations of probability distribution functions consider the approximation:
n AR ( t ) n FR ( t ) = α t ℓ − 1 .
With Eq.6 and Eq.9 and after a straightforward calculation one gets the following:
n AR ( t ) = α β n RE ( t ) t ⇒ n RE ( t ) = β t α n AR ( t ) .
From assumptions done above, Eq.10 express the fact about n RE ( t ) and n AR ( t ) they are proportional to each other. Such proportionality is dictated by the quantity ( β / α ) t dependent on time. (It should be noted the role of free parameters α and β at the set up of equations and their physical meaning.) Some restrictions on them can be given as at the case when α ≫ β t the scenario where the number of nanoparticles free of interaction is bigger than the ones have arrived to target. Then one can write down:
β t α ≈ β t α − β t α 3 + . . . . = sin β t α ,
⇒ n RE ( t ) = sin β t α n AR ( t ) .
with β / α with units of frequency. The sinusoid behavior of the rate n RE ( t ) / n AR ( t ) can be understood in terms of electrical oscillations originated from Coulomb forces as shall be seen next section.

4.2. Weibull and Lorentzian Distributions

The Gaussian distribution might not be the unique distribution that models the efficiency of nanoparticles. For instance, putting Eq.9 into Eq.7 one gets:
E ( t ) = α t ℓ − 1 Exp − β t ℓ
that takes the form of the well-known Weibull distributions. Eq.13 express the fact that the efficiency of injected nanoparticles acquires a maximum for some values of free parameters α and β , that would give the peaks of distributions.
Turning now to Eq.4, one can see that the replacements from Eq.7 and Eq.9 yields:
E ( t ) = α t ℓ − 1 1 + β t ℓ .
It is evident that a peaked behavior emerges with ℓ=2. Such form is known as the Lorentzian distribution with the change t → t − t C and it reads:
E ( t ) | ℓ = 2 = α t − t C 1 + β ( t − t C ) 2 ,
with t C the critical time as written in Eq.8. Furthermore more distributions can be generated. Consider for example the definition:
n AR ( t ) n FR ( t ) = γ ( t ) ,
As consequence from this Eq.7 can be rewritten as:
E ( t ) = γ Exp − ( β t ) ℓ .
In contrast to Eq.7 now one can see that β with units of t − 1 and it is also affected by the exponent ℓ. Inspired in deterministic relation F / m v = d v / d s with F and m the mechanical force and mass of nanoparticles, β = v s . In conjunction to this γ = g ( v , s , ℓ ) that conveys to write down an equation for the efficiency as follows:
E ( t ) = g ( v , s , ℓ ) Exp − v t s ℓ .
with v the velocity of nanoparticles (that is assumed to be same of blood in artery). The function g ( v , s , ℓ ) is not fully unknown. This can be derived from the existence of a flux of probability F ( t ) that can be written below as:
F ( t ) = Exp − v t s ℓ .
Because there is a degradation of initial volume of injected nanoparticles at time the negative derivative of flux with respect to velocity restores the efficiency and it reads:
E ( t ) = − d F ( t ) d v = − ℓ v v t s ℓ − 1 Exp − v t s ℓ .
Therefore, γ = g ( v , s , ℓ ) = − ℓ v v t s ℓ − 1 . It is noteworthy that E ( t ) can be related to a Weibull distribution. For example the case when ℓ=2, one arrives to:
E ( t ) = d F ( t ) d v = 2 t s Exp − v t s 2 .
It is clear that the TDD scheme is not based in a single group velocity along the bloodstream. Instead the efficiency is constituted by the finite contribution of a set of velocities corresponding to several segments s j as:
E ( t ) = ∑ j = 1 J 2 t j s j Exp − v j t j s j 2 .
As seen in [15], injected drug delivery would exhibit different dynamics depending on the transit along the arteries in conjunction to the different cells that undergoes interactions with nanoparticles. Thus for example, the drug absorption is a consequence of the net efficiency among the channels vascular, extracellular and antigen-binding. In virtue to repulsion and attraction forces among nanoparticles because the Coulomb law (Eq. 31 of Ref.[16]), one can assume that v j = v 0 sin v j t j s j . Inserting this into Eq.22 one gets for J aggregations of nanoparticles:
E ( t ) = ∑ j = 1 J 2 t j s j Exp − v 0 t j sin v j t j s j s j 2 .
and for t j → t that means all aggregations of nanoparticles are arriving same velocity and time (with s j → s ), then the efficiency gets the form:
E ( t ) = 2 t × J s Exp − v 0 t sin ( x − s c ) t s τ s 2 .
It is noted that the velocity v was rewritten as ( x − s c ) / τ . With s c the critical distance that plays the role as phase in the sense that exists a minimal time that makes different the arrival of nanoparticles to target. In Figure 2 the cases of up to 3 critical distances when v 0 t / s = 1 have been plotted.
E ( t ) = 4 π ( r 1 r 2 ) 3 e − 2 x R 9 ϵ R a AR e v D s + a AR e − v D s 2 4 π ( r 1 r 2 ) 3 e − 2 x R 9 ϵ R a FR e v D s + a FR e − v D s 2 + 4 π ( r 1 r 2 ) 3 e − 2 x R 9 ϵ R a RE e v D s ¯ + a RE e − v D s ¯ 2
In a minimal model (it is nanoparticles defined as a AR , a RE and a FR exhibit same difusion and electrodynamics) the term 4 π ( r 1 r 2 ) 3 e − 2 x R 9 ϵ R is common to all them. Then one arrives to a compact form of efficiency:
= 1 a FR a AR e v D s + a AR e − v D s 2 e v D s + e − v D s 2 + a RE a FR e v D s ¯ + e − v D s ¯ 2 .
Consider the change s → s ¯ by which rejected nanoparticles acquire a random distance s ¯ after to fail to be internalize tumor. Here it should be noted that exists the possibility that nanoparticles have could enter through tumor but into the hypoxia region. This is against the purpose of TDD schemes. Only the evidence at the patient’s outcomes as to the effect of injected dose delivery and its relation to the percent in the tumor degradation can be relevant to estimate the randomness of scheme. Consider now a optimistic scenario by which a AR ≫ a FR then Eq.42 depends directly of the quantity of nanoparticles at the assumed cases and the fraction: a RE a AR , because this Eq.42 is rewritten E ( t ) =
e v D s + e − v D s 2 e v D s + e − v D s 2 + a RE a AR 2 e v D s ¯ + e − v D s ¯ 2 .
To provide an interpretation of Eq.43, special attention has been paid on the term that give accounts of rejected ones. Some approximations have been done, for example D ≫ v × s and with this the numerator gets the value of 2. Besides, as assumed above the fraction a FR a AR ≈ 0 . As usual D has units of L 2 / T . The exponential part s ¯ D v with v → v 0 sin 2 ( κ s ) then from above s ¯ D v 0 sin 2 ( κ s ) = s ¯ D v 0 sin ( κ s ) = t τ sin ( κ s ) with τ = ℓ 2 s ¯ v 0 approximated to be 1 in units of time. With these calculations one can rewrite Eq.43 as E ( t ) = 2 ( exp [ t sin ( s ) ] + exp [ − t sin ( s ) ] ) 2 with κ with units of L − 1 and wit the value 1. The why of the sinusoid approximation is because the expected flipping property producing either attraction or rejection. In Figure 3 the corresponding contours plot Eq.43 are displayed. It is easy to see that in a scenario dictated by determinism, one would get only lines showing the linearities of a simple dynamics of nanoparticles by following same blood velocity. However, left-side and right-side panels are showing a non-trivial morphology, fact that allows to incorporate probabilistic aspects as a direct counterpart of determinism. As seen in left-side panel Figure 3 the contour plot exhibited the maximum value of efficiency has turned out to be of 12% that is favorable in the sense that a small efficiency translates as a poor Coulomb interaction among the nanoparticles so that one has the chance that a substantial fraction of them might be arriving to their target with a minimal electrical interaction. In other words, electrical interactions would trigger noise or background to the TDD scheme. One can see in right-side panel arrows pointing the values of a null efficiency due to Coulomb forces that are against the propagation of nanoparticles (the reader should be note that so far it is presented a hybrid description combing probability, electrodynamics and diffusion). In fact, for distances 6.6 to 7.8 (a.u.) and for times of 2.5 (a.u.) one can see that the supposed flux of nanoparticles are exhibiting a slow displacement that is free of Coulomb interactions. In contrast to other space-time regions the fact that the nanoparticles are traveling fast, it might not be guaranteeing a optimal drug delivery, instead it would be affected by Coulomb interactions as well as randomness.

5. Usage of Bayes’s Theorem

It is not difficult to corroborate that Eq.43 has some extent the structure of Bayes’s theorem known as:
B = P A ⊗ P B P A ⊗ P B + ( 1 − P A ) ⊗ P W ,
that applied onto Eq.43 acquires the following meaning if and only if T = N + M : with T the total number of sent nanoparticles.
  • P A probability that N nanoparticles arrive to tumor.
  • P B probability that all of them achieve to internalize tumor.
  • 1 − P A probability that M nanoparticles fail to reach the tumor.
  • P W probability that 1 − P A is wrong and nanoparticles were scattered off tumor.
This is resumed in cartoon of Figure 4. It is clear that a number of nanoparticles N can be internalize (even into the hypoxic zone) with M the ones that are rejected due to minimal permeation as well as chemical unbalance due to tumor microenvironment [30]. By taking into account all these items, then the direct correspondence with Eq.42 turns out to be:
P A ⊗ P B = e v D s + e − v D s 2
( 1 − P A ) ⊗ P W = a RE a AR 2 e v D s ¯ + e − v D s ¯ 2
and P W opts to be random since not any tool would allow to measure the verification if 1 − P A is wrong or true. This is related to the capability for enhancing the permeability of nanoparticles (see Ref. [31]). Indeed, the expansion: e − v D s ¯ ≈ 1 - v D s ¯ is used and with this Eq.46 acquires the form:
( 1 − P A ) ⊗ P W = 1 − v D s ¯ + e v D s ¯ 2 ⊗ a RE a AR 2 .
In Eq.45 one can note that P A = P B . This is encompassing the employed theory of paper: Both arrival and internalization are dictated by equation of diffusion and electrodynamics. On the other hand, the probability of confirmation is delayed to P A at the sense that only evidence at the effects of injected drugs in patients can serve as a strong indicator of this mathematical abstraction.
In this manner, from Eq.47, the coefficients a RE and a AR can both be estimated from electrodynamics. Consider the Coulomb force for rejection (with ϵ B =1.) F RE = q BS N RE Q RE x RE 2 with q BS the net electric charge from free ions at the blood stream and over target (or tumor) and Q RE the net charge of rejected nanoparticles. With the definition ρ = N RE Q RE / V RE then F RE = q BS ρ RE V RE x RE 2 that implies that ρ RE = a RE = F RE x RE 2 q BC V RE . Same procedure is applied to estimate a AR that is also expressed in terms of density as: ρ AR = F AR x AR 2 q BC V AR , so that a RE a AR 2 = ρ RE ρ AR 2 = F RE x RE 2 V AR F AR x AR 2 V RE 2 . Now Eq.43 can be finally written as the conditional probability of internalization in according to sketch of Figure 4 and it reads as follows:
P INT ( t ) = e v D s + e − v D s 2 e v D s + e − v D s 2 + F RE x RE 2 V AR F AR x AR 2 V RE 2 1 − v D s ¯ + e v D s ¯ 2 .

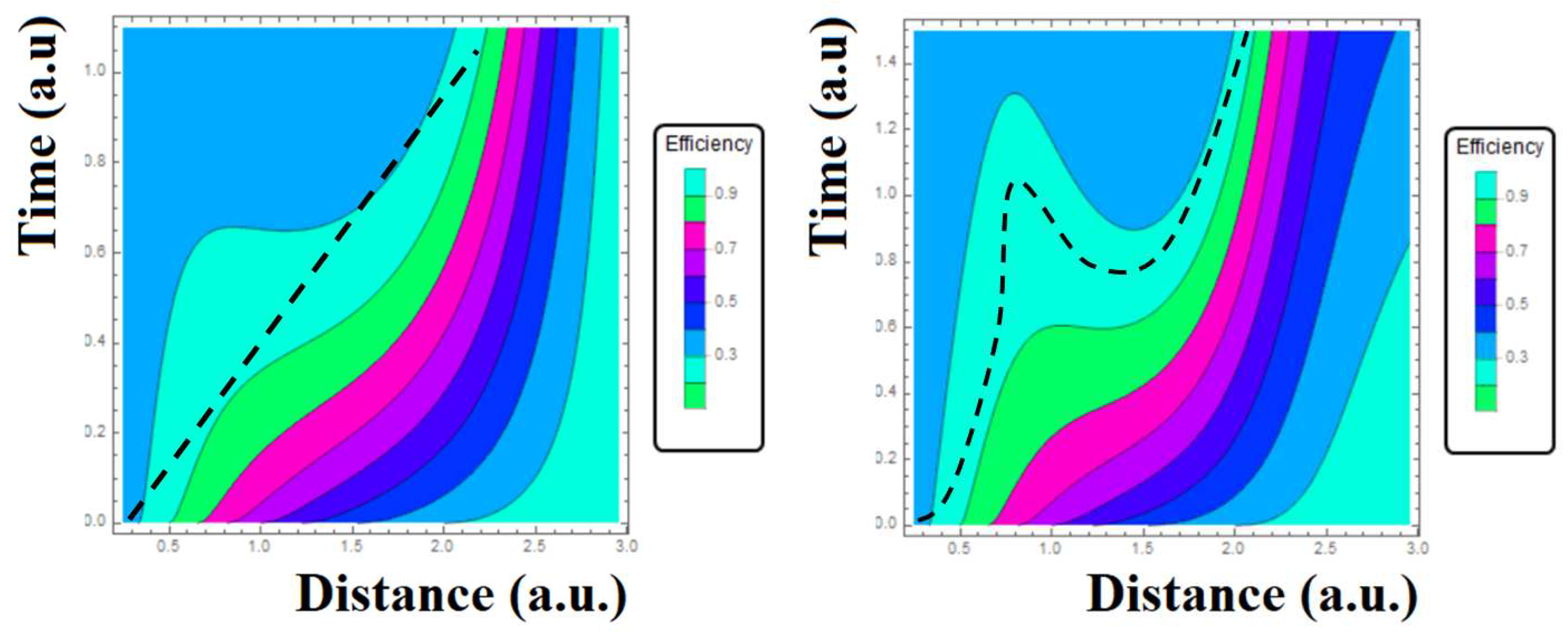
5.1. Bayesian Behavior Inside Linear Scenarios

In Figure 5 Eq.48 or Bayes probability has been plotted for two scenarios. In both cases one can see the deformation of linear region as a consequence that dynamics of nanoparticles abandoning its deterministic behavior. In this subsection also the choice κ = 1 was used. In left-side panel the dashed line is superimposed to contour plot to note the transition between determinism and probability where Bayes’s theorem would apply well (in the sense that the efficiency becomes now a probability). Here is used the approximation F RE x RE 2 V AR F AR x AR 2 V RE 2 ≈ x RE 2 as well as e − v D s → sin ( x ) that also affect the exponentials functions. The dashed line is crossing the region with a high Bayes probability in around 90%. Indeed, it can be seen as a linearity between time and distance yielding a constant velocity against the picture of classical forces (Coulomb-like for examples) governed by accelerated nanoparticles because Newtonian forces. A different case is presented in right-side panel where it was used e − v D s → sin 2 ( s ) . The dashed line does not follows a linear behavior, instead it is demonstrating the nonlinearity of internalization in an entire Bayes scheme. For small s then one has sin 2 ( s ) ≈ ( s − 1 / 6 s 3 ) 2 = s 2 − s 3 / 3 + s 6 / 36 . These nonlinearities would be in according to the events where nanoparticles would arrive to the hypoxia zones [32]. This is of importance in the sense to estimate the percent of nanoparticles that turned to be lost and differencing them from those that were scattered off tumor surface. In addition one can anticipate the percent of fail against the ones that would exhibit a high probability to internalize tumor or objective tissue [33–35]. Thus, the difference between the percent of tumor degradation and the percent of density of injected nanoparticles would provide a test in which TDD is either purely a stochastic or determinism process. This also would reach studies at angiogenesis [36,37]. Finally, the processes against internalization such as retention and accumulation although not directly observed all of them would exhibit a side not favorable as to the usage of targeting drug delivery [38] whose usage should come finally from observed outcomes of oncological treatment of patient.

6. Conclusion

In this paper, a hybrid theoretical approach that have ended with the inclusion of Bayesian concepts in the action of internalization of drug delivery scheme, was presented. In essence, it has been build a chain of formalisms in the sense that the probability-electrodynamics-diffusion can be a solid ground to face the problem in the fail of targeted drug delivery method. Although the presented study has consisted in the formulation of equations, it is noteworthy that the Bayes’s theorem has emerged as being inherent at the basic formulation of efficiency. The contour plots has yielded that the internalization of nanoparticles might be subject to aspects that combines the linearity and nonlinearities at the TDDs scheme. Also the hypothesis that drug delivery might be touching a territory based on randomness would be an additional idea in a next study. Nevertheless, the experimental input is deeply needed as to validate to some extent the theoretical predictions. In a subsequent study, under the umbrella of the developed theory of this paper, the randomness of TDD shall be measured in order to estimate the patient recovery [39,40] and the relation with the success probability of TDD techniques.

References

  1. Zhang N, Xiong G and Liu Z (2022), Toxicity of metal-based nanoparticles: Challenges in the nano era. Front. Bioeng. Biotechnol. 10:1001572. [CrossRef]
  2. Marina A. Dobrovolskaia, et.al, Interaction of colloidal gold nanoparticles with human blood: effects on particle size and analysis of plasma protein binding profiles, Nanomedicine. 2009 June ; 5(2): 106–117. [CrossRef]
  3. Niloofar Ajdari and et.al, Gold nanoparticle interactions in human blood: a model evaluation, Nanomedicine: Nanotechnology, Biology, and Medicine 13 (2017) 1531–1542. Nanomedicine: NBM 2017;13:1531-1542. [CrossRef]
  4. Dobrovolskaia MA, Neun BW, Man S, Ye X, Hansen M, Patri AK, et al. Protein corona composition does not accurately predict haemocompatibility of colloidal gold nanoparticles. Nanomedicine 2014, 10, 1453–63. [CrossRef] [PubMed]
  5. Mosesson, M. W. Fibrinogen and fbrin structure and functions. Journal of Trombosis and Haemostasis 2005, 3, 1894–1904. [Google Scholar] [CrossRef] [PubMed]
  6. Kharazian, B., Lohse, S.E., Ghasemi, F. et al. Bare surface of gold nanoparticle induces inflammation through unfolding of plasma fibrinogen. Sci Rep 2018, 8, 12557. [CrossRef] [PubMed]
  7. Deng, Z. J., Liang, M., Monteiro, M., Toth, I. and Minchin, R. F. Nanoparticle-induced unfolding of fbrinogen promotes Mac-1 receptor activation and infammation. Naturenanotechnology 2011, 6, 39–44.
  8. Valerie Forest and Jeremie Pourchez. Preferential binding of positive nanoparticles on cell membranes is due to electrostatic interactions: A too simplistic explanation that does not take into account the nanoparticle protein corona. Materials Science and Engineering: C, 2017, 70, pp.889 - 896. [CrossRef]
  9. Zhao, F.; Zhao, Y.; Liu, Y.; Chang, X.; Chen, C.; Zhao, Y. Cellular uptake, intracellular trafficking, and cytotoxicity of nanomaterials. Small Weinh. Bergstr. Ger. 2011, 7, 1322–1337. [Google Scholar] [CrossRef] [PubMed]
  10. Panariti, A.; Miserocchi, G.; Rivolta, I. The effect of nanoparticle uptake on cellular behavior: disrupting or enabling functions? Nanotechnol. Sci. Appl. 2012, 5, 87–100. [Google Scholar] [PubMed]
  11. Barisik, M.; Atalay, S.; Beskok, A.; Qian, S. Size Dependent Surface Charge Properties of Silica Nanoparticles. J. Phys. Chem. C. 2014, 118, 1836–1842. [Google Scholar] [CrossRef]
  12. Cobanoglu MC, Liu C, Hu F, Oltvai ZN, Bahar I. Predicting drug-target interactions using probabilistic matrix factorization. J Chem Inf Model. 2013, 53, 3399–409. [CrossRef] [PubMed]
  13. Liu, X.; Huang, N.; Li, H.; Jin, Q.; Ji, J. Surface and size effects on cell interaction of gold nanoparticles with both phagocytic and nonphagocytic cells. Langmuir 2013, 29, 9138–9148. [Google Scholar] [CrossRef] [PubMed]
  14. Ajdari, N. and et.al, B. G. Gold nanoparticle interactions in human blood: A model evaluation. Nanomedicine: Nanotechnology, Biology and Medicine 2017, 13, 1531–1542. [CrossRef] [PubMed]
  15. Y. Chahibi and I. F. Akyildiz, "Molecular Communication Noise and Capacity Analysis for Particulate Drug Delivery Systems," in IEEE Transactions on Communications, vol. 62, no. 11, pp. 3891-3903, Nov. 2014. [CrossRef]
  16. Y. Chahibi, I. F. Akyildiz, S. Balasubramaniam and Y. Koucheryavy, "Molecular Communication Modeling of Antibody-Mediated Drug Delivery Systems". IEEE Transactions on Biomedical Engineering 2015, 62, 1683–1695. [CrossRef] [PubMed]
  17. Jon Won Park, et.al., Structural Study of Citrate Layers on Gold Nanoparticles: Role of Intermolecular Interactions in Stabilizing. J. Am. Chem. Soc. 2014, 136, 1907–1921. [CrossRef] [PubMed]
  18. Hoshyar N, Gray S, Han H, Bao G. The effect of nanoparticle size on in vivo pharmacokinetics and cellular interaction. Nanomedicine 2016, 11, 673–92. [CrossRef] [PubMed]
  19. Louis Jose, Scott D. Baalrud; A generalized Boltzmann kinetic theory for strongly magnetized plasmas with application to friction. Physics of Plasmas 2020, 27, 112101. [CrossRef]
  20. Nagy, A. Shannon entropy density as a descriptor of Coulomb systems. Chemical Physics Letters 2013, 556, 355–358. [Google Scholar] [CrossRef]
  21. J. Yu, D. Jin and L. Zhang, Mobile paramagnetic nanoparticle-based vortex for targeted cargo delivery in fluid, 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 2017, pp. 6594-6599. [CrossRef]
  22. Matthew J. Webber, E. Thomas Pashuck, (Macro)molecular self-assembly for hydrogel drug delivery. Advanced Drug Delivery Reviews 2021, 172, 275–295. [CrossRef] [PubMed]
  23. M. Howard Lee, Fick’s Law, Green-Kubo Formula, and Heisenberg’s Equation of Motion, Phys. Rev. Lett. 85, 2422.
  24. S. Martens, G. Schmid, L. Schimansky-Geier, and P. Hänggi, Entropic particle transport: Higher-order corrections to the Fick-Jacobs diffusion equation. Phys. Rev. E 2011, 83, 051135. [CrossRef] [PubMed]
  25. N. Roxhed, B. Samel, L. Nordquist, P. Griss and G. Stemme, "Painless Drug Delivery Through Microneedle-Based Transdermal Patches Featuring Active Infusion," in IEEE Transactions on Biomedical Engineering, vol. 55, no. 3, pp. 1063-1071, March 2008. [CrossRef]
  26. McGinty, S. McKee, R. M. Wadsworth and C. McCormick, "Modelling drug-eluting stents," in Mathematical Medicine and Biology: A Journal of the IMA, vol. 28, no. 1, pp. 1-29, March 2011. [CrossRef]
  27. Y. Chahibi, M. Pierobon, S. O. Song and I. F. Akyildiz, "A Molecular Communication System Model for Particulate Drug Delivery Systems," in IEEE Transactions on Biomedical Engineering, vol. 60, no. 12, pp. 3468-3483, Dec. 2013. [CrossRef]
  28. Y. Chahibi, M. Pierobon and I. F. Akyildiz, "Pharmacokinetic Modeling and Biodistribution Estimation Through the Molecular Communication Paradigm," in IEEE Transactions on Biomedical Engineering, vol. 62, no. 10, pp. 2410-2420, Oct. 2015. 2015. [CrossRef]
  29. Available online: https://www.wolframalpha.com/.
  30. McDonald, P. C., Chafe, S. C., Brown, W. S., Saberi, S., Swayampakula, M., Venkateswaran, G., et al. (2019). Regulation of pH by carbonic anhydrase 9 mediates survival of pancreatic cancer cells with activated KRAS in response to hypoxia. Gastroenterology 157, 823–837. [CrossRef]
  31. Gao Q, Zhang J, Gao J, Zhang Z, Zhu H and Wang D (2021), Gold Nanoparticles in Cancer Theranostics, Front. Bioeng. Biotechnol. 9:647905. ibid M. Femminella, G. Reali and A. V. Vasilakos*, "A Molecular Communications Model for Drug Delivery," in IEEE Transactions on NanoBioscience, vol. 14, no. 8, pp. 935-945, Dec. 2015, doi: 10.1109/TNB.2015.2489565. [CrossRef]
  32. Muz B, de la Puente P, Azab F, Azab AK. The role of hypoxia in cancer progression, angiogenesis, metastasis, and resistance to therapy. Hypoxia (Auckl). 2015 Dec 11;3:83-92. [CrossRef] [PubMed]
  33. Yang Y, Zheng X, Chen L, Gong X, Yang H, Duan X, Zhu Y. Multifunctional Gold Nanoparticles in Cancer Diagnosis and Treatment. Int J Nanomedicine. 2022;17:2041-2067. [CrossRef]
  34. Bharti S, Kaur G, Jain S, Gupta S, Tripathi SK. Characteristics and mechanism associated with drug conjugated inorganic nanoparticles. J Drug Target. 2019;27(8):813–829. [CrossRef]
  35. Kim H, Nguyen VP, Manivasagan P, et al. Doxorubicin-fucoidan-gold nanoparticles composite for dual-chemo-photothermal treatment on eye tumors. Oncotarget. 2017;8(69):113719–113733. [CrossRef]
  36. Darweesh RS, Ayoub NM, Nazzal S. Gold nanoparticles and angiogenesis: molecular mechanisms and biomedical applications. Int J Nanomedicine. 2019 Sep 19;14:7643-7663. [CrossRef] [PubMed]
  37. Carmeliet P, Jain RK. Molecular mechanisms and clinical applications of angiogenesis. Nature. 2011;473(7347):298–307. [CrossRef]
  38. Gacche RN, Meshram RJ. Angiogenic factors as potential drug target: efficacy and limitations of anti-angiogenic therapy. Biochim Biophys Acta Rev Cancer. 2014;1846(1):161–179. [CrossRef]
  39. Yan L, Shen J, Wang J, Yang X, Dong S, Lu S. Nanoparticle-Based Drug Delivery System: A Patient-Friendly Chemotherapy for Oncology. Dose Response. 2020 Jul 10;18(3):1559325820936161. [CrossRef] [PubMed]
  40. Yang Z, Xie J, Zhu J, et al. Functional exosome-mimic for delivery of siRNA to cancer: in vitro and in vivo evaluation. J Control Release 2016, 243, 160–171. [CrossRef] [PubMed]
Preprints 82746 g001
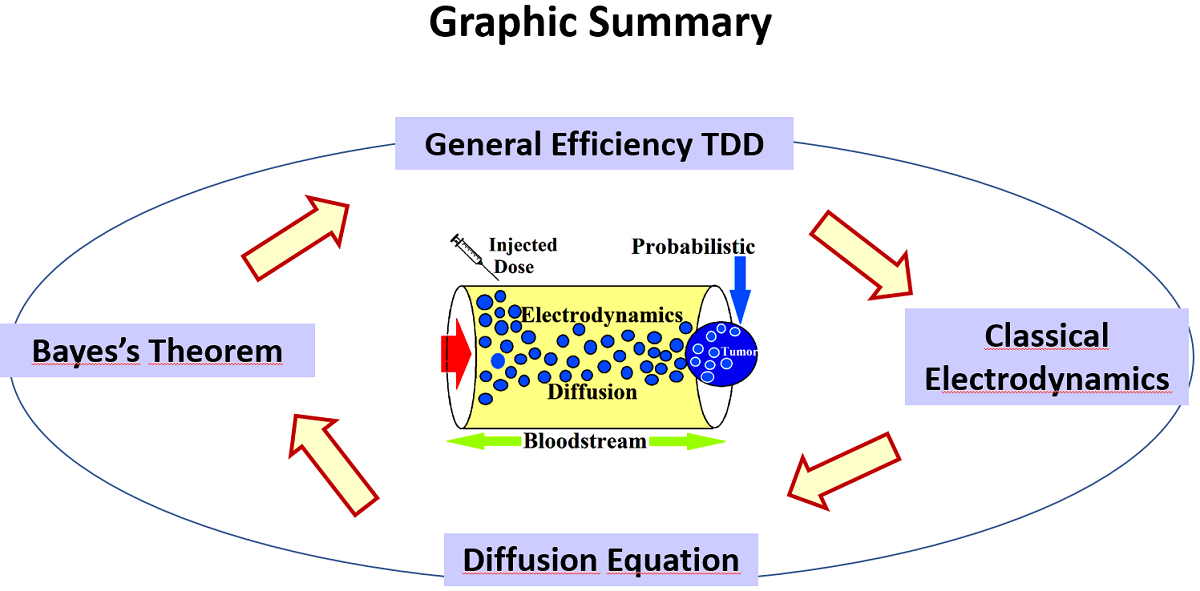
Figure 1. Sketch of a three-phases process: (a) injection, (b) diffusion, transit, (c) arrival and internalization, of nanoparticles into blood stream. It is hypothesized the hybrid view of paper by which the entire process would consist in electrodynamics and diffusion and globally dictated by probabilistic rules.
Figure 1. Sketch of a three-phases process: (a) injection, (b) diffusion, transit, (c) arrival and internalization, of nanoparticles into blood stream. It is hypothesized the hybrid view of paper by which the entire process would consist in electrodynamics and diffusion and globally dictated by probabilistic rules.
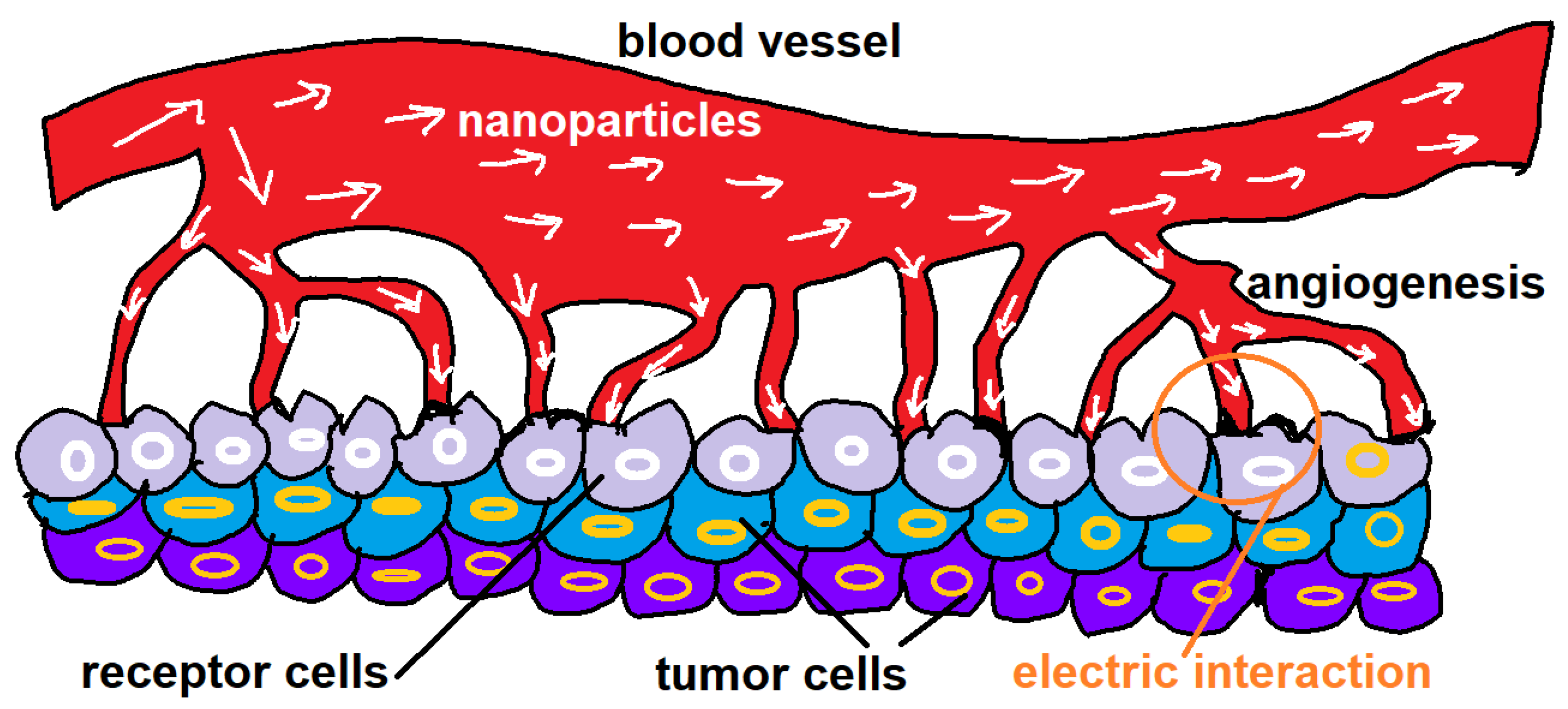
Preprints 82746 g001
Preprints 82746 g002
Figure 2. The theoretical efficiency of arrival up to for 3 different critical distances. While these distances are increasing, the efficiencies turns out to be reduced as a consequence of scattering of nanoparticles at the blood stream. Thus one observes a transition from Weibull (sc=3.5 and sc=4.0) to Gaussian distributions (sc=5.0).
Figure 2. The theoretical efficiency of arrival up to for 3 different critical distances. While these distances are increasing, the efficiencies turns out to be reduced as a consequence of scattering of nanoparticles at the blood stream. Thus one observes a transition from Weibull (sc=3.5 and sc=4.0) to Gaussian distributions (sc=5.0).
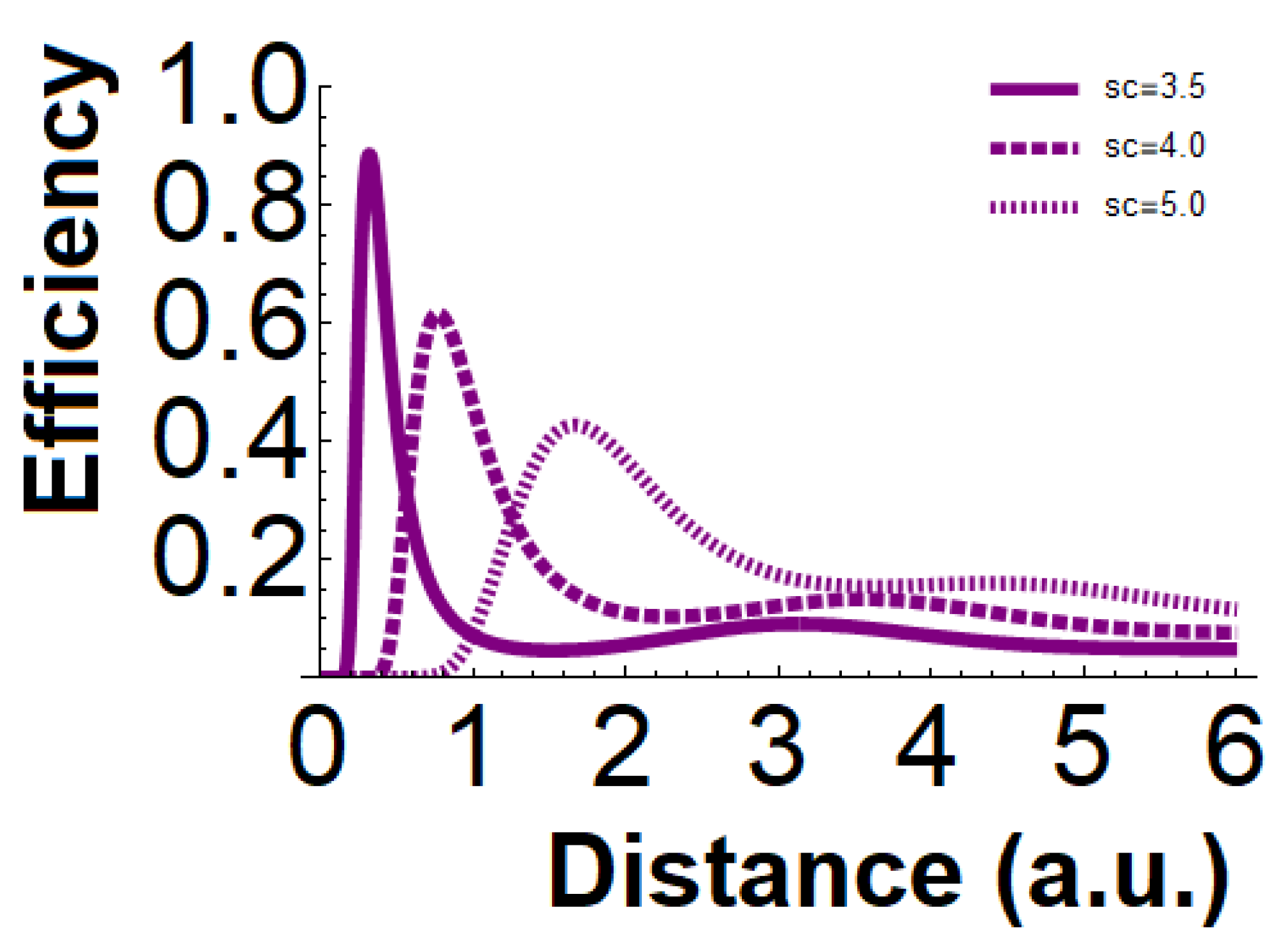
Preprints 82746 g002
Preprints 82746 g003
Figure 3. Contour plots of Eq.43 as function of argument v / D × s Left-side: the case when v = s / t ≈ 0 displaying the maximum efficiency of order of 12%. Right-side: the case with the approximation sin ( κ s ) is applied (see text below) displaying zones of a null efficiency due Coulomb effects at the injected nanoparticles. Arrows are indicating the transition of a null efficiency to one of order of 20%. Plots were done with package of Ref. [29].
Figure 3. Contour plots of Eq.43 as function of argument v / D × s Left-side: the case when v = s / t ≈ 0 displaying the maximum efficiency of order of 12%. Right-side: the case with the approximation sin ( κ s ) is applied (see text below) displaying zones of a null efficiency due Coulomb effects at the injected nanoparticles. Arrows are indicating the transition of a null efficiency to one of order of 20%. Plots were done with package of Ref. [29].
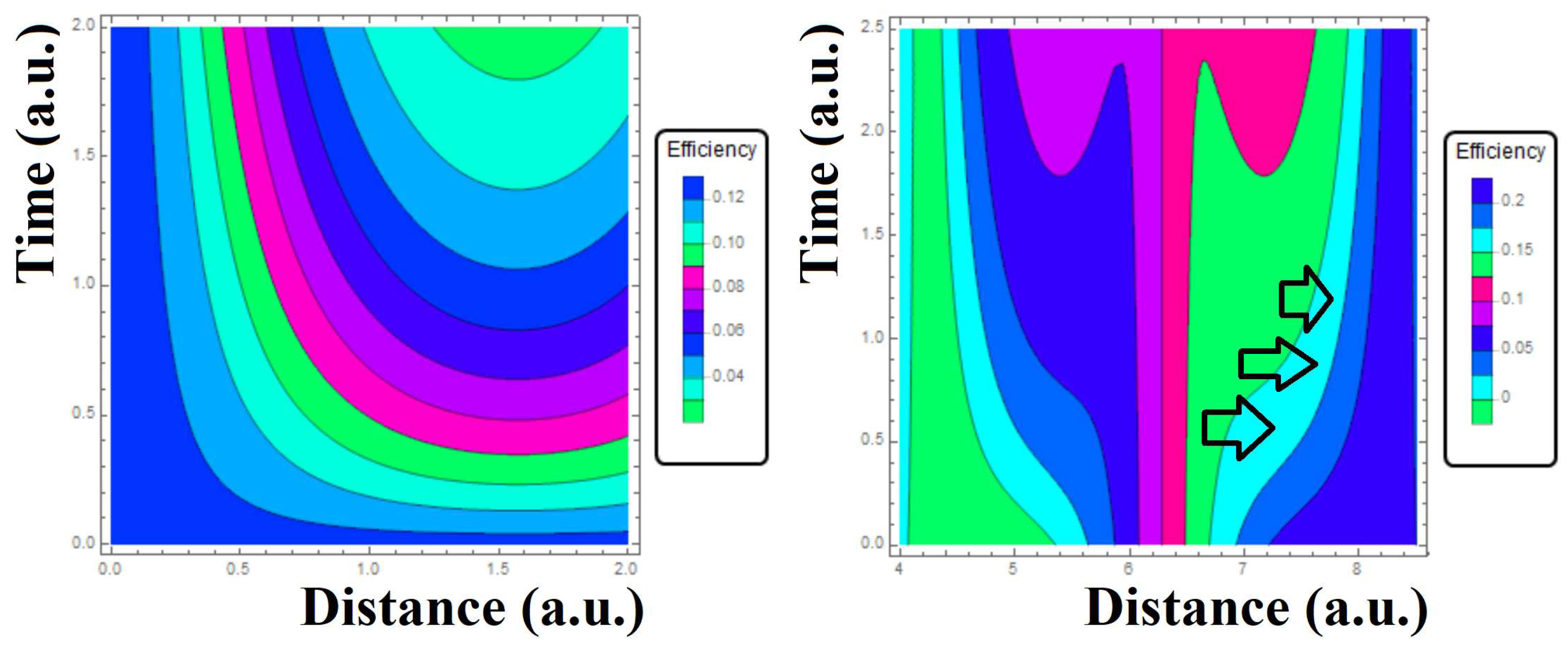
Preprints 82746 g003
Preprints 82746 g004
Figure 4. Sketch for the probabilistic interpretation of Eq.43 by which it is proposed the possible probabilistic behavior of nanoparticles arriving to target tumor. Here it is expressed the fact that exists the firm scenarios of rejection and internalization in conjunction to the ones inside the hypoxic region.
Figure 4. Sketch for the probabilistic interpretation of Eq.43 by which it is proposed the possible probabilistic behavior of nanoparticles arriving to target tumor. Here it is expressed the fact that exists the firm scenarios of rejection and internalization in conjunction to the ones inside the hypoxic region.
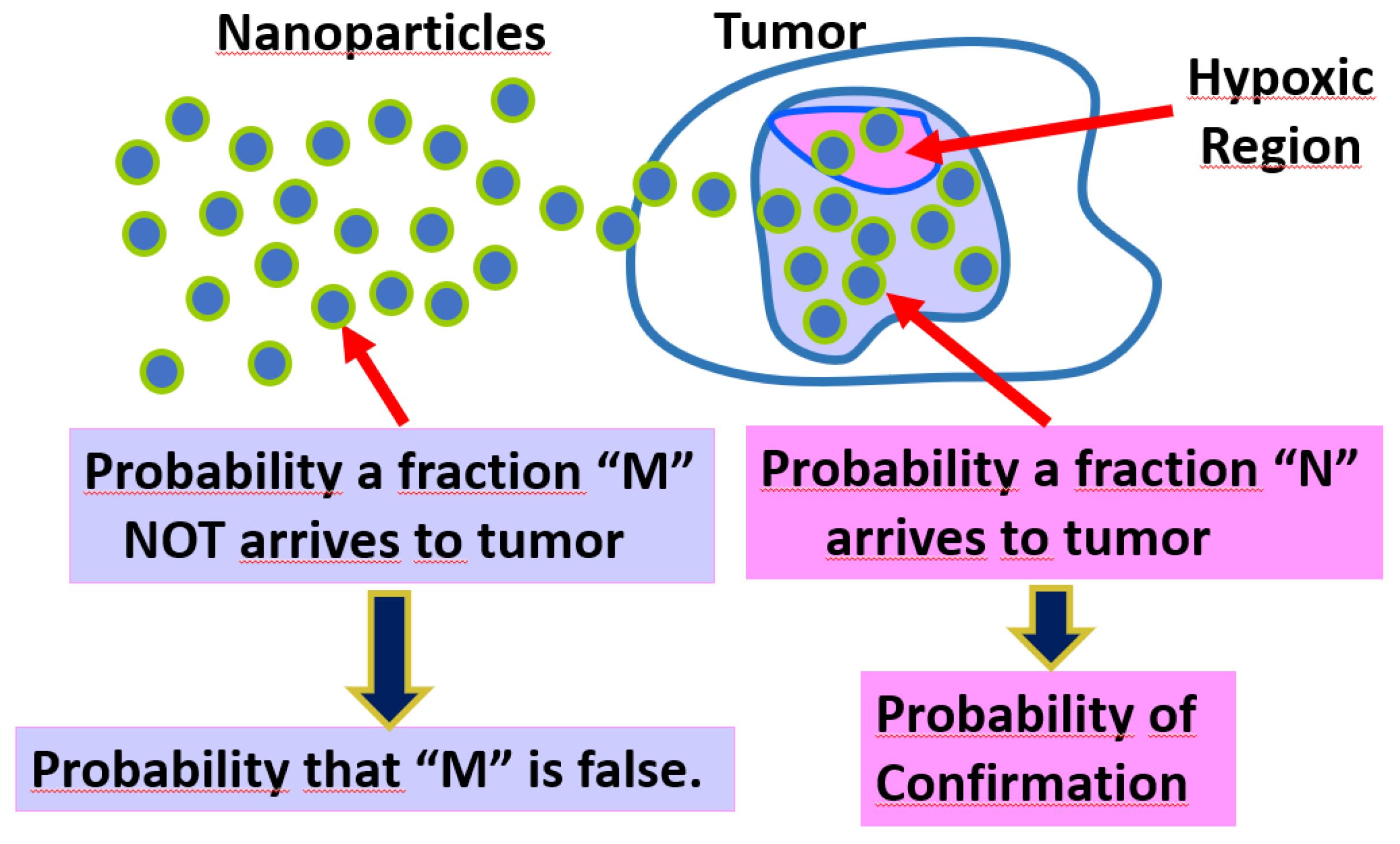
Preprints 82746 g004
Preprints 82746 g005
Figure 5. Contour plots of Eq.48 showing the apparition of nonlinearities despite the linear relation between time and space traveled by nanoparticles. Left-side: the case where the exponential was approximated to be sinusoidal sin(x). Here it is noted a linearity between the relation space-time (dashed line). Right-side: the case where it was opted by the sin 2 (x) expressing nonlinearity between space and time as consequence of electrical forces hypothetically due to either rejection or attraction. Plots were done with package of Ref. [29].
Figure 5. Contour plots of Eq.48 showing the apparition of nonlinearities despite the linear relation between time and space traveled by nanoparticles. Left-side: the case where the exponential was approximated to be sinusoidal sin(x). Here it is noted a linearity between the relation space-time (dashed line). Right-side: the case where it was opted by the sin 2 (x) expressing nonlinearity between space and time as consequence of electrical forces hypothetically due to either rejection or attraction. Plots were done with package of Ref. [29].
Preprints 82746 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated