Prerpints.org logo
Preprint
Article

Determination of Optimal Spatial Sample Sizes for Fitting Negative Binomial-Based Crash Prediction Models with Consideration of Statistical Modeling Assumptions

Altmetrics

Downloads

105

Views

53

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

17 August 2023

Posted:

21 August 2023

You are already at the latest version

Alerts
Abstract
Transportation authorities aim to boost road safety by identifying risky locations and applying suitable safety measures. The Highway Safety Manual (HSM) is a vital resource for US transportation professionals, aiding in the creation of Safety Performance Functions (SPFs), which are predictive models for crashes. These models rely on Negative Binomial distribution-based regression and misinterpreting them due to unmet statistical assumptions can lead to erroneous conclusions, including inaccurately assessing crash rates or missing high-risk sites. The Florida Department of Transportation (FDOT) has introduced context classifications to HSM SPFs, complicating assumption violation identification. This study, part of an FDOT-sponsored project, investigates established statistical diagnostic tests to identify model violations and proposes a novel approach to determine optimal spatial regions for Empirical Bayes adjustment. This adjustment aligns HSM-SPFs with regression assumptions. The study employs a case study involving Florida roads. Results indicate that a 20-mile radius offers an optimal spatial sample size for modeling crashes of all injury levels, ensuring accurate assumptions. For severe injury crashes, which are less frequent and harder to predict, a 60-mile radius is suggested to fulfill statistical modeling assumptions. This methodology guides FDOT practitioners in assessing the conformity of HSM-SPFs with intended assumptions and determining appropriate region sizes.
Keywords: 
Subject: Engineering  -   Safety, Risk, Reliability and Quality

1. Introduction

Predictive crash models are used extensively by local and state transportation officials to understand the effects of various roadway and traffic-based factors on the roadway crash rates, frequencies, and severities and to determine and assess the effectiveness of potential safety countermeasures. Lord et al conducted a study in 2005 that examined the performance of different regression models to predict crash frequency, whereas the current study intends to focus primarily on a particular type of predictive model used by Highway Safety Manual HSM [1]. HSM contains quantitative analytical tools, entitled, safety performance functions (SPFs), that predict average number of crashes per year at a roadway facilities (i.e., intersections and segments) by incorporating known information about a roadway entity into an equation [2]. The SPFs in the HSM have been developed through extensive research and statistical analysis of data collected across the United States roadways and are valuable to state and local transportation agencies for their ability to detect areas with safety concerns [3,4,5,6].
SPFs are log-linear regression models based on a Negative Binomial distribution to predict the frequency of crashes on roadway segments or intersections [7]. SPFs for segments are the subject of this study, and the basic form of the SPF equation consists of Annual Average Daily Traffic (AADT) and segment length as the regressors. Due to the noticeable spatial difference across the U.S. in terms of driving behavior, environmental characteristics, and roadway conditions, The American Association of State Highway and Transportation Official (AASHTO) recommends that the HSM SPFs require to be calibrated to better present regional conditions using multiplication Crash Modification Factors (CMFs) and Calibration Factors (CFs) [2]. Some states in US calibrated the prediction models in Part C of the HSM using their own data, including crash frequency and traffic and geometric features of the roadway. Some other jurisdictional agencies would like to develop their own SPFs instead of calibrating the existing ones from elsewhere to represent crash characteristics better [8,9,10]. In order to avoid additional costs and efforts for developing local SPFs, Srinivasan et al. in 2016, proposed a methodology to develop calibration function in case individual calibration factors were unable to provide a proper estimation for actual local crash data [11]. Subsequently, Farid et al. confirmed the proficiency of an innovative approach for developing calibration functions by employing K-Nearest Neighbor (KNN) regression [12].
While a considerable number of studies have focused on developing calibration methods to improve the effectiveness of SPFs, limited effort has been devoted to investigating the statistical reasons behind inaccurate crash frequency predictions that may also cause wrong interpretation of safety countermeasures in terms of their effectiveness to potential decrease in crash frequency. There may be instances where certain crash prediction statistical model assumptions may not be met in practice depending on the observed data; while, this does may not invalidate the analysis results, it is crucial that the practitioner is aware of the limitations [13]. To diagnose common modeling violations that may occur when using Negative Binomial-based SPFs with geocoded crash data, this paper examines several well-known statistical tests. It presents a new approach to determining the optimal spatial regional size (that determines how many segments are contained within the historical data) for implementing Empirical Bayes adjustments for SPF crash prediction, in order to satisfy the regression assumptions of the model. The issues with model form adequacy (linearity), overdispersion, and undercounting of zeros in modeling crash data with SPF models are studied and explicit diagnostic tests are developed. The methodology would be helpful for the transportation practitioners to understand whether the intended modeling assumptions of the HSM SPF equations are satisfied with the crash data observed in the field.
To demonstrate the methodology, a case study that focused on modeling roadway segment crashes in the FDOT District 4 (including Broward, Indian River, Martin, Palm Beach, and St. Lucie counties) was presented. Multivehicle non-driveway crashes from years 2015, 2016, 2017 and 2018 occurring on divided two-way 4-lane urban and suburban arterial segments (U4D) of the study region are studied. SPFs crash models are estimated and assessed using generalized linear models. Throughout the following sections, we will discuss past calibration studies of SPFs, potential statistical violations in crash models, data we used for our research, methodology, results, and conclusions.

2. Literature Review

The application of the HSM SPFs have been confirmed for predicting crash counts by roadway facility classification, crash severity, and crash type. However, their overall efficiency in various regions comparing to the ones similar to the base conditions is still under debate. To aid inter-jurisdictional transferability, recent studies have investigated the possibility of developing new SPF calibration methods instead of redeveloping SPFs [8]. For instance, Srinivasan and Carter conducted an extensive research to calibrate the SPFs suggested by HSM for North Carolina for 9 crash types that occurred on 16 roadway types [5]. They also proposed a method to re-develop or re-calibrate SPFs in the future due to the expected changes in vehicle technology, engineering treatments, reporting practices, etc. In another research project, Sun et al., calibrated the HSM functions for local conditions in Missouri due to the significant variation in gathering required data in this across the state [14]. A highway safety management tool, named Safety Analyst™, was adopted by Kweon and Lim using SPFs developed and calibrated for multilane highway and freeway segments in Virginia [15]. Moreover, SPFs provided in HSM have been regionalized by Donnell et al., for: (1) rural two-lane highways segments and intersections; (2) rural multilane highway segments and intersections; and (3) Urban and suburban arterial (non-freeway) segments and intersections in Pennsylvania [16]. Thanks to the sufficient number of available data associated with segments and intersections, they could calibrate the SPFs at the county, planning organization (metropolitan and rural), and engineering district levels [16]. Khattak et al., [17] and Al-Deek et al., [18] also developed their own calibrated functions to forecast the expected crash frequency for various roadway facility types, for Tennessee and Florida, respectively.
Crash modification factors (CMFs) are applied to account for the effects of site-specific geometric design (lane width, shoulder width, horizontal curves, etc.) and traffic control features (automated speed enforcement) and estimate crash frequencies for facilities which have design variations from the base conditions which SPFs were developed [19]. SPFs were developed for roadway facilities using base conditions for number of lanes, lane widths, median widths, lighting conditions, etc. The SPFs should be adjusted accordingly when a roadway facility has a design that differs from the base conditions. The CMF for each geometric design or traffic control feature based on the SPF base condition is one, whereas features associated with higher crash frequencies than the base condition have CMFs that are greater than one, and features associated with lower crash frequencies than the base condition have CMFs that are less than one. Despite extensive efforts to develop and calibrate SPFs in HSM, some over/under prediction were observed in states with significant differences in gathering required data, instruction for completion of crash reports by officers, etc. For example, Brimley et al., investigated the prediction ability of the models and identified that the SPFs in HSM typically under predicted the crash counts for rural two-lane two-way roadway segments based on their study in Utah [20]. Moreover, Gross et al. proposed a guideline in developing CMFs based on the available data and discussed the process for selecting an appropriate evaluation methodology [21].
In addition to the aforementioned CMFs, a multiplicative calibration factor (CF) has been defined by HSM to improve SPF crash predictions by maintaining the original form of the model and the relation between independent variables and crashes. The HSM recommends that agencies used an unbiased sample of 30 to 50 sites to determine the jurisdiction calibration factor (CF) [2]. Srinivasan et al. provides a comprehensive step-by-step guideline to develop SPFs and CFs [22]. Some jurisdictions may have substantial variations in conditions within the jurisdiction (e.g., snowy winter driving, variations in driving population, etc.). Hence, any SPF calibration must consider these localized variations. The purpose of the calibration factors is to modify the predicted average crash frequency from the default manual predictions to local conditions (i.e. Florida conditions) accounting for regional characteristics such as climate, driver populations, animal populations, crash reporting thresholds, and crash reporting system procedures [2].
Aside from the application of the CMFs and CFs to the base SPF equation, which enables practitioners to predict the number of crashes at sites with similar characteristics, HSM recommends that an Empirical Bayes (EB) adjustment be applied as a result of the recognition that the safety of a particular site can be more accurately assessed by taking into account the historical number of crashes previously observed at that location. This procedure enables us to avoid regression-to-the-mean effects caused by the natural tendency to select for treatment the sites with high observed crash frequency. The EB method has been applied to HSMs’ SPFs for many years and attracted even more attention in literature [20]. As part of our study, we also reviewed the Empirical Bayes method for dealing with overdispersed counts in crash prediction which included Hauer et al [23], Hauer et al [24], Lord and Mannering [25]. More recently, Farid et al. proposed the Modified Empirical Bayes (MEB) method to develop segment-specific calibration factors for calibrating SPF [26]. The results indicated that the MEB method outperformed the calibration factor [26]; however, MEB’s practicality remains limited, since it requires sufficient observed crash data to provide a reliable prediction. Furthermore, Persaud et al., (2010) proposed a Fully Bayesian (FB) for before-after treatment evaluations for situations where it is difficult to acquire large sufficient reference observations to calibrate existing SPFs required for the traditional EB approach by enhancing more flexibility in utilizing crash frequency distributions [27]. While their approach enables traffic safety analysts to better account for uncertainty in the sample data than the EB approach, it was identified as a complex alternative [27].
In the current approach to the EB adjustment of SPFs, the study region from which the data are collected is assumed to be known, which is typically an entire state or a district. Das et al. developed new rules-based SPFs for low-volume rural local roadways on the basis of segment length and AADT as the most contributing factors and proposed a method to improve the model accuracy in terms of R-Square and cumulative residual (CURE) plot [28]. However, choosing the study region too large or too small can cause issues with the validity of the HSM-specified model form (goodness of fit) or the overdispersion parameter. Several authors have studied the effects of sample size with respect to goodness of fit [29] and overdispersion assumption [30], however, a systematic approach to determine a spatial sample size approach for specific SPF model has not been studied. To address this gap, this research effort proposes a new method to determine the optimal spatial sample size in applying EB adjustment for SPF crash prediction analyses.

3. Study Area and Data Sources

The application of the diagnostic tests and the proposed spatial sample selection method is illustrated on crash data collected from, Florida Department of Transportation (FDOT) District 4 (including Broward, Indian River, Martin, Palm Beach, and St. Lucie counties). The current study intends to explore crashes involving multiple vehicles that occurred away from all types of intersection and were not under their influences. Accordingly, the proposed method filtered out the crash data using the attributes that represent the number of vehicles involved in the crash, and remove crashes involving a single vehicle, pedestrians and bicycles, and intersections. The required crash dataset for the study area is acquired and assembled according to the following steps: (1) Filtering out intersection-related crashes and excluding them from the data set on the basis of a crash-related attribute that represents crashes that occurred at an intersection, influenced by an intersection, in a driveway access, and at a railroad crossing; (2) Creating a 250 ft. buffer around the center of signalized intersections and removing crashes completely located within the buffer areas. A buffer of 250 feet around the center of an intersection is set as the default size for the intersection’s influence zone, according to the HSM [2]; (3) Extracting of multivehicle non-driveway related and not pedestrian/bicyclist-related crash types occurring on the divided two-way 4-lane urban and suburban arterial segments (U4D); (4) Utilizing AADT line feature shapefile for segmentation and assigning crash count to 50-feet buffer areas along the divided two-way 4-lane urban and suburban arterial segments.
SPFs for two separate crash severities were calibrated for the final crash data set: (1) All crash types occurring on the U4D arterial segments, and (2) Fatal-and-Injury crash types occurring on the U4D arterial segments. Fatal-and-Injury (FI) crashes involve all levels of injury severity i.e., fatalities (K), incapacitating injuries (A), non-incapacitating injuries (B), and possible injuries (C). A crash count can be determined by implementing the EB-based method on appropriate SPF data by counting the crash points and assigning them to the associated U4D arterial segments. Multivehicle non-driveway crashes from years 2015, 2016, 2017, and 2018 are obtained from crash reports maintained by the Florida Department of Highway Safety and Motor Vehicles (FLHSMV). Crash data comprises points scattered along the roadway network, each representing a vehicle crash and mapped to the GIS shapefile using longitude and latitude coordinates. Table 1 summarizes the crash data categorized with respect to their associated KABCO scale that occurred in Florida District 4 during the study period. Furthermore, Figure 1 illustrates how the aforementioned crashes are distributed throughout the study area.
To follow the objectives of the research, the HSM SPFs, constructed for multiple-vehicle non-driveway crashes for U4D arterial segments, were examined to conduct a diagnostic test. The aforementioned SPFs formulate the predicted crash frequency based on several traffic and roadway geometric factors, including Average Annual Daily Traffic (AADT), segment length in mile, number of lane, etc. The traffic and geometric features are usually provided by the responsible branches of departments of transportation in the format of shapefiles or as-built drawings of roadway geometrics. The current research validates the SPFs using data from following databases: (1) historical AADT volume measurements for state roadways through the FDOT Telemetered Traffic Monitoring Sites (TTMS) databases maintained by Transportation Data and Analytics (TDA) office and (2) the FDOT Geographic Information System (GIS) system for roadway variables (e.g., speed limit, number of lanes, intersect angle) [31]. For the District 4 study area, we utilized the AADT shapefile for segmentation, which are calculated based on the average AADTs during the study period, i.e., 2015 to 2018. According to this segmentation criteria, District 4 has 1,067 roadway segments. Based on the methodology described in the following section, the size of the geographical sub-region to be used in SPF modeling is identified.

4. Methodology

The Highway Safety Manual (HSM) provides a procedure in which 18 steps can be followed to estimate the expected average crash frequency using SPF crash prediction models [2]. The main objective of this study was to develop diagnostic tests for identifying modeling violations that may be encountered in using the Negative Binomial-based HSM SPFs in crash count modeling. As such, we intend to propose a methodology to determine the optimal size of the crash data set according to the associated level of injury in order to ensure that the modeling assumptions for SPF crash prediction are reasonably accurate when implementing the Empirical Bayes (EB) method. Figure 2 provides a schematic overview of the steps of creating a data set and applying the SPF for crash prediction within the proposed methodology for the case study of multivehicle non-driveway crashes occurring along U4D arterial segments.
Accordingly, a subset of crash data including multiple-vehicle crashes that were not affected by intersections and driveways was prepared. To simplify the estimation and avoid applying Crash Modification Factors (CMF) associated with base conditions, SPFs are constructed for multiple-vehicle non-driveway crashes for divided two-way (2 lanes in each directions) 4-lane urban and suburban arterial segments in the study regions under the base condition (i.e., absence of automated speed enforcement, prohibited on-street parking, no lighting, no roadside fixed object density). According to HSM’s definition, U4D segments have four lanes with continuous cross-sectional areas of two lanes in each direction of travel, where the lanes are physically separated by distance or barrier [2]. The FDOT GIS database provides a shapefile containing a spatial attribute representing the number of lanes [31]. HSM recommends the following Negative Binomial regression model for predicting multiple-vehicle non-driveway crashes:
N S P F = e x p [ β 0 + β 1 l n ( A A D T ) + l n ( L ) ]
where AADT is the annual average daily traffic, L is the segment length (miles), β 0 , and β 1 are the regression coefficients. HSM develops the regression coefficients for various crash types in terms of the highest level of injury [2]. Hence, we categorize the crash data based on the KABCO scale and utilize the appropriate regression coefficients recommended by HSM to predict crash frequency. Table 2 presents the values of the coefficients β 0 , and β 1 reported in HSM to be used in applying Equation (1) for U4D segments.
In order to enhance the accuracy of SPFs’ prediction results, a calibration is performed by applying a multiplicative Calibration Factor (CF), therefore its aggregate crash prediction within a whole jurisdiction is equal to the aggregate number of observed crashes. Accordingly, the observed crash data that occurred in the study area between 2015 and 2018 is counted by creating a buffer of 50-feet wide along the homogenous roadway segments and counting the crashes that are located within the buffer and assigning them to the segments. Calibrating the model preserves the original model form and modifies the predicted average crash frequency from the default manual predictions to account for local characteristics (i.e., Florida). According to the FDOT’s recommendations, the CF for an urban four-lane divided roadway (U4D) is equal to 1.63 [32].
Since our data have accurate locations of the observed crashes, the Site-Specific EB Method is applicable. Therefore, Equation (2) has been also adopted to apply the empirical Bayes method on the basis of the recognition that the safety of a site is best estimated by considering both the number of observed crashes at the site and the number of crashes at sites with similar characteristics, as predicted by the SPF. For District 4, the average crash frequency is predicted based on the crashes that occurred between 2015 and 2017 and validated using the observed crashes in 2018.
N E x p e c t e d = w × N S P F + ( 1.00 − w ) × N O b s e r v e d
where w is a weight factor defined as a function of the SPFs overdispersion parameter (see Table 2), k, to combine the two estimates:
w = 1 1 + k ∑ i ∈ A l l S t u d y A r e a Y e a r s N P r e d i c t e d , i
To test the adequacy of the SPF model, we fit a Negative Binomial (NB) regression model to the data using the functional form and the variables specified in the SPF for each crash severity and assess the adequacy of the model using statistical diagnostic tests. In particular, we employ three model adequacy tests: A test for linearity (adequacy of the functional form) of the NB model, a test for the closeness of the estimated overdispersion parameter to the HSM value and a test for excess zeros in the NB model. For linearity, we employ a chi-square goodness of fit (GOF) test, which asks whether the assumed linear model functional form is adequate. Assuming that the model is valid, the deviance of the NB model is distributed with a chi-square distribution of degree of freedom equal to n-p. For a NB regression [33], deviance is calculated using Equation (4) the test rejects the hypothesis that the model functional form is adequate if the p-value of the test, found using Equation (5) is below some level of significance (typically 0.05).
D = 2 ∑ i = 1 n [ y i l o g ( y i μ i ^ ) − y i μ i ^ ]
p G O F = P ( χ n − p 2 > D )
Therefore, for a given geographical region, if p G O F is close to one, the functional form of the HSM-specified NB model is adequate. The second test checks whether the overdispersion parameter estimated from the data agrees well with the overdispersion values provided by HSM published for a given facility (roadway segment or intersection) and crash type (See Table 2). The overdispersion parameter is estimated based on Equation (6):
k ^ = 1 n − p ∑ i = 1 n ( y i − μ i ^ ) 2 μ i ^
where n is the number of years of data used to fit the model and p is the number of explanatory variables in the SPF, y i and μ i ^ are observed crash counts and crash counts predicted by SPF, respectively. For the HSM specified NB model to be adequate in terms of overdispersion parameter we want k ^ to be close to k H S M , the HSM published overdispersion parameters for a given facility (See Table 2). The third test, determines whether there is a larger number of zeros or small counts in the crash data than what the NB regression model can represent. If the data set contains a large number of zeros, the zero-inflation problem, the predictive capability of the NB regression model can be adversely impacted. The likelihood ratio test compares the fit of a zero inflated NB regression model (which contains a hurdle part) to a NB regression for the given data [33]. The two parts of the zero inflated model, the hurdle (the zero) model and the count (the nonzero) model, can have different sets of explanatory variables. The likelihood ratio test based on Equation (7) determines whether a hurdle part, that models only the zeros using a binary logit, is needed in the NB regression model.
L L R = 2 ( l n L 1 − l n L 2 )
L 1 is the maximized likelihood of a zero inflated NB regression model (model 1), that includes the hurdle part, and L 2 is the maximized likelihood of the NB regression model (model 2) that does not include the hurdle part. Since the two models are hierarchical (model 1 contains model 2) the likelihood ratio test statistic will follow a χ 2 distribution with degrees of freedom equal to the difference in number of parameters p 1 − p 2 if both models 1 and 2 fit equally well (i.e., the hurdle part does not improve the fit of the model). If the p-value of the likelihood ratio test, defined as Equation (8) is significant (e.g., smaller than 0.05) then we conclude that there are excess zeros or small counts in the data and a zero inflated NB should instead be used to model the crash data.
p Z I = P ( χ p 1 − p 2 2 ) > L L R
Utilizing the statistical diagnostic tests, this paper proposes a new spatial scan method in order to determine the best region size to use in estimating an EB adjusted SPF model. The method considers a sequence of overlapping circular subregions and uses all the historical crash counts observed for the segments within the segment to fit an SPF model. For a circular subregion radius, a subregion i is constructed by pooling in all crash data for 3 years (2015-2017), the AADT and length data for the i t h segment and all segments contained within a subregion with a radius of R miles. A Negative Binomial model (both ordinary and zero-inflated) of the form given in Equation (1) is fitted to the data and the linearity test p-value p G O F , i is computed with Equation (5) and the overdispersion parameter k ^ i is computed with Equation (6). The scanning is repeated for n overlapping circular subregions in the study region and the metrics are computed for i = 1 , 2 , … , n . To combine the metrics obtained from all n subregions in the entire study region with a single number, the following summary metrics are defined.
S o v e r d i s p = 1 n ∑ i = 1 n ( k ^ i k H S M − 1 ) 2
S n o n l i n e a r = 1 n ∑ i = 1 n ( p G O F , i − 1 ) 2
S o v e r a l l = S o v e r d i s p + S n o n l i n e a r
S o v e r d i s p combines the deviations of the estimated overdispersion parameters k ^ i using subregions of radius of R miles from the ideal HSM overdispersion parameter k H S M . S n o n l i n e a r combines the deviations goodness of fit p-value p G O F , i using subregions of radius of R miles from the ideal value of 1, which implies the linear SPF model form is a perfect fit. The analysis is repeated and S o v e r a l l is calculated for increasing R values. The goal of the spatial scan analysis is to identify a good subregion size that satisfies the statistical modeling assumptions and identify the subregions within the study region that cannot be adequately represented using a NB regression model. Therefore, a large value of the combined metric S o v e r a l l indicates that the subregion radius R used in modeling could be revised (to a smaller or larger value) so that so that the modeling assumptions are better satisfied. The empirical results from the study area reveal that the subregion radius R has small impact on the zero-inflation test results. Therefore, in this method, a summary metric for the zero-inflation test is not included.

5. Results and Discussions

In this section, we present the diagnostic results of the SPFs with data extracted from Florida roadways. Note that the objective of the diagnostic tests is to determine whether the N S P F functional form that was shown by Equation (1) earlier represents the observed crash data well. To compute the diagnostic test statistics, the coefficients are estimated from observed crash data, using the generalized linear modeling suite in the R statistical computing language. The estimated coefficients may therefore be different from values given in HSM (see Table 2) depending on the observed crash counts. In addition, the overdispersion parameter estimated from data using Equation (6) is compared to the HSM value (k=1.32) provided in Table 2.
Negative Binomial regression models are fitted to crash count, AADT and segment length data for 2015, 2016, and 2017 in this subregion. According to the fitted models for a sample segment, the residual diagnostic tests results are found as shown in Table 3. The results indicate that the linearity of the NB model with a 10-mile radius is better than the NB model with a 15 miles radius (p-value of 10-mile radius model is larger than 15 mile radius model). The Likelihood Ratio Test (LRT) for the zero inflated NB model with a 10-mile radius is also better than the NB model with a 15 miles radius (p-value of 10-mile radius model is larger than 15-mile radius model). The estimated overdispersion parameter of the 15-mile radius model is closer to the HSM overdispersion parameter than the 10-mile radius model.
From this single case, it appears that a smaller subregion is better in terms of the functional form accuracy and the excess zeros; however, larger subregion is better in terms of the overdispersion parameter estimation. To extend the analysis performed on a single roadway segment, the model fitting and diagnostic testing steps are repeated for all roadway segments within the study region considering the roadway network distance between the centroid of the adjacent segments. A spatial scan of all roadway segments in the study region is conducted and the diagnostic metrics are computed from overlapping circular subregions centered at the roadway segments. The scanning analysis is conducted for each of the 1,068 roadway segments in the study area and all crash counts. Each summary metric, defined as Equation (9) to Equation (11), combines the deviations of the subregion models from an ideal model and to have a good overall performance the value of the summary metric would be close to zero. Figure 3 illustrates segments within the study area that violate the diagnostic criteria based on the test statistics considering a variety of values for the radius. For nonlinearity in negative binomial regression (Figure 3-a), the segments for which p G O F , i < 0.015 are highlighted. For low overdispersion (Figure 3-b), the segments for which k ^ i < 0.55 k H S M are highlighted (i.e., 55% of the HSM value is considered to be a cut-off value). For zero-inflation (Figure 3-c) the segments for which p Z I , i < 0.05 are highlighted. It is worth mentioning that for a radius less than 20 mile zero inflated models are not estimable and for these radius values the maps for the zero-inflation test p-values are not shown.
The aforementioned results indicate that the number of segments violating the assumptions changes depending on the subregion radius. Edges of the region appear to have some effect on the diagnostic metric values. A very large radius makes the linear model unable to capture the variation in the crash counts and nonlinearity becomes an issue. Too small region results in inaccuracies with the overdispersion representation. Increasing the radius generally helps overdispersion but negatively affects linearity. The subregions with overdispersion issues usually are less bad when we use a larger radius. That is, a region identified as less overdispersed than the HSM value may not be such if we used a larger radius. When using a smaller neighborhood radius, the subregions with nonlinearity issues tend to be less problematic. This means that a region defined as nonlinear may not actually be so if a smaller radius was used. As the radius increases, the zero-inflation issue remains unchanged.
The same procedure has been followed for KABC crashes and the obtained results indicate that the zero inflation problem is more prominent than was observed with all crashes since the KABC crashes occur less frequently (See Table 1). However, the linearity in model parameters and overdispersion assumptions are more closely satisfied. Moreover, the summary measures (Equation (9) to Equation (11)) are computed for a wide range of radius values and shown in Figure 4. The overall summary measures are computed for 7, 10, 13, 16, 20, and 25-mile radius and plotted in Figure 4-a. The results indicate that concerning all crash data, the 20-mile radius provides the best tradeoff between nonlinearity and overdispersion (See Figure 4-a). Note that because the summary metrics are defined as averages of the model result from all segments in the study area, the recommended 20-mile radius is a good enough subregion size to analyze any roadway segment regardless of its location within District 4. Our recommendation is to use HSM-recommended SPF with a 20-mile radius for all segments except for the segments shown in purple in Figure 3-c, for which a zero-inflated NB regression is recommended. While, for the KABC crashes, Figure 4-b illustrates that the overall summary metrics continue to decrease with increasing subregion radius; however, the decrease in the reduction tapers off around a 60-mile radius. Therefore, for modeling KABC crashes, at least a 60-mile radius region is recommended to satisfy the assumptions of the SPF model. Summary measures are computed for 20, 30, 40, 50, 60, and 80-mile radius are shown in Figure 4-b.

6. Conclusions and Future Work

This paper intended to develop an innovative diagnostic test to determine how and to what extent crash data could probably violate the statistical assumptions associated with nonlinearity in negative binomial regression, overdispersion, and zero-inflation. Based on the methodology developed in this research, the size of the geographical subregion to be used in SPF modeling is identified. We concluded that if the interest is in SPF prediction of any type of crash, crash data for 3 years from all roadway segments in a 20-mile radius around the roadway segment that is under study should be used to implement the EB method. By contrast, if the interest is on predicting severe injury crashes (KABC), which is a rarer event, data should be gathered from a larger region which should have at least 60-mile radius. Knowledge gained from this study can help practitioners to decide on taking a corrective action to satisfy the assumptions. If the linearity in model parameters assumption is in question, different algebraic transformations of AADT and/or length, such as square-root or reciprocal, may be tried instead of logarithmic transformations. If the overdispersion parameter is in question, then the overdispersion parameter estimated from the data, instead of the HSM recommendation, may be used. If the excess zeros is in question than a zero-inflated NB regression may be used. In practice, some of the modeling assumptions would not be met depending on the observed data; however, this does not invalidate the analysis results as long as the practitioner is aware of the limitations. Some of the assumptions would have small impacts while others would be more detrimental on crash modeling. While the proposed radiuses of 20 and 60 ensure that the statistical assumptions associated with HSM-SPFs are met, the relatively large region probably contributes to the unexplained heterogeneity within the specified region in terms of its special, geometric, and traffic characteristics. In order to resolve this issue, the FDOT developed and implemented a classification method that categorizes roadway segments based on the existing land use and development pattern into eight main categories, that is, C1-Natural, C2-Rural, C2T-Rural Town, C3R-Suburban Residential, C3C-Suburban Commercial, C4-Urban General, C5-Urban Center, and C6-Urban Core [18,34,35]. Therefore, the results obtained by this research enable us to conduct a stratified analysis by the context classification system implemented by the FDOT which categorizes roadway network facilities. Moreover, the proposed method for determining an appropriate sample size could be integrated with machine learning-based validation methods to enhance the accuracy and consistency of predictive tools for network screening [36].

Author Contributions

The authors confirm contribution to the paper as follows:“Conceptualization, M.K., O.A.V., E.E.O., R.M., R.G., and B.J.; methodology, M.K., S.R.A., O.A.V., E.E.O., R.M., R.G., and B.J.; software, M.K. and O.A.V.; validation, M.K., S.R.A., O.A.V., E.E.O., and R.M.; formal analysis, M.K. and O.A.V.; investigation, M.K., O.A.V., E.E.O., and R.M.; resources, O.A.V., R.G., and B.J.; data creation, M.K.; writing—original draft preparation, M.K., O.A.V., E.E.O., and R.M.; writing—review and editing, M.K., O.A.V., E.E.O., and R.M.; visualization, M.K.; supervision, O.A.V., E.E.O., R.M., R.G., and B.J.; project administration, O.A.V.; funding acquisition, O.A.V.. All authors have read and agreed to the published version of the manuscript.”

Funding

This study was sponsored by the State of Florida Department of Transportation (FDOT) grant BDV30-945-001. The opinions, findings, and conclusions expressed in this paper are those of the authors and not necessarily those of the State of Florida Department of Transportation.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The necessary crash data were acquired from the FDOT Safety Office through the Department of Highway Safety and Motor Vehicles (DHSMV) Crash Analysis Reporting (CAR) system. Access to this source is limited to authorized users, including FDOT staff, consultants, governmental agencies, and universities, pending approval by FDOT. As this paper is affiliated with the FDOT project (grant BDV30-945-001), the authors possess access to the database.

Conflicts of Interest

The authors declare that they have no competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Lord, D.; Washington, S.P.; Ivan, J.N. Poisson, Poisson-gamma and zero-inflated regression models of motor vehicle crashes: Balancing statistical fit and theory. Accident Analysis & Prevention 2005, 37, 35–46. [Google Scholar] [CrossRef]
  2. AASHTO. Highway Safety Manual; 2010. [Google Scholar]
  3. Abdel-Aty, M.A.; Lee, C.; Park, J.; Wang, J.H.; Abuzwidah, M.; Al-Arifi, S. Validation and application of highway safety manual (part D) in Florida; Technical report; 2014. [Google Scholar]
  4. Alluri, P.; Saha, D.; Liu, K.; Gan, A. Improved processes for meeting the data requirements for implementing the Highway Safety Manual (HSM) and Safety Analyst in Florida; Technical report; 2014. [Google Scholar]
  5. Srinivasan, R.; Carter, D. Development of Safety Performance Functions for North Carolina; 2011; p. 88. [Google Scholar]
  6. Wang, J.H.; Abdel-Aty, M.; Lee, J. Examination of the Transferability of Safety Performance Functions for Developing Crash Modification Factors: Using the Empirical Bayes Method. Transportation Research Record: Journal of the Transportation Research Board 2016, 2583, 73–80. [Google Scholar] [CrossRef]
  7. Poch, M.; Mannering, F. Negative Binomial Analysis of Intersection-Accident Frequencies. Journal of Transportation Engineering 1996, 122, 105–113. [Google Scholar] [CrossRef]
  8. Lu, J.; Haleem, K.; Alluri, P.; Gan, A.; Liu, K. Developing local safety performance functions versus calculating calibration factors for SafetyAnalyst applications: A Florida case study. Safety Science 2014, 65, 93–105. [Google Scholar] [CrossRef]
  9. Ulak, M.B.; Ozguven, E.E.; Karabag, H.H.; Ghorbanzadeh, M.; Moses, R.; Dulebenets, M. Development of Safety Performance Functions for Restricted Crossing U-Turn Intersections. Journal of Transportation Engineering, Part A: Systems 2020, 146. [Google Scholar] [CrossRef]
  10. Young, J.; Park, P.Y. Benefits of small municipalities using jurisdiction-specific safety performance functions rather than the Highway Safety Manual’s calibrated or uncalibrated safety performance functions. Canadian Journal of Civil Engineering 2013, 40, 517–527. [Google Scholar] [CrossRef]
  11. Srinivasan, R.; Colety, M.; Bahar, G.; Crowther, B.; Farmen, M. Estimation of Calibration Functions for Predicting Crashes on Rural Two-Lane Roads in Arizona. Transportation Research Record: Journal of the Transportation Research Board 2016, 2583, 17–24. [Google Scholar] [CrossRef]
  12. Farid, A.; Abdel-Aty, M.; Lee, J. A new approach for calibrating safety performance functions. Accident Analysis and Prevention 2018, 119, 188–194. [Google Scholar] [CrossRef] [PubMed]
  13. Dong, Q.; Jiang, X.; Huang, B.; Richards, S.H. Analyzing Influence Factors of Transverse Cracking on LTPP Resurfaced Asphalt Pavements through NB and ZINB Models. Journal of Transportation Engineering 2013, 139, 889–895. [Google Scholar] [CrossRef]
  14. Sun, C.; Brown, H.; Edara, P.; Claros, B.; Nam, K. Calibration of the HSM’s SPFs for Missouri; Publication CMR14-007; Missouri Department of Transportation, 2014. [Google Scholar]
  15. Kweon, Y.j.; Lim, I.k. Development of Safety Performance Functions for Multilane Highway and Freeway Segments Maintained by the Virginia Department of Transportation. Technical report, 2014.
  16. Donnell, E.T.; Gayah, V.V.; Li, L. Regionalized Safety Performance Functions. Final report for the Pennsylvania Department of Transportation, FHWA-PA-2016-001-PSU WO 17 2016.
  17. Khattak, A.; Ahmad, N.; Mohammadnazar, A.; MahdiNia, I.; Wali, B.; Arvin, R. Highway Safety Manual Safety Performance Functions& Roadway Calibration Factors: Roadway Segments Phase 2, Part 2020.
  18. Al-Deek, H.; Sandt, A.; Gamaleldin, G.; McCombs, J.; Blue, P. A Roadway Context Classification Approach for Developing Safety Performance Functions and Determining Traffic Operational Effects for Florida Intersections. Technical report, 2020.
  19. Kitali, A.E.; Sando, T.; Castro, A.; Kobelo, D.; Mwakalonge, J. Using Crash Modification Factors to Appraise the Safety Effects of Pedestrian Countdown Signals for Drivers. Journal of Transportation Engineering, Part A: Systems 2018, 144. [Google Scholar] [CrossRef]
  20. Brimley, B.; Saito, M.; Schultz, G. Calibration of highway safety manual safety performance function: Development of New Models for Rural Two-Lane Two-Way Highways, 2012. [CrossRef]
  21. Gross, F.; Persaud, B.; Lyon, C. A Guide to Developing Quality Crash Modification Factors. Technical report, 2010.
  22. Srinivasan, R.; Bauer, K. Safety Performance Function Development Guide: Developing JurisdictionSpecific SPFs. Technical report, 2013.
  23. Hauer, E. Overdispersion in modelling accidents on road sections and in Empirical Bayes estimation. Accident Analysis & Prevention 2001, 33, 799–808. [Google Scholar] [CrossRef]
  24. Hauer, E.; Harwood, D.W.; Council, F.M.; Griffith, M.S. Estimating Safety by the Empirical Bayes Method: A Tutorial. Transportation Research Record: Journal of the Transportation Research Board 2002, 1784, 126–131. [Google Scholar] [CrossRef]
  25. Lord, D.; Mannering, F. The statistical analysis of crash-frequency data: A review and assessment of methodological alternatives. Transportation Research Part A: Policy and Practice 2010, 44, 291–305. [Google Scholar] [CrossRef]
  26. Farid, A.; Abdel-Aty, M.; Lee, J. Comparative analysis of multiple techniques for developing and transferring safety performance functions. Accident Analysis & Prevention 2019, 122, 85–98. [Google Scholar] [CrossRef]
  27. Persaud, B.; Lan, B.; Lyon, C.; Bhim, R. Comparison of empirical Bayes and full Bayes approaches for before–after road safety evaluations. Accident Analysis & Prevention 2010, 42, 38–43. [Google Scholar] [CrossRef]
  28. Das, S.; Tsapakis, I.; Khodadadi, A. Safety performance functions for low-volume rural minor collector two-lane roadways. IATSS Research 2021, 45, 347–356. [Google Scholar] [CrossRef]
  29. Wood, G. Generalised linear accident models and goodness of fit testing. Accident Analysis & Prevention 2002, 34, 417–427. [Google Scholar] [CrossRef]
  30. Lord, D. Modeling motor vehicle crashes using Poisson-gamma models: Examining the effects of low sample mean values and small sample size on the estimation of the fixed dispersion parameter. Accident Analysis & Prevention 2006, 38, 751–766. [Google Scholar] [CrossRef]
  31. Florida Department of Transportation (FDOT). Statewide Traffic Data Files, 2022.
  32. FDOT Safety Office. FDOT Highway Safety Manual User Guide 2015, 2015.
  33. Faraway, J.J. Extending the Linear Model with R; Chapman and Hall/CRC, 2016. [Google Scholar] [CrossRef]
  34. Florida Department of Transportation. FDOT Context Classification Guide. Technical report, 2020.
  35. Gamaleldin, G.; Al-Deek, H.; Sandt, A.; El-Urfali, A.; Kayes, M.I.; Gamero, V. Roadway Context Classification Approach for Developing Regional Safety Performance Functions for Florida Intersections. Transportation Research Record 2020, 2674, 191–202. [Google Scholar] [CrossRef]
  36. Tayebikhorami, S.; Sacchi, E. Validation of Machine Learning Algorithms as Predictive Tool in the Road Safety Management Process: Case of Network Screening. Journal of Transportation Engineering, Part A: Systems 2022, 148. [Google Scholar] [CrossRef]
Preprints 82714 g001
Figure 1. Crash distribution for all levels of injury in District 4 during years 2015-2018.
Figure 1. Crash distribution for all levels of injury in District 4 during years 2015-2018.
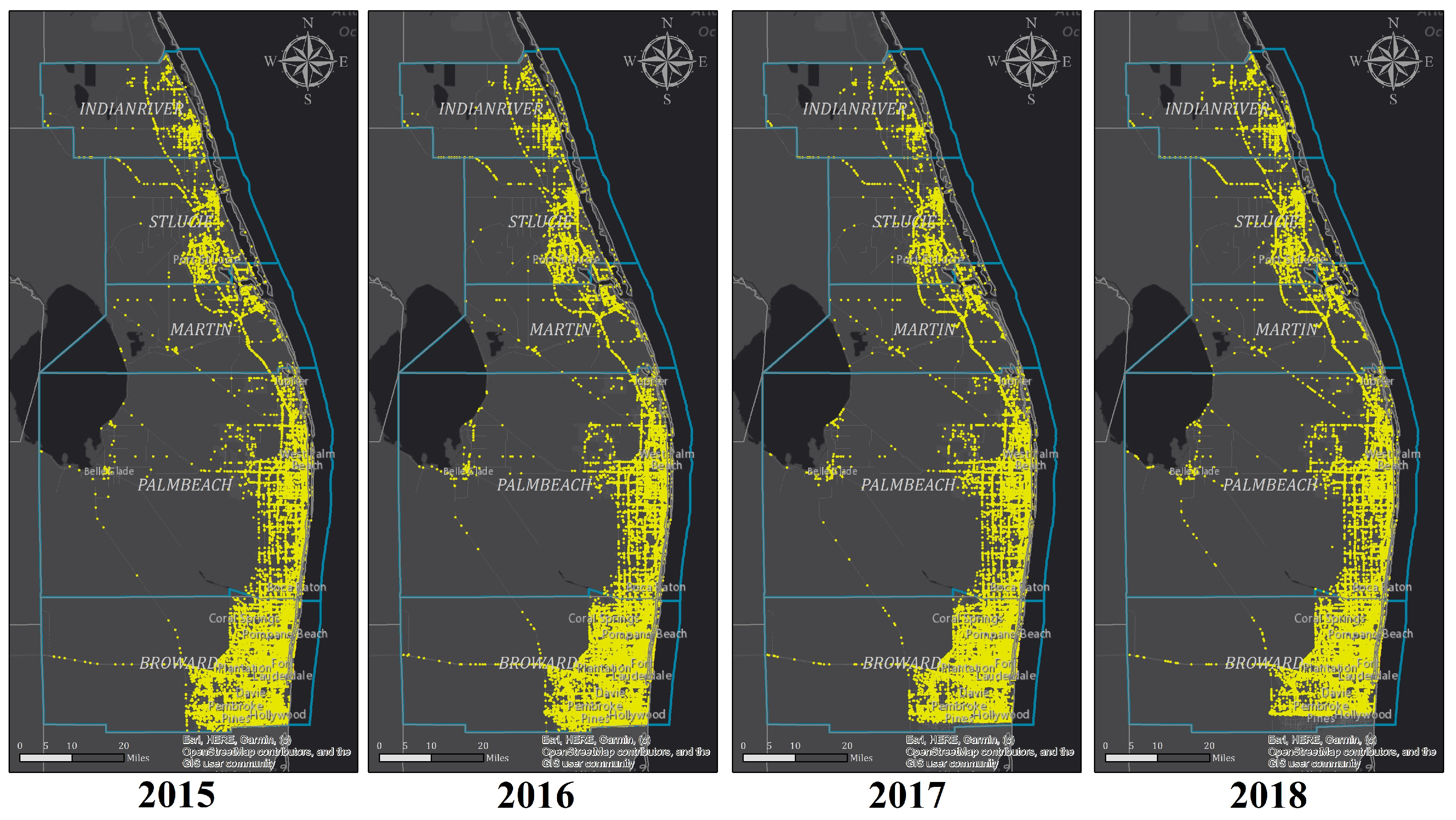
Preprints 82714 g001
Preprints 82714 g002
Figure 2. Schematic overview of the methodology.
Figure 2. Schematic overview of the methodology.
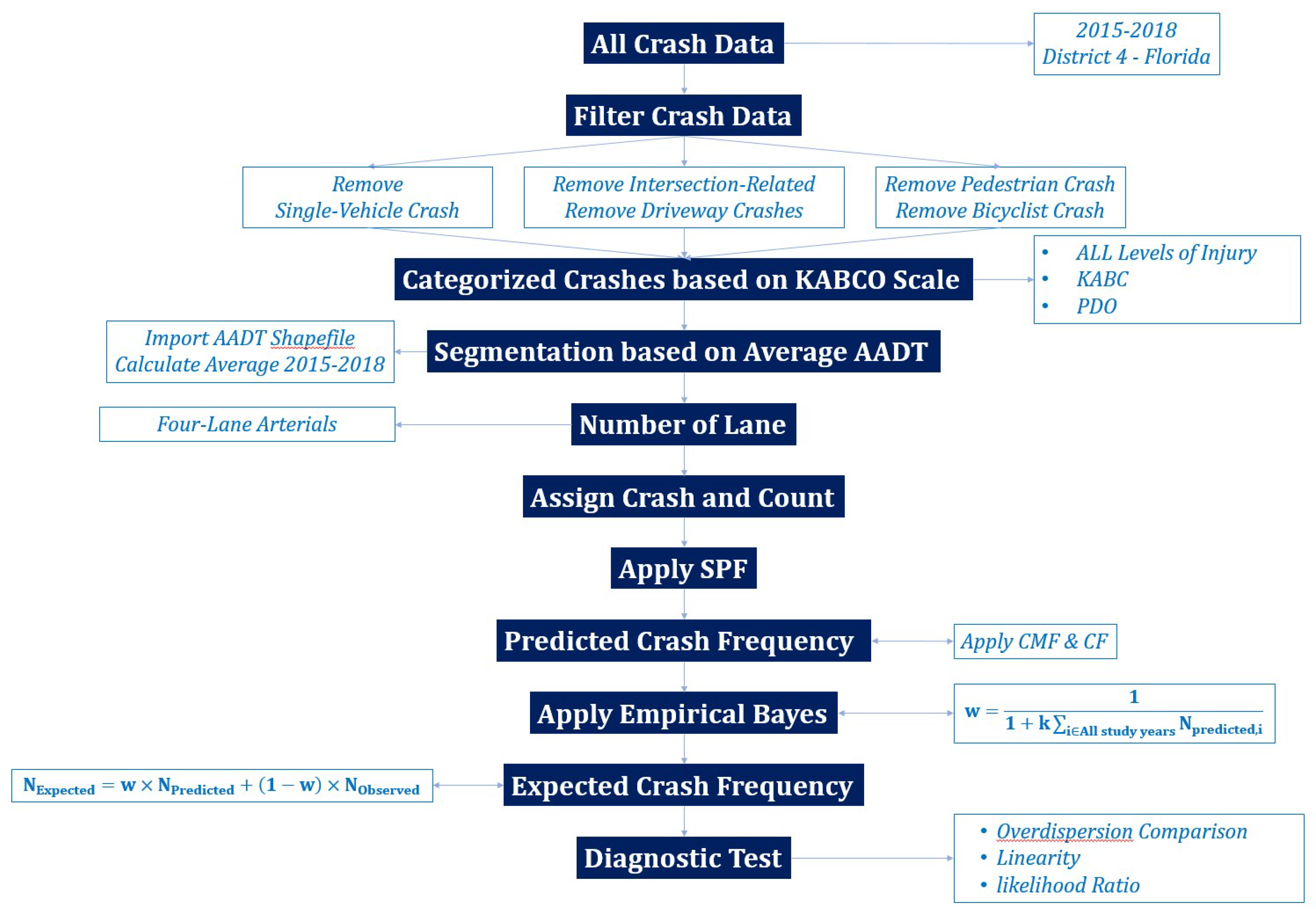
Preprints 82714 g002
Preprints 82714 g003
Figure 3. Map of subregion centroids that do not meet statistical assumptions: (a) Segments with severe nonlinearity in negative binomial regression, (b) Segments with low overdispersion, and (c) Segments with zero-inflation (for radius < 20 miles zero-inflated models are not estimable).
Figure 3. Map of subregion centroids that do not meet statistical assumptions: (a) Segments with severe nonlinearity in negative binomial regression, (b) Segments with low overdispersion, and (c) Segments with zero-inflation (for radius < 20 miles zero-inflated models are not estimable).
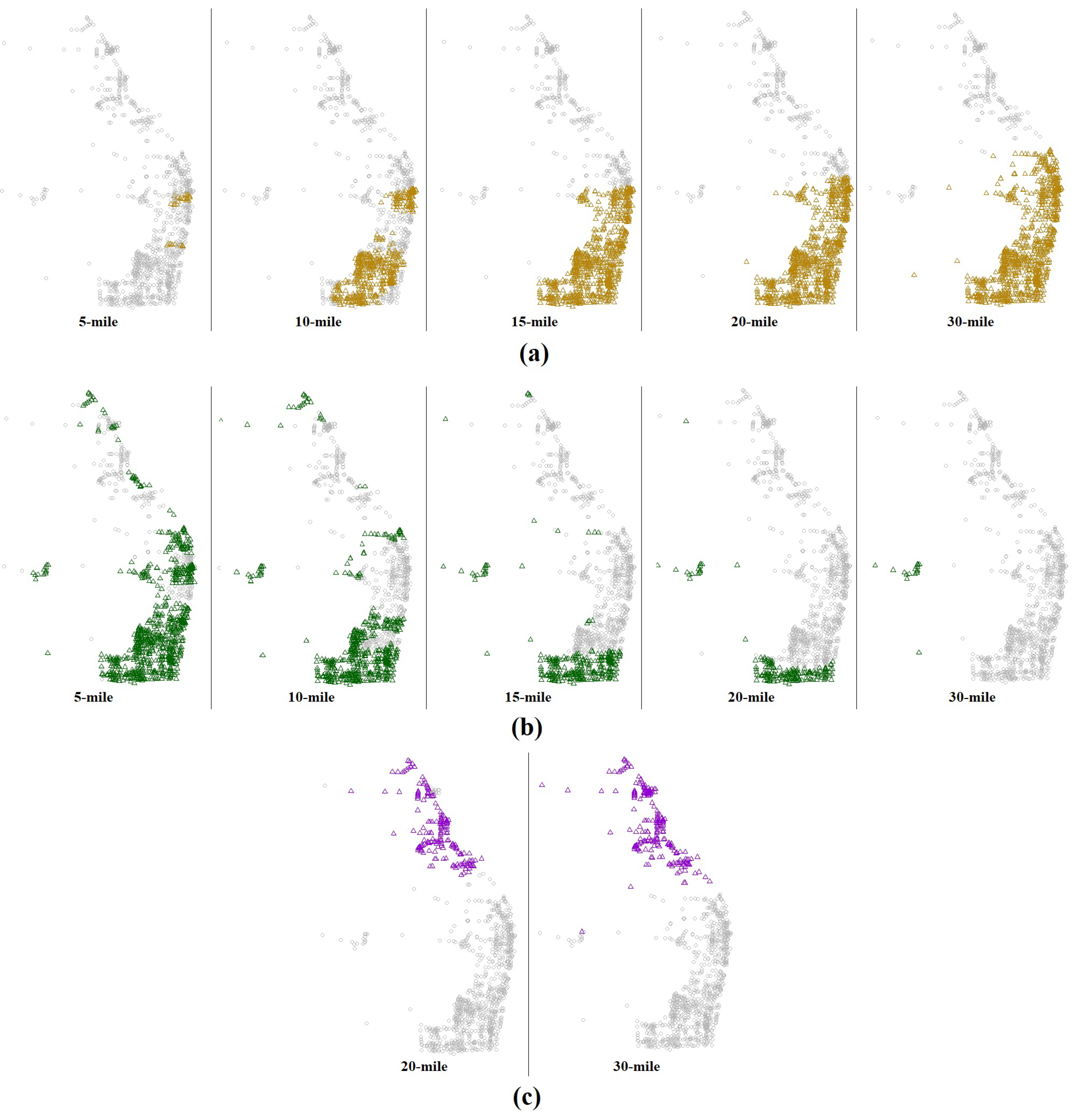
Preprints 82714 g003
Preprints 82714 g004
Figure 4. Summary measures for increasing subregion radii in District 4: (a) All crashes and (b) KABC crashes.
Figure 4. Summary measures for increasing subregion radii in District 4: (a) All crashes and (b) KABC crashes.
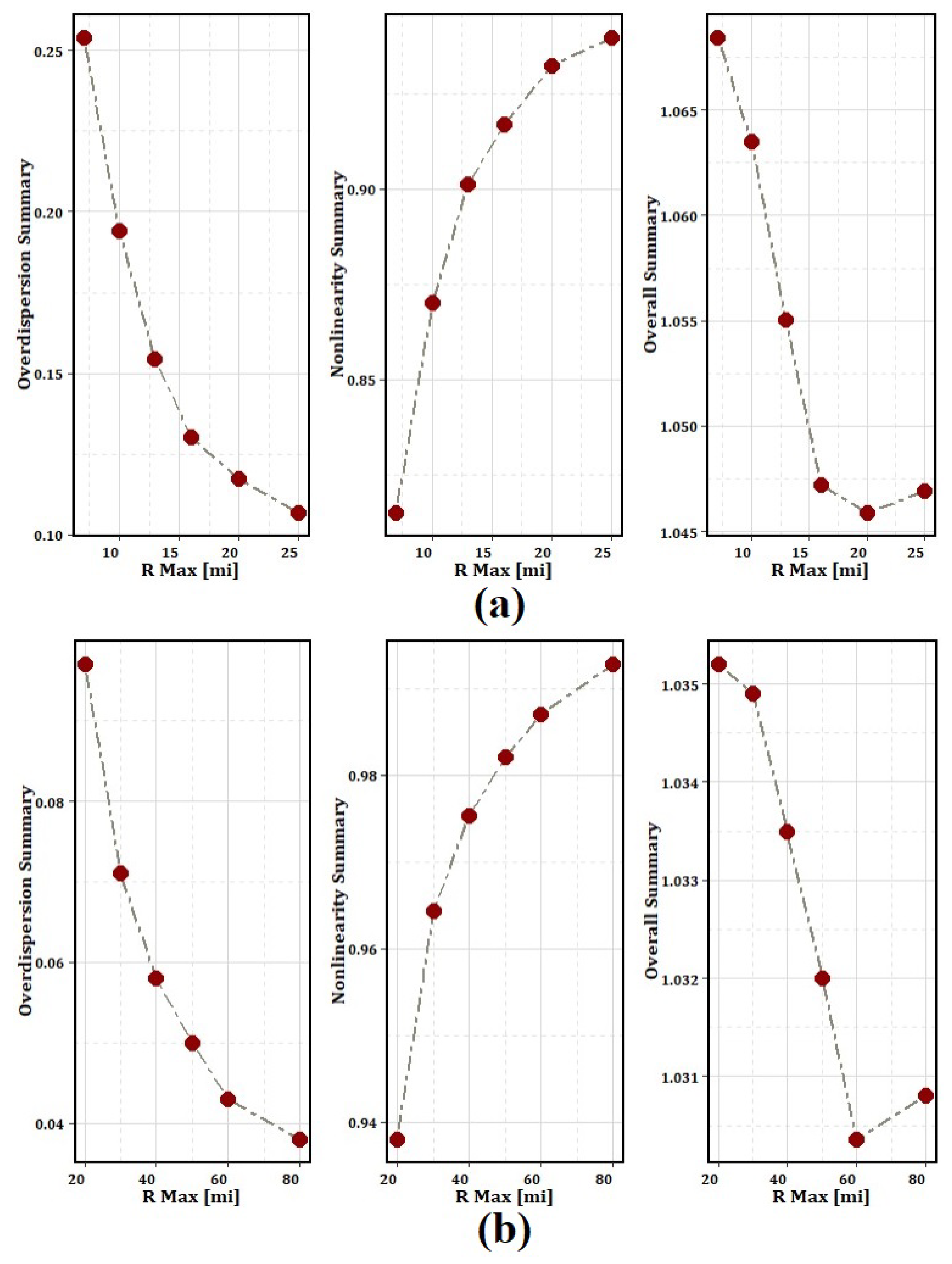
Preprints 82714 g004
Table 1. Annual crash counts for District 4 during 2015 to 2018.
Table 1. Annual crash counts for District 4 during 2015 to 2018.
Crash Type 2015 2016 2017 2018
All Crash in Florida 374,342 395,785 402,385 403,626
All Crash in District 4 76,025 85,611 83,688 86,596
All Considered Crash* 31,013 37,003 34,538 38,630
All Considered Crash on U4D 6,154 7,538 6,474 6,289
U4D KABC Crash** 1,334 1,647 1,440 1,371
U4D PDO Crash*** 3,870 4,881 4,163 4,113
* Multiple Vehicle Non-Driveway Not at Intersection No Pedestrian and No Bicyclist; ** KABC Crash: Fatal (K), Incapacitating(A), Non-Incapacitating(B), and Possible Injury (C); *** PDO Crash: Property Damage Only Crash.
Table 2. HSM SPF Coefficients for multiple-vehicle nondriveway crashes on U4D [2].
Table 2. HSM SPF Coefficients for multiple-vehicle nondriveway crashes on U4D [2].
KABCO Scale Crash Type (Level of Injury) β 0 β 1 Overdispersion Parameter
KABCO Total Crashes −12.34 1.36 1.32
KABC Fatal-and-Injury Crashes −12.76 1.28 1.31
PDO Property Damage Only Crashes −12.81 1.38 1.34
Table 3. Diagnostic tests for 10 mile and 15 mile radius for a sample segment.
Table 3. Diagnostic tests for 10 mile and 15 mile radius for a sample segment.
Diagnostic Test 10 miles 15 miles
GOF test p-value 0.0204 0.0054
Estimated k 0.6469 0.6600
Zero Inflation p-value 0.9851 0.2623
HSM k-value 1.32 1.32
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated