Research on Automatic Vertical Parking Path Planning Algorithm for Narrow Parking Spaces

Preprint

Article

Research on Automatic Vertical Parking Path Planning Algorithm for Narrow Parking Spaces

This version is not peer-reviewed.

Yanfeng Wu^*

,Xuan Li,

Jianping Gao,Xinling Yang

Yanfeng Wu^*

,Xuan Li,

Jianping Gao,Xinling Yang

This version is not peer-reviewed.

Altmetrics

Downloads

132

Views

Comments

Submitted:

20 August 2023

Posted:

21 August 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

The narrow parking space will result in difficulties in path planning and spot turning caused by sudden changes and discontinuities in path curvature. To address the problem, this paper investigates the performance of three path planning algorithms and proposes a path optimization algorithm. First, the narrow parking space is defined based on single-step parking of the arc-line combination parking algorithm. Second, to compare the arc-line combination algorithm, Hybrid A* algorithm, and particle swarm optimization parking algorithm under different narrow parking spaces, a multi-objective evaluation function is proposed, including three evaluation indicators, namely, the path length, the number of positive and negative conversions of vehicle speed, and the smoothness of the path. Their performance is compared by simulation conducted in MATLAB, the results show that the Hybrid A* algorithm is the better than others for narrow parking spaces. Third, to smooth the planning path, a path optimization algorithm based on the cubic B-spline curve and gradient descent is proposed. Finally, the simulation is conducted between the proposed algorithm and Hybrid A* algorithm, the result shows that the proposal can effectively eliminate the curvature mutation point and constrain the path curvature to meet the requirements of a smooth path.

Keywords:

Subject:

Engineering - Automotive Engineering

1. Introduction

With the continuous rise of car ownership, the availability of parking spaces is decreasing, leading to increasingly narrow parking areas, which will cause the parking difficult and inefficient for drivers, even result in collision between the vehicle and the surroundings. It can also cause traffic jams and even traffic accidents. Therefore, automatic parking technology under narrow parking spaces has gradually become the research focus.

The automatic parking system mainly uses sensors of the vehicle to measure the relative distance, speed, and angle between the vehicle and the surrounding objects. It calculates the operation process through the on-board computing or cloud computing platform. It controls the vehicle’s steering, acceleration and deceleration to achieve automatic parking. The parking process can be divided into four steps, namely, environmental perception, parking space detection and recognition, parking path planning, parking path following control. Among them, path planning is to plan a path avoiding collision under vehicle dynamics constraints based on environment and location information and is executed on the vehicle [1].

At present, there are three kinds of vertical parking path planning algorithms commonly used in traditional standard parking spaces. One is the geometric algorithm. Zhao, B et al. [2] used arc lines as transition paths in local path planning to park a vehicle, including arcs and line segments based on the optimal parking starting point node, although the parking path is shortened, it is only suitable for single-step parking. Jiang, M et al. [3] proposed a vertical parking path planning algorithm based on polynomial curve optimization to improve the safety and success rate of automatic vertical parking in complex environments, although it can solve the problem of not being able to single step parking, this algorithm requires a wider parking space. Zhang, J et al. [4] proposed a vertical parking trajectory planning algorithm based on a cycloid curve, decoupling the vertical parking trajectory planning problem into a path planning problem and a velocity planning problem, but it can only be used in slightly narrow parking spaces. The arc-line combination algorithm in the geometric algorithm has accurate characteristics, which can accurately calculate the driving trajectory of the vehicle in the parking process so that the vehicle can accurately park into the specified parking space.

The second is a random search algorithm. Yu, L et al. [5] adopted a particle swarm optimization algorithm to solve equality constraints based on parking boundary, inequality constraints based on curvature, collision avoidance, and parking space reduction. It obtained optimized, smooth, and curvature continuous programming path curve expressions by taking the weighted sum of maximum curvature and the absolute value of the horizontal coordinate of the starting position of parking as the objective function. However, due to the large number of parameters, the path search efficiency is low Kim, M et al. [6] proposed a Target Tree RRT* algorithm in complex environments, which uses the clothoid path to design the target tree to deal with curvature discontinuity. To further reduce the planning time, a cost function is defined to initialize an appropriate target tree considering obstacles. Combining the optimal variable RRT and searching for the shortest path, the Target Tree RRT* algorithm obtains an approximately optimal path as the sampling time increases, although the path search time is shortened, the smoothness of the path cannot be guaranteed. Zhang, J et al. [7] proposed a parallel parking path planning algorithm based on the improved particle swarm optimization, comprehensively considered the non-holonomic kinematics constraints of the 4WS by wire vehicle, process constraints and boundary constraints of the power and steering subsystems, obstacle avoidance constraints, initial parking posture, and target parking posture constraints, and established a parallel parking path planning constraint optimization problem to minimize the total duration of the parking process, the particle swarm optimization, which can deal with equality constraints and inequality constraints, is used to solve the problem and obtain the optimal parallel parking path, although it can solve the problem of non-smooth path, it is not suitable for narrow parking spaces. The search process of the particle swarm optimization algorithm in the random search algorithm performs parallel search, the computational efficiency is high, and the parking path that meets the conditions can be found in a short time. The principle of the particle swarm optimization algorithm is simple, and the parameter adjustment is relatively simple. For different parking scenarios, only a few parameters need to be adjusted.

The third type is the graph search algorithm. Sedighi, S et al. [8] proposed an efficient computational algorithm that combines the Hybrid A* search algorithm with visibility graph planning to find the shortest non-holonomic path in a mixed (continuous-discrete) environment for automatic parking, although the relatively short path can be searched, the search time is increased. Bai, J et al. [9] proposed a directed Hybrid A* global path planning algorithm based on the generalized Vinor map for the path planning problem of autonomous valet parking systems, which accurately and effectively generates a collision-free path from the entrance of the parking lot to the starting point of parking. Xiong, L et al. [10] improved the Hybrid A* by adding a penalty term for obstacle distance on the Reeds-shepp (RS) curve, which improved the problem of the RS curve being too close to obstacles and improved the effectiveness of parking. The Hybrid A* algorithm in the graph search algorithm is a heuristic search in a continuous coordinate system, which can ensure that the generated trajectory satisfies the vehicle non-integrity constraint (kinematic constraint). It can deal with non-smooth obstacles and find the optimal global solution. By combining the discrete node network with the exploration of continuous space, the calculation amount and search time can be reduced.

These three algorithms can improve parking efficiency, reduce search time, adapt to traditional standard parking spaces. However, their applications on automatic vertical parking in narrow spaces is rare and their performance is uncertain. In addition, there is no standard for the narrow parking space and no evaluation index for automatic parking in narrow spaces.

For the reasons mentioned above, the contributions of this study are summarized as follows.

The narrow parking space is defined based on the single-step parking limitation of the arc-line combination parking algorithm. The parking space is defined as a narrow parking space, and the width of the narrow parking space is approximately 1.25-1.35 times the width of the vehicle body.
A multi-objective evaluation function of narrow parking spaces is proposed. The parking route planning algorithms of three various types (arc-line combination, particle swarm optimization, and Hybrid A*) are simulated and examined by the function under different narrow degrees. The simulated parking path curve and curvature are evaluated, and the advantages and disadvantages of the three algorithms in narrow parking space parking planning are analyzed.
A path optimization algorithm based on a cubic B-spline curve and gradient descent is proposed to optimize the path planned by the parking algorithm.

The remainder of this paper is organized as follows. Section 2 introduces the establishment of the vehicle motion model, the principle of three parking algorithms, and the multi-objective function. The path planning simulation of three algorithms in different narrow parking space widths and the comparative analysis of multi-objective function values are discussed in Section 3. Section 4 proposes a parking path and path curvature algorithm based on a cubic B-spline curve and gradient descent, while the experimental results and their analysis are provided in Section 4. The conclusion is drawn in the last section.

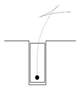
2. Vehicle Kinematics Model

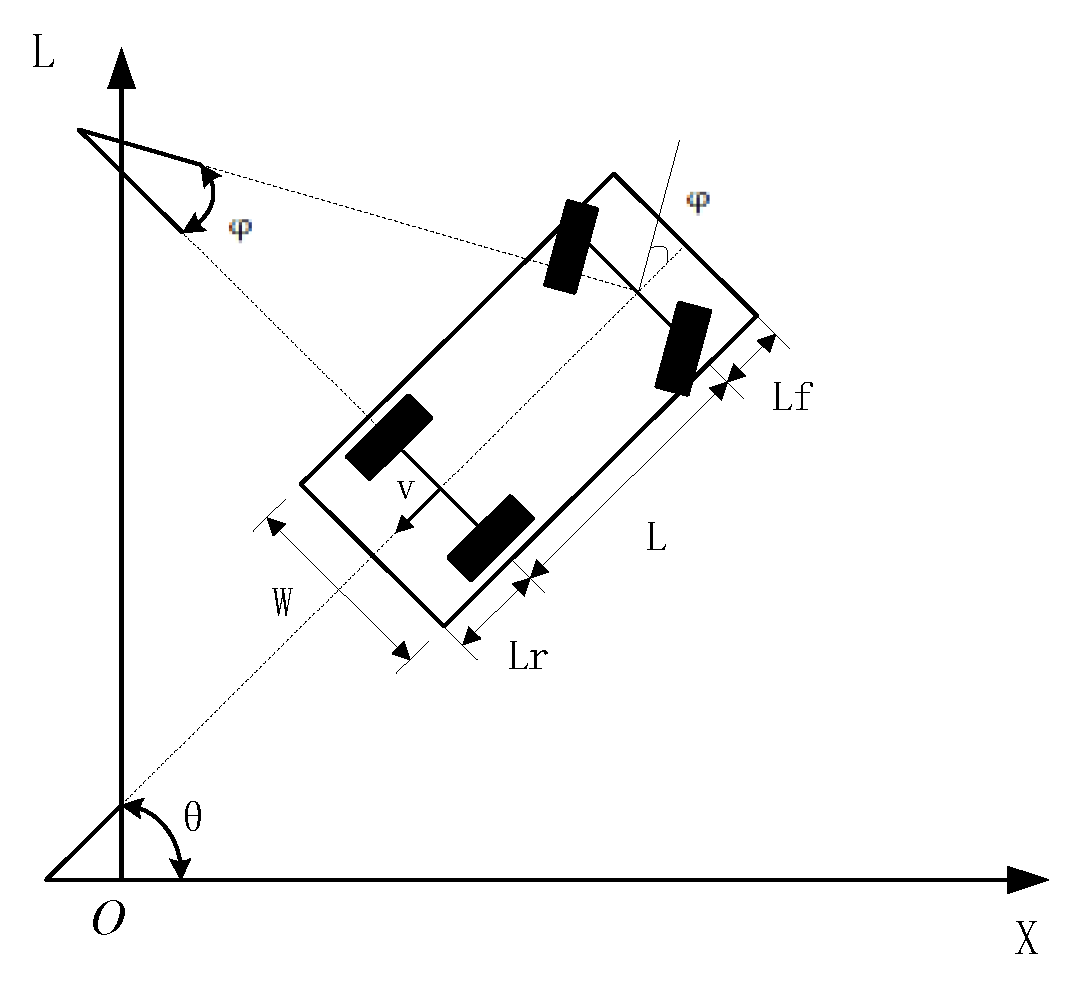
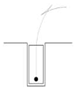
During the automatic parking process, the vehicle speed is relatively low, usually at 2km/h, and the lateral sliding generated during the parking process can be ignored [11]. The center of the vehicle’s rear axle is the base point, and the vehicle kinematics is modeled, as shown in Figure 1.

The following differential equation can be obtained by selecting the center of the equivalent vehicle rear axle as the reference point, referring to Figure 1.

{\dot{x}}_{N} s i n θ - {\dot{y}}_{N} s i n θ = 0

(1)

The kinematics equation of the center point of the equivalent rear axle is obtained from equation (1), which can be expressed as

[\begin{matrix} {\dot{x}}_{N} \\ {\dot{y}}_{N} \\ \dot{θ} \end{matrix}] = [\begin{matrix} c o s θ \\ s i n θ \\ t a n φ / L \end{matrix}] v

(2)

Where

θ

is the heading angle of the vehicle,

φ

is the Ackermann angle of the vehicle, which is the front wheel steering angle of the vehicle,

L

is the wheelbase of the vehicle,

V

is the speed at the center point of the rear axle of the vehicle.

3. Automatic Parking Path Planning Method

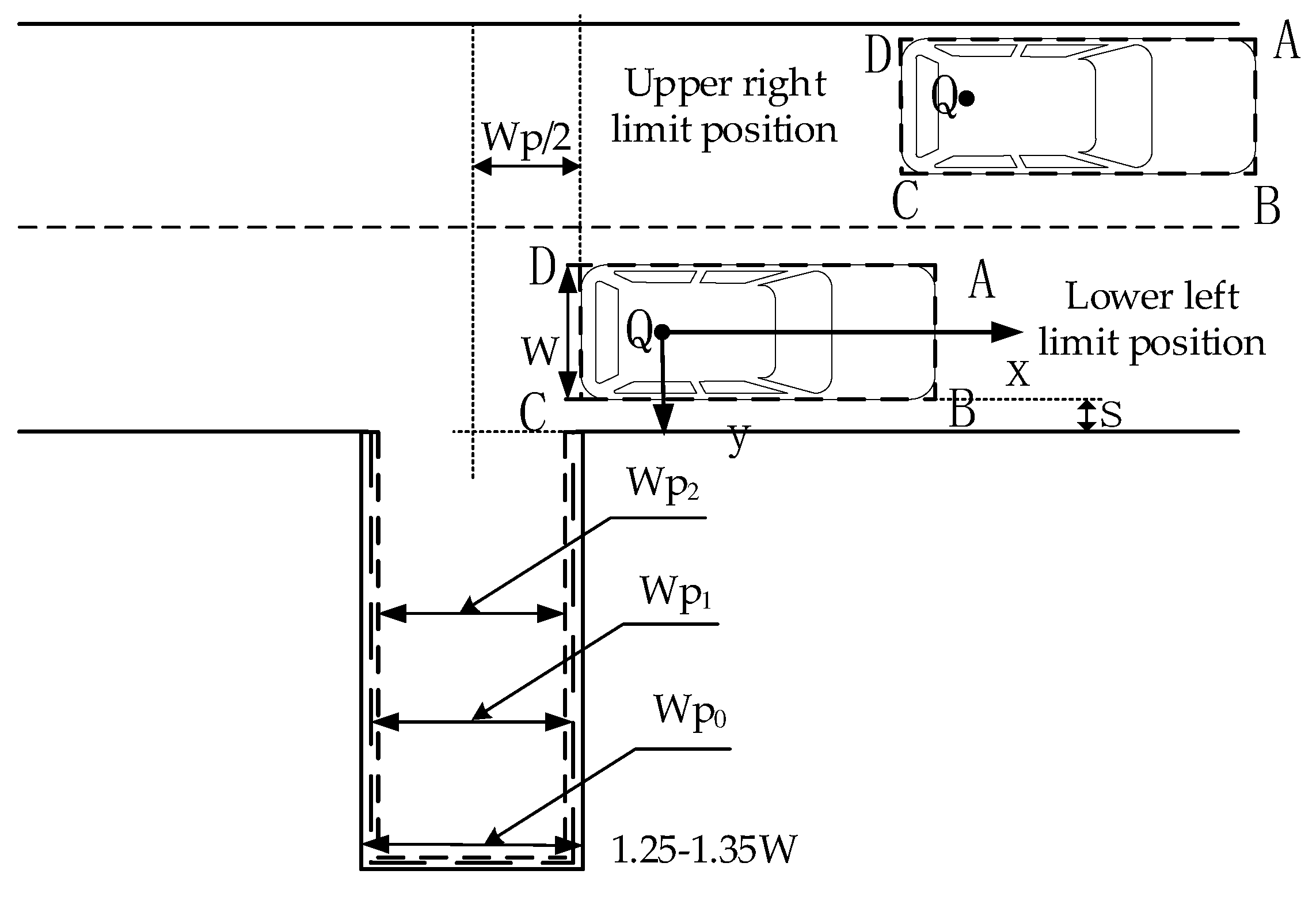
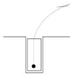
3.1. Narrow Parking Spaces

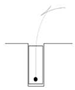
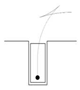
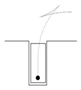
The size of standard parking space is regulated considering the factors such as the width of the vehicle, the minimum turning radius of the vehicle and parking safety. Let the width of the standard parking space be

W_{P_{0}}

, generally, any parking space narrower than

W_{P_{0}}

can be called a narrow parking space. However, the degrees of narrowness affects the parking path planning. If the width of the parking space

W_{P}

is slightly narrower than

W_{P_{0}}

, namely,

W_{P_{0}} \leq W_{P} \leq W_{P_{1}}

as shown in Figure 2, the vehicle can be parked one step using arc-line combination parking algorithm. When

W_{P_{1}} \leq W_{P} \leq W_{P_{2}}

, the vehicle cannot be parked within one step and the vehicle cannot be parked when

W_{P_{2}} \leq W_{P}

. In this study, we only consider the multi-step parking, namely,

W_{P_{1}} \leq W_{P} \leq W_{P_{2}}

as the narrow parking space, which is approximately 1.25-1.35 times the width of the vehicle body

W_{V}

, namely,

W_{P_{1}} \approx 1.35 W_{V}

and

W_{P_{2}} \approx 1.25 W_{V}

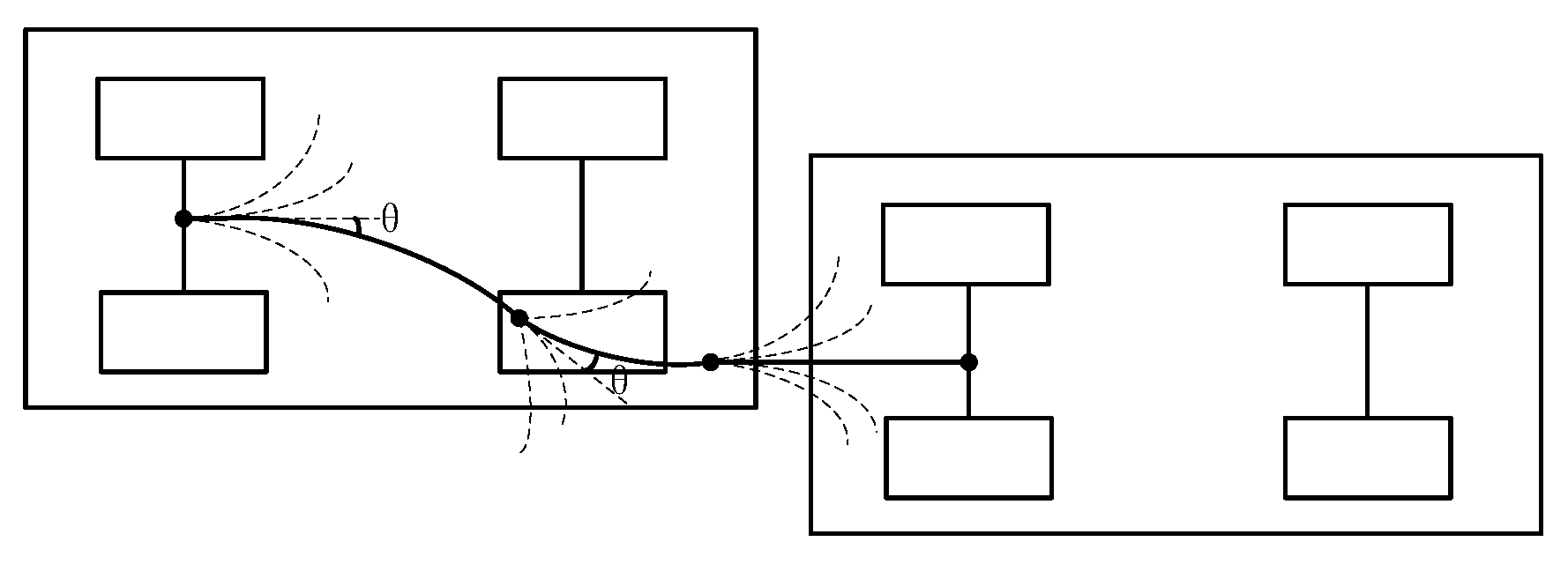
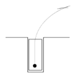
3.2. Principles of Arc-Line Combination Planning Algorithm

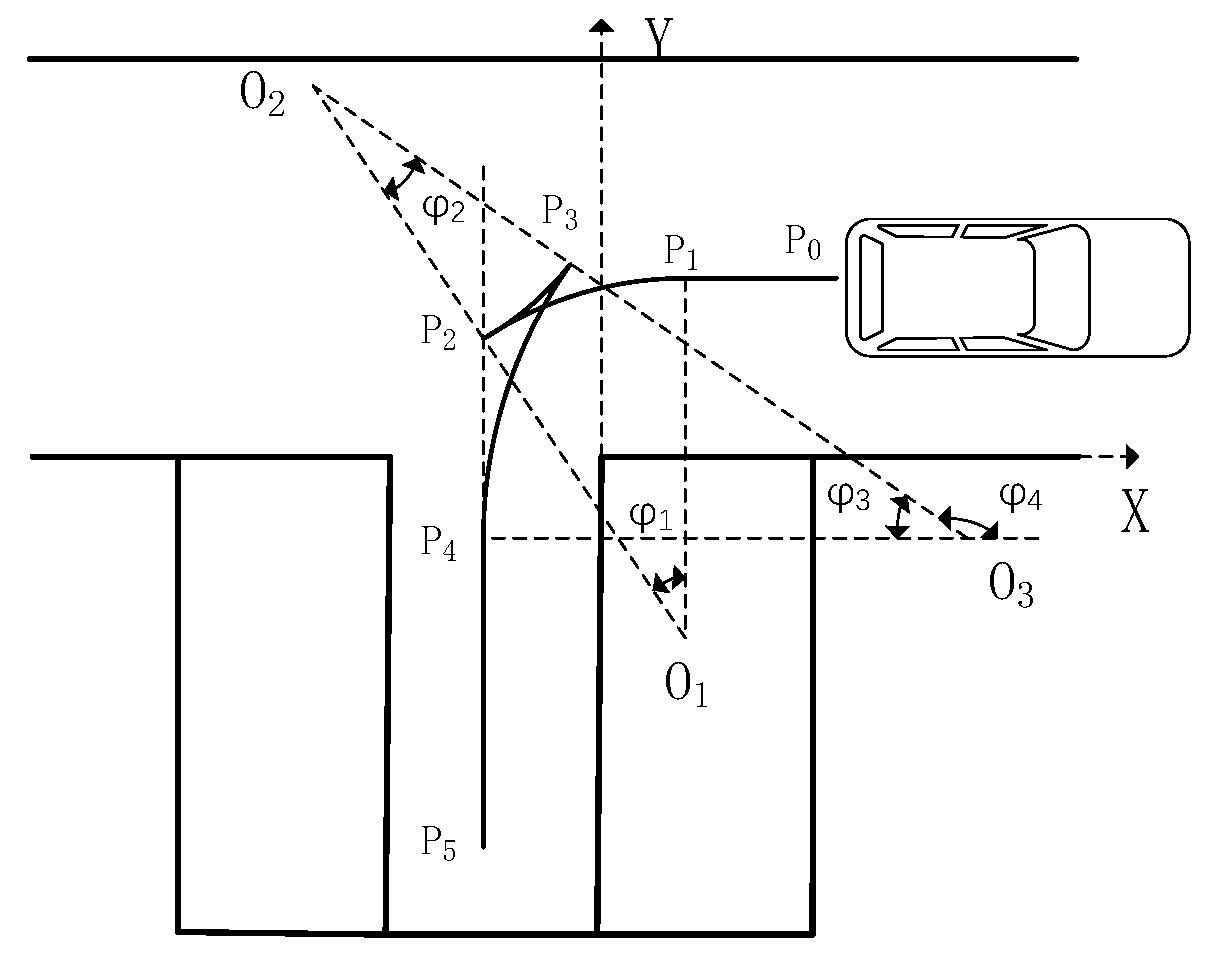
The arc-line combination vertical parking algorithm is a geometric algorithm, which is composed of multiple straight lines and arcs. The radius of the arc is the minimum turning radius of the vehicle. The arc-line combination multi-step vertical parking path planning diagram is shown in Figure 3. The parking path consists of straight lines P₀P₁, P₄P₅ and arcs P₁P₂, P₂P₃, and P₃P₄. The start parking position is point P₀, and the end parking position is point P₅.

The first arc path is P₁P₂.

The vehicle reaches the initial parking position P₀ and starts parking within a safety threshold ψ; when the left rear of the vehicle and the left side of the parking space reach the safety threshold, the first arc P₁P₂ parking is completed.

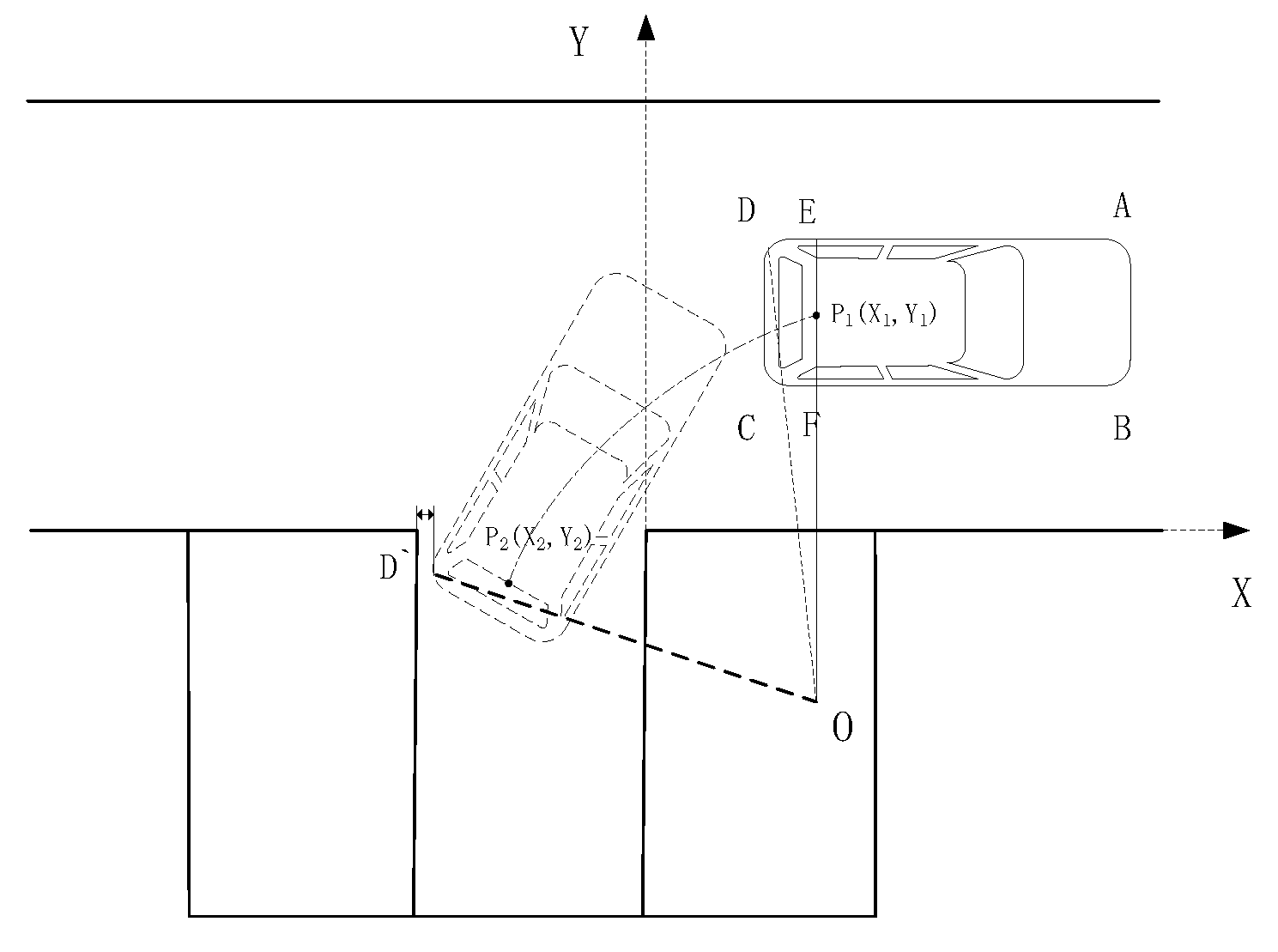
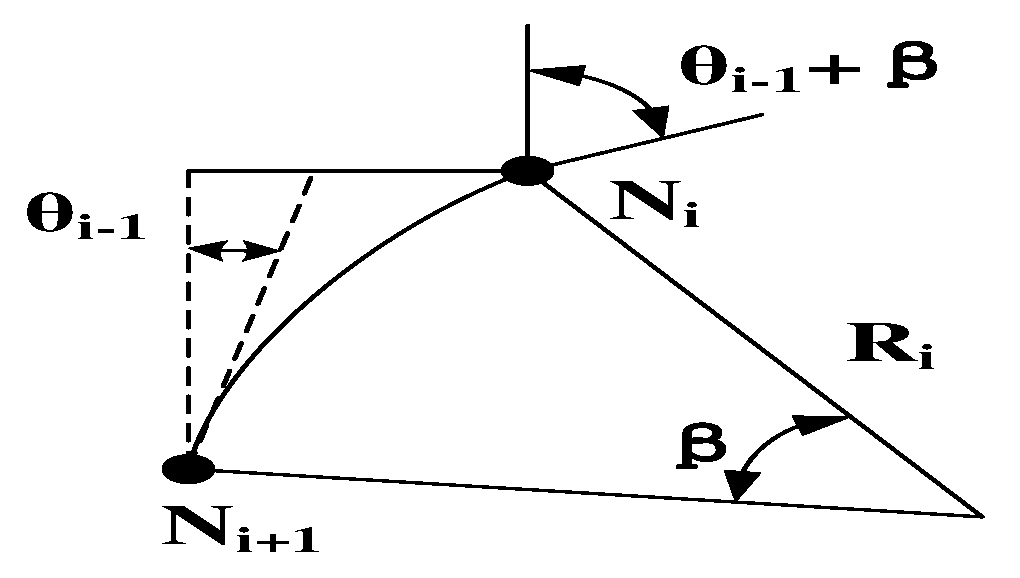
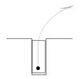
The arcs are obtained by their parameters. The angle parameter

φ_{0}

between the straight-line OE and the straight-line OD is obtained from Equation (3) and as shown in Figure 4.

φ_{0} = a r c t a n (\frac{D E}{O E})

(3)

The parameter corresponding to the first arc P₁P_2, is

φ_{1}

, and the vehicle reverses from the initial parking position P₀. When the vehicle's left rear and left side of the parking space reach the safety threshold, the left parking space vertex coordinates are D’ (X_D’, Y_D’). Based on the D’ horizontal coordinate value and the rear axle center coordinate, the angle of the first arc can be obtained.

φ_{1} = a r c s i n (\frac{X_{1} - X_{D ’}}{O D}) - φ_{0}

(4)

The second arc path is P₂P₃.

The parameters corresponding to the second arc path P₂P₃ are O₂ and

φ_{2}

. The coordinates of the circle's center O2 (xo2, yo2) can be obtained from the coordinates of the center Q₂ of the vehicle's rear axle and the vehicle's heading angle. The relationship between the center O₂ and center O₃ can be obtained from the geometric relationship between the tangent of the second and third arcs.

{(x_{o 3} - x_{o 2})}^{2} + {(y_{o 3} - y_{o 2})}^{2} = {(2 R_{m i n})}^{2}

(5)

The parameters corresponding to the third arc are O₃ and

φ_{3}

. Since the arc P₃P₄ is tangent to the straight line P₄P₅, the coordinates of O₃ (x_o3, y_o3) can be obtained.

Based on the above analysis, the angle

φ_{2}

corresponding to the second arc path, P₂P₃ can be obtained.

φ_{3} = a r c t a n (\frac{y_{o 2} - y_{o 3}}{x_{o 3} - x_{o 2}})

(6)

φ_{2} = \frac{π}{2} - φ_{3} - φ_{1}

(7)

3.3. Principles of Particle Swarm Optimization Planning Algorithm

The particle swarm optimization (PSO) algorithm is a random search algorithm with high precision, fast convergence speed, few parameters, and easy implementation. Through cooperation, the population is optimized. Each potential solution of an optimization problem is considered a bird in the search space, called a “particle” [12]. Each particle has a moderate value determined by an objective function and a speed to determine the flight distance and direction. All particles follow the current optimal particle to search in the solution space, which means finding the optimal solution through multiple iterations.

Assuming that an optimization problem is defined in D-dimensional space, the number of particles in the population is

S_{k}

, and the position, velocity, and cost function values of the particles are

X_{i} = (x_{i 1}, x_{i 2}, \dots, x_{i D})

V_{i} = (v_{i 1}, v_{i 2}, \dots, v_{i D})

f (X_{i})

, respectively. The optimal population is

P_{i}

, which refers to the particle with the smallest cost function value of the current particle in all iterations. The global optimal is

P_{g}

, which refers to the particle with the smallest cost function value in the optimal particle.

The velocity and position update formulas of the particles are as follows.

v_{i d} (k + 1) = {η v}_{i d} (k) + c_{1} r_{2} [P_{i d} - x_{i d} (k)] + c_{2} r_{2} [P_{g d} - x_{i d} (k)]

(8)

x_{i d} (k + 1) = x_{i d} (k) + v_{i d} (k + 1), 1 \leq k \leq k_{m a x}, 1 \leq i \leq N_{P}, 1 \leq d \leq D

(9)

η (k) = \frac{(η_{i n i} - ω_{e n d}) (k_{m a x} - k)}{k_{m a x}} + η_{e n d}

(10)

Among them,

N_{P}

is the number of particles, the larger the particle swarm size, the easier it is to find the global optimal solution;

k_{m a x}

is the maximum number of iterations,

v_{i d} (k)

is the d-dimensional velocity component of the k-th population particle

i

x_{i d} (k)

is the d-dimensional position component of the k-th population particle

i

P_{i d}

is the d-dimensional position component of the optimal particle

i

;

P_{g d}

is the global optimal d-dimensional position component,

r_{1}

and

r_{2}

are random functions that generate random numbers between 0 and 1. The η is the inertia weight. Introducing inertia weight gives the particle swarm a more vital global search ability in the early stage and a more vital local optimization ability in the later stage and increasing η can improve global search ability, and reducing η can improve local search ability; reasonable η is the key to achieving efficient search and avoiding falling into local optima. The

c_{1}

and

c_{2}

are acceleration coefficients to determine particle and global optimization guidance weights, where

c_{1}

affects the optimal local value and

c_{2}

affects the optimal global value.

PSO stop criterion: the end of the particle swarm optimization algorithm is either the number of iterations reaches the maximum value or the optimization result reaches the error threshold.

The particle swarm optimization algorithm must find an optimal parking position and angle in vertical parking. Therefore, in the particle swarm optimization algorithm, the position and angle of the vehicle are used as parameters of the objective function; specifically, the position and angle of the vehicle are used as the state vectors of the particles, and the objective function is the path function of arc straight line planning. After determining the independent variable of the minimum value of the objective function and the starting point of parking, the parking point position information is obtained based on the vehicle's minimum turning radius and the objective function's minimum value. The objective function is used to judge its position, and the optimal solution is searched through continuous attempts and adjustments, achieving a fast and efficient vertical parking process.

3.4. Principles of Hybrid A* Planning Algorithm

The Hybrid A* algorithm is different from the traditional A* algorithm. It is a state space heuristic algorithm. It can introduce heuristic information in the search process, the search path conforms to vehicle kinematics, the parking environment is gridded, and each search location in the gridded state space is evaluated to get the best position and then perform the following search from this position to the destination [13,14,15].

The Hybrid A* algorithm is often used in various path planning, including automatic parking path planning. The Hybrid A* extends from the parent node with various steering operations (left turn, right turn, or no turn), and combines the vehicle kinematics model to determine new nodes, thus ensuring the motion continuity requirements between the child node and the parent node. Therefore, the path generated in this way can meet the needs of vehicle driving, as shown in Figure 5.

In path planning, three-dimensional coordinates

(x, y, θ)

to describe the vehicle's posture. In the formula,

x

is the horizontal coordinate,

y

is the vertical coordinate,

θ

is the heading angle of the vehicle. The node expansion process of the Hybrid A* algorithm is shown in Figure 6, where

N_{i - 1}

and

N_{i}

respectively represent the previous node and the current node. The basic principle is shown in Equations (11)–(15).

β = (\frac{L_{a r c}}{W}) \times t a n α

(11)

R_{i} = \frac{L_{a r c}}{β}

(12)

x_{i} = x_{i + 1} + R_{i} [s i n (θ_{i + 1} + β) - s i n (θ_{i - 1})]

(13)

y_{i} = x_{i + 1} - R_{i} [c o s (θ_{i + 1} + β) + c o s (θ_{i - 1})]

(14)

θ_{i} = θ_{i - 1} + β

(15)

Where,

L_{a r c}

is the step size of each extension of the Hybrid A* algorithm,

α

is the steering angle of the vehicle,

W

is the track width, the angle of

β

corresponding to the arc between

N_{i - 1}

and

N_{i}

nodes can also be directly set as the minimum turning radius of the vehicle during expansion.

The Hybrid A* algorithm considers the influence of the front wheel angle on the node expansion to form a three-dimensional coordinate

(x, y, θ)

. At the same time, two heuristic functions are considered: unconstrained heuristic function and constrained heuristic function. Among them, the unconstrained heuristic function ignores the non-holonomic constraints of the vehicle, considers the environmental obstacles. Therefore, it is not necessary to consider the kinematic constraints of the vehicle, such as the heading angle. The constrained heuristic function ignores environmental obstacles, considers vehicle non-integrity constraints. The unconstrained heuristic function value is used to calculate the constrained heuristic function value, and the Reeds-Shepp curve is used to calculate the size of the heuristic function value.

3.5. Parking Path Evaluation function

Planned path length is commonly used as index to measure the performance of standard spaces parking. However, it is not suitable for evaluating the narrow spaces parking because of the frequent changes in speed and direction. In this paper, we propose a multi-objective evaluation function for narrow parking space paths to evaluate the comprehensive performance of parking algorithms.

The number of positive and negative transitions in vehicle speed. The number of positive and negative vehicle speed transitions $R$ is obtained by judging the speed direction of the previous and subsequent moments.
The total length of the path.

$L = \sum_{i = 1}^{N} {({(x (i + 1) - x (i))}^{2} + {(y (i + 1) - y (i))}^{2})}^{\frac{1}{2}}$

(16)
Path Smoothness.

The minimum curvature of the path curve can represent the smoothness of the path curve. The smaller the minimum curvature, the better the smoothness of the path curve. The average minimum curvature of the entire parking path curve can be compared.

\bar{ρ} = m i n (ρ_{i 1 m i n}, ρ_{i 2 m i n}, ρ_{i 3 m i n})

(17)

where

ρ_{i 1 m i n}

is the minimum curvature of the first path curve of the i-th path point;

ρ_{i 2 m i n}

is the minimum curvature of the second segment of the curve at the i-th path point;

ρ_{i 3 m i n}

is the minimum curvature of the third segment of the curve at the i-th path point.

The above three evaluation indicators values are calculated separately and weighting summation. The multi-objective evaluation function value S of the planning route of these three planning algorithms is obtained as follows,

S = ω_{l} L + ω_{r} R + ω_{ρ} \bar{ρ}

(18)

where

ω_{l}

is the weighted coefficient of the total path length;

ω_{r}

is the weighted coefficient of the number of positive and negative conversions of vehicle speed;

ω_{ρ}

is the weighted coefficient of the planned path curvature.

4. Path Planning Simulation

4.1. Parking Scene Settings

According to the “Specification for the Setting of Parking Spaces on Urban Roads,” (GA/T 850—2021 of China) the size of vertical parking spaces for small cars is 2.5-2.7 * the size is 5-6 meters. The width of the single-lane turning lane is not less than 3.5 meters, while the width of the double lane is not less than 5 meters. The turning section should meet the needs of one vehicle turning at a time. This paper selects a small sedan as the research object, with a width of 1.737m, a length of 4.579m, and a minimum turning radius of 5.6m, and the safety threshold between vehicle and parking space ψ, ψ = 0.1m. According to the above definition of narrow parking spaces, this paper sets the parameters for narrow parking spaces, as shown in Table 1.

4.2. Simulation

In this paper, the path planning algorithm is simulated in MATLAB. Firstly, based on the three established planning models, the arc straight line, the Hybrid A*, and the particle swarm optimization paths for a 2.5m wide standard parking space are simulated at a given starting point. Then, the path planning simulation for narrow parking spaces is compared, and the curvature of each arc of the three is compared.

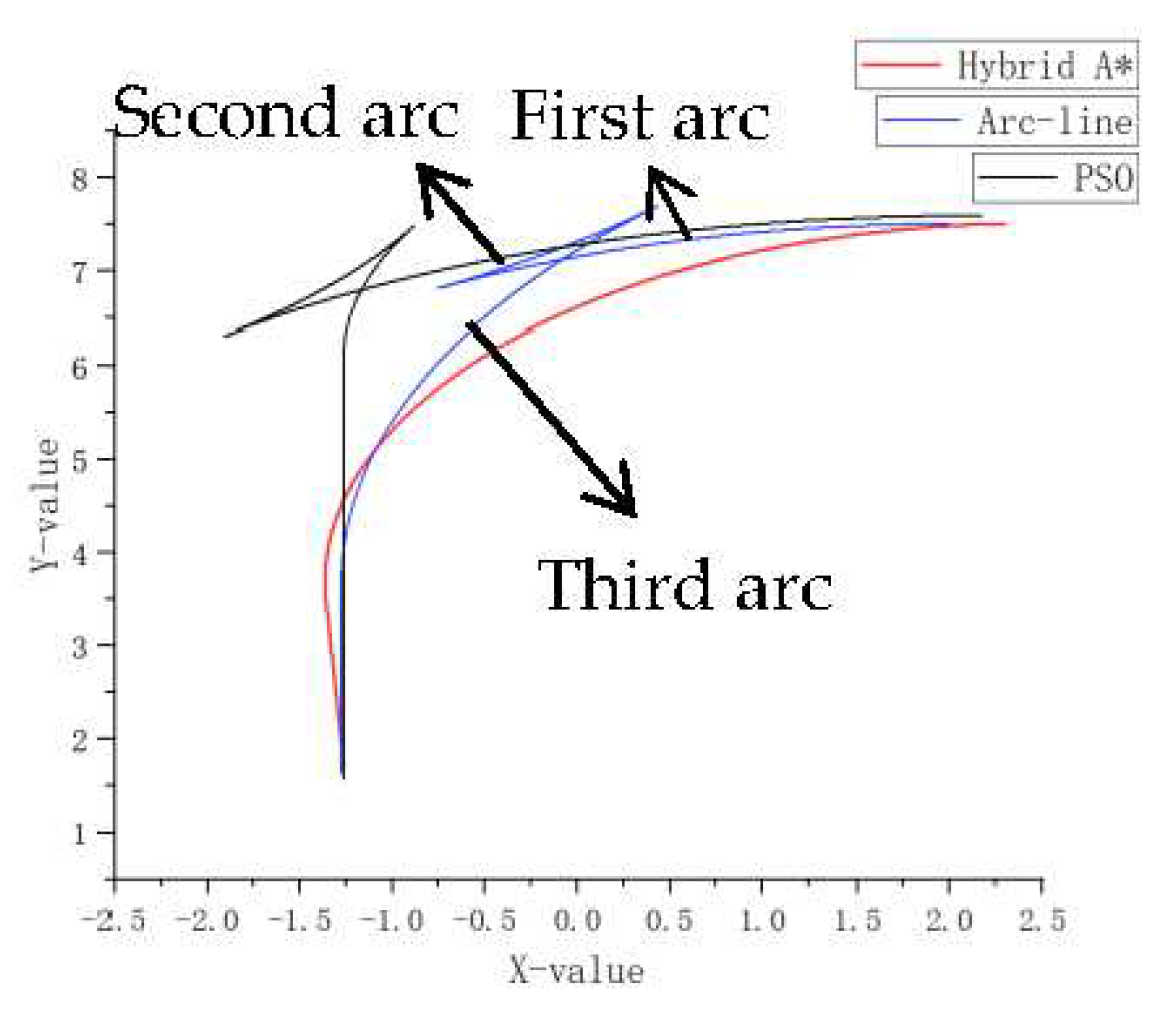
The following is a comparison of the paths planned by the three algorithms when the parking space width is a standard size of 2.5m, as shown in Figure 7.

It can be seen that the path planned by the Hybrid A* includes two arcs and a straight line, and the path planned by arc-line combination and particle swarm optimization includes three arcs and a straight line. Moreover, the first arc of the Hybrid A* planning is much smaller than the arc-line combination and particle swarm optimization. In this way, to complete the parking operation, the path of the Hybrid A* planning needs to be adjusted once outside the library to enter the library, while the arc straight line and the particle swarm need to be adjusted twice outside the library. The following will simulate and compare the width of different parking spaces.

The path curve can be discretized into many path points containing

(x, y)

coordinate values. Then, according to the path length calculation formula in the parking path evaluation index in Section 2.3, the arc-line combination, Hybrid A*, and particle swarm optimization path length can be calculated. Based on each coordinate point, the curvature calculation formula can be used to obtain the curvature value corresponding to each arc segment.

4.2.1. Arc-Line Combination

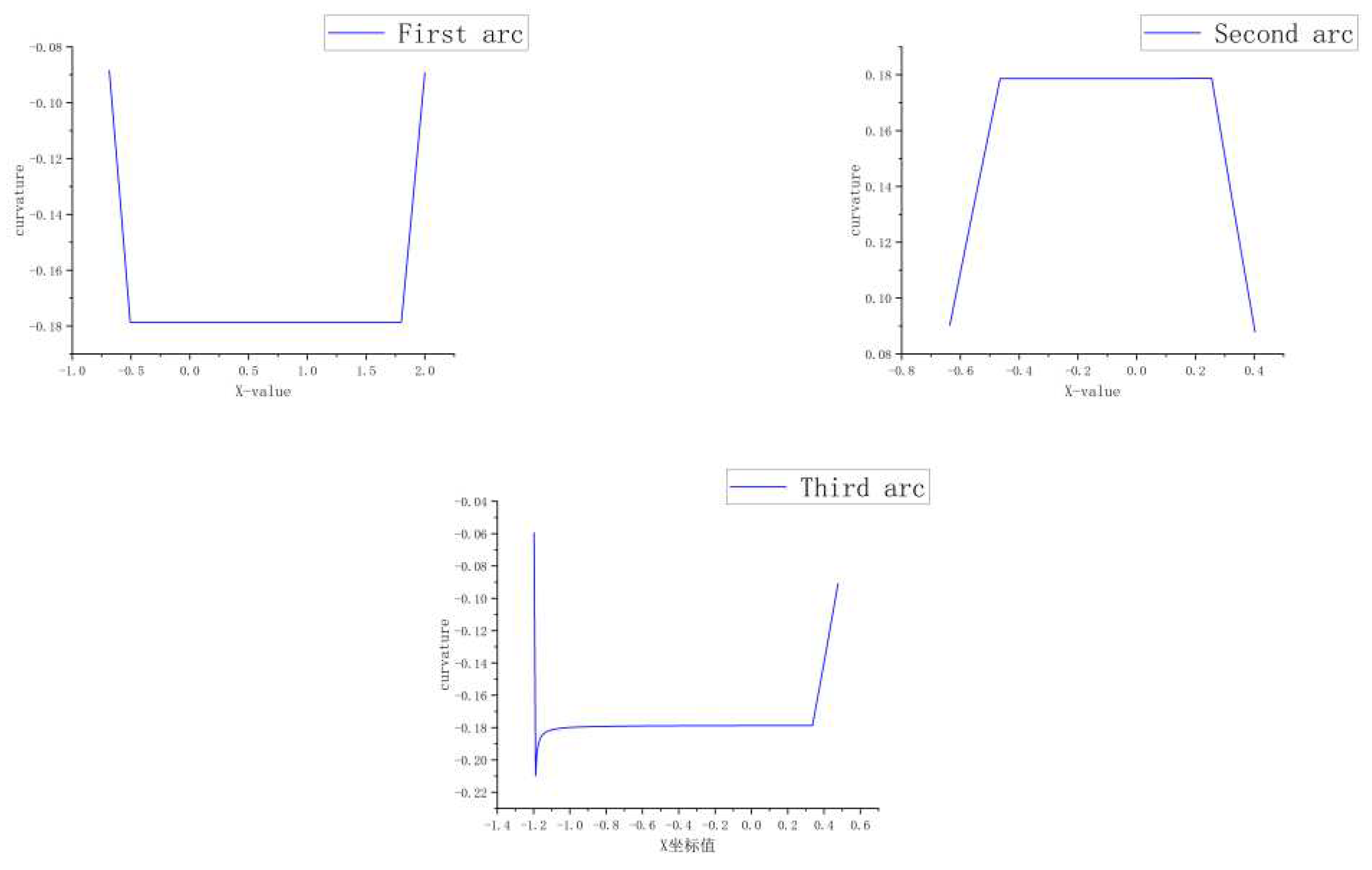
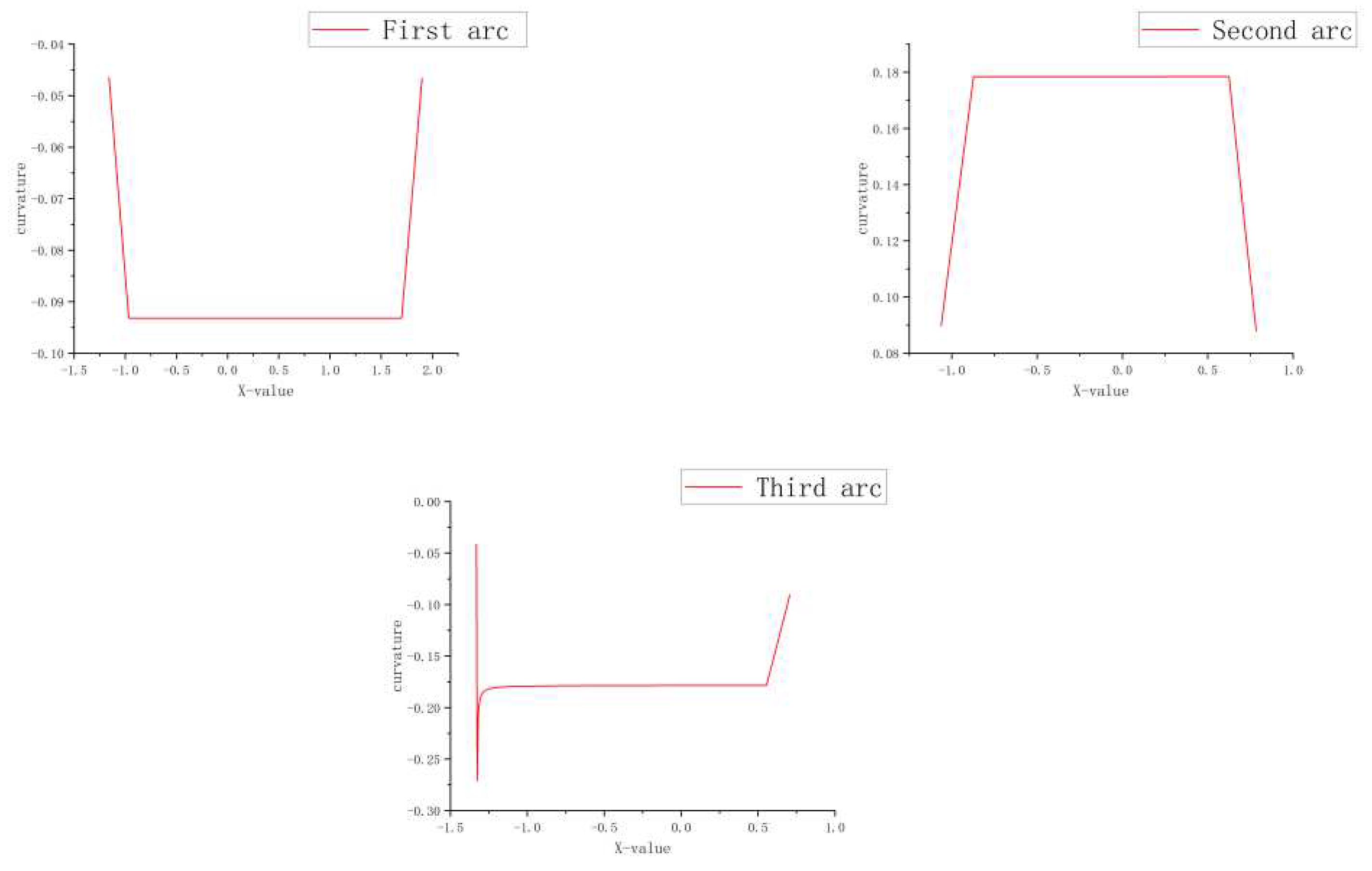
The path length and curvature for arc-line combination planning are simulated based on different parking space widths in MATLAB simulation, as shown below.

The above is the curvature diagram of the simulated path using the arc line planning algorithm in three narrow parking spaces with different widths. Although the parking spaces have different widths, the curvature mutation is the same. From Figure 8, the curvature of the first arc has two mutation points, the second arc has two mutation points, and the third arc has two mutation points. The comparison information of path length and reverse times simulated by MATLAB under different parking space widths can be seen in Table 2.

4.2.2. Hybrid A*

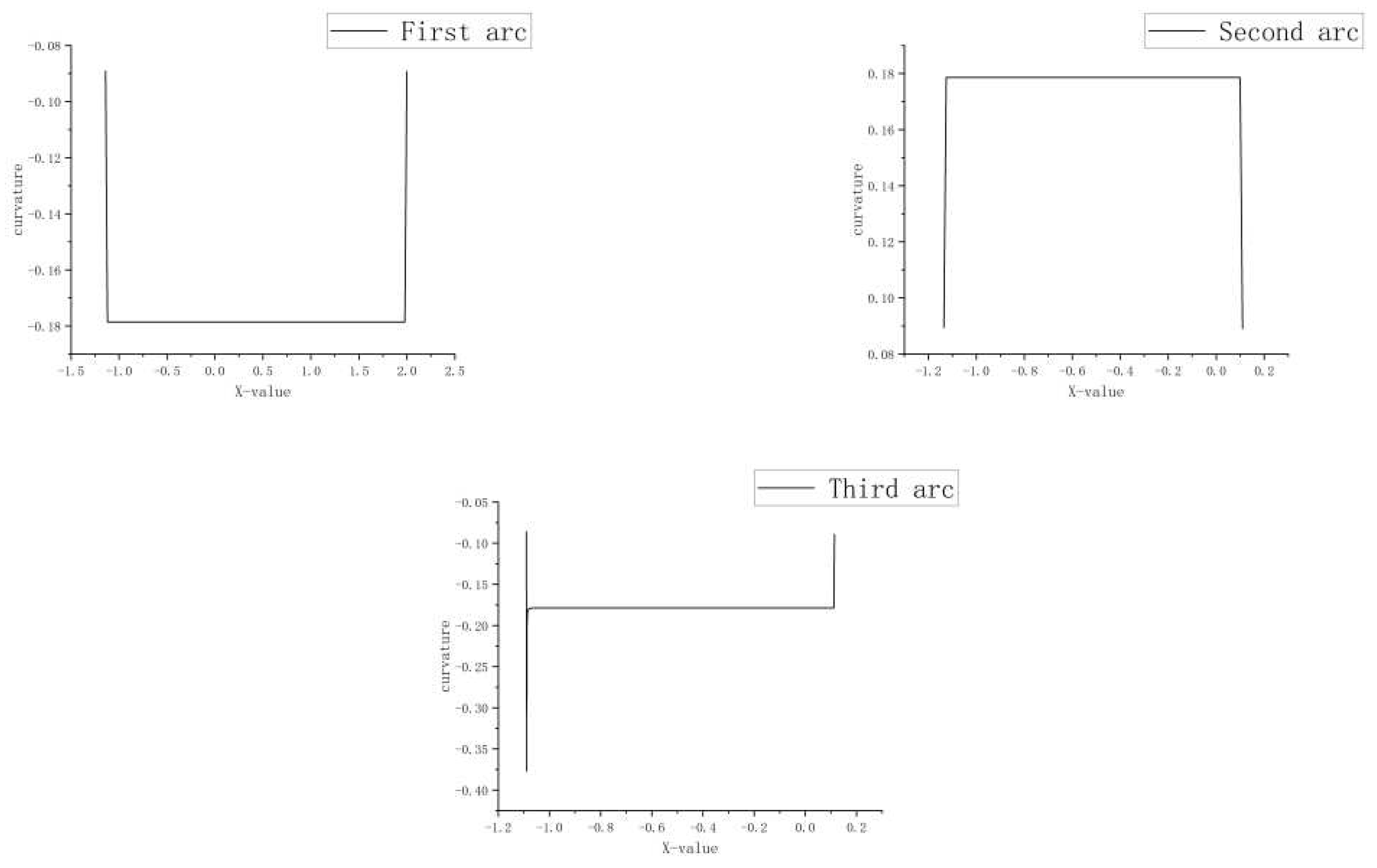
The path length and curvature of Hybrid A* planning is based on different parking space widths in MATLAB simulation, as shown below.

The above is the curvature map of the simulated path using the Hybrid A* planning algorithm in three narrow parking spaces with different widths. Although the parking spaces have different widths, the curvature mutation is the same. From Figure 9, the curvature of the first arc has two mutation points, the second arc has two mutation points, and the third arc has two mutation points. The comparison information of path length and reverse times simulated by MATLAB under different parking space widths can be seen in Table 3.

4.2.3. Particle Swarm Optimization

The particle swarm parameters are set reasonably with reference to practical engineering experience. The path length and curvature of particle swarm optimization are based on different parking space widths in MATLAB simulation, as shown below.

The above is the curvature diagram of the simulation path using the particle swarm optimization algorithm in narrow parking spaces. From Figure 10, the curvature of the first arc has two mutation points, the second arc has two mutation points, and the third arc has two mutation points. The path curvature map planned by the particle swarm optimization algorithm is very similar to the arc line planning algorithm, but the curvature of the segmented arc in Figure 10 changes relatively faster than that of the arc line, and the curvature is less smooth; the second mutation in the third arc is relatively more severe than the mutation in the straight arc. The comparison information of path length and reverse times simulated by MATLAB under different parking space widths can be seen in Table 4.

Through the above simulation results, it can be found that the path needs to be adjusted multiple times to park smoothly due to the narrow space, whether using circle arc- straight line, Hybrid A*, or particle swarm optimization algorithms. From the three tables, the path planned by circular arc straight lines is the longest, and the three planning algorithms have the same number of positive and negative vehicle speed conversions, that is, reverse times. By analyzing the path length, the number of positive and negative vehicle speed transitions, and the number of vehicle position adjustments outside the depot in Figure 7, the parking operation time of the path planned by the geometric algorithm is relatively long, and the efficiency is relatively low.

By analyzing the paths in Figure 7 and the tables, it can be found that the Y values of the adjusted coordinates for the arc straight line and particle swarm planning paths outside the garage are relatively large, which means that the vehicle’s position is farther away from the garage compared to Hybrid A*, and the width of the driving lane is 5m. In this way, further away from the garage increases the risk of vehicles touching the curb, opposite vehicles, or walls, leading to parking failure.

The simulation results of selecting different narrow-width parking spaces show that only the Hybrid A* algorithm successfully parks when the parking space width is 2.1m, the arc-line combination and Hybrid A* algorithm parking successfully at 2.2m. All three algorithms were successfully parked at 2.3m. This indicates that Hybrid A* is most suitable when the parking environment is relatively narrow. Selecting a width of 2.3m parking space, the weighting coefficients adopted in this article are

ω_{l}

=1.25,

ω_{r}

=1,

ω_{ρ}

=400. Based on the multi-objective evaluation function, the results of three parking planning algorithms are compared, as shown in Table 5.

Based on comprehensive analysis, the arc-line combination planning has the longest path among the three evaluation indicators, and the particle swarm optimization has the shortest path; The number of positive and negative vehicle speed transitions is the same. The average minimum curvature of the three arcs of Hybrid A* is the smallest, and the particle swarm is the largest. The final evaluation function S has the lowest score of Hybrid A*, while the arc straight line has the highest score and significantly differs from the two other planning algorithms. This indicates that the arc straight line planning algorithm is unsuitable for narrow parking spaces. Although the particle swarm optimization algorithm has the same evaluation score as Hybrid A* in a 2.3m vast parking space and the shortest path, the path is not smooth relative to Hybrid A*, and the curvature mutation is more significant. Therefore, the Hybrid A * planning algorithm is more suitable for narrow parking spaces.

Although the Hybrid A* planning algorithm is better overall, it also has the problem that the curvature discontinuity of the path curve leads to the spot turn. In order to solve the problem of curvature discontinuity of the planned path, it is necessary to smooth the path optimization.

5. Path Smoothing Optimization of the B-spline Curve and Gradient Descent Algorithm

The Gradient descent is a numerical optimization algorithm with a small storage capacity and high stability. The gradient of the function (the tangent slope of the function at this point) can well indicate the direction in which the function value drops the fastest so that each step can effectively approach the optimal solution. It can optimize the curvature of the smoother curve and adjust the curvature of the curve to meet the kinematic requirements of vehicle driving. If the curve is not smooth in some places, there may be no gradient in these places, which makes the gradient descent algorithm unable to optimize in these places.

A series of control points, including the starting point and the end point of the curve, are selected. The B-spline curve, with multiple control points, has the characteristics of multi-order derivative continuity. Therefore, the B-spline curve can be used for path smoothing, which makes up for the shortcomings of the gradient descent algorithm that cannot be optimized in the non-smooth path. However, the parking paths are composed of multi-segment arcs and straight lines for narrow parking spaces. In this way, B-spline curves are used to optimize each arc of multi-step parking, and then the optimized smooth curve is used to limit the path curvature by the gradient descent algorithm.

5.1. Path Smoothing Optimization Based on the B-Spline Curve

The B-spline curve is an improved curve based on the Bézier curve [16]. It can not only change the order of the curve but also realize the local change of the curve. Assuming that there are

n

control vertices, the k-order B-spline curve function is expressed as follows.

P (u) = \sum_{i = 0}^{n} P_{i} N_{i, k} (u)

(19)

In the above formula,

k = {0, 1, 2, . . ., n}

U = {u_{0}, u_{1}, . . ., u_{(n + k + 1)}}

is the node vector sequence,

P_{i}

is the ith curve equation corresponding to this point, and

N_{(i, k)} (u)

is the k-th B-spline basis function. The recurrence formula is as follows.

\{\begin{array}{l} d e f i n e \frac{0}{0} = 0 \\ N_{i, 0} (u) = \{\begin{matrix} 1, u_{i} ≪ u ≪ u_{i + 1} \\ 0, o t h e r \end{matrix} \\ N_{i, k} (u) = \frac{(u - u_{i}) N_{i, k - 1} (u)}{u_{i + k} - u_{i}} + \frac{{(u}_{i + k + 1} - u) N_{i + 1, k - 1} (u)}{u_{i + k + 1} - u_{i - 1}}, u_{k} \leq u \leq u_{n + 1} \end{array}

(20)

According to the structure of the B-spline curve, its shape is determined by the node vector and the control point of the piecewise mixed function. Then, according to the distribution of the midpoint of the node vector sequence U, the B-spline curve can be divided into four types [17]: uniform B-spline curve, quasi-uniform B-spline curve, piecewise Bézier curve, non-uniform B-spline curve.

When optimizing the parking path, the starting point and the endpoint of the parking cannot be ignored. The quasi-uniform B-spline curve meets the requirements of passing through the starting and endpoints. It is closer to the original trajectory, which can maintain the shape of the original path to the maximum extent. Therefore, this paper chooses this curve to optimize the parking path. When the value of

k

in Equation (21) is 3, the expression of cubic quasi-uniform B-spline can be obtained.

P (u) = \sum_{i = 0}^{3} P_{i} N_{i, k} (u)

(21)

Then, this paper uses the B-spline curve to fit each path arc to obtain a smooth path. The specific algorithm process is as follows: first, the path planning is carried out to obtain the path point set, and the opposite change position of the vehicle movement direction is judged; more, multiple arc path curves are obtained by segmenting the complete path, and B-spline curves are used to optimize each path curve. Finally, the final smooth path is obtained by stitching the optimized path curves.

5.2. Path Curvature Optimization Based on the Gradient Descent

To ensure that the curve curvature satisfies the minimum turning radius constraint of the vehicle for the optimized path

X_{i} = (x_{i}, y_{i})

i \in [i, N]

of the B-spline curve, the following objective function is designed for re-optimization, and the planned path curvature is controlled to be not more significant than the maximum turning curvature of the vehicle.

F = ω_{c} \sum_{i = 1}^{N - 1} σ_{c} (\frac{Δ \emptyset_{i}}{|Δ X_{i}|} - k_{m a x})

(22)

Where

\emptyset_{i}

represents the change of the tangential angle at the vertex;

ω_{c}

represents the weight of the curvature term;

σ_{c}

is the penalty function,

Δ X_{i} = X_{i} - X_{i - 1}

, is the displacement at point

X_{i}

;

Δ \emptyset_{i}

is the angle change of the path at the point

X_{i}

;

k_{m a x}

is the maximum curvature of the vehicle turning; among them:

Δ \emptyset_{i} = |{t a n}^{- 1} (\frac{Δ y_{i + 1}}{Δ x_{i + 1}}) + {t a n}^{- 1} (\frac{Δ y_{i}}{Δ x_{i}})|

(23)

Because the curvature is affected by the derivative of the three points

X_{i}

X_{i + 1}

X_{i - 1}

, and the curvature

k_{i} = \frac{Δ \emptyset_{i}}{|Δ X_{i}|}

, therefore:

Δ \emptyset_{i} = {c o s}^{- 1} (\frac{Δ X_{i}^{T} Δ X_{i + 1}}{|X_{i}^{T}| |Δ X_{i + 1}|})

(24)

The partial derivatives of curvature to

X_{i}

X_{i + 1}

X_{i - 1}

are calculated respectively, and the following results are obtained:

\frac{\partial k_{i}}{\partial X_{i}} = - \frac{1}{|Δ X_{i}|} \frac{\partial Δ \emptyset_{i}}{\partial c o s (Δ \emptyset_{i})} \frac{\partial c o s (Δ \emptyset_{i})}{\partial X_{i}} - \frac{\partial Δ \emptyset_{i}}{Δ X_{i}^{2}} \frac{\partial Δ X_{i}}{\partial X_{i}}

(25)

\frac{\partial k_{i}}{\partial X_{i + 1}} = - \frac{1}{|Δ X_{i}|} \frac{\partial Δ \emptyset_{i}}{\partial c o s (Δ \emptyset_{i})} \frac{\partial c o s (Δ \emptyset_{i})}{\partial X_{i + 1}}

(26)

\frac{\partial k_{i}}{\partial X_{i - 1}} = - \frac{1}{|Δ X_{i}|} \frac{\partial Δ \emptyset_{i}}{\partial c o s (Δ \emptyset_{i})} \frac{\partial c o s (Δ \emptyset_{i})}{\partial X_{i - 1}} - \frac{\partial Δ \emptyset_{i}}{Δ X_{i}^{2}} \frac{\partial Δ X_{i}}{\partial X_{i - 1}}

(27)

The gradient formula of curvature is:

\frac{\partial F}{\partial X_{i}} = ω_{c} (ω_{i - 1} \frac{\partial k_{i}}{\partial X_{i - 1}} + ω_{i} \frac{\partial k_{i}}{\partial X_{i}} + ω_{i + 1} \frac{\partial k_{i}}{\partial X_{i + 1}})

(28)

For formulas (25)–(27), according to the curvature gradient formula can be obtained:

\frac{\partial Δ \emptyset_{i}}{\partial c o s} = \frac{\partial {c o s}^{- 1} (c o s (Δ \emptyset_{i}))}{\partial c o s (Δ \emptyset_{i})} = \frac{- 1}{{(1 - {c o s}^{2} (Δ \emptyset_{i}))}^{1 / 2}}

(29)

In summary, the curvature of each path point is calculated according to the current path sequence and input as a curvature penalty term, and the weighted sum is used as the overall objective function. In each iteration, the coordinate correction value of each point on the path is obtained by gradient derivation of the objective function. Then the coordinate value of each point on the original path is added with the correction value to obtain a new path optimized by one gradient descent. The algorithm will converge to the new path within the set total number of iterations M.

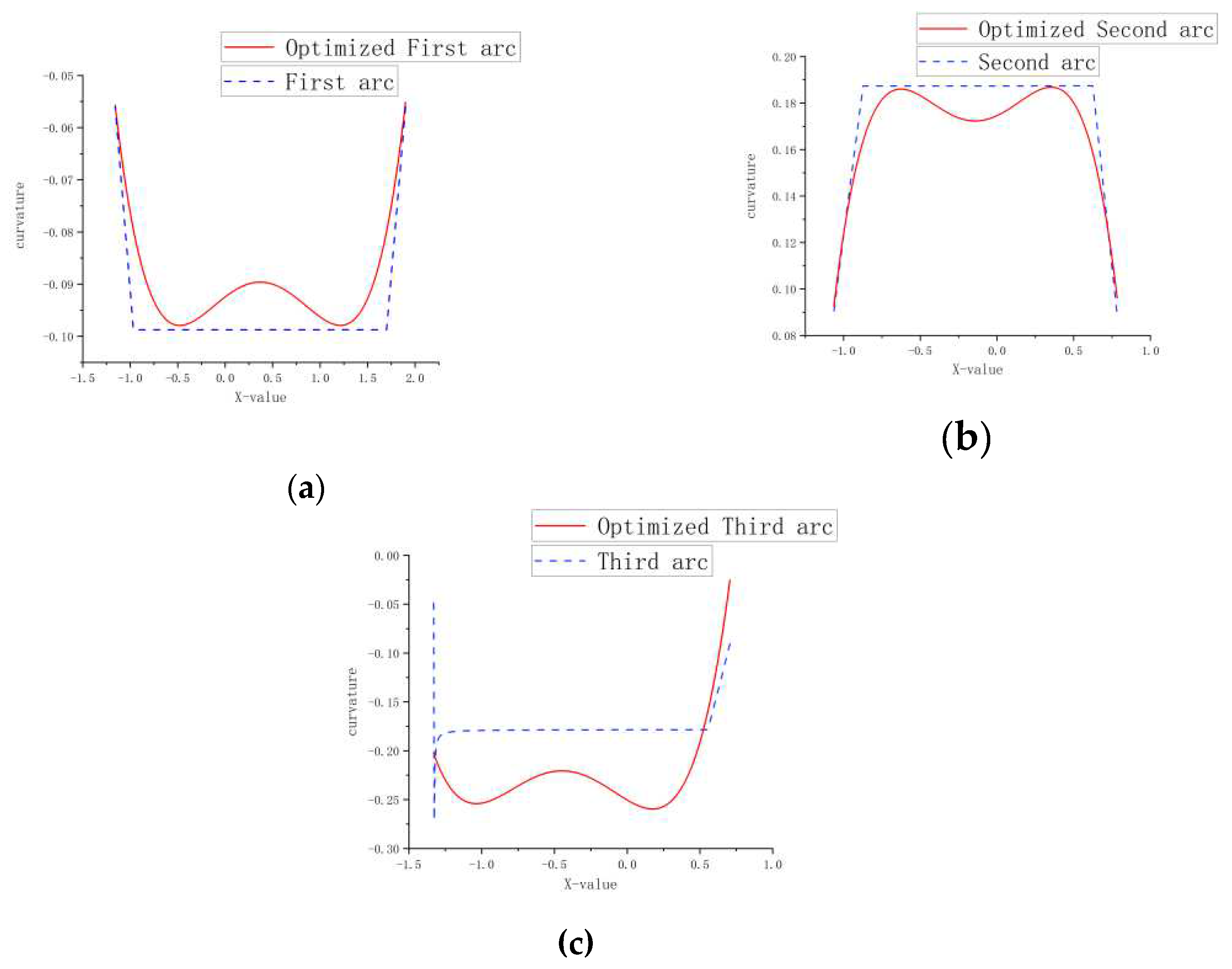
According to the same path information of Hybrid A* in Section 3.2, and MATLAB simulation, the following figure is the curvature comparison after Hybrid A* path optimization.

Figure 11a is the comparison of the curvature of the first arc parking path of the Hybrid A* before and after the B-spline curve and the gradient descent algorithm; Figure 11b is the comparison of the curvature of the second arc parking path of the Hybrid A* before and after the B-spline curve and the gradient descent algorithm. Figure 11c compares the curvature of the third arc parking path of the Hybrid A* before and after the B-spline curve and the gradient descent algorithm. The mean curvature of Figure 11a,b becomes smaller. Although the curvature in Figure 11c becomes more significant, the curvature of the three path curves is continuous without mutation and meets the requirements of continuous curvature change of parking path planning and the minimum turning radius constraint of the vehicle.

The Hybrid A* path curve with a width of 2.3m and the optimized path curve of 3.2 parking spaces are selected. The multi-objective evaluation function compares the multi-objective function S values before and after optimization. The simulation results can be seen in Table 6.

Based on comprehensive analysis, the curvature of the Hybrid A* path is optimized by the B-spline curve and the gradient descent algorithm. The average value of the minimum curvature is less than the curvature before optimization, which is reduced by 0.005 m⁻¹, and less than the curvature of the arc straight line and the particle swarm optimization algorithm. Although the Hybrid A* increases the path length by 1.54 m after optimization, the function value after optimization is less than before optimization, which is reduced by 0.07. The simulation results show that in the narrow parking environment, the path of the Hybrid A* planning optimized by the B-spline curve and the gradient descent algorithm proposed in this paper is better overall.

6. Conclusions

This paper defines a narrow parking space. The single-step parking failure of the arc-line combination parking algorithm is taken as the standard. The parking space is defined as a narrow parking space, and the width of the narrow parking space is approximately 1.25-1.35 times the width of the vehicle body, namely,

W_{P_{1}} \approx 1.35 W_{P}

and

W_{P_{2}} \approx 1.25 W_{P}

. And, aiming at the narrow parking space and narrow parking environment, a multi-objective function is proposed to evaluate the applicability of three planning algorithms, namely arc straight line, hybrid A * and particle swarm optimization, in narrow parking space.

The curvature of the parking path curve is discontinuous, and severe mutations result in spot turns according to the simulation results and the analysis of narrow parking environments. This paper proposes a algorithm based on the B-spline curve and gradient descent algorithm to optimize the path to solve the problem of discontinuous and abrupt curvature of the path curve. The optimized path curvature is smooth and satisfies the minimum turning radius constraint of the vehicle.

However, this paper does not consider the speed planning of parking, parking space detection and recognition and parking path following control. In the future, the variable speed planning and the recognition of narrow parking spaces by vehicle and the following control of vehicle will be considered.

References

Xie, S.; Chen, H.; Zhang, J. Path Planning Algorithm for Parallel Parking. In Proceedings of the 2014 China Society of Automotive Engineering Annual Meeting, Beijing, China, 16 April 2014; pp. 637–640. [Google Scholar]
Zhao, B.; Xin, C.; Man, J.; Liang, C.; Jing, J. A novel Path Planning Methodology for Automated Valet Parking Based on Directional Graph Search and Geometry Curve. Robot Auton Syst 2020, 132, 103606. [Google Scholar]
Jiang, M.; Peng, Y.; Huang, W.; Xu, D. Polynomial Curve-optimized Vertical Parking Path Planning and Tracking. J F Univ (Nat Sci Ed) 2023, 51, 76–82. [Google Scholar]
Zhang, J.; Zhao, J.; Shi, Z.; Yang, X. Trajectory Planning and Tracking Control for Perpendicular Parking Based on Clothoid Curve. J S Univ (Nat Sci Ed) 2020, 50, 182–191. [Google Scholar]
Yu, L.; Wang, X.; Wu, B.; Hou, Z.; Wu, Y. Path Planning Optimization and Tracking of Parallel Parking for Driverless Vehicles. J J Univ (Nat Sci Ed) 2022, 43, 519–523. [Google Scholar]
Kim, M.; Ahn, J.; Park, J. Target Tree-RRT*. Continuous-Curvature Path Planning Algorithm for Autonomous Parking in Complex Environments. IEEE T Autom Sci Eng 2022, 1–12. [Google Scholar]
Zhang, J.; Bu, C.; Wang, C.; Zhao, J. Parallel Parking Path Planning and Tracking Control for Wire-four-wheel Steering Vehicle. J H Univ (Nat Sci Ed) 2021, 48, 44–50. [Google Scholar]
Sedighi, S.; Nguyen, D.-V.; Kuhnert, K.-D. Guided Hybrid A-star Path Planning Algorithm for Valet Parking Applications. In Proceedings of the 2019 5th International Conference on Control, Automation and Robotics, Beijing, China, 19 April 2019. [Google Scholar]
Bai, J.; Xu, Y.; Ji, J.; Chen, Y.; Zhang, Y. Path Planning for Automated Valet Parking Based on Graph Search and Geometry Curve. J C Univ of Technol (Nat Sci Ed) 2022, 36, 115–125. [Google Scholar]
Xiong, L.; Gao, J.; Fu, Z.; Xiao, K. Path Planning for Automatic Parking Based on Improved Hybrid A Algorithm. In Proceedings of the 2021 5th CAA International Conference on Vehicular Control and Intelligence, Tianjin, China, 29 October 2021. [Google Scholar]
Hu, J.; Zhu, L.; Chen, R.; Zhong, X.; Xu, W.; Zhang, M. Research on Parallel Parking Path Planning Algorithm for Narrow Parking Space. AE 2022, 44, 1041–1048. [Google Scholar]
Van Nguyen, L.; Phung, M.D.; Ha, Q.P. Game Theory-Based Optimal Cooperative Path Planning for Multiple UAVs. IEEE Access 2022, 10, 108034–108045. [Google Scholar] [CrossRef]
Ren, B.; Wang, X.; Deng, W.; Nan, J.; Zhong, R.; Ding, J. Path Optimization Algorithm for Automatic Parking Based on Hybrid A* and Reeds-Shepp Curve with Variable Radius. China J. Highw. Transp 2022, 35, 317–327. [Google Scholar]
Bi, J.; Kaoru, H.; Xiang, D.; Ya, P.; Zhi, Y. Path Planning Based on Improved Hybrid A∗ Algorithm. J Adv Comput Intell. 2021, 25, 64–72. [Google Scholar]
Huang, J.; Liu, Z.; Xue, M.; Feng, H.; Hong, Y. Search-Based Path Planning Algorithm for Autonomous Parking: Multi-Heuristic Hybrid A*. In Proceedings of the 2022 34th Chinese Control and Decision Conference, Hefei, China, 15 August 2022. [Google Scholar]
Zhao, L.; Mao, R.; Bai, Y. Local Path Planning for Unmanned Surface Vehicles based on Hybrid A* and B-spline. In Proceedings of the 2022 IEEE International Conference on Unmanned Systems, Guangzhou, China, 28 October 2022. [Google Scholar]
Zeng, D.; Yu, Z.; Zhang, P.; Chen, H. Cubic B-spline Curve for Obstacle Avoidance Trajectory Planning of Unmanned Vehicle. J T Univ (Nat Sci Ed) 2019, 47, 159–163. [Google Scholar]

Figure 1. The simplified vehicle kinematics model.

Figure 2. Vehicle parking position diagram and Narrow parking space diagram.

Figure 3. Multi step path planning.

Figure 4. The first arc path P₁P₂.

Figure 5. Hybrid A* extended node diagram.

Figure 6. New nodes generation principle of Hybrid A*.

Figure 7. Paths of the three algorithms.

Figure 8. Three-segments arc path curvatures of arc-line combination algorithm.

Figure 9. Three-segments arc path curvature of Hybrid A* algorithm.

Figure 10. Three-segments arc path curvature of particle swarm optimization algorithm.

Figure 11. Three arc path curvatures of optimized Hybrid A*.

Table 1. Parameters of narrow parking scenarios.

Scene parameters	Parking space width S_W/m	Parking space length S_L/m	Length of driving passage L/m	Width of driving passage W/m	Vehicle’s Initial heading angle θ_min/(°)
Value	2.3~2.1	5.0	9.0	5.0	-10~10

Table 2. Planned paths of arc-line combination algorithm under different parking spaces.

Parking Space width/m	2.3	2.2	2.1
Total path length/m	11.39	11.37	11.21
Speed positive and negative conversion times/time	2	2	2
Security threshold/m	0.2	0.1	0.09
Planned path

Table 3. Planned paths of Hybrid A* algorithm under different parking spaces.

Parking Space width/m	2.3	2.2	2.1
Total path length/m	9.48	9.50	9.53
Speed positive and negative conversion times/time	2	2	2
Security threshold/m	0.2	0.1	0.09
Planned path

Table 4. Planned paths of particle swarm optimization algorithm under different parking spaces.

Parking space width/m	2.3	2.2	2.1
Total path length/m	9.47	9.48	9.50
Speed positive and negative conversion times/time	2	2	2
Security threshold/m	0.1	0.09	0.08
Planned path

Table 5. Performance of the three algorithms.

Algorithm	Total Path Length/m	Speed Positive and Negative Conversion Times/Time	$\bar{ρ}$	S
Arc-line combination	11.39	2	0.159	79.84
Hybrid A*	9.48	2	0.151	74.25
PSO	9.47	2	0.161	78.24

Table 6. Performance comparison between optimized Hybrid A* and the other.

Algorithm	Total Path Length/m	Speed Positive and Negative Conversion Times/Time	$\bar{ρ_{i}}$	S
Hybrid A*(without optimization)	9.48	2	0.151	74.25
Hybrid A*(optimization)	11.02	2	0.146	74.18
PSO	9.47	2	0.161	78.24
Circular arc straight line	11.39	2	0.159	79.84

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Research on Automatic Vertical Parking Path Planning Algorithm for Narrow Parking Spaces

Abstract

Keywords:

Subject:

1. Introduction

2. Vehicle Kinematics Model

3. Automatic Parking Path Planning Method

3.1. Narrow Parking Spaces

3.2. Principles of Arc-Line Combination Planning Algorithm

3.3. Principles of Particle Swarm Optimization Planning Algorithm

3.4. Principles of Hybrid A* Planning Algorithm

3.5. Parking Path Evaluation function

4. Path Planning Simulation

4.1. Parking Scene Settings

4.2. Simulation

4.2.1. Arc-Line Combination

4.2.2. Hybrid A*

4.2.3. Particle Swarm Optimization

5. Path Smoothing Optimization of the B-spline Curve and Gradient Descent Algorithm

5.1. Path Smoothing Optimization Based on the B-Spline Curve

5.2. Path Curvature Optimization Based on the Gradient Descent

6. Conclusions

References

MDPI Initiatives

Important Links

Subscribe