Modeling and Dynamical Analysis of a Fractional Order Predator-Prey System with Anti-Predator Behaviour and Holling Type IV Functional Response

Preprint

Article

Modeling and Dynamical Analysis of a Fractional Order Predator-Prey System with Anti-Predator Behaviour and Holling Type IV Functional Response

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 August 2023

Posted:

21 August 2023

You are already at the latest version

Alerts

Abstract

We here investigate the dynamical behavior of a fractional-order predator-prey system with anti-predator behavior and Holling IV type functional response. First we study the non-negativity, existence, uniqueness, and boundedness of solutions to the system from a mathematical analysis perspective. Then, we analyze the stability of its equilibrium points and the possibility of bifurcations using stability analysis methods and bifurcation theory, and prove the existence of a supercritical Hopf bifurcation in the system. After providing numerical simulations to illustrate the conclusions theoretically derived, by summarizing those various analytical results obtained, we finally present three interesting conclusions that can contribute to better understanding and preservation of ecological systems.

Keywords:

Subject: Computer Science and Mathematics - Mathematical and Computational Biology

MSC: 39A28; 39A30

1. Introduction

The study of predator-prey system can be traced back to the 18th century. However, the establishment of predator-prey system in the modern sense is primarily attributed to the work of Alfred J. Lotka and Vito Volterra in the early 20th century, who independently proposed models for predator-prey systems and conducted in-depth research on their dynamical behavior. Their researches laid the important theoretical foundation for the dynamics of predator-prey system. The Lotka-Volterra systems described the interactions between predator and prey, and quickly became a hot topic in dynamical research. Even today, studying the dynamical relationship between predator and prey remains an important subject. To comprehend the intricate dynamical properties presented in predator-prey systems, numerous researchers have dedicated themselves to studying predator-prey models in depth. During the course of the research, they have found multitudes of fascinating dynamical properties among various systems [1–8]. Although we may subconsciously assume that prey is inherently disadvantaged in a predator-prey system, there are many instances where prey can resist predation and causes harm to predator, even leads to the death of predator. The existence of such scenarios underscores the significance of determining which entitles hold for the advantage of prey in a predator-prey system [9].

The anti-predator behavior of prey is widely observed in the natural world. Many scholars have conducted researches on the anti-predator behavior of prey and have identified two main ways in which prey exhibits such behaviors: (a) through morphological or behavioral changes [10,11], or (b) by actively attacking the predator [12–14].

In 1987, Ives and Dobson [15] proposed the following system to simulate the anti-predator behavior (a)

\{\begin{matrix} \frac{d x}{d t} = α x (1 - \frac{x}{k}) - β - \frac{e^{- γ β} q x y}{1 + a x}, \\ \frac{d y}{d t} = \frac{b e^{- γ β} q x y}{1 + a x} - d y, \end{matrix}

(1.1)

where the meanings of all parameters are presented in Table 1.

The requirement on the prey by anti-predator behavior (b) is higher, as it not only demands that adult prey can resist predation by predator but also requires adult prey to have the ability to kill the juveniles of the predators. However, there have been few studies on anti-predator behavior (b). In 2015, Tang and Xiao [16] proposed a system to simulate anti-predator behavior (b), and considered the following Holling type IV functional response function system

\{\begin{matrix} \frac{d u}{d t} = a u (1 - \frac{u}{k}) - \frac{b u v}{h + u^{2}}, \\ \frac{d v}{d t} = \frac{c b u v}{h + u^{2}} - d v - g u v, \end{matrix}

(1.2)

where the meanings of all parameters are given in Table 2.

The concept of fractional derivative can be traced back to the 18th century, and the mathematician who first proposed fractional derivative was Liouville [17]. In the 20th century, the mathematician Riesz made the initial reference to the concept of fractional derivative and conducted research on its properties in the reference [18], combining the studies of Liouville and Riesz to establish the Riesz-Liouville definition of fractional derivative that we use today. Subsequently, the mathematician Caputo introduced the Caputo definition of fractional derivative in the reference [19].

In the past two decades, due to the superiority of fractional derivative in studying various ecological system genetic effects, numerous mathematicians have turned their attention to investigating fractional-order ecological systems, finding many interesting dynamical properties presenting in fractional-order ecological systems [20–27]. Currently, a relatively comprehensive research framework has been established for mathematical model of integer order ecosystem, while the study for fractional order ecosystems is still not very mature. Therefore, the authors of this paper intend to introduce Caputo fractional derivation to system (1.2) and extend system (1.2) to a fractional order ecosystem. We’d like to use the Caputo definition of fractional derivative to analyze how the anti-predator behavior and Holling type IV functional response function in fractional order ecosystem will impact the dynamics of the system. As a result, we introduce the following fractional order predator-prey system with Holling type IV functional response and anti-predator behaviors

\{\begin{matrix} _{0}^{C} D_{t}^{α} u (t) = a u (1 - \frac{u}{k}) - \frac{b u v}{h + u^{2}}, \\ _{0}^{C} D_{t}^{α} v (t) = \frac{c b u v}{h + u^{2}} - d v - g u v, \end{matrix}

(1.3)

where the meanings of all parameters are presented in Table 2. For the method of introducing Caputo fractional differential equation into ecosystem model, the reference [28] may be consulted.

The overall structure of this paper is described as follows: In Section 2, some preliminaries are provided for some defintions, lemmas and theorems that will be used to analyze the dynamical properties of the system (1.3). In Section 3, the well-posedness of the system (1.3) is analyzed. In Section 4, the existence and stability of the equilibrium points of the system (1.3) are investigated along with a bifurcation analysis. In Section 5, numerical simulations are performed to validate the results of our theoretical analysis. In Section 6, interesting conclusions are drawn based on some findings from the previous sections.

2. Preliminaries

In this section, we primarily introduce the definition and some conclusions of Caputo fractional derivative that are necessary for our subsequent research.

Definition 2.1.

[29]

Under the definition of Caputo fractional derivative, the fractional derivative of function

f (ξ) \in A C^{n} ([0, + \infty], R)

is given as

_{0}^{C} D_{ξ}^{α} f (ξ) = \int_{0}^{ξ} \frac{f^{(n)} (ϑ)}{Γ (n - α) {(ξ - ϑ)}^{α - n + 1}} d ϑ,

where α represents the order of the fractional derivative.

When

n = 1

, the fractional derivative

_{0}^{C} D_{ξ}^{α} f (ξ)

takes the form of

_{0}^{C} D_{ξ}^{α} f (ξ) = \int_{0}^{ξ} \frac{f (ϑ)}{Γ (1 - α) {(ξ - ϑ)}^{α}} d ϑ .

Definition 2.2.

[29]

The Mittag-Leffler function

M_{i}

, when the order i of

M_{i}

is positive, is defined as

M_{i} (ζ) = \sum_{j = 0}^{\infty} \frac{ζ_{j}}{Γ (j i + 1)}, ζ_{j} \in C,

as the sequence converges.

Lemma 2.1.

[30]

For

_{0}^{C} D_{ξ}^{α} f (ξ) \in A C ([0, Ξ], R)

, if

f (ξ_{1}) = 0

and

f (ξ_{0}) > 0

(all

ξ_{0} \in [0, ξ_{1}))

, then

_{0}^{C} D_{ξ}^{α} f (ξ_{1}) < 0

Lemma 2.2.

[31]

For fractional order system

_{0}^{C} D_{ξ}^{α} Y (ξ) = Z (ξ, Y), ξ \geq 0,

with initial condition

Y (0) = (u (0), v (0))

, where

0 < α \leq 1

Z : [0, + \infty) \times τ \to R^{n}

τ \subseteq R

, if

Z (ξ, Y)

fulfills the local Lipschitz condition for

Z \in R_{n}

∥ Z (ξ, Y) - Z (ξ, \tilde{Y}) ∥ \leq Δ \cdot ∥ Y - \tilde{Y} ∥,

then the system has a unique solution on

[0, + \infty) \times τ

, and

∥ Y (y_{1}, y_{2}, y_{3}, \dots, y_{n}) - Y (\tilde{y_{1}}, \tilde{y_{2}}, \tilde{y_{3}}, \dots, \tilde{y_{n}}) ∥ \leq \sum_{i = 1}^{n} | y_{i} - \tilde{y_{i}} |,

for

i = 1, 2, 3, \dots, n, y_{i}, \tilde{y_{i}} \in R .

Theorem 2.1.

[32]

The Laplace transform of

_{0}^{C} D_{ξ}^{α} f (ξ)

L [_{0}^{C} D_{ξ}^{α} f (ξ)] = ϑ^{α} F (ϑ) - \sum_{j = 0}^{n - 1} ϑ^{α - j - 1} f^{j} (0),

where

F (ϑ) = L [f (ξ)]

α \in (n - 1, n), n \in Z_{+}

Theorem 2.2.

[33]

Assume

α > 0

β > 0

and

K \in C^{n \times n}

, then

L [ξ^{β - 1} E_{α, β} (K ξ^{α})] = \frac{ϑ^{α - β}}{ϑ^{α} - K},

for

R e (ϑ) > {∥ K ∥}^{\frac{1}{α}}

, where

R e (ϑ)

is the real part of complex number ϑ and

E_{α, β}

is the Mittag-Leffler function.

Theorem 2.3.

[34]

For the following fractional order system

_{0}^{C} D_{ξ}^{α} f (ξ) = g (f (ξ)), f (0) = f_{0} \in R^{N}, α \in (0, 1),

where

f (ξ) = {(f_{1} (ξ), f_{2} (ξ), f_{3} (ξ), \dots, f_{n} (ξ))}^{T} \in R^{n}

and

g = {(g_{1}, g_{2}, g_{3}, \dots, g_{n})}^{T} : R^{n} \to R^{n}

. If

g (f^{*}) = 0

, then

f^{*}

is an equilibrium point. Set

J (f^{*})

is the Jacobian matrix

J = \frac{\partial g}{\partial f} = \frac{\partial (g_{1}, g_{2}, g_{3}, \dots, g_{n})}{\partial (f_{1}, f_{2}, f_{3}, \dots, f_{n})}

for

f = f^{*}

. If the characteristic values

λ_{i} (i = 1, 2, 3, \dots, n)

J (f^{*})

meet

| a r g (λ_{i}) | > \frac{α π}{2} (i = 1, 2, 3, \dots, n)

, then

f^{*}

is locally asymptotically stable.

Theorem 2.4.

[35]

We say that a fractional-order system undergoes a fractional Hopf bifurcation if there exists a critical value

β = β_{c}

such that the following conditions are satisfied:

λ_{1} (β_{c})

and

λ_{2} (β_{c})

satisfy

| a r g (λ_{i} (β_{c})) | = \frac{π α}{2}, (i = 1, 2)

| a r g (λ_{i} (β_{c})) | \neq \frac{π α}{2}, (i = 3, 4, 5, \dots, n)

\frac{d}{d β} | a r g (λ_{i} (β)) {| |}_{β = β_{c}} \neq 0, (i = 1, 2)

where λ represents the eigenvalues of the Jacobian matrix of the system.

3. Analysis of Well-Posedness of the System (1.3)

In this section, we consider the uniqueness, non-negativity and boundedness of solutions of the system (1.3).

Theorem 3.1.

For the initial condition

(u (0), v (0)) \in A,

the system (1.3) owns a unique solution

U (t) = (u (t), v (t)) \in A

for all

t \geq 0

, where

A = {(u, v) \in R^{2} : m a x {| u |, | v |} < γ_{1}, m i n {| u |, | v |} > γ_{2}}

Proof.

Consider the time interval

[0, t_{1}], t_{1} < + \infty

. Construct a mapping

G (U) = {(G_{1} (U), G_{2} (U))}^{T}

, where

U = {(u, v)}^{T}

and

\{\begin{matrix} G_{1} (U) = a u (1 - \frac{u}{k}) - \frac{b u v}{h + u^{2}}, \\ G_{2} (U) = \frac{c b u v}{h + u^{2}} - d v - g u v . \end{matrix}

For

U, \tilde{U} \in A

, we have

\begin{matrix} ∥ G (U) - G (\tilde{U}) ∥ \\ = | G_{1} (U) - G_{1} (\tilde{U}) | + | G_{2} (U) - G_{2} (\tilde{U}) | \\ = | a u (1 - \frac{u}{k}) - \frac{b u v}{h + u^{2}} - a \tilde{u} (1 - \frac{\tilde{u}}{k}) + \frac{b \tilde{u} \tilde{v}}{h + {\tilde{u}}^{2}} | \\ + |\frac{c b u v}{h + u^{2}} - d v - g u v - \frac{c b \tilde{u} \tilde{v}}{h + {\tilde{u}}^{2}} - d \tilde{v} - g \tilde{u} \tilde{v}| \\ \leq a | u - \tilde{u} | + \frac{a}{k} | u + \tilde{u} | | u - \tilde{u} | + |\frac{b u v (h + {\tilde{u}}^{2}) - b \tilde{u} \tilde{v} (h + u^{2})}{(h + u^{2}) (h + {\tilde{u}}^{2})}| \\ + |\frac{c b u v (h + {\tilde{u}}^{2}) - c b \tilde{u} \tilde{v} (h + u^{2})}{(h + u^{2}) (h + {\tilde{u}}^{2})}| + d | v - \tilde{v} | + g | u v - \tilde{u} \tilde{v} |, \end{matrix}

\begin{matrix} = a | u - \tilde{u} | + \frac{a}{k} | u + \tilde{u} | | u - \tilde{u} | \\ + (1 + c) |\frac{b h u (v - \tilde{v}) + b h \tilde{v} (u - \tilde{u})}{(h + u^{2}) (h + {\tilde{u}}^{2})} + \frac{b u^{2} \tilde{u} (v - \tilde{v}) - b u \tilde{u} v (u - \tilde{u})}{(h + u^{2}) (h + {\tilde{u}}^{2})}| \\ + d | v - \tilde{v} | + g | u (v - \tilde{v}) + \tilde{v} (u - \tilde{u}) |, \\ \leq (a + g γ_{1} + \frac{2 a γ_{1}}{k} + \frac{b (1 + c) (h γ_{2} + γ_{2}^{3})}{{(h + γ_{2}^{2})}^{2}}) | u - \tilde{u} | \\ + (d + g γ_{1} + \frac{b (1 + c) (h γ_{2} + γ_{2}^{3})}{{(h + γ_{2}^{2})}^{2}}) | v - \tilde{v} |, \\ = L_{1} | u - \tilde{u} | + L_{2} | v - \tilde{v} | \leq L ∥ U - \tilde{U} ∥, \end{matrix}

where

L = m a x {L_{1}, L_{2}}

with

L_{1} = a + g γ_{1} + \frac{2 a γ_{1}}{k} + \frac{b (1 + c) (h γ_{2} + γ_{2}^{3})}{{(h + γ_{2}^{2})}^{2}}

and

L_{2} = d + g γ_{1} + \frac{b (1 + c) (h γ_{2} + γ_{2}^{3})}{{(h + γ_{2}^{2})}^{2}}

Hence,

G (U)

conforms the condition of local Lipschitz, then the system (1.3) owns a unique solution by Lemma 2.2. □

Theorem 3.2.

All solutions of the system (1.3) initiating from

(u (0), v (0)) \in R^{+}

are non-negative and bounded in the region W, where

W = \{(u (t), v (t) \in R_{+}^{2}) ∥ 0 \leq u (t) + \frac{v (t)}{c} \leq \frac{k {(a + d)}^{2}}{4 a d}\} .

Proof.

First, let us prove the non-negativity of the solution. Assume that there exists a constant

μ (> 0)

that satisfies

\{\begin{matrix} u (t) > 0, t \in [0, μ), \\ u (μ) = 0, \\ u (μ^{+}) < 0 . \end{matrix}

We can easily find out

_{0}^{C} D_{t}^{α} {u (t) |}_{μ} = 0

, and derive

u (μ^{+}) = 0

from Lemma 2.1, which obviously contradicts

u (μ^{+}) < 0

. Thus

u (t) > 0

for any

t \in [0, + \infty)

. Similarly, we can prove

v (t) > 0

for

\forall t \in [0, + \infty)

Now construct a function

X (t) = u (t) + \frac{v (t)}{c}

, which will help us prove the boundedness of the solution. The Caputo fractional derivative of

X (t)

with order

α

\begin{matrix} _{0}^{C} D_{t}^{α} X (t) & = a u (t) - \frac{a u {(t)}^{2}}{k} - \frac{d v (t)}{c} - \frac{g u v}{c}, \\ = a u (t) (1 - \frac{u (t)}{k}) - \frac{g u (t) v (t)}{c} - d (X (t) - u (t)) . \end{matrix}

Then

\begin{matrix} _{0}^{C} D_{t}^{α} X (t) + d X (t) & = a u (t) (1 - \frac{u (t)}{k}) - \frac{g u (t) v (t)}{c} + d u (t) \\ \leq \frac{k {(a + d)}^{2}}{4 a} - {(u (t) \sqrt{\frac{a}{k}} - \frac{(a + d)}{2} \sqrt{\frac{k}{a}})}^{2} \\ \leq \frac{k {(a + d)}^{2}}{4 a}, \end{matrix}

i.e.

\begin{matrix} _{0}^{C} D_{t}^{α} X (t) + d X (t) \leq \frac{k {(a + d)}^{2}}{4 a} . \end{matrix}

Applying Theorem 2.1 and making Laplace transform on both sides of the above inequality at the same time, one has

L [_{0}^{C} D_{t}^{α} X (t) + d X (t)] \leq L [\frac{k {(a + d)}^{2}}{4 a}] .

This leads to

ϑ^{α} F (ϑ) - ϑ^{α - 1} X (0) + d F (ϑ) \leq \frac{1}{ϑ} \frac{k {(a + d)}^{2}}{4 a},

where

F (ϑ) = L [X (t)]

. Hence,

\begin{matrix} F (ϑ) \leq \frac{k {(a + d)}^{2}}{4 ϑ a (ϑ^{α} + d)} + \frac{ϑ^{α - 1}}{ϑ^{α} + d} X (0) . \end{matrix}

By using the inverse Laplace transform on both sides of the above inequality, we may derive

\begin{matrix} L^{- 1} [F (ϑ)] \leq T L^{- 1} [\frac{1}{ϑ (ϑ^{α} + d)}] + X (0) L^{- 1} [\frac{ϑ^{α - 1}}{ϑ^{α} + d}], \\ \Rightarrow & X (t) \leq T L^{- 1} [\frac{ϑ^{- 1}}{ϑ^{α} + d}] + X (0) L^{- 1} [\frac{ϑ^{α - 1}}{ϑ^{α} + d}], \end{matrix}

where

T = \frac{k {(a + d)}^{2}}{4 a}

. From Theorem 2.2, one obtains

\begin{matrix} X (t) \leq T t^{α} E_{α, α + 1} (- d t^{α}) + X (0) E_{α, 1} (- d t^{α}) . \end{matrix}

According to the properties of the Mittag–Leffer function, we get

\begin{matrix} E_{α, 1} (- d t^{α}) = - d t^{α} E_{α, α + 1} (- d t^{α}) + \frac{1}{Γ (1)}, \end{matrix}

i.e.,

\begin{matrix} - \frac{1}{d} [E_{α, 1} (- d t^{α}) - 1] = t^{α} E_{α, α + 1} (- d t^{α}), \end{matrix}

which displays

\begin{matrix} X (t) \leq (X (0) - \frac{T}{d}) E_{α, 1} (- d t^{α}) + \frac{T}{d} . \end{matrix}

Notice that

E_{α, 1} \to 0

when

t \to \infty

. Thus, we have

X (t) \leq \frac{T}{d}

for large t, i.e.,

X (t) \leq \frac{k {(a + d)}^{2}}{4 a d}

for large t. Accordingly, all solutions of the system (1.3) are bounded in the region

\begin{matrix} W = \{(u (t), v (t)) \in R_{+}^{2} ∥ 0 \leq u (t) + \frac{v (t)}{c} \leq \frac{k {(a + d)}^{2}}{4 a d}\} . \end{matrix}

The proof is over. □

4. Stability and Bifurcation of the System (1.3)

In this section, we first identify the equilibrium points of the system (1.3), then analyze their stability, and finally investigate the existence of bifurcation of its positive equilibrium points.

4.1. Existence of Equilibrium Point

We first can easily observe that the two points

Q_{0} (0, 0)

and

Q_{k} (k, 0)

always are equilibrium points of the system (1.3).

Next, we consider the positive equilibrium points of the system (1.3). It is evident that the positive equilibrium solutions of the system (1.3) satisfy the following equations

\{\begin{matrix} a (1 - \frac{u}{k}) - \frac{b v}{h + u^{2}} = 0, \\ \frac{c b u}{h + u^{2}} - d - g u = 0 . \end{matrix}

(4.1)

By performing a transformation on the second equation, we find that the component u of positive equilibrium point (u,v) meets the following equation

p (u) = g u^{3} + d u^{2} + (g h - c b) u + d h = 0

(4.2)

while the positive component

v = \frac{a}{b} (1 - \frac{u}{k}) (h + u^{2})

. Therefore, the problem of finding positive equilibrium points of the system (1.3) is transferred to that of solving the positive solutions of the equation (4.2). It is easy to derive

p^{^{'}} (u) = 3 g u^{2} + 2 d u + g h - c b, p^{^{''}} (u) = 6 g u + 2 d .

(4.3)

Obviously,

p^{^{''}} (u) > 0

always holds for

u > 0

. This implies

p^{^{'}} (u)

is monotonically increasing for

u > 0

. Now consider the solutions of

p (u) = 0

according to the following two cases.

Case 1: $g h - c b \geq 0$ . Then $p^{^{'}} (u) > 0$ , indicating that $p (u)$ is monotonically increasing. Again $p (0) = d h > 0$ . Therefore, there are no positive solutions of $p (u) = 0$ for $g h - c b \geq 0$ , which then implies that the system (1.3) has no positive equilibrium points.
Case 2: $g h - c b < 0$ . Then $p^{^{'}} (u) = 0$ has a unique positive solution, denoted by $u^{*}$ , where $u^{*} = \frac{- d + \sqrt{d^{2} - 3 g (g h - c b)}}{3 g}$ . Furthermore, since $p^{^{'}} (u)$ is monotonically increasing, we can conclude that $p (u)$ is monotonically decreasing in the interval $(0, u^{*})$ whereas monotonically increasing in the interval $(u^{*}, + \infty)$ . So, the function $p (u)$ takes the minimum at $u = u^{*}$ for $u \in (0, \infty)$ . Substituting $u^{*}$ into (4.2), we obtain

$\begin{matrix} p (u^{*}) = & \frac{1}{27 g^{2}} [R^{3} + 3 (3 h g^{2} - 3 b c g - d^{2}) R + 3 (d^{2} + 3 b c d g + 6 d h g^{2})] \\ = & \frac{1}{27 g^{2}} [- 2 R^{3} + 3 (d^{2} + 3 b c d g + 6 d h g^{2})] = \frac{2}{27 g^{2}} (R_{0}^{3} - R^{3}), \end{matrix}$

where $R = \sqrt{d^{2} - 3 g (g h - c b)}$ and $R_{0} = \sqrt[3]{\frac{3}{2} (d^{2} + 3 b c d g + 6 d h g^{2})}$ . Then we can discuss the positive solution of $p (u) = 0$ in view of the following three subcases:
Subcase 1. $p (u^{*}) > 0 ⟺ R < R_{0}$ . This means that the equation $p (u) = 0$ has no positive roots.
Subcase 2. $p (u^{*}) = 0 ⟺ R = R_{0}$ . This indicates that there is only one positive solution $u^{*}$ of the equation $p (u) = 0$ .
Subcase 3. $p (u^{*}) < 0 ⟺ R > R_{0}$ . This means that there are two positive roots of the equation $p (u) = 0$ , denoted by $u_{1}$ and $u_{2}$ . Namely,

$\begin{matrix} u_{1} = \frac{- d + \sqrt{R} (c o s (\frac{o}{3}) - \sqrt{3} s i n (\frac{o}{3}))}{3 g}, \\ u_{2} = \frac{- d + \sqrt{R} (c o s (\frac{o}{3}) + \sqrt{3} s i n (\frac{o}{3}))}{3 g}, \end{matrix}$

where $o = a r c c o t (J)$ , $J = \frac{2 d R^{2} - 3 g T}{2 R^{3}} (J \in (- 1, 1))$ and $T = d (g h - c b) - 9 g h d$ . Evidently, $0 < u_{1} < u^{*} < u_{2}$ .

Denote the two positive equilibria as

Q_{i} (u_{i}, v_{i})

u_{i} < k, i = 1, 2

. Summarizing the above analysis, we can obtain the following result.

Theorem 4.1.

Let

R, R_{0}, u^{*}, u_{1}, u_{2}

be respectively defined in Case 2 and Case 3. For the existence of equilibrium point of the system (1.3), the following statements hold.

Regardless of any value of parameters taking, the system (1.3) always has a trivial equilibrium point $Q_{0} (0, 0)$ and a boundary equilibrium point $Q_{k} (k, 0)$ .
When $g h - c b \geq 0$ , the system (1.3) does not have positive equilibrium points.
When $g h - c b < 0$ , we further have the following conclusions.
If $R_{0} > R$ , then the system (1.3) does not have positive equilibrium points.

(b)

R_{0} = R

, then, for

0 < k \leq u^{*}

, the system (1.3) does not have positive equilibrium points; for

u^{*} < k

, the system (1.3) has one positive equilibrium point

Q_{*} (u^{*}, v^{*})

(c)

R_{0} < R

, then, for

0 < k \leq u_{1}

, the system (1.3) does not have positive equilibrium points; for

u_{1} < k \leq u_{2}

hold, the system (1.3) has only one positive equilibrium point

Q_{1} (u_{1}, v_{1})

; for

u_{2} < k

, the system (1.3) has two positive equilibrium points

Q_{1} (u_{1}, v_{1})

and

Q_{2} (u_{2}, v_{2})

Next we analyze the stability of these equilibrium points of the system (1.3).

4.2. Stability of Equilibrium Point

The Jacobian matrix of the system (1.3) at any equilibrium

Q (u, v)

is as follows

J (u, v) = (\begin{matrix} a (1 - \frac{2 u}{k}) - \frac{b v}{h + u^{2}} + \frac{2 b u^{2} v}{{(h + u^{2})}^{2}} & - \frac{b u}{h + u^{2}} \\ \frac{b c v (h - u^{2})}{{(h + u^{2})}^{2}} - g v & \frac{b c u}{h + u^{2}} - d - g u \end{matrix}) .

4.2.1. The Stability of Trivial Equilibrium Point $Q_{0} (0, 0)$

Theorem 4.2.

The trivial equilibrium point

Q_{0} (0, 0)

is a saddle.

Proof.

Substituting the trivial equilibrium point

Q_{0} (0, 0)

into the Jacobian matrix

J (u, v)

, we obtain

J (Q_{0}) = (\begin{matrix} a & 0 \\ 0 & - d \end{matrix}),

it is easy to see that the Jacobian matrix

J (Q_{0})

has two eigenvalues:

λ_{1} = a > 0

and

λ_{2} = - d < 0

. Since

| a r g (λ_{1}) | = 0 < \frac{α π}{2}

and

| a r g (λ_{2}) | = π > \frac{α π}{2}

, the trivial equilibrium point

Q_{0}

is a saddle. □

4.2.2. The Stability of Boundary Equilibrium $Q_{k} (k, 0)$

Theorem 4.3.

The boundary equilibrium point

Q_{k} (k, 0)

is a stable node for

\frac{c b k}{h + k^{2}} - g k < d

while a saddle for

\frac{c b k}{h + k^{2}} - g k > d

Proof.

Substituting boundary equilibrium point

Q_{k} (k, 0)

into the Jacobian matrix

J (u, v)

, we have

J (Q_{k}) = - a \frac{- b k}{h + k^{2}} [5 p t] 0 \frac{c b k}{h + k^{2}} - d - g k .

Now divide into the following two cases for discussion:

Case 1: $\frac{c b k}{h + k^{2}} - g k > d$ . Then we obtain the two eigenvalues of the Jacobian matrix $J (Q_{k})$ : $λ_{1} = - a < 0$ and $λ_{2} = \frac{c b k}{h + k^{2}} - d - g k > 0$ . Thereout, $| a r g (λ_{1}) | = π > \frac{α π}{2}$ and $| a r g (λ_{2}) | = 0 < \frac{α π}{2}$ . So, the boundary equilibrium point $Q_{k}$ is a saddle.
Case 2: $\frac{c b k}{h + k^{2}} - g k < d$ . Then the two eigenvalues of the Jacobian matrix $J (Q_{k})$ are $λ_{1} = - a < 0$ and $λ_{2} = \frac{c b k}{h + k^{2}} - d - g k < 0$ . Because of $| a r g (λ_{1}) | = π > \frac{α π}{2}$ and $| a r g (λ_{2}) | = π > \frac{α π}{2}$ , the boundary equilibrium point $Q_{k}$ is a stable node.

□

4.2.3. The Stability of Positive Equilibrium $Q_{i} (u_{i}, v_{i}) (i = 1, 2)$

Theorem 4.4.

The positive equilibrium point

Q_{1} (u_{1}, v_{1})

is stable for

k > \frac{h + 3 u_{1}^{2}}{2 u_{1}}

and unstable for

k < \frac{h + 3 u_{1}^{2}}{2 u_{1}}

; the postive equilibrium point

Q_{2} (u_{2}, v_{2})

is always a saddle point.

Proof.

For readers’ better comprehension, let’s begin to analyze the stability of the positive equilibrium point

Q_{2} (u_{2}, v_{2})

Substituting the point

Q_{2} (u_{2}, v_{2})

into the Jacobian matrix

J (u, v)

, one obtains

J (Q_{2}) = (\begin{matrix} - a \frac{u_{2}}{k} + \frac{2 b u_{2}^{2} v_{2}}{{(h + u_{2}^{2})}^{2}} & - \frac{b u_{2}}{h + u_{2}^{2}} \\ \frac{b c v_{2} (h - u_{2}^{2})}{{(h + u_{2}^{2})}^{2}} - g v_{2} & 0 \end{matrix}),

from which, we can easily derive the following result

\begin{matrix} | J (Q_{2}) | = \frac{b u_{2} v_{2}}{h + u_{2}^{2}} (\frac{b c (h - u_{2}^{2})}{{(h + u_{2}^{2})}^{2}} - g) . \end{matrix}

(4.4)

From (4.2), we can deduce

h = \frac{b c u_{2}}{g u_{2} + d} - u_{2}^{2} .

(4.5)

Substituting (4.5) into (4.4) obtains

| J (Q_{2}) | = \frac{(g u_{2} + d) v_{2}}{b c^{2} u_{2}} (b c d - 2 g^{2} u_{2}^{3} - 4 g d u_{2}^{2} - 2 d^{2} u_{2}) .

(4.6)

Let

q (u_{2}) = b c d - 2 g^{2} u_{2}^{3} - 4 g d u_{2}^{2} - 2 d^{2} u_{2}

. Since

p^{^{'}} (u^{*}) = 0

p (u^{*}) < 0

and

q (u_{2})

is monotonically decreasing, we can obtain

\begin{matrix} q (u_{2}) < q (u^{*}) & = b c d - 2 g^{2} {u^{*}}^{3} - 4 g d {u^{*}}^{2} - 2 d^{2} u^{*} \\ = g (d h - 2 g {u^{*}}^{3} - d {u^{*}}^{2}) \\ < g (- 2 g {u^{*}}^{3} - d {u^{*}}^{2} - g {u^{*}}^{3} - d {u^{*}}^{2} - (g h - c b) u^{*}) \\ = g u^{*} (- 3 g {u^{*}}^{2} - 2 d u^{*} - g h + c b) = 0 . \end{matrix}

(4.7)

This verifies that

| J (Q_{2}) | < 0

holds if

Q_{2}

exists, which reads

λ_{1} λ_{2} < 0

. Accordingly,

λ_{1} > (<) 0 \Rightarrow | a r g (λ_{1}) | < (>) \frac{α π}{2}

and

λ_{2} < (>) 0 \Rightarrow | a r g (λ_{1}) | > (<) \frac{α π}{2}

. Thus the postive equilibrium point

Q_{2} (u_{2}, v_{2})

is always a saddle.

Similarly, for the postive equilibrium point

Q_{1} (u_{1}, v_{1})

, we have

\begin{matrix} q (u_{1}) & = b c d - 2 g^{2} u_{1}^{3} - 4 g d u_{1}^{2} - 2 d^{2} u_{1} \\ > g (d h - 2 g {u^{*}}^{3} - d {u^{*}}^{2}) \\ > g u^{*} (- 3 g {u^{*}}^{2} - 2 d u^{*} - g h + c b) = 0 . \end{matrix}

(4.8)

So,

| J (Q_{1}) | > 0

, which reads

λ_{1} λ_{2} > 0

. In order to determine the signs of

λ_{1}

and

λ_{2}

, we need further consider the sign of the trace of matrix

J (Q_{1})

. Note that the trace of

J (Q_{1})

t r (J (u_{1}, v_{1})) = - a \frac{u_{1}}{k} + \frac{2 b u_{1}^{2} v_{1}}{{(h + u_{1})}^{2}}

. Notice

\frac{c b u_{1} v_{1}}{h + u_{1}^{2}} - d v_{1} - g u_{1} v_{1} = 0

and

v_{1} = \frac{a}{b} (1 - \frac{u_{1}}{k}) (h + u_{1}^{2})

. So,

t r (J (u_{1}, v_{1})) = \frac{2 a u_{1}^{2}}{k (h + u_{1}^{2})} (k - \frac{h + 3 u_{1}^{2}}{2 u_{1}}) > (=, <) 0 \Leftrightarrow k > (=, <) \frac{h + 3 u_{1}^{2}}{2 u_{1}} .

Therefore, we can conclude: if

k < \frac{h + 3 u_{1}^{2}}{2 u_{1}}

, then

λ_{1} < 0 (\Rightarrow | a r g (λ_{1}) | > \frac{α π}{2}

) and

λ_{2} < 0 (\Rightarrow | a r g (λ_{2}) | > \frac{α π}{2}

), so, the system (1.3) is stable at

Q_{1} (u_{1}, v_{1})

; if

k > \frac{h + 3 u_{1}^{2}}{2 u_{1}}

, then

λ_{1} > 0 (\Rightarrow | a r g (λ_{1}) | = 0 < \frac{α π}{2}

) and

λ_{2} > 0 (\Rightarrow | a r g (λ_{2}) | = 0 < \frac{α π}{2}

), hence the system (1.3) is unstable at

Q_{1} (u_{1}, v_{1})

For readers’ convenience, we summarize the stability of equilibrium points of the system (1.3) in Table 3. □

4.3. Bifurcation Analysis

In this section, we utilize Theorem 2.4 to investigate the bifurcations occurring at point

Q_{1} (u_{1}, v_{1})

of the fractional-order system (1.3).

In the third section, we see that the Jacobian matrix of the system (1.3) at the point

Q_{1} (u_{1}, v_{1})

is as follows:

J (Q_{1}) = (\begin{matrix} - a \frac{u_{1}}{k} + \frac{2 b u_{1}^{2} v_{1}}{{(h + u_{1}^{2})}^{2}} & - \frac{b u_{1}}{h + u_{1}^{2}} \\ \frac{c b v_{1} (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g v_{1} & 0 \end{matrix}) .

The characteristic equation of the Jacobian matrix

J (Q_{1})

is given by

λ^{2} - (- a \frac{u_{1}}{k} + \frac{2 b u_{1}^{2} v_{1}}{{(h + u_{1}^{2})}^{2}}) λ + \frac{b u_{1}}{h + u_{1}^{2}} (\frac{c b v_{1} (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g v_{1}) = 0 .

(4.9)

Substituting

v_{1} = \frac{a}{b} (1 - \frac{u_{1}}{k}) (h + u_{1}^{2})

into equation (4.9), we have

\begin{matrix} λ^{2} - a u_{1} (\frac{2 k u_{1} - 3 u_{1}^{2} - h}{k (h + u_{1}^{2})}) λ + a u_{1} (1 - \frac{u_{1}}{k}) (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g) = 0 . \end{matrix}

(4.10)

Take k as bifurcation parameter of the system (1.3). If k takes a critical value

k_{0} > 0

such that the corresponding eigenvalues

λ_{k_{0}} = r e^{i γ}

, where

γ = \pm \frac{α π}{2}

, then a bifurcation occurs. Now we look for

k_{0}

such that

λ_{k_{0}}

satisfies the equation (4.10).

Substituting

λ_{k_{0}}

into (4.10), we can obtain the following equation

\begin{matrix} r^{2} e^{2 i γ} - a u_{1} (\frac{2 k_{0} u_{1} - 3 u_{1}^{2} - h}{k_{0} (h + u_{1}^{2})}) r e^{i γ} + a u_{1} (1 - \frac{u_{1}}{k_{0}}) (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g) = 0 . \end{matrix}

Namely,

\begin{matrix} r^{2} (c o s (2 γ) + i s i n (2 γ)) - a u_{1} (\frac{2 k_{0} u_{1} - 3 u_{1}^{2} - h}{k_{0} (h + u_{1}^{2})}) r (c o s γ + i s i n γ) \\ + a u_{1} (1 - \frac{u_{1}}{k_{0}}) (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g) = 0 . \end{matrix}

Hence,

\begin{matrix} \begin{matrix} \{\begin{matrix} r^{2} c o s (2 γ) - a u_{1} (\frac{2 k_{0} u_{1} - 3 u_{1}^{2} - h}{k_{0} (h + u_{1}^{2})}) r c o s γ + a u_{1} (1 - \frac{u_{1}}{k_{0}}) (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g) = 0, \\ r^{2} s i n (2 γ) - a u_{1} (\frac{2 k_{0} u_{1} - 3 u_{1}^{2} - h}{k_{0} (h + u_{1}^{2})}) r s i n γ = 0 . \end{matrix} \end{matrix} . \end{matrix}

(4.11)

Since we are interested in non-zero solutions for r, from the second equation of (4.11) we can derive

r = a u_{1} (\frac{2 k_{0} u_{1} - 3 u_{1} - h}{2 c o s γ k_{0} (h + u_{1}^{2})})

, after which is substituted into the first equation of (4.11), one has

{(\frac{2 k_{0} u_{1} - 3 u_{1}^{2} - h}{k_{0} (h + u_{1}^{2})})}^{2} \frac{- a^{2} u_{1}^{2}}{4 c o s^{2} γ} + a u_{1} (1 - \frac{u_{1}}{k_{0}}) (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g) = 0 .

So,

a u_{1} {(\frac{2 k_{0} u_{1} - 3 u_{1}^{2} - h}{k_{0} (h + u_{1}^{2})})}^{2} = 4 c o s^{2} γ (1 - \frac{u_{1}}{k_{0}}) (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g),

namely,

\begin{matrix} ω_{1} k_{0}^{2} - ω_{2} k_{0} + ω_{3} = 0, \end{matrix}

(4.12)

where

\begin{matrix} ω_{1} = 4 a u_{1}^{3} - 4 c o s^{2} γ (c b (h - u_{1}^{2}) - g {(h + u_{1}^{2})}^{2}), \\ ω_{2} = 4 a u_{1}^{2} (3 u_{1}^{2} + h) - 4 c o s^{2} γ u_{1} (c b (h - u_{1}^{2}) - g {(h + u_{1}^{2})}^{2}), \\ ω_{3} = a u_{1} {(3 u_{1}^{2} + h)}^{2} > 0 . \end{matrix}

| J (Q_{1}) | > 0

implies

c b (h - u_{1}^{2}) - g {(h + u_{1}^{2})}^{2} > 0

. Let

S_{0} = \frac{a {u_{1}}^{3}}{c b (h - u_{1}^{2}) - g {(h + u_{1}^{2})}^{2}}

. Then

S_{0} > 0

. After a lengthy and tedious calculation, we can classify the following three cases for further discussion:

Case 1: $c o s^{2} γ > S_{0}$ . Then we have $ω_{1} < 0$ . Due to $k_{0} > 0$ , we can obtain $k_{0} = \frac{ω_{2} - \sqrt{ω_{2}^{2} - 4 ω_{1} ω_{3}}}{2 ω_{1}}$ .
Case 2: $c o s^{2} γ = S_{0}$ . Then $ω_{1} = 0$ . Noticing $k_{0} > 0$ , we can obtain $k_{0} = \frac{ω_{3}}{ω_{2}}$ .
Case 3: $c o s^{2} γ < S_{0}$ . Then we have $ω_{1} > 0$ and $ω_{2} > 0$ . Calculate $ω_{2}^{2} - 4 ω_{1} ω_{3}$ to obtain

$\begin{matrix} ω_{2}^{2} - 4 ω_{1} ω_{3} \\ = 16 u_{1} c o s^{2} γ [u_{1} c o s γ^{2} (c b (h - u_{1}^{2}) - g (h + u_{1}^{2})) + a (3 u_{1}^{2} + h) (u_{1}^{2} + h)] \\ > 0 . \end{matrix}$

Then we can derive that $k_{0}$ has two values $\frac{ω_{2} \pm \sqrt{ω_{2}^{2} - 4 ω_{1} ω_{3}}}{2 ω_{1}}$ .

Regardless of any case, the critical value

k_{0}

always esixts. Next, we prove that the system (1.3) satisfies the conditions of Theorem 2.4 at the positive equilibrium point

Q_{1} (u_{1}, v_{1})

From the existence of

k_{0}

, we see that

| a r g (λ_{i} (k_{0})) | = \frac{α π}{2} (i = 1, 2)

, hence, the first condition in Theorem 2.4 holds true. Because the Jacobian matrix of the system (1.3) has only two eigenvalues, we do not need to consider the second condition in Theorem 2.4. Next, we focus on proving that the system (1.3) satisfies the third condition of Theorem 2.4. Taking the derivative of equation (4.10) with respect to k to obtain

\begin{matrix} 2 λ \frac{d λ}{d k} - a u_{1} (\frac{2 u_{1}}{h + u_{1}^{2}} - \frac{3 u_{1}^{2} + h}{k (h + u_{1}^{2})}) \frac{d λ}{d k} - a u_{1} \frac{3 u_{1}^{2} + h}{k^{2} (h + u_{1}^{2})} λ + \\ \frac{a u_{1}^{2}}{k^{2}} (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g) = 0 . \end{matrix}

(4.13)

Thus,

\begin{matrix} \frac{d λ}{d k} = \frac{\frac{a u_{1} (3 u_{1}^{2} + h)}{k^{2} (h + u_{1}^{2})} λ - \frac{a u_{1}^{2}}{k^{2}} (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g)}{2 λ + \frac{3 a u_{1}^{3} + a u_{1} h - 2 a k u_{1}^{2}}{k (h + u_{1}^{2})}} \end{matrix}

(4.14)

It suffices for us to verify

λ_{1, k_{0}} = r e^{i \frac{α π}{2}}

. Substituting

k = k_{0}

and

λ_{1, k_{0}} = r e^{i \frac{α π}{2}}

into the right side of (4.14) gets

\begin{matrix} \frac{d λ}{d k} |_{k = k_{0}} & = \frac{\frac{a u_{1} (3 u_{1}^{2} + h)}{k_{0}^{2} (h + u_{1}^{2})} r e^{i γ} - \frac{a u_{1}^{2}}{k_{0}^{2}} (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g)}{2 r e^{i γ} + \frac{3 a u_{1}^{3} + a u_{1} h - 2 a k_{0} u_{1}^{2}}{k_{0} (h + u_{1}^{2})}}, \\ = \frac{\frac{a u_{1} (3 u_{1}^{2} + h)}{k_{0}^{2} (h + u_{1}^{2})} r (c o s γ + i s i n γ) - \frac{a u_{1}^{2}}{k_{0}^{2}} (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g)}{2 r (c o s γ + i s i n γ) + \frac{3 a u_{1}^{3} + a u_{1} h - 2 a k_{0} u_{1}^{2}}{k_{0} (h + u_{1}^{2})}}, \\ = \frac{ψ_{1} + ψ_{2} i}{ψ_{3}^{2} + ψ_{4}^{2}} \end{matrix}

(4.15)

where

\begin{matrix} ψ_{1} = (\frac{a u_{1} (3 u_{1}^{2} + h)}{k_{0}^{2} (h + u_{1}^{2})} r c o s γ - \frac{a u_{1}^{2}}{k_{0}} (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g)) \\ \times (2 r c o s γ + \frac{3 a u_{1}^{3} + a u_{1} h - 2 a k_{0} u_{1}^{2}}{k_{0} (h + u_{1}^{2})}) + \frac{a u_{1} (3 u_{1}^{2} + h)}{k_{0}^{2} (h + u_{1}^{2})} 2 r^{2} s i n^{2} γ, \\ ψ_{2} = (\frac{a (3 u_{1}^{2} + h) (3 u_{1}^{2} + h - 2 k_{0} u_{1})}{k_{0}^{3} {(h + u_{1}^{2})}^{2}} + \frac{2}{k_{0}} (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g)) a u_{1}^{2} r s i n γ, \\ ψ_{3} = 2 r c o s γ + \frac{3 a u_{1}^{3} + a u_{1} h - 2 a k_{0} u_{1}^{2}}{k_{0} (h + u_{1}^{2})}, ψ_{4} = 2 r s i n γ . \end{matrix}

Denote

λ (k) = m (k) + i n (k)

, then

a r g (λ (k)) = a r c t a n (\frac{n}{m})

. By differentiating

a r g (λ (k))

with respect to k, we get

\begin{matrix} \frac{d}{d k} a r g (λ (k)) = \frac{m n^{^{'}} - n m^{^{'}}}{m^{2} + n^{2}} = \frac{W (m, n)}{{| λ (k) |}^{2}} \end{matrix}

(4.16)

where

W (m, n) = |\begin{matrix} m & n \\ m^{^{'}} & n^{^{'}} \end{matrix}|

Therefore,

\begin{matrix} \frac{d}{d k} a r g (λ (k)) |_{k = k_{0}} & = \frac{W (m (k_{0}), n (k_{0}))}{| λ (k_{0}) |^{2}} \\ = \frac{1}{| λ (k_{0}) |^{2}} |\begin{matrix} m (k_{0}) & n (k_{0}) \\ m^{^{'}} (k_{0}) & n^{^{'}} (k_{0}) \end{matrix}| \\ = \frac{1}{| λ (k_{0}) |^{2}} |\begin{matrix} r c o s γ & r s i n γ \\ \frac{ψ_{1}}{ψ_{3}^{2} + ψ_{4}^{2}} & \frac{ψ_{2}}{ψ_{3}^{2} + ψ_{4}^{2}} \end{matrix}| . \end{matrix}

(4.17)

We can easily deduce that when

k_{0}

exists,

| λ (k_{0}) |^{2} \neq \infty

hold true.

Next, we prove the conditions under which

W (m, n) (k_{0}) \neq 0

holds true.

In fact,

\begin{matrix} W (m, n) (k_{0}) = |\begin{matrix} r c o s γ & r s i n γ \\ \frac{ψ_{1}}{ψ_{3}^{2} + ψ_{4}^{2}} & \frac{ψ_{2}}{ψ_{3}^{2} + ψ_{4}^{2}} \end{matrix}| \neq 0 \\ ⟺ \frac{1}{ψ_{3}^{2} + ψ_{4}^{2}} (r c o s γ ψ_{2} - r s i n γ ψ_{1}) \neq 0 \\ ⟺ c o s γ ψ_{2} - s i n γ ψ_{1} \neq 0 \\ ⟺ 4 u_{1} r c o s γ (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g) + \\ u_{1} (\frac{c b (h - u_{1}^{2})}{{(h + u_{1}^{2})}^{2}} - g) (\frac{3 a u_{1}^{3} + a u_{1} h - 2 a k_{0} u_{1}^{2}}{k_{0} (h + u_{1}^{2})}) - 2 r^{2} \frac{3 u_{1}^{2} + h}{k_{0} (h + u_{1}^{2})} \neq 0, \\ ⟺ k_{0} \neq k_{h}, \end{matrix}

(4.18)

where

k_{h} = \frac{2 r^{2} (3 u_{1}^{2} + h) {(h + u_{1}^{2})}^{2} - u_{1} (c b (h - u_{1}^{2}) - g (h + u_{1}^{2})) (3 a u_{1}^{3} + a u_{1} h)}{u_{1} (c b (h - u_{1}^{2}) - g (h + u_{1}^{2})) (4 r c o s γ (h + u_{1}^{2}) - 2 a u_{1}^{2})} .

(4.19)

This is true by adding the assumption

k_{0} \neq k_{h}

. So, summarizing the above analysis, one has the following results.

Theorem 4.5.

Suppose that all parameters in the system (1.3) are positive. Let

R_{0}, R, k_{0}, k_{h}

be defined as above. If

g h - c b < 0

R_{0} < R

u_{1} < k

k_{0} \neq k_{h}

, then the system (1.3) undergoes a fractional Hopf bifurcation at point

Q_{1} (u_{1}, v_{1})

5. Numerical Simulation

In this section, we perform numerical simulations for the dynamical behaviors of the system (1.3) using Matlab, aiming to provide readers with a more intuitive understanding to the dynamics of the system (1.3).

In Figure 1, the parameter values in the system (1.3) take as

r = 0.015

k = 0.3

a = 0.1

b = 0.9

d = 0.3

e = 0.2

m = 0.1

and

α = 0.98

. Figure 1(a) displays the trajectories of the system (1.3) starting from different points. Although it can be observed that the system (1.3) exhibits a saddle at the origin, it is not entirely clear. To provide a more clear representation of the behavior of the system (1.3) at the origin, we construct the streamline plots, depicted in Figure 1(b). From Figure 1(b), it is evident that the system (1.3) possesses a saddle at the origin.

In Figure 2(a)-(b), the parameter values of the system (1.3) are

r = 0.9

k = 10

b = 0.2

a = 3

m = 0.9

d = 0.2

e = 0.2

and

α = 0.98

, which satisfy

\frac{c b k}{h + k^{2}} - d - g k < 0

. Figure 2(a) shows the behavior of the system (1.3) regardless of starting from the point

(30, 10)

(30, 12)

(30, 14)

, it will eventually converge to the point (10, 0). Figure 2(b) demonstrates how the populations of prey and predator change for time when starting from the point

(30, 10)

. We can observe that as time increases, the population of prey tends to 10, while the population of predator goes extinct. In Figure 2(c), the parameter values of the system (1.3) are

r = 0.6

k = 1

b = 0.5

a = 0.1

m = 0.6

d = 0.1

e = 0.1

and

α = 0.98

, which satisfy

\frac{c b k}{h + k^{2}} - d - g k > 0

. We can clearly see that the system (1.3) exhibits a saddle at the boundary equilibrium point

(1, 0)

For the positive equilibrium point of the system (1.3), we are interested in its bifurcation behavior. In Figure 3, the parameter values of the system (1.3) are

r = 0.6

b = 0.5

a = 0.1

m = 0.6

d = 0.1

e = 0.1

and

α = 0.98

. Figure 3(a) and (b) show that the positive equilibrium

Q_{1} (u_{1}, v_{1})

is a stable focus and an unstable focus when

k = 1

and

k = 10

, respectively. And we can see from Figure 3(b) that when k crosses the critical value, a stable limit cycle emerges, indicating the occurrence of a supercritical bifurcation in the system(1.3).

6. Conclusion

In this paper, we propose a fractional order predator-prey model with a Holling IV functional response and anti-predator behavior. We analyze the dynamical behavior of the model, including the feasibility, the existence of equilibrium points, the stability of equilibrium points and the possibility of bifurcations of the system. Numerical simulations are conducted, aiming to provide readers with a more intuitive understanding towards the dynamics of the system (1.3). By analyzing the dynamical behavior of the system (1.3), we can obtain the following conclusions:

(1) By analyzing the stability of the equilibrium point

Q_{0} (0, 0)

and conducting numerical simulations, we can determine that the equilibrium point

Q_{0} (0, 0)

is a saddle point. This implies that under any conditions existing in nature, the simultaneous extinction of predator and prey does not occur.

(2) Through the study of the dynamical behavior of the boundary equilibrium point

Q_{k} (k, 0)

and numerical simulations, we have found that when d is large, it leads to the extinction of predator. In this case, the prey population tends towards a stable density. On the other hand, when d is small, the extinction of predator does not occur, and the prey population tends towards a stable state. This indicates that when a detrimental condition for the survival of predator and prey arises in nature, predator may tend towards extinction, while the prey population, although it may decrease, does not tend towards extinction. Instead, it stabilizes at a certain level.

(3) Based on the analysis and numerical simulations of the positive equilibrium point

Q_{1} (u_{1}, v_{1})

, we can draw the following conclusions: When the parameter k exceeds a critical value, the system exhibits a stable limit cycle. This implies that the interaction between predator and prey leads to periodic oscillations. The presence of this limit cycle indicates that the system exhibits rich dynamic behavior, and under specific conditions, the populations of predator and prey undergo periodic fluctuations. Therefore, we can achieve a coexistence steady state and eliminate the limit cycle by reducing the environmental carrying capacity of the prey.

Author Contributions

All authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.

Funding

This work is partly supported by the National Natural Science Foundation of China (61473340), the Distinguished Professor Foundation of Qianjiang Scholar in Zhejiang Province (F703108L02), the Natural Science Foundation of Zhejiang University of Science and Technology ( F701108G14)

Data Availability Statement

There is no applicable data associated with this manuscript.

Conflicts of Interest

The authors declare that they have no competing interests.

References

Berryman, A.A. The orgins and evolution of predator-prey theory. Ecology 1992, 73, 1530–1535. [Google Scholar] [CrossRef]
Wang, W.; Chen, L. A Predator-Prey System with Stage-Structure for Predator. Computers Math. Applic. 1997, 33, 83–91. [Google Scholar] [CrossRef]
Ba, Z.; Li, X. Period-doubling bifurcation and Neimark-Sacker bifurcation of a discrete predator-prey model with Allee effect and cannibalism. Electronic Research Archive 2023, 31, 1405–1438. [Google Scholar] [CrossRef]
Liu, Y.; Li, X. Dynamics of a discrete predator-prey model with Holling-II functional response. International Journal of Biomathematics 2021, 14, 2150068. [Google Scholar] [CrossRef]
Qi, H.; Meng, X. Threshold behavior of a stochastic predator–prey system with prey refuge and fear effect. Applied Mathematics Letters 2021, 113, 106846. [Google Scholar] [CrossRef]
Blasius, B.; Rudolf, L.; et al. Long-term cyclic persistence in an experimental predator–prey system. Nature 2020, 577, 226–230. [Google Scholar] [CrossRef]
Mukherjee, D. Role of fear in predator–prey system with intraspecific competition. Mathematics and Computers in Simulation 2020, 177, 263–275. [Google Scholar] [CrossRef]
Qiu, H.; Guo, S.; et al. Stability and Bifurcation in a Predator–Prey System with Prey-Taxis. International Journal of Bifurcation and Chaos 2020, 30, 2050022. [Google Scholar] [CrossRef]
Perc, M.; Grigolini, P. Collective behavior and evolutionary games–An introduction,Chaos. Solitons & Fractals 2013, 56, 1–5. [Google Scholar]
Lima, S.L. Stress and Decision Making under the Risk of Predation: Recent Developments from Behavioral, Reproductive, and Ecological Perspectives. Advances in the study of behavior 1998, 27, 215–290. [Google Scholar]
Tollrian, R. Predator-Induced Morphological Defenses: Costs, Life History Shifts, and Maternal Effects in Daphnia Pulex. Ecology 1995, 76, 1691–1705. [Google Scholar] [CrossRef]
Choh, Y.; Lgnacio, M.; et al. Predator-prey role reversals, juvenile experience and adult antipredator behaviour. Laboratory of Applied Entomology 2012, 2, 728. [Google Scholar] [CrossRef]
Janssen, A.; Faraji, F.; et al. Interspecific infanticide deters predators. Ecology Letters 2002, 5, 490–494. [Google Scholar] [CrossRef]
Saito, Y. Prey kills predator: Counter-attack success of a spider mite against its specific phytoseiid predator. Experimental & Applied Acarology 1986, 2, 47–62. [Google Scholar]
Ives, A.; Dobson, A. Antipredator behavior and the population dynamics of simple predator-prey systems. The American Naturali 1987, 130, 431–447. [Google Scholar] [CrossRef]
Tang, B.; Xiao, Y. Bifurcation analysis of a predator–prey model with anti-predator behaviour. Chaos, Solitons & Fractals 2015, 70, 58–68. [Google Scholar]
Liouville. Troisième mémoire sur le développement des fonctions ou parties de fonctions en séries dont les divers termes sont assujettis à satisfaire à une même équation différentielle du second ordre, contenant un paramètre variable. Journal de Mathématiques Pures et Appliquées 1837, 2, 418–436. [Google Scholar]
Riesz, M. L’intégrale de Riemann-Liouville et le problème de Cauchy pour l’équation des ondes. Bulletin de la S. M. F. 1939, 67, 153–170. [Google Scholar] [CrossRef]
Caputo, M. Linear Models of Dissipation whose Q is almost Frequency Independent-II, Geophys. J. R. astr. 1976, 13, 529–539. [Google Scholar] [CrossRef]
Li, H.; Zhang, L.; et al. Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J. Appl. Math. Comput. 2017, 54, 435–449. [Google Scholar] [CrossRef]
Bonyah, E.; Atangana, A.; et al. A fractional model for predator-prey with omnivore. Chaos 2019, 29, 013136. [Google Scholar] [CrossRef]
Kumar, S.; Kumar, R.; et al. Chaotic behaviour of fractional predator-prey dynamical system. Chaos, Solitons and Fractals 2020, 135, 109811. [Google Scholar] [CrossRef]
Das, M.; Samanta, G. A delayed fractional order food chain model with fear effect and prey refuge. Mathematics and Computers in Simulation 2020, 20, 30217–2. [Google Scholar] [CrossRef]
Barman, D.; Roy, J.; et al. Impact of predator incited fear and prey refuge in a fractional order prey predator model. Chaos, Solitons and Fractals 2021, 142, 110420. [Google Scholar] [CrossRef]
Das, M.; Samanta, G. A prey-predator fractional order model with fear effect and group defense. International Journal of Dynamics and Control 2021, 9, 334–349. [Google Scholar] [CrossRef]
Yousef, F.; Yousef, A.; et al. Effects of fear in a fractional-order predator-prey system with predator density-dependent prey mortality. Chaos, Solitons and Fractals 2021, 145, 110711. [Google Scholar] [CrossRef]
Zhang, N.; Kao, Y.; et al. Impact of fear effect and prey refuge on a fractional order prey–predator system with Beddington–DeAngelis functional response. Chaos 2022, 32, 043125. [Google Scholar] [CrossRef]
Majumdar, P.; Mondal, B.; et al. Controlling of periodicity and chaos in a three dimensional prey predator model introducing the memory effect. Chaos, Solitons and Fractals 2022, 164, 112585. [Google Scholar] [CrossRef]
Kai, D. The analysis of fractional differential equations (an application-oriented exposition using differential operators of Caputo type); Springer Scienc & Business Media, 2010; pp. 237–244. [Google Scholar]
Cieck, M.; Yakar, C.; et al. Stability, Boundedness, and Lagrange Stability of Fractional Differential Equations with Initial Time Difference. The Scientific World Journal 2014, 2014, 939027. [Google Scholar]
Odibat, Z.; Shawagfeh, N. Generalized Taylor’s formula. Applied Mathematics and Computation 2007, 186, 286–293. [Google Scholar] [CrossRef]
Liang, S.; Wu, R.; et al. Laplace transform of fractional order differential equations. Electronic Journal of Differential Equations 2015, 2015, 1–15. [Google Scholar]
Kexue, L.; Jigen, P. Laplace transform and fractional differential equations. Applied Mathematics Letters 2011, 24, 2019–2023. [Google Scholar] [CrossRef]
Petráš. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation, Beijing, 2011.
Deshpande, A.; Daftardar-Gejji, V.; et al. On Hopf bifurcation in fractional dynamical systems. Chaos, Solitons and Fractals 2017, 98, 189–198. [Google Scholar] [CrossRef]

Figure 1. (a) shows the trajectories of the system (1.3) starting from points

(0.8, 0.4)

(0.7, 0.3)

, and

(0.6, 0.35)

, respectively; (b) represents the streamline plots of the system (1.3) at the origin.

Figure 1. (a) shows the trajectories of the system (1.3) starting from points

(0.8, 0.4)

(0.7, 0.3)

, and

(0.6, 0.35)

, respectively; (b) represents the streamline plots of the system (1.3) at the origin.

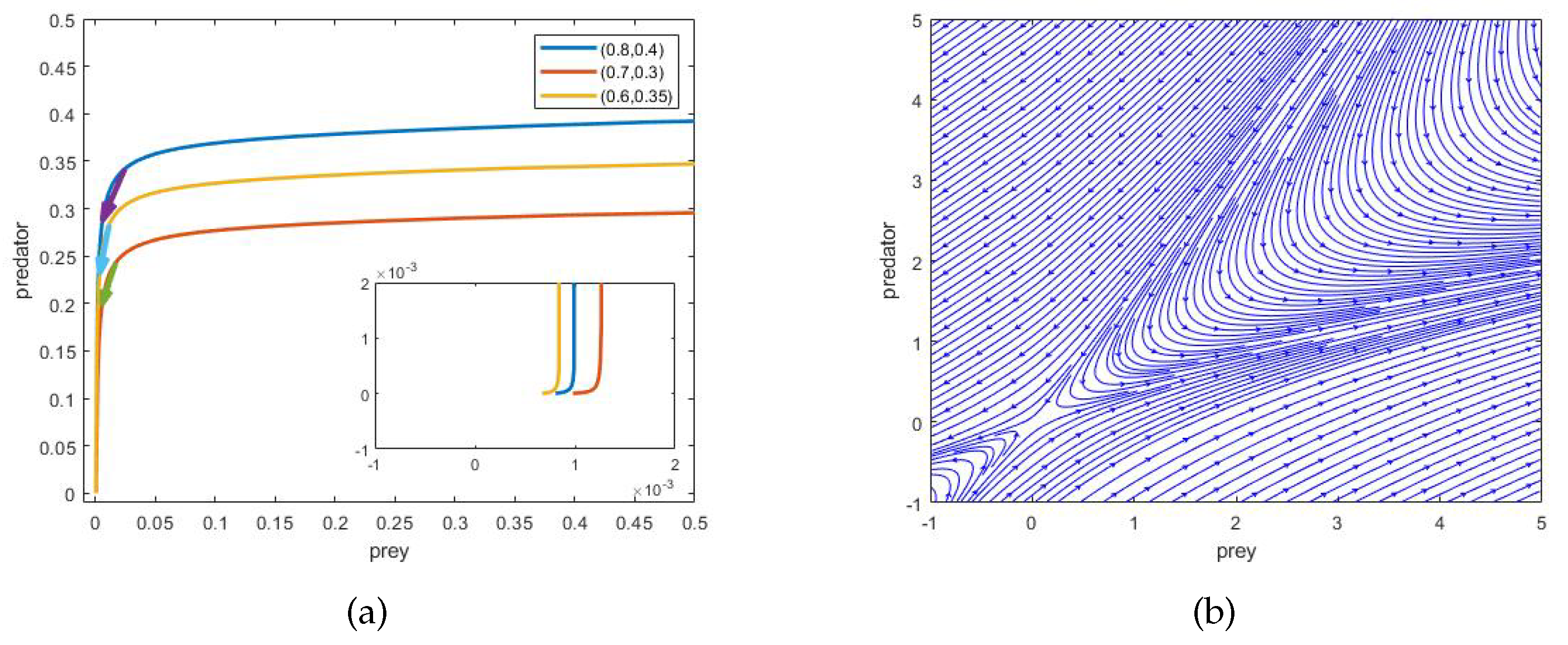
Figure 2. (a) when

\frac{c b k}{h + k^{2}} - d - g k < 0

, the property of the system (1.3) at the boundary equilibrium point (10,0); (b) shows starting from the point

(30, 10)

, the quantities of prey and predator vary with time; (c)when

\frac{c b k}{h + k^{2}} - d - g k > 0

, the property of the system (1.3) at the boundary equilibrium point (1,0).

Figure 2. (a) when

\frac{c b k}{h + k^{2}} - d - g k < 0

, the property of the system (1.3) at the boundary equilibrium point (10,0); (b) shows starting from the point

(30, 10)

, the quantities of prey and predator vary with time; (c)when

\frac{c b k}{h + k^{2}} - d - g k > 0

, the property of the system (1.3) at the boundary equilibrium point (1,0).

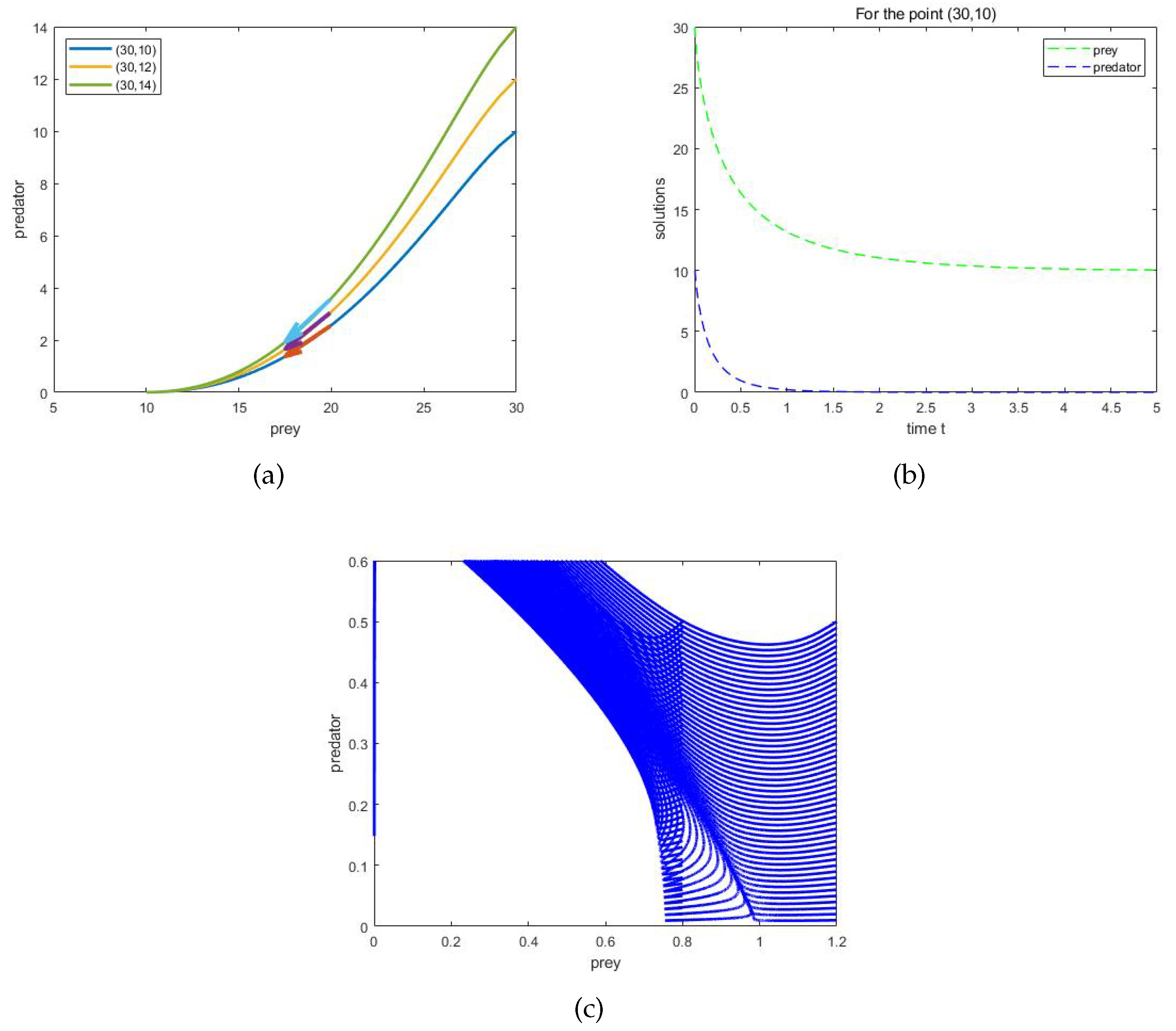
Figure 3. The existence of the supercritical Hopf bifurcation of the system (1.3) with the parameter values

r = 0.6

b = 0.5

a = 0.1

m = 0.6

d = 0.1

e = 0.1

α = 0.98

and

k = 1

for (a) while

k = 10

for (b).

Figure 3. The existence of the supercritical Hopf bifurcation of the system (1.3) with the parameter values

r = 0.6

b = 0.5

a = 0.1

m = 0.6

d = 0.1

e = 0.1

α = 0.98

and

k = 1

for (a) while

k = 10

for (b).

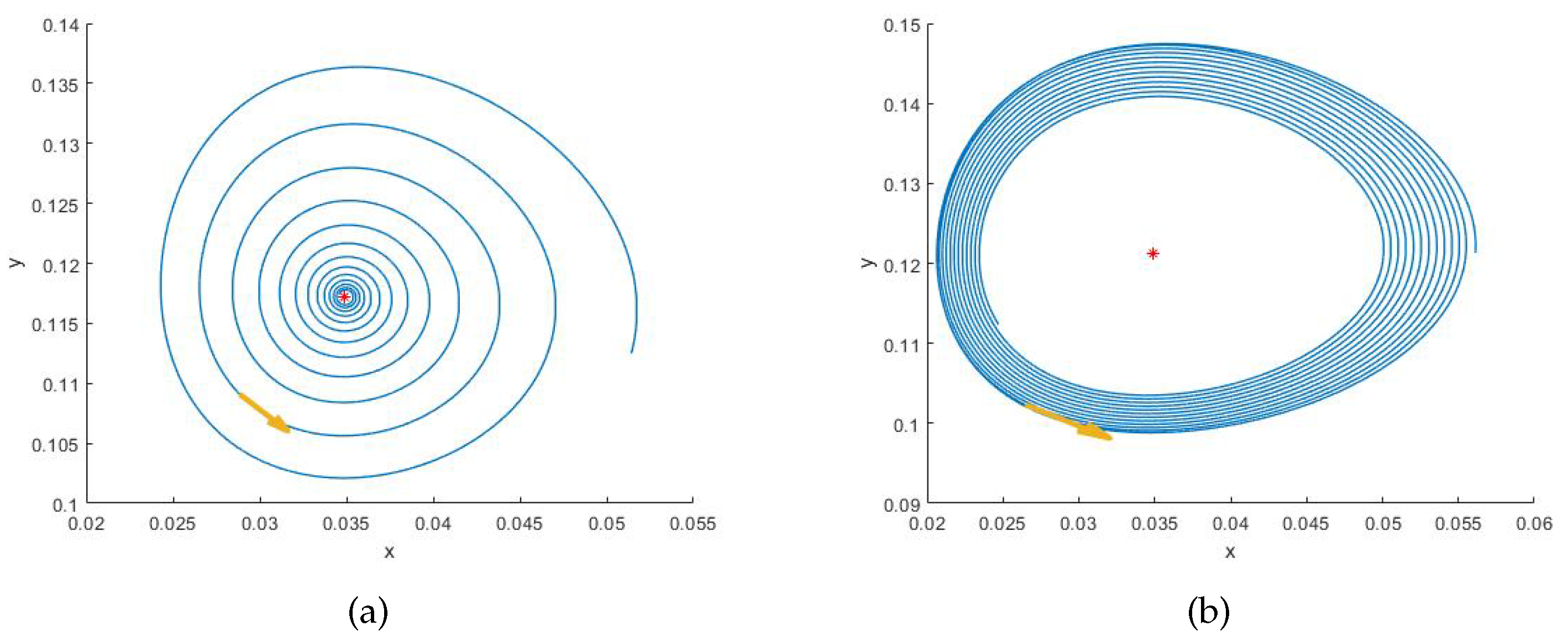
Table 1. Biological meanings of all parameters in the system (1.1).

Parameter	Meaning
x	Prey population density
y	Predator population density
$α > 0$	Natality of prey population
$k > 0$	Carrying capacity of the environment to prey
$β > 0$	Cost incurred by the prey as a result of anti-predator behavior
$γ > 0$	Effects resulting from the anti-predator behavior of prey
$\frac{q x}{1 + a x}, q > 0, a > 0$	Holling II functional response function
$b > 0$	Conversion rate of prey consumed into predator
$d > 0$	Death rate of predator population

Table 2. Biological meanings of parameters in the systems (1.2) and (1.3).

Parameter	Meaning
u	Prey population density
v	Predator population density
$a > 0$	Natality of prey population
$k > 0$	Carrying capacity of the environment to prey
$b > 0$	Predator’s capture rate
$c > 0$	Conversion rate of prey into predator
$\frac{b u}{h + u^{2}}$ , h>0	Holling type IV functional response function
$d > 0$	Death rate of predator
$g > 0$	Mortality rate of predator due to the anti-predator effects of prey
$0 < α \leq 1$	Order of fractional-order derivative

Table 3. The stability of equilibrium points of the system (1.3).

Point	Conditions	Properties
$Q_{0} (0, 0)$		saddle
$Q_{k} (k, 0)$	$d > \frac{b c k}{h + k^{2}} - g k$	stable
	$d < \frac{b c k}{h + k^{2}} - g k$	saddle
$Q_{1} (u_{1}, v_{1})$	$k < \frac{h + 3 u_{1}^{2}}{2 u_{1}}$	unstable
	$k > \frac{h + 3 u_{1}^{2}}{2 u_{1}}$	stable
$Q_{2} (u_{2}, v_{2})$		saddle

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Modeling and Dynamical Analysis of a Fractional Order Predator-Prey System with Anti-Predator Behaviour and Holling Type IV Functional Response

Abstract

1. Introduction

2. Preliminaries

3. Analysis of Well-Posedness of the System (1.3)

4. Stability and Bifurcation of the System (1.3)

4.1. Existence of Equilibrium Point

4.2. Stability of Equilibrium Point

4.2.1. The Stability of Trivial Equilibrium Point Q 0 ( 0 , 0 )

4.2.2. The Stability of Boundary Equilibrium Q k ( k , 0 )

4.2.3. The Stability of Positive Equilibrium Q i ( u i , v i ) ( i = 1 , 2 )

4.3. Bifurcation Analysis

5. Numerical Simulation

6. Conclusion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4.2.1. The Stability of Trivial Equilibrium Point $Q_{0} (0, 0)$

4.2.2. The Stability of Boundary Equilibrium $Q_{k} (k, 0)$

4.2.3. The Stability of Positive Equilibrium $Q_{i} (u_{i}, v_{i}) (i = 1, 2)$