Prerpints.org logo
Preprint
Article

The Accuracy Assessment of Lithospheric Density Models

Altmetrics

Downloads

107

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 August 2023

Posted:

22 August 2023

You are already at the latest version

Alerts
Abstract
The Earth’s synthetic gravitational and density models can be used to validate numerical procedures applied for a global (or large-scale regional) gravimetric forward and inverse modelling. Since the Earth’s lithospheric structure is better constrained by tomographic surveys than a deep mantle, most of existing 3-D density models describe only a lithospheric density structure, while 1-D density models are typically used to describe a deep mantle density structure below the lithosphere-asthenosphere boundary. The accuracy of currently available lithospheric density models is examined in this study. The error analysis is established to assess the accuracy of modelling the sub-lithospheric mantle geoid, while focusing on the largest errors (according to our estimates) that are attributed to lithospheric thickness and lithospheric mantle density uncertainties. Since a forward modelling of the sub-lithospheric mantle geoid comprises also numerical procedures of adding and subtracting gravitational contributions of similar density structures, the error propagation is derived for actual rather than random errors (that are described by the Gauss’ error propagation law). Possible systematic errors then either lessen or sum up after applying particular corrections to a geoidal geometry that are attributed to individual lithospheric density structures (such as sediments) or density interfaces (such as a Moho density contrast). The analysis indicates that errors in modelling of the sub-lithospheric mantle geoid attributed to lithospheric thickness and lithospheric mantle density uncertainties could reach several hundreds of meters, particularly at locations with the largest lithospheric thickness under cratonic formations. This numerical finding is important for a calibration and further development of synthetic density models of which mass equals the Earth’s total mass (excluding the atmosphere). Consequently, the (long-to-medium wavelength) gravitational field generated by a synthetic density model should closely agree with the Earth’s gravitational field.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

Gravimetric forward and inverse modelling techniques are essential numerical tools applied in physical geodesy and gravimetric geophysics. In physical geodesy applications, these methods are used to compute topographic and terrain gravity corrections in a gravimetric geoid modelling—e.g., [1,2,3,4,5,6,7,8,9,10,11] and compile isostatic gravity maps—e.g., [12]. In gravimetric geophysics, these methods are used to compile Bouguer and mantle gravity maps—e.g., [13,14,15,16,17,18]. Furthermore, numerous techniques have been developed and applied for a gravimetric interpretation of the Earth’s inner structure—e.g., [19,20,21].
Whereas the gravimetric inverse modelling is applied to determine an unknown density structure or density interface from observed gravity data, the gravimetric forward modelling is used to compute gravitational field quantities generated by a known density structure or density interface. Several different methods have been developed for a local and regional gravimetric forward modelling based on solving the Newton’s volume integral in the spatial domain by applying numerical, semi-analytical, and analytical methods—e.g., [2,[22,23,24,25,26,27,28,29,30,31,32]]. In global (and large-scale regional) applications, methods of solving the Newton’s volume integral in the spectral domain utilize a spherical harmonic analysis and synthesis of gravity and density structure models—e.g., [33,34,35,36,37,38,39,40,41,42].
The validation of accuracy and numerical efficiency of newly developed methods for a gravimetric forward and inverse modelling is often done by comparing results with solutions obtained from existing (and typically well-established) numerical methods and procedures. Alternatively, simple or more refined synthetic density models (designed for various configurations of different geometrical density bodies) have been more recently used for testing and validation of spatial methods developed for a local and regional gravimetric forward modelling and inversion by adopting a planar approximation. For global (or large-scale regional) applications, synthetic density models should mimic more realistically the Earth’s actual shape and inner density structure. Such synthetic density models have already been used to validate numerical techniques involved in a gravimetric geoid modelling—e.g., [43,44,45]. Other examples of possible applications could be given in studies of the sediment bedrock morphology—e.g., [46], the lithospheric and mantle density structure—e.g., [16,47], the crustal thickness—e.g., [16,18,[47,48,49,50,51,52], the dynamic and residual topography—e.g., [53,54,55], or the oceanic lithosphere thermal contraction and its isostatic rebalance—e.g., [56]. To construct a global synthetic density model that closely resembles the Earth’s shape and inner structure, available global topographic and density structure models could be used for this purpose together with additional models that provide information about the Earth’s inner structure (such as crust and lithospheric thickness models). Moreover, constraints have to be applied so that the mass of Earth’s synthetic model is equal to the Earth’s total mass (excluding the atmosphere), and the gravitational field generated by the Earth’s synthetic model closely agrees with the Earth’s gravitational field (in terms of a geoidal geometry, gravity, and gravity gradient).
A number of seismic velocities and mass density models have been developed based on the analysis of tomographic data, while incorporating geophysical, geochemical, and geothermal constraints—e.g., [57,58,59,60,61,62,63,64]; for an overview of these models see also Trabant [65]. A practical application of global 1-D density models, such as the PREM [58] or AK135-F [60], is limited by the absence of a lateral density information. To address this issue, 1-D reference density models could be refined by incorporating 2-D or 3-D global lithospheric and mantle density models to achieve a more realistic representation of the Earth’s inner density structure. Whereas reliable 3-D mantle density models are rare, a number of 3-D crustal and lithospheric density models have been developed and published. Nataf and Ricard [66] derived the crustal and upper-mantle density model based on the analysis of seismic data and additional constrains such as heat flow and chemical composition. Mooney et al. [67] compiled the CRUST5.0 global crustal model with a 5°×5° spatial resolution. Later, the updated global crustal model CRUST2.0 was compiled with a 2°×2° resolution by Bassin et al. [68]. The CRUST1.0 is the most recent version, complied globally with a 1°×1° resolution—e.g., [69]. The CRUST2.0 and CRUST1.0 incorporate also a lateral density structure within the uppermost mantle. Pasyanos et al. [70] compiled the LITHO1.0 global lithospheric model (including the asthenosphere). This model was prepared to fit the high-resolution (Love and Rayleigh) surface wave dispersion maps by using the CRUST1.0 crust data and the LLNL-G3D upper mantle model [71] as the a priori information. Compared to similar 3-D density and velocity models, this model provides also information on the lithosphere-asthenosphere boundary (LAB). Hirt and Rexer [72] constructed the Earth2014 global model consisting of topographic, bathymetric, inland bathymetric, and polar glacier bedrock relief datasets. Chen and Tenzer [73] compiled the Earth’s Spectral Crustal Model 180 (ESCM180) by augmenting the Earth2014 and CRUST1.0 models.
Since many parts of the world are not yet sufficiently covered by tomographic surveys, the refinement of 1-D reference density models by incorporating 2-D or 3-D global lithospheric and mantle density models is not simple. Moreover, the direct relation between seismic velocities and mass densities does not exist because a density distribution depends on many other factors (such us temperature, mineral composition, and pressure). In spite of these practical and theoretical limitations, the development of synthetic density models that more or less realistically approximate the Earth’s shape and inner density structure is essential for a more comprehensive assessment of gravimetric forward and inverse modelling techniques (then that based on using simplistic, typically geometric density models). Moreover, input data uncertainties should be known in order to realistically assess the accuracy of synthetic density models.
To inspect possibilities of refining the Earth’s synthetic density model, the accuracy of published lithospheric density models is assessed based on a novel approach presented in this study. This novel approach allows to formulate the error propagation and consequently provide rough error estimates in a gravimetric forward modelling that are attributed to lithospheric density and geometry uncertainties. A gravimetric forward modelling is applied to determine a long-wavelength geoidal geometry that is corrected for gravitational contributions of lithospheric density and thickness variations. Expressions for a gravimetric forward modelling are presented in Section 2, and then used to derive the error analysis in Section 3. Numerical results are briefly presented in Section 4, and the accuracy of results is discussed in Section 5. Major findings are concluded in Section 6.

2. Numerical model

We applied methods for a spherical harmonic analysis and synthesis of gravitational and lithospheric density models to compute the sub-lithospheric mantle geoid. Details on theoretical aspects are given below.

2.1. Geoid

The geoid height N is defined by—e.g., [74]
N ( Ω ) = T ( r g , Ω ) γ 0 ( φ )
where the disturbing potential T (i.e., the difference between values of the actual and normal gravity potential W and U respectively; T = W − U ) is stipulated at the geoid surface ( r g , Ω ) . The normal gravity γ 0 in Eq. (1) is computed at the ellipsoid surface according to Somigliana-Pizzetti’s theory [75,76] for the GRS80 [77] parameters. The 3-D position in Eq. (1) and thereafter is defined in the spherical coordinate system ( r , Ω ) , where r is the radius and Ω = ( φ , λ ) denotes the spherical direction with the spherical latitude φ and longitude λ . In the context of interpreting long-wavelength features in the geoidal geometry attributed to a sub-lithospheric mantle density structure, the disturbing potential T in Eq. (1) can approximately (cf. Wieczorek [19,78]; Tenzer et al., [79]) be computed by using the following expression—e.g., [74]
T ( r g , Ω ) ≅ GM R ∑ n = 0 n ¯ ∑ m = − n n T n , m Y n , m ( Ω )
where GM = 3986005 × 10 8 m3 s-2 is the geocentric gravitational constant, R = 6371 × 10 3 m is the Earth’s mean radius, T n , m are the (fully-normalized) disturbing potential coefficients, Y n , m are the (fully-normalized) surface spherical functions of degree n and order m, and n ¯ is the upper summation index of spherical harmonics.

2.2. Sub-lithospheric mantle geoid

In the forward modelling scheme, the gravitational contribution of lithospheric density heterogeneities is subtracted from a geoidal geometry in order to enhance a gravitational signature of density structures within the mantle below the lithosphere (i.e., within the sub-lithospheric mantle). This procedure yields the sub-lithospheric mantle geoid N SM , defined by
N SM ( Ω ) = N ( Ω ) + T SM ( r g , Ω ) γ 0 ( ϕ )
The computation of the sub-lithospheric mantle disturbing potential T SM in Eq. (3) is realized in numerical steps explained next.

2.2.1. Bouguer disturbing potential

The Bouguer disturbing potential T B is obtained from the disturbing potential T after subtracting the gravitational potentials of topography V T , bathymetry V B , and polar glaciers V I . We then write (cf. Tenzer et al., [48,50])
T B = T − V T − V B − V I
The gravitational potentials of atmosphere [80] and lakes [81] are completely negligible when compared to values of the gravitational potentials V T , V B , and V I .
The topographic potential in Eq. (4) is often computed individually for a uniform and anomalous topographic density. The topographic potential V T , ρ T for a uniform topographic density reads [12]
V T , ρ T ( r g , Ω ) = GM R ∑ n = 0 n ¯ ∑ m = − n n V n , m T , ρ T Y n , m ( Ω )
The potential coefficients V n , m T , ρ T in Eq. (5) are given by
V n , m T , ρ T = 3 2 n + 1 ρ T ρ ¯ Earth ∑ k = 0 n + 2 ( n + 2 k ) 1 k + 1 H n , m ( k + 1 ) R k + 1
where ρ ¯ Earth = 5500 kg.m-3 is the Earth’s mean mass density, and ρ T is the average (constant) topographic density. The Laplace harmonics H n of topographic heights H are defined by the following integral convolution
H ( Ω ) = ∑ n = 0 ∞ H n ( Ω ) ,
H n ( Ω ) = 2 n + 1 4 π ∬ Φ ρ T H ′ P n ( t ) d Ω ′ = ∑ m = − n n H n , m Y n , m ( Ω ) ,
where H n , m are the topographic coefficients, P n is the Legendre polynomial for the argument t of cosine of the spherical angle ψ between two points ( r , Ω ) and ( r ′ , Ω ′ ) ; i.e., t = cos ψ . The infinitesimal surface element on the unit sphere is denoted as d Ω ′ = cos φ ′ d φ ′ d λ ′ , and Φ = { Ω ′ = ( φ ′ , λ ′ ) : φ ′ ∈ [ − π / 2 , π / 2 ] ∧ λ ′ ∈ [ 0 , 2 π ) } is the full spatial angle. The corresponding higher-order terms { H n , m ( k ) : k = 2 , 3 , ... } read
H n ( k ) ( Ω ) = 2 n + 1 4 π ∬ Φ H ′ k P n ( t ) d Ω ′ = ∑ m = − n n H n , m ( k ) Y n , m ( Ω )
The topographic potential V g T , δ ρ T for an anomalous lateral topographic density is computed from
V T , δ ρ T ( r g , Ω ) = GM R ∑ n = 0 n ¯ ∑ m = − n n V n , m T , δ ρ T Y n , m ( Ω )
where
V n , m T , δ ρ T = 3 2 n + 1 1 ρ ¯ Earth ∑ k = 0 n + 2 ( n + 2 k ) 1 k + 1 δ ρ T K n , m ( k + 1 ) R k + 1
The topographic density-heights coefficients { δ ρ T K n ( k ) : k = 1 , 2 , 3 , ... } in Eq. (10) are given by
δ ρ T K n ( k ) ( Ω ) = 2 n + 1 4 π ∬ Φ δ ρ T ( Ω ′ ) K ′ k P n ( t ) d Ω ′ = ∑ m = − n n δ ρ T K n , m ( k ) Y n , m ( Ω )
The height K in Eq. (11) equals the topographic height H except for areas covered by polar glaciers. In this case, the height K is defined as the topographic height minus the ice thickness. The anomalous lateral topographic density δ ρ T in Eq. (11) is taken with respect to the average topographic density ρ T , so that δ ρ T ( Ω ) = ρ T − ρ T ( Ω ) .
The bathymetric potential V B in Eq. (4) is defined by [82,83]
V B ( r g , Ω ) = GM R ∑ n = 0 n ¯ ∑ m = − n n V n , m b Y n , m ( Ω )
The bathymetric coefficients V n , m b read
V n , m b = 3 2 n + 1 Δ ρ 0 w ρ ¯ Earth ( F n , m b − a 1 β Δ ρ 0 w R F n , m b 1 − a 2 β Δ ρ 0 w R 2 F n , m b 2 )
where Δ ρ 0 w is the nominal value of the surface seawater density contrast; and β , a 1 , and a 2 denote parameters of the depth-dependent seawater density developed by Gladkikh and Tenzer [84]. The numerical coefficients F n , m b , F n , m b 1 , and F n , m b 2 in Eq. (13) are computed from
F n , m b ≅ D n , m R − ( n + 2 ) D n , m ( 2 ) 2 R 2 + ( n + 2 ) ( n + 1 ) D n , m ( 3 ) 6 R 3
− ( n + 2 ) ( n + 1 ) n D n , m ( 4 ) 24 R 4 + ( n + 2 ) ( n + 1 ) n ( n − 1 ) D n , m ( 5 ) 120 R 5
+ ∑ k = 5 n + 2 ( n + 2 k ) ( − 1 ) k k + 1 D n , m ( k + 1 ) R k + 1   ,
F n , m b 1 ≅ D n , m ( 2 ) 2 R 2 − ( n + 2 ) D n , m ( 3 ) 3 R 3 + ( n + 2 ) ( n + 1 ) D n , m ( 4 ) 8 R 4
− ( n + 2 ) ( n + 1 ) n D n , m ( 5 ) 30 R 5 + ∑ k = 4 n + 2 ( n + 2 k ) ( − 1 ) k k + 2 D n , m ( k + 2 ) R k + 2
+ ∑ k = 3 n + 2 ( n + 2 k ) ( − 1 ) k k + 3 D n , m ( k + 3 ) R k + 3
The coefficients D n , m of global bathymetric model are defined by
D n ( Ω ) = 2 n + 1 4 π ∬ Φ D ( Ω ′ ) P n ( cos ψ ) d Ω ′ = ∑ m = − n n D n , m Y n , m ( Ω ) ,
and their higher-order terms { D n ( i ) : i = 2 , 3 , 4 } read (ibid.)
D n ( i ) ( Ω ) = 2 n + 1 4 π ∬ Φ D k ( Ω ′ ) P n ( cos ψ ) d Ω ′ = ∑ m = − n n D n , m ( i ) Y n , m ( Ω ) ,
where D denotes the bathymetric depth.
The ice potential V I in Eq. (4) is computed from (cf. Foroughi and Tenzer [85])
V I ( r g , Ω ) = GM R ∑ n = 0 n ¯ ∑ m = − n n V n , m I Y n , m ( Ω )
The ice coefficients V n , m I in Eq. (19) read
V n , m I = 3 2 n + 1 δ ρ I ρ ¯ Earth ( F u n , m − F l n , m ) ,
where the numerical coefficients F l n , m and F u n , m are given by
F l n , m = ∑ k = 0 n + 2 ( n + 2 k ) 1 k + 1 L n , m ( k + 1 ) R k + 1
F u n , m = ∑ k = 0 n + 2 ( n + 2 k ) 1 k + 1 H n , m ( k + 1 ) R k + 1
The coefficients F l n , m utilize the spherical lower-bound functions L n of a volumetric mass density contrast layer and their higher-order terms [82,83]
L n ( k + 1 ) ( Ω ) = 2 n + 1 4 π ∬ Φ H L k + 1 ( Ω ′ ) P n ( t ) d Ω ′ = ∑ m = − n n L n , m ( k + 1 ) Y n , m ( Ω )
Since the upper-bound of glaciers is identical with the topographic surface, the numerical coefficients F u n , m are generated directly from the height coefficients { H n ( k ) : k = 1 , 2 , ... }. The ice density contrast δ ρ I in Eq. (20) is taken with respect to a uniform topographic density ρ T , i.e. δ ρ I = ρ T − ρ I , where ρ I denotes the density of polar glaciers.

2.2.2. Crust-stripped disturbing potential

The gravitational potential of consolidated-crust density contrast V C and the gravitational potential of sediment density contrast V S are subtracted from the Bouguer disturbing potential T B in order to remove the gravitational contribution of density heterogeneities within the whole crust. This procedure yields the crust-stripped disturbing potential T CS (cf. Tenzer et al. [48])
T CS = T B − V S − V C
The potentials V S and V C in Eq. (23) are computed according to a method developed by Tenzer et al. [82] that utilizes the expression for a gravitational potential V generated by an arbitrary volumetric mass layer with a variable depth and thickness while having laterally distributed vertical mass density variations. It reads
V ( r g , Ω ) = GM R ∑ n = 0 n ¯ ∑ m = − n n V n , m Y n , m ( Ω )
The potential coefficients V n , m in Eq. (24) are defined by
V n , m = 3 2 n + 1 1 ρ ¯ Earth ∑ i = 0 I ( F l n , m ( i ) − F u n , m ( i ) )
where the coefficients { F l n , m ( i ) , F u n , m ( i ) : i = 0 , 1 , ... , I } are computed from
F l n , m ( i ) = ∑ k = 0 n + 2 ( n + 2 k ) ( − 1 ) k k + 1 + i L n , m ( k + 1 + i ) R k + 1 ,
F u n , m ( i ) = ∑ k = 0 n + 2 ( n + 2 k ) ( − 1 ) k k + 1 + i U n , m ( k + 1 + i ) R k + 1
The terms ∑ m = − n n L n , m Y n , m and ∑ m = − n n U n , m Y n , m in Eq. (26) define the spherical lower-bound and upper-bound laterally distributed radial density variation functions L n and U n of degree n . These numerical coefficients combine information on the geometry and mass density (or density contrast) distribution within a volumetric layer. The computation of these coefficients is realized to a certain degree of spherical harmonics from discrete data of the spatial mass density distribution (typically provided by means of density, depth and thickness data) of a particular structural component of the Earth’s interior.
The spherical functions L n and U n including their higher-order terms { L n ( k + 1 + i ) , U n ( k + 1 + i ) : k = 0 , 1 , ... ; i = 1 , 2 , ... , I } in Eq. (26) are defined by
L n ( k + 1 + i ) ( Ω ) = { 2 n + 1 4 π ∬ Φ ρ ( D U , Ω ′ ) D L k + 1 ( Ω ′ ) P n ( t ) d Ω ′ = ∑ m = − n n L n , m ( k + 1 ) Y n , m ( Ω )                 i = 0     2 n + 1 4 π ∬ Φ β ( Ω ′ ) α i ( Ω ′ ) D L k + 1 + i ( Ω ′ ) P n ( t ) d Ω ′ = ∑ m = − n n L n , m ( k + 1 + i ) Y n , m ( Ω )               i = 1 , 2 , ... , I
and
U n ( k + 1 + i ) ( Ω ) = { 2 n + 1 4 π ∬ Φ ρ ( D U , Ω ′ ) D U k + 1 ( Ω ′ ) P n ( t ) d Ω ′ = ∑ m = − n n U n , m ( k + 1 ) Y n , m ( Ω )                 i = 0     2 n + 1 4 π ∬ Φ β ( Ω ′ ) α i ( Ω ′ ) D U k + 1 + i ( Ω ′ ) P n ( t ) d Ω ′ = ∑ m = − n n U n , m ( k + 1 + i ) Y n , m ( Ω )               i = 1 , 2 , ... , I
For a specific volumetric layer, the mass density ρ is either constant ρ , laterally-varying ρ ( Ω ′ ) or - in the most general case - approximated by the laterally distributed radial density variation model by using the following polynomial function (for each lateral column)
ρ r ′ , Ω ′ = ρ D U , Ω ′ + β Ω ′ ∑ i = 1 I α i Ω ′ R − r ′ i
f o r   R − D U ( Ω ′ ) ≥ r ′ > R − D L ( Ω ′ )
The nominal value of lateral density ρ ( D U , Ω ′ ) is stipulated at the depth D U . This density distribution describes a radial density variation (in terms of coefficients { α i : i = 1 , 2 , ... , I } and β ) within a volumetric mass layer at a location Ω ′ . Alternatively, when modeling a gravitational field of anomalous density structures (in this case, the density contrast of sediments and consolidated crust), the density contrast Δ ρ of volumetric mass layer relative to the reference density ρ c is defined by
Δ ρ ( r ′ , Ω ′ ) = ρ c − ρ ( r ′ , Ω ′ )
= Δ ρ ( D U , Ω ′ ) − β ( Ω ′ ) ∑ i = 1 I α i ( Ω ′ ) ( R − r ′ ) i ,
f o r   R − D U ( Ω ′ ) ≥ r ′ > R − D L ( Ω ′ )
where Δ ρ ( D U , Ω ′ ) is the nominal value of lateral density contrast stipulated at the depth D U . Here the reference density ρ c of homogenous crust is used.

2.2.3. Mantle disturbing potential

To reveal a gravitational signature attributed to a mantle density structure, the Moho geometry signature has to be subtracted from the crust-stripped disturbing potential. This procedure yields the mantle disturbing potential. According to Tenzer et al. [50], the mantle disturbing potential T M is obtained from the crust-stripped disturbing potential T CS after subtracting the gravitational potential of Moho geometry V M , Δ ρ c / m . We then write
T M = T CS − V M , Δ ρ c / m
The potential V M , Δ ρ c / m (for the average Moho density contrast Δ ρ c / m ) is defined in the following form
V M , Δ ρ c / m ( r g , Ω ) = 3 GM R ρ ¯ Earth ∑ n = 0 n ¯ ∑ m = − n n F n , m Δ ρ M Y n , m ( Ω ) ,
where the numerical coefficients F n , m Δ ρ M are given by
F n , m Δ ρ M = − Δ ρ c / m ( 2 n + 1 ) ( n + 3 ) ∑ k = 1 n + 3 ( n + 3 k ) ( − 1 ) k R k M ^ n , m ( k )
The Moho depth spherical functions M ^ n and their higher-order terms { M ^ n ( k ) : k = 2 , 3 , ... } read
M ^ n ( k ) = 2 n + 1 4 π ∬ Φ M k ( Ω ′ ) P n ( t ) d Ω ′
= ∑ m = − n n M ^ n , m ( k ) Y n , m ( Ω )
As seen in Eq. (34), the coefficients { M n , m ( k ) : k = 1 , 2 , ... } are generated from values of the Moho depth M . The Moho density contrast in Eq. (33) is defined as the average lithospheric mantle density ρ LM from which the (constant) reference crustal density ρ c is subtracted. Hence
Δ ρ c / m = ρ LM − ρ c

2.2.4. Lithosphere-stripped disturbing potential

The lithosphere-stripped disturbing potential T CL is obtained from the mantle disturbing potential T M by subtracting the lithospheric-mantle gravitational potential V L M , so that
T CL = T M − V L M
For a lateral density distribution function within the lithospheric mantle, the lithospheric-mantle gravitational potential V L M is defined by
V L M ( r g , Ω ) = 3 GM R ρ ¯ Earth ∑ n = 0 n ¯ 1 2 n + 1
× ∑ k = 0 n + 2 ( n + 2 k ) ( − 1 ) k R k + 1 ( k + 1 ) ∑ m = − n n ( L n , m ( k + 1 ) − M n , m ( k + 1 ) ) Y n , m ( Ω )
where the Moho coefficients M n , m ( k + 1 ) describe the geometry and lateral density (contrast) distribution at the Moho interface, and the LAB coefficients L n , m ( k + 1 ) describe the geometry and lateral density (contrast) distribution at the LAB.
The Moho coefficients M n , m ( k + 1 ) in Eq. (37) are defined in the following form
∑ m = − n n M n , m ( k ) Y n , m ( Ω ) = 2 n + 1 4 π ∬ Φ δ ρ L M ( Ω ′ ) M k ( Ω ′ ) P n ( t ) d Ω ′
where M denotes the Moho depth (see Eq. 34). The (lateral) lithospheric mantle density contrast δ ρ L M in Eq. (38) is computed as the difference between the adopted (lithospheric mantle) reference density ρ LM and the lithospheric mantle density ρ L M ; i.e., δ ρ L M ( Ω ′ ) = ρ LM − ρ L M ( Ω ′ ) .
The LAB coefficients L n , m ( k + 1 ) in Eq. (37) read
∑ m = − n n L n , m ( k ) Y n , m ( Ω ) = 2 n + 1 4 π ∬ Φ δ ρ L M ( Ω ′ ) L k ( Ω ′ ) P n ( t ) d Ω ′
where L is the LAB depth. If we consider a current resolution of global lithospheric density models (1×1 arc-deg or lower) that corresponds (by means of a half wavelength) to a spectral resolution up to the degree 180 of spherical harmonics, the lithospheric-mantle gravitational potential can sufficiently be computed by using binomial series in Eq. (37) up to only the third-order term.

2.2.5. Sub-lithospheric mantle disturbing potential

The computation of the lithosphere-stripped disturbing potential T CL in Eq. (36) enhanced a signature of the LAB geometry that has to be removed in order to enhance a gravitational signature of the sub-lithospheric mantle density structure. This procedure is realized by stripping the lithosphere with respect to the density contrast between the reference (lithospheric mantle) density and the asthenosphere density in order to obtain the sub-lithospheric mantle disturbing potential. The sub-lithospheric mantle disturbing potential T SM is then computed as
T SM = T CL − V L A B ,
where the potential V L A B of LAB geometry is defined by
V L A B ( r g , Ω ) = 3 GM R ρ ¯ Earth ∑ n = 0 n ¯ 1 2 n + 1
× ∑ k = 0 n + 2 ( n + 2 k ) ( − 1 ) k R k + 1 ( k + 1 ) ∑ m = − n n L ^ n , m ( k + 1 ) Y n , m ( Ω )
The coefficients L ^ n , m ( k + 1 ) in Eq. (41) read
∑ m = − n n L ^ n , m ( k ) Y n , m ( Ω ) = 2 n + 1 4 π Δ ρ L / A ∬ Φ L k ( Ω ′ ) P n ( t ) d Ω ′ ,
where L is the LAB depth (see also Eq. 39), and the LAB density contrast Δ ρ L / A = ρ A − ρ LM is defined as the difference between the lithospheric mantle density ρ L and the asthenospheric density ρ A . We note that the computation of V L A B can again be restricted up to the third-order terms of a binomial series (as in the case of computing V L M in Eq. 37).

3. Model uncertainties

The numerical model presented in Section 2 was used in this section to derive the error propagation in modelling of the sub-lithospheric mantle geoid. According to results presented in Section 4 (see Table 1), the gravitational contributions of lithospheric mantle and LAB are one order of magnitude larger than the corresponding contributions of topographic and crustal density structures. We, therefore, focused only on the estimation of errors due to lithospheric mantle density and lithospheric thickness uncertainties, while disregarding much smaller (in absolute sense) modelling errors due to crustal density uncertainties.

3.1. Errors due to lithospheric thickness uncertainties

In the sub-lithospheric mantle geoid modelling, the lithospheric thickness information is used to compute the lithospheric-mantle gravitational potential V L M (in Eq. 39) and the LAB potential V L A B (in Eq. 41). We then established a relation between the error of sub-lithospheric mantle geoid ε N SM and the error of lithospheric thickness ε L in the following form
ε N SM = − 1 γ 0 ( ∂ V L M ∂ L + ∂ V L A B ∂ L ) ε L
= − 3 γ 0 GM R ρ ¯ Earth ∑ n = 0 n ¯ 1 2 n + 1 ∑ k = 0 n + 2 ( n + 2 k ) ( − 1 ) k R k + 1 ( k + 1 ) ∑ m = − n n ( L n , m ( k + 1 ) + L ^ n , m ( k + 1 ) ) Y n , m ( Ω )
= − 3 γ 0 4 π GM R ρ ¯ Earth ∑ n = 0 n ¯ ∑ k = 0 n + 2 ( n + 2 k ) ( − 1 ) k R k + 1 ( k + 1 )
× ∬ Φ [ δ ρ L M ( Ω ′ ) + Δ ρ L / A ] ( k + 1 ) L k ( Ω ′ ) ε L ( Ω ′ ) P n ( t ) d Ω ′
After disregarding terms k ≥ 1 , the expression in Eq. (43) simplifies to
ε N SM ≅ − 3 γ 0 4 π GM R 2 ρ ¯ Earth ∬ Φ [ δ ρ L M ( Ω ′ ) + Δ ρ L / A ] ε L ( Ω ′ ) ∑ n = 0 n ¯ P n ( t ) d Ω ′
For n = 0, we have
ε N SM ≅ − 3 γ 0 4 π GM R 2 ρ ¯ Earth ∬ Φ [ δ ρ L M ( Ω ′ ) + Δ ρ L / A ] ε L ( Ω ′ ) d Ω ′
When assuming that the largest contribution to the error ε N SM comes from lithospheric thickness uncertainties in the vicinity of computation point (for which the error is estimated), the global integration domain in Eq. (45) could be disregarded. Instead, we reduce a functional relation only for a position of computation point. We then write
ε N SM ≈ − 3 γ 0 4 π GM R 2 ρ ¯ Earth ( δ ρ L M + Δ ρ L / A ) ε L
Inserting for γ 0 ≈ GM / R 2 in Eq. (46), we arrive at
ε N SM ≈ − 3 4 π ( δ ρ L M + Δ ρ L / A ρ ¯ Earth ) ε L

3.2. Errors due to lithospheric mantle density uncertainties

The lithospheric mantle density information is used to compute the Moho density contrast Δ ρ c / m (Eq. 35), the lithospheric mantle density variations δ ρ L M (Eq. 38), and the LAB density contrast Δ ρ L / A (Eq. 42). This involves the computation of the Moho potential V M , Δ ρ c / m (in Eq. 32), the lithospheric-mantle gravitational potential V L M (in Eq. 39), and the LAB potential V L A B (in Eq. 41). The error propagation for the lithospheric mantle density uncertainties is then established in the following form
ε N SM = − 1 γ 0 ( ∂ V M , Δ ρ c / m ∂ Δ ρ c / m ε Δ ρ c / m + ∂ V L M ∂ δ ρ L M ε δ ρ L M + ∂ V L A B ∂ Δ ρ L / A ε Δ ρ L / A )
= − 3 γ 0 4 π GM R ρ ¯ Earth ∑ n = 0 n ¯ ∑ k = 0 n + 2 ( n + 2 k ) ( − 1 ) k R k + 1 ( k + 1 )
× ∬ Φ { ε Δ ρ c / m M k + 1 ( Ω ′ ) + [ ε δ ρ L M ( Ω ′ ) L k + 1 ( Ω ′ ) − ε δ ρ L M ( Ω ′ ) M k + 1 ( Ω ′ ) ] ε Δ ρ L / A L k + 1 ( Ω ′ ) } P n ( t ) d Ω ′ ,
where ε Δ ρ c / m , ε δ ρ L M and ε Δ ρ L / A denote, respectively, the errors in the Moho density contrast Δ ρ c / m , the anomalous lithospheric mantle density δ ρ L M , and the LAB density contrast Δ ρ L / A .
After disregarding terms k ≥ 1 in Eq. (48), we arrive at
ε N SM ≅ − 3 γ 0 4 π GM R 2 ρ ¯ Earth ∬ Φ { ε Δ ρ c / m M k + 1 ( Ω ′ ) + ε δ ρ L M ( Ω ′ ) L k + 1 ( Ω ′ )
− ε δ ρ L M ( Ω ′ ) M k + 1 ( Ω ′ ) + ε Δ ρ L / A L k + 1 ( Ω ′ ) } ∬ Φ ∑ n = 0 n ¯ P n ( t ) d Ω ′
Considering that n = 0 and γ 0 ≈ GM / R 2 , we get
ε N SM ≅ − 3 4 π ρ ¯ Earth ∬ Φ { ε Δ ρ c / m M k + 1 ( Ω ′ ) + ε δ ρ L M ( Ω ′ ) L ( Ω ′ ) − ε δ ρ L M ( Ω ′ ) M ( Ω ′ ) + ε Δ ρ L / A L ( Ω ′ ) } d Ω ′
By analogy with Eq. (46), the expression in Eq. (50) is further simplified to
ε N SM ≈ − 3 4 π ρ ¯ Earth [ ε Δ ρ c / m M + ε δ ρ L M ( L − M ) + ε Δ ρ L / A L ]
As seen in Eq. (51), the sub-lithospheric mantle geoid error ε N SM in this case depends on the accuracy of anomalous lithospheric mantle density δ ρ L M . In addition, the errors ε Δ ρ L / A and ε Δ ρ c / m in adopted values of the LAB density contrast Δ ρ L / A and the Moho density contrast Δ ρ c / m affect the accuracy.

4. Results

Tenzer and Chen [81] applied numerical procedures (described in Section 2) to compute the global sub-lithospheric mantle geoid globally with a spectral resolution up to degree 180 of spherical harmonics. They used the EIGEN-6C4 [86] global gravitational model, the Earth2014 topographic, bathymetric, and glacial bedrock relief datasets [72], the UNB_TopoDens global lateral topographic density model [87], the total sediment thickness data for the world's oceans and marginal seas [88], the CRUST1.0 [69] global seismic crustal model updated for the sediment and crustal layers of the Antarctic lithosphere by Baranov et al. [89], and the LITHO1.0 [70] global seismic lithospheric model. They adopted the reference density values 2670 kg.m-3 (cf. Hinze [90]; Artemjev et al. [91)) for the crust above the geoid, 2900 kg.m-3 for the crust below the geoid, and 3300 kg.m-3 for the lithospheric mantle. To further improve the accuracy of forward modelling, they defined the ocean density contrast for a depth-dependent seawater density function [47,84], and applied a density model of marine sediments [92] under marginal seas and oceans.
The gravitational contributions of individual lithospheric density structures are plotted in Figure 1, with the statistical summary of results in Table 1. Modifications of the geoidal geometry after subtracting gravitational contributions of individual lithospheric density structures are presented in Figure 2, with the statistical summary in Table 2.
A long-wavelength geoidal geometry (Figure 2a) reflects mainly a mantle density structure—e.g., [93,94], while a signature of crustal density and geometry variations (including a topographic surplus of large orogenic formations) is less prominent. After removing the gravitational contributions topography and lithospheric density and geometry (i.e., LAB) variations, the resulting (sub-lithospheric mantle) geoidal geometry (see Figure 2f) should (optimally) enhance the gravitational signature of sub-lithospheric mantle.
It is well known fact that a spatial pattern in dynamic topography models—e.g., [54,55],[95,96,97,98] mainly reflects a mantle convection flow, with maxima marking locations of the African and South Pacific superplumes that represent large-scale regions characterized by an elevated topography and shallow ocean-floor depts caused by a low-density upwelling mantle material from the core-mantle boundary. The corresponding minima are explained by a high-density mantle downwelling flow. Tomographic studies—e.g., [99] indicate that superplumes coincide with locations of large low-shear-velocity provinces (LLSVPs) beneath Africa (called Tuzo) and the South Pacific (called Jason). Since the gravitational contributions of lithospheric density and thickness variations have been modelled and consequently removed in our forward modelling procedure, the sub-lithospheric mantle geoid should mainly reflect deep mantle density anomalies. Consequently, the spatial pattern of sub-lithospheric mantle geoid (especially its long-wavelength spectrum up to degree 5 of spherical harmonics; see Figure 3) does not closely agree with a spatial pattern of dynamic topography models (cf. Tenzer and Chen [81]). A comparative study of spatial patterns in the sub-lithospheric mantle geoid and dynamic topography models is thus not meaningful for the assessment of errors in our gravimetric forward modelling.
As seen in Figure 3, the long-wavelength pattern in the sub-lithospheric mantle geoid is characterized by a large positive anomaly in the Central Pacific and a less pronounced anomaly in the Central Atlantic with a prolonged shape across the Atlantic Ocean and further extending across the South Indian Ocean towards West Australia. These two positive anomalies are coupled by negative anomalies in the Equatorial East Pacific and across South and East Eurasia. An additional negative anomaly is detected in Antarctica. If we consider that a spatial pattern of the sub-lithospheric mantle geoid should mainly manifest sub-lithospheric mantle density heterogeneities, it becomes clear that a long-wavelength pattern in Figure 3 might be affected by large errors especially at locations with a maximum lithospheric thickness. This becomes even more evident when inspecting the sub-lithospheric mantle geoid in Figure 2f, where a maximum lithospheric deepening is clearly manifested in the geoidal geometry. This indicates a possible presence of large errors attributed to lithospheric model uncertainties used in the gravimetric forward modelling. These errors are estimated in the next section.

5. Error analysis

Large errors are expected in the CRUST1.0 and LITHO1.0 models used for a gravimetric forward modelling in this study. As already mentioned in the preceding section, this is particularly evident from pronounced positive sub-lithospheric mantle geoid anomalies (Figure 2f) that are also still partially exhibited in its long-wavelength pattern (Figure 3). These positive anomalies correspond with the largest cratonic lithospheric thickness (the Laurentian Shield in North America, the Amazonian Shield and São Francisco Craton in South America, the West African Craton, the East European and Siberian Cratons and the Baltic Shield in Eurasia, and the West Australian Craton).
As seen in Eq. (47), the lithospheric thickness uncertainties propagate almost linearly to the sub-lithospheric mantle geoid uncertainties. We can, therefore, readily estimate the geoid errors for particular lithospheric thickness uncertainties. According to the LITHO1.0 model, the lithospheric mantle density varies roughly from 3000 to 3450 kg.m-3. From these density variations we can assume that δ ρ L M is mostly within ±200 kg.m-3. The boundary between the lowermost lithosphere and the uppermost asthenosphere (i.e., the LAB) is rheological, conventionally taken at the 1300°C isotherm, above which the mantle behaves in a rigid fashion and below which behaves in a ductile fashion [100]. Studies suggest the existence of a compositional or chemical density contrast 0-20 kg.m-3 [101], except probably the cratonic mantle. In addition to a possibly chemical density contrast, a strong thermal density contrast 30-60 kg.m-3 occurs when the asthenosphere is locally uplifted by rifting. We, therefore, assume that the density variations Δ ρ L / A at the boundary between the lithosphere and the asthenosphere are mostly within ±30 kg.m-3. For δ ρ L M + Δ ρ L / A = ± 230 kg.m-3, the errors in the lithospheric thickness estimates of ε L ≈ ± 10 km cause errors in the sub-lithospheric mantle geoid roughly ε N SM ≈ ± 0.1 km.
The lithospheric thickness models vary significantly. Pasyanos et al. [70], for instance, found large differences between their LITHO1.0 model and that prepared by Conrad and Lithgow-Bertelloni [102]. They also provided explanation that these large differences are due to applying different methods, assumptions, and input data. To get a rough idea about a magnitude of these errors, we compared the lithospheric thickness models SLNAAFSA [103], SL2013sv [104], LITHO1.0 [70], CAM2016 [105,106], and 3D2015-07Sv [107], and used their differences to estimate (sub-lithospheric mantle) geoid errors. We note here that the SLNAAFSA model was prepared by Hoggard et al. [103] by merging regional updates from North America [108], Africa [109], and South America [110] into the global SL2013sv model. The lithospheric thickness models are shown in Figure 4, with their statistical summary given in Table 3. The statistics of differences between individual lithospheric thickness models are summarized in Table 4.
As seen in Table 4, differences between lithospheric thickness models exceed several hundreds of meters. If we consider that average uncertainties in the lithospheric thickness ε L are about ±40 km (the average of the Root-Mean-Square (RMS) of differences in Table 4), the sub-lithospheric mantle geoid errors ε N SM could reach or even exceed ±0.4 km.
Tomographic images of the lithosphere have a limited accuracy and resolution. Moreover, the conversion between seismic wave velocities and rock densities is not unique—e.g., [58,111]. Hager and Richards [112], for instance, mentioned that a lithospheric mantle composition and seismic anisotropy is more complex than a deep mantle structure, making it harder to convert seismic anomalies to density anomalies or buoyancy (cf. also Simmons et al., [113]). We, therefore, expect also large (sub-lithospheric mantle) geoid modelling errors due to lithospheric mantle density uncertainties.
According to Eq. (51), the sub-lithospheric mantle geoid error ε N SM depends on the accuracy of anomalous lithospheric mantle density δ ρ L M , and additional errors ε Δ ρ L / A and ε Δ ρ c / m in adopted values of the LAB density contrast Δ ρ L / A and the Moho density contrast Δ ρ c / m . Large density variations occur within the lithospheric mantle, although in comparison to the crust, fewer constraints exist on the composition of the lithospheric mantle. Petrological models for the origin of basalt are used to compile models of the oceanic lithospheric mantle. An undepleted peridotitic source that partially melts to produce the mid-ocean ridge basalt, leaves behind a depleted residue (a harzburgite), the thickness of which depends on the degree of a partial melt. As the oceanic lithosphere cools, the undepleted mantle becomes part of the lithospheric column and its thickness increases with the ocean-floor age. The composition of the continental lithospheric mantle depends on a tectonic province and its age. Jordan [114] proposed that the lithospheric mantle might be cold and buoyant in the thickest cratonic portions of very fast seismic velocity (see also Gung et al., [115]). These conditions require the presence of a depleted layer overlying an undepleted upper mantle layer. Based on the LITHO1.0 lithospheric mantle density variations (roughly within ±200 kg.m-3) and the previously summarized studies, we can anticipate that lithospheric mantle density uncertainties ε δ ρ L M are mostly within ±100 kg.m-3. We further assume that uncertainties in the average LAB density contrast ε Δ ρ L / A are roughly ±15 kg.m-3.
Results from seismic and gravimetric studies revealed that the Moho density contrast varies substantially. Artemieva [116] demonstrated that the in situ density contrast between the crystalline crust and the lithospheric upper mantle differs substantially between the Cratonic and the Phanerozoic crust within the European part of the Eurasian tectonic plate, approximately 500 kg.m-3 for the crust beneath Western Europe, between 300 and 350 kg.m-3 for most of the Precambrian crust, and by as little as 150-250 kg.m-3 for some parts of the Baltic and the Ukrainian Shields. Sjöberg and Bagherbandi [117] provided the average values 678±78 and 334±108 kg.m-3 of the Moho density contrast for the continental and oceanic areas respectively. According to these studies, we speculate that the errors of Moho density contrast ε Δ ρ c / m could be roughly ±50 kg.m-3. Adopting the above error estimates of ε δ ρ L M ≈ ± 100 kg.m-3, ε Δ ρ L / A ≈ ± 15 kg.m-3, and ε Δ ρ c / m ≈ ± 50 kg.m-3 and considering the lithospheric thickness L ~100 km and the Moho depth M of ~30 km, the geoid modelling error ε N SM could, according to Eq. (51), reach or even exceed ±0.5 km.
To confirm the above theoretical estimates, we rearranged the error propagation in Eq. (51) into the form that directly incorporates density uncertainties within the uppermost asthenosphere and the lowermost crust. Inserting for Δ ρ c / m = ρ LM − ρ c , δ ρ L M = ρ LM − ρ L M and Δ ρ L / A = ρ A − ρ LM in Eq. (51), we get
ε N SM ≈ − 3 4 π ρ ¯ Earth [ ( ε ρ LM − ε ρ c ) M + ( ε ρ LM − ε ρ L M ) ( L − M ) + ( ε ρ A − ε ρ LM ) L ]
≈ − 3 4 π ρ ¯ Earth [ ε ρ LM M − ε ρ c M + ε ρ LM L − ε ρ LM M − ε ρ L M ( L − M ) + ε ρ A L − ε ρ LM L ]
≈ 3 4 π ρ ¯ Earth [ ε ρ c M + ε ρ L M ( L − M ) + ε ρ A L ] ,
where ε ρ c and ε ρ A are errors in the average crustal ρ c and asthenospheric ρ A densities respectively. As seen in Eq. (52), the modelling error ε N SM depends on the accuracy of lithospheric mantle density distribution as well as adopted average densities of the crust and the asthenosphere, while errors in adopted value of the average lithospheric mantle density ρ LM cancel.
Christensen and Mooney [111] reported the average value 2835 kg.m-3 for the continental crustal density. Tenzer et al. [50] provided a very similar value 2790 kg.m-3. The oceanic crust, composed primarily of mafic rocks, is typically heavier than the continental crust—e.g., [118]. Tenzer et al. [50] estimated that the average density of the oceanic crust (without marine sediments) is 2860 kg.m-3. Carlson and Raskin [119] provided the estimate of 2890 kg.m-3. Tenzer and Gladkikh [92] confirmed a similar value (when disregarding marine sediments) of 2900 kg.m-3 based on the analysis of global samples of marine bedrock densities. If we focus only on the lowermost crustal density uncertainties, the density according to the CRUST1.0 varies from 2850 kg.m-3 under Himalayas to 3050 kg.m-3 under oceans with a standard deviation ~70 kg.m-3. Christensen and Mooney [111] provided the uncertainty of ±50 kg.m-3 for the crystalline crust that could be reduced to ~±30 kg.m-3 when considering only the lowermost crust. The error ε ρ c of ±50 kg.m-3 could then be a realistic expectation for an average density within the lowermost crust.
Density variations within the asthenosphere are probably controlled by a mantle flow pattern. Large density variations attributed to mantle plumes, for instance, were detected under Iceland, Hawaii, Azores, and elsewhere—e.g., [120]. Seismic tomography results indicate also relatively large density heterogeneities and density discontinuities in the mantle transition zone at depths approximately between 410 to 660 km—e.g., [121,122]. Based on petrological evidences, Griffin et al. [123] reported density variations 3300-3400 kg.m-3 in the asthenosphere. From these estimates, we could assume that the error ε ρ A in the average asthenosphere density is roughly ±30 kg.m-3. Assigning these density uncertainties to Eq. (52), the geoid modelling errors ε N SM within ±0.6 km closely corresponds with the estimated value of ±0.5 km according to Eq. (51).
To check the correctness of our initial assumption that the lithospheric mantle density uncertainties ε δ ρ L M are mostly within ±100 kg.m-3, we used differences between the lithospheric thickness models (in Table 4) to reversely estimate errors of lithospheric mantle density. The computation was done approximately by using a simple relation for the gravitational potential V of an infinite planar plate that is computed from the density ρ and thickness s values as follows
V ≈ 2 π G R ρ s
The error propagation model for Eq. (53) reads
ε V ≈ 2 π G R ( s ε ρ + ρ ε s ) ,
where ε ρ is a density uncertainty, and ε s is a thickness uncertainty.
Since we here inspect the propagation only between errors ε δ ρ L M and ε N SM (or equivalently ε V ), the error ε s in Eq. (54) is disregarded. We then write
ε V ≈ 2 π G R s ε ρ
Defining the potential errors ε V in Eq. (55) in terms of geoid uncertainties ε N , we arrive at
ε N = ε V γ o ε V ≈ 2 π γ o G R s ε ρ ≈ 2 π G R GM / R 2 s ε ρ ≈ 2 π R 3 M s ε ρ ,
where M = 5.9722 x 1024 kg is the Earth’s total mass.
According to Table 4, the RMS of differences between the lithospheric thickness models is on average roughly ±0.4 km. This RMS corresponds to the density error ε ρ of ~ ±160 kg.m-3. As seen, this error estimate agrees quite closely with the error analysis according to Eq. (51), where we assumed density errors within a similar range (i.e., ε δ ρ L M ≈ ± 100 kg.m-3, ε Δ ρ L / A ≈ ± 15 kg.m-3, and ε Δ ρ c / m ≈ ± 50 kg.m-3).
As confirmed in this study, the sub-lithospheric mantle geoid modelling is affected mainly by errors in lithospheric thickness and lithospheric mantle density. Since we disregarded density variations within the asthenosphere, additional errors in our result are possibly attributed to temperature anomalies and small-scale convection patterns within the asthenosphere. It is also clear from Eq. (52) that the geoid modelling errors due to lithospheric mantle density uncertainties increase almost linearly with the increasing lithospheric thickness. Consequently, both uncertainties likely propagate into maximum geoid errors at locations characterized by the largest continental lithospheric deepening under cratonic formations that are manifested by large positive anomalies of the sub-lithospheric mantle geoid model (Figure 2e). At these locations, errors could according to our estimates reach (or even exceed) ±0.5 km.
These theoretical findings indicate that the sub-lithospheric mantle geoid presented in Figure 2f (or Figure 3) might be very inaccurate, especially at locations with a maximum lithospheric deepening where these errors reach maxima. In reality, modifications of the geoidal geometry by sub-lithospheric mantle density heterogeneities are probably much smaller than those seen in Figure 2f. This is due to the fact that relative lateral density variations within the mantle are up to only a few percent—e.g., [124,125,126,127,128,129].

6. Summary and concluding remarks

We have analyzed errors of computing the sub-lithospheric mantle geoid based on applying a gravimetric forward modelling and by using lithospheric density and thickness models as input data. The principle of this method is to model and subsequently remove the gravitational contributions of topography and lithospheric density and geometry variations in order to enhance a gravitational signature of the sub-lithospheric mantle density structure in the geoidal geometry. The expressions in the spectral domain, that utilize methods for a spherical harmonic analysis and synthesis of gravitational and lithospheric density structure models, were then used to establish the error propagation between geoid modelling errors and lithospheric mantle and lithospheric thickness uncertainties.
According to our analysis, errors in modelling of sub-lithospheric mantle geoid due to lithospheric thickness and lithospheric mantle density uncertainties could reach or even exceed ±0.5 km, particularly at locations with a maximum lithospheric thickness under cratons where both errors could magnify significantly. Theoretical error analysis and numerical results, therefore, suggest that actual modifications of the geoidal geometry by lateral mantle density variations below the lithosphere-asthenosphere boundary are much smaller than those computed and presented in Figure 2f (or in Figure 3).
This finding is indicative for a possible improvement of the Earth’s synthetic density and gravitational models based on a density calibration within individual lithospheric and underlying deeper mantle layers so that a sum of volumetric mass densities within the Earth’s synthetic model provides the value that closely agrees with the Earth’s total mass (excluding the atmosphere). Equivalently, the Earth’s synthetic density model should generate the gravitational field that closely agree with the Earth’s gravitational field. This issue will be addressed in the forthcoming study, where we will compile a synthetic model that closely fulfills both requirements.

Author Contributions

Conceptualization, R.T.; methodology, R.T.; software, W.Ch.; validation, W.Ch.; formal analysis, W.Ch.; data curation, W.Ch.; writing—original draft preparation, R.T.; writing—review and editing, R.T.; visualization, W.Ch.. All authors have read and agreed to the published version of the manuscript.

Funding

Dr. Tenzer R conducted this research during his sabbatical leave at the German Research Centre for Geosciences - GFZ Potsdam in Germany. Dr. Chen W was funded by the National Natural Science Foundation of China (NSFC Grant Number: 42264001), Jiangxi University of Science and Technology High-level Talent Research Startup Project (205200100588).

Data Availability Statement

The data presented in this study are available upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Forsberg, R.; Tscherning, C.C. Topographic effects in gravity field modelling for BVP. Geodetic boundary value problems in view of the one centimeter geoid 1997, 239–272. [Google Scholar]
  2. Hwang, C.; Wang, C.G.; Hsiao, Y.S. Terrain correction computation using Gaussian quadrature. Computers & Geosciences 2003, 29, 1259–1268. [Google Scholar]
  3. Ågren, J. Regional geoid determination methods for the era of satellite gravimetry: numerical investigations using synthetic earth gravity models. Doctoral dissertation, Infrastruktur 2004. [Google Scholar]
  4. Hwang, C.; Hsiao, Y.S.; Shih, H.C. Geodetic and geophysical results from a Taiwan airborne gravity survey: Data reduction and accuracy assessment. Journal of Geophysical Research: Solid Earth 2007, 112. [Google Scholar] [CrossRef]
  5. Makhloof, A.A.sE. The use of topographic-isostatic mass information in geodetic applications. Doctoral dissertation, Universitäts-und Landesbibliothek Bonn 2007. [Google Scholar]
  6. Makhloof, A.A.; Ilk, K.H. Effects of topographic–isostatic masses on gravitational functionals at the Earth’s surface and at airborne and satellite altitudes. Journal of Geodesy 2008, 82, 93–111. [Google Scholar] [CrossRef]
  7. Tsoulis, D.; Novák, P.; Kadlec, M. Evaluation of precise terrain effects using high-resolution digital elevation models. Journal of Geophysical Research: Solid Earth 2009, 114. [Google Scholar] [CrossRef]
  8. Flury, J.; Rummel, R. On the geoid–quasigeoid separation in mountain areas. Journal of Geodesy 2009, 83, 829–847. [Google Scholar] [CrossRef]
  9. Tziavos, I.N.; Sideris, M.G. Topographic reductions in gravity and geoid modeling. In Geoid Determination; Springer: Berlin, Heidelberg, 2013; pp. 337–400. [Google Scholar]
  10. Jiang, T.; Dang, Y.; Zhang, C. Gravimetric geoid modeling from the combination of satellite gravity model, terrestrial and airborne gravity data: a case study in the mountainous area, Colorado. Earth, Planets and Space 2020, 72, 1–15. [Google Scholar] [CrossRef]
  11. Tenzer, R.; Chen, W.; Rathnayake, S. The effect of anomalous global lateral topographic density on the geoid-to-quasigeoid separation. Journal of Geodesy 2021, 95, 1–20. [Google Scholar] [CrossRef]
  12. Tenzer, R.; Hirt, C.; Novák, P. Contribution of mass density heterogeneities to the geoid-to-quasigeoid separation. J. Geod. 2016, 90, 1–65. [Google Scholar] [CrossRef]
  13. Artemieva, I.M.; Mooney, W.D. Thermal thickness and evolution of Precambrian lithosphere: a global study. J. Geophys. Res 2001, 106, 16837–16414. [Google Scholar] [CrossRef]
  14. Kaban, M.K.; Schwintzer, P.; Artemieva, I.M. Density of the continental roots: compositional and thermal contributions. Earth Planet. Sci. Lett 2003, 209, 53–69. [Google Scholar] [CrossRef]
  15. Artemieva, I.M. Global 1°×1° thermal model TC1 for the continental lithosphere: Implications for lithosphere secular evolution. Tectonophysics 2006, 416, 245–277. [Google Scholar] [CrossRef]
  16. Tenzer, R.; Hamayun; Vajda, P. Global map of the gravity anomaly corrected for complete effects of the topography, and of density contrasts of global ocean, ice, and sediments. Contributions to Geophysics and Geodesy 2008, 38, 357–370. [Google Scholar]
  17. Mooney, W.D; Kaban, M.K. The North American upper mantle: density, composition, and evolution. J. Geophys. Res 2010, 115, B12424. [Google Scholar] [CrossRef]
  18. Tenzer, R.; Chen, W. Mantle and sub-lithosphere mantle gravity maps from the LITHO1.0 global lithospheric model. Earth-Sci. Rev 2019, 194, 38–56. [Google Scholar] [CrossRef]
  19. Wieczorek, M.A. Gravity and topography of the terrestrial planets. Treatise on geophysics 2007, 10, 165–206. [Google Scholar]
  20. Uieda, L.; Barbosa, V.C.; Braitenberg, C. Tesseroids: Forward-modeling gravitational fields in spherical coordinates. Geophysics 2016, 81, F41–F48. [Google Scholar] [CrossRef]
  21. Yang, M.; Hirt, C.; Pail, R. TGF: a new MATLAB-based software for terrain-related gravity field calculations. Remote sensing 2020, 12, 1063. [Google Scholar] [CrossRef]
  22. Nagy, D. The gravitational attraction of a right rectangular prism. Geophysics 1966, 31, 362–371. [Google Scholar] [CrossRef]
  23. Nagy, D.; Papp, G.; Benedek, J. The gravitational potential and its derivatives for the prism. Journal of Geodesy 2000, 74, 552–560. [Google Scholar] [CrossRef]
  24. Forsberg, R.; Tscherning, C.C. The use of height data in gravity field approximation by collocation. Journal of Geophysical Research: Solid Earth 1981, 86, 7843–7854. [Google Scholar] [CrossRef]
  25. Götze, H.J.; Lahmeyer, B. Application of three-dimensional interactive modeling in gravity and magnetics. Geophysics 1988, 53, 1096–1108. [Google Scholar] [CrossRef]
  26. Denker, H. Regional gravity field modeling: theory and practical results. In Sciences of geodesy-II; Springer: Berlin, Heidelberg, 2003; pp. 185–291. [Google Scholar]
  27. Tsoulis, D. Terrain modeling in forward gravimetric problems: a case study on local terrain effects. Journal of Applied Geophysics 2003, 54, 145–160. [Google Scholar] [CrossRef]
  28. Novák, P.; Grafarend, E.W. The effect of topographical and atmospheric masses on spaceborne gravimetric and gradiometric data. Studia geophysica et geodaetica 2006, 50, 549–582. [Google Scholar] [CrossRef]
  29. Asgharzadeh, M.F.; Von Frese, R.R. B.; Kim, H.R. Spherical prism gravity effects by Gauss-Legendre quadrature integration. Geophysical Journal International 2007, 169, 1–11. [Google Scholar] [CrossRef]
  30. Heck, B.; Seitz, K. A comparison of the tesseroid, prism and point-mass approaches for mass reductions in gravity field modelling. Journal of Geodesy 2007, 81, 121–136. [Google Scholar] [CrossRef]
  31. D’Urso, M.G. On the evaluation of the gravity effects of polyhedral bodies and a consistent treatment of related singularities. Journal of Geodesy 2013, 87, 239–252. [Google Scholar] [CrossRef]
  32. Grombein, T.; Seitz, K.; Heck, B. Optimized formulas for the gravitational field of a tesseroid. Journal of Geodesy 2013, 87, 645–660. [Google Scholar] [CrossRef]
  33. Parker, R.L. The rapid calculation of potential anomalies. Geophysical Journal International 1972, 31, 447–455. [Google Scholar] [CrossRef]
  34. Colombo, O.L. Numerical Methods for Harmonic Analysis on the Sphere. OSU report No. 310, Department of Geodetic Science and Surveying 1981.
  35. Forsberg, R. A study of terrain reductions, density anomalies and geophysical inversion methods in gravity field modelling. Report 355, Department of Geodetic Science and Surveying, Ohio State University, Columbus 1984.
  36. Wieczorek, M.A.; Phillips, R.J. Potential anomalies on a sphere: Applications to the thickness of the lunar crust. Journal of Geophysical Research: Planets 1998, 103, 1715–1724. [Google Scholar] [CrossRef]
  37. Chambat, F.; Valette, B. Earth gravity up to second order in topography and density. Physics of the Earth and Planetary Interiors 2005, 151, 89–106. [Google Scholar] [CrossRef]
  38. Eshagh, M. Comparison of two approaches for considering laterally varying density in topographic effect on satellite gravity gradiometric data. Acta Geophysica 2010, 58, 661–686. [Google Scholar] [CrossRef]
  39. Tenzer, R.; Novák, P.; Vajda, P. Uniform spectral representation of the Earth’s inner density structures and their gravitational field. Contributions to Geophysics and Geodesy 2011, 41, 191–209. [Google Scholar] [CrossRef]
  40. Balmino, G.; Vales, N.; Bonvalot, S. Spherical harmonic modelling to ultra-high degree of Bouguer and isostatic anomalies. Journal of Geodesy 2012, 86, 499–520. [Google Scholar] [CrossRef]
  41. Hirt, C.; Kuhn, M. Evaluation of high-degree series expansions of the topographic potential to higher-order powers. Journal of Geophysical Research: Solid Earth 2012, 117. [Google Scholar] [CrossRef]
  42. Novák, P.; Tenzer, R.; Eshagh, M. Evaluation of gravitational gradients generated by Earth's crustal structures. Computers & Geosciences 2013, 51, 22–33. [Google Scholar]
  43. Haagmans, R. A synthetic Earth for use in geodesy. Journal of Geodesy 2000, 74, 503–511. [Google Scholar] [CrossRef]
  44. Kuhn, M.; Featherstone, W.E. Construction of a synthetic Earth gravity model by forward gravity modelling. In A Window on the Future of Geodesy: Proceedings of the International Association of Geodesy IAG General Assembly Sapporo, Japan June 30–July 11, 2003; Springer: Berlin Heidelberg, 2005; pp. 350–355. [Google Scholar]
  45. Baran, I.; Kuhn, M.; Claessens, S.J. A synthetic Earth gravity model designed specifically for testing regional gravimetric geoid determination algorithms. Journal of Geodesy 2006, 80, 1–16. [Google Scholar] [CrossRef]
  46. Kitterød, N.O.; Leblois, É. Modelling Bedrock Topography. Earth Surface Dynamics Discussions 2019, 1–36. [Google Scholar]
  47. Tenzer, R.; Bagherbandi, M.; Gladkikh, V. Signature of the upper mantle density structure in the refined gravity data. Comput. Geosci. 2012, 16, 975–986. [Google Scholar] [CrossRef]
  48. Tenzer, R.; Hamayun; Vajda, P. Global maps of the CRUST2.0 crustal components stripped gravity disturbances. J Geophys Res 2009, 114, B05408. [Google Scholar]
  49. Tenzer, R.; Hamayun; Vajda, P. Global maps of the step-wise topography corrected and crustal components stripped geoids using the CRUST2.0 model. Contributions to Geophysics and Geodesy 2009, 39, 1–18. [Google Scholar] [CrossRef]
  50. Tenzer, R.; Chen, W.; Jin, S. Effect of upper mantle density structure on Moho geometry. Pure and Applied Geophysics 2015, 172, 1563–1583. [Google Scholar] [CrossRef]
  51. Tenzer, R.; Chen, W.; Baranov, A. Gravity maps of Antarctic lithospheric structure from remote-sensing and seismic data. Pure and Applied Geophysics 2018, 175, 2181–2203. [Google Scholar] [CrossRef]
  52. Sjöberg, L.E.; Majid, A. The uncertainty of CRUST1.0: Moho depth and density contrast models. J Appl Geod. 2021, 15, 143–152. [Google Scholar] [CrossRef]
  53. Steinberger, B. Effects of latent heat release at phase boundaries on flow in the Earth’s mantle, phase boundary topography and dynamic topography at the Earth’s surface: Physics Earth Planet. Inter 2007, 164, 2–20. [Google Scholar] [CrossRef]
  54. Müller, R.D.; Flament, N.; Matthews, K.J. Formation of Australian continental margin highlands driven by plate-mantle interaction. Earth Planet. Sci. Lett. 2016, 441, 60–70. [Google Scholar] [CrossRef]
  55. Rubey, M.; Brune, S.; Heine, C. Global patterns in Earth's dynamic topography since the Jurassic: the role of subducted slabs. Solid Earth 2017, 8, 899–919. [Google Scholar] [CrossRef]
  56. Tenzer, R.; Chen, W.; Tsoulis, D. Analysis of the refined CRUST1. 0 crustal model and its gravity field. Surveys in geophysics 36, 139–165. [CrossRef]
  57. Dziewonski, A.M.; Hales, A.L.; Lapwood, E.R. Parametrically simple Earth models consistent with geophysical data. Physics of the Earth and Planetary Interiors 1975, 10, 12–48. [Google Scholar] [CrossRef]
  58. Dziewonski, A.M.; Anderson, D.L. Preliminary Reference Earth Model. Physics Earth Planet, Inter 1981, 25, 297–356. [Google Scholar] [CrossRef]
  59. Kennett, B.L. N.; Engdahl, E.R. Traveltimes for global earthquake location and phase identification. Geophysical Journal International 1991, 105, 429–465. [Google Scholar] [CrossRef]
  60. Kennett, B.L.; Engdahl, E.R.; Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophysical Journal International 1995, 122, 108–124. [Google Scholar] [CrossRef]
  61. Montagner, J.P.; Kennett, B.L. N. How to reconcile body-wave and normal-mode reference Earth models. Geophysical Journal International 1996, 125, 229–248. [Google Scholar] [CrossRef]
  62. Van der Lee, S.; Nolet, G. Upper mantle S velocity structure of North America. Journal of Geophysical Research: Solid Earth 1997, 102, 22815–22838. [Google Scholar] [CrossRef]
  63. Kustowski, B.; Ekström, G.; Dziewoński, A.M. Anisotropic shear-wave velocity structure of the Earth's mantle: A global model. Journal of Geophysical Research: Solid Earth 2008, 113. [Google Scholar] [CrossRef]
  64. Simmons, N.A.; Forte, A.M.; Boschi, L. GyPSuM: a joint tomographic model of mantle density and seismic wave speeds. J. Geophys. Res. Solid Earth 2010, 115, B12310. [Google Scholar] [CrossRef]
  65. Trabant, C.; Hutko, A.R.; Bahavar, M. Data products at the IRIS DMC: Stepping stones for research and other applications. Seismological Research Letters 2012, 83, 846–854. [Google Scholar] [CrossRef]
  66. Nataf, H.C.; Ricard, Y. 3SMAC: an a priori tomographic model of the upper mantle based on geophysical modeling. Physics of the Earth and Planetary Interiors 1996, 95, 101–122. [Google Scholar] [CrossRef]
  67. Mooney, W.D.; Laske, G.; Masters, T.G. CRUST 5.1: A global crustal model at 5× 5. Journal of Geophysical Research: Solid Earth 1998, 103, 727–747. [Google Scholar] [CrossRef]
  68. Bassin, C. The current limits of resolution for surface wave tomography in North America. Eos Trans. AGU 2000, 81, F897. [Google Scholar]
  69. Laske, G.; Masters, G.; Ma, Z. et al. Update on CRUST1.0-A 1-degree global model of Earth’s crust. In Geophysical research abstracts; EGU General Assembly: Vienna, Austria, 2013; Volume 15, p. 2658. [Google Scholar]
  70. Pasyanos, M.E.; Masters, T.G.; Laske, G. LITHO1.0: An updated crust and lithospheric model of the Earth. J. Geophys. Res. 2014, 119, 2153–2173. [Google Scholar] [CrossRef]
  71. Simmons, N.A.; Myers, S.C.; Johannesson, G. LLNL-G3Dv3: Global P wave tomography model for improved regional and teleseismic travel time prediction. Journal of Geophysical Research: Solid Earth 2012, 117. [Google Scholar] [CrossRef]
  72. Hirt, C.; Rexer, M. Earth2014: 1 arc-min shape, topography, bedrock and ice-sheet models - available as gridded data and degree-10,800 spherical harmonics. Int. J. Appl. Earth. Obs. and Geoinf 2015, 39, 103–112. [Google Scholar] [CrossRef]
  73. Chen, W.; Tenzer, R. Harmonic coefficients of the Earth’s spectral crustal model 180–ESCM180. Earth Science Informatics 2015, 8, 147–159. [Google Scholar] [CrossRef]
  74. Heiskanen, W.A.; Moritz, H. Physical geodesy. Freeman W.H., New York 1967.
  75. Pizzetti, P. Sopra il calcolo teorico delle deviazioni del geoide dall` ellissoide. Atti. R. Accad. Sci. Torino 1911, 46, 331–350. [Google Scholar]
  76. Somigliana, C. Teoria generale del campo gravitazionale dell'ellissoide di rotazione. Memorie della società astronomica italiana 1929, 4, 425. [Google Scholar]
  77. Moritz, H. Geodetic Reference System 1980. J. Geod 2000, 74, 128–162. [Google Scholar] [CrossRef]
  78. Wieczorek, M.A. Gravity and Topography of the Terrestrial Planets. Treatise on Geophysics: Second Edition 2015, 10, 153–193. [Google Scholar]
  79. Tenzer, R.; Foroughi, I.; Sjöberg, L.E. Definition of physical height systems for telluric planets and moons. Surveys in Geophysics 2018, 39, 313–335. [Google Scholar] [CrossRef]
  80. Tenzer, R.; Vajda, P.; Hamayun. Global atmospheric corrections to the gravity field quantities. Contr Geophys. Geod. 2009, 39, 221–236. [Google Scholar] [CrossRef]
  81. Tenzer, R.; Chen, W. Comparison of gravimetric, isostatic, and spectral decomposition methods for a possible enhancement of the mantle signature in the long-wavelength geoidal geometry. Remote Sensing, Special issue: Satellite Missions for Earth and Planetary Exploration, Space-Geodetic Techniques II 2023.
  82. Tenzer, R.; Novák, P.; Vajda, P. Spectral harmonic analysis and synthesis of Earth’s crust gravity field. Comput. Geosc. 2012, 16, 193–207. [Google Scholar] [CrossRef]
  83. Tenzer, R.; Gladkikh, V.; Vajda, P. Spatial and spectral analysis of refined gravity data for modelling the crust-mantle interface and mantle-lithosphere structure, Surv. Geophys 2012, 33, 817–839. [Google Scholar]
  84. Gladkikh, V.; Tenzer, R. A mathematical model of the global ocean saltwater density distribution. Pure Appl. Geophys 2011, 169, 249–257. [Google Scholar]
  85. Foroughi, I.; Tenzer, R. Comparison of different methods for estimating the geoid-to-quasigeoid separation. Geophys. J. Int 2017, 210, 1001–1020. [Google Scholar] [CrossRef]
  86. Förste, Ch.; Bruinsma, S.L.; Abrikosov, O. et al. EIGEN-6C4 The latest combined global gravity field model including GOCE data up to degree and order 2190 of GFZ Potsdam and GRGS Toulouse. GFZ Data Services, Ed: Tapley B.D., Bettadpur S., Watkins M 2014.
  87. Sheng, M.B.; Shaw, C.; Vaníček, P. Formulation and validation of a global laterally varying topographical density model. Tectonoph 2019, 762, 45–60. [Google Scholar] [CrossRef]
  88. Divins, D.L. Total Sediment Thickness of the World's Oceans & Marginal Seas. NOAA National Geophysical Data Center, Boulder, CO 2003.
  89. Baranov, A.; Tenzer, R.; Bagherbandi, M. Combined gravimetric-seismic crustal model for Antarctica. Surv. Geophys 2018, 39, 1–23. [Google Scholar] [CrossRef]
  90. Hinze, W.J. Bouguer reduction density, why 2.67? Geophys 2003, 68, 5–1559. [Google Scholar] [CrossRef]
  91. Artemjev, M.E.; Kaban, M.K.; Kucherinenko, V.A. Subcrustal density inhomogeneities of northern Eurasia as derived from the gravity data and isostatic models of the lithosphere. Tectonophysics 1994, 240, 248–280. [Google Scholar] [CrossRef]
  92. Tenzer, R.; Gladkikh, V. Assessment of density variations of marine sediments with ocean and sediment depths. Sci. World J. 2014, 2014, 823296. [Google Scholar] [CrossRef]
  93. Hager, B.H. Subducted slabs and the geoid: Constraints on mantle rheology and flow. Journal of Geophysical Research: Solid Earth 1984, 89, 6003–6015. [Google Scholar] [CrossRef]
  94. Panasyuk, S.V.; Hager, B. Models of isostatic and dynamic topography, geoid anomalies, and their uncertainties. J. Geophys. Res. 2000, 105, 28199–28209. [Google Scholar] [CrossRef]
  95. Barnett-Moore, N.; Hassan, R.; Müller, R.D. Dynamic topography and eustasy controlled the paleogeographic evolution of northern Africa since the mid-Cretaceous. Tectonics 2017, 36, 929–944. [Google Scholar] [CrossRef]
  96. Flament, N.; Gurnis, M.; Williams, S. Topographic asymmetry of the South Atlantic from global models of mantle flow and lithospheric stretching. Earth Planet. Sci. Lett 2014, 387, 107–119. [Google Scholar] [CrossRef]
  97. Flament, N.; Gurnis, M.; Müller, R.D. Influence of subduction history on South American topography. Earth Planet. Sci. Lett 2015, 430, 9–18. [Google Scholar] [CrossRef]
  98. Cao, W.; Flament, N.; Zahirovic, S. The interplay of dynamic topography and eustasy on continental flooding in the late Paleozoic. Tectonophysics 2019, 761. [Google Scholar] [CrossRef]
  99. Lithgow-Bertelloni, C.; Silver, P.G. Dynamic topography, plate driving forces and the African superswell. Nature 1998, 395, 269–272. [Google Scholar] [CrossRef]
  100. Self, S.; Rampino, M. The Crust and Lithosphere. Geological Society of London 2012. [Google Scholar]
  101. Turcotte, D.L.; Schubert, G. Geodynamics - 2nd Edition. Cambridge University Press 2002, pp. 472.
  102. Conrad, C.P.; Lithgow-Bertelloni, C. Influence of continental roots and asthenosphere on plate-mantle coupling. Geophys. Res. Lett 2006, 33, L05312. [Google Scholar] [CrossRef]
  103. Hoggard, M.J.; Czarnota, K.; Richards, F.D. Global distribution of sediment-hosted metals controlled by craton edge stability. Nature Geoscience 2020, 13, 504–510. [Google Scholar] [CrossRef]
  104. Schaeffer, A.J.; S. Lebedev. Global shear speed structure of the upper mantle and transition zone. Geophysical Journal International 2013, 194, 417–449. [Google Scholar] [CrossRef]
  105. Ho, T.; K. Priestley; E. Debayle. A global horizontal shear velocity model of the upper mantle from multimode love wave measurements. Geophysical Journal International 2016, 207, 542–561. [Google Scholar] [CrossRef]
  106. Priestley, K.; McKenzie, D.; Ho, T. A lithosphere–asthenosphere boundary—A global model derived from multimode surface-wave tomography and petrology. Lithospheric discontinuities 2018, 111–123. [Google Scholar]
  107. Debayle, E.; F. Dubuffet; S. Durand. An automatically updated S-wave model of the upper mantle and the depth extent of azimuthal anisotropy. Geophysical Research Letters 2016, 43, 674–682. [Google Scholar] [CrossRef]
  108. Schaeffer, A.J.; S. Lebedev. Imaging the North American continent using waveform inversion of global and USArray data. Earth and Planetary Science Letters 2014, 402, 26–41. [Google Scholar] [CrossRef]
  109. Celli, N.L.; S. Lebedev, A.J. Schaeffer. et al. African cratonic lithosphere carved by mantle plumes. Nature Communications 2020a, 11.
  110. Celli, N.L.; S. Lebedev, A.; J. Schaeffer, M. et al. The upper mantle beneath the South Atlantic Ocean, South America and Africa from waveform tomography with massive data sets. Geophysical Journal International 2020, 221, 178–204. [CrossRef]
  111. Christensen, N.I.; Mooney, W.D. Seismic velocity structure and composition of the continental crust: A global view. Journal of Geophysical Research: Solid Earth 1995, 100, 9761–9788. [Google Scholar] [CrossRef]
  112. Hager, B.H.; Richards, M.A. Long-wavelength variations in Earth’s geoid - physical models and dynamical implications. Phil. Trans. R. Soc. Lond., Ser. A 1989, 328, 309–327. [Google Scholar]
  113. Simmons, A.J.; Willett, K.M.; Jones, P.D. Low-frequency variations in surface atmospheric humidity, temperature, and precipitation: Inferences from reanalyses and monthly gridded observational data sets. Journal of Geophysical Research: Atmospheres 2010, 115. [Google Scholar] [CrossRef]
  114. Jordan, T.H. The continental tectosphere. Rev. Geophys 1975, 13, 1–12. [Google Scholar] [CrossRef]
  115. Gung, Y.C.; Panning, M.; Romanowicz, B. Global anisotropy and the thickness of continents. Nature 2003, 422, 707–711. [Google Scholar] [CrossRef] [PubMed]
  116. Artemieva, I.M. Dynamic topography of the East European craton: Shedding light upon lithospheric structure, composition and mantle dynamics. Glob. Planet. Change 2007, 58, 411–434. [Google Scholar] [CrossRef]
  117. Sjöberg, L.E.; Bagherbandi, M. A method of estimating the Moho density contrast with a tentative application by EGM08 and CRUST2.0. Acta Geophys. 2011, 59, 3–502. [Google Scholar] [CrossRef]
  118. Rogers, N.; Blake, S.; Burton, K. An introduction to our dynamic planet. Cambridge University Press 2008. [Google Scholar]
  119. Carlson, R.L.; Raskin, G.S. Density of the ocean crust. Nature 1984, 311, 555–558. [Google Scholar] [CrossRef]
  120. Hoggard, M.J.; White, N.; Al-Attar, D. Global dynamic topography observations reveal limited influence of large-scale mantle flow. Nature-Geoscience 2016, 9, 456–463. [Google Scholar] [CrossRef]
  121. Simmons, N.A.; Gurrola, H. Multiple seismic discontinuities near the base of the transition zone in the Earth’s mantle. Nature 2000, 405, 559–562. [Google Scholar] [CrossRef]
  122. Lawrence, J.F.; Shearer, P.M. Constraining seismic velocity and density for the mantle transition zone with reflected and transmitted waveforms, Geochem. Geophys. Geosyst 2006, 7, Q10012. [Google Scholar] [CrossRef]
  123. Griffin, W.L.; O’Reilly, S.Y.; Afonso, J.C. The Composition and Evolution of Lithospheric Mantle: a Re-evaluation and its Tectonic Implications. J. Petrolog 2009, 50, 7–1185. [Google Scholar] [CrossRef]
  124. Ishii, M.; Tromp, J. Normal-mode and free-air gravity constraints on lateral variations in velocity and density of Earth's mantle. Science 1999, 285, 1231–1236. [Google Scholar] [CrossRef]
  125. Kuo, C.; Romanowicz, B. Density and seismic velocity variations determined from normal mode spectra, EOS, Trans. Am. geophys. Un. 1999, 80, S14. [Google Scholar]
  126. Panasyuk, S.; Ishii, M.; O'Connell, R. Constraints on the density and viscosity structure of the earth, EOS, Trans. Am. geophys. Un. 1999, 80, F28. [Google Scholar]
  127. Resovsky, J.S.; Ritzwoller, M.H. Regularization uncertainty in density models estimated from normal mode data. Geophys. Res. Lett. 1999, 26, 2319–2322. [Google Scholar] [CrossRef]
  128. Romanowicz, B. Can we resolve 3-D density heterogeneity in the lower mantle? Geophys. Res. Lett. 2001, 28, 1107–1110. [Google Scholar] [CrossRef]
  129. Kuo, C.; Romanowicz, B. On the resolution of density anomalies in the Earth's mantle using spectral fitting of normal-mode data. Geophys. J. Int. 2002, 150, 162–179. [Google Scholar] [CrossRef]
Preprints 82929 g001
Figure 1. Global maps of the gravitational potentials of: (a) topography V T , (b) ice V I , (c) bathymetry V B , (d) sediments V S , (e) consolidated crust V C , (f) Moho geometry   V M , Δ ρ c / m , (g) lithospheric mantle V L M , and (h) LAB geometry   V L A B .
Figure 1. Global maps of the gravitational potentials of: (a) topography V T , (b) ice V I , (c) bathymetry V B , (d) sediments V S , (e) consolidated crust V C , (f) Moho geometry   V M , Δ ρ c / m , (g) lithospheric mantle V L M , and (h) LAB geometry   V L A B .
Preprints 82929 g001
Preprints 82929 g002
Figure 2. Global maps of: (a) the geoid N , (b) the Bouguer geoid N B , (c) the crust-stripped geoid N C S , (d) the mantle geoid N M , (e) the lithosphere-stripped geoid N C L , and (f) the sub-lithospheric mantle geoid N S M .
Figure 2. Global maps of: (a) the geoid N , (b) the Bouguer geoid N B , (c) the crust-stripped geoid N C S , (d) the mantle geoid N M , (e) the lithosphere-stripped geoid N C L , and (f) the sub-lithospheric mantle geoid N S M .
Preprints 82929 g002
Preprints 82929 g003
Figure 3. The sub-lithospheric mantle geoid computed up to degree 5 of spherical harmonics (and calibrated so its mean value equals zero).
Figure 3. The sub-lithospheric mantle geoid computed up to degree 5 of spherical harmonics (and calibrated so its mean value equals zero).
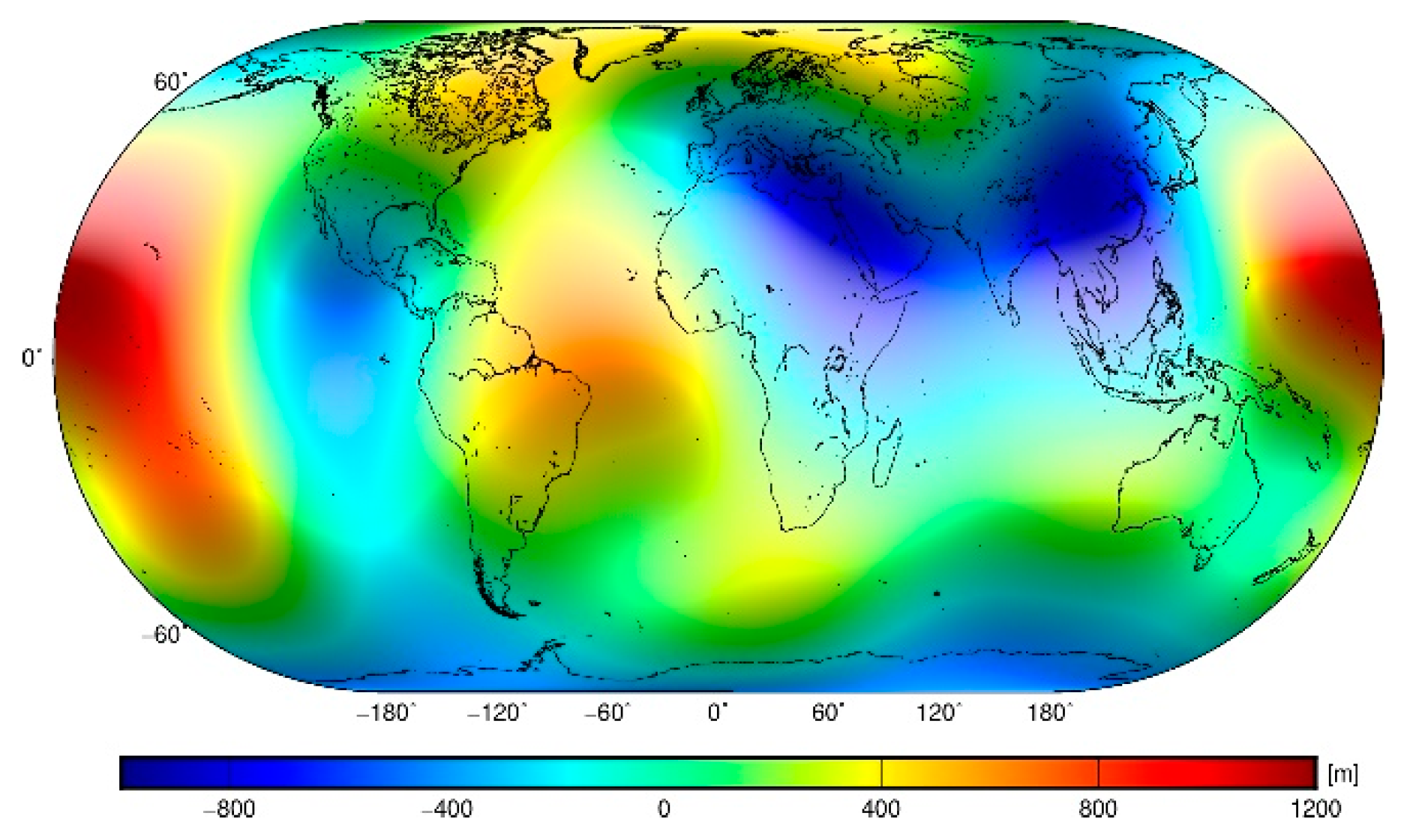
Preprints 82929 g003
Preprints 82929 g004
Figure 4. Lithospheric thickness models: (a) SLNAAFSA, (b) SL2013sv, (c) LITHO1.0, and (d) CAM2016, and (e) 3D2015-07Sv.
Figure 4. Lithospheric thickness models: (a) SLNAAFSA, (b) SL2013sv, (c) LITHO1.0, and (d) CAM2016, and (e) 3D2015-07Sv.
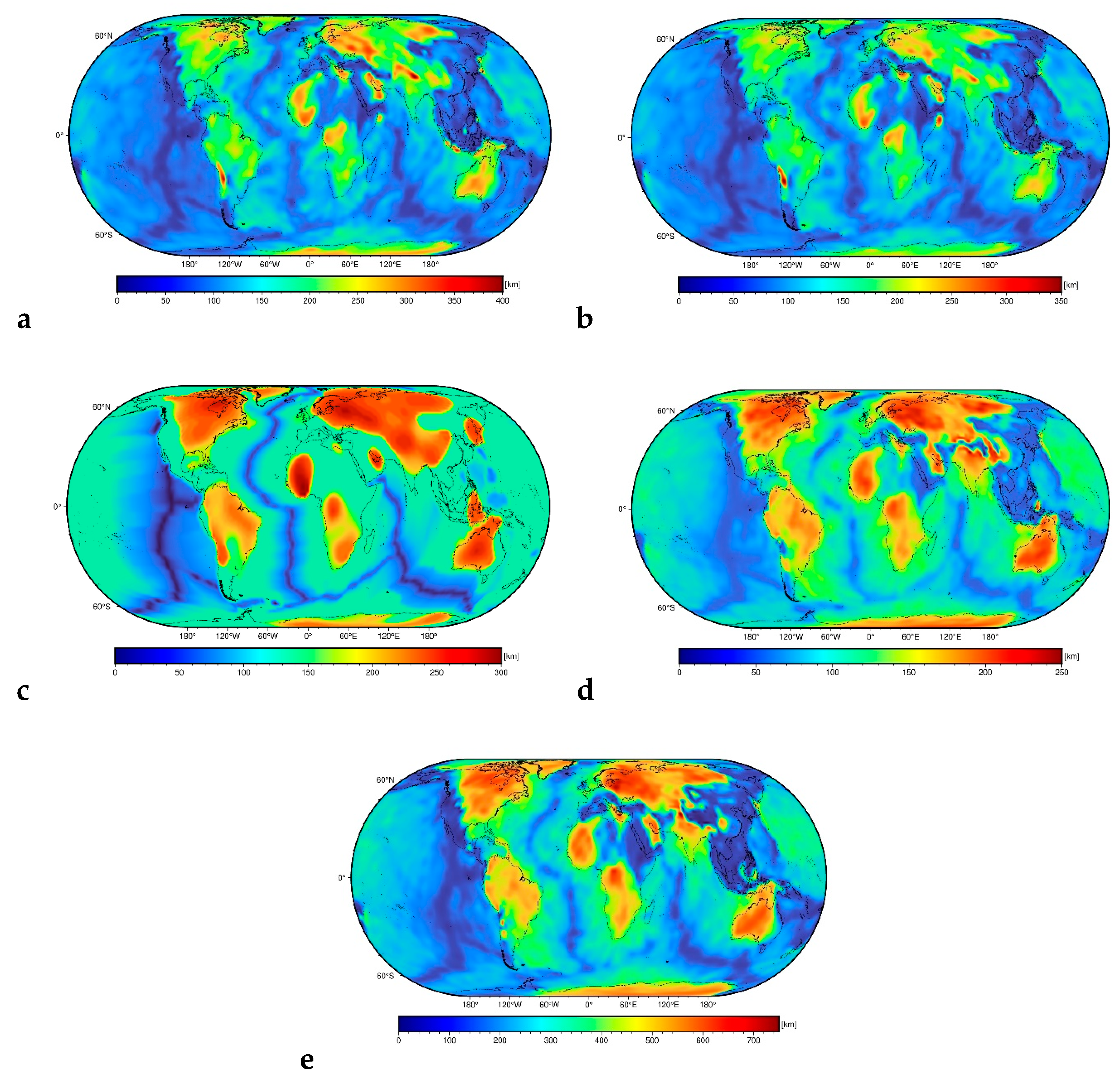
Preprints 82929 g004
Table 1. Statistics of gravitational potentials used to compute the sub-lithospheric mantle gravity disturbances. For notation used, see legend in Figure 1.
Table 1. Statistics of gravitational potentials used to compute the sub-lithospheric mantle gravity disturbances. For notation used, see legend in Figure 1.
Gravitational potential Min [m2.s-2] Max [m2.s-2] Mean [m2.s-2] STD [m2.s-2]
V T 2226 8494 3589 1114
V I -3472 -312 -731 729
V B -28533 -16402 -22386 3185
V S -3862 -1937 -2719 444
V C 11529 25075 15661 2741
V M , Δ ρ c / m -69885 -46423 -55734 5832
V L M -262661 -174276 -213366 17795
V L A B 168987 244558 203311 16194
Table 2. Statistics of geoid models. For notation used, see legend in Figure 2.
Table 2. Statistics of geoid models. For notation used, see legend in Figure 2.
Refined geoid Min [m] Max [m] Mean [m] STD [m]
N -106 85 -1 29
N B 1198 2946 2269 356
N C S -1358 1743 671 630
N M 5772 6617 6358 128
N C L 24009 33222 28130 1835
N S M 6445 8388 7384 372
Table 3. Statistics of the lithospheric thickness models SLNAAFSA, SL2013sv, LITHO1.0, CAM2016, and 3D2015-07Sv.
Table 3. Statistics of the lithospheric thickness models SLNAAFSA, SL2013sv, LITHO1.0, CAM2016, and 3D2015-07Sv.
Lithospheric thickness model Min [km] Max [km] Mean [km] STD [km]
SLNAAFSA 38 364 115 57
SL2013sv 40 350 112 52
LITHO1.0 7 271 114 55
CAM2016 38 241 111 46
3D2015-07Sv 36 703 110 51
Table 4. Statistics of differences between the lithospheric thickness models SLNAAFSA, SL2013sv, LITHO1.0, CAM2016, and 3D2015-07Sv.
Table 4. Statistics of differences between the lithospheric thickness models SLNAAFSA, SL2013sv, LITHO1.0, CAM2016, and 3D2015-07Sv.
Lithospheric thickness model differences Min [km] Max [km] Mean [km] RMS [km]
SLNAAFSA - SL2013sv -237 303 3 11
SLNAAFSA - LITHO1.0 -196 289 1 77
SLNAAFSA - CAM2016 -160 307 4 26
SLNAAFSA - 3D2015-07Sv -638 309 5 26
SL2013sv - LITHO1.0 -195 298 -1 74
SL2013sv - CAM2016 -160 306 1 22
SL2013sv - 3D2015-07Sv -637 303 3 24
LITHO1.0 - CAM2016 -184 206 2 71
LITHO1.0 - 3D2015-07Sv -603 206 4 74
CAM2016 - 3D2015-07Sv -561 195 2 18
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated