Submitted:
02 September 2023
Posted:
05 September 2023
You are already at the latest version
Abstract

Keywords:
1. Introduction
1.1. Aerial Imaging
1.2. Unmanned Aerial Imaging
1.3. Preserving Wildlife
2. Proposed Approach
2.1. Background theory
2.1.1. Differential Techniques:
- A. Horn– Schunck method:
- B. Lucas–Kanade method:


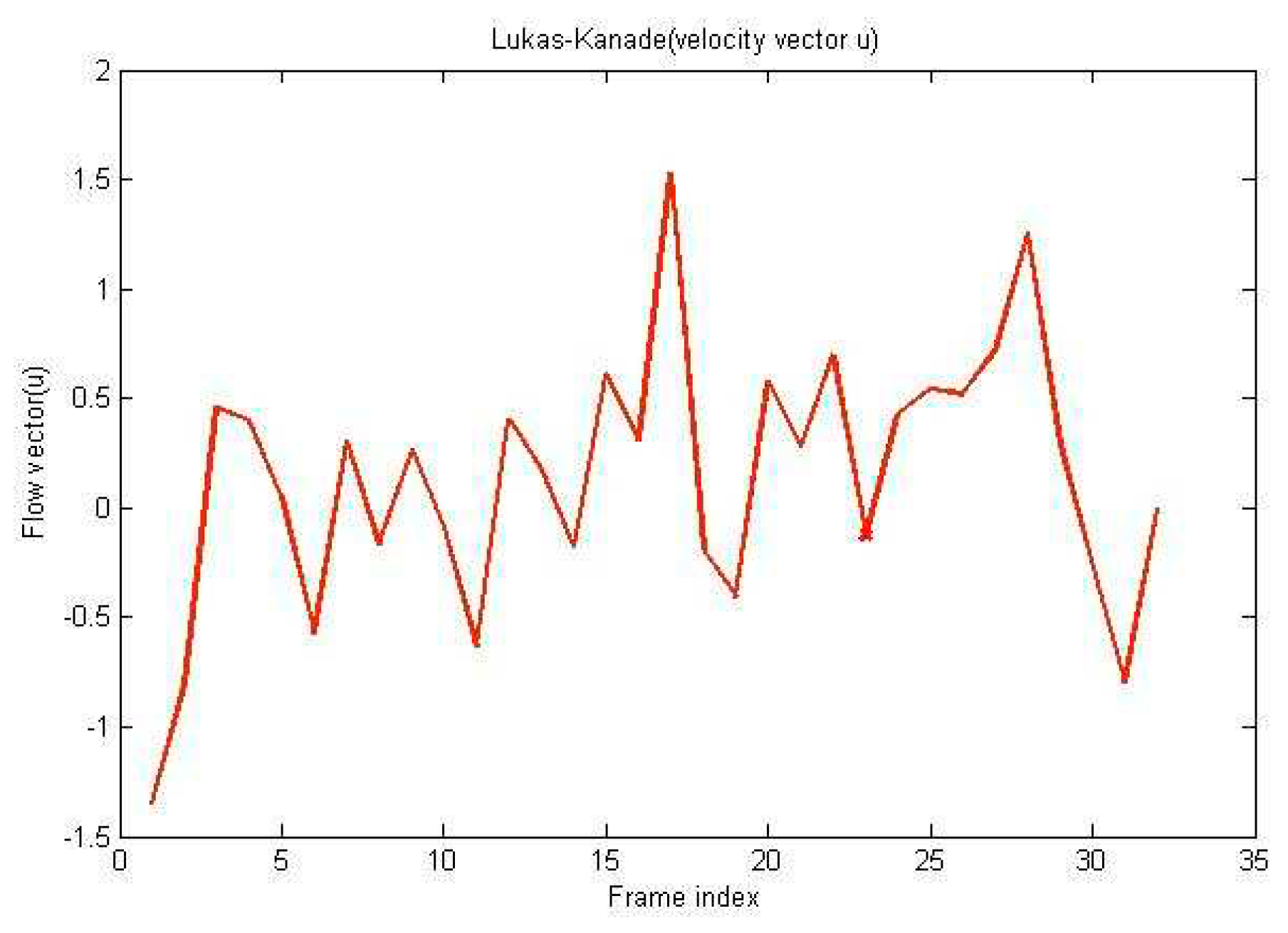
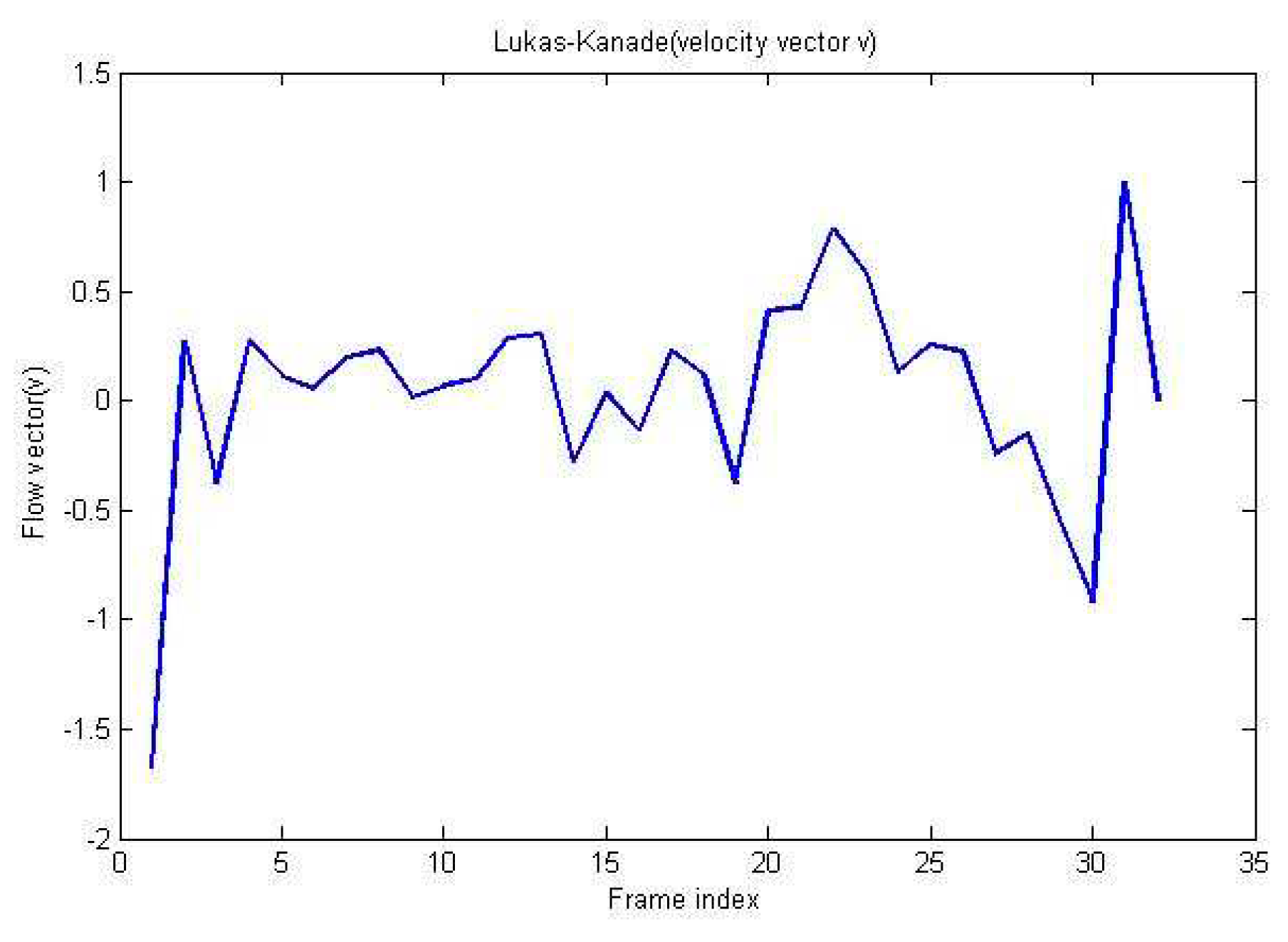
3. Experimental results
4. Conclusion

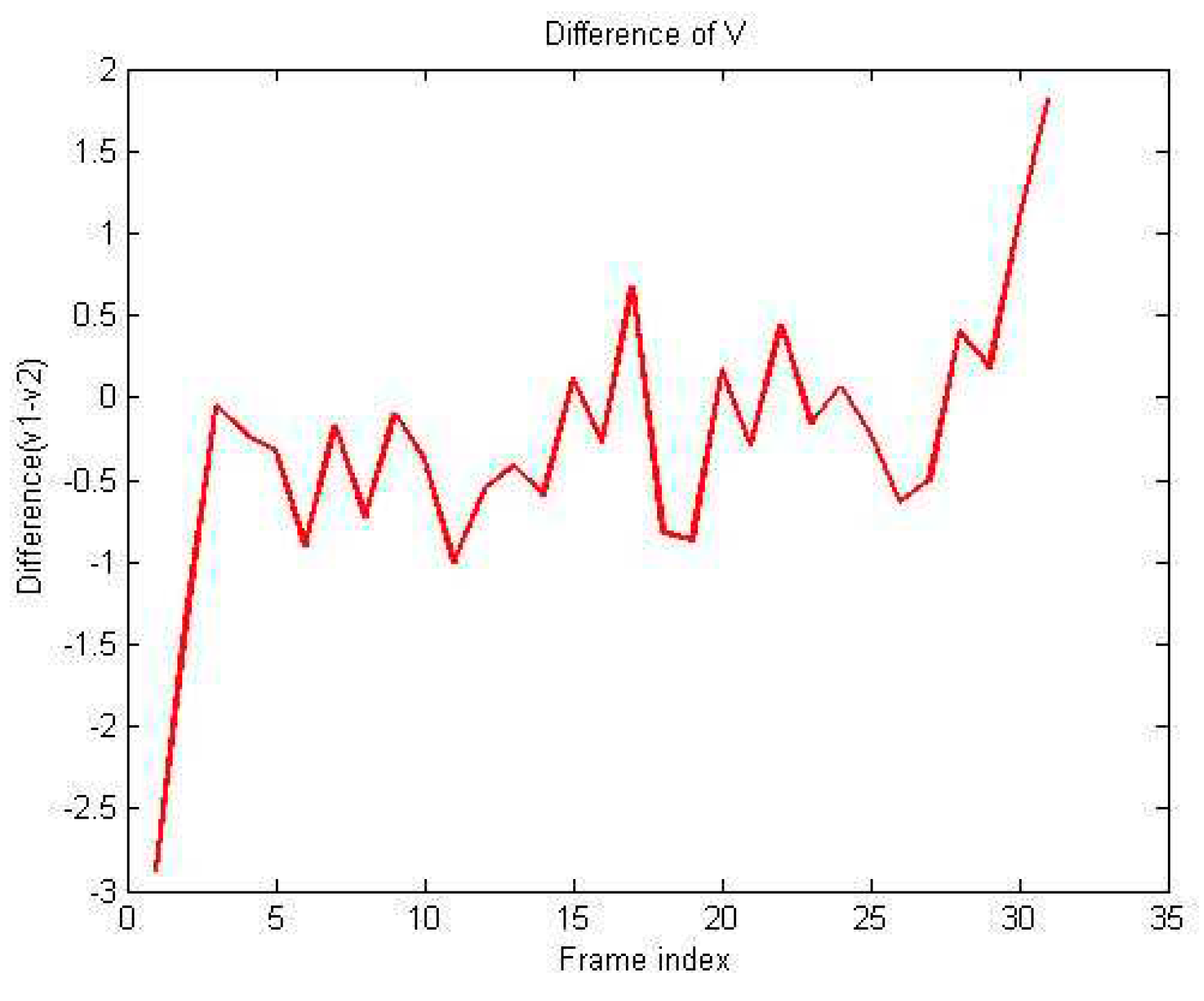

References
- Counting Wildlife Manual, WWF-Southern Africa Regional Programme Office, Zimbabwe, January (2004).
- M. Israel, “AUAV-based Roe Deer Fawn detection system”, Conference on Unmanned Aerial Vehicle in Geomatics, Zurich, Switzerland, (2011).
- P. Christiansen, K. A. Steen, R. N. Jørgensen, H. Karstoft, “Automated Detection and Recognition of Wildlife Using Thermal Cameras”, Sensors, vol. 14 no. 8, pp 13778-13793, 2014. [CrossRef]
- M. Leonardo, A. M. Jensen, C.Coopmans, M. McKee, Y. Chen “A Miniature Wildlife Tracking UAV Payload System Using Acoustic Biotelemetry”, International Design Engineering Technical Conferences, (2013).
- M. Jensen, D. K Geller, YangQuanChen,“Monte Carlo Simulation Analysis of Tagged Fish Radio Tracking Performance by Swarming Unmanned Aerial Vehicles in Fractional Order Potential Fields”, Journal of Intelligent & Robotic Systems, vol. 74, no. 1-2, pp. 287-307, (2013). [CrossRef]
- W. Selby, P. Corke, D.Rus, “Autonomous Aerial Navigation and Tracking of Marine Animals”,Australasian Conference on Robotics and Automation, (2011).
- J. Linchant, C. Vermeulen, P. Lejeune, J. Semeki, J. Lisein, “Are unmanned aircraft systems (UASs) the future of wildlife monitoring? A review of accomplishments and challenges”, Laboratory of Tropical & Subtropical Forestry, Passage des Déportés, (2015). [CrossRef]
- R. C. Gonzales, R. E. Woods, and S. L. Eddins. Digital image processing using MATLAB.Pearson Prentice Hall, (2004).
- Helmut Mayer, Automatic Object Extraction from Aerial Imagery—A Survey Focusing on Buildings. January 28, (1999). [CrossRef]
- Andr´e Fischer, Thomas H. Kolbe, Extracting Buildings from Aerial Images Using Hierarchical Aggregation in 2D and 3D. July 7, (1998).
- Stuart L. Pimm,1,* Sky Alibhai. Emerging Technologies to Conserve Biodiversity.
- Martin Wikelski1, Roland W. Kays . Going wild: what a global small-animal tracking system could do for experimental biologists. 26 October (2006). [CrossRef]
- YunfeiFanga, Shengzhi Dub. Motion Based Animal Detection in Aerial Videos.
- Siyi Li, Dit-Yan Yeung . Visual Object Tracking for Unmanned Aerial Vehicles: A Benchmark and New Motion Models. [CrossRef]
- J. L. Barron, D. J. Fleet, and S. S. Beauchemin, “Performance of optical flow techniques,” Int. J. Comput. Vis., vol. 12, no. 1, pp. 43–77, 1994. [CrossRef]
- Bruhn, J. Weickert, and C. Schnörr, “Lucas/Kanade meets Horn/Schunck: Combining local and global optic flow methods,” Int. J. Comput. Vis., vol. 61, no. 3, pp. 1–21, 2005. [CrossRef]
- M. G. Pinto, A. P. Moreira, P. G. Costa, and M. V. Correia, “Revisiting Lucas-Kanade and Horn-Schunck,” J. Comput. Eng. Informatics, vol. 1, no. 2, pp. 23–29, 2013. [CrossRef]
- S. Negahdaripour, “Revised definition of optical flow: integration of radiometrie and geometric cues for dynamic scene analysis,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 20, no. 9, pp. 961–979, 1998.
- L. Fennema and W. B. Thompson, “Velocity determination in scenes containing several moving objects,” Computer Graphics and Image Processing, vol. 9, no. 4. pp. 301–315, 1979. [CrossRef]
- Kim, Nam-In, et al. "Piezoelectric Sensors Operating at Very High Temperatures and in Extreme Environments Made of Flexible Ultrawide-Bandgap Single-Crystalline AlN Thin Films." Advanced Functional Materials 33.10 (2023): 2212538. [CrossRef]

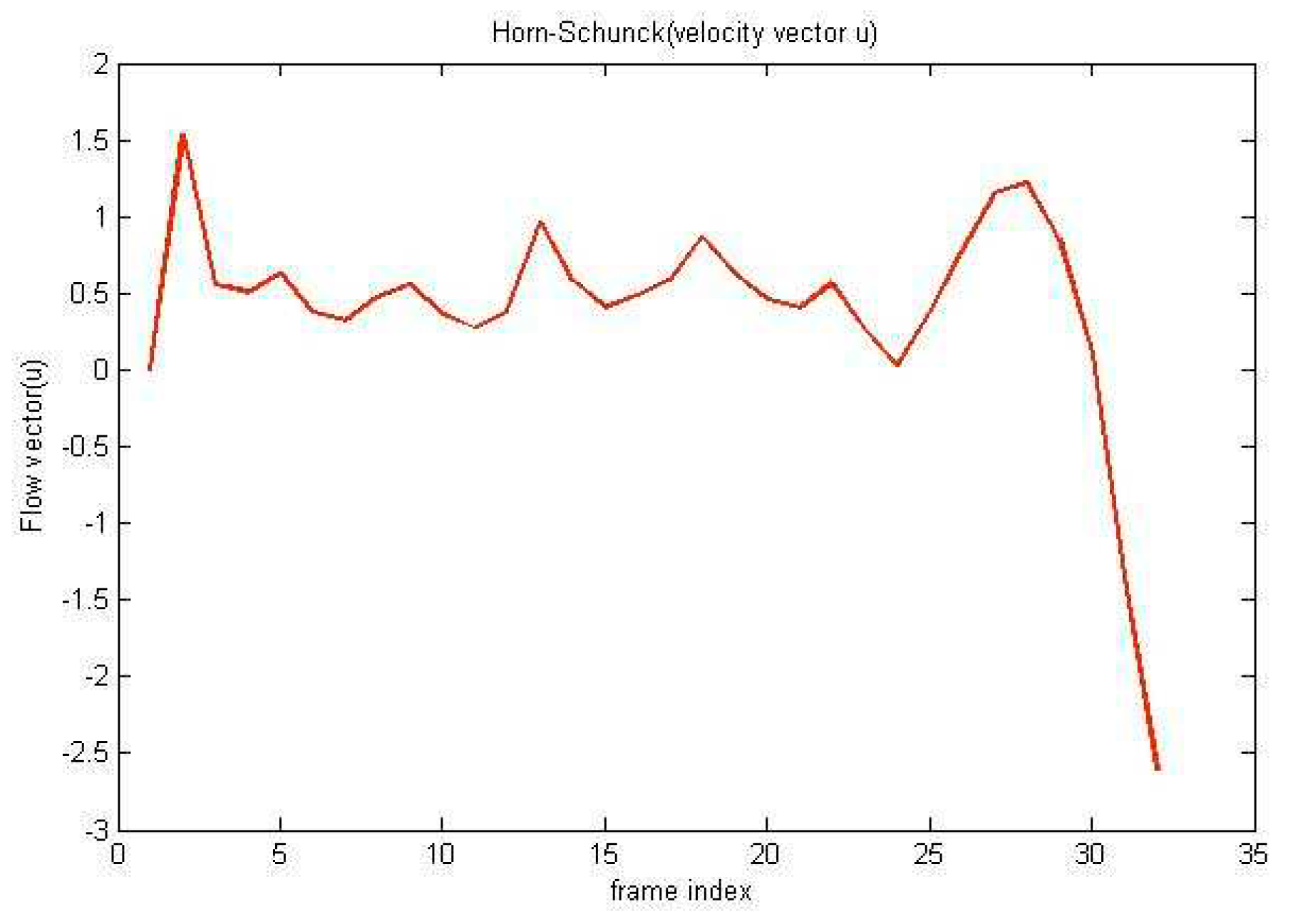
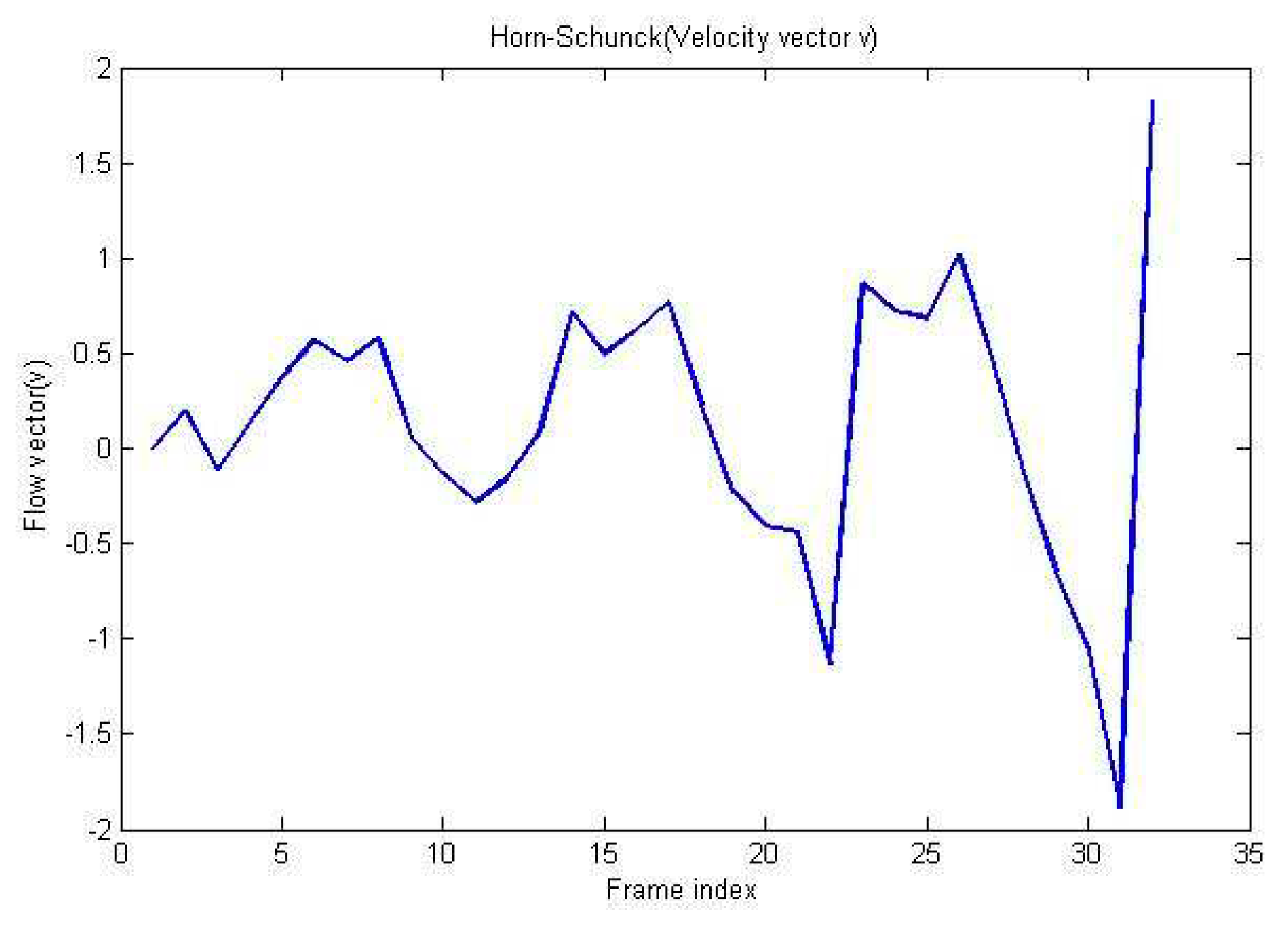
| Method | Lucas-Kande | Horn-schunck | Difference | |||
|---|---|---|---|---|---|---|
| optical flow between frame (i & i+1) | optical flow between frame (i & i+1) | |||||
| Frame(i) | U1 | V1 | U2 | V2 | U1-U2 | V1-V2 |
| 1 | -1.68 | -1.35 | 0.19 | 1.53 | -1.87 | -2.88 |
| 2 | 0.28 | -0.81 | -0.11 | 0.56 | 0.39 | -1.37 |
| 3 | -0.37 | 0.46 | 0.13 | 0.51 | -0.50 | -0.05 |
| 4 | 0.27 | 0.40 | 0.37 | 0.63 | -0.09 | -0.23 |
| 5 | 0.12 | 0.06 | 0.57 | 0.38 | -0.45 | -0.32 |
| 6 | 0.06 | -0.57 | 0.46 | 0.32 | -0.40 | -0.90 |
| 7 | 0.20 | 0.31 | 0.58 | 0.48 | -0.38 | -0.17 |
| 8 | 0.23 | -0.16 | 0.05 | 0.56 | 0.18 | -0.72 |
| 9 | 0.02 | 0.27 | -0.13 | 0.37 | 0.15 | -0.10 |
| 10 | 0.07 | -0.09 | -0.28 | 0.28 | 0.35 | -0.37 |
| 11 | 0.10 | -0.63 | -0.16 | 0.38 | 0.26 | -1.01 |
| 12 | 0.28 | 0.40 | 0.09 | 0.97 | 0.20 | -0.56 |
| 13 | 0.31 | 0.18 | 0.72 | 0.59 | -0.41 | -0.41 |
| 14 | -0.28 | -0.18 | 0.50 | 0.41 | -0.78 | -0.59 |
| 15 | 0.03 | 0.61 | 0.62 | 0.49 | -0.59 | 0.12 |
| 16 | -0.14 | 0.31 | 0.77 | 0.59 | -0.90 | -0.27 |
| 17 | 0.23 | 1.53 | 0.23 | 0.86 | -0.00 | 0.67 |
| 18 | 0.12 | -0.19 | -0.23 | 0.63 | 0.35 | -0.82 |
| 19 | -0.38 | -0.41 | -0.40 | 0.46 | 0.03 | -0.87 |
| 20 | 0.41 | 0.58 | -0.44 | 0.40 | 0.85 | 0.17 |
| 21 | 0.43 | 0.28 | -1.13 | 0.56 | 1.55 | -0.29 |
| 22 | 0.78 | 0.70 | 0.86 | 0.26 | -0.08 | 0.45 |
| 23 | 0.58 | -0.13 | 0.72 | 0.03 | -0.14 | -0.16 |
| 24 | 0.13 | 0.43 | 0.68 | 0.37 | -0.56 | 0.06 |
| 25 | 0.26 | 0.54 | 1.02 | 0.76 | -0.76 | -0.22 |
| 26 | 0.22 | 0.52 | 0.48 | 1.15 | -0.25 | -0.63 |
| 27 | -0.24 | 0.72 | -0.13 | 1.22 | -0.12 | -0.50 |
| 28 | -0.15 | 1.26 | -0.65 | 0.85 | 0.50 | 0.40 |
| 29 | -0.55 | 0.29 | -1.06 | 0.10 | 0.51 | 0.18 |
| 30 | -0.91 | -0.27 | -1.88 | -1.35 | 0.97 | 1.08 |
| 31 | 1.00 | -0.79 | 1.83 | -2.60 | -0.83 | 1.81 |
| Method | Horn Schunck | Lucas-kanade | Difference |
|---|---|---|---|
| u | 4.2616 | 1.4227 | 2.8389 |
| v | 12.7478 | 4.2467 | 8.5011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





