Numerical Analysis of Cracked Double-Beam Systems

Preprint

Article

Numerical Analysis of Cracked Double-Beam Systems

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 August 2023

Posted:

23 August 2023

You are already at the latest version

Alerts

Abstract

Based on the elasticity theory, this paper deals with the static analysis of a cracked double beam system in presence of a Winkler medium. The double-beam system is also supposed to be constrained at both ends by elastically flexible springs, with transverse and rotational stiffness. Using a variational formulation, the static governing equations are derived and solved by using analytical and numerical approaches. In the first approach, the closed-form solutions for the displacements functions are obtained based on the Euler-Bernoulli beam theory. In the second approach, the Cell-Discretization Method (CDM) is performed, according to which the two beams are reduced to a set of rigid bars linked together by means of elastic constraints, where the bending stiffness of the bars is concentrated. The resulting stiffness matrix is easily deduced, and the governing equations of the static problem can be immediately solved. A comparative analysis is performed in order to verify the accuracy and validity of the proposed method. This study focuses on the effect of various parameters including the crack depth and position, boundary conditions, elastic medium and slenderness. The validity of the proposed analysis is confirmed by comparing the present results with those obtained from the other approach. In particular, the results obtained by closed-form solution and Cell-discretization method (CDM) are compared by Finite element method (FEM). Accuracy of the results has been evaluated by making comparisons with the results in literature and reported in bibliography. It is demonstrated that the proposed algorithm provides a simple and powerful tool in dealing with the static analysis of a double-beam system. Finally, some concluding remarks are made.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

The literature regarding the mechanical behaviour of beams is very rich. In the majority of the earliest papers, the solutions presented in the literature can be divided into theoretical and numerical ones. In this context, there exist a lot of studies on evaluating the bending, buckling, post-buckling and vibration behaviours of beams using Euler- Bernoulli and Timoshenko beams models [1–10].

It is well-known that the structural behaviour of beams is sensitive to presence of cracks. In a beam, their occurrence, introduces local flexibility, a localised increase in the bending flexibility, which may lead to excessive deflections and unexpected failures. Because of their practical relevance, many studies are performed to explore the static deflection and vibration response of the beams with different boundary conditions and resting on various elastic foundations [11–17]. Some works are cited herein. In [11] Biondi and Caddemi have studied the problem of the integration of the static governing equations for uniform Euler−Bernoulli beam with two types discontinuities and have presented a closed form solutions of governing differential equations. Cicirello and Palmeri [12] dealt with the static analysis of pre-damaged Euler−Bernoulli beams with any number of unilateral cracks and subjected to tensile or compression forces combined with arbitrary transverse loads. Khaji et al. in [13] have developed an analytical approach for crack identification procedure in uniform Timoshenko beams with an open edge crack, based on bending vibration measurements. Ghannadiasl and Khodapanah in [14] have presented an analytical solution of dynamic analysis of cracked Euler-Bernoulli beam on the elastic foundation subjected to the concentrated load. Also, the effects of depth and location of the crack on natural frequency and deflection of the cracked beam on an elastic foundation have been evaluated. In his PhD thesis [15], Batihan dealt with the transverse vibration of a cracked beam on an elastic foundation and the effect of crack and foundation parameters on transverse vibration natural frequencies has been presented. Yang et al. have studied the bending deformation of the Timoshenko beam with switching cracks and the influence of the beam slenderness ratio, the crack depth, and the external load on the crack state and bending performances of the cracked beam have been assessed [16]. Finally, Alijani et al. have investigated the static behavior of cracked Euler−Bernoulli beams resting on an elastic foundation implementing analytical, approximate and numerical approaches [17].

Although the single beam models under various kind of loadings and boundary conditions are the most studied structural solutions, they cannot be employed in many engineering applications, such as sandwich or composites beams, nanostructures, adhesively bonded joints, floating-slab tracks, continuous dynamic vibration absorbers. Starting from these assumptions, double-beam systems have attracted much attention from researchers and engineers and they play an important role in many fields of structural and foundation engineering.

Double Beam System (BS) models are structural models consisting of two parallel beams structure interconnected by a uniformly distributed elastic layer which is generally considered as Winkler elastic medium. Beam theories are assumed to govern the beams and elastic foundation models are assumed to represent the elastic layers. Thanks to their remarkable structural properties, such as better vibration absorption than a single beam, lighter weight, and higher strength and stiffness, led to an explosion of interest within the scientific community. As a result, progressive research activities regarding BS have been ongoing in recent years, and they have been used widely in many engineering fields. For instance, special configurations of multiple pipeline systems, auxiliary underground structures (i.e. passageway and drainage systems) can be represented by double Beam System (BS) models. In civil engineering field, this system helps to reduce the energy from the earthquake and based on this peculiar characteristic, many vibration absorbers have been developed. Although static and vibration analysis of beams resting on elastic foundation is a widely studied topic, few works for static analysis of elastically connected system can be found in the literature. In this sense, applying theoretical and numerical methods, some significant results have been obtained in the study of beams and nanotubes [18–23].

The present paper deals with the static analysis of a uniform cracked double beam system in presence of a Winkler medium. The structure is also supposed to be constrained at both ends by elastically flexible springs, with transverse stiffness and rotational stiffness. Energy principle is formulated for the static analysis of the double beam system and the goverming equations is solved analytically and numerically. Cell-Discretization Method (CDM) is employed to discretize and solve the governing equations and boundary conditions. This numerical method has already been used by the authors [23–26], by Raithel and Franciosi [27] and Franciosi and Franciosi [28] for different structural problems. The analysis is performed reducing the two beams to a set of rigid bars linked together by means of elastic sections (elastic cells), in which the stiffness of the beam is properly concentrated. In this way, the structure is reduced to a system with finite number of degrees of freedom, and the global stiffness matrix can be easily calculated.

Numerical examples are then given to demonstrate the reliability and effectiveness of the current model. Also, in order to outline the efficiency of the proposed computational model, the Authors have considered the derivation of a beam finite element and have presented the derivation of stiffness matrix for cracked double-beam system. The results obtained by closed-form solution are compared by Cell-discretization method (CDM) and Finite element method (FEM). Accuracy of the results has been evaluated by making comparisons with the results in literature and reported in bibliography. Also, the effects of different parameters, such as crack depth and position, boundary conditions, elastic medium stiffness, slenderness on the static behaviour of the structure are investigated. It is demonstrated that the proposed algorithm provides a simple and powerful tool in dealing with the static analysis of a double-beam system. Finally, some concluding remarks are made.

2. Problem formulation

Let us consider the system which is composed of two parallel beams, having the same length L and translational and rotational elastic constraints at their ends, as shown in Figure 1. Assuming that the material and geometrical properties of the two beams are the same, let be E and I the Young’s modulus and moment of inertia, respectively. It is assumed that the two beams are joined by a Winkler-type medium with modulus

k_{m}

. The upper beam is subjected to a uniformly distributed load, q.

Based on the Euler-Bernoulli theory and applying the variational formulation, the total potential energy of the system under consideration assumes the following form:

\begin{matrix} E_{1} + P = & \frac{1}{2} \sum_{i = 1}^{2} \int_{0}^{L} [{EI}_{j} {(\frac{\partial^{2} v_{j} (z)}{\partial z^{2}})}^{2}] dz + \frac{1}{2} k_{jRL} v_{j}^{^{'} 2} (z = 0) + \frac{1}{2} k_{jTL} v_{j}^{2} (z = 0) + \\ \frac{1}{2} k_{jRR} v_{j}^{^{'} 2} (z = L) + \frac{1}{2} k_{jTR} v_{j}^{2} (z = L) - \int_{0}^{L} q v_{1} (z) dz + \frac{1}{2} k_{jds} {(Δ v_{j}^{^{'}} (L_{jc}))}^{2} \end{matrix}

(1)

E_{2} = \frac{1}{2} \int_{0}^{L} [k_{m} {(v_{2} (z) - v_{1} (z))}^{2}] dz

(2)

where

E_{1}

is strain energy of two beams, P is potential energy of applied load and

E_{2}

the elastic energy which includes the contribution of the elastic medium. Let v(z) the transverse displacement, z is the spatial coordinate,

k_{jRL}

and

k_{jTL}

are rotational and translational stiffness at z=0 and

k_{jRR}

k_{jTR}

rotational and translational stiffnesses at z=L, respectively, with j=1,2. The index j=1,2 refers to the order of the beams: the upper beam is indicated by j=1 and the lower beam by j=2, respectively. Finally,

k_{jds}

is equivalent rotational springs stiffness of the two corresponding sections of two beams and

L_{jc}

is their abscissa.

Applying the principle of stationary potential energy, the following dimensionless form of the static governing equations of the Euler−Bernoulli beam model is obtained:

\begin{matrix} v_{1}^{''''} (ζ) + \frac{k_{m} L^{4}}{EI} (v_{1} (ζ) - v_{2} (ζ)) = \frac{q L^{4}}{EI} \\ v_{2}^{''''} (ζ) + \frac{k_{m} L^{4}}{EI} (v_{2} (ζ) - v_{1} (ζ)) = 0 \end{matrix}

(3)

in which

ζ = \frac{z}{L}

. In this way, we shift the domain [0,L] to the domain [0,1] .

As it is known, the presence of a crack or concentrated force introduces a discontinuity and therefore the displacement function of two beams is not a smooth function of z. Consequently, in order to calculate the displacement function of the two beams, a separate differential equations system must be written for each beam segment between the discontinuities. Let n be the number of discontinuities of the upper section and s those of the lower section,

n + s + 1 = m

differential equations systems are written. Therefore the number of systems of equations is the sum of the discontinuities between the upper and lower sections of the two beams.

For the double beam system under consideration, one gets:

\begin{matrix} v_{1}^{''''} (ζ) + \frac{k_{m} L^{4}}{EI} (v_{1} (ζ) - v_{m + 1} (ζ)) = \frac{q L^{4}}{EI} 0 < ζ < γ_{1} \\ v_{m + 1}^{''''} (ζ) + \frac{k_{m} L^{4}}{EI} (v_{m + 1} (ζ) - v_{1} (ζ)) = 0 0 < ζ < γ_{1} \end{matrix}

(4)

\begin{matrix} v_{i}^{''''} (ζ) + \frac{k_{m} L^{4}}{EI} (v_{i} (ζ) - v_{m + i} (ζ)) = \frac{q L^{4}}{EI} γ_{i - 1} < ζ < γ_{i} i = 2, . . ., m - 1 \\ v_{m + i}^{''''} (ζ) + \frac{k_{m} L^{4}}{EI} (v_{m + i} (ζ) - v_{i} (ζ)) = 0 γ_{i - 1} < ζ < γ_{i} i = 2, . . ., m - 1 \end{matrix}

(5)

\begin{matrix} v_{m}^{''''} (ζ) + \frac{k_{m} L^{4}}{EI} (v_{m} (ζ) - v_{2 m} (ζ)) = \frac{q L^{4}}{EI} γ_{m - 1} < ζ < 1 \\ v_{2 m}^{''''} (ζ) + \frac{k_{m} L^{4}}{EI} (v_{2 m} (ζ) - v_{m} (ζ)) = 0 γ_{m - 1} < ζ < 1 \end{matrix}

(6)

From the first equations of (4)–(6) the displacements

v_{m + i}

(

ζ

) and

v_{2 m} (ζ)

are obtained, respectively, which substituted in the second equation of (4)–(6), lead to:

v_{m + 1} (ζ) = \frac{v_{1}^{''''} (ζ)}{α^{4}} + v_{1} (ζ) - \frac{p}{α^{4}}

(7)

v_{m + i} (ζ) = \frac{v_{i}^{''''} (ζ)}{α^{4}} + v_{i} (ζ) - \frac{p}{α^{4}} i = 2, . . ., m - 1

(8)

v_{2 m} (ζ) = \frac{v_{m}^{''''} (ζ)}{α^{4}} + v_{m} (ζ) - \frac{p}{α^{4}}

(9)

and the following system of equations yields:

v_{1}^{''''''''} (ζ) + 2 α^{4} v_{1}^{^{''''}} (z) = p α^{4} 0 < ζ < γ_{1}

(10)

v_{i}^{''''''''} (ζ) + 2 α^{4} v_{i}^{^{''''}} (z) = p α^{4} γ_{i - 1} < ζ < γ_{i} i = 2, . . ., m - 1

(11)

v_{m}^{''''''''} (ζ) + 2 α^{4} v_{m}^{^{''''}} (z) = p α^{4} γ_{m - 1} < ζ < 1

(12)

setting

α = \sqrt[4]{\frac{k_{m} L^{4}}{EI}}; p = \frac{q L^{4}}{EI}

(13)

The general solutions are:

\begin{matrix} v_{i} (ζ) = & a_{1 + (i - 1) 8} + a_{2 + (i - 1) 8} ζ + a_{3 + (i - 1) 8} ζ^{2} + a_{4 + (i - 1) 8} ζ^{3} + \\ a_{5 + (i - 1) 8} Cos h [\frac{α}{\sqrt[4]{2}} ζ] Sin [\frac{α}{\sqrt[4]{2}} ζ] + a_{6 + (i - 1) 8} Cos h [\frac{α}{\sqrt[4]{2}} ζ] Cos [\frac{α}{\sqrt[4]{2}} ζ] + \\ a_{7 + (i - 1) 8} Sin h [\frac{α}{\sqrt[4]{2}} ζ] Sin [\frac{α}{\sqrt[4]{2}} ζ] + a_{8 + (i - 1) 8} Sin h [\frac{α}{\sqrt[4]{2}} ζ] Cos [\frac{α}{\sqrt[4]{2}} ζ] + \\ \frac{p ζ^{4}}{48} i = 1, m \end{matrix}

(14)

where

a_{j}

are eight constants that are determined, for each segment, by imposing the boundary conditions. At the n discontinuity point for the upper beam with traslational and rotational constraints, the boundary conditions are defined as:

\begin{matrix} v_{1}^{^{''}} (ζ = 0) - K_{1 RL} v_{1}^{^{'}} (ζ = 0) = 0 \\ v_{1}^{^{'''}} (ζ = 0) + K_{1 TL} v_{1} (ζ = 0) = 0 \end{matrix}

(15)

\begin{matrix} v_{i} (ζ = γ_{i}) - v_{i + 1} (ζ = γ_{i}) = 0 i = 2, m - 1 \\ v_{1}^{^{'}} (ζ = γ_{i}) - v_{i + 1}^{^{'}} (ζ = γ_{i}) + \frac{Ψ}{L} v_{1}^{^{''}} (ζ = γ_{i}) = 0 \\ v_{i}^{^{''}} (ζ = γ_{i}) - v_{i + 1}^{^{''}} (ζ = γ_{i}) = 0 \\ v_{i}^{^{'''}} (ζ = γ_{i}) - v_{i + 1}^{^{'''}} (ζ = γ_{i}) + F_{t} = 0 \end{matrix}

(16)

\begin{matrix} v_{m}^{^{''}} (ζ = 1) + K_{1 RR} v_{m}^{^{'}} (ζ = 1) = 0 \\ v_{m}^{^{'''}} (ζ = 1) - K_{1 TR} v_{m} (ζ = 1) = 0 \end{matrix}

(17)

For the lower beam, having translational and rotational elastic constraints at the ends and subjected to a concentrated force, the boundary conditions are:

\begin{matrix} v_{m + 1}^{^{''}} (ζ = 0) - K_{2 RL} v_{m + 1}^{^{'}} (ζ = 0) = 0 \\ v_{m + 1}^{^{'''}} (ζ = 0) + K_{2 TL} v_{m + 1} (ζ = 0) = 0 \end{matrix}

(18)

\begin{matrix} v_{m - 1 + i} (ζ = γ_{i}) - v_{m + i} (ζ = γ_{i}) = 0 i = 2, m \\ v_{m - 1 + i}^{^{'}} (ζ = γ_{i}) - v_{m + i}^{^{'}} (ζ = γ_{i}) + \frac{Ψ}{L} v_{m - 1 + i}^{^{''}} (ζ = γ_{i}) = 0 \\ v_{m - 1 + i}^{^{''}} (ζ = γ_{i}) - v_{m + i}^{^{''}} (ζ = γ_{i}) = 0 \\ v_{m - 1 + i}^{^{'''}} (ζ = γ_{i}) - v_{m + i}^{^{'''}} (ζ = γ_{i}) + F_{t} = 0 \end{matrix}

(19)

\begin{matrix} v_{2 m}^{^{''}} (ζ = 1) + K_{2 RR} v_{2 m}^{^{'}} (ζ = 1) = 0 \\ v_{2 m}^{^{'''}} (ζ = 1) - K_{2 TR} v_{2 m} (ζ = 1) = 0 \end{matrix}

(20)

where

\begin{matrix} F_{t} = \frac{F L^{3}}{EI} K_{j RL} = \frac{k_{jRL} L}{EI}; K_{j RR} = \frac{k_{jRR} L}{EI}; \\ K_{jTL} = \frac{k_{jTL} L^{3}}{EI}; K_{jTR} = \frac{k_{jTR} L^{3}}{EI}; j = 1, 2 \end{matrix}

(21)

denote dimensionless parameters of rotational and translational stiffnesses at two ends, for

ζ

=0 and

ζ

=1, respectively and taking into account the presence of concentrated non-dimensional force.

By substituting the following equations

v_{m + 1} (ζ = 0) = \frac{v_{1}^{''''} (ζ)}{α^{4}} + v_{1} (ζ) - \frac{p}{α^{4}}

(22)

v_{m + i} (ζ = γ_{i}) = \frac{v_{i}^{''''} (ζ)}{α^{4}} + v_{i} (ζ) - \frac{p}{α^{4}}

(23)

v_{2 m} (ζ) = \frac{v_{n}^{''''} (ζ)}{α^{4}} + v_{m} (ζ) - \frac{p}{α^{4}}

(24)

into the equations (18-20), one obtains the following system of equations:

\begin{matrix} \frac{v_{1}^{^{''''''}} (ζ = 0)}{α^{4}} + v_{1}^{^{''}} (ζ = 0) - K_{2 RL} (\frac{v_{1}^{^{'''''}} (ζ = 0)}{α^{4}} + v_{1}^{^{'}} (ζ = 0)) = 0 \\ \frac{v_{1}^{^{'''''''}} (ζ = 0)}{α^{4}} + v_{1}^{^{'''}} (ζ = 0) + K_{2 TL} (\frac{v_{1}^{^{''''}} (ζ = 0)}{α^{4}} + v_{1} (ζ = 0) - \frac{p}{α^{4}}) = 0 \end{matrix}

(25)

\begin{matrix} \frac{v_{i}^{^{''''}} ((ζ = γ_{i})}{α^{4}} + v_{i} (ζ = γ_{i}) - \frac{v_{i + 1}^{^{''''}} (ζ = γ_{i})}{α^{4}} - v_{i + 1} (ζ = γ_{i}) = 0 i = 2, m - 1 \end{matrix}

(26)

\begin{matrix} \frac{v_{i}^{^{'''''}} (ζ = γ_{i})}{α^{4}} + v_{i}^{^{'}} (ζ = γ_{i}) - \frac{v_{2}^{^{'''''}} (ζ = γ_{i})}{α^{4}} + \\ - v_{2}^{^{'}} (ζ = γ_{i}) + \frac{Ψ}{L} (\frac{v_{1}^{^{''''''}} (ζ = γ_{i})}{α^{4}} + v_{1}^{^{''}} (ζ = γ_{i})) = 0 \end{matrix}

(27)

\begin{matrix} \frac{v_{i}^{^{''''''}} (ζ = γ_{i})}{α^{4}} + v_{i}^{^{''}} (ζ = γ_{i}) - \frac{v_{2}^{^{''''''}} (ζ = γ_{i})}{α^{4}} - v_{2}^{^{''}} (ζ = γ_{i}) = 0 \end{matrix}

(28)

\begin{matrix} \frac{v_{1}^{^{'''''''}} (ζ = γ_{i})}{α^{4}} + v_{i}^{^{'''}} (ζ = γ_{i}) - \frac{v_{2}^{^{'''''''}} (ζ = γ_{i})}{α^{4}} - v_{2}^{^{'''}} (ζ = γ_{i}) + F_{t} = 0 \end{matrix}

(29)

\begin{matrix} \frac{v_{m}^{^{''''''}} (ζ = 1)}{α^{4}} + v_{m}^{^{''}} (ζ = 1) + K_{2 RR} (\frac{v_{m}^{^{'''''}} (ζ = 1)}{α^{4}} + v_{m}^{^{'}} (ζ = 1)) = 0 \\ \frac{v_{m}^{^{'''''''}} (ζ = 1)}{α^{4}} + v_{m}^{^{'''}} (ζ = 1) - K_{2 TR} (\frac{v_{m}^{^{''''}} (ζ = 1)}{α^{4}} + v_{m} (ζ = 1) - \frac{p}{α^{4}}) = 0 \end{matrix}

(30)

3. Cracks: modelling and method of solution

3.1. Modelling of cracks: an overview of the discrete spring model

The identification of the location and depth of a crack in beam type structures is an important topic of structural health monitoring and has been the subject of a significant body of research. The literature concerning the modelling of cracks is very rich and various models, such as local stiffness reduction, discrete spring models, and complex models in two or three dimensions, have been proposed in the technical literature. In this topic, the state of the art can be found in a review works by Alijani et al. [17] and by Palmeri and Cicirello [29]. In both papers the authors report a coherent yet concise review of as many of these publications as possible and the main themes treated are the modelling and simulation of static behaviour of cracked beams.

According to the classification by Friswell and Penny [30], the proposed approach falls in the broad category of “discrete spring models”, being equivalent to an internal hinge coupled with a linear elastic spring. This model is widely adopted when the focus of the structural analysis is on the global performance of frames and trusses, rather than on phenomena of crack initiation and crack propagation. Although very simple, the discrete spring model proves to be very efficient for static problems. The idea of treating cracked beams with equivalent linear springs at the cracks position is based on the partition of each member into undamaged pieces between two consecutive cracks. One of the main advantages of this model is the effective representation of the crack in terms of position and severity. Different attempts can be found in the literature to provide the values for the rotational spring stiffness using crack parameters as depth or geometry. Among them, Palmeri and Cicirello [29] have investigated the static analysis of multi-cracked Euler–Bernoulli and Timoshenko beams using this relationship. Afterward, Okamura et al. [31] have showed the buckling behavior of cracked columns with a rectangular cross-section. Furthermore, Ricci and Viola [32] have extended the method of Kienzler and Herrmann [33] to evaluate stress intensity factors of cracked beams and bars and have derived two relationships between stress intensity factor and rotational spring stiffness. In the following analysis, two relationships between stress intensity factor and rotational spring stiffness have been considered, so as introduced by Alijani et al. in [17].

Figure 2 shows a beam with a crack in the non-dimensional position

γ_{i}

and depth a. Also, it is assumed that the shear effect as well as axial and torsional loads are neglected. According to this assumption, the stress intensity factors may be evaluated through the following equations:

K_{I} = \frac{6 M}{b h^{2}} \sqrt{π a} F_{m} (ξ) 0 \leq ξ \leq 0.6, ξ = \frac{a}{h}

(31)

K_{I} = \frac{3.99 M}{b h \sqrt{h} \sqrt{{(1 - ξ^{2})}^{3}}} 0.6 \leq ξ \leq 1.0, ξ = \frac{a}{h}

(32)

where

F_{m} (ξ)

is given from the following geometric function

F_{M} (ξ) = \sqrt{(\frac{2}{π ξ}) tan \frac{π ξ}{2}} \frac{0.923 + 0.199 {(1 - sin (\frac{π ξ}{2}))}^{4}}{cos (\frac{π ξ}{2})}

(33)

Finally, the following relationship is defined:

\frac{1}{k_{ds}} = \frac{2 b (1 - \lor^{2})}{E} \int_{0}^{a} {(\frac{K_{I}}{M})}^{2} d a

(34)

which is used to determine a rotational spring stiffness factor equivalently in terms of the geometric and material parameters of the crack and where

Ψ

of Equation (27) is equal to

\frac{EI}{k_{ds}}

and

k_{ds}

is the stiffness of the i-th equivalent spring.

In the present paper the rotational spring stiffness factor is assumed to be different for each beam. In particular

Ψ_{1}

and

Ψ_{2}

indicate the rotational spring stiffness factor for upper and lower beams, respectively.

3.2. Method of Solution: Cell-discretization method (CDM)

The Cell-discretization method (CDM) is an efficient numerical method for the solution of linear partial differential equations. It has been becoming an important tool in field of the structural engineering, thanks to its approximation abilities and easiness to be implemented. The advent of sophisticated and totally generalized discretization tools, such as Finite Element method (FEM), Boundary Element Method (BEM), allowed to simulate the behaviour of structures taking into account several variables due to the removal of as many as simplified hypotheses, but on the other hand such procedures may induce to lose the physical sense of the real behaviour of the structures that should be always at the basis of engineering studies. In this sense, the CDM may be regarded as a technique able to address such issues. Since the beginning of the 20th century, this method found several applications, for instance: the dynamics and stability of arches; masonry arches; static and dynamical analysis of Euler-Bernoulli beams under several load and boundary conditions; static and dynamical analysis of Timoshenko and Rayleigh beams; static analysis of plates under several load and boundary conditions [23–28]. More recently, some of the present authors applied the method to the dynamical analysis of single- and double-walled carbon nanotubes, by taking into account non - local effects [23,26] and they obtained results showing that the method is able to describe the nanostructure behaviour satisfactorily with a little computational effort. In several papers, the procedure is shown to be very versatile and able to work in any case on a finite number of Lagrangian parameters by bringing the solution into the alveo of the usual numerical analysis methods.

In the present paper, the two beams are reduced to a set of t rigid bars with the same length

l

, linked together by n=t+1 elastic cells (see Figure 3). The moment of inertia

I_{j}

, with j=1,2, will be evaluated at the cells abscissa, obtaining the concentrated stiffness

k_{1 i} = \frac{{EI}_{1 i}}{l}

and

k_{2 i} = \frac{{EI}_{2 i}}{l}

, for the upper and lower beams, respectively. Both these quantities can be organized into the so-called unassembled stiffness diagonal matrix

k_{j}

with dimension (n x n), j=1,2, for each two beams.

If the cross-section is non-uniform, for each rigid section of length

l

the average of the inertia across the elastic cell can be considered.

In this way, the structure is reduced to a classical holonomic system, with 2n degrees of freedom, in particular, n vertical displacements

v_{1 i}

for the upper beam, and n vertical displacements

v_{2 i}

, for the lower beam, at the cells abscissa will be conveniently assumed as Lagrangian coordinates and will be organized into the 2n-dimensional vector v. Moreover, for the upper and lower beams the n-1 rotations of the rigid bars can be calculated as a function of the Lagrangian coordinates as follows:

\begin{matrix} ϕ_{1, i} = \frac{v_{1, i + 1} - v_{1, i}}{l} \\ ϕ_{2, i} = \frac{v_{2, i + 1} - v_{2, i}}{l} \end{matrix}

(35)

or, in matrix form

ϕ_{1} =

v_{1}

and

ϕ_{2} =

v_{2}

where

V

is a rectangular transfer matrix with n-1 rows and n columns.

The relative rotations between the two faces of the elastic cells are given by:

ψ_{j, 1} = ϕ_{j, 1}, ψ_{j, i} = ϕ_{j, i} - ϕ_{j, i - 1}, ψ_{j, n} = - ϕ_{j, n - 1}

(36)

or, in matrix form

ψ_{1}

Δ

ϕ_{1}

for upper rigid bar and

ψ_{2}

Δ

ϕ_{2}

, for lower rigid bar, where

Δ

is another rectangular transfer matrix with n rows and n-1 columns.

The strain energies

L_{je}

, with j=1,2, (the first two terms of Equation (1)) are given by:

\begin{matrix} L_{1 e} = \frac{1}{2} \sum_{i = 1}^{n} k_{1, ii} ψ_{1, i}^{2} \\ L_{2 e} = \frac{1}{2} \sum_{i = 1}^{n} k_{2, ii} ψ_{2, i}^{2} \end{matrix}

(37)

and they are concentrated at the cells of the upper and lower beams, respectively.

The strain energies should be expressed as functions of the Lagrangian coordinates as follows:

\begin{matrix} L_{1 e} = \frac{1}{2} ψ_{1}^{T} k_{1} ψ_{1} = \frac{1}{2} ϕ_{1}^{T} Δ^{T} k_{1} Δ ϕ_{1} = \frac{1}{2} {v_{1}}^{T} (V^{T} Δ^{T} k_{1} Δ V) v_{1} \\ L_{2 e} = \frac{1}{2} ψ_{2}^{T} k_{2} ψ_{2} = \frac{1}{2} ϕ_{2}^{T} Δ^{T} k_{2} Δ ϕ_{2} = \frac{1}{2} {v_{2}}^{T} (V^{T} Δ^{T} k_{2} Δ V) v_{2} \end{matrix}

(38)

so that, the total strain energy can be expressed as:

L_{e} = \frac{1}{2} v^{T} (\begin{matrix} K_{1} & 0 \\ 0 & K_{2} \end{matrix}) v

(39)

where

K_{1}

(V^{T} Δ^{T} k_{1} Δ V)

and

K_{2}

(V^{T} Δ^{T} k_{2} Δ V)

. The global assembled stiffness matrix K,with 2n rows and 2n columns, assumes the following form:

K = (\begin{matrix} K_{1} & 0 \\ 0 & K_{2} \end{matrix})

(40)

The potential energy, as function of the Lagrangian coordinates, is given by:

P_{1} = \sum_{i = 1}^{n} q_{i} v_{1, i}

(41)

Being the double beam system subjected to a uniformly distributed load q

q = (q_{1}, . . ., q_{i}, . . ., q_{n})

(42)

with

\begin{matrix} q_{1} = q l / 2; q_{n} = q l / 2; \\ q_{i} = q l i = 2, . . ., n - 1 \end{matrix}

(43)

the global assembled load matrix Q with 2n rows and 2n columns, assumes the following form:

Q = (\begin{matrix} q & 0 \\ 0 & 0 \end{matrix})

(44)

The strain energy due to the elastic medium, Equation (2), can be expressed as:

E_{2} = \frac{1}{2} v^{T} C v_{1} + \frac{1}{2} v_{2}^{T} C v_{2} - v_{1}^{T} C v_{2}

(45)

The terms of matrix

C

are given by:

\begin{matrix} C_{i, i} = 2 \frac{l}{3} k_{m}, i = 3, n - 3 \\ C_{i + 1, i} = C_{i i, + 1} = \frac{l}{3} k_{m}, i = 2, n - 2 \\ C_{1, 1} = \frac{l}{6} k_{m}, C_{2, 2} = \frac{l}{3} k_{m}, C_{1, 2} = C_{2, 1} = \frac{l}{12} k_{m} \end{matrix}

(46)

The matrix

C

with n rows and n columns and have half-band widths equal to 2 takes the following form:

C_{t} = (\begin{matrix} C & - C \\ - C & C \end{matrix})

(47)

Finally, the static governing equation can be written as:

K_{t} v = Q

(48)

with

K_{t}

is the global assembled stiffness matrix:

K_{t} = K + C_{t}

(49)

3.2.1. Boundary conditions in presence of a crack

Finally, starting to the strain energy terms of the flexible constraints at the ends in the eq (1), the assembled stiffness matrix K must be modified as follows:

\begin{matrix} K [1, 1] = K [1, 1] + k_{1 TL}; \\ K [n, n] = K [n, n] + k_{1 TR}; \\ K [n + 1, n + 1] = K [n + 1, n + 1] + k_{2 TL}; \\ K [2 n, 2 n] = K [2 n, 2 n] + k_{2 TR}; \end{matrix}

(50)

The rotational stiffnesses of the constraints of each beam can be taken into account by summing up the corresponding flexibilities of the rigid bars and one gets:

\begin{matrix} k_{1} [1, 1] = \frac{k_{1} [1, 1] k_{1 RL}}{k_{1 RL} + k_{1} [1, 1]} \\ k_{1} [n, n] = \frac{k [n, n] k_{1 RR}}{k_{1 RR} + k_{1} [n, n]} \\ k_{2} [1, 1] = \frac{k_{2} [1, 1] k_{2 RL}}{k_{2 RL} + k_{2} [1, 1]} \\ k_{2} [n, n] = \frac{k_{2} [n, n] k_{2 RR}}{k_{2 RR} + k_{2} [n, n]} \end{matrix}

(51)

These terms will be organized in two matrices

k_{1}

and

k_{2}

furnished in (40). In presence of a crack at the

j^{ma}

cell abscissa, the local stiffness of the upper beam is given by:

k_{1} [j + 1, j + 1] = \frac{k_{1} [j + 1, j + 1] k_{1 ds}}{k_{1 ds} + k_{1} [j + 1, j + 1]}

(52)

whereas at the

s^{ma}

cell abscissa relative to the lower beam, the local stiffness is:

k_{2} [s + 1, s + 1] = \frac{k_{2} [s + 1, s + 1] k_{2 ds}}{k_{2 ds} + k_{2} [s + 1, s + 1]}

(53)

if the height of crack is different in the two beams. The values

k_{1 ds}

and

k_{2 ds}

are derived from Equation (34).

3.3. Method of solution: Finite Element Method (FEM)

In order to outline the efficiency of the proposed computational model (CDM), the Authors considered the derivation of a beam finite element for static analysis of a cracked double-beam system. In particular, a finite element of a cracked double-beam system has been developed on the basis of a variational approach and the shape functions for rotational and translational displacements have been used to develop the stiffness matrix in presence and absence of cracks.

For the structure under consideration (see Figure 4), the total potential energy is given by:

\begin{matrix} E_{t} = & \frac{1}{2} \int_{0}^{L} {EI}_{1} {(\frac{\partial^{2} v_{1} (z)}{\partial z^{2}})}^{2} dz + \int_{0}^{L} {EI}_{2} {(\frac{\partial v (z)}{\partial z^{2}})}^{2} dz - \int_{0}^{L} q v_{1} (z) dz + \\ \frac{1}{2} \int_{0}^{L} k_{m} {(v_{2} (z) - v_{1} (z))}^{2} dz \end{matrix}

(54)

Using the cubic polynomial functions for the transverse displacements, the following shape functions are derived:

N_{i} = (\begin{matrix} 1 - \frac{3 z^{2}}{L^{2}} + \frac{2 z^{3}}{L^{3}} \\ - z + \frac{2 z^{2}}{L} - \frac{z^{3}}{L^{2}} \\ \frac{3 z^{2}}{L^{2}} - \frac{2 z^{3}}{L^{3}} \\ \frac{z^{2}}{L} - \frac{z^{3}}{L^{2}} \end{matrix});

(55)

where i=1,2 refers to the upper and lower beams, respectively. The transverse displacements are thus given as:

v_{i} (z) = N_{i}^{T} d_{i}

(56)

where

d_{i}

denotes the vector of nodal displacements and is given by:

d_{i} = {(V_{1}^{(i)}, Θ_{1}^{(i)}, V_{2}^{(i)}, Θ_{2}^{(i)})}^{T}

(57)

Deriving the nodal displacements respect to spatial coordinate z, the following expressions are obtained:

\frac{{dv}_{i} (z)}{dz} = N_{i}^{^{'} T} d_{i}; \frac{d^{2} v_{i} (z)}{{dz}^{2}} = N_{i}^{’ ’ T} d_{i}

(58)

which substituted into Equation (54) leads to:

\begin{matrix} E_{t} = & \frac{1}{2} d_{1}^{T} (\int_{0}^{L} N_{1}^{’ ’} EI N_{1}^{’ ’ T} dz) d_{1} + \frac{1}{2} d_{2}^{T} (\int_{0}^{L} N_{2}^{’ ’} EI N_{2}^{’ ’ T} dz) d_{2} - d_{1}^{T} \int_{0}^{L} q N_{1} dz + \\ \frac{1}{2} d_{1}^{T} (\int_{0}^{L} N_{1} k_{m} N_{1}^{T} dz) d_{1} + \frac{1}{2} d_{2}^{T} (\int_{0}^{L} N_{2} k_{m} N_{2}^{T} dz) d_{2} + \\ - d_{1}^{T} (\int_{0}^{L} N_{1} k_{m} N_{2}^{T} dz) d_{2} - d_{2}^{T} (\int_{0}^{L} N_{2} k_{m} N_{1}^{T} dz) d_{1} \end{matrix}

(59)

Applying the principle of stationary potential energy, one gets:

\begin{matrix} (\int_{0}^{L} N_{1}^{’ ’} EI N_{1}^{’ ’ T} dz) d_{1} + (\int_{0}^{L} N_{1} k_{m} N_{1}^{T} dz) d_{1} - (\int_{0}^{L} N_{1} k_{m} N_{2}^{T} dz) d_{2} = \int_{0}^{L} q N_{1} dz \\ (\int_{0}^{L} N_{2}^{’ ’} EI N_{2}^{’ ’ T} dz) d_{2} + (\int_{0}^{L} N_{2} k_{m} N_{2}^{T} dz) d_{2} - (\int_{0}^{L} N_{2} k_{m} N_{1}^{T} dz) d_{1} = 0 \end{matrix}

(60)

rearrangement the terms in

d_{1}

and

d_{2}

, one gets:

\begin{matrix} (\int_{0}^{L} N_{1}^{’ ’} EI N_{1}^{’ ’ T} dz + \int_{0}^{L} N_{1} k_{m} N_{1}^{T} dz) d_{1} - (\int_{0}^{L} N_{1} k_{m} N_{2}^{T} dz) d_{2} = \int_{0}^{L} q N_{1} dz \\ \int_{0}^{L} N_{2}^{’ ’} EI N_{2}^{’ ’ T} dz + (\int_{0}^{L} N_{2} k_{m} N_{2}^{T} dz) d_{2} - (\int_{0}^{L} N_{2} k_{m} N_{1}^{T} dz) d_{1} = 0 \end{matrix}

(61)

(\begin{matrix} K_{11} & - K_{12} \\ - K_{21} & K_{22} \end{matrix}) (\begin{matrix} d_{1} \\ d_{2} \end{matrix}) = (\begin{matrix} Q \\ 0 \end{matrix})

(62)

being

\begin{matrix} K_{11} = \int_{0}^{L} N_{1}^{’ ’} EI N_{1}^{’ ’ T} dz + \int_{0}^{L} N_{1} k_{m} N_{1}^{T} dz; \\ K_{12} = \int_{0}^{L} N_{1} k_{m} N_{2}^{T} dz; \\ K_{21} = \int_{0}^{L} N_{2} k_{m} N_{1}^{T} dz; \\ K_{22} = \int_{0}^{L} N_{2}^{’ ’} EI N_{2}^{’ ’ T} dz + \int_{0}^{L} N_{2} k_{m} N_{2}^{T} dz; \\ Q = \int_{0}^{L} q N_{1} dz . \end{matrix}

(63)

Equation (62) can be rewritten as:

\begin{matrix} K_{11} d_{1} - K_{12} d_{2} = Q \\ - K_{21} d_{1} + K_{22} d_{2} = 0 \end{matrix}

(64)

From the second Equation (64) we obtain

d_{1}

which substituted in the first equation leads to:

\begin{matrix} d_{2} = K_{22}^{- 1} K_{21} d_{1}; \\ (K_{11} - K_{12} K_{22}^{- 1} K_{21}) d_{1} = Q \end{matrix}

(65)

\begin{matrix} d_{1} = {(K_{11} - K_{22}^{- 1} K_{12} K_{21})}^{- 1} Q; \\ d_{2} = K_{22}^{- 1} K_{12} d_{1} \end{matrix}

(66)

In presence of a crack the stiffness matrix of finite element with a crack must be modified. Several investigators have been derived the stiffness matrix for a cracked beam element and the crack effect on the stiffness matrix has been investigated (see for example [34,35]). In the present analysis the structure under consideration has been analyzed implementing beam finite elements that have not taken the effect of shear forces into account. Therefore the stiffness matrix, which represents the relationship between nodal force vector and nodal displacements vector, can be expressed as:

\begin{matrix} K_{c} = \frac{EI}{δ} (\begin{matrix} 12 a_{11} & - 6 a_{12} & - 12 a_{13} & - 6 a_{14} \\ - 6 a_{21} & a_{22} & 6 a_{23} & a_{24} \\ - 12 a_{31} & 6 a_{32} & 12 a_{33} & 6 a_{34} \\ - 6 a_{41} & a_{42} & 6 a_{43} & a_{44} \end{matrix}) \end{matrix}

(67)

so as deduced in [35] (see formula 22), where

k_{r} = \frac{EI}{Ψ}

δ

is given by:

δ = L (k_{r} L^{3} + EI (12 L_{1}^{2} - 12 L L_{1} + L^{2} 4))

(68)

and where

\begin{matrix} a_{11} = a_{33} = (EI + k_{r} L); \\ a_{22} = (12 EI L_{1}^{2} + k_{r} L^{3} 4); \\ a_{44} = (12 EI {(L - L_{1})}^{2} + 4 k_{r} L^{3}); \\ a_{12} = a_{21} = (k_{r} L^{2} + 2 EI L_{1}); \\ a_{13} = a_{31} = (EI + k_{r} L); \\ a_{14} = a_{41} = (k_{r} L^{2} + 2 EI (L - L_{1})); \\ a_{23} = a_{32} = (k_{r} L^{2} + 2 EI L_{1}); \\ a_{24} = a_{42} = (12 EI (L - L_{1}) L_{1} + 2 k_{r} L^{3}); \\ a_{34} = a_{43} = (k_{r} L^{2} + 2 EI (L - L_{1})) . \end{matrix}

(69)

This matrix will be translated into

K_{22}

at the appropriate abscissa.

4. Numerical examples: results and discussion

In order to evaluate the effects of crack, taper ratio, elastic medium parameter, boundary conditions and rotational and traslational stiffness on the two beams deflection, several numerical examples are presented, using a general code developed in Mathematica [36]. The solutions in terms of deflection function are derived by using analytical and numerical approaches. The results obtained using the Euler-Bernoulli beam model are also presented to show the validity and reliability of the proposed approach (CDM).

In all numerical examples, the structure under consideration is composed of two parallel beam having the same length L equal to 2.5 m and the following material properties: Young’s modulus is 30 GPa and Poisson’s ratio

ν

=0.3. The cross-section of two beams is a rectangular with base and height dimensions of b=0.10 m and height 0.18 m, respectively. Also, let be

k_{m}

=1 MPa the media-type foundation modulus and q=100 kN/m a uniformly distributed load applied to the upper beam.

4.1. Case 1: Simply supported-simply supported double-beam system in presence of a crack, on the lower beam, and a uniformly distributed load applied to the upper beam

In the first numerical example, static deflections of a simply supported-simply supported (SS-SS) double-beam system, in presence of a crack and a uniformly distributed load, has been investigated, by using a large number of cells, i.e. n = 300. The crack is introduced at the dimensionless abscissa z=1.25 m from the left end of the lower beam. The non-dimensional crack height is assumed to be

ξ

=0.5. The upper beam is loaded with a uniformly distributed load q=100 kN/m.

Figure 5 displays the dimensionless transverse displacements of two beams. Particularly, the dashed line refers to the vertical displacements of the upper beam, whereas the solid line shows the displacements of the lower beam. As can be seen the maximum value of transverse displacement

v_{1}

is equal to 0.0291243 m, at the dimensionless abscissa z=1.25 m, whereas the transverse displacement

v_{2}

at the crack position (z=1.25 m) is equal to 0.00890037. In order to check the correctness of the numerical calculations of CDM, a numerical comparison with the results given by closed-form solutions is proposed. Applying the exact procedure the tranverse displacements values of two beams are

v_{1}

(z=1.25 m)=0.0291244 m and

v_{2}

(z=1.25 m)=0.00890037 m, respectively. As can be seen, the deflections of two beams show that there is an excellent agreement among the results obtained by the theoretical and numerical procedures. Also, in Figure 4 is shown the influence of the crack position on the deflection of SS−SS two beams. This figure emphasizes that the deflection will be maximized if the position of crack approaches the midspan of the beam.

In order to show the robustness,the accuracy and reliability of the proposed numerical method, the structure under consideration has also been analyzed implementing beam finite element.

In a first case the structure has been analyzed implementing beam finite element that takes the effect of a crack and distributed load into account. The crack is introduced in the midspan of the lower beam (

L_{1} = 0.5 L

) and a uniformly distributed load is applied to the upper beam only. For different values of Winkler-type medium stiffness

k_{m}

, the maximum displacements of the beam system have been calculated by means Finite element method (FEM), closed-form solution and CD method and the results obtained are quoted in Table 1. As can be easily seen from the table, using the proposed analytical approach and numerical methods, the estimated values of maximum displacements of double beam system are in excellent agreement with numerical calculations based on the FE method. Also, the results obtained show that the displacements decrease as

k_{m}

increases.

In the second case, the structure has been analyzed implementing beam finite element that have not taken the effect of crack into account. Particularly, a simply supported-simply supported (SS-SS) double-beam system submitted to a uniformly distributed load, acting on the upper beam only, has been considered. For different values of

k_{m}

the maximum displacements of the beam system have been calculated and the results obtained from the closed-form procedure and numerical methods based on the Cell-Discretization Method (CDM) and Finite Element method (FEM) are compared and quoted in Table 2.

As shown from the table, the estimated values of maximum displacements of double beam system are in excellent agreement with numerical calculations based on the FE method. Also, the results obtained show that the displacements decrease as

k_{m}

increases.

4.2. Case 2: Simply supported-simply supported double-beam system in presence of a uniformly ditributed load, on the upper beam, and of a crack, on the upper and lower beams

In the second example, a simply supported-simply supported (SS-SS) double-beam system with two transverse cracks has been considered. The transverse cracks are applied to the upper and lower beams at the non-dimensional distances of z=0.5 m and z=1.75 m, respectively. The upper beam is loaded with a uniformly distributed load q=100 kN/m.

In Figure 6 the deflections of two beams have been reported. Particularly, the vertical displacements of the upper beam are represented with a dashed line, whereas the solid line shows the displacements of the lower beam. As can be noted, for the upper beam the maximum value of transverse displacement

v_{1}

is equal to 0.0321605 m, at the dimensionless abscissa z=1.18 m, whereas, for the lower beam, the transverse displacement

v_{2}

at the crack position (z=1.2375 m) is equal to 0.00847839. The closed-form solution, on the other hand, provides the following results: the maximum value of deflection

v_{1}

(z=1.18 m)=0.0321452 m, for the upper beam, and the maximum value of deflection

v_{2}

(z=1.2375 m)=0.0084943 m, for lower beam. It can be seen that the predicted results of CDM are in excellent agreement the closed-form solutions.

4.3. Case 3: Effect of elastic constraints and crack on the static behaviour of double-beam system

This example considers a double-beam system with the same geometrical and material properties of the previous numerical examples. The beams are elastically restrained against translational and rotational at either ends, with the following fixed values

k_{1 TL}

= k_{2 TL}

= k_{1 TR}

k_{2 TR} = 10^{10}

and varying the non-dimensional rotational stiffness in the range [0-

10^{4}]

. The transverse crack is located at the mid-span of the lower beam. A uniformly distributed load q=100 kN/m is applied to the upper beam. Table 3 presents the deflections first value for simply supported double beam system, for different values of the non-dimensional stiffnesses. In Table 3, results involving respective maximum transverse displacements

v_{1 max}

and

v_{2 max}

, at the midspan for the upper and lower beams, are presented. As can be noted, as the stiffnesses values increase, deflections decrease throughout the two beams, especially near the crack. An analogy between increasing the stiffness and decreasing the deflections is illustrated in Figure 7 which represents the clamped-clamped beam case.

4.4. Case 4: Effect of taper ratio coefficient and crack on the static behaviour of double-beam system

This numerical example considers the influence of taper ratio and crack on the static behaviour of two non-uniform double-beam system, having the following law of moment of inertia:

I (z) = I_{0} {((β - 1) \frac{z}{L} + 1)}^{4}

(70)

with

β <

1 cross-section decreases with the abscissa, on the contrary if

β >

1 cross-section increaes with the abscissa. A uniformly distributed load, q=100 kN/m, is applied to the upper beam and a crack is introduced at the midspan of the lower beam. For varying

β

in the range [0.5-2], the effect of taper ratio is evaluated as obtained by using CDM. In Figure 8 and Figure 9, the displacements diagrams are depicted, for

β

=0.5, 1, respectively. The upper beam is simply supported at the left end and clamped at the right end, while the lower beam is simply supported at either ends.

For

β

=1.5,2, in Figure 10 and Figure 11 the displacements diagrams are plotted. The upper beam is simply-supported at either ends, while the lower beam is simply-supported, at the left end, and clamped, at the right end.

For varying

β

=0.5-2, in Table 4 the maximum deflections values for two beams are quoted. It is interesting to note that the maximum deflections value decreases when the taper ratio coefficient increases.

4.5. Case 5: Effect of a concentrated force and crack located at the midspan of upper and lower beams, respectively

In this numerical example, the effect of concentrated force is evaluated. Consider a simply supported-simply supported (SS-SS) double-beam system in presence of a crack. The transverse crack is located at the midspan of the lower beam and a concentrated force F is located at the midspan of the upper beam. Table 5 shows the maximum deflections values for different values of the concentrated force and in absence of a distributed load. As can be noted, as the value of the concentrated force F increases, the values of displacements at the midspan of the two beams increase.

For the same numerical example, fixed the force value F=

10^{4}

N and varying the nondimensional height of crack

ξ = \frac{a}{h}

, located at the mid-distance of the lower beam, the maximum deflections are calculated and listed in Table 6. It is interesting to note that the maximum deflections value increases as the nondimensional height of crack increases.

4.6. Case 6: Effect of the slenderness $λ$ on the deflections for both upper and lower beams in presence of a crack

In this numerical example, to study the effects of the slenderness

λ = \frac{L}{h}

on displacements and rotations, considers a simply-supported double beam system having the same geometrical and material properties of the previous numerical examples. The beam system is submitted to a uniformly distributed load q=100 kN/m acting on the upper beam only. A crack is introduced in the midspan of the lower beam.

Setting

Γ = \frac{h}{b} = 1.8

and being

λ = \frac{L}{h}

, the expressions of the parameters of Eq. (13) became:

α = λ \sqrt[4]{\frac{12 k_{m} Γ}{E}}; p = \frac{12 q Γ λ^{4}}{E}

(71)

Eq. (71) denotes the relationship between the deflection and slenderness.

For different values of slenderness

λ

of the two beams, the maximum displacements and the rotations at the left and right ends (for

ζ

=0 and

ζ

=1), respectively, are calculated. The results obtained from the closed-form solution and numerical method based on the Cell-Discretization Method (CDM) are compared and listed in Table 7. As can be easily seen from the table, the displacements values are in excellent agreement. Also, the results obtained show that the displacements increase as the slenderness

λ = \frac{L}{h}

of the two beams increases.

5. Concluding remarks

In the present paper, the static behaviour of a double-beam system, in the presence of Winkler medium, carrying a crack, at generic position, on the lower beam, and subjected to a distributed load, on the upper beam, have been studied. The double-beam system is also supposed to be constrained at the ends by elastically flexible springs, with transverse stiffness and rotational stiffness. According to the Euler-Bernoulli beam theory, the static governing equations are derived using an variational formulation and have been solved through implementing analytical and numerical approaches. Among numerical approach, the Cell-Discretization Method (CDM) is employed to solve the governing equations, in which the beam is reduced to a set of rigid bars linked together by means of elastic constraints. A comparative analysis has been performed in order to verify the accuracy and validity of the proposed numerical method. The effects of crack, taper ratio, elastic medium parameter, boundary conditions and rotational and traslational stiffness on the two beams deflections through theoretical and numerical approaches have been presented. Through the obtained results, the following observations apply:

-: if the transverse stiffness value increase the maximum deflections value decreases;
-: if the taper ratio coefficient increases the maximum deflections value decreases;
-: the crack plays a key role for static behaviour of double-beam system: the maximum deflections value increases when the crack increases.

Finally, the numerical examples demonstrate that the results determined by CDM perfectly match with the solutions from the governing equations of the double-beam model and are in good agreement with the results obtained by FEM. It is shown that the CD method has a good and rapid convergence regardless of the beam theory, crack and elastic foundation parameters.

Author Contributions

Conceptualization, M.A. D.R., M.L.; methodology, M.A.D.R., M.L.; software, M.A. D.R.; validation, M.A. D.R., M.L.; formal analysis, M.A. D.R.; investigation, M.L.; resources, M.A.D.R., M.L.; data curation, M.A.D.R. and M.L..; writing—original draft preparation, M.L.; writing—review and editing, M.A. D.R. and M.L.; visualization, M.A. D.R..; supervision, M.A.D.R.; project administration, X.X.; funding acquisition, Y.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Conflicts of Interest

The authors declare no conflict of interest.

References

Chun, KR. Free vibration of a beam with one end spring-hinged and the other free. J. of Appl. Mech. 1972., 39, 1154–1155. [Google Scholar] [CrossRef]
Lee, TW. Vibration frequencies for a uniform beam with one end spring-hinged and carrying a mass at the other free end. J. of Appl. Mech. 1973, 40, 813–815. [Google Scholar] [CrossRef]
De Rosa MA, Lippiello M, Non-classical boundary conditions and DQM for double-beams. Mech. Research. Comm. 2007, 34, 538–544. [CrossRef]
Emam SA, Nayfeh AH. Post-buckling and free vibrations of composite beams. Composite Structures, 88, 2009, 636-642.
De Rosa MA, Lippiello M, Maurizi MJ, Martin HD. Free vibration of elastically restrained cantilever tapered beams with concentrated viscous damping and mass. Mech. Research. Comm. 37 (2), 2010, 261-264.
Chen JZ,. Wang YG. Free vibrations of a beam with elastic end restraints subject to a constant axial load. Arch. of Appl. Mech. 83 (2), 2013, 241-252.
Auciello N, Lippiello M. Vibration analysis of rotating non-uniform Rayleigh beams using “CDM” method”. Global Virtual Conference. 2013.
Sinira BG, Ozhanb BB, Reddy JN. Buckling configurations and dynamic response of buckled Euler-Bernoulli beams with non-classical supports. Lat. Am. J. Solids Struct. 11 (14) 2014.
De Rosa MA, Lippiello M, Armenio G, De Biase G, Savalli S. Dynamic analogy between Timoshenko and Euler–Bernoulli beams. Acta Mech. 231, 2020, 4819-4834.
Yesilce, Y. Differential transform method and numerical assembly technique for free vibration analysis of the axial-loaded Timoshenko multiple-step beam carrying a number of intermediate lumped masses and rotary inertias. Struct. Eng. Mech., 53(3), 2015, 537-573.
Biondi B, Caddemi S. Closed form solutions of Euler-Bernoulli beam with singularities. Int. J. Solids Struct. 42, 2005, 3027-3044.
Cicirello A, Palmeri A. Static analysis of Euler-Bernoulli beams with multiple unilateral cracks under combined axial and transverse loads. Int. J. Solids Struct. 51, 2014, 1020-1029.
Khaji N, Shafiei M, Jalalpour M. Closed-form solutions for crack detection problem of Timoshenko beams with various boundary conditions. Int J of Mech Sci, 51(9-10), 2009, 667-681.
Ghannadiasl, A. , Khodapanah Ajirlou S. Dynamic Response of Multi-cracked Beams Resting on Elastic Foundation. Int. J. of Engineering 31(11), 2018, 1830-1837.
Batihan, AC. Vibration analysis of cracked beams on elastic foundation using Timoshenko beam theory. Thesis to the graduate school of natural and applied science Midlle East Techinical University 2011.
Yang X, Huang J, Ouyang Y. Bending of Timoshenko beam with effect of crack gap based on equivalent spring model. Appl. Math. and Mech. 2016, 1–16.
Alijani A, Mastan Abadi M, Darvizeh A, Abadi M. Kh. Theoretical approaches for bending analysis of founded Euler-Bernoulli cracked beams. Arch Appl Mech 88, 2018, 875-895.
Chung MP, Lin K.C. Model and analysis method for machine components in contact. Conference Proceedings of Computational Mechanics 8, Eds (S. N. Atluri, G.Yagawa), 1, 1988, 957-958.
Brito WKF, Maia CDCD, Maciel WGM, Static analysis of a double-beam system by finite element method, in: Proceedings of the 6th International Congress on Technology, Engineering and Science, Kuala Lumpur, Malaysia, 2018.
Brito WKF, Maia CDCD, Mendonca AV. Bending analysis of elastically connected Eulerernoulli double-beam system using the direct boundary element method. Appl. Math Model 74, 2019, 387-408.
Yoon J, Ru CQ, Mioduchowski A. Vibration of an embedded multiwall carbon nanotube. Comp. Sci. and Tech. 63 (11), 2003, 1533-1542.
Xu KY, Aifantis EC, Yan YH. Vibrations of double walled carbon nanotubes with different boundary conditions between inner and outer tubes. J. of Appl. Mech. 75(2) 2008, 0210131–0210139.
De Rosa MA, Lippiello M. Free Vibration Analysis of DWCNTs Using CDM and Rayleigh-Schmidt Based on Nonlocal Euler-Bernoulli Beam Theory. The Scientific World Journal Volume 2014, Article ID 194529, 13 pages.
De Rosa MA, Lippiello M, Natural vibration frequencies of tapered beams, Engineering Transactions 57 (1) 2009, 44-66.
Auciello NM, Lippiello M, Vibration analysis of rotating non-uniform Rayleigh beams using “CDM” method, News in Engineering, Volume 1, Issue 1, 2013, Sci-Pub, ISSN: 1339-4886. 30 November.
De Rosa MA, Lippiello M. Free vibration analysis of SWCNT using CDM in the presence of nonlocal effect. International Journal of Engineering and Innovative Technology (IJEIT) 4(4) 2014.
Raithel A, Franciosi C, Dynamic analysis of arches using Lagrangian approach, J. of Struct. Eng. 110 (4) 1984, 847–858.
Franciosi V, Franciosi C. The cells method in masonry arch analysis, 8th International Brick/Block masonry conference, Dublin 19-21 September (1988), Vol. III 1290–1301.
Palmeri A, Cicirello A. Physically-based Dirac’s delta functions in the static analysis of multi-cracked Euler–Bernoulli and Timoshenko beams. Int. J. of Solids and Struct. 48, 2011, 2184-2195.
Friswel M, Penny J. Crack modeling for structural health monitoring. Int. J. of Solids and Struct. 1, 2002, 139–148.
Okamura H, Liu HW, Chu CS, Liebowitz H. A cracked column under compression. J. Eng. Fract. Mech. 1, 1969, 547–564.
Ricci P, Viola E. Stress intensity factors for cracked T-sections and dynamic behavior of T-beams. J. Eng. Fract. Mech. 73, 2006, 91–111.
Kienzler R, Herrmann G. An elementary theory of defective beams. J. Acta Mech. 1986, 62, 37–46. [CrossRef]
Viola E, Nobile L, Federici L. Formulation of cracked beam element for structural anlysis. J. Eng. Mech. 2002, 128, 220–230.
Skrinar M, Plibersek T. New finite element for transversely cracked slender beams subjected to transverse loads. Comp. Mat. Scie. 2007, 39, 250–260. [CrossRef]
S. Wolfram, The Mathematica 8. Wolfram media Cambridge: Cambridge University Press; (2010).

Figure 1. Double-beam system constrained at the ends by elastically flexible springs and in presence of a Winkler-type elastic medium.

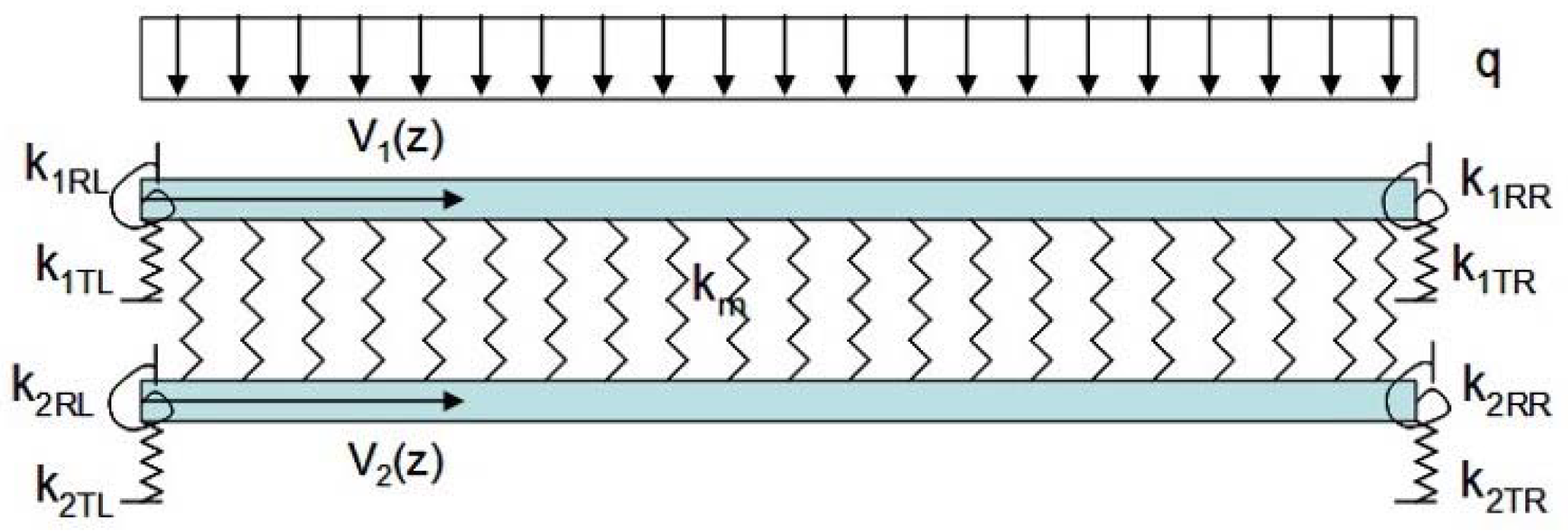
Figure 2. Geometry of beam with crack.

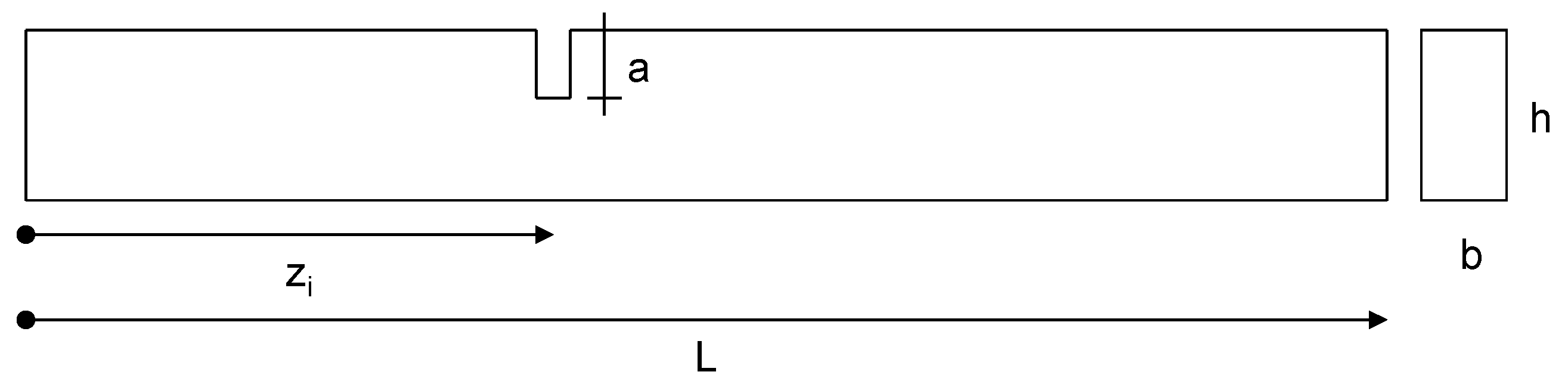
Figure 3. Structural system discretization CD method.

Figure 4. Structural system discretization FE method.

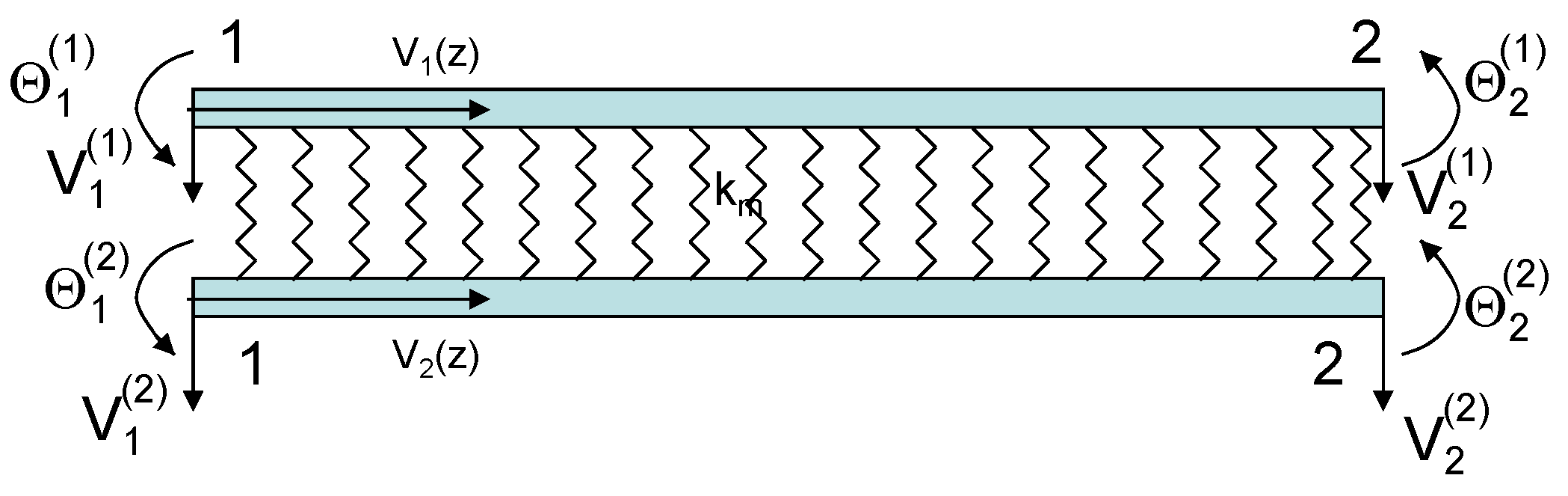
Figure 5. Displacements and rotations diagrams of two beams, at the crack position z=1.25 m.

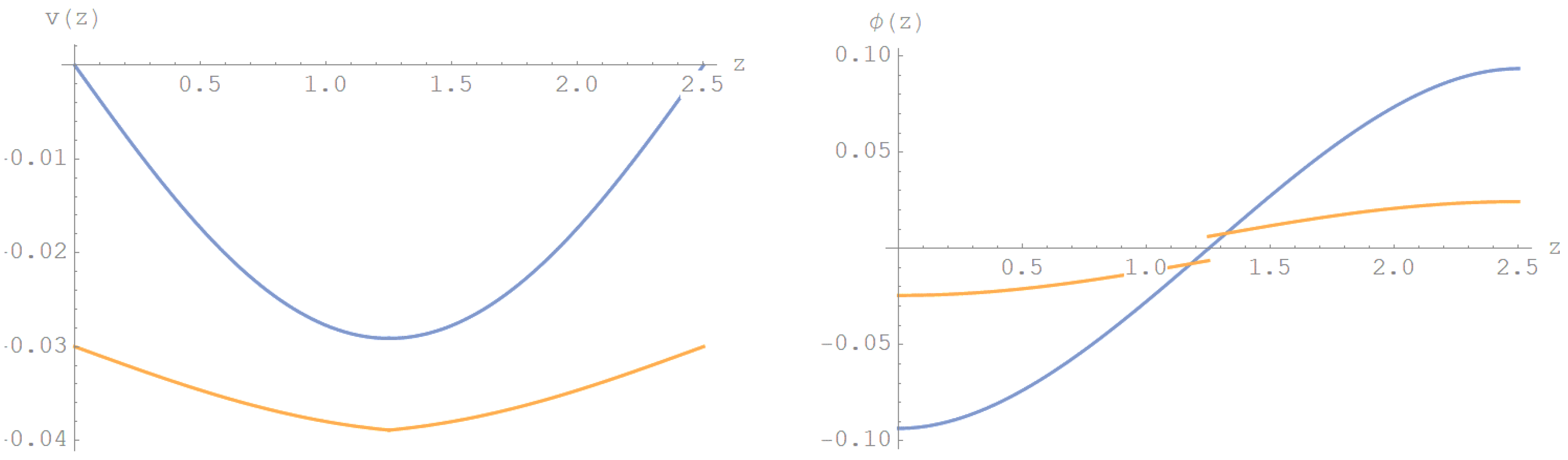
Figure 6. Displacements diagram of two beams, at the crack position z=0.5 m and z=1.75 m.

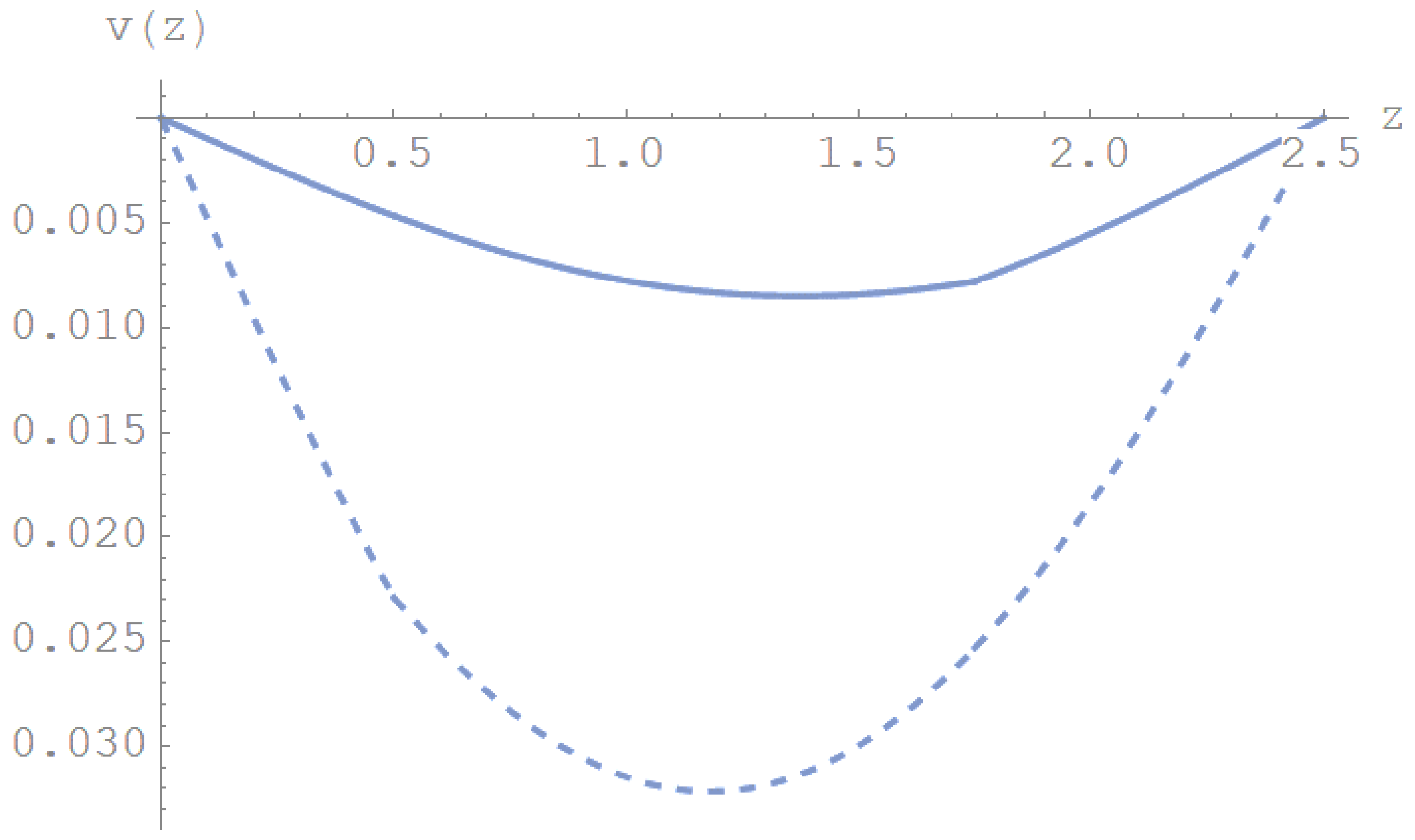
Figure 7. Displacements diagram for a clamped-clamped double beam system with a crack on the lower beam and a uniformly distributed load applied to the upper beam.

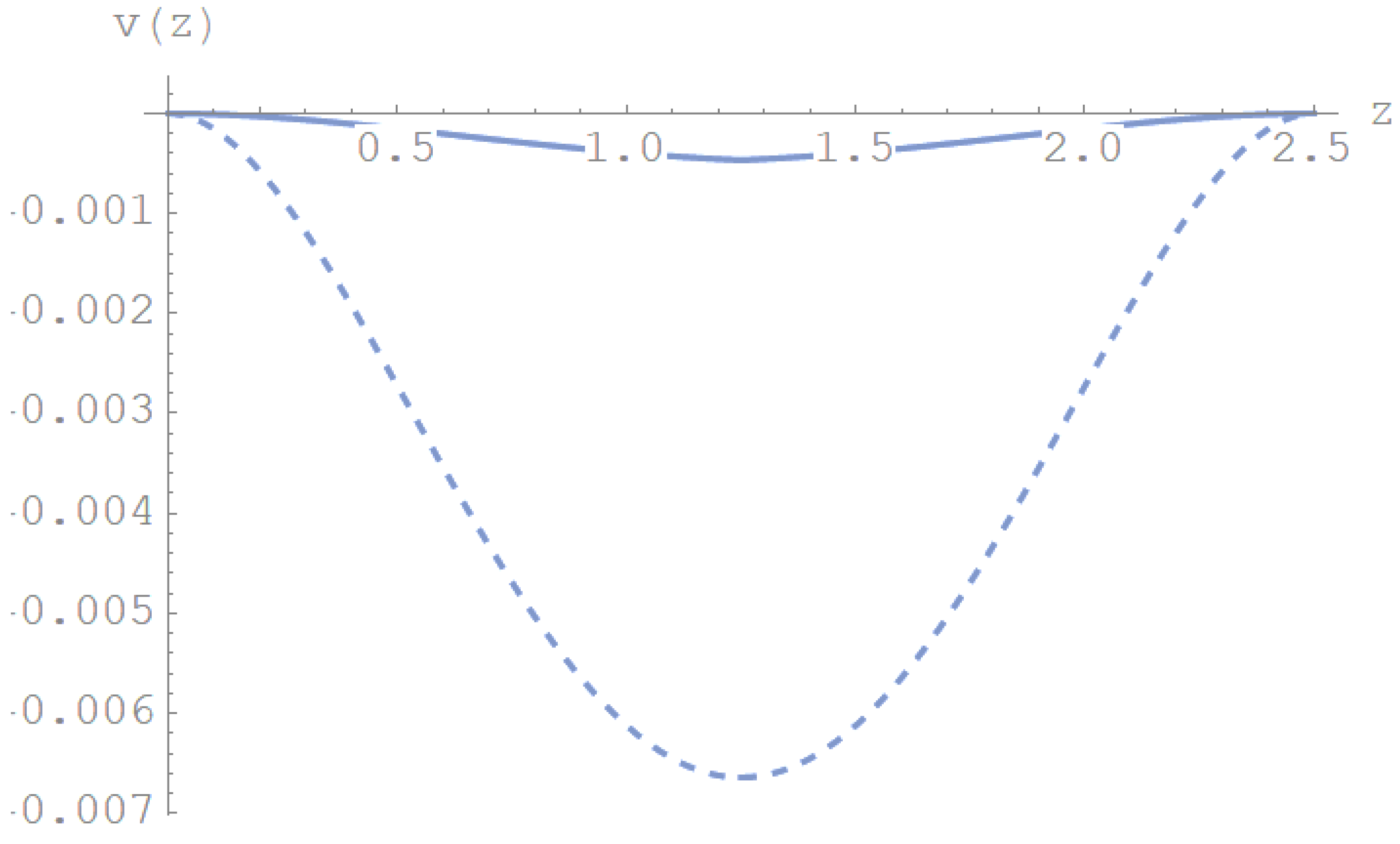
Figure 8. Displacements diagram for a tapered double beam system with different boundary conditions and for

β

=0.5.

Figure 8. Displacements diagram for a tapered double beam system with different boundary conditions and for

β

=0.5.

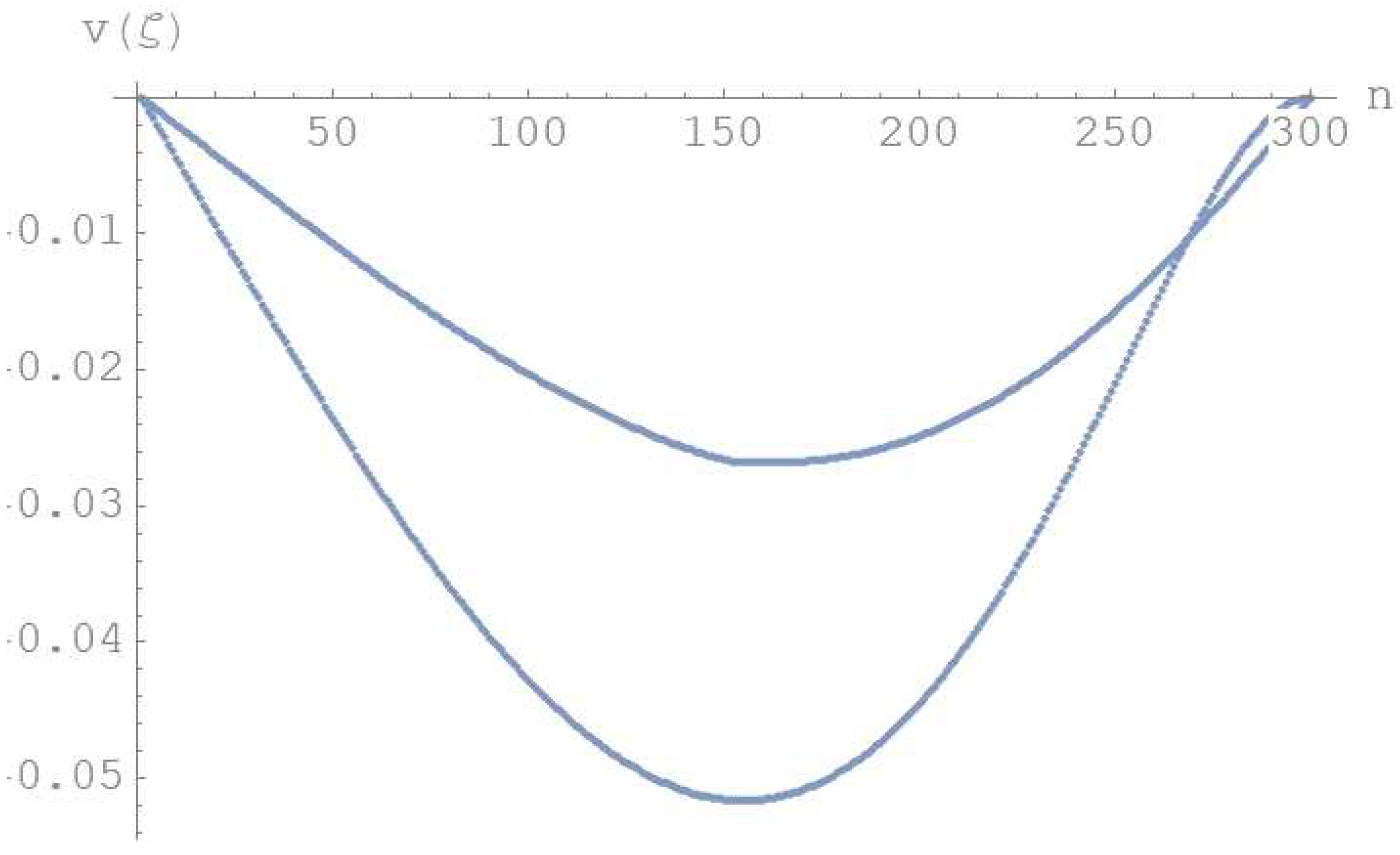
Figure 9. Displacements diagram for a uniform double beam system with different boundary conditions and for

β

=1.

Figure 9. Displacements diagram for a uniform double beam system with different boundary conditions and for

β

=1.

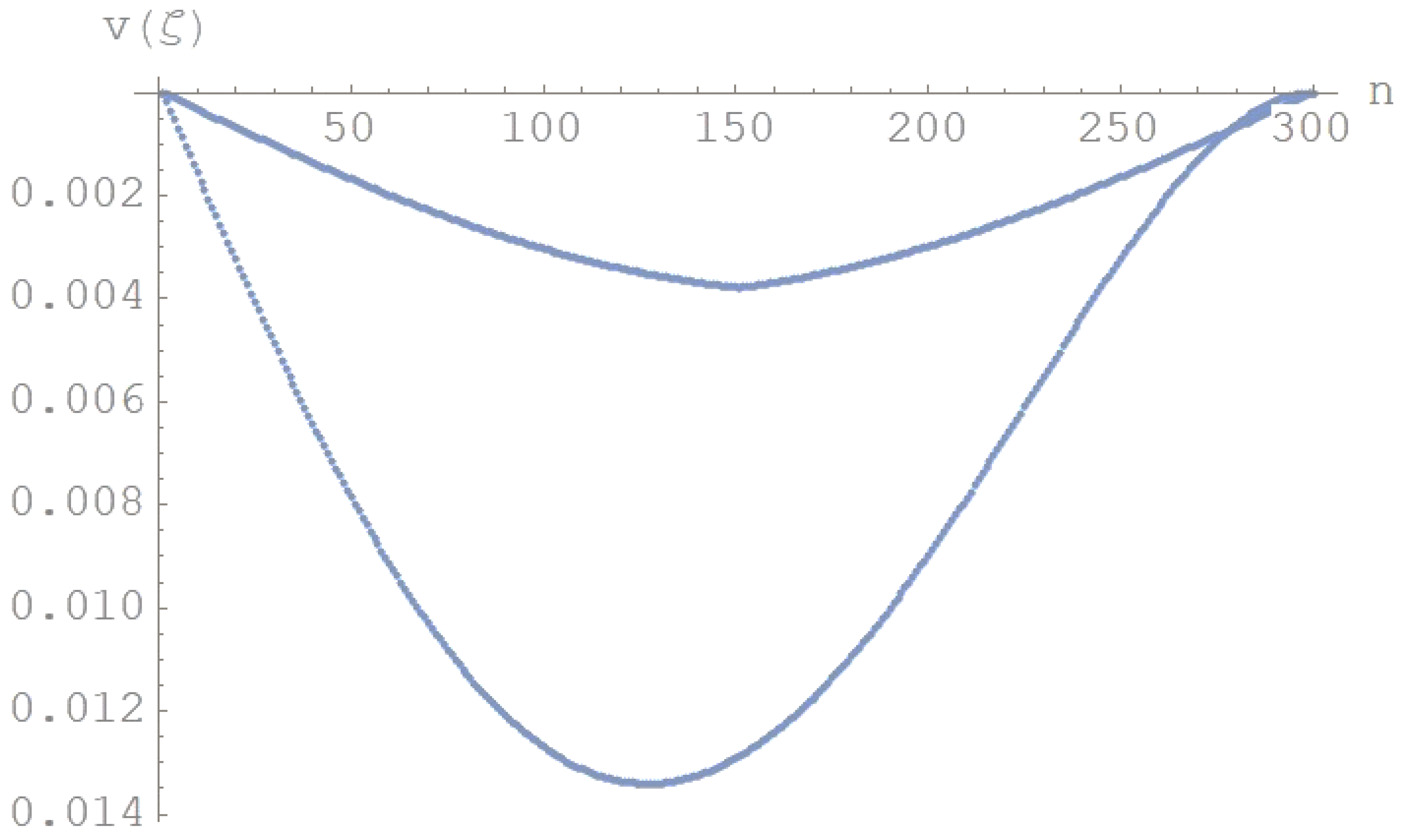
Figure 10. Displacements diagram for a uniform double beam system with different boundary conditions and for

β

=1.5.

Figure 10. Displacements diagram for a uniform double beam system with different boundary conditions and for

β

=1.5.

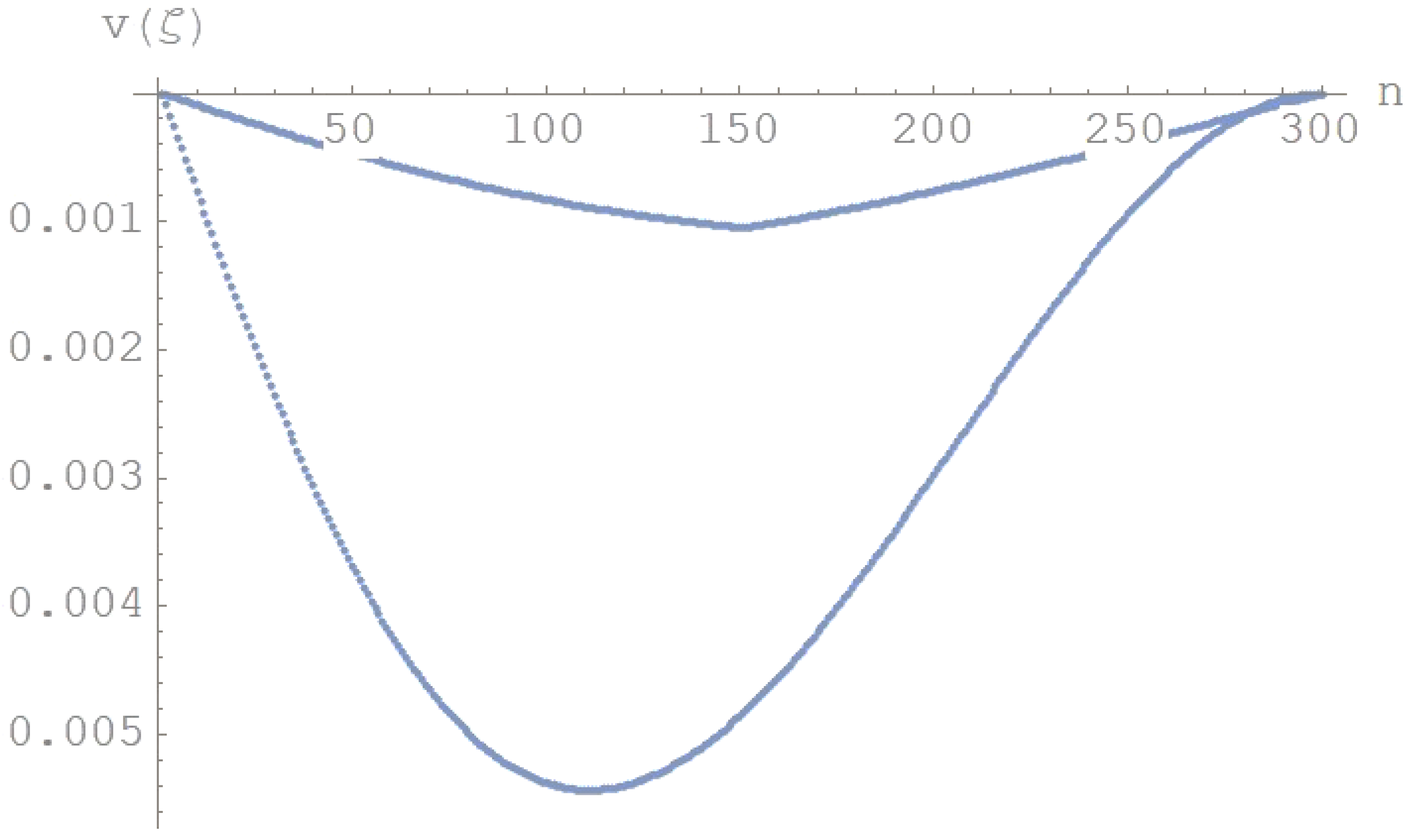
Figure 11. Displacements diagram for a uniform double beam system with different boundary conditions and for

β

=2.

Figure 11. Displacements diagram for a uniform double beam system with different boundary conditions and for

β

=2.

Table 1. Maximum deflections values of two beams varying

k_{m}

in the range

[10^{2}, 10^{3}, 10^{4}, 10^{5}]

and with a crack acting on the lower beam, where C-FS=Closed-form solution, C=CDM, F=FEM.

Table 1. Maximum deflections values of two beams varying

k_{m}

in the range

[10^{2}, 10^{3}, 10^{4}, 10^{5}]

and with a crack acting on the lower beam, where C-FS=Closed-form solution, C=CDM, F=FEM.

$k_{m}$	$v_{1 max} (C - FS)$	$v_{2 max} (C - FS)$	$v_{1 max} (C)$	$v_{2 max} (C)$	$v_{1 max} (F)$	$v_{2 max} (F)$
$10^{2}$	0.0348842	1.489 $10^{- 6}$	0.0348842	1.489 $10^{- 6}$	0.0348842	9.631 $10^{- 7}$
$10^{3}$	0.0348756	0.0000149	0.0348754	0.0000149	0.0348756	0.0000149
$10^{4}$	0.0347895	0.0001479	0.0347894	0.0001479	0.0347895	0.0001479
$10^{5}$	0.0339827	0.0013952	0.0339826	0.0013952	0.0340380	0.0013964

Table 2. Maximum deflections values of two beams varying

k_{m}

in the range

[10^{2}, 10^{3}, 10^{4}, 10^{5}]

and in absence of crack, where C-FS=Closed-form solution, C=CDM, F=FEM.

Table 2. Maximum deflections values of two beams varying

k_{m}

in the range

[10^{2}, 10^{3}, 10^{4}, 10^{5}]

and in absence of crack, where C-FS=Closed-form solution, C=CDM, F=FEM.

$k_{m}$	$v_{1 max} (C - FS)$	$v_{2 max} (C - FS)$	$v_{1 max} (C)$	$v_{2 max} (C)$	$v_{1 max} (F)$	$v_{2 max} (F)$
$10^{2}$	0.0348842	9.631 $10^{- 7}$	0.0348842	9.631 $10^{1} 0^{- 7}$	0.0348842	9.631 $10^{- 7}$
$10^{3}$	0.0348756	9.626 $10^{- 6}$	0.0348754	9.626 $10^{- 6}$	0.0348756	9.626 $10^{- 6}$
$10^{4}$	0.0347894	0.0000958	0.0347893	0.0000958	0.0347895	0.0000958
$10^{5}$	0.0339723	0.0000913	0.0339721	0.0000913	0.0339271	0.0000913

Table 3. Maximum deflections values of two beams varying the non-dimensional rotational stiffness

K_{1 RL}

= k_{1 RR}

= k_{2 RL}

k_{2 RR}

K_{R}

in the range

[0, 1, 10, 10^{2}, 10^{3}, 10^{4}, 10^{10}]

Table 3. Maximum deflections values of two beams varying the non-dimensional rotational stiffness

K_{1 RL}

= k_{1 RR}

= k_{2 RL}

k_{2 RR}

K_{R}

in the range

[0, 1, 10, 10^{2}, 10^{3}, 10^{4}, 10^{10}]

$K_{R}$	$v_{1 max}$	$v_{2 max}$
0	0.0291244	0.00890045
1	0.0220762	0.00509119
10	0.0107519	0.00119981
$10^{2}$	0.00713561	0.000536748
$10^{3}$	0.00669172	0.000474023
$10^{4}$	0.00666452	0.000467836
$10^{10}$	0.00664013	0.000467150

Table 4. The maximum deflections value for different value of

β

Table 4. The maximum deflections value for different value of

β

$β$	$v_{1 max}$	$v_{2 max}$	Figure
0.5	0.051597	0.026785	7
1	0.013401	0.003783	8
1.5	0.005433	0.0010456	9
2	0.002697	0.0004161	10

Table 5. The maximum deflections value for different values of dimensional concentrated force F and for height of crack “a”=0.09 m.

$F (N)$	$v_{1 max}$	$v_{2 max}$
10	1.87065 $10^{- 6}$	5.59848 $10^{- 7}$
$10^{2}$	1.87065 $10^{- 5}$	5.59848 $10^{- 6}$
$10^{3}$	1.87065 $10^{- 4}$	5.59848 $10^{- 5}$
$10^{4}$	1.87065 $10^{- 3}$	5.59848 $10^{- 4}$
$10^{5}$	1.87065 $10^{- 2}$	5.59848 $10^{- 3}$

Table 6. The maximum deflections for different values of crack depth and for a non-dimensional concentrated force

F_{t}

0.107167

Table 6. The maximum deflections for different values of crack depth and for a non-dimensional concentrated force

F_{t}

0.107167

$ξ$	$v_{1 max}$	$v_{2 max}$
0.1	0.00184331	0.000397534
0.2	0.00184666	0.000417421
0.3	0.00185267	0.000453055
0.4	0.00186293	0.000513990
0.5	0.00187065	0.000559848

Table 7. Numerical comparison among the closed-form solutions (C-FS) and numerical results based on the CDM, for different values of length

λ

and (

ζ

=0.5).

Table 7. Numerical comparison among the closed-form solutions (C-FS) and numerical results based on the CDM, for different values of length

λ

and (

ζ

=0.5).

$λ$	$v_{1} (C - F S)$	$v_{2} (C - F S)$	$v_{1} (C D M)$	$v_{2} (C D M)$
2	0.00001500	8.5277 $10^{- 9}$	0.000014500	8.5276 $10^{- 9}$
3	0.00007589	1.6061 $10^{- 7}$	0.00007589	1.6061 $10^{- 7}$
5	0.00058326	6.7375 $10^{- 6}$	0.00058326	6.7374 $10^{- 6}$
7	0.00221279	0.00007947	0.00221279	0.00007947
9	0.00588599	0.00048809	0.00588599	0.00048808
13.8889	0.0291243	0.00890046	0.02912429	0.00890037

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Numerical Analysis of Cracked Double-Beam Systems

Abstract

1. Introduction

2. Problem formulation

3. Cracks: modelling and method of solution

3.1. Modelling of cracks: an overview of the discrete spring model

3.2. Method of Solution: Cell-discretization method (CDM)

3.2.1. Boundary conditions in presence of a crack

3.3. Method of solution: Finite Element Method (FEM)

4. Numerical examples: results and discussion

4.1. Case 1: Simply supported-simply supported double-beam system in presence of a crack, on the lower beam, and a uniformly distributed load applied to the upper beam

4.2. Case 2: Simply supported-simply supported double-beam system in presence of a uniformly ditributed load, on the upper beam, and of a crack, on the upper and lower beams

4.3. Case 3: Effect of elastic constraints and crack on the static behaviour of double-beam system

4.4. Case 4: Effect of taper ratio coefficient and crack on the static behaviour of double-beam system

4.5. Case 5: Effect of a concentrated force and crack located at the midspan of upper and lower beams, respectively

4.6. Case 6: Effect of the slenderness λ on the deflections for both upper and lower beams in presence of a crack

5. Concluding remarks

Author Contributions

Funding

Informed Consent Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4.6. Case 6: Effect of the slenderness $λ$ on the deflections for both upper and lower beams in presence of a crack