Prerpints.org logo
Preprint
Article

REM-Based Indoor Localization with the Extra Tree Regressor

Altmetrics

Downloads

124

Views

55

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 August 2023

Posted:

23 August 2023

You are already at the latest version

Alerts
Abstract
As an established and widely available infrastructure, wireless local area networks (WLANs) have emerged as a viable option for indoor localization of both mobile and stationary users. In planning a mobile communications network and radio system design, the critical role of coverage prediction becomes evident, empowering network operators to optimize cellular networks and elevate the overall customer experience. Moreover, WLANs present several challenges that must be fulfilled when it comes to localization based on Wi-Fi signals to get a proper coverage prediction map. This paper presents a study based on application of the extra trees regression (ETR) for indoor localization by using coverage prediction maps. The aim of the proposed method is to accurately estimate a user’s position within a radio environment map (REM) area using collected received signal strength indicator (RSSI) values. The proposed scheme investigates several machine learning (ML) regression algorithms for localization, where the training dataset is obtained from the REM by using the nearest neighbors method. Parameter tuning is conducted to optimize the performance of the ETR scheme by using 10-fold cross-validation. In the numerical results, we first demonstrate the effectiveness of utilizing ML regression techniques for generating coverage maps, which enables accurate estimation of the Wi-Fi signal strength in indoor environments. Then, we showcase the superior performance of the proposed ETR-based method compared to several other ML schemes for indoor localization using the REM. ML algorithms, including decision tree regression and the ETR, are compared to evaluate the system model. Based on error metrics, the proposed ETR-based approach exhibits the best performance among the evaluated techniques. The combination of coverage map generation and localization using regression techniques offers a powerful approach for analyzing the radio frequency (RF) environment in indoor spaces.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The Radio Environment Map (REM), a digital map that offers details on the radio frequency (RF) environment in a certain area, is made by employing RF sensors to find and examine signals from wireless devices like Wi-Fi networks and cell towers. Along with information on interference and noise levels, it displays the location and strength of RF signals. This information is crucial for optimal performance, dependability, and interference-free operation of wireless equipment. The REM is crucial to many wireless systems, including Internet of Things (IoT) gadgets and autonomously driven automobiles. However, since the number of devices and data volumes continue to increase dramatically, the quick commercialization of fifth-generation (5G) technology poses substantial problems to current communication networks. Therefore, increasing the data rate remains a major requirement in cellular networks [1]. Offering location-based services has received a lot of attention recently since they are thought to be the next step in contextual awareness, network management, customized information delivery, and healthcare monitoring [2,3,4,5,6]. To augment the precision and dependability of device localization, a REM can be employed, which offers an intricate blueprint of the RF environment. By comparing the received signal strength (RSS) at different locations with the signal strength map stored in the REM, a device can estimate its location with a high degree of accuracy.
Reliable and optimized service coverage is crucial for accessing the RF spectrum, and accurate estimation of propagation path loss (PL) plays a vital role in achieving this. Various propagation models based on theory or experimentation have been reported in the literature to estimate the PL of signal coverage [7]. Indoor and outdoor REMs are the two main divisions. An outdoor REM covers an outdoor area [8], whereas an indoor REM is a digital map that offers details about the RF environment inside a building or structure [9]. An indoor coverage map is used to help with indoor wireless communication system planning, design, and optimization in malls, hospitals, or office buildings. Network designers can create wireless networks that are more effective and efficient, arrange wireless devices optimally, and solve signal coverage and interference issues by using the indoor coverage map [10].
One way to improve the utilization of radio resources is to use REMs for insights into the propagation environment and to help understand its characteristics [11]. The REM can optimize wireless network deployment by identifying strong/weak signal coverage and interference, improving network efficiency and effectiveness [12]. Meanwhile, the REM aids RF spectrum management by identifying high- and low-RF activity, leading to efficient spectrum resource allocation and interference avoidance [13]. Furthermore, the REM can detect and locate unauthorized RF activity for security and emergency responses, and can be used for many things by detecting and evaluating the distribution of RF signals in a specific area, especially with the importance of localizing objects or devices in a particular context in today’s technological environment. According to measurements of the signal strength or other aspects of wireless signals, localization in the context of wireless communication systems often entails calculating the location of a mobile device or other wireless devices.
The localization process requires calculating an object’s coordinates inside a predetermined reference frame, such as its latitude, longitude, and height. In order to determine an object’s precise position, the localization process often gathers and interprets data from numerous sources. These sources may include wireless signals, such as a global positioning system (GPS) [14], sensors [15], Bluetooth [16], Wi-Fi [17], landmarks, or infrastructure. GPS-based localization is commonly used for outdoor positioning and relies on signals from satellites. By receiving signals from multiple satellites, a GPS can triangulate its position with high accuracy [14]. For indoor environments, Wi-Fi-based localization is commonly used. It leverages Wi-Fi signals and access points (APs) strategically placed within the building to estimate the position of devices [17]. By measuring the signal strength or utilizing fingerprinting techniques, a device’s indoor location can be determined. Bluetooth-based localization uses signals and beacons to determine the proximity and position of devices within a limited range. Bluetooth beacons are small devices that transmit signals, allowing other devices to detect their presence and estimate their location [16]. RF identification (RFID)-based localization relies on tags and readers. RFID tags are attached to objects, and readers detect the tags to track and locate objects within a specific area [18]. Sensor-based localization encompasses a range of sensors that are utilized by mobile robots and other devices to gather data, including motion. The primary objective is to determine the user’s location by analyzing motion, orientation, and visual surroundings [15].
Vendors and companies have been inspired to create solutions that support the rising number of location-based services (LBSs). Indoor localization has applicability across several IoT sectors, whether as a core service or a complementary one. It is possible to aggregate and evaluate the locations of several users or objects by using ML algorithms and crowdsourcing data. Such expertise can improve the overall user experience, forecast human behavior for future planning, and avoid problems. The great potential of LBSs in IoT applications, including smart cities, healthcare, commerce, and security, is confirmed by market surveys. Incorporation of an IPS into IoT settings makes it possible to develop creative, context-aware services that meet the various demands of users and promotes IoT technology [19].
Indoor localization estimates the coordinates or relative positions of objects within a defined space and poses unique challenges and requirements [20]. Overall, localization technologies play a crucial role in improving efficiency, enhancing user experiences, and enabling a wide range of location-based applications across various industries.
Our main aim is to propose a new and improved method for indoor coverage map localization. We utilize received signal strength indicator (RSSI) values and an ML algorithm, leveraging real data collected from field strength measurements. The data were obtained using a robot named Turtlebot3 Burger in a room at the University of Ulsan, South Korea. To achieve localization by using the indoor coverage map, we developed a model employing ML regression. We developed a methodology for constructing the REM, which is utilized to obtain a training dataset for our ML-based approach to indoor localization. By employing this framework, we create accurate indoor localization for the coverage map, and determine user locations on the map.
The novelty of our approach is summarized as follows.
  • We propose an ML-based approach to obtain the indoor coverage map and accurately localize users by harnessing the potential of RSSI signals.
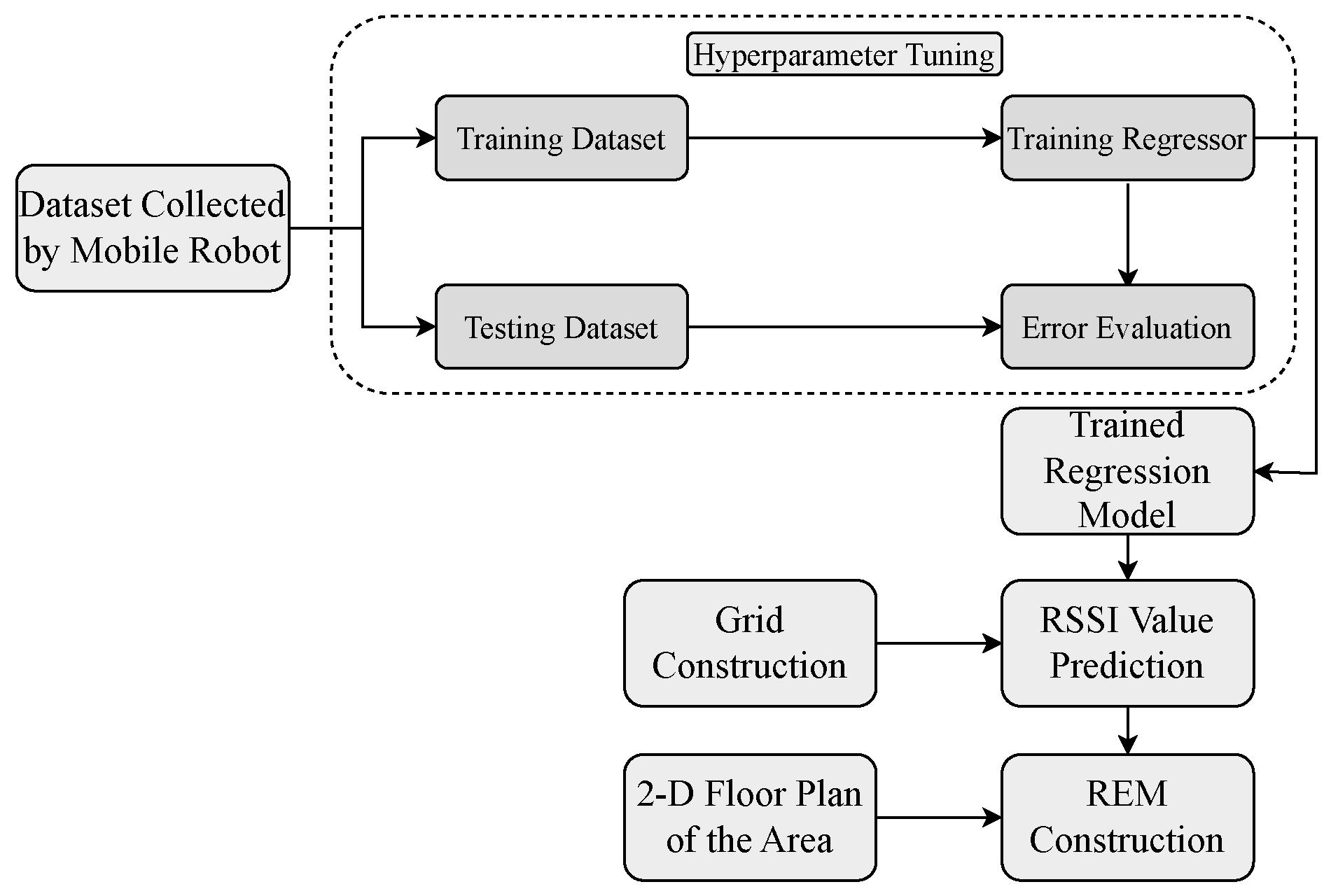
  • Construction of the REM is based on an ML scheme using a single AP to collect RSSI measurements from a mobile robot. This strategic approach enables operators to gain clear visibility into coverage prediction and identify potential shadow areas on the indoor REM. In our study, we focus on localization by leveraging a coverage prediction map specifically considering RSSI signals within an indoor environment of the University of Ulsan.
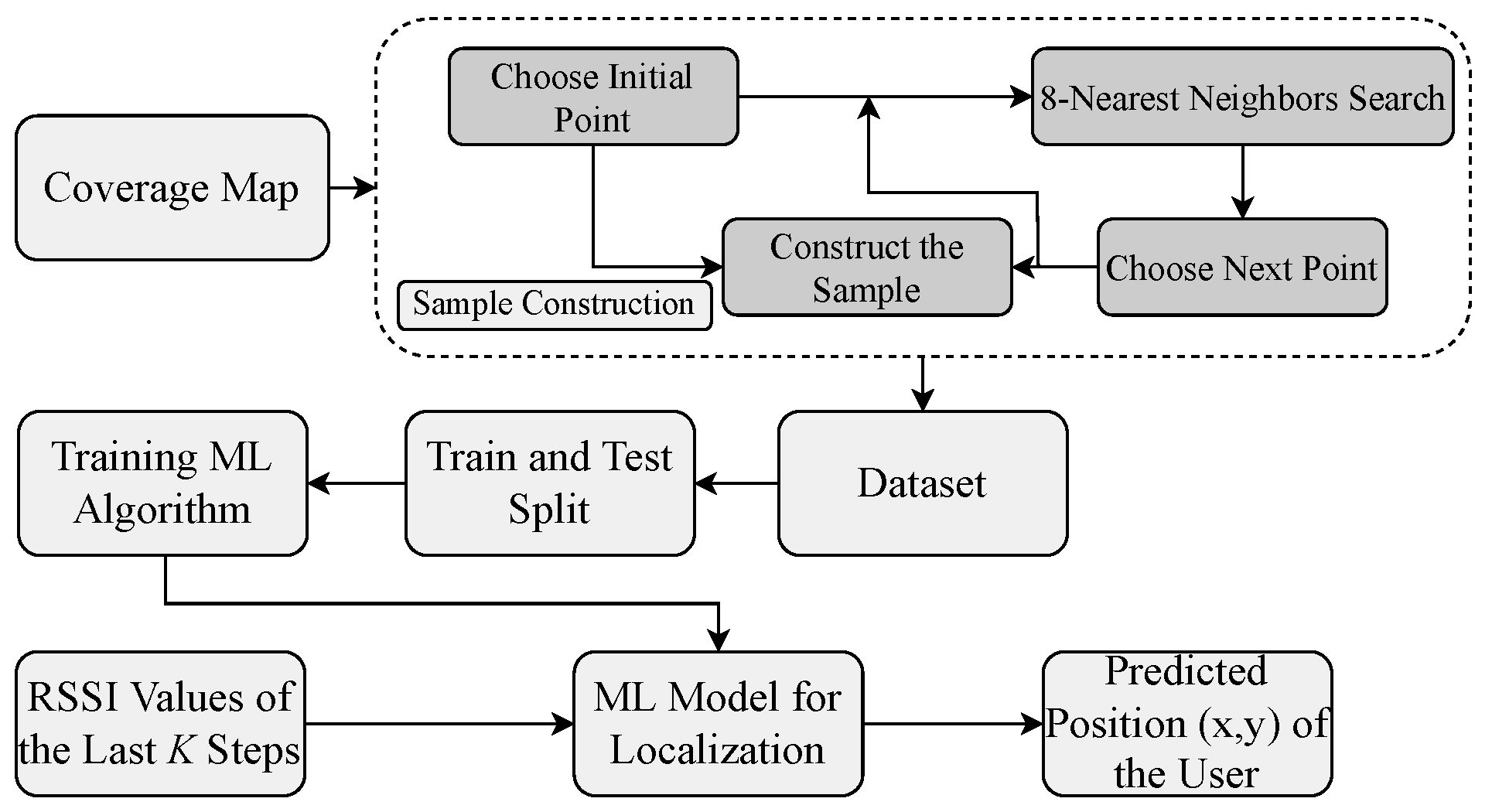
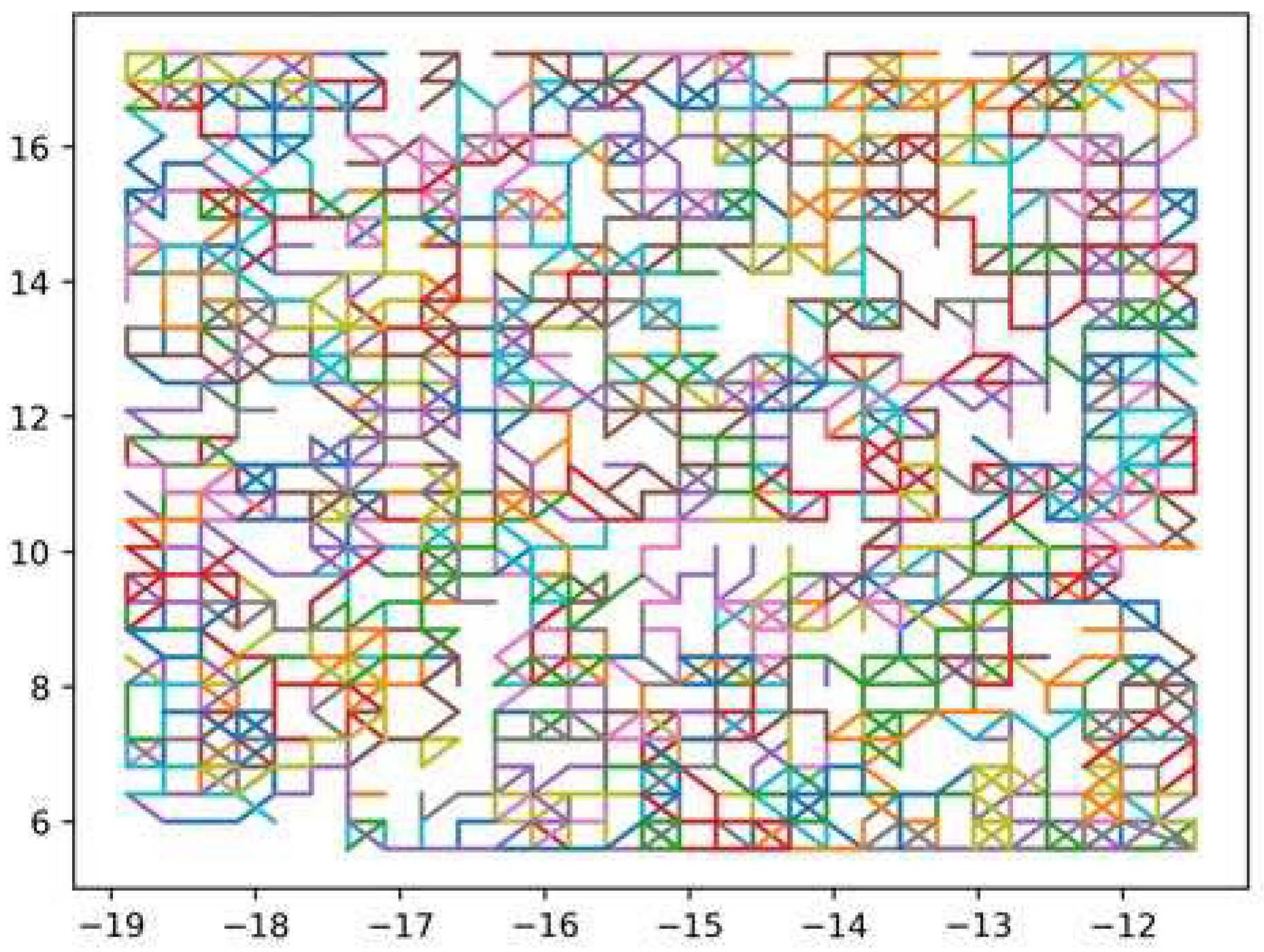
  • To construct the dataset used to train our ML algorithm for localization, the selection of each step is primarily based on a nearest neighbors search. Within each sample, we choose the first point randomly and then obtain eight nearest neighbors to determine the next step. This iterative process continues for K steps. By diligently following this procedure, we construct a single sample. This process is repeated until we reach the defined number of samples for the dataset.
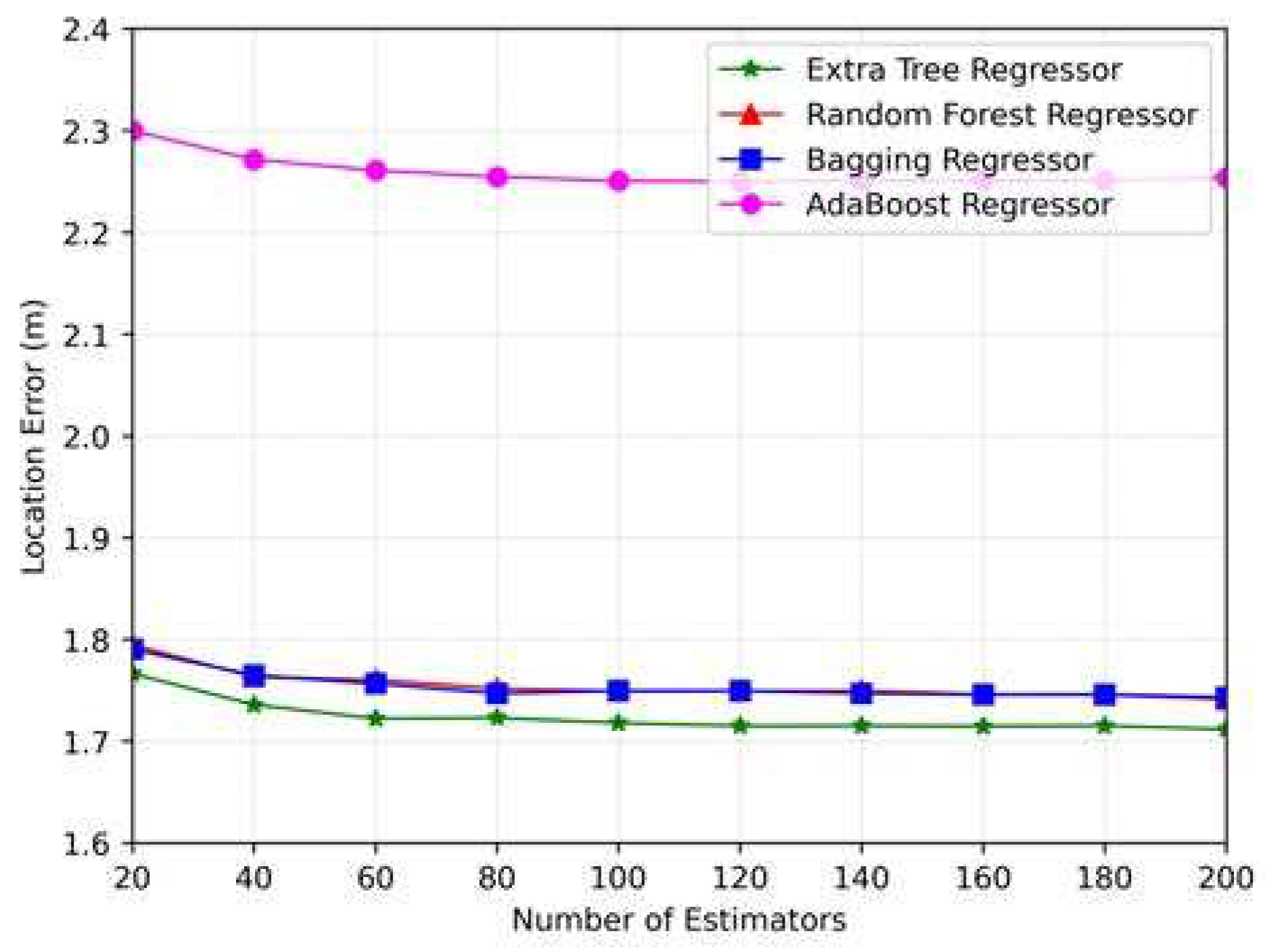
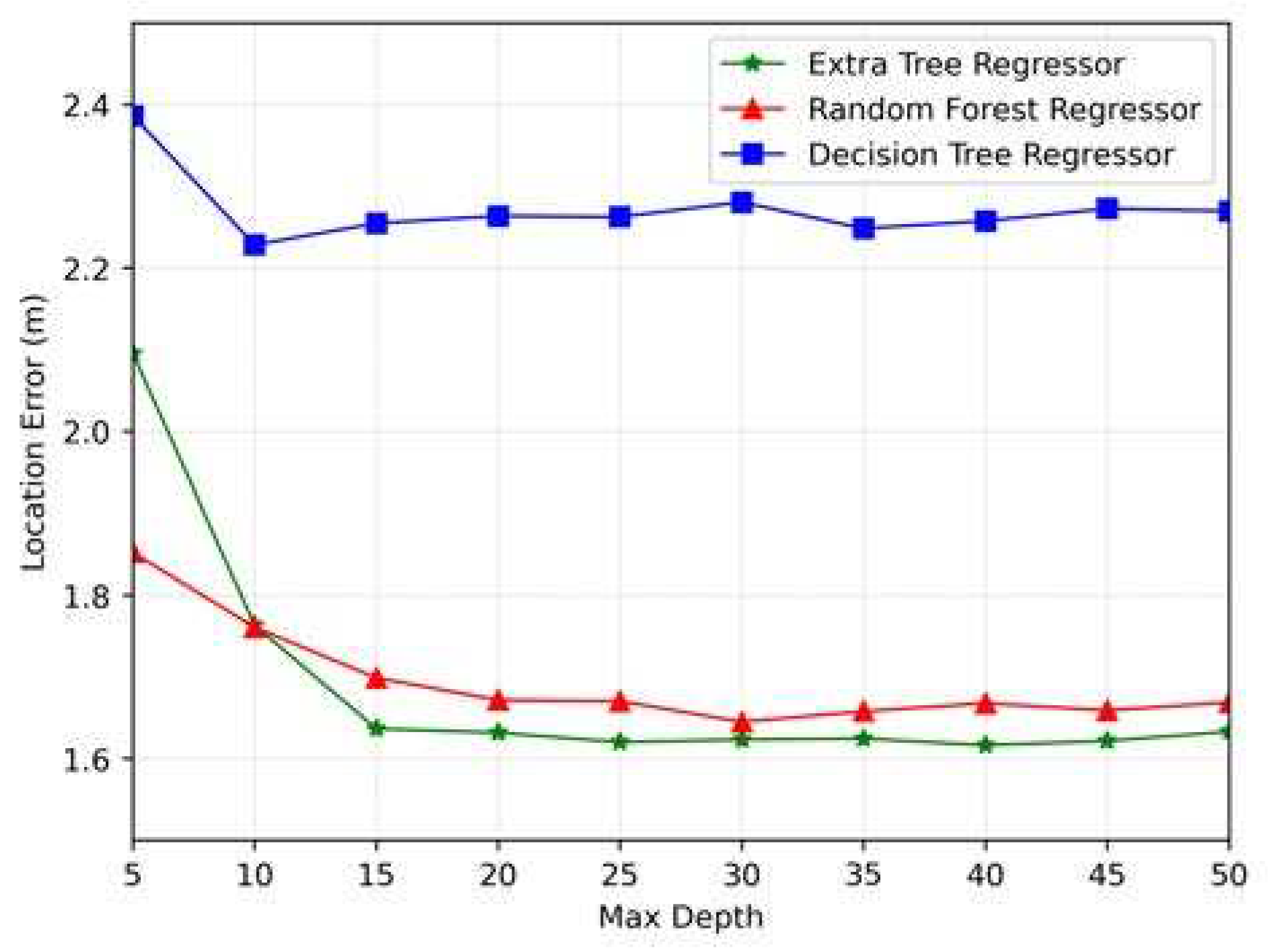
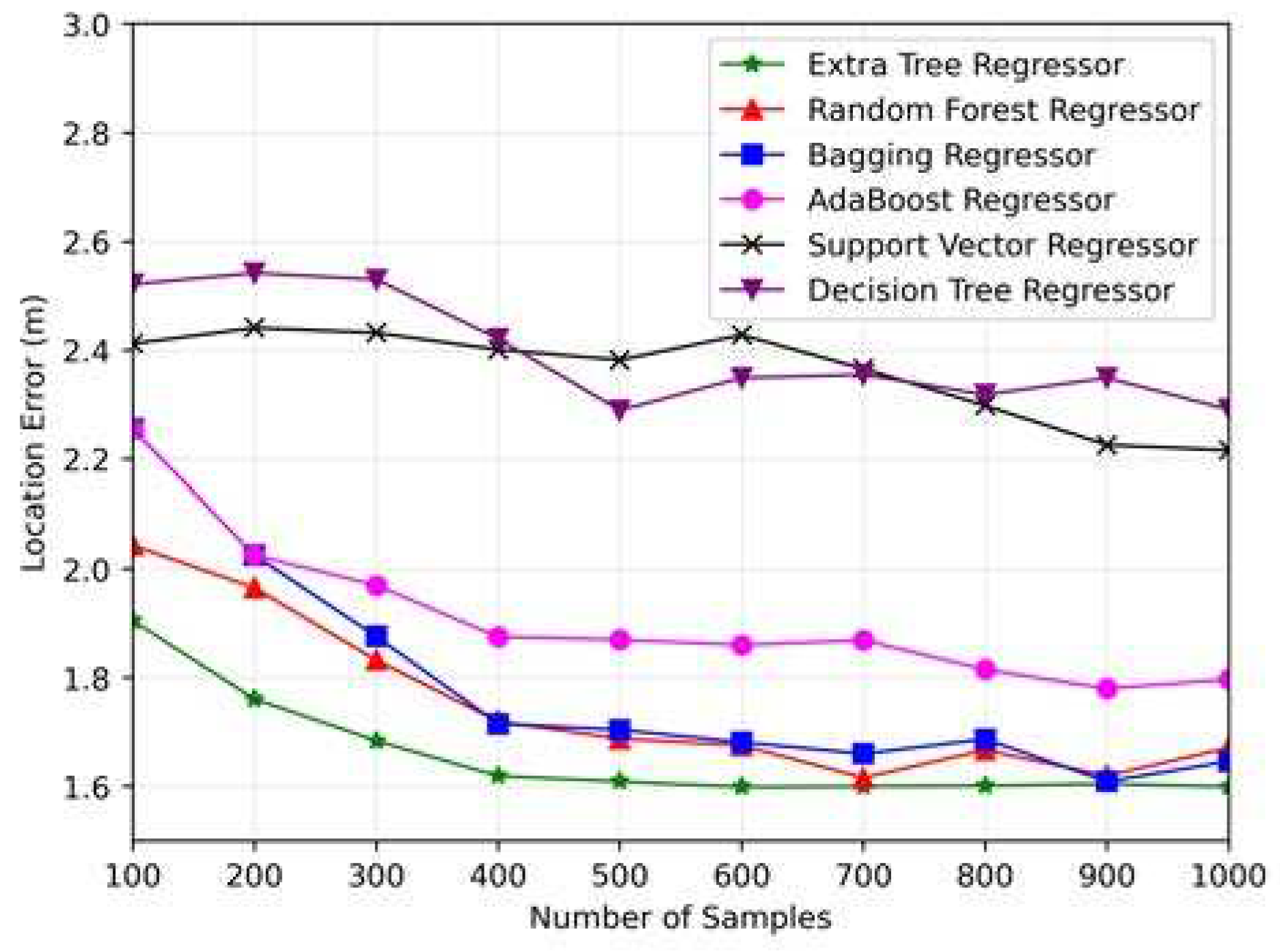
  • We meticulously analyzed several prominent ML algorithms, namely the random forest regression [21], decision tree regression [22], extra trees regression (ETR) [20], and adaBoost regression [23], etc. Through the rigorous application of the 10-fold cross-validation technique, we aim to identify the optimal regressor algorithm for our proposed approach by considering the localization error.

2. Related Work

Different models for locating a user in an indoor environment are available in the localization field, implementing methods such as the REM [9]. First, we explore major research based on conventional statistical methods. Using RSSI parameters and neural network technology, Gadhgadhi et al. [24] presented localization strategies. Two methods—the artificial neural network (ANN) and the decision tree—were used to compare the outcomes of the resulting location estimate. In the beginning, three inputs along with the ANN were used to estimate the position for each RSSI triplet and calculate the mean error value of overall positions acquired. Using a four-input ANN architecture, the same process estimated the location for each set of four inputs and determined the mean error value for the estimated position. In the study, they used neural networks to perform localization based on RSSI parameters. They compared the ANN and decision tree using an RSSI dataset from a previous study. The ANN with four inputs showed better accuracy and reduced computation, proving that increasing the number of sensors improves accuracy.
Low-precision indoor localization (LIL) and high-precision indoor localization (HIL), two Bluetooth-based techniques introduced by Wang et al. [25], used RSSI data to define a limited region that corresponds to a specific position of the Bluetooth-enabled device. They discovered via their tests that HIL performs better than LIL in terms of accuracy in the majority of instances, mostly because of an additional data training phase. In conclusion, HIL provided better performance than LIL when implementing the extra data training phase was possible.
Based on the most recent research findings, Billa et al. [26] presented a review paper with a thorough overview of many commonly used IPSs. The report goes into detail about their uses, accuracy, benefits, and drawbacks. It found that as system complexity and implementation costs grow, so does the accuracy. The performance of an IPS has been improved by researchers merging various systems, which resulted in the creation of hybrid models that provide effective IPS solutions. One survey examined several algorithms put forth for the online phase of fingerprinting technologies, including the most advanced Bluetooth version (Bluetooth Low Energy [BLE]), an ultrasonic indoor positioning system (UIPS), and indoor localization using ultra-wideband (UWB) technology. The merits and disadvantages of each algorithm are covered in detail, along with examples of how they could be used in different situations. The authors suggested that to get efficient outcomes, the algorithm that will be used must be well thought out.
Huang et al. [27] proposed a self-training indoor localization system with non-line-of-sight (NLOS) mitigation. To infer pedestrian paths, the system makes use of data from maps, inertial sensors, and UWB transceivers. This technique enabled automated data collection, categorization, and learning by merging multisensory information. Weak labels for UWB data are created and repeatedly improved via self-training, which dramatically lowers the labor cost compared to conventional supervised learning techniques. Experimental results showed significant improvements in localization accuracy, NLOS range error reduction, and multi-base station localization under mixed LOS/NLOS circumstances. The work emphasized how self-training techniques may provide indoor localization and tracking with high precision at a cheap cost. In order to tackle larger-scale issues, the authors stated that future work requires enhancing experimental settings and gathering massive amounts of data through crowdsourcing. Moreover, to improve feature representation and model performance, the authors suggested that more investigation is required into advanced ML techniques like the gradient boosting decision tree, the convolutional neural network, and the minimax risk classifier. To further improve the localization system, the authors investigated the fusion of other RF signals like 5G, Wi-Fi, and Bluetooth as well as the inclusion of signal metrics like intensity, phase, and fingerprint.
Dargie et al. [28] investigated the use of recursive estimation, which deals with interior localization of mobile robots. The study explored several kinds of errors and explained the presumptions that underpin the estimating assignment. The two objectives of the estimation assignment are to: (1) align the mean of the estimated random component with the robot’s real position, and (2) reduce the variance (uncertainty) in the estimated random variable. The study emphasized that both prediction and measurement components are involved in recursive estimation strategies. The prediction component is stated abstractly in a Kalman filter, whereas it is expressed explicitly as a transition probability, p x t ∣ x t − 1 , in Bayesian estimation and particle filters. It was stressed that faults in the robot’s driving configuration, which are recorded as process defects in Kalman filter formulation, frequently impact the transition probability. It is important for an estimation assignment to note the importance of model parameters and the suitability of the statistics used to describe them. The research also shows how process, measurement, and prediction statistics may be established for two different sensing systems: the inertial measurement unit (IMU) and UWB.
Sadowski et al. [29] investigated k-nearest neighbors (KNN) and naive Bayes, two memoryless methods coupled with trilateration, for their possible application in an indoor localization system. The methods were classified for accuracy, precision, and complexity in three rooms with varied amounts of interference during the tests. Three wireless technologies (ZigBee, BLE, and Wi-Fi) were used throughout the trials to verify the findings. According to the results, KNN with k = 4 outperformed all other localization algorithms in terms of accuracy and precision. Naive Bayes also performed well, but it needed more time to execute because it uses a database for its computations, giving it an O(mn) complexity. Despite being the least efficient technique overall, trilateration had the best O(1) complexity and needed the least amount of running time for position computations.
In the Android Pie mobile operating system, Han et al. [30] proposed a LOS detection technique that focuses on Wi-Fi Fine Timing Measurement (FTM). The support vector machine FTM algorithm (SVM-FTM) was created primarily to use multilateration techniques for indoor localization. A hypothesis test framework and the SVM are used to identify LOS signals, and multipath error is considered to distinguish between low and high-quality signals. In a sample size of 99, the average identification rate of high-quality signals was 92.4%, whereas in a sample size of 29, it was 78.3%. Localization performance significantly improved by a factor of 24.4 when using only high-quality signals in comparison to the ideal LOS detector. When compared to SVM-RSS, the suggested SVM-FTM LOS identification method showed an average gain in identification accuracy of 8.33% and a drop in localization root mean square error (RMSE) of 20.3%.
Fifth-generation commercial networks are currently being installed in large numbers in the mid-band, mostly in the Band n78 frequency range between 3.3 GHz and 3.8 GHz. Garcia et al. [31] proposed the extremely randomized trees regressor (ERTR) algorithm for forecasting the coverage of outdoor-to-indoor propagation in 5G mid-band operational networks. Following that, a REM is created to make it simpler to view the outcomes and find coverage gaps and traffic hotspots. This is accomplished using a collection of channel measurements from a Sapienza University building in Rome, Italy. Additionally, the ERTR-based strategy was evaluated using three error metrics: relative error, mean absolute error (MAE), and RMSE. The efficacy of five more ML regression algorithms was assessed for comparison, and the ERTR-based method outperformed the baseline schemes in all cases. Furthermore, the authors constructed a REM based on ERTR for outdoor environments [31]. Specifically, the authors utilized actual measurement data from Ikoyi, Lagos, and Victoria Island, Nigeria.
Garcia et al. [32] proposed construction of a REM and coverage prediction for 5G networks in band n78. They proposed a novel approach using the ERTR algorithm to predict outdoor-to-indoor coverage for 5G mid-band networks. The results showed that the proposed ERTR technique outperformed other machine learning regression algorithms, enhancing the accuracy of coverage prediction in various scenarios. Additionally, the performance of five ML-based schemes (RF, KNN, Ridge, DT, and Bagging) was studied to evaluate the proposed ERTR system model. Their proposed scheme outperformed the benchmark methods in terms of relative error, MAE, and RMSE with 10-fold cross-validation. Moreover, the constructed REM validated the superiority of the ERTR algorithm in identifying favorable propagation conditions and potential shadow areas. The authors concluded that the proposed ERTR method outperformed the baseline schemes in all error metrics and with lower computational complexity.
As per our understanding, there is no research paper regarding the specific approach of utilizing the user’s steps for localization based on REM construction that has been mentioned previously. To evaluate REM construction, three error matrices are used: RMSE, R 2 , and MAE. Moreover, motivated by the benefits of the ETR in providing high accuracy when predicting coverage for both outdoor [31] and indoor environments [32], this paper proposes a novel approach based on the ETR and nearest neighbors techniques for indoor localization. Furthermore, for this purpose, we construct a REM of the area of interest by applying the ETR algorithm. In addition, we focus on studying ML regression algorithms like decision tree regression and the support vector regressor to compute the coverage map and evaluate the localization techniques by using 10-fold cross-validation with a distance evaluation metric.
The rest of the paper is structured as follows. Section 3 contains a description of the methodology. In Section 4, the proposed methodology has been described along with the data construction and our proposed ETR-based scheme. In Section 5, we have included a broad description of several regression techniques. The error matrices with appropriate graphical explanations regarding the hyper-parameter tuning are presented in the numerical results and also include some graphical results of REM building in Section 6. Section 7 narrates the conclusions of our paper.

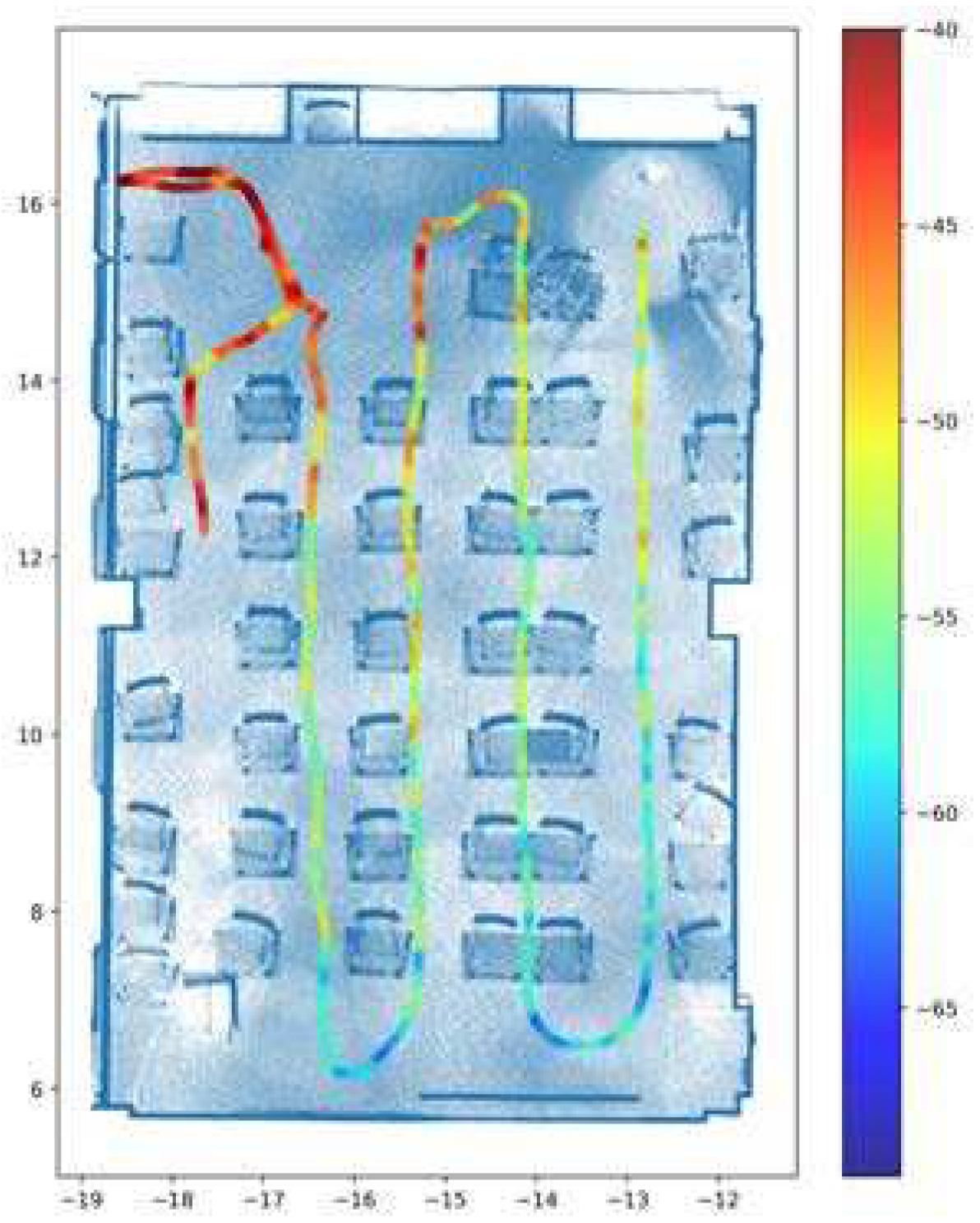
3. Measurement Methodology

This section provides a detailed explanation of the experimental data collection and configuration process used to acquire measured data for indoor localization and constructing a REM. The focus is on discussing the mobile robot utilized in the study and the methods employed for data collection.
A mobile robot is a versatile system utilized in various industries to enhance productivity and perform tasks efficiently. It is highly functional, with a sensor that is very accurate, navigational systems, and decision-making algorithms, along with its feature of free movement and completion of tasks in an accurate manner.
In our experiment, we employed Turtlebot-3 Burger [33] as the mobile robot, which is shown in Figure 1. This robot consists of several essential components, including a single-board computer (SBC), an embedded controller, the LDS-02 360 laser distance sensor, an IMU sensor, an encoder, and the Robot Operating System (ROS). The SBC, powered by Raspberry Pi, allows for algorithm configuration within a Linux environment. ROS, an open-source meta-operating system for robots, facilitates seamless communication between different processes. The embedded controller, utilizing OpenCR, takes on the primary responsibility of controlling the robot’s movement and utilizing the array of sensors. The LDS-02 accurately measures the time it takes to reflect the laser pulses emitted, enabling precise position estimation by calculating the position of the reflector. Additionally, the DYNAMIXEL encoder provides electrical signals that offer position and speed information for both rotary and linear motion.
These integrated components empower the mobile robot to navigate its surroundings, make informed calculations, and efficiently execute tasks. With the help of the mobile robot, a lot of data were collected to create a simple view of the room under study at the University of Ulsan. In Figure 2, a 2D visual representation of the floor plan shows where the AP was located and illustrates the layout used for collecting measurements.
The experimental data collection process involved obtaining RSSI data using the built-in Wi-Fi module of Raspberry Pi. The iwconfig command line tool displays information about the wireless network interface, including SSID, signal frequency, quality, and strength. The encoder and IMU sensor data merge with Lidar data to create ROS odometry. RSSI and location estimation data are collected separately using a shell script in Linux and synchronized using timestamps.
The merging process synchronizing the two data sets ensures the data are collected simultaneously while the mobile robot is in operation, and ensures that RSSI and localization data align correctly.
The localization of indoor REM data utilized in this paper consisted of X and Y coordinates along with corresponding RSSI values. Localization data play a crucial role in navigation and location-based services, enabling precise determination of the robot’s physical position. The experiment used the integrated Lidar and Wi-Fi interface in Turtlebot3 Burger to collect both localization data and RSSI values.

4. Proposed Methodology

4.1. General Overview

Our proposed method conducts REM localization by initially using the x- and y-axis values as features along with signal values as labels for REM construction. We employed various regression techniques to our dataset where the ETR yielded excellent results compared to the others. Our primary focus in this paper is on localization where we utilize the user’s steps in conjunction with RSSIs taken from the REM which were evaluated using regression algorithms.
The ETR is a supervised learning algorithm that relies for training on a labeled dataset containing input features and corresponding target values. Specifically, the ETR algorithm uses the input features to predict a continuous target variable. This algorithm proves particularly valuable when dealing with complex regression problems.
In our system model, we utilize RSSI signals to generate the coverage map, which is subsequently employed to construct our proposed ML-based framework for indoor localization. RSSI values provide insights into signal quality and are applied in tasks such as network planning, signal mapping, and device localization [34]. Our experiment primarily focuses on utilizing Wi-Fi technology to obtain RSSI measurements.

4.2. Dataset Construction

We collected the data using the mobile robot, ensuring it encompassed a wide range of data types. This dataset was carefully selected to meet our specific requirements for localization and the construction of the indoor REM. The colored path in Figure 3 shows the path direction of the mobile robot, where the start point is near the access point. The start point is colored red because the access point is located in that place. The values corresponding to the x-axis and y-axis were designated as features and RSSI as labels in order to create the coverage map.
Next, we preprocessed the data by employing training and testing datasets split for error evaluation. The ML algorithm was used for the prediction of RSSI values, as illustrated in Figure 4 to establish a grid construction that covers the area of interest with a uniform interval. Then, by applying the ML algorithm, the RSSI values were predicted at each point on the grid for a graphical image of REM. Subsequently, we compared various regression algorithms to generate the 2-D floor plan of REM, employing advanced techniques to ensure accurate modeling.
For localization, we utilized the already constructed REM based on RSSI signals as features, while the x- and y-axis values were used as labels. The data were then organized by associating the RSSI values with the REM. Our proposed approach to construct the dataset is based on the 8-nearest neighbors scheme illustrated in Figure 5. The dataset is composed of multiple steps from the REM, where each step contains the RSSI value and the corresponding position x , y to identify the user’s location. A sample in the dataset represents a collection of K steps. For example, the first sample includes features RSSI 1 , RSSI 2 , … , RSSI K and the position of the final step serves as the target position to be predicted x K , y K . The selection of each step is based on the nearest neighbors search. In each sample, the first point is randomly selected. Then, eight nearest neighbors are obtained. From these neighbors, the second point is randomly chosen. This process continues by obtaining eight nearest neighbors for the second point and randomly selecting the third point from these neighbors. This iterative process was repeated until K steps were obtained, forming one sample. The final dataset was created by collecting multiple samples. We gathered 1000 samples to obtain a broad range of paths and user locations.
Following the above process, we trained ML algorithms and assessed the performance of our system model employing 10-fold cross-validation.
The dataset for the indoor localization scheme using 8-nearest neighbors is presented in Figure 6. Each line corresponds to a single sample from the dataset, wherein a sample comprises a collection of several users’ steps. Within our system model, we meticulously incorporated a total of 600 samples, with each sample encompassing 8 distinct steps. By following this rigorous procedure, the dataset was meticulously prepared to facilitate the process of indoor localization.

4.3. ETR Framework for Indoor Localization

There are numerous supervised classification techniques available, including ensemble learning methods, among which random forest and the ETR have gained significant popularity as effective approaches to addressing supervised classification and regression problems. The methods harness the collective strength of multiple models to enhance performance[20]. These algorithms create independent base learners through the utilization of various training algorithms and by introducing randomization during the tree construction process. The incorporation of randomization techniques promotes greater tree diversity, leading to reduced correlation among the trees and improved independence. However, the construction of ensembles can present computational challenges, especially when dealing with large datasets. To overcome this issue, the focus has shifted towards the faster ETR algorithm [31,32]. In this research paper, we propose an ETR that presents an innovative approach to predicting indoor localization. The ETR algorithm combines predictions from individual trees, with each tree constructed using the entire training dataset. It employs a top-down learning approach, starting from the root node and subsequently traversing branches and child nodes. Setting itself apart from the random forest technique, the ETR incorporates two distinctive characteristics: the random selection of feature subsets for each tree and the random selection of splitting values.
Comprising a multitude of individual decision trees, the ETR utilizes the complete training dataset for each tree. A decision tree consists of interconnected root, child, and leaf nodes forming the hierarchical structure depicted in Figure 7. The ETR algorithm initiates at the root node and progressively determines split rules by leveraging a randomized subset of features and a partially random cut point. This iterative process is perpetuated at each subsequent child node until the traversal reaches a leaf node, encapsulating the decision-making process within the decision tree.
Formally, given a training dataset, X = x 1 , x 2 , … , x n , where n takes values from 1 to N samples and x N represents a K + 2 -dimensional vector composed of K features and two target values to be predicted, the ETR algorithm generates M independent decision trees. Within each decision tree, subset D r of training dataset X is assigned to each child node r. At each node r, the ETR algorithm selects the optimal split based on training subset D r and a random subset of features, following the algorithm outlined in Table 1.
To elaborate, subset D r at child node r is divided into two sets: D r r i g h t , comprising the samples that satisfy the split rule, and D r l e f t , consisting of the remaining training samples. The selection of the best-split MSE is used as a scoring function. This process is repeated at each child node until it reaches the minimum number of samples required for splitting n m i n , or until all the samples in subset D r possess the same label. Finally, the label of the samples in subset D r represents each leaf node. During the testing phase, a test sample progresses through each decision tree and traverses each child node. The best splits guide the test sample toward either the left or right child node until it arrives at a leaf node.

5. Machine Learning Regression Baseline Schemes

Regression techniques, which are a collection of statistical methods that establish a connection between one or more independent variables and a dependent variable, vary in terms of their assumptions about the data, about the nature of the relationship they model, and the complexity of the model. These techniques include linear regression, the ETR, decision tree regression, ridge regression, and AdaBoost regression. Overall, regression techniques are effective tools for understanding the relationships between variables and making predictions about the future based on past data. This section provides a brief description of some ML baseline schemes.

5.1. Random Forest Regressor

The aim of the random forest regressor is to build a reliable and precise predictive model for tasks involving classification or regression. In a random forest, the ensemble is made up of many decision trees that have been generated and assembled. A random subset of the data and the features is used to train each decision tree, adding diversity and lowering overfitting. By combining all the individual trees’ predictions, either through majority voting (for classification) or averaging (for regression), the random forest’s final forecast is created. The random forest technique is renowned for its capacity to process large amounts of data, capture complex correlations between variables, and make accurate predictions. We utilized estimators in this regression technique that take into consideration the number of trees, the maximum depth introduced as the deepest level of a tree, and other factors [21].

5.2. AdaBoost Regressor

The AdaBoost regressor, which performs especially well when there is an abundance of noisy or complex data, is adaptable for a variety of regression applications because it can handle continuous and categorical variables. The regressor seeks to build a strong and robust regression model that can precisely predict the target variable by merging numerous weak regressors [23].

5.3. Decision Tree Regressor

The decision tree regressor, a regression methodology that uses a decision tree model to predict continuous target variables, divides the data into subsets based on the values of independent variables and builds a tree structure by repeatedly splitting the data until each subset is as pure as possible and contains values for the target variable. This method can handle continuous and categorical targets, with the predicted value for continuous targets being the average value in each leaf node. Decision tree regression has a number of benefits, including being simple to understand, accommodating linear and non-linear relationships, handling missing variables, and working well [22].

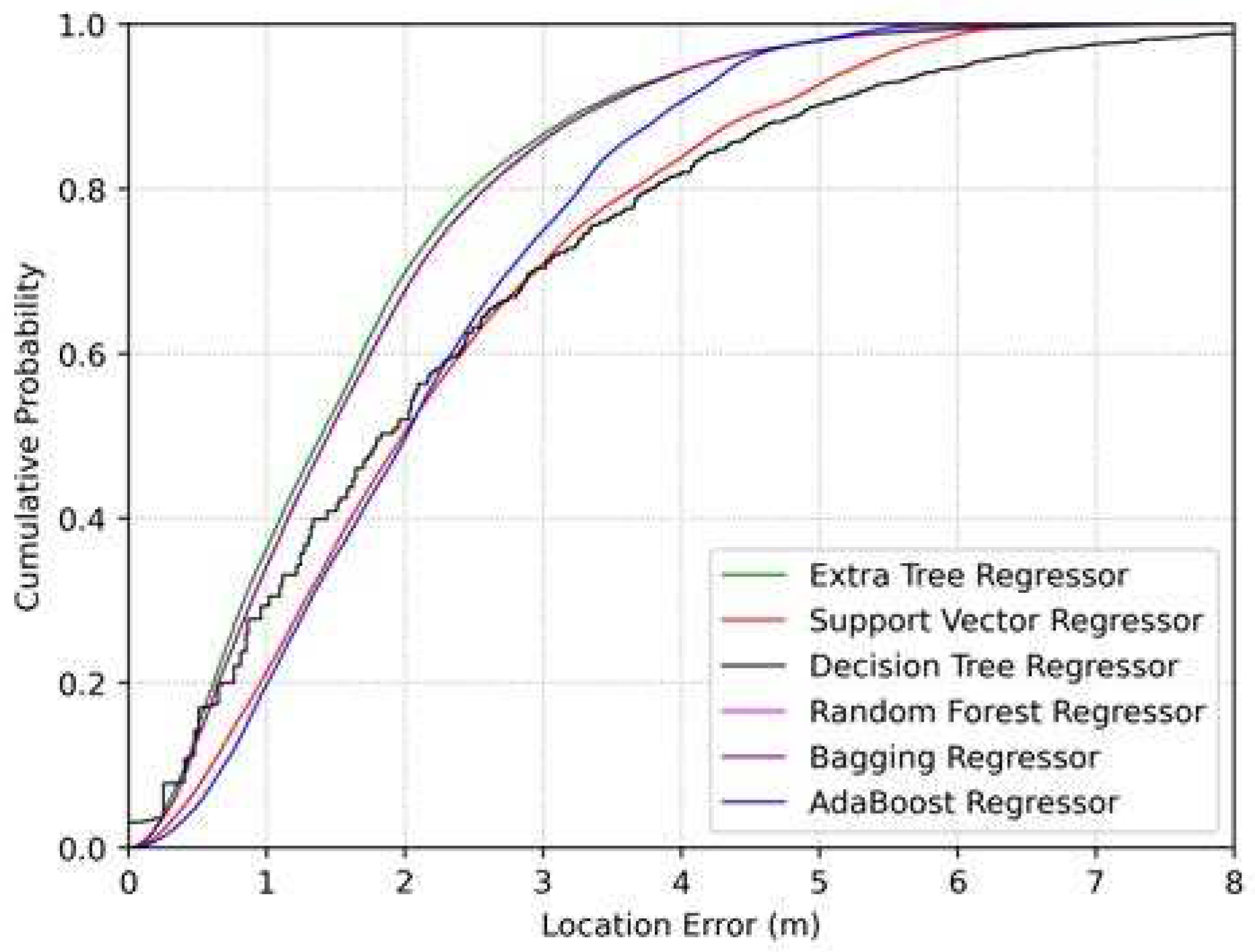
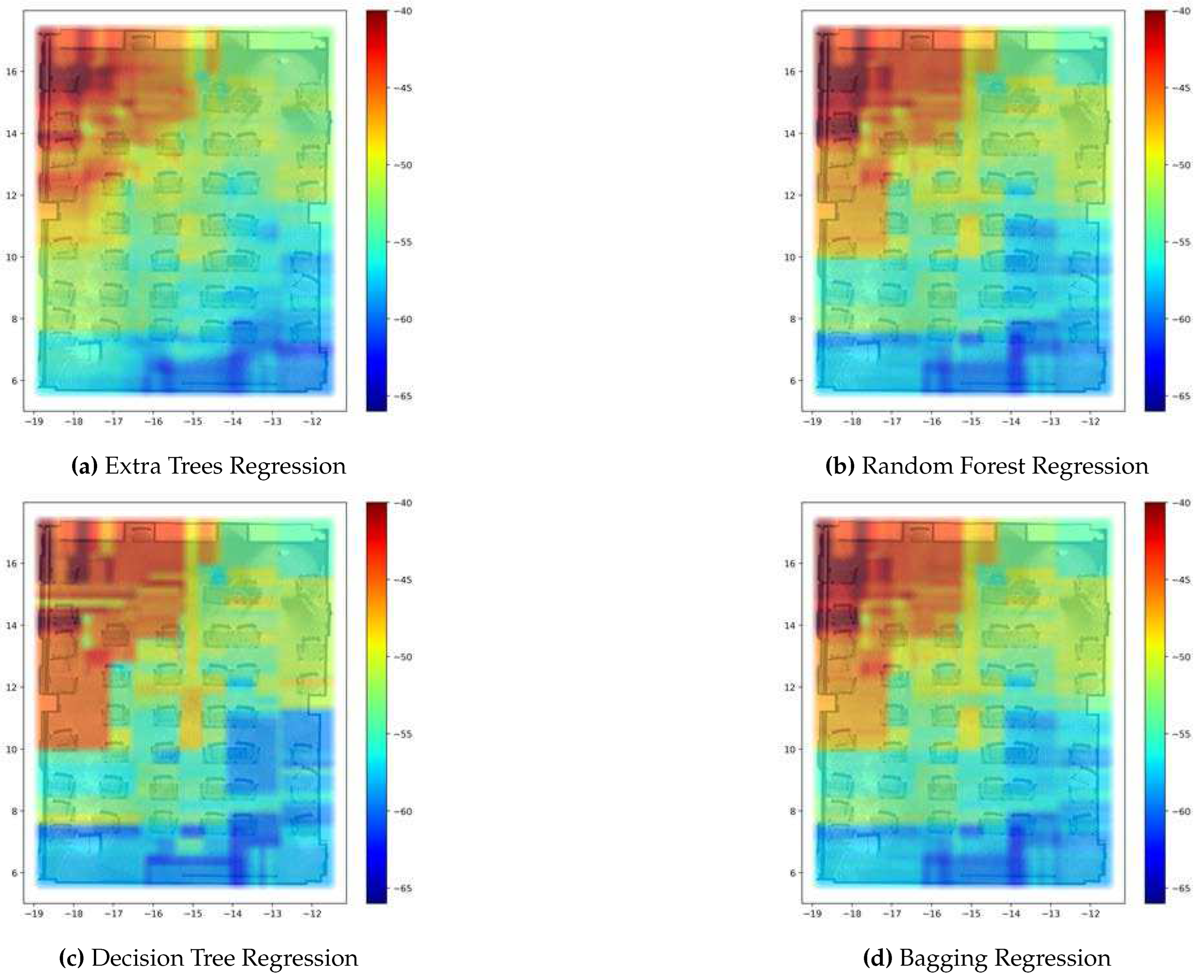
6. Numerical Results

In this section, we provide a detailed description of the performance of the proposed approach and the process of hyperparameter tuning. Additionally, we present graphical representations comparing the model’s performance using different regression techniques. To evaluate the performance of REM construction, we employ various error metrics, including RMSE, MAE, and R 2 , and present the results in Table 2. Furthermore, we assess the accuracy of indoor localization using location error measurements.

6.1. Model Evaluation

In this subsection, we provide a detailed description of the error metrics used to evaluate REM construction and the ML-based approach to indoor localization.
A measurement that depicts the average error of the estimates is mean absolute error. To determine how well the predictions match the actual values, MAE calculates the absolute difference between the actual value, designated as y i , and the corresponding predicted measure of the RSSI value, denoted as y ^ i [35]. Then, MAE can be expressed by
M A E = ∑ i = 1 N y i − y ^ i N ,
where N is the total number of data samples for equations (1), (2), (3), and (4).
The square root of the average of the squared discrepancies between predicted RSSI values y ^ i and corresponding actual observations y i is used to calculate the root mean square error, a metric that measures the error rate. RMSE gives an indication of how well predictions reflect the actual numbers calculated by:
R M S E = ∑ i = 1 N y i − y ^ i 2 N .
For equations (1) and (2), the performance of the system model will be considered good if the result is lower, whereas R 2 is totally opposite; it is good when the R 2 result is higher:
R 2 = 1 − ∑ i = 1 N y i − y ^ i 2 ∑ i = 1 N y i − y ¯ i ,
where y ¯ i is the average target value.
The numerator of the second term is the mean error determined by the sum of squares of the residual prediction errors, and the denominator is the variance [36,37]. The fundamental goal of the R 2 score is to quantify how much of the variation in the target-dependent variable is predictable by the independent variables in a regression model. The score has no lower range (indicating that forecasts can be severely erroneous) and an upper bound of 1, which denotes a fully accurate prediction. When the score is close to 0, it may be compared to making a random estimate about the mean y ¯ i . According to the described equation, all of them will analyze a comprehensive evaluation of the system model’s performance because each statistic distinguishes different aspects of the model’s correctness and data fit.
We evaluate the performance of the algorithms for indoor localization by using the location error equation, defined by:
Location Error = ∑ i = 1 N ∥ Predicted Location i − Actual Location i ∥ N .
First, we evaluate the REM construction based on RMSE, R 2 , and MAE. In the ML algorithm, we set the following parameters: 50 for the maximum depth, 200 for the estimators, and 2 for the minimum sample split parameter. Table 2 shows the performance from REM construction, which can be evaluated based on the errors obtained for different regression techniques. We can see that the proposed ETR-based scheme achieved the lowest error among the comparative schemes, followed by random forest and the bagging regressor. However, support vector and AdaBoost regression models showed higher errors, suggesting comparatively poorer performance in this specific scenario.
We evaluated the performance of the proposed ETR-based scheme for indoor localization using the location error in Equation (4). In addition, we compared the performance of the ETR-based scheme with multiple regression techniques as alternative approaches to indoor localization.
Table 2. Performance comparison between the proposed ETR algorithm and other regression techniques based on REM error calculations.
Table 2. Performance comparison between the proposed ETR algorithm and other regression techniques based on REM error calculations.
Algorithm RMSE R 2 MAE
Extra Trees Regression 0.997 0.975 0.421
Random Forest Regression 1.067 0.971 0.49
Decision Tree Regression 1.218 0.963 0.47
Bagging Regression 1.064 0.972 0.492
Support Vector Regression 2.977 0.779 2.317
AdaBoost Regression 2.874 0.794 2.301
The proposed scheme used K features and two labels to implement indoor localization. Then, we employed two ML-based regressors to handle the two target variables. Each ML regressor takes as features the RSSI values obtained in K steps, denoted as RSSI 1 , RSSI 2 , … , RSSI K , and predicts the corresponding target value. The first ML model predicts the position of the final K-th step in the x-coordinate, while the second ML model predicts the position in the y-coordinate. We evaluated the algorithm’s performance by using the location error described in Equation (4). Multiple regression techniques have been used for selection and comparison of algorithm performance as well.
This paper presents various figures showcasing the utilization of the parameters, max depth, and number of estimators in different regression algorithms. Fine-tuning of hyperparameters was performed to achieve optimal system performance. In Figure 8, the number of estimators was varied from 20 to 200, and location error calculations were performed by using 10-fold cross-validation with different regression techniques. This visual representation clearly demonstrates the superior performance of the ETR compared to other regression techniques. Notably, at 140 estimators, the ETR still exhibited a lower error rate with the rate remaining the lowest thereafter.
Figure 9 compares the location error versus maximum depth for the ETR, random forest, and decision tree regressors. Once again, the ETR demonstrated better performance. The error gradually decreased after a max depth of 15, reaching the lowest error rate at 40.
Simulations were conducted for the significance of the number of samples to determine the behavior of the ML-based regressor from different dataset sizes. Figure 10 illustrates the location error versus the number of samples. An array of regressors, including the ETR and random forest, bagging, AdaBoost, support vector, and decision trees regressors, were employed to compare their performance. We can see that the system performs optimally with a sample size of 600.
In conclusion, the best parameters for our proposed ETR-based model were selected by fine-tuning the hyperparameters of ML-based regressors, and the ETR showed better performance than the compared algorithms.
Next, we evaluate localization performance in indoor environments by using a cumulative distribution function (CDF) graph (Figure 11). The graph provides an insightful performance comparison among the various regression techniques used in the study, namely the ETR and decision tree, random forest, AdaBoost, bagging, and support vector regression. Upon analyzing the CDF graph, we can see that the proposed ETR outperformed the other regression methods in terms of localization accuracy. This implies that the ETR-based algorithm consistently provided more precise estimations of user locations. By demonstrating the superior performance of the ETR approach, the CDF graph highlights its efficacy in achieving accurate localization results, emphasizing its potential for real-world applications in various fields requiring precise location estimation. Notably, the system exhibits a remarkable level of precision, whereby approximately 90% of localization errors were found below the three-meter threshold.

6.2. Computational Complexity Analysis

The computational complexity of the proposed ETR-based approach and the random forest regressor and bagging regressor comparison systems are examined in this subsection. The results show the number of regression trees, the number of features, the number of samples, and the maximum depth of the trees affect the computational complexity of the proposed ETR. In further detail, O V · K · P · l d may be used to approximate the computational complexity of the ETR, where V denotes the number of trees, K is the number of features, P is the number of training samples, and l d is the maximum tree depth. When choosing the optimal split in our simulations, we considered G = K = 8 and the maximum tree depth to be l d = 40 .
The computational complexity of the random forest regressor is similarly determined by O V · K · P · l d [38]. Nevertheless, compared to the random forest regressor, the ETR takes less time to compute since it employs a random threshold rather than trying to find the best practicable threshold to split the data at each node. For the bagging regressor, the computational complexity can be expressed by O G B · K B [38] where G B is the total number of base regressors, and K B is the computational difficulty of training a base regressor. We utilized the decision tree regressor, which has a complexity of K B = O K · P · l d , as the basis estimator in our simulations.

6.3. Graphical Results of REM Construction

Using several regression algorithms, this section using a graphical depiction of the REM. A grid of 50×50 points was created covering the whole area of interest and populated with RSSI-predicted values obtained from the trained regression algorithms, spanning the region of interest.
Upon examining Figure 12, which depicts coverage prediction maps for the RSSI target value on 2-D maps, we can discern the outcomes yielded by our proposed ETR-based algorithm, as well as random forest, decision tree, and bagging regressors. We observe from Figure 12(b), (c), and (d) that the random forest regressor, the decision tree regressor, and the bagging regressor exhibited abrupt changes in the RSSI values across the REM, rendering it challenging to identify critical points where the signal strength experienced a decline. Consequently, the reliability of the coverage prediction is compromised. In contrast, the REM generated by the ETR algorithm displays a tendency to offer more generalized prediction points, enabling a gradual depiction of degradation in signal strength without abrupt transitions. This characteristic of the ETR allows for better discernment of the quality of signal reception, enabling identification of areas with satisfactory reception as well as shadow areas. It is crucial to highlight that a variety of factors, including the quality and quantity of training data, the method used to create the maps, and the complexity of the environment being mapped, affect how well REMs created using ML techniques perform.

7. Conclusion

The proposed scheme showcased a practical application of a REM in predicting a user’s position within the REM coverage area using a set of collected RSSI signal values. The study demonstrated the effectiveness of ML-based regression techniques for REM construction and for accurately estimating a user’s location in an indoor environment. The main contribution of the paper is utilization of the REM to train the proposed ETR-based scheme for user localization. This was achieved based on a collection of several user steps while using data measurements from a single AP. The research successfully generated precise coverage maps that provide valuable insights into the RF environment of a specific area. These coverage maps were then exploited for the proposed indoor localization framework. Numerical results indicated that the proposed ML-based approach can effectively predict a user’s current position within the coverage area. The system model was evaluated using several ML algorithms, including decision tree regressor, random forest, AdaBoost and support vector regression. Based on the localization error, the ETR outperformed the other techniques. This research provides accurate information on the RF environment that can be applied to indoor navigation, asset tracking, and wireless communications to improve network performance.

References

  1. Zhang, K.; Zhao, J.; Liu, P.; Yin, C. Radio Environment Map Enhanced Intelligent Reflecting Surface Systems Beyond 5G. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops). IEEE; 2021; pp. 1–6. [Google Scholar]
  2. McGuire, M.; Plataniotis, K.N.; Venetsanopoulos, A.N. Data fusion of power and time measurements for mobile terminal location. IEEE Transactions on Mobile Computing 2005, 4, 142–153. [Google Scholar] [CrossRef]
  3. Sytems, C. Wi-Fi based real-time location tracking: Solutions and technology. In CISCO Syt.; 2006.
  4. Patterson, C.A.; Muntz, R.R.; Pancake, C.M. Challenges in location-aware computing. IEEE Pervasive Computing 2003, 2, 80–89. [Google Scholar] [CrossRef]
  5. Rodríguez, M.D.; Favela, J.; Martínez, E.A.; Muñoz, M.A. Location-aware access to hospital information and services. IEEE Transactions on information technology in biomedicine 2004, 8, 448–455. [Google Scholar] [CrossRef] [PubMed]
  6. Harroud, H.; Ahmed, M.; Karmouch, A. Policy-driven personalized multimedia services for mobile users. IEEE Transactions on Mobile computing 2003, 2, 16–24. [Google Scholar] [CrossRef]
  7. Pahlavan, K.; Levesque, A.H. Wireless information networks; John Wiley & Sons, 2005.
  8. Moreta, C.E.G.; Acosta, M.R.C.; Koo, I. Prediction of digital terrestrial television coverage using machine learning regression. IEEE Transactions on Broadcasting 2019, 65, 702–712. [Google Scholar] [CrossRef]
  9. Suga, N.; Maeda, Y.; Sato, K. Indoor Radio Map Construction via Ray Tracing With RGB-D Sensor-Based 3D Reconstruction: Concept and Experiments in WLAN Systems. IEEE Access 2023, 11, 24863–24874. [Google Scholar] [CrossRef]
  10. Kliks, A.; Kryszkiewicz, P.; Umbert, A.; PéRez-Romero, J.; Casadevall, F.; Kułacz. Application of radio environment maps for dynamic broadband access in TV bands in urban areas. IEEE access 2017, 5, 19842–19863. [Google Scholar] [CrossRef]
  11. Santana, Y.H.; Plets, D.; Alonso, R.M.; Nieto, G.G.; Martens, L.; Joseph, W. Radio Environment Map of an LTE Deployment Based on Machine Learning Estimation of Signal Levels. In Proceedings of the 2022 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB). IEEE; 2022; pp. 01–06. [Google Scholar]
  12. Chou, S.F.; Yen, H.W.; Pang, A.C. A REM-enabled diagnostic framework in cellular-based IoT networks. IEEE Internet of Things Journal 2019, 6, 5273–5284. [Google Scholar] [CrossRef]
  13. Gavrilovska, L.M.; Atanasovski, V.M. Dynamic REM towards flexible spectrum management. In Proceedings of the 2013 11th International Conference on Telecommunications in Modern Satellite, Cable and Broadcasting Services (TELSIKS). IEEE, Vol. 1; 2013; pp. 287–296. [Google Scholar]
  14. Cheng, B.; Du, R.; Yang, B.; Yu, W.; Chen, C.; Guan, X. An accurate GPS-based localization in wireless sensor networks: A GM-WLS method. In Proceedings of the 2011 40th International conference on parallel processing workshops. IEEE; 2011; pp. 33–41. [Google Scholar]
  15. Goyal, R.; Krishna, K.M.; Bhuvanagiri, S. Sensor Based Localization for Mobile Robots by Exploration and Selection of Best Direction. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics. IEEE; 2006; pp. 846–851. [Google Scholar]
  16. Zhuang, Y.; Zhang, C.; Huai, J.; Li, Y.; Chen, L.; Chen, R. Bluetooth localization technology: Principles, applications, and future trends. IEEE Internet of Things Journal 2022, 9, 23506–23524. [Google Scholar] [CrossRef]
  17. Hernández, N.; Ocaña, M.; Alonso, J.M.; Kim, E. WiFi-based indoor localization and tracking of a moving device. In Proceedings of the 2014 Ubiquitous Positioning Indoor Navigation and Location Based Service (UPINLBS). IEEE; 2014; pp. 281–289. [Google Scholar]
  18. Ni, L.M.; Zhang, D.; Souryal, M.R. RFID-based localization and tracking technologies. IEEE Wireless Communications 2011, 18, 45–51. [Google Scholar] [CrossRef]
  19. Farahsari, P.S.; Farahzadi, A.; Rezazadeh, J.; Bagheri, A. A survey on indoor positioning systems for IoT-based applications. IEEE Internet of Things Journal 2022, 9, 7680–7699. [Google Scholar] [CrossRef]
  20. Acosta, M.R.C.; Ahmed, S.; Garcia, C.E.; Koo, I. Extremely randomized trees-based scheme for stealthy cyber-attack detection in smart grid networks. IEEE access 2020, 8, 19921–19933. [Google Scholar] [CrossRef]
  21. Jaiswal, J.K.; Samikannu, R. Application of random forest algorithm on feature subset selection and classification and regression. In Proceedings of the 2017 world congress on computing and communication technologies (WCCCT). Ieee; 2017; pp. 65–68. [Google Scholar]
  22. Saltykov, S. Algorithm of Building Regression Decision Tree Using Complementary Features. In Proceedings of the 2020 13th International Conference" Management of large-scale system development"(MLSD). IEEE; 2020; pp. 1–5. [Google Scholar]
  23. Sembina, G. Building a Scoring Model Using the Adaboost Ensemble Model. In Proceedings of the 2022 International Conference on Smart Information Systems and Technologies (SIST). IEEE; 2022; pp. 1–6. [Google Scholar]
  24. Gadhgadhi, A.; HachaÏchi, Y.; Zairi, H. A machine learning based indoor localization. In Proceedings of the 2020 4th International Conference on Advanced Systems and Emergent Technologies (IC_ASET). IEEE; 2020; pp. 33–38. [Google Scholar]
  25. Wang, Y.; Ye, Q.; Cheng, J.; Wang, L. RSSI-based bluetooth indoor localization. In Proceedings of the 2015 11th international conference on mobile ad-hoc and sensor networks (MSN). IEEE; 2015; pp. 165–171. [Google Scholar]
  26. Billa, A.; Shayea, I.; Alhammadi, A.; Abdullah, Q.; Roslee, M. An overview of indoor localization technologies: Toward IoT navigation services. In Proceedings of the 2020 IEEE 5th International Symposium on Telecommunication Technologies (ISTT). IEEE; 2020; pp. 76–81. [Google Scholar]
  27. Huang, Y.; Mazuelas, S.; Ge, F.; Shen, Y. Indoor localization system with NLOS mitigation based on self-training. IEEE Transactions on Mobile Computing 2022. [Google Scholar] [CrossRef]
  28. Dargie, W.; Wen, J. Examination of Indoor Localization Techniques and Their Model Parameters. In Proceedings of the 2021 IEEE 18th International Conference on Mobile Ad Hoc and Smart Systems (MASS). IEEE; 2021; pp. 364–373. [Google Scholar]
  29. Sadowski, S.; Spachos, P.; Plataniotis, K.N. Memoryless techniques and wireless technologies for indoor localization with the internet of things. IEEE Internet of Things Journal 2020, 7, 10996–11005. [Google Scholar] [CrossRef]
  30. Han, K.; Yu, S.M.; Kim, S.L. Smartphone-based indoor localization using Wi-Fi fine timing measurement. In Proceedings of the 2019 International Conference on Indoor Positioning and Indoor Navigation (IPIN). IEEE; 2019; pp. 1–5. [Google Scholar]
  31. GARCÍA, C.E.; Koo, I. Extremely Randomized Trees Regressor Scheme for Mobile Network Coverage Prediction and REM Construction. IEEE Access 2023. [Google Scholar] [CrossRef]
  32. Garcia, C.E.; Koo, I. Coverage Prediction and REM Construction for 5G Networks in Band n78. In Proceedings of the 2023 15th International Conference on Computer and Automation Engineering (ICCAE). IEEE; 2023; pp. 125–129. [Google Scholar]
  33. Hwang, T.; Acosta, M.R.C.; Moreta, C.E.G.; Koo, I. Estimating Indoor Radio Environment Maps with Mobile Robots and Machine Learning. The International Journal of Advanced Smart Convergence 2023, 12, 92–100. [Google Scholar]
  34. Wu, R.H.; Lee, Y.H.; Tseng, H.W.; Jan, Y.G.; Chuang, M.H. Study of characteristics of RSSI signal. In Proceedings of the 2008 IEEE International Conference on Industrial Technology. IEEE; 2008; pp. 1–3. [Google Scholar]
  35. Schneider, P.; Xhafa, F. Anomaly detection classification and CEP with ML methods. Anomaly Detection and Complex Event Processing over IoT Data Streams, 2022, pp. 193–233.
  36. Klemme, F.; Amrouch, H. Scalable machine learning to estimate the impact of aging on circuits under workload dependency. IEEE Transactions on Circuits and Systems I: Regular Papers 2022, 69, 2142–2155. [Google Scholar] [CrossRef]
  37. Parmar, J.; Patel, S.K.; Katkar, V.; Natesan, A. Graphene-based refractive index sensor using machine learning for detection of mycobacterium tuberculosis bacteria. IEEE Transactions on NanoBioscience 2022, 22, 92–98. [Google Scholar] [CrossRef] [PubMed]
  38. Abdar, M.; Acharya, U.R.; Sarrafzadegan, N.; Makarenkov, V. NE-nu-SVC: a new nested ensemble clinical decision support system for effective diagnosis of coronary artery disease. Ieee Access 2019, 7, 167605–167620. [Google Scholar] [CrossRef]
Preprints 83015 g001
Figure 1. Turtlebot-3 Burger.
Figure 1. Turtlebot-3 Burger.
Preprints 83015 g001
Preprints 83015 g002
Figure 2. Layout of the classroom under study at the University of Ulsan.
Figure 2. Layout of the classroom under study at the University of Ulsan.
Preprints 83015 g002
Preprints 83015 g003
Figure 3. The data collection path of the mobile robot.
Figure 3. The data collection path of the mobile robot.
Preprints 83015 g003
Preprints 83015 g004
Figure 4. Flow chart for REM construction.
Figure 4. Flow chart for REM construction.
Preprints 83015 g004
Preprints 83015 g005
Figure 5. The proposed ML-based indoor localization framework.
Figure 5. The proposed ML-based indoor localization framework.
Preprints 83015 g005
Preprints 83015 g006
Figure 6. Illustration of the dataset for indoor localization using 8-nearest neighbors.
Figure 6. Illustration of the dataset for indoor localization using 8-nearest neighbors.
Preprints 83015 g006
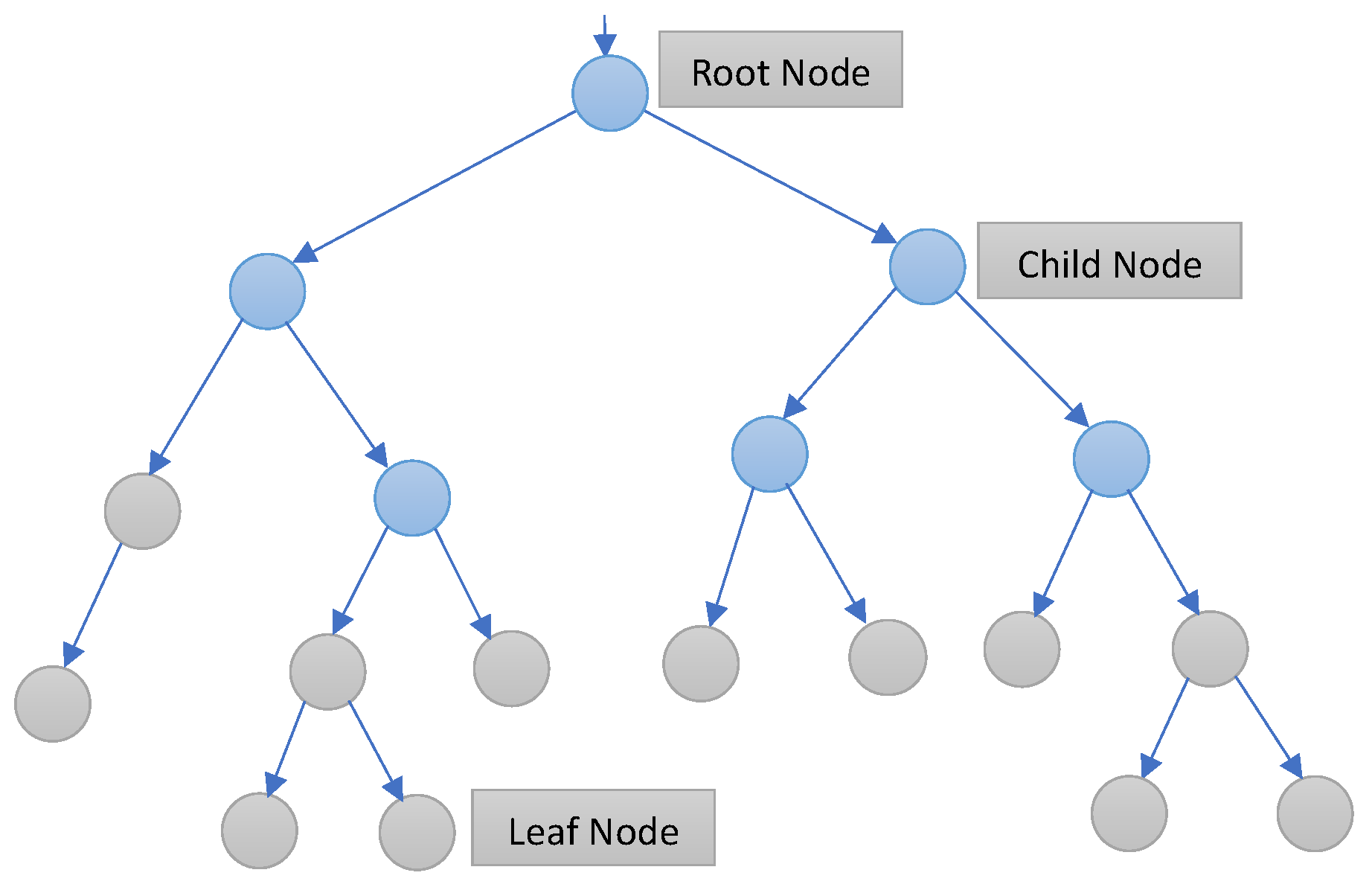
Preprints 83015 g007
Figure 7. The decision tree scheme.
Figure 7. The decision tree scheme.
Preprints 83015 g007
Preprints 83015 g008
Figure 8. Number of estimators vs. location error.
Figure 8. Number of estimators vs. location error.
Preprints 83015 g008
Preprints 83015 g009
Figure 9. Number of errors (max depth vs. location).
Figure 9. Number of errors (max depth vs. location).
Preprints 83015 g009
Preprints 83015 g010
Figure 10. Number of errors (samples vs. location).
Figure 10. Number of errors (samples vs. location).
Preprints 83015 g010
Preprints 83015 g011
Figure 11. Cumulative distribution function of location error from indoor localization.
Figure 11. Cumulative distribution function of location error from indoor localization.
Preprints 83015 g011
Preprints 83015 g012
Figure 12. Coverage prediction maps from using different regression techniques.
Figure 12. Coverage prediction maps from using different regression techniques.
Preprints 83015 g012
Table 1. Selection of the split rule in the ETR-based scheme.
Table 1. Selection of the split rule in the ETR-based scheme.
1. Input: training subset D r = d 1 , d 2 , … , d W r
                         K-dimensional vector made from sample d k = f 1 , f 2 , … , f K
                          G = numerous attributes selected randomly
                          n min = node to be split as required at the minimum number of samples
2. If  W r < n min or the node has a label for each observation it contains.
             When splitting is complete, classify the node as a leaf node.
3. Else
              Choose a random subset of G features f l , f 2 … , f G from among the original K features.
               ( G ≤ K )
4.         For each feature g in the subgroup Do:
                     Find f g min , and f g max as the higher and lower rates of feature g in subset D r .
                     Obtain a random cut-point, f g c c , uniformly in the range f g min , f g max
                     Set f g < f g c
               End for
5.          Select a split f * < f * c such that MSE f * c = min g = 1 , 2 , … , G MSE f g c
6. Output: Best split f * < f * c at child node r.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated