Preprint

Article

An Efficient and Fast Sparse Grid Algorithm for High-Dimensional Numerical Integration

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 August 2023

Posted:

23 August 2023

You are already at the latest version

Alerts

Abstract

This paper is concerned with developing an efficient numerical algorithm for fast implementation of the sparse grid method for computing the $d$-dimensional integral of a given function. The new algorithm, called the MDI-SG ({\em multilevel dimension iteration sparse grid}) method, implements the sparse grid method based on a dimension iteration/reduction procedure, it does not need to store the integration points, nor does it compute the function values independently at each integration point, instead, it reuses the computation for function evaluations as much as possible by performing the function evaluations at all integration points in a cluster and iteratively along coordinate directions. It is shown numerically that the computational complexity (in terms of CPU time) of the proposed MDI-SG method is of polynomial order $O(Nd^3 )$ or better, compared to the exponential order $O(N(\log N)^{d-1})$ for the standard sparse grid method, where $N$ denotes the maximum number of integration points in each coordinate direction. As a result, the proposed MDI-SG method effectively circumvents the curse of dimensionality suffered by the standard sparse grid method for high-dimensional numerical integration.

Keywords:

Subject: Computer Science and Mathematics - Computational Mathematics

1. Introduction

With rapid developments in nontraditional applied sciences such as mathematical finance [1], image processing [2], economics [3], and data science [4], there is an ever increasing demand for efficient numerical methods for computing high-dimensional integration which also becomes crucial for solving some challenging problems. Numerical methods (or quadrature rules) mostly stem from approximating the Riemann sum in the definition of integrals, hence, they are grid-based. The simplest and most natural approach for constructing numerical quadrature rules in high dimensions is to apply the same 1-d rule in each coordinate direction, this then leads to tensor-product (TP) quadrature rules. It is well known (and easy to check) that the number of integration points (and function evaluations) grows exponentially in the dimension d, such a phenomenon is known as the curse of dimensionality (CoD). Mitigating or circumventing the CoD has been the primary goal when it comes to constructing efficient high-dimensional numerical quadrature rules. A lot of progress has been made in this direction in the past fifty years, this includes sparse grid (SG) methods [1,5,6,7], Monte Carlo (MC) methods [8,9], Quasi-Monte Carlo (QMC) methods [10,11,12,13,14], deep neural network (DNN) methods [15,16,17,18,19]. To some certain extent, those methods are effective for computing integrals in low and medium dimensions (i.e.,

d ≲ 100

), but it is still a challenge for them to compute integrals in very high dimensions (i.e.,

d \approx 1000

This is the second installment in a sequel [20] which aims at developing fast numerical algorithms for high-dimensional numerical integration. As mentioned above, the straightforward implementation of the TP method will evidently run into the CoD dilemma. To circumvent the difficulty, we proposed in [20] a multilevel dimension iteration algorithm (called MDI-TP) for accelerating the TP method. The ideas of the MDI-TP algorithm are to reuse the computation of function evaluation as much as possible in the tensor product method by clustering computations, which allows an efficient and fast function evaluations at integration points together, and to do clustering by a simple dimension iteration/reduction strategy, which is possible because of the lattice structure of the TP integration points. Since the idea of the MDI strategy essentially applied to any numerical integration rule whose integration points have a lattice-like structure, this indeed motivates the work of this paper by applying the MDI idea to accelerate the sparse grid method. We recall that, unlike the existing numerical integration methods, the MDI algorithm is not aiming to providing a new numerical integration method per se, instead, it is an acceleration algorithm for an efficient implementation of any tensor-product-like existing method. Thus, the MDI is not a “discretization" method but a “solver" (borrowing the numerical PDE terminologies). A well suited analogy would be high order polynomial evaluations, that is, to compute

p_{0} : = p (x_{0}) = a_{k} x_{0}^{k} + a_{k - 1} x_{0}^{k - 1} + \dots + a_{1} x_{0} + a_{0}

for a given real number input

x_{0}

. It is well known that such a high order polynomial evaluation on a computer is notoriously unstable, inaccurate (due to roundoff errors) and expensive, however, those difficulties can be easily overcome by a simple nested iteration (or Horner’s algorithm. cf. [21]), namely, set

p_{0} \leftarrow a_{k}

and for

j = k, k - 1, \dots, 1

, set

p_{0} \leftarrow p_{0} x_{0} + a_{j - 1}

. From the cost saving and efficiency point view, the reason for the nested iteration to be efficient and fast is that it reuses many multiplications involving

x_{0}

compared to the direct evaluations of each term in

p (x_{0})

. Conceptually, this is exactly the main idea of the MDI algorithm, i.e., to reuse computations of the function evaluations in an existing method as much as possible to save the computation cost and hence to make it efficient and fast.

The sparse grid (SG) method, which was first proposed by Smolyak in [22], only uses a (small) subset of the TP integration points while still maintains a comparable accuracy of the TP method. As mentioned earlier, the SG method was one of few successful numerical methods which can mitigate the CoD in high-dimensional computation, including computing high-dimensional integration and solving high-dimensional PDEs [1,5,6,7]. The basic idea in application to high-dimensional numerical integration stems from Smolyak’s general method for multivariate extensions of univariate operators. Based on this construction, the midpoint rule [23], the rectangle rule [24], the trapezoidal rule [25], the Clenshaw-Curtis rule [26,27], and the Gaussian-Legendre rule [28,29] have been used as a one-dimensional numerical integration method. A multivariate quadrature rule is then constructed by forming the TP method of each of these one-dimensional rules on the underlying sparse grid. Like TP method, the SG method is quite general and easy to implement. But unlike the TP method, its computational cost is much lower because the number of its required function evaluations grows exponentially with a smaller base. A key observation is that the function evaluations of the SG method involve a lot of computation in each coordinate direction which can be shared because each coordinate

ξ_{j}

of every integration point

ξ = (ξ_{1}, ξ_{2}, \dots, ξ_{d}) \in R^{d}

is shared by many other integration points due to their tensor product structure. This observation motivates us to compute the required function evaluations in cluster and iteratively in each coordinate direction instead of computing them at the integration points independently.

The goal of this paper is to apply the MDI strategy to the SG method, the resulting algorithm, which is called the MDI-SG algorithm, provides a fast algorithm for an efficient implementation of the SG method. The MDI-SG method incorporates the MDI nested iteration idea into the sparse grid method which allows the reuse of the computation in the function evaluations at the integration points as much as possible. This saving significantly reduces the overall computational cost for implementing the sparse grid method from an exponential growth to a low-order polynomial growth.

The rest of this paper is organized as follows. In Section 2, we first briefly recall the formulation of the sparse grid method and some known facts. In Section 3, we introduce our MDI-SG algorithm, first in two and three dimensions to explain the main ideas of the algorithm, and then generalize it to arbitrary dimensions. In Section 4 and Section 5, we present various numerical experiments to test the performance of the proposed MDI-SG algorithm and compare its performances to the standard SG method and the classical MC method. These numerical tests show that the MDI-SG algorithm is much faster in low and medium dimensions (i.e.

d ≲ 100

) and in very high dimensions (i.e.

d \approx 1000

). It still works even when the MC method fails to compute. We also provide numerical tests to measure the influence of parameters in the proposed MDI-SG algorithm, including dependencies on the choice of underlying 1-d quadrature rule, and the choice of iteration step size. In Section 6 we numerically estimate the computational complexity of the MDI-SG algorithm. This is done by using standard regression technique to discover the relationship between CPU time and dimension. It is showed that the CPU time grows at most in a polynomial order

O (d^{3} N)

, where d and N stand for respectively the dimension of integration domain and the maximum number of integration points in each coordinate direction. As a result, the proposed MDI-SG method effectively circumvents the curse of dimensionality. Finally, the paper is concluded with some concluding remarks given in Section 7.

2. Preliminaries

In this paper,

f (x) : \bar{Ω}

\to R

denote a given continuous function on

\bar{Ω} \subset R^{d}

for

d > > 1

, then

f (x)

has pointwise values at every

x = (x_{1}, x_{2}, \dots, x_{d}) \in \bar{Ω} .

Without loss of the generality, we set

Ω : = {[- 1, 1]}^{d}

and consider the basic and fundamental problem of computing the integral

I_{d} (f) : = \int_{Ω} f (x) d x .

(1)

As mentioned in Section 1, the goal of this paper is to develop a fast algorithm for computing above integral based on the sparse grid methodology. To that end, below we briefly recall the necessary elements of sparse grid methods.

2.1. The sparse grid method

We now recall the formulation of the sparse grid method for approximating (1) and its tensor product reformulation formula which will be crucially used later in the formulation of our fast MDI-SG algorithm.

For each positive integer index

l \geq 1

, let

n_{l}

be a positive integer which denotes the number of grid points at level l and

Γ_{1}^{l} : = \{x_{1}^{l} < x_{2}^{l} < \dots < x_{n_{l}}^{l}\} \subset [- 1, 1]

(2)

denote a sequence of the level l grid points in

[- 1, 1]

. The grid sets

{Γ_{1}^{l}}

is said to be nested provided that

Γ_{1}^{l} \subset Γ_{1}^{l + 1}

. The best known example of the nested grids is the following dyadic grids:

Γ_{1}^{l} = \{x_{i}^{l} : = \frac{i}{2^{l - 1}} : i = - 2^{l - 1}, \dots, 0, 1, \dots, 2^{l - 1}\} .

(3)

For a given positive integer q, the tensor product

G_{d}^{q} : = Γ_{1}^{q} \times Γ_{1}^{q} \times \dots \times Γ_{1}^{q}

then yields a standard tensor product grid on

Ω = {[- 1, 1]}^{d}

. Notice that here the qth level is used in each coordinate direction. To reduce the number of grid points in

G_{d}^{q}

, the sparse grid idea is to restrict the total level to be q in the sense that

q = l_{1} + l_{2} + \dots + l_{d}

, where

l_{i}

is the level used in the ith coordinate direction, its corresponding tensor product grid is

Γ_{1}^{l_{1}} \times Γ_{1}^{l_{2}} \times \dots \times Γ_{1}^{l_{d}}

. Obviously, the decomposition

q = l_{1} + l_{2} + \dots + l_{d}

is not unique, so all such decomposition must be considered. The union

Γ_{d}^{q} : = ⋃_{l_{1} + \dots + l_{d} = q} Γ_{1}^{l_{1}} \times \dots \times Γ_{1}^{l_{d}}

(4)

then yields the famous Smolyak sparse grid (imbedded) on

Ω = {[- 1, 1]}^{d}

(cf. [6]). We remark that the underlying idea of going from

G_{d}^{q}

Γ_{d}^{q}

is exactly same as going from

Q_{q} (Ω)

P_{q} (Ω)

, where

Q_{q}

denotes the set of polynomials whose degrees in all coordinate directions not exceeding q and

P_{q}

denotes the set of polynomials whose total degrees not exceeding q.

After having introduced the concept of sparse grids, we then can define the sparse grid quadrature rule. For a univariate function g on

[- 1, 1]

, we consider d one-dimensional quadrature formula

J_{1}^{l_{i}} (g) : = \sum_{j = 1}^{n_{l_{i}}} w_{j}^{l_{i}} g (x_{j}^{l_{i}}), i = 1, \dots, d,

(5)

where

{x_{j}^{l_{i}}, j = 1, \dots, n_{l_{i}}}

and

{w_{j}^{l_{i}}, j = 1, \dots, n_{l_{i}}}

denote respectively the integration points/nodes and weights of the quadrature rule, and

n_{l_{i}}

denotes the number of integration points in the ith coordinate direction in

[- 1, 1]

. Define

\begin{matrix} l & : = [l_{1}, l_{2}, \dots, l_{d}], | l | : = l_{1} + l_{2} + \dots + l_{d}, \\ N_{d, s} & : = \{l = [l_{1}, \dots, l_{d}] : | l | = s, s \geq d\} . \end{matrix}

For example

N_{2, 4} = \{[1, 3], [2, 2], [3, 1]\}

Then, the sparse grid quadrature rule with accuracy level

q \in N

for d-dimensional integration (1) on

{[- 1, 1]}^{d}

is defined as (cf. [1])

Q_{d}^{q} (f) : = \sum_{q - d + 1 \leq | l | \leq q} {(- 1)}^{q - | l |} (\begin{matrix} d - 1 \\ q - | l | \end{matrix}) \sum_{l \in N_{d, | l |}} (J_{1}^{l_{1}} \otimes J_{1}^{l_{2}} \otimes \dots \otimes J_{1}^{l_{d}}) f,

(6)

where

(J_{1}^{l_{1}} \otimes J_{1}^{l_{2}} \otimes \dots \otimes J_{1}^{l_{d}}) f : = \sum_{j_{1} = 1}^{n_{l_{1}}} \dots \sum_{j_{d} = 1}^{n_{l_{d}}} w_{j_{1}}^{l_{1}} \dots w_{j_{d}}^{l_{d}} f (x_{j_{1}}^{l_{1}}, \dots, x_{j_{d}}^{l_{d}}) .

(7)

We note that each term

(J_{1}^{l_{1}} \otimes J_{1}^{l_{2}} \otimes \dots \otimes J_{1}^{l_{d}}) f

in (7) is the tensor product quadrature rule which uses

n_{l_{i}}

integration points in the ith coordinate direction. To write

Q_{d}^{q} (f)

more compactly, we set

n_{d}^{q} : = \sum_{q - d + 1 \leq | l | \leq q} n_{l_{1}} \dots n_{l_{d}},

which denotes the total number of integration points in

Ω = {[- 1, 1]}^{d}

. Let

w_{k}, k = 1, \dots, n_{d}^{q}

, denote the corresponding weights and define the bijective mapping

\{x^{k} : k = 1, \dots, n_{d}^{q}\} ⟶ \{(x_{j_{1}}^{l_{1}}, \dots, x_{j_{d}}^{l_{d}}) : j_{i} = 1, \dots, n_{l_{i}}, q - d + 1 \leq | l | \leq q\} .

Then, the sparse grid quadrature rule

Q_{d}^{q} (f)

can be rewritten as

Q_{d}^{q} (f) = \sum_{k = 1}^{n_{d}^{q}} w_{k} f (x^{k}) .

(8)

We also note that some weights

w_{k}

may become negative even though the one-dimensional weights

w_{j_{1}}^{l_{1}}, \dots, w_{j_{d}}^{l_{d}}

are positive. Therefore, it is no longer possible to interpret

Q_{d}^{q} (f)

as a discrete probability measure. Moreover, the existence of negative weights in (8) may cause numerical cancellation, hence, loss of significant digits. To circumvent such a potential cancellation, it is recommended in [7] that the summation is carried out by coordinates, this then leads to the following tensor product reformulation of

Q_{d}^{q} (f)

Q_{d}^{q} (f) = \sum_{l_{1} = 1}^{q - 1} \sum_{l_{2} = 1}^{γ_{1}^{q}} \dots \sum_{l_{d} = 1}^{γ_{d - 1}^{q}} \sum_{j_{1} = 1}^{n_{l_{1}}} \dots \sum_{j_{d} = 1}^{n_{l_{d}}} w_{j_{1}}^{l_{1}} \dots w_{j_{d}}^{l_{d}} f (x_{j_{1}}^{l_{1}}, \dots, x_{j_{d}}^{l_{d}}),

(9)

where the upper limits are defined recursively as

γ_{0}^{q} : = q, γ_{j}^{q} : = γ_{j - 1}^{q} - l_{j}, j = 1, 2, \dots, d .

In the nested mesh case (i.e.,

Γ_{1}^{l}

is nested), nested integration points are selected to form the sparse grid. We remark that different 1-d quadrature rules in (5) will lead to different sparse grid methods in (6). We also note that the tensor product reformulation (9) will play a crucial role later in the construction of our MD-SG algorithm.

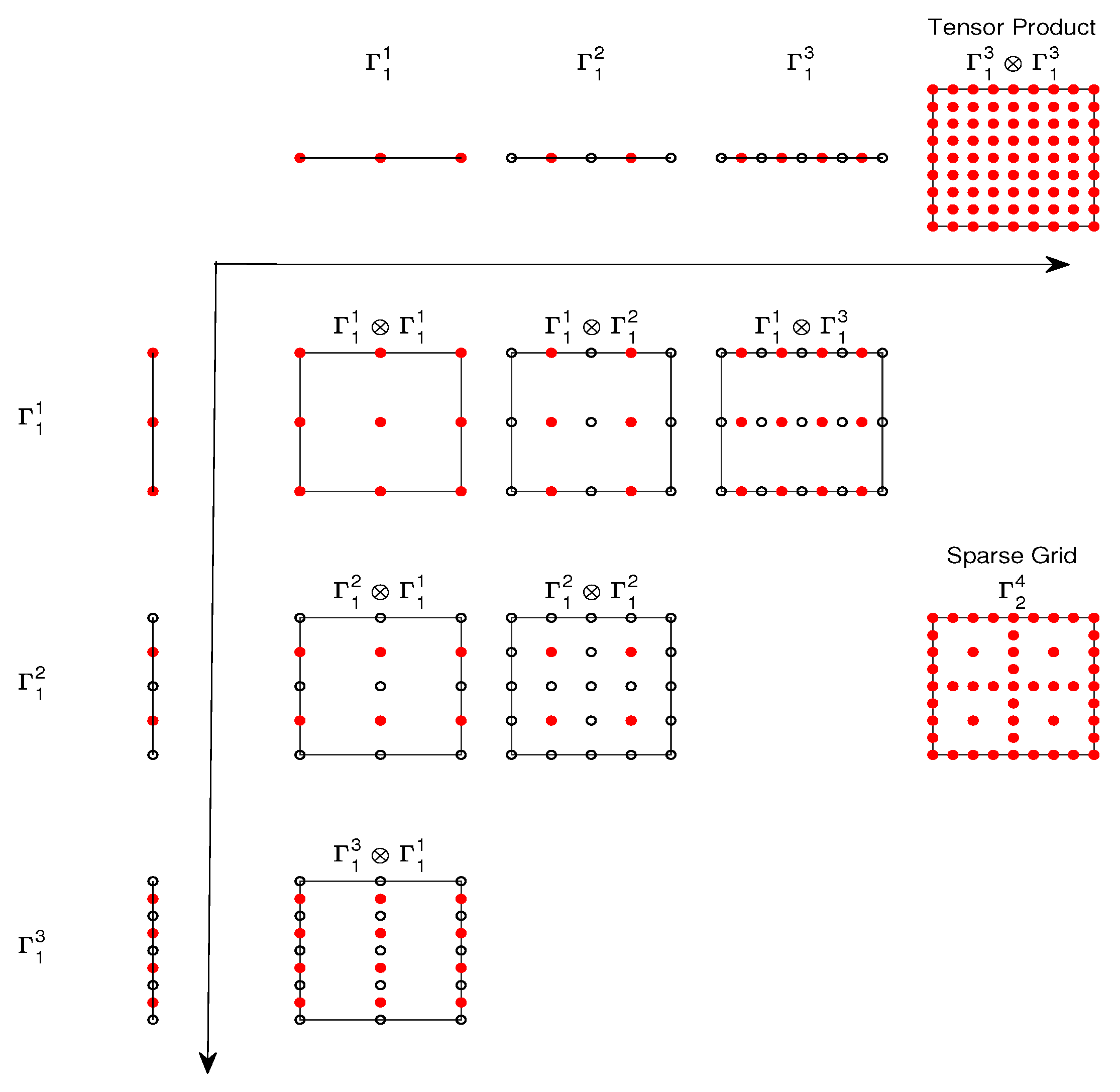
Figure 1 demonstrates the construction of a sparse grid according to the Smolyak rule when

d = 2

and

q = 4

. The meshes are nested, namely,

Γ_{1}^{l_{i}} \subset Γ_{1}^{l_{i + 1}}

. The 1-d integration-point sequence

Γ_{1}^{l_{1}}

(

l_{1} = 1, 2, 3

, and

n_{l_{1}} = 3, 5, 9

) and

Γ_{1}^{l_{2}}

(

l_{2} = 1, 2, 3

, and

n_{l_{2}} = 3, 5, 9

) are shown at the top and left of the figure, and the tensor product points

Γ_{1}^{3} \otimes Γ_{1}^{3}

are shown in the upper right corner. From (6) we see that the sparse grid rule is a combination of the low-order tensor product rule on

Γ_{1}^{i} \otimes Γ_{1}^{j}

with

3 \leq i + j \leq 4

. The point sets of these products and the resulting sparse grid

Γ_{2}^{4}

are shown in the lower half of the figure. We notice that some points in the sparse grid

Γ_{2}^{4}

are repeatedly used in

Γ_{1}^{i} \otimes Γ_{1}^{j}

with

3 \leq i + j \leq 4

. Consequently, we would avoid the repeated points (i.e., only using the red points in Figure 1) and use the reformulation (9) which does not involve repetition in the summation.

2.2. Examples of sparse grid methods

As mentioned earlier, different 1-d quadrature rules in (5) lead to different sparse grid quadrature rules in (9). Below we introduce four widely used sparse grid quadrature rules which will be the focus of this paper.

Example 1: The classical trapezoidal rule. The 1-d trapezoidal rule is defined by (cf. [25])

J_{1}^{q} (g) = \sum_{l = 1}^{q - 1} \sum_{j = 1}^{n_{l}}^{''} w_{j}^{l} g (x_{j}^{l})

(10)

with

q \geq 2

and

n_{1} = 1, n_{l} = 2^{l - 1} + 1, w_{j}^{l} = 2^{2 - l}, x_{j}^{l} = (j - 1) \cdot 2^{2 - l} - 1

. Where the

\sum^{''}

indicates that the first and last terms in the sum are halved. The following theorem gives the error estimate, its proof can be found in [7, pages 3-5].

Theorem 1.

Suppose

g \in C^{2} : = \{g : Ω \to R, ∥ \frac{\partial^{s} g}{\partial x^{s}} ∥_{\infty} < \infty, s \leq 2\}

, then there holds

|I_{1} (g) - J_{1}^{q} (g)| \leq C 2^{- 2 q} .

(11)

Example 2: The classical Clenshaw-Curtis rule. This quadrature rule reads as follows (cf. [26,27]):

J_{1}^{q} (g) = \sum_{l = 1}^{q - 1} \sum_{j = 1}^{n_{l}} w_{j}^{l} g (x_{j}^{l})

(12)

with

q \geq 2, n_{1} = 1, n_{l} = 2^{l - 1} + 1, x_{j}^{l} = - cos (π (j - 1) / (n_{l} - 1)), j = 1, \dots, n_{l}

and the weights

w_{1}^{l} = w_{n_{l}}^{l} = \frac{1}{n_{l} (n_{l} - 2)}, w_{j}^{l} = \frac{2}{n_{l} - 1} (1 + 2 \sum_{k = 1}^{\frac{n_{l} - 1}{2}}^{'} \frac{1}{1 - 4 k^{2}} cos \frac{2 π (j - 1) k}{n_{l} - 1})

for

2 \leq j \leq n_{l} - 1

. Where

\sum^{'}

indicates that the last term in the summation is halved.

The following error estimate holds and see [26, Theorem 1] for its proof.

Theorem 2.

Suppose

g \in C^{r} : = \{g : Ω \to R, ∥ \frac{\partial^{s} g}{\partial x^{s}} ∥_{\infty} < \infty, s \leq r\}

, then there holds

|I_{1} (g) - J_{1}^{q} (g)| \leq C {(n_{1}^{q})}^{- r}, w h e r e n_{1}^{q} : = n_{1} + n_{2} + \dots + n_{q - 1} .

(13)

Example 3: The Gauss-Patterson rule. This quadrature rule is defined by (cf. [28,29])

J_{1}^{q} (g) = \sum_{l = 1}^{q - 1} \sum_{j = 1}^{n_{l}} w_{j}^{l} g (x_{j}^{l})

(14)

with

q \geq 2, n_{l} = 2^{l} (n + 1) - 1

, and

{x_{j}^{l}}_{j = 1}^{n_{l}}

being the union of the zeroes of the polynomial

P_{n} (x)

and

G_{i} (x), 1 \leq i < l

, where

P_{n} (x)

is the n-th order Legendre polynomial and

G_{1} (x)

is the

(n + 1)

-th order Stieltjes polynomial and the

G_{i} (x)

is orthogonal to all polynomials of degree less than

2^{l - 1} (n + 1)

with respect to the weight function

P_{n} (x) (\prod_{j = 1}^{i - 1} G_{j} (x))

{w_{j}^{l}}_{j = 1}^{n_{l}}

are defined similarly to the Gauss-Legendre case, see [29] for details. Gauss-Patterson rules are a sequence of nested quadrature formulas with the maximal order of exactness. Its error estimate is given by the following theorem, see [27,28, Theorem 1].

Theorem 3.

Suppose

g \in C^{r} : = \{g : Ω \to R, ∥ \frac{\partial^{s} g}{\partial x^{s}} ∥_{\infty} < \infty, s \leq r\}

, then there holds

|I_{1} (g) - J_{1}^{q} (g)| \leq C {(n_{1}^{q})}^{- r}, w h e r e n_{1}^{q} : = n_{1} + n_{2} + \dots + n_{q - 1} .

(15)

Example 4: The classical Gauss-Legendre rule. This classical quadrature rule is defined by

J_{1}^{q} (g) = \sum_{l = 1}^{q - 1} \sum_{j = 1}^{n_{l}} w_{j}^{l} g (x_{j}^{l})

(16)

with

q \geq 2, n_{l} = l

for

l \geq 1

{x_{j}^{l}}_{j = 1}^{n_{l}}

are the zeroes of the

n_{l}

th order Legendre polynomial

P_{n_{l}} (x)

, and

{w_{j}^{l}}_{j = 1}^{n_{l}}

are the corresponding weights.

The following theorem gives the error estimate, its proof can be found in [7, pages 3-5].

Theorem 4.

Suppose

g \in C^{r} : = \{g : Ω \to R, ∥ \frac{\partial^{s} g}{\partial x^{s}} ∥_{\infty} < \infty, s \leq r\}

, then there holds

|I_{1} (g) - J_{1}^{q} (g)| \leq C {(n_{1}^{q})}^{- r}, w h e r e n_{1}^{q} : = n_{1} + n_{2} + \dots + n_{q - 1} .

(17)

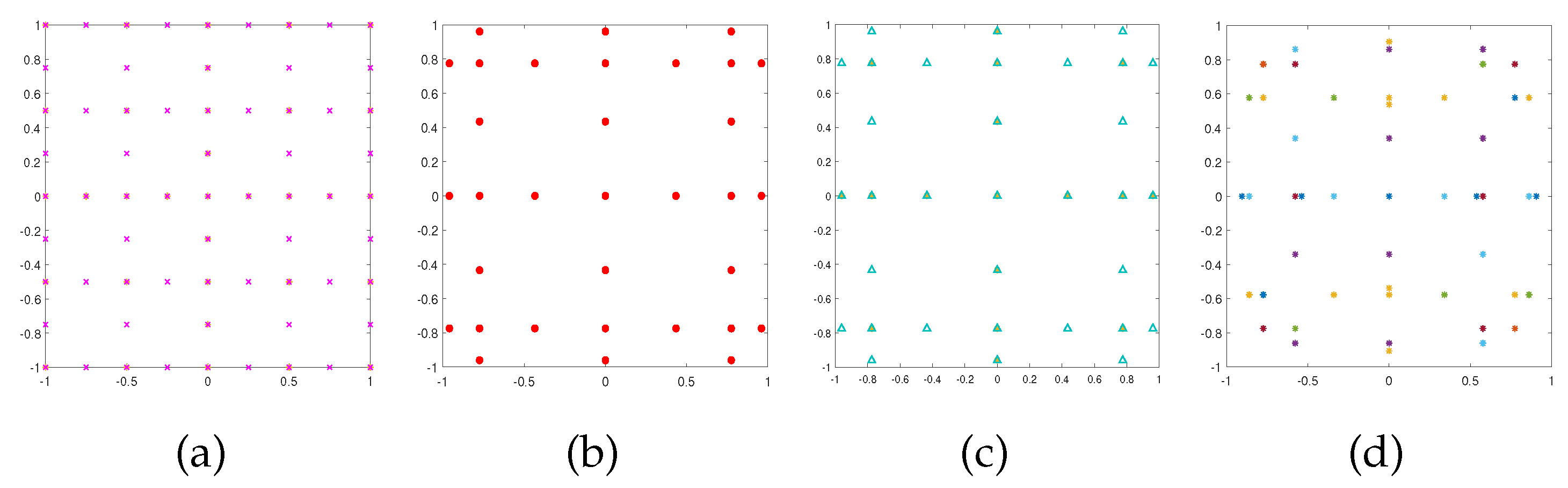
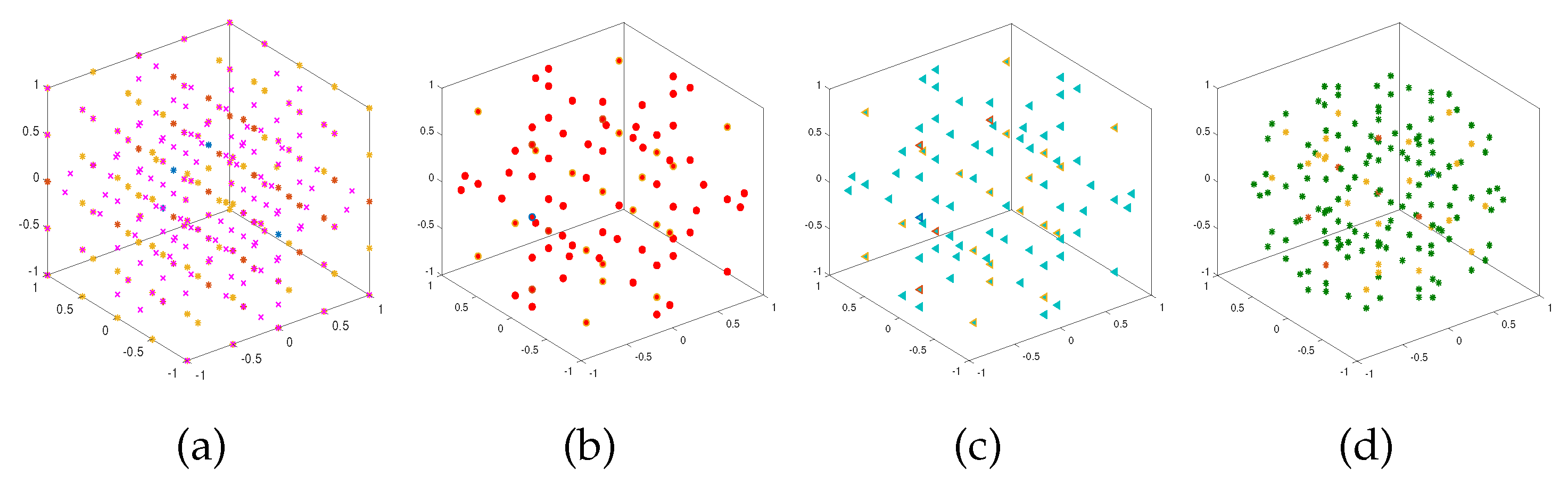
Figure 2 and Figure 3 show the resulting sparse grids of the above four examples in both 2-d and 3-d cases with

q = 6

and

q = 7

respectively. We note that these four sparse grids have different structures.

We conclude this section by remarking that the error estimates of the above quadrature rules can be easily translate to error estimates for the sparse grid method (9). For example, in the case of the Clenshaw-Curtis, Gauss-Patterson, and Gauss-Legendre quadrature rule, there holds (cf. [26, Corollary 1])

|I_{d} (f) - Q_{d}^{q} (f)| \leq C {(n_{d}^{q})}^{- r} \cdot {(log (n_{d}^{q}))}^{(d - 1) (r + 1)} \forall f \in W_{d}^{r},

(18)

where

n_{d}^{q} : = \sum_{q - d + 1 \leq | l | \leq q} n_{l_{1}} \dots n_{l_{d}},

W_{d}^{r} : = {f : Ω \to R; | \frac{\partial^{| l |} f}{\partial x_{1}^{l_{1}} \dots \partial x_{d}^{l_{d}}} |_{\infty} < \infty, l_{i} \leq r, i = 1, 2, \dots, d\} .

We note that the above estimate indicates that the error of the sparse grid method still deteriorates exponentially in the dimension d, but with a smaller base

log (n_{d}^{q})

3. The MDI-SG algorithm

The goal of this section is to present an efficient and fast implementation algorithm (or solver), called the MDI-SG algorithm, for evaluating the sparse grid quadrature rule (6) via its reformulation (9) in order to circumvent the curse of dimensionality which hampers the usage of the sparse grid method (6) in high dimensions. To better understand the main idea of the MDI-SG method, we first consider the simple two and three dimensional cases and then to formulate the algorithm in arbitrary dimensions.

Recall that

f (x) : \bar{Ω}

\to R

denote a continuous function on

\bar{Ω} \subset R^{d}

, we assume that f has a known expression.

3.1. Formulation of the MDI-SG algorithm in two dimensions

Let

d = 2

Ω = {[- 1, 1]}^{2}

, and

x = (x_{1}, x_{2}) \in Ω

. By Fubini’s Theorem we have

I_{2} (f) : = \int_{{[- 1, 1]}^{2}} f (x) d x = \int_{- 1}^{1} (\int_{- 1}^{1} f (x_{1}, x_{2}) d x_{1}) d x_{2} .

(19)

Then, the two-dimensional SG quadrature rule (9) takes the form

Q_{2}^{q} (f) = \sum_{l_{1} = 1}^{q - 1} \sum_{l_{2} = 1}^{γ_{1}^{q}} \sum_{j_{1} = 1}^{n_{l_{1}}} \sum_{j_{2} = 1}^{n_{l_{2}}} w_{j_{1}}^{l_{1}} w_{j_{2}}^{l_{2}} f (x_{j_{1}}^{l_{1}}, x_{j_{2}}^{l_{2}}),

(20)

where

γ_{1}^{q} = q - l_{1}

. Motivated by (and mimicking) the Fubini’s formula (19), we rewrite (20) as

\begin{matrix} Q_{2}^{q} (f) & = \sum_{l_{2} = 1}^{γ_{1}^{q}} \sum_{j_{2} = 1}^{n_{l_{2}}} w_{j_{2}}^{l_{2}} (\sum_{l_{1} = 1}^{q - 1} \sum_{j_{1} = 1}^{n_{l_{1}}} w_{j_{1}}^{l_{1}} f (x_{j_{1}}^{l_{1}}, x_{j_{2}}^{l_{2}})) \\ = \sum_{l_{2} = 1}^{γ_{1}^{q}} \sum_{j_{2} = 1}^{n_{l_{2}}} w_{j_{2}}^{l_{2}} f_{1} (x_{j_{2}}^{l_{2}}), \end{matrix}

(21)

where

f_{1} (s) : = \sum_{l_{1} = 1}^{q - 1} \sum_{i = 1}^{n_{l_{1}}} w_{i}^{l_{1}} f (x_{i}^{l_{1}}, s) .

We note that the evaluation of

f_{1} (x_{2})

is amount to applying the 1-d formula (5) to approximate the integral

\int_{- 1}^{1} f (x_{1}, x_{2}) d x_{1} .

However, the values of

{f_{1} (x_{j_{2}}^{l_{2}})}

will not be computed by the 1-d quadrature rule in our MDI-SG algorithm, instead,

f_{1}

is formed as a symbolic function, so the 1-d quadrature rule can be called on

f_{1}

. Therefore, we still use the SG method to select the integration points, and then use our MDI-SG algorithm to perform function evaluations at the integration points collectively to save computation, which is the main idea of the MDI-SG method.

Let W and X denote the weight and node vectors of the 1-d quadrature rule on

[- 1, 1]

n_{l_{i}}

represents the number of integration points in the

x_{i}

direction and we use a parameter

r \in {1, 2, 3, 4}

to indicate one of the four quadrature rule. The following algorithm implements the sparse grid quadrature formula (21).

We note that the first do-loop forms the symbolic function

f_{1}

which encodes all computations involving the

x_{1}

-components at all integration points. The second do-loop evaluates the 1-d quadrature rule for the function

f_{1}

. As mentioned above, in this paper we only focus on the four well-known 1-d quadrature rules: (i) trapezoidal rule; (ii) Clenshaw-Curtis rule; (iii) Gauss-Patterson rule; (iv) Gauss-Legendre rule. They will be represented respectively by

r = 1, 2, 3, 4

Below we use a simple 2-d example to explain the mechanism of above 2d-MDI-SG algorithm. It is clear that to directly compute the SD sum

\sum_{i_{1} = 1}^{n_{1}} \sum_{i_{2} = 1}^{n_{2}} f (ξ_{i_{1}}, ξ_{i_{2}}) = f (ξ_{1}, ξ_{1}) + f (ξ_{1}, ξ_{2}) + \dots + f (ξ_{n_{1}}, ξ_{n_{2}}),

(22)

it is necessary to compute the function values of

f (x_{1}, x_{2})

n_{1} n_{2}

points, which are often done independently. On the other hand, the 2d-MDI-SD algorithm is based on rewriting the sum as

\sum_{i_{1} = 1}^{n_{1}} \sum_{i_{2} = 1}^{n_{2}} f (ξ_{i_{1}}, ξ_{i_{2}}) = \sum_{i_{1} = 1}^{n_{1}} f_{1} (ξ_{i_{1}}),

(23)

where

f_{1} (x_{1}) = \sum_{i_{2}}^{n_{2}} f (x_{1}, ξ_{i_{2}})

denotes the symbolic function obtained in the first do-loop. Hence, the algorithm performs two separate do-loops. In the first d-loop, symbolic computations are performed to obtain the symbolic function

f_{1} (x_{1})

which is saved. In the second do-loop, the single sum

\sum_{i_{1} = 1}^{n_{1}} f_{1} (ξ_{i_{1}})

is done. When computing the symbolic function

f_{1} (x_{1})

, a lot of computations have been reused for computing the coefficients in

f_{1} (x_{1})

, and those coefficients are constants in the second do-loop. Efficiently generating the symbolic function and using it to compute the SG sum are the main reasons of saving computation and computer memory.

Take

f (x_{1}, x_{2}) = x_{1}^{2} + x_{1} x_{2} + x_{2}^{2}

as a concrete example. The direct computation the SG sum in (22) requires to compute the function value

f (ξ_{1}, ξ_{2}) = ξ_{1}^{2} + ξ_{1} ξ_{2} + ξ_{2}^{2}

at each node

(ξ_{1}, ξ_{2})

, this in turn requires three multiplications and two additions. With a total of

n_{1} n_{2}

nodes, then computing the sum requires a total of

3 n_{1} n_{2}

multiplications and

3 n_{1} n_{2} - 1

additions. On the other hand, when using the 2d-MDI-SD algorithm to compute the same sum, in the first do-loop, we compute the symbolic function

f_{1} (x_{1}) = \sum_{i_{2} = 1}^{n_{2}} f (x_{1}, ξ_{i_{2}})

which requires

n_{2}

“symbolic multiplications" of

ξ_{i_{2}} x_{1}

(no real multiplication is needed because of its linear dependence on

ξ_{u_{2}}

) and

n_{2}

multiplications of

ξ_{i_{2}}^{2}

, as well as

3 n_{2} - 1

additions. In the second do-loop, computing the

\sum_{i_{1} = 1}^{n_{1}} f_{1} (ξ_{i_{1}})

requires

n_{1}

multiplications of

ξ_{i_{1}}^{2}

and

n_{1}

multiplications of

ξ_{i_{1}} {\bar{ξ}}_{i_{2}}

, as well as

3 n_{1} - 1

additions. Thus, the 2d-MDI-SD algorithm requires a total of

2 (n_{1} + n_{2})

multiplications and

3 (n_{1} + n_{2} - \frac{4}{3})

additions. Therefore, the 2d-MDI-SG algorithm computes the SD sum much cheaper than the standard implementation, and this advantage will become more significant in high dimensions. See Section 3.2 and Section 3.3 for details.

3.2. Formulation of the MDI-SG algorithm in three dimensions

In the subsection we extend the formulation of the above 2d-MDI-SGI algorithm to the 3-d case by highlighting its main steps, in particular, how the above 2-d algorithm is utilized. First, recall that Fubini’s Theorem is given by

I_{3} (f) : = \int_{{[- 1, 1]}^{3}} f (x) d x = \int_{{[- 1, 1]}^{2}} (\int_{- 1}^{1} f (x) d x_{1}) d x^{'},

(24)

where

x^{'} = (x_{2}, x_{3})

Second, notice that the SG quadrature rule (9) in 3-d takes the form

Q_{3}^{q} (f) = \sum_{l_{1} = 1}^{q - 1} \sum_{l_{2} = 1}^{γ_{1}^{q}} \sum_{l_{3} = 1}^{γ_{2}^{q}} \sum_{j_{1} = 1}^{n_{l_{1}}} \sum_{j_{2} = 1}^{n_{l_{2}}} \sum_{j_{3} = 1}^{n_{l_{3}}} w_{j_{1}}^{l_{1}} w_{j_{2}}^{l_{2}} w_{j_{3}}^{l_{3}} f (x_{j_{1}}^{l_{1}}, x_{j_{2}}^{l_{2}}, x_{j_{3}}^{l_{3}}) .

(25)

where

γ_{2}^{q} = q - l_{1} - l_{2}

. Mimicking the above Fubini’s formula, we rewrite (25) as

\begin{matrix} Q_{3}^{q} (f) & = \sum_{l_{3} = 1}^{γ_{2}^{q}} \sum_{j_{3} = 1}^{n_{l_{3}}} \sum_{l_{2} = 1}^{γ_{1}^{q}} \sum_{j_{2} = 1}^{n_{l_{2}}} w_{j_{3}}^{l_{3}} w_{j_{2}}^{l_{2}} (\sum_{l_{1} = 1}^{q - 1} \sum_{j_{1} = 1}^{n_{l_{1}}} w_{j_{1}}^{l_{1}} f (x_{j_{1}}^{l_{1}}, x_{j_{2}}^{l_{2}}, x_{j_{3}}^{l_{3}})) \\ = \sum_{l_{3} = 1}^{γ_{2}^{q}} \sum_{j_{3} = 1}^{n_{l_{3}}} \sum_{l_{2} = 1}^{γ_{1}^{q}} \sum_{j_{2} = 1}^{n_{l_{2}}} w_{j_{3}}^{l_{3}} w_{j_{2}}^{l_{2}} f_{2} (x_{j_{2}}^{l_{2}}, x_{j_{3}}^{l_{3}}), \end{matrix}

(26)

where

f_{2} (s, t) : = \sum_{l_{1} = 1}^{q - 1} \sum_{j_{1} = 1}^{n_{l_{1}}} w_{j_{1}}^{l_{1}} f (x_{j_{1}}^{l_{1}}, s, t) .

(27)

We note that

f_{2}

is formed as a symbolic function in our MDI-SG algorithm and the right-hand side of (26) is viewed as a 2-d sparse grid quadrature formula for

f_{2}

, it can be computed either directly or recursively by using Algorithm 1. The following algorithm implements the SG quadrature formula (26).

Algorithm 1 2d-MDI-SG(f,

Ω, r, q, X, W

)

Initialize $Q = 0$ , $f_{1} = 0$ .
for $l_{1} = 1 : q$ do
for $j_{1} = 1 : n_{l_{1}}$ do
$f_{1} = f_{1} + W_{j_{1}}^{l_{1}} f ((X_{j_{1}}^{l_{1}}, \cdot))$ .
end for
end for
for $l_{2} = 1 : q - l_{1}$ do
for $j_{2} = 1 : n_{l_{2}}$ do
$Q = Q + W_{j_{2}}^{l_{2}} \cdot f_{1} (X_{j_{2}}^{l_{2}})$ .
end for
end for
returnQ.

Where

P_{3}^{2}

denotes the orthogonal projection (or natural embedding):

x = (x_{1}, x_{2}, x_{3})

\to x^{'} = (x_{2}, x_{3})

, W and X stand for the weight and node vectors of the underlying 1-d quadrature rule.

From Algorithm 2 we can see the mechanism of the MDI-SG algorithm. It is based on two main ideas: (i) to use the sparse grid approach to select integration points; (ii) to use the discrete Fubini formula to efficiently compute the total sparse grid sum by reducing it to calculation of a low-dimensional (i.e., 2-d) sparse grid sum, which allows us to recursively call the low-dimensional MDI-SG algorithm.

Algorithm 2 3d-MDI-SG(f,

Ω, r, q, X, W

)

Initialize $Q = 0, f_{2} = 0$ .
for $l_{1} = 1 : q$ do
for $j_{1} = 1 : n_{l_{1}}$ do
$f_{2} = f_{2} + W_{j_{1}}^{l_{1}} \cdot f ((X_{j_{1}}^{l_{1}}, \cdot, \cdot))$ .
end for
end for
$Ω_{2} = P_{3}^{2} Ω, γ_{1}^{q} = q - l_{1}$ .
$Q =$ 2d-MDI-SG $(f_{2}, Ω_{2}, r, γ_{1}^{q}, X, W)$ .
returnQ.

3.3. Formulation of the MDI-SG algorithm in arbitrary d-dimensions

The goal of this subsection is to extend the 2-d and 3-d MDI-SG algorithms to arbitrary d-dimensions. We again start with recalling the d-dimensional Fubini’s Theorem

I_{d} (f) = \int_{Ω} f (x) d x = \int_{Ω_{d - m}} (\int_{Ω_{m}} f (x) d x^{''}) d x^{'},

(28)

where

1 \leq m < d

Ω = {[- 1, 1]}^{d}, Ω_{m} = ρ_{d}^{m} Ω = {[- 1, 1]}^{m}

and

Ω_{d - m} = P_{d}^{d - m} Ω = {[- 1, 1]}^{d - m}

in which

ρ_{d}^{m}

and

P_{d}^{d - m}

denote respectively the orthogonal projections (or natural embeddings):

x = (x_{1}, x_{2}, \dots, x_{d}) \to x^{''} = (x_{1}, x_{2}, \dots, x_{m})

and

x = (x_{1}, x_{2}, \dots, x_{d}) \to x^{'} = (x_{m + 1}, x_{m + 2}, \dots, x_{d})

. The integer m denotes the dimension reduction step length in our algorithm.

Mimicking the above Fubini’s Theorem, we rewrite the d-dimensional SG quadrature rule (9) as follows:

\begin{matrix} Q_{d}^{q} (f) & = \sum_{l_{d} = 1}^{γ_{d - 1}^{q}} \sum_{j_{d} = 1}^{n_{l_{d}}} \dots \sum_{l_{m + 1} = 1}^{γ_{m}^{q}} \sum_{j_{m + 1}}^{n_{l_{m + 1}}} w_{j_{m + 1}}^{l_{m + 1}} \dots w_{j_{d}}^{l_{d}} (\sum_{l_{m} = 1}^{γ_{m - 1}^{q}} \dots \sum_{j_{1} = 1}^{n_{l_{1}}} w_{j_{1}}^{l_{1}} \dots w_{j_{m}}^{l_{m}} f (x_{j_{1}}^{l_{1}}, \dots, x_{j_{d}}^{l_{d}})) \\ = \sum_{l_{d} = 1}^{γ_{d - 1}^{q}} \sum_{j_{d} = 1}^{n_{l_{d}}} \dots \sum_{l_{m + 1} = 1}^{γ_{m}^{q}} \sum_{j_{m + 1} = 1}^{n_{l_{m + 1}}} w_{j_{m + 1}}^{l_{m + 1}} \dots w_{j_{d}}^{l_{d}} f_{d - m} (x_{j_{m + 1}}^{l_{m + 1}}, \dots, x_{j_{d}}^{l_{d}}), \end{matrix}

(29)

where

\begin{matrix} f_{d - m} (s_{1}, \dots, s_{d - m}) = \sum_{l_{m} = 1}^{γ_{m - 1}^{q}} \sum_{j_{m} = 1}^{n_{l_{m}}} \dots \sum_{l_{1} = 1}^{q - 1} \sum_{j_{1} = 1}^{n_{l_{1}}} w_{j_{1}}^{l_{1}} \dots w_{j_{m}}^{l_{m}} f (x_{j_{1}}^{l_{1}}, \dots, x_{j_{m}}^{l_{m}}, s_{1}, \dots, s_{d - m}) . \end{matrix}

(30)

We note that in our MDI-SG algorithm

f_{d - m}

defined by (30) is a symbolic function and the right-hand side of (29) is a

(d - m)

-order multi-summation, which itself can be evaluated by employing the dimension reduction strategy. Dimensionality can be reduced by iterating

k : = [\frac{d}{m}]

times until

d - k m \leq m

. To implement this process, we introduce the following conventions.

If $t = 1$ , set MDI-SG $(t, f_{t}, Ω_{t}, m, s, r, q, X, W) : = J_{1}^{q} (f)$ , which is computed by using the one-dimensional quadrature rule (5).
If $t = 2$ , set MDI-SG $(t, f_{t}, Ω_{t}, m, s, r, q, X, W) : =$ 2d-MDI-SG $(f_{t}, Ω_{t}, r, q, X, W)$ .
If $t = 3$ , set MDI-SG $(t, f_{t}, Ω_{t}, m, s, r, q, X, W) : =$ 3d-MDI-SG $(f_{t}, Ω_{t}, r, q, X, W)$ .

We note that when

t = 1, 2, 3

, the parameter m becomes a dummy variable and can be given any value. Recall that

P_{t}^{t - m}

denotes the natural embedding from

R^{t}

R^{t - m}

by deleting the first m components of vectors in

R^{t}

. The following algorithm implements the sparse grid quadrature via (29).

Where

\begin{matrix} f_{t - m} (s_{1}, \dots, s_{t - m}) = \sum_{l_{m} = 1}^{γ_{m - 1}^{q}} \sum_{j_{m} = 1}^{n_{l_{m}}} \dots \sum_{l_{1} = 1}^{q - 1} \sum_{j_{1} = 1}^{n_{l_{1}}} w_{j_{1}}^{l_{1}} \dots w_{j_{m}}^{l_{m}} \cdot f (x_{j_{1}}^{l_{1}}, \dots, x_{j_{m}}^{l_{m}}, s_{1}^{}, \dots, s_{t - m}) . \end{matrix}

(31)

We remark that Algorithm 3 recursively generates a sequence of symbolic functions

f_{d}, \dots, f_{d - k m}, f_{d - k m - s}, \dots, f_{d - k m - k_{1} s}

, each function has m fewer arguments than its predecessor. As mentioned earlier, our MDI-SG algorithm does not perform the function evaluations at all integration points independently, but rather iteratively along m-coordinate directions, hence, the function evaluation at any integration point is not completed until the last step of the algorithm is executed. As a result, many computations are reused in each iteration, which is the main reason for the computation saving and to achieve a faster algorithm.

Algorithm 3 MDI-SG

(d, f, Ω, m, s, r, q, X, W)

$Ω_{d} = Ω, f_{d} = f, k = [\frac{d}{m}], γ_{d}^{q} = q - 1$ .
for $t = d : - m : d - k m$ (the index is decreased by m at each iteration) do
$Ω_{d - m} = P_{t}^{t - m} Ω_{t}, γ_{d - m}^{q} = γ_{t}^{q} - l_{1} - \dots - l_{m}$ .
(Construct symbolic function $f_{t - m}$ by (31) below).
$MDI - SG (t, f_{t}, Ω_{t}, m, s, r, γ_{t}^{q}, X, W) : = MDI - SG (t - m, f_{t - m}, Ω_{t - m}, m, s, r, γ_{t - m}^{q}, X, W)$
end for
$d = d - k m, s = 1 (o r 2, 3), f_{d} = f_{t}, k_{1} = [\frac{d - k m}{s}]$ .
for $t = d : s : d - k_{1} s$ (the index is decreased by s at each iteration) do
$Ω_{d - s} = P_{t}^{t - s} Ω_{t}, γ_{d - s}^{q} = γ_{t}^{q} - l_{1} - \dots - l_{s}$ .
(Construct symbolic function $f_{t - s}$ by (31) below).
$MDI - SG (t, f_{t}, Ω_{t}, m, s, r, γ_{t}^{q}, X, W) : = MDI - SG (t - s, f_{t - s}, Ω_{t - s}, m, s, r, γ_{t - s}^{q}, X, W)$
end for
$Q = MDI - SG (d - k_{1} s, f_{d - k_{1} s}, Ω_{d - k_{1} s}, m, s, r, γ_{d - k_{1} s}^{q}, X, W) .$
return Q.

4. Numerical performance tests

In this section, we present extensive numerical tests to guage the performance of the proposed MDI-SG algorithm and to compare it with the standard sparse grid (SG) and classical Monte Carlo (MC) methods. All numerical tests show that MDI-SG algorithm outperforms both SG and MC methods in low and medium high dimensions (i.e.

d ≲ 100

), and can compute very high-dimensional (i.e.

d \approx 1000

) integrals while others fail.

All our numerical experiments are done in Matlab 9.4.0.813654(R2018a) on a desktop PC with Intel(R) Xeon(R) Gold 6226R CPU 2.90GHz and 32GB RAM.

4.1. Two and three-dimensional tests

We first test our MDI-SG algorithm on simple 2-d and 3-d examples and compare its performance (in terms of CPU time) with SG methods.

Test 1. Let

Ω = {[- 1, 1]}^{2}

and consider the following 2-d integrands:

f (x) : = exp (5 x_{1}^{2} + 5 x_{2}^{2}); \hat{f} (x) : = sin (2 π + 10 x_{1}^{2} + 5 x_{2}^{2}) .

(32)

Let q denote the accuracy level of the sparse grid. The larger q is, the more integration points we need for the 1-d quadrature rule, and the higher the accuracy of the MDI-SG quadrature. The base 1-d quadrature rule is chosen to be the Gauss-Patterson rule, hence, parameter

r = 3

in the algorithm.

Table 1 and Table 2 present the computational results (errors and CPU times) of the MDI-SG and SG methods for approximating

I_{2} (f)

and

I_{2} (\hat{f})

, respectively.

From Table 1 and Table 2, we observe that these two methods use very little CPU time, although the SG method in both tests outperforms, but the difference is almost negligible, so both methods do well in 2-d case.

Test 2. Let

Ω = {[- 1, 1]}^{3}

and we consider the following 3-d integrands:

f (x) = exp (5 x_{1}^{2} + 5 x_{2}^{2} + 5 x_{3}^{2}), \hat{f} (x) = sin (2 π + 10 x_{1}^{2} + 5 x_{2}^{2} + 5 x_{3}) .

(33)

We compute the integral of these two functions over

Ω = {[- 1, 1]}^{3}

using the MDI-SG and SG methods. Likewise, let q denote the accuracy level of the sparse grid, choose parameters

r = 3

and

m = 1

in the algorithm.

The test results are given in Table 3 and Table 4. We again observe that both methods use very little CPU time although the SG method again slightly outperforms in both tests. However, as q increases, the number of integration points increases, and the CPU times used by these two methods get closer. We would like to point out that both methods are very efficient and their difference is negligible in the 3-d case.

4.2. High-dimensional tests

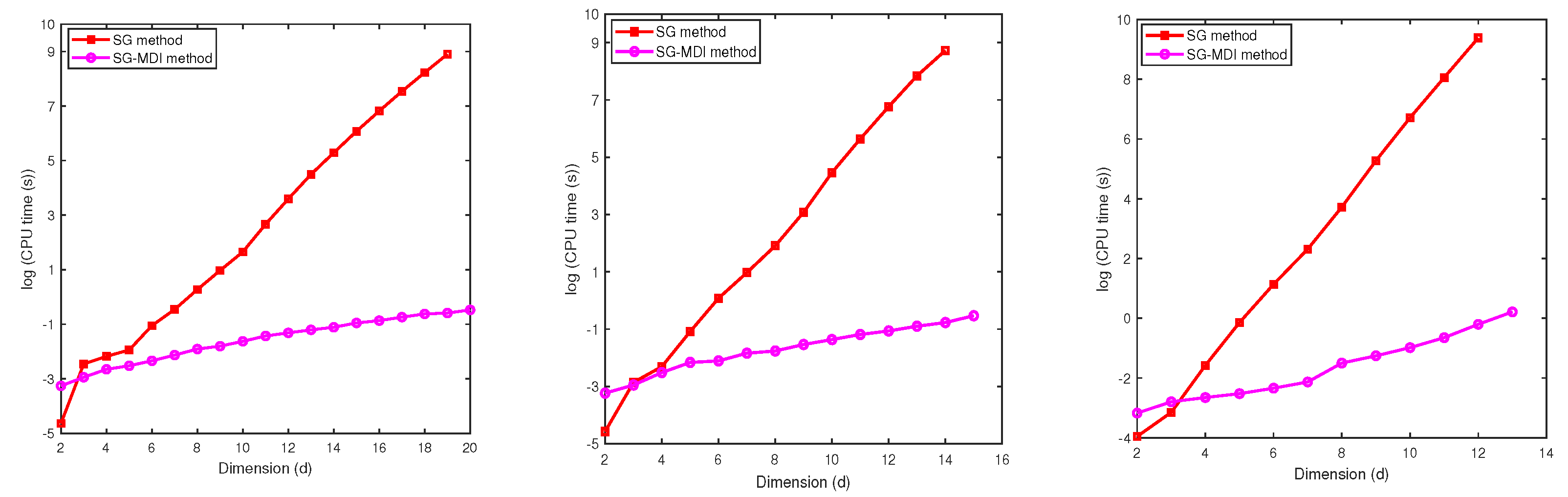
In this section we evaluate the performance of the MDI-SG method for

d > > 1

. First, we test and compare the performance of the MDI-SG and SG methods in computing Gaussian integrals for dimensions

2 \leq d \leq 20

because

d \approx 20

is the highest dimension that the SG method is able to compute a result on our computer. We then provide a performance comparison (in terms of CPU time) of the MDI-SG and classical Monte Carlo (MC) methods in computing high-dimensional integrals.

Test 3. Let

Ω = {[- 1, 1]}^{d}

for

2 \leq d \leq 20

and consider the following Gaussian integrand:

f (x) = \frac{1}{\sqrt{2 π}} exp (- \frac{1}{2} {| x |}^{2}),

(34)

where

| x |

stands for the Euclidean norm of the vector

x \in R^{d}

We compute the integral

I_{d} (f)

by using the MDI-SG and SG methods, as done in Test 1-2. Both methods are based on the same 1-d Gauss-Patterson rule (i.e., the parameter

r = 3

). We also set

m = 1, s = 1

in the MDI-SG method and use two accuracy levels

q = 10, 12

, respectively.

Table 5 gives the relative error and CPU time for approximating

I_{d} (f)

using MDI-SG and SG methods with accuracy level

q = 10

, and Table 6 gives the corresponding results for

q = 12

. We observe that the errors should be the same for both methods (since they use the same integration points), but their CPU times are quite different. The SG method is more efficient for

d \leq 4

when

q = 8, 10

and for

d \leq 3

when

q = 12

, but the MDI-SG method excels for

d \geq 4

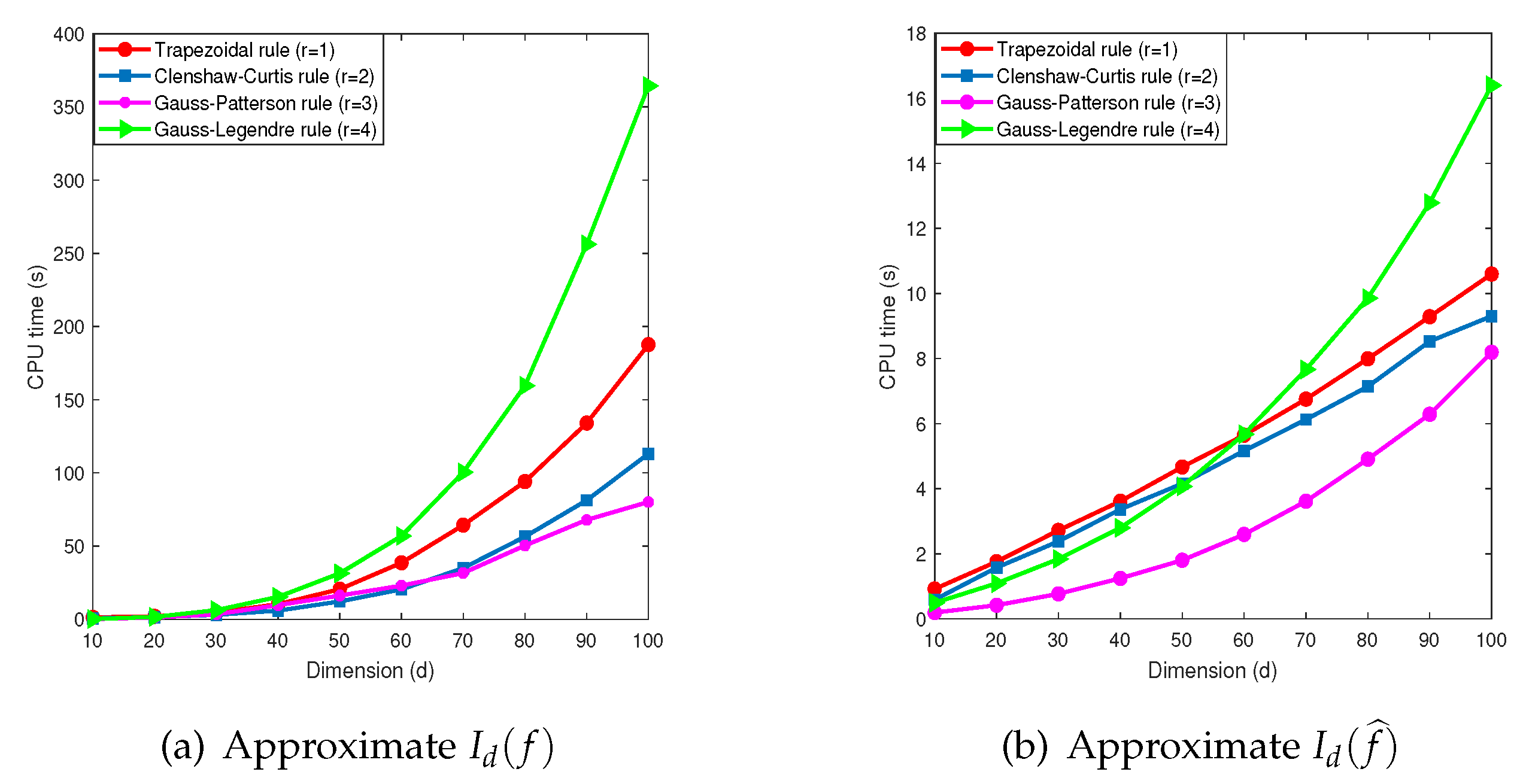
and the winning margin becomes significant as d and q increase (also see Figure 4). For example, when

d = 14

and

q = 10

, the CPU time required by the SG method is about 6167 seconds, which is about 2 hours, but the CPU time of the MDI-SG method is less than 1 second! Also, when

d = 13

and

q = 12

, the SG method fails to compute the integral due to running out of computer memory because too large number of integration points must be saved and function evaluations must be performed, but the MDI-SG method only needs about 2 seconds to complete the computation!

The classical (and quasi) Monte Carlo (MC) method is often the preferred/default method for computing high-dimensional integrals. However, due to its low order of convergence, to achieve the accuracy, a large number of function evaluations are required at randomly sampled integration points and the number grows rapidly as dimension d increases (due to the rapid growth of variance). Below we compare the performance of the MDI-SG (with parameters

r = 3, q = 10, m = 10, s = 1

) and classical MC method. In the test, when

d \geq 10

, we use the iteration step length

m > 1

to iterate faster until

d - k m \leq m

to reach the stage 2 of the iteration. We refer the reader to Section 5.2 for a detailed analysis.

Test 4. Let

Ω = {[- 1, 1]}^{d}

and choose the following integrands:

f (x) = \prod_{i = 0}^{d} \frac{1}{0 . 9^{2} + {(x_{i} - 0.6)}^{2}}, \hat{f} (x) = \frac{1}{\sqrt{2 π}} exp (- \frac{1}{2} {| x |}^{2}) .

(35)

We use relative error as a criterion for comparison, that is, we determine a required (minimum) number of random sampling points for the MC method so that it produces a relative error comparable to that of the MDI-SG method. The computed results for

I_{d} (f)

and

I_{d} (\hat{f})

are respectively given in Table 7 and Table 8.

From Table 7 and Table 8, we clearly see that there is a significant difference in the CPU time of these two methods for computing

I_{d} (f)

and

I_{d} (\hat{f})

. When

d > 30

, the classical MC method fails to produce a computed result with a relative error of order

10^{- 5}

. As explained in [20], the MC method requires more than

10^{10}

randomly sampled integration points and then needs independently to compute their function values, which is a tall order to do on a regular workstation.

Next, we come to address a natural question that asks how high the dimension d can be handled by the MDI-SG method. Obviously, the answer must be computer-dependent, and that given below is obtained using the workstation at our disposal.

Test 5. Let

Ω = {[- 1, 1]}^{d}

and consider the following integrands:

f (x) = \frac{1}{2^{d}} exp (\sum_{i = 1}^{d} {(- 1)}^{i + 1} x_{i}), \hat{f} (x) = \prod_{i = 0}^{d} \frac{1}{0 . 9^{2} + {(x_{i} - 0.6)}^{2}} .

(36)

We then compute

I_{d} (f)

and

I_{d} (\hat{f})

using the MDI-SG algorithm for an increasing sequence of d up to 1000 with parameters

r = 3, q = 10, m = 10, s = 1

. The computed results are shown in Table 9. We stop the computation at

d = 1000

since it is already quite high and use

q = 10, m = 10, s = 1

to minimize the computation in each iteration. This test demonstrates the promise and capability of the MDI-SG algorithm for efficiently computing high-dimensional integrals. When computing the integral of a 1000-dimensional function by the SG method, the SG sum contains

5.6 \times 10^{601}

function evaluations, but the MDI-SG algorithm does not compute them one by one. Instead, the symbolic functions are efficiently degenerated through dimension iterations by reusing/sharing many calculations. It should be noted that the MDI-SG algorithm does use of a lot of computer memory when computing high-dimensional integrals.

5. Influence of parameters

There are four parameters in the d-dimensional MDI-SG algorithm, they are respectively

r, m, s

, and q. Where

r \in {1, 2, 3, 4}

represents the choice of one-dimensional numerical quadrature rule, namely, the (composite) trapezoidal rule (

r = 1

), Clenshaw-Curtis rule (

r = 2

), Gauss-Patterson rule (

r = 3

), and Gauss-Legendre rule (

r = 4

). The parameter m stands for the multi-dimensional iteration step size in the first stage of the algorithm so the dimension of the integration domain is reduced by m in each iteration. In practice,

1 \leq m \leq q

, and it is preferred to be close to q. In this section we shall evaluate the performance of the MDI-SG algorithm when

m < q, m = q, m > q

. It should be noted that after

k : = [\frac{d}{m}]

iterations, the algorithm enters to its second stage and the iteration step size is changed to s. Since after the first stage, the remaining dimension

d - k m

small, so

s \in {1, 2, 3}

. It should be noted that after

k_{1} : = [\frac{d - k m}{s}]

iterations, the residual dimension satisfies

d - k m - k_{1} s \leq s

. Then in case

s = 2

or 3, one has two options to complete the algorithm. One either just continues the dimension reduction by calling 3d-MDI-SG or 2d-MDI-SG as explained in the definition of Algorithm 3 or compute the remaining 2- or 3-dimensional integral directly. The effect of these two choices will be tested in this section. Finally, the parameter q represents the precision level of the sparse grid method. Obviously, the larger q is, the higher accuracy of the computed results, the trade-off is more integration points must be used, hence, adds more cost. In this section we shall also test the impact of q value to the MDI-SG algorithm.

5.1. Influence of parameter r

We first examine the impact of one-dimensional quadrature rules, which are indicated by

r = 1, 2, 3, 4

, in the MDI-SG algorithm.

Test 6: Let

Ω = {[- 1, 1]}^{d}

and choose the integrand f as

f (x) = exp (\sum_{i = 1}^{d} {(- 1)}^{i + 1} x_{i}), \hat{f} (x) = \prod_{i = 0}^{d} \frac{1}{0 . 9^{2} + {(x_{i} - 0.6)}^{2}} .

(37)

Below we compare the performance of the MDI-SG algorithm with different r in computing

I_{d} (f)

and

I_{d} (\hat{f})

with the accuracy level

q = 10

and step size

m = 10

Figure 5 (a) shows the computed results of

I (f)

by the MDI-SG algorithm. We observe that the choice of one-dimensional quadrature rules has a significant impact on the accuracy and efficiency of the MDI-SG algorithm. The trapezoidal rule (

r = 1

) has the lowest precision and uses the most integration points, the Clenshaw-Curtis rule (

r = 2

) is the second lowest, and the Gauss-Patterson (

r = 3

) and Gauss-Legendre rule (

r = 4

) have the highest precision. Both the Clenshaw-Curtis and Gauss-Patterson rule use the nested grids, that is, the integration points of the

(q + 1)

th level contain those of the qth level. Although they use the same number of integration points, the Gauss-Patterson rule is more efficient than the Clenshaw-Curtis rule. Moreover, the Gauss-Patterson rule is more efficient than the Gauss-Legendre rule (

r = 4

) which uses the most CPU time and produces the most accurate solution. This comparison suggests that the Gauss-Patterson rule is a winner among these four rules when they are used as the building blocks in the MDI-SG algorithm for high-dimensional integration.

Figure 5 (b) shows the computational results of

I_{d} (\hat{f})

by the MDI-SG algorithm. Similarly, the choice of one-dimensional quadrature rules has a significant impact on the accuracy and efficiency of the MDI-SG algorithm. Because the integrand

\hat{f} (x)

is simple, the MDI-SG algorithm with all four 1-d quadrature rules computes this integral very fast. Again, the trapezoidal rule is least accurate and the other three rules all perform very well, but a closer look shows that the Gauss-Patterson rule is again the best performer.

Figure 5. Performance comparison of the MDI-SG algorithm with

q = 10, m = 10, s = 1

, and

r = 1, 2, 3, 4

Figure 5. Performance comparison of the MDI-SG algorithm with

q = 10, m = 10, s = 1

, and

r = 1, 2, 3, 4

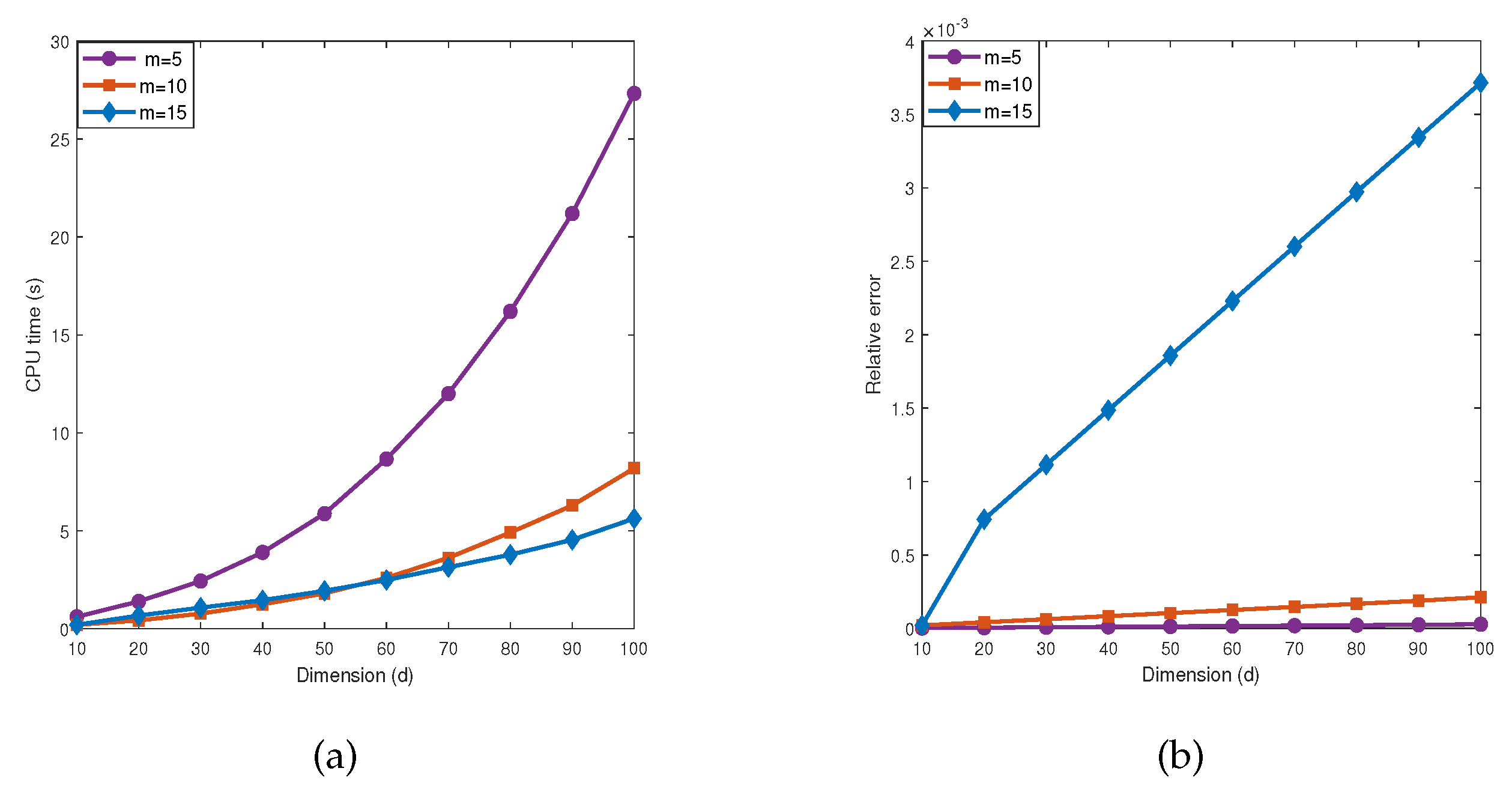
5.2. Influence of parameter m

From the Table 5 and Table 6 and Figure 6 and Figure 7, we observe that when

m = 1

is fixed, as the dimension d increases, the number of iterations by the MDI-SG algorithm also increases, and the computational efficiency decreases rapidly. In practice, the step size m of the MDI-SG algorithm in the first stage iteration should not be too large or too small. One strategy is to use variable step sizes. After selecting an appropriate initial step size m, it can be decreased during the dimension iteration. The next test presents a performance comparison of the MDI-SG algorithm for

m < q, m = q, m > q

Test 7. Let

Ω = {[- 1, 1]}^{d}

, f and

\hat{f}

be the same as in (35).

We compute these integrals using the MDI-SG algorithm with

s = 1, r = 3

(Gauss-Patterson rule) and

q = 10

Figure 6 presents the computed results of integral

I (f)

in Test 7 by the MDI-SG algorithm. It is easy to see that the accuracy and efficiency of the MDI-SG algorithm with different m are different, this is because the step size m affects the number of iterations in the first stage. It shows that the larger step size m, the smaller the number of iterations and the number of symbolic functions that need to be saved, and the fewer CPU time are used, but at the expense of decreasing accuracy and higher truncation error. On the other hand, the smaller step size m, the more accurate of the computed results, but at the expense of more CPU time. To explain this observation, we notice that when the step size m is large, each iteration reduces more dimensions, and the number of symbolic functions that need to be saved is less, but the truncation error generated by the system is larger, although the used CPU time is small. When the step size is small, however, more symbolic functions need to be saved. This is because each iteration reduces a small number of dimensions, the error of computed result is smaller, but the used CPU time is larger. We also observed that the MDI-SG algorithm with step size

m \approx q

achieves a good balance between CPU time and accuracy.

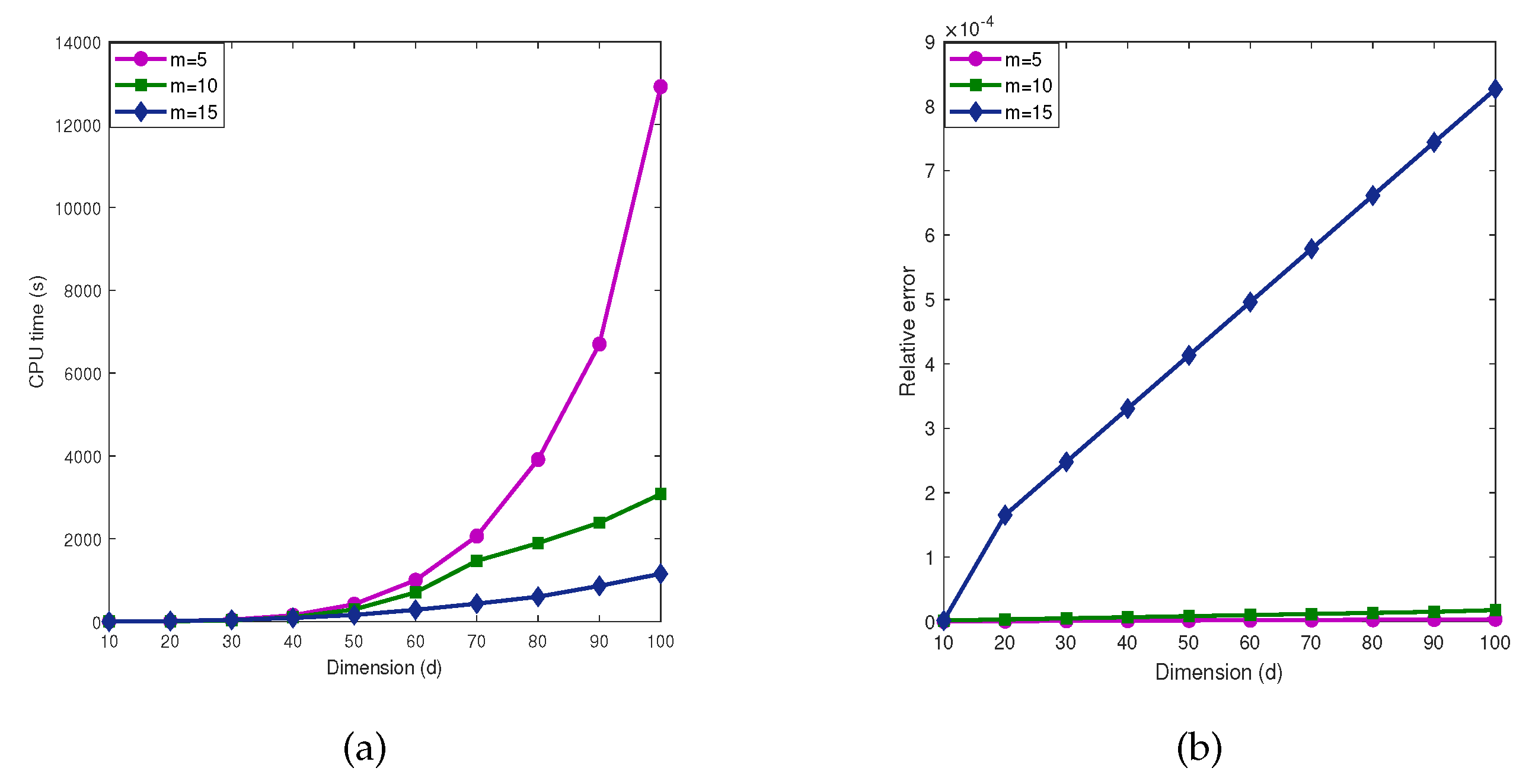
Figure 7 shows the computed results of

I_{d} (\hat{f})

in Test 7 the MDI-SG algorithm. As expected, choosing different parameters m has a significant impact on the accuracy and efficiency of the MDI-SG algorithm. Since function evaluation of the integrand

\hat{f} (x)

is more complicated, the influence of different parameters m on the MDI-SG algorithm is dramatic. Again, the MDI-SG algorithm with step size

m \approx q

strikes a balance between CPU time and accuracy.

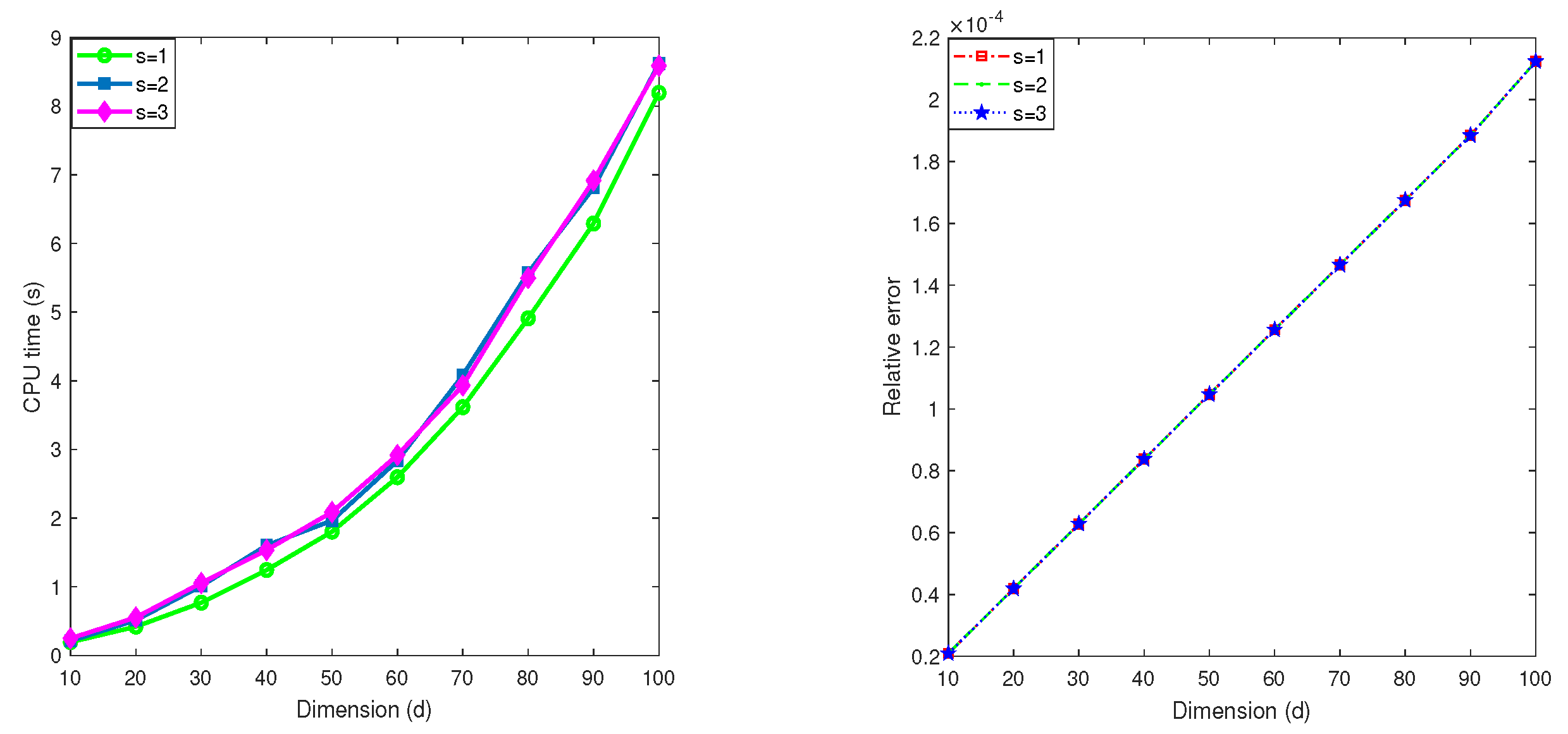
5.3. Influence of the parameter s

In this subsection, we test the impact of the step size s used in the second stage of the MDI-SG algorithm. Recall that the step size

m \approx q

works well in the first stage. After

k : = [\frac{d}{m}]

iterations, the dimension of the integration domain is reduced to

d - k m

which is relatively small, hence, s should be small. In practice, we have

1 \leq s \leq 3

. The goal of the next test is to provide a performance comparison of the MDI-SG algorithm with

s = 1, 2, 3

Test 8. Let

Ω = {[- 1, 1]}^{d}

, and choose the integrand f as

f (x) = \prod_{i = 0}^{d} \frac{1}{0 . 9^{2} + {(x_{i} - 0.6)}^{2}} .

(38)

We compute this integral

I (f)

using the MDI-SG algorithm with

m = 10, r = 3

(Gauss-Patterson rule) and

q = 10

. Figure 8 displays the computed results. We observe that the same accuracy is achieved in all cases

s = 1, 2, 3

, which is expected. Moreover, the choice of s has little effect on the efficiency of the algorithm. An explanation for this observation is that because

d - k m

becomes small after the first stage iterations, so the number of the second stage iterations is small, the special way of performing function evaluations in the MDI-SG algorithm is not sensitive to the small variations in the choice of

s = 1, 2, 3

5.4. Influence of the parameter q or N

Finally, we examine the impact of the accuracy level q on the MDI-SG algorithm. Recall that the parameter q in the SG method is related to the number of integration points N in one coordinate direction on the boundary. It is easy to check that for the trapezoidal (

r = 1

) and Clenshaw Curtis (

r = 2

) quadrature rules,

q = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

correspond to

N = 1, 3, 5, 9, 9, 17, 17, 17, 17, 33

, for the Gauss-Patterson quadrature rule (

r = 3

q = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10

correspond to

N = 1, 3, 3, 7, 7, 7, 15, 15, 15, 15

, and for the Gauss-Legendre quadrature rule (

r = 4

q = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14

correspond to

N = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14

. Therefore, we only need to examine the impact of the parameter N on the MDI-SG algorithm. To the end, we consider the case

m = 1, s = 1

, and

r = 4

(Gauss-Legendre rule) in the next test.

Test 8. Let

Ω = {[- 1, 1]}^{d}

and choose the following integrands:

\begin{matrix} f (x) = exp (\sum_{i = 1}^{d} {(- 1)}^{i + 1} x_{i}), \hat{f} (x) = cos (2 π + \sum_{i = 1}^{d} x_{i}), \tilde{f} (x) = \prod_{i = 0}^{d} \frac{1}{0 . 9^{2} + {(x_{i} - 0.6)}^{2}} . \end{matrix}

Table 10, Table 11, and Table 12 present respectively the computed results for

d = 5, 10

and

N = 4, 6, 8, 10, 12, 14

. We observe that the quality of approximations also depends on the behavior of the integrand. For very oscillatory and rapidly growing functions, more integration points must be used to achieve good accuracy.

6. Computational complexity

6.1. The relationship between the CPU time and N

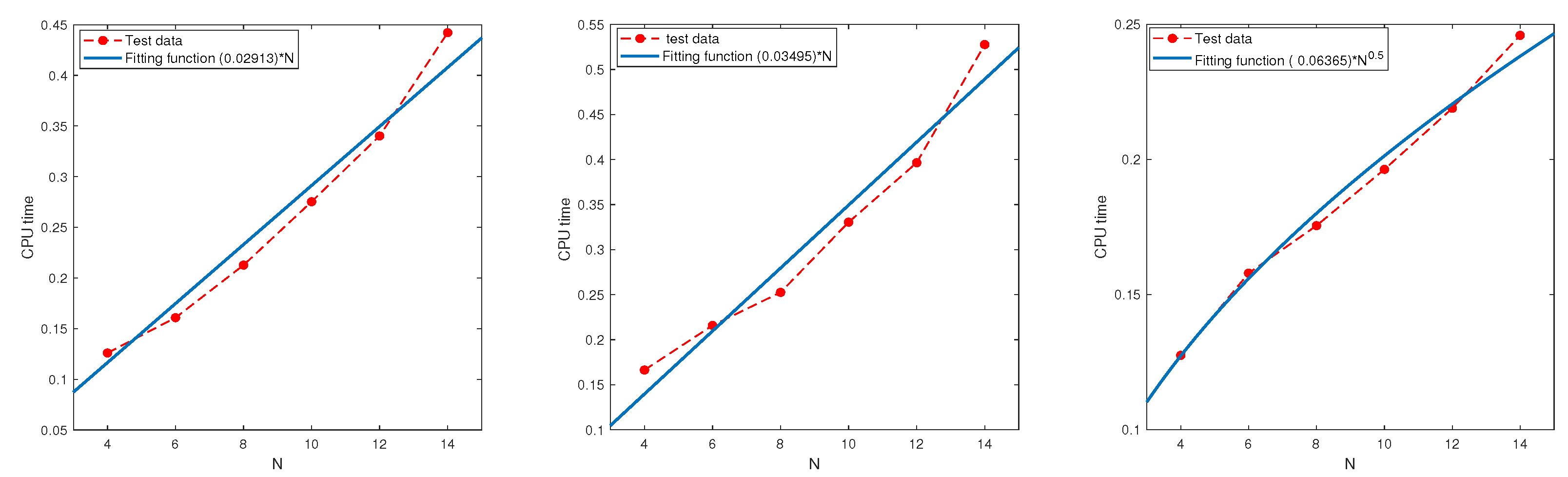
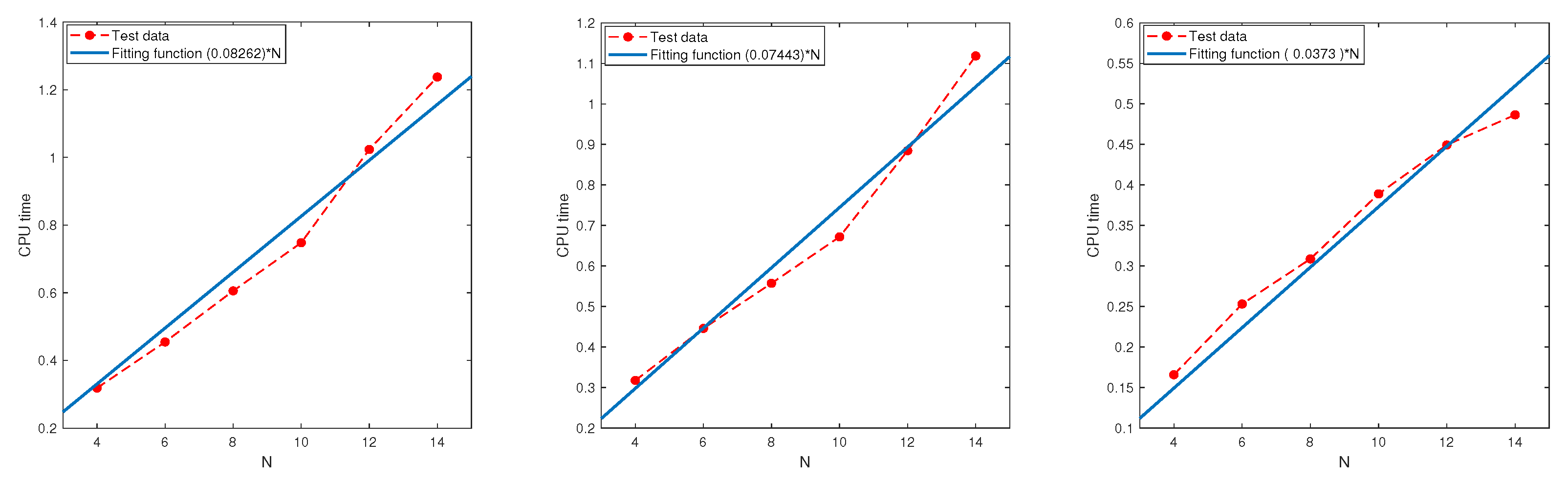
In this subsection, we examine the relationship between the CPU time and parameter N using the regression technique based on the test data.

Test 9. Let

Ω, f, \tilde{f}

, and

\tilde{f}

be the same as in Test 8.

Figure 9 and Figure 10 show the CPU time as a function of N obtained by the least square method and the fitting functions are given in Table 13. All the results indicate that the CPU time grows at most linearly in N.

6.2. The relationship between the CPU time and the dimension d

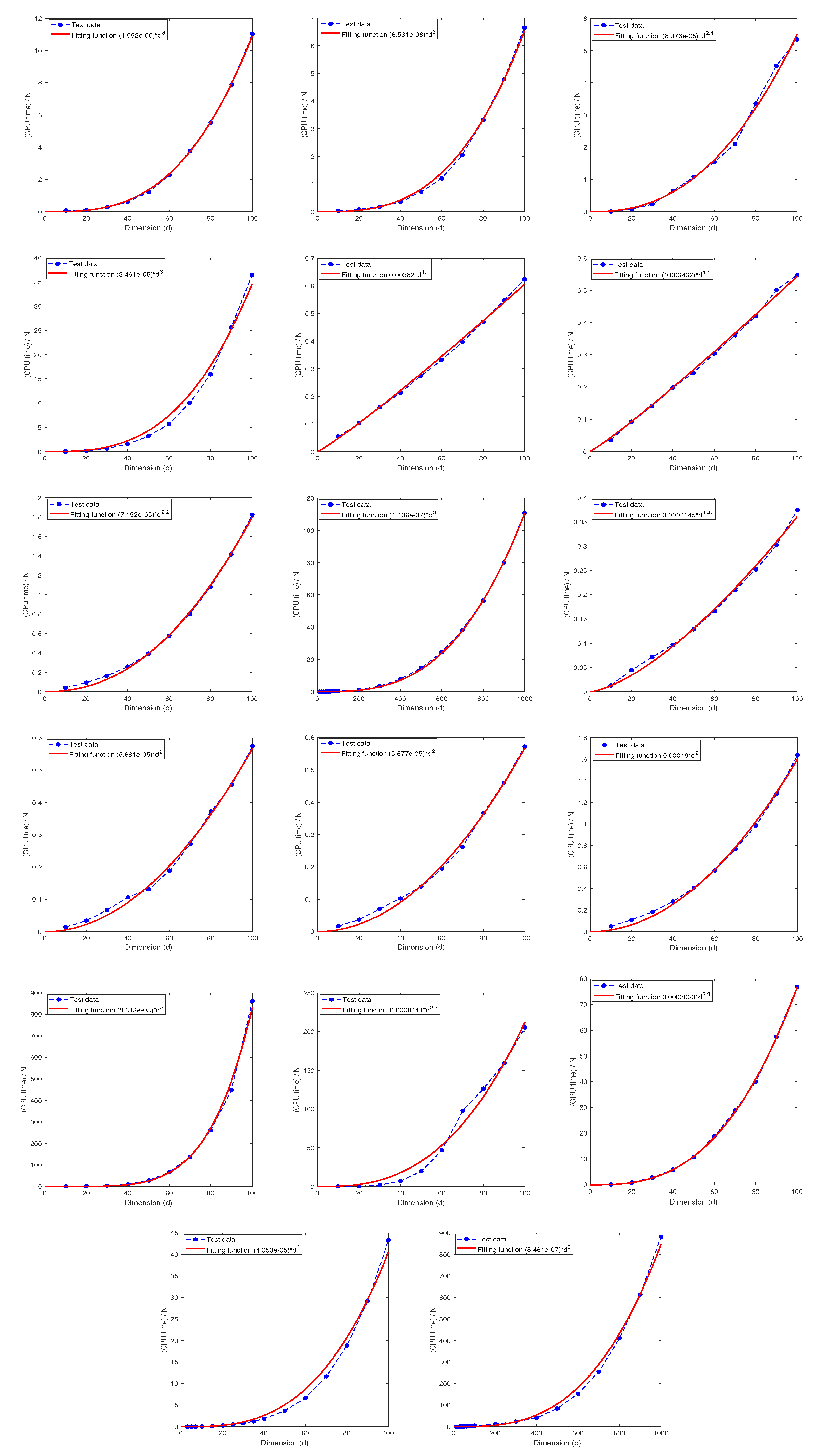
Recall that the computational complexity of the sparse grid method is of the order

O (N \cdot {(log N)}^{d - 1})

for computing

I_{d} (f)

, which grows exponentially in d with base

log N

. The numerical tests presented above overwhelmingly and consistently indicate that the MDI-SG algorithm has hidden capability to overcome the curse of dimensionality which hampers the sparse grid method. The goal of this subsection is to find out the computational complexity of the MDI-SG algorithm (in terms of CPU time as a function of d) using the regression technique based on numerical test data.

Test 10. Let

Ω = {[0, 1]}^{d}

and consider the following five integrands:

\begin{matrix} f_{1} (x) = exp (\sum_{i = 1}^{d} {(- 1)}^{i + 1} x_{i}), & f_{2} (x) = \prod_{i = 0}^{d} \frac{1}{0 . 9^{2} + {(x_{i} - 0.6)}^{2}}, \\ f_{3} (x) = \frac{1}{\sqrt{2 π}} exp (- \frac{1}{2} {| x |}^{2}), & f_{4} (x) = cos (2 π + \sum_{i = 1}^{d} x_{i}), \\ f_{5} (x) = \frac{1}{2^{d}} exp (\sum_{i = 1}^{d} {(- 1)}^{i + 1} x_{i}) . \end{matrix}

Figure 11 displays the CPU time as functions of d obtained by the least square regression method whose analytical expressions are given in Table 14. We note that the parameters of the MDI-SG algorithm only affect the coefficients of the fitting functions, but not their orders in d.

We also quantitatively characterize the performance of the fitted curve by the R-square in Matlab, which is defined as R-

square = 1 - \frac{\sum_{i}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}}{\sum_{i}^{n} {(y_{i} - \bar{y})}^{2}}

. Where

y_{i}

represents a test data output,

{\hat{y}}_{i}

refers to the predicted value, and

\bar{y}

indicates the mean value of

y_{i}

. Table 14 also shows that the R-square of all fitting functions is very close to 1, which indicates that the fitting functions are quite accurate. These results suggest that the CPU time grows at most cubically in d. Combining the results of Test 8 in Section 5.4 we conclude that the CPU time required by the proposed MDI-SG algorithm grows at most in the polynomial order

O (d^{3} N)

7. Conclusions

This paper presented an efficient and fast implementation algorithm (or solver), called the MDI-SG algorithm, for high-dimensional numerical integration using the sparse grid method. It is based on combining the idea of dimension iteration/reduction combined with the idea of computing the function evaluations at all integration points in cluster so many computations can be reused. It was showed numerically that the computational complexity (in terms of the CPU time) of the MDI-SG algorithm grows at most cubically in the dimension d, and overall in the order

O (N d^{3})

, where N denotes the maximum number of integration points in each coordinate direction. This shows that the MDI-SG algorithm could effectively circumvent the curse of the dimensionality in high-dimensional numerical integration, hence, makes sparse grid methods not only become competitive but also can excel for the job. Extensive numerical tests were provided to examine the performance of the MDI-SG algorithm and to carry out performance comparisons with the standard sparse grid method and with the Monte Carlo (MC) method. It was showed that the MDI-SG algorithm (regardless the choice of the 1-d base sparse grid quadrature rules) is faster than the MC method in low and medium dimensions (i.e.,

d ≲ 100

), much faster in very high dimensions (i.e.,

d \approx 1000

), and succeeds even when the MC method fails. An immediate application of the proposed MDI-SG algorithm is to solve high-dimensional linear PDEs based on the integral equation formulation, which will be reported in a forthcoming work.

Author Contributions

Conceptualization, X.F.; methodology, H.Z. and X.F.; code and simulation. H.Z.; writing—original draft preparation, H.Z..; writing—revision and editing, X.F. All authors have read and agreed to the published version of the manuscript.

Funding

The work of X.F. was partially supported by the NSF grants: DMS-2012414 and DMS-230962.

Data Availability Statement

All datasets generated during the current study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

M. Griebel and M. Holtz, Dimension-wise integration of high-dimensional functions with applications to finance, J. Complexity, 26:455–489, 2010.
S. M. LaValle, K. J. Moroney and S. A. Hutchinson, Methods for numerical integration of high-dimensional posterior densities with application to statistical image models, IEEE transactions on image processing, 6(12): 1659–1672, 1997.
J. Barraquand and D. Martineau, Numerical valuation of high dimensional multivariate American securities, Journal of financial and quantitative analysis, 30(3): 383–405, 1995.
J . Quackenbush, Extracting biology from high-dimensional biological data, Journal of Experimental Biology, 210(9):1507–1517, 2007.
H.-J. Bungartz and M. Griebel, Sparse grids, Acta Numer., 13:147–269, 2014.
J. Dos Santos Azevedo and S. Pomponet Oliveira, A numerical comparison between quasi-Monte Carlo and sparse grid stochastic collocation methods, Commun. Comput. Phys., 12:1051–1069, 2012.
T. Gerstner and M. Griebel, Numerical integration using sparse grids, Numerical algorithms, 18(3): 209–232, 1998.
R. E. Caflisch, Monte Carlo and quasi-Monte Carlo methods, Acta Numer., 7:1–49, 1998.
Y. Ogata, A Monte Carlo method for high dimensional integration, Numer. Math., 55:137–157, 1989.
J. Dick, F. Y. Kuo, and I. H. Sloan, High-dimensional integration: the quasi-Monte Carlo way, Acta Numer., 22:133–288, 2013.
F. J. Hickernell, T. Müller-Gronbach, B. Niu, and K. Ritter, Multi-level Monte Carlo algorithms for infinite-dimensional integration on R^N, J. Complexity 26:229–254, 2010.
F. Y. Kuo, C. Schwab, and I. H. Sloan, Quasi-Monte Carlo methods for high-dimensional integration: the standard (weighted Hilbert space) setting and beyond, ANZIAM J., 53:1–37, 2011.
J. Lu and L. Darmofal, Higher-dimensional integration with Gaussian weight for applications in probabilistic design, SIAM J. Sci. Comput., 26:613–624, 2004.
A. Wipf, High-Dimensional Integrals, in Statistical Approach to Quantum Field Theory, Springer Lecture Notes in Physics, 100:25–46, 2013.
W. E and B. Yu, The deep Ritz method: A deep learning-based numerical algorithm for solving variational problems, Commun. Math. and Stat., 6:1–12, 2018.
J. Han, A. Jentzen, and W. E, Solving high-dimensional partial differential equations using deep learning, PNAS, 115:8505–8510, 2018.
L. Lu, X. Meng, Z. Mao, and G. E. Karniadakis, DeepXDE: A deep learning library for solving differential equations, SIAM Rev., 63:208–228, 2021.
J. Sirignano and K. Spiliopoulos, DGM: A deep learning algorithm for solving partial differential equations, J. Comput. Phys., 375:1339–1364, 2018.
J. Xu, Finite neuron method and convergence analysis, Commun. Comput. Phys, 28:1707–1745, 2020.
X. Feng and H. Zhong, A fast multilevel dimension iteration algorithm for high dimensional numerical integration. preprint.
R. L. Burden and J. D. Faires, Numerical Analysis, 10th edition, Cengage Learning, 2015.
S. A. Smolyak, Quadrature and interpolation formulas for tensor products of certain classes of functions, Russian Academy of Sciences., 148(5): 1042–1045, 1963.
G. Baszenki and F. -J. Delvos, Multivariate Boolean midpoint rules, Numerical Integration IV, Birkhäuser, Basel, 1–11, 1993.
S. H. Paskov, Average case complexity of multivariate integration for smooth functions, Journal of Complexity, 9(2): 291–312, 1993.
T. Bonk, A new algorithm for multi-dimensional adaptive numerical quadrature,Adaptive Methods—Algorithms, Theory and Applications, Vieweg+ Teubner Verlag, Wiesbaden, 54–68, 1994.
E. Novak and K. Ritter, High dimensional integration of smooth functions over cubes, Numerische Mathematik, 75(1):79–97, 1996.
E. Novak and K. Ritter, The curse of dimension and a universal method for numerical integration,Multivariate approximation and splines. Birkhäuser, Basel, 177–187, 1997.
E. Novak and K. Ritter, Simple cubature formulas for d-dimensional integrals with high polynomial exactness and small error, Report, Institut für Mathematik, Universität Erlangen–Nürnberg, 1997.
T. N. L. PattersonThe optimum addition of points to quadrature formulae, Math. Comp., 22(104): 847–856, 1968.

Figure 1. Construction of a nested sparse grid in two dimensions.

Figure 2. Sparse grids corresponding to the trapezoidal rule (a), Clenshaw-Curtis rule (b), Gauss-Patterson rule (c), and Gauss-Legendre rule (d) when

d = 2, q = 6

Figure 2. Sparse grids corresponding to the trapezoidal rule (a), Clenshaw-Curtis rule (b), Gauss-Patterson rule (c), and Gauss-Legendre rule (d) when

d = 2, q = 6

Figure 3. Sparse grids corresponding to the trapezoidal rule (a), Clenshaw-Curtis rule (b), Gauss-Patterson rule (c), and Gauss-Legendre rule (d) when

d = 3, q = 7

Figure 3. Sparse grids corresponding to the trapezoidal rule (a), Clenshaw-Curtis rule (b), Gauss-Patterson rule (c), and Gauss-Legendre rule (d) when

d = 3, q = 7

Figure 4. CPU time comparison of MDI-SG and SG tests:

q = 8

(left),

q = 10

(middle),

q = 12

(right).

Figure 4. CPU time comparison of MDI-SG and SG tests:

q = 8

(left),

q = 10

(middle),

q = 12

(right).

Figure 6. Efficiency and accuracy comparison of the MDI-SG algorithm with

q = 10

r = 3, s = 1

and

m = 5, 10, 15

for approximating

I_{d} (f)

Figure 6. Efficiency and accuracy comparison of the MDI-SG algorithm with

q = 10

r = 3, s = 1

and

m = 5, 10, 15

for approximating

I_{d} (f)

Figure 7. Efficiency and accuracy comparison of the MDI-SG algorithm with

q = 10

r = 3, s = 1

and

m = 5, 10, 15

for approximating

I_{d} (\hat{f})

Figure 7. Efficiency and accuracy comparison of the MDI-SG algorithm with

q = 10

r = 3, s = 1

and

m = 5, 10, 15

for approximating

I_{d} (\hat{f})

Figure 8. Efficiency comparison of the MDI-SG algorithm with

r = 3

and

s = 1, 2, 3

Figure 8. Efficiency comparison of the MDI-SG algorithm with

r = 3

and

s = 1, 2, 3

Figure 9. The relationship between the CPU time and parameter N when

d = 5

for computing

I_{d} (f)

(left),

I_{d} (\hat{f})

(middle),

I_{d} (\tilde{f})

(right).

Figure 9. The relationship between the CPU time and parameter N when

d = 5

for computing

I_{d} (f)

(left),

I_{d} (\hat{f})

(middle),

I_{d} (\tilde{f})

(right).

Figure 10. The relationship between the CPU time and parameter N when

d = 10

for computing

I_{d} (f)

(left),

I_{d} (\hat{f})

(middle),

I_{d} (\tilde{f})

(right).

Figure 10. The relationship between the CPU time and parameter N when

d = 10

for computing

I_{d} (f)

(left),

I_{d} (\hat{f})

(middle),

I_{d} (\tilde{f})

(right).

Figure 11. The relationship between the CPU time and dimension d.

Table 1. Relative errors and CPU times of MDI-SG and SG tests with

m = 1

for approximating

I_{2} (f)

Table 1. Relative errors and CPU times of MDI-SG and SG tests with

m = 1

for approximating

I_{2} (f)

		MDI-SG		SG
Accuracy level $(q)$	Total nodes	Relative error	CPU time(s)	Relative error	CPU time(s)
6	33	$1.0349 \times 10^{- 1}$	0.0512817	$1.0349 \times 10^{- 1}$	0.0078077
7	65	$2.3503 \times 10^{- 3}$	0.0623538	$2.3503 \times 10^{- 3}$	0.0084645
9	97	$8.1019 \times 10^{- 4}$	0.0644339	$8.1019 \times 10^{- 4}$	0.0095105
10	161	$1.8229 \times 10^{- 6}$	0.0724491	$1.8229 \times 10^{- 6}$	0.0106986
13	257	$2.0720 \times 10^{- 7}$	0.0913161	$2.0720 \times 10^{- 7}$	0.0135131
14	321	$4.3279 \times 10^{- 7}$	0.1072016	$4.3279 \times 10^{- 7}$	0.0155733

Table 2. Relative errors and CPU times of MDI-SG and SG tests with

m = 1

for approximating

I_{2} (\hat{f}

Table 2. Relative errors and CPU times of MDI-SG and SG tests with

m = 1

for approximating

I_{2} (\hat{f}

		MDI-SG		SG
Accuracy level $(q)$	Total nodes	Relative error	CPU time(s)	Relative error	CPU time(s)
9	97	$4.7425 \times 10^{- 1}$	0.0767906	$4.7425 \times 10^{- 1}$	0.0098862
10	161	$1.4459 \times 10^{- 3}$	0.0901238	$1.4459 \times 10^{- 3}$	0.0102700
13	257	$1.9041 \times 10^{- 5}$	0.1025934	$1.9041 \times 10^{- 5}$	0.0152676
14	321	$2.3077 \times 10^{- 5}$	0.1186194	$2.3077 \times 10^{- 5}$	0.0144737
16	449	$3.1236 \times 10^{- 6}$	0.1353691	$3.1236 \times 10^{- 6}$	0.0177445
20	705	$2.4487 \times 10^{- 6}$	0.1880289	$2.4487 \times 10^{- 6}$	0.0355606

Table 3. Relative errors and CPU times of MDI-SG and SG tests with

m = 1

for approximating

I_{3} (f)

Table 3. Relative errors and CPU times of MDI-SG and SG tests with

m = 1

for approximating

I_{3} (f)

		MDI-SG		SG
Accuracy level $(q)$	Total nodes	Relative error	CPU time(s)	Relative error	CPU time(s)
9	495	$3.2467 \times 10^{- 2}$	0.0669318	$3.2467 \times 10^{- 2}$	0.0235407
10	751	$1.8956 \times 10^{- 3}$	0.0886774	$1.8956 \times 10^{- 3}$	0.0411750
11	1135	$3.9146 \times 10^{- 4}$	0.0902602	$3.9146 \times 10^{- 4}$	0.0672375
13	1759	$4.7942 \times 10^{- 6}$	0.1088353	$4.7942 \times 10^{- 6}$	0.0589584
14	2335	$1.8013 \times 10^{- 6}$	0.1381728	$1.8013 \times 10^{- 6}$	0.0704032
15	2527	$1.2086 \times 10^{- 6}$	0.1484829	$1.2086 \times 10^{- 6}$	0.0902680
16	3679	$3.6938 \times 10^{- 7}$	0.1525743	$3.6938 \times 10^{- 7}$	0.1143728

Table 4. Relative errors and CPU times of MDI-SG and SG tests with

m = 1

for approximating

I_{3} (\hat{f})

Table 4. Relative errors and CPU times of MDI-SG and SG tests with

m = 1

for approximating

I_{3} (\hat{f})

		MDI-SG		SG
Accuracy level $(q)$	Total nodes	Relative error	CPU time(s)	Relative error	CPU time(s)
12	1135	$5.5057 \times 10^{- 1}$	0.0921728	$5.5057 \times 10^{- 1}$	0.0495310
13	1759	$8.9519 \times 10^{- 3}$	0.1031632	$8.9519 \times 10^{- 3}$	0.0644124
15	2527	$1.8063 \times 10^{- 3}$	0.1771094	$1.8063 \times 10^{- 3}$	0.0891040
16	3679	$1.1654 \times 10^{- 4}$	0.1957219	$1.1654 \times 10^{- 4}$	0.1159222
17	4447	$2.4311 \times 10^{- 5}$	0.2053174	$2.4311 \times 10^{- 5}$	0.1443184
19	6495	$5.4849 \times 10^{- 6}$	0.4801467	$5.4849 \times 10^{- 6}$	0.2259950
20	8031	$1.5333 \times 10^{- 6}$	0.6777698	$1.5333 \times 10^{- 6}$	0.2632516

Table 5. Relative errors and CPU times of MDI-SG and SG tests with

m = 1, s = 1

, and

q = 10

for approximating

I_{d} (f)

Table 5. Relative errors and CPU times of MDI-SG and SG tests with

m = 1, s = 1

, and

q = 10

for approximating

I_{d} (f)

		MDI-SG		SG
Dimension (d)	Total nodes	Relative error	CPU time(s)	Relative error	CPU time(s)
2	161	$1.0163 \times 10^{- 8}$	0.0393572	$1.0163 \times 10^{- 8}$	0.0103062
4	2881	$2.0310 \times 10^{- 8}$	0.0807326	$2.0310 \times 10^{- 8}$	0.0993984
8	206465	$1.3429 \times 10^{- 7}$	0.1713308	$1.3429 \times 10^{- 7}$	6.7454179
10	1041185	$1.6855 \times 10^{- 6}$	0.2553576	$1.6855 \times 10^{- 6}$	86.816883
12	4286913	$1.8074 \times 10^{- 5}$	0.3452745	$1.8074 \times 10^{- 5}$	866.1886366
14	5036449	$2.1338 \times 10^{- 4}$	0.4625503	$2.1338 \times 10^{- 4}$	6167.3838002
15	12533167	$7.1277 \times 10^{- 4}$	0.5867914	failed	failed

Table 6. Relative errors and CPU times of MDI-SG and SG tests with

m = 1, s = 1

, and

q = 12

for approximating

I_{d} (f)

Table 6. Relative errors and CPU times of MDI-SG and SG tests with

m = 1, s = 1

, and

q = 12

for approximating

I_{d} (f)

		MDI-SG		SG
Dimension (d)	Total nodes	Relative error	CPU time(s)	Relative error	CPU time(s)
2	161	$1.0198 \times 10^{- 8}$	0.0418615	$1.0198 \times 10^{- 8}$	0.0191817
4	6465	$2.0326 \times 10^{- 8}$	0.0704915	$2.0326 \times 10^{- 8}$	0.2067346
6	93665	$3.0487 \times 10^{- 8}$	0.0963325	$3.0487 \times 10^{- 8}$	3.1216913
8	791169	$4.0881 \times 10^{- 8}$	0.2233707	$4.0881 \times 10^{- 8}$	41.3632962
10	5020449	$4.0931 \times 10^{- 8}$	0.3740873	$4.0931 \times 10^{- 8}$	821.6461622
12	25549761	$1.1560 \times 10^{- 6}$	0.8169479	$1.1560 \times 10^{- 6}$	11887.797686
13	29344150	$5.2113 \times 10^{- 6}$	1.2380811	failed	failed

Table 7. CPU times of the MDI-SG and MC tests with comparable relative errors for approximating

I_{d} (f)

Table 7. CPU times of the MDI-SG and MC tests with comparable relative errors for approximating

I_{d} (f)

		MC		MDI-SG
Dimension (d)	Relative error	CPU time(s)	Relative error	CPU time(s)
5	$1.3653 \times 10^{- 5}$	62.1586394	$1.3653 \times 10^{- 5}$	0.0938295
10	$2.0938 \times 10^{- 5}$	514.1493073	$2.0938 \times 10^{- 5}$	0.1945813
20	$4.2683 \times 10^{- 5}$	1851.0461899	$4.1876 \times 10^{- 5}$	0.4204564
30	$6.2814 \times 10^{- 5}$	15346.222011	$6.2814 \times 10^{- 5}$	0.7692118
35	$7.3283 \times 10^{- 5}$	failed	$7.3283 \times 10^{- 5}$	0.9785784
40	$8.3752 \times 10^{- 5}$		$8.3752 \times 10^{- 5}$	1.2452577
60	$1.2562 \times 10^{- 4}$		$1.2562 \times 10^{- 4}$	2.5959174
80	$1.6750 \times 10^{- 4}$		$1.6750 \times 10^{- 4}$	4.9092032
100	$2.1235 \times 10^{- 4}$		$2.1235 \times 10^{- 4}$	8.1920274

Table 8. CPU times of the MDI-SG and MC tests with comparable relative errors for approximating

I_{d} (\hat{f})

Table 8. CPU times of the MDI-SG and MC tests with comparable relative errors for approximating

I_{d} (\hat{f})

		MC		MDI-SG
Dimension (d)	Relative error	CPU time(s)	Relative error	CPU time(s)
5	$9.4279 \times 10^{- 7}$	85.2726354	$9.4279 \times 10^{- 7}$	0.0811157
10	$1.6855 \times 10^{- 6}$	978.1462121	$1.6855 \times 10^{- 6}$	0.295855
20	$3.3711 \times 10^{- 6}$	2038.138555	$3.3711 \times 10^{- 6}$	6.3939110
30	$5.0567 \times 10^{- 6}$	16872.143255	$5.0567 \times 10^{- 6}$	29.5098187
35	$5.8995 \times 10^{- 6}$	failed	$5.8995 \times 10^{- 6}$	62.0270714
40	$6.7423 \times 10^{- 6}$		$6.7423 \times 10^{- 6}$	106.1616486
80	$1.3484 \times 10^{- 5}$		$1.3484 \times 10^{- 5}$	1893.8402620
100	$1.7825 \times 10^{- 5}$		$1.7825 \times 10^{- 5}$	3077.1890005

Table 9. Computed results for

I_{d} (f)

and

I_{d} (\hat{f})

by the MDI-SG algorithm.

Table 9. Computed results for

I_{d} (f)

and

I_{d} (\hat{f})

by the MDI-SG algorithm.

		$I_{d} (f)$		$I_{d} (\hat{f})$
Dimension (d)	Approximate Total nodes	Relative error	CPU time(s)	Relative error	CPU time(s)
10	$1.0411 \times 10^{6}$	$1.4725 \times 10^{- 6}$	0.1541	$2.0938 \times 10^{- 5}$	0.1945
100	$1.4971 \times 10^{60}$	$1.5125 \times 10^{- 5}$	80.1522	$2.1235 \times 10^{- 4}$	8.1920
300	$3.3561 \times 10^{180}$	$4.5377 \times 10^{- 5}$	348.6000	$6.3714 \times 10^{- 4}$	52.0221
500	$7.5230 \times 10^{300}$	$7.7786 \times 10^{- 5}$	1257.3354	$1.0621 \times 10^{- 3}$	219.8689
700	$1.6767 \times 10^{421}$	$1.0890 \times 10^{- 4}$	3827.5210	$1.4869 \times 10^{- 3}$	574.9161
900	$3.7524 \times 10^{541}$	$1.4001 \times 10^{- 4}$	9209.119	$1.9117 \times 10^{- 3}$	1201.65
1000	$5.6136 \times 10^{601}$	$1.5557 \times 10^{- 4}$	13225.14	$2.3248 \times 10^{- 3}$	1660.84

Table 10. Performance comparison of the MDI-SG algorithm with

q, N = 4, 6, 8, 10, 12, 14

for computing

I_{d} (f)

Table 10. Performance comparison of the MDI-SG algorithm with

q, N = 4, 6, 8, 10, 12, 14

for computing

I_{d} (f)

$q (N)$	$d = 5$			$d = 10$
$q (N)$	Approximate total nodes	Relative error	CPU time(s)	Approximate total nodes	Relative error	CPU time(s)
4(4)	241	$3.8402 \times 10^{- 3}$	0.1260	1581	$5.7516 \times 10^{- 2}$	0.3185
6(6)	2203	$1.6039 \times 10^{- 5}$	0.1608	40405	$2.3524 \times 10^{- 3}$	0.4546
8(8)	13073	$1.7195 \times 10^{- 8}$	0.2127	581385	$3.6774 \times 10^{- 5}$	0.6056
10(10)	58923	$6.4718 \times 10^{- 12}$	0.2753	5778965	$2.2885 \times 10^{- 7}$	0.7479
12(12)	218193	$1.8475 \times 10^{- 12}$	0.3402	44097173	$2.2746 \times 10^{- 9}$	1.0236
14(14)	695083	$8.0013 \times 10^{- 12}$	0.4421	112613833	$3.8894 \times 10^{- 11}$	1.2377

Table 11. Performance comparison of the MDI-SG algorithm with

q, N = 4, 6, 8, 10, 12, 14

for computing

I_{d} (\hat{f})

Table 11. Performance comparison of the MDI-SG algorithm with

q, N = 4, 6, 8, 10, 12, 14

for computing

I_{d} (\hat{f})

$q (N)$	$d = 5$			$d = 10$
$q (N)$	Approximate total nodes	Relative error	CPU time(s)	Approximate total nodes	Relative error	CPU time(s)
4(4)	241	$1.4290 \times 10^{- 2}$	0.1664	1581	$8.1129 \times 10^{- 1}$	0.3174
6(6)	2203	$6.1319 \times 10^{- 5}$	0.2159	40405	$3.6823 \times 10^{- 2}$	0.4457
8(8)	13073	$6.6347 \times 10^{- 8}$	0.2526	581385	$5.8931 \times 10^{- 4}$	0.5571
10(10)	58923	$2.5247 \times 10^{- 11}$	0.3305	5778965	$3.8749 \times 10^{- 6}$	0.6717
12(12)	218193	$1.7163 \times 10^{- 12}$	0.3965	44097173	$2.2490 \times 10^{- 8}$	0.8843
14(14)	695083	$8.2889 \times 10^{- 12}$	0.5277	112613833	$8.7992 \times 10^{- 10}$	1.1182

Table 12. Performance comparison of the MDI-SG algorithm with

q, N = 4, 6, 8, 10, 12, 14

for computing

I_{d} (\tilde{f})

Table 12. Performance comparison of the MDI-SG algorithm with

q, N = 4, 6, 8, 10, 12, 14

for computing

I_{d} (\tilde{f})

$q (N)$	$d = 5$			$d = 10$
$q (N)$	Approximate total nodes	Relative error	CPU time(s)	Approximate total nodes	Relative error	CPU time(s)
4(4)	241	$6.1894 \times 10^{- 4}$	0.1275	1581	$1.5564 \times 10^{- 2}$	0.1657
6(6)	2203	$1.9354 \times 10^{- 3}$	0.1579	40405	$1.0163 \times 10^{- 2}$	0.2530
8(8)	13073	$1.5488 \times 10^{- 4}$	0.1755	581385	$2.2076 \times 10^{- 3}$	0.3086
10(10)	58923	$1.7878 \times 10^{- 6}$	0.1963	5778965	$1.4304 \times 10^{- 4}$	0.3889
12(12)	218193	$7.0609 \times 10^{- 7}$	0.2189	44097173	$9.3339 \times 10^{- 6}$	0.4493
14(14)	695083	$1.7194 \times 10^{- 8}$	0.2459	112613833	$2.4671 \times 10^{- 7}$	0.4864

Table 13. The relationship between the CPU time and parameter N.

Integrand	r	m	d	Fitting function	R-square
$f (x)$	3	1	5	$h_{1} (N) = (0.02913) * N$	0.9683
$\hat{f} (x)$	3	1	5	$h_{2} (N) = (0.03495) * N$	0.9564
$\tilde{f} (x)$	3	1	5	$h_{3} (N) = (0.06365) * N^{\frac{1}{2}}$	0.9877
$f (x)$	3	1	10	$h_{4} (N) = (0.08262) * N$	0.9692
$\hat{f} (x)$	3	1	10	$h_{5} (N) = (0.07443) * N$	0.9700
$\tilde{f} (x)$	3	1	10	$h_{6} (N) = (0.0373) * N$	0.9630

Table 14. The relationship between CPU time as a function of the dimension d.

Integrand	r	m	s	$q (N)$	Fitting function	R-square
$f_{1}$	1	10	1	10(33)	$g_{1} = (1.092 e - 05) * N d^{3}$	0.9995
	2	10	1	10(33)	$g_{2} = (6.531 e - 06) * N d^{3}$	0.9977
	3	10	1	10(15)	$g_{3} = (8.076 e - 05) * N d^{2.4}$	0.9946
	4	10	1	10(10)	$g_{4} = (3.461 e - 05) * N d^{3}$	0.9892
$f_{2}$	1	10	1	10(33)	$g_{5} = 0.003820 * N d^{1.1}$	0.9985
	2	10	1	10(33)	$g_{6} = 0.003432 * N d^{1.1}$	0.9986
	3	5	1	10(15)	$g_{6} = (7.152 e - 05) * N d^{2.2}$	0.9983
	3	10	1	10(15)	$g_{9} = (1.106 e - 07) * N d^{3}$	0.9998
	3	15	1	10(15)	$g_{7} = 0.0004145 * N d^{1.47}$	0.9955
	3	15	2	10(15)	$g_{7} = (5.681 e - 05) * N d^{2}$	0.9961
	3	15	3	10(15)	$g_{7} = (5.677 e - 05) * N d^{2}$	0.9962
	4	10	1	10(10)	$g_{8} = 0.00016 * N d^{2}$	0.9965
$f_{3}$	3	5	1	10(15)	$g_{11} = (8.312 e - 08) * N d^{3}$	0.9977
	3	10	1	10(15)	$g_{12} = 0.0008441 * N d^{2.7}$	0.9844
	3	15	1	10(15)	$g_{13} = 0.0003023 * N d^{2.8}$	0.9997
$f_{4}$	3	10	1	10(15)	$g_{18} = (4.053 e - 05) * N d^{3}$	0.9903
$f_{5}$	3	10	1	10(15)	$g_{19} = (8.461 e - 07) * N d^{3}$	0.9958

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Efficient and Fast Sparse Grid Algorithm for High-Dimensional Numerical Integration

Abstract

1. Introduction

2. Preliminaries

2.1. The sparse grid method

2.2. Examples of sparse grid methods

3. The MDI-SG algorithm

3.1. Formulation of the MDI-SG algorithm in two dimensions

3.2. Formulation of the MDI-SG algorithm in three dimensions

3.3. Formulation of the MDI-SG algorithm in arbitrary d-dimensions

4. Numerical performance tests

4.1. Two and three-dimensional tests

4.2. High-dimensional tests

5. Influence of parameters

5.1. Influence of parameter r

5.2. Influence of parameter m

5.3. Influence of the parameter s

5.4. Influence of the parameter q or N

6. Computational complexity

6.1. The relationship between the CPU time and N

6.2. The relationship between the CPU time and the dimension d

7. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe