Prerpints.org logo
Preprint
Article

Buddy System Based Alpha Numeric Weight Based Clustering Algorithm with User Threshold

Altmetrics

Downloads

102

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Decision-Making and Data Mining for Sustainable Computing

Submitted:

23 August 2023

Posted:

24 August 2023

You are already at the latest version

Alerts
Abstract
Data is present in the data sources like Files and Data bases, Retrieval of information from that data sources is one of the important issue nowadays. So for retrieval information from the data sources clustering is used. In the present market different types of clustering algorithms were available. But opting of the clustering is based on user requirements. This paper focuses on the study of hierarchical clustering approach on different conditions or measures or with customer choices like clustering process number of clusters generated at each level, number of levels, attributes range for performing the clustering on the given data set. In brief overview we discuss the hierarchical approach for clustering algorithm with the user opting choices.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

I. Introduction

Clustering is a collecting of grouping set of objects where all similar come into one group and dissimilar objects will come into other group [1]. Clustering is a one of the method which is used in the data mining process, feature extraction and data classification. Among all the clustering algorithms, hierarchical clustering approach is a hot topic in the current era. Hierarchical clustering approaches are of two kinds. They were Agglomerative clustering approach and Divisive clustering approach [2]. Divisive approach is a top down approach for clustering the given data set and forms a hierarchical clustering tree. In order to get good clusters from the given data set, we have to go for user preferences. Clustering Process Creates 2 Groups of clusters. They were
Table 1. Types of Objects in the clustering Process.
Table 1. Types of Objects in the clustering Process.
Objects Group Details
Similar All Objects of same type
Dissimilar All Objects of different type
Clustering Distances
For the given data set, the distance between any two clusters is called as Clustering Distance. It is of two types. They were Inter-cluster and Intra cluster Distance.
Table 2. Types of cluster Distances.
Table 2. Types of cluster Distances.
Type of cluster Distance Details
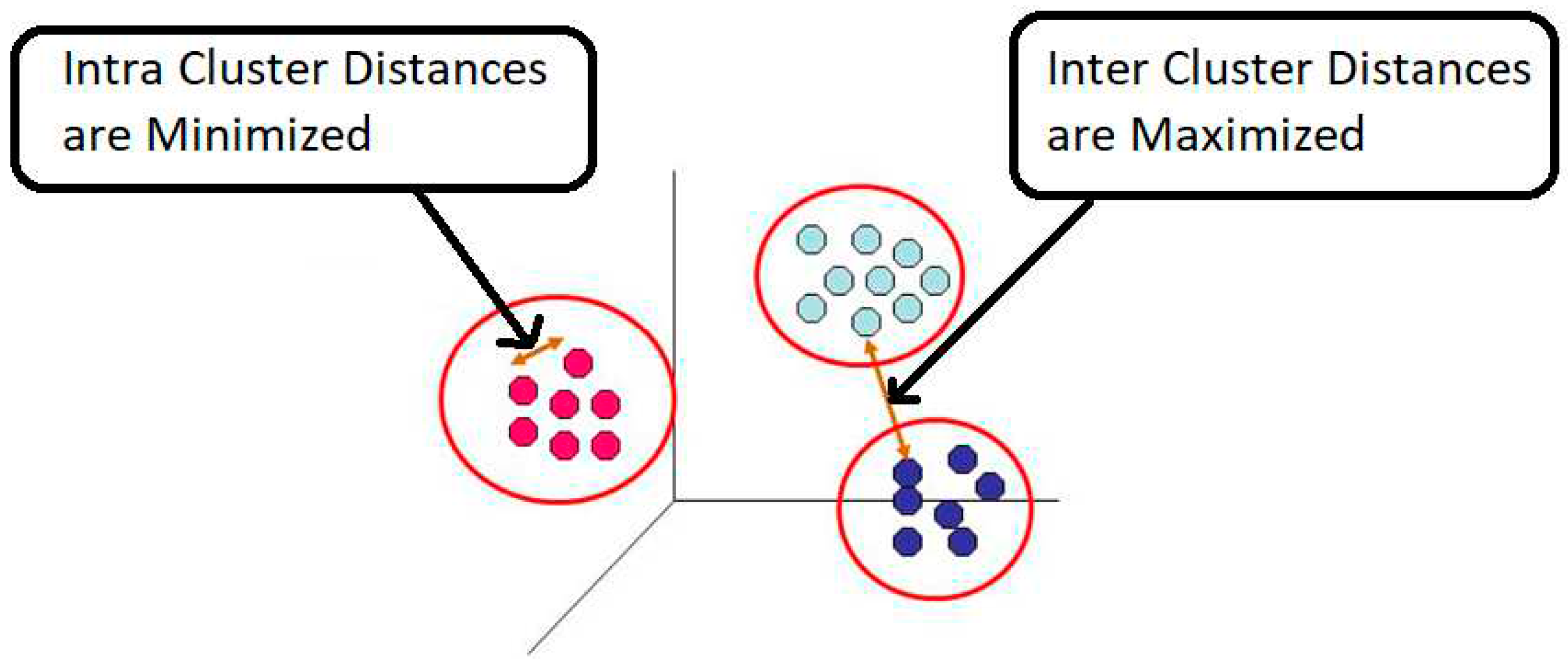
Intra cluster It is the distance between the centroid of a cluster and a data item present within a cluster.
Inter cluster It is the distance between the data items in distinct clusters.
Preprints 83116 g001
Figure 1. Types of cluster Distances.
Figure 1. Types of cluster Distances.
Preprints 83116 g001
Table 3. Clustering Outline.
Table 3. Clustering Outline.
Techniques of Data Mining Clustering, Classification, Association mining, Text mining, Sequential patterns, prediction, Decision trees, and Regression.
Technique Unsupervised
Classes Used for Finite set of classes
Data Mining Task Descriptive
Goal Used for finding similarities in the data set.
Data Set Used for finite set of data
Objects Similarity Defined by similarity function
Table 4. Outline of Supervised and Unsupervised Learning [3].
Table 4. Outline of Supervised and Unsupervised Learning [3].
Property Supervised Learning Unsupervised Learning
Definition It uses datasets which are labeled on algorithms to train, classify data or predict outcomes correctly. Machine learning is used in the Unsupervised Learning concepts to understand, cluster unlabeled datasets.
Number of Classes Unknown Unknown
Labeling Input data Labeled Input data unlabeled
Output Known Unknown
Uses Training Data Set Input Data set
Knowledge Required on Training Set No previous knowledge
Classify Used for later observations data understanding
performance Measure Accurately Indirect / Qualitative
Used for Analysis Prediction
Examples Classification, regression e.t.c Clustering, Association e.t.c
Types of Hierarchical Clustering
It is of two types. They were Divisive and Agglomerative.
Preprints 83116 g002
Figure 2. Types of Hierarchical Clustering.
Figure 2. Types of Hierarchical Clustering.
Preprints 83116 g002
Divisive
It starts with complete data set and divides it into successfully small clusters [4].
Preprints 83116 g003
Figure 3. Divisive Clustering Example.
Figure 3. Divisive Clustering Example.
Preprints 83116 g003
Agglomerative
It starts with single element as a unique cluster and combines them into successfully big clusters [5].
I.e. Data mining means extraction of data from data sources. So, whatever the data extracted will be used by the user. So, we have to take the preferences of the user before the clustering process. So, at the end of the clustering the user will get good Clustering resultsfrom a given dataset.
Preprints 83116 g004
Figure 4. Agglomerative Clustering Example.
Figure 4. Agglomerative Clustering Example.
Preprints 83116 g004
Preprints 83116 g005
Figure 5. Agglomerative and Divisive clustering indicating dendrograms.
Figure 5. Agglomerative and Divisive clustering indicating dendrograms.
Preprints 83116 g005
Applications of Clustering
In the current era the data in the servers is growing day by day so Clustering is used in many Areas such Market Analysis, Outlier Detection, Classification of Documents, Data Mining Function, Pattern Recognition, Image Processing, Anomaly Detection, Medical Image processing, Grouping of Search Results, for the Analysis of Social Networks e.t.c.
Table 5. Clustering Application Areas.
Table 5. Clustering Application Areas.
Clustering Application Areas Clustering Purpose
Market Analysis It is used to identify different groups of people in the Market and to identify their requirement to provide the products Required by the Customers [6].
Outlier Detection It is used in outlier detection applications. Example of credit card fraud [7].
Classification Of Documents It is used to classify the documents in WWW (world wide web) [8].
Data Mining Function It is used in cluster analysis (to observe characteristics of each cluster) [9].
Pattern Recognition It is used in traffic Pattern Recognition to clear traffic problems [10].
Image Processing It is used in Image Processing for segmentation of image [11].
Anomaly Detection It is used in anomaly detection is to study normal modes in the data available and it is used to point out anomalous are there or not [12].
Medical Imaging It is used in Medical Imaging for segmentation of the images and analyzes it [13].
Search Result Grouping It is used in the grouping of search results from the WWW when the users so the Search [14].
Social Network Analysis It is used to merge the entities of a social network into distinct Classes depends on their relationships and links between the classes [15].
e.t.c
Stages of Clustering
Total there are three stages in the clustering process [16]. They were
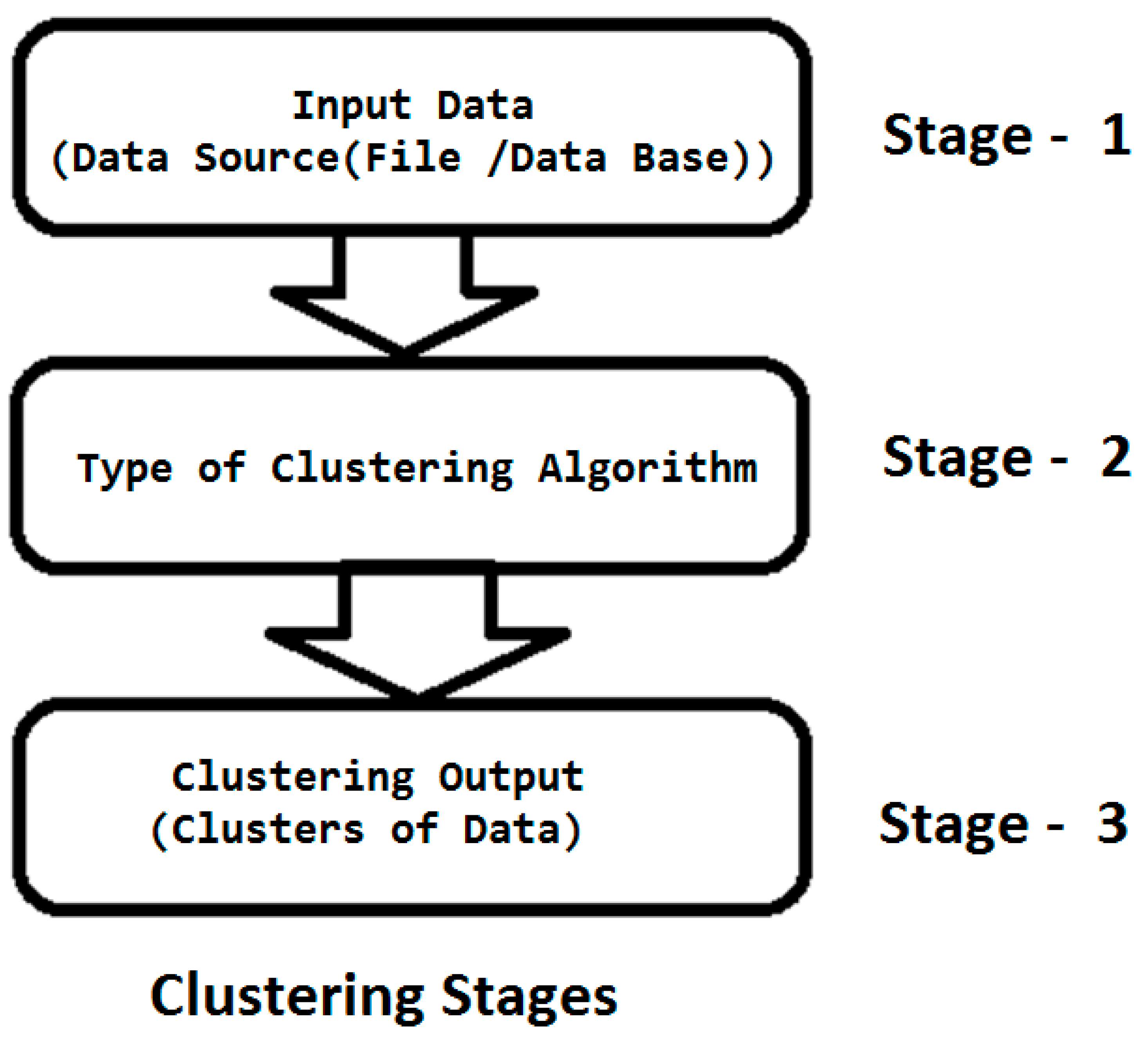
Preprints 83116 g006
Figure 6. Stage of clustering.
Figure 6. Stage of clustering.
Preprints 83116 g006
Note:
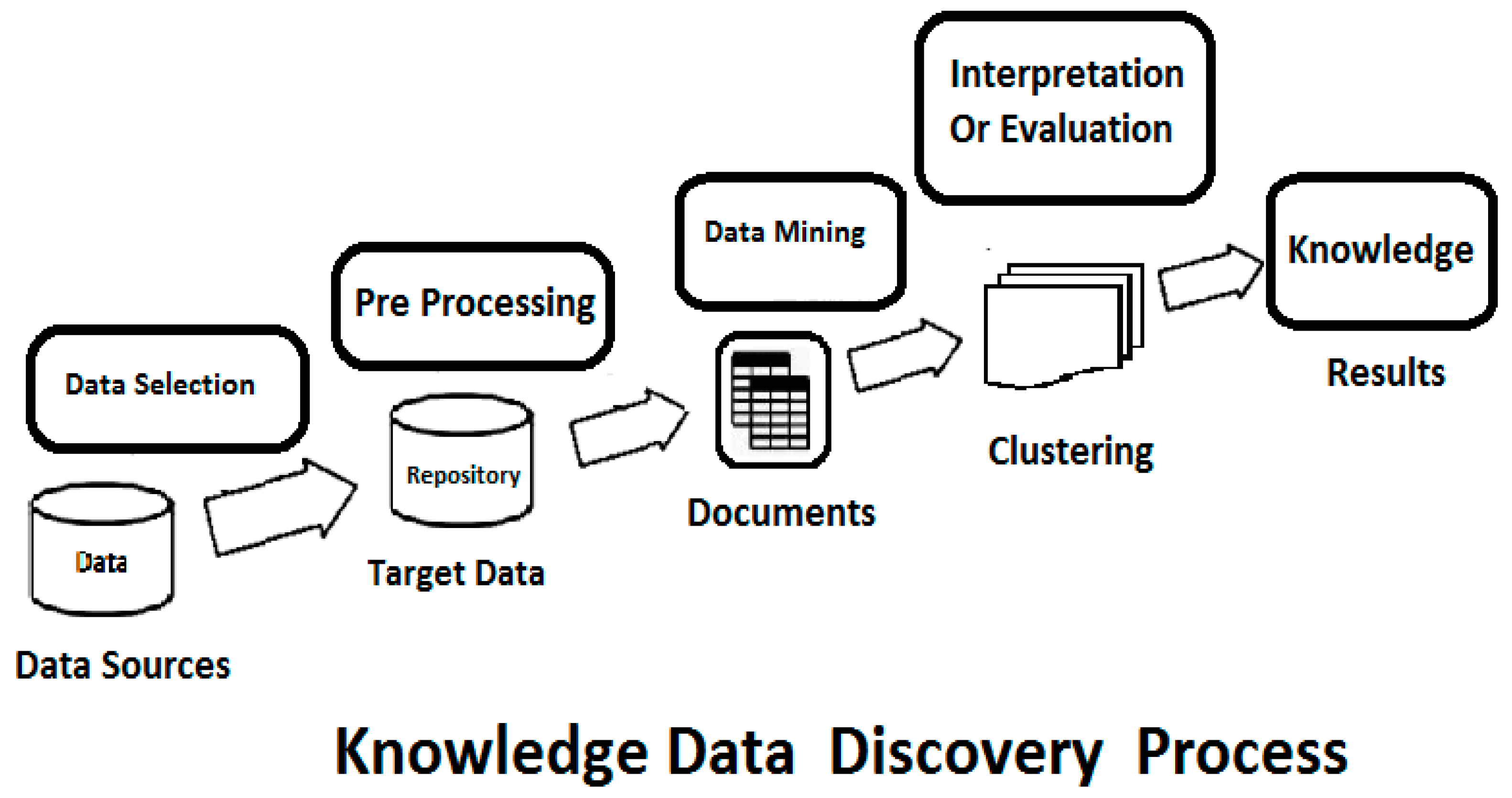
  • In the stage one, Input Data to clustering algorithm is collected from a file or a data base.
  • In the stage two, Different Types of clustering algorithm are utilized to process the stage 1data.In the current ERA different types of clustering algorithms are available in the market like Constraint Based Method, Soft Computing, Partitioning, Hierarchical, Density Based, Grid Based, Model Based, Bi-clustering, Graph Based, e.t.c.
  • In Knowledge Discovery in Database clustering is a part of it [17].
  • Data Preprocessing Techniques [18].
Preprints 83116 g007
Figure 7. Knowledge Data Discovery Process.
Figure 7. Knowledge Data Discovery Process.
Preprints 83116 g007
It includes Data Reduction, Cleaning and Transformation.
Table 6. Techniques of Data preprocessing.
Table 6. Techniques of Data preprocessing.
Techniques of Data preprocessing Handle Operations
Data Cleaning [19] Missing Data, Noisy Data
Data Reduction [20] 1. Attribute Subset Selection (Attributes).
2. Numerosity Reduction (Reduces data by replacing original data by smaller form of data representation).
3. Dimensionality Reduction (Compression the data).
Data Transformation [21] 1. Smoothing (Remove Noise).
2. Aggregation (Generates Attributes summary).
3. Generalization (Converts Low level data to high level data).
4. Normalization (Scales the Attributes).
5. Attribute Construction (Create New Attributes).

II. Literature Survey

In the market Different types clustering methods were there proposed by different researcher’s persons. For each clustering method there will be one or more sub clustering Algorithms. Each sub clustering algorithm will have its own constraints. The major clustering methods available in the market were
Table 7. Types of Clustering.
Table 7. Types of Clustering.
S. No Clustering Type Details Sub Clustering Methods
1. Partitioning It is used to group data by moving objects from one group to another using relocation technique [22]. 1. CLARA.
2. CLARANS.
3. EMCLUSTERING.
4. FCM.
5. K MODES.
6. KMEANS.
7. KMEDOIDS.
8. PAM.
9. XMEANS.
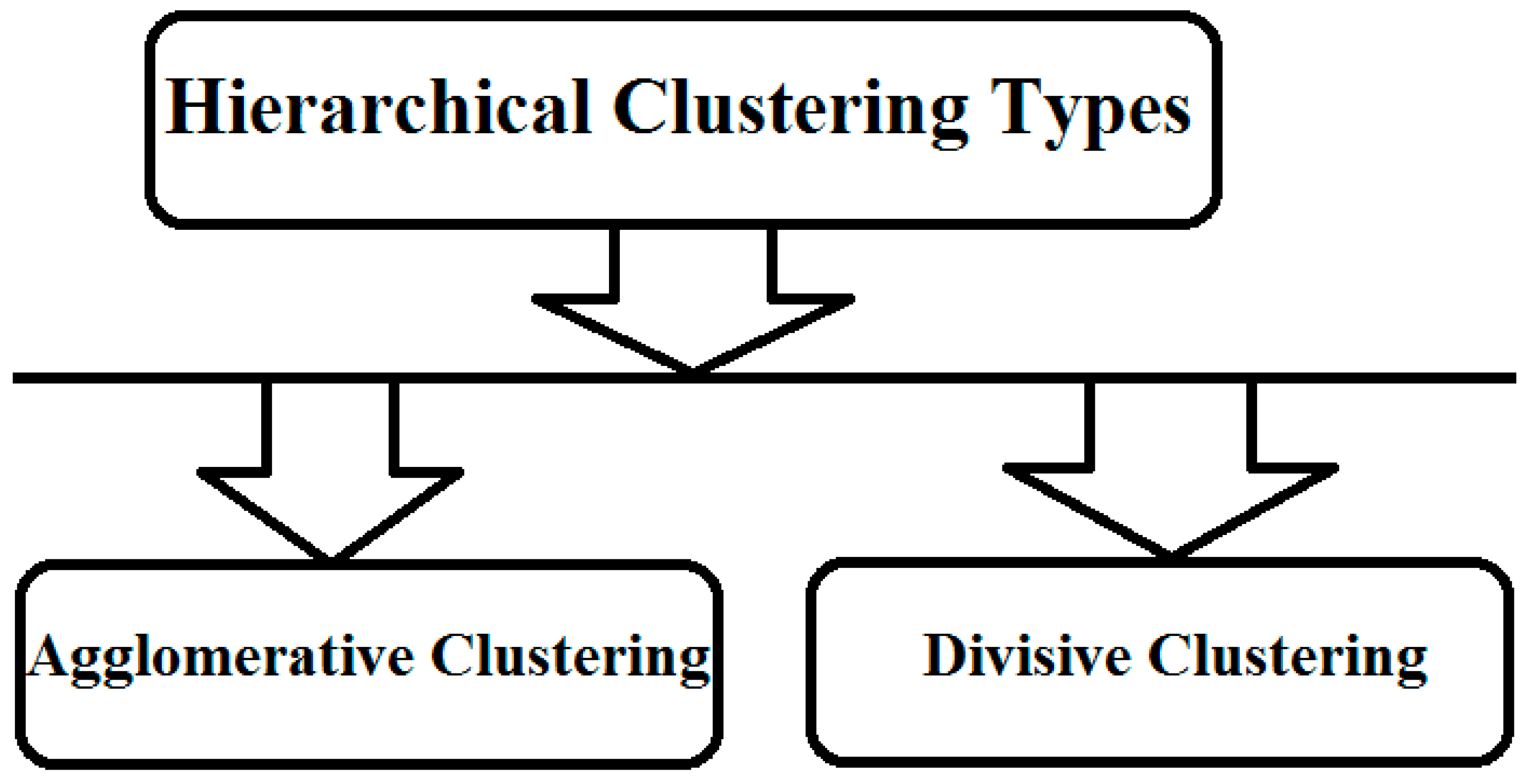
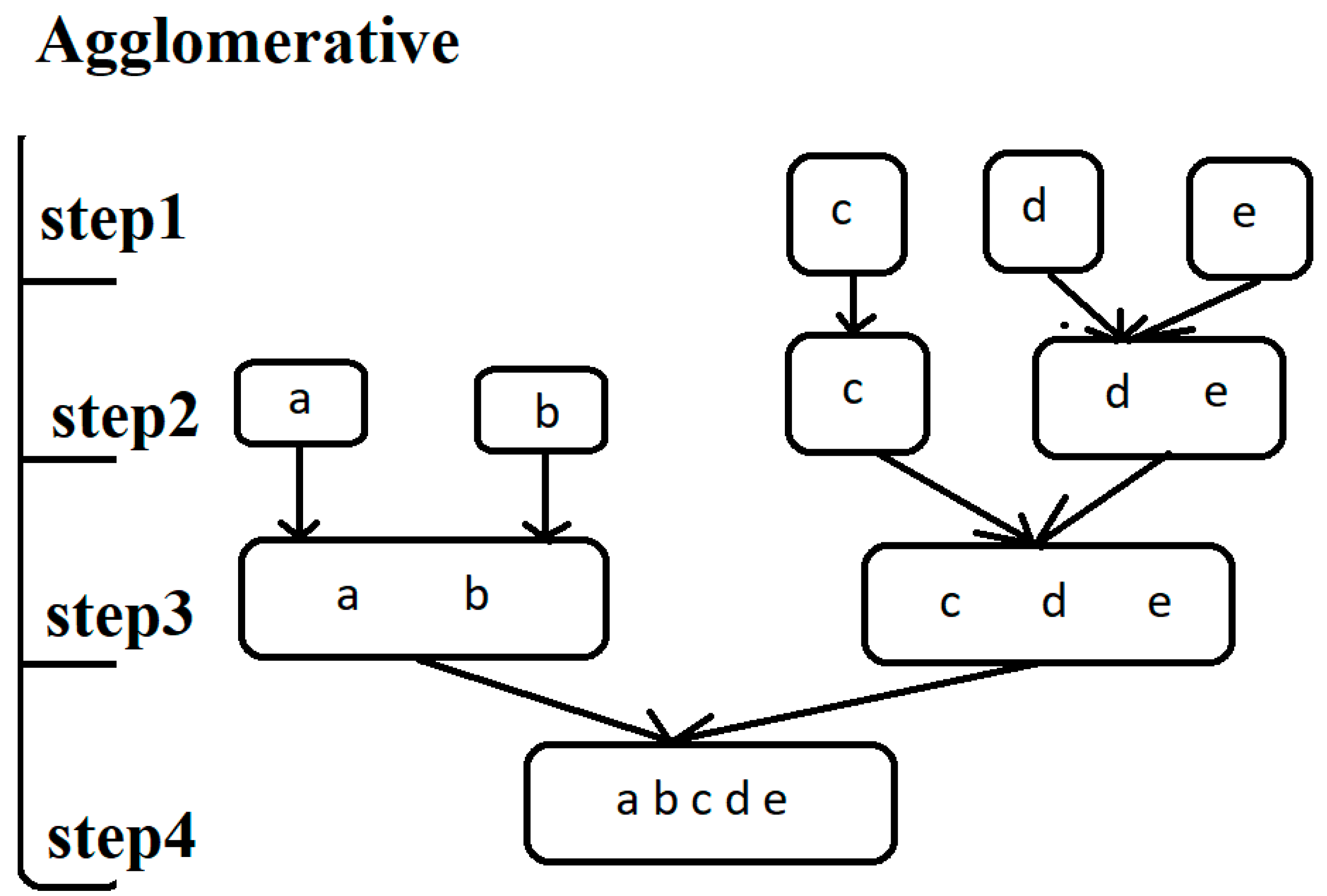
2. Hierarchical It is used to create clusters based on a particular similarity in the objects [23]. It is of two types. They were Agglomerative and Divisive.
Agglomerative clustering clusters the data based on combining clusters up.
Divisive clustering clusters the data based on merging clusters down. Other names for hierarchical clustering are hierarchical cluster analysis or HCA.		 1. AGNES.
2. BIRCH.
3. CHAMELEON.
4. CURE.
5. DIANA.
6. ECHIDNA.
7. ROCK.
3. Density Based It is used radius as a constraint to group the data. Here data points within a particular radius are considered as a group and remaining points are considered as noise [24]. 1. DBSCAN.
2. OPTICS.
3. DBCLASD.
4. DENCLUE.
5. CENCLUE.
4. Grid Based Grid Based calculates the density of cells and based on the cells densities values clustering is done [25]. 1. CLIQUE.
2. OPT GRID.
3. STING.
4. WAVE CLUSTER.
5. Model Based It uses a statistical approach for clustering the data where each object is assigned a weight (probability distribution) which is used to cluster the data [26]. 1. EM.
2. COBWEB.
3. CLASSIT.
4. SOMS.
6. Soft Computing In Soft Computing, clusters individual data points are assigned to more than one cluster and after clustering the clusters will have minimum similarity [27]. 1. FCM.
2. GK.
3. SOM.
4. GA Clustering.
7. Biclustering It is the clustering of the rows and columns of a matrix simultaneous using a data mining technique [28]. 1. OPSM.
2. Samba.
3. JSa.
8. Graph Based Graph is a collection of nodes (vertices). Clustering of these nodes of a graph based on certain weights assigned to the nodes is called as Graph Based Clustering [29]. 1. Click.
9 Hard Clustering In Hard Clustering individual data points are assigned to a unique cluster and after clustering clusters will have maximum similarity [30]. 1. KMEANS.
Each Clustering method calculates different types of parameters for doing the Clustering on a given data set. The time and space complexity of the algorithms are different for different clustering algorithms.
Similarity Measures Used by Different Clustering Methods [50]
Similarity measures are used to identify the good clusters in the given data set. There are so many Similarity measures used in the current market. They were Average Distance, Canberra Metric, Chord, Clustering coefficient, Cosine, Czekanowski Coefficient, Euclidean distance,
Index of Association, Kmean, KullbackLeibler Divergence, Mahalanobis, Manhattan distance or City blocks distance, Mean Character Difference, Minkowski Metric, Pearson coefficient,
Weighted Euclidean e.t.c
Table 8. Similarity measures in Clustering.
Table 8. Similarity measures in Clustering.
S.No Similarity measures Name Details
1 Average Distance It is the Euclidean distance but a modified version [31].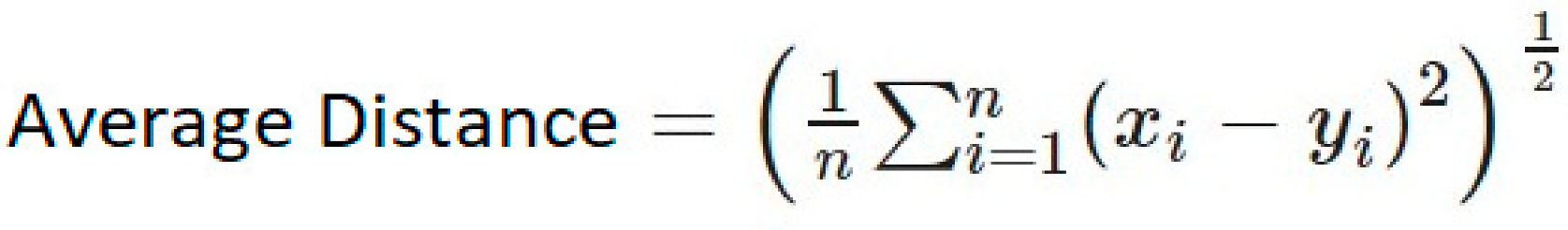Preprints 83116 i003
Here x, y are data points in n-dimensional space
2 Weighted Euclidean It is the modified version of Euclidean distance [32].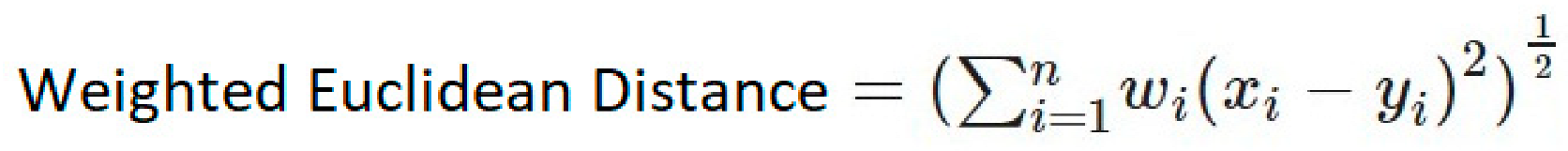
Preprints 83116 i004
3 Chord It is the length calculated between two points which are normalized within a hypersphere of radius one [33].
4 Mahalanobis It is the distance sample point (outlier) and a distribution [34].
5 Mean Character Difference It is calculated using all points in the given space [35].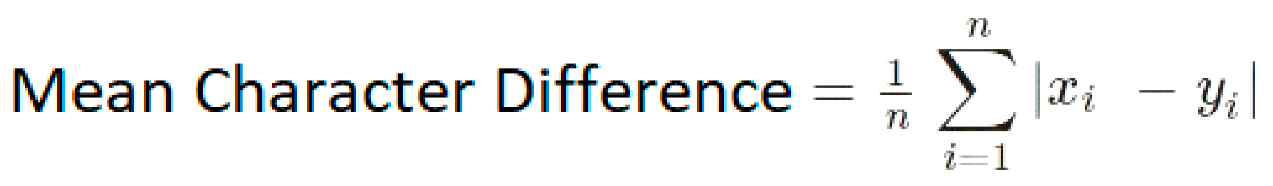
Preprints 83116 i005
6 Index of Association It is calculated using all points in the given space [36].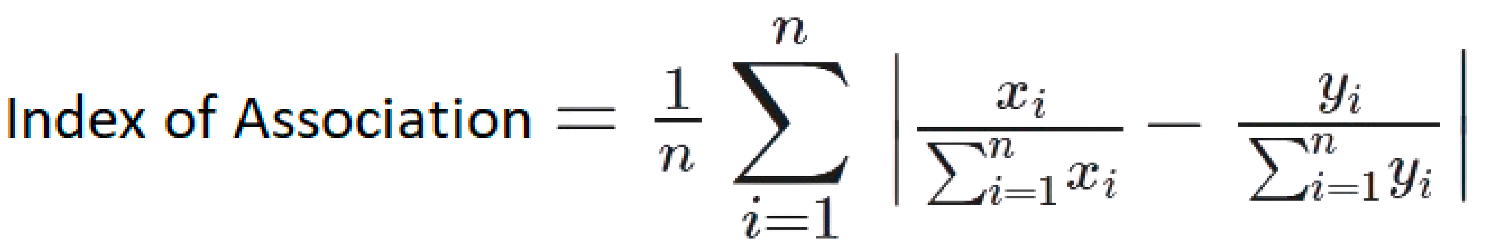
Preprints 83116 i006
7 Canberra Metric It is calculated using all points in the given space [37].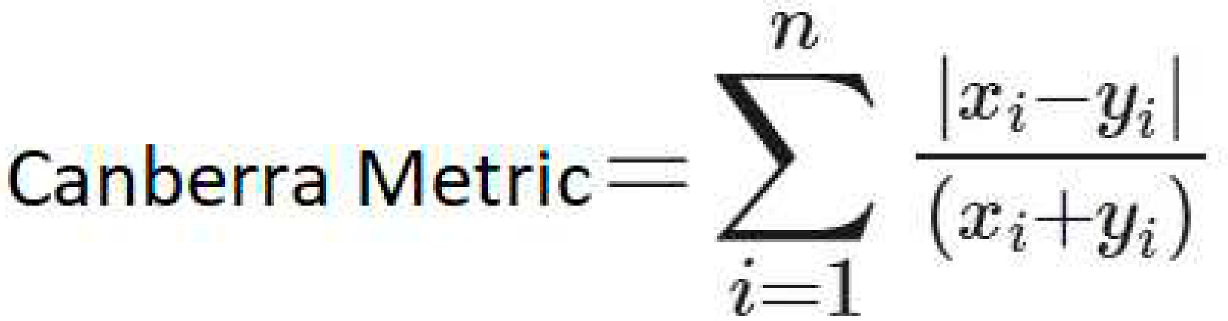
Preprints 83116 i007
8 Czekanowski Coefficient It is calculated using all points in the given space [38].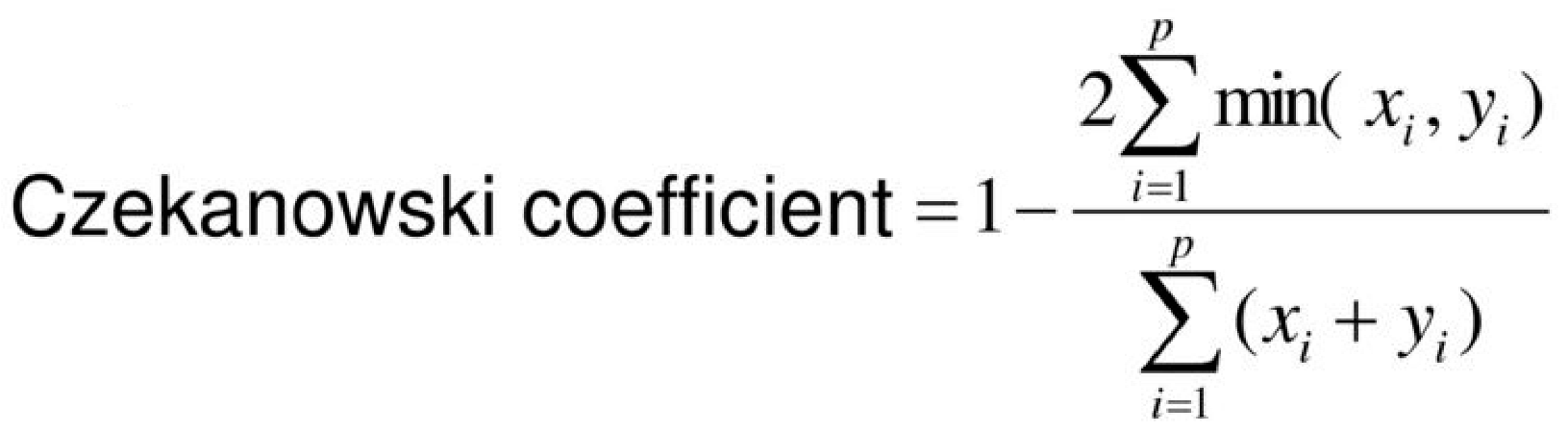
Preprints 83116 i008
9 Pearson coefficient It is calculated using all points in the given space [39].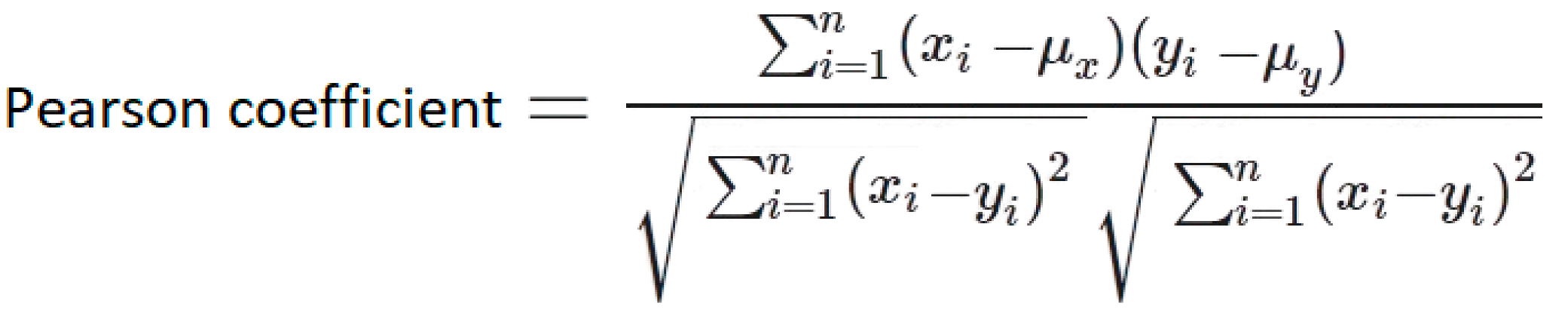
Preprints 83116 i009
10 Minkowski Metric Minkowski Distance/metric are the distance between two vectors and it’s a generalization of both the Manhattan and Euclidean distance [40].
11 Manhattan distance or City blocks distance It is the distance between vectors.
It is equal to the one-norm of the distance between the vectors [41].
12 Euclidean distance Euclidean distance is also known as Pythagorean distance. It is the distance between any two points (Cartesian coordinates) in the Euclidean space [42].
13 KullbackLeibler Divergence KullbackLeibler Divergence is used to calculate the distance between two independent discrete probability distributions (data and cluster center point). It is used to create cluster group by combining multiple Fuzzy c-means clustering’s results [43].
14 Clustering coefficient It is used to calculate how the nodes of a graph are connected along with the degree [44].
15 Cosine It is the replacement of Euclidean distance with cosine function [45].
16 Kmean It is the mean of all the coordinates or points in the in the Euclidean space [46].
Inputs and Outputs in Clustering Process
In every clustering algorithm the user gives so many parameters as inputs to the clustering algorithm and gets the outputs.
Table 9. Inputs and Outputs in clustering process.
Table 9. Inputs and Outputs in clustering process.
S.NO Inputs and Outputs Details
1 Number of Inputs for the clustering process Clustering Algorithm, Algorithm Constraints, Number of Levels and clusters per each level.
2 Number of Levels In the entire clustering.
3 Number of clusters At each stage
4 Sum of Square Error (SSE) or other errors It is a measure of difference between the data obtained by the prediction model that has been done before. [47]
5 Likelihood of Clusters It is the similarity of clusters in the data points. [48]
6 Unlikelihood of Clusters It is the dissimilarity of clusters in the data points.
7 Number of variable parameters at each level These are the input parameters which are changed during the running of the algorithm like threshold.
8 outlier In the clustering process any object doesn’t belong to any cluster it is called as a outlier. [48]
9 Output Clusters

III. Proposed Algorithm

Buddy Memory Allocation Technique invented by Harry Markowitz for Memory Allocation Technique in the year 1963. Buddy memory allocation technique is used to divide memory into 2 halves and gives a best fit and is easy to implement it [51]. Here Modified Buddy system is used for clustering on Alpha numeric weighted based sorted records for clustering.
Preprints 83116 g008
Figure 8. Example of Buddy System.
Figure 8. Example of Buddy System.
Preprints 83116 g008
The problem with the buddy system is it works for the even number of records. But it is difficult to work with odd number of records. So I our algorithm it works for both even and odd record count.
Buddy System with Alpha Numeric Weighted Based Clustering Algorithm
  • Take a Sample data set.
  • Calculate The Weight of Individual Object by Position of an attribute of a particular column for all records.
    • Object individual position is calculated using ASCII Character Binary Table.
    • Formula for calculating the Alpha Numeric Weight based Object Positional Value for a Term/Field (ANWAPVT) of a record.
    • ANWAPVT = (First Char) ASCII value ∗ n + (second Char) ASCII value ∗ (n-1) ------- (Last char-3) + (Last char-2) ASCII value ∗ 3 + (Last char-1) ASCII value ∗ 2 + Last char ∗ ASCII value ∗ 1
    • Example: Term is AB·AB = 65 ∗ 2 + 66 ∗ 1 = 130 + 66 = 196
    • Here “A” ASCII value is 65 and “B” ASCII value is 66.
3.
Sort the records/data in ascending order as per the Alpha Numeric Weight based Object individual position values. For that call the Sort Function or write a sort function to sort the records.
4.
Compute the number of records (N) in the Data source (data base/set/File). Specify Number of levels (L) that should be generated in the clustering process which should be always 2L < N.
5.
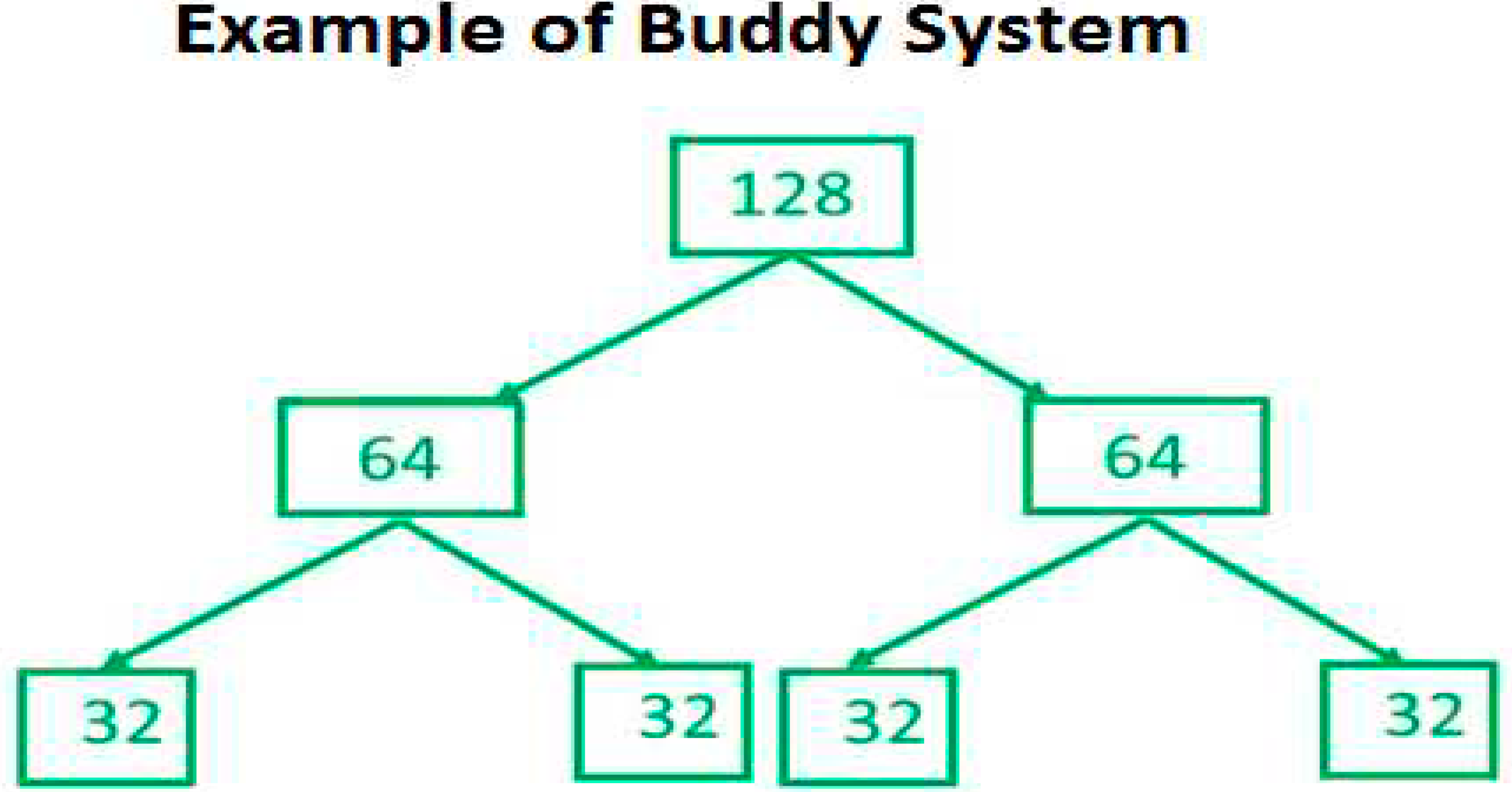
Use Modified buddy system for level wise cluster generation. I.e. At each level, every cluster is splits into two sub clusters and adds computed clusters to a list. Here list index indicates the cluster number.
Table 10. Example of Modified buddy system.
Table 10. Example of Modified buddy system.
If No. of elements (N) Elements in Cluster1 Elements in Cluster2
Even N/2 N/2
Odd N/2 N/2 + 1
I.e. cluster1 is divided into two clusters (cluster2 and cluster3).
6.
Repeat the step5 till 2L< N. Where
  • L = Number of levels that has to be generated using buddy system.
  • N = Number of records in the data set.
7.
Assign the elements to each cluster in a based on the list from the sorted data set.
8.
Use the list to generate a pie circle chart.
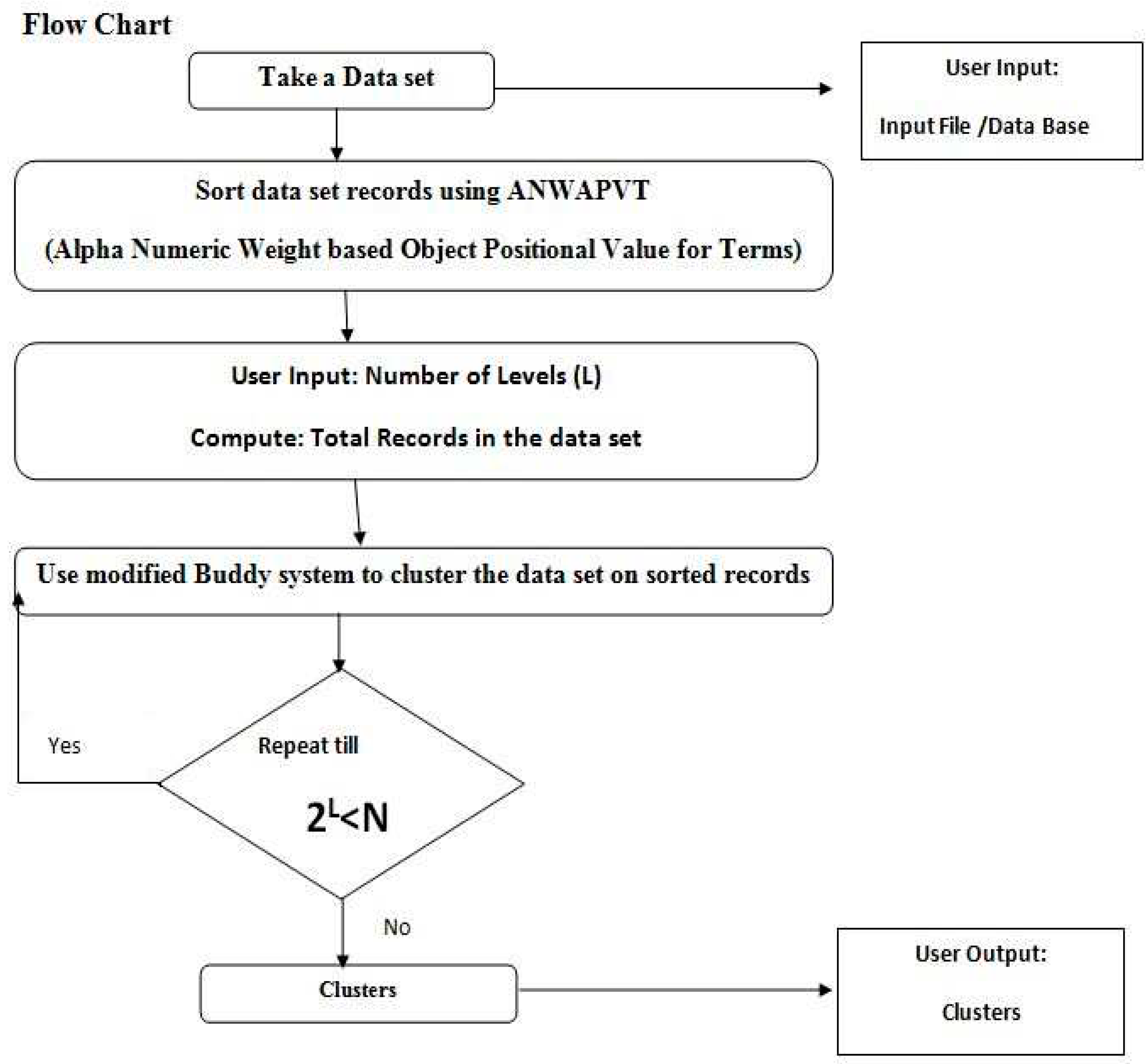
Preprints 83116 g009
Figure 9. Buddy System Based Alpha Numeric Weight Based Clustering Algorithm with User Threshold.
Figure 9. Buddy System Based Alpha Numeric Weight Based Clustering Algorithm with User Threshold.
Preprints 83116 g009
Note
  • The number of elements in each cluster can be known using algorithm.
  • Data set can be collected/downloaded from freely available public repositories. i.e The data set which we have used is twitter data set.
  • At each level the numbers of clusters are equal to 2L (Where number of levels L is required by the user.)
  • Data preprocessing techniques applied on the collected data set. This data set will be the input for the proposed Algorithm [52].
  • Clustering output will be saved in the output file/Data base.
  • Data preprocessing has to be done on the data set before clustering algorithm starts [53].
  • Data preprocessing can also be done on multiple data sources to get required data for clustering algorithm [54].
  • Formatted data is given as input for the clustering process and output is patterns [55].
  • Data mining output is the input for the clustering algorithm input.
  • Each clustering algorithm will be associated with a time complexity [56].
  • Patterns can be explored and filtered [57].
  • After data clustering the data is used for visualization and interpretation of results [58].
  • Clustering is used in Association rules [59] and classification [60].

IV. Results

Results are being generated using python.
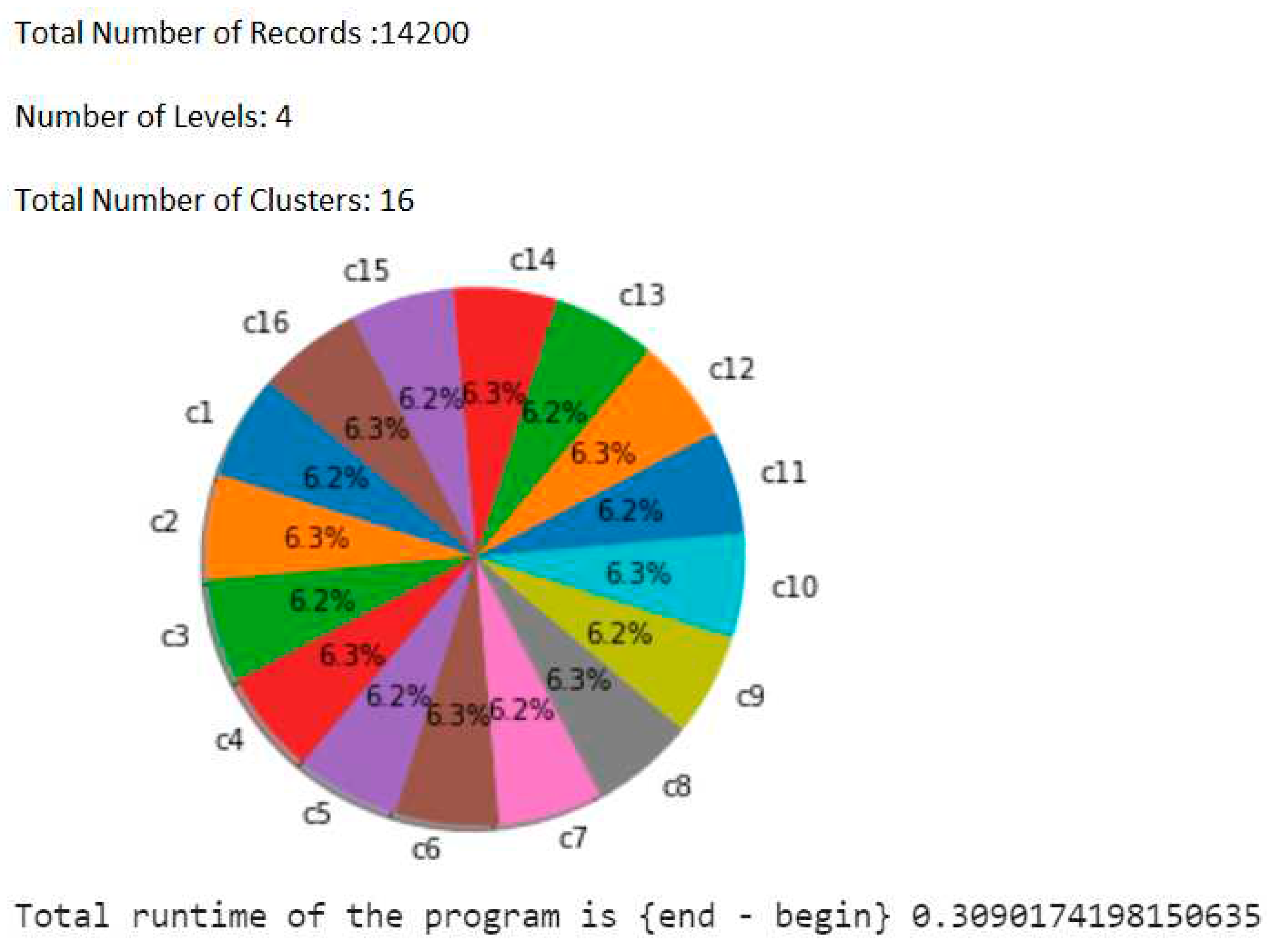
Preprints 83116 g010
Figure 10. Clustering Result.
Figure 10. Clustering Result.
Preprints 83116 g010

V. Conclusion

Here we are going to implement Buddy system with Alpha numeric weighted based clustering Algorithm with user preferences to get good clusters. So the efficiency of the clustering algorithm depends on the metrics (Buddy system, Alpha numeric weight of the object with user preferences and number of levels) used in the clustering algorithm.

References

  1. Bindra, K.; Mishra, A. A detailed study of clustering algorithms. In Proceedings of the 2017 6th international conference on reliability, infocom technologies and optimization (trends and future directions)(ICRITO); 2017. [Google Scholar]
  2. Liu, F.; Wei, Y.; Ren, M.; Hou, X.; Liu, Y. An agglomerative hierarchical clustering algorithm based on global distance measurement. In Proceedings of the 2015 7th International Conference on Information Technology in Medicine and Education (ITME); 2015. [Google Scholar]
  3. Sathya, R.; Abraham, A. Comparison of Supervised and Unsupervised Learning Algorithms for Pattern Classification. International Journal of Advanced Research in Artificial Intelligence 2013, 2, 34–38. [Google Scholar] [CrossRef]
  4. Lahane, S.V.; Kharat, M.U.; Halgaonkar, P.S. Divisive approach of Clustering for Educational Data. In Proceedings of the 2012 Fifth International Conference on Emerging Trends in Engineering and Technology; 2012. [Google Scholar]
  5. Makrehchi, M. Hierarchical Agglomerative Clustering Using Common Neighbours Similarity. In Proceedings of the 2016 IEEE/WIC/ACM International Conference on Web Intelligence (WI); 2016. [Google Scholar]
  6. Pranata, I.; Skinner, G. Segmenting and Targeting Customers through Clusters Selection & Analysis. In Proceedings of the 2015 International Conference on Advanced Computer Science and Information Systems (ICACSIS); 2015. [Google Scholar]
  7. Ahmed, M.; Mahmood, A.N. A Novel Approach for Outlier Detection and Clustering Improvement. In Proceedings of the 2013 IEEE 8th Conference on Industrial Electronics and Applications (iciea); 2013. [Google Scholar]
  8. Madaan, V.; Kumar, R. An Improved Approach for Web Document Clustering. In Proceedings of the 2018 International Conference on Advances in Computing, Communication Control and Networking (ICACCCN); 2018. [Google Scholar]
  9. Shen, H.; Duan, Z. Application Research of Clustering Algorithm Based on K-Means in Data Mining. In Proceedings of the 2020 International Conference on Computer Information and Big Data Applications (CIBDA); 2020. [Google Scholar]
  10. Chen, Y.; Kim, J.; Mahmassani, H.S. Pattern recognition using clustering algorithm for scenario definition in traffic simulation-based decision support systems. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC); 2014. [Google Scholar]
  11. Coleman, G.B.; Andrews, H.C. Image segmentation by clustering. Proceedings of the IEEE 1979, 67, 773–785. [Google Scholar] [CrossRef]
  12. Sharma, M.; Toshniwal, D. Pre-Clustering Algorithm for Anomaly Detection and Clustering that uses variable size buckets. In Proceedings of the 2012 1st International Conference on Recent Advances in Information Technology (RAIT); 2012. [Google Scholar]
  13. Zhan, Y.; Pan, H.; Han, Q.; Xie, X.; Zhang, Z.; Zhai, X. Medical image clustering algorithm based on graph entropy. In Proceedings of the 2015 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD); 2015. [Google Scholar]
  14. Suneetha, M.; Fatima, S.S.; Pervez, S.M.Z. Clustering of web search results using Suffix tree algorithm and avoidance of repetition of same images in search results using L-Point Comparison algorithm. In Proceedings of the 2011 International Conference on Emerging Trends in Electrical and Computer Technology; 2011. [Google Scholar]
  15. Prabhu, J.; Sudharshan, M.; Saravanan, M.; Prasad, G. Augmenting Rapid Clustering Method for Social Network Analysis. In Proceedings of the 2010 International Conference on Advances in Social Networks Analysis and Mining; 2010. [Google Scholar]
  16. Panapakidis, I.P.; Alexiadis, M.C.; Papagiannis, G.K. Three-Stage Clustering Procedure for Deriving the Typical Load Curves of the Electricity Consumers. In Proceedings of the 2013 IEEE Grenoble Conference; 2013. [Google Scholar]
  17. Iiritano, S.; Ruffolo, M. Managing the Knowledge Contained in Electronic Documents: a Clustering Method for Text Mining. In Proceedings of the 12th International Workshop on Database and Expert Systems Applications; 2001. [Google Scholar]
  18. Dwivedi, S.K.; Rawat, B. A Review Paper on Data Preprocessing: A Critical Phase in Web Usage Mining Process. In Proceedings of the 2015 International Conference on Green Computing and Internet of Things (ICGCIoT); 2015. [Google Scholar]
  19. Ratnadeep R. Deshmukh and Vaishali Wangikar. Data Cleaning: Current Approaches and Issues.
  20. Reddy, G.T.; Reddy, M.P.K.; Lakshmanna, K.; Kaluri, R.; Rajput, D.S.; Srivastava, G.; Baker, T. Analysis of Dimensionality Reduction Techniques on Big Data. IEEE Access 2020, 8, 54776–54788. [Google Scholar] [CrossRef]
  21. Schelling, B.; Plant, C. Dataset-Transformation: improving clustering by enhancing the structure with DipScaling and DipTransformation. Knowledge and Information Systems 2020, 62, 457–484. [Google Scholar] [CrossRef]
  22. Dharmarajan, A.; Velmurugan, T. Applications of Partition based Clustering Algorithms: A Survey. In Proceedings of the 2013 IEEE International Conference on Computational Intelligence and Computing Research; 2013. [Google Scholar]
  23. Nagpal, A.; Jatain, A.; Gaur, D. Review based on data clustering algorithms. In Proceedings of the 2013 IEEE conference on information & communication technologies; 2013. [Google Scholar]
  24. Singh, P.; Meshram, P.A. Survey of Density Based Clustering Algorithms and its Variants. In Proceedings of the 2017 International conference on inventive computing and informatics (ICICI); 2017. [Google Scholar]
  25. Amini, A.; Wah, T.Y.; Saybani, M.R.; Yazdi, S.R.A.S. A study of density-grid based clustering algorithms on data streams. In Proceedings of the 2011 Eighth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD); 2011. [Google Scholar]
  26. Xu, D.; Tian, Y. A Comprehensive Survey of Clustering Algorithms. Annals of Data Science 2015, 2, 165–193. [Google Scholar] [CrossRef]
  27. Srutipragayn Swain and Manoj Kumar DasMohapatra. A review paper on soft computing based clustering algorithm.
  28. Madeira, S.C.; Oliveira, A.L. Biclustering Algorithms for Biological Data Analysis: A Survey. IEEE/ACM transactions on computational biology and bioinformatics 2004, 1, 24–45. [Google Scholar] [CrossRef] [PubMed]
  29. Zhou, M.; Hui, H.; Qian, W. A graph-based clustering algorithm for anomaly intrusion detection. In Proceedings of the 2012 7th International Conference on Computer Science & Education (ICCSE); 2012. [Google Scholar]
  30. Christina, J.; Komathy, K. Analysis of hard clustering algorithms applicable to regionalization. In Proceedings of the 2013 IEEE conference on information & communication technologies; 2013. [Google Scholar]
  31. Andonovski, G.; Škrjanc, I. Evolving clustering algorithm based on average cluster distance CAD. In Proceedings of the 2022 IEEE International Conference on Evolving and Adaptive Intelligent Systems (EAIS); 2022. [Google Scholar]
  32. Lei, M.; Ling, Z.H.; Dai, L.R. Minimum Generation Error Training With Weighted Euclidean Distance On Lsp For Hmm-Based Speech Synthesis. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing; 2010. [Google Scholar]
  33. Yang, Y.; Guo, S.Z.; Hu, G.Y.; Li, H.B. An improved Hybrid P2P Control Model Based on Chord. In Proceedings of the 2012 Second International Conference on Instrumentation, Measurement, Computer, Communication and Control; 2012. [Google Scholar]
  34. Fattah, H.A.; Al Masba, M.; Hasan, K.A. Sentiment Clustering By Mahalanobis Distance. In Proceedings of the 2018 4th International Conference on Electrical Engineering and Information & Communication Technology (iCEEiCT); 2018. [Google Scholar]
  35. Koh, Z.; Zhou, Y.; Lau, B.P.L.; Liu, R.; Chong, K.H.; Yuen, C. Clustering and Analysis of GPS Trajectory Data Using Distance-Based Features. IEEE Access 2022, 10, 125387–125399. [Google Scholar] [CrossRef]
  36. Cui, H.; Zhang, K.; Fang, Y.; Sobolevsky, S.; Ratti, C.; Horn, B.K. A Clustering Validity Index Basedon Pairing Frequency. IEEE Access 2017, 5, 24884–24894. [Google Scholar] [CrossRef]
  37. Raeisi, M.; Sesay, A.B. A Distance Metric for Uneven Clusters of Unsupervised K-Means Clustering Algorithm. IEEE Access 2022, 10, 86286–86297. [Google Scholar] [CrossRef]
  38. Guan, C.; Yuen, K.K.F.; Coenen, F. Particle swarm Optimized Density-based Clustering and Classification: Supervised and unsupervised learning approaches. Swarm and evolutionary computation 2019, 44, 876–896. [Google Scholar] [CrossRef]
  39. xue Huang, F.; Zhao, X.; Li, C. Clustering Effect of Style based on Pearson correlation. In Proceedings of the 2010 International Conference on Internet Technology and Applications; 2010. [Google Scholar]
  40. Svetlova, L.; Mirkin, B.; Lei, H. MFWK-Means: Minkowski Metric Fuzzy Weighted K-Means for high dimensional data clustering. In Proceedings of the 2013 IEEE 14th International Conference on Information Reuse & Integration (IRI); 2013. [Google Scholar]
  41. Roopa, H.; Asha, T. Segmentation of X-ray image using city block distance measure. In Proceedings of the 2016 International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT); 2016. [Google Scholar]
  42. Bouhmala, N. How Good Is The Euclidean Distance Metric For The Clustering Problem. In Proceedings of the 2016 5th IIAI international congress on advanced applied informatics (IIAI-AAI); 2016. [Google Scholar]
  43. Martins, A.M.; Neto, A.D.; de Melo, J.D.; Costa, J.A.F. Clustering using neural networks and Kullback-Leibler divergency. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541); 2004. [Google Scholar]
  44. Ren, S.; Fan, A. K-means clustering algorithm based on coefficient of variation. In Proceedings of the 2011 4th International Congress on Image and Signal Processing; 2011. [Google Scholar]
  45. Popat, S.K.; Deshmukh, P.B.; Metre, V. A Hierarchical document clustering based on cosine similarity measure. In Proceedings of the 2017 1st International Conference on Intelligent Systems and Information Management (ICISIM); 2017. [Google Scholar]
  46. Chi, D. Research on the Application of K-Means Clustering Algorithm in Student Achievement. In Proceedings of the 2021 IEEE International Conference on Consumer Electronics and Computer Engineering (ICCECE); 2021. [Google Scholar]
  47. Kaur, J.; Singh, H. Performance Evaluation of a Novel Hybrid Clustering Algorithm using Birch and K-Means. In Proceedings of the 2015 Annual IEEE India Conference (INDICON); 2015. [Google Scholar]
  48. Rai, U.K.; Sharma, K. Maximum Likelihood Estimation based Clustering Algorithm on Wireless Sensor Network-A Review. In Proceedings of the 2017 International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS); 2017. [Google Scholar]
  49. Pamula, R.; Deka, J.K.; Nandi, S. An Outlier Detection Method based on Clustering. In Proceedings of the 2011 second international conference on emerging applications of information technology; 2011. [Google Scholar]
  50. Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. Clustering algorithms and validity measures. In Proceedings of the Thirteenth International Conference on Scientific and Statistical Database Management. SSDBM 2001; 2001. [Google Scholar]
  51. Chang, J.M.; Gehringer, E.F. A High-Performance Memory Allocator for Object-Oriented Systems. IEEE Transactions on Computers 1966, 45, 357–366. [Google Scholar] [CrossRef]
  52. Çelik, O.; Hasanbaşoğlu, M.; Aktaş, M.S.; Kalıpsız, O.; Kanli, A.N. Implementation of Data Preprocessing Techniques on Distributed Big Data Platforms. In Proceedings of the 2019 4th International Conference on Computer Science and Engineering (UBMK); 2019. [Google Scholar]
  53. Sreenivas, P.; Srikrishna, C.V. An Analytical approach for Data Preprocessing. In Proceedings of the 2013 International Conference on Emerging Trends in Communication, Control, Signal Processing and Computing Applications (C2SPCA); 2013. [Google Scholar]
  54. Mhon, G.G.W.; Kham, N.S.M. ETL Preprocessing with Multiple Data Sources for Academic Data Analysis. In Proceedings of the 2020 IEEE Conference on Computer Applications (ICCA); 2020. [Google Scholar]
  55. Cooley, R.; Mobasher, B.; Srivastava, J. Web Mining: Information and Pattern Discovery on the World Wide WebR. In Proceedings of the ninth IEEE international conference on tools with artificial intelligence; 1997. [Google Scholar]
  56. Venkatkumar, I.A.; Shardaben, S.J.K. Comparative study of Data Mining Clustering algorithms. In Proceedings of the 2016 International Conference on Data Science and Engineering (ICDSE); 2016. [Google Scholar]
  57. Bertini, E.; Lalanne, D. Investigating and reflecting on the integration of automatic data analysis and visualization in knowledge discovery. Acm Sigkdd Explorations Newsletter 2010, 11, 9–18. [Google Scholar] [CrossRef]
  58. Venkatkumar, I.A.; Shardaben, S.J.K. Comparative study of Data Mining Clustering algorithms. In Proceedings of the 2016 International Conference on Data Science and Engineering (ICDSE); 2016. [Google Scholar]
  59. Yildirim, N.; Uzunoglu, B. Association Rules for Clustering Algorithms for Data Mining of Temporal Power Ramp Balance. In Proceedings of the 2015 International Conference on Cyberworlds (CW); 2015. [Google Scholar]
  60. Kesavaraj, G.; Sukumaran, S. A study on classification techniques in data mining. In Proceedings of the 2013 fourth international conference on computing, communications and networking technologies (ICCCNT); 2013. [Google Scholar]

Short Biography of Authors

Preprints 83116 i001 Dr. Srikanth Thota received his Ph.D in Computer Science Engineering for his research work in Collaborative Filtering based Recommender Systems from J.N.T.U, Kakinada. He received M.Tech. Degree in Computer Science and Technology from Andhra University. He is presently working as an Associate Professor in the department of Computer Science and Engineering, School of Technology, GITAM University, Visakhapatnam, Andhra Pradesh, India. His areas of interest include Machine learning, Artificial intelligence, Data Mining, Recommender Systems, Soft computing.
Preprints 83116 i002 Mr. MaradanaDurgaVenkata Prasad received his B.TECH (Computer Science and Information Technology) in 2008 from JNTU, Hyderabad and M.Tech. (Software Engineering) in 2010 from Jawaharlal Nehru Technological University, Kakinada, He is a Research Scholar with Regd No: 1260316406 in the department of Computer Science and Engineering, Gandhi Institute Of Technology And Management (GITAM) Visakhapatnam, Andhra Pradesh, India. His Research interests include Clustering in Data Mining, Big Data Analytics, and Artificial Intelligence. He is currently working as an Assistant Professor in Department of Computer Science Engineering, CMR Institute of Technology, Ranga Reddy, India.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated