Preprint
Article
AlphaFold Blindness to Topological Barriers Affects Its Ability to Correctly Predict Proteins’ Topology
Altmetrics
Downloads
190
Views
78
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
23 August 2023
Posted:
24 August 2023
You are already at the latest version
Alerts
Abstract
AlphaFold is a groundbreaking Deep Learning tool for protein structure prediction. It achieved remarkable accuracy in modeling the many 3D structures while taking as the input only the known amino acid sequence of proteins in question. Intriguingly though, in the early steps of each individual structure prediction procedure, AlphaFold is not respecting topological barriers that in real proteins result from the reciprocals impermeability of polypeptide chains. This study aims to investigate how this non-respecting of topological barriers affects AlphaFold predictions with respect to the topology of protein chains. We focus on such classes of proteins that during their natural folding form reproducibly the same knot type on their linear polypeptide chain as revealed by their crystallographic analysis. We use partially artificial test constructs in which the mutual non-permeability of polypeptide chains should not permit the formation of such knots during natural protein folding. We find that despite the formal impossibility that the protein folding process could produce such knots, AlphaFold predicts these proteins to be knotted. Our study underscores the necessity for cautious interpretation and further validation of topological features in protein structures predicted by AlphaFold.
Keywords:
Subject: Biology and Life Sciences - Biochemistry and Molecular Biology
1. Introduction
AlphaFold [1,2,3] has revolutionized protein structure prediction, achieving unprecedented accuracy and surpassing other competitors in two editions of the Critical Assessment of Structure Prediction (CASP) competition [4,5]. The quantitative leap was possible due to utilizing deep learning algorithms and large databases. This, in turn, fostered numerous modifications and implementations [6,7,8,9,10,11,12,13,14]. Following the success, the authors and developers of AlphaFold have created a broadly available, comprehensive database of predicted 3D protein structures, starting from the whole human proteome [15] and later expanding it to over 200 million entries offering a vast potential for exploration.
One problem, which can be studied in such a vast database is the existence of proteins of non-trivial topology. In fact, protein chains can reproducibly self-tie into an open-knotted structure [16], or shoelace-like spliknots [17]. Including many-chain structures and disulfide bonds, one can identify links and other more complex topologically non-trivial structures in proteins [18,19,20,21,22,23,24,25]. However, in the known proteome, only a dozen of knotted protein families (about 2% of known structures) were identified and those families represent five different knot types [26,27,28]. It was therefore very tempting to search for new knotted families and knot topologies among the structures predicted by AlphaFold.
In this spirit, Brems et al identified two new knot topologies, with 5 and 7 crossings in minimal crossing projection (, and knots), the latter being the most complex knot up to date [29]. Yet another knot type, a symmetric knot with 6 crossings ( knot) was identified by Perlinska et al [30]. It is worth mentioning, that all those knots, if identified also in an experiment, would disprove the long-standing hypothesis, that all protein knots are formed by single threading through a twist loop (so-called “twist knots”) [31]. Finally, the topology of all the structures predicted by AlphaFold was analyzed and gathered in the AlphaKnot database [32]. Yet, there remains the question, how probable are AlphaFold predictions in terms of topology. In fact, the topological analysis is a very delicate matter, as switching the position of two close chains may completely change the protein topology. To be conscious of AlphaFold limitations it is necessary to understand its algorithm.
In short, AlphaFold consists of two blocks. One, called Evoformer builds an abstract protein representation from protein sequence and its homologs. The second block is the structure module, which aim is to build a complete 3D structure starting from the abstract representation produced by Evoformer [1]. The abstract representation produced by Evoformer is a set of rotations and translations one has to perform to move each of the amino acids from the initial position (same for each residue) to a desired place. The movement is being done in the structure block. Remarkably, during adjusting the structure, all the residues can move freely (called suggestively “residue gas”) and the peptide bond geometry is not conserved. The violation of geometrical constraints and chain connectivity is important from the viewpoint of the algorithm, as it simplifies greatly the calculations. The backbone geometry is corrected only in the last step, during fine-tuning of the structure within the Amber force field, which aim is only to remove stereochemical violations.
As a result, the continuity of modeled polypeptide chain, which provides a basic topological constraint, is deliberately not maintained. This, in some specific cases, may negatively affect the algorithm’s predictions concerning the topology of polypeptide chains. In particular, when AlphFold predicts that a polypeptide chain of a given protein forms a knot of a given topological type this may not reflect the reality.
To address the problem of structure correctness, the proposed models are assessed based on the pLDDT metric (a version of lDDT - Local Distance Difference Test metric [33]). The metric calculates, how optimal are inter-residue distances, where the optimum is taken from known, homologous structures. The metric attains values in the range of 0-100, where values larger than 70 are treated as “a generally good backbone prediction”, while those with pLDDT higher than 90 are “modeled to high accuracy”. The metric is local in the sense, that it is calculated for each residue individually, however, usually the mean value is presented to assess the structure, which may be insufficient for judging the topology, as it depends on local chain placement.
In this work we analyze, how the AlphaFold intrinsic, algorithm-based limitations translate to the correctness of topology prediction. In particular, we construct a series of examples of artificial protein structures that were predicted to be knotted by AlphaFold despite the fact that the formation of these knots was for kinetic and topological reasons not realizable. As a result, we postulate to treat the AlphaFold results with caution, especially when investigating topological aspects of protein structures.
2. Materials and Methods
2.1. Software and Hardware
We utilized AlphaFold 2.3.2 as a Docker image on the Google Cloud Platform, employing n1-highmem-8 instances with one NVIDIA Tesla K80 GPU. The Life Sciences API and Cloud Shell facilitated job execution, with output saved in a dedicated Google Cloud Storage bucket. All necessary scripts are available in the GitLab project repository (https://gitlab.com/pdabrowskitumanski/alphafoldwrapper). A full version of BFD and the monomer protocol of AlphaFold were utilized when running the jobs.
2.2. Structures and Sequences
Amino acid sequences testing AlphaFold predictions of protein structures were downloaded from the RCSB database or modified accordingly. A detailed list of the sequences used, along with the corresponding models obtained and their topology, is available in the GitLab project repository. UCSF Chimera [34] was employed for structure analysis and visualization.
3. Results
3.1. AlphaFold Builds Protein Structures Forming Arbitrary Complex Knots
To consider the theoretical possibilities of forming knotted polypeptide chains during protein folding let us briefly discuss how such knots can be formed. Although a great majority of proteins fold into their native structure without forming knots on their polypeptide chains, there are also families of proteins whose polypeptide chains get reproducibly knotted during their folding [16,26,28,35]. In contrast to the entropically driven formation of various knots on long polymeric chains such as on long linear DNA molecules packed inside phage heads [36,37,38], the knots formed during protein folding are highly specific, where a given protein species always form the same type of knot, which in the majority of knotted proteins is a simple trefoil () knot with just three crossings in its minimal crossing diagram. However, the knots in proteins can also be more complex, and for example, the polypeptide chain of bacterial -haloacid dehalogenase always forms a complex knot with 6 crossings in its minimal crossing diagram [39]. The formed knot is known as Stevedore’s knot and has a topological notation once the two ends of the linear knots are connected with each other without introducing additional crossings. In addition to forming a unique type of knot characteristic to a given protein species, knotted portions of polypeptide chains take practically the same shape in each copy of a given knotted protein and can even be required for the formation of active sites of these proteins [40].
Most of the knots observed in proteins are shallow which means that the intra-chain interlacing leading to the formation of knots is located very close to at least one of the ends of the polypeptide chain. It is assumed that shallow protein knots form during the final stages of protein folding when the protein chain compacts into a globule and one or both of its termini interlace with the distally located portions of the same polypeptide chain. Alternatively, the loop can move with respect to the tail in a mouse-trap-like mechanism [41,42,43]. Less frequent than shallow knots are deep knots in which intrachain interlacing leads to the formation of the knot located further than ca 20 amino acids from the nearest termini of the knotted polypeptide chain [44].
Deep knots are unlikely to form by such a simple mechanism as shallow knots. Conformational changes involving motions of the entire folded domains with respect to each other were proposed to cause an entire terminal portion of the folding chain to interlace with distal portions of the same chain [45]. It was also proposed that ribosome-driven, active polypeptide chain translocation resulting from the vectorial process of nascent polypeptide chain growth during co-translational folding may drive the formation of deep knots [46,47].
Alternatively, a conformational change resulting from domain duplication, in which two domains interlace, was proposed as a mechanism of single deep knot formation [48]. However, the on-ribosome folding can produce only a single deep knot, as each knot requires a twisted loop surrounding the ribosome exit tunnel. It is highly doubtful, that two such loops would attach to the ribosome surface in the desired conformation. Similarly, domain swapping results in a single knot as it is an outcome of swapping the termini position. Threading the tail could in principle lead to two consecutive knotted domains (as there are two chains to be threaded – Figure 1A).
Formation of a higher number of consecutive knots would require passing very long tails or already folded, knotted domains through the twisted loop, which again seems doubtful. Eventually, the combination of on-ribosome folding (Figure 1B) or domain swapping with tail threading could lead to maximally 3 consecutive knots (Figure 1C) – two shallow on the termini and a deep in the center.
As a consequence, proteins with three or more consecutive deep knots should not be realizable through protein folding.
We, therefore, tested the ability of AlphaFold to predict the folded structure of an artificial protein in which the polypeptide chain is composed of multiple tandem repeats of polypeptide chains of naturally knotted proteins. We started from MJ0366 from Methanocaldococcus jannaschii (PDB code: 2efv) which is known to form a shallow trefoil knot. Interestingly, AlphaFold predicted that the structure of multiple repeats of will MJ0366 sequence forms a composite knot where each of MJ0366 domains forms a trefoil knot (see Figure 2). For practical reasons (computer memory requirements and calculation time), we limited our tests to polypeptide chains with up to 10 tandem repeats, but it seems that constructs with any arbitrary number of MJ0366 repeats would be predicted by AlphaFold to form proteins with the corresponding number of linearly arranged trefoil-forming polypeptide blocks (Figure 2).
It needs to be mentioned here that although in its native form, the polypeptide chain of a single domain of MJ0366 from Methanocaldococcus jannaschii forms a shallow trefoil knot, in the artificial construct tested here only the two terminal repeats could form shallow knots by the interlacing of their free ends with some accessible polypeptide chain portions of the same protein. Moreover, apart from the two terminal knots, during folding, such a construct would most probably create multiple slipknots, where the internal domains, evolutionarily optimized for shallow threading would not have the means to cause complete threading of long portions of polypeptide chains. This is, however, not the case in the modeled structure.
Although slipknots are present in numerous proteins, the structure predicted by AlphaFold for this tandem repeat of MJ0366 is not composed of multiple slip knot-forming portions but of portions forming complete knots. Obtaining such a structure would require threading the whole domain through the twisted loop, which is impossible in a natively shallowly knotted protein.
We also tested AlphaFold predictions for artificial structures composed of multiple repeats of amino acid blocks that in a natural setting form deep knots in polypeptide chains. We used trimeric (3x) and pentameric (5x) amino acid sequences taken from the protein YibK (PDB code: 1j85) that naturally forms a deep trefoil knot. As shown in Figure 3 AlphaFold predicted that these constructs will fold into forms with three and five knots respectively, which again suggests that it can produce a chain with an arbitrary number of consecutive knots. Again, such structures are impossible using the known mechanisms of knot formation in proteins.
In our study, the domains were connected usually with a flexible, nine-glycine linker, to remove a possible influence of the linker on the domain structure. However, for the completeness of the study, we also tested various linker types (using glycine-serine linkers and proline-reach linkers) and lengths (in the range of 1-17 residues). Apart from conformational variablity of linkers, we always obtained topologically equivalent results. AlphaFold also provides a multimer algorithm, which was created to model proteins composed of several disjoined subunits. We tested also this algorithm, again obtaining the same protein topologies.
3.2. AlphaFold Predicts Impossibly Densely Packed Structures
The structures presented before were multidomain chains. We also thought if it is possible to obtain a falsely knotted, single-domain structure. In order to produce one, we started again from YibK protein, which naturally forms a trefoil knot. We have, however, shortened the twisted loop through which the terminal portion of the chain would need to thread to form a knot. If the twisted loop is too short the threading should become impossible and knots should not form.
However, even after the removal of 8 residues from the twisted loop (around 40%) AlphaFold still predicted a knotted structure with no significant conformational change apart from the missing part of the loop (Figure 4A). In addition, we were able to exchange small residues for bulky tryptophans producing an extremely dense packing within the twisted loop pierced by the threaded portion of the knotted polypeptide chain. Although no stereochemical clashes were observed within the twisted loop, any movement needed for threading seems impossible (Figure 4B). The structure predicted shoed no significant conformational changes relative to the native structure.
4. Discussion
In this study, we demonstrated, that AlphaFold can predict protein constructs to form complex knots even in cases where the formation of such complex knots by natural protein folding is not feasible. We have analyzed two cases of multidomain proteins with composite knots, and a single-domain proteins with modified knotted core. Overall, the results show, that not respecting topological barriers in the early steps of the protein modeling procedure hinders AlphaFold ability to predict topologically valid structures.
The non-respecting of the topology is a very deeply rooted feature of the algorithm, as it is required to treat the chain in a reduced form of rotations and translations predicted by one of the AlphaFold modules. Therefore, fixing the topological problem would require changing the deep learning architecture of the tool. As a result, additional validation of predicted topologies is imperative in any studies of AlphaFold-predicted structures, where the topology is important.
Most importantly, such validation has to be motivated biologically. Assessing the final structure using any metric seems to be insufficient. In particular, assessing the structure by mean pLDDT for a given chain (standard metric used in AlphaFold) may be highly confusing. In particular, all of the structures analyzed in this work have mean pLDDT larger than 76, and in most cases larger than 80, and therefore are classified as modeled reasonably. The reason is, that in the case of knotted structures, crucial in structure validation is the mutual location of the loop and threading chain - the information which, being local, is easily lost while averaging the pLDDT metric over the whole chain.
However, calculating the per-residue pLDDT does not solve the problem. In fact, in our cases, the lowest pLDDT is obtained for the linkers, while for each knotted core the pLDDT is always relatively large (Figure 5). This is, however, expected, as pLDDT measures how optimal are the distances, where the optimum is taken from the reference structures. Therefore, the more similar is each knotted core to the native structure, the higher the pLDDT score.
This is the general problem with local measures such as pLDDT - locally, each domain and knotted core has the correct structure. These are the global features of the protein (existence of a few domains), which makes the whole structure wrong. Therefore, to fully assess the predicted structure, some global metric, taking into account the whole backbone at once should be used.
There is also another problem with local metrics such as pLDDT, which may be seen in multidomain proteins. If the studied domain exists in some experimental structures as a homodimer, then pLDDT would increase if any two repeats of the domain were placed closely. In particular, when predicting the structure of a homotrimer, AlphaFold will try to locate two domains in the same place relative to the third domain, as in this case, the distances between the third and two other domains would match those in the homodimer. This may lead to the overlaying of the domains. In fact, although we did not find such structures in the best-ranked AlphaFold models, we indeed found such trimers with overlayed domains among models with a lower ranking (Figure 6). It is worth mentioning, that such structures also have mean pLDDT larger than 70, so they should be regarded as reliably modeled.
The experiment with the tight loop in the YibK artificial mutant showed another problem of AlphaFold, that small changes in the sequence, although potentially having a drastic effect on the topology, have only limited influence on the structure predicted by AlphaFold. This effect was studied before in the case of missense mutations [49,50], but it shows, that AlphaFold is of limited use in the case of lasso-like proteins [51,52], where the topology can change when introducing, or removing single cysteine residue.
The whole analysis shows, that AlphaFold, by design allowing chain passage, is not suited to model structures with topological features such as knots. Yet, some knotted structures identified among AlphaFold results may still be real. The and knots identified by Brems et al [29] are single-domain structures with no visible dense residue packing. The knot found by Perlinska et al [30] is a double-domain knot, however, the domains are swapped. A similar effect was already observed in the analysis of possible evolutionary pathway of deep knot, another topologically symmetric structure [31].
In general, however, caution should be exercised when interpreting AlphaFold’s predictions in terms of protein topology, considering the potential for false-positive identification of knots and other topological features.
Author Contributions
Conceptualization, P.D.T and A.S; Methodology, P.D.T and A.S; Software, P.D.T; Investigation, P.D.T and A.S; Writing – Original Draft Preparation, A.S; Writing – Review & Editing P.D.T and A.S; Visualization, P.D.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding
Data Availability Statement
Initial data (protein sequences and 3D structures) can be found in RCSB database. Obtained results can be found in the GitLab repository https://gitlab.com/pdabrowskitumanski/alphafoldwrapper.
Acknowledgments
We acknowledge the developers of AlphaFold for providing open access to their tool, the authors of the RCSB database for maintaining a valuable resource for protein structures, Google Cloud Platform for supporting us with free credits, and Nobuhisa Misue from Google for clear instructions on running AlphaFold on Google Cloud.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.; Bridgland, A.; et al. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.; Bridgland, A.; et al. Protein structure prediction using multiple deep neural networks in the 13th Critical Assessment of Protein Structure Prediction (CASP13). Proteins: structure, function, and bioinformatics 2019, 87, 1141–1148. [Google Scholar] [CrossRef] [PubMed]
- Kryshtafovych, A.; Schwede, T.; Topf, M.; Fidelis, K.; Moult, J. Critical assessment of methods of protein structure prediction (CASP)—Round XIII. Proteins: Structure, Function, and Bioinformatics 2019, 87, 1011–1020. [Google Scholar] [CrossRef]
- Kryshtafovych, A.; Schwede, T.; Topf, M.; Fidelis, K.; Moult, J. Critical assessment of methods of protein structure prediction (CASP)—Round XIV. Proteins: Structure, Function, and Bioinformatics 2021, 89, 1607–1617. [Google Scholar] [CrossRef] [PubMed]
- Mirdita, M.; Schütze, K.; Moriwaki, Y.; Heo, L.; Ovchinnikov, S.; Steinegger, M. ColabFold: making protein folding accessible to all. Nature methods 2022, 19, 679–682. [Google Scholar] [CrossRef]
- Luebbert, L.; Pachter, L. Efficient querying of genomic reference databases with gget. Bioinformatics 2023, 39, btac836. [Google Scholar] [CrossRef]
- Evans, R.; O’Neill, M.; Pritzel, A.; Antropova, N.; Senior, A.; Green, T.; Žídek, A.; Bates, R.; Blackwell, S.; Yim, J.; et al. Protein complex prediction with AlphaFold-Multimer. biorxiv 2021, pp. 2021–10.
- Baek, M.; Anishchenko, I.; Humphreys, I.; Cong, Q.; Baker, D.; DiMaio, F. Efficient and accurate prediction of protein structure using RoseTTAFold2. bioRxiv 2023, pp. 2023–05.
- Baek, M.; Baker, D. Deep learning and protein structure modeling. Nature methods 2022, 19, 13–14. [Google Scholar] [CrossRef]
- Baek, M.; DiMaio, F.; Anishchenko, I.; Dauparas, J.; Ovchinnikov, S.; Lee, G.R.; Wang, J.; Cong, Q.; Kinch, L.N.; Schaeffer, R.D.; et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021, 373, 871–876. [Google Scholar] [CrossRef]
- Hekkelman, M.L.; de Vries, I.; Joosten, R.P.; Perrakis, A. AlphaFill: enriching AlphaFold models with ligands and cofactors. Nature Methods 2023, 20, 205–213. [Google Scholar] [CrossRef]
- Terwilliger, T.C.; Poon, B.K.; Afonine, P.V.; Schlicksup, C.J.; Croll, T.I.; Millán, C.; Richardson, J.S.; Read, R.J.; Adams, P.D. Improved AlphaFold modeling with implicit experimental information. Nature methods 2022, 19, 1376–1382. [Google Scholar] [CrossRef] [PubMed]
- Ahdritz, G.; Bouatta, N.; Kadyan, S.; Xia, Q.; Gerecke, W.; O’Donnell, T.J.; Berenberg, D.; Fisk, I.; Zanichelli, N.; Zhang, B.; et al. OpenFold: Retraining AlphaFold2 yields new insights into its learning mechanisms and capacity for generalization. bioRxiv 2022, pp. 2022–11.
- Tunyasuvunakool, K.; Adler, J.; Wu, Z.; Green, T.; Zielinski, M.; Žídek, A.; Bridgland, A.; Cowie, A.; Meyer, C.; Laydon, A.; et al. Highly accurate protein structure prediction for the human proteome. Nature 2021, 596, 590–596. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski-Tumanski, P.; Rubach, P.; Goundaroulis, D.; Dorier, J.; Sułkowski, P.; Millett, K.C.; Rawdon, E.J.; Stasiak, A.; Sulkowska, J.I. KnotProt 2. 0: a database of proteins with knots and other entangled structures. Nucleic acids research 2019, 47, D367–D375. [Google Scholar]
- King, N.P.; Yeates, E.O.; Yeates, T.O. Identification of rare slipknots in proteins and their implications for stability and folding. Journal of molecular biology 2007, 373, 153–166. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski-Tumanski, P.; Sulkowska, J.I. Topological knots and links in proteins. Proceedings of the National Academy of Sciences 2017, 114, 3415–3420. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Goundaroulis, D.; Stasiak, A.; Sulkowska, J.I. q-curves in proteins. arXiv, preprint. arXiv:1908.05919 2019.
- Dabrowski-Tumanski, P. Niemyska,W.; Pasznik, P.; Sulkowska, J.I. LassoProt: server to analyze biopolymers with lassos. 2016, 44, W383–W389. Nucleic acids research 2016, 44, W383–W389. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Jarmolinska, A.I.; Niemyska, W.; Rawdon, E.J.; Millett, K.C.; Sulkowska, J.I. LinkProt: a database collecting information about biological links. Nucleic acids research 2016, p. gkw976.
- Zhao, Y.; Chwastyk, M.; Cieplak, M. Structural entanglements in protein complexes. The Journal of Chemical Physics 2017, 146. [Google Scholar] [CrossRef]
- Baiesi, M.; Orlandini, E.; Trovato, A.; Seno, F. Linking in domain-swapped protein dimers. Scientific reports 2016, 6, 33872. [Google Scholar] [CrossRef]
- Liang, C.; Mislow, K. Topological features of protein structures: knots and links. Journal of the American Chemical Society 1995, 117, 4201–4213. [Google Scholar] [CrossRef]
- Liang, C.; Mislow, K. Knots in proteins. Journal of the American Chemical Society 1994, 116, 11189–11190. [Google Scholar] [CrossRef]
- Jackson, S.E.; Suma, A.; Micheletti, C. How to fold intricately: using theory and experiments to unravel the properties of knotted proteins. Current opinion in structural biology 2017, 42, 6–14. [Google Scholar] [CrossRef] [PubMed]
- Faísca, P.F. Knotted proteins: A tangled tale of structural biology. Computational and structural biotechnology journal 2015, 13, 459–468. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski-Tumanski, P.; Sulkowska, J.I. To tie or not to tie? That is the question. Polymers 2017, 9, 454. [Google Scholar] [PubMed]
- Brems, M.A.; Runkel, R.; Yeates, T.O.; Virnau, P. AlphaFold predicts the most complex protein knot and composite protein knots. Protein Science 2022, 31, e4380. [Google Scholar] [CrossRef]
- Perlinska, A.P.; Niemyska, W.H.; Gren, B.A.; Bukowicki, M.; Nowakowski, S.; Rubach, P.; Sulkowska, J.I. AlphaFold predicts novel human proteins with knots. Protein Science 2023, 32, e4631.
- Taylor,W.R. Protein knots and fold complexity: some new twists. Computational biology and chemistry 2007, 31, 151–162. [CrossRef]
- Niemyska,W.; Rubach, P.; Gren, B.A.; Nguyen, M.L.; Garstka,W.; Bruno da Silva, F.; Rawdon, E.J.; Sulkowska, J.I. AlphaKnot: server to analyze entanglement in structures predicted by AlphaFold methods. Nucleic Acids Research 2022, 50, W44–W50.
- Mariani, V.; Biasini, M.; Barbato, A.; Schwede, T. lDDT: a local superposition-free score for comparing protein structures and models using distance difference tests. Bioinformatics 2013, 29, 2722–2728. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—a visualization system for exploratory research and analysis. Journal of computational chemistry 2004, 25, 1605–1612. [Google Scholar] [CrossRef]
- Flapan, E.; Heller, G. Topological complexity in protein structures. Computational and Mathematical Biophysics 2015, 3. [Google Scholar] [CrossRef]
- Arsuaga, J.; Vazquez, M.; McGuirk, P.; Trigueros, S.; Sumners, D.W.; Roca, J. DNA knots reveal a chiral organization of DNA in phage capsids. Proceedings of the National Academy of Sciences 2005, 102, 9165–9169. [Google Scholar] [CrossRef] [PubMed]
- Marenduzzo, D.; Micheletti, C.; Orlandini, E.; Sumners, D.W. Topological friction strongly affects viral DNA ejection. Proceedings of the National Academy of Sciences 2013, 110, 20081–20086. [Google Scholar] [CrossRef] [PubMed]
- Reith, D.; Cifra, P.; Stasiak, A.; Virnau, P. Effective stiffening of DNA due to nematic ordering causes DNA molecules packed in phage capsids to preferentially form torus knots. Nucleic acids research 2012, 40, 5129–5137. [Google Scholar] [CrossRef]
- Bölinger, D.; Sułkowska, J.I.; Hsu, H.P.; Mirny, L.A.; Kardar, M.; Onuchic, J.N.; Virnau, P. A Stevedore’s protein knot. PLoS computational biology 2010, 6, e1000731. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Stasiak, A.; Sulkowska, J.I. In search of functional advantages of knots in proteins. PloS one 2016, 11, e0165986. [Google Scholar] [CrossRef]
- Beccara, S.; Škrbi´c, T.; Covino, R.; Micheletti, C.; Faccioli, P. Folding pathways of a knotted protein with a realistic atomistic force field. PLoS computational biology 2013, 9, e1003002. [Google Scholar] [CrossRef] [PubMed]
- Chwastyk, M.; Cieplak, M. Multiple folding pathways of proteins with shallow knots and co-translational folding. The Journal of chemical physics 2015, 143. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Jarmolinska, A.; Sulkowska, J. Prediction of the optimal set of contacts to fold the smallest knotted protein. Journal of Physics: Condensed Matter 2015, 27, 354109. [Google Scholar]
- Lim, N.C.; Jackson, S.E. Molecular knots in biology and chemistry. Journal of Physics: Condensed Matter 2015, 27, 354101. [Google Scholar]
- Lim, N.C.; Jackson, S.E. Mechanistic insights into the folding of knotted proteins in vitro and in vivo. Journal of molecular biology 2015, 427, 248–258. [Google Scholar] [CrossRef]
- Dabrowski-Tumanski, P.; Piejko, M.; Niewieczerzal, S.; Stasiak, A.; Sulkowska, J.I. Protein knotting by active threading of nascent polypeptide chain exiting from the ribosome exit channel. The Journal of Physical Chemistry B 2018, 122, 11616–11625. [Google Scholar] [CrossRef] [PubMed]
- Chwastyk, M.; Cieplak, M. Cotranslational folding of deeply knotted proteins. Journal of Physics: Condensed Matter 2015, 27, 354105. [Google Scholar] [CrossRef] [PubMed]
- Taylor,W. R. A deeply knotted protein structure and how it might fold. Nature 2000, 406, 916–919.
- Buel, G.R.; Walters, K.J. Can AlphaFold2 predict the impact of missense mutations on structure? Nature Structural & Molecular Biology 2022, 29, 1–2. [Google Scholar]
- Pak, M.A.; Markhieva, K.A.; Novikova, M.S.; Petrov, D.S.; Vorobyev, I.S.; Maksimova, E.S.; Kondrashov, F.A.; Ivankov, D.N. Using AlphaFold to predict the impact of single mutations on protein stability and function. Plos one 2023, 18, e0282689. [Google Scholar] [CrossRef] [PubMed]
- Niemyska,W.; Dabrowski-Tumanski, P.; Kadlof, M.;, Haglund, E.;, Sułkowski, P. Complex lasso: new entangled motifs in proteins. 2016, 6, 36895.
- Haglund, E.; Sulkowska, J.I.; Noel, J.K.; Lammert, H.; Onuchic, J.N.; Jennings, P.A. Pierced lasso bundles are a new class of knot-like motifs. PLoS computational biology 2014, 10, e1003613. [Google Scholar] [CrossRef]
Figure 1.
Proposed mechanisms of knot formation. A) Direct threading of the tail can produce up to two knots, most possibly shallow. B) On-ribosome knotting requires attaching the loop to the ribosome surface and therefore allows the formation of a single deep knot. C) Composition of threading and on-ribosome folding allows the creation of three consecutive knots (separated by dashed lines) – one deep in the center surrounded by up to two, most possibly shallow knots formed by the termini. The colors in panels B and C show large and small subunits of a ribosome. Green is the protein chain. The arrows indicate the chain movement leading to a knot.
Figure 1.
Proposed mechanisms of knot formation. A) Direct threading of the tail can produce up to two knots, most possibly shallow. B) On-ribosome knotting requires attaching the loop to the ribosome surface and therefore allows the formation of a single deep knot. C) Composition of threading and on-ribosome folding allows the creation of three consecutive knots (separated by dashed lines) – one deep in the center surrounded by up to two, most possibly shallow knots formed by the termini. The colors in panels B and C show large and small subunits of a ribosome. Green is the protein chain. The arrows indicate the chain movement leading to a knot.
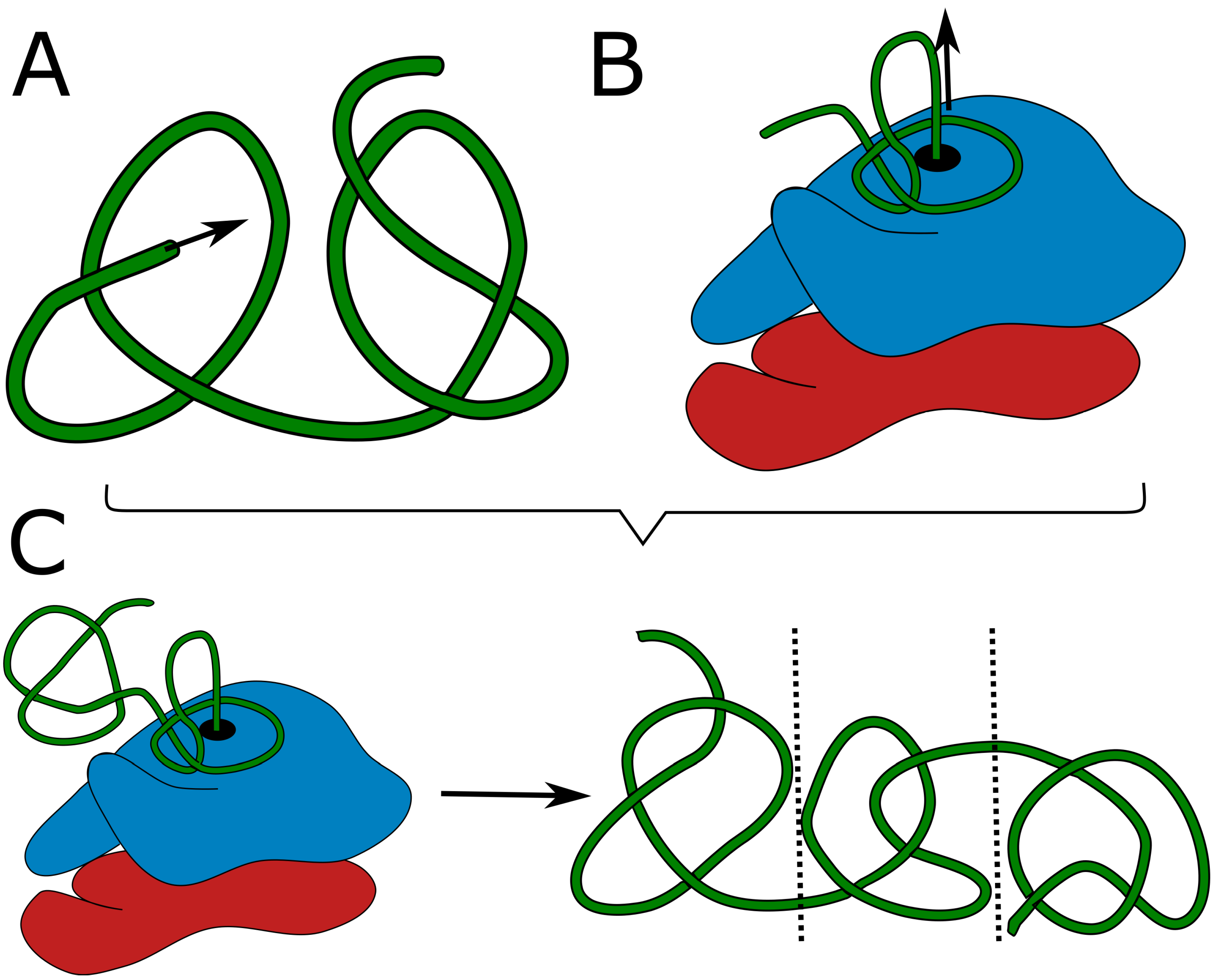
Figure 2.
Structures of MJ0366 (PDB code 2efv) multimers. A) trimer with 3 consecutive knots, B) pentamer with 5 consecutive knots, C) decamer with 10 consecutive knots. In each panel, the domains are depicted in different colors. Black strands denote the glycine linkers.
Figure 2.
Structures of MJ0366 (PDB code 2efv) multimers. A) trimer with 3 consecutive knots, B) pentamer with 5 consecutive knots, C) decamer with 10 consecutive knots. In each panel, the domains are depicted in different colors. Black strands denote the glycine linkers.
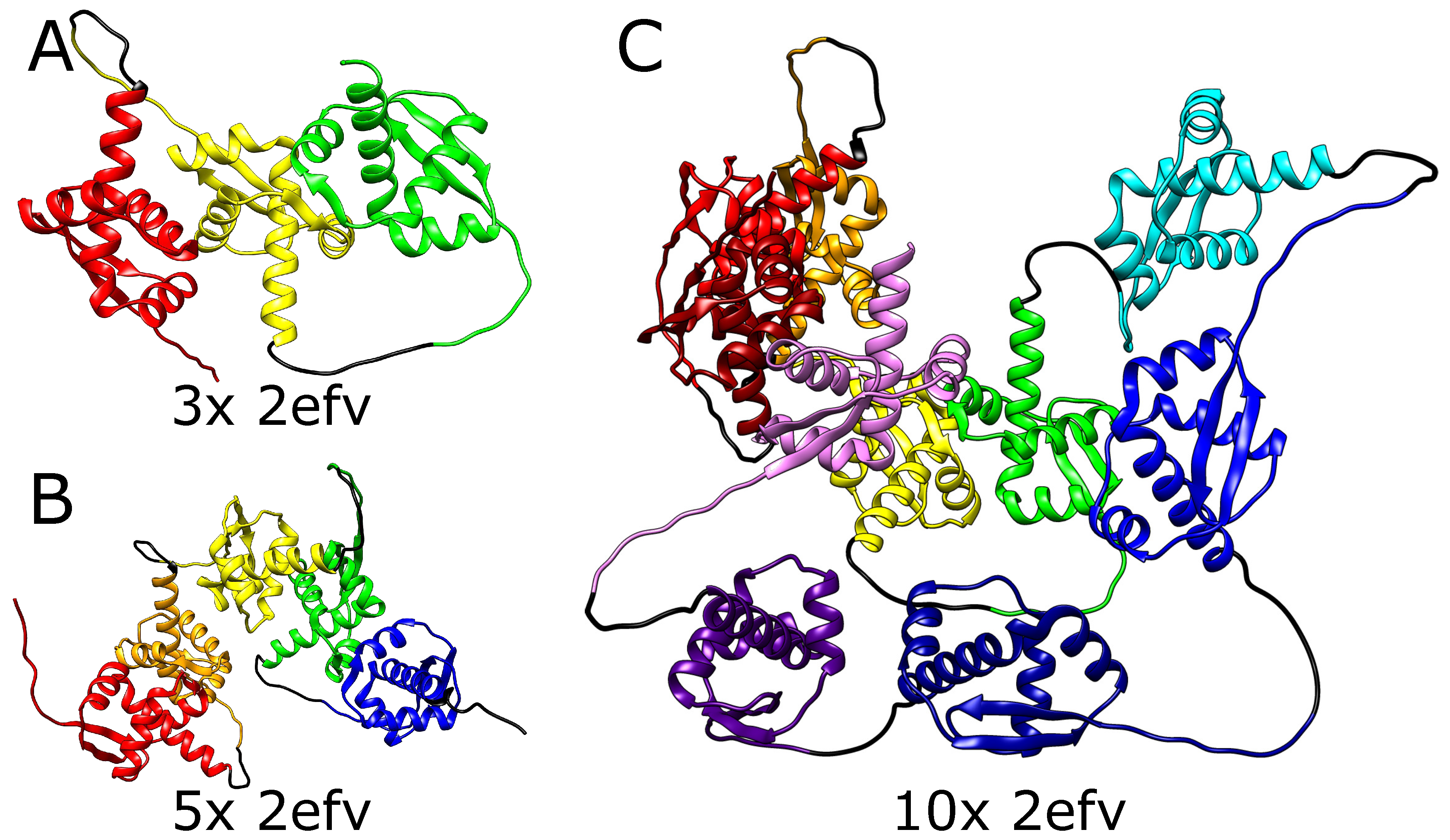
Figure 3.
The structures of multimers of deeply knotted YibK protein (PBD code 1j85). A) trimer with 3 consecutive trefoil knots, B) pentamer with 5 consecutive trefoil knots. In both panels, the tandemly repeated protein blocks are represented with different pastel colors. The darker colors indicate the knotted core. The glycine linkers are presented in black.
Figure 3.
The structures of multimers of deeply knotted YibK protein (PBD code 1j85). A) trimer with 3 consecutive trefoil knots, B) pentamer with 5 consecutive trefoil knots. In both panels, the tandemly repeated protein blocks are represented with different pastel colors. The darker colors indicate the knotted core. The glycine linkers are presented in black.
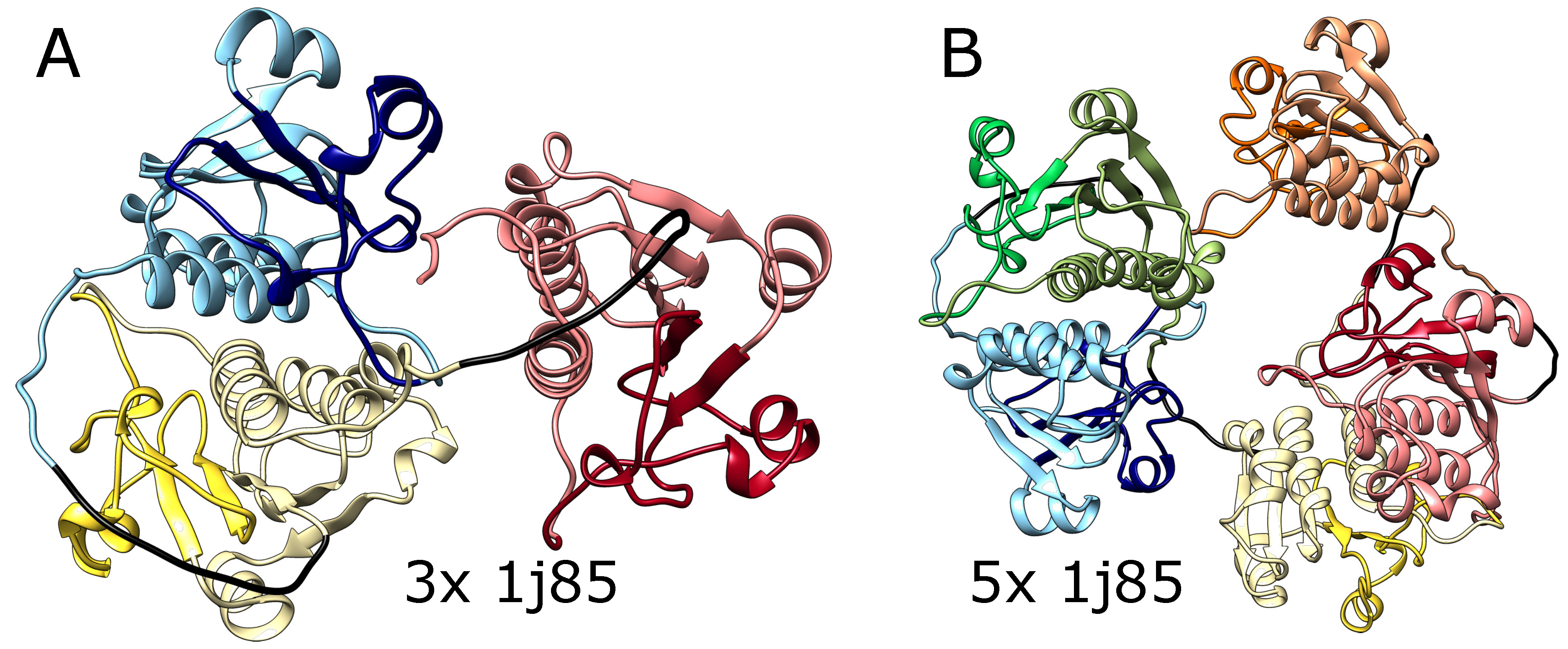
Figure 4.
Modified YibK protein with shortened loop. A) The native (blue) structure of YibK overlayed with the structure with 40% of residues removed from the twisted loop (red). The structures differ only in the region of the modified loop. B) The loop (green) with the threaded tail (yellow) with all the atoms explicitly showed. In the top left corner - the schematic depiction of the threading.
Figure 4.
Modified YibK protein with shortened loop. A) The native (blue) structure of YibK overlayed with the structure with 40% of residues removed from the twisted loop (red). The structures differ only in the region of the modified loop. B) The loop (green) with the threaded tail (yellow) with all the atoms explicitly showed. In the top left corner - the schematic depiction of the threading.
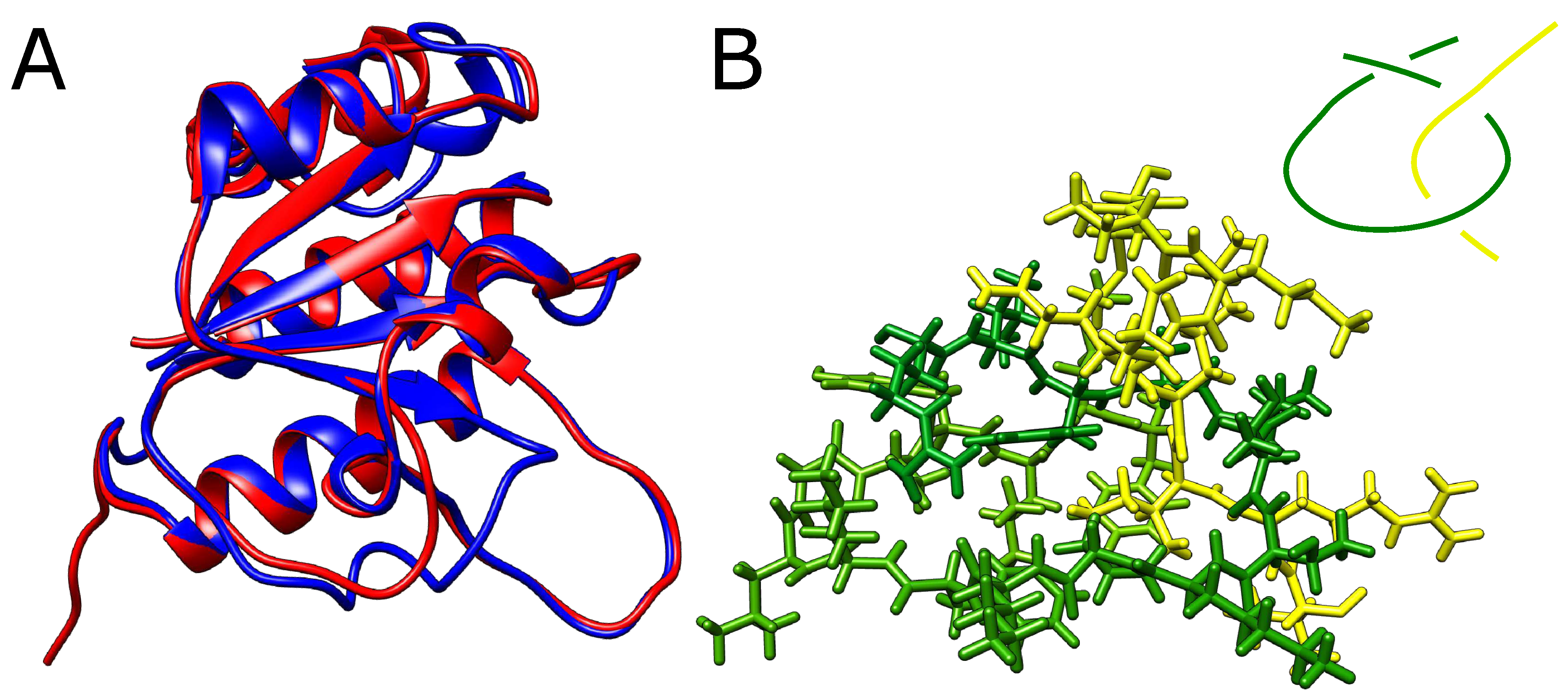
Figure 5.
The predicted structures of tandem triple repeats colored by pLDDT. A) 2efv trimer and B) 1j85 trimer (right). Both structures have three consecutive trefoil knots. The lowest pLDDT (blue) can be seen in the linkers which are flexible and do not have homologs with well-defined structures. The knotted cores pLDDT is relatively high (red) indicating those regions are modeled reliably. The white parts are the tails with medium values of pLDDT.
Figure 5.
The predicted structures of tandem triple repeats colored by pLDDT. A) 2efv trimer and B) 1j85 trimer (right). Both structures have three consecutive trefoil knots. The lowest pLDDT (blue) can be seen in the linkers which are flexible and do not have homologs with well-defined structures. The knotted cores pLDDT is relatively high (red) indicating those regions are modeled reliably. The white parts are the tails with medium values of pLDDT.
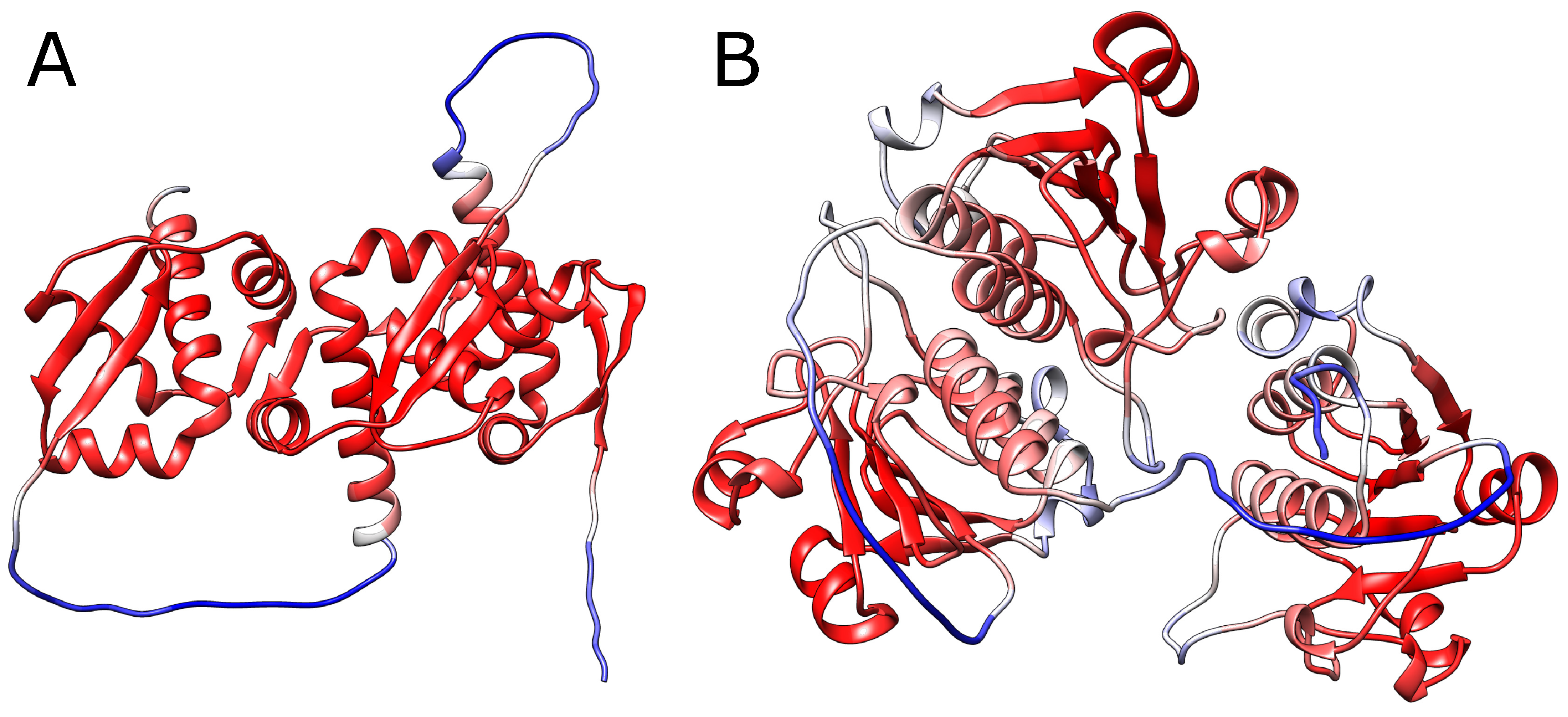
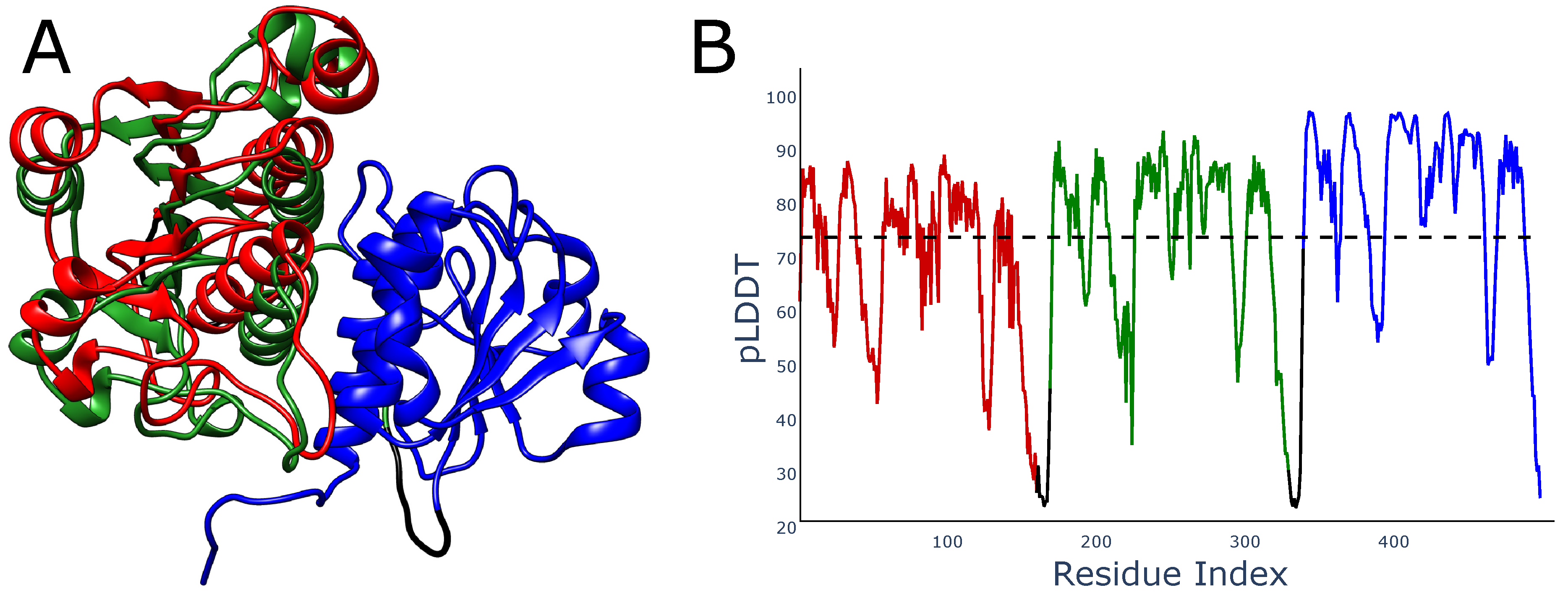
Figure 6.
Wrong structure with overlayed domains. A) the model proposed by AlphaFold for the 1j85 trimeric repeat ranked in second place. The terminal domains - red and green - are almost overlayed. B) the plot of pLDDT for the structure. The dashed line denotes the mean pLDDT score equal to 74. The colors in panel A match those in panel B.
Figure 6.
Wrong structure with overlayed domains. A) the model proposed by AlphaFold for the 1j85 trimeric repeat ranked in second place. The terminal domains - red and green - are almost overlayed. B) the plot of pLDDT for the structure. The dashed line denotes the mean pLDDT score equal to 74. The colors in panel A match those in panel B.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






