Prerpints.org logo
Preprint
Article

Numerical Analysis of Solid Core Photonic Crystal Fiber Based on Plasmonic Materials for Analytes Refractive Index Sensing

Altmetrics

Downloads

127

Views

36

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

24 August 2023

Posted:

25 August 2023

You are already at the latest version

Alerts
Abstract
In this study, we presented a simple highly sensitive sensor based on commercially available solid core photonic crystal fiber (PCF) and surface plasmon resonance (SPR) for measuring the refractive index (RI) of analytes. The numerical simulation based on the finite element method (FEM) has been examined to compute the optical properties such as confinement loss, power spectrum, and transmission intensity of the sensor. The most sensitive and inert plasmonic materials (gold and silver) have been assumed to be coated inside the fiber with the range of analytes RI from 1.32 to 1.40. The performance of the proposed sensor has been evaluated by tracing the several optical features like wavelength sensitivity, amplitude sensitivity, resolution of the sensor, and figure of merit. As a result, the comparative study between silver and gold elements has been carried out in which the maximum sensitivity received as 1.15 μm/RIU and 1.10 μm/RIU respectively. Whereas, on the base of power spectrum the obtained sensitivity was 513 μm/RIU for the gold layer. Moreover, the effect of other structural parameters (air holes and plasmonic layers thickness) on the sensing performance has been taken into an account. According to the simulation analysis and results, this sensor would have a great potential in various sensing applications of biomedical and liquid refractive index.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

Introduction

In the past few decades, the development of surface plasmon based sensing (SPR) techniques has been emphasized as an effective optical detection phenomenon owing to high sensitivity, label free, and real time monitoring [1]. Particularly, SPR is highly attractive to refractive index (RI) deviations, which performs as a suitable sensor for measuring the chemical, biological, and physical parameters [2,3]. The working principle of SPR sensing method can be well explained among the interface of metal and dielectric materials when the light signals and the free electrons jointly overlap at the same frequency [4]. Mostly commonly functional SPR-sensing platform rely on prism structure and optical fiber technology. However, prism structure demands mechanical and optical modules, these devices have massive arrangements that cause high cost and are not valuable for the integration of practical applications [5,6].
On the other hand, conventional optical fiber based SPR sensors have progressed a lot due to their high resolution, a miniaturized structure, and reliability in remote sensing applications [7,8]. But these types of fibers are single mode or multimode fibers which consist of core and cladding section; therefore, the external part of the fiber is chemically or physically isolated to reveal the core region to enhance the linking among the surface plasmon polariton (SPP) mode and core mode [9,10].
The invention of photonic crystal fiber (PCF) was a prominent breakthrough in optical fiber technology which is utilized in various fields such as spectroscopy, biomedical, and industrial machinery [11]. PCF has fascinated attraction over the conventional optical fiber due to their remarkable performance such as large effective area, nonlinearity, low loss, multi-parameter sensors, endlessly single mode, tunable dispersion, high index contrast and extensive range of environmental monitoring [12,13]. Therefore, the combination of PCF-based SPR sensing mechanism pays much attention to many researchers due to their flexibility structures and controllable light [14]. The air holes in the core and cladding region moderate the effective refractive index of the core which enhances the phase matching between the SPP and core modes [15]. The selection of plasmonic elements is also an important factor for PCF-SPR sensor, commonly there are gold, graphene, silver, copper, aluminum, and titanium nitride [16,17]. Among these materials, mostly silver and gold have created extreme and developing concern in the research study of PCF-SPR sensor to develop the precious optical features [18]. Silver approaches a high sensitivity, but it becomes oxidized in the presence of humid environment that can be improved by coating a layer of other elements like graphene, gold, or titanium oxide. Contrary, gold is chemically stable, biocompatible, and more appropriate for microfluidic liquids sensing [19].
Recently, many groups of researchers have proposed microstructure fibers based SPR sensor with various configuration of PCF where analytes or layer of plasmonic materials placed inside or outside the fiber to measure the different parameters [20]. In 2017, Weng et al. introduced the D-shape hole with dual cladding photonic crystal fiber based on surface plasmon resonance for sensing the temperature parameters [21]. In 2018, Ahmed et al. proposed the plasmon resonance PCF biosensor based on Titanium Nitride (TiN) to achieve the RI sensitivity as 7700 nm/RIU [22]. Furthermore, a dual channel photonic crystal fiber based on gold plasmonic material has been numerically investigated with the sensitivity of 3750 nm/RIU for RI measurement [23]. In 2020, a multi-channel PCF sensor based on surface plasmon resonance with multi-analytes channel has been studied with the sensitivity of 3083 nm/RIU [24]. Additionally, for the detection and quantification of coronavirus a photonic crystal fiber based on the plasmonic material is theoretically examined in 2022. The obtained sensitivity was 2009 nm/RIU, 2745 nm/RIU, 1984 nm/RIU, for the analytes RBD, RNA, and IgG respectively [25].
From the above literature review it has been seen that mostly researchers work with the complex structure of PCF’s which are not available commercially and need specific arrangements to fabricate which could be lengthy and costly. Further, the single or multiple plasmonic materials are utilized at the same structure of PCF to measure the sensitivity whereas the comparative study still is missing among the two materials at the same structure of PCF.
In this study, we introduced a broad analysis of commercially available solid core photonic crystal fiber based on plasmonic materials for liquid refractive index sensing. The Finite element method (FEM) has been applied to compute the sensing performance and the guiding properties of light spectrum. The most highly sensitive plasmonic materials silver and gold are utilized with the analytes refractive index range of 1.32-1.40. The proposed sensor is explored by finding the different optical properties of confinement loss, wavelength sensitivity, amplitude sensitivity, power spectrum and transmission intensity which creates the shift of peaks wavelength. The maximum sensitivities achieved as 1.15 μm/RIU, 1.10 μm/RIU for gold and silver materials respectively. On the other hand, by analyzing the power spectrum the obtained sensitivity was 513μm/RIU. Moreover, the comparative study of plasmonic particles and the effect of size of air holes and metal layers also has been investigated.

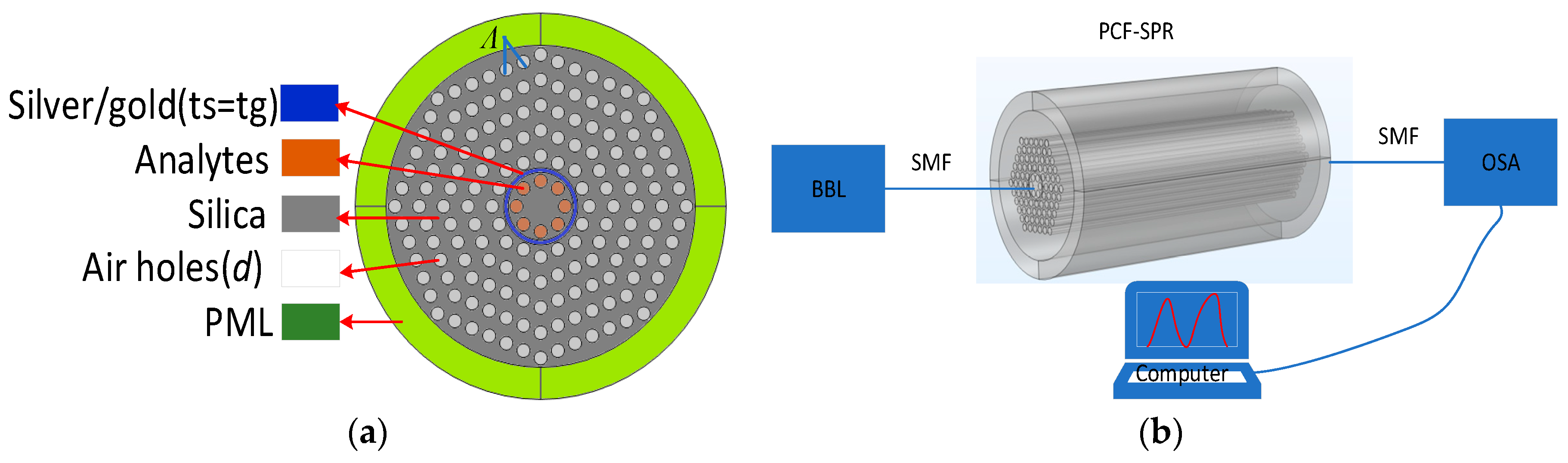
Geometrical Structure and Design

The cross-section view of 2-dimension proposed PCF-SPR design with the hexagonal arrangements of five layers of cladding air holes has been depicted in Figure 1a. The central part consists of the core region and the holes filled with analytes which are covered by a layer of plasmonic material (silver/gold). The size of the cladding air holes and the silver/gold layer are denoted by d (1.0 μm) and tg,ts (26 nm) respectively. The distance between two adjacent air holes is expressed as pitch Λ (2.2 μm). Silica is used as background material. The outer part of the fiber contains the perfectly matched layer (PML) which is applied to absorb the light spectrum occurring at various points. Moreover, the schematic diagram of 3-D PCF-SPR structure has been shown in Figure 1b which involves the sensing setup. The broadband light source (BBL) transmits the light signal with lead in single mode fiber (SMF) to the PCF-SPR sensor which leads out by SMF at the optical spectrum analyzer (OSA). Finally, the transmitted signals are displayed on the screen. All the parameters are optimized to achieve the maximum sensitivity of the proposed model.
The benefit of this kind of fiber is a commercially available and simple structure for a manufacturing process. The air holes surrounding the core region act to minimize the loss of light spectrum. The proposed structure can be fabricated by employing a high-temperature furnace in a standard fiber drawing tower. After preparing the fiber preform, silica rods and capillaries are compiled with the stack and draw procedure [26].
After fabrication process, the coating of silver or gold layer inside the fiber is the most important subject that demands a high temperature in some deposition methods such as thermal evaporation, sputtering, and radio frequency. As this PCF-SPR structure is assumed to be coated or filled internally with metal and analytes, that creates a little complexity in fabrication process, but it also leads to solidity and a stable sensor which prevents the external influences. Therefore, the most common and valuable technique of chemical vapor deposition (CVD) can be exploited to integrate the metal layer and analytes efficiently [27].

Materials and Methodology

The PCF-SPR design sensor involves cladding air holes with a refractive index of 1, and the background materials is silica whose refractive index can be analyzed by the sellimeier equation. The light dispersion of the sellimeier method can be calculated by the following equation [28].
s i l i c a n = 1 + A 1 λ 2 λ 2 − B 1 + A 2 λ 2 λ 2 − B 2 + A 3 λ 2 λ 2 − B 3
where n is the effective refractive index of the pure silica glass, the values for the constant variables are A1 = 0.6961663, A2 = 0.4079426, A3 = 0.8974794, B1 = 0.0684043, B2 = 0.1162414, B3 = 98.96161. λ is the operating wavelength in (μm).
Moreover, silver/gold has been selected as one of the promising candidates for plasmonic material which improves the detection capacity of the sensor. The advantages of these materials are no interband shift at visible wavelength, narrow resonance peak, and low optical damping. The material dispersion of plasmonic materials to realize the metal-dielectric behavior is illustrated by the Drude–Lorentz model [29].
E A u = E ∞ – ω D 2 ω ω + j γ D – ∆ ε . Ω L 2 ω 2 − Ω L 2 + j Γ L ω
where ɛAu is the permittivity of gold, ɛ∞ = 5.9673 is the permittivity of gold at high frequency, ω =2πc/λ is known as the angular frequency where c is the velocity of light, ωD = 2113.6 THz ⨯ 2π is known as plasma frequency, γD = 15.92 THz is known as damping frequency and Δɛ = 1.09 is denoted by the weighting factor. ΩL= 650.07 ⨯ 2π THz and ГL =104.86 ⨯ 2π THz are known as Lorentz oscillator strength and spectral width, respectively.
In the simulation study, the finite element method (FEM) based on the COMSOL Multiphysics Software is applied to investigate and evaluate the light transmission of the proposed PCF-SPR sensor. In computation, the physics-controlled way of fine mesh analysis is studied which consists of the number of 499097 solved elements for both domain and boundary elements. The distribution of electric fields in the core mode for X and Y polarization has been shown in Figure 2a,b respectively which illustrates the maximum light confining into the core region. On the other hand, Figure 2c,d shows the light spectrum for the SPP modes. The arrows indicate the direction of light in X and Y polarization respectively.
A broadband wavelength ranges from 1.30 μm to 1.70 μm is carried out for the whole simulation analysis. By using the silver material Figure 3a demonstrates the distribution of the light transmission among the SPP and fundamental core modes in which the RI of analytes, size of air holes, and the thickness has been fixed at RI=1.33, d=1.0 μm, and ts=26 nm respectively. In this graph, the confinement loss (CL) and the real part of the effective refractive index (neff) are taken from the right and left side respectively. The red line exhibits the loss peak for core mode whereas the black and blue solid lines represent the effective refractive index of fundamental modes and SPP modes respectively. It has been noticed that at the wavelength of 1.44 μm, the same refractive index of SPP and core mode intersect with each other which creates the resonance wavelength. At the resonance wavelength, the maximum light is transferred from the fundamental mode to SPP mode, where the sharp loss peak is monitored which is called phase matching condition. The unidentified samples can be detected by varying this peak to a longer or a shorter wavelength with the refractive index of different analytes. As the wavelength is going to increase the effective refractive index for the core and SPP mode is steadily decreased. So, the maximum refractive index is achieved at the minimum wavelength. Likewise, the short dash line in Figure 3b illustrates the loss spectra with respect to wavelength for gold material. Here the same parameters have been fixed like silver analysis but the resonance peak shifts towards the higher wavelength with higher refractive index and minimum loss. Usually, the core and SPP modes work at visible and infrared radiation respectively. The propagation of light has been evaluated for core-X and core-Y polarization spectrum. Both polarization spectrums have the same mechanism of light transmission. Therefore, core-X-polarized mode is considered to explore the sensor schemes for further study.

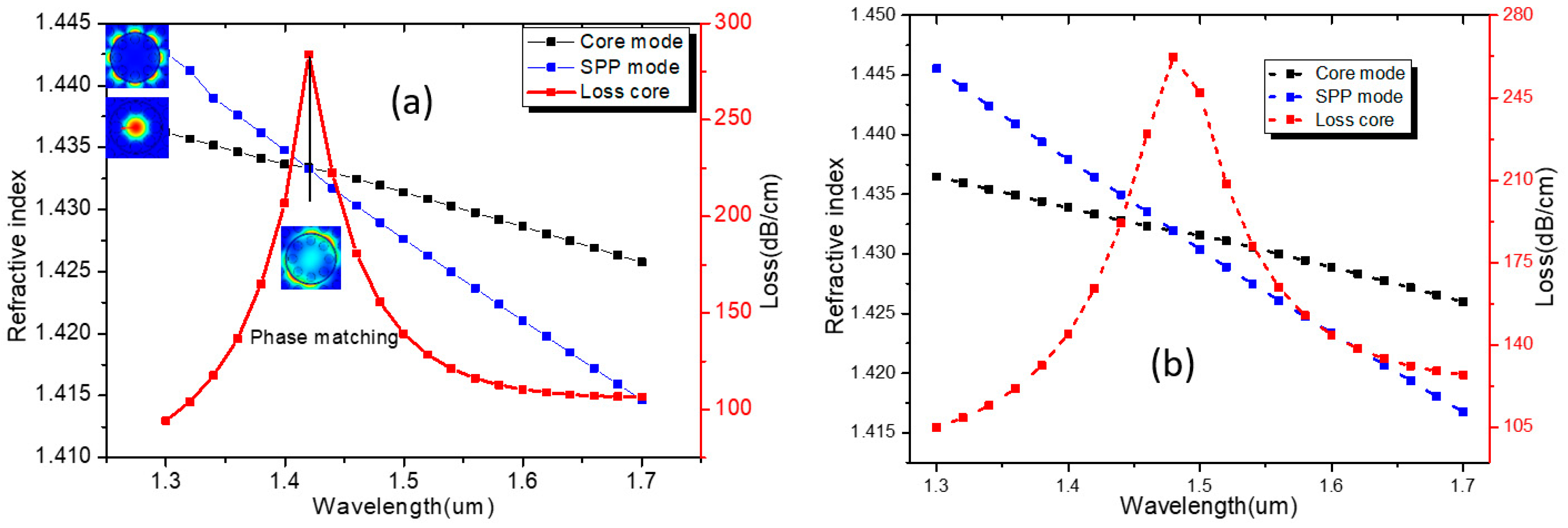
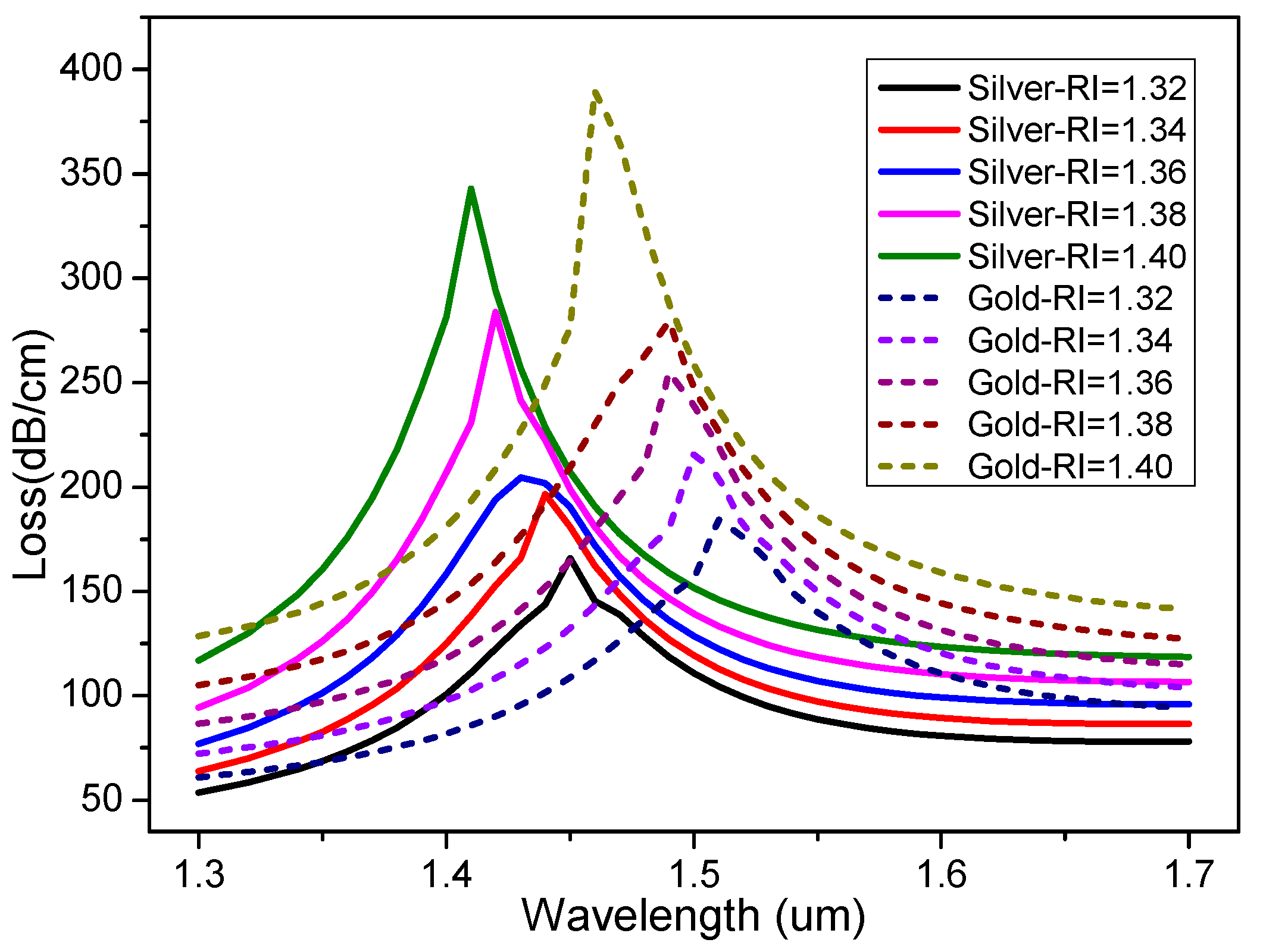
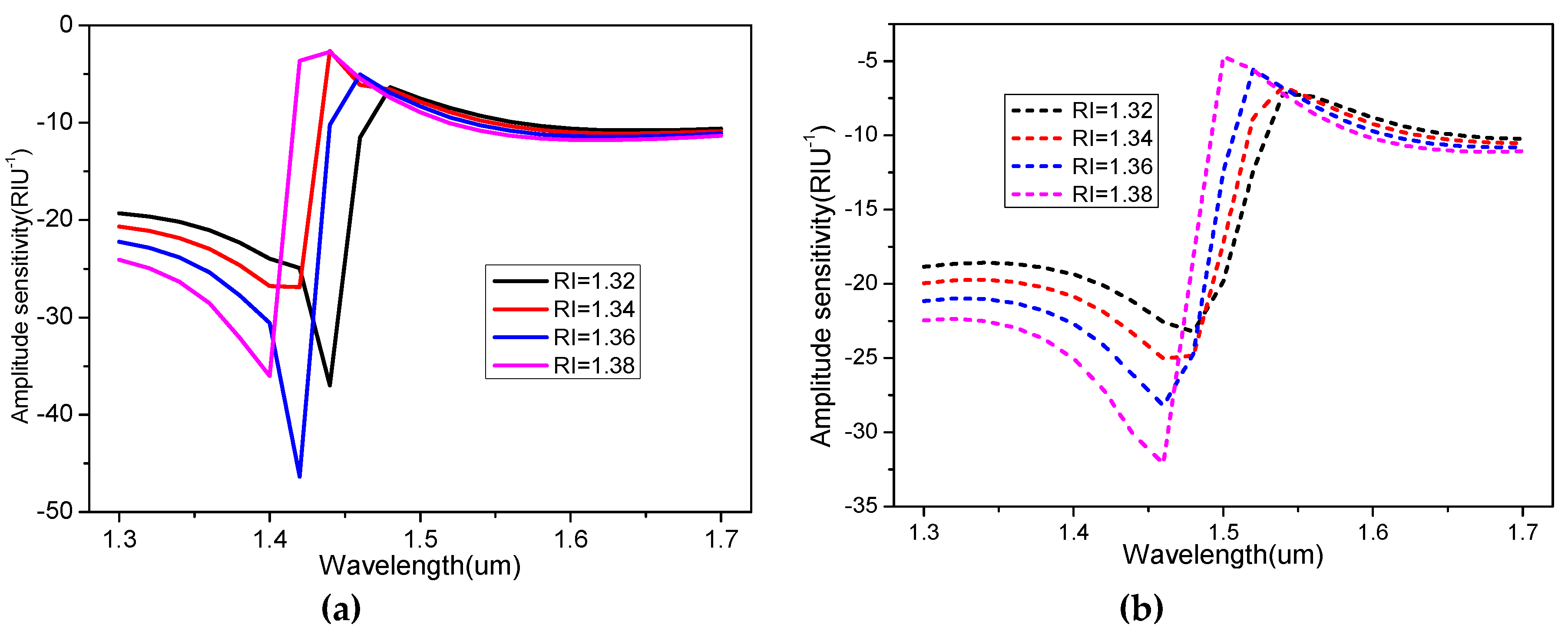
Results and Discussions

Moreover, the change of direction of light coupling shifts between the core and SPP mode happens at the resonance wavelength. Basically, the computation and examinations of the proposed PCF-SPR sensor have been explored by CL, one of the most important aspects in evaluating the function of the sensor. The CL of the fundamental mode can be calculated by the following equation [30].
C L d B c m = 8.686 × 2 π λ × I m n e f f × 10 4 ,
Where k 0 = 2 π λ is the free space of wave number, λ is the operating wavelength (μm), and I m n e f f is the imaginary part of effective refractive index.
To realize the sensing mechanism of the proposed PCF-SPR structure, the properties of the analytes RI have been examined. The effective refractive index of the SPP mode is highly responsive to the surrounding environment. The small variation of RI of analytes makes a significant shift of the real part of core mode. The comparatively confinement loss of silver and gold as a function of wavelength due to the alteration of analyte RI from 1.32 to 1.40 is shown in Figure 4. This graph depicts the solid lines to indicate the silver resonance wavelength. At the minimum RI (1.32) with sliver material, the small loss peak (162 dB/cm) is observed. By increasing the RI of analytes, the loss peak is going to increase at the higher RI (1.40), the maximum loss peak (340 dB/cm) is obtained. The resonance wavelength shifts move towards the shorter wavelength with the increment of analytes RI. Similarly, the same phenomena of loss spectra with short dash lines of gold material have been shown in Figure 4. The resonance wavelength shift attained at the higher wavelength as compared to silver analysis also the higher loss peak (386 dB/cm) is achieved at the RI of 1.40. During the analysis of loss spectrum with the variation of analytes RI, the rest of parameters like metal layer thickness (tg=26 nm) and air holes (d=1.0 μm) were kept constant.
Furthermore, the effect of air holes and the thickness of plasmonic layers has been evaluated. Figure 5a describes the solid and short dash lines of the variation of silver and gold layer (22 nm to 34 nm) with the change of each step 4nm respectively. It seems that by increasing the thickness of the silver and gold layer the resonance wavelength is moving towards the shorter wavelength and comparatively both have higher resonance wavelength. In both cases (silver and gold) at the thickness of (ts,tg=26 nm) the highest loss peak (269 dB/cm) appears, and at the maximum thickness (ts,tg=34 nm) the minimum loss (119 dB/cm) and (135 dB/cm) is achieved respectively. As a result, the alteration of plasmonic layers has a great impact on the sensing phenomena.
Correspondingly, in Figure 5b different sizes of air holes (0.96 μm to 1.0 μm) with the interval step of 0.02 μm have been considered for both silver and gold material. Here the maximum loss peak (252 dB/cm) is attained at the size of (1.0 μm) for gold metal.
Sensitivity is the most important factor to validate the actual performance of the sensor that depends on the peak wavelength shift and the variation of the analytes RI. The following equation can be employed to determine the sensitivity (S) of analytes [31].
S λ μ m R I U = ∆ λ p e a k ∆ n a
Where, ∆ λ p e a k is the resonance wavelength shift, and ∆ n a is the variation of analytes RI.
Another meaningful feature is the Resolution (R) of the sensor which is applied to identify the minor variation of analyte RI. The resolution of a sensor can be determined by the following equation [32].
R = Δ n a × ∆ λ m i n ∆ λ p e a k
Where, ∆ λ m i n represents the difference between two resonance peak wavelength, Δ n a is the alteration of analytes RI, and ∆ λ p e a k is the maximum peak of resonance wavelength.
Furthermore, for practical execution of sensors, the inquiry of amplitude approach is modest and efficient. Amplitude sensitivity can be estimated by operating the following equation [33].
S A = − 1 α λ , n a ∂ ∝ λ , n a ∂ n a
Where α λ , n a is the confinement loss as a function of the wavelength and RI of analytes. ∂ ∝ λ , n a is the difference between two loss peaks under two different refractive indexes at the same wavelength. The values of amplitude sensitivity have been calculated by tracing Figure 4.
Figure 6a implies the amplitude sensitivity of the refractive index of different analytes for silver layer. At the refractive index of (1.36) the maximum amplitude sensitivity (-46 RIU-1) is achieved. On the other hand, Figure 6b indicates the amplitude sensitivity for the gold layer. Here the maximum amplitude sensitivity (-32 RIU-1) is obtained at the resonance wavelength (1.46 μm) with the RI of (1.38).
Figure of merit (FOM) is the significant attribute to value the function of any type of sensors. The following equation is employed to find the FOM [34].
F O M = S λ F W H M
Where S λ   is the wavelength sensitivity measured in μm/RIU, and FWHM is the full width at half-maximum calculated in nanometers from the resonance wavelength. Figure 7a shows the function of FOM with the variation of analytes RI for silver layer. The maximum FOM attained as 25 RIU-1 at the analyte RI of 1.34. Next in Figure 7b the variation of analyte RI for gold layer has been depicted. Here the maximum FOM 31 RIU-1 obtained at the RI of 1.32 which is comparatively higher than the silver analysis.
On the basis of the above equations (4,5,6,7) the wavelength sensitivity, amplitude sensitivity, resolution, and FOM of proposed PCF-SPR sensor has been calculated. Table 1 explains the comparative results among the silver and gold in which the performance of the gold metal secured higher sensitivity than silver layer.
Additionally, the birefringence, coupling length, power spectrum, and transmission intensity also has a great influence to validate the working function of the sensors. Therefore, these parameters have been calculated based on the difference of effective refractive index of the X and Y polarization mode. Here the explanation of the most important aspects such as power and transmission intensity have been considered.
The optical power variations operate from one mode to another, along with the proposed sensor. The expression of birefringence and coupling length define the power spectrum. The power spectrum ensures the sensor ability, which is measured by using the following equation [35].
P o u t = s i n 2 B × π × L λ
Where B is the birefringence, L is the coupling length, and λ is the operating wavelength.
Figure 8a shows the power spectrum as a function of wavelength with the variation of analytes RI (1.32 to 1.40). By increasing the RI of analytes, the power peak spectrum moves towards the shorter wavelength. The maximum sensitivity obtained is 1.13 μm/RIU at the refractive index of 1.32.
The transmission intensity plays a significant role in calculating the sensitivity of the proposed PCF-SPR sensor. The change of intensity propagation has been manipulated. The whole plasmonic impression extensively fluctuates on the transmittance. However, the wavelength sensitivity of the designed sensor can be figured out through the alteration of the sharp peak of the transmittance curve with the change of the refractive index. The transmittance spectrum can be evaluated by using the following equation [36].
T r ( d B ) = 10 × l o g 10 P o u t P i n
where Tr is the transmission of light, Pin is the maximum power as a fraction of Pout.
The transmission spectrum with respect to wavelength by varying the analyte RI has been depicted in Figure 8b. This graph explains the variation of resonance wavelength to shorter wavelength as the refractive index increases. With the increases of analyte refractive index, the transmission is going to higher wavelength. For the transmission spectrum the attained sensitivity is 1.21 μm/RIU.
A linear reaction is a valuable mechanism for sensor execution as it allocates to resolve the unidentified quantities by regular data extrapolation. Therefore, by considering the good results of Figure 4 and the Figure 8a (power spectrum) with gold material has been explored for linear regressions. Figure 9a illustrates the linear fitting curve of loss function with respect to the resonance wavelength and the variation of analytes RI. In this graph the slope values consider the sensitivity of the sensor which is obtained as 513 μm/RIU with the adjacent R2 of 0.997. Similarly, Figure 9b exhibits the linear regression of power spectrum as a function of wavelength shift and the variation of analyte RI. The achieved sensitivity was 0.706 μm/RIU with an R-square value of 0.979.
A comparison study of the proposed structure and the previous work done based on RI sensing has been drawn in Table 2, which consists of the sensitivity results. In the overall analysis, the PCF-SPR sensor has a remarkable impact in refractive index sensing, particularly gold has higher sensitivity than silver layer. Moreover, this designed structure enhances solidity and stability for sensing applications. By tuning the structural parameters and sensing materials, the results can be further improved.

Conclusions

In conclusion, we proposed and numerically computed the PCF-SPR sensor based on plasmonic material to examine the analytes RI sensing. To investigate the sensing mechanism of optical guiding properties such as confinement loss, power spectrum, and transmission intensity, the finite element method (FEM) based on mode solver is employed. The comparative study has been carried out by utilizing the properties of gold and silver in which the range of analytes RI is taken from 1.32 to 1.40. For the gold analysis, the maximum achieved wavelength sensitivity, amplitude sensitivity, and resolution are 1.15 μm/RIU, -32 RIU-1, and 0.0145 RIU-1 respectively. Additionally, power spectrum analysis has been examined with higher sensitivity of 513 μm/RIU. Moreover, the impact of several fundamental parameters like air holes and thickness of the plasmonic layer on this sensor have been analyzed. The numerical analysis and the exploration of this proposed sensor illustrate a suitable candidate for several applications for liquid and biological sensing.

Data Availability Statement

The simulation data are available from the corresponding and first author upon request.

Acknowledgment

This research was supported by the Tecnológico de Monterrey, Monterrey, N.L. 64849, México.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Al Mahfuz, M.; Hossain, M.A.; Haque, E.; Hai, N.H.; Namihira, Y.; Ahmed, F. A Bimetallic-Coated, Low Propagation Loss, Photonic Crystal Fiber Based Plasmonic Refractive Index Sensor. Sensors 2019, 19, 3794. [Google Scholar] [CrossRef] [PubMed]
  2. Gomez-Cardona, N.; Reyes-Vera, E.; Torres, P. High Sensitivity Refractive Index Sensor Based on the Excitation of Long-Range Surface Plasmon Polaritons in H-Shaped Optical Fiber. Sensors 2020, 20, 2111. [Google Scholar] [CrossRef] [PubMed]
  3. Liu, C.; Yang, L.; Su, W.; Wang, F.; Sun, T.; Liu, Q.; Mu, H.; Chu, P.K. Numerical analysis of a photonic crystal fiber based on a surface plasmon resonance sensor with an annular analyte channel. Opt. Commun. 2017, 382, 162–166. [Google Scholar] [CrossRef]
  4. Kamrunnahar, Q.M.; Mou, J.R.; Momtaj, M. Dual-core gold coated photonic crystal fiber plasmonic sensor: Design and analysis. Results Phys. 2020, 18, 103319. [Google Scholar] [CrossRef]
  5. Yu, H.; Peng, Y.; Yang, Y.; Li, Z.Y. Plasmon-enhanced light–matter interactions and applications. Comput. Mater. 2019, 5, 1–14. [Google Scholar] [CrossRef]
  6. Yan, X.; Li, B.; Cheng, T.; Li, S. Analysis of High Sensitivity Photonic Crystal Fiber Sensor Based on Surface Plasmon Resonance of Refractive Indexes of Liquids. Sensors 2018, 18, 2922. [Google Scholar] [CrossRef]
  7. Sharma, A.K.; Jha, R.; Gupta, B.D. Fiber-optic sensors based on surface plasmon resonance: A comprehensive review. IEEE Sens. J. 2007, 7, 1118–1129. [Google Scholar] [CrossRef]
  8. Sharma, A.K.; Pandey, A.K.; Kaur, B. A Review of advancements (2007–2017) in plasmonics-based optical fiber sensors. Opt. Fiber Technol. 2018, 43, 20–34. [Google Scholar] [CrossRef]
  9. Lv, W.; Yao, J.; Wang, R.; Luan, N. Surface plasmon resonance sensor based on D-shaped microstructured optical fiber with hollow core. Opt. Express 2015, 23, 8576–8582. [Google Scholar]
  10. Jin, W.; Li, X.; Wu, S.; Fu, X.; Fu, G.; Bilal, M.M.; Bi, W. Highly sensitive temperature sensing probes based on liquid cladding elliptical micro/nanofibers. Opt. Express 2020, 28, 20062–20073. [Google Scholar] [CrossRef]
  11. Bilal, M.M.; Bi, W.; Jaleel, F.; Luwen, Y.; Sohail, M.N.; Irshad, M.; Madni, H.A. Magnetic fluid-based photonic crystal fiber for temperature sensing. Opt. Eng. 2019, 58, 072008. [Google Scholar] [CrossRef]
  12. Taghizadeh, M.; Bozorgzadeh, F.; Ghorbani, M. Designing magnetic field sensor based on tapered photonic crystal fibre assisted by a ferrofluid. Sci. Rep. 2021, 11, 1–9. [Google Scholar]
  13. Bilal, M.M.; Bi, W.; Liu, X.; Yang, L.; Wa, J.; Madni, H.A. Magnetic field sensor based on the magnetic fluid infiltration into the cladding air holes of the solid-core photonic crystal fiber. Opt. Eng. 2019, 58, 096107. [Google Scholar] [CrossRef]
  14. Gamal, Y.; Younis, B.M.; Hegazy, S.F.; Badr, Y.; Hameed, M.F.O.; Obayya, S.S.A. Highly Sensitive Multi-Functional Plasmonic Biosensor Based on Dual Core Photonic Crystal Fiber. IEEE Sens. J. 2022, 22, 6731–6738. [Google Scholar] [CrossRef]
  15. Abdelghaffar, M.; Gamal, Y.; El-Khoribi, R.A.; Soliman, W.; Badr, Y.; Hameed, M.F.O.; Obayya, S.S.A. Highly sensitive V-shaped SPR PCF biosensor for cancer detection. Opt. Quantum Electron. 2023, 55, 1–20. [Google Scholar] [CrossRef]
  16. Han, Y.; Gao, J.; Lu, J.; Li, Y.; Liu, Y. D-shaped photonic crystal fiber plasmonic refractive index sensor based on gold grating. Appl. Opt. 2018, 57, 5268–5272. [Google Scholar]
  17. Momota, M.R.; Hasan, M.R. Hollow-core silver coated photonic crystal fiber plasmonic sensor. Opt Mater 2018, 76, 287–294. [Google Scholar] [CrossRef]
  18. Liu, Q.; Lv, J.; Yi, Z.; Liu, C.; Liu, W.; Fu, H.; Hu, C.; Lv, Y.; Wu, X.; Yang, L.; et al. HE1,1 mode excited surface plasmon resonance for high-sensitivity sensing by photonic crystal fibers. JOSA A 2023, 40, 35–44. [Google Scholar]
  19. Shafkat, A. Analysis of a gold coated plasmonic sensor based on a duplex core photonic crystal fiber. Sens. Biosensing Res. 2020, 28, 100324. [Google Scholar] [CrossRef]
  20. Mittal, S.; Sharma, T.; Tiwari, M. Surface plasmon resonance based photonic crystal fiber biosensors: A review. Mater. Today Proc. 2021, 43, 3071–3074. [Google Scholar] [CrossRef]
  21. Weng, S.; Pei, L.I.; Wang, J.; Ning, T.; Li, J. High sensitivity D-shaped hole fiber temperature sensor based on surface plasmon resonance with liquid filling. Photonics Res. 2017, 5, 103–107. [Google Scholar] [CrossRef]
  22. Khalil, A.E.; El-Saeed, A.H.; Ibrahim, M.A.; Hashish, M.E.; Abdelmonem, M.R.; Hameed, M.F.O.; Azab, M.Y.; Obayya, S.S.A. Highly sensitive photonic crystal fiber biosensor based on titanium nitride. Opt. Quantum Electron. 2018, 50, 1–12. [Google Scholar] [CrossRef]
  23. Kaur, V.; Singh, S. A dual-channel surface plasmon resonance biosensor based on a photonic crystal fiber for multianalyte sensing. J. Comput. Electron. 2019, 18, 319–328. [Google Scholar] [CrossRef]
  24. Yasli, A.; Ademgil, H.; Haxha, S.; Aggoun, A. Multi-Channel Photonic Crystal Fiber Based Surface Plasmon Resonance Sensor for Multi-Analyte Sensing. IEEE Photonics J. 2020, 12, 6800515. [Google Scholar] [CrossRef]
  25. Islam, A.; Haider, F.; Ahmed, R.; Aoni, R.A. Plasmonic photonic biosensor: In situ detection and quantification of SARS-CoV-2 particles. Opt. Express 2022, 30, 40277–40291. [Google Scholar] [CrossRef]
  26. Rahman, M.M.; Rana, M.M.; Anower, M.S.; Rahman, M.S.; Paul, A.K. Design and analysis of photonic crystal fiber-based plasmonic microbiosensor: An external sensing scheme. SN Appl. Sci. 2020, 2, 1–11. [Google Scholar] [CrossRef]
  27. Hasan, M.R.; Akter, S.; Rifat, A.A.; Rana, S.; Ali, S. A Highly Sensitive Gold-Coated Photonic Crystal Fiber Biosensor Based on Surface Plasmon Resonance. Photonics 2017, 4, 18. [Google Scholar] [CrossRef]
  28. Al Mahfuz, M.; Hossain, M.A.; Haque, E.; Hai, N.H.; Namihira, Y.; Ahmed, F. Dual-Core Photonic Crystal Fiber-Based Plasmonic RI Sensor in the Visible to Near-IR Operating Band. IEEE Sens. J. 2020, 20, 7692–7700. [Google Scholar] [CrossRef]
  29. Bilal, M.M.; López-Aguayo, S.; Szczerska, M.; Madni, H.A. Multi-functional sensor based on photonic crystal fiber using plasmonic material and magnetic fluid. Appl. Opt. 2022, 61, 10400–10407. [Google Scholar] [CrossRef]
  30. Ramola, A.; Van, V.; Singh, S.; Shakya, A.K. Design of an ultra-sensitive bimetallic anisotropic PCF SPR biosensor for liquid analytes sensing. Opt. Express 2022, 30, 9233–9255. [Google Scholar]
  31. Zha, F.; Li, J.; Sun, P.; Ma, H. Highly sensitive selectively coated D-shape photonic crystal fibers for surface plasmon resonance sensing. Phys. Lett. A 2019, 383, 1825–1830. [Google Scholar] [CrossRef]
  32. Sharif, V.; Pakarzadeh, H. High-performance surface plasmon resonance fiber sensor based on cylindrical vector modes. Sci. Rep. 2023, 13, 1–9. [Google Scholar]
  33. Sharif, V.; Pakarzadeh, H. Terahertz Hollow-Core Optical Fibers for Efficient Transmission of Orbital Angular Momentum Modes. J. Light. Technol. 2021, 39, 4462–4468. [Google Scholar] [CrossRef]
  34. Ayyanar, N.; Raja, G.T.; Sharma, M.; Kumar, D.S. Photonic Crystal Fiber-Based Refractive Index Sensor for Early Detection of Cancer. IEEE Sens. J. 2018, 18, 7093–7099. [Google Scholar] [CrossRef]
  35. Ahmed, K.; Jabin, M.A.; Paul, B.K. Surface plasmon resonance-based gold-coated biosensor for the detection of fuel adulteration. J. Comput. Electron. 2020, 19, 321–332. [Google Scholar] [CrossRef]
  36. Ahmed, K.; Haque, M.J.; Jabin, M.A.; Paul, B.K.; Amiri, I.S.; Yupapin, P. Tetra-core surface plasmon resonance based biosensor for alcohol sensing. Phys. B Condens. Matter 2019, 570, 48–52. [Google Scholar] [CrossRef]
  37. Momota, M.R.; Hasan, M.R. Hollow-core silver coated photonic crystal fiber plasmonic sensor. Opt Mater 2018, 76, 287–294. [Google Scholar] [CrossRef]
  38. Hasan, M.R.; Akter, S.; Rifat, A.A.; Rana, S.; Ahmed, K.; Ahmed, R.; Subbaraman, H.; Abbott, D. Spiral photonic crystal fiber-based dual-polarized surface plasmon resonance biosensor. IEEE Sens. J. 2018, 18, 133–140. [Google Scholar] [CrossRef]
  39. S. Akter and S. M. Abdur Razzak, Highly sensitive open-channels based plasmonic biosensor in visible to near-infrared wavelength. Results Phys. 2019, 13, 102328. [Google Scholar] [CrossRef]
  40. Zuhayer, A.; Shafkat, A. Design and analysis of a gold-coated dual-core photonic crystal fiber bio-sensor using surface plasmon resonance. Sens. Biosensing Res. 2012, 33, 100432. [Google Scholar] [CrossRef]
  41. Sakib, M.N.; Hossain, M.B.; Al-tabatabaie, K.F.; Mehedi, I.M.; Hasan, M.T.; Hossain, M.A.; Amiri, I.S. High performance dual core D-shape PCF-SPR sensor modeling employing gold coat. Results Phys. 2019, 15, 102788. [Google Scholar] [CrossRef]
Preprints 83192 g001
Figure 1. (a) The cross-section view of the proposed 2-D PCF structure, and (b) the 3-D schematic diagram of sensing mechanism of PCF-SPR sensor.
Figure 1. (a) The cross-section view of the proposed 2-D PCF structure, and (b) the 3-D schematic diagram of sensing mechanism of PCF-SPR sensor.
Preprints 83192 g001
Preprints 83192 g002
Figure 2. Electric field distribution of the fundamental mode with (a) X, and (b) Y polarization. SPP mode light spectrum c) X and d) Y polarization.
Figure 2. Electric field distribution of the fundamental mode with (a) X, and (b) Y polarization. SPP mode light spectrum c) X and d) Y polarization.
Preprints 83192 g002
Preprints 83192 g003
Figure 3. The phase matching point of SPP and core mode as a function of wavelength with (a) silver and, (b) gold materials.
Figure 3. The phase matching point of SPP and core mode as a function of wavelength with (a) silver and, (b) gold materials.
Preprints 83192 g003
Preprints 83192 g004
Figure 4. Confinement loss spectra of silver and gold with the variation of analytes RI at d=0.98μm, and layer=26nm.
Figure 4. Confinement loss spectra of silver and gold with the variation of analytes RI at d=0.98μm, and layer=26nm.
Preprints 83192 g004
Preprints 83192 g005
Figure 5. (a) The variation of silver and gold layers with respect to loss at RI=1.33, d=0.98. (b) the influence of air holes of silver and gold at RI=1.33, layer=26nm.
Figure 5. (a) The variation of silver and gold layers with respect to loss at RI=1.33, d=0.98. (b) the influence of air holes of silver and gold at RI=1.33, layer=26nm.
Preprints 83192 g005
Preprints 83192 g006
Figure 6. (a) amplitude sensitivity as a function of RI for silver element, and (b) amplitude sensitivity for gold element.
Figure 6. (a) amplitude sensitivity as a function of RI for silver element, and (b) amplitude sensitivity for gold element.
Preprints 83192 g006
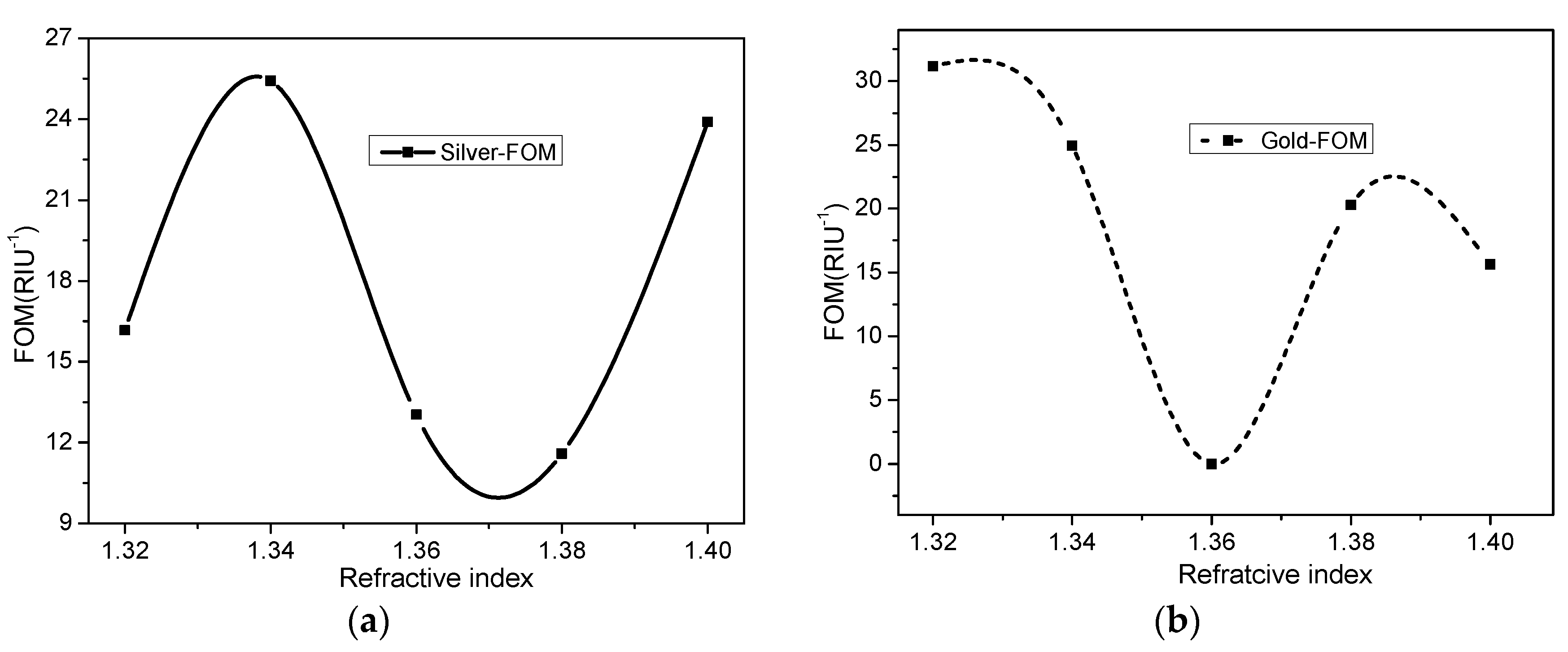
Preprints 83192 g007
Figure 7. The function of FOM with the respect to variation of analytes RI for a) silver, and b) gold.
Figure 7. The function of FOM with the respect to variation of analytes RI for a) silver, and b) gold.
Preprints 83192 g007
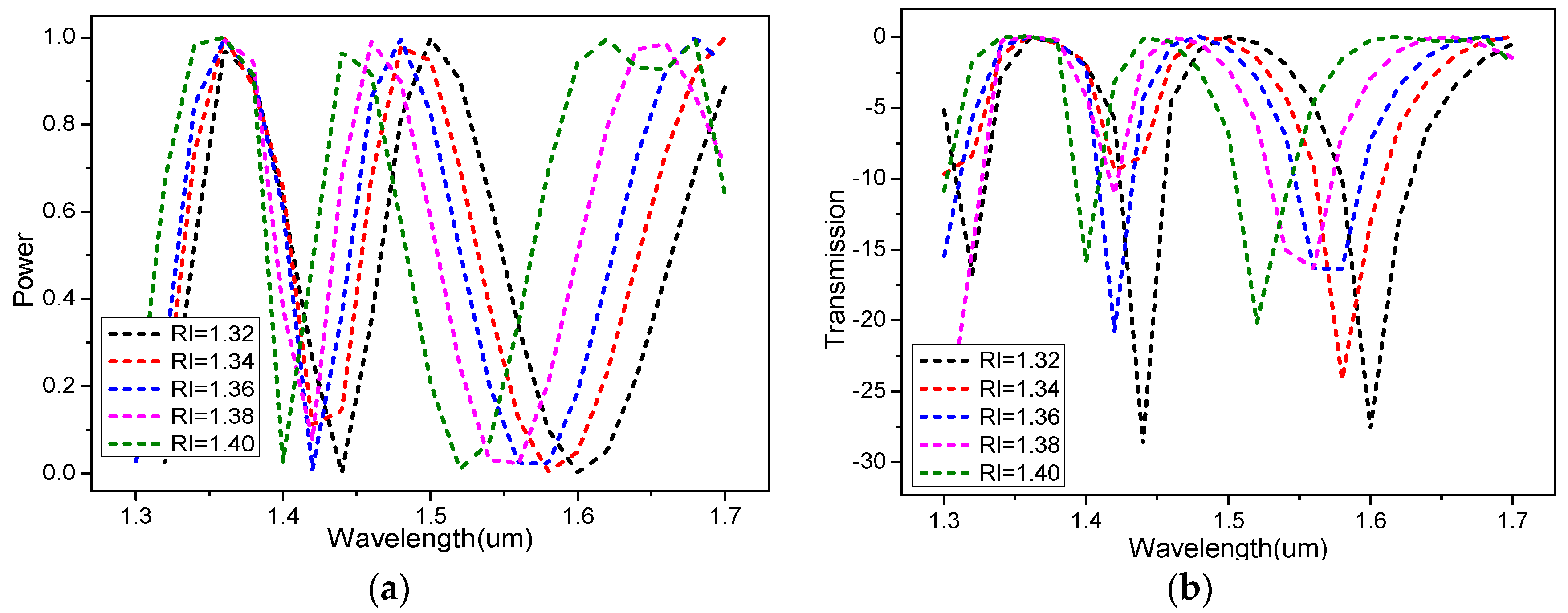
Preprints 83192 g008
Figure 8. The variation of analytes RI as a function of wavelength with respect to (a) power spectrum, and (b) transmission intensity.
Figure 8. The variation of analytes RI as a function of wavelength with respect to (a) power spectrum, and (b) transmission intensity.
Preprints 83192 g008
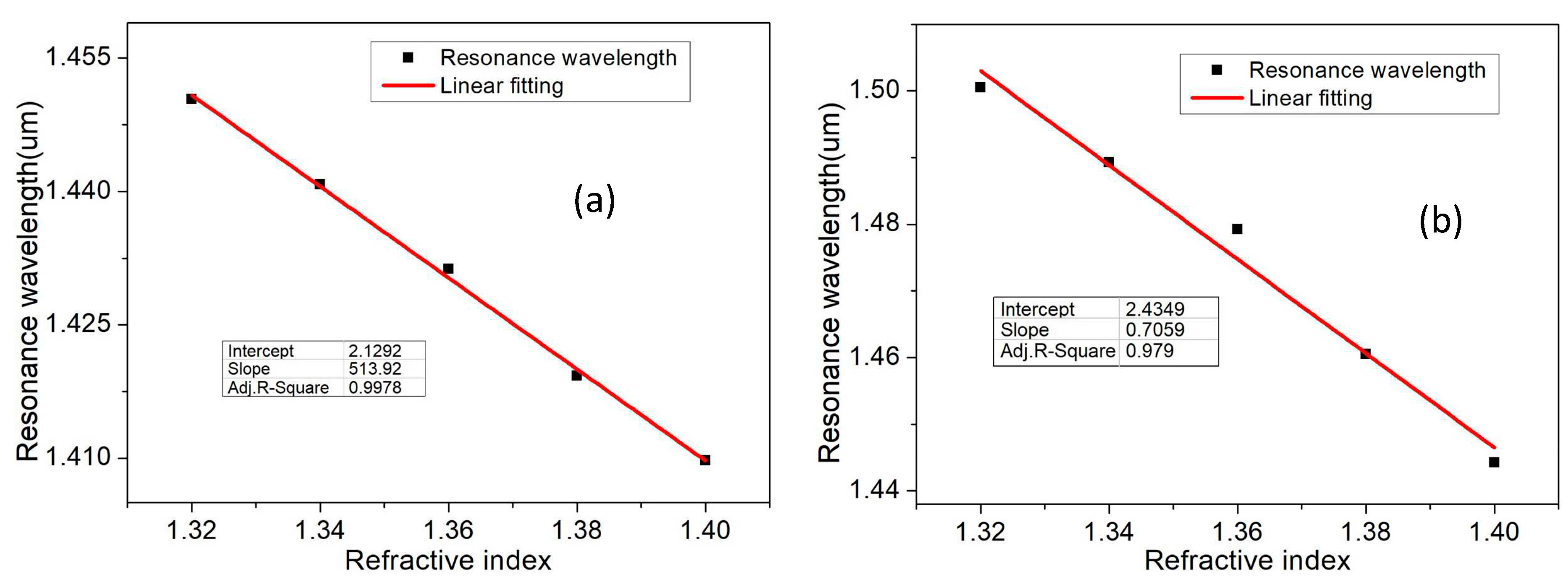
Preprints 83192 g009
Figure 9. The function of linear fitting regression with respect to resonance wavelength and variation of refractive index for (a) loss peaks, and (b) power spectrum.
Figure 9. The function of linear fitting regression with respect to resonance wavelength and variation of refractive index for (a) loss peaks, and (b) power spectrum.
Preprints 83192 g009
Table 1. The performance of PCF-SPR sensor with WS, resolution, AS, and FOM among gold and silver.
Table 1. The performance of PCF-SPR sensor with WS, resolution, AS, and FOM among gold and silver.
RI λpeak[μm] Sλ[μm/RIU] R[RIU] AS[RIU-1] FOM [RIU-1]
silver gold silver gold silver gold s i l v e r gold s i l v e r gold
1.32 1.451 1.519 1.100 1.151 0.010 0.0145 -36 -23 16 31
1.34 1.439 1.502 1.074 1.121 0.007 0.0106 -27 -24 25 24
1.36 1.430 1.490 1.052 1.096 0.010 0.0087 -46 -27 12 -0.2
1.38 1.420 1.481 1.029 1.073 0.010 0.0111 -35 -32 11 20
1.40 1.409 1.469 1.006 1.049 ---- ---- ---- ---- 23 15
Table 2. The comparison study between the proposed sensor and the previous work done.
Table 2. The comparison study between the proposed sensor and the previous work done.
RI range WS AS [RIU-1] R [RIU] FOM [RIU-1] Ref
1.33-1.37 4200 nm/RIU 300 3.33×10-5 ---- [37]
1.33-1.38 4600 nm/RIU 420 2.17×10-5 ---- [38]
1.33-1.40 5000 nm/RIU 396 2.0×10-5 47 [39]
1.35-1.40 8000 nm/RIU 1443 12.2×10-6 ---- [40]
1.45-1.48 8000 nm/RIU 700 1.78×10-5 138 [41]
1.32-1.40 513 μm/RIU -46 0.0145 31 Proposed work
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated