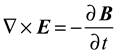Rendering Maxwell Equations into the Compressible Inviscid Fluid Dynamics Form

Preprint

Communication

Rendering Maxwell Equations into the Compressible Inviscid Fluid Dynamics Form

Altmetrics

Downloads

114

Views

Comments

PETER VADASZ^*

This version is not peer-reviewed

Submitted:

24 August 2023

Posted:

25 August 2023

You are already at the latest version

Alerts

Abstract

Maxwell equations governing electromagnetic effects are being shown to be equivalent to the compressible inviscid Navier-Stokes equations applicable in fluid dynamics and representing conservation of mass and linear momentum. The latter applies subject to a generalized Beltrami condition to be satisfied by the magnetic field. This equivalence indicates that the compressible inviscid Navier-Stokes equations are Lorentz invariant as they derive directly from the Lorentz invariant Maxwell equations subject to the same Beltrami condition. In addition, the derivation results provide support for the claim that electromagnetic potentials have physical significance as demonstrated by Aharonov-Bohm effect, and are not only a convenient mathematical formulation.

Keywords:

Subject: Physical Sciences - Fluids and Plasmas Physics

1. Introduction

Electromagnetic effects are related to fluid dynamics via applications of Magneto-Hydro-Dynamics (MHD) to a variety of fields, such as liquid metals [1-4], nanofluids [5,6], non-Newtonian fluids [7], and many others.

Electromagnetic phenomena, such as electromagnetic waves propagate in space following the solution of Maxwell equations. The latter are a set of four partial differential equations for the unknown variables of the electric field, magnetic field, charge density, and current density (charge flux). The solution to these set of equations is typically obtained via a gauge theory, i.e. introducing a scalar and a vector potential related to the electric and magnetic fields and solving the resulting wave equations for these potentials. Once the solution for the potentials is obtained a reverse transformation leads to the solution to the electric and magnetic fields. This procedure is similar to introducing scalar and vector potentials in attempting to solve fluid dynamics problems, although the latter are typically much more difficult. Also the introduction of a stream function for solving two-dimensional fluid dynamics flows is also a similar procedure, although in this case much simpler than the electromagnetic one. In all these cases the introduced potentials are defined up to an integrating constant or for a vector potential, up to a gradient of an arbitrary function. The latter has no significance as long as the physically significant variables are the electromagnetic fields and not the potentials. Therefore, the introduction of the potentials was seen as a convenient mathematical solution method and the potentials themselves were not given any physical interpretation. Aharonov-Bohm effect (Aharonov and Bohm [8, 9]) which was confirmed both theoretically as well as experimentally suggested the opposite, i.e. that the potentials do have physical significance, although no explanation for the latter nor the precise physical meaning of these potentials was provided.

Vadasz [10] showed that a continuous mass distribution for a general variable gravitational field

g (t, x)

is equivalent to a form identical to Maxwell equations from electromagnetism, subject to a modified Beltrami condition. Attempts at deriving equations thar are identical to Maxwell equations for continuous media have been presented particularly with application to fluid dynamics. For example, Marmanis [11] uses an equation derived by Lamb [12] from the incompressible Navier-Stokes equations and uses it in deriving a new theory of turbulence. A similar approach was used by Sridhar [13] in order to “formulate the problem of advection and diffusion of a passive tracer by an arbitrary, incompressible velocity field”, to find that the “problem is identical to the diffusive dynamics of a charged particle in electromagnetic fields constructed from the velocity field.” Rousseaux et al. [14] tested experimentally and theoretically the concept of “hydrodynamic charge” in the case of a “coherent structure such as the Burgers vortex”. These attempts apply to the incompressible fluid Navier-Stokes equations without the gravitational field and result in a form identical to Maxwell equations having the following correspondence: electromagnetic vector potential converts into velocity, magnetic field converts into vorticity, electric field converts into Lamb vector (

l = - v \times \nabla \times v

), where

v (t, x)

is the velocity, and the electric charge converts into a “hydrodynamic charge”

q_{H}

identical to the divergence of the Lamb vector, i.e.

q_{H} = \nabla \cdot l

The present paper shows that Maxwell equations in free space governing electromagnetic phenomena are equivalent to the compressible inviscid Navier-Stokes equations subject to a generalized Beltrami condition. Consequently, a clear explanation of what physical meaning could be associated with these potentials is provided at the end of the paper.

2. Governing Equations

The following derivations use the definition of the mass to charge density ratio, assumed constant and assumed to take a linear form such as

β_{q} = \frac{ρ}{|ρ_{q}|} = \frac{m_{q}}{|q|} = const . [k g / C]

(1)

where

ρ

is the mass density

[kg / m^{3}]

related to the total mass , and

ρ_{q}

[C / m^{3}]

is the electric charge density related to the electric charge

q

Then the definition of the electromagnetic momentum density (i.e. electromagnetic momentum per unit volume) is introduced in the form carrying units of , and where the vector

A

[N / A]

is related to the magnetic field

B

[T]

by the relationship

B = - \nabla \times A

(2)

The electromagnetic momentum density will be shown to be identical to the current density (charge flux)

J_{q} = ρ_{q} A / β_{q}

[C / m^{2} s]

. Equation (1) produces the Gauss law for the magnetic field expressed in the form

\nabla \cdot B = 0

(3)

because the curl of the divergence of any vector is always zero.

Then, by using the Coulomb law in field form together with the Ampere law as follows

\nabla \cdot E = \frac{1}{ε_{o}} ρ_{q}

(4)

c_{o}^{2} \nabla \times B = \frac{1}{ε_{o}} ρ_{q} \frac{A}{β_{q}} + \frac{\partial E}{\partial t}

(5)

where

E

is the electric field in units of

[N / C]

ε_{o}

is the permittivity of vacuum in units of

[F / m]

t

is time in units of

[s]

, and

c_{o}

is the speed of light in free space. The Faraday law of induction is presented in the form

(6)

Equations (3), (4), (5), and (6) form the Maxwell equations governing electromagnetic phenomena in free space.

3. Converting the Governing Equations into a Maxwell form

By applying the divergence operator on equation (5) yields

0 = \frac{1}{ε_{o}} \nabla \cdot (ρ_{q} \frac{A}{β_{q}}) + \frac{\partial}{\partial t} (\nabla \cdot E)

(7)

Substituting (4) into (7) leads to

\frac{\partial ρ_{q}}{\partial t} + \nabla \cdot (ρ_{q} \frac{A}{β_{q}}) = 0

(8)

Equation (8) represents the conservation of electric charge, or the electric charge continuity equation while

A / β_{q}

represents the electric charge velocity.

Also, the following equation for the conservation of the electromagnetic momentum leads directly to Faraday law of induction (6), as follows

ρ_{q} [\frac{\partial A}{\partial t} + (A \cdot \nabla) A] = - c_{o}^{2} β_{q} \nabla ρ_{q} + ρ_{q} E

(9)

Dividing equation (9) by

ρ_{q}

produces

\frac{\partial A}{\partial t} + (A \cdot \nabla) A = - \nabla [s_{q} c_{o}^{2} β_{q} \ln |ρ_{q}|] + E

(10)

where

s_{q} = q / |q| = + 1 if q > 0 & - 1 if q < 0

. By using the following identity

(A \cdot \nabla) A = \frac{1}{2} \nabla (A \cdot A) - A \times (\nabla \times A)

(11)

into equation (10) yields

\frac{\partial A}{\partial t} = - \nabla [s_{q} c_{o}^{2} β_{q} \ln |ρ_{q}| + \frac{1}{2} (A \cdot A)] + A \times (\nabla \times A) + E

(12)

Taking the curl (

\nabla \times

) of equation (12) and using equation (2) leads to

- \frac{\partial B}{\partial t} = \nabla \times E - \nabla \times [A \times B]

(13)

Subject to satisfying the following generalized Beltrami condition (Rousseaux et al. [12], Yoshida et al.[13], Mahajan and Yoshida [14], Gerner [15], Amari et al. [16], Bhattacharjee [17], Lakhatakia [18])

\nabla \times [A \times B] = 0

(14)

equation (13) converts into the Faraday law of induction in the form

- \frac{\partial B}{\partial t} = \nabla \times E

(15)

The generalized Beltrami condition (in fluid dynamics) is satisfied when one of the following occurs

(a) B = - \nabla \times A = 0

(16)

then the flow is irrotational, and in electromagnetism it implies no magnetic field.

(b) A \times B = 0

(17)

i.e. the electromagnetic vector potential

A

and the magnetic field

B

are parallel (Beltrami condition). In this case

A

cannot be two-dimensional.

(c) \nabla \times [A \times B] = 0

(14)

which is the generalized Beltrami condition implying the existence of a scalar potential

ψ

such that

A \times B = \nabla ψ

(18)

satisfying identically the generalized Beltrami condition (14). This scalar potential can be in particular (not necessarily)

ψ = - \frac{1}{2} A \cdot A

(19)

in which case (18) converts by using (1) and (19) into

A \times (\nabla \times A) = \nabla (\frac{1}{2} A \cdot A)

(20)

In all these cases the term

(A \cdot \nabla) A

in equations (9) and (10) vanishes.

Equations (8) and (9) that emerged directly from the Maxwell equations have a form identical to the compressible inviscid Navier-Stokes equations from fluid dynamics with following equivalence

ρ \to ρ_{q}

v \to A / β_{q}

v_{o}^{2} \to c_{o}^{2}

g \to E

ξ = - \nabla \times v \to B = - \nabla \times A

, where

v

is the velocity vector,

ξ

is the vorticity vector,

g

is the variable gravitational field, and

v_{o}

is the speed of propagation of the pressure wave

p

, i.e. by using a linear constitutive relationship between pressure and mass density

p = p_{o} + v_{o}^{2} (ρ - ρ_{o})

(21)

Therefore if the vector-potential

A

is linearly related to the electric charge velocity in the form

v = \frac{A}{β_{q}}

(22)

identifying the electromagnetic momentum

ρ_{q} A

to the electric current density (charge flux)

J_{q}

[A / m^{2}]

, i.e.

J_{q} = ρ_{q} v = ρ_{q} \frac{A}{β_{q}}

(23)

and assuming a linear relationship between the mass density and the charge density, such as the one presented in equation (3), and if the generalized Beltrami condition (14) is satisfied, then by using (21), equations (8) and (9) become

\frac{\partial ρ}{\partial t} + \nabla \cdot (ρ v) = 0

(24)

ρ [\frac{\partial v}{\partial t} + (v \cdot \nabla) v] = - \nabla p + ρ_{q} E

(25)

Equations (24) and (25) are the compressible inviscid Navier-Stokes equations for a charged continuum identical to a fluid. They were derived directly from the Maxwell equations subject to the generalized Beltrami condition and assuming linear relationships between the electromagnetic vector potential

A

and charge velocity

v

, and between the mass density

ρ

and charge density

ρ_{q}

This result may be linked to the Aharonov-Bohm effect (Aharonov and Bohm [8, 9]), which conceptually challenges the view that expressing the Maxwell equations in terms of potentials and hence converting them into a gauge theory is only a mathematical reformulation with no physical consequences because the scalar and vector potentials have no apparent physical significance. The result presented in the present paper supports Aharonov and Bohm [8, 9] claim of the physicality of electromagnetic potentials

Φ

= s_{q} c_{o}^{2} β_{q} \ln |ρ_{q}| + \frac{1}{2} (A \cdot A)

and

A

by illustrating that the former is related to a reduced pressure, while the latter is related to the electric charge velocity, as shown above.

4. Conclusions

The Maxwell equations were shown to convert into the compressible inviscid Navier-Stokes equations subject to the magnetic field satisfying a generalized Beltrami condition. Since Maxwell equations are Lorentz invariant, the latter suggests that subject to the same condition the compressible inviscid Navier-Stokes equations are Lorentz invariant too. Finally, the results also support the claim that electromagnetic potentials have physical significance as demonstrated by Aharonov-Bohm effect, and are not only a convenient mathematical formulation.

References

Gupta, A.; Jog, C.S. A Monolithic Finite Element Formulation for Magnetohydrodynamics Involving a Compressible Fluid. Fluids 2022, 7, 27. [Google Scholar] [CrossRef]
Suponitsky, V.; Khalzov, I.V.; Avital, E.J. Magnetohydrodynamics Solver for a Two-Phase Free Surface Flow Developed in OpenFOAM. Fluids 2022, 7, 210. [Google Scholar] [CrossRef]
Smolentsev, S. Physical Background, Computations and Practical Issues of the Magnetohydrodynamic Pressure Drop in a Fusion Liquid Metal Blanket. Fluids 2021, 6, 110. [Google Scholar] [CrossRef]
Vlachomitrou, M.; Pelekasis, N. Numerical Study of a Liquid Metal Oscillating inside a Pore in the Presence of Lorentz and Capillary Forces. Fluids 2020, 5, 12. [Google Scholar] [CrossRef]
Nabwey, H.A.; El-Kabeir, S.M.M.; Rashad, A.M.; Abdou, M.M.M. Effectiveness of Magnetized Flow on Nanofluid Containing Gyrotactic Micro-Organisms over an Inclined Stretching Sheet with Viscous Dissipation and Constant Heat Flux. Fluids 2021, 6, 253. [Google Scholar] [CrossRef]
Mahdy, A.; El-Zahar, E.R.; Rashad, A.M.; Saad, W.; Al-Juaydi, H.S. The Magneto-Natural Convection Flow of a Micropolar Hybrid Nanofluid over a Vertical Plate Saturated in a Porous Medium. Fluids 2021, 6, 202. [Google Scholar] [CrossRef]
Sarada, K.; Gowda, R.J.P.; Sarris, I.E.; Kumar, R.N.; Prasannakumara, B.C. Effect of Magnetohydrodynamics on Heat Transfer Behaviour of a Non-Newtonian Fluid Flow over a Stretching Sheet under Local Thermal Non-Equilibrium Condition. Fluids 2021, 6, 264. [Google Scholar] [CrossRef]
Aharonov, Y.; Bohm, D. Significance of electromagnetic potentials in quantum theory. Phys. Rev. 1959, 115, 485–491. [Google Scholar] [CrossRef]
Aharonov, Y.; Bohm, D. Further considerations on electromagnetic potentials in quantum theory. Phys. Rev. 1961, 123, 1511–1524. [Google Scholar] [CrossRef]
Vadasz, P. “Newtonian gravitational waves from a continuum”, submitted for publication. 2023. Available online: http://ssrn.com/abstract=4499000.
Lamb, H. On the conditions of steady motion of a fluid. Proc. Lond. Math. Soc. 1877, 1–9, 91–93. [Google Scholar] [CrossRef]
Rousseaux, G.; Seifer, S.; Steinberg, V.; Wiebel, A. On the Lamb vector and the hydrodynamic charge. Exp. Fluids 2006, 42, 291–299. [Google Scholar] [CrossRef]
Marmanis, H. Analogy between the Navier-Stokes equations and Maxwell equations: Application to turbulence. Phys. Fluids 1998, 10, 1428–1437. [Google Scholar] [CrossRef]
Sridhar, S. Turbulent transport of a tracer: An electromagnetic formulation. Phys. Rev. E 1998, 58, 522–525. [Google Scholar] [CrossRef]
Yoshida, Z.; Ohsaki, S.; Ito, A.; Mahajan, S.M. Stability of Beltrami flows. J. Math. Phys. 2003, 44, 2168–2178. [Google Scholar] [CrossRef]
Mahajan, S.M.; Yoshida, Z. Double curl Beltrami flow: Diamagnetic structures. Phys. Rev. Lett. 1998, 81, 4863–4866. [Google Scholar] [CrossRef]
Gerner, W. Typical field lines of Beltrami flows and boundary field line behaviour of Beltrami flows on simply connected, compact, smooth manifolds with boundary. Ann. Glob. Anal. Geom. 2021, 60, 65–82. [Google Scholar] [CrossRef]
Amari, T.; Boulbe, C.; Boulmezaoud, T.Z. Computing Beltrami fields. SIAM J. Sci. Comput. 2009, 31, 3217–3254. [Google Scholar] [CrossRef]
Bhattacharjee, C. Beltrami-Bernoulli equilibria in weakly rotating self-gravitating fluid. J. Plasma Phys. 2022, 88, 175880101. [Google Scholar] [CrossRef]
Lakhatakia, A. Viktor Trkal, Beltrami fields, and Trkalian flows. Czechoslov. J. Phys. 1994, 44, 89–96. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Rendering Maxwell Equations into the Compressible Inviscid Fluid Dynamics Form

Abstract

1. Introduction

2. Governing Equations

3. Converting the Governing Equations into a Maxwell form

4. Conclusions

References

MDPI Initiatives

Important Links

Subscribe