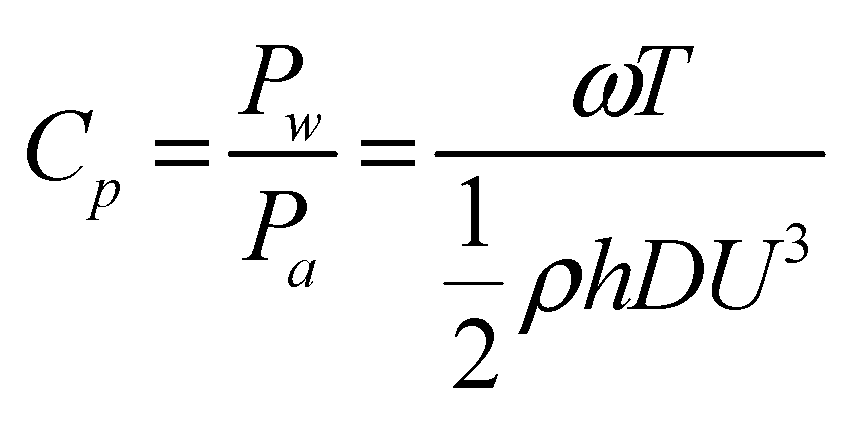Prerpints.org logo
Preprint
Article

Investigating Overlap Ratio Effect on Performance of a Modified Savonius Wind Turbine: An Experimental Study

Altmetrics

Downloads

269

Views

122

Comments

0

This version is not peer-reviewed

Advances in Wind Energy Technology

Submitted:

25 August 2023

Posted:

29 August 2023

You are already at the latest version

Alerts
Abstract
A Savonius wind turbine is one of the simplest vertical-axis turbines. Several researchers have been attracted to it because of its simple structure, low noise, appropriate torque, and independence from wind direction. SR3345 and SR5050 blade profiles will be investigated for their effects on the performance of Savonius wind turbines. First, the fabricated wind turbine is placed in front of an open circuit wind tunnel with a velocity of 6 m/s. Furthermore, governing relationships are used to calculate power and torque coefficients as well as tip speed. In this study, the power and torque coefficients of the turbine are compared with the two profiles considered based on overlap ratios between 0 and 0.3. Despite its increased stability, the central shaft reduced the power coefficient of the turbine. For blade SR3345, the best performance occurs at tip speed ratios of less than 1, while for blade SR5050, the best performance occurs at higher tip speed ratios. Both blades SR3345 and SR5050 achieve the highest power coefficients at overlap ratios of 0 and 0.18 when a central shaft is present.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

Engineers are studying alternative energy sources and their applications in order to develop alternative energy sources as a result of the excessive use of fossil fuels and the growing demand for energy. It has become increasingly popular to use wind power as a clean and accessible source of energy in recent years [1,2]. A vertical-axis wind turbine (VAWT) is more efficient at low speeds than horizontal-axis wind turbines (HAWTs) [3]. It has therefore been the focus of many researchers to design and optimize wind turbines for regions with low wind speeds in order to maximize the use of wind energy. As a result of the high number of geometric variables involved in turbomachinery, optimization problems are advantageous for obtaining the best performance [4,5]. Due to its simplified design, the Savonius wind turbine is one of the most important VAWTs. It is also important to note that Savonius wind turbines are independent of wind direction and have automatic start-up at low wind speeds, both of which are important performance parameters As a consequence, numerous studies have been conducted to examine the performance of the Savonius wind turbine as one of the most important turbomachines [6,7,8,9,10]. Below are some examples of Savonius wind turbine applications.
It is reported that Alexander and Holownia [11] added end plates to the turbine design in order to examine the effects of the aspect, overlap, and gap ratios on the performance of the turbine in a wind tunnel. Avonius turbines with two blades outperformed 3- and 4-bladed designs when aspect and overlap ratios were increased. Aspect and overlap ratios were tested by Roth [12] and optimal values were calculated as 0.77 and 0.22, respectively. It should be noted, however, that Modi et al. [13] also reported values of 0.77 and 0.25 for the same parameters. According to Fujisawa [14], the effects of flow and overlap ratio on wind turbine performance were studied. The results indicated that an overlap ratio of 0.15 improved the static torque performance of the wind turbine. Using numerical and experimental methods, Fujisawa [15] examined numerically and experimentally the effect of flow behavior around Savonius blades at various overlap ratios in another study. According to the study, the overlap coefficient is directly related to flow sensitivity and the formation of vortices near the blades. Furthermore, it was found that increasing the rate of flow passing through the overlap distance increased the pressure on the concave surface of the returning blade, and decreasing the vortex width increased the torque. To prevent air escape from the blades, Altan et al. [16] considered two plates above and beneath the blades and concluded that larger plates offer better performance. Okulov and Van Kuik [17] propose that the maximum power coefficient is theoretically 0.593 for any wind machine. The Betz limit [18] can only be reached when the wind velocity over the blade is one-third of the free-flow wind speed.
With two cylindrical blades, Savonius wind turbines achieve a maximum power coefficient of 0.31 [19]. Many researchers have studied the effects of different parameters on the performance of turbines since then. Consequently, Simonds et al. [20] designed a Savonius wind turbine that incorporates the blades and achieves a maximum power ratio of 0.14 with a tip speed ratio of 0.7. According to Kamoji et al. [21], a modified Savonius blade with an overlap ratio of zero and an aspect ratio of 0.5 produced the maximum power coefficient of 0.21 at a specific wind speed when it was subjected to an examination of the effects of overlap ratio, aspect ratio, and Reynolds number on Savonius blade performance. The numerous studies on the effect of blade shape on turbine performance suggest that elliptical blades can increase the power coefficient of the turbine by up to 10.7% compared to cylindrical blades [22].
Based on numerical analysis, Alom et al. [23] proposed an elliptical geometry for the blades. As a result of their study, they demonstrated that cylindrical blades improved turbine efficiency by 18.18% at a given overlap ratio and speed. As compared to conventional wind turbines, Savonius turbine blades feature elliptical blades. Drag is the primary factor affecting Savonius blades. The blades begin to rotate as soon as the wind collides with their concave segment due to the greater drag force experienced by the concave segment. It is, however, the negative blade torque that is responsible for the low efficiency of this type of turbine. As a result, Mari et al. [24] presented three elliptical designs to replace the circular ones and conducted numerical calculations, resulting in an increase of 21.5% in the power coefficient. Savonius wind turbine performance is affected by the optimum overlap ratio. At an overlap ratio of zero, Damak et al. [25] constructed two types of experimental and theoretical helical blades for the Savonius turbine and obtained a power coefficient of 0.2 at a tip speed ratio of almost 0.87. Tartuferi et al. [26] improved the Savonius wind turbine by proposing a novel design for the blade airfoils and employing a deflector as an accessory. Due to its aerodynamic thickness and cross-section, this blade geometry is the only one with a variable thickness along the camber line, allowing the high and low-pressure regions to change simultaneously.
Even though some experimental and numerical research has been conducted on the performance of Savonius wind turbines, little is known about how geometrical parameters affect wind turbine performance. Specifically, the literature review summarized above suggests a lack of research on the effect of overlap ratio on Savonius wind turbines with and without shaft rotors. The air will flow in all directions when the wind pounds the Savonius wind turbine’s rotor. As a result, the rotor shaft can influence the performance of a turbine. This study is intended to investigate the effect of a shaft rotor on the performance of Savonius wind turbines with two different blade profiles at variable overlap ratios. This can affect wind generator power output. In order to measure the performance of Savonius wind turbines, power, and torque coefficients, as well as tip speed ratio, can be used. A conventional wind turbine was used as a benchmark for calculating flow characteristics, and experimental results were used to validate the results. Finally, the experimental test with the modified wind turbine revealed that the wind turbine with a shaft rotor achieved the highest power coefficient for both SR3345 and SR5050 blades at overlap ratios of 0 and 0.18, respectively.

2. Geometric Data

Savonius wind turbine includes a central shaft for torque transmission and two attached twisted blades, designed using Solidworks. Using a 3D printer, the turbine blades were manufactured from PLA (Polylactic Acid) with a diameter of 300 mm and a height of 300 mm. By keeping the extruded plastic warm, the 3D structure of the turbine shape is manufactured using a 3D printer’s robotic heating bed (Quantum Generous Pro). The Quantum Generous Pro printer has an accuracy of 50 microns, and its largest dimensions are 300 mm in x, 250 mm in y, and 300 mm in z. Also, the layer thickness in 3D printing is set to 200 microns. 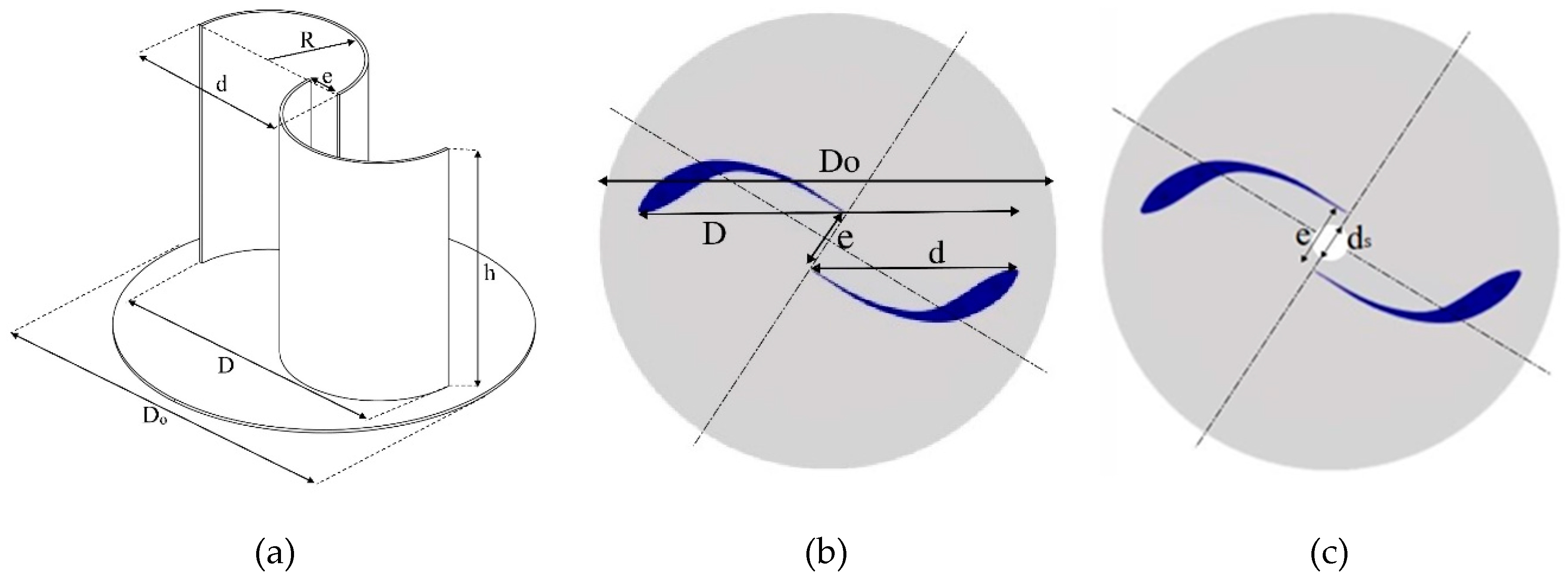Table 1 and Figure 1 illustrate the dimensions and operating parameters of the model and the 3D wind turbine model used in the test rig. By blocking the flow of air out of the upper and lower turbines, a concave blade is intended to generate greater force.
As a first step in setting up the experimental conditions, the turbine was positioned in the center of the test section, and variable wind speeds were adjusted. For accurate measurement of turbine performance at different torques, an optical tachometer was preferred over a dynamic tachometer. The turbine torque was calculated dynamically. By securing the blades with end plates, their efficiency is increased. Additionally, the diameter of the end plates should be 10% greater than the total length of the two blades. Based on this suggestion, the end plate diameter was calculated. A more substantial thickness was considered for the lower plate (10 mm) than for the upper plate (5 mm). To investigate the effect of overlap in practice, the location of the blades on the plates was designed so that they could be effortlessly removed and installed at their specific positions using nuts and bolts. A laser cutting machine was used to cut plexiglass of the thicknesses outlined previously. This was due to the number of holes in the secured plates and their requirements for high accuracy.

3. Problem description

To explore the effect of overlap ratio on the performance of the Savonius wind turbine with or without a rotor shaft, this study examines two different blade profiles (SR3345 & SR5050) in a two-bladed Savonius wind turbine. Savonius VAWTs’ power is influenced significantly by the overlap ratio. Because the double-bladed Savonius turbine offers the best efficiency, this study examined Savonius wind turbines as a case study. Simulated and designed 3D models of the SR3345 and SR5050 airfoils and defined their dimensions and distinctive camber lines.
The following equations were used for the calculation of the power and torque coefficients, denoted by Cp and CT, respectively. The power coefficient is defined as the ratio of the power generated by the wind turbine (Pw) to the power available in the wind (Pa):
Preprints 83327 i001
Which should never exceed a value of 59.3% according to Betz’s law [18]. Which ω represents the rotational speed of the turbine, T the power generated by the turbine, ρ the air density, U the velocity of the free flow colliding the turbine blades, and h and D respectively show the height and diameter of the turbine. Similarly, the torque coefficient is defined as the ratio of the generated torque (T) to the theoretical torque (Tw):
Preprints 83327 i002
where As is the vertically projected area of the blade, calculated by h×D, where d is the diameter of each blade.
The tip speed ratio (α) is also defined as:
Preprints 83327 i003
Based on the rotational speed and diameter of each blade, it is possible to calculate the speed of the blade at its tip. As a result, the speed of the wind turbine is proportional to the operating point at which the maximum amount of power is generated. Aspect ratio refers to the ratio of the height of the turbine blades to the diameter of the turbine.
As shown in Figure 1a, in the case where the blades diverge along the direction perpendicular to the curvature line at the connection point, the overlap ratio (δ=e/d) is defined as the ratio of the spacing of the blades along this direction (e) to the length of the blade cord. Turbine torque, top rotational speed, automatic startup speed, and turbine power are all highly dependent on this ratio. In Figure 1b,c, the critical parameters that affect the performance of a wind turbine with and without a shaft are shown.

4. Experimental setup

Tests of the Savonius wind turbines were conducted under realistic conditions, such as low flow disturbances, in order to evaluate the accuracy of the experimental results. For these experiments, the open-circuit wind tunnel at Shiraz University of Technology was used. The tunnel and testing chamber measured 800×300×240 mm and 300×60×60 mm, respectively.
Figure 2a,b illustrate the experimental setup for the Savonius wind turbine study. It is possible to adjust the fluid velocity of the test chamber up to 40 m/s. For realistic operating conditions, the turbine can be placed outside the test chamber at a certain distance from the outlet, as shown in Figure 2b. Based on velocity measurements at specific locations, the distance between the outlet and turbine is selected to achieve optimal velocity. Vibrations and applied torques should be minimized when designing the power transmission system. Design decisions are influenced greatly by the material and diameter of the main shaft, the length of the bases, the ball bearings, and the connecting flanges. Figure 2c illustrates how these factors are considered in the design process.

5. Experimental validation and error analysis

A mathematical problem generally involves one or more constants, some of which are derived from approximate solutions to other mathematical problems. As a result of the representation of these numbers, errors may propagate during arithmetic operations. Doubts regarding a result’s validity are described as uncertainty. Measurement uncertainties serve as indicators of measurement quality. Consequently, an estimation of the real values can only be considered complete if it is accompanied by uncertainty. When reporting the results of a physical quantity, it is necessary to provide quantitative notes regarding the quality of the measurement results.
Uncertainty (σf) can be expressed by σ f = ∂ f ∂ x 2 . σ x 2 + ∂ f ∂ y 2 . σ y 2 according to the error propagation law [27]. Based on the equations presented and the errors regarding the specifications of the measurement devices, parameter errors can now be calculated. The measured parameters and errors are presented in Table 2. Variables h, D, and R are measured with a precision of 1 mm, and other variables are calculated according to their respective catalogs.
Where σx and σy are the uncertainties in variables x and y. In this way, based on σf, uncertainty for power and torque coefficient be determined as follows:
σ C p = ∂ C p ∂ h 2 . σ h 2 + ∂ C p ∂ D 2 . σ D 2 + ∂ C p ∂ v 2 . σ v 2 + ∂ C p ∂ m 2 . σ m 2 + ∂ C p ∂ S 2 . σ S 2 + ∂ C p ∂ R 2 . σ R 2 + ∂ C p ∂ ω 2 . σ ω 2
σ C t = ∂ C t ∂ h 2 . σ h 2 + ∂ C t ∂ D 2 . σ D 2 + ∂ C t ∂ v 2 . σ v 2 + ∂ C t ∂ m 2 . σ m 2 + ∂ C t ∂ S 2 . σ S 2 + ∂ C t ∂ R 2 . σ R 2
A coefficient error can be accurately determined by obtaining the equations for the power and torque coefficients, implicit differentiation, and substitution of the measured values.
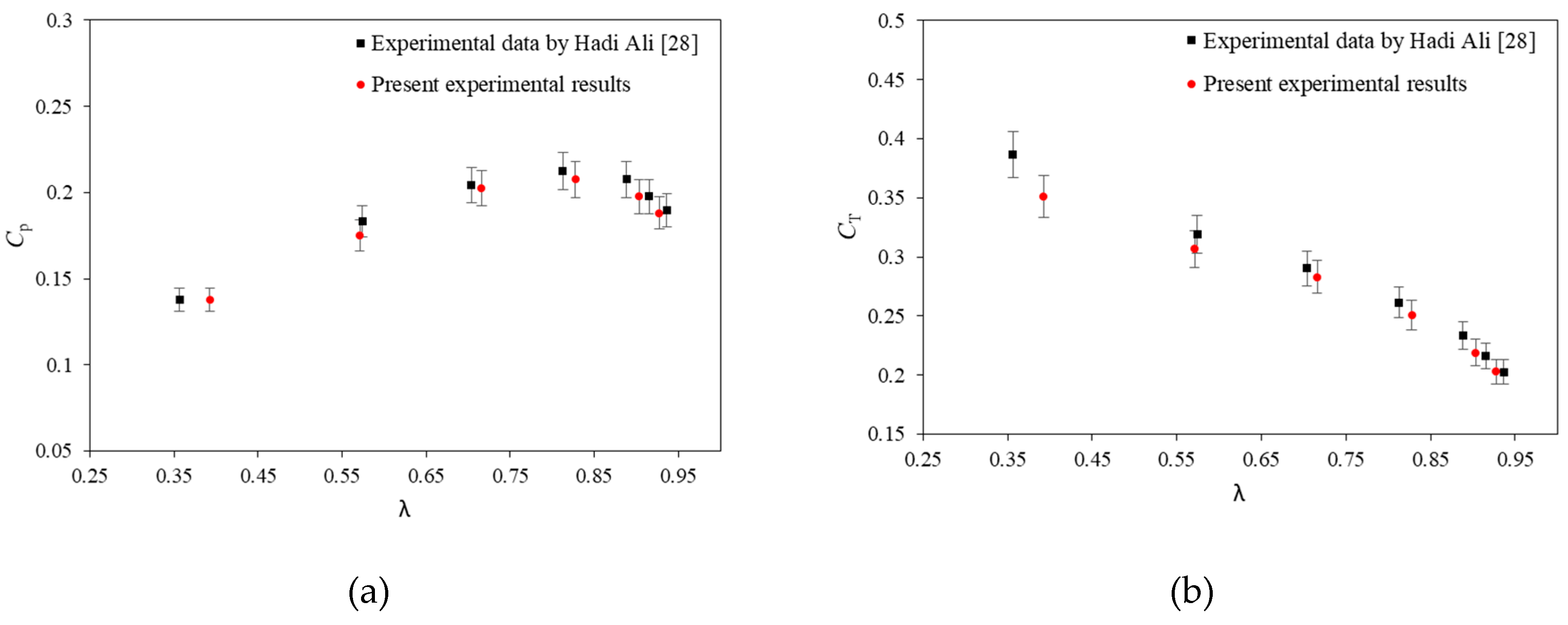
The results of a conventional wind turbine are compared with the experimental data presented by Hadi Ali [28] to evaluate the accuracy and validity of the data. Below is a comparison of the power coefficient and torque coefficient of conventional Savonius wind turbines.
In Figure 3a,b, the power and torque coefficients are shown as a function of the tip speed ratio. In terms of the power coefficient, the maximum and average relative errors are 5.68% and 1.95%, respectively, and for the torque coefficient, the maximum and average relative errors are 7.93% and 3.44%, respectively. Results in the model being able to predict the flow conditions in an appropriate manner. There is a slight difference between the results at low tip speed ratios, approximately less than 0.55. Consequently, friction has an even more notable effect on device performance at low tip speed ratios. The present power and torque coefficient may, in some cases, be lower than the experimental one due to some losses in the testing process.

6. Results and discussions

In order to determine the characteristics of the Savonius wind turbine, a series of experimental tests were conducted to examine the effects of the overlap ratio on the performance of the Savonius wind turbine with and without a shaft for the SR3345 and SR5050 rotors. Furthermore, we discuss the effects of mounting a rotor shaft at the center of a Savonius wind turbine on its overall performance.

6.1. Savonius wind turbine with a shaft rotor

The center of the plates was placed with a shaft in order to investigate the effect of placing a shaft at the center of the plates on turbine performance. As a result of the inclusion of the shaft in the center of the turbine, air behavior is complicated, and the turbine’s strength and stability are increased.
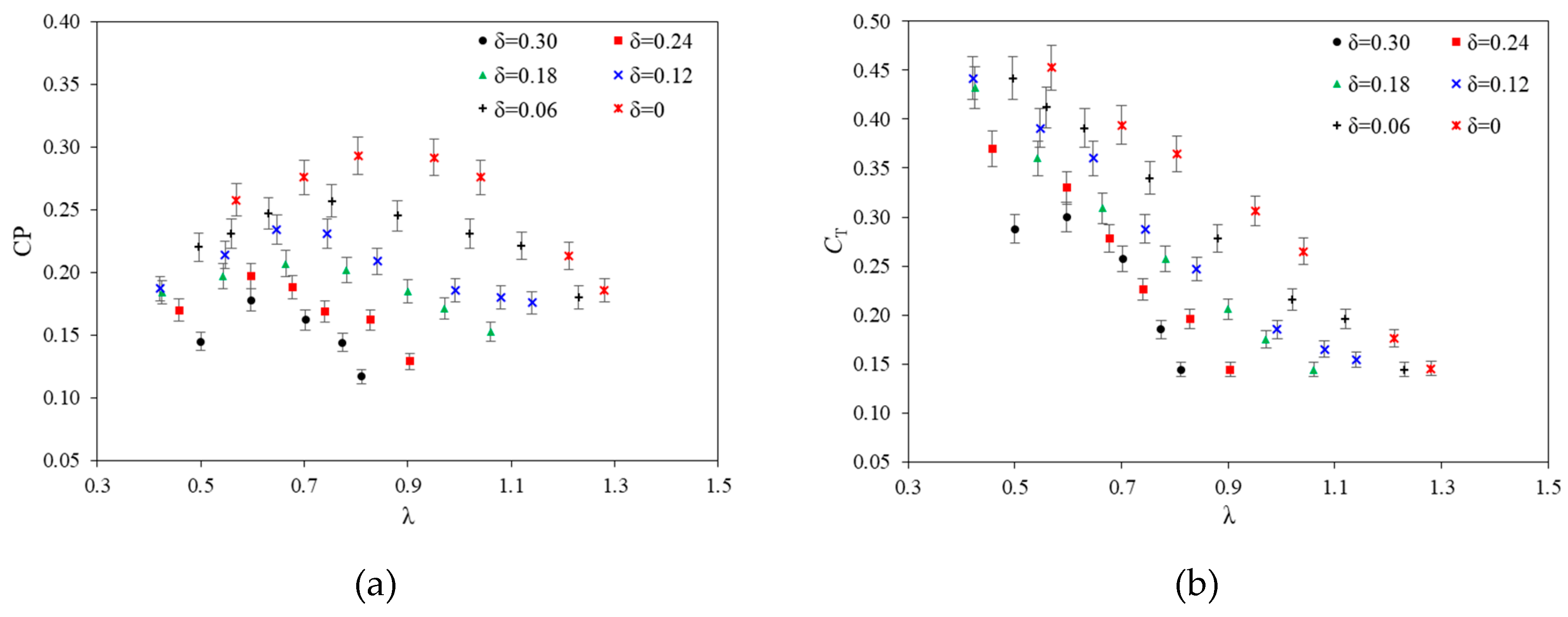
The main challenge associated with the performance of a Savonius wind turbine is the management of its power and torque coefficients [29,30]. A comparison of the performance of the Savonius wind turbine equipped with blades of SR3345 and a shaft rotor at overlap ratios of 0 to 0.3 is presented in Figure 4a,b. In the experiment test with the zero-overlap ratio, the tip speed ratio and the power coefficient ranged from 0.5 to 1.3 and 0.14 to 0.26, respectively.
According to Figure 4a, the power coefficient increases initially and then decreases as the tip speed ratio increases. At an overlap ratio of 0 and a tip speed ratio of 0.9 to 1, the maximum power coefficient (Cp=0.26) occurs. As a result of increasing the overlap ratio and the distance between the two blades, the drag force acting upon the blades is reduced, resulting in a smaller amount of wind energy being absorbed by the turbine. Further, the negative pressure behind the wind turbine causes an inverse pressure gradient, which separates the flow and generates vortices, thereby reducing the turbine’s performance.
Increasing the overlap ratio will reduce the rotational speed of the wind turbine, so the high tip speed ratio and maximum power coefficient will decrease at lower tip speed ratios for a given overlap ratio, which will result in a reduction in the rotational speed ratios, so, at an overlap ratio of 0.3, the maximum power coefficient (Cp=0.16) occurs at a tip speed ratio of 0.6. In the experiment test, raising the load at a wind speed of 6 m/s started to enhance the rotational speed, causing the tip speed ratio to decline from its highest value to its lowest value.
According to Figure 4b, increasing the load increases the torque coefficient and decreases the tip speed ratio. The torque coefficient does, however, experience a slight decrease at overlap ratios of 0.18 and 0.3 after reaching its peak value. With an overlap ratio of 0 and a tip speed ratio of 0.52, the torque coefficient peaks at approximately 0.45. The torque coefficient decreases as the overlap ratio increases at a given tip speed ratio.
Variations of the power and torque coefficient against the tip speed ratio for the Savnius wind turbine equipped with SR5050 profile blade and a shaft rotor at overlap ratios of 0 to 0.3 with a step size of 0.06 are plotted in Figure 5a,b, respectively.
It can be seen in Figure 5a that decreasing the tip speed ratio and increasing the load results in a somewhat linear behavior. Once the power coefficient reaches its peak, a declining trend is observed. A comparison of overlap ratios between 0 and 0.3 with a step size of 0.06 reveals that although the overlap ratio does not significantly impact the turbine’s performance, increasing the overlap ratio up to 0.18 increases the maximum power coefficient, such that the power coefficient reaches a value of 0.25 when the overlap ratio is roughly 0.18 and the tip speed ratio is approximately 1. When the overlap ratio is increased beyond 0.18, the maximum power coefficient decreases to almost 0.02. As a result, the highest power coefficient is not achieved at an overlap ratio of 0, as is the case for SR3345 blades. Also, the power coefficient assumes similar values at overlap ratios of 0.06 to 0.18, which leads to a maximum power coefficient at the end of this range, similar to reports suggesting that cylindrical blades have a maximum power ratio between 0.18 and 0.24.
In contrast, no significant changes in the torque coefficient are observed when the overlap coefficient ranges from 0 to 0.18. Furthermore, the maximum torque coefficient is almost 0.41 at overlaps of 0 to 0.24 and tip speed ratios of 0.26 to 0.43. The smallest value is 0.15 when the overlap ratio is zero (Figure 5b).

6.2. Savonius wind turbine without a shaft rotor

This section examines the performance of the Savonius wind turbine, which consists of two types of blades and end plates. The same analysis can be conducted in this case, except for the removal of the central shaft, which decreases the strength of the turbine and allows the air to behave more predictably.
Figure 6a shows the power coefficients for the aforementioned overlap ratios at different tip speed ratios for the SR3345 rotor without a shaft. As compared to the previous case (Figure 4a) at high tip speed ratios, the power coefficient increases significantly. As the ratio decreases, however, the power coefficient decreases to values close to a wind turbine equipped with a shaft rotor. This suggests that the shaft’s impact is substantially reduced to negligible levels as the wind turbine’s load increases and the rotational speed declines. As the overlap ratio increases, both with and without a shaft, the power coefficient is closer to that of wind turbines equipped with SR3345 rotors. As a result, it can be concluded that the power coefficient is not significantly affected by mounting a shaft rotor at a high overlap ratio.
Figure 6b illustrates torque coefficients for tip speed ratios of 0.1, 0.06, 0.12, 0.18, 0.24, and 30. The highest torque coefficient of 0.453 corresponds to zero overlap ratios at a tip speed ratio of 0.58. Further, as the overlap ratio increases, the range of tip speed ratios and the maximum torque coefficient decrease, indicating that the turbine has a lower performance range. A comparison of Figure 6b and Figure 4b clearly illustrate that removing the turbine’s central shaft does not decrease its torque coefficient after reaching its maximum value at an overlap ratio of 0.18, which indicates that the torque ratio is continuously increasing.
Figure 7a illustrates the effect of demounting a rotor shaft on the power coefficient of the blade of the SR5050. A rotor shaft also plays a significant role in determining the maximum power coefficient of a wind turbine. With a rotor shaft overlap of zero, the highest power coefficient for the wind turbine is approximately 0.26, which occurs at tip speed ratios between 1 and 1.2. A decrease in the power coefficient becomes negligible below a tip speed ratio of 0.8 as the overlap ratio increases.
Up to a tip speed ratio of 0.9, the torque coefficient is higher at an overlap ratio of zero than at other ratios. As shown in Figure 7b, however, as the tip speed ratio decreases and the overlap ratio increases, the torque coefficient continues to increase until it reaches its peak (CT=0.427) at λ=0.3.

7. Conclusions

An experimental study was conducted using a Savonius wind turbine under different conditions (with and without a shaft) in order to determine the impact of geometric parameters on wind turbine performance. An extensive range of effective parameters has been taken into account in this study. This model has been validated against wind tunnel data published in the literature for turbines with shafts first, and then without shafts to determine the optimum overlap ratio. It may be helpful for designers to improve the efficiency of Savonius wind turbines by describing some important geometrical parameters, as the development of a Savonius wind turbine is a very challenging undertaking. In this study, the objective was to evaluate the effect of mounting a rotor shaft and overlap ratio on the performance of a Savoius wind turbine. Overall, the present study can be summarized as follows:
  • At a tip speed ratio broader than 1.06, blade SR5050 achieved a maximum power coefficient of approximately 0.263. In contrast, blade type SR3345 achieved a maximum power coefficient of 0.293 at a tip speed ratio of less than 1.06.
  • The power coefficient of both blade types is reduced when a shaft rotor is added at the center of the turbine as a barrier.
  • In blade SR 3345, when tip speed ratios were less than 1, and overlap ratios were zero, maximum power coefficients were 0.254; whereas, in blade SR5050, the maximum power coefficient was 0.247 when tip speed ratios were higher than 1, and overlap ratios were approximately 0.18. Due to the larger curvature of the blades and shaft rotor, the wind turbine behaves similarly to those with cylindrical blades.
  • The results indicate deterioration of the turbine performance and more intense effects of using the shaft.

Funding

There is no funding source.

Conflict of Interests

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

References

  1. J. Zare, S. E. Hosseini, and M. R. Rastan, “Airborne dust-induced performance degradation in NREL phase VI wind turbine: a numerical study,” https://doi.org/10.1080/15435075.2023.2246544, pp. 1–20, Aug. 2023. [CrossRef]
  2. J. Zare, S. E. Hosseini, and M. R. Rastan, “NREL Phase VI wind turbine in the dusty environment,” Apr. 2023, Accessed: Aug. 25, 2023. [Online]. Available: https://arxiv.org/abs/2304.06285v1.
  3. S. Roy and U. K. Saha, “Wind tunnel experiments of a newly developed two-bladed Savonius-style wind turbine,” Appl. Energy, 2015. [CrossRef]
  4. M. H. Shojaeefard, S. E. Hosseini, and J. Zare, “Numerical simulation and multi-objective optimization of the centrifugal pump inducer,” Modares Mech. Eng., vol. 17, no. 7, pp. 205–216, 2018.
  5. M. H. Shojaeefard, S. E. Hosseini, and J. Zare, “CFD simulation and Pareto-based multi-objective shape optimization of the centrifugal pump inducer applying GMDH neural network, modified NSGA-II, and TOPSIS,” Struct. Multidiscip. Optim., vol. 60, no. 4, pp. 1509–1525, May 2019. [CrossRef]
  6. K. M. Youssef, A. M. El Kholy, A. M. Hamed, N. A. Mahmoud, A. M. El Baz, and T. A. Mohamed, “An innovative augmentation technique of savonius wind turbine performance,” Wind Eng., vol. 44, no. 1, pp. 93–112, Feb. 2020. [CrossRef]
  7. P. Mohan Kumar, M. M. R. Surya, S. Narasimalu, and T. C. Lim, “Experimental and numerical investigation of novel Savonius wind turbine,” https://doi.org/10.1177/0309524X18780392, vol. 43, no. 3, pp. 247–262, Jun. 2018. [CrossRef]
  8. M. P. Thomai, S. Sivamani, and H. Venkatesan, “Experimental and Numerical Investigation to Assess the Performance of Helical Bach Vertical Axis Wind Turbine at Low Wind Velocity Conditions,” J. Sol. Energy Eng. Trans. ASME, vol. 144, no. 5, Oct. 2022. [CrossRef]
  9. M. Ahmad, A. Shahzad, and S. I. A. Shah, “Experimental investigation and analysis of proposed hybrid vertical axis wind turbine design,” https://doi.org/10.1177/0958305X231181675, Jun. 2023. [CrossRef]
  10. K. Pietrykowski, N. Kasianantham, D. Ravi, M. Jan Gęca, P. Ramakrishnan, and M. Wendeker, “Sustainable energy development technique of vertical axis wind turbine with variable swept area—An experimental investigation,” Appl. Energy, vol. 329, p. 120262, Jan. 2023. [CrossRef]
  11. J. Alexander and B. P. Holownia, “Wind tunnel tests on a savonius rotor,” J. Wind Eng. Ind. Aerodyn., 1978. [CrossRef]
  12. N. J. Roth, “Prototype Design and Performance of Savonius Rotor Based on Irrigation System,” The University of British Columbia, 1985.
  13. V. J. Modi, N. J. Roth, and M. S. U. K. Fernando, “Optimum-configuration studies and prototype design of a wind-energy-operated irrigation system,” J. Wind Eng. Ind. Aerodyn., 1984. [CrossRef]
  14. N. Fujisawa, “On the torque mechanism of Savonius rotors,” J. Wind Eng. Ind. Aerodyn., 1992. [CrossRef]
  15. N. Fujisawa, “Velocity measurements and numerical calculations of flow fields in and around Savonius rotors,” J. Wind Eng. Ind. Aerodyn., 1996. [CrossRef]
  16. D. Altan, M. Atilgan, and A. Özdamar, “An experimental study on improvement of a Savonius rotor performance with curtaining,” Exp. Therm. Fluid Sci., 2008. [CrossRef]
  17. V. L. Okulov and G. A. M. Van Kuik, “The Betz-Joukowsky limit: On the contribution to rotor aerodynamics by the British, German and Russian scientific schools,” Wind Energy, 2012. [CrossRef]
  18. J. R. P. Vaz and D. H. Wood, “Performance analysis of wind turbines at low tip-speed ratio using the Betz-Goldstein model,” Energy Convers. Manag., vol. 126, pp. 662–672, Oct. 2016. [CrossRef]
  19. V. J. Modi and M. S. U. K. Fernando, “On the Performance of the Savonius Wind Turbine,” J. Sol. Energy Eng., vol. 111, no. 1, pp. 71–81, Feb. 1989. [CrossRef]
  20. M. H. Simonds, A. Bodek, and B. R. Institute., Performance test of a Savonius rotor. Ste. Anne de Bellevue, Quebec: Brace Research Institute, Macdonald College of McGill University, 1964.
  21. M. A. Kamoji, S. B. Kedare, and S. V Prabhu, “Performance tests on helical Savonius rotors,” Renew. Energy, vol. 34, no. 3, pp. 521–529, 2009.
  22. Banerjee, S. Roy, P. Mukherjee, and U. K. Saha, “Unsteady Flow Analysis Around an Elliptic-Bladed Savonius-Style Wind Turbine,” ASME 2014 Gas Turbine India Conf. GTINDIA 2014, Feb. 2015. [CrossRef]
  23. N. Alom, S. C. Kolaparthi, S. C. Gadde, and U. K. Saha, “Aerodynamic Design Optimization of Elliptical-Bladed Savonius-Style Wind Turbine by Numerical Simulations.” Jun. 2016. [CrossRef]
  24. M. Mari, M. Venturini, and A. Beyene, “A Novel Geometry for Vertical Axis Wind Turbines Based on the Savonius Concept,” J. Energy Resour. Technol., vol. 139, no. 6, Jul. 2017. [CrossRef]
  25. Damak, Z. Driss, and M. S. Abid, “Optimization of the helical Savonius rotor through wind tunnel experiments,” J. Wind Eng. Ind. Aerodyn., vol. 174, pp. 80–93, 2018.
  26. M. Tartuferi, V. D’Alessandro, S. Montelpare, and R. Ricci, “Enhancement of savonius wind rotor aerodynamic performance: A computational study of new blade shapes and curtain systems,” Energy, 2015. [CrossRef]
  27. S. Shamim and S. Anwar, “Error Analysis in the Experimental Physics Lab,” Lab Monogr. Introd. Exp. Phys., p. 11, 2009.
  28. M. Hadi Ali, “Experimental Comparison Study for Savonius Wind Turbine of Two & Three Blades At Low Wind Speed,” Int. J. Mod. Eng. Res. www.ijmer.com, 2013.
  29. H. L. Bai, C. M. Chan, X. M. Zhu, and K. M. Li, “A numerical study on the performance of a Savonius-type vertical-axis wind turbine in a confined long channel,” Renew. Energy, vol. 139, pp. 102–109, Aug. 2019. [CrossRef]
  30. E. Antar and M. Elkhoury, “Parametric sizing optimization process of a casing for a Savonius Vertical Axis Wind Turbine,” Renew. Energy, vol. 136, pp. 127–138, Jun. 2019. [CrossRef]
Preprints 83327 g001
Figure 1. (a) Schematic view of the parameters of the Savonius wind turbine with a semicircular blade, (b) important parameters in defining the overlap ratio for the shaftless turbine blade and (c) for the turbine blade with a shaft.
Figure 1. (a) Schematic view of the parameters of the Savonius wind turbine with a semicircular blade, (b) important parameters in defining the overlap ratio for the shaftless turbine blade and (c) for the turbine blade with a shaft.
Preprints 83327 g001
Preprints 83327 g002
Figure 2. (a) Schematic of the tunnel at Shiraz University of Technology, (b) placement of the turbine in front of the windtunnel outlet, and (c) Close up of the power transmission system.
Figure 2. (a) Schematic of the tunnel at Shiraz University of Technology, (b) placement of the turbine in front of the windtunnel outlet, and (c) Close up of the power transmission system.
Preprints 83327 g002
Preprints 83327 g003
Figure 3. Comparison of the experimental results of (a) power and (b) torque coefficient with the experimental data by Hadi Ali [28].
Figure 3. Comparison of the experimental results of (a) power and (b) torque coefficient with the experimental data by Hadi Ali [28].
Preprints 83327 g003
Preprints 83327 g004
Figure 4. Effects of overlap ratio on the (a) power and (b) torque coefficient of the Savonius wind turbine equipped with blade of SR3345 and a shaft rotor at overlap ratios of 0 to 0.3 with a step size of 0.06.
Figure 4. Effects of overlap ratio on the (a) power and (b) torque coefficient of the Savonius wind turbine equipped with blade of SR3345 and a shaft rotor at overlap ratios of 0 to 0.3 with a step size of 0.06.
Preprints 83327 g004
Preprints 83327 g005
Figure 5. Effects of overlap ratio on the (a) power and (b) torque coefficient of the Savonius wind turbine equipped with blade of SR5050 and a shaft rotor at overlap ratios of 0 to 0.3 with a step size of 0.06.
Figure 5. Effects of overlap ratio on the (a) power and (b) torque coefficient of the Savonius wind turbine equipped with blade of SR5050 and a shaft rotor at overlap ratios of 0 to 0.3 with a step size of 0.06.
Preprints 83327 g005
Preprints 83327 g006
Figure 6. Variations of (a) the power and (b) the torque coefficient of the Savonius wind turbine equipped with blade of SR3345 without a shaft rotor at overlap ratios of 0 to 0.3 with a step size of 0.06.
Figure 6. Variations of (a) the power and (b) the torque coefficient of the Savonius wind turbine equipped with blade of SR3345 without a shaft rotor at overlap ratios of 0 to 0.3 with a step size of 0.06.
Preprints 83327 g006
Preprints 83327 g007
Figure 7. Variations of (a) the power and (b) the torque coefficient of the Savonius wind turbine equipped with blade of SR5050 without a shaft rotor at overlap ratios of 0 to 0.3 with a step size of 0.06.
Figure 7. Variations of (a) the power and (b) the torque coefficient of the Savonius wind turbine equipped with blade of SR5050 without a shaft rotor at overlap ratios of 0 to 0.3 with a step size of 0.06.
Preprints 83327 g007
Table 1. Geometric parameters of the Savonius rotor.
Table 1. Geometric parameters of the Savonius rotor.
Geometric parameters Value
End plate (D0) 330 mm
Rotor diameter (D) 300 mm
Rotor height (h) 300 mm
Number of blades 2
Overlap ratio 0
Aspect ratio 1
Table 2. Precision of measurements of variables.
Table 2. Precision of measurements of variables.
ω (rad/s) R (m) S (kg) M (kg) v (m/s) D (m) h (m) Variable
0.0105 0.001 0.005 0.005 0.2 0.001 0.001 Measurement error
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated