Processing of Porous Core Materials Mimicking Bone’s Microstructure: A Permeability and Mechanical Strength Analysis

1. Introduction

To produce bone implants that meet special characteristics, the development of porous materials with localized porosity has attracted much attention [1,2]. For two decades, the most widely used manufacturing materials for the manufacture of porous materials have been mainly bioglasses [3] and metal alloys [4,5,6,7]. Depending on the specific characteristics of the bone to be replaced or improved and its respective location, materials that may be the most suitable are chosen. Currently, one of the most used techniques for the manufacture of porous materials is, additive manufacturing is one of the most prominent, but the cost is strongly limiting [1,2,8]. In order to imitate the real porosity of bone, there is a process that favors the formation of pores with subsequent sintering, presented as a cheaper alternative for the manufacture of porous systems [9,10,11,12,13]. Titanium alloys are the most studied materials because of its high specific strength, an excellent corrosion resistance, and an exceptional biocompatibility. The main problem that is solved by scaffolds configuration is the reduction on the mechanical properties, which is a major concern in order to reduce the phenomenon called stress-shielding. Likewise, this phenomenon is one of the main causes of aseptic loosening, which is generated by the difference in rigidity between the bone and the implant [14]. It is well establishing that mechanical properties of materials are reduced as much as the volume fraction of pores increases, generally, following a power law, as that proposed by Gibson and Ashby [15]. Other works have found that pore characteristics could influence the reduction of mechanical properties such as size and shape. They have proposed models including parameters of the pore characteristics that are not easy to obtain and most of them were projected from 2D images, which increases the incertitude of such models [16,17]. Recently, Cabezas et al. suggested that the exponent in the power law proposed by Gibson and Ashby can be adjusted to find a good response for porous Ti6Al4V materials fabricated by powder metallurgy with the space holder technique [12]. To produce a successful implant, it must have mechanical properties, biocompatibility, and adequate osseointegration. Biocompatibility refers to the material’s ability to be accepted by the human body, this property is limited by the material’s cytotoxicity (release of hazardous ions). Therefore, Ti is one of the materials with the best demonstrated biocompatibility [18]. On the other hand, osseointegration is the ability of the material to facilitate bone growth through it. A property called permeability is of paramount importance as it allows the flow of nutrients and osteocytes and also removes metabolic wastes as they are transported through the porosity of bone, which is associated with bone adaptation and regeneration [19]. In addition, interconnected pores enhance anchorage and vascularization, thus, a better mechanical adhesion between implant and bone can be achieved [20,21,22,23]. Different authors have evaluated the permeability of scaffolds, which increases as a function of the pore size and volume fraction [24,25,26]. Olmos et al. [26] investigated permeability of porous samples fabricated by the space holder technique. Demonstrate that there is anisotropy when measuring permeability depending on the orientation, longitudinal or transversal, which is consistent with what has been reported for bones [27].

Most of the reports in the literature have linked the pore volume fraction and the pore characteristics to mechanical and flow properties as well as to cell and/or bone ingrowth for components with a uniform porosity. Nonetheless, real bone microstructure includes porosity gradients that enable specific cell migration during tissue regeneration, vascularization, and tissue ingrowth by facilitating gas diffusion, nutrient supply, and waste removal. Only a few studies have investigated the fabrication of two-layer components by powder metallurgy. M. Dewidar and Kim [28] and Lee et al. [29] produced Ti-based systems consisting of a solid core and a porous outer shell, where they studied the compressive behavior of these two-phase systems. On the other hand, Ahmadi and Sadrnezhaad [30] they present a component that has a configuration similar to bone, where there are porous cores and dense outer layers. They included a variation in the diameter of the porous core from 6 to 14 mm, while the external diameter remained constant at 16 mm. From this study, it was shown that the elastic modulus depends linearly on the thickness of the porous core.

The present work is focused on multilayer components with graded porosity fabricated by conventional sintering of Ti6Al4V alloy powders. Mechanical properties of the components are evaluated by compression tests. Pore features are studied by X ray microtomography at different resolutions and permeability values are deduced from 3D images through numerical simulations.

2. Materials and Methods

2.1. Sample preparation

Prealloyed Ti-6Al-4V spherical powder with particle size distribution 0-45 μm, manufactured by Raymor, Canada, was used as the base material. For the generation of large pores, ammonium bicarbonate salt ((NH₄)HCO₃) with a particle size of between 100-500 μm of irregular shape was used. Provided by Alfa Aesar, USA. First, monolayer samples were fabricated with or without pore formers by successive die pressing and sintering. Powders of Ti6Al4V without pore formers were mixed with a solution of polyvinyl alcohol (PVA) as a binder at 1 wt.% and then, simply poured into an 8 mm diameter steel die and compacted with a pressure of 500 MPa. The PVA was subsequently removed at 500 °C with 30 minutes of residence in an argon atmosphere, thus, the resulting green density of these compacts was around 70 The poreless monolayers are prepared from the Ti64 mixture with a 30, 40 and 50% volume fraction of the salt particles ((NH₄)HCO₃). 1% PVA was also added as a binder, and the mixture was subsequently compacted at 500 MPa pressure in a cylindrical stainless-steel mold of 8 mm in diameter. Salts particles were eliminated at 180°C for 6 h under argon atmosphere. This samples were used to obtain mechanical properties as a reference to the bilayer components.

Secondly, bilayer samples were fabricated by combining layers of dense and porous materials by using the configuration of porous core and dense shell of samples. Porous core corresponds to the samples with the center of compacts with the mixture of Ti6Al4V and salt particles.

In order to obtain two-layer samples, stainless steel tubes of two different diameters 3 and 5.66 mm were placed at the center of the 8 mm diameter stainless steel die. The size of diameter allows to have two ratios of the volume corresponding to each layer, 85/15 and 50/50 respectively. Different quantities of pores were obtained in the porous core by adding 30, 40 and 50 % of salt particles. The mixture of Ti6Al4V and salt particles was poured inside the tubes then a punch was used to flatten the surface. Then, the Ti6Al4V powders filled the outer section to obtain a denser layer, the procedure to fabricate bilayer samples was detailed elsewhere [31]. Afterwards, the samples were pressed at 500 MPa. Finally, the salt was removed as described.

The sintering process of all the green samples was carried out in a Linseis L75V vertical dilatometer at 25 °C/min until reaching 1260 °C, remaining 1 hour in Argon atmosphere. The dilatometer was purged to remove the air by flowing high purity argon for 30 minutes before starting the heating. After sintering, the relative density of samples was obtained by measuring the volume of samples and weighing them to obtain the pore volume fraction.

2.2. Microstructure characterization

The sintered samples were cut and metallographically prepared with SiC abrasive paper and alumina powder to obtain a surface roughness Ra of 70 nm. The microstructure was observed with a field emission scanning electron microscope (FE-SEM) Tescan MIRA 3 LMU, with a voltage of 20 keV.

A study of macroporosity was carried out from 3D images acquired by computerized microtomography (CMT) in a Zeiss Xradia 510 Versa 3D X-ray microtomograph. In order to observe the 8 mm diameter Ti64 samples, an intensity of 120 kV was used. 1600 projections were obtained around the samples in 360°, with a CCD camera of 1025×1025 pixels. The resulting voxel size of approximately 9 μm, in order to be able to observe the entire sample. This resolution allowed an analysis of the pores created by the ammonium bicarbonate salt particles.

The 3D images were manually processed to obtain binary images at a constrained threshold, based on the relative density, previously obtained from the actual mass and volume. Once the binary images were obtained, the solid and porous phases were represented with a voxel intensity of 255 and 0 respectively. From the processed images, the porosity characteristics were obtained, such as the volume fraction, the size distribution, and the size of the channels, according to the process explained by L. Olmos [26].

2.3. Compression tests

After 3D image analysis, simple compression tests were performed according to ASTM D695-02 with an Instron 1150 universal testing machine, the strain rate was 0.5 mm/min. The elastic modulus (E) and the elastic limit (σy) were calculated from the load displacement data provided by the machine. For stress calculation, a data correction was performed assuming that the volume was constant during the test, this assumption is reasonable for low strains where E and σy are estimated.

2.4. Numerical permeability simulation

The flow properties of the porous samples were evaluated by numerical simulation of permeability using the Avizo® software on the 3D reconstructed binary images obtained by tomography. To run the numerical simulations, a minimum representative volume (MRV) was obtained by selecting a 20x20x20 voxel volume cube from the center of the 3D image, then relative density for this volume was calculated. The operations carried out were repeated in 20 voxels per side of the volume of the cube until reaching a relatively constant relative density, a similar method was proposed by Okuma et al. [32]. To save numerical simulation time due to computational limitations, a minimum volume was calculated to obtain a maximum of precision. A volume of 2503 voxels³ was obtained in which the relative density reached an almost constant value A volume of 300x300x300 voxels is used, (20 mm³ of the real volume). The numerical simulations were carried out in three directions, where the Cartesian axes X and Y are the horizontal planes and Z the vertical axis.

The Avizo® software performs numerical simulations based on Darcy’s law, solving the Navier Stokes equations by finite volume method. The simulation considers a Newtonian fluid in steady state, representing the blood with a viscosity of 0.045 Pa*s. The pressure conditions used at the inlet and outlet were 130 and 100 kPa respectively.

3. Results and discussion

3.1. Dilatometry analysis

The axial strain during the sintering cycle of monolayer and bilayer samples is plotted as a function of the time and temperature in Figure 1a. It is found that curves show at first a dilation until the sintering is activated at 680 °C. Then, the slope of the curve changes to be negative, which indicates a shrinkage of the compacts that has an exponential behavior until the end of the isothermal stage. Finally, the stage of cooling added a small shrinkage due to the thermal contraction of samples. It is found that the final strain is larger for the porous sample, and the one obtained for the bilayer is in the middle between the porous and dense monolayer samples. It can also be noted that the shrinkage of the bilayer with the porous core with a ratio with the dense shell of 50/50 is larger than the one with a ratio of 85/15. This behavior indicates that densification is due to a combination of both layers. This can be confirmed by the strain rate of the bilayer samples that increases as the diameter of porous core does it, see Figure 1b. High strain rate is reached in the porous sample because the macroscopic deformation is due to the sintering effects; necks formation and growing, and by the deformation of large pores due to the sintering stresses developed by the densification.

The sintered relative density of all samples is listed in Table 1, and as it was expected, the values of the bilayer samples are in between of the monolayer sample. However, in order to establish if the relative density of samples corresponds to the volume of each layer, the rule of mixtures is used to estimate the relative density. The rule of mixture can be written as follows:

$$D_b=f_c{D}_c+f_s{D}_s$$

(1)

In where, the D_b, D_c and D_s means the relative density of the bilayer, core and shell samples, respectively. D_c and D_s will be assumed to be the relative density of the monolayer samples obtained at the same fabrication conditions of the bilayer samples. And fc and fs mean the volume fraction of the core and shell samples, respectively. The volume fractions of the porous core and dense shell layers correspond to 15, 50 % and 85, 50 %, respectively. It is found that all the relative densities estimated by the rule of mixtures are higher than the ones measured. This suggests that more interparticle porosity is obtained, which is generated by the stresses generated at the interface of both layers. Although this difference can be as high as 10 times from the porous to the dense samples, delamination of the core layer was not observed [30,33,34]. The larger ratios of the DR-M/D (see Table 1) found in bilayer 85/15 samples indicate that the dense layer should be more affected for this effect. Therefore, the relative density of bilayers is lower than the one predicted by the rule of mixtures.

Figure 1. Dilatometry of the bilayer layers of Ti64 samples a) axial strain and b) strain rate.

Figure 1. Dilatometry of the bilayer layers of Ti64 samples a) axial strain and b) strain rate.

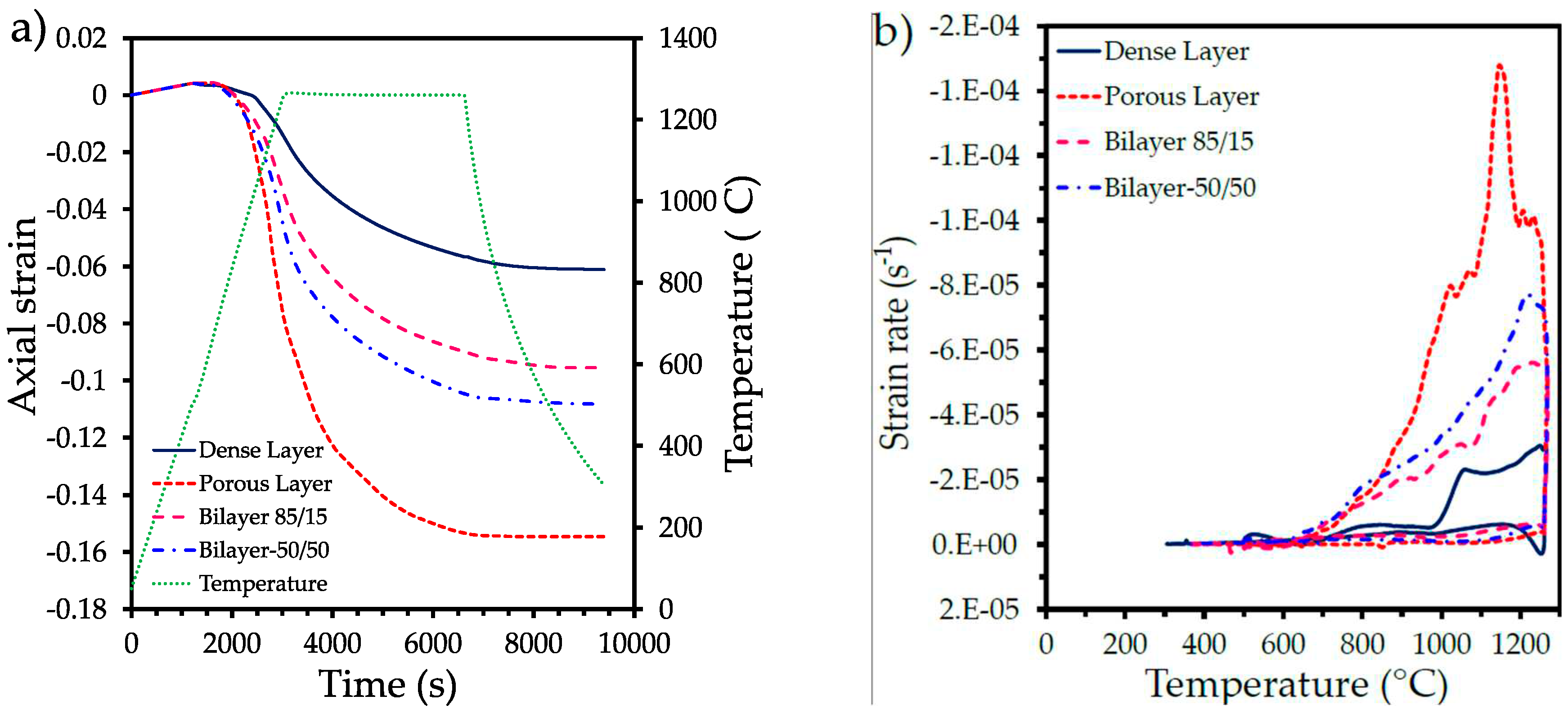
Table 1. Relative density measured and estimated by the rule of mixtures (R-M).

Sample	Relative density (D)	Relative density (R-M)	Ratio DR-M/D
Ti6Al4V P0	0.9633	--
Ti6Al4V P30	0.5436	--
Ti6Al4V P40	0.3972	--
Ti6Al4V P50	0.3378	--
Bilayer 85/15 P30	0.7706	0.9043	1.17
Bilayer 85/15 P40	0.7544	0.8837	1.17
Bilayer 85/15 P50	0.7238	0.8753	1.20
Bilayer 50/50 P30	0.6557	0.7532	1.14
Bilayer 50/50 P40	0.6026	0.6800	1.12
Bilayer 50/50 P50	0.5827	0.6502	1.11

Table 1. Relative density measured and estimated by the rule of mixtures (R-M).

Sample	Relative density (D)	Relative density (R-M)	Ratio DR-M/D
Ti6Al4V P0	0.9633	--
Ti6Al4V P30	0.5436	--
Ti6Al4V P40	0.3972	--
Ti6Al4V P50	0.3378	--
Bilayer 85/15 P30	0.7706	0.9043	1.17
Bilayer 85/15 P40	0.7544	0.8837	1.17
Bilayer 85/15 P50	0.7238	0.8753	1.20
Bilayer 50/50 P30	0.6557	0.7532	1.14
Bilayer 50/50 P40	0.6026	0.6800	1.12
Bilayer 50/50 P50	0.5827	0.6502	1.11

3.2. Tomography analysis

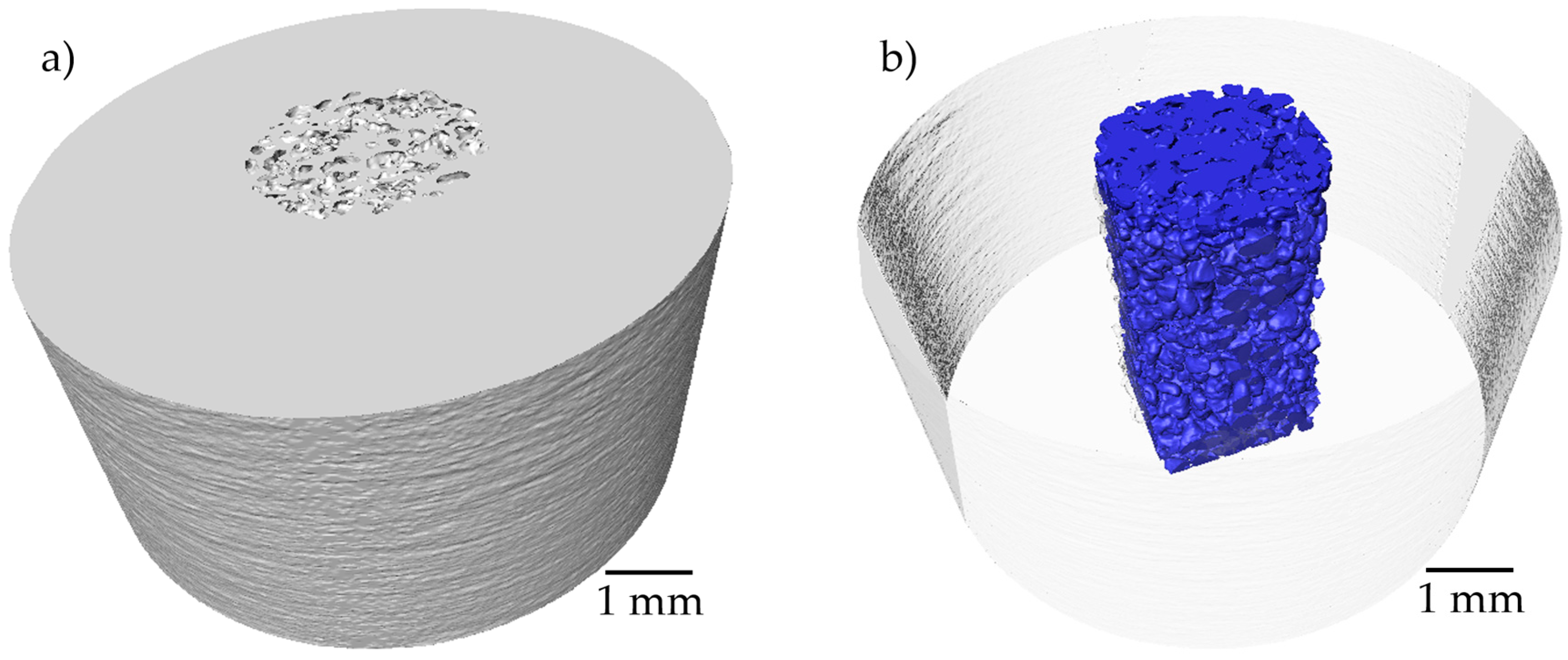
Virtual 2D slices of bilayer samples showing the distribution of large pores illustrate the interface between the porous core and the dense shell, Figure 2. Large pores are well located in the middle of the samples and two different diameters can be distinguished. Because of the voxel resolution of the 3D images; is not possible to observe the interparticle porosity remaining after sintering. Nevertheless, this analysis is more focused on the location of the large pores and, to confirm that no fissures or delamination are found at the interface. It can also be qualitative noticed that the strut size in the porous core is reduced as the pore volume increased. A 3D rendering of the bilayer samples fabricated with 30 and 50 vol.% of salts and 85/15 and 50/50 diameter ratio of the core are shown in Figure 3a-3b and 3c-3d, respectively. It can be notice that the core has a cylindrical shape that goes from the top to the bottom. Also, the connectivity of pores is illustrated by a color code that indicates if large pores are connected to each other. As it can be observed, the porosity created is fully interconnected, which is according to that found for monolithic porous samples in [12].

The pore volume fraction in the porous core in bilayer samples shows an increment with respect to the volume fraction of pore formers used, see Table 2. This is mainly because the interaction of the pore formers particles induces additional interparticle porosity. The pore size distribution of the porous core in bilayer samples was estimated from the 3D images and it is very similar no matter the quantity of pore formers used, Figure 4a. This suggests that salts particles are randomly distributed without big agglomerates that could form larger pores. A wide pore size distribution from 50 to 580 µm is found (see Table 2), which corresponds to the size of pore formers. The pore size (d₅₀) measured range was from 168 to 184 µm (see Table 2), which indicates that pore formers particles were surrounded by the Ti64 particles. On the contrary, the median strut size shows a reduction as the pore volume of pore formers increases from 97 to 61 µm, see Table 2. This represents a reduction of 38 % for an increment in the pore volume of 44 % indicating a linear behavior for the strut size with respect to the pore volume fraction. The pore and strut size are lower than those obtained in scaffolds fabricated for additive manufacturing (AM), which ranged between 350 to 1400 µm for pores and 466 to 941 µm for struts depending on the AM technique used [35,36,37]. However, the pore size distribution is suitable to allow the cell adhesion and the formation of mineralization tissues that lead to the bone ingrowth [38,39,40].

Figure 2. 2D virtual slices of bilayer samples, a) and b) porous core 30% of pore formers and c) and d) porous core 50% of pore formers.

Figure 2. 2D virtual slices of bilayer samples, a) and b) porous core 30% of pore formers and c) and d) porous core 50% of pore formers.

Figure 3. Rendering 3D of bilayer samples and simulated flow paths in the porous core; a), b) and e) porous core 30% of pore formers and c), d) and f) porous core 50% of pore formers.

Figure 3. Rendering 3D of bilayer samples and simulated flow paths in the porous core; a), b) and e) porous core 30% of pore formers and c), d) and f) porous core 50% of pore formers.

Permeability was estimated from numerical simulations on the 3D microstructure issue from the porous core and the values are listed in Table 2. As expected, the permeability increases as the volume fraction does. The behavior corresponds to a cubic power law with respect to the pore volume fraction as it is shown in Figure 4b. This is consistent with different models proposed to estimate the permeability based on the Kozeny-Carman model [41,42]. It can also be noted from the flow lines a more tortuous path for the samples with 30 vol.% of pore formers in comparison to the ones with 50 vol.% of pore formers, Figure 3e and 3f. This confirms the reduction in the tortuosity measured from the 3D images and listed in Table 2. The permeability values also are in the range of that reported for human bones. For example, it is 3.10−11 to 5.10−10 m² for human proximal femur and 10-8 to 10-9 m² for human vertebral body, according to Nauman et al. [27].

Figure 4. Pore and strut size distributions a) and b) permeability as a function of the pore volume fraction of the porous core layer with different volume fractions of bilayer samples.

Figure 4. Pore and strut size distributions a) and b) permeability as a function of the pore volume fraction of the porous core layer with different volume fractions of bilayer samples.

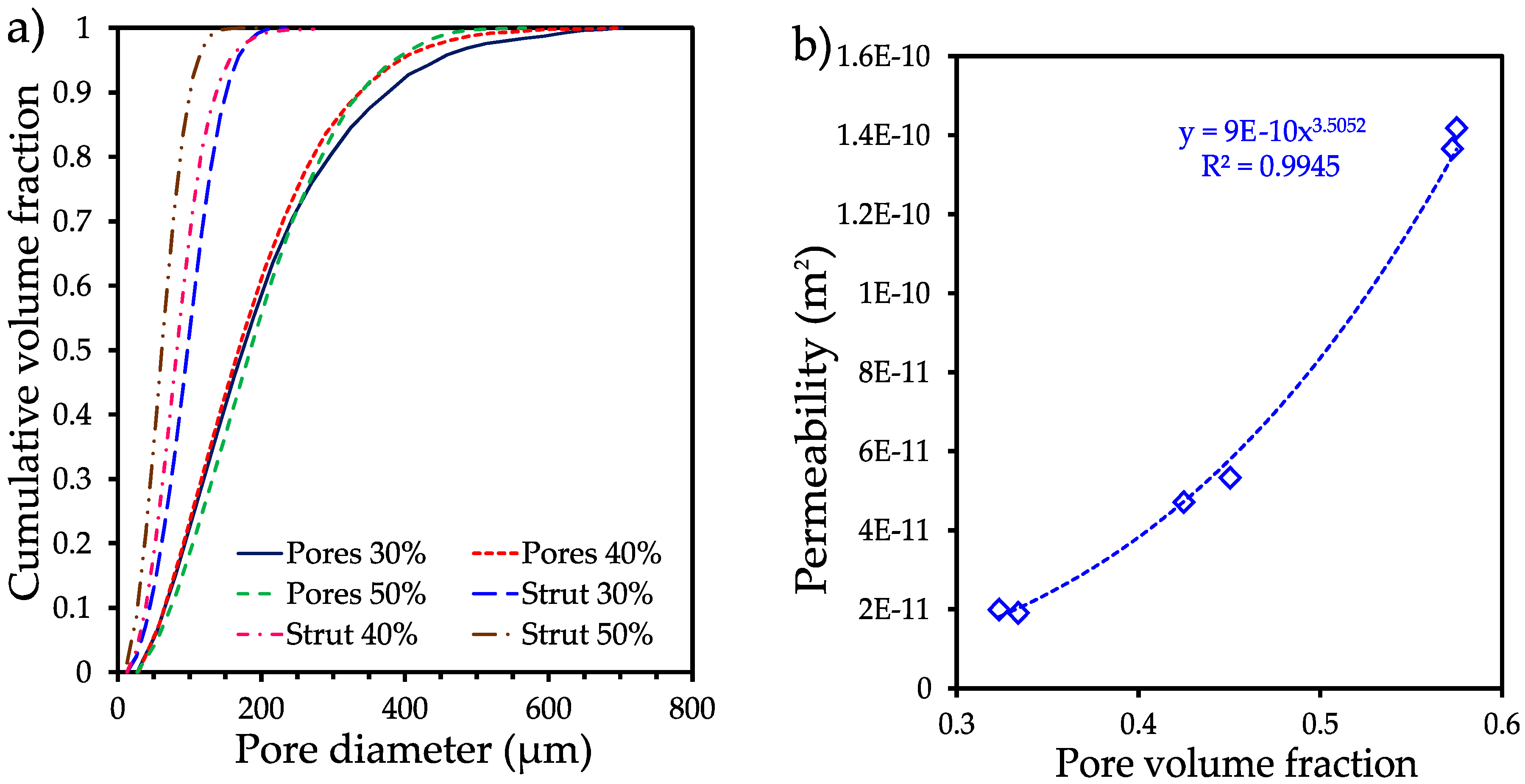
Table 2. Pore characteristics of the porous core layers fabricated with different quantities of pore formers.

Volume fraction of pore formers (%)	Pore volume fraction (%)	Median pore size (d50 µm)	Median strut size (d50 µm)	Permeability (m2 E-10)	Tortuosity
30	32.32	174.10	97.12	0.19	1.82
40	42.50	168.36	82.26	0.47	1.58
50	57.26	184.79	61.27	1.36	1.37

Table 2. Pore characteristics of the porous core layers fabricated with different quantities of pore formers.

Volume fraction of pore formers (%)	Pore volume fraction (%)	Median pore size (d50 µm)	Median strut size (d50 µm)	Permeability (m2 E-10)	Tortuosity
30	32.32	174.10	97.12	0.19	1.82
40	42.50	168.36	82.26	0.47	1.58
50	57.26	184.79	61.27	1.36	1.37

3.3. Mechanical strength analysis

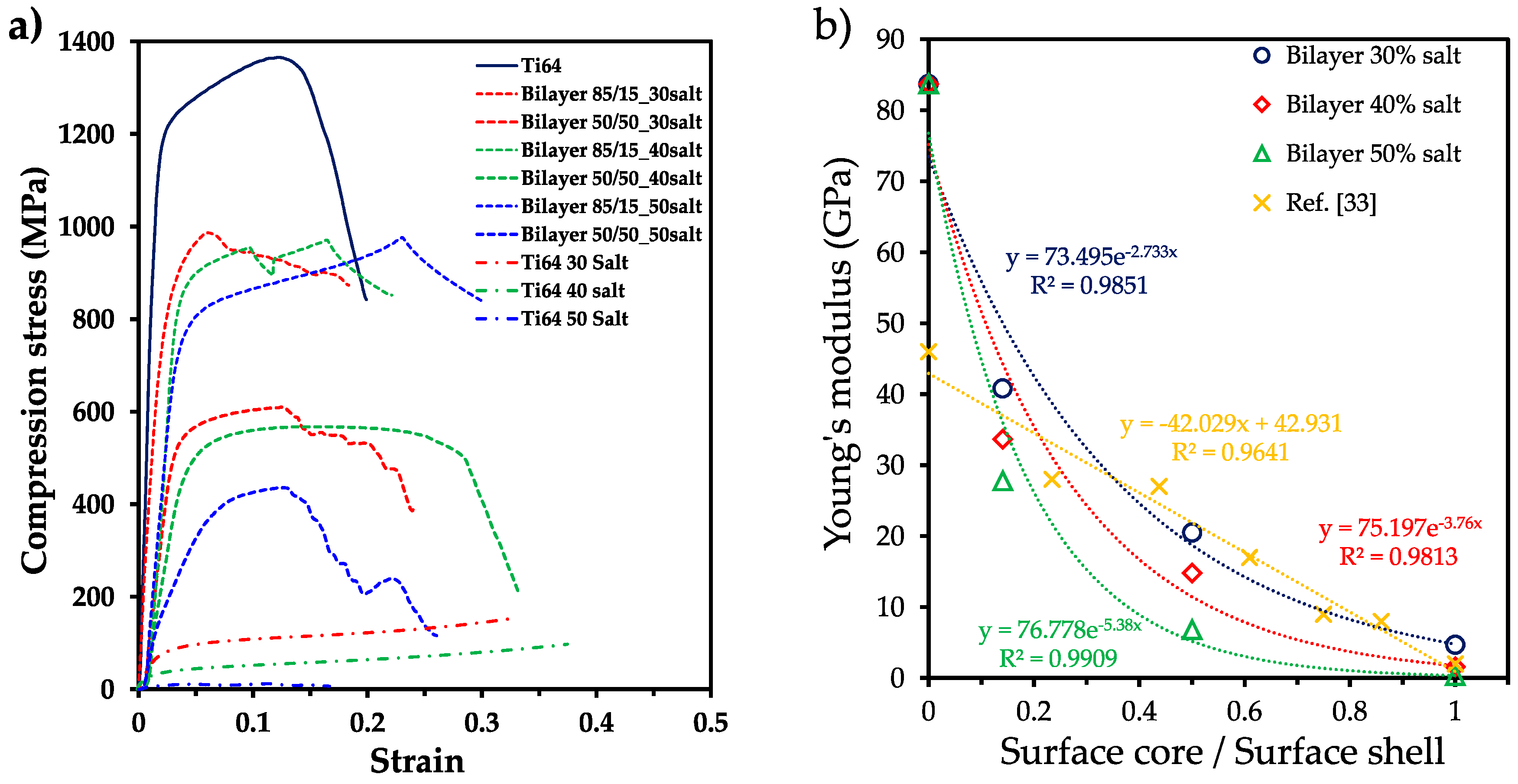
The compression behavior of bilayer samples is shown in the stress-strain curves in Figure 5a. As a reference, the monolithically samples are also plotted. As expected, the strength decreases as the pore formers and the core diameter increase. It can also be noticed that ductility is reduce because the strain of bilayers is reduced by the effect of the dense shell. The elastic modulus (E) and the yield stress (σy) were estimated from the elastic part of the curves in Figure 5a and the values are listed in Table 3. Monolithically samples show a high reduction as the pore volume increases showing the lowest value of E, 0.32 GPa and σy, 9.7 MPa. Although, the values of E deduced from the stress–strain curves should be taken with caution because they are frequently underestimated in comparison to the ones reported by ultrasonic method [33,43]. The E values of the bilayer samples also show a reduction that shows an exponential behavior as a function of the ratio between the surface of the porous core and the dense shell, Figure 5b. This behavior is different to the lineal one reported by Ahmadi and Sadrnezhaad [33], whose values are also plotted in Figure 5b as a comparison. It can be noticed that lower values were obtained in this work for similar porous core diameter, which is due to the quantity of pores generated by the pore formers. The E value was calculated using the rule of mixture, as it was done above for the density, with the aim to understand the behavior of the samples under compression. The rule of mixture can be re-written as follows:

$$E_b=f_c{E}_c+f_s{E}_s$$

(2)

In where, the Eb, Ec and Es means the elastic modulus of the bilayer, core and shell samples, respectively. Ec and Es will be assumed to be the E of the monolayer samples obtained at the same fabrication conditions of the bilayer samples. And fc and fs mean the volume fraction of the core and shell samples, respectively. The ER-M values are higher than those measured from the stress-strain curves, see Table 3. This is consistent with the values of the relative density estimated from the rule of mixtures, however the ER-M/E the ratio is larger than that obtained from the density.

Figure 5. Stress-strain compression curves of bilayer samples with different ratio of porous core diameter.

Figure 5. Stress-strain compression curves of bilayer samples with different ratio of porous core diameter.

On the other hand, the σy values of bilayer samples also show a reduction as the core diameter increases, as expected. Nevertheless, the behavior is close to be linear, instead of exponential as found for E. The σy was also estimated by the rule of mixture as it was made for the E:

$${\sigma }_{yb}=f_c{\sigma }_{yc}+f_s{\sigma }_{ys}$$

(3)

In where, the σ_yb, σ_yc and σ_ys mean the yield stress of the bilayer, core and shell samples, respectively. σ_yc and σ_ys will be assumed to be the σ_y of the monolayer samples listed in Table 3. It was also found that the rule of mixture overestimates the σ_y measured, however, σ_y R-M/ σ_y the ratio is close to one. This indicates that the σ_y follows a linear trend since the rule of mixture is a linear equation. In addition, the admissible strain (σy/E), which should be as high as possible to improve the mechanical behavior of a bone implant, as suggested in [44], is also shown in Table 3. The values go from 10 E^-3 to 43 E^-3, the highest being for the Bilayer 50/50 P50. These values are in the range reported for human bones (from 0.011 for compact bone to 0.035 for trabecular vertebra [1].

Table 3. Mechanical properties of monolayer and bilayer samples.

Sample	E (GPa)	ER-M (GPa)	ER-M/E	σy (MPa)	σy R-M (MPa)	σy R-M/ σy	σy/E (10-3)
Ti6Al4V P0	83.7	--		846.5			10.11
Ti6Al4V P30	4.7	--		58			12.34
Ti6Al4V P40	1.6	--		31.3			19.56
Ti6Al4V P50	0.32	--		9.7			30.31
Bilayer 85/15 P30	40.8	72.59	1.77	643.9	735.61	1.14	15.78
Bilayer 85/15 P40	33.7	44.15	2.15	445.5	451.81	1.01	21.73
Bilayer 85/15 P50	27.8	72.15	2.14	615.5	731.86	1.18	18.26
Bilayer 50/50 P30	20.5	42.60	2.87	399.8	438.44	1.09	27.01
Bilayer 50/50 P40	14.8	71.97	2.58	608.5	728.82	1.19	21.88
Bilayer 50/50 P50	6.83	42.60	6.23	299	438.44	1.46	43.77

Table 3. Mechanical properties of monolayer and bilayer samples.

Sample	E (GPa)	ER-M (GPa)	ER-M/E	σy (MPa)	σy R-M (MPa)	σy R-M/ σy	σy/E (10-3)
Ti6Al4V P0	83.7	--		846.5			10.11
Ti6Al4V P30	4.7	--		58			12.34
Ti6Al4V P40	1.6	--		31.3			19.56
Ti6Al4V P50	0.32	--		9.7			30.31
Bilayer 85/15 P30	40.8	72.59	1.77	643.9	735.61	1.14	15.78
Bilayer 85/15 P40	33.7	44.15	2.15	445.5	451.81	1.01	21.73
Bilayer 85/15 P50	27.8	72.15	2.14	615.5	731.86	1.18	18.26
Bilayer 50/50 P30	20.5	42.60	2.87	399.8	438.44	1.09	27.01
Bilayer 50/50 P40	14.8	71.97	2.58	608.5	728.82	1.19	21.88
Bilayer 50/50 P50	6.83	42.60	6.23	299	438.44	1.46	43.77

Different models have been proposed to predict the elastic modulus of porous materials as a function of pore volume fraction [15,45,46,47]. Some of them are considering the pore shape by introducing shape factors that are generally measured from 2D postmortem images, which makes difficult to englobe the different porous materials. Cabezas et al. [12] found that the Gibson and Ashby [15] power law can accurately predict the E values by fitting the exponent of the power law to be 4 instead of the original 2 proposed, resulting in:

$$E=E_{0}D^4$$

(4)

where E₀ is the elastic modulus of the fully dense materials. Thus, the E values of monolayer and bilayer samples are depicted in Figure 6a, and it is found a good accuracy with the model to predict the E values by considering the relative density. This could suggest that stiffness on the bilayer samples is driven by the porosity in the samples. This can be confirmed from the fractured images shown in Figure 7, in where pores in the core layer are closed during the deformation process can be noted. It can also notice that the fracture shows a 45° angle, which is formed at the shell, Figure 7a and 7c, no matter the core diameter, nor the pore volume fraction.

On the contrary, the values of the σ_y for the bilayer samples does not follow the behavior estimated for the same power law proposed in [12]. These values are much higher, which suggests that σ_y is more depending on the dense shell. This could confirm that stiffness and strength in bilayer samples cannot be simply estimated by the rule of mixtures since the interaction of both layers play a role in the mechanical behavior. In where, the deformation of pores gives a more elasticity, as it can be noticed from the fractured images in Figure 7b and 7d. Meanwhile, the dense shell gives a high resistance as suggested by the fracture path in Figure 7a and 7c.

From the results obtained and discussed above, it can be said that bilayer samples with a volume ratio of core to shell of 50/50 and beyond, can be used for bone implants since their microstructure, permeability and mechanical characteristics can better mimic the human bones values.

Figure 6. a) Young’s modulus and b) yield stress as a function of the relative density.

Figure 6. a) Young’s modulus and b) yield stress as a function of the relative density.

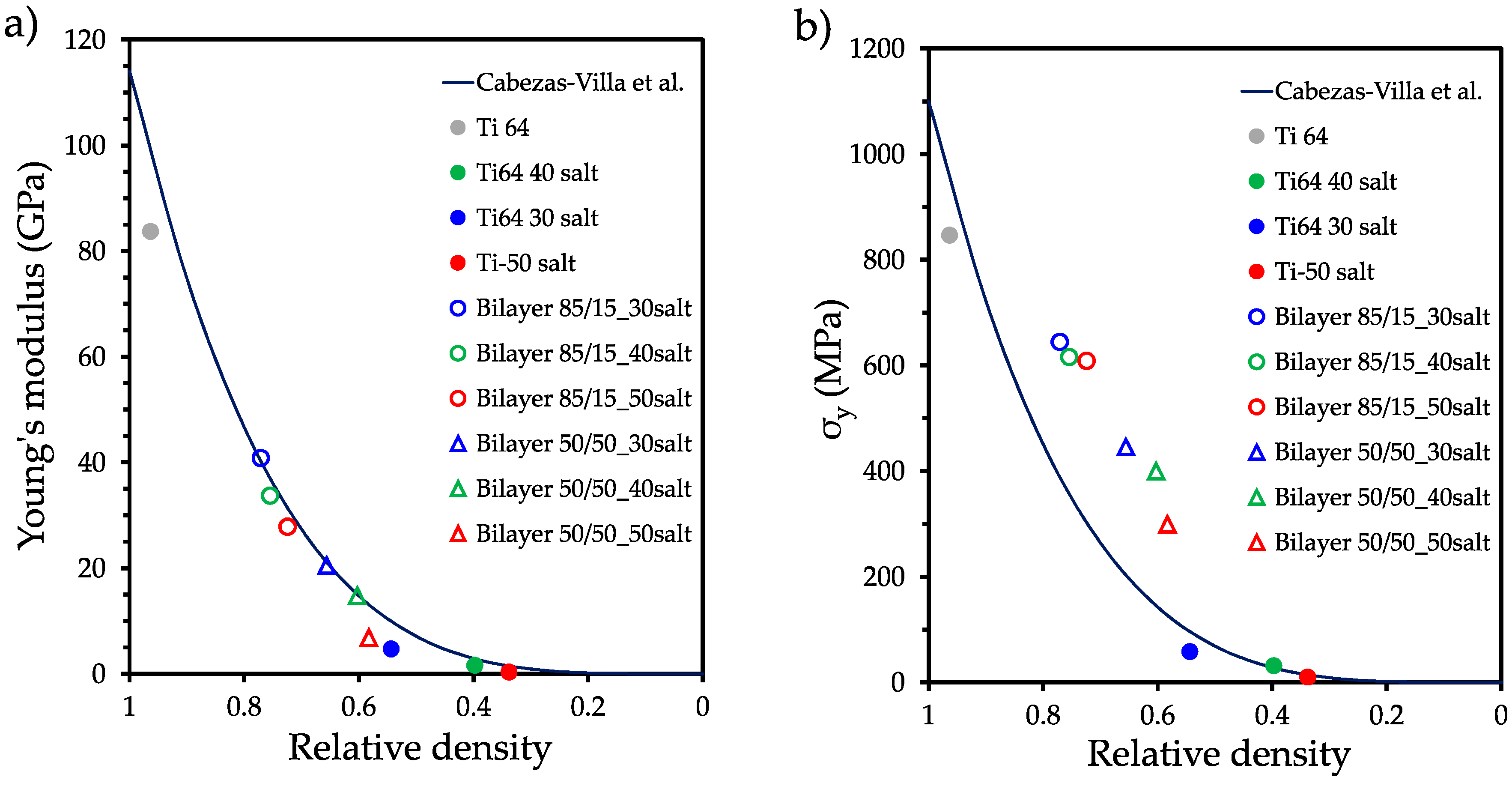
Figure 7. SEM images of the fractured samples after compression tests, a) and b) porous core 30% of pore formers and c) and d) porous core 50% of pore formers.

Figure 7. SEM images of the fractured samples after compression tests, a) and b) porous core 30% of pore formers and c) and d) porous core 50% of pore formers.

4. Conclusions

A process to fabricate materials with a porous core that can mimic the microstructure of human bones was successfully developed by pressing and sintering steps. No cracks were formed during sintering because the porous core and the dense shell are composed of the same kind of particles, which generate interparticle bonds at the interface of both layers. It is also concluded that stiffness of bilayer components is driven by the porous core, meanwhile, the presented strength resulted from the combination of both layers. This gives materials with permeability and mechanical properties as well as high admissible strain (σ_y /E) similar to that of the human bones. In order to obtain specifically values of mechanical or permeability, the quantity of pores or the porous core diameter should be adjusted for optimization according to the power laws proposed.