Preprint
Article
An Analysis of Primary Care Physician Accessibility and Medical Resource Distribution in Eastern Quebec: Utilizing an Enhanced Two-Step Floating Catchment Area (E2SFCA) Methodology
Altmetrics
Downloads
159
Views
51
Comments
0
This version is not peer-reviewed
Submitted:
27 August 2023
Posted:
29 August 2023
You are already at the latest version
Alerts
Abstract
This study evaluates the accessibility of primary care physicians (PCPs) in Eastern Quebec using an enhanced two-step floating catchment area (E2SFCA) methodology. The E2SFCA methodology considers both the population supply of PCPs and the travel time between PCPs and dissemination areas, and was found to be effective in identifying possibly underserved areas. The availability of primary care services is contingent upon the presence of adequate road infrastructure, and populations residing in areas with limited access to main road networks may experience compromised access to primary care. The study concludes that the E2SFCA methodology can facilitate the identification of areas experiencing a shortage of PCPs, and this information can be used to inform the development of regional medical workforce programs and support the establishment of rural residency initiatives.
Keywords:
Subject: Social Sciences - Geography, Planning and Development
Introduction
The provision of adequate healthcare services in the province of Québec presents a significant challenge due to its unique geographic location and expansive size. There are notable disparities in healthcare delivery within the province, with rural and remote populations facing considerable disadvantages. These individuals often must travel long distances to access healthcare services (Desmeules et al., 2006; Browne, 2010) and frequently experience shortages of healthcare professionals (Romanow, 2002). For many rural and remote populations, access to healthcare is a critical concern (McGrail and Humphreys, 2009).
Limited availability of rural healthcare services frequently impedes access to necessary care. This lack of access to services disproportionately affects aging populations in rural communities (Arpin-Simonetti, 2018), and a higher prevalence of diabetes has been observed. Additionally, rural areas exhibit elevated mortality rates for a range of pathologies (INSPQ, 2019).
The limited availability of healthcare services in remote areas contributes to the poor health of populations residing far from major centers (Starfield et al., 2005: W5-100), compounded by difficulties in accessing primary care physicians and specialists (Romanow, 2002). The addition of one family physician per 10,000 population nationally would reduce mortality by 34.6% (Starfield et al., 2005: W5-100). The shortage of healthcare providers in rural areas has been well-documented (Pong et al., 2005; Pampalon et al., 209), and the absence of clinicians is a major concern for individuals residing in these regions.
To meet the healthcare needs of a population, dedicated healthcare resources must be both available and accessible. Optimal access to healthcare can only be achieved if service offerings are sufficient and located within an acceptable proximity. Availability and proximity should be considered in tandem when assessing access to healthcare services. This concept is referred to as “spatial accessibility” and forms the foundation for a more comprehensive measure of access.
Although nearly 90% of the rural and remote population would technically have access to a family physician or CLSC (community health centre) within a 15-minute drive (INSPQ, 2009), the number of health care providers tends to decrease from urban to rural areas. This is illustrated by the variation in general practitioners (GP) utilization rates per head of population (McGraill and Humphreys, 2009). Earlier research observations posit that patients who grapple with geographic obstacles to primary care may be hospitalized more frequently (Gao et al., 2021), particularly in the instance of patients living in clinically underserved zones.
The literature has extensively documented the disparity in healthcare access between urban and rural populations. A preponderance of research indicates that rural areas generally have limited access to healthcare services (Laditka et al., 2009; McGrail and Humphreys, 2009). However, there is a paucity of studies investigating the impact of geographic remoteness on healthcare access. For example, Hausdorf et al. (2008) observed that residents of remote areas reported lower levels of satisfaction with their access to healthcare. Additionally, Laditka et al. (2009) found that hospitalization rates increased with greater degrees of rurality.
While the majority of research on healthcare accessibility has focused on urban regions (Fone et al., 2006; HQO, 2007; Luo & Qi, 2009), several studies have evaluated accessibility in rural areas (Farrington and Farrington, 2005; Arcury et al. 2006; Smith et al. 2008; Laditka et al. 2009; Jankowski & Brown 2014; McGrail & Humphreys 2009, 2014). One issue that has received limited attention is the variation between urban and rural contexts, which might be of importance, considering that 59,4%% of the population in our study area is considered rural (SRQ, 2018), 2018). Salze et al (2011) conducted a study in France that highlighted the significance of rurality in reducing access. Furthermore, numerous studies have corroborated the association between rural residency and reduced access to and utilization of healthcare services (Hicks, 1991; Farrington and Farrington, 2005; Hausdorf et al., 2008; Al-Taiar et al., 2010).
In Quebec province, the government has implemented programs to mitigate the difficulties rural populations face in accessing healthcare services, albeit with limited success. These programs continue to utilize administrative boundaries at the regional or local level, exacerbating the issue of access by obscuring underserved rural areas (Mcgrail, 2012). The majority of these programs focus on providing primary care services, as they serve as the primary entry point into the healthcare system for most individuals seeking care. Despite these efforts, the number of emergency room visits appears to substantiate the scarcity of available family physicians (VGQ, 2020), with 71% of emergency room visits in 2019 being related to non-urgent consultations. However, without an advanced tool for measuring access, it is difficult to accurately assess the impact of these programs and quantify their effectiveness.
To address this issue, we will employ an advanced access measurement method capable of identifying underserved areas while circumventing the limitations inherent in traditional access measures based on crude administrative boundaries. Specifically, we will compare the population-to-provider ratio using administrative boundaries to the E2SFCA in order to investigate healthcare access in the eastern region of Quebec province. We will first examine the rationale behind gravity-based access measurement methods before delving into a detailed discussion of the method employed in this research, the characteristics of our study area, and the results obtained when utilizing a more sophisticated method in comparison to the traditional administrative approach based on fixed population-to-provider ratios within administrative areas.
Literature overview
According to the framework proposed by Joseph and Phillips (1984), measures of potential access can be categorized into two distinct approaches: regional availability and regional accessibility. The regional availability approach, commonly referred to as the provider-to-population ratio (Brabyn and Barnett 2004; Rosenthal, Zaslavsky, and Newhouse 2005), assesses the potential for access within rigid administrative units and has been extensively employed in government initiatives and academic literature to identify areas with shortages of healthcare providers (Guagliardo et al. 2004). In addition to being relatively straightforward to interpret, population-provider ratios offer a simple analysis of spatial access values. However, their utility is constrained by two major assumptions. Firstly, they only account for variations within fixed geopolitical boundaries. Secondly, they are predicated on the assumption that individuals do not seek healthcare services outside of their designated administrative unit (Joseph and Phillips, 1984; Guagliardo, 2004; Luo, 2004).
The degree of internal variation increases as the level of aggregation of rational service areas (i.e., the size of the areal unit) increases, while the issue of permeability decreases. The inverse is true for lower levels of aggregation. Consequently, calculating population-provider ratios within administrative borders can significantly impact the results when working at different scales, giving rise to a well-documented source of statistical bias in geography known as the modifiable areal unit problem (MAUP). As such, research utilizing population-provider ratios has yielded inconsistent results and has been subject to the effects of the modifiable areal unit problem (MAUP) (Openshaw, 1984).
In contrast to regional availability measures, regional accessibility measures are often more challenging to compute (Joseph & Phillips, 1984). This is due in part to the complexity of the issue, as both supply and demand are spatially distributed and may overlap, and competition exists among both suppliers and consumers (Huff, 1963, 1964).
When assessing accessibility to services, it is crucial to incorporate some form of travel impedance to measure the distance between supply (i.e., physicians) and demand (i.e., population) (Brabyn and Barnett 2004; Hiscock et al. 2008; Charreire and Combier 2009). Travel impedance, expressed in terms of distance, time, or cost to the nearest service or facility from an individual’s residence or population center, is a simple, intuitive, and widely employed measure of spatial accessibility (Fortney et al. 2000; Rosero-Bixby 2004). When utilizing travel impedance to calculate access, an increase in travel distance generally corresponds to a decrease in accessibility. Travel impedance can be calculated using various distance measures, including Euclidean (i.e., straight-line) distance; Manhattan (i.e., rectangular) distance or distance along two sides of a right-angled triangle opposite the hypotenuse (Apparicio et al. 2003; Apparicio et al. 2008); the shortest travel distance along a transportation network (Ottensmann 1994); and the shortest travel time along a transportation network (Morris and Verdini. 1979). Due to the fact that Euclidean distance measures presuppose linear trajectories, their capacity to accurately represent the modes of travel utilized by individuals is limited. Consequently, their utility as a tool may be restricted.. With advancements in GIS technology, road distance and travel time have become the most commonly used measures of travel impedance.
Due to the conflicting nature of the two assumptions, utilizing population-to-provider ratios as a means of calculating spatial accessibility is considered overly simplistic (Fortney et al., 2000; Guagliardo, 2004; Luo and Wang, 2003; Pong & Pitblado, 2001). To address some of the limitations inherent in distance-based accessibility measures, gravity models were developed. These models, in conjunction with population-provider ratios and nearest service analysis, have frequently been employed to assess potential spatial accessibility to health services. In contemporary health literature, population demand is commonly represented by the geographic or population-weighted centroid of a given area (Langford & Higgs, 2006), while physician supply is determined by the actual location of services and is typically geocoded to a specific address or zip code aggregation.
In an effort to address the issues associated with regional availability measures, a variety of techniques, commonly referred to as gravity models, have been developed. These models are designed to predict the potential interaction between population location and all available service points within a reasonable distance (Guagliardo, 2004). Such models provide a measure that accounts for both proximity and availability (Joseph & Phillips, 1984). At their core, gravity models examine flows or movements between two sites, such as a patient’s residential location and a doctor’s office. As the distance between the provider and consumer increases, the number of interactions decreases, thereby reducing the attractiveness of a service and increasing the associated travel impedance. These techniques reveal greater spatial variation as they utilize finer-resolution spatial data and eliminate issues associated with rigidly defined borders. The gravity model is considered to be the most reliable method for measuring spatial access because it takes into account the decreased likelihood of access with increased distance from service sites and has been employed in other studies related to spatial access to health care.
The primary limitation of using the gravity model is the distance decay coefficient (β), which requires different values for measuring urban and rural access to PHC physicians. A high value indicates that individuals are less likely to travel far for a service, while a lower value indicates that individuals are willing to travel greater distances for a service. The latter results in lower variance of accessibility scores and thus stronger spatial smoothing (Wang 2007).
Despite being conceptually more rigorous and comprehensive, the majority of criticism directed towards the gravity model has focused on its lack of intuitive interpretation, its requirement for more data input to calculate, and its sensitivity to zone size (Joseph and Phillips 1984; Luo and Wang 2003; Guagliardo 2004; Luo and Qi 2009; Schuurman et al. 2010). Additional criticism pertains to the difficulty in selecting or empirically determining the distance-decay function (Guagliardo, 2004; Joseph & Phillips, 1984; Luo & Wang, 2003).
The floating catchment area (FCA) method employs circular buffers around census tract population centroids to compute a physician-to-population ratio based on the number of enclosed facilities. Utilizing this method, the radius of the buffer represents the catchment and reveals the distance that individuals are willing to travel to access health care services. Services located within the catchment area are considered fully available within that catchment. However, this assumption is inherently flawed. A physician within the catchment may not be fully available to serve residents within the catchment because he or she may also serve residents located nearby but outside of the catchment.
Similar to earlier iterations of the gravity model, the FCA method was criticized for only accounting for supply and neglecting the demand side of the equation. In light of its numerous limitations, the FCA method was subsequently improved upon. In 2000, Radke and Mu addressed the supply-demand issue with the development of a spatial decomposition method that was later termed the 2SFCA method by Luo and Wang (2003). Rather than producing ratios of physicians to population within a neighborhood, this method acknowledges that individuals may seek care in a neighborhood other than their own by using a buffer around medical clinics to calculate a provider-to-population ratio. In the second step, population catchments are calculated by identifying all physician services that fall within a threshold distance and summing the ratios from the first step. This ratio is considered to represent the spatial accessibility for the population location (Wang &Luo, 2005; Higgs, 2004).
Despite the variations among the numerous FCA versions, there are several characteristics that they all share. All FCA methods are enhancements of the advanced gravity model and thus belong to the category of gravity-based spatial accessibility models. They incorporate information regarding supply (i.e., health care services), demand (i.e., population), and distance, and they combine elements of both regional availability (i.e., supply-demand ratios) and regional accessibility.
The 2SFCA method, also developed by Luo and Wang (2003), is a widely recognized and utilized approach that originated from earlier versions of the FCA methods, with a specific focus on primary care in rural areas. This method has been employed in numerous recent studies to measure healthcare accessibility (Guagliardo, 2004; Wang and Luo 2005; Bagheri et al. 2006; Yang et al., 2006; Langford and Higgs, 2006; Wang, 2007; Cervigni et al., 2008 ; Wang et al., 2008; McGrail and Humphreys, 2009; Schuurman et al., 2010; Ngui and Apparicio, 2011; Wang and Roisman, 2011).
The 2SFCA method retains many of the advantages of a gravity model while also being intuitive to interpret as it generates a specific form of physician-to-population ratio (Luo and Wang, 2003). To accurately capture spatial accessibility, which encompasses both proximity and availability, the 2SFCA method employs two distinct elements in its calculation: the location of primary care services and the population as well as the number of services and population size at each location. Distance impedance is treated as a dichotomous measure in the 2SFCA method; any distance within a threshold is considered equally accessible while any distance beyond the threshold is considered equally inaccessible. The first step of the 2SFCA method involves determining the population that falls within the catchment area of each service provider (i.e., the potential population size being “served”). The second step involves allocating services to the population by identifying the services that fall within the catchment area of each population radius. The calculation of both steps produces a familiar population-to-provider ratio.
The 2SFCA method employs floating catchment areas (windows) rather than fixed boundaries. The size of the window is determined by the maximum travel impedance, with all services contained within considered accessible. A notable characteristic of the 2SFCA method is that, irrespective of the threshold value selected, the sum of the weighted mean values of GP ratios is equivalent to the supply and demand ratio in the larger study area.
Despite its widespread use, the 2SFCA method has several limitations (Luo and Wang, 2003). For instance, it does not account for distance decay within catchments and relies on fixed catchment sizes for all physician (i.e., supply) and population (i.e., demand) locations (McGrail & Humphreys, 2009). Distance decay is assumed to be negligible within a catchment, which may not hold true in large geographical regions with widely dispersed populations and extensive catchments. This effect is particularly pronounced in rural areas. Catchment sizes for both supply and demand are not differentiated between densely populated metropolitan areas and sparsely populated rural or remote areas. The results of the 2SFCA method are highly sensitive to the size of the unit of analysis (i.e., census tract). Another significant limitation is the assumption that all residents of a catchment area utilize services equally, regardless of population characteristics. However, recent demographic studies have shown that health service utilization varies by age group, highlighting the importance of accounting for such variations when modeling access to healthcare services. The demand amount is assumed to be constant, but in reality, demand at one service site may decrease when other sites are available simultaneously. As a result, the 2SFCA method may overestimate demand for some service sites, with the overestimation effect increasing with the number of service sites in the vicinity (e.g., in urban areas with high concentrations of medical sites). Additionally, the method employs a dichotomous measure (i.e., all locations outside of the catchment have no access at all), which can lead to underestimation of accessibility in larger (i.e., rural) study areas and overestimation in smaller (i.e., urban) study areas, particularly in large or irregularly shaped study areas.
To address the limitations of the 2SFCA method, Luo and Qi (2009) developed an enhancement that incorporates a distance decay function into the floating catchments of both algorithmic steps. The original 2SFCA method was constrained by the assumption of equal access within catchments and the assumption that locations outside of the catchment have no access. To overcome these limitations, the authors proposed an update to the 2SFCA method that included a distance-decay parameter. By assigning weights to steps one and two within the 2SFCA method, the model was able to address the issues previously identified in the health service literature. Each catchment is divided into multiple sub-catchments, with varying weights defined by a weight function that can be adjusted depending on the type or importance of a service. This approach acknowledges that services closer to the census tract centroid are more accessible. Furthermore, the magnitude of the Gaussian weights used in analysis can be varied according to research context or service type (i.e., primary care, specialized care, etc.).
The distance decay function measures the relationship between service usage and distance, assuming that other factors influencing service usage remain constant. Health care service utilization tends to decrease with increasing distance from a service provider (Joseph and Phillips, 1984), similar to other forms of spatial interaction. Estimating the β parameter in the distance decay function is crucial as it specifies the impedance to travel created by distance or the willingness of individuals to travel between zones. Omitting this parameter is equivalent to assuming that distance (i.e., time) is a negligible barrier within a catchment. While many studies employ exponential or power functions with arbitrary values depending on the type of area (Luo and Whippo, 2012; Luo and Wang, 2003; Schuurman et al., 2010), fewer attempt to identify the optimal function type and value by fitting the function to utilization data (Skov-Petersen, 2001; de Vries et al., 2004). However, such data are often unavailable, leading researchers to use arbitrarily determined impedance coefficients when calculating potential spatial access to medical services.
Distance decay may be implemented using a discrete stepped model approach (e.g., Luo and Qi, 2009; Wan et al., 2012) or a continuous mathematical function (Langford et al., 2012). However, in either case, the question arises as to the precise nature of the distance-decay function that should be adopted (McGrail and Humphreys, 2009). Wang defined six different distance-decay functions, with the crude 2SFCA method characterized by its use of a binary discrete function that exhibits no decay within a catchment and complete decay outside of a catchment. Kwan (1998) identified the three most common forms as the inverse-power function, Gaussian function, and the the negative exponential function (Figure 1).
Langford et al. (2012) also noted two other commonly used distance decay weightings: linear decay and Butterworth filter. There is limited evidence to support the selection of one decay function over another, which can be problematic as accessibility (Luo and Wang 2003; Wan et al. 2012). Efforts are ongoing to identify the most appropriate parameters for a distance decay function that can accurately capture changes in travel behavior across different urban and rural settings.
The Enhanced Two-Step Floating Catchment Area (E2SFCA) method offers several advantages over the original 2SFCA method. By employing multiple distance decay weights in place of the dichotomous 0 and 1 values used in the 2SFCA method, the E2SFCA method is able to differentiate accessibility within catchments and is more closely aligned with the gravity model. The E2SFCA method treats more distant providers as less accessible through the use of distance decay coefficients and measures distance in travel time through the actual road network. As a result, the E2SFCA method is now widely regarded as the gold standard of FCA methods.
Method
Measures of accessibility register the range individuals must surmount to access the resource, while measures of availability evaluate the level or bulk of services attainable, frequently in relation to the size of people that must be accommodated (Bryant et Delamater, 2019). Provider-to-population ratio (Kindig et al., 1992; Brabyn and Barnett 2004; Rosenthal et al., 2005), measures the potential for access within strict administrative units and has been widely utilized in government initiatives and available literature for identifying health shortage areas (Guagliardo 2004). Policymakers frequently interpret scarcity areas by determining PPR per physician zone, for the straightforward motive that it is an easy calculation and gives a handily intelligible figure of accessibility (Dewulf et al., 2013). Thus, the need for healthcare is often established by basic population counts per administrative area, excluding the curable morbidity as the more suitable proxy (Bauer et al., 2020). Besides being relatively easy to interpret, population-provider ratios provide a straightforward analysis of spatial access values but are limited in their use by two major assumptions. First, they only account for variations within strict administrative boundaries. Second, they are limited by the assumption that individuals do not seek services outside of their administrative unit (Joseph and Phillips, 1984; Guagliardo, 2004; Luo, 2004).
In response to those problems, a range of techniques, often referred to as gravity models, have been developed. These models are meant to predict the potential interaction between population location and all available service points within reasonable distance (Guagliardo, 2004). Those models provide a measure that accounts for both proximity and availability (Joseph & Phillips, 1984). Most broadly, gravity models examine flows or movements between two sites, such as a patient's residential location and a doctor’s office. Physicians cohabit in a mesh of imbricated catchments, and people are unimpeded to consider healthcare where they please and from who they want (Dewulf et al., 2013) but as the distance between the provider and consumer increases, the number of interactions decreases, thus diminishing the attractiveness of a service and increasing the associated travel impedance. These techniques reveal more spatial variation as they utilize finer-resolution spatial data and remove issues of rigidly defined borders.
The E2SFCA method treats more distant providers as less accessible, through the use of distance decay coefficients, while distance is measured in travel time through the actual road network. The advantage of the enhanced two-step floating catchment area method is that distance decay weights substitute the dichotomous 0 and 1 in 2SFCA. Through such a strategy, it is accepted that services that are closer to the census tract centroid are more accessible. In addition, the magnitude of the Gaussian weights used during analyses can be varied according to research context or the nature of the service type (i.e., primary care, specialized care, etc.; Joseph and Phillips, 1984; Pirie, 1979; Millward and Spinney, 2013). Consequently, it solves the issue of not differentiating accessibility within the catchment and is theoretically more analogous to the gravity model, thus improving the finer discrimination analysis capacity of the method. As such, localized, and often hidden, over or under deserved areas can be enlightened, most particularly in rural areas.
The E2SFCA has been identified as the most sensitive method to use in the rural environment, particularly for geographic access to primary care (McGrail and Humphreys, 2009). Incidentally, results from Bauer et al. (2020) posit that FCA methods work best especially in non-emergency contexts, as time is less of the essence. In an emergency, only the closest facility will be "available" while in a non-emergency context, one might be more inclined to access another facility for other reasons (insurance coverage, past experience, etc.).
Data and methodology
In measuring access to primary care, it is essential to consider the location and size of both providers and population by calculating the proximity between them. Population data and location were obtained from the 2016 Canadian national census, using dissemination areas (DAs), which are the smallest standard geographic areas containing all census data (in our study, DAs had an average population of 496 and a size of 342km2).
Data and location for all general practitioners (GPs) were obtained from the Ministry of Health Directory and the College of Physicians data (2021), which are updated annually. To verify the accuracy of this information, every medical clinic in our study was contacted in fall 2022, with a 98% agreement rate with the official data.
The geographical scope of our study encompasses the four easternmost regions of the province of Quebec. These regions are predominantly rural in nature, with the exception of several small urban centers that serve as administrative hubs, including Saguenay, Rimouski, Gaspé, and Sept-Îles. Two small universities located within these regions offer training for select health professions; however, individuals seeking to become general practitioners must complete formal medical education in Quebec City or beyond. Externships and portions of residency programs may be completed within these regions. Nursing education is more readily accessible, with numerous small colleges situated in smaller population centers throughout Eastern Quebec.
The Côte-Nord region, encompassing a land area of 247,655 km², constitutes a significant portion of the northern shore of the Saint Lawrence River estuary. As per the 2016 Canadian Census, the region’s population amounted to 92,518 individuals, distributed among 33 municipalities. This region had the equivalent of 77 full time general practitioners to deserve the entire area, giving a ratio 0,83 GP per 1000 inhabitants, but can go as high as 1.39 and 1.37 for the Manicouagan and Minganie area. The regional economy is primarily driven by industries such as mining (predominantly iron ore), lumbering, aluminum production, and tourism. The region is home to several large mining companies, including ArcelorMittal Mines Canada and Cliffs Natural Resources. Additionally, fourteen hydroelectric dams supply Hydro-Québec with more than 10 gigawatts of power. These dams play a crucial role in meeting the energy needs of Quebec and contribute significantly to the province’s economy.
The Gaspésie-Iles-de-la-Madeleine region encompasses a land area of 20 272 km² and has a population of 92 403. To serve this region, 131 general practitioners were calculated for a ratio of 1,45 GP per 1000 inhabitants, but this ratio can go as high as 2.70 in the Avignon area. The interior of the peninsula is characterized by a rugged northward extension of the Appalachian Mountains known as the Chic-Chocs. Historically, the peninsula’s economy has been centered on industries such as fishing, agriculture, and forestry. The region includes the Gaspé Peninsula and the Îles-de-la-Madeleine archipelago and lies at the eastern extreme of southern Quebec.
The Bas-Saint-Laurent region is delineated by the Saint Lawrence River to the north, New Brunswick and Maine to the south, and the Gaspé Peninsula to the east. Spanning an area of 28,319 km², it has a population of 197,385. For this region, it is 227 general practitioners that were enumerated for a ratio of 1.15 GP per 1000 inhabitants, and up to 2.30 for the Basques region. Since the early 20th century, the region has undergone a transition towards secondary and tertiary processing of its resources and is actively seeking to establish new markets in fields such as marine technology, biotechnology, sustainable construction, and peat utilization. Comprised of eight regional county municipalities and 114 municipalities.
Saguenay–Lac-Saint-Jean is characterized by the Saguenay Fjord, which is formed by the estuary of the Saguenay River and extends through much of the region. With a land area of 98,713 km², it has a population of 275,552. 288 general practitioners for the whole region gives a ratio of 1.04 GP per 1000 inhabitants, and up to 1.34 for the Maria-Chapdelaine area, ans 1.31 for the Domaine-du-Roy area. The manufacturing, education, health and social assistance, and trade sectors collectively account for nearly half of the region’s GDP.
To measure access in those regions, we will be using the floating catchment area (FCA) method. This methods uses circular buffers around census tract population centroids to compute a physician-to-population ratio from the number of enclosed facilities (Figure 1) to anticipate the potential interaction between population location and all accessible service points within sensible distance (Guagliardo, 2004, Luo and Qi, 2009). When distance between physicians and patients grows, the number of interactions drops. The model then takes the following form:
where, A represents the sum of the spatial accessibility from population i, Sj is the number of general practitioners at location j, dij constitutes the travel time between i and j and V is the population demand defined as following:
where, Pk is population demand at location k, dkj is travel time between k and j while β is the distance decay (travel impedance) coefficient.
Through this methodology, the buffer radius can represent catchment and reveals the distance that individuals are willing to travel in order to access healthcare services on the principle of a cost-minimization behavior (Paez, 2019).
Services falling within the catchment area are considered fully available within that catchment. In light of its many limitations, the FCA method was improved upon. In 2000, Radke and Mu were able to address the supply-demand issue with the development of a spatial decomposition method that was later termed the 2SFCA method by Luo and Wang (2003).
Using the "closest facility" tool of the Network Analysis module of QGIS with the TravelTime (™) API, we determined network routes and calculated proximity within a maximum catchment size of 100 minutes between geocoded medical clinics and the population centroid of the dissemination area. Distance between 60 minutes and 120 minutes is generally accepted as the most sensible choice in a rural context (Amiri et al., 2020; Crooks and Schuurman, 2012; McGrail, 2012; Wan et al., 2012). Data for the road network were obtained from Open Streets, and travel time, instead of distance, was used by combining road length with average speed. The E2SFCA method was used on the exported data with a spreadsheet. Our beta coefficient was linear and corresponds to a 1% decrease in access per driven minute. Linear coefficient are often used in a rural context (Amiri et al., 2020; Crooks and Schuurman 2012; Higgs et al., 2017; Schuurman et al., 2010), and are easier to calculate, while maintaining the internal rationale of the beta coefficient in the E2SFCA method. Categories on our maps were made using thresholds of the lower and upper family physicians’ ratios recommended in the literature.
Indeed, ideal ratio of general practitioners to population can vary, but the most often recommended ratios are situated between 2.25 to 4.05 family physicians per 1 000 inhabitants (COGME, 1995; Cooper et al., 2002; Dill and Salsberg, 2008; GMENAC, 1981; Hicks and Glenn, 1991; Markit, 2021, ratios that can easily be converted to population per physician, as used in the E2SFCA method. This interval being quite wide, it will be used as the lower and upper limit upon which access will be deemed insufficient (under 2.25) or overprovisioned (4.05). This will create 3 categories of access that can demonstrate the level of access offered to the population. Those thresholds will be used in the E2SFCA method and the administrative map using the classic PPR.
The E2SFCA method makes possible the aggregation of those elements to create an accessibility measure. To start, a ratio of population to provider needs to be calculated for each healthcare clinic by including all population locations that are within our defined threshold (in this case, 100 minutes). There is no distance decay in the first part, as every clinic is static. Then, in step two, another population-to-provider ratio is calculated, but this time for every population centroid in each of the DA while using a distance decay of β that represents distance friction. The impedance function reflects reality as it translates the cost of traveling further as a barrier to access, putting far away clinics as less accessible to the population. Otherwise, access would be the same for everyone in the catchment area, which is not realistic. Additionally, it is imperative to maintain the level of access on the map, even in unorganized areas known as TNOs (Territoire non organisé). These regions, located in Canada, are not incorporated as municipalities or Indian reserves. The primary level of governance in these areas is typically provincial or territorial, although adjacent localities may also provide governance. Populations often traverse these regions for access or reside there permanently, despite the absence of municipal services. These areas may also become part of an existing community (McGrail & Humphreys, 2009, 2012; Luo, 2009).
Results
Utilization of the E2SFCA method necessitates two parameters: a maximum catchment time and a distance decay. In this article, we compared the population-to-provider ratio using administrative boundaries to the E2SFCA to investigate healthcare access in the Eastern part of Quebec province.
According to data from Statistics Canada in 2016, there were 14 Dissemination Areas (DAs) in which over 20% of the population had a commute time exceeding one hour to reach their workplace. Moreover, in 13 DAs, no residents had a commute time of less than 15 minutes. Given the longer commute time to work, it is not surprising that access to primary medical care may also take longer due to the vast area one must traverse to access any kind of service. Private automobiles were the predominant mode of transportation to work, accounting for 75% of all transportation in over 90% of DAs. Furthermore, in more than 77% of DAs, less than 10% of the population commuted to work by walking, and in 48% of DAs, no residents walked to their workplace.
In rural areas, the absence of public transit often means that even a 10-minute commute can represent a significant barrier to access, particularly for more vulnerable individuals without access to a car. Many studies utilizing the E2SFCA method do not apply space decay for the first 10 minutes (Amiri et al., 2020; Barrett, 2016; Crooks and Schuurman, 2012; McGrail, 2012; McGrail et Humphreys, 2009; Schuurman, Bérubé et Crooks, 2010), which may seem reasonable as 10 minutes is generally considered a short time to travel to access a healthcare clinic.
As such, we deliberately applied our distance decay from the first minute of travel time. As for the upper limit, many studies (Bauer et al., 2018; Bauer and Groneberg, 2016; Donohoe et al., 2016; Luo and Whippo, 2012; McGrail, 2012; McGrail and Humphreys, 2009; Naylor et al., 2019; Wan et al., 2012) use a 60-minute maximum catchment size, which again, might make sense as an hour seems like a long time to travel to access a general practitioner. The reality, however, is that many rural inhabitants are willing to drive farther than that to consult their physicians (Amiri et al., 2020; Barrett, 2016; Crooks and Schuurman, 2012; Schuurman et al., 2010). As such, the 100-minute upper limit in our study coupled with a distance decay of 1% per driven minute made things elegant and easier to understand and above all, simpler to interpret.
Figure 2 illustrates the access level when using the recommended general practitioner lower and upper limit threshold applied within fixed administrative boundaries as used by the Ministry of Health. Using this method, primary care access appears quite homogenous and difficulties in accessing care would seem minimal and exceptional rather than the norm.
The use of the E2SFCA method increased the sensitivity in identifying medically underserved or oversupplied rural areas, as shown in Figure 3. As expected, the southeast and most populated areas benefit from better access, while the opposite is true for less populous and more remote regions. Populations from small towns near main roads can access general physicians from nearby small towns, as evidenced by patients consulting emergency rooms or medical clinics in neighboring towns, thereby increasing their actual medical access. This is not reflected when using the traditional PPR method. Conversely, individuals living further from main roads and relying on unnumbered rural roads and dirt roads experience a significant decrease in access.
Figure 3.
Measure of geographic access to general practitioners with service delimitation and population demand.
Figure 3.
Measure of geographic access to general practitioners with service delimitation and population demand.
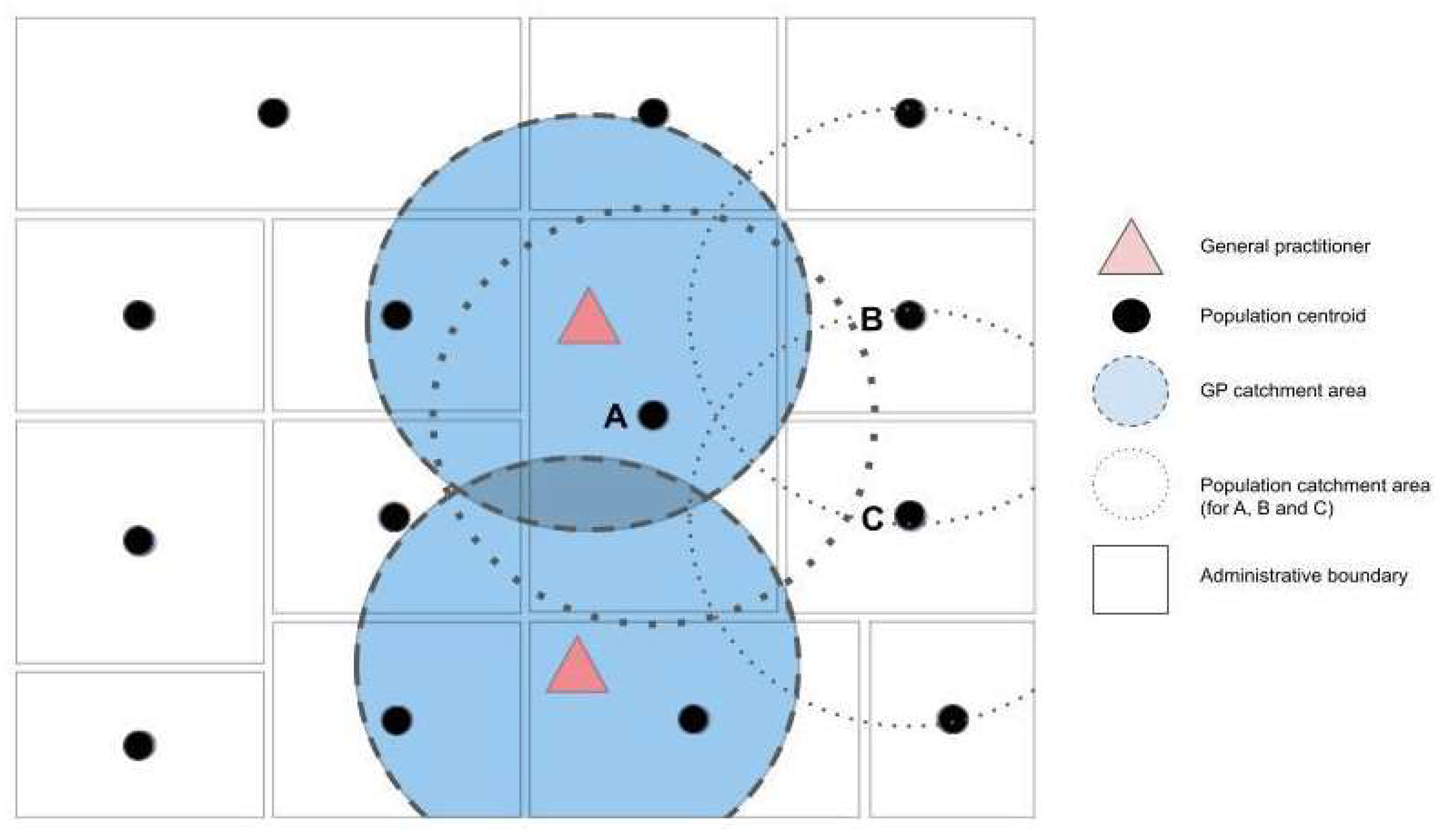
Figure 4.
Level of access to general practitioners using the provider to population ratio method.
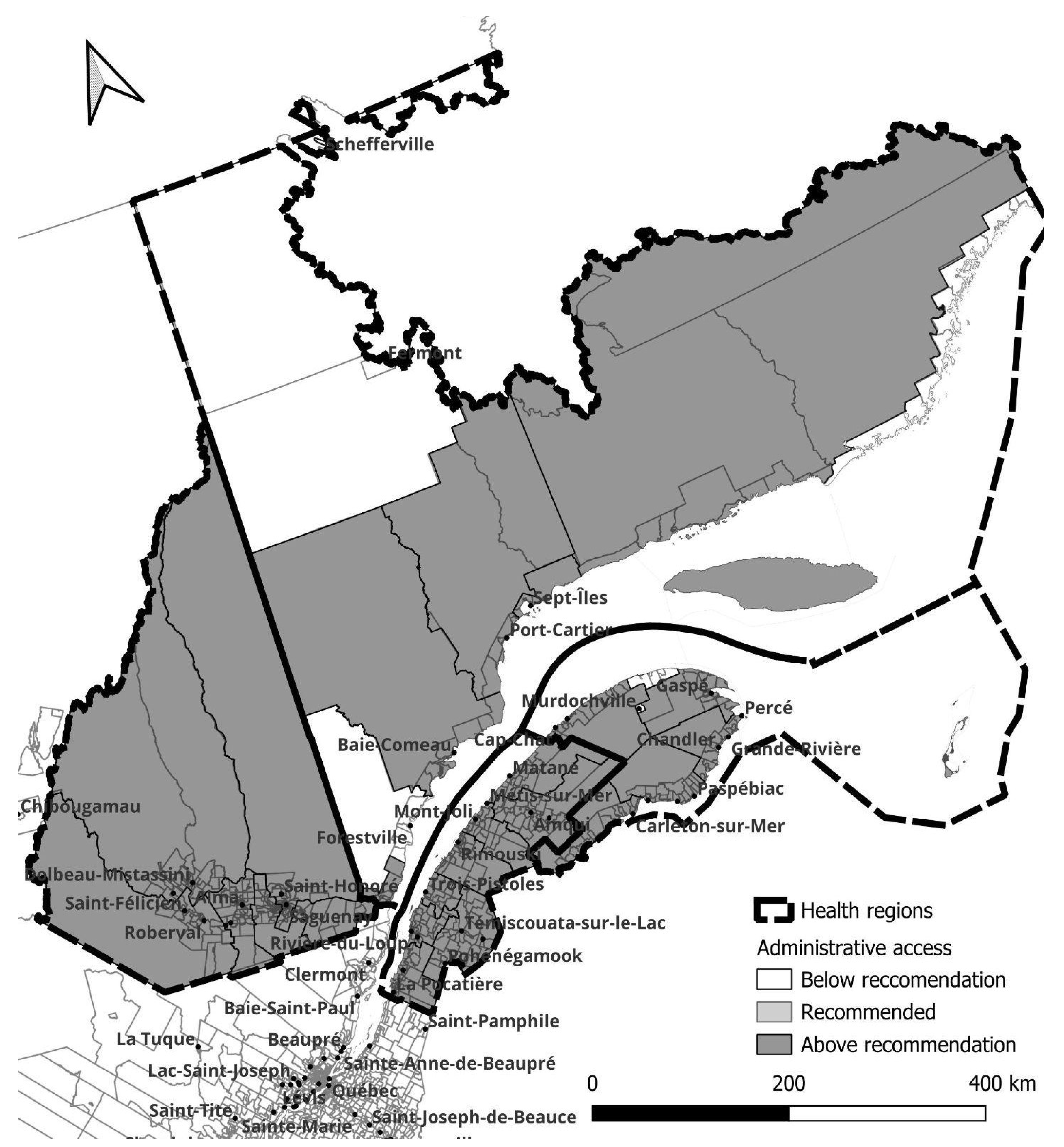
Figure 5.
Level of access to general practitioners using the enhanced two-step floating catchment area method.
Figure 5.
Level of access to general practitioners using the enhanced two-step floating catchment area method.
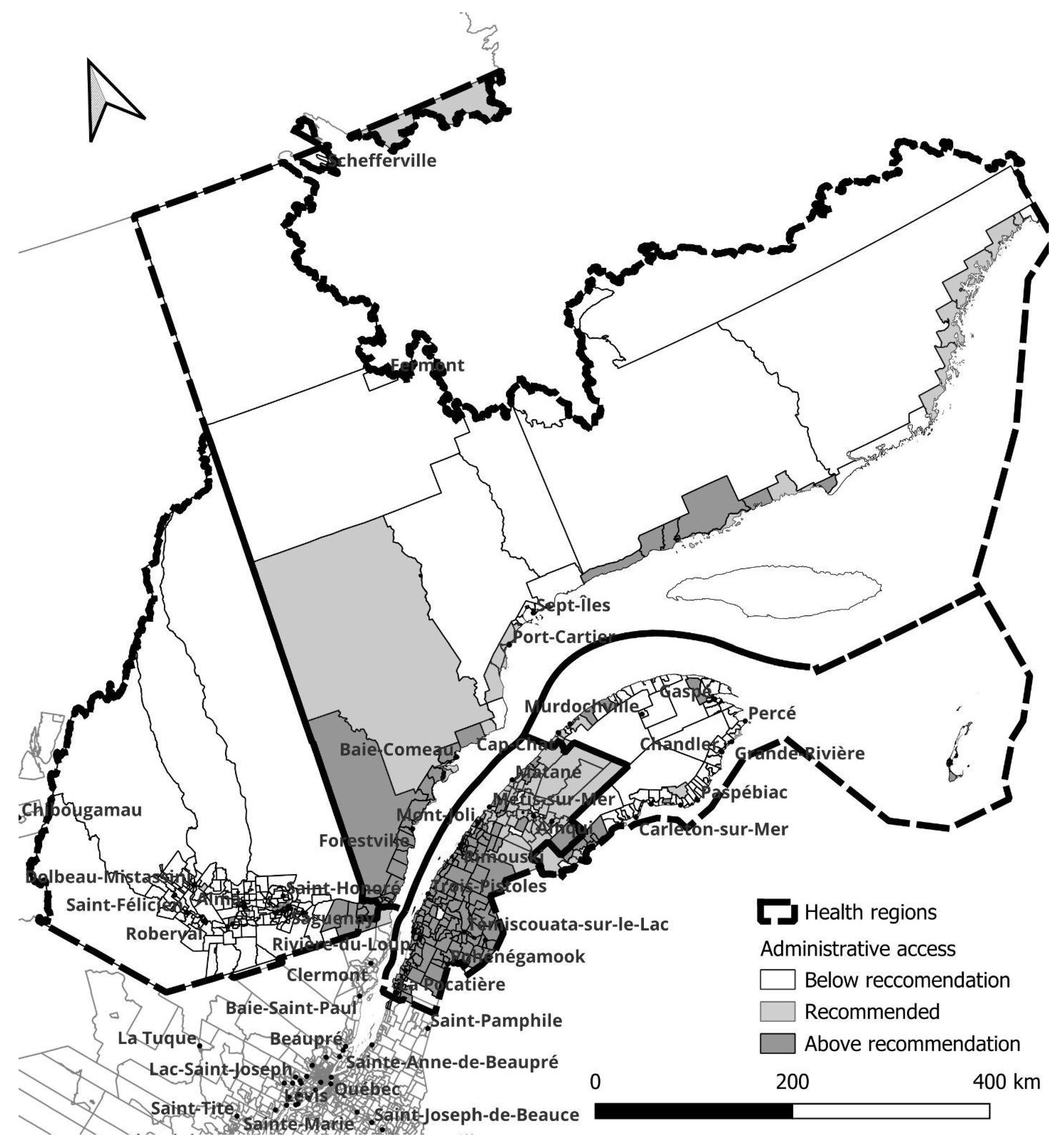
The most notable discrepancy in accessibility, when contrasting the two methodologies, is the reduction in accessibility further from the provincial capital (lower left) as demonstrated by the E2SFCA. In contrast, the conventional PPR method indicates minimal accessibility issues except for a few regions in the northernmost part of the studied area and on the north side of the Gaspesie peninsula. The E2SFCA unequivocally illustrates that a well-developed road network is crucial for optimal accessibility, as evidenced by improved accessibility in regions with highway access and diminished accessibility as the road network transitions from highways to regular roads, rural roads, and ultimately dirt roads.
Figure 6.
Level of access: PPR on the left and E2SFCA on the right.
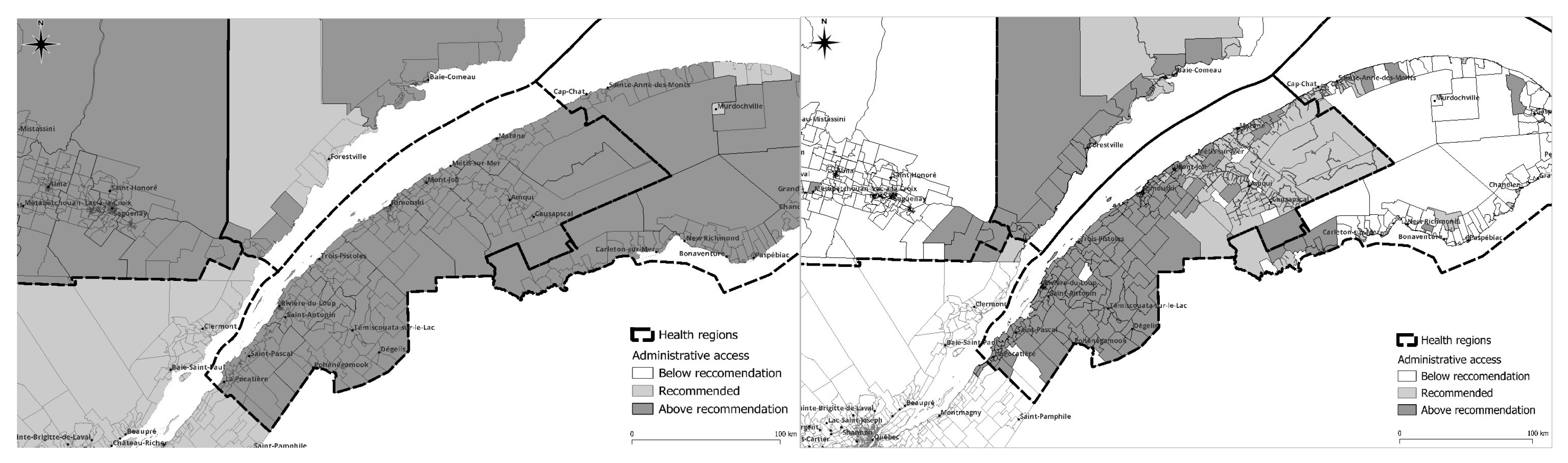
In the Bas-Saint-Laurent region, an analysis using the E2SFCA method indicates satisfactory primary care accessibility up to the end of the Transnational Highway. However, as one progresses eastward, there is a subsequent reduction in accessibility. This reduction in primary care accessibility is also evident in smaller towns that lack direct access to the highway. According to the E2SFCA method, 5.4% of the dissemination areas have low access to primary medical care. In contrast, the PPR method does not indicate any such deficiency in access. This highlights the limitations of the PPR method in accurately reflecting regional and rural real access levels.
The region of Saguenay presents a unique case within the context of our study. It is the most populous area under examination, with the majority of its inhabitants residing in the southeastern part of the Lake. As illustrated in Figure 7, when distance is incorporated into the methodology for assessing access to healthcare, it becomes apparent that the number of general practitioners may be insufficient to serve the entire population. In fact, 94.9% of the dissemination areas fall below the recommended physician-to-population ratio. This stands in contrast to the results obtained using the PPR method, which overstates average access by indicating better than recommended ratios for all dissemination areas. Additionally, it is important to note that the road network beyond the City of Saguenay, which circumnavigates the lake, does not extend significantly into the mainland. This results in a pronounced deficiency in primary care accessibility for rural areas.
Figure 7.
Level of access: PPR on the left and E2SFCA on the right.
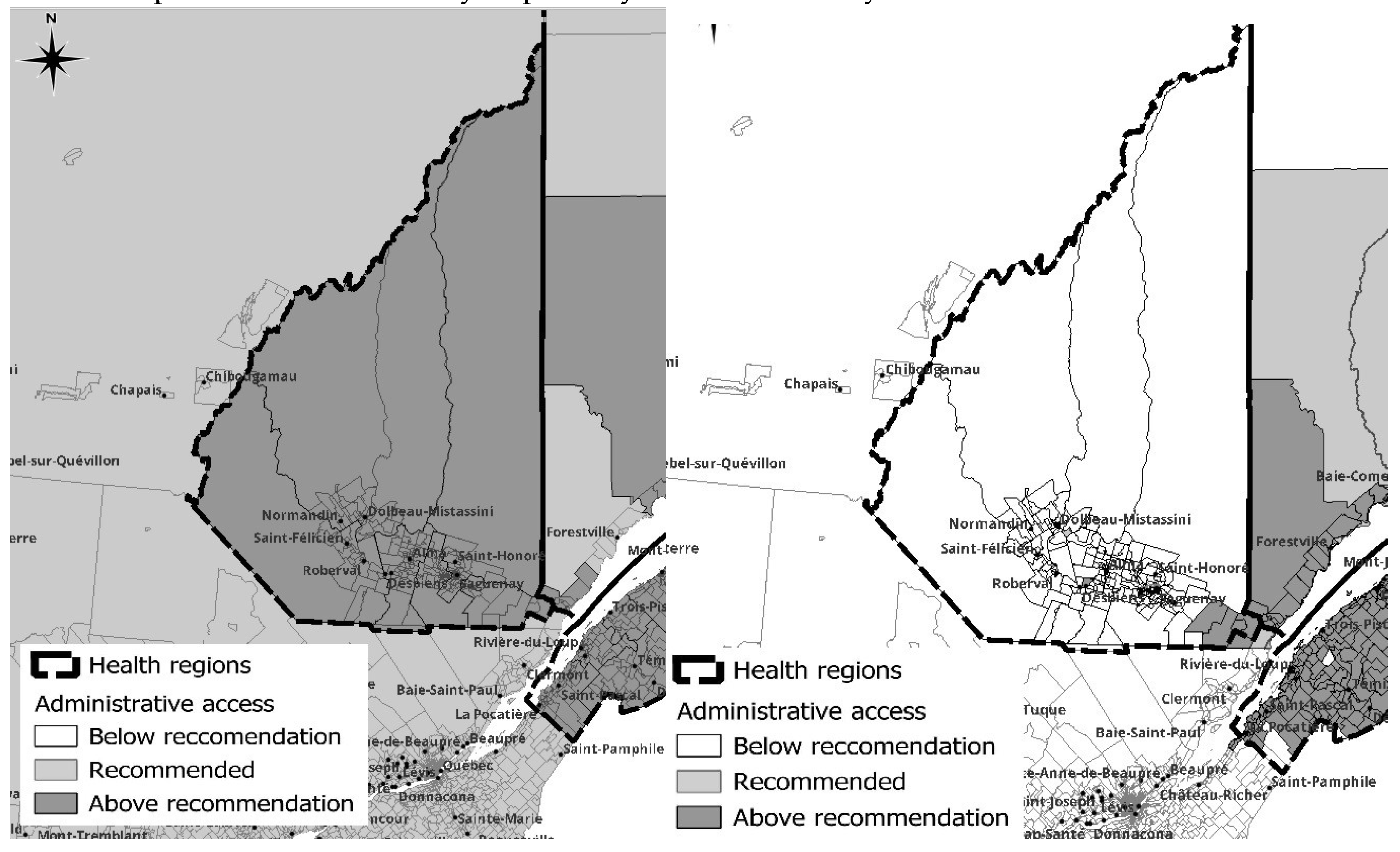
Figure 8.
Level of access: PPR on the left and E2SFCA on the right.
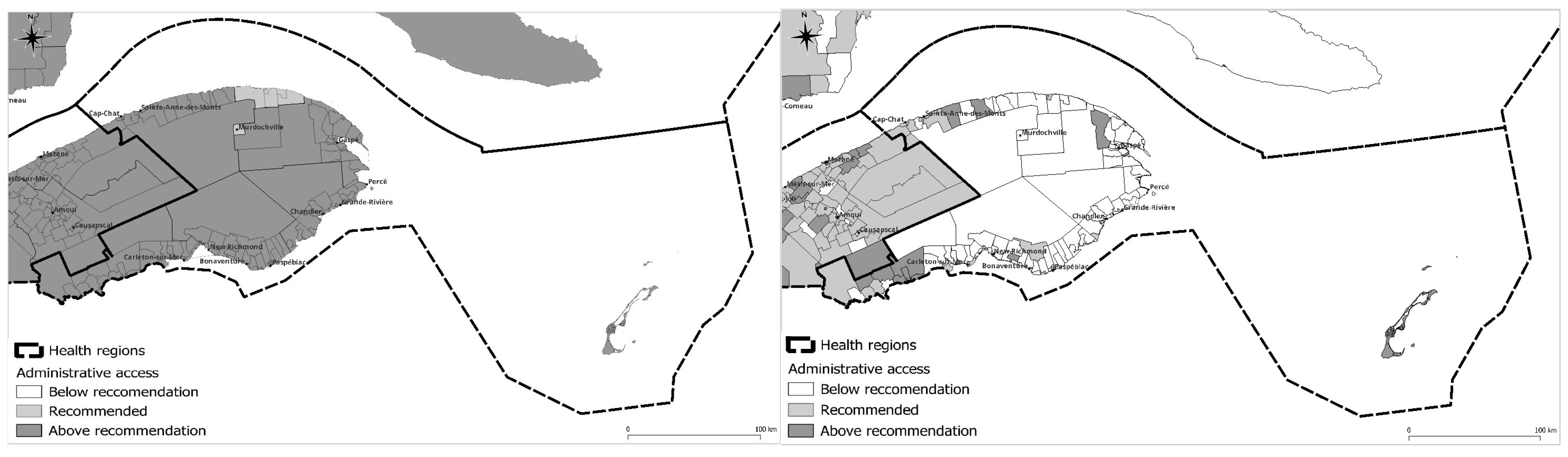
In the Gaspesie region, the incorporation of distance into the assessment of primary care accessibility reveals a marked deficiency in access. Even the easternmost Gaspé region exhibits suboptimal primary care accessibility. The only area within the region that fares marginally better is the southwestern portion, which is in proximity to the Bas-Saint-Laurent region and the province of New Brunswick. While the PPR method does not indicate any access deficit, an analysis using the E2SFCA method reveals a staggering 58.3% of all dissemination areas in the Gaspesie region with low levels of access to primary care.
Figure 9.
Level of access: PPR on the left and E2SFCA on the right.
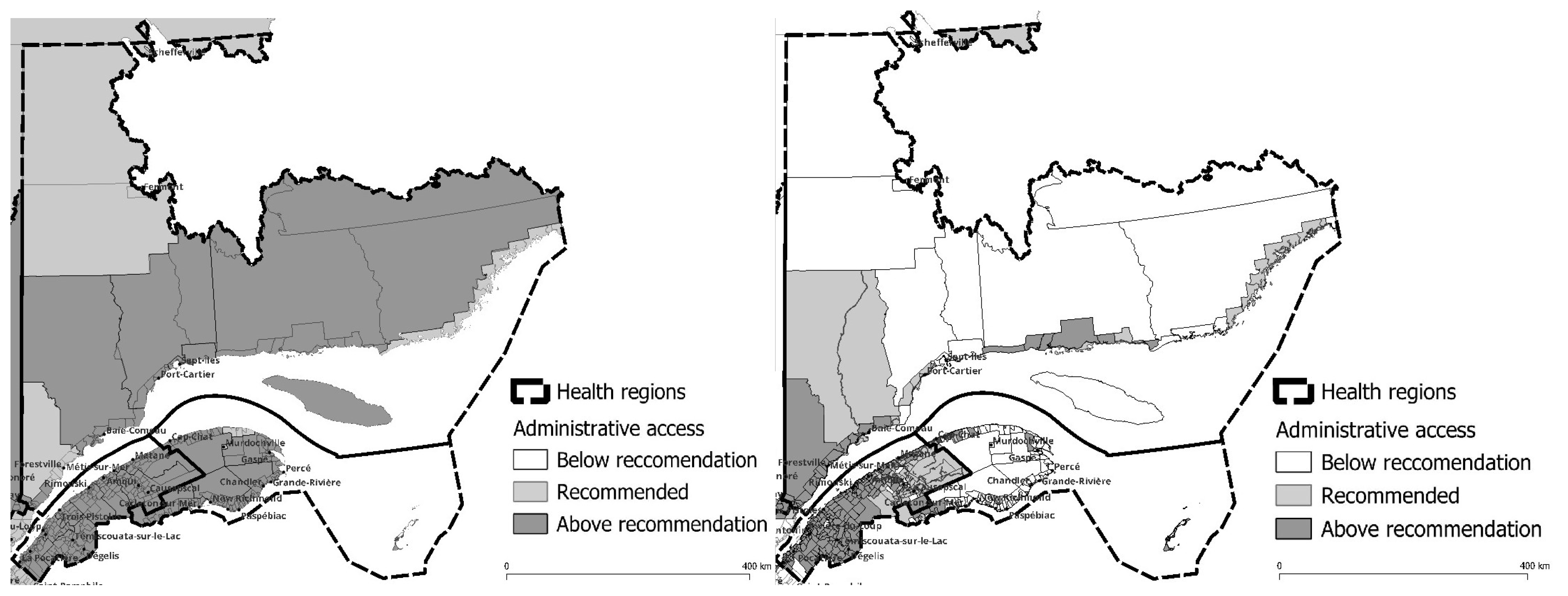
A similar pattern to that observed in the other regions is also evident in the Côte-Nord region, where diminished road access correlates with reduced primary care accessibility. The areas surrounding Baie-Comeau and Sept-Iles, which are the two largest population centers in the region, exhibit better accessibility to primary care. However, as one ventures further inland, primary care accessibility deteriorates significantly. Utilizing the E2SFCA method to assess access reveals that 28.8% of the region lacks sufficient access to primary care. This stands in stark contrast to the results obtained using the PPR method, which did not indicate any access deficit whatsoever.
The differences between the Enhanced Two-Step Floating Catchment Area (E2SFCA) and Provider-to-Population Ratio (PPR) methodologies for assessing primary care accessibility are significant and have important implications. The E2SFCA method is a spatial accessibility measure that takes into account multiple transportation modes, providing a more realistic representation of accessibility. This method is particularly effective in revealing concealed accessibility issues that are frequently correlated with actual problems in accessing primary care.
In contrast, the conventional PPR method considers everyone within an area as having equal access to primary care, regardless of factors such as distance or transportation options. This can result in the concealment of accessibility issues, particularly in remote and rural areas where distance can be a critical factor in accessing primary care. As such, the PPR method is inadequate for evaluating primary care access in these areas.
From an equity standpoint, the E2SFCA method is distinctly superior to the PPR method. By revealing concealed accessibility issues, it provides a more accurate picture of primary care access and can inform policy decisions aimed at improving equity in healthcare. In light of these considerations, it is important to carefully consider the choice of methodology when assessing primary care accessibility and to question the political implications of utilizing one approach over the other.
Discussion:
Our results clearly demonstrate the need for an improved tool to measure access in rural Canada. Current government programs aimed at improving rural health access rely on administrative boundaries at the regional or local level, which exacerbates the access problem by obscuring underserved rural areas.
Our research increased the level of detection of variations by capturing small area variations in rural areas using the smallest possible geographical scale (dissemination area), thereby enhancing sensitivity in identifying underserved primary care areas. Unlike most studies that continue to use fixed administrative areas, compounding the Modifiable Areal Unit Problem (MAUP), the E2SFCA method is better suited to identifying underserved areas. In this study, we clearly observed that the larger the areal unit, the more severe the internal variation problem becomes. Calculating PPRs with predefined administrative borders introduces a clear bias against rural access to primary care. As a result, the use of population-provider ratios should not be encouraged (Neutens, 2015) as micro-level data are essential for understanding relationships at their closest level of interaction. Relying on simple measures such as PPRs perpetuates inequity (Neutens, 2015).
The E2SFCA method has the potential to enhance the current planning tool that underpins the equitable allocation of funding for rural health. The increased sensitivity of the E2SFCA method in detecting variations in access is demonstrated in Figures 3 to 7, which compare its results with current administrative classifications for the population of Eastern Quebec. This comparison reveals that access to primary care within existing healthcare regions is not homogenous and that there is a significant discrepancy between the levels of access determined by the traditional method and those determined by the E2SFCA method across most of the territory.
This article introduces a novel method for measuring access that is more effective in evaluating shortage areas than traditional administrative methods. These advancements are associated with improvements in the 2SFCA method, including the implementation of a distance decay function and the avoidance of arbitrary catchment sizes with uniform access levels. Furthermore, the method overcomes the limitations of using administrative borders by establishing “borderless” areas of primary care access. While geographical access is crucial for primary care, it is important to note that the method assumes equal utilization of services by all residents, irrespective of population characteristics. This assumption results in a constant demand amount that does not account for variations in healthcare needs among different areas based on their socio-economic characteristics.
Measuring access is a complex undertaking, particularly when considering actual service utilization by the population and perceived barriers to healthcare such as suitability, affordability, awareness, and equity in service provision. These dimensions are more challenging to measure within small areas and often necessitate large-scale surveys. The incorporation of these indicators into the measurement process would increase its complexity and diminish the advantages of using the E2SFCA method. One potential solution is to employ a social and material deprivation index when feasible (Pampalon, 2003). Despite its limitations, the E2SFCA method provides a convenient framework for developing a refined measure of spatial access in primary healthcare.
Conclusion
The aim of this study was to evaluate the accessibility of primary care physicians (PCPs) in Eastern Quebec using an enhanced 2-step floating catchment area (E2SFCA) methodology. This approach facilitated the assessment of primary care access patterns that are not easily discernible through traditional access measures. The E2SFCA methodology took into account dissemination area-level population supply of PCPs and travel time between PCPs and dissemination area-level population, employing a linear distance (β) decay function based on distance traveled by car. This was particularly pertinent given the inadequate public transportation system in the region under study, and its absence in the most remote and vulnerable parts of the area.
The results of our study demonstrate that the E2SF-CA method is better able to identify medically underserved primary care areas than the traditional PPR method by enabling the calculation of spatial accessibility at a much finer spatial resolution. The E2SFCA approach can assist in the identification of PCP shortage areas, the development of regional medical workforce programs (plans régionaux d’effectifs médicaux), and the establishment of rural residency programs.
Our research illustrates the application of the 2SFCA method in the province of Quebec, using primary care access as the primary driver, and reveals variations in spatial access patterns that were not visible using the current administrative approach employed by the Ministry of Health.
From a methodological perspective, this study represents the first application of the E2SFCA method to measure spatial accessibility to primary care facilities in Québec outside of an urban environment. In practical terms, the study provides a fundamental understanding of inpatient care status within the studied area by revealing variations in accessibility scores across the territory and identifying areas with poor accessibility. This information is valuable for guiding policymakers and local managers. In Québec, a significant amount of public funding is allocated in the form of incentives to facilitate the recruitment of physicians in remote areas with shortages of primary care providers. Our results demonstrate that the E2SFCA method offers a superior alternative to the PPR method for allocating such resources in the context of resource scarcity. Incorporating deprivation data to improve equity of access to primary care could enhance fairness for vulnerable populations.
References
- Al-Taiar, A., Clark, A., Longenecker, J.C., Whitty, C.J., 2010. Research Physical accessibility and utilization of health services in Yemen, 8.
- Amiri, S.; Espenschied, J.R.; Roll, J.M.; Amram, O. Access to Primary Care Physicians and Mortality in Washington State: Application of a 2-Step Floating Catchment Area. J. Rural. Health 2019, 36, 292–299. [CrossRef]
- Apparicio, P.; Shearmur, R.; Brochu, M.; Dussault, G. The measure of distance in a social science policy context: Advantages and costs of using network distances in eight Canadian metropolitan areas. Journal of Geographic Information and Decision Analysis 2003, 7, 105–131. [Google Scholar]
- Apparicio, P.; Abdelmajid, M.; Riva, M.; Shearmur, R. Comparing alternative approaches to measuring the geographical accessibility of urban health services: Distance types and aggregation-error issues. Int. J. Health Geogr. 2008, 7, 7. [CrossRef]
- Arcury, T.A.; Preisser, J.S.; Gesler, W.M.; Powers, J.M. Access to Transportation and Health Care Utilization in a Rural Region. J. Rural. Health 2005, 21, 31–38. [CrossRef]
- Arpin-Simonetti, E. Développement régional: Un Québec en morceaux. Relations 2018, 798, 14–16. [Google Scholar]
- Bagheri, N., Benwell, G.L., Holt, A., 2005 Measuring spatial accessibility to primary health care 6. Actes de colloque de la Spatial Information Research Centre de la Otago University tenu en novembre 2005, 6.
- Barrett, O., 2016. Measuring Accessibility to Primary Health Care Across the Urban-rural Continuum in the Province of Alberta. [CrossRef]
- Bauer, J.; Müller, R.; Brüggmann, D.; Groneberg, D.A. Spatial Accessibility of Primary Care in England: A Cross-Sectional Study Using a Floating Catchment Area Method. Health Serv. Res. 2018, 53, 1957–1978. [CrossRef]
- Bauer, J.; Groneberg, D.A. Measuring Spatial Accessibility of Health Care Providers – Introduction of a Variable Distance Decay Function within the Floating Catchment Area (FCA) Method. PLOS ONE 2016, 11, e0159148. [CrossRef]
- Bauer, J.; Klingelhöfer, D.; Maier, W.; Schwettmann, L.; Groneberg, D.A. Prediction of hospital visits for the general inpatient care using floating catchment area methods: a reconceptualization of spatial accessibility. Int. J. Health Geogr. 2020, 19, 29. [CrossRef]
- Brabyn, L.; Barnett, R. Brabyn, L.; Barnett, R. Population need and geographical access to general practitioners in rural New Zealand 2004, 117, 13.
- Browne, A., 2010. Issues affecting access to health services in northern, rural and remote regions of Canada. Northern Article Series. Prince George, BC: University of Northern British Columbia.
- Bryant, J.; Delamater, P.L. Examination of spatial accessibility at micro- and macro-levels using the enhanced two-step floating catchment area (E2SFCA) method. Ann. GIS 2019, 25, 219–229. [CrossRef]
- Canadian Institute for Health Information. A profile of physicians in Canada, 2020 [infographic].
- Cervigni, F.; Suzuki, Y.; Ishii, T.; Hata, A. Spatial Accessibility to Pediatric Services. J. Community Health 2008, 33, 444–448. [CrossRef]
- Charreire, H.; Combier, E. Poor prenatal care in an urban area: A geographic analysis. Health Place 2009, 15, 412–419. [CrossRef]
- COGME, Physician Workforce Funding Recommendations for Department of Health and Human Services’ Programs, Seventh Report, 1995.
- Cooper, R.A.; Getzen, T.E.; McKee, H.J.; Laud, P.; Dill, M.J.; Pankow, S.; Erikson, C.; Shipman, S.; Nyweide, D.J.; Anthony, D.L.; et al. Economic And Demographic Trends Signal An Impending Physician Shortage. Health Aff. 2002, 21, 140–154. [CrossRef]
- Crooks, V.A.; Schuurman, N. Interpreting the results of a modified gravity model: examining access to primary health care physicians in five Canadian provinces and territories. BMC Health Serv. Res. 2012, 12, 230. [CrossRef]
- DesMeules, M., Pong, R., Lagacé, C., Heng, D., Manuel, D., Pitblado, R., Bollman, R., Guernsey, J., Kazanjian, A., Koren, I., 2006. How healthy are rural Canadians? An assessment of their health status and health determinants. Canadian Institute for Health Information.
- de Vries, J.J.; Nijkamp, P.; Rietveld, P. Exponential or Power Distance-Decay for Commuting? An Alternative Specification. Environ. Plan. A: Econ. Space 2009, 41, 461–480. [CrossRef]
- Dewulf, B.; Neutens, T.; De Weerdt, Y.; Van de Weghe, N. Accessibility to primary health care in Belgium: an evaluation of policies awarding financial assistance in shortage areas. BMC Fam. Pr. 2013, 14, 122. [CrossRef]
- Dill, M.J. and Salsberg, E.S., 2008. The complexities of physician supply and demand: projections through 2025. Association of American Medical Colleges.
- Donohoe, J.; Marshall, V.; Tan, X.; Camacho, F.T.; Anderson, R.T.; Balkrishnan, R. Spatial Access to Primary Care Providers in Appalachia. J. Prim. Care Community Health 2016, 7, 149–158.
- Farrington, J.; Farrington, C. Rural accessibility, social inclusion and social justice: towards conceptualisation. Journal of Transport geography 2005, 13, 1–12. [Google Scholar] [CrossRef]
- Fone, D.L.; Christie, S.; Lester, N. Comparison of perceived and modelled geographical access to accident and emergency departments: a cross-sectional analysis from the Caerphilly Health and Social Needs Study. Int. J. Health Geogr. 2006, 5, 16. [CrossRef]
- Fortney, J.; Rost, K.; Warren, M.J. Comparing Alternative Methods of Measuring Geographic Access to Health Services. Health Serv. Outcomes Res. Methodol. 2000, 1, 173–184. [CrossRef]
- Gao, F.; Languille, C.; Karzazi, K.; Guhl, M.; Boukebous, B.; Deguen, S. Efficiency of fine scale and spatial regression in modelling associations between healthcare service spatial accessibility and their utilization. Int. J. Health Geogr. 2021, 20, 22. [CrossRef]
- 1981.
- Guagliardo, M.F. Spatial accessibility of primary care: Concepts, methods and challenges. Int. J. Health Geogr. 2004, 13. [CrossRef]
- Hausdorf, K.; Rogers, C.; Whiteman, D.; Newman, B.; Coxeter, P.; Youl, P.; Aitken, J. Rating access to health care: Are there differences according to geographical region?. Aust. New Zealand J. Public Health 2008, 32, 246–249. [CrossRef]
- Health Quality Ontario, 2016. Interventions to Improve Access to Primary Care for People Who Are Homeless: A Systematic Review, 2016. . Ont Health Technol Assess Ser 16, 1–50.
- Hicks, L.L.; Glenn, J.K. Rural Populations and Rural Physicians: Estimates of Critical Mass Ratios, by Specialty. J. Rural. Health 1991, 7, 357–371. [CrossRef]
- Higgs, G.; Zahnow, R.; Corcoran, J.; Langford, M.; Fry, R. Modelling spatial access to General Practitioner surgeries: Does public transport availability matter?. J. Transp. Health 2017, 6, 143–154. [CrossRef]
- Higgs, G.; Langford, M.; Jarvis, P.; Page, N.; Richards, J.; Fry, R. Using Geographic Information Systems to investigate variations in accessibility to ‘extended hours’ primary healthcare provision. Health Soc. Care Community 2018, 27, 1074–1084. [CrossRef]
- Hiscock, R. Hiscock, R., Pearce, J., Blakely, T., Witten, K., 2008. Is Neighborhood Access to Health Care Provision Associated with Individual-Level Utilization and Satisfaction? Health Services Research 43, 2183–2200.
- Huff, D.L. A Probabilistic Analysis of Shopping Center Trade Areas. Land Econ. 1963, 39, 81. [CrossRef]
- Institut national de santé publique du Québec. Rapport Annuel de Gestion 2008-2009. Québec; 2009.
- Institut national de santé publique du Québec. Rapport Annuel de Gestion 2018-2019. Québec; 2019.
- Jankowski, P.; Brown, B. Health Care Accessibility Modeling: Effects of Change in Spatial Representation of Demand for Primary Health Care Services. Quaest. Geogr. 2014, 33, 39–53. [CrossRef]
- Joseph, A.E., Phillips, D.R., 1984. Accessibility and utilization: geographical perspectives on health care delivery. Harper & Row, London.
- Kindig, D.A.; Schmelzer, J.R.; Hong, W. Age distribution and turnover of physicians in nonmetropolitan counties of the United States. Health services research 1992, 27, 565. [Google Scholar] [PubMed]
- Laditka, J.N.; Laditka, S.B.; Probst, J.C. Health care access in rural areas: Evidence that hospitalization for ambulatory care-sensitive conditions in the United States may increase with the level of rurality. Health Place 2009, 15, 761–770. [CrossRef]
- Langford, M.; Higgs, G. Measuring Potential Access to Primary Healthcare Services: The Influence of Alternative Spatial Representations of Population. Prof. Geogr. 2006, 58, 294–306. [CrossRef]
- Langford, M.; Fry, R.; Higgs, G. Measuring transit system accessibility using a modified two-step floating catchment technique. Int. J. Geogr. Inf. Sci. 2012, 26, 193–214. [CrossRef]
- Luo, W. Using a GIS-based floating catchment method to assess areas with shortage of physicians. Health Place 2003, 10, 1–11. [CrossRef]
- Luo, W.; Qi, Y. An enhanced two-step floating catchment area (E2SFCA) method for measuring spatial accessibility to primary care physicians. Health Place 2009, 15, 1100–1107. [CrossRef]
- Luo, W.; Wang, F. Measures of Spatial Accessibility to Health Care in a GIS Environment: Synthesis and a Case Study in the Chicago Region. Environ. Plan. B: Plan. Des. 2003, 30, 865–884. [CrossRef]
- Luo, W.; Whippo, T. Variable catchment sizes for the two-step floating catchment area (2SFCA) method. Health Place 2012, 18, 789–795. [CrossRef]
- Markit, I., 2021. The complexities of physician supply and demand: projections from 2019 to 2034. Washington, DC: AAMC.
- McGrail, M.R. Spatial accessibility of primary health care utilising the two step floating catchment area method: an assessment of recent improvements. Int. J. Health Geogr. 2012, 11, 50. [CrossRef]
- McGrail, M.R.; Humphreys, J.S. The index of rural access: an innovative integrated approach for measuring primary care access. BMC Health Serv. Res. 2009, 9, 124. [CrossRef]
- McGrail, M.R.; Humphreys, J.S. Measuring spatial accessibility to primary health care services: Utilising dynamic catchment sizes. Appl. Geogr. 2014, 54, 182–188. [CrossRef]
- Millward, H.; Spinney, J. Urban–Rural Variation in Satisfaction with Life: Demographic, Health, and Geographic Predictors in Halifax, Canada. Appl. Res. Qual. Life 2012, 8, 279–297. [CrossRef]
- Morris, J.G.; Verdini, W.A. Minisum I p Distance Location Problems Solved via a Perturbed Problem and Weiszfeld’s Algorithm. Operations Research 1979, 27, 1180–1188. [Google Scholar] [CrossRef]
- Naylor, K.B.; Tootoo, J.; Yakusheva, O.; Shipman, S.A.; Bynum, J.P.W.; Davis, M.A. Geographic variation in spatial accessibility of U.S. healthcare providers. PLOS ONE 2019, 14, e0215016. [CrossRef]
- Neutens, T. Accessibility, equity and health care: review and research directions for transport geographers. J. Transp. Geogr. 2015, 43, 14–27. [CrossRef]
- Ngui, A.N.; Apparicio, P. Optimizing the two-step floating catchment area method for measuring spatial accessibility to medical clinics in Montreal. BMC Health Serv. Res. 2011, 11, 166. [CrossRef]
- Openshaw, S. Ecological Fallacies and the Analysis of Areal Census Data. Environ. Plan. A Econ. Space 1984, 16, 17–31. [CrossRef]
- Ottensmann, J.R. Evaluating Equity in Service Delivery in Library Branches. J. Urban Aff. 1994, 16, 109–12. [CrossRef]
- Paez, A.; Higgins, C.D.; Vivona, S.F. Demand and level of service inflation in Floating Catchment Area (FCA) methods. PLOS ONE 2019, 14, e0218773. [CrossRef]
- Pampalon, R.; Raymond, G. Indice de défavorisation matérielle et sociale: son application au secteur de la santé et du bien-être. Santé société et solidarité 2003, 2, 191–208. [Google Scholar] [CrossRef]
- Pampalon, R., Hamel, D., Gamache, P., 2009. Une comparaison de données socioéconomiques individuelles et géographiques pour la surveillance des inégalités sociales de santé au Canada. Statistique Canada.
- Pirie, G.H. Measuring Accessibility: A Review and Proposal. Environ. Plan. A: Econ. Space 1979, 11, 299–312. [CrossRef]
- Pong, R.W., Pitblado, J.R., Canadian Institute for Health Information, 2005. Geographic distribution of physicians in Canada beyond how many and where. Canadian Institute for Health Information = Institut canadien d’information sur la santé, Ottawa, Ont, 148.
- Radke, J.; Mu, L. Spatial Decompositions, Modeling and Mapping Service Regions to Predict Access to Social Programs. Ann. GIS 2000, 6, 105–112. [CrossRef]
- Reibling, N.; Ariaans, M.; Wendt, C. Worlds of Healthcare: A Healthcare System Typology of OECD Countries. Health Policy 2019, 123, 611–620. [CrossRef]
- Romanow, R.J., 2002. Commission sur l’avenir des soins de santé au Canada, Guidé par nos valeurs: l’avenir des soins de santé au Canada. Commission sur l’avenir des soins de santé au Canada, Saskatoon.
- Rosenthal, M.B.; Zaslavsky, A.; Newhouse, J.P. The Geographic Distribution of Physicians Revisited. Health Serv. Res. 2005, 40, 1931–1952. [CrossRef]
- Rosero-Bixby, L. Spatial access to health care in Costa Rica and its equity: a GIS-based study. Soc. Sci. Med. 2004, 58, 1271–1284. [CrossRef]
- Salze, P.; Banos, A.; Oppert, J.-M.; Charreire, H.; Casey, R.; Simon, C.; Chaix, B.; Badariotti, D.; Weber, C. Estimating spatial accessibility to facilities on the regional scale: an extended commuting-based interaction potential model. Int. J. Health Geogr. 2011, 10, 2. [CrossRef]
- Schuurman, N.; Bérubé, M.; Crooks, V.A. Measuring potential spatial access to primary health care physicians using a modified gravity model. 2010, 54, 29–45. [CrossRef]
- Skov-Petersen, H., 2001. Estimation of distance-decay parameters: GIS-based indicators of recreational accessibility., in: ScanGIS. pp. 237–258.
- Smith, K.B.; Humphreys, J.S.; Wilson, M.G.A. Addressing the health disadvantage of rural populations: How does epidemiological evidence inform rural health policies and research?. Aust. J. Rural. Health 2008, 16, 56–66. [CrossRef]
- Solidarité rurale du Québec. 2018. Les Milieux ruraux du Québec: portraits régionaux. 90p.
- Starfield, B. Measurement of Outcome: A Proposed Scheme. Milbank Q. 2005, 83, 11. [CrossRef]
- Vérificateur Général du Québec. Rapport Du Vérificateur Général du Québec à l’Assemblée Nationale 2020-2021. Québec; 2020.
- Wan, N.; Zou, B.; Sternberg, T. A three-step floating catchment area method for analyzing spatial access to health services. Int. J. Geogr. Inf. Sci. 2012, 26, 1073–1089. [CrossRef]
- Wang, L. Immigration, ethnicity, and accessibility to culturally diverse family physicians. Health Place 2007, 13, 656–671. [CrossRef]
- Wang, F.; Luo, W. Assessing spatial and nonspatial factors for healthcare access: towards an integrated approach to defining health professional shortage areas. Health Place 2005, 11, 131–146. [CrossRef]
- Wang, F.; McLafferty, S.; Escamilla, V.; Luo, L. Late-Stage Breast Cancer Diagnosis and Health Care Access in Illinois∗. Prof. Geogr. 2008, 60, 54–69. [CrossRef]
- Wang, L.; Roisman, D. Modeling Spatial Accessibility of Immigrants to Culturally Diverse Family Physicians. Prof. Geogr. 2011, 63, 73–91. [CrossRef]
- Wittevrongel, K., Shaw, M.L., 2020. A Prescription for Quebec’s Doctor Shortage.
- Yang, D.-H.; Goerge, R.; Mullner, R. Comparing GIS-Based Methods of Measuring Spatial Accessibility to Health Services. J. Med Syst. 2006, 30, 23–32. [CrossRef]
Figure 1.
Inverse-power function on the left, Gaussian function in the middle and negative exponential function on the right.
Figure 1.
Inverse-power function on the left, Gaussian function in the middle and negative exponential function on the right.
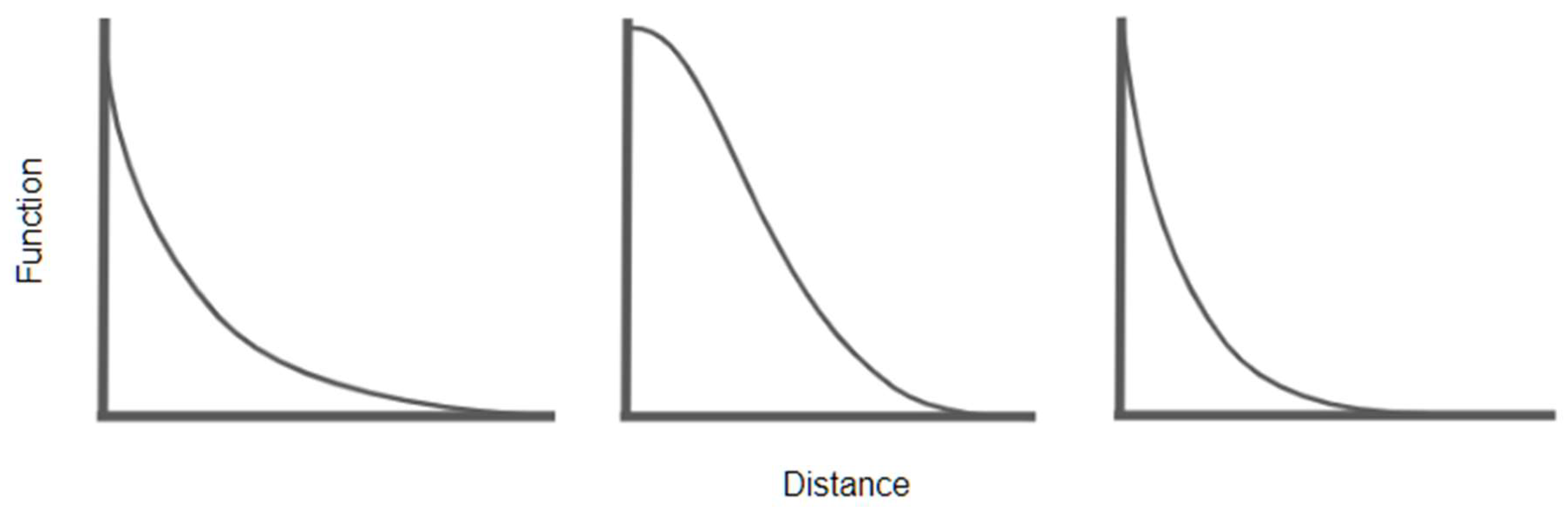
Figure 2.
Eastern Quebec map; Cote-Nord area North; Gaspesie area East; Saguenay area West and Bas St-Laurent South.
Figure 2.
Eastern Quebec map; Cote-Nord area North; Gaspesie area East; Saguenay area West and Bas St-Laurent South.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





