Preprint
Article
Enhanced Clustering and Indoor Movement Path Generation from Wi-Fi Fingerprint Data Using Bounding Boxes and Grid Cells
This version is not peer-reviewed.
Submitted:
28 August 2023
Posted:
29 August 2023
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
Recently, various applications of indoor location-based services using Wi-Fi fingerprint data have been studied. However, since fingerprint data collected at a specific location does not have continuous information between signals and correlation information between signals, path data cannot exist in principle. Therefore, most indoor positioning technologies are based on predicting the position of a stationary positioner at a specific location based on signal data collected at a specific location in the indoor space. Due to the discontinuous nature of these signals, they are unable to account for user movement. Therefore, there is a need for techniques to improve the accuracy of indoor positioning in moving situations. This paper proposes a method for enriching all data points with relevant information to obtain improved indoor positioning results and an improved technique for generating movement path data. The proposed technique generates relevant information with continuity by expressing data points as Bounding Boxes (BB) and subsequently clustering them using grid cells. Through the proposed method, we represented and expanded the indoor location data, which consists of data points, as BB. However, data points represented by BB do not have any adjacency information with each other, and as a result, it is not possible to create a movement path between neighboring BB. To solve the problem, we used clustering, a machine learning technique that categorizes data points into groups, to group BBs. This was done by constructing a YOLO (You Only Look Once) grid cell that included all BBs and clustered them into grid cells that were divided into specific regions through the suggestion phase. The clustering results align with the indoor structure of the building, indicating that the data points have been appropriately clustered. BBs inside a grid cell are contained within a moveable area and have related information. We also generated association information between neighboring grid cells through the proposal technique, and then generated path information that can be traveled between grid cells. In this paper, we use the movement path information generated from a dataset as training data for machine learning, and through this, we propose an enhanced indoor positioning technology.
Keywords:
Subject:
Computer Science and Mathematics - Computer Science1. Introduction
Recently, Wi-Fi fingerprinting has been used to build indoor positioning systems[1-8]. In this approach, a dataset from a Wi-Fi fingerprinting system uses received signal strength indication (RSSI) information from access points (APs) collected at a specific location point as data to determine location. At this time, the location is calculated by comparing the surrounding RSSI values of the location determination point with the previously collected fingerprinting data as input data. However, the RSSI value of a Wi-Fi AP contains irregularities in the noise caused by obstacles, which can lead to erroneous results. Therefore, many studies are conducted to improve the location accuracy [9].
Location determination methods are studied for Wi-Fi signals collected by the built in sensors of smart devices [10]. But the approaches in many studies suffer from the disadvantages of requiring assistive devices and complex configuration [11]. Therefore, another approach to improve location accuracy is to use RSSI along with the mobile terminal's movement path [12,13,14]. For trajectory estimation along the path of movement, approaches have been proposed that either use dead reckoning trajectories generated from a mounted inertial measurement unit (IMU) or fuse RSSI from Wi-Fi signals and position estimation from a global positioning system (GPS) [13]. There is also a study that presents a Wi-Fi RSSI dataset that includes sequentially collected trajectories[14]. Although datasets with trajectories can enhance location accuracy, their practical application in real world environments is challenging due to the substantial additional costs associated with dataset preparation and processing. Additionally, these datasets are limited by the fact that they solely represent the paths traveled during the collection process. In datasets where trajectories are not available (e.g., collected Wi-Fi fingerprints), it is difficult to estimate the mobile device's path of movement. It is possible to create a movement path by using a Recurrent Neural Network (RNN) model that can learn time series information from a machine learning algorithm [9]. RNNs extract features from high-dimensional time series input data and can be applied to classification and regression problems. RNN models are supervised learning algorithms that can take into account the continuity of the data [15,16,17]. However, RNNs do not have long-term memory and suffer from the vanishing gradient problem. To solve this problem, variants models such as LSTM (Long Short-Term Memory) and GRU (Gated Recurrent Unit) are used [18]. These networks can take into account the continuous movement of the terminal in the indoor localization to more accurately determine its current position or predict its next movement. The use of LSTMs in indoor positioning systems requires sequential RSSI inputs along the terminal's path of movement. However, the datasets provided for most indoor positioning studies do not contain sequential path information.
In this paper, we propose an enhanced Wi-Fi fingerprinting-based method for generating movement path data, building upon previous research. Visualize a Wi-Fi fingerprint dataset and use BB and grid cell to create clusters that separate indoor location areas. A grid cell is a cluster formed from a dataset. This adjacency was determined by calculating the state transition probability for the BBs within the grid cell, which was then used to generate path data. In the process, we improved upon the problems with parameterization for thresholding in our previous paper. Instead of solely relying on Wi-Fi fingerprinting information, the proposed machine learning model utilizes the movement path data generated through the proposed method. This allows the RSSI of the previous location to influence the positioning of the current location. The performance of the technique was verified through experiments, enhancing the algorithm and refining the movement path generation structure from the previous paper.
This paper is organized as follows: Chapter 2 describes BB, IoU, and grid cell. Chapter 3 describes the proposed technology, which visualizes all data points as BB used for image object detection, groups and classifies BBs into grid cells based on the results obtained by combining and expanding BBs, and calculates the association information between grid cells to generate movement path data. Chapter 4 describes the performance evaluation of the proposed localization algorithm. Finally, Chapter 5 presents the conclusions and future work of this study.
2. Materials and Methods
We describe the techniques required for the indoor localization technique proposed in this thesis. In our previous paper, there is a possibility of errors in cluster formation during the process of clustering adjacent data points, and there is a problem in calculating the distance between clusters that include data points. This can be caused by measuring the distance between clusters and using an arbitrary threshold to connect clusters that are within a certain distance to establish a path. This problem can lead to the establishment of adjacencies between data points that are not actually adjacent to each other, forming incorrect clusters and generating movement paths that have structurally untraversable configurations. To solve the problem, this paper improves the adjacency of BB by representing data points as BBs and completely removing the threshold for adjacency judgment through IoU operations. We also applied grid cells to form clusters of BBs. Below we briefly describe the BB, IoU, and grid cell used in our proposed technique.
2.1. IoU(Intersection over Union)
Computational vision is being advanced by CNNs, and various studies are being conducted to detect objects in images. The most basic element used to detect objects in an image is the BB. Object detection uses the BB for the entity and the predicted BB to predict the object in the image, and detects the entity by finding and correcting for losses. IoU is the most popular way to compensate for this loss [19]. Extensions to this technique include Generalized IoU (GIoU), Distance IoU (DIoU), and Complete IoU (CIoU), which are basically based on IoU [19,20].
Figure 1 compares the difference between IoU and GIoU presented in the GIoU paper in a situation where the values of -Norm and -Norm are the same. -Norm is the distance between the upper right point (, ) of the green box corresponding to BBGT in (a) and the upper right point (, ) in (a), and -Norm is the distance between the two boxes in (b), with (, ) as the center of the two boxes and w, h as the width and height of the boxes. (a) shows a case where two BBs have the same -Norm, but different IoU and GIoU values, and (b) shows that the same -Norm can result in different IoU and GIoU values.
In this paper, to create a path using Wi-Fi signals, all data points, which are Wi-Fi signals, are treated as images. Each point is represented as a BB, and IoU is used as a criterion for merging and extending neighboring BBs.
2.2. YOLO(You Only Look Once)
YOLO [21] is one of the deep learning algorithms for detecting objects in images. YOLO divides the image into grids, and for each grid cell, it predicts the class and BB information of the object it contains. YOLO uses relative position information within grid cells to estimate BB. This means that the coordinates of the BB are expressed as a value relative to the upper left corner of the grid cell. Because of this, YOLO predicts an offset, which is a value representing relative position information. For example, if BB is predicted to be (0.2, 0.3, 0.4, 0.5) within one grid cell, this is the location information relative to the upper left corner of that grid cell. Therefore, in order to calculate the coordinates of the bounding box within the actual image, we need to calculate the absolute coordinate values using the location information of the corresponding grid cells and the predicted offset values. By using this relative position information, YOLO is a technique for predicting the position of objects in an image. In YOLO, the Anchor Box is a box that predefines the shape and size of the BB predicted in each grid cell. Anchor boxes are used to detect objects with different sizes and proportions. The size and shape of the anchor boxes are predefined in YOLO, and these values are set differently depending on the dataset. Each grid cell can have multiple anchor boxes, which allows to detect objects of different sizes and shapes. By calculating the difference between the predicted BB and the anchor box, YOLO accurately predicts the position and size of the object. Direct location prediction in YOLOv2 [22] predicts the BB as a 5-dimensional vector in a cell according to the anchor box, constraining the BB to not deviate from the grid cell, and if the original YOLO predicted the center of the grid, v2 predicts how far it moves from the top left vertex.
In this paper, the Wi-Fi data points represented by BBs are represented by one grid cell containing all of them, and the BBs are divided into grid cells containing the minimum number of BBs to represent the clusters of BBs and calculate the correlation of each grid cell. This grid cell is called a cell in this paper.
3. Suggested techniques
The technology introduced in this paper begins by generating associative information between non-contiguous data points. The process of representing all data points as BB, calculating the IoU between BBs, combining nested BBs, and scaling the size of the BBs is repeated until the target BB size is reached. And they are represented as cells to cluster the extended BBs. In this process, all BBs are designated as a single cell, and a cell division process is carried out to generate visualization information that represents the clustering of adjacent BBs. For movement path generation, the continuity of neighboring cells is calculated to generate adjacency information to determine whether a path can be created between cells. Finally, the movement path is generated utilizing the adjacency information of the cells. This process enhances the movement path generation algorithm from our previous paper to create the entire path. Thus, the proposed technique improves on the problems associated with clustering in our prior work and provides a basis for stable path computation. The following describes each step of the proposed technique in detail.
3.1. Bounding Box
We used BB to visualize and represent the Wi-Fi fingerprint data used for the experiment as image information based on X, Y coordinates. This process is divided into initial BB setup and BB joining, and the BB joining process consists of BB expansion and merge.
3.1.1. Initial Bounding Box Setup
All data points on the coordinate plane are replaced by BBs with a size of BBi from the initial fingerprint dataset D, as specified in Table 1. This creates a BB for all data points, and the coordinate values (X, Y) of the data points are the center of the BB. The initial data D is equal to Equation 1. In this formula, n is the number of RSSI signal values, N is the number of APs, and k is the number of data contained in the dataset. Let be the x (or l) coordinate of the i-th data point, and be the y (or m) coordinate of the i-th data point.
3.1.2. Merging and expanding bounding boxes
BB merging is a two-step process. First, the merge process combines two nested BBs to consolidate them. Secondly, there is an expansion process that increases the size of an independent BB that does not overlap with other BBs, allowing it to be merged with other BBs. The ratio variable for scaling BB in this process is m_factor, let's call it . BB size is , which is the initial size of the BB. The maximum size of the BB, max_factor, is , the IoU Threshold is , the information of each BB is , is the x-axis position, is the y-axis position, is the width, is the height, and is the dataset index included in the BB. Accordingly, BB information is represented as . The initial BB setup is as shown in Equation 2 below.
Next, calculate the IoU value between the input BBs using Equation 3.
To save the status information of the merging process, we set up a BB List to store and manage the BBs created in the current stage, and checked whether the merging or expanding process was performed. At this point, if any merging or expanding process is performed in the current step, it will proceed to the next step. If all BBs are larger than max_factor, the process will terminate immediately without proceeding with the merging and expanding process of the next step. Therefore, if the size of all BBs does not yet meet the termination condition, the process of combining and enlarging BBs will be repeated for the number of initial BBs. In this iteration, the IoU value of the current BB and other BBs is calculated and the BBs that are greater than the IoU Threshold value are merged. This checks to see if the current BB is already a combined BB, and at every iteration it checks for combining or expanding information per BB. It then calculates the minimum BB size of the current BB and the other selected BB to calculate the minimum BB that contains both BBs, creating a new combined BB and adding it to the BB List. The BB List is then used to update the status information of the BBs used in the union, specifying that they are the BBs used in the union. If BBs have an IoU value that is less than the IoU Threshold required for joining, they do not have overlapping regions and can be judged to be independently located BBs. Thus, independent BBs expand their size to merge with other BBs around them. It sets the expanded BB information to the BB List and updates the status of the current BB. The expansion of a BB is done by multiplying the current size of the BB by m_factor. In our previous paper, we set a threshold in the form of a constant to prove neighboring data points [9]. If this is applied to the BB of this paper, the proximity of independent BBs can be determined using GIoU. However, when using GIoU, the same issue as using a threshold constant value arises. We solved this problem by extending the nested BBs using IoU. BBs that were not used for merging and expansion are processed in the next step. Checks for BBs that have not been merged or expanded in the current staff and saves them to the BB List. Finally, as a condition for ending the merge and expand phase, the BB List information is checked to determine whether the iteration should continue or end. The behavior for merging and expanding BBs is shown in Algorithm 1. The hyperparameter definitions used in this algorithm are tabulated in Chapter 4.
| Algorithm 1 Combination bounding box Algorithm |
|
Input: Bounding Box set , m_factor , IoU Threshold , max_factor Output: updated Bounding Box set , doRepeat doRepeat ← False; IoU ← getIoU(); ; ; Initialize ; for iter ← 1 to do if then doRepeat ← True; ; ; if then ; ; ; ; ; ; ; ; else if then ; ; ; ; ; ; end end ; end |
3.2. Cell Division
After the BBs are combined and extended, a grouping operation is required to show their proximity to each other in a clustered form. To do this, neighboring BBs are clustered into cells, and each cell lays the foundation for the generation of path information. YOLO's grid cell refers to a box that predefines the shape and size of the predicted BBs. We initially represented the entire coordinate plane of the data points as a single cell, and then divide the cell into sub-cells for clustering the BBs. In other words, we used cell for clustering BBs.
Let be a cell, and for each state j, denote the cell information by . The minimum size of the cell is called min_factor and is represented by . Let be the minimum width and the minimum height of the cell. The variable for limiting the number of BBs per direction within a cell is max_overlap_factor, letting be the number of BBs. This allows the initialization of the first cell to be and c1 to be equal to Equation 4.
Cells are used to cluster BBs because BBs have overlapping regions in neighboring cells or the IoU value between BBs is 0. In other words, if BBs are independent and not overlapping, it is difficult to generate adjacency information between BBs based on BBs alone. Therefore, we group BBs into cells and determine if they can be moved to a neighboring cell. At this time, we determined where the BB is located inside the cell (top, bottom, left, right, etc.) and expressed the adjacency to create a movement path between cells. Therefore, cells are divided based on BBs, and as a result, in regions where the initial data points are not densely located, the cell size becomes relatively large. In this case, the problem of assigning adjacency to non-adjacent BBs and generating incorrect movement paths has been resolved.
The construction of a cell below describes the process of setting up an initial cell to represent all data points represented by BBs as a single cell, and then iteratively dividing the entire cell into sub-cells consisting of adjacent BBs.
3.2.1. Initial cell Settings
We display all the BBs that have been merged and expanded as images on the coordinate plane and set up a single cell of a size that encompasses the entire BB. Unlike the checkerboard cell setup typically used by cell in YOLO, we start with a single cell and iterate through the cell, dividing it based on the BBs clustered inside the cell.
3.2.2. Dividing into Sub-cells
The input values for dividing cells are the current cell size and current BB information, followed by the minimum size of the divided cell, the number of BBs the cell contains, and finally the data points. The result of the cell partitioning process is the partitioned cell information table C. Basically, one cell is divided into 4 equal parts, and the size of the divided cell is compared with, which represents the min_factor, to check. In this case, two conditions arise: firstly, the division proceeds if the size of the divided cell is greater than , and secondly, the division stops if the size of the divided cell is smaller than and the division condition is not met. The division process for each condition is as follows:
- Dividing process: First, perform a dividing condition discovery process. Temporarily divide the cell into four parts based on the center point of the current cell. The number of BBs included in the temporarily divided area is calculated, and if the count is greater than β, which is the max_overlap_factor, the division is confirmed. At this point, the divided cell information is recorded in the table, and the division process is repeated based on the divided cell. If the number of BBs in each divided region is less than β, the division process is terminated.
- End of division: Records the size of the current cell where the division ended and the BB information contained in the current cell in the declared cell information table. Check where in the cell the BB contained in the current cell is located. This checks the location of nine regions inside the current cell, categorized as top, bottom, left, right, and each corner. Check the BBs contained in the categorized location and store and update that information in the cell information table.
The behavior of performing cell segmentation of the combined BB based on all data points is shown in Algorithm 2. The hyperparameters used in this algorithm are defined in a table in Chapter 4.
| Algorithm 2 cell Segmentation Algorithm |
|
Input: cell infomation Bounding Box set , , , Output: cell set , doDivision ← False; IoU ← getIoU(); ; Initialize ; if then halfW ← ; halfH ← ; leftL ← ; rightL ← +; topM ← +; bottomM ← ; ; BBOverlapNum ← ; for iter ← 1 to do if then doDivision ← True; break; end end end if doDivision =True then ; for iter ← 1 to do ; end else ; end |
3.3. Adjacency check
The adjacency check determines whether a route can be established to a neighboring cell based on the positions of BBs inside the cell. This means that even if cells are adjacent to each other, a route should not be created if the BBs inside the cell are not adjacent. In this case, we need the direction in which the cell is activated to find the cell's adjacency. To do this, we define the directionality as . This is a function that returns the position of the BB contained in the i-th cell region in 8 directions, as determined according to Algorithm 3.
| Algorithm 3 cell direction Algorithm |
|
Input: cell information Bounding Box set , Output: cell direction /* The order of direction information is up, down, left, right, top left, bottom right, bottom left, top right. */ ; heightOneThird ← ; widthOneThird ← ; ; for i ← 1 to do for j ← 1 to do ; if max( then ; break; end end end ; /* top left */ ; /* bottom right */ ; /* bottom left */ ; /* top right */ |
3.3.1. Calculating adjacency
Adjacency generation defines the space for movement path generation as an adjacency matrix , where each element is either 0 or 1, as shown in Equation 5.
where represents the (i, j)-th element, and the diagonal element (i=j) has a value if and only if BB exists.
The calculation order is iterated over the number of cells in the adjacency matrix, and if a cell contains a BB, it is checked whether the current cell and its neighboring cell are adjacent to each other. Algorithm 4 demonstrates the process of checking if there is a BB inside the current cell and its neighboring cells that matches the adjacent direction. If the condition is met, it is registered in the adjacency list.
| Algorithm 4 cell Adjacency Algorithm |
|
Input: cell information set Bounding Box set Output: cell adjacency matrix ; Initialize ; for i ← 1 to do ;/*algorithm 3*/ end for i ← 1 to do then ; ; ; ; ; for j ← to do ; ; ; ; direction_idx ← 0; if then direction_idx ← 1; else if then direction_idx ← 2; else if then direction_idx ← 3; else if then direction_idx ← 4; else if then direction_idx ← 5; else if then direction_idx ← 6; else if then direction_idx ← 7; else if then direction_idx ← 8; end if then ; if then ; else ; end if then ; ; end end end end end |
3.3.2. Movement Path Generation
The process of generating movement paths is iterated for each training data point. The process begins by selecting a random cell and sampling the data points within that cell. This is followed by a random walk in the neighbor matrix of the current cell. A random walk samples the data points contained in a cell at a specific location. If this cell is the last one in the path to be generated, the corresponding coordinate values (x, y) are used as the label. The algorithm for this is a refinement of Algorithm 3 from our previous paper [9], expressed as Algorithm 5. Algorithm 5 is a movement path data generation algorithm. It takes a dataset D, the state transition matrix P from the previous paper, the length of the movement path, cell information, and cell adjacency matrix A as inputs. The algorithm produces an output dataset defined as . It collects the data points contained within cells and uses the cell number of the last point. Separate datasets are created for training and testing purposes. Accordingly, the output data and each element t are defined by Equation 6.
| Algorithm 5 Movement Path Generation Algorithm[9] |
|
Input state transition matrix P , Path length path , , cell information set , cell adjacency matrix Output: ; for iter ← 1 do cellidx ← ; ; for pathiter ← 2 to path do cellidx ← ; end ; end |
4. Experiment
4.1. Experimental Environment
We analyze the performance of the proposed techniques using publicly available Wi-Fi fingerprint datasets. The dataset used is from a 2019 paper [23].
The dataset used in this paper contains RSSI, latitude, longitude, and layer information. Specifically, latitude and longitude data were calculated as datapoint locations. The training dataset includes 3852 data from the 0th floor and 3323 data from the 1st floor, with a total of 489 indoor positioning points used. The dataset also contains 443 unique APs. However, in this paper, we only used data from floor 0 because we do not consider interfloor movement. Considering only layer 0 data, the number of unique APs was found to be 173. The following hyperparameters are used to calculate the movement paths according to the proposed method.
Table 1 lists the hyperparameters required for merging BBs. Here, BBi size refers to the size of the initial BB, m_factor represents the multiplier used for expanding the BB when there are no neighboring BBs around it, and max_factor is the maximum size for combining and expanding the BB, which cannot exceed 5m. The IoU threshold is 0. Non-overlapping BBs cannot be merged with neighboring BBs, only expanded.
Table 2 presents the hyperparameters required to divide cells, where the minimum size of the divided cell is 5 meters and the maximum number of BBs contained in the cell is limited to 2. If this limit is exceeded, the cell is divided.
The information of the dataset needed for training is shown in Table 3, where the units are counts. Use Algorithm 5 to visit cells along the movement path from a random cell and collect RSSI data for each cell. The RSSI data from the visited cell is gathered by splitting it into train and test datasets. The last visited cell is numbered Y. Based on this data, we trained a model for the classification problem, utilizing a single slot on an Nvidia DGX A100 as the training environment.
Table 4 displays the range of hyperparameters we employed for training, subsequently serving as the search space for the Bayesian optimizer. The Bayesian optimizer is a method that predicts the optimal values of hyperparameters based on a prior probability distribution, which was used to find the optimal hyperparameters. The optimal hyperparameters calculated from the experiments are summarized in Table 5.
The initial data distribution before training the LSTM on the Wi-Fi fingerprint data used in the experiment is shown in Figure 2. This shows the distribution of data based on the Wi-Fi signal alone, regardless of the indoor structure.
4.2. Experimental Results
Based on the RSSI signal data, the proposed technique is applied to represent the BB, and the final BB is obtained through the process of merging and expanding the BB. The result is then divided into cells, as shown in (a) of Figure 3. The initial cell is sized to encompass all BBs placed within the floor, and the distribution of BBs across the cells demonstrates that the BBs and cells form the foundation for generating movement paths. This is (b) in Figure 3. As a result, we can observe that the BBs positioned within the entire cell represent the gathered dataset as BBs, and they are organized and divided in a manner consistent with the actual indoor structure of the floor.
When the placement of these BBs is plotted against the arrangement of the original data points, we can observe that they are correctly distributed within the cell region. This proves the appropriateness of the cell division, as the clustering of the replaced BBs is correctly represented within the cells. Therefore, our cell division technique is the basis for computing the movement path. In Figure 4, (a) shows that the division of the cells made sense when merged with the original data points.
Based on the BB's location within the cell calculated in (b) of Figure 3 and the neighboring cells where the BB exists, the cell adjacency calculation algorithm determines the adjacency. The movement path was then computed based on cells whose adjacency was confirmed through the path generation algorithm. The result is depicted in (b) of Figure 4, and we confirmed that the calculated paths match the actual paths taken in the real building.
Training was carried out by utilizing the computed movement path dataset and the specified hyperparameters. The results are shown in Table 6, which are the experimental results of the proposed method based on the 2019 dataset [23]. The experimental results express the accuracy of the computed paths. The training data and test data were trained with the LSTM model, and the accuracy of the training results is shown as the mean, deviation, maximum, and minimum values. We can see that the difference between the maximum and minimum accuracy is only 0.24% for the training data and 0.59% for the test data, and the deviation is low, so the accuracy remains constant.
5. Conclusions
In this paper, we proposed a method to generate movement path data based on data without continuity information of signals collected by Wi-Fi RSSI. We confirmed the applicability of the proposed technology as a technique to reduce the positioning error of indoor location-based services. We proposed a technique for generating movement path data by representing the data points of Wi-Fi fingerprint data as Bounding Boxes, merging and expanding BBs using IoU, and forming clusters of data points based on grid cells. Wi-Fi fingerprint data for indoor environments lack sequence information. Therefore, the input data for learning should consist of continuous datasets rather than isolated RSSI values. To solve this problem, this paper constructs BBs from indoor positioning points of Wi-Fi fingerprint data. Based on this, grid cells are created to divide the dataset area. Adjacency is calculated based on the BBs distributed within each cell, enabling the creation of movement paths. In the previous paper, the cluster size was not constant, the number of clusters was fixed, the shape of the cluster was not standardized, and data points that should not be included in the cluster were included. As a result, a problem was identified where the movement path was inaccurately generated due to clustering errors. In this paper, we have proposed improvements to address these issues. The experimental results utilizing the proposed technique demonstrate that the cluster size is a minimum of 5 meters. Consequently, the number of clusters can be adjusted flexibly based on the data point distribution. The clustering process utilizes a cell structure to prevent the inclusion of incorrect data points. As a result, it was verified that the movement path exhibited accuracy and a standardized cluster structure. Through experimentation, it was confirmed that an accurate movement path was established within an indoor positioning environment that necessitates time-series information. In addition, we were able to enhance the reliability of the adjacency calculation by addressing the issue of establishing connections between unrelated data points, which arose from the use of an arbitrary threshold in calculating data point adjacencies. And as a result of verifying the similarity between the Wi-Fi fingerprint data and the building structure from which it was collected, we were able to cluster the data points accurately compared to the unsupervised learning clustering method. In the future, research needs to be expanded to include three-dimensional movement path calculations using a voxel structure for generating paths within a three-dimensional environment.
Author Contributions
Conceptualization, H.-G.S., D.-S.L., C.-G.H., and C.-P.Y.; methodology, C.-G.H., and C.-P.Y.; software, H.-G.S., and C.-P.Y.; validation, H.-G.S.,C.-G.H, and C.-P.Y.; formal analysis, C.-G.H., and C.-P.Y.; investigation, D.-S.L., and C.-G.H.; resources, H.-G.S.; data curation, D.-S.L., and C.-G.H.; writing—original draft preparation, H.-G.S., and C.-P.Y.; writing—review and editing, C.-G.H., and C.-P.Y.; visualization, H.-G.S., D.-S.L., C.-G.H., and C.-P.Y.; supervision, C.-G.H., and C.-P.Y.; project administration, C.-G.H., and C.-P.Y.; funding acquisition, C.-P.Y. All authors have read and agreed to the published version of the manuscript.
Funding
None.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the authors.
Acknowledgments
None.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Feng, C.; Au, W.S.A.; Valaee, S.; Tan, Z. Received-signal-strength-based indoor positioning using compressive sensing. IEEE Trans. Mob. Comput. 2011, 11, 1983–1993. [Google Scholar] [CrossRef]
- Sahar, A.; Han, D. An LSTM-based indoor positioning method using Wi-Fi signals. In Proceedings of the ACM International Conference on Vision, Image and Signal Processing (ICVISP); ACM: Las Vegas, NV, USA; 2018. [Google Scholar]
- Shrestha, S.; Talvitie, J.; Lohan, E.S. Deconvolution-based indoor localization with WLAN signals and unknown access point locations. In Proceedings of the International Conference on Localization and GNSS (ICL-GNSS), Turin, Italy, 25–27 June 2013. [Google Scholar]
- Park, C.U.; Shin, H.-G.; Choi, Y.-H. A parallel artificial neural network learning scheme based on radio wave fingerprint for indoor localization. In Proceedings of the 10th International Conference on Ubiquitous and Future Networks (ICUFN), Prague, Czech Republic, 3–6 July 2018. [Google Scholar]
- Tian, Z.; Tang, X.; Zhou, M.; Tan, Z. Fingerprint indoor positioning algorithm based on affinity propagation clustering. EURASIP J. Wirel. Commun. Netw. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, K.; Zhang, W.; Zhang, Y.; Gu, J. Wi-Fi positioning based on deep learning. In Proceedings of the IEEE International Conference on Information and Automation (ICIA), Hailar, China, 28–30 July 2014; pp. 1176–1179. [Google Scholar]
- Jarawan, T.; Kamsing, P.; Tortceka, P.; Manuthasna, S.; Hematulin, W.; Chooraks, T.; Phisannupawong, T.; Sanzkarak, S.; Munakhud, S.; Somjit, T. Wi-Fi Received Signal Strength-based Indoor Localization System Using K-Nearest Neighbors fingerprint integrated D*algorithm. In Proceedings of the 23rd International Conference on Advanced Communication Technology (ICACT), PyeongChang, Korea, 7–10 February 2021; pp. 242–247. [Google Scholar]
- Wang, G.; Abbasi, A.; Liu, H. Wi-Fi-based Environment Adaptive Positioning with Transferable Fingerprint Features. In Proceedings of the IEEE 11th Annual Computing and Communication Workshop and Conference (CCWC), Virtual Conference, 27–30 January 2021; pp. 123–128. [Google Scholar]
- SHIN, Hong-Gi; CHOI, Yong-Hoon; YOON, Chang-Pyo. Movement path data generation from Wi-Fi fingerprints for recurrent neural networks. Sensors 2021, 21, 2823]. [Google Scholar] [CrossRef]
- Gao, K.; Wang, H.; Nazarko, J.; Chobanov, G. Indoor Trajectory Prediction Algorithm Based on Communication Analysis of Built-In Sensors in Mobile Terminals. IEEE Sens. J. 2021, 1–8. [Google Scholar] [CrossRef]
- Wang, P.; Koike-Akino, T.; Orlik, P. Fingerprinting-Based Indoor Localization with Commercial MMWave Wi-Fi: NLOS Propagation. In Proceedings of the IEEE Global Communications Conference 2020 (IEEE Globecom 2020), Taipei, Taiwan, 7–11 December 2020. [Google Scholar]
- Echizenya, K.; Kondo, K.; Kitagawa, T. Evaluation of the real-time indoor location and motion direction estimation system applying DNN to RSSI Fingerprints of BLE beacons. In Proceedings of the IEEE 9th Global Conference on Consumer Electronics (GCCE), Kobe, Japan, 13–16 October 2020. [Google Scholar]
- Gu, Y.; Zhou, C.; Wieser, A.; Zhou, Z. Trajectory Estimation and Crowdsourced Radio Map Establishment from Foot-Mounted IMUs,Wi-Fi Fingerprints, and GPS Positions. IEEE Sens. J. 2019, 19, 1104–1113. [Google Scholar] [CrossRef]
- Khassanov, Y.; Nurpeiissov, M.; Sarkytbayev, A.; Kuzdeuov, A.; Varol, H. Finer-level Sequential Wi-Fi-based Indoor Localization. In Proceedings of the 2021 IEEE/SICE International Symposium on System Integration (SII), Iwaki, Fukushima, Japan, 11–14 January 2021; pp. 163–169. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. In Proceedings of the International Conference on Artificial Neural Networks (ICANN); IET: Edinburgh, UK; 1999. [Google Scholar]
- Mikolov, T.; Karafiat, M.; Burget, L.; Cernocky, J.; Khudanpur, S. Recurrent neural network-based language model. In Proceedings of the Annual Conference of the International Speech Communication Association (INTERSPEECH 2010); International Speech Communication Association; International Speech Communication Association: Chiba, Japan; 2010. [Google Scholar]
- Van, H.G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar]
- R. Hamid Rezatofighi, T. Nathan, J.Y. Gwak, S. Amir, R. Ian, S. Silvio, “Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression,”. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2019; pp. 658–666.
- Z. Zheng, P. Wang, W. Liu, J. Li, R. Ye, and D. Ren, Distance-IoU loss: Faster and better learning for bounding box regression. In Proceedings of the AAAI conference on artificial intelligence; 2020; 34, pp. 12993–13000.
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- González, J.L.S.; Morillo, L.M.S.; Álvarez-García, J.A.; Ros, F.E.D.S.; Ruiz, A.R.J. Energy-efficient indoor localization Wi-Fi-fingerprint system: An experimental study. IEEE Access 2019, 7, 162664–162682. [Google Scholar] [CrossRef]
Figure 1.
Comparison of IoU and GIoU [19].
Figure 1.
Comparison of IoU and GIoU [19].
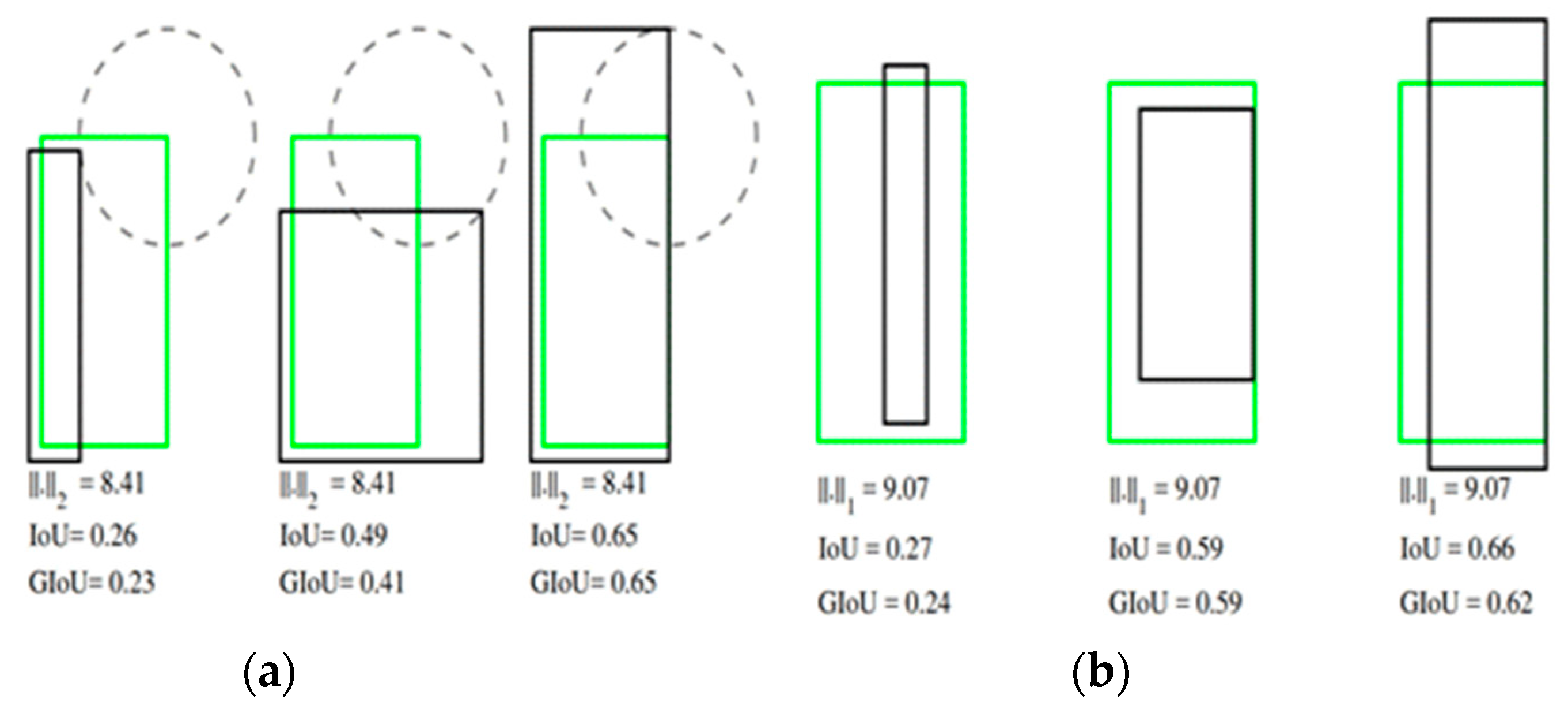
Figure 2.
Distributions of initial data points.
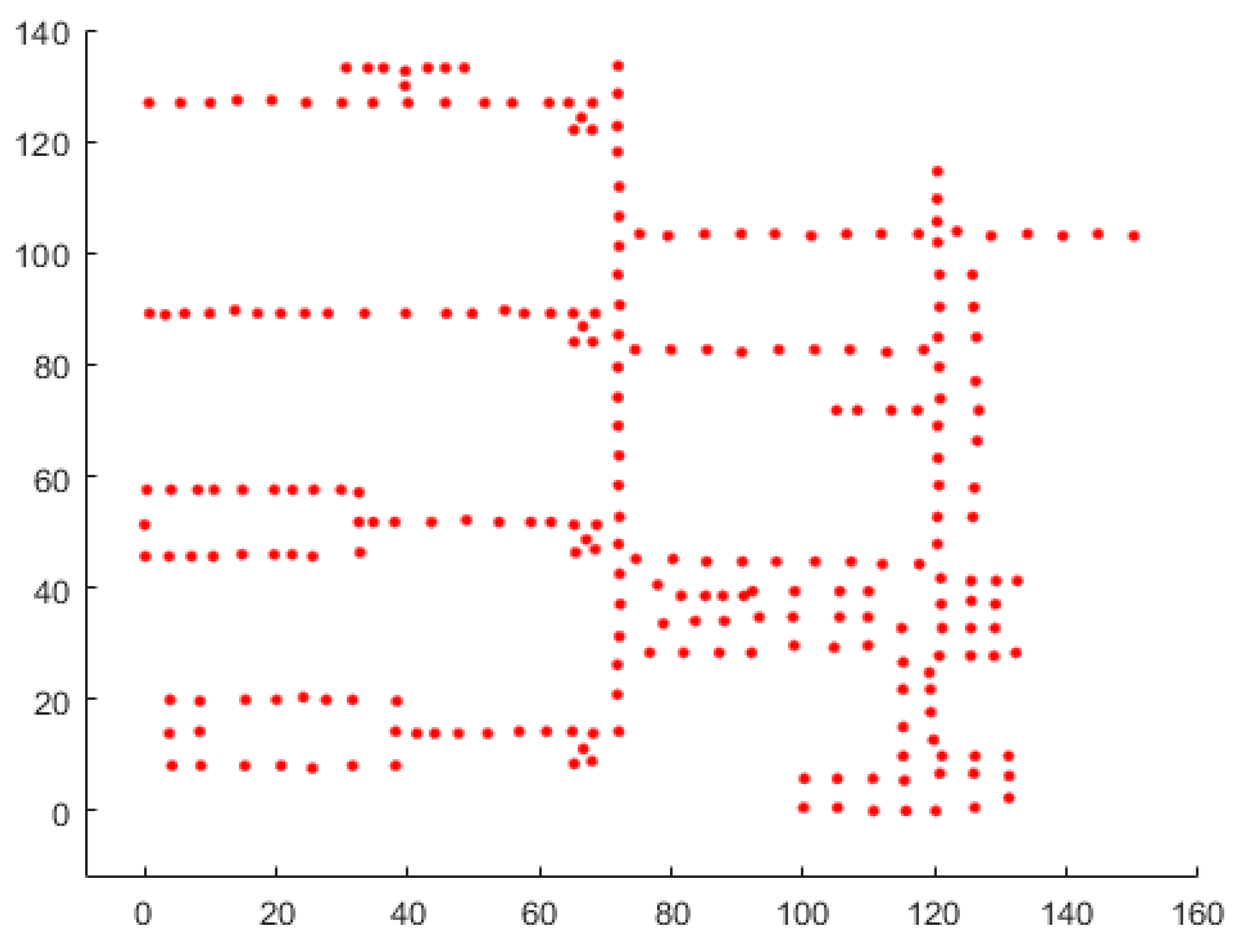
Figure 3.
BB and cell division. (a) The result of merging and expanding the BB. (b) The result of merging the BB from (a) with the structure of the cells divided by the cell division algorithm.
Figure 3.
BB and cell division. (a) The result of merging and expanding the BB. (b) The result of merging the BB from (a) with the structure of the cells divided by the cell division algorithm.
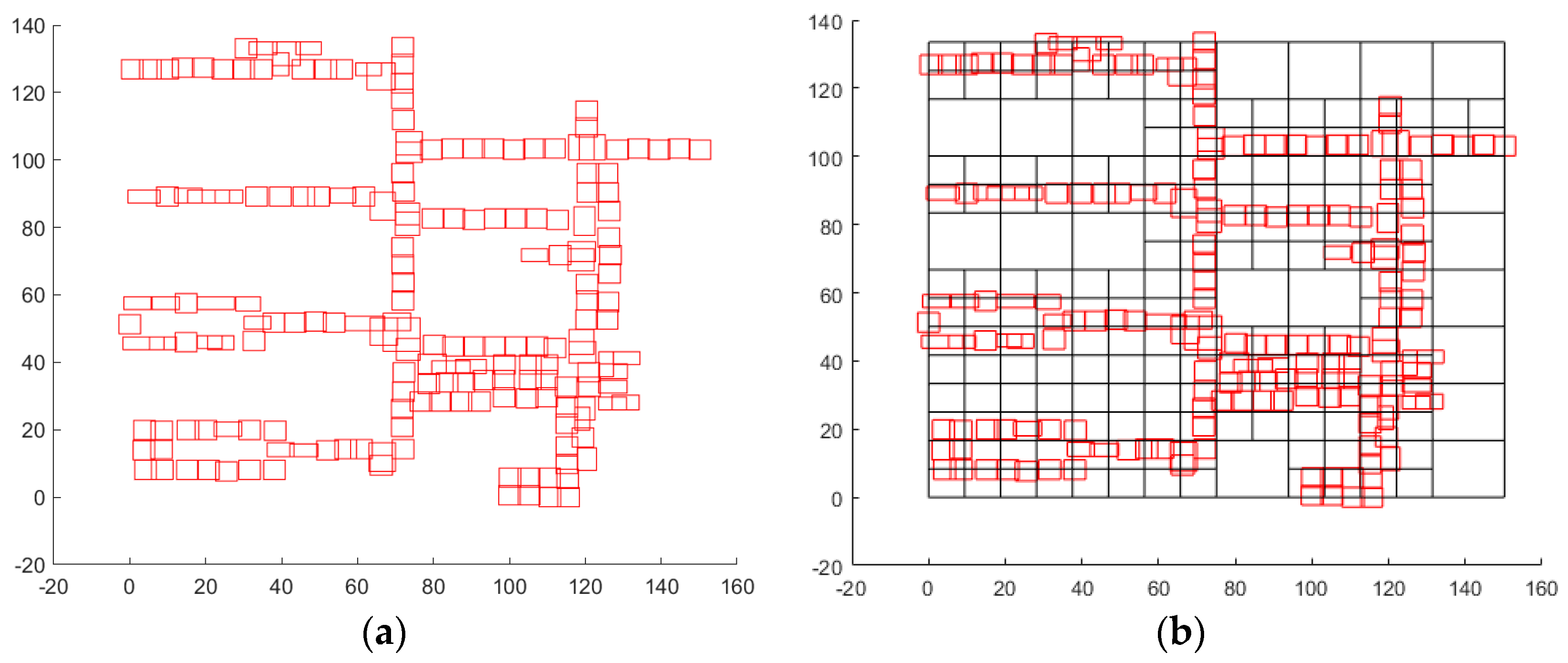
Figure 4.
cell division and movement path computation: (a) Distribution the initial data with the cell structure divided by the cell algorithm. (b) Paths generated by the movement path generation algorithm.
Figure 4.
cell division and movement path computation: (a) Distribution the initial data with the cell structure divided by the cell algorithm. (b) Paths generated by the movement path generation algorithm.
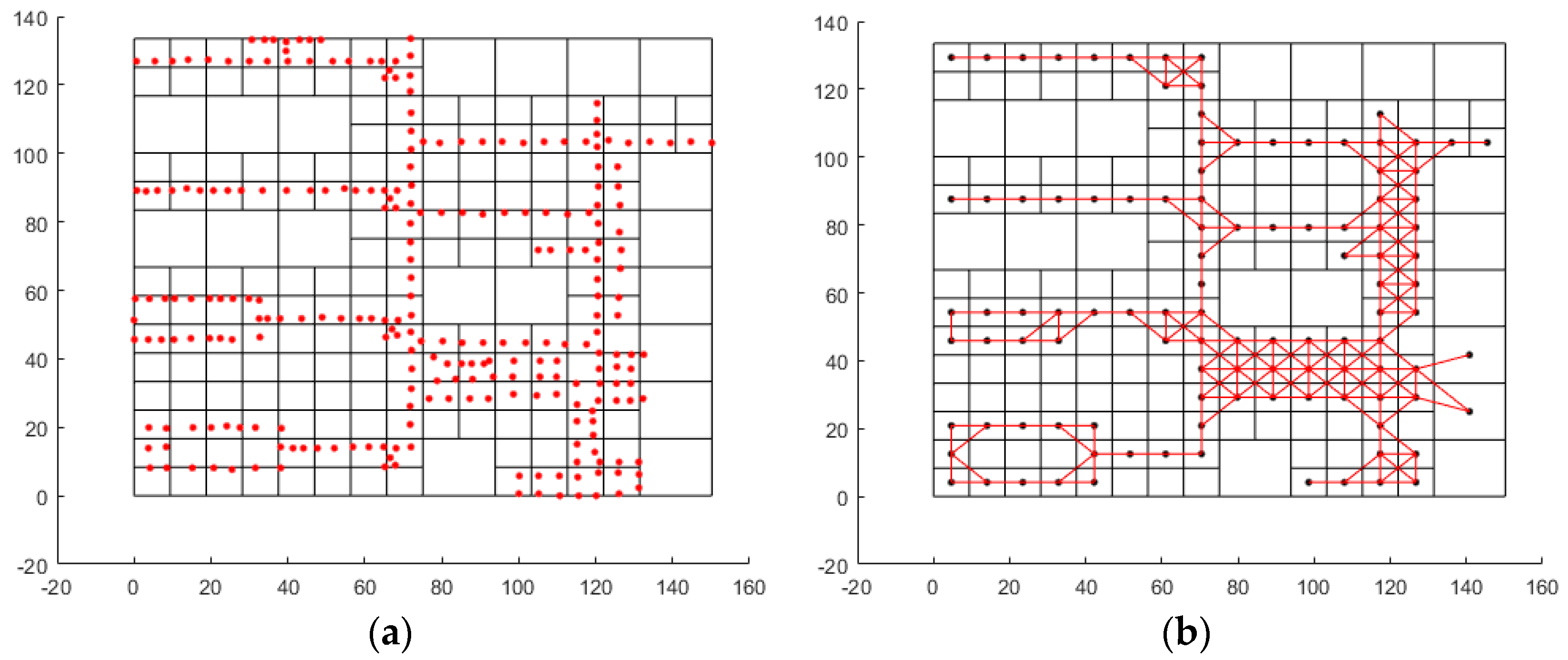
Table 1.
Hyperparameters required for merging BBs.
| hyper parameter | BBi size | m_factor | max_factor | IoU Threshold |
|---|---|---|---|---|
| value | 0.5m x 0.5m | x1.5 | 5m | 0.0 |
Table 2.
Hyperparameters for Dividing cells.
| hyper parameter | min_factor | max_overlap_factor |
|---|---|---|
| Value | 5 m | 2 |
Table 3.
Hyperparameters for the dataset.
| hyper parameter | Data Point | APs | Path | Training Data | Test Data |
|---|---|---|---|---|---|
| Value | 3,852 | 173 | 5 | 30,000 | 5,000 |
Table 4.
Range of hyperparameters.
| hyper parameter |
Learning Rate | Dropout | LSTM Length | Hidden cell | Epoch | RSSI Normalize |
Batch Size |
|---|---|---|---|---|---|---|---|
| value | 0.00001~0.01 | 0.0~0.4 | [2–7] | [64,128,256,512,1024] | 50~5,000 | [True, False] | [64,128,256,512,1024] |
Table 5.
Best Model in Learning.
|
hyper parameter |
Learning Rate | Dropout | LSTM Length | Hidden cell | Epoch |
RSSI Normalize |
Batch Size |
| value | 0.000676 | 0.188579 | 3 | 64 | 3,552 | True | 1024 |
Table 6.
Experimental results (unit: Accuracy %).
| Average | Deviation | Max | Min | |
|---|---|---|---|---|
| Learning | 99.75 | 0.001123832728 | 99.85 | 99.61 |
| Test | 92.94 | 0.002634387974 | 93.19 | 92.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated







