In South Korea, the residential real estate market is influenced not just by traditional supply and demand dynamics, but also by external factors such as housing policies and macroeconomic conditions. Given the significant role of housing assets in individual wealth, market fluctuations can have profound implications. While prior research has utilized variables like GDP growth rate, patent issuance, and birth rates, and employed models like LSTM and ARIMA for housing price predictions, many overlook key localized factors. Notably, the impact of subway stations and living SOC facilities on housing prices, especially in metropolitan areas, remains underexplored. This study addresses these gaps by analyzing usage trends across subway stations, assessing the influence of living SOC facilities on housing values, and identifying the optimal machine learning model for price predictions near transport hubs. Through a comparative analysis of machine learning techniques, we aim to provide insights for more informed housing price determinations, promoting a more stable real estate market.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

The housing market, an intricate nexus of activities including purchasing and selling of homes, real estate transactions, and price determination, significantly contributes to the dynamics of a nation’s economy [1,2,3]. It is notably susceptible to an array of determinants such as overarching economic health, fluctuating interest rates, consumer demand, and shifts in government policies. As such, the condition of the housing market can be interpreted as a barometer of a country’s economic vitality: a robust housing market often signals a prosperous economy while a frail one can suggest impending economic downturns [2,4,5,6].

In South Korea, the housing market is integral to the overall economy, with its stability resonating across a wide spectrum of stakeholders, not just homeowners. This ripple effect touches landlords, construction firms, lenders, policymakers, and has broader implications for the community at large. Within this context, areas close to subway stations, known as `station proximity areas’, have garnered significant attention. The convenience and accessibility offered by these areas have made them highly sought after, leading to a pronounced impact on housing prices [7,8,9,10,11,12,13,14]. Given the importance of the housing market to the nation’s economy, the stability of housing prices in station proximity areas becomes even more crucial. Therefore, understanding and predicting the dynamics of housing prices in these areas is of paramount importance for all involved entities and the broader economic landscape of the country.

Predictive modeling for housing prices in South Korean station areas is a critical area of research that can provide numerous benefits. Accurate price forecasting can empower individuals and organizations with valuable insights for informed decision-making when buying, selling, or investing in real estate. More than just providing transactional benefits, effective prediction models can curtail the volatility associated with housing prices [15,16,17,18,19,20,21]. Furthermore, these models can serve as important tools for regulators and policymakers in identifying, monitoring, and mitigating anomalies within the housing market. This has the potential to contribute to reducing the turbulence associated with housing prices, thereby fostering a more stable and predictable market environment.

In this study, we aim to construct a comprehensive prediction model for housing prices in South Korean station areas. We employ machine learning methods predicated on regression models. Regression models, statistically sophisticated tools that predict a dependent variable based on the values of one or more independent variables, have been proven effective in identifying and mapping complex interdependencies among variables [22,23]. By harnessing the capabilities of these models, we endeavor to build a robust and accurate housing price prediction model that uses actual data from areas surrounding subway stations.

A distinctive aspect of our research is the integration of the Living Social Overhead Capital (SOC) facilities as stable factors into the predictive modeling process. SOC facilities represent the core infrastructures and services, including transportation systems, communication networks, energy and water supply, schools, and hospitals. These are provided by both governmental and private sectors to buttress economic growth and enhance societal welfare [24,25,26]. As these facilities are less susceptible to rapid changes and upheavals, incorporating them into our model as stable predictors can enhance the model’s predictive accuracy and reliability.

In pursuit of a more stable housing market, this study sets out to develop an advanced and precise housing price prediction model using stable factors, such as facilities with low volatility and distinct regional characteristics. By accomplishing this, we hope to provide valuable insights and a blueprint for future research aimed at enhancing the predictability and stability of housing prices in the station areas in South Korea. In turn, this could contribute to a more predictable and stable housing market, better informed stakeholders, and an overall more resilient economy.

2. Related Research

The housing market, with its myriad influencing factors, especially around station areas, has been the subject of extensive academic exploration [27,28,29,30,31,32,33,34,35]. To provide a comprehensive context for our research within this vast domain, it’s imperative to delve into the methodologies, findings, and implications of prior studies. This section aims to review the literature, highlighting the evolution of predictive modeling in the housing market and the integration of machine learning techniques.

Historically, predictions in the housing market were deeply rooted in traditional econometric models [36,37]. These models primarily emphasized macroeconomic indicators. A notable study [36] delved into the complexities of the Japanese housing market, shedding light on the challenges faced by the average Japanese individual when purchasing a house. This research introduced the innovative "asset market approach," which conceptualized houses as unique asset classes. By combining the consumption capital asset pricing model with housing and residential land supply functions, a robust theoretical framework was crafted. However, the study’s focus on data from the 1970s and 1980s and its primary emphasis on the Japanese context might limit its applicability to contemporary global housing markets.

Mikhed and Zemčík’s research [38] provided a fresh perspective on the U.S. housing market. They meticulously investigated whether house prices genuinely reflected their underlying economic fundamentals. Their findings, derived from both aggregate and panel data, revealed significant discrepancies between house prices and their determinants, especially evident before the 2006 market correction. While their insights were invaluable, the study’s reliance on traditional statistical methodologies suggests potential enhancements through the integration of modern machine learning techniques.

Genesove and Han’s work [39] is particularly noteworthy for its in-depth exploration of housing market liquidity. By leveraging a unique dataset spanning diverse geographical areas and timeframes, they offered a panoramic view of market dynamics. Their innovative approach to understanding demand shocks and their subsequent impact on liquidity was groundbreaking. However, the study’s reliance on data from the National Association of Realtors and its traditional methodologies indicate areas for potential improvement.

The hedonic pricing model, a cornerstone in real estate economics, has been instrumental in understanding how various factors, such as location and amenities, influence property values. Building on this foundation, several studies have investigated the relationship between housing prices and transportation infrastructure [12,32,40,41,42,43,44]. The study in Beijing [32] emphasized the positive correlation between proximity to rail transit systems and elevated property values. Another research in Tianjin [40] highlighted the transformative impact of subway systems on urban landscapes and housing prices.

Machine learning’s integration into housing price predictions has been a game-changer [45,46,47,48,49,50]. A recent study [45] showcased the potential of various algorithms, with the RIPPER algorithm standing out for its superior predictive capabilities. This research underscored the transformative power of machine learning, suggesting a paradigm shift from traditional methodologies.

By 2018, the field of housing market research had matured considerably, with researchers employing more intricate datasets and refining their methodologies. A testament to this progression is a seminal work by [46]. This study provided a fresh perspective on the subject, specifically focusing on Ames, Iowa. The authors meticulously dissected the Ames Housing dataset, employing regression-based supervised learning methodologies to predict housing prices. Through a rigorous comparative analysis of multiple models, they identified an optimal model, which they then used as a foundation for amalgamating predictions. Their innovative approach to feature engineering and categorization stands out, offering a blueprint for future research in the domain. They delved deep into the intricacies of the dataset, exploring factors such as neighborhood characteristics, property age, and amenities. Despite achieving a commendable rank on Kaggle.com’s public leaderboard, the study acknowledges its limitations, emphasizing the need for broader validation and exploration. This work underscores the burgeoning potential of machine learning in real estate economics, reinforcing the notion that as datasets grow and computational techniques advance, the horizon of possibilities in housing market research continues to expand.

Fast-forwarding to 2023, the research landscape witnessed further advancements. H. Peng et al.’s study [49] introduced LUCE, a novel predictive model tailored for the Toronto housing market. LUCE was designed to address two pivotal challenges in real estate evaluation: the scarcity of recent sales prices and the sparsity of housing data. The model’s ingenuity lies in its ability to structure housing data in a Heterogeneous Information Network (HIN), where graph nodes represent crucial housing entities and attributes pivotal for price evaluation. By leveraging Graph Convolutional Networks (GCNs), LUCE extracts spatial information from the HIN, such as geographical locations of houses. Subsequently, the model employs Long Short Term Memory (LSTM) networks to capture the temporal dependencies in housing transaction data over time. This dual approach allows LUCE to provide a comprehensive, up-to-date housing evaluation dataset, significantly simplifying downstream appraisal tasks.

In the same year, another groundbreaking study [50] presented at the European Conference on Social Media delved into the nexus between social media sentiment and housing prices. This research probed the influence of Twitter sentiment, specifically pertaining to the Covid-19 pandemic, on the resale prices of Housing Development Board (HDB) apartments in Singapore. The study utilized the VADER lexicon-based tool for sentiment analysis and employed the Granger Causality method to discern the relationship between sentiment scores and reported Covid-19 cases. The research harnessed the power of neural networks for prediction, emphasizing the advantages of using Twitter sentiment over traditional predictors. The findings revealed that the incorporation of Twitter sentiment augments the prediction accuracy, surpassing models that rely solely on traditional predictors. This study underscored the pivotal role of sentiment analysis derived from Twitter data in urban economics, shedding light on the profound capability of social media platforms to encapsulate the behavioral economic nuances of a populace.

In the vast landscape of housing market research, several studies have delved into various factors influencing housing prices, from traditional econometric models to the integration of modern machine learning techniques. While many have explored the impact of transportation infrastructure, such as proximity to rail transit systems, and others have investigated the influence of social media sentiment, few have combined these with the significance of Living Social Overhead Capital (SOC) facilities.

Our research stands distinct in its approach. While previous studies have either focused on transportation infrastructure or the significance of SOC facilities separately, our study amalgamates these two pivotal factors. By integrating data from both SOC facilities and subway stations, we provide a more holistic view of the determinants influencing housing prices. Furthermore, our application of advanced machine learning techniques, tailored to handle the intricacies of such combined data, sets our work apart.

In Chapter 3, we delve into the meticulous process of data collection and preprocessing for our research. We gathered a diverse range of data, encompassing both SOC facilities and subway stations. This data underwent rigorous preprocessing to ensure its accuracy and relevance. We addressed missing values, outliers, and potential biases to craft a robust dataset that truly reflects the urban landscape and its impact on housing prices. The integration of these datasets was a pivotal step, ensuring that our machine learning models had a comprehensive view of the factors influencing housing prices.

With our dataset in place, we embarked on a comparative analysis of eight advanced machine learning models. Each model was trained and tested on our integrated dataset, with the aim of identifying the most accurate and efficient model for housing price prediction. Through rigorous evaluation metrics and cross-validation, we identified the optimal model that showcased superior predictive capabilities.

3. The Proposed Scheme

3.1. Raw Data

In this study, we aim to construct a model to predict housing prices in areas in close proximity to railway systems, a significant component of Traffic Social Overhead Capital (SOC) facilities. We utilized the Metro-Adjacent Residential Transaction data, provided by the Korea Real Estate Board and available on the National Transportation Data Open Market, as our primary input variables. This dataset, as shown in Table 1, comprises actual housing transaction data extracted from the Ministry of Land, Infrastructure and Transport’s real estate transaction disclosure system, specifically transactions that occurred within 500 meters of subway stations. Based on this dataset, we incorporated additional data on SOC facilities and life convenience facilities as independent variables in our analysis, considering them as constant factors that could influence housing prices.

For data partitioning, we utilized approximately one year’s worth of data, from November 2021 to November 2022, as our training dataset, while we used about one month’s data from December 2022 as our testing dataset. Given the scope and objectives of our study, we chose to focus solely on sales data. Hence, out of the total 360,084 instances in our training dataset, we utilized 58,342 instances of sales data, and out of the 25,622 instances in our testing dataset, we utilized 2,804 instances of sales data. We noted that there were missing values observed in our dataset, specifically in the `BLDG_YEAR’ variable. In the training dataset, we identified 810 missing instances, and in the testing dataset, 35 missing instances were found. The specific approach for handling these missing values will be detailed in the subsequent methodology subsection of this study.

3.2. Pre-Processing Data

This subsection discusses the pre-processing steps performed on the data prior to our analysis. Data pre-processing is a crucial step in any data-driven project. It helps to clean, normalize, and transform the raw data into a format suitable for further analysis or model training. These steps are essential to ensure the quality and reliability of the results derived from the data. We outline the specific pre-processing techniques used in our study, detailing why each step was necessary and how it contributes to the overall analysis.

3.2.1. Variable Modification and Reduction1

During our pre-processing, we conducted both variable elimination and modification to optimize our dataset for further analysis. We identified a set of variables, as presented in Table 1, that either contained duplicate information or were not applicable to our study. The variables `SIGUNGU_CD’, `EMDL_CD’, `CLL’, `MNO’, and `SNO’ encapsulate address-related information, which is already sufficiently represented by the `ADRES’ variable. To avoid redundancy, these overlapping variables were eliminated. Additionally, we removed variables such as `GRNTE_AMOUNT’ and `MTHRNT_AMOUNT’, irrelevant to sale transactions, from our analysis. This streamlined our dataset and ensured that our model would only train on features pertinent to our research objectives.

After variable elimination, we modified the `HUS_TP’ variable, which represents the property type of each transaction. `HUS_TP’ consists of three unique categories: `Apartment’, `Studio’, and `Multi-family residential’. To allow machine learning algorithms to process this categorical data more effectively, we applied the one-hot encoding technique. This process converted each category into a separate column assigned a binary value of 1 (presence of the feature) or 0 (absence of the feature). This transformation allowed our model to utilize the property type data effectively without any inherent order or priority.

3.2.2. Log-Scaling of the Target Variable

Following the variable elimination, we then proceeded with the log-scaling of our target variable, `DLNG_AMOUNT’. This variable, representing the sale price, exhibited a right-skewed nature with low normality and a long tail on the right. Log-scaling involves the transformation of variable values to their logarithmic scale and is typically applied to variables with large values or are heavily skewed. In many cases, a few large values dominate the distribution of feature values. By applying log transformation to `DLNG_AMOUNT’, we could convert these values to a more normalized distribution, potentially enhancing the performance of our machine learning model. The visual representation of the log-scaling process is demonstrated in Figure 1.

3.2.3. Geocoding and Distance Calculation

Following the log-scaling, we utilized Geocoding to pinpoint the geographic locations related to the housing transactions. Geocoding converts addresses into their corresponding positions on the Earth’s surface (i.e., latitude and longitude), enabling the mapping and analysis of geographical data [51,52,53]. For the geocoding process, we leveraged the AI·NAVER API from the Naver Cloud Platform to convert the `ADRES’ variable from our base dataset into geographical coordinates.

With the geocoded locations of the housing transactions, we used the Haversine formula to determine the distance between the houses and the surrounding SOC facilities [54,55]. The Haversine formula calculates the great-circle distance between two points on a sphere’s surface, like the Earth, taking into account its curvature. This makes it more suitable than regular flat-plane distance calculations. The formula is as follows:

\begin{matrix} a & = {sin}^{2} (\frac{Δ ϕ}{2}) + cos (ϕ_{1}) cos (ϕ_{2}) {sin}^{2} (\frac{Δ λ}{2}) \\ c & = 2 \cdot a t a n 2 (\sqrt{a}, \sqrt{1 - a}) \\ d & = R \cdot c \end{matrix}

where

ϕ

is latitude,

λ

is longitude, and R is Earth’s radius (mean radius = 6,371km). For instance, to find the distance between Seoul (coordinates 37.5665° N, 126.9780° E) and Busan (coordinates 35.1796° N, 129.0756° E) in South Korea, this formula can be used. For our study, we aggregated facilities within a 500-meter radius, typically considered a 5-10 minute walk and thus, within walking distance. Given that we used geocoded coordinates for our calculations, the Haversine formula was essential for accurate distance calculation.

3.2.4. Socio-Environmental Determinants of Housing Prices

The socio-environmental context of a region plays a pivotal role in determining real estate values. Specifically, properties in areas that boast high-quality public services, such as esteemed educational institutions and healthcare facilities, and have robust transportation networks often fetch higher prices than those in areas lacking these amenities. Conversely, areas deficient in public transportation or quality public services typically experience diminished real estate demand, leading to reduced property prices [56,57,58]. Recognizing the importance of these determinants, we have incorporated the condition of local infrastructure and amenities surrounding a property into our dataset under the term `local living facilities’.

Educational institutions are paramount in the homebuying decisions, especially for families with school-going children. The proximity of schools to a residence is often a primary consideration for such families. In light of this, our dataset includes the count of elementary and middle schools within a 500 m radius from the property, represented as `ELET_SCH’ and `MDL_SCH’. Furthermore, urban amenities like parks and libraries, which elevate the quality of life, also have a bearing on property prices. We have quantified the number of urban parks and libraries within a 500-meter radius from the property and integrated this data as variables named `CNT_PARK’ and `CNT_LIB’ in our dataset.

Subsequent to the inclusion of these socio-environmental determinants, we undertook a regional clustering exercise to visually compare real estate prices across different areas. The visual representation of this clustering is depicted in Figure 2. It’s a general understanding that owning property in affluent areas necessitates a proportionate income. Thus, we expected a strong correlation between the average regional income and property prices. To substantiate this, we analyzed the total reported salary by region based on the end-of-year tax settlement of earned income. This analysis yielded the average annual salary per person by region, which we represented as the variable `INC_BY_RGN’ in our dataset. This addition further enriched our understanding of the interplay between property prices and regional income.

3.2.5. The Influence of Housing Brands on Property Value

For potential homebuyers, the brand reputation of a residential property often plays a pivotal role in their decision-making process. Specifically, properties developed by renowned construction firms are typically associated with higher quality and standards, which can subsequently influence their market prices. This sentiment is corroborated by data from the Korea Corporate Brand Reputation’s apartment brand reputation analysis in January 2023 [59], which ranked Hillstate as the top brand, followed by Prugio and Xi.

Given the evident significance of housing brands in the real estate market, our study sought to incorporate this factor into our analysis. We referenced the `Top 20 Apartment Brand Preferences’ as provided by the Korea Corporate Reputation Research Institute. Using the `COMP_NM’ variable, we identified whether a particular property was developed by one of the major construction companies. This binary representation serves to capture the brand value of the property, indicating if it was constructed by a leading developer in the industry.

3.2.6. Assessing the Importance of Subway Stations and Data Processing

Subway station passenger traffic varies based on diverse user intentions, reflecting the significance of stations that serve various destinations, including offices, residences, hospitals, entertainment venues, and more. In this study, our objective is to gauge the importance of each subway station by analyzing passenger entry and exit volumes.

Our primary data source was the `Standard Station Information’ provided by the Rail Portal as of January 2023. However, during the data collection process, we encountered several challenges. A notable disparity existed in the operating institutions across different subway lines within the metropolitan area. Additionally, acquiring data from subway lines operated by the private sector was challenging since these entities are not mandated to disclose such information. Furthermore, some public datasets contained inaccuracies, attributed to issues like turnstile errors, which complicated the precise extraction of data. To address these challenges, we compiled a comprehensive list of subway line-specific operating institutions in the metropolitan area, facilitating our data collection. This list is detailed in Table 2.

While our primary focus was on the 2022 passenger volume data, we supplemented missing data from certain private-sector-operated subway lines using the ’Integrated Transport Card Big Data System’ managed by the Ministry of Land, Infrastructure, and Transport. For stations that lacked 2022 data, we referred to the 2021 dataset. During data preprocessing, we made transformations using the `NEAR_SUBW_NM’ variable to enhance its linkage with the passenger volume data. This involved reconciling station names that had changed over time and resolving duplicate station names across different lines. We standardized these names to a consistent `Line_StationName’ format. Lastly, to evaluate the significance of subway stations, the primary variable, passenger volume, was normalized using the MinMaxScaler. This technique, widely used in machine learning, scales and normalizes data to fall between 0 and 1.

3.2.7. Interplay between Housing Prices and Financial Market Dynamics

The dynamics of housing prices are influenced by a myriad of factors, one of which is the prevailing financial climate [1,2,3,4,5,6]. Among various indicators representing the financial health of an economy, the policy rate emerges as a pivotal gauge reflecting a nation’s monetary policy and the broader economic sentiment. In South Korea, the Bank of Korea is responsible for setting and adjusting this rate. Recognizing the significance of the policy rate in our study, we incorporated it as a primary variable to understand the intricate interplay between the monetary policy landscape and housing prices.

Given the time-series nature of our foundational dataset, it is essential to consider the timing of housing transactions. By combining the `CTRT_YRMTH’ and `CTRT_DAY’ variables, we introduced a new variable, `PLC_RATE’, which corresponds to the policy rate prevailing on the specific date of the transaction. This integration offers a nuanced reflection of the financial context at the time of each housing transaction. However, an inherent limitation must be acknowledged. The funding mechanisms employed for housing purchases might not always align with the contemporaneous policy rate. For instance, prospective homeowners might secure financing well in advance, potentially under different interest rate conditions. Thus, solely examining the interplay between the policy rate and housing prices might provide an oversimplified perspective, highlighting the need for more comprehensive studies to delve deeper into this complexity.

3.2.8. Addressing Missing data and Incorporating Building Age

The concurrent development of housing and associated infrastructures, such as roads and sewage systems, provides distinct efficiency benefits compared to sequential development. This integrated approach in housing projects streamlines approval processes, eliminating the need for multiple approval stages and thereby accelerating the overall development timeline [60,61]. Given this backdrop, it is logical to infer missing values by observing analogous developmental patterns within the dataset.

In relation to the `BLDG_YEAR’ variable from Table 1, we identified a total of 845 missing values across both the training and testing datasets. To address this, we employed the KNN imputer method, leveraging inherent data similarities. The KNN imputer works by pinpointing the K-nearest neighboring data points and then imputing the missing value based on the average of these neighbors. For our study, we utilized the KNN Imputer from scikit-learn, setting it to consider the five nearest data points for imputation purposes. The age of a building is undeniably a pivotal factor in real estate purchasing decisions. To encapsulate this aspect, we introduced the `AGE_BLDG’ variable, which is derived by subtracting the building’s construction year from the contract year.

3.3. Modeling Process

In this section, we delve into the intricacies of our modeling process, starting with an assessment of the input variables. Our model incorporates a total of 15 input variables. Among these, three variables -`NEAR_SUB_DIST’, `FLR’, and `XUAR’ - are directly extracted from Table 1 of our foundational dataset. They represent the distance from a subway station (within 500 m), the floor number of the building, and the exclusive area of the house, respectively. The remaining variables have been refined through various preprocessing steps. For instance, the `WTD_SUBW_RANK’ variable was derived by summing the boarding and alighting counts at subway stations and then normalizing these values. A significant aspect of this preprocessing involved geocoding based on the ‘ADRES’ variable, which allowed us to utilize the resulting latitude and longitude coordinates. We also introduced the `INC_BY_REG’ variable, which is based on the 2021 wage income settlement details specific to the housing’s region, be it a city or district. The `PLC_RATE’ variable reflects the benchmark interest rate set by the Bank of Korea on the transaction day. Furthermore, the variables `ELET_SCH’ and `MDL_SCH’ denote the count of elementary and middle schools, respectively, within a 500 m radius. In a similar vein, `CNT_PARK’ and `CNT_LIB’ variables capture the number of parks and libraries, respectively, within the same proximity. Lastly, the `COMP_NM’ variable serves as an indicator, signifying whether the housing was constructed by a renowned construction company. A comprehensive list of the input variables utilized in our final model can be found in Table 3.

3.3.1. Multicollinearity and Its Mitigation

As we progress through the modeling process, it’s imperative to ensure the validity and reliability of our model. One potential pitfall in multiple regression models that can compromise reliability is the presence of multicollinearity. Multicollinearity is a phenomenon observed in multiple regression analyses when several independent variables are highly correlated with each other. In models burdened with high multicollinearity, deciphering the distinct influence of each independent variable becomes intricate, potentially leading to unreliable coefficient estimates [62,63]. Such scenarios can inflate the standard errors of the regression coefficients, rendering it challenging to attain statistically significant results.

To address the issue of multicollinearity in our analysis, the Variance Inflation Factor (VIF) was employed. The VIF calculates the magnitude of multicollinearity among independent variables. Specifically, it sets each independent variable as the dependent variable and conducts a regression analysis against other variables, using the

R^{2}

value for its computation. Typically, a VIF value exceeding 10 indicates significant multicollinearity between the variable in question and others.

Utilizing the statsmodels.api library in Python, VIF values for all independent variables were determined. The computed VIF values for the modeling input variables are depicted in Figure 3. However, after performing one-hot encoding (OHE) on the original `HUS_TP’ variable, we observed potential multicollinearity. Given the inherent nature of OHE, which transforms a single variable into multiple binary columns, it is not uncommon to encounter high multicollinearity among the generated features. Recognizing this, we excluded the highly correlated variables and re-evaluated the VIF. Upon inspecting the revised VIF values for each feature, all variables demonstrate a VIF less than 10.

3.3.2. Optimal Model Determination

Upon addressing multicollinearity, our next step involved evaluating the efficacy of eight distinct machine learning models using cross-validation. A concise overview of these models and their unique characteristics is provided in Table 4.

Model validation is an integral component of the modeling process. Cross-validation, a foundational technique in machine learning, gauges a model’s performance by partitioning the dataset into multiple training and test subsets. This approach is instrumental in preventing overfitting. However, our dataset presents a unique challenge due to its inherent time series nature. Resorting to standard Cross-Validation methods would be problematic, as it poses the risk of unintentionally leveraging future data to forecast past or present events. To navigate this intricacy, we adopt the Time Series Nested Cross-Validation (TS-Nested CV) strategy [64]. This specific validation approach is tailored for data with temporal dependencies. It ensures that the training dataset always precedes the validation set in chronological order. As such, instead of the conventional k-fold techniques, the TS-Nested CV is preferred. We implement this process using the Time Series Split tool available in the scikit-learn library. A schematic depiction of the approach can be found in Figure 4.

Choosing the right evaluation metric is crucial for assessing a model’s performance accurately. These metrics offer quantitative insights into a model’s predictive accuracy. In our study, due to the target variable’s deviation from normality during preprocessing, we applied a logarithmic transformation. Consequently, we selected RMSLE (Root Mean Squared Log Error) over RMSE as our primary evaluation metric. RMSLE is advantageous as it reduces the impact of outliers in predictions by calculating the squared logarithmic difference between predicted and actual values.

RMSLE = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(log (p_{i} + 1) - log (a_{i} + 1))}^{2}}

Where

p_{i}

represents the predicted values and

a_{i}

denotes the actual values.

Using the TS-Nested CV method, we compared the eight models based on the RMSLE metric. For this assessment, we primarily used the default hyperparameters for each model. The results are illustrated in Figure 5. Among the evaluated models, the LightGBM model emerged as the top performer, registering an RMSLE score of 0.23427. Based on this outcome, we identified LightGBM as the most suitable predictive model for our study.

3.4. Hyperparameter Tuning of LightGBM and Feature Importance Analysis

To further refine the performance of the chosen LightGBM model, hyperparameter tuning is essential. For this task, we utilized the OPTUNA library, an open-source Python tool designed specifically for hyperparameter optimization. While it shares similarities with GridSearch, RandomSearch, and BayesianOptimization, OPTUNA offers a more streamlined and efficient approach to optimize both machine learning and deep learning models. It significantly reduces the time and effort typically required for model selection and hyperparameter adjustment.

Given that a lower RMSLE signifies better accuracy, our optimization objective was set to `minimize’. To balance optimization quality with computational efficiency, we limited the number of iterations to

n_t r i a l = 100

. Post-optimization, the model’s accuracy saw a marked improvement, with the RMSLE value decreasing from the initial 0.23427 to 0.22317.

In our analysis using the LightGBM model, we sought to identify the most influential features affecting housing prices. The determined feature importances are depicted in Figure 6. Notably, the `WTD_SUBW_RANK’ emerged as the most influential factor, representing the weighted significance of subway stations. The `INC_BY_REG’ variable, which denotes the income percentile of the property’s administrative district, was the second most impactful feature. Delving into the property-specific attributes, both the `AGE_BLDG’and `XUAR”variables, representing the building’s age and property area respectively, were significant in shaping housing prices.

These findings suggest that location-related external factors, especially transit accessibility, have a more pronounced impact on housing prices than the inherent attributes of the properties. Additionally, the age and size of a property play crucial roles in its valuation. This underscores the importance of location and surrounding amenities, particularly transportation links, in urban real estate valuation. Further exploration into the diverse factors influencing housing prices presents a valuable direction for future research.

Armed with these insights, stakeholders in the real estate market, both buyers and sellers, can make more informed decisions, especially concerning location and transportation accessibility. As we transition to the concluding remarks, it’s vital to contemplate the broader implications of our findings, especially in the realms of urban planning, policy formulation, and emerging real estate trends. This sets the foundation for the discussions in the subsequent sections.

4. Discussion

In the rapidly changing field of housing market research, our study offers a fresh perspective by examining the interplay between traditional econometric models and the latest machine learning techniques. By combining data from SOC facilities and subway stations, we present a comprehensive method to understand the multifaceted factors influencing housing prices.

Our integration of diverse datasets provides a holistic view of urban amenities and their impact on housing prices. The rigorous preprocessing and data integration methods we employed can serve as a reference point for future studies, emphasizing robustness and reliability. Moreover, our comparative evaluation of eight advanced machine learning models highlights the transformative potential of machine learning in reshaping housing price predictions. Our model not only delivers superior predictive accuracy but also illuminates the intricate relationships between various determinants.

Although many studies have focused either on transportation infrastructure or the significance of SOC facilities, our research stands out with its integrated approach. We move beyond traditional approaches, offering a deeper understanding of housing prices by considering both subway accessibility and the importance of SOC facilities. This comprehensive perspective ensures a more accurate prediction model, setting our research apart from others.

While our study has made significant contributions to housing price prediction, we recognize that the vast landscape of urban economics still holds many areas ripe for exploration. Our research provides valuable insights and charts a path for future inquiries. By emphasizing the importance of a comprehensive approach and the potential of machine learning, we hope to inspire continued innovation in housing market research.

Author Contributions

Conceptualization, J.P. and S.B.; methodology, J.P., S.B. and J.K.; software, S.B. and J.K.; validation, S.B., J.K. and K.K.; formal analysis, J.P.; investigation, S.B. and J.K.; resources, S.B. and J.K.; data curation, S.B., J.K. and K.K.; writing—original draft preparation, S.B. and J.K.; writing—review and editing, J.P. and K.K.; visualization, S.B. and J.K.; supervision, J.P.; project administration, J.P.; funding acquisition, J.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education (NRF-2021R1F1A1064073).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Metro-Adjacent Residential Transaction data, Available on the National Transportation Data Open Market, https://www.bigdata-transportation.kr/frn/prdt/detail?prdtId=PRDTNUM_000000020052, Apartment brand January 2023 big data analysis results, Available on Korea Corporate Brand Reputation, https://brikorea.com/bbs/board.php?bo_table=rep_1&wr_id=2126, Korea Railroad Corporation, https://info.korail.com/info/selectBbsNttView.do;jsessionid=Zr2b7ZEC5zImD31IuWd5VAK72TuaxwQfUAppAfGsTzlsebEobzZT8I13TT5RPdpD?key=867&bbsNo=425&nttNo=15252&searchCtgry=&searchCnd=all&searchKrwd=&integrDeptCode=&pageIndex=1, Seoul Metro Corporation, http://www.seoulmetro.co.kr/kr/board.do?menuIdx=548&bbsIdx=2215619, Incheon Metro Corporation, https://www.ictr.or.kr/main/bbs/bbsMsgDetail.do?msg_seq=253&bcd=data, Namyangju City Urban Corporation, https://www.ncuc.or.kr/jj_line/1734?action=read&action-value=313f7ca5e6d4b76452aef867a71a1f2e, Rail Portal, https://data.kric.go.kr/rips/M_01_01/detail.do?id=32, Traffic Card Big Data System, https://www.stcis.go.kr/wps/main.do, Railway industry Information Center, http://www.kric.go.kr/jsp/industry/rss/citystapassList.jsp?q_org_cd=A010010042&q_fdate=2022

Conflicts of Interest

The authors declare no conflict of interest.

References

Zhang, W.; Chen, S.; Guo, D.; Li, B. The impact of internet real estate intermediary platform on the real estate market. Proceedings of The 4th International Conference on Crowd Science and Engineering, Jinan, China, 132–139., 18–21 October 2019. [Google Scholar]
Chen, C.-J.; Zhai, H.; Wang, A.; Ma, S.; Sun, J.; Wu, C.; Zhang, Y. Experimental research on the impact of interest rate on real estate market transactions. Discrete Dyn. Nat. Soc. 2022, 9946703. [Google Scholar] [CrossRef]
Li, Y. The impact of COVID-19 on China’s real estate industry and the outlook for industry trends. BCP Business & Management 2022, 34, 337–343. [Google Scholar]
Kurihara, Y. Demand for money under low interest rates in Japan. J. Economics and Financial Studies 2016, 04, 12–19. [Google Scholar] [CrossRef]
Ofor, T. N.; Alagba, O. S.; Ifurueze, M.S. Housing finance market and economic growth of West Africa region: a study of Nigeria and Ghana. Int. J. Business & Economic Development 2018, 6, 49–60. [Google Scholar]
Ayan, E.; Eken,S. Detection of price bubbles in Istanbul housing market using LSTM autoencoders: a district-based approach. Soft Comput. 2021, 25, 7957–7973. [Google Scholar] [CrossRef]
Bajic, V. The effects of a new subway line on housing prices in metropolitan Toronto. Urban Stud. 1983, 20, 147–1583. [Google Scholar] [CrossRef]
Agostini, C. A.; Palmucci, G. A. ; The anticipated capitalisation effect of a new metro line on housing prices. Fisc. Stud. 2008, 29, 233–256. [Google Scholar] [CrossRef]
Wang, L. Impact of urban rapid transit on residential property value. Chinese Economy 2010, 43, 33–52. [Google Scholar] [CrossRef]
Sun, W.; Zheng, S.; Wang, R. The capitalization of subway access in home value: A repeat-rentals model with supply constraints in Beijing. Transp. Res. Part A Policy Pract. 2015, 80, 104–115. [Google Scholar] [CrossRef]
Trojanek, R.; Gluszak, M. Spatial and time effect of subway on property prices. J. Hous. Built Environ. 2018, 33, 359–384. [Google Scholar] [CrossRef]
Wen, H.; Gui, Z.; Tian, C.; Xiao, Y.; Fang, L. Subway opening, traffic accessibility, and housing prices: A quantile hedonic analysis in Hangzhou, China. Sustainability 2018, 10, 2254. [Google Scholar] [CrossRef]
Li, S.; Chen, L.; Zhao, p. The impact of metro services on housing prices: a case study from Beijing. Transportation 2019, 46, 1291–1317. [Google Scholar] [CrossRef]
Zhou, Z.; Chen, H.; Han, L.; Zhang, A. The effect of a subway on house prices: evidence from Shanghai. ” Real Estate Econ. 2021, 49, 199–234. [Google Scholar] [CrossRef]
Choi, M.; Byeon, S. Comparison on forecasting performance of housing price prediction models in Seoul. Seoul Studies 2016, 17, pp. 75–89. [Google Scholar]
Lee, T. H.; Jun, M. Prediction of Seoul house price index using deep learning algorithms with multivariate time series data. SH Urban Research & Insight 2018, 8, 39–56. [Google Scholar]
Bae, S. Y.; Chung, E.-C.; Lee, S. Y. Effects of urban railway transportation services on housing prices: case of apartments in Gyeonggi Province. J. of the Korea Real Estate Analysts Association 2018, 24, 85–98. [Google Scholar] [CrossRef]
Bae, S. W. Forecasting property prices using the machine learning methods: model comparisons. Ph.D. dissertation, Dept. of Urban Planning and Real Estate, Dankook University, Gyeonggi Province, South Korea, 2019.
Kim, H.; Kwon, Y.; Choi, Y. Assessing the impact of public rental housing on the housing prices in proximity: Based on the regional and local level of price prediction models using long short-term memory (LSTM). Sustainability 2020, 12, 7520. [Google Scholar] [CrossRef]
Song, Y. S.; Kim, H.; Cho, O.-S. Investigation of prediction of house price change in Seoul based on demographics with back propagation algorithm. J. The Inst. Elec. Inf. Eng. 2020, 57, 27–33. [Google Scholar]
Kim, H.-S. Machine learning forecasting of residential market: the case of innovation clusters. MBA thesis, Dept. Business Adminidtration, Hanyang University, Seoul, South Korea, 2021.
Snee, R. D. Validation of regression models: methods and examples. Technometrics 1977, 19, 415–428. [Google Scholar] [CrossRef]
Fahrmeir, L.; Kneib, T.; Lang, S.; Marx, B. Regression. Springer: Berlin, Heidelberg, 2013, pp. 21–72.
Koukouli, S.; Vlachonikolis, IG.; Philalithis, A. Socio-demographic factors and self-reported funtional status: the significance of social support. BMC Health Services Research 2002, 2, 20. [Google Scholar] [CrossRef]
Chiesura, A. The role of urban parks for the sustainable city. Landsc. Urban Plan. 2004, 68, 129–138. [Google Scholar] [CrossRef]
Vera-Toscano, E.; teca-Amestoy, V. The relevance of social interactions on housing satisfaction. Soc. Indic. Res. 2008, 86, 257. [Google Scholar] [CrossRef]
Cervero, R.; Duncan, M. Benefits of proximity to rail on housing markets: experiences in Santa Clara County. J. Public Transp. 2002, 5, 1–18. [Google Scholar] [CrossRef]
McMillen, P. D.; McDonald, J. Reaction of house prices to a new rapid transit line: Chicago’s Midway Line, 1983–1999. Real Estate Econ. 2004, 32, 463–486. [Google Scholar] [CrossRef]
Andersson, D. E.; Shyr, O. F.; Fu, J. Does high-speed rail accessibility influence residential property prices? Hedonic estimates from southern Taiwan. J. Transp. Geogr. 2010, 18, 166–174. [Google Scholar] [CrossRef]
Debrezion, G.; Pels, E.; Rietveld, P. The impact of rail transport on real estate prices: an empirical analysis of the Dutch housing market. Urban Stud. 2010, 48, 997. [Google Scholar] [CrossRef]
Efthymiou, D.; Antoniou, C. How do transport infrastructure and policies affect house prices and rents? Evidence from Athens, Greece. Transp. Res. Part A Policy Pract. 2013, 52, 1–22. [Google Scholar] [CrossRef]
Dai, X.; Bai, X.; Xu, M. The influence of Beijing rail transfer stations on surrounding housing prices. Habitat Int. 2016, 55, 79–88. [Google Scholar] [CrossRef]
Tan, R.; He, Q.; Zhou, K.; Xie, P. The effect of new metro stations on local land use and housing prices: the case of Wuhan, China. J. Transp. Geogr. 2019, 79, 102488. [Google Scholar] [CrossRef]
Berawi, M. A.; Miraj, P.; Saroji, G.; Sari, M. Impact of rail transit station proximity to commercial property prices: utilizing big data in urban real estate. J Big Data 2020, 7, 71. [Google Scholar] [CrossRef]
Yang, L.; Liang, Y.; He, B.; Yang, H.; Lin, D. COVID-19 moderates the association between to-metro and by-metro accessibility and house prices. Transp. Res. Part D Transp. Environ. 2023, 114, 103571. [Google Scholar] [CrossRef]
Okumura, T.; Ueda, K.; Iwamoto, Y.; Kanemoto, Y.; Shibata, A.; Yoshida, A.; Maquito, F. Housing investment and residential land supply in Japan:an asset market approach. J. Jpn. Int. Econ. 1997, 11, 27–54. [Google Scholar] [CrossRef]
Gonzalez, A. Resilience of microfinance institutions to national macroeconomic events: an econometric analysis of MFI asset quality. MIX Discussion Paper No. 1, Jul. 2007. Available online. [CrossRef]
Mikhed, V.; Zemčík, P. Do house prices reflect fundamentals? aggregate and panel data evidence. J. Hous. Econ. 2009, 18, 140–149. [Google Scholar] [CrossRef]
Genesove, D.; Han, L. Search and matching in the housing market. J. Urban Econ. 2012, 72, 31–45. [Google Scholar] [CrossRef]
Sun, H.; Wang, Y.; Li, Q. The impact of subway lines on residential property values in Tianjin: an empirical study based on hedonic pricing model. Discrete Dyn. Nat. Soc. 2016, 1478413. [Google Scholar] [CrossRef]
Hawkins, J.; Habib, K. N. Spatio-temporal hedonic price model to investigate the dynamics of housing prices in contexts of urban form and transportation services in Toronto. Transp. Res. Rec. 2018, 2672, 21–30. [Google Scholar] [CrossRef]
Lisi, G. Hedonic pricing models and residual house price volatility. L. Spat. Resour. Sci. 2019, 12, 133–142. [Google Scholar] [CrossRef]
Lieske, N. S.; Nouwelant, R.; Han, J. H.; Pettit, C. A novel hedonic price modelling approach for estimating the impact of transportation infrastructure on property prices. Urban Stud. 2021, 58, 182–202. [Google Scholar] [CrossRef]
Luo, H.; Zhao, S.; Yao, R. Determinants of housing prices in Dalian city, China: empirical study based on hedonic price model. J. Urban Plann. Dev. 2021, 147, 05021017. [Google Scholar] [CrossRef]
Park, B.; Bae, J. K. Using machine learning algorithms for housing price prediction: the case of Fairfax County, Virginia housing data. Expert Syst. Appl. 2015, 42, 2928–2934. [Google Scholar] [CrossRef]
Fan, C.; Cui, Z.; Zhong, X. 25–31 July 2020, House prices prediction with machine learning algorithms. In Proceesdings of The 37th International Conference on Machine Learning Conference, Vienna, Austria, , 6–10.
Varma, A.; Sarma, A.; Doshi, S.; Nair, R. House price prediction using machine learning and neural networks. Proceedings of Second International Conference on Inventive Communication and Computational Technologies, Coimbatore, India, 1936–1939., 20-21 April 2018. [Google Scholar]
Zhang, Q. Housing price prediction based on multiple linear regression. Sci. Program. 2021, 7678931. [Google Scholar] [CrossRef]
Peng, B.; Li, J.; Wang, Z.; Yang, R.; Liu, M.; Zhang, M.; Yu, P. S.; He, L. Lifelong property price prediction: A case study for the Toronto real sstate market. IEEE Trans. Knowl. Data Eng. 2023, 35, 2765–2780. [Google Scholar] [CrossRef]
Durai, S. A.; Wang, Z. Resale HDB price prediction considering covid-19 through sentiment analysis. In Proceedings of the 10th European Conference on Social Media, Krakow, Poland, 276–285., 18–19 May 2023. [Google Scholar]
Fan, C.; Wu, F.; Mostafavi, A. A hybrid machine learning pipeline for automated mapping of events and locations from social media in disasters. IEEE Access 2020, 8, 10478–10490. [Google Scholar] [CrossRef]
Monir, n.; Rasam, A.; Ghazali, R.; Suhandri, S. F. Address geocoding services in geospatial-based epidemiological analysis: a comparative reliability for domestic disease mapping. Int. J. Geoinformatics 2021, 17, 156–166. [Google Scholar]
Panecki, T. Mapping imprecision: how to eeocode data from inaccurate historic maps. ISPRS Int. J. Geo-Information 2023, 12, 149. [Google Scholar] [CrossRef]
Chopde, N. R.; Nichat, M. K. Landmark based shortest path detection by using a* and haversine formula. Int. J. Innov. Res. Comput. Commun. Eng. 2013, 1, 298–302. [Google Scholar]
Alam, C. N.; Manaf, K.; Atmadja, A. R.; Aurum, D. K. Implementation of haversine formula for counting event visitor in the radius based on Android application. In Proceedings of the th International Conference on Cyber and IT Service Management, Bandung, Indonesia, 1-6., 26-27 April 2016. [Google Scholar]
Aliyu, A.; Kemiki, O.; Bello, M. Transportation accessibility benefit and the dynamic pattern of real estate prices: emerging literature. Path of Sci. 2018, 4, 1001–1016. [Google Scholar] [CrossRef]
Liu, F.; Chen, K.; Zhang, T.; Zhang, Y.; Song, Y. Will good service quality promote real estate value? evidence from Beijing, China. Land 2022. 11, 166. [CrossRef]
Gupta, A.; Nieuwerburgh, S. V.; Kontokosta, C. Take the Q train: value capture of public infrastructure projects. J. Urban Econ. 2022, 129, 103422. [Google Scholar]
Goo, C.-H. Apartment brand 23 big data analysis results. Available online: https://brikorea.com/bbs/board.php?bo_table=rep_1&wr_id=2126. 20 January.
Kamp, H. Transport infrastructures and sustainability of urban development. J. Irish Urban Stud. 2002, 1, 37–46. [Google Scholar]
Lieske, S. N.; McLeod, D. M.; Coupal, R. H. Infrastructure development, residential growth and impacts on public service expenditure. Appl. Spatial Anal. Policy 2015, 8, 113. [Google Scholar] [CrossRef]
Farrar, D. E.; Glauber, R. R. Multicollinearity in regression analysis: the problem revisited. Rev. Econ. Stat. 1967, 49, 92–107. [Google Scholar] [CrossRef]
Dupuis, D. J.; Victoria-Feser, M.-P. Robust VIF regression with application to variable selection in large data sets. Ann. Appl. Stat. 2013, 7, 319–341. [Google Scholar] [CrossRef]
Donate, J. P.; Cortez, P.; Sánchez, G. G.; Miguel, A. S. Time series forecasting using a weighted cross-validation evolutionary artificial neural network ensemble. Neurocomputing 2013, 109, 27–32. [Google Scholar] [CrossRef]

1	In this paper, the terms ’variable’ and ’feature’ are used interchangeably.

Figure 1. Logarithmic scaling of the target variable, DLNG_AMOUNT (Sales Price). The left figures represent the data before scaling, while the right figures illustrate the data after the application of logarithmic scaling.

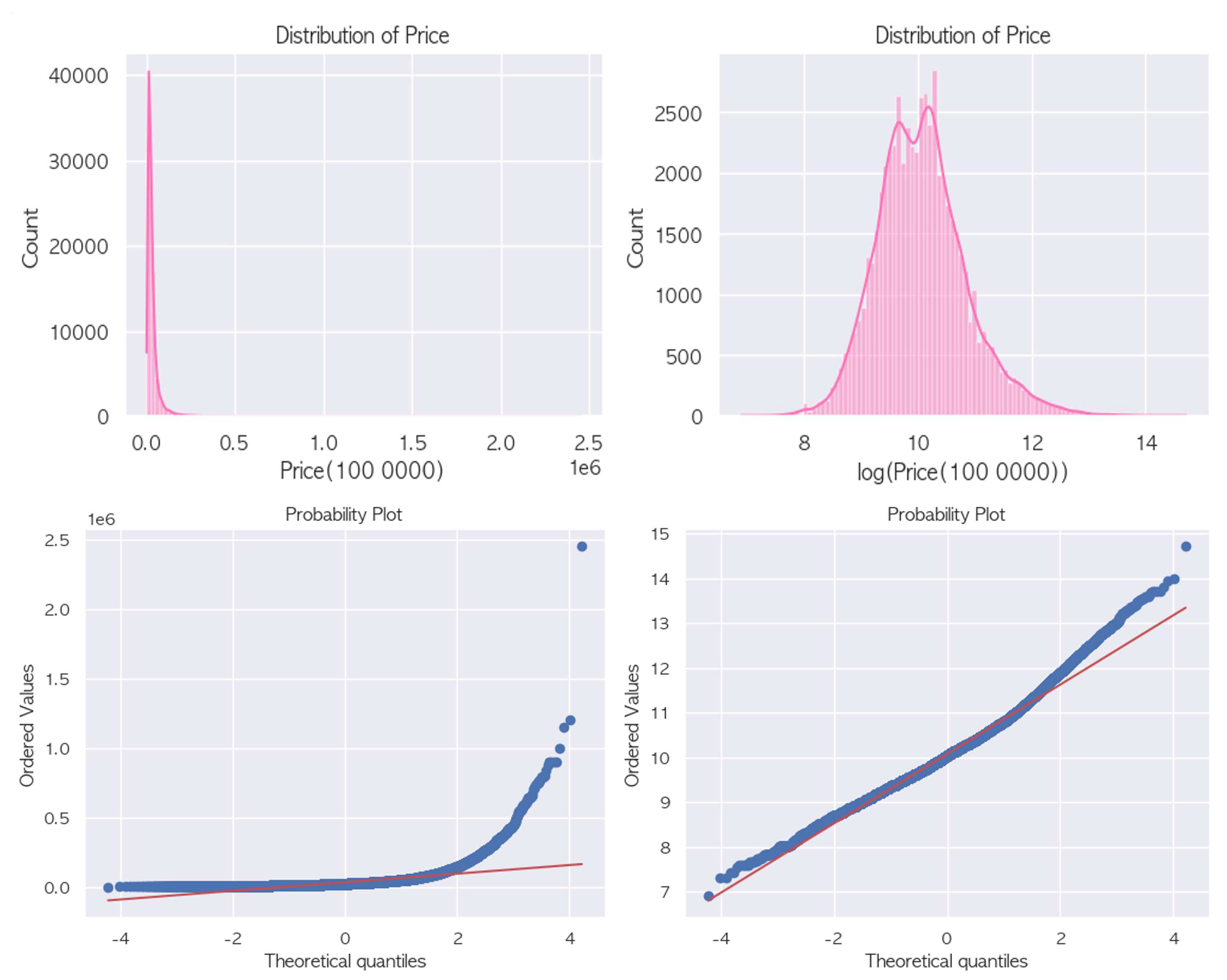
Figure 2. Bar chart illustrating the ranking of real estate prices per square meter in different regions based on actual transaction data. Each bar represents a different region, and the length of the bar denotes the price per square meter. The regions are ranked from highest to lowest based on their respective prices per square meter. This visualization highlights the spatial variations in real estate prices.

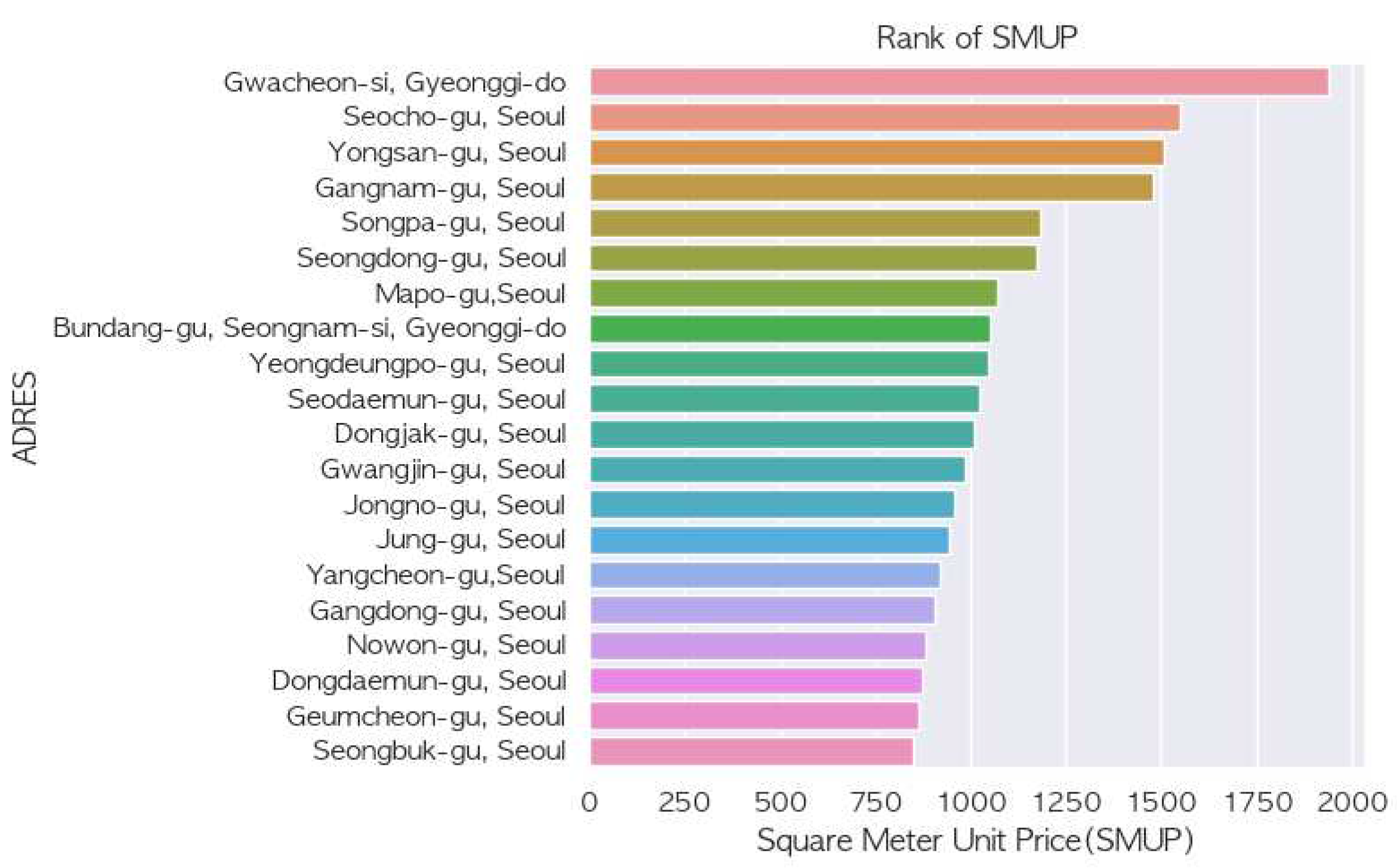
Figure 3. Variance Inflation Factor (VIF) values for all features: Assessing multicollinearity among input variables in the modeling process.

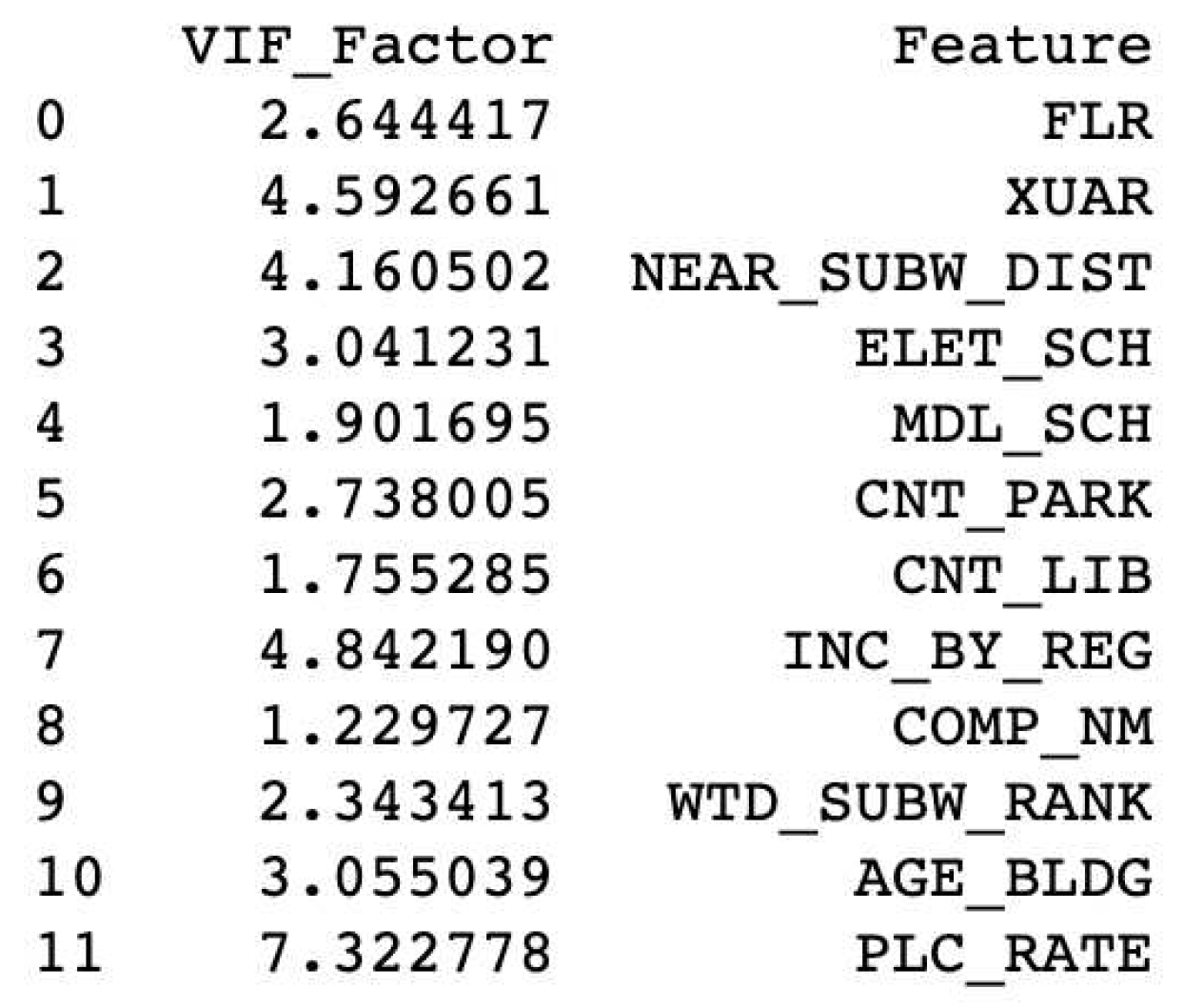
Figure 4. Nested Cross-Validation Process: Illustration of the step-by-step splitting of training and test datasets, emphasizing the hierarchical structure of hyperparameter tuning within the inner loop and performance evaluation in the outer loop.

Figure 5. Bar chart comparison of the average RMSLE values across eight models using cross-validation.

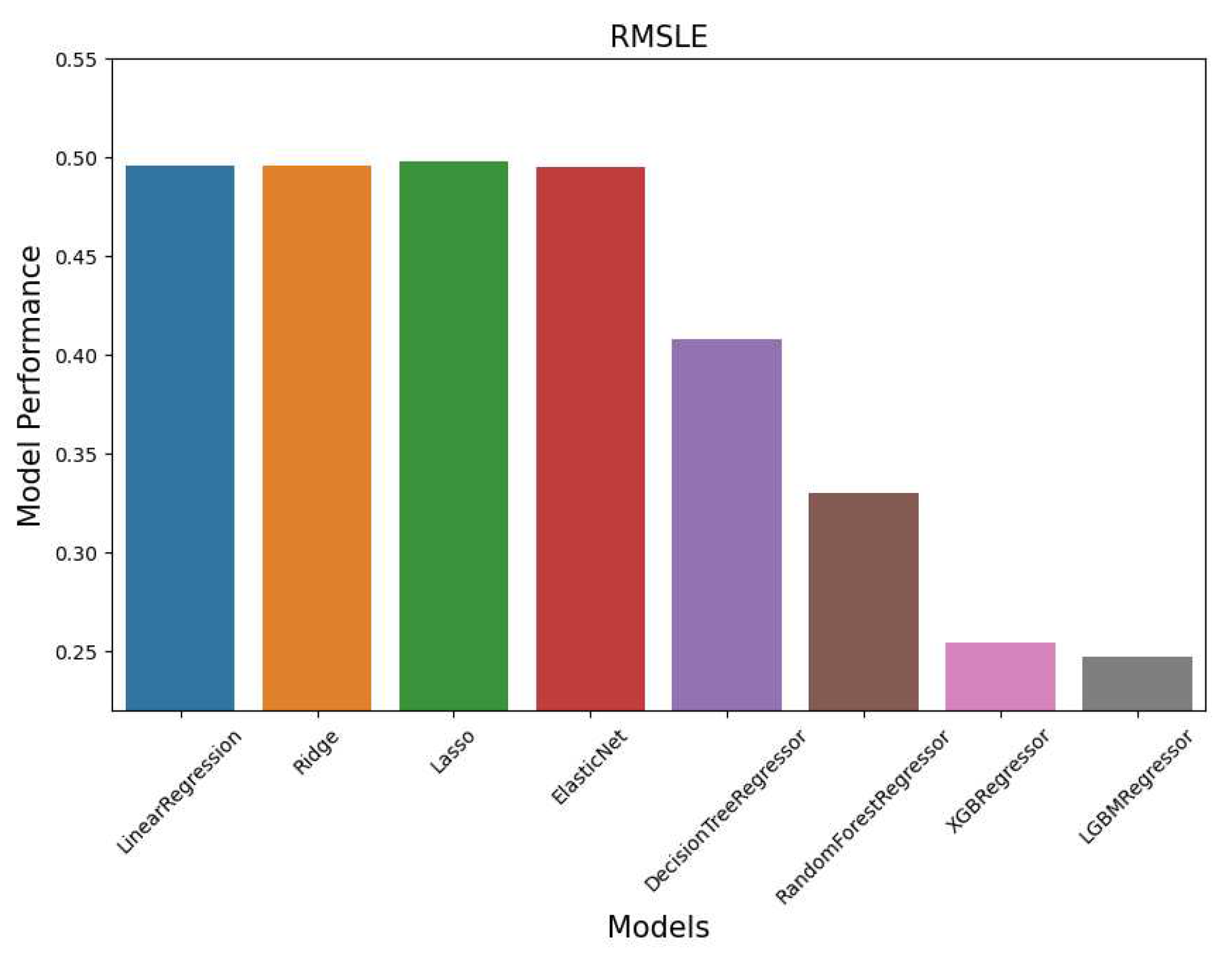
Figure 6. Feature importance rankings derived from the LightGBM model for housing prices.

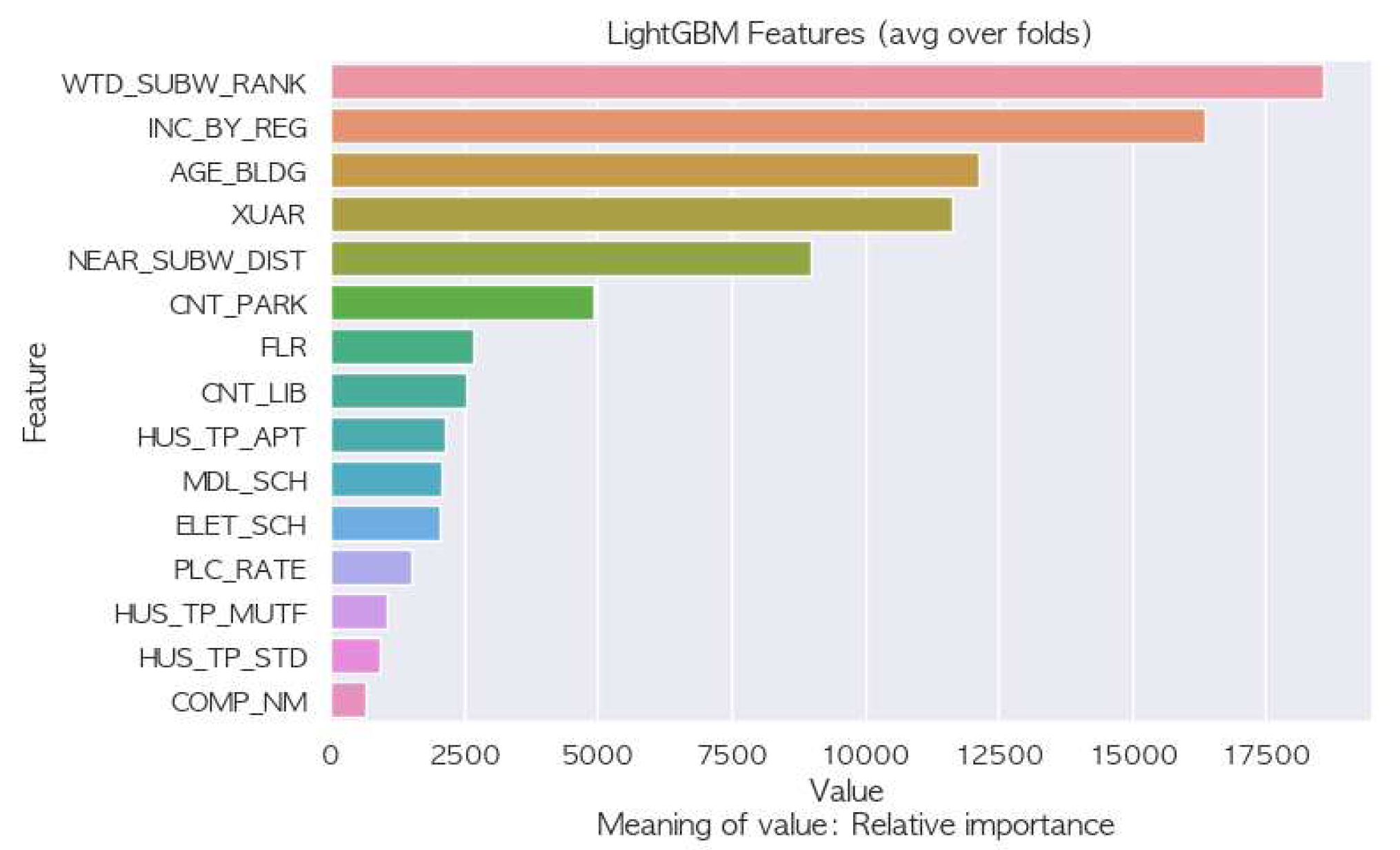
Table 1. Data Set Specification of Metro-Adjacent Residential Transaction provided by the Korea Real Estate Board.

Feature	Feature Description
SIGUNGU_CD	Municipality Code ¹
EMDL_CD	Submunicipality Code ²
CLL	Land Lot Classification (1: Regular, 2: Mountain)
MNO	Land Lot Number (Main) ³
SNO	Land Lot Number (Sub) ³
ADRES	Address Name (Legal District)
HUS_TP	Type of Multi-unit Housing (Apartment, Multi-family, Studio)
COMP_NM	Complex (Building) Name
BLDG_YEAR	Year of Construction
FLR	Floor Information
XUAR	Exclusive Area ( $m^{2}$ )
CTRT_YRMTH	Contract Year and Month
CTRT_DAY	Contract Day
TRANSCT_TYPE	Transaction Type (Sale, Jeonse ⁴, Monthly Rent)
DLNG_AMOUNT	Sale Price (in 10,000 KRW)
GRNTE_AMOUNT	Security Deposit (in 10,000 KRW)
MTHRNT_AMOUNT	Monthly Rent (in 10,000 KRW)
NEAR_SUBW_NM	Nearest Subway Station Name
NEAR_SUBW_DIST	Straight-line Distance to the Nearest Subway Station

¹ The `Municipality Code’ in this context is a unique identifier used specifically for designating administrative divisions in South Korea. ² The `Submunicipality Code’ is the hierarchical levels of administrative divisions in South Korea, from smaller (township/town/neighborhood) to larger (city/county/district). It’s used to identify specific areas within a city or county. ³ These terms refer to the identifiers used in the addressing system in Korea, similar to street names and house numbers in Western addressing systems. ⁴ In South Korea, it denotes a distinctive rental system where a large lump-sum deposit is made in lieu of monthly rent.

Table 2. Subway Operating Institutions by Line.

Line	Operating Institution
Incheon Subway Line 1 & 2, Urban Railway Line 7	Incheon Transit Corporation
Everline	Yongin Light Rail Corporation
Incheon International Airport Line	Airport Railroad Corporation
Ui LRT	Ui LRT Corporation
Shinbundang Line	DX Line
Greater Capital Area Light Rail Sillim Line	ROTEM SRS Co., Ltd.
Maglev	Incheon International Airport Terminal
Gimpo Gold Line	Gimpo Gold Line Co., Ltd.
Jinjeop Line	Namyangju City Corporation
Seoul Metro Lines 1-8 (part of Line 9)	Seoul Metro
Greater Capital Area Metro Line 9	Seoul Metro Line 9 Corporation
Uijeongbu LRT	Uijeongbu Light Rail Co., Ltd.
Gyeonggang Line, Gyeongbu Line, Janghang Line, Gyeongwon Line, Gyeongui Central Line, Gyeongin Line, Gyeongchun Line, Bundang Line, Suin Line, Gwacheon Line, Ansan Line, Ilsan Line, West Sea Line, Itx-Gyeongchun Line	Korea Railroad Corporation

Table 3. Summary of Input Features Utilized in the Modeling Process After Complete Preprocessing

Feature	Feature Description
WTD_SUBW_RANK	Ranking of subway stations based on weighted passenger volume
NEAR_SUBW_DIST	Distance between the property and the nearest subway station
INC_BY_REG	Ranked region based on weighted average income
PLC_RATE	Policy interest rate corresponding to the contract date
ELET_SCH	Number of elementary schools
MDL_SCH	Number of middle schools
CNT_PART	Number of parks
CNT_LIB	Number of libraries
FLR	Floor Information
XUAR	Exclusive Area ( $m^{2}$ )
COMP_NM	Branded construction company status
HUS_TP_APT	Apartment status
HUS_TP_STD	Studio status
HUS_TP_MUTF	Multi-Family status
LOG_PRICE	Log-transformed sale price
AGE_BLDG	Building age

Table 4. Overview of the Eight Machine Learning Models Employed in the Study, Highlighting Their Unique Characteristics and Features.

Model	Description
Linear Regression	A general linear regression learning model that reflects the correlation between explanatory and dependent variables.
Ridge Regression	A linear regression learning model with L1 regularization.
Lasso Regression	A linear regression learning model with L2 regularization.
ElasticNet Regression	A linear regression learning model that combines both L1 and L2 regularization.
Decision Tree	A tree-based learning model that branches in the direction of lower impurity and learns to minimize this impurity.
Random Forest	Utilizing Bagging, this tree-based learning model selects variables randomly, preventing overfitting typically seen in Decision Trees.
XGBoost	An ensemble tree-based learning model that utilizes boosting techniques. It inputs the loss of the previous model into the learning data and uses the gradient method to correct errors.
LightGBM	A tree-based learning model that minimizes error loss by employing methods like GOSS, EFB, and Leaf Wise.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Optimal Machine Learning Model for SOC Facilities’ Impact on Housing Prices

Abstract