Preprint
Article
The Improved Microwave Absorption Performance of the 3D Porous (Ni@NO-C)n/No-C Composite Absorber
Altmetrics
Downloads
77
Views
18
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
29 August 2023
Posted:
30 August 2023
You are already at the latest version
Alerts
Abstract
Microwave absorbers with lightweight, good stability and high efficiency have attracted much attention for their applications in many contemporary fields. In this work, the 3D porous (Ni@NO-C)n/NO-C composite absorber was prepared by a wet chemistry method with Ni chains and melamine as precursors, in which NO-C (N,O-doped carbon) encapsulated Ni particles are homogenously dispersed in the 3D porous networks of NO-C in the form of (Ni@NO-C)n chains. The special microstructure of the as-prepared material is proved to be benefit for the improvement of its microwave adsorption performance. The as-synthesized (Ni@NO-C)n/NO-C composite ab-sorber exhibited an effective absorption bandwidth of 4.1 GHz and an extremely large reflection loss of -72.3 dB. The excellent microwave absorbing performances can be ascribed to the coopera-tive consequence of dielectric loss and magnetic loss along with the balance between attenuation capability and impedance match.
Keywords:
Subject: Chemistry and Materials Science - Other
1. Introduction
Microwave absorbers (MAs) have attracted much attention for their applications in military defense, information safety and wireless data communication, etc. [1]. In contrast to traditional electromagnetic shielding reflection materials, MAs can convert electromagnetic waves into heat and other kinds of energy or dissipate them through interference [2]. In line with classical electromagnetic theory, electromagnetic waves are composed of rapidly oscillating electric field and magnetic field [3], and the absorption characteristics of MAs are highly dependent on their dielectric loss, magnetic loss and impedance matching [4]. Normally, the MAs with large dielectric losses are barium titanate ceramics [5], silicon carbide [6], conductive polymers [7], carbon materials [8], transition metal sulfides [9], whereas these with great magnetic losses are mainly composed of magnetic metals and their alloys or compounds[10,11].
To date, MAs with a single dielectric or magnetic loss are far from meeting the rapidly expending demands, and it is an effective way to improve the performance of electromagnetic wave absorption by constructing dual/multiple-component composite MAs, making full use of the loss mechanism of various materials [12]. As one of the most typical dual-component composite MAs, the magnetic metal/carbon composite has become the research focus in the field of electromagnetic wave absorption. Carbon materials, a kind of very important dielectric loss MAs, have the advantages of low density, excellent chemical stability, diverse microscopic morphology, adjustable dielectric constant and strong dielectric loss ability, etc. [13]. On the other hand, magnetic metals usually show strong magnetic loss ability because of their high saturation magnetization, Snoek limit and low coercivity [14]. It has been expected that the composite of magnetic metals and carbon materials can not only maintain the magnetic losses of magnetic metals but also strengthen the dielectric losses of carbon materials via high-intensity interface polarization, dipolar-oriented polarization and other polarization relaxation mechanism. Moreover, the impedance matching characteristics of the magnetic metal/carbon composites could be optimized by regulation of their microstructures and component metal/carbon ratios [15,16], and carbon materials are composited with magnetic metal in the form of coating, which can not only slow down the oxidation and corrosion rate of metal materials, but also reduce the overall density of composite materials. Therefore, researchers have conducted a lot of research on the preparation of magnetic metal/carbon composites. Li et al. [17] fabricated yolk−shell structured Co3Fe7@C with the precursor of (Co0.9Fe0.1)Fe2O4@phenolic resin, in which carbon shell can effectively prevent the oxidation and agglomeration of encapsulated metal alloy particles. Shen et al. [18] prepared porous Ni/NiO/carbon nanofibers by successive electrospinning, vacuum calcination and chemical etching, which exhibited a maximum reflection loss of -47.9 dB at 9.5 GHz. Sha et al. [19] constructed chemical Ni−C bonding by a microwave welding method at the interface between carbon nanotubes and Ni nanoparticles, which could induce a strong microwave absorption band in the range of 10 to 18 GHz. Ding et al. [20] synthesized Co nanoparticles loaded carbon nanosheets via a simple swelling and carbonization treatment of cellulose fibril and confirmed that the anisotropy derived from the lamellar structure of two-dimensional carbon materials was responsible for magnetic resonance. Qi et al. [21] prepared the composite of Co/CoO/LSC (lotus seedpod carbon) by carbonization of lotus seedpods and hydrogen reduction of Co3O4, in which the 3D porous biomass-derived carbon was proved to be conducive to microwave absorption for the improvement of impedance match and multiple scattering. All of the above works are based on the composites of 0D magnetic metals (or their alloys and oxides) and 0-3D carbon materials. Recently, Zhao et al [22] fabricated the triple-component composite of graphene aerogels, carbon nanotubes and CoNi chains (GA-CNT-CoNi) through a facile freeze-drying strategy and followed by thermal reduction, which demonstrated superior EM wave absorption performances because of the bridging roles played by 1D CoNi chains and CNTs to link graphene nanosheets for the construction of a conductive and macroscopic network.
On the basis of structural engineering, heteroatom doping/modification of carbon materials offers an effective approach to adjust the microwave absorption properties of the composites of magnetic metals/carbon materials [23,24]. Different from carbon atoms in atomic size, bond length, number of nuclear electrons and electron spin density, heteroatoms, e.g. B, N, P and S, could introduce a large number of point defect groups in the vicinity of carbon atoms, changing the surface electronic structure and forming an abundant defect dipoles to enhance dipole polarization in carbon materials [25]. Wang et al. [26] synthesized novel bowknot-like N doped carbon encapsulated Co nanoparticles, which exhibited excellent absorbing performance with a minimum reflection loss of -47.6 dB at 11.0 GHz. Zhang et al. [27] fabricated hollow N-doped carbon polyhedron (NCP) encapsulated CoNi@NC nanoparticles with zeolitic imidazolate frameworks-67 (ZIF-67) as a solid template and speculated that the C−N species on the surfaces of N-doped carbon contributed a lot to the dipole polarizations. Liu et al. [28] prepared cobalt nanoparticles decorated in N-doped carbon nanofibers (Co/N-C NFs) by electrospinning and annealing methods, whose excellent microwave absorption properties were ascribed to the proper impedance matching via adjusting the composition of the absorber and higher Co content. In addition, boron and nitrogen co-doped graphene nanosheets (BCN) [29] as well as sulfur doped graphene (S-GS) [30] were also prepared, in which the contributions of heteroatom doping to the microwave absorption properties of graphene were verified.
Herein, Ni chains were initially synthesized by a wet chemical method with the assistance of a hydrophilic polymer template. Subsequently, Ni chains and melamine were annealed in an inert atmosphere, and a composite microwave absorber consistent of NO-C encapsulated Ni nanoparticles (Ni@NO-C) and 3D NO-C was obtained. The as prepared Ni/ NO-C composite has a special microstructure and displays a largely improved microwave absorption performance both in the maximum reflection loss and in the effective absorption bandwidth, which might largely be owing to the in-situ grown (Ni@NO-C)n chains and the 3D porous networks of NO-C. The novel porous 3D magnetic metal/carbon composite fabricated in this work has the advantages over the previously reported 3D porous Ni chain networks [31] in lighter weight, better stability and more effective microwave absorption efficiency.
2. Materials and Methods
2.1. Materials
Nickel chloride hexahydrate (NiCl2·6H2O), hydrazine monohydrate (N2H4·H2O), and polyvinylpyrrolidone (PVP) were purchased from Shanghai Macklin Biochemical Co., Ltd. (Shanghai, China). Melamine, ethylene glycol (EG), anhydrous ethanol and ethanol were purchased from Tianjin Fuyu Fine Chemical Co., Ltd. (Tianjin, China). All the chemicals were analytical reagent grade and used without further purification.
2.2. Preparation of Ni nanoparticle-assembled chains
Ni nanoparticle-assembled chains were prepared by a templated wet chemical method [31] with PVP as soft template and ethylene glycol as solvent. Typically, after 1.08 g NiCl2·6H2O and 4 g PVP were completely dissolved in 300 ml ethylene glycol, a mixture of 1 ml hydrazine hydrate and 9 ml anhydrous ethanol was added dropwise under intensive stirring. With the color of the solution changed from grass green to blue, the reaction mixture was kept stirring for 30 min and then transferred to a three-necked flask. After refluxing for 1h in an oil bath, the gray participates were magnetically separated and washed with deionized water and ethanol for several times, and then dried at 313 K in vacuum oven for 12 h.
2.3. Fabrication of the 3D porous (Ni@NO-C)n/NO-C composite absorber
0.2 g Ni nanoparticle-assembled chains and 2.5 g melamine were homogeneously mixed in an agate mortar by vigorous grinding for 15 min, and then transferred to a quartz boat. Under the protection of argon gas, the powder mixture was heated in a tubular furnace to 750 ℃ at a heating rate of 5 ℃/min. After keeping for 3 h at 750 ℃, the black mixture was naturally cooled down to collect the 3D porous (Ni@NO-C)n/NO-C composite absorber.
2.4. Characterization methods
SEM and TEM were conducted on a field-emission scanning electron microscope (QUANTA 200S, FEI, Holland) and a transmission electron microscope (JEM2100, JEOL, Japan), respectively. Data of X-ray diffraction were collected by an X-ray diffractometer (XRD, D8 Advance, Bruker, German), and Raman scattering was recorded on a confocal Raman spectroscopic system (In Via, Renishaw, Britain) excited with a laser of 458 nm. The elemental composition and functional groups of materials were analyzed by a X-ray photoelectron spectrometer (Kratos-AXIS ULTRA DLD, SHIMADZU, Japan).
The electromagnetic parameters are obtained by a microwave vector network analyzer (N5230A, Agilent, America) in the frequency range of 2~18 GHz. The samples used for microwave absorption tests were composed of 3D porous (Ni@NO-C)n/NO-C composite absorber and paraffin with a mass ratio of 1:2, which were pressed into a ring with outer diameter, inner diameter and thickness of 7, 3 and 2 mm, respectively.
3. Results
The microstructure and morphology of the as-prepared Ni chains and the 3D porous (Ni@NO-C)n/NO-C composite absorber was characterized by SEM observation. As shown in Figure 1a, spherical Ni nanoparticles, whose mean diameter is about 100 nm, assembly to form bead chains with various lengths under the assistance of PVP molecular templates. In comparison to those reported previously [31], smaller Ni particles and shorter bead chains were achieved. Instead of aggregating to 3D nickel chain nets through the cross-linking with each other for longer nickel chains, the shorter Ni chains have smoother surfaces and are well isolated. It can be seen from Figure 1b that after pyrolysis at 750℃ with melamine the Ni chains are coated with N,O-C material which are derived from melamine. Moreover, the N,O-C coated Ni chains and N,O-doped carbon form 3D porous networks, in which Ni chains are homogenously dispersed in the porous nets of N,O-C material. On one hand, this magnetic metal/carbon composite with novel microstructure could be a kind of microwave absorber with high stability and lightweight. On the other hand, it could also be a kind of microwave absorber with high electromagnetic wave absorption efficiency because of its adjustable conductivity leaded the balance between impedance match and attenuation capability.
Shown in Figure 2a are the powder X-ray diffraction (XRD) patterns of Ni chains and the 3D porous (Ni@NO-C)n/NO-C composite absorber, in which the strong diffraction peaks observed at 44.5°, 51.9° and 76.4°could be indexed to the (111), (200) and (220) lattice planes of fcc-Ni (JCPDS 04-0850), respectively. For Ni chains, there are not any other observable diffraction peaks, indicating that the prepared Ni chains are of single phase and not obviously oxidized. For the 3D porous (Ni@NO-C)n/NO-C composite absorber, the weak diffraction peaks detected at 37.5°, 43.4° and 63.2°could be assigned to the (111), (200) and (220) lattice planes of fcc-NiO (JCPDS 47-1049), respectively. One can also find a small diffraction peak at 26.5°, which is ascribed to the (002) lattice plane of graphite, confirming the partial graphitization of carbon component in melamine. In line with Mering-Maire equation [32], the degree of graphitization was calculated to be 46.1%. Additionally, the full width at half maximum (FWHM) of the 3D porous (Ni@NO-C)n/NO-C composite absorber is much narrower than that of Ni chains, implying that the Ni crystallite size of the former is expected to be much larger than that of the later.
From the Raman spectrum of the 3D porous (Ni@NO-C)n/NO-C composite absorber displayed in Figure 2b, featured D, G and G’ bands are clearly observed at 1350, 1582 and 2700 cm-1, respectively. Based on the position (2700 cm-1) and multiple secondary structures of the G’ band, it can be concluded that multilayered graphite is formed via pyrolysis of melamine. Particularly, the disorder-induced D band is normally associated with the presence of in-plane substitutional heteroatoms, vacancies, grain boundaries, or other defects, and the intensity ratio of D and G bands (ID/IG) has been regarded as a direct indicator of the crystalline symmetry of carbon materials [33]. The ID/IG in area integral intensity is measured to be 1.6, which can be attributed to the plentiful defects and low crystalline symmetry for the carbon materials in the 3D porous (Ni@NO-C)n/NO-C composite absorber.
Displayed in Figure 3a is a typical TEM image of a Ni@NO-C particle in the 3D porous (Ni@NO-C)n/NO-C composite absorber. It is obvious that Ni nanoparticle is encapsulated in N,O-C material, in which the crystalline nickel core and partially graphited N,O-C layers could be clearly distinguished. This core-shell structured Ni@NO-C composite particle endows the composite of Ni chains and N,O-C with much improved stability. From the HR-TEM displayed in Figure 3b, it can be observed that the lattice spacing of crystalline Ni core is 0.203 nm, corresponding to the (111) lattice plane of fcc–Ni crystal, whereas the lattice spacing of partially graphited N,O-C layers is around 0.34 nm, corresponding to the (002) lattice plane of graphite. It should be noted that incomplete carbon layers grow unevenly around Ni nanoparticle, which might be a result of the competitive effect of neighbouring Ni particles in the same Ni chain. Moreover, the elemental mapping images shown in Figs. 3c–f evidence that the core is made of nickel and that nitrogen and oxygen are evenly distributed in the partially graphited carbon layers, offering solid supports both to the elemental composition and the core-shell structure of the Ni@NO-C composite particle.
The surface chemical state and elemental composition of the 3D porous (Ni@NO-C)n/NO-C composite absorber was investigated by XPS. From the survey XPS spectrum illustrated in Figure 4a, it can be seen that elements including Ni, C, N and O are present in the composite of Ni chains and N,O-doped carbon, whose relative molar contents are estimated to be 17.25%, 69.96%, 8.70% and 4.09%, respectively. In the deconvoluted Ni 2p spectrum (Figure 4b), the two main peaks at 853.9 and 871.6 eV correspond to the characteristic Ni 2p3/2 and Ni 2p1/2 ones of Ni, whereas the two peaks at 855.9 and 873.7 eV correspond to the characteristic Ni 2p3/2 and Ni 2p1/2 ones of NiO, and the two satellites detected around 860.8 and 879.5 eV offer further support for the presence of Ni atoms and Ni2+ ions in the 3D porous (Ni@NO-C)n/NO-C composite absorber. In the deconvoluted C 1s spectrum (Figure 4c), the peaks at 284.6, 285.4 and 288.5 eV are ascribed to C-C/C=C, C-N and C-O, respectively, indicating that the partially graphitized carbon layers are co-doped with nitrogen and oxygen elements. In the deconvoluted N 1s spectrum (Figure 4d), the peaks at 398.8, 400.8 and 403.1 eV are owing to the pyridinic, pyrrolic and graphitic nitrogen atoms, respectively. Of importance to note that the vast majority of nitrogen atoms are doped in the margins (pyridinic N) or defects (pyrrolic N) of the partially graphitized carbon layers. In the deconvoluted O 1s spectrum (Figure 4e), the peaks at 529.4, 532.1 and 533.8 eV can be attributed to Ni-O, C-O and C = O, respectively. It is assumed that oxygen atoms are covalently bonded to the surface of partially graphited carbon layers, apart from those bonded with Ni. Thus, XPS characterization confirms the nitrogen doping leaded high-density margins as well as oxygen-containing functional groups in the partially graphitized carbon layers.
When EM waves radiated to MAs, the impedance matching between MAs and free space is crucial, since only those MAs that satisfy impedance matching will allow as much radiated EM wave as possible to enter their interiors, paving the way for the subsequent absorption of EM wave. The complex permittivity and permeability of MAs play a significant role in microwave absorption. When the frequency of EM wave and the thickness of MAs are fixed, the impedance matching is only related to the complex permittivity and the complex permeability. Figure 5a illustrates the frequency dependence of the complex permittivity for the paraffin-based composite with 30 wt % (Ni@NO-C)n/NO-C over the 2.0-18.0 GHz frequency range. The real part of complex permittivity depicts the electrical energy storage due to the polarization of the electrical dipole, and the imaginary part of permittivity stands for energy conversion caused by relaxation of various polarizations. It can be found that the value of the real part (ε’) decreases largely from 12.06 at 2.0 GHz to 6.73 at 18.0 GHz with the increase in frequency, whereas the value of imaginary part (ε’’) changes from 3.44 to 2.16 in an oscillatory mode. In comparison with the real part (ε’), little variation is observed for the imaginary part (ε’’) of the paraffin-based composite with 30 wt% (Ni@NO-C)n/NO-C in the frequency range of 2–18 GHz, implying that the as-prepared EM absorbent has relatively stable dielectric loss ability. In line with Debye theory and free electron theory, the dielectric loss ability and relative complex permittivity of MAs are determined by their conductive loss and polarization relaxation behaviors. The conductive loss is associated with their electric conductivity, whereas polarization relaxation includes ionic polarization, electronic polarization, dipole orientation polarization and interfacial polarization. Since ionic polarization and electronic polarization usually occur in the high frequency range of 103 – 106 GHz, the interfacial polarization and intrinsic electric dipole polarization play important roles for the polarization relaxation of MAs. The multiple hierarchical interfaces (the barriers at defects, edges/boundaries or seams) in the composite of paraffin and (Ni@NO-C)n/NO-C contribute a lot to the multiple resonances observed in Figure 5a. On the other hand, the electrons undergoing dipolar polarization are usually associated with crystal defects, heterogeneous interfaces and the regions where the polarization of electron cloud occurs. For the (Ni@NO-C)n/NO-C absorbent, the dipoles originated from positive Ni2+ ions with their surrounding negative O2− ions, N,O-containing functional groups and plentiful defects in multi-layered graphite also contribute to dielectric constant (ε′) through dipolar polarization and to dielectric loss (ε″) through dipole relaxation, thus improving the dielectric loss ability of the microwave adsorption material [34,35].
In line with Debye relaxation theory, the relationship between ε´ and ε″ could be described by the following equation [36]:
where, εs is the static dielectric constant and ε∞ is the dielectric constant at infinite high frequency. Taking ε’’ as the ordinate and ε’ as the abscissa, the obtained curve is called Cole-Cole plot, in which each downward semicircle represents a dipole polarization relaxation process. In the Cole-Cole plot shown in Figure 5b, multiple semicircles are observed, confirm the existence of multiple dielectric relaxations in the paraffin-based composite with 30 wt% (Ni@NO-C)n/NO-C.
Displayed in Figure 5c is the frequency dependence of the complex permeability of the composite of paraffin and (Ni@NO-C)n/NO-C in the frequency range of 2–18 GHz. The real part of complex permeability depicts the magnetic energy storage, and the imaginary part of permeability stands for energy conversion. From Figure 5c, it can be seen that the real part (μ′) decreases oscillatingly from 1.12 at 2 GHz to 1.04 at 8.32 GHz and then increases oscillatingly to 1.23 at 18 GHz. Whereas, the imaginary part (μ″) increases oscillatingly from 0.078 at 2 GHz to 0.21 at 4.48 GHz and then decreases oscillatingly to 0.072 at 18 GHz. In contrast to the arc-discharged Ni@CNOs [37], the (Ni@NO-C)n/NO-C EM absorbent demonstrates positive value of imaginary part imaginary part (μ″ ), indicating its effective magnetic dissipation capacity. In addition, the fluctuation amplitude of the value of μ″ is much smaller than that of μ′ in the frequency range of 8–18 GHz, indicating that the as-prepared EM absorbent also has relative stable magnetic loss ability. According to the related theory of magnetic loss, magnetic loss involves a series of complex mechanisms, mainly including eddy current loss, exchange resonance, natural resonance, domain wall resonance and hysteresis loss. Since the domain wall resonance and hysteresis losses are negligible in the gigahertz range, the permeability of the composite of paraffin and (Ni@NO-C)n/NO-C might be mainly owing to eddy current loss, natural resonance and exchange resonance rather than magnetic hysteresis or domain wall resonance.
In order to explore the magnetic loss type of the sample, the eddy current coefficient C0 is calculated by the following equation [38]:
where, f is the frequency of incident electromagnetic waves. If the eddy current effect is the only origin of magnetic loss, the value of C0 will be a constant in the corresponding frequency range [39]. As shown in Figure 5d, the value of C0 fluctuates greatly in the frequency range of 2.0–18.0 GHz, indicating that natural resonance and exchange resonance contribute greatly to the magnetic loss mechanism. As a matter of fact, the nine peaks observed in Figure 5c are indicative of various ferromagnetic resonance modes. The relatively sharp resonance peaks between 2.0 and 11.0 GHz are attributed to the natural resonance from static magnetic energy, while the relatively broad resonance peaks between 11.0 and 18.0 GHz belong to exchange resonance among different magnetic nanoparticles [40]. It is widely accepted that natural resonance is affected by the inherent properties of the material itself, such as size, morphology and other factors. The multiple natural resonances of (Ni@NO-C)n/NO-C can be attributed to the discrete distributions of different-sized NO-C encapsulated Ni@NO-C nanoparticles or their (Ni@NO-C)n chains. On the other hand, exchange resonance is usually associated with spin-wave excitations, small size effect, and surface effect of small-size magnetic nanoparticles in the higher frequency range [40]. For the as-prepared (Ni@NO-C)n/NO-C EM absorbent, the Ni cores (or short Ni chains) are insulated by nitrogen and oxygen co-doped graphite layers, which can intensely suppress the eddy current effect. Therefore, the magnetic loss of the as-prepared (Ni@NO-C)n/NO-C EM absorbent are mainly originated from resonance loss.
The as-prepared (Ni@NO-C)n/NO-C absorbent exhibits a remarkable microwave absorption performance. Shown in Figure 6a is the 3D plot of reflection loss (RL) values versus frequency and thickness for the paraffin-based composite with 30 wt% (Ni@NO-C)n/NO-C. The RL values are calculated based on transmit line theory according to the experimentally measured complex permittivity and permeability [10]. At a thickness of 2.0 mm, the effective absorption bandwidth reaches 4.3 GHz (11.7 to 16.0GHz) and the maximum reflection loss reaches -20.3 dB at 13.28 GHz. When the thickness is 2.5 mm, the frequency band that can achieve effective absorption is from 8.4 to 12.4 GHz, and the maximum of reflection loss reached to -58.1 dB at 10.9 GHz. At a thickness of 2.9 mm, the effective absorption bandwidth reaches 4.2 GHz (6.9 to 11.1 GHz) and the maximum reflection loss reaches -72.3 dB at 8.2 GHz. When the thickness is 4.0 mm, the frequency band that can achieve effective absorption is from 5.4 to 7.4 GHz, and the maximum of reflection loss reached to -71.8 dB at 5.7 GHz. For comparison, Table 1 lists the microwave absorption data of typical Ni/carbon composite absorbers reported in recent years. It is obvious that the microwave absorption performance of the as-prepared (Ni@NO-C)n/NO-C is superior to most reported Ni/carbon composite absorbers.
The excellent microwave absorption performance can be attributed to the cooperative consequence of dielectric loss and magnetic loss owing to the specific microstructure of the (Ni@NO-C)n/NO-C composite EM absorbent. To evaluate the loss ability of the electromagnetic energy, the dielectric loss tangent (tan δε = ε″/ε′) and magnetic loss tangent (tan δμ = μ″/μ′) are calculated and shown in Figure 6b. It is obvious that tan δε is larger than tan δμ in the measured frequency range, indicating that dielectric losses play more important roles than magnetic losses for the as-prepared (Ni@NO-C)n/NO-C absorbent. Moreover, multiple resonances are observed for tan δε, which do not incompletely appear in pairs with those of tan δμ at the same frequency, implying an unbalanced energy conversion between complex permittivity and complex permeability [51]. In comparison with those magnetic metal/carbon composites reported previously [37,52,53,54], the as-prepared Ni@NO-C)n/NO-C EM composite material exhibits the richest multiple resonances, which might be attributed to its special microstructure and the doping effect of nitrogen and oxygen in multi-layered graphite. From Figure 6b, it can also be seen that there are several maxima in the magnetic loss tangent (tan δμ)−frequenc curve, indicating also that the magnetic loss is mostly attributed to multiple magnetic resonances, i.e. natural resonance and exchange resonance. Of interest to note that the as-prepared (Ni@NO-C)n/NO-C composite exhibits much narrower gap between tan δε and tan δμ at the same frequency than the arc-discharged Ni@CNOs composite nanoparticles [55], and it is expected that matched characteristic impedance would lead more radiated EM wave to enter the interiors of the as-prepared (Ni@NO-C)n/NO-C absorbent, which is benefit for the subsequent absorption of EM wave.
Strong attenuation capability is a crucial factor for excellent EMW absorption materials. The attenuation constant α determines the total loss ability of absorption materials and features the amplitude attenuation of EM waves. The attenuation constant α of the as-prepared (Ni@NO-C)n/NO-C absorbent can be calculated by the following equation [56]:
where, c is the velocity of EM waves in free space. It can be seen from Figure 6c that the attenuation constant of the as-prepared (Ni@NO-C)n/NO-C absorbent fluctuatingly increases from 28.0 at 2.0 GHz to 203.6 at 18.0 GHz with the increase in frequency, among which some maxima appear at 4.8, 7.3, 10.2 and 13.5 GHz. The attenuation constant value of the as-prepared (Ni@NO-C)n/NO-C absorbent is lower than that of yolk−shell structured Co3Fe7@C [17], which could be ascribed to the nitrogen and oxygen doping effect leaded the decrease in conductivity, whereas it is comparable to the waxberry-like hierarchical Ni@C microspheres [55].
Good impedance matching is another crucial factor for excellent EMW absorption materials. The coefficient of impedance match determines whether the EMW can enter the interior of the absorber, which is expressed by the following equation [57,58]:
where Zin is the input impedance, Z0 is the wave impedance in free space, μr is the complex permeability, εr is the complex permeability, j is the complex unit, f is the frequency, d is the thickness, and c is the velocity of EM waves in free space. When the input impedance Zin is numerically equal to the wave impedance in free space, the normalized input impedance Z value is equal to 1 and then the microwave can enter the absorbing material to the greatest extent. Therefore, the absorber shows better impedance match when Z is close to 1. Displayed in Figure 6d are the 3D Z values of the as-prepared (Ni@NO-C)n/NO-C absorbent calculated in the thickness range of 1.0 – 5.5 mm and in the frequency range of 2 – 18 GHz. It is obvious that good impedance matching could be achieved for the as-prepared absorbent by adjusting thickness and frequency to get Z value close to 1, and the thinner the sample is the higher the impedance matching frequency is. The four black dots observed in Figure 6d mark the thickness and frequency corresponding to the maximum reflection losses and the widest effective absorption bandwidth of the as-prepared sample (see Figure 6a), whose impedance matching coefficient (Z) are in the range of 0.60 – 1.18, showing the balance between attenuation capability and impedance match. .
4. Conclusions
In summary, 3D porous (Ni@NO-C)n/NO-C composite absorber was prepared by pyrolysis of Ni chains and melamine, whose unique microstructure contributes greatly to its quite good microwave wave absorption performance. The NO-C materials contribute a tailored dielectric loss through conductivity modification and multiple interfacial and intrinsic electric dipole polarizations, while the (Ni@NO-C)n chains dispersed in the 3D porous networks of NO-C material offer a proper magnetic loss owing to natural and exchange resonances. Moreover, the multiple resonances observed in the curves of dielectric loss tangent and magnetic loss tangent make it easy to achieve good impedance match, which is benefit for the improvement of the maximum reflection loss and the effective absorption bandwidth of the as-prepared 3D porous (Ni@NO-C)n/NO-C composite absorber. It is believed that the microwave absorption performances of the as-prepared absorber could be further improved by complete optimization of its composition and microstructure, and the 3D porous (Ni@NO-C)n/NO-C composite material has the potential as a high-efficiency microwave adsorption absorber with lightweight and high stability.
Author Contributions
Xinmeng Jia: Conceptualization, Investigation, Writing - original draft, Writing - review & editing. Chao Ruan: Conceptualization,Validation. Zhigang Li: Resources. Yongfu Lian: Supervision,Writing - review & editing, Funding acquisition.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 51572071), and the Program for Innovative Research Team in University (Grant No. T–1237), Ministry of Education,China.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Zhang:, D.; Deng, Y.; Han, C.; Zhu, H.; Yan, C.; Zhang, H. Enhanced Microwave Absorption Bandwidth in Graphene-Encapsulated Iron Nanoparticles with Core-Shell Structure. Nanomaterials. 2020, 10, 931. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Jiang, C.; Duan, X.; Song, J.; Yuan, Y.; Chen, N. Fe3O4/carbonized cellulose micro-nano hybrid for high-performance microwave absorber. Carbohydr. Polym. 2020, 245, 116531. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; . Li, Y.; Zhang, H.-B; Zhang, Y.; Luo, J.-Q.; Liu, L.-X.; Yu, Z.-Z. Lightweight Fe@C hollow microspheres with tunable cavity for broadband microwave absorption. Composites Part B: Eng. 2019, 177, 107346. [Google Scholar] [CrossRef]
- Adam, M.; Hart, A.; Stevens, L.A.; Wood, J.; Robinson, J.P.; Rigby, S.P. Microwave synthesis of carbon onions in fractal aggregates using heavy oil as a precursor. Carbon. 2018, 138, 427–435. [Google Scholar] [CrossRef]
- Cui, L.; Tian, C.; Tang, L.; Han, X.; Wang, Y.; Liu, D.; Xu, P.; Li, C.; Du, Y. Space-Confined Synthesis of Core-Shell BaTiO3@Carbon Microspheres as a High-Performance Binary Dielectric System for Microwave Absorption. ACS Appl. Mater. Interfaces. 2019, 11, 31182–31190. [Google Scholar] [CrossRef]
- Lv, X.; Ye, F.; Cheng, L.; Zhang, L. 3D printing “wire-on-sphere” hierarchical SiC nanowires / SiC whiskers foam for efficient high-temperature electromagnetic wave absorption. J. Mater. Sci. Technol. 2022, 109, 94–104. [Google Scholar] [CrossRef]
- Li, C.; Sui, J.; Jiang, X.; Zhang, Z.; Yu, L. A sustainable construction of an efficient lightweight microwave absorber from polymeric sponge. Ceram. Int. 2019, 45, 18572–18582. [Google Scholar] [CrossRef]
- Inagaki, M.; Toyoda, M.; Soneda, Y.; Morishita, T. Nitrogen-doped carbon materials. Carbon. 2018, 132, 104–140. [Google Scholar] [CrossRef]
- Bai, X.; Wang, L.; Lin, Y. Hierarchical N, S-codoped honeycomb-like porous C@Co9S8@CNTs structure as high-performance microwave absorber. Mater Lett. 2020, 264, 27342. [Google Scholar] [CrossRef]
- Shen, Z.; Yang, H.; Xiong, Z.; Xie, Y.; Liu, C. Hollow core-shell CoNi@C and CoNi@NC composites as high-performance microwave absorbers. J. Alloys Compd. 2021, 871, 159574. [Google Scholar] [CrossRef]
- Park, J.-H.; Lee, S.; Chul, J.; Ro, S.-J. Suh, Yolk–shell Fe–Fe3O4@C nanoparticles with excellent reflection loss and wide bandwidth as electromagnetic wave absorbers in the high-frequency band. Appl. Surf. Sci. 2022, 573, 151469. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Q.; Fu, Y.; Liu, T. A review on carbon/magnetic metal composites for microwave absorption. J. Mater. Sci. Technol. 2021, 86, 91–109. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Z.; Qi, L.; Liao, Q.; Kang, Z.; Zhang, Y. Toward the Application of High Frequency Electromagnetic Wave Absorption by Carbon Nanostructures. Adv Sci (Weinh). 2019, 6, 1801057. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, X.; Quan, B.; Ji, G.; Liang, X.; Liu, W.; Du, Y. A facile self-template strategy for synthesizing 1D porous Ni@C nanorods towards efficient microwave absorption. Nanotechnology. 2017, 28, 115704. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Di, X.; Gao, X.; Wu, X.; Wang, P. Rational construction of Co@C polyhedrons covalently-grafted on magnetic graphene as a superior microwave absorber. J. Alloys Compd. 2020, 843, 156031. [Google Scholar] [CrossRef]
- Yan, J.; Huang, Y.; Yan, Y.; Zhao, X.; Liu, P. The composition design of MOF-derived Co-Fe bimetallic autocatalysis carbon nanotubes with controllable electromagnetic properties. Compos. Part A Appl.Sci. Manufacturing. 2020, 139, 106107. [Google Scholar] [CrossRef]
- Li, H.; Bao, S.; Li, Y.; Huang, Y.; Chen, J.; Zhao, H.; Jiang, Z.; Kuang, Q.; Xie, Z. Optimizing the Electromagnetic Wave Absorption Performances of Designed Co3Fe7@C Yolk-Shell Structures. ACS Appl. Mater. Interfaces. 2018, 10, 28839–28849. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, F.; Song, P.; Zhang, Y.; Zhang, T.; Wen, X.; Ma, J.; Zhang, D.; Du, X. Design and synthesis of magnetic porous carbon nanofibers with excellent microwave absorption. J. Alloys Compd. 2022, 903, 163971. [Google Scholar] [CrossRef]
- Sha, L.; Gao, P.; Wu, T.; Chen, Y. Chemical Ni-C Bonding in Ni-Carbon Nanotube Composite by a Microwave Welding Method and Its Induced High-Frequency Radar Frequency Electromagnetic Wave Absorption. ACS Appl. Mater. Interfaces. 2017, 9, 40412–40419. [Google Scholar] [CrossRef]
- Ding, Y.; Bai, J.; Liu, H.; Zhang, Y.; Li, K.; Yang, P.-a.; Zhang, Y.; Bao, Z. Nitrogen-doped carbon nanosheets homogeneously embedded with Co nanoparticles via biostructure confinement as highly efficient microwave absorbers. Appl. Surf. Sci. 2022, 590, 153119. [Google Scholar] [CrossRef]
- Qi, Y.; Qin, Y.; Kimura, H.; Wang, Y.; Yang, Y.; Ni, C.; Yu, X.; Huang, C.; Tian, J.; Liu, R.; Du, W.; Xie, X. Co/CoO/Lotus Seedpod Nanoporous Carbon Composites Reduced from Co3O4 for High-Performance Microwave Absorbers. ACS Applied Nano Materials. 2023, 6, 4681–4692. [Google Scholar] [CrossRef]
- Zhao, B.; Li, Y.; Ji, H.; Bai, P.; Wang, S.; Fan, B.; Guo, X.; Zhang, R. Lightweight graphene aerogels by decoration of 1D CoNi chains and CNTs to achieve ultra-wide microwave absorption. Carbon. 2021, 176, 411–420. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, C.; Xian, G.; Zhu, Z.; Liu, Y.; Kong, L.B. Synthesis of nitrogen-doped polyaniline-derived carbon/Ni3Fe nanocomposites as high-performance microwave absorbers. J. Alloys Compd. 2022, 924, 166585. [Google Scholar] [CrossRef]
- Ning, M.; Li, J.; Kuang, B.; Wang, C.; Su, D.; Zhao, Y.; Jin, H.; Cao, M. One-step fabrication of N-doped CNTs encapsulating M nanoparticles (M = Fe, Co, Ni) for efficient microwave absorption. Appl. Surf. Sci. 2018, 447, 244–253. [Google Scholar] [CrossRef]
- Dai, W.; Luo, F. H.; Xiong, Y.; Wang, X.; Cheng, Y.; Gong, R. Synthesis of yolk-shell structured carbonyl iron@void@nitrogen doped carbon for enhanced microwave absorption performance. J. Alloys Compd. 2020, 812, 152083. [Google Scholar] [CrossRef]
- Wang, J.; Li, Q.; Ren, J.; Zhang, A.; Zhang, Q.; Zhang, B. Synthesis of bowknot-like N-doped Co@C magnetic nanoparticles constituted by acicular structural units for excellent microwave absorption. Carbon. 2021, 181, 28–39. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, F.; Zhang, S.; Yuan, H.; Zhu, C.; Zhang, X.; Chen, Y. Hollow N-Doped Carbon Polyhedron Containing CoNi Alloy Nanoparticles Embedded within Few-Layer N-Doped Graphene as High-Performance Electromagnetic Wave Absorbing Material. ACS Appl. Mater. Interfaces. 2018, 10, 24920–24929. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Li, Y.; Yuan, M.; Sun, G.; Li, H.; Ma, S.; Liao, Q.; Zhang, Y. In Situ Preparation of Cobalt Nanoparticles Decorated in N-Doped Carbon Nanofibers as Excellent Electromagnetic Wave Absorbers. ACS Appl. Mater. Interfaces. 2018, 10, 22591–22601. [Google Scholar] [CrossRef]
- Kang, Y.; Chu, Z.; Zhang, D.; Li, G.; Jiang, Z.; Cheng, H.; Li, X. Incorporate boron and nitrogen into graphene to make BCN hybrid nanosheets with enhanced microwave absorbing properties. Carbon, 2013, 61, 200–208. [Google Scholar] [CrossRef]
- Tan, L.; Zhu, M.; Li, X.; Feng, H.; Chen, N.; Zhao, D. Lightweight excellent microwave absorption properties based on sulfur doped graphene, J. Saudi Chem. Soc. 2020, 24, 9–19. [Google Scholar] [CrossRef]
- Liu, J.; Cao, M.S.; Luo, Q.; Shi, H.L.; Wang, W.Z.; Yuan, J. Electromagnetic Property and Tunable Microwave Absorption of 3D Nets from Nickel Chains at Elevated Temperature. ACS Appl. Mater. Interfaces. 2016, 8, 22615–22622. [Google Scholar] [CrossRef] [PubMed]
- Heckmann, A.; Fromm, O.; Rodehorst, U.; Münster, P.; Winter, M.; Placke, T. New insights into electrochemical anion intercalation into carbonaceous materials for dual-ion batteries: impact of the graphitization degree. Carbon. 2018, 131, 201–212. [Google Scholar] [CrossRef]
- Yi, P.; Yao, Z.; Zhou, J.; Wei, B.; Lei, L.; Tan, R.; Fan, H. Facile synthesis of 3D Ni@C nanocomposites derived from two kinds of petal-like Ni-based MOFs towards lightweight and efficient microwave absorbers. Nanoscale. 2021, 13, 3119–3135. [Google Scholar] [CrossRef] [PubMed]
- He, G.; Duan, Y.; Pang, H. Microwave Absorption of Crystalline Fe/MnO@C Nanocapsules Embedded in Amorphous Carbon. Nanomicro. Lett. 2020, 12, 57. [Google Scholar] [CrossRef]
- Di, X.; Wang, Y.; Fu, Y.; Wu, X.; Wang, P. Wheat flour-derived nanoporous carbon@ZnFe2O4 hierarchical composite as an outstanding microwave absorber. Carbon. 2021, 173, 174–184. [Google Scholar] [CrossRef]
- Yang, R.; Yuan, J.; Yu, C.; Yan, K.; Fu, Y.; Xie, H.; Chen, J.; Chu, P.; Wu, X. Efficient electromagnetic wave absorption by SiC/Ni/NiO/C nanocomposites. J. Alloys Compd. 2020, 816, 152519. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, Q.; Zhao, H.; Ruan, C.; Wang, Y.; Li, Z.; Lian, Y. The arc-discharged Ni-cored carbon onions with enhanced microwave absorption performances. Mater Lett. 2020, 265, 16374–16385. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Xiang, Z.; Zhu, X.; Dong, Y.; Huang, C.; Cai, L.; Lu, W. Biconical prisms Ni@C composites derived from metal-organic frameworks with an enhanced electromagnetic wave absorption. Carbon, 2021, 184, 115–126. [Google Scholar] [CrossRef]
- Wu, N.; Liu, D.; Xu, J.; Liu, W.; Shao, Q.; Guo, Z. Enhanced Electromagnetic Wave Absorption of Three-Dimensional Porous Fe3O4/C Composite Flowers, ACS Sustain. Chem. Eng. 2018, 6, 12471–12480. [Google Scholar]
- Su, X.G.; Han, M.J.; Wang, J.; . Wu, Q.L; Duan, H.J.; Liang, C.B.; Zhang, S.C.; Pu, Z.Z.; Liu, Y.Q. Regulated dielectric loss based on core-sheath carbon-carbon hierarchical nanofibers toward the high-performance microwave absorption, J. Colloid Interface Sci. 2022, 624, 619–628. [Google Scholar] [CrossRef]
- Qiu, Y.; Lin, Y.; Yang, H.; Wang, L.; Wang, M.; Wen, B. Hollow Ni/C microspheres derived from Ni-metal organic framework for electromagnetic wave absorption. Chem. Eng. J. 2020, 383. [Google Scholar] [CrossRef]
- Li, J.; Zhang, F.; Lu, H.; Guo, W.; He, X.; Yuan, Y. Heterogeneous rod-like Ni@C composites toward strong and stable microwave absorption performance. Carbon, 2021, 181, 358–369. [Google Scholar] [CrossRef]
- Li, S.-T.; Shi, G.-M.; Li, Q.; Shi, F.-N.; Wang, X.-L.; Yang, L.-M. One-step synthesis and performances of Ni@CN nanocapsules with superior dual-function as electrocatalyst and microwave absorbent. Colloids Surf. Physicochem. Eng. Asp. 2021, 615, 126162. [Google Scholar] [CrossRef]
- Hu, S.; Zhou, Y.; He, M.; Liao, Q.; Yang, H.; Li, H.; Xu, R.; Ding, Q. Hollow Ni-Co layered double hydroxides-derived NiCo-alloy@g-C3N4 microtubule with high-performance microwave absorption. Mater Lett. 2018, 231, 171–174. [Google Scholar] [CrossRef]
- Xie, P.; Li, H.; He, B.; Dang, F.; Lin, J.; Fan, R.; Hou, C.; Liu, H.; Zhang, J.; Ma, Y.; Guo, Z. Bio-gel derived nickel/carbon nanocomposites with enhanced microwave absorption. J. Mater. Chem. C 2018, 6, 8812–8822. [Google Scholar] [CrossRef]
- Qiu, S.; Lyu, H.; Liu, J.; Liu, Y.; Wu, N.; Liu, W. Facile Synthesis of Porous Nickel/Carbon Composite Microspheres with Enhanced Electromagnetic Wave Absorption by Magnetic and Dielectric Losses. ACS Appl. Mater. Interfaces. 2016, 8, 20258–20266. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, X.; Quan, B.; Ji, G.; Liang, X.; Liu, W.; Du, Y. A facile self-template strategy for synthesizing 1D porous Ni@C nanorods towards efficient microwave absorption. Nanotechnology. 2017, 28, 115704. [Google Scholar] [CrossRef]
- Liu, W.; Shao, Q.; Ji, G.; Liang, X.; Cheng, Y.; Quan, B.; Du, Y. Metal–organic-frameworks derived porous carbon-wrapped Ni composites with optimized impedance matching as excellent lightweight electromagnetic wave absorber. Chem. Eng. J. 2017, 313, 734–744. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, G.; Luo, J.; Hu, Y.; Hao, G.; Guo, H.; Guo, F.; Wang, S.; Jiang, W. A MOFs-derived 3D superstructure nanocomposite as excellent microwave absorber. Chem. Eng. J. 2021, 426, 130725. [Google Scholar] [CrossRef]
- Han, X.; Huang, Y.; Ding, L.; Song, Y.; Li, T.; Liu, P. Ti3C2Tx MXene Nanosheet/Metal–Organic Framework Composites for Microwave Absorption. ACS Appl. Nano Mater. 2020, 4, 691–701. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, S.-J.; Li, D.-S.; Jiang, L. Lightweight and recoverable ANF/rGO/PI composite aerogels for broad and high-performance microwave absorption. Compos. B Eng. 2021, 213, 108701. [Google Scholar] [CrossRef]
- Feng, J.; Pu, F.; Li, Z.; Li, X.; Hu, X.; Bai, J. Interfacial interactions and synergistic effect of CoNi nanocrystals and nitrogen-doped graphene in a composite microwave absorber. Carbon, 2016, 104, 214–225. [Google Scholar] [CrossRef]
- Li, X.-P.; Deng, Z.; Li, Y.; Zhang, H.-B.; Zhao, S.; Zhang, Y.; Wu, X.-Y.; Yu, Z.-Z. Controllable synthesis of hollow microspheres with Fe@Carbon dual-shells for broad bandwidth microwave absorption. Carbon 2019, 147, 172–181. [Google Scholar] [CrossRef]
- Li, W.; Li, W.C.; Ying, Y.; Yu, J.; Zheng, J.; Qiao, L.; Li, J.; Che, S. Multifunctional flower-like core-shell Fe/Fe4N@SiO2 composites for broadband and high-efficiency ultrathin electromagnetic wave absorber. J. Mater. Sci. Technol. 2023, 132, 90–99. [Google Scholar] [CrossRef]
- Liu, D.; Du, Y.; Xu, P.; Wang, F.; Wang, Y.; Cui, L.; Zhao, H.; Han, X. Rationally designed hierarchical N-doped carbon nanotubes wrapping waxberry-like Ni@C microspheres for efficient microwave absorption. J. Mater. Chem. A. 2021, 9, 5086–5096. [Google Scholar] [CrossRef]
- Liu, X.; Hao, C.; Jiang, H.; Zeng, M.; Yu, R. Hierarchical NiCo2O4/Co3O4/NiO porous composite: a lightweight electromagnetic wave absorber with tunable absorbing performance. J. Mater. Chem. C. 2017, 5, 3770–3778. [Google Scholar] [CrossRef]
- Liu, S.; Yu, M.; Zheng, Q.; Liang, X.; Xie, S.; Xu, Y.; Wang, C. Optimized impedance matching and enhanced microwave absorbing performance of porous flaky Fe4N wrapped with SiO2. J. Magn. Magn. Mater. 2021, 536, 168119. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, R.; Cui, W.-G.; Lu, Z.; Yang, Y.; Pan, H.; Che, R. Heterostructure design of 3D hydrangea-like Fe3O4/Fe7S8@C core-shell composite as a high-efficiency microwave absorber. Carbon. 2023, 210, 118043. [Google Scholar] [CrossRef]
Figure 1.
SEM images of the as-prepared Ni chains (a) and the 3D porous (Ni@NO-C)n/NO-C composite absorber (b).
Figure 1.
SEM images of the as-prepared Ni chains (a) and the 3D porous (Ni@NO-C)n/NO-C composite absorber (b).

Figure 2.
The XRD patterns of Ni chains (black) and the 3D porous (Ni@NO-C)n/NO-C composite absorber (red) (a) and Raman spectrum of the 3D porous (Ni@NO-C)n/NO-C composite absorber (b).
Figure 2.
The XRD patterns of Ni chains (black) and the 3D porous (Ni@NO-C)n/NO-C composite absorber (red) (a) and Raman spectrum of the 3D porous (Ni@NO-C)n/NO-C composite absorber (b).
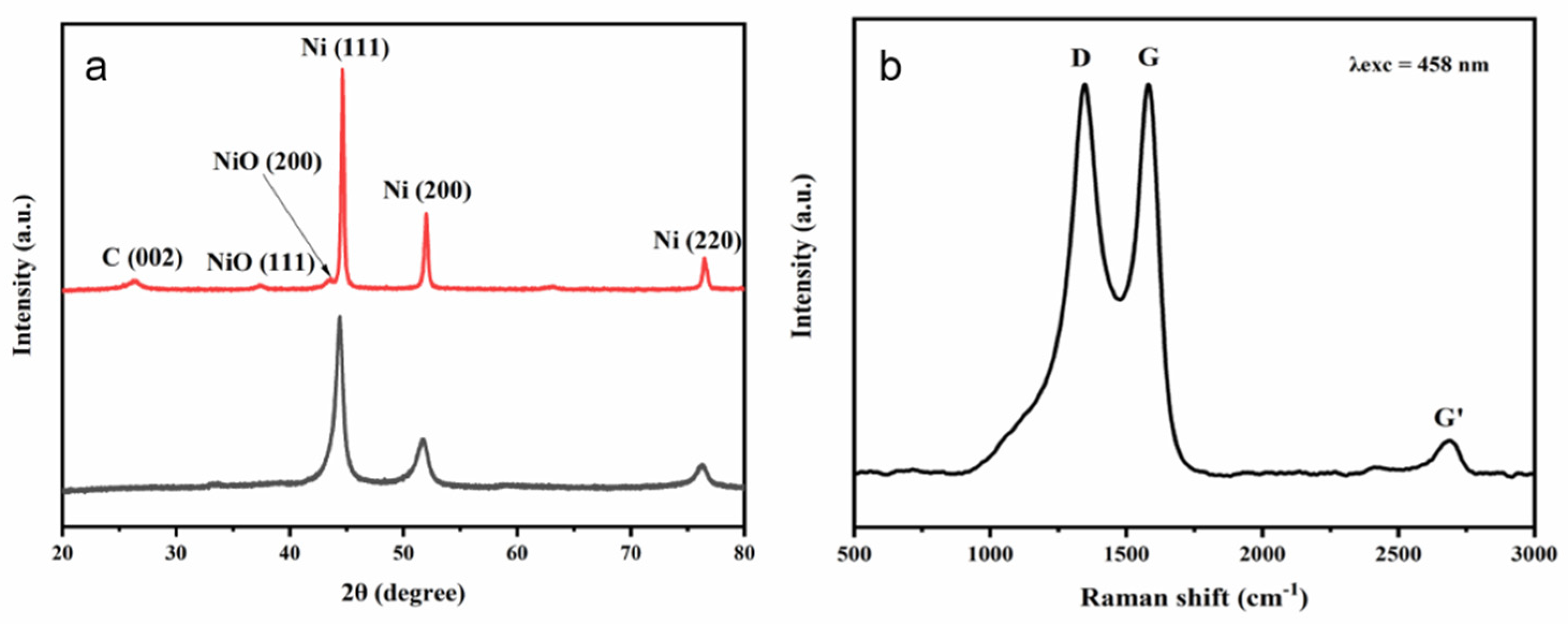
Figure 3.
TEM (a), HR-TEM (b) and elemental mapping (c–f) images of the 3D porous (Ni@NO-C)n/NO-C composite absorber.
Figure 3.
TEM (a), HR-TEM (b) and elemental mapping (c–f) images of the 3D porous (Ni@NO-C)n/NO-C composite absorber.

Figure 4.
The survey (a) and deconvoluted Ni 2p (b), C 1s (c), N 1s (d) and O 1s (e) XPS spectra of the 3D porous (Ni@NO-C)n/NO-C composite absorber.
Figure 4.
The survey (a) and deconvoluted Ni 2p (b), C 1s (c), N 1s (d) and O 1s (e) XPS spectra of the 3D porous (Ni@NO-C)n/NO-C composite absorber.
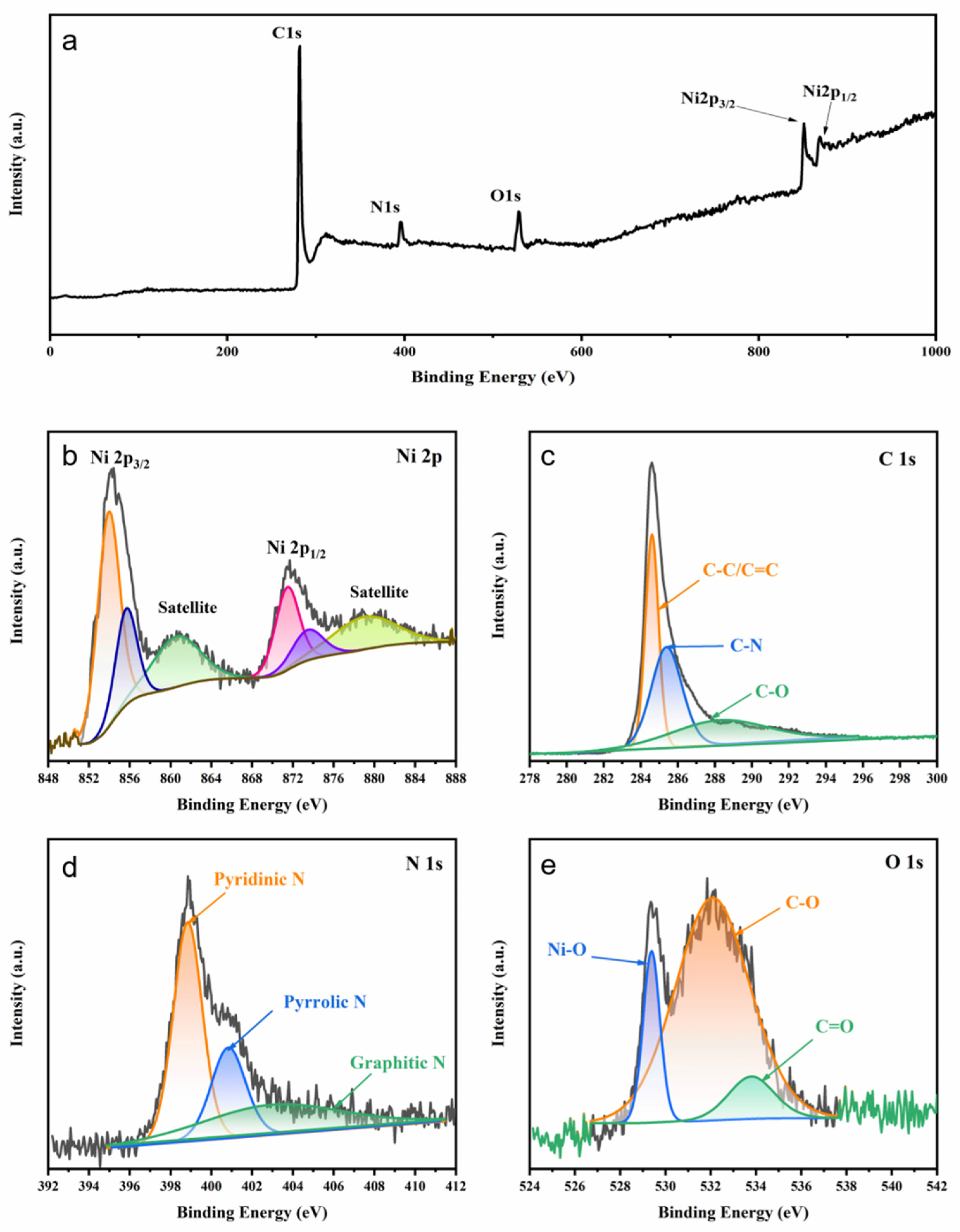
Figure 5.
The complex permittivity (a), Cole-Cole curve (b), complex permeability (c) and C0 curve (d) for the paraffin-based composite with 30 wt% (Ni@NO-C)n/NO-C.
Figure 5.
The complex permittivity (a), Cole-Cole curve (b), complex permeability (c) and C0 curve (d) for the paraffin-based composite with 30 wt% (Ni@NO-C)n/NO-C.
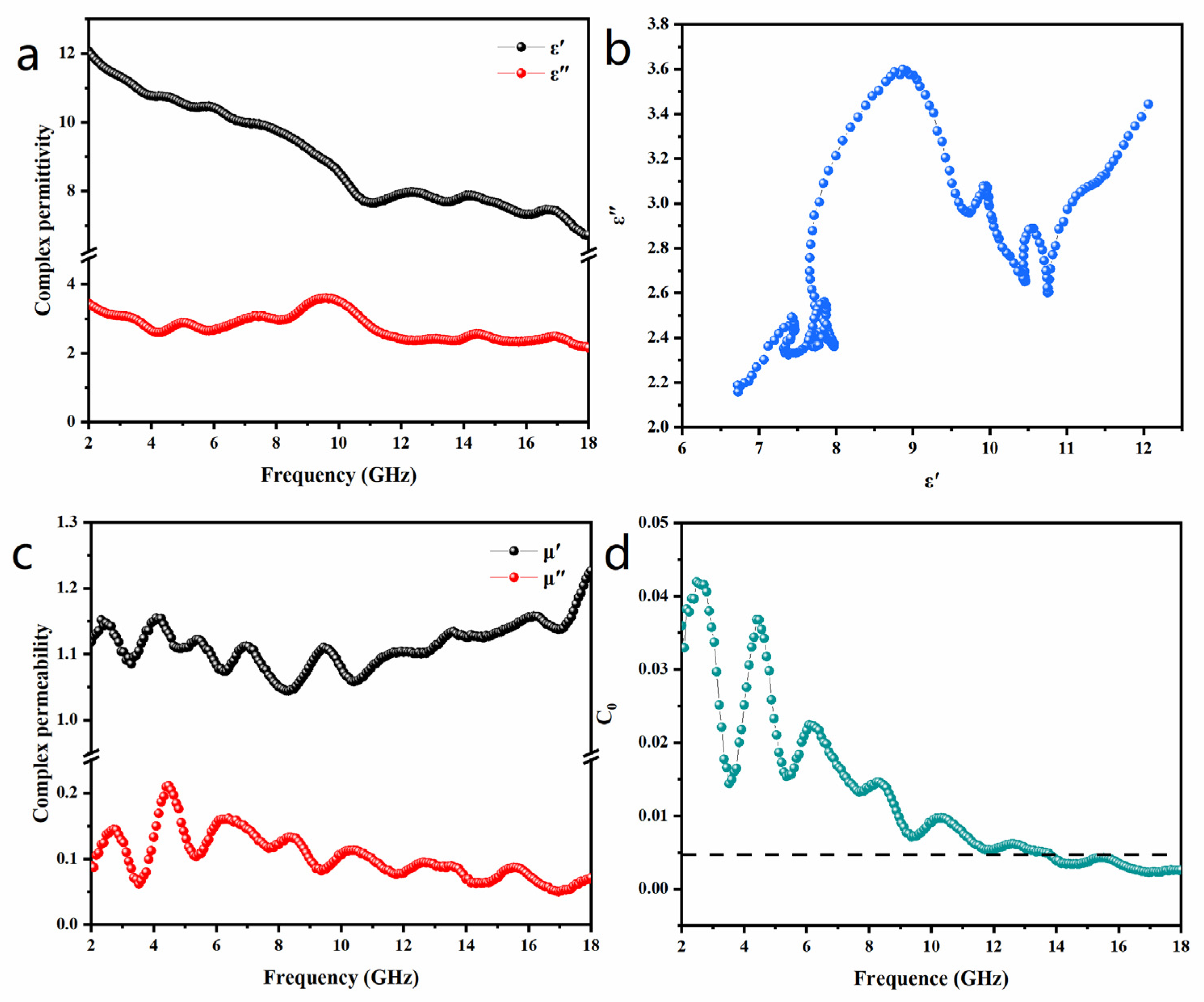
Figure 6.
3D representation of the reflection losses values (a), dielectric loss tangent and magnetic loss tangent (b), Attenuation constant α (c), and normalized impedance Z (d) of the 3D porous (Ni@NO-C)n/NO-C composite absorber .
Figure 6.
3D representation of the reflection losses values (a), dielectric loss tangent and magnetic loss tangent (b), Attenuation constant α (c), and normalized impedance Z (d) of the 3D porous (Ni@NO-C)n/NO-C composite absorber .
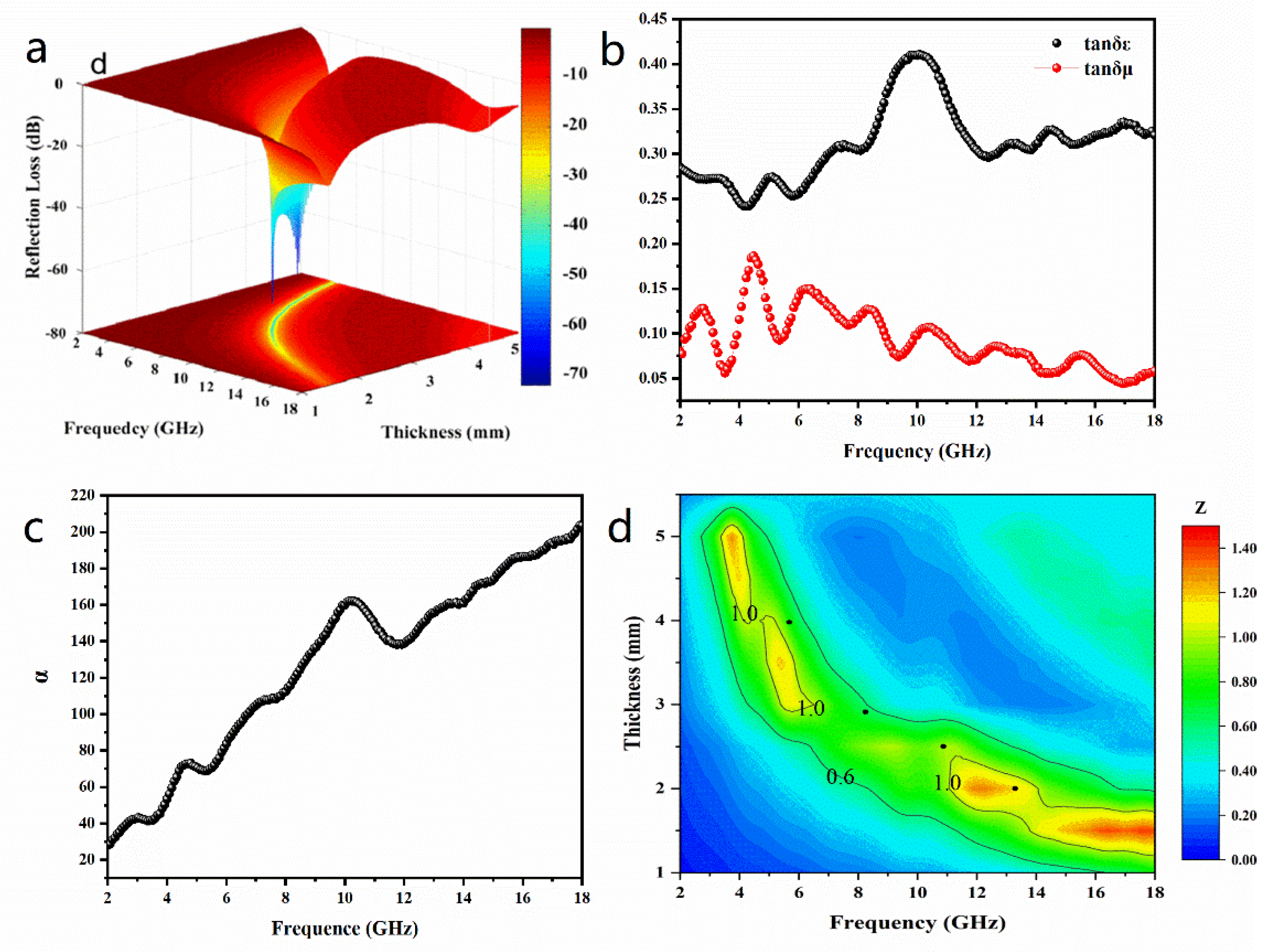
Table 1.
Comparison of the microwave absorptions of typical Ni/carbon composite absorbers.
| Materials | Filler loading (wt%) | Matching thickness (mm) | RLmax (dB) | EAB (GHz) | Refs. |
|---|---|---|---|---|---|
| Ni/C hollow microspheres | 30 | 1.80 | -57.25 | 5.10 | [41] |
| Ni@C nanorods | 30 | 1.66 | -58.7 | 4.4 | [42] |
| Ni@CN nanocapsules | - | 2.3 | -35.8 | ≈3.5 | [43] |
| NiCo@g-C3N4 | 20 | 2.0 | -35.05 | 4.80 | [44] |
| Ni/C | 30 | 1.5 | ≈-17.6 | 4.8 | [45] |
| Ni/C microsphere | 75 | 1.8 | -28.40 | 4.90 | [46] |
| Ni@C nanorods | 40 | 1.7 | ≈-22 | 5.2 | [47] |
| Ni/C composite(s500) | 40 | 2.60 | -51.80 | 3.48 | [48] |
| MXene/Ni/N-CNT(HM1) | - | 1.49 | -57.78 | 2.08 | [49] |
| MXene@Ni-CZIF | 50 | 3.4 | -64.11 | ≈1.7 | [50] |
| MXene@Ni-CZIF | 33 | 4.8 | -34.52 | 1.48 | [50] |
| (Ni@NO-C)n/NO-C | 30 | 2.5 | -57.9 | 4.0 | Herein |
| (Ni@NO-C)n/NO-C | 30 | 2.9 | -72.3 | 4.2 | Herein |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






