Prerpints.org logo
Preprint
Review

Anomaly Detection in Power System State Estimation: Review and New Directions

Altmetrics

Downloads

159

Views

49

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 August 2023

Posted:

30 August 2023

You are already at the latest version

Alerts
Abstract
Foundational and state-of-the-art anomaly detection methods through power system state estimation are reviewed. The traditional components for bad data detection such as chi-square testing, residual-based methods, and hypothesis testing are discussed to explain the motivations for recent anomaly detection methods given the increasing complexity of power grids, energy management systems, and cyber-threats. In particular, state estimation anomaly detection based on data-driven quickest change detection and artificial intelligence are discussed and directions for research are suggested with particular emphasis on considerations of the future smart grid.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Since its introduction by Schweppe in the late 1960s [1,2], power system state estimation has proved an integral component of Energy Management Systems (EMS). Schweppe’s proposed nonlinear static state estimation (SSE) provides estimates of the actual network status which could then be leveraged for subsequent analysis, including contingency evaluation and power flow studies [3]. Soon after, strategies for mitigating erroneous measurement data [4,5] were developed to ensure fidelity of the power system state estimates. SSE and dynamic state estimation (DSE) both share a rich history of research [6,7,8], however SSE has seen more real-world implementation. Nevertheless, DSE shows great promise as an enhancing role to legacy SSE based EMS [9], especially with increased adoption of synchrophasor measurements [10], and thus anomaly detection methods using both approaches are surveyed.
Numerous sources of gross errors have been identified and formulated in the literature, including measurement, parameter, and topology discrepancies with respect to the system model. More recently, with the integration of EMS into sophisticated computer networks, the potential for cyber-security vulnerabilities became apparent. What new considerations must be made when bad data is malicious? False data injection attacks [11], for example, were formulated as an exercise in fooling legacy bad data detection schemes. That said, attacks on cyber-physical systems have yielded very real consequences, including equipment damage and rolling blackouts [12]. Anomaly detection techniques that can properly handle these manufactured instances of bad data, and thus improve bad data processing in state estimation generally, are surveyed in this review. This review also hopes to highlight some considerations for future approaches of anomaly detection in state estimation, including implementation-based research in the face of increasingly dynamic load and generation profiles, complexity of distributed cyber-physical infrastructure, and pushes for combined SSE and DSE approaches for higher fidelity EMS information to improve control, efficiency, and stability in the future smart grid.

2. Power System State Estimation

2.1. Static State Estimation

One of the most common methods of performing power system SE is the Weighted Least Squares (WLS) estimator [7]. A power system with n buses and d measurements can be modeled through a set of nonlinear algebraic equations in the measurement model:
z = h ( x ) + e
where z ∈ R 1 × d is the measurement vector, x ∈ R 1 × N the state variables vector, h : R 1 × N → R 1 × d a continuous nonlinear differentiable function, and e ∈ R 1 × d the measurement error vector. Each measurement error e i is assumed to follow a zero mean Gaussian distribution. N = 2 n − 1 is the number of unknown state variables, i.e., the complex voltages at each bus.
In the traditional WLS approach, the best state vector estimate in (1) is determined by minimizing the weighted norm of the residual, represented with the cost function J ( x ) :
J ( x ) = ∥ z − h ( x ) ∥ W 2 = [ z − h ( x ) ] T W [ z − h ( x ) ]
where W = R − 1 is the inverse covariance matrix of the measurements, otherwise known as the weight matrix.
Linearizing the measurement model (1) yields:
Δ z = H Δ x + e
where H = ∂ h ∂ x is the Jacobian matrix of h at the current state estimate. The estimate of the linearized state vector is then given by:
Δ x ^ = ( H T W H ) − 1 H T W Δ z
The estimated value of the measurement vector mismatch Δ z is given by:
Δ z ^ = H Δ x ^ = P Δ z
where P = H ( H T W H ) − 1 H T W denotes the linear projection or "hat" matrix. The idempotent matrix P also has the following properties [7]:
(6a) P H = H (6b) ( I − P ) H = 0
These properties facilitate an expression for the measurement residuals:
(7a) r = Δ z − Δ z ^ (7b)   = ( I − P ) Δ z (7c)   = ( I − P ) ( H Δ x + e ) (7d)   = ( I − P ) e [ Using Equation ( 6 b ) ] (7e)   = S e
where S is known as the residual sensitivity matrix, which was first recognized in [5] for representing the sensitivity of the measurement residual to the measurement error during bad data processing. Also useful is the residual covariance matrix Ω [7]
(8a) E r = E Se = 0 (8b) C o v r = E rr T = S ee T S T (8c)   = SR = Ω
The residual covariance matrix is used for the detection and identification of bad data, as well as providing insight into degree of interaction, concepts that will be elaborated upon further in Section 3.

2.2. Dynamic State Estimation

SSE does not consider any history of the measurement vector z , but instead provides a snapshot of the system. This "memoryless" assumption of SSE proved sufficient for real-time monitoring in early EMS. For one, older power networks were not as regimented at the distribution level–with far fewer microgrids, distributed energy resources, and net load dynamics compared to today’s systems. Secondly, the measurement data fed to the state estimator almost always came from measurement devices with slow sampling rates, such as the 2-4 second range of SCADA. One might argue, then, that the true bottleneck for capturing dynamic behavior in state estimation was slow metering rates. That said, Schweppe’s formulation arrived just shortly after the introduction of the Kalman filter in 1961 [13], which inspired power researchers to seek formulations beyond the still-developing SSE. The practical hangup of slow meter sampling rates would be relieved somewhat with the introduction of synchronized phasor measurements in the 1980s [10]. Phasor Measurement Units (PMUs) provide higher sampling rates when compared to SCADA, but also GPS coordination to avoid uncertainty associated with asynchronicity.
Like SSE, dynamic state estimation (DSE) encompasses a wide range of methods. Early DSE formulations considered the same set of measurements and state variables as those used in SSE: active and/or reactive power flow and injections, and complex bus voltages. Other approaches seek to better capture load dynamics by considering generator rotor angle and speed as differential-algebraic state variables [9,14,15], however this review will primarily consider DSE-based anomaly detection implementations that use algebraic state variables.
DSE can be accomplished by modeling the power system as a discrete time dynamic system. The Kalman filter is used [16] to estimate the state variables at time k through prediction and measurement update steps upon each iteration:
Predict:
x ^ k | k − 1 = A k x ^ k − 1 | k − 1
F k | k − 1 = A k F k − 1 | k − 1 A k T + Q k
Update:
K k = F k | k − 1 H k T H k F k | k − 1 H k T + R k − 1
x ^ k | k = x ^ k | k − 1 + K k z k − H k x ^ k | k − 1
F k | k = F k | k − 1 − K k H k F k | k − 1
where, at time k, A k is the state transition matrix, K k the Kalman gain matrix, and H k the measurement matrix. F k | k and F k | k − 1 denote the state covariance matrix estimates based on measurements up to times k and k − 1 . Q k and R k are the process and observation noise covariance matrices, respectively.
The authors of the first Kalman filter power system DSE approach [17] hinted at its compatibility with anomaly detection methods which, at the time, were under study for SSE. Early work soon after [18,19] formulated bad data detection by analyzing the innovation process
v k = y k − h ( x ^ k | k − 1 )
Additional approaches for bad data processing in DSE include asymmetry analysis based on the skewness of the normalized estimation error [16,20]. DSE anomaly detection research remains an active field [15,21], especially since dynamic load and generation profiles are commonplace in microgrid systems with distributed energy resources (DERs).

3. Bad Data Types and Considerations

Bad data can be classified as either single or multiple. For single bad data, one measurement in the system is corrupted with a large error. Multiple bad data describes more than one measurement being in error, and can be further classified by degree of interaction and conformity [7]. Multiple bad data is said to be interacting when the residuals are highly correlated, whereas conformity describes the degree to which gross errors are "masked" in the residual (i.e., nonconforming errors present as high normalized residuals) [8]. Another illustration of how error does not always reflect fully in the residual is the concept of leverage points [22,23,24,25], which can hinder the effectiveness of largest residual methods. Leverage points arise as a consequence of system topology, parameter values, and measurement placement, and are usually caused by the following: i) injection and flow measurements near branches with small X/R ratio; ii) injection measurements near busses with a large number of incident branches; and iii) a measurement having a large weight [6,26]. Even a single leverage point can compromise bad data detectability.
Gross errors that exist beyond the acceptable noise limit of the state estimation model can be categorized into three types: measurement, parameter, and topology. Each of these errors suggests a discrepancy between the measurement data and model, and are described further below.

3.1. Measurement Error

Measurement error is an inevitability given the limitations of metering equipment accuracy. Meters can fail or degrade, introducing bias and compromising both accuracy and Gaussian error assumption: empirical studies of synchrophasor error have yielded heavy-tailed error distributions such as Cauchy, Student’s t, logistic, and Laplace [27,28]. Further, the communications infrastructure itself may contribute to measurement error in the case of failure or interference [7]. Particularly egregious measurement errors that suggest physically impossible grid conditions, such as negative bus voltage magnitudes or magnitudes several times larger or shorter than nominal values, are filtered through pre-processing [8], but more "agreeable" measurement errors can nevertheless affect the accuracy of state estimates.

3.2. Parameter Error

Parameter errors suggest discrepancies between measurement data and the system model. While Schweppe in his original formulation [1] did recognize the impact of erroneous model parameters, such errors were not permitted in the network model. For example, a parameter error might arise when the variability in a line impedance value due to extreme weather conditions is not taken into account. The mismatch between the measurement data and the line impedance database value, which is used in the Y-admittance matrix for power flow calculations, would reflect in the state estimation error.
A simple alteration of (1) yields an augmented model [29] and linearization:
z i = h i ( x , p 0 ) + e i ≈ h i ( x , p ) + ∂ h i ∂ p Δ p + e i
where p is the true parameter value, p 0 the erroneous parameter value, and Δ p = p 0 − p the parameter error.
Stuart and Herget [30] investigated the impact of parameter errors on SSE by simulating erroneous values for line impedance, measurement error variance, and transformer tap settings. Of particular note was an observed relationship between the severity of error and lightly loaded lines.
Parameter errors can be thought of as a special case of multiple bad data in which only the measurements pertaining to the erroneous model parameter are in error. As such, studies have been performed with of goal of differentiating between the two. In [31], it was shown through analysis of the state estimation error distribution that parameter errors reflect only in the measurement functions with erroneous parameter values. Parameter estimation itself has been treated as a process separate from state estimation. A practical implementation of this was first developed in [32], in which a sensitivity-based WLS estimation approach is used to both identify and estimate parameter error.

3.3. Topology Error

Like parameter errors, topology errors suggest discrepancies in the measurement model. System topology describes the bus-branch network configuration at the time of state estimation. Topology processing, which precedes state estimation, normally determines the correct status of manual switching and circuit breaking apparatus. A topological discrepancy, such as a branch outage unaccounted for by the topology processor, would reflect in the Jacobian measurement matrix H , which requires accurate bus-branch connection logic for power flow calculation. Topology errors can significantly compromise state estimation accuracy through multiple conforming bad data [7]. Early work showed that such topology errors can reflect in the state estimation error [33,34], and that normalized residual methods could be used for detection. Other approaches suggest incorporating statuses of switching devices themselves as additional state variables [35], aiding in the identification of topology errors as such.

4. Bad Data Detection

To preserve the accuracy of state variable estimates, bad data must be detected, identified, and either eliminated or corrected. Whether the source of the bad data is measurement, parameter, or topology-based, detection is the first step. The classical components of bad data detection can be broadly categorized into three main branches, and are often used in conjunction with one another: chi-square χ 2 testing, residual-based methods, and hypothesis testing.

4.1. Chi-Squared χ 2 Test

For a set of d random variables { X i , i = 1 , 2 , … d } with unit Gaussian distribution X i ∼ N ( 0 , 1 ) , a new random variable with χ 2 distribution is defined Y = ∑ i = 1 d X i 2 [6]. This follows the form of the cost function defined in (2), and can be written as the performance index
J ( x ^ ) = ∑ i = 1 d z i − h i ( x ^ ) σ i 2
assuming that the measurement errors are independent and distributed e i ∼ N ( 0 , σ 2 ) . J ( x ^ ) then follows a χ 2 distribution with d − N degrees of freedom, which d the number of measurements and N the number of unknown state variables.
A critical value C = χ ( d − N ) , p 2 can then be obtained based on the degrees of freedom d − N and the desired detection confidence with probability p = 1 − α , where α is a constraint on false probability. If J ( x ^ ) ≥ C then bad data is suspected, otherwise the measurements are assumed free of bad data. χ 2 testing has proved valuable for detection of bad data even in the early history of SSE [5], where it was quickly realized that χ 2 and normalized residual methods can outperform one another generally, but that χ 2 often proved better for multiple bad data.

4.2. Residual-Based Methods

The χ 2 test soon became commonplace for detection of bad data detection in WLS SSE for a specified constraint on false probability α , after which residual analysis could be performed for identification of the measurement(s) in error [36]. However, in the case of single bad data in larger networks, analysis of both the weighted and normalized residuals also proved viable for detection due to a more pronounced response in the presence of gross errors when compared to χ 2 testing. The use of normalized residuals for bad data detection was introduced in [5]. Using the residual covariance matrix Ω i i = d i a g ( Ω ) , the normalized residuals can be defined
r i N = | r i | Ω i i
It was shown in [5] that, after bad data had been detected through means such as the χ 2 test, a list of the normalized residuals in descending order could be obtained. The largest normalized residual could be used to identify the measurement in error, after which the measurement was removed and the state estimation re-run. If bad data was still detected, the procedure would repeat until all erroneous measurements were eliminated. Further techniques were developed to correct measurements contaminated with bad data, rather than eliminating them [8]. Correction keeps the measurement structure intact, which is especially important in cases of limited redundancy.
Both detection and identification for bad data can be achieved without χ 2 testing by comparing the largest normalized residual to a statistical threshold depending on the desired sensitivity [7]. The case studies in [5] demonstrated that, in the case of multiple bad data, either interacting or noninteracting, no consensus could be developed as to whether χ 2 testing or the largest normalized residual test proved superior for bad data detection detection. A geometric interpretation of the normalized residuals was developed in [37], significantly improving the generalizability of multiple interacting bad data detection. The residual difference between estimated and actual measurements continues to be a vital component in state estimation anomaly detection, including in newer formulations to be expanded upon in Section 6.

4.3. Hypothesis Testing

Hypothesis testing is a statistical method for deciding between accepting a null hypothesis H 0 or an alternative hypothesis H 1 based on available observations. In power system state estimation, the hypotheses are formulated as:
  • H 0 :   z i is a valid measurement.
  • H 1 :   z i is a measurement in error.
The first work to use hypothesis testing identification (HTI) for bad data in power system state estimation [38] developed regions of acceptance between H 0 and H 1 by comparing the estimation error to a threshold dependent on the measurement standard deviation and a pre-selected constraint on false probability α . New results of this HTI method were presented in [39], where the optimality of the linear estimator is established along with a decision strategy based on a constraint for missed detection β . In [40] the authors bridge the gaps between theory and practicality by implementing the HTI on eight test systems, showcasing its strengths in detecting multiple interacting bad data. For bad data identification, HTI methods show significant advantages over methods bad on normalized residuals, which may be strongly correlated [7]. HTI techniques also demonstrated potential for discerning error type, such as in topology error identification [41,42].

5. When Bad Data Becomes Malicious

The introduction of the concept of false data injection attacks (FDIAs) [11] helped to highlight the limitations of classical bad data detection methods. What if bad data is malicious and/or statistically derived to avoid conventional detection? The basic idea of FDIAs is that an attacker can design an injection of multiple interacting bad data, which is then applied to the measurement vector z . Consider the representation z a = z + a , where a = ( a 1 , a 2 , ⋯ , a m ) T is a vector of malicious data. The attacker’s goal is to design a to alter the state estimates, which EMS use to make operating decisions, but without triggering bad data detection. Ramifications of undetected attacks include compromised system stability [12] and negative economic impact [43]. The success of such attacks is largely dependent on the information available to the attacker, such as number of meters compromised, state estimates, system topology, and Jacobian structure, to name a few.
Denial-of-service (DoS) attacks are another source of mismatch between the measurement data fed to the state estimator and the true power system state. Causes for DoS attacks are numerous [44], including communication channel jamming, packet flooding, and compromising of metering devices such as SCADA and PMUs so that data is not updated for that region of the power grid. For state estimation, DoS attacks are typically modelled as a set of measurements that are no longer available, which can negatively impact state variable accuracy. If stealthiness is desired, care would need to be taken on the attacker’s part so as not to render the system unobservable. FDIAs can also be designed to create a topology error attack [45,46,47], in which a conventionally nondetectable mismatch between measurement data and topology processing can lead to compromised system stability and cost-effective operation.
The authors of [48] present FDIA strategies from attacker and defender perspectives. For the attacker, it is typically assumed that there is a cost associated with information obtained. With this in mind, an algorithm is presented to find the minimal set of measuring devices required to manufacture an unobservable attack.
In [49], a comparative analysis of FDIA impact between so-called DC and AC SSE is conducted. DC SSE considers active power measurements only, with bus voltage angles as the state variables. In contrast, the complete AC SSE considers both active and reactive power measurements, with bus voltage magnitudes and angles as the state variables. Such a study was important due to the DC model warranting far more attention in the FDIA research space at the time, despite the full nonlinear AC model finding use in real-world EMS applications [50,51].
Impacts of FDIAs on Kalman filter DSE approaches were studied in [52], where it was found that the unscented Kalman filter (UKF) [53] yielded better performance compared to the extended Kalman filter (EKF) [54] and enhanced EKF [55]. Further, an on-line nonparametric cumulative sum (CUSUM) approach was proposed to detect anomalies based on distribution changes of the state estimation error. This is related to quickest change detection approaches, which will be elaborated upon further in Section 6.1. A Kalman filter state estimation approach was proposed in [56], where a Euclidean detector was used to overcome the shortcomings of the χ 2 test for detecting statistically derived FDIAs as well as DoS attacks.
The FDIA formulation and its derivatives largely indicated a need for new bad data detection techniques. Further, with the increasing push towards cyber-physical operation of the smart grid [57], many new points of entry for cyber-attack became apparent, such as Internet of Things (IoT) infrastructure [58], communication channels [59], and distributed computing [60]. The intersection of model-based and data-driven solutions would grow to better handle the bad data detection limitations posed by FDIAs. With state estimation anticipated to remain a vital component to EMS, new formulations based on quickest change detection and AI would be developed for improved anomaly detection.

6. Recent Approaches

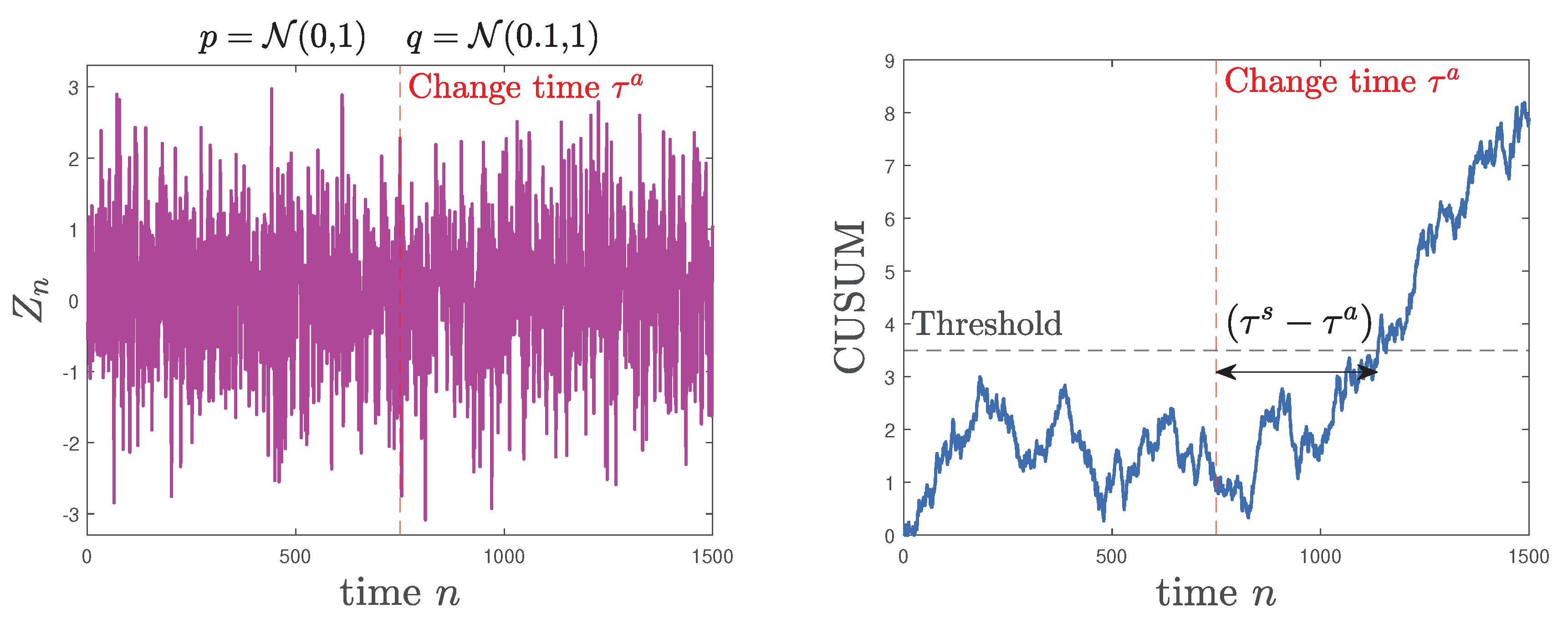
6.1. Quickest Change Detection

Quickest change detection (QCD) is concerned with detecting a possible change in the distribution of a monitored observation sequence [61], indicative of an anomaly in a stochastic environment. The general goal in QCD theory is to design algorithms to detect these changes with the smallest detection delay possible, subject to a constraint on false alarm.
Three main ingredients are needed in the QCD problem [62]: an observed stochastic process { X n , n = 1 , 2 , … } , a change time τ a at which the statistical properties of the process undergo change, and a decision maker that declares a change time τ s based on observations of the stochastic process. False alarm is defined as an instance of the decision maker declaring a change before the change occurs: I { τ s < τ a } . The constraint on false alarm follows from the Neyman-Pearson hypothesis testing formulation [63] which is foundational to the QCD problem.
The Neyman-Pearson Lemma [64] establishes the optimal test for binary hypothesis testing, involving the null ( H 0 ) and alternate ( H 1 ) hypotheses. For a single observation X:
  • H0: X has pdf p.
  • H1: X has pdf q.
Then comparing the likelihood ratio  q ( X ) / p ( X ) to a threshold value is the most powerful test in terms of deciding which hypothesis is true while minimizing missed detection subject to a constraint on false alarm [65]. The likelihood ratio plays a fundamental role in recursive sequential change detection algorithms such as Page’s CUSUM [66] and the Shiryaev-Roberts procedure [67], each of which enjoy optimality properties in terms of minimizing false alarm and detection delay ( τ s − τ a ) + max ( 0 , τ s − τ a ) . These properties are given proper discussion in [61].
QCD approaches have shown great promise for power system anomaly detection applications, such as line outage detection and identification [68,69,70]. QCD has further application in detecting changes in the state estimation error, which has been proposed for fault and FDIA detection. The first QCD approach for state estimation FDIA detection implemented an adaptive approach using the CUSUM statistic
S n = max { 0 , S n − 1 + L ( Z n ) } , n ≥ 1 , withS 0 = 0 .
where { Z n , n = 1 , 2 , … } is the observed stochastic process and L the log-likelihood ratio. Sample plots of a subtle change in a Gaussian observation process along with the corresponding CUSUM statistic are included in Figure 1.
Because the exact form of the post-change distribution q is not known, the authors in [71,72] use a Rao test based approximation [73] of the generalized likelihood ratio test for CUSUM-based FDIA detection. A low-complexity Orthogonal Matching Pursuit CUSUM (OMP-CUSUM) approach in [74] accounts for the unknown change distribution by maximizing the cumulative log-likelihood ratio to detect FDIAs that are sparse (i.e., only a small number of meters are assumed accessible to the attacker).
Both centralized and distributed CUSUM-based approaches for FDIA detection are proposed in [75], replacing the unknown parameters of the post-change distribution with their maximum likelihood estimates (MLEs). For the centralized case, the observed stochastic process of interest is the projection of the measurement vector on the orthogonal Jacobian space component R ⊥ ( H ) . This is expressed as y ˜ n ≜ P n y n , where P is the previously defined linear projection matrix. The distributed case partitions the power system into areas and estimates the state variables through the alternating direction method of multipliers (ADMM) [76], where each area i has its own observed process { y ˜ n i , n = 1 , 2 , … } . These approaches outperformed the adaptive-CUSUM approach in [71,72] due in part to improved detection of FDIAs with negative and larger elements of the attack vector a .
The work in [77] incorporates a Kalman filter approach and seperately evaluates DoS attacks and FDIAs. Better detection performance was observed for stealth FDIAs in particular, in which perfect system topology knowledge allows an attacker to inject false data along the column space of H . Four Kalman filtering techniques in [52] were evaluated using nonparametric CUSUM, in which both pre and post-change distributions p and q are unknown. Hybrid FDIA/jamming attacks are assessed for the Kalman filter CUSUM-based detector in [78]. The distinction between persistent and non-persistent attacks was made as well. Most CUSUM-based detectors assume persistence in the change of the observed stochastic process, and so an intermittent attack series could be designed to increase detection delay. Thus the Generalized Shewhart Test, which can detect significant increases in L, is presented as a countermeasure against stealthy, non-persistent FDIAs. A relaxed generalized CUSUM (RGCUSUM) algorithm is presented in [79] for FDIA detection. A relaxation on maximizing the post-change likelihood over the unknown parameters yielded a more computationally efficient algorithm than its generalized CUSUM counterpart. A Normalized Rao CUSUM-based detector with a time-varying dynamic model was employed in [80] to better distinguish between FDIA and sudden load changes.
The work in [81] also assesses the Shiryaev-Roberts (SR) procedure along with CUSUM for change detection. In contrast to CUSUM, the optimality of the SR procedure pertains to detecting τ at a distant time horizon [82,83]. The SR procedure is defined recursively as
T n = exp L ( Z n ) [ T n − 1 + 1 ] , n ≥ 1 , with T 0 = 0 .
Further, modified CUSUM and SR procedure algorithms [84] are employed in the same work as evaluation benchmarks for a so-called DeepQCD algorithm for online cyber-attack detection, which uses deep recurrent neural networks to detect changes in transient cases and with autocorrelated observations.

6.2. AI Approaches

FDIA detection can be framed as a binary classification problem in which the measurement vector z is determined to be either normal (negative class) or anomalous (positive class). One of the first to use semi-supervised and supervised learning for FDIA detection [85] explored perceptron, support vector machine (SVM), k-nearest neighbors (k-NN), and sparse logistic regression algorithms for supervised learning. Semi-supervised learning, in which unlabelled test data in incorporated in training, was explored with semi-supervised SVMs. Many valuable takeaways were garnered from this work, including considerations of power system size and and computational complexity, however stealthy FDIAs were not considered. An Extended Nearest Neighbors (ENN) algorithm was proposed in [86] to better handle the imbalanced data problem, (i.e., cases in which the number of negative class samples greatly exceeds or is significantly less than the number of positive class samples). Classification performance was then compared to SVM and k-NN algorithms. The work in [87] used a method based on the margin-setting algorithm, typically used in image processing applications, in which hypersphere decision boundaries were formed through labeled PMU time-series data. The MSA approached yielded superior classification performance compared to standard artificial neural networks (ANN) and SVM.
Unsupervised principal component analysis (PCA) showed utility in the construction of stealthy and blind FDIAs as well and in developing robust detection methods [88,89]. PCA is again employed in [90] as a preprocessing step to project higher dimensional correlated measurement data to a lower dimension, removing correlation between data and magnifying the distance between normal and anomalous measurements. For performance comparison, the authors implemented a supervised distributed ADMM-based SVM, which could only outperform the PCA-based anomaly detection when the training set was large. Mahalanobis distance based ensemble detection methods demonstrated success for FDIA detection in [91,92,93,94], including in high-fidelity real-time simulation.
Reinforcement learning (RL) based QCD approaches are explored in [81,95]. The QCD problem can be formulated as a case of optimal stopping, in which a decision to exercise must be made to minimize cost [96,97]. In QCD, this is understood as declaring a stop time τ s at a cost relative to the actual stop time τ a . For the Markov Decision Process (MDP) component of RL, one can either seek to maximize reward or minimize cost [98]. Two components for the cost are constructed [96]: one for continuing (associated with missed detection) and one for stopping (associated with false alarm). The authors in [95] use a model-free state–action–reward–state–action (SARSA) approach to learn the expected future cost for each state-action pair in a Q-table. The authors opt for a quantization scheme for learning when faced with the continuous observation space. Because the actual change time τ a is a hidden state, a partially observable Markov decision process (POMDP) formulation is used. This RL approach significantly outperformed the Euclidean [56] and cosine-similarity metric [99] based detectors in terms of minimizing mean probability of false alarm and detection delay for various cyber-attack types, including hybridFDI/jamming, DoS, and network topology attacks.
Neural network and deep learning approaches also show promise for malicious and standard bad data detection. A Deep Belief Network based classifier is proposed in [100] using Conditional Gaussian-Bernoulli Restricted Boltzmann Machines in the hopes of revealing higher-dimensional temporal features of stealthy FDIAs. The temporal correlation between measurements to the state estimator is analyzed through Recurrent Neural Networks (RNN) for FDIA detection in [101]. A nonlinear autoregressive exogenous (NARX) model configuration for ANNs is explored in [102] for stealthy optimized FDIA detection. The authors in [103] consider a limited set of target labels for attacked measurement data, an example of semi-supervised learning. Autoencoders, used for dimensionality reduction and feature extraction, are integrated into a generative adversarial network. The framework compensates for the limited labelled data set by using two neural networks: one generative, responsible for creating fake samples, and other discriminative, responsible for distinguishing between real and generated samples.

7. Conclusions and Suggestions for Future Work

A survey of legacy bad data detection procedures has been presented along with limitations with respect to malicious bad data. Cyber-attack formulations such as FDIA highlight the need for better data detection by pointing out the theoretical manipulation of grid operating procedures by bad actors. Even if one argues that the FDIA formulation is more of a theoretical exercise than a practical concern, it still points to shortcomings in legacy bad data detection. Standard bad data and physical line-faults under the leverage point conditions discussed earlier are difficult to detect for similar reasons as statistically derived stealth FDIAs. Newer methods such as QCD and AI seek to overcome legacy bad data detection techniques by leveraging features such as measurement data temporal patterns and probability density changes in the state estimation error.
Increased access to real state estimation measurement data would aid greatly in accessing the practicality of QCD and AI anomaly detection formulations. For example, a QCD formulation assuming independent and identically distributed (i.i.d.) observations may be compromised under dynamic load and generation profiles, in which case the measurement data exhibits complicating factors like autocorrelation as investigated in [81]. Robustness of newer anomaly detection strategies to asynchronous measurement data should also be investigated. Until synchronized measurement data for state estimation becomes standard, uncertainty quantification of this type should considered so as not to be considered a false-positive source of anomalous behavior. Availability of time-series data such as SCADA and/or PMU measurements for multi-bus systems would aid state estimation researchers in quantifying uncertainty and measurement correlation. It is also recommended that future work incorporate dynamic load and generation profiles to better reflect the future directions of the modern smart grid. This was a motivation in the work [80], which highlighted the importance of discerning anomalies from dynamic behavior such as large load shifts.

7.1. Climate changes and impacts on power and energy systems

Climate change presents additional challenges, motivations, and considerations for anomaly detection in state estimation. The leading cause of power outages in the United States is extreme weather events [104], which are expected to increase in frequency with climate change [105]. Greater instances of inclement weather also have a direct impact on state estimation accuracy, such as the increased uncertainty associated with temperature-dependent transmission line model parameters [106,107]. Further, as climate change increases the need for decarbonization efforts, so too does the shift towards renewable DERs. As a result, the future micro-grid distribution level is anticipated to become increasingly complex, with greater dynamics in load and generation profiles. This calls legacy bad data techniques into question, as many were formulated with relatively quasi-static conditions in mind. This highlights the need for improved anomaly detection, as climate change will bring with it a greener but nevertheless more complicated power grid.

References

  1. Schweppe, F.C.; Wildes, J. Power System Static-State Estimation, Part I: Exact Model. IEEE Transactions on Power Apparatus and Systems, -89. [CrossRef]
  2. Filho, M.; da Silva, A.; Falcao, D. Bibliography on power system state estimation (1968-1989). IEEE Transactions on Power Systems 1990, 5, 950–961. [Google Scholar] [CrossRef]
  3. Schellstede, G.; Beissler, G. A Software Package for Security Assessment Functions. In Power Systems and Power Plant Control; Pingyang, W., Ed.; IFAC Symposia Series; Pergamon: Oxford, 1987; pp. 277–284. [Google Scholar] [CrossRef]
  4. Merrill, H.M.; Schweppe, F.C. Bad Data Suppression in Power System Static State Estimation. IEEE Transactions on Power Apparatus and Systems, 2718; -90. [Google Scholar] [CrossRef]
  5. Handschin, E.; Schweppe, F.; Kohlas, J.; Fiechter, A. Bad data analysis for power system state estimation. IEEE Transactions on Power Apparatus and Systems 1975, 94, 329–337. [Google Scholar] [CrossRef]
  6. Monticelli, A. State estimation in electric power systems: a generalized approach; Springer, 2012.
  7. Abur, A.; Expósito, A.G. Power System State Estimation: Theory and Implementation, 1 ed.; CRC Press, 2004. [CrossRef]
  8. Bretas, A.; Bretas, N.; London Jr, J.B.; Carvalho, B. ; others. Cyber-Physical Power Systems State Estimation, 2021. [Google Scholar]
  9. Zhao, J.; Gómez-Expósito, A.; Netto, M.; Mili, L.; Abur, A.; Terzija, V.; Kamwa, I.; Pal, B.; Singh, A.K.; Qi, J.; Huang, Z.; Meliopoulos, A.P.S. Power System Dynamic State Estimation: Motivations, Definitions, Methodologies, and Future Work. IEEE Transactions on Power Systems 2019, 34, 3188–3198. [Google Scholar] [CrossRef]
  10. Phadke, A. Synchronized phasor measurements-a historical overview. IEEE/PES Transmission and Distribution Conference and Exhibition, 2002, Vol. 1, pp. 476–479 vol.1. [CrossRef]
  11. Liu, Y.; Ning, P.; Reiter, M.K. False Data Injection Attacks against State Estimation in Electric Power Grids 2011. 14.
  12. Musleh, A.S.; Chen, G.; Dong, Z.Y. A Survey on the Detection Algorithms for False Data Injection Attacks in Smart Grids. IEEE Transactions on Smart Grid 2020, 11, 2218–2234. [Google Scholar] [CrossRef]
  13. Kalman, R.E.; Bucy, R.S. New Results in Linear Filtering and Prediction Theory. Journal of Basic Engineering 1961, 83, 95–108. [Google Scholar] [CrossRef]
  14. Zhao, J.; Singh, A.K.; Mir, A.S.; Taha, A.; Rouhani, A.; Gomez-Exposito, A.; Meliopoulos, A.; Pal, B.; Kamwa, I.; Qi, J.; Mili, L.; Mohd Ariff, M.A.; Netto, M.; Glavic, M.; Yu, S.; Wang, S.; Bi, T.; Van Cutsem, T.; Terzija, V.; Huang, Z. Power system dynamic state and parameter estimation-transition to power electronics-dominated clean energy systems: IEEE task force on power system dynamic state and parameter estimation 2021.
  15. Liu, Y.; Singh, A.K.; Zhao, J.; Meliopoulos, A.P.S.; Pal, B.; Ariff, M.A.b.M.; Van Cutsem, T.; Glavic, M.; Huang, Z.; Kamwa, I.; Mili, L.; Mir, A.S.; Taha, A.; Terzija, V.; Yu, S. Dynamic State Estimation for Power System Control and Protection. IEEE Transactions on Power Systems 2021, 36, 5909–5921. [Google Scholar] [CrossRef]
  16. Bretas, N. An iterative dynamic state estimation and bad data processing. International Journal of Electrical Power & Energy Systems 1989, 11, 70–74. [Google Scholar] [CrossRef]
  17. Debs, A.S.; Larson, R.E. A Dynamic Estimator for Tracking the State of a Power System. IEEE Transactions on Power Apparatus and Systems, 1670; -89. [Google Scholar] [CrossRef]
  18. Nishiya, K.I.; Takagi, H.; Hasegawa, J.; Koike, T. Dynamic state estimation for electric power systems—introduction of a trend factor and detection of innovation processes. Electrical Engineering in Japan 1976, 96, 79–87. [Google Scholar] [CrossRef]
  19. Nishiya, K.; Hasegawa, J.; Koike, T. Dynamic state estimation including anomaly detection and identification for power systems. IEE Proceedings C Generation, Transmission and Distribution 1982, 129, 192–198. [Google Scholar] [CrossRef]
  20. Bretas, A.S.; Bretas, N.G.; Massignan, J.A.D.; London Junior, J.B.A. Hybrid Physics-Based Adaptive Kalman Filter State Estimation Framework. Energies 2021, 14. [Google Scholar] [CrossRef]
  21. Jin, Z.; Zhao, J.; Ding, L.; Chakrabarti, S.; Gryazina, E.; Terzija, V. Power system anomaly detection using innovation reduction properties of iterated extended kalman filter. International Journal of Electrical Power & Energy Systems 2022, 136, 107613. [Google Scholar] [CrossRef]
  22. Mili, L.; Phaniraj, V.; Rousseeuw, P. Least median of squares estimation in power systems. IEEE Transactions on Power Systems 1991, 6, 511–523. [Google Scholar] [CrossRef]
  23. Celik, M.; Abur, A. A robust WLAV state estimator using transformations. IEEE Transactions on Power Systems 1992, 7, 106–113. [Google Scholar] [CrossRef]
  24. Majumdar, A.; Pal, B.C. Bad Data Detection in the Context of Leverage Point Attacks in Modern Power Networks. IEEE Transactions on Smart Grid 2018, 9, 2042–2054. [Google Scholar] [CrossRef]
  25. Mili, L.; Cheniae, M.; Vichare, N.; Rousseeuw, P. Robust state estimation based on projection statistics [of power systems]. IEEE Transactions on Power Systems 1996, 11, 1118–1127. [Google Scholar] [CrossRef]
  26. Zhao, J.; Mili, L. Vulnerability of the Largest Normalized Residual Statistical Test to Leverage Points. IEEE Transactions on Power Systems 2018, 33, 4643–4646. [Google Scholar] [CrossRef]
  27. Wang, S.; Zhao, J.; Huang, Z.; Diao, R. Assessing Gaussian Assumption of PMU Measurement Error Using Field Data. IEEE Transactions on Power Delivery 2018, 33, 3233–3236. [Google Scholar] [CrossRef]
  28. Huang, C.; Thimmisetty, C.; Chen, X.; Stewart, E.; Top, P.; Korkali, M.; Donde, V.; Tong, C.; Min, L. Power Distribution System Synchrophasor Measurements With Non-Gaussian Noises: Real-World Data Testing and Analysis. IEEE Open Access Journal of Power and Energy 2021, 8, 223–228. [Google Scholar] [CrossRef]
  29. Zarco, P.; Exposito, A. Power system parameter estimation: a survey. IEEE Transactions on Power Systems 2000, 15, 216–222. [Google Scholar] [CrossRef]
  30. Stuart, T.A.; Herczet, C.J. A Sensitivity Analysis of Weighted Least Squares State Estimation for Power Systems. IEEE Transactions on Power Apparatus and Systems, 1696; -92. [Google Scholar] [CrossRef]
  31. Bretas, A.S.; Bretas, N.G.; Carvalho, B.E. Further contributions to smart grids cyber-physical security as a malicious data attack: Proof and properties of the parameter error spreading out to the measurements and a relaxed correction model. International Journal of Electrical Power & Energy Systems 2019, 104, 43–51. [Google Scholar] [CrossRef]
  32. Liu, W.H.E.; Lim, S.L. Parameter error identification and estimation in power system state estimation. IEEE Transactions on Power Systems 1995, 10, 200–209. [Google Scholar] [CrossRef]
  33. Costa, I.; Leao, J. Identification of topology errors in power system state estimation. IEEE Transactions on Power Systems 1993, 8, 1531–1538. [Google Scholar] [CrossRef]
  34. Wu, F.; Liu, W.H. Detection of topology errors by state estimation (power systems). IEEE Transactions on Power Systems 1989, 4, 176–183. [Google Scholar] [CrossRef] [PubMed]
  35. Korres, G.N.; Manousakis, N.M. A state estimation algorithm for monitoring topology changes in distribution systems. 2012 IEEE Power and Energy Society General Meeting, 2012, pp. 1–8. [CrossRef]
  36. Koglin, H.J.; Neisius, T.; Bei<i>β</i>ler, G.; Schmitt, K. Bad data detection and identification. International Journal of Electrical Power & Energy Systems 1990, 12, 94–103. [Google Scholar] [CrossRef]
  37. Clements, K.A.; Davis, P.W. Multiple Bad Data Detectability and Identifiability: A Geometric Approach. IEEE Transactions on Power Delivery 1986, 1, 355–360. [Google Scholar] [CrossRef]
  38. Cutsem, T.V.; Ribbens-Pavella, M.; Mili, L. Hypothesis Testing Identification: A New Method For Bad Data Analysis In Power System State Estimation. IEEE Transactions on Power Apparatus and Systems, 3239. [Google Scholar] [CrossRef]
  39. Mili, L.; Van Cutsem, T.; Ribbens-Pavella, M. Decision Theory Applied to Bad Data Identification in Power System State Estimation. IFAC Proceedings Volumes 1985, 18, 945–950. [Google Scholar] [CrossRef]
  40. Mili, L.; Van Cutsem, T. Implementation of the hypothesis testing identification in power system state estimation. IEEE Transactions on Power Systems 1988, 3, 887–893. [Google Scholar] [CrossRef]
  41. Lourenco, E.; Costa, A.; Clements, K. Bayesian-based hypothesis testing for topology error identification in generalized state estimation. IEEE Transactions on Power Systems 2004, 19, 1206–1215. [Google Scholar] [CrossRef]
  42. Wu, W.B.; Cheng, M.X.; Gou, B. A Hypothesis Testing Approach for Topology Error Detection in Power Grids. IEEE Internet of Things Journal 2016, 3, 979–985. [Google Scholar] [CrossRef]
  43. Xie, L.; Mo, Y.; Sinopoli, B. Integrity Data Attacks in Power Market Operations. IEEE Transactions on Smart Grid 2011, 2, 659–666. [Google Scholar] [CrossRef]
  44. Amin, S.; Cárdenas, A.A.; Sastry, S.S. Safe and Secure Networked Control Systems under Denial-of-Service Attacks. Hybrid Systems: Computation and Control; Majumdar, R., Tabuada, P., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2009; pp. 31–45. [Google Scholar]
  45. Kim, J.; Tong, L. On Topology Attack of a Smart Grid: Undetectable Attacks and Countermeasures. IEEE Journal on Selected Areas in Communications 2013, 31, 1294–1305. [Google Scholar] [CrossRef]
  46. Liu, X.; Li, Z. Local Topology Attacks in Smart Grids. IEEE Transactions on Smart Grid 2017, 8, 2617–2626. [Google Scholar] [CrossRef]
  47. Liang, G.; Weller, S.R.; Luo, F.; Zhao, J.; Dong, Z.Y. Generalized FDIA-Based Cyber Topology Attack With Application to the Australian Electricity Market Trading Mechanism. IEEE Transactions on Smart Grid 2018, 9, 3820–3829. [Google Scholar] [CrossRef]
  48. Kosut, O.; Jia, L.; Thomas, R.J.; Tong, L. Malicious Data Attacks on Smart Grid State Estimation: Attack Strategies and Countermeasures. 2010 First IEEE International Conference on Smart Grid Communications, 2010, pp. 220–225. [CrossRef]
  49. Hug, G.; Giampapa, J.A. Vulnerability Assessment of AC State Estimation With Respect to False Data Injection Cyber-Attacks. IEEE Transactions on Smart Grid 2012, 3, 1362–1370. [Google Scholar] [CrossRef]
  50. Nuthalapati, S. State Estimation Performance Monitoring. https://www.nerc.com/pa/rrm/Resources/Monitoring_and_Situational_Awareness_Conference1/10.%20Monitoring%20SE%20Performance%20at%20ERCOT_Sarma%20Nuthalapati_ERCOT.pdf, 2015. Accessed: 2023-06-03.
  51. ETAP State Estimation Software. https://etap.com/product/state-estimation-software, 2015. Accessed: 2023-06-03.
  52. Yang, Q.; Chang, L.; Yu, W. On false data injection attacks against Kalman filtering in power system dynamic state estimation. Security and Communication Networks 2016, 9, 833–849. [Google Scholar] [CrossRef]
  53. Valverde, G.; Terzija, V. Unscented Kalman filter for power system dynamic state estimation. IET Generation, Transmission & Distribution 2011, 5, 29–37. [Google Scholar] [CrossRef]
  54. Ghahremani, E.; Kamwa, I. Dynamic State Estimation in Power System by Applying the Extended Kalman Filter With Unknown Inputs to Phasor Measurements. IEEE Transactions on Power Systems 2011, 26, 2556–2566. [Google Scholar] [CrossRef]
  55. Shih, K.R.; Huang, S.J. Application of a robust algorithm for dynamic state estimation of a power system. IEEE Transactions on Power Systems 2002, 17, 141–147. [Google Scholar] [CrossRef]
  56. Manandhar, K.; Cao, X.; Hu, F.; Liu, Y. Detection of Faults and Attacks Including False Data Injection Attack in Smart Grid Using Kalman Filter. IEEE Transactions on Control of Network Systems 2014, 1, 370–379. [Google Scholar] [CrossRef]
  57. Faheem, M.; Shah, S.; Butt, R.; Raza, B.; Anwar, M.; Ashraf, M.; Ngadi, M.; Gungor, V. Smart grid communication and information technologies in the perspective of Industry 4.0: Opportunities and challenges. Computer Science Review 2018, 30, 1–30. [Google Scholar] [CrossRef]
  58. Yilmaz, Y.; Uludag, S. Mitigating IoT-based Cyberattacks on the Smart Grid. 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), 2017, pp. 517–522. [CrossRef]
  59. Yan, Y.; Qian, Y.; Sharif, H.; Tipper, D. A Survey on Cyber Security for Smart Grid Communications. IEEE Communications Surveys & Tutorials 2012, 14, 998–1010. [Google Scholar] [CrossRef]
  60. Kurt, M.N.; Yılmaz, Y.; Wang, X. Secure Distributed Dynamic State Estimation in Wide-Area Smart Grids. IEEE Transactions on Information Forensics and Security 2020, 15, 800–815. [Google Scholar] [CrossRef]
  61. Xie, L.; Zou, S.; Xie, Y.; Veeravalli, V.V. Sequential (Quickest) Change Detection: Classical Results and New Directions. IEEE Journal on Selected Areas in Information Theory 2021, 2, 494–514. [Google Scholar] [CrossRef]
  62. Veeravalli, V.V.; Banerjee, T. , Quickest change detection. In Academic Press Library in Signal Processing; Elsevier, 2014; Vol. 3, pp. 209–255. [CrossRef]
  63. Poor, H.V. An introduction to signal detection and estimation, 2 ed.; Springer Texts in Electrical Engineering, Springer-Verlag: New York, 1994. [Google Scholar]
  64. Neyman, J.; Pearson, E.S. IX. On the problem of the most efficient tests of statistical hypotheses. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 1933, 231, 289–337. [Google Scholar] [CrossRef]
  65. Moulin, P.; Veeravalli, V.V. Statistical Inference for Engineers and Data Scientists; Cambridge University Press, 2018. [CrossRef]
  66. Page, E.S. Continuous Inspection Schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
  67. Polunchenko, A.S.; Tartakovsky, A.G. On Optimality of the Shiryaev-Roberrts Procedure for Detecting a Change in Distribution. The Annals of Statistics 2010, 38, 3445–3457. [Google Scholar] [CrossRef]
  68. Banerjee, T.; Chen, Y.C.; Dominguez-Garcia, A.D.; Veeravalli, V.V. Power system line outage detection and identification — A quickest change detection approach. 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2014, pp. 3450–3454. [CrossRef]
  69. Rovatsos, G.; Jiang, X.; Domínguez-García, A.D.; Veeravalli, V.V. Comparison of statistical algorithms for power system line outage detection. 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2016, pp. 2946–2950. [CrossRef]
  70. Yang, X.; Chen, N.; Zhai, C. A Control Chart Approach to Power System Line Outage Detection Under Transient Dynamics. IEEE Transactions on Power Systems 2021, 36, 127–135. [Google Scholar] [CrossRef]
  71. Huang, Y.; Li, H.; Campbell, K.A.; Han, Z. Defending false data injection attack on smart grid network using adaptive CUSUM test. 2011 45th Annual Conference on Information Sciences and Systems, 2011, pp. 1–6. [CrossRef]
  72. Huang, Y.; Tang, J.; Cheng, Y.; Li, H.; Campbell, K.A.; Han, Z. Real-Time Detection of False Data Injection in Smart Grid Networks: An Adaptive CUSUM Method and Analysis. IEEE Systems Journal 2016, 10, 532–543. [Google Scholar] [CrossRef]
  73. De Maio, A. Rao Test for Adaptive Detection in Gaussian Interference With Unknown Covariance Matrix. IEEE Transactions on Signal Processing 2007, 55, 3577–3584. [Google Scholar] [CrossRef]
  74. Akingeneye, I.; Wu, J. Low Latency Detection of Sparse False Data Injections in Smart Grids. IEEE Access 2018, 6, 58564–58573. [Google Scholar] [CrossRef]
  75. Li, S.; Yılmaz, Y.; Wang, X. Quickest Detection of False Data Injection Attack in Wide-Area Smart Grids. IEEE Transactions on Smart Grid 2015, 6, 2725–2735. [Google Scholar] [CrossRef]
  76. Kekatos, V.; Giannakis, G.B. Distributed Robust Power System State Estimation. IEEE Transactions on Power Systems 2013, 28, 1617–1626. [Google Scholar] [CrossRef]
  77. Kurt, M.N.; Yılmaz, Y.; Wang, X. Distributed Quickest Detection of Cyber-Attacks in Smart Grid. IEEE Transactions on Information Forensics and Security 2018, 13, 2015–2030. [Google Scholar] [CrossRef]
  78. Kurt, M.N.; Yılmaz, Y.; Wang, X. Real-Time Detection of Hybrid and Stealthy Cyber-Attacks in Smart Grid. IEEE Transactions on Information Forensics and Security 2019, 14, 498–513. [Google Scholar] [CrossRef]
  79. Zhang, J.; Wang, X. Low-Complexity Quickest Change Detection in Linear Systems With Unknown Time-Varying Pre- and Post-Change Distributions. IEEE Transactions on Information Theory 2021, 67, 1804–1824. [Google Scholar] [CrossRef]
  80. Nath, S.; Akingeneye, I.; Wu, J.; Han, Z. Quickest Detection of False Data Injection Attacks in Smart Grid with Dynamic Models. IEEE Journal of Emerging and Selected Topics in Power Electronics 2022, 10, 1292–1302. [Google Scholar] [CrossRef]
  81. Kurt, M.N. Data-Driven Quickest Change Detection. PhD thesis, Columbia University, 2020. [CrossRef]
  82. Moustakides, G.V.; Polunchenko, A.S.; Tartakovsky, A.G. Numerical Comparison of CUSUM and Shiryaev–Roberts Procedures for Detecting Changes in Distributions. Communications in Statistics - Theory and Methods 2009, 38, 3225–3239. [Google Scholar] [CrossRef]
  83. Pollak, M.; Tartakovsky, A.G. Exact optimality of the Shiryaev-Roberts procedure for detecting changes in distributions. 2008 International Symposium on Information Theory and Its Applications, 2008, pp. 1–6. [CrossRef]
  84. Polunchenko, A.S.; Raghavan, V. Comparative performance analysis of the Cumulative Sum chart and the Shiryaev-Roberts procedure for detecting changes in autocorrelated data. Applied Stochastic Models in Business and Industry 2018, 34, 922–948. [Google Scholar] [CrossRef]
  85. Ozay, M.; Esnaola, I.; Yarman Vural, F.T.; Kulkarni, S.R.; Poor, H.V. Machine Learning Methods for Attack Detection in the Smart Grid. IEEE Transactions on Neural Networks and Learning Systems 2016, 27, 1773–1786. [Google Scholar] [CrossRef]
  86. Yan, J.; Tang, B.; He, H. Detection of false data attacks in smart grid with supervised learning. 2016 International Joint Conference on Neural Networks (IJCNN), 2016, pp. 1395–1402. [CrossRef]
  87. Wang, Y.; Amin, M.M.; Fu, J.; Moussa, H.B. A Novel Data Analytical Approach for False Data Injection Cyber-Physical Attack Mitigation in Smart Grids. IEEE Access 2017, 5, 26022–26033. [Google Scholar] [CrossRef]
  88. Yu, Z.H.; Chin, W.L. Blind False Data Injection Attack Using PCA Approximation Method in Smart Grid. IEEE Transactions on Smart Grid 2015, 6, 1219–1226. [Google Scholar] [CrossRef]
  89. Hao, J.; Piechocki, R.J.; Kaleshi, D.; Chin, W.H.; Fan, Z. Sparse Malicious False Data Injection Attacks and Defense Mechanisms in Smart Grids. IEEE Transactions on Industrial Informatics 2015, 11, 1–12. [Google Scholar] [CrossRef]
  90. Esmalifalak, M.; Liu, L.; Nguyen, N.; Zheng, R.; Han, Z. Detecting Stealthy False Data Injection Using Machine Learning in Smart Grid. IEEE Systems Journal 2017, 11, 1644–1652. [Google Scholar] [CrossRef]
  91. Trevizan, R.D.; Ruben, C.; Nagaraj, K.; Ibukun, L.L.; Starke, A.C.; Bretas, A.S.; McNair, J.; Zare, A. Data-driven Physics-based Solution for False Data Injection Diagnosis in Smart Grids. 2019 IEEE Power & Energy Society General Meeting (PESGM), 2019, pp. 1–5. [CrossRef]
  92. Ruben, C.; Dhulipala, S.; Nagaraj, K.; Zou, S.; Starke, A.; Bretas, A.; Zare, A.; McNair, J. Hybrid data-driven physics model-based framework for enhanced cyber-physical smart grid security. IET Smart Grid 2020, 3, 445–453. [Google Scholar] [CrossRef]
  93. Nagaraj, K.; Zou, S.; Ruben, C.; Dhulipala, S.; Starke, A.; Bretas, A.; Zare, A.; McNair, J. Ensemble CorrDet with adaptive statistics for bad data detection. IET Smart Grid 2020, 3, 572–580. [Google Scholar] [CrossRef]
  94. Vega-Martinez, V.; Cooper, A.; Vera, B.; Aljohani, N.; Bretas, A. Hybrid Data-Driven Physics-Based Model Framework Implementation: Towards a Secure Cyber-Physical Operation of the Smart Grid. 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I&CPS Europe), 2022, pp. 1–5. [CrossRef]
  95. Kurt, M.N.; Ogundijo, O.; Li, C.; Wang, X. Online Cyber-Attack Detection in Smart Grid: A Reinforcement Learning Approach. IEEE Transactions on Smart Grid 2019, 10, 5174–5185. [Google Scholar] [CrossRef]
  96. Tsitsiklis, J.; van Roy, B. Optimal stopping of Markov processes: Hilbert space theory, approximation algorithms, and an application to pricing high-dimensional financial derivatives. IEEE Transactions on Automatic Control 1999, 44, 1840–1851. [Google Scholar] [CrossRef]
  97. Chen, S.; Devraj, A.M.; Bušić, A.; Meyn, S. Zap Q-Learning for Optimal Stopping. 2020 American Control Conference (ACC), 2020, pp. 3920–3925. [CrossRef]
  98. Meyn, S. Control Systems and Reinforcement Learning; Cambridge University Press, 2022. [CrossRef]
  99. Chen, P.Y.; Yang, S.; McCann, J.A.; Lin, J.; Yang, X. Detection of false data injection attacks in smart-grid systems. IEEE Communications Magazine 2015, 53, 206–213. [Google Scholar] [CrossRef]
  100. He, Y.; Mendis, G.J.; Wei, J. Real-Time Detection of False Data Injection Attacks in Smart Grid: A Deep Learning-Based Intelligent Mechanism. IEEE Transactions on Smart Grid 2017, 8, 2505–2516. [Google Scholar] [CrossRef]
  101. Ayad, A.; Farag, H.E.Z.; Youssef, A.; El-Saadany, E.F. Detection of false data injection attacks in smart grids using Recurrent Neural Networks. 2018 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), 2018, pp. 1–5. [CrossRef]
  102. Ganjkhani, M.; Fallah, S.N.; Badakhshan, S.; Shamshirband, S.; Chau, K.w. A Novel Detection Algorithm to Identify False Data Injection Attacks on Power System State Estimation. Energies 2019, 12. [Google Scholar] [CrossRef]
  103. Zhang, Y.; Wang, J.; Chen, B. Detecting False Data Injection Attacks in Smart Grids: A Semi-Supervised Deep Learning Approach. IEEE Transactions on Smart Grid 2021, 12, 623–634. [Google Scholar] [CrossRef]
  104. Chen, H.; Bresler, F.S.; Bryson, M.E.; Seiler, K.; Monken, J. Toward Bulk Power System Resilience: Approaches for Regional Transmission Operators. IEEE Power and Energy Magazine 2020, 18, 20–30. [Google Scholar] [CrossRef]
  105. Fischer, E.M.; Sippel, S.; Knutti, R. Increasing probability of record-shattering climate extremes. Nature Climate Change 2021, 11, 689–695. [Google Scholar] [CrossRef]
  106. Cecchi, V.; Miu, K.; Leger, A.S.; Nwankpa, C. Study of the impacts of ambient temperature variations along a transmission line using temperature-dependent line models. 2011 IEEE Power and Energy Society General Meeting, 2011, pp. 1–7. [CrossRef]
  107. Cecchi, V.; Knudson, M.; Miu, K. System impacts of temperature-dependent transmission line models. 2014 IEEE PES General Meeting | Conference & Exposition, 2014, pp. 1–1. [CrossRef]
Preprints 83306 g001
Figure 1. Example of a small mean shift observation sequence with corresponding CUSUM evolution.
Figure 1. Example of a small mean shift observation sequence with corresponding CUSUM evolution.
Preprints 83306 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated