Prerpints.org logo
Preprint
Article

Medium Energy Proton Detector Onboard FY-4B Satellite

Altmetrics

Downloads

108

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 August 2023

Posted:

30 August 2023

You are already at the latest version

Alerts
Abstract
: This work introduces the instrument design of the medium energy proton detector (MEPD, detection range: 30keV-5MeV) mounted on the Chinese Fengyun-4B (FY-4B) satellite. Compared with the similar detector on the Fengyun-3E (FY-3E) satellite, the instrument has undergone significant changes due to the different orbital radiation environment and solar lighting conditions. Based on the calculation of radiation model AP8, the geometry factor is reduced to 0.002 cm2sr, while the MEPD on FY-3E satellite is 0.005 cm2sr. Another difference is that sensors in some directions is exposed to direct sunlight for 80 minutes every day on this orbit, depending on the attitude angle of the satellite, which is much worse than that on FY-3E satellite. According to the calculation results of permeability of photons through different materials, a 100 nm thickness nickel film is added in front of sensors in order to eliminate light pollution completely. The experiment on the solar simulator shows that the measure is effective and the detector has no error counts when the solar irradiance coefficient is 1.0. In addition, Geant4 software is applied to simulate particle transportation process under complete machine condition so that to check the contamination of electrons on sensors among all directions after magnetic deflection. Data obtained in orbit shows that the instrument works properly, and the data is in good agreement with the AP8 model. The observations of the MEPD on board the FY-4B satellite can provide important support for the safety of the spacecraft and the theoretical research related to space weather.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

Located at the geostationary orbit, Fengyun-4 series of satellites is the second generation of meteorological satellite of China. The observation data from FY-4 is real-time and continuous, so it is an ideal platform for space environment monitoring and alarm service, including numerical weather prediction, disaster weather warning, climate prediction service, ecological environment monitoring, communication and navigation safety and other fields. Launched on June 3rd, 2021, the FY-4B satellite is the first operational satellite of this series, on which many payloads in the space environment monitoring instruments package are newly added or optimized compared with FY-4A satellite, such as medium energy proton detectors (MEPD), medium energy electron detectors (MEED), plasma analyzer, fluxgate magnetometer and radiation dosimeter. Together with the FY-4A satellite, the double star network will further meet the service needs of China and the countries and regions along the Belt and Road for meteorological monitoring and forecasting, emergency disaster prevention and mitigation. 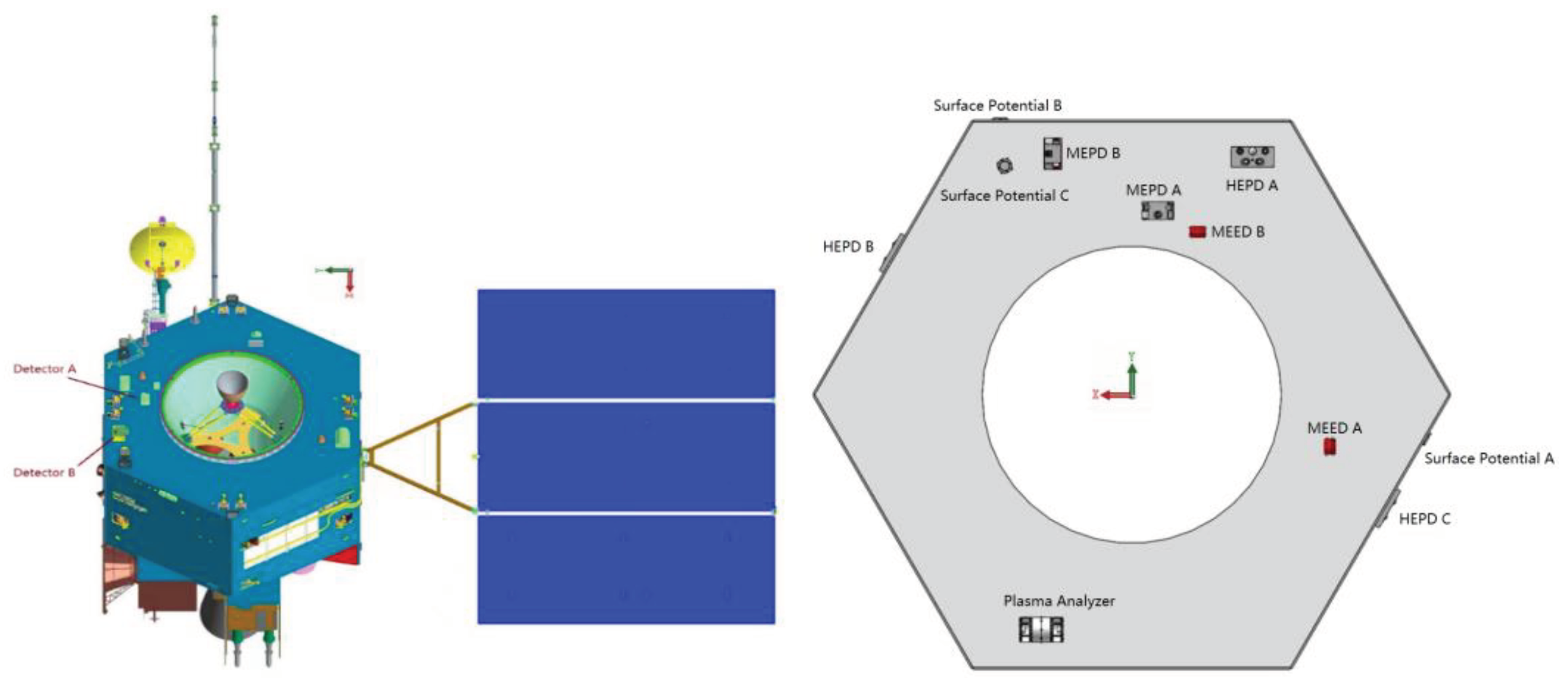Figure 1 shows all the detectors in the space environment instrument package.
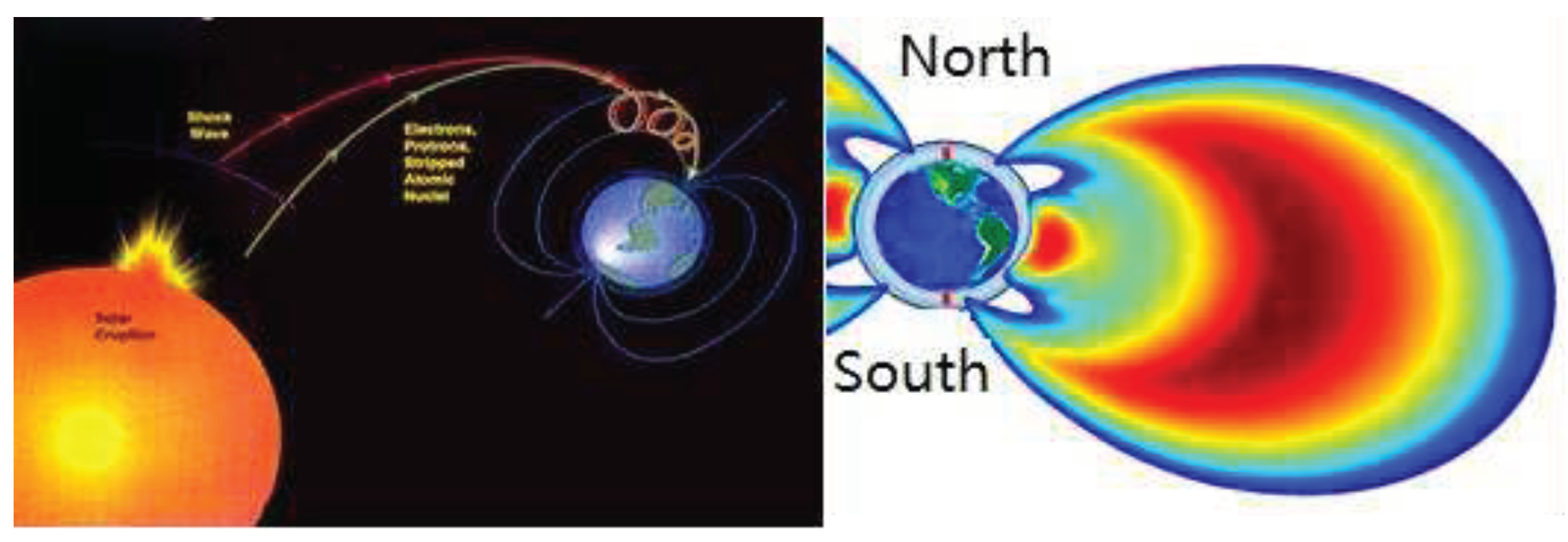
The orbit lies at the edge of outer radiation belt and it has a strong electron radiation background (Figure 2), which disturbs frequently [1]. Three-axis stabilized attitude of the satellite makes it possible to monitor solar activity, and medium-high energy particle, solar energetic charged particles, and galactic cosmic ray particles can be monitored on this space-based platform [2-4].
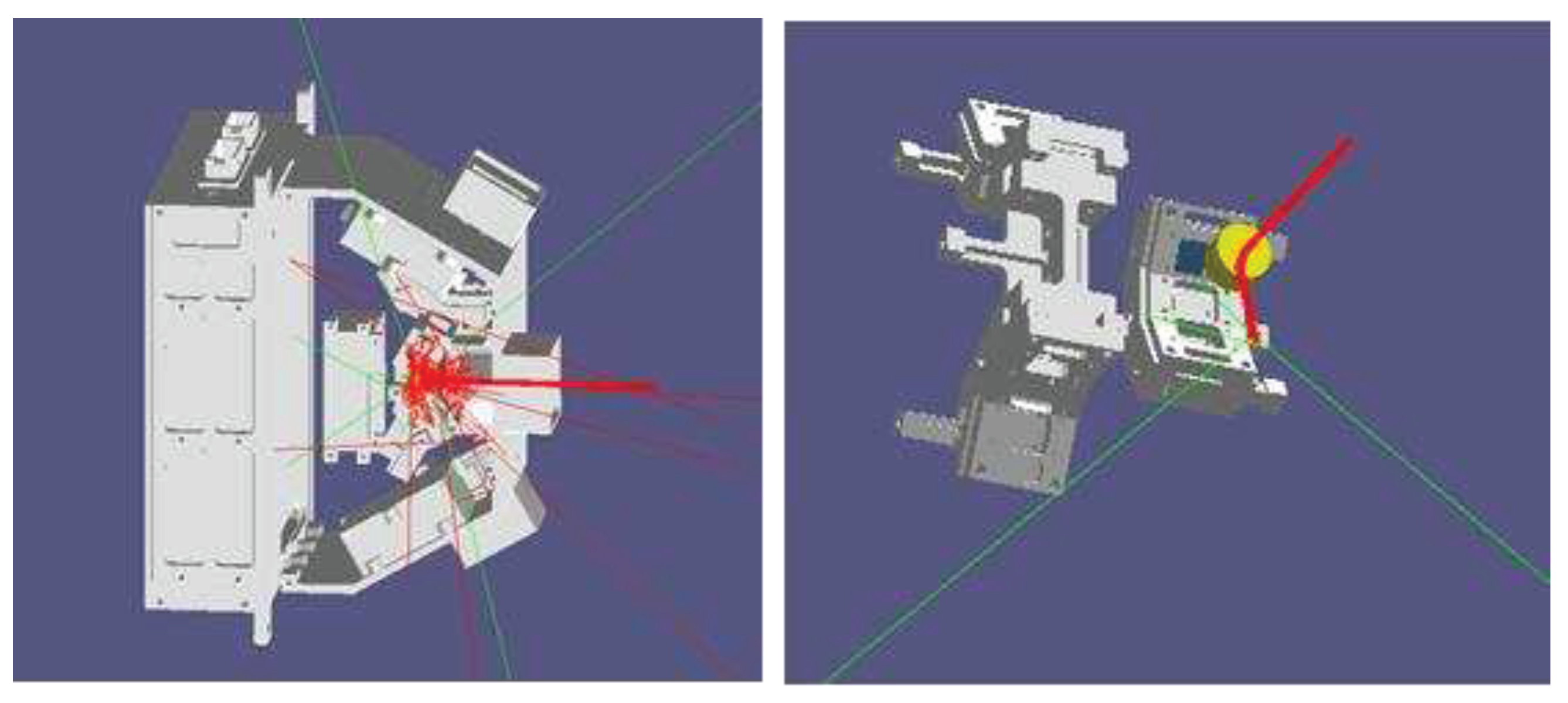
Joint observation of medium energy particle and high energy particle on this orbit can realize seamless and precise measurement of full spectrum with high resolution so as to monitor the transfer and distribution of the particles, which is extremely meaningful for studying the energy transport from the magnetotail to the earth and global radiation environment modeling [5]. The MEPD on FY-4B satellite is equipped with two components, detector A and detector B, both of which are installed on the top panel of the satellite. The field of view (FOV) of each detector is a 180°×20° sector (composed of nine 20°×20° FOV), which is parallel to the equatorial plane for detector A and parallel to the meridian plane for detector B. Figure 3 shows the overall layout of satellite (left) and the partial enlarged view of installation diagram of the two detectors (right).
This article is organized as follows: Section 2 introduces the mission requirements mainly scientific indicators of the MEPD. Section 3 briefly describes the detector design as a whole and focuses on the geometry factor design and light blocking layer design. Section 4 discusses the calibration and the testing results on the ground. Section 5 provides some results of in-orbit detection during the initial launch phase to verify the performance of the instrument.
The ground calibration results indicate that these two detectors exhibit excellent performance, and the design of the detector meets the requirements of detection tasks. Preliminary on-orbit observations data shows that the proton spectra measured are in good agreement with the results given by radiation belt model AP8.

2. Mission requirements

The task objective of MEPD on the FY-4B satellite is to achieve a wide energy spectrum detection of 30keV -1MeV in 18 directions, nine directions divided along the meridian plane and another nine directions divided along the equatorial plane, and to divide them into 12 energy channels in each direction. The actual measurement range is consistent with the detector on FY-3E satellite, which is 30keV-5MeV. The detailed scientific indicators are shown in Table 1.

3. Instrument Design

3.1. System composition

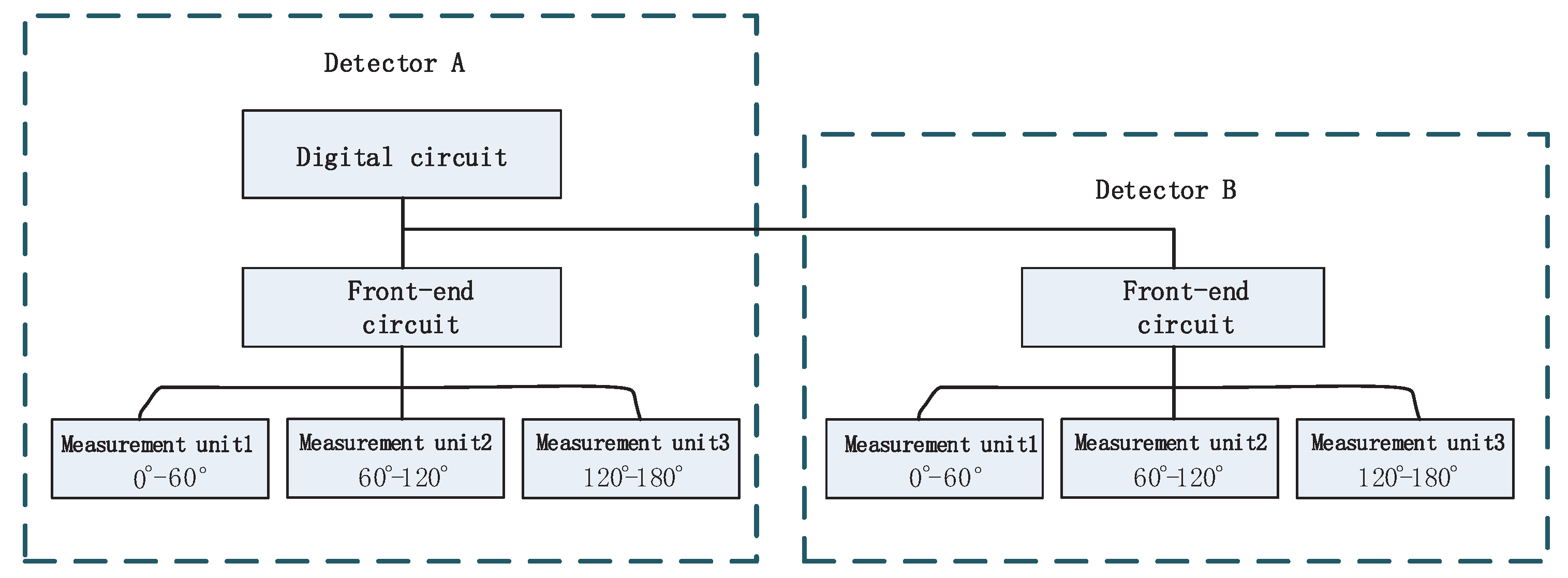
Similar to the MEPD on FY-3E satellite [6], this instrument consists of two parts, and the connection relationship is shown in Figure 4, in which detector A includes digital circuit for data acquisition and data processing besides the three measurement units and their matching front-end circuit, and detector B only includes three measurement units and their matching front-end circuits. The data packet including data of the two detectors is transmitted to RTU (Remote Terminal Unit, responsible for communication between detectors and satellite platform) by communication interface of detector A.
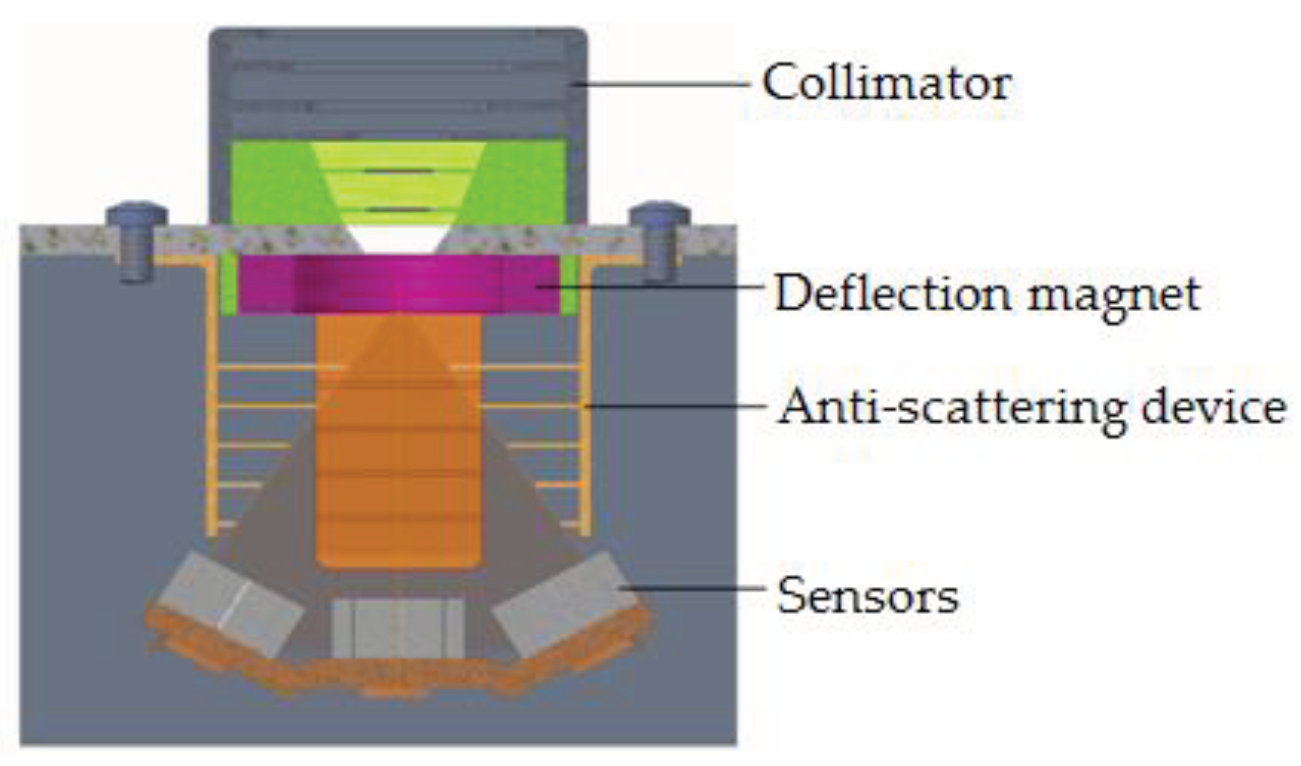
Each component is composed of three measurement units and each measurement unit has three groups of sensors organized in a fan-shaped arrangement. The internal structure of a measurement unit is shown in Figure 5. The field of view of each measurement unit is 20° × 60°, which is combined from three detection directions.

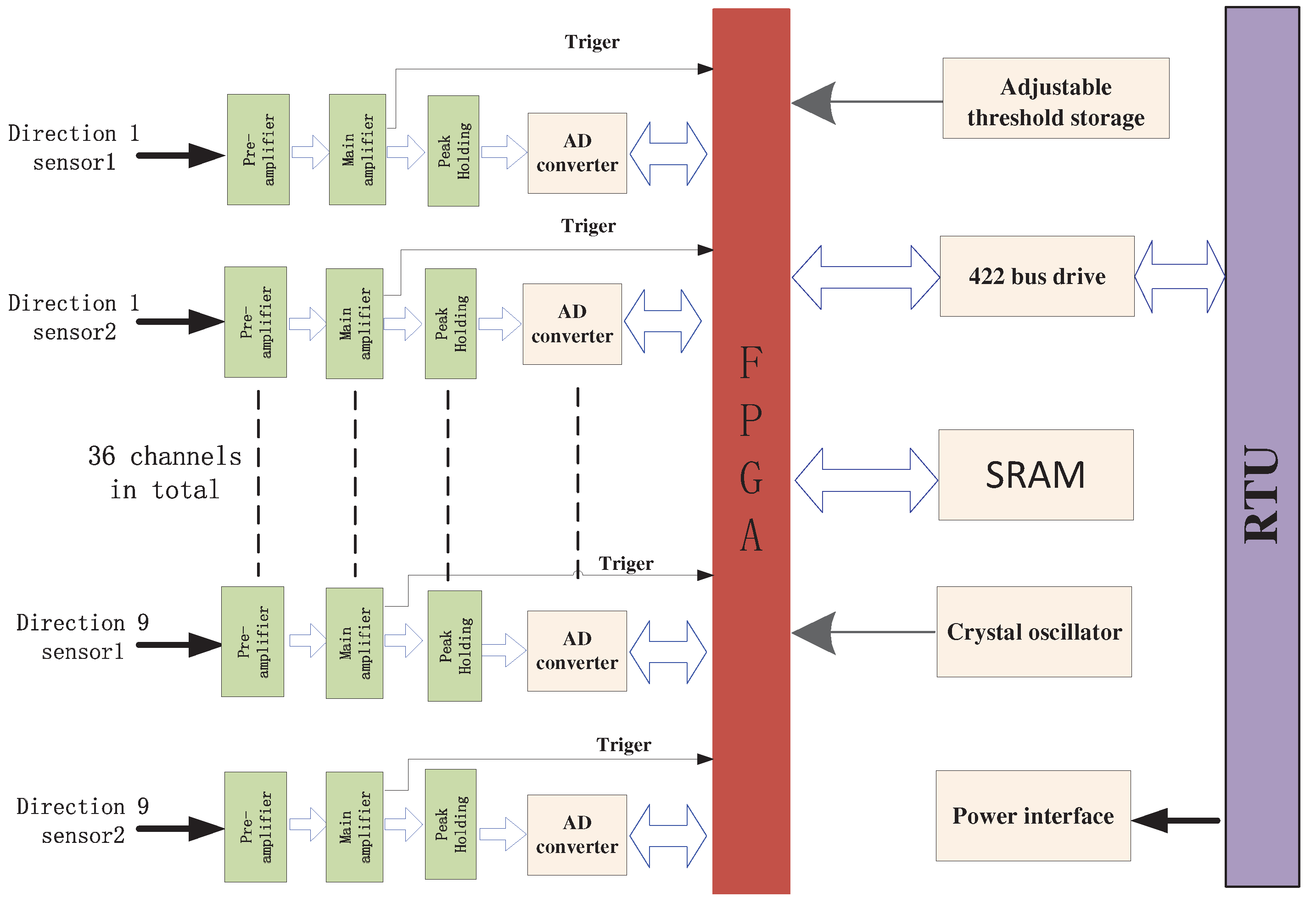
3.2. Electronics design

Two sensors form a group, which realizes the proton detection of one direction, and each sensor is connected to an independent front-end signal processing circuit. Thus, the whole instrument has a total of 36 front-end electronics circuits, which include pre-amplifier circuits、main amplifier circuits and peak holding circuits. Besides the front-end circuits, the electronics system also includes AD acquisition circuits, FPGA data processing module, communication circuits and power module. The working principle block diagram of detector A is shown in Figure 6.
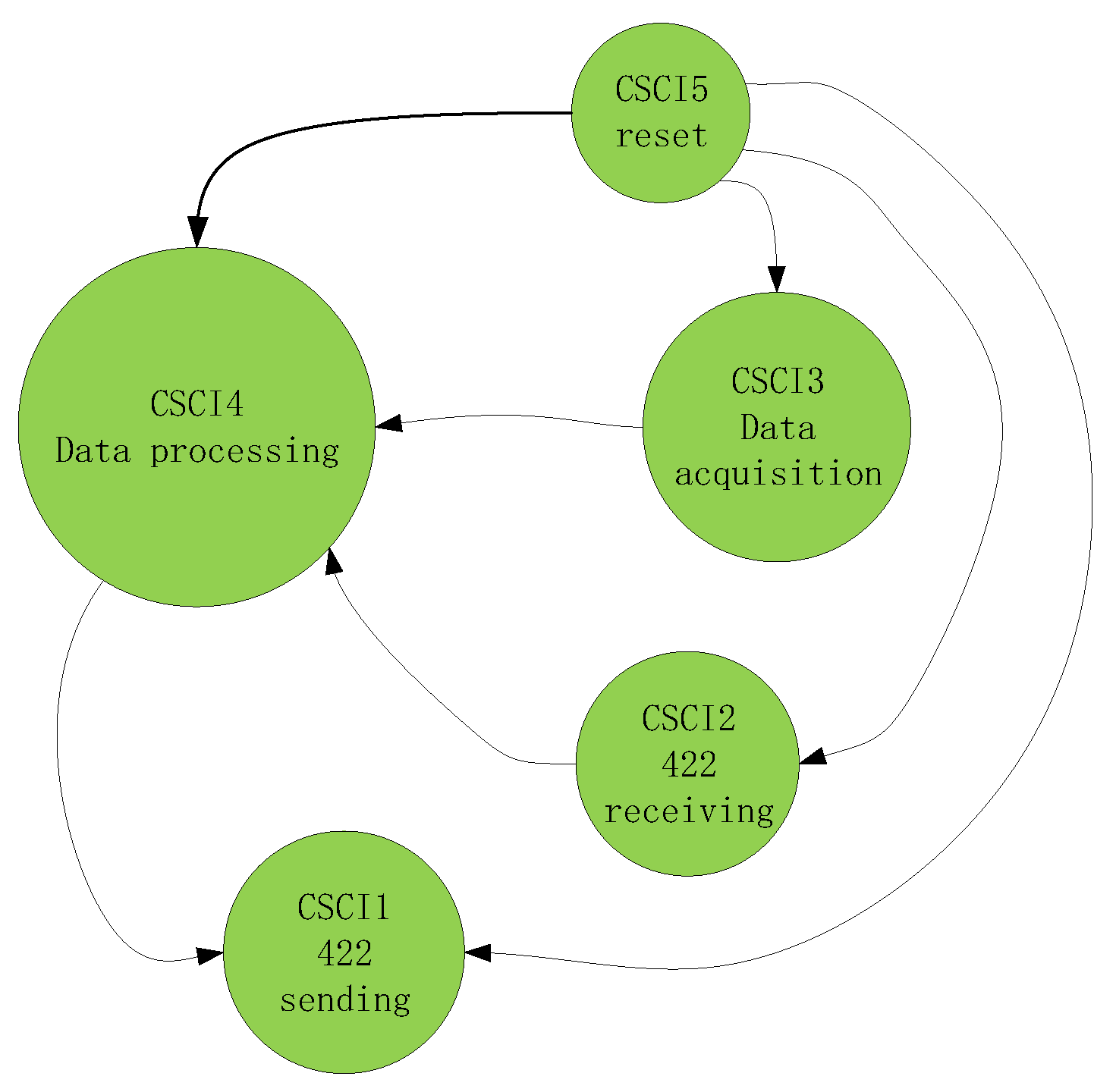
An FPGA (Field Programmable Gate Array) device AX1000-1CQ352M is used to realize logical control. In software design, five function modules are included: reset module, science data and engineering parameter acquisition module, data processing module, 422 bus receiving module and 422 bus sending module. Figure 7 shows the relationship of the function modules, in which the CSCI is the abbreviation of computer software configuration item.
The software workflow is as follows: 422 bus receives the data acquisition command, which marks beginning of the 1s cycle, then the six analog-to-digital converters (ADC128S, 8 channels in each device) start to work in trigger mode under the time-sharing strategy (Figure 8), which means that 18 sensor signals from detector A are acquired in the first 0.45s, the 18 sensor signals of detector B are acquired in another 0.45s, so time factor should be considered when normalizing the data. After that, in the following 0.1s, the engineering parameters such as sensor noise monitoring signals, power supply voltages monitoring signals of 5V and ±12V are collected and stored into a SRAM. Then the FPGA waits for the “data sending” command and clears the SRAM after sending the data. Every two ADs are responsible for a measurement unit (three directions), and the priority for each direction depends on the sequence of the incoming trigger signals.

3.3. Sensor system

3.3.1. Light blocking layer

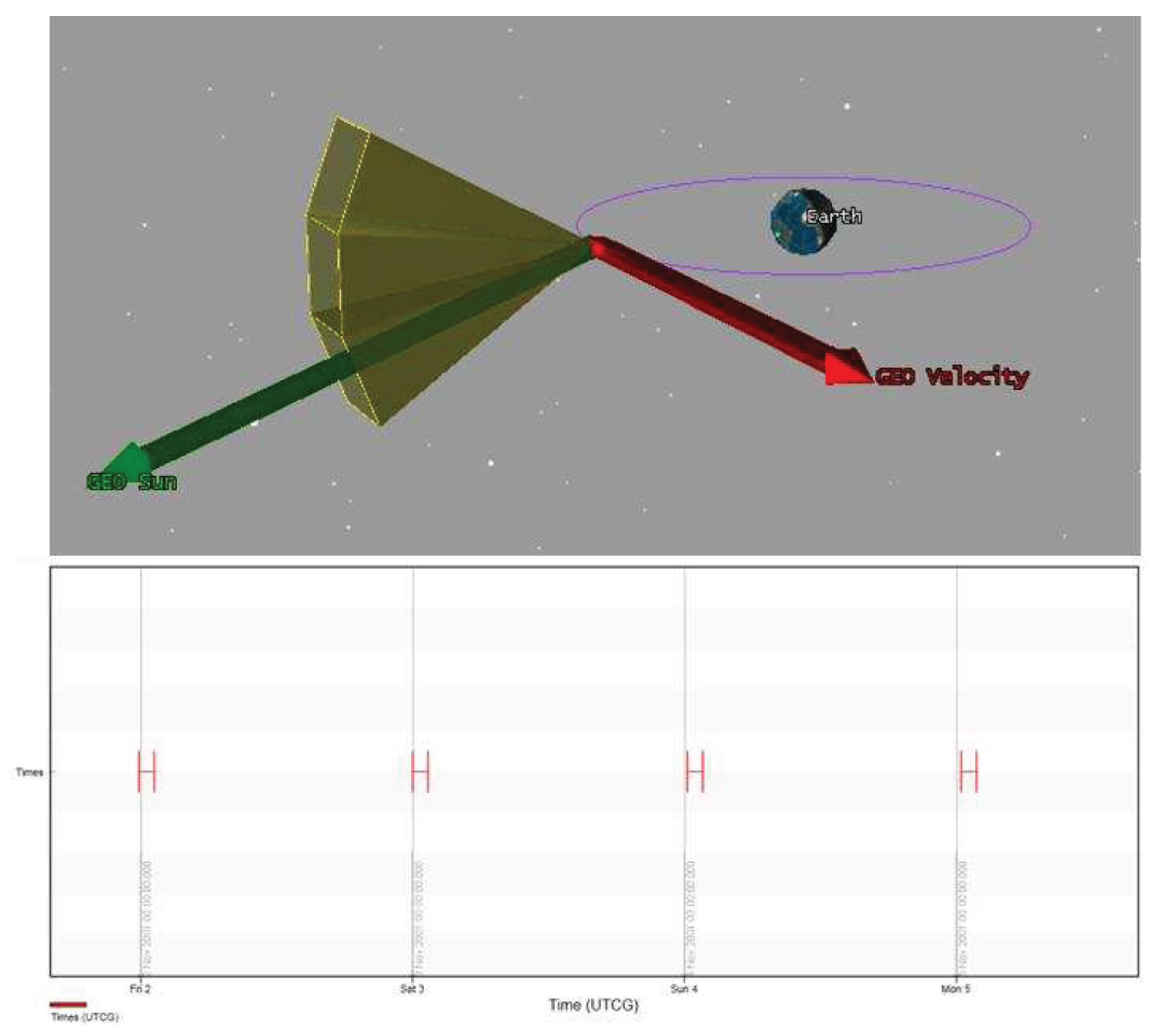
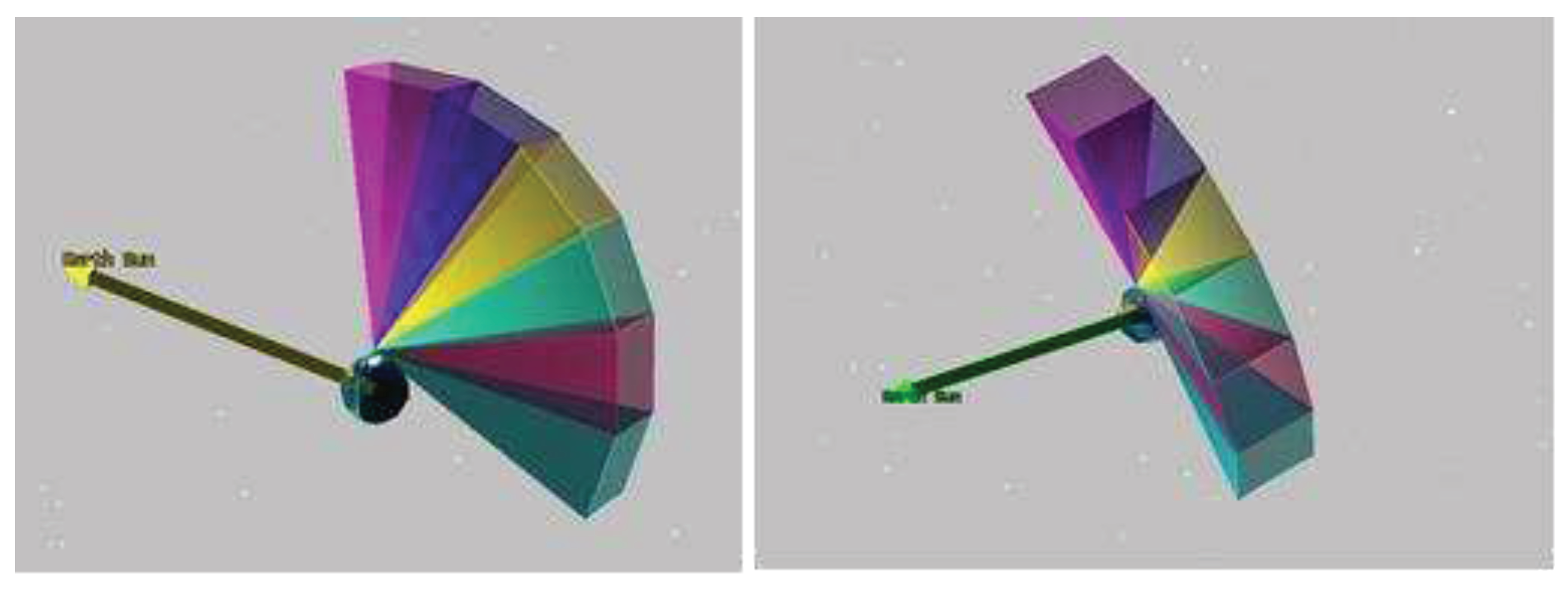
Commonly used light-blocking layer is not applicable here because it can greatly reduce the energy of incoming protons, especially when the energy of the incident proton is low, so the MEPD on FY-3E satellite used a 100nm thick aluminum coating on the surface of the sensor to shield the noise interference of visible light. When sunlight does not directly enter the sensors (like MEPD on FY-3E satellite，on which the two detectors are installed on the -X direction and +Y direction, respectively), the thickness of aluminum plated is enough to prevent stray light from entering sensors, and the influence of sunlight on the detection results can be ignored. But in FY-4 orbit, according to satellite trajectory simulation, sensors in certain directions expose to direct sunlight for 80 minutes every day. Figure 9 shows the scene of sensors illuminated by sunlight simulated with STK (satellite tool kit). Figure 11 shows that on FY-3E satellite, neither detector of MEPD has a chance to be exposed to sunlight directly.
From Figure 9 we can see that the time of sensors exposing to direct sunlight is not negligible. According to the experimental results of the detector on a solar simulator in vacuum tank, there are interference counting output in channel P1 and channel P2, and this may be caused by uneven coating thickness of aluminum. The lighting interference counting greatly affects the use of scientific data, and on the other hand, lighting will reduce the lifespan of sensors, so extra measures must be taken to shield the sunlight.
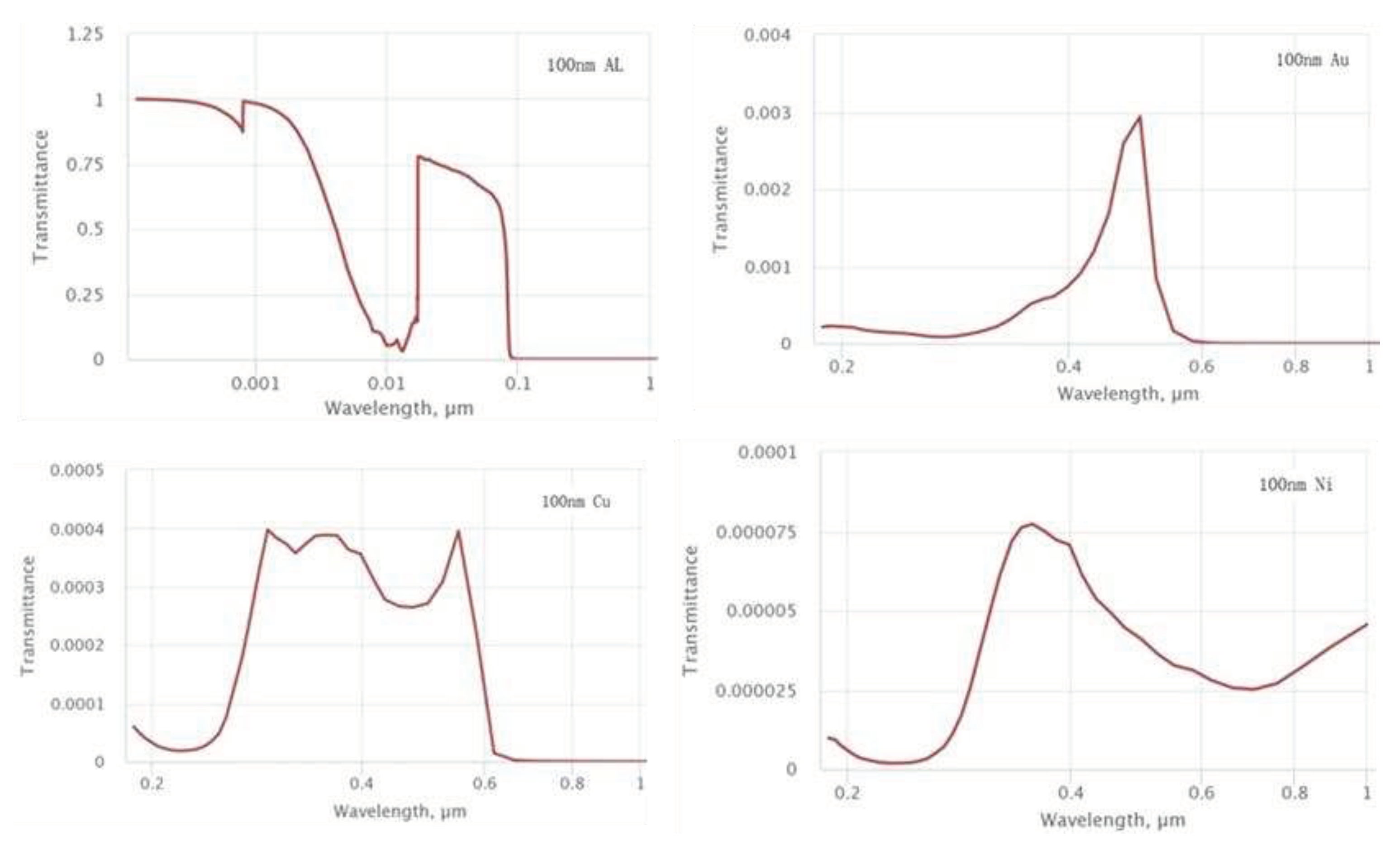
Compared with other material, nickel film has superior shading performance. Figure 11 shows the comparison of light blocking ability of four materials: Al、Au、Cu、Ni (the data is obtained from https://refractiveindex.info/). As can be seen from the Figure, when the wave length of light is less than 100nm, Cu and Ni have lower light penetration rate and at wavelength greater than 100nm, Al and Ni perform better. Considering the blocking effect of materials on protons, nickel is the best light barrier material, so besides the aluminum coating, another 100nm nickel film light barrier is added in front of the sensors.
After adding nickel film in front of the sensors, the lighting test of MEPD is carried out under the illumination of the solar simulator, which is provided by Beijing Institute of Spacecraft Environment Engineering. Adjusting the angle between the parallel light beam and the normal direction of the sensor sensitive surface to 0°,30°,60°,90°, no counting output in all the energy channels of the detector. Figure 12 shows the lighting test scenario of MEPD.
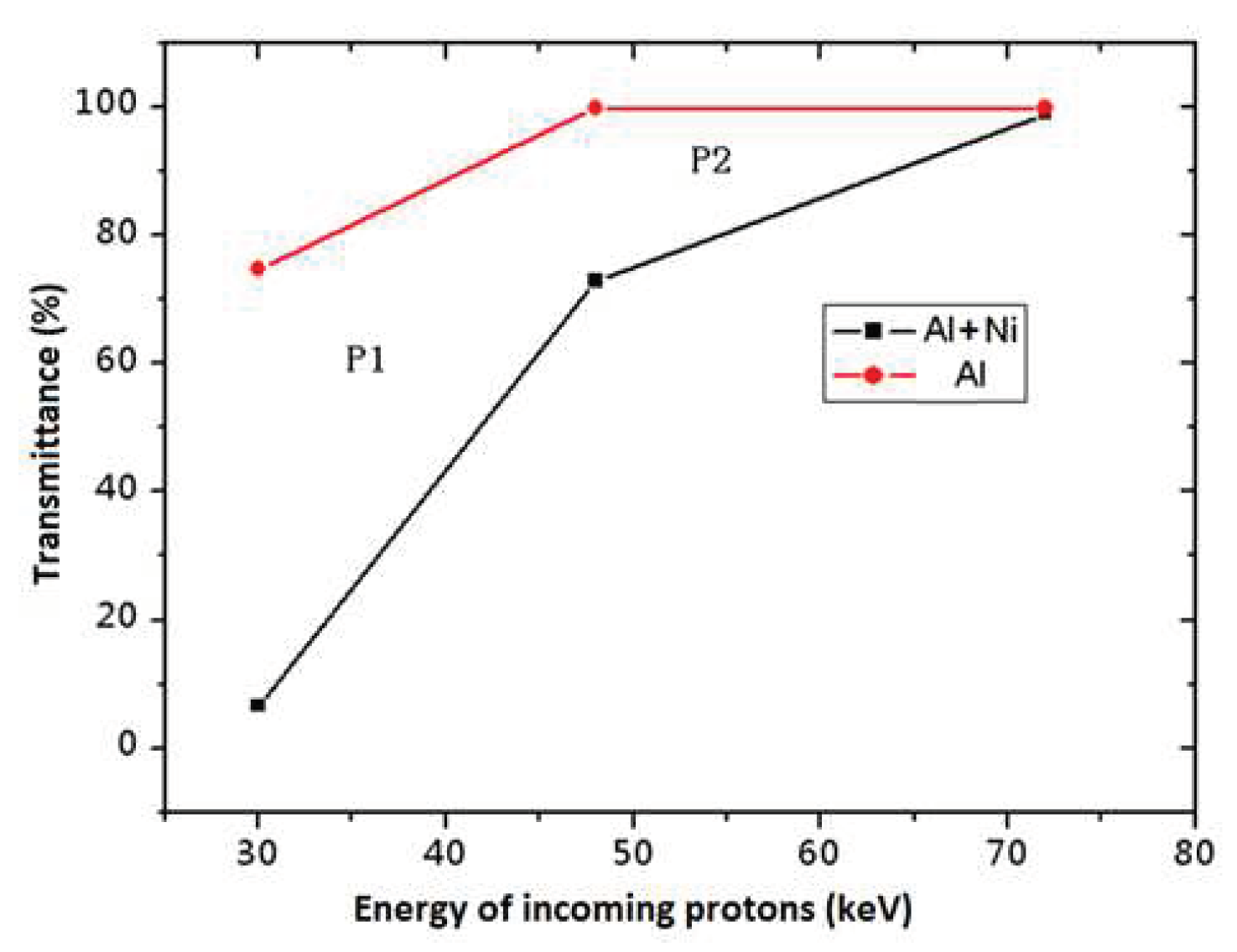
However, using 100nm thickness nickel film in front of the sensors to block the light will reduce the detection efficiency greatly, especially for channel P1 and channel P2. Figure 13 shows the transmittance of protons with or without the addition of another 100nm nickel film respectively.
As shown in Figure 13, when a 100 nm nickel film added, the detection efficiency has significantly decreased in channel P1 and channel P2, so it is necessary to make corrections when using data of these two channels.

3.3.2. Proton transportation simulation

Same with MEPD on FY-3E satellite, ion implantation-type semiconductor sensors are used in the detectors. The sensor is 300um thick and the sensitive area is 8×8 mm, with a 100nm thickness aluminum coating. In each direction, sensor D1 is used as a pulse amplitude analyzer for energy division, and D2 is used as an anti-coincidence detector to exclude the interference of high-energy protons and high-energy electrons. Due to the wide dynamic range, the output signal of D1 is amplified in two stages to output energy channels P1-P6 and P7-P12, respectively.
In front of the sensor, there is a total of 100nm thick nickel film and 100nm thick aluminum coating. Figure 14 simulates the energy deposit of 30keV proton in silicon after passing through the above-mentioned materials.
We can see that with these light blocking materials, the mean energy left for 30keV proton is only about 7.8keV, almost half of the deposited energy when a 30keV proton is incident on the MEPD sensor of FY-3E satellite.

3.3.3. Deflecting magnet

The function of deflecting magnet is to exclude the interference of medium and low energy electrons [7]. For medium energy protons and electrons of the same energy, their energy loss in the silicon semiconductor sensor is almost the same, and they cannot be identified by the circuit. Therefore, deflecting magnet is used inside the collimator to deflect the electrons so that they cannot come into the silicon sensor. The deflecting magnet used here is a permanent annular magnet structure which can exclude electronic interference below 1.5MeV. Due to the elastic scattering of electrons, the deflected electrons may enter sensors in other directions, causing interference with measurements in other directions. Geant4 software [8-9] was used to establish a model of the entire machine and simulate the trajectory of electrons to obtain the proportion of deflected electrons entering sensors of other direction. The simulation results showed that interference ratio is far less than 1% within the full energy range, thus the influence of the deflected electrons on other sensors can be ignored. Deflection scene of 1.5MeV electrons passing through the magnetic field is shown in Figure 15.
Electrons with higher energy (> 1.5 MeV) still had a certain probability to enter the detector after being deflected by the magnetic field. The interference ratio of electrons to medium energy protons can be effectively reduced to within 2% by the anti-coincidence sensor. This is why two sensors are used in each direction.

3.4. Geometry factor

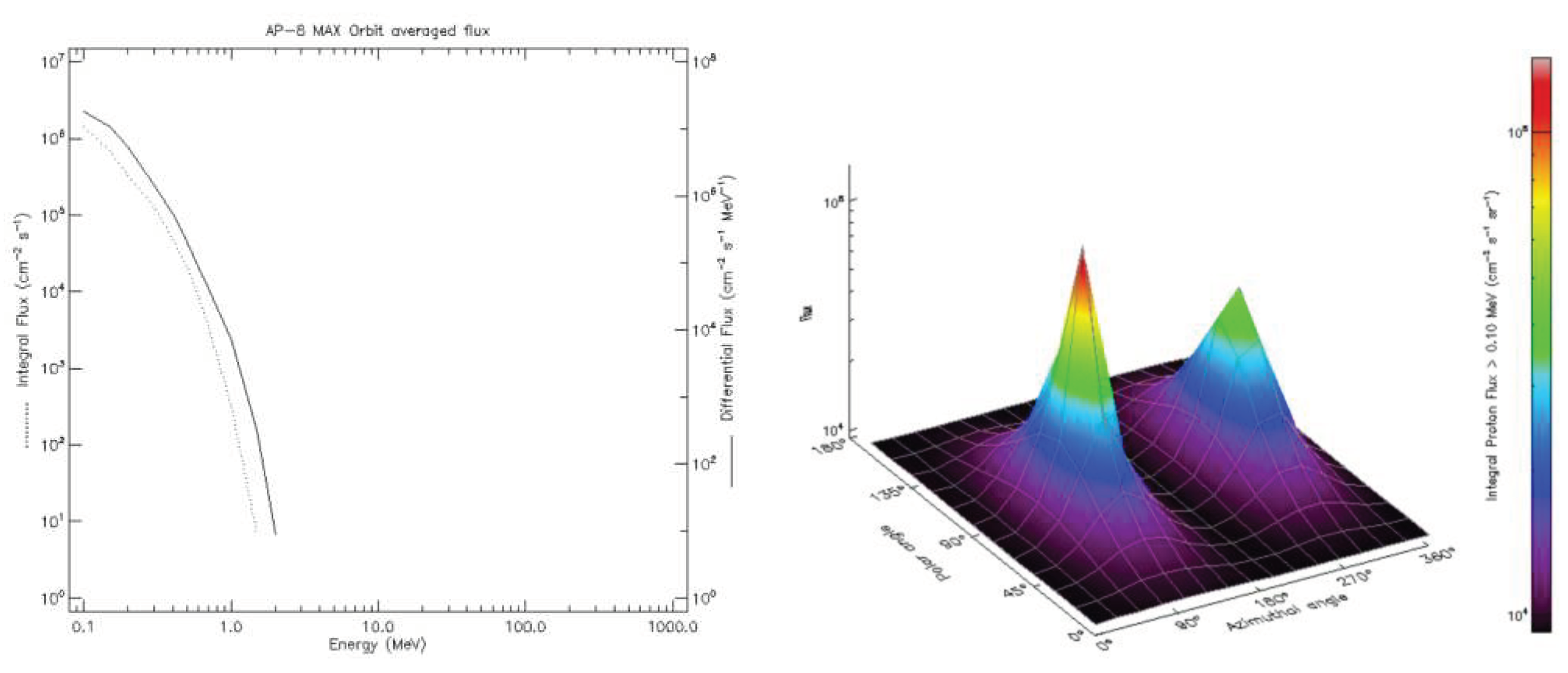
The geometry factor is decided by the structure of sensor system. The field of view (FOV), which mainly depends on the collimator, is the key factor to determine the geometry factor. A good collimator can provide shielding conditions to prevent the interference of particles obliquely incident from the side to the sensor [10]. According to radiation model AP8-MAX, the integral flux of protons above 100keV in this orbit is up to 106cm-2s-1, and trapped proton unidirectional flux at 100keV is greater than 105cm-2sr-1s-1, as shown in Figure 16. At present, there is no available model or measured data for reference for medium energy protons with energy lower than 100keV. Extrapolation was carried out according to the model and with a certain margin, the integral proton anisotropy flux greater than 30keV is approximately 107cm-2 sr-1s-1. Since the maximum suitable counting rate of the electrics is 5×104/s, the geometry factor can be set to 0.005 cm2sr at most theoretically. Considering the counting error of electronics at high counting rates, here we set the geometry factor to 0.002 cm2sr in order to ensure that electronics has an appropriate counting rate.

4. Ground calibration

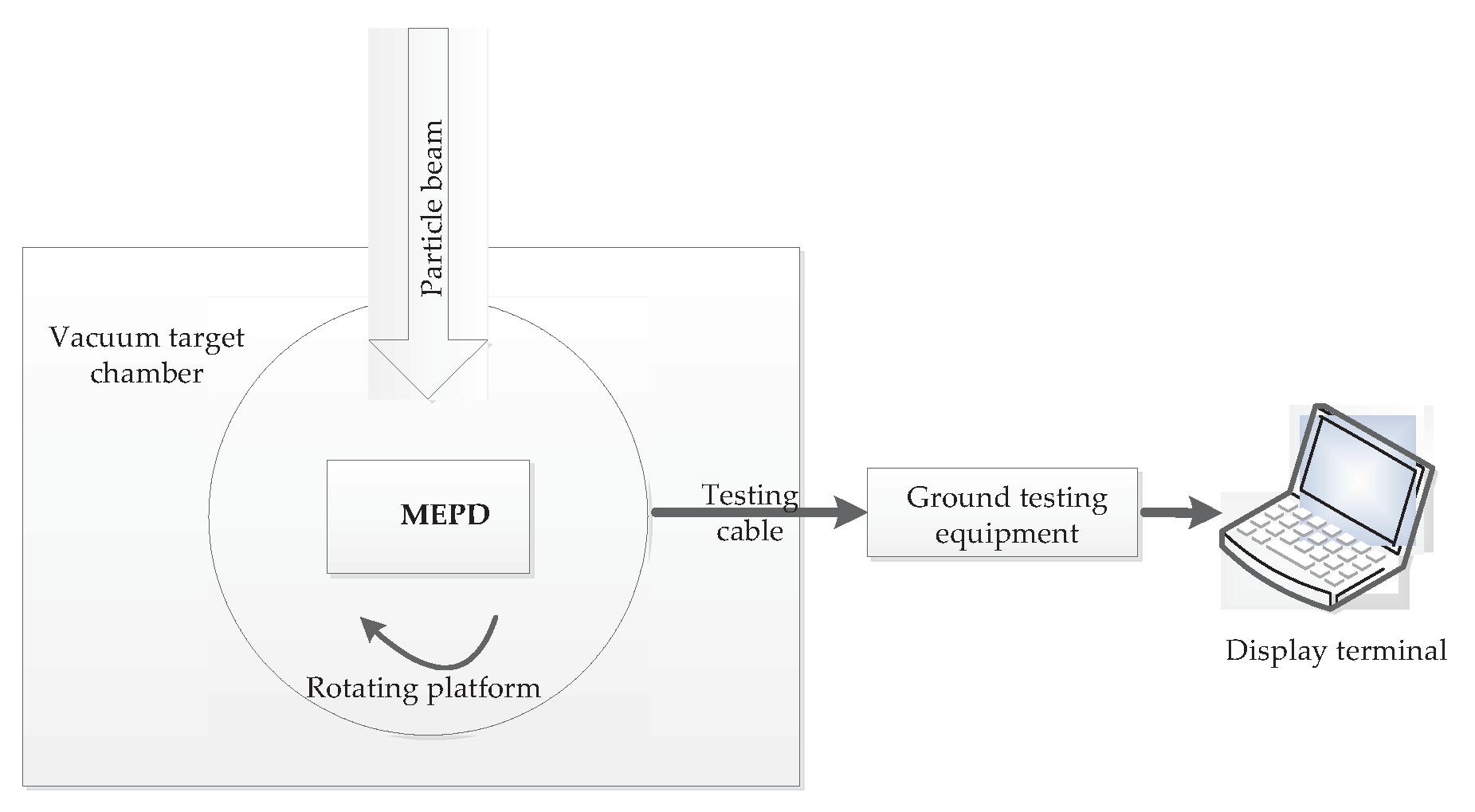
4.1. Calibration Method

The calibration method is the same as that of similar particle detectors [11-15]. The calibration items include the energy spectra range, energy linearity, energy resolution, particle flux accuracy and the test of the sensor thickness, size, field of view, and the particle identification capability etc.al. Detailed introduction of calibration method and test contents can be found in the article [6]. The calibration was carried out on the 200 keV and 2 MeV accelerators of the “Space Payload Test and Calibration Platform” in Huairou District, Beijing. The block diagram and calibration scenario of the calibration testing system are shown in Figure 17 and Figure 18. The main calibration results are given here in this article.

4.2. Calibration Results

Since the calibration results of 18 directions of the MEPD are highly consistent in the energy spectra range, linearity, and energy resolution, the ground testing results of the MEPD in direction one are given here to verify its performance.

4.2.1. Energy Linearity & Energy Resolution

The energy linearity is obtained by following steps. Firstly, select the electron beam with determined energy Ei for incident, and record the energy deposition spectrum of electrons in the silicon sensor through a multi-channel system. Then, using multi-channel measurement results, Gaussian fitting is adopted to obtain the center value λ i. Meanwhile, through Geant4 simulation, the energy loss (Δ Ei ) of incident electrons with energy of Ei is obtained. After that, use a series of Δ Ei and λ i results (n points, n>5) for linear fitting with a formula of y = k x + b . Finally, energy linearity χ for each direction can be calculated as follows:
χ = 1 n ∑ i = 1 i = n | Δ E i − y i Δ E i |
Energy resolution refers to the energy broadening measured by the detector for particles with fixed energy and it is equal to the ratio of the full width at half maximum (FHWM) to the center value λ 0, as shown in Equation (2):
η = Δ λ λ 0 × 100 %
In Equation (2), λ0 is the abscissa of Gaussian peak position and Δ λ   is FHWM of Gaussian fitting curve.
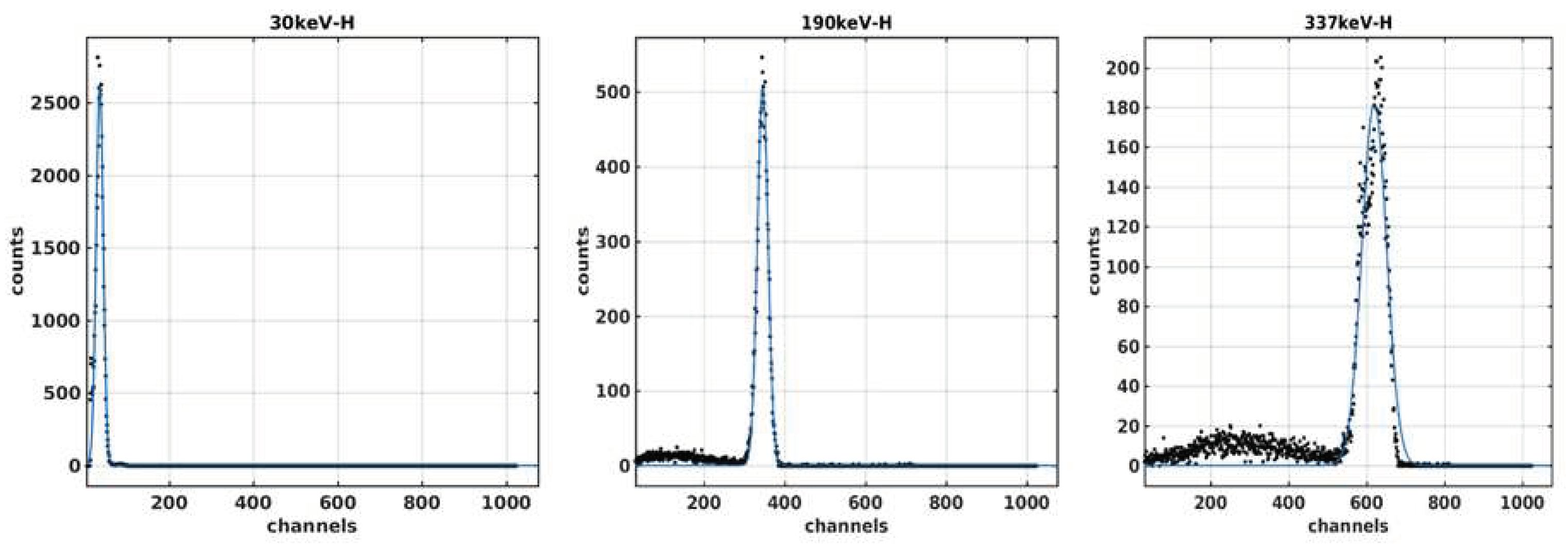
Part of the Gaussian fitting results of the measured data of low energy sections (30keV, 190keV, 337keV) in the multi-channel analysis mode in direction one are shown in Figure 19, where the ordinate of the black points is the multi-channel counting data corresponding to the fixed incident electron energy, the abscissa is the channel number, and the blue curve is the fitting result.
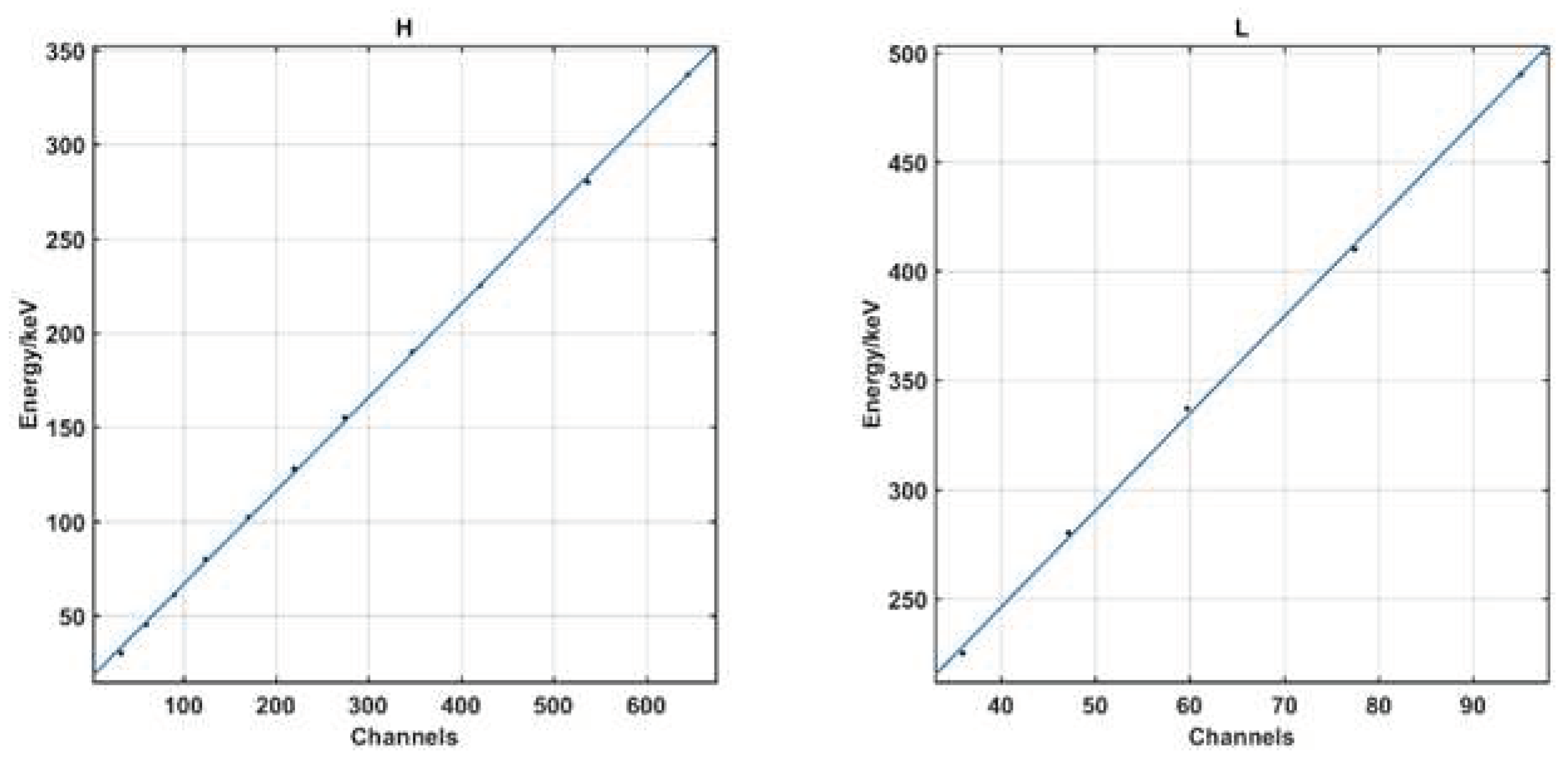
The linear fitting results for energy bands with incident particle energy<350keV and energy bands with energy>350keV are shown in Figure 20, respectively. The linear fitting formula for low energy section (high gain) is y = 0.5827 x + 16.07 and for high energy section (low gain): y = 6.651 x + 81.86 , where x is channel position and y is energy loss in keV.Table 2 lists the calibration results of energy resolution and energy linearity in all directions.

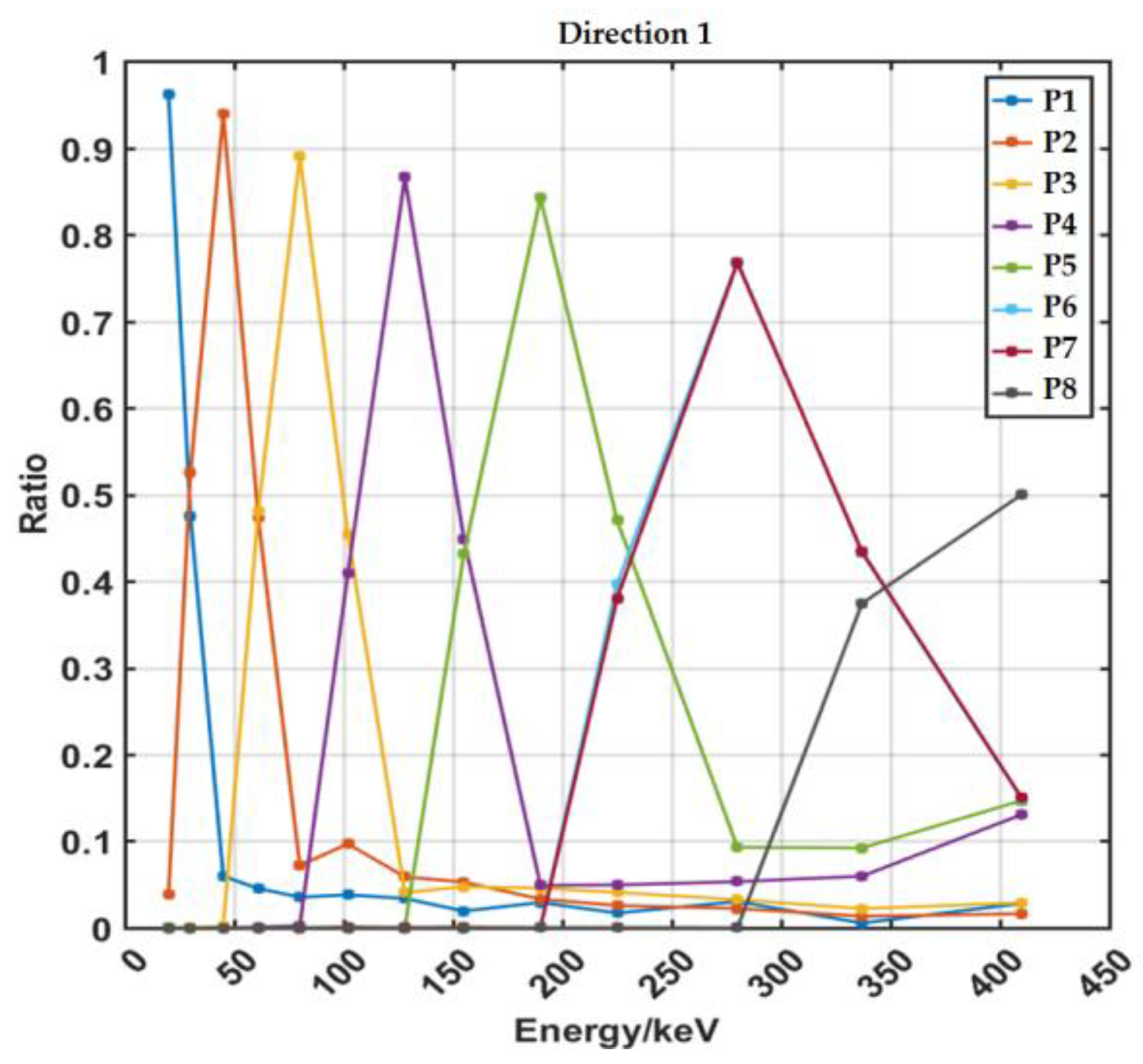
4.2.2. Energy Channel Division

The actual demarcation points of energy channels are determined by the count change between two adjacent energy channels. Normalizing the counts of the two energy channels to obtain the proportion of counts in each energy channel, the central intersection point can be found according to the changing trend of the counting ratio. The actual obtained boundary values are shown in Table 3. The error range of energy channels division is calculated by Equation (3):
δ=|Ca-Cd|/Cd.
In the formula, Ca is the actual energy boundary position, Cd is the designed energy boundary position, and δ is the error range.
According to the energy channel division in Table 3, we set the threshold voltage corresponding to the actual energy boundary in the software. Then we remove the deflecting magnet of measurement unit 1 and select electrons of multiple energies (30keV to 450keV) on the accelerator to test the detector. The response of each energy channel of the detector is very good, especially the P6 and P7 energy channels, which almost completely overlap and are consistent with the design, as shown in Figure 21. This test verified the detector's energy response performance.

4.2.3. Flux calibration

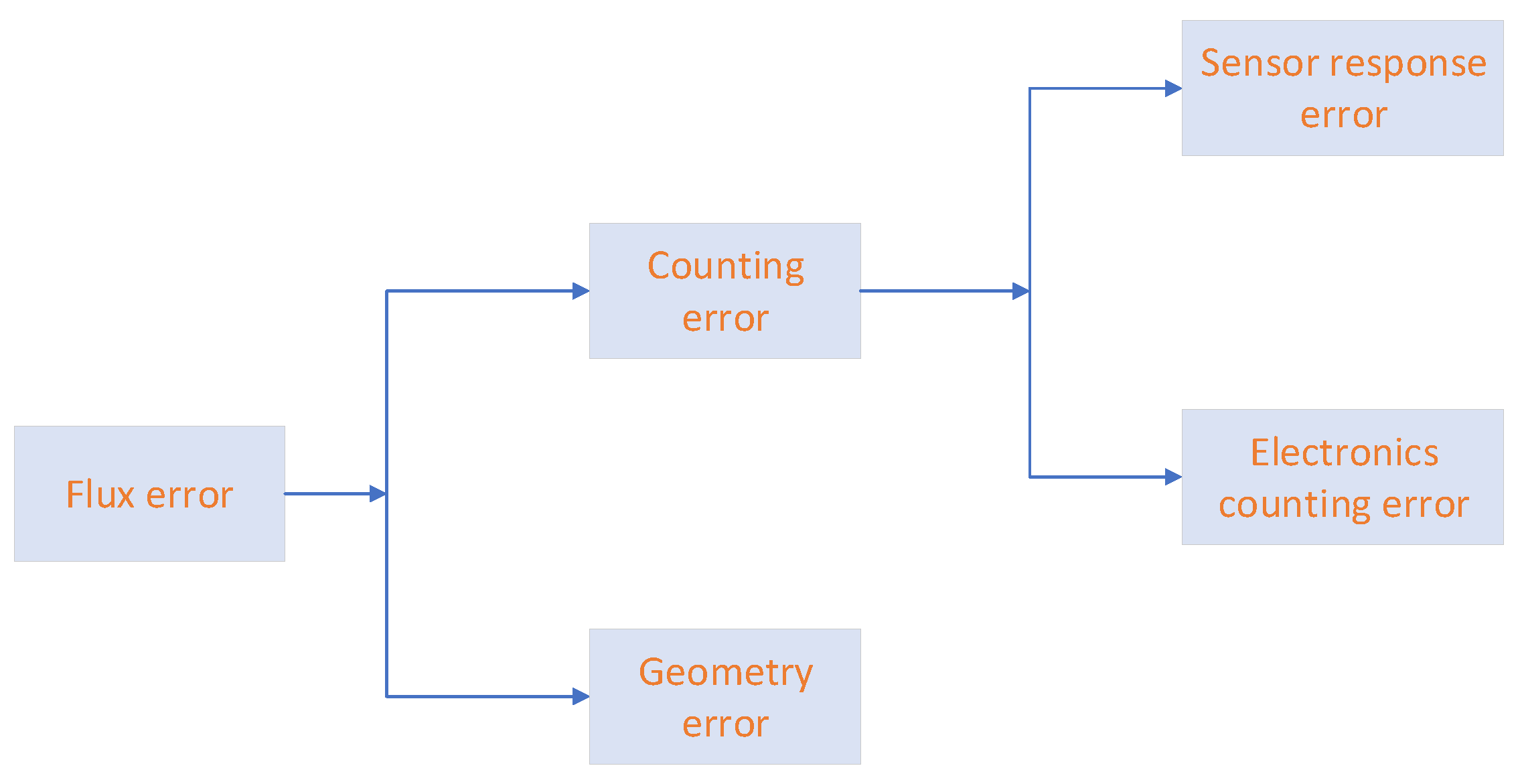
Flux calibration is used to correct in-orbit counting rate measurement results and verify instrument response under high flux conditions. Figure 22 shows the composition of flux error.
According to the system error transfer function:
σ y 2 = ∑ i ( ∂ y ∂ x ) 2 σ xi 2
The total flux error:
σ F 2 = σ N 2 + σ G 2
Where σ F is Flux error, σ N     is counting error, and σ G is geometry error.
The calculation method of geometric factors can be referenced in reference [16]. Because this process is a calculation method based on random numbers, there will inevitably be computational errors. The specific calculation method is to obtain a series of geometric factor values G i through multiple identical calculations, and calculate the average to obtain the final geometric factor. The variance of the geometric factor sample is the accuracy of the geometric factor. Due to the use of large sample sampling simulation, the simulation shows that the calculation accuracy of the geometric factor is better than 3%.
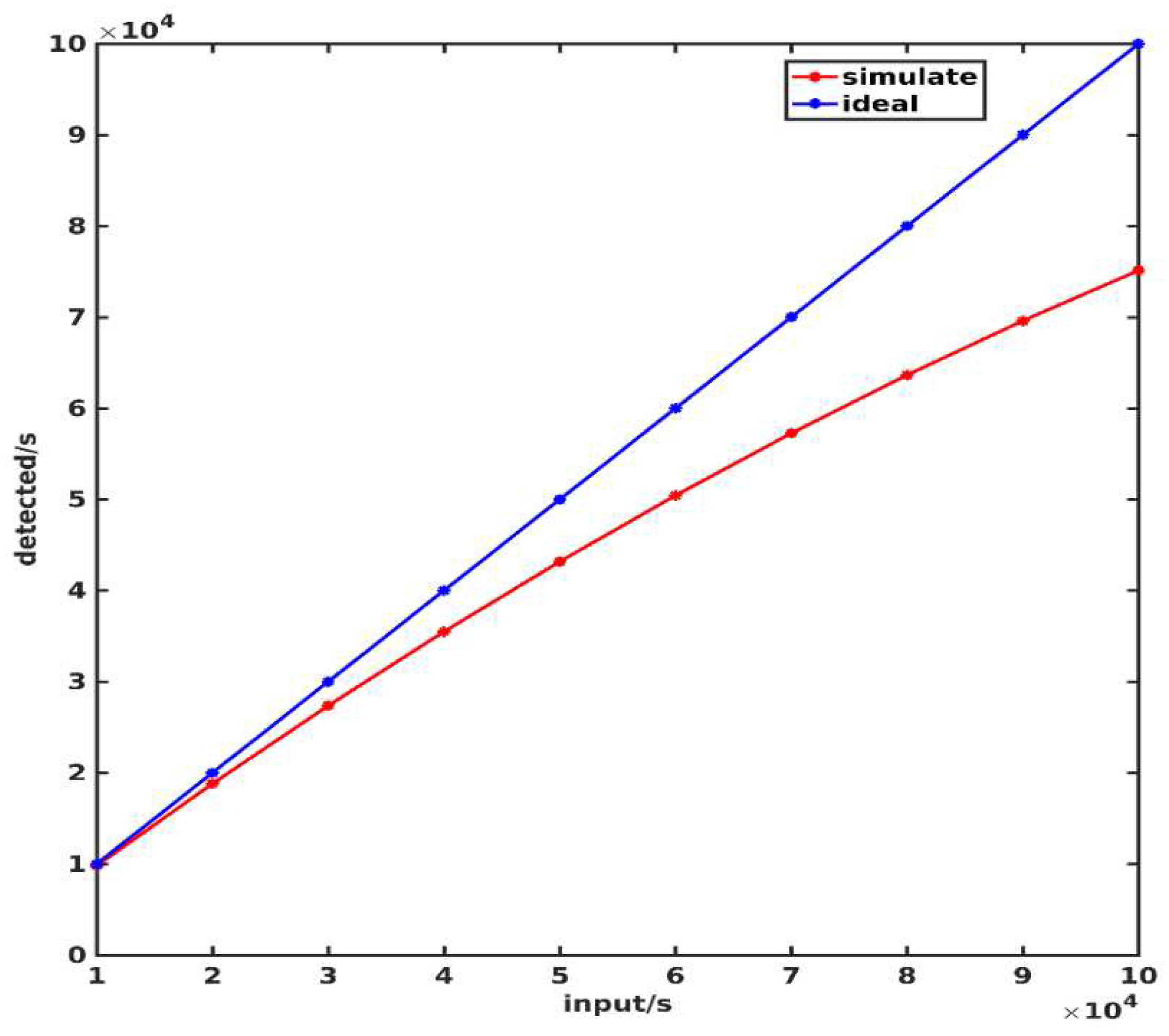
The detector counting error consists of the sensor response error and electronic counting error, based on which the counting error can be calculated according to formula 4. The electronic counting error mainly depends on the time required for the detector to process a single particle. The time resolution of the detector is 6µs. When the time interval between incident particles is less than 6µs, the detector will not be able to distinguish between two particle signals, which will result in count loss. The relationship between the number of incident particles and the output count is simulated, shown in Figure 23.
By fitting the simulation results, the relationship between the output counts and the number of incident particles can be obtained as follows:
y = − 2.17 × 10 − 6 x 2 + 0.9644 × x + 380
In which x is incident particle number, y is fitting result of average output counts.
The true value of incident particles number can be obtained by inferring the fitted curve, with a maximum electronics counting error of 1.57%.
When calculating the sensor response error, we use 207Bi radiation source to irradiate the sensor multiple times, and record the total count n i per unit time, the counting response error of the sensors is obtained by calculating the standard deviation:
σ s = 1 n − 1 ∑ i = 1 n ( n i − n ¯ ) 2
The sensor response error is 4.8% in this case.
According to formula 4, the total flux error of MEPD is 9.37%.

5. Observation results in orbit

After the launch of FY-4(02) satellite in June 2021, the first-hand data obtained shows that the distribution of medium energy protons is consistent with the AP8 model. Electron mixing and light pollution have been well suppressed.
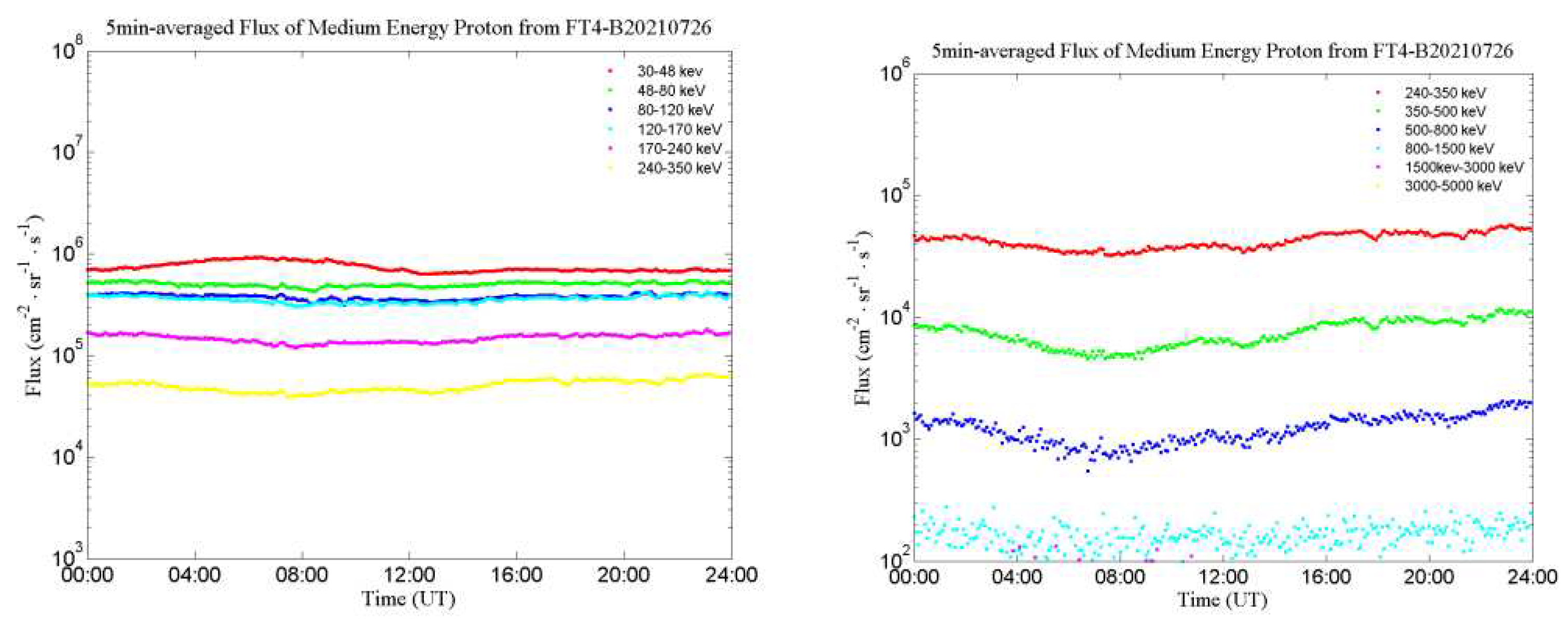
Figure 24 shows the proton flux observation results for each channel in direction 5. As shown in the Figure, the flux of each energy channel in this direction shows temporal changes at different time scales, indicating that the detector can continuously observe the flux of energy protons in space, and fully realize the function of medium energy proton detection.
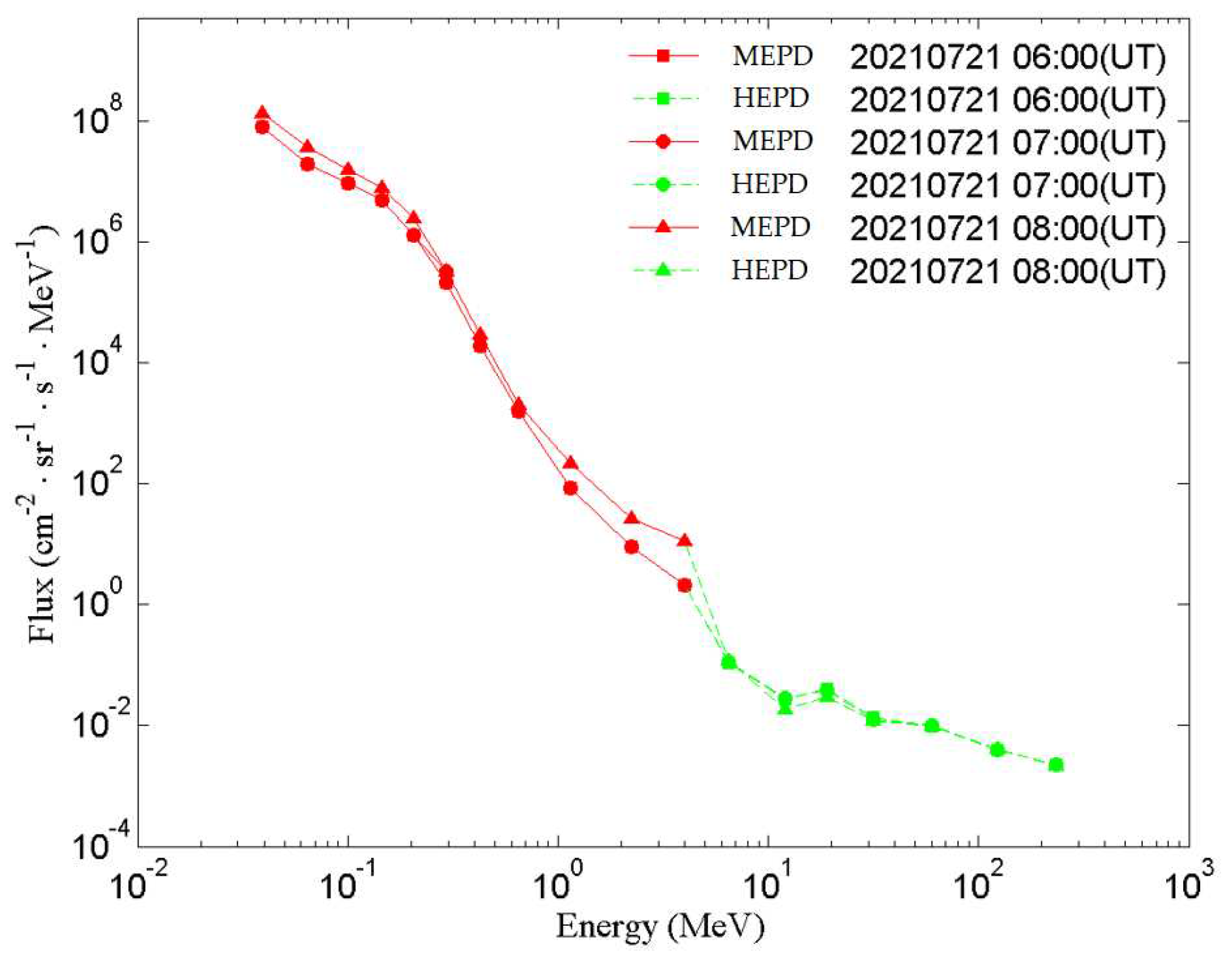
Combined with the results of high-energy proton detection on the satellite, data of protons with a wide energy spectrum spanning 4 orders of magnitude (30keV～300MeV) is obtained for the first time in China (shown in Figure 25).

6. Conclusion

This paper discusses the design and development of electronic system and sensor system of MEPD on FY-4 satellite in detail. Compared with MEPD on FY-3(05) satellite, the ability to eliminate the light pollution is further improved by using a 100nm nickel film. The experiment under the lighting of solar simulator shows that all proton channels are not contaminated by photons. The geometric factor is redesigned according to the characteristics of orbital radiation environment. The data obtained in orbit shows that this instrument works properly and the data is in good agreement with the results calculated by the AP8 model.

Author Contributions

Conceptualization, H.Z.; Funding acquisition, W.Z.; Project administration, X.Z.; Data curation, A.C.; Methodology, S.Z.; Investigation, L.Z.; Supervision, R.Z.; Resources, J.G.; writing—original draft preparation, H.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by China National Space Administration (CNSA D050103).

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Acknowledgments

We thank the following facilities and personnel for supporting the calibration of the MEPD: NSSC-SEF (National Space Science Center-Space Electron Facility), China; Irradiation facility dedicated for Heavy Ion-Induced Single-Event Effect, CIAE (China Institute of Atomic Energy), China; HIRFL Heavy Ion Research Facility in Lanzhou, China. We thank Gang Guo/CIAE and Jie Liu/HIRFL for providing the service of calibration.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chang Z, Wang Y M, Tian T,et al. Causal Analysis Between Geosynchronous Satellite Anomalies and Space Environment[J].Yuhang Xuebao/journal of Astronautics, 2017, 38(4):435-442. [CrossRef]
  2. Matéo-Vélez J-C, Sicard A, Payan D, Ganushkina N, Meredith NP, Sillanpäa I. Spacecraft surface charging induced by severe environments at geosynchronous orbit. Space Weather, 2018, 16: 89– 106. [CrossRef]
  3. Nagai T, Shinohara I, Singer H J,et al.Proton and Electron Injection Path at Geosynchronous Altitude[J].Journal of Geophysical Research, A. Space Physics: JGR, 2019(6):124. [CrossRef]
  4. B.T. Tsurutani, J.K. B.T. Tsurutani, J.K. Arballo, X.-Y. Zhou, C. Galvan, J.K. Chao. A: Electromagnetic electron and proton cyclotron waves in geospace, 2002; 12. [Google Scholar] [CrossRef]
  5. Baker, D. N. et al. High-Energy Magnetospheric Protons and Their Dependence on Geomagneticand Interplanetary Conditions, J. Geophys, 1979, Res. 84, 7138.
  6. Zhang, H.; Zhang, X.; Wang, J.; Huang, C.; Li, J.; Zong, W.; Shen, G.; Zhang, S.; Yang, Y.; Zhang, P. Design and Development of Medium Energy Proton Detector Onboard FY-3E Satellite. Aerospace 2023, 10, 321. [Google Scholar] [CrossRef]
  7. Zhang S Y,Wang S J.Design of the sweeping magnet in the space particle detector.Chinese J.Geophys. 6: Chinese), 2007, 50(3), 2007.
  8. Geant4 Collaboration. Geant4’s Guide for Application Developers, Version Geant4.10. 2013.
  9. Guo J,Banjac, Saša,Röstel, Lennart,et al.Implementation and validation of the GEANT4/AtRIS code to model the radiation environment at Mars[J].Journal of Space Weather and Space Climate, 2019, 9. [CrossRef]
  10. Yando, K., R. Millan, J. Green, and D. Evans. A Monte Carlo simulation of the NOAA POES Medium Energy Proton and Electron Detector instrument, J. Geophys. Res., 2011, 116, A10231. [Google Scholar] [CrossRef]
  11. Hou Donghui, Zhang Shenyi, Zhang Xiaoxin, Zong Weiguo. 9: Design Optimization of Novel Collimator for Detector of Space High Energy Electron: A Simulation Study, Chinese Journal of Vacuum Science and Technology, 2020,10, 2020. [CrossRef]
  12. Grupen, C. , and B. Shwartz. Particle Detectors, Cambridge Monogr. on Part. Phys., Nucl. Phys. and Cosmol., 2008,vol. 26, 2nd ed., Cambridge Univ. Press, Cambridge, U. K.
  13. McFadden, J. , et al. In-flight instrument calibration and performance verification, in Calibration of Particle Instruments in Space Physics, ISSI Sci. Rep., 2007,vol. SR-007, pp. 277–385, Eur. Space Agency, Paris.
  14. Juan, V. Rodriguez1,2,*, Michael H. Denton3,4, and Michael G. Henderson. On-orbit calibration of geostationary electron and proton flux observations for augmentation of an existing empirical radiation model. J. Space Weather Space Clim. J. Space Weather Space Clim. 2020, 10, 28 JV Rodriguez et al, Published by EDP Sciences 2020. [Google Scholar] [CrossRef]
  15. Jo, G. B. , Sohn, J., Choi, C. R., Yi, Y., Min, K. W., Kang, S. B., Na, G. W., & Shin, G. H. Development of High Energy Particle Detector for the Study of Space Radiation Storm. Journal of Astronomy and Space Sciences, 2014, 31 (3) The Korean Space Science Society. [CrossRef]
  16. Zhang S Y, Zhang X G, Wang C Q, et al. The geometric factor of high energy protons detector on FY-3 satellite. 2: Science China: Earth Sciences, 2014, 57, 2014. [CrossRef]
Preprints 83544 g001
Figure 1. Detectors onboard FY-4B satellite.
Figure 1. Detectors onboard FY-4B satellite.
Preprints 83544 g001
Preprints 83544 g002
Figure 2. Space environment on FY-4 satellite orbit.
Figure 2. Space environment on FY-4 satellite orbit.
Preprints 83544 g002
Preprints 83544 g003
Figure 3. The MEPD installation on FY-4B satellite.
Figure 3. The MEPD installation on FY-4B satellite.
Preprints 83544 g003
Preprints 83544 g004
Figure 4. Connection diagram of the MEPD.
Figure 4. Connection diagram of the MEPD.
Preprints 83544 g004
Preprints 83544 g005
Figure 5. Internal structure of a measurement unit.
Figure 5. Internal structure of a measurement unit.
Preprints 83544 g005
Preprints 83544 g006
Figure 6. Schematic diagram of detector A.
Figure 6. Schematic diagram of detector A.
Preprints 83544 g006
Preprints 83544 g007
Figure 7. FPGA modules function relationship.
Figure 7. FPGA modules function relationship.
Preprints 83544 g007
Preprints 83544 g008
Figure 8. Time division of software workflow.
Figure 8. Time division of software workflow.
Preprints 83544 g008
Preprints 83544 g009
Figure 9. Simulation of the visibility of MEPD sensors to the sun on FY-4B orbit.
Figure 9. Simulation of the visibility of MEPD sensors to the sun on FY-4B orbit.
Preprints 83544 g009
Preprints 83544 g010
Figure 10. Simulation of the visibility of MEPD sensors to the sun on FY-3E orbit.
Figure 10. Simulation of the visibility of MEPD sensors to the sun on FY-3E orbit.
Preprints 83544 g010
Preprints 83544 g011
Figure 11. Comparison of light blocking ability of 100nm thickness metal films of different materials.
Figure 11. Comparison of light blocking ability of 100nm thickness metal films of different materials.
Preprints 83544 g011
Preprints 83544 g012
Figure 12. Lighting test of MEPD with solar simulator in vacuum tank.
Figure 12. Lighting test of MEPD with solar simulator in vacuum tank.
Preprints 83544 g012
Preprints 83544 g013
Figure 13. Transmittance of protons with (black line) or without (red line) the addition of another 100nm nickel film.
Figure 13. Transmittance of protons with (black line) or without (red line) the addition of another 100nm nickel film.
Preprints 83544 g013
Preprints 83544 g014
Figure 14. Geant4 simulation of energy deposit of 30keV proton in sensors.
Figure 14. Geant4 simulation of energy deposit of 30keV proton in sensors.
Preprints 83544 g014
Preprints 83544 g015
Figure 15. Deflection scene of 1.5 MeV electrons passing through the magnetic field.
Figure 15. Deflection scene of 1.5 MeV electrons passing through the magnetic field.
Preprints 83544 g015
Preprints 83544 g016
Figure 16. The integral/differential proton flux (left) and the integral proton anisotropy flux (right) on FY-4 orbit calculated by AP8 Model.
Figure 16. The integral/differential proton flux (left) and the integral proton anisotropy flux (right) on FY-4 orbit calculated by AP8 Model.
Preprints 83544 g016
Preprints 83544 g017
Figure 17. The block diagram of the calibration testing system.
Figure 17. The block diagram of the calibration testing system.
Preprints 83544 g017
Preprints 83544 g018
Figure 18. The calibration scenario of MEPD.
Figure 18. The calibration scenario of MEPD.
Preprints 83544 g018
Preprints 83544 g019
Figure 19. The Gaussian fitting results of accelerator test data.
Figure 19. The Gaussian fitting results of accelerator test data.
Preprints 83544 g019
Preprints 83544 g020
Figure 20. The linear fitting results of energy loss and multi-channel addresses.
Figure 20. The linear fitting results of energy loss and multi-channel addresses.
Preprints 83544 g020
Preprints 83544 g021
Figure 21. Energy response performance testing.
Figure 21. Energy response performance testing.
Preprints 83544 g021
Preprints 83544 g022
Figure 22. Composition diagram of flux error.
Figure 22. Composition diagram of flux error.
Preprints 83544 g022
Preprints 83544 g023
Figure 23. Detector measured counts VS input particle number.
Figure 23. Detector measured counts VS input particle number.
Preprints 83544 g023
Preprints 83544 g024
Figure 24. Observations of medium Energy Proton Flux in Direction 5.
Figure 24. Observations of medium Energy Proton Flux in Direction 5.
Preprints 83544 g024
Preprints 83544 g025
Figure 25. Observational results of medium-high protons (30keV-300MeV) on FY-4(02) satellite.
Figure 25. Observational results of medium-high protons (30keV-300MeV) on FY-4(02) satellite.
Preprints 83544 g025
Table 1. Scientific indicators of MEPD.
Table 1. Scientific indicators of MEPD.
No. Parameter MEPD on FY-4B Remarks
1 Energy range 30 keV-5 MeV Channel P6 and channel P7 are overlapping in order to verify the long-term consistency of the two energy sections
12 channels:
Low energy section:
P1:30 keV-48 keV;
P2:48 keV-80 keV;
P3:80 keV-120 keV;
P4:120 keV-170 keV;
P5:170 keV-240 keV;
P6:240 keV-350 keV.
High energy section:
P7:240 keV-350 keV;
P8:350 keV-500 keV;
P9:500 keV-800 keV;
P10:800 keV-1500 keV;
P11:1500 keV-3000 keV;
P12:3000 keV-5000 keV.
2 Detection directionsand field of view 18 Detector A: directions 1-9
(20°×20° for each direction) Detector B: directions 10-18
Table 2. Calibration results of energy resolution and energy linearity.
Table 2. Calibration results of energy resolution and energy linearity.
Detector Direction Energy Linearity Energy Resolution
A 1 1.69% 4.55%（@280keV）
2 1.57% 4.62%（@280keV）
3 1.54% 4.27%（@280keV）
4 2.43% 4.19%（@280keV）
5 3.57% 8.16%（@280keV）
6 2.19% 5.08%（@280keV）
7 1.67% 4.11%（@280keV）
8 3.94% 7.42%（@280keV）
9 1.74% 4.2%（@280keV）
B 10 1.10% 4.86%（@280keV）
11 0.79% 6.50%（@280keV）
12 1.11% 6.27%（@280keV）
13 2.78% 10.56%（@280keV）
14 1.84% 6.44%（@280keV）
15 0.94% 6.72%（@280keV）
16 1.20% 5.98%（@280keV）
17 0.40% 4.77%（@280keV）
18 0.76% 4.86%（@280keV）
Table 3. Energy demarcation points and error range.
Table 3. Energy demarcation points and error range.
Energy Channel Designed Boundary (keV) Actual Boundary (keV) Error Range (%)
P1 30–48 48.2 0.42%
P2 48–80 48.2-79.9 0.42%/0.12%
P3 80–120 79.9-120.9 0.21%/0.75%
P4 120–170 120.9-171.8 0.75%/1.06%
P5 170–240 171.8-243.6 1.06%/1.50%
P6 240–350 243.6-355.8 1.50%/1.66%
P7 240–350 244.2-356.3 1.75%/1.80%
P8 350–500 356.3-502.3 1.80%/0.46%
P9 500–800 502.3-790.7 0.46%/1.16%
P10 800–1500 790.7-1495.8 1.16%/0.28%
P11 1500–3000 1495.8-2997.5 0.28%/0.08%
P12 3000–5000 2997.5-4996.3 0.08%/0.03%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated