1. Introduction:
To determine an approximation of the hemodynamics in liver sinusoid using a numerical model with relevant anatomical features (variable lumen section, variable porosity, presence of the space of Disse, presence of lymphatic drainage) and varying pressure.
In liver lobules, blood enters the sinusoids from the portal triad (PT) and flows towards the central vein (CV). Sinusoids are approximately 275 µm long and 5-15 µm wide (Ehrlich et al., 2019),(Cogger et al., 2020). Particularly, the periportal zone (zone 1) of the sinusoid has lumen with narrower diameter with respect to the perivenous zone (zone 3) while intermediate width characterizes the zone in between(zone 2) ((Wake et al., 1988), (MacPhee et al., 1995), (Komatsu et al., 1990)).
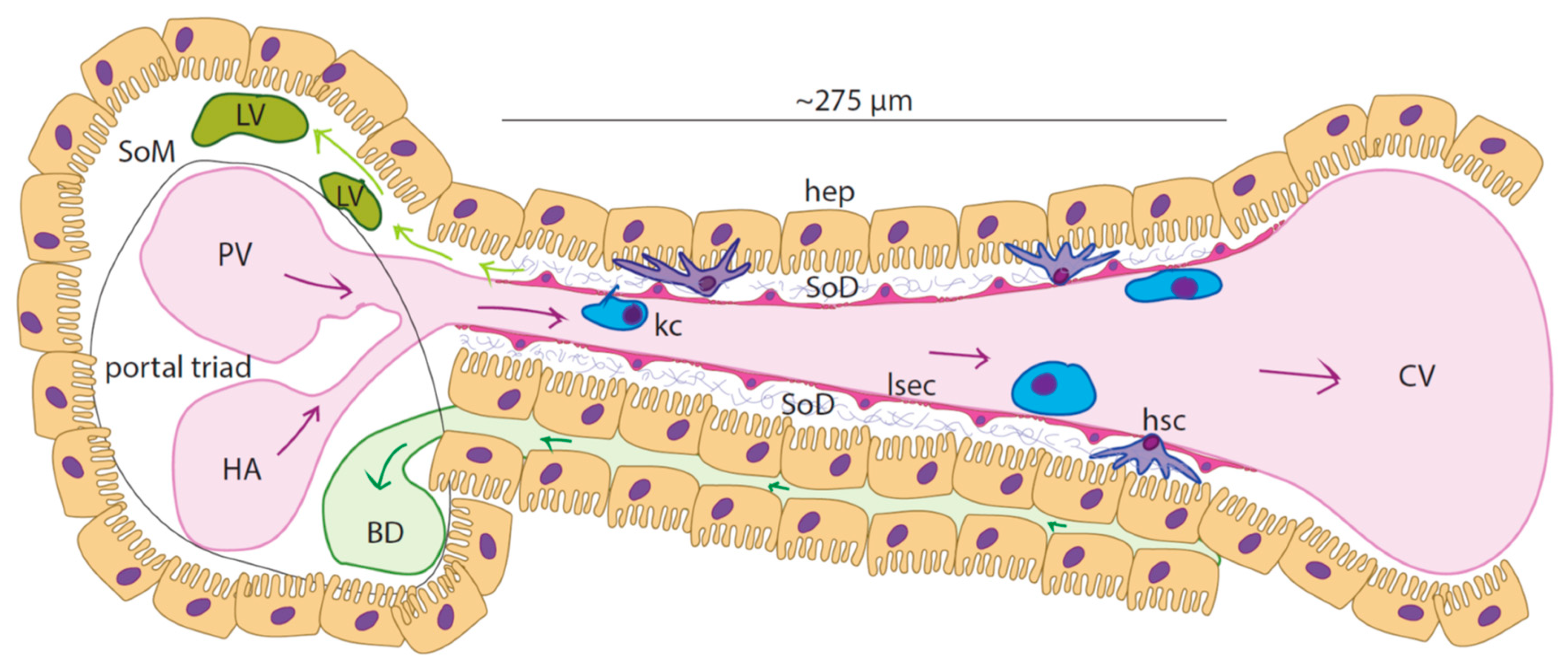
Figure 1.1.
Schematic of the liver sinusoid: Liver sinusoid endothelial cells (LSECs) form the highly specialized and fenestrated endothelium of the sinusoids. Resident macrophages (Kupffer cells - KCs) populate the sinusoidal lumen while hepatic stellate cells can be found within the space of Disse (SoD), an approximately 1µm thick region with sparse extracellular matrix (grey bundles-proteoglycans and collagen type III) that separates the LSECs from the hepatocytes (hep). Blood rich in nutrients and oxygen flows from the portal vein (PV) and the hepatic artery (HA) towards the central vein (CV). Bile is formed in the hepatocytes and flows through the bile canaliculi that are situated between hepatic cords. Lymph is largely (ca 80%) formed from the filtrate in the Space of Disse (SoD)and flows into the lymphatic vasculature LV, which is in the Space of Mall (SoM).
Figure 1.1.
Schematic of the liver sinusoid: Liver sinusoid endothelial cells (LSECs) form the highly specialized and fenestrated endothelium of the sinusoids. Resident macrophages (Kupffer cells - KCs) populate the sinusoidal lumen while hepatic stellate cells can be found within the space of Disse (SoD), an approximately 1µm thick region with sparse extracellular matrix (grey bundles-proteoglycans and collagen type III) that separates the LSECs from the hepatocytes (hep). Blood rich in nutrients and oxygen flows from the portal vein (PV) and the hepatic artery (HA) towards the central vein (CV). Bile is formed in the hepatocytes and flows through the bile canaliculi that are situated between hepatic cords. Lymph is largely (ca 80%) formed from the filtrate in the Space of Disse (SoD)and flows into the lymphatic vasculature LV, which is in the Space of Mall (SoM).
Studies on rat models showed that mean linear flow rate of the bloodstream within the hepatic microvasculature is roughly 144 µm/s, the flow speed and fluidic resistance increasing from periportal to perivenous zone (Ehrlich et al., 2019), (Komatsu et al., 1990), (Eguchi et al., 1987)). Conversely, the pressure along the sinusoid decreases from 70 mmHg (9333 Pa) inside zone 1 down to 30 mmHg (2666 Pa) in zone 3 (Komatsu et al., 1990).
Hepatic zonation also affects endothelial porosity, the area fraction of the endothelium covered by fenestrations, with fewer and narrower fenestrations in the periportal zone relative to the pericentral zone (Cogger et al., 2020), (HORN et al., 1986),(Vidal-Vanaclocha & Barberá-Guillem, 1985),(Wack et al., 2001),(Wisse et al., 1983). This zonation of porosity was found inversely correlated with expression of CD45 along the sinusoid and could be recognized in isolated liver sinusoidal endothelial cells (LSEC) sorted by CD45 expression (Xie et al., 2010).
Table 1.1.
Partial summary of the literature concerning sinusoidal dimensions and flow parameters.
Table 1.1.
Partial summary of the literature concerning sinusoidal dimensions and flow parameters.
| Reference |
i) model ii) method III) sinusoid dimensions iv) flow v) pressure vi) fenestrations |
| Vidal-Vanaclocha & Barbera-Guillem 1985 |
i) rat ii) SEM vi) zone 3 has wider fenestrations (94-121nm vs 73-101nm) and higher frequency (10.21-10.68fenestrations/µm2 vs 5.74-6.26 fenestrations/µm2) than zone 1 and greater number of sieve plates (1.73 fold). |
| Komatsu 1990 |
i) rat ii) in vivo fluorescence microscopy III) the diameter of the sinusoid increases from zone 1 to zone 2 to zone 3, 6.4µm-7µm-8.3µm iv) the flow rate increases along the sinusoid, 143-221-331µm/s v) interpolated values of pressure within sinusoids: zone 1 68-50, zone 2 50-40, zone 3 40-28 mmHg. |
| Horn 1986 |
i) human ii) SEM vi) in zone 3 fenestrations are more numerous (23.5 vs 19.2%) than in zone 1, porosity is higher in zone 3 than in zone 1 (9.1 vs7.6%) |
| Henriksen&Lassen 1988 |
i) theoretical model iv) shape of the sinusoid does not affect the flow profile which is characterized by increasing speed moving from zone 1 to zone 3 v) in humans the pressure drop between portal and central vein is between 3-5mmHg (450Pa). |
| Ryou 2020 |
v) clinical portal hypertension has pressure above 5mmHg(666Pa) while normal pressure is around 3.4mmHg(450Pa). |
| MacPhee 1995 |
i) mouse and rat ii) high resolution in vivo microscopy iv) flow speed is highly variable due to interactions between blood-cells and the cells of the sinusoid, generally the velocity in zone 3 is greater than in zone 1. |
| Wake 1988 |
i) rat ii) light and electron microscopy iii) centrilobular LSEC are larger (longer, wider) than periportal LSEC. |
| Yoon 2013 |
i) mouse ii) computed tomography iii) zone 1 features a smaller diameter (8.8 vs 13.7µm) than zone 3 vi) zone 1 has lower porosity than zone 3. |
| Wisse 1983 |
i) rat ii) SEM vi) porosity is higher and fenestrations have wider diameters in zone 3 than in zone 1 (97.92 vs 76.57nm & 11.63 vs 6.81%). |
The liver is the main site of lymph production in the body, with about 80% being formed here (ref). Hepatic lymph generation begins with the filtration of blood through the fenestrations of the sinusoidal lining followed by drainage through the lymphatic vasculature beginning in the Space of Mall (SoM) a region of the portal tract situated between outermost hepatocytes and the hepatic stroma (Tanaka & Iwakiri, 2016), (Jeong et al., 2022), (Santambrogio, 2018)). Lymph production is correlated with the hydrostatic pressure within the sinusoids, where even slight changes to pressure will increase lymph production and flow ((Tanaka & Iwakiri, 2016, 2018), Jeong et al. (2022)). This physiological consequence, particularly evident in pathological conditions such as portal hypertension, is due to the high permeability of the sinusoids (Hsu & Itkin, 2016)).
Given the inaccessibility of the liver sinusoids to sensors that could directly measure hemodynamic variables, CFD simulations have been attempted to describe the flow field within the elementary units of the liver lobule, the sinusoids(Table 1.2). Traditional approaches for numerical models of the liver sinusoids are based upon anatomical structures imported from imaging carried out on either animal or human liver specimens. The resulting models generally represent the sinusoidal lumen and do not consider other elements (e.g. the Space of Disse, fenestrations). These left out characteristic features of the liver sinusoids could play significant roles in the hemodynamics of the liver. In models endothelial porosity is commonly introduced in numerical models that simulate flow over an entire lobule, modelling porosity as porous medium. In general computational models of the liver sinusoid lack generality and do not provide adequate flexibility to assess flow through the sinusoid.
Table 1.2.
Most significant studies on numerical models of liver sinusoid or lobule. v = velocity; FR = flow rate; WSS = wall sheqr stress; P = pressure; 2D = bidimensional; 3D = tridimensional.
Table 1.2.
Most significant studies on numerical models of liver sinusoid or lobule. v = velocity; FR = flow rate; WSS = wall sheqr stress; P = pressure; 2D = bidimensional; 3D = tridimensional.
| Ref. |
Mod.
Obj.
|
Dim. |
Origin |
Bound.
Cond.
|
Eval.
Param.
|
Highlights |
Piergiovanni
(2017) |
sinusoidal
network |
3D |
in vivo images, mouse |
phys. |
vmean, FRmass, WSS |
local hemodynamics,
investigation for different occlusion degree |
| Hu (2017) |
lobule |
3D |
numerical |
phys.,
path. (fibrosis, cirrhosis) |
P, vmean, FRvol |
porous media approach,
fibrotic-cirrhotic lobule |
| Debbaut (2012) |
3 lobules |
3D |
3 human lobule cast digitized with micro-CT scanner |
phys. |
P, permeability, preferential flow pathways, WSS
|
liver circulation anisotropy estimation |
| Bonfiglio (2010), Siggers (2014) |
lobule |
2D |
numerical |
phys., post-resection, lymph production |
P, blood flow distribution (v), lymph flow |
infinite lattice of hexagonal lobules, sinusoid space as porous medium, resection effect, anisotropy and shear-dependent tissue deformation, lymph production |
There are few models of the fluid dynamics of the liver or hepatic sinusoids that account for the presence of fenestrations (Rani et al., 2006) with most simulating whole lobules, or larger areas of the liver ((Rohan et al., 2019), (Debbaut et al., 2011, 2012), (Ricken et al., 2010), (Hu et al., 2017), (Siggers et al., 2014), (Piergiovanni et al., 2017), (Ahmadi-Badejani et al., 2020), (Mosharaf-Dehkordi, 2019), (Bonfiglio et al., 2010), (Schwen et al., 2014, 2015), (Barléon et al., 2018), (Rezania et al., 2016)) and as such account for porosity in a more general way (as porous medium) in their models. No one has to our knowledge added variable porosity to their models as such.
We therefore believe there is value added in a model that looks at the single sinusoid level, investigating the contributions made by the overall shape and the distribution of fenestrations (porosity) in a computational fluid dynamics model of a single sinusoid.
This is especially on account of the effects found in microfluidics of variable increasing versus constant porosity on fluid flow velocity magnitude through a micro-channel (Brainerd et al., 2019.). Brainerd et al found that in a micro-channel lined with pores, the outflow velocity magnitude dropped significantly along its length if the porosity (% area fraction covered by open pores) was even along the length, while to achieve an even outflow from the channel, porosity needed to increase along the length. Taken together with the electron microscopic observations made on liver tissue samples, porosity was expected to contribute to fluid dynamics in the liver sinusoid.
2. Modeling and methods
CFD simulations were performed using Ansys® software and a laptop with the following features:
Table 2.1.
Hardware specifications.
Table 2.1.
Hardware specifications.
| Processor |
Intel i5-10300H |
| Clock Freq. [GHz] |
2.50 |
| Core # |
8 |
| Ram [GB] |
8 |
Essentially, the numerical 2D models utilized in the simulations were two half sections of a simplified sinusoid having either constant luminal radius (named C = constant radius sinusoid) or diverging luminal radius (named D = diverging sinusoid).
Each model was tested in different configurations of porosity and inlet pressure (physiological vs pathological pressure).
The effect of a lymphatic outflow in the portal tract of the SoD was explored for each model as well.
Linear porosity was defined as the ratio between the length given by the sum of the fenestrations and the length of the sinusoid.
Zonal linear porosity was defined as the ratio between the length given by the sum of the fenestrations in a certain zone and the length of the zone itself.
All the three zones (periportal (1), perivenous (3) and intermediate (2)) were set to the same length (275/3 = 91.667µm).
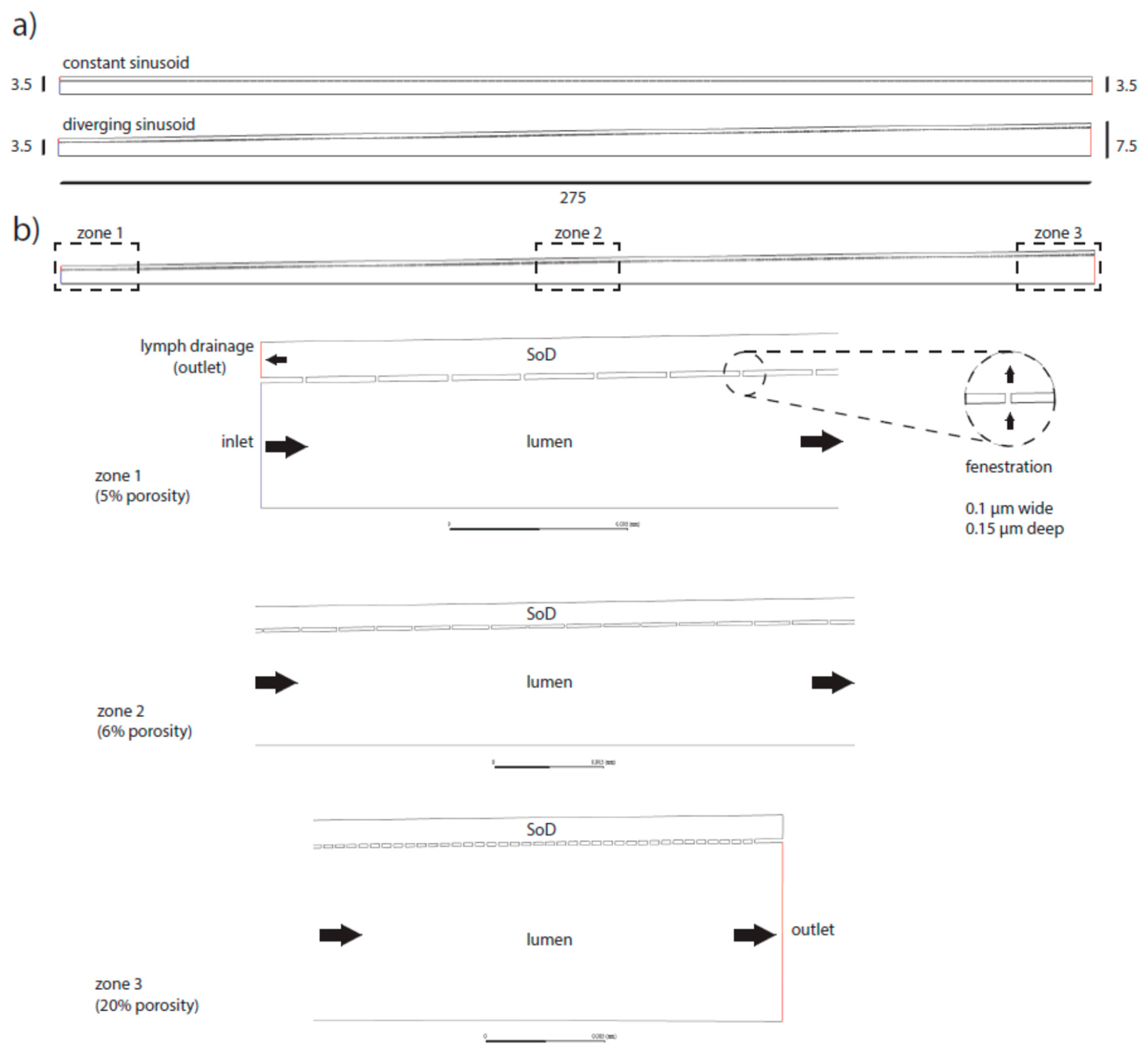
Numerical models with constant porosity were obtained arranging fenestrations with constant pitch along the whole length of the sinusoid. When variable porosity was applied, the fenestration pitch varied zone by zone (but keeping fenestrations evenly spaced inside the zone itself). Zone 1, 2 and 3 of the sinusoid had porosity 5%, 6% and 20% respectively. Thus, porosity changes were applied just by raising the number of fenestrations rather than enlarging their diameter (see Figure 2.1).
Figure 2.1.
Schematics of the numerical models of the sinusoid. The model was designed as a half section. Two main versions were adopted, constant radius and diverging sinusoid (a). Sizes are in microns. Example of the more complete model adopted in the simulations (b): diverging section including variable porosity (5%, 6%, 20%) and an extra outlet at the portal side of the space of Disse (SoD) to mimic lymphatic drainage (dark arrows indicate the flow direction).
Figure 2.1.
Schematics of the numerical models of the sinusoid. The model was designed as a half section. Two main versions were adopted, constant radius and diverging sinusoid (a). Sizes are in microns. Example of the more complete model adopted in the simulations (b): diverging section including variable porosity (5%, 6%, 20%) and an extra outlet at the portal side of the space of Disse (SoD) to mimic lymphatic drainage (dark arrows indicate the flow direction).
The numerical 2D models of the sinusoid were designed to meet both computational capabilities of the hardware and anatomical likelihood.
The Sinusoid was designed as a half section 275µm long. Two half sections
were evaluated, constant radius (3.5µm) and linearly rising radius (in- let/outlet radii respectively set to 3.5µm and 7.5µm).
The Space of Disse (SoD) was modeled as a 2D chamber 1µm thick surrounding the sinusoid lumen and communicating with it via fenestrations.
Fenestrations were modeled as 100nm long and 150nm high channels connecting the sinusoidal lumen with the SoD (see Figure 2.2).
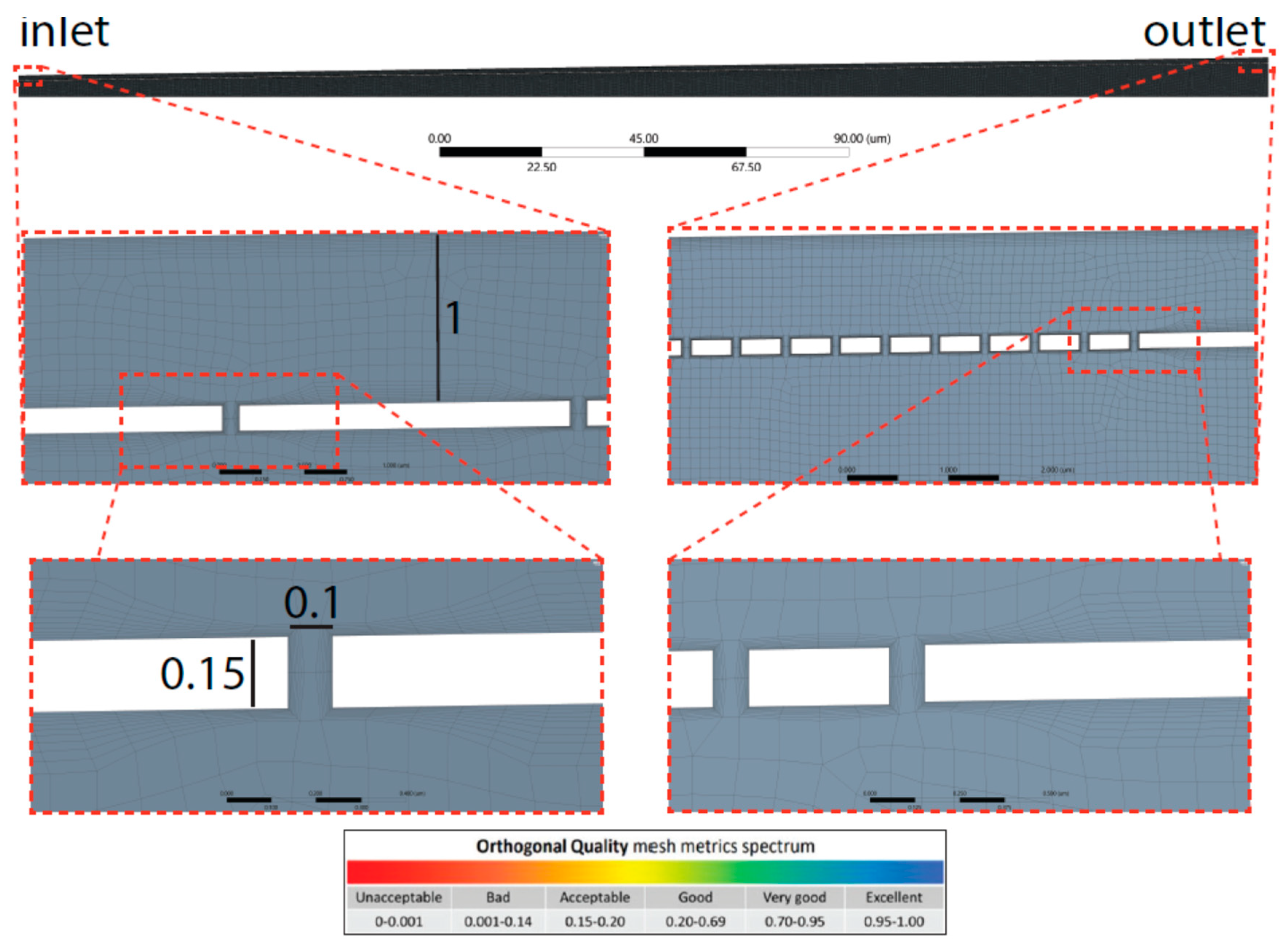
Figure 2.2.
Mesh highlights shown for diverging sinusoid model. The side of each element of the mesh was set to 0.1µm max size. Further, bottom panel, the quality spectrum for orthogonality metric is reported.
Figure 2.2.
Mesh highlights shown for diverging sinusoid model. The side of each element of the mesh was set to 0.1µm max size. Further, bottom panel, the quality spectrum for orthogonality metric is reported.
Proper geometry is essential to facilitate the meshing process (discretization of the whole surface into tiny sub-surfaces defined by nodes for which the solver computes the solutions of the fluid dynamic equations). Main design strategies to obtain the geometry of the sinusoid follow:
Main walls (sinusoid lumen and space of Disse lumen) were formed as 2 coaxial rectangles (or trapezoids when sinusoid had diverging section).
Fenestrations were modeled as a linear pattern.
The sketch was converted to a surface and a symmetry axis was introduced (model halving).
The finite element method (FEM) facilitates a complex system’s numerical simulation. This involves the discretization of a continuous system into small elements (named cells, which are defined by nodes) over which to solve the equations. The obtained local solutions are ultimately integrated to produce a global solution over entire domains and bodies. Thus, the quality of those solutions generated by the solver strictly depend on the quality of the mesh, which defines size, distribution and shape of the finite elements. Reduced number of elements lead to coarse solution with low computational costs. A high number of elements gives accurate solution which requires time consuming calculations. The obtained mesh had a good quality (
Figure 2.3) in this way ensuring accurate solutions. However, the mesh can be further improved by reducing the size of the elements (set here to 0.1µm).
The laminar flow module of a pressure based solver, which couples the mass and momentum conservation with no-slip boundary conditions, was applied to disclose pressure and linear speed profiles of a steady flow for incompressible fluid (blood).
Fluent solver (by Ansys) was utilized setting laminar-flow module with no-slip condition at the boundaries (v = 0 at the walls). Blood at 37◦C was selected as material (η = 0.0035 kg/ms-1, ρ = 1060 kg/m3). Since the computational model was based on a pressure-driven flow, the physiological pressures were set to 1067 and 800 Pa, respectively at the inlet/outlet (Ryou et al., 2020). Pathological conditions (e.g., portal hypertension) were introduced elevating inlet pressure up to 2400Pa (Ryou et al., 2020). To simulate lymphatic drainage a pressure outlet was added at the portal region (zone 1) of the SoD and the selected out- pressure was set to 100Pa (Heppell et al., 2015). The equations were solved through COUPLED algorithm (keeping default under-relaxation factors). The solutions convergenced after 105 which were initially set to 2000 iterations.
The physics of the numerical model can be explained with the following partial differential equations (PDEs):
That is the mass conservation equation for incompressible fluid where ρ is the density (kg/m−3) and u is the 3D velocity vector (m/s)
Which is the momentum equation for Newtonian fluids (constant µ) where P is the pressure (Pa), µ is the dynamic viscosity (Pa · s).
3. Results:
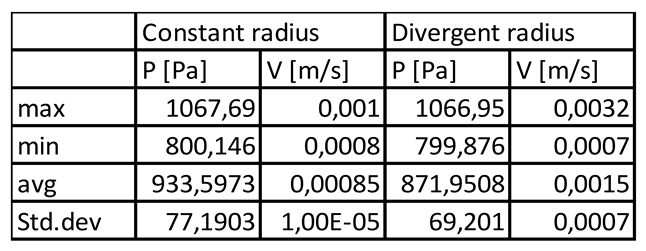
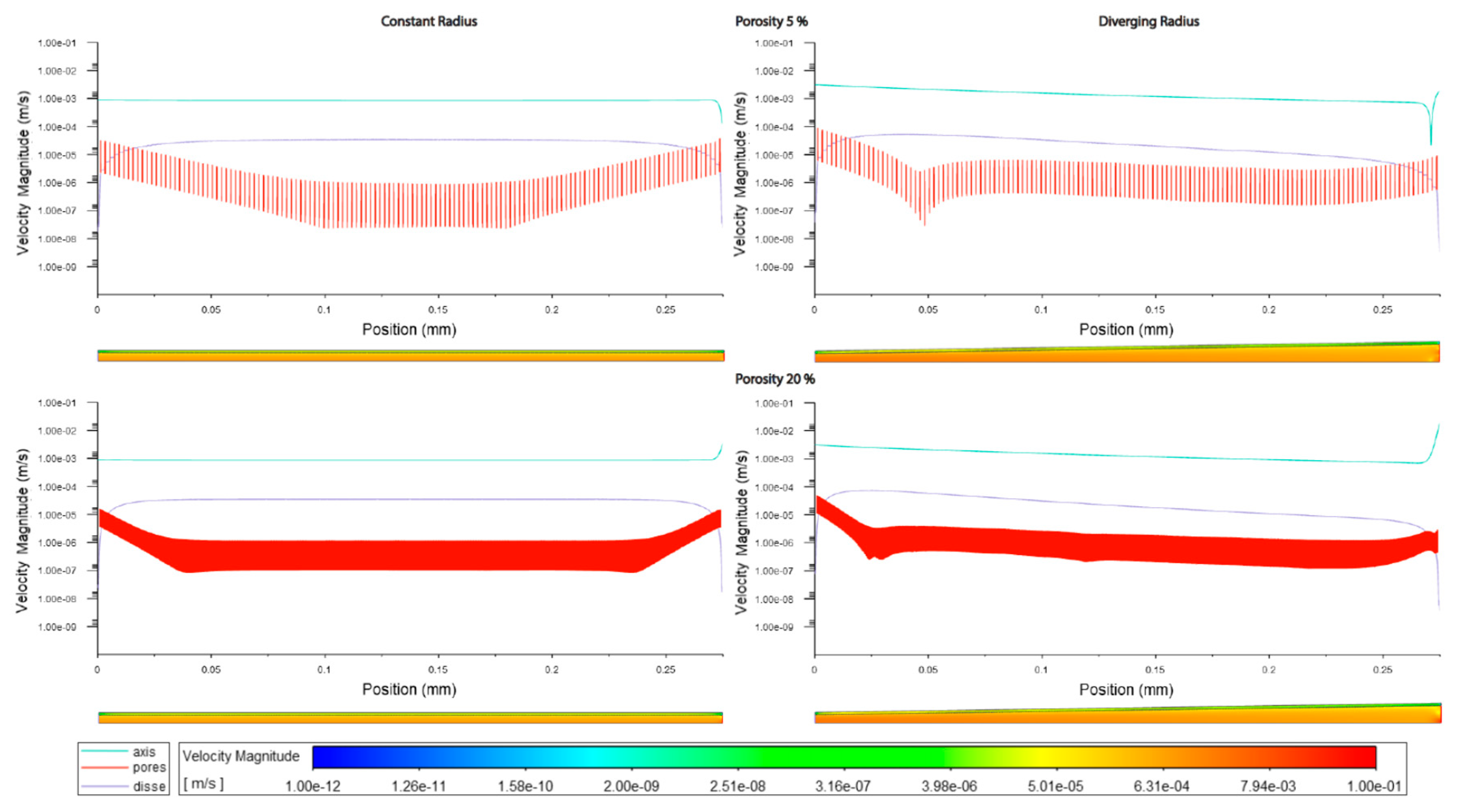
In general velocity magnitude was greater through the divergent models compared with the constant radii models, with velocity modules through the lumen centre-line being approximately 2-fold higher in the divergent models. (Figures 3.1,2,5, Tables 3.1,2,3).
Table 3.1.
Quantitative evaluation of pressure (P) and velocity (V) at the axis of the simplified models of the sinusoid without fenestrations or lymphatic drainage (constant radius and diverging radius microchannel).
Table 3.1.
Quantitative evaluation of pressure (P) and velocity (V) at the axis of the simplified models of the sinusoid without fenestrations or lymphatic drainage (constant radius and diverging radius microchannel).
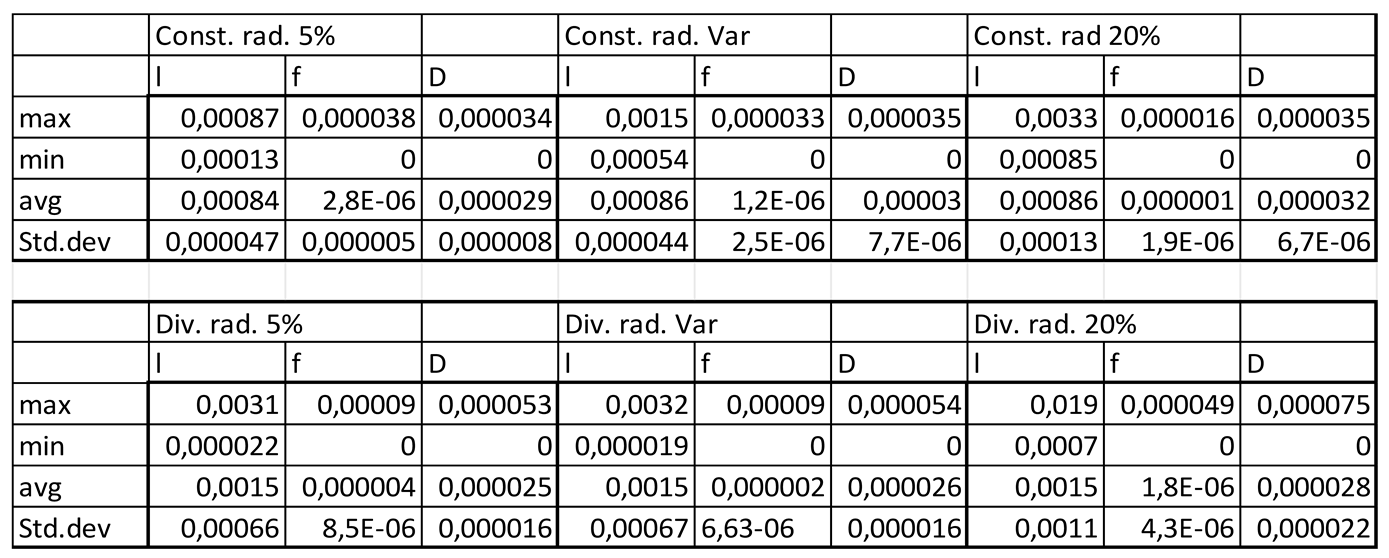
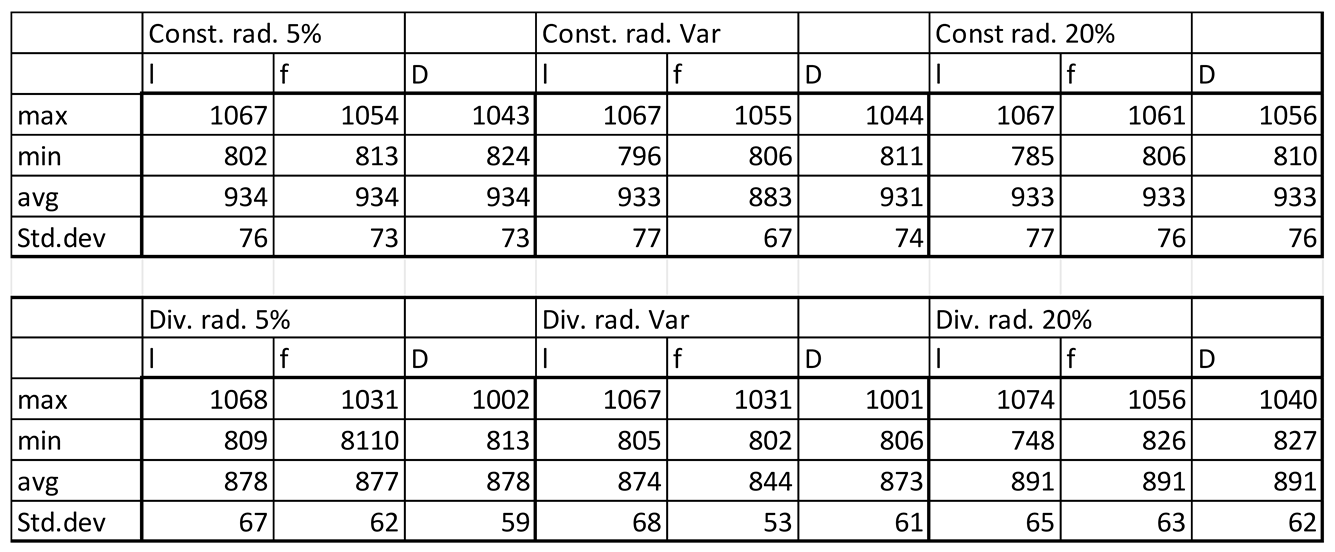
Table 3.2.
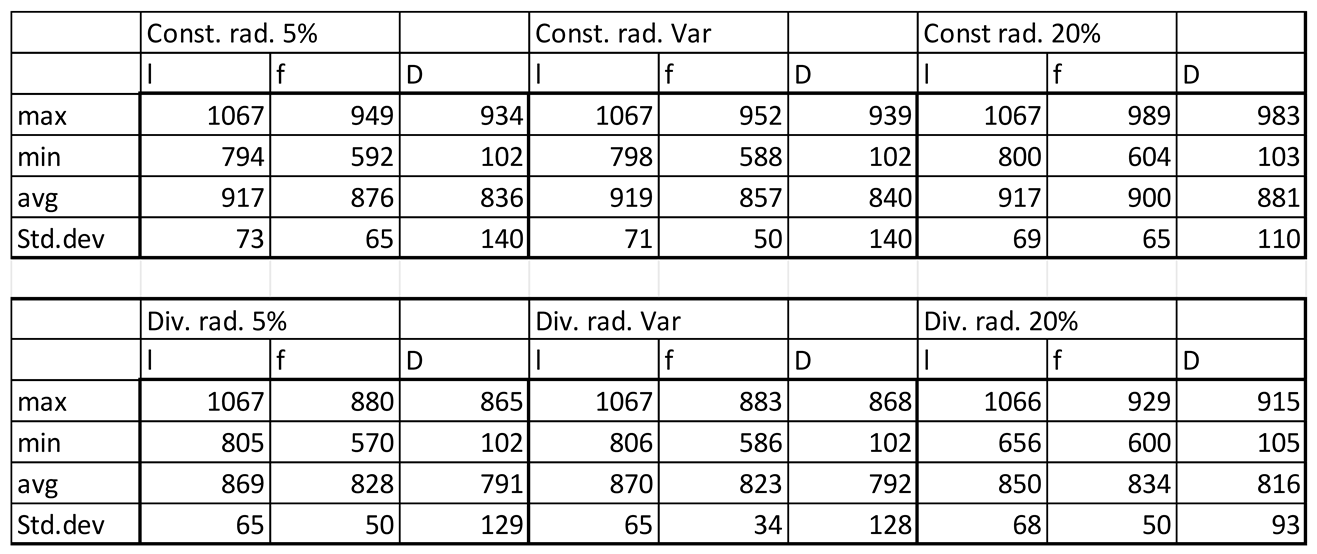
Velocity magnitudes in sinusoids modelled without lymphatic drainage, Const. rad. = constant radius, Div. rad. = diverging radius, porosity given as %, Var = variable increasing porosity 5-20%, l=lumen centreline, f=fenestrations, D=Space of Disse.
Table 3.2.
Velocity magnitudes in sinusoids modelled without lymphatic drainage, Const. rad. = constant radius, Div. rad. = diverging radius, porosity given as %, Var = variable increasing porosity 5-20%, l=lumen centreline, f=fenestrations, D=Space of Disse.
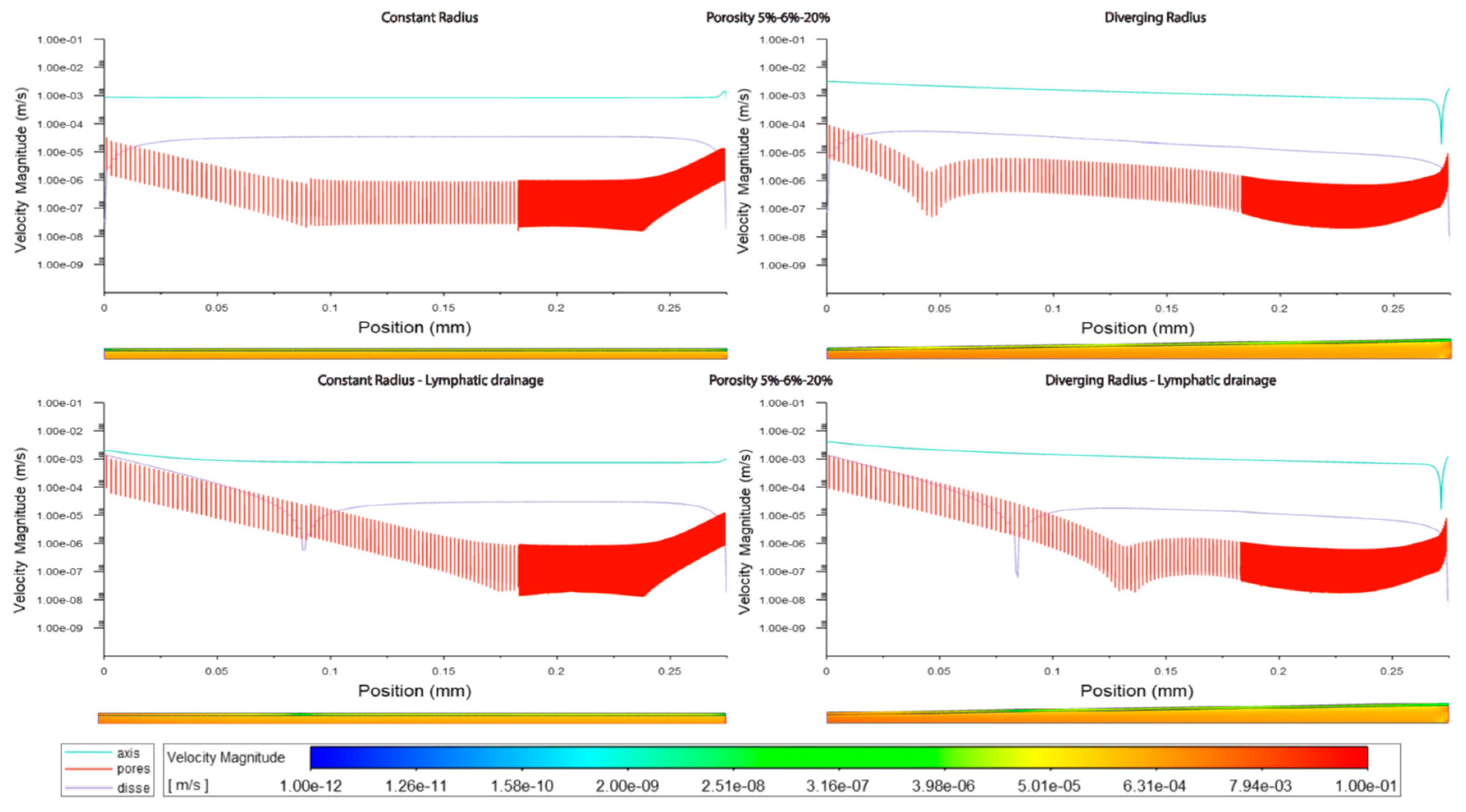
Figure 3.1.
Velocity magnitudes along sinusoids modelled without lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical) and low (5%) porosity or high (20%) porosity.
Figure 3.1.
Velocity magnitudes along sinusoids modelled without lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical) and low (5%) porosity or high (20%) porosity.
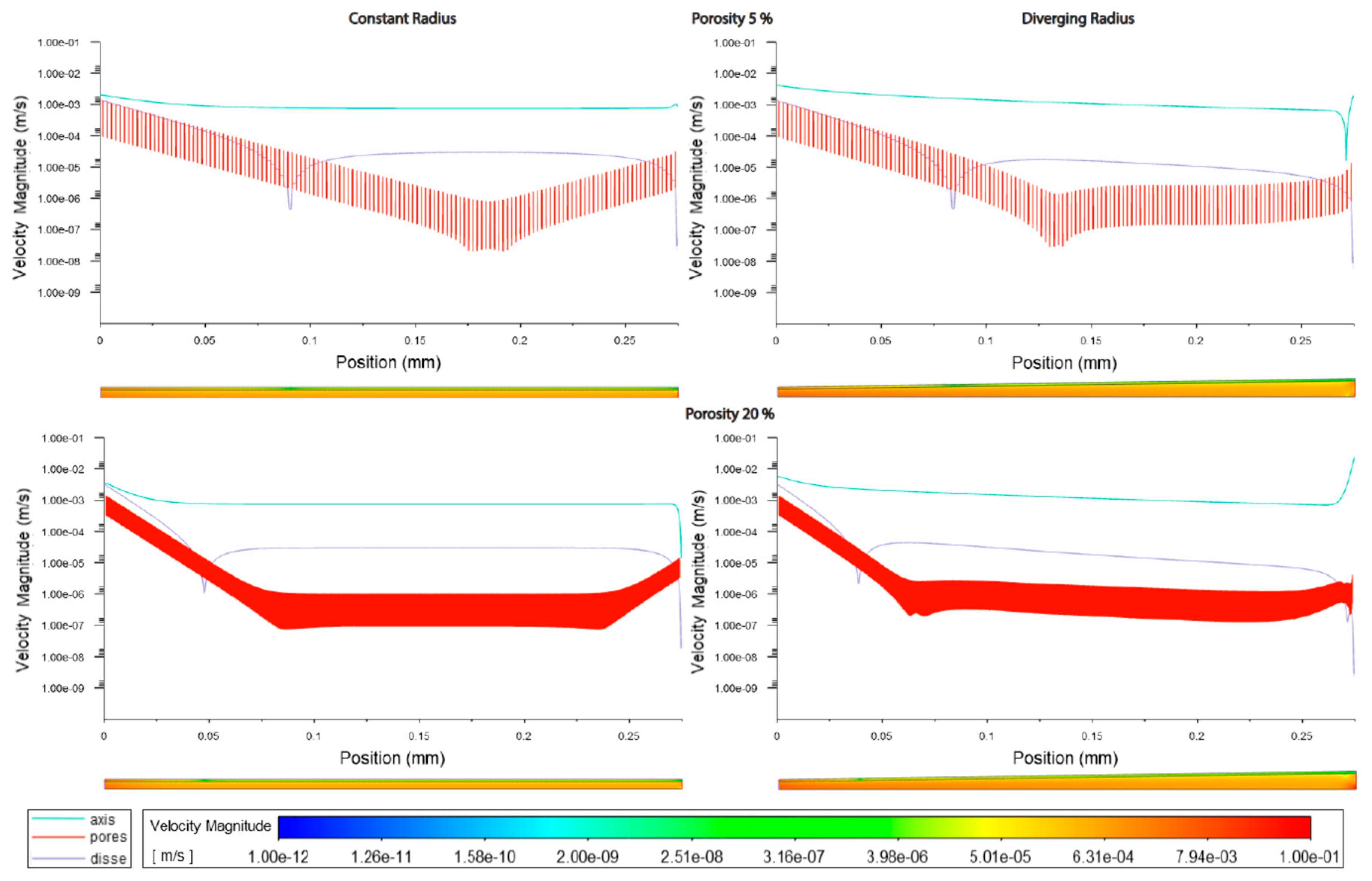
The increment of zonal porosity increased the velocity in the space of Disse slightly, whilst decreasing velocity through fenestrations, there was a modest decrease in luminal velocity in cylindrical models, whilst a slight increase in divergent models. Velocity magnitudes through the space of Disse were higher in models with lymphatic drainage than in those without (Figures3.1,2,5 Tables3.3,2).
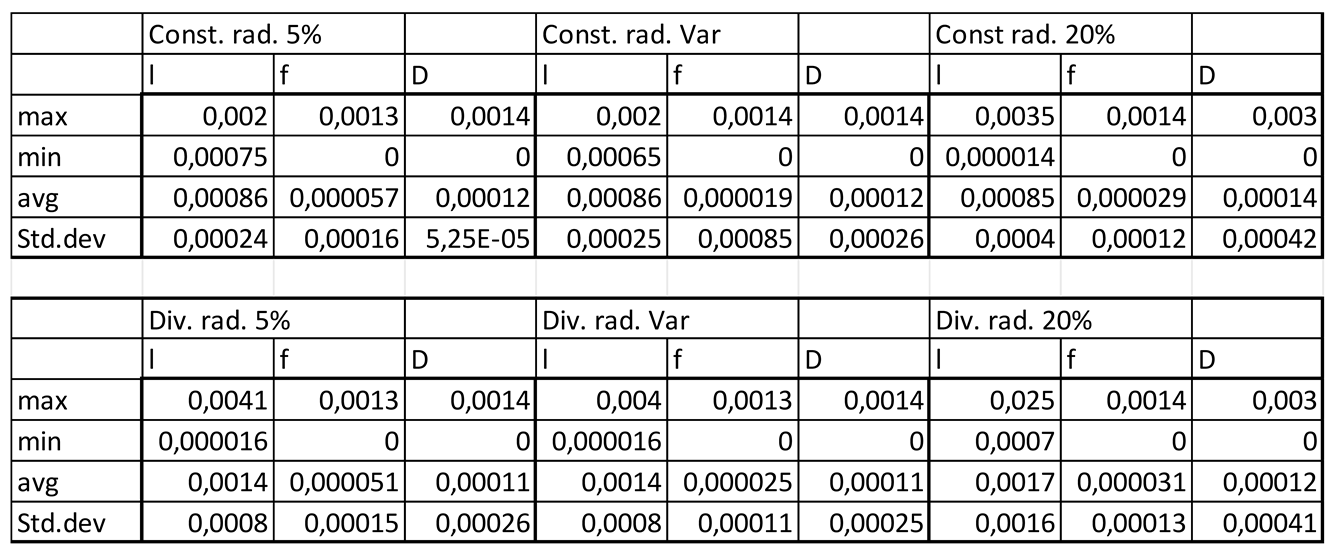
Table 3.3.
Velocity magnitudes in sinusoids modelled with lymphatic drainage, Const. rad. = constant radius, Div. rad. = diverging radius, porosity given as %, Var = variable increasing porosity 5-20%, l=lumen centreline, f=fenestrations, D=Space of Disse.
Table 3.3.
Velocity magnitudes in sinusoids modelled with lymphatic drainage, Const. rad. = constant radius, Div. rad. = diverging radius, porosity given as %, Var = variable increasing porosity 5-20%, l=lumen centreline, f=fenestrations, D=Space of Disse.
Figure 3.2.
Velocity magnitudes along sinusoids modelled with lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical) and low (5%) porosity or high (20%) porosity.
Figure 3.2.
Velocity magnitudes along sinusoids modelled with lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical) and low (5%) porosity or high (20%) porosity.
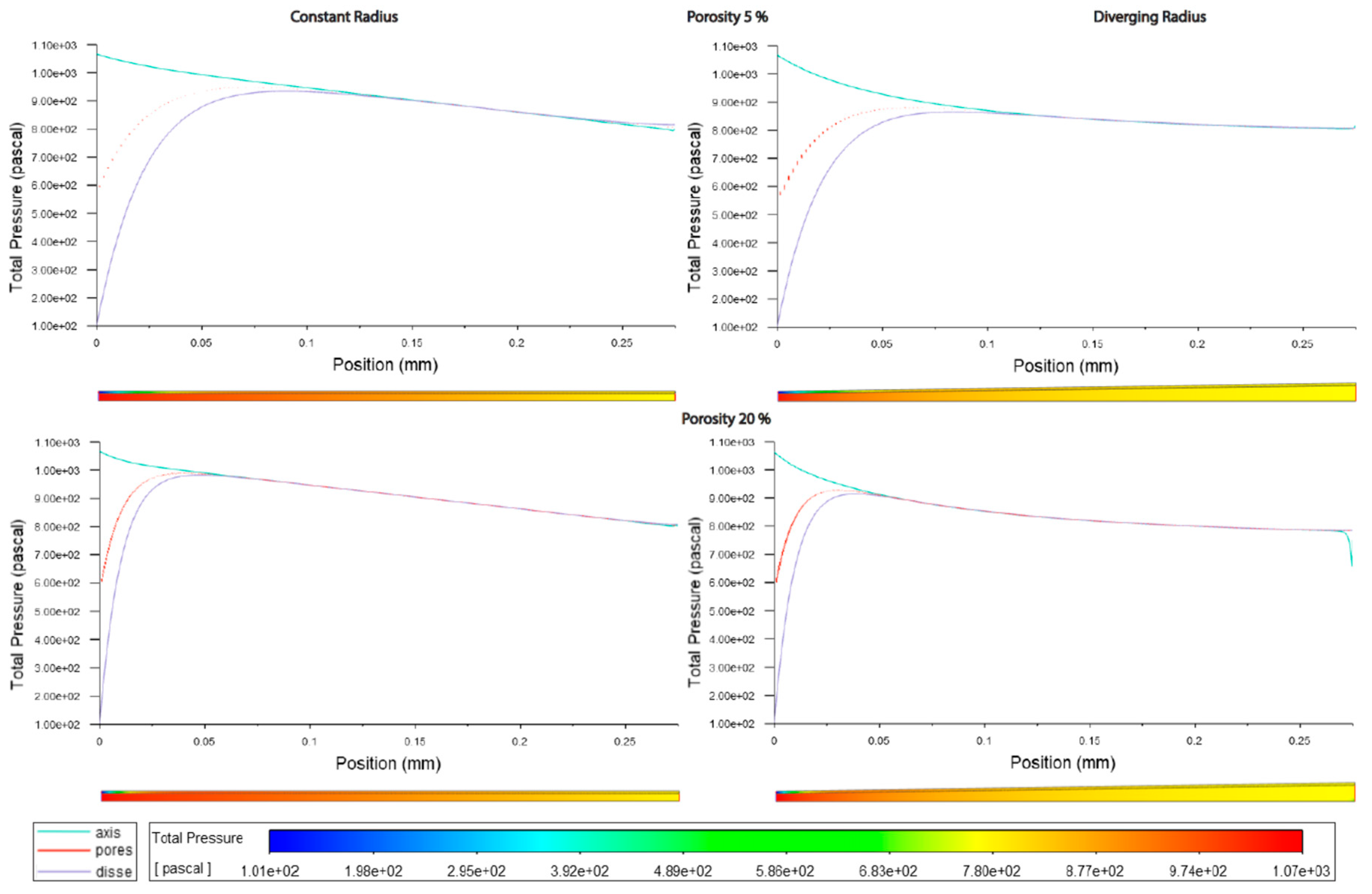
Figure 3.3.
Pressure along sinusoids modelled without lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical), and low (5%) porosity or high (20%) porosity.
Figure 3.3.
Pressure along sinusoids modelled without lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical), and low (5%) porosity or high (20%) porosity.
Velocity magnitudes through the fenestrations were lower with higher porosity (high=20%) in models without lymphatic drainage, whilst in models with lymphatic drainage velocities were higher in low porosity (low=5%) than in high porosity, velocities were lower in variable porosity (variable=5,6,20%) than either low or high porosity models (Figures 3.1,2,5 Tables 3.2,3)
Figure 3.4.
Pressure along sinusoids modelled with lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical) and low (5%) porosity or high (20%) porosity, (top/bottom).
Figure 3.4.
Pressure along sinusoids modelled with lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical) and low (5%) porosity or high (20%) porosity, (top/bottom).
Luminal velocity magnitude was slightly higher in constant radii models without lymphatic drainage, with high and variable porosity, and unchanged in divergent radii models. In constant radii models with lymphatic drainage, luminal velocity was higher in low and variable porosity models. Luminal velocity in divergent radii models was higher when models had high porosity and lymphatic drainage, and equal in all others (Figures 3.1,2,5 Tables 3.2,3).
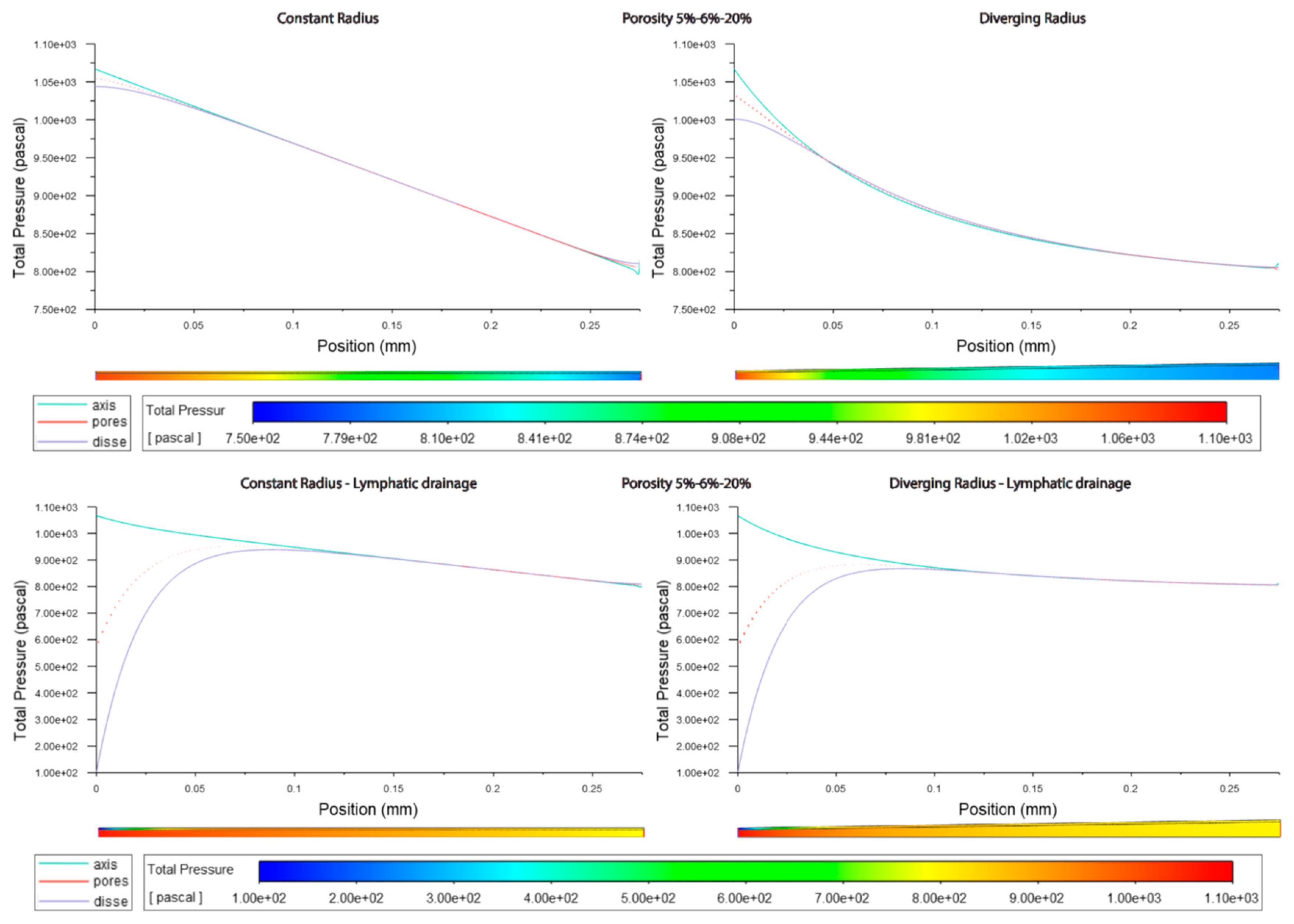
Figure 3.5.
Velocity along sinusoids modelled with variable porosity (5, 6, 20%). Models are with constant radius (cylinder) or with diverging radius (conical) and with or without lymphatic drainage.
Figure 3.5.
Velocity along sinusoids modelled with variable porosity (5, 6, 20%). Models are with constant radius (cylinder) or with diverging radius (conical) and with or without lymphatic drainage.
Average pressure in the lumen was about 7% lower in the divergent models relative to the cylindrical models. For models without lymphatic drainage with divergent radii luminal pressure was lowest in variable porosity models, while for constant radii models with lymphatic drainage variable porosity models had slightly higher luminal pressure. In divergent models with lymphatic drainage variable porosity had the highest average pressure, with lower pressure in low porosity models, and lower still in high porosity models (Figures 3.3,4 Tables 3.4,5).
Figure 3.6.
Pressure along sinusoids modelled with variable porosity (5, 6, 20%). Models are with constant radius (cylinder) or with diverging radius (conical) and with or without lymphatic drainage.
Figure 3.6.
Pressure along sinusoids modelled with variable porosity (5, 6, 20%). Models are with constant radius (cylinder) or with diverging radius (conical) and with or without lymphatic drainage.
Pressure across fenestrations was lower in variable porosity models relative to low and high porosity models, else pressure across fenestrations was higher in higher porosity than in low porosity models(Figures3.3,4,6 Tables3.4,5).
Table 3.4.
Pressure in sinusoids modelled without lymphatic drainage, Const. rad. = constant radius, Div. rad. = diverging radius, porosity given as %, Var = variable increasing porosity 5-20%, l=lumen centreline, f=fenestrations, D=Space of Disse.
Table 3.4.
Pressure in sinusoids modelled without lymphatic drainage, Const. rad. = constant radius, Div. rad. = diverging radius, porosity given as %, Var = variable increasing porosity 5-20%, l=lumen centreline, f=fenestrations, D=Space of Disse.
Table 3.5.
Pressure in sinusoids modelled with lymphatic drainage, Const. rad. = constant radius, Div. rad. = diverging radius, porosity given as %, Var = variable increasing porosity 5-20%, l=lumen centreline, f=fenestrations, D=Space of Disse.
Table 3.5.
Pressure in sinusoids modelled with lymphatic drainage, Const. rad. = constant radius, Div. rad. = diverging radius, porosity given as %, Var = variable increasing porosity 5-20%, l=lumen centreline, f=fenestrations, D=Space of Disse.
In models without lymphatic drainage the pressure in the space of Disse was always lower in the variable porosity models, whereas in models with lymphatic drainage pressure increased from low to variable to high (Figures3.3,4,6 Tables 3.4,5).
In general the variable porosity model had velocity and pressure curves in between low and high constant porosity, being somewhat closer to low constant porosity (Figures 3.1-6)
In total the overall shape of the vessel (Figures 3.1-6, Tables 3.1-5) and presence or absence of lymphatic drainage in the periportal zone had the largest effects of flow parameters, whilst porosity had some effects these were less pronounced.
Modelling with a pathological (elevated) pressure regimen did not show any changes in pressure or flow behaviour. Increasing input/output pressure to 2400/800Pa as per Ryou2020, only rescaled proportionally to increases in pressure, the same patterns as for physiological pressures, that is differences between them were merely rescaled.
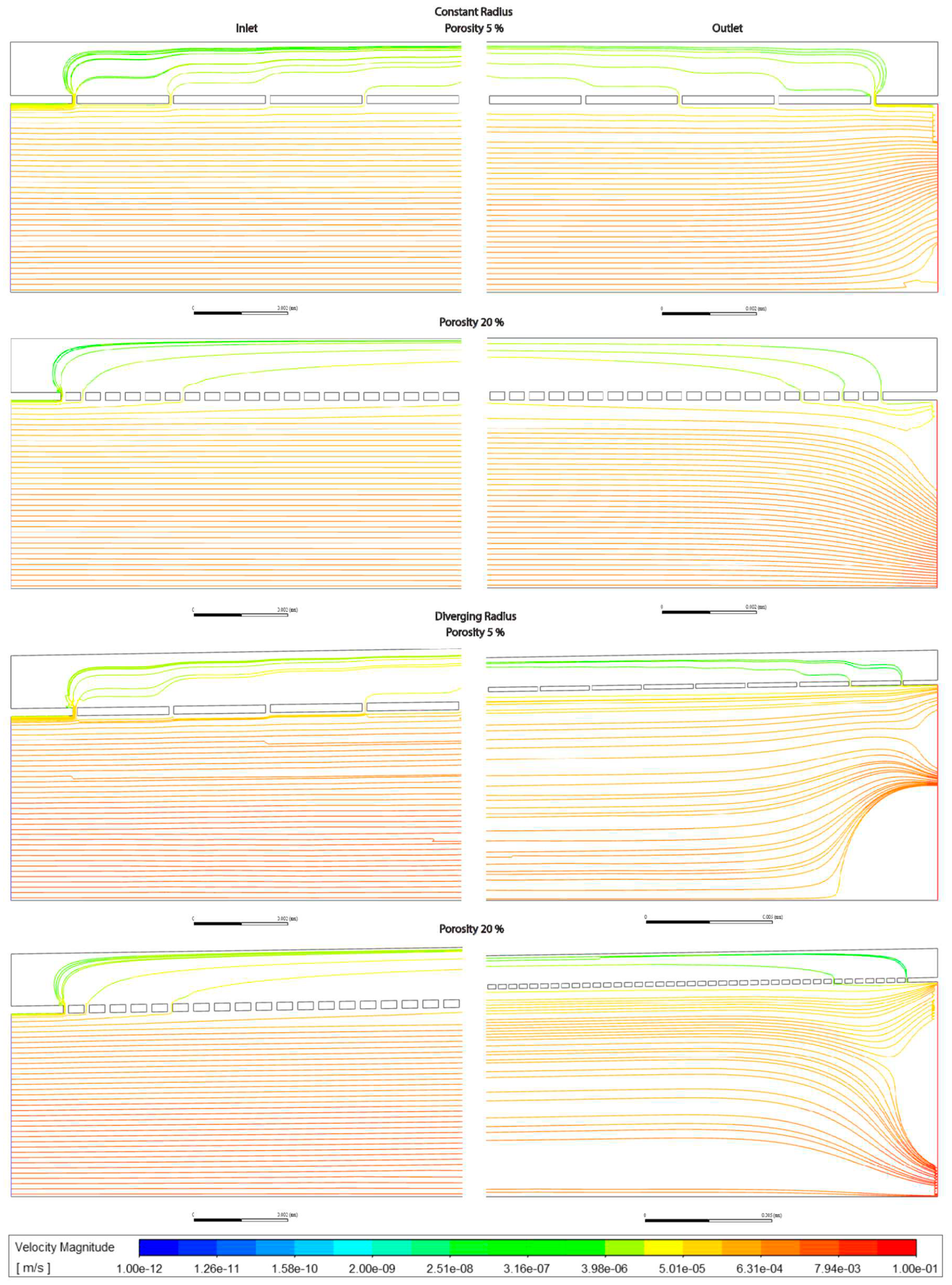
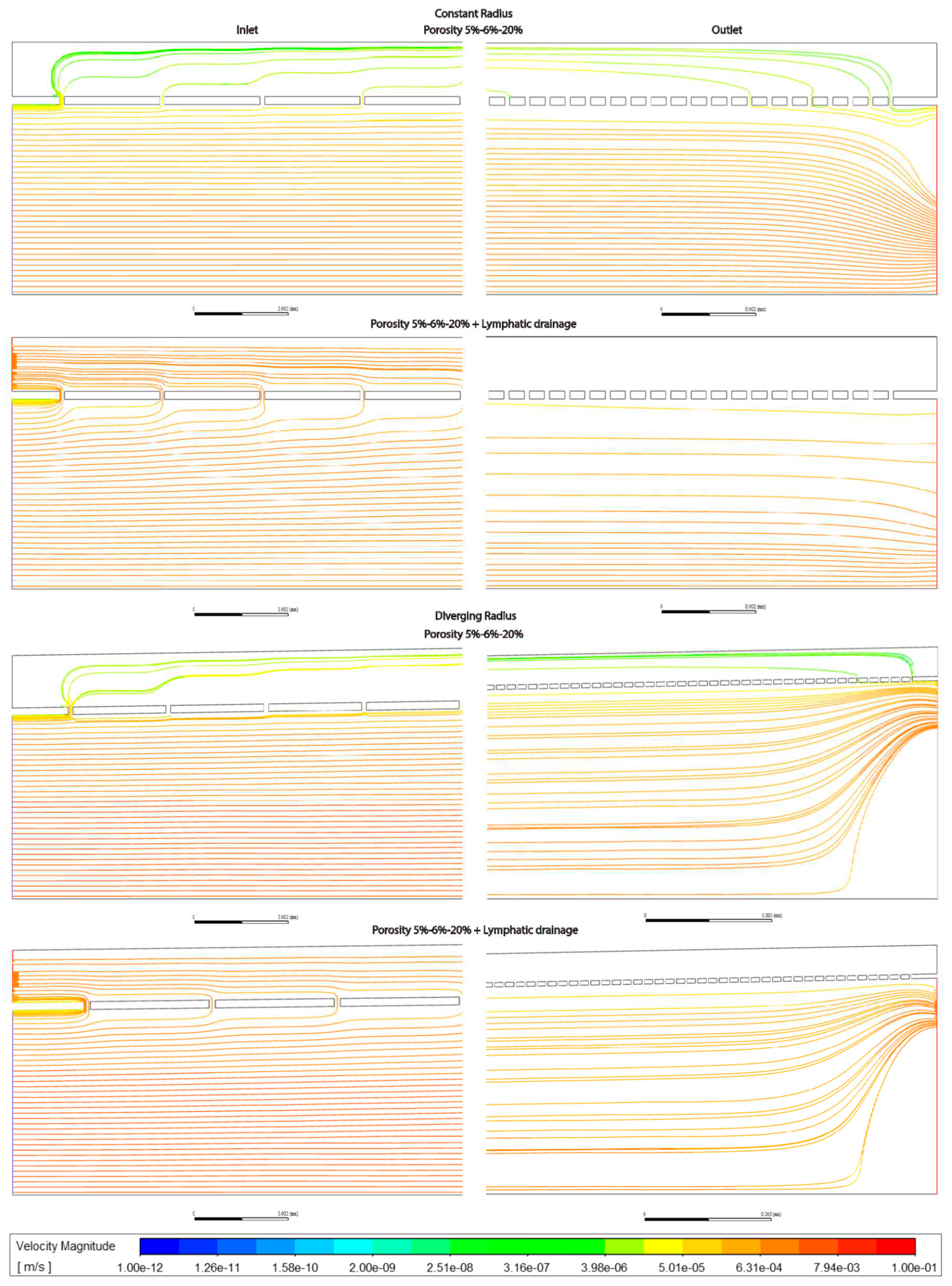
Admixing: Observing flowlines, the addition of a lymphatic drainage in the periportal zone leads to more fluid moving through the space of Disse and more admixing relative to models without, whereas porosity only has a modest effect when comparing models with low, high or variable porosity (Figures 3.7-9). Divergent models show stronger vortice formation at the outlet, compared with constant radii models.
Figure 3.7.
Streamlines at Inlet (left hand side) and Outlet (right hand side) for sinusoids modelled without lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical) and low (5%) porosity or high (20%) porosity.
Figure 3.7.
Streamlines at Inlet (left hand side) and Outlet (right hand side) for sinusoids modelled without lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical) and low (5%) porosity or high (20%) porosity.
Figure 3.8.
Streamlines at Inlet (left hand side) and Outlet (right hand side) for sinusoids modelled with lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical), and low (5%) porosity or high (20%) porosity.
Figure 3.8.
Streamlines at Inlet (left hand side) and Outlet (right hand side) for sinusoids modelled with lymphatic drainage. Models are with constant radius (cylinder) or with diverging radius (conical), and low (5%) porosity or high (20%) porosity.
Figure 3.9.
Streamlines at Inlet (left hand side) and Outlet (right hand side) for sinusoids modelled with variable porosity (5-6-20%), constant (cylinder) or diverging (conical) radius, and with or without lymphatic drainage.
Figure 3.9.
Streamlines at Inlet (left hand side) and Outlet (right hand side) for sinusoids modelled with variable porosity (5-6-20%), constant (cylinder) or diverging (conical) radius, and with or without lymphatic drainage.
Discussion & Future Perspectives:
Four physiologically relevant 2D models of the hepatic sinusoids were generated for CFD simulations to disclose possible hemodynamics insights. Simulations were carried out considering a laminar and steady flow of blood (constant dynamic viscosity) generated by a differential pressure between sinusoid inlet and outlet.
Velocity and pressure trends have been collected for all models in conditions of physiological and pathophysiological (elevated) pressures. Also, an extra outlet was added to the model to reproduce the lymphatic drainage in the portal zone of the SoD.
a. Pressure decreases linearly in constant radius models (Cmods) and exponentially in diverging radius models (Dmods).
b. Dmods generally have lower pressure all throughout, compared with Cmods.
c. Increased porosity in the pericentral zone implies a generalized pressure reduction, mostly borne by SoD.
d. Lymphatic drainage reduces with the pressure within the sinusoid, especially inside the SoD. This effect might be exaggerated by the model (see below in General considerations).
e. Pathological conditions, elevated pressure, (PatCs) merely re-scale the same pressure behavior obtained with physiological conditions (PhyCs).
f. In terms of average pressure, sinusoidal lumen and SoD have comparable pressure while through the fenestration pressure is generally lower.
a. In general, Cmods have constant luminal velocity and almost constant velocity within the SoD. Velocity through the fenestration develops along the sinusoid with parabolic trend: higher values at the inlet/outlet (where flow enters/exit the SoD).
In general, Dmods demonstrate slowly decreasing velocity along the sinusoidal lumen and along the SoD. Through the fenestrations, velocity goes down within the first 50-100µm and then follows a sinusoidal trend with rising values in proximity of the outlet.
Globally, Dmods produced greater velocity in all compartments of the sinusoid compared with Cmods.
b. Some of the models (especially but not only the Dmods) present a reverse flow at the outlet.
c. Porosity augmentation in perivenous zone mostly affects velocity of the SoD and through fenestrations (no effect on luminal speed - flow through fenestration and SoD looks to compensate for the porosity changes). Generally, velocity increases within SoD while it decreases through the fenestrations.
d. Adding lymphatic drainage to the perivenous zone generated a shift of velocity trend towards the outlet. Average flow speed through the fenestrations reaches higher values and decreases slower within the first half of the sinusoid (increased flow exchange between lumen and SoD). Similarly, flow along the SoD is characterized by higher average speed.
e. PatCs merely re-scale the same velocity behavior obtained with PhyCs.
a. Lymphatic drainage in the SoD was modeled as a depressurization. This affects the flow within the entire sinusoid. Since lymphatic flow rate is estimated to be 100-500 times less than the flow rate of blood (Swartz, 2001), it might be necessary to adjust the pressure value at the drainage outlet (i.e., current flow speed within the SoD is too high).
b. Lymphatic drainage is expected to be much higher in pathological conditions (Jeong et al. (2022), Tanaka and Iwakiri (2018)) and this aspect was not taken into account in our simulations (i.e., drainage outlet was set to the same pressure value rather than a lower one).
c. With the current boundary conditions (PhyCs, PatCs), porosity variations seems to be fully compensated through flow exchange between lumen and SoD via fenestrations without affecting flow velocity inside the lumen. In the model the elevated pressure seen in pathologies is not causing alterations to the flow pattern with unchanged geometries. While the model does not account for cellular responses to elevated pressure and flow velocity, it shows the sinusoidal geometry needs to be altered for flow patterns to change.
d. Instead of a homogeneous variation of porosity, with evenly spaced fenestrations a stochastic porosity model might be applied (more complex geometry) for greater realism. We believe the simplification in our model is justified for our application, but others will need to evaluate the realism required by their inquiry.
f. Further degrees of complexity can be added using non constant viscosity (for example: Carreau model) and pulsatile flow, requiring a user defined function. This however requires better data on pulsatile flow in the sinusoid.
g. The resolution of the model (in terms of # element in the mesh) might be increased to provide more accurate solution (which might be necessary when modeling shear stress) though this too makes the model more computationally heavy. For our case of determining a general trend this is sufficient, but other applications might need a finer mesh.
h. The model simplifies the sinusoid to a straight line, whereas the real case would be curved and branching. This simplification is necessary to home in on the focus of this article, variable porosity and diameter in and of the sinusoid, but is also a departure from reality in this regard.
Main insights:
Luminal flow and pressure are mainly affected by the overall shape, i.e. evolution of vessel diameter, with porosity, from fenestrations affecting nigh exclusively flow in the Space of Disse.
An increasing porosity, with higher porosity towards the pericentral/zone 3, modestly (4% in divergent model) increases flow velocity through the SoD, relative to a constant porosity model, but also decreases velocity through fenestrations significantly (reduced by 50% in the divergent model). Pressure in likewise modestly reduced (-4% in divergent model) through fenestrations and the space of Disse in the variable porosity model relative to a constant porosity model.
Simulating lymphatic drainage by adding an outlet increased flow velocity and exchange between lumen and Space of Disse. More detailed studies of how this parameter evolves are required.
Some effects may be underestimated in the model on account of parameter reduction, as pulsatile flow, curved geometry, tissue compressibility and obstruction of flow by migrating blood cells (MacPhee 1995, Wisse 1985) are left out to home in on two parameters, porosity zonation and vessel shape. The addition of some of these to the model may be feasible with better computational hardware available. Adding fenestrations with realistic porosity to a larger more detailed model such as that used by Piergiovanni 2017 would also be worth doing, perhaps helping elucidate distribution patterns of various solutes and colloids at the sinusoid level, but would make much greater requirements in terms of both time and hardware.
Future Perspectives
Our model did not account for pulsatility of flow, as is the case for blood-flow, or elasticity of the tissue itself, which can compress in response to pressure. Lymphatic outflow was also approximated as constant which is unlikely the real case, but was good enough for our investigation pertaining to flow and pressure relations.
Adding a few of these more computationally heavy elements may yield better results, the geometry and simplifications therein of the model however we feel are accurate enough for further use.
The model shows differences in fluid flow velocity through the SoD between constant and increasing porosity along the sinusoid-model, this may have implications towards solute exchange between the blood stream and the hepatocytes.
There would be benefit in generating a more accurate and detailed model of the sinusoid. These should account for: branching (ideally in 3 dimensions) and elasticity of the tissue itself ,double inlet (arterial and venous contribution) pulsatile flow, blood cells which would barely fit the initial diameter of the sinusoid (RBCs and leukocytes which adhere slightly to the endothelial lining), lymphatic drainage is probably related to the pulsatility of flow (probably intermittent outflow into lymphatics, based on pressure maxima in sinusoid), with mixing and flow-paths described in the case of pulsatile flow with blood cells in the sinusoid (the contributions this makes theorized by Wisse (Wisse et al., 1985)).
Acknowledgements
Special thanks are given to professor Peter McCourt and Karolina Szafranska for linguistic input. This project was funded in part by Horizon 2020 MSCA ITN DeLIVER(grant no. 766181) and the Faculty of Health Sciences UiT.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ahmadi-Badejani, R. , Mosharaf-Dehkordi, M., & Ahmadikia, H. (2020). An image-based geometric model for numerical simulation of blood perfusion within the liver lobules. Computer Methods in Biomechanics and Biomedical Engineering, 23, 987–1004. [CrossRef]
- Barléon, N. , Clarke, R. J., & Ho, H. (2018). Novel methods for segment-specific blood flow simulation for the liver. Computer Methods in Biomechanics and Biomedical Engineering, 21, 780–783. [CrossRef]
- Bonfiglio, A. , Leungchavaphongse, K., Repetto, R., & Siggers, J. H. (2010). Mathematical modeling of the circulation in the liver lobule. Journal of Biomechanical Engineering, 132. [CrossRef]
- Brainerd, C. , Gorti, V., Janes, M., Jones, K., Khayat, S., Liu, A., Noonan-shueh, M., & Rao, S. (n.d.). Title of Document : VARIABLE FENESTRATION OF A 3D NANOPRINTED LIVER SINUSOID ON A CHIP Dr. Ryan D. Sochol Department of Mechanical Engineering.
- Cogger, V. C. , Hunt, N. J., & Le Couteur, D. G. (2020). Fenestrations in the Liver Sinusoidal Endothelial Cell. In The Liver (pp. 435–443). Wiley. [CrossRef]
- Debbaut, C. , Monbaliu, D., Casteleyn, C., Cornillie, P., Van Loo, D., Van Hoorebeke, L., Simoens, P., Pirenne, J., & Segers, P. (2011). Multiscale Modeling of the Blood Circulation in the Human Liver Using Vascular Corrosion Casting and Micro-CT Imaging Techniques. ASME 2011 Summer Bioengineering Conference, Parts A and B, 451–452. [CrossRef]
- Debbaut, C. , Vierendeels, J., Casteleyn, C., Cornillie, P., Van Loo, D., Simoens, P., Van Hoorebeke, L., Monbaliu, D., & Segers, P. (2012). Perfusion Characteristics of the Human Hepatic Microcirculation Based on Three-Dimensional Reconstructions and Computational Fluid Dynamic Analysis. Journal of Biomechanical Engineering, 134. [CrossRef]
- Eguchi, H. , Sato, N., Matsumura, T., Minamiyama, M., Kawano, S., & Kamada, T. (1987). The microcirculatory properties around the hepatic periportal and pericentral regions of rats. Fourth World Congress for Microcirculation.
- Ehrlich, A. , Duche, D., Ouedraogo, G., & Nahmias, Y. (2019). Challenges and Opportunities in the Design of Liver-on-Chip Microdevices. Annual Review of Biomedical Engineering, 21(June), 219–239. [CrossRef]
- Heppell, C., Roose, T., & Richardson, G. (2015). A Model for Interstitial Drainage Through a Sliding Lymphatic Valve. Bulletin of Mathematical Biology, 77, 1101–1131. [CrossRef]
- HORN, T. , HENRIKSEN, J. H., & CHRISTOFFERSEN, P. (1986). The sinusoidal lining cells in “normal” human liver. A scanning electron microscopic investigation. Liver, 6, 98–110. [CrossRef]
- Hsu, M. C., & Itkin, M. (2016). Lymphatic Anatomy. Techniques in Vascular and Interventional Radiology, 19, 247–254. [CrossRef]
- Hu, J. , Lü, S., Feng, S., & Long, M. (2017). Flow dynamics analyses of pathophysiological liver lobules using porous media theory. Acta Mechanica Sinica/Lixue Xuebao, 33, 823–832. [CrossRef]
- Jeong, J. , Tanaka, M., & Iwakiri, Y. (2022). Hepatic lymphatic vascular system in health and disease. Journal of Hepatology. [CrossRef]
- Komatsu, H., Koo, A., & Guth, P. H. (1990). Leukocyte flow dynamics in the rat liver microcirculation. Microvascular Research, 40, 1–13. [CrossRef]
- MacPhee, P. J. , Schmidt, E. E., & Groom, A. C. (1995). Intermittence of blood flow in liver sinusoids, studied by high-resolution in vivo microscopy. American Journal of Physiology - Gastrointestinal and Liver Physiology, 269(5 32-5). [CrossRef]
- Mosharaf-Dehkordi, M. (2019). A fully coupled porous media and channels flow approach for simulation of blood and bile flow through the liver lobules. Computer Methods in Biomechanics and Biomedical Engineering, 22, 901–915. [CrossRef]
- Piergiovanni, M. , Bianchi, E., Capitani, G., Li Piani, I., Ganzer, L., Guidotti, L. G., Iannacone, M., & Dubini, G. (2017). Microcirculation in the murine liver: a computational fluid dynamic model based on 3D reconstruction from in vivo microscopy. Journal of Biomechanics, 63, 125–134. [CrossRef]
- Rani, H. P. , Sheu, T. W. H., Chang, T. M., & Liang, P. C. (2006). Numerical investigation of non-Newtonian microcirculatory blood flow in hepatic lobule. Journal of Biomechanics, 39, 551–563. [CrossRef]
- Rezania, V. , Coombe, D., & Tuszynski, J. A. (2016). A physiologically-based flow network model for hepatic drug elimination III: 2D/3D DLA lobule models. Theoretical Biology and Medical Modelling, 13, 1–22. [CrossRef]
- Ricken, T., Dahmen, U., & Dirsch, O. (2010). A biphasic model for sinusoidal liver perfusion remodeling after outflow obstruction. Biomechanics and Modeling in Mechanobiology, 9, 435–450. [CrossRef]
- Rohan, E., Turjanicová, J., & Lukeš, V. (2019). Multiscale modelling of liver perfusion. 15th International Conference on Computational Plasticity. Fundamentals and Applications, COMPLAS 2019, 343–353.
- Ryou, M., Stylopoulos, N., & Baffy, G. (2020). Nonalcoholic fatty liver disease and portal hypertension. Exploration of Medicine, 1, 149–169. [CrossRef]
- Santambrogio, L. (2018). The Lymphatic Fluid (pp. 111–133). [CrossRef]
- Schwen, L. O. , Krauss, M., Niederalt, C., Gremse, F., Kiessling, F., Schenk, A., Preusser, T., & Kuepfer, L. (2014). Spatio-Temporal Simulation of First Pass Drug Perfusion in the Liver. PLoS Computational Biology, 10. [CrossRef]
- Schwen, L. O. , Schenk, A., Kreutz, C., Timmer, J., Rodríguez, M. M. B., Kuepfer, L., & Preusser, T. (2015). Representative sinusoids for hepatic four-scale pharmacokinetics simulations. PLoS ONE, 10, 1–39. [CrossRef]
- Siggers, J. H. , Leungchavaphongse, K., Ho, C. H., & Repetto, R. (2014). Mathematical model of blood and interstitial flow and lymph production in the liver. Biomechanics and Modeling in Mechanobiology, 13, 363–378. [CrossRef]
- Swartz, M. A. (2001). The physiology of the lymphatic system. Advanced Drug Delivery Reviews, 50(1–2), 3–20. [CrossRef]
- Tanaka, M. , & Iwakiri, Y. (2016). The Hepatic Lymphatic Vascular System: Structure, Function, Markers, and Lymphangiogenesis. Cmgh, 2, 733–749. [CrossRef]
- Tanaka, M., & Iwakiri, Y. (2018). Lymphatics in the liver. Current Opinion in Immunology, 53, 137–142. [CrossRef]
- Vidal-Vanaclocha, F., & Barberá-Guillem, E. (1985). Fenestration patterns in endothelial cells of rat liver sinusoids. Journal of Ultrastructure Research and Molecular Structure Research, 90, 115–123. [CrossRef]
- Wack, K. E., Ross, M. A., Zegarra, V., Sysko, L. R., Watkins, S. C., & Stolz, D. B. (2001). Sinusoidal ultrastructure evaluated during the revascularization of regenerating rat liver. Hepatology, 33, 363–378. [CrossRef]
- Wake, K. , Motomatsu, K., Dan, C., & Kaneda, K. (1988). Three-dimensional structure of endothelial cells in hepatic sinusoids of the rat as revealed by the Golgi method. Cell and Tissue Research, 253, 563–571. [CrossRef]
- Wisse, E., De Zanger, R. B., Jacobs, R., & McCuskey, R. S. (1983). Scanning Electron Microscope Observations on the Structure of Portal Veins, Sinusoids and Central Veins in Rat Liver. Scanning Electron Microscopy, v(pt 3), 1441–1452.
- Wisse, E. , De Zanger, R., Charles, K., Van Der Smissen, P., & McCuskey, R. (1985). The Liver Sieve : Considerations Concerning the Structure and Function of Endothelial Fenestrae, the Sinusoidal Wall and the Space of Disse. Hepatology, 5.
- Xie, G. , Wang, L., Wang, X., Wang, L., & DeLeve, L. D. (2010). Isolation of periportal, midlobular, and centrilobular rat liver sinusoidal endothelial cells enables study of zonated drug toxicity. American Journal of Physiology - Gastrointestinal and Liver Physiology, 299, 1204–1210. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).