Preprint
Article
Riemann–Hilbert Problems, Polynomial Lax Pairs, Integrable Equations and Their Soliton Solutions
Altmetrics
Downloads
134
Views
38
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
25 August 2023
Posted:
30 August 2023
You are already at the latest version
Alerts
Abstract
The standard approach to integrable nonlinear evolution equations (NLEE) usually uses the following steps: 1) Lax representation $[L,M]=0$; 2)~construction of fundamental analytic solutions (FAS);
3) reducing the inverse scattering problem (ISP) to a Riemann-Hilbert problem (RHP) $\xi^+(x,t,\lambda) =\xi^-(x,t,\lambda) G(x,t\lambda)$ on a contour $\Gamma$ with sewing function $G(x,t,\lambda)$; 4) soliton solutions and possible applications.Step 1) involves several assumptions: the choice of the Lie algebra $\mathfrak{g}$ underlying $L$, as well as its
dependence on the spectral parameter, typically linear or quadratic in $\lambda$.
In the present paper we propose another approach which substantially extends the classes of integrable NLEE.Its first advantage is that one can effectively use any polynomial dependence in both $L$ and $M$. We use the following steps: A) Start with canonically normalized RHP with predefined contour $\Gamma$; B) Specify the $x$ and $t$ dependence of the sewing function defined on $\Gamma$; C) Introduce convenient parametrization for the solutions $ \xi^\pm(x,t,\lambda)$
of the RHP and formulate the Lax pair and the nonlinear evolution equations (NLEE); D) use Zakharov-Shabat dressing method to derive their soliton solutions. This needs correctly taking into account the symmetries of the RHP. E) Define the resolvent of the Lax operator and use it analyze its spectral properties.
Keywords:
Subject: Physical Sciences - Mathematical Physics
1. Introduction
In 1968 one of the great discoveries in mathematical physics took place. Its authors: P. Lax, C. S. Gardner, J. M. Greene, M. D. Kruskal, R. M. Miura and N. J. Zabusky after several years of analysis proved that the KdV equation can be exactly solved by the inverse scattering method (ISM). This was the first and for some time, the only NLEE that could be solved exactly. Soon after that it was demonstrated that the KdV is completely integrable infinite-dimensional Hamiltonian system; its action-angle variables were found by Zakharov and Faddeev [137]. The whole story is well described by N. J. Zabusky in his review paper [128].
The second big step in this direction followed in 1971 by the seminal paper of Zakharov and Shabat who discovered the second equation integrable by the ISM: the nonlinear Schrödinger (NLS) equation [132]; in 1973 the same authors demonstrated that the NLS equation is integrable also under nonvanishing boundary conditions [133]. Both versions of NLS equations described interesting and important physical applications in nonlinear optics, plasma physics, hydrodynamics and others. This inspired many scientists, mathematicians and physicists alike to join the scientific community interested in the study of soliton equations. As a result new soliton equations started to appear one after another. Here we only mention the modified KdV (mKdV) equation [125], the N-wave equations [131], the Manakov system known also as the vector NLS equation [92] and many others. Many of them have already been included in monographs: see e.g. [1,10,18,64,104] and the numerous references therein.
The first few NLEE were related to the algebra , so the corresponding inverse scattering problem could be solved using the famous Gelfand-Levitan-Marchenko (GLM) equation. For the Manakov system it was necessary to use block matrix Lax operator, so the GLM equation was naturally generalized also for that case. However, the ISM for the N-wave system came up to be substantially more difficult. Indeed, for the (block) matrix Lax operator the Jost solutions possess analyticity properties which are basic for the GLM eq. However the Lax pair for the N-wave system is the generalized Zakharov-Shabat system:
where and are real constants such that , . Without restrictions we can assume that . In this case only the first and the last column of the corresponding Jost solutions allow analytic extension in the spectral parameter . This, however, was not enough to derive GLM equation. It was Shabat who discovered the way out of this difficulty [106,107]. He was able to modify the integral equations for the Jost solutions into integral equations that provide the fundamental analytic solutions (FAS) and of L which allowed analytic extensions for and respectively. As a result the interrelation between the FAS and the sewing function :
can be reformulated as Riemann-Hilbert problem (RHP). Now we can solve the ISP for L by using the RHP with canonical normalization:
The normalization condition (1.4) ensures that the RHP has unique regular solution [104]. It also allowed Zakharov and Shabat to develop their dressing method, which enables one to calculate the N-soliton solutions not only for the N-wave system, but also for the whole hierarchy of NLEE related to L (1.1); see [134,135] and also [32,104]. In short, the dressing Zakharov-Shabat factor came up as one of the most effective methods for a) constructing soliton solutions, and b) understand that the dressed Lax operator has some additional discrete eigenvalues, as well as the explicit form of the dressed FAS.
The GZS system has natural reductions after which the potential and J belong either to or to algebra. Other reductions were proposed by Mikhailov [96] which substantially enlarged the classes of integrable NLEE. Some of these reductions require that J has complex-valued eigenvalues. Constructing FAS for such systems poses additional difficulties, which were overcome by Beals and Coifman [7] for the GZS systems related to algebra. Later the results of [7] were extended first for the systems related to or to algebra, (see [64]) as well as to Mikhailov’s reductions [57,64].
The FAS play an important role in soliton theory. Indeed, they can be used to introduce
- 1.
-
Scattering data The minimal sets of scattering data are determined by the asymptotics ofHere and are the factors of the Gauss decompositions of the scattering matrix .
- 2.
- Resolvent The FAS determine the kernel of the resolvent of L. Applying contour integration method on one can derive the spectral expansions for L, i.e. the completeness relation of FAS.
- 3.
- Dressing method Zakharov-Shabat dressing method is a very effective and convenient method to construct the class of reflectionless potentials of L and to derive the soliton solutions of the NLEE. The simplest dressing factor has pole singularities at , which determine the new discrete eigenvalues that are added to the spectrum of the initial Lax operator.
- 4.
- Generalized Fourier transforms Here we start with GZSh system related to a simple Lie algebra with Cartan-Weyl basis , [67] and construct the so-called 'squared solutions'where is the projector onto the image of the operator . It is known that the 'squared solution' are complete set of functions in the space of allowed potentials [30]. In particular, if we expand the potential over the 'squared solutions' the expansion coefficients will provide the minimal set of scattering data. Similarly, the expansion coefficients of are the variations of the minimal set of scattering data. Therefore the 'squared solutions' can be viewed as FAS in the adjoint representation of , see [2,12,30,45,59,62,63,64,78,108,121] as well as [12,24,39,65].
- 5.
- Hierarchies of Hamiltonian structures The GFT described above allow one to prove that each of the NLEE related to L allows a hierarchy of Hamiltonian structures. More precisely, each NLEE allows a hierarchy of Hamiltonians and a hierarchy of symplectic forms (or a hierarchy of Poisson brackets) such that for any n they produce the relevant NLEE. [30,81,86]
- 6.
- Complete integrability and action-angle variables. Starting from the famous paper by Zakharov and Faddeev [137] it is known that some of the NLEE allow action-angle variables. The difficulty here is that these NLEE are Hamiltonian system with infinitely many degrees of freedom. Therefore the strict derivation of the proof must be based on the completeness relation for the 'squared solutions'. In fact VG and E. Khristov [45,59] (see also [63]) proposed the so-called 'symplectic basis' of squared solutions, which maps the variation of the potential of the AKNS system to the variation of the action-variables. Unfortunately for many multi-component systems such bases are not yet known.
The above arguments lead us to the hypothesis that we could use more effective approach to the integrable NLEE which starts from the RHP rather than from a specific Lax operator. In the first part of this paper we will demonstrate that FAS could be constructed and used also for quadratic pencils. We also formulate explicitly the corresponding RHP. For quadratic pencils we have additional natural symmetry which maps . This symmetry is also inherent in the contour in the complex -plane, on which the RHP is defined.
In Section 2 we first demonstrate that the well known methods for analysis of NLEE can be generalized also for Lax operators quadratic in , see eq. (2.28) below. On this level we for the first time meet with purely algebraic problem for constructing two commuting quadratic pencils. For polynomial pencils of higher orders those problems will be more and more difficult to solve. In particular we outline the construction of the FAS and which are analytic in and respectively, see Figure 4 below. As a result, the continuous spectrum of these Lax operators fill up the union of the real and imaginary axis of the complex -plane. As a consequence contours of the corresponding RHP will be unless an additional factor complicates the picture. Thus we see that the symmetries of the NLEE or of its Lax pair determine the contour of the RHP.
In Section 3 we remind the notion of Mikhailov’s reduction group and briefly outline characteristic contours of the relevant RHP. We also demonstrate that Zakharov–Shabat theorem is valid for a larger class of Lax operators than it was proved before. It is important to request that the RHP is canonically normalized. This ensures that the RHP has unique regular solution, which is important for the application of the Zakharov-Shabat dressing method.
Another important factor in formulating the RHP is Mikhailov’s reduction group. In Section 4 we outline some of the obvious effects which the reduction group may have on the contour of the RHP. Therefore it is not only the order of the polynomial in , but also the symmetry (the reduction group) which determine the contour of the RHP. For example, if we add an additional Mikhailov’s symmetry that maps then the corresponding Lax operator will be polynomial in and which in turn will require adjustments in the techniques for deriving the dressing factors and soliton solutions.
In Section 5 we propose a parametrization of the solutions of RHP for the class of RHP related to homogeneous spaces, see eq. (5.1). Here we require that the coefficients provide local coordinates of the corresponding homogeneous space. Thus we are able to derive a new systems of N-wave equations, see also [36,52,53,56,74]. We also demonstrate that the dressing Zakharov-Shabat method [100,129,134,135,136] can be naturally extended to derive the soliton solutions of these new N-wave equations. At the same time the structure of the dressing factors depends substantially on the symmetries of the Lax operators. Thus even for the one-soliton solutions we need to solve linear block-matrix equations. The situation when we have two involutions: the Hermitian one and the symmetry are typical for Lax operators L related to the algebras . But if we request in addition that L is related to symplectic or orthogonal Lie algebra then we have to deal with three involutions, and the corresponding linear equations get more involved. That is why we focus first on the one-soliton solutions. The derivation of the N soliton solutions is discussed later.
Section 6 is devoted to the MNLS equations which require the use of symmetric spaces, see Refs. [21,40,67,92,94,118,119,122,126]. We start again with the parametrization of the RHP which now must be compatible with the structure of the symmetric spaces. To us it was natural to limit ourselves to the four classes Hermitian symmetric spaces related to the non-exceptional Lie algebras, see [67]. Again we parametrize the coefficients as local coordinates of the corresponding symmetric spaces. In fact must have the same grading as the symmetric space, but we were able to apply additional reductional requesting , see eq. (6.11) below. Thus we formulate the typical MNLS equations related to the four classes of symmetric spaces.
In Section 7 we derive the one soliton solutions of MNLS. Again, like in Section 5, we treat separately the MNLS related to A.III type symmetric spaces, because the corresponding FAS have only two involutions. The MNLS related to C.I and D.III symmetric spaces possess three involutions; the corresponding linear equations are similar to the ones for the class of N-wave equations, but the solutions are different. The symmetric spaces of BD.I class are treated separately, because their typical representation is provided by block matrices, so many of the calculations are indeed different. At the end of this Section we derive the soliton interactions for the BD.I class of MNLS [41]. More precisely we use the asymptotic of the dressing factor for applying it to the two-soliton solution in order to calculate the center-of-mass and the phase shifts of the solitons.
In Section 8 we introduce the resolvent of the Lax operators in terms of the FAS. The diagonal of the resolvent after a regularization can be expressed in terms of the solution of the RHP by ; here by 'hat' we denote the inverse matrix. It can be viewed as generating functional of the integrals of motion.
We end the paper by discussion and conclusions. Some technical aspects in the calculations such as the structure of the symmetric spaces, and the root systems of the simple Lie algebras as well as the Gauss decompositions of the elements of the simple Lie groups are given in the appendices.
2. From the Lax representation to the RHP
2.1. N-waves according to Manakov and Zakharov
The N-wave equations were discovered by Manakov and Zakharov in 1974 [131]. The Lax operator is the classical Zakharov-Shabat system:
with real-valued diagonal . The second operator in the Lax representation is also linear in
with real-valued diagonal . Then the N-wave equations, which are the compatibility condition take the form:
For some time solving the ISP for the Lax operator was an open problem. However in 1974 Shabat [106,107] proved that has fundamental solutions and which are analytic in the upper- and lower-half of .
Let us briefly outline the construction of FAS proposed by A. B. Shabat [106,107]; for more details see also [32,104]. We will assume for simplicity that the potential is defined on the whole axis and satisfies the following conditions:
- C.1
- By we mean that possesses smooth derivatives of all orders and falls off to zero for faster than any power of x:
- C.2
- is such that the corresponding operator L has only a finite number of simple discrete eigenvalues.
We will impose also the typical reduction of the Lax operator: the GZSs with -reduction:
We start by introducing the Jost solutions of L:
and the scattering matrix:
The Jost solutions satisfy the following Volterra type integral equations:
where and . It is well known that Volterra type equations possess solutions provided the integrals of the equations are convergent. In our case this will be true for real . Indeed, in this case the exponential factors in the equations (2.7) will be bounded and the convergence of the integrals is ensured by the fact that satisfies Condition 1. However, for complex the exponential factors are not growing only for the first and the last columns of the Jost solutions.
Shabat introduced the FAS of L by modifying the integral equations for them as follows:
where
Now it is not difficult to check that all exponential factors in the integrands of (2.8) are falling off for , while the exponential factors in the integrands of (2.9) are falling off for . In other words, allows analytic extensions for in the upper complex half-plane, while is analytic for in the lower complex half-plane. Obviously and are FAS of a slightly modified Lax operator:
Theorem 1.
Let satisfies conditions (C.1), (C.2) and let the matrix elements of J be ordered . Then the solution of the eqs. (2.8) (resp. of the eqs. (2.9)) exists and allows analytic extension for (resp. for ).
Remark 1.
Due to the fact that in eq. (2.8) we have both ∞ and as lower limits the equations are rather of Fredholm than of Volterra type. Therefore we have to consider also the Fredholm alternative, i.e. there may exist finite number of values of for which the solutions have zeroes and pole singularities in λ. The points in fact are the discrete eigenvalues of in .
The reduction condition (2.4) with means that the FAS and the scattering matrix satisfy:
Each fundamental solution of the Lax operator is uniquely determined by its asymptotic for or . Therefore in order to determine the linear relations between the FAS and the Jost solutions for we need to calculate the asymptotics of FAS for . Taking the limits in the right hand sides of the integral equations (2.8) and (2.9) we get:
This can be written in compact form using (2.10):
where the matrices , and are of the form:
Let us now relate the factors , and to the scattering matrix . Comparing (2.14) with (2.6) we find
i.e. , and are the factors in the Gauss decomposition of .
It is well known how given one can construct explicitly its Gauss decomposition, see the Appendix B. Here we need only the expressions for :
where are the principal upper and lower minors of of order j.
Remark 2.
Corollary 1.
The upper (resp. lower) principal minors (resp. of are analytic functions of λ for (resp. for ).
Proof.
Follows directly from theorem 1, from the limits:
and from (2.15b) and (2.17). □
Thus the solution of the ISP for was reduced to a RHP:
on the real axis of . The solutions defined by (2.10) satisfy an alternative RHP:
which is canonically normalized, i.e.
2.2. MNLS equations according to Manakov, Fordy and Kulish
The first MNLS:
where is a 2-component vector, was proposed by Manakov [92] in 1974. Later in their seminal paper [21] Fordy and Kulish demonstrated the deep relations between the MNLS equations and the symmetric spaces [67]. As a result the Lax representation for the MNLS takes the form:
For the Manakov model (2.22) and . Special role here is played by the Cartan element J of the corresponding simple Lie algebra. It determines the Cartan involution, which picks up the symmetric space from the corresponding Lie algebra. The Manakov model is related to the symmetric space . The symmetric spaces have been classified about a century ago by E. Cartan, see e.g. [67].
In 1976 Kaup and Newell [81] derived the generalizations of NLS corresponding to Lax operator, quadratic in . This generalization of NLS now is known as the derivative NLS (DNLS), because its nonlinear terms depend on the x-derivative of q. Another form of the DNLS eq. is known since 1978 as the Gerdjikov-Ivanov (GI) equation [42,58], see also [14,19,20,90] and the references therein. It is gauge equivalent to DNLS and besides the terms with x-derivative, contains also nonlinearities of 5-th order. In Section 6 below we describe the multi-component generalizations to GI equations.
2.3. Generic Lax representation
We start with the idea of constructing more general polynomial Lax pairs:
The compatibility condition of the pair (2.24) holds for any and has the form:
Here we will assume that both and . In addition we will fix up the gauge by requiring that
where J and K are constant diagonal matrices.
Eq. (2.25) must hold identically with respect to the spectral parameter . Thus here there comes the first technical difficulty related with the parametrization of L and M. Indeed, let us consider the example where and . The the left hand side of (2.25) is a polynomial of order 6 with respect to , whose highest 4 coefficients are given by
The coefficient at is vanishing because J and K are diagonal. The vanishing of the coefficient at is means that is expressed through . Indeed, if we put and then
The next two relations coming from and are not so easy to satisfy.
Gel’fand and Dickey [15,25,26,27,28] provide a very effective solution to the problem. They suggest a general construction for the Lax pairs of the form (2.24) using the fractional powers of the Lax operator. Below we will outline, along with the effective parametrization of the RHP, an equivalently effective method for generic Lax representations.
2.4. Jost solutions and FAS of L
Here we start with generic Lax operator, quadratic in with vanishing boundary conditions and canonical gauge. In our case this is:
Remark 3.
For the potentials and we assume that they matrices which are smooth functions of x for all values of t, tending to 0 fast enough for ; for simplicity we could take them to be Schwartz-type functions
The Jost solutions to (2.28) are defined as follows:
Both Jost solutions are fundamental solutions: indeed they are non-degenerate matrix-valued functions. In what follows we will choose the potentials and to take values in a given simple Lie algebra . Then the fundamental solutions and will belong to the corresponding simple Lie group .
It is also well known that any two fundamental solutions are linearly related. In other words:
The matrix belongs to the Lie group .
The integral equations for the Jost solutions take the form:
where and and is the unit matrix. In components we have:
Note that both integral equations are Volterra type equations.
The boundary conditions on the potentials and in Remark 3 ensure that equations (2.31) always have solutions provided the exponentials do not grow for or . Obviously, this holds true for , i.e. for . As we will see below, this is the continuous spectrum of L (2.28).
However the equations (2.31) allow also for important exceptions. These will be easier seen if we use the equations (2.32). Let us, for example consider the equations for the first (resp. for the last) columns of the Jost solutions; So we have to consider the equations (2.32) for (resp. for ). Let us assume also that , i.e. is in the second or fourth quadrant of the complex -plane. Then it is easy to check that the exponential factors in all the equations for , decay for . The same holds true also for the equations for , . Therefore we find that the first column of and the last column of allow analytic extensions to the second and fourth quadrants of . Similarly we find, that the first column of and the last column of allow analytic extensions for , or to the first and third quadrants of . The other columns of and are defined only on the continuous spectrum of L. Indeed, the corresponding set of equations (2.32) some of the exponential factors will decay, but others will grow up.
Nevertheless our aim will be to demonstrate that one can construct fundamental analytic solutions (FAS) for L. These will be matrix solutions, one of which allows analytic extension for and the other one – for . This can be done using Shabat’s method [106,107] based on proper modification of the integral equations (2.32). So let be fundamental solutions of L, i.e. and let us introduce . These solutions will be different from the Jost solutions, because, as we will see, their behavior for is different.
Following Shabat’s idea we define as the solution of the following set of integral equations:
Likewise, are defined as the solution of the following set of integral equations:
Note that the only difference with the equations (2.32) is in index inequalities in the right hand sides; this changes the signs of the factors .
There is an alternative possibility to introduce FAS with a minor change of the integral equations (2.33) and (2.34)
Likewise, are defined as the solution of the following set of integral equations:
Figure 1.
The continuous spectrum of the Lax operator (2.28) and the contour of the related Riemann-Hilbert problem .
Figure 1.
The continuous spectrum of the Lax operator (2.28) and the contour of the related Riemann-Hilbert problem .
Now we have to establish the linear relations between the FAS and the Jost solutions.
The first consequence of the equations (2.33), (2.34), (2.35) and (2.36) concerns the limits of their diagonal matrix elements for , namely:
Obviously the matrices and are x and t independent and in addition they are analytic for ; analogously and are analytic for .
Next we find that:
where and (resp. and ) are upper-triangular matrices (resp. lower triangular) with 1 on the diagonal. Remember, since the Jost solutions and the FAS belong to the Lie group , then all the limits in (2.38) must also belong to .
From (2.38) it follows that the FAS are related to the Jost solutions as follows:
More detailed analysis shows that these triangular and diagonal matrices are in fact the factors in the Gauss decompositions of the scattering matrix :
see Appendix B.
Remark 4.
Let us consider cubic pencils in λ assuming that the leading terms and of L and M respectively are such that J and K have different real eigenvalues. Their FAS can be constructed quite analogously as we did above for the quadratic pencils. The substantial difference between the cubic and the quadratic cases are in the regions of analyticity. The solutions (resp. ) for the cubic pencils are analytic for (resp. ), see sectors (resp. sectors ) on Figure 4.
2.5. The time-dependence of
The Lax representation of a given NLEE requires the commutativity of two ordinary differential operators:
where L is given by (2.28). We assume that M has the same form as L:
Below we will treat also M-operators that are higher order polynomials of . The first remark is that the commutativity condition (2.41) must hold identically with respect to . Note also that (2.41) holds true for any in (2.42). We will use this fact to determine the t-dependence of the scattering matrix .
Indeed, let us consider where is the Jost solution in (2.29) and let us take the limit in (2.42). Due to the vanishing boundary conditions we get:
i.e. . Thus we determined the function for this choice of the M-operator. Let us now take the limit in (2.42). This gives:
i.e.
From eq. (2.45) there follow also the time-dependence of the Gauss factors:
For the diagonal factors we get:
In other words we have two sets of functions of that are t-independent. Note also, that from the canonical normalization of FAS there follows that . Obviously they will generate integrals of motion. Indeed, let us consider their asymptotic expansions:
Obviously . As we shall see below each of the integrals can be expressed as an integral of the potentials and . The advantage of the choice (2.47) is that the integrands of are local, i.e. they depend only on and and their x-derivatives.
Above we described the time dependence for the N-wave equations related to the Lax operators (2.28). In general, each of these operators generates a hierarchy of NLEE. Indeed the NLEE is determined by fixing up along with L also the second operator M in the Lax pair. For example, if we want to treat DNLS-type equations we need, to specify two things. First, the structure of L must be compatible with a Hermitian symmetric space [21], and second, the potential of M must polynomial of order 4 in with leading term . Then and the time dependence of the scattering data will be given by:
Then from eq. (2.49) there follow also the time-dependence of the Gauss factors:
More details about this we will give in the Section devoted to the DNLS type equations.
3. RHP and integrable NLEE
The simplest nontrivial Lax operators, i.e. the ones that are linear in have been studied in detail by now, see [18,63,104] and the numerous references therein. That is why in this paper we will concentrate mostly on Lax operators that are quadratic in like (2.28). In the previous section we constructed the FAS of this operators for the case of vanishing boundary conditions and the result was as follows. The continuous spectrum of L fills up the union of the real and purely imaginary axis , see Figure 1; The analyticity regions for the FAS of (2.28) are for and for , where by , we denote the quadrants of the complex -plane.
3.1. Uniqueness of the regular solution of RHP
The FAS derived above are also linearly related to each other. From equations (2.39) there easily follows that:
These relations allow us to relate the Lax pair to a RHP. Indeed, our FAS are not very suitable because for large they strongly oscillate (like ). In order to avoid these singularities we introduce . Then the RHP can be formulated as:
which allows canonical normalization:
In the previous Subsections we outlined how, starting with the Lax representation one can derive the RHP. Here, following Zakharov and Shabat we will demonstrate how starting from the RHP one can derive the relevant Lax representation. We will use slightly modified RHP with canonical normalization:
compare with (3.2).
We will say that the solution is regular if and have neither zeroes nor singularities in their regions of analyticity.
Corollary 2.
The RHP (3.4) with canonical normalization has unique regular solution.
Proof.
Let us assume that is another regular solution to the RHP (3.4). Consider:
we remind that . Using (3.4) we easily find that:
i.e. is analytic in the whole complex plane . In addition, it tends to for . Then according to the great Liouville theorem, . □
Remark 5.
The RHP (3.4) obviously allows the trivial regular solution when . In this case the corresponding FAS of L will take the form:
3.2. Zakharov-Shabat theorem
Theorem 2
(Zakharov-Shabat [135]). Let satisfy the RHP (3.4). Then are FAS of L (2.28) and M (2.42).
Proof.
Let us introduce the functions
Then, from eqs. (3.4) we find:
Thus are analytic in the whole complex plane . The canonical normalization of the RHP means, however, that are singular for . More specifically, is linear function of . Using again the great Liouville theorem we conclude that there must exist the linear in function such that:
i.e.
Multiplying both sides of (3.11) by we find that the solutions to the RHP (3.4) must satisfy the ODE:
It remains to insert into eq. (3.12) to obtain that are FAS of eq. (2.28).
Applying the same considerations on the second function we find that it is analytic on the whole complex -plane and has the form:
This means that must satisfy also
and therefore are FAS of the M-operator (2.42). □
Remark 6.
Zakharov-Shabat theorem initially was proven for Lax operators with linear dependence on the spectral parameter λ. The above proof is elementary generalization of the original idea. Obviously it can easily be extended for any polynomial Lax pair, see e.g. (2.24). The details of these generalizations are left to the readers.
4. Mikhailov’s reduction groups and the contours of RHP
4.1. General theory
The reduction groups introduced by [96] are a powerful tool for deriving new integrable equations, admitting Lax representation. It has been substantially developed since its discovery, see [9,22,31,37,88,89,120,127]. Mikhailov’s reductions were used in the seminal paper of Drinfeld and Sokolov [16] as an important tool to analyze the gradings of simple Lie algebras and their consequences for the integrable equations. It also stimulated the development of the infinite dimensional Lie algebras and Kac-Moody algebras [8,16,67].
A reduction group is a finite group acting on the solution set of (2.24) which preserves the Lax representation [96], i.e. it ensures that the reduction constraints are automatically compatible with the evolution. must have two realizations: i) and ii) , i.e. as conformal mappings of the complex -plane. To each we relate a reduction condition for the Lax pair as follows [96]:
where and are the images of and or depending on the choice of . Since is a finite group then for each there exist an integer such that .
The finite subgroups of were classified by Klein, see [13]. They consist of two infinite series: i) - cyclic group of order h; ii) - dihedral group of order ; and the groups related to the Platonic solids: tetrahedron, cube, octahedron, dodecahedron and icosahedron. In what follows we will most attention to and ; although examples of systems with Platonic solids as group of reductions are also known, [82,88,89,95]
It is important to note that the form of the equations depends not only on the chosen reduction group, but also on its realization.
It is well known, that every finite group can be imbedded as a subgroup of some finite symmetric group ; this is the group of permutations of the numbers . The group consists of all cyclic permutations of the numbers .
The symmetric group is the commutator subgroup of the symmetric group with index 2 and has therefore elements. It is the kernel of the signature group homomorphism explained under symmetric group. It is isomorphic to .
Generically each of these groups is rigorously defined by their genetic codes. In other words one introduces one or more generating elements of the group and defines the relationes they must satisfy. For the two types of groups we have:
These are the formal definitions of these groups. Below we will outline their realizations as subgroups of the group of automorphisms of the algebra , as well as subgroups of the conformal group. These realizations are specific both for the explicit form of the corresponding NLEE as well as for the spectral properties of their Lax operators.
Other important facts are the orbits and the fundamental domains of the groups. Each element of is of finite order, i.e. there exist an integer such that . Acting on a point, say it produces an orbit in the complex -plane consisting of the points . Then by fundamental domain of we mean the manifold which contains only one point of each orbit. The orbits depend not only on the element , but also on the specific realization of . Below we will specify the fundamental domains for each of the realizations of the reduction groups.
We start with -reductions, (or involutions) for two of the best known classes of NLEE:
4.2. Involutive reductions
We will start with typical reductions (involutions) on the Lax representations (2.24) [96]:
By above we have denoted involutive automorphisms of the simple Lie algebra in which and take values.
Working with Lax operators which are quadratic pencils it is natural to impose two basic symmetries: i) the Hermitian symmetry 1) in (4.3) with and ; and the symmetry 2) in (4.3) mapping . A third involution iii) may appear if we request in addition that U and V belong to a simple Lie algebra of the series , or . This means:
where the matrices are introduced in the Appendix A.
Note that equations (4.3) in fact take into account the all typical external automorphisms of the simple Lie algebras. Therefore we need to consider only those realizations of which are elements of the Weyl group of , or belong to the Cartan subgroup of . This means that may have the form:
where the roots are all orthogonal to each other. This will ensure that is an involution: . Similarly the vector must be such that , where are nonnegative integers and are the fundamental weights of . Then the similarity transformations with will also have the property .
Figure 2.
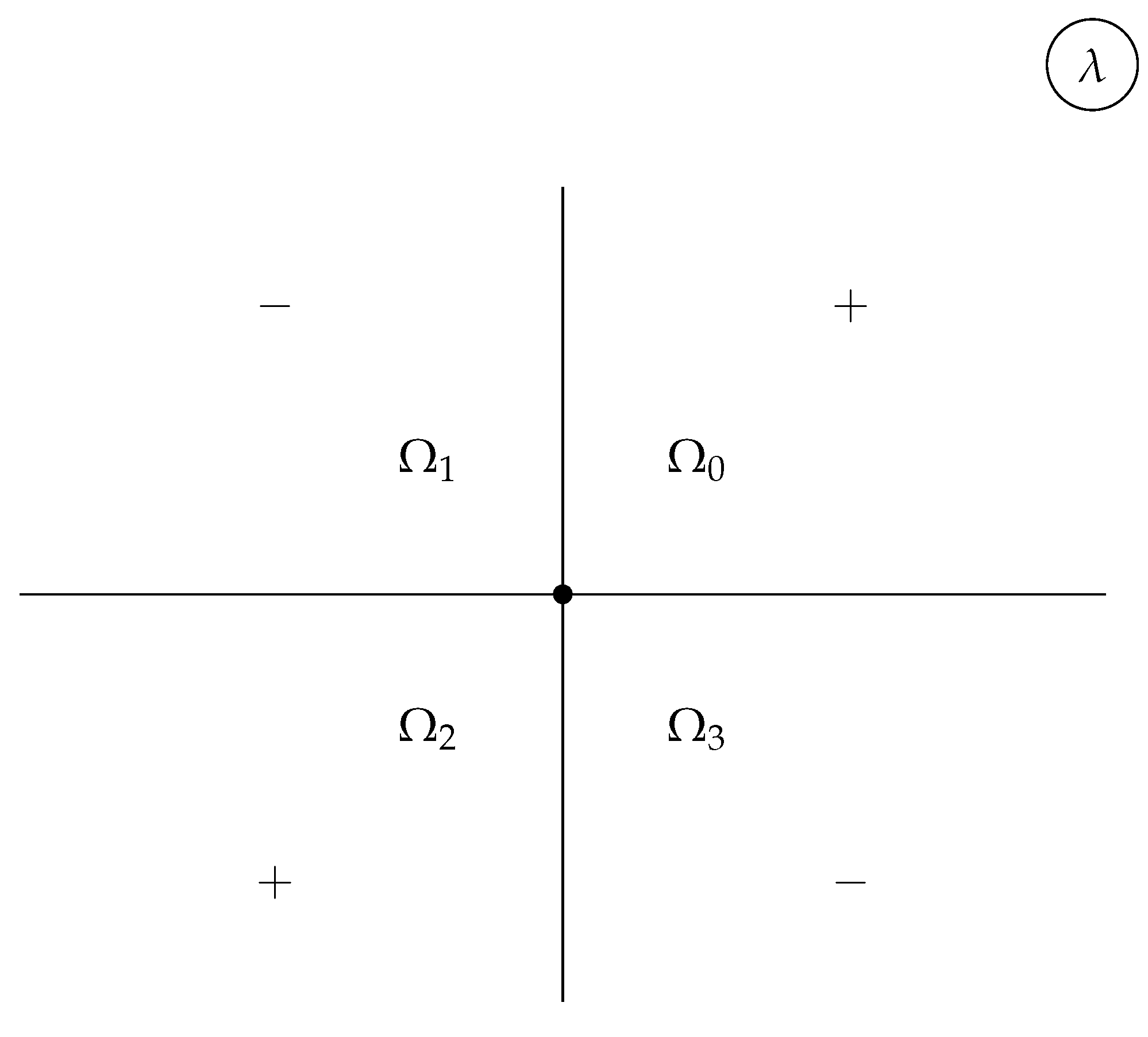
Examples of involutions for Lax operators linear in . The continuous spectrum fills up the real axis; the FAS are analytic for respectively. Left panel: for reductions of types and the discrete eigenvalues come in complex-conjugate pairs, shown by × and ∘; Right panel: for reductions of type and there are two types of eigenvalues: pairs of purely imaginary ones shown by ∘; quadruplets and shown by ×
Figure 2.
Examples of involutions for Lax operators linear in . The continuous spectrum fills up the real axis; the FAS are analytic for respectively. Left panel: for reductions of types and the discrete eigenvalues come in complex-conjugate pairs, shown by × and ∘; Right panel: for reductions of type and there are two types of eigenvalues: pairs of purely imaginary ones shown by ∘; quadruplets and shown by ×
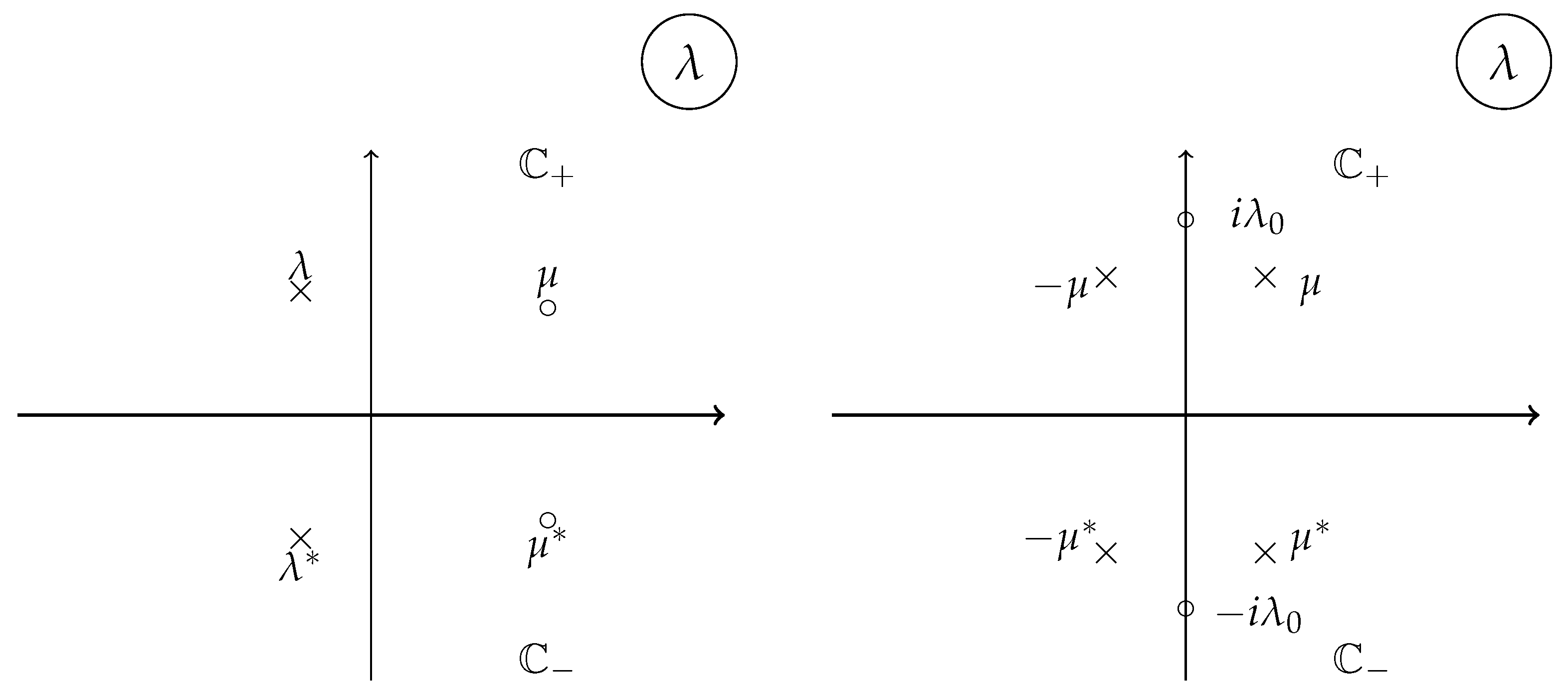
Figure 3.
Examples of involutions for Lax operators quadratic in ; the continuous spectrum fills up . Left panel: for reductions of types and the discrete eigenvalues come in complex-conjugate pairs, shown by ×; for reductions of type they come in pairs shown by ∘. In both cases the contour of the RHP is the real axis. Right panel: the first involution maps ; or to ; the second one maps or to . In both cases the contour of the RHP is given by the unit circle ,119]
Figure 3.
Examples of involutions for Lax operators quadratic in ; the continuous spectrum fills up . Left panel: for reductions of types and the discrete eigenvalues come in complex-conjugate pairs, shown by ×; for reductions of type they come in pairs shown by ∘. In both cases the contour of the RHP is the real axis. Right panel: the first involution maps ; or to ; the second one maps or to . In both cases the contour of the RHP is given by the unit circle ,119]
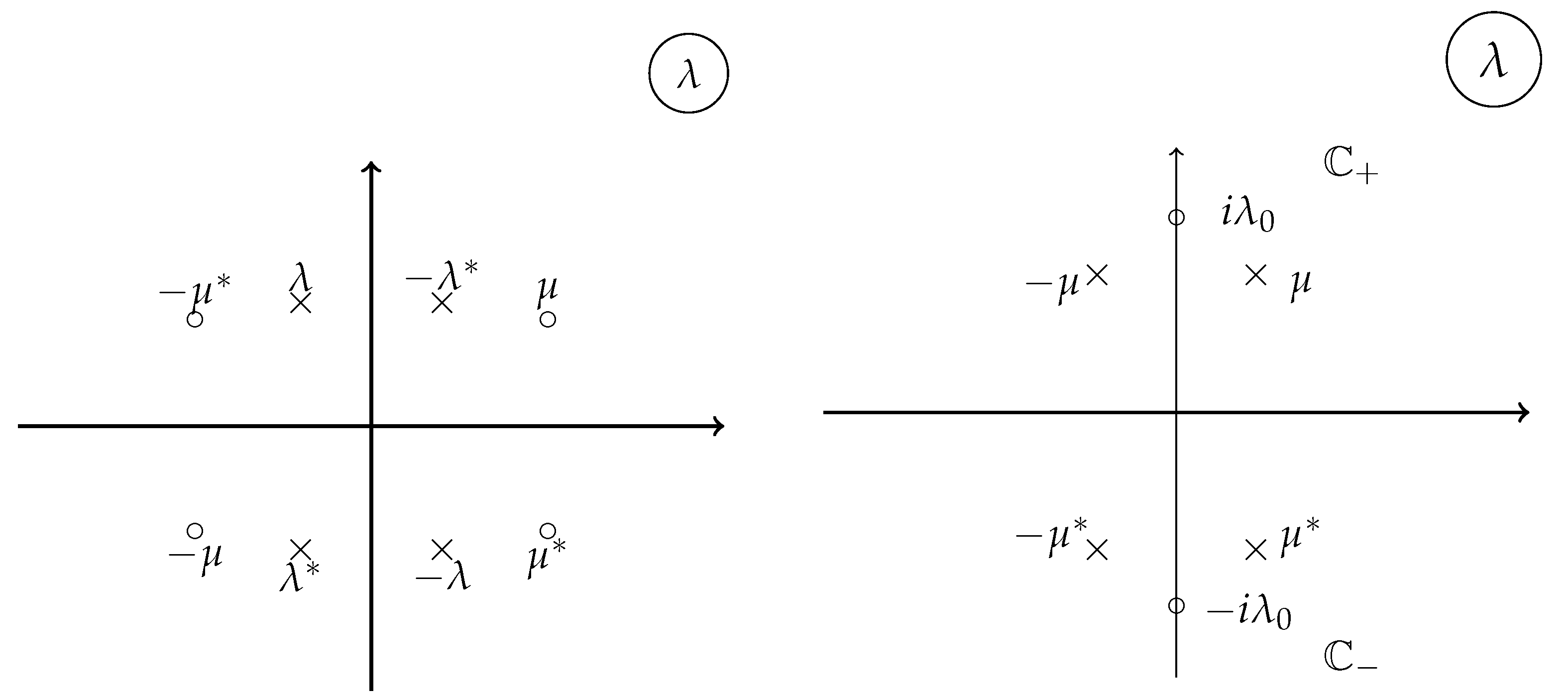
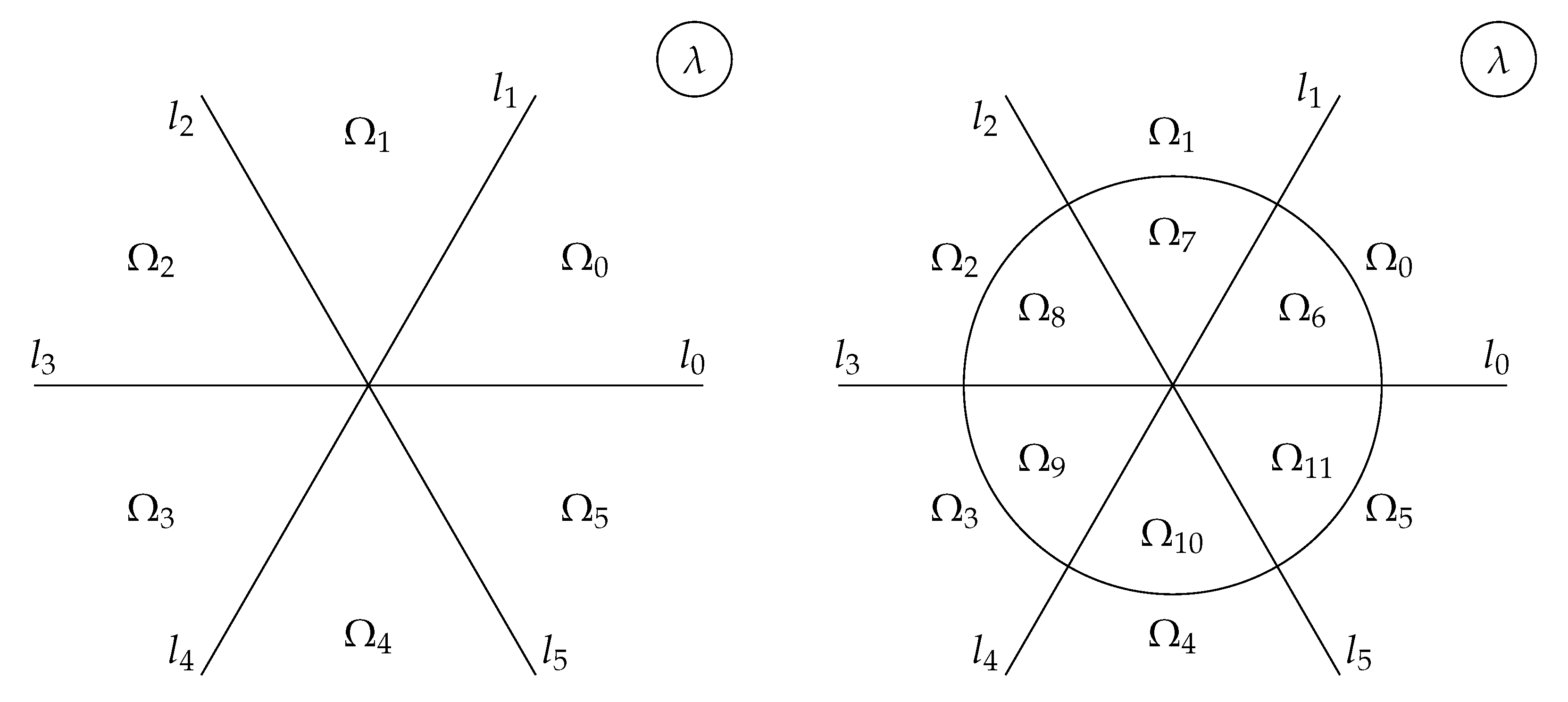
Figure 4.
Left panel: contour of a RHP with symmetry. The FAS is analytic in the sectors , while is analytic in the sectors ; Right panel: contour of a RHP with symmetry with additional involution mapping .
Figure 4.
Left panel: contour of a RHP with symmetry. The FAS is analytic in the sectors , while is analytic in the sectors ; Right panel: contour of a RHP with symmetry with additional involution mapping .
Another important factor for the correct realization of the reduction groups is – the leading power in the Lax operator (2.24). In the majority of cases people consider generalized Zakharov-Shabat systems, i.e. . Let us combine this choice with real-valued eigenvalues of J and vanishing boundary conditions on . Then the analysis of the corresponding integral equations for the Jost solutions show that the FAS (resp. ) of have analyticity properties for (resp. ). That means that the contour of the corresponding RHP coincides with the real axis . Then the spectrum of consists of continuous part filling up and pairs of complex-valued discrete eigenvalues , see Figure 3. As fundamental domain of this group we can choose the upper half-plane of the complex -plane.
In what follows we will concentrate on Lax operators with ; most often we will have . In Section 2 we proved that (resp. ) of L (2.28) have analyticity properties for (resp. ). That means that the contour of the corresponding RHP coincides with the union of the real and purely imaginary axis . Then the spectrum of L consists of continuous part filling up . Typically such Lax operators have additional symmetry , so the discrete eigenvalues come in quadruplets and , see Figure 3. Effectively in these cases we deal with = Then as fundamental domain of this realizations of the group we can choose the first quadrant of the complex -plane.
4.3. reduction groups
We will consider here the cyclic groups of order . These groups have only one generating elements:
The cyclic group has h elements: ; typically its realization on the complex -plane is given by , where .
4.4. reduction groups
We will consider here the dihedral groups of order . These groups have two generating elements:
The dihedral group has elements: and allows several inequivalent realization on the complex -plane. Some of them are:
where again and . An important realization in the case of a reduction group is given by
5. Parametrizing the RHP with canonical normalization
An important tool in our investigation is the theory of the simple Lie algebras and the methods of their gradings.
The reason to limit our selves with the simple Lie algebras is due to the fact, that we need to have unique solution of the inverse spectral problem of the Lax operator. The mapping between the potential and the scattering matrix for generic, linear in operators have been studied using the Wronskian relations [10,30,63]. They require the existence of a non-degenerate metric. A metric, characteristic for the Lie algebras is the famous Killing form, which is non-degenerate for the semi-simple Lie algebras. In fact we will limit ourselves by considering only the simple Lie algebras.
We will limit ourselves also by considering only two families of NLEE. The first family is known as the N-wave equations, discovered by Zakharov and Manakov [131], see Section 2.1 above. Typically they contain first order derivatives in both x and t and quadratic nonlinearities. In this Section we will describe a new class of N-wave equations whose Lax operators are both quadratic in [36,52]. We will see, that they have higher order nonlinearities.
The second family of NLEE we will focus on are the multi-component NLS (MNLS) equations. It is well known that they are related to the symmetric spaces [21]. Their Lax operators will also be quadratic in , so they will be multicomponent generalizations of the derivative MLS eq. [81] and GI equations [19,20,42,58].
5.1. Generic parametrization of the RHP with canonical normalization
We can introduce a parametrization for using its asymptotic expansion:
Obviously, if we want that be elements of a simple Lie group , then the coefficients must be elements of the corresponding simple Lie algebra . In addition we request that provides local coordinates of the corresponding homogeneous space. Besides, the solution is canonically normalized, because
The most general parametrization of requires that are generic elements of the algebra . However such approach has a disadvantage: the corresponding NLEE involve too many independent functions. There are two ways to avoid it: first, we can fix up the gauge of the Lax operators; second we can and will impose reductions of Mikhailov type. Typically we will fix the gauge by requesting that the leading terms in the Lax operators are chosen as diagonal constant matrices, i.e. constant elements of the Cartan subalgebra . Another important issue is to explain how, using from eq. (5.1) we can parameterize any generic Lax pair related to that RHP.
Let us choose, following the ideas of Gel’fand and Dickey
where the subscript + means that we retain only the non-negative in terms in the right hand sides of (5.3) and explain how one can calculate and . First, we remind that since and , then both . From the general theory of Lie algebras we know that
where , etc. The first few coefficients in these expansions take the form:
Thus we see that and are parameterized by the first few coefficients .
Another formula from the general theory of Lie algebras which we will need below is:
In general:
The first few coefficients are:
The effectiveness of the general form of the Lax pair (5.3) follows from the relation which is easy to check:
because the matrices K and J are diagonal. Therefore, the commutator must contain only negative powers of .
In addition we may impose on Mikhailov type reductions. Each of them uses a finite order automorphism, which introduces a grading in the algebra . Below we will use several types of -reductions based on automorphisms of order 2 of the Lie algebra:
compare with (4.3). The last reduction is typical for Lax operators which are quadratic in .
Another important reduction is provided by the Cartan involutions , which determines the hermitian symmetric spaces [67] and acts on as follows:
5.2. The family of N-wave equations with cubic nonlinearities
If we generalize to Lax pairs quadratic in we find:
where , , Q again belong to a simple Lie algebra , J and K are constant elements of . Examples of N-wave type equations will be given below; here we just note that they contain first order derivatives with respect to x and t and cubic (not quadratic) nonlinearities with respect to .
Below we will impose two types of Mikhailov reductions:
where
and , . In particular for the n-wave equations (see eqs. (2.3) and (2.1), (2.2)), we get and J and K must be real. For the FAS and the scattering matrix these reductions give:
see [36,52].
First we will derive the N-wave equations in general form; then we will illustrate them by a couple of examples. Using the generic parametrization (5.1) we obtain:
The compatibility condition in this case is:
It must hold identically with respect to . It is easy to check that the coefficients at and vanish. Some more efforts are needed to check that the coefficient at :
also vanishes identically due to the proper parametrization of U and V. The compatibility conditions must hold identically with respect to . The first three of these relations:
are satisfied identically due to the correct parametrization of . In more details
The last two coefficients at and vanish provided and satisfy the following N-wave type equations:
Note, that while and are linear in , and are quadratic in . Therefore the nonlinearities in this N-wave equations are cubic in .
We assume that the root system of is split into , such that
We also denote positive and negative roots by a plus or minus superscript. Then considering (5.12) we must have:
It is easy to check that this choice of is compatible with the following two involutions of the RHP
which means that
Example 1
(6-wave type equations: ). The involution is given by
The potentials are:
The corresponding NLEE ensure that the coefficients at and also vanish. These give:
where and
Example 2
(4-wave type equations: ). The involution is given by
We first choose the potentials , , J, K and the involution as follows:
It is easy to check that and , and consequently the FAS of (5.11) satisfies . The corresponding equations (5.20) become:
and
5.3. The main idea of the dressing method
In this section we will generalize Zakharov-Shabat dressing method [134,135] for the quadratic pencils. We will start with the simplest possible form of the dressing factor which generates the one-soliton solutions. We do this for two reasons. The first one is that due to the additional involutions inherent in the quadratic pencils the dressing factors for the one-soliton solutions require solving block-matrix linear equations. The other reason is that we will be able to calculate the asymptotics of the one-soliton dressing factors which will allow us to study the soliton interactions for the corresponding NLEE. The N-soliton solutions can be derived either by repeating N-times the one-soliton dressing or by considering dressing factors whose pole singularities determined by , . In this case one has to solve much more complicated block-matrix linear equations.
In order to avoid unnecessary repetitions of formulae we will introduce the notations for the 'naked' and one-soliton solutions FAS of the Lax pairs.
where and are the Lax pair whose potentials and are vanishing. By and we denote the Lax pair whose potentials are provided by the one-soliton solutions of the corresponding NLEE. Each time from the context it will be clear which specific La pair we are considering.
For the N-wave systems the 'naked' FAS are given by:
while for the NLS-type equations
where the dressing factor will be calculated below for each of the relevant cases. The specific form of J and K in (5.34) depends on the specific choice of the corresponding homogeneous space. Likewise the specific form of J in (5.35) is determined by the choice of the relevant symmetric space.
Each dressing factor is a fractional linear function of the spectral parameter . As such we will use:
Indeed, comes up naturally due to the symmetry . By we denote constants such that ; i.e . As we shall see below , and their hermitian conjugate determine the discrete eigenvalues of .
The generic form of the dressing factors is the same for both types of NLEE considered above. If we impose only types of symmetries on L and M, such as:
and similar relations for . Here is constant diagonal matrix such that . Then must satisfy:
then and its inverse have the form
Here the 'polarization' vectors , , and determine the residues of u and . These residues for the one-soliton case will be evaluated explicitly below for each of the NLEE we consider.
5.4. Dressing of N-wave equations: two involutions
We start with the N-wave type on homogeneous spaces with two involutions. Using the equations (5.33) we derive the following equation for the dressing factor:
which also must hold identically with respect to . This can be verified by taking the residues of the left hand sides of (5.40) for and equating them to 0. This gives:
from which one easily finds, see e q. (5.34):
Similarly, we can use the equation satisfied by which reads:
Putting the residue of (5.43) at to 0 we get:
The result is, see eq. (5.34):
Remark 7.
We note that the vectors , , and are constants, which must satisfy the (5.38). Due to the same reductions we must also have . We have also chosen to be constant diagonal matrix whose matrix elements equal .
Thus, if we know the regular solutions then we have derived explicitly the x and t dependence of the vectors and . In addition we know that also must hold identically with respect to . That means that the residues:
must vanish. Inserting u and from eq. (5.39) we obtain the equations:
In the specific calculations below we will use more convenient notations, namely:
where and . The functions and are linear functions of x and t; for each specific example they will be given explicitly.
The last step we need to do is to determine the corresponding singular potentials and . To this end we come back to the equation (5.40) for the dressing factor and study its limit for . Its left hand side is a quadratic polynomial of . Skipping the details we obtain:
We we put we get simplified expression for the one-soliton solution:
More explicit expressions for and in terms of hyper-trigonometric functions will be given below for each of the examples.
Example 3
(One soliton solutions, case). The Lax representation in that case is provided by the operators (5.11) where J, K, and are given by (5.26). The 'naked' polarization vectors (5.42) and (5.45) become:
Taking into account the typical hermitian reduction of L and M we find and . The dressed polarization vectors defined by (5.47) are equal to:
They also satisfy . Therefore
where and . In addition
5.5. Dressing of N-wave equations: three involutions
Here we will consider only the cases, when the two above involutions are combined with condition that or . Then the dressing factors take the form:
where . Inserting into (5.57) we get:
Since the dressing factor is mapping a regular solution to the RHP into a singular solution of the same problem, it must satisfy the reductions (5.24), i.e
In addition one can check that the conditions:
are identically satisfied. The second condition in (5.60) ensures that belongs to the orthogonal group if ; for belongs to the symplectic group.
Note that the new dressing factors and their inverse satisfy the same differential equations (5.40) and (5.43) respectively. These equations must be satisfied identically with respect to . This means that all the residues of these equations at the poles of u and must vanish.
Thus we obtain the generalizations of eqs. (5.45) and (5.42) for the three involutions case:
where , , and are constant polarization vectors. We assume that we know which are related to the regular solutions of the RHP. Typically they correspond to vanishing potentials and ; thus we must have:
In addition we need to ensure that the expressions for and hold identically with respect to . The presence of the third involution makes this problem more difficult, because these expressions have second order poles at the points . It is easy to see that these residues simplify to:
Remember that these vectors depend on x and t and the conditions (5.63) must be identities. But we also know that these polarization vectors must satisfy (5.61). Therefore we have:
The proof that all other scalar products in (5.63) are x and t independent is done similarly. Thus the conditions (5.63) in fact impose restrictions only on the initial polarization vectors:
The last condition that is imposed on the polarization vectors comes from eq. (5.59) and reads
Taking the residues at leads to
i.e., transposing the first of the above equations we find:
By the way, , so
Thus eq. (5.68) is rewritten as:
where the block matrices and are given by:
The inverse of the matrix in the right hand side of eq. (5.69) is given by:
and
i.e., we introduce the relations and the notations
Using the fact that S and commute we can simplify the matrix in (5.71) into:
where
Thus we find the following expressions for and in terms of and :
It remains to calculate the potentials. To this end we rewrite eq. (5.40) in the form:
where we have assumed and . Taking the limit of (5.77) we obtain:
where
Figure 5.
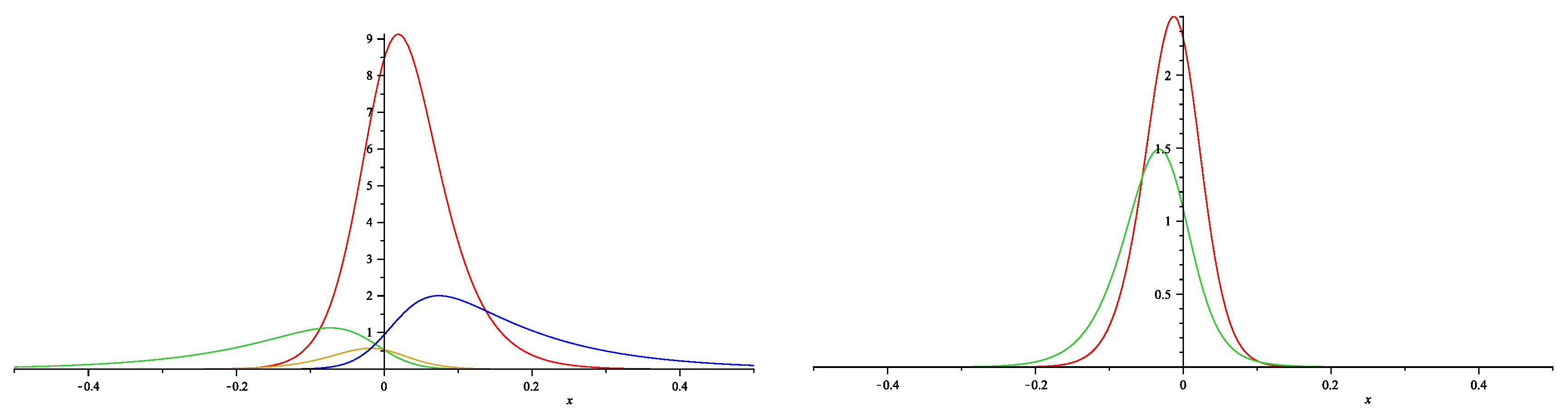
One soliton solution for the 6-wave equations: (blue), (red), (green) and (yellow) on the left panel; (green) and (red) are on the right panel. All functions are evaluated for . The values of the parameters are , , , , , .
Figure 5.
One soliton solution for the 6-wave equations: (blue), (red), (green) and (yellow) on the left panel; (green) and (red) are on the right panel. All functions are evaluated for . The values of the parameters are , , , , , .
Example 4
(One soliton solutions, case). We start with the 'naked' polarization vectors:
where . In addition the constant polarization vectors must satisfy eqs. (5.64). For convenience we choose the following parametrization of , , and :
where the real constants , , and satisfy the relations:
With polarization constants the relations (5.64) are automatically satisfied; in addition the relations (5.66) are also satisfied. With these notations for the scalar products of the 'naked' polarization vectors we obtain:
The 'dressed' polarization vectors:
where
Note that are real constants. Skipping the details we find:
where , provided in general by eq. (5.75) now takes the form:
Thus we obtain the dressed polarization vectors as follows:
where
It remains to use eq. (5.78) and calculate the corresponding one-soliton solutions of the 4-wave NLEE (5.31) and (5.32). The result is:
and
6. MNLS family and symmetric spaces
We already pointed out the importance of the seminal paper of Fordy and Kulish [21] for the NNLS equations. Each symmetric space is generated by a Cartan involution [67], which determines the principal symmetry for the Lax pair and for the solution of the RHP. For this family of NLEE it will be more convenient to use another parametrization of :
This is similar to the parametrization in (5.1), however now each of the coefficients provides local coordinates for the relevant symmetric space. The typical reduction here is to assume that is anti-hermitian:
In the appendix we briefly describe the root systems of the simple Lie algebras, as well as the Cartan involutions that generate the corresponding Hermitian spaces. We remind that the Cartan involution is determined by a special element of the Cartan subalgebra . By we will denote the vector in the space which is dual to J. Using we can split the positive roots of into two subsets:
Below we specify the Cartan involutions for the four classes of Hermitian symmetric spaces and their realizations as factor groups:
in A.III case . The corresponding vectors and the subsets of roots are given by:
where .
The Cartan involution splits the root system of the relevant simple Lie algebra into two subsets:
In the appendix we will briefly describe the roots systems and the Cartan involutions corresponding to these symmetric spaces. Here we just note that for the A.III, C.I and D.III symmetric spaces we can introduce local coordinates, which in the typical representation is given by block matrices:
Indeed, for the A.III type symmetric spaces the blocks and may be arbitrary, apart from the fact that they must be hermitian conjugate to each other. For the symmetric spaces of type C.I and D.III these blocks must be constrained in such a way that the corresponding matrix must be an element of the or algebra.
The fourth hermitian symmetric space is has different block-matrix structure. In this case we a dealing with the root system of algebras and the Cartan involution is provided by J which is dual to . As a result we have:
As a result, in the typical representation the local coordinates are provided by a block matrices with the following structure:
For these reasons we will consider separately these two types of symmetric space.
Here we assume that the exponent provides the local coordinates of the corresponding hermitian symmetric space; we also assume that it is an odd function of . In short:
Note that if we evaluate the exponential in (6.11) we will have two types of terms. The even powers of will be block diagonal matrices which are even functions of ; the odd powers of will be block-off-diagonal matrices which will be odd functions of . As we shall see below, this will give us more 'economic' way for the MNLS equations. Indeed, the equations that we will derive will be parametrized solely by the coefficients of . In addition we have additional symmetry due to the fact that and . This means that
Let us now consider Lax operators which are quadratic in , e.g. (2.28). The construction of their FAS is outlined in Subsection 2.4 above. Obviously the solutions and of the equations (2.33) are analytic for and respectively. This means that now is analytic in the first and third quadrant of the complex -plane, while is analytic in the second and the third quadrant, see Figure 1.
6.1. Lax pairs on symmetric spaces. Generic case
We start with the realization of Cartan involution which are convenient for Lax pairs. Here we assume that the reader is familiar with the theory of simple Lie algebras and their root systems [67,87]. We already mentioned above that the Cartan involution is determined by the Cartan subalgebra element J which provides the leading terms of the operators in the Lax pair. Below we will assume that L is quadratic in ; then M must be a quartic polynomial of :
This Lax pair has the form of (5.3), only now . Therefore for . Then the compatibility condition takes the form:
and equate to zero the terms with the different powers of . It is easy to check that the terms at , and vanish identically. The rest of the terms are given by:
where we used the traditional . The first two of the above equations allow us to express and in terms of Q and .
Here we assume that functions , , belong to the simple Lie algebra ; J is a constant elements in the Cartan subalgebra . The classification of all symmetric spaces, and therefore, of all possible Cartan involutions has been done by Cartan more than a century ago and can be found in many monographs, see e.g. [67]. The Cartan involution introduces a -grading in , i.e.
Let us assume that and . Then:
In particular this means that the Cartan involution splits the roots system into two subsets, which are determined by the choice of J:
In particular this means, that the generic elements and take the form:
The Cartan involution can be realized as a similarity transformation by the Cartan subgroup element which acts on X and Y above by:
Therefore the imposed reduction can be written as:
Note that this is in agreement with the chosen parametrization (5.1).
Remark 8.
Note that the mapping maps and ; as a result its preserves the analyticity regions of both and . The mapping maps and , i.e. it maps the analyticity region of into the analyticity region of .
6.2. NLEE on symmetric spaces: A.III
Here we will consider multicomponent derivative NLS-type (DMNLS) equations [81,123] and multicomponent GI (MGI) equations [42,58]. Note that the RHP for the DMNLS equations is not canonically normalized which requires slight modifications in applying the dressing method. However DMNLS and MGI equations are gauge equivalent.
For L linear in we get the well known multicomponent NLS equations, see [21]. For the symmetric spaces of the types A.III, C.I and D.III the Cartan involution is fixed up by the choice of the matrix J which takes the form [67]:
The coefficients of the Lax operators are:
The first of the equations in (6.15) is satisfied if
Comparing this expression for with the one from (6.23) we find that
Inserting into the expression for in (6.23) we find:
The corresponding MNLS is obtained from the third of the equations (6.15). Taking into account that
and
we obtain the MNLS in the form:
If we put the equations obtain more familiar form:
It remains to analyze the last of the equations (6.15). To this end we need:
Then the last of the equations (6.15) become:
It is easy to check that eq. (6.29) directly follows from (6.27).
Up to now in this subsection we treated the matrix as generic rectangular matrix. However below we would like to outline the special case: the vector NLS known also as the Manakov model. Then and the number of vector components1 can be any:
6.3. MNLS equations related to D.III and C.I symmetric spaces
Eq. (6.28) provides the NLEE related to the A.III type symmetric spaces. Similar considerations may be applied to other two classes of symmetric spaces: D.III and C.I. Indeed the block structure of the Lax pair for these two classes of symmetric spaces is the same as the one of (6.23) and J has the form of (6.22) where the unit matrices have equal dimensions N. The substantial difference between these symmetric spaces is in the fact that they are subject of additional reduction. Indeed, for D.III we must require that which means that they must satisfy in addition (see [16]):
Therefore and
For C.I type symmetric spaces we must have which means that
Therefore and
The reasons for such choice of the definitions of the algebras and is that the Cartan subalgebras are represented by diagonal matrices. The explicit form of and are given in [16], see also the Appendix.
For example, the NLEE related to the symmetric spaces C.I and D.III related to and respectively are obtained by inserting into the equation below:
the following matrices for :
In both cases such substitutions into (6.28) can be viewed as special reductions to 6-component MNLS. Of course these MNLS can not be equivalent since they are related to non-isomorphic symmetric spaces. The parametrizations in eq. (6.36) have been obtained using the Cartan-Weyl basis given in Appendix A.
6.4. MNLS related to BD.I-type symmetric spaces
The basic parametrization for BD.I which is isomorphic to has different block matrix form from the one for A.III, namely:
Here the matrices are , while are -component vectors; this fixes up the block-structure of the matrices in this subsection. We also introduce
where
We have used the following notations above:
The potentials are:
Since the first of the equations (6.15) gives:
which in components give:
The second equation in (6.15) is identically satisfied as a consequence of (6.45).
Finally the equations of motion:
Since in addition we put we get [38]:
One can check that the second equation in (6.46) holds identically as a consequence of (6.47).
7. Soliton solutions of the MNLS equations
7.1. Dressing for NLEE on symmetric spaces: A.III case
In this case the dressing factor satisfies two involutions:
then and its inverse have the form
Here the 'polarization' vectors , , and determine the residues of u and . They must satisfy eq. (5.40) which must be valid identically with respect to . Repeating the arguments as in Subsection 5.4 we find the x and t dependence of the polarization vectors:
where , , and are constant polarization vectors. We assume that we know which are related to the regular solutions of the RHP. Typically they correspond to vanishing potentials and ; thus we must have:
We will need also to impose the proper normalization conditions on the polarization vectors so that
Thus we find the following expressions for and in terms of and :
It remains to calculate the potentials. To this end we must consider the limit of eq. (5.40) for , which takes the form:
where we have assumed and . Taking the limit of (7.7) we obtain:
Skipping the details we find:
Example 5
(A.III type symmetric spaces, generic case). Let us specify the form of the naked polarization vectors:
Therefore the scalar products are given by:
As a result:
The corresponding will be given by:
The coefficient is expressed through the matrix elements of by:
Example 6
(A.III type symmetric spaces, VNLS case). Now the naked polarization vectors:
Therefore the scalar products are given by:
Therefore
The corresponding will be given by:
The coefficient is expressed through the matrix elements of by:
The Figure 6 shows that the one soliton solution of (6.28) has two maxima. Another important difference as compare with the scalar case is that the phase of the A.III type soliton is not linear in x.
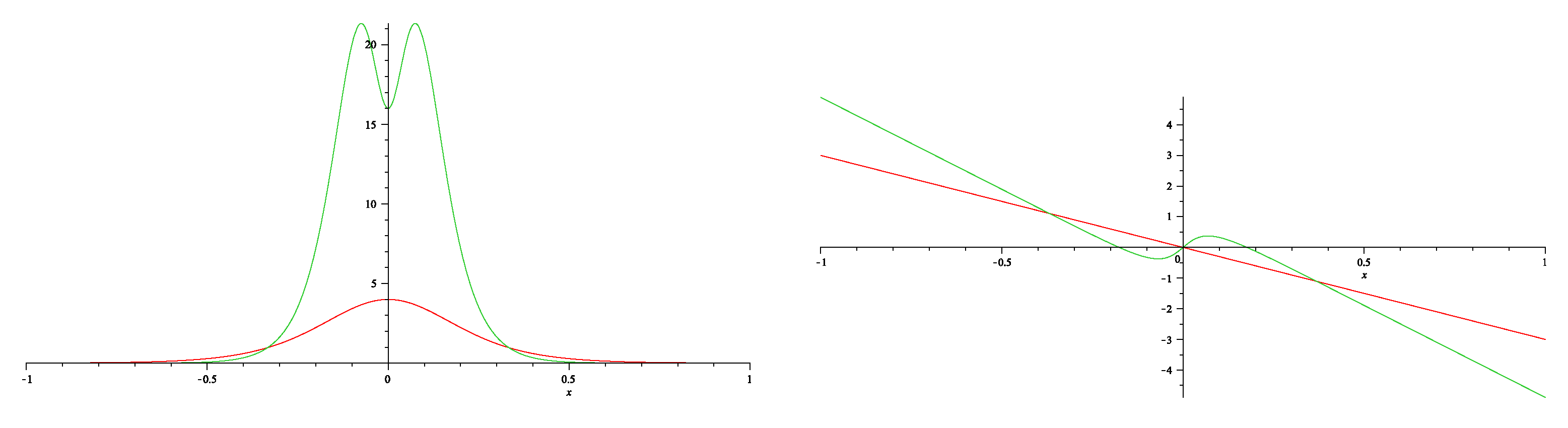
Figure 6.
The one-soliton solution for the A.III type vector NLS (6.28). From eq. (7.18) one finds that all components of are proportional to the same function, whose modulus squared is plotted on the left panel in green. For comparison we have plotted also the modulus squared of the scalar NLS (red). On the right panel we have plotted the phase for both equations: in green is the phase of (6.28), while in red is phase of the scalar NLS. The plots are done for and .
Figure 6.
The one-soliton solution for the A.III type vector NLS (6.28). From eq. (7.18) one finds that all components of are proportional to the same function, whose modulus squared is plotted on the left panel in green. For comparison we have plotted also the modulus squared of the scalar NLS (red). On the right panel we have plotted the phase for both equations: in green is the phase of (6.28), while in red is phase of the scalar NLS. The plots are done for and .
7.2. Dressing for NLEE on symmetric spaces: C.I and D.III cases
In this case the dressing factors are subject to three involutions. Therefore the dressing factor must also satisfy these involutions. They determine the structure of the dressing factors. The first two involutions are the same as in eq. (6.23). The third involution comes from the requirement that the FAS and the dressing factors belong to the corresponding Lie group ( or ), see Appendix A.
The dressing factors that satisfy the above constraints take the form
First we need to ensure that and in (7.20) map a FAS of into a FAS of and vice versa. This will be true if they satisfy the equations:
identically with respect to . But we have chosen fraction linear dependence on , it is easy to guess that eqs. (7.21) will hold true if all the residues in the left hand sides of (7.21) vanish. For example, taking the residue at we get:
Thus it is easy to check, that the left hand sides of eq. (7.22) vanish if:
where , , and are constant polarization vectors. Analogously, using the symmetries we find that all the other residues of eq. (7.21) vanish.
Next we check that and obviously satisfy conditions b) and c). However it is far from obvious that they belong to the corresponding group. Since the expression for is obtained using the group properties of it is enough to check that . Note that the product contains residues of second order. It is easy to see that these residues simplify to:
Remember that these vectors depend on x and t and the conditions (7.24) must be identities. But we also know that these polarization vectors must satisfy (5.42) and (5.45). Therefore we have:
The proof that all other scalar products in (7.24) are x and t independent is done similarly. Thus the conditions (7.24) in fact impose restrictions only on the initial polarization vectors:
The last condition that is imposed on the polarization vectors comes from eq. (5.59) and reads
Assuming that the regular solution of the Lax operator corresponds to vanishing potentials which means that
and using for the eigenvalues and the polarization vectors the parametrization above we obtain
and the notations and normalization conditions on the polarization vectors are the same as in (7.5)
Taking the residues at leads to
which can be written down as the following sets of linear equations:
Here the block matrices and are given by:
where , . This system is solved similarly as eqs. (5.86) and (5.73). Using the fact that we can simplify the result into:
where
Thus we find the following expressions for and in terms of and :
It remains to calculate the potentials. To this end we use the first equation in (7.21) for , assuming and . In this limit the term vanishes and the rest of the equation is linear in . Thus we obtain:
where
After some calculations we get:
The expression for coincides with from eq. (6.23).
Figure 7.
The one-soliton solution for the C.I type NLS (6.28). The plots are done for and . Left panel: – red, – green, – orange; Right panel: – red, – green, – orange. In both cases , and , , , , ,.
Figure 7.
The one-soliton solution for the C.I type NLS (6.28). The plots are done for and . Left panel: – red, – green, – orange; Right panel: – red, – green, – orange. In both cases , and , , , , ,.
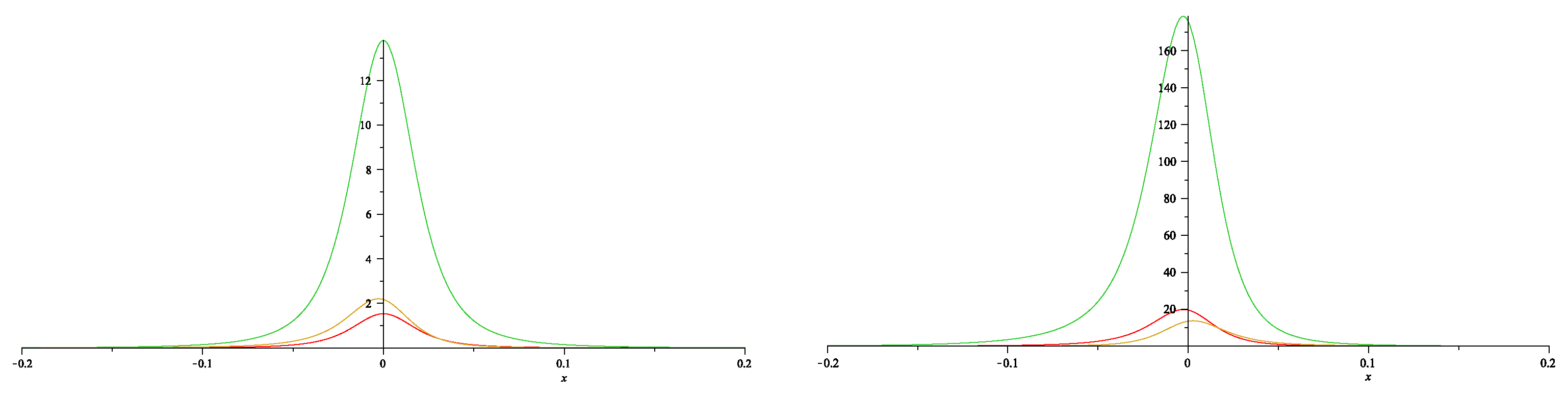
Figure 8.
The one-soliton solution for the D.III type NLS (6.28). The plots are done for and . Left panel: – red, – green, – orange, – blue; Right panel: – red, – green. In both cases , and , , , , ,, , .
Figure 8.
The one-soliton solution for the D.III type NLS (6.28). The plots are done for and . Left panel: – red, – green, – orange, – blue; Right panel: – red, – green. In both cases , and , , , , ,, , .
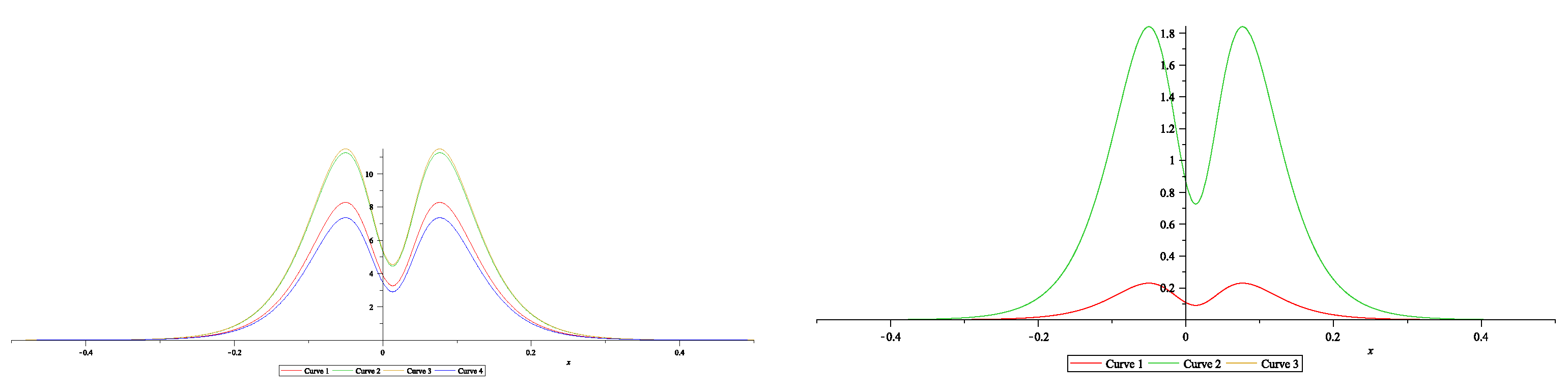
Figure 9.
The same as in Figure 8 but now and .
Figure 9.
The same as in Figure 8 but now and .
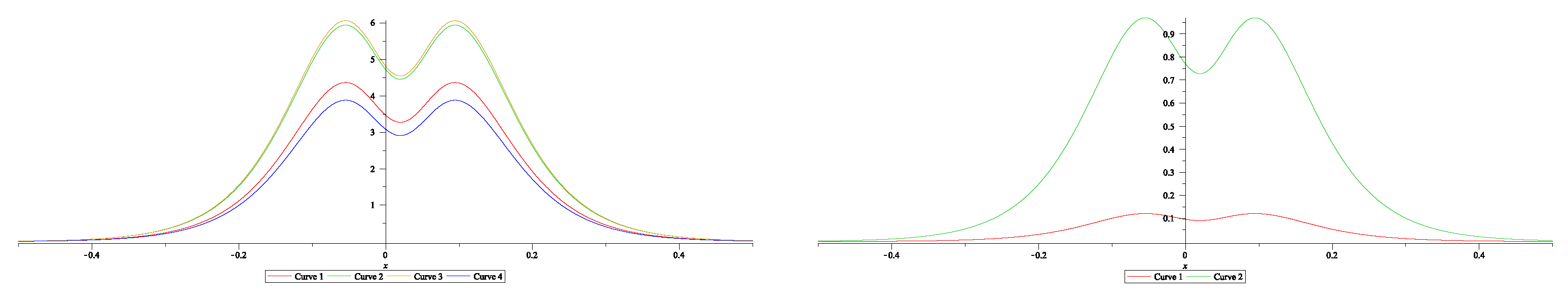
7.3. Dressing for NLEE on symmetric spaces: BD.I cases
The Cartan involution is given by a matrix , with
The dressing factors are like in (7.20)
where the polarization vectors , , and have components. The explicit form of is:
The involutions can then be written as
Note also, that .
The dressing factors subject to three involutions are presented in (7.20). Applying the same technique as above we first derive the constraints on the polarization vectors that annihilate the second order poles in :
7.4. N-soliton solutions and soliton interactions of MNLS equations
As you could see from the above even the derivation of the one-soliton solutions is not very easy. The N-soliton solutions however can be derived using one the following suggestions.
The first to try and repeat the dressing method starting however from the one soliton solution, rather than from the naked one . Thus:
where has the same form as (7.20) but now:
Solving the algebraic equations you can use the same formulae from above, only now the expressions for , , will be more complicated. Thus you will be able to derive the 2-soliton solution for the corresponding MNLS eq.
Another way to derive the N-soliton solutions will be to use a more complicated dressing factor:
Then you will obtain a more complicated linear algebraic system of equations for and in terms of and .
Besides we need the scalar products and the definition of . We assume here that we are considering or algebras and that
8. Multi-soliton solutions
We will outline the dressing method for the N-soliton solutions of MNLS in the case of three involutions.
The dressing factors for N solitons in that case take the form:
where
The N-soliton dressing factor must satisfy eq. (7.21) which must hold identically with respect to . That means that all residues for must vanish. Repeating the analysis in Subsection 7.2 we obtain the analogues of eqs. (7.23):
Next we must ensure that . It is obvious that here we encounter residues of second order. Vanishing or these residues requires set of conditions generalizing eq. (7.24):
for all . Using the fact that the solutions and are elements of the orthogonal or symplectic groups one can check that the constraints (8.4) in fact affect only the 'naked' polarization vectors:
Analyzing the residues of first order and requiring them to vanish we derive a set of linear equations which allow us to find explicit expressions for the 'dressed' polarization vectors and in terms of and . Below we will derive this equations for the simplest nontrivial case: :
and
where
In order to find the 2-soliton solution we need to solve eq. (8.8) and invert the block matrix; then
The explicit calculation of the right hand side of eq. (8.10) will be published elsewhere.
9. The resolvent and spectral properties of Lax operators
In this Section following [32] we briefly address the spectral properties of the Lax operators. We intend to demonstrate that the notion of the resolvent introduced in [32] for the generalized Zakharov-Shabat systems can be naturally extended to the class of quadratic pencils that we have studied above.
Below for simplicity we assume that the function (5.1) which introduces the parametrization of the RHP is a smooth matrix-valued function of x satisfying the following conditions:
- C.1
- possesses smooth derivatives of all orders with respect to x and falls off to zero for faster than any power of x:
- C.2
- is such that the corresponding RHP has finite index. For the class of RHP that we have been dealing with this means that the solution of the RHP must have finite number of simple zeroes and pole singularities.
Remark 9.
Let us assume that the zeroes and the pole singularities of (resp. ) are located at the points (resp. at ). Taking into account the symmetries of the FAS (5.14) we conclude that:
- 1.
- if is a zero or pole of , then there must exist which is also a zero or pole of ;
- 2.
- if is a zero or pole of , then there must exist which is also zero or pole of .
- 3.
- if is a zero or pole of , then there must exist which is a zero or pole of .
Choosing proper enumeration of the zeroes and poles we can arrange them so that , , , , , and , .
The FAS of which are related to the solution of the RHP by allow one to construct the resolvent of the operator L and then to investigate its spectral properties. By resolvent of we understand the integral operator with kernel which satisfies
where is an n-component vector function in with bounded norm, i.e. .
From the general theory of linear operators [5,17] we know that the point in the complex -plane is a regular point if is the kernel of a bounded integral operator. In each connected subset of regular points must be analytic in .
The points which are not regular constitute the spectrum of . Roughly speaking the spectrum of consist of two types of points:
- i) the continuous spectrum of consists of all points for which is an unbounded integral operator;
- ii) the discrete spectrum of consists of all points for which develops pole singularities.
Let us now show how the resolvent can be expressed through the FAS of . Here and below we will limit ourselves with Lax operators L which are quadratic pencils of and have the form (5.3) (i.e. ). Assuming that the eigenvalues of J are different and real we can always order them so that
In Section 2 above we constructed the FAS of such operators. Using them we can write down in the form:
the kernel of the resolvent is given by:
where
where is the number of positive eigenvalues of J, see (9.2). Due to the condition , is fixed up uniquely.
The next theorem establishes that is indeed the kernel of the resolvent of .
Theorem 3.
Let satisfy conditions (C.1) and (C.2) and let be the simple zeroes of the solutions of the RHP. Let and let be defined as in eq. (9.5). Then:
- 1.
- will be FAS of a quadratic pencil of the form (5.11) whose coefficients will be expressed through as in (5.15).
- 2.
- is a kernel of a bounded integral operator for ;
- 3.
- is uniformly bounded function for and provides a kernel of an unbounded integral operator;
- 4.
- satisfy the equation:
Idea of the proof.
□
- is obvious from the fact that are the FAS of (5.11). It is also easy to see that if satisfies conditions (C.1) and (C.2) then and will also satisfy condition C1. In addition obviously will satisfy condition C2 and will have poles and zeroes at the points , see Remark 9.
-
Assume that and consider the asymptotic behavior of for . From equations (5.11) we find thatWe use the fact that has triangular asymptotics for and (see eq. (2.38)). With the choice of (9.5) we check that the right hand side of (9.7) falls off exponentially for and arbitrary choice of y. All other possibilities are treated analogously.
- For the arguments of 2) can not be applied because the exponentials in the right hand side of (9.7) only oscillate. Thus we conclude that for is only a bounded function of x and thus the corresponding operator is an unbounded integral operator.
- The proof of eq. (9.6) follows from the fact that and
If the algebra then and its inverse do not have common poles. In this case condition C2 is valid also for . However this is not true for the orthogonal or symplectic algebras; in this case may have poles of second order, which require additional care.
Now we can derive the completeness relation for the eigenfunctions of the Lax operator L by applying the contour integration method (see e.g. [2,46,47]) to the integral:
where the contours are shown on the Figure 10. The idea is to calculate first using the Cauchy residue theorem. Taking into account that the contours and are positively oriented, while and are negatively oriented we obtain:
We can also evaluate integrating along the contours. The integration along the real and purely imaginary axis provides the contribution coming from the continuous spectrum of L. The integration along the infinite arcs of the contours can be evaluated explicitly. To this end we use the fact that are canonically normalized we find:
Adding these two answers and using the definitions of we find
Equating the two answers for we find the following completeness relations for the FAS of L:
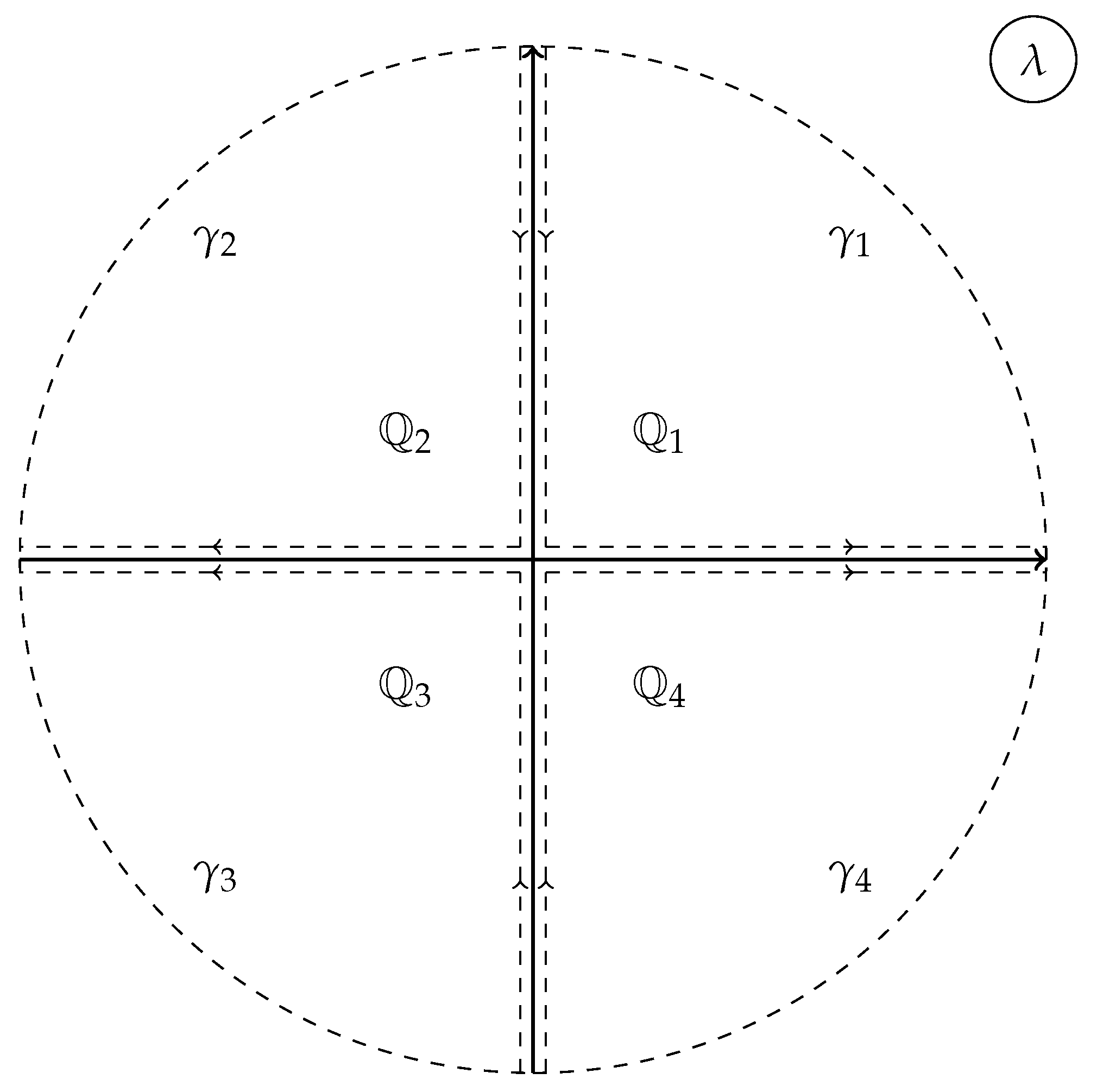 This relation (9.14) allows one to expand any vector-function over the eigenfunctions of the system (5.11). If we multiply (9.14) on the right by and integrate over y we get:
where the expansion coefficients are of the form:
This relation (9.14) allows one to expand any vector-function over the eigenfunctions of the system (5.11). If we multiply (9.14) on the right by and integrate over y we get:
where the expansion coefficients are of the form:
Figure 10.
The contours of the related Riemann-Hilbert problem .

Corollary 3.
The discrete spectrum of the Lax operator (5.11) consists of the poles of the resolvent which are described in Remark 9.
Remark 10.
Here we used also the fact that all eigenvalues of J are non-vanishing. In the case when one (or several) of them vanishes we can prove completeness of the eigenfunctions only on the image of which is a subspace of .
Remark 11.
The authors are aware that these type of derivations need additional arguments to be made rigorous. One of the real difficulties is to find explicit conditions on the potentials and that are equivalent to the condition (C.2). Nevertheless there are situations (e.g., the reflectionless potentials) when all these conditions are fulfilled and all eigenfunctions of can be explicitly calculated. Another advantage of this approach is the possibility to apply it to Lax operators with more general dependence on λ, e.g. polynomial and rational.
10. Discussion and conclusions
Our idea is to remind some of the old papers which were milestones in the past, but for various reasons tend to be forgotten. Another motivation to do this is our intention to generalize these results for quadratic pencils and pencils of higher degrees.
Of course. many of the results we mention below were first introduced for the GZSh system. One of the important results is the resolvent for the Lax operator L [29,32,33] expressed in terms of the FAS. Combined with the contour integration method it allows one to to construct the spectral decompositions of L. They also allow one to prove that the poles and zeroes of FAS provide the discrete eigenvalues of L. Rigorous proofs would hardly be possible with these methods, but their importance is in the fact that can be applied to wide class of non-self-adjoint Lax operators.
In the Introduction we already listed a number of results about the interpretation of the ISM as GFT and ISM for the GZaSha systems. Our comment on it is that this idea can be generalized also for the quadratic pencils considered as Lax operators above. We intend to continue the idea in our next publications. Of course it will have its versions for the homogeneous as well as for the symmetric spaces.
The initial ideas that we have extended above for quadratic pencils have been developed before by other influential scientists, see some of theirs reviews and monographs [18,32,33,63,70,71,91,101,104,130]. It is important to note that these ideas are applicable also to discrete evolution equations as Ablowitz-Ladik system [3,43].
Another important approach to integrable NLEE has been developed by Shabat, Mikhailov, Yamilov, Svinolupov et al, see [98,99,101,138]. It allows one to derive systems of equations that possess higher symmetries, or higher integrals of motion. Lately this method has been used by Zhao [138], who covered all integrable systems in two independent functions. Some of these equations were shown to possess Lax representations related to the twisted Kac-Moody algebras [54].
Special attention must be paid to the NLEE with deep Mikhailov reduction groups, like and . Typically by h we denote the Coxeter number of the corresponding simple Lie algebra. Here we include the families of KdV and MKdV eqs., as well as 2-dimensional Toda field theories [4,49,50,51,55,79,80,97,102,103] as well as some Camassa-Holm type eqs. [11,44,66,68,69,75,76].
Kulish-Sklyanin system, or in other words the 3-component NLS related to the BD.I symmetric space has important applications to the spin-1 Bose-Einstein condensate, see [23,24,34,38,41,60,61,72,73,84,85,105,113,114,115,116,117,124,116]. Using the dressing method in [35,41] we calculated the limit of the dressing factor for . This allowed us to describe the soliton interactions, i.e. to calculate the center-of-mass and the phase shifts in the soliton interactions.
In our final remarks we mention the generalizations to dimensions [48,62,83,93], the MNLS related to spectral curves [6,11,77,109,110,111,112] and the hierarchies of Hamiltonian structures. It is known that one can relate Poisson brackets on the quadratic pencils which, along with the integrals of motion allow one to interprete the NLEE in the hierarchy as Hamiltonian equations of motion. Such Poisson brackets have been introduced for the polynomial pencils by Kulish and Reyman [86]. Of course they allow generalization to any semi-simple Lie algebra. We already mentioned that for the generalized Zakharov-Shabat systems this has been already done. In fact the spectral theory of the recursion operators has been constructed which generate all NLEE along with its Hamilton formulation. For the quadratic pencils the recursion operators have not yet been constructed; we hope that this problem will be solved soon.
Acknowledgments
The authors are grateful to professors R. I. Ivanov and G. G. Grahovski for careful reading of the manuscript and for many useful suggestions. Financial support of the Bulgarian National Science Foundation, contract KP-06N42-2 is acknowledged.
Appendix A. Root systems of simple Lie algebras
This is assumed to be well known material which we display without proofs and in a manner suitable for pedestrians in Lie algebras; for proofs and more details see [8,67]. The fundamental ideas of Cartan and Weil are based on:
- The Cartan subalgebras of all simple Lie algebras can be represented by diagonal matrices;
- There is an one-to-one mapping between the elements of and the vectors in r-dimensional Euclidean space ;
- The Weil generators are defined as eigenvectors of all the elements of , i.e.where . Here is the vector corresponding to H, and is a root of the algebra belonging to its system of roots .
Skipping the details we will describe the roots systems for all classical series , , and of simple Lie algebras.
- Root systems
- Dynkin diagrams
- Cartan-Weyl basis
- Automorphisms of finite order
Basic properties of the root systems.
- If then is also a root, .
- Each roots system is split into positive and negative roots:
- In each root systems one can introduce a basis, known as system of simple roots. By definition , are simple roots if: i) they are linearly independent and form a basis in ; ii) they are positive roots such that ;
- Each positive root can be expressed as sum of simple roots where all are integers;
- There is a maximal (resp. minimal) root (resp ) such that (resp. ) is not a root;
-
Symmetry properties of and Weyl group. Introduce the Weyl reflections by:The Weyl reflections form a finite group, which preserves , i.e. .
Appendix A.1. The root system of A r ≃sl(r+1) algebras
The algebras can be represented by matrices whose trace is equal to 0. Their Cartan subalgebras are provided by diagonal matrices whose trace vanishes . Therefore the vector dual to H belongs to the dimensional Euclidean space which is orthogonal to the vector , where form the orthonormal basis in . The Weil generators are provided by the matrices which have only one non-vanishing entry at position equal to 1, i.e.:
It is easy to check that the commutation relations between the Cartan elements H and the Weyl generators can be written down as:
It coincides with (A.1) where the root . Thus we find that the root system of consists of the vectors:
Obviously each root is a vector orthogonal to . We will need also to split the root system into positive and negative roots:
i.e. to the positive (resp. negative) roots there correspond upper triangular (resp., lower) triangular matrices. Note that all roots are orthogonal to the vector , so they span r-dimensional subspace of .
The simple roots of are provided by , . The Dynkin diagram of is:

The basis of the Cartan subalgebra consists of , . The Weyl generators were given above in (A.2).
Remark 12.
For the orthogonal and symplectic Lie algebras we will use slightly different but equivalent definition. Typically the orthogonal algebras are represented as the algebras of skew-symmetric matrices, i.e.
In what follows we will use slightly different but equivalent definition, namely:
where the matrix is given by:
Note that . For the symplectic algebras we have:
where
Now . The advantage of these definitions is, that now the Cartan subalgebras of both and are represented by diagonal matrices.
Appendix A.2. The root system of B r ≃so(2r+1) algebras
Using Remark 12 we find that with the new definition of the antisymmetry is with respect to the second diagonal. The Cartan subalgebra elements are given by the following matrices:
The Cartan-Weyl basis in the typical representation basis is given by:
where .
The commutation relations (A.1) show that the root system of is provided by:
The simple roots are given by:
The Dynkin diagram is:

Appendix A.3. The root system of C r ≃sp(2r) algebras
The Cartan subalgebra elements of are given by the following matrices:
The Cartan-Weyl basis in the typical representation basis is given by:
where .
The commutation relations (A.1) show that the root system of is provided by:
The simple roots are given by:
The Dynkin diagram is:

Appendix A.4. The root system of D r ≃so(2r) algebras
Using Remark 12 we find that with the new definition of the antisymmetry is with respect to the second diagonal. The Cartan subalgebra elements are given by the following matrices:
The Cartan-Weyl basis in the typical representation basis is given by:
where .
The commutation relations (A.1) show that the root system of is provided by:
The simple roots are given by:
The Dynkin diagram is:
Appendix B. Gauss decompositions
The Gauss decompositions have natural group-theoretical interpretation and can be generalized to any semi-simple Lie algebra:
i.e. , and are the factors in the Gauss decomposition of . It is well known that if given group element allows Gauss decompositions then its factors are uniquely determined. Below we write down the explicit expressions for the matrix elements of , , through the matrix elements of :
where
is the minor of order k of formed by the rows , , ..., and the columns , , ..., ; by we mean that p is missing.
From the formulae above we arrive to the following
Corollary 4.
In order that the group element allows the first (resp. the second) Gauss decomposition (B.1) is necessary and sufficient that all upper- (resp. lower-) principle minors (resp. ) are not vanishing.
These formulae hold true also if we need to construct the Gauss decomposition of an element of the orthogonal group. Here we just note that if then
where
One can check that if satisfies (B.11) then each of the factors , and also satisfy (B.11) and thus belong to the same group . In addition we have the following interrelations between the principal minors of :
References
- M. A. Ablowitz and P. A. Clarkson. Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, 1991. [CrossRef]
- M. J. Ablowitz, D. J. Kaup, A. C. Newell, and H. Segur. The inverse scattering transform- Fourier analysis for nonlinear problems. Studies in Appl. Math., 53(4):249–315, 1974. [CrossRef]
- M. J. Ablowitz and J. F. Ladik. Nonlinear differential–difference equations and fourier analysis. Journal of Mathematical Physics, 17(6):1011–1018, 1976. [CrossRef]
- M. Adler. On a trace functional for pseudo-differential operators and the symplectic structure of the Korteweg-de Vries equation. Invent. Math, 50:219–248, 1979.
- N. I. Akhiezer and I. M. Glazman. Theory of Linear operators in Hilbert space. Dover Publications, New York, (1961-1963). Translated from Russian.
- Dubrovin B. A. Matrix finite-zone operators. J. Soviet Math., 28(1):20–50, 1985. [CrossRef]
- R. Beals and R. R. Coifman. Scattering and inverse scattering for first order systems. Commun. Pure & Appl. Math., 37:39, 1984. [CrossRef]
- N. Bourbaki. Elements of mathematics. Lie Groups and Lie Algebras.Chapters 4-6. Springer, Berlin, Heidelberg, New York, 2002.
- R.T. Bury. Automorphic Lie Algebras, Corresponding Integrable Systems and Their Soliton Solutions. PhD thesis, University of Leeds, 2010.
- F. Calogero and A. Degasperis. Spectral transform and solitons. i. In Studies in Mathematics and its Applications, volume 13. Elsevier, North Holland, 1982.
- Q.U. Changzheng, Junfeng Song, and Ruoxia Yao. Multi-component integrable systems and invariant curve flows in certain geometries. SIGMA, 9:1–20, 2013. [CrossRef]
- A. Constantin, V. S. Gerdjikov, and R. I. Ivanov. Generalized fourier transform for the camassa-holm equation. Inverse Problems, 23:1565–1597, 2007.
- H. Coxeter and W Moser. Generators and relations for discrete groups (3ed). Springer, 1972.
- H. H. Dai and E. G. Fan. Variable separation and algebro-geometric solutions of the Gerdjikov-Ivanov equation. Chaos, Solitons, Fractals, 22:93–101, 2004. [CrossRef]
- L. A. Dickey. Soliton Equations and Hamiltonian Systems. World scientific, 2003.
- V. G. Drinfel’d and V. V. Sokolov. Lie algebras and equations of korteweg-de vries type. Sov. J. Math., 30:1975–2036, 1985. [CrossRef]
- N. Dunford and J. T. Schwartz. Spectral theory. Self-adjoint operators in Hilbert space, volume 2 of Linear operators. Interscience Publishers, Inc., NY, 1963.
- L. D. Faddeev and L. A. Takhtadjan. Hamiltonian Methods in the Theory of Solitons. Springer Verlag, Berlin, 1987.
- E.G. Fan. Darboux transformation and solion-like solutions for the gerdjikov-ivanov equation. J. Phys. A, 33:6925–6933, 2000.
- E.G. Fan. A family of completely integrable multi-hamiltonian systems explicitly related to some celebrated equations. J. Math. Phys., 42:4327–4344, 2001. [CrossRef]
- A. P. Fordy and P. P. Kulish. Nonlinear schrödinger equations and simple lie algebras. Commun. Math. Phys., 89:427–443, 1983. [CrossRef]
- A. V. Mikhailov G. Berkeley and P. Xenitidis. Darboux transformations with tetrahedral reduction group and related integrable systems. Journal of Mathematical Physics, 57:092701, 2016.
- S. Gaiarin, A. M. Perego, E. P. da Silva, F. Da Ros, and D. Zibar. Experimental demonstration of dual polarization nonlinear frequency division multiplexed optical transmission system. In 2017 European Conference on Optical Communication (ECOC), pages 1–3, 2017. [CrossRef]
- S. Gaiarin, A. M. Perego, E. P. da Silva, F. Da Ros, and D. Zibar. Dual-polarization nonlinear fourier transform-based optical communication system. Optica, 5(3):263–270, Mar 2018. [CrossRef]
- I. M. Gel’fand and L. A. Dikii. Fractional powers of operators and hamiltonian systems. Funct. Anal. Appl., 10(4):259–273, 1976. [CrossRef]
- I. M. Gel’fand and L. A. Dikii. The resolvent and hamiltonian systems. Funct. Anal. Appl., 11(2):93–105, 1977.
- I. M. Gel’fand and L. A. Dikii. The calculus of jets and nonlinear hamiltonian systems. Funct. Anal. Appl., 12(2):81–94, 1978. [CrossRef]
- I. M. Gel’fand and L. A. Dikii. Integrable nonlinear equations and the liouville theorem. Funct. Anal. Appl., 13(1):6–15, 1979. [CrossRef]
- V. S. Gerdjikov. On the spectral theory of the integro-differential operator λ, generating nonlinear evolution equations. Lett. Math. Phys., 6(6):315–324, 1982.
- V. S. Gerdjikov. Generalised fourier transforms for the soliton equations. gauge covariant formulation. Inverse Problems, 2(1):51–74, 1986. [CrossRef]
- V. S. Gerdjikov. zn–reductions and new integrable versions of derivative nonlinear schrödinger equations. In M. Lakshmanan A. P. Fordy, A. Degasperis, editor, Nonlinear evolution equations: integrability and spectral methods, pages 367–379. Manchester University Press, 1991.
- V. S. Gerdjikov. Algebraic and analytic aspects of n-wave type equations. Contemporary Mathematics, 301:35–68, 2002.
- V. S. Gerdjikov. Basic aspects of soliton theory. In A. C. Hirshfeld. I. M. Mladenov, editor, Geometry, Integrability and Quantization, pages 78–125. Sortex, Sofia, 2005.
- V. S. Gerdjikov. Bose-einstein condensates and spectral properties of multicomponent nonlinear schrödinger equations. Discrete and Continuous Dynamical Systems, 4(5):1181–1197, 2011. [CrossRef]
- V. S. Gerdjikov. On soliton interactions of vector nonlinear schrödinger equations. In AMITANS conference, AIP 1404, pages 57–67, 2011.
- V. S. Gerdjikov. Riemann-hilbert problems with canonical normalization and families of commuting operators. Pliska Stud. Math. Bulgar, 21:201–216, 2012.
- V. S. Gerdjikov. Derivative nonlinear schrödinger equations with Zn and Dn–reductions. Romanian Journal of Physics, 58:573–582, 2013.
- V. S. Gerdjikov. Kulish-sklyanin type models: integrability and reductions. Theoretical and Mathematical Physics, 192(2):1097–1114, 2017. [CrossRef]
- V. S. Gerdjikov. On nonlocal models of kulish-sklyanin type and generalized fourier transforms. In K. Georgiev, M. Todorov, and I. Georgiev, editors, Advanced Computing in Industrial Mathematics. Studies in Computational Intelligence, volume 681, pages 37–52. springer, 2017.
- V. S. Gerdjikov and G.G. Grahovski. Multi-component nls models on symmetric spaces: Spectral properties versus representations theory. SIGMA, 6:44–73, 2010. [CrossRef]
- V. S. Gerdjikov and G.G. Grahovski. Two soliton interactions of bd.i multicomponent nls equations and their gauge equivalent. AIP Conf. Proc., 1301:561–572, 2010. [CrossRef]
- V. S. Gerdjikov and M. I. Ivanov. The quadratic bundle of general form and the nonlinear evolution equations. i. expansions over the “squared” solutions are generalized fourier transforms. Bulgarian J. Phys, 10:13–26, 1983.
- V. S. Gerdjikov, M. I. Ivanov, and P. P. Kulish. Expansions over the "squared” solutions and difference evolution equations. J. Math. Phys., 25(1):25–34, 1984.
- V. S. Gerdjikov and R. I. Ivanov. Multicomponent fokas-lenells equations on hermitian symmetric spaces. Nonlinearity, 34:939, 2021. [CrossRef]
- V. S. Gerdjikov and E. Kh. Khristov. On the evolution equations solvable with the inverse scattering problem. i. the spectral theory. Bulgarian J. Phys., 7(1):28–41, 1979.
- V. S. Gerdjikov and P. P. Kulish. Complete integrable hamiltonian systems related to the non–self–adjoint dirac operator. Bulgarian J. Phys., 5(4):337–349, 1978.
- V. S. Gerdjikov and P. P. Kulish. The generating operator for the n×n linear system. Physica D, 3D(3):549–564, 1981.
- V. S. Gerdjikov, Nianhua Li, V. B. Matveev, and A. O. Smirnov. On soliton solutions and soliton interactions of kulish-sklyanin and hirota-ohta systems. Theoretical and Mathematical Physics, 213(1):1331–1347, 2022. [CrossRef]
- V. S. Gerdjikov, D. M. Mladenov, A. A. Stefanov, and S. K. Varbev. Mkdv-type of equations related to b2(1) and a4(2). In Mihaela Kouteva-Guentcheva Boyka Aneva, editor, Nonlinear Mathematical Physics and Natural Hazards. Springer Proceedings in Physics 163, pages 59–69. Springer, 2015.
- V. S. Gerdjikov, D. M. Mladenov, A. A. Stefanov, and S. K. Varbev. On mkdv equations related to the affine kac-moody algebra a5(2). J. Geom. Sym. Phys, 39:17–31, 2015. [CrossRef]
- V. S. Gerdjikov, D. M. Mladenov, A. A. Stefanov, and S. K. Varbev. Soliton equations related to the affine kac-moody algebra d4(1). Eur. Phys. J. Plus, 130:106–123, 2015. [CrossRef]
- V. S. Gerdjikov and A. A. Stefanov. New types of two component nls-type equations. Pliska Studia Mathematica, 26:53–66, 2016.
- V. S. Gerdjikov and A. A. Stefanov. On an example of derivative nonlinear schrödinger equation with D2 reduction. Pliska Stud. Math., 30:99–108, 2019.
- V. S. Gerdjikov, A. A. Stefanov, I. D. Iliev, G. P. Boyadjiev, A. O. Smirnov, V. B. Matveev, and M. V. Pavlov. Recursion operators and the hierarchies of mkdv equations related to d4(1), d4(2) and d4(3) kac-moody algebras. Theoretical and Mathematical Physics, 204(3):1110–1129, 2020.
- V. S. Gerdjikov and A. B. Yanovski. On soliton equations with Zh and Dh reductions: conservation laws and generating operators. J. Geom. Symmetry Phys, 31:57–92, 2013.
- V. S. Gerdjikov and A. B. Yanovski. Riemann-hilbert problems, families of commuting operators and soliton equations. Journal of Physics: Conference Series, 482:012017, 2014. [CrossRef]
- V. S. Gerdjikov and A. B. Yanovski. Cbc systems with mikhailov reductions by coxeter automorphism. i. spectral theory of the recursion operators. Studies in Applied Mathematics, 134:145–180, 2015. [CrossRef]
- V.S. Gerdjikov and M.I. Ivanov. The quadratic bundle of general form and the nonlinear evolution equations. ii. hierarchies of hamiltonian structures. Bulgarian J. Phys, 10:130–143, 1983.
- V.S. Gerdjikov and E.Kh. Khristov. On the evolution equations solvable with the inverse scattering problem. ii. hamiltonian structures and backlund transformations. Bulgarian J. Phys., 7(2):119–133, 1979.
- V.S. Gerdjikov, N.A. Kostov, and T.I. Valchev. Bose-einstein condensates with f=1 and f=2. reductions and soliton interactions of multi-component nls models. In Solomon M. Saltiel, Alexander A. Dreischuh, and Ivan P. Christov, editors, Proceedings of SPIE, volume 7501. SPIE, 2009.
- V.S. Gerdjikov, N.A. Kostov, and T.I. Valchev. Solutions of multi-component nls models and spinor bose-einstein condensates. Physica D, 238:1306–1310, 2009. [CrossRef]
- V.S. Gerdjikov, A.O. Smirnov, and V.B. Matveev. From generalized fourier transforms to spectral curves for the manakov hierarchy. i. generalized fourier transforms. Eur. Phys. J. Plus, 135(8):659, 2020.
- V.S. Gerdjikov, G. Vilasi, and A. B. Yanovski. Integrable Hamiltonian Hierarchies. Spectral and Geometric Methods, volume 748 of Lecture Notes in Physics. Springer Verlag, Berlin, Heidelberg, New York, 2008.
- V.S. Gerdjikov and A.B. Yanovski. Completeness of the eigenfunctions for the caudrey–beals–coifman system. J. Math. Phys., 35(7):3687–3725, 1994.
- J.V. Goossens, M. Yousefi, Y. Jaouën, and H. Haffermann. Polarization-division multiplexing based on the nonlinear Fourier transform. Optic Express, 25(22):437–462, 2017.
- J. Haberlin and T. Lyons. Solitons of shallow-water models from energy-dependent spectral problems. Eur. Phys. J. Plus, 133:16, 2018. [CrossRef]
- S. Helgasson. Differential geometry, Lie groups and symmetric spaces, volume 34 of Graduate Studies in Mathematics. AMS, Providence, Rhode Island, 2012.
- D. Holm and R. Ivanov. Smooth and peaked solitons of the ch equation. J. Phys. A: Math. Theor, 43:434003–434003–, 2010.
- D. Holm and R. Ivanov. Two-component ch system: Inverse scattering, peakons and geometry. Inverse Problems, 27:045013–045032, 2011. [CrossRef]
- D. D. Holm. Geometric Mechanics Part I: Dynamics and Symmetry. Imperial College Press, London, 2011.
- D. D. Holm. Geometric Mechanics Part II: Rotating, Translating and Rolling. Imperial College Press, London, 2011.
- J. Ieda, T. Miyakawa, and M. Wadati. Exact analysis of soliton dynamics in spinor bose-einstein condensates. Phys. Rev Lett., 93:194102, 2004. [CrossRef]
- J. Ieda, T. Miyakawa, and M. Wadati. Matter-wave solitons in an f=1 spinor bose-einstein condensate. J. Phys. Soc. Jpn, 73:2996, 2004.
- R. Ivanov. On the dressing method for the generalised zakharov-shabat system. Nuclear Physics B, 694:509–524, 2004. [CrossRef]
- R. Ivanov and T. Lyons. Integrable models for shallow water with energy dependent spectral problems. Journal of Nonlinear Mathematical Physics, 19:1240008–12400025, 2012. [CrossRef]
- R. I. Ivanov. Nls-type equations from quadratic pencil of lax operators: Negative flows. Chaos, Solitons & Fractals, 161:112299, 2022. [CrossRef]
- V. Z. Enol’skii J. C. Eilbeck and N. A. Kostov. Quasiperiodic and periodic solutions for vector nonlinear schrödinger equations. J. Math. Phys., 41(12):8236, 2000.
- D. J. Kaup. Closure of the squared zakharov–shabat eigenstates. J. Math. Annal. Appl., 54(3):849–864, 1976. [CrossRef]
- D. J. Kaup. The three-wave interaction - a nondispersive phenomenon. Stud. Appl. Math, 55:9–44, 1976. [CrossRef]
- D. J. Kaup. On the inverse scattering problem for cubic eigenvalue problems of the class ψxxx+6qψx+6rψ=λψ. Stud. Appl. Math, 62:189–216, 1980.
- D. J. Kaup and A. C. Newell. An exact solution for a derivative nonlinear schr6dinger equation. J. Math. Phys., 19(4):798–801, 1978.
- V. Knibbeler, S. Lombardo, and J. A. Sanders. Higher-dimensional automorphic lie algebras. Found. Comput. Math, 17:987–1035, 2017. [CrossRef]
- B.G. Konopelchenko. Solitons in Multidimensions. Inverse Spectral Transform Method. World Scientific, Singapore, 1993. [CrossRef]
- N. A. Kostov, V. A. Atanasov, V. S. Gerdjikov, and G. G. Grahovski. On the soliton solutions of the spinor bose-einstein condensate. In Peter A. Atanasov, Tanja N. Dreischuh, Sanka V. Gateva, and Lubomir M. Kovachev, editors, Proceedings of SPIE 6604, 2007.
- P. P. Kulish and E.K. Sklyanin. O(N)-invariant nonlinear Schrodinger equation – A new completely integrable system. Phys. Lett. A, 84(7):349–352, 1981. [CrossRef]
- P.P. Kulish and A.G. Reiman. Hamiltonian structure of polynomial bundles. Journal of Soviet Mathematics, 28(4):505–513, 1985. [CrossRef]
- A. N. Leznov and M. V. Saveliev. Two-dimensional nonlinear equations of the string type and their complete integration. Theoret. and Math. Phys., 54(3):323–337, 1983.
- S. Lombardo and A. V. Mikhailov. Reductions of integrable equations: Dihedral group. J. Phys. A, 37:7727–7742, 2004. [CrossRef]
- S. Lombardo and A. V. Mikhailov. Reduction groups and automorphic lie algebras. Communication in Mathematical Physics, 258:179–202, 2005. [CrossRef]
- Jinghua Luo and Engui Fan. ∂¯-dressing method for the coupled gerdjikov?ivanov equation. Applied Mathematics Letters, 110:106589, 2020.
- B. Prinari M. J. Ablowitz and A. D. Trubach. Discrete and Continuous Nonlinear Schrödinger Systems. London Mathematical Society Lecture Note Series. Cambridge University press, 2004.
- S. V. Manakov. On the theory of two-dimensional stationary self-focusing of electromagnetic waves. Sov. Phys. JETP, 38:248, 1974.
- S. V. Manakov and V. E. Zakharov. Soliton theory. In I. M. Khalatnikov, editor, Sov.Sci.Rev.A, volume 1, pages 133–190, London, 1979.
- V.B. Matveev and A.O. Smirnov. AKNS hierarchy, MRW solutions, Pn breathers, and beyond. J. Math. Phys., 59(9):091419, 2018.
- A. V. Mikhailov. Reductions in integrable systems. the reduction group. JETP Lett., 32(2):187–192, 1980. [CrossRef]
- A. V. Mikhailov. The reduction problem and the inverse scattering problem. Physica D, 3D:73–117, 1981. [CrossRef]
- A. V. Mikhailov, M. A. Olshanetsky, and A. M. Perelomov. Two-dimensional generalized toda lattice. Comm. Math. Phys, 79:473–488, 1981. [CrossRef]
- A. V. Mikhailov, A. B. Shabat, and R. I. Yamilov. The symmetry approach to the classification of non-linear equations. complete lists of integrable systems. Russian Math. Surveys, 42:3–53, 1987. [CrossRef]
- A. V. Mikhailov, A. B. Shabat, and R. I. Yamilov. Extension of the module of invertible transformations. classification of integrable systems. Commun. Math. Phys, 115:1–19, 1988. [CrossRef]
- A. V. Mikhailov and V. E. Zakharov. On the integrability of classical spinor models in two-dimensional space–time. Commun. Math. Phys, 74:21–40, 1980. [CrossRef]
- A.V. Mikhailov, A.B. Shabat, and V.V. Sokolov. The symmetry approach to classification of integrable equations. In V.E. Zakharov, editor, What Is Integrability? Springer Series in Nonlinear Dynamics, pages 115–184. Springer, Berlin, 1991.
- R. Constantinescu N. C. Babalic and V. Gerdjikov. On the solutions of a family of tzitzeica equations. J. Geom. Symm. Physics, 37:1–24, 2015.
- R. Constantinescu N. C. Babalic and V. S. Gerdjikov. On tzitzeica equation and spectral properties of related lax operators. Balkan Journal of Geometry and Its Applications, 19:11–22, 2014.
- S. Novikov, S. Manakov, L. Pitaevskii, and V. Zakharov. Theory of Solitons: The Inverse Scattering Method. Plenum, Consultants Bureau, New York, 1984. [CrossRef]
- T. Ohmi and K. Machida. Bose-einstein condensation with internal degrees of freedom in alkali atom gases. J. Phys. Soc. Jpn, 67:1822, 1998.
- A. B. Shabat. A one-dimensional scattering theory. i. Differ. Uravn., 8:164–178, 1972. [CrossRef]
- A. B. Shabat. The inverse scattering problem for a system of differential equations. Funkts. Anal. Prilozhen, 9:75–78, 1975.
- A. O. Smirnov, V. S. Gerdjikov, and V. B. Matveev. From generalized fourier transforms to spectral curves for the manakov hierarchy. ii. spectral curves for the manakov hierarchy. Eur. Phys. J. Plus, 135(7):561, 2020. [CrossRef]
- A.O. Smirnov. Spectral curves for the derivative nonlinear Schrodinger equations. Symmetry, 13(7):1203, 2021. [CrossRef]
- A.O. Smirnov, E.A. Frolov, and V.S. Gerdjikov. Spectral curves for the multi-phase solutions of manakov system. In IOP Conf Ser: Mater. Sci. Eng., volume 862, page 052041. IOP, 2020. [CrossRef]
- A.O. Smirnov, V.S. Gerdjikov, and E.E. Aman. The kulish-sklyanin type hierarchy and spectral curves. In IOP Conf. Ser.: Mater. Sci. Eng. 1047, page 012114, 2021. [CrossRef]
- A.O. Smirnov and A.S. Kolesnikov. Dubrovin’s method and ablowitz-kaup-newell-segur hierarchy. In IOP Conf. Ser.: Mat. Sci. Eng. 1181, page 012028, 2021.
- A. Streche-Pauna, A. Florian, and V. S. Gerdjikov. On generalized kulish-sklyanin models. Physics AUC, 30(2):175–195, 2020.
- M. Uchiyama, J. Ieda, and M. Wadati. Dark solitons in f=1 spinor bose–einstein condensate. J. Phys. Soc. Jpn, 75:064002, 2006.
- M. Uchiyama, J. Ieda, and M. Wadati. Multicomponent bright solitons in f=2 spinor bose-einstein condensates. J. Phys. Soc. Japan, 76(7):74005, 2007. [CrossRef]
- M. Ueda and M. Koashi. Theory of spin-2 bose-einstein condensates: Spin correlations, magnetic response, and excitation spectra. Phys. Rev. A, 65:063602, 2002. [CrossRef]
- G. G. Grahovski V. A. Atanasov, V. S. Gerdjikov and N. A. Kostov. Fordy-kulish models and spinor bose-einstein condensates. J. Nonlinear Math. Phys., 15(3):291–298, 2008.
- R. Ivanov V. Gerdjikov and G. Grahovski. On integrable wave interactions and lax pairs on symmetric spaces. Wave Motion, 71:53–70, 2017.
- R. Ivanov V. Gerdjikov and A. Stefanov. Riemann-hilbert problem, integrability and reductions. Journal of Geometric Mechanics, 11:167–185, 2019.
- G. G. Grahovski V. S. Gerdjikov, A. V. Mikhailov, and T. I. Valchev. On soliton interactions for the hierarchy of a generalised heisenberg ferromagnetic model on su(3)/s(u(1)× u(2)) symmetric space. Journal of Geometry and Symmetry in Physics, 25:23–55, 2012.
- M. I. Ivanov V. S. Gerdzhikov and P. P. Kulish. Quadratic bundle and nonlinear equations. Theoretical and Mathematical Physics, 44(3):784–795, 1980.
- T. I. Valchev. On certain reductions of integrable equations on symmetric spaces. AIP Conference Proceedings, 1340:154–164, 2011. [CrossRef]
- T. I. Valchev. Dressing method and quadratic bundles related to symmetric spaces. vanishing boundary conditions. Journal of Mathematical Physics, 57:021508, 2016.
- N.A. Kostov V.S. Gerdjikov and T.I. Valchev. Solutions of multi-component NLS models and Spinor Bose-Einstein condensates. Physica D, 238:1306–1310, 2009.
- M. Wadati. The exact solution of the modified Korteweg de Vries equation. J. Phys. Soc. Japan, 1972. [CrossRef]
- O.H. Warren and J.N. Elgin. The vector nonlinear Schrödinger hierarchy. Physica D, 228:166–171, 2007.
- A. B. Yanovski and T. I. Valchev. Pseudo-hermitian reduction of a generalized heisenberg ferromagnet equation. i. auxiliary system and fundamental properties. Journal of Nonlinear Mathematical Physics, 25:324–350, 2018.
- Norman J. Zabusky. Fermi–pasta–ulam, solitons and the fabric of nonlinear and computational science: History, synergetics, and visiometrics. Chaos, 15:015102, 2005. [CrossRef]
- V. E. Zakharov. The inverse scattering method. In R. K. Bullough and P. J. Caudrey, editors, Solitons, pages 243–286. Springer-Verlag, Berlin, 1980.
- V. E. Zakharov. Integrable systems in multidimensional spaces. In Mathematical Problems in Theoretical Physics, Lecture Notes in Phys. 153, pages 190–216. Springer-Verlag, Berlin, 1982.
- V. E. Zakharov and S. V. Manakov. On the theory of resonance interactions of wave packets in nonlinear media. Zh. Exp. Teor. Fiz, 69:1654–1673, 1975.
- V. E. Zakharov and A. B. Shabat. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Soviet Physics-JETP, 34:62–69, 1972.
- V. E. Zakharov and A. B. Shabat. Interaction between solitons in a stable medium. Sov. Phys. JETP, 37(5):823–828, 1973.
- V. E. Zakharov and A. B. Shabat. A scheme for integrating nonlinear evolution equations of mathematical physics by the inverse scattering method. i. Funkts. Anal. Prilozhen., 8:43–53, 1974.
- V. E. Zakharov and A. B. Shabat. Integration of the nonlinear equations of mathematical physics by the inverse scattering method. Funkts. Anal. Prilozhen, 13:13–22, 1979.
- V.E. Zakharov. Exact solutions of the problem of parametric interaction of wave packets. Dokl. Akad. Nauk SSSR, 228:1314–1316, 1976.
- V.E. Zakharov and L.D. Faddeev. Korteweg-de vries equation: A completely integrable hamiltonian system. Functional Analysis and Its Applications, 5(4):280–287, 1971. [CrossRef]
- Guangxiu Zhao. Integrability of Two-component Systems of Partial Differential Equations. PhD thesis, Loughborough University, 2020.
| 1 | Manakov proposed the first vector NLS equation with only 2 components [92]. The reason was that he wanted to treat a special case of VNLS which described the propagation of birefringent optical pulses in optical fibers. Since our Lax operator above is a quadratic pencil, the equation (6.30) we derived is a vector generalization of GI equation. Of course the method of solution of the VNLS is easily generalized to p-component vectors. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





