Prerpints.org logo
Preprint
Article

Hybrid Approach to Colony-Forming Unit Counting Problem using Multi-Loss U-Net Reformulation

Altmetrics

Downloads

103

Views

41

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 August 2023

Posted:

30 August 2023

You are already at the latest version

Alerts
Abstract
The Colony-Forming Unit (CFU) counting problem remains a complex issue without a universal solution in biomedical and food safety domains. A multitude of sophisticated heuristics and segmentation-driven approaches have been proposed by numerous researchers. Among those, U-Net is the most frequently cited and popular Deep Learning method. The latter approach provides a segmentation output map and requires an additional counting procedure which accounts for unique segmented regions and detected microbial colonies. However, because of pixel-based targets it tends to generate irrelevant artifacts or errant pixels, leading to inaccurate and mixed post-processing results. In response to these challenges, we propose a novel hybrid counting approach, incorporating a multi-loss U-Net reformulation and a post-processing Petri dish localization algorithm. First of all, our unique innovation lies in the multi-loss U-Net reformulation. We introduce an additional loss term at the bottleneck U-Net layer, focusing on delivering an auxiliary signal indicating where to look for distinct CFUs. Second, our novel localization algorithm accurately incorporates an agar plate and its bezel into the CFU counting routines. Finally, our proposition is further enhanced by the integration of a fully automated solution. This comprises a specially designed uniform Petri dish illumination system and a counting web application. The latter application is capable of directly receiving images from the camera, which are subsequently processed, and the segmentation results are sent back to the user. This feature provides an opportunity to correct the CFU counts, offering a feedback loop that contributes to the continued development of the Deep Learning model. Through extensive experimentation, we have found that all probed multi-loss U-Net architectures incorporated in our hybrid approach consistently outperform their single-loss counterparts which utilize exclusively the combination of Tversky and Cross-Entropy training losses at the output U-Net layer. We report further significant improvements by the means of our novel localization algorithm. This reaffirms the effectiveness of our proposed hybrid solution in addressing contemporary challenges of the precise in-vitro CFU counting.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

Colony-Forming Unit (CFU) detection and counting is a process typically used in microbiology or cell biology to measure the number of viable initial cells in a culture or sample [1]. It is particularly useful for assessing the viability of bacteria or cell colonies during the development of cultures in the laboratory. It involves isolating and counting the number of visible bacterial or cell colonies growing on a solid or semi-solid surface (agar plate) inoculated with the sample [2]. Some popular CFU-counting applications include assessing the viability of a bacterial culture following exposure to a toxic compound or measuring the number of cells in a tissue sample following cellular transfection.
For many decades Colony-Forming Unit (CFU) detection and counting problem was merely a human expert’s prerogative and responsibility. A diverse set of possible lighting and environmental conditions were preventing a successful automation by the means of image analysis techniques. Furthermore, CFU segmentation seems to suffer from drifting image acquisition conditions, background noise, an extreme variability of backgrounds, bacteria types, possible shapes and textures of agar plates being collected under varying conditions [3]. Nevertheless, following the latest advances in the CFU segmentation and counting domain using Deep Learning techniques and more specifically U-Net architectures [4,5,6], one has allowed for greater accuracy in biomedical probing, drug testing or food safety applications. Moreover, the Deep Learning approach, which renders the CFU segmentation as an image recognition process, has achieved higher precision and accuracy levels leading to substantial improvements in the CFU counting domain even with a single-cell resolution. Additionally to different U-Net architectures, which have been employed to increase the accuracy of the aforementioned segmentation task, one can combine several pre- and post-processing techniques to eliminate image artifacts and focus on the results within visible bounds of an agar plate. While U-Net models can improve CFU segmentation by combining both feature extraction and classification tasks, different edge detection and image processing techniques can even further reinforce the counting approach by smoothing exterior CFU edges as well as distilling the localization of an agar plate.
From a general standpoint, the U-Net architecture lies at the heart of image segmentation in the biomedical domain, which in turn can be seen as a highly complex and error-prone task requiring state-of-the-art techniques to achieve accurate results. Recent advances in Deep Learning have highlighted a significant progress in this area, leading to the development of specialized Convolutional Neural Networks (CNNs) [7,8] such as U-Nets, Deep Reinforcement Learning (DRL) [9,10] models, and Generative Adversarial Networks (GANs) [11,12]. These models are used to accurately label objects in images for a variety of biomedical applications such as object detection, object recognition, and image classification. In addition, these techniques are used to identify subtle differences between similar images, and to separate different components of a biomedical scene or an image. All of these approaches are greatly reducing the need for a manual intervention and making the image segmentation process more time-efficient and less labor-intensive.
Our paper proposes a novel hybrid approach to the CFU counting problem. Our main idea is grounded in the multi-loss and multi-layer U-Net training objective tailored to provide an auxiliary signal of where to look for distinct CFUs. This objective introduces an additional term at the bottom-most bottleneck U-Net layer, where the receptive field of an encoder pathway typically extracts the most high-level and coarse-grained visual features. To enhance our training objective and attain the finest and sharpest level of granularity, we combine different loss functions, such as the Dice Similarity Coefficient and the Cross-Entropy, together with our novel counting-tailored objective. Finally, we employ a novel Petri dish localization technique which identifies its bezel and a corresponding reflection zone within an image and outputs a segmentation mask for an accurate and precise estimate of CFUs growing in the refection zone and deep within an agar plate. The latter constitutes another innovative algorithm being proposed by the following paper.
For practical reasons our proposed approach is compared only to some latest advanced CFU counting approaches, such as the Self-Normalized Density Map [13] which has been shown to be effective in counting tasks, as well as object detection methods, such as YOLOv6 [14] which can count CFUs in terms of detected bounding boxes. Back to [13], the authors proposed a novel method of combining the statistical properties of the density segmentation maps with the baseline U 2 -Net model [15]. For a fair comparison, we take their best attained scores and show how our proposed and other baseline methods compare to theirs. Additionally, we make a comparative analysis of all examined U-Net models with and without an improved multi-loss reformulation, as well as with and without our Petri dish localization technique, to highlight the superiority of the proposed approach. The improvements of the Petri dish localization algorithm are clearly presented in our ablation study in Section 3.3 and they imperatively highlight the importance of applying proper post-processing and artifact removing techniques.
The remainder of this paper is organized as follows. The proposed methods along with the datasets (materials) and experimental setup are discussed in Section 2, where two core improvements along with a web application to the CFU counting problem are illustrated in detail. The experimental results are presented in Section 3. In Section 4 we discuss the obtained results, pros and cons of the proposed approach and future work. Finally, Section 5 concludes the paper.

2. Materials and Methods

In this section we introduce our hybrid CFU counting approach. It consists of two essential components and could be seen as a pipeline with several steps. The first one accounts for the CFU segmentation task in which we propose a novel improved Multi-Loss U-Net learning objective. The second one focuses on the Petri dish localization and detection task. The latter approach allows for a more fine-grained counting of expected CFUs within a valid surface only by identifying its bezel and a corresponding reflection zone where visible CFUs could be duplicated. This second major step drastically reduces the latent levels of noise, e.g. flipped pixels, segmented out artifacts and other pixel-based errors inherent to image segmentation tasks where targets are defined on a per-pixel basis. In between of these two primary pipeline steps we have other post- and preprocessing procedures responsible for removing artifacts within a single detected CFU region, e.g. smoothing exterior CFU edges.

2.1. Multi-Loss U-Net

This section introduces our proposed reformulation of the well-known U-Net architecture, which accommodates for a supplemental loss function term in the training objective. In order to provide an auxiliary signal for the U-Net model on where to locate CFUs, we define a second ground-truth segmentation output map Y m i d , which constitutes the result of a binary mapping F ↦ R 2 of all CFU centroids from the input 2D space to the re-sized 64 × 64 output 2D space of the bottom-most bottleneck U-Net layer. In the case of two or more CFUs which map to the same 2D spatial cell, we still keep its value unchanged and activated1. The examples of both ground-truth output maps (corresponding to the same image) can be found in Figure 1.
Depending on the number of down-sampling blocks (e.g., max-pooling or convolution layers with a stride greater than 1), we might end up with a different number of 2D spatial features at the middle layer. All of our probed U-Net models are restricted to have 1024 × 1024 input spatial dimensions, 5 down-sampling blocks with a stride of 2, and a 64 × 64 2D spatial resolution at the bottom-most U-Net middle layer. Moreover, to align the number of model-dependent feature maps at the middle layer, we apply an averaging procedure across these maps to arrive at a single feature map. Finally, to achieve a better alignment between the aforementioned ground-truth segmentation map Y m i d and the latter 64 × 64 averaged feature map X m i d of the middle layer, we introduce the following loss function:
L m i d ( X m i d , Y m i d ) = − ∥ X m i d · Y m i d ∥ 1 , 1 ∥ X m i d ∥ F ∥ Y m i d ∥ F ,
where ∥ · ∥ F relates to the Frobenius norm, ∥ · ∥ 1 , 1 to the entry-wise matrix norm and · denotes an element-wise multiplication. The latter loss function promotes similarity between output maps, thus enforcing the extraction of meaningful features only around pertinent CFU-containing regions of the input 2D space.
To arrive at the final training objective, we combine our optimization objective in Eq.1 with typical segmentation-tailored losses, such as the Dice Similarity Coefficient L D S C and the Cross-Entropy L C E , defined solely for the output layer X o u t and the ground-truth segmentation Y o u t maps, which match the input dimensions:
L ( X m i d , X o u t , Y m i d , Y o u t ) = L m i d ( X m i d , Y m i d ) + L C E ( X o u t , Y o u t ) + L D S C ( X o u t , Y o u t ) ,
where the last two loss terms are defined as follows:
L C E ( X o u t , Y o u t ) = − ∑ c = 1 2 ∥ Y c o u t · log ( X c o u t ) ∥ 1 , 1
L D S C ( X o u t , Y o u t ) = 1 − ∑ c = 1 2 ∥ X c o u t · Y c o u t ∥ 1 , 1 ∥ X c o u t ∥ 1 , 1 ∥ Y c o u t ∥ 1 , 1 + ϵ ,
where c spans an index of the target segmentation class, which, in retrospect, boils down to the foreground and background classes only, and ϵ = 10 − 5 is a normalization constant to prevent exploding or imploding gradients.
To summarize our findings, we introduce a novel multi-loss and multi-layer U-Net training objective which comprises the well-known loss functions from the literature [6] as well as a novel loss term which builds upon an additional auxiliary signal. We do not optimize any coefficients of the individual loss terms as their values are constrained to the − 1 , 1 interval and are well-balanced.

2.2. Petri Dish Localization

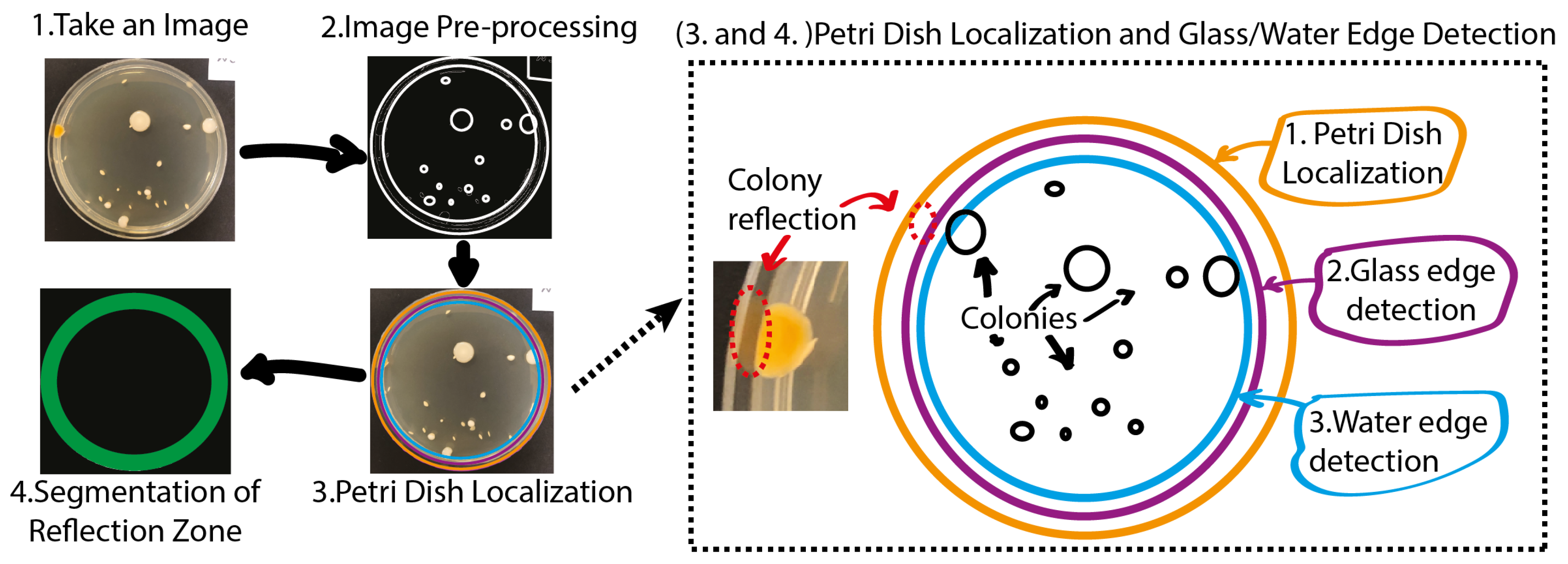
The aforementioned approach is used for the Petri dish localization task and is meant for the downstream removal of bacterial colony reflections on an agar plate. The proposed approach constitutes the three instrumental parts: Image Preprocessing, Petri Dish Localization and Segmentation of the Reflection Zone (see Figure 2).
The bacterial colony image preprocessing task consists of two parts: edge segmentation and blurring. The blurring procedure removes some of the image noise and small artifacts [16]. Bacterial colony images can be smoothed by using a Gaussian blur. The Gaussian blur filter [17] can be formulated by using the Gaussian probability distribution function calculus in a two-dimensional space as in Eq.5:
G ( x , y ) = 1 2 π σ 2 e − x 2 + y 2 2 σ 2 ,
where x and y - two-dimensional coordinates; σ - standard deviation (affects the strength of smoothing: a higher standard deviation value means stronger smoothing). The high frequency component suppression (the removal of small details) is performed by this procedure. In this way, blurring prepares bacterial colony images for the further analysis and downstream segmentation tasks.
The next important step is an edge-based segmentation, which allows for the detection of sharp transitions in brightness levels in CFU images. The edge-based segmentation can be performed by using a Canny edge detector [18]. Moreover, the latter segmentation prepares images for the further agar plate localization task.
The aforementioned task of the Petri dish localization holds an immense significance as its outcome contributes to enhancing the precision of automated bacterial colony counting routines. An agar plate usually has the shape of a circle. Therefore, the proposed localization method is based on the general equation of a circle in Eq.6:
( x − x 0 ) 2 + ( y − y 0 ) 2 = r 2 ,
where x and y – two-dimensional coordinates of the circumference; x 0 and y 0 – two-dimensional coordinates of the circumference’s center; r – the circumference radius. Furthermore, the main purpose of this method is to find parameters x 0 , y 0 , r which produce a circumference that closely matches an observed bezel. Furthermore, it may be possible to use the circle Hough transform [19] for this purpose. At the beginning of the Petri dish localization step, the length of the dish radius is not known. Accordingly, the 3 D Hough space [19] should be used for the circle Hough transform. The 3D Hough space is done by using an accumulator array A ( x 0 , y 0 , r ) .
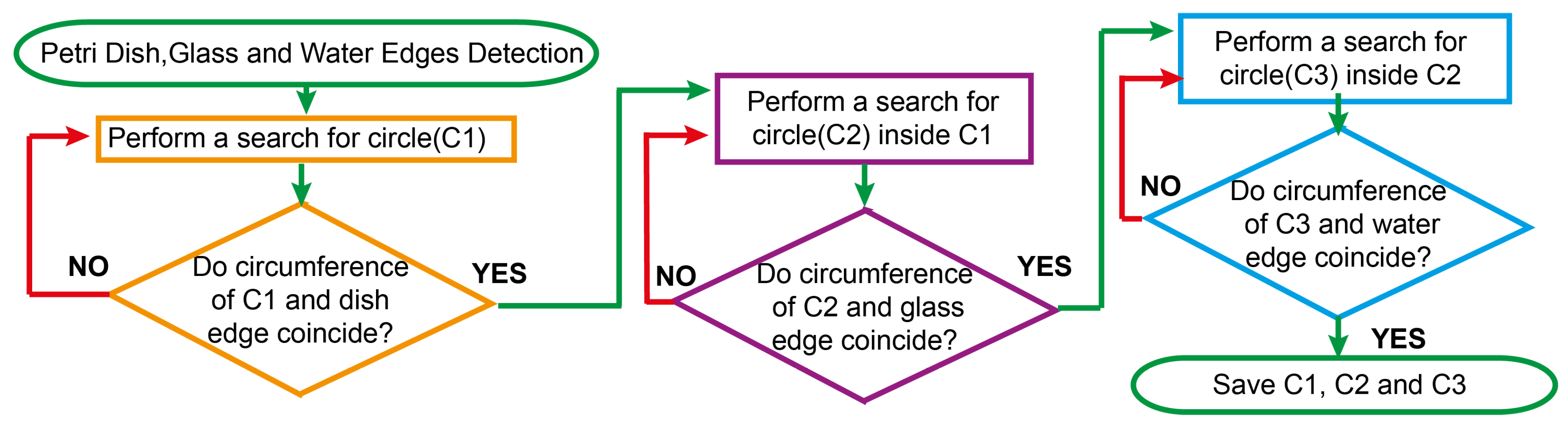
The next stage involves the segmentation of two reflection zones: the glass reflection and the water reflection. The Figure 3 shows a schematic flow-diagram of the reflection zone detection routine. First, the Petri dish edge is being detected. Next, the glass edge is being detected and finally, the water edge is being localized. The latter approach allows for performing a complete Petri dish localization task while reducing the influence of highly disrupting CFU reflections on our hybrid counting approach. An outcome of the algorithm presented above in Figure 3 for one random sample can be found in Figure 4.

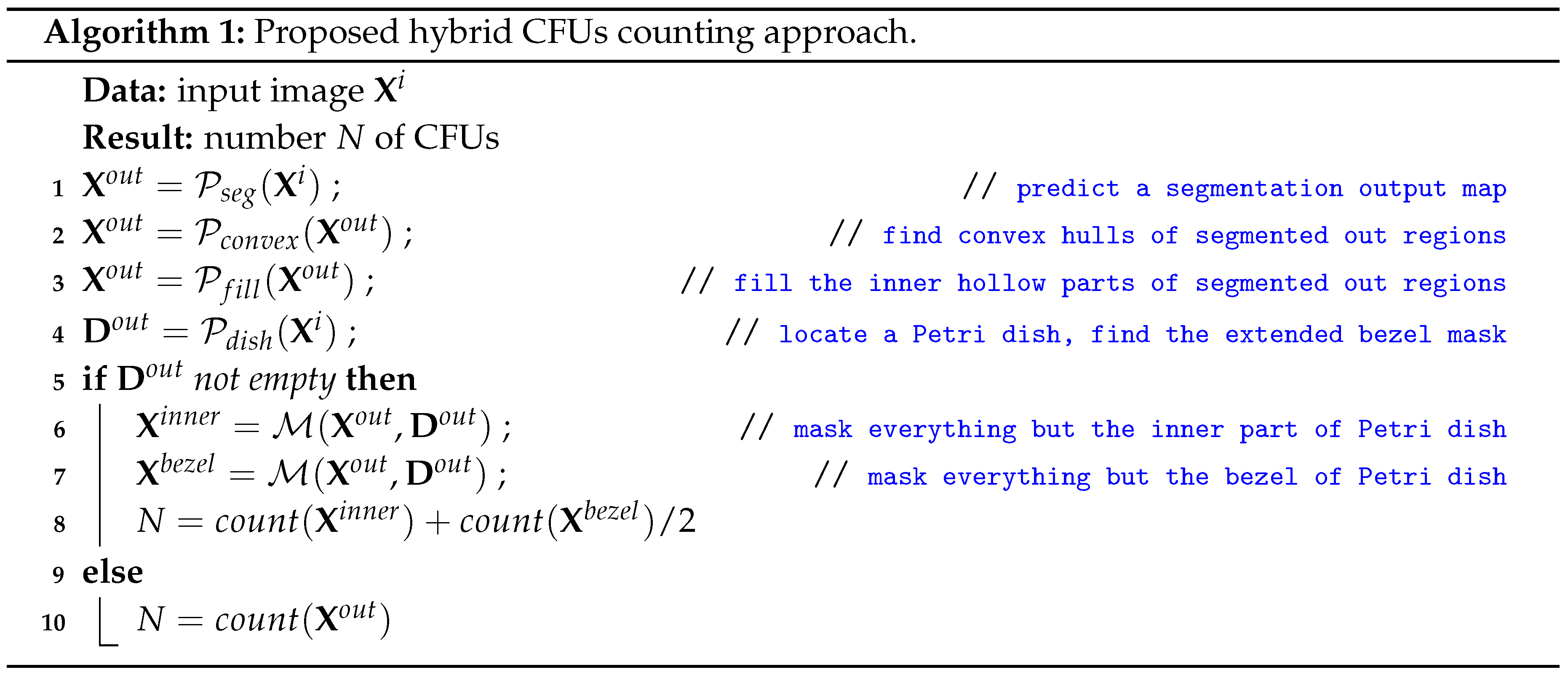
2.3. Hybrid Approach

In this section we present our hybrid approach which can be postulated as a sequence of algorithmic steps. We present a simplified version of our approach step-by-step in Algorithm 1.
Preprints 83699 i001
The breakdown of our Algorithm 1 can be outlined using several crucial steps which should be preserved for a successful application. The first step constitutes the actual prediction of the segmentation output map X o u t by our multi-loss U-Net model P s e g . A few next steps are designated for post-processing the predicted CFU regions such that we do not have any artifacts within (such as holes) or at the border of such a region. The latter could be done by finding convex hulls and filling the inner holes by the means of scikit-image software library. Finally, we proceed to the Petri dish localization step defined by the function P d i s h . The latter function derives a full segmentation mask spanning an area between the outer agar plate bezel and the water edge within. The very final step depends on whether we have found a valid mask by the means of P d i s h or not. In case of a success, we count CFUs laying completely inside the Petri dish but outside of the found mask and halve the count of detected colonies inside the mask. Otherwise, we proceed to the normal counting routine c o u n t ( X o u t ) on the initial post-processed X o u t segmentation map.

2.4. CFU Counting Application

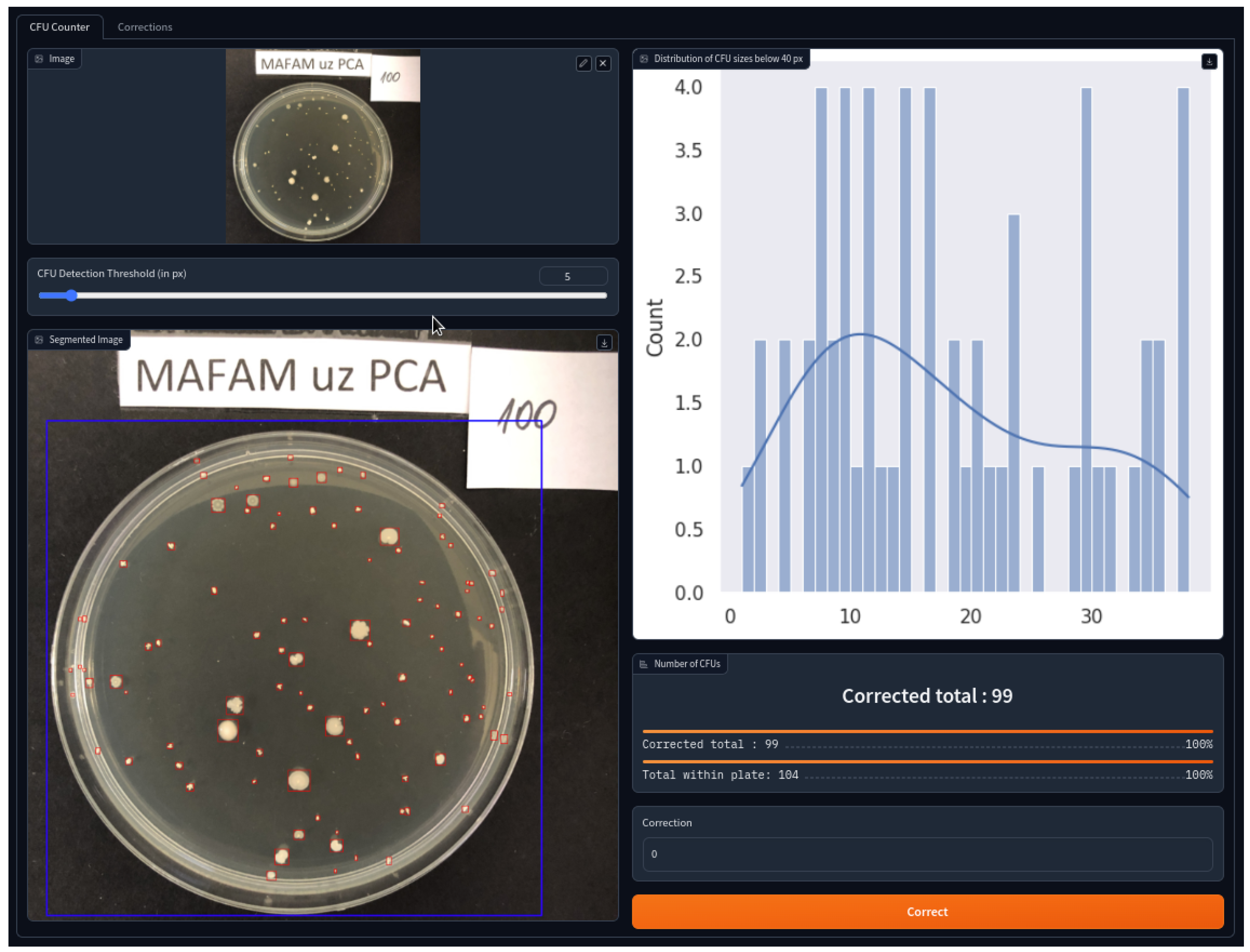
To enhance and bolster the acceptance of our novel approach we have developed a web application which hosts our hybrid approach and provides a seamless access to it. Within one tap and a single shot from anyone’s smartphone in a lab, one can more accurately estimate the CFU count withing the localized agar plate. This way significantly streamlines the working process and boosts the productivity of any lab personnel. In Figure 5 we can find a complete user interface of such an application. Web UI is composed of several integral widgets such as the one used for uploading images (top left) or viewing the statistics on the distribution of CFU sizes (top right). The other controls constitute the slider with the threshold in pixels on the minimum considered area of the bacterial colony as well as submitting the correction. Other widgets represent the outcome of our hybrid approach such as an image with bounding boxes of CFUs (in red) or an agar plate (in blue) as well as estimated2 and corrected3 CFU counts within an agar plate. Web application is developed using Gradio framework [20].

2.5. Datasets

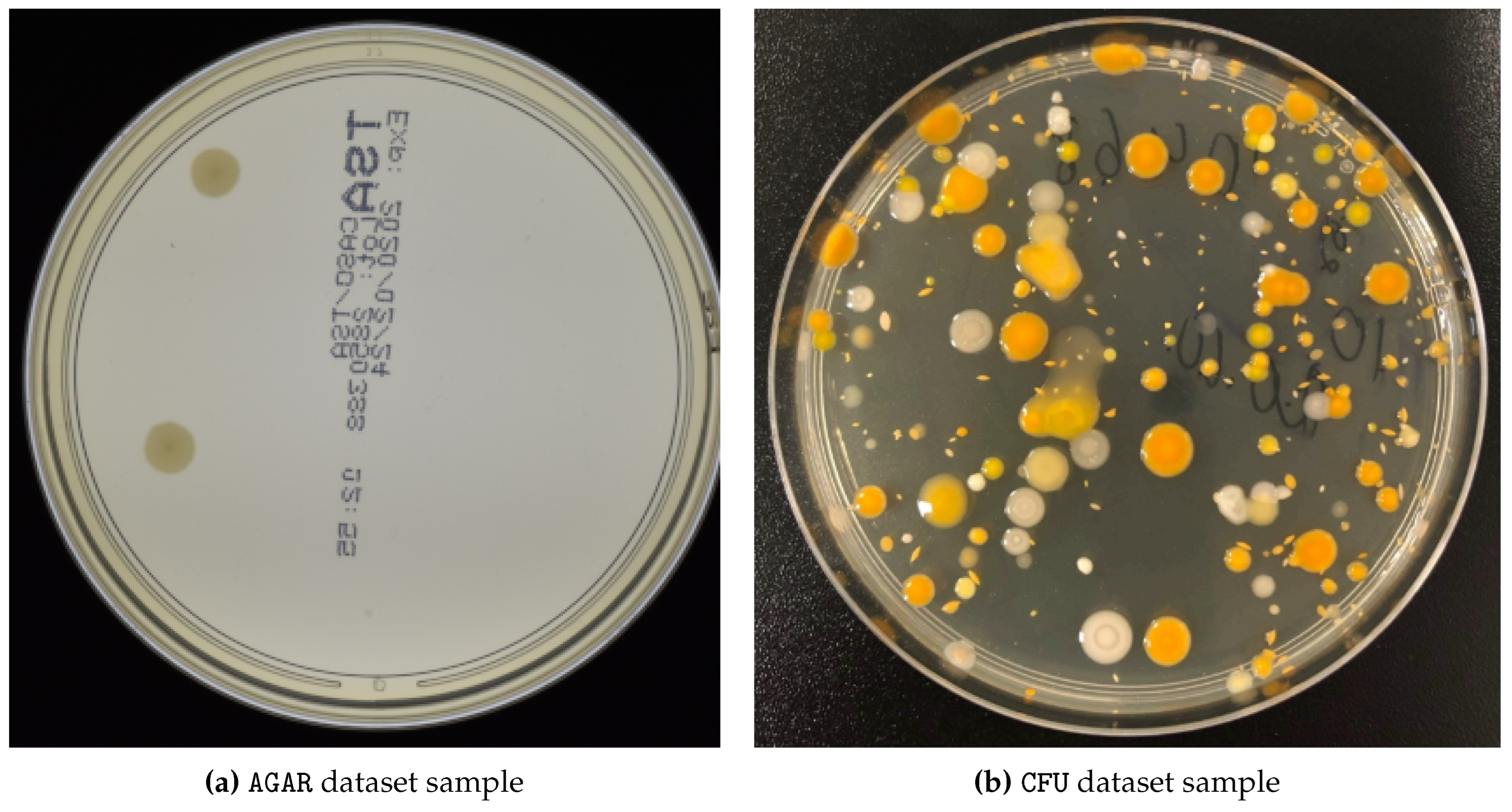
We use two different CFU datasets, one of which is publicly available. The Annotated Germs for Automated Recognition (AGAR) dataset [21] is an image database of microbial colonies cultured on an agar plate. It contains 18,000 photos of five different microorganisms, taken under diverse lighting conditions with two different cameras. Following the experimental setup of [13], we took only high-resolution images. Moreover, we do not follow their setup of providing ground-truth density maps by the means of Gaussian blurring of the provided CFU-centroids but rather we draw a circle up to one-tenth of the minimal height or width (of the corresponding bounding box) in radius around it. The other proprietary dataset is comprised of Colony-Forming Unit (CFU) images with different types of bacteria being cultivated on an agar plate for later segmentation and estimation of the number of initially present CFUs. This dataset was collected in-house by our project partner ("Laboratorija Auctoritas LTD"). A brief summary of all datasets is given in Table 1 with the corresponding characteristics. The example images of both datasets can be found in Figure 6.

2.6. Experimental Setup

All models were tested under the same experimental setup, which envisioned a 5-fold cross-validation or a random split with fixed-size training, validation, and test sets. During the training stage, we proceeded with a fixed number of epochs, where for each epoch, the model performance on the validation set was tracked and the best-performing model4 was saved as a checkpoint. For the AGAR dataset, we merged all higher resolution training and validation images originally provided and then took 3 random splits, where 10% was used as a test set, 18% as a validation, and 72% as a training set. For the proprietary CFU dataset, we had only 150 annotated images and 242 test images with CFU counts only. For the latter dataset we performed a 5-fold cross-validation split across 150 annotated images and evaluated the checkpointed best-performing model on a test set. Splits for all models were identical to ensure the comparability of all approaches. No thresholding on the minimal region sizes or other than in Algorithm 1 post-processing steps where performed. All images were re-scaled to 1024 × 1024 input spatial dimensions to match the setup in [13], and the standard z-score normalization technique was applied, i.e., each RGB channel was normalized according to the channel-wise mean and standard deviation:
z = X − μ σ .
For all datasets, we report the Mean Absolute Error (MAE, Eq.8) and the symmetric Mean Absolute Percentage Error (sMAPE, Eq.9) of the CFU counts across all test images (agar plates). Additionally we report all the performance metrics for the images with ground-truth CFU counts below 100 as it was originally done in [13] to preserve the comparability across approaches. Finally, we report results for YOLOv6 model in the similar experimental setting on both datasets at the best found confidence threshold (for the CFU dataset it was 0.2 and for the AGAR one: 0.16). For YOLOv6 we followed the setup provided in [14] and created a hardcoded split only once by fixing the training, validation and test sets to the mentioned above ones for all datasets. The well-established region counting algorithm from the scikit-image software library was used to keep track of all CFU counts; it was applied across output segmentation maps to get the predicted n i ˜ CFU counts per image while n i was taken from JSON annotation files for the AGAR dataset or provided by a human expert for the proprietary CFU dataset.
M A E = 1 N ∑ i = 1 N | n i − n i ˜ |
s M A P E = 100 % N ∑ i = 1 N | n i − n i ˜ | | n i + n i ˜ |
The maximum number of epochs for the CFU dataset was set to 200 while for the AGAR dataset we set it to 15. As our main optimization objective for X o u t , we use the sum of Tversky [22] and Cross-Entropy losses for all probed U-Net architectures, and we name such an architecture as Single-Loss if only one ground-truth segmentation map Y o u t is used. The Tversky loss is initialized with α = 0.5 and β = 0.5 , which effectively reduces it to a smoothed version of the Dice Similarity Coefficient. We call an architecture Hybrid if Algorithm 1 is being used and P s e g is being provided by such an architecture. We use Adam optimizer [23] for training all the models, and our initial learning rate is set to 0.001 . During the training stage, we gradually decrease the learning rate using a time-based decay scheduler. All experiments were performed using TensorFlow [24] framework and MIScnn [25] library for the variations of the U-Net model. YOLOv6 model and the corresponding experimental setup infrastructure was taken from the corresponding repository. All the code together with Petri dish localization library was containerized and ran using Docker [26] infrastructure. We used Nvidia GeForce 1080 Ti GPU card with 11 GB of RAM for training all the models. Other hardware specifications are as follows: Xeon e5-2696v3 CPU with 18 cores, 128 GB of RAM at 2133 MHz and Linux (Ubuntu 20.04 LTS) operating system. The source code was dockerized and put on Docker Hub; it is freely available by using the following command: docker pull jumutc/cfu_analysis. All our code is distributed under GPLv3 license and doesn’t include any referenced datasets.

3. Results

3.1. Main Results

In Table 2 we report our experimental results (without any stratification by the ground-truth CFU counts) for the CFU dataset, and in Table 3 we demonstrate the performance on the AGAR dataset. We report average MAE (Eq.8) and sMAPE (Eq.9) scores with standard deviations across CV-folds or random splits. We experiment with five diverse U-Net architectures along with the YOLOv6 model5 to provide a sufficient outlook on the possibilities and performance gains one can achieve using our proposed approach. We aggregate results across single-loss, hybrid (ours) and multi-loss (ours) formulations for U-Net++ [27], Plain U-Net [6], Residual U-Net [28], and Dense U-Net [29] and MultiRes U-Net [30] architectures. In bold we highlight the best attained scores across all U-Net architectures.
As one can notice from Table 2 and Table 3, our proposed hybrid approach is clearly outperforming every single counterpart and also the object detection YOLOv6 model by a large margin. We can notice consistent performance gains when using a U-Net model paired with Algorithm 1 which is indicated by the Hybrid prefix. This clearly justifies the usage and practical importance of the Petri dish localization approach described in Section 2.2.
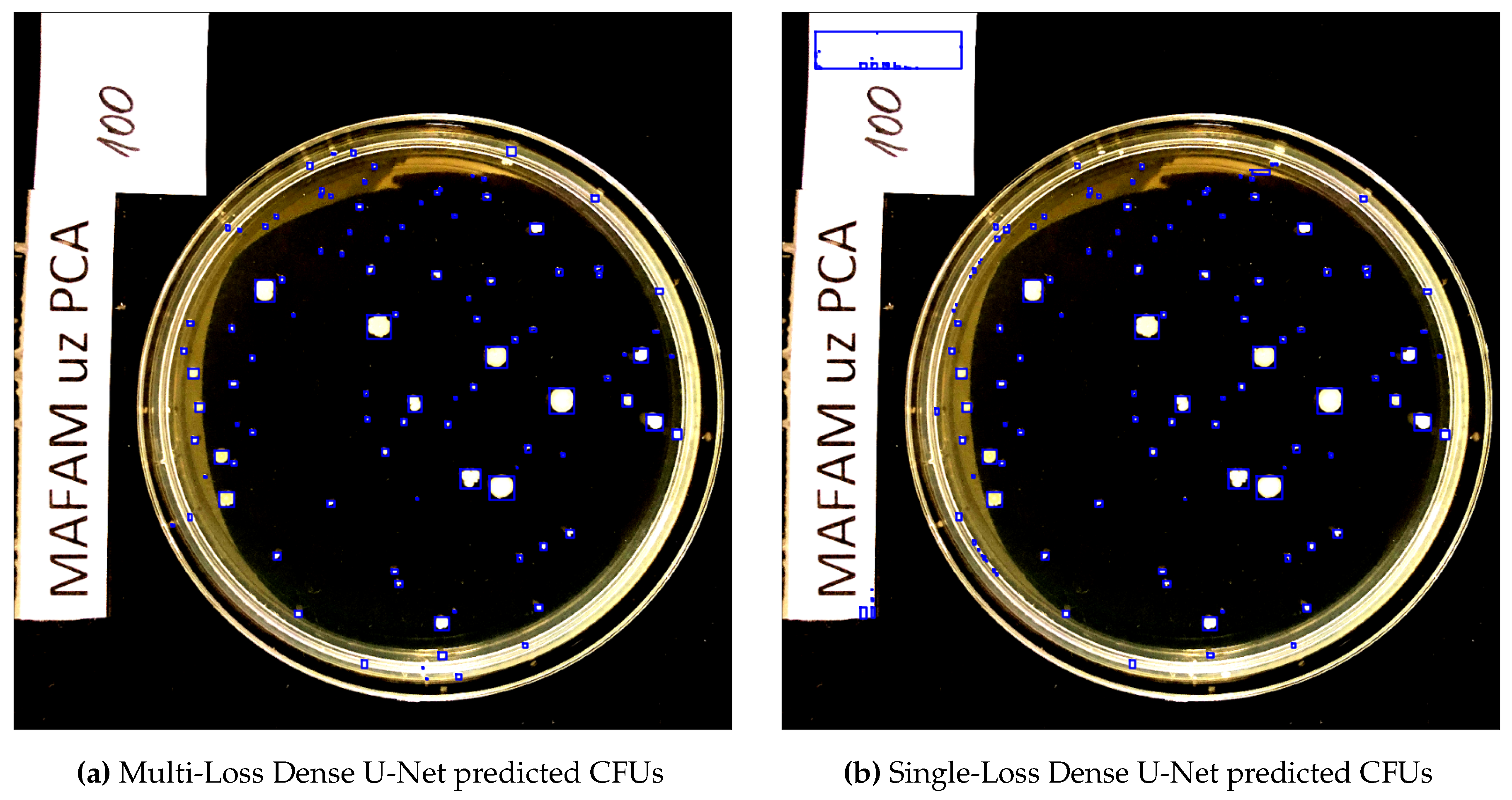
In Figure 7 we compare two predicted segmentation output maps from the Dense U-Net architectures for one of the CFU test set images. The actual CFU count is 100, our Multi-Loss reformulation even without further rectification via Algorithm 1 detected 101 CFUs and the Single-Loss counterpart detected 140 CFUs. As we can clearly see, our proposed Multi-Loss reformulation is much more precise and accurate in terms of segmented CFU regions. Not a single artifact (on the left side of the image) is segmented, resulting in an almost ideal estimation of the CFU count: 101 colonies, compared to the 100 actual human-counted ones.

3.2. Stratified Results

Finally, we highlight the results for the same experimental setup and for the same CFU and AGAR datasets to showcase the efficacy and achieved performance gains of our proposed approach on the ground-truth strata where mistakes are more profound, i.e. on the samples with less than 100 ground-truth CFUs. These results were collected from the same models and the same test sets as of Table 2 and Table 3 with an additional sample filtering on the top. In hindsight, these results allow us for a direct comparison with [13] as they restricted their subset of the entire AGAR dataset to only those samples.
If we compare the scores from Table 5 to the results from [13], we can note a major improvement, as the best MAE attained for their proposed Self-Normalized Density Map approach6 is 3.65 and their best sMAPE is 4.05%. We should underscore one U-Net architecture which is especially notable for the AGAR dataset: Plain U-Net. Even with a single-loss approach, it attains much better MAE and sMAPE scores. This observation is contrasting to the much worse performance results (compared to other architectures) on the proprietary CFU dataset and might indicate that this architecture is performing the best on homogeneous datasets, such as the AGAR one, while lacking generalization capabilities for more difficult ones, such as CFU, or where we might have some co-variate shift problems.
For the proprietary CFU dataset in Table 4 we can clearly spot a major improvement as well. We can notice that all models alleviated with our Algorithm 1 as well as our promising Multi-Loss U-Net reformulation consistently outperform baseline architectures and are delivering very profound improvements rooted in the hybrid approach.
Table 4. CFU dataset’s stratified (under 100 CFUs) counting results for YOLOv6, U-Net++, Plain U-Net, Dense U-Net, Residual U-Net and MultiRes U-Net architectures.
Table 4. CFU dataset’s stratified (under 100 CFUs) counting results for YOLOv6, U-Net++, Plain U-Net, Dense U-Net, Residual U-Net and MultiRes U-Net architectures.
Architecture MAE sMAPE
YOLOv6 10.21 14.75
Single-Loss U-Net++ 15.59±4.94 19.11±5.07
Single-Loss Plain U-Net 38.08±6.22 23.30±3.05
Single-Loss Residual U-Net 18.88±8.46 20.79±7.89
Single-Loss Dense U-Net 17.57±3.81 19.28±3.47
Single-Loss MultiRes U-Net 10.90±2.68 13.25±3.47
Hybrid Single-Loss U-Net++ (ours) 11.44±2.85 14.98±3.49
Hybrid Single-Loss Plain U-Net (ours) 30.84±2.67 26.49±2.20
Hybrid Single-Loss Residual U-Net (ours) 15.33±6.32 18.10±6.51
Hybrid Single-Loss Dense U-Net (ours) 14.30±3.34 16.47±3.32
Hybrid Single-Loss MultiRes U-Net (ours) 9.04±1.73 11.39±2.65
Hybrid Multi-Loss U-Net++ (ours) 8.85±0.90 11.87±1.11
Hybrid Multi-Loss Plain U-Net (ours) 22.41±2.34 21.89±2.02
Hybrid Multi-Loss Residual U-Net (ours) 7.28±0.35 9.37±0.65
Hybrid Multi-Loss Dense U-Net (ours) 10.62±1.15 9.71±0.68
Hybrid Multi-Loss MultiRes U-Net (ours) 9.11±2.85 11.24±2.92
Table 5. AGAR dataset’s stratified (under 100 CFUs) counting results for Self-Normalized Density Map, YOLOv6, U-Net++, Plain U-Net, Dense U-Net, Residual U-Net and MultiRes U-Net architectures.
Table 5. AGAR dataset’s stratified (under 100 CFUs) counting results for Self-Normalized Density Map, YOLOv6, U-Net++, Plain U-Net, Dense U-Net, Residual U-Net and MultiRes U-Net architectures.
Architecture MAE sMAPE
Self-Normalized Density Map 3.65 4.05
YOLOv6 4.27 11.71
Single-Loss U-Net++ 10.29±3.90 34.19±17.42
Single-Loss Plain U-Net 1.23±0.17 2.69±0.23
Single-Loss Residual U-Net 6.68±1.46 15.95±3.78
Single-Loss Dense U-Net 11.78±6.40 25.90±10.12
Single-Loss MultiRes U-Net 3.84±1.00 9.40±2.34
Hybrid Single-Loss U-Net++ (ours) 10.35±3.87 34.32±17.46
Hybrid Single-Loss Plain U-Net (ours) 1.33±0.17 2.95±0.34
Hybrid Single-Loss Residual U-Net (ours) 6.15±1.47 15.48±3.69
Hybrid Single-Loss Dense U-Net (ours) 11.19±6.15 25.97±10.18
Hybrid Single-Loss MultiRes U-Net (ours) 3.06±0.74 8.03±1.98
Hybrid Multi-Loss U-Net++ (ours) 5.81±1.37 16.78±4.29
Hybrid Multi-Loss Plain U-Net (ours) 0.88±0.05 2.17±0.13
Hybrid Multi-Loss Residual U-Net (ours) 3.61±0.32 10.08±1.72
Hybrid Multi-Loss Dense U-Net (ours) 3.30±0.32 9.46±0.44
Hybrid Multi-Loss MultiRes U-Net (ours) 2.90±0.52 7.67±1.48

3.3. Ablation Study

To justify a practical use of Algorithm 1 and its constituents we perform an ablation study of dissecting it into two major alternatives: counting everything uniformly inside of X i n n e r ∪ X b e z e l ; counting CFUs inside of X i n n e r and X b e z e l separately as described in Algorithm 1. The experimental setup and dataset cross-validation splits were kept identical to the ones in Section 2.6. Table 6 and Table 7 accumulate the obtained results only for our Multi-Loss hybrid architectures.
As one can clearly conclude from Table 6, our proposed hybrid approach outperforms other ablated variants by a clear margin in terms of the MAE and sMAPE scores. Additionally, in Table 7 we can notice that for some architectures on the AGAR dataset our full hybrid approach slightly worsens the observed MAE and sMAPE scores. The latter can be attributed to the absence of small CFUs and corresponding reflections at the bezel. In such a clean setting any additional CFU count manipulations can only deteriorate the metrics. For future research directions, we might look for a better reformulation of Eq.1, as different datasets might require more specialized and intricate handling.

3.4. Comparative Study

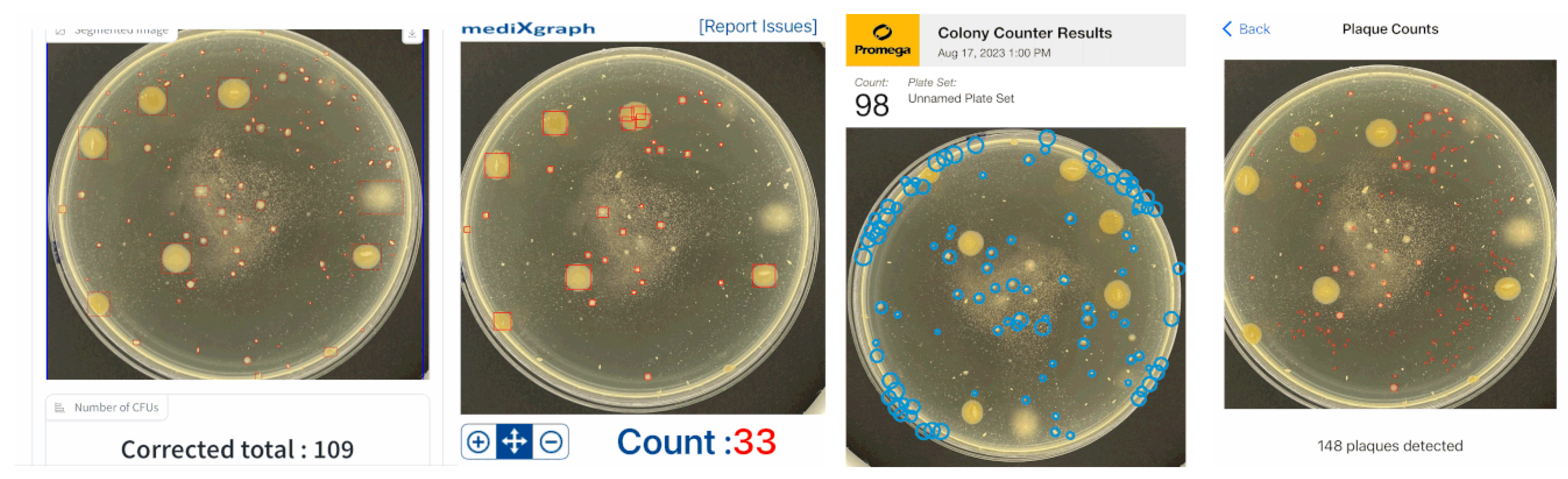
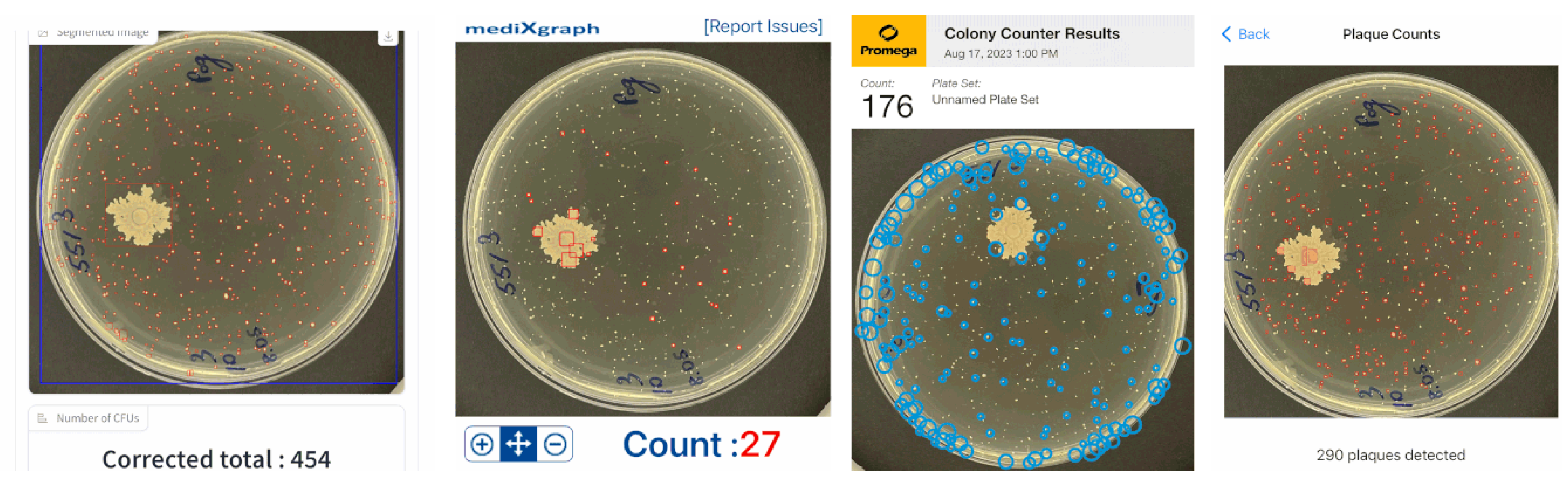
To test our developed hybrid approach on real lab examples, three additional iOS applications were tested. Since the uttermost benefit of using automated counting tools is more prominent for higher number of colonies, the two cases with CFU counts of 97 (in Figure 8) and 439 (in Figure 9) were tested. Other tests showed a similar qualitative and quantitative precision.
The test in Figure 8 shows a typical situation when an agar substance has impurities which slightly affect the proposed system’s accuracy. ColonyCount application’s result is almost exact, but most of the found colonies are false. The second case has a perfectly clear agar plate with one big irregularly formed colony. None of the compared applications (apart from our proposed one), including ColonyCount, CFU.Ai and OnePetri, could detect it. All of the compared approaches for Figure 9 output by far less detected CFUs than the actual ground-truth one or our developed application in Section 2.4.
Our proposed approach was shown to have some errors in the merged colonies and small artifacts on an agar substance. The latter could be solved using a threshold parameter, which could sieve out all smaller segmented regions. This parameter could be usable as well in the lab when single-strain colonies are studied. In the latter situation, scientists are counting only large colonies, filtering out small CFUs of other strains which grow much slower due to an unsuitable agar.
We would like to express an additional disclaimer that all experiments where performed in the restricted laboratory setup with our own choice of bacterial strains and lightning conditions, hence we do not want to generalize our observations for the compared iOS applications over the entire spectrum of possible CFU imaging sources.

4. Discussion

This paper discussed a novel hybrid approach to the CFU counting problem. Our approach is rooted in the multi-loss and multi-layer U-Net training objective tailored to provide an auxiliary signal of where to look for distinct CFUs. With a novel training objective, which introduces an auxiliary term at the bottom-most bottleneck U-Net layer, we enrich the receptive field of an encoder pathway. Additionally, we combine different loss functions, such as the Dice Similarity Coefficient and the Cross-Entropy, together with our novel counting-tailored objective to boost the overall training convergence and consistency. To conclude our approach, we came up with a novel Petri dish localization technique which identifies different edges within an agar plate and outputs a segmentation mask for an accurate and precise estimate of CFUs growing in the refection zone and deep within a Petri dish.
Empirical evaluation of the considered approach on the proprietary CFU and public AGAR datasets underpins our findings. The overall performance of all tested U-Net models with our innovative loss term starkly surpasses the one of any Single-Loss models, which brings us to the conclusion that having an additional signal guidance is always beneficial. On the other hand, post-processing can be rendered as another integral part of the observed improvement as our ablation studies suggest. Altogether, different parts of Algorithm 1 are building up an extended advantage of our proposed hybrid approach over all other existing solutions.
Compared to the previous studies of Graczyk et al. [13], our demonstrated hybrid approach delivers drastically better performance metrics and is much simpler in terms of practical implementation as it embarks on standard U-Net architectures. Anyone can take an existing state-of-the-art U-Net model, train it, and finally embed it seamlessly to our CFU counting application without knowing any internal details.
To wrap up the discussion section we summarize the pros and cons of the proposed approach as follows.
  • Pros of the proposed approach:
    • Possibility to improve seamlessly any U-Net architecture.
    • Enhanced post-processing routines which allow for improving the contours and regions of segmented out CFUs.
    • Petri dish localization algorithm which allows for CFU counting only on a valid agar plate.
  • Cons of the proposed approach:
    • Multiple losses at the training time which might require a weighting scheme.
    • Increased post-processing time and consumed resources.

5. Conclusions

In this paper, we have investigated a novel multi-loss and multi-layer U-Net reformulation which focuses on providing an auxiliary signal of where to look for distinct CFUs while solving an ubiquitous CFU counting problem. We proposed an additional loss term for the bottom-most bottleneck U-Net layer, where the architecture extracts the most high-level and coarse-grained visual features. This novel loss function couples together an averaged feature map of the aforementioned middle layer and a second ground-truth segmentation indicator map of CFU positions in the input space. An additional Petri dish localization routine (along with other post-processing steps) is proposed to enhance the overall performance and counting efficiency of the discussed hybrid approach.
A comprehensive empirical evaluation of our solution on two diverse CFU datasets supports our findings. Additionally, we compare our approach to the recently published one and show that we can achieve some notable performance gains while using a simplified problem statement and a basic Plain U-Net reformulation embedded into Algorithm 1. Some potential future research directions might include investigations into applying similar principles for the multi-scale U-Net architectures, such as previously mentioned U 2 -Net [15] or recently proposed Multi-Path U-Net [31] models.

Funding

Research is funded by the European Regional Development Fund project "Fast and cost-effective machine learning based system for microorganism growth analysis" (agreement No:1.1.1.1/19A/147).

Data Availability Statement

The AGAR dataset is available at https://agar.neurosys.com.

Acknowledgments

Bacterial tests and CFU counting were performed at the laboratory of our project partner - LTD "Laboratorija Auctoritas" in Riga, Latvia.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Brugger, S.D.; Baumberger, C.; Jost, M.; Jenni, W.; Brugger, U.; Mühlemann, K. Automated Counting of Bacterial Colony Forming Units on Agar Plates. PLOS ONE 2012, 7, 1–6. [Google Scholar] [CrossRef] [PubMed]
  2. Mandal, P.; Biswas, A.; K, C.; Pal, U. Methods for Rapid Detection of Foodborne Pathogens: An Overview. American Journal of Food Technology 2011, 6. [Google Scholar] [CrossRef]
  3. ul Maula Khan, A.; Torelli, A.; Wolf, I.; Gretz, N. AutoCellSeg: robust automatic colony forming unit (CFU)/cell analysis using adaptive image segmentation and easy-to-use post-editing techniques. Scientific Reports 2018, 8, 1–10. [Google Scholar] [CrossRef]
  4. Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Medical Image Computing and Computer-Assisted Intervention (MICCAI); Springer, 2015; Vol. 9351, LNCS; pp. 234–241. [Google Scholar]
  5. Sun, F.; V, A.K.; Yang, G.; Zhang, A.; Zhang, Y. Circle-U-Net: An Efficient Architecture for Semantic Segmentation. Algorithms 2021, 14. [Google Scholar] [CrossRef]
  6. Isensee, F.; Maier-Hein, K.H. An attempt at beating the 3D U-Net. CoRR 2019, abs/1908.02182, [1908.02182]. [Google Scholar]
  7. Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Advances in Neural Information Processing Systems; Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Eds. Curran Associates, Inc., 2012; Vol. 25. [Google Scholar]
  8. Yadav, S.S.; Jadhav, S.M. Deep convolutional neural network based medical image classification for disease diagnosis. Journal of Big Data 2019, 6, 113. [Google Scholar] [CrossRef]
  9. Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press, 2018. [Google Scholar]
  10. Zhou, S.K.; Le, T.H.N.; Luu, K.; Nguyen, H.V.; Ayache, N. Deep reinforcement learning in medical imaging: A literature review. CoRR 2021, abs/2103.05115, [2103.05115]. [Google Scholar] [CrossRef] [PubMed]
  11. Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Advances in neural information processing systems 2014, 2672–2680. [Google Scholar]
  12. Ahmad, W.; Ali, H.; Shah, Z.; Azmat, S. A new generative adversarial network for medical images super resolution. Scientific Reports 2022, 12, 9533. [Google Scholar] [CrossRef] [PubMed]
  13. Graczyk, K.M.; Pawłowski, J.; Majchrowska, S.; Golan, T. Self-normalized density map (SNDM) for counting microbiological objects. Scientific Reports 2022, 12. [Google Scholar] [CrossRef] [PubMed]
  14. Li, C.; Li, L.; Jiang, H.; Weng, K.; Geng, Y.; Li, L.; Ke, Z.; Li, Q.; Cheng, M.; Nie, W.; Li, Y.; Zhang, B.; Liang, Y.; Zhou, L.; Xu, X.; Chu, X.; Wei, X.; Wei, X. YOLOv6: A Single-Stage Object Detection Framework for Industrial Applications. arXiv 2022, arXiv:cs.CV/2209.02976. [Google Scholar]
  15. Qin, X.; Zhang, Z.; Huang, C.; Dehghan, M.; Zaiane, O.R.; Jagersand, M. U2-Net: Going deeper with nested U-structure for salient object detection. Pattern Recognition 2020, 106, 107404. [Google Scholar] [CrossRef]
  16. Krig, S. Computer Vision Metrics: Survey, Taxonomy, and Analysis; Apress OPEN, 2014.
  17. Das, A.; Medhi, A.; Karsh, R.K.; Laskar, R.H. Image splicing detection using Gaussian or defocus blur. International Conference on Communication and Signal Processing (ICCSP), 2016, pp. 1237–1241. [CrossRef]
  18. Hao, G.; Min, L.; Feng, H. Improved Self-Adaptive Edge Detection Method Based on Canny. 5th International Conference on Intelligent Human-Machine Systems and Cybernetics, 2013, Vol. 2, pp. 527–530. [CrossRef]
  19. Chen, X.; Lu, L.; Gao, Y. A new concentric circle detection method based on Hough transform. 7th International Conference on Computer Science and Education (ICCSE), 2012, pp. 753–758. [CrossRef]
  20. Abid, A.; Abdalla, A.; Abid, A.; Khan, D.; Alfozan, A.; Zou, J. Gradio: Hassle-Free Sharing and Testing of ML Models in the Wild. arXiv 2019, arXiv:cs.LG/1906.02569. [Google Scholar]
  21. Majchrowska, S.; Pawłowski, J.; Guła, G.; Bonus, T.; Hanas, A.; Loch, A.; Pawlak, A.; Roszkowiak, J.; Golan, T.; Drulis-Kawa, Z. arXiv 2021, arXiv:cs.CV/2108.01234.
  22. Mohseni Salehi, S.S.; Erdogmus, D.; Gholipour, A. Tversky loss function for image segmentation using 3D fully convolutional deep networks. International Workshop on Machine Learning in Medical Imaging. Springer, Springer, 2017, p. 379–387.
  23. Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings; Bengio, Y.; LeCun, Y., Eds., 2015.
  24. Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Goodfellow, I.; Harp, A.; Irving, G.; Isard, M.; Jia, Y.; Jozefowicz, R.; Kaiser, L.; Kudlur, M.; Levenberg, J.; Mané, D.; Monga, R.; Moore, S.; Murray, D.; Olah, C.; Schuster, M.; Shlens, J.; Steiner, B.; Sutskever, I.; Talwar, K.; Tucker, P.; Vanhoucke, V.; Vasudevan, V.; Viégas, F.; Vinyals, O.; Warden, P.; Wattenberg, M.; Wicke, M.; Yu, Y.; Zheng, X. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015. Software available from tensorflow.org.
  25. Müller, D.; Kramer, F. MIScnn: a framework for medical image segmentation with convolutional neural networks and deep learning. BMC Medical Imaging 2021, arXiv:eess.IV/1910.09308]21, arXiv:eess. [Google Scholar] [CrossRef] [PubMed]
  26. Merkel, D. Docker: lightweight linux containers for consistent development and deployment. Linux journal 2014, 2014, 2. [Google Scholar]
  27. Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. , UNet++: A Nested U-Net Architecture for Medical Image Segmentation: 4th International Workshop, DLMIA 2018, and 8th International Workshop, ML-CDS 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, September 20, 2018, Proceedings; 2018; Vol. 11045, pp. 3–11. [CrossRef]
  28. Zhang, Z.; Liu, Q. Road Extraction by Deep Residual U-Net. IEEE Geoscience and Remote Sensing Letters 2017, PP. [Google Scholar] [CrossRef]
  29. Kolařík, M.; Burget, R.; Uher, V.; Říha, K.; Dutta, M.K. Optimized High Resolution 3D Dense-U-Net Network for Brain and Spine Segmentation. Applied Sciences 2019, 9. [Google Scholar] [CrossRef]
  30. Ibtehaz, N.; Rahman, M.S. MultiResUNet : Rethinking the U-Net architecture for multimodal biomedical image segmentation. Neural Networks 2020, 121, 74–87. [Google Scholar] [CrossRef] [PubMed]
  31. Jumutc, V.; Bļizņuks, D.; Lihachev, A. Multi-Path U-Net Architecture for Cell and Colony-Forming Unit Image Segmentation. Sensors 2022, 22. [Google Scholar] [CrossRef] [PubMed]
1
for the binary mapping this means Y i j m i d = 1
2
raw counting based on the output of step 3 in Algorithm 1
3
using Algorithm 1 compeltely
4
according to MAE score in Eq.8 on the validation dataset
5
we report scores only for a single split
6
we report only reference numbers from [13]
Preprints 83699 g001
Figure 1. The examples of the original segmentation output map Y o u t and the one defined by the binary mapping F ↦ R 2 as Y m i d .
Figure 1. The examples of the original segmentation output map Y o u t and the one defined by the binary mapping F ↦ R 2 as Y m i d .
Preprints 83699 g001
Preprints 83699 g002
Figure 2. Preprocessing (2), Petri dish localization (3) and segmentation of the reflection zone (4).
Figure 2. Preprocessing (2), Petri dish localization (3) and segmentation of the reflection zone (4).
Preprints 83699 g002
Preprints 83699 g003
Figure 3. A schematic flow-diagram of an underlying algorithm for the reflection zone detection routine. We can underpin several blocks, such as search for C1 - Petri dish edge, C2 - glass edge and C3 - water edge. The final mask of the localized Petri dish bezel constitutes an area between C1 and C3 as can be noted from Figure 2 (3-4) as well.
Figure 3. A schematic flow-diagram of an underlying algorithm for the reflection zone detection routine. We can underpin several blocks, such as search for C1 - Petri dish edge, C2 - glass edge and C3 - water edge. The final mask of the localized Petri dish bezel constitutes an area between C1 and C3 as can be noted from Figure 2 (3-4) as well.
Preprints 83699 g003
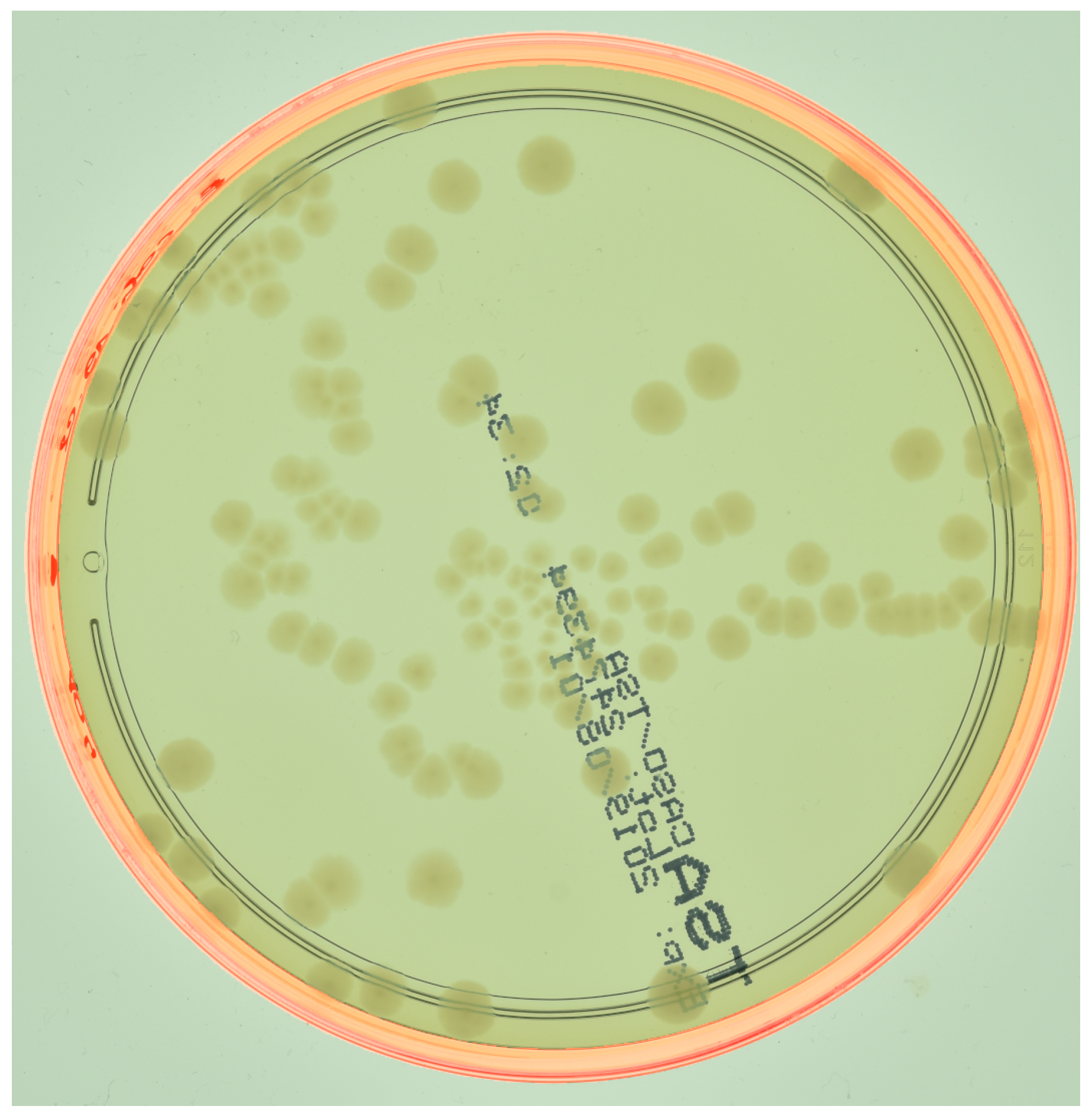
Preprints 83699 g004
Figure 4. The bezel localization mask of an agar plate (from the AGAR dataset described in Section 2.5) is outlined in red. For visual clarity, better viewed in color.
Figure 4. The bezel localization mask of an agar plate (from the AGAR dataset described in Section 2.5) is outlined in red. For visual clarity, better viewed in color.
Preprints 83699 g004
Preprints 83699 g005
Figure 5. CFU acounting web application. Web UI is composed of different widgets such as the one used for uploading images (top left) or viewing the statistics on the distribution of CFU sizes (top right). The slider is used to control the minimum considered area in pixels of the bacterial colony. Submitting input and button is used to provide a user feedback on the ground-truth CFU count. Other widgets represent the outcome of our hybrid approach such as an image with bounding boxes of CFUs (in red) or an agar plate (in blue) as well as estimated and corrected CFU counts. For visual clarity, better viewed in color.
Figure 5. CFU acounting web application. Web UI is composed of different widgets such as the one used for uploading images (top left) or viewing the statistics on the distribution of CFU sizes (top right). The slider is used to control the minimum considered area in pixels of the bacterial colony. Submitting input and button is used to provide a user feedback on the ground-truth CFU count. Other widgets represent the outcome of our hybrid approach such as an image with bounding boxes of CFUs (in red) or an agar plate (in blue) as well as estimated and corrected CFU counts. For visual clarity, better viewed in color.
Preprints 83699 g005
Preprints 83699 g006
Figure 6. Magnified examples of AGAR (a) and proprietary CFU (b) datasets.
Figure 6. Magnified examples of AGAR (a) and proprietary CFU (b) datasets.
Preprints 83699 g006
Preprints 83699 g007
Figure 7. The predicted segmentation output for the CFU test set image from the Dense U-Net architectures, i.e. Multi-Loss versus Single-Loss. The results are represented by blue bounding boxes around the segmented CFUs. All images are given in the normalized RGB spectrum, as described in Section 2.6. For visual clarity, better viewed in color.
Figure 7. The predicted segmentation output for the CFU test set image from the Dense U-Net architectures, i.e. Multi-Loss versus Single-Loss. The results are represented by blue bounding boxes around the segmented CFUs. All images are given in the normalized RGB spectrum, as described in Section 2.6. For visual clarity, better viewed in color.
Preprints 83699 g007
Preprints 83699 g008
Figure 8. CFU counting accuracies using our proposed hybrid system (leftmost) and three dedicated iOS applications: CFU.Ai (second to left), ColonyCount (second to right), OnePetri (rightmost). The ground-truth CFU count: 97.
Figure 8. CFU counting accuracies using our proposed hybrid system (leftmost) and three dedicated iOS applications: CFU.Ai (second to left), ColonyCount (second to right), OnePetri (rightmost). The ground-truth CFU count: 97.
Preprints 83699 g008
Preprints 83699 g009
Figure 9. CFU counting accuracies using our proposed hybrid system (leftmost) and three dedicated iOS applications: CFU.Ai (second to left), ColonyCount (second to right), OnePetri (rightmost). The ground-truth CFU count: 439.
Figure 9. CFU counting accuracies using our proposed hybrid system (leftmost) and three dedicated iOS applications: CFU.Ai (second to left), ColonyCount (second to right), OnePetri (rightmost). The ground-truth CFU count: 439.
Preprints 83699 g009
Table 1. Dataset characteristics.
Table 1. Dataset characteristics.
Dataset Number of Images Image Sizes
AGAR high-resolution 6990 3632 × 4000 × 3
Proprietary CFU 392 3024 × 3024 × 3
Table 2. CFU dataset’s counting results for YOLOv6, U-Net++, Plain U-Net, Dense U-Net, Residual U-Net and MultiRes U-Net architectures.
Table 2. CFU dataset’s counting results for YOLOv6, U-Net++, Plain U-Net, Dense U-Net, Residual U-Net and MultiRes U-Net architectures.
Architecture MAE sMAPE
YOLOv6 19.69 12.41
Single-Loss U-Net++ 18.54±4.33 14.12±3.51
Single-Loss Plain U-Net 40.44±7.04 23.30±3.05
Single-Loss Residual U-Net 21.24±5.58 15.38±5.04
Single-Loss Dense U-Net 19.14±3.07 14.14±2.36
Single-Loss MultiRes U-Net 15.14±1.70 10.37±2.21
Hybrid Single-Loss U-Net++ (ours) 15.93±2.76 11.47±2.41
Hybrid Single-Loss Plain U-Net (ours) 32.57±3.43 19.93±1.63
Hybrid Single-Loss Residual U-Net (ours) 18.51±3.24 13.53±3.88
Hybrid Single-Loss Dense U-Net (ours) 16.52±2.26 12.17±2.14
Hybrid Single-Loss MultiRes U-Net (ours) 14.13±1.13 9.20±1.61
Hybrid Multi-Loss U-Net++ (ours) 13.06±0.81 9.21±0.76
Hybrid Multi-Loss Plain U-Net (ours) 24.72±2.46 16.42±1.49
Hybrid Multi-Loss Residual U-Net (ours) 12.17±0.22 7.73±0.35
Hybrid Multi-Loss Dense U-Net (ours) 14.10±0.84 9.71±0.68
Hybrid Multi-Loss MultiRes U-Net (ours) 13.42±1.82 8.91±1.85
Table 3. AGAR dataset’s counting results for YOLOv6, U-Net++, Plain U-Net, Dense U-Net, Residual U-Net and MultiRes U-Net architectures.
Table 3. AGAR dataset’s counting results for YOLOv6, U-Net++, Plain U-Net, Dense U-Net, Residual U-Net and MultiRes U-Net architectures.
Architecture MAE sMAPE
YOLOv6 7.93 12.28
Single-Loss U-Net++ 17.70±5.10 36.08±17.39
Single-Loss Plain U-Net 3.05±0.08 3.11±0.22
Single-Loss Residual U-Net 11.93±1.85 17.33±3.83
Single-Loss Dense U-Net 17.74±6.70 27.31±9.84
Single-Loss MultiRes U-Net 7.55±1.75 10.34±2.48
Hybrid Single-Loss U-Net++ (ours) 17.76±5.07 36.20±17.43
Hybrid Single-Loss Plain U-Net (ours) 3.19±0.07 3.37±0.32
Hybrid Single-Loss Residual U-Net (ours) 11.57±1.96 16.98±3.82
Hybrid Single-Loss Dense U-Net (ours) 17.33±6.44 27.48±9.91
Hybrid Single-Loss MultiRes U-Net (ours) 6.91±1.57 9.12±2.18
Hybrid Multi-Loss U-Net++ (ours) 10.82±1.70 18.23±4.30
Hybrid Multi-Loss Plain U-Net (ours) 1.89±0.04 3.25±0.15
Hybrid Multi-Loss Residual U-Net (ours) 7.67±0.32 11.10±1.56
Hybrid Multi-Loss Dense U-Net (ours) 6.78±0.81 10.24±0.57
Hybrid Multi-Loss MultiRes U-Net (ours) 6.64±1.49 8.68±1.78
Table 6. Ablation study results for the CFU dataset. By Multi-Loss only we denote a U-Net architecture without any additional post-processing. By Multi-Loss (1) we denote a Multi-Loss architecture where CFU counting is done uniformly inside of X i n n e r ∪ X b e z e l . By Multi-Loss (2) we denote a full approach outlined in Algorithm 1.
Table 6. Ablation study results for the CFU dataset. By Multi-Loss only we denote a U-Net architecture without any additional post-processing. By Multi-Loss (1) we denote a Multi-Loss architecture where CFU counting is done uniformly inside of X i n n e r ∪ X b e z e l . By Multi-Loss (2) we denote a full approach outlined in Algorithm 1.
Architecture Multi-Loss only Multi-Loss (1) Multi-Loss (2)
MAE sMAPE MAE sMAPE MAE sMAPE
U-Net++ 16.00±1.90 13.01±2.22 13.63±0.87 9.93±0.77 13.06±0.81 9.21±0.76
Plain U-Net 28.65±2.79 18.61±1.58 27.84±2.83 18.02±1.56 24.72±2.46 16.42±1.49
Residual U-Net+ 12.87±0.49 8.75±0.59 12.75±0.45 8.64±0.54 12.18±0.22 7.73±0.35
Dense U-Net 15.73±1.17 11.08±0.83 15.36±1.11 10.80±0.79 14.10±0.84 9.71±0.68
MultiRes U-Net 14.90±3.08 10.33±2.65 14.44±2.65 9.90±2.25 13.42±1.82 8.91±1.85
Table 7. Ablation study results for the AGAR dataset. By Multi-Loss only we denote a U-Net architecture without any additional post-processing. By Multi-Loss (1) we denote a Multi-Loss architecture where CFU counting is done uniformly inside of X i n n e r ∪ X b e z e l . By Multi-Loss (2) we denote a full approach outlined in Algorithm 1.
Table 7. Ablation study results for the AGAR dataset. By Multi-Loss only we denote a U-Net architecture without any additional post-processing. By Multi-Loss (1) we denote a Multi-Loss architecture where CFU counting is done uniformly inside of X i n n e r ∪ X b e z e l . By Multi-Loss (2) we denote a full approach outlined in Algorithm 1.
Architecture Multi-Loss only Multi-Loss (1) Multi-Loss (2)
MAE sMAPE MAE sMAPE MAE sMAPE
U-Net++ 10.72±1.70 17.97±4.21 10.78±1.70 18.09±4.23 10.82±1.70 18.22±4.30
Plain U-Net 1.74±0.06 2.07±0.15 1.81±0.05 2.20±0.12 1.89±0.04 2.35±0.15
Residual U-Net+ 7.76±0.21 11.38±1.39 7.72±0.24 11.23±1.57 7.67±0.32 11.10±1.56
Dense U-Net 7.13±1.13 10.88±0.91 6.92±0.96 10.54±0.74 6.79±0.81 10.24±0.57
MultiRes U-Net 6.56±1.48 8.96±1.69 6.60±1.49 8.63±1.81 6.64±1.49 8.68±1.78
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated