Field Experiment for Prequalification Scheme of Distribution System Operator on Distributed Energy Resource Aggregations

1. Introduction

In order to drive cost-effective investment in distribution grid while increasing shares of renewable energy, authorities and utilities are exploring ways to increase hosting capacities using connect-and-manage connection arrangements or non-wire alternatives with battery storages [1]. In the past, traditional connect-and-forget connections arrangements have been based on a worst-case scenario, with limited hosting capacities that would not be a problem without any operational action. However, recent changes in grid connection policy have led to a situation where distribution system operators (DSOs) are forced to actively take operational measures in the event of distribution constraints, even though this allows more renewable energy to be accommodated on the same line capacity [2,3].

Meanwhile, regulators around the world are considering ways to increase the visibility of distributed energy resources (DERs) and integrate them into the governance of wholesale markets by providing higher levels of economic compensation to DERs that contribute to the grid to improve system reliability [4,5,6]. This literature contains ideas for institutionalizing participation in wholesale electricity markets by aggregating many small DERs that physically connect the distribution grid through new market participants such as distributed energy resource aggregators (DERAs) or virtual power plants (VPPs). This research was motivated by the fact that the space in which DERAs are financially rewarded is the wholesale market at the transmission level, but the resources they manage are physically distributed widely across the distribution grid. If there is enough DERs connected to the grid that may cause distribution constraints, and they want to participate in the wholesale market through a DERA, the DSO needs to prequalify the DERA's bidding actions. The prequalification process allows DSOs to receive DERA's day-ahead and real-time market bids in advance, review them for potential grid constraint events, and implement a system where only bids that pass the process are forwarded to the wholesale market. In the absence of such a system, DERA may act only to maximize revenue in the wholesale market without considering distribution constraints, causing a situation where the reliability of the distribution grid is greatly threatened.

Previous studies have implemented and studied various forms of such schemes. In one study, the DSO calculates power flows based on the VPP's bids and responds by performing grid reconfiguration if it anticipates a constraint problem, and if there is still a problem, it calculates the sensitivity of each VPP's resources and the amount of violation and delivers it to the VPP. The VPP will then adjust their scheduling and submit it to the DSO. In this case, it is characterized by utilizing a periodic rolling horizon update method to respond to future uncertainties [7]. Another study proposed a scheme in which the DSO and TSO each operate an own balancing market, and DER bids go directly to the TSO market bids if they do not cause problems on the distribution grid, and if they do, they are cleared within the DSO's balancing market first and the adjusted bids go to the TSO market [8]. On the other hand, [9] and [10] proposed a system for DSOs to verify bids of DERAs based on robust optimization for handling uncertainty in generation and load. These two papers are unique in that they propose an interaction scheme designed based on the legal authority of each entity in the real world, and they present the idea of converting a robust optimization based on chance-constrained optimization into a cooperative solution based on linearized information exchange between entities. In the most recent work, the DSO calculates and communicates the expected distribution system constraints according to the VPP's bidding plan, and the VPP also estimates its own distribution system constraints based on multiple scenario forecasts and utilizes them in actual operations. In this paper, the process of the DSO communicating distribution system constraints to the VPP occurs only once and does not include an iteration process [11].

In addition to the above theoretical research, field experiments are also being conducted in various countries. The EU's SmartNet project sought to design an optimized interaction scheme between TSO-DSOs and proposed five representative TSO-DSO coordination schemes: Centralized AS market model, Local AS market model, Shared balancing responsibility model, Common TSO-DSO AS market model, and Inte-grated flexibility market model [12]. OMI Polo Español S.A., an electricity market operator in Iberia, conducted the IREMEL project to define the operating model for the regional electricity market and to design and demonstrate mechanisms to address distribution system constraints that arise from the participation of distributed resources in the wholesale market [13]. The COOIDINET project in Spain, Sweden, and Greece is a demonstration of DSOs and TSOs working together to implement a cooperative system in a reliable and efficient manner. The project designed a TSO-DSO cooperation system in which congestion management in the distribution system is first addressed at the local DSO level, with priority access to local flexibility resources, and only unused bids are forwarded to the higher level system operator [14]. These demonstration projects took into account the market rules and power industry structure in each jurisdiction where the demonstration was conducted.

In Korea, a demonstration study of the TSO-DSO-DERA coordination scheme was conducted from August 2019 to August 2023, leaded by KEPCO, considering the current Korean power industry structure and market rules. In particular, this project focused on the interaction between DSO and DERAs who want to participate in the TSO's market, and conducted a demonstration of prequalification scheme on two distribution lines of KEPCO. The reference [9] and [10] are the deliverables from this demonstration project. In addition to the day-ahead prequalification, this project also included a demonstration of the direct control scheme of the DSO in a real-time situation, which is beyond the scope of this paper and is not described. This paper aims to summarize and share practical algorithm improvements and lessons learned based on the algorithm in the previous study in [9], as well as validation through real-world demonstration sites.

In Section 2, roles and responsibilities of relevant actors in the proposed scheme are presented. Section 3 and 4 describe the overall scheme of the proposed prequalification process and details of internal prequalification algorithm of DSO, respectively. Section 5 provides results of field experiment of the prequalification scheme on the real demonstration sites in Korea. Section 6 presents the concluding remarks of this study.

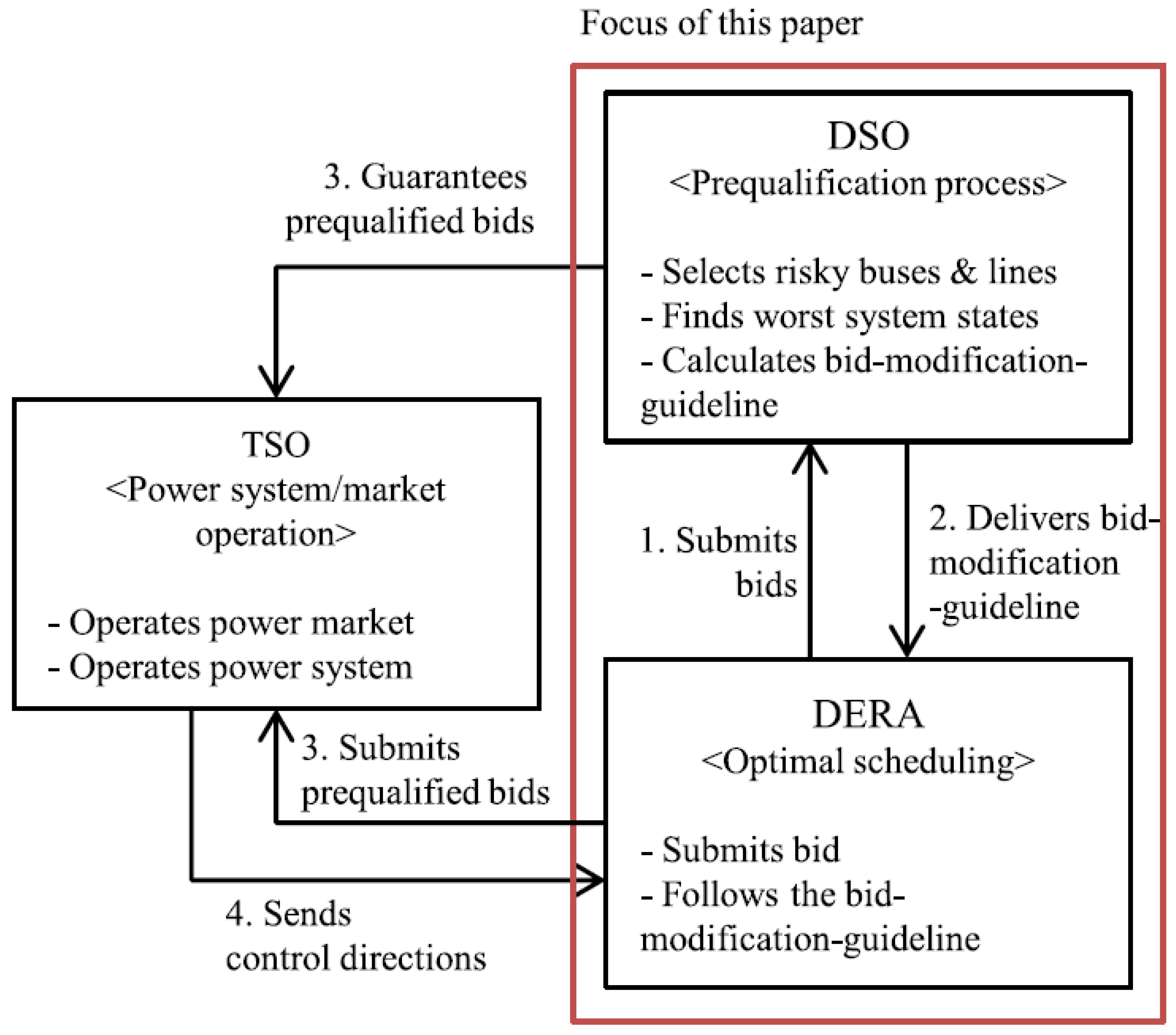
2. Role and Responsibilities of Relevant Actors

In this section, we describe the roles and responsibilities of each actor involved in the DSO's prequalification scheme assumed in this study. This can be depicted as shown in Figure 1.

In order to understand the demonstration results of this paper, it is necessary to first understand the theoretical content of the prequalification scheme that the entire consortium research team was trying to implement, as well as the governance of the Korean electricity industry. The governance and actor-specific roles and responsibilities assumptions in this study are not based on exploring all the theoretically possible cases as in other previous studies, but rather on the premise of minimal effort to maintain as much as possible within the current structure and the recently revised laws and regulations. It can be said that the focus was on ensuring that there is not much difference between what was tested in the demonstration study and the system that will be implemented in the real world in the future.

In Korea, the DSO, the entity that actually implements and operates the prequalification scheme, is the state-owned power company, KEPCO. It directly operates transmission, distribution, and sales businesses and has six power generation companies as subsidiaries with a portfolio of large traditional power generation sources [15]. Retail business license raises a conflict of interest argument for KEPCO to act as a DSO, but the South Korean government attempts to control this through direct oversight. In practice, the resources of KEPCO's generation companies are mainly large coal, nuclear, and gas-fired generation, and they rarely enter the distribution-level DER market.

Meanwhile, South Korea recently enacted a special law to promote the installation of DERs, which will take effect in 2024. The law explicitly stipulates the operating rights and responsibilities of distribution business license holders. Currently, KEPCO is the sole distribution business license holder. The law allows DSOs to forcibly disconnect loads or DERs in emergency situations where reliability is threatened, but the right to curtail on a regular basis was excluded from the National Assembly's discussion. Therefore, individual arrangements for output control between DERs or DERAs representing them and DSOs are needed to resolve potential distribution constraints caused by DERs.

Because DERA is a private entity that recruits DERs to directly participate in the wholesale market and earn revenue, it is not responsible for the reliability of the distribution or transmission grid, but through the national grid code and the network access agreement with KEPCO, it can be disconnected due to the decision of a certain TSO or DSO if it threatens the reliability of the network. From DERA's perspective, it has an motivation to coordinate with DSOs to trade off the risk of total disconnection for the bounded risk of partial curtailment.

In South Korea, the Korea Power Exchange (KPX) operates the wholesale market and transmission system, similar to independent system operators in the United States. They are not directly responsible for coordinating and managing distribution system constraints caused by DERs, unless the constraints extend to transmission system issues, as the Electricity Business Act delegates operational responsibility for the power system below 154kV to KEPCO.

Table 1. Operator in power system by voltage levels in Korea.

Voltage Level	Operator
≥ 154kV	ISO (KPX)
70kV and 22.9 kV Dedicated transmission line	TO (KEPCO)
≤ 22.9kV distribution line	DSO (KEPCO)

Table 1. Operator in power system by voltage levels in Korea.

Voltage Level	Operator
≥ 154kV	ISO (KPX)
70kV and 22.9 kV Dedicated transmission line	TO (KEPCO)
≤ 22.9kV distribution line	DSO (KEPCO)

3. Overall Prequalification Scheme of DSO on Market Participation of DERA

The DSO's prequalification module designed in the demonstration project interacts with DERA's bidding module as shown in the following figure. Before the DERA submits a bid to the wholesale market, the DERA requests a prequalification procedure for the bid to the DSO, and the DSO's prequalification module uses an internal algorithm to review the potential constraints of the distribution system based on the expected generation of the DER under the DERA's bid.

Figure 2. Overall interaction process of DSO and DEAR in the proposed prequalification scheme.

Figure 2. Overall interaction process of DSO and DEAR in the proposed prequalification scheme.

Here is a breakdown of the entire process shown in the figure above.

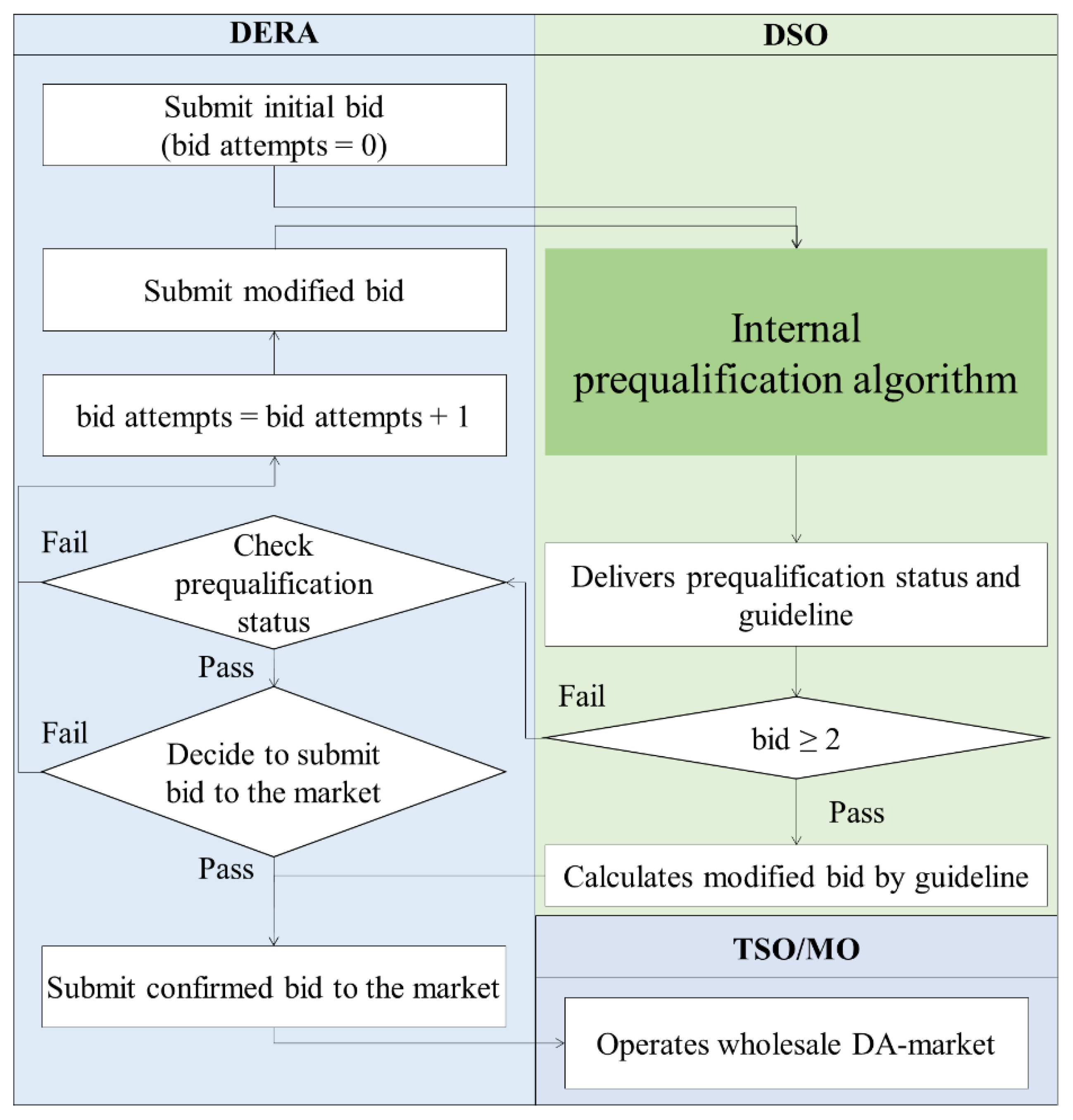
1) 

Submission of initial bids to DSO by DERA 

The DERA submits bids to the DSO prior to the participation of wholesale market between 00:00 and 09:00 on D-1. The DERA determines and submits initial energy and reserve bids based on the generation forecast of the DERs managed by itself and its bidding strategy. It is allowed to continuously modify the bids during these hours.

2) 

Execution of internal prequalification algorithm of DSO 

The proposed day-ahead prequalification algorithm is executed as a module of the DSO's internal distribution operation system. The algorithm is completed within 15 minutes between 09:00 and 09:15 on D-1. The algorithm performs robust optimization by considering the initial bids submitted by DERAs, the load of each distribution node predicted by the DSO itself, and the forecast error range of each node. The DSO performs the optimization with the goal of maximizing the sum of the DERAs' 24-hour generation in order to minimize the output curtailment of the DERAs. The result of the algorithm is the maximum biddable capacity of the DERs at each node and the upper and lower bounds of the biddable output for storage resources. The resulting bid-modification-guideline values are passed to the DERA. The DERA is obliged to comply with the modification guidelines for bids that are determined to threaten the reliability of the distribution system according to the grid access agreement with the DSO.

3) 

Iteration of DERA’s bid modification and DSO’s re-prequalification under the bid-modification-guidelines 

The DERA will modify the output setpoints of each resource in light of the bid-modification-guidelines received from the DSO and resubmit them to the DSO. The first modified bid submission will take place during D-1 09:15-09:30, and the prequalification algorithm for it will take place between 09:30-09:45. The second modified bid submission will take place between D-1 09:45 and 10:00, and the prequalification algorithm for it will take place between D-1 10:00 and 10:15. Since the second modified bid submission is the third bid submitted by the DERA, if it does not pass prequalification by this time, the DSO will be forced to apply the last provided bid-modification-guidelines to end the process. This is because, due to time constraints in real-world system operation, it is not possible to give an infinite number of chances, so in this demonstration study, we set a total of three chances including the initial bidding after trial and error. This can be customized according to the market operation timeline of each jurisdiction applying prequalification.

4) 

Start of existing transmission-level wholesale market with the qualified bids of DERAs

Qualified Bid will be delivered to the transmission-level wholesale market as the one of bids from conventional market participants.

4. Efficient Prequalification Algorithm of DSO based on Robust Optimization

In this section, we detail the formulation of the prequalification and the algorithm to solve it efficiently, based on robust optimization approach, so that the DSO can support the market participation of DERAs while maintaining the reliability of the distribution system. For this purpose, we use the following nomenclature.

Sets and Indices
$b,i, j, k$	Subscripts for buses
$l$	Subscripts for lines
$b_{rsk}, l_{rsk}$	Subscripts for risky buses and lines
$t, a$	Subscripts for DER and DERA
$s, s\text{'}$	Subscripts for iterations
$\mathcal{N},\mathcal{L}$	Set of buses and lines
${\mathcal{N}}_{rsk\_ovv}, {\mathcal{N}}_{rsk\_udv}, {\mathcal{L}}_{rsk\_uof}, {\mathcal{L}}_{rsk\_dof}$	Set of overvoltage, undervoltage risky buses and upper overflow, down overflow risky lines
${\mathcal{G}}_i^a\supset {\mathcal{S}}_i^a,{\mathcal{R}}_i^a$	Set of DER, storage, and DER with reserve of DERA a on bus i
$\mathcal{A}$	Set of DERA
${\mathcal{X}}_{PF}^s, {\mathcal{X}}_{V\_OV}^s, {\mathcal{X}}_{V\_UV}^s, {\mathcal{X}}_{F\_UF}^s, {\mathcal{X}}_{F\_DF}^s, {\mathcal{X}}_{bid}^s$	Set of result of power flow, worst overvoltage state, worst undervoltage state, worst upper overflow state, worst down overflow state and revised bidding in iteration s
Parameters
$G_{ij}, B_{ij}$	Conductance and susceptance of the line between bus i and j [p.u.]
$\overline{V}, \underset{\_}{V}$	Upper and lower limit of the voltage magnitude [p.u.]
${\overline{S}}_{f,l}$	Upper rate capacity of line l [p.u.]
${\overline{P}}_{g,t}$	Rate capacity of DER t [p.u.]
${\overline{∆P}}_{g,t},{\underset{\_}{∆P}}_{g,t}$	Increase and decrease controllable amount of DRES t [p.u.]
$p_{g,t}^{ini},q_{g,t}^{ini}$	Active and reactive power of DRES t in initial bidding of CVPP [p.u.]
$r_{u,t}^{ini},r_{d,t}^{ini}$	Ramp up and down reserve power of DRES t in initial bidding of CVPP [p.u.]
$\overline{p_{g,t}^{ini}},\underset{\_}{p_{g,t}^{ini}}$	Upper and lower active power of DRES t in initial bidding of CVPP [p.u.]
${\overline{P}}_{d,i},{\overline{Q}}_{d,i}$	Demand forecast of bus i [p.u.]
$\underset{\_}{\mathrm{p}\mathrm{f}}$	A lower limit of the power factor
${\sigma }_{g,t}^{high}, {\sigma }_{g,t}^{low}$	Upper and lower uncertainty range of output of DER t [p.u.]
${\sigma }_{d,t}^{high}, {\sigma }_{d,i}^{low}$	Upper and lower uncertainty range of demand forecast of bus i [p.u.]
${OV}_{i,a}^s, {UV}_{i,a}^s$	Overvoltage and Undervoltage violation on bus i of DERA a in iteration s [p.u.]
${UF}_{l,a}^s, {DF}_{l,a}^s$	Upper overflow and down overflow violation on line l of DERA a in iteration s [p.u.]
$S{n}_{ovp,i,j}^s,S{n}_{ovq,i,j}^s$	Overvoltage magnitude sensitivity of active and reactive power on bus j to bus i to in iteration s at overvoltage worst case
$S{n}_{uvp,i,j}^s,S{n}_{uvq,i,j}^s$	Undervoltage magnitude sensitivity of active and reactive power on bus j to bus i to in iteration s at undervoltage worst case
$S{n}_{usp,l,k}^s,S{n}_{usq,l,k}^s$	Squared complex flow sensitivity of active and reactive power on bus k to line l to in iteration s at upper overflow worst case
$S{n}_{dsp,l,k}^s,S{n}_{dsq,l,k}^s$	Squared complex flow sensitivity of active and reactive power on bus k to line l to in iteration s at down overflow worst case
${Allc}_{ov,i,a}^s,{Allc}_{uv,i,a}^s$	Allocation factor of overvoltage and undervoltage violation on bus i of DERA a in iteration s
${Allc}_{uf,l,a}^s,{Allc}_{df,l,a}^s$	Allocation factor of upper and down overflow violation on line l of DERA a in iteration s
${ϵ}_V, {ϵ}_F, {ϵ}_{Bid}$	Criteria of overvoltage security, overflow security and convergence of bid revision
Decision Variables
$p_{g,t}^s, q_{g,t}^s$	Active and reactive power of DER t in iteration s [p.u.]
$r_{u,t}^s, r_{d,t}^s$	Ramp up and ramp down reserve power of DER t in iteration s [p.u.]
$\overline{p_{g,t}^s},\underset{\_}{p_{g,t}^s}$	Upper and lower active power of DER t in iteration s [p.u.]
${∆p}_{g,t}^s, {∆q}_{g,t}^s$	Adjustment of active and reactive power of DER t in iteration s [p.u.]
$\overline{{∆p}_{g,t}^s}, \underset{\_}{{∆p}_{g,t}^s}$	Adjustment of Upper and lower active power of DER t in iteration s [p.u.]
$p_i^s, q_i^s$	Active and reactive injected power on bus i in iteration s [p.u.]
$\left|v_i^s\right|, {\theta }_i^s$	Magnitude and angle of voltage on bus i in iteration s [p.u.]
${\xi }_{g,i}^s, {\xi }_{d,i}^s$	Forecast error rate of the DER output and demand on bus i in iteration s
$s_{f,l}^s, p_{f,l}^s, q_{f,l}^s$	Complex, active and reactive power flow on line l in iteration s [p.u.]
${\theta }_{ij}^s,{\theta }_l^s$	Angle of voltage between bus i and bus j or on line l in iteration s [p.u.]
$u_{g,t}^s$	Dropout binary variable of DER t in iteration s
Auxiliary Variables
$p_{g,t}^{s,ab}, q_{g,t}^{s,ab}$	Absolute value of active and reactive power difference of DER t between initial bid and iteration s [p.u.]
$r_{u,t}^{s,ab}, r_{d,t}^{s,ab}$	Absolute value of Ramp up and ramp down reserve power difference of DER t between initial bid and iteration s [p.u.]
$p_{st,t}^{s,dch}, q_{st,t}^{s,dch}$	Active and reactive discharging power of storage DER t in iteration s [p.u.]
$p_{st,t}^{s,ch}, q_{st,t}^{s,ch}$	Active and reactive charging power of storage DER t in iteration s [p.u.]
$v_{st,t}^s$	Charging state binary variable of storage DER t in iteration s
Binary Variables
${\xi }_{g,i}^s, {\xi }_{d,i}^s$	Forecast error rate of the DER output and demand on bus i in iteration s

4.1. Original formulation for prequalification

We assumed that the distribution grid has the following three properties:

• DSOs are regulated entities and strive to be neutral, and as public entities, they strive to maximize social welfare;
• The load is inflexible and is supplied with electricity at a fixed tariff. It is important to note that this is not very different from the actual empirical environment in Korea;
• Only DERs based on renewable energy sources with zero-marginal-cost characteristics are connected to the distribution grid, and they are also price-takers.

By the first property, the basic objective function of DSO can be formulated as social welfare maximization. If we restrict a region of the distribution system under the DSO's jurisdiction to one ecosystem, the social welfare of this ecosystem can be expressed as the sum of the surplus of customers and producers. In this environment, consumer surplus is invariant with respect to the amount of electricity generation because the second property assumes that customers are price takers and not price responsive. Producers' surplus is constrained by the physical environment of the distribution grid, and their surplus can be maximized by generating as much as possible under these constraints. Considering the uncertainty inherent in the output of DERs, the social welfare maximization problem in this environment can be formulated as a chance-constrained problem with the following equations, which has already been presented in [9].

$\underset{X}{\max }\mathbb{E}\left[\sum _{i\in \mathcal{G}}{\tilde{p}}_{g,i}\right]$ (1a)

subject to

${\tilde{p}}_{g,i}=p_{g,i}\bullet {\xi }_{g,i}$, $\forall i\in \mathcal{G}$ (1b)

${\tilde{q}}_{g,i}=q_{g,i}\bullet {\xi }_{g,i}$, $\forall i\in \mathcal{G}$ (1c)

${\tilde{P}}_{d,i}={\overline{P}}_{d,i}\bullet {\xi }_{d,i}$, $\forall i\in \mathcal{N}$ (1d)

${\tilde{Q}}_{d,i}={\overline{Q}}_{d,i}\bullet {\xi }_{d,i}$, $\forall i\in \mathcal{N}$ (1e)

$\mathrm{P}\mathrm{r}\left\{\left|v_i\left(\xi \right)\right|\le \overline{V}\right\}\ge 1-ϵ, \forall i\in \mathcal{N}\setminus \left\{1\right\}$ (1f)

$\mathrm{P}\mathrm{r}\left\{{\left|s_{f,l}\left(\xi \right)\right|}^2\le {{\overline{S}}^2}_{f,l}\right\}\ge 1-ϵ, \forall i\in \mathcal{L}$ (1g)

$G\left({\mathit{p}}_{\mathit{g}},{\mathit{q}}_{\mathit{g}},\left|{\mathit{v}}_{\mathit{i}}\left(\mathit{\xi }\right)\right|,\left|{\mathit{s}}_{\mathit{f},\mathit{l}}\left(\mathit{\xi }\right)\right|,\mathit{x}\left(\mathit{\xi }\right),\mathit{\xi }\right)\le 0$ (1h)

$H\left({\mathit{p}}_{\mathit{g}},{\mathit{q}}_{\mathit{g}},\left|{\mathit{v}}_{\mathit{i}}\left(\mathit{\xi }\right)\right|,\left|{\mathit{s}}_{\mathit{f},\mathit{l}}\left(\mathit{\xi }\right)\right|,\mathit{x}\left(\mathit{\xi }\right),\mathit{\xi }\right)=0$ (1i)

Assume that ${{\mathit{p}}^{\mathit{*}}}_{\mathit{g}}$ and ${{\mathit{q}}^{\mathit{*}}}_{\mathit{g}}$ are the optimal solution of eq. (1), then we obtain ${\xi }^{*,i}$ and ${\xi }^{*,l}$ which can maximize $\left|{\mathit{v}}_{\mathit{i}}\left(\mathit{\xi }\right)\right|$ and $\left|{\mathit{s}}_{\mathit{f},\mathit{l}}\left(\mathit{\xi }\right)\right|$, respectively. ${{\mathit{p}}^{\mathit{*}}}_{\mathit{g}}$ and ${{\mathit{q}}^{\mathit{*}}}_{\mathit{g}}$ will satisfy the chance-constraints eq. (1f, 1g). Then, in this optimal case, the chance constraints can be rewritten into a deterministic form, which can be presented in following eq. (2):

$\left|v_i\left(\xi \right)\right|\le \overline{V}$, $\forall i\in \mathcal{N}\setminus \left\{1\right\}$ (2a)

${\left|s_{f,l}\left(\xi \right)\right|}^2\le {{\overline{S}}^2}_{f,l}$, $\forall i\in \mathcal{L}$ (2b)

The essence of the algorithm proposed in the reference [9] is that a simple examination of the overvoltage and overflow cases is sufficient to find a solution close to the optimal solution of Eq. (1). The bus voltages in the grid are positively correlated with each other, and so are the line flow on each line. This has already been proven in section V-D of [9]. Applying this tendency, we can find the worst overvoltage case ${\xi }^{v, rsk}$ by finding the scenario that maximizes the sum of the voltages of each risky bus for ${\mathcal{N}}_{rsk}$, the set of buses that are likely to exceed the constraint, and the worst overflow case ${\xi }^{f, rsk}$ by finding the scenario that maximizes the sum of the usage rates for ${\mathcal{L}}_{rsk}$. The same principle can be applied to undervoltage. Once the power generation vectors of each node corresponding to ${\xi }^{v, rsk}$ and ${\xi }^{f, rsk}$ have been determined, the effect of the change in active and reactive power of each node on the voltage of each node and line flow of each line around these values can be formulated as a linear approximation using the sensitivity matrix from power flow equation, and this approximation can be substituted into Eq. (2) to find the bid-modification-guideline, which is the active and reactive power setpoint for each node that does not exceed the constraints of the distribution system. This idea is the main finding of reference [9]. Using this idea, [9] solves a complex full robotization problem like Eq. (1), but instead of solving a complex problem, they proposed an efficient algorithm that consists of a series of simple computations to obtain the desired solution.

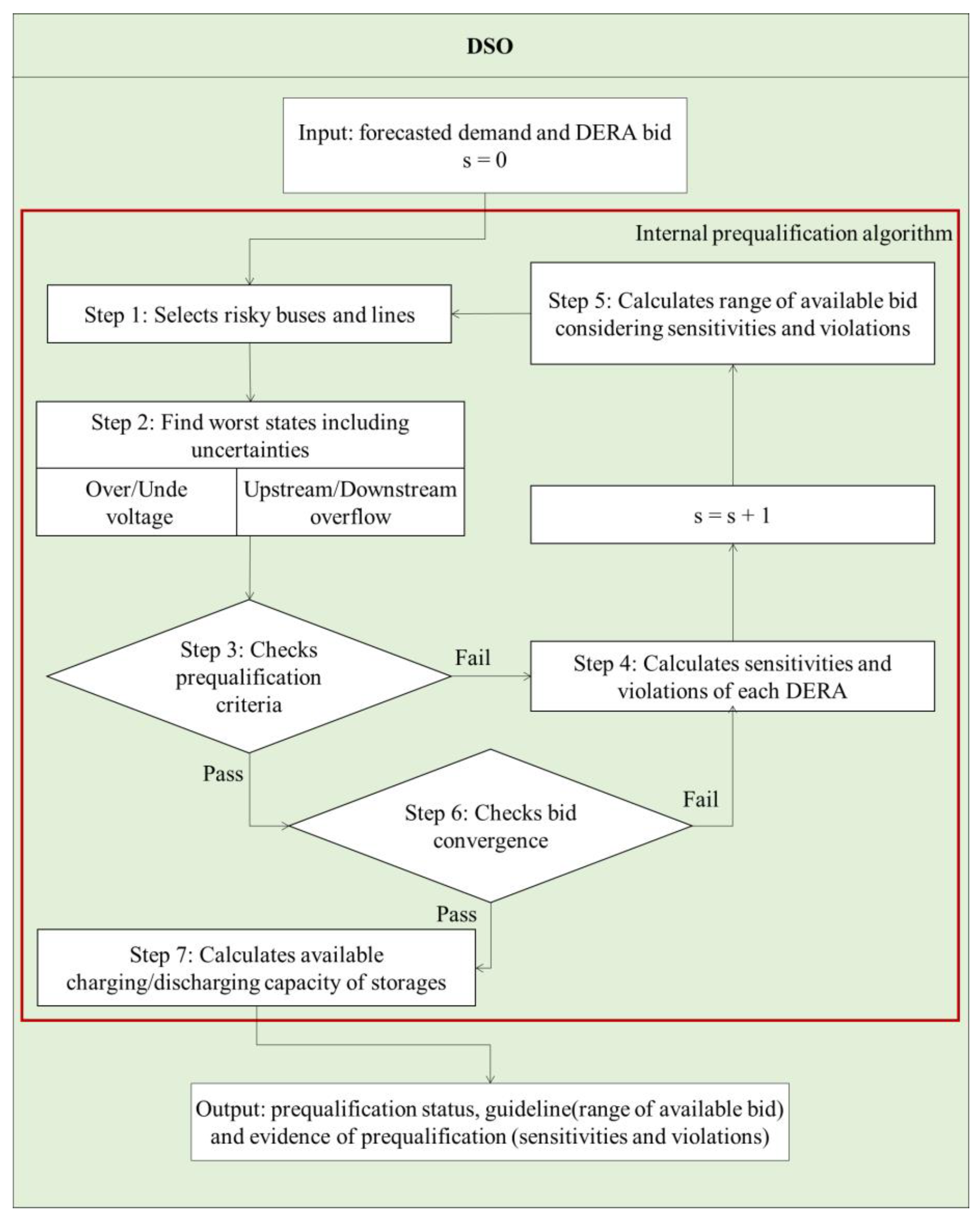
4.2. Efficient prequalification algorithm implemented in field experiment

In this paper, we have adapted the algorithm from the reference [9] for field experiment and summarized it with step-by-step formulas. The specific differences from the previous paper are summarized in the following subsections 4.3.

• Step 1: Selection of risky nodes and lines 

The DSO conducts a power flow calculation of the distribution system under its jurisdiction, based on the bidding information submitted by DERA and own load forecast of the DSO. From the results of the power flow calculation, the risky set is determined by determining which lines exceed the overvoltage/undervoltage risk threshold or the reverse/forward overflow risk threshold.

${\theta }_1^s=0, \left|v_1^s\right|=1$ (3a)

$p_i^s=\left|v_i^s\right|\sum _{j\in \mathcal{N}}\left|v_j^s\right|\left(G_{ij}\cos {\theta }_{ij}^s+B_{ij}\sin {\theta }_{ij}^s\right), \forall i\in \mathcal{N}$ (3b)

$q_i^s=\left|v_i^s\right|\sum _{j\in \mathcal{N}}\left|v_j^s\right|\left(G_{ij}\sin {\theta }_{ij}^s-B_{ij}\cos {\theta }_{ij}^s\right), \forall i\in \mathcal{N}$ (3c)

$p_{f,l}^s=\left|v_i^s\right|\left|v_j^s\right|\left(G_{ij}\cos {\theta }_{ij}^s+B_{ij}\sin {\theta }_{ij}^s\right)-G_{ij}{\left|v_i^s\right|}^2, \forall \left(i,j\right)=\forall l\in \mathcal{L}$ (3d)

$q_{f,l}^s=\left|v_i^s\right|\left|v_j^s\right|\left(G_{ij}\sin {\theta }_{ij}^s-B_{ij}\cos {\theta }_{ij}^s\right)+B_{ij}{\left|v_i^s\right|}^2, \forall \left(i,j\right)=\forall l\in \mathcal{L}$ (3e)

${\left|s_{f,l}^s\right|}^2={\left(p_{f,l}^s\right)}^2+{\left(q_{f,l}^s\right)}^2, \forall l\in \mathcal{L}$ (3f)

$p_i^s=\sum _{t\in {\mathcal{G}}_i}{p}_{g,t}^s-{\overline{P}}_{d,i}, \forall i\in \mathcal{N}$ (3g)

$q_i^s=\sum _{t\in {\mathcal{G}}_i}{q}_{g,t}^s-{\overline{Q}}_{d,i}, \forall i\in \mathcal{N}$ (3h)

${\mathcal{N}}_{rsk\_ovv}^s=\left\{b_{rsk}^{s^{\text{'}}}|b_{rsk}^{s^{\text{'}}}=\underset{b\in \mathcal{N}}{\arg \max }\left(\left|v_b^{s^{\text{'}}}\right|-\overline{v}\right), \left|v_b^{s^{\text{'}}}\right|\in \left|{\mathit{v}}^{s^{\text{'}}}\right|\in {\mathcal{X}}_{PF}^{s^{\text{'}}}, \forall s^{\text{'}}\le s\right\}$ (4a)

(${\mathcal{N}}_{rsk\_udv}^s=\left\{b_{rsk}^{s^{\text{'}}}|b_{rsk}^{s^{\text{'}}}=\underset{b\in \mathcal{N}}{\arg \min }\left(\left|v_b^{s^{\text{'}}}\right|-\overline{v}\right), \left|v_b^{s^{\text{'}}}\right|\in \left|{\mathit{v}}^{s^{\text{'}}}\right|\in {\mathcal{X}}_{PF}^{s^{\text{'}}}, \forall s^{\text{'}}\le s\right\}$ (4b)

${\mathcal{L}}_{rsk\_uof}^s=\left\{l_{rsk}^{s^{\text{'}}}|l_{rsk}^{s^{\text{'}}}=\underset{l\in \mathcal{L}}{\arg \max }\left(\frac{\left|s_{f,l}^{s^{\text{'}}}\right|-{\overline{S}}_{f,l}}{{\overline{S}}_{f,l}}\right), \left|s_{f,l}^{s^{\text{'}}}\right|\in \left|{\mathit{s}}^{s^{\text{'}}}\right|\in {\mathcal{X}}_{PF}^{s^{\text{'}}}, \forall s^{\text{'}}\le s,p_{f,l}^{s^{\text{'}}}\in R^{-} \right\}$ (4c)

${\mathcal{L}}_{rsk\_dof}^s=\left\{l_{rsk}^{s^{\text{'}}}|l_{rsk}^{s^{\text{'}}}=\underset{l\in \mathcal{L}}{\arg \max }\left(\frac{\left|s_{f,l}^{s^{\text{'}}}\right|-{\overline{S}}_{f,l}}{{\overline{S}}_{f,l}}\right), \left|s_{f,l}^{s^{\text{'}}}\right|\in \left|{\mathit{s}}^{s^{\text{'}}}\right|\in {\mathcal{X}}_{PF}^{s^{\text{'}}}, \forall s^{\text{'}}\le s,p_{f,l}^{s^{\text{'}}}\in R^{+} \right\}$ (4d)

• Step 2: Exploration of worst-case scenario considering uncertainty ranges 

The DSO considers the forecast error of DERs and loads, and the amount each DER responds to the frequency control signal from the TSO. For each of the four cases, overvoltage, undervoltage, reverse overflow, and forward overflow, the worst-case scenario is explored where each value of the risky nodes and lines within the considered uncertainty ranges causes the greatest violation of grid constraints.

$\underset{{\mathcal{X}}_{V\_\mathit{OV}}^s}{\max }\sum _{i\in {\mathcal{N}}_{rsk\_ovv}^s}\left|v_i^s\right|$ (5a)

subject to

(3a-3c)

$1-{\sigma }_{d,i}^{low}\le {\xi }_{d,i}^s\le 1+{\sigma }_{d,i}^{high}, \forall i\in \mathcal{N}$ (5b)

$1-\frac{\sum _{t\in {\mathcal{G}}_i-{\mathcal{R}}_i}{p}_{g,t}^s{\sigma }_{g,i}^{low}+\sum _{t\in {\mathcal{R}}_i}{r}_{d,t}^s}{\sum _{t\in {\mathcal{G}}_i}{p}_{g,t}^s}\le {\xi }_{g,i}^s\le 1+\frac{\sum _{t\in {\mathcal{G}}_i-{\mathcal{R}}_i}{p}_{g,t}^s{\sigma }_{g,i}^{high}+\sum _{t\in {\mathcal{R}}_i}{r}_{u,t}^s}{\sum _{t\in {\mathcal{G}}_i}{p}_{g,t}^s}, \forall i\in \mathcal{N}$ (5c)

$p_i^s={\xi }_{g,i}^s\sum _{t\in {\mathcal{G}}_i}{p}_{g,t}^s-{\overline{P}}_{d,i}{\xi }_{d,i}^s, \forall i\in \mathcal{N}$ (5d)

$q_i^s={\xi }_{g,i}^s\sum _{t\in {\mathcal{G}}_i}{q}_{g,t}^s-{\overline{Q}}_{d,i}{\xi }_{d,i}^s, \forall i\in \mathcal{N}$ (5e)

$\underset{{\mathcal{X}}_{V\_\mathit{UV}}^s}{\min }\sum _{i\in {\mathcal{N}}_{rsk\_udv}^s}\left|v_i^s\right|$ (6)

subject to

(3a-3c, 5b-5e)

$\underset{{\mathcal{X}}_{F\_\mathit{UF}}^s}{\max }\sum _{l\in {\mathcal{L}}_{rsk\_uof}^s}{\left|s_{f,l}^s\right|}^2/{\left|{\overline{S}}_{f,l}\right|}^2$ (7)

subject to

(3a – 3f, 5b – 5e)

$\underset{{\mathcal{X}}_{F\_\mathit{DF}}^s}{\max }\sum _{l\in {\mathcal{L}}_{rsk\_dof}^s}{\left|s_{f,l}^s\right|}^2/{\left|{\overline{S}}_{f,l}\right|}^2$ (8)

subject to

(3a-3f, 5b-5e)

• Step 3: Check of grid constraint violation 

The DSO verifies that all grid constraints are not violated in all worst-case scaenrios found in Step 2. If any violations occurred, go to Step 4; if none existed, go directly to Step 6.

${OV}_i^s=\left|v_i^s\right|-\overline{v}, \forall i\in \mathcal{N},\left|v_i^s\right|\in \left|{\mathit{v}}^s\right|\in {\mathcal{X}}_{V_{OV}}^s$ (9a)

${UV}_i^s=\underset{\_}{v}-\left|v_i^s\right|, \forall i\in \mathcal{N},\left|v_i^s\right|\in \left|{\mathit{v}}^s\right|\in {\mathcal{X}}_{V\_UV}^s$ (9b)

${UF}_l^s={\left|s_{f,l}^s\right|}^s-{\left|{\overline{S}}_{f,l}\right|}^2, \forall l\in \mathcal{L},\left|s_{f,l}^s\right|\in \left|{\mathit{s}}_f^s\right|\in {\mathcal{X}}_{F\_UF}^s$ (9c)

${DF}_l^s={\left|s_{f,l}^s\right|}^s-{\left|{\overline{S}}_{f,l}\right|}^2, \forall l\in \mathcal{L},\left|s_{f,l}^s\right|\in \left|{\mathit{s}}_f^s\right|\in {\mathcal{X}}_{F\_DF}^s$ (9d)

$\mathit{max}{\mathit{O}\mathit{V}}^s\le {ϵ}_V$ (10a)

$\mathit{max}{\mathit{U}\mathit{V}}^s\le {ϵ}_V$ (10b)

$\mathit{max}{\mathit{U}\mathit{F}}^s\le {ϵ}_F$ (10c)

$\mathit{max}{\mathit{D}\mathit{F}}^S\le {ϵ}_F$ (10d)

• Step 4: Calculation of sensitivity matrix of each DERA and allocation of violation information 

The DSO calculates the sensitivity matrix regarding the impacts of DERs on each node and line for each worst-case scenario. Based on this information, the DSO allocates the violation information to each DERA.

$\left[\begin{array}{c}∆{\mathit{\theta }}_{-1}^s\\ ∆{\left|{\mathit{v}}_{-1}\right|}^s\end{array}\right]={\left.{\left[\begin{array}{cc}{\mathit{J}}_{p\theta }^s\left(\mathit{x}\right)& {\mathit{J}}_{p\left|v\right|}^s\left(\mathit{x}\right)\\ {\mathit{J}}_{q\theta }^s\left(\mathit{x}\right)& {\mathit{J}}_{q\left|v\right|}^s\left(\mathit{x}\right)\end{array}\right]}^{-1}\right|}_{\mathit{x}={\mathcal{X}}_{V\_OV}^s}\left[\begin{array}{c}∆{\mathit{p}}_{-1}^s\\ ∆{\mathit{q}}_{-1}^s\end{array}\right]=\left[\begin{array}{cc}{\mathit{S}\mathit{n}}_{o\theta p}^s\left(\mathit{x}\right)& {\mathit{S}\mathit{n}}_{ovp}^s\left(\mathit{x}\right)\\ {\mathit{S}\mathit{n}}_{o\theta q}^s\left(\mathit{x}\right)& {\mathit{S}\mathit{n}}_{ovq}^s\left(\mathit{x}\right)\end{array}\right]\left[\begin{array}{c}∆{\mathit{p}}_{-1}^s\\ ∆{\mathit{q}}_{-1}^s\end{array}\right]$ (11a)

$\left[\begin{array}{c}∆{\mathit{\theta }}_{-1}^s\\ ∆{\left|{\mathit{v}}_{-1}\right|}^s\end{array}\right]={\left.{\left[\begin{array}{cc}{\mathit{J}}_{p\theta }^s\left(\mathit{x}\right)& {\mathit{J}}_{p\left|v\right|}^s\left(\mathit{x}\right)\\ {\mathit{J}}_{q\theta }^s\left(\mathit{x}\right)& {\mathit{J}}_{q\left|v\right|}^s\left(\mathit{x}\right)\end{array}\right]}^{-1}\right|}_{\mathit{x}={\mathcal{X}}_{V\_UV}^s}\left[\begin{array}{c}∆{\mathit{p}}_{-1}^s\\ ∆{\mathit{q}}_{-1}^s\end{array}\right]=\left[\begin{array}{cc}{\mathit{S}\mathit{n}}_{o\theta p}^s\left(\mathit{x}\right)& {\mathit{S}\mathit{n}}_{ovp}^s\left(\mathit{x}\right)\\ {\mathit{S}\mathit{n}}_{o\theta q}^s\left(\mathit{x}\right)& {\mathit{S}\mathit{n}}_{ovq}^s\left(\mathit{x}\right)\end{array}\right]\left[\begin{array}{c}∆{\mathit{p}}_{-1}^s\\ ∆{\mathit{q}}_{-1}^s\end{array}\right]$ (11b)

${Sn}_{usp,l,k}^s=\frac{\partial {\left|s_{f,l}\right|}^2}{\partial p_k}={\left.2\left(p_{f,l}^s\frac{\partial p_{f,l}}{\partial p_k}+q_{f,l}^s\frac{\partial q_{f,l}}{\partial p_k}\right)\right|}_{\mathit{x}={\mathcal{X}}_{F\_UF}^s}, \forall l\in \mathcal{L}$ (12a)

${Sn}_{usq,l,k}^s=\frac{\partial {\left|s_{f,l}\right|}^2}{\partial q_k}={\left.2\left(p_{f,l}^s\frac{\partial p_{f,l}}{\partial q_k}+q_{f,l}^s\frac{\partial q_{f,l}}{\partial q_k}\right)\right|}_{\mathit{x}={\mathcal{X}}_{F\_UF}^s}, \forall l\in \mathcal{L}$ (12b)

${Sn}_{dsp,l,k}^s=\frac{\partial {\left|s_{f,l}\right|}^2}{\partial p_k}={\left.2\left(p_{f,l}^s\frac{\partial p_{f,l}}{\partial p_k}+q_{f,l}^s\frac{\partial q_{f,l}}{\partial p_k}\right)\right|}_{\mathit{x}={\mathcal{X}}_{F\_DF}^s}, \forall l\in \mathcal{L}$ (12c)

${Sn}_{dsq,l,k}^s=\frac{\partial {\left|s_{f,l}\right|}^2}{\partial q_k}={\left.2\left(p_{f,l}^s\frac{\partial p_{f,l}}{\partial q_k}+q_{f,l}^s\frac{\partial q_{f,l}}{\partial q_k}\right)\right|}_{\mathit{x}={\mathcal{X}}_{F\_DF}^s}, \forall l\in \mathcal{L}$ (12d)

${OV}_i^s=\sum _{a\in \mathcal{A}}{OV}_{i,a}^s, \forall i\in \mathcal{N}$ (13a)

${UV}_i^s=\sum _{a\in \mathcal{A}}{UV}_{i,a}^s, \forall i\in \mathcal{N}$ (13b)

${UF}_l^s=\sum _{a\in \mathcal{A}}{UF}_{l,a}^s, \forall l\in \mathcal{L}$ (13c)

${DF}_l^s=\sum _{a\in \mathcal{A}}{DF}_{l,a}^s, \forall l\in \mathcal{L}$ (13d)

${OV}_{i,a}^s=\frac{{OV}_i^s*{Allc}_{ov,i,a}^s}{\sum _{a\in \mathcal{A}}{Allc}_{ov,i,a}^s}, \forall i\in \mathcal{N}$ (14a)

${UV}_{i,a}^s=\frac{{UV}_i^s*{Allc}_{uv,i,a}^s}{\sum _{a\in \mathcal{A}}{Allc}_{uv,i,a}^s}, \forall i\in \mathcal{N}$ (14b)

${UF}_{l,a}^s=\frac{{UF}_l^s*{Allc}_{uf,l,a}^s}{\sum _{a\in \mathcal{A}}{Allc}_{uf,l,a}^s}, \forall l\in \mathcal{L}$ (14c)

${DF}_{l,a}^s=\frac{{DF}_l^s*{Allc}_{df,l,a}^s}{\sum _{a\in \mathcal{A}}{Allc}_{df,l,a}^s}, \forall l\in \mathcal{L}$ (14d)

${Allc}_{ov,i,a}^s=\sum _{j\in \mathcal{N}}\left({Sn}_{ovp,i,j}^s\sum _{t\in {\mathcal{G}}_j^a}{p}_{g,t}^s\right), \forall i\in \mathcal{N},\forall a\in \mathcal{A}$ (15a)

${Allc}_{uv,i,a}^s=\sum _{j\in \mathcal{N}}\left({Sn}_{uvp,i,j}^s\sum _{t\in {\mathcal{G}}_j^a}{p}_{g,t}^s\right), \forall i\in \mathcal{N},\forall a\in \mathcal{A}$ (15b)

${Allc}_{uf,l,a}^s=\sum _{j\in \mathcal{N}}\left({Sn}_{usp,l,k}^s\sum _{t\in {\mathcal{G}}_k^a}{p}_{g,t}^s\right), \forall l\in \mathcal{L},\forall a\in \mathcal{A}$ (15c)

${Allc}_{df,l,a}^s=\sum _{k\in \mathcal{N}}\left({Sn}_{dsp,l,k}^s\sum _{t\in {\mathcal{G}}_k^a}{p}_{g,t}^s\right), \forall l\in \mathcal{L},\forall a\in \mathcal{A}$ (15d)

• Step 5: Calculation of maximum allowable bids based on sensitivity matrix and constraints violations 

This step calculates the maximum allowable bids for each DERA, taking into account the sensitivity of the DERs calculated in Step 4 and the amount of constraint violations distributed among the DERAs. The objective function of the DERA is set to minimize the difference between the initial bid and the revised bid based on the iterative process.

$-{OV}_{i,a}^s\ge \sum _{j\in \mathcal{N}}\left({Sn}_{ovp,i,j}^s\sum _{t\in {\mathcal{G}}_j^a}\overline{{∆p}_{g,t}^s}+{Sn}_{ovq,i,j}^s\sum _{t\in {\mathcal{G}}_j^a}{∆q}_{g,t}^s\right), \forall i\in \mathcal{N}$ (16a)

$-{OV}_{i,a}^s\ge \sum _{j\in \mathcal{N}}\left({Sn}_{ovp,i,j}^s\sum _{t\in {\mathcal{G}}_j^a}\underset{\_}{{∆p}_{g,t}^s}+{Sn}_{ovq,i,j}^s\sum _{t\in {\mathcal{G}}_j^a}{∆q}_{g,t}^s\right), \forall i\in \mathcal{N}$ (16b)

$-{UV}_{i,a}^s\ge \sum _{j\in \mathcal{N}}\left({Sn}_{uvp,i,j}^s\sum _{t\in {\mathcal{G}}_j^a}\overline{{∆p}_{g,t}^s}+{Sn}_{uvq,i,j}^s\sum _{t\in {\mathcal{G}}_j^a}{∆q}_{g,t}^s\right), \forall i\in \mathcal{N}$ (16c)

$-{UV}_{i,a}^s\ge \sum _{j\in \mathcal{N}}\left({Sn}_{uvp,i,j}^s\sum _{t\in {\mathcal{G}}_j^a}\underset{\_}{{∆p}_{g,t}^s}+{Sn}_{uvq,i,j}^s\sum _{t\in {\mathcal{G}}_j^a}{∆q}_{g,t}^s\right), \forall i\in \mathcal{N}$ (16d)

$-{UF}_{l,a}^s\ge \sum _{k\in \mathcal{N}}\left({Sn}_{usp,l,k}^s\sum _{t\in {\mathcal{G}}_k^a}\overline{{∆p}_{g,t}^s}+{Sn}_{usq,l,k}^s\sum _{t\in {\mathcal{G}}_k^a}{∆q}_{g,t}^s\right), \forall l\in \mathcal{L}$ (16e)

$-{UF}_{l,a}^s\ge \sum _{k\in \mathcal{N}}\left({Sn}_{usp,l,k}^s\sum _{t\in {\mathcal{G}}_k^a}\underset{\_}{{∆p}_{g,t}^s}+{Sn}_{usq,l,k}^s\sum _{t\in {\mathcal{G}}_k^a}{∆q}_{g,t}^s\right), \forall l\in \mathcal{L}$ (16f)

$-{DF}_{l,a}^s\ge \sum _{k\in \mathcal{N}}\left({Sn}_{dsp,l,k}^s\sum _{t\in {\mathcal{G}}_k^a}\overline{{∆p}_{g,t}^s}+{Sn}_{dsq,l,k}^s\sum _{t\in {\mathcal{G}}_k^a}{∆q}_{g,t}^s\right), \forall l\in \mathcal{L}$ (16g)

$-{DF}_{l,a}^s\ge \sum _{k\in \mathcal{N}}\left({Sn}_{dsp,l,k}^s\sum _{t\in {\mathcal{G}}_k^a}\underset{\_}{{∆p}_{g,t}^s}+{Sn}_{dsq,l,k}^s\sum _{t\in {\mathcal{G}}_k^a}{∆q}_{g,t}^s\right), \forall l\in \mathcal{L}$ (16h)

$\underset{{\mathcal{X}}_{\mathit{bm}}^s}{\mathit{min}}\sum _{t\in {\mathcal{G}}^a-{\mathcal{S}}^a}\left(\left|p_{g,t}^{ini}-p_{g,t}^s\right|+\left|q_{g,t}^{ini}-q_{g,t}^s\right|\right)+m\sum _{t\in {\mathcal{S}}^a}\left(\left|p_{g,t}^{ini}-p_{g,t}^s\right|+\left|q_{g,t}^{ini}-q_{g,t}^s\right|\right)+\sum _{t\in {\mathcal{R}}^a}\left(\left|r_{u,t}^{ini}-r_{u,t}^s\right|+\left|r_{d,t}^{ini}-r_{d,t}^s\right|\right)$ (17a)

Subject to

(16)

$\overline{p_{g,t}^s}=\left\{\begin{array}{cc}{p}_{g,t}^s+r_{u,t}^s,& \forall t\in {\mathcal{R}}^a\\ p_{g,t}^s,& \forall t\in {\mathcal{G}}^a-{\mathcal{R}}^a\end{array}\right.$ (17b)

$\underset{\_}{p_{g,t}^s}=\left\{\begin{array}{cc}{p}_{g,t}^s-r_{u,t}^s,& \forall t\in {\mathcal{R}}^a\\ p_{g,t}^s,& \forall t\in {\mathcal{G}}^a-{\mathcal{R}}^a\end{array}\right.$ (17c)

$\overline{p_{g,t}^s}=\overline{p_{g,t}^{s-1}}+\overline{{∆p}_{g,t}^s}, \forall t\in {\mathcal{G}}^a$ (17d)

$\underset{\_}{p_{g,t}^s}=\underset{\_}{p_{g,t}^{s-1}}+\underset{\_}{{∆p}_{g,t}^s}, \forall t\in {\mathcal{G}}^a$ (17e)

$\left(\overline{p_{g,t}^{ini}}-{\underset{\_}{∆P}}_{g,t}\right)u_{g,t}^s\le \overline{p_{g,t}^s}\le \left(\overline{p_{g,t}^{ini}}+{\overline{∆P}}_{g,t}\right)u_{g,t}^s, \forall t\in {\mathcal{G}}^a$ (17f)

$\left(\overline{p_{g,t}^{ini}}-{\underset{\_}{∆P}}_{g,t}\right)u_{g,t}^s\le \underset{\_}{p_{g,t}^t}\le \left(\overline{p_{g,t}^{ini}}+{\overline{∆P}}_{g,t}\right)u_{g,t}^s, \forall t\in {\mathcal{G}}^a$ (17g)

$\left(q_{g,t}^{ini}-{\underset{\_}{∆Q}}_{g,t}\right)u_{g,t}^s\le q_{g,t}^s\le \left(q_{g,t}^{ini}+{\overline{∆Q}}_{g,t}\right)u_{g,t}^s, \forall t\in {\mathcal{G}}^a$ (17h)

${\mathit{max}\left(\left|\overline{p_{g,t}^s}\right|,\left|\underset{\_}{p_{g,t}^s}\right|\right)}^2+{\left(q_{g,t}^s\right)}^2\le {\overline{P}}_{g,t}^2, \forall t\in {\mathcal{G}}^a$ (17i)

$\left|q_{g,t}^s\right|\le \left|p_{g,t}^s\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)\right|, \forall t\in {\mathcal{G}}^a$ (17j)

$p_{g,t}^{s,ab}\ge p_{g,t}^{ini}-p_{g,t}^s, \forall t\in {\mathcal{G}}^a$ (18a)

$p_{g,t}^{s,ab}\ge -p_{g,t}^{ini}+p_{g,t}^s, \forall t\in {\mathcal{G}}^a$ (18b)

$q_{g,t}^{s,ab}\ge q_{g,t}^{ini}-q_{g,t}^s, \forall t\in {\mathcal{G}}^a$ (18c)

$q_{g,t}^{s,ab}\ge -q_{g,t}^{ini}+q_{g,t}^s, \forall t\in {\mathcal{G}}^a$ (18d)

$r_{u,t}^{s,ab}\ge r_{u,t}^{ini}-r_{u,t}^s, \forall t\in {\mathcal{R}}^a$ (18e)

$r_{u,t}^{s,ab}\ge -r_{u,t}^{ini}+r_{u,t}^s, \forall t\in {\mathcal{R}}^a$ (18f)

$r_{d,t}^{s,ab}\ge r_{d,t}^{ini}-r_{d,t}^s, \forall t\in {\mathcal{R}}^a$ (18g)

$r_{d,t}^{s,ab}\ge -r_{d,t}^{ini}+r_{d,t}^s, \forall t\in {\mathcal{R}}^a$ (18h)

$q_{g,t}^s\ge \frac{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}{\sqrt{{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}^2+1}-1}\left(\overline{p_{g,t}^s}-{\overline{P}}_{g,t}\right), \forall t\in {\mathcal{G}}^a$ (19a)

$q_{g,t}^s\le -\frac{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}{\sqrt{{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}^2+1}-1}\left(\overline{p_{g,t}^s}-{\overline{P}}_{g,t}\right), \forall t\in {\mathcal{G}}^a$ (19b)

$q_{g,t}^s\ge -\frac{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}{\sqrt{{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}^2+1}-1}\left(\underset{\_}{p_{g,i}^s}+{\overline{P}}_{g,t}\right), \forall t\in {\mathcal{G}}^a$ (19c)

$q_{g,t}^s\le \frac{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}{\sqrt{{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}^2+1}-1}\left(\underset{\_}{p_{g,i}^s}+{\overline{P}}_{g,t}\right), \forall t\in {\mathcal{G}}^a$ (19d)

$q_{g,t}^s\ge \left\{\begin{array}{cc}-p_{g,t}^s\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right),& if p_{g,t}^s\ge 0\\ p_{g,t}^s\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right),& otherwise\end{array}\right., \forall t\in {\mathcal{G}}^a$ (20a)

$q_{g,t}^s\le \left\{\begin{array}{cc}{p}_{g,t}^s\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right),& if p_{g,t}^s\ge 0\\ -p_{g,t}^s\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right),& otherwise\end{array}\right., \forall t\in {\mathcal{G}}^a$ (20b)

$q_{g,t}^s\ge -p_{g,t}^s\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right), \forall t\in {\mathcal{G}}^a-{\mathcal{S}}^a$ (21a)

$q_{g,t}^s\le p_{g,t}^s\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right), \forall t\in {\mathcal{G}}^a-{\mathcal{S}}^a$ (21b)

$p_{g,t}^s=p_{st,t}^{s,dch}-p_{st,t}^{s,ch}, \forall t\in {\mathcal{S}}^a$ (22a)

$q_{g,t}^s=q_{st,t}^{s,dch}-q_{st,t}^{s,ch}, \forall t\in {\mathcal{S}}^a$ (22b)

$p_{st,t}^{s,dch}\le {\overline{P}}_{g,t}{v}_{st,t}^s, \forall t\in {\mathcal{S}}^a$ (22c)

$p_{st,t}^{s,ch}\le {\overline{P}}_{g,t}\left(1-v_{st,t}^s\right), \forall t\in {\mathcal{S}}^a$ (22d)

$q_{st,t}^{s,dch}\ge -p_{st,t}^{s,dch}\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right), \forall t\in {\mathcal{S}}^a$ (23a)

$q_{st,t}^{s,dch}\le p_{st,t}^{s,dch}\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right), \forall t\in {\mathcal{S}}^a$ (23b)

$q_{st,t}^{s,ch}\ge -p_{st,t}^{s,ch}\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right), \forall t\in {\mathcal{S}}^a$ (23c)

$q_{st,t}^{s,ch}\le p_{st,t}^{s,ch}\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right), \forall t\in {\mathcal{S}}^a$ (23d)

$\underset{{\mathcal{X}}_{\mathit{bid}}^s}{\mathit{min}}\sum _{t\in {\mathcal{G}}^a-{\mathcal{S}}^a}\left(p_{g,t}^{s,ab}+q_{g,t}^{s,ab}\right)+m\sum _{t\in {\mathcal{S}}^a}\left(p_{g,t}^{s,ab}+q_{g,t}^{s,ab}\right)+\sum _{t\in {\mathcal{G}}^a}\left(r_{u,t}^{s,ab}+r_{d,t}^{s,ab}\right)$ (24)

subject to

(16, 17b-17h, 18, 19, 21-23)

• Step 6: Check the convergence of modified bids

This step checks that the bid value is not too different from the bid value of the previous iteration if it passed the criteria in Step 3. Since the power flow equation is nonlinear and we consider it by linearizing it in the form of sensitivity, there may be an error from the actual optimal value. To reduce this, this iteration step is performed.

$\mathit{max}\left\{\left|\overline{p_{g,t}^s}-\overline{p_{g,t}^{s-1}}\right||t\in {\mathcal{G}}^a\right\}\le {ϵ}_{Bid}$ (25a)

$\mathit{max}\left\{\left|\underset{\_}{p_{g,t}^s}-\underset{\_}{p_{g,t}^{s-1}}\right||t\in {\mathcal{G}}^a\right\}\le {ϵ}_{Bid}$ (25b)

$\mathit{max}\left\{\left|q_{g,t}^s-q_{g,t}^{s-1}\right||t\in {\mathcal{G}}^a\right\}\le {ϵ}_{Bid}$ (25c)

• Step 7: Additional calculation of upper and lower bounds for outputs of storage resources 

It is a step for the DSO to calculate and communicate to DERAs the upper and lower bounds of storage output that will not affect the reliability of the grid.

$\underset{\begin{array}{c}{\mathit{p}}_{\mathit{st}}, {\mathit{q}}_{\mathit{st}}\\ {∆\mathit{p}}_{\mathit{st}}, {∆\mathit{q}}_{\mathit{st}}\end{array}}{\mathit{max}}\sum _{t\in {\mathcal{S}}^a}{p}_{st,t}$ (26a)

Subject to

$p_{st,t}=p_{g,t}^{end}+{∆p}_{st,t}, \forall t\in {\mathcal{S}}^a$ (26b)

$q_{st,t}=q_{g,t}^{end}+{∆q}_{st,t}, \forall t\in {\mathcal{S}}^a$ (26c)

$\overline{p_{g,t}^{ini}}-{\underset{\_}{∆P}}_{g,t}+r_{d,t}^{end}\le p_{st,t}\le \overline{p_{g,t}^{ini}}+{\overline{∆P}}_{g,t}-r_{u,t}^{end}, \forall t\in {\mathcal{S}}^a$ (26d)

$q_{g,t}^{ini}-{\underset{\_}{∆Q}}_{g,t}\le q_{st,t}\le q_{g,t}^{ini}+{\overline{∆Q}}_{g,t}, \forall t\in {\mathcal{S}}^a$ (26e)

$-{OV}_{i,a}^{end}\ge \sum _{j\in \mathcal{N}}\left({Sn}_{ovp,i,j}^{end}\sum _{t\in {\mathcal{S}}_j^a}{∆p}_{st,t}+{Sn}_{ovq,i,j}^{end}\sum _{t\in {\mathcal{S}}_j^a}{∆q}_{st,t}\right), \forall i\in \mathcal{N}$ (26f)

$-{UV}_{i,a}^{end}\ge \sum _{j\in \mathcal{N}}\left({Sn}_{uvp,i,j}^{end}\sum _{t\in {\mathcal{S}}_j^a}{∆p}_{st,t}+{Sn}_{uvq,i,j}^{end}\sum _{t\in {\mathcal{S}}_j^a}{∆q}_{st,t}\right), \forall i\in \mathcal{N}$ (26g)

$-{UF}_{l,a}^{end}\ge \sum _{k\in \mathcal{N}}\left({Sn}_{usp,l,k}^{end}\sum _{t\in {\mathcal{S}}_k^a}{∆p}_{st,t}+{Sn}_{usq,l,k}^{end}\sum _{t\in {\mathcal{S}}_k^a}{∆q}_{st,t}\right), \forall l\in \mathcal{L}$ (26h)

$-{DF}_{l,a}^{end}\ge \sum _{k\in \mathcal{N}}\left({Sn}_{dsp,l,k}^{end}\sum _{t\in {\mathcal{S}}_k^a}{∆p}_{st,t}+{Sn}_{dsq,l,k}^{end}\sum _{t\in {\mathcal{S}}_k^a}{∆q}_{st,t}\right), \forall l\in \mathcal{L}$ (26i)

$\mathit{max}\left({\left(p_{st,t}+r_{u,t}^{end}\right)}^2,{\left(p_{st,t}-r_{d,t}^{end}\right)}^2 \right)+{\left(q_{st,t}\right)}^2\le {\overline{P}}_{g,t}^2, \forall t\in {\mathcal{S}}^a$ (26j)

$\left|q_{st,t}\right|\le \left|p_{st,t}\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)\right|, \forall t\in {\mathcal{S}}^a$ (26k)

$q_{st,t}\ge \frac{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}{\sqrt{{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}^2+1}-1}\left(p_{st,t}+r_{u,t}^{end}-{\overline{P}}_{g,t}\right), \forall t\in {\mathcal{S}}^a$ (27a)

$q_{st,t}\le -\frac{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}{\sqrt{{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}^2+1}-1}\left(p_{st,t}+r_{u,t}^{end}-{\overline{P}}_{g,t}\right), \forall t\in {\mathcal{S}}^a$ (27b)

$q_{st,t}\ge -\frac{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}{\sqrt{{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}^2+1}-1}\left(p_{st,t}-r_{d,t}^{end}+{\overline{P}}_{g,t}\right), \forall t\in {\mathcal{S}}^a$ (27c)

$q_{st,t}\le \frac{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}{\sqrt{{\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right)}^2+1}-1}\left(p_{st,t}-r_{d,t}^{end}+{\overline{P}}_{g,t}\right), \forall t\in {\mathcal{S}}^a$ (27d)

$p_{st,t}=p_{st,t}^{dch}-p_{st,t}^{ch}, \forall t\in {\mathcal{S}}^a$ (28a)

$q_{st,t}=q_{st,t}^{dch}-q_{st,t}^{ch}, \forall t\in {\mathcal{S}}^a$ (28b)

$p_{st,t}^{dch}\le {\overline{P}}_{g,t}{v}_{st,t}, \forall t\in {\mathcal{S}}^a$ (28c)

$p_{st,t}^{ch}\le {\overline{P}}_{g,t}\left(1-v_{st,t}\right), \forall t\in {\mathcal{S}}^a$ (28d)

$q_{st,t}^{dch}\ge -p_{st,t}^{dch}\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right), \forall t\in {\mathcal{S}}^a$ (29a)

$q_{st,t}^{dch}\le p_{st,t}^{dch}\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right), \forall t\in {\mathcal{S}}^a$ (29b)

$q_{st,t}^{ch}\ge -p_{st,t}^{ch}\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right), \forall t\in {\mathcal{S}}^a$ (29c)

$q_{st,t}^{ch}\le p_{st,t}^{ch}\mathit{tan}\left({\mathit{cos}}^{-1}\left(\underset{\_}{pf}\right)\right), \forall t\in {\mathcal{S}}^a$ (29d)

A flow chart representation of the entire algorithm from step1 to step6 is shown in Figure 3.

4.3. Improvements in the implemented algorithm compared to previous work

This demonstration study tried to improve some settings and shorten the execution time of the proposed algorithm in the previous theoretical studies through the trial and error in the practical implementation. In this section, we will express and explain the meaning of the additions for each group of formulars in the previous section compared to that of the algorithm in [9].

• Equation (4b), (4d), (6), (8), (9b), (9d), (10b), and (10d)

The previous study [9] did not consider the possibility of undervoltage or forward overcurrent problems in a distribution system with a lot of DERs, but in the actual demonstration environment, there were very rare cases of such situations due to tap adjustment of transformer voltage or the influence of other existing voltage control facilities, and the algorithm was modified to prepare for all cases. Therefore, when selecting cases that exceed the risk criteria, overvoltage, undervoltage, reverse overcurrent, and forward overcurrent are all checked by adding the eq. (4b) and eq. (4d).

• Equation (5c) 

While the previous algorithm in [9] have treated the participation of DERs in ancillary services as an uncertainty for the DSO, this study changes the formula to take into account the reserve bidding as well as uncertainty of DERs.

• Equation (13a)-(13d), (14a)-(14d), (15a)-(15d), and (16a)-(16h) 

In the original theoretical study [9], the algorithm was designed so that the DSO would deliver a sensitivity matrix with grid information to a DERA as a bid-modification guideline. The intention in the scheme was to convey as much information as possible and allow the DERA to formulate a bid strategy with maximum discretion. However, during the course of the demonstration project, the DERAs participating in the demonstration claimed that too much discretion given to them entailed high costs and project management uncertainty in the early project stages, and that they preferred a bid-modification guideline in the form of a range of absolute output values given by the DSO. This allowed the iteration process to proceed but limited the information exchanged by modifying the initial algorithm to a range of absolute output values in a matrix. In the future, as more capable and strategic DERAs enter the market, we expect to see an evolution back toward more discretion, similar to the form of the original study. In addition, while the original study only considered a single DERA, we have added formulas to distribute the information in the case of multiple DERAs by calculating their contribution to the amount of violations.

• Equation (17a)-(17j)

In the existing algorithm, even if the DERA makes a bid modification, in each iteration the DSO calculates the bid-modification-guideline for the purpose of Eq. (1a), the field experiment results show that the decision of DERA to reduce its output is ignored. When the DERA has a storage and strategically intends to reduce its output at a certain time and increase its sales at another time, the DSO makes a decision regardless of the DERA's intention. This was a violation of the DERA's free-will and discretion, so we added the equations above to modify the prequalification to best honor the DERA's strategy in the original bid.

• Equation (18a)-(18h), (19a)-(19d), (20a), (20b), (21a), (21b), (22a)-(22d), (23a)-(23d), and (24) 

In this paper, auxiliary variables were used to linearize the objective function and conditional constraints in absolute value form in the DSO control procedure, and the power factor operating range of the DERs were linearized to avoid considering regions that cannot be solved in the first place. These measures were taken to improve the speed of the algorithm during the validation process.

• Equation (25a)-(25c) 

In addition, real-world demonstration results showed that the process of calculating corrective bids in the algorithm did not converge and oscillated with large deviations in value, so we added a function that finds a corrective bid that does not cause a violation and terminates itself when this happens.

• Equation (26a)-(26k), (27a)-(27d), (28a)-(28d), and (29a)-(29d) 

The existing algorithm does not explicitly assume the existence of DERA's storage resources. The prequalification process does not converge in a limited number of iteration if all operations of storages are autonomously left to DERAs. Therefore, during the demonstration process, we devised the method that allows the DERA to schedule storage resources for its own benefit but allows DSOs to calculate and communicate the upper and lower biddable output limits in a contextualized manner that does not threaten the grid.

• Others 

On the other hand, in the real-world demonstration process, there was a problem of computational speed compared to the theoretical simulation in the lab. This was caused by the problem of using an open-source solver instead of a commercial solver due to license issues, which was managed by improving the performance of the algorithm. In particular, the existing algorithm performed sequential computations for all time indices, but the improved algorithm was modified to run the algorithm in parallel for multiple time indices by increasing the processor of the computer for demonstration.

5. Results of Field Experiment

We conducted a demonstration using a real distribution line as the target site to verify the validity of the proposed prequalification scheme. In this section, we describe the configuration of the demonstration site and show that the proposed scheme works well in the real world through the demonstration results.

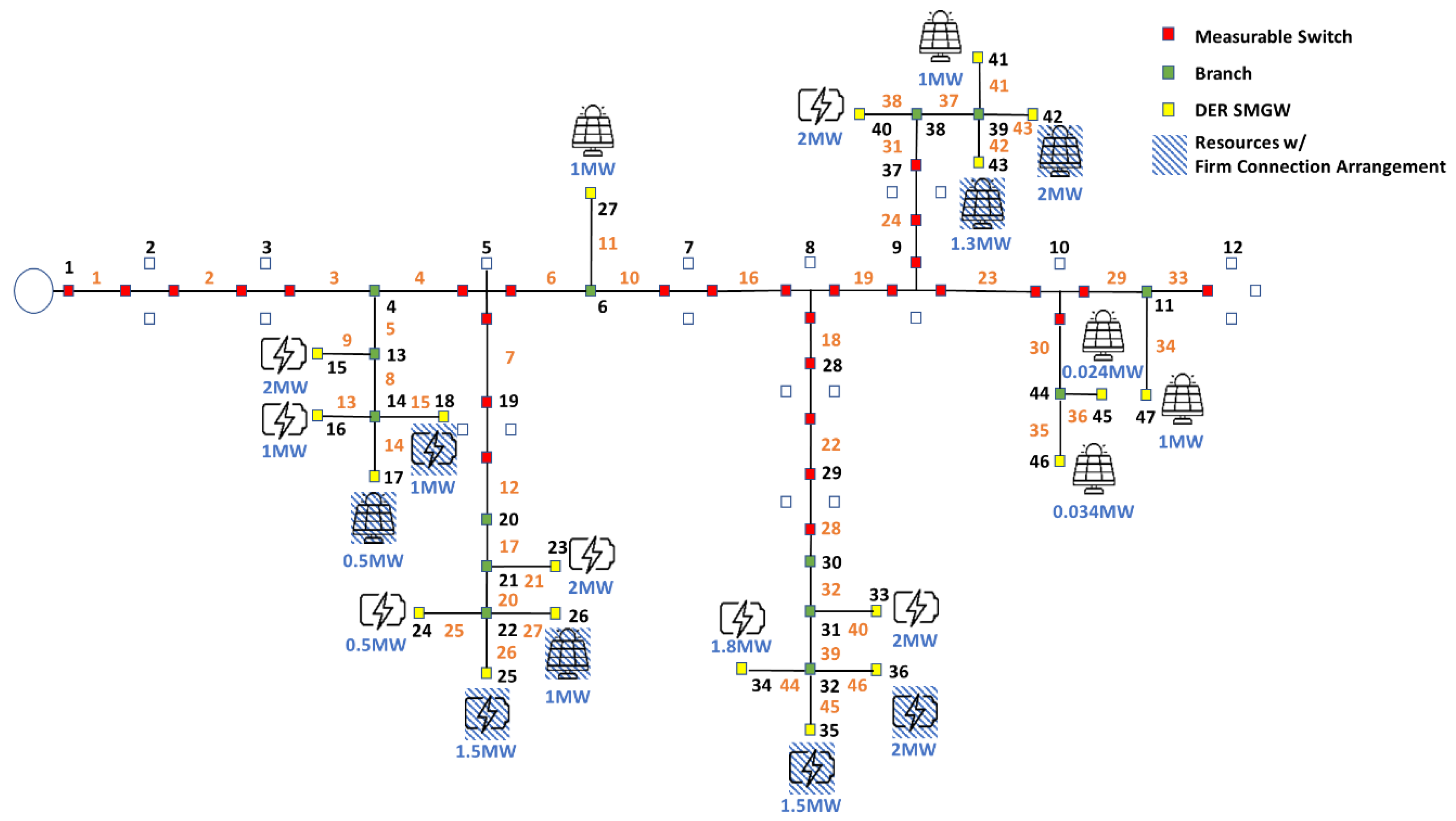
5.1. System configurations

The demonstration was conducted on a 22.9kV line named Oh-ryong D/L in the city of Gwangju, Korea. The grid diagram of this D/L is shown in the Figure 4. There are 7.858 MW of photovoltaic system (PV) connected to this D/L, of which 4.8 MW are already under firm-connection arrangements with KEPCO and cannot be contractually controlled. These resources are shown in the grid diagram with a dotted line. In addition, a total of 17.3 MW/69.2 MWh of energy storage system (ESS) are connected, of which 6 MW/24 MWh are not participating in the demonstration and have existing contractual charge and discharge scheduling arrangements with the utility. These resources are also shown on the grid map with oblique lines on the item. If all of the connected PV and ESS were to fully output, the total generation of D/L would exceed the capacity of 10 MW, which could potentially result in a grid constraint violation. This situation is not allowed under KEPCO's existing connection regulations, but we temporarily set it up like this for the demonstration purposes. As there was no device to measure the output of each DER, the voltage of the point, and the phase angle, and to deliver the information to the operating system, this project installed smart meter gateway devices in the yellow-colored part of the grid map and collected the information.

5.2. Scenario configuration

First, it was assumed that there was only one DERA participating in the prequalification that took place the day before. This was necessary because there was only one entity involved in the project as DERA. This DERA wants to bid into the wholesale market using its contracted DERs, and before doing so, it submits its bid information to the DSO for prequalification to ensure that it does not cause problems with the reliability of the distribution system. The missed resources, which are marked in the oblique lines in the Figure 4, that are not included in this scheme are recognized as negative loads.

In this study, we show the operation results for 24 hours on a sunny day in the winter season during the demonstration period. On that day, the net-load of the entire D/L had the following pattern when measured at the node 1 in the network, and the solar power generation had the pattern shown in the following figure.

Figure 5. (a) Net-load pattern of the Oh-ryong D/L and (b) PV utilization rate pattern at a sunny day in the winter season. 

Figure 5. (a) Net-load pattern of the Oh-ryong D/L and (b) PV utilization rate pattern at a sunny day in the winter season. 

In this situation, the DERA, which wants to participate in the wholesale market by aggregating the resources existing in this system, acted according to the procedure described in Section 3 of this paper.

The scheme proposed in this study takes a robust approach to manage the uncertainty of load and generation with 5% uncertainty from the day-ahead forecast values, and the robustness of the scheme is verified by the actual load and generation realized in the real-time operation stage. As a constraint of the distribution system, we set a criteria to keep the voltage between 0.95 p.u. and 1.05 p.u.. Additionally, in step 1 of Section 4, which selects the risky bus and risky line, the voltage is less than or equal to 0.96 and more than 1.04 to select the risky bus, and the voltage is more than 60% of the line capacity to select the risky line. These appropriate criteria were established through a lot of trial and error.

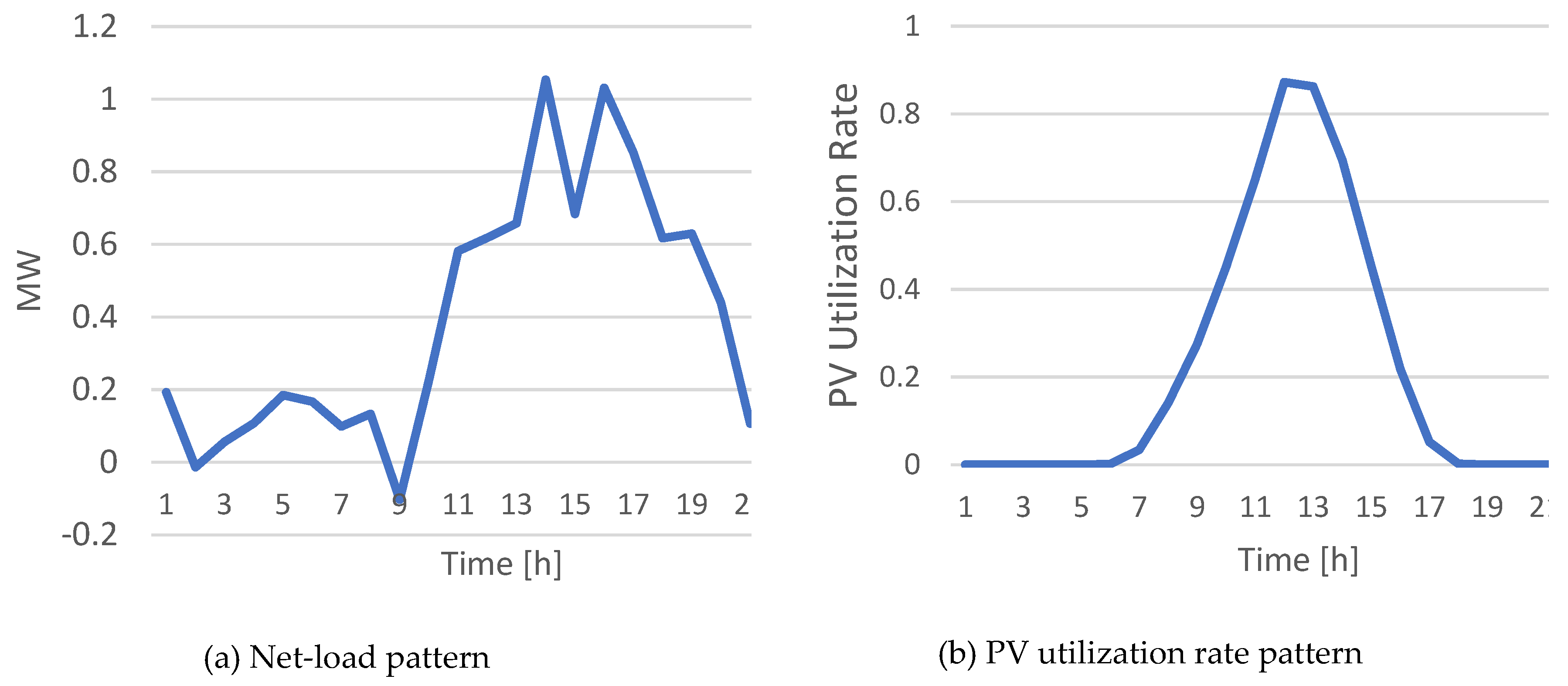
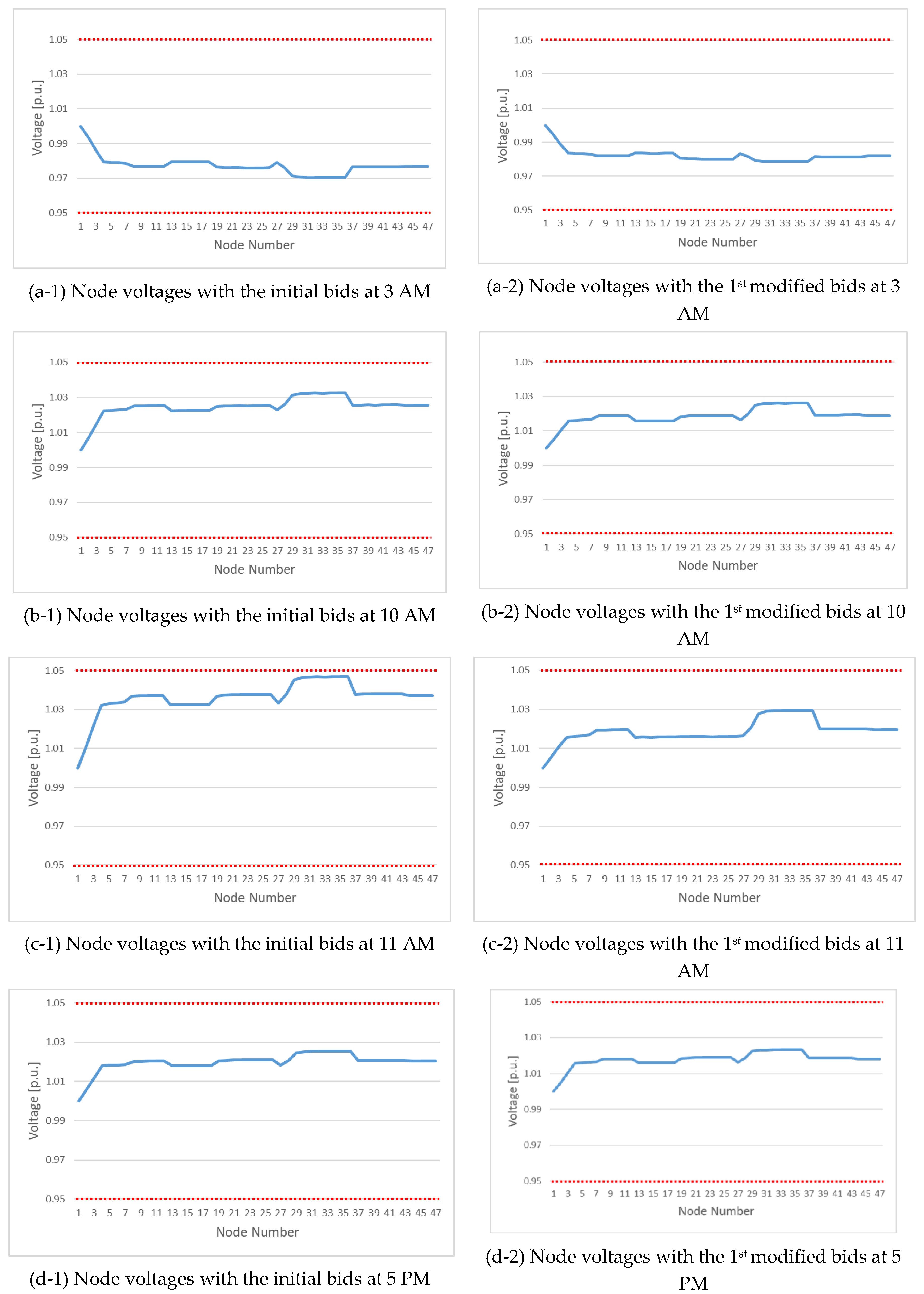
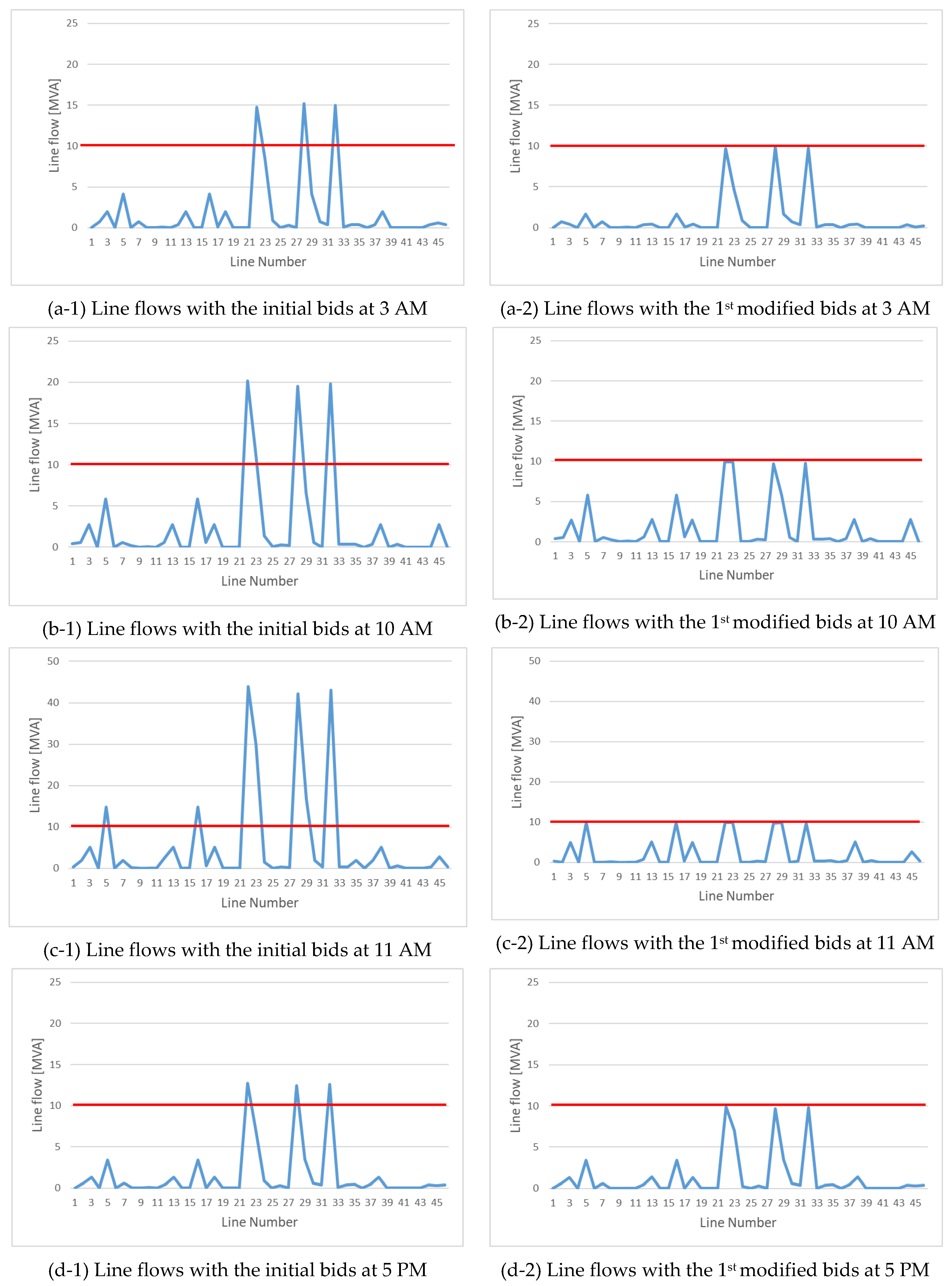
5.3. Verification of the proposed scheme

Out of the total 24 hours of the prequalification scheme operation, we will show the results for 3 AM, 10 AM, 11 AM, and 5 PM, when constraint violations occurred due to DERA's initial bids, for voltages or line flows, respectively.

It can be seen from Figure 6 that the site did not experience any explicit voltage violations from the initial bids for these four time slots, and that guidelines were communicated to resolve possible constraints on line flows, and the DERA responded with modified bids, resulting in a margin on the voltage side.

However, as shown in Figure 7, the initial bids of the DERA were analyzed to cause line flow violations in all four time slots. The result of 3AM was a forward overflow and all other time slots showed reverse overflows. The DSO predicted this situation in advance through the prequalification algorithm proposed in this paper and provided bid-modification guidelines to DERA. This information was provided to the DERA in the form of the guidelines shown in Table 2, and the DERA modified its bid within the ranges presented in the guidelines and resubmitted it to the DSO. The result was that all constraints are resolved in the next iteration, as shown in Figure 7. Through this process, the DERA was validated by the DSO that its bid does not threaten the reliability of the distribution grid. What we wanted to verify through this demonstration was whether the overall algorithm results could ensure the reliability of the distribution system in a real system, and whether the interaction process between DSO and DERA could be completed within a limited time. It can be concluded that satisfactory results were obtained for the above situations.

Table 2. Example of bid-modification-guideline for DERA from the prequalification algorithm of DSO at 11 AM.

DER Index	DER Type	Hour Index	Max. Allowable Generation Power [kW]	Max. Allowable Discharging Power [kW]	Max. Allowable Charging Power [kW]
15	ESS	11	-	-1,909.22	-1,940.00
16	ESS	11	-	970.00	-970.00
23	ESS	11	-	-1,940.00	-1,940.00
24	ESS	11	-	-43.71	-485.00
27	PV	11	8.77	-	0
33	ESS	11	-	1,940.00	-1,940.00
34	ESS	11	-	1,746.00	-1,746.00
40	ESS	11	-	0	-1,940.00
41	PV	11	746.10	0	0
45	PV	11	17.91	0	0
46	PV	11	25.37	0	0
47	PV	11	454.26	0	0

Table 2. Example of bid-modification-guideline for DERA from the prequalification algorithm of DSO at 11 AM.

DER Index	DER Type	Hour Index	Max. Allowable Generation Power [kW]	Max. Allowable Discharging Power [kW]	Max. Allowable Charging Power [kW]
15	ESS	11	-	-1,909.22	-1,940.00
16	ESS	11	-	970.00	-970.00
23	ESS	11	-	-1,940.00	-1,940.00
24	ESS	11	-	-43.71	-485.00
27	PV	11	8.77	-	0
33	ESS	11	-	1,940.00	-1,940.00
34	ESS	11	-	1,746.00	-1,746.00
40	ESS	11	-	0	-1,940.00
41	PV	11	746.10	0	0
45	PV	11	17.91	0	0
46	PV	11	25.37	0	0
47	PV	11	454.26	0	0