Prerpints.org logo
Preprint
Article

Estimation of Two-Component Activities of Binary Liquid Alloys by the Pair Potential Energy Containing a Polynomial of the Partial Radial Distribution Function

Altmetrics

Downloads

86

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

28 August 2023

Posted:

31 August 2023

You are already at the latest version

Alerts
Abstract
An investigation of pair partial radial distribution functions and molecular pair potentials within a system has established that the existing potential functions are rooted in the assumption of a static arrangement of atoms, overlooking their distribution and vibration. In this study, Hill’s proposed radial distribution function polynomials are applied for the pure gaseous state to a binary liquid alloy system to derive the pair potential energy. The partial radial distribution functions of 36 binary liquid alloy systems reported in literature were examined and then validated using four thermodynamic models. Results show that the molecular interaction volume model (MIVM) and regular solution model (RSM) outperform other models when an asymmetric method is used to calculate the partial radial distribution function. The MIVM exhibits a mean standard deviation (SD) of 0.095 and a mean absolute relative difference (ARD) of 32.2%. Similarly, the RSM demonstrates a mean SD of 0.078 and an ARD of 32.2%. The Wilson model yields a mean SD of 0.124 and a mean ARD of 226%. The nonrandom two-liquid (NRTL) model exhibits a mean SD of 0.225 and a mean ARD of 911%. On applying the partial radial distribution function symmetry method, the MIVM and RSM outperform the other approaches, with a mean SD of 0.143 and a mean ARD of 165.9% for the MIVM. The RSM yields a mean SD of 0.117 and an ARD of 208.3%. The Wilson model exhibits the mean values of 0.133 and 305.6% for SD and ARD, respectively. The NRTL model shows an average SD of 0.200 and an average ARD of 771.8%. Based on this result, the influence of the symmetry degree on the thermodynamic model is explored by examining the symmetry degree as defined by the experimental activity curves of the two components.
Keywords: 
Subject: Chemistry and Materials Science  -   Metals, Alloys and Metallurgy

1. Introduction

Pair potentials play a fundamental role in comprehending the static and dynamic properties of gases, liquids, and solids [1]. The main objective of studying pair potentials is to develop accurate and reliable models that describe intermolecular interactions and enable simulation, prediction, and explanation of the behavior and properties of molecular systems. Various computational simulation studies, such as for protein folding, drug–receptor interactions, and material property prediction, are conducted using molecular pair potentials to ascertain the underlying mechanisms of molecular interactions, explore novel material properties, and optimize drug design. Materials science and surface science researchers have investigated molecular potentials to thoroughly understand phenomena such as material structure, stability, crystal defects, and surface adsorption. Understanding intermolecular interactions is essential in material design, catalyst development, and comprehending material interfaces and surface phenomena. Molecular pair potential models encompass widely used semiempirical potentials such as the Lennard–Jones potential [2], Morse potential [3], and Born–Mayer potential [4] as well as molecular force fields, quantum mechanical descriptions, and statistical mechanics methods. Different factors affect the selection and examination of these models, including application needs and accuracy considerations [5,6,7]. Accurate pair potentials provide a comprehensive description of energy, geometric structure, and spectral properties of molecules and serve as the basis for investigating collision and chemical-reaction dynamics, such as those for molecular collisions. Thus, an in-depth study of potential pair functions holds significant physical implications and offers broad applications. This study reveals a direct correlation between the radial distribution function (RDF) and molecular pair potential. Herein, we establish a unified approach by exploiting the analogy between the computational procedure for the RDF in a pure gas and its application to the molecular pair potential in a binary liquid system. To substantiate our framework, we rigorously analyzed the RDF using 36 binary liquid alloys.

2. Thermodynamic Model

2.1. Regular Solution Model (RSM)

Hildebrand proposed the RSM in 1929 [8]. According to this model, the molar excess volume and mixing entropy are zero and the molar excess mixing Gibbs free energy is equal to the molar excess mixing enthalpy [9]. The expression for the molar excess Gibbs free energy for a binary system is as follows; the activity coefficient of the component i is ln γ i .
Δ G m E = Δ H m = Ω i j x i x j
ln γ i = Ω i j x j 2
Here, x i and x i are the mole fractions of components i and j , respectively, and Ω i j is the interaction parameter between components i and j . Ω i j is only related to temperature and does not change with the composition of components.

2.2. Wilson model

In 1964, Wilson [10] introduced a semiempirical and semitheoretical model based on the local concept. This model assumes that “local concentrations” (represented as volume fractions) primarily determine molecular interactions. These concentrations are defined in relation to the Boltzmann distribution probability term for energy. The excess free energy associated with the concentrations can be expressed as follows.
G m E R T = − x i ln ( x i + A j i x j ) − x j ln ( x j + A i j x i )
ln γ i = − ln ( x i + A i j x j ) + x j A i j x i + A i j x j − A j i x j + A j i x i
Here, A i j and A j i are the interaction parameters between components i and j , which are only related to temperature and do not change with the composition of components [11].

2.3. Nonrandom two-liquid (NRTL) model

The NRTL model, introduced by Renon and Prausnitz in 1968 [12], has been extensively used in correlating thermodynamic data, computing thermodynamic properties, and predicting phase equilibrium for diverse fluid systems in chemical processes. This model, based on the concept of local concentration, permits the determination of molar excess Gibbs free energy. The activity coefficient of the component i is ln γ i .
G m E R T = x i x j τ j i G j i x i + x j G j i + τ i j G i j x j + x i G i j
ln γ i = x j 2 τ j i G j i 2 ( x i + x j G j i ) 2 + τ i j G i j ( x j + x i G i j ) 2
τ i j = g i j − g j j R T   τ j i = g j i − g i i R T  
G i j = exp ( − α τ i j )   G j i = exp ( − α τ j i )
Here, A i j and A j i are energy parameters characterizing the interaction between components i and j; α is related to nonrandomness in the mixture, independent of temperature and composition of a solution. Moreover, the characteristic parameter of a solution depends on the solution type. When the mixture is entirely random, many binary system experimental data show that α varies from 0.2 to 0.47. In this study, α = 0.3.

2.4. Molecular Interaction Volume Model (MIVM)

In 2000, Tao introduced the volume model of molecular interaction [13], which uses statistical thermodynamics and fluid phase equilibrium theory to describe the motion of liquid molecules. This model yields the following expression:
G m E R T = x i ln V m i x i V m i + x j V m j B j i + x j ln V m j x j V m j + x i V m i B i j − x i x j 2 Z i B j i ln B j i x i + x j B j i + Z j B i j ln B i j x j + x i B i j
The activity coefficients of the components i is ln γ i .
ln γ i = 1 + ln V m i V m i x i + V m j B j i x j − x i V m i V m i x i + x j V m j B j i − x j V m i B i j V m j x j + x i V m i B i j − x j 2 2 Z i B j i 2 ln B j i ( x i + x j B j i ) 2 + Z j B i j ln B i j ( x j + B i j x i ) 2
Here, Z i and Z j are the first coordination numbers of i and j pure substances, respectively, and V m i and V m j are the molar volumes of i and j , respectively. B i j and B j i are the interaction parameters of i − j and j − i , respectively. k is the Boltzmann constant, and T is the temperature.

3. Pair potential energy polynomials of the binary liquid

In an extremely diluted pure gas, the correlation between the intermolecular potential energy and RDF can be expressed as follows [14]:
lim ρ 0 → 0 g 12 ( r ) = exp − ε 12 k T
However, in practical scenarios, the RDF and intermolecular potential energy strongly depend on the number density of the system. The relation between the RDF and pair potential energy can be expanded using a polynomial expression in terms of the number density ρ 0 :
g 12 ( r , ρ 0 , T ) = e − ε / k T 1 + ρ 0 g 1 ( R , T ) + ρ 0 2 g 2 ( R , T ) + ⋯
In this case, we consider a pure gas system comprising three molecules labeled 1, 2, and 3 (Figure 1). These molecules afford six molecular distributions: 1–1, 1–2, 1–3, 2–2, 2–3, and 3–3. Among these distributions, the RDF of 1–2 represents the spatial distribution of molecule 1 around molecule 2. However, g 12 ( r , ρ 0 , T ) is influenced by molecule 3 and is centered around this molecule, thereby affecting molecules 1 and 2 in g 12 ( r , ρ 0 , T ) . Consequently, based these observations, a connection can be established between the RDF and pair potential energy.
g 12 ( r , ρ 0 , T ) = e − ε 12 / k T exp ρ 0 ∫ V [ e − ε 13 / k T − 1 ] [ e − ε 23 / k T − 1 ] d r 3 = e − ε 12 / k T 1 + ρ 0 ∫ V [ e − ε 13 / k T − 1 ] [ e − ε 23 / k T − 1 ] d r 3
Consequently, the expansion based on ρ 0 is 1 + ρ 0 ∫ V [ e − ε 13 / k T − 1 ] [ e − ε 23 / k T − 1 ] d r 3 . Equation (13) is compared with Equation (12).
g 1 ( r 12 , T ) = ∫ V [ e − ε 13 / k T − 1 ] [ e − ε 23 / k T − 1 ] d r 3 = ∫ V [ e − ε 13 / k T e − ε 23 / k T − e − ε 23 / k T − e − ε 13 / k T + 1 ] d r 3 = ∫ V e − ε 13 / k T e − ε 23 / k T d r 3 − ∫ V e − ε 23 / k T d r 3 − ∫ V e − ε 13 / k T d r 3 + ∫ V d r 3
This knowledge is applied to binary liquid alloys based on the understanding of molecular interactions in pure gases. The molecular distribution in the binary liquid system is characterized by three scenarios: i − i , i − j , and j − j . The RDF i − j describes the distribution of molecule i around molecule j in a binary system (Figure 1). However, the remaining molecule i influences the i molecule in the RDF i − j , while the remaining molecule j affects the j molecule in the RDF i − j . Unlike pure gas centered on the remaining molecules 3 affecting the RDF 1–2. In a binary system, the spatial positioning of the remaining molecules i and j influences the RDF i − j for molecules i and j . That is, the i molecule in the RDF affecting i − j is centered on the other i molecules, while the j molecule in the RDF affecting i − j is centered on the other j molecules.
If the RDF in a binary liquid system can be expanded as a polynomial based on number density, then Equation (14) takes the following form:
g 1 ( r i j , T ) = ∫ V e − ε i i / k T d r × ∫ V e − ε j j / k T d r − ∫ V e − ε i i / k T d r − ∫ V e − ε j j / k T d r + ( ∫ V d r i i + ∫ V d r j j )
Suppose that the subradial distribution function g 1 ( r i j , T ) of the principal RDF g i j ( r , ρ 0 , T ) conforms to ρ 0 → 0 , i.e., i − j is the primary RDF, then i − i and j − j conform to ρ 0 → 0 and the subradial distribution function is:
g i i ( r ) = exp − ε i i k T g j j ( r ) = exp − ε j j k T
Substituting Equation (16) into Equation (15), we obtain:
g 1 ( r i j , T ) = ∫ V g i i ( r ) d r × ∫ V g j j ( r ) d r − ∫ V g i i ( r ) d r − ∫ V g j j ( r ) d r + ∫ V d r i i + ∫ V d r j j
Then substituting Equation (17) into Equation (13), we obtain:
g i j ( r , ρ 0 , T ) = e − ε i j / k T exp ρ 0 ∫ V g i i ( r ) d r × ∫ V g j j ( r ) d r − ∫ V g i i ( r ) d r − ∫ V g j j ( r ) d r + ( ∫ V d r i i + ∫ V d r j j ) = e − ε i j / k T 1 + ρ 0 ∫ V g i i ( r ) d r × ∫ V g j j ( r ) d r − ∫ V g i i ( r ) d r − ∫ V g j j ( r ) d r + ( ∫ V d r i i + ∫ V d r j j )
The relation between the RDF and potential energy can be obtained using Equation (18):
− ε i j k T = ln g i j ( r , ρ 0 , T ) 1 + ρ 0 ∫ V g i i ( r ) d r × ∫ V g j j ( r ) d r − ∫ V g i i ( r ) d r − ∫ V g j j ( r ) d r + ( ∫ V d r i i + ∫ V d r j j )
Pair potential energy between molecules can be accurately calculated using the RDF. This function represents the ratio of the probability of finding another molecule at a distance r to the random distribution [15]. In the double distribution function, for a system with N molecules and volume V , the probability of a molecule appearing in the element d r i is ( N / V ) d r i , the probability of a molecule appearing at the distance d r j is ( N / V ) d r j , and the probability of molecular pairs appearing at a distance r is ( N / V ) 2 d r i d r j . The double distribution function is given as follows:
p ( 2 ) ( r ) d r i d r j = ( N V ) 2 d r i d r j
In the system, the average potential energy ε between each molecule is:
ε = ∬ V ε i j ( r ) p ( 2 ) ( r ) d r i d r j
However, in the RDF of binary systems, the probability of having molecule i in d r i at r i and molecule j in d r j at r j is p ( 2 ) ( r ) d r i d r j . The potential energy is ε , and the average value of ε is the sum of all possible times of the probabilities:
ε i j ¯ = 1 V 2 ∬ V ε i j ( r ) g i j ( r ) d r i d r j = 1 V 2 ∫ V d r i ∫ ε i j ( r ) g i j ( r ) d r j = 1 V ∫ ε i j ( r ) g i j ( r ) 4 π r 2 d r = 4 π ∫ ε i j ( r ) g i j ( r ) r 2 d r 4 π ∫ r 2 d r = ∫ ε i j ( r ) g i j ( r ) r 2 d r ∫ r 2 d r
Substituting Equation (19) into Equation (22) yields the potential energy between molecules:
− ε i j ¯ k T = ∫ g i j ( r ) r 2 ln g i j ( r ) 1 + ρ 0 ∫ V g i i ( r ) d r × ∫ V g j j ( r ) d r − ∫ V g i i ( r ) d r − ∫ V g j j ( r ) d r + ( ∫ V d r i i + ∫ V d r j j ) d r ∫ r 2 d r
The peak value of the RDF signifies the disparity between the local and bulk molar fractions. As the mole fraction increases, the contributions of the second and third RDF peaks diminish while the contribution of the first peak amplifies. The pair potential energy is then calculated using Equation (23) and the area of the first peak of the skewed RDF. The biased RDF used in this study is defined by three key coordinates: r 0 (which represents the starting point of g(r) before reaching zero), r m (the transverse coordinate of the first peak of g(r)), and r 1 (the transverse coordinate of the first valley of g(r)). The asymmetric method of calculating the RDF involves integrating the area between r 0 and r 1 , while the symmetric method involves integrating the area between r 0 and r m (Figure 2). The trapezoidal method [16] is used to compute these areas (Equation (24)). Table 1 lists the references for the partial RDFs of 36 binary liquid alloys.
∫ r 1 r 0 g ( r ) d r ≈ b − a 2 N ∑ n = 1 N g ( r n ) + g ( r n + 1 ) = b − a 2 N g ( r ) + 2 g ( r 2 ) + ....... + 2 g ( r N ) + g ( r N + 1 )
The RSM has a tunable parameter Ω i j . The average coordination number Z ¯ [52] is obtained using the pure coordination number of the two components. Additionally, the temperature T documented in literature and the calculated parameter Ω i j can be referred to calculate the parameter Ω i j ' at the desired temperature T ' .
Z ¯ = 1 2 ( Z i + Z j )
Ω i j = k T Z ¯ ε i j ¯ − 1 2 ( ε i i ¯ + ε j j ¯ )
T ln Ω i j = T ' ln Ω i j '
The parameters A i j and A j i of Wilson equation are given. Additionally, the values of parameters A i j ' and A j i ' at the desired temperature T ' can be obtained using the temperature T from the literature that was employed to calculate the corresponding parameters A i j and A j i .
A i j = V i V j exp − ε i j ¯ − ε j j ¯ R T   A j i = V j V i exp − ε j i ¯ − ε i i ¯ R T
T ln A i j = T ' ln A i j '     T ln A j i = T ' ln A j i '
The NRTL has two parameters τ i j and τ j i . These parameters obtained using the temperature T mentioned in the literature are employed to calculate the parameters τ i j ' and τ j i ' , respectively, at the required temperature T ' .
τ i j = − ε i j ¯ − ε j j ¯ k T   τ j i = − ε j i ¯ − ε i i ¯ k T
T ln τ i j = T ' ln τ i j '     T ln τ j i = T ' ln τ j i '
The MIVM involves parameters B i j and B j i , representing the interaction parameters for i–j and j–i interactions, respectively. Using B i j and B j i values obtained at temperature T , the corresponding parameters B i j ' and B j i ' can be calculated at the desired temperature T ' .
B i j = exp − ε i j ¯ − ε j j ¯ k T   B j i = exp − ε j i ¯ − ε i i ¯ k T
T ln B i j = T ' ln B i j '     T ln B j i = T ' ln B j i '

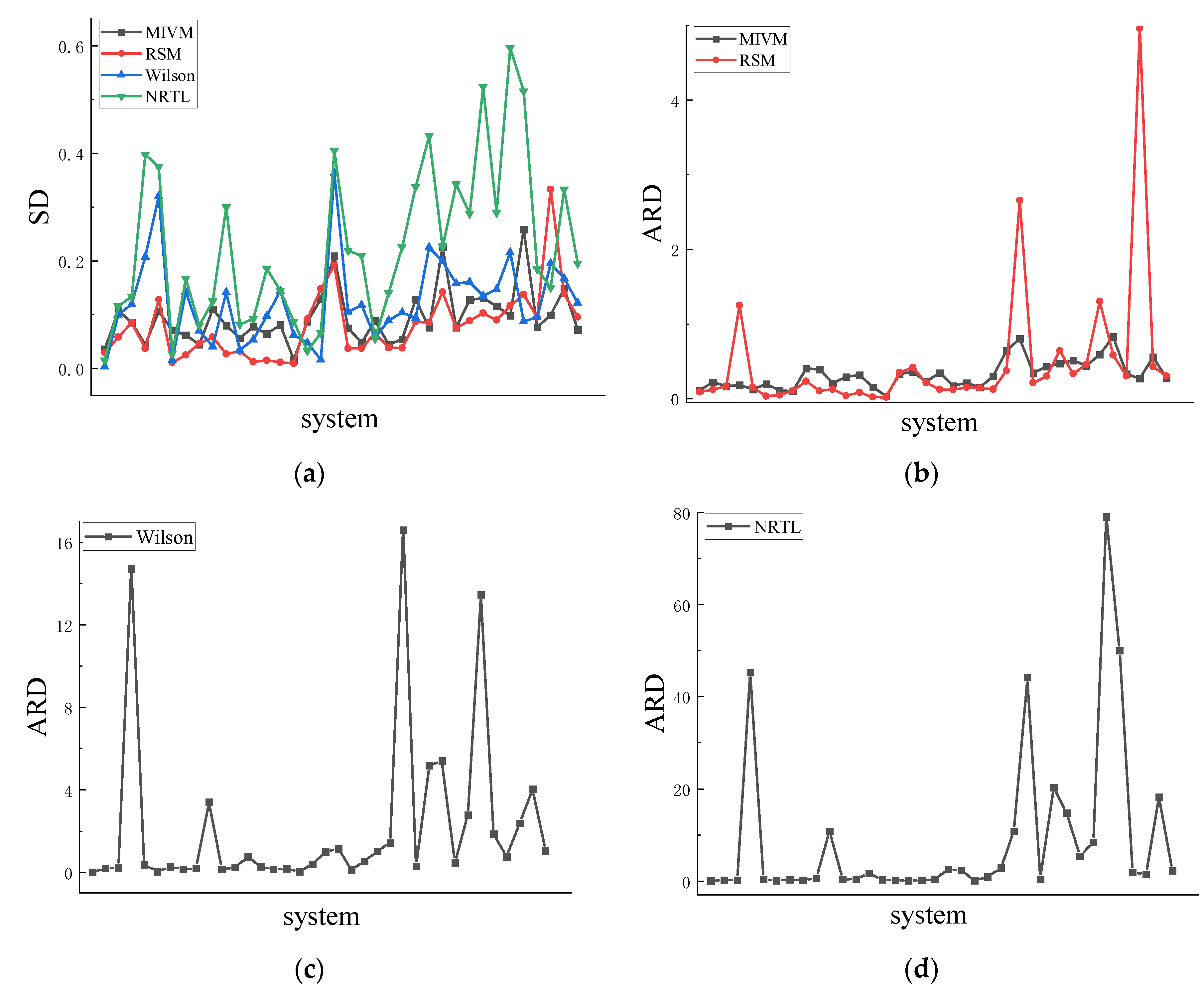
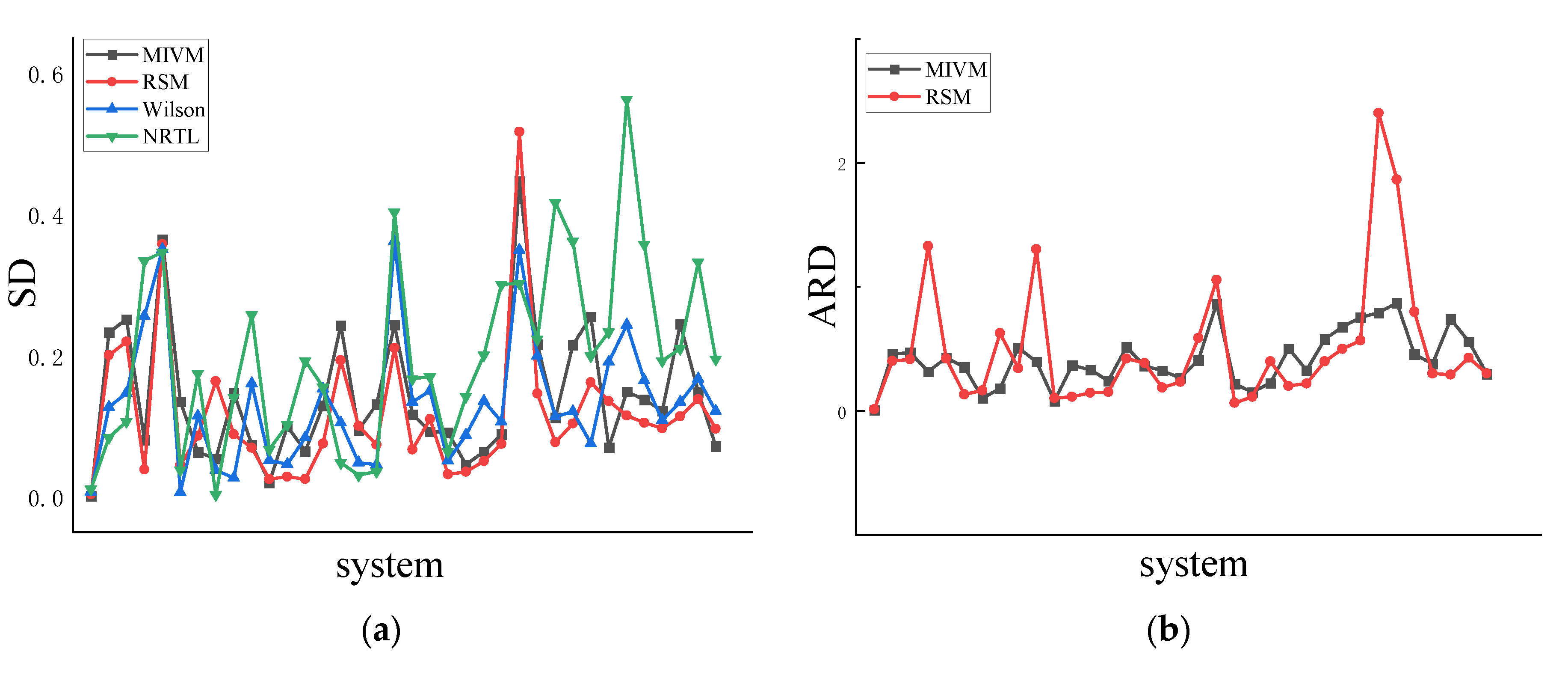
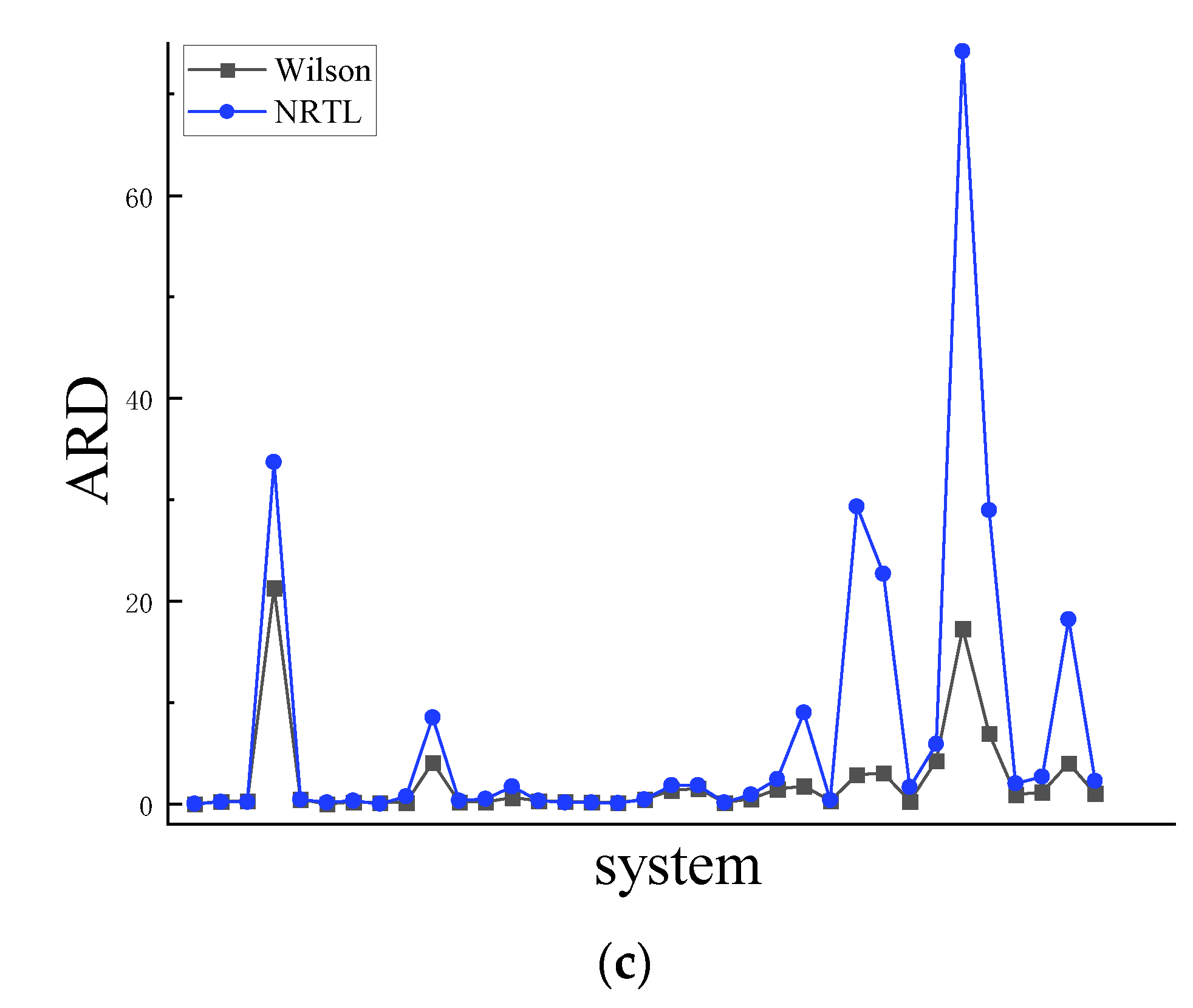
4. Result analysis

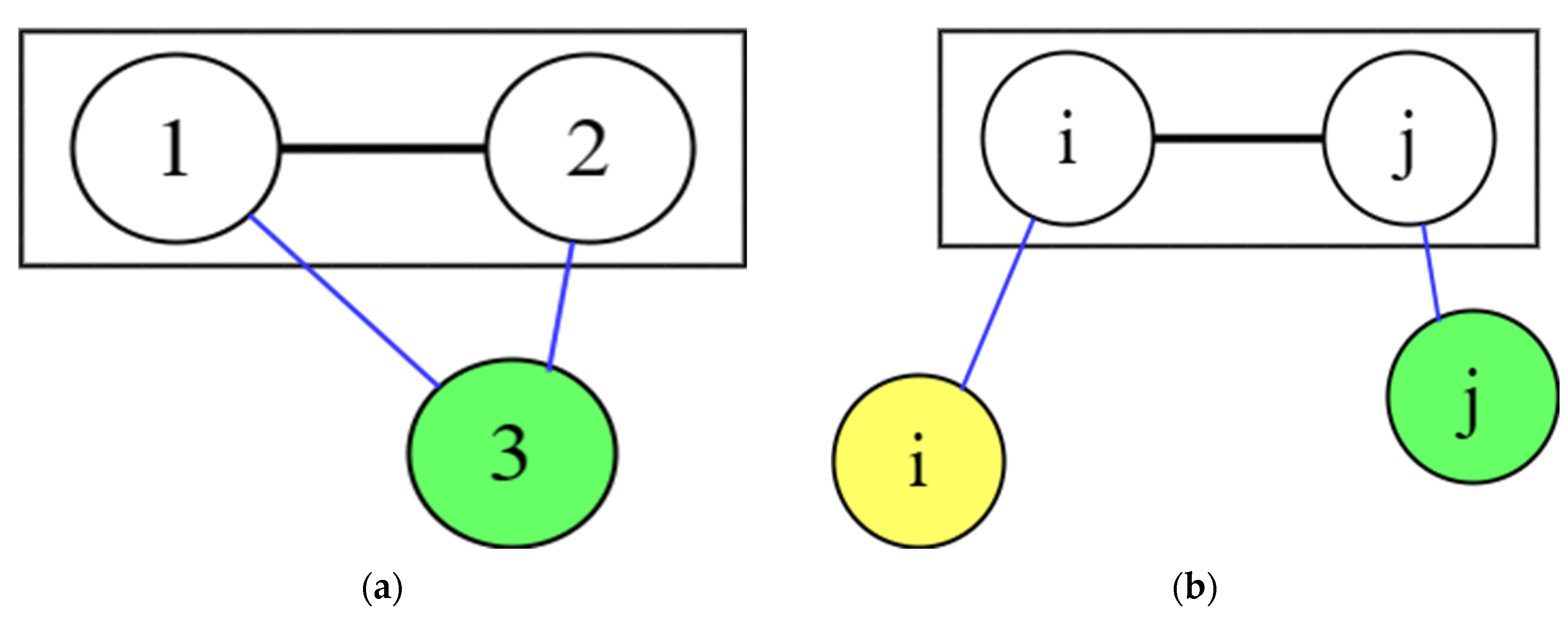
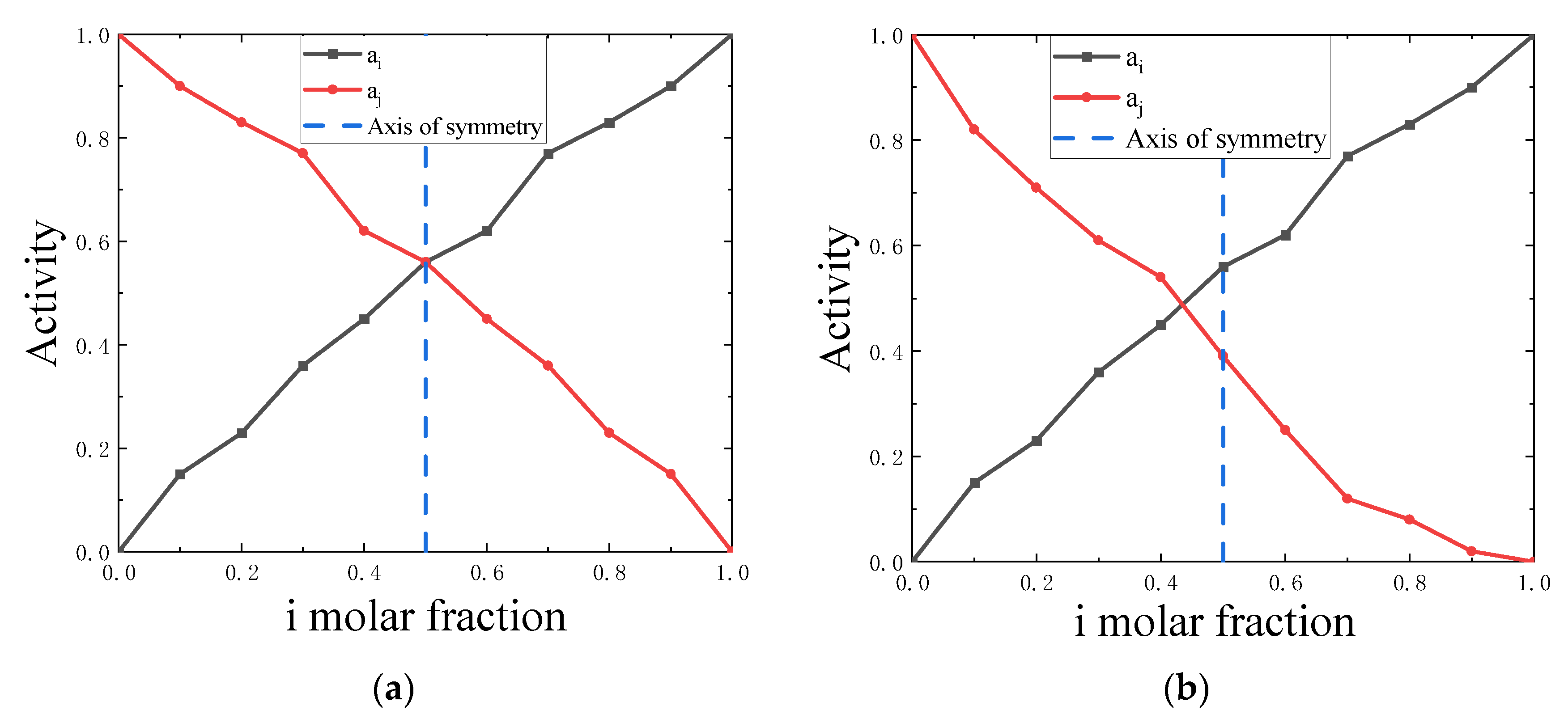
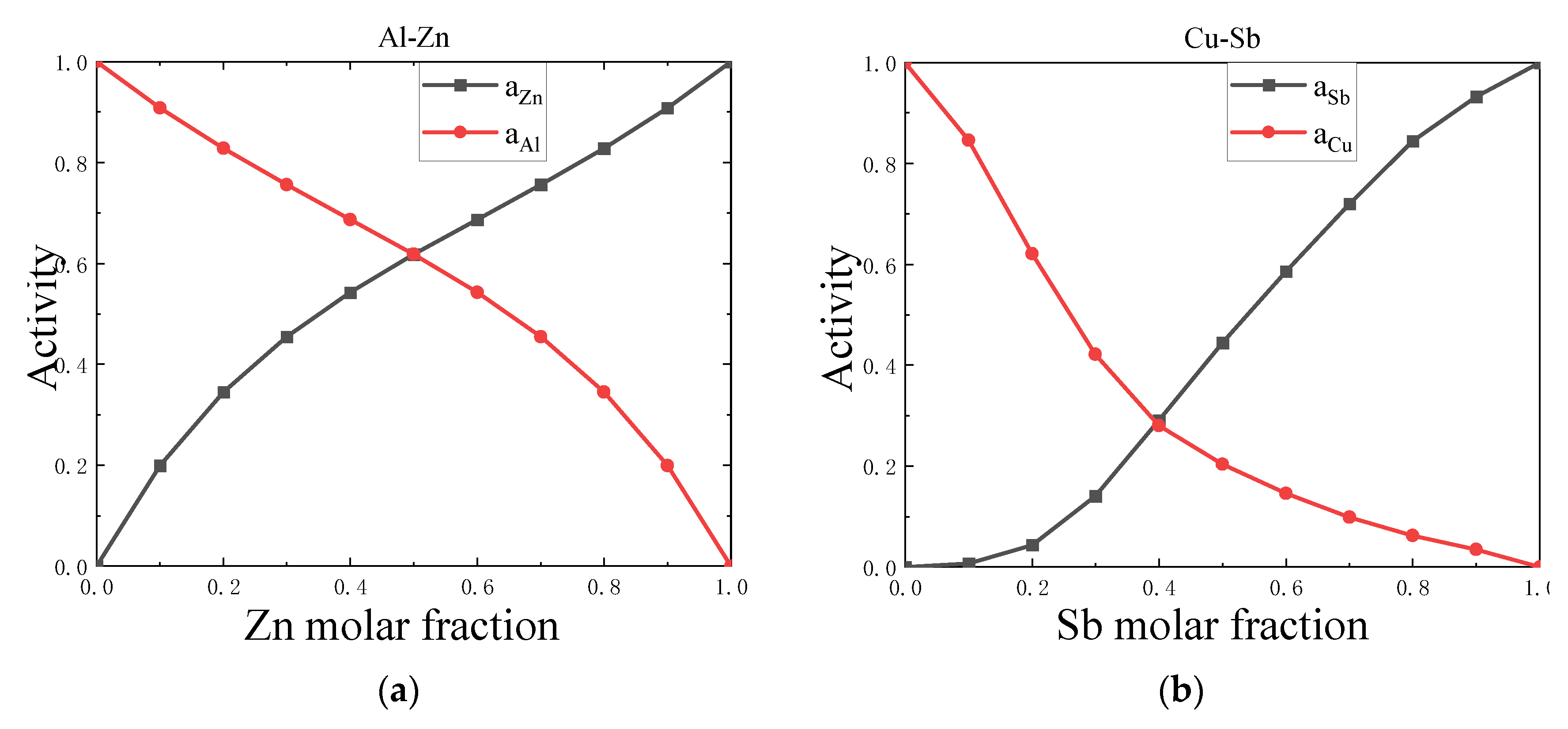
4.1. Symmetry

Figure 3 shows the molar fraction x i = x j = 0.5 of the two components as the symmetry axis of their activity curve. The symmetry degree of the activity curve can be defined as the average absolute value of the activity difference between the two components at the same concentration. In this context, S represents the measure of symmetry.
S i j = ∑ l = 1 m ( a i − a j ) x i = x j l m
The symmetry increases as the S value decreases. At S = 0 , the system exhibits complete symmetry, where a i and a j denote the experimental activity of components i and j, respectively, and m represents the number of experimental activities. This definition also applies to similar geometric figures. Table 3 presents the symmetry degrees of the activity curves for the 36 systems based on the aforementioned definitions.

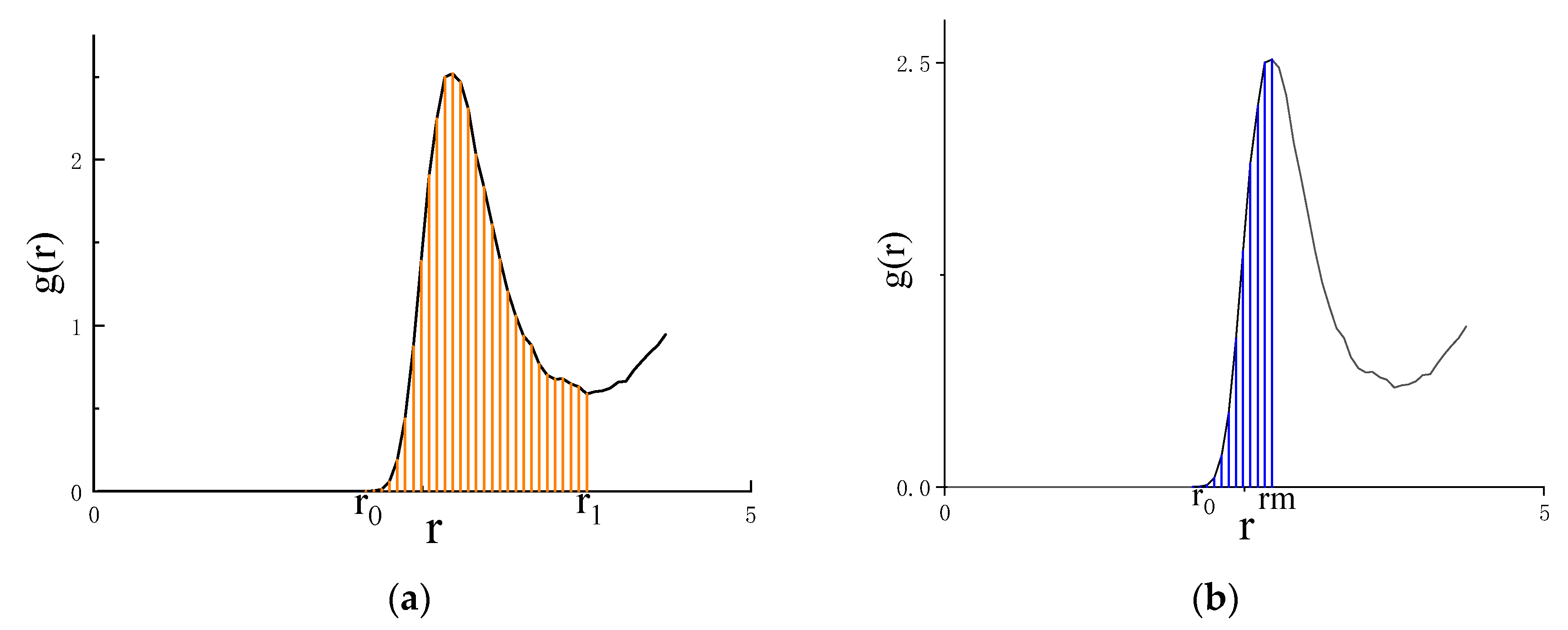
4.2. Asymmetric method for calculating the RDF

The asymmetric method uses the area between r 0 and r 1 presented in Figure 2 and Equation (23) to determine the parameters for each model. Table 4 and Table 5 and Figure 5 demonstrate that among the first 12 systems, the RSM performs better than other models for 7 systems. The average standard deviation (SD) is 0.033, and the average absolute relative deviation (ARD) is 8.9%. In case of the 12 systems with moderate symmetry, the RSM outperforms the other three models in 8 systems, resulting in a mean SD of 0.054 and a mean ARD of 13.7%. Notably, the MIVM also performs well, with a mean SD of 0.084 and an average ARD of 25.5%. For the 12 systems with low symmetry, the RSM outperforms the other three models in 6 systems, yielding an average SD of 0.115 and an average ARD of 36%. Additionally, the RSM outperforms the other three models in 5 systems when the systems have even lower symmetry, with an average SD of 0.103 and an average ARD of 41.5%. Considering the average performance across all 36 binary liquid alloy systems, the Wilson and NRTL models exhibit the poorest performance, displaying larger SD and ARD values than the other models. As shown in Figure 5, the SD and ARD values generally increase with decreasing symmetry, albeit not significantly. Further analysis of high, medium, and low-symmetry systems reveals a strong correlation between the RSM and symmetry.

4.3. Symmetric method for calculating the RDF

The methodology based on symmetry involves deriving parameters for each model using the region from r 0 to r m (Figure 6) and Equation (23). Analysis of data presented in Table 6 and Table 7 and Figure 6 reveals that among the 12 systems characterized by high symmetry, the MIVM outperforms the other three models with an average SD of 0.127 and an average ARD of 30.5%. Conversely, the RSM exhibits an average SD of 0.111 and an average ARD of 44.6%. In the 12 systems with medium symmetry, the RSM outperforms the other three models, yielding a mean SD of 0.088 and an ARD of 32.9%. By contrast, the MIVM exhibits a mean SD of 0.118 and an ARD of 36.7%. For the 12 systems with low symmetry, the RSM and MIVM surpass the other three models. The RSM exhibits an average SD of 0.118 and an average ARD of 73.4%, and the MIVM shows a mean SD of 0.159 and a mean ARD of 58.4%. Each model exhibits distinct performance characteristics depending on the system representation. The data comparison indicates an increasing trend in ARD values with decreasing symmetry.

5. Conclusion

This study uses polynomials to describe the partial RDF in pure gases and extends this approach to binary liquid systems. The primary aim of this study is to characterize the molecular distribution and unravel intermolecular interactions, which are essential for accurate thermodynamic calculations. The RDF exhibits irregularities when the symmetric method is used instead of the asymmetric one for RDF calculation. Notably, the estimation of binary liquid alloy activity favors using the asymmetric method, especially when considering the average results obtained from both methods for the 36 binary liquid alloy systems investigated in this study. We selected and compared four thermodynamic models based on their symmetry degree. Data analysis reveals that the RSM exhibits the highest dependency on the symmetry degree. Conversely, the MIVM demonstrates superior adaptability to symmetric and asymmetric systems.

Author Contributions

Dongping Tao: Theoretical guidance, review; Jiulong Hang: Conceptualization, Writing-original draft, Writing—review & editing.

Acknowledgments

The authors would like to acknowledge the valuable theoretical guidance provided by Mr. TAO, the research facilities provided by the School of Metallurgy and Energy at Kunming University of Technology. This work was financially supported by the National Natural Science Foundation of China under Grant No. 51464022.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Xie, J.C.; Kar, T.; Xie, R.-H. An Accurate Pair Potential Function for Diatomic Systems. Chemical Physics Letters 2014, 591, 69–77. [Google Scholar] [CrossRef]
  2. Lennard-Jones, J.E. Cohesion. Proc. Phys. Soc. 1931, 43, 461. [Google Scholar] [CrossRef]
  3. Morse, P.M. Diatomic Molecules According to the Wave Mechanics. II. Vibrational Levels. Phys. Rev. 1929, 34, 57–64. [Google Scholar] [CrossRef]
  4. Born, M.; Mayer, J.E. Zur Gittertheorie der Ionenkristalle. Z. Physik 1932, 75, 1–18. [Google Scholar] [CrossRef]
  5. Ter Horst, M.A.; Schatz, G.C.; Harding, L.B. Potential Energy Surface and Quasiclassical Trajectory Studies of the CN+H 2 Reaction. The Journal of Chemical Physics 1996, 105, 558–571. [Google Scholar] [CrossRef]
  6. Hirst, D.M. Ab Initio Potential Energy Surfaces for Excited States of the NO2+ Molecular Ion and for the Reaction of N+ with O2. The Journal of Chemical Physics 2001, 115, 9320–9330. [Google Scholar] [CrossRef]
  7. Grandinetti, F.; Vinciguerra, V. Adducts of NF2+ with Diatomic and Simple Polyatomic Ligands: A Computational Investigation on the Structure, Stability, and Thermochemistry. International Journal of Mass Spectrometry 2002, 216, 285–299. [Google Scholar] [CrossRef]
  8. Hildebrand, J.H. SOLUBILITY. XII. REGULAR SOLUTIONS 1. J. Am. Chem. Soc. 1929, 51, 66–80. [Google Scholar] [CrossRef]
  9. Hildebrand, J.H.; Prausnitz, J.M.; Scott, R.L. Regular and Related Solutions : The Solubility of Gases Liquids, and Solids/Joel H. Hildebrand, John M. Prausnitz, Robert L. Scott.
  10. Wilson, G.M. Vapor-Liquid Equilibrium. XI. A New Expression for the Excess Free Energy of Mixing. J. Am. Chem. Soc. 1964, 86, 127–130. [Google Scholar] [CrossRef]
  11. Fan, T.X.; Yang, G.J.; Chen, J.Q.; Zhang, D. Model Prediction of Thermodynamics Activity in Multicomponent Liquid Alloy. KEM 2006, 313, 19–24. [Google Scholar] [CrossRef]
  12. Renon, H.; Prausnitz, J.M. Local Compositions in Thermodynamic Excess Functions for Liquid Mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
  13. Tao, D.P. A New Model of Thermodynamics of Liquid Mixtures and Its Application to Liquid Alloys. Thermochimica Acta 2000, 363, 105–113. [Google Scholar] [CrossRef]
  14. Hill, T.L. Statistical Mechanics : Principles and Selected Applications/Terrell L. Hill. Journal of Chemical Education 1957. [Google Scholar]
  15. Hu, Y. . Molecular thermodynamics of fluids [M]. Higher Education Press, 1982.
  16. S.-T. Yeh, Using Trapezoidal Rule for the Area under a Curve Calculation, (n.d.).
  17. Chanda, S.; Ahmed, A.Z.Z.; Bhuiyan, G.M.; Barman, S.K.; Sarker, S. A Test of Distribution Function Method in the Case of Liquid Transition Metals Alloys. Journal of Non-Crystalline Solids 2011, 357, 3774–3780. [Google Scholar] [CrossRef]
  18. Trybula, M.; Jakse, N.; Gasior, W.; Pasturel, A. Structural and Physicochemical Properties of Liquid Al–Zn Alloys: A Combined Study Based on Molecular Dynamics Simulations and the Quasi-Lattice Theory. The Journal of Chemical Physics 2014, 141, 224504. [Google Scholar] [CrossRef]
  19. Hongri, C.; Xiufang, B.; Hui, L.; Li, W. Molecular Dynamics Simulation on Structures of Cu-Ni Alloy. cjcp 2002, 15, 288–294. [Google Scholar]
  20. Belova, I.V.; Ahmed, T.; Sarder, U.; Yi Wang, W.; Kozubski, R.; Liu, Z.-K.; Holland-Moritz, D.; Meyer, A.; Murch, G.E. Computer Simulation of Thermodynamic Factors in Ni-Al and Cu-Ag Liquid Alloys. Computational Materials Science 2019, 166, 124–135. [Google Scholar] [CrossRef]
  21. Wang, H.; Wei, B. Understanding Atomic-Scale Phase Separation of Liquid Fe-Cu Alloy. Chin. Sci. Bull. 2011, 56, 3416–3419. [Google Scholar] [CrossRef]
  22. Goto, R.; Shimojo, F.; Munejiri, S.; Hoshino, K. Structural and Electronic Properties of Liquid Ge–Sn Alloys: Ab Initio Molecular-Dynamics Simulations. J. Phys. Soc. Jpn. 2004, 73, 2746–2752. [Google Scholar] [CrossRef]
  23. Song, B.; Xu, N.; Jiang, W.; Yang, B.; Chen, X.; Xu, B.; Kong, L.; Liu, D.; Dai, Y. Study on Azeotropic Point of Pb–Sb Alloys by Ab-Initio Molecular Dynamic Simulation and Vacuum Distillation. Vacuum 2016, 125, 209–214. [Google Scholar] [CrossRef]
  24. Qin, J.; Pan, S.; Qi, Y.; Gu, T. The Structure and Thermodynamic Properties of Liquid Al–Si Alloys by Ab Initio Molecular Dynamics Simulation. Journal of Non-Crystalline Solids 2016, 433, 31–37. [Google Scholar] [CrossRef]
  25. Kbirou, M.; Mazroui, M.; Hasnaoui, A. Atomic Packing and Fractal Behavior of Al-Co Metallic Glasses. Journal of Alloys and Compounds 2018, 735, 464–472. [Google Scholar] [CrossRef]
  26. Canales, M.; González, D.J.; González, L.E.; Padró, J.A. Static Structure and Dynamics of the Liquid Li-Na and Li-Mg Alloys. Phys. Rev. E 1998, 58, 4747–4757. [Google Scholar] [CrossRef]
  27. Pu, Z.; Zhang, H.; Li, Y.; Yang, B. Study on Sn-Sb Alloy by Ab-Initio Molecular Dynamic Simulation. IOP Conf. Ser.: Mater. Sci. Eng. 2018, 394, 032098. [Google Scholar] [CrossRef]
  28. Jakse, N.; Pasturel, A. Local Order and Dynamic Properties of Liquid and Undercooled Cu x Zr 1 − x Alloys by Ab Initio Molecular Dynamics. Phys. Rev. B 2008, 78, 214204. [Google Scholar] [CrossRef]
  29. Korkmaz, Ş.; Korkmaz, S.D. Structure and Inter-Diffusion Coefficients of Liquid Na x K1−x Alloys. J. Phase Equilib. Diffus. 2010, 31, 15–21. [Google Scholar] [CrossRef]
  30. Ishii, Y.; Takanaga, T. Atomic and Electronic Structures and Dynamics in Liquid Alloys near Eutectic Point. J. Phys. Soc. Jpn. 2000, 69, 3334–3341. [Google Scholar] [CrossRef]
  31. Wang, C.C.; Wong, C.H. Short-to-Medium Range Order of Al–Mg Metallic Glasses Studied by Molecular Dynamics Simulations. Journal of Alloys and Compounds 2011, 509, 10222–10229. [Google Scholar] [CrossRef]
  32. Korkmaz, S.D.; Korkmaz, Ş. A Study for Structure and Inter-Diffusion Coefficient of Liquid K 1− xCs xMetal Alloys. Physics and Chemistry of Liquids 2011, 49, 801–810. [Google Scholar] [CrossRef]
  33. Costa Cabral, B. First Principles Molecular Dynamics of a Liquid Li–Na Alloy. Journal of Molecular Structure: THEOCHEM 1999, 463, 145–149. [Google Scholar] [CrossRef]
  34. Bai, Y.W.; Zhao, X.L.; Bian, X.F.; Song, K.K.; Zhao, Y. Structure Evolution of Au50Cu50 Alloy from Melt to the Disordered Solid Solution. MSF 2020, 993, 273–280. [Google Scholar] [CrossRef]
  35. Shi, L.; Jia, L.; Ning, P.; Sun, X.; Wang, C.; Ma, Y.; Wang, F.; Qu, T.; Li, K. Vacuum Distillation and Ab Initio Molecular Dynamic Simulation of Al–Li Alloys. Vacuum 2023, 210, 111877. [Google Scholar] [CrossRef]
  36. Yang, S.J.; Hu, L.; Wang, L.; Wei, B. Molecular Dynamics Simulation of Liquid Structure for Undercooled Zr-Nb Alloys Assisted with Electrostatic Levitation Experiments. Chemical Physics Letters 2018, 701, 109–114. [Google Scholar] [CrossRef]
  37. Özdemir Kart, S.; Tomak, M.; Uludoğan, M.; Çağın, T. Liquid Properties of Pd–Ni Alloys. Journal of Non-Crystalline Solids 2004, 337, 101–108. [Google Scholar] [CrossRef]
  38. Liu, D.; Qin, J.Y.; Gu, T.K. The Structure of Liquid Mg–Cu Binary Alloys. Journal of Non-Crystalline Solids 2010, 356, 1587–1592. [Google Scholar] [CrossRef]
  39. Rao, R.V.G.; Venkatesh, R. Investigations of the Dynamic Properties of the Liquid Phase of Glassy CaAl Alloys. phys. stat. sol. (b) 1992, 170, 39–46. [Google Scholar] [CrossRef]
  40. Mendelev, M.I.; Kramer, M.J.; Hao, S.G.; Ho, K.M.; Wang, C.Z. Development of Interatomic Potentials Appropriate for Simulation of Liquid and Glass Properties of NiZr 2 Alloy. Philosophical Magazine 2012, 92, 4454–4469. [Google Scholar] [CrossRef]
  41. Roik, O.S.; Yakovenko, O.M.; Kazimirov, V.P.; Sokol’skii, V.E.; Golovataya, N.V.; Kashirina, Ya.O. Structure of Liquid Al Sn Alloys. Journal of Molecular Liquids 2021, 330, 115570. [Google Scholar] [CrossRef]
  42. Roik, O.S.; Samsonnikov, O.V.; Kazimirov, V.P.; Sokolskii, V.E.; Galushko, S.M. Medium-Range Order in Al-Based Liquid Binary Alloys. Journal of Molecular Liquids 2010, 151, 42–49. [Google Scholar] [CrossRef]
  43. Chen, F.; Cao, C.; Zhong, Q.; Liu, J.; Yang, L.; Chen, Z. Ab Initio Molecular Dynamics Study on Local Structure and Dynamic Properties of Liquid Ni62Nb38 Alloy. Materials Today Communications 2021, 27, 102207. [Google Scholar] [CrossRef]
  44. Gruner, S.; Kaban, I.; Kleinhempel, R.; Hoyer, W.; Jóvári, P.; Delaplane, R.G. Short-Range Order and Atomic Clusters in Liquid Cu–Sn Alloys. Journal of Non-Crystalline Solids 2005, 351, 3490–3496. [Google Scholar] [CrossRef]
  45. Jakse, N.; Nguyen, T.L.T.; Pasturel, A. Local Order and Dynamic Properties of Liquid Au x Si1− x Alloys by Molecular Dynamics Simulations. The Journal of Chemical Physics 2012, 137, 204504. [Google Scholar] [CrossRef] [PubMed]
  46. Chou, C.-Y.; Kim, H.; Hwang, G.S. A Comparative First-Principles Study of the Structure, Energetics, and Properties of Li–M (M = Si, Ge, Sn) Alloys. J. Phys. Chem. C 2011, 115, 20018–20026. [Google Scholar] [CrossRef]
  47. Li, X.; Wang, J.; Qin, J.; Dong, B.; Pan, S. The Reassessment of the Structural Transition Regions along the Liquidus of Fe–Si Alloys and a Possible Liquid–Liquid Structural Transition in FeSi2 Alloy. Physics Letters A 2018, 382, 2655–2661. [Google Scholar] [CrossRef]
  48. Bhuiyan, G.M.; Ali, I.; Rahman, S.M.M. Atomic Transport Properties of AgIn Liquid Binary Alloys. Physica B: Condensed Matter 2003, 334, 147–159. [Google Scholar] [CrossRef]
  49. Weber, H.; Schumacher, M.; Jóvári, P.; Tsuchiya, Y.; Skrotzki, W.; Mazzarello, R.; Kaban, I. Experimental and Ab Initio Molecular Dynamics Study of the Structure and Physical Properties of Liquid GeTe. Phys. Rev. B 2017, 96, 054204. [Google Scholar] [CrossRef]
  50. Peng, H.L.; Voigtmann, Th.; Kolland, G.; Kobatake, H.; Brillo, J. Structural and Dynamical Properties of Liquid Al-Au Alloys. Phys. Rev. B 2015, 92, 184201. [Google Scholar] [CrossRef]
  51. Guo, F.; Tian, Y.; Qin, J.; Xu, R.; Zhang, Y.; Zheng, H.; Lv, T.; Qin, X.; Tian, X.; Sun, Y. Structure of Liquid Cu–Sb Alloys by Ab Initio Molecular Dynamics Simulations, High Temperature X-Ray Diffraction, and Resistivity. J Mater Sci 2013, 48, 4438–4445. [Google Scholar] [CrossRef]
  52. Dorini, T.T.; Eleno, L.T.F. Liquid Bi–Pb and Bi–Li Alloys: Mining Thermodynamic Properties from Ab-Initio Molecular Dynamics Calculations Using Thermodynamic Models. Calphad 2019, 67, 101687. [Google Scholar] [CrossRef]
  53. Franke, P.L. , & Neuschütz, D. Binary Systems. “Binary Systems. Part 1-5.
Preprints 83460 g001
Figure 1. (a) is the molecular distribution diagram of pure substance, (b) is the molecular distribution diagram of the binary system.
Figure 1. (a) is the molecular distribution diagram of pure substance, (b) is the molecular distribution diagram of the binary system.
Preprints 83460 g001
Preprints 83460 g002
Figure 2. an illustration of the non-symmetric method of integration of radial distribution functions, b graphical representation of the non-symmetric method of integration of a radial distribution function.
Figure 2. an illustration of the non-symmetric method of integration of radial distribution functions, b graphical representation of the non-symmetric method of integration of a radial distribution function.
Preprints 83460 g002
Preprints 83460 g003
Figure 3. (a) means that the activity curve is entirely symmetric, (b) means that the activity curve is asymmetric.
Figure 3. (a) means that the activity curve is entirely symmetric, (b) means that the activity curve is asymmetric.
Preprints 83460 g003
Preprints 83460 g004
Figure 4. (a) is an entirely symmetric system, (b) is the system with the worst symmetry in this paper.
Figure 4. (a) is an entirely symmetric system, (b) is the system with the worst symmetry in this paper.
Preprints 83460 g004
Preprints 83460 g005
Figure 5. (a) is the SD of 36 systems, (b) is the ARD of MIVM and RSM models of 36 systems, (c) is the ARD of the Wilson equation of 36 systems, and (d) is the ARD of the NRTL equation of 36 systems.
Figure 5. (a) is the SD of 36 systems, (b) is the ARD of MIVM and RSM models of 36 systems, (c) is the ARD of the Wilson equation of 36 systems, and (d) is the ARD of the NRTL equation of 36 systems.
Preprints 83460 g005
Preprints 83460 g006aPreprints 83460 g006b
Figure 6. (a) is the SD of 36 systems, (b) is the ARD of MIVM and RSM models of 36 systems, (c) is the ARD of Wilson and NRTL equation of 36 systems.
Figure 6. (a) is the SD of 36 systems, (b) is the ARD of MIVM and RSM models of 36 systems, (c) is the ARD of Wilson and NRTL equation of 36 systems.
Preprints 83460 g006aPreprints 83460 g006b
Table 1. Partial radial distribution function of binary liquid alloys References.
Table 1. Partial radial distribution function of binary liquid alloys References.
System Co-Ni [17] Al-Zn [18] Cu-Ni [19] Al-Ni [20] Cu-Fe [21] Ge-Sn [22] Ag-Cu [20] Pb-Sb [23] Al-Si [24] Al-Co [25]
System Li-Mg [26] Sb-Sn [27] Cu-Zr [28] K-Na [29] Pb-Sn [30] Al-Mg [31] Cs-K [32] Li-Na [33] Au-Cu [34] Al-Li [35]
System Nb-Zr [36] Ni-Pd [37] Cu-Mg [38] Al-Ca [39] Ni-Zr [40] Al-Sn [41] Al-Cu [42] Nb-Ni [43] Cu-Sn [44] Au-Si [45]
System Li-Sn [46] Fe-Si [47] Ag-In [48] Ge-Te [49] Al-Au [50] Cu-Sb [51]
Table 3. Symmetry of the 36 systems from highest to lowest.
Table 3. Symmetry of the 36 systems from highest to lowest.
System Co-Ni Al-Zn Cu-Ni Al-Ni Cu-Fe Ge-Sn Ag-Cu Pb-Sb Al-Si Al-Co
S i j 0 0 0.0028 0.0034 0.0048 0.007 0.0088 0.0096 0.0102 0.0114
System Li-Mg Sb-Sn Cu-Zr K-Na Pb-Sn Al-Mg Cs-K Li-Na Au-Cu Al-Li
S i j 0.0114 0.0115 0.0119 0.0136 0.0158 0.0177 0.0228 0.0336 0.0364 0.0452
System Nb-Zr Ni-Pd Cu-Mg Al-Ca Ni-Zr Al-Sn Al-Cu Nb-Ni Cu-Sn Au-Si
S i j 0.0473 0.0494 0.0597 0.0724 0.0807 0.0823 0.1116 0.1334 0.1342 0.139
System Li-Sn Fe-Si Ag-In Ge-Te Al-Au Cu-Sb
S i j 0.14 0.1454 0.1483 0.1548 0.160 0.208
Table 4. Model parameters of the non-symmetric method.
Table 4. Model parameters of the non-symmetric method.
System MIVM RSM Wilson NRTL
B i j ' B j i ' Ω i j ' = Ω j i ' A i j ' A j i ' τ i j ' τ j i '
Co-Ni 0.964 0.977 0.343 0.964 0.977 -0.036 -0.023
Al-Zn 1.246 0.743 0.423 1.166 0.795 0.220 -0.297
Cu-Ni 1.086 0.863 0.374 0.999 0.938 0.082 -0.147
Al-Ni 1.493 1.649 -5.203 0.991 2.485 0.401 0.500
Cu-Fe 0.943 0.805 1.512 0.943 0.805 -0.059 -0.217
Ge-Sn 0.740 1.273 0.266 1.214 0.776 -0.302 0.241
Ag-Cu 0.675 1.194 1.225 0.471 1.709 -0.394 0.177
Pb-Sb 1.558 0.517 1.046 1.457 0.553 0.443 -0.660
Al-Si 1.405 1.077 -1.856 1.226 1.235 0.340 0.074
Al-Co 1.112 1.884 -4.213 0.802 2.612 0.106 0.633
Li-Mg 1.357 0.914 -1.095 1.469 0.844 0.305 -0.090
Sb-Sn 0.769 1.545 -0.847 0.735 1.618 -0.262 0.435
Cu-Zr 0.908 1.669 -2.277 1.782 0.851 -0.096 0.512
K-Na 0.700 1.176 1.018 0.366 2.252 -0.357 0.162
Pb-Sn 1.044 0.912 0.267 0.932 1.021 0.043 -0.092
Al-Mg 0.820 1.123 0.459 1.162 0.793 -0.198 0.116
Cs-K 1.204 0.635 1.310 0.801 0.955 0.185 -0.454
Li-Na 0.764 0.999 1.347 1.416 0.539 -0.270 -0.001
Au-Cu 1.163 1.444 -2.877 0.812 2.068 0.151 0.368
Al-Li 1.136 1.379 -2.356 1.485 1.055 0.128 0.321
Nb-Zr 0.814 1.255 -0.110 1.048 0.975 -0.206 0.227
Ni-Pd 1.168 1.087 -1.307 1.590 0.798 0.153 0.080
Cu-Mg 1.312 1.258 -2.781 2.575 0.641 0.272 0.230
Al-Ca 2.202 1.259 -5.761 5.826 0.476 0.789 0.230
Ni-Zr 1.522 1.730 -5.373 3.247 0.811 0.420 0.548
Al-Sn 0.624 1.440 0.598 1.024 0.877 -0.471 0.365
Al-Cu 1.568 1.530 -5.209 2.192 1.152 0.476 0.450
Nb-Ni 1.772 1.071 -3.558 1.070 1.774 0.572 0.069
Cu-Sn 1.987 0.849 -2.904 0.874 1.932 0.687 -0.163
Au-Si 1.224 1.684 -3.129 1.034 1.993 0.202 0.521
Li-Sn 3.396 2.186 -10.225 4.263 1.742 1.223 0.782
Fe-Si 5.678 1.776 -9.822 4.695 2.148 1.737 0.574
Ag-In 1.595 0.925 -2.227 2.476 0.596 0.467 -0.078
Ge-Te 0.409 1.891 1.285 0.912 0.848 -0.894 0.637
Al-Au 1.680 1.660 -5.740 2.287 1.219 0.519 0.507
Cu-Sb 1.804 0.881 -2.315 0.757 2.098 0.590 -0.127
Table 5. Deviation and relative error of each model in the non-symmetric method.
Table 5. Deviation and relative error of each model in the non-symmetric method.
System MIVM RSM Wilson NRTL
SD ARD/% SD ARD/% SD ARD/% SD ARD/%
Co-Ni 0.036 10.8 0.029 8.8 0.003 0.8 0.015 4.4
Al-Zn 0.108 22 0.058 12.1 0.100 20.5 0.116 23.7
Cu-Ni 0.085 16.5 0.085 16.5 0.120 23.1 0.134 25.7
Al-Ni 0.044 18.3 0.037 125 0.208 1472 0.398 4520
Cu-Fe 0.106 12.5 0.128 15.1 0.321 37.5 0.375 44
Ge-Sn 0.071 19.4 0.011 3.1 0.016 4.1 0.027 7.5
Ag-Cu 0.062 10.8 0.025 4.6 0.143 26.1 0.167 30.5
Pb-Sb 0.044 9.9 0.047 10.5 0.070 15.9 0.080 18.1
Al-Si 0.110 40.5 0.058 23.2 0.041 18.5 0.125 63.3
Al-Co 0.080 39.2 0.027 10.5 0.142 341 0.300 1085
Li-Mg 0.056 20.7 0.032 12.3 0.035 14.2 0.082 34.9
Sb-Sn 0.078 29.3 0.012 3.6 0.054 24.5 0.093 44.2
Cu-Zr 0.064 31.6 0.015 8.4 0.098 74.4 0.185 162
K-Na 0.081 15.3 0.012 2 0.144 27.8 0.145 28
Pb-Sn 0.016 3.2 0.009 1.7 0.063 14.3 0.087 19.6
Al-Mg 0.087 32.9 0.092 34.9 0.048 17 0.033 11.2
Cs-K 0.129 36 0.148 41.7 0.016 3.3 0.066 16.9
Li-Na 0.210 22.9 0.192 21.3 0.364 40.5 0.405 45.2
Au-Cu 0.076 34.5 0.038 12.1 0.105 101 0.219 255
Al-Li 0.048 17 0.037 12.2 0.118 115 0.209 236
Nb-Zr 0.089 21.1 0.066 15.1 0.058 13 0.056 12.4
Ni-Pd 0.044 15 0.039 14.1 0.090 53.7 0.140 91
Cu-Mg 0.054 30.2 0.038 12.4 0.104 103 0.226 286
Al-Ca 0.129 64.3 0.087 37.4 0.094 144 0.338 1081
Ni-Zr 0.076 80.2 0.085 266 0.225 1661 0.433 4415
Al-Sn 0.226 34.4 0.142 21.3 0.199 30.4 0.226 34.5
Al-Cu 0.076 43 0.075 30.1 0.158 516 0.343 2031
Nb-Ni 0.128 47.2 0.089 64 0.161 540 0.288 1478
Cu-Sn 0.131 51.2 0.103 33.3 0.135 48 0.524 544
Au-Si 0.116 44 0.090 45.6 0.147 279 0.290 847
Li-Sn 0.098 59.1 0.117 130 0.216 1347 0.596 7906
Fe-Si 0.259 82.9 0.137 58.3 0.088 186 0.516 5003
Ag-In 0.077 32.8 0.095 30.3 0.095 76 0.185 191
Ge-Te 0.099 27.3 0.333 496 0.195 239 0.150 148
Al-Au 0.149 55.9 0.139 42.7 0.168 405 0.333 1822
Cu-Sb 0.072 28 0.096 30.4 0.122 104 0.196 229
Ave 0.095 32.2 0.078 47.4 0.124 226 0.225 911
S D = ∑ ( a p r e − a exp ) 2 N ; A R D = 1 N ∑ | a p r e − a exp a exp | × 100 % . a p r e —calculated value of the activity; a exp [53]—experimental activity value.
Table 6. Parameters of each model of the weighting method.
Table 6. Parameters of each model of the weighting method.
System MIVM RSM Wilson NRTL
B i j ' B j i ' Ω i j ' = Ω j i ' A i j ' A j i ' τ i j ' τ j i '
Co-Ni 1.089 0.900 0.118 1.089 0.900 0.085 -0.106
Al-Zn 1.317 0.938 -1.162 1.232 1.003 0.275 -0.064
Cu-Ni 1.391 0.877 -1.138 1.280 0.953 0.330 -0.132
Al-Ni 1.155 2.099 -5.114 0.766 3.163 0.144 0.742
Cu-Fe 0.890 1.145 -0.103 0.890 1.145 -0.117 0.135
Ge-Sn 0.562 1.573 0.545 0.923 0.958 -0.576 0.453
Ag-Cu 1.309 0.582 1.538 0.914 0.833 0.269 -0.542
Pb-Sb 1.231 0.810 0.017 1.151 0.866 0.207 -0.211
Al-Si 1.534 1.140 -2.499 1.338 1.307 0.428 0.131
Al-Co 0.830 1.774 -2.218 0.551 2.673 -0.186 0.573
Li-Mg 1.087 0.988 -0.363 1.177 0.912 0.083 -0.012
Sb-Sn 0.825 1.576 -1.288 0.788 1.650 -0.192 0.455
Cu-Zr 1.206 1.206 1.206 1.206 1.206 1.206 1.206
K-Na 0.562 1.364 1.390 0.293 2.613 -0.577 0.311
Pb-Sn 1.601 0.830 -1.549 1.430 0.929 0.471 -0.186
Al-Mg 0.808 1.126 0.528 1.144 0.796 -0.213 0.119
Cs-K 1.642 0.660 -0.391 1.092 0.992 0.496 -0.416
Li-Na 0.728 1.069 1.245 1.350 0.577 -0.317 0.067
Au-Cu 2.423 0.515 -1.229 1.692 0.737 0.885 -0.664
Al-Li 0.813 1.374 -0.580 1.062 1.051 -0.208 0.318
Nb-Zr 0.671 1.414 0.279 0.864 1.098 -0.399 0.346
Ni-Pd 1.174 1.105 11.250 -1.445 1.599 0.811 0.159
Cu-Mg 0.882 1.538 -1.689 1.731 0.783 -0.126 0.430
Al-Ca 2.423 0.515 -1.229 1.692 0.737 0.885 -0.664
Ni-Zr 0.607 1.260 1.484 1.296 0.591 -0.499 0.231
Al-Sn 0.649 1.393 0.566 1.065 0.849 -0.433 0.332
Al-Cu 1.963 1.534 -6.647 1.472 2.180 0.714 0.453
Nb-Ni 3.602 1.064 -7.456 2.174 1.763 1.281 0.062
Cu-Sn 4.758 0.617 -5.972 2.091 1.403 1.560 -0.484
Au-Si 1.438 0.875 -0.992 1.214 1.036 0.363 -0.134
Li-Sn 2.077 2.672 -8.741 2.608 2.129 0.731 0.983
Fe-Si 1.534 1.843 -4.414 1.268 2.228 0.428 0.611
Ag-In 1.066 1.467 -2.560 1.654 0.946 0.064 0.384
Ge-Te 0.636 3.025 -3.272 1.419 1.356 -0.452 1.107
Al-Au 1.903 0.844 -2.370 0.799 2.011 0.643 -0.169
Cu-Sb 1.743 1.017 -3.207 1.743 1.017 0.556 0.017
Table 7. Model deviations and relative errors of weighting methods.
Table 7. Model deviations and relative errors of weighting methods.
System MIVM RSM Wilson NRTL
SD ARD/% SD ARD/% SD ARD/% SD ARD/%
Co-Ni 0.002 0.4 0.004 1.1 0.007 2.1 0.011 3.3
Al-Zn 0.233 45.8 0.201 40 0.128 26 0.085 17.5
Cu-Ni 0.252 46.9 0.220 41.3 0.147 28.3 0.107 20.8
Al-Ni 0.081 31.7 0.039 133 0.257 2130 0.335 3370
Cu-Fe 0.365 42.8 0.359 42 0.351 41.2 0.347 40.7
Ge-Sn 0.135 35.4 0.045 13.2 0.007 1.6 0.039 10.8
Ag-Cu 0.063 10.2 0.087 16.3 0.115 21.2 0.175 31.8
Pb-Sb 0.054 17.9 0.164 62.6 0.038 13.3 0.004 0.9
Al-Si 0.147 50.8 0.089 34.2 0.027 12.1 0.142 72.6
Al-Co 0.074 39.6 0.070 130 0.161 411 0.258 852
Li-Mg 0.020 7.9 0.026 10.2 0.052 21.7 0.067 28.5
Sb-Sn 0.100 36.5 0.029 11.3 0.046 20.7 0.103 49.6
Cu-Zr 0.065 33 0.026 14.4 0.084 62.1 0.193 171
K-Na 0.130 24.3 0.076 15.2 0.154 29.6 0.156 29.9
Pb-Sn 0.244 51.4 0.194 42 0.105 23.7 0.049 11
Al-Mg 0.095 36.2 0.101 38.4 0.049 17.5 0.031 10.7
Cs-K 0.132 32.3 0.074 18.8 0.046 11.5 0.036 8.9
Li-Na 0.244 26.7 0.211 23.4 0.363 40.4 0.404 45.1
Au-Cu 0.117 40.7 0.067 58.8 0.135 137 0.168 181
Al-Li 0.093 86.2 0.110 106 0.151 156 0.171 182
Nb-Zr 0.092 21.6 0.032 6.3 0.052 11.5 0.065 14.7
Ni-Pd 0.046 15.2 0.036 11.3 0.088 52.4 0.143 93.2
Cu-Mg 0.065 22.3 0.051 40 0.136 144 0.202 245
Al-Ca 0.089 50.3 0.075 20 0.107 175 0.301 901
Ni-Zr 0.447 4520 0.518 5760 0.350 3200 0.303 2560
Al-Sn 0.216 32.8 0.147 21.9 0.200 30.6 0.224 34.3
Al-Cu 0.113 57.6 0.078 39.9 0.114 289 0.417 2930
Nb-Ni 0.216 67.7 0.104 49.9 0.121 302 0.363 2270
Cu-Sn 0.255 75.4 0.163 56.7 0.076 28 0.200 167
Au-Si 0.070 79 0.136 240 0.192 425 0.234 591
Li-Sn 0.150 86.9 0.116 187 0.244 1730 0.564 7420
Fe-Si 0.138 45.8 0.105 79.9 0.165 693 0.358 2900
Ag-In 0.122 37.9 0.097 30.1 0.109 90.8 0.193 204
Ge-Te 0.245 73.9 0.114 29.1 0.135 118 0.211 268
Al-Au 0.149 55.9 0.139 42.7 0.168 405 0.333 1820
Cu-Sb 0.072 29.9 0.097 30 0.122 105 0.196 228
Ave 0.143 165.9 0.117 208.3 0.133 305.6 0.200 771.8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated