Preprint
Article
Hardware Implementations of Elliptic Curve Cryptography Using Shift-Sub Based Modular Multiplication Algorithms
Altmetrics
Downloads
310
Views
144
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
30 August 2023
Posted:
31 August 2023
You are already at the latest version
Alerts
Abstract
Elliptic curve cryptography (ECC) over prime fields relies on scalar point multiplication realized by point addition and point doubling. Point addition and point doubling operations consist of many modular multiplications of large operands (256 bits for example), especially in projective and Jacobian coordinates which eliminate the modular inversion required in affine coordinates for every point addition or point doubling operation. Accelerating modular multiplication is therefore important for high-performance ECC. This paper presents the hardware implementations of modular multiplication algorithms, including 1) Interleaved modular multiplication (IMM), 2) Montgomery modular multiplication (MMM), 3) Shift-sub modular multiplication (SSMM), 4) SSMM with advance preparation (SSMMPRE), and 5) SSMM with CSAs and sign detection (SSMMCSA) algorithms, and evaluates their execution time (the number of clock cycles and clock frequency) and required hardware resources (ALMs and registers). Experimental results show that SSMM is 1.76 times faster than IMM, and SSMMCSA is 3.21 times faster than IMM. We also present the ECC hardware implementations based on the Secp256k1 protocol in affine, projective, and Jacobian coordinates using the IMM, SSMM, SSMMPRE, and SSMMCSA algorithms, and investigate their cost and performance. Our ECC implementations can be applied to the design of hardware security module systems.
Keywords:
Subject: Computer Science and Mathematics - Security Systems
1. Introduction
The use of elliptic curves in cryptography is proposed by Neal Koblitz and Victor S. Miller independently in 1985 [1,2]. Elliptic curve cryptography (ECC) over finite field of a prime number m relies on the fact that scalar point multiplication can be computed, but it is almost impossible to compute the multiplicand d given only the original point P and the point of the product Q. Scalar point multiplication can be done with point addition (adding two points) and point doubling [3]. In conventional affine coordinates, point addition and point doubling require computing the slope of a line involving division. In both projective and Jacobian coordinates, divisor multiplication is calculated such that division is eliminated during scalar point multiplication. One final division is required to convert a point from projective or Jacobian coordinates to affine coordinates to obtain the shared secret key based on the elliptic curve Diffie-Hellman (ECDH) key exchange. ECDH is a variant of the Diffie-Hellman key agreement protocol using ECC between two parties to establish a shared secret key over an insecure network [4,5]. A modular inversion algorithm calculating is given in [3]. Based on it, this paper provides a Verilog HDL implementation to calculate . It can be used in affine coordinates to calculate the line slope, or in projective and Jacobian coordinates to convert points to affine coordinates in the final step for obtaining the shared secret key.
Point addition and point doubling operations consist of many modular multiplications, especially in projective and Jacobian coordinates. Accelerating modular multiplication is therefore important for high-performance ECC. Interleaved modular multiplication (IMM) algorithm [6] eliminates the need for division and has lower hardware cost. Montgomery modular multiplication (MMM) algorithm [7] performs multiplication in Montgomery domain and is very efficient for modular exponentiation used by RSA cryptography. Shift-sub modular multiplication (SSMM) algorithm [8,9] performs modular multiplication with shift and subtraction. An algorithm using CSA (Carry save adder) [10] is proposed but it requires either a modular computation after the iterations or a pre-computed look-up table for fixed multiplier and moduli (Y and M in the algorithm). This paper proposes two enhanced versions of SSMM: SSMM with advance preparation (SSMMPRE) and SSMM with CSAs and sign detection (SSMMCSA) algorithms. This paper also presents the ECC implementations based on Secp256k1 [4] protocol which is used in Bitcoin where a 256-bit is used as the modulus.
The new contributions of this paper are summarized below. 1) Based on SSMM, we propose SSMMPRE (SSMM with advance preparation) and SSMMCSA (SSMM with CSAs and sign detection) algorithms that have lower latency than SSMM. 2) The hardware implementations of IMM, MMM, SSMM, SSMMPRE, and SSMMCSA algorithms are presented and their cost (required adaptive logic modules (ALMs) and registers) and performance (the number of clock cycles and clock frequency) are evaluated. 3) The hardware implementations of ECC in affine, projective, and Jacobian coordinates using the IMM, SSMM, SSMMPRE, and SSMMCSA algorithms are presented and their cost and performance are evaluated. And 4) some important Verilog HDL source codes and their simulation waveform are included. Compared to RSA cryptography, ECC provides stronger encryption with shorter key lengths. The ECC implementations described in this paper can be applied to the design of HSM (Hardware security module) systems.
The rest of the paper is organized as follows. Section 2 introduces the background of ECC, including the point addition, point doubling, scalar point multiplication, ECDH key agreement protocol, and affine, projective, and Jacobian coordinates. Section 3 describes the modular multiplication algorithms, including the IMM, MMM, SSMM, SSMMPRE, and SSMMCSA algorithms. Section 4 presents hardware implementations of modular multiplications and ECC and evaluates their cost and performance. And Section 5 concludes the paper. Verilog HDL codes for SSMM and modular inversion are listed in appendixes.
2. Elliptic Curve Cryptography Algorithms
This section describes ECC algorithms and ECDH that underlie this work. A top view of the relationship between these algorithms is shown in Figure 1.
The interesting computations in ECC are point addition and point doubling. We first introduce these two computations in an elliptic curve over the real numbers. In the real number field, an elliptic curve can be defined in Weierstrass form as
Note that this curve is symmetrical about the x-axis. If point is on an elliptic curve, then is also on the same elliptic curve.
2.1. ECC Point Addition and Doubling in Affine Coordinates
Affine coordinates use two coordinates to represent an elliptic curve point, as shown by, for example, and . We will see that the ECC point addition and point doubling in affine coordinates require expensive divisions.
2.1.1. ECC Point Addition in Affine Coordinates
Figure 2 shows the point addition on an elliptic curve . Given two distinct points and on the curve, if the line through P and Q intersects the curve in , then is defined as and . Because , the line through S and R is a vertical line.
Below we show how to get formulas to calculate and based on , , , and for . The formula of the line through P and Q is
where is the slope of the line . Squaring both the left side and right side of (2), we get . Then replacing of (1) with , we have
Because P, Q, and S are three points on the curve, meaning that , , and are three roots of (3), based on Vieta’s formulas, we have
Expanding (4) gives:
Then from (3) and (5) we have . That is, and . Considering the line slope , , and , we summarize the formulas for point addition on elliptic curve as follows.
For , the line through P and does not intersect the elliptic curve at the third point. For this reason, the point O at infinity is included in the group of elliptic curves and defined as . By this definition, .
In practice, a group of elliptic curves over a finite field of or is used, where contains numbers from 0 to and uses n-bit binary numbers. In the case of , the results of all the above calculations are modularized by m, where m is usually a prime number. For example, Secp256k1 [4] elliptic curve used in Bitcoin uses a 256-bit . Secp256k1 defines and gives a point on the elliptic curve as follows.
a = 0x0000000000000000000000000000000000000000000000000000000000000000
b = 0x0000000000000000000000000000000000000000000000000000000000000007
m = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
x = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
y = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
By considering , we give the point addition algorithm over the finite field of in Algorithm 1. In our implementation, O is denoted as . In the case of , we perform the point doubling (line 6 in the algorithm).

An example of point addition on the Secp256k1 curve is shown below where , , and in affine coordinates.
Px = 0xe493dbf1c10d80f3581e4904930b1404cc6c13900ee0758474fa94abe8c4cd13
Py = 0x51ed993ea0d455b75642e2098ea51448d967ae33bfbdfe40cfe97bdc47739922
Qx = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
Qy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
Rx = 0x2f8bde4d1a07209355b4a7250a5c5128e88b84bddc619ab7cba8d569b240efe4
Ry = 0xd8ac222636e5e3d6d4dba9dda6c9c426f788271bab0d6840dca87d3aa6ac62d6
2.1.2. ECC Point Doubling in Affine Coordinates
Figure 3 shows the point doubling on an elliptic curve . Compared to the point addition shown in Figure 2, here we have and . Given a point on the curve, if the tangent line through P intersects the curve in , then is defined as and .
Below we show how to get formulas to calculate and based on , , and a for . The formula of the line through P is
where is the slope of the line . Squaring both the left side and right side of (9), we get . Then replacing of (1) with , we have
Because P, Q (), and S are three points on the curve, meaning that , , and are three roots of (10), based on Vieta’s formulas, we have
Expanding (11) gives:
Then from (10) and (12) we have . That is, and . The slope of tangent line of at P can be obtained as follows.
Considering and , we summarize the formulas for point doubling on elliptic curve as follows.
We give the point doubling algorithm over the finite field of in Algorithm 2. For , the tangent at P is vertical and does not intersect the elliptic curve at any other point. By definition, for such a point P (line 2 in the algorithm).

An example of point doubling on the Secp256k1 curve is shown below where , and in affine coordinates.
Px = 0xb91dc87409c8a6b81e8d1be7f5fc86015cfa42f717d31a27d466bd042e29828d
Py = 0xc35b462fb20bec262308f9d785877752e63d5a68e563e898b4f82f47594680fc
Rx = 0x2d4fca9e0dff8dec3476a677d555896a0980ebccc6bc595a23675496dcc33bb5
Ry = 0xcce413eee9496094256e446b22fd234c03d9258330d77fc8b0d318a6aedba8cb
2.2. ECC Point Addition and Doubling in Projective Coordinates
Point addition and point doubling in affine coordinates require modular inversion (division) to calculate the line slope . We can eliminate the expensive modular inversion during calculations by using projective coordinates. In projective coordinates, a point is defined as . Initially, we can convert a point in affine coordinates to a point in projective coordinates by . Then we calculate in projective coordinates using formulas that do not contain division. At the very final step, we can get the point in affine coordinates with the transformation of and , which require divisions.
The formulas for ECC point addition and doubling in projective coordinates can be derived based on the formulas in affine coordinates. A point P in projective coordinates is represented by the triple , corresponding to the point in affine coordinates. That is, and . We derive the point doubling formulas for in projective coordinates as follows.
From (17), we have
From (18), we have
Let . Because , i.e., , then
From (19), we have
Because , i.e., , then
Given , the formulas for point doubling in projective coordinates are summarized below.
We can use the similar method to derive the formulas for point addition in projective coordinates. The derivation is omitted here but the calculations are shown in the following algorithm. It can be seen that the calculations require many more multiplications. Algorithm 3 gives the algorithm for point addition in projective coordinates. And Algorithm 4 gives the algorithm for point doubling in projective coordinates.


An example of point addition on the Secp256k1 curve is shown below where , , and in projective coordinates.
Px = 0x61bac660b055382e5906bd6e56e316542194b799b7bcf5ad05ee2171fd81735a
Py = 0xbe44ac0a2b712ccb6bb3ea933e4db0a4213c139078aef594cf8c2c5c2924d54d
Pz = 0x2b6da6fb02877584dc4d5111c88783772d7be5ac2866cce3707d53913384bf49
Qx = 0x6789c1137724f1f3f585337a1814eebc23ea329a0390fd9b1b9ece7af3e71ce1
Qy = 0xc9563c5035ccafec8673f56185141f720073ab3063bb417bf0e70e9d9128c232
Qz = 0x58990cd022b711912676c0451bdab6be04a06c1871b0139214bdbe81fd965555
Rx = 0xf4e9cb9ba9c18876b7b0ad000ce921b35e23139456f4f6c3f70e2fea149500a0
Ry = 0xc06176a9221b6d8b49a22130fb934b21358a1775df68d93ec308aca3ece072b5
Rz = 0x878fb153f0690416ba0ee136ec663debf8472f3ee92d350f9b3a42b4fd53fb27
An example of point doubling on the Secp256k1 curve is shown below where and in projective coordinates.
Px = 0x24fd537e9a5125438a02848f6b74725f678723f5c1450b8fb82a68f0c88c9764
Py = 0xe42e83a1d3d7c2241535b5c0ba5f2462c24bd87aaf9f15b05f3775d168b9bf6c
Pz = 0xe00794d20b32e0e94472c36b89cf5e5d6ec769b53dd6c1422e9467090c272305
Rx = 0x24d00c48ac8bbe61ceb0ac5daf5defd913af9220a07650642a3a41cad9030ee6
Ry = 0x75d429714ea6ce1ab3811d9adc16961a219e2812210fa8465042c18ecd5a0de6
Rz = 0x644a5a2964435364b74d7fa79fe0f06a5b1d2782e7f7b8d1e835db6d6b8786bc
2.3. ECC Point Addition and Doubling in Jacobian Coordinates
A point P in Jacobian coordinates is represented by the triple , corresponding to the point [2] (Page 424) in affine coordinates. That is, and . We derive the point doubling formulas for in Jacobian coordinates as follows.
From (17), we have
From (18), we have
Let . Because , we have
From (19), we have
Because , we have
Given , the formulas for point doubling in Jacobian coordinates are summarized below.
An example of point doubling on the Secp256k1 curve is shown below where and in Jacobian coordinates.
Px = 0xe43306185ef298127aef469d577aed78acafaddfc28ad0857491c38ffbedc475
Py = 0x4d83871239769596f65c180546c170a28cffca37bf6393025c457f406f54c517
Pz = 0xdafa620812722dceda7d93a91158dadbe11fee894e71eafa054d5f5fd274377e
Rx = 0x7d7cd6974d7e127a5fdf3f3c9c9eb5dcd9c15e033794466de63bcf2b9548ff85
Ry = 0x8f967b514296945a6dd052bca59ec1418a35cde3c6dd7b269d2e71daa80f851e
Rz = 0xcf89daf8b6c736cc851882b7e85c8ea8f703a9323a3d627909582b7904766035
Based on formulas (6), (7), and (8), and and , the formulas for point addition in Jacobian coordinates can be derived which are omitted here. An example of point addition on the Secp256k1 curve is shown below where , , and in Jacobian coordinates.
Px = 0xb7bae589ec8a8c722c1ffb2c37fd4bbeda59074675c3eb50f1673ed46bbedfbe
Py = 0x81dee3398bdd718591c10762f61a0e41c4d609dffddcbeeb3894b8c4ce75e027
Pz = 0x51ec57b21350ad3d3466be5a7d28742279fbac1146fb4143767ee368a7dc741e
Qx = 0x0aa20a04dba4788e9b99e10f2e9f4d43b7f53916a5cacf2050dc70bc34c18d21
Qy = 0x60f318d01180b303f4b20a49c2b7e2b498405f88bd423a9a7cb92bab5f1b6abf
Qz = 0x3e1dcb6efa88b113f40b5858ea8c3cb5ddae2277c4683af9487e27023cba690d
Rx = 0x348248c47ad5d3186bd807c382659263840ba7ea13e61128d24337db9b0e5278
Ry = 0xb38573698dd6fef9ec93a9d68ae0a997191b678474cc00a13961defa3ed763e9
Rz = 0x76da2008046aae9901e6b96a7b54c42fd480de5cbc8cef6c0d0a9b3d7086f0f4
The point in affine coordinates can be transformed from Jacobian coordinates by and . This is only performed one time at the final step. It can be done with the modular inversion which we will introduce next.
2.4. Modular Inversion
In affine coordinates, the point addition and point doubling algorithms must compute the slope of a line. Projective and Jacobian coordinates require the point to be transformed into affine coordinates at the final step to obtain the shared secret key. These calculations or transformations require division and modulo operations.
Generally, the modular inversion calculates , where m is an n-bit odd number and . An example of modular inversion is shown below.
b = 0x9cfa1c993911914be0f15bd74a878abe0079c6254b961b82e1abda76387d1d85
a = 0xd5076ae274e874c2eb0f7778717c39460236549ddd9fc651e68a0c0e787b4ce8
m = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
c = 0xe8e5ac2e1d3358894ce1b3342737b38c39b89059dd55d3c4741626de8270228e
Algorithm 2.22 in [3] gives an algorithm to calculate using the extended Euclidean algorithm. Based on it, we give a Verilog HDL implementation of the modular inversion that calculates in Appendix B. Figure B1 shows the simulation waveform generated with ModelSim.
In affine coordinates, every point addition or point doubling invokes modular inversion to calculate the line slope . In projective or Jacobian coordinates, this modular inversion can be removed during point addition or point doubling calculations, but a final division is required to transform a point from projective or Jacobian to affine coordinates to obtain the shared secret key. This division can be achieved using modular inversion.
2.5. Scalar Point Multiplication
Scalar point multiplication performs where P and Q are elliptic curve points and is an n-bit scalar. Scalar point multiplication is also called point multiplication, it can be done with “double-and-add” method [3]. Algorithm 5 formally gives the algorithm for scalar point multiplication. The algorithm invokes point addition and point doubling. Point doubling can be calculated simultaneously with point addition.

Below we give a small example to show the calculation steps of the scalar point multiplication. For a 4-bit , we calculate in 4 steps to get .
| Weight | Point addition | Point doubling | |
| Initial | |||
| 1 | |||
| 2 | |||
| 4 | |||
| 8 |
2.6. Elliptic Curve Diffie-Hellman Key Exchange
Elliptic curve Diffie-Hellman (ECDH) is a variant of the Diffie-Hellman key agreement protocol using ECC between two parties to establish a shared secret key over an insecure network [4,5]. Then this shared secret key can be used by the two parties to encrypt and decrypt subsequent communications using a fast symmetric-key cryptography over the insecure network.
The ECDH key exchange protocol is shown in Table 1. Because , , and , we have . Below shows an ECDH key exchange example using Secp256k1. We can see that two parties have a same shared secret key (Qabx = Qbax).
da = 0x650aa7095daeaa37ab9051541f0ce304f8969a6d88bb3bebb4fe680fca9a2595
db = 0xedc68f194c4e30d6ef90467df822b00e5ef122dea48c9d1c54817080d1a341f4
Qax = 0x167d2537aa6bbd8d978b58be0f9466520b7b184e205ff96a9ff567b35b32c7b7
Qay = 0xde3961553d36551f92726fee0e332133960edddccd2784b98b2af730d2fc6e14
Qbx = 0x839da64a414c2243a5526230603109be9c615613a9e98c3d650bb0488580bbda
Qby = 0x96e88e99304a5afcdd77c4f3b3327a28162627ebe08194baa0c78dfb67a11042
Qabx = 0x1f254c7da15899275cdcab9d992f58251a4ab630fe9864d20cf317ab57749947
Qaby = 0xd6cb400b3c49d33d3df28f9d34fa09f8b6c8edf117a378c5a45d0a51e6c0debc
Qbax = 0x1f254c7da15899275cdcab9d992f58251a4ab630fe9864d20cf317ab57749947
Qbay = 0xd6cb400b3c49d33d3df28f9d34fa09f8b6c8edf117a378c5a45d0a51e6c0debc
3. Modular Multiplication Algorithms
Point addition and point doubling use many modular multiplications. This section describes interleaved modular multiplication (IMM), Montgomery modular multiplication (MMM), and shift-sub modular multiplication (SSMM) algorithms, and proposes shift-sub modular multiplication with advance preparation (SSMMPRE) and shift-sub modular multiplication with CSAs and sign detection (SSMMCSA) algorithms.
3.1. Interleaved Modular Multiplication Algorithm
The IMM algorithm [6] is formally given in Algorithm 6. It computes where , , and m is an n-bit odd number. That is, the ()th bit and 0th bit of n-bit m are 1. IMM begins with checking the ()th bit of multiplier b. Therefore, in each iteration, the product p is shifted to the left by one bit (line 3). Because , (lines 3 and 4). Therefore, it is enough to subtract from (lines 5 and 6), ensuring .

Figure 4 shows a possible hardware implementation of Algorithm 6. Red squares are registers, others are combinational circuits. Clearly, the critical path is the right part that computes the new p in each iteration. It consists of three carry-propagate adders (CPAs) and three multiplexers. The most significant bit of the adder output (sign) can be used as the select signal of multiplexers. Note that can be realized by suitable wiring.
3.2. Montgomery Modular Multiplication Algorithm
The MMM algorithm [7] performs modular multiplication in Montgomery domain. It is very efficient for modular exponentiation used by RSA cryptography. MMM calculates , where , , and m is an n-bit odd number with . It performs reduction during the multiplication because a and b are represented in Montgomery domain as follows.
where and are the operands in the conventional domain. Such a reduction ensures that the product p is an operand still in Montgomery domain:
MMM is widely used in RSA cryptography where the modular exponentiation is realized with the repeated modular multiplications. MMM algorithm is formally given in Algorithm 7. We perform in n iterations and divide p by 2 in each iteration. Line 3 performs multiplication. Line 4 makes p even for the reduction where is the least significant bit of p. Line 5 shifts p to right by one bit (). Line 6 ensures . The reason is shown below. Suppose after the 0th iteration. For , , , , if .

Figure 5 shows a possible hardware implementation of Algorithm 7. Red squares are registers, others are combinational circuits. Clearly, the critical path is the right part that computes the new p in each iteration. It consists of three CPAs and three multiplexers. The most significant bit of the adder output (sign) or the least significant bit of p can be used as the select signal of multiplexers. Note that can be realized by suitable wiring.
3.3. Shift-Sub Modular Multiplication Algorithm
The SSMM algorithm [8,9] is given in Algorithm 8. It begins with checking the 0th bit of multiplier b to calculate . Therefore, in each iteration, the multiplicand u () is shifted to the left by one bit (line 5). Because , (line 3). Therefore, it is enough to subtract m from (line 4), ensuring . Because , (line 5). Therefore, it is enough to subtract m from (line 6), ensuring .

Figure 6 shows a possible hardware implementation of Algorithm 8. Red squares are registers, others are combinational circuits. Compared to Figure 4 and Figure 5, here we reduce critical path to two CPAs and two multiplexers. The bit (b[cnt] in the figure) is used as a selection signal for the last (bottom) multiplexer. If it is a 0, the value in register p is selected (unchanged). The register u and its corresponding combinational circuits are added for performing lines 5 and 6 in Algorithm 8. Note that the implementation is slightly different from the algorithm. Regardless of , we calculate and first. If is non-negative, select it, otherwise select . Finally, the value selected by is written to register p.
Note that instead of using a multiplexer in the bottom, the bit can be used as a write enable for register p. That is, if , we just keep the content of register p unchanged.
3.4. Shift-Sub Modular Multiplication with Advance Preparation Algorithm
From the implementation of the SSMM algorithm, we can see that the critical path is the computation of . m is a modulus and does not change during the multiplication. u is the multiplicand and doubles with each iteration. Then we can prepare in advance in the previous iteration. u is generated as follows. If is non-negative, is written to register u; otherwise, is written to register u, where is the value of u in the previous iteration. In the current iteration, we have two cases for . Case 1: if is negative. Case 2: if is non-negative. Then we just prepare and , and store them in registers. That is, if , ; otherwise . The algorithm SSMMPRE is formally given in Algorithm 9.
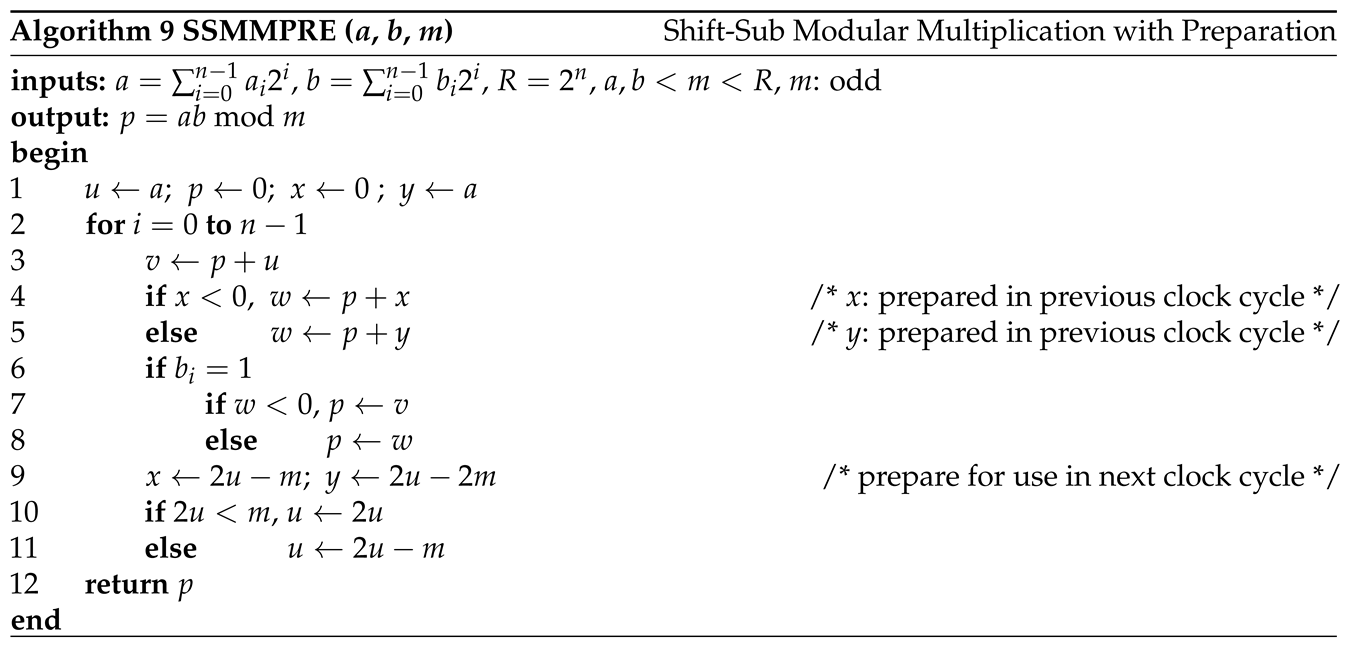
Figure 7 shows the hardware implementation of Algorithm 9. Registers x and y hold and , respectively, where is the value of u in the previous iteration.
3.5. Shift-Sub Modular Multiplication with CSAs and Sign Detection Algorithm
The algorithm SSMMCSA (SSMM with CSAs and sign detection) is formally given in Algorithm 10. Figure 8 shows the implementation of SSMMCSA. The two CPAs in Figure 6 are replaced with CSAs. Through our hardware implementation, we find that the part of CSAs that generates c and s is no longer the critical path. We use another register q to store calculated with a CPA, and generate p from q. The critical path of this circuit contains a CPA and a multiplexer. The output of CSAs consists of carry c and sum s. The result value p will be . We will later propose an easy way to determine the sign of from c and s without using CPA to calculate . The upper CSA performs and the other CSA performs , corresponding to and in Figure 6. One CSA’s output will be selected with the “csasign” (CSA’s sign) signal and stored to the CS register.

Note that we can get from m quickly. Usually where needs a CPA. But here m is an n-bit odd value (), so that we can invert the left bits of m and leave the least-significant-bit unchanged, that is, ’b.
Now we describe how to generate the signal of “csasign”. Figure 9 shows an example of determining the sign of from 17-bit C and S for a 16-bit when using CSAs. We divide the 17 bits to 4 windows, namely , , , and . has 5 bits and each of , , and has 4 bits. We use one 5-bit and three 4-bit CPAs, carry-lookahead adders (CLAs) for instance, to perform additions in 4 windows simultaneously as follows. Note that each of adders generates a 5-bit result.
| = | + | (Add 5-bit, 5-bit sum) | ||||
| = | + | (Add 4-bit, 5-bit sum) | ||||
| = | + | (Add 4-bit, 5-bit sum) | ||||
| = | + | (Add 4-bit, 5-bit sum) |
We summarize the three cases shown in Figure 9 as follows. The signal “sign_inverse” is true means that the original sign () is inverted when ’b1111.
| sign_inverse | = | Case 2 | ||||||
| | | ’b | & | Case 1 | |||||
| | | ’b | & | ’b | & | Case 0 |
The sign bit is a 1 if is negative; a 0 otherwise. When is a 0 and “sign_inverse” is true, the sign will be 1 at the condition of ’b1111. Similarly, when is a 1 and “sign_inverse” is true, the sign will be 0 at the condition of ’b1111. Thus we have the following expression for determining the “csasign”.
The symbol ⊕ denotes an eXclusive OR (XOR) operation. When ’b1111, the sign equals , regardless any case for , , or . Note that , , and are sums of two 4-bit values c and s, so they do not have the pattern 5’b11111. The maximum sum is 5’b11110 when both c and s have a maximum value of 4’b1111.
In the example described above, the window size is 4. We can let the window size be 2 or 8. Then we can use eight 2-bit adders or two 8-bit adders to determine the sign of . The former has a shorter latency introduced by adders, but the logic equation for determining the sign is more complicated. On the other hand, the latter has a simpler logic equation but the adder has a longer latency to determine the sign.
For a 256-bit ECC, there are more options for the number of adder bits and the number of windows. In order to design a low-cost and high-performance circuit, we instigate the cost (the number of ALMs) and performance (the circuit frequency) of the sign detection circuit for using CSAs in 256-bit ECC on FPGA (Field-programmable gate array) chip. There are 7 configurations. The experimental results are shown in Table 2 and Figure 10.
In general, decreasing CPA bits increases frequency. However, in our simulations, the frequency of the last configuration (128 windows and 2-bit adder) is lower than the configuration with 64 windows and 4-bit adder. This is because the logic equation for sign detection becomes complicated. We can also see that larger adders require more ALMs.
Based on the experimental results, our 256-bit ECC implementations use 4-bit adders, so there are 64 windows (). A frequency of 392.46 MHz is measured when the FPGA chip implements only the sign detection circuitry. Implementing both the sign detection circuit and the CSAs results in a frequency of 343.76 MHz, lower than 392.46 MHz. The latency of the CSAs is the same as that of a 1-bit full adder. Clearly, it is less than that of the sign detection circuit. These experimental results imply that the frequency decreases as the circuit gets larger.
Note that the sign detection circuit itself is a combinational circuit. If we want to test its latency we can add registers on both the input and output sides. These registers are for testing purposes only and should be removed for ECC implementations. Otherwise, there will be a delay of two clock cycles, resulting in incorrect timing.
4. Hardware Implementations of Modular Multiplications and ECC
We have implemented modular multiplication algorithms and ECC in Verilog HDL. Unlike sequential program code in software, hardware modules can operate simultaneously. Considering data dependency, we must handle the synchronization between hardware modules using signals such as “start” and “ready”. This section describes these implementations and evaluates their cost and performance.
4.1. Hardware Implementations of Modular Multiplications
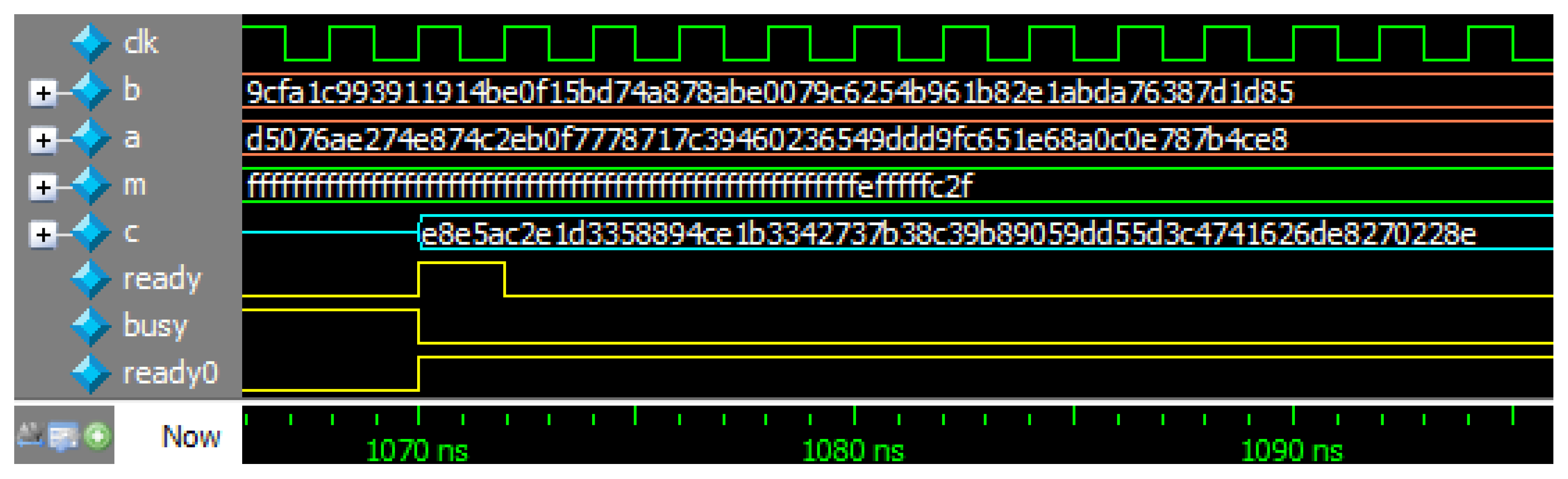
We have implemented the five modular multiplication algorithms described in the previous section. Since we use the 256-bit key proposed in Secp256k1 [4], the Verilog HDL code for modular multiplication also uses 256-bits. As an example of Verilog HDL code shown in Appendix A, the circuit calculates , where m is a 256-bit odd number and , as described in Algorithm 8 (SSMM). “start” is a one clock cycle active signal that tells the module to start modular multiplication. “ready”, “busy”, and “ready0” are synchronization signals with other modules. The simulation waveform generated with ModelSim can be found in Figure A1. It is easy to develop Verilog HDL code for other modular multiplication algorithms by referring to the SSMM example code.
Table 3 gives the cost-performance of the five modular multiplication algorithms. The column of clock cycles shows the required number of clock cycles when executing the modular multiplication algorithm. The column of frequency (MHz) shows the frequency in MHz at which the circuit can work. The column of latency (s) shows the time in microsecond, that is calculated by dividing the clock cycles by the clock frequency. The column of ALMs shows the required number of adaptive logic modules. And the column of registers shows the required number of flip-flops.
Figure 11 plots the relative cost-performance of the modular multiplication algorithms to that of IMM. From this figure and table, we can see that SSMMCSA provides the highest frequency and lowest latency at the highest hardware cost.
4.2. Hardware Implementations of ECC
We have implemented ECC in affine, projective, and Jacobian coordinates using the IMM, SSMM, SSMMPRE, and SSMMCSA modular multiplication algorithms.
MMM is very efficient for modular exponentiation as the basic operation for RSA cryptography because it does not require modular (division). The modular exponentiation can be calculated by repeatedly calling MMM. However, transformations to the Montgomery domain are required before the calculations, and a transformation back to the normal domain is also required to obtain the final result. Domain transformation requires the value which is calculated by costly modular operations. ECC in projective or Jacobian coordinates also does not require modular (division) during scalar point multiplication. Getting the key requires a final division to convert the point to affine coordinates. For these reasons, ECC using MMM is not implemented in this work.
Referring to Algorithm 5, in affine coordinates, the module of scalar point multiplication (scalarmult) invokes the module of point addition (addpoints) and the module of point doubling (doublepoint), as follows (simplified).
module scalarmult (clk, rst_n, start, x, y, d, m, a, rx, ry, ready);
addpointsap(clk,rst_n,start_ap,x1,y1,x2,y2,m,a,apx,apy,ready_ap);
doublepointdp(clk,rst_n,start_dp,x1,y1,m,a,dpx,dpy,ready_dp);
endmodule
Based on the start signal of module scalarmult, we can generate the start signals of start_ap for addpoints and start_dp for doublepoint. An important synchronization is to allow addpoints to start only after the previous iteration’s doublepoint has finished. After 256 iterations, the addition point [apx, apy] is the result point [rx, ry]. The modules of scalar point multiplication in projective and Jacobian coordinates invoke the point addition and doubling modules in projective and Jacobian coordinates, respectively.
In addpoints and doublepoint modules, the result point is calculated based on the algorithms of point addition and point doubling, as described in Algorithm 1 (or 3) and Algorithm 2 (or 4). These modules invoke
(1) modadd (modular addition),
(2) modsub (modular subtraction),
(3) modmul (modular multiplication), and
(4) modinv (modular inversion).
The first two modules are combinational circuits which take one clock cycle. The last two modules are sequential circuits for which we must generate the start signals. The Verilog HDL source codes of these two modules are given in the appendices Appendix A and Appendix B.
Referring to Table 1, in affine coordinates, x of the and can be used as the shared secret key for two parties. In projective and Jacobian coordinates, x must be calculated once by and respectively. Such calculations can be performed using modmul and modinv as shown in the appendices Appendix A and Appendix B. Table 4 gives the cost-performance of the ECC in affine, projective, and Jacobian coordinates using the IMM, SSMM, SSMMPRE, and SSMMCSA modular multiplication algorithms.
The relative cost-performance of the ECC in affine, projective, and Jacobian coordinates are plotted in the Figure 12, Figure 13 and Figure 14, where the cost-performance of IMM is set to 1.0.
As shown in Table 3, the circuit SSMMCSA has the highest frequency, but applying it to the ECC design does not achieve a higher frequency than the other circuits, such as SSMM. This is because, in ECC design, there are other modules that have longer latency than CSAs and sign detection. For example, modadd takes one clock cycle to perform an addition on two operands a and b, a subtraction (subtracting the modulus m from the sum), and a selection using a multiplexer based on the sign of the subtraction result. Such calculations take longer time than the CSAs and sign detection operations. Meanwhile, SSMMCSA circuit is larger than SSMM, this also decreases the frequency.
Figure 15 shows the relative latency to IMM for ECC implementations. All SSMM-related implementations have lower latency than IMM. We can see that the SSMM in projective coordinates has the lowest latency. This is because, SSMMPRE and SSMMCSA use a lot of hardware resources, which reduces the frequency. Interestingly, the latency in projective coordinates is lower than that in Jacobian coordinates. The formulas for point addition and point doubling in Jacobian coordinates look simpler than those in projective coordinates, but from Formula 24, the calculation of depends on , resulting in a sequential execution. On the other hand, and in projective coordinates can be calculated in parallel (Formula 21 and Formula 20).
5. Concluding Remarks
This paper introduced ECC modular multiplication algorithms and their hardware implementations. Experimental results show that SSMMCSA (Shift-sub modular multiplication with CSAs and sign detection) has lower latency than SSMM (Shift-sub modular multiplication). We also investigated ECC implementations in affine, projective, and Jacobian coordinates using the IMM (Interleaved modular multiplication), SSMM, SSMMPRE (Shift-sub modular multiplication with advance preparation) , and SSMMCSA algorithms. Experimental results show that ECC in projective coordinates with SSMM has the lowest latency among all implementations.
The SSMMCSA circuit itself has a higher frequency than SSMM, but the ECC circuits using SSMMCSA have the same or even lower frequency than that using SSMM. The next challenge is to make the SSMMCSA ECC circuit faster than the SSMM ECC circuit.
Appendix A. Verilog HDL Code of Shift-Sub Modular Multiplication (SSMM)

This code implements Algorithm 8. Its block diagram is shown in Figure 6. The signal “start” is active for one clock cycle to tell the module to start modular multiplication. The signal “ready” remains active for one clock cycle to indicate that the modular multiplication result is available. “ready0” remains active until the multiplier is cleared. This signal is used to confirm the readiness of multiple modules to initiate another module’s operation. Figure A1 shows the simulation waveform generated with ModelSim.
Figure A1.
Waveform of SSMM that calculates . The Verilog HDL code is given in Appendix A.
Figure A1.
Waveform of SSMM that calculates . The Verilog HDL code is given in Appendix A.
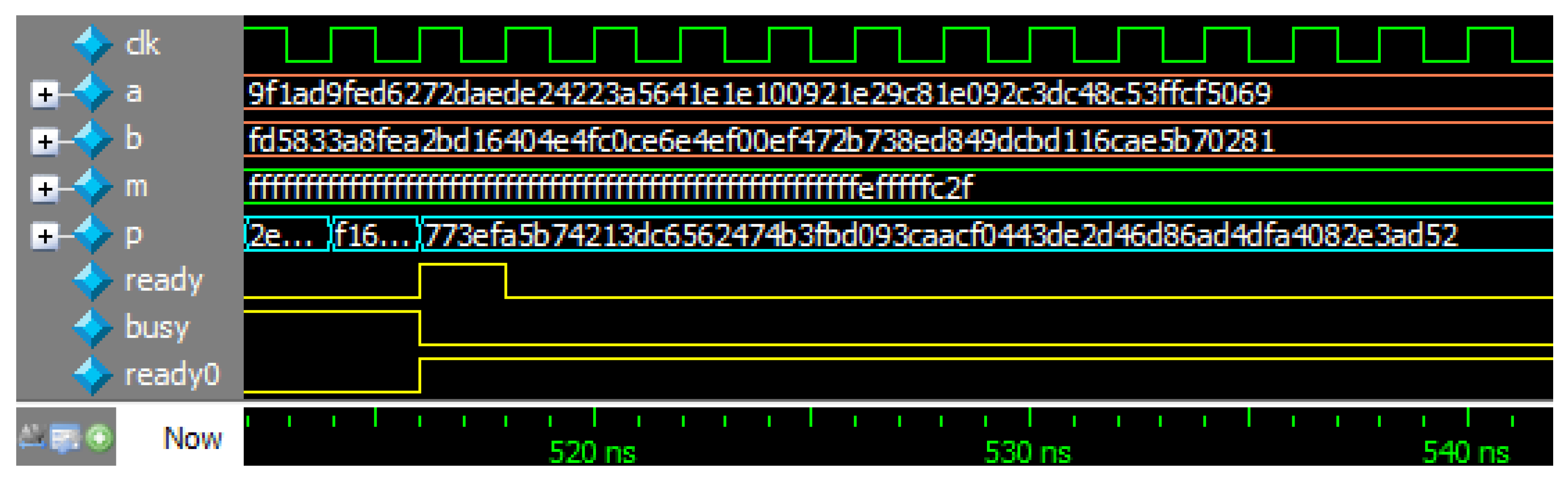
Appendix B. Verilog HDL Code of Modular Inversion

This code is developed based on Algorithm 2.22 in [3]. The signal “start” is active for one clock cycle to tell the module to start modular inversion. The signal “ready” remains active for one clock cycle to indicate that the modular inversion result is available. “ready0” remains active until the multiplier is cleared. This signal is used to confirm the readiness of multiple modules to initiate another module’s operation. The testbench is listed below.

Figure B1 shows the simulation waveform generated with ModelSim.
Figure B1.
Waveform of modular inversion that calculates . The Verilog HDL code is given in Appendix B.
Figure B1.
Waveform of modular inversion that calculates . The Verilog HDL code is given in Appendix B.
References
- Koblitz, N. Elliptic curve cryptosystems. Mathematics of Computation 1987, 48, 203–209. https://www.ams.org/journals/mcom/1987-48-177/S0025-5718-1987-0866109-5/S0025-5718-1987-0866109-5.pdf.
- Miller, V.S. Use of Elliptic Curves in Cryptography. In Proceedings of the Advances in Cryptology — CRYPTO ’85 Proceedings, Berlin, Heidelberg, 1986; pp. 417–426. https://link.springer.com/content/pdf/10.1007/3-540-39799-X_31.pdf?pdf=inline%20link.
- Hankerson, D.; Menezes, A.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer-Verlag: New York Inc, 2004. [CrossRef]
- Certicom Corp. Standards for Efficient Cryptography. SEC 2: Recommended Elliptic Curve Domain Parameters; http://www.secg.org/sec2-v2.pdf, 2010.
- Barker, E.; Chen, L.; Roginsky, A.; Vassilev, A.; Davis, R. SP 800-56A Rev. 3, Recommendation for Pair-Wise Key-Establishment Schemes Using Discrete Logarithm Cryptography; National Institute of Standards and Technology, 2018. https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-56Ar3.pdf.
- Blakely, G.R. A Computer Algorithm for Calculating the Product AB Modulo M. IEEE Transactions on Computers 1983, C-32, 497–500. [CrossRef]
- Montgomery, P.L. Modular Multiplication Without Trial Division. Mathematics of Computation 1985, 44, 519–521. https://www.ams.org/journals/mcom/1985-44-170/S0025-5718-1985-0777282-X/S0025-5718-1985-0777282-X.pdf.
- Li, Y.; Chu, W. Shift-Sub Modular Multiplication Algorithm and Hardware Implementation for RSA Cryptography. In Proceedings of the 17th International Conference on Information Assurance and Security, Lecture Notes in Networks and Systems, Cham, 2021; pp. 541–552. [CrossRef]
- Li, Y.; Chu, W. Verilog HDL Implementation for an RSA Cryptography using Shift-Sub Modular Multiplication Algorithm. Journal of Information Assurance and Security 2022, 17, 113–121. http://www.mirlabs.org/jias/secured/Volume17-Issue3/Paper11.pdf.
- Bunimov, V.; Schimmler, M. Area and time efficient modular multiplication of large integers. In Proceedings of the Proceedings IEEE International Conference on Application-Specific Systems, Architectures, and Processors, 2003, pp. 400–409. [CrossRef]
- Chen, L.; Moody, D.; Regenscheid, A.; Robinson, A.; Randall, K. Recommendations for Discrete Logarithm-based Cryptography: Elliptic Curve Domain Parameters. NIST Special Publication NIST SP 800-186, 2023. https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-186.pdf. [CrossRef]
Figure 1.
ECDH and ECC algorithms. The ECDH Key Exchange invokes a Scalar Point Multiplication that uses two computations - Point Addition and Point Doubling. Four primitive modular calculations (Addition, Subtraction, Multiplication, and Inversion) are used for these two computations.
Figure 1.
ECDH and ECC algorithms. The ECDH Key Exchange invokes a Scalar Point Multiplication that uses two computations - Point Addition and Point Doubling. Four primitive modular calculations (Addition, Subtraction, Multiplication, and Inversion) are used for these two computations.
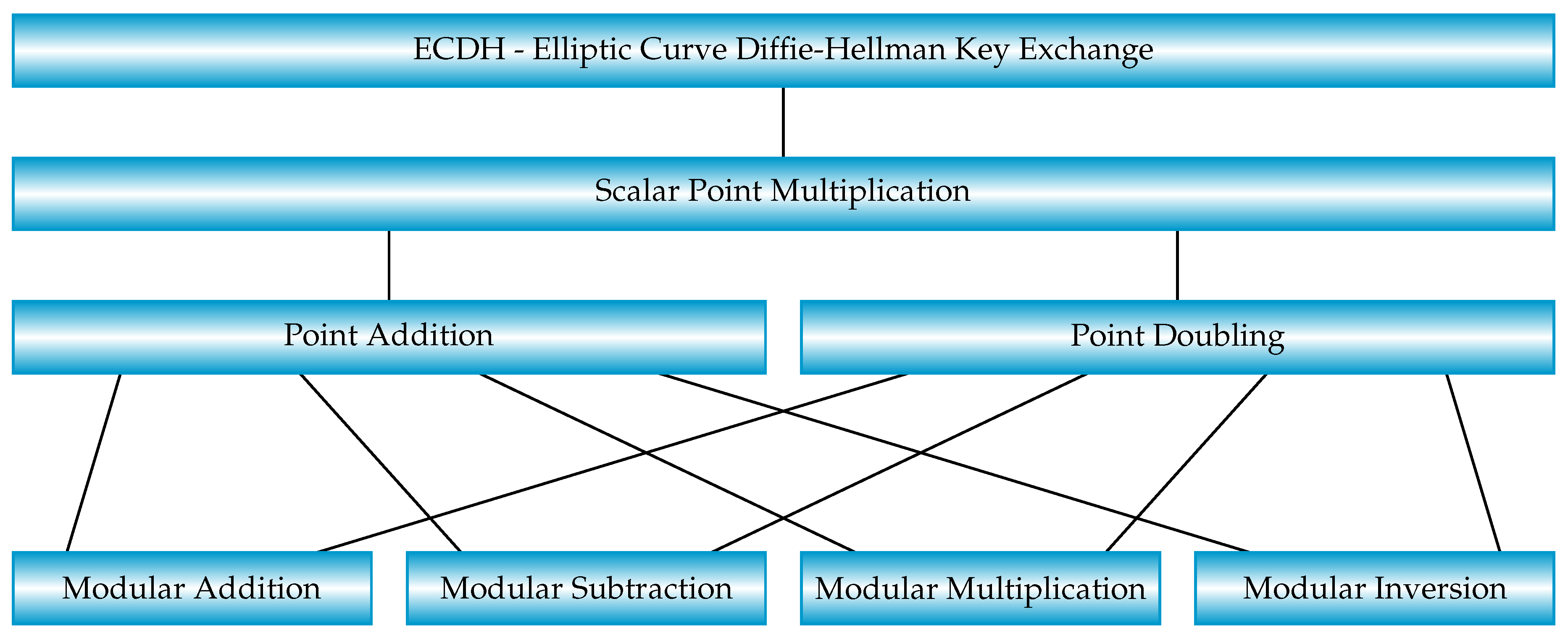
Figure 2.
Point addition on an elliptic curve in the real number field.
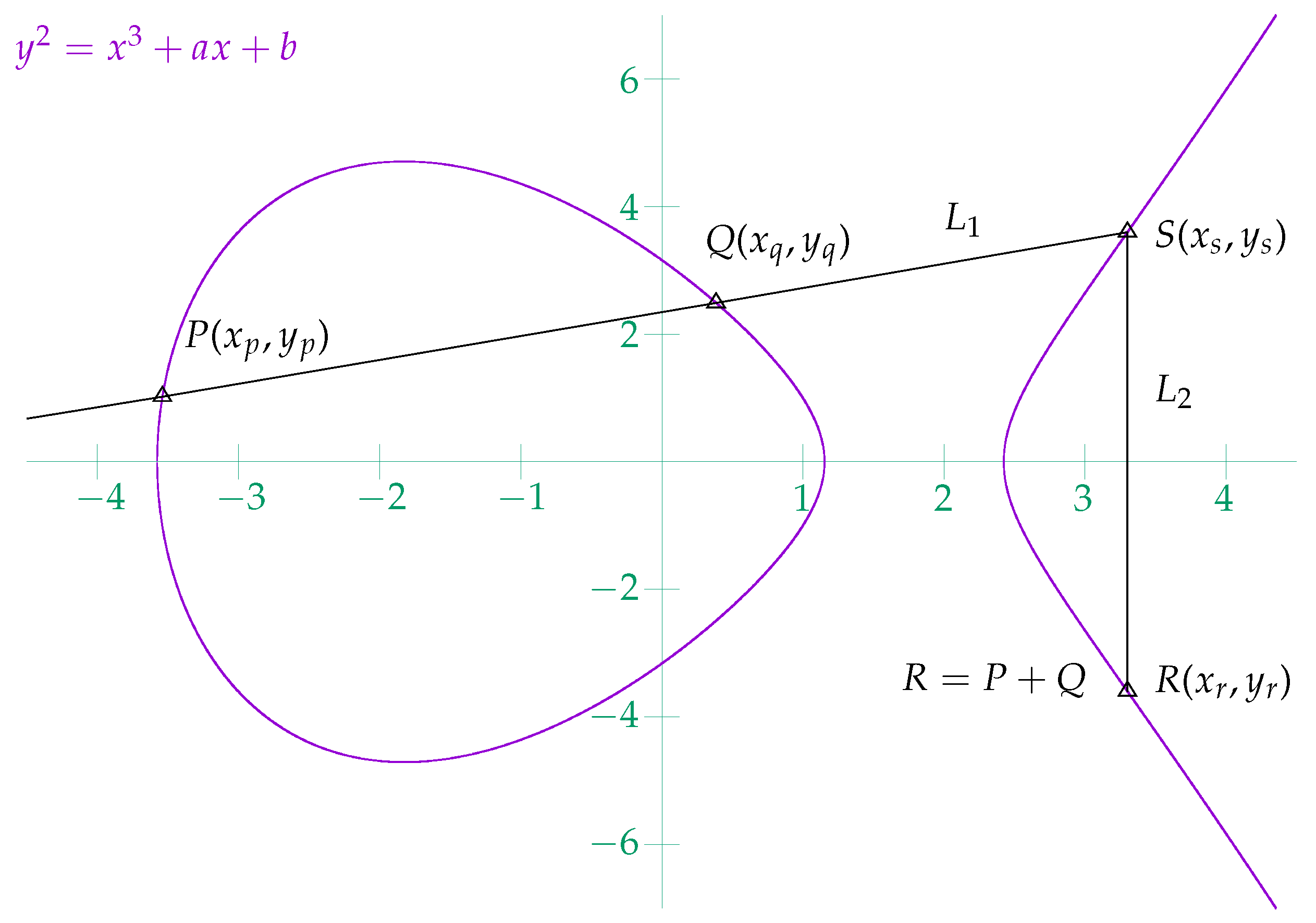
Figure 3.
Point doubling on an elliptic curve in the real number field.
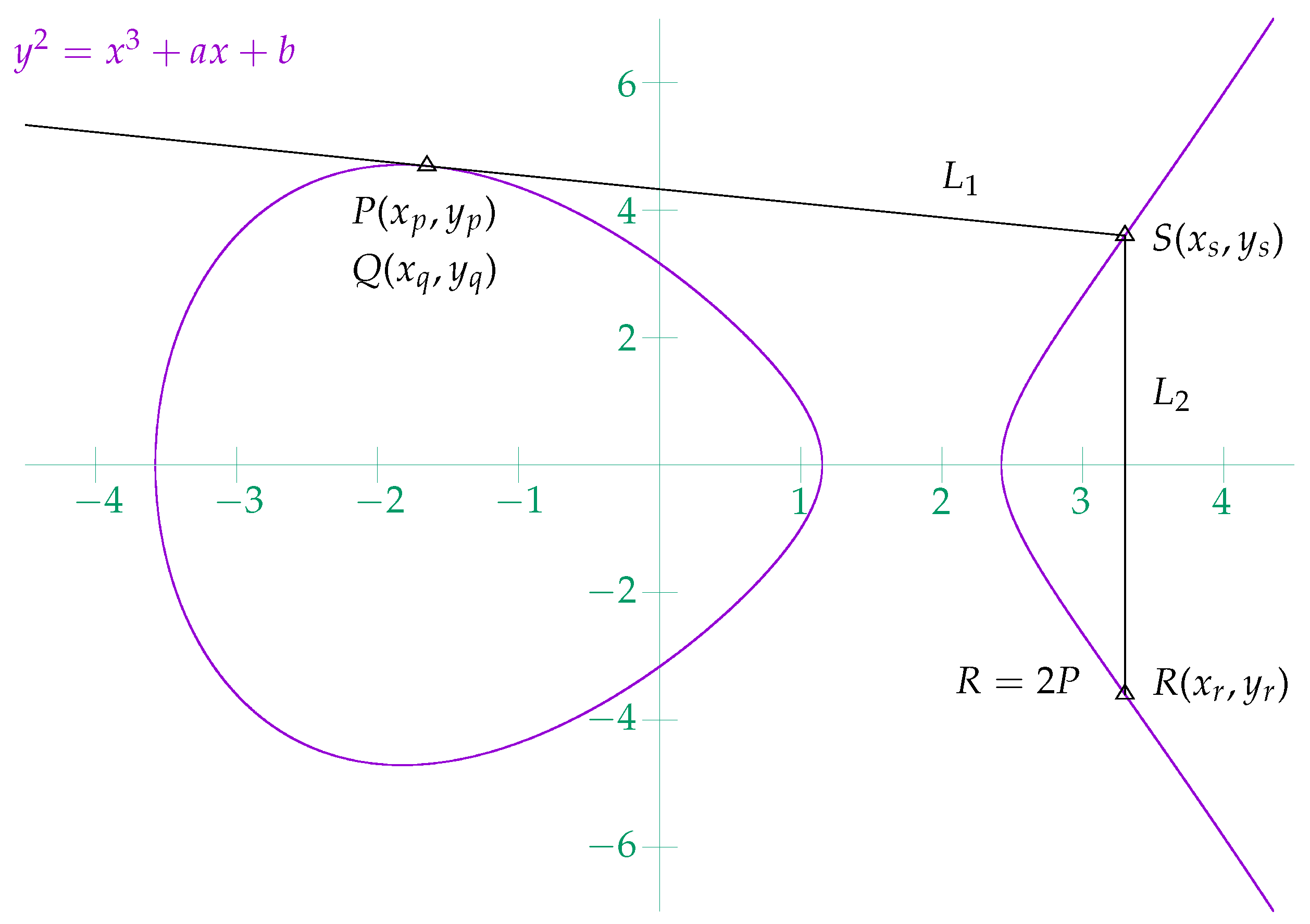
Figure 4.
Block diagram of interleaved modular multiplication (IMM). It implements Algorithm 6.
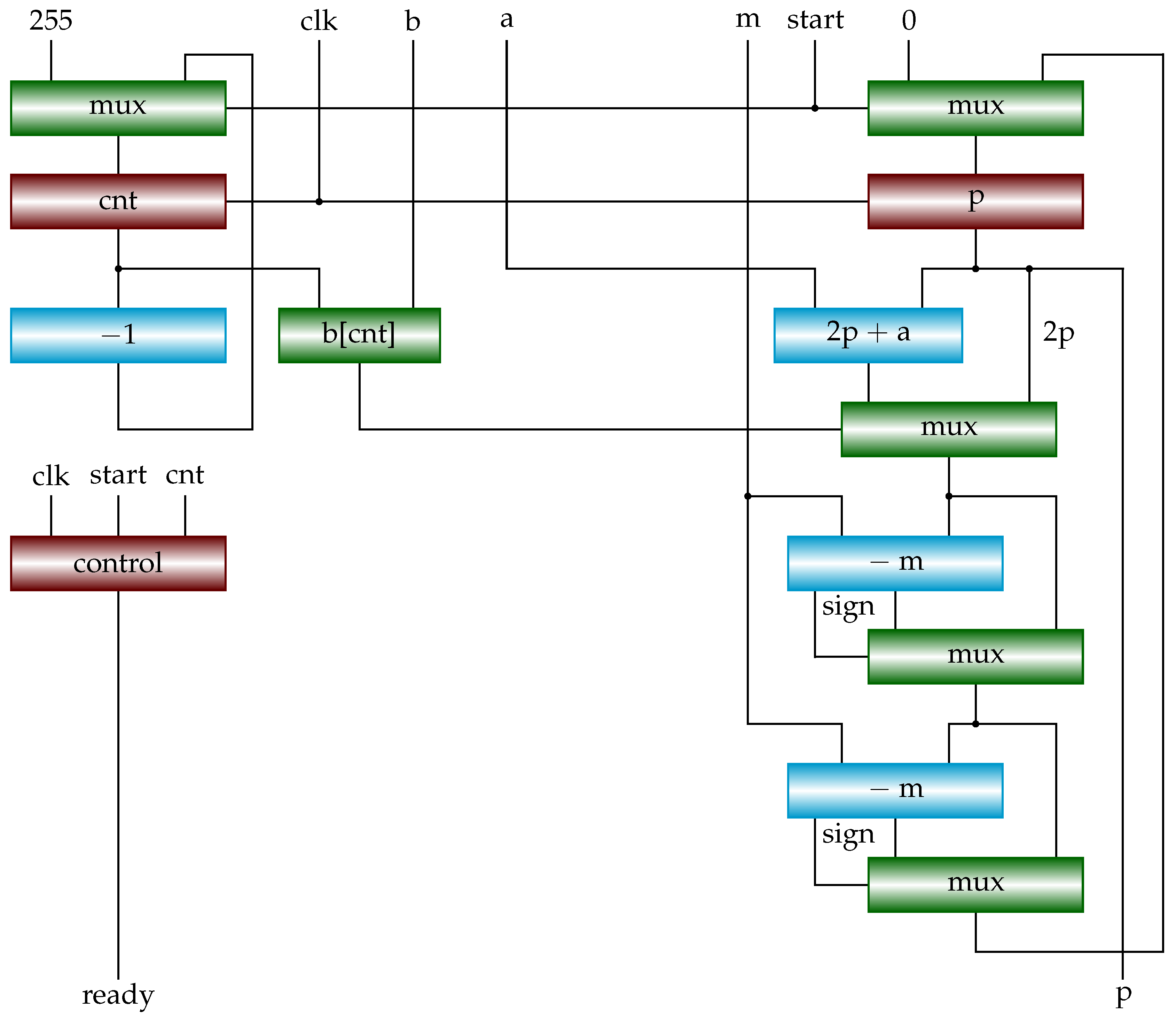
Figure 5.
Block diagram of Montgomery modular multiplication (MMM). It implements Algorithm 7.
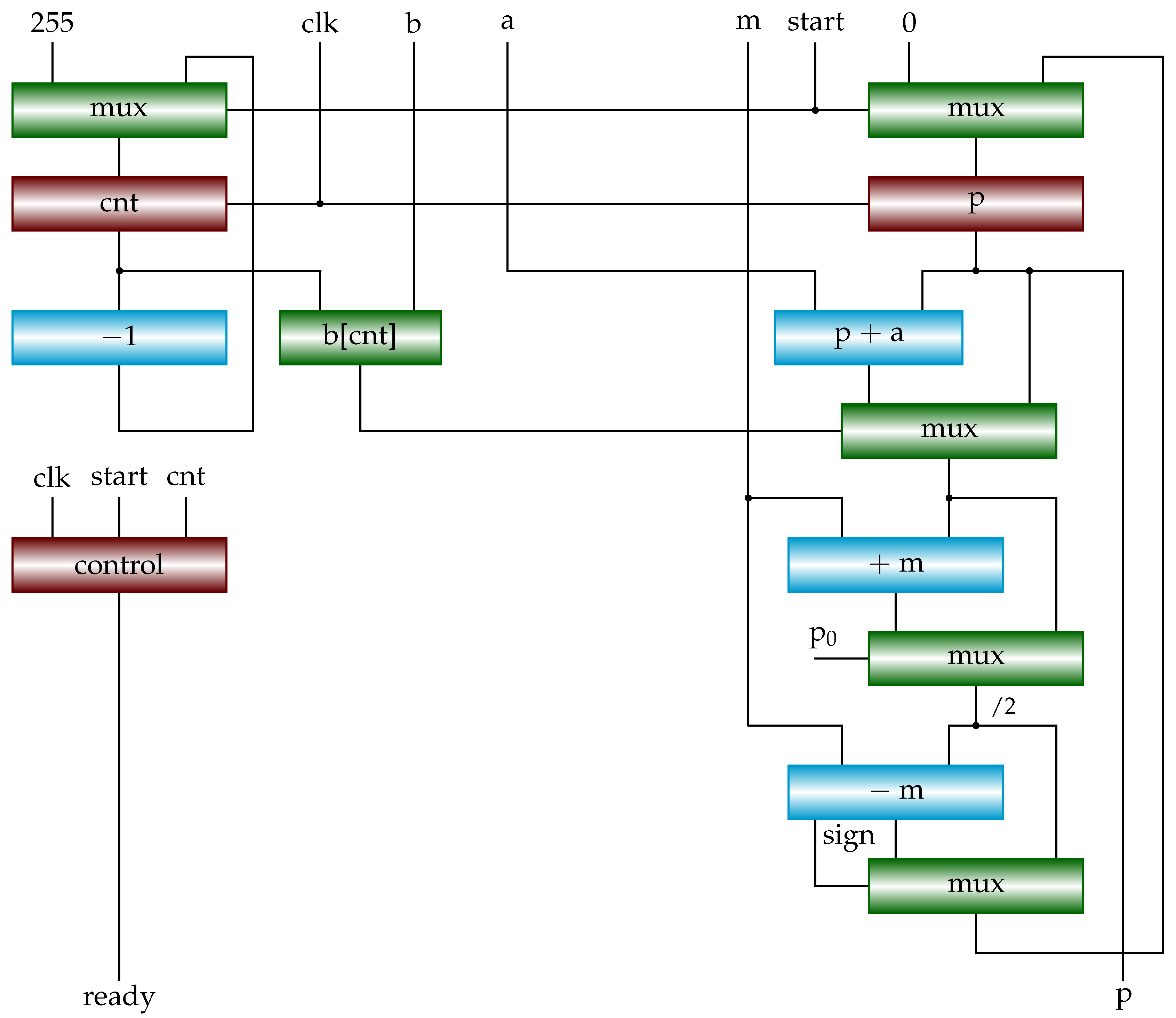
Figure 6.
Block diagram of shift-sub modular multiplication (SSMM). It implements Algorithm 8.
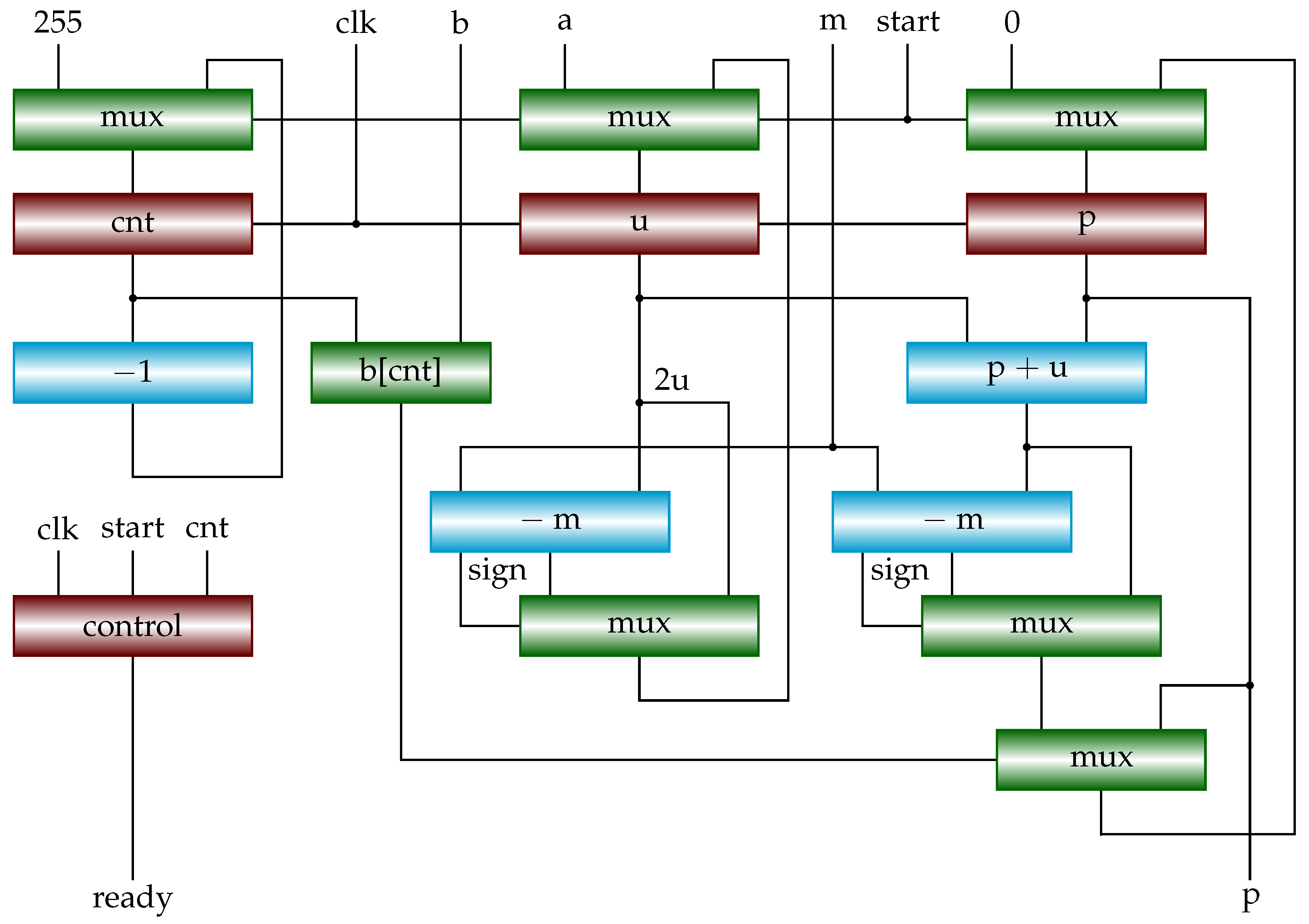
Figure 7.
Block diagram of shift-sub modular multiplication with advance preparation (SSMMPRE). It implements Algorithm 9.
Figure 7.
Block diagram of shift-sub modular multiplication with advance preparation (SSMMPRE). It implements Algorithm 9.
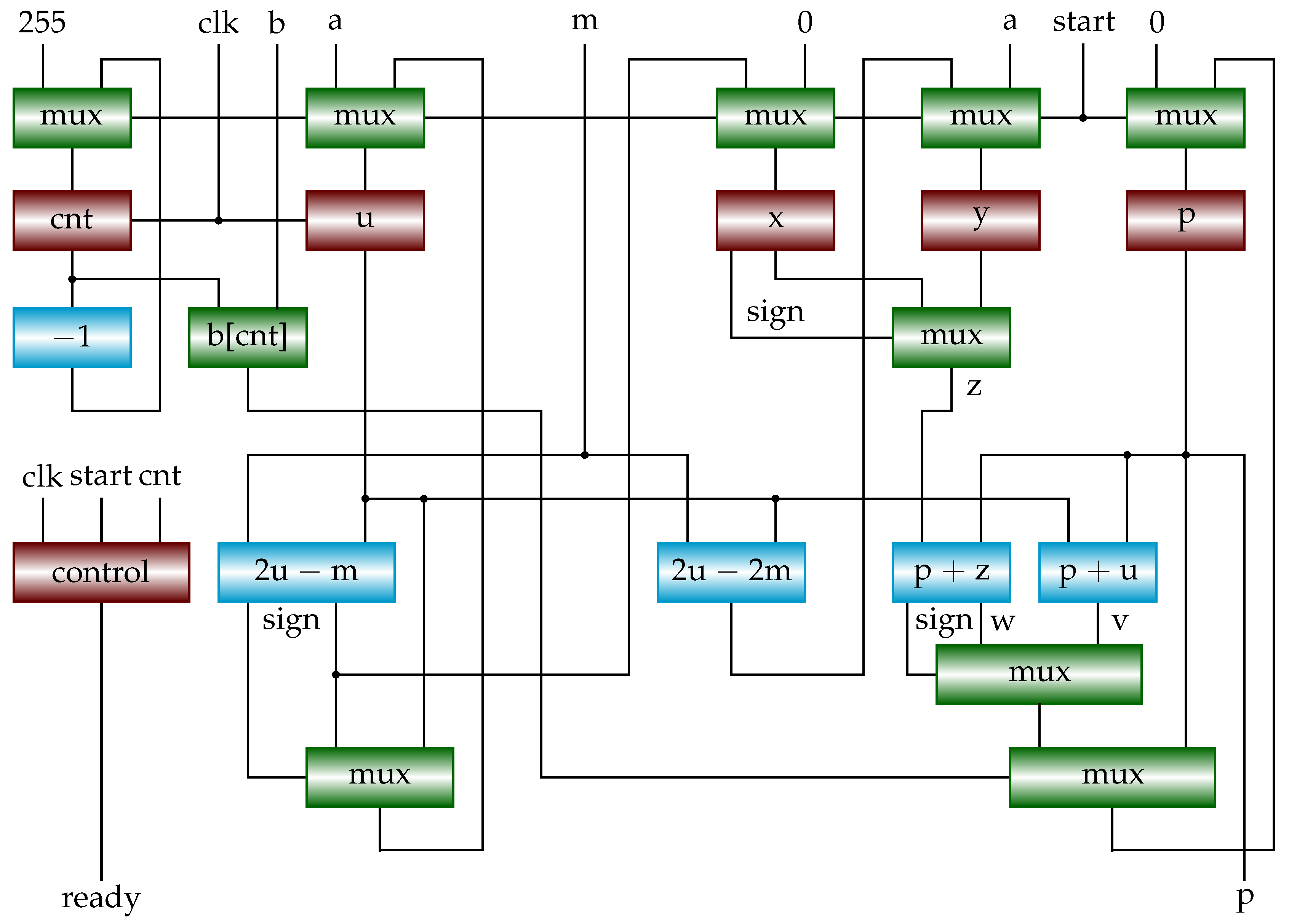
Figure 8.
Block diagram of shift-sub modular multiplication with CSAs and sign detection (SSMMCSA). It implements Algorithm 10.
Figure 8.
Block diagram of shift-sub modular multiplication with CSAs and sign detection (SSMMCSA). It implements Algorithm 10.
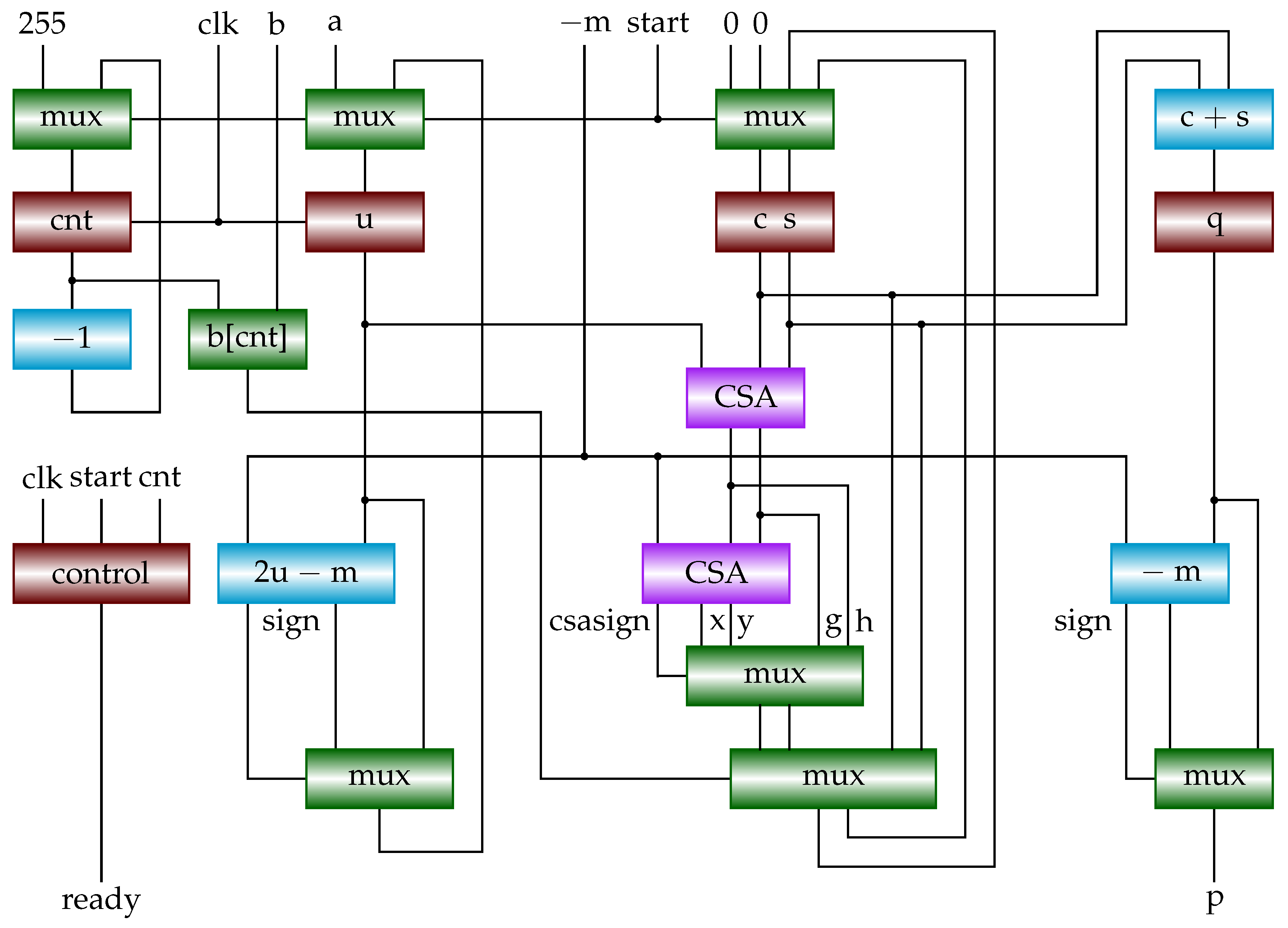
Figure 9.
Determining the sign of based on the 17-bit outputs C and S of CSAs. We divide 17 bits to four windows. There are five bits in the left-most window. Each of other three windows has four bits. The C and S are inputs; others are outputs of adders. indicates the sign except for Case 0, Case 1, or Case 2, where the sign is the inverse of when ’b1111.
Figure 9.
Determining the sign of based on the 17-bit outputs C and S of CSAs. We divide 17 bits to four windows. There are five bits in the left-most window. Each of other three windows has four bits. The C and S are inputs; others are outputs of adders. indicates the sign except for Case 0, Case 1, or Case 2, where the sign is the inverse of when ’b1111.
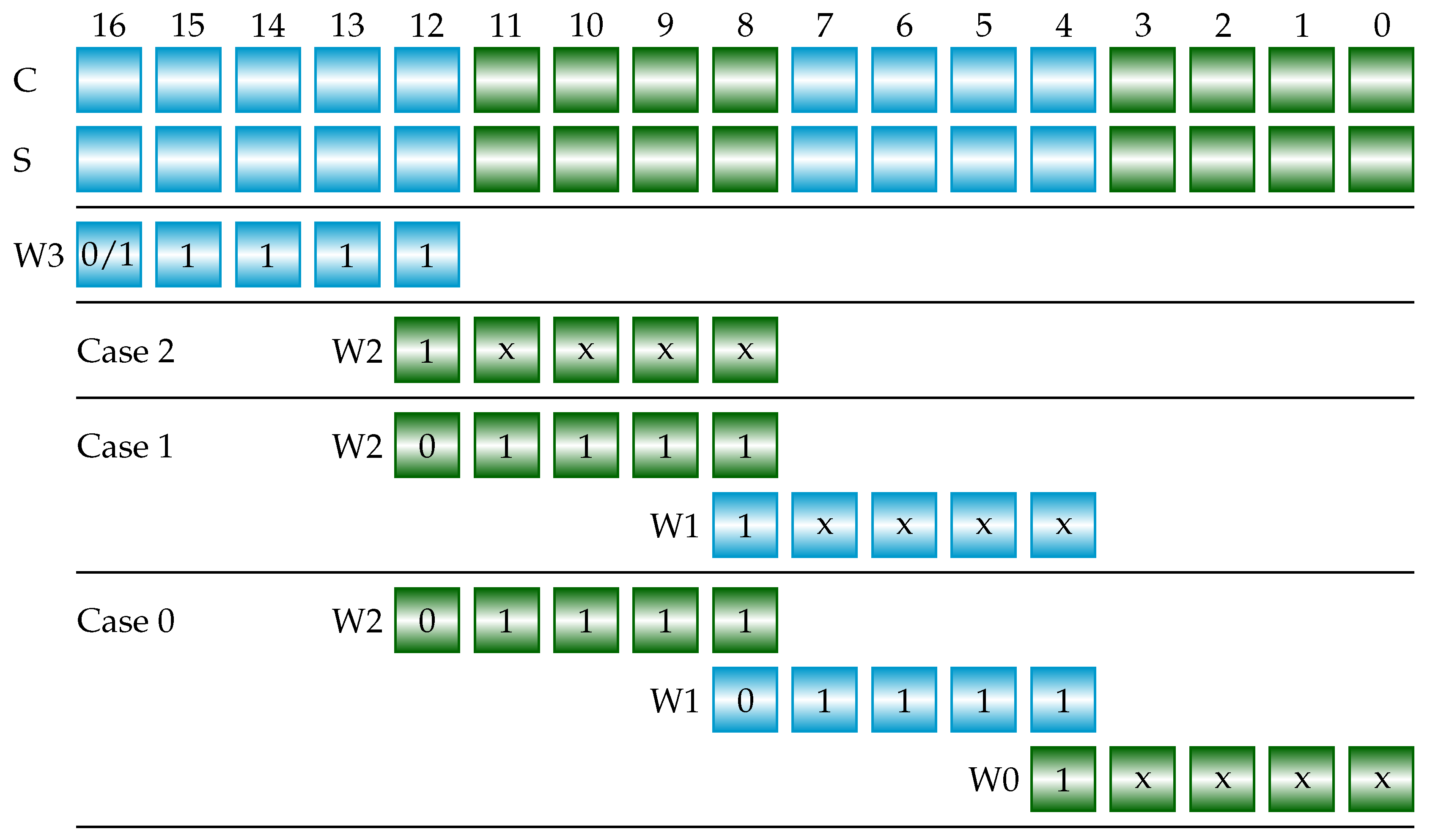
Figure 10.
Cost and performance of sign detection with different configurations.
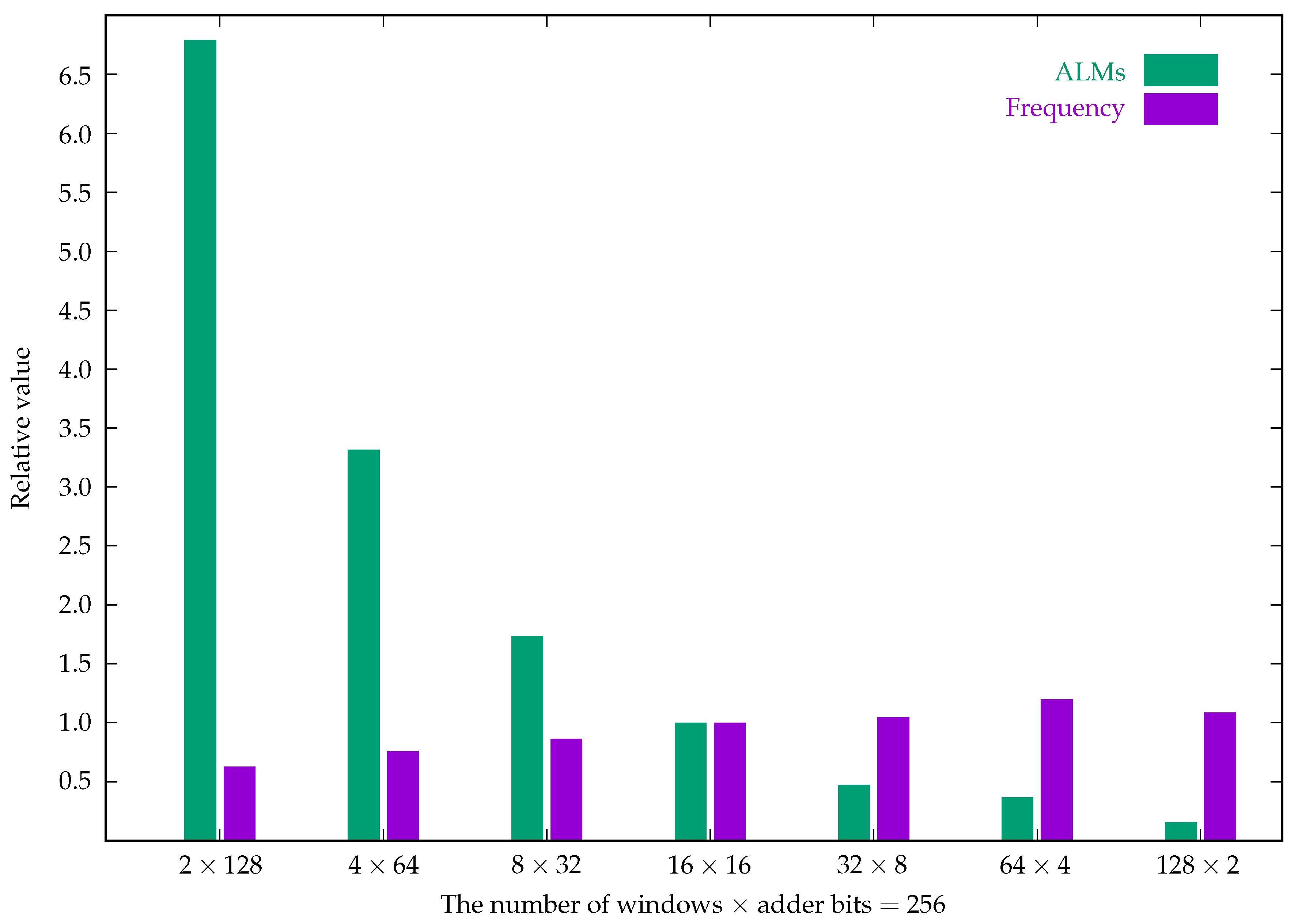
Figure 11.
Cost performance comparison of modular multiplication algorithms.
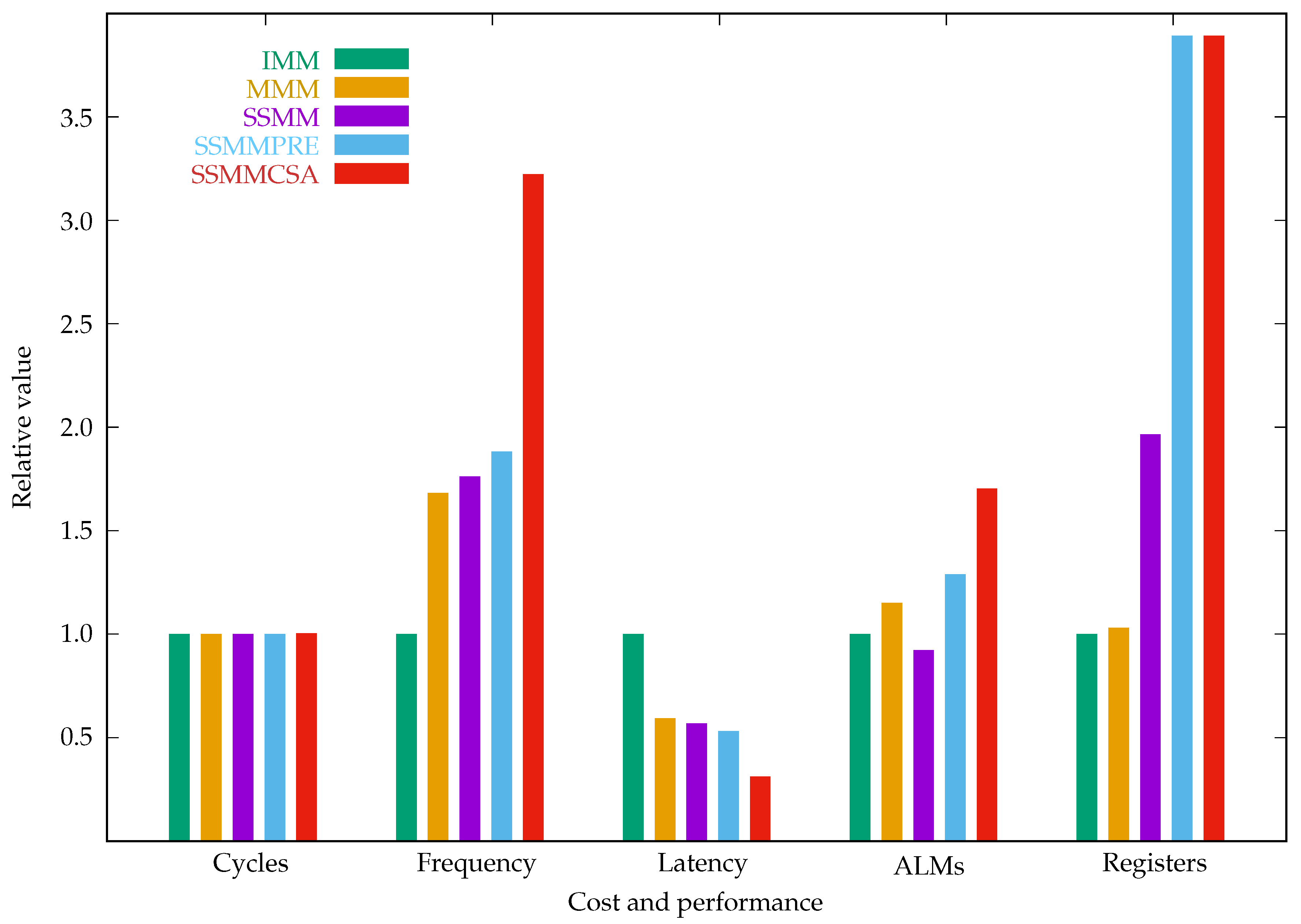
Figure 12.
Cost performance comparison of ECC in affine coordinates.
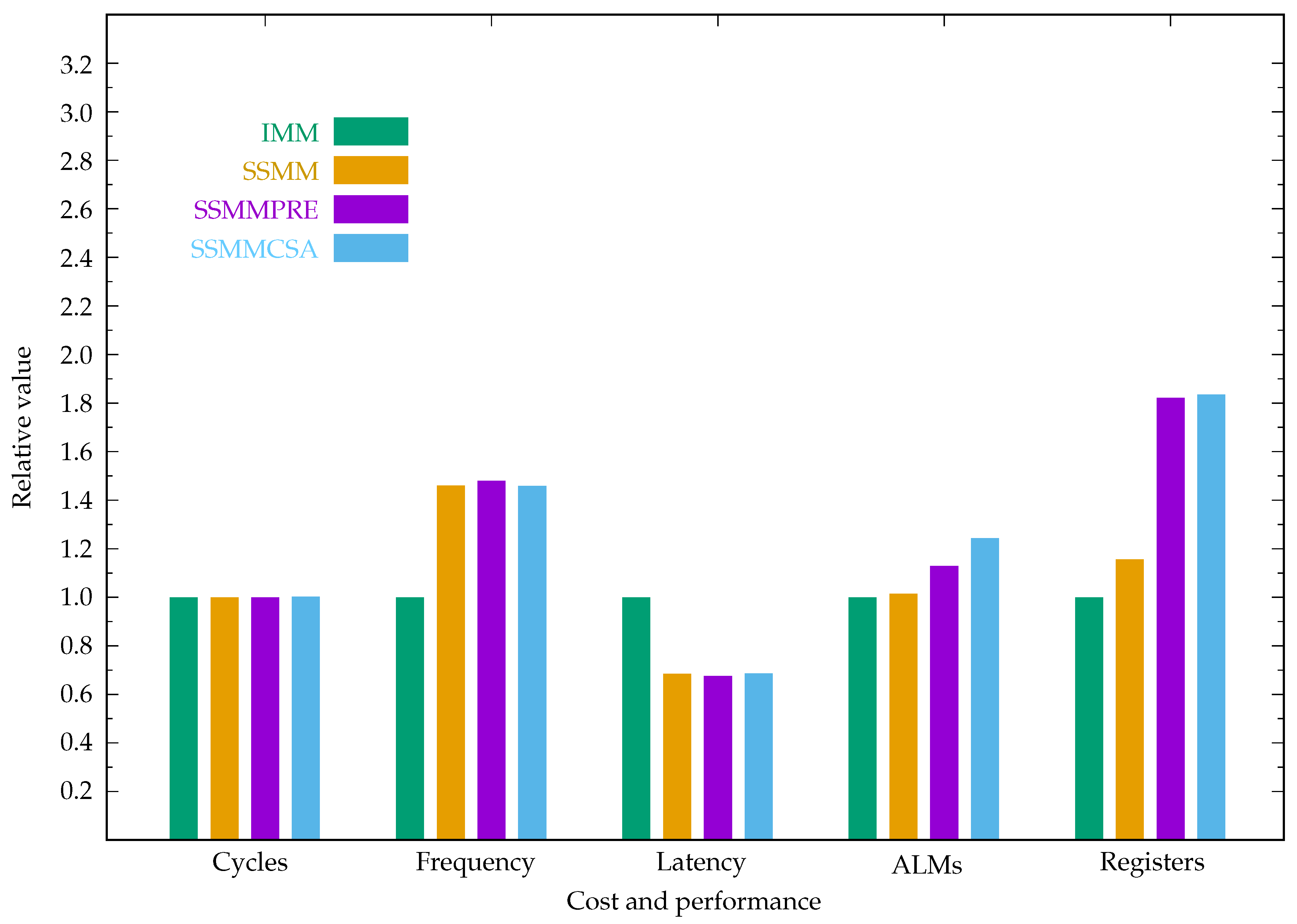
Figure 13.
Cost performance comparison of ECC in projective coordinates.
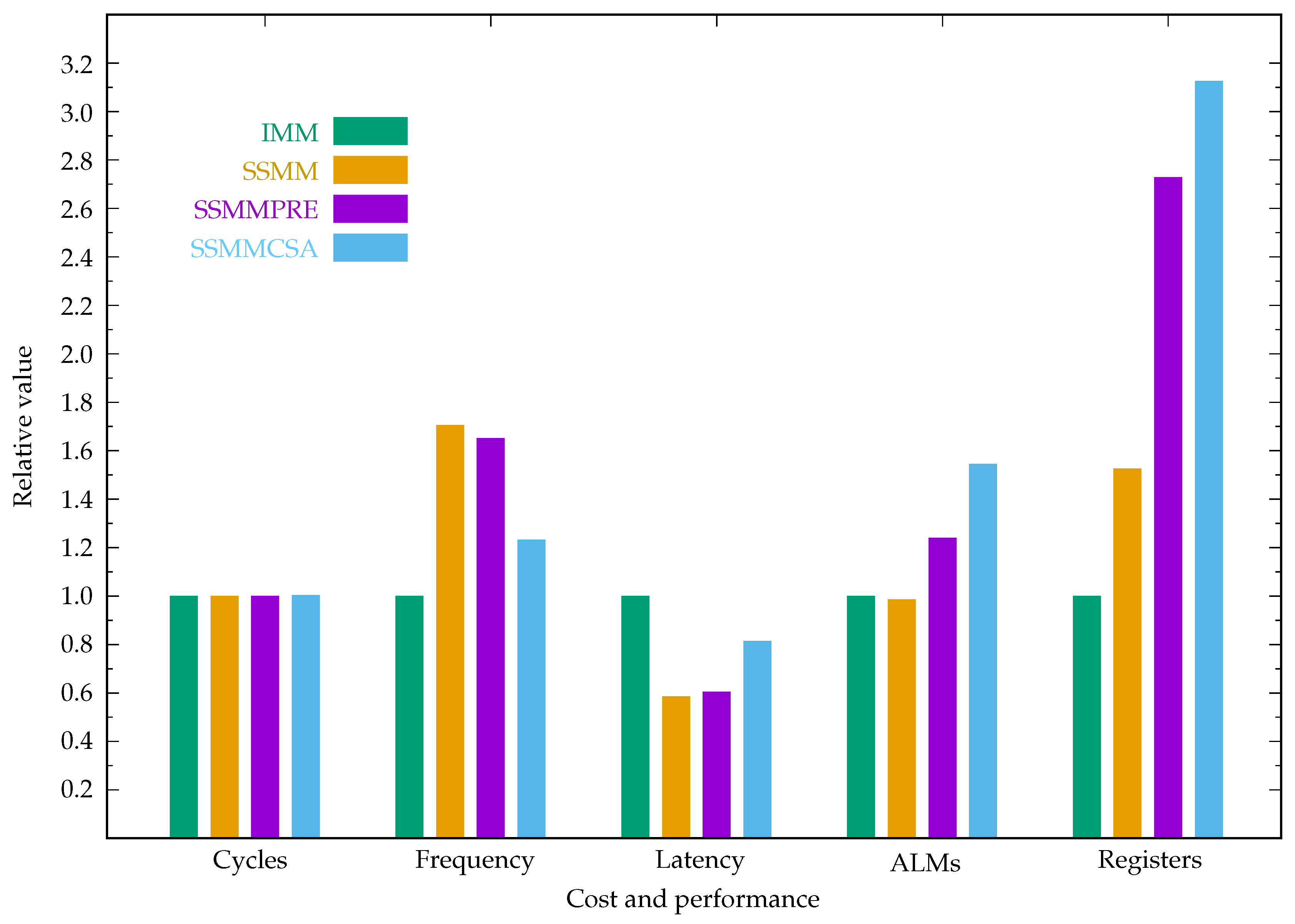
Figure 14.
Cost performance comparison of ECC in Jacobian coordinates.
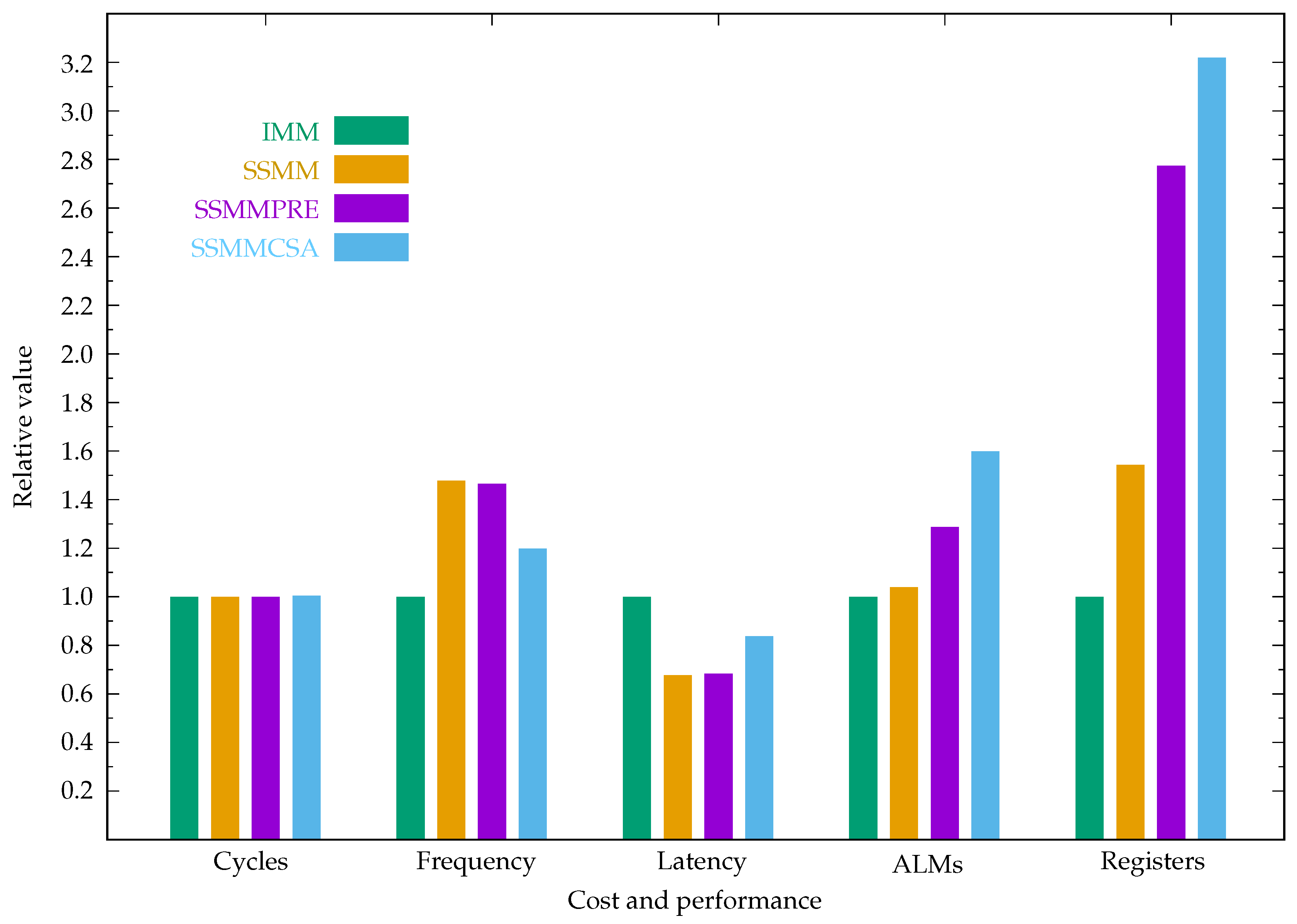
Figure 15.
Relative latency of ECC. The SSMM in projective coordinates has the lowest latency.
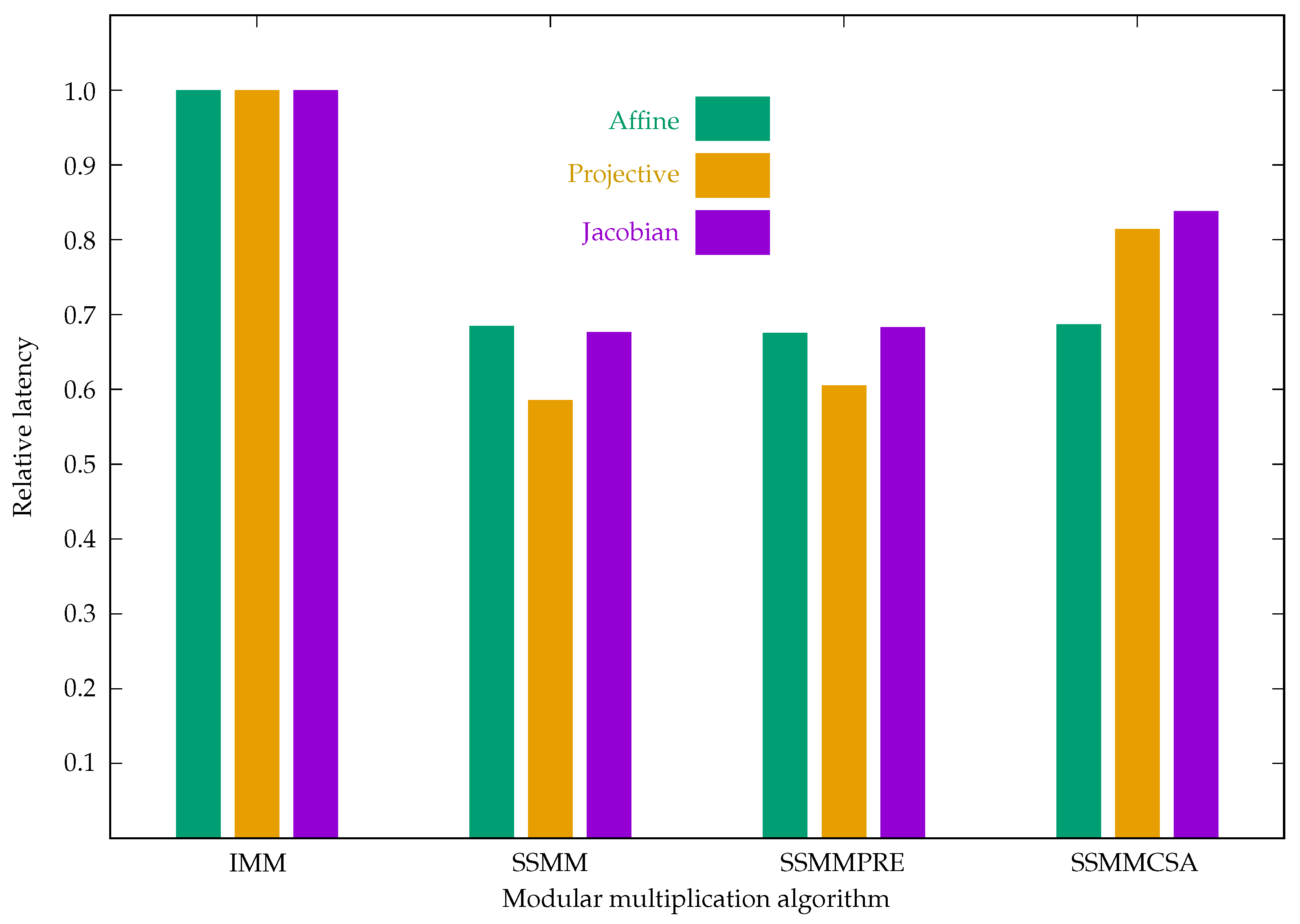
Table 1.
Elliptic curve Diffie-Hellman key exchange.
| Expose an elliptic curve and a point P on the elliptic curve to the world | |
| Alice | Bob |
| Generate a secret | Generate a secret |
| Calculate (Algorithm 5) | Calculate (Algorithm 5) |
| Expose | Expose |
| Get from Bob | Get from Alice |
| Calculate (Algorithm 5) | Calculate (Algorithm 5) |
| Use x of as the key | Use x of as the key |
Table 2.
Cost and performance of sign detection with different configurations. The FPGA chip device is Cyclone V / 5CGXFC7D7F31C8.
Table 2.
Cost and performance of sign detection with different configurations. The FPGA chip device is Cyclone V / 5CGXFC7D7F31C8.
| Windows × Adder bits | |||||||
| ALMs | 129 | 63 | 33 | 19 | 9 | 7 | 3 |
| Frequency (MHz) | 205.30 | 248.57 | 282.09 | 326.90 | 342.58 | 392.46 | 355.75 |
Table 3.
Comparison of modular multiplication algorithms. SSMM is 1.76 times faster than IMM and SSMMCSA is 3.21 times faster than IMM. The FPGA chip device is Cyclone V / 5CGXFC7D7F31C8.
Table 3.
Comparison of modular multiplication algorithms. SSMM is 1.76 times faster than IMM and SSMMCSA is 3.21 times faster than IMM. The FPGA chip device is Cyclone V / 5CGXFC7D7F31C8.
| Algorithm | Clock cycles | Frequency (MHz) | Latency (s) | ALMs | Registers |
| IMM | 258 | 35.15 | 7.34 | 657 | 268 |
| MMM | 258 | 59.12 | 4.36 | 756 | 276 |
| SSMM | 258 | 61.92 | 4.17 | 606 | 527 |
| SSMMPRE | 258 | 66.16 | 3.90 | 847 | 1043 |
| SSMMCSA | 259 | 113.29 | 2.29 | 1119 | 1043 |
Table 4.
Comparison of ECC in different coordinates with different modular multiplication algorithms. The FPGA chip device is Cyclone V / 5CGXFC7D7F31C8.
Table 4.
Comparison of ECC in different coordinates with different modular multiplication algorithms. The FPGA chip device is Cyclone V / 5CGXFC7D7F31C8.
| Algorithm | Clock cycles | Frequency (MHz) | Latency (ms) | ALMs | Registers |
| ECC in Affine Coordinates | |||||
| IMM | 402,146 | 13.98 | 28.77 | 14,816 | 6,995 |
| SSMM | 402,146 | 20.41 | 19.70 | 15,032 | 8,085 |
| SSMMPRE | 402,146 | 20.69 | 19.44 | 16,723 | 12,743 |
| SSMMCSA | 403,166 | 20.40 | 19.76 | 18,416 | 12,834 |
| ECC in Projective Coordinates | |||||
| IMM | 396,550 | 17.28 | 22.95 | 30,291 | 15,352 |
| SSMM | 396,550 | 29.49 | 13.45 | 29,878 | 23,434 |
| SSMMPRE | 396,550 | 28.54 | 13.89 | 37,545 | 41,902 |
| SSMMCSA | 398,080 | 21.31 | 18.68 | 46,831 | 47,984 |
| ECC in Jacobian Coordinates | |||||
| IMM | 369,079 | 14.31 | 25.79 | 27,884 | 14,068 |
| SSMM | 369,079 | 21.15 | 17.45 | 28,978 | 21,708 |
| SSMMPRE | 369,079 | 20.95 | 17.62 | 35,864 | 39,024 |
| SSMMCSA | 370,502 | 17.14 | 21.62 | 44,591 | 45,298 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





